Ngân hàng bài tập phần Thống kế toán | Đề cương ôn tập môn Xác suất thống kê | Học viện Ngân hàng

Bài tập phần Th ng kê ố Toán
Phần I. Bài toán ước lượng
1. Trong một cuộc điều tra 150 người nghiện thuốc lá được chọn ngẫu nhiên, người ta tính được
số điếu thuốc hút trong một tuần của họ có trung bình là 97 và độ lệch tiêu chuẩn là 36. Biết số
điếu thuốc hút trong một tuần của người nghiện thuốc là biến ngẫu nhiên có phân phối (xấp xỉ)
chuẩn. Với độ tin cậy 95%, ước lượng:
a) Số điếu thuốc trung bình một người hút trong 1 tuần bằng khoảng tin cậy đối xứng.
b) Phương sai của số điếu thuốc một người hút trong một tuần bằng khoảng tin cậy bên phải.
2. Tuổi thọ của một loại bóng đèn do một dây chuyền sản xuất ra có độ lệch chuẩn là 95 giờ. Điều
tra 50 bóng đèn loại này tính được tuổi thọ trung bình là 350 giờ. Giả thiết tuổi thọ của bóng đèn
là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn. a) Với ộ
đ tin cậy 95%, hãy ước lượng tuổi thọ trung bình tối đa của loại bóng đèn này.
b) Nếu muốn ước lượng tuổi thọ trung bình của loại bóng đèn đạt độ chính xác là 25 giờ và độ
tin cậy 98% thì cần điều tra bao nhiêu bóng?
3. Chỉ tiêu A của một loại sản phẩm là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn. Mẫu điều tra
về chỉ tiêu A (tính bằng %) của sản phẩm này được cho trong bảng: Xi 0 – 5
5 – 10 10 – 15 15 – 20 20 – 25 25 – 30 30 – 35 35 – 40 ni 7 12 20 25 18 12 5 1
a) Ước lượng trung bình, phương sai chỉ tiêu A của sản phẩm đó . b) Với ộ
đ tin cậy 95%, ước lượng trung bình chỉ tiêu A bằng khoảng tin cậy đối xứng.
c) Hãy ước lượng trung bình tối thiểu của chỉ tiêu A với ộ đ tin cậy 95%.
d) Nếu muốn ước lượng trung bình chỉ tiêu A đạt độ tin cậy 95% và độ chính xác 1,2% thì cần
điều tra thêm bao nhiêu sản phẩm nữa?
e) Nếu sử dụng mẫu này để ước lượng trung bình các sản phẩm đạt độ chính xác 1% thì đảm
bảo độ tin cậy là bao nhiêu?
f) Những sản phẩm có chỉ tiêu A không quá 10% là loại 2. Hãy ước lượng trung bình chỉ tiêu
A các sản phẩm loại 2 với độ tin cậy 95%, biết rằng chỉ tiêu A các sản phẩm loại 2 là biến
ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
4. Cơ quan cảnh sát giao thông kiểm tra hệ thống phanh của 100 chiếc xe tải trên đường quốc lộ.
Họ phát hiện 35 chiếc có phanh chưa đảm bảo.
a) Tìm khoảng tin cậy 95% cho tỉ lệ xe tải có phanh chưa an toàn.
b) Tìm khoảng tin cậy 98% cho tỉ lệ xe tải có phanh tốt.
5. Điều tra ngẫu nhiên thu nhập của 100 nhân viên công ty A thu được kết quả sau:
Thu nhập (triệu đồng/tháng) 3,0 3,2 3,4 3,6 3,8 4,0 1 Số nhân viên 5 15 25 30 20 5
a) Ước lượng mức thu nhập trung ì
b nh của nhân viên công ty A với ộ đ tin cậy 0,95.
b) Hãy ước lượng tỉ lệ nhân viên công ty A có thu nhập không quá 3,6 triệu đồng/tháng với ộ đ tin cậy 0,95.
Biết thu nhập/tháng của nhân viên công t y này là biến ngẫu nhiên có phân phôi (xấpxỉ) chuẩn.
6. Điều tra doanh thu trong tuần (triệu đồng) của một số cửa hàng bán tạp phẩm ở vùng A, người
ta thu được số liệu sau: Doanh thu trong tuần 21 22 23 24 25 26 Số cửa hàng 7 17 29 27 15 5 Với ộ đ tin cậy 95% hãy:
a) Tìm khoảng tin cậy cho doanh thu/tuần trung bình tối thiểu của mỗi cửa hàng tạp phẩm ở vùng A.
b) Tìm khoảng tin cậy cho độ phân tán của doanh thu/tuần.
c) Tìm khoảng tin cậy cho tỉ lệ số cửa hàng có doanh thu/tuần dưới 23 triệu đồng.
7. Để nghiên cứu nhu cầu về một loại hàng ở một khu vực, người ta tiến hành khảo sát về nhu cầu
mặt hàng này ở 400 hộ gia đình, kết quả cho trong bảng:
Nhu cầu (kg/tháng) 0 – 1 1 – 2 2 – 3 3 – 4 4 – 5 5 – 6 6 – 7 7 – 8 Số hộ 10 35 86 132 78 31 18 10
Giả sử khu vực nghiên cứu có 4000 hộ và nhu cầu về loại hàng này là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
a) Ước lượng nhu cầu trung bình về mặt hàng này của toàn khu vực trong một năm với độ tin cậy 95%.
b) Khi ước lượng nhu cầu trung bình về mặt hàng này của toàn khu vực trong một năm, nếu ta
muốn độ tin cậy đạt được 99% và độ chính xác là 4,8 tấn thì cần khảo sát nhu cầu loại hàng
này thêm bao nhiêu hộ gia đình trong vùng này nữa?
8. Lãi suất cổ phiếu của một công ty là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn. Giá trị trong
10 năm qua (đơn vị: %) là: 15, 12, 20, 8,10, 16, 14, 22, 18, 19. Với độ tin cậy 95%, hãy ước lượng:
a) Độ phân tán (phương sai) của lãi suất cổ phiếu này.
b) Độ phân tán tối đa của lãi suất cổ phiếu này.
c) Độ phân tán tối thiểu của lãi suất cổ phiếu này.
9. Kết quả quan sát về hàm lượng vitamin C của một loại trái cây cho ở bảng sau:
Hàm lượng vitamin C(%) 3 – 7 8 – 10 11 – 13 14 – 16 17 – 19 20 – 24 Số trái cây 5 10 20 35 25 5 2
Biết hàm lượng vitamin C ở trái cây này là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
a) Với độ tin cậy 95%, hãy tìm khoảng tin cậy đối xứng của hàm lượng vitamin C trung bình trong mỗi trái;
b) Qui ước những trái cây có hàm lượng vitamin C từ 17% trở lên là loại 1. Nếu muốn độ chính
xác khi ước lượng hàm lượng vitamin C trung bình là 𝜀1 ≤ 0,5 và độ chính xác khi ước
lượng tỉ lệ trái cây loại 1 là 𝜀2 ≤ 0,05 với cùng độ tin cậy 95% thì cần mẫu có kích thước tối thiểu bao nhiêu?
10. Để đánh giá trữ lượng cá trong hồ người ta đánh bắt 2000 con cá, đánh dấu rồi thả xuống hồ.
Sau đó bắt lại 400 con thì thấy có 80 con có dấu. a) Với ộ
đ tin cậy 95%, hãy ước lượng trữ lượng cá trong hồ.
b) Nếu muốn sai số của ước lượng giảm đi một nửa thì lần sau phải đánh bắt bao nhiêu con?
11. Lô hàng có rất nhiều sản phẩm loại A và 1000 sản phẩm loại B. Lấy ngẫu nhiên 400 sản phẩm
từ lô hàng để kiểm tra thì thấy có 36 sản phẩm loại B . a) Với ộ
đ tin cậy 0,95, hãy ước lượng số sản phẩm loại A có trong lô hàng.
b) Nếu muốn ước lượng tỉ lệ sản phẩm loại A có trong lô hàng đạt được độ chính xác 5% thì độ
tin cậy đạt được bao nhiêu %?
12. Để ước lượng số tờ bạc giả của một loại giấy bạc người ta đánh dấu 200 tờ bạc giả loại này rồi
tung vào lưu thông. Sau một thời gian ngắn kiểm tra 600 tờ bạc giả loại này có 15 tờ được đánh dấu. Với ộ
đ tin cậy 95%, hãy ước lượng số tờ bạc giả loại này.
Phần II. Bài toán Kiểm định giả thuyết
1. Khối lượng trung bình của một gói đường do một máy tự động đóng gói theo thiết kế là 500
gam/gói. Nghi ngờ máy đóng gói đường làm việc không bình thường làm cho khối lượng của
gói đường có xu hướng giảm sút. Người ta lấy ngẫu nhiên 30 gói cân thử được khối lượng trung
bình là 495 gam và độ lệch chuẩn s =10 gam. Với mức ý nghĩa 5%, hãy kết luận về nghi ngờ trên.
2. Chỉ tiêu chất lượng A của một loại sản phẩm là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
Một mẫu điều tra được kết quả cho trong bảng: xi (gam) 200 220 240 260 280 Số sản phẩm 3 7 16 17 7
a) Có tài liệu cho rằng trung bình chỉ tiêu A các sản phẩm loại này là 250 gam. Cho nhận xét
về tài liệu này với mức ý nghĩa 5%.
b) Những sản phẩm có chỉ tiêu A nhỏ hơn 240 gam là loại 2. Có tài liệu cho rằng trung bình chỉ
tiêu A các sản phẩm loại 2 là 220 gam. Hãy cho nhận xét về tài liệu này với mức ý nghĩa
2%. Giả thiết chỉ tiêu A của sản phẩm loại 2 có phân phối chuẩn. 3
3. Điều tra doanh số bán hàng X (đơn vị: triệu đồng/tháng) của các hộ kinh doanh một loại hàng năm nay cho số liệu:
Doanh số (tr.đồng/tháng 11 11,5 12 12,5 13 13,5 Số hộ 10 15 20 30 15 10
a) Những hộ có doanh số trên 12,5 triệu đồng/tháng là những hộ có doanh số cao. Có tài liệu
cho rằng tỉ lệ hộ có doanh số cao là 35%. Cho nhận xét về tỉ lệ trong tài liệu đó với mức ý nghĩa 5%?
b) Năm trước doanh số bán hàng trung bình của các hộ này là 120 triệu/1 năm. Có thể cho rằng
doanh số bán hàng của các hộ này năm nay tăng lên không, với mức ý nghĩa 1%?
4. Nếu áp dụng phương pháp công nghệ thứ nhất thì tỉ lệ phế phẩm là 9%, còn áp dụng phương
pháp công nghệ thứ hai thì trong 100 sản phẩm có 4 phế phẩm. Với mức ý nghĩa 5%, có thể cho
rằng áp dụng phương pháp công nghệ thứ hai cho tỉ lệ phế phẩm thấp hơn không?
5. Lô hàng đủ tiêu chuẩn xuất khẩu nếu tỉ lệ phế phẩm không vượt quá 3%. Kiểm tra ngẫu nhiên
400 sản phẩm của lô hàng thấy có 14 phế phẩm. Với mức ý nghĩa 0,05 có cho phép lô hàng xuất khẩu được không?
6. Tỉ lệ phế phẩm do một máy tự động sản xuất là 5%. Kiểm tra một mẫu ngẫu nhiên 300 sản phẩm
thấy có 24 sản phẩm là phế phẩm. Từ đó có ý kiến cho rằng tỉ lệ phế phẩm do máy đó sản xuất
có chiều hướng tăng lên. Hãy kết luận ý kiến nêu trên với mức ý nghĩa 0,05.
7. Một nhà máy sản xuất bóng đèn cho rằng chất lượng bóng đèn loại này được coi là đồng đều
nếu tuổi thọ của các bóng đèn có độ lệch chuẩn bằng 1000 giờ hoặc ít hơn. Lấy ngẫu nhiên 10
bóng để kiểm tra thì tìm được độ lệch chuẩn mẫu s = 1150. Vậy với mức ý nghĩa 5% có thể coi
chất lượng bóng đèn loại này do công ty sản xuất là đồng đều hay không. Biết tuổi thọ của bóng
đèn là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
8. Khối lượng của con gà lúc mới nở là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn. Nghi ngờ độ
đồng đều về trọng lượng gà con giảm sút người ta cân thử 12 con và tìm được s2 = 11,41 (gam)2.
Với mức ý nghĩa 0,05, hãy kết luận về điều nghi ngờ trên biết rằng độ phân tán của khối lượng gà con là σ2 = 10 (gam)2.
Phần III. Bài tập tổng hợp
1. Năng suất lúa của vùng A là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn. Thu hoạch ngẫu nhiên
100 ha của vùng trong vụ này tính được năng suất trung bình là 𝑥 = 37,9 (tạ/ha) và ∑100(𝑥 ) 𝑖=1 𝑖 − 𝑥 2 = 1059.
a) Hãy ước lượng năng suất lúa trung bình của vùng với độ tin cậy 95%.
b) Nếu vụ trước năng suất lúa trung bình của vùng này là 35 (tạ/ha), thì với mức ý nghĩa 5% có
thể cho rằng năng suất lúa vụ này cao hơn được không? 4
2. Năng suất một giống lúa chất lượng cao tại vùng A là biến ngẫu nhiên có phân phối (xấp xỉ)
chuẩn. Thu hoạch ngẫu nhiên 256 ha lúa vùng được các số liệu: 𝑥 = 15,027 (tạ/ha), ∑256( 𝑖=1 𝑥 ) 𝑖 − 𝑥 2 = 148,809.
a) Hãy ước lượng năng suất trung bình tối thiểu của giống lúa trên với độ tin cậy 0,95.
b) Khi mới đưa ra sản xuất, phương sai của năng suất giống lúa trên tại vùng A là 5 (tạ/ha)2.
Người ta nghi ngờ giống lúa trên đã bị thoái hóa nên nó không ổn định so với trước đây. Dựa
vào mẫu trên hãy kết luận về nghi ngờ trên với mức ý nghĩa 5%.
3. Khảo sát về thu nhập của một số người làm việc ở một công ty, người ta thu được bảng số liệu: Thu nhập
20 – 26 26 – 30 30 – 34 34 – 38 38 – 42 42 – 50 (triệu đồng/năm) Số người 20 50 130 110 60 30
a) Những người có thu nhập không quá 30 triệu đồng/năm là những người có thu nhập thấp.
Với độ tin cậy 96%, hãy tìm khoảng tin cậy đối xứng của tỉ lệ người có thu nhập thấp của công ty.
b) Nếu công ty báo cáo mức thu nhập bình quân của một người là 3 triệu đồng/tháng thì có tin
cậy được không (kết luận với mức ý nghĩa 5%)?
c) Nếu muốn ước lượng thu nhập trung bình của một người ở công ty này với ộ đ chính xác 0,5
triệu đồng/năm thì độ tin cậy đạt được bao nhiêu?
4. Thu nhập hàng tháng của một công nhân ở xí nghiệp N là biến ngẫu nhiên có phân phối (xấp xỉ)
chuẩn. Năm nay, điều tra ngẫu nhiên 100 công nhân thu được số liệu sau: Thu nhập 5 5,5 6 6,5 7 7,5 8
(triệu đồng/tháng) Số công nhân 5 15 20 30 15 9 6
a) Biết xí nghiệp N có 1000 công nhân, ước tính thu nhập hàng tháng trung bình của toàn bộ
công nhân ở xí nghiệp này;
b) Với độ tin cậy 95%, ước lượng thu nhập hàng tháng trung bình tối thiểu của 1 công nhân xí nghiệp N.
c) Nếu trước đó 1 năm tỉ lệ công nhân có thu nhập trên 7 triệu đồng/tháng là 10% thì với mức
ý nghĩa 5% có thể cho rằng tỉ lệ này năm nay đã tăng lên không?
5. Mẫu điều tra về giá bán X (đơn vị: 1000 đồng) của mỗi cổ phiếu A trên thị trường chứng khoán
trong các phiên giao dịch được cho ở bảng sau: xi
11 – 13 13 – 15 15 – 17 17 – 19 19 – 21 21 – 23 23 – 25 Số phiên 5 17 23 33 25 16 2
Biết giá bán X là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
a) Với độ tin cậy 95%, hãy tìm khoảng tin cậy đối xứng của doanh thu trung bình khi bán 10000
cổ phiếu A trên thị trường với độ tin cậy 95%. 5
b) Nếu muốn ước lượng giá bán của một cổ phiếu A đạt độ chính xác là 500 đồng với độ tin
cậy 95% thì cần điều tra thêm bao nhiêu phiên nữa?
c) Với độ tin cậy 95%, hãy ước lượng tỉ lệ tối thiểu cổ phiếu A có giá bán từ 17 nghìn đồng trở lên. d) Với ộ
đ tin cậy 90%, hãy tìm khoảng tin cậy của phương sai giá bán một cổ phiếu A.
e) Biết rằng trước kia độ phân tán của giá bán cổ phiếu A là √11 nghìn đồng. Với mức ý nghĩa
2%, có thể cho rằng độ phân tán về giá bán của loại cổ phiếu này có xu hướng giảm xuống
so với trước đây không?
6. Xét nghiệm 100 chai nước Luvia trong một nhà kho, thấy tỉ lệ chất A trong một chai như sau:
Tỉ lệ chất A (%) [0; 5) [5; 10) [10; 15) [15; 20) [20; 25) [25; 30) [30; 35) [35; 40) Số chai 7 12 20 25 18 12 5 1
Biết rằng tỉ lệ chất A (%) ở một chai nước Luvia là biến ngẫu nhiên X có phân phối (xấp xỉ) chuẩn.
a) Với độ tin cậy 95%, trung bình tỉ lệ chất A trong mỗi chai nước Luvia không bé hơn bao nhiêu?
b) Nếu dùng mẫu này để ước tính trung bình tỉ lệ chất A của mỗi chai nước Luvia với độ chính
xác là 1% thì độ tin cậy là bao nhiêu? (biết𝑢0,11 ≈ 1,2393).
c) Nếu muốn ước tính trung bình tỉ lệ chất A đạt độ tin cậy 96% và độ chính xác là 1,2% thì
phải xét nghiệm thêm bao nhiêu chai nước Luvia nữa?
d) Những chai nước Luvia có lượng chất A nhỏ hơn 10% thì không đạt yêu cầu. Biết rằng nhà
kho có 1000 chai nước Luvia, hãy ước tính số chai Luvia không đạt yêu cầu cảu kho ấy với độ tin cậy 96%.
e) Với mức ý nghĩa 5%, cho biết tỉ lệ chai nước Louvia đạt yêu cầu trong kho có trên 80% không?
7. Khảo sát về mức thưởng của một số người làm việc ở một công ti, người ta thu được bảng số liệu:
Mức thưởng (triệu đồng/năm) 20 – 26 26 – 30 30 - 34 34 – 38 38 – 42 42 - 50 Số người 20 50 130 110 60 30
a) Những người có mức thưởng không quá 30 triệu đ/năm là những người có mức thưởng thấp.
Với độ tin cậy 95%, hãy tìm khoảng tin cậy đối xứng của tỉ lệ người có mức thưởng thấp của công ti;
b) Nếu công ti báo cáo mức mức thưởng bình quân của một người là 3 triệu đồng/tháng thì có
tin cậy được không (kết luận với mức ý nghĩa 5%)?
c) Nếu muốn ước lượng mức thưởng trung bình của một người ở công ti này với độ chính xác
0,5 triệu đồng/năm thì độ tin cậy đạt được bao nhiêu?
8. Từ một lô hàng gồm 4000 sản phẩm, người ta chọn ngẫu nhiên 400 sản phẩm để kiểm tra thì 6
thấy có 350 sản phẩm loại I.
a) Nếu cho rằng số sản phẩm loại I của lô hàng là 3700 thì có chấp nhận được không (với mức ý nghĩa 5%)?
b) Nếu muốn ước lượng tỉ lệ sản phẩm loại I của lô hàng đạt được độ chính xác 3,5% và độ tin
cậy 95% thì cần kiểm tra bao nhiêu sản phẩm nữa?
9. Theo dõi giá bán hàng ngày của mặt hàng A cho kết quả sau
Giá bán (triệu đồng) 34,2 34,3 34,4 34,5 34,6 34,7 34,8 34,9 35 Số ngày 5 8 12 17 21 15 12 7 3
Biết giá bán hàng ngày có phân phối chuẩn N(; 2). Viết đáp số cho các câu hỏi sau:
1/ Xác định trung bình mẫu và độ lệch chuẩn mẫu?
2/ Ước lượng tỷ lệ ngày có giá bán tối đa 34,8 triệu?
3/ Với độ tin cậy 95%, ước lượng tối đa giá bán trung bình?
4/ Với độ tin cậy 95%, tìm khoảng ước lượng của độ phân tán về thu nhập?
5/ Với độ tin cậy 95%, tìm giá trị lớn nhất của tỷ lệ ngày bán dưới 34,5 triệu đồng?
6/ Muốn ước tỷ lệ ngày có giá bán cao hơn 34,5 triệu đồng với độ chính xác không quá 0,06
thì cần điều tra tối thiểu bao nhiêu người?
7/ Tỷ lệ ngày có giá bán thấp hơn 34,4 triệu trước đây là 15%. Có ý kiến cho rằng tỷ lệ trên
cao hơn hiện nay. Xác định cặp giả thuyết để kiểm định ý kiến trên?
8/ Tính giá trị quan sát cho kiểm định tại phần 7?
9/ Có ý kiến cho rằng độ phân tán về giá bán mặt hàng A là 0,035 (triệu đồng2). Xác định cặp
giả thuyết để kiểm định ý kiến trên?
10/ Với mức ý nghĩa 5%, nêu kết luận cho kiểm định tại phần 9?
10. Điều tra doanh số bán hàng (đơn vị: triệu đồng/tháng) của các hộ kinh doanh mặt hàng A năm 2022, được số liệu: Doanh số 110 115 120 125 130 135 Số hộ gia đình 10 15 20 30 15 10
Đưa ra kết quả cho những câu hỏi dưới đây (các phép tính làm tròn đến 4 chữ số thập phân).
1) Khi ước lượng trung bình của doanh số bán hàng một tháng của mỗi hộ ?
2) Với độ tin cậy 95%, doanh số bán hàng trung bình của mỗi hộ trong một tháng không vượt quá bao nhiêu?
3) Những hộ có doanh số trên 125 triệu đồng /tháng là những hộ có doanh số cao. Với độ tin
cậy 95%, tỉ lệ hộ có doanh số cao không thấp hơn bao nhiêu? 7
4) Nếu muốn ước lượng tỉ lệ hộ có doanh số cao với độ chính xác 0,05 và độ tin cậy 95% thì
phải điều tra thêm bao nhiêu hộ nữa?
5) Khi ước lượng phương sai của doanh số bán hàng bằng khoảng tin cậy hai phía (giả thiết
doanh số bán hàng của các hộ kinh doanh mặt hàng A là biến ngẫu nhiên có phân phối (xấp
xỉ) chuẩn) thì dùng công thức nào?
6) Có tài liệu cho rằng tỉ lệ hộ có doanh số cao năm 2022 là 30%. Khi kiểm định xem tỉ lệ trong
tài liệu đó có chấp nhận được không thì giá trị quan sát của TCKĐ là bao nhiêu?
7) Năm 2021 trung bình của doanh số bán hàng các hộ này là 1,44 tỷ đồng/năm. Kí hiệu 𝜇 là
doanh số bán hàng trung bình năm 2022. Khi kiểm định rằng doanh số bán hàng trung bình
của các hộ năm 2022 có tăng lên hay không thì cặp giả thuyết là gì ?
8) Với mức ý nghĩa 5%, có thể chấp nhận báo cáo cho rằng độ biến động về doanh số bán hàng
của các hộ kinh doanh mặt hàng A là 50 (triệu đồng)2? Giả thiết doanh số bán hàng của các
hộ kinh doanh mặt hàng A là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
9) Với độ tin cậy 95%, số gia đình có mức doanh thu trên 120 triệu đồng/ tháng ở vùng này
không nhỏ hơn bao nhiêu? Biết rằng toàn vùng có 1000 hộ kinh doanh mặt hàng A.
10) Khi ước lượng trung bình của doanh số bán hàng các hộ này bởi trung bình mẫu với độ
chính xác 5 triệu đồng/ tháng thì độ tin cậy là bao nhiêu? 8
Bảng giá trị hàm 𝜱 𝒖
𝟎(𝒖) = 𝟏 ∫ 𝒆−𝒛𝟐 𝟐 𝒅𝒛 √𝟐𝝅 𝟎 9
Bảng giá trị tới h n chu ạ n
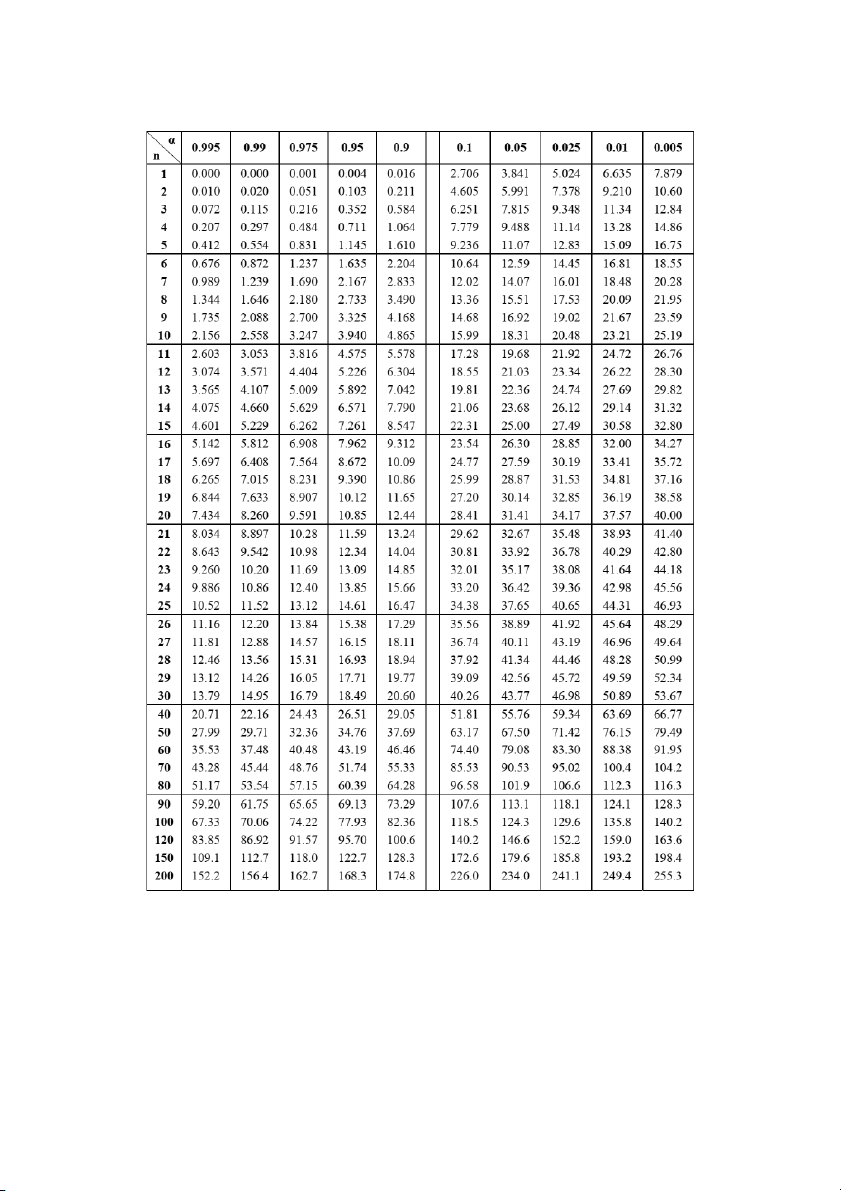
ẩ 𝒖𝜶: 𝑷(𝑼 > 𝒖𝜶) = 𝜶 10
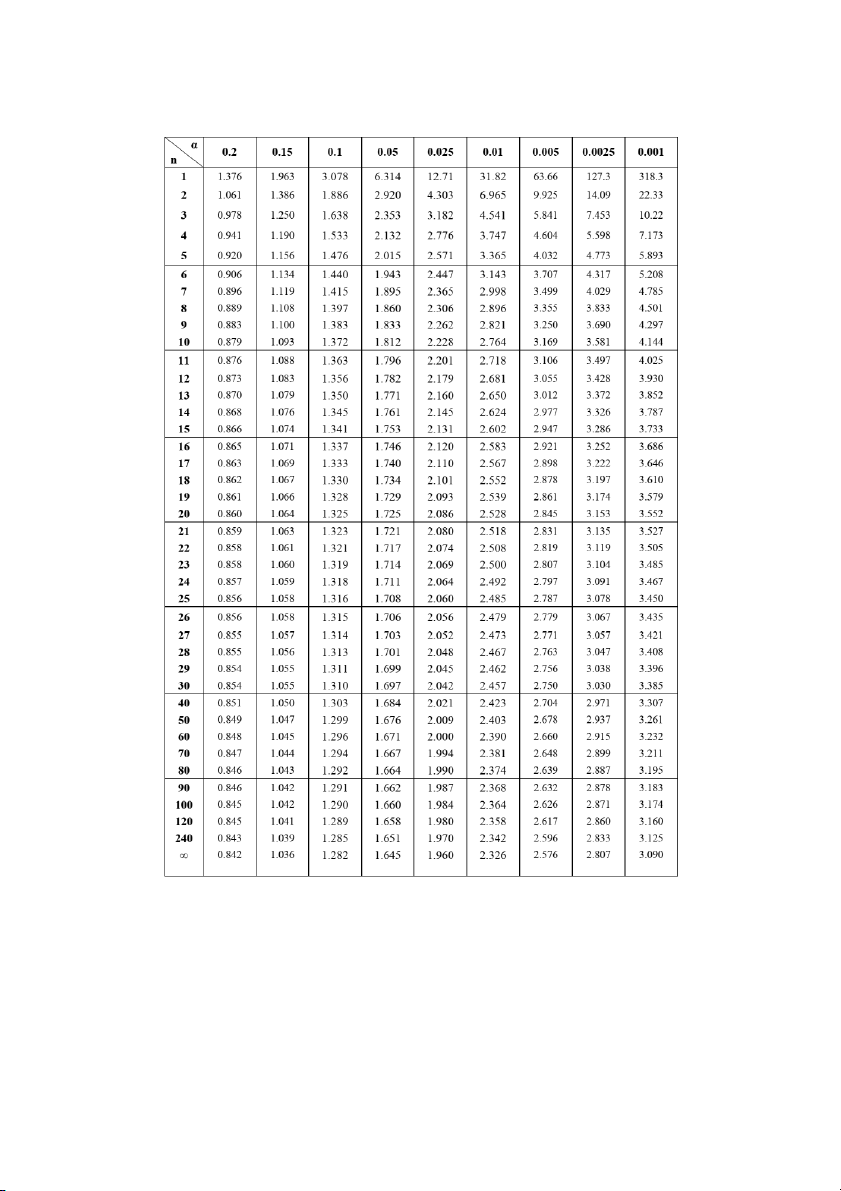
Bảng giá trị tới hạn phân phối Student 𝒕(𝒏) 𝜶 11
Bảng giá trị tới hạn phân phối Khi bình phương 𝝌𝟐(𝒏) 𝜶 12
SỬ DỤNG EXCEL 2010 ĐỂ TRA CÁC GIÁ TRỊ TỚI HẠN
1. 𝛷0(𝑢) = NORM.S.DIST(𝑢,TRUE) − 0.5
2. Giá trị tới hạn chuẩn: 𝑢𝛼 = −1 ∗ NORM.S.INV(𝛼 )
3. Tìm 𝛼 khi biết 𝑢𝛼 : 𝛼 = 1 − NORM.S.DIST(𝑢𝛼,TRUE)
4. Giá trị tới hạn Student: 𝑡
(𝑛)𝛼 = T.INV.2T(2 ∗ 𝛼, 𝑛)
5. Giá trị tới hạn Khi bình phương: 𝜒2(𝑛) 𝛼 = CHISQ.INV.RT(𝛼, 𝑛)
6. Tìm giá trị tới hạn Fisher: Fα(n1, n2) = F. INV. RT(α, n1, n2) (𝑛) (𝑛)
7. Tìm α khi biết n và 𝑡 : 𝛼 = T.DIST.RT(𝑡 , 𝑛) 𝛼 𝛼
SỬ DỤNG MÁY TÍNH CASIO 570 VN PLUS TÍNH CÁC GIÁ TRỊ
CỦA PHÂN PHỐI CHUẨN
1. Tính 𝛷0(𝑢), chẳng hạn với 𝑢 = 1,26
MODE  3  1  AC  SHIFT  1  5  2  1.26  =
Kết quả hiển thị trên màn hình, giá trị 𝛷0(1.26) là: 0.3961 7
2. Tìm 𝑢 khi biết 𝛷0(𝑢) = 0.17
MODE  ▼  3  3  0.33  =  =  =
Kết quả hiển thị trên màn hình: –0.4399131231.
Giá trị của u là: –1 × (–0.4399131231) = 0.4399131231.
(chú ý: 0.33 là kết quả của phép toán 0.5 – 0.17).
3. Tính giá trị của 𝑢𝛼 khi biết 𝛼, chẳng hạn 𝛼 = 0.025
MODE  ▼  3  3  0.025  =  =  =
Kết quả hiện thị trên màn hình: : –1.959964028
Giá trị cần tìm là: 𝑢0.025 = −1 × (– 1.959964028) = 1.959964028
4. Tìm 𝛼 khi biết giá trị của 𝑢𝛼. Ví dụ: Biết 𝑢𝛼 = 1.65, tìm 𝛼?
MODE  3  1  AC  0.5  – (dấu trừ)  SHIFT  1  5  2  1.65  =
Kết quả hiển thị trên màn hình, giá trị 𝛼 là: 0.04947 13