Nghiên Cứu về Doanh Số Điện Thoại | Tiểu Luận Kinh Tế Lượng Ứng Dụng

lOMoAR cPSD| 45740153 lOMoAR cPSD| 45740153 LỜI MỞ ĐẦU
Thế kỉ 21 đang là kỉ nguyên của việc chạy đua công nghệ. Vì vậy nhu cầu sử
dụng điện thoại của mỗi người ngày càng tăng hay nói cách khác điện thoại chính là
một trong những thứ không thể thiếu trong cuộc sống, công việc,…Chính vì thế điện
thoại ngày càng được các doanh nghiệp chú trọng phát triển về mẫu mã, tính năng,
giá cả để có thể đáp ứng được nhu cầu của khách hàng và cạnh tranh nhau trên thị trường.
Tuy nhiên giá cả của một chiếc điện thoại có thể được xem là một trong những yếu
tố quan trọng nhất để người tiêu dùng quyết định xem có nên mua hay không bởi nó
phụ thuộc vào mức thu nhập của mỗi người. Giá cả của một chiếc điện thoại bị chi
phối bởi nhiều yếu tố khác nhau (một trong những yếu tố đó là chi phí nghiên cứu
phát triển và chi phí lắp ráp linh kiện). Xuất phát từ thực tế khách quan và nhu cầu
cấp thiết đó, nhóm em tiến hành khảo sát mô hình hồi quy để tìm ra sự ảnh hưởng
của chi phí nghiên cứu phát triển và chi phí lắp ráp linh kiện đến doanh số bán hàng
điện thoại của doanh nghiệp.
Đối tượng nghiên cứu
Doanh số bán điện thoại của doanh nghiệp.
Phạm vi nghiên cứu
Thị trường tại Việt Nam.
Mục tiêu nghiên cứu
• Xác định yếu tố chi phí nghiên cứu phát triển và chi phí lắp ráp linh
kiện tác động như thế nào đến doanh số bán điện thoại.
• Tìm ra các giải pháp để cải thiện doanh số bán điện thoại của doanh nghiệp. 2 lOMoAR cPSD| 45740153
Kết cấu đề tài bao gồm 3 chương:
• Chương I: Cơ sở lý luận của phương pháp OLS (Phương pháp bình phương nhỏ nhất)
• Chương II: Thực trạng của doanh nghiệp
• Chương III: Các giải pháp
CHƯƠNG I: CƠ SỞ LÝ LUẬN CỦA PHƯƠNG PHÁP OLS
(PHƯƠNG PHÁP BÌNH PHƯƠNG NHỎ NHẤT) 1) Khái niệm
Bình phương nhỏ nhất thông thường (ordinary least squares – OLS) là một
phương pháp phổ biến để ước lượng các tham số của mô hình hồi quy tuyến
tính, mô tả mối quan hệ giữa một hay nhiều biến định lượng độc lập và một
biến phụ thuộc (hồi quy đơn biến hay hồi quy đa biến).
2) Phương pháp và công thức của mô hình hồi quy hai biến (hồi quy ba biến)
• Bắt đầu từ mô hình hồi quy hai biến trở lên thì mô hình có nhiều sai số đáng
kể => Phải có U.
• Mô hình hồi quy tổng thể ngẫu nhiên Yi = β1 + β2X2 + β3X3 + U1
• Hàm hồi quy mẫu (với giả thiết Ûi=0): Ŷi = β̂1+β̂2X2+β̂3X3
• Ý nghĩa của hệ số hồi quy riêng: cho biết ảnh hưởng của từng biến độc
lập lên giá trị trung bình của biến phụ thuộc khi các biến còn lại được giữ không đổi.
• Ý nghĩa của mô hình: 3 lOMoAR cPSD| 45740153
-Khi biến độc lập X2; X3 = 0  ước lượng Ŷi = β̂1.
-Nếu 𝑋2 không đổi => Khi 𝑋3 tăng lên 1 đơn vị thì 𝑌̂ 𝑖 tăng lên 1 khoản chính bằng 𝛽̂ 3.
- Nếu 𝑋3 không đổi => Khi 𝑋2 tăng lên 1 đơn vị thì 𝑌̂ 𝑖 tăng lên 1 khoản chính bằng 𝛽̂ 2.
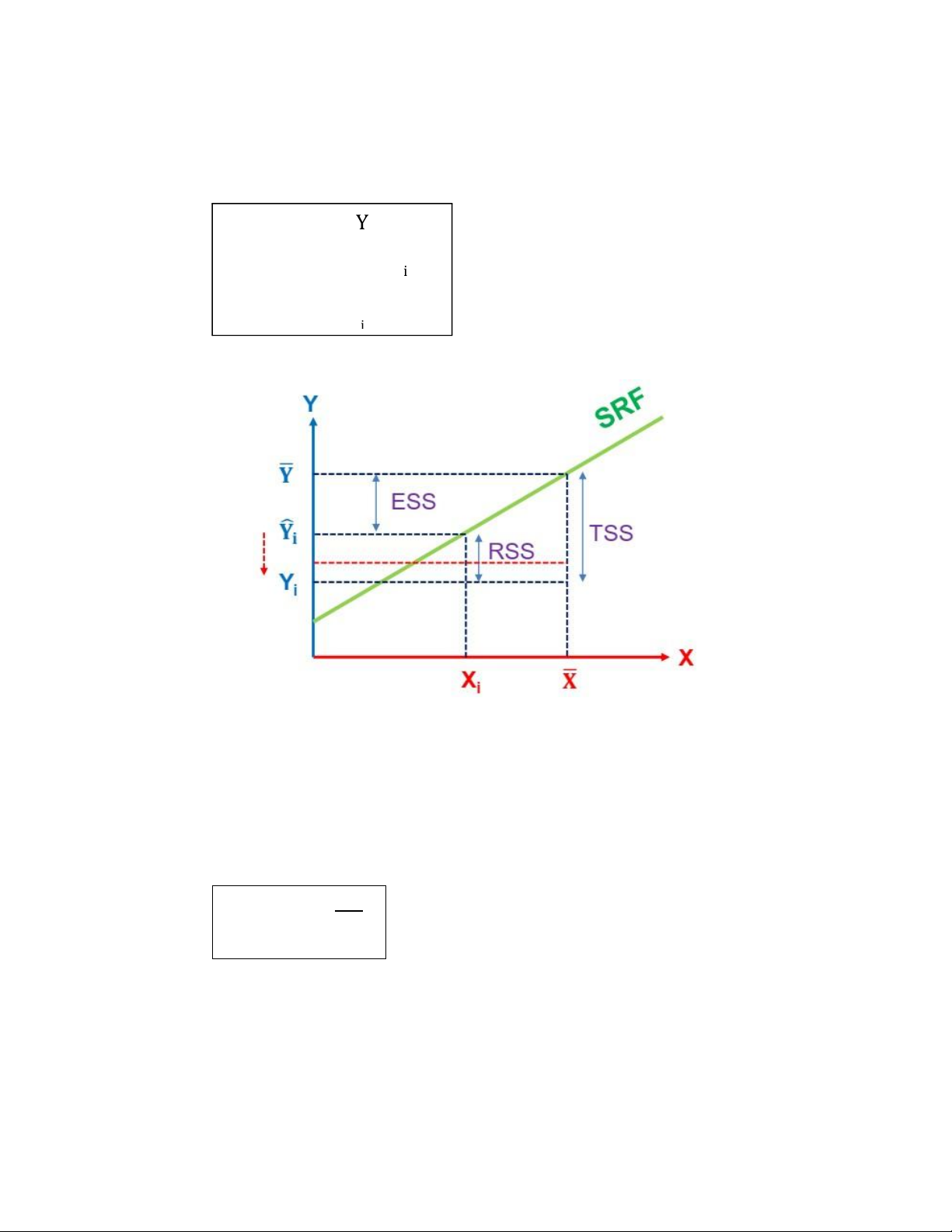
• Tổng bình phương các độ lệch:
-TSS (Total Sum of Squares): Tổng bình phương các độ sai lệch giữa giá
trị quan sát 𝑌̂𝑖 và giá trị trung bình 𝑌̂ của chúng.
-ESS (Explained Sum of Squares): Tổng bình phương các độ sai lệch giữa
giá trị ước lượng 𝑌̂ 𝑖 và giá trị trung bình 𝑌̂ của chúng. 4 lOMoAR cPSD| 45740153
-RSS (Residual Sum of Squares): Tổng bình phương các độ sai lệch giữa
giá trị quan sát 𝑌̂𝑖 và giá trị ước lượng 𝑌̂ 𝑖. TSS
ESS = ∑(Ŷi − Y)2 = β̂2 ∑ yix2i + β̂3 ∑ yix3i RSS = TSS - ESS
• Hệ số xác định 𝑅2: ESS β̂ 𝑅2 = = 2 ∑ yix2i +2β 3 ∑ yix3i TSS ∑ yi
• Hệ số xác định hiệu chỉnh 𝑅 2 (đối với mô hình hồi quy đa biến thì không
tìm r vì không biết lấy dấu của 𝛽̂ nào và không biết Y sẽ phụ thuộc vào X nào): ▪ Lập luận:
𝑅2>> => Mô hình => hoàn hảo
-Thực tế: khi ước lượng mô hình 1 biến thường ít chính xác do còn
quá nhiều biến độc lập (X) khác tác động đến biến phụ thuộc (Y).
-Ví dụ: Biến doanh thu (Y) phụ thuộc bởi các biến độc lập như 𝑋1:
Chi phí quảng cáo, 𝑋2: Chi phí sản xuất, 𝑋3: chị phí nhân công,… -
Do đó: người ta tìm cách tăng 𝑅2 càng nhiều càng tốt => Hiệu chỉnh 𝑅2 bằng 𝑅 2.
-Công thức tính hệ số xác định hiệu chỉnh:
𝑅 2=1 - (1 - 𝑅2)[𝑛−1] k: tham số của mô hình, kể cả hệ số tự do 𝑛−𝑘
-Hệ số xác định hiệu chỉnh 𝑅 2có các tính chất:
+ k càng lớn => 𝑅 2 càng nhỏ hơn 𝑅2.
+ Khi k>1  𝑅 2 ≤ 𝑅2 ≤ 1 5 lOMoAR cPSD| 45740153
+ 𝑅 2 𝑐ó 𝑡ℎể (−).Trường hợp này quy ước: 𝑅 2 = 0 Tóm lại:
-Dùng 𝑅 2 thay thế cho 𝑅2 để xét thêm biến độc lập (X) vào mô hình;
-Nếu thêm biến mà làm 𝑅 2 tăng và các tham số ≠ 0 => nên đưa thêm biến.
• Phương sai của các hệ số hồi quy:
-Phương sai (Var-Variance) là phép đo mức chênh lệch giữa các số liệu
trong một tập dữ liệu trong thống kê. Nó đo khoảng cách giữa mỗi số liệu
với nhau và đến giá trị trung bình của tập dữ liệu.
-Sai số chuẩn (SE-Standard Error) là một thuật ngữ thống kê đo lường độ
chính xác mà phân phối mẫu đại diện cho một tổng thể bằng cách sử dụng độ lệch chuẩn.
-Phương sai nhiễu của tổng thể kí hiệu: 𝜎̂ 2 -Công thức: 6 lOMoAR cPSD| 45740153
• Công thức khoảng tin cậy (khoảng tin cậy - Confidence Interval là một
phạm vi các giá trị có khả năng chứa một tham số tổng thể không xác
định) của hệ số hồi quy 𝛽̂ 1 và 𝛽̂ 2 và 𝛽̂ 3
β̂1 ± tnα−/23.Sê(β̂1) β - n − 3 . + n − 3 .
1 ∈ [ β 1 t α / 2 Se ( β 1 ) ; β 1 t α / 2 Se ( β 1 ) ]
β̂2 ± tnα−/23.Sê(β̂2) β - n − 3 . + n − 3 .
2 ∈ [ β 2 t α / 2 Se ( β 2 ) ; β 2 t α / 2 Se ( β 2 ) ] 7 lOMoAR cPSD| 45740153
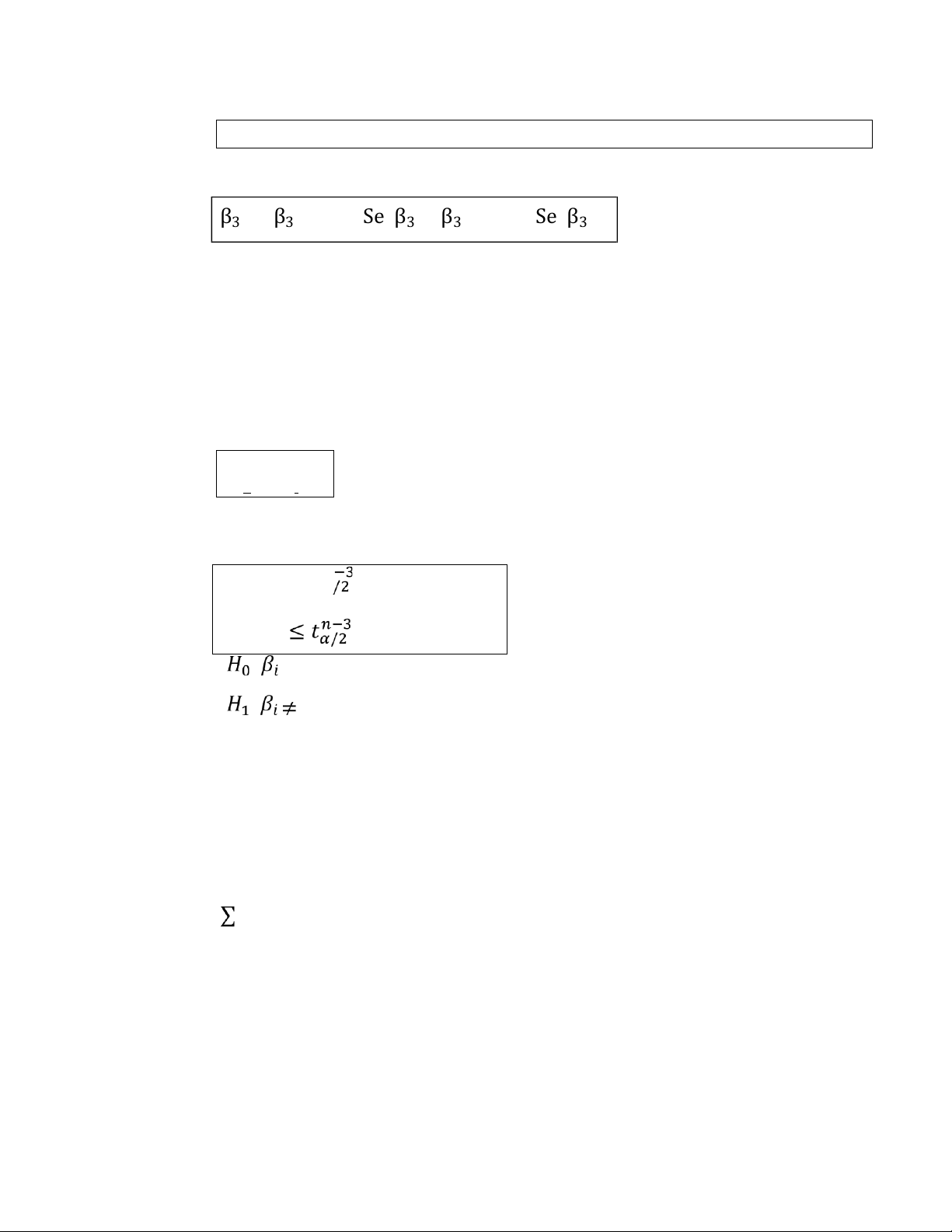
β̂3 ± tnα−/23.Sê(β̂3) β - n − 3 . + n − 3 .
3 ∈ [ β 3 t α / 2 Se ( β 3 ) ; β 3 t α / 2 Se ( β 3 ) ]
Với: 𝛼 (mức ý nghĩa của mô hình) – Tra bảng thống kê t - Student n – Bậc tự do
• Kiểm định giả thiết về tham số (hệ số hồi quy)
Trong thống kê “t” được xác định bằng công thức: t =
𝛽̂Sê1(−𝛽̂ 𝛽̂1𝑖0)
Nguyên tắc quyết định:
Nếu |𝑡𝑖| > 𝑡𝛼𝑛 : Bác bỏ 𝐻0 Nếu |𝑡𝑖| : Chấp nhận 𝐻0
- : = 0 (Biến độc lập 𝑋𝑖 không ảnh hưởng đến biến phụ thuộc 𝑌̂𝑖)
- : 0 (Biến độc lập 𝑋𝑖 có ảnh hưởng đến biến phụ thuộc 𝑌̂𝑖)
3) Phương pháp và công thức của mô hình hồi quy đơn biến (hồi quy hai biến)
• Giả sử có n cặp quan sát (𝑋𝑖, 𝑌̂𝑖). Tìm giá trị 𝑌̂ 𝑖 sao cho 𝑌̂ 𝑖 gần giá trị 𝑌̂𝑖
nhất, tức 𝑒𝑖=|𝑌̂𝑖 − 𝑌̂ 𝑖| càng nhỏ càng tốt. •
𝑒𝑖 thường rất nhỏ và thậm chí bằng 0 vì chúng triệt tiêu lẫn nhau. Để tránh
tình trạng này, ta dùng phương pháp bình phương nhỏ nhất.
• Tính chất của hàm hồi quy mẫu (SRF):
-Hàm hồi quy mẫu SRF luôn đi qua điểm trung bình mẫu (𝑋 ; 𝑌̂ )
-Giá trị trung bình của các phần dư (ngẫu nhiên) 𝑈̅ = 0 8 lOMoAR cPSD| 45740153
-𝑈̅ 𝑖 và 𝑌̂ 𝑖 không tương quan với nhau
-𝑈̅ 𝑖 và 𝑋𝑖 không tương quan với nhau •
Mô hình ước lượng: 𝑌̂ 𝑖 = 𝛽̂ 1 + 𝛽̂ 2𝑋2
• Ý nghĩa của mô hình:
-𝛽̂ 1: Cho biết giá trị trung bình của biến phụ thuộc Y là bao nhiêu khi biến
độc lập X nhận giá trị 0.
-𝛽̂ 2: Cho biết giá trị trung bình của Y sẽ thay đổi (tăng hoặc giảm) bao
nhiêu đơn vị khi giá trị của X (tăng hoặc giảm) 1 đơn vị với điều kiện các
yếu tố khác không đổi. • Công thức: X n Y = ∑ Yi n β̂2 = ∑ ∑YXi2iX −i n−.n(X̅.X̅)Y̅2 β̂1 = Y - β̂2 X xi = Xi - X yi = Yi - Y
Với 𝑥𝑖 và 𝑦𝑖 gọi là độ lệch giá trị của biến so với giá trị trung bình mẫu
• Tổng bình phương độ lệch
-TSS (Total Sum of Squares): Tổng bình phương các độ sai lệch giữa giá
trị quan sát 𝑌̂𝑖 và giá trị trung bình 𝑌̂ của chúng.
-ESS (Explained Sum of Squares): Tổng bình phương các độ sai lệch giữa
giá trị ước lượng 𝑌̂ 𝑖 và giá trị trung bình 𝑌̂ của chúng. 9 lOMoAR cPSD| 45740153
- RSS (Residual Sum of Squares): Tổng bình phương các độ sai lệch giữa
giá trị quan sát 𝑌̂𝑖 và giá trị ước lượng 𝑌̂ 𝑖. TSS = ∑ Y i 2 - n (Y ) 2 ESS = β 2 ( 2 2 ∑ X i 2 – n . X i ) RSS = ∑ ( Y ) 2 i − Y i
• Từ đồ thị ta có thể đưa ra nhận xét: khi ESS càng lớn hơn RSS =>giá trị
ước lượng 𝑌̂ 𝑖 càng gần đúng với giá trị quan sát 𝑌̂𝑖 => mô hình ước
lượng có giá trị đúng rất cao (hoàn hảo) và ngược lại.
• Đặt 𝑅2 là đại lượng đo mức độ phù hợp của SRF với các giá trị quan sát là
𝑋𝑖 và 𝑌̂𝑖: Ta gọi đó là hệ số xác định (Coefficient of determination). 𝑅2 = 1 - 𝑅𝑆𝑆 = 𝐸𝑆𝑆 𝑇𝑆𝑆 𝑇𝑆𝑆
• Hệ số xác định 𝑅2 có các tính chất sau:
-𝑅2 ∈ (0;1). Thông thường: 0 < 𝑅2 ≤ 1 Với:
-R2 = 1: Mô hình hồi quy hoàn hảo 10 lOMoAR cPSD| 45740153
-R2 = 0: Mô hình hồi quy không phù hợp
Thực tế: Ít khi R2 = 0 hoặc R2 = 1 mà thường là gần bằng 1 hoặc gần bằng 0
-R2 ≥ 0.9: Mô hình có độ chính xác cao
-0.7 ≤ R2 < 0.9: Mô hình có độ chính xác khá cao
-0.5 < R2 < 0.7: Mô hình có độ chính xác khá -R2
= 0.5: Mô hình có độ chính xác trung bình
-R2 < 0.5: Mô hình có độ chính xác kém
(Ngoài ra người ta còn dựa trên R2 để làm cơ sở phỏng đoán độ tin cậy)
• Hệ số tương quan r (Correlation Coefficient)
-Để xác định X và Y có quan hệ chặt chẽ với nhau hay không. Ta dùng hệ số tương quan r.
-Công thức xác định hệ số tương quan r như sau: r = ± √ 𝑅 2
(Điều kiện: r cùng dấu với 𝛽̂ 2) -Nếu:
▪ r nhận giá trị (+) => X và Y có quan hệ đồng biến
▪ r nhận giá trị (-) => X và Y có quan hệ nghịch biến
• Các tính chất của hệ số hồi quy -Thứ nhất:
▪ 𝛽̂ 1 và 𝛽̂ 2 là ước lượng của 𝛽̂1 và 𝛽̂2 => Giá trị của 𝛽̂ 1 và 𝛽̂ 2 sau khi
tìm được bằng phương pháp OLS mang ý nghĩa đại diện cho n cặp
quan sát (𝑋𝑖 và 𝑌̂𝑖) -Thứ hai:
▪ 𝛽̂ 1 và 𝛽̂ 2 là đại lượng ngẫu nhiên => Với mẫu khác nhau, chúng sẽ có giá trị khác nhau 11 lOMoAR cPSD| 45740153
 𝛽̂ 1 và 𝛽̂ 2 có sự biến động
-Để đánh giá mức độ biến động 𝛽̂ 1 và 𝛽̂ 2 người ta dùng phương sai (Var-
Variance) và sai số chuẩn (Se-standard error) với:
+Phương sai (Var-Variance) là phép đo mức chênh lệch giữa các số liệu
trong một tập dữ liệu trong thống kê. Nó đo khoảng cách giữa mỗi số liệu
với nhau và đến giá trị trung bình của tập dữ liệu.
+Sai số chuẩn (SE-Standard Error) là một thuật ngữ thống kê đo lường độ
chính xác mà phân phối mẫu đại diện cho một tổng thể bằng cách sử dụng độ lệch chuẩn.
-Công thức tính phương sai-Var cho 𝛽̂ 1 và 𝛽̂ 2: Var( β . σ 2 1 ) = ∑ X i2 n ∑ x 2 (1) i Var( β 2 ) = σ 2 ∑ x 2 (2) i σ2 = RSS n−2
-Do 𝜎̂ 2 là ước lượng của 𝜎̂2 nên khi thay σ 2 vào (1) và (2) ta được:
Var(β̂1) = ∑nX2i .∑σ x22i σ 2 Var(β̂2) = ∑ x2i
-Công thức tính sai số chuẩn-Se cho 𝛽̂ 1 và 𝛽̂ 2: 12 lOMoAR cPSD| 45740153 𝑆𝑒 ( β ) = 1 √ Var ( β 1 ) 𝑆𝑒 ( β ) = 2 √ Var ( β 2 )
• Công thức tính khoảng tin cậy (khoảng tin cậy - Confidence Interval là một
phạm vi các giá trị có khả năng chứa một tham số tổng thể không xác
định) của hệ số hồi quy 𝛽̂ 1 và 𝛽̂ 2:
β̂1 ± tnα−/22. Sê(β̂1) β - n − 2 . ( ) ; n − 2 . ( )
1 ∈ [ β 1 t α / 2 Se β 1 β 1 + t α / 2 Se β 1
β̂2 ± tnα−/22. Sê(β̂2) β - n − 2 . ( ) ; n − 2 . ( )
2 ∈ [ β 2 t α / 2 Se β 2 β 2 + t α / 2 Se β 2
Với: 𝛼 (mức ý nghĩa của mô hình): tra bảng thống kê t – Student n: Bậc tự do
• Kiểm định giả thiết (Kiểm định sự phù hợp của mô hình)
𝑌̂ 𝑖 = 𝛽̂ 1 + 𝛽̂ 2𝑋2
-Đặt: Ký hiệu 𝜃 để chỉ 𝛽̂1 hoặc 𝛽̂2
𝜃 để chỉ 𝛽̂ 1 hoặc 𝛽̂ 2 -Kiểm định 2 phía:
Giả thiết thống kê 𝐻0: 𝜃 = 𝜃0 và 𝐻1: 𝜃 ≠ 𝜃0(Với 𝜃0 là 1 giá trị cho trước). -Kiểm định phía phải: 13 lOMoAR cPSD| 45740153
Giả thiết thống kê 𝐻0: 𝜃 = 𝜃0 và 𝐻1: 𝜃 > 𝜃0 -Kiểm định phía trái:
Giả thiết thống kê 𝐻0: 𝜃 = 𝜃0 và 𝐻1: 𝜃 < 𝜃0 4)
Ứng dụng trong thực tế:
Trong thực tế, người ta có thể sử dụng hồi quy tuyến tính trong nhiều trường hợp:
▪ Khí tượng học, nếu người ta cần dự đoán nhiệt độ hoặc lượng mưa
dựa trên các yếu tố bên ngoài.
▪ Sinh học, nếu người ta cần dự đoán số lượng cá thể còn lại trong một
loài dựa trên số lượng động vật ăn thịt hoặc nguồn sống.
▪ Về kinh tế, nếu người ta cần dự đoán doanh thu của một công ty dựa
trên số lượng hàng được bán ra,… Bảng t – Student 14 lOMoAR cPSD| 45740153
CHƯƠNG II: THỰC TRẠNG DOANH NGHIỆP 15 lOMoAR cPSD| 45740153
CÔNG TY ĐIỆN TỬ SAM SUNG
Phần 1: Tổng quan về doanh nghiệp
1. Phạm vi hoạt động
Theo hãng nghiên cứu thị trường TrendForce, Samsung Electronics Co. là nhà sản
xuất điện thoại thông minh dẫn đầu toàn cầu trong quý III/2020, khi nhu cầu đối với 16 lOMoAR cPSD| 45740153
thiết bị di động của hãng này gia tăng tại các thị trường phát triển trong bối cảnh đại
dịch COVID-19 diễn biến phức tạp.
Sản lượng điện thoại thông minh của Samsung Electronics trong quý III/2020 đạt 78
triệu chiếc, tăng 42% so với quý trước đó và chiếm 23,2% thị phần.
Nhắc đến samsung, người ta sẽ liên tưởng ngay đến các dòng điện thoại thời thượng
và đẳng cấp. Chính vì thế Samsung luôn là một trong những dòng được yêu chuộng
nhất tại Việt Nam. Điều đó có thể thấy rõ nhất qua việc vào năm 2020 Samsung tiếp
tục giữ ngôi vương thị phần điện thoại ở Việt Nam.
Cụ thể, Samsung vẫn đang đứng đầu thị trường Việt với 24% thị phần
Tính đến nay, sự hiện diện của Samsung tại Việt Nam bao gồm 6 nhà máy, 1 trung
tâm Nghiên cứu & Phát triển (R&D) và 1 đơn vị bán lẻ, trong đó SEV (Bắc Ninh) và
SEVT (Thái Nguyên) là 2 nhà máy sản xuất điện thoại di động lớn nhất của Samsung
trên toàn cầu, SEHC (Thành phố Hồ Chí Minh) là nhà máy điện tử gia dụng lớn nhất
tại Đông Nam Á, và SVMC là Trung tâm R&D lớn nhất của Samsung tại Đông Nam 17 lOMoAR cPSD| 45740153
Á. Trong chiến lược phát triển của Samsung, Việt Nam đóng vai trò quan trọng là cứ
điểm toàn cầu không chỉ trong sản xuất mà còn với các hoạt động nghiên cứu và phát triển R&D.
Để đáp nhu cầu của khách hàng cũng như là cải thiện về dịch vụ samsung cũng đã
mở rộng các chuỗi cửa hàng trải nghiệm nhằm tư vấn, hỗ trợ phần mềm cũng như
sửa chửa, chăm sóc thiết bị điện thoại, tại Việt Nam đã có 5 cửa hàng trải nghiệm
Samsung (1 cửa hàng ở miền bắc và 4 cửa hàng ở miền nam):
- Cửa Hàng Trải Nghiệm Samsung Thái Hà: 98 Thái Hà, Quận Đống Đa, Hà Nội
- Cửa Hàng Trải Nghiệm Samsung Crescent Mall: Tầng 3, Crescent Mall, 101
Tôn Dật Tiên, P. Tân Phú, Q.7, TP.HCM
- Cửa Hàng Trải Nghiệm Samsung Biên Hòa: 91 Đồng Khởi, P. Tam Hiệp, TP. Biên Hòa, Đồng Nai
- Cửa Hàng Trải Nghiệm Samsung Bình Dương: 459 Đại lộ Bình Dương, P.
Phú Cường, TP. Thủ Dầu Một, Bình Dương
- Cửa Hàng Trải Nghiệm Samsung Kiên Giang: 570 Nguyễn Trung Trực, P.
Vĩnh Lạc, TP. Rạch Giá, Kiên Giang
Ngoài ra, điện thoại samsung chính hãng còn được phối bởi các doanh nghiệp và cửa hàng khác 18 lOMoAR cPSD| 45740153
2. Sứ mệnh và giá trị cốt lõi - Sứ mệnh:
Samsung đi theo triết lý kinh doanh đơn giản: cống hiến tài năng và công nghệ của
mình để tạo ra các sản phẩm và dịch vụ vượt trội đóng góp cho một xã hội toàn cầu 19 lOMoAR cPSD| 45740153
tốt đẹp hơn. Để đạt được điều này, Samsung hết sức coi trọng con người và công nghệ của mình.
Năm 2017, Samsung Việt Nam tập trung hỗ trợ tư vấn các doanh nghiệp hoạt động
trong lĩnh vực công nghiệp kỹ thuật cao và mở rộng phạm vi tư vấn đến các công ty đối tác nội địa.
Với 12 doanh nghiệp Việt Nam tham gia chương trình tư vấn trong năm 2017,
Samsung sẽ cử các chuyên gia Hàn Quốc giàu kinh nghiệm trong lĩnh vực công nghệ
sản xuất thành phẩm và quản lý chất lượng sản xuất sang trực tiếp hướng dẫn trong
12 tuần. Theo đó, các chuyên gia Hàn Quốc sẽ khảo sát, đánh giá các doanh nghiệp
Việt trong thời gian hai tuần và trực tiếp tư vấn, làm việc cùng doanh nghiệp Việt
trong mười tuần tiếp theo nhằm cải tiến quy trình sản xuất và hoàn thiện các tiêu
chuẩn trong việc cung ứng sản phẩm, linh kiện cho các nhà máy của Samsung tại Việt Nam.
Ông Han Myoung Sup, Tổng Giám đốc Tổ hợp Samsung Việt Nam cho biết
“Trong suốt hai năm qua, Samsung đã luôn nỗ lực hỗ trợ các doanh nghiệp Việt Nam
gia tăng năng lực cạnh tranh về sản xuất và chất lượng sản phẩm của mình. Việc
chuyển hướng tư vấn và hỗ trợ sang ngành công nghiệp kỹ thuật cao giúp các doanh
nghiệp Việt sản xuất được các linh kiện phức tạp hơn và tham gia vào chuỗi giá trị
cao hơn chính là sự khẳng định mạnh mẽ cho cam kết đầu tư lâu dài và bền vững tại
thị trường Việt Nam của Samsung”. - Giá trị:
+Con người: Là nền tảng cốt lõi của công ty, Samsung luôn đào tạo nhân viên của
mình trở thành những cá nhân tài giỏi nhất, xuất sắc nhất và ứng xử có văn hóa. 20