Nội dung ôn tập giữa HK2 Toán 10 năm 2020 – 2021 trường Trần Phú – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
NỘI DUNG ÔN TẬP GIỮA HỌC KÌ II
TRƯỜNG THPT TRẦN PHÚ-HOÀN KIẾM Môn: TOÁN Khối : 10
Năm học 2020-2021
I – PHẦN ĐẠI SỐ
Bài 1: Giải các bất phương trình sau: 2 3 4 x  2x  5 x  
1  x  2  x  6 a)  x  3 b)  0 x  4
x 73 x  22 2 x  2 x  3 x  4x 15 c)  2
x  x   2 3 2
x  5x  6  0 d)   2 1 x x 1 x 1
Bài 2: Giải các hệ bất phương trình sau: 2    2  x 3x 4
x  x 12  0 2 3
 x 10x 3  0   0 a)  b)  c) 2  x  3 2x 1  0 2
x  6x 16  0  2
x  x  2  0 2x  3 1  x 1 2 x  2x  7 2 1 x  2x  2 d)  e) 4   1 f)  1
 x  22x  4 2 x 1 2    13 x 5x 7 0   x 1
Bài 3: Giải các phương trình và bất phương trình sau: a) 2
x  5x  4  x  4 b) 2
x  5 x 1 1  0 c) 2
x 1  2x  0 2 x  4x
d) 1 4x  2x 1 e) 2x  5  7  4x f) 1 2 x  x  2
Bài 4: Giải các phương trình và bất phương trình sau: a) 2
3x  9x 1  x  2 b) 2
x  x 12  7  x c) 2
21 4x  x  x  3 2 x 16 5  x  x  d)  x  3  e) 2
x 8x 12  x  2 4 3 4 f)  2 x  3 x  3 x
Bài 5: Tìm tất cả các giá trị của m để mỗi biểu thức sau luôn dương với mọi x. a) 2
x  4x  m  5 b) 2
x  m  2 x  8m 1 c) m   2
1 x  2m  
1 x  3m  2
Bài 6: Tìm tất cả các giá trị của m để mỗi biểu thức sau luôn âm với mọi x. a) m   2
4 x  m  
1 x  2m 1 b) m   2
2 x  5x  4 c) 2
x  m   2 4 1 x 1 m
Bài 7: Tìm tất cả các giá trị của tham số m để mỗi bất phương trình sau nghiệm đúng với mọi giá trị x: a) m   2
1 x  2m  
1 x  3m  3  0 b)  2
m  m   2 4
5 x  2 m   1 x  2  0 1 2 x  8x  20 c)  0 2
mx  2 m   1 x  9m  4
Bài 8: Tìm tất cả các giá trị của m để phương trình: a) 2
x  2m  
1 x  9m  5  0 có hai nghiệm âm phân biệt b) m   2
2 x  2mx  m  3  0 có hai nghiệm dương phân biệt. c) m   2
5 x  3mx  m 1  0 có hai nghiệm trái dấu
Bài 9. Tìm tất cả các giá trị của m sao cho phương trình: 4
x    m 2 2 1 2
x  m 1  0 a) vô nghiệm
b) Có hai nghiệm phân biệt c) Có bốn nghiệm phân biệt
Bài 10. Tìm tất cả các giá trị của tham số m để hệ bất phương trình sau vô nghiệm: 2
x 10x 16  0 
mx  3m 1
Bài 11. Biểu diễn hình học tập nghiệm của các bất phương trình sau:
a) 2x  y  1 b) 3
 x  y  2  0 c) 2x  3y  5  0
Bài 12. Biểu diễn hình học tập nghiệm của các hệ bất phương trình sau:
x  3y  0 3   y  0  a) 
b) x  2 y  3 
2x  3y 1  0 x  y  2 
x  y  2  0 
Bài 13. Cho hệ bất phương trình:  H  x  y 1  0
2x  y 1 0 
a) Biểu diễn hình học tập nghiệm của hệ bất phương trình
b) Tìm x, y thỏa mãn (H) sao cho F = 2x+3y đạt giá trị lớn nhất, giá trị nhỏ nhất.
II - PHẦN HÌNH HỌC
Bài 1: Cho  ABC có a = 7, b = 8, c = 5. Tính : góc Â; diện tích S của tam giác ABC; đường
cao ha kẻ từ đỉnh A; đường trung tuyến kẻ từ đỉnh A; bán kính đường tròn ngoại tiếp, nội tiếp của tam giác ABC.
Bài 2: Cho tam giác ABC có AB = 6, AC= 8 và 0 ˆA  60
a) Tính diện tích S, đường cao ha, trung tuyến ma của tam giác ABC.
b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC
c) Tính độ dài đường phân giác trong của góc A.
Bài 3: Tam giác ABC có Bˆ  600 Cˆ ;
 450; BC  a .Tính theo a độ dài hai cạnh AB, AC và
bán kính đường tròn nội tiếp,ngoại tiếp tam giác ABC.
Bài 4: Cho tam giác ABC có a = 5, b = 6, c = 3. Trên đoạn AB, BC lần lượt lấy các
điểm M, K sao cho BM = 2, BK = 2. Tính độ dài MK.
Bài 5: Cho tam giác ABC, các trung tuyến AA1 = 3, BB1 = 6 và hợp với nhau một góc 600.
Tính độ dài các cạnh của tam giác ABC. 2
Bài 6: Cho tam giác ABC có BC  a;CA  b; AB  c và đường trung tuyến AM = c = AB. Chứng minh rằng: a) 2 a   2 2
2 b  c  b) 2 sin A   2 2 sin B 2  sin C
Bài 7: Cho tam giác ABC có các cạnh a, b, c thỏa mãn: 2 2 2
5c  a  b .Chứng minh rằng: Tam
giác có hai đường trung tuyến AA1 và BB1 vuông góc với nhau.
Bài 8: Cho tam giác ABC có 𝑎 = 7, 𝑏 = 8, 𝑐 = 5. Chứng minh rằng: ∆𝐴𝐵𝐶 có một góc bằng 600.
b3  c3  3  a  a2
Bài 9: Chứng minh rằng: ∆𝐴𝐵𝐶 đều   b  c  a a  b 2 cos C
Bài 10: Khoảng cách từ A đến C không thể đo được trực tiếp vì phải qua một đầm lầy nên
người ta làm như sau: Xác định một điểm B có khoảng cách AB = 12m và đo được góc 𝐴𝐶𝐵 ̂ =
370. Hãy tính khoảng cách AC biết rằng BC = 5m.
III - PHẦN BÀI TẬP TRẮC NGHIỆM
Câu 1: Tìm tập nghiệm S của bất phương trình 2 x  4  0 .
A. S   ;  2
 2; B. S   2  ;2
C. S   ;  2  2;
D. S   ;
 04;
Câu 2: Tìm tập nghiệm S của bất phương trình 2
x  4x  4  0 . A. S  \   2 B. S 
C. S  2; D. S  \   2
Câu 3: Tìm khẳng định đúng trong các khẳng định sau?
A. f  x 2
 3x  2x  5 là tam thức bậc hai.
B. f  x  2x  4 là tam thức bậc hai.
C. f  x 3
 3x  2x 1 là tam thức bậc hai.
D. f  x 4 2
 x  x 1 là tam thức bậc hai.
Câu 4: Cho f  x 2
 ax  bx  ca  0 và 2
  b  4ac . Cho biết dấu của khi f  x
luôn cùng dấu với hệ số a với mọi x . A. < 0. B. = 0. C. > 0. D. 0.
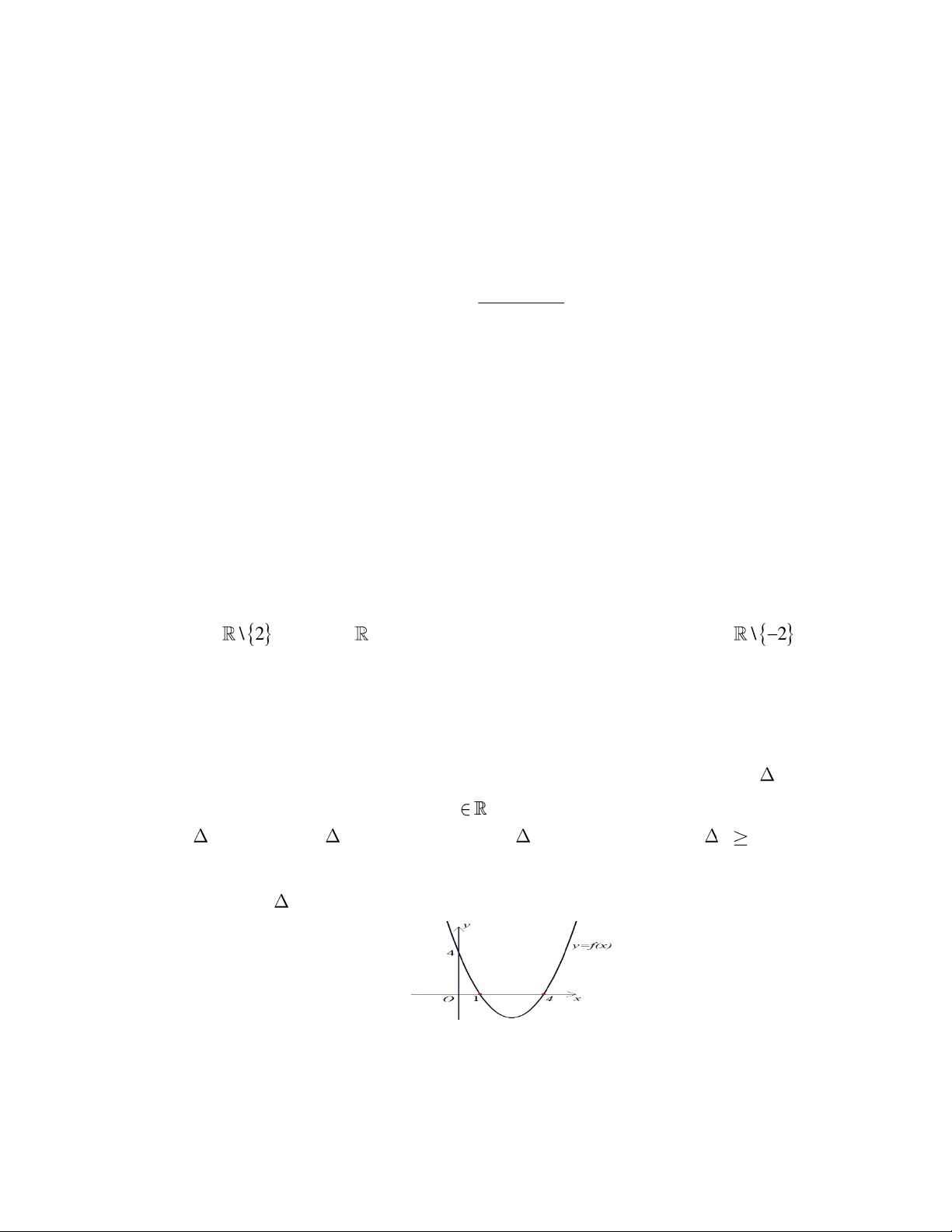
Câu 5: Cho hàm số    2 y
f x  ax  bx  c có đồ thị như hình vẽ. Đặt 2
  b  4ac , tìm dấu của a và .
A. a  0,   0 B. a  0,   0
C. a  0,   0
D. a  0,   0
Câu 6: Tìm giá trị của tham số m để phương trình 2
x  m   2
2 x  m  4m  0 có hai nghiệm trái dấu. 3
A. 0  m  4
B. m  0 hoặc m  4 C. m  2 D. m  2
Câu 7: Tìm các giá trị của tham số m để phương trình 2
x  mx  4m  0 vô nghiệm.
A. 0  m  16 B. 4   m  4
C. 0  m  4
D. 0  m  16
Câu 8: Tìm tất cả các giá trị của a để 2 a  a
A. a  0 hoặc a  1
B. 0  a  1
C. a  1 D. a 
Câu 9: Tìm tất cả các giá trị của tham số m để bất phương trình 2
x  x  m  0 vô nghiệm. 1 1 1 A. m  B. m C. m  D. m  4 4 4
Câu 10: Giá trị x thỏa mãn bất phương trình 2  x  6  0 là? A. x  2 . B. x  3 .
C. x  4 . D. x  5 . 1
Câu 11: Điều kiện của bất phương trình  x  2 là? 2 x  4 A. x  2  . B. x  2 . C. x  2 . D. x  0 .
Câu 12: Nghiệm của bất phương trình 2x 10  0 là?
A. x  5 . B. x  5 . C. x  5 . D. x  8 .
Câu 13: Tìm tập nghiệm S của bất phương trình 4  x 16  0 ?
A. S  4; . B. S  4; .
C. S   ;  4.
D. S   ;  4   .
Câu 14: Nhị thức f  x  2x  6 dương trong ?
A. S  3; . B. S   ;3   .
C. S  3;.
D. S    ;3 .
Câu 15: Tập nghiệm của bất phương trình  x  
1  x  3  0 là? A. . B.  ;   
3 1; . C.  3   ;1 . D. 1; . 4  x
Câu 16: Tập nghiệm của bất phương trình  0 là? 3  x  6 A. 2;4 . B.  ;
 24;. C. 2;4 .
D. 2; 4 . x 
Câub 17: Tập nghiệm của bất phương trình 1 1là? x  3
A. S  3; . B. S  .
C. S   .
D. S   ;3   .
Câu18: Bất phương trình nào sau đây là bậc nhất một ẩn? 2
A. 3x 1 2x B.  3  x
C. 2x  y  1
D. 2x 1  0 x x 
Câu 19: Tìm điều kiện của bất phương trình 2 3  x 1la? 2x  3 3 3 2 2 A. x   . B. x  .
C. x   . D. x  . 2 2 3 3 4 2x  3
Câu 20: Tìm điều kiện của bất phương trình  x  2 là? 6  3x A. x  2 . B. x  2 . C. x  2 . D. x  2 .
Câu 21: Tập nghiệm của bất phương trình 2  3x  x  6 là? A. S   1
 ; . B. S   ;    1 .
C. S    ;1 .
D. S  1; .
Câu 22: Giá trị x  2
 là nghiệm của hệ bất phương trình nào sau đây? 2x  3 1
2x  5  3x 2x  4  3
2x  3  3x  5 A.  . B.  . C.  . D.  . 3   4x  6  4x 1  0 1   2x  5 2x  3 1
Câu 23: Cho f  x  2x  4 , khẳng định nào sau đây là đúng?
A. f  x  0  x  2  ; .
B. f  x  0  x  ;  2 .
C. f  x  0  x 2;  .
D. f  x  0  x  2  . x 
Câu 24: Tập nghiệm của bất phương trình 3 2x   4x 1là? 5  8   8  A. S  ;    . B. S   ;     . 11   11  4   2  C. S  ;    . D. S   ;   .   11   11
Câu 25: Tập nghiệm của bất phương trình 5  x2x  3  0 là?  3   3   3    A. S   ;  5;   B. S  ;5   C. S  5;  
 . D. S     3 ; 5  ;    .  2   2   2   2  x 
Câu 26: Tập nghiệm của bất phương trình 4 2  0? 6  2x
A. S  2;3
B. S  2;  3
C. S   ;
 23; D. S   ;  23;
Câu 27: Tìm m để f  x  m  2 x  2m 1 là nhị thức bậc nhất? m  2  A. m  2 B.  1
C. m  2 D. m  2 m   2
Câu 28: Tập nghiệm của bất phương trình 2x 1  1 ? 1 
A. S  0  ;1 B. S  ;1  
C. S    ;1
D. S   ;   1 1; 2 
Câu 29: Tập nghiệm của bất phương trình 3x 1  2 ?    1   1 
A. S    1 ;1  ;  
 .B. S   C. S  1  ;   D. S  ;     3   3   3  5
Câu 30: Tập nghiệm của bất phương trình 2
x  2  x 1 ?  1  1  A. S   B. S   ;    
C. S  1; D. S  ;     2  2 
Câu 31: Trong tam giác ABC có:
A. a2  b2  c2  bc cos A B. a2  b2  c2  bc cos A
C. a2  b2  c2  bc 2
cos A D. a2  b2  c2  bc 2 cos A
Câu 32: Nếu tam giác ABC có 2 2 2
a  b  c thì:
A. Aˆ là góc tù B. Aˆ là góc vuông
C. Aˆ là góc nhọn D. Aˆ là góc nhỏ nhất
Câu 33: Trong tam giác ABC có:
A. a  2R cos A B. a  2R sin A
C. a  2R tan A D. a  Rsin A
Câu 34: Trong tam giác ABC có 0 ˆ AB  2 , m AC  1 ,
cm A  60 Khi đó độ dài cạnh BC là:
A. 1cm B. 2 cm C. 3 cm D. 5 cm
Câu 35: Tam giác ABC có: 𝑎 = 5; 𝑏 = 3; 𝑐 = 5. Số đo của góc 𝐵𝐴𝐶 ̂ là: A. 0 ˆA  60 B. 0 ˆA  30 C. 0 ˆA  45 D. 0 ˆA  90
Câu 36: Tam giác ABC có AB = 8cm, BC = 10cm, CA = 6cm. Đường trung tuyến AM của
tam giác đó có độ dài bằng:
A. 4cm B. 5 cm C. 6 cm D. 7 cm
Câu 37: Tam giác ABC vuông tại A có AB = 6cm, BC = 10cm. Đường tròn nội tiếp tam giác đó có bán kính r là:
A. 1cm B. 2 cm C. 2 cm D. 3 cm
Câu 38: Tam giác ABC có : a  cm 3 ,b  cm 2 , c  cm 1
.Đường trung tuyến ma có độ dài là: 5 3
A. 1cm B. 1,5 cm C. cm D. cm 2 2
Câu 39: Tam giác đều nội tiếp đường tròn bán kính R = 4cm có diện tích là: A. 2 12 3cm B. 2 13 2cm C. 2 13cm D. 2 15cm
Câu 40: Tam giác ABC vuông cân tại A có AB = a. Đường tròn nội tiếp tam giác ABC có bán kính r bằng: a a a a A. B. C. D. 2 2 2  2 3
Câu 41: Tam giác ABC có ba cạnh thỏa mãn điều kiện: a  b  ca  b  c  ab 3 . Khi đó số đo của góc 𝐶̂ là: A. 0 120 B. 0 30 C. 0 45 D. 0 60
Câu 42: Hình bình hành ABCD có AB  ; a BC  a 2, . Khi đó hình bình hành có diện tích là: A. 2 2a B. 2 a 2 C. 2 a D. 2 a 3 6
Câu 43: Tam giác ABC vuông cân tại A có AB = AC = a. Đường trung tuyến BM có độ dài là: 3 a 5 A.
a B. a 2 C. a 3 D. 2 2
Câu 44: Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R bằng: a 3 a 3 a 2 a 3 A. B. C. D. 2 3 3 4
Câu 45: Bán kính đường tròn nội tiếp tam giác đều cạnh a bằng: a 3 a 2 a 3 a 5 A. B. C. D. 6 5 4 7
Câu 46: Trong tam giác ABC có: b  c b  c b  c A. m  B. m  C. m 
D. m  b  c a 2 a 2 a 2 a
Câu 47: Tam giác ABC có 0
ˆA 120 thì câu nào sau đây đúng
A. a2  b2  c2  bc 3
B. a2  b2  c2  bc
C. a2  b2  c2  bc 3
D. a2  b2  c2  bc
Câu 48: Tam giác ABC có a  ; 8 b  ;
7 c  5 Diện tích của tam giác là
A. 5 3 B. 8 3 C. 10 3 D. 12 3
Câu 49: Diện tích của tam giác ABC, biết ˆ A  600;b  ; 10 c  20 là:
A. 50 3 B. 50 C. 50 2 D. 50 5
Câu 50: Cho tam giác ABC có a  ;
2 b  6;c  1 3 Góc Bˆ là A. 0 115 B. 0 75 C. 0 60 D. 530 ' 32
Câu 51: Cho tam giác ABC có a  ;
2 b  6;c  1 3 Góc Aˆ là: A. 0 30 B. 0 45 C. 0 68 D. 0 75
Câu 52: Cho tam giác ABC, các đường cao h , h , h thỏa mãn hệ thức h 3  h 2  h . Tìm hệ a b c a b c thức giữa a, b, c. 3 2 1 3 2 1 A.   B. a 3  b
2  c C. a 3  b 2  c D.   a b c a b c
Câu 53: Cho tam giác ABC, nếu h 2
 h  h thì a b c 2 1 1 A.  
B. 2sin A  sin B  sin C sin A sin B sin C 2 1 1
C. sin A  2sin B  2sin C D.   sin A sin B sin C
Câu 54: Diện tích S của tam giác sẽ thỏa mãn hệ thức nào trong hai hệ thức sau đây ? I.
S 2  pp  ap  bp  c II. S 2 16
 a  b  ca  b  ca b  cb  c  a
A. Chỉ I B. Chỉ II C. Cả I và II D. Không có 7
Câu 55: Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R. Gọi r là bán kính đườ R
ng tròn nội tiếp tam giác ABC. Khi đó tỉ số bằng r 2  2 2 1 2 1 A. 1 2 B. C. D. 2 2 2 8