lOMoAR cPSD| 46831624
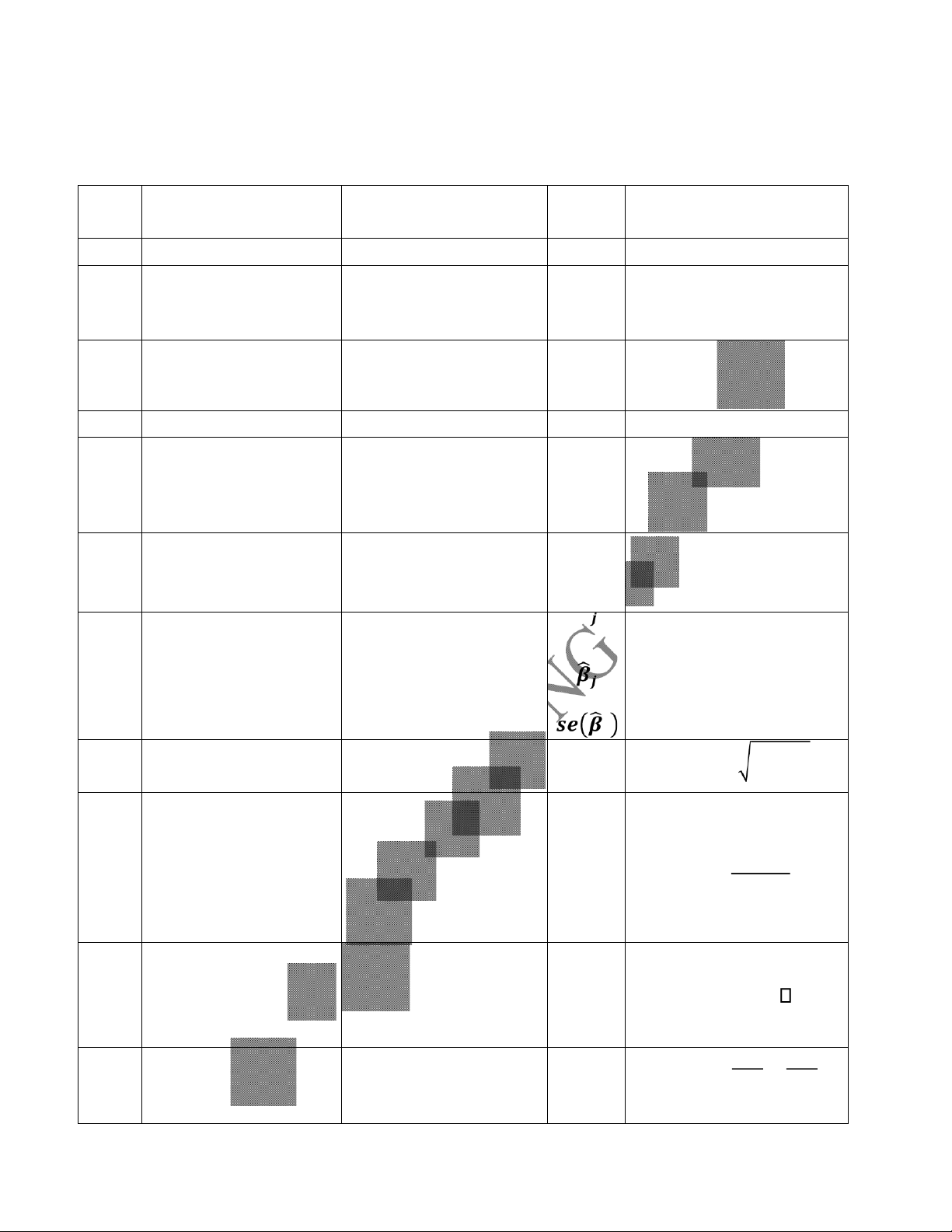
Ý NGHĨA BẢNG HỒI QUY MÔ HÌNH BẰNG PHẦN MỀM EVIEWS CẦN KÍ TÊN CÔNG THỨC TÍNH XEM Ý NGHĨA HIỆU 1 Dependent Variable Tên biến phụ thuộc Y Phương pháp bình
Method: Least Squares phương tối thiểu (nhỏ OLS nhất) Date - Time Ngày giờ thực hiện Sample Số liệu mẫu Included 2 Observations Cỡ mẫu (số quan sát) n Các biến giải thích có 3 Cột Variable trong mô hình (trong
đó C là hệ số bị chặn)
Giá trị các hệ số hồi quy 4 Cột Coefficient
Sai số chuẩn của các hệ 5 Cột Std. Error = var số hồi quy
Giá trị thống kê t tương
ứng (trong đó t là đại lương ngẫu 6 Cột t-Statistic nhiên có phân phối hoặc = Student với bậc tự do (n-k)) Giá trị xác p –
suất của thống value 7 p-valuej = P(t tj) Cột Prob kê t tương ứng = 1 − = 8 R - Squared
Hệ số xác định mô hình ℎ = , lOMoAR cPSD| 46831624
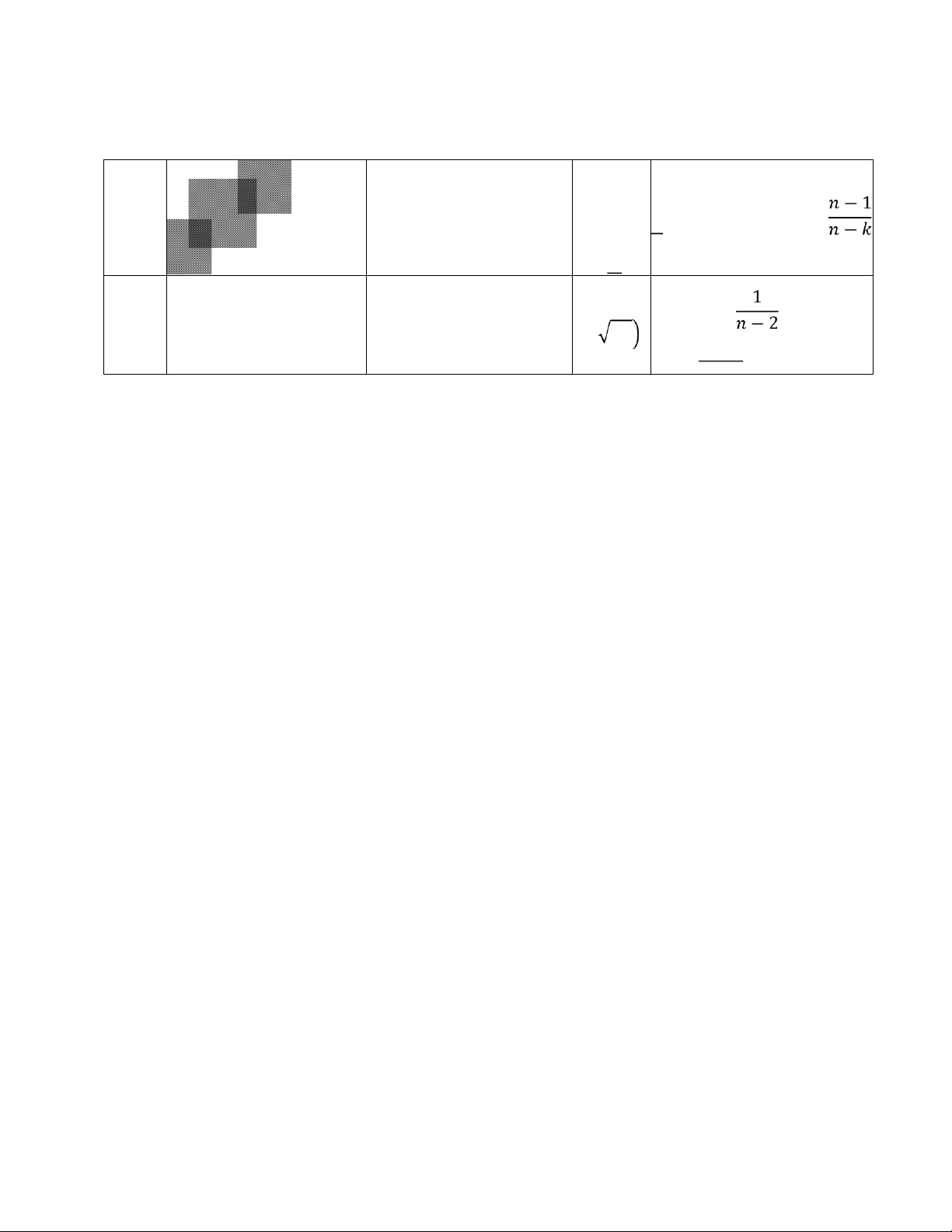
Hệ số xác định có hiệu 9 Adjusted R- chỉnh = 1 − (1 − ) Squared Sai số chuẩn của hồi 10 S.E of regression
quy (giá trị ước lượng = cho ) = =−, − lOMoAR cPSD| 46831624 = Tổng bình phương các 11 Sum squared resid RSS sai lệch (phần dư) = − = − = −, Tiêu chuẩn ước lượng hợp lý (Logarit của Log likelihood L hàm hợp lý) Durbin – Watson Thống kê Durbin - 12 Stat d Watson Giá trị trung bình mẫu
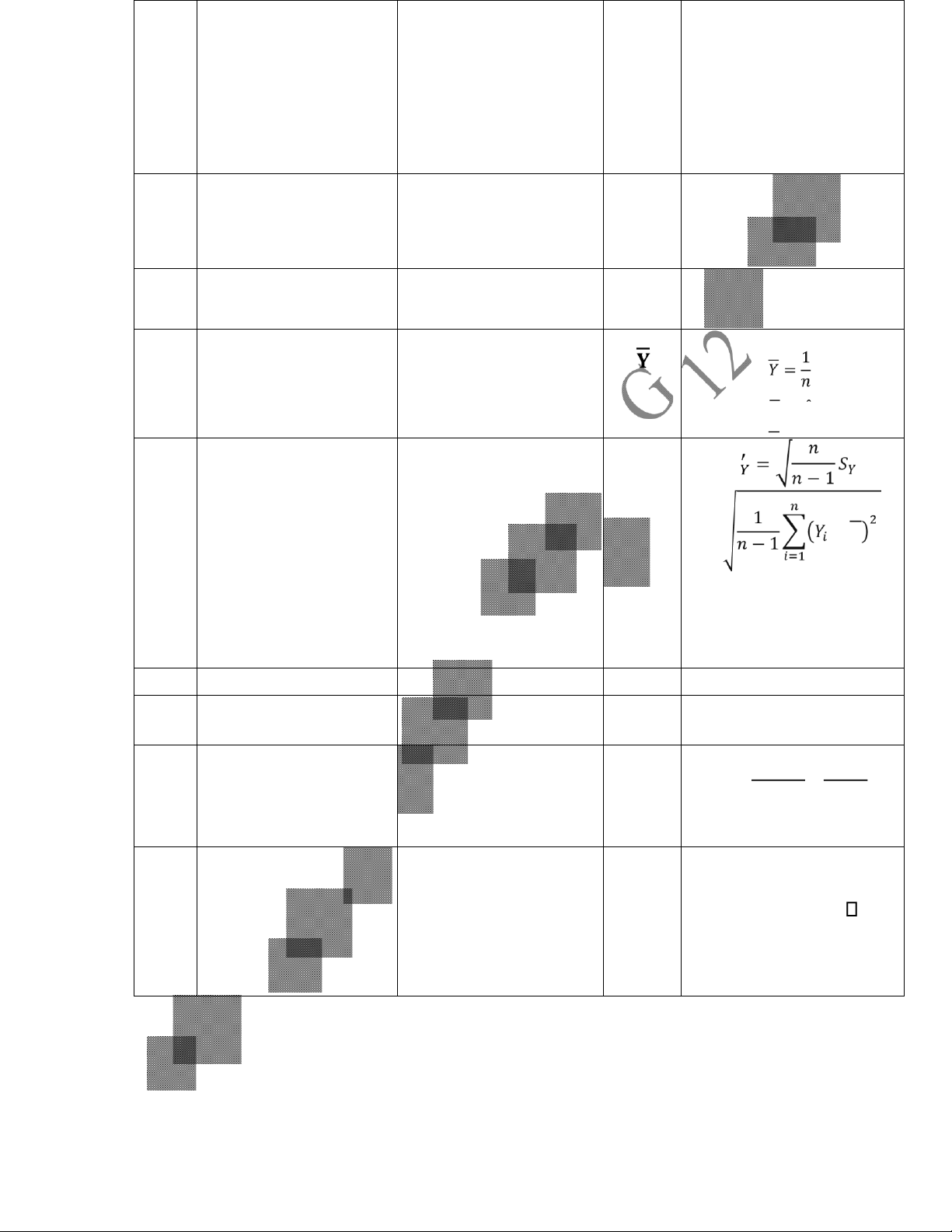
13 Mean dependent var của biến phụ thuộc và = +
Độ lệch chuẩn mẫu có hiệu chỉnh của biến 14 S.D dependent var phụ thuộc S 2 = − Akaike info criterion Tiêu chuẩn Akaike AIC
Schwarz info criterion Tiêu chuẩn Schwarz SC − = . 15 F - Statistic Giá trị của thống kê F − − F Giá trị xác suất của thống kê F tương ứng (với F là biến ngẫu p-value = P(F 16
Prob (F – Statistic) nhiên có phân phối pvalue FStatistic) Fisher có bậc tự do (k- 1, n-k)) lOMoAR cPSD| 46831624
ÔN TẬP CÁCH GIẢI ĐỀ THI KINH TẾ LƯỢNG CÂU YÊU CẦU CÁCH GIẢI
MÔ HÌNH HỒI QUY HAI BIẾN a) Tìm mô hình nβ + β ∑ X = ∑ Y hồi quy tuyến
Cách 1: Giải hpt sau tìm được β ∑ X + β ∑ X = ∑(XY)
tính mẫu của Y β , β Þ Hàm hồi quy tuyến tính mẫu (SRF) : = + theo X
Cách 2: Sử dụng S , S , r,, X, Y để tìm β , β S β = r, . S và β = Y − β X
Þ Hàm hồi quy tuyến tính mẫu (SRF) : = +
Cách 3: Dựa vào bảng hồi quy mô hình bằng Eviews ta có được
β , β Þ Hàm hồi quy tuyến tính mẫu (SRF) : = + b) Nêu ý nghĩa của
: Nếu không có X (X = 0) thì Y trung bình là đơn vị. các hệ số hồi
: Khi X tăng lên 1 đơn vị thì Y tăng trung bình là đơn vị. quy
c) Tính hệ số xác Cách 1: = , hay R = 1 − = trong đó
định mô hình TSS = n. S ; ESS = n. β . S ; RSS = n 1 − r, S
Cách 2: Dựa vào bảng hồi quy mô hình bằng Eviews ta có được (R – Squared).
d) Nêu ý nghĩa hệ R (= ): sự biến thiên của X giải thích xấp xỉ a% sự biến thiên
số xác định mô của Y (khoảng 1- a% chưa giải thích được). hình lOMoAR cPSD| 46831624
e) Tìm khoảng tin Ta dùng thống kê sau: T = ~ St(n − 2); j = 1,2 cậy cho các hệ
số hồi quy tổng Với = 1 − cho trước ta tìm được C = t ⁄ Khoảng thể, với độ tin
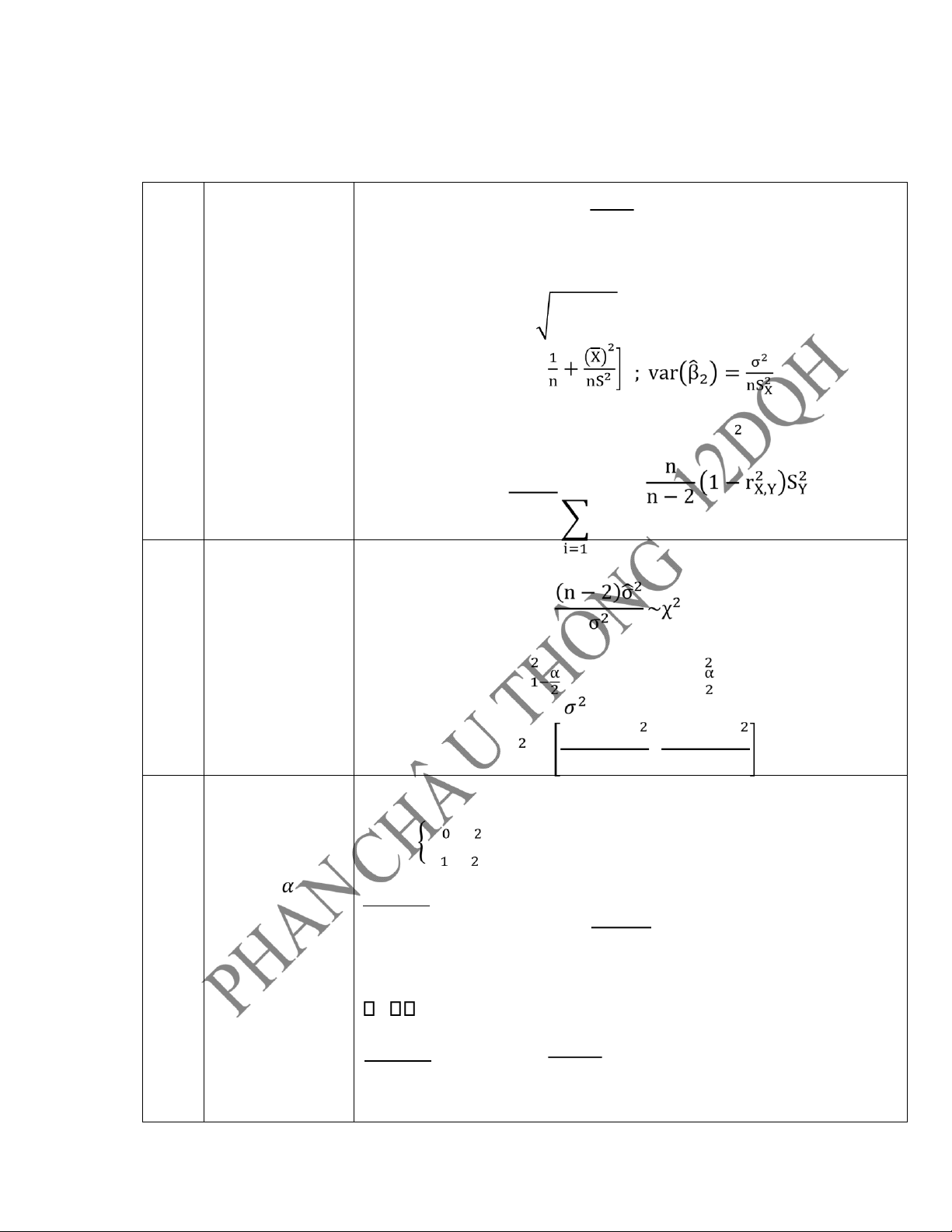
ước lượng cho : β Î [β − Cse β ; β + Cse β ] cậy Trong đó: se β = var β Ta có: var β = σ trong đó σ thay bằng σ 1 σ = e = n − 2 f)
Hãy ước lượng Ta dùng thống kê sau: phương sai của sai số ngẫu Y = (n − 2) nhiên tổng thể
Với α = 1 − γ cho trước ta có (hay tìm khoảng a = χ (n − 2) ; b = χ (n − 2) tin cậy cho phương sai Khoảng ước lượng cho : nhiễu) với độ (n − 2)σ (n − 2)σ σ ∈ ; b a tin cậy
g) Khi X thay đổi Bài toán kiểm định: có ảnh hưởng
H : β = 0 (X thay đổi không ảnh hưởng tới Y) tới Y hay không với mức ý
H : β ¹ 0 (X thay đổi có ảnh hưởng tới Y) nghĩa
Cách 1: Nếu H0 đúng, ta có thống kê β T = ~ St(n − 2) se β
Với cho trước ta tìm được C = t ⁄ Nếu T C, bác bỏ H0. Cách 2: Ta có t =
Dựa vào bảng hồi quy mô hình bằng Eviews ta có: lOMoAR cPSD| 46831624
p-value2 = P (|t| t2), trong đó t ~ St(n − 2) Với
cho trước, nếu p-value , bác bỏ H0.
h) Mô hình có phù Bài toán kiểm định: hợp hay không
H : R = 0 (Mô hình không phù hợp) với mức ý nghĩa
H : R > 0 (Mô hình phù hợp)
Cách 1: Ta dùng thống kê (n − 2)R F = ~ F(1, n − 2) 1 − R
Với cho trước ta tìm được C = f (1, n − 2) Nếu F C, bác bỏ H0. Cách 2: Ta có F = ( )
Dựa vào bảng hồi quy mô hình bằng Eviews ta có: p-
value = P(F F-Statistic), trong đó F ~ F(1,n − 2)
Với cho trước, nếu p-value , bác bỏ H0. lOMoAR cPSD| 46831624 i) Dự báo giá trị
Với X0 cho trước ta tìm được Y dựa vào phương trình
trung bình của Y = β + β X . Y khi X = X0,
Để dự báo giá trị trung bình của Y, ta dùng thống kê với độ tin cậy cho trước Y − E(Y X = X ) T = ~St(n − 2) se(Y ) Độ lệch chuẩn của Y se Y = var Y = nS Trong đó: σ = 1 − r, S
Với = 1 − cho trước ta tìm được C = t ⁄
Khoảng dự báo cho giá trị trung bình của Y E(Y X = X ) Î Y − Cse Y ; Y + Cse Y lOMoAR cPSD| 46831624 j) Dự báo giá trị
Với X0 cho trước ta tìm được Y dựa vào phương trình cá biệt của Y Y = β + β X .
khi X = X0, với Để dự báo giá trị cá biệt của Y, ta dùng thống kê độ tin cậy cho Y − Y trước T = ~St(n − 2) se(Y − Y )
Độ lệch chuẩn của (Y − Y ) se(Y − Y ) = Trong đó: var Y = σ và: σ = 1 − r,
Với = 1 − cho trước ta tìm được C = t
Khoảng dự báo cho giá trị cá biệt của Y
Y ∈ Y − Cse(Y − Y ); Y + Cse(Y − Y ) k) Tính hệ số co
Hệ số co giãn của Y theo X: giãn của Y theo ∂Y X X X tại điểm ε = . X, Y và giải Y = β . Y thích kết quả ∂X nhận được Tại điểm X, Y ta có X ε = β . Y
Ý nghĩa: Khi X tăng lên 1% thì Y tăng ε% nếu ε > 0 hoặc giảm ε% nếu ε < 0 l) Hãy viết lại
Khi Y và X thay đổi đơn vị trở thành Y∗ và X∗ thì ta có hàm hồi quy khi Y∗ = k Y và X∗ = k X
đơn vị tính thay Các hệ số hồi quy tổng thể thay đổi: đổi k β = k . β và β =. β k
Mô hình được viết lại như sau: Y∗ = β + β . X∗
MÔ HÌNH HỒI QUY BỘI (NHIỀU BIẾN) lOMoAR cPSD| 46831624 a) Tìm mô hình hồi β quy tuyến tính
Cách 1: Giải hpt sau β = (X X) .(X Y) = β mẫu của Y theo β X (xét hàm 3 biến)
tìm được β , β , β Þ Hàm hồi quy tuyến tính mẫu (SRF): = + + Trong đó: ⎡ n X ⎢ ⎞ X X = ⎢ X X ⎟⎟ ⎢ ⎢ X X X ⎠ ⎣ = + + b) Nêu ý nghĩa của
: Nếu không có X2 và X3 (X2 = X3 = 0) thì Y trung bình là đơn các hệ số hồi vị. quy
: Trong điều kiện các yếu tố khác không đổi, khi X2 tăng lên 1
đơn vị thì Y tăng trung bình là đơn vị.
: Trong điều kiện các yếu tố khác không đổi, khi X3 tăng lên 1
đơn vị thì Y tăng trung bình là đơn vị. lOMoAR cPSD| 46831624
c) Tính hệ số xác Cách 1: R = 1 − = trong đó định mô hình TSS = Y Y − n Y = ∑ − n Y = n.S ; ESS = . (X Y) − n Y ; RSS = TSS − ESS
Cách 2: Dựa vào bảng hồi quy mô hình bằng Eviews ta có được (R – Squared). d) Nêu ý nghĩa hệ
R (= ): Mô hình giải thích khoảng a% bộ số liệu (khoảng 1- a% số xác định mô
chưa giải thích được). hình
e) Tìm khoảng tin Ta dùng thống kê sau: T = ~ St(n − k); j = 1, k cậy cho các hệ số
hồi quy tổng thể, Với = 1 − cho trước ta tìm được C = t ⁄ Khoảng ước với độ tin cậy lượng cho β : β Î [β − Cse β ; β + Cse β ] Trong đó: se β = var β RSS σ = n − k f) Hãy ước lượng phương sai của
Ta dùng thống kê sau: Y = ( ) ~χ (n − k) sai số ngẫu
Với α = 1 − γ cho trước ta có nhiên tổng thể (hay tìm khoảng a = χ (n − k) ; b = χ (n − k) tin cậy cho Khoảng ước lượng cho : phương sai (n − k)σ (n − k)σ nhiễu) với độ tin σ ∈ ; b a cậy lOMoAR cPSD| 46831624
g) Khi Xj thay đổi Bài toán kiểm định: có ảnh hưởng tới
H : β = 0 X thay đổi không ảnh hưởng tới Y Y hay không với mức ý nghĩa
H : β ¹ 0 X thay đổi có ảnh hưởng tới Y
Cách 1: Nếu H0 đúng, ta có thống kê β T = ~ St(n − k) se β
Với cho trước ta tìm được C = t ⁄ Nếu T C, bác bỏ H0. Cách 2: Ta có t =
Dựa vào bảng hồi quy mô hình bằng Eviews ta có:
p-valuej = P (|t| tj), trong đó t ~ St(n − k)
Với cho trước, nếu p-value , bác bỏ H0.
h) Mô hình có phù Bài toán kiểm định: hợp hay không
H : R = 0 (Mô hình không phù hợp) với mức ý nghĩa
H : R > 0 (Mô hình phù hợp)
Cách 1: Ta dùng thống kê R n − k F = . ~ F(k − 1, n − k) 1 − R k − 1
Với cho trước ta tìm được C = f (k − 1, n − k) Nếu F C, bác bỏ H0. Cách 2: Ta có F = .
Dựa vào bảng hồi quy mô hình bằng Eviews ta có:
p-value = P(F F-Statistic), trong đó F ~ F(k − 1, n − k) Với
cho trước, nếu p-value , bác bỏ H0. lOMoAR cPSD| 46831624 i) Dự báo giá trị trung bình của Y khi X = X0, với độ tin cậy cho trước ~St(n − k) σ (X ) (X X) X
Với = 1 − cho trước ta tìm được C = t ⁄
Khoảng dự báo cho giá trị trung bình của Y E(Y X = X ) Î Y − Cse Y ; Y + Cse Y lOMoAR cPSD| 46831624 j) Dự báo giá trị cá 1
biệt của Y khi X Với X0 = X
cho trước ta tìm được Y dựa vào phương trình = X0, với độ tin X cậy cho trước 1 Y = β X = (β β β ). X X
Để dự báo giá trị cá biệt của Y, ta dùng thống kê Y − Y T = ~St(n − k) se(Y − Y )
Độ lệch chuẩn của (Y − Y ) se(Y − Y ) = var(Y − Y ) = σ + var Y Trong đó: var Y = σ (X ) (X X) X và σ =
Với = 1 − cho trước ta tìm được C = t ⁄
Khoảng dự báo cho giá trị cá biệt của Y
Y ∈ Y − Cse(Y − Y ); Y + Cse(Y − Y )
k) Chọn mô hình Cách 1: Nếu đề bài cho R và R ở hai mô hình thì chọn mô hình
nào là phù hợp nào có R lớn hơn. nhất dựa vào dữ liệu bài toán n − 1
trong đó: R = 1 − (1 − R ) n − k
Cách 2: Nếu đề bài cho RSS và RSS ở hai mô hình thì chọn mô
hình nào có RSS nhỏ hơn. lOMoAR cPSD| 46831624 l)
Tìm khoảng tin Ta dùng thống kê sau: cậy cho hai hệ β ± β − (β ± β ) T = ~ St(n − k); j = 1, k se β ± β
Với = 1 − cho trước ta tìm được C = t ⁄ Khoảng ước lượng cho β ± β : (β ± β ) Î [ β ± β − Cse β ± β ; β ± β số (β ± β ) + Cse β ± β ] Trong đó: se β ± β = var β ± β = se β + se β ± 2cov β , β m) Kiểm định giả Bài toán kiểm định: thuyết cho rằng
H : β = β∗ X tăng 1 đơn vị thì Y tăng β∗ đơn vị khi Xj tăng 1 đơn vị thì Y
H : β ¹ β∗ X tăng 1 đơn vị thì Y không tăng β∗ đơn vị Nếu H0
tăng β∗ đơn vị đúng, ta có thống kê β − β∗ T = ~ St(n − k) se β
Với cho trước ta tìm được C = t ⁄ Nếu T C, bác bỏ H0. n) Kiểm định giả Bài toán kiểm định:
thuyết cho rằng H : β = β∗ hay β ≤ β∗X tăng 1 đơn vị thì Y không tăng hơn β đơn vị khi X j tăng 1 đơn vị thì Y
H :β > β∗ X tăng 1 đơn vị thì Y tăng hơn β đơn vị
tăng lớn hơn β∗ Nếu H0 đúng, ta có thống kê đơn vị
Với cho trước ta tìm được C = t Nếu T C, bác bỏ H0. lOMoAR cPSD| 46831624 o) Kiểm định giả Bài toán kiểm định:
thuyết cho rằng H : β = β∗ hay β ≥ β∗X tăng 1 đơn vị thì Y không tăng ít hơn β∗ đơn vị khi X j tăng 1 đơn vị thì Y
H :β < β∗ X tăng 1 đơn vị thì Y tăng ít hơn β∗ đơn vị tăng ít hơn β∗
Nếu H0 đúng, ta có thống kê đơn vị β − β∗ T = ~ St(n − k) se β
Với cho trước ta tìm được C = t Nếu -T C, bác bỏ H0. lOMoAR cPSD| 46831624 p) Kiểm định ý
Cách 1: Bài toán kiểm định: kiến cho rằng
H : β = 0 nên loại m biến ra khỏi MH (hoặc không thêm m biến vào MH) có nên loại bỏ m biến ra khỏi
H : β ¹ 0 không nên loại m biến ra khỏi mô hình (hoặc nên thêm m biến vào MH) Ta có thống kê mô hình (hoặc RSS − RSS n − k R − R n − k thêm m biến F = . = . ~F(k − 1, n − k) vào mô hình) RSS m 1 − R m hay không
Với cho trước ta tìm được C = f (k − 1, n − k) Nếu F C, bác bỏ H0.
Cách 2: Kiểm định Wald (loại bớt biến ra khỏi mô hình)
H : β = 0 (nên loại biến ra khỏi mô hình)
H : β ¹ 0(không nên loại biến ra khỏi mô hình)
Dựa vào bảng kiểm định Wald ta có: p-value = P(F
FStatistic), trong đó F ~ F(k − 1, n − k)
Với cho trước, nếu p-value , bác bỏ H0. lOMoAR cPSD| 46831624
MÔ HÌNH HỒI QUY VỚI BIẾN GIẢ
Mô hình quan hệ giữa chi tiêu cá nhân với thu nhập và giới tính của cá nhân đó Thành lập mô Y = β + βX + β D (1) hình
Trong đó: Y là chi tiêu, X là thu nhập
D = 1: nam giới, D = 0: nữ giới
❖ Mở rộng mô hình: Với mô hình trên, khi thu nhập cá nhân
tăng 1 đơn vị thì chi tiêu tăng β đơn vị bất kể là nam hay nữ.
Nhưng với giả thiết cho rằng nếu thu nhập tăng 1 đơn vị
thì mức chi tiêu tăng thêm của nam và nữ khác nhau thì β phải là: β = β + β . D
Lúc này mô hình (1) được viết lại: Y = β + β + β . D X + β D Hay: = + + + ( )
Trong đó: XD được gọi là biến tương tác giữa X và D.
- Khi D = 1: Y = β + β + β + β X
Đây là hồi quy chi tiêu - thu nhập của nam. - Khi D = 0: Y = β + β X
Đây là hồi quy chi tiêu - thu nhập của nữ. lOMoAR cPSD| 46831624 a) Nếu ý nghĩa của các hệ số hồi
β : khi không có thu nhập chi tiêu trung bình của một người nữ quy là β đơn vị.
β : khi thu nhập của một người nữ tăng 1 đơn vị thì chi tiêu
trung bình của họ tăng β đơn vị.
β : khi không có thu nhập thì chi tiêu trung bình của một người
nam chênh lệch so với của một người nữ là β đơn vị (hay
chênh lệch về hệ số tung độ gốc giữa hàm hồi qui cho nam và hàm hồi qui cho nữ).
β : khi thu nhập của một người nam tăng 1 đơn vị thì chi tiêu
của họ tăng nhiều hơn của nữ β đơn vị (nếu β > 0) hay tăng ít
hơn của nữ β đơn vị (nếu β
< 0) (hay chênh lệch về hệ số
độ dốc giữa hàm hồi qui cho nam và hàm hồi qui cho nữ). b) Hãy ước lượng các hệ số hồi Ta dùng thống kê sau: T = ~ St(n − k); j = 1, k quy, với độ tin
Với = 1 − cho trước ta tìm được C = t cậy ⁄ Khoảng
ước lượng cho : β Î [β − Cse β ; β + Cse β ] Trong đó: se β = var β c) Kiểm định sự Bài toán kiểm định: phù hợp của mô
H : R = 0 (Mô hình không phù hợp) hình hồi quy, với mức ý nghĩa α
H : R > 0 (Mô hình phù hợp) Ta dùng thống kê R n − k F = . ~ F(k − 1, n − k) 1 − R k − 1
Với cho trước ta tìm được C = f (k − 1, n − k) Nếu F C, bác bỏ H0. lOMoAR cPSD| 46831624 d) Chi tiêu về loại
❖ Bài toán kiểm định: hàng A của nam H : β = β
= 0: (Chi tiêu nam nữ giống nhau) và nữ có giống nhau hay không
H : β ≠ 0 ∪ β ≠ 0: (Chi tiêu nam nữ không giống nhau) ❖ ? Kết luận với Kiểm định giả thiết: mức ý nghĩa α
H : β = 0: (Biến D thay đổi không ảnh hưởng tới Y)
H : β ≠ 0: (Biến D thay đổi có ảnh hưởng tới Y) Ta có thống kê: t = ~ st(n − k)
Với cho trước ta tìm được C = t ⁄ Nếu T C, bác bỏ H0.
❖ Kiểm định giả thiết: H : β
= 0: (Biến XD thay đổi không ảnh hưởng tới Y)
H : β ≠ 0: (Biến XD thay đổi có ảnh hưởng tới Y) Ta có thống kê: t = ~ st(n − k)
Với cho trước ta tìm được C = t ⁄ Nếu T C, bác bỏ H0. ❖ Kết luận:
Nếu kết quả hai kiểm định trên cùng chấp nhận H0 thì chi
tiêu nam nữ không khác nhau (giống nhau). Ngược lại, nếu kết
quả hai kiểm định trên cùng bác bỏ hoặc vừa có chấp nhận và
bác bỏ H0 thì chi tiêu nam nữ khác nhau.
KIỂM ĐỊNH GIẢ THUYẾT MÔ HÌNH
1. Phương sai thay đổi lOMoAR cPSD| 46831624 a) Kiểm định Giả thuyết: Park
H : β = 0 (không có hiện tượng phương sai thay đổi) (ước lượng mô hình hồi quy
H : β ¹ 0 (có hiện tượng phương sai thay đổi) lne = β + β
Cách 1: Nếu H0 đúng, ta có thống kê β lnX + ε ) T = ~ St(n − 2) se β
Với cho trước ta tìm được C = t ⁄ Nếu T C, bác bỏ H0. Cách 2: Ta có t =
Dựa vào bảng kiểm định Park bằng phần mềm Eviews ta
có được: p-value2 = P (|t| t2), trong đó t ~ St(n − 2) Với
cho trước, nếu p-value , bác bỏ H0. b) Kiểm định Giả thuyết: Glejser
H : (không có hiện tượng phương sai thay đổi)
H : (có hiện tượng phương sai thay đổi)
Cách 1: Với α cho trước ta tìm được: ( − 1) (tra bảng phân phối Chi bình phương). Nếu nR2
( − 1), bác bỏ giả thuyết H0.
Cách 2: Dựa vào bảng kiểm định Glejser bằng phần mềm
Eviews ta có được: p-value = P ( ( − 1)).
Với cho trước, nếu p-value , bác bỏ H0. c) Giả thuyết: Kiểm định
H : (không có hiện tượng phương sai thay đổi) White
H : (có hiện tượng phương sai thay đổi)
Cách 1: Với α cho trước ta tìm được: ( − 1) (tra bảng phân phối Chi bình phương). Nếu nR2
( − 1), bác bỏ giả thuyết H0.
Cách 2: Dựa vào bảng kiểm định White bằng phần mềm
Eviews ta có được: p-value = P ( ( − 1)).
Với cho trước, nếu p-value , bác bỏ H0. 2. Đa cộng tuyến