













Preview text:
Chương 1. BIẾN CỐ - XÁC SUẤT CỦA BIẾN CỐ
Bài 1. Phép thử và biến cố - Quan hệ giữa các biến cố
I. Phép thử và biến cố -
Phép thử là hành động mà kết quả của nó là ngẫu nhiên (không dự đoán được một cách chắc chắn). -
Ví dụ: Tung 1 con xúc xắc, bắn 1 viên đạn vào bia,… -
Biến cố là kết quả của phép thử. -
Ví dụ: Tung 1 con xúc xắc là 1 phép thử. Ta có các biến cố:
“Xuất hiện mặt 1 chấm”
“Xuất hiện mặt 2 chấm” ….
“Xuất hiện mặt 6 chấm”
“Xuất hiện mặt chẵn chấm”
“Xuất hiện mặt có số chấm lớn hơn 3”
* Một số khái niệm -
Biến cố sơ cấp: là biến cố đơn, không thể phân tách chia nhỏ được nữa. Ngoài các biến cố sơ cấp ta,
còn có các biến cố là phức hợp của các biến cố sơ cấp. -
Không gian mẫu: là tập hợp tất cả các biến cố sơ cấp, kí hiệu là (omega). -
Mỗi biến cố sơ cấp làm cho biến cố A xảy ra được gọi là 1 kết quả thuận lợi cho biến cố A. Tập hợp tất
cả các kết quả thuận lợi cho biến cố A kí hiệu là A Nhận xét:
Với mọi biến cố A ta có: A hay A
* Phân loại biến cố -
Biến cố chắc chắn: là biến cố nhất định xảy ra sau phép thử, kí hiệu là U hoặc . -
Biến cố bất khả: là biến cố không thể xảy ra sau phép thử, kí hiệu là V hoặc Ø. -
Biến cố ngẫu nhiên: là biến cố có thể xảy ra hoặc không xảy ra sau phép thử, thường được ký hiện là A, B, C,… hoặc A , 1 A , 2 A ,…. 3
II. Quan hệ giữa các biến cố 1. Quan hệ kéo theo -
Định nghĩa: Biến cố A được gọi là kéo theo biến cố B nếu biến cố A xảy ra thì biến cố B cũng xảy ra sau phép thử. - Kí hiệu: A B -
Ví dụ: Gieo 1 con xúc xắc B
Gọi Ai là biến cố “Xuất hiện mặt i chấm”, i = 1 ;6 A B
B là biến cố “Xuất hiện mặt lẻ chấm” A Ta có: A1 B, A 2 B A1 B
2. Quan hệ tương đương A B A = B B A
3. Tổng các biến cố (Có ít nhất một, hoặc)
* Định nghĩa 1: Tổng của 2 biến cố A
và B là biến cố xảy ra khi có ít nhất một trong hai biến cố A và B xảy
ra sau phép thử, ký hiện là A + B.
VD1: Có 2 người, mỗi người bắn 1 viên đạn vào cùng 1 bia.
Gọi Ai là biến cố “Người thứ I bắn trúng bia”, i = 1 ;2
B là biến cố “Bia bị trúng đạn”
Nhận thấy B xảy ra khi có ít nhất 1 trong 2 biến cố A và 1 A xảy ra nên ta có: B = 2 A + 1 A2 A B A + B (A B) (A hợp B)
* Định nghĩa 2: Tổng của n biến cố
VD2: Một nhà máy sản xuất 3 sản phẩm.
Gọi Ai là biến cố “Sản phẩm thứ i đạt yêu cầu”, i = 1 ;3
B là biến cố “Có ít nhất 1 sản phẩm đạt yêu cầu” Ta có: B = A + 1 A + 2 A3
Chú ý: Nếu biến cố B xảy ra khi hoặc A xảy ra, hoặc 1
A2 xảy ra,…. hoặc A xảy ra thì ta có: n B = A + 1 A + … + 2 An
VD3: Xét VD mục II.1 ta có B = A + 1 A + 3 A5
4. Tích các biến cố (Cả 2, tất cả, và)
* Định nghĩa 1: Tích của 2 biến cố A và B là biến cố xảy ra khi cả hai biến cố A và B cùng xảy ra sau phép thử, ký hiệu là AB. VD: Xét VD mục II.3.
Gọi C là biến cố “Cả 2 người bắn trúng bia” thì C = A1A .2 A B AB (A B) (A giao B)
* Định nghĩa 2: Tích của n biến cố
5. Quan hệ xung khắc
* Định nghĩa 1: Hai biến cố A và B được gọi là xung khắc nhau nếu chúng không thể đồng thời xảy ra sau phép thử. Tức là AB = V. VD1: Gieo 1 con xúc xắc.
Gọi A là biến cố “Xuất hiện mặt chẵn chấm”
B là biến cố “Xuất hiện mặt lẻ chấm”
Ta có A và B xung khắc nhau. VD2: Xét VD mục II.3. Ta có A và 1 A không xung khắc nhau. 2
* Định nghĩa 2: Các biến cố A1, A2,…, A nđược gọi là xung khắc từng đôi nếu 2 biến cố bất kỳ trong các
biến cố đó đều xung khắc nhau. VD3: Xét VD mục II.1 Ta có A , 1 A ,…, 2
A6 là các biến cố xung khắc từng đôi.
6. Quan hệ đối lập
Định nghĩa: Cho biến cố A. Khi đó biến cố “Không phải A” được gọi là biến cố đối lập của biến cố A. Kí hiệu A VD1: Gieo 1 con xúc xắc
Gọi A là biến cố “Xuất hiện mặt chẵn chấm”
A là biến cố “Xuất hiện mặt lẻ chấm”
Gọi B là biến cố “Xuất hiện mặt có số chấm lớn hơn 3”
B là biến cố “Xuất hiện mặt có số chấm nhỏ hơn hoặc bằng 3”
VD2: Rút 4 quân bài từ bộ bải 52 quân.
Gọi A là biến cố “Rút được ít nhất 1 quân Át”
A là biến cố “Không rút được quân Át nào”
Gọi B là biến cố “Cả 4 quân bài rút ra màu đỏ”
B là biến cố “Rút được ít nhất 1 quân bài màu đen” hoặc “Rút được nhiều nhất 4 quân bài màu đỏ” Minh họa A U = Tính chất: A + A = U = A. A = V = Ø
Chú ý: Nếu đối lập thì xung khắc. Nhưng xung khắc thì chưa chắc đối lập nhau.
VD: A “Xuất hiện mặt 1 chấm”
B “ Xuất hiện mặt 2 chấm”
A xung khắc B nhưng chưa đối lập B
C “Không xuất hiện mặt 1 chấm” đối lập với A. VD3: Gieo 1 con xúc xắc
A: “Xuất hiện mặt có số chấm lớn hơn 3”
B: “Xuất hiện mặt có số chấm nhỏ hơn 3”
A và B xung khắc nhau nhưng không đối lập nhau (thiếu mặt 3 chấm).
7. Hiệu hai biến cố A\B xảy ra
A xảy ra A xảy ra A B xảy ra B không xảy ra B xảy ra A\B A B AB A B A\B = A. B\A = B. = .B
A + B = A.B + A.B + A.B
8. Hệ đầy đủ các biến cố
Định nghĩa: Các biến cố A1, A2,…, An được gọi là hệ đầy đủ các biến cố nếu có một và chỉ một biến cố
trong các biến cố đó xảy ra sau phép thử. VD: Xét VD mục II.1 …. A2 Ta có A , A 1 ,…, A 2
là hệ đầy đủ các biến cố. 6 A A U = 1
Chú ý: Với mọi biến cố A ta có: n
A và A là hệ đầy đủ các biến cố. A U =
9. Một số tính chất
- Tính chất 1 (luật phủ định của phủ định¿ : ´A=A
- Tính chất 2 (luật lũy đẳng) A+ A= A A . A= A
- Tính chất 3 (luật đồng nhất) A+U =U ; A+V =A A . U = A ; A . V =V
- Tính chất 4 (luật giao hợp): A+B=B+ A
- Tính chất 5 (luật phân phối): ( A+B).C= AC+BC
- Tính chất 6 (luật đối ngẫu): o
Đối lập của 1 tổng bằng tích các đối lập: A+B= A . B o
Đối lập của 1 tích bằng tổng các đối lập: ABC= A + B+C
Bài 2. Xác suất của biến cố
I. Khái niệm về xác suất
Xác suất của một biến cố là con số đặc trưng cho khả năng xảy ra của biến cố đó. Biến cố nào có xác
suất lớn hơn thì có khả năng xảy ra lớn hơn và ngược lại.
II. Một số định nghĩa về xác suất
1. Định nghĩa xác suất theo quan điểm cổ điển (đòi hỏi đồng khả năng)
Định nghĩa: Giả sử phép thử có n kết cục đồng khả năng và lập thành hệ đầy đủ các biến cố, trong đó có
m(A) kết cục thuận lợi cho biến cố A. Khi đó xác suất của biến cố A được ký hiệu và xác định như sau:
P (A )= m( A) n
VD1.1: Gieo 2 con xúc xắc cân đối và đồng chất. Tính xác suất để tổng số chấm xuất hiện bằng 8.
Gọi A: “Tổng số chấm xuất hiện bằng 8”
Ta có: = {(i ; j) : 1 i ; j ≤ ≤ 6} n = 36
Ta có A = {(2;6) ; (6;2) ; (3;5) ; (5;3) ; (4;4)} m(A) = 5
P (A )= 5 ≈ 0,13889 36
Nhắc lại về tổ hợp: Số cách lấy ra r phần tử từ một tập hợp gồm n phần tử là C rn C 0= n=1 ;
C 1= n−1=n n C C n n n VD1.2: 7 đỏ / 3 xanh lấy 4 ra
Ta có: n = C4 và m(A) = C2. C2 10 7 3 C 2. C2
Gọi A: “Trong 4 bi lấy ra có 2 đỏ và 2 xanh” P (A )= 7 3 =0,3 4 C 10 VD1.3: n = C 1 = 1 = N N và m = CM M
Gọi B: “Lấy được phần tử mang đặc tính A” C1
P (B )= M= M C1 N N Nhận xét:
Khi lấy ngẫu nhiên 1 phần tử của 1 tập hợp thì xác suất lấy được phần tử
mang đặc tính A chính là tỉ lệ
phần tử mang đặc tính A của tập hợp đó.
2. Định nghĩa xác suất theo quan điểm thống kê (không đòi hỏi đồng khả năng)
Khái niệm tần suất: thực hiện n phép thử T mà trong mỗi phép thử có thể xuất hiện hoặc không xuất hiện
biến cố A. Gọi X là số lần xuất hiện biến cố A trong n phép thử đó.
Khi đó: f ( A )= X được gọi là tần suất xuất hiện biến cố A trong n phép thử T. n
VD: Một người bắn 100 viên đạn thấy có 70 lần bắn trúng mục tiêu. Vậy tần suất bắn trúng mục tiêu của
người đó trong 100 lần bắn là f = 70 =0,7 100
Định nghĩa xác suất theo tần suất: thực hiện n phép thử T mà trong mỗi phép thử đều có thể xuất hiện
hoặc không xuất hiện biến cố A. Khi n đủ lớn thì tần suất xuất hiện biến cố A thường dao động rất ít xung
quanh 1 số cố định p nào đó. Số p được gọi là tần suất của biến cố A.
Theo định nghĩa này thì ta không biết p do đó ta lấy: P (A )= p=f ( A)= X (n đủ lớn) n
3. Định nghĩa xác suất theo tiên đề
III. Một số tính chất của xác suất
Tính chất 1: 0 ≤ P(A) ≤ 1 ∀ A Tính chất 2: P(U) = 1 Tính chất 3: P(V) = 0
Tính chất 4: P(A) + P( A) = 1 Tính chất 5: Nếu A , A 1 ,…, A 2
là hệ đầy đủ các biến cố thì: n P(A1) + P(A2) +….+ P(A ) = 1 n
Phương pháp phần bù: P(A) = 1−P( A)
VD1.4: 7 đỏ / 5 xanhh lấy 4
Gọi A là biến cố “Lấy được ít nhất 1 bi xanh” C4
A là biến cố “Cả 4 bi lấy ra đều là bi đỏ”
P (A )= 7 = 7 C4 99 12
P(A) = 1−P( A) ≈ 0,92929
Bài 3. Các công thức tính xác suất
I. Xác suất có điều kiện
1. Khái niệm xác suất có điều kiện
Khái niệm: Xác suất của 1 biến có được tính trong điều kiện đã biết một hoặc một số biến cố khác đã xảy ra
được gọi là xác suất có điều kiện.
Ký hiệu: Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được ký hiệu là P(A/B) (P của A với điều kiện B).
VD: Rút 1 quân bài từ bộ bài 52 quân.
Gọi A: “Rút được quân Át bích”
B: “Rút được quân bài màu đen” 1 1 Ta có: P(A/B) = ; P(A) = 36 52
Công thức xác suất có điều kiện: P( AB)
P( A / B)= (điều kiện P(B) 0) P( B)
2. Khái niệm về sự phụ thuộc và độc lập của các biến cố
Định nghĩa 1: Biến cố A được gọi là độc lập với biến cố B nếu P(A/B) = P(A) -
Tính chất 1: Nếu biến cố A độc lập với biến cố B thì ta chứng minh được biến cố B cũng độc lập với
biến cố A. Do đó ta nói A và B độc lập nhau. -
Tính chất 2: Nếu A và B độc lập nhau thì: o
A và B cũng độc lập với nhau o
A và B cũng độc lập với nhau o
A và B cũng độc lập với nhau
Định nghĩa 2: Các biến cố độc lập từng đôi
Định nghĩa 3: Các biến cố độc lập toàn phần (độc lập trong toàn bộ, độc lập nhau)
Chú ý: Ta có thể hiểu các biến cố độc lập nhau là các biến cố mà khả năng xảy ra của biến cố này không
phụ thuộc vào các biến cố khác đã xảy ra hay không.
VD: Có 3 người, mỗi người bắn 1 viên đại vào bia. Gọi Ai là biến cố “Người thứ I bắn trúng bia”, i =1 ;3 . Ta có A , 1 A , 2 A độc lập nhau. 3
II. Xác suất của tích các biến cố P(A A 1 ….A 2 n) = P(A ).P(A 1 /A 2 1)….P(A /A n 1A ….A 2 n-1) Nếu A , A 1 ,…, A 2 n độc lập nhau thì: P(A1A ….A 2 n) = P(A ).P(A 1 )….P(A 2 ) n VD1.5:
Gọi Ai là biến cố “Người thứ i bắn trúng bia”, i = 1 ;2 Ta có A ,
1 A2 độc lập nhau và P(A ) = 0,8 ; P(A 1 2)= 0,9
Gọi B là biến cố “Cả 2 người bắn trúng bia” Ta có B = A1A2 Do đó: P(B) = P(A1A ) = P(A 2 1).P(A2) = 0,8.0,9 = 0,62
VD1.6: 7 tốt / 3 xấu lấy 1 tốt 5 tốt / 4 xấu lấy 1
Gọi Ai là biến cố “Sản phẩm lấy ở hộp thứ i là sản phẩm tốt”, 1 ;2
B là biến cố “Cả 2 sản phẩm lấy ra đều là sản phẩm tốt” Ta có B = A1A2 7 6 Suy ra: P(B) = P(A1A ) = P(A 2 ). P(A 1 2/A ) = 1 × =0,42 10 10
III. Xác suất của tổng các biến cố
2 biến cố: P(A + B) = P(A) + P(B) – P(AB)
3 biến cố: P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC)
Đặc biệt: Nếu A , 1 A ,…, 2
An xung khắc từng đôi thì: P(A +A 1 2+…+An) = P(A ) + P(A 1 ) +…+P(A 2 n)
Chú ý: Nếu các biến cố A , 1 A2,…, An
thì để tính xác suất của biến cố B = độc lập nhau A1+ A +…+ 2 A ta nên n
dùng phương pháp phần bù: P(B) = 1 – P(B)
= 1 – P( A 1+ A 2+…+ A n)
= 1 – P( A 1). P( A 2)… P( An) Hệ quả:
(1) P(A.B ) = P(A) – P(AB) ; P(AB) = P(B) – P(AB)
(2) P(A/ B ¿ = 1 – P(A/B)
(3) P(ABC) = P(AB) – P(ABC)
(4) P(A BC ¿ = P(A) – P(AB) – [ P(AC) – P(ABC) ]
IV. Công thức xác suất đầy đủ và công thức Bayes Cho A , 1 A ,…, A 2 n là
1 hệ đầy đủ các biến cố và B là 1 biến cố bất kỳ trong cùng phép thử với hệ đầy đủ đã cho. Ta có: -
Công thức xác suất đầy đủ n
P (B )=∑ P (Ai ) . P(B/ Ai) i=1 - Công thức Bayes
P ( Ai ). P( B/ Ai)
P( Ai / B)=
, i = 1 ;n P( B) Chú ý: -
Ta dùng công thức xác suất đầy đủ khi biến cố cần tính xác suất phụ thuộc 1 hệ đầy đủ các biến cố. -
Ta áp dụng công thức Bayes khi cần tính xác suất có điều kiện mà biến cố cần tính xác suất là thành
phần hệ đầy đủ các biến cố. Công thức Bayes thường đi kèm với công thức xác suất đầy đủ.
Chương 2. ĐẠI LƯỢNG NGẪU NHIÊN
Bài 1. Đại lượng ngẫu nhiên - Phân phối xác suất
của đại lượng ngẫu nhiên
I. Định nghĩa và phân loại đại lượng ngẫu nhiên Định nghĩa
Đại lượng X được gọi là đại lượng ngẫu nhiên nếu: -
X có thể nhận giá trị trong 1 tập hợp số thực nào đó. -
Trước khi thực hiện phép thử ta không biết được X sẽ nhận giá trị nào trong các giá trị mà nó có thể
nhận. Tức là giá trị của X sau phép thử là ngẫu nhiên, không dự đoán được 1 cách chắc chắn. Một số ký hiệu - Đại lượng ngẫu nhiên X,
thường được ký hiệu là Y, Z,… hoặc X1, X , X 2 ,…. 3 -
Các giá trị có thể có của đại lượng ngẫu nhiên X được ký hiệu là x1, x , x 2 3 khi đó ta viết: ,… X: x , x 1 2, x3,… Ví dụ
VD1. Tung 1 con xúc xắc. Gọi X là số chấm xuất hiện ở mặt trên con xúc xắc. Ta có X là 1 đại lượng ngẫu
nhiên và X: 1, 2, 3, 4, 5, 6.
VD2. Tung 1 đồng xu cho tới khi xuất hiện mặt sấp thì dừng lại. Gọi Y là số lần tung đồng xu. Ta có Y là 1
đại lượng ngẫu nhiên và Y: 1, 2, 3, …
VD3. Thời lượng đèn đỏ ở 1 ngã tư là 60 giây. Gọi Z là thời gian chờ đèn đỏ của 1 phương tiện giao thông ở
ngã tư đó (đơn vị: giây). Ta có Z là 1 đại lượng ngẫu nhiên và Z : [0,60].
Phân loại đại lượng ngẫu nhiên -
ĐLNN rời rạc: là đại lượng ngẫu nhiên mà tập các giá trị có thể có của nó là 1 tập hữu hạn hoặc vô hạn đếm được. -
ĐLNN liên tục: là đại lượng ngẫu nhiên mà tập các giá trị có thể có của nó có thể lấp đầy 1 hoặc 1 số
khoảng nào đó trên trục số và xác suất để đại lượng ngẫu nhiên đó nhận giá trị từng điểm đều bằng 0.
Nghĩa là: P(X = xi) = 0, xi R. Nhận xét -
Đối với ĐLNN rời rạc ta có thể liệt kê được các giá trị mà đại lượng ngẫu nhiên có thể nhận. -
Đối với ĐLNN liên tục ta không thể liệt kê được các giá trị mà đại lượng ngẫu nhiên có thể nhận. -
Nếu X là ĐLNN liên tục thì ta có: P(x1 < X < x ) = P(x 2 ≤ X < x 1 ) = P(x 2 < X ≤ x 1 ) = P(x 2 ≤ X ≤ x 1 ) 2
II. Phân phối xác suất của đại lượng ngẫu nhiên
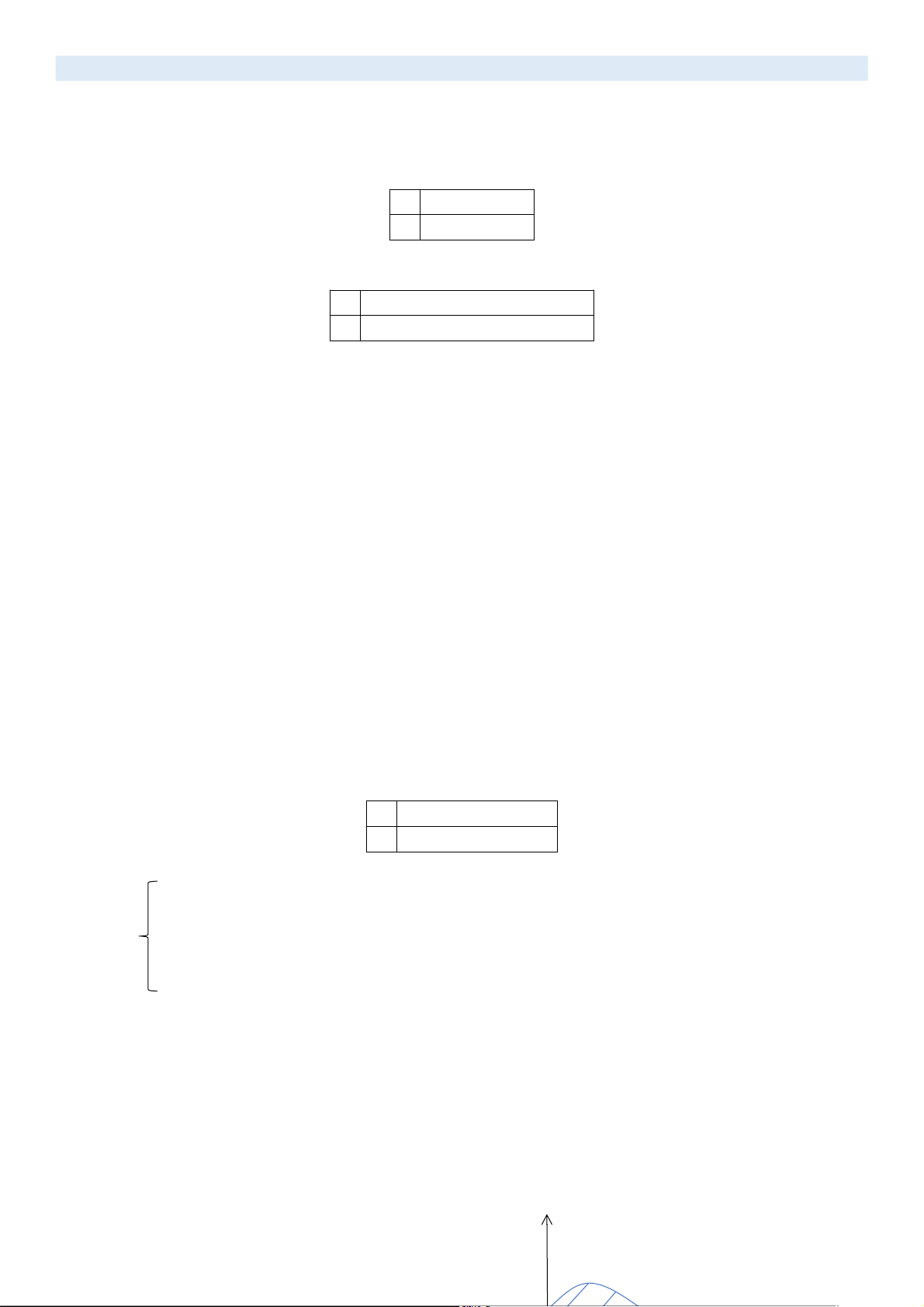
1. Bảng phân phối xác suất của ĐLNN rời rạc Định nghĩa 1:
Giả sử X là 1 đại lượng ngẫu nhiên rời rạc và X có thể nhận các giá trị x ,1 x ,…, 2 xn với các xác suất tương ứng là p , p 1 ,…, p 2
. Khi đó bảng sau được gọi là bảng phân phối xác suất của X. n X x1 x … x 2 n P p1 p … p 2 n Ví dụ
Gọi X là số chấm xuất hiện khi tung 1 con xúc xắc cân đối và đồng chất thì X có bảng phân phối xác suất là: X 1 2 3 4 5 6 P 1/6 1/6 1/6 1/6 1/6 1/6 Nhận xét -
Bảng phân phối xác suất chỉ có được đối với ĐLNN rời rạc, ĐLNN liên tục không có bảng phân phối xác suất. -
Bảng phân phối xác suất cho biết các giá trị mà ĐLNN có thể nhận và phân phối xác suất của ĐLNN tại từng giá trị đó.
2. Hàm phân phối xác suất của ĐLNN
Định nghĩa: Cho X là 1 đại lượng ngẫu nhiên khi đó hàm số F(x) = P(X < x), x
R được gọi là hàm phân phối xác suất của X.
Ý nghĩa hình học: Giá trị của hàm F(x) cho ta biết phân phối xác suất của ĐLNN ở bên trái giá trị x.
Công thức tính xác suất khi biết hàm PPXS P(x1 ≤ x < x ) = F(x 2 ) – F(x 2 ) 1 Tính chất -
Tính chất 1: 0 ≤ F(x) ≤1, x R - Tính chất 2: F(+) = 1 và F( ) = 0 - Tính chất 3:
F(x) là 1 hàm không giảm trên R - Tính chất 4:
Nếu X là ĐLNN liên tục thì F(x) là hàm liên tục trên R.
Xác định hàm PPXS khi biết bảng PPXS VD: Cho X có bảng PPXS: X 1 2 3 4 P 0,1 0,3 0,4 0,2 Hàm PPXS của X là: 0 khi x ≤ 1 0,1 khi 1 < x ≤ 2 F(x) = 0,4 khi 2 < x ≤ 3 0,8 khi 3 < x ≤ 4 1 khi x > 4
3. Hàm mật độ xác suất của ĐLNN liên tục
Định nghĩa: Cho X là ĐLNN liên tục có hàm PPXS là F(x). Nếu hàm số F(x) có đạo hàm bậc nhất tại x thì
đạo hàm đó được gọi là mật độ xác suất của X tại x.
Hàm số f(x) = F’(x), ∀x được gọi là hàm mật độ xác suất của ĐLNN X. Nhận xét -
Hàm MĐXS chỉ có đối với ĐLNN liên tục. ĐLNN rời rạc không có hàm MĐXS. -
Hàm MĐXS cho ta biết PPXS của ĐLNN liên tục tại từng giá trị của ĐLNN đó. Tính chất - Tính chất 1: f(x) ≥ 0, ∀x y f(x) x +∞ - Tính chất 2:
∫ f ( x)dx=1 −∞
Bài 2. Một số tham số đặc trưng của đại lượng ngẫu nhiên
I. Kỳ vọng (Expectation – Expected Value)
Định nghĩa 1: Giả sử X là có bảng PPXS: ĐLNN rời rạc X x1 x … x 2 n P p1 p … p 2 n n
Khi đó, kỳ vọng của X được ký hiệu và xác định như sau: E (X )=∑ x p i i i=1
Định nghĩa 2: Giả sử X là ĐLNN liên tục có hàm MĐXS là f(x). Khi đó, kỳ vọng của X được ký hiệu và xác định như sau: + ∞
E( X)=∫ x . f (x )dx −∞ Ý nghĩa -
Kỳ vọng của ĐLNN là trung bình có trọng số của các giá trị mà ĐLNN có thể nhận (trọng số chính
là các xác suất tương ứng). Do đó kỳ vọng đặc trưng cho giá trị trung bình của ĐLNN. -
Trong kinh tế, kỳ vọng đặc trưng cho lợi nhuận trung bình mà nhà đầu tư có thể đạt được khi tham
gia 1 chiến lược kinh doanh. Tính chất -
Tính chất 1: E(C) = C, với C là 1 hằng số. -
Tính chất 2: E(CX) = C.E(X), với C là 1 hằng số. - Tính chất 3: E(X ± Y) = E(X) ± E(Y) - Tính chất 4:
Nếu X và Y độc lập nhau thì: E(X.Y) = E(X).E(Y) n
Chú ý: Nếu X là ĐLNN rời rạc thì: E ( 2 X2 )=∑ x . p i i i=1
II. Phương sai (Dispersion – Variance)
Định nghĩa: Cho X là ĐLNN có E(X) = a. Khi đó, phương sai của X được ký hiệu và xác định như sau:
D (X )=E [(X−a)2]
Nhận xét: Phương sai của ĐLNN là trung bình bình phương sai lệch của các giá trị mà ĐLNN có thể
nhận so với kỳ vọng của nó. Ý nghĩa -
Phương sai của ĐLNN đặc trưng cho mức độ tập trung hay phân tán của các giá trị mà ĐLNN có
thể nhận so với kỳ vọng của nó.
Nếu phương sai nhỏ thì độ phân tán nhỏ, độ tập trung lớn, các giá trị của ĐLNN thường gần kỳ vọng của nó.
Nếu phương sai lớn thì độ phân tán lớn, độ tập trung nhỏ, các giá trị của ĐLNN thường xa kỳ vọng của nó. -
Trong kinh tế, phương sai đặc trưng cho mức độ rủi ro khi tham gia 1 chiến lược kinh doanh. Nếu 1
chiến lược kinh doanh có phương sai của lợi nhuận (hay tỉ suất lợi nhuận) càng lớn thì rủi ro càng cao và ngược lại. Nhận xét -
Nếu phương sai càng lớn thì độ phân tán, độ rủi ro, độ biến động, … càng lớn và ngược lại. -
Nếu phương sai càng lớn thì độ đồng đều, độ chính xác, độ ổn định, … càng nhỏ và ngược lại. Tính chất - Tính chất 1:
D(C) = 0, với C là 1 hằng số. - Tính chất 2: D(CX) = C2 , với C là 1 hằng số. .D(X) - Tính chất 3:
Nếu X & Y độc lập nhau thì: D(X Y) = D(X) + D(Y) Hệ quả: D(X C) = D(X) , với C là 1 hằng số.
Cách tính phương sai:
D (X )=E( X2)−[ E (X )] 2
Lưu ý: Đơn vị đo của phương sai bằng bình phương đơn vị đo của ĐLNN.
III. Độ lệch tiêu chuẩn
Định nghĩa: Cho X là ĐLNN. Khi đó, độ lệch tiêu chuẩn của X được ký hiệu và xác định như sau:
σ (X )=√ D(X )
Ý nghĩa: Độ lệch tiêu chuẩn có ý nghĩa giống ý nghĩa của phương sai. Tuy nhiên, đơn vị của độ lệch tiêu
chuẩn giống đơn vị của ĐLNN. Do đó, khi cần đánh giá mức độ phân tán theo đơn vị đo người ta thường
dùng độ lệch tiêu chuẩn.
IV. Hệ số biến thiên (Coefficient of Variation)
Định nghĩa: Cho X là ĐLNN. Khi đó, hệ số biến thiên của X được ký hiệu và xác định như sau: √ D( X)
VC (X ) = σ ( X ) × 100 %= × 100 % |E(X )| |E( X)| Ý nghĩa -
Hệ số biến thiên là thước đo độ phân tán trên mỗi đơn vị kỳ vọng. Hệ số biến thiên càng lớn thì độ
phân tán càng cao và ngược lại. -
Trong kinh tế, hệ số biến thiên là thước đo độ rủi ro trên mỗi đơn vị sinh lời kỳ vọng. Hệ số biến
thiên càng cao thì độ rủi ro càng lớn và ngược lại. -
Hệ số biến thiên thường được dùng để so sánh độ phân tán, rủi ro, độ đồng đều, độ chính xác,…
Nhất là khi các ĐLNN có đơn vị tính khác nhau hoặc quy mô khác nhau. -
Trong trường hợp đặc biệt, nếu ĐLNN có cùng đơn vị tính và có quy mô như nhau thì để so sánh độ
phân tán, độ rủi ro,… ta có thể so sánh phương sai hoặc độ lệch tiêu chuẩn.
NOTE: Hỏi độ phân tán so sánh hệ số biến thiên V. Mốt Định nghĩa -
Mốt của ĐLNN là giá trị của ĐLNN có khả năng xảy ra nhiều nhất. -
Mốt của ĐLNN rời rạc là giá trị mà tại đó xác suất tương ứng là lớn nhất. -
Mốt của ĐLNN liên tục là giá trị mà tại đó hàm mật độ xác suất đạt giá trị cực đại. Ký hiệu: Mod (X)
VI. Giá trị tới hạn
Định nghĩa: Cho X là ĐLNN liên tục và 0 ≤ 1. ≤
Khi đó số thực x thỏa mãn: P(X > x) = . Được gọi
là giá trị tới hạn mức của X.
Bài 3. Đại lượng ngẫu nhiên hai chiều I. Định nghĩa
Định nghĩa: Cho X, Y là các ĐLNN khi đó cặp (X;Y) được gọi là đại lượng ngẫu nhiên hai chiều. Phân loại -
Nếu X & Y là các ĐLNN rời rạc thì (X;Y) được gọi là ĐLNN hai chiều rời rạc. -
Nếu X & Y là các ĐLNN liên tục thì (X;Y) được gọi là ĐLNN hai chiều liên tục.
II. PPXS của ĐLNN hai chiều
1. Bảng PPXS của ĐLNN hai chiều rời rạc
Định nghĩa: Cho ĐLNN hai chiều rời rạc (X;Y). Giả sử X: x , x 1 2,…, xm và Y: y , y 1 ,…, y 2 . n
Đặt pij (X = xi ; Y = yj), i = 1 ;m và j = 1 ;n P(X = xi ; Y = yj) P[(X = xi).(Y = yi)] P[(X ; Y) = (xi ; yi)]
Khi đó, bảng sau được gọi là bảng PPXS của ĐLNN 2 chiều (X ; Y) Y y X 1 y2 … yn Tổng x1 p11 p12 … p1n h1 x2 p21 p22 … p2n h2 (1) … … … … … … xm pm1 Pm2 … pmn hm Tổng c1 c2 … cn 1 m n
Chú ý: ∑∑ p =1 ij i=1 j=1
Nhận xét: Ta có thể lập được bảng PPXS của X & Y như sau: X x1 x … x 2 m h1 + h2 + … + hm = 1 P h1 h2 … hm Y y1 y2 … yn c + c 1 + … + c 2 = 1 P c n 1 c2 … cn
2. Hàm PPXS của ĐLNN 2 chiều
3. Hàm MĐXS của ĐLNN 2 chiều liên tục
III. PPXS có điều kiện
Bài toán: Cho ĐLNN 2 chiều rời rạc (X ; Y) có bảng PPXS như bảng (1). Giả sử đã biết Y = y hãy lập bảng 1 PPXS của X. - Bước 1: Tính P(Y = y ) = c 1 1 -
Bước 2: Tính các xác suất điều kiện:
P( X =x ; Y = y )
P (X =x /Y = y )= m 1 m 1 P(Y = y ) 1 -
Ta có bảng PPXS của X với điều kiện Y = y là: 1 X / Y = y1 x1 x2 … xm p p p P 11 21 … m 1 c c c 1 1 1
Chú ý: Sau khi lập bảng PPXS có điều kiện ta có thể tính được kỳ vọng có điều kiện: p p p
E (X /Y = y )=x . 11 +x . 21 +…+x . m1 1 1 c 2 c m c 1 1 1
IV. Mômen tương quan và hệ số tương quan
1. Mômen tương quan (Hiệp phương sai – Covariance)
Định nghĩa: Cho (X;Y) là ĐLNN 2 chiều. Khi đó mômen tương quan (Hiệp phương sai) của X và Y được
ký hiệu và xác định như sau:
cov (X , Y )=μ ( X , Y )=E {[ X−E (X )]. [Y −E (Y )] }
Công thức tính hiệp phương sai: cov ( X , Y )=E (XY )−E ( X) . E(Y ) m n
Với bảng PPXS (1) thì ta có: E (XY )=∑ ∑ x y p i j ij i=1 j =1
Tính chất: Nếu X & Y độc lập nhau thì: cov(X;Y) = 0
cov(X;X) = E(X ) – [E(X)] 2 = D(X) 2
Công thức tính phương sai của tổng, hiệu: D(aX bY) = a D(X) + b 2 D(Y) 2 2ab.cov(X;Y)
Nếu X và Y độc lập nhau thì: D(aX bY) = a D(X) + b 2 2D(Y)
2. Hệ số tương quan
Định nghĩa: Cho (X;Y) là ĐLNN 2 chiều. Khi đó, hệ số tương quan giữa X và Y được ký hiệu và xác định như sau:
ρ (X , Y )= cov ( X ; Y )
σ ( X ). σ (Y ) Tính chất: - Tính chất 1:
ρ (X , Y ) không phụ thuộc đơn vị đo của X & Y. - Tính chất 2:
|ρ( X ,Y )|≤1 Ý nghĩa -
ρ (X , Y ) đặc trưng cho mức độ tương quan tuyến tính giữa X và Y (tính đường thẳng càng gần 1 thì càng thẳng)
Nếu |ρ( X , Y )| càng lớn (gần 1) thì X và Y tương quan tuyến tính càng chặt (càng mạnh).
Nếu |ρ( X , Y )| càng nhỏ (gần 0) thì X và Y tương quan tuyến tính càng lỏng (càng yếu). Quy ước: 0 – 0,2: rất yếu ; 0,2 – 0,4: yếu ; 0,4 – 0,6: trung bình 0,6 – 0,8: mạnh ; 0,8 – 1: rất mạnh -
Nếu ρ (X , Y ) > 0 thì X và Y tương quan cùng chiều.
Nếu ρ (X , Y ) < 0 thì X và Y tương quan ngược chiều.
Nếu ρ (X , Y ) = 0 thì X và Y không tương quan với nhau.
Bài 4. Một số quy luật phân phối xác suất thông dụng
I. Quy luật phân phối 0 – 1 Ký hiệu: X ~ A(p)
Tham số đặc trưng: E(X) = p D(X) = pq với q = 1 - p
II. Quy luật phân phối nhị thức (Binomial Distribution) 1. Dãy thử Bernoulli
Định nghĩa: Dãy thử Bernoulli là dãy phép thử thỏa mãn 2 điều kiện: -
Các phép thử độc lập nhau. -
Trong mỗi phép thử đều có thể xuất hiện hoặc không xuất hiện biến cố A và xác suất xuất hiện biến
cố A trong mỗi phép thử đều bằng nhau.
VD: Một người bắn 5 viên đại vào 1 mục tiêu. Xác suất bắn trúng mục tiêu của người đó là 0,7. Đây là 1 dãy phép thử Bernoulli.
Chú ý: Nếu số phần tử trong 1 tập hợp rất lớn so với số phần tử lấy ra thì lấy không hoàn lại được coi là lấy có hoàn lại. 2. Bài toán Bernoulli
Bài toán: Xét dãy phép thử Bernoulli với số lượng phép thử là n và xác suất xuất hiện biến cố A trong mỗi
phép thử là p. Gọi X là số lần xuất hiện biến cố A trong dãy phép thử đó. Hãy lập bảng PPXS của X. Ta có: X: 0, 1, …, n
Nhận xét: P (X=m)=Cm m n . p .qn−m Vậy X có bảng PPXS là: X 0 1 …. m …. n (1) P C0
1 . p1 .qn−1 …. Cm. pm . qn−m …. Cn
n. p0 . qn C n n n. pn . q0
3. Định nghĩa quy luật phân phối nhị thức
Định nghĩa: ĐLNN có bảng PPXS như bảng (1) được gọi là có phân phối nhị thức với 2 tham số n và p. Ký hiệu: X ~ B(n ; p)
Nhận xét: Nếu X là số lần xuất hiện biến cố A trong dãy phép thử Bernoulli thì X ~ B(n ; p). Ở đó:
n: số lượng phép thử
p: xác suất xuất hiện biến cố A trong mỗi phép thử.
4. Công thức tính xác suất
Nếu X ~ B(n ; p) thì ta có:
Công thức Bernoulli: : P (X=m)=Cm . pm .qn−m n m2 Và:
P (m ≤ X ≤ m )= ∑ P(X =m) 1 2 m=m1
5. Tham số đặc trưng - Nếu X ~ B(n ; p) thì: E(X) = n.p ; D(X) = npq ;
σ (X )=√npq -
Nếu X ~ B(n ; p) thì để tìm Mốt của X ta tính: x0 = (n + 1).p
Nếu x0 Z thì Mod(X) = [x ] (phần nguyên của x 0
0: là số nguyên lớn nhất không vượt quá x ) 0 Nếu x0 Z thì: Mod1(X) = x0 và Mod2(X) = x – 1 0
III. Quy luật phân phối Poission
Định lý Poission: Cho X ~ B(n ; p). Khi n khá lớn (n > 100) và p khá gần 0 (p
≤ 0,005) thì X có phân phối
xấp xỉ phân phối Poission P( với ) = np. Khi đó: e−λ . λm
P( X=m)≈ m!
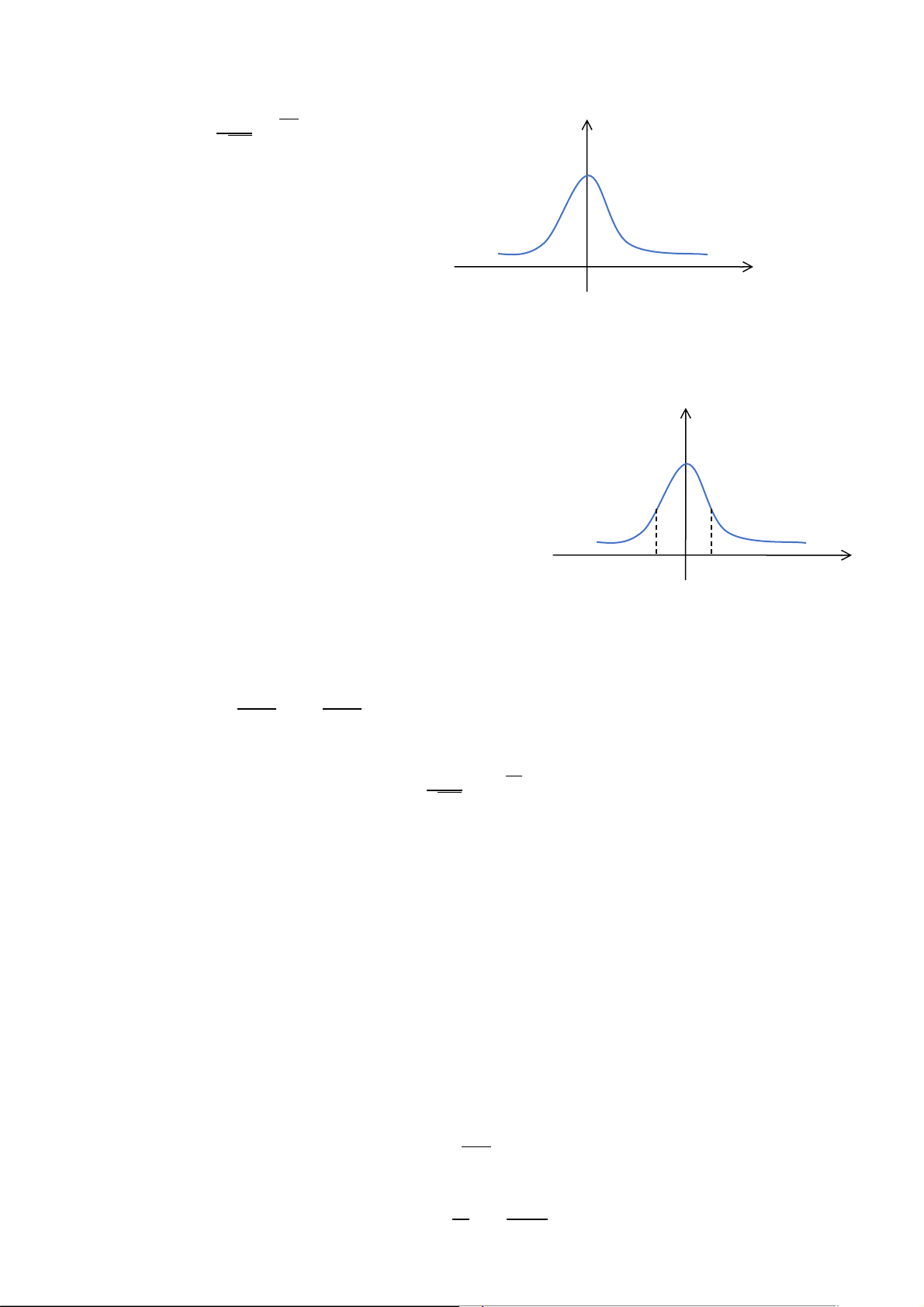
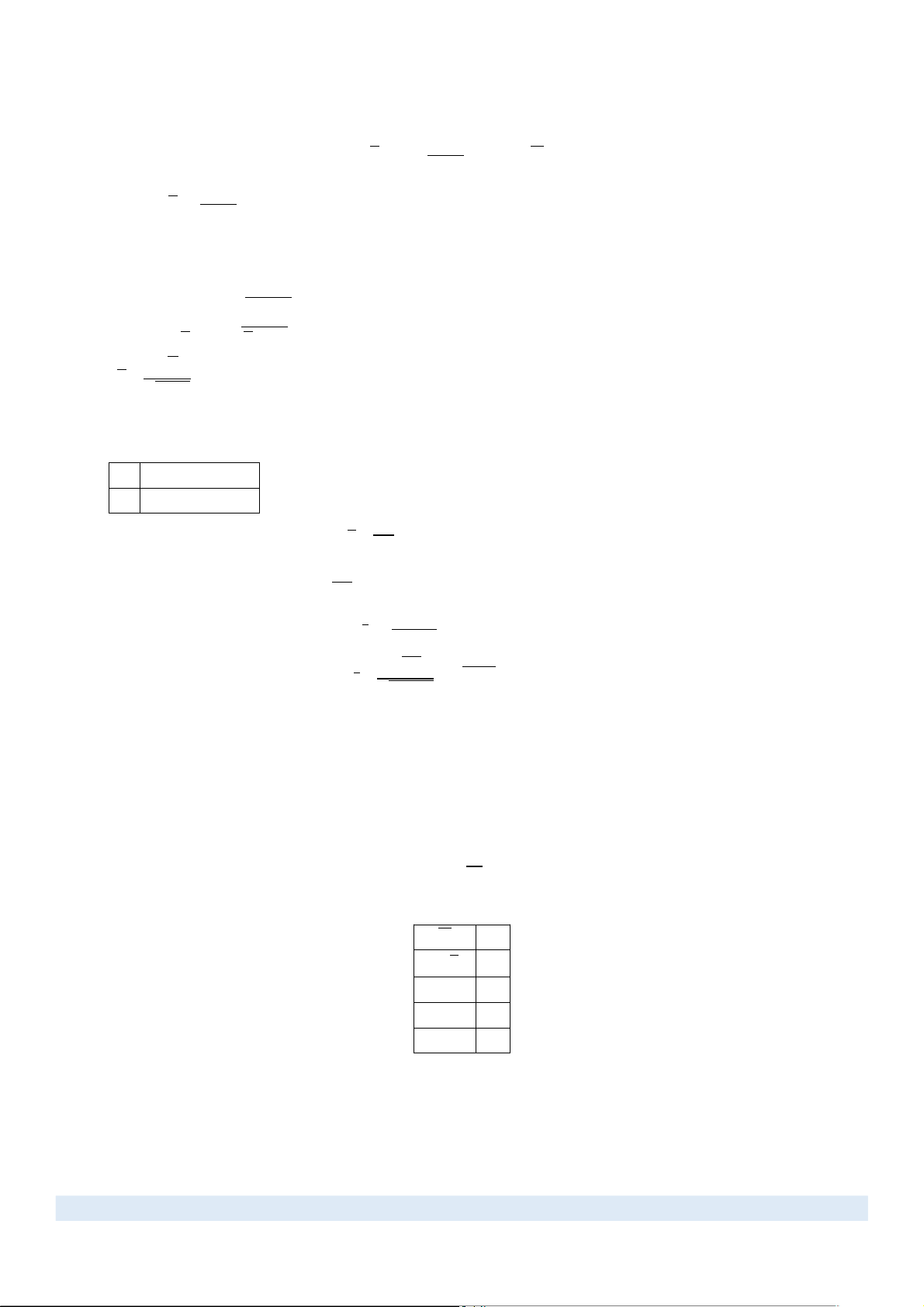
IV. Quy luật phân phối chuẩn (Normal Distribution) 1. Định nghĩa
Định nghĩa: ĐLNN X được gọi là có phân phối chuẩn với 2 tham số a và ( > 0) nếu hàm MĐXS của X −( x−a)2 có dạng: f (x )= 1
×e 2σ2 , ∀ x ∈ R σ√2 π Ký hiệu: X ~ N(a ; 2) a f(x) 0 a x
Đặc biệt: Nếu a = 0, = 1 thì ta nói X có phân phối chuẩn tắc, ký hiệu N(0 ; 1). Khi đó, hàm mật độ xác −x2
suất của X là: φ(x )= 1 2 y √ × e 2 π f(x) x 0
2. Tham số đặc trưng
Nếu X ~ N(a ; ) thì ta có: 2 E(X) = a D(X) = 2 y (X) = Mod(X) = a
Nhận xét: Nếu X ~ N(a ; ) thì ta có: 2 -
a là kỳ vọng của X, a đặc trưng cho giá trị trung bình của X. S = S = - 2 là phương sai của X. -
là độ lệch tiêu chuẩn của X. u
Giá trị tới hạn chuẩn: Giá trị tới hạn chuẩn mức ký hiệu là u u 1- 0 x u1- = – u
3. Công thức tính xác suất
Công thức: Nếu X ~ N(a ; ) thì ta có: 2
P (α< X <β)=Φ(β−a)−Φ(α−a ) σ σ P ¿ x −t2 Φ( x)= 1 2 √
×∫ e dt , ∀ x∈ R 2 π 0
Chú ý: Trong CT ở trên, nếu tại các dấu bất đẳng thức có thêm dấu bằng thì kết quả vẫn không thay đổi.
Tính chất của hàm Φ( x) : -
Hàm Φ (x) là hàm lẻ trên R nên Φ(−x)=−Φ ( x) , ∀ x ∈ R -
Ta có: lim Φ( x)=0,5 (ta còn viết là Φ(+∞ )=0,5 ¿ x→+∞ -
Khi x đủ lớn (x > 5) thì ta lấy Φ( x) ≈ 0,5 4. Quy tắc 3 Nếu X ~ N(a ; )
2 thì hầu chắc chắn (với xác suất 0,9973) đại lượng ngẫu nhiên X sẽ nhận giá trị trong khoảng (a - 3 ; a + 3)
5. Định lý Moivre – Laplace
Định lý: Cho X ~ B(n ; p). Khi n khá lớn, p không quá gần 0, không quá gần 1 (0,005 < p < 0,995) thì X có
phân phối xấp xỉ phân phối chuẩn với a = n.p và = √npq Do đó ta có: 1
P (X=m) ≈ ❑ ×φ(m−a ) σ −a −a
P(m ≤ X ≤ m ) ≈ Φ (m2 )−Φ(m2 ) 1 2 σ σ
V. Quy luật phân phối Student
X có giới hạn Student với k bậc tự do: X ~ T(k)
Giá trị tới hạn Student mức với k bậc tự do: t(k) t1-(k) = – t(k)
VI. Quy luật phân phối Khi bình phương
X có phân phối Khi bình phương với k bậc tự do: X ~ χ2(k)
Giá trị tới hạn Khi bình phương mức với k bậc tự do: 2 χ ( k) α
VII. Quy luật phân phối Fisher – Snedecor
X có phân phối Fisher – Snedecor với k và k 1 bậc tự do: 2 X ~ F(k1,k ) 2
Giá trị tới hạn Fisher – Snedecor với k và k 1 2 bậc tự do: f(k1,k ) 2 Tính chất: f (k , k )= 1 α 1 2 f ( k ,k ) 1−α 2 1
Chương 3. Ước lượng tham số
Bài 1. Tham số đám đông – Tham số mẫu
I. Đám đông – Mẫu
Đám đông (Tổng thể nghiên cứu) là tập hợp các phần tử mà ta muốn nghiên cứu. Số phần tử của đám đông
được gọi là kích thước của đám đông, ký hiệu là N.
Mẫu là tập hợp các phần tử lấy ra từ đám đông để nghiên cứu. Số phần tử của mẫu được gọi là kích thước mẫu, ký hiệu là . n Dãy thống kê:
Giả sử cần nghiên cứu dấu hiệu X của 1 đám đông. Từ đám đông ta lấy mẫu kích thước n để nghiên cứu.
Gọi xi là giá trị của X ở phần tử thứ i trong mẫu (i = 1, 2,…, n). Trong các giá trị này có thể có các giá trị
giống nhau. Để cho gọn, ta chỉ viết các giá trị giống nhau 1 lần kèm theo số lần xuất hiện tương ứng ta được
dãy thống kê dạng điểm cho dưới dạng tần số: X x1 x … x 2 k (1) m m1 m … m 2 k Chú ý: m1 + m +…+ m 2 k = n
II. Tham số đám đông
* Giả sử: cần nghiên cứu dấu hiệu X của 1 đám đông (X là 1 ĐLNN). Đặt: E(X) = a ; D(X) = 2 ; (X) = Khi đó:
a là kỳ vọng của X a đặc trưng cho giá trị trung bình của X trong đám đông.
2 là phương sai của X 2 đặc trưng cho độ phân tán các giá trị của X trong đám đông so với kỳ vọng của nó.
là độ lệch tiêu chuẩn của X.
a, 2, đều mang thông tin cô đọng của đám đông nên chúng được coi là các tham số đám đông.
* Giả sử: đám đông cần nghiên cứu chỉ có 2 loại phần tử là các phần tử mang đặc tính A và các phần tử
không mang đặc tính A. Gọi M là số phần tử mang đặc tính A trong đám đông: p= M N
p là tỉ lệ phần tử mang đặc tính A trong đám đông (p chính là xác suất lấy được phần tử mang đặc tính A
khi lấy ngẫu nhiên 1 phần tử của đám đông).
p cũng mang thông tin cô đọng của đám đông nên p cũng được gọi là tham số đám đông. III. Tham số mẫu
Mẫu ngẫu nhiên – Mẫu cụ thể:
Giả sử cần nghiên cứu dấu hiệu X của 1 đám đông. Từ đám đông ta dự định lấy mẫu, kích thước n để nghiên
cứu. Gọi Xi là giá trị của X ở phần tử thứ I trong mẫu, i = 1 ;n
Vì mẫu chưa chọn cụ thể nên mỗi Xi sẽ là 1 ĐLNN (X1, X , …, X 2
n) gọi là mẫu ngẫu nhiên.
Khi đã lấy mẫu thì Xi nhận giá trị cụ thể là xi. Khi đó (x1, x2, …, x )
n được gọi là mẫu cụ thể. 1. Trung bình mẫu
Định nghĩa: Với mẫu ngẫu nhiên (X1, X2,…, Xn) thì trung bình mẫu của X được ký hiệu và xác định như sau: n X = 1 ∑ X n i i=1
Ý nghĩa: X đặc trưng cho giá trị trung bình của X ở trong mẫu
X là hình ảnh thu hẹp của a. Nhận xét:
X là 1 ĐLNN (giá trị của X chưa cố định, giá trị của X phụ thuộc vào mẫu lấy ra).
Với mẫu cụ thể (x , x 1 ,…, x 2 ) thì n
X nhận giá trị cụ thể là: n x= 1 ∑ x n i i=1
Với dãy thống kê (1) thì ta có:
x= 1 (x m +x m +…+ x m ) n 1 1 2 2 k k
2. Phương sai mẫu và phương sai mẫu điều chỉnh a) Phương sai mẫu
Định nghĩa: Với mẫu ngẫu nhiên (X1, X ,…, 2
Xn) thì phương sai mẫu của X được ký hiệu và xác định như sau n
S2( X )= 1 ∑ ( X ¿¿ i−X )2¿ n i=1
Ý nghĩa: S2 đặc trưng cho mức độ phân tán các giá trị của X ở trong mẫu so với trung bình mẫu của nó
S2 là hình ảnh thu hẹp của 2. Nhận xét: S2 là 1 ĐLNN.
Với các mẫu cụ thể (x , x 2 1 2,…, x ) thì S n nhận giá trị cụ thể: n
s2= 1 ∑ (x¿¿ i−x)2 ¿ n i=1
Với dãy số thống kê điểm cho dưới dạng tần số thì ta có:
s2= 1 ( x2m +x2m +…+x2 m )−( x )2 n 1 1 2 2 k k
b) Phương sai mẫu điều chỉnh
Định nghĩa: Với mẫu ngẫu nhiên (X ,1 X ,…, 2 X )
n thì phương sai mẫu điều chỉnh của X được ký hiệu và xác định như sau: n
S2 ( X )= 1 ∑ (X −X )2 n−1 i i=1 Nhận xét: S2= n S2 n−1
3. Độ lệch tiêu chuẩn mẫu và Độ lệch tiêu chuẩn mẫu điều chỉnh Định nghĩa: -
Đại lượng S(X) = √S2(X ) được gọi là độ lệch tiêu chuẩn mẫu của X. -
Đại lượng S (X ) =√S2( X ) được gọi là độ lệch tiêu chuẩn mẫu điều chỉnh của X. √n S=√ S n−1
VD1: Điều tra điểm môn xác suất của 10 sinh viên HVTC ta được số liệu như sau: 7 8 6 9 7 7 6 8 6 7
Gọi X là số điểm môn xác suất của sinh viên HVTC. Ta có dãy thống kê: X 6 7 8 9 m 3 4 2 1
x= 1 (6.3+7.4 +8.2+9.1 )=7,1 10
s2= 1 (62.3+72.4 +82 .2+ 92.1)−7,12=0,89 10
s2= 10 ×0,89 ≈ 0,98889 10−1 √10 s= √
× √0,89 ≈ 0,99443 10−1 4. Tần suất mẫu
Định nghĩa: Giả sử đám đông nghiên cứu chỉ có 2 loại phần tử là các phần tử mang đặc tính A và các phần
tử không mang đặc tính A.
Từ đám đông ta dự định lấy mẫu kích thước n để nghiên cứu.
Gọi m là số phần tử mang đặc tính A trong mẫu. Khi đó tần suất mẫu được xác định và ký hiệu như sau: f = m n
Ý nghĩa: f là tỉ lệ phần tử mang đặc tính A trong mẫu f là hình ảnh thu hẹp của p. X a S2 , S2 2 s f p *
Bài 2. Ước lượng điểm một số tham số đám đông
I. Khái niệm ước lượng điểm
Giả sử nghiên cứu 1 đám đông với tham số chưa biết. Từ đám đông ta lấy mẫu để nghiên cứu. Với mỗi
mẫu lấy ra thì tham số mẫu * nhận một giá trị cụ thể. Ta dùng giá trị cụ thể này để ước lượng cho . Việc
ước lượng cho tham số như vậy được gọi là ước lượng điểm.
II. Ước lượng chệch và Ước lượng không chệch
Định nghĩa: Giả sử ta dùng tham số mẫu * để ước lượng điểm cho tham số của đám đông. -
Nếu E(*) = thì * được gọi là ước lượng không chệch của . -
Nếu E(*) thì được gọi là ước lượng chệch của * .
III. Ước lượng điểm một số tham số đám đông Một số kết quả:
X là ước lượng không chệch của a. 2
S2 là ước lượng chệch của .
S2 là ước lượng không chệch của 2.
f là ước lượng không chệch p.
Bài 3. Ước lượng khoảng một số tham số đám đông
I. Một số khái niệm mở đầu
Giả sử: cần nghiên cứu 1 đám đông với tham số chưa biết. Từ đám đông ta lấy kích thước n để nghiên
cứu. Giả sử ta có các đại lượng thống kê ❑¿, ❑¿ thỏa mãn: 1 2 ¿ ¿
P (❑ <θ<❑ ) =γ 1 2
Khi đó: ta gọi khoảng (¿¿ ;❑¿)¿ là khoảng tin cậy của với độ tin cậy . ( càng lớn càng đáng tin cậy) 1 2
Trường hợp đặc biệt: Nếu ta có tham số mẫu * và một số > 0 thỏa mãn:
P (θ¿−ε <θ< θ¿+ ε) =P(|θ¿−θ|<ε )=γ
Thì khoảng (θ¿−ε; θ¿+ε) được gọi là khoảng tin cậy đối xứng của với độ tin cậy và được gọi là sai số
cho phép của ước lượng.
Trong phần tiếp theo ta sẽ ký hiệu α=1−γ
II. Ước lượng kỳ vọng (ước lượng giá trị trung bình) Bài toán:
Giả sử cần nghiên cứu dấu hiệu X của 1 đám đông có E(X) = a ; D(X) = 2 với a chưa biết. Để ước lượng a,
từ đám đông ta lấy mẫu kích thước n để nghiên cứu. Khi đó, với độ tin cậy ta có khoảng tin cậy đối xứng a
được xác định như sau: 1) Trường hợp n và 30
chưa biết (trường hợp mẫu lớn): ( s s x−u ; x +u α × √ α × ) n √ n 2 2 s ε=u × α √n 2 u α
α : giá trị tới hạn chuẩn mức 2 2
2) Trường hợp n < 30 và X ~ N(a ; 2 với ) chưa biết: ( s s
x−t (n−1) ×
; x +t ( n−1)× α √ α √ ) n 2 n 2 s
ε=t (n−1)× α √n 2 t ( n−1) α α
: giá trị tới hạn Student mức với (n – 1) bậc tự do. 2 2
Chú ý: Khoảng tin cậy của a là: ( s s x−u × ; x+u × α √ α √ ) 2 n−1 2 n−1
III. Ước lượng phương sai (ước lượng độ phân tán, độ đồng đều, độ chính xác, độ rủi
ro, độ biến động, độ ổn định,…)
Bài toán: Giả sử cần nghiên cứu X của 1 đám đông. Ở đó X ~ N(a ; 2) với chưa 2
biết. Để ước lượng 2,
từ đám đông ta lấy mẫu kích thước n để nghiên cứu. Khi đó, trong trường chưa biết a với độ tin cậy ta có
khoảng tin cậy của được xác định như sau: 2 ( ns2 ns2 (n−1)s2 ; ; 2 2 2 2 χ ( n−1) χ
(n−1 ))=( (n−1)s2
χ ( n−1) χ (n−1) ) α α 1− α 1− α 2 2 2 2 χ2 (n−1 ) α α
: Giá trị tới hạn Khi bình phương mức với (n – 1) bậc tự do. 2 2
IV. Ước lượng xác suất (ước lượng tỉ lệ)
Bài toán: Giả sử đám đông cần nghiên cứu có tỉ lệ phần tử mang đặc tính A là p chưa biết. Để ước lượng p,
từ đám đông ta lấy mẫu kích thước n để nghiên cứu. Khi đó, trong trường hợp n f (1−f )≥ 20 0 0 thì độ tin cậy
ta có khoảng tin cậy đối xứng của p được xác định như sau: ( √f (1−f ) √ (1−f ) 0 f 0 f −u 0 0 × ; f +u × ) 0 α √n 0 α √n 2 2 √f (1−f ) 0 ε =u 0 α × √n 2
Chú ý: Giả sử ta đã tìm được khoảng tin cậy của p là (p ; p 1 ). 2 M Ta có: p < p < p 1 2 p1 < < p N 2 -
Bài toán 1: Cho N và yêu cầu ước lượng M (ước lượng số phần tử mang đặc tính A của đám đông). -
Bài toán 2: Cho M và yêu cầu ước lượng N (ước lượng số phần tử của đám đông).
Đặc điểm chung: Ước lượng số phần tử.
Chương 4. Kiểm định giả thuyết thống kê
Bài 1. Khái quát về bài toán kiểm định giả thuyết thống kê
- Trong thực tế, đôi khi ta gặp tình huống phải lựa chọn 1 trong 2 giả thuyết về cùng 1 vấn đề. Giả thuyết
ban đầu ký hiệu là H , giả thuyết còn lại gọi là 0
đối thuyết ký hiệu là H1.
- Để đi đến quyết định chấp định H 0hay H ,1 từ
đám đông ta lấy mẫu để nghiên cứu và dựa vào kết quả
thu được ở mẫu cùng quy tắc kiểm định đã được xây dựng để kết luận.
- Khi kết luận như vậy ta có thể mắc sai lầm. Có 2 loại sai lầm ta có thể mắc phải như sau: