Ôn tập công thức- Môn nguyên lý thống kê| Đại học Kinh Tế Quốc Dân

Đại học Kinh tế Quốc dân với những kiến thức và thông tin bổ ích giúp các bạn định hướng và họp tập dễ dàng hơn. Mời bạn đọc đón xem. Chúc bạn ôn luyện thật tốt và đạt điểm cao trong kì thi sắp tới.

105 53 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Nguyên lý thống kê

Trường: Đại học Kinh Tế Quốc Dân

Thông tin:

38 trang 5 tháng trước

Tác giả:

Profile Hà Việt Anh
ÔN T P MÔN NGUYÊN LÝ TH NG KÊẬ Ố
Ậ
Phân t v i các kho ng cách t b ng nhau. ổ ớ ả ổ ằ
max min
i i
i
X X
h
n
Trong đó:
i
h
: Tr s kho ng cách t . ị ố ả ổ
max
i
X
: ng bi n l n nh t c a tiêu th c phân t . Lượ ế ớ ấ ủ ứ ổ
min
i
X
: Lượng biến nhỏ nhất của tiêu thức phân tổ.
n
: S t c n chia. ố ổ ầ
ác bước phân tổ thống kê:
Bước 1: Lựa ch n tiêu th c phân t . ọ ứ ổ
Bước 2: Xác định số tổ cần phân và khoảng cách t . ổ
Bước 3: Phân ph vào t ng t . ối các đơn vị ừ ổ
Ố
ST
T
Công th c ứ
ơn
vị
Chú thích
ố tu t đối t ời v số tu t đối t ời đi
1
§ §
T G
T
§
TLH
T
1
§ §
0
T G
y
T
y
§
1
i
TLH
i
y
T
y
%,
pđv
1
y
: M c a hi ng k nghiên c u. ức độ ủ n tượ ứ
0
y
: M c a hi ng k g ức độ ủ n tượ ốc.
§ §
T G
T
: S nh g c (T nh g c). ố tương đối động t ái đị ố ốc độ PT đị ố
§
TLH
T
: S ng thái liên hoàn (T PT liên hoàn). ố tương đối độ ốc độ
2
KH
T
0
KH
KH
y
T
y
%,
pđv
KH
T
: S i nhi m v k ho ch. ố tương đố ụ ế ạ
TK
T
: S hoàn thành k ho ch. ố tương đối ế ạ
TK
T
1
TK
KH
y
T
y
Hệ qu : ả
DT KH TK
T T T
DT
TK
KH
T
T
T
v
DT
KH
TK
T
T
T
KH
y
: M c a hi ng k k ho ch. ức độ ủ n tượ ế ạ
0
y
: M c t c a ch tiêu kức độ thự ế ủ ỉ ở g c so sánh. ố
1
y
: M c a hi ng k báo cáo. ức độ ủ n tượ
3
KC
T
bq
KC
TT
y
T
y
%,
pđv
bq
y
: M c a b ph n. ức độ ủ ộ ậ
TT
y
: M c a t ng th . ức độ ủ ổ
4
CD
T
§
C
m
T
n
%,
pđv
m
: M c a hi ng c bi n. ức độ ủ n tượ ần đán giá p ổ ế
n
: M c a hi ức độ ủ n tượng n o đó có liên quan.
5
KG
T
1
2
KG
x
T
x
%,
pđv
1
x
: M c a hi ng không gian th nh t c n phân tích. ức độ ủ n tượ ở ứ ấ ầ
2
x
: M c a hi ng không gian th so ức độ ủ n tượ ở ứ ai dùng l cơ sở
sánh.
1
X
1
n
i
i
X
X
n
đvt
i
X
: Lượ ến (i=1, 2, …, n)ng bi
n
: S trong t ng th . ố đơn vị ổ
2
X
1
1
n
i i
i
n
i
i
X f
X
f
đvt
i
X
: Lượ ến (i=1, 2, …, n)ng bi
i
f
: Quy n s n s ) ề ố (Tầ ố
i i
X f
: Gia quy n ề
8
g
X
ax min
2
m
g
X X
X
(với lượng biến có khoảng cách tổ)
đvt
axm
X
: Lượng biến lớn nhất của tổ.
min
X
: Lượng biến nhỏ nhất của tổ.
3
t
X
1
1
k
i i
i
t
k
i
i
X n
X
n
đvt
i
X
: S bình quân t ố ổ i.
i
n
: Quy n s ho c s t ề ố ặ ố đơn vị ổ i.
K: S ố lượng t . ổ
4
X
1
1
n
i
i
n
i
i
i
M
X
M
X
Khi:
1 2
...
n
M M M M
thì:
1
1
n
i
i
n
X
X
đvt
i i i
M X f
: Gia quy n. ề
(Vậ ầ ố ầ ố ẩn d t tụng i c ưa biế n s hay t n s n)
1
X
1
1 2 3
. . .....
n
n
i
i
n
n
X X
X X X X
đvt
i
X
: Lượng bi ến (i=1, 2, 3,…,n)
n
: S ( S ng bi n). ố đơn vị ố lượ ế
2
X
1
21
1
1 2
. .....
n
i
i
i
n
i
ii
n
f
f
i
i
f
f f fn
n
X X
X X X
đvt
i
X
: Lượ ến (i=1, 2, 3,…,n)ng bi
i
f
: T n s ng. ầ ố tương ứ
1
Số trung v (MEDIAN - ị
e
M
)
+)Với dãy s ng bi n ố có lượ ế
không có kho ng cách tả ổ:
*
2 1,
e q
n k k N M x
(
q
là t ổ ở giữa)
*
2 ,
2
q p
e
x x
n k k N M
(
,q p
là t ổ ở giữa)
+)Với dãy s ng bi n ố lượ ế có
khoả ổng cách t :
*Xác định tổ chứa
e
M
: C ng d n t n s n khi nào b ng ho t quá ộ ồ ầ ố (S
i
) đế ằ ặc vượ
2
i
f
thì d ng. ừ
*Giá tr g a s trung v nh theo công th ị ần đúng củ ố ị được xác đị ức:
min
1
2
e
e e
e
i
M
e M M
M
f
S
M X h
f
14
Số M t (MODE - ố
o
M
)
+)Với dãy s ng bi n ố lượ ế
không có kho ng cách tả ổ:
axim
o
M X
(Mốt l lượ ất trong dã lượng biến lớn nh ng biến)
+)Với dã lượng biến có
khoả ổng cách t :
TH có kho ng cách t : ả ổ đều nhau
TH kho ng cách t . ả ổ không đều nhau
*Tổ a m t là t có t n s l n nhchứ ố ổ ầ ố ớ ất
max
f
Tæ
.
*Giá tr g a m c tính theo công th ị ần đúng củ ốt đượ ức:
min
1
1 1
o o
o o
o o o o
M M
o M M
M M M M
f f
M X h
f f f f
*Tổ a M t là t có m phân ph là l n nh tchứ ố ổ ật độ ối ớ ấ
PP
max
M
Tæ
.
i
i
PP
i
f
M
h
rong đó:
i
PP
M
: M phân ph i c a t ật độ ố ủ ổ i.
i
f
: T n s c a t ầ ố ủ ổ i.
i
h
: Tr s kho ng cách t c a t ị ố ả ổ ủ ổ i.
*Giá tr g a M c tính: ị ần đúng củ ốt đượ
min
1
1 1
M Mo
o
o o
M M M M
o o o o
PP PP
o M M
PP PP PP PP
M M
M X h
M M M M
1
Khoảng bi n thiên ế
(
R
)
ax minm
R X X
đvt
axm
X
: Lượng biến lớn nhất.
min
X
: Lượng biến nhỏ nhất.
Ố Q
(
e
)
16
+)TH không có quy n s : ề ố
1
n
i
i
X X
e
n
+)TH có quy n s :ề ố
1
1
.
n
i i
i
n
i
i
X X f
e
f
17
Phương sai (
2
)
+)TH không có quy n s : ề ố
+)TH có quy n s : ề ố
2
2
1
n
i
i
X X
n
2
2
1
1
n
i i
i
n
i
i
X X f
f
18
ộ lệch chuẩn (
)
2
19
Hệ s ố biến thiên
100
e
e
V
X
100V
X
20
CÁC THAM S U TH HÌNH DÁNG C A THAM S Ố BIỂ Ị Ủ Ố
Cách 1: So sánh 3 ch ỉ
tiêu đặc trưng.
+)Nếu đườ ối đống cong phân ph i xứng thì:
e o
X M M
+)Nếu đườ ng cong phân phối l ch phải thì:
e o
X M M
+)Nếu đườ ng cong phân phối l ch trái thì:
e o
X M M
Cách 2: Tính h không ệ
đố ứi x ng.
o
A
X M
K
*Khi
A
K
>0 là phân ph i l ch ph ố ải.
*Khi
A
K
<0 là phân ph i l ch trái. ố
*Khi
A
K
=0 là phân ph i chu n i x ng. ố ẩ đố ứ
H i x ng tính ra càng l n dãy s phân ph i x ng. đố ứ ớ ố ối c ng ông đố ứ
: ỀU TRA CHỌN MẪU
3.1 T NG TH CHUNG VÀ T NG TH M U Ổ Ể Ổ Ể Ẫ
Chỉ tiêu
Tổng th chung ể
Tổng th m u ể ẫ
Quy mô m (số ẫu)
N
n
Số bình quân
X
Tỷ l theo m t tiêu th c ộ ứ
p
f
P ương sai
2 2 2
X
2
2 2
o
X X
P ương sai củ a tổng th mẫu:
2
2
2
1 1
1 1
n n
i i i i
i i
o
n n
i i
i i
X n X n
n n
Hoặc
2
2
1
1
( )
n
i i
i
o
n
i
i
X X n
n
3.2 SAI S N MỐ CHỌ ẪU
Cách ch n ọ
Suy r ộng
Chọ ạn hoàn l i
(Chọn nhiều l ần)
Chọ ạn không hoàn l i
(Chọn 1 l ần)
Bình quân
Tổng th
2
X
n
Tổng th
2
1
X
n
n N
Mẫu
2
1
o
X
n
Mẫu
2
1
1
o
X
n
n N
Tỷ l ệ
Tổng th
1
p
p p
n
Tổng th
1
1
p
p p
n
n N
Mẫu
1
1
f
f f
n
Mẫu
1
1
1
f
f f
n
n N
,
p
X
: Các sai s bình quân n m ng s bình quân và t l . ố chọ ẫu i ước lượ ố ỷ
3.3 N C U TRA CH N M U O Ả ỦA Ề Ọ Ẫ
* CÔNG TH C T NG QUÁT Ứ Ổ
. 2
. 2
X
X
p f
P X z z
P f p z z
(*)
V iớ
.
.
.
X
X
p f
z
z
z
(**)
rong đó:
X
X
z
và
f
p
z
: phạm vi sai số chọn mẫu bình quân và tỷ l
z
: h s tin c ố ậy.
-Nếu
30n
thì
,
i i
X f
tuân theo quy lu t phân ph i chu n. Tra b ng 1: Phân ph i chu n ậ ố ẩ ả ố ẩ
-Nếu
30n
thì
i
X
tuân theo quy lu t phân ph i Student. Tra b ng 2: Phân ph i Student. ậ ố ả ố
Dạng
Tên
Tóm t t ắ
Cách gi i ả
Bài toán 1
Suy r ng tài li u tra n m u. ộ u điề chọ ẫ
Bài toán tìm
& p
biết
...P a
Từ thi : giả ết tín (*) v (**) đ
+)Suy r ng bình quân: ộ
X X
X X
+)Suy r ng t l ộ ỷ :
p p
f p f
Bài toán 2
Tìm xác su tin c y) khi suy rất (Độ ậ ộng
tài li u tra ch n m u điề ọ ẫu.
Bài toán tìm
... ?P
biết
&
X p
Từ công th c (**) ta có: ứ
? ... 2 ?
X
X
p
f
z
z P z
z
Bài toán 3
Tính s t ng th m u (ố lượng đơn vị ổ ẫ
n
)
Bài toán tìm n
biết
...P a
và
Theo gi thi t ta suy ra: ả ế
... 2 ? ?P z z z
Tìm n = ? d ng f thay p n u p không th ) (Lưu ý: ử ụ ế xđ
Suy
rộng
Chọ ạn hoàn l i
Chọ ạn không hoàn l i
Bình
quân
2 2
2
X
z
n
2 2
2 2 2
X
Nz
n
N z
Tỷ l
2
2
1
p
z p p
n
2
2 2
1
1
p
Nz p p
n
N z p p
3.4 N M U NG U NHIÊN P P P Ọ Ẫ Ẫ
* CH N M U C I (M U CHÙM) Ọ Ẫ Ả KHỐ Ẫ
Công th c ứ
Chú gi i ả
Suy r ng ộ
bình quân
2
1
X
X
R r
r R
+) N u s các kh i không b ng nhau: ế ố đơn vị ố ằ
2
2
.
i i
X
i
x x n
n
+)Nếu s các kh i b ng nhau: ố đơn vị ố ằ
2
2
i
X
x x
r
2
X
: P ương sai giữa các số bình
quân kh c ch n. ối đượ ọ
i
x
: S bình quân c a m i khố ủ ỗ ối được
chọn (i=1,2,…,r).
x
: S bình quân c a các khố ủ ối được
chọn.
Suy r ng t l ộ ỷ ệ
1
1
r r
f
f f
R r
r R
+)Nếu s các kh i không b ng nhau: ố đơn vị ố ằ
i i
r
i
f n
f
n
+)Nếu s các kh i b ng nhau: ố đơn vị ố ằ
i
r
f
f
r
r
f
: T l bình quân c a các khỷ ủ ối
đượ ọc ch n.
Với
1,2,...,i r
là t l c a m i khỷ ủ ỗ ối
đượ ọc ch n.
3.5 PHÂN TÍCH CÁC THÀNH PH N C A DÃY S I GIAN Ầ Ủ Ố THỜ
PHÂN TÍCH CÁC THÀNH PH N C A DÃY SẦ Ủ Ố THỜI GIAN
+)Kết h p c ng: ợ ộ
t t t t
y f s z
.
+)Kết h p nhân: ợ
. .
t t t t
y f s z
.
Trong đó:
+) Xu thế:
t
f
.
+) Th i vờ ụ:
t
s
.
+)Ngẫu nhiên:
t
z
.
+)Hàm xu th có d ng: ế ạ
.
i
f t t T
0 1t
f a a t
Với
1,2,3,...t
thứ t ự
thời gian trong dãy s . ố
1
2
12 1
2.. 1
S n
a T
m mm n n
n
: S ố nă .
m
: S ố quý trong nă
4m
0 1
. 1
. 2
T m n
a a
m n
1. Phân tích các thành ph n theo k t h p c ng ầ ế ợ ộ
2. Phân tích các thành ph n theo k t h p nhânầ ế ợ
0 1
1
2
t j j
m
s s y y a j
với
1,2,3,4j
t t t t
z y f s
i
T T
.
t j
s s H
j
m
H
s
t
j
t
y
s
y
.
i
S t T
0
4
i
y
y
i
i
y
y
n
t
t
t
y
y
s
.
t
t
t t
y
z
f s
Ể Ị IV: KI NH GIẢ THUYẾT
Cặp gi thuyả ết:
0
1 0
H : Gi¶ thuyÕt gèc
H : Gi¶ thuyÕt ®èi cña H
Kiểm định phía phải
Kiểm định phía trái
Kiểm định 2 phía
0 0
1 0
:
:
H
H
0 0
1 0
:
:
H
H
0 0
1 0
:
:
H
H
2. Nếu
Z
miền bác bỏ ỏ: Bác b
0
H
, ch p nhấ ận
1
H
.
3. N ếu
Z
miền bác bỏ: c ưa đủ cơ sở bác bỏ
0
H
(chấp nh n giậ ả thuyết
0
H
).
1. KIỂM ỊNH VÀ SO SÁNH S TRUNG BÌNH Ố
a/ Ki nh giá tr trung bình ểm đị ị
C tặp gi thuyả ế
2
đã biết
2
chưa biết với
( 30)n
2
chưa biết với
( 30)n
So sánh
Tiêu chu n ki ẩ ểm định
So sánh
Tiêu chu n ki ẩ ểm định
So sánh
0 0
1 0
:
:
H
H
0
X n
Z
0,5
Z Z
0
0
X n
Z
Với
2
0 0
1
n
n
0
: Độ l ch tiêu chuẩn
mẫu điều chỉnh.
0,5
Z Z
0
X n
t
S
Với
S
(hay
0
): Độ l ch
chuẩn m u chẫu điề ỉnh.
, 1
n
t t
0 0
1 0
:
:
H
H
0,5
Z Z
0,5
Z Z
, 1
n
t t
0 0
1 0
:
:
H
H
0,5 2
Z Z
0,5 2
Z Z
2, 1
n
t t
Miề ừn th a nh n ậ
Miề ừn th a nh n ậ
Miề ừn th a nh n ậ
b/ Ki nh 2 giá tr trung bình c a 2 m c l p ểm đị ị ủ ẫu độ ậ
C gi tặp ả thuyế
2 2
1 2
,
đã biết
2 2
1 2
,
chưa biết với
1 2
30, 30n n
2 2
1 2
,
chưa biết với
1 2
30, 30n n
Tiêu chu n ki ẩ ểm định
So sánh
Tiêu chu n ki ẩ ểm định
So sánh
Tiêu chu n ki ẩ ểm định
So sánh
0 1 2
1 1 2
:
:
H
H
1 2
2 2
1 2
1 2
X X
Z
n n
0,5
Z Z
1 2
1 2
2 2
0 0
1 2
X X
Z
n n
0,5
Z Z
1 2
2 2
1 2
X X
t
s s
n n
1 2
1 2
1 1
X X
s
n n
;
Với
2
s
là giá tr chung c a 2 ị ủ
p ương sai ẫu
2 2
01 02
,
:
2 2
1 01 2 022
1 2
1 1
2
n n
s
n n
1 2
, 2n n
t t
0 1 2
1 1 2
:
:
H
H
0,5
Z Z
0,5
Z Z
1 2
, 2n n
t t
0 1 2
1 1 2
:
:
H
H
0,5 2
Z Z
0,5 2
Z Z
1 2
2, 2n n
t t
c/ Ki nh 2 giá tr trung bình c a 2 m u ph thu c ểm đị ị ủ ẫ ụ ộ
Cặp gi thuy t ả ế
Tiêu chu n ki ẩ ểm định
So sánh
0 0
1 0
:
:
d
d
H
H
0
0
d
d n
t
d
Trung bìn các độ l ch gi a các c p giá tr c a 2 mữ ặ ị ủ ẫu
rong đó
2
2
2
0 0
.
1 1 1
d d
i
i
d
d
n
d
n n d
n n n
, 1
n
t t
0 0
1 0
:
:
d
d
H
H
, 1
n
t t
0 0
1 0
:
:
d
d
H
H
2, 1
n
t t
2. KIỂ ỊNH VÀ SO SÁNH TỶ L (p)
KIỂ ỊNH T L C A 1 TT CHUNG Ỷ Ủ
ĐK áp dụng:
n
đủ lớn
0 0
. 5 1 5 n p n p
KIỂ ỊNH 2 T L CỶ ỦA 2 TT CHUNG
ĐK áp dụng: Khi
1 2
,n n
đủ lớn
1 1 1 1 2 2 2 2
; 1 ; ; 1 5 n f n f n f n f
Cặp gi thuy t ả ế
Tiêu chu n ki ẩ ểm định
So sánh
Cặp gi thuy t ả ế
Tiêu chu n ki ẩ ểm định
So sánh
0 0
1 0
:
:
H p p
H p p
0
0 0
1
f p n
Z
p p
Với
x
n
f
n
0,5
Z Z
0 1 2
1 1 2
:
:
H p p
H p p
1 2
1 2
1 1
1
f f
Z
f f
n n
Với: (f: t l chung c a 2 mỷ ủ ẫu)
1 21 1 2 2
1 2 1 2
x x
n nn f n f
f
n n n n
0,5
Z Z
0 0
1 0
:
:
H p p
H p p
0,5
Z Z
0 1 2
1 1 2
:
:
H p p
H p p
0,5
Z Z
0 0
1 0
:
:
H p p
H p p
0,5 2
Z Z
0 1 2
1 1 2
:
:
H p p
H p p
0,5 2
Z Z
: DÃ SỐ THỜI GIAN
5. ỐNG KÊ DÃY SỐ THỜI GIAN
STT
CHỈ TIÊU
1s
Số bình quân c ng theo ộ
thời gian
1/ Dãy s i k ố thờ ỳ
1
n
i
i
y
y
n
2/ Dãy s m ố thời điể
a/ TH k/c i gian b ng nhau thờ ằ
1
2 1
...
2 2
1
n
n
yy
y y
y
n
b/ TH k/c th i gian không b ng nhau ờ ằ
1
1
.
n
i i
i
n
i
i
y t
y
t
2
ượng tăng (giảm) tuyệt
đối
(CT M i liên hố ệ:
1
n
i n
i
)
1/ Liên hoàn
1i i i
y y
/ ịnh gốc
1i i
y y
3/ Bình quân
2 1
1 1 1
n
i
i n n
y y
n n n
3
Tốc độ phát triển
(CT M i liên hố ệ:
2
n
i n
i
t T
và
1
i
i
i
T
t
T
)
1/ Liên hoàn
1
i
i
i
y
t
y
/ ịnh gốc
1
i
i
y
T
y
3/ Bình quân
1 1
1
1
2 3
2
1
. .....
n
n
n n
n
n
i n i n
i
y
t t t t t T
y
4
Tốc độ tăng (giả m)
tương đối
1/ Liên hoàn
1
1 1
1
i i i
i i
i i
y y
a t
y y
100,%
i i
a t
/ ịnh gốc
1
1 1
1
i i
i i
y y
A T
y y
100,%
i i
A T
3/ Bình quân
1
i i
a t
(lần)
100
i i
a t
(%)
5
Số m) tuytăng (giả ệt đối
ứ ớng v i 1% t ốc độ tăng
(giảm)
1/ Liên hoàn
1
1
(%) 100
.100
i i i
i
i
i
i
y
g
a
y
/ ịnh gốc
1 1
1
.
ons
.100 100
.100
i i
i
i
i
y y
g c t
y
5. 2 U HI NG BI NG C A HI P P P Ể X Ớ Ế Ủ ỢNG
1. M r ng kho ng th i ở ộ ả ờ gian (quý, 6 tháng, năm…)
2. Dãy s t ố bình quân trượ
1/ Số bìn quân trượt cho nhóm 3 m ức độ
1
1 2 3
2 2
2 3 4
3 3
2 1
1 1
( ) :
( ) :
3
( ):
3
...
( ) :
3
( ) :
n n n
n n
n
y
y y y
y y
y y y
y y
y y y
y y
y
2/ Số t cho nhóm 4 m bìn quân trượ ức độ
1
2
1 2 3 4
3 3
2 3 4 5
4 4
4 3 2 1
2 2
3 2 1
1 1
( ) :
( ):
( ):
4
( ):
4
...
( ) :
4
( ) :
4
( ) :
n n n n
n n
n n n n
n n
n
y
y
y y y y
y y
y y y y
y y
y y y y
y y
y y y y
y y
y
3. s i v Phương pháp chỉ ố thờ ụ
0
i
TVi
y
I
y
TVi
I
: Ch s i v c a thỉ ố thờ ụ ủ ời gian
i
.
i
y
: S trung bình các m c a các th i gian cùng tên ố ức độ ủ ờ
i
.
0
y
: S trung bình c a tố ủ ất c các m trong dãy sả ức độ ố.
5.3 M T S NG KÊ NG N H Ố P P P DỰ O Ố Ắ Ạ (dưới 3 năm)
1. D ự đoán dựa vào lượng tăng (giả ệt đốm) tuy i bình quân
2. D a vào t phát tri n bình quânự đoán dự ốc độ ể
Mô hình d ự đoán:
.
n L n
y y L
Với
1
1
n
y y
n
n
y
: M i cùng trong dãy s ức độ cuố ố
thời gian
: Lượng tăng (giả t đốm) tuy i bình
quân.
L
: Th i gian d ờ ự đoán (tầm xa dự
đoán).
Mô hình d ự đoán:
( )
L
n L n
y y t
Với
1
1
n
n
y
t
y
n
y
: M i cùng trong dãy s ức độ cuố ố
thời gian
: Lượng tăng (giả t đốm) tuy i bình
quân.
L
: Th i gian d ờ ự đoán (tầm xa dự
đoán).
t
: T c phát tri n bình quân.ố độ
3. D a vào hàm xu th và bi ng th i v ự đoán dự ế ến độ ờ ụ
4. D ự đoán theo phương pháp san bằng mũ giản đơn
a/ Hàm xu th k t h p c ng và bi n ế ế ợ ộ ế
độ ờ ụng th i v
ttt
sfY
ˆ
ˆˆ
b/ Hàm xu th k t h p nhân và bi n ế ế ợ ế
độ ờ ụng th i v
ttt
sfY
ˆ
.
ˆˆ
Mô hình d ự đoán:
11
ˆ
..
ˆ
ttt
YyY
Với
)1(
t
Y
ˆ
: M d báo cho th i gian t ức độ ự ờ
1
ˆ
t
Y
: Mức độ dự báo cho th i gian t-ờ 1
: H s san b ố ằng ũ
y
t-1
: M c t c a th i gian t-1 ức độ thự ế ủ ờ
5. D a vào hàm xu th ự đoán dự ế
-)Từ Ptr đường thẳng:
x
y a bx
-)Vận d ng trong dãy s i gian ta có Ptr: ụ ố thờ
t
y a bt
-)Xác định
,a b
CÁCH 1: Áp dụng p ương p áp bìn p ương n ỏ nhất gi i Hpt: CÁCH 2: ả
2
y na b t
ty a t b t
2
.
t
a y bt
ty t y
b
Mô hình d ự đoán:
n L
y a b t L
: Ỉ SỐ ( Passche)
/ P P P Ỉ SỐ
3. Phương
pháp ch s ỉ ố
cá th ể
1/ Ch s cá th ỉ ố ể chất lượng
1
0
p
p
i
p
Số tuy i: t đố
1 0
p
p p
2/ Ch s cá th s ỉ ố ể ố lượng
1
0
q
q
i
q
Số tuy i: t đố
1 0
q
q q
4. Phương
pháp ch s ỉ ố
chung
. Phương pháp
chỉ s liên h p ố ợ
1/ Ch s liên h p ch ỉ ố ợ ất lượng
1 1
0 1
.
.
p
p q
I
p q
Số tuy t đối:
1 1 0 1
. .
pq
p q p q
Số tương đối:
1 1 0 1
0 0 0 0
. .
%
. .
pq
pq
p q p q
p q p q
2/ Ch s liên h p s ng ỉ ố ợ ố lượ
0 1
0 0
.
.
q
p q
I
p q
Số tuy t đối:
0 1 0 0
. .
pq
p q p q
Số tương đối:
0 1 0 0
0 0 0 0
. .
%
. .
pq
pq
p q p q
p q p q
. Phương pháp
chỉ s bình quân ố
1/ Ch tiêu ch ng ỉ ất lượ (bình quân gia
quy n)ề
1
0 1
0 11 1
0
0 1 0 1 0 1
.
.
p
p
p
p q
i p q
p q
p
I
p q p q p q
1/ Ch tiêu ch ng ỉ ất lượ (bình quân
điều hòa)
1 1 1 1 1 1
0
0 1
1 1
1 1
1
.
1
.
p
p
p q p q p q
I
p
p q
p q
p q
i
p
2/ Ch tiêu s ng ỉ ố lượ (bình quân gia
quy n)ề
1
0 0
0 00 1
0
0 0 0 0 0 0
.
.
q
q
q
p q
i p q
p q
q
I
p q p q p q
2/ Ch tiêu s ng ỉ ố lượ (bình quân điều
hòa)
0 1 0 1 0 1
0
0 0
0 1
0 1
1
.
1
.
q
q
p q p q p q
I
q
p q
p q
p q
i
q
2.3 Phương pháp
1/ Ch s chung v ỉ ố ề chất lượng
2/ Ch s chung v s ỉ ố ề ố lượng
g p p
tính ch s theo ch ỉ ố ỉ
tiêu bình quân
1
0
X
X
I
X
g ợ g
1 1
1
1
0 0
0
0
.
.
p
p q
q
p
I
p q
p
q
Số tuy t đối:
1 0 1
*
pq
p p q
Số tương đối
0 0
%
.
pq
pq
p q
g ợ g
1 1
1
1
0 0
0
0
.
.
q
p q
p
q
I
p q
q
p
Số tuy t đối:
1 0 0
*
pq
q q p
Số tương đối
0 0
%
pq
pq
p q
II/ H NG CH THỐ Ỉ SÔ
/ Phương
trình kinh
tế
D P Q
D
: Doanh thu.
P
: Giá bán.
Q
: Sản lượng.
WQ N
Q
: S ng s n xuản lượ ả ất.
W
: Năng suất lao động.
N
: S nhân công, lao ố động (người).
F L N
F
: Qu ỹ tiền lương.
L
: Đơn giá lương trên 1 công n ân.
N
: Số n ân công, lao động (người).
C z Q
C
: Chi phí s n xuả ất.
z
: Giá t n đơn vị sản phẩm.
Q
: S ng s n xuản lượ ả ất.
2/ H ệ
thống chỉ
số phát
triển
Chỉ s phát tri n = Ch s hoàn thành kố ể ỉ ố ế ch hoạ
Chỉ s ố
nhi hoệ ụm v kế ạch
Chỉ s phát tri n doanh thu: ố
1 1 1 1 1
0 0 1 0 0
. . .
. . .
KH
KH
p q p q p q
p q p q p q
Chỉ s doanh thu = Chố ỉ s giá c ố ả
Chỉ s ng bán ra. ố lượ
.
pq p q
I I I
1 1 1 1 0 1
0 0 0 1 0 0
. . .
. . .
p q p q p q
p q p q p q
3/ Phân
tích ch s ỉ ố
1/ 2 nhân t ố ảnh hưởng
1 1 1 1 0 1
0 0 0 1 0 0
*
xf x f
x f x f x f
I I I
x f x f x f
(1) (2) (3)
Biến động tuy t đối:
1 1 0 0 1 1 0 1 0 1 0 0
( ) ( )x f x f x f x f x f x f
Biến động tương đối:
2/ 3 nhân t ố ảnh hưởng
1 1 1
011
0 0 001 0
* *
xf x f
x f f
xx
I I I
x f f
x x
(1) (2) (3) (4)
Biến động tuy t đối:
1 1 0 0 1 01 1 01 0 1 1 0 0
( ) ( ) ( )x f x f x x f x x f f f x
Biến động tương đối:
1 1 0 0 1 01 1 01 0 1 1 0 0
0 0 0 0 0 0 0 0
( ) ( ) ( )x f x f x x f x x f f f x
x f x f x f x f
1 1 0 0 1 1 0 1 0 1 0 0
0 0 0 0 0 0
( ) ( )x f x f x f x f x f x f
x f x f x f
- s (1): Ph n ánh bi ng c a t ng bi n Chỉ ố ả ến độ ủ ổng lượ ế
tiêu th c do ng c a t t c các nhân t ứ ản ưở ủ ấ ả ố
- s (2): Ph n ánh bi n d ng c a t ng bi n Chỉ ố ả ế ộ ủ ổng lượ ế
tiêu th c do nhân t ng ứ ố chất lượ
- s (3): Ph n ánh bi n d ng c a t ng bi n Chỉ ố ả ế ộ ủ ổng lượ ế
tiêu th c do nhân t s ng ứ ố ố lượ
VD: Xét TH Qu ỹ tiền lương có nhân tố ảnh hưở ng ta có:
Chỉ số:
F L N
I I I
Phân tích 2 nhân t ố ản ưởng:
011 1
0 01 0
F
FF F
I
F F F
Với:
01 0 1
.
F L N
1 1 1 1 0 1
0 0 0 1 0 0
. . .
. . .
F
L N L N L N
I
L N L N L N
+)Số tuy t đối:
1 0 1 01 01 0
F F F F F F F
+)Số tương đối:
1 0 1 01 01 0
0 0 0
%
F F F F F F
F
F F F
- s (1): Ph n ánh bi ng c a t ng bi n tiêu th c do ng cChỉ ố ả ến độ ủ ổng lượ ế ứ ản ưở ủa t t c các ấ ả
nhân t ố
- s (2): Ph n ánh bi ng c ng bi n tiêu th c nghiên c u do ng cChỉ ố ả ến độ ủa lượ ế ứ ứ ản ưở ủa
nhân t ố chất lượng
- s (3): Ph n ánh bi ng c a k t c u t ng th do nhân t s ng Chỉ ố ả ến độ ủ ế ấ ổ ố ố lượ
- s (4): Ph n ánh bi ng c a quy mô t ng th ng t i bi n bi ng cChỉ ố ả ến độ ủ ổ ản ưở ớ ế ến độ ủa
tổng lượng tiêu thức
VD: Xét TH S ng s n xu t ra ch u 3 nhân tản lượ ả ấ ị ố ảnh hưởng:
1 1 1
011
0 0 001 0
W .
W
W
W .
W W
Q
N N
I
N N
Với:
1 1
1
1
W .
W
N
N
0 1
01
1
W .
W
N
N
0 0
0
0
W .
W
N
N
+)Số tuy t đối:
1 1 0 0 1 01 1 01 0 1 1 0 1
W . W . W W . W W . .WQ N N N N N N
+)Số tương đối:
0 1 1 01 0 1
1 0 0
1 1 0 0
0 0 0 0 0 0 0 0
W W . W W .
.W
W . W .
%
W . W . W . W .
N N
N N
N N
Q
N N N N
| 1/38
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ÔN TẬP MÔN NGUYÊN LÝ THỐNG KÊ Ậ
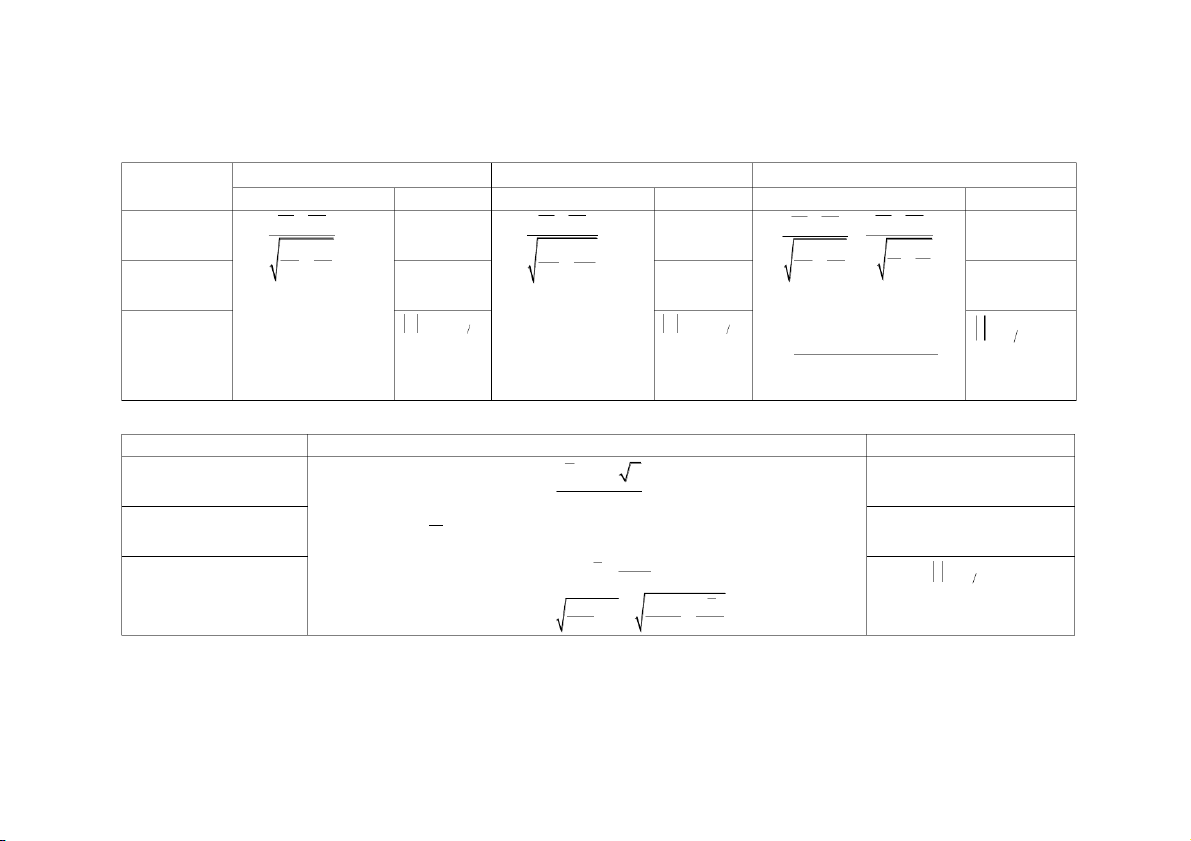
Phân tổ với các khoảng cách tổ bằng nhau. Trong đó:
h : Trị số khoảng cách tổ. i XX m i ax m i in h X
: Lượng biến lớn nhất của tiêu thức phân tổ. i imax n X
: Lượng biến nhỏ nhất của tiêu thức phân tổ. imin
n : Số tổ cần chia.
ác bước phân tổ thống kê:
Bước 1: Lựa chọn tiêu thức phân tổ.
Bước 2: Xác định số tổ cần phân và khoảng cách tổ.
Bước 3: Phân phối các đơn vị vào từng tổ. Ố ST ơn T Tên Công thức vị Chú thích
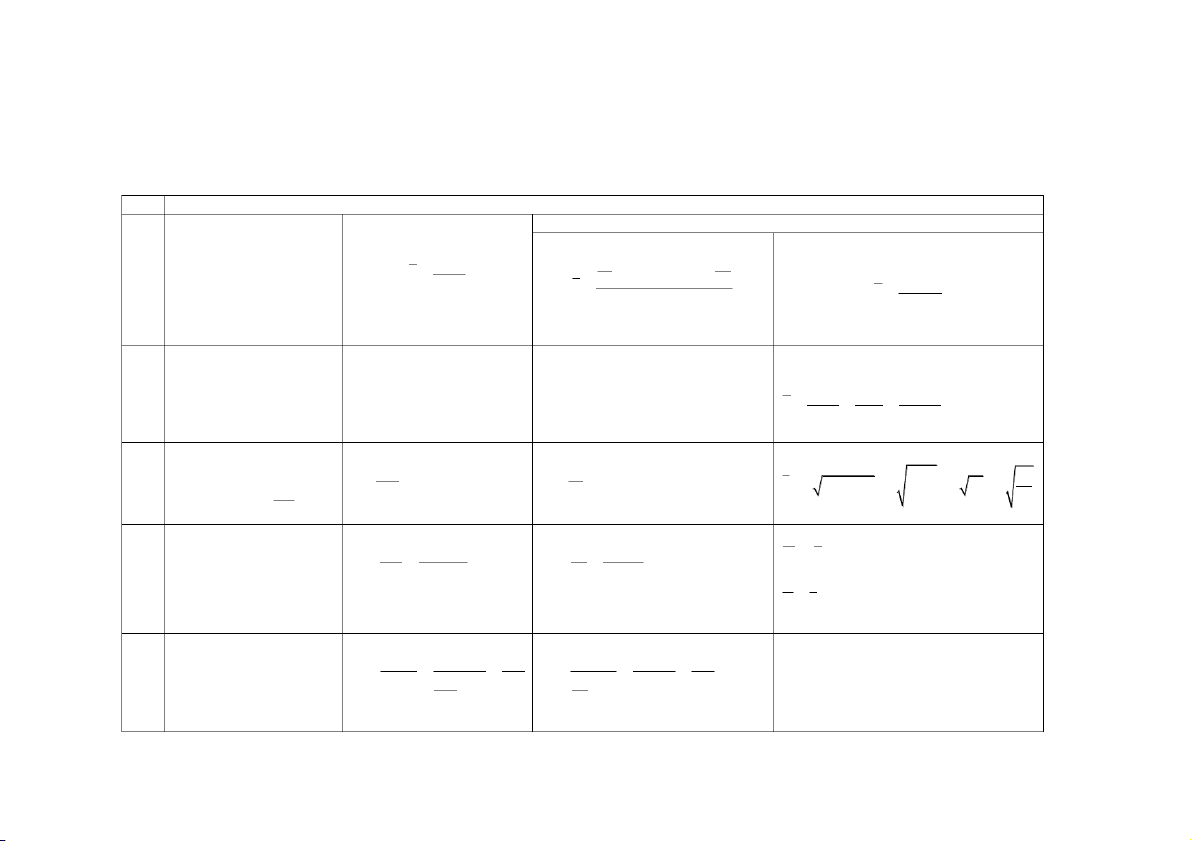
ố tu t đối t ời v số tu t đối t ời đi y %, ức độ ủ n tượ ứ 1 y : M c a hi ng k nghiên c u. Số tương đối động T  1 §T §G y pđv 0
y : Mức độ của hi n tượng k gốc . 1 thái 0 y ( T  i
ố tương đối động t ái đị ố ốc độ PT đị ố § T : S nh g c (T nh g c). § T G § T ), ( § T ) T G § TLH §TLH yi1 ố tương đối độ ốc độ § T : S ng thái liên hoàn (T PT liên hoàn). TLH Số tương đối kế y %, T
: Số tương đối nhi m vụ kế hoạch. KH TKH 2 hoạch KH pđv 0 y
T : Số tương đối hoàn thành kế hoạch. ( T ), TK KH ( T ) y y
: Mức độ của hi n tượng k kế hoạch. TK 1 TKH TK yKH
y : Mức độ thực tế của chỉ tiêu ở k gốc so sánh. 0
Hệ quả: ức độ ủ n tượ 1 y : M c a hi ng k báo cáo. TT T DT KH TK T T DTT  v DT TTK T KH T KH TK
Số tương đối kết cấu y %,
y : Mức độ của bộ phận. 3 bq Tbq ( T ) KC pđv KC y y
: Mức độ của tổng th . TT TT Số tương đối cường m %,
m : Mức độ của hi n tượng cần đán giá p ổ biến. 4 T  độ ( T ) C § n
pđv n : Mức độ của hi n tượng n o đó có liên quan. CD Số tương đối không x %, 1
x : Mức độ của hi n tượng ở không gian thứ nhất cần phân tích. T  1 5 gian KG pđv 2 x
x : Mức độ của hi n tượng ở không gian thứ ai dùng l cơ sở so 2 ( T ) KG sánh. Số bình quân cộng n  đvt
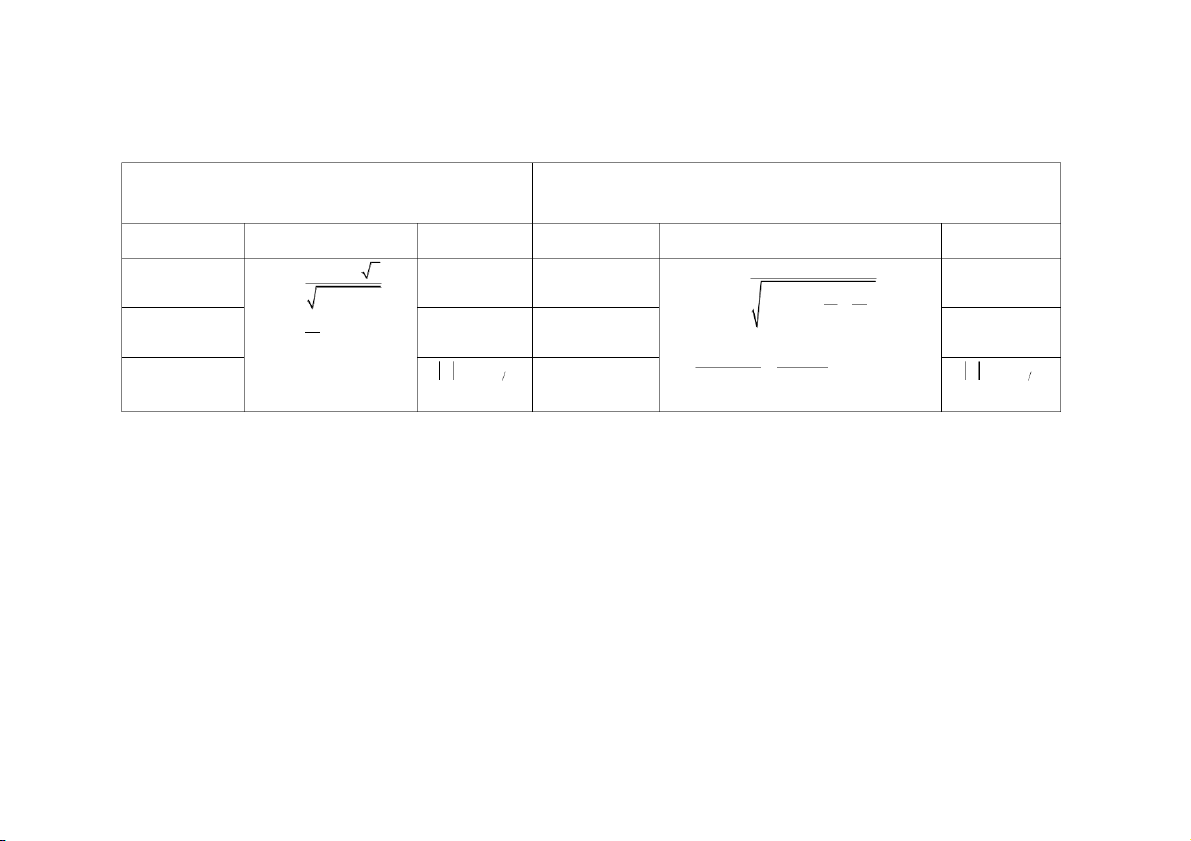
X : Lượng biến (i=1, 2, …, n) i 1 giản đơn X i ố đơn vị ổ i 1   n : S trong t ng th . ( X X ) n n đvt
X : Lượng biến (i=1, 2, …, n) X fi Số bình quân cộng i i 2 i 1 ề ố (Tầ ố X   f : Quy n s n s ) i gia quyền ( X ) n f
X f : Gia quyền i i i i 1  Trị số giữa XX đvt X
: Lượng biến lớn nhất của tổ. max min  a m x 8 X ( g X ) 2 X
: Lượng biến nhỏ nhất của tổ. g
(với lượng biến có khoảng cách tổ) min k đvt ố ổ i. Số bình quân chung  X : S bình quân t X n i i i 3
từ các số bình quân tổ i 1 ề ố ặ ố đơn vị ổ i. X   n : Quy n s ho c s t i t k (X )  K: Số lượng tổ. t ni i 1  n đvt
M X f : Gia quyền. Mi i i i
(Vận dụng i c ưa biết tần số hay tần số ẩn) i1 X n M i Số bìn quân điều  X 4 hoà gia quyền i 1  i
Khi: M M  ...   thì: ( M M X ) 1 2 n n X n 1  i 1  X i đvt Số bình quân nhân n
X : Lượng biến (i=1, 2, 3,…,n)  i n X X  1 giản đơn i
n : Số đơn vị ( Số lượng biến). i 1  ( X ) n
X .X .X ..... 1 2 3 X n n n  đvt
X : Lượng biến (i=1, 2, 3,…,n) i f fi i  1 i  Số bình quân nhân X Xi
f : Tần số tương ứng. 2 i 1 i gia quyền ( X ) n fi f f fn i 1 i 2  X . X ..... 1 2 X n
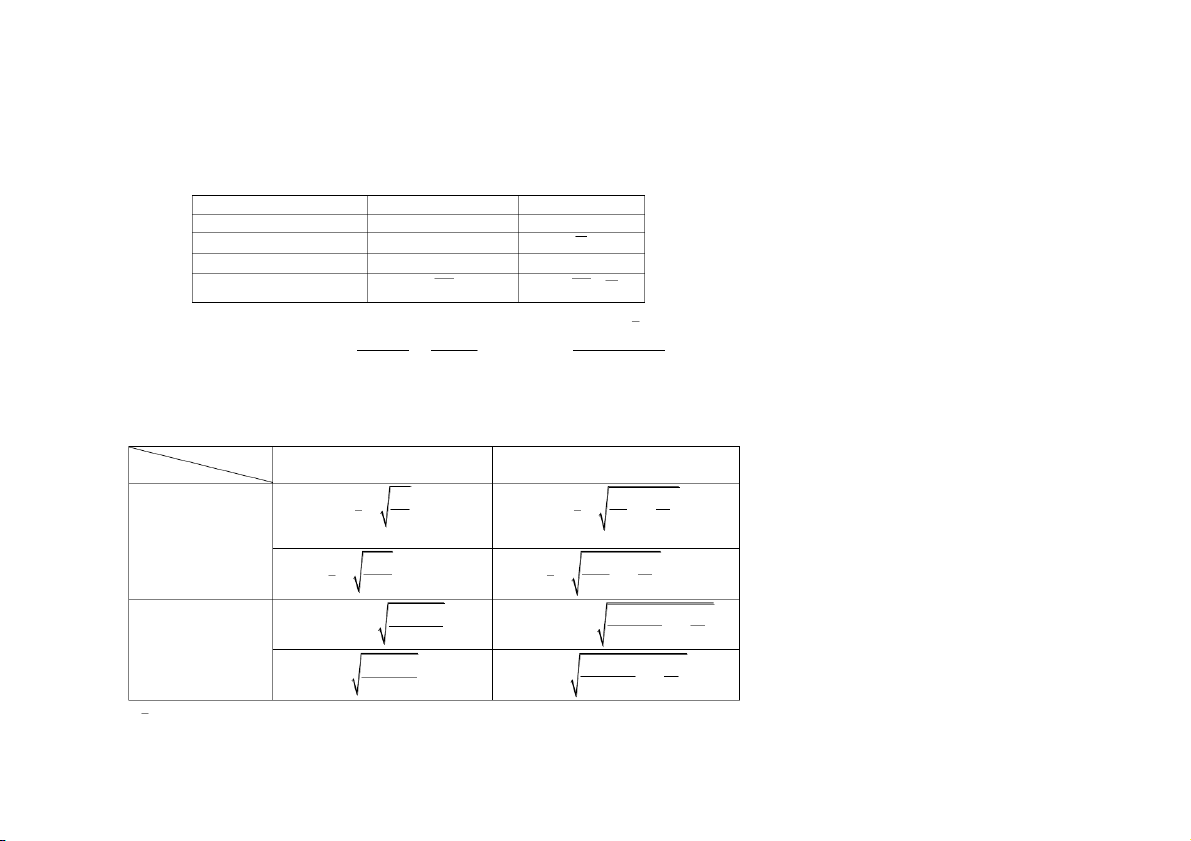
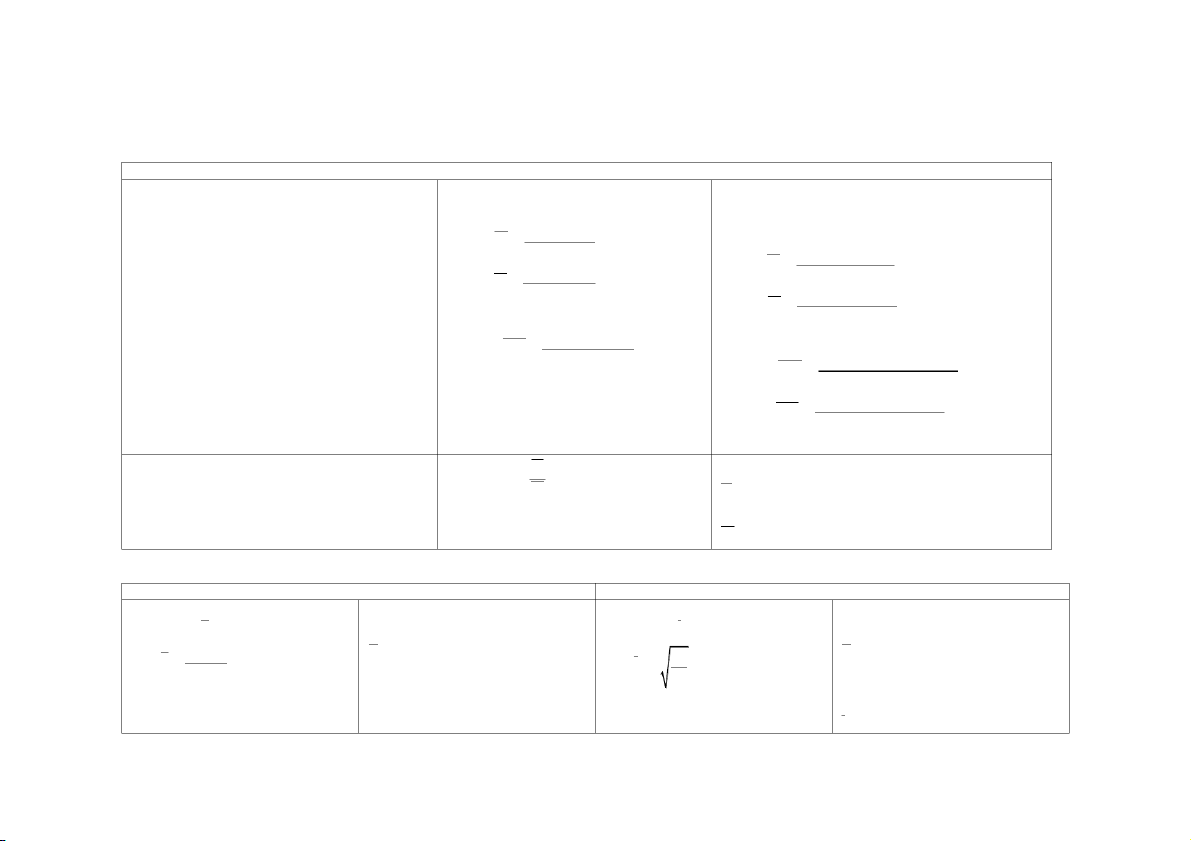
Số trung vị (MEDIAN - M ) e
n k   * 2
1, k N   M x (q là tổ ở giữa)
+)Với dãy số có lượng biến e q
không có khoảng cách tổ: x xn k  * 2 , k N q pM  ( ,
q p là tổ ở giữa) e 2 1 f
*Xác định tổ chứa M : Cộng dồn tần số (S i
i) đến khi nào bằng hoặc vượt quá thì dừng. e 2
+)Với dãy số lượng biến có
*Giá trị gần đúng của số trung vị được xác định theo công thức :
khoảng cách tổ: fi   SM 1 2  e M Xh e M M m e in e f e M 14
Số Mốt (MODE - M ) o
+)Với dãy số lượng biến M X o i a m x
không có khoảng cách tổ:
(Mốt l lượng biến lớn nhất trong dã lượng biến)
TH có khoảng cách tổ đều nhau:
TH khoảng cách tổ không đều nhau.
*Tổ chứa mốt là tổ có tần số lớn nhất Tæ .
*Tổ chứa Mốt là tổ có mật độ phân phối là lớn nhất fmax 
*Giá trị gần đúng của mốt được tính theo công thức : Tæ . M PPmax  f iff M P iP M M 1 h o o M Xh i o M M m o in of f   rong đó: f f M M 1 M M o o   1 o o
+)Với dã lượng biến có ật độ ố ủ ổ i.
khoảng cách tổ: M : M phân ph i c a t P i P
f : Tần số của tổ i. i
h : Trị số khoảng cách tổ của tổ i. i
*Giá trị gần đúng của Mốt được tính: MM PP PP 1  M Mo o M Xh o M M m o in oM MMM PP PP PP PP M M 1 o o   M M 1 o oR XX đvt X
: Lượng biến lớn nhất. 1
Khoảng biến thiên a m x min a m x ( R ) X
: Lượng biến nhỏ nhất. min Ố Q ( e )
+)TH không có quyền số:
+)TH có quyền số: n n  
X X . f i i 16 X X i 1  i e i 1 e   n n fi i 1  17 Phương sai ( 2  )
+)TH không có quyền số:
+)TH có quyền số: n  n X X X X f i 2 i 2 i 2 i 1    2 i 1    n n fi i1 18
ộ lệch chuẩn ( )    2 e V  1  00 e 19
Hệ số biến thiên XV  100  X
CÁC THAM SỐ BIỂU THỊ HÌNH DÁNG CỦA THAM SỐ
+)Nếu đường cong phân phối đối xứng thì:
X M M e o
Cách 1: So sánh 3 chỉ
+)Nếu đường cong phân phối l ch phải thì: tiêu đặc trưng.
X M M e o
+)Nếu đường cong phân phối l ch trái thì: 20
X M M e o X M o K A
Cách 2: Tính hệ không *Khi K >0 là phân phối l ch phải. A đối xứng.
*Khi K <0 là phân phối l ch trái. A
*Khi K =0 là phân phối chuẩn đối xứng. A
 H đối xứng tính ra càng lớn dãy số phân phối c ng ông đối xứng.
: ỀU TRA CHỌN MẪU
3.1 TỔNG THỂ CHUNG VÀ TỔNG THỂ MẪU Chỉ tiêu
Tổng thể chung
Tổng thể mẫu Quy mô (số mẫu) N n Số bình quân  X
Tỷ l theo một tiêu thức p f P ương sai 2 2 2   X  2 2 2
  X X o 2  n n    n 2  X n X n  2    
(X X) n i i i i i i
P ương sai của tổng th mẫu: 2  i 1 i 1         2 i 1    o n n     o n n n    nii   Hoặc i i 1   i 1    i 1 
3.2 SAI SỐ CHỌN MẪU Cách chọn
Chọn hoàn lại
Chọn không hoàn lại Suy rộng
(Chọn nhiều lần)
(Chọn 1 lần) 2  2  n Tổng th   Tổng th     1   X n X n N Bình quân 2  2  n Mẫu o   Mẫu o     1   X n 1  X n 1  N p 1 p
p 1 p   Tổng th   Tổng th   1 np   n p nN
Tỷ lệ f 1  f
f 1 f   n  Mẫu   Mẫu   1 f   n 1 f n  1  N
 , : Các sai số bình quân chọn mẫu i ước lượng số bình quân và tỷ l . X p
3.3 O ẢN CỦA ỀU TRA CHỌN MẪU
* CÔNG THỨC TỔNG QUÁT
P X    
z    z X  . 2   X  (*)  P rong đó:
  f p  
z    z p  . 2 f  
  z và   z : phạm vi sai số chọn mẫu bình quân và tỷ l   Xpz. X f Với   . X X z    (**)   .z  ố ậy. p f z : h s tin c
-Nếu n  30thì X , f tuân theo quy luật phân phối chuẩn. Tra bảng 1: Phân phối chuẩn i i
-Nếu n  30 thì X tuân theo quy luật phân phối Student. Tra bảng 2: Phân phối Student. i Dạng Tên Tóm tắt Cách giải Bài toán 1
Suy rộng tài li u điều tra chọn mẫu.
Bài toán tìm  & p
Từ giả thiết tín (*) v (**) đ : biết +)Suy rộng bình quân:
P ...  a
X     X  X X +)Suy rộng tỷ l : f  
p f  p p Bài toán 2
Tìm xác suất (Độ tin cậy) khi suy rộng Bài toán tìm P ...  ?
Từ công thức (**) ta có:
tài li u điều tra chọn mẫu. biết     X X & p z    X
   z  ?  P...  2  z  ? p z     f  Bài toán 3
Tính số lượng đơn vị tổng th mẫu ( n ) Bài toán tìm n Theo giả thiết ta suy ra:
biết P ...  a và  P .. 
.  2 z  z  ? z  ? 
Tìm n = ? (Lưu ý: ử dụng f thay p nếu p không th xđ ) Suy Chọn hoàn lại Chọn không hoàn lại rộng Bình 2 2 z  2 2 Nz n n  quân 2  2 2 2 N  z X X 2 z p1  p 2 Nz p 1  p Tỷ l n n  2  2 2
N  z p1 p pp
3.4 P P P ỌN MẪU NGẪU NHIÊN
* CHỌN MẪU CẢ KHỐI (MẪU CHÙM) Công thức Chú giải Suy rộng 2  2   
 : P ương sai giữa các số bình bình quân R r X   X   X quân khối được chọn. r R 1 
+) Nếu số đơn vị các khối không bằng nhau:
x : Số bình quân của mỗi khối được i  chọn (i=1,2,…,r). x x n i 2 . 2 i  
x : Số bình quân của các khối được X n  chọn. i
+)Nếu số đơn vị các khối bằng nhau:  x  2 x 2 i   X r
Suy rộng tỷ lệ ff   
f : Tỷ l bình quân của các khối r 1 r R r   r f   rR 1   được chọn. Với là tỷ l của mỗi khối
+)Nếu số đơn vị các khối không bằng nhau:
i  1, 2,..., r được chọn. f ni i f r ni
+)Nếu số đơn vị các khối bằng nhau: fi f r r
3.5 PHÂN TÍCH CÁC THÀNH PHẦN CỦA DÃY SỐ THỜI GIAN
PHÂN TÍCH CÁC THÀNH PHẦN CỦA DÃY SỐ THỜI GIAN Trong đó:
+)Kết hợp cộng: y f s z . +) Xu thế: f . t t t t t
+)Kết hợp nhân: y f .s .z . +) Thời vụ: s . t t t t t +)Ngẫu nhiên: z . t
+)Hàm xu thế có dạng: f t   t.T i  
f a a t Với t  1, 2, 3,... thứ tự 12  S n  1  n : Số nă . t 0 1 a   T thời gian trong dãy số. 1  
m : Số quý trong nă m.n  2 n   1  m 2.m  m  4 T . m n 1   0 a 1 a m.n 2
1. Phân tích các thành phần theo kết hợp cộng
2. Phân tích các thành phần theo kết hợp nhân  m 1
s s .H
s s y y a j  với j 1, 2, 3, 4 t j t j j 0 1  2    m H
z y f s t t t ts j T Ti yt s j yt S t.Ty i t y  t yst i y  0 4 y t z   t f . y s t t i y i n
IV: KIỂ ỊNH GIẢ THUYẾT Cặp giả thuyết:  H : Gi¶ thuyÕt gèc  0
H : Gi¶ thuyÕt ®èi cña H 1 0
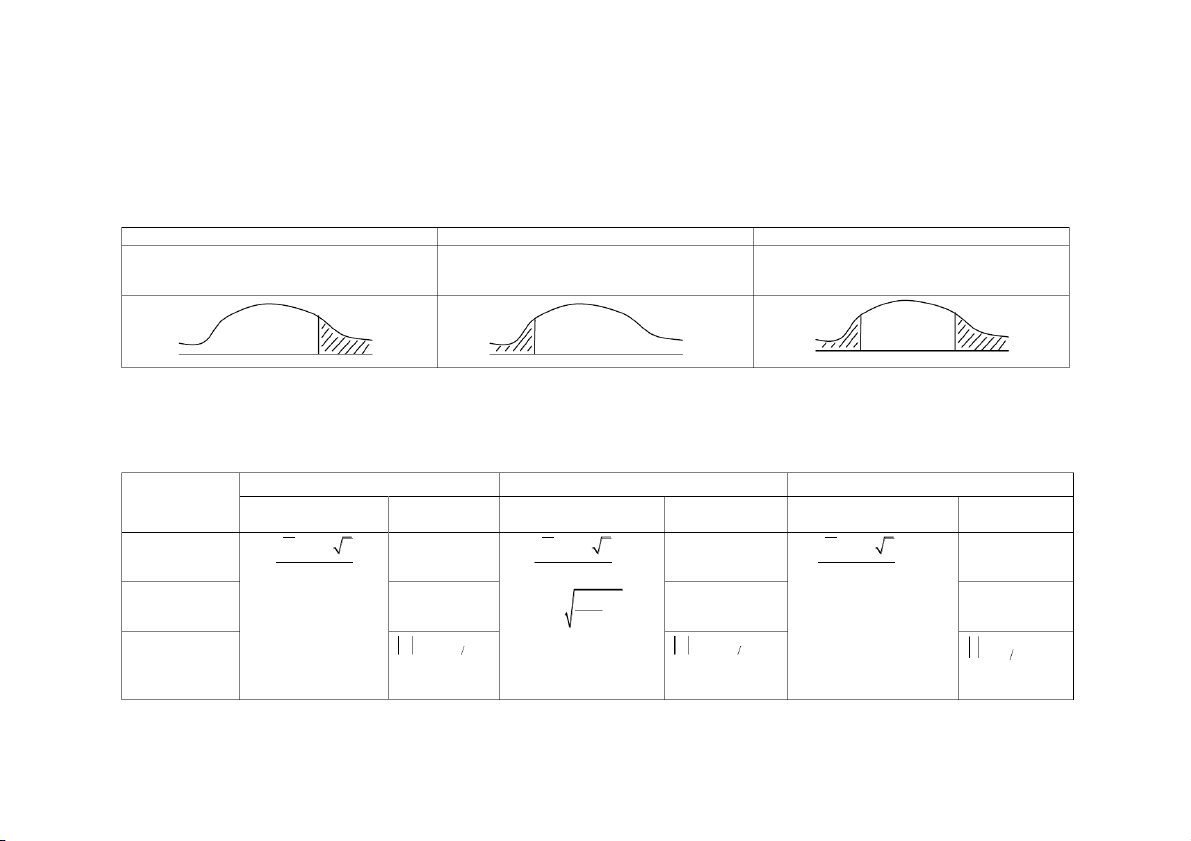
Kiểm định phía phải
Kiểm định phía trái
Kiểm định 2 phía H :    H :    H :    0 0  0 0  0 0  H :     H :     H :     1 0 1 0 1 0 Miền thừa nhận Miền thừa nhận Miền thừa nhận
2. Nếu Z miền bác bỏ: Bác bỏH , chấp nhận 0 H . 1
3. Nếu Z miền bác bỏ: c ưa đủ cơ sở bác bỏ H (chấp nhận giả thuyết 0 H ). 0
1. KIỂM ỊNH VÀ SO SÁNH SỐ TRUNG BÌNH
a/ Kiểm định giá trị trung bình
Cặp giả thuyết 2  đã biết 2
 chưa biết với (n  30) 2
 chưa biết với (n  30)
Tiêu chuẩn kiểm So sánh
Tiêu chuẩn kiểm định So sánh
Tiêu chuẩn kiểm định So sánh định H :    Z Z Z Z t  0 0 X    X     X  t 0  0  0  n 0,5 n 0,5 n    , n  1  Z Z t H :     1 0   S 0 H :    Z  Z Z    Z  Với  ): Độ l ch t   0 0 n S (hay 0,5 0 t  0,5   , n  Với 2    1  0 0 chuẩn mẫu điều chỉnh. H :     1 0 n  1 H :    Z Z
 : Độ l ch tiêu chuẩn Z  0 0  0 Z t t  0,5  2 0,5 2  2, n  1  H   mẫu điều chỉnh. :   1 0
b/ Kiểm định 2 giá trị trung bình của 2 mẫu độc lập
Cặp giả thuyết 2 2  , đã biết 2 2
 , chưa biết với n  30,n  30 2 2
 , chưa biết với n  30,n  30 1 2 1 2 1 2 1 2 1 2
Tiêu chuẩn kiểm định So sánh
Tiêu chuẩn kiểm định So sánh
Tiêu chuẩn kiểm định So sánh H :    Z Z Z Z 0 1 2 X X 0,5 X XX X X X t t  1 2 Z  1 2 Z  0,5 1 2 t  1 2  ; , n1 n  2 2   H :     2 2 2 2 2 2 1 1 2      s  1 1 1 2  s 1 0 2 0   s      Z  Z Z  Z n n H : 0 1 2 1 n 2 n n n  1 n 2 n 0,5 1 2 1 2 t t   0,5 , 1 n  2 n 2 H :    Với 2
s là giá trị chung của 2  1 1 2 p ương sai ẫu 2 2  , H :    Z Z  01 02 : 0 1 2 Z Z   0,5 2 0,5 2 t
t 2,n n 2 1 2  H :   
n  1   n  1  2   2   2 1 01 2 02  1 1 2 s  n n  2 1 2
c/ Kiểm định 2 giá trị trung bình của 2 mẫu phụ thuộc
Cặp giả thuyết
Tiêu chuẩn kiểm định So sánh H :    t  0 d  n t 0  d 0  ,  n 1   H :     t  1 d 0 0dH :    t   0 t d 0   , n  1  d H :   
Trung bìn các độ l ch giữa các cặp giá trị của 2 mẫu  1 d 0  dH :    t  0 d 0  d i t   n  2,n 1   H  :    1 d 0  rong đó 2 2  nd 2 i n .d       0 0  d n 1 d n 1  n 1 
2. KIỂ ỊNH VÀ SO SÁNH TỶ L (p)
KIỂ ỊNH TỶ L CỦA 1 TT CHUNG
KIỂ ỊNH 2 TỶ L CỦA 2 TT CHUNG
ĐK áp dụng: nđủ lớn  .
n p  5  n 1 p  5
ĐK áp dụng: Khi n , n đủ lớn n f ;n 1 f ;n f ;n 1 f  5 1 1 1  1  2 2 2  2   0  0   1 2
Cặp giả thuyết
Tiêu chuẩn kiểm định So sánh
Cặp giả thuyết
Tiêu chuẩn kiểm định So sánh H :   f p Z Z f Z  
H : p p f Z  0  0 p 0 p n 0,5 0 1 2 1 2 0,5  Z   Z
H : p pH :   1 1  1 0 p 1 p p  0  p0  1 1 2 f 1  f     H :  Z  ZH :  Z  Z 0 p 0 p 0,5 0 1 p p2  1 n 2 n    Với f nx  0,5
Với: (f: tỷ l chung của 2 mẫu)
H : p p n
H : p p 1 0  1 1 2 n f n f n n
H : p p 1 1 2 2 1 x 2 x   f Z Z H : p p   Z  0 0  0 1 2   Z  0,5 2  0,5  2 1 n 2 n 1 n 2 n H :   H :  1 p 0 p  1 1 p p2
: DÃ SỐ THỜI GIAN
5. ỐNG KÊ DÃY SỐ THỜI GIAN STT CHỈ TIÊU 1s
Số bình quân cộng theo 1/ Dãy số thời kỳ
2/ Dãy số thời điểm thời gian n
a/ TH k/c thời gian bằng nhau
b/ TH k/c thời gian không bằng nhau yi y y n i 1 1 n y y  ...  2 yy. n 1  t i i n 2 2 y i 1 y n 1 n ti i 1  2
ượng tăng (giảm) tuyệt 1/ Liên hoàn / ịnh gốc 3/ Bình quân đối
  y y
  y y n i i i 1  i i 1
(CT Mối liên hệ:
i y y i 2 n n 1 n          ) n 1  n 1 n 1 i n i 1 3
Tốc độ phát triển 1/ Liên hoàn / ịnh gốc 3/ Bình quân
(CT Mối liên hệ: y y n i i y n t T n 1  n 1  n T i i t t .t .....  n 1 tt T n 1   i 2 3 n i n t T
và i t ) y y i 1  1 i 2  y i n i 1 i 2  Ti 1  4
Tốc độ tăng (giảm) 1/ Liên hoàn / ịnh gốc 3/ Bình quân tương đối y yy y i i i1 a t 1 a    t 1 i i 1 A   T 1 (lần) i i i i y y i i y y i 1  i 1  1 1
a t 100, % i i
a t 100(%) i i
A T 100, % i i 5
Số tăng (giảm) tuyệt đối 1/ Liên hoàn / ịnh gốc
ứng với 1% tốc độ tăng   y   .y y i i i 1  i i 1 1 (giảm) g    g     const i a (%)  i   i .100 100 i i 100 .100 .100 i y y i 1  1
5. 2 P P P ỂU HI X ỚNG BIẾ NG CỦA HI ỢN G
1. Mở rộng khoảng thời gian (quý, 6 tháng, năm…)
2. Dãy số bình quân trượt
1/ Số bìn quân trượt cho nhóm 3 mức độ
2/ Số bìn quân trượt cho nhóm 4 mức độ (y ) :  ( y ) :  1 1   ( y ) :  1 y 2 y 3 y (y ) :  2 2 y2 3    1 y 2 y 3 y 4 y   ( y ) :  3 3 y 2 y 3 y 4 y ( 4 y ) :  3 y3 3 y    2 y3 y4 y5 ( y ) :  ... 4 4 y 4 yy y ... n2 n 1 (y ) :  n yn 1  n 1  3 yyyy n 4 n3 n 2 n 1 ( y ) : y   (y ) :  n  2 n  2 4 n yyyy n 3  n 2  n 1 ( y ) :  n yn 1  n 1  4 ( y ) :  n
3. Phương pháp chỉ số thời vụ y I
: Chỉ số thời vụ của thời gian i . i I TVi TVi y0
y : Số trung bình các mức độ của các thời gian cùng tên i i .
y : Số trung bình của tất cả các mức độ trong dãy số. 0
5.3 M T SỐ P P P DỰ O ỐNG KÊ NGẮN HẠ (dưới 3 năm)
1. Dự đoán dựa vào lượng tăng (giảm) tuyệt đối bình quân
2. Dự đoán dựa vào tốc độ phát triển bình quân Mô hình dự đoán:
y : Mức độ cuối cùng trong dãy số Mô hình dự đoán:
y : Mức độ cuối cùng trong dãy số n n yy  .L thời gian y
y (t)L thời gian nL n nL n
 : Lượng tăng (giảm) tuy t đối bình
 : Lượng tăng (giảm) tuy t đối bình Với y y n 1   y Với n t n 1  n  1 quân. quân. y
L : Thời gian dự đoán (tầm xa dự 1
L : Thời gian dự đoán (tầm xa dự đoán). đoán).
t: Tốc độ phát tri n bình quân.
3. Dự đoán dựa vào hàm xu thế và biến động thời vụ
4. Dự đoán theo phương pháp san bằng mũ giản đơn
a/ Hàm xu thế kết hợp cộng và biến
b/ Hàm xu thế kết hợp nhân và biến Mô hình dự đoán:
Yˆ : Mức độ dự báo cho thời gian t độ t
ng thời vụ
động thời vụ ˆ ˆ Y   .y   .Y t t 1  t 1
ˆY : Mức độ dự báo cho thời gian t-1
Yˆ  fˆ  sˆ
Yˆ  fˆ s .ˆ 1 (  )  t 1  t t t t t t Với   : H số san bằng ũ
yt-1: Mức độ thực tế của thời gian t-1
5. Dự đoán dựa vào hàm xu thế
-)Từ Ptr đường thẳng: y a bx x
-)Vận dụng trong dãy số thời gian ta có Ptr: y a bt t -)Xác định , a b
CÁCH 1: Áp dụng p ương p áp bìn p ương n ỏ nhất giải Hpt: CÁCH 2:
a y bt
  y na bt   2 ty t .y ty  a t  b t   b 2 t
Mô hình dự đoán: y
a b t L nL  
: Ỉ SỐ (Passche)
/ P P P Ỉ SỐ 3. Phương
1/ Chỉ số cá thể chất lượng
2/ Chỉ số cá thể số lượng
pháp chỉ số 1 p q1 cá thể i i p q 0 p 0 q
Số tuy t đối:   p p
Số tuy t đối:   q q p 1 0 q 1 0 4. Phương
pháp chỉ số chung . Phương pháp
1/ Chỉ số liên hợp chất lượng
2/ Chỉ số liên hợp số lượng
chỉ số liên hợp p .  p .  1 1 q q I  0 1 I p p  .q q p  .q 0 1 0 0 Số tuy t đối: Số tuy t đối:   p .q p .q     p .q p .q   pq 1 1 0 1 pq 0 1 0 0 Số tương đối: Số tương đối:  p .q   p .q   p .q   p .qpq 1 1 0 1 %   pq 0 1 0 0 %   pqpq p .qp .  p .qp . 0 0 0 q0 0 0 0 q0 . Phương pháp
1/ Chỉ tiêu chất lượng (bình quân gia 2/ Chỉ tiêu số lượng (bình quân gia
chỉ số bình quân quyền) quyền) 1 p q p  1  0 1 qp q p .q 0 0 p i p q   p .q q i p q  1 1 0 p 0 1 I    0 1 0 q 0 0 I    p p  .q p q p q   q p  .q p q p q   0 1 0 1 0 1 0 0 0 0 0 0
1/ Chỉ tiêu chất lượng (bình quân
2/ Chỉ tiêu số lượng (bình quân điều điều hòa) hòa) p .   1 1 q 1 p 1 q 1 p 1 q I    p p  .q p 1 0 1 0   p .qp qp q p q p q  0 1 0 1 0 1 1 1 1 1 I    q 1 p ip .q q 1 p 0 0 0  p q 0 1 0 p 1 q 1 q iq 2.3 Phương pháp
1/ Chỉ số chung về chất lượng
2/ Chỉ số chung về số lượng g p p g ợ g g ợ g
tính chỉ số theo chỉ p .  p . 1 1 q 1 q1 tiêu bình quân pq qp 1 1 1 1 X I   I   1 I p pp .q q qp .q X 0 0 0 0 0 0 0 X   0 q 0 p Số tuy t đối: Số tuy t đối:   p p q    q q ppq  * 1 0  pq  * 1 0  1 0 Số tương đối Số tương đối   % pq   % pq   pq p .  pq 0 0 q  0p 0q
II/ H THỐNG CHỈ SÔ / Phương
D P Q D : Doanh thu. trình kinh P : Giá bán. tế
Q : Sản lượng.
Q  W N
Q : Sản lượng sản xuất. W : Năng suất lao động.
N : Số nhân công, lao động (người).
F L N
F : Quỹ tiền lương.
L : Đơn giá lương trên 1 công n ân.
N : Số n ân công, lao động (người).
C z Q
C : Chi phí sản xuất.
z : Giá t n đơn vị sản phẩm.
Q : Sản lượng sản xuất. 2/ Hệ
Chỉ số phát triển = Chỉ số hoàn thành kế hoạch Chỉ số
Chỉ số doanh thu = Chỉ số giá cả Chỉ số lượng bán ra.
thống chỉ
nhiệm vụ kế hoạch II .I pq p q số phát
Chỉ số phát tri n doanh thu:
p .q p .q p . triển q p  .q p  .q p q  1 1 1 1 0 1 KH . 1 1 1 1 1     
p .q p .q p .q p .qp .q p . 0 0 0 1 0 0 0 0 q KH 1 0 0 3/ Phân
1/ 2 nhân tố ảnh hưởn g
2/ 3 nhân tố ảnh hưởn g
tích chỉ số
 1x 1f  1x 1f  0x 1f x f fx xII I   1 1 1 1 01 II I   xf x f * * xf x f * x f x f x f    x fx x f  0 0 0 1 0 0 0 0 01 0 0 (1) (2) (3) (1) (2) (3) (4) Biến động tuy t đối: Biến động tuy t đối: x f x f  ( x f x f )  ( x f x f )
 1 1  0 0  1 1  0 1  0 1  0 0 x f x f  (x x ) f (x x ) f ( f  f ) 1 1 0 0 1 01 1 01 0 1 1 0 x0
Biến động tương đối:
Biến động tương đối:
x f  x f (x x ) f (x x ) f ( f  f )x 1 1 0 0 1 01 1 01 0 1 1 0 0    x fx fx fx f 0 0 0 0 0 0 0 0
x f x f (x f x f ) ( x f  x f ) - Chỉ số (1): Phản ánh biến động của tổng lượng biến tiêu thức do ản ưởng của tất cả các 1 1 0 0 1 1 0 1 0 1 0 0   nhân tố x  0 f0 x  0 f0 x  0 f0
- Chỉ số (2): Phản ánh biến động của lượng biến tiêu thức nghiên cứu do ản ưởng của nhân tố chất lượng
- Chỉ số (1): Phản ánh biến động của tổng lượng biến
- Chỉ số (3): Phản ánh biến động của kết cấu tổng th do nhân tố số lượng
tiêu thức do ản ưởng của tất cả các nhân tố
- Chỉ số (4): Phản ánh biến động của quy mô tổng th ản ưởng tới biến biến động của
- Chỉ số (2): Phản ánh biến dộng của tổng lượng biến tổng lượng tiêu thức
tiêu thức do nhân tố chất lượng
VD: Xét TH Sản lượng sản xuất ra chịu 3 nhân tố ảnh hưởng:
- Chỉ số (3): Phản ánh biến dộng của tổng lượng biến W. 
tiêu thức do nhân tố số lượng 1 1 N W W 1 N 1 01 I     Q W .N W W N  0 0 01 0 0
VD: Xét TH Quỹ tiền lương có nhân tố ảnh hưởng ta có: W .N  Chỉ số:   Với: 1 1 W  1 I I I F L N N  1
Phân tích 2 nhân tố ản ưởng: W .N  1 F 1 F 0 F 1 0 1 W  I    01 F  1 N 0 F 0 F 1 0 F Với: W . F   L . N 01 0 1 N 0 0 W  0   N L .N
L .N L . 0 1 1 1 1 0 1 N I    +)Số tuy t đối: F L  .N L  .N L  . 0 0 0 1 0 0 N Q
  W .N W .N  W W .N  W W .N   N   N .W 1 1 0 0   1 01 1  01 0 1  1 0  +)Số tuy t đối: 1 +)Số tương đối: F        1 F 0 F  1 F 0 F 1   0 F 1 0 F  W .N  W . W W . N W W . N N     N N .W   1 1 0 0  0 1  1  01 0  +)Số tương đối: 1  1 0  0         % Q 1 0 1 01 01 0 % F F F F F F   W .N  W .N  W .N  W .N F    0 0 0 0 0 0 0 0 0 F 0 F 0 F