Ôn tập cuối kỳ Thống kê ứng dụng | Trường Đại học Kinh tế – Luật

lOMoAR cPSD| 46348410
PHẦN I. CÁC CÂU HỎI TRẮC NGHIỆM (5 điểm)
Câu 1: Trong bài báo (Thuộc tính hấp dẫn của điểm đến Đà Nẵng đối với khách nội địa trong bối cảnh
Covid-19 – Lê Thái Phượng và cộng sự, 2022) có câu hỏi sau:
Q1. Bạn hãy cho biết vùng/ miền bạn đang sinh sống ?...........
Dữ liệu của câu Q1 thuộc vào thang đo nào sau đây? A. Định danh (nominal) C. Khoảng (interval) B. Thứ bậc (ordinal) D. Tỷ lệ (ratio)
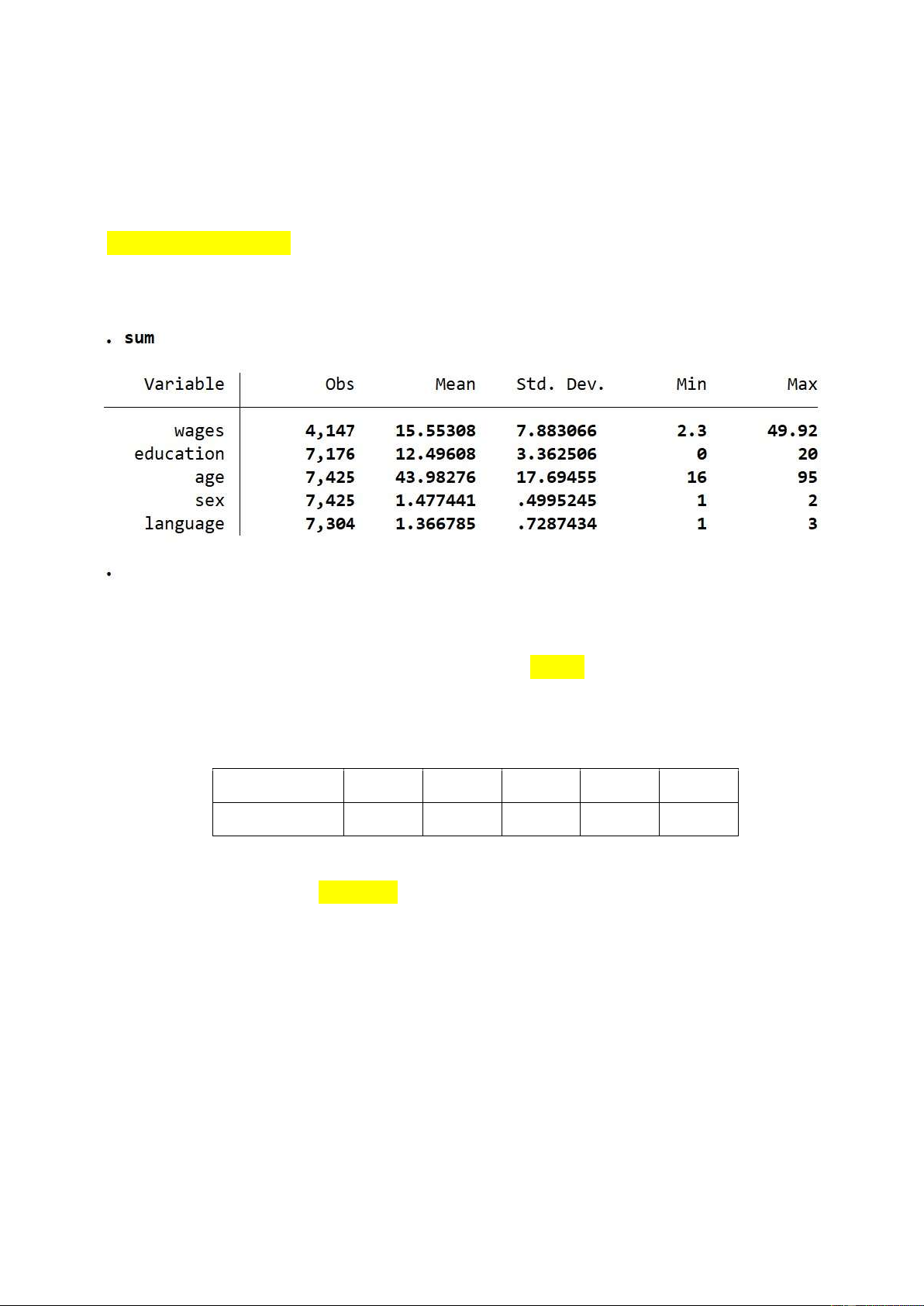
Câu 2: Cho bảng kết quả thống kê mô tả từ Stata như sau:
Biến nào có phương sai cao nhất? A. wages B. educationD. sex C. age
Cột Std. Dev. -> age có gtri lớn nhất
Câu 3: Cho bảng dữ liệu về chiều cao của 50 SV UEL ngẫu nhiên được chọn như sau:
Chiều cao (cm) 140-145 145-150 150-155 155-160 160-165 Số lượng SV 5 10 22 7 6
Số yếu vị (mode) của bộ dữ liệu trên là bao nhiêu cm? A. B. 152.22 150C. 153.35 D. 154.5
ModX = 150 + 5 x (((22-10):((22-10)+(22-7)))= 152,(2)
Bài toán sau dành cho câu 4, 5: Với X (Thu nhập) có kết quả từ phần mềm Stata như sau 1 lOMoAR cPSD| 46348410
Câu 4: Tìm đáp án ĐÚNG (dựa trên so sánh trung bình và trung vị)
A. Dữ liệu phân phối đối xứng hoàn toàn C. Dữ liệu lệch phải B. Dữ liệu lệch trái D. Mode là 60
Trung vị (Med) là giá trị đứng ở vị trí giữa trong một dãy số đã được sắp xếp có thứ tự, theo hình
Med là 180 ứng với 50%, và Mean là 173, 6667. Vì Mean < Med -> lệch trái.
Câu 5: Hệ số biến thiên (CV) là A. 1.71% C. 5.2% B. 300% D. 33.29%
CV= S/ (X) = 57,81228 : 173, 6667 = 33,29%
Câu 6: Cho bảng dữ liệu về chiều dài của 50 con cá như sau:
Chiều dài (mm) Số lượng 300-350 10 350-400 20 400-450 15 450-500 5 Tổng 50
Tính Med (trung vị) (đơn vị mm) của bộ dữ liệu này? A. 400 B. 375.8 C. 387.5 D. Đáp án khác
Bảng có 50 con cá, nên khoảng 25 26 sẽ là Med -> trong khoảng từ 350 -400.
Med = 350 + 50 x ((50/2-10)/20) = 387,5
Câu 7: Trong dây chuyền sản xuất nước đóng chai tuân theo quy luật phân phối chuẩn, người ta tính được
khối lượng trung bình của chai nước là 450g và độ lệch chuẩn là 15g. Hỏi có bao nhiêu sản phẩm (xấp xỉ)
có khối lượng nằm trong khoảng (420, 480) g biết có 10000 sản phẩm được sản xuất? A. 9500 B. 8900 C. 9970 D. 9350 2 lOMoAR cPSD| 46348410
P(420 bấm máy tính Distribution – Normal CD với cận dưới -2, cận trên 2,
muy = 0 và xích ma = 1 ra 0,95445. Vậy số sp thỏa là 9544,5. -> A
Bài toán sau dành cho câu 8, 9: Thu nhập (USD/tuần) của các hộ gia đình được tóm tắt trong bảng sau Variable Obs Mean Std. dev. Min Max thu_nhap 40 143.5 40.5 80 200
Câu 8: Hãy ước lượng mức thu nhập trung bình của một hộ gia đình với độ tin cậy 95% với số liệu được
tóm tắt trong bảng trên, cho biết thu nhập tuân theo phân phối chuẩn.
A. (130.949; 166.051) C. (120.949; 156.051)
B. (120.949; 166.051) D. (130.949; 156.051)
Áp dụng công thức ước lượng 1 mẫu, trường hợp ước lượng trung bình muy, có phương sai tổng
thể xích ma, có kqua là 143,5 +/- 40,5:(căn bậc hai 40)x1,96 -> D
Câu 9: Nếu muốn ước lượng mức thu thập trung bình của một hộ gia đình có độ chính xác (sai số) là 10
(USD/tuần) thì cần khảo sát THÊM ít nhất bao nhiêu hộ gia đình nữa với độ tin cậy 95%. A. 24 B. 64 C. 34 D. 54
Sai số : epsilon = 1,96 x 40,5 / (căn bậc 2 của n) = 10 -> n = 63,01 -> lấy ít nhất 64.
Đề hỏi THÊM -> 64 – 40= 24.
Câu 10: Một cửa hàng được gọi là có DOANH THU CAO (dt_cao) nếu doanh thu lớn hơn 290 triệu
đồng/ngày. Bài toán ước lượng nên được sử dụng trong trường hợp này nếu muốn tìm hiểu về tỷ lệ các
cửa hàng có doanh thu cao với độ tin cậy 95% là:
A. Bài toán ước lượng tỷ lệ trên một tổng thể và
p∈(0.5966;0.8537)
B. Bài toán ước lượng tỷ lệ trên một tổng thể và p∈(0.26;0.74)
C. Bài toán ước lượng trung bình trên một tổng thể và μ∈(0.5966;0.8537)
D. Bài toán ước lượng trung bình trên một tổng thể trên một tổng thể và p∈(0.26;0.74)
Bảng ở trên thể hiện khảo sát 50 cửa hàng, trong đó 13 cửa hàng có giá trị 0 là k có doanh thu cao
và ngược lại với 1. Bảng này đánh lừa, k có liên quan tới câu hỏi. 3 lOMoAR cPSD| 46348410
Bảng thứ 2, cho thấy tỉ lệ cửa hàng có dthu cao, tin cậy 95% ở góc phải. -> A
Câu 11: Muốn đánh giá trọng lượng trung bình của trẻ sơ sinh, người ta tiến hành điều tra ngẫu nhiên 100
trẻ sơ sinh và thu được kết quả như sau:
Với độ tin cậy 95%, hãy ước lượng phương sai trọng lượng (kg2) của trẻ sơ sinh. A. (0.052; 0.122) C. (0.1896; 0.3312) B. (0.3667; 0.5585) D. (0.1345; 0.3119)
Hê hê bài này lười gthich quá =))))))
Thì nó là trường hợp mình ước lượng 1 mẫu tìm phương sai tổng thể, trường hợp chưa có muy.
Tìm S bấm máy tính, nhớ set cái Frequency trước khi vào MODE – 3 – 1 (1-VAR), đối với máy tính
570 (còn 580 tự mò tại k có máy đó) sẽ ra S=0,4983.
Áp dụng công thức ước lượng sẽ đụng tới bảng phụ lục 6 – chi bình phương, làm đúng là khi tra và
dùng 2 số 129,6 và 74,22.
Kqua: 99 x (0,4983)^2 / 129,6 ; 99 x (0,4983)^2 / 74,22
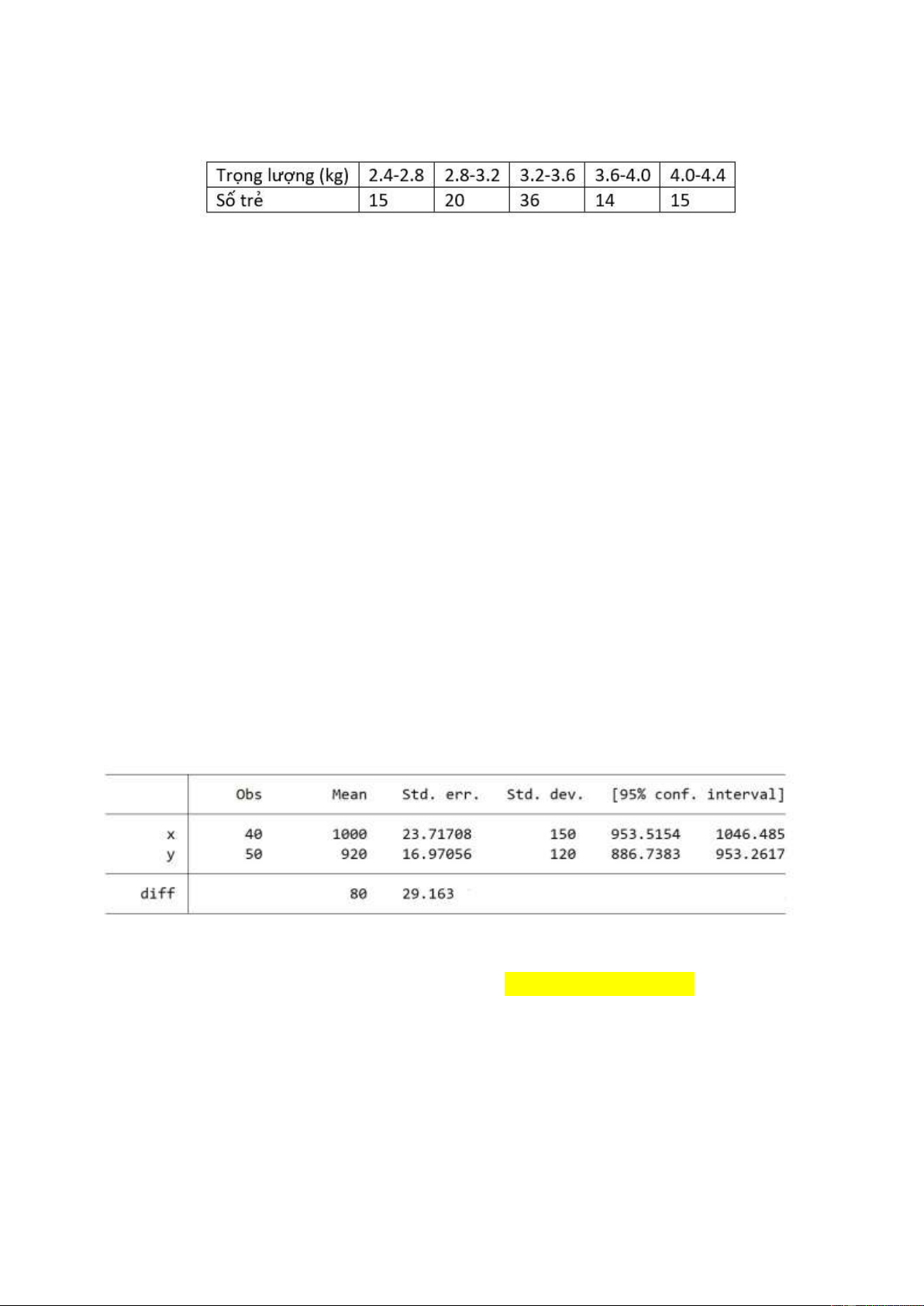
Câu 12: Hãy ước lượng sự khác biệt số tiền trung bình có trong tài khoản ATM của khách hàng tại 2 ngân
hàng X, Y từ kết quả trên phần mềm Stata với độ tin cậy 95%. Cho biết số tiền có trong tài khoản ATM
của khách hàng tại mỗi ngân hàng có phân phối chuẩn.
A. (22.8405; 147.1595) C. (32.8405; 147.1595) B. (32.8405; 137.1595) D. (22.8405; 137.1595)
Này là áp dụng ước lượng 2 mẫu, trường hợp chưa biết phương sai tổng thể nhưng n1 và n2 đều >30.
Sai số epsilon = 1,96 x (căn bậc hai (150^2 /40 + 120^2 /50)) = 57,16…. (ĐTC 95% nên z = 1,96)
KTC cho muy1- muy2 = 1000 – 920 +/- 57,16 = ….
Câu 13: Nam và nữ được hỏi về việc họ sẽ làm gì nếu nhận được tờ 500k qua đường bưu điện, gửi cho
hàng xóm nhưng lại bị gửi nhầm cho họ. Liệu họ có trả lại nó cho hàng xóm của họ không? Trong số 69
nam giới được hỏi, 52 người nói “có” và trong số 131 phụ nữ được hỏi, 120 người nói “có”. 4 lOMoAR cPSD| 46348410
Tìm khoảng tin cậy 95% cho sự khác biệt về tỷ lệ giữa nam (pnam) và nữ (pnữ) nói “có”.
A. pnam – pnữ ∈(−0.2746,0.0502) C.
pnam – pnữ ∈(0.0502,0.2746)
B. pnam– pnữ∈(−0.2746,−0.0502) D. Một đáp án khác
Sử dụng ước lượng sự khác biệt tỷ lệ 2 tổng thể (p1-p2) f 1 =
52/69 ; f 2 = 120/131; f ngang = (52+120)/(69+131) = 0,86.
Sai số epsilon = căn bậc hai ( f ngang x (1 - f ngang) x (1/n1 + 1/n2)) x z = căn bậc hai ( 0,86 x 0,14 x
(1/69 + 1/131) x 1,96 = 0,10116…
Kqua (52/69 – 120/131 – 0,10116; 52/69 – 120/131 + 0,10116).
Update: Có 2 công thức tính trường hợp ‘ước lượng sự khác biệt tỷ lệ 2 tổng thể (p1-p2)’
Nếu mà áp dụng cthuc trong giáo trình thống kê thì đáp án sẽ là B.
Câu 14: Chiều cao trung bình của nam giới trưởng thành ở một quốc gia là 170 cm. Người ta nghi ngờ rằng
ở một thành phố nào đó ở quốc gia đó có thể có chiều cao trung bình của nam giới khác 170 cm do một số
yếu tố môi trường. Họ chọn một mẫu ngẫu nhiên gồm 9 người đàn ông trưởng thành trong thành phố đó và
nhận được các giá trị sau cho chiều cao của họ (tính bằng cm):
176.2; 157.9; 160.1; 180.9; 165.1; 167.2; 162.9; 155.7; 166.2
Giả sử rằng chiều cao tuân theo phân phối chuẩn, với mức ý nghĩa 5%, hãy tính giá trị t kiểm định và đưa
ra quyết định tương ứng với H0: μ=170?
A. ttest = -1.52, bác bỏ H0 C. ttest = 2.31, bác bỏ H0
B. ttest = -1.52, chấp nhận H0 D. t
test = -2.31, chấp nhận H0
H (alpha) : muy khác 170.
Theo công thức, bác bỏ Ho nếu t-test < - z hay t-test > z.
Z = 1,96 (vì mức ý nghĩa 5%, tra z của 0.025 ở bảng), trung bình mẫu X ngang = 165,8 ; phương sai
mẫu = 8,24697… (bấm máy)
t-test = (165,8 – 170)/(8,24697/ căn 9) = -1,52. Do t-test thuộc (-1,96;1,96) nên là k có căn cứ bác bỏ Ho.
Câu 15: Với ý kiến cho rằng thu nhập bình quân tại tỉnh A là 10 triệu đồng/tháng, kết quả kiểm định trên phần mềm Stata như sau
Hãy cho biết p-value là bao nhiêu ? 5 lOMoAR cPSD| 46348410 A. 0.9812
B. 0.0188D. Đáp án khác C. 0.0375
Câu 16: Có ý kiến cho rằng mức chi tiêu trung bình của một người dân tỉnh A ít nhất là 7 triệu đồng/tháng.
Kết quả kiểm định trên phần mềm Stata như sau Tìm đáp án SAI
A. Giá trị kiểm định là 6.3246 C. Bác bỏ H0
B. Chưa có cơ sở bác bỏ H0 D. p-value là 1.000
Theo đề thì Ho là mean >= 7, Ha là mean < 7.
A. Đúng do góc bên phải, z = 6,3246.
B. p-value ở Ha: mean < 7 là 1,0000 lớn hơn mức ý nghĩa alpha 5% -> k bác bỏ đc Ho.
C. Vì B đúng nên C sai. D. Theo hình.
Câu 17: Người ta muốn kiểm tra nhận định tỷ lệ ô tô nước ngoài chiếm 40% nên đã thử trên một mẫu thì
được kết quả như sau:
Nhận định nào dưới đây là SAI?
A. Giá trị kiểm định là -1.8034 (Đ)
B. Với mức ý nghĩa 10%, có thể chấp nhận ý kiến cho rằng tỷ lệ ô tô nước ngoài chiếm ít nhất là 40%
C. Số lượng ô tô của mẫu là 74 (number of obs = số quan sát = 74) (Đ)
D. Giá trị của p-value trong trường hợp H1: p<0.4 là 0.0357 (Đ, quá rõ)
Về câu B, Ho là p>= 0,4; Ha là p<0,4. Kiểm định p-value theo hình là 0,0357 < 10%. Bác bỏ Ho.
Câu 18: Kết quả kiểm định phương sai trên một mẫu từ phần mềm Stata như sau One-sample test of variance 6 lOMoAR cPSD| 46348410
Obs Mean Std. err. Std. dev. [98% conf. interval] x 10 . 47.43416 150 . .
sd = sd(x) c = chi2 = 7.0069 H0: sd = 170 Degrees of freedom = 9
Ha: sd < 170 Ha: sd != 170 Ha: sd > 170
Pr(C < c) = 0.3636 2*Pr(C < c) = 0.7272 Pr(C > c) = 0.6364 Tìm đáp án ĐÚNG
A. Giá trị kiểm định Chi-square là 9
C. Độ lệch chuẩn mẫu hiệu chỉnh là 150
B. p-value của kiểm định 2 phía là 0.3636
D. Cỡ mẫu quan sát là 150
A. 9 -> 7,0069 – S B. 0,3636 -> 0,7272 C. Đ D. Obs = 10.
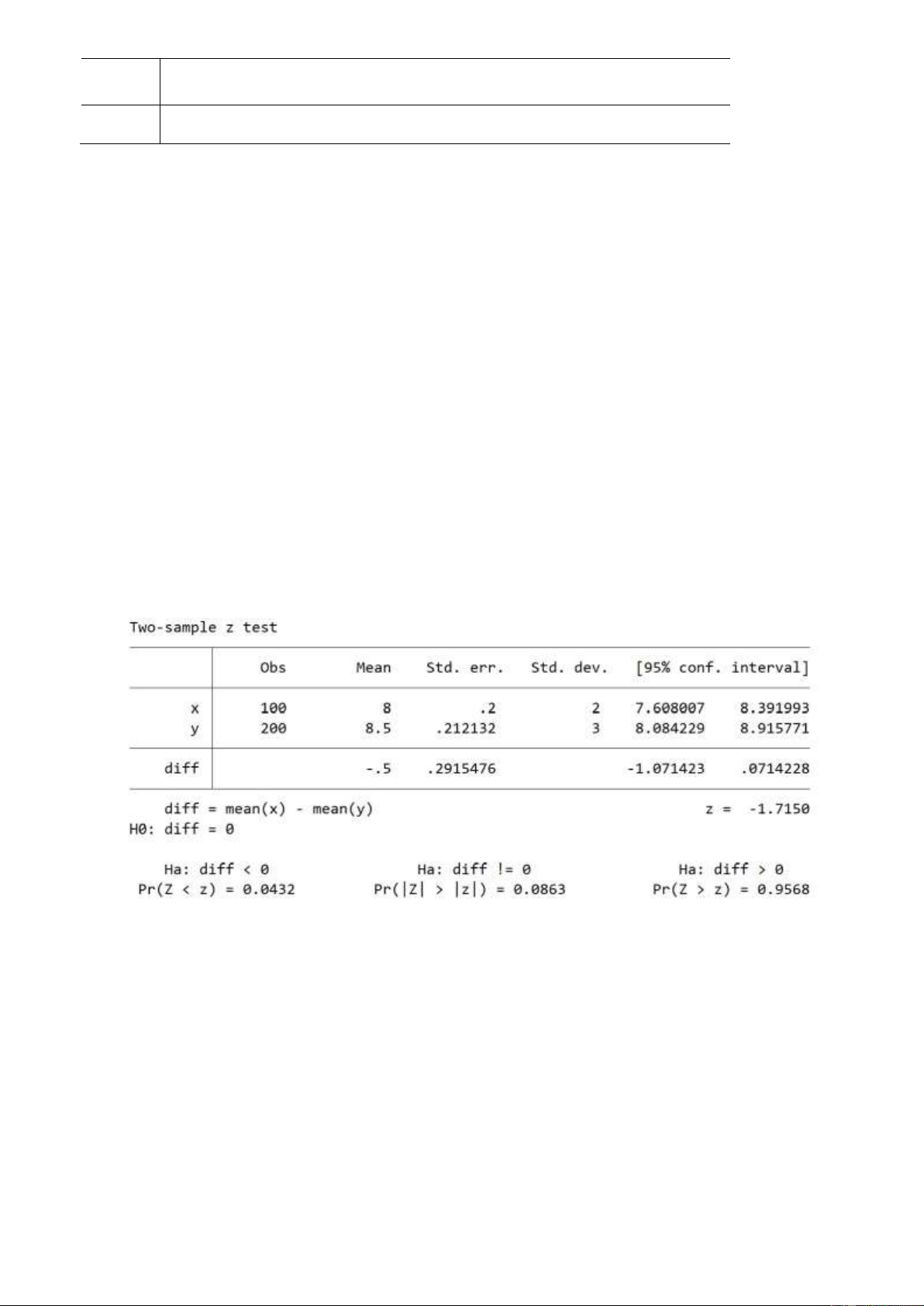
Câu 19: Có ý kiến cho rằng có sự khác biệt về thu nhập trung bình của người dân tại 2 tỉnh X và Y. Kết
quả kiểm định trên phần mềm Stata như sau Ta có các phát biểu sau
i. Giá trị kiểm định là -1.7150 (Đ) ii. p-
value là 0.0863 (Đ) iii. Chấp nhận H0 với mức ý nghĩa 5% (Đ) Đếm số phát biểu SAI A. 0 B. 1 C. 2 D. 3
iii. Ho là diff = 0, Ha là diff khác 0. Do p-value là 0,0863 > mức ý nghĩa 0,05 nên k có cơ sở bác bỏ Ho. 7 lOMoAR cPSD| 46348410
Câu 20: Có ý kiến cho rằng tỷ lệ sinh viên ra trường có việc làm tại trường X cao hơn trường Y. Kết quả
kiểm định trên phần mềm Stata như sau Ta có các phát biểu sau
i. Giá trị kiểm định là 1.9819 (Đ) ii. p-value là 0.0475 (X>Y
nên là diff >0, p-value 0,0237 – S)
iii. Chấp nhận H0 với mức ý nghĩa 1% (Vì p-value = 0,0237 > 1% nên k có cơ sở bác bỏ Ho - Đ) Đếm số phát biểu SAI A. 0 B. 1 C. 2 D. 3 8 lOMoAR cPSD| 46348410
PHẦN II. CÁC CÂU HỎI TỰ LUẬN (5 điểm)
Câu 21 (4 điểm): Khảo sát về thu nhập của người dân tại tỉnh A, người ta thu được kết quả trong bảng sau
Thu nhập (triệu đồng/tháng) 3 – 6 6 – 9 9 – 15 15 – 21 21 – 27 Số người 5 20 30 30 20
a) Hãy ước lượng mức thu nhập trung bình của người dân tại tỉnh A với độ tin cậy 95%.
b) Có ý kiến cho rằng tỷ lệ người có thu nhập dưới 6 triệu đồng/tháng của tỉnh A là 4%.
Hãykiểm định ý kiến này với mức ý nghĩa 5%.
c) Hãy ước lượng mức độ biến động (phương sai) thu nhập của người dân tỉnh A với độ tincậy
95%. Cho biết các giá trị tới hạn χ20.025;104=134.11; χ20.975;104=77.67.
d) Khảo sát thu nhập của người dân tỉnh B trên mẫu 200 người dân thì thu được thu nhậptrung
bình là 20 triệu đồng/tháng và độ lệch chuẩn mẫu hiệu chỉnh là 7.5 triệu đồng/tháng. Hãy
kiểm định ý kiến cho rằng thu nhập tỉnh B cao hơn tỉnh A với mức ý nghĩa 5%.
Câu 22 (1 điểm): Có thông tin cho rằng tình hình kinh tế thế giới tại thời điểm hiện nay đang bước
vào “suy thoái kinh tế”. Bằng kiến thức của môn thống kê ứng dụng, bạn hãy trình bày các bài
toán để minh họa, biểu thị thông tin trên.