
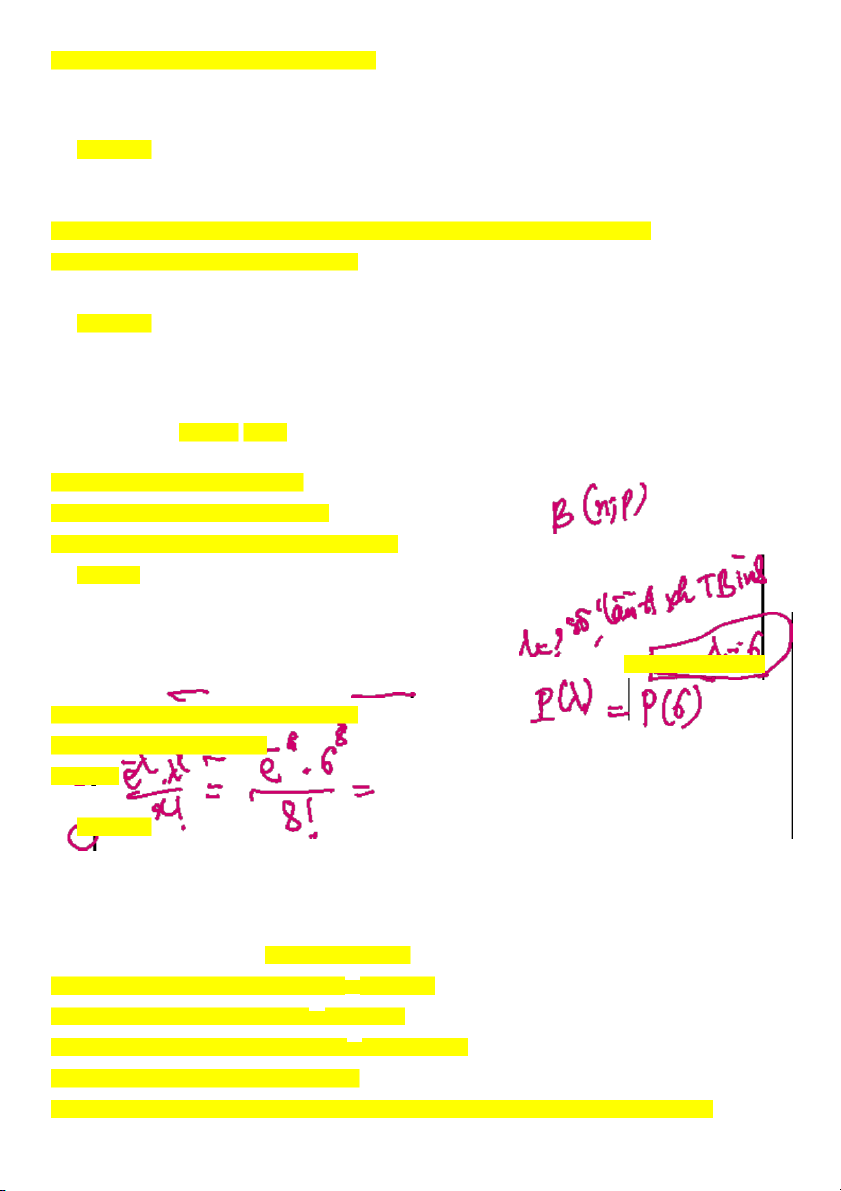

Preview text:
Câu 1: Tôn giáo của 50 người là biến gì: A. Định tính B. Định lượng C. Cả 2 đều đúnee D. Cả 2 đều sai
Câu 2: Màu tóc của người dân ở 1 khu cách ly là biến sử dụng thang đo nào: A. thang tỷ lệ B. thang danh nghĩa C. Thang thứ hạng D. Thang đo khoảng
Câu 3: Trong 50 người khảo sát có 10 người có độ tuổi từ 25- 30. Tần suất của lớp trên là: 10:50*100=20% A. 7% B. 10% C. 20% D. 27%
Câu 4: Độ rộng của lớp dữ liệu từ [16-20] là: 20-16+1=5 A. 4 B. 5 C. 6 D. 7
Câu 5: Cho dữ liệu về điểm thi toán của 10 học sinh như sau: 9; 6; 7; 10; 6; 9; 4; 6; 5; 7.
Điểm trung bình của 10 học sinh trên là: A. 5.8 B. 6.9 C. 7.1 D. 8.4
Câu 6: Dữ liệu về nhóm máu của 15 người được cho như sau:
A, AB, O, O, A, AB, B, B, O, O, AB, O, A, O, O.
Giá trị Mode( là giá trị có tần số lớn nhất, xuất hiện nhiều lần nhất) của nhóm dữ liệu trên là: A. A B. B C. O D. AB
Câu 7: Một doanh nhân có 1 bộ sưu tập ô tô gồm 7 chiếc Porsche và 12 chiếc BMW. Người này
bốc thăm 4 chiếc ngẫu nhiên để làm từ thiện. Xác suất cả 4 chiếc đều là BMW là:
P (lấy được 4 chiếc BMW) =12C4 : 19C4= A. 0,243 B. 0,574 C. 0,004 D. 0,128
Câu 8: Có 26% khách hàng của siêu thị A rất thích mua táo ở siêu thị này. Xác suất để trong 1
nhóm 5 người khách bất kỳ không có ai thích mua táo ở siêu thị là:
Gọi X là số người thích mua táo ở siêu thị. X tuân theo pp Nhị thức B(5; 0.26)
P(X=0) = 5C0* (0.26)^0 * (1-0.26)^5= A. 0,222 B. 0,333 C. 0,444 D. 0,518
Câu 9: Một nghiên cứu cho rằng, ở quốc gia X có 63% người từ 65 tuổi trở lên bị cúm hàng
năm. Một nhóm gồm 30 người có độ tuổi từ 65 trở lên được chọn ngẫu nhiên. Xác suất để
trong nhóm người này có một nửa mắc cúm là:
Gọi X là số người mắc bệnh cúm
X tuân theo pp Nhị thức B(30; 0.63)
P(X=15)= 30C15* (0.63)^15* (1-0.63)^15= A. 0,05 B. 0,15 C. 0,25 D. 0,55
Câu 10: Số cá mà một người câu được ở một khúc sông trong một giờ là phân phối Poisson
với trung bình là 6 con/ giờ. Xác suất để trong giờ tới người này câu được 8 con cá là:
Gọi X số cá người đó câu được trong 1h X tuân theo pp Poisson P(6) P(X=8)= A. 0,276 B. 0,103 C. 0,351 D. 0,606
Câu 11: Dân số thành phố A là 100000 người . thành phố có 2 tờ nhật báo A và B. tỷ lệ người
dân của thành phố đọc các tờ nhật báo trên là 10% đọc tờ A và 30% đọc tờ B, 8% đọc cả 2 tờ
A và B. có bao nhiêu người chỉ đọc một tờ báo nói trên .
Gọi A biến cố người dân đọc tờ báo A P(A)=0.1
B biến cố người dân đọc tờ báo B P(B)= 0.3
A.B là biến cố ng dân đọc cả 2 tờ báo P(A.B)= 0.08
Biến cố chỉ đọc một tờ báo là: A\B +B\A
P(A\B + B\A)= P(A\B) + P(B\A)= P(A)- P(A.B) + P(B)- P(A.B)= 0.1+ 0.3- 2* 0.08= 0.24
TRong 100000 người , số người chỉ đọc 1 tờ báo là : 100000* 0.24 =24000
Câu 12: Một công ty bán hàng nhận được trung bình 3 cuộc gọi mỗi giờ trên số điện thoại
miễn phí. Tìm xác suất để trong một giờ có tối đa 3 cuộc gọi.
X số cuộc gọi…..trong 1 giờ. X tuân theo pp Poisson P(3)
Xác suất trong 1 giờ có tối đa 3 cuộc gọi P(X<=3) =0.647
Câu 13: cho A ,B là 2 biến cố bất kỳ trong đó P(A)=0.4, P(B)=0.8, P(A.B)=0,2 Tìm P(A+B), P(A\B), P(B|A).
P(A+B)= P(A)+ P(B)- P(A.B)= 0.4+ 0.8-0.2 =1
P(A\B)= P(A)- P(A.B)=0.4 – 0.2 = 0.2
P(B|A)= P(A.B): P(A)= 0.2: 0.4 =0.5




