





















Preview text:
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Điện thoại: 0946798489 ĐỀ Đ Ề SỐ S 1. 1 ÔN THI T ĐG Đ NL ĐHQ Đ G H À NỘI I202 0 1 2 -2 - 02 0 2 2
• |FanPage: Nguyễn Bảo Vương
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
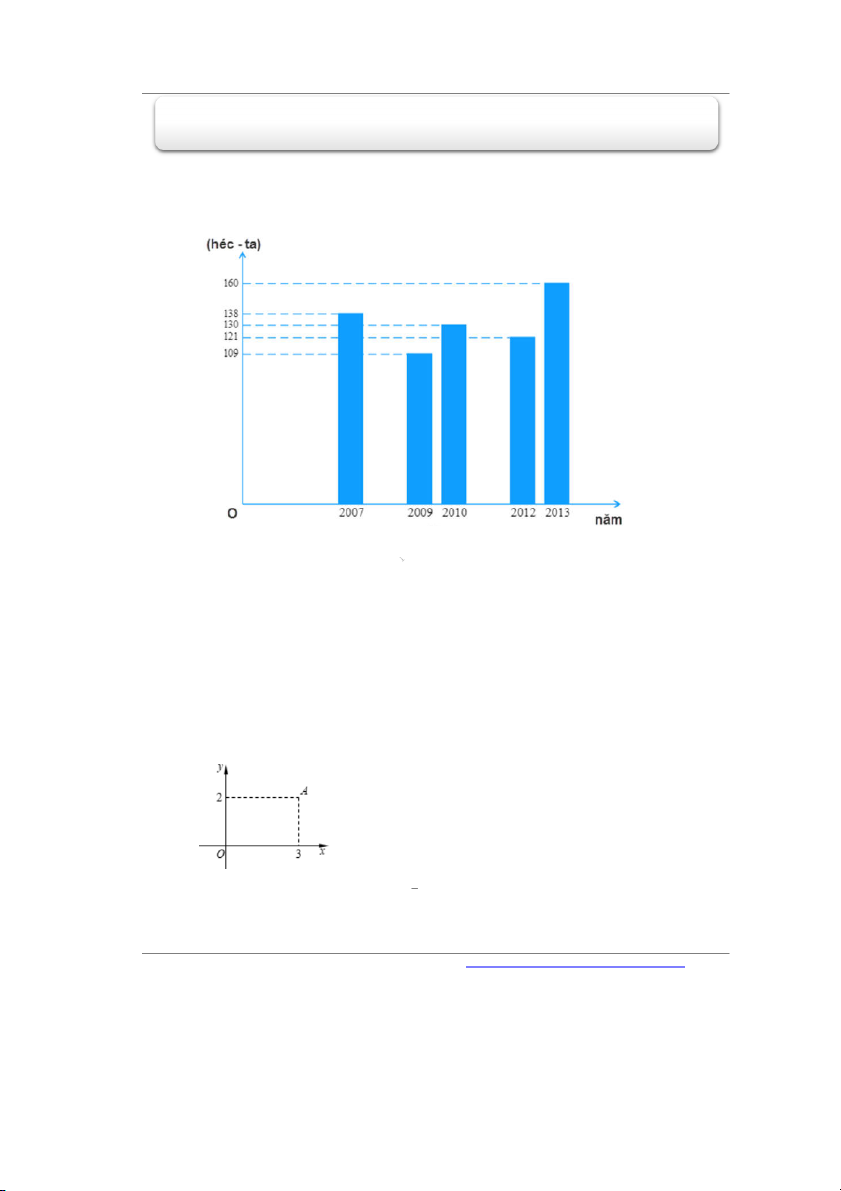
Câu 1. Người ta thống kê diện tích trồng lúa của một địa phương trong các năm tính theo héc-ta rồi
biểu diễn thành biểu đồ ở trên.
Diện tích trồng lúa ít nhất trong các năm là bao nhiêu (héc - ta)? A. 160. B. 138 C. 121. D. 109
Câu 2. Một ô tô đang chuyển động đều với vận tốc am / s thì phanh. Từ thời điểm đó ô tô chuyển động
chậm dần đều với phương trình vận tốc vt 5
t am / s . Biết rằng từ lúc phanh đến khi xe
dừng hẳn ô tô đi được 40m . Tính vận tốc xe khi chưa phanh? A. a 80m / s . B. a 20m / s. C. a 25m / s . D. a 40m / s .
Câu 3. Tập hợp nghiệm của bất phương trình log x 1 3 là: 2 A. S ; 9 B. S 1;9 C. S 1;10 D. S ; 1 0 2 2
x 3xy y 2x 3y 6 0
Câu 4. Hệ phương trình có nghiệm là: 2x y 3 A. 3;3. B. 2;1, 3;3. C. Vô nghiệm. D. 2;1.
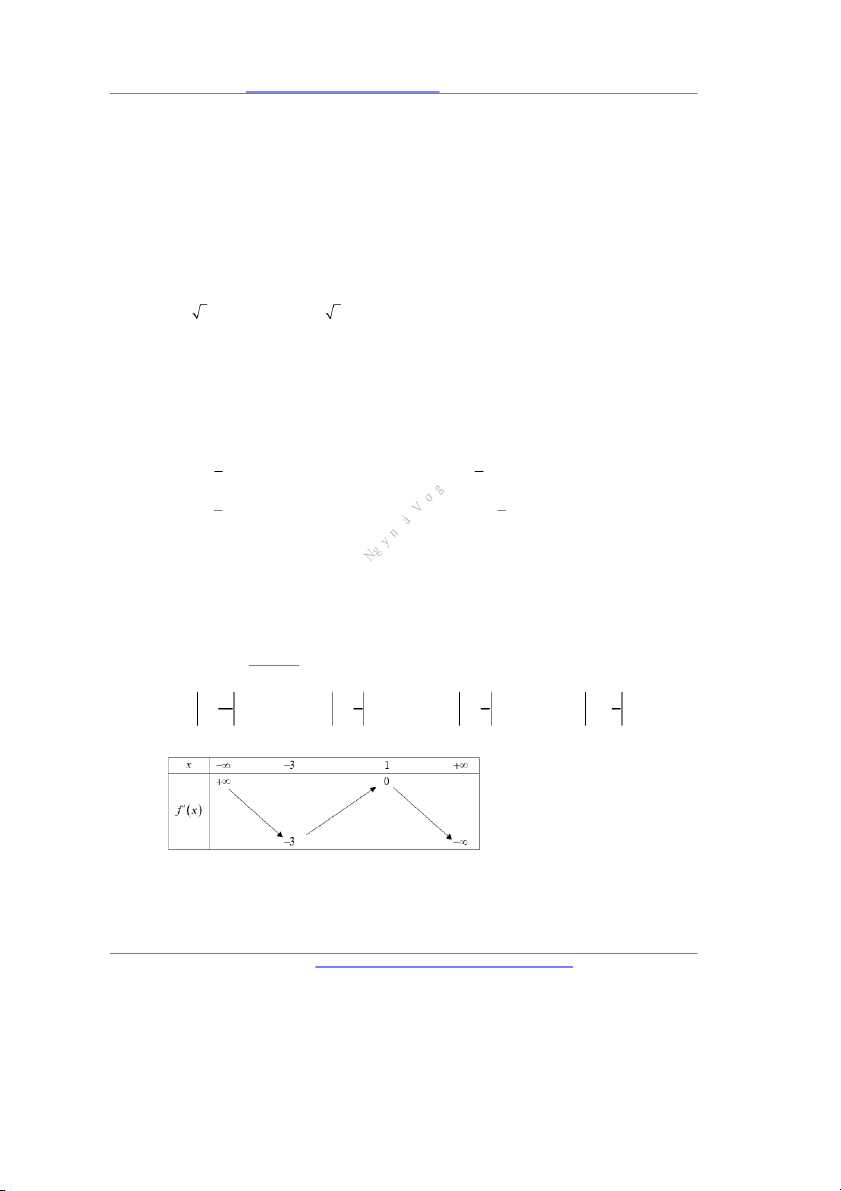
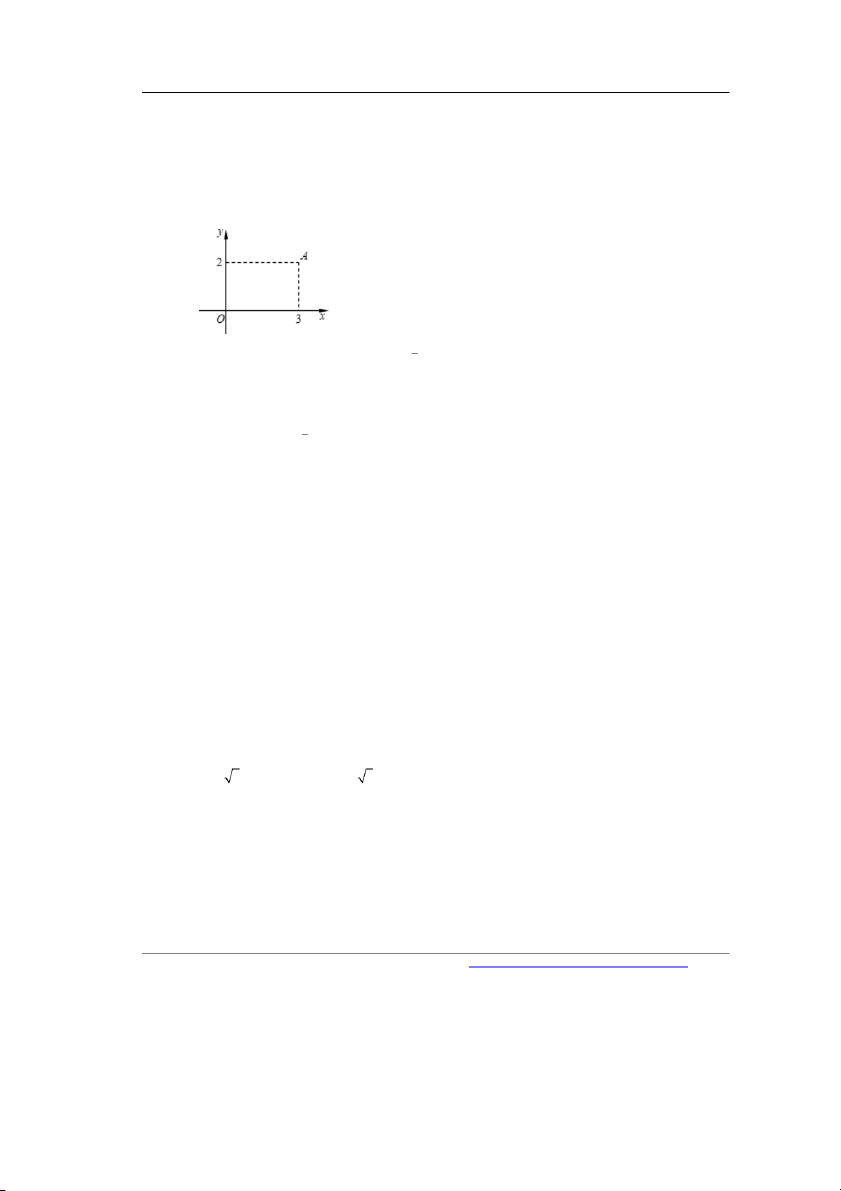
Câu 5. Điểm A trong hình vẽ bên biểu diễn cho số phức z . .
Tìm phần thực và phần ảo của số phức z .
A. Phần thực là 3 và phần ảo là 2 . B. Phần thực là 3 và phần ảo là 2 .
C. Phần thực là 3 và phần ảo là 2 i . D. Phần thực là 3 và phần ảo là 2i .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2;4; 1 , B 1 ;1;3 và mặt phẳng
P: x 3y 2z 5 0. Viết phương trình mặt phẳng Q đi qua hai điểm A , B và vuông góc với mặt phẳng P .
A. Q : 2y 3z 11 0 B. Q : 2x 3z 11 0
C. Q : 2y 3z 12 0 D. Q : 2y 3z 10 0 Câu 7.
Trong không gian với hệ tọa độ Oxyz , cho hai điểm A3; 1 ; 1 , B4;2; 3
. Gọi A là hình
chiếu vuông góc của A trên mặt phẳng Oxy và B là hình chiếu vuông góc của B trên
mặt phẳng Oyz . Độ dài đoạn thẳng A B bằng A. 2 3 . B. 3 3 . C. 2 . D. 3 .
Câu 8. Tam thức bậc hai f x 2
x 3x 2 nhận giá trị không âm khi và chỉ khi A. x 1;2 . B. x ; 1 2; . C. x 1;2 . D. x ; 1 2; .
Câu 9. Tìm tất cả các giá trị của tham số m để phương trình m
2 sin 2x m 1 vô nghiệm. 1 1 A. m ;2 2; . B. m ; . 2 2 1 1 C. m ;2 . D. m ; 2; . 2 2
Câu 10. Ông A gửi 120 triệu đồng tiền vào ngân hàng với lãi suất 6% / năm. Biết rằng nếu không rút tiền
ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp
theo. Hỏi sau 10 năm, tổng số tiền mà ông A nhận được là bao nhiêu, giả định trong khoảng thời
gian này lãi suất không thay đổi và ông A không rút tiền ra? (Lấy kết quả gần đúng đến hàng phần trăm)
A. 214,90 triệu đồng. B. 224,10 triệu đồng.
C. 234,90 triệu đồng. D. 215,10 triệu đồng. 2 x 1 Câu 11. Nguyên hàm bằng. x 2 x 1 1 1 1 1 A. ln x C . B. ln x C . ln x C D. 2 ln x C . 2 x x C. x . x
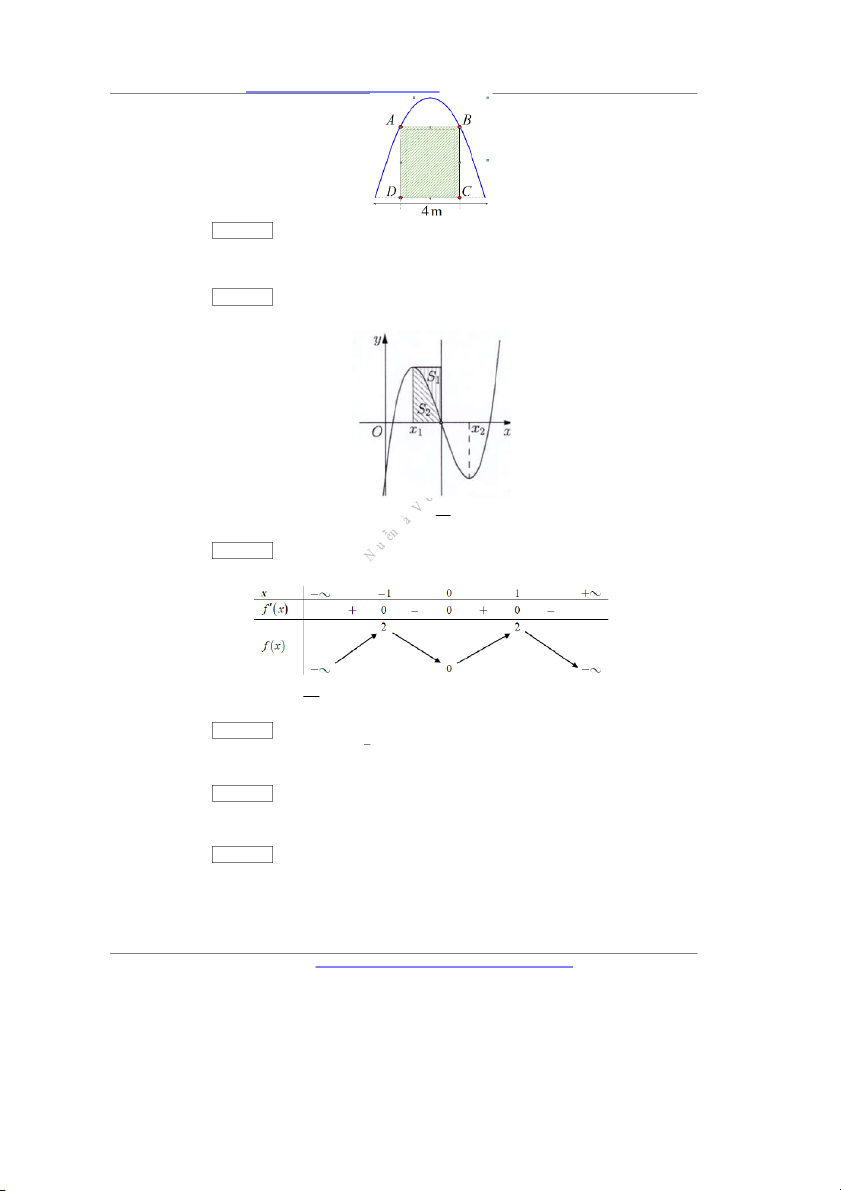
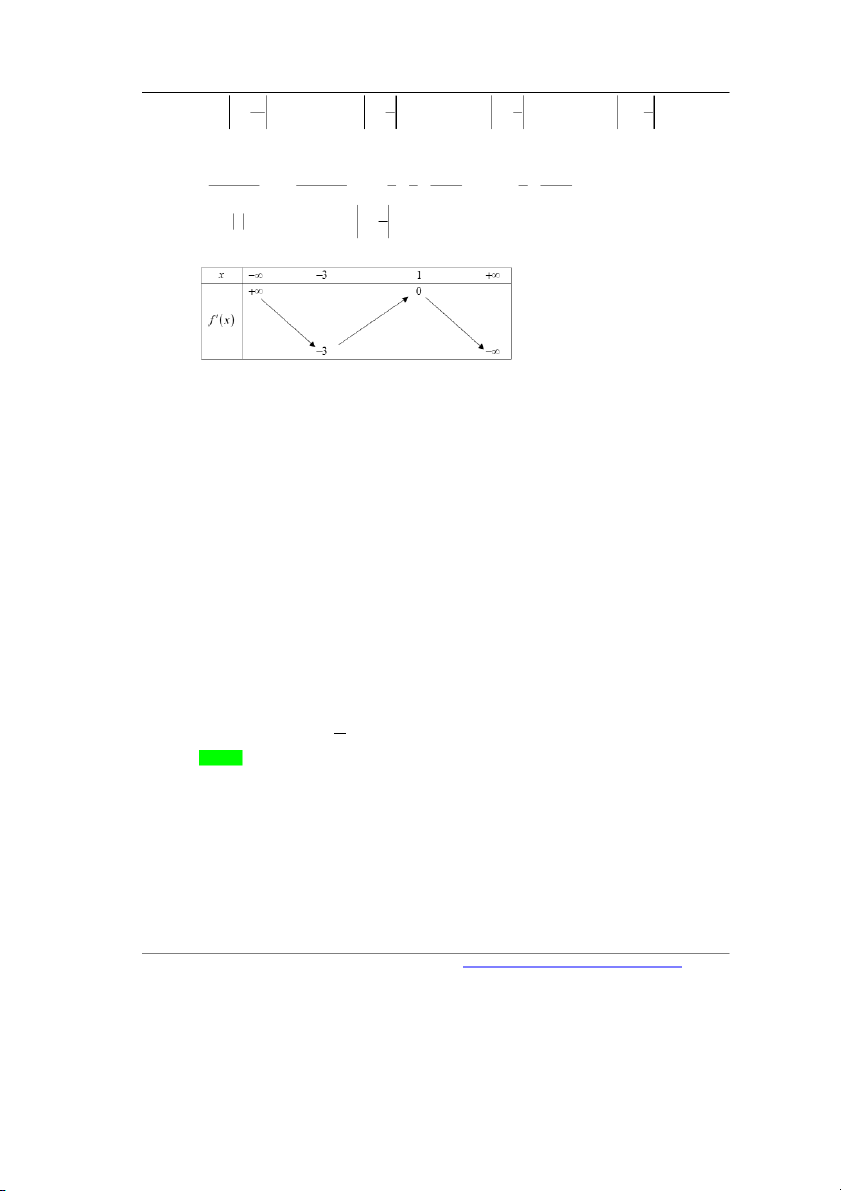
Câu 12. Cho hàm số y f x có đạo hàm trên . Hàm số y f
x có bảng biến thiên như sau:
Bất phương trình 2 x f x
e m đúng với mọi x 1 ; 1 khi và chỉ khi A. m f 1 2e. B. m f 1 e. C. m f 1 2e. D. m f 1 2e .
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Câu 13. Một xe ô tô đang chạy với vận tốc 20m/s thì người lái xe nhìn thấy chướng ngại vật nên đạp
phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc là vt 2 t 20 , trong đó
t là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà ô tô đi được trong 15 giây cuối cùng bằng A. 75m. B. 200 m. C. 100 m. D. 125 m.
Câu 14. Bạn Hùng trúng tuyển vào trường đại học A nhưng vì do không đủ nộp học phí nên Hùng quyết
định vay ngân hàng trong 4 năm mỗi năm vay 3.000.000 đồng để nộp học phí với lãi suất 3%
/năm. Sau khi tốt nghiệp đại học bạn Hùng phải trả góp hàng tháng số tiền T (không đổi) cùng với
lãi suất 0,25%/ tháng trong vòng 5 năm. Số tiền T hàng tháng mà bạn Hùng phải trả cho ngân
hàng (làm tròn đến kết quả hàng đơn vị) là: A. 309604 đồng. B. 232518 đồng. C. 232289 đồng. D. 215456 đồng.
Câu 15. Phương trình log x 1 2 có nghiệm là: 3 A. x 8 . B. x 10 . C. x 7 . D. x 5 .
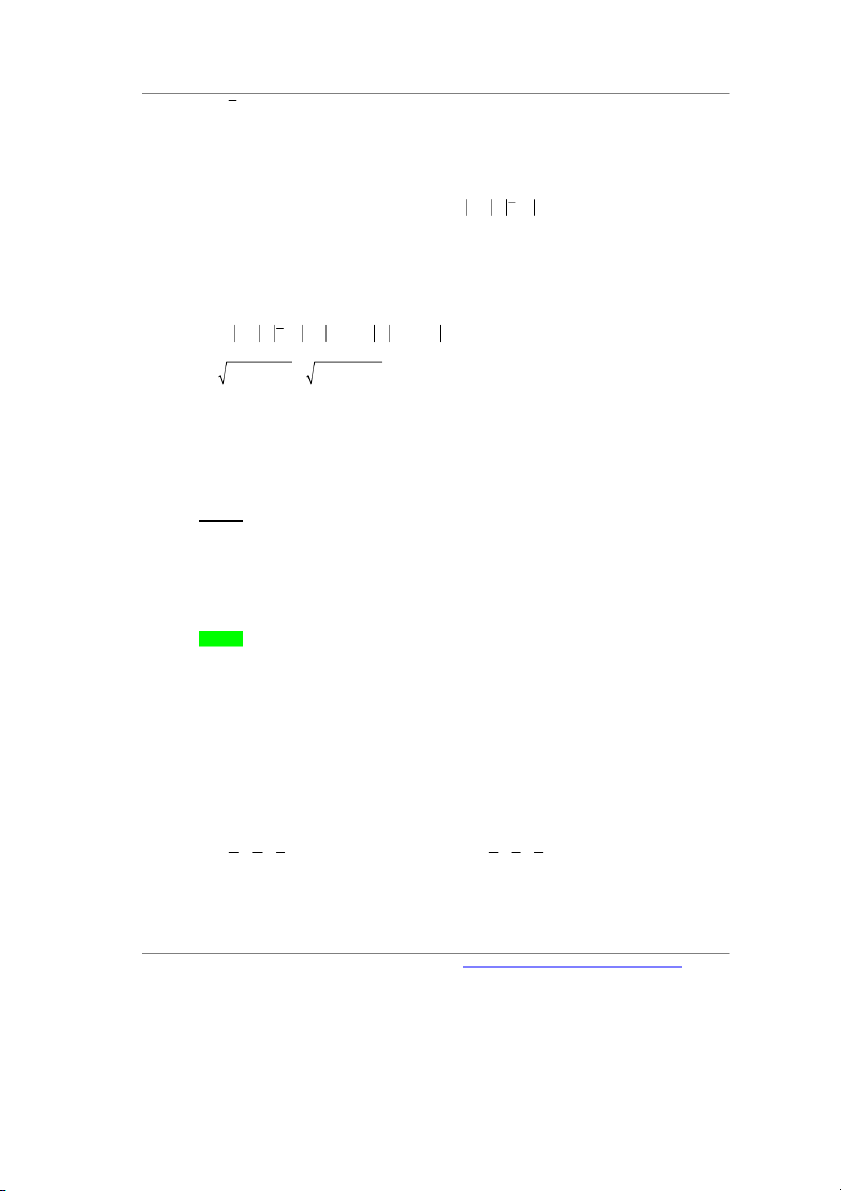
Câu 16. Cho hình phẳng A giới hạn bởi các đường ,x y e – x
y e và x 1. Thể tích của khối tròn xoay
tạo thành khi quay hình A quanh trục hoành là. 2 2 e 2 2 e A. e e ( 1) . ( 1) 2 2 B. 2 2 . 2 2 e 2 2 e C. e e ( 1) . D. ( 1) . 2 2 2 2
Câu 17. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y x x mx 1 đồng biến trên ; . A. 1 m . B. 4 m . C. 4 m . D. 1 m . 3 3 3 3
Câu 18. Tìm số phức z thỏa mãn iz 2z 9 3i . A. z 5 i . B. z 5 i . C. z 1 5i. D. z 1 5i .
Câu 19. Tập hợp điểm biểu diễn các số phức z thỏa mãn z i z 3 trong mặt phẳng Oxy là:
A. Đường thẳng :x y 4 0 .
B. Đường thẳng : 3x y 4 0 .
C. Đường thẳng :x y 4 0.
D. Đường thẳng : 3x y 4 0 .
Câu 20. Tìm tọa độ giao điểm của 2 đường thẳng sau đây: x 3 4t x 1 4t ' : và : 1 y 2 2 5t y 7 5t ' A. (1; 3). B. (5; 1). C. (1; 7). D. (3; 2). Câu 21. Cho phương trình 2 2 x y 2x 2my 1
0 0 1. Có bao nhiêu số nguyên m 0;1 0 để 1 là
phương trình của đường tròn? A. 8 . B. không có. C. 6 . D. 7.
Câu 22. Trong không gian cho điểm M (1; 3;2).Có bao nhiêu mặt phẳng đi qua M và cắt các trục tọa độ tại , A ,
B C mà OA OB OC 0 A. 2. B. 3. C. 4. D. 1.
Câu 23. Một khối nón có đường sinh bằng 2a và diện tích xung quanh của mặt nón bằng 2 a . Tính thể
tích của khối nón đã cho? 3 a 15 3 a 15 3 a 15 3 a 7 A. V . B. V . C. V . D. V . 8 12 24 24
Câu 24. Cho hình lập phương ABCD.A B C D
có O và O lần lượt là tâm của hình vuông ABCD và ABC D
. Gọi V là thể tích khối nón tròn xoay có đỉnh là trung điểm của OOvà đáy là đường 1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
tròn ngoại tiếp hình vuông ABCD ; V là thể tích khối trụ tròn xoay có hai đáy là hai đường tròn 2
nội tiếp hình vuông ABCD và A B C D
. Tỉ số thể tích V1 là V2 1 1 1 1 A. B. C. D. 3 4 6 2 Câu 25. Cho lăng trụ AB . C A B C
có đáy là tam giác đều cạnh a, AA b và AA tạo với mặt đáy một
góc 60. Tính thể tích khối lăng trụ. 3 3 3 1 A. 2 a b . B. 2 a b . C. 2 a b . D. 2 a b . 4 8 8 8
Câu 26. Cho tứ diện ABCD , G là trọng tâm tam giác ABD . Trên đoạn BC lấy điểm M sao cho
MB 2MC . Khẳng định nào sau đây đúng? A. MG song song ACB. B. MG song song BCD . C. MG song song ACD. D. MG song song ABD .
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A1;1;2 , B 1
;0;4, C 0;1;3 và điểm
M thuộc mặt cầu S x y z 2 2 2 : 1 1. Nếu biểu thức 2 2 2
MA MB MC đạt giá trị nhỏ
nhất thì độ dài đoạn AM bằng A. 6 . B. 2 . C. 6 . D. 2 .
Câu 28. Cho hai điểm A 3;3;1, B 0; 2;1 và mặt phẳng : x y z 7 0. Đường thẳng d nằm
trên sao cho mọi điểm của d cách đều 2 điểm , A B có phương trình là x 2t x t x t x t A. y 7 3t . B. y 7 3t. C. y 7 3t . D. y 7 3t. z t z 2t z 2t z 2t
Câu 29. Cho hàm số y f (x 2) 2 có đồ thị như hình bên dưới. Tìm số điểm cực trị của hàm số g x 3 2 f x 3x trên (0; ) . 2 A. 5. B. 4. C. 2. D. 3.
Câu 30. Trong không gian Oxyz cho mặt cầu S x 2 y 2 z 2 : 1 2 3 9 và mặt phẳng
P:2x 2y z 3 0 . Gọi M ; a ;
b c là điểm trên mặt cầu sao cho khoảng cách từ M đến
P lớn nhất. Khi đó: A. a b c 8. B. a b c 5. C. a b c 6 . D. a b c 7. 1 1
Câu 31. Cho hàm số f x 4 3 2
x x x 2020 , số điểm cực trị của hàm số y f x là 4 3 A. 2 . B. 3. C. 4 . D. 5.
Câu 32. Để phương trình sau có nghiệm duy nhất 2 2
2x 3x 2 5a 8x x , giá trị của tham số a là
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 49 57 A. a 15 . B. a 1 2 . C. a . D. a . 60 80 x 2 1 khi x 0 Câu 33. Cho hàm số f x . sin x 1 khi x 0 2 Tính I f 2 x f 2x sin x dx 0 A. 3 I 1 . B. 3 2 I C. 3 I 2 D. 3 I 2 4 4 3 4 4
Câu 34. Một bình đựng 8 viên bi xanh và 4 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi. Xác suất để có được ít
nhất hai viên bi xanh là bao nhiêu? 28 41 14 42 A. . B. . C. . D. . 55 55 55 55
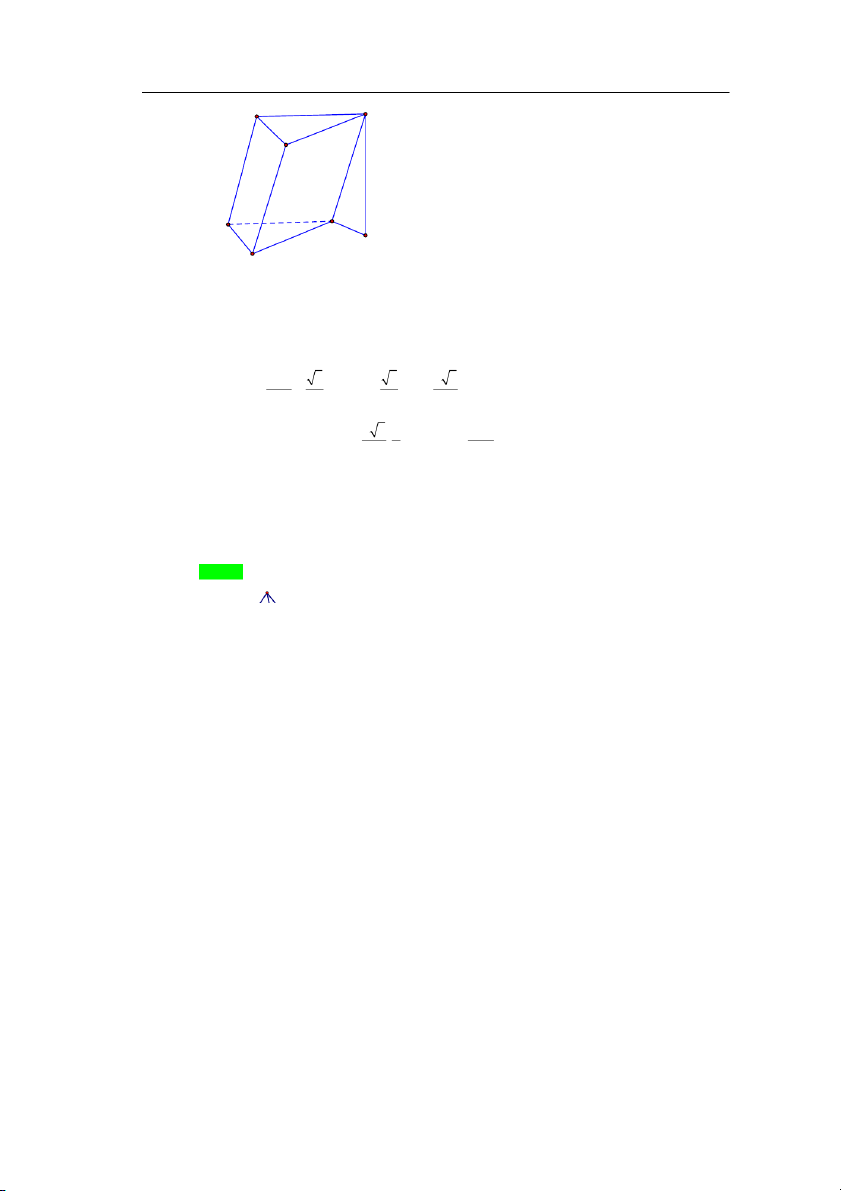
Câu 35. Cho lăng trụ đều ABC.AB C
có tất cả các cạnh bằng 2 . Gọi M, N và P lần lượt là trung điểm của A B ; B C
và CA . Thể tích của khối đa diện lồi có các đỉnh là các điểm , A B,C, M , N, P bằng A. 3 3 . B. 3 3 . C. 3 3 . D. 3 3 . 16 8 4 2 B. ĐIỀN KHUYẾT (15 CÂU)
Câu 36. Viết phương trình tiếp tuyến của đồ thị hàm số 3 2
y x 3x 6x 11 tại giao điểm của đồ thị với trục tung. Đáp án: …………..
Câu 37. Cho hàm số y f
x có đạo hàm f x x 2 x 4 1
2 x 4 . Số điểm cực trị của hàm số y f x là? Đáp án: …………..
Câu 38. Trong không gian với hệ tọa độ Oxy, cho P : 2 x 2y z 3 0 và điểm M 1;2;1, khi đó
khoảng cách từ điểm M đến mặt phẳng P bằng: Đáp án: …………..
Câu 39. Một đội thanh niên tình nguyện có 15 người,gồm 12 nam và 3 nữ.Hỏi có bao nhiêu cách phân
công đội thanh niên tình nguyện đó về giúp đỡ 3 tỉnh miền núi, sao cho mỗi tỉnh có 4 nam và một nữ? Đáp án: ………….. f x 16 2 f x 16 4
Câu 40. Cho hàm số f x xác định trên thỏa mãn lim 12 . Giới hạnlim x2 x 2 2 x2 x x 6 bằng Đáp án: …………..
Câu 41. Trong đợt hội trại “Khi tôi 18 ” được tổ chức tại trường THPT X, Đoàn trường có thực hiện một
dự án ảnh trưng bày trên một pano có dạng parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu
các lớp gửi hình dự thi và dán lên khu vực hình chữ nhật ABCD có kích thước AB 2 ,
m AD 3m ABCD, phần còn lại sẽ được trang trí hoa văn cho phù hợp và pano được đặt
sao cho cạnh CD tiếp xúc với mặt đất. Hỏi vị trí cao nhất của pano so với mặt đất là bao nhiêu?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Đáp án: …………..
Câu 42. Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số 4 y x 2 m 2 4 x 3 có 1 cực
trị. Số phần tử của tập S là Đáp án: …………..
Câu 43. Cho hình vẽ bên dưới biết y f x là hàm đa thức bậc 3 và phần gạch chéo là diện tích S , S . 1 2 S
Cho biết f x f x 0 và x x 4. Tỷ số 1 bằng 1 2 2 1 S 2 Đáp án: ………….. Câu 44. Cho hàm số y
f x có bảng biến thiên như sau Số nghiệm thuộc đoạn 9 0;
của phương trình f f cos x 2 là 2 Đáp án: …………..
Câu 45. Xét các số phức z thỏa mãn (2 z)(z i) là số thuần ảo. Tập hợp các điểm biểu diễn của z trong
mặt phẳng tọa độ là: Đáp án: …………..
Câu 46. Cho hình lập phương AB .
CD A' B 'C 'D . Gọi M là trung điểm của BB . Tính cosin của góc giữa
hai đường thẳng AM và AC Đáp án: …………..
Câu 47. Trong không gian Oxyz, cho điểm A 2;0; 2 , B 3;1; 4 ,C 2;2; 0 . Điểm D trong mặt
phẳng Oyz có cao độ âm sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D
đến mặt phẳng Oxy bằng 1. Khi đó có tọa độ điểm D thỏa mãn bài toán là
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Đáp án: …………..
Câu 48. Xét các số thực a , b thỏa măn a b 1 . Tm giá trị nhỏ nhất P của biểu thức min 2 a P a . a 2 log 3logb b b Đáp án: ………….. Câu 49. Cho hình chóp .
S ABC có SA ABC , SA 3a , AB 10a , BC 14a, AC 6a . Gọi M là 3
trung điểm AC , N là điểm thuộc đoạn thẳng AB sao cho AN
AB. Tính theo a khoảng cách 5
giữa hai đường thẳng SM và CN . Đáp án: …………..
Câu 50. Cho hình chóp tứ giác đều S .ABCD có độ dài cạnh bên bằng 2 . Gọi là góc giữa cạnh bên của
hình chóp và mặt đáy. Tính sin để thể tích của khối chóp S.ABCD lớn nhất? Đáp án: …………..
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Lời giải tham khảo
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Người ta thống kê diện tích trồng lúa của một địa phương trong các năm tính theo héc-ta rồi biểu
diễn thành biểu đồ ở trên.
Diện tích trồng lúa ít nhất trong các năm là bao nhiêu (héc - ta)? A. 160. B.138 C. 121. D.109 Lời giải Chọn D
Câu 2. Một ô tô đang chuyển động đều với vận tốc am / s thì phanh. Từ thời điểm đó ô tô chuyển động
chậm dần đều với phương trình vận tốc v t 5
t a m / s . Biết rằng từ lúc phanh đến khi xe
dừng hẳn ô tô đi được 40m . Tính vận tốc xe khi chưa phanh? A. a 80m / s . B. a 20m / s . C. a 25m / s . D. a 40m / s. Lời giải Chọn B a Ta có 5 t a 0 t 5 a a 5 5 2 a t S 40 v t 5 5
dt 40 (5t a )dt 40 at 40 0 2 0 0 2 a 5 2 2 2 2 25 a a a a 2 40 40
40 a 400 a 20. 2 5 10 5 10
Câu 3. Tập hợp nghiệm của bất phương trình log x 1 3 là: 2 A. S ;9 B. S 1;9 C. S 1;10 D. S ; 10 Lời giải Chọn B x 1 0 x 1 Ta có: log x 1 3 . 2 3 x 1 2 x 9 2 2 x
3xy y 2x 3y 6 0
Câu 4. Hệ phương trình có nghiệm là: 2 x y 3
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 A. 3;3. B. 2;1, 3;3. C. Vô nghiệm. D. 2;1. Lời giải Chọn B
Ta có : y x x 3x x x 2 2 2 3 2 3 2 3 2x 32x 3 6 0 2
x 5x 6 0 x 2; x 3
x 2 y 1, x 3 y 3
Câu 5. Điểm A trong hình vẽ bên biểu diễn cho số phức z . .
Tìm phần thực và phần ảo của số phức z .
A. Phần thực là 3 và phần ảo là 2 . B. Phần thực là 3 và phần ảo là 2 .
C. Phần thực là 3 và phần ảo là 2 i . D. Phần thực là 3 và phần ảo là 2i . Lời giải Chọn A
Ta có z 3 2i z 3 2i .
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2;4; 1 , B 1;1; 3 và mặt phẳng
P : x3 y 2 z 5 0. Viết phương trình mặt phẳng Q đi qua hai điểm A, B và vuông góc
với mặt phẳng P .
A. Q: 2 y 3z11 0 B. Q: 2x 3z 11 0
C. Q: 2 y 3 z12 0 D. Q: 2 y 3 z10 0 Lời giải Chọn A
Ta có AB 3;3;2 , P có vtpt n 1; 3
;2 . Q có vtpt k AB,n 4 0;2; 3 .
Q : 2y 3z 11 0.
Câu 7. Trong không gian với hệ tọa độOxyz , cho hai điểm A3;1; 1 , B4;2; 3
. Gọi A là hình chiếu
vuông góc của A trên mặt phẳng Oxyvà B là hình chiếu vuông góc của B trên mặt phẳng
Oyz . Độ dài đoạn thẳng A B bằng A. 2 3 . B. 3 3 . C. 2 . D. 3. Lời giải Chọn B
Do A là hình chiếu vuông góc của A 3; 1
;1 trên mặt phẳng Oxy nên A3; 1 ;0. B 4; 2; 3
Do B là hình chiếu vuông góc của
trên mặt phẳng Oyz nên B0;2; 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Ta có A B 3;3; 3 A B
2 2 2 3 3 3 3 3 .
Câu 8. Tam thức bậc hai f x 2
x 3x 2 nhận giá trị không âm khi và chỉ khi A. x 1;2 . B. x ;1 2; . C. x 1; 2 . D. x ; 1 2; . Lời giải Chọn A Ta có f x 2
0 x 3x 2 0 1 x 2 .
Câu 9. Tìm tất cả các giá trị của tham số m để phương trình m 2sin 2x m 1 vô nghiệm. 1 1 A. m ;2 2; . B. m ; . 2 2 1 1 C. m ;2 . D. m ; 2; . 2 2 Lời giải Chọn B
TH1. Với m 2, phương trình m 2sin 2x m 1 0 3 : vô lý.
Suy ra m 2 thì phương trình đã cho vô nghiệm. m
TH2. Với m 2, phương trình m 1
2 sin 2x m 1 sin 2x . m 2 m 1 1 m 2 m 1 Để phương trình vô nghiệm m 2 1;1 1 . m 2 m 1 m 2 1 2 m 2
Kết hợp hai trường hợp, ta được 1
m là giá trị cần tìm. 2
Câu 10. Ông A gửi 120 triệu đồng tiền vào ngân hàng với lãi suất 6% / năm. Biết rằng nếu không rút tiền
ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp
theo. Hỏi sau 10 năm, tổng số tiền mà ông A nhận được là bao nhiêu, giả định trong khoảng thời
gian này lãi suất không thay đổi và ông A không rút tiền ra? (Lấy kết quả gần đúng đến hàng phần trăm)
A. 214,90 triệu đồng. B. 224,10 triệu đồng.
C. 234,90 triệu đồng. D. 215,10 triệu đồng. Lời giải Chọn A
Ta có a 120 triệu đồng.
Đặt T là số tiền nhận được sau n năm. n
Sau 1 năm số tiền có được (cả gốc và lãi) là T a a.6% a 1 0,06 . 1
Sau 2 năm số tiền có được là T a 1 0,062 . 2
Gọi T là tổng tiền mà A nhận được sau 10 năm. T a 10 10 1 0,06 120.1.06 214,90 . 2 x 1 Câu 11. Nguyên hàm bằng. x 2 x 1
Trang 10 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 1 1 1 A. ln x C . B. ln x C . ln x C D. 2 1 ln x C . 2 x x C. x . x Lời giải Chọn C 2 2 x 1 x 1 2 1 2 2 x 1 2 x x dx dx dx dx 2 x 1 x 2 x 2 2 1 x x x 1 x x 1 . ln x ln 1 2
x 1 C ln x C. x
Câu 12. Cho hàm số y f
x có đạo hàm trên . Hàm số y f x có bảng biến thiên như sau:
Bất phương trình 2 x f x
e m đúng với mọi x 1 ; 1 khi và chỉ khi A. m f 1 2e . B. m f 1 e. C. m f 1 2e . D. m f 1 2e . Lời giải Chọn C
Ta có 2 x , 1 ; 1 2 x f x e m x f x e , m x 1 ; 1 (*)
Đặt 2 x g x f x
e . Khi đó, 2 x g x f x e .
Từ bảng biến thiên của hàm số y f x suy ra f x 0, x 1 ; 1
Suy ra 2 x g x f x e 0, x 1 ; 1 .
Do đó, (*) min g x m m g 1 m f 1 2e . 1;1
Câu 13. Một xe ô tô đang chạy với vận tốc 20m/s thì người lái xe nhìn thấy chướng ngại vật nên đạp
phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc là v t 2 t 20 , trong đó
t là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà ô tô đi được trong 15 giây cuối cùng bằng A. 75m. B. 200 m. C. 100 m. D. 125 m. Lời giải Chọn B
Từ khi người lái xe đạp phanh đến lúc xe dừng hẳn thì vt 0 2t 20 0 t 10.
Do đó quãng đường ô tô đi được trong 15 giây cuối cùng là 10
s 20.5 2t 2 0 dt 200m. 0
Câu 14. Bạn Hùng trúng tuyển vào trường đại học A nhưng vì do không đủ nộp học phí nên Hùng quyết
định vay ngân hàng trong 4 năm mỗi năm vay 3.000.000 đồng để nộp học phí với lãi suất 3%
/năm. Sau khi tốt nghiệp đại học bạn Hùng phải trả góp hàng tháng số tiền T (không đổi) cùng với
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
lãi suất 0,25%/ tháng trong vòng 5 năm. Số tiền T hàng tháng mà bạn Hùng phải trả cho ngân
hàng (làm tròn đến kết quả hàng đơn vị) là: A. 309604 đồng. B. 232518 đồng. C. 232289 đồng. D. 215456 đồng. Lời giải Chọn C
Vậy sau 4 năm bạn Hùng nợ ngân hàng số tiền là: s 4 3 2 3000000 3% 3%
3% 12927407,43.
Lúc này ta coi như bạn Hùng nợ ngân hàng khoản tiền ban đầu là 12.927.407,43 đồng, số tiền này
bắt đầu được tính lãi và được trả góp trong 5 năm. Ta có công thức:
N r n .r 12927407,40,002 60 5 .0,0025 232289 . r n 0,0025 60
Câu 15. Phương trình log x 1 2 có nghiệm là: 3 A. x 8 . B. x 10 . C. x 7 . D. x 5 . Lời giải Chọn A
Ta có: log x 1 2 x 1 9 x 8. 3
Câu 16. Cho hình phẳng A giới hạn bởi các đường x y e , – x
y e và x 1. Thể tích của khối tròn xoay
tạo thành khi quay hình A quanh trục hoành là. 2 2 e 2 2 e A. e e ( 1) . ( 1) 2 2 B. 2 2 . 2 2 e 2 2 e C. e e ( 1) . D. ( 1) . 2 2 2 2 Lời giải Chọn B
Hoành độ giao điểm của x y e và – x y e là x 0.. 1 1 2 x 2 x e e 2x 2 e e 2 2 ( x V e e )dx ( ) ( 1) . 0 2 2 2 2 0
Câu 17. Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y x x mx 1 đồng biến trên ; . A. 1 m . B. 4 m . C. 4 m . D. 1 m . 3 3 3 3 Lời giải Chọn A
Tập xác định: D . 2 y 3x 2 x m . 1
Hàm số đã cho đồng biến trên ; y' 0; x ' 1 3m 0 m . 3
Câu 18. Tìm số phức z thỏa mãn iz 2z 9 3i. A. z 5 i . B. z 5 i . C. z 1 5i . D. z 1 5i . Lời giải Chọn A Gọi z a bi ( ;
a b ). Suy ra: z a b .i Ta có:
Trang 12 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
iz 2z 9 3i i a bi 2 a bi 9 3i
2a b a 2b i 9 3i 2 a b 9 a 5 . a 2b 3 b 1 Vậy z 5 i .
Câu 19. Tập hợp điểm biểu diễn các số phức z thỏa mãn z i z 3 trong mặt phẳng Oxy là:
A. Đường thẳng :x y 4 0 .
B. Đường thẳng : 3x y 4 0 .
C. Đường thẳng :x y 4 0.
D. Đường thẳng : 3x y 4 0 . Lời giải Chọn B
Gọi z x yi với x , y . Khi đó điểm M ;
x y là điểm biểu diễn cho số phức z .
Ta có z i z 3 x yi i x yi 3
x y 2 x 2 2 2 1
3 y 6x 2y 8 0 3x 2 y 4 0 .
Vậy tập hợp điểm biểu diễn số phức z là đường thẳng :3x y 4 0 .
Câu 20. Tìm tọa độ giao điểm của 2 đường thẳng sau đây: x 3 4t x 1 4t ' : và : 1 y 2 2 5t y 7 5t ' A. (1; 3). B. (5; 1). C. (1; 7). D. (3; 2). Lời giải Chọn C 3 4t 1 4t t 1 Xét hệ: giao điểm A1;7. 2 5t 7 5t t ' 0 Câu 21. Cho phương trình 2 2
x y 2x 2my 10 0 1. Có bao nhiêu số nguyên m 0;1 0 để 1 là
phương trình của đường tròn? A. 8 . B. không có. C. 6 . D. 7. Lời giải Chọn C m 3
Điều kiện để 1 là phương trình đường tròn: 2 1 m2 2
10 0 m 9 . m 3
Như vậy trong khoảng 0;10 có 6 giá trị nguyên của m là 4;5;6;7;8; 9 .
Câu 22. Trong không gian cho điểm M(1;3;2) .Có bao nhiêu mặt phẳng đi qua M và cắt các trục tọa độ tại , A ,
B C mà OA OB OC 0 A. 2. B. 3. C. 4. D. 1. Lời giải Chọn B Giả sử mặt phẳng ( ) cần tìm cắt O , x O , y Oz lần lượt tại
A(a,0,0),B(0,b,0),C(0,0c)(a,b,c 0) x y z 1 3 2
( ) : 1; ( ) qua M(1; 3
;2) nên: ( ) : 1(*) a b c a b c
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ a b c (1) a b c (2) OA OB OC 0 a b c 0 a b c(3) a b c (4)
Thay (1) vào (*) ta có phương trình vô nghiệm 3
Thay (2),(3),(4) vào (*) ta được tương ứng a 4 ,a 6,a 4 Vậy có 3 mặt phẳng.
Câu 23. Một khối nón có đường sinh bằng 2a và diện tích xung quanh của mặt nón bằng 2 a . Tính thể
tích của khối nón đã cho? 3 a 15 3 a 15 3 a 15 3 a 7 A. V . B. V . C. V . D. V . 8 12 24 24 Lời giải Chọn C 2 2 2 a a a S rl a r . xq l .2a 2 2 a a 15 2 2 2 h l r 4a . 4 2 2 3 1 2 1 a a 15 a 15 V r .h . . . 3 3 4 2 24
Câu 24. Cho hình lập phương ABCD.A B C D
có Ovà O lần lượt là tâm của hình vuông ABCD và AB C D
. Gọi V là thể tích khối nón tròn xoay có đỉnh là trung điểm của OO và đáy là đường 1
tròn ngoại tiếp hình vuông ABCD; V là thể tích khối trụ tròn xoay có hai đáy là hai đường tròn 2 V
nội tiếp hình vuông ABCD và AB C D
. Tỉ số thể tích 1 là V2 1 1 1 1 A. B. C. D. 3 4 6 2 Lời giải Chọn A
Gọi hình lập phương ABCD.A B C D
có cạnh bằng a. Khi đó 2 3 1 a 2 a a 2 3 a a V 1 Ta có V . ; V .a suy ra 1 . 1 3 2 2 12 2 2 4 V 3 2 Câu 25. Cho lăng trụ AB . C AB C
có đáy là tam giác đều cạnh a , AA b và AA tạo với mặt đáy một
góc 60. Tính thể tích khối lăng trụ. 3 3 3 1 A. 2 a b . B. 2 a b . C. 2 a b . D. 2 a b . 4 8 8 8 Lời giải Chọn B
Trang 14 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 C' A' B' A C H B
Kẻ A H ABC tại H
Suy ra góc giữa AA và đáy bằng AAH 60 AH 3 3 b 3 sin 60 A H A A . A A 2 2 2 b 3 1 2 3a b Do đó V A H .S 2 . a sin 60 . ABC .A B C ABC 2 2 8
Câu 26. Cho tứ diện ABCD, G là trọng tâm tam giác ABD . Trên đoạn BC lấy điểm M sao cho
MB 2MC . Khẳng định nào sau đây đúng? A. MG song song ACB . B. MG song song BCD . C. MG song song ACD . D. MG song song ABD. Lời giải Chọn C A B D G M C
Vì MG//CD nên MG // ACD .
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A1;1;2, B 1 ;0; 4, C0; 1 ;3 và điểm
M thuộc mặt cầu S 2 2
: x y z12 1 . Nếu biểu thức 2 2 2
MA MB MC đạt giá trị nhỏ
nhất thì độ dài đoạn AM bằng A. 6 . B. 2 . C. 6 . D. 2 . Lời giải Có AB 2 ; 1 ; 2 ; AC 1 ; 2; 1 nên ba điểm ,
A B,C không thẳng hàng. Gọi G là trọng
tâm tam giác ABC. Suy ra G 0;0;3 . Nhận thấy G nằm ngoài mặt cầu. 2 2 2 2 2 2 2 2 2 2 2 2 2 2
MA MB MC MA MB MC 3MG GA GB GC 3MG GA GB GC
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Biểu thức 2 2 2
MA MB MC đạt giá trị nhỏ nhất MG đạt giá trị nhỏ nhất M là giao
điểm của đoạn IG và mặt cầu, với I 0;0; 1 là tâm của mặt cầu. x 0
Đường thẳng IG nhận IG 0;0;2 là VTCP nên có phương trình là y 0 . z 12t
Tọa độ giao điểm của đường thẳng IG và mặt cầu là nghiệm của hệ x 0 x 0 y 0 y 0 z 1 2t z x y z 12 0 2 2 1 z 2
Với M 0;0;0 thì MG 3 ;
Với M 0;0; 2 thì MG 1 ;
Do đó MG đạt giá trị nhỏ nhất với M 0;0;
2 . Khi đó AM 2 2 2 1 0 1 0 2 2 2
Câu 28. Cho hai điểm A 3;3;1, B 0; 2;1 và mặt phẳng : x y z 7 0. Đường thẳng d nằm
trên sao cho mọi điểm của d cách đều 2 điểm , A B có phương trình là x 2t x t x t x t A. y 7 3t . B. y 7 3t. C. y 7 3t . D. y 7 3t. z t z 2t z 2t z 2t Lời giải Chọn B
Mọi điểm trên d cách đều hai điểm ,
A B nên d nằm trên mặt phẳng trung trực của đoạn AB . 3 5 Có AB 3 ; 1
;0 và trung điểm AB là I ; ;1
nên mặt phẳng trung trực của AB là: 2 2 3 5 3 x y 0 3x y 7 0 . 2 2 3x y 7 0 y 7 3x
Mặt khác d nên d là giao tuyến của hai mặt phẳng: . x y z 7 0 z 2 x x t
Vậy phương trình d : y 7 3t t . z 2t
Câu 29. Cho hàm số y f (x 2) 2 có đồ thị như hình bên dưới. Tìm số điểm cực trị của hàm số g x 3 2 f x 3x trên (0; ) . 2
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 A. 5. B. 4. C. 2. D. 3. Lời giải Chọn D
Từ đồ thị của hàm số y f (x 2) 2 , tịnh tiến lên trên 2 đơn vị rồi tịnh tiến sang phải 2 đơn vị,
ta được đồ thị của hàm y f x như sau 3
Ta có g x 3x 2 3 f x 3x 2 x 1 x 1 3 x 3 0 x 2 g x 3 2 0 3 x 3x 0 x 0 . 2 f x 3x 0 2 2 x 1 3 3 2 x 3x 3 2 x 1 3
Ta thấy đây đều là các nghiệm đơn, do đó hàm số y g x có 5 điểm cực trị. 3 Vậy hàm số g x 2 f x 3x
có 3 điểm cực trị trên (0; ) . 2
Câu 30. Trong không gian Oxyz cho mặt cầu S x 2 y 2 z 2 : 1 2 3 9 và mặt phẳng
P:2x 2y z 3 0. Gọi M a;b;c là điểm trên mặt cầu sao cho khoảng cách từ M đến
P lớn nhất. Khi đó: A. a b c 8. B. a b c 5 . C. a b c 6 . D. a b c 7. Lời giải Chọn D
Mặt S cầu có tâm I 1;2; 3 , R 3 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
d I P 2.1 2.2 3 3 4 ,
R mặt phẳng cắt mặt cầu theo một đường tròn 2 2 2 3 2 2 1 Gọi M a; ; b
c là điểm trên mặt cầu sao cho khoảng cách từ M đến P lớn nhất. Khi M thuộc
đường thẳng vuông đi qua M và vuông góc với P x 1 2t
: y 2 2t . Thay vào mặt cầu S t2 t2 t2 2 2 2
9 9t 9 t 1 z 3 t 2.3 2.0 4 3 10
Với t 1 M 3;0;4 d M ;P 2 2 2 3 2 2 1 2. 1 2.4 2 3 1 Với t 1
M 1;4;2 d M; P 2 2 2 3 2 2 1
Vậy M3;0;4 a b c 7. 1 1
Câu 31. Cho hàm số f 4 3 2
x x x x 2020, số điểm cực trị của hàm số y f x là 4 3 A. 2 . B. 3. C. 4 . D. 5 . Lời giải Chon B Phương pháp x
y f x y .f x nên ta có nhận xét sau: x
-Hàm số đạt cực trị tại điểm x 0
-Số điểm cực trị dương của hàm số y f
x là n thì số điểm cực trị của hàm số y f x là 2n 1 f 3 2 x x x 2x x x 1 x 2 Ta có x 0 f x 0 x 1 x 2 Hàm số y f
x có một cực trị dương nên hàm số y f x có ba cực trị.
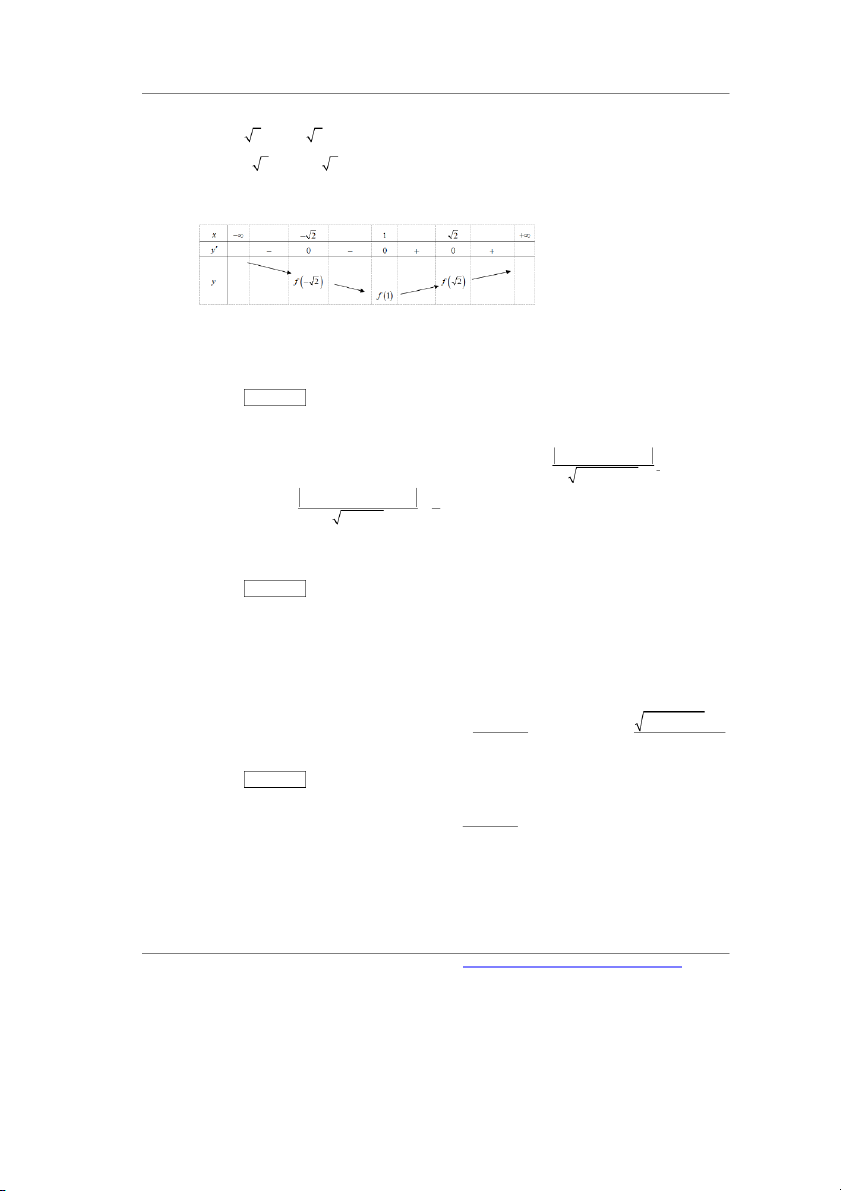
Câu 32. Để phương trình sau có nghiệm duy nhất 2 2 2 x 3 x 2 5 a 8
x x , giá trị của tham số a là A. a 15 . B. a 1 2 . C. 49 a . D. 57 a . 60 80 Lời giải Chọn C
Phương trình tương đương với 2 2
2x 3x 2 x 8x 5a 1 2
3x 5x 2 khi x , x 2
Xét hàm số y f x 2 2 2
2x 3x 2 x 8x 1 2
x 11x 2 khi x 2 2
Suy ra, bảng biến thiên của hàm y f x 2 2
2x 3x 2 x 8x như sau:
Trang 18 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 5 1 11 x 6 2 2 2 2 3x 5x 2 2 2 x 11x 2 3x 5x 2 y 49 12 49 49
Yêu cầu bài toán 5a a . 12 60 x 2 1 khi x 0 Câu 33. Cho hàm số f x . sin x 1 khi x 0 2 Tính I f 2 x f 2x sin x dx 0 A. 3 I 1 . B. 3 2 I C. 3 I 2 D. 3 I 2 4 4 3 4 4 Lời giải 2 2 2 2 2 3 cos2 x +) Ta có: I f x dx sin x s 2 in x 1 dx 2 sin x dx 1 2 2 0 0 0 3 2 4 2 2 +) Ta có: I f 2 x sin x dx 4 x 1 sin x dx 3 2 0 0 3 Vậy I I I 1. 1 2 4
Câu 34. Một bình đựng 8 viên bi xanh và 4 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi. Xác suất để có được ít
nhất hai viên bi xanh là bao nhiêu? 28 41 14 42 A. . B. . C. . D. . 55 55 55 55 Lời giải Chọn D
Số trường hợp có thể là: n 3 C 220 . 12
Gọi A là biến cố “Lấy được ít nhất 2 viên bi xanh”
TH1: Lấy được 2 viên bi xanh và 1 viên bi đỏ có: 2 1 C .C 112 (Cách). 8 4
TH2: Lấy được 3 viên bi xanh có: 3 C 56 (Cách). 8 Suy ra: n( )
A 112 56 168 (Cách). 168 42
Vậy xác suất để có được ít nhất hai viên bi xanh là: ( P ) A . 220 55
Câu 35. Cho lăng trụ đều ABC.ABC có tất cả các cạnh bằng 2 . Gọi M , N và P lần lượt là trung điểm của A B ; B C
và CA . Thể tích của khối đa diện lồi có các đỉnh là các điểm , A B,C, M , N, P bằng 3 3 3 3 3 3 3 3 A. 16 . B. 8 . C. 4 . D. 2 . Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Chọn D 2 2 3
Thể tích khối lăng trụ ABC.ABC là V AA .S . A B C 2. 2 3 4
Gọi thể tích của khối đa diện lồi có các đỉnh là các điểm , A B,C, M , N, Plà V . 1 Ta có V V V . V V 1 AA MP BB MN CC N P 1 1 1 1 V AA .S . .AA . S V AA MP A MP A' B'C' 3 3 4 12 1 1 1 1 V . BB .S .BB . S V BB MN B ' 3 MN 3 4 A B C 12 1 1 1 1 V . CC S CC S V CC NP . C NP . . 3 3 4 A B C 12 3 3 3 3 3 Vậy V V V V V V V V .2 3 . 1 AA MP BBMN CCNP 12 4 4 2 B. ĐIỀN KHUYẾT (15 CÂU)
Câu 36. Viết phương trình tiếp tuyến của đồ thị hàm số 3 2
y x 3x 6x 11 tại giao điểm của đồ thị với trục tung. Đáp án: ………….. Lời giải
Đồ thị hàm số giao với trục tung tại điểm A0;1 1 Xét 2
y 3x 6x 6 Hệ số góc của tiếp tuyến là k y 0 6
Vậy phương trình tiếp tuyến cần tìm là y 6 x 0 1 1 hay y 6 x 11.
Câu 37. Cho hàm số y f x có đạo hàm f x x 2 x 4 1
2 x 4 . Số điểm cực trị của hàm số y f x là? Đáp án: ………….. Lời giải 2
Ta có f x x 2 x 4 0 1 2 x 4 0 x 2 x 2 1 2 x 2 0 .
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 x 1, y f 1 x 2, y f 2 . x 2, y f 2 Bảng biến thiên. .
Dựa vào bảng biến thiên, ta có hàm số chỉ có 1 cực trị.
Câu 38. Trong không gian với hệ tọa độ Oxy, cho P : 2 x 2y z 3 0 và điểm M 1;2; 1 , khi đó
khoảng cách từ điểm M đến mặt phẳng P bằng: Đáp án: ………….. Lời giải
Công thức cần nhớ: cho điểm M x ; y ; z
P: ax by cz d 0 0 0 0 và mặt phẳng . ax by cz d
Thì ta có khoảng cách từ M đến mặt phẳng P là: d M ;P 0 0 0 . 2 2 2 a b c 2.1 2 2 1 3 2 Vậy d M ; P . 4 4 1 3
Câu 39. Một đội thanh niên tình nguyện có 15 người,gồm 12 nam và 3 nữ.Hỏi có bao nhiêu cách phân
công đội thanh niên tình nguyện đó về giúp đỡ 3 tỉnh miền núi, sao cho mỗi tỉnh có 4 nam và một nữ? Đáp án: ………….. Lời giải Có 4
C cách phân công 4 nam về tỉnh thứ nhất 12
Với mỗi cách phân công trên thì có 4
C cách phân công 4 nam về tỉnh thứ hai và có 4 C cách phân 8 4
công 4 nam còn lại về tỉnh thứ ba.
Khi phân công nam xong thì có 3! cách phân công ba nữ về ba tỉnh đó. Vậy có tất cả 4 4 4
C .C .C .3! 4989600 cách phân công. 12 8 4 f x 16 2 f x 16 4
Câu 40. Cho hàm số f x xác định trên thỏa mãn lim 12 . Giới hạnlim x2 x 2 2 x2 x x 6 bằng Đáp án: ………….. Lời giải f x 16
Từ giả thiết f x xác định trên thỏa mãn lim 12 f 2 16 x 2 x 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ 2 f x 16 4 2 f x 1 6 1 6 Ta có: lim lim 2 x 2 x x 6 x 2 2
x x 6 2 f x 16 4 2 f x 16 f x 16 2 3 lim lim . . x2 x 2 x
3 2 f x 16 4 x2 x 2 x 3
2 f x 16 4 5
Câu 41. Trong đợt hội trại “Khi tôi 18 ” được tổ chức tại trường THPT X, Đoàn trường có thực hiện một
dự án ảnh trưng bày trên một pano có dạng parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu
các lớp gửi hình dự thi và dán lên khu vực hình chữ nhật ABCD có kích thước AB 2 ,
m AD 3m ABCD, phần còn lại sẽ được trang trí hoa văn cho phù hợp và pano được đặt
sao cho cạnh CD tiếp xúc với mặt đất. Hỏi vị trí cao nhất của pano so với mặt đất là bao nhiêu? Đáp án: ………….. Lời giải
Xây dựng hệ trục tọa độ như hình vẽ:
Bản chất của bài toán: xác định tung độ đỉnh của parabol 2
y ax bx c , biết parabol đi qua
các điểm O 0;0 , A 1;3, B 3;3 . . a0 . b0 c 0 a 1
Ta có hệ phương trình: . a1 . b1 c 3 b 4 .a9 .b3 c 3 c 0 parabol 2
y x 4x có đỉnh I 2; 4 .
Vậy vị trí cao nhất của pano so với mặt đất là 4m .
Câu 42. Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số 4 y x 2 m 2 4 x 3 có 1 cực
trị. Số phần tử của tập S là Đáp án: ………….. Lời giải x 0 Ta có: 3 y x 2 4
2 m 4 x y 0 2 2 2 x 2 x m 4 2 0 . 2 m 4 x 2
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 2 m 4
Hàm số đã cho có 1 cực trị y 0 có nghiệm duy nhất x 0 2 x có nghiệm kép 2 bằng 0 hoặc vô nghiệm 2 m 4 2 0 m 4 2
m 2 mà m S 2 ;1;0;1; 2 . 2
Vậy số phần tử của S là 5.
Câu 43. Cho hình vẽ bên dưới biết y f x là hàm đa thức bậc 3 và phần gạch chéo là diện tích S , S . 1 2 Cho biết S
f x f x 0 và x x 4. Tỷ số 1 bằng 1 2 2 1 S 2 Đáp án: ………….. Lời giải
Từ giả thiết ta có f x a x x x x a x x x x 4 a x x 2 4a x x với 1 2 1 1 1 1 a 0 . a
Suy ra f x x x 3 2a x x 2 C . 1 1 3 a 32
Từ đây ta tính được f x C và f x x x 2a x x C a C 2 2 1 3 2 1 2 1 3 3 32a 16a Do vậy f x f x
, kết hợp với f x f x 0, ta có: f x C . 1 1 2 1 2 3 3 a
Do đó, f x x x 3 6x x 2 16 1 1 3 . S S S S Ta có: 1 1 1 1 . S S S S 2 f x S 32 2 1 2 1 1 1 a S1 3 x1 2 1 x 2 a Mà S f x dx
x x 3 6 x x 216dx t x x , ta được 1 , đổi biến 1 1 3 1 x1 x1 2 a S 20a 2 t 6t 16 . 1 3 3 0 20a S S 3 5 Vậy 1 1 . S 32 32 20a 3 2 a S a 1 3 3 3 Câu 44. Cho hàm số y
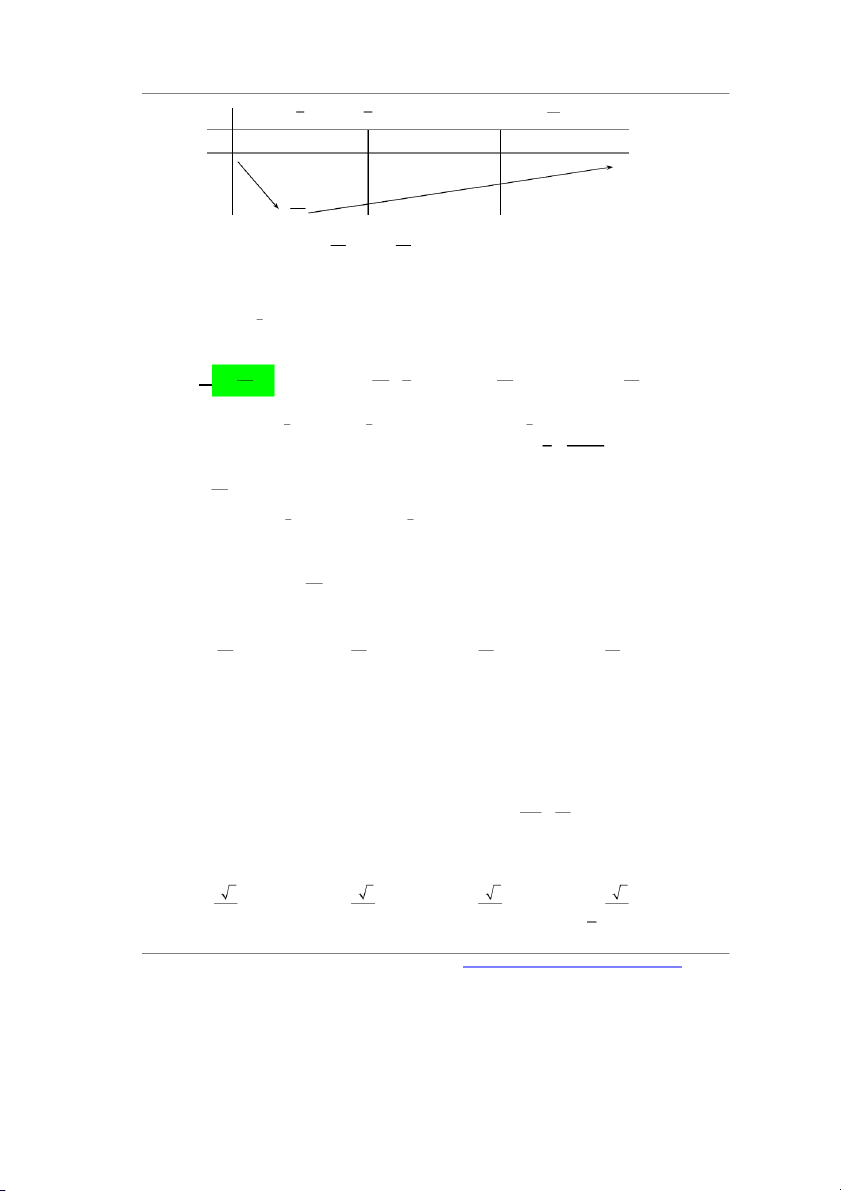
f x có bảng biến thiên như sau
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Số nghiệm thuộc đoạn 9 0;
của phương trình f f cos x 2 là 2 Đáp án: ………….. Lời giải
Cách 1: Phương pháp ghép trục Đặt u cos x 1;1 x 0 x Vì 9 x 0; nên
u sin x 0 x 2 2 x 3 x 4
Từ bảng biến thiên suy ra tổng số nghiệm phương trình đã cho là 9.
Cách 2: Tự luận truyền thống f cosx 1
Từ bảng biến thiên ta suy ra: f f cosx 2 f cosx 1 TH1: f cos x 1 Đặt t cos x ,t 1;1
Khi đó phương trình f cos x 1 trở thành f t 1, với t 1;1 .
Đây là phương trình có hoành độ giao điểm của đồ thị hàm số y
f t và đường thẳng y 1. t a 1
Dựa vào bảng biến thiên, ta có f t 1 phương trình vô nghiệm. t b 1 TH2: f cos x 1 Tương tự TH1: Đặt t cos x , t 1;1 t m ; 1 loaïi t n 1;0 f t 1 t p 0;1 t q 1; loaïi + Với t n 1; 0
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Ứng với mỗi giá trị t 1;0 thì phương trình cos x
t có 4 nghiệm phân biệt thuộc 9 0; . 2 + Với t p 0;1 Ứng với mỗi giá trị t 0;1 thì phương trình cos x
t có 5nghiệm phân biệt thuộc 9 0; . 2
Hiển nhiên, 9 nghiệm trong những trường hợp trên đều khác nhau.
Vậy phương trình đã cho có 9 nghiệm thuộc đoạn 9 0; . 2
Câu 45. Xét các số phức z thỏa mãn (2 z)(z i) là số thuần ảo. Tập hợp các điểm biểu diễn của z trong
mặt phẳng tọa độ là: Đáp án: ………….. Lời giải
Gọi số phức z x yi , x y z x y . i
Thay vào điều kiện ta được: (2 z )(z i ).
(2 x yi)(x yi i).
2 x yi x 1 yi .
(2 x)x y(1 y) (2 x)(1 y) xyi.
(2 z)(z i)là số thuần ảo khi và chỉ khi: (2 ) x x ( y 1 y) 0. 2 2
x y 2x y 0 . 1 5
Vậy số phức z x yi thuộc đường tròn tâm I 1; , bán kính R . 2 2
Câu 46. Cho hình lập phương AB .
CD A' B'C ' D . Gọi M là trung điểm của BB. Tính cosin của góc giữa
hai đường thẳng AM và A C Đáp án: ………….. Lời giải
+ Ta có A'C '/ /AC nên góc giữa AM và AC là góc giữa AC và AM .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ 2 2 2 a 2 a 5 MA MC MB AB a + Xét tam giác AMC có: 2 2 ; 2 2 AC AB BC a 2
Áp dụng định lí cosin trong tam giác AMC , ta có: 2 2 2 cos AM AC AM AC MC AC a 2 10 , 2 . MA AC 2MA a 5 5 2. 2
Câu 47. Trong không gian Oxyz , cho điểm A2;0; 2 , B3; 1 ; 4 , C 2
;2;0 . Điểm D trong mặt
phẳng Oyz có cao độ âm sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D
đến mặt phẳng Oxy bằng 1. Khi đó có tọa độ điểm D thỏa mãn bài toán là Đáp án: ………….. Lời giải
Vì D Oyz D 0;b;c , do cao độ âm nên c 0. c Khoảng cách từ D0; ;
b c đến mặt phẳng Oxy : z 0 bằng 1 1 c 1 do c 0. 1 Suy ra tọa độ D 0; ; b 1 . Ta có: AB 1; 1 ; 2 , AC 4 ;2;2; AD 2 ; ; b 1 A , B AC 2;6; 2 A , B AC. AD 4
6b 2 6b 6 6 b 1
1 V AB AC AD b ABCD , . 1 6 b 3 D 0;3; 1 Mà V 2 b 1 2
. Chọn đáp án D 0;3;1. . ABCD b 1 D 0; 1 ; 1
Câu 48. Xét các số thực a, b thỏa măn a b 1 . Tm giá trị nhỏ nhất P của biểu thức min 2 a P a . a 2 log 3logb b b Đáp án: ………….. Lời giải
Với điều kiện đề bài, ta có 2 2 a a a 2 a P log a a b a 2 3logb 2loga 3logb 4 log a . 3log b b b b b b b b 2 a 4 1 log b a 3log b . b b 3 3
Đặt t log b 0 (vì a b 1 ), ta có P 41 t2 2
4t 8t 4 f t . a t t b 8t 2t 1 2 3 2 4t t 6t 3 3 8 3 Ta có f (t) 8t 8 2 2 2 t t t 1 Vậy f t 1 0 t
. Khảo sát hàm số, ta có P f 15 . 2 min 2
Trang 26 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Câu 49. Cho hình chóp S.ABC có SA ABC, SA 3a , AB 10a, BC 14a , AC 6a . Gọi M là 3
trung điểm AC , N là điểm thuộc đoạn thẳng AB sao cho AN AB . Tính theo a khoảng cách 5
giữa hai đường thẳng SM và CN . Đáp án: ………….. Lời giải Ta có 2 2 2 AB AC BC 1 + cos BAC BAC 120o . 2 A B BC 2 3 + AN AB 6 a . 5 1 + AM AC 3a . 2
Gọi E là trung điểm AN ME //NC (EM là đường trung bình của ANC ). NC// EM
NC// SEM mà SM SEM d CN ,SM d N,SEM . EM SEM d N, SEM AE AN SEM E . d
1 d N, SEM d , A SEM , A SEM EN
Gọi F là hình chiếu của A lên EM F là trung điểm của EM AE AM 3a
Gọi H là hình chiếu của A lên SF d , A SEM AH . a + 3 AF AE cos EAF . 2 1 1 1 3a 5 + AH . 2 2 2 AH AS AF 5 Vậy d SM CN 3a 5 , . 5
Câu 50. Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh bên bằng 2 . Gọi là góc giữa cạnh bên của
hình chóp và mặt đáy. Tính sin để thể tích của khối chóp S.ABCD lớn nhất? Đáp án: ………….. Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Ta có SC 1 SO (ABCD) Do SC ABCD ; SCO . SC (ABCD) C AC Mà OC 2.cos
; SO 2.sin ; AC 2OC 4.cos ; AB 2 2.cos . 2 Nên 2 2 S AB . ABCD 8.cos 1 16 16 Vì vậy 2 2 V SO S . S ABCD . . ABCD .sin .cos .sin .(1 sin ) . 3 3 3 16 16 t sin Xét hàm 2 y ( t 1 t ) 3t t với 3 3 0 t 1 16 3 y 2 3
t 1; y 0 t . 3 3 Bảng biến thiên:
Dựa vào bảng biến thiên ta tìm được 3 t
thì hàm số y đạt giá trị lớn nhất. 3 3 3 32 3 Như vậy sin
thể tích của khối chóp S.ABCD lớn nhất và V y . 3 max 3 27
• XEM THÊM ĐỀ CƯƠNG ÔN THI TẠI:
• https://www.nbv.edu.vn/2022/01/de-cuong-danh-gia-nang-luc-dhqg-ha-noi.html
Theo dõi Fanpage: Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hoặc Facebook: Nguyễn Vương https://www.facebook.com/phong.baovuong
Tham gia ngay: Nhóm Nguyễn Bào Vương (TÀI LIỆU TOÁN) https://www.facebook.com/groups/703546230477890/
Ấn sub kênh Youtube: Nguyễn Vương
https://www.youtube.com/channel/UCQ4u2J5gIEI1iRUbT3nwJfA?view_as=subscriber
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Tải nhiều tài liệu hơn tại: https://www.nbv.edu.vn/
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 30 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31




