Ôn thi đánh giá năng lực(Đề 6) | Trường đại học Quốc gia Hà Nội

 Ôn thi đánh giá năng lực(Đề 6) | Trường đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Đánh giá năng lực

Trường: Đại học Quốc gia Hà Nội

Thông tin:

27 trang 2 tháng trước

Tác giả:

Profile Kim Oanh
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Điện thoại: 0946798489
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuong Trang 1
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Thống kê điểm môn toán trong một kì thi của 500 em học sinh thấy số bài được điểm 9 tỉ lệ
2%. Hỏi tần số của giá trị x
i
=9 là bao nhiêu?
A. B. C. D. 10 20 30 5
Câu 2. Một ôtô đang chạy thì người lái đạp phanh, từ thời điểm đó, ôtô chuyển động chậm dần đều với
vận tốc
12 24 / s
v t t m
, trong đó là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu t
đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét?
A.
20 m
. B.
18 m
. C.
24 m
. D.
15 m
.
Câu 3. Nghiệm của phương trình
log 1 2
x
là.
A.
1025
.
B.
2 1
e
.
C.
2
1e
. D.
101
.
Câu 4. Nghiệm của hệ phương trình:
2 2
5
6
xy x y
x y y x
là:
A.
1;2 , 2;1 .
B.
0;1 , 1; 0 .
C.
0; 2 , 2;0
. D.
1 1
2; , ;2 .
2 2
Câu 5. Tìm tọa độ điểm
M
là điểm biểu diễn số phức
z
biết
z
thỏa mãn phương trình
1 3 5i z i
.
A.
1; 4
M
. B.
1; 4
M
. C.
1; 4
M
. D.
1; 4
M
.
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
3; 1; 2M
và mặt phẳng
:3 2 4 0x y z
. Phương trình nào dưới đây là phương trình mặt phẳng đi qua
M
và song
song với
?
A.
3 2 6 0x y z
. B.
3 2 6 0x y z
.
C.
3 2 4 0x y z
. D.
3 2 14 0x y z
.
Câu 7. Trong không gian , cho điểm Oxyz
4; 1;3A
và đường thẳng
1 1 3
:
2 1 1
x y z
d
. Tọa độ
điểm là điểm đối xứng với điểm qua M A d là
A.
2; 5;3
M
. B.
M
. C.
M
. D.
0; 1;2
M
.
Câu 8. Tập nghiệm của bất phương trình
2 4
1 3
x x
x x
là:
A.
1
; 1;3
2

. B.
1
;1 1;3
2
S
.
C.
1
;1 3;
2
S

. D.
1
; 1;3
2
S

.
Câu 9. Cho phương trình
2
1 cos cos 2 cos sin
0
cos 1
x x x x
x
. Tính tổng các nghiệm nằm trong khoảng
0;2018
của phương trình đã cho?
A.
2035153
. B.
1017072
. C.
1019090
. D.
2037171
.
Câu 10.
Cho cấp số nhân
n
u
cố công bội
q
và
1
0u . Điểu kiện của
q
để cấp số nhân
n
u
có ba số
hạng liên tiếp là độ dài ba cạnh của một tam giác là :
ĐỀ
ĐỀ
ĐỀ
ĐỀ ĐỀ
SỐ
SỐ
SỐ
SỐ SỐ
6.
6.
6.
6. 6.
Ô
Ô
Ô
ÔÔ
N
N
N
N N
THI
THI
THI
THITHI
ĐG
ĐG
ĐG
ĐGĐG
N
N
N
NN
L
L
L
L L
ĐHQ
ĐHQ
ĐHQ
ĐHQĐHQ
G
G
G
GG
H
H
H
H H
À
À
À
À À
NỘ
NỘ
NỘ
NỘNỘ
I
I
I
I I
2
2
2
22
021
021
021
021021
-2
-2
-2
-2-2
022
022
022
022022
• |FanPage: Nguyễn Bảo Vương
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 2 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
A.
0 1 q
B.
2
51
1
q
C.
1q
.
D.
1 5 1 5
2 2
q
Câu 11. Họ tất cả các nguyên hàm của hàm số
2 1
1
x
f x
x
trên khoảng
;1
là
A.
2
3
2
1
x C
x
. B.
2 3ln 1 x x C
.
C.
2
3
2
1
x C
x
. D.
2 3ln 1 x x C
.
Câu 12. Cho hàm số
y f x
liên tục trên
R
và có đồ thị như hình vẽ dưới đây. Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình
6 6
4 sin cos 1f x x m có nghiệm.
A.
6
. B.
5
. C.
4
. D.
3
.
Câu 13. Một tay đua đang điều khiển chiếc xe đua của mình với vận tốc
180( / )km h
. Tay đua nhấn ga để
về đích, kể từ đó xe chạy với gia tốc
2
( ) 2 1 ( / )a t t m s . Hỏi rằng sau
4s
sau khi tay đua nhấn
ga thì xe đua chạy với vận tốc bao nhiêu km/h
A.
200( / )km h
. B.
252( / )km h
.
C.
288( / )km h
. D.
243( / )km h
.
Câu 14. Một người gửi tiết kiệm ngân hàng
20
triệu với lãi suất không đổi là
7,2%
trên năm và tiền lãi
hàng tháng được nhập vào vốn. Hỏi sau ít nhất bao nhiêu năm người đó thu về được tổng số tiền
lớn hơn
345
triệu đồng?
A.
33
năm.
B.
41
năm.
C.
50
năm.
D.
10
năm.
Câu 15.
Giải phương trình
3
log 2 211x
.
A.
211
3 2x
. B.
3
211 2x
. C.
3
211 2x
. D.
211
3 2x
.
Câu 16. Cho hình phẳng
H
giới hạn bởi các đường
, y x y x
và
4x
. Thể tích của khối tròn
xoay tạo thành khi quay hình
H
quanh trục hoành nhận giá trị nào sau đây:
A.
38
3
V
. B.
41
3
V
. C.
41
2
V
. D.
40
3
V
.
Câu 17. Có tất cả bao nhiêu giá trị nguyên của
m
để hàm số
3
4
x
y
x m
nghịch biến trên khoảng
2;
A.
2
B.
1
C.
3
D. Vô số
Câu 18. Tìm số phức
z
thỏa mãn
2
2 1 1 1 z z i z
và
1.z
A.
3 1
10 10
z i
. B.
z i
. C.
3 1
10 10
z i
. D.
z i
.
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 3
Câu 19. Trên mặt phẳng tạo độ
Oxy
, tập hợp điểm biểu diễn số phức
z
thỏa mãn
z i iz
là
A. Đường thẳng
2
y
. B. Đường thẳng
1
2
y
.
C. Đường thẳng
1
2
y
. D. Đường tròn tâm
0; 1
I
.
Câu 20. Cho đường thẳng
d
:
2
1 3
x t
y t
và
2
điểm
(
1 ; 2 , .)
2 ;
A B m
Định
m
để
A
và
B
nằm cùng
phía đối với
.d
A.
13
m
. B.
13
m
. C.
13
m
. D.
13
m
.
Câu 21. Trong mặt phẳng toạ độ cho ba điểm
(4;0), (0;2),C(1,6;3,2)
A B
. Tính bán kính đường tròn ngoại
tiếp tam giác.
A.
5
. B.
4,75
. C.
2 5
. D.
4,5
.
Câu 22. Trong không gian
O xyz
, cho các điểm
1;0;1 ; 5;2;3
M N
và mặt phẳng
:2 7 0
Q x y z
.
Vectơ pháp tuyến của mặt phẳng
P
đi qua các điểm
,M N
và vuông góc với mặt phẳng
Q
là
A.
1;0; 2
n
. B.
1;0; 2
n
. C.
4;0;8
n
. D.
8;0;4
n
.
Câu 23. Cho hình nón có thiết diện qua trục là tam giác đều. Gọi
1
V
,
2
V
lần lượt là thể tích của khối cầu
ngoại tiếp và nội tiếp hình nón đã cho. Tính tỉ số
1
2
V
V
.
A.
4
. B.
16
. C.
8
. D.
2
.
Câu 24. Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ như hình vẽ bên. Các kích thước
được ghi (cùng đơn vị
dm
). Tính thể tích của bồn chứa.
.
A.
5 2
4 3
. B.
3
3
4
3
. C.
2 5
4 .3
. D.
2
5
4
3
.
Câu 25. Cho hình lăng trụ
.
ABC A B C
có đáy là tam giác đều cạnh
a
,
3
2
a
AA
. Biết rằng hình chiếu
vuông góc của
A
lên
ABC
là trung điểm
BC
. Tính thể tích
V
của khối lăng trụ đó.
A.
3
2
3
a
V
. B.
3
3
4 2
a
V
. C.
3
3
2
V a
. D.
3
V a
.
Câu 26. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
8AB a
,
8SA SB SC SD a
.
Gọi
N
là trung điểm cạnh
SD
. Tính diện tích thiết diện của hình chóp
.
S ABCD
cắt bởi mặt
phẳng
ABN
.
A.
2
24a
. B.
2
12 11
a
. C.
2
12a
. D.
2
6 11
a
.
Câu 27. Trong không gian
Oxyz
cho mặt cầu
2 2 2
: 2 1 1 9
S x y z
và điểm
; ;
M a b c S
sao cho biểu thức
2 2P a b c
đạt giái trị nhỏ nhất. Khi đó giá trị biểu thức
T a b c
bằng
A.
1T
. B.
2T
. C.
1T
. D.
2T
.
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 4 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Câu 28. Trong không gian với hệ trục tọa độ
Oxyz
, cho tam giác
ABC
có
1;1;1A
,
4; 3;1B
và
1;1;2
C
. Đường phân giác trong của góc
A
có phương trình là:
A.
1 3
1 4
1 5
x t
y t
z t
. B.
4 3
3 4
6 5
x t
y t
z t
. C.
1 3
1 4
1 5
x t
y t
z t
. D.
4 3
3 4
6 5
x t
y t
z t
.
Câu 29. Cho hàm số
y f x
có đạo hàm
f x
trên
, phương trình
0f x
có
4
nghiệm thực và
đồ thị hàm số
f x
như hình vẽ. Tìm số điểm cực trị của hàm số
2
y f x
.
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 30. Trong không gian
Oxyz
, cho ba điểm
1; 2;1A
,
5; 0; 1B
,
3;1; 2C
và mặt phẳng
:3 3 0Q x y z
. Gọi
; ;M a b c
là điểm thuộc
Q
thỏa mãn
2 2 2
2MA MB MC
nhỏ
nhất. Tính tổng
5a b c
.
A.
14
. B.
11
. C.
9
. D.
15
.
Câu 31. Cho hàm số
)(xfy
có bảng xét dấu của
f x
như hình vẽ.
Có bao nhiêu số nguyên
m
để hàm số
mxfy
có đúng
3
cực trị.
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 32. Tìm
m
để phương trình:
4 2 2
3 3 0x m x m
có đúng
3
nghiệm:
A.
m
. B.
3m
. C.
3m
. D.
3m
.
Câu 33. Cho hàm số
y f x
liên tục trên
\ 0;1
thoả mãn:
2
2
2 1
1 2 , 0;1
x x
x x f x x x f x x
x
và
4
3 ln 3
9
f
.
Biết
2 ln2 ,f a b a b
. Giá trị
2
9a b
bằng.
A.
4
. B.
7
. C.
2
. D. 8.
Câu 34. Một hộp đựng 3 viên bi màu xanh, 5 viên bi màu đỏ, 6 viên bi màu trắng và 7 viên bi màu đen.
Chọn ngẫu nhiên đồng thời từ hộp 4 viên bi, tính xác suất để 4 viên được chọn không nhiều hơn 3
màu và luôn có bi màu xanh?
A.
2085
5985
. B.
2058
5985
. C.
2295
5985
. D.
2259
5985
.
Câu 35. Cho hình lăng trụ
.ABCD A B C D
có đáy là hình bình hành. Gọi
M
,
N
,
P
,
Q
lần lượt là trọng
tâm các tam giác
A AD
,
A CD
,
A CB
,
A BA
. Gọi
O
là điểm bất kỳ trên mặt đáy
ABCD
. Biết
thể tích khối chóp
.O MNPQ
bằng
V
. Tính theo
V
thể tích khối lăng trụ
.ABCD A B C D
.
A.
27
8
V
. B.
81
4
V
. C.
81
2
V
. D.
27
4
V
.
O
x
y
4
2
1
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 5
B. ĐIỀN KHUYẾT (15 CÂU)
Câu 36. Tiếp tuyến với đồ thị
3 2
1y x x tại điểm có hoành độ
0
1x có phương trình là:
Đáp án: …………..
Câu 37. Cho hàm số
y f x
có đạo hàm
2
1 2 3f x x x x
. Hàm số đã cho có bao nhiêu điểm
cực trị?
Đáp án: …………..
Câu 38. Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
với
1; 2; 1
A
,
0; 3; 4
B
,
2; 1; 1C
. Độ dài đường cao từ đến A
BC
bằng:
Đáp án: …………..
Câu 39. Lớp 10A4 cử đại diện 3 học sinh, 11A5 cử đại diện 4 học sinh, 12A6 cử đại diện 5 học sinh đi đại
hội (ngồi bàn tròn). Hỏi có bao nhiêu cách xếp 12 học sinh vào bàn sao cho các thành viên của
mỗi lớp ngồi cạnh nhau ?
Đáp án: …………..
Câu 40. Cho hàm số
f x
liên tục trên
thỏa mãn
1
( ) 5
lim 2
1
x
f x
x
. Tìm
m
để hàm số
2
2 ( ) 7 ( ) 1
1
5
1
2 1
khi x
g
f x f x
x
mx khi
x
x
liên tục tại
1x
?
Đáp án: …………..
Câu 41. Cho
a
,
b
,
c
là 3 số thực thỏa mãn
0
4 9 24 0
a
a b c
. Gọi
1
x ,
2
x lần lượt là hoành độ giao điểm
của parabol
2
: 2 3 4P y ax bx c
với trục hoành. Tìm giá trị nhỏ nhất của biểu thức
1 2
T x x
.
Đáp án: …………..
Câu 42. Tìm tất cả tham số thực của
m
để hàm số
3 2
1 1
2 2
3 3
y m x x mx
có cực đại, cực tiểu.
Đáp án: …………..
Câu 43. Cho hàm số
y f x
liên tục trên
và có đồ thị
f x
như hình vẽ
Đặt
0 6 2S f f f a f a
. Tập giá trị của
S
chứa tối đa bao nhiêu số nguyên?
Đáp án: …………..
Câu 44. Cho hàm số
y f x
xác định trên
và có bảng biến thiên như sau
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 6 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Số nghiệm thuộc đoạn
3 ;3
của phương trình
cos 1f x
là
Đáp án: …………..
Câu 45. Cho
1
z ,
2
z là hai trong các số phức
z
thỏa mãn điều kiện
5 3 5z i
, đồng thời
1 2
8z z
.
Tập hợp các điểm biểu diễn của số phức
1 2
w z z trong mặt phẳng tọa độ
Oxy
là đường tròn có
phương trình nào dưới đây?
Đáp án: …………..
Câu 46. Cho hình vuông
ABCD
và tam giác đều
SAB
cạnh
a
nằm trong hai mặt phẳng vuông góc với
nhau. Tính sin góc giữa đường thẳng
SC
và mặt phẳng
SAD
.
Đáp án: …………..
Câu 47. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 3
:
2 2 1
x y z
và điểm
1; 2; 0A
. Khoảng cách từ điểm
A
đến đường thẳng
bằng:
Đáp án: …………..
Câu 48. Cho ba số thực
a
,
b
,
1
;1
4
c
. Tìm giá trị nhỏ nhất
min
P
của biểu thức.
1 1 1
log log log
4 4 4
a b c
P b c a
.
Đáp án: …………..
Câu 49. Cho hình chóp
.S ABCD
có đáy là hình thoi có
ABC
mặt bên
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi
, ,H M N
lần lượt là trung điểm các cạnh
, ,AB SA SD
và
G
là trọng tâm tam giác
.SBC
Tính khoảng cách từ
G
đến mặt phẳng
( )HMN
biết khối chóp
.S ABCD
có thể tích
3
4
a
V
Đáp án: …………..
Câu 50. Cho hình hộp chữ nhật
.ABCD A B C D
có
2A D
,
,( 0)A B x x
. Góc giữa đường thẳng
AC
và mặt phẳng
ABB A
bằng
60
. Tính giá trị lớn nhất
max
V của thể tích khối hộp chữ nhật
.
ABCD A B C D
.
Đáp án: …………..
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 7
Lời giải tham khảo
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Thống kê điểm môn toán trong một kì thi của 500 em học sinh thấy số bài được điểm 9 tỉ lệ
2%. Hỏi tần số của giá trị x
i
=9 là bao nhiêu?
A.10 B. C. 20 30 D. 5
Lời giải:
Chọn A
tần số x
i
=9 là:
2%.500
10
100%
Câu 2. Một ôtô đang chạy thì người lái đạp phanh, từ thời điểm đó, ôtô chuyển động chậm dần đều với vận
tốc
12 24 / s
v t t m
, trong đó
t
là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp
phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét?
A.
20 m
. B.
18 m
. C.
24 m
. D.
15 m
.
Lời giải
Chọn C
Ta có:
12 24 0 2
v t t t
. Quản đường ôtô di chuyển từ lúc đạp phanh đến lúc dừng
hẳn là :
2
0
12 24 24
S t dt
.
Câu 3. Nghiệm của phương trình
log 1 2
x
là.
A.
1025
.
B.
2 1
e
.
C.
2
1
e
. D.
101
.
Lời giải
Chọn D
log 1 2
x
2
1 10 101
x x
Câu 4. Nghiệm của hệ phương trình:
2 2
5
6
xy x y
x y y x
là:
A.
B.
0;1 , 1; 0 .
C.
0; 2 , 2;0
. D.
1 1
2; , ; 2 .
2 2
Lời giải
Chọn A
Đặt
2
, 0
4S x y P xy S P
Ta có :
5
6
P S
PS
,S P
là nghiệm của phương trình
2
5 6 0 2; 3
X X XX
Khi
S P
(loại)
Khi
S P
thì
,x y
là nghiệm phương trình
2
3 2 0
XX
1; 2
X X
Vậy nghiệm của hệ là
1;2 , 2;1
.
Câu 5. Tìm tọa độ điểm
M
là điểm biểu diễn số phức
z
biết
z
thỏa mãn phương trình
1 3 5i z i
.
A.
M
. B.
1; 4
M
. C.
1; 4
M
. D.
1; 4
M
.
Lời giải
Chọn B
Ta có:
3 5
1 4
1
i
z i
i
1 4z i
1;4
M
.
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 8 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
3; 1; 2M
và mặt phẳng
:3 2 4 0
x y z
. Phương trình nào dưới đây là phương trình mặt phẳng đi qua
M
và song
song với
?
A.
3 2 6 0x y z
. B.
3 2 6 0x y z
.
C.
3 2 4 0x y z
. D.
3 2 14 0x y z
.
Lời giải
Chọn A
Mặt phẳng đi qua
3; 1; 2M
và song song với
có phương trình:
3 3 1 2 2 0 3 2 6 0x y z x y z
.
Câu 7. Trong không gian Oxyz, cho điểm
4; 1;3A
và đường thẳng
1 1 3
:
2 1 1
x y z
d
. Tọa độ điểm
M là điểm đối xứng với điểm qua A d là
A.
2; 5;3
M
. B.
1;0;2
M
. C.
2; 3;5
M
. D.
0; 1;2
M
.
Lời giải
Chọn C
Đường thẳng d có vectơ chỉ phương
(2; 1;1)a
và phương trình tham số
1 2
1
3
x t
y t
z t
.
Gọi là trung điểm của , khi đó nằm trên đường thẳng nên H AM H d
1 2 ; 1 ;3H t t t
2 3; ;AH t t t
. 0 2(2 3) 0 6 6 0 1AH d AH a t t t t t

Do đó tọa độ điểm
3; 2;4H
.
Mà là trung điểm của nên H AM
M
.
Câu 8. Tập nghiệm của bất phương trình
2 4
1 3
x x
x x
là:
A.
1
; 1;3
2

. B.
1
;1 1;3
2
S
.
C.
1
;1 3;
2
S

. D.
1
; 1;3
2
S

.
Lời giải
Chọn A
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 9
Ta có
2 3 1 4
2 4 2 4
0 0
1 3 1 3 1 3
x x x x
x x x x
x x x x x x
2 2
6 3 4
0
1 3
x x x x
x x
4 2 2 1
0 0
1 3 1 3
x x
x x x x
Lập bảng xét dấu ta có
1
; 1;3
2

x
.
Câu 9. Cho phương trình
2
1 cos cos 2 cos sin
0
cos 1
x x x x
x
. Tính tổng các nghiệm nằm trong khoảng
0;2018
của phương trình đã cho?
A.
2035153
. B.
1017072
. C.
1019090
. D.
2037171
.
Lời giải
Chọn B
Điều kiện:
2 ,x k k
.
2
1 cos cos 2 cos sin
0
cos 1
x x x x
x
2
1 cos cos2 cos 1 cos
0
cos 1
x x x x
x
cos2 cos 1 cos 0
x x x
cos2 1x
,x k k
. Đối chiếu điều kiện ta thấy với
k
lẻ sẽ không thỏa. Vậy các nghiệm thuộc
0;2018
của phương trình là
Khi đó,
2 ;4 ; 6 ;...;2016
, có tất cả
1008
nghiệm.
Tổng tất cả các nghiệm thuộc khoảng
0;2018
:
1 2 1008
...
S x x x
1008
2 2016 1017072
2
.
Câu 10. Cho cấp số nhân
n
u
cố công bội
q
và
1
0
u
. Điểu kiện của
q
để cấp số nhân
n
u
có ba số
hạng liên tiếp là độ dài ba cạnh của một tam giác là :
A.
0 1 q
B.
2
51
1
q
C.
1
q
.
D.
1 5 1 5
2 2
q
Lời giải
Chọn D
Giả sử ba số hạng liên tiếp là
1 2
1 1 1
, ,
n n n
u q u q u q
. Ba số hạng này là độ dài ba cạnh của một tam
giác
2 1 2
1 1 1
1 2 2
1 1 1
21 2
1 1 1
0 1 0
1 5 1 5
0 1 0
2 2
1 0
0
n n n
n n n
n n n
u q u q u q q q
u q u q u q q q q
q q
u q u q u q
.
Câu 11. Họ tất cả các nguyên hàm của hàm số
2 1
1
x
f x
x
trên khoảng
;1
là
A.
2
3
2
1
x C
x
. B.
2 3ln 1
x x C
.
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 10 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
C.
2
3
2
1
x C
x
. D.
2 3ln 1 x x C
.
Lời giải
Chọn D
Ta có
2 1 3
d d 2 d 2 3ln 1
1 1
x
f x x x x x x C
x x
.
Câu 12. Cho hàm số
y f x
liên tục trên
R
và có đồ thị như hình vẽ dưới đây. Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình
6 6
4 sin cos 1f x x m có nghiệm.
A.
6
. B.
5
. C.
4
. D.
3
.
Lời giải
Chọn B
Đặt
6 6 2 2
3
4 sin cos 1 4 1 sin 2 1 3 3sin 2
4
t x x x x
0;3t
Phương trình
6 6
4 sin cos 1f x x m có nghiệm khi và chỉ khi phương trình
f t m
có
nghiệm thuộc
0;3 4 0m
có 5 giá trị nguyên
Câu 13. Một tay đua đang điều khiển chiếc xe đua của mình với vận tốc
180( / )km h
. Tay đua nhấn ga để
về đích, kể từ đó xe chạy với gia tốc
2
( ) 2 1 ( / )a t t m s . Hỏi rằng sau
4s
sau khi tay đua nhấn
ga thì xe đua chạy với vận tốc bao nhiêu km/h
A.
200( / )km h
. B.
252( / )km h
.
C.
288( / )km h
. D.
243( / )km h
.
Lời giải
Chọn B
Đổi đơn vị
180( / ) 50(m/ s)km h
.
Từ khi tay đua nhấn ga, xe chạy với vận tốc
2
( ) (2 1)v t t dt t t C
.
Tại
0, (0) 50(m/ s)t v C
2
( ) 50.v t t t
Sau khi tay đua nhấn ga
4s
thì xe chạy với vận tốc
2
(4) 4 4 50 70( / ).v m s
Đổi đơn vị
70( / ) 252( / ).m s km h
Câu 14. Một người gửi tiết kiệm ngân hàng
20
triệu với lãi suất không đổi là
7,2%
trên năm và tiền lãi
hàng tháng được nhập vào vốn. Hỏi sau ít nhất bao nhiêu năm người đó thu về được tổng số tiền
lớn hơn
345
triệu đồng?
A.
33
năm.
B.
41
năm.
C.
50
năm.
D.
10
năm.
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 11
Lời giải
Chọn B
Từ giả thiết ta suy ra người đó đã gửi ngân hàng theo hình thức lãi kép nên ta có công thức
1
n
T A r
với
20
A
triệu là số tiền ban đầu,
345
T
triệu là số tiền người đó nhận được sau
n
năm gửi,
7,2% 0,072
r
là lãi xuất hàng năm.
Ta có
1,072
69 69
345 20.1,072 1,072 log 40,96
4 4
n n
n
Vậy sau ít nhất
41
năm người đó thu về được tổng số tiền lớn hơn
345
triệu đồng
Câu 15. Giải phương trình
3
log 2 211
x
.
A.
211
3 2
x
. B.
3
211 2
x
. C.
3
211 2
x
. D.
211
3 2
x
.
Lời giải
Chọn D
Ta có:
3
log 2 211
x
211
2 3
x
211
3 2
x
.
Câu 16. Cho hình phẳng
H
giới hạn bởi các đường
,
y x y x
và
4
x
. Thể tích của khối tròn
xoay tạo thành khi quay hình
H
quanh trục hoành nhận giá trị nào sau đây:
A.
38
3
V
. B.
41
3
V
. C.
41
2
V
. D.
40
3
V
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm:
2
0
0
x
x x x
x x
.
Thể tích khối tròn xoay cần tìm là
4
2
0
Ox
V x x dx
.
Xét phương trình
2
0
0
1
x
x x
x
.
Do đó
1 4 1 4
2 2 2 2
0 1 0 1
Ox
V x x dx x x dx x x dx x x dx
.
1 4
3 2 3 2
0 1
41
3 2 3 2 3
x x x x
(đvtt).
Câu 17. Có tất cả bao nhiêu giá trị nguyên của
m
để hàm số
3
4
x
y
x m
nghịch biến trên khoảng
2;
A.
2
B.
1
C.
3
D. Vô số
Lời giải
Chọn B
TXĐ:
\ 4D m
2
4 3
'
4
m
y
x m
Hàm số
3
4
x
y
x m
nghịch biến trên khoảng
2;
0 2;y x
4 3 0
4 2;
m
m
3
4
4 2
m
m
3
4
1
2
m
m
1 3
2 4
m
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vì
m
nên
0
m
. Vậy có
1
giá trị
m
thỏa mãn yêu cầu bài toán.
Câu 18. Tìm số phức
z
thỏa mãn
2
2 1 1 1
z z i z
và
1.
z
A.
3 1
10 10
z i
. B.
z i
. C.
3 1
10 10
z i
. D.
z i
.
Lời giải
Chọn C
Gọi
z x yi
với
x
,
y
.
Ta có
2 2
z 1 x y 1
.
Và
2
2 2
2 z 1 z 1 1 i z 2 x yi 1 x yi 1 1 i x y
2 2 2 2
x y 3x 1 y x y i 0
2 2
2 2
3 1 0
0
x y x
x y y
2
10x 3x 0
y 3x 1
3
x
10
1
y
10
Vậy
3 1
z i
10 10
.
Câu 19. Trên mặt phẳng tạo độ
Oxy
, tập hợp điểm biểu diễn số phức
z
thỏa mãn
z i iz
là
A. Đường thẳng
2
y
. B. Đường thẳng
1
2
y
.
C. Đường thẳng
1
2
y
. D. Đường tròn tâm
0; 1
I
.
Lời giải
Chọn C
Gọi số phức
z a bi
,a b
.
Ta có:
z i iz
a bi i i a bi
1
a b i b ai
2
2 2 2
1
a b b a
2 1 0
b
.
Vậy tập hợp điểm biểu diễn số phức
z
thỏa mãn điều kiện bài toán là đường thẳng
1
2
y
.
Câu 20. Cho đường thẳng
d
:
2
1 3
x t
y t
và
2
điểm
(
1 ; 2 , .)
2 ;
A B m
Định
m
để
A
và
B
nằm cùng
phía đối với
.d
A.
13
m
. B.
13
m
. C.
13
m
. D.
13
m
.
Lời giải
Chọn B
Phương trình tổng quát của đường thẳng
:3( 2) 1( 1) 0.
d x y
hay
:3x 7 0
d y
.
,A B
cùng phía với
(3 7)(3 7) 0 2( 13 ) 0 13.
A A B B
d x y x y m m
Câu 21. Trong mặt phẳng toạ độ cho ba điểm
(4;0), (0; 2),C(1,6;3,2)
A B
. Tính bán kính đường tròn ngoại
tiếp tam giác.
A.
5
. B.
4,75
. C.
2 5
. D.
4,5
.
Lời giải
Chọn A
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 13
Gọi
( ; )I a b
là tâm đường tròn ngoại tiếp tam giác
Ta có
2 2
2 2
2 2 2
2
4 2
4 1,6 3,2
x y x y
IA IB
IA IC
x y x y
2 3 2
(2;1) 2; 1 5
0, 3 0,4 0, 2 1
x y x
I IA R IA
x y y

.
Câu 22. Trong không gian
O xyz
, cho các điểm
1;0;1 ; 5;2;3
M N
và mặt phẳng
:2 7 0
Q x y z
.
Vectơ pháp tuyến của mặt phẳng
P
đi qua các điểm
,M N
và vuông góc với mặt phẳng
Q
là
A.
1;0; 2
n
. B.
1;0; 2
n
. C.
4;0;8
n
. D.
8;0;4
n
.
Lời giải
Chọn B
Ta có
4;2;2
MN
và vectơ pháp tuyến của mặt phẳng
Q
là
2; 1;1
Q
n
.
Mà
và
P Q
nên vectơ pháp tuyến của mặt phẳng
P
là
n
thỏa mãn:
( )
( )
, 4;0; 8
Q
Q
n MN
n MN n
n n

.
Vậy vectơ pháp tuyến của mặt phẳng
P
là
1;0; 2
n
.
Câu 23. Cho hình nón có thiết diện qua trục là tam giác đều. Gọi
1
V
,
2
V
lần lượt là thể tích của khối cầu
ngoại tiếp và nội tiếp hình nón đã cho. Tính tỉ số
1
2
V
V
.
A.
4
. B.
16
. C.
8
. D.
2
.
Lời giải
Chọn C
Giả sử hình nón đã cho có đường sinh
l a
.
Ta có khối cầu ngoại tiếp và khối cầu nội tiếp hình nón có bán kính lần lượt là
3
3
a
R
và
3
6
a
r
.
Gọi
1
V
,
2
V
lần lượt là thể tích của khối cầu ngoại tiếp và nội tiếp hình nón.
Ta có
1
2
4
3
4
V
V
3
8
R
r
.
Câu 24. Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ như hình vẽ bên. Các kích thước
được ghi (cùng đơn vị
dm
). Tính thể tích của bồn chứa.
a
r
R
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 14 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
.
A.
5 2
4 3
. B.
3
3
4
3
.
C.
2 5
4 .3
. D.
2
5
4
3
.
Lời giải
Chọn C
Gọi
1
V
là thể tích hình trụ có đường cao
36 dm
và bán kính đường tròn đáy 9 (dm).
2
V
là thể tích nửa hình cầu có bán kính
9 dm
.
Ta có
2
1
.9 .36 2916V
3
dm
và
3
2
2
.9 486
3
V
3
cm .
.
Do đó
1 2
2 3888V V V
3 2 5 3
dm 4 .3 dm
.
Câu 25. Cho hình lăng trụ
.ABC A B C
có đáy là tam giác đều cạnh
a
,
3
2
a
AA
. Biết rằng hình chiếu
vuông góc của
A
lên
ABC
là trung điểm
BC
. Tính thể tích
V
của khối lăng trụ đó.
A.
3
2
3
a
V
. B.
3
3
4 2
a
V
. C.
3
3
2
V a
.
D.
3
V a
.
Lời giải
Chọn B
Gọi
H
là trung điểm
BC
, ta có:
A H ABC
.
Xét tam giác
ABC
ta có:
3
2
a
AH
.
Xét tam giác
AA H
vuông tại
H
,
2 2
6
2
a
A H AA AH
.
Vậy thể tích khối lăng trụ:
2 3 3
3 6 3 2 3
. .
4 2 8
4 2
LT ABC
a a a a
V S A H
.
Câu 26. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
8AB a
,
8SA SB SC SD a
.
Gọi
N
là trung điểm cạnh
SD
. Tính diện tích thiết diện của hình chóp
.S ABCD
cắt bởi mặt
phẳng
ABN
.
A.
2
24a
. B.
2
12 11a
.
C.
2
12a
. D.
2
6 11a
.
Lời giải
Chọn B
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 15
Mặt phẳng
ABN
chứa
//AB CD
nên cắt mặt phẳng
SCD
theo giao tuyến
//NM CD
và
M
cũng là trung điểm của
SC
. Suy ra thiết diện cần tìm là hình thang cân
ABMN
.
Hạ
NI AB
. Ta có
2 2 2
NI AN AI
với
8 3
4 3
2
a
AN a
.
2
AI AB MN
8 4 4 2a a a AI a
. Từ đó suy ra
2 11
NI a
.
Vậy
1
.
2
ABMN
S AB MN NI
2
1
8 4 2 11 12 11
2
a a a a
.
Câu 27. Trong không gian
Oxyz
cho mặt cầu
2 2 2
: 2 1 1 9
S x y z
và điểm
; ;
M a b c S
sao cho biểu thức
2 2P a b c
đạt giái trị nhỏ nhất. Khi đó giá trị biểu thức
T a b c
bằng
A.
1T
. B.
2T
. C.
1T
. D.
2T
.
Lời giải
Chọn A
Ta có
2 2 6 2 2 1 2 1
P a b c P a b c
.
Áp dụng bất đẳng thức Bunhiacopski ta có
2
2 2 2 2
2 2 2
6 2 2 1 2 1 1 2 2 2 1 1
P a b c a b c
2
6 81 9 6 9 3 15
P P P
. Từ đó
min
2 1 1
1 2 23
2 2 1 2 1 9
a b c
P
a b c
1
9 2 9
1
2 1 1
1
1 2 2
a
a
b
a b c
c
Vậy
P
đạt giá trị nhỏ nhất khi
1; 1; 1 1
M T a b c
.
Câu 28. Trong không gian với hệ trục tọa độ
Oxyz
, cho tam giác
ABC
có
1;1;1
A
,
4; 3;1
B
và
1;1;2
C
. Đường phân giác trong của góc
A
có phương trình là:
A.
1 3
1 4
1 5
x t
y t
z t
. B.
4 3
3 4
6 5
x t
y t
z t
. C.
1 3
1 4
1 5
x t
y t
z t
. D.
4 3
3 4
6 5
x t
y t
z t
.
Lời giải
Chọn B
M
N
O
D
B
C
A
S
I
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
3; 4;0
AB
,
0;0;1
AC
,
5
AB AB

,
1
AC AC

.
Nhận xét:
0
AB AC

⇒
AB AC
⇒
ABC
vuông tại
A
.
Trên cạnh
AB
lấy
B
sao cho
1
AB
⇒
1 1 3 4
3; 4;0 ; ;0
5 5 5 5
AB AB
.
Đường phân giác trong của góc
A
là
AD
có một vectơ chỉ phương là:
3 4 1
; ;1 3; 4;5 3; 4;5
5 5 5
AD AC AB
 
.
Vậy phương trình đường phân giác của góc
A
là:
1 3
: 1 4
1 5
x t
AD y t
z t
.
Cho
1
t
4; 3;6E AD
4 3
: 3 4
6 5
x t
AD y t
z t
.
Câu 29. Cho hàm số
y f x
có đạo hàm
f x
trên
, phương trình
0
f x
có
4
nghiệm thực và
đồ thị hàm số
f x
như hình vẽ. Tìm số điểm cực trị của hàm số
2
y f x
.
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn C
Ta có:
2
2 .
y x f x
0
y
2
2
2
2
2 0
0
1
2
4
x
x
x
x
x
0
0
1
2
2
x
x
x
x
x
Do
2
0
f x
2
2
4
0 1
x
x
2
2
1 1
x
x
x
O
x
y
4
2
1
A
D
B
C
B'
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 17
Vậy hàm số có 5 điểm cực trị.
Câu 30. Trong không gian
Oxyz
, cho ba điểm
1; 2;1A
,
5; 0; 1B
,
3;1; 2C
và mặt phẳng
:3 3 0Q x y z
. Gọi
; ;M a b c
là điểm thuộc
Q
thỏa mãn
2 2 2
2MA MB MC
nhỏ
nhất. Tính tổng
5a b c
.
A.
14
. B.
11
. C.
9
. D.
15
.
Lời giải
Chọn C
Gọi
E
là điểm thỏa mãn
2 0EA EB EC
 
3;0;1E
.
Ta có:
2 2 2
2S MA MB MC
2 2 2
2MA MB MC
 
2 2 2
2ME EA ME EB ME EC
   
2 2 2 2
4 2ME EA EB EC
.
Vì
2 2 2
2EA EB EC
không đổi nên
S
nhỏ nhất khi và chỉ khi
ME
nhỏ nhất.
M
là hình chiếu vuông góc của
E
lên
Q
.
Phương trình đường thẳng
:ME
3 3
1
x t
y t
z t
.
Tọa độ điểm
M
là nghiệm của hệ phương trình:
3 3
1
3 3 0
x t
y t
z t
x y z
0
1
2
1
x
y
z
t
.
0; 1;2
M
0a
,
1b
,
2c
.
5 0 1 5.2a b c 9
.
Câu 31. Cho hàm số
)(xfy
có bảng xét dấu của
f x
như hình vẽ.
Có bao nhiêu số nguyên
m
để hàm số
mxfy
có đúng
3
cực trị.
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Ta có bảng xét dấu của hàm số
y f x m
:
Hàm số
mxfy
có đúng
3
cực trị khi và chỉ khi hàm số
mxfy
có đúng
1
cực trị
dương
24
02
04
m
m
m
.
Vì
m
nguyên nên
2;3 m
.
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 18 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Vậy có
2
giá trị
m
cần tìm.
Câu 32. Tìm
m
để phương trình:
4 2 2
3 3 0x m x m
có đúng
3
nghiệm:
A.
m
. B.
3
m
. C.
3
m
. D.
3
m
.
Lời giải
Chọn B
Đặt
2
, 0t x t
, phương trình trở thành
2 2
3 3 0t m t m
(*)
Phương trình đã cho có đúng nghiệm khi phương trình (*) có 1 nghiệm bằng
0
và
1
nghiệm
dương.
Khi
2
0 0 3 0 3t x m m
.
3m
phương trình
4
0 0x x
(không thỏa).
3m
phương trình
4 2 2 2
0
2 3 0 2 3 0
2 3
x
x x x x
x
(thỏa).
Vậy
3m
thỏa yêu cầu.
Câu 33. Cho hàm số
y f x
liên tục trên
\ 0;1
thoả mãn:
2
2
2 1
1 2 , 0;1
x x
x x f x x x f x x
x
và
4
3 ln 3
9
f
.
Biết
2 ln2 ,f a b a b
. Giá trị
2
9a b
bằng.
A.
4
. B.
7
. C.
2
. D. 8.
Lời giải
Xét
1x
ta có:
2
2
3
2 2
3
2 2
2
2
2
2
2 1
1 2 .
2 1
2
1
2 1
2
.
1 1 1
2 2
1
1
2
1
2
1
2ln
1
x x
x x f x x x f x
x
x x
x
f x f x
x x x
x x
x x x
f x f x
x x x x x
x x x x
f x f x
x x
x
x x
f x
x x
x x
f x dx
x x
x
f x x x C
x
Mà
9
3 ln 3
4
f
nên ta có
9 9
. ln 3 3 2 ln 3 3
2 4
C C
.
Suy ra
2
2
2ln 3 1
1 1
2 ln2 9 2.
4 2
x x x
f x f a b
x
Câu 34. Một hộp đựng 3 viên bi màu xanh, 5 viên bi màu đỏ, 6 viên bi màu trắng và 7 viên bi màu đen.
Chọn ngẫu nhiên đồng thời từ hộp 4 viên bi, tính xác suất để 4 viên được chọn không nhiều hơn 3
màu và luôn có bi màu xanh?
A.
2085
5985
. B.
2058
5985
. C.
2295
5985
. D.
2259
5985
.
3
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 19
Lời giải
Chọn C
Tổng số bi là:
3 5 6 7 21
(viên).
Tổng số bi không tính màu xanh là:
5 6 7 18
(viên).
Chọn ngẫu nhiên 4 viên có:
4
21
5985C
(cách).
Số cách chọn 4 viên có đủ 4 màu là:
3.5.6.7 630
(cách).
Số cách chọn 4 viên không có viên bi màu xanh là:
4
18
3060C
(cách).
Số cách chọn để 4 viên được chọn không nhiều hơn 3 màu và luôn có bi màu xanh là:
5985 630 3060 2295
.
Vậy xác suất cần tìm là:
2295
5985
.
Câu 35. Cho hình lăng trụ
.ABCD A B C D
có đáy là hình bình hành. Gọi
M
,
N
,
P
,
Q
lần lượt là trọng
tâm các tam giác
A AD
,
A CD
,
A CB
,
A BA
. Gọi
O
là điểm bất kỳ trên mặt đáy
ABCD
. Biết
thể tích khối chóp
.O MNPQ
bằng
V
. Tính theo
V
thể tích khối lăng trụ
.ABCD A B C D
.
A.
27
8
V
. B.
81
4
V
. C.
81
2
V
. D.
27
4
V
.
Lời giải
Chọn C
Gọi
M
,
N
,
P
,
Q
lần lượt là trung điểm của các cạnh
, , ,AD DC CB BA
.
Ta có
2
2 1 2
. . .S .S
3 9 2 9
MNPQ M N P Q ABCD ABCD
S S
.
Đường cao của khối chóp
.O MNPQ
là:
. .
1
3
O MNPQ A ABCD
h h
.
2
27
A ABCD
V V
.
Ta lại có
. ' ' ' '
1
3
A ABCD ABCDA B C D
V V
.
Suy ra
. .
2 81
81 2
ABCD A B C D ABCD A B C D
V V V V
.
B. ĐIỀN KHUYẾT (15 CÂU)
Câu 36. Tiếp tuyến với đồ thị
3 2
1y x x tại điểm có hoành độ
0
1x có phương trình là:
Đáp án: …………..
Lời giải.
Tọa độ tiếp điểm:
0 0
1 1x y . Tiếp điểm
1; 1M
.
Hệ số góc của tiếp tuyến:
2
3 2 1 1y x x y
.
Tiếp tuyến tại điểm có hoành độ
0
1x có phương trình:
1 1y x y x
.
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 37. Cho hàm số
y f x
có đạo hàm
2
1 2 3
f x x x x
. Hàm số đã cho có bao nhiêu điểm
cực trị?
Đáp án: …………..
Lời giải
Số điểm cực trị của hàm số là số nghiệm đơn của
0
f x
2
0
1 2 3 0 1
3
2
x
x x x x
x
1x
là nghiệm kép,
3
0,
2
x x
là nghiệm đơn.
Câu 38. Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
với
1; 2; 1
A
,
0; 3; 4
B
,
2; 1; 1
C
. Độ dài đường cao từ
A
đến
BC
bằng:
Đáp án: …………..
Lời giải
2; 2; 5 , 1; 1; 5
BC BA
.
,
50
33
BC BA
AH
BC
 

.
Câu 39. Lớp 10A4 cử đại diện 3 học sinh, 11A5 cử đại diện 4 học sinh, 12A6 cử đại diện 5 học sinh đi đại
hội (ngồi bàn tròn). Hỏi có bao nhiêu cách xếp 12 học sinh vào bàn sao cho các thành viên của
mỗi lớp ngồi cạnh nhau ?
Đáp án: …………..
Lời giải
Ghép 3 học sinh lớp 10A4 thành một nhóm.
Ghép 4 học sinh lớp 11A5 thành một nhóm.
Ghép 5 học sinh lớp 12A6 thành một nhóm.
Xếp 3 nhóm quanh bàn tròn có
2!
cách, hoán vị 3 học sinh lớp 10A4 có
3!
cách, hoán vị 4 học
sinh lớp 11A5 có
4!
cách, hoán vị 5 học sinh lớp 12A6 có
5!
cách. Theo quy tắc nhân có
2.3!4!5!
cách xếp thỏa mãn yêu cầu bài toán.
Câu 40. Cho hàm số
f x
liên tục trên
thỏa mãn
1
( ) 5
lim 2
1
x
f x
x
. Tìm
m
để hàm số
2
2 ( ) 7 ( ) 1
1
5
1
2 1
khi x
g
f x f x
x
mx khi
x
x
liên tục tại
1x
?
Đáp án: …………..
Lời giải.
Vì
1 1 1
( ) 5
lim 2 lim[ ( ) 5] 0 lim ( ) 5
1
x x x
f x
f x f x
x
Ta có: +)
1 2
g m
+)
2
1 1 1
2 ( ) 7 ( ) 15 [2 ( ) 3][ ( ) 5]
lim lim lim
1 1
x x x
f x f x f x f
g x
x
x x
1 1
( ) 5
lim lim[2 ( ) 3]
1
x x
f x
f x
x
2(2.5 3) 26
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 21
Hàm số
g x
liên tục tại
1x
khi:
1
lim 1
x
g x g
2 26
m
24
m
Câu 41. Cho
a
,
b
,
c
là 3 số thực thỏa mãn
0
4 9 24 0
a
a b c
. Gọi
1
x
,
2
x
lần lượt là hoành độ giao điểm
của parabol
2
: 2 3 4P y ax bx c
với trục hoành. Tìm giá trị nhỏ nhất của biểu thức
1 2
T x x
.
Đáp án: …………..
Lời giải
Phương trình hoành độ giao điểm của
P
với trục hoành là
2
2 3 4 0
ax bx c
(1).
P
cắt trục hoành tại hai điểm khi và chỉ khi phương trình (1) có nghiệm, tức là ta có
2
9 32 0
b ac
Khi đó hoành độ giao điểm
1
x
,
2
x
của
P
với trục hoành là nghiệm của (1), suy ra
2
1 2
2
9 32
2 4
b ac
T x x
a a
(2)
Theo bài ra ta có
1 9
4 9 24 0
6 24
a b c c a b
(3).
Thay (3) vào (2) ta có
2
2
2
9 4 3 1 1
3 1
4 3 2 3
3
b b b
T
a a a
,
Dấu “=” xảy ra khi và chỉ khi
3 3
1 0 12
2 2
b
a b c
a
.
Vậy giá trị nhỏ nhất của
T
bằng
1
3
.
Câu 42. Tìm tất cả tham số thực của
m
để hàm số
3 2
1 1
2 2
3 3
y m x x mx
có cực đại, cực tiểu.
Đáp án: …………..
Lời giải
2
1
2 2
3
y m x x m
.
Hàm số có cực đại, cực tiểu khi phương trình
0
y
có hai nghiệm phân biệt
0
2 0
m
2
1 2
1 0
3 3
2
m m
m
3 1
2
m
m
3 2
m
hoặc
2 1
m
.
Câu 43. Cho hàm số
y f x
liên tục trên
và có đồ thị
f x
như hình vẽ
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 22 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
0 6 2
S f f f a f a
. Tập giá trị của
S
chứa tối đa bao nhiêu số nguyên?
Đáp án: …………..
Lời giải
Ta có:
6
0 2
d d
a
a
S f x x f x x
1 2 3 4
S S S S .
Do đó:
2 2 4 6 2
( 0)4
2 2 2 2
a m n a n
m
S
3 10n m a
.
Do
0
2 6
m a
a n
nên
2 6n m
Suy ra:
4 3 10 8
a n m a a
Vậy
S
có tối đa 11 giá trị nguyên.
Câu 44. Cho hàm số
y f x
xác định trên
và có bảng biến thiên như sau
Số nghiệm thuộc đoạn
3 ;3
của phương trình
cos 1f x
là
Đáp án: …………..
Lời giải
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 23
Ta có
0 cos 1x
. Khi đó từ bảng biến thiên ta được
cos 1
cos 0
cos 1
cos 0 1
cos 1
f x
x
f x
x a a
f x
Vẽ đồ thị hàm số
cos ; 3 ; 3g x x x
.
Từ đồ thị ta có
Phương trình
cos 0x
có 6 nghiệm.
Phương trình
cos (0 1)x a a
có 12 nghiệm.
Vậy ta có tổng cộng 18 nghiệm.
Câu 45. Cho
1
z ,
2
z là hai trong các số phức
z
thỏa mãn điều kiện
5 3 5z i
, đồng thời
1 2
8z z
.
Tập hợp các điểm biểu diễn của số phức
1 2
w z z trong mặt phẳng tọa độ
Oxy
là đường tròn có
phương trình nào dưới đây?
Đáp án: …………..
Lời giải
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 24 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
A
,
B
,
M
là các điểm biểu diễn của
1
z ,
2
z ,
w
. Khi đó
A
,
B
thuộc đường tròn
2 2
: 5 3 25
C x y
và
1 2
8AB z z
.
C
có tâm
5;3I
và bán kính
5R
, gọi
T
là trung điểm của $AB$ khi đó
T
là trung điểm
của $OM$ và
2 2
3IT IA TA
.
Gọi
J
là điểm đối xứng của
O
qua
I
suy ra
10;6J
và $IT$ là đường trung bình của tam giác
OJM
, do đó
2 6
JM IT
.
Vậy
M
thuộc đường tròn tâm
J
bán kính bằng
6
và có phương trình
2 2
10 6 36x y
.
Câu 46. Cho hình vuông
ABCD
và tam giác đều
SAB
cạnh
a
nằm trong hai mặt phẳng vuông góc với
nhau. Tính sin góc giữa đường thẳng
SC
và mặt phẳng
SAD
.
Đáp án: …………..
Lời giải
Gọi
I
là trung điểm của
AB
. Khi đó
SI ABCD
.
Ta có
AD AB
AD SI
AD SAB
mà
AD SAD
suy ra
SAD SAB
.
Dựng
BH SA
tại
H
suy ra
SH SAD
.
Trong mặt phẳng
SAD
kẻ
/ /Hx AD
. Trong mặt phẳng
,
BC Hx
qua
C
kẻ đường thẳng song
song với
BH
cắt
Hx
tại
K
thì
CK SAD
. Suy ra
SK
là hình chiếu vuông góc của
SC
trên
x
S
I
K
H
D
C
B
A
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 25
mặt phẳng
SAD
nên góc giữa đường thẳng
SC
và mặt phẳng
SAD
là góc
CSK
. Ta có
3
2
a
BH CK
. Trong tam giác
SCI
có
2 2
2 2
3 5
2
4 4
a a
SC SI IC a
.
Suy ra
3
6
2
sin
4
2
a
CK
CSK
SC
a
Câu 47. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1 2 3
:
2 2 1
x y z
và điểm
1; 2; 0
A
. Khoảng cách từ điểm
A
đến đường thẳng
bằng:
Đáp án: …………..
Lời giải
Gọi
H
là hình chiếu vuông góc của
A
trên
, ta có
1 2 ; 2 2 ; 3
H t t t
,
t
.
2 2 ; 2 ; 3
AH t t t

Một vectơ chỉ phương của
là
2; 2; 1
u
.
. 0 4 4 4 3 0AH u t t t
7
9
t
.
4 14 20
; ;
9 9 9
AH
16 196 400 2 17
81 81 81 3
AH
.
Vậy
2 17
;
3
d A
.
Câu 48. Cho ba số thực
a
,
b
,
1
;1
4
c
. Tìm giá trị nhỏ nhất
min
P
của biểu thức.
1 1 1
log log log
4 4 4
a b c
P b c a
.
Đáp án: …………..
Lời giải
Vợi mọi
1
;1
4
x
ta có
2
2 2
1 1 1
0
4 2 4
x x x x x
.
Lấy logarit 2 vế, ta được
2
1
log log
4
t t
x x
(với
0;1
t
(*).
Áp dụng BĐT (*) ta được:
2
1
log log 2log
4
a a a
b b b
.
2
1
log log 2log
4
b b b
c c c
.
2
1
log log 2log
4
c c c
a a a
.
Suy ra
3
min
2 log log log 2.3 log .log .log 6
a b c a b c
P b c a b c a P
.
Câu 49. Cho hình chóp
.
S ABCD
có đáy là hình thoi có
60 ,
ABC
mặt bên
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi
, ,H M N
lần lượt là trung điểm các cạnh
, ,AB SA SD
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Trang 26 Fanpage Nguyễn Bảo Vương
https://www.facebook.com/tracnghiemtoanthpt489/
và
G
là trọng tâm tam giác
.SBC
Tính khoảng cách từ
G
đến mặt phẳng
( )HMN
biết khối chóp
.S ABCD
có thể tích
3
4
a
V
Đáp án: …………..
Lời giải
Gọi
x
là cạnh hình thoi, ta có:
3 3
3
, 3,
2
1 1
. . .
3 2 4 4
x
AC x BD x SH
x a
V AC BD SH x a
Dựng
/ / , , .
MK SH KI HO KJ MI KJ HMN
Chứng minh được
/ /SBC
; ; ; 2 ; 2 .d G d S d A d K KJ
Tính được
1 3 3 3
. , .
4 2 8 2 4
a a SH a
KI MK
Suy ra
2 2
. 15
.
20
KI KM a
KJ
KI KM
Vậy
15 15
; 2 2. .
20 10
a a
d G KJ
Câu 50. Cho hình hộp chữ nhật
.ABCD A B C D
có
2A D
,
,( 0)A B x x
. Góc giữa đường thẳng
AC
và mặt phẳng
ABB A
bằng
60
. Tính giá trị lớn nhất
max
V của thể tích khối hộp chữ nhật
.
ABCD A B C D
.
Đáp án: …………..
Lời giải
O
K
M
N
P
H
B
C
A
D
S
I
J
G
Điện thoại: 0946798489 TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Facebook Nguyễn Vương
https://www.facebook.com/phong.baovuongTrang 27
Ta có
, , 60
AC ABB A AC AB B AC
.
Xét tam giác
AB C
vuông tại
B
có
2
.cot60
3
AB B C
.
Xét tam giác
ABB
vuông tại
B
có
2 2 2
4
3
BB AB AB x
.
Thể tích của khối hộp chữ nhật
.
ABCD A B C D
là
2 2
2
4
4 4
3
. . 2 2.
3 2 3
x x
V AA A D BB x x
Vậy giá trị lớn nhất của thể tích khối hộp chữ nhật
.
ABCD A B C D
là
max
4
3
V
.
• XEM THÊM ĐỀ CƯƠNG ÔN THI TẠI:
• https://www.nbv.edu.vn/2022/01/de-cuong-danh-gia-nang-luc-dhqg-ha-noi.html
Theo dõi Fanpage: Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hoặc Facebook: Nguyễn Vương https://www.facebook.com/phong.baovuong
Tham gia ngay: Nhóm Nguyễn Bào Vương (TÀI LIỆU TOÁN)
https://www.facebook.com/groups/703546230477890/
Ấn sub kênh Youtube: Nguyễn Vương
https://www.youtube.com/channel/UCQ4u2J5gIEI1iRUbT3nwJfA?view_as=subscriber
Tải nhiều tài liệu hơn tại: https://www.nbv.edu.vn/
| 1/27
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Điện thoại: 0946798489 ĐỀ Đ Ề SỐ S 6. 6 ÔN THI T ĐG Đ NL ĐHQ Đ G H À NỘI I202 0 1 2 -2 - 02 0 2 2
• |FanPage: Nguyễn Bảo Vương
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Thống kê điểm môn toán trong một kì thi của 500 em học sinh thấy số bài được điểm 9 tỉ lệ
2%. Hỏi tần số của giá trị xi =9 là bao nhiêu? A. 10 B. 20 C. 30 D. 5
Câu 2. Một ôtô đang chạy thì người lái đạp phanh, từ thời điểm đó, ôtô chuyển động chậm dần đều với
vận tốc v t   12t  24 m / s , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét? A. 20 m . B. 18 m . C. 24 m . D. 15 m .
Câu 3. Nghiệm của phương trình logx   1  2 là. A. 1025. B. 2e 1. C. 2 e 1. D. 101.  xy x y  5
Câu 4. Nghiệm của hệ phương trình:  là: 2 2  x y y x 6 A.      1;2,2;  1 . B. 0;  1 ,1; 0 . C. 0; 2,2;0. D. 1 1 2; , ;2 .      2   2 
Câu 5. Tìm tọa độ điểm M là điểm biểu diễn số phức z biết z thỏa mãn phương trình 1 i z  3  5i . A. M  1  ;  4. B. M 1; 4 . C. M 1; 4 . D. M 1; 4  .
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho điểm M 3;1; 2 và mặt phẳng
:3x y 2z 4 0 . Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song song với  ?
A. 3x  y  2z  6  0 . B. 3x  y  2z  6  0 .
C. 3x  y  2z  4  0 . D. 3x  y  2z 14  0. x 1 y 1 z  3
Câu 7. Trong không gian Oxyz, cho điểm A4;1;3 và đường thẳng d :   . Tọa độ 2 1 1
điểm M là điểm đối xứng với điểm A qua d là A. M 2;5;3 . B. M  1  ; 0; 2 . C. M 2;3;5 . D. M 0;1;2 . x  2 x  4
Câu 8. Tập nghiệm của bất phương trình  là: x 1 x  3 A.  1  1  ;       1;3. B. S   ;1    1;3 .  2  2   1  1 C.   S   ;1  3;   . D. S  ;    1;3.  2   2    x x  x 2 1 cos cos 2 cos  sin Câu 9. Cho phương trình
x  0 . Tính tổng các nghiệm nằm trong khoảng cos x 1
0;2018  của phương trình đã cho? A. 2035153 . B. 1017072 . C. 1019090 . D. 2037171 . Câu 10.
Cho cấp số nhân u cố công bội q và u  0 . Điểu kiện của q để cấp số nhân u có ba số n  n  1
hạng liên tiếp là độ dài ba cạnh của một tam giác là :
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ 1  5 A. 0  q  1 B. 1  q  2 1   5 1 5 C. q  1.  q  D. 2 2 x 
Câu 11. Họ tất cả các nguyên hàm của hàm số f  x 2 1 
trên khoảng ;1 là x 1 3 A. 2 x  . B. 2x  3ln x 1  C C . x 12 3 C. 2x  . D. 2x  3l  n x   1   C C. x  2 1
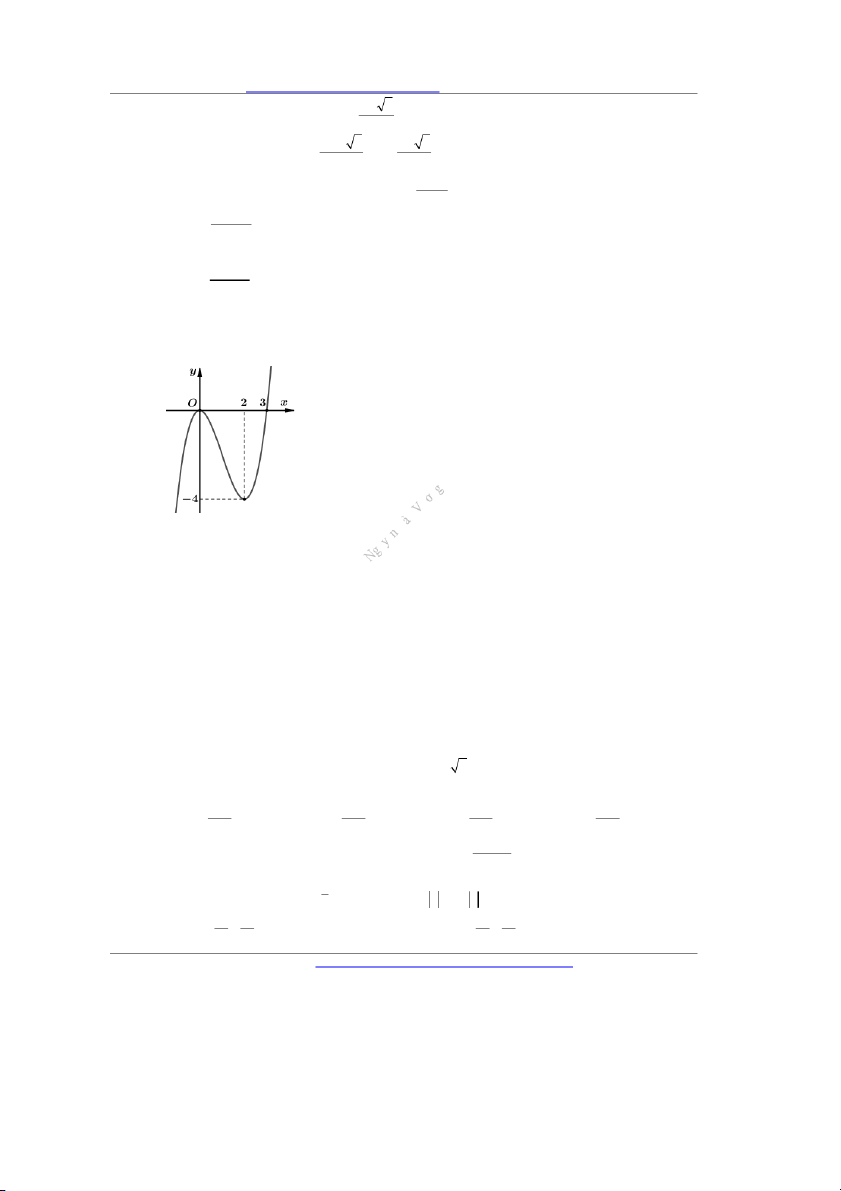
Câu 12. Cho hàm số y  f x liên tục trên R và có đồ thị như hình vẽ dưới đây. Có bao nhiêu giá trị
nguyên của tham số m để phương trình f   6 6
4 sin x  cos x  1  m có nghiệm. A. 6 . B. 5. C. 4 . D. 3.
Câu 13. Một tay đua đang điều khiển chiếc xe đua của mình với vận tốc 180(km / h). Tay đua nhấn ga để
về đích, kể từ đó xe chạy với gia tốc 2
a(t)  2t 1 (m / s ) . Hỏi rằng sau 4s sau khi tay đua nhấn
ga thì xe đua chạy với vận tốc bao nhiêu km/h A. 200(km / ) h . B. 252(km / ) h . C. 288(km / h) . D. 243(km / ) h .
Câu 14. Một người gửi tiết kiệm ngân hàng 20 triệu với lãi suất không đổi là 7,2% trên năm và tiền lãi
hàng tháng được nhập vào vốn. Hỏi sau ít nhất bao nhiêu năm người đó thu về được tổng số tiền
lớn hơn 345 triệu đồng? A. 33 năm. B. 41 năm. C. 50 năm. D. 10 năm.
Câu 15. Giải phương trình log x  2  211. 3   A. 211 x  3  2 . B. 3 x  211  2 . C. 3 x  211  2 . D. 211 x  3  2 .
Câu 16. Cho hình phẳng H  giới hạn bởi các đường y  x, y  x và x  4 . Thể tích của khối tròn
xoay tạo thành khi quay hình H  quanh trục hoành nhận giá trị nào sau đây: 38 41 41 40 A. V  . B. V  . C. V  . D. V  . 3 3 2 3 x 3
Câu 17. Có tất cả bao nhiêu giá trị nguyên của m để hàm số y 
nghịch biến trên khoảng 2;   x  4m A. 2 B. 1 C. 3 D. Vô số
Câu 18. Tìm số phức z thỏa mãn z   z    i 2 2 1 1 1 z và z  1. 3 1 3 1 A. z    i . B. z  i . C. z    i . D. z  i . 10 10 10 10
Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Câu 19. Trên mặt phẳng tạo độ Oxy , tập hợp điểm biểu diễn số phức z thỏa mãn z  i  iz là
A. Đường thẳng y  2 . B. Đường thẳng 1 y   . 2 C. Đường thẳng 1
y  . D. Đường tròn tâm I 0;  1 . 2 x 2 t
Câu 20. Cho đường thẳng d : 
và 2 điểm A 1 ; 2, B(2 ; m .) Định m để A và B nằm cùng y   1 3t phía đối với d . A. m  13 . B. m  13 . C. m  13. D. m  13.
Câu 21. Trong mặt phẳng toạ độ cho ba điểm ( A 4; 0), (
B 0; 2),C(1, 6;3, 2) . Tính bán kính đường tròn ngoại tiếp tam giác. A. 5 . B. 4,75. C. 2 5 . D. 4,5.
Câu 22. Trong không gian Oxyz , cho các điểm M 1;0;  1 ; N5;2; 
3 và mặt phẳngQ:2x y z7 0.
Vectơ pháp tuyến của mặt phẳng Pđi qua các điểm M , N và vuông góc với mặt phẳng Q là A. n   1  ;0; 2   . B. n   1;0;  2 . C. n   4;0;  8 . D. n  8;0;  4 .
Câu 23. Cho hình nón có thiết diện qua trục là tam giác đều. Gọi 1 V , 2
V lần lượt là thể tích của khối cầu
ngoại tiếp và nội tiếp hình nón đã cho. Tính tỉ số 1 V . 2 V A. 4 . B. 16 . C. 8. D. 2.
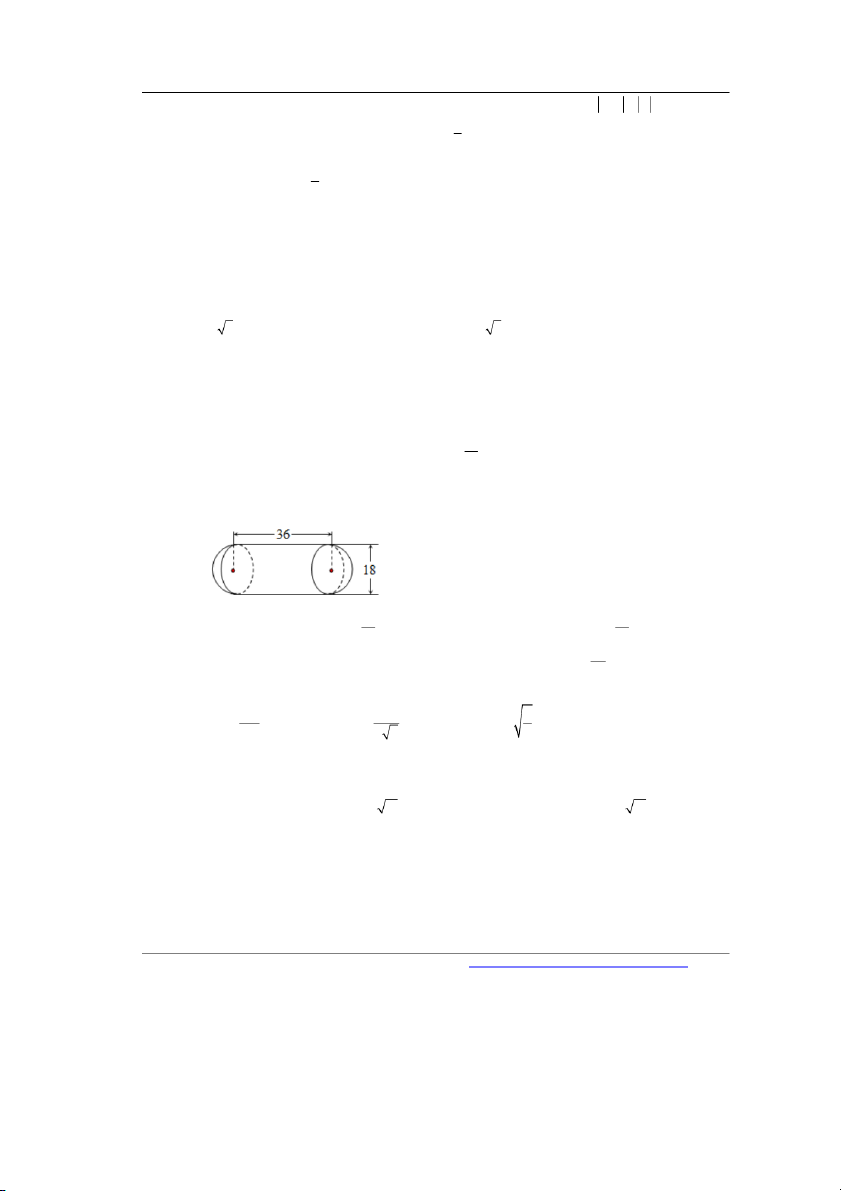
Câu 24. Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ như hình vẽ bên. Các kích thước
được ghi (cùng đơn vị dm ). Tính thể tích của bồn chứa. . 3 4 2 4 A. 5 2  4  3 . B.  . C. 2 5  4 .3 . D.  . 3 3 5 3 3
Câu 25. Cho hình lăng trụ a ABC.A B  C
  có đáy là tam giác đều cạnh a , AA  . Biết rằng hình chiếu 2
vuông góc của A lên ABC  là trung điểm BC . Tính thể tích V của khối lăng trụ đó. 3 2a 3 3a A. V  . B. V  . C. 3 3 V  a . D. 3 V  a . 3 4 2 2
Câu 26. Cho hình chóp S .ABCD có đáy ABCD là hình vuông cạnh AB  8a, SA  SB  SC  SD  8a .
Gọi N là trung điểm cạnh SD. Tính diện tích thiết diện của hình chóp S .ABCD cắt bởi mặt phẳng ABN  . A. 2 24a . B. 2 12 a 11 . C. 2 12a . D. 2 6a 11. Câu 27. Trong không gian 2 2 2
Oxyz cho mặt cầu  S : x 2   y  1   z  1  9 và điểm
M a;b;c  S  sao cho biểu thức P  a  2b  2c đạt giái trị nhỏ nhất. Khi đó giá trị biểu thức T  a  b  c bằng A. T  1 . B. T  2 . C. T  1 . D. T  2.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Câu 28. Trong không gian với hệ trục tọa độ Oxyz , cho tam giác ABC có A 1;1;1, B 4;  3;1 và
C 1;1; 2 . Đường phân giác trong của góc A có phương trình là:  x 1 3t  x  4  3t  x 1 3t x  4 3t A.      y  1 4t . B.  y 3  4 t . C. y 1 4t . D. y  3 4t .  z  1 5t     z  6  5t  z  1 5t  z  6  5t 
Câu 29. Cho hàm số y  f  x có đạo hàm f  x trên , phương trình f  x  0 có 4 nghiệm thực và đồ thị hàm số 2
f x  như hình vẽ. Tìm số điểm cực trị của hàm số y  f x  . y 2 4 O x 1 A. 3 . B. 4 . C. 5 . D. 6 . A 1;  2;1
B 5; 0; 1 C 3;1;  2
Câu 30. Trong không gian Oxyz , cho ba điểm , , và mặt phẳng
Q :3x  y  z 3  0 M  ; a ; b c  Q . Gọi là điểm thuộc thỏa mãn 2 2 2 MA  MB  2MC nhỏ
nhất. Tính tổng a  b  5c. A. 14 . B. 11. C. 9 . D. 15 .
Câu 31. Cho hàm số y  f (x) có bảng xét dấu của f   x như hình vẽ.
Có bao nhiêu số nguyên m để hàm số y  f x  m  có đúng 3cực trị. A. 1. B. 2 . C. 3. D. 4 . Câu 32. Tìm 4 2 2
m để phương trình: x  m  3 x  m  3  0 có đúng 3 nghiệm: A. m   . B. m   3 . C. m  3 . D. m  3 .
Câu 33. Cho hàm số y  f   x liên tục trên \0;  1 thoả mãn: 2 x  2 x 1 2 x x 1
  f  x x x 2 f x      , x   0;  1 và f   4 3  ln 3 . x 9 Biết f   2  a bln 2  , a b  . Giá trị 2 a  9b bằng. A. 4. B. 7. C. 2. D. 8.
Câu 34. Một hộp đựng 3 viên bi màu xanh, 5 viên bi màu đỏ, 6 viên bi màu trắng và 7 viên bi màu đen.
Chọn ngẫu nhiên đồng thời từ hộp 4 viên bi, tính xác suất để 4 viên được chọn không nhiều hơn 3
màu và luôn có bi màu xanh? 2085 2058 2295 2259 A. . B. . C. . D. . 5985 5985 5985 5985
Câu 35. Cho hình lăng trụ AB . CD A B  C  D
  có đáy là hình bình hành. Gọi M , N , P , Q lần lượt là trọng tâm các tam giác A A  D , A CD  , A CB 
, A BA . Gọi O là điểm bất kỳ trên mặt đáy ABCD . Biết thể tích khối chóp .
O MNPQ bằng V . Tính theo V thể tích khối lăng trụ AB . CD ABC D   . 27 81 81 27 A. V . B. V . C. V . D. V . 8 4 2 4
Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 B. ĐIỀN KHUYẾT (15 CÂU)
Câu 36. Tiếp tuyến với đồ thị 3 2
y  x  x 1 tại điểm có hoành độ x  1 có phương trình là: 0 Đáp án: ………….. Câu 37. Cho hàm số 2
y  f x có đạo hàm f  x  x  x  
1 2x 3 . Hàm số đã cho có bao nhiêu điểm cực trị? Đáp án: …………..
Câu 38. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A1; 2;   1 , B0; 3; 4 ,
C 2; 1; 1 . Độ dài đường cao từ A đến BC bằng: Đáp án: …………..
Câu 39. Lớp 10A4 cử đại diện 3 học sinh, 11A5 cử đại diện 4 học sinh, 12A6 cử đại diện 5 học sinh đi đại
hội (ngồi bàn tròn). Hỏi có bao nhiêu cách xếp 12 học sinh vào bàn sao cho các thành viên của
mỗi lớp ngồi cạnh nhau ? Đáp án: ………….. f (x )  5
Câu 40. Cho hàm số f x  liên tục trên thỏa mãn lim
 2 . Tìm m để hàm số x 1  x 1 2  2 f (x)  7 f (x) 15   g x  khi x 1   x 1 liên tục tại x  1 ? m  x  2 khi x 1 Đáp án: ………….. a  0
Câu 41. Cho a , b , c là 3 số thực thỏa mãn 
. Gọi x , x lần lượt là hoành độ giao điểm 4a  9b 24c 0 1 2 của parabol   2
P : y  2ax  3bx  4c với trục hoành. Tìm giá trị nhỏ nhất của biểu thức T   . 1 x x2 Đáp án: ………….. 1 1
Câu 42. Tìm tất cả tham số thực của m để hàm số y   m  2 3 2 x  x 
mx  2 có cực đại, cực tiểu. 3 3 Đáp án: …………..
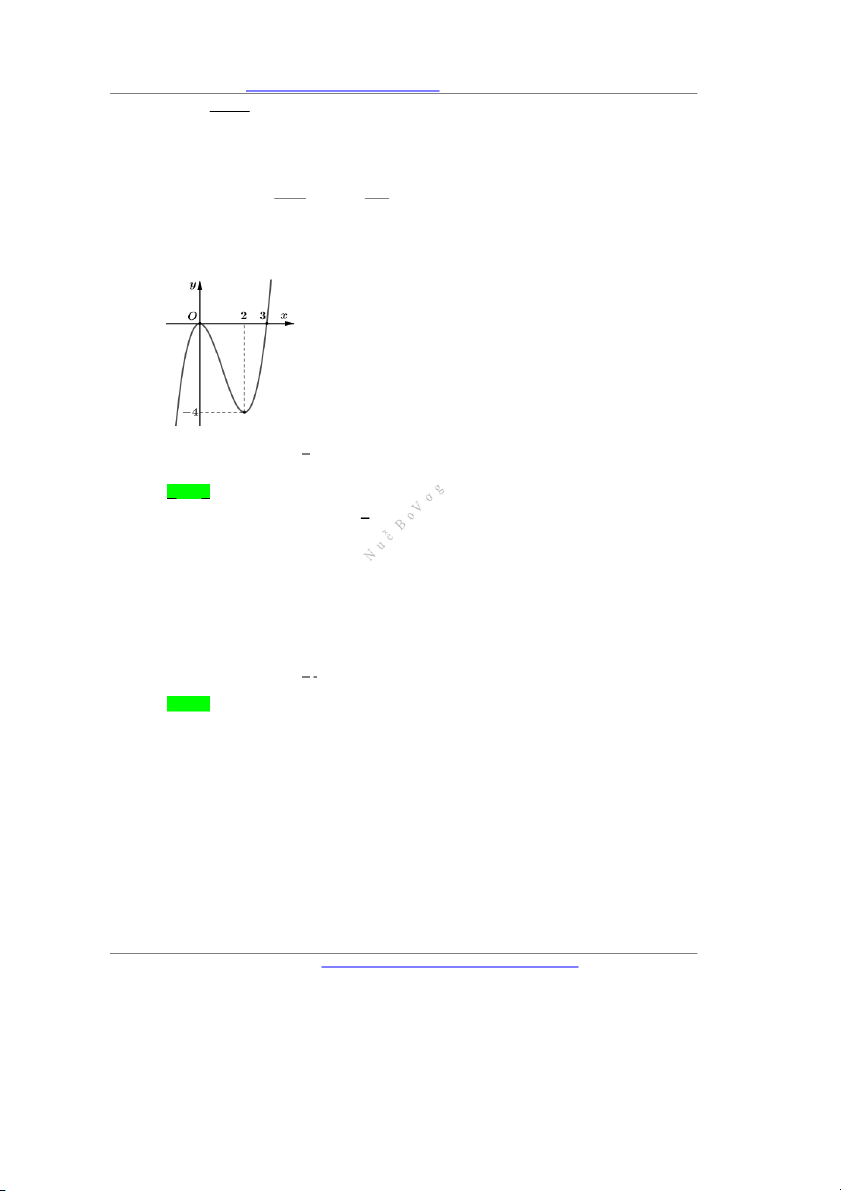
Câu 43. Cho hàm số y  f  x liên tục trên và có đồ thị f  x như hình vẽ
Đặt S  f 0 f 6 f a f a  2 . Tập giá trị của S chứa tối đa bao nhiêu số nguyên? Đáp án: …………..
Câu 44. Cho hàm số y  f  x xác định trên và có bảng biến thiên như sau
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Số nghiệm thuộc đoạn  3 ;3  của phương trình f  cos x 1 là Đáp án: …………..
Câu 45. Cho z , z là hai trong các số phức  
 , đồng thời z  z  8 . 1 2
z thỏa mãn điều kiện z 5 3i 5 1 2
Tập hợp các điểm biểu diễn của số phức w  z  z trong mặt phẳng tọa độ Oxy là đường tròn có 1 2
phương trình nào dưới đây? Đáp án: …………..
Câu 46. Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc với
nhau. Tính sin góc giữa đường thẳng SC và mặt phẳng SAD . Đáp án: ………….. x  1 y  2 z  3
Câu 47. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng :   và điểm 2 2  1
A1; 2; 0 . Khoảng cách từ điểm A đến đường thẳng  bằng: Đáp án: …………..  1 Câu 48. Cho ba số thực  a, b , c  ;1 
. Tìm giá trị nhỏ nhất P của biểu thức. 4    min  1  1  1  P  log b   log c   log a  . a  4 b  4 c  4        Đáp án: …………..
Câu 49. Cho hình chóp S.ABCD có đáy là hình thoi có ABC  60, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi H , M , N lần lượt là trung điểm các cạnh , AB S , A SD
và G là trọng tâm tam giác SBC. Tính khoảng cách từ G đến mặt phẳng (HMN) biết khối chóp 3 a S.ABCD có thể tích V  4 Đáp án: …………..
Câu 50. Cho hình hộp chữ nhật AB . CD A B  C  D  có A D    2 , A B
   x, (x  0) . Góc giữa đường thẳng
AC và mặt phẳng  ABB A
  bằng 60. Tính giá trị lớn nhất m V
của thể tích khối hộp chữ nhật ax ABCD .A B  C  D   . Đáp án: …………..
Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Lời giải tham khảo
A. TRẮC NGHIỆM KHÁCH QUAN (35 CÂU)
Câu 1. Thống kê điểm môn toán trong một kì thi của 500 em học sinh thấy số bài được điểm 9 tỉ lệ
2%. Hỏi tần số của giá trị xi =9 là bao nhiêu? A.10 B. 20 C. 30 D. 5 Lời giải: Chọn A 2%.500 tần số xi =9 là: 10 100%
Câu 2. Một ôtô đang chạy thì người lái đạp phanh, từ thời điểm đó, ôtô chuyển động chậm dần đều với vận tốc vt  1
 2t  24 m/ s , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp
phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét? A. 20 m . B. 18 m . C. 24 m . D. 15 m . Lời giải Chọn C Ta có: v t   1
 2t  24  0  t  2 . Quản đường ôtô di chuyển từ lúc đạp phanh đến lúc dừng 2 hẳn là : S   1  2t 24 dt  24  . 0
Câu 3. Nghiệm của phương trình logx   1  2 là. A. 1025 . B. 2e 1  . C. 2 e 1  . D. 101. Lời giải Chọn D log  2
x1  2  x 1  10  x  101 x  y  x  y  5
Câu 4. Nghiệm của hệ phương trình:  là: 2 2 x y  y x   6 A. 1;2, 2;  1 . B. 0;1, 1; 0. C. 0; 2, 2;0. D.  1   1  2; , ; 2 .  2   2      Lời giải Chọn A
Đặt S  x y P  xy  2 , S  4P  0   P  S  5 Ta có :  PS   6
 S, P là nghiệm của phương trình 2
X  5X  6  0  X  2; X  3 Khi S  2, P  3 (loại)
Khi S  3, P  2 thì x, y là nghiệm phương trình 2
X  3 X  2  0  X  1; X  2
Vậy nghiệm của hệ là 1;2,  2;1 .
Câu 5. Tìm tọa độ điểm M là điểm biểu diễn số phức z biết z thỏa mãn phương trình 1 i z  3 5i . A. M  1  ;  4 . B. M  1  ; 4  . C. M 1; 4 . D. M 1; 4  . Lời giải Chọn B 3 5 Ta có: i z 
 1 4i  z  1 4i  M  1  ;4 . 1 i
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho điểm M 3;1; 2  và mặt phẳng
:3x y 2z 4 0 . Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song song với  ?
A. 3x  y  2z  6  0 . B. 3x  y  2z  6  0 .
C. 3x  y  2z  4  0 . D. 3x  y  2z 14  0 . Lời giải Chọn A
Mặt phẳng đi qua M 3;1; 
2 và song song với   có phương trình: 3 x   3  y  
1  2 z  2  0  3x  y  2z  6  0. x 1 y 1 z 3
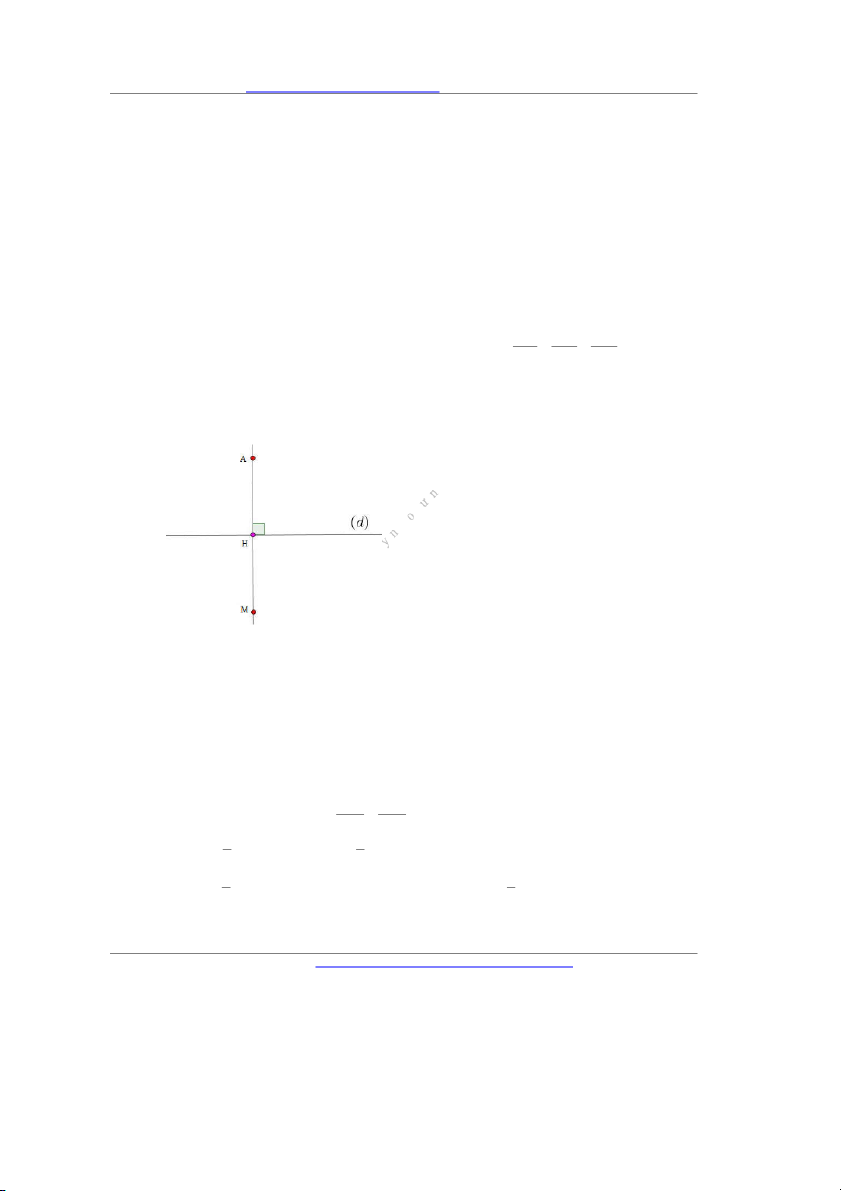
Câu 7. Trong không gian Oxyz, cho điểm A 4;1;3 và đường thẳng d :   . Tọa độ điểm 2 1  1
M là điểm đối xứng với điểm A qua d là A. M 2;5;3 . B. M 1;0;2 . C. M 2; 3  ;5 . D. M 0; 1  ;2  . Lời giải Chọn C  x  1 2t 
Đường thẳng d có vectơ chỉ phương a  (2;1;1) và phương trình tham số  y  1 t .  z 3 t 
Gọi H là trung điểm của AM, khi đó H nằm trên đường thẳng d nên H 1 2t;1 t;3  t AH  2t  3; t  ;t 
AH  d  AH . a  0  2(2t  3)  t  t  0  6t  6  0  t  1
Do đó tọa độ điểm H 3;2;4.
Mà H là trung điểm của AM nên M 2; 3;5 . x  2 x  4
Câu 8. Tập nghiệm của bất phương trình  là: x 1  x 3  1  1 A. ;      
1;3 . B. S   ;1    1;3 . 2    2   1  1 C.   S   ;1  3;   . D. S  ;   1;3.  2  2   Lời giải Chọn A
Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 x  2 x  4 x  2 x  4  x   2  x   3  x   1  x   4 Ta có     0   0 x 1 x  3 x 1 x  3  x  1 x   3 2 x  x    2 6 x  3 x  4      4x 2 2x 1     0   0 x  x  0 1 3  x  1 x   3  x  1 x   3  1 
Lập bảng xét dấu ta có x  ;   1; 3. 2     x  x  x  2 1 cos cos 2 cos sin Câu 9. Cho phương trình
x  0 . Tính tổng các nghiệm nằm trong khoảng cos x1
0;2018 của phương trình đã cho? A. 2035153 . B. 1017072 . C. 1019090 . D. 2037171 . Lời giải Chọn B
Điều kiện: x   k 2 ,  k  .   2 x x  x 2 1 cos cos 2 cos  sin x
1 cos xcos2x cos x 1 cos x  0   0 cos x 1 cos x1
 cos 2x  cosx 1 cosx  0  cos 2x  1  x  k , k  . Đối chiếu điều kiện ta thấy với k
lẻ sẽ không thỏa. Vậy các nghiệm thuộc 0;2018  của phương trình là
Khi đó,  2 ;4 ; 6 ;...;2016, có tất cả 1008 nghiệm.
Tổng tất cả các nghiệm thuộc khoảng 0;2018 : 1008 S  x  x  ...  x  2 2016  1017072   . 1 2 1008 2
Câu 10. Cho cấp số nhân u cố công bội
u  0 . Điểu kiện của u có ba số n  q và 1
q để cấp số nhân  n 
hạng liên tiếp là độ dài ba cạnh của một tam giác là : 1  5 A. 0  q  1 B. 1  q  2 1   5 1 5 C. q  1 .  q  D. 2 2 Lời giải Chọn D
Giả sử ba số hạng liên tiếp là n n 1  n 2 u q , u q ,
. Ba số hạng này là độ dài ba cạnh của một tam 1 1 1 u q n n 2 n 1  2      1 u q 1 u q 1 u q 0 q  q 1 0       1   5 1  5 giác  n n 1 n 2 2  1 u q  1 u q  1 u q  0 1   q q  0  q . 2 2  n1 n 2 n  2 u q  u q  u q  0 q  q  1 0  1 1 1   x 
Câu 11. Họ tất cả các nguyên hàm của hàm số f x  2 1 
trên khoảng ;1 là x 1  3 A. 2x   . B. 2x  3ln x   1   C C . x  2 1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ 3 C. 2 x  C. D. 2x  3ln x   1  C. x  2 1 Lời giải Chọn D 2x 1  3 Ta có  f xdx dx 2 d     x  2x 3ln    x   1 C . x 1   x 1  
Câu 12. Cho hàm số y  f x liên tục trên R và có đồ thị như hình vẽ dưới đây. Có bao nhiêu giá trị
nguyên của tham số m để phương trình f   6 6
4 sin x  cos x  1  m có nghiệm. A. 6 . B. 5. C. 4 . D. 3 . Lời giải Chọn B  3 Đặt  t  4 6 6 sin x cos x 2 2
1  4 1  sin 2x 1  3 3sin 2x   t   0;  3 4    Phương trình f   6 6 4 sin x  cos x  
1  m có nghiệm khi và chỉ khi phương trình f t   m có
nghiệm thuộc 0;3  4
  m  0  có 5 giá trị nguyên
Câu 13. Một tay đua đang điều khiển chiếc xe đua của mình với vận tốc 180(km / h). Tay đua nhấn ga để
về đích, kể từ đó xe chạy với gia tốc 2
a(t)  2t 1 (m / s ) . Hỏi rằng sau 4s sau khi tay đua nhấn
ga thì xe đua chạy với vận tốc bao nhiêu km/h A. 200(km / ) h . B. 252(km / ) h . C. 288(km / h) . D. 243(km / ) h . Lời giải Chọn B
Đổi đơn vị 180(km / h)  50(m/ s) .
Từ khi tay đua nhấn ga, xe chạy với vận tốc 2
v(t)  (2t 1)dt  t  t  C  .
Tại t  0, v(0)  C  50(m/ s) 2  v(t)  t  t  50.
Sau khi tay đua nhấn ga 4s thì xe chạy với vận tốc 2
v(4)  4  4  50  70(m / s).
Đổi đơn vị 70(m / s)  252(km / h).
Câu 14. Một người gửi tiết kiệm ngân hàng 20 triệu với lãi suất không đổi là 7,2% trên năm và tiền lãi
hàng tháng được nhập vào vốn. Hỏi sau ít nhất bao nhiêu năm người đó thu về được tổng số tiền
lớn hơn 345 triệu đồng? A. 33 năm. B. 41 năm. C. 50 năm. D. 10 năm.
Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Lời giải Chọn B
Từ giả thiết ta suy ra người đó đã gửi ngân hàng theo hình thức lãi kép nên ta có công thức  1 n T A r
với A  20 triệu là số tiền ban đầu, T  345 triệu là số tiền người đó nhận được sau
n năm gửi, r  7, 2% 0, 072 là lãi xuất hàng năm. 69 69
Ta có 345  20.1,072n  1,072n   n  log  40,96 1,072 4 4
Vậy sau ít nhất 41 năm người đó thu về được tổng số tiền lớn hơn 345 triệu đồng
Câu 15. Giải phương trình log x 2  211. 3  A. 211 x  3  2 . B. 3 x  211 2 . C. 3 x  211  2 . D. 211 x  3  2. Lời giải Chọn D Ta có: log x 2  211 211  x  2  3 211  x  3  2 . 3  
Câu 16. Cho hình phẳng H  giới hạn bởi các đường y  x, y  x và x 4. Thể tích của khối tròn
xoay tạo thành khi quay hình H  quanh trục hoành nhận giá trị nào sau đây: 38 41 41 40 A. V  . B. V  . C. V  . D. V  . 3 3 2 3 Lời giải Chọn B  x   0
Phương trình hoành độ giao điểm: x  x    x  0. 2  x  x 4
Thể tích khối tròn xoay cần tìm là 2 V   x  x dx  . Ox 0 x  0 Xét phương trình 2 x  x  0   . x  1 1 4 1 4 Do đó 2 2 V
  x  x dx   x  x dx   x  x dx   x  x dx     . Ox  2   2  0 1 0 1 1 4 3 2 3 2  x x   x x  41          (đvtt). 3 2   3 2  3     0 1 
Câu 17. Có tất cả bao nhiêu giá trị nguyên của x m để hàm số 3 y 
nghịch biến trên khoảng 2;   x  4m A. 2 B. 1 C. 3 D. Vô số Lời giải Chọn B TXĐ: D  \  4   m 4m  3 y '   x  4m2 x 3 Hàm số y 
nghịch biến trên khoảng 2;    y  0x  2;  x  4m  3  3 m    4m3 0 m   4 1 3 4       m  m  2;   4  1  4  m  2 m    2 4  2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Vì m  nên m  0. Vậy có 1 giá trị m thỏa mãn yêu cầu bài toán.
Câu 18. Tìm số phức z thỏa mãn z    z    i 2 2 1 1 1 z và z  1. 3 1 3 1 A. z    i . B. z  i . C. z    i . D. z  i . 10 10 10 10 Lời giải Chọn C
Gọi z  x  yi với x , y . Ta có 2 2 z  1  x  y  1.
Và          2            2 2 2 z 1 z 1 1 i z 2 x yi 1 x yi 1 1 i x  y    2 2      2 2 x y 3x 1 y  x  y i  0  3 2 2  x   x  y  3x  1 0 2 10x   3x  0   10     2 2 x  y  y  0  y 3x 1  1  y   10 3 1 Vậy z    i . 10 10
Câu 19. Trên mặt phẳng tạo độ Oxy , tập hợp điểm biểu diễn số phức z thỏa mãn z  i  iz là 1
A. Đường thẳng y  2 . B. Đường thẳng y   . 2 1
C. Đường thẳng y  . D. Đường tròn tâm I 0;  1 . 2 Lời giải Chọn C
Gọi số phức z  a  bi  a,b   .
Ta có: z  i  iz  a bi i  i a bi   a  b   1 i  b   ai  a  b  2 2 2 2 1  b  a  2  b 1  0 .
Vậy tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện bài toán là đường thẳng 1 y  . 2 x  2 t
Câu 20. Cho đường thẳng d :  và 2 điểm A 1 ;  2 , B( 2
 ; m .) Định m để A và B nằm cùng y  1 3t  phía đối với d . A. m  13. B. m  13 . C. m  13 . D. m 13 . Lời giải Chọn B
Phương trình tổng quát của đường thẳng d : 3(x  2) 1(y 1)  0. hay d : 3x  y  7  0. ,
A B cùng phía với d  (3x  y  7)(3x  y  7)  0  2(13 m)  0  m  13. A A B B
Câu 21. Trong mặt phẳng toạ độ cho ba điểm A(4;0),B (0; 2),C(1,6;3, 2) . Tính bán kính đường tròn ngoại tiếp tam giác. A. 5 . B. 4,75 . C. 2 5 . D. 4,5 . Lời giải Chọn A
Trang 12 Fanpage Nguyễn Bảo Vương 
 https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Gọi I (a;b) là tâm đường tròn ngoại tiếp tam giác I  A  IB  x   2 2 2
4  y  x  y  2 2 Ta có    I  A  IC  x    2 4  y  x  1,  2 6  y  3,  2 2 2  2x  y  3  x  2      I(2;1)  IA2;  1  R  IA  5 . 0, 3x  0, 4y  0, 2 y  1  
Câu 22. Trong không gian Oxyz , cho các điểm M 1;0;  1 ; N5;2; 
3 và mặt phẳngQ:2x y z7 0.
Vectơ pháp tuyến của mặt phẳng Pđi qua các điểm M , N và vuông góc với mặt phẳng Q là A. n   1  ;0; 2   . B. n  1;0; 2   . C. n  4;0;8 . D. n  8;0;4  . Lời giải Chọn B Ta có MN   4;2; 
2 và vectơ pháp tuyến của mặt phẳng Q  là n   Q  2; 1; 1 .
Mà MN  P  vàP  
Q nên vectơ pháp tuyến của mặt phẳng P là n thỏa mãn: n  MN   n   MN ,  ( n Q)   4;0;  8   . n n(Q) 
Vậy vectơ pháp tuyến của mặt phẳng P là n  1;0; 2   .
Câu 23. Cho hình nón có thiết diện qua trục là tam giác đều. Gọi 1 V , 2
V lần lượt là thể tích của khối cầu V
ngoại tiếp và nội tiếp hình nón đã cho. Tính tỉ số 1 . 2 V A. 4 . B. 16 . C. 8. D. 2. Lời giải Chọn C a r R
Giả sử hình nón đã cho có đường sinh l  a . a 3
Ta có khối cầu ngoại tiếp và khối cầu nội tiếp hình nón có bán kính lần lượt là R  và 3 a 3 r  . 6 Gọi 1 V , 2
V lần lượt là thể tích của khối cầu ngoại tiếp và nội tiếp hình nón. 4 3  R 3 Ta có   1 V 3  R   8   . V 4 3   2 r  r 3
Câu 24. Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ như hình vẽ bên. Các kích thước
được ghi (cùng đơn vị dm ). Tính thể tích của bồn chứa.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ . 3 4 2 4 A. 5 2  4  3 . B.  . C. 2 5 4 .3 . D.  . 3 3 5 3 Lời giải Chọn C
Gọi V là thể tích hình trụ có đường cao 36 dm và bán kính đường tròn đáy 9 (dm). 1
V là thể tích nửa hình cầu có bán kính 9 dm . 2 2 Ta có 2
V  .9 .36  2916  3 dm  và 3 V   .9  486  3 cm .. 1 2 3 Do đó V V 2V 3888     3 2 5    3 dm 4 .3 dm . 1 2 3
Câu 25. Cho hình lăng trụ a AB . C A B  C
  có đáy là tam giác đều cạnh a , AA  . Biết rằng hình chiếu 2
vuông góc của A lên  ABC là trung điểm BC . Tính thể tích V của khối lăng trụ đó. 3 2 3 3a A. a V  . B. V  . C. 3 3 V  a . D. 3 V  a . 3 4 2 2 Lời giải Chọn B
Gọi H là trung điểm BC , ta có: A H   ABC. a 3
Xét tam giác ABC ta có: AH  . 2 Xét tam giác a AA H  vuông tại H , 2 2 6 A H   AA  AH  . 2 2 3 3 a 3 a 6 3a 2 3
Vậy thể tích khối lăng trụ:  .  . a V S A H    . LT ABC 4 2 8 4 2
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh AB  8a , SA  SB  SC  SD  8a .
Gọi N là trung điểm cạnh SD . Tính diện tích thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng ABN . A. 2 24a . B. 2 12a 11 . C. 2 12a . D. 2 6a 11. Lời giải Chọn B
Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 S M N B C I O A D
Mặt phẳng ABN  chứa AB//CD nên cắt mặt phẳng SCD theo giao tuyến NM //CD và M
cũng là trung điểm của SC . Suy ra thiết diện cần tìm là hình thang cân ABMN . 8a 3 Hạ NI  AB . Ta có 2 2 2 NI  AN  AI với AN   4a 3 . 2
2AI  AB  MN  8a  4a  4a  AI  2a . Từ đó suy ra NI 2 a 11 . 1 1 Vậy S  AB  MN NI  8a 4a  2 2a 11 12a 11 . ABMN  . 2 2 Câu 27. Trong không gian 2 2 2
Oxyz cho mặt cầu  S : x 2   y  1   z  1  9 và điểm
M a;b;c  S  sao cho biểu thức P  a  2b  2c đạt giái trị nhỏ nhất. Khi đó giá trị biểu thức T  a  b  c bằng A. T  1 . B. T  2 . C. T  1 . D. T  2. Lời giải Chọn A
Ta có P a 2b 2c P 6 a   2 2b   1 2c   1 .
Áp dụng bất đẳng thức Bunhiacopski ta có P  2  a 
 b    c   2   
    a  2 b  2 c  2 2 2 2 6 2 2 1 2 1 1 2 2 2 1 1      P 2
6  81 9  P  6  9  3  P  15. Từ đó  a  2 b 1 c 1 9  a   2  9  a  1      P  3   1 2 2       b  1  min  a 2 b 1 c 1     
 a 2 2 b 1 2 c 1 9  1 2 2 c  1 
Vậy P đạt giá trị nhỏ nhất khi M 1; 1  ;   1  T  a  b c  1  .
Câu 28. Trong không gian với hệ trục tọa độ Oxyz , cho tam giác ABC có A1;1;  1 ,  B 4; 3  ;1 và
C 1;1; 2 . Đường phân giác trong của góc A có phương trình là: x  1 3t x  4 3  t x 1 3t x  4  3t A.     y   1 4t . B. y    3 4t . C. y  1 4t . D. y   3 4t . z  1     5t z  6   5t z 1   5t z  6   5t Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ C D A B' B AB 3; 4  ; 
0 , AC 0;0;1 , AB  AB  5, AC  AC  1.
Nhận xét: AB AC  0 ⇒ AB  AC ⇒ A  BC vuông tại A. 1 1 3 4  
Trên cạnh AB lấy B sao cho AB  1 ⇒ AB  AB  3; 4  ;0  ; ;0  . 5 5 5 5 
Đường phân giác trong của góc A là AD có một vectơ chỉ phương là:  3 4  1 AD  AC  AB  ; ;1   
 3;4; 5   3;4;  5 .  5 5  5 x   1 3t
Vậy phương trình đường phân giác của góc 
A là: AD : y 1  4t . z   1 5t   x  4  3t  Cho t 1   E 4; 3
 ;6 AD  AD:  y  3  4t .  z  6   5t
Câu 29. Cho hàm số y  f  x có đạo hàm f  x  trên , phương trình f  x  0 có 4 nghiệm thực và đồ thị hàm số 2
f  x  như hình vẽ. Tìm số điểm cực trị của hàm số y  f  x  . y 2 4 O x 1 A. 3. B. 4 . C. 5 . D. 6 . Lời giải Chọn C Ta có: y x f  2 2 .  x  2 x 0  x  0  2  x  0  x   0 y  0 2   x 1   x  1    2  x  2  x   2  2  x   4  x  2  x  2 2  x  4 Do  f  2 x   0    x  2  2 0    x  1  1   x   1
Trang 16 Fanpage Nguyễn Bảo Vương 
 https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Vậy hàm số có 5 điểm cực trị.
A 1;  2;1 B 5; 0; 1 C 3;1; 2
Câu 30. Trong không gian Oxyz , cho ba điểm , , và mặt phẳng
Q :3x  y  z 3  0 M  ; a ; b c  Q . Gọi là điểm thuộc thỏa mãn 2 2 2 MA  MB  2MC nhỏ
nhất. Tính tổng a  b  5c . A. 14. B. 11. C. 9 . D. 15 . Lời giải Chọn C
Gọi E là điểm thỏa mãn EA  EB  2EC  0  E 3;0;  1 . 2 2 2 Ta có: 2 2 2
S  MA  MB  2MC  MA  MB  2MC
 ME  EA2  ME  EB2  ME  EC 2 2 2 2 2 2
 4ME  EA  EB  2EC . Vì 2 2 2
EA  EB  2EC không đổi nên S nhỏ nhất khi và chỉ khi ME nhỏ nhất.
 M là hình chiếu vuông góc của E lên Q . x  3 3t 
Phương trình đường thẳng ME : y  t . z 1  t  x  3  3t x  0    y  t y  1 
Tọa độ điểm M là nghiệm của hệ phương trình:    . z  1 t  z  2   3  x  y  z  3 0 t   1 
 M 0;1;2  a  0, b  1, c  2.
 a  b  5c  0 1 5.2  9 .
Câu 31. Cho hàm số y  f (x) có bảng xét dấu của f  x như hình vẽ.
Có bao nhiêu số nguyên m để hàm số y  f  x  m  có đúng 3cực trị. A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn B
Ta có bảng xét dấu của hàm số y f x m :
Hàm số y  f  x  m có đúng 3cực trị khi và chỉ khi hàm số y  f x   m có đúng 1 cực trị m 4 0 dương    4 m  2. m 2 0 
Vì m nguyên nên m  ; 3 2  .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Vậy có 2 giá trị m cần tìm. Câu 32. Tìm 4 2 2
m để phương trình: x  m  3 x  m  3  0 có đúng 3 nghiệm: A. m   . B. m   3 . C. m  3 . D. m  3 . Lời giải Chọn B Đặt 2 2 2
t  x ,t  0 , phương trình trở thành t  m  3t  m  3  0 (*)
Phương trình đã cho có đúng 3 nghiệm khi phương trình (*) có 1 nghiệm bằng 0 và 1 nghiệm dương. Khi 2
t  0  x  0  m  3  0  m   3 . m  3  phương trình 4
x  0  x  0 (không thỏa).  x  0
m   3  phương trình 4 2 2 x  2 3x  0  x  2 x  2 3  0   (thỏa).  x   2 3
Vậy m   3 thỏa yêu cầu.
Câu 33. Cho hàm số y  f   x liên tục trên \0;  1 thoả mãn: 2 x  2 x 1 2
x x  1 f  x  x x  2  f x      ,x  0;  1 và f   4 3  ln 3 . x 9 Biết f   2  a bln 2  , a b . Giá trị 2 a  9b bằng. A. 4. B. 7. C. 2. D. 8. Lời giải Xét x  1ta có: 2 x  2 x  1 2
x x  1 f  x  x x  2  f x      . x x 2 x  2 x 1  f x  f x      x  x   3 1 x 2 2      x 2     f  x x x 2x 1 x f x   x  x  . 3 1 x  1 x x  1  2 2 x    f x  x 2x x 2   2 f x  x 1 x   1 x 2   x    f x  x 2     x1  x 2 x     f  x x 2  dx    x 1  x  2 x 
f  x  x  2ln x  C x 1 Mà f   9 3  ln 3 nên ta có 9 9
. ln 3  3 2 ln 3 C  C   3 . 4 2 4 x  2ln x 3 x 1  1 1 Suy ra f x      f 2 2
   ln2 a 9b 2. 2 x 4 2
Câu 34. Một hộp đựng 3 viên bi màu xanh, 5 viên bi màu đỏ, 6 viên bi màu trắng và 7 viên bi màu đen.
Chọn ngẫu nhiên đồng thời từ hộp 4 viên bi, tính xác suất để 4 viên được chọn không nhiều hơn 3
màu và luôn có bi màu xanh? 2085 2058 2295 2259 A. . B. . C. . D. . 5985 5985 5985 5985
Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Lời giải Chọn C
Tổng số bi là: 3 5 6  7  21 (viên).
Tổng số bi không tính màu xanh là: 5  6  7  18 (viên).
Chọn ngẫu nhiên 4 viên có: 4 C  5985 (cách). 21
Số cách chọn 4 viên có đủ 4 màu là: 3.5.6.7  630 (cách).
Số cách chọn 4 viên không có viên bi màu xanh là: 4 C  3060 (cách). 18
Số cách chọn để 4 viên được chọn không nhiều hơn 3 màu và luôn có bi màu xanh là:
5985  630  3060  2295. 2295
Vậy xác suất cần tìm là: . 5985
Câu 35. Cho hình lăng trụ AB . CD A B  C  D
  có đáy là hình bình hành. Gọi M , N , P , Q lần lượt là trọng tâm các tam giác A A  D , A CD  , A CB 
, ABA . Gọi O là điểm bất kỳ trên mặt đáy ABCD. Biết thể tích khối chóp .
O MNPQ bằng V . Tính theo V thể tích khối lăng trụ AB . CD ABC D  . 27 81 81 27 A. V . B. V . C. V . D. V . 8 4 2 4 Lời giải Chọn C
Gọi M  , N , P, Q lần lượt là trung điểm của các cạnh AD , DC ,CB, BA . 2  2   1 2 Ta có S  S   . MNPQ .   MNP Q . .S ABCD .S  3  9 2 9 ABCD 1 2
Đường cao của khối chóp . O MNPQ là: h    . . h V V O MNPQ A. 3 ABCD . 27 A ABCD 1 Ta lại có V  V . A .ABCD ABCDA 'B 'C 'D ' 3 2 81 Suy ra V  V      V      V . ABCD .A B C D ABCD . 81 A B C D 2 B. ĐIỀN KHUYẾT (15 CÂU)
Câu 36. Tiếp tuyến với đồ thị 3 2
y  x  x 1 tại điểm có hoành độ x  1 có phương trình là: 0 Đáp án: ………….. Lời giải.
Tọa độ tiếp điểm: x  1 y  1. Tiếp điểm M 1;  1 . 0 0
Hệ số góc của tiếp tuyến: 2
y  3x  2x  y   1  1.
Tiếp tuyến tại điểm có hoành độ x  1 có phương trình: y   x   1 1  . 0 y x
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/ Câu 37. Cho hàm số 2
y  f  x có đạo hàm f  x  x x  
1 2x 3 . Hàm số đã cho có bao nhiêu điểm cực trị? Đáp án: ………….. Lời giải
Số điểm cực trị của hàm số là số nghiệm đơn của f  x  0  x  0 
 x x 122x 3  0  x 1   3 x    2 3
x  1là nghiệm kép, x 0, x   là nghiệm đơn. 2
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC với A1; 2;   1 , B 0; 3; 4 , C 2; 1;  
1 . Độ dài đường cao từ A đến BC bằng: Đáp án: ………….. Lời giải BC  2; 2  ; 5  ,BA  1; 1  ; 5  . BC, BA   50 AH   . BC 33
Câu 39. Lớp 10A4 cử đại diện 3 học sinh, 11A5 cử đại diện 4 học sinh, 12A6 cử đại diện 5 học sinh đi đại
hội (ngồi bàn tròn). Hỏi có bao nhiêu cách xếp 12 học sinh vào bàn sao cho các thành viên của
mỗi lớp ngồi cạnh nhau ? Đáp án: ………….. Lời giải
Ghép 3 học sinh lớp 10A4 thành một nhóm.
Ghép 4 học sinh lớp 11A5 thành một nhóm.
Ghép 5 học sinh lớp 12A6 thành một nhóm.
Xếp 3 nhóm quanh bàn tròn có 2! cách, hoán vị 3 học sinh lớp 10A4 có 3!cách, hoán vị 4 học
sinh lớp 11A5 có 4!cách, hoán vị 5 học sinh lớp 12A6 có 5!cách. Theo quy tắc nhân có 2.3!4!5!
cách xếp thỏa mãn yêu cầu bài toán.  Câu 40. Cho hàm số f (x) 5 f x liên tục trên thỏa mãn lim
 2 . Tìm m để hàm số x 1  x 1  2  2 f (x) 7 f (x) 1  5   g  x khi x 1   x 1 liên tục tạix  1 ? mx 2 khi x  1 Đáp án: ………….. Lời giải. f (x)  5 Vì lim
 2  lim[ f (x) 5] 0  lim f (x)  5 x 1  x 1  x 1 x 1   Ta có: +) g   1  m  2 2 2 f ( ) x 7 f( ) x 1  5 [2 f( ) x 3][ f( ) x 5] +) lim g x  lim  lim x 1  x 1  x 1 x 1   x 1  f ( ) x 5  lim  lim[2 f ( )
x  3]  2(2.5  3)  26 x 1 x1 x 1
Trang 20 Fanpage Nguyễn Bảo Vương 
 https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Hàm số g x  liên tục tại x  1 khi: lim g x  g  1 x 1 
 m  2  26  m  24 a  0
Câu 41. Cho a , b, c là 3 số thực thỏa mãn  . Gọi 4 1 x , 2
x lần lượt là hoành độ giao điểm a 9b 24c   0 của parabol P  2
: y  2ax  3bx  4c với trục hoành. Tìm giá trị nhỏ nhất của biểu thức T   . 1 x x2 Đáp án: ………….. Lời giải
Phương trình hoành độ giao điểm của P  với trục hoành là 2 2 ax  3bx 4 c 0 (1).
P  cắt trục hoành tại hai điểm khi và chỉ khi phương trình (1) có nghiệm, tức là ta có 2   9b 32ac  0
Khi đó hoành độ giao điểm
với trục hoành là nghiệm của (1), suy ra 1 x , 2 x của P  2  9b  32ac T  x    (2) 1 x 2 2 2 a 4a Theo bài ra ta có 1 9
4a 9b  24c  0 c   a  b (3). 6 24 2 2 Thay (3) vào (2) ta có 9 b b 4  3b  1 1 T   3    1   , 2 4   a a 3  2a  3 3 3b 3
Dấu “=” xảy ra khi và chỉ khi
 1 0  a   b  12c . 2a 2 1
Vậy giá trị nhỏ nhất của T bằng . 3 1 1
Câu 42. Tìm tất cả tham số thực của m để hàm số y   m  2 3 2 x  x 
mx  2 có cực đại, cực tiểu. 3 3 Đáp án: ………….. Lời giải y   m   2 1 2 x  2x  m . 3
Hàm số có cực đại, cực tiểu khi phương trình y  0 có hai nghiệm phân biệt  1 2     0 2 1   m  m 0  3   m 1     3 3    3  m  2  hoặc  2  m  1. m 2  0   m  2  m  2  
Câu 43. Cho hàm số y  f x liên tục trên và có đồ thị f  x như hình vẽ
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Đặt S  f 0  f 6  f a  f a  2 . Tập giá trị của S chứa tối đa bao nhiêu số nguyên? Đáp án: ………….. Lời giải a 6
Ta có: S   f  xdx  f   xdx    S    . 1 S 2 S 3 S4 0 a  2
(m  0)4 a  m2 n  a  24 6 n2 Do đó: S    
 3 n  m  a 10 . 2 2 2 2 0 m  a Do  nên 2  n  m  6 a   2  n  6 Suy ra: 4
  a  3n  m  a 10  8  a
Vậy S có tối đa 11 giá trị nguyên.
Câu 44. Cho hàm số y  f  x xác định trên và có bảng biến thiên như sau
Số nghiệm thuộc đoạn  3 ;3  của phương trình f  cos x 1 là Đáp án: ………….. Lời giải
Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
Ta có 0  cos x 1. Khi đó từ bảng biến thiên ta được  f cos x     f  x  1 cos x 0 cos 1      f cos x  1  cos x  a   0  a 1
Vẽ đồ thị hàm số g  x  cos x ; x   3  ; 3 . Từ đồ thị ta có
Phương trình cos x  0 có 6 nghiệm.
Phương trình cos x  a (0  a  1) có 12 nghiệm.
Vậy ta có tổng cộng 18 nghiệm.
Câu 45. Cho z , z là hai trong các số phức z thỏa mãn điều kiện z  5  3i  5 , đồng thời z  z  8 . 1 2 1 2
Tập hợp các điểm biểu diễn của số phức w  z 
trong mặt phẳng tọa độ 1 z 2 Oxy là đường tròn có
phương trình nào dưới đây? Đáp án: ………….. Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
Gọi A , B , M là các điểm biểu diễn của z , z , w. Khi đó 1 2 A , B thuộc đường tròn
C x  2  y  2 : 5
3  25 và AB  z  z  8. 1 2
C  có tâm I 5;3 và bán kính R  5, gọi T là trung điểm của $AB$ khi đó T là trung điểm của $OM$ và 2 2 IT  IA  TA  3 .
Gọi J là điểm đối xứng của O qua I suy ra J 10;6 và $IT$ là đường trung bình của tam giác
OJM , do đó JM  2 IT  6 . Vậy 2 2
M thuộc đường tròn tâm J bán kính bằng 6 và có phương trình  x 1  0  y   6  36 .
Câu 46. Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc với
nhau. Tính sin góc giữa đường thẳng SC và mặt phẳng SAD . Đáp án: ………….. Lời giải S K x H A D I C B
Gọi I là trung điểm của AB. Khi đó SI   ABCD . AD  AB Ta có 
 AD   SAB mà AD  SAD  suy ra SAD  SAB  .  AD  SI
Dựng BH  SA tại H suy ra SH  SAD .
Trong mặt phẳng SAD kẻ Hx / / AD. Trong mặt phẳng  BC, Hx qua C kẻ đường thẳng song
song với BH cắt Hx tại K thì CK  SAD . Suy ra SK là hình chiếu vuông góc của SC trên
Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022
mặt phẳng SAD nên góc giữa đường thẳng là góc
SC và mặt phẳng  SAD  CSK . Ta có a 3 2 2 3a 5a BH  CK  . Trong tam giác SCI có 2 2 SC  SI  IC    a 2 . 2 4 4 a 3 CK 6 Suy ra 2 sin CSK    SC a 2 4 x 1 y  2 z  3
Câu 47. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng  :   và điểm 2 2 1  A 1
 ; 2; 0 . Khoảng cách từ điểm A đến đường thẳng  bằng: Đáp án: ………….. Lời giải
Gọi H là hình chiếu vuông góc của A trên , ta có H 1 2t; 2 2t; 3 t , t  .
AH   2  2t;  2t; 3 t
Một vectơ chỉ phương của  là u  2; 2; 1.
AH.u  0  4  4t  4t  3  t  7 0  t   . 9  4 14 20  16 196 400 2 17 AH  ; ;    AH     .  9 9 9  81 81 81 3 Vậy d  A  2 17 ;  . 3 Câu 48. Cho ba số thực   a , b , 1 c  ;1 
 . Tìm giá trị nhỏ nhất P của biểu thức.  4  min  1  1  1  P  log b   log c   log a  . a  4 b  4  c  4        Đáp án: ………….. Lời giải 2 1  1  1 Vợi mọi  1  2 2 x  ;1 
 ta có x  x   x   0  x  x    .  4  4  2  4
Lấy logarit 2 vế, ta được 2  1 log  x  log x  (với t 0;1 (*). t t  4     1 
Áp dụng BĐT (*) ta được: 2 log b   log b  2 log b . a   4  a a   1  2 log c  c    c . b logb 2log  4 b   1  2 log a   log a  2 log a . c   4  c c 
Suy ra P  2 log b log c log a 3  2.3 log . b log . c log a  6  P . a b c a b c min
Câu 49. Cho hình chóp S.ABCD có đáy là hình thoi có ABC  60, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi H, M , N lần lượt là trung điểm các cạnh A , B S , A SD
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Blog: Nguyễn Bảo Vương: https://nguyenbaovuong.blogspot.com/
và G là trọng tâm tam giác SBC. Tính khoảng cách từ G đến mặt phẳng (HMN) biết khối chóp 3 a S.ABCD có thể tích V  4 Đáp án: ………….. Lời giải S N M J A D G K H I O P B C
Gọi x là cạnh hình thoi, ta có: x 3 AC  , x BD  x 3, SH  2 3 3 1 1   . . . x a V AC BD SH    x  a 3 2 4 4
Dựng MK / /SH , KI  HO, KJ  MI  KJ   HMN   .
Chứng minh được  SB  C / / 
  d G;    d S;    d  ;
A    2d  K;    2KJ . 1 a 3 a 3 SH a 3 Tính được KI  .  , MK   . 4 2 8 2 4 K . I KM a 15 Suy ra KJ   . 2 2 20 KI KM Vậyd G   a 15 a 15 ;  2KJ  2.  . 20 10
Câu 50. Cho hình hộp chữ nhật AB . CD A B  C  D  có A D    2 , A B
   x, (x  0) . Góc giữa đường thẳng
AC và mặt phẳng  ABB A
  bằng 60. Tính giá trị lớn nhất m V
của thể tích khối hộp chữ nhật ax ABCD.A B  C  D   . Đáp án: ………….. Lời giải
Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/ Điện thoại: 0946798489
TÀI LIỆU ÔN THI ĐGNL ĐHQG HÀ NỘI 2021-2022 Ta có AC, ABB A   
  AC,AB   B AC  60.
Xét tam giác ABC vuông tại B có 2
AB  B C.cot 60  . 3
Xét tam giác ABB vuông tại B có 2 2 4 2 BB  AB  AB   x . 3
Thể tích của khối hộp chữ nhật ABCD.A B  C  D   là 4 2 2   4 x x 3 4 2 V  AA .A D  .BB  2x  x  2.  3 2 3
Vậy giá trị lớn nhất của thể tích khối hộp chữ nhật 4 ABCD.A B  C  D   là m V  . ax 3
• XEM THÊM ĐỀ CƯƠNG ÔN THI TẠI:
• https://www.nbv.edu.vn/2022/01/de-cuong-danh-gia-nang-luc-dhqg-ha-noi.html
Theo dõi Fanpage: Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hoặc Facebook: Nguyễn Vương 
 https://www.facebook.com/phong.baovuong
Tham gia ngay: Nhóm Nguyễn Bào Vương (TÀI LIỆU TOÁN)  https://www.facebook.com/groups/703546230477890/
Ấn sub kênh Youtube: Nguyễn Vương
 https://www.youtube.com/channel/UCQ4u2J5gIEI1iRUbT3nwJfA?view_as=subscriber
Tải nhiều tài liệu hơn tại: https://www.nbv.edu.vn/
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27