Phần 2: Tổng Hợp Lý Thuyết Phần Tự Luận Trong Bài Thi Cuối Kỳ môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

PHẦN 2: TỔNG HỢP LÝ THUYẾT PHẦN TỰ LUẬN TRONG BÀI THI CUỐI KỲ
Câu 1. Định nghĩa vecto gia tốc. Nêu đặc điểm và ý nghĩa của các vecto gia tốc tiếp tuyến, gia tốc pháp tuyến
Định nghĩa vecto gia tốc :
Vecto gia tốc là đại lượng vectơ biểu thị
cho gia tốc. Gia tốc là đại lượng vật lý đặc
trưng cho sự biến thiên nhanh hay chậm của vận tốc. Gia tốc tiếp tuyến: +Đặc điểm:
- Có phương trùng với tiếp tuyến của quỹ đạo tại M
- Có phương là chiều chuyển động khi v tăng
và ngược lại khi v giảm dv
-Có độ lớn bằng đạo hàm vận tốc theo thời gian adt t
+ ý nghĩa: Vecto gia tốc tiếp tuyến đặc trưng cho sự biến thiên của vecto vận tốc về giá trị Gia tốc pháp tuyến: +Đặc điểm:
- Có phương vuông góc với tiếp tuyến quỹ đạo tại M
- Có chiều hướng vào tâm v - Độ lớn bằng: aR  2 n
+ý nghĩa: Vecto gia tốc pháp tuyến đặc trưng cho sự biến thiên về phương của vecto vận tốc Bài toán:
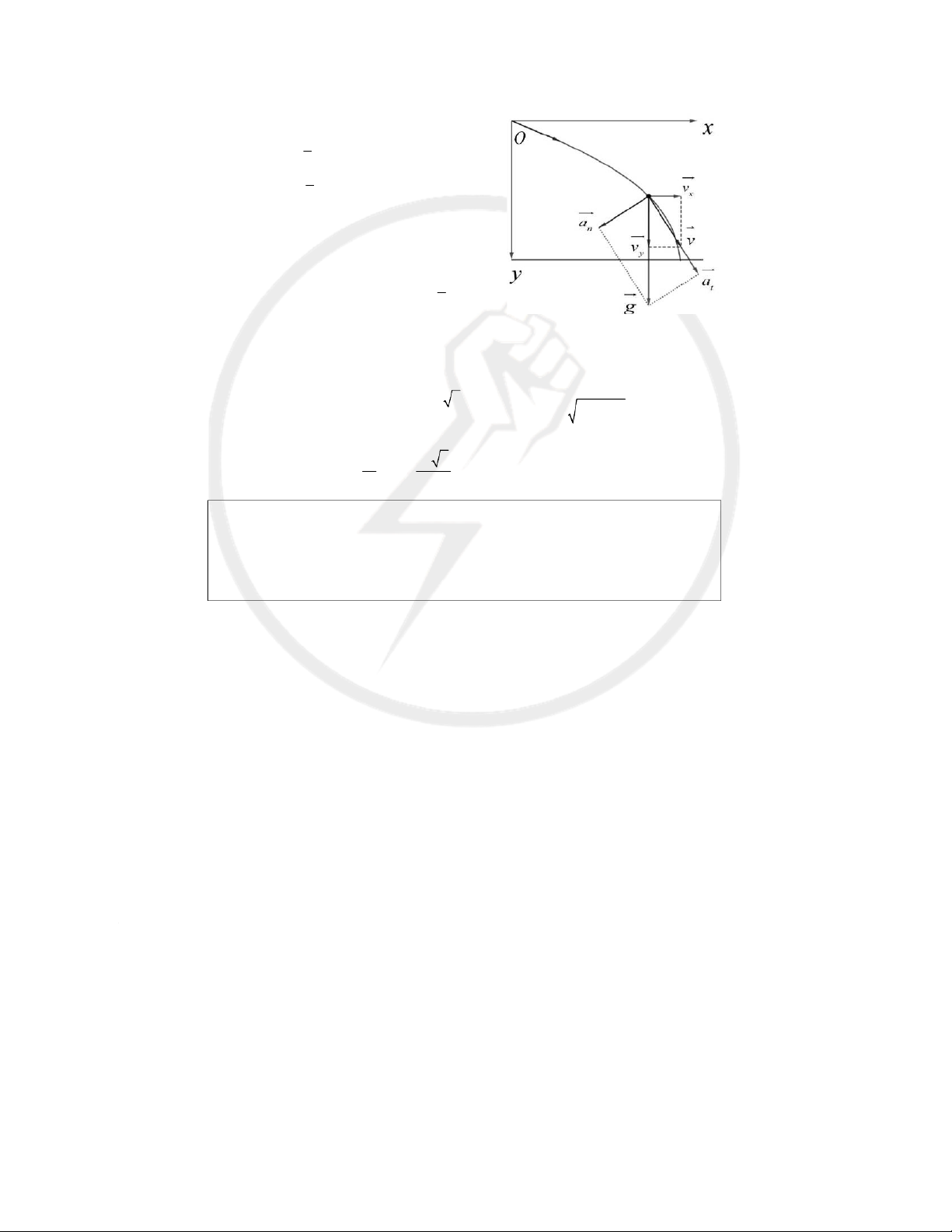
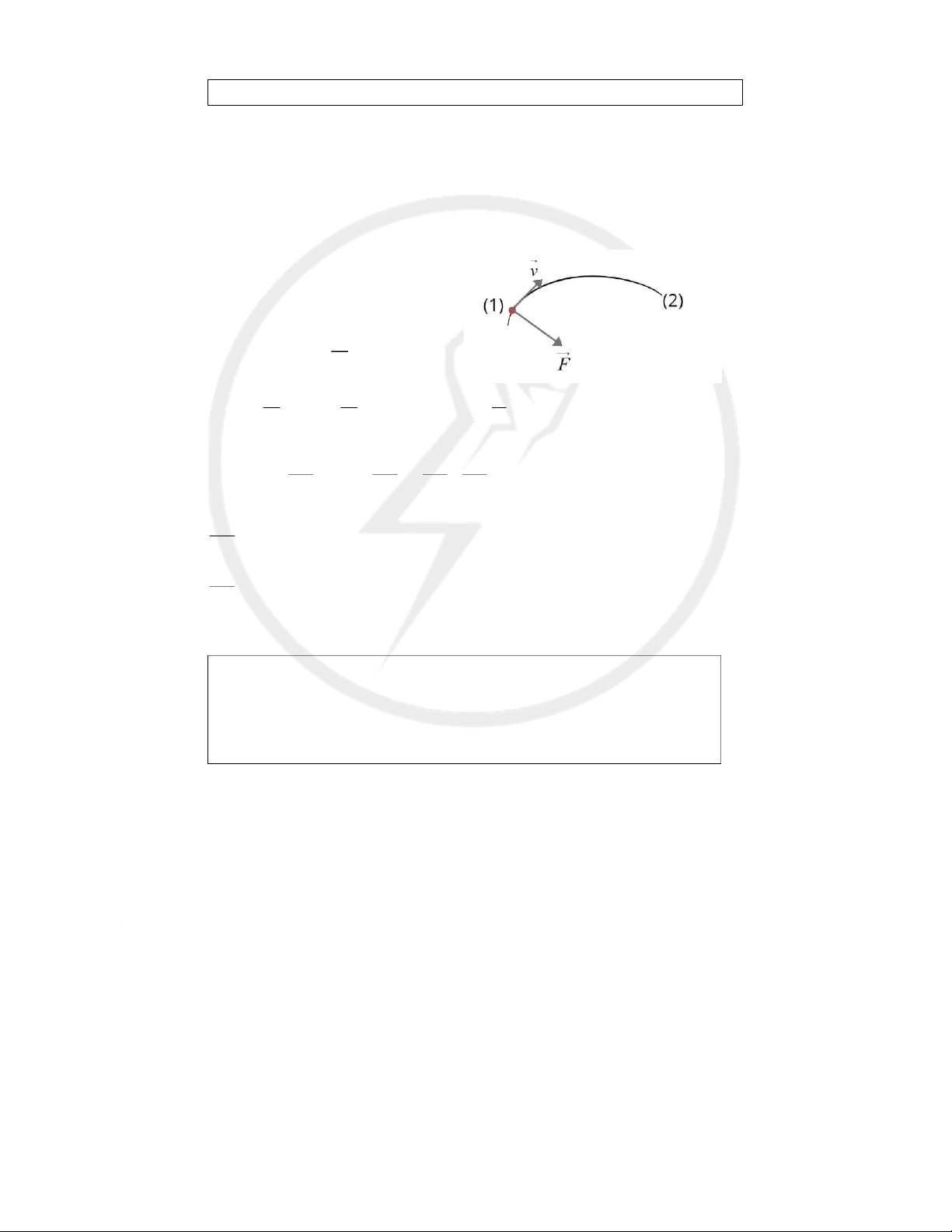
Từ đỉnh tháp có độ cao h, người ta ném một hòn đá xuống dưới đất với vận tốc ban đầu v
theo phương hợp với phương thẳng đứng một góc  ( hình vẽ) 0
a. Viết phương trình chuyển động của hòn đá trong hệ tọa độ vuông góc, với gốc tọa
độ tại điểm bắt đầu ném ( hình vẽ) b.  Cho h  m v  m  g 
m s Tìm thời gian bay và tốc độ 30 ; 20 / 2; 60o; 9, 8 / . 2
của hòn đá khi chạm đất. 0
Tìm gia tốc pháp tuyến tại điểm chạm đất. Bỏ qua lực cản của không khí 61 bkkhongsotach.edu.vn Giải:
Chọn hệ tọa độ như hình vẽ :    1 2 x x v t a t  0 0 x x 2  1 2 y  y v  t a t 0 0 y y  2 x 0 0 yx v  0 t 0  sin . v v   x  sin 0 0 0 Với    1 2 v v   y v t gt  yo cos cos . 2 0 0  ax 0 a g  y  +Tính thời gian bay: 2 y  h 4,t9 t 1  0  30 0; tính  ra t s 1, 66 v   v  m s x sin 10 3 / Tốc độ khi chạm đất 0    2 2  v  v v m s x y 31, 47 / v v  gt m s  y cos 26, 27 /  0 v +Ta có : x 10 3 2 a  g   g  m s n sin 9, 8 5, 39 / v 31, 47
Câu 2: Trình bày các vấn đề sau:
a. Hệ quy chiếu quán tính và nguyên lí tương đối Galileo.
b. Hệ quy chiếu không quán tình và lực quán tính ly tâm. Trả lời:
a. +Định nghĩa: Là hệ quy chiếu mà trên hệ quy chiếu đó, các định luật quán tính của Newton được nghiệm đúng
+ Nguyên lý tương đối Galileo:
- Mọi hệ quy chiếu chuyển động thẳng đều đối với hệ quy chiếu quán tính cũng là hệ quy
chiếu quán tính hay các định luật Niuton được nghiệm đúng trong hệ quy chiếu chuyển động
thẳng đều đối với hệ quy chiếu quán tính. 62 bkkhongsotach.edu.vn
Điều đó có nghĩa là: các phương trình động lực học trong các hệ quy chiếu quán tính có dạng
như nhau, các phương trình cơ học bất biến đối với phép biến đổi Galileo.
b. Trong 1 hệ quy chiếu chuyển động có gia tốc so với 1 hệ quy chiếu quán tính, các định
luật Niuton không được nghiệm đúng nữa là hệ quy chiếu không quán tính.
Lực quán tính ly tâm và lực quán tính xuất hiện trên 1 vật nằm yên trong hệ quy chiếu quay
so với 1 hệ quy chiếu quán tính.   F  m  .aht
Lực quán tính ly tâm có cùng độ lớn nhưng ngược chiều với lực hướng tâm. Bài toán:
Người ta chèo một con thuyền qua sông theo hướng vuông góc với bờ sông với vận tốc 7,2
km/h. Nước chảy đã mang con thuyền về phía xuôi dòng một khoảng 150m. Tìm:
a) Vận tốc của dòng nước đối với bờ sông;
b) Thời gian cần để thuyền qua được sông. Cho biết chiều rộng của sông bằng 0,5 km. Giải: 
+) v là vận tốc thuyền so với nước 0 
+) u là vận tốc dòng nước 
+) v là vận tốc thuyền so với bờ a) v 7  ,2 km 2 /h m/s 0 BC ut u tan .     AB v t v 0 0 BC u u v m s Mà 150 0, 3 0, 3 0, 3. 0.6 /        0   AB v 500 0 63 bkkhongsotach.edu.vn AB
b) Thời gian cần để qua sông: 500 t s   250   v 2 0 Câu 3:
a. Nêu định nghĩa động lượng ,thiết lập các định lí về động lượng của chất điểm, ý
nghĩa của động lượng và xung lượng của lực.
b. Trình bày định luật bảo toàn động lượng của hệ chất điểm cô lập và định luật bảo
toàn động lượng theo một phương của hệ chất điểm. Trả lời:
a.- Định nghĩa: Động lượng của một chất điểm là đại lượng vật lý được xác định bằng tích số
giữa khối lượng và vận tốc của chất điểm đó.   Vectơ động lượng: K mv   
- Định lý 1: Theo định luật II Newton, ta có: F m a .     d mv dv    d K  m F   F  F . dt dt dt
Vậy: Đạo hàm động lượng của 1 chất điểm đối với thời gian có giá trị bằng lực (hay tổng hợp
lực) tác dụng lên chất điểm đó.
- Định lý 2: Theo định lý I:  K t    2 2 d K   dt  F  d K  Fdt  d K  Fdt   K t 1 1 t     2   K  K K F  dt  ( F.  t nếu F không đổi). 2 1 t1 t  2  Fdt 
gọi là xung lượng của lực F trong khoảng thời gian t t  . 1 2 t1
Vậy: Độ biến thiên động lượng của 1 chất điểm trong một khoảng thời gian nào đó có giá trị
bằng xung lượng của lực (hay tổng hợp lực) tác dụng lên chất điểm trong khoảng thời gian đó.
- Ý nghĩa của động lượng:
+ Động lượng đặc trưng cho chuyển động về mặt động lực học và vận tốc cũng đặc trưng cho
chuyển động về mặt động học.
+ Động lượng đặc trưng cho khả năng truyền chuyển động. 64 bkkhongsotach.edu.vn  
- Ý nghĩa của xung lượng: K F.t  .
+ Xung lượng của một lực trong khoảng thời gian t
 đặc trưng cho tác dụng của lực trong khoảng thời gian đó.
b.Định luật bảo toàn của hệ chuyển động cô lập và theo phương.
+ Của hệ chất điểm (chuyển động)
Theo định lý 2 về động lượng ta có d          1 m 1 v 2 m 2 v ... n nm v  F (1) dt 
F - tổng hợp các ngoại lực tác dụng lên hệ .     
 Xét hệ cô lập thì: F  0 , tức là m v  m v  ... n nm v  const . 1 1 2 2
 tổng động lượng của 1 hệ cô lập là đại lượng không đổi – được bảo toàn
 Theo 1 phương của hệ chất điểm   
m v  m v   m v  const . x x ... 1 1 2 2 n nx
Khi đó: Hình chiếu của tổng động lượng của một hệ lên phương x đó là một đại lượng được bảo toàn. Bài toán: m
Hai hòn bi có khối lượng m1, và m2 = 1 được treo bằng 2 sợi dây có cùng chiều dài l = 2
6(m) vào một điềm. Kéo lệch hòn bi m1, cho đến khi dây treo nam ngang rồi thả ra để nó
va chạm vào bi m2. Sau va chạm hai hòn bi dính vào nhau và lên tới độ cao cực đại là? ( cho g = 9,8(m /s2)) Giải:
Bảo toàn cơ năng( mốc thế năng tại vị trí cân bằng của hòn bi 1 trước va chạm) m v 1 1 0  m gl   0 2  v gl (1) 1 2
Ngay sau va chạm cả hai hòn bi có cùng vận tốc v'. bảo toàn động lượng ta có: m v m v 2 2 1 1 m v  (m  m )v'  v  '    v 2gl (2) 1 1 2 m m m 3 3 1 2 1 m1 2
Động năng của hệ hai hòn bi sau va chạm là 65 bkkhongsotach.edu.vn 2 2 m v ' m v ' 3 1 2 1 2 2 2 W '    m  v m  v mgl d ' 1 1 2 2 4 3 3
Sau va chạm hai hòn bi dính vào nhau và tiếp nối chuyển động tròn ban đầu của hòn bi
l.Động năng W’d của hệ hai hòn bi chuyển động thành thế năng 3 W '  m  m g h
m gh của hai hòn bi ở độ cao tối đa h ( chọn mốc tính thế năng như t ( ) 2 1 2 1 trên) 2 3 4 W '  W  m gl  m gh  h l m d t ' 2, 667( ) 1 1 3 2 9
Câu 4: Nêu quan niệm về không gian và thời gian trong cơ học Newton. Phép biến đổi
Galileo. Phát biểu nguyên lí tương đối Galileo. Trả lời:
* Chuyển động tương đối và nguyên lý Galileo 
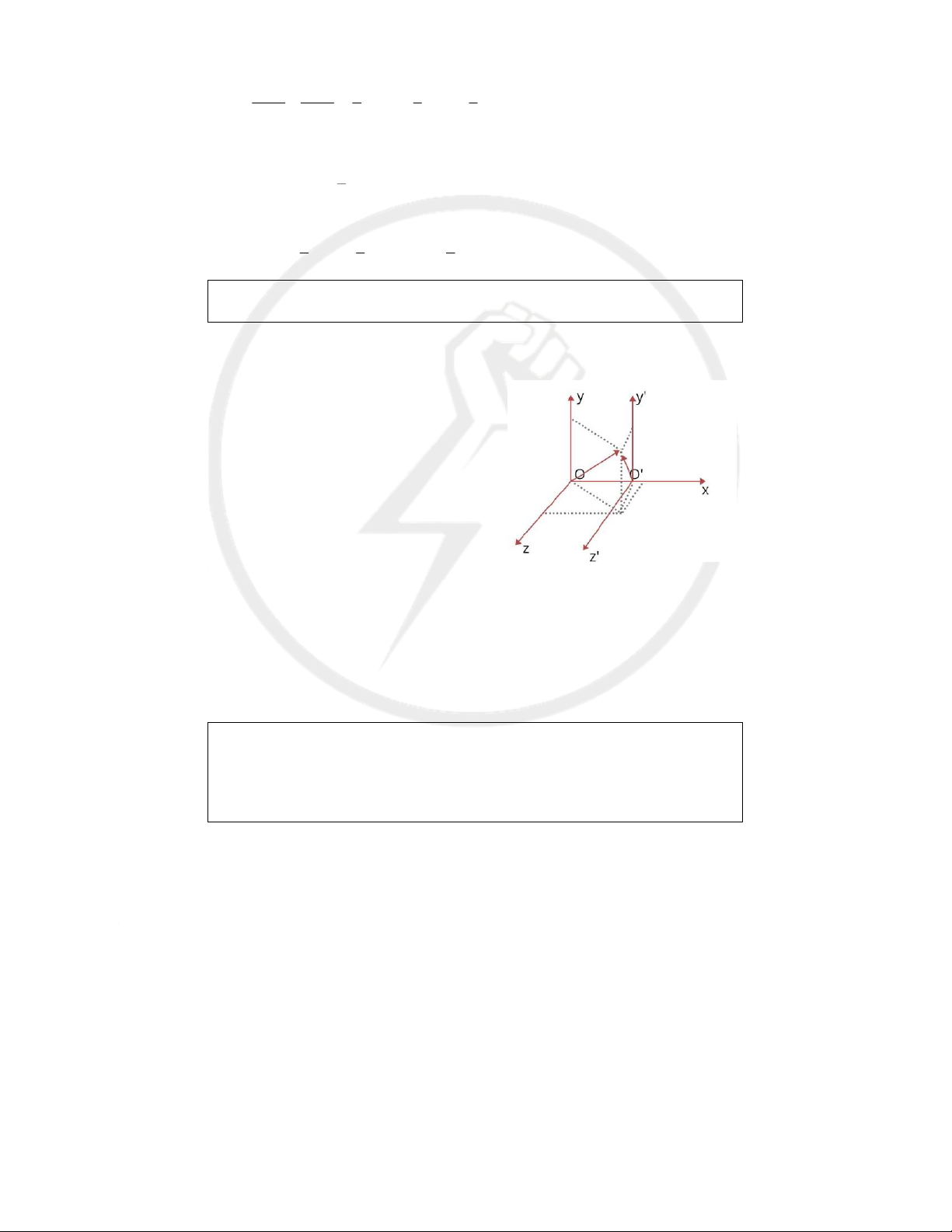
+) Xét hqc O chuyển động dọc theo Ox với vận tốc v ; O ; y // O y Oz // O z . 0
+) Thời gian là tuyệt đối: t t
+) Không gian là tương đối: x  x    x v  t 0 y y   
chuyển động là tương đối. z z 
x  x  v t x x x x l l
+) Khoảng không gian là tuyệt đối: 1 1 0        . 2 1 2 1 x  x  v t  2 2 0 
+ Nguyên lý tương đối Galileo:
- Mọi hệ quy chiếu chuyển động thẳng đều đối với hệ quy chiếu quán tính cũng là hệ quy
chiếu quán tính hay các định luật Niuton được nghiệm đúng trong hệ quy chiếu chuyển động
thẳng đều đối với hệ quy chiếu quán tính.
Điều đó có nghĩa là: các phương trình động lực học trong các hệ quy chiếu quán tính có dạng
như nhau, các phương trình cơ học bất biến đối với phép biến đổi Galileo.
Bài toán: Một người đang chạy với tốc độ v  2 m/s thì ném tới trước một hòn đá với tốc
độ so với người là v 5 m/s. Bỏ qua mọi ma sát và chiều cao của người. 0
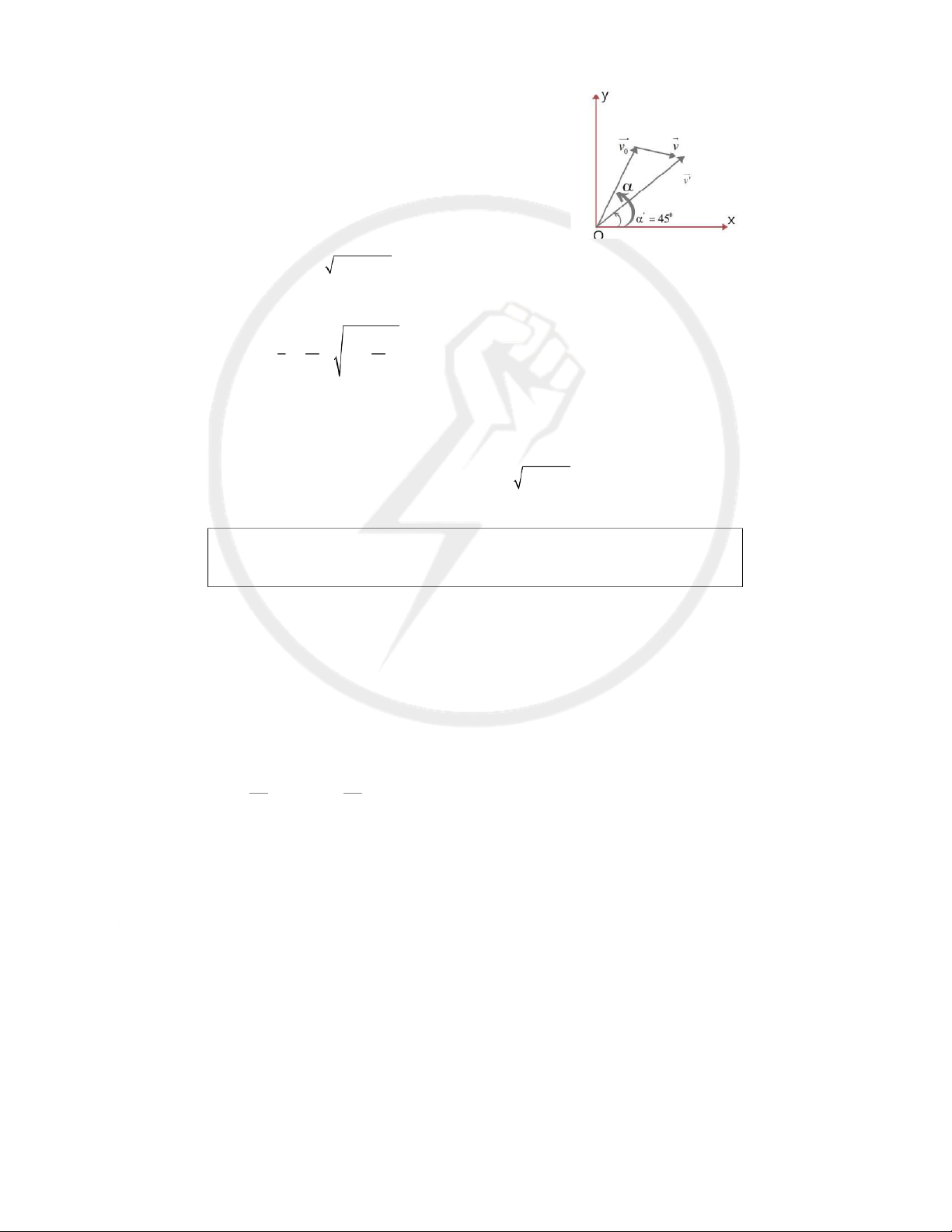
a) Tìm góc nghiêng  của vận tốc hòn đá so với người để hòn đá có tầm bay xa cực đại.
b) Tính tốc độ v của hòn đá so với mặt đất trong trường hợp câu a. Trả lời: 66 bkkhongsotach.edu.vn a) Góc     v v  v (1) 0 
Để hòn đá có tầm bay xa cực đại thì v phải hợp với phương ngang góc 45 . Do đó: vv . x y
Chiếu (1) lên 2 phương Ox và Oy: v cos s  inv   v  0 0 2  v cos  v  v  1 cos 0 0 2 2 2 2  2v cos  2  vvcos  v v   0 0 0 0   2 1 v v      cos 2        (2) 2  v v    0 0       Thay số: cos  
 0, 478   61, 45 . b) Tính v : 2 2 2 v v v   2 vv cos  0 0
Thay (2) vào biểu thức trên, ta tìm được: 2 2 2 2 v v  v 2 v v 0 0 Thay số: v 6,2 m/s
Câu 5: Trình bày định lý về mômen động lượng của một chất điểm và của một hệ chất
điểm đối với gốc tọa độ. Định luật bảo toàn mômen động lượng của chất điểm và hệ chất điểm. Trả lời:
Mômen động lượng của một chất điểm là 1 đại lượng vectơ xác định bằng tích có hướng giữa
vectơ bán kính quỹ đạo và vectơ động lượng của chất điểm đó.  
+ Với chất điểm chuyển động tròn: L  I w (I: mômen quán tính).     + Với hệ chất điểm: L   L  r k  . i i i
- Định lý về mômen động lượng:
+ Theo định lý về động lượng ta có:   d k d k      F  r  r  F dt dt 67 bkkhongsotach.edu.vn  d        d L r k r F   M  . dt dt
Vậy: Đạo hàm theo thời gian của mômen động lượng đối với gốc O của 1 chất điểm chuyển
động bằng tổng mômen đối với O của các lực tác dụng lên chất điểm.  L t    2 2 d L     Từ dt  M d L Mdt d L L   L Mdt   2 1 L t1 1 t  2    L  M  dt  . Nếu M không đổi  L   M.t . t1
Vậy: Độ biến thiên mômen động lượng trong 1 khoảng thời gian bằng xung lượng của
mômen lực tác dụng lên chất điểm trong khoảng thời gian đó.
- Định luật bảo toàn Mômen động lượng   Từ: d L    thì d L    M nếu M O  O  Lconst . dt dt
Vậy: Đối với 1 hệ chất điểm cô lập, hoặc chịu tác dụng của các ngoại lực nhưng tổng mômen
của các ngoại lực ấy đối với gốc O bằng 0, thì tổng mômen động lượng của 1 hệ là 1 đại lượng bảo toàn.
Với hệ chất điểm quay xung quanh 1 trục cố định: d         Nếu:       1 I w 1 w 2I 2 ... w n n I  M O  I wI w I ..w . n n con st dt 1 1 2 2   
 Vật rắn quay quanh 1 trục cố định M O I wconst . 68 bkkhongsotach.edu.vn
Câu 6: Tính công của lực hấp dẫn khi một vật có khối lượng m chuyển động trong trường  
hấp dẫn gây bởi một vật có khối lượng M từ vị trí r đến vị trí r (Xem các vật như chất 1 2
điểm, có vẽ hình). Từ đó chứng minh trường hấp dẫn là trường thế? Trả lời:  22 r r   2 2   Mm A  dA  F   .d r. dr  F      G  r d    r 1  2 1 r r 1 1  Mm M  m   1 1
 A G     G   GM  m  t  W W t        . 1 2 r r r r       1 2 1 2
 Công của lực F không phụ thuộc vào dạng đường đi mà chỉ phụ thuộc vào điểm đầu, điểm cuối.
 Trường hấp dẫn là trường thế. Bài toán:
Tính thế năng hấp dẫn của một vật m cách Trái đất (có khối lượng M) một khoảng r tính từ
tâm trái đất. Từ đó tính thế năng của vật có khối lượng m khi vật m cách bề mặt trái đất một khoảng h R
, lấy mốc thế năng tại mặt đất bằng không. Trả lời:
+ Thế năng của một vật m cách Trái đất (M) một khoảng r tính từ tâm trái đất: WGMm r  C   r
+ Lấy mốc tính thế năng là mặt đất, biểu thức tính thế năng của chất điểm trong trường hấp GMm r R  
dẫn của trái đất là: W  rR GMm
+ Khi r  R hh, tRa  có: r R   h và R r W 2  R   h  mg h với 2 0 R GM g   m l / à s2 029, 8
gia tốc trọng trường trên mặt đất. R 69 bkkhongsotach.edu.vn
Câu 7: Thiết lập các định lý về mômen động lượng (2 định lý) của vật rắn quay quanh trục cố định. Trả lời:        Vật rắn: L  L  r  m  v  m  r   r  i i i i i i i i i i        L m  r       r   m r i i i i  2 . .  i i i      L I  .   d L d  d   * Định lý I: 
I I  I   . dt dt dt 
Vậy: Đạo hàm mômen động lượng L theo thời gian bằng tổng mômen lực tác dụng lên vật rắn theo trục đó.  d L    . dt  
* Định lý II: Ta có: d L  .dt
Xét  tác dụng trong khoảng thời gian t t t 2 1 t    2   L  L L  dt   Xung lượng mômen. 2 1 t1
Vậy: Độ biến thiên mômen động lượng của vật rắn quay quanh 1 trục có giá trị bằng xung
lượng của mômen lực tác dụng lên vật rắn trong thời gian t .   Nếu    const L  t  . 70 bkkhongsotach.edu.vn Bài toán:
Một thanh chiều dài l = 0,9(m), khối lượng M = 6(kg) có thể quay tự do xung quanh một
trục nằm ngang đi qua một đầu của thanh. Một viên đạn khối lượng m= 0,01(kg) bay theo
hướng nằm ngang với vận tốc = 300(m /s) tới xuyên vào đầu kia của thanh và mắc vào
thanh. Vận tốc gốc của thanh ngay sau khi viên đạn đập vào đầu thanh là bao nhiêu ? Giải:   
Xét hệ trưóc va chạm: Tổng động lượng cả hệ: p m
v ( vì mỗi viên đạn có vận tốc v
mô men động lượng trước khi va chạm là: L = r.p.sinα = l.p = mvl
Vậy moomen quán tinh của hệ vật sau va chạm: Lsau = I1ω+I2ω
- I1 là moment chất điềm (viên đạn) đối với trục quay I1 = ml2 l 2 M 2 2 ( ) Ml Ml -I '2
2 là moment quán tính của thanh mảnh I   2 12 12 3 2 Ml  2 L  I I   ml   S ( ) ( ) 1 2 3
Áp dụng định luật bảo toàn momen động lượng 2   Ml mvl v 2 L  L mvl  ml      rad s t s 1, 658( / ) 2   3(1 ) Ml  l M 2 ml m 3 3 71 bkkhongsotach.edu.vn
Câu 8: Định lý về động năng của chất điểm. Nêu ý nghĩa của động năng. Trả lời:
- Định nghĩa: Động năng là phần cơ năng tương ứng với chuyển động của các vật. Là đại
lượng thể hiện mối phụ thuộc vào vận tốc chuyển động của vật thể do công ngoại lực tác dụng. - Định lý động năng: 
+ Xét 1 chất điểm khối lượng m, chịu tác dụng của một lực F , chuyển rời từ vị trí (1) tới vị 
trí (2). Công của lực F thực hiện là: 2    A Fd s  (1) 1     dv Lại có: F  m a m dt thay vào (1) ta có:           2 2 2 2 2 dv d s    v A m s d d m d v mvdv m              dt dt 2 1 1  1   1     22 2 2   v    2 2 mv mv mv mv 2 1 A d      d       (2).   2   v 2 2 2 1    1   2
mv2 : động năng của chất điểm ở vị trí (2). 2 2
mv1 : động năng của chất điểm ở vị trí (1). 2
Từ (2) ta có: Độ biến thiên động năng của 1 chất điểm trong 1 quãng đường nào đó có giá trị
bằng công của ngoại lực tác dụng lên chất điểm sinh ra từ quãng đường đó.
Bài toán:Một quả cầu khối lượng 2kg, chuyển động với vận tốc 3 m/s, va chạm xuyên
tâm với một quả cầu thứ hai khối lượng 3kg đang chuyển động cùng chiều với quả cầu
thứ nhất với vận tốc 1 m/s. Tìm vận tốc của các quả cầu sau va chạm nếu:
a) Va chạm là hoàn toàn đàn hồi.
b) Va chạm là không đàn hồi (mềm). Trả lời:
a) Va chạm hoàn toàn đàn hồi     +) BTĐL: m v m v m  v m  v   1 1 2 2 1 1 2 2 72 bkkhongsotach.edu.vn t   m v v    m  v v  (1) 1  1 1  2 2 2  2 2 2 2 m v m v m v  m v + BTCN: 1 1 2 2 1 1 2 2    2 2 2 2  m  2 2 v v   m   2 2 v v (2) 1 1 1 2 2 2  2
  v v v v 1  1 1 2 2  vv  2 (3) 2 1  m v v   m  2 v  v 1  1 1  2  1 2   6 2  vv6   3  3 1 1 3  v m/s 1 5 13  v m/s. 2 5 b) Va chạm mềm m v  m v +) m v  m v  m  m V 9 1 1 2 2  Vm  m .  m/s 1 1 2 2 1  2  5 1 2
Câu 9: Nêu các đặc điểm động học của chuyển động tịnh tiến và chuyển động quay
quanh một trục cố định của vật rắn.
Trả lời:a. Đặc điểm động học của chuyển động tịnh tiến:
- Khi vật rắn chuyển động tịnh tiến, mọi điểm của vật rắn vạch ra quỹ đạo giống nhau.
- Tại mỗi thời điểm, mọi điểm của vật rắn đều có cùng vận tốc và gia tốc. 
Gọi a là gia tốc chung cho các điểm của vật rắn m , ,
m ..., m chịu sự tác dụng của 1 2 n    F , F ,..., F . Khi đó ta có: 1 2 n   m a  F 1 1   m a  F 2 2   … m a  F n n 73 bkkhongsotach.edu.vn
 Để nghiên cứu chuyển động tịnh tiến của 1 vật rắn, ta chỉ cần nghiên cứu chất điểm bất kì
là đủ, người ta thường chọn khối tâm.
* Chuyển động của vật rắn quay quanh 1 trục cố định:
- Mọi điểm của vật rắn vạch ra quỹ đạo là 1 đường tròn, nằm trong mặt phẳng vuông góc với
trục quay có tâm nằm trên trục quay.
- Trong cùng 1 khoảng thời gian, mọi điểm trên vật rắn cùng quay được 1 góc.
- Tại thời điểm, 1 điểm của vật rắn có cùng ,  : 2 d d d     ;   2 dt dt dt  
- Tại thời điểm t, vectơ vận tốc dài v và a của chất điểm cách trục quay 1 khoảng r, được t
xác định bởi công thức:    v r     t a r  Bài toán:
Một quả cầu đặc có khối lượng m = l,4(Kg), lăn không trượt với vận tốc V1 = 10(m/s) thành
tường rồi bật ra với vận tốc V2 = 8(m/s). Nhiệt lượng tỏa ra trong va chạm đó là Giải:
Sau va chạm động năng của vật giảm. Độ giảm động năng này tỏa ra dưới dạng nhiệt
Khi chuyển động, quả cầu vừa có động năng tịnh tiến, vừa có động năng quay
Động năng của quả cầu đặc, đồng chất, lăn không trượt:   W 1 2 1 2 2 2 1 2 2 1 2  I   m  R  .   mR    mv dp 2 2 5 5 2
Moment quán tính của quả cầu đặc đồng chất: 2 2 I mR  5 2 mv
Động năng tịnh tiến của quả cầu đặc: W  d tt  2  W W 1 1 7     mv  mv mv dd q  d W 2 2 2 tt   5 2 10
Nhiệt lượng tỏa ra do va chạm: Q  W 7 7  2 2  m v v       J d   2 2 .1, 4. 10 8 35, 25 2 1    10 10 74 bkkhongsotach.edu.vn
Câu 10: Viết phương trình cơ bản trong chuyển động quay của vật rắn với một trục cố định?
giải thích đại lượng ? Nếu đặc điểm của momen quán tính? Trả lời:
-Phương trình cơ bản trong chuyển động quay của vật rắn với một trục cố định:   
M I . với M là momen ngoại lực(N/m);I là momen quán tính của vật 2 (k.g ) m ; 
 là gia tốc góc của chuyển động 2 (rad / s )
Đặc điểm của momen quán tính:
+)là đại ượng vật lý đặc trưng cho tính bảo toàn trạng thái của hệ trong chuyển động quay.
+)Momen quán tính phụ thuộc vào khối lượng của các thành phần trong hệ và khoảng cách
giữa các thành phần trong hệ đến trục quay. Bài toán Một vật m k 1 g 
được nối với một đầu dây cuốn vào một trụ đặc và được thả rơi xuống
như hình vẽ. Trụ có bán kính  R c 1 m 0 và có khối lượng M  kg6 . Bỏ qua lực ma sát và khối lượng của dây.
a) Tìm độ lớn gia tốc dài của vật m và lực căng của dây. Cho g m/s2 10 . 
b) Tìm công thực hiện bởi lực căng của dây khi trụ quay được một góc (kể từ lúc bắt 4 đầu thả vật). 75 bkkhongsotach.edu.vn Giải:
a) Tính a và T. Có hệ phương trình: P  T ma  . . a T  R I  I  r mg Trong đó: 1 1 I  MR 2 2 T  Ma a   2, m 5 /s 2 2 1 m M  2 Sức căng 1  T Ma  . 7, N 5 2  b) Công 0, 75 A    T .R. J  0,59 J.   4
Câu 11: Thiết lập biểu thức tính công của ngoại lực trong chuyển động quay của vật rắn
xung quang một trục cố định. Suy ra định lý về động năng của vật rắn trong chuyển động quay. Trả lời: +Có dA  F m d à s d d r   dA  . r F d d M  t. s t
+ Công toàn phần của vật rắn quay từ vị trí 1 đến 2 2 2 2 2 2 2 d  d A  d  A M  I. d   I. .d   . I d      dt 2 1 1 1 1 1 1 1 2 2  A I I  W W  2 1 dq2d 1 q 2 2
+ Định lý động năng của vật rắn quay:
Độ biến thiên động năng của vật rắn quay trong 1 khoảng thời gian có giá trị bằng công của
ngoại lực tác dụng lên chất điểm trong thời gian đó. 76 bkkhongsotach.edu.vn
Bài toán: Một cột đồng chất có chiều cao h m
 5 , đang ở vị trí thẳng đứng thì bị đổ xuống. Xác định:
a) Vận tốc dài của đỉnh cột khi nó chạm đất;
b) Vị trí của điểm M trên cột sao cho khi M chạm đất thì vận tốc của nó đúng bằng vận tốc
chạm đất của một vật thả rơi tự do từ vị trí M. mgh
Giải:a) Ở vị trí thẳng đứng, cột thế năng w1 . Khi đổ tới mặt đất thì thế năng này 3
biến thành động năng quay của cột ở vị trí chạm đất 1 2
 , trIong đó I là momen quán d 2 2 mh
tính của cột đối với trục qua gốc của cột: I,
 là vận tốc góc của cột lúc chạm đất. 3
Áp dụng định luật bảo toàn cơ năng sẽ tính được  , từ đó suy ra vận tốc của đỉnh cột lúc chạm đất v h   3 gh.
b) Gọi x là độ cao của điểm M khi cột ở vị trí thẳng đứng. Áp dụng công thức tính vận tốc
của vật rơi tự do, ta có: v lúc chạm đất  2 . 2 T g h x
eo điều kiện của đầu bài: x g  . 2 Từ x đó suy ra: x h M  3
Câu 12: Thiết lập phương trình dao động tắt dần của con lắc lò xo dưới tác dụng của
lực cản có độ lớn tỷ lệ với tốc độ. Tìm công thức tính giảm lượng loga của dao động tắt dần. Trả lời:
* Thiết lập phương trình dao động tắt dần của con lắc lò xo.   F  k x
Các lực tác dụng lên vật: kv  F rv c    
Viết phương trình Niuton với quả cầu:  F  F  ma   kx rv ma  kv c 2 d x d x hay m  k  xr  . 2 dt dt 2 d x r x d k x   . 0   . 2 dt m dt m k r Đặt 2   hay . 2  0 m m 77 bkkhongsotach.edu.vn 2 d x d x x 2   2 0     . 0 dt dt
Nghiệm của phương trình trên có dạng:  t x      0 A co e s
 t  đó là phương trình dao động tắt dần với 2 2      . 0
Giảm lượng loga: loga tự nhiên của số 2 biên độ dao động liên tiếp cách nhau 1 chu kỳ T. Đặt  t A  A .e  0 A t  t A e  . Giảm lượng loga: 0 T   ln l     T . A  nt  ln e    t T T  A .e0
Câu 13: Trình bày định luật phân bố phân tử theo vận tốc Maxwell. Từ đó suy ra công
thức tính vận tốc có xác suất lớn nhất và vận tốc trung bình của phân tử khí (không phải
tích phân). Cho biết ý nghĩa của các loại vận tốc này. Trả lời:
* Định luật phân bố phân tử theo vận tốc của Maxwell
+) Thực nghiệm chứng tỏ rằng các phân tử khí có vận tốc rất lớn 0  v  . Giả sử khí có n
phân tử, dn là số phân tử có vận tốc trong khoảng v dv  dn  dn là s% ố p 
hần trăm phần tử có vận tốc nằm trong khoảng này hay là xác suất tìm n n
thấy phần tử có vận tốc nằm trong khoảng v d v .
+) F v  là một hàm phụ thuộc vào v, gọi là hàm phân bố. dn
+) F v dv là xác suất phân tử có vận tốc trong khoảng  ,vv  dv   F v dv    n  dn    F   v dv n   n F v dv    n 0 0 0   F   là v điề  dv u kiệ 1
n chuẩn hóa của hàm phân bố. 0 3 2 m v 22 0  m  
Từ đó Maxwell tìm được: F v  4. 02 kT   v e  2kT     78 bkkhongsotach.edu.vn dF v  2k2 T T R +) Xét  0 F v  đạt max tại v v 
 (xác suất phân tử có v dv xs m  s x 0 là cao nhất).  kT kT
 Vận tốc trung bình: v  F v  8 8 vdv  m     00  2 kT kT T
Vận tốc căn quân phương: 2 2 v  v  F v v dv   v  c c    3 3 3 R m m  00 0 +) sv  v v  . x c
Bài toán: Khối lượng riêng của một chất khí  = 5.10-2 (kg / m3); vận tốc căn quân
phương của các phân tử khí này là v = 450(m /s). Áp suất của khối khí tác dụng lên thành bình là: Giải PV n PV RT PV P P
Áp dụng PT trạng thái khí lí tưởng: nRT    RT   m  m    V 2 RT RT v
Vận tốc căn quản phương của các phân tử khí: 3 c v    c   3 2 2 P v v c c 2    P .  3375( / N m )  3 3 79 bkkhongsotach.edu.vn
Câu 14: Trình bày nội dung cơ bản của thuyết động học phân tử khí lí tưởng. Viết phương
trình giữa áp suất và nhiệt độ của khối khí đó. Từ đó tính nội năng khí lí tưởng. Trả lời: * Nội dung:
+) Các chất cấu tạo gián đoạn và gồm 1 số lớn các phân tử.
+) Các phân tử chuyển động liên hoàn không ngừng. Cường độ chuyển động biểu hiện nhiệt độ của hệ.
+) Kích thước phân tử rất nhỏ so với khoảng cách giữa chúng, có thể coi là chất điểm.
+) Các phân tử không tương tác, chỉ va chạm theo cơ học Newton.
* Phương trình cơ bản của thuyết động học phân tử chất khí. n +) n  n 1 .v .t s
  Số phân tử vc với đáy trục n    n0v t  . s  0 6 6  
+) Xung lg do 1 phân tử:  t   m v  m v  2m v 0 2 0 1 0 2 2 m v m v 2 1 mv 1 0 0     F  n   . .n v t  s  2  n m v s 0 t t t 6 0 0 3 F 1 2  P  n m v . 0 0 s  3 2 nRT 3n R 3T R n T * Hệ quả: P n w w     0 3 v 2 2n v N 0 RT Mà N  n N  w 3 3 .2 2   kT A N A Với 23
N : số phân tử trong 1 mol. A 6.023.10 R 23 kN  1, 23.10 : Hằng số Boltzman. A Thay vào: 2 P  n w  n. kT 0 0 3 +) w 3  (đkT
ộng năng trung bình tịnh tiến). 2 80 bkkhongsotach.edu.vn