Phân dạng và bài tập phân thức đại số Toán 8 Kết Nối Tri Thức Với Cuộc Sống

Tài liệu gồm 101 trang, được tổng hợp và biên soạn bởi thầy giáo Nguyễn Bỉnh Khôi, phân dạng và tuyển chọn các bài tập chuyên đề phân thức đại số trong chương trình môn Toán 8 bộ sách Kết Nối Tri Thức Với Cuộc Sống, có đáp án và lời giải chi tiết. Mời các bạn đón đọc!

21 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 8

Môn: Toán 8

Thông tin:

101 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
1
PHÂN THỨC ĐẠI SỐ
6
Chûúng
PHÂN THỨC ĐẠI SỐ
PHÂN THỨC ĐẠI SỐ
21
Baâi
A
AA TRỌNG TÂM KIẾN THỨC
1 Phân thức đại số
Một phân thức đại số (hay nói gọn là phân thức) là biểu thức có dạng
A
B
, trong đó A, B là những đa thức và
B khác đa thức 0, A được gọi là tử thức (hay tử), B được gọi là mẫu thức (hay mẫu).
Nhận xét. Mỗi đa thức cũng được coi là một phân thức với mẫu thức bằng 1. Đặc biệt, số 0 và số 1 cũng là
phân thức đại số.
2 Hai phân thức bằng nhau
Hai phân thức
A
B
và
C
D
gọi là bằng nhau nếu A · D = B · C.
A
B
=
C
D
nếu A · D = B · C .
3 Điều kiện xác định và giá trị của phân thức tại một giá trị đã cho của biến
Khi thay các biến của phân thức đại số bằng các giá trị nào đó (sao cho phân thức xác định), rồi thực hiện các
phép tính thì ta nhận được giá trị của phân thức đại số đó tại các giá trị của biến.
Như vậy, để tính giá trị của phân thức tại những giá trị cho trước của biến ta thay các giá trị cho trước của
biến vào phân thức đó rồi tính giá trị của biểu thức số nhận được.
Điều kiện xác định của phân thức
A
B
là điều kiện của biến để mẫu thức B khác 0.
Ta chỉ cần quan tâm đến điều kiện xác định khi tính giá trị của phân thức.
Khi xét phân thức mà không nói gì thêm thì ta hiểu các biến chỉ nhận các giá trị làm cho phân thức xác
định.
A
BB CÁC DẠNG BÀI TẬP
Dạng 1. Nhận biết phân thức, xác định tử thức và mẫu thức
1/101 1/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
21. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
2
c Ví dụ 1. Chỉ ra các phân thức trong các biểu thức sau đây
2x + 1
x − 3
;
ab
a + b
; x
2
+ 2x + 1;
√
5;
√
x
x + 1
.
Lời giải.
Trong các biểu thức trên,
2x + 1
x − 3
;
ab
a + b
; x
2
+ 2x + 1;
√
5 là phân thức.
Biểu thức
√
x
x + 1
không phải là phân thức, vì
√
x không phải là đa thức. □
c Ví dụ 2.
a) Cách viết nào sau đây không cho một phân thức?
6y
3
z
x
2
;
xy + z
−3
;
y + z
0
;
0
x + 1
; x
3
− xy.
b) Viết mẫu thức của mỗi phân thức trong các cách viết trên.
Lời giải.
a) Trong các cách viết trên,
y + z
0
không phải là phân thức
b) Các phân thức
6y
3
z
x
2
;
xy + z
−3
;
0
x + 1
; x
3
− xy có mẫu lần lượt là x
2
; −3; x + 1; 1.
□
c Ví dụ 3. Trong các cặp phân thức sau, cặp phân thức nào có cùng mẫu thức?
−20x
3y
2
và
4x
3
5y
2
;a)
5x − 10
x
2
+ 1
và
5x − 10
x
2
− 1
;b)
5x + 10
4x − 8
và
4 − 2x
4(x − 2)
.c)
Lời giải.
Cặp phân thức có cùng mẫu thức là
5x + 10
4x − 8
và
4 − 2x
4(x − 2)
. □
c Ví dụ 4. Trong những biểu thức sau, biểu thức nào là phân thức?
2x + 1
x + 4
.a)
xy
x + 2y
.b)
1
x
x
2
+ 1
.c)
x
2
y + xy
2
x − y
.d)
x
2
− 2
1
x
.e)
Lời giải.
a) Do 2x + 1 và x + 4 là các đa thức và đa thức x + 4 khác đa thức 0 nên biểu thức
2x + 1
x + 4
là phân thức.
b) Do xy và x + 2y là các đa thức và đa thức x + 2y khác đa thức 0 nên biểu thức
xy
x + 2y
là phân thức.
c) Do biểu thức
1
x
không phải là đa thức nên biểu thức
1
x
x
2
+ 1
không phải là phân thức.
d) Do x
2
y + xy
2
và x −y là các đa thức và đa thức x −y khác đa thức 0 nên biểu thức
x
2
y + xy
2
x − y
là phân thức.
2/101 2/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
3
e) Do biểu thức
1
x
không phải là đa thức nên biểu thức
x
2
− 2
1
x
không phải là phân thức.
□
Dạng 2. Điều kiện xác định và giá trị của phân thức tại một giá trị đã cho của biến
c Ví dụ 5. Viết điều kiện xác định của mỗi phân thức sau
3x + 4
x − 2
;a)
x − y
x + y
;b)
x − 3
x + 2
;c)
1
2a + 4
;d)
xy
2
x − 2y
.e)
Lời giải.
a) Phân thức xác định khi x − 2 = 0 hay x = 2.
b) Phân thức xác định khi x + y = 0 (nghĩa là tại các giá trị của x và y thoả mãn x + y = 0).
c) Điều kiện xác định của phân thức là x + 2 = 0 hay x = −2.
d) Điều kiện xác định của phân thức
1
2a + 4
là 2a + 4 = 0 hay a = −2.
e) Điều kiện xác định của phân thức
xy
2
x − 2y
là x − 2y = 0 hay x = 2y.
□
c Ví dụ 6. Viết điều kiện xác định của phân thức
x + 1
x − 1
và tính giá trị của phân thức tại x = 2.
Lời giải.
Điều kiện xác định của phân thức là x − 1 = 0 hay x = 1.
Giá trị của phân thức tại x = 2 là
2 + 1
2 − 1
= 3. □
c Ví dụ 7. Tính giá trị của phân thức
x
2
− x − 1
x
2
+ 3x
tại x = 2; x = 1.
Lời giải.
○ Tại x = 2, phân thức có giá trị là
2
2
− 2 − 1
2
2
+ 3 · 2
=
1
10
.
○ Tại x = 1, phân thức có giá trị là
1
2
− 2 − 1
1
2
+ 3 · 1
=
−1
4
.
□
c Ví dụ 8. Cho phân thức P =
x
2
− 1
2x + 1
.
a) Tính giá trị của phân thức tại x = 0; x = 1; x = 2.
b) Tại x = −
1
2
thì phân thức có xác định không? Tại sao?
Lời giải.
3/101 3/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
21. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
4
a) Tại x = 0, P =
0 − 1
2 · 0 + 1
= −1.
Tại x = 1, P =
1
2
− 1
2 · 1 + 1
= 0.
Tại x = 2, P =
2
2
− 1
2 · 2 + 1
=
3
5
.
b) Với x = −
1
2
thì giá trị của mẫu thức là 2 ·
Å
−
1
2
ã
+ 1 = −1 + 1 = 0 nên phân thức không xác định.
□
c Ví dụ 9. Tìm giá trị của phân thức
x
2
− 2x + 1
x + 2
tại x = −3, x = 1;a)
xy − 3y
2
x + y
tại x = 3, y = −1.b)
Lời giải.
a) Với x = −3, ta có
(−3)
2
− 2(−3) + 1
−3 + 2
=
9 + 6 + 1
−1
=
16
−1
= −16.
Với x = 1, ta có
1
2
− 2 · 1 + 1
1 + 2
=
0
3
= 0.
b) Với x = 3, y = −1, ta có
3 · −1 − 3 · (−1)
2
3 + −1
=
3 · −1 − 3 · 1
2
=
−3 − 3
2
=
−6
2
= −3.
□
Dạng 3. Hai phân thức bằng nhau
c Ví dụ 10. Mỗi cặp phân thức sau đây có bằng nhau không? Tại sao?
xy
2
xy + y
và
xy
x + 1
;a)
xy − y
x
và
xy − x
y
;b) A =
3x
2
− 9x
x
2
− 9
và B =
3x
x + 3
;c)
x
5
và
x
2
− x
5x − 5
;d)
3 + x
3 + 2x
và
1
2
;e)
x + y
x
2
− y
2
và
1
x − y
;f)
x
x
2
− 1
và
1
x − 1
;g)
1
x
2
+ x + 1
=
1 − x
1 − x
3
;h)
1 + x
1 − x
2
=
1
1 − x
.i)
Lời giải.
a) Ta có
®
(xy
2
) · (x + 1) = x
2
y
2
+ xy
2
(xy + y) · xy = x
2
y
2
+ xy
2
.
Do đó (xy
2
) · (x + 1) = (xy + y) · xy.
Vậy
xy
2
xy + y
=
xy
x + 1
;
b) Ta có
®
(xy − y) · y = xy
2
− y
2
x · (xy − x) = x
2
y − x
2
.
.
Do đó (xy −y) · y = x · (xy − x).
Vậy hai phân thức
xy − y
x
và
xy − x
y
không bằng nhau.
4/101 4/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
5
c) Ta có
®
3x
2
− 9x
· (x + 3) = 3x
3
+ 9x
2
− 9x
2
− 27x = 3x
3
− 27x
x
2
− 9
· 3x = 3x
3
− 27x.
Vậy
3x
2
− 9x
· (x + 3) =
x
2
− 9
· 3x.
Do đó
3x
2
− 9x
x
2
− 9
=
3x
x + 3
, hay A = B.
d) Ta có: x · (5x − 5) = 5x
2
− 5x và 5 ·
x
2
− x
= 5x
2
− 5x nên x · (5x − 5) = 5 ·
x
2
− x
.
Vậy
x
5
=
x
2
− x
5x − 5
.
e) Ta có: (3 + x) ·2 = 6 + 2x và (3 + 2x) ·1 = 3 + 2x. Do 6 + 2x = 3 + 2x nên hai phân thức
3 + x
3 + 2x
và
1
2
không
bằng nhau.
f) Ta có: (x + y) · (x − y) = x
2
− y
2
và
x
2
− y
2
· 1 = x
2
− y
2
nên (x + y) · (x − y) =
x
2
− y
2
· 1. Vậy
x + y
x
2
− y
2
=
1
x − y
.
g) Ta có: x · (x − 1) = x
2
− 1 và
x
2
− 1
· 1 = x
2
− 1
nên x · (x − 1) =
x
2
− 1
· 1. Vậy
x
x
2
− 1
=
1
x − 1
.
h) Ta có
1
x
2
+ x + 1
=
1 − x
1 − x
3
vì 1 · (1 − x
3
) = (1 − x)(x
2
+ x + 1).
i) Vì (1 + x)(1 − x) = (1 − x
2
) · 1 nên
1 + x
1 − x
2
=
1
1 − x
.
□
c Ví dụ 11. Dùng định nghĩa hai phân thức bằng nhau, chứng tỏ rằng:
3y
4
=
6xy
8x
;a)
x + y
3x
=
3x(x + y)
2
9x
2
(x + y)
;b)
x + 1
x + 3
=
x
2
+ 4x + 3
x
2
+ 6x + 9
.c)
Lời giải.
a) Ta có 3y · 8x = 4 · 6xy nên
3y
4
=
6xy
8x
.
b) Ta có (x + y) · 9x
2
(x + y) = 3x · 3x(x + y)
2
nên
x + y
3x
=
3x(x + y)
2
9x
2
(x + y)
.
c) Ta có
(x + 1)
x
2
+ 6x + 9
= (x + 1)(x + 3)
2
.
(x + 3) ·
x
2
+ 4x + 3
= (x + 3)(x + 3)(x + 1) = (x + 1)(x + 3)
2
.
Do đó (x + 1)
x
2
+ 6x + 9
= (x + 3) ·
x
2
+ 4x + 3
.
Suy ra
x + 1
x + 3
=
x
2
+ 4x + 3
x
2
+ 6x + 9
.
□
c Ví dụ 12. Chứng minh đẳng thức
x − 2
−x
=
8 − x
3
x (x
2
+ 2x + 4)
.
Lời giải.
5/101 5/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
21. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
6
Ta có x
2
+ 2x + 4 = x
2
+ 2x + 1 + 3 = (x + 1)
2
+ 3 > 0 nên
x − 2
−x
=
(x − 2) ·
x
2
+ 2x + 4
−x · (x
2
+ 2x + 4)
=
x
3
− 8
−x (x
2
+ 2x + 4)
=
8 − x
3
x (x
2
+ 2x + 4)
.
Vế trái bằng vế phải. Đẳng thức đã được chứng minh. □
c Ví dụ 13. Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong đẳng thức
A
x
2
− 4
=
x
x + 2
Lời giải.
Ta có
(x + 2) = x ·
x
2
− 4
A · (x + 2) = x · (x − 2) · (x + 2).
Suy ra A = x · (x − 2). □
c Ví dụ 14. Dùng tính chất cơ bản của phân thức, hãy điền một đa thức thích hợp vào chỗ trống trong đẳng
thức
(x + 1)
2
x
2
+ x
=
. . .
x
.
Lời giải.
Ta có
(x + 1)
2
x
2
+ x
=
(x + 1)
2
x(x + 1)
=
(x + 1)
2
: (x + 1)
x(x + 1) : (x + 1)
=
x + 1
x
.
Vậy đa thức cần tìm là x + 1. □
Dạng 4. Tìm giá trị nhỏ nhất, giá trị lớn nhất của phân thức
○ Với a > 0 (a là hằng số)
P (x) = m + a[F (x)]
2
≥ m; giá trị nhỏ nhất của P (x) bằng m khi F (x) = 0.
P (x) = m − a[F (x)]
2
≤ m; giá trị lớn nhất của P (x) bằng m khi F (x) = 0.
○ Với a > 0 (a là hằng số), P (x) > 0 thì
a
P (x)
nhỏ nhất (hoặc lớn nhất) khi P (x) lớn nhất (hoặc nhỏ
nhất).
c Ví dụ 15.
a) Tìm giá trị nhỏ nhất của phân thức A =
x
2
+ 2x + 3
4
.
b) Tìm giá trị lớn nhất của phân thức B =
4 − 4x
2
+ 4x
5
.
Lời giải.
a) A =
x
2
+ 2x + 3
4
có giá trị nhỏ nhất ⇔ x
2
+ 2x + 3 có giá trị nhỏ nhất.
Mà x
2
+ 2x + 3 = (x + 1)
2
+ 2 ≥ 2, nên giá trị nhỏ nhất của x
2
+ 2x + 3 là 2 khi x = −1.
Vậy giá trị nhỏ nhất của phân thức A là
2
4
=
1
2
, đạt được khi x = −1.
b) B =
4 − 4x
2
+ 4x
5
có giá trị lớn nhất ⇔ 4 − 4x
2
+ 4x có giá trị lớn nhất.
6/101 6/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
7
Mà 4 − 4x
2
+ 4x = 5 − (2x − 1)
2
≤ 5 nên giá trị lớn nhất của 4 − 4x
2
+ 4x là 5 khi x =
1
2
.
Vậy giá trị lớn nhất của B là
5
5
= 1, đạt được khi x =
1
2
.
□
c Ví dụ 16. Tìm giá trị lớn nhất của P =
10
x
2
− 2x + 2
.
Lời giải.
Tử thức 10 > 0 và mẫu thức x
2
− 2x + 2 = (x − 1)
2
+ 1 > 0 nên P lớn nhất ⇔ x
2
− 2x + 2 nhỏ nhất.
Mà x
2
− 2x + 2 = (x − 1)
2
+ 1 ≥ 1, nên giá trị nhỏ nhất của x
2
− 2x + 2 là 1 khi x = 1.
Vậy giá trị lớn nhất của P là
10
1
= 10, đạt được khi x = 1. □
Dạng 5. Vận dụng
c Ví dụ 17. Cho hình chữ nhật ABCD và MNP Q như hình vẽ (các số đo trên hình tính theo đơn vị
centimét).
D
B
x + 3
x + 1
A
C
Q
N
x + 1
x
M
P
a) Viết phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật MNP Q.
b) Tính giá trị của phân thức đó tại x = 2 và tại x = 5.
Lời giải.
a) Diện tích của hình chữ nhật ABCD là (x + 3) · (x + 1).
Diện tích của hình chữ nhật MN P Q là (x + 1) · x.
Do đó phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật MN P Q là
(x + 3) · (x + 1)
(x + 1) · x
.
b)
○ Với x = 2, phân thức trên có giá trị là
(2 + 3) · (2 + 1)
(2 + 1) · 2
=
5
2
.
○ Với x = 5, phân thức trên có giá trị là
(5 + 3) · (5 + 1)
(5 + 1) · 5
=
8
5
.
□
c Ví dụ 18. Giá thành trung bình của một chiếc áo sơ mi được một xí nghiệp sản xuất cho bởi biểu thức
C(x) =
0,0002x
2
+ 120x + 1000
x
, trong đó x là số áo được sản xuất và C tính bằng nghìn đồng. Tính C khi
x = 100, x = 1000.
Lời giải.
7/101 7/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
21. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
8
• Khi x = 100, giá thành trung bình mỗi áo sẽ là
C(100) =
0,0002 · 100
2
+ 120 · 100 + 1000
100
=
2 + 12000 + 1000
100
=
13002
100
= 130,02.
Vậy giá thành trung bình mỗi áo là 130,02 nghìn đồng.
• Khi x = 1000, giá thành trung bình mỗi áo sẽ là
C(1000) =
0,0002 · 1000
2
+ 120 · 1000 + 1000
1000
=
200 + 120000 + 1000
1000
=
121200
1000
= 121,2.
Vậy giá thành trung bình mỗi áo là 121,2 nghìn đồng.
□
c Ví dụ 19. Chị Hà mở một xưởng thủ công với vốn đầu tư ban đầu (xây dựng nhà xưởng, mua máy móc,...)
là 80 triệu. Biết chi phí để sản xuất (tiền mua vật liệu, lương nhân công) của 1 sản phẩm là 15 nghìn đồng.
Gọi x là số sản phẩm mà xưởng của chị Hà làm được.
a) Viết phân thức biểu thị số tiền thực (đơn vị là nghìn đồng) đã bỏ ra để làm được x sản phẩm.
b) Viết phân thức biểu thị chi phí thực (đơn vị là nghìn đồng) để tạo ra 1 sản phẩm theo x.
c) Tính chi phí thực để tạo ra 1 sản phẩm nếu x = 100; x = 1 000. Nhận xét về chi phí thực để tạo ra 1
sản phẩm nếu x ngày càng tăng.
Lời giải.
Đổi 80 triệu = 80 000 (nghìn đồng).
a) Phân thức biểu thị số tiền thực (đơn vị là nghìn đồng) đã bỏ ra để làm được x sản phẩm là 80 000 + 15 · x
(nghìn đồng).
b) Phân thức biểu thị chi phí thực (đơn vị là nghìn đồng) để tạo ra 1 sản phẩm theo x là
80 000 + 15 · x
x
(nghìn
đồng).
c)
○ Chi phí thực để tạo ra 1 sản phẩm nếu x = 100 là
80 000 + 15 · 100
100
= 815 (nghìn đồng).
○ Chi phí thực để tạo ra 1 sản phẩm nếu x = 1 000 là
80 000 + 15 · 1000
1000
= 95 (nghìn đồng).
Vậy chi phí thực để tạo ra 1 sản phẩm sẽ ngày càng giảm nếu x ngày càng tăng.
□
A
CC BÀI TẬP VẬN DỤNG
c Bài 1. Viết tử thức và mẫu thức của phân thức
5x − 2
3
.
Lời giải.
Tử thức là 5x − 2.○ Mẫu thức là 3.○
□
8/101 8/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
9
c Bài 2. Trong các cặp phân thức sau, cặp phân thức nào có mẫu giống nhau?
−20x
3y
2
và
4x
5y
2
;a)
3x − 1
x
2
+ 1
và
3x − 1
x + 1
;b)
x − 1
3x + 6
và
x + 1
3(x + 2)
.c)
Lời giải.
Phân thức có mẫu giống nhau là
x − 1
3x + 6
và
x + 1
3(x + 2)
. □
c Bài 3. Trong các biểu thức sau, biểu thức nào là phân thức?
3x + 1
2x − 1
; 2x
2
− 5x + 3;
x +
√
x
3x + 2
.
Lời giải.
3x + 1
2x − 1
; 2x
2
− 5x + 3 là các phân thức.
x +
√
x
3x + 2
không phải là phân thức vì x +
√
x không phải là một đa thức. □
c Bài 4. Cho A là một đa thức khác 0 tùy ý. Hãy giả thích vì sao
0
A
= 0 và
A
A
= 1.
Lời giải.
Ta có
0
A
= 0 vì 0 = 0 · A.○ Ta có
A
A
= 1 vì A = 1 · A.○
□
c Bài 5. Viết điều kiện xác định của các phân thức sau
4x − 1
2x − 6
;a)
x − 10
x + 3y
;b) 3x
2
− x + 7;c)
y
3y + 3
;d)
4x
x
2
+ 16
;e)
x + y
x − y
.f)
Lời giải.
a) Phân thức xác định khi 2x − 6 = 0 hay x = 3.
b) Phân thức xác định khi x + 3y = 0 hay x = −3y.
c) Phân thức 3x
2
− x + 7 là một đa thức nên xác định với mọi x.
d) Điều kiện để giá trị của phân thức
y
3y + 3
được xác định là 3y + 3 = 0.
e) Điều kiện để giá trị của phân thức
4x
x
2
+ 16
được xác định là x
2
+ 16 = 0.
f) Điều kiện để giá trị của phân thức
x + y
x − y
được xác định là x − y = 0.
□
c Bài 6. Viết điều kiện xác định của phân thức
x
2
+ x − 2
x
3
+ 2
. Tính giá trị của phân thức trên lần lượt tại
x = 0; x = 1; x = 2.
Lời giải.
Điều kiện xác định của phân thức
x
2
+ x − 2
x
3
+ 2
là x
3
+ 2 = 0.
9/101 9/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
21. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
10
○ Giá trị của phân thức tại x = 0 là
0
2
+ 0 − 2
0
3
+ 2
= −1.
○ Giá trị của phân thức tại x = 1 là
1
2
+ 1 − 2
1
3
+ 2
= 0.
○ Giá trị của phân thức tại x = 2 là
2
2
+ 2 − 2
2
3
+ 2
=
2
5
.
□
c Bài 7. Tìm giá trị của phân thức
A =
3x
2
+ 3x
x
2
+ 2x + 1
tại x = −4;a) B =
ab − b
2
a
2
− b
2
tại a = 4, b = −2.b)
Lời giải.
a) Với x = −4 ta có
A =
3(−4)
2
+ 3(−4)
(−4)
2
+ 2(−4) + 1
=
3 · 16 − 12
16 − 8 + 1
=
36
9
= 4.
b) Với a = 4 và b = −2 ta có
B =
4 · (−2) − (−2)
2
4
2
− (−2)
2
=
−8 − 4
16 − 4
=
−12
12
= −1.
□
c Bài 8. Vì sao các kết luận sau đây đúng?
−6
−4y
=
3y
2y
2
;a)
x + 3
5
=
x
2
+ 3x
5x
;b)
3x(4x + 1)
16x
2
− 1
=
−3x
1 − 4x
.c)
Lời giải.
a) Ta có
−6
−4y
=
3y
2y
2
vì −6 · 2y
2
= 3y · (−4y).
b) Ta có
x + 3
5
=
x
2
+ 3x
5x
vì (x + 3) · 5x = (x
2
+ 3x) · 5.
c) Ta có
3x(4x + 1)
16x
2
− 1
=
−3x
1 − 4x
vì 3x(4x + 1) · (1 − 4x) = (−3x) · (16x
2
− 1).
□
c Bài 9. Mỗi cặp phân thức sau có bằng nhau không? Tại sao?
3ac
a
3
b
và
6c
2a
2
b
;a)
3ab − 3b
2
6b
2
và
a − b
2b
.b)
Lời giải.
a) Ta có 3ac · 2a
2
b = 6a
3
bc và a
3
b · 6c = 6a
3
bc.
Do đó 3ac · 2a
2
b = a
3
b · 6c.
Vậy
3ac
a
3
b
=
6c
2a
2
b
.
b) (3ab − 3b
2
) · 2b = 6ab
2
− 6b
3
và (a − b) · 6b
2
= 6ab
2
− 6b
3
.
Do đó (3ab − 3b
2
) · 2b = (a − b) · 6b
2
.
Vậy
3ab − 3b
2
6b
2
=
a − b
2b
.
□
10/101 10/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
11
c Bài 10. Tìm đa thức thích hợp thay vào ? trong các đẳng thức sau
2x + 1
x − 1
=
?
x
2
− 1
;a)
x
2
+ 2x
x
3
+ 8
=
?
x
2
− 2x + 4
.b)
Lời giải.
a) Ta có
2x + 1
x − 1
=
(2x + 1) · (x + 1)
(x − 1) · (x + 1)
=
2x
2
+ 3x + 1
x
2
− 1
.
Vậy ? là 2x
2
+ 3x + 1.
b) Ta có
x
2
+ 2x
x
3
+ 8
=
x(x + 2)
(x + 2)(x
2
− 2x + 4)
=
x
x
2
− 2x + 4
.
Vậy ? là x.
□
c Bài 11. Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
3x
2
=
15xy
10y
;a)
3x − 3y
2y − 2x
=
−3
2
;b)
x
2
− x + 1
x
=
x
3
+ 1
x · (x + 1)
.c)
Lời giải.
a) Ta có: 3x · 10y = 30xy và 2 · 15xy = 30xy nên 3x · 10y = 2 · 15xy. Vậy
3x
2
=
15xy
10y
.
b) Ta có: (3x − 3y) · 2 = 6x − 6y và (2y − 2x) · (−3) = 6x − 6y
nên (3x − 3y) · 2 = (2y − 2x) · (−3). Vậy
3x − 3y
2y − 2x
=
−3
2
.
c) Ta có:
x
2
− x + 1
· x · (x + 1) = x ·
x
3
+ 1
nên
x
2
− x + 1
x
=
x
3
+ 1
x · (x + 1)
.
□
c Bài 12.
a) Tìm đa thức A, cho biết
A
x − 2
=
x
2
+ 3x + 2
x
2
− 4
.
b) Tìm đa thức M, cho biết
M
x − 1
=
x
2
+ 3x + 2
x + 1
.
Lời giải.
Dùng định nghĩa, ta có
A = x + 1.a) M = x
2
+ x − 2.b)
□
c Bài 13. Tìm giá trị lớn nhất của phân thức P , biết P =
15
x
2
− 2x + 4
.
Lời giải.
Ta có P =
15
x
2
− 2x + 4
=
15
(x − 1)
2
+ 3
≤
15
3
= 5.
Suy ra giá trị lớn nhất của P là 5 khi x = 1. □
11/101 11/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
21. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
12
c Bài 14. Tìm giá trị nhỏ nhất của phân thức Q, biết Q =
18
4x − x
2
− 7
.
Lời giải.
Q =
18
−x
2
+ 4x − 7
nhỏ nhất khi
18
x
2
− 4x + 7
lớn nhất, mà
18
x
2
− 4x + 7
=
18
(x − 2)
2
+ 3
≤
18
3
= 6.
Vậy giá trị nhỏ nhất của Q là −6 khi x = 2. □
c Bài 15. Tìm giá trị nguyên của x để phân thức
6
2x + 1
nhận giá trị nguyên.
Lời giải.
6
2x + 1
nhận giá trị nguyên khi 2x + 1 ∈ Ư(6).
Mà 2x + 1 lẻ với x ∈ Z nên 2x + 1 ∈ {1; 3; −1; −3}.
Do đó x ∈ {0; 1; −1; −2}. □
c Bài 16. Tìm số nguyên dương n nhỏ nhất sao cho
n − 2
2n + 1
khác 0 và không tối giản.
Lời giải.
n − 2
2n + 1
khác 0 và không tối giản khi nghịch đảo của nó
2n + 1
n − 2
tồn tại và không tối giản.
Ta có
2n + 1
n − 2
=
2(n − 2) + 5
n − 2
.
Vì 5 là số nguyên tố nên phân số không tối giản khi n − 2 là bội của 5, do đó n − 2 = 5 hay n = 7 (vì n là số
nguyên dương nhỏ nhất). □
c Bài 17. Một ô tô chạy với vận tốc trung bình là x (km/h).
a) Viết biểu thức biểu thị thời gian ô tô (tính bằng giờ) chạy hết quãng đường 120 km.
b) Tính thời gian ô tô đi được 120 km trong trường hợp vận tốc trung bình của ô tô là 60 km/h.
Lời giải.
a) Biểu thức biểu thị thời gian ô tô (tính bằng giờ) chạy hết quãng đường 120 km là
t =
120
x
(h).
b) Thời gian ô tô đi được 120 km trong trường hợp vận tốc trung bình của ô tô là 60 km/h là
t =
120
60
= 2 (h).
□
c Bài 18. Lúc 6 giờ sáng, bác Vinh lái ô tô xuất phát từ Hà Nội đi huyện Tỉnh Gia (Thanh Hoá). Khi đến
Phủ Lý (Hà Nam), cách Hà Nội khoảng 60 km, bác Vinh dừng lại ăn sáng trong 20 phút. Sau đó, bác Vinh
tiếp tục đi về Tĩnh Gia và phải tăng vận tốc thêm 10 km/h để đến nơi đúng giờ dự định.
a) Gọi x (km/h) là vận tốc ô tô đi trên quãng đường Hà Nội - Phủ Lý. Hãy viết các phân thức biểu thị thời
gian bác Vinh chạy xe trên các quãng đường Hà Nội - Phủ Lý và Phủ Lý - Tĩnh Gia, biết rằng quãng
đường Hà Nội - Tĩnh Gia có chiều dài khoảng 200 km.
b) Nếu vận tốc ô tô đi trên quãng đường Hà Nội - Phủ Lý là 60 km/h thì bác Vinh đến Tĩnh Gia lúc mấy
12/101 12/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
13
giờ?
Lời giải.
a) Thời gian bác Vinh chạy xe trên quãng đường Hà Nội - Phủ Lý là
60
x
(giờ).
Quãng đường từ Phủ Lý đến Tĩnh Gia là 200 − 60 = 140 (km).
Thời gian bác Vinh chạy xe trên quãng đường Phủ Lý - Tĩnh Gia là
140
x + 10
(giờ).
b) Thời gian bác Vinh chạy xe trên quãng đường Hà Nội - Phủ Lý là
60
60
= 1 (giờ).
Thời gian bác Vinh chạy xe trên quãng đường Phủ Lý - Tĩnh Gia là
140
60 + 10
= 2 (giờ).
Vậy bác Vinh đến Tĩnh Gia vào lúc 9 giờ 20 phút.
□
c Bài 19. Để loại bỏ x (tính theo %) chất gây ô nhiễm không khí từ khí thải của một nhà máy, ước tính
cần chi phí là
1,7x
100 − x
(tỉ đồng).
a) Nếu muốn loại bỏ 90% chất gây ô nhiễm từ khí thải nhà máy thì cần chi phí là bao nhiêu?
b) Viết điều kiện xác định của phân thức
1,7x
100 − x
. Hỏi có thể loại bỏ được 100% chất gây ô nhiễm từ khí
thải nhà máy hay không?
Lời giải.
a) Muốn loại bỏ 90% chất gây ô nhiễm từ khí thải nhà máy thì cần chi phí là
1,7x · 90
100 − 90
= 15,3 (tỉ đồng).
b) Điều kiện xác định của phân thức là 100 − x = 0 hay x = 100.
Do đó, không thể loại bỏ được 100% chất thải gây ô nhiễm từ khí thải của nhà máy.
□
13/101 13/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
14
PHÂN THỨC ĐẠI SỐ
22
Baâi
A
AA TRỌNG TÂM KIẾN THỨC
1 Tính chất cơ bản của phân thức
○ Tính chất cơ bản:
— Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức 0 thì được một phân
thức mới bằng phân thức đã cho
A
B
=
A · M
B · M
(M là đa thức khác đa thức 0).
— Nếu chia cả tử và mẫu của một phân thức cho một nhân tử chung của chúng thì được một phân
thức mới bằng phân thức đã cho
A
B
=
A : N
B : N
(N là nhân tử chung).
○ Quy tắc đổi dấu: Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức bằng phân thức
đã cho
A
B
=
−A
−B
2 Rút gọn phân thức
Muốn rút gọn một phân thức, ta có thể:
○ Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung
○ Chia cả tử và mẫu cho nhân tử chung.
Chú ý: Có khi cần đổi dấu ở tử hoặc mẫu để nhận ra nhân tử chung của tử và mẫu (lưu ý tới tính
chất A = −(−A)).
3 Quy đồng mẫu nhiều phân thức
14/101 14/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
15
○ Tìm mẫu thức chung
Muốn tìm mẫu thức chung, ta có thể làm như sau:
— Phân tích mẫu thức của các phân thức đã cho thành nhân tử
— Mẫu thức chung cần tìm là một tích mà các nhân tử được chọn như sau:
+ Nhân tử bằng số của mẫu thức chung là tích các nhân tử bằng số ở các mẫu thức của các phân
thức đã cho (nếu các nhân tử bằng số ở các mẫu thức là những số nguyên dương thì nhân tử
bằng số của mẫu thức chung là BCNN của chúng)
+ Với mỗi lũy thừa của cùng một biểu thức có mặt trong các mẫu thức, ta chọn lũy thừa với số
mũ cao nhất.
○ Quy đồng mẫu thức
Muốn quy đồng mẫu thức nhiều phân thức, ta có thể làm như sau:
— Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung
— Tìm nhân tử phụ của mỗi phân thức
— Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
A
BB CÁC DẠNG BÀI TẬP
Dạng 1. Rút gọn phân thức
c Ví dụ 1. Rút gọn các phân thức sau:
3x
2
+ 6xy
6x
2
;a)
2x
2
− x
3
x
2
− 4
;b)
x + 1
x
3
+ 1
;c)
x
2
− xy
3 (xy
2
− y
3
)
.d)
Lời giải.
3x
2
+ 6xy
6x
2
=
3x · (x + 2y)
3x · x
=
x + 2y
x
.a)
2x
2
− x
3
x
2
− 4
=
−x
2
· (x − 2)
(x − 2)(x + 2)
=
−x
2
x + 2
.b)
x + 1
x
3
+ 1
=
x + 1
(x + 1) · (x
2
− x + 1)
=
1
x
2
− x + 1
.c)
x
2
− xy
3 (xy
2
− y
3
)
=
x(x − y)
3y
2
(x − y)
=
x
3y
2
.d)
□
c Ví dụ 2. Rút gọn phân thức
2x
2
y
5
3x
4
y
2
;a)
3x(x − y)
3
2x
2
(x − y)
2
;b)
3x
2
y + 4xy
2
6x + 8y
;c)
−3x
2
− 6x
4 − x
2
.d)
Lời giải.
2x
2
y
5
3x
4
y
2
=
2y
3
· x
2
y
2
3x
2
· x
2
y
2
=
2y
3
3x
2
.a)
3x(x − y)
3
2x
2
(x − y)
2
=
3(x − y)x(x − y)
2
2x · x(x − y)
2
=
3(x − y)
2x
.b)
3x
2
y + 4xy
2
6x + 8y
=
xy · (3x + 4y)
2 · (3x + 4y)
=
xy
2
.c)
−3x
2
− 6x
4 − x
2
=
3x
2
+ 6x
x
2
− 4
=
3x(x + 2)
(x − 2)(x + 2)
=
3x
x − 2
.d)
□
c Ví dụ 3. Rút gọn phân thức
A =
x − y
x
−
y
3
;a) B =
18x
2
x
2
− 2xy + y
2
27 (x
4
− x
3
y)
;b)
15/101 15/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
16
x
2
+ 2x
x
2
+ 4x + 4
;c)
x
2
y − xy
2
x
2
− y
2
.d)
Lời giải.
Ta có
a) A =
x − y
x
−
y
3
=
x − y
(x − y)(x
2
+ xy + y
2
)
=
1
x
2
+ xy + y
2
.
b) B =
18x
2
x
2
− 2xy + y
2
27 (x
4
− x
3
y)
=
2 · 9x
2
(x − y)
2
3 · 9x
3
(x − y)
=
2(x − y)
3x
.
c)
x
2
+ 2x
x
2
+ 4x + 4
=
x · (x + 2)
(x + 2)
2
=
x
x + 2
.
d)
x
2
y − xy
2
x
2
− y
2
=
xy · (x − y)
(x + y) · (x − y)
=
xy
x + y
.
□
c Ví dụ 4. Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao có thể viết:
3
4 − x
=
−3
x − 4
;a)
x − y
xy − x
=
y − x
x − xy
;b)
3x + y
y
=
3xy + y
2
y
2
.c)
Lời giải.
a) Ta có:
3
4 − x
=
3 · (x − y)
(4 − x) · (−1)
=
−3
x − 4
. Vậy
3
4 − x
=
−3
x − 4
.
b) Ta có:
x − y
xy − x
=
(x − y) · (−1)
(xy − x) · (−1)
=
y − x
x − xy
. Vậy
x − y
xy − x
=
y − x
x − xy
.
c)
3x + y
y
=
(3x + y) · y
y · y
=
3xy + y
2
y
2
.
□
Dạng 2. Chứng minh đẳng thức
○ Phân tích tử và mẫu của phân thức ở vế trái (vế phải) của đẳng thức đã cho rồi rút gọn phân thức.
○ So sánh kết quả ở hai vế.
c Ví dụ 5. Chứng minh các đẳng thức sau:
x − y
y
2
− x
2
=
−1
x + y
;a)
2x
−x + 4
=
−2x
x − 4
;b)
−12a
2
bc
9ab
3
=
−4ac
3b
2
;c)
30xy
2
(x − y)
45xy(x − y)
2
=
2y
3(x − y)
.d)
Lời giải.
x − y
y
2
− x
2
=
−(y − x)
(y + x)(y − x)
=
−1
x + y
.a)
2x
−x + 4
=
2x(−1)
(−x + 4)(−1)
=
−2x
x − 4
.b)
−12a
2
bc
9ab
3
=
(−4) · 3 · a · a · b · c
3 · 3 · a · b · b
2
=
−4ac
3b
2
.c)
30xy
2
(x − y)
45xy(x − y)
2
=
2 · 15xyy(x − y)
3 · 15xy(x − y)(x − y)
=
2y
3(x − y)
.d)
□
16/101 16/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
17
c Ví dụ 6. Chứng minh đẳng thức
2x − 2xy − 3 + 3y
1 − 3y + 3y
2
− y
3
=
2x − 3
(1 − y)
2
.
Lời giải.
Ta có
2x − 2xy − 3 + 3y
1 − 3y + 3y
2
− y
3
=
2x(1 − y) − 3(1 − y)
(1 − y)
3
=
(1 − y) · (2x − 3)
(1 − y)
3
=
2x − 3
(1 − y)
2
.
Vế trái bằng vế phải, đẳng thức được chứng minh. □
c Ví dụ 7. Chứng tỏ hai phân thức
a
2
− b
2
a
2
b + ab
2
và
a − b
ab
bằng nhau.
Lời giải.
Ta có
a
2
− b
2
a
2
b + ab
2
=
(a − b)(a + b)
ab(a + b)
=
a − b
ab
. □
Dạng 3. Tính giá trị biểu thức
○ Rút gọn biểu thức đã cho.
○ Thay giá trị của biến vào biểu thức đã rút gọn, rồi thực hiện các phép tính.
c Ví dụ 8. Cho phân thức P =
x
3
− x
(1 + xy)
2
− (x + y)
2
với x = ±1 và y = ±1.
a) Rút gọn phân thức P .
b) Tìm giá trị của biểu thức P với x = −12, y = 99.
Lời giải.
a) Ta có
P =
x
3
− x
(1 + xy)
2
− (x + y)
2
=
x
x
2
− 1
(1 + xy − x − y)(1 + xy + x + y)
=
x(x + 1)(x − 1)
[(1 − x) − y(1 − x)][(1 + x) + y(1 + x)]
=
x(x + 1)(x − 1)
(1 − x)(1 − y)(1 + x)(1 + y)
=
x
(1 + y)(y − 1)
b) Với x = −12, y = 99, ta được
P =
−12
(1 + 99)(99 − 1)
=
−12
100.98
=
−3
2450
.
□
c Ví dụ 9. Cho phân thức Q =
x
2
− 4y
2
· (x − 2y)
x
2
− 4xy + 4y
2
với x = 2y.
a) Rút gọn phân thức Q.
b) Tính giá trị của phân thức tại x = −9998 và y = −1.
Lời giải.
17/101 17/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
18
a) Rút gọn phân thức
Q =
x
2
− 4y
2
· (x − 2y)
x
2
− 4xy + 4y
2
=
(x + 2y)(x − 2y)(x − 2y)
(x − 2y)
2
= x + 2y
b) Với x = −9998; y = −1; (x = 2y), ta được
Q = −9998 + 2 · (−1) = −10000
□
c Ví dụ 10. Biết x > y > 0 và 3x
2
+ 3y
2
= 10xy. Tính P =
y − x
y + x
.
Lời giải.
Cách 1:
3x
2
+ 3y
2
= 10xy, nên 3x
2
− 9xy − xy + 3y
2
= 0 ⇔ (3x − y)(x − 3y) = 0.
Mà x > y > 0 nên 3x > y, do đó x = 3y.
Suy ra P =
y − x
y + x
=
y − 3y
y + 3y
=
−2y
4y
= −
1
2
.
Cách 2:
Xét P
2
=
x
2
+ y
2
− 2xy
x
2
+ y
2
+ 2xy
mà 3x
2
+ 3y
2
= 10xy hay x
2
+ y
2
=
10
3
xy nên ta có
P
2
=
10
3
xy − 2xy
10
3
xy + 2xy
=
4
16
=
1
4
.
Mặt khác x > y > 0 nên P < 0, do đó p = −
1
2
.
Nhận xét.
○ Cách 1: Phương pháp giải là phân tích đa thức thành nhân tử. Sau đó biểu diễn biến này theo biến kia rồi
thay vào phân thức.
○ Cách 2: Bình phương biểu thức cần tính, rồi thay thế. Tuy nhiên phải nhận xét dấu của biểu thức để chọn
giá trị thích hợp, nếu không sẽ mắc sai lầm.
□
c Ví dụ 11. Cho a, b thỏa mãn 3a − b = 5. Tính giá trị
M =
5a − b
2a + 5
−
3b − 3a
2b − 5
với a = −2,5; b = 2,5.
Lời giải.
Từ 3a − b = 5, ta có b = 3a − 5.
Do đó
M =
5a − (3a − 5)
2a + 5
−
3(3a − 5) − 3a
2(3a − 5) − 5
=
2a + 5
2a + 5
−
6a − 15
6a − 15
= 1 − 1 = 0
Nhận xét. Ngoài cách trên, bạn cũng có thể thay 5 = 3a −b vào biểu thức rồi rút gọn, ta cũng được kết quả
như trên.
□
Dạng 4. Chứng minh giá trị biểu thức không phụ thuộc vào biến
Rút gọn các phân thức đại số để phân thức đã rút gọn không còn chứa biến.
18/101 18/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
19
c Ví dụ 12. Chứng minh giá trị các biểu thức sau đây không phụ thuộc vào giá trị của x và y.
a)
x
2
− 4y
2
(x + 2y)(mx − 2my)
b)
9x
2
− 1
1 − 3x
+
3xy − 3x + 2y − 2
y − 1
với x =
1
3
; y = 1.
Lời giải.
a) Ta có
x
2
− 4y
2
(x + 2y)(mx − 2my)
=
(x + 2y)(x − 2y)
(x + 2y)(x − 2y)m
=
1
m
.
Vậy giá trị biểu thức không phụ thuộc vào giá trị của x; y.
b) Ta có
9x
2
− 1
1 − 3x
+
3xy − 3x + 2y − 2
y − 1
=
(3x − 1)(3x + 1)
−(3x − 1)
+
3x(y − 1) + 2(y − 1)
y − 1
=
3x + 1
−1
+
(3x + 2)(y − 1)
y − 1
= −3x − 1 + 3x + 2 = 1
Vậy giá trị biểu thức không phụ thuộc vào giá trị của x; y.
□
Dạng 5. Tìm x thỏa mãn đẳng thức cho trước
○ Đưa đẳng thức về dạng ax = b.
○ Tìm x =
b
a
(với a = 0).
○ Rút gọn biểu thức
b
a
.
c Ví dụ 13. Tìm x, biết a
2
x + 3ax + 9 = a
2
với a = 0; a = −3.
Lời giải.
a
2
x + 3ax + 9 = a
2
hay a(a + 3) · x = a
2
− 9.
Vì a = 0; a = −3, do đó chia cả hai vế cho a(a + 3) ta được
x =
a
2
− 9
a(a + 3)
=
(a − 3)(a + 3)
a(a + 3)
=
a − 3
a
□
c Ví dụ 14. Cho a, b, c là các số thực khác 0 và
a + b − c
c
=
a − b + c
b
=
−a + b + c
a
.
Đặt x =
(a + b)(b + c)(c + a)
abc
. Tính giá trị của x.
Lời giải.
Cộng 2 vào các vế của đẳng thức cho, ta được
a + b + c
c
=
a + b + c
b
=
a + b + c
a
(1)
Nếu a + b + c = 0; x =
(−c)(−a)(−b)
abc
= −1.
Nếu a + b + c = 0, từ (1) suy ra a = b = c và x =
2a · 2b · 2c
abc
= 8 > 0.
Nhận xét. Sẽ là thiếu sót nếu ta chỉ có a = b = c.
□
19/101 19/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
20
Dạng 6. Quy đồng mẫu thức
Xem phần trọng tâm kiến thức.
c Ví dụ 15. Quy đồng mẫu thức của các phân thức sau:
−7y
12xz
2
,
11z
18x
2
y
,
5x
6y
2
z
a)
6
7xy
2
z
,
11
14x
2
y
3
z
3
b)
Lời giải.
a) Mẫu thức chung là 36x
2
y
2
z
2
.
Ta có
−7y
12xz
2
=
−7y · 3xy
2
12xz
2
.3xy
2
=
−21xy
3
36x
2
y
2
z
2
11z
18x
2
y
=
11z.2yz
2
18x
2
y.2yz
2
=
22yz
3
36x
2
y
2
z
2
5x
6y
2
z
=
5x · 6x
2
z
6y
2
z · 6x
2
z
=
30x
3
z
36x
2
y
2
z
2
b) Mẫu thức chung là 36x
2
y
2
z
2
.
Ta có
6
7xy
2
z
=
6.2xyz
2
7xy
2
z.2xyz
2
=
12xyz
2
14x
2
y
3
z
3
;
11
14x
2
y
3
z
3
để nguyên.
□
c Ví dụ 16. Quy đồng mẫu thức của các phân thức sau:
5
3x + 15
;
3
x
2
− 25
a)
x
2
− x
x
2
− 1
;
3x + 3
x
3
+ 2x
2
+ x
;
2x
x
3
b)
Lời giải.
a) 3x + 15 = 3(x + 5); x
2
− 25 = (x + 5)(x − 5)
MTC: 3(x + 5)(x − 5).
Ta có
5
3(x + 5)
=
5(x − 5)
3(x + 5)(x − 5)
3
x
2
− 25
=
3.3
3.(x + 5)(x − 5)
=
9
3(x + 5)(x − 5)
b) Rút gọn các phân thức đã cho, ta được
x
x + 1
;
3
x(x + 1)
;
2
x
2
MTC: x
2
(x + 1).
x
x + 1
=
x · x
2
(x + 1)x
2
=
x
3
x
2
(x + 1)
3
x(x + 1)
=
3x
x
2
(x + 1)
2
x
2
=
2(x + 1)
x
2
(x + 1)
Nhận xét. Trước khi quy đồng, bạn nên rút gọn phân thức (nếu có thể).
□
20/101 20/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
21
c Ví dụ 17. Quy đồng mẫu thức hai phân thức
3
5x
3
+ 5x
2
và
−7
2x
3
+ 4x
2
+ 2x
.
Lời giải.
Ta có 5x
3
+ 5x
2
= 5x
2
· (x + 1) và 2x
3
+ 4x
2
+ 2x = 2x ·
x
2
+ 2x + 1
= 2x · (x + 1)
2
.
Mẫu thức chung là 10x
2
(x + 1)
2
.
Nhân tử phụ của 5x
3
+ 5x
2
là
MTC :
5x
3
+ 5x
2
= 10x
2
(x + 1)
2
:
5x
2
(x + 1)
= 2(x + 1).
Nhân tử phụ của 2x
3
+ 4x
2
+ 2x là
MTC :
2x
3
+ 4x
2
+ 2x
= 10x
2
(x + 1)
2
:
2x(x + 1)
2
= 5x.
Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng, ta có
3
5x
3
+ 5x
2
=
3 · 2(x + 1)
10x
2
(x + 1)
2
=
6(x + 1)
10x
2
(x + 1)
2
và
−7
2x
3
+ 4x
2
+ 2x
=
−7 · 5x
10x
2
(x + 1)
2
=
−35x
10x
2
(x + 1)
2
□
c Ví dụ 18. Quy đồng mẫu thức hai phân thức
1
3x
2
− 3
và
1
x
3
− 1
.
Lời giải.
Ta có 3x
2
− 3 = 3(x − 1)(x + 1) và x
3
− 1 = (x − 1)(x
2
+ x + 1).
MTC là 3(x − 1)(x + 1)(x
2
+ x + 1).
Khi đó,
1
3x
2
− 3
=
x
2
+ x + 1
3(x − 1)(x + 1)(x
2
+ x + 1)
và
1
x
3
− 1
=
3(x + 1)
3(x − 1)(x + 1)(x
2
+ x + 1)
. □
c Ví dụ 19. Quy đồng mẫu thức các phân thức:
1
3x − 6
,
2
3x + 6
và
3
4 − x
2
.
Lời giải.
Ta có:
3
4 − x
2
=
−3
x
2
− 4
;
3x − 6 = 3 (x − 2) ;
3x + 6 = 3 (x + 2) ;
x
2
− 4 = (x − 2) (x + 2) .
Chọn MTC là: 3 (x − 2) (x + 2).
Nhân tử phụ của các mẫu thức trên lần lượt là: x + 2 ; x − 2 ; 3.
Vậy:
1
3x − 6
=
1
3 (x − 2)
=
x + 2
3 (x − 2) (x + 2)
;
2
3x + 6
=
2
3 (x + 2)
=
2 (x − 2)
3 (x − 2) (x + 2)
;
3
4 − x
2
=
−3
x
2
− 4
=
−3
(x − 2) (x + 2)
=
−9
3 (x − 2) (x + 2)
.
□
Dạng 7. Vận dụng
c Ví dụ 20. Cho hình chữ nhật ABCD và MNP Q như hình vẽ (các số đo trên hình tính theo đơn vị
centimét).
21/101 21/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
22
D
B
x + 3
x + 1
A
C
Q
N
x + 1
x
M
P
a) Viết phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật MNP Q.
b) Tính giá trị của phân thức đó tại x = 2 và tại x = 5.
Lời giải.
a) Diện tích của hình chữ nhật ABCD là (x + 3) · (x + 1).
Diện tích của hình chữ nhật MN P Q là (x + 1) · x.
Do đó phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật MN P Q là
(x + 3) · (x + 1)
(x + 1) · x
.
b)
○ Với x = 2, phân thức trên có giá trị là
(2 + 3) · (2 + 1)
(2 + 1) · 2
=
5
2
.
○ Với x = 5, phân thức trên có giá trị là
(5 + 3) · (5 + 1)
(5 + 1) · 5
=
8
5
.
□
c Ví dụ 21. Chị Hà mở một xưởng thủ công với vốn đầu tư ban đầu (xây dựng nhà xưởng, mua máy móc,...)
là 80 triệu. Biết chi phí để sản xuất (tiền mua vật liệu, lương nhân công) của 1 sản phẩm là 15 nghìn đồng.
Gọi x là số sản phẩm mà xưởng của chị Hà làm được.
a) Viết phân thức biểu thị số tiền thực (đơn vị là nghìn đồng) đã bỏ ra để làm được x sản phẩm.
b) Viết phân thức biểu thị chi phí thực (đơn vị là nghìn đồng) để tạo ra 1 sản phẩm theo x.
c) Tính chi phí thực để tạo ra 1 sản phẩm nếu x = 100; x = 1 000. Nhận xét về chi phí thực để tạo ra 1
sản phẩm nếu x ngày càng tăng.
Lời giải.
Đổi 80 triệu = 80 000 (nghìn đồng).
a) Phân thức biểu thị số tiền thực (đơn vị là nghìn đồng) đã bỏ ra để làm được x sản phẩm là 80 000 + 15 · x
(nghìn đồng).
b) Phân thức biểu thị chi phí thực (đơn vị là nghìn đồng) để tạo ra 1 sản phẩm theo x là
80 000 + 15 · x
x
(nghìn
đồng).
c)
○ Chi phí thực để tạo ra 1 sản phẩm nếu x = 100 là
80 000 + 15 · 100
100
= 815 (nghìn đồng).
○ Chi phí thực để tạo ra 1 sản phẩm nếu x = 1 000 là
80 000 + 15 · 1000
1000
= 95 (nghìn đồng).
Vậy chi phí thực để tạo ra 1 sản phẩm sẽ ngày càng giảm nếu x ngày càng tăng.
□
22/101 22/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
23
A
CC BÀI TẬP VẬN DỤNG
c Bài 1. Dùng tính chất cơ bản của phân thức, giải thích vì sao
2x + 2
x
2
− 1
=
2
x − 1
;a)
−x
1 − x
=
x
x − 1
;b)
(x − 2)
3
x
2
− 2x
=
(x − 2)
2
x
;c)
1 − x
−5x + 1
=
x − 1
5x − 1
.d)
Lời giải.
Áp dụng tính chất cơ bản của phân thức, ta có
a)
2x + 2
x
2
− 1
=
2(x + 1)
(x − 1)(x + 1)
=
2
x − 1
.
b) Do −(−x) = x và 1 − x = −(x − 1) nên
−x
1 − x
=
x
x − 1
.
c)
(x − 2)
3
x
2
− 2x
=
(x − 2)
3
x(x − 2)
=
(x − 2)
2
x
.
d)
1 − x
−5x + 1
=
−(x − 1)
−(5x − 1)
=
x − 1
5x − 1
.
□
c Bài 2. Tìm đa thức thích hợp thay cho dấu "?".
y − x
4 − x
=
?
x − 4
Lời giải.
Ta có
y − x
4 − x
=
−(x − y)
−(4 − x)
=
x − y
4 − x
. Do đó ? = x − y. □
c Bài 3. Tìm a sao cho hai phân thức sau bằng nhau:
5x
x + 1
và
ax(x − 1)
(1 − x)(x + 1)
Lời giải.
Ta có
ax(x − 1)
(1 − x)(x + 1)
=
ax(x − 1)
−(x − 1)(x + 1)
=
−ax
x + 1
.
Do đó −a = 5 hay a = −5. □
c Bài 4. Tìm mẫu thức chung của hai phân thức
2x
x
2
+ 3x + 2
;
3x
x
2
+ 4x + 3
Lời giải.
Ta có x
2
+ 3x + 2 = x
2
+ x + 2x + 2 = (x + 1)(x + 2)
x
2
+ 4x + 3 = x
2
+ x + 3x + 3 = (x + 1)(x + 3)
nên mẫu thức chung là (x + 1)(x + 2)(x + 3). □
c Bài 5. Rút gọn các phân thức sau:
5x + 10
25x
2
+ 50
;a)
45x(3 − x)
15x(x − 3)
3
;b)
x
2
− 1
2
(x + 1) (x
3
+ 1)
.c)
23/101 23/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
24
Lời giải.
a)
5x + 10
25x
2
+ 50
=
5(x + 2)
25(x
2
+ 2)
=
x + 2
5(x
2
+ 2)
;
b)
45x(3 − x)
15x(x − 3)
3
=
−3 · 15x(x − 3)
15x(x − 3)
3
=
−3
(x − 3)
2
;
c)
x
2
− 1
2
(x + 1) (x
3
+ 1)
=
(x − 1)
2
(x + 1)
2
(x + 1) (x + 1) (x
2
− x + 1)
=
(x − 1)
2
x
2
− x + 1
.
□
c Bài 6. Rút gọn mỗi phân thức sau:
8
2
+ 4x
1 − 4x
2
;a)
x
3
− xy
2
2x
2
+ 2xy
;b)
24x
2
y
2
16xy
3
;c)
6x − 2y
9x
2
− y
2
.d)
Lời giải.
a)
8
2
+ 4x
1 − 4x
2
=
4x · (2x + 1)
(1 − 2x) · (1 + 2x)
=
4x
1 − 2x
.
b)
x
3
− xy
2
2x
2
+ 2xy
=
x ·
x
2
− y
2
2x · (x + y)
=
x · (x − y) · (x + y)
2x · (x + y)
=
x − y
2
.
c)
24x
2
y
2
16xy
3
=
3x
2y
.
d)
6x − 2y
9x
2
− y
2
=
2 · (3x − y)
(3x − y) · (3x + y)
=
2
3x + y
.
□
c Bài 7. Cho phân thức P =
x + 1
x
2
− 1
.
a) Rút gọn phân thức đã cho, kí hiệu Q là phân thức nhận được.
b) Tính giá trị của P và Q tại x = 11. So sánh hai kết quả đó.
Lời giải.
a) Ta có P =
x + 1
x
2
− 1
=
x + 1
(x − 1)(x + 1)
=
1
x − 1
= Q.
b) P (11) =
1
10
và Q(11) =
1
10
. Vậy P (11) = Q(11).
□
c Bài 8. Quy đồng mẫu thức các phân thức sau:
1
x
3
− 8
và
3
4 − 2x
;a)
x
x
2
− 1
và
1
x
2
+ 2x + 1
;b)
5
2x
2
y
3
và
3
xy
4
;c)
3
2x
2
− 10x
và
2
x
2
− 25
;d)
2
x − 3y
và
3
x + 3y
;e)
7
4x + 24
và
13
x
2
− 36
.f)
Lời giải.
a) Ta có x
3
− 8 = (x − 2)(x
2
+ 2x + 4) và 4 − 2x = −2(x − 2).
Do đó, MTC là 2(x − 2)(x
2
+ 2x + 4).
Ta có
1
x
3
− 8
=
2
2(x − 2)(x
2
+ 2x + 4)
và
3
4 − 2x
=
−6(x
2
+ 2x + 4)
2(x − 2)(x
2
+ 2x + 4)
.
24/101 24/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
25
b) Ta có x
2
− 1 = (x − 1)(x + 1) và x
2
+ 2x + 1 = (x + 1)
2
.
Do đó, MTC là (x − 1)(x + 1)
2
.
Ta có
x
x
2
− 1
=
x(x + 1)
(x − 1)(x + 1)
2
và
1
x
2
+ 2x + 1
=
x − 1
(x − 1)(x + 1)
2
.
c) Ta chọn MTC là 2x
2
y
4
. Khi đó:
5
2x
2
y
3
=
5 · y
2x
2
y
3
· y
=
5y
2x
2
y
4
.
3
xy
4
=
3 · 2x
xy
4
· 2x
=
6x
2x
2
y
4
.
d) Ta có: 2x
2
− 10x = 2x · (x − 5) và x
2
− 25 = (x − 5) · (x + 5).
Ta chọn MTC là 2x · (x − 5) · (x + 5). Khi đó:
3
2x
2
− 10x
=
3
2x · (x − 5)
=
3 · (x + 5)
2x · (x − 5) · (x + 5)
=
3x + 15
2x · (x − 5) · (x + 5)
.
2
x
2
− 25
=
2
(x − 5) · (x + 5)
=
2 · 2x
(x − 5) · (x + 5) · 2x
=
4x
2x · (x − 5) · (x + 5)
.
e) Ta chọn MTC là (x − 3y) · (x + 3y). Khi đó:
2
x − 3y
=
2 · (x + 3y)
(x − 3y) · (x + 3y)
.
3
x + 3y
=
3 · (x − 3y)
(x − 3y) · (x + 3y)
.
f) Ta có: 4x + 24 = 4 · (x + 6) và x
2
− 36 = (x − 6) · (x + 6).
Ta chọn MTC là 4 · (x − 6) · (x + 6). Khi đó:
7
4x + 24
=
7
4 · (x + 6)
=
7 · 4 (x − 6)
4 · (x − 6) · (x + 6)
=
28 · (x − 6)
4 · (x − 6) · (x + 6)
.
13
x
2
− 36
=
13
(x − 6) · (x + 6)
=
13 · 4
4 · (x − 6) · (x + 6)
=
52
4 · (x − 6) · (x + 6)
.
□
c Bài 9. Quy đồng mẫu thức các phân thức sau:
1
x + 2
;
x + 1
x
2
− 4x + 4
và
5
2 − x
.a)
1
3x + 3y
;
2x
x
2
− y
2
và
x
2
− xy + y
2
x
2
− 2xy + y
2
.b)
Lời giải.
a) Ta có x + 2 = x + 2; x
2
− 4x + 4 = (x − 2)
2
và 2 − x = −(x − 2).
Do đó, MTC là (x + 2)(x − 2)
2
.
Ta có
1
x + 2
=
(x − 2)
2
(x + 2)(x − 2)
2
;
x + 1
x
2
− 4x + 4
=
(x + 2)(x + 1)
(x + 2)(x − 2)
2
và
5
2 − x
=
−5(x − 2)(x + 2)
(x + 2)(x − 2)
2
.
b) Ta có 3x + 3y = 3(x + y); x
2
− y
2
= (x + y)(x − y) và x
2
− 2xy + y
2
= (x − y)
2
.
Do đó, MTC là 3(x − y)
2
(x + y).
Ta có
1
3x + 3y
=
(x − y)
2
3(x − y)
2
(x + y)
;
2x
x
2
− y
2
=
6x(x − y)
3(x − y)
2
(x + y)
và
x
2
− xy + y
2
x
2
− 2xy + y
2
=
3(x + y)(x
2
− xy + y
2
)
3(x − y)
2
(x + y)
.
□
c Bài 10. Quy đồng mẫu thức của các phân thức sau:
2x + 1
6xy
3
và
3x
9x
2
y
a)
3x
2
− 4x + 1
x
2
− 25
;
x − 3
5 − x
;
4x
x + 5
b)
25/101 25/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
26
Lời giải.
a) Mẫu thức chung là 18x
2
y
3
.
Nhân tử phụ tương ứng là 18x
2
y
3
: 6xy
3
= 3x
18x
2
y
3
: 9x
2
y = 2y
2
.
Ta có
2x + 1
6xy
3
=
(2x + 1) · 3x
6xy
3
· 3x
=
3x(2x + 1)
18x
2
y
3
3x
9x
2
y
=
3x · 2y
2
9x
2
y · 2y
2
=
6xy
2
18x
2
y
3
b) Mẫu thức chung là (x − 5)(x + 5) = x
2
− 25.
Ta có
3x
2
− 4x + 1
x
2
− 25
để nguyên.
x − 3
5 − x
=
3 − x
x − 5
=
(3 − x)(x + 5)
(x − 5)(x + 5)
=
(3 − x)(x + 5)
x
2
− 25
4x
x + 5
=
4x(x − 5)
(x + 5)(x − 5)
=
4x(x − 5)
x
2
− 25
.
□
c Bài 11. Cho hai phân thức
9x
2
+ 3x + 1
27x
3
− 1
và
x
2
− 4x
16 − x
2
.
a) Rút gọn hai phân thức đã cho.
b) Quy đồng mẫu thức hai phân thức nhận được ở câu a.
Lời giải.
a) Ta có
9x
2
+ 3x + 1
27x
3
− 1
=
9x
2
+ 3x + 1
(3x − 1)(9x
2
+ 3x + 1)
=
1
3x − 1
.
Ta có
x
2
− 4x
16 − x
2
=
x(x − 4)
(4 − x)(4 + x)
=
−x
x + 4
.
b) Ta có MTC là (3x − 1)(x + 4).
Ta có
1
3x − 1
=
x + 4
(3x − 1)(x + 4)
−x
x + 4
=
−x(3x − 1)
(3x − 1)(x + 4)
.
□
c Bài 12. Một ô tô chạy với vận tốc trung bình là x (km/h).
a) Viết biểu thức biểu thị thời gian ô tô (tính bằng giờ) chạy hết quãng đường 120 km.
b) Tính thời gian ô tô đi được 120 km trong trường hợp vận tốc trung bình của ô tô là 60 km/h.
Lời giải.
a) Biểu thức biểu thị thời gian ô tô (tính bằng giờ) chạy hết quãng đường 120 km là
t =
120
x
(h).
b) Thời gian ô tô đi được 120 km trong trường hợp vận tốc trung bình của ô tô là 60 km/h là
t =
120
60
= 2 (h).
□
26/101 26/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
27
c Bài 13. Lúc 6 giờ sáng, bác Vinh lái ô tô xuất phát từ Hà Nội đi huyện Tỉnh Gia (Thanh Hoá). Khi đến
Phủ Lý (Hà Nam), cách Hà Nội khoảng 60 km, bác Vinh dừng lại ăn sáng trong 20 phút. Sau đó, bác Vinh
tiếp tục đi về Tĩnh Gia và phải tăng vận tốc thêm 10 km/h để đến nơi đúng giờ dự định.
a) Gọi x (km/h) là vận tốc ô tô đi trên quãng đường Hà Nội - Phủ Lý. Hãy viết các phân thức biểu thị thời
gian bác Vinh chạy xe trên các quãng đường Hà Nội - Phủ Lý và Phủ Lý - Tĩnh Gia, biết rằng quãng
đường Hà Nội - Tĩnh Gia có chiều dài khoảng 200 km.
b) Nếu vận tốc ô tô đi trên quãng đường Hà Nội - Phủ Lý là 60 km/h thì bác Vinh đến Tĩnh Gia lúc mấy
giờ?
Lời giải.
a) Thời gian bác Vinh chạy xe trên quãng đường Hà Nội - Phủ Lý là
60
x
(giờ).
Quãng đường từ Phủ Lý đến Tĩnh Gia là 200 − 60 = 140 (km).
Thời gian bác Vinh chạy xe trên quãng đường Phủ Lý - Tĩnh Gia là
140
x + 10
(giờ).
b) Thời gian bác Vinh chạy xe trên quãng đường Hà Nội - Phủ Lý là
60
60
= 1 (giờ).
Thời gian bác Vinh chạy xe trên quãng đường Phủ Lý - Tĩnh Gia là
140
60 + 10
= 2 (giờ).
Vậy bác Vinh đến Tĩnh Gia vào lúc 9 giờ 20 phút.
□
c Bài 14. Để loại bỏ x (tính theo %) chất gây ô nhiễm không khí từ khí thải của một nhà máy, ước tính
cần chi phí là
1,7x
100 − x
(tỉ đồng).
a) Nếu muốn loại bỏ 90% chất gây ô nhiễm từ khí thải nhà máy thì cần chi phí là bao nhiêu?
b) Viết điều kiện xác định của phân thức
1,7x
100 − x
. Hỏi có thể loại bỏ được 100% chất gây ô nhiễm từ khí
thải nhà máy hay không?
Lời giải.
a) Muốn loại bỏ 90% chất gây ô nhiễm từ khí thải nhà máy thì cần chi phí là
1,7x · 90
100 − 90
= 15,3 (tỉ đồng).
b) Điều kiện xác định của phân thức là 100 − x = 0 hay x = 100.
Do đó, không thể loại bỏ được 100% chất thải gây ô nhiễm từ khí thải của nhà máy.
□
27/101 27/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
28
PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
23
Baâi
A
AA TRỌNG TÂM KIẾN THỨC
1 Cộng hai phân thức cùng mẫu thức
Quy tắc: muốn cộng hai phân thức cùng mẫu thức, ta cộng các tử thức với nhau và giữ nguyên mẫu thức
A
C
+
B
C
=
A + B
C
.
Kết quả của phép cộng hai phân thức được gọi là tổng của hai phân thức đó. Ta thường viết tổng dưới dạng
rút gọn.
2 Cộng hai phân thức khác mẫu
Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đổng mẫu thức rổi cộng các phân thức có cùng mẫu
thức vừa tìm được.
3 Trừ hai phân thức
○ Muốn trừ hai phân thức có cùng mẫu thức ta trừ các tử thức và giữ nguyên mẫu thức.
○ Muốn trừ hai phân thức có mẫu thức khác nhau, ta quy đổng mẫu thức rổi trừ các phân thức có cùng
mẫu thức vừa tìm được.
Cũng như phép trừ phân số, ta có thể chuyển phép trừ phân thức thành phép cộng phân thức như sau:
A
B
−
C
D
=
A
B
+
−C
D
.
4 Cộng, trừ nhiều phân thức đại số
Vì trừ một phân thức cũng là cộng với phân thức đối của phân thức đó nên các biểu thức gổm các phép
tính cộng, trừ phân thức cũng có thể xem là chỉ gổm các phép cộng phân thức. Chẳng hạn, biểu thức P =
2x + 1
x + 1
+
x
x − 1
−
1
x
2
− 1
có thể viết thành
P =
2x + 1
x + 1
+
x
x − 1
+
−1
x
2
− 1
Cũng như phép cộng phân số, phép cộng phân thức cũng có các tính chất giao hoán, kết hợp. Vì vậy, khi làm
tính với một biểu thức chỉ gổm các phép cộng phân thức ta có thể đổi chỗ, nhóm (kết hợp) các số hạng một
cách tuỳ ý.
Trong các biểu thức ta có thể đổi chỗ các số hạng kèm theo dấu của nó.
Quy tắc dấu ngoặc
○ Nếu trước dấu ngoặc có dấu “+” thì bỏ dấu ngoặc và giữ nguyên các số hạng.
○ Nếu trước dấu ngoặc có dấu "-" thì bỏ dấu ngoặc và đổi dấu các số hạng trong dấu ngoặc.
28/101 28/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
29
A
BB CÁC DẠNG BÀI TẬP
Dạng 1. Cộng, trừ các phân thức cùng mẫu thức
○ Cộng,trừ các tử thức với nhau;
○ Giữ nguyên mẫu thức
A
C
±
B
C
=
A ± B
C
.
c Ví dụ 1. Thực hiện phép tính sau:
x + y
3x
+
x − 2y
3x
;a)
x
2
+ 4
x − 2
+
4x
2 − x
;b)
3x + 1
2xy
−
x − 2
2xy
;c)
xy
2x − y
−
2x
2
y − 2x
.d)
Lời giải.
a)
x + y
3x
+
x − 2y
3x
=
x + y + x − 2y
3x
=
2x − y
3x
.
b)
x
2
+ 4
x − 2
+
4x
2 − x
=
x
2
+ 4
x − 2
+
−4x
x − 2
=
x
2
+ 4 − 4x
x − 2
=
(x − 2)
2
x − 2
= x − 2.
c)
3x + 1
2xy
−
x − 2
2xy
=
3x + 1 − x + 2
2xy
=
2x + 3
2xy
.
d)
xy
2x − y
−
2x
2
y − 2x
=
xy
2x − y
+
2x
2
2x − y
=
xy + 2x
2
2x − y
.
□
c Ví dụ 2. Thực hiện các phép cộng, trừ phân thức sau:
x + y
xy
+
x − y
xy
;a)
x
2
+ 5x
x + 2
−
x − 4
x + 2
;b)
3x + 2y
x
2
− y
2
−
x
x
2
− y
2
;c)
5x
2
x − 1
+
5 − 10x
x − 1
.d)
Lời giải.
a)
x + y
xy
+
x − y
xy
=
x + y + x − y
xy
=
2x
xy
=
2
y
;
b)
x
2
+ 5x
x + 2
−
x − 4
x + 2
=
x
2
+ 5x − (x − 4)
x + 2
=
x
2
+ 5x − x + 4
x + 2
=
x
2
+ 4x + 4
x + 2
=
(x + 2)
2
x + 2
=
(x + 2)(x + 2)
x + 2
= x + 2;
c)
3x + 2y
x
2
− y
2
−
x
x
2
− y
2
=
3x + 2y − x
x
2
− y
2
=
2x + 2y
(x + y)(x − y)
=
2(x + y)
(x + y)(x − y)
=
2
x − y
.
d)
5x
2
x − 1
+
5 − 10x
x − 1
=
5x
2
+ 5 − 10x
x − 1
=
5(x − 1)
2
x − 1
= 5(x − 1).
□
c Ví dụ 3. Thực hiện phép tính:
x − 7
x
2
y
+
y + 7
x
2
y
.a)
x − 2y
x
2
+ xy
+
x + 2y
x
2
+ xy
.b)
3x − 2y
x + y
−
2x − 3y
x + y
.c)
Lời giải.
29/101 29/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
30
a) Ta có
x − 7
x
2
y
+
y + 7
x
2
y
=
(x − 7) + (y + 7)
x
2
y
=
x − 7 + y + 7
x
2
y
=
x + y
x
2
y
.
b) Ta có
x − 2y
x
2
+ xy
+
x + 2y
x
2
+ xy
=
x − 2y + x + 2y
x
2
+ xy
=
2x
x
2
+ xy
=
2x
x(x + y)
=
2
x + y
.
c)
3x − 2y
x + y
−
2x − 3y
x + y
=
(3x − 2y) − (2x − 3y)
x + y
=
3x − 2y − 2x + 3y
x + y
=
x + y
x + y
= 1.
□
c Ví dụ 4. Thực hiện phép tính:
x − 2y
x − y
−
y
y − x
;a)
x
2
+ y
2
x
2
− y
2
−
2xy
y
2
− x
2
;b)
4x + 3y
x
2
− y
2
−
3x + 4y
x
2
− y
2
,c)
Lời giải.
a)
x − 2y
x − y
−
y
y − x
=
x−2y
x−y
+
Å
−
y
y − x
ã
=
x − 2y
x − y
+
y
x − y
=
x − 2y + y
x − y
=
x − y
x − y
= 1.
b)
x
2
+ y
2
x
2
− y
2
−
2xy
y
2
− x
2
=
x
2
+ y
2
x
2
− y
2
+
Å
−
2xy
y
2
− x
2
ã
=
x
2
+ y
2
x
2
− y
2
+
2xy
x
2
− y
2
=
x
2
+2xy+y
2
x
2
−y
2
=
(x+y)
2
(x−y)(x+y)
=
x+y
x−y
.
c)
2xy − 3y
2
x
2
− 3xy
−
x
3x − 9y
=
2xy − 3y
2
x(x − 3y)
−
x
3(x − 3y)
=
3 · (2xy − 3y
2
)
3x(x − 3y)
−
x · x
3x(x − 3y)
=
6xy − 9y
2
− x
2
3x(x − 3y)
=
−(x − 3y)
2
3x(x − 3y)
=
3y − x
3x
.
□
c Ví dụ 5. Rút gọn biểu thức sau
A =
x
4
− (x − 1)
2
(x
2
+ 1)
2
− x
2
+
x
2
−
x
2
− 1
2
x
2
(x + 1)
2
− 1
+
x
2
(x − 1)
2
− 1
x
4
− (x + 1)
2
Lời giải.
Ta có
A =
x
2
− x + 1
x
2
+ x − 1
(x
2
+ 1 − x) (x
2
+ 1 + x)
+
x + x
2
− 1
x − x
2
+ 1
(x
2
+ x − 1) (x
2
+ x + 1)
+
x
2
− x − 1
x
2
− x + 1
(x
2
− x − 1) (x
2
+ x + 1)
=
x
2
+ x − 1
x
2
+ x + 1
+
x − x
2
+ 1
x
2
+ x + 1
+
x
2
− x + 1
x
2
+ x + 1
=
x
2
+ x + 1
x
2
+ x + 1
= 1
Nhận xét. Nếu mỗi phân thức có thể rút gọn được, bạn nên rút gọn trước khi thực hiện phép tính.
□
c Ví dụ 6. Cho a, b, c thõa mãn abc = 1. Tính
M =
a
ab + a + 1
+
b
bc + b + 1
+
c
ac + c + 1
.
Lời giải.
30/101 30/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
31
Thay 1 = abc vào biểu thức, ta có
M =
a
ab + a + 1
+
abc · b
bc + abc · b + abc
+
c
ac + c + abc
=
a
ab + a + 1
+
ab
1 + ab + a
+
1
a + 1 + ab
=
ab + a + 1
ab + a + 1
= 1
Nhận xét.
○ Lời giải trên tinh tế khi giữ nguyên một mẫu thức và thay số 1 vào vị trí hợp lí để rút gọn phân thức, đưa
các phân thức về cùng mẫu.
○ Sử dụng kỹ thuật trên, bạn có thể giải được bài toán sau
Cho a, b, c, d thỏa mãn abcd = 1. Tính giá trị của biểu thức
N =
1
1 + 2a + 3ab + 4abc
+
1
2 + 3b + 4bc + bcd
+
1
3 + 4c + cd + 2cda
+
1
4 + d + 2da + 3dab
.
□
Dạng 2. Cộng, trừ các phân thức không cùng mẫu thức
○ Quy đồng mẫu thức để đưa về các phân thức có cùng mẫu.
○ Cộng, trừ tử thức với nhau và giữ nguyên mẫu thức.
c Ví dụ 7. Thực hiện phép tính:
5
x
và
3
1 − x
;a)
2x + 1
x
−
y − 1
y
;b)
1 − x
xy + x
2
+
1
x + y
;c)
1
x
2
+ xy
+
1
xy + y
2
;d)
xy + 5
x
2
+ xy
−
y
x + y
;e)
2
a
+
1
a − 3
;f)
2x
x
2
− 4
−
1
x − 2
;g)
x
xy − y
2
−
y
x
2
− xy
.h)
Lời giải.
a)
5
x
+
3
1 − x
=
5(1 − x)
x(1 − x)
+
3x
x(1 − x)
=
5(1 − x) + 3x
x(1 − x)
=
5 − 2x
x(1 − x)
.
b)
2x + 1
x
−
y − 1
y
=
(2x + 1)y
xy
−
x(y − 1)
xy
=
(2x + 1)y − x(y − 1)
xy
=
xy + x + y
xy
.
c)
1 − x
xy + x
2
+
1
x + y
=
1 − x
x(y + x)
+
1
x + y
=
1 − x
x(x + y)
+
x
x(x + y)
=
1 − x + x
x(x + y)
=
1
x(x + y)
.
d)
1
x
2
+ xy
+
1
xy + y
2
=
1
x(x + y)
+
1
y(x + y)
=
y
xy(x + y)
+
x
xy(x + y)
=
x + y
xy(x + y)
=
1
xy
.
e)
xy + 5
x
2
+ xy
−
y
x + y
=
xy + 5
x(x + y)
−
y
x + y
=
xy + 5
x(x + y)
−
xy
x(x + y)
=
xy + 5 − xy
x(x + y)
=
5
x(x + y)
.
f)
2
a
+
1
a − 3
=
2(a − 3)
a(a − 3)
+
a
a(a − 3)
=
2a − 6 + a
a(a − 3)
=
3a − 6
a(a − 3)
=
3(a − 2)
a(a − 3)
;
g)
2x
x
2
− 4
−
1
x − 2
=
2x
(x + 2)(x − 2)
−
(x + 2)
(x + 2)(x − 2)
=
2x − (x + 2)
(x + 2)(x − 2)
=
x − 2
(x + 2)(x − 2)
=
1
x + 2
;
h)
x
xy − y
2
−
y
x
2
− xy
=
x
y(x − y)
−
y
x(x − y)
=
x
2
xy(x − y)
−
y
2
xy(x − y)
=
x
2
− y
2
xy(x − y)
=
(x + y)(x − y)
xy(x − y)
=
x + y
xy
.
□
31/101 31/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
32
c Ví dụ 8. Thực hiện các phép cộng, trừ phân thức sau:
a
a − 3
−
3
a + 3
;a)
1
2x
+
2
x
2
;b)
4
x
2
− 1
−
2
x
2
+ x
;c)
2xy − 3y
2
x
2
− 3xy
−
x
3x − 9y
.d)
Lời giải.
a)
a
a − 3
−
3
a + 3
=
a(a + 3)
(a − 3)(a + 3)
−
3(a − 3)
(a − 3)(a + 3)
=
a
2
+ 3a − 3a + 9
a
2
− 9
=
a
2
+ 9
a
2
− 9
;
b)
1
2x
+
2
x
2
=
x
2x
2
+
2 · 2
2x
2
=
x + 4
2x
2
;
c)
4
x
2
− 1
−
2
x
2
+ x
=
4
(x − 1)(x + 1)
−
2
x(x + 1)
=
4x
x(x − 1)(x + 1)
−
2(x − 1)
x(x − 1)(x + 1)
=
4x − 2x + 2
x(x − 1)(x + 1)
=
2x + 2
x(x − 1)(x + 1)
=
2(x + 1)
x(x − 1)(x + 1)
=
2
x(x − 1)
.
d)
4x + 3y
x
2
− y
2
−
3x + 4y
x
2
− y
2
=
4x + 3y − 3x − 4y
x
2
− y
2
=
x − y
(x − y)(x + y)
=
1
x + y
.
□
c Ví dụ 9. Thực hiện phép tính sau
3
4xy
+
5x
2y
2
z
+
7
6yz
2
;a)
x
2
x
2
+ 3x
+
3
x + 3
+
3
x
.b)
Lời giải.
a)
3
4xy
+
5x
2y
2
z
+
7
6yz
2
=
9yz
2
12xy
2
z
2
+
30x
2
z
12xy
2
z
2
+
14xy
12xy
2
z
2
=
9yz
2
+ 30x
2
z + 14xy
12xy
2
z
2
.
b)
x
2
x
2
+ 3x
+
3
x + 3
+
3
x
=
x
2
x(x + 3)
+
3x
x(x + 3)
+
3(x + 3)
x(x + 3)
=
x
2
+ 3x + 3
x(x + 3)
=
(x + 3)
2
x(x + 3)
=
x + 3
x
.
□
c Ví dụ 10. Thực hiện các phép tính sau
3x
5x + 5y
−
x
10x − 10y
;a)
1
3x − 2
−
4
3x + 2
−
3x − 6
4 − 9x
2
;b)
2a
(a + 1)
2
+
a
a + 1
+
1 − a
a
2
+ 2a + 1
.c)
Lời giải.
a)
3x
5x + 5y
−
x
10x − 10y
=
3x
5(x + y)
−
x
10(x − y)
=
6x(x − y)
10(x + y)(x − y)
−
x(x + y)
10(x + y)(x − y)
=
6x
2
− 6xy − x
2
− xy
10(x + y)(x − y)
=
5x
2
− 7xy
10(x + y)(x − y)
.
b)
1
3x − 2
−
4
3x + 2
−
3x − 6
4 − 9x
2
=
3x + 2
(3x − 2)(3x + 2)
−
4(3x − 2)
(3x − 2)(3x + 2)
+
3x − 6
(3x − 2)(3x + 2)
=
3x + 2 − 12x + 8 + 3x − 6
(3x − 2)(3x + 2)
=
−6x + 4
(3x − 2)(3x + 2)
=
−2(3x − 2)
(3x − 2)(3x + 2)
=
−2
3x + 2
.
32/101 32/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
33
c)
2a
(a + 1)
2
+
a
a + 1
+
1 − a
a
2
+ 2a + 1
=
2a
(a + 1)
2
+
1 − a
(a + 1)
2
+
a
a + 1
=
a + 1
(a + 1)
2
+
a
a + 1
=
1
a + 1
+
a
a + 1
=
1 + a
a + 1
= 1
□
Dạng 3. Tìm x thõa mãn đẳng thức cho trước
Chuyển hạng tử không chứa x về một vế, ta được biểu thức của x.
Rút gọn biểu thức của x.
c Ví dụ 11. Tìm x biết
x −
1
a + 1
=
2
a
2
− 1
(a là hằng số)
Lời giải.
x −
1
a + 1
=
2
a
2
− 1
x =
2
a
2
− 1
+
1
a + 1
=
2 + a − 1
(a − 1)(a + 1)
=
a + 1
(a − 1)(a + 1)
=
1
a − 1
□
c Ví dụ 12. Tìm x biết
x +
1
a
2
− a
=
a
a − 1
; (a là hằng số).
Lời giải.
x =
a
a − 1
−
1
a
2
− a
=
a
2
a(a − 1)
−
1
a(a − 1)
=
a
2
− 1
a(a − 1)
=
(a − 1)(a + 1)
a(a − 1)
=
a + 1
a
.
□
c Ví dụ 13. Nếu cho X +
a
2
+ 2
· a
a
3
− 1
− 1 =
2
a
2
+ a + 1
thì X là phân thức nào?
Lời giải.
Ta có X =
2
a
2
+ a + 1
−
a
2
+ 2
a
a
3
− 1
+ 1 =
2(a − 1) − a
3
− 2a + a
3
− 1
a
3
− 1
=
−3
a
3
− 1
. □
Dạng 4. Rút gọn và tính giá trị biểu thức
○ Sử dụng phép cộng, trừ phân thức để rút gọn biểu thức.
○ Thay giá trị của biến đã cho vào biểu thức đã rút gọn và thực hiện các phép tính.
c Ví dụ 14. Rút gọn biểu thức P =
1
x
+
1
y
−
1
x
Lời giải.
Ta có P =
1
x
+
1
y
−
1
x
=
1
x
+
1
y
+
−1
x
=
1
x
+
−1
x
+
1
y
= 0 +
1
y
=
1
y
. □
33/101 33/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
34
c Ví dụ 15. Rút gọn biểu thức P =
3
2x + 1
+
ï
5
4x − 1
−
Å
5
4x − 1
+
3
2x + 1
ãò
.
Lời giải.
Ta có P =
3
2x + 1
+
ï
5
4x − 1
−
Å
5
4x − 1
+
3
2x + 1
ãò
=
3
2x + 1
+
ï
5
4x − 1
−
5
4x − 1
−
3
2x + 1
ò
=
3
2x + 1
+
5
4x − 1
−
5
4x − 1
−
3
2x + 1
=
Å
3
2x + 1
−
3
2x + 1
ã
+
Å
5
4x − 1
−
5
4x − 1
ã
= 0.
□
c Ví dụ 16. Rút gọn biểu thức
A =
x + 2
x
2
+ x + 1
−
2
x − 1
−
2x
2
+ 4
1 − x
3
.
Lời giải.
Ta có A =
(x + 2)(x − 1)
(x − 1) (x
2
+ x + 1)
−
2
x
2
+ x + 1
(x − 1) (x
2
+ x + 1)
+
2x
2
+ 4
(x − 1) (x
2
+ x + 1)
=
x
2
+ 2x − x − 2 − 2x
2
− 2x − 2 + 2x
2
+ 4
(x − 1) (x
2
+ x + 1)
=
x
2
− x
(x − 1) (x
2
+ x + 1)
=
x(x − 1)
(x − 1) (x
2
+ x + 1)
=
x
x
2
+ x + 1
.
Nhận xét. Trong khi thực hiện phép tính cộng, trừ các phân thức đại số, nếu có hai đa thức ở mẫu đối nhau,
bạn nên áp dụng quy tắc đổi dấu một trong hai phân thức đó.
□
c Ví dụ 17. Rút gọn biểu thức
A =
20x
2
+ 120x + 180
(3x + 5)
2
− 4x
2
+
5x
2
− 125
9x
2
− (2x + 5)
2
−
(2x + 3)
2
− x
2
3 (x
2
+ 8x + 15)
.
Lời giải.
Ta có A =
20(x + 3)
2
(x + 5).5(x + 1)
+
5(x − 5)(x + 5)
5(x + 1)(x − 5)
−
(x + 3) · 3 · (x + 1)
3(x + 3)(x + 5)
=
4(x + 3)
2
(x + 5) · (x + 1)
+
x + 5
x + 1
−
x + 1
x + 5
=
4(x + 3)
2
+ (x + 5)
2
− (x + 1)
2
(x + 1)(x + 5)
=
4x
2
+ 24x + 36 + x
2
+ 10x + 25 − x
2
− 2x − 1
(x + 1)(x + 5)
=
4(x + 3)
x + 1
.
Nhận xét. Trong khi thực hiện phép tính cộng, trừ các phân thức đại số, nếu phân thức nào rút gọn được,
bạn nên rút gọn trước khi thực hiện.
□
c Ví dụ 18. Rút gọn rồi tính giá trị của biểu thức
P =
6x
2
+ 8x + 7
x
3
− 1
+
x
x
2
+ x + 1
−
6
x − 1
với x =
1
2
.
34/101 34/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
35
Lời giải.
Rút gọn biểu thức
P =
6x
2
+ 8x + 7
x
3
− 1
+
x
x
2
+ x + 1
−
6
x − 1
=
6x
2
+ 8x + 7
(x − 1) (x
2
+ x + 1)
+
x(x − 1)
(x − 1) (x
2
+ x + 1)
−
6
x
2
+ x + 1
(x − 1) (x
2
+ x + 1)
=
6x
2
+ 8x + 7 + x
2
− x − 6x
2
− 6x − 6
(x − 1) (x
2
+ x + 1)
=
x
2
+ x + 1
(x − 1) (x
2
+ x + 1)
=
1
x − 1
.
Với x =
1
2
, ta có P =
1
1
2
− 1
= −2. □
c Ví dụ 19. Tính giá trị của biểu thức
P =
10
(x + 2)(3 − x)
−
12
(3 − x)(3 + x)
−
1
(x + 3)(x + 2)
tại x = −0,75.
Lời giải.
Ta có P =
10 · (x + 3) − 12 · (x + 2) − (3 − x)
(x + 2)(3 − x)(x + 3)
=
3 − x
(x + 2)(3 − x)(x + 3)
=
1
(x + 2)(x + 3)
.
Với x = 0,75 thì giá trị của P =
1
(−0, 75 + 2)(−0, 75 + 3)
=
16
45
. □
c Ví dụ 20. Rút gọn biểu thức
B =
1
a − b
+
1
a + b
+
2a
a
2
+ b
2
+
4a
3
a
4
+ b
4
+
8a
7
a
8
+ b
8
.
Lời giải.
B =
2a
a
2
− b
2
+
2a
a
2
+ b
2
+
4a
3
a
4
+ b
4
+
8a
7
a
8
+ b
8
=
4a
3
a
4
− b
4
+
4a
3
a
4
+ b
4
+
8a
7
a
8
+ b
8
=
8a
7
a
8
− b
8
+
8a
7
a
8
+ b
8
=
16a
15
a
16
− b
16
.
□
c Ví dụ 21. Cho a + b + c = 0. Rút gọn biểu thức
a) A =
a
2
a
2
− b
2
− c
2
+
b
2
b
2
− a
2
− c
2
+
c
2
c
2
− a
2
− b
2
;
b) B =
1
b
2
+ c
2
− a
2
+
1
c
2
+ a
2
− b
2
+
1
a
2
+ b
2
− c
2
.
Lời giải.
a) Ta có a = −b − c nên a
2
= b
2
+ 2bc + c
2
⇒ a
2
− b
2
− c
2
= 2bc.
Tương tự ta có b
2
− a
2
− c
2
= 2ac
c
2
− a
2
− b
2
= 2ab.
Do đó A =
a
2
2bc
+
b
2
2ac
+
c
2
2ab
⇒ A =
a
3
+ b
3
+ c
3
2abc
(1)
35/101 35/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
36
Xét a
3
+ b
3
+ c
3
= a
3
+ b
3
− (a + b)
3
= −3ab(a + b) = 3abc (2)
Vậy từ (1) và (2) ta có A =
3abc
2abc
=
3
2
.
b) Ta có b + c = −a nên b
2
+ c
2
+ 2bc = a
2
⇒ b
2
+ c
2
− a
2
= −2bc.
Tương tự ta có c
2
+ a
2
− b
2
= −2ac
a
2
+ b
2
− c
2
= −2ab.
Do đó ta có B =
1
−2bc
+
1
−2ac
+
1
−2ab
=
a + b + c
−2abc
= 0.
Nhận xét.
○ Bài toán không quá khó, chỉ sử dụng biến đổi một cách linh hoạt các mẫu thức mà cần sử dụng giả thiết.
○ Bạn nên nhớ đẳng thức đẹp: Cho a + b + c = 0 thì ta có a
3
+ b
3
+ c
3
= 3abc.
□
Dạng 5. Chứng minh giá trị biểu thức không phụ thuộc vào biến. Chứng minh đẳng thức
a) Thực hiện phép cộng, trừ các phân thức để rút gọn biểu thức không còn chứa biến.
b) Chứng minh đẳng thức
○ Từ đẳng thức đã cho ta biến đổi một vế bằng vế còn lại.
○ Hoặc biến đổi cả hai vế cùng bằng một biểu thức.
c Ví dụ 22. Chứng tỏ giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x.
P =
2x
x
2
+ 4x + 4
+
x + 1
x + 2
+
2 − x
x
2
+ 4x + 4
.
Lời giải.
P =
2x
x
2
+ 4x + 4
+
x + 1
x + 2
+
2 − x
x
2
+ 4x + 4
=
Å
2x
x
2
+ 4x + 4
+
2 − x
x
2
+ 4x + 4
ã
+
x + 1
x + 2
=
2x + 2 − x
x
2
+ 4x + 4
+
x + 1
x + 2
=
x + 2
(x + 2)
2
+
x + 1
x + 2
=
1
x + 2
+
x + 1
x + 2
=
1 + x + 1
x + 2
=
x + 2
x + 2
= 1.
□
c Ví dụ 23. Chứng tỏ giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x, y.
x
2
+ y
2
− 1
x
2
+ 2xy + y
2
+
2y
x + y
+
1 − 2y
2
x
2
+ 2xy + y
2
.
Lời giải.
Ta có
x
2
+ y
2
− 1
x
2
+ 2xy + y
2
+
2y
x + y
+
1 − 2y
2
x
2
+ 2xy + y
2
=
x
2
+ y
2
− 1 + 1 − 2y
2
x
2
+ 2xy + y
2
+
2y
x + y
=
x
2
− y
2
(x + y)
2
+
2y
x + y
=
(x + y)(x − y)
(x + y)
2
+
2y
x + y
=
x − y
x + y
+
2y
x + y
=
x − y + 2y
x + y
=
x + y
x + y
= 1.
□
36/101 36/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
37
c Ví dụ 24. Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị biến x.
A =
x + 1
x − 1
+
x − 1
x + 1
−
4
x
2
− 1
với x = 1; x = −1.
Lời giải.
Ta có A =
(x + 1)
2
(x − 1)(x + 1)
+
(x − 1)
2
(x − 1)(x + 1)
−
4
(x − 1)(x + 1)
=
x
2
+ 2x + 1 + x
2
− 2x + 1 − 4
x
2
− 1
= 2.
Vậy giá trị biểu thức A đã cho không phụ thuộc vào giá trị của x. □
c Ví dụ 25. Chứng minh đẳng thức
x − 5y
2x − 3y
−
24xy
4x
2
− 9y
2
−
x + 8y
3y − 2x
=
2x − 3y
2x + 3y
..
Lời giải.
x − 5y
2x − 3y
−
24xy
4x
2
− 9y
2
−
x + 8y
3y − 2x
=
x − 5y
2x − 3y
+
x + 8y
2x − 3y
−
24xy
(2x − 3y)(2x + 3y)
=
2x + 3y
2x − 3y
−
24xy
(2x − 3y)(2x + 3y)
=
(2x + 3y)
2
− 24xy
(2x − 3y)(2x + 3y)
=
(2x − 3y)
2
(2x − 3y)(2x + 3y)
=
2x − 3y
2x + 3y
.
□
c Ví dụ 26. Chứng minh đẳng thức
x
x + y
+
2xy
x
2
− y
2
−
y
x + y
=
x
2
+ y
2
x
2
− y
2
.
Lời giải.
x
x + y
+
2xy
x
2
− y
2
−
y
x + y
=
x
x + y
−
y
x + y
+
2xy
(x − y)(x + y)
=
x − y
x + y
+
2xy
(x − y)(x + y)
=
(x − y)
2
(x − y)(x + y)
+
2xy
(x − y)(x + y)
=
x
2
− 2xy + y
2
+ 2xy
x
2
− y
2
=
x
2
+ y
2
x
2
− y
2
.
□
c Ví dụ 27. Chứng minh đẳng thức
a
2
+ 3ab
a
2
− 9b
2
+
2a
2
− 5ab − 3b
2
6ab − a
2
− 9b
2
=
a
2
+ ab + ac + bc
3bc − a
2
− ac + 3ab
.
Lời giải.
Biến đổi vế phải
V P =
(a + b)(a + c)
3b(c + a) − a(a + c)
=
(a + b)(a + c)
(a + c)(3b − a)
=
a + b
3b − a
(1)
Biến đổi vế trái
V T =
a(a + 3b)
(a − 3b)(a + 3b)
+
(a − 3b)(2a + b)
−(a − 3b)
2
=
a
a − 3b
−
2a + b
a − 3b
=
−a − b
a − 3b
=
a + b
3b − a
(2)
Từ (1) và (2) ta có vế trái bằng vế phải, suy ra điều phải chứng minh. □
37/101 37/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
38
Dạng 6. Vận dụng
c Ví dụ 28. Tại một cuộc đua thuyền diễn ra trên một khúc sông từ A đến B dài 3 km. Mỗi đội thực hiện
một vòng đua, xuất phát từ A đến B, rồi quay về A là đích. Một đội đua đạt tốc độ (x + 1) km/h khi xuôi
dòng từ A đến B và đạt tốc độ (x − 1) km/h khi ngược dòng từ B về A.
Viết biểu thức tính tổng thời gian đi và về, chênh lệch thời gian giữa đi và về của đội đua thuyền. Tính giá
trị của các đại lượng này khi v = 6 km/h.
Lời giải.
Quãng đường từ A đến B dài 3 km. Ta có: Thời gian =
quãng đường
vận tốc
.
Khi xuôi dòng, tốc độ của đội đua là (x + 1) km/h nên thời gian đi (thời gian xuôi dòng) là
3
x + 1
h.
Khi ngược dòng, tốc độ của đội đua là (x − 1) km/h nên thời gian về (thời gian ngược dòng) là
3
x − 1
h.
○ Tổng thời gian đi và về của đội đua thuyền là
3
x + 1
+
3
x − 1
h.
○ Chênh lệch thời gian giữa đi và về là
3
x − 1
−
3
x + 1
h.
○ Khi v = 6 km/h tức là x = 6. Khi đó
— Tổng thời gian đi và về của đội đua thuyền là
3
6 + 1
+
3
6 − 1
=
36
35
h.
— Chênh lệch thời gian giữa đi và về là
3
6 − 1
−
3
6 + 1
=
6
35
h.
Tức là đi khi đội đua thuyền đi về thời gian lâu hơn khi đội đi là
6
35
giờ.
□
c Ví dụ 29. Một đoàn tàu chở khách đi một quãng đường 500 km, trong đó có 50 km đường qua thành phố
và 450 km đường qua vùng rừng núi. Biết tốc độ tàu khi chạy qua thành phố kém 30 km/h so với tốc độ tàu
khi chạy qua vùng rừng núi. Gọi x (km/h) là tốc độ tàu chạy qua vùng rừng núi. Viết phân thức biểu thị theo
x:
a) Thời gian tàu chạy qua vùng rừng núi;
b) Thời gian tàu chạy qua thành phố;
c) Thời gian tàu chạy trên cả quãng đường.
Lời giải.
a) Phân thức biểu thị thời gian tàu chạy qua vùng rừng núi là
450
x
(giờ).
b) Tốc độ tàu chạy qua thành phố là x − 30 (km/h).
Phân thức biểu thị thời gian tàu chạy qua thành phố là
50
x − 30
(giờ).
c) Thời gian tàu chạy trên cả quãng đường là
450
x
+
50
x − 30
=
450(x − 30) + 50x
x(x − 30)
=
500x − 13500
x(x − 30)
(giờ).
Vậy phân thức biểu thị thời gian tàu chạy trên cả quãng đường là
500x − 13500
x(x − 30)
(giờ).
□
38/101 38/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
39
c Ví dụ 30. Một tàu du lịch chạy xuôi dòng 15 km, sau đó quay ngược lại để trở về điểm xuất phát và kết
thúc chuyến du lịch. Biết rằng vận tốc của tàu khi nước yên lặng là 10 km/h và vận tốc của dòng nước là x
(km/h).
a) Hãy viết các phân thức biểu thị theo x thời gian xuôi dòng, thời gian ngược dòng và tổng thời gian tàu
chạy.
b) Tính tổng thời gian tàu chạy khi vận tốc dòng nước là 2 km/h.
Lời giải.
a) Ta có vận tốc của tàu du lịch khi nước xuôi dòng là 10 + x (km/h) (x > 0). Suy ra thời gian xuôi dòng là
t
x
=
15
10 + x
(h).
Tương tự vận tốc của tàu di lịch khi nước ngược dòng là 10 − x (km/h) (x > 0). Suy ra thời gian ngược
dòng là t
n
=
15
10 − x
(h).
Vậy tổng thời gian tàu chạy là
t =
15
10 + x
+
15
10 − x
=
15 · 20
100 − x
=
300
100 − x
(h)
b) Khi vận tốc dòng nước là 2 km/h thay vào ta có
t =
300
100 − 2
=
150
49
(h).
□
A
CC BÀI TẬP VẬN DỤNG
c Bài 1. Thực hiện các phép cộng, trừ phân thức sau:
a − 1
a + 1
+
3 − a
a + 1
;a)
b
a − b
+
a
b − a
;b)
(a + b)
2
ab
−
(a − b)
2
ab
.c)
Lời giải.
a)
a − 1
a + 1
+
3 − a
a + 1
=
a − 1 + 3 − a
a + 1
=
2
a + 1
;
b)
b
a − b
+
a
b − a
=
b
a − b
−
a
a − b
=
b − a
a − b
= −1;
c)
(a + b)
2
ab
−
(a − b)
2
ab
=
(a
2
+ 2ab + b
2
) − (a
2
− 2ab + b
2
)
ab
=
4ab
ab
= 4.
□
c Bài 2. Tính
7x + 2
5x − 2
−
2 − 2x
5x − 2
;a)
5x − 2
4x
2
y
−
x − 2
4x
2
y
;b)
xy
x
2
− y
2
−
x
2
y
2
− x
2
;c)
x + 4
x
2
− 4
−
1
x
2
+ 2x
.d)
Lời giải.
a)
7x + 2
5x − 2
−
2 − 2x
5x − 2
=
7x + 2 − 2 + 2x
5x − 2
=
9x
5x − 2
.
b)
5x − 2
4x
2
y
−
x − 2
4x
2
y
=
5x − 2 − x + 2
4x
2
y
=
4x
4x
2
y
=
1
xy
.
39/101 39/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
40
c)
xy
x
2
− y
2
−
x
2
y
2
− x
2
=
xy
x
2
− y
2
+
x
2
x
2
− y
2
=
xy + x
2
x
2
− y
2
=
x(x + y)
(x + y)(x − y)
=
x
x − y
.
d)
x(x + 4) − (x − 2)
x(x + 2)(x − 2)
=
x + 1
x(x − 2)
.
□
c Bài 3. Thực hiện các phép cộng, trừ phân thức sau:
1
2a
+
2
3b
;a)
x − 1
x + 1
−
x + 1
x − 1
;b)
x + y
xy
−
y + z
yz
;c)
2
x − 3
−
12
x
2
− 9
;d)
1
x − 2
+
2
x
2
− 4x + 4
;e)
1
x + 1
−
1
x
3
+ 1
+
1
x
2
− x + 1
.f)
Lời giải.
a)
1
2a
+
2
3b
=
3b
6ab
+
4a
6ab
=
4a + 3b
6ab
;
b)
x − 1
x + 1
−
x + 1
x − 1
=
(x − 1)
2
(x + 1)(x − 1)
−
(x + 1)
2
(x + 1)(x − 1)
=
(x
2
− 2x + 1) − (x
2
+ 2x + 1)
(x + 1)(x − 1)
=
−4x
x
2
− 1
;
c)
x + y
xy
−
y + z
yz
=
z(x + y)
xyz
−
x(y + z)
xyz
=
xz + yz − xy − xz
xyz
=
y(z − x)
xyz
=
z − x
xz
;
d)
2
x − 3
−
12
x
2
− 9
=
2(x + 3)
(x − 3)(x + 3)
−
12
(x − 3)(x + 3)
=
2x + 6 − 12
(x − 3)(x + 3)
=
2(x − 3)
(x − 3)(x + 3)
=
2
x + 3
;
e)
1
x − 2
+
2
x
2
− 4x + 4
=
1
x − 2
+
2
(x − 2)
2
=
x − 2
(x − 2)
2
+
2
(x − 2)
2
=
x − 2 + 2
(x − 2)
2
=
x
(x − 2)
2
.
f)
1
x + 1
−
1
x
3
+ 1
+
1
x
2
− x + 1
=
x
2
− x + 1
x
3
+ 1
−
1
x
3
+ 1
+
x + 1
x
3
+ 1
=
x
2
+ 1
x
3
+ 1
.
□
c Bài 4. Thực hiện các phép tính sau:
x + 2
x − 1
−
x − 3
x − 1
+
x − 4
1 − x
;a)
1
x + 5
−
1
x − 5
+
2x
x
2
− 25
;b) x +
2y
2
x + y
− y.c)
Lời giải.
a)
x + 2
x − 1
−
x − 3
x − 1
+
x − 4
1 − x
=
(x + 2) − (x − 3)
x − 1
−
x − 4
x − 1
=
5 − (x − 4)
x − 1
=
9 − x
x − 1
;
b)
1
x + 5
−
1
x − 5
+
2x
x
2
− 25
=
x − 5
(x + 5)(x − 5)
−
x + 5
(x + 5)(x − 5)
+
2x
(x + 5)(x − 5)
=
(x − 5) − (x + 5) + 2x
(x + 5)(x − 5)
=
2x − 10
(x + 5)(x − 5)
=
2(x − 5)
(x + 5)(x − 5)
=
2
x + 5
;
c) x +
2y
2
x + y
− y =
x(x + y)
x + y
+
2y
2
x + y
−
y(x + y)
x + y
=
x
2
+ xy + 2y
2
− xy − y
2
x + y
=
x
2
+ y
2
x + y
.
□
40/101 40/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
41
c Bài 5. Thực hiện phép tính
5x − 4
9
+
4x + 4
9
;a)
x
2
y − 6
2x
2
y
+
6 − xy
2
2x
2
y
;b)
x + 1
x
2
− 5x
+
x − 18
x
2
− 5x
+
x + 2
x
2
− 5x
;c)
7y
3
−
7y − 5
3
;d)
4x − 1
3xy
2
−
7x − 1
3xy
2
;e)
3y − 2x
x − 2y
−
x − y
2y − x
.f)
Lời giải.
a)
5x − 4
9
+
4x + 4
9
=
5x − 4 + 4x + 4
9
=
9x
9
= x.
b)
x
2
y − 6
2x
2
y
+
6 − xy
2
2x
2
y
=
x
2
y − 6 + 6 − xy
2
2x
2
y
=
x
2
y − xy
2
2x
2
y
=
xy(x − y)
2x
2
y
=
x − y
2x
.
c)
x + 1
x
2
− 5x
+
x − 18
x
2
− 5x
+
x + 2
x
2
− 5x
=
x + 1 + x − 18 + x + 2
x
2
− 5x
=
3x − 15
x
2
− 5x
=
3(x − 5)
x(x − 5)
=
3
x
.
d)
7y
3
−
7y − 5
3
=
7y − 7y + 5
3
=
5
3
.
e)
4x − 1
3xy
2
−
7x − 1
3xy
2
=
4x − 1 − 7x + 1
3xy
2
=
−3x
3xy
2
=
−1
y
2
.
f)
3y − 2x
x − 2y
−
x − y
2y − x
=
3y − 2x
x − 2y
+
x − y
x − 2y
=
3y − 2x + x − y
x − 2y
=
2y − x
x − 2y
=
−(x − 2y)
x − 2y
= −1.
□
c Bài 6. Thực hiện phép tính
4x + 2
4x − 4
+
3 − 6x
6x − 6
;a)
y
2x
2
− xy
+
4x
y
2
− 2xy
;b)
x
x − y
+
y
x + y
+
2y
2
x
2
− y
2
;c)
x
2
+ 2
x
3
− 1
+
x
x
2
+ x + 1
+
1
1 − x
.d)
Lời giải.
a)
4x + 2
4x − 4
+
3 − 6x
6x − 6
=
4x + 2
4(x − 1)
+
3 − 6x
6(x − 1)
=
12x + 6 + 6 − 12x
12(x − 1)
=
12
12(x − 1)
=
1
x − 1
.
b)
y
2x
2
− xy
+
4x
y
2
− 2xy
=
y
x(2x − y)
+
4x
y(y − 2x)
=
y
2
− 4x
2
xy(2x − y)
=
(y − 2x)(y + 2x)
−xy(y − 2x)
=
−y − 2x
xy
c)
x
x − y
+
y
x + y
+
2y
2
x
2
− y
2
=
x(x + y) + y(x − y) + 2y
2
(x − y)(x + y)
=
x
2
+ xy + xy − y
2
+ 2y
2
(x − y)(x + y)
=
x
2
+ 2xy + y
2
(x − y)(x + y)
=
(x + y)
2
(x − y)(x + y)
=
x + y
x − y
.
d)
x
2
+ 2
x
3
− 1
+
x
x
2
+ x + 1
+
1
1 − x
=
x
2
+ 2 + x(x − 1) − (x
2
+ x + 1)
(x − 1)(x
2
+ x + 1)
=
x
2
− 2x + 1
(x − 1)(x
2
+ x + 1)
=
(x − 1)
2
(x − 1)(x
2
+ x + 1)
=
x − 1
x
2
+ x + 1
.
□
41/101 41/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
42
c Bài 7. Thực hiện phép tính
1
x − 2
−
1
x + 1
;a)
12
x
2
− 9
−
2
x − 3
;b)
1
xy − x
2
−
1
y
2
− xy
;c)
2x
x
2
− 1
−
3
2 + 2x
+
1
2 − 2x
.d)
Lời giải.
a)
1
x − 2
−
1
x + 1
=
x + 1
(x − 2)(x + 1)
−
x − 2
(x − 2)(x + 1)
=
x + 1 − (x − 2)
(x − 2)(x + 1)
=
x + 1 − x + 2
(x − 2)(x + 1)
=
3
(x − 2)(x + 1)
.
b)
12
x
2
− 9
−
2
x − 3
=
12
(x + 3)(x − 3)
−
2
x − 3
=
12
(x + 3)(x − 3)
−
2(x + 3)
(x + 3)(x − 3)
=
12 − 2(x + 3)
(x + 3)(x − 3)
=
12 − 2x − 6
(x + 3)(x − 3)
=
6 − 2x
(x + 3)(x − 3)
=
−3(x − 3)
(x + 3)(x − 3)
=
−3
x + 3
.
c)
1
xy − x
2
−
1
y
2
− xy
=
1
x(y − x)
−
1
y(y − x)
=
y
xy(y − x)
−
x
xy(y − x)
=
y − x
xy(y − x)
=
1
xy
.
d)
2x
x
2
− 1
−
3
2 + 2x
+
1
2 − 2x
=
2x
(x + 1)(x − 1)
−
3
2(x + 1)
−
1
2(x − 1)
=
4x
2(x + 1)(x − 1)
−
3(x − 1)
2(x + 1)(x − 1)
−
x + 1
2(x + 1)(x − 1)
=
(4x − 3x − x) + (3 − 1)
2(x + 1)(x − 1)
=
2
2(x + 1)(x − 1)
=
1
(x + 1)(x − 1)
.
□
c Bài 8. Thực hiện phép tính
x
2
− 3x + 1
2x
2
+
5x − 1 − x
2
2x
2
.a)
y
x − y
+
x
x + y
.b)
x
2x − 6
+
9
2x(3 − x)
.c)
Lời giải.
a)
x
2
− 3x + 1
2x
2
+
5x − 1 − x
2
2x
2
=
2x
2x
2
=
1
x
.
b)
y
x − y
+
x
x + y
=
y(x + y)
x
2
− y
2
+
x(x − y)
x
2
− y
2
=
x
2
+ y
2
x
2
− y
2
.
c)
x
2x − 6
+
9
2x(3 − x)
=
x
2
2x(x − 3)
+
9
2x(3 − x)
=
x
2
2x(x − 3)
−
9
2x(x − 3)
=
(x − 3)(x + 3)
2x(x − 3)
=
x + 3
2x
.
□
42/101 42/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
43
c Bài 9. Thực hiện phép tính
5 − 3x
x + 1
−
−2 + 5x
x + 1
.a)
x
x − y
−
y
x + y
.b)
3
x + 1
−
2 + 3x
x
3
+ 1
.c)
Lời giải.
a)
5 − 3x
x + 1
−
−2 + 5x
x + 1
=
7 − 8x
x + 1
.
b)
x
x − y
−
y
x + y
=
x(x + y)
x
2
− y
2
−
y(x − y)
x
2
− y
2
=
x
2
+ y
2
x
2
− y
2
.
c)
3
x + 1
−
2 + 3x
x
3
+ 1
=
3(x
2
− x + 1)
(x + 1)(x
2
− x + 1)
−
2 + 3x
(x + 1)(x
2
− x + 1)
=
3x
2
− 6x + 1
(x + 1)(x
2
− x + 1)
.
□
c Bài 10. Thực hiện phép tính
a)
1
x
+
2
x + 1
+
3
x + 2
−
1
x
−
2
x − 1
−
3
x + 2
.
b)
2x − 1
x
+
1 − x
2x + 1
+
3
x
2
− 9
+
1 − 2x
x
+
x − 1
2x + 1
−
3
x + 3
.
Lời giải.
a)
1
x
+
2
x + 1
+
3
x + 2
−
1
x
−
2
x − 1
−
3
x + 2
=
2
x + 1
−
2
x − 1
=
2(x − 1) − 2(x + 1)
(x − 1)(x + 1)
=
4
(x
2
− 1
.
b)
2x − 1
x
+
1 − x
2x + 1
+
3
x
2
− 9
+
1 − 2x
x
+
x − 1
2x + 1
−
3
x + 3
=
3
(x − 3)(x + 3)
−
3(x − 3)
(x − 3)(x + 3)
=
12 − 3x
x
2
− 9
.
□
c Bài 11. Thực hiện phép tính
a)
x
2
+ 4x + 4
x
2
− 4
+
x
2 − x
+
4 − x
5x − 10
.
b)
x
x
2
+ 1
−
Å
3
x + 6
+
2 − x
x + 4
ã
+
ï
3
x + 6
−
Å
1
x
2
+ 1
−
x − 2
x + 4
ãò
.
Lời giải.
a) Ta có:
x
2
+ 4x + 4
x
2
− 4
+
x
2 − x
+
4 − x
5x − 10
=
(x + 2)
2
(x − 2)(x + 2)
−
x
x − 2
+
4 − x
5(x − 2)
=
x + 2
x − 2
−
x
x − 2
+
4 − x
5(x − 2)
=
5(x + 2)
5(x − 2)
−
5x
5(x − 2)
+
4 − x
5(x − 2)
=
14 − x
5x − 10
.
b) Ta có:
x
x
2
+ 1
−
Å
3
x + 6
+
2 − x
x + 4
ã
+
ï
3
x + 6
−
Å
1
x
2
+ 1
−
x − 2
x + 4
ãò
43/101 43/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
44
=
x
x
2
+ 1
−
3
x + 6
+
x − 2
x + 4
+
3
x + 6
−
1
x
2
+ 1
+
x − 2
x + 4
=
Å
x
x
2
+ 1
−
1
x
2
+ 1
ã
+
Å
−
3
x + 6
+
3
x + 6
ã
+
2(x − 2)
x + 4
=
x − 1
x
2
+ 1
+
2(x − 2)
x + 4
□
c Bài 12. Thực hiện phép tính
x − y
xy
+
y − z
yz
+
z − x
zx
.a)
x
(x − y)
2
+
y
y
2
− x
2
.b)
Lời giải.
a) Ta có:
x − y
xy
+
y − z
yz
+
z − x
zx
=
z(x − y) + x(y − z) + y(z − x)
xyz
=
zx − zy + xy − xz + yz − yx
xyz
=
(zx − xz) + (−zy + yz) + (xy − yx)
xyz
= 0
b) Ta có:
x
(x − y)
2
+
y
y
2
− x
2
=
x
(x − y)
2
+
y
(y − x)(x + y)
=
x(x + y)
(x − y)
2
(x + y)
−
y(x − y)
(x − y)
2
(x + y)
=
x
2
+ xy − yx + y
2
(x − y)
2
(x + y)
=
x
2
+ y
2
(x + y)(x − y)
2
.
□
c Bài 13. Tính:
5x − 2
15
+
2x + 2
15
;a)
2 − 2x
6x
3
y
+
3 + 2y
6x
3
y
+
2x − 5
6x
3
y
;b)
x
2
x + y
+
y
2
y + z
+
−y
2
x + y
+
−z
2
y + z
.c)
Lời giải.
a)
5x − 2
15
+
2x + 2
15
=
5x − 2 + 2x + 2
15
=
7x
15
.
b)
2 − 2x
6x
3
y
+
3 + 2y
6x
3
y
+
2x − 5
6x
3
y
=
2 − 2x + 3 + 2y + 2x − 5
6x
3
y
=
2y
6x
3
y
=
1
3x
3
c)
x
2
x + y
+
y
2
y + z
+
−y
2
x + y
+
−z
2
y + z
=
x
2
− y
2
x + y
+
y
2
− z
2
y + z
=
(x + y)(x − y)
x + y
+
(y + z)(y − z)
y + z
=x − y + y − z
=x − z.
44/101 44/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
45
□
c Bài 14. Tính
4x − 2
7xy
2
+
x + 2
7xy
2
;a)
1
x
+
1
2x
+
1
3x
;b)
2x − 1
x
+
x + 3
2
.c)
Lời giải.
a)
4x − 2
7xy
2
+
x + 2
7xy
2
=
4x − 2 + x + 2
7xy
2
=
5x
7xy
2
=
5
7y
2
.
b)
1
x
+
1
2x
+
1
3x
=
6
6x
+
3
6x
+
2
6x
=
11
6x
.
c)
2x − 1
x
+
x + 3
2
=
2(2x − 1)
2x
+
x(x + 3)
2x
=
4x − 2 + x
2
+ 3x
2x
=
x
2
+ 7x − 2
2x
.
□
c Bài 15. Viết phân thức P =
4x
2
− 2x + 3
2x − 1
dưới dạng tổng một đa thức và một phân thức có tử thức là
hằng số.
Lời giải.
P =
4x
2
− 2x + 3
2x − 1
=
4x
2
− 2x
2x − 1
+
3
2x − 1
= 2x +
3
2x − 1
.
□
c Bài 16. Cho phân thức P =
4x
2
− 2x + 7
2x − 1
. Tìm giá trị nguyên của x để giá trị của phân thức P là một
số nguyên.
Lời giải.
Ta có P = 2x +
7
2x − 1
; x ∈ Z.
Để P nhận giá trị nguyên thì 2x − 1 ∈ Ư(7).
Do đó 2x − 1 = 1 ⇒ x = 1
2x − 1 = 7 ⇒ x = 4
2x − 1 = −1 ⇒ x = 0
2x − 1 = −7 ⇒ x = −3
□
c Bài 17. Cho biểu thức P =
25x
2
− 1
1 − 5x
+
5xy − 15x + y − 3
y − 3
với x =
1
5
; y = 3. Tính giá trị của P .
Lời giải.
Ta có P =
(5x − 1)(5x + 1)
−(5x − 1)
+
(y − 3) · (5x + 1)
y − 3
= −5x − 1 + 5x + 1 = 0. □
c Bài 18. Cho (a + b + c)
2
= a
2
+ b
2
+ c
2
. Rút gọn biểu thức
P =
a
2
a
2
+ 2bc
+
b
2
b
2
+ 2ac
+
c
2
c
2
+ 2ab
.
Lời giải.
Từ (a + b + c)
2
= a
2
+ b
2
+ c
2
, ta có
a
2
+ b
2
+ c
2
+ 2(ab + bc + ca) = a
2
+ b
2
+ c
2
nên ab + bc + ca = 0.
45/101 45/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
46
Xét a
2
+ 2bc = a
2
+ 2bc − ab − bc − ca = a
2
− ab − ca + bc
= (a − b)(a − c)
.
Tương tự ta có b
2
+ 2ac = (b − a)(b − c)
c
2
+ 2ab = (c − a)(c − b).
Do đó ta có P =
a
2
(a − b)(a − c)
+
b
2
(b − a)(b − c)
+
c
2
(c − a)(c − b)
⇒ P = −
a
2
(b − c) + b
2
(c − a) + c
2
(a − b)
(a − b)(b − c)(c − a)
.
Phân tích tử thức thành nhân tử, ta có
P = −
(a − b)(b − c)(a − c)
(a − b)(b − c)(c − a)
= 1.
□
c Bài 19. Chứng minh giá trị của biểu thức sau không phụ thuộc vào x.
A =
x + 4
2x + 4
−
x − 2
x
2
− 4
.
Lời giải.
A =
x + 4
2(x + 2)
−
x − 2
(x + 2)(x − 2)
=
x + 4
2(x + 2)
−
1
x + 2
=
x + 4 − 2
2(x + 2)
=
1
2
. □
c Bài 20.
a) Thực hiện phép tính
1
x
−
1
x + 1
.
b) Thu gọn biểu thức
A =
1
x
2
+ x
+
1
x
2
+ 3x + 2
+
1
x
2
+ 5x + 6
+
1
x + 3
.
Lời giải.
a)
1
x(x + 1)
.
b) Phân tích mẫu thức thành nhân tử rồi áp dụng câu a.
Ta có A =
1
x(x + 1)
+
1
(x + 1)(x + 2)
+
1
(x + 2)(x + 3)
+
1
x + 3
=
1
x
−
1
x + 1
+
1
x + 1
−
1
x + 2
+
1
x + 2
−
1
x + 3
+
1
x + 3
=
1
x
.
□
c Bài 21.
a) Rút gọn biểu thức: A =
2x
2
+ 1
x
3
+ 1
+
1 − x
x
2
− x + 1
−
1
x + 1
;
b) Tính giá trị của biểu thức A tại x = −3.
Lời giải.
46/101 46/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
47
a) Rút gọn biểu thức A như sau:
A =
2x
2
+ 1
x
3
+ 1
+
1 − x
x
2
− x + 1
−
1
x + 1
=
2x
2
+ 1
(x + 1) (x
2
− x + 1)
+
1 − x
x
2
− x + 1
−
1
x + 1
=
2x
2
+ 1
(x + 1) (x
2
− x + 1)
+
(1 − x)(x + 1)
(x + 1) (x
2
− x + 1)
−
x
2
− x + 1
(x + 1) (x
2
− x + 1)
=
2x
2
+ 1 + (1 − x)(x + 1) −
x
2
− x + 1
(x + 1) (x
2
− x + 1)
=
2x
2
+ 1 + 1 − x
2
− x
2
+ x − 1
(x + 1) (x
2
− x + 1)
=
x + 1
(x + 1) (x
2
− x + 1)
=
1
x
2
− x + 1
.
b) Điều kiện xác định của phân thức
1
x
2
− x + 1
là x
2
− x + 1 = 0.
Với x = −3 ta thấy x
2
− x + 1 = (−3)
2
− (−3) + 1 = 91 = 0.
Do đó, giá trị của biểu thức A tại x = −3 là
1
(−3)
2
− (−3) + 1
=
1
91
.
□
c Bài 22. Cùng đi từ thành phố A đến thành phố B cách nhau 450 km, xe khách chạy với tốc độ x km/h;
xe tải chạy với tốc độ y km/h (x > y). Nếu xuất phát cùng lúc thì xe khách đến thành phố B sớm hơn xe tải
bao nhiêu giờ?
Lời giải.
Quãng đường đi từ thành phố A đến thành phố B cách nhau 450 km.
Xe khách chạy với tốc độ x km/h nên thời gian xe khách đi hết quãng đường AB là
450
x
h.
Xe tải chạy với tốc độ y km/h nên thời gian xe tải đi hết quãng đường AB là
450
y
h.
Thời gian xe khách đến thành phố B sớm hơn xe tải là
450
y
−
450
x
=
450x − 450y
xy
h. □
c Bài 23.
Có ba hình hộp chữ nhật A, B, C có chiều dài, chiều rộng
và thể tích được cho như Hình 2. Hình B và C có các kích
thước giống nhau, hình A có cùng chiều rộng với B và C.
a) Tính chiều cao của các hình hộp chữ nhật. Biểu thị
chúng bằng các phân thức cùng mẫu số.
b) Tính tổng chiều cao của hình A và C, chênh lệch chiều
cao của hình A và B.
A
E
D
C G
H
K
F
IJ
L
M N
P Q
a cm
3
b cm
3
x cm
y cm
z cm
A
C
B
?
Hình 2
?
Lời giải.
a) Ta có V = Chiều dài · Chiều rộng · Chiều cao ⇒ Chiều cao =
V
Chiều dài · Chiều rộng
. Dựa vào Hình 2 ta
thấy:
○ Khối hộp chữ nhật A có thể tích là a cm
3
, chiều dài là x cm và chiều rộng là z cm nên chiều cao là
a
xz
=
ay
xyz
cm.
○ Khối hộp chữ nhật B có thể tích là b cm
3
, chiều dài là y cm và chiều rộng là z cm nên chiều cao là
b
yz
=
bx
xyz
cm.
47/101 47/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
48
○ Khối hộp chữ nhật C có kích thước giống khối hộp B nên chiều cao là
bx
xyz
cm.
b) Tổng chiều cao của hình A và C là
ay
xyz
+
bx
xyz
=
ay + bx
xyz
cm.
Ta có
ay
xyz
−
bx
xyz
=
ay − bx
xyz
nên hình A cao hơn hình B là
ay − bx
xyz
cm.
□
c Bài 24. Một xí nghiệp dự định sản xuất 10 000 sản phẩm trong x ngày. Khi thực hiện, xí nghiệp đã làm
xong sớm hơn 1 ngày so với dự định và còn làm thêm được 80 sản phẩm. Viết phân thức biểu thị theo x:
a) Số sản phẩm xí nghiệp làm trong 1 ngày theo dự định;
b) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế;
c) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế nhiều hơn số sản phẩm xí nghiệp làm trong 1 ngày
theo dự định.
Lời giải.
a) Số sản phẩm xí nghiệp làm trong 1 ngày theo dự định là
10 000
x
(sản phẩm).
b) Số sản phẩm xí nghiệp đã hoàn thành trên thực tế là 10 000 + 80 = 10 080 (sản phẩm).
Số ngày xí nghiệp đã hoàn thành trên thực tế là x − 1 (ngày).
Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế là
10 080
x − 1
(sản phẩm)
c) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế nhiều hơn số sản phẩm xí nghiệp làm trong 1 ngày
theo dự định là
10000
x
−
10080
x − 1
= 80
Å
125
x
−
126
x − 1
ã
= 80
Å
125(x − 1)
x(x − 1)
−
126x
x(x − 1)
ã
= 80 ·
125x − 125 − 126x
x(x − 1)
=
−80x − 10000
x(x − 1)
(sản phẩm).
□
c Bài 25. Người ta mở hai vòi nước cùng chảy vào bể không chứa nước. Thời gian để vòi thứ nhất chảy một
mình đầy bể ít hơn thời gian để vòi thứ hai chảy một mình đầy bể là 2 giờ. Gọi x (giờ) là thời gian vòi thứ
nhất chảy một mình để đầy bể. Viết phân thức biểu thị theo x:
a) Thời gian vòi thứ hai chảy một mình đầy bể;
b) Phần bể mà mỗi vòi chảy được trong 1 giờ;
c) Phần bể mà cả hai vòi chảy được trong 1 giờ.
Lời giải.
a) Theo đề bài, thời gian để vòi thứ nhất chảy một mình đầy bể ít hơn thời gian để vòi thứ hai chảy một mình
đầy bể là 2 giờ.
Hay thời gian để vòi thứ hai chảy một mình đầy bể nhiều hơn thời gian để vòi thứ nhất chảy một mình đầy
bể là 2 giờ.
Do đó, thời gian vòi thứ hai chảy một mình đầy bể là x + 2 (giờ).
b) Số phần bể mà vòi thứ nhất chảy được trong 1 giờ là
1
x
(bể).
Số phần bể mà vòi thứ hai chảy được trong 1 giờ là
1
x + 2
(bể).
48/101 48/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
49
c) Số phần bể mà cả hai vòi chảy được trong 1 giờ là
1
x
+
1
x + 2
=
x + 2
x(x + 2)
+
x
x(x + 2)
=
x + 2 + x
x(x + 2)
=
2x + 2
x(x + 2)
(bể).
□
c Bài 26. Để hưởng ứng phong trào Tết trồng cây, chi đoàn thanh niên dự định trồng 120 cây xanh. Khi
bắt đầu thực hiện, chi đoàn được tăng cường thêm 3 đoàn viên. Gọi x là số đoàn viên ban đầu của chi đoàn
và giả sử số cây mỗi đoàn viên trồng là như nhau. Viết phân thức biểu thị theo x:
a) Số cây mỗi đoàn viên trồng theo dự định;
b) Số cây mỗi đoàn viên trồng theo thực tế;
c) Số cây mỗi đoàn viên trồng theo dự định nhiều hơn số cây mỗi đoàn viên trồng theo thực tế.
Lời giải.
a) Theo dự định, chi đoàn thanh niên trồng 120 cây xanh, ban đầu chi đoàn có x đoàn viên.
Do đó, phân thức biểu thị số cây mỗi đoàn viên trồng theo dự định là
120
x
(cây).
b) Theo thực tế, chi đoàn được tăng cường thêm 3 đoàn viên.
Khi đó, số đoàn viên của chi đoàn theo thực tế là x + 3 (đoàn viên).
Do đó, phân thức biểu thị số cây mỗi đoàn viên trồng theo thực tế là
120
x + 3
(cây).
c) Số cây mỗi đoàn viên trồng theo dự định nhiều hơn số cây mỗi đoàn viên trồng theo thực tế là
120
x
−
120
x + 3
=
120(x + 3) − 120x
x(x + 3)
=
120x + 360 − 120x
x(x + 3)
=
360
x(x + 3)
(cây).
Vậy phân thức biểu thị số cây mỗi đoàn viên trồng theo dự định nhiều hơn số cây mỗi đoàn viên trồng theo
thực tế là
360
x(x + 3)
(cây).
□
c Bài 27. Gia đình cô Lương nuôi ba con lợn. Cả ba con lợn đều ăn cùng một loại thức ăn gia súc. Biểu đồ
cột ở hình dưới biểu diễn số ngày mà mỗi con lợn ăn hết một bao thức ăn. Hỏi cả ba con lợn ăn trong x ngày
(x ∈ N
∗
) thì cần bao nhiêu thức ăn?
O
1
2
3
4
5
6
7
số ngày
Con
thứ nhất
Con
thứ hai
Con
thứ ba
Con
lợn
49/101 49/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
50
Lời giải.
Dựa vào biểu đồ cột, ta có
○ Con lợn thứ nhất ăn 3 ngày hết 1 bao thức ăn.
Khi đó, mỗi ngày con lợn thứ nhất ăn hết
1
3
bao thức ăn.
Do đó, con lợn thứ nhất ăn trong x ngày hết
x
3
bao thức ăn.
○ Con lợn thứ hai ăn 6 ngày hết 1 bao thức ăn.
Khi đó, mỗi ngày con lợn thứ hai ăn hết
1
6
bao thức ăn.
Do đó, con lợn thứ hai ăn trong x ngày hết
x
6
bao thức ăn.
○ Con lợn thứ ba ăn 4 ngày hết 1 bao thức ăn.
Khi đó, mỗi ngày con lợn thứ hai ăn hết
1
4
bao thức ăn.
Do đó, con lợn thứ hai ăn trong x ngày hết
x
4
bao thức ăn.
Cả ba con lợn ăn trong x ngày (x ∈ N
∗
) thì cần
x
3
+
x
6
+
x
4
=
4x
12
+
2x
12
+
3x
12
=
9x
12
=
3x
4
(bao thức ăn).
Vậy cả ba con lợn ăn trong x ngày (x ∈ N
∗
) thì cần
3x
4
bao thức ăn. □
50/101 50/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
51
PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
24
Baâi
A
AA TRỌNG TÂM KIẾN THỨC
1 Phép nhân các phân thức đại số
○ Quy tắc: Muốn nhân hai phân thức, ta nhân các tử thức với nhau, các mẫu thức với nhau
A
B
·
C
D
=
A · C
B · D
.
○ Phép nhân các phân thức có các tính chất:
— Giao hoán:
A
B
·
C
D
=
C
D
·
A
B
.
— Kết hợp:
Å
A
B
·
C
D
ã
·
E
F
=
A
B
·
Å
C
D
·
E
F
ã
;
— Phân phối đối với phép cộng:
A
B
Å
C
D
+
E
F
ã
=
A
B
·
C
D
+
A
B
·
E
F
2 Phân thức nghịch đảo
○ Hai phân thức được gọi là nghịch đảo của nhau nếu tích của chúng bằng 1.
○ Tổng quát, nếu
A
B
là phân thức khác 0 thì
A
B
·
B
A
= 1, do đó
A
B
là phân thức nghịch đảo của phân thức
B
A
.
3 Phép chia
Muốn chia phân thức
A
B
cho phân thức
C
D
khác 0, ta nhân
A
B
với phân thức nghịch đảo của
C
D
.
A
B
:
C
D
=
A
B
·
D
C
với
C
D
= 0.
A
BB CÁC DẠNG BÀI TẬP
Dạng 1. Thực hiện phép nhân, phép chia các phân thức
c Ví dụ 1. Thực hiện các phép tính sau:
18x
2
y
2
15z
·
5z
3
9x
3
y
2
;a)
5x + 5y
4x − 4y
·
6x − 6y
25x + 25y
;b) 3x
3
y
4
·
Å
−
7z
9xy
5
ã
.c)
Lời giải.
a)
18x
2
y
2
15z
·
5z
3
9x
3
y
2
=
18x
2
y
2
· 5z
3
15z · 9x
3
y
2
=
2z
2
3x
.
51/101 51/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
52
b)
5x + 5y
4x − 4y
·
6x − 6y
25x + 25y
=
5 · (x + y) · 6 · (x − y)
4 · (x − y) · 25 · (x + y)
=
3
10
.
c) 3x
3
y
4
·
Å
−
7z
9xy
5
ã
=
3x
3
y
4
· (−7z)
9xy
5
= −
7x
2
z
3y
.
□
c Ví dụ 2. Thực hiện phép tính sau
x
2
− 25
x
2
− 3x
:
x
2
+ 5x
x
2
− 9
;a) −
25x
2
y
5
3x
: 15xy
2
;b) (x
2
+ y
2
) :
x
3
y + xy
3
x
4
y
.c)
Lời giải.
a)
x
2
− 25
x
2
− 3x
:
x
2
+ 5x
x
2
− 9
=
x
2
− 25
x
2
− 3x
·
x
2
− 9
x
2
+ 5x
=
(x + 5)(x − 5)(x + 3)(x − 3)
x(x − 3)x(x + 5)
=
(x − 5)(x + 3)
x
2
.
b) −
25x
2
y
5
3x
: 15xy
2
=
−25x
2
y
5
3x
·
1
15xy
2
=
−5y
3
9
.
c) (x
2
+ y
2
) :
x
3
y + xy
3
x
4
y
= (x
2
+ y
2
) ·
x
4
y
xy(x
2
+ y
2
)
= x
3
.
□
c Ví dụ 3. Thực hiện phép tính
x + 1
x + 2
:
x + 2
x + 3
:
x + 3
x + 1
.
Lời giải.
x + 1
x + 2
:
x + 2
x + 3
:
x + 3
x + 1
=
x + 1
x + 2
·
x + 3
x + 2
·
x + 1
x + 3
=
(x + 1)
2
(x + 2)
2
.
□
Dạng 2. Rút gọn biểu thức
Thực hiện phép nhân, phép chia các phân thức đại số để rút gọn biểu thức.
c Ví dụ 4. Cho K =
Å
x + 1
x − 1
−
x − 1
x + 1
+
x
2
− 4x − 1
x
2
− 1
ã
·
x + 2003
x
a) Rút gọn K.
b) Tìm số nguyên x để K nhận giá trị nguyên.
Lời giải.
a) Ta có
K =
(x + 1)
2
− (x − 1)
2
+ x
2
− 4x − 1
(x − 1)(x + 1)
·
x + 2003
x
K =
x
2
+ 2x + 1 − x
2
+ 2x − 1 + x
2
− 4x − 1
(x − 1)(x + 1)
·
x + 2003
x
K =
x
2
− 1
x
2
− 1
·
x + 2003
x
.
Vậy K =
x + 2003
x
.
52/101 52/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
53
b) Điều kiện xác định: x = 0; x = 1; x = −1. Ta có K = 1 +
2003
x
.
Để K ∈ Z thì
2003
x
∈ Z ⇒ x ∈ Ư(2003) và x = 1; x = −1.
Vậy x ∈ {−2003; 2003} thì K nhận giá trị nguyên.
□
c Ví dụ 5. Thực hiện phép tính sau
a) P =
12x + 5
x + 9
·
4x + 3
360x + 150
+
12x + 5
x + 9
·
6 − 3x
360x + 150
.
b) P =
x + 3y
3x + y
·
4x − 2y
x − y
−
x + 3y
3x + y
·
x − 3y
x − y
.
Lời giải.
a) Dùng tính chất phân phối, ta có
P =
12x + 5
x + 9
·
Å
4x + 3
360x + 150
+
6 − 3x
360x + 150
ã
=
12x + 5
x + 9
·
x + 9
30(12x + 5)
=
1
30
.
b) Dùng tính chất phân phối, ta có
P =
x + 3y
3x + y
·
Å
4x − 2y
x − y
−
x − 3y
x − y
ã
=
x + 3y
3x + y
·
3x + y
x − y
=
x + 3y
x − y
.
□
c Ví dụ 6. Rút gọn biểu thức
R =
3a
2
− 2ab − b
2
2a
2
+ ab − b
2
:
3a
2
− 4ab + b
2
3a
2
+ 2ab − b
2
.
Lời giải.
R =
(a − b)(3a + b)
(2a − b)(a + b)
:
(a − b)(3a − b)
(3a − b)(a + b)
R =
3a + b
2a − b
.
□
c Ví dụ 7. Cho x = 0, x = ±2. Rút gọn rồi tính giá trị biểu thức
A =
Å
4
x − 2
−
3
x + 2
ã
:
x + 14
x
2
với x = −3.
Lời giải.
Rút gọn biểu thức ta có
A =
Å
4(x + 2)
(x − 2)(x + 2)
−
3(x − 2)
(x − 2)(x + 2)
ã
·
x
2
x + 14
=
4x + 8 − 3x + 6
x
2
− 4
·
x
2
x + 14
=
x + 14
x
2
− 4
·
x
2
x + 14
=
x
2
x
2
− 4
.
Thay x = −3 vào biểu thức rút gọn ta được
A =
(−3)
2
(−3)
2
− 4
=
9
5
.
□
53/101 53/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
54
Dạng 3. Tìm x thỏa mãn đẳng thức cho trước
○ Tìm x từ đẳng thức x : A = B, ta có x = A · B.
○ Tìm x từ đẳng thức A · x = B, ta có x = B : A.
○ Rút gọn biểu thức B : A dựa vào phép chia phân thức.
c Ví dụ 8. Tìm biểu thức x, biết
x :
a
2
+ a + 1
2a + 2
=
a + 1
a
3
− 1
.
Lời giải.
x :
a
2
+ a + 1
2a + 2
=
a + 1
a
3
− 1
⇒ x =
a + 1
a
3
− 1
·
a
2
+ a + 1
2a + 2
x =
a + 1
(a − 1)(a
2
+ a + 1)
·
a
2
+ a + 1
2(a + 1)
x =
1
2(a − 1)
.
□
c Ví dụ 9. Tìm x, biết
a + 1
a + 2
· x =
a
2
− 1
a
2
+ 2a
, với a là hằng số; a = 1; a = −1; a = 0; a = −2.
Lời giải.
a =
a
2
− 1
a
2
+ 2a
:
a + 1
a + 2
=
(a − 1)(a + 1)
a(a + 2)
·
a + 2
a + 1
=
a − 1
a
.
□
Dạng 4. Chứng minh giá trị biểu thức không phụ thuộc vào giá trị của biến
Thực hiện phép tính các phân thức để rút gọn biểu thức không còn chứa biến.
c Ví dụ 10. Cho ab + bc + ca = 1. Chứng minh rằng tích sau không phụ thuộc vào biến số
A =
(a + b)
2
1 + a
2
·
(b + c)
2
1 + b
2
·
(c + a)
2
1 + c
2
.
Lời giải.
Ta có
1 + a
2
= ab + bc + ca + a
2
= (a + b)(a + c).
Tương tự ta có
1 + b
2
= (b + a)(b + c)
1 + c
2
= (c + a)(c + b).
Thế vào A, ta được
A =
(a + b)
2
(a + b)(a + c)
·
(b + c)
2
(b + c)(b + a)
·
(c + a)
2
(c + a)(c + b)
= 1.
Vậy giá trị biểu thức A không phụ thuộc vào giá trị của biến. □
54/101 54/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
55
c Ví dụ 11. Cho a + b + c = 0. Chứng minh rằng tích sau không phụ thuộc vào biến số
M =
4bc − a
2
bc + 2a
2
·
4ca − b
2
ca + 2b
2
·
4ab − c
2
ab + 2c
2
;a) N =
1 +
a
b
·
Å
1 +
b
c
ã
·
1 +
c
a
.b)
Lời giải.
a) Ta có
4bc − a
2
bc + 2a
2
=
4bc − (b + c)
2
bc + 2a(b + c)
=
−(b
2
− 2bc + c
2
)
bc + a
2
− ab − ac
=
−(b − c)
2
(a − b)(a − c)
.
Tương tự ta có
4ca − b
2
ca + 2b
2
=
−(c − a)
2
(b − a)(b − c)
4ab − c
2
ab + 2c
2
=
−(a − b)
2
(c − a)(c − b)
.
Thế vào M, ta được
M =
4bc − a
2
bc + 2a
2
·
4ca − b
2
ca + 2b
2
·
4ab − c
2
ab + 2c
2
=
−(a − b)
2
(b − c)
2
(c − a)
2
−(a − b)
2
(b − c)
2
(c − a)
2
= 1.
Vậy giá trị biểu thức M không phụ thuộc vào giá trị của biến.
b) Ta có
N =
1 +
a
b
·
Å
1 +
b
c
ã
·
1 +
c
a
=
a + b
b
·
b + c
c
·
a + c
a
=
(−c) · (−a) · (−b)
abc
= −1.
Vậy giá trị biểu thức N không phụ thuộc vào giá trị của biến.
□
Dạng 5. Vận dụng
c Ví dụ 12. Đường sắt và đường bộ đi từ thành phố A đến thành phố B có độ dài bằng nhau và bằng s
(km). Thời gian để đi từ A đến B của tàu hỏa là a (giờ), của ô tô khách là b (giờ) (a < b). Tốc độ của tàu hỏa
gấp bao nhiêu lần tốc độ của ô tô? Tính giá trị này khi s = 350, a = 5, b = 7.
Lời giải.
Vận tốc tàu hỏa:
s
a
(km/h).
Vận tốc ô tô:
s
b
(km/h).
Vận tốc tàu hỏa gấp vận tốc ô tô:
s
a
:
s
b
=
s
a
·
b
s
=
b
a
(lần).
Giá trị cần tính là
b
a
=
7
5
. □
55/101 55/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
56
c Ví dụ 13. Máy A xát được x tấn gạo trong a giờ, máy B xát được y tấn gạo trong b giờ.
a) Viết các biểu thức biểu thị số tấn gạo mỗi máy xát được trong 1 giờ (gọi là công suất của máy).
b) Công suất của máy A gấp bao nhiêu lần máy B? Viết biểu thức biểu thị số lần này.
c) Tính giá trị biểu thức ở câu b khi x = 3, a = 5, y = 2, b = 4.
Lời giải.
a) Công suất máy A là
x
a
, Công suất máy B là
y
b
.
b) Công suất của máy A gấp máy B:
x
a
:
y
b
=
x
a
·
b
y
=
xb
ay
(lần).
c) Tính giá trị biểu thức ở câu b khi x = 3, a = 5, y = 2, b = 4.
xb
ay
=
3 · 4
5 · 2
=
6
5
.
□
c Ví dụ 14. Một ca nô đi xuôi dòng trên một khúc sông từ A đến B dài 20 km rồi lại đi ngược dòng từ B
về A. Biết tốc độ dòng nước là 3 km/h. Gọi x( km/h) là tốc độ của ca nô. Viết phân thức biểu thị theo x:
a) Thời gian ca nô đi xuôi dòng từ A đến B;
b) Thời gian ca nô đi ngược dòng từ B về A;
c) Tỉ số của thời gian ca nô đi xuôi dòng từ A đến B và thời gian ca nô đi ngược dòng từ B về A.
Lời giải.
a) Do tốc độ ca nô đi xuôi dòng là x + 3( km/h) nên phân thức biểu thị thời gian ca nô đi xuôi dòng từ A đến
B là
20
x + 3
(giờ).
b) Do tốc độ ca nô đi ngược dòng là x − 3( km/h) nên phân thức biểu thị thời gian ca nô đi ngược dòng từ B
về A là
20
x − 3
(giờ).
c) Tỉ số của thời gian ca nô đi xuôi dòng từ A đến B và thời gian ca nô đi ngược dòng từ B về A là
20
x + 3
:
20
x − 3
=
20
x + 3
·
x − 3
20
=
x − 3
x + 3
·
Vậy phân thức biểu thị tỉ số thời gian ca nô đi xuôi dòng từ A đến B và thời gian ca nô đi ngược dòng từ
B về A là
x − 3
x + 3
·
□
c Ví dụ 15. Bác Châu vay ngân hàng 1,2 tỉ đồng để mua nhà theo hình thức trả góp. Số tiền bác Châu phải
trả mỗi tháng bao gồm số tiền gốc phải trả hằng tháng (bằng số tiền gốc chia đều cho số tháng vay) và số
tiền lãi phải trả hằng tháng (bằng số tiền gốc nhân với lãi suất tháng).
a) Gọi r là l¯ai suất năm của khoản vay trả góp này. Tính số tiền x (triệu đồng) mà bác Châu phải trả mỗi
tháng theo số tháng vay y (tháng) và lãi suất năm r. Từ đó suy ra công thức tính lãi suất năm r theo
x và y.
b) Tính giá trị của r tại x = 30, y = 48 rồi cho biết, nếu trả góp mỗi tháng 30 triệu đồng trong vòng 4 năm
thì lãi suất năm (tính theo %) của khoản vay này là bao nhiêu?
Lời giải.
56/101 56/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
57
a) x =
1, 2 · 10
3
y
+ 1, 2 · 10
3
·
r
12
⇒ r =
Å
x −
1, 2 · 10
3
y
ã
: 10
2
.
b) r =
Å
30 −
1, 2 · 10
3
48
ã
: 10
2
= 0, 05 = 5%.
□
A
CC BÀI TẬP TỰ LUYỆN
c Bài 1. Tính
3x + 6
4x − 16
·
8 − 2x
x + 2
;a)
3x
2
5y
3
·
Å
−10y
3
9x
3
ã
.b)
Lời giải.
a)
3x + 6
4x − 16
·
8 − 2x
x + 2
=
3(x + 2)
4(x − 4)
·
2(4 − x)
x + 2
= −
3
2
.
b)
3x
2
5y
3
·
Å
−10y
3
9x
3
ã
=
3x
2
· (−10y
3
)
5y
3
· 9x
3
= −
2
3x
.
□
c Bài 2. Thực hiện các phép tính sau
M =
x
5
+ 2x
2
+ 3
3x
3
+ 3
·
4x
x
2
− 4
·
5x
3
+ 5
x
5
+ 2x
2
+ 3
;a) A =
x
2
+ 2x
3x − 6
·
2x − 4
x
2
+ 4x + 4
.b)
Lời giải.
a) M =
x
5
+ 2x
2
+ 3
3x
3
+ 3
·
4x
x
2
− 4
·
5x
3
+ 5
x
5
+ 2x
2
+ 3
=
x
5
+ 2x
2
+ 3
3(x
3
+ 1)
·
4x
x
2
− 4
·
5(x
3
+ 1)
x
5
+ 2x
2
+ 3
=
20x
3(x
2
− 4)
.
b) A =
x
2
+ 2x
3x − 6
·
2x − 4
x
2
+ 4x + 4
=
x(x + 2)
3(x − 2)
·
2(x − 2)
(x + 2)
2
=
2x
3(x + 2)
.
□
c Bài 3. Rút gọn rồi tính giá trị của biểu thức
P =
x
2
− 1
x + 5
·
2x + 10
x
2
− x
với x = 99.
Lời giải.
Ta có
P =
x
2
− 1
x + 5
·
2x + 10
x
2
− x
=
(x + 1)(x − 1)
x + 5
·
2(x + 5)
x(x − 1)
=
2(x + 1)
x
.
Thế x = 99, ta được P =
200
99
. □
c Bài 4. Hãy điền phân thức thích hợp vào dấu . . . trong đẳng thức sau
1
x
·
x
x + 1
·
x + 1
x + 2
·
x + 2
x + 3
·
x + 3
x + 4
·
x + 4
x + 5
· . . . = 1.
Lời giải.
57/101 57/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
58
Ta có
1
x
·
x
x + 1
·
x + 1
x + 2
·
x + 2
x + 3
·
x + 3
x + 4
·
x + 4
x + 5
=
1
x + 5
.
Vậy phân thức cần điền là x + 5. □
c Bài 5. Cho x + y + z = 1. Chứng minh rằng giá trị biểu thức sau không phụ thuộc vào giá trị của biến số
P =
(x + y)
2
xy + z
·
(y + z)
2
yz + x
·
(z + x)
2
zx + y
.
Lời giải.
Ta có
xy + z = xy + z(x + y + z) = xy + xz + yz + z
2
= (z + x)(z + y).
Tương tự ta có
yz + x = (x + y)(x + z)
zx + y = (y + x)(y + z).
Thế vào P , ta được
P =
(x + y)
2
(z + x)(z + y)
·
(y + z)
2
(x + y)(x + z)
·
(z + x)
2
(y + x)(y + z)
= 1.
Vậy giá trị biểu thức P không phụ thuộc vào giá trị của biến. □
c Bài 6. Thực hiện các phép tính
a) A =
1
4
+ 4
3
4
+ 4
·
5
4
+ 4
7
4
+ 4
·
9
4
+ 4
11
4
+ 4
· . . . ·
17
4
+ 4
19
4
+ 4
;
b) B =
1
4
+
1
4
2
4
+
1
4
·
3
4
+
1
4
4
4
+
1
4
·
5
4
+
1
4
6
4
+
1
4
· . . . ·
29
4
+
1
4
30
4
+
1
4
.
Lời giải.
a) Ta có
k
4
+ 4 = (k
2
+ 2)
2
− 4k
2
= (k
2
+ 2 + 2k)(k
2
+ 2 − 2k) =
(k + 1)
2
+ 1
(k − 1)
2
+ 1
.
Áp dụng kết quả, ta được
A =
1
4
+ 4
3
4
+ 4
·
5
4
+ 4
7
4
+ 4
·
9
4
+ 4
11
4
+ 4
· . . . ·
17
4
+ 4
19
4
+ 4
=
(2
2
+ 1)(0
2
+ 1)
(4
2
+ 1)(2
2
+ 1)
·
(6
2
+ 1)(4
2
+ 1)
(8
2
+ 1)(6
2
+ 1)
·
(10
2
+ 1)(8
2
+ 1)
(12
2
+ 1)(10
2
+ 1)
· . . . ·
(18
2
+ 1)(16
2
+ 1)
(20
2
+ 1)(18
2
+ 1)
=
1
20
2
+ 1
=
1
401
.
b) Ta có
k
4
+
1
4
=
Å
k
4
+ k
2
+
1
4
ã
− k
2
=
Å
k
2
+
1
2
ã
2
− k
2
=
Å
k
2
+ k +
1
2
ãÅ
k
2
− k +
1
2
ã
=
ñ
Å
k +
1
2
ã
2
+
1
4
ôñ
Å
k −
1
2
ã
2
+
1
4
ô
.
Áp dụng kết quả vào B, ta tính được B =
1
1861
.
58/101 58/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
59
□
c Bài 7. Thực hiện phép tính
3x + 9
x
2
− 4
:
x + 3
x − 2
;a)
5x
2
+ 10xy
x
2
+ 2xy + 4y
2
:
x + 2y
x
3
− 8y
3
.b)
Lời giải.
a)
3x + 9
x
2
− 4
:
x + 3
x − 2
=
3(x + 3)
(x + 2)(x − 2)
·
x − 2
x + 3
=
3
x + 2
.
b)
5x
2
+ 10xy
x
2
+ 2xy + 4y
2
:
x + 2y
x
3
− 8y
3
=
5x(x + 2y)
x
2
+ 2xy + 4y
2
·
(x − 2y)(x
2
+ 2xy + 4y
2
)
x + 2y
= 5x(x − 2y).
□
c Bài 8. Tính
4x
2
− 1
x
: (1 − 2x);a) (x + y) :
y
2
+ xy
x − y
.b)
Lời giải.
a)
4x
2
− 1
x
: (1 − 2x) =
(2x + 1)(2x − 1)
x(1 − 2x)
=
−2x − 1
x
.
b) (x + y) :
y
2
+ xy
x − y
=
(x + y)(x − y)
y(x + y)
=
x − y
y
.
□
c Bài 9. Thực hiện phép chia
a) A =
x + y + z
(x + y)
2
− (x + y)z
:
x
2
+ y
2
− z
2
+ 2xy
2x + 2y
;
b) B =
6x − 3
x
:
4x
2
− 1
3x
2
;
c) C =
x
2
− 12xy + 36y
2
x
2
+ 12xy + 36y
2
:
3x − 18y
3x + 18y
.
Lời giải.
a) A =
x + y + z
(x + y)
2
− (x + y)z
·
2(x + y)
(x + y)
2
− z
2
=
x + y + z
(x + y)(x + y − z)
·
2(x + y)
(x + y + z)(x + y − z)
=
2
(x + y − z)
2
.
b) B =
6x − 3
x
·
3x
2
4x
2
− 1
=
3(2x − 1)
x
·
3x
2
(2x − 1)(2x + 1)
=
9x
2x + 1
.
c) C =
x
2
− 12xy + 36y
2
x
2
+ 12xy + 36y
2
·
3x + 18y
3x − 18y
=
(x − 6y)
2
(x + 6y)
2
·
3(x + 6y)
3(x − 6y)
=
x − 6y
x + 6y
.
□
c Bài 10. Hãy điền phân thức thích hợp vào dấu . . . trong đẳng thức sau
x
x + 1
:
x + 1
x + 2
:
x + 2
x + 3
:
x + 3
x + 4
:
x + 4
x + 5
: . . . = 1.
59/101 59/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
60
Lời giải.
Kết quả của 4 phép chia đầu là
x
x + 1
:
x + 1
x + 2
:
x + 2
x + 3
:
x + 3
x + 4
:
x + 4
x + 5
=
x
x + 1
·
x + 2
x + 1
·
x + 3
x + 2
·
x + 4
x + 3
·
x + 5
x + 4
=
x(x + 5)
(x + 1)
2
.
Vậy phân thức cần điền vào chỗ trống là
x(x + 5)
(x + 1)
2
. □
c Bài 11. Tìm x, biết
3a
4
· x =
4a
5
với a = 0.a)
a + 2
a + 1
· x =
a
2
− 4
a
2
+ a
với a /∈ {−1; 0; −2}.b)
Lời giải.
a) x =
4a
5
:
3a
4
=
4a
5
·
4
3a
=
16
15
.
b) x =
a
2
− 4
a
2
+ a
:
a + 2
a + 1
=
a
2
− 4
a
2
+ a
·
a + 1
a + 2
=
(a + 2)(a − 2)(a + 1)
a(a + 1)(a + 2)
=
a − 2
a
.
□
c Bài 12. Tính A =
5
2
− 1
3
2
− 1
:
9
2
− 1
7
2
− 1
:
13
2
− 1
11
2
− 1
: . . . :
57
2
− 1
55
2
− 1
.
Lời giải.
Ta có
A =
5
2
− 1
3
2
− 1
·
7
2
− 1
9
2
− 1
·
11
2
− 1
13
2
− 1
· . . . ·
55
2
− 1
57
2
− 1
=
4 · 6
2 · 4
·
6 · 8
8 · 10
·
10 · 12
12 · 14
· . . . ·
54 · 56
56 · 58
=
6 · 6
2 · 58
=
9
29
.
□
c Bài 13. Tâm đạp xe từ nhà đến câu lạc bộ câu cá có quãng đường dài 15 km với tốc độ x (km/h). Lượt
về thuận chiều gió nên tốc độ nhanh hơn lượt đi 4 (km/h).
a) Viết biểu thức biểu thị tổng thời gian T hai lượt đi và về.
b) Viết biểu thức biểu thị hiệu thời gian t lượt đi đối với lượt về.
c) Tính T và t với x = 10.
Lời giải.
a) Viết biểu thức biểu thị tổng thời gian T hai lượt đi và về.
Thời gian đi
15
x
(h).
Thời gian về
15
x + 4
(h).
Vậy T =
15
x
+
15
x + 4
.
b) Viết biểu thức biểu thị hiệu thời gian t lượt đi đối với lượt về:
t =
15
x
−
15
x + 4
.
60/101 60/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
61
c) Tính T và t với x = 10.
T =
15
x
+
15
x + 4
=
15
10
+
15
14
=
18
7
.
t =
15
x
−
15
x + 4
=
15
10
−
15
14
=
3
7
.
□
c Bài 14. Một xí nghiệp theo kế hoạch cần phải sản xuất 120 tấn hàng trong một số ngày quy định. Do cải
tiến kĩ thuật nên xí nghiệp đã hoàn thành kế hoạch sớm hơn thời gian quy định 1 ngày và làm thêm được 5
tấn hàng. Gọi x là số ngày xí nghiệp cần làm theo dự định. Viết phân thức biểu thị theo x:
a) Số tấn hàng xí nghiệp làm trong 1 ngày theo dự định;
b) Số tấn hàng xí nghiệp làm trong 1 ngày trên thực tế;
c) Tỉ số của số tấn hàng xí nghiệp làm trong 1 ngày trên thực tế và số tấn hàng xí nghiệp làm trong 1 ngày
theo dự định.
Lời giải.
a) Số tấn hàng xí nghiệp làm trong 1 ngày theo dự định là
120
x
tấn hàng.
b) Số tấn hàng xí nghiệp làm trong 1 ngày trên thực tế là
120
x − 1
+ 5 tấn hàng.
c) Tỉ số của số tấn hàng xí nghiệp làm trong 1 ngày trên thực tế và số tấn hàng xí nghiệp làm trong 1 ngày
theo dự định là
Å
120
x − 1
+ 5
ã
:
120
x
=
5x + 115
x − 1
·
x
120
=
x(x + 23)
24(x − 1)
·
□
c Bài 15. Một xe ô tô chở hàng đi từ địa điểm A đến địa điểm B hết x giờ. Sau khi trả hàng tại địa điểm
B, xe quay ngược trở lại địa điểm A nhưng thời gian xe chạy về đến A chỉ là x −1 giờ. Biết quãng đường AB
dài 160 km, viết phân thức biểu thị theo x:
a) Tốc độ xe ô tô khi chạy từ A đến B;
b) Tốc độ xe ô tô khi chạy từ B về A;
c) Tỉ số của tốc độ xe ô tô khi chạy từ A đến B và tốc độ xe ô tô khi chạy từ B về A.
Lời giải.
a) Tốc độ xe ô tô khi chạy từ A đến B là
160
x
km/h.
b) Tốc độ xe ô tô khi chạy từ B về A là
160
x − 1
km/h.
c) Tỉ số của tốc độ xe ô tô khi chạy từ A đến B và tốc độ xe ô tô khi chạy từ B về A là
160
x
:
160
x − 1
=
x − 1
x
·
□
c Bài 16. Bác Châu vay ngân hàng 1,2 tỉ đồng để mua nhà theo hình thức trả góp. Số tiền bác Châu phải
trả mỗi tháng bao gồm số tiền gốc phải trả hằng tháng (bằng số tiền gốc chia đều cho số tháng vay) và số
tiền lãi phải trả hằng tháng (bằng số tiền gốc nhân với lãi suất tháng).
a) Nếu mỗi tháng bác Châu trả 15 triệu đồng trong 10 năm thì lãi suất năm (tính theo %) là bao nhiêu?
61/101 61/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
62
Hãy cho biết tổng số tiền thực tế bác Châu phải trả chênh lệch bao nhiêu so với khoản vay 1,2 tỉ đồng.
b) Trong công thức tính lãi suất năm nói trên, hai biến x, y phải thoả mãn các điểu kiện x > 0, y > 0,
xy > 1200. Em hãy giải thích ý nghĩa thực tiễn của các điều kiện này.
Lời giải.
a) r =
Å
15 −
1, 2 · 10
3
120
ã
: 10
2
= 0, 05 = 5%.
10 năm tương đương 120 tháng.
Số tiền bác Châu phải trả hàng tháng là 15.120 = 1 800 ( triệu đồng)=1,8 (tỉ đồng).
Số tiền chêch lệch so với số tiền thực tế là 600 triệu đồng.
b) x là số tiền trả hàng tháng nên x > 0.
y là số tháng trả hết tiền nên y > 0.
1200 ở đây được hiểu hiểu là 1200 triệu hay 1,2 tỉ đồng khi trả cho ngân hàng thì ngân hàng phải có lời để
duy trì hoạt động do đó xy > 1200.
□
62/101 62/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
63
LUYỆN TẬP CHUNG
A
AA TRỌNG TÂM KIẾN THỨC
○ Mỗi biểu thức là một phân thức hoặc biểu thị một dãy phép toán cộng, trừ, nhân, chia trên những phân
thức gọi là biểu thức hữu tỉ.
○ Nhờ các quy tắc của các phép toán cộng, trừ, nhân, chia các phân thức, ta có thể biến đổi biểu thức hữu
tỉ thành một phân thức.
○ Điều kiện của biến để giá trị tương ứng của mẫu thức khác 0 là điều kiện để giá trị của phân thức được
xác định.
A
BB CÁC DẠNG BÀI TẬP
Dạng 1. Tìm điều kiện của biến để phân thức xác định
Ta tìm các giá trị của biến sao cho giá trị tương ứng của mẫu thức khác 0.
c Ví dụ 1. Với giá trị nào của x thì giá trị của phân thức được xác định?
5x
3x − 6
;a)
x − 2
x
2
+ 8x
;b)
x
2
− 1
16x
2
− 25
.c)
Lời giải.
a) Giá trị của phân thức
5x
3x − 6
được xác định khi 3x − 6 = 0 hay 3x = 6, suy ra x = 2.
b) Giá trị của phân thức
x − 2
x
2
+ 8x
được xác định khi x
2
+ 8x = 0 hay x(x + 8) = 0, suy ra x = 0 và x = −8.
c) Giá trị của phân thức
x
2
− 1
16x
2
− 25
được xác định khi 16x
2
− 25 = 0 hay x
2
=
25
16
, suy ra x =
5
4
và x = −
5
4
.
□
Dạng 2. Tìm giá trị của x để phân thức bằng 0
Giá trị của phân thức bằng 0 khi tử có giá trị bằng 0 và mẫu có giá trị khác 0.
A(x)
B(x)
= 0 khi A(x) = 0 và B(x) = 0.
c Ví dụ 2. Tìm giá trị của x để giá trị phân thức sau bằng 0.
x
2
− 1
x
2
+ 2x + 1
;a)
x
2
− 5x + 6
x
2
− 4
.b)
Lời giải.
Phân thức bằng 0 khi tử thức bằng 0, mẫu thức khác 0.
a)
x
2
− 1
x
2
+ 2x + 1
= 0 khi
®
x
2
− 1 = 0
(x + 1)
2
= 0
suy ra x = 1.
63/101 63/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
64
b)
x
2
− 5x + 6
x
2
− 4
=
(x − 2)(x − 3)
(x + 2)(x − 2)
= 0 khi
®
(x − 2)(x − 3) = 0
(x + 2)(x − 2) = 0
suy ra x = 3.
□
Dạng 3. Rút gọn biểu thức
Thực hiện phép nhân và phép chia các phân thức đại số để rút gọn biểu thức.
c Ví dụ 3. Rút gọn biểu thức
B =
Å
1
x − 1
−
1
x
ã
:
Å
x + 1
x − 2
−
x + 2
x − 1
ã
.
Lời giải.
Điều kiện x = 0; x = 1; x = 2. Ta có
B =
x − (x − 1)
x(x − 1)
:
(x − 1)(x + 1) − (x + 2)(x − 2)
(x − 1)(x − 2)
=
1
x(x − 1)
:
x
2
− 1 − x
2
+ 4
(x − 1)(x − 2)
=
1
x(x − 1)
·
(x − 1)(x − 2)
3
=
x − 2
3x
.
□
c Ví dụ 4. Cho biểu thức A =
Å
x + 2
x
2
− x
+
x − 2
x
2
+ x
ã
·
x
2
− 1
x
2
+ 2
.
Rút gọn A.a) Tính giá trị của A với x = 100.b)
Lời giải.
a) Điều kiện x = 0; x = ±1.
Ta có
A =
(x + 2)(x + 1) + (x − 2)(x − 1)
x(x + 1)(x − 1)
·
x
2
− 1
x
2
+ 2
A =
x
2
+ 2x + x + 2 + x
2
− 2x − x + 2
x(x + 1)(x − 1)
·
x
2
− 1
x
2
+ 2
A =
2x
2
+ 4
x(x
2
− 1)
·
x
2
− 1
x
2
+ 2
=
2
x
.
b) Với x = 100, ta có A =
2
100
=
1
50
.
□
c Ví dụ 5. Rút gọn biểu thức
a) A =
Å
1 +
b
2
+ c
2
− a
2
2bc
ã
·
1 +
a
b + c
1 −
a
b + c
·
b
2
+ c
2
− (b − c)
2
a + b + c
.
b) B =
Ü
y
2
− yz + z
2
x
+
x
2
y + z
−
3
1
y
+
1
z
ê
·
2
y
+
2
z
1
xy
+
1
yz
+
1
zx
+ (x + y + z)
2
.
Lời giải.
64/101 64/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
65
a) A =
Å
1 +
b
2
+ c
2
− a
2
2bc
ã
·
1 +
a
b + c
1 −
a
b + c
·
b
2
+ c
2
− (b − c)
2
a + b + c
=
(b + c)
2
− a
2
2bc
·
b + c + a
b + c − a
·
b
2
+ c
2
− b
2
+ 2bc − c
2
a + b + c
=
(a + b + c)(b + c − a)
2bc
·
b + c + a
b + c − a
·
2bc
a + b + c
= a + b + c.
b) B =
Ü
y
2
− yz + z
2
x
+
x
2
y + z
−
3
1
y
+
1
z
ê
·
2
y
+
2
z
1
xy
+
1
yz
+
1
zx
+ (x + y + z)
2
=
Å
y
2
− yz + z
2
x
+
x
2
y + z
−
3yz
y + z
ã
·
2(y + z)
yz
x + y + z
xyz
+ (x + y + z)
2
=
(y + z)(y
2
− yz + z
2
) + x
3
− 3xyz
x(y + z)
·
2x(y + z)
x + y + z
+ (x + y + z)
2
=
x
3
+ y
3
+ z
3
− 3xyz
1
·
2
x + y + z
+ (x + y + z)
2
=
2(x + y + z)(x
2
+ y
2
+ z
2
− xy − yz − xz)
x + y + z
+ (x + y + z)
2
= 2x
2
+ 2y
2
+ 2z
2
− 2xy − 2yz − 2xz + x
2
+ y
2
+ z
2
+ 2xy + 2yz + 2zx
= 3x
2
+ 3y
2
+ 3z
2
.
□
Dạng 4. Vận dụng
c Ví dụ 6. Hôm qua, thanh long được bán với giá a đồng mỗi kilôgam. Hôm nay, người ta đã giảm giá 1000
đồng cho mỗi kilôgam thanh long. Với cùng số tiền b đồng thì hôm nay mua được nhiều hơn bao nhiêu kilôgam
thanh long so với hôm qua?
Lời giải.
Gọi a − 1000 (đồng) là số tiền mỗi kilôgam thanh long ngày hôm nay.
Số kilôgam thanh long mua được với số tiền b đồng ngày hôm qua là
b
a
kilôgam.
Số kilôgam thanh long mua được với số tiền b đồng ngày hôm nay là
b
a − 1000
kilôgam.
Số kilôgam thanh long mua được nhiều hơn so với hôm qua là
b
a
−
b
a − 1000
kilôgam. □
c Ví dụ 7. Hai người thợ cùng sơn một bức tường. Nếu một mình sơn xong bức tường thì người thứ nhất
làm xong lâu hơn người thứ hai là 2 giờ. Gọi x là số giờ mà người thứ nhất một mình sơn xong bức tường.
Viết phân thức biểu thị tổng số phần của bức tường sơn được mà người thứ nhất sơn trong 3 giờ và người thứ
hai sơn trong 4 giờ theo x.
Lời giải.
Gọi x là số giờ mà người thứ nhất một mình sơn xong bức tường.
⇒ 1 giờ người thứ nhất sơn được
1
x
bức tường.
⇒ 3 giờ người thứ nhất sơn được
3
x
bức tường.
65/101 65/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
66
⇒ người thứ hai một mình sơn xong bức tường mất x − 2 giờ.
⇒ 1 giờ người thứ hai sơn được
1
x − 2
bức tường.
⇒ 4 giờ người thứ hai sơn được
4
x − 2
bức tường.
Do đó, số phần của bức tường sơn được mà người thứ nhất sơn trong 3 giờ và người thứ hai sơn trong 4 giờ là
3
x
+
4
x − 2
=
3(x − 2) + 4x
x(x − 2)
=
7x − 6
x(x − 2)
.
□
c Ví dụ 8. Số tiền hằng năm A (triệu đô la Mỹ) mà người Mỹ chi cho việc mua đồ ăn, đồ uống khi ra khỏi
nhà và dân số P (triệu người) hằng năm của Mỹ từ năm 2000 đến năm 2006 lần lượt được cho bằng công thức
sau
A =
−8 242,58t + 348 299,6
−0,06t + 1
với 0 ≤ t ≤ 6.
P = 2,71t + 282,7 với 0 ≤ t ≤ 6.
Trong đó, t là số năm tính từ năm 2000, t = 0 tương ứng với năm 2000.
(Nguồn: U.S. Bureau of Economic Analysis and U.S. Census Bureau)
Viết phân thức biểu thị (theo t) số tiền bình quân hằng năm mà mỗi người Mỹ đã chi cho việc mua đồ ăn, đồ
uống khi ra khỏi nhà.
Lời giải.
Số tiền bình quân hằng năm mà mỗi người Mỹ đã chi cho việc mua đồ ăn, đồ uống khi ra khỏi nhà là
A
P
=
−8 242,58t + 348 299,6
(−0,06t + 1) (2,71t + 282,7)
với 0 ≤ t ≤ 6.
□
A
CC BÀI TẬP VẬN DỤNG
c Bài 1. Giá trị của phân thức
2x − 1
x
2
− 4
được xác định khi nào?
Lời giải.
Giá trị của phân thức
2x − 1
x
2
− 4
được xác định khi x
2
− 4 = 0 hay (x + 2)(x − 2) = 0, suy ra x = ±2. □
c Bài 2. Tìm giá trị của x để giá trị của phân thức
2x
2
+ 10x + 12
x
3
− 4x
bằng 0.a)
x
3
+ x
2
− x − 1
x
3
− 2x
2
+ x
bằng 0.b)
Lời giải.
a)
2x
2
+ 10x + 12
x
3
− 4x
=
2(x + 2)(x + 3)
x(x + 2)(x − 2)
= 0 khi
®
2(x + 2)(x + 3) = 0
x(x + 2)(x − 2) = 0
suy ra x = −3.
b)
x
3
+ x
2
− x − 1
x
3
− 2x
2
+ x
=
(x + 1)
2
(x − 1)
x(x − 1)
2
= 0 khi
®
(x + 1)
2
(x − 1) = 0
x(x − 1)
2
= 0
suy ra x = −1.
□
66/101 66/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
67
c Bài 3. Thực hiện các phép tính sau.
a)
1
xy
+
1
yz
+
1
zx
;
b)
x
2x − y
+
y
2x + y
+
3xy
y
2
− 4x
2
.
Lời giải.
a)
1
xy
+
1
yz
+
1
zx
=
z
xyz
+
x
xyz
+
y
xyz
=
x + y + z
xyz
;
b)
x
2x − y
+
y
2x + y
+
3xy
y
2
− 4x
2
=
x (2x + y)
(2x + y) (2x − y)
+
y (2x − y)
(2x + y) (2x − y)
−
3xy
(2x + y) (2x − y)
=
2x
2
+ xy + 2xy − y
2
− 3xy
(2x + y) (2x − y)
=
2x
2
− y
2
4x
2
− y
2
.
□
c Bài 4. Thực hiện các phép tính sau.
a)
4x − 6
5x
2
− x
·
25x
2
− 10x + 1
27 − 8x
3
;
b)
2x + 10
(x − 3)
2
:
(x + 5)
3
x
2
− 9
.
Lời giải.
a)
4x − 6
5x
2
− x
·
25x
2
− 10x + 1
27 − 8x
3
=
2 (2x − 3)
x (5x − 1)
·
(5x − 1)
2
(3 − 2x) (9 + 6x + 4x
2
)
=
−2 (5x − 1)
x (9 + 6x + 4x
2
)
;
b)
2x + 10
(x − 3)
2
:
(x + 5)
3
x
2
− 9
=
2x + 10
(x − 3)
2
·
x
2
− 9
(x + 5)
3
=
2 (x + 5)
(x − 3)
2
·
(x − 3) (x + 3)
(x + 5)
3
=
2 (x + 3)
(x − 3) (x + 5)
2
.
□
c Bài 5. Thực hiện các phép tính sau.
a)
4x
2
− 1
16x
2
− 1
Å
1
2x + 1
+
1
2x − 1
+
1
1 − 4x
2
ã
;
b)
Å
x + y
xy
−
2
x
ã
x
3
y
3
x
3
− y
3
.
Lời giải.
a) Ta có
1
2x + 1
+
1
2x − 1
+
1
1 − 4x
2
=
2x − 1
(2x − 1) (2x + 1)
+
2x + 1
(2x − 1) (2x + 1)
−
1
(2x − 1) (2x + 1)
=
2x − 1 + 2x + 1 − 1
(2x − 1) (2x + 1)
=
4x − 1
(2x − 1) (2x + 1)
67/101 67/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
68
Do đó
4x
2
− 1
16x
2
− 1
Å
1
2x + 1
+
1
2x − 1
+
1
1 − 4x
2
ã
=
4x
2
− 1
(4x
2
− 1) (4x
2
+ 1)
Å
4x − 1
(2x − 1) (2x + 1)
ã
=
1
4x
2
+ 1
Å
4x − 1
(2x − 1) (2x + 1)
ã
=
1
4x
2
+ 1
Å
4x − 1
(4x
2
− 1)
ã
=
4x − 1
(16x
2
− 1)
.
b)
Å
x + y
xy
−
2
x
ã
x
3
y
3
x
3
− y
3
=
Å
1
x
+
1
y
−
2
x
ã
x
3
y
3
x
3
− y
3
=
Å
1
y
−
1
x
ã
x
3
y
3
(x − y) (x
2
+ xy + y
2
)
=
x − y
xy
x
3
y
3
(x − y) (x
2
+ xy + y
2
)
=
x
2
y
2
x
2
+ xy + y
2
.
□
c Bài 6. Cho biểu thức P =
x
2
− 6x + 9
9 − x
2
+
4x + 8
x + 3
.
a) Rút gọn P .
b) Tính giá trị của P tại x = 7.
c) Chứng tỏ P = 3 +
2
x + 3
. Từ đó tìm tất cả các giá trị nguyên của x sao cho biểu thức đã cho nhận giá
trị nguyên.
Lời giải.
a) P =
x
2
− 6x + 9
9 − x
2
+
4x + 8
x + 3
=
(x − 3)
2
(3 − x) (x + 3)
+
4x + 8
x + 3
=
3 − x + 4x + 8
x + 3
=
3x + 11
x + 3
.
b) Thay x = 7 vào biểu thức P ta được P =
3 · 7 + 11
7 + 3
=
32
10
.
c) P =
3x + 11
x + 3
=
3x + 9 + 2
x + 3
= 3 +
2
x + 3
.
Với x nguyên, P nhận giá trị nguyên khi (x + 3) ∈ Ư (2) = {±1; ±2}.
○ x + 3 = 1 ⇒ x = −2.
○ x + 3 = −1 ⇒ x = −4.
○ x + 3 = 2 ⇒ x = −1.
○ x + 3 = −2 ⇒ x = −5.
Vậy các giá trị nguyên của x để P nguyên là {−5; −4; −2; −1}.
□
c Bài 7. Cho N =
2x − 10
x
2
− 7x + 10
−
2x
x
2
− 4
+
1
2 − x
.
a) Rút gọn N.
b) Tìm giá trị nguyên của x để N nhận giá trị nguyên.
Lời giải.
68/101 68/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
69
a) Điều kiện x = ±2; x = 5.
N =
2(x − 5)
(x − 2)(x − 5)
−
2x
x
2
− 4
−
1
x − 2
=
2
x − 2
−
1
x − 2
−
2x
x
2
− 4
=
x + 2 − 2x
(x − 2)(x + 2)
=
2 − x
(x − 2)(x + 2)
=
−1
x + 2
.
b) Để N nhận giá trị nguyên thì x + 2 ∈ Ư(−1).
Suy ra x + 2 ∈ {−1; 1} hay x ∈ {−3; −1}, thỏa mãn điều kiện.
Vậy với x ∈ {−3; −1} thì N nhận giá trị nguyên.
□
c Bài 8. Rút gọn các biểu thức sau
a) A =
ï
1
a
2
+
1
b
2
+
2
a + b
·
Å
1
a
+
1
b
ãò
·
ab
(a + b)
2
.
b) B =
ï
1
(2x − y)
2
+
2
4x
2
− y
2
+
1
(2x + y)
2
ò
·
4x
2
+ 4xy + y
2
16x
.
Lời giải.
a) A =
ï
1
a
2
+
1
b
2
+
2
a + b
·
Å
1
a
+
1
b
ãò
·
ab
(a + b)
2
=
ï
1
a
2
+
1
b
2
+
2
ab
ò
·
ab
(a + b)
2
=
a
2
+ b
2
+ 2ab
a
2
b
2
·
ab
(a + b)
2
=
a + b)
2
a
2
b
2
·
ab
(a + b)
2
=
1
ab
.
b) B =
ï
1
(2x − y)
2
+
2
4x
2
− y
2
+
1
(2x + y)
2
ò
·
4x
2
+ 4xy + y
2
16x
=
ï
1
(2x − y)
2
+
2
(2x − y)(2x + y)
+
1
(2x + y)
2
ò
·
(2x + y)
2
16x
=
ï
(2x − y)
2
+ 2(2x − y)(2x + y) + (2 x + y)
2
(2x − y)
2
(2x + y)
2
ò
·
(2x + y)
2
16x
=
[(2x − y) + (2x + y)]
2
(2x − y)
2
·
1
16x
=
16x
2
(2x − y)
2
· 16x
=
x
(2x − y)
2
.
□
c Bài 9. Rút gọn biểu thức sau
x
x − y
−
y
x + y
y
x − y
+
x
x + y
.
Lời giải.
Ta có
x
x − y
−
y
x + y
=
x − y + y
x − y
−
x + y − x
x + y
= 1 +
y
x − y
− 1 +
x
x + y
=
y
x − y
+
x
x + y
.
69/101 69/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
70
Suy ra
x
x − y
−
y
x + y
y
x − y
+
x
x + y
= 1.
□
c Bài 10. Trên một dòng sông, một con thuyền đi xuôi dòng với tốc độ (x + 3) km/h và đi ngược dòng với
tốc độ (x − 3) km/h (x > 3).
a) Xuất phát từ bến A, thuyền đi xuôi dòng trong 4 giờ, rồi đi ngược dòng trong 2 giờ. Tính quãng đường
thuyền đã đi. Lúc này thuyền cách bến A bao xa?
b) Xuất phát từ bến A, thuyền đi xuôi dòng đến bến B cách bến A 15 km, nghỉ 30 phút, rồi quay về bến
A. Sau bao lâu kể từ lúc xuất phát thì thuyền quay về đến bến A?
Lời giải.
a) Quãng đường thuyền đi xuôi dòng trong 4 giờ là 4(x + 3) (km).
Quãng đường thuyền đi ngược dòng trong 2 giờ là 2(x − 3) (km).
Quãng đường thuyền đã đi là 4(x + 3) + 2(x − 3) = 4x + 12 + 2x − 6 = 6x + 6 (km).
Vì lúc đầu thuyền đi xuôi dòng và quay về đi ngược dòng nên quãng đường còn cách bến A là 4(x+3)−2(x−3) =
4x + 12 − 2x + 6 = 2x + 18 (km).
b) Đổi 30 (phút) bằng
1
2
(h).
Thời gian thuyền đi xuôi dòng từ A đến B là
15
x + 3
(h).
Thời gian thuyền đi ngược dòng từ B đến A là
15
x − 3
(h).
Thời gian thuyền đi kể từ lúc xuất phát đến khi thuyền quay về đến bến A là
15
x + 3
+
1
2
+
15
x − 3
(h).
□
c Bài 11. Một xưởng may lập kế hoạch may 80 000 bộ quần áo trong x ngày. Nhờ cải tiến kĩ thuật, xưởng
đã hoàn thành kế hoạch sớm 11 ngày và may vượt kế hoạch 100 bộ quần áo.
a) Hãy viết phân thức theo biến x biểu thị số bộ quần áo mỗi ngày xưởng may được theo kế hoạch.
b) Viết phân thức biểu thị số bộ quần áo thực tế xưởng may được mỗi ngày.
c) Viết biểu thức biểu thị số bộ quần áo mỗi ngày xưởng may được nhiều hơn so với kế hoạch.
d) Nếu theo kế hoạch, mỗi ngày xí nghiệp may 800 bộ quần áo thì nhờ cải tiến kĩ thuật, mỗi ngày xưởng
may được nhiều hơn so với kế hoạch bao nhiêu bộ quần áo.
Lời giải.
a) Theo kế hoạch xưởng may 80 000 bộ quần áo trong x ngày nên số bộ quần áo mỗi ngày xưởng may được
theo kế hoạch là
80 000
x
(bộ).
b) Thực tế, thời gian xưởng may là x − 11 (ngày) và số bộ quần áo may được là 80 000 + 100 = 80 100 (bộ).
Do đó số bộ quần áo thực tế xưởng may được mỗi ngày là
80 100
x − 11
(bộ).
c) Số bộ quần áo mỗi ngày xưởng may được nhiều hơn so với kế hoạch là
80 100
x − 11
−
80 000
x
=
80 100x − 80 000x + 880 000
x (x − 11)
=
100x + 880 000
x (x − 11)
(bộ).
70/101 70/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
71
d) Theo kế hoạch, mỗi ngày xí nghiệp may 800 bộ quần áo nên
80 000
x
= 800 suy ra x = 100.
Khi đó, số bộ quần áo mỗi ngày xưởng may được nhiều hơn so với kế hoạch là
100 · 100 + 880 000
100 (100 − 11)
= 100 (bộ).
□
c Bài 12. Một xe ô tô đi từ Hà Nội đến Vinh với vận tốc trung bình là 60 km/h và dự kiến sẽ đến Vinh sau
5 giờ chạy xe. Tuy nhiên, sau 2
2
3
giờ chạy với vận tốc 60 km/h, xe dừng nghỉ 20 phút. Sau khi dừng nghỉ, để
đến Vinh đúng thời gian dự kiến, xe phải tăng vận tốc so với chặng đầu.
a) Tính độ dài quãng dường Hà Nội - Vinh.
b) Tính độ dài quãng đường còn lại sau khi dừng nghỉ.
c) Cho biết ở chặng thứ hai xe tăng vận tốc thêm x (km/h). Hãy viết biểu thức P biểu thị thời gian (tính
bằng giờ) thực tế xe chạy hết chặng đường Hà Nội - Vinh.
d) Tính giá trị của P lần lượt tại x = 5 ; x = 10; x = 15, từ đó cho biết ở chặng thứ hai sau khi xe dừng
nghỉ:
○ Nếu tăng vận tốc thêm 5km/h thì xe đến Vinh muộn hơn dự kiến bao nhiêu giờ?
○ Nếu tăng vận tốc thêm 10km/h thì xe đến Vinh có đúng thời gian dự kiến không?
○ Nếu tăng vận tốc thêm 15km/h thì xe đến Vinh sớm hơn dự kiến bao nhiêu giờ?
Lời giải.
a) Độ dài quãng đường Hà Nội - Vinh: 60 · 5 = 300 km.
b) Độ dài quãng đường còn lại sau khi dừng nghỉ: 300 − 60 · 2
2
3
= 140 km
c) P = 2
2
3
+
1
3
+
140
60 + x
= 3 +
140
60 + x
.
d) Thay x = 5 vào biểu thức P ta được P = 3 +
140
65
=
67
13
. Như vậy xe sẽ đến Vinh muộn hơn
67
13
− 5 =
28
13
giờ nếu tăng vận tốc thêm 5 km/h.
Thay x = 10 vào biểu thức P ta được P = 3 +
140
70
= 5. Như vậy xe sẽ đến đúng giờ dự kiến nếu tăng vận
tốc thêm 10km/h.
Thay x = 15 vào biểu thức P ta được P = 3 +
140
75
=
73
15
. Như vậy xe sẽ đến Vinh muộn hơn 5 −
73
15
=
2
15
giờ nếu tăng vận tốc thêm 15 km/h.
□
71/101 71/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
72
ÔN TẬP CHƯƠNG VI
A
AA BÀI TẬP RÈN LUYỆN
c Bài 1. Rút gọn phân thức
P =
54x(x − 3)
3
63(3 − x)
2
.a) Q =
x
2
− 3xy
21y
2
− 7xy
.b)
Lời giải.
a) P =
54x(x − 3)
3
63(3 − x)
2
=
54x(x − 3)
3
63(x − 3)
2
=
6x(x − 3)
7
.
b) Q =
x
2
− 3xy
21y
2
− 7xy
=
−x(3y − x)
7y(3y − x)
=
−x
7y
.
□
c Bài 2. Tính tổng
y
2x
2
− xy
+
4x
y
2
− 2xy
.
Lời giải.
y
2x
2
− xy
+
4x
y
2
− 2xy
=
y
x(2x − y)
+
4x
y(y − 2x)
=
y
2
− 4x
2
xy(2x − y)
=
(y + 2x)(y − 2x)
xy(2x − y)
=
−(2x + y)
xy
.
□
c Bài 3. Cho biểu thức P =
2x + y
2x
2
− xy
+
2x − y
2x
2
+ xy
−
16x
4x
2
− y
2
. Chứng tỏ rằng giá trị biểu thức P không phụ
thuộc giá trị của biến y.
Lời giải.
Ta có
P =
2x + y
x(2x − y)
+
2x − y
x(2x + y)
−
16x
(2x − y)(2x + y)
=
(2x + y)
2
+ (2x − y)
2
− 16x
2
x(2x − y)(2x + y)
=
−8x
2
+ 2y
2
x(2x − y)(2x + y)
=
−2(4x
2
− y
2
)
x(4x
2
− y
2
)
=
−2
x
.
Vậy giá trị biểu thức P không phụ thuộc vào giá trị của biến y. □
c Bài 4. Tính giá trị của biểu thức M =
x − xy − y + y
2
y
3
− 3y
2
+ 3y − 1
, với x = −
3
4
; y =
1
2
.
Lời giải.
Điều kiện y = 1.
M =
x(1 − y) − y(1 − y)
(y − 1)
3
=
(x − y)(1 − y)
−(1 − y)
3
=
y − x
(1 − y)
2
.
72/101 72/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
73
Thay x = −
3
4
; y =
1
2
, ta có M =
1
2
+
3
4
Å
1 −
1
2
ã
2
= 5. □
c Bài 5. Tính giá trị biểu thức Q =
x − y
x + y
, biết x
2
− 2y
2
= xy và x = 0; x + y = 0.
Lời giải.
Từ x
2
− 2y
2
= xy ta có x
2
− xy − 2y
2
= 0 ⇔ (x + y) (x − 2y) = 0.
Do x + y = 0 nên x − 2y = 0 ⇔ x = 2y.
Vậy Q =
x − y
x + y
=
2y − y
2y + y
=
1
3
. □
c Bài 6. Tính giá trị biểu thức sau
P =
2003
2
· 2013 + 31 · 24 − 1
(2003 · 2008 + 4)
2004 · 2005 · 2006 · 2007 · 2008
.
Lời giải.
Đặt x = 2003, ta có
P =
x
2
(x + 10) + 31(x + 1) − 1
· [x(x + 5) + 4]
(x + 1)(x + 2)(x + 3)(x + 4)(x + 5)
=
x
3
+ 10x
2
+ 31x + 30
x
2
+ 5x + 4
(x + 1)(x + 2)(x + 3)(x + 4)(x + 5)
.
Phân tích đa thức thành nhân tử ta được
P =
(x + 1)(x + 2)(x + 3)(x + 4)(x + 5)
(x + 1)(x + 2)(x + 3)(x + 4)(x + 5)
= 1.
Nhận xét. Phương pháp giải bài trên là đại số hóa bằng cách đặt x = 2003, sau đó rút gọn phân thức đại số.
Nhiều biểu thức số ta có thể giải bằng đại số như trên.
□
c Bài 7. Cho a
1
; a
2
; a
3
; . . . ; a
2007
; a
2008
là 2008 số thực thỏa mãn
a
K
=
2K + 1
(K
2
+ K)
2
với K = 1; 2; 3; . . . 2008.
Tính tổng S
2008
= a
1
+ a
2
+ a
3
+ . . . + a
2007
+ a
2008
.
Lời giải.
Ta có
a
K
=
2K + 1
(K
2
+ K)
2
=
(K + 1)
2
− K
2
K
2
(K + 1)
2
=
1
K
2
−
1
(K + 1)
2
Do đó
S
2008
= a
1
+ a
2
+ a
3
+ . . . + a
2007
+ a
2008
=
1
1
2
−
1
2
2
+
1
2
2
−
1
3
2
+
1
3
2
−
1
4
2
+ . . . +
1
2008
2
−
1
2009
2
= 1 −
1
2009
2
=
4036080
4036081
.
□
73/101 73/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
74
c Bài 8. Cho
a
b + c
+
b
c + a
+
c
a + b
= 1. Chứng minh rằng
a
2
b + c
+
b
2
c + a
+
c
2
a + b
= 0.
Lời giải.
Ta có
a
b + c
+
b
c + a
+
c
a + b
= 1
⇒
Å
a
b + c
+
b
c + a
+
c
a + b
ã
(a + b + c) = a + b + c
⇒
a
2
b + c
+ a +
b
2
c + a
+ b +
c
2
a + b
+ c = a + b + c
⇒
a
2
b + c
+
b
2
c + a
+
c
2
a + b
= 0.
Nhận xét. Quan sát mẫu thức b + c; c + a; a + b ta thấy chúng không thể cùng dấu được. Do đó ta có thể
kết luận: trong ba số a, b, c có ít nhất một số âm, ít nhất một số dương.
□
c Bài 9. Biết x = −y, y = −z, z = −x, rút gọn biểu thức sau
A =
x
2
− yz
(x + y)(x + z)
+
y
2
+ xz
(y + x)(y + z)
+
z
2
+ xy
(z + x)(z + y)
.
Lời giải.
Nhận xét rằng
x
2
− yz
(x + y)(x + z)
=
x
2
+ xy − xy − yz
(x + y)(x + z)
=
x
x + z
−
y
x + y
.
Tương tự ta có
y
2
+ xz
(y + x)(y + z)
=
y
x + y
−
z
y + z
z
2
+ xy
(z + x)(z + y)
=
z
y + z
−
x
x + z
.
Do đó ta được
A =
x
x + z
−
y
x + y
+
y
x + y
−
z
y + z
+
z
y + z
−
x
x + z
= 0.
□
c Bài 10. Biết x, y, z đôi một khác nhau, chứng minh rằng
y − z
(x − y)(x − z)
+
z − x
(y − z)(y − x)
+
x − y
(z − x)(z − y)
=
2
x − y
+
2
y − z
+
2
z − x
.
Lời giải.
Nhận xét rằng
y − z
(x − y)(x − z)
=
x − z + y − x
(x − y)(x − z)
=
1
x − y
+
1
z − x
.
Tương tự ta có
z − x
(y − z)(y − x)
=
1
y − z
+
1
x − y
;
x − y
(z − x)(z − y)
=
1
z − x
+
1
y − z
.
Công vế theo vế ta được điều phải chứng minh.
74/101 74/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
75
Nhận xét. Kỹ thuật của bài là tách mỗi phân thức vế trái thành tổng hai phân thức mà mẫu thức giống một
mẫu thức vế phải. Ngoài ra bạn cũng có thể biến đổi từng vế bằng cách quy đồng mẫu thức, ta cũng được kết
quả khá đẹp.
□
c Bài 11. Chứng minh rằng
x − y
1 + xy
+
y − z
1 + yz
+
z − x
1 + zx
=
x − y
1 + xy
·
y − z
1 + yz
·
z − x
1 + zx
.
Lời giải.
x − y
1 + xy
+
y − z
1 + yz
+
z − x
1 + zx
=
x − y
1 + xy
+
y − x + x − z
1 + yz
+
z − x
1 + zx
=
x − y
1 + xy
−
x − y
1 + yz
+
x − z
1 + yz
−
x − z
1 + zx
= (x − y)
ï
1
1 + xy
−
1
1 + yz
ò
+ (x − z)
ï
1
1 + yz
−
1
1 + zx
ò
= (x − y)
yz − xy
(1 + xy)(1 + yz)
+ (x − z)
zx − yz
(1 + yz)(1 + zx)
=
(x − y)(z − x)
1 + yz
ï
y
1 + xy
−
z
1 + zx
ò
=
(x − y)(z − x)
1 + yz
y − z
(1 + xy)(1 + xz)
=
x − y
1 + xy
·
y − z
1 + yz
·
z − x
1 + zx
.
□
c Bài 12. Cho biểu thức A =
x
x − 5
−
10x
x
2
− 25
−
5
x + 5
.
a) Tìm tập xác định và rút gọn biểu thức A.
b) Tính giá trị của A khi x = 9.
Lời giải.
a) Tập xác định x = ±5.
A =
x
x − 5
−
10x
x
2
− 25
−
5
x + 5
=
x(x + 5) − 10x − 5(x − 5)
(x + 5)(x − 5)
=
x
2
− 10x + 25
(x + 5)(x − 5)
=
x − 5
x + 5
.
b) Thay x = 9, ta được A =
9 − 5
9 + 5
=
4
14
=
2
7
.
□
c Bài 13. Cho biểu thức B =
Å
4
x
3
− 4x
+
1
x + 2
ã
:
2x − 4 − x
2
2x
2
+ 4x
.
a) Tìm tập xác định và rút gọn biểu thức B.
b) Tính giá trị của B tại x = 1.
75/101 75/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
76
c) Tìm giá trị nguyên của x để biểu thức B nhận giá trị nguyên.
Lời giải.
a) Tập xác định x = 0; x = ±2.
B =
Å
4
x
3
− 4x
+
1
x + 2
ã
:
2x − 4 − x
2
2x
2
+ 4x
=
Å
4
x(x + 2)(x − 2)
+
x(x − 2)
x(x + 2)(x − 2)
ã
:
2x − 4 − x
2
2x(x + 2)
=
4 + x
2
− 2x
x(x + 2)(x − 2)
·
2x(x + 2)
−(4 + x
2
− 2x)
=
−2
x − 2
=
2
2 − x
.
b) Thay x = 1, ta được B =
2
2 − 1
= 2.
c) Để B nhận giá trị nguyên thì 2 − x ∈ Ư(2) ⇒ 2 − x ∈ {2; −2; 1; −1} ⇔ x ∈ {0; 4; 1; 3}.
Đối chiếu với tập xác định suy ra B nhận giá trị nguyên khi x ∈ {4; 1; 3}.
□
c Bài 14. Cho biểu thức P =
Å
2x
2
+ 1
x
3
− 1
−
1
x − 1
ã
:
Å
1 −
x
2
+ 4
x
2
+ x + 1
ã
.
a) Rút gọn biểu thức P .
b) Tính giá trị của P tại x = −6.
c) Tìm giá trị nguyên của x để P nhận giá trị nguyên.
Lời giải.
a) Tập xác định x = 1.
P =
Å
2x
2
+ 1
x
3
− 1
−
1
x − 1
ã
:
Å
1 −
x
2
+ 4
x
2
+ x + 1
ã
=
Å
2x
2
+ 1 − (x
2
+ x + 1)
(x − 1)(x
2
+ x + 1)
ã
:
Å
x
2
+ x + 1 − x
2
− 4
x
2
+ x + 1
ã
=
Å
x
2
− x
(x − 1)(x
2
+ x + 1)
ã
:
Å
x − 3
x
2
+ x + 1
ã
=
Å
x(x − 1)
(x − 1)(x
2
+ x + 1)
ã
·
Å
x
2
+ x + 1
x − 3
ã
=
x
x − 3
.
b) Thay x = −6, ta được P =
−6
−6 − 3
=
2
3
.
c) Ta có P =
x
x − 3
= 1 +
3
x − 3
.
Do đó, P nhận giá trị nguyên khi x − 3 ∈ Ư(3) ⇒ x − 3 ∈ {3; −3; 1; −1} ⇒ x ∈ {6; 0; 4; 2}.
Vậy với x ∈ {6; 0; 4; 2} thì P nhận giá trị nguyên.
□
c Bài 15. Cho Q =
12x − 45
x
2
− 7x + 12
−
x + 5
x − 4
+
2x + 3
3 − x
.
76/101 76/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
77
a) Rút gọn biểu thức P .
b) Tính giá trị Q tại |x| = 3.
c) Tìm giá trị nguyên của x để Q nhận giá trị nguyên.
Lời giải.
a) Tập xác định x = 3; x = 4.
Q =
12x − 45
x
2
− 7x + 12
−
x + 5
x − 4
+
2x + 3
3 − x
=
12x − 45
(x − 3)(x − 4)
−
x + 5
x − 4
−
2x + 3
x − 3
=
12x − 45 − (x + 5)(x − 3) − (2x + 3)(x − 4)
(x − 3)(x − 4)
=
−3x
2
+ 15x − 18
(x − 3)(x − 4)
=
−3(x − 2)(x − 3)
(x − 3)(x − 4)
=
−3(x − 2)
x − 4
.
b) Ta có |x| = 3 ⇔
ñ
x = 3 (loại)
x = −3 (nhận)
.
Thế x = −3, ta được Q =
−3(−3 − 2)
−3 − 4
=
−15
7
.
c) Ta có Q =
−3(x − 2)
x − 4
= −3 −
6
x − 4
.
Do đó, Q nhận giá trị nguyên khi
x − 4 ∈ Ư(6) ⇒ x − 4 ∈ {6; −6; 3; −3; 2; −2; 1; −1} ⇒ x ∈ {10; −2; 7; 1; 6; 2; 5; 3}
Đối chiếu với tập xác định suy ra Q nhận giá trị nguyên khi x ∈ {10; −2; 7; 1; 6; 2; 5}.
□
c Bài 16. Cho a
1
; a
2
; . . . ; a
9
được xác định bởi công thức
a
k
=
3k
2
+ 3k + 1
(k
2
+ k)
3
với k ⩾ 1.
Hãy tính giá trị của tổng 1 + a
1
+ a
2
+ . . . + a
9
.
Lời giải.
Ta có
a
k
=
3k
2
+ 3k + 1
(k
2
+ k)
3
=
(k + 1)
3
− k
3
k
2
(k + 1)
3
=
1
k
3
−
1
(k + 1)
3
Do đó
S = 1 + a
1
+ a
2
+ . . . + a
9
= 1 +
Å
1
1
3
−
1
2
3
ã
+
Å
1
2
3
−
1
3
3
ã
+ . . . +
Å
1
9
3
−
1
10
3
ã
= 2 −
1
10
3
=
1999
1000
.
□
77/101 77/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
78
c Bài 17. Tính
1986
2
− 1992
1986
2
+ 3972 − 3
· 1987
1983 · 1985 · 1988 · 1989
.
Lời giải.
Đặt x = 1986
P =
x
2
− x − 6
·
x
2
+ 2x − 3
· (x + 1)
(x − 3)(x − 1)(x + 2)(x + 3)
=
(x − 3) (x + 2) (x − 1) (x + 3) (x + 1)
(x − 3)(x − 1)(x + 2)(x + 3)
= x + 1.
Suy ra
1986
2
− 1992
1986
2
+ 3972 − 3
· 1987
1983 · 1985 · 1988 · 1989
= 1987.
□
c Bài 18. Đặt a + b + c = 2p. Chứng minh rằng
1
p − a
+
1
p − b
+
1
p − c
−
1
p
=
abc
p(p − a)(p − b)(p − c)
.
Lời giải.
1
p − a
+
1
p − b
+
1
p − c
−
1
p
=
p − b + p − a
(p − a)(p − b)
+
p − p + c
p(p − c)
=
c
(p − a)(p − b)
+
c
p(p − c)
=
c [p(p − c) + (p − a)(p − b)]
p(p − a)(p − b)(p − c)
=
c
2p
2
− p(a + b + c) + ab
p(p − a)(p − b)(p − c)
=
abc
p(p − a)(p − b)(p − c)
.
□
c Bài 19. Biết a = −b, b = −c, c = −a. Chứng minh rằng
b
2
− c
2
(a + b)(a + c)
+
c
2
− a
2
(b + c)(b + a)
+
a
2
− b
2
(c + a)(c + b)
=
b − c
b + c
+
c − a
c + a
+
a − b
a + b
.
Lời giải.
Ta có
b
2
− c
2
(a + b)(a + c)
=
b
2
− a
2
(a + b)(a + c)
+
a
2
− c
2
(a + b)(a + c)
=
b − a
a + c
+
a − c
a + b
.
Tương tự ta có
c
2
− a
2
(b + c)(b + a)
=
c − b
b + a
+
b − a
b + c
a
2
− b
2
(c + a)(c + b)
=
a − c
c + b
+
c − b
c + a
.
Cộng vế theo vế ta được điều phải chứng minh. □
A
BB BÀI TẬP BỔ SUNG
78/101 78/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
79
c Bài 20. Cho a + b + c = 0 và a, b, c đều khác 0. Rút gọn biểu thức
A =
ab
a
2
+ b
2
− c
2
+
bc
b
2
+ c
2
− a
2
+
ca
c
2
+ a
2
− b
2
.
Lời giải.
Từ a + b + c = 0 suy ra a + b = −c.
Bình phương hai vế, ta được a
2
+ b
2
+ 2ab = c
2
nên a
2
+ b
2
− c
2
= −2ab.
Tương tự, b
2
+ c
2
− a
2
= −2bc và c
2
+ a
2
− b
2
= −2ca.
Do đó, A =
ab
−2ab
+
bc
−2bc
+
ca
−2ca
= −
1
2
−
1
2
−
1
2
= −
3
2
. □
c Bài 21. Rút gọn biểu thức
A =
1
1 − x
+
1
1 + x
+
2
1 + x
2
+
4
1 + x
4
+
8
1 + x
8
.
Lời giải.
Do đặc điểm của bài toán, ta không quy đồng mẫu tất cả các phân thức mà cộng lần lượt từng phân thức.
A =
2
1 − x
2
+
2
1 + x
2
+
4
1 + x
4
+
8
1 + x
8
=
4
1 − x
4
+
4
1 + x
4
+
8
1 + x
8
=
8
1 − x
8
+
8
1 + x
8
=
16
1 − x
16
.
□
c Bài 22. Rút gọn biểu thức
B =
3
(1 · 2)
2
+
5
(2 · 3)
2
+ ··· +
2n + 1
[n(n + 1)]
2
.
Lời giải.
Đương nhiên không thể quy đồng mẫu tất cả các phân thức. Ta tìm cách tách mỗi phân thức thành hiệu của hai
phân thức rồi dùng phương pháp khử liên tiếp. Ta có
2k + 1
k
2
(k + 1)
2
=
(k + 1)
2
− k
2
k
2
(k + 1)
2
=
1
k
2
−
1
(k + 1)
2
.
Do đó
B =
1
1
2
−
1
2
2
+
1
2
2
−
1
3
2
+ ··· +
1
n
2
−
1
(n + 1)
2
= 1 −
1
(n + 1)
2
=
n(n + 2)
(n + 1)
2
.
□
c Bài 23. Xác định các số a, b, c sao cho
1
(x
2
+ 1)(x − 1)
=
ax + b
x
2
+ 1
+
c
x − 1
. (1)
Lời giải.
Thực hiện phép cộng ở vế phải của (1) ta được
(ax + b)(x − 1) + c(x
2
+ 1)
(x
2
+ 1)(x − 1)
=
ax
2
− ax + bx − b + cx
2
+ c
(x
2
+ 1)(x − 1)
=
(a + c)x
2
+ (b − a)x + (c − b)
(x
2
+ 1)(x − 1)
.
79/101 79/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
80
Đồng nhất phân thức trên với phân thức
1
(x
2
+ 1)(x − 1)
, ta được
a + c = 0
b − a = 0
c − b = 1
⇒
®
c + b = 0
c − b = 1
⇒ c =
1
2
, b = −
1
2
.
Do đó a = −
1
2
. Như vậy
1
(x
2
+ 1)(x − 1)
=
−
1
2
x −
1
2
x
2
+ 1
+
1
2
x − 1
. □
c Bài 24. Cho A =
1
(x + y)
3
Å
1
x
4
−
1
y
4
ã
,
B =
2
(x + y)
4
Å
1
x
3
−
1
y
3
ã
,
C =
2
(x + y)
5
Å
1
x
2
−
1
y
2
ã
.
Thực hiện phép tính A + B + C.
Lời giải.
Ta có
A =
y
4
− x
4
x
4
y
4
(x + y)
3
=
(y
2
+ x
2
)(y
2
− x
2
)
x
4
y
4
(x + y)
3
=
(y
2
+ x
2
)(y − x)
x
4
y
4
(x + y)
2
.
B + C =
2
(x + y)
4
Å
1
x
3
−
1
y
3
+
1
x + y
·
y
2
− x
2
x
2
y
2
ã
=
2
(x + y)
4
Å
1
x
3
−
1
y
3
+
y − x
x
2
y
2
ã
=
2
(x + y)
4
·
y
3
− x
3
+ xy(y − x)
x
3
y
3
=
2
(x + y)
4
·
(y − x)(y
2
+ 2yx + x
2
)
x
3
y
3
=
2(y − x)
(x + y)
2
x
3
y
3
.
Do đó,
A + B + C =
(y
2
+ x
2
)(y − x)
x
4
y
4
(x + y)
2
+
2(y − x)
(x + y)
2
x
3
y
3
=
(y
2
+ x
2
)(y − x) + 2xy(y − x)
x
4
y
4
(x + y)
2
=
(y − x)(y
2
+ x
2
+ 2xy)
x
4
y
4
(x + y)
2
=
y − x
x
4
y
4
.
□
c Bài 25. Thực hiện các phép tính
a)
x + 3
x + 1
−
2x − 1
x − 1
−
x − 3
x
2
− 1
;
b)
1
x(x + y)
+
1
y(x + y)
+
1
x(x − y)
+
1
y(y − x)
.
Lời giải.
a)
x + 3
x + 1
−
2x − 1
x − 1
−
x − 3
x
2
− 1
=
(x + 3)(x − 1) − (2x − 1)(x + 1) − (x − 3)
x
2
− 1
=
−x
2
+ 1
x
2
− 1
= −1.
b)
1
x(x + y)
+
1
y(x + y)
+
1
x(x − y)
+
1
y(y − x)
=
x + y
xy(x + y)
+
y − x
xy(x − y)
=
1
xy
−
1
xy
= 0.
80/101 80/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
81
□
c Bài 26. Thực hiện phép tính
a) A =
1
(a − b)(a − c)
+
1
(b − a)(b − c)
+
1
(c − a)(c − b)
;
b) B =
1
a(a − b)(a − c)
+
1
b(b − a)(b − c)
+
1
c(c − a)(c − b)
;
c) C =
bc
(a − b)(a − c)
+
ac
(b − a)(b − c)
+
ab
(c − a)(c − b)
;
d) D =
a
2
(a − b)(a − c)
+
b
2
(b − a)(b − c)
+
c
2
(c − a)(c − b)
.
Lời giải.
a) A =
1
(a − b)(a − c)
+
1
(b − a)(b − c)
+
1
(c − a)(c − b)
=
c − b + a − c + b − a
(a − b)(b − c)(c − a)
= 0.
b) Ta có
B =
1
a(a − b)(a − c)
+
1
b(b − a)(b − c)
+
1
c(c − a)(c − b)
=
bc(b − c) − ac(a − c) + ab(a − b)
abc(a − b)(b − c)(a − c)
=
c(b
2
− bc − a
2
+ ac) + ab(a − b)
abc(a − b)(b − c)(a − c)
=
c [(b − a)(b + a) − c(b − a)] + ab(a − b)
abc(a − b)(b − c)(a − c)
=
(a − b)(−cb − ca + c
2
) + ab(a − b)
abc(a − b)(b − c)(a − c)
=
(a − b)(−cb − ac + c
2
+ ab)
abc(a − b)(b − c)(a − c)
=
(a − b)(b − c)(a − c)
abc(a − b)(b − c)(a − c)
=
1
abc
.
c) Ta có
C =
bc
(a − b)(a − c)
+
ac
(b − a)(b − c)
+
ab
(c − a)(c − b)
=
bc(b − c) − ac(a − c) + ab(a − b)
abc(a − b)(b − c)(a − c)
=
c(b
2
− bc − a
2
+ ac) + ab(a − b)
(a − b)(b − c)(a − c)
=
c [(b − a)(b + a) − c(b − a)] + ab(a − b)
(a − b)(b − c)(a − c)
=
(a − b)(−cb − ca + c
2
) + ab(a − b)
(a − b)(b − c)(a − c)
=
(a − b)(−cb − ac + c
2
+ ab)
(a − b)(b − c)(a − c)
=
(a − b)(b − c)(a − c)
(a − b)(b − c)(a − c)
= 1.
81/101 81/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
82
d) Ta có
D =
a
2
(a − b)(a − c)
+
b
2
(b − a)(b − c)
+
c
2
(c − a)(c − b)
=
a
2
(b − c) − b
2
(a − c) + c
2
(a − b)
(a − b)(b − c)(a − c)
=
a
2
(b − c) − b
2
a + b
2
c + c
2
a − c
2
b
(a − b)(b − c)(a − c)
=
a
2
(b − c) − a(b
2
− c
2
) + bc(b − c)
(a − b)(b − c)(a − c)
=
(b − c)(a
2
− ab − ac + cb)
(a − b)(b − c)(a − c)
=
(b − c) [a(a − b) − c(a − b)]
(a − b)(b − c)(a − c)
=
(b − c)(a − b)(a − c)
(a − b)(b − c)(a − c)
= 1.
□
c Bài 27. Cho a, b, c là các số nguyên khác nhau đôi một. Chứng minh rằng biểu thức sau có giá trị là một
số nguyên:
P =
a
3
(a − b)(a − c)
+
b
3
(b − a)(b − c)
+
c
3
(c − a)(c − b)
.
Lời giải.
Ta có
P =
a
3
(a − b)(a − c)
+
b
3
(b − a)(b − c)
+
c
3
(c − a)(c − b)
=
a
3
(b − c) + b
3
(c − a) + c
3
(a − b)
(a − b)(b − c)(a − c)
.
Phân tích tử thành nhân tử
a
3
(b − c) + b
3
(c − a) + c
3
(a − b) = a
3
b − a
3
c + b
3
c − b
3
a + c
3
(a − b)
= (a
3
b − b
3
a) − (a
3
c − b
3
c) + c
3
(a − b)
= ab(a − b)(a + b) − c(a − b)(a
2
+ ab + b
2
) + c
3
(a − b)
= (a − b)(a
2
b + ab
2
− ca
2
− cb
2
− abc + c
3
)
= (a − b)
(c
3
− cb
2
) − (abc − ab
2
) + (a
2
b − ca
2
)
= (a − b)(b − c)(−cb − c
2
+ ab + a
2
)
= (a − b)(b − c)
(ab − cb) + (a
2
− c
2
)
= (a − b)(b − c)(a − c)(a + b + c).
Vậy P = a + b + c. □
c Bài 28. Cho 3y − x = 6. Tính giá trị biểu thức A =
x
y − 2
+
2x − 3y
x − 6
.
Lời giải.
A =
x
y − 2
+
2x − 3y
x − 6
=
3y − 6
y − 2
+
2x − x − 6
x − 6
= 3 + 1 = 4. □
c Bài 29. Tìm x, y, z biết rằng
x
2
2
+
y
2
3
+
z
2
4
=
x
2
+ y
2
+ z
2
5
.
82/101 82/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
83
Lời giải.
Từ
x
2
2
+
y
2
3
+
z
2
4
=
x
2
+ y
2
+ z
2
5
suy ra
Å
x
2
2
−
x
2
5
ã
+
Å
y
2
3
−
y
2
5
ã
+
Å
z
2
4
−
z
2
5
ã
= 0.
Cho nên
3x
2
10
+
2y
2
15
+
z
2
20
= 0. Do đó, x = y = z = 0. □
c Bài 30. Tìm x, y biết rằng x
2
+ y
2
+
1
x
2
+
1
y
2
= 4.
Lời giải.
Ta có
x
2
+ y
2
+
1
x
2
+
1
y
2
= 4 ⇒
Å
x
2
− 2 +
1
x
2
ã
+
Å
y
2
− 2 +
1
y
2
ã
= 0
⇒
Å
x −
1
x
ã
2
+
Å
y −
1
y
ã
2
= 0
⇒
x −
1
x
= 0
y −
1
y
= 0
⇒
®
x
2
= 1
y
2
= 1.
Có bốn đáp án như bảng sau
x 1 1 −1 −1
y 1 −1 1 −1
□
c Bài 31. Cho biết
1
a
+
1
b
+
1
c
= 2, (1)
1
a
2
+
1
b
2
+
1
c
2
= 2. (2)
Chứng minh rằng a + b + c = abc.
Lời giải.
Từ (1) suy ra
1
a
2
+
1
b
2
+
1
c
2
+ 2
Å
1
ab
+
1
bc
+
1
ca
ã
= 4.
Do (2) nên
1
ab
+
1
bc
+
1
ca
= 1 suy ra
a + b + c
abc
= 1.
Do đó a + b + c = abc. □
c Bài 32. Cho
x
a
+
y
b
+
z
c
= 0, (1)
và
a
x
+
b
y
+
c
z
= 2. (2)
Tính giá trị biểu thức
a
2
x
2
+
b
2
y
2
+
c
2
z
2
.
Lời giải.
Từ (1) suy ra bcx + acy + abz = 0.
Từ (2) suy ra
a
2
x
2
+
b
2
y
2
+
c
2
z
2
+
Å
ab
xy
+
bc
yz
+
ca
zx
ã
= 4.
Do đó
a
2
x
2
+
b
2
y
2
+
c
2
z
2
= 4 − 2
abz + acy + bcx
xyz
= 4. □
c Bài 33. Cho (a + b + c)
2
= a
2
+ b
2
+ c
2
và a, b, c khác 0. Chứng minh rằng
1
a
3
+
1
b
3
+
1
c
3
=
3
abc
.
83/101 83/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
84
Lời giải.
Từ giả thiết suy ra ab + bc + ca = 0 ⇒ b + c = −
bc
a
.
Do đó
ab + bc + ca
abc
= 0, tức là
1
a
+
1
b
+
1
c
= 0. Suy ra
1
a
= −
Å
1
b
+
1
c
ã
⇒
1
a
3
= −
Å
1
b
+
1
c
ã
3
= −
1
b
3
−
1
c
3
− 3
Å
1
b
2
c
+
1
bc
2
ã
⇒
1
a
3
+
1
b
3
+
1
c
3
= −
3(b + c)
b
2
c
2
=
3bc
ab
2
c
2
=
3
abc
.
□
c Bài 34. Cho
a
b
+
b
c
+
c
a
=
b
a
+
a
c
+
c
b
. Chứng minh rằng trong ba số a,b,c tồn tại hai số bằng nhau.
Lời giải.
Từ giả thiết suy ra
a
2
c + b
2
a + c
2
b = b
2
c + a
2
b + c
2
a ⇒ a
2
(c − b) − a(c
2
− b
2
) + bc(c − b) = 0
⇒ (c − b)(a
2
− ac − ab + bc) = 0
⇒ (c − b)(a − c)(a − b) = 0.
Tồn tại một trong các thừa số c − b, a − c, a − b bằng 0. Do đó, trong ba số a, b, c tồn tại hai số bằng nhau. □
c Bài 35. Tìm các giá trị nguyên của x để phân thức sau có giá trị là số nguyên:
a) A =
2x
3
− 6x
2
+ x − 8
x − 3
;
b) B =
x
4
− 2x
3
− 3x
2
+ 8x − 1
x
2
− 2x + 1
;
c) C =
x
4
+ 3x
3
+ 2x
2
+ 6x − 2
x
2
+ 2
.
Lời giải.
a) A =
2x
3
− 6x
2
+ x − 8
x − 3
= 2x
2
+ 1 −
5
x − 3
.
A nguyên khi x nguyên, x − 3 nguyên và nó là ước của 5.
Suy ra x − 3 = 1 hoặc x − 3 = −1 hoặc x − 3 = 5 hoặc x − 3 = −5.
Hay x = 4 hoặc x = 2 hoặc x = 8 hoặc x = −2.
b) B =
x
4
− 2x
3
− 3x
2
+ 8x − 1
x
2
− 2x + 1
= x
2
− 4 +
3
(x − 1)
2
.
B nguyên khi x nguyên, (x − 1)
2
nguyên và nó là ước của 3.
Suy ra (x − 1)
2
= 1 hoặc (x − 1)
2
= 3.
Hay x − 1 = −1 hoặc x − 1 = 1 hay x = 0 hoặc x = 2.
c) C =
x
4
+ 3x
3
+ 2x
2
+ 6x − 2
x
2
+ 2
= x
2
+ 3x −
2
x
2
+ 2
.
C nguyên khi x nguyên, x
2
+ 2 nguyên và nó là ước của 2.
Suy ra x
2
+ 2 = 2 hay x = 0.
□
84/101 84/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
85
c Bài 36. Rút gọn biểu thức sau với x =
a
3a + 2
A =
x + 3a
2 − x
+
x − 3a
2 + x
−
2a
4 − x
2
+ a.
Lời giải.
A =
x + 3a
2 − x
+
x − 3a
2 + x
−
2a
4 − x
2
+ a =
6ax + 4x − 2a
4 − x
2
+ a =
2x(3a + 2) − 2a
4 − x
2
+ a = a. □
c Bài 37. Rút gọn biểu thức
A =
2
a − b
+
2
b − c
+
2
c − a
+
(a − b)
2
+ (b − c)
2
+ (c − a)
2
(a − b)(b − c)(c − a)
.
Lời giải.
Đặt a − b = x, b − c = y, c − a = z thì x + y + z = 0.
Ta có A =
2
x
+
2
y
+
2
z
+
x
2
+ y
2
+ z
2
xyz
=
(x + y + z)
2
xyz
= 0. □
c Bài 38. Cho biết
a + b − c
ab
−
b + c − a
bc
−
c + a − b
ca
= 0. Chứng minh rằng trong ba phân thức ở vế trái,
có ít nhất một phân thức bằng 0.
Lời giải.
Ta có
a + b − c
ab
−
b + c − a
bc
−
c + a − b
ca
= 0 ⇔ c(a + b − c) − a(b + c − a) − b(c + a − b) = 0
⇔ a
2
+ b
2
− 2ab − c
2
= 0
⇔ (a − b)
2
− c
2
= 0
⇔ (a − b + c)(a − b − c) = 0.
Vậy a − b + c = 0 hoặc a − b − c = 0. □
c Bài 39. Xác định các số a, b, c sao cho:
a)
1
x(x
2
+ 1)
=
a
x
+
bx + c
x
2
+ 1
;
b)
1
x
2
− 4
=
a
x − 2
+
b
x + 2
;
c)
1
(x + 1)
2
(x + 2)
=
a
x + 1
+
b
(x + 1)
2
+
c
x + 2
.
Lời giải.
a) Ta có
a
x
+
bx + c
x
2
+ 1
=
a(x
2
+ 1) + (bx + c)x
x(x
2
+ 1)
=
(a + b)x
2
+ cx + a
x(x
2
+ 1)
.
Đồng nhất với phân thức
1
x(x
2
+ 1)
ta được
a + b = 0
c = 0
a = 1
⇒
a = 1
b = −1
c = 0.
b) Ta xó
a
x − 2
+
b
x + 2
=
a(x + 2) + b(x − 2)
x
2
− 4
=
(a + b)x + 2(a − b)
x
2
− 4
.
85/101 85/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
86
Đồng nhất với phân thức
1
x
2
− 4
ta được
a + b = 0
a − b =
1
2
⇒
a =
1
4
b = −
1
4
.
c) Ta có
a
x + 1
+
b
(x + 1)
2
+
c
x + 2
=
a(x + 1)(x + 2) + b(x + 2) + c(x + 1)
2
(x + 1)
2
(x + 2)
=
(a + c)x
2
+ (3a + b + 2c)x + a + 2b + c
(x + 1)
2
(x + 2)
.
Đồng nhất với phân thức
1
(x + 1)
2
(x + 2)
ta được
a + c = 0
3a + b + 2c = 0
a + 2b + c = 1
⇒
a = −1
b = 1
c = 1.
□
c Bài 40. Rút gọn biểu thức
B = (ab + bc + ca)
Å
1
a
+
1
b
+
1
c
ã
− abc
Å
1
a
2
+
1
b
2
+
1
c
2
ã
.
Lời giải.
B = (ab + bc + ca)
Å
1
a
+
1
b
+
1
c
ã
− abc
Å
1
a
2
+
1
b
2
+
1
c
2
ã
= (ab + bc + ca)
bc + ca + ab
abc
− abc
b
2
c
2
+ c
2
a
2
+ a
2
b
2
a
2
b
2
c
2
=
(bc + ca + ab)
2
abc
−
b
2
c
2
+ c
2
a
2
+ a
2
b
2
abc
=
2abc(a + b + c)
abc
= 2(a + b + c).
□
c Bài 41. Cho a, b, c khác nhau đôi một và
1
a
+
1
b
+
1
c
= 0. Rút gọn các biểu thức:
a) M =
1
a
2
+ 2bc
+
1
b
2
+ 2ac
+
1
c
2
+ 2ab
;
b) N =
bc
a
2
+ 2bc
+
ac
b
2
+ 2ac
+
ab
c
2
+ 2ab
;
c) P =
a
2
a
2
+ 2bc
+
b
2
b
2
+ 2ac
+
c
2
c
2
+ 2ab
.
Lời giải.
Từ giả thiết suy ra ab + bc + ac = 0 nên
a
2
+ 2bc = a
2
+ bc + (−ab − ac) = a(a − b) − c(a − b) = (a − b)(a − c).
Tương tự, b
2
+ 2ac = (b − a)(b − c) và c
2
+ 2ab = (c − a)(c − b).
a) M =
1
a
2
+ 2bc
+
1
b
2
+ 2ac
+
1
c
2
+ 2ab
=
1
(a − b)(a − c)
+
1
(b − a)(b − c)
+
1
(c − a)(c − b)
=
b − c + c − a + a − b
(a − b)(b − c)(a − c)
= 0.
86/101 86/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
87
b) N =
bc
a
2
+ 2bc
+
ac
b
2
+ 2ac
+
ab
c
2
+ 2ab
=
bc
(a − b)(a − c)
+
ac
(b − a)(b − c)
+
ab
(c − a)(c − b)
=
bc(b − c) + ac(c − a) + ab(a − b)
(a − b)(b − c)(a − c)
=
−c(a
2
− b
2
) + c
2
(a − b) + ab(a − b)
(a − b)(b − c)(a − c)
=
(a − b)(−ac − cb + c
2
+ ab)
(a − b)(b − c)(a − c)
=
(a − b) [−c(a − c + b(a − c)]
(a − b)(b − c)(a − c)
=
(a − b)(b − c(a − c))
(a − b)(b − c)(a − c)
= 1.
c) P =
a
2
a
2
+ 2bc
+
b
2
b
2
+ 2ac
+
c
2
c
2
+ 2ab
=
a
2
(a − b)(a − c)
+
b
2
(b − a)(b − c)
+
c
2
(c − a)(c − b)
=
a
2
(b − c) + b
2
(c − a) + c
2
(a − b)
(a − b)(b − c)(a − c)
=
ab(a − b) − c(a
2
− b
2
) + c
2
(a − b)
(a − b)(b − c)(a − c)
=
(a − b)(ab − ac − bc + c
2
)
(a − b)(b − c)(a − c)
=
(a − b)(b − c)(a − c)
(a − b)(b − c)(a − c)
= 1.
□
c Bài 42. Cho các số a, b, c khác nhau đôi một và
a + b
c
=
b + c
a
=
c + a
b
. Tính giá trị biểu thức
M =
1 +
a
b
Å
1 +
b
c
ã
1 +
c
a
.
Lời giải.
Ta có
a + b
c
=
b + c
a
=
c + a
b
=
a + b + b + c + c + a
a + b + c
=
2(a + b + c)
a + b + c
.
Nếu a + b + c = 0 thì tỉ số trên bằng 2. Suy ra a + b = 2c, b + c = 2a.
Do đó a − c = 2(c − a) nên c = a, trái với đề bài.
Vậy a + b + c = 0. Ta có M =
a + b
b
·
b + c
c
·
c + a
a
=
−c
b
·
−a
c
·
−b
a
= −1. □
c Bài 43. Cho a
3
+ b
3
+ c
3
= 3abc và a + b + c = 0. Tính giá trị của biểu thức
N =
a
2
+ b
2
+ c
2
(a + b + c)
2
.
Lời giải.
Ta có a
3
+ b
3
+ c
3
− 3abc = (a + b + c)(a
2
+ b
2
+ c
2
− ab − bc − ca).
Do a
3
+ b
3
+ c
3
= 3abc và a + b + c = 0 nên đẳng thức trên trở thành a
2
+ b
2
+ c
2
− ab − bc − ca = 0.
Lại có
a
2
+ b
2
+ c
2
− ab − bc − ca = (a
2
− 2ab + b
2
) + (b
2
− 2bc + c
2
) + (c
2
− 2ca + a
2
)
= (a − b)
2
+ (b − c)
2
+ (c − a)
2
.
Như vậy từ a
2
+ b
2
+ c
2
− ab − bc − ca = 0 suy ra a = b = c.
Do đó, N =
3a
2
(3a)
2
=
3a
2
9a
2
=
1
3
. □
c Bài 44. Rút gọn biểu thức A =
Å
1 −
1
2
2
ãÅ
1 −
1
3
2
ãÅ
1 −
1
4
2
ã
···
Å
1 −
1
n
2
ã
.
Lời giải.
87/101 87/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
88
Ta có
A =
Å
1 −
1
2
2
ãÅ
1 −
1
3
2
ãÅ
1 −
1
4
2
ã
···
Å
1 −
1
n
2
ã
=
1 · 3
2
2
·
2 · 4
3
2
·
3 · 5
4
2
···
(n − 1)(n + 1)
n
2
=
1 · 2 · 3 ···(n − 1)
2 · 3 · 4 ···n
·
3 · 4 · 5 ···(n + 1)
2 · 3 · 4 ···n
=
1
n
·
n + 1
2
=
n + 1
2n
.
□
c Bài 45. Rút gọn biểu thức B =
1
2
2
2
− 1
·
3
2
4
2
− 1
·
5
2
6
2
− 1
···
(2n + 1)
2
(2n + 2)
2
− 1
.
Lời giải.
Ta có
B =
1
2
2
2
− 1
·
3
2
4
2
− 1
·
5
2
6
2
− 1
···
(2n + 1)
2
(2n + 2)
2
− 1
=
1
2
1 · 3
·
3
2
3 · 5
·
5
2
5 · 7
···
(2n + 1)
2
(2n + 1)(2n + 3)
=
1
2
· 3
2
· 5
2
···(2n + 1)
2
1 · 3
2
· 5
2
···(2n + 1)
2
· (2n + 3)
=
1
(2n + 3)
.
□
c Bài 46. Rút gọn biểu thức
1
1 · 2
+
1
2 · 3
+
1
3 · 4
+ ··· +
1
(n − 1)n
.
Lời giải.
Ta có
1
1 · 2
+
1
2 · 3
+
1
3 · 4
+ ··· +
1
(n − 1)n
=
1
1
−
1
2
+
1
2
−
1
3
+
1
3
−
1
4
+ ··· +
1
n − 1
−
1
n
= 1 −
1
n
=
n − 1
n
.
□
c Bài 47. Rút gọn biểu thức
1
2 · 5
+
1
5 · 8
+
1
8 · 11
+ ··· +
1
(3n + 2)(3n + 5)
.
Lời giải.
Ta có
1
(3n + 2)(3n + 5)
=
1
3
Å
1
3n + 2
−
1
3n + 5
ã
.
Do đó
1
2 · 5
+
1
5 · 8
+
1
8 · 11
+ ··· +
1
(3n + 2)(3n + 5)
=
1
3
Å
1
2
−
1
5
+
1
5
−
1
8
+
1
8
−
1
11
+ ··· +
1
3n + 2
−
1
3n + 5
ã
=
1
3
Å
1
2
−
1
3n + 5
ã
=
1
3
·
3n + 5 − 2
2(3n + 5)
=
n + 1
2(3n + 5)
.
□
c Bài 48. Rút gọn biểu thức
1
1 · 2 · 3
+
1
2 · 3 · 4
+
1
3 · 4 · 5
+ ··· +
1
(n − 1)n(n + 1)
.
Lời giải.
Ta có
1
(n − 1)n(n + 1)
=
1
2
ï
1
(n − 1)n
−
1
n(n + 1)
ò
.
Do đó
1
1 · 2 · 3
+
1
2 · 3 · 4
+
1
3 · 4 · 5
+ ··· +
1
(n − 1)n(n + 1)
88/101 88/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
89
=
1
2
ï
1
1 · 2
−
1
2 · 3
+
1
2 · 3
−
1
3 · 4
+
1
3 · 4
−
1
4 · 5
+ ··· +
1
(n − 1)n
−
1
n(n + 1)
ò
=
1
2
ï
1
2
−
1
n(n + 1)
ò
=
1
2
·
n(n + 1) − 2
2n(n + 1)
=
(n − 1)(n + 2)
4n(n + 1)
.
□
c Bài 49. Chứng minh rằng với mọi số tự nhiên n ≥ 1, ta luôn có
1
2
2
+
1
4
2
+
1
6
2
+ ··· +
1
(2n)
2
<
1
2
.
Lời giải.
Ta có
A =
1
2
2
+
1
4
2
+
1
6
2
+ ··· +
1
(2n)
2
=
1
4
Å
1
1
2
+
1
2
2
+
1
3
2
+ ··· +
1
n
2
ã
.
Suy ra A <
1
4
Å
1 +
1
1 · 2
+
1
2 · 3
+ ··· +
1
(n − 1)n
ã
.
Lại có 1 +
1
1 · 2
+
1
2 · 3
+ ··· +
1
(n − 1)n
= 1 +
1
1
−
1
n
= 2 −
1
n
.
Do đó A <
1
4
Å
2 −
1
n
ã
, suy ra A <
1
2
. □
c Bài 50. Chứng minh rằng với mọi số tự nhiên n ≥ 1, ta luôn có
1
3
2
+
1
5
2
+
1
7
2
+ ··· +
1
(2n + 1)
2
<
1
4
.
Lời giải.
Ta có
B =
1
3
2
+
1
5
2
+
1
7
2
+ ··· +
1
(2n + 1)
2
<
1
3
2
− 1
+
1
5
2
− 1
+
1
7
2
− 1
+ ··· +
1
(2n + 1)
2
− 1
.
Lại có
1
3
2
− 1
+
1
5
2
− 1
+
1
7
2
− 1
+ ··· +
1
(2n + 1)
2
− 1
=
1
2 · 4
+
1
4 · 6
+
1
6 · 8
+ ··· +
1
2n(2n + 2)
=
1
2
Å
1
2
−
1
4
+
1
4
−
1
6
+
1
6
−
1
8
+ ··· +
1
2n
−
1
2n + 2
ã
=
1
2
Å
1
2
−
1
2n + 2
ã
.
Do đó B <
1
2
Å
1
2
−
1
2n + 2
ã
, suy ra B <
1
4
. □
c Bài 51. Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta luôn có
A =
1
2
2
+
1
3
2
+
1
4
2
+ ··· +
1
n
2
<
2
3
.
Lời giải.
Nhận xét, với mọi số tự nhiên n ≥ 2 ta luôn có
1
n
2
<
4
4n
2
− 1
= 2
Å
1
2n − 1
−
1
2n + 1
ã
.
Khi đó
A < 2
Å
1
3
−
1
5
+
1
5
−
1
7
+
1
7
−
1
9
+ ··· +
1
2n − 1
−
1
2n + 1
ã
.
89/101 89/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
90
Lại có
1
3
−
1
5
+
1
5
−
1
7
+
1
7
−
1
9
+ ··· +
1
2n − 1
−
1
2n + 1
=
1
3
−
1
2n + 1
.
Do đó A < 2
Å
1
3
−
1
2n + 1
ã
, suy ra A <
2
3
. □
c Bài 52. Chứng minh rằng với mọi số tự nhiên n ≥ 3, ta luôn có
B =
1
3
3
+
1
4
3
+
1
5
3
+ ··· +
1
n
3
<
1
12
.
Lời giải.
Với mọi số tự nhiên n ≥ 3, ta luôn có
1
n
3
<
1
n
3
− n
=
1
(n − 1)n(n + 1)
=
1
2
·
(n + 1) − (n − 1)
(n − 1)n(n + 1)
=
1
2
ï
1
(n − 1)n
−
1
n(n + 1)
ò
.
Khi đó
B <
1
2
ï
1
2 · 3
−
1
3 · 4
+
1
3 · 4
−
1
4 · 5
+
1
4 · 5
−
1
5 · 6
+ ··· +
1
(n − 1)n
−
1
n(n + 1)
ò
.
Lại có
1
2 · 3
−
1
3 · 4
+
1
3 · 4
−
1
4 · 5
+
1
4 · 5
−
1
5 · 6
+ ··· +
1
(n − 1)n
−
1
n(n + 1)
=
1
6
−
1
n(n + 1)
.
Do đó B <
1
2
ï
1
6
−
1
n(n + 1)
ò
, suy ra B <
1
12
. □
c Bài 53. Chứng minh rằng với mọi số tự nhiên n ≥ 1, ta luôn có
A =
Å
1 +
1
1 · 3
ãÅ
1 +
1
2 · 4
ãÅ
1 +
1
3 · 5
ã
···
Å
1 +
1
n(n + 2)
ã
< 2.
Lời giải.
Với mọi số tự nhiên n ≥ 1, ta có 1 +
1
n(n + 2)
=
n(n + 2) + 1
n(n + 2)
=
n
2
+ 2n + 1
n(n + 2)
=
(n + 1)
2
n(n + 2)
.
Khi đó
A =
2
2
1 · 3
·
3
2
2 · 4
·
4
2
3 · 5
···
(n + 1)
2
n(n + 2)
=
2 · 3 · 4 ···(n + 1)
1 · 2 · 3 ···n
·
2 · 3 · 4 ···(n + 1)
3 · 4 · 5 ···(n + 2)
=
n + 1
1
·
2
n + 2
= 2 ·
n + 2 − 1
n + 2
= 2
Å
1 −
1
n + 2
ã
.
Do đó A < 2. □
c Bài 54. Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta luôn có
B =
Å
1 −
2
6
ãÅ
1 −
2
12
ãÅ
1 −
2
20
ã
···
Å
1 −
2
n(n + 1)
ã
>
1
3
.
Lời giải.
Với mọi số tự nhiên n ≥ 2, ta có 1 −
2
n(n + 1)
=
n(n + 1) − 2
n(n + 1)
=
n
2
+ n − 2
n(n + 1)
=
(n − 1)(n + 2)
n(n + 1)
.
Khi đó
B =
Å
1 −
2
6
ãÅ
1 −
2
12
ãÅ
1 −
2
20
ã
···
Å
1 −
2
n(n + 1)
ã
=
1 · 4
2 · 3
·
2 · 5
3 · 4
·
3 · 6
4 · 5
···
(n − 1)(n + 2)
n(n + 1)
=
1 · 2 · 3 ···(n − 1)
2 · 3 · 4 · n
·
4 · 5 · 6 ···(n + 2)
3 · 4 · 5 ···(n + 1)
=
1
n
·
n + 2
3
=
1
3
Å
1 +
2
n
ã
.
Do đó B >
1
3
. □
90/101 90/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
91
c Bài 55. Rút gọn biểu thức A =
3
2
− 1
5
2
− 1
·
7
2
− 1
9
2
− 1
·
11
2
− 1
13
2
− 1
···
43
2
− 1
45
2
− 1
.
Lời giải.
Ta có
A =
3
2
− 1
5
2
− 1
·
7
2
− 1
9
2
− 1
·
11
2
− 1
13
2
− 1
···
43
2
− 1
45
2
− 1
=
2 · 4
4 · 6
·
6 · 8
8 · 10
·
10 · 12
12 · 14
···
42 · 44
44 · 46
=
2
46
=
1
23
.
□
c Bài 56. Chứng minh rằng A =
2
3
+ 1
2
3
− 1
·
3
3
+ 1
3
3
− 1
·
4
3
+ 1
4
3
− 1
···
9
3
+ 1
9
3
− 1
<
3
2
.
Lời giải.
Ta có
n
3
+ 1
n
3
− 1
=
(n + 1)(n
2
− n + 1)
(n − 1)(n
2
+ n + 1)
=
(n + 1)
(n − 0,5)
2
+ 0,75
(n − 1) [(n + 0,5)
2
+ 0,75]
.
Khi đó
A =
3(1,5
2
+ 0,75)
1(2,5
2
+ 0,75)
·
4(2,5
2
+ 0, 75)
2(3,5
2
+ 0,75)
·
5(3,5
2
+ 0,75)
3(4,5
2
+ 0,75)
···
10(8,5
2
+ 0,75)
8(9,5
2
+ 0,75)
=
3 · 4 · 5 ···10
1 · 2 · 3 ···8
·
1,5
2
+ 0,75
9,5
2
+ 0,75
=
9 · 10
1 · 2
·
3
91
=
3
2
·
90
91
.
Do đó A <
3
2
. □
c Bài 57. Chứng minh rằng với mọi số tự nhiên n ≥ 2, luôn có
B =
2
3
− 1
2
3
+ 1
·
3
3
− 1
3
3
+ 1
·
4
3
− 1
4
3
+ 1
···
n
3
− 1
n
3
+ 1
>
2
3
.
Lời giải.
Với mọi số tự nhiên n ≥ 2, ta có
n
3
− 1
n
3
+ 1
=
(n − 1)(n
2
+ n + 1)
(n + 1)(n
2
− n + 1)
=
(n − 1)
(n + 0,5)
2
+ 0,75
(n + 1) [(n − 0,5)
2
+ 0,75]
.
Khi đó
B =
1(2,5
2
+ 0,75)
3(1,5
2
+ 0,75)
·
2(3,5
2
+ 0,75)
4(2,5
2
+ 0, 75)
·
3(4,5
2
+ 0,75)
5(3,5
2
+ 0,75)
···
(n − 1)
(n + 0,5)
2
+ 0,75
(n + 1) [(n − 0,5)
2
+ 0,75]
=
1 · 2 · 3 ···(n − 1)
3 · 4 · 5 ···(n + 1)
·
(n + 0,5)
2
+ 0,75
1,5
2
+ 0,75
=
1 · 2
n · (n + 1)
·
n
2
+ n + 1
3
=
2
3
·
n
2
+ n + 1
n
2
+ n
.
Do đó B >
2
3
. □
c Bài 58. Rút gọn biểu thức P =
1
4
+ 4
5
4
+ 4
9
4
+ 4
···
21
4
+ 4
(3
4
+ 4) (7
4
+ 4) (11
4
+ 4) ···(23
4
+ 4)
.
Lời giải.
Ta có
n
4
+ 4 = (n
2
+ 2)
2
− 4n
2
= (n
2
− 2n + 2)(n
2
+ 2n + 2) =
(n − 1)
2
+ 1
(n + 1)
2
+ 1
.
Khi đó
P =
(0
2
+ 1)(2
2
+ 1)
(2
2
+ 1)(4
2
+ 1)
·
(4
2
+ 1)(6
2
+ 1)
(6
2
+ 1)(8
2
+ 1)
·
(8
2
+ 1)(10
2
+ 1)
(10
2
+ 1)(12
2
+ 1)
···
(20
2
+ 1)(22
2
+ 1)
(22
2
+ 1)(24
2
+ 1)
=
0
2
+ 1
24
2
+ 1
=
1
577
.
□
91/101 91/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
92
c Bài 59. Rút gọn biểu thức
M =
1
a
2
− 5a + 6
+
1
a
2
− 7a + 12
+
1
a
2
− 9a + 20
+
1
a
2
− 11a + 30
.
Lời giải.
Ta có
M =
1
(a − 2)(a − 3)
+
1
(a − 3)(a − 4)
+
1
(a − 4)(a − 5)
+
1
(a − 5)(a − 6)
=
1
a − 3
−
1
a − 2
+
1
a − 4
−
1
a − 3
+
1
a − 5
−
1
a − 4
+
1
a − 6
−
1
a − 5
=
1
a − 6
−
1
a − 2
=
4
(a − 2)(a − 6)
.
□
c Bài 60. Rút gọn biểu thức
Å
n − 1
1
+
n − 2
2
+
n − 3
3
+ ··· +
2
n − 2
+
1
n − 1
ã
:
Å
1
2
+
1
3
+
1
4
+ ··· +
1
n
ã
.
Lời giải.
Ta có
n − 1
1
+
n − 2
2
+
n − 3
3
+ ··· +
2
n − 2
+
1
n − 1
=
n − 1
1
+
n − 2
2
+
n − 3
3
+ ··· +
n − (n − 2)
n − 2
+
n − (n − 1)
n − 1
=
n
1
+
n
2
+
n
3
+ ··· +
n
n − 2
+
n
n − 1
− 1 − 1 − 1 − ··· − 1 − 1
= n +
n
2
+
n
3
+ ··· +
n
n − 1
− (n − 1)
=
n
2
+
n
3
+
n
4
+ ··· +
n
n − 1
+
n
n
= n
Å
1
2
+
1
3
+
1
4
+ ··· +
1
n − 1
+
1
n
ã
.
Do đó
Å
n − 1
1
+
n − 2
2
+
n − 3
3
+ ··· +
2
n − 2
+
1
n − 1
ã
:
Å
1
2
+
1
3
+
1
4
+ ··· +
1
n
ã
= n.
□
c Bài 61. Rút gọn biểu thức
A
B
=
1
1 · (2n − 1)
+
1
3 · (2n − 3)
+
1
5 · (2n − 5)
+ ··· +
1
(2n − 3) · 3
+
1
(2n − 1) · 1
1 +
1
3
+
1
5
+ ··· +
1
2n − 1
.
Lời giải.
Ta có nhận xét
1
k(2n − k)
=
1
2n
Å
1
k
+
1
2n − k
ã
.
Khi đó
A =
1
2n
ïÅ
1
1
+
1
2n − 1
ã
+
Å
1
3
+
1
2n − 3
ã
+ ··· +
Å
1
2n − 3
+
1
3
ã
+
Å
1
2n − 1
+
1
1
ãò
=
1
2n
· 2
Å
1 +
1
3
+
1
5
+ ··· +
1
2n − 1
ã
=
1
n
Å
1 +
1
3
+
1
5
+ ··· +
1
2n − 1
ã
=
B
n
.
92/101 92/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
93
Do đó
A
B
=
1
n
. □
c Bài 62. Cho abc = 1 và a + b + c =
1
a
+
1
b
+
1
c
. Chứng minh rằng trong ba số a, b, c tồn tại một số bằng
1.
Lời giải.
Từ đẳng thức a + b + c =
1
a
+
1
b
+
1
c
suy ra a + b + c =
ab + bc + ca
abc
.
Mà abc = 1 nên a + b + c = ab + bc + ca.
Để chứng minh trong ba số a, b, c tồn tại một số bằng 1, ta cần chứng minh
(a − 1)(b − 1)(c − 1) = 0.
Ta có
(a − 1)(b − 1)(c − 1) = (ab − a − b + 1)(c − 1) = abc − ab − ac + a − bc + b + c − 1
= (abc − 1) + (a + b + c) − (ab + bc + ca).
Vì abc = 1 và a + b + c = ab + bc + ca nên biểu thức trên bằng 0.
Do đó, tồn tại một trong ba thừa số a − 1, b − 1, c − 1 bằng 0.
Vậy tồn tại một trong ba số a, b, c bằng 1. □
c Bài 63. Chứng minh rằng nếu x + y + z = a và
1
x
+
1
y
+
1
z
=
1
a
thì tồn tại một trong ba số x, y, z bằng a.
Lời giải.
Từ giả thiết suy ra a = 0. Khi đó
1
x
+
1
y
+
1
z
=
1
x + y + z
hay
xy + yz + zx
xyz
=
1
x + y + z
.
Suy ra (xy + yz + zx)(x + y + z) − xyz = 0. (1)
Ta có
(xy + yz + zx)(x + y + z) − xyz = x
2
y + xy
2
+ xyz + xyz + y
2
z + yz
2
+ x
2
z + xyz + xz
2
− xyz
= x
2
y + xy
2
+ xyz + y
2
z + xyz + yz
2
+ x
2
z + xz
2
= xy(x + y) + yz(x + y) + yz(x + z) + xz(x + z)
= y(x + y)(x + z) + z(x + z)(x + y)
= (x + y)(y + z)(z + x).
Từ (1) suy ra (x + y)(y + z)(z + x) = 0. Do đó x = −y hoặc y = −z hoặc z = −x.
○ Với x = −y thì từ
1
x
+
1
y
+
1
z
=
1
a
suy ra z = a.
○ Với y = −z thì từ
1
x
+
1
y
+
1
z
=
1
a
suy ra x = a.
○ Với z = −x thì từ
1
x
+
1
y
+
1
z
=
1
a
suy ra y = a.
Vậy tồn tại một trong ba số x, y, z bằng a. □
c Bài 64. Các biểu thức x + y + z và
1
x
+
1
y
+
1
z
có thể cùng có giá trị bằng 0 được hay không?
Lời giải.
93/101 93/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
94
Giả sử x + y + z = 0 và
1
x
+
1
y
+
1
z
= 0.
Ta có
1
x
+
1
y
+
1
z
=
xy + yz + zx
xyz
. Mà
1
x
+
1
y
+
1
z
= 0 nên xy + yz + zx = 0.
Từ x + y + z = 0 suy ra (x + y + z)
2
= 0 hay x
2
+ y
2
+ z
2
+ 2(xy + yz + zx) = 0.
Vì xy + yz + zx = 0 nên x
2
+ y
2
+ z
2
= 0, suy ra x = y = z = 0. Điều này vô lí vì khi đó
1
x
,
1
y
,
1
z
không xác định.
Vậy x + y + z và
1
x
+
1
y
+
1
z
không thể cùng có giá trị bằng 0. □
c Bài 65. Tính giá trị của biểu thức M =
1
x + 2
+
1
y + 2
+
1
z + 2
, biết rằng
2a = by + cz; 2b = ax + cz; 2c = ax + by và a + b + c = 0.
Lời giải.
Cộng theo từng vế ba đẳng thức 2a = by + cz; 2b = ax + cz; 2c = ax + by ta được
a + b + c = ax + by + cz = ax + 2a = a(x + 2).
Suy ra
1
x + 2
=
a
a + b + c
.
Tương tự,
1
y + 2
=
b
a + b + c
,
1
z + 2
=
c
a + b + c
.
Do đó M =
a + b + c
a + b + c
= 1. □
c Bài 66. Cho abc = 2. Rút gọn biểu thức M =
a
ab + a + 2
+
b
bc + b + 1
+
2c
ac + 2c + 2
.
Lời giải.
Với abc = 2, ta có
M =
a
ab + a + 2
+
b
bc + b + 1
+
2c
ac + 2c + 2
=
a
ab + a + 2
+
ab
abc + ab + a
+
2c
ac + 2c + abc
=
a
a + ab + 2
+
ab
a + ab + 2
+
2
a + ab + 2
=
a + ab + 2
a + ab + 2
= 1.
□
c Bài 67. Cho abc = 1. Rút gọn biểu thức N =
a
ab + a + 1
+
b
bc + b + 1
+
c
ac + c + 1
.
Lời giải.
Với abc = 1, ta có
N =
a
ab + a + 1
+
b
bc + b + 1
+
c
ac + c + 1
=
a
a + ab + 1
+
ab
abc + ab + a
+
c
ac + c + abc
=
a
a + ab + 1
+
ab
a + ab + 1
+
1
a + ab + 1
=
a + ab + 1
a + ab + 1
= 1.
□
c Bài 68. Cho
a
c
=
a − b
b − c
, a = 0, c = 0, a − b = 0, b − c = 0. Chứng minh rằng
1
a
+
1
a − b
=
1
b − c
−
1
c
.
Lời giải.
94/101 94/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
95
Từ giả thiết suy ra a(b − c) = c(a − b). (1)
Ta có
1
c
+
1
a − b
=
a − b + c
c(a − b)
. (2)
1
b − c
−
1
a
=
a − b + c
a(b − c)
. (3)
Từ (1), (2), (3) suy ra điều phải chứng minh. □
c Bài 69. Cho a + b + c = 0 (a = 0, b = 0, c = 0). Rút gọn biểu thức A =
a
2
bc
+
b
2
ca
+
c
2
ab
.
Lời giải.
Ta có
A =
a
2
bc
+
b
2
ca
+
c
2
ab
=
a
3
+ b
3
+ c
3
abc
=
(a + b + c)(a
2
+ b
2
+ c
2
− ab − bc − ca) + 3abc
abc
=
3abc
abc
= 3.
□
c Bài 70. Cho a + b + c = 0 (a = 0, b = 0, c = 0). Rút gọn biểu thức
B =
a
2
a
2
− b
2
− c
2
+
b
2
b
2
− c
2
− a
2
+
c
2
c
2
− a
2
− b
2
.
Lời giải.
Từ a + b + c = 0 suy ra b + c = −a. Khi đó b
2
+ 2bc + c
2
= a
2
hay a
2
− b
2
− c
2
= 2bc.
Tương tự, b
2
− c
2
− a
2
= 2ca, c
2
− a
2
− b
2
= 2ab.
Do đó
B =
a
2
2bc
+
b
2
2ca
+
c
2
2ab
=
a
3
+ b
3
+ c
3
2abc
=
(a + b + c)(a
2
+ b
2
+ c
2
− ab − bc − ca) + 3abc
2abc
=
3abc
2abc
=
3
2
.
□
c Bài 71. Cho biết a + b + c = 0, hãy tính giá trị của biểu thức
A =
Å
a − b
c
+
b − c
a
+
c − a
b
ãÅ
c
a − b
+
a
b − c
+
b
c − a
ã
.
Lời giải.
Đặt M =
a − b
c
+
b − c
a
+
c − a
b
, ta có
M ·
c
a − b
= 1 +
c
a − b
Å
b − c
a
+
c − a
b
ã
= 1 +
c
a − b
·
b
2
− bc + ac − a
2
ab
= 1 +
c
a − b
·
(a − b)(c − a − b)
ab
= 1 +
2c
2
ab
= 1 +
2c
3
abc
.
Tương tự, M ·
a
b − c
= 1 +
2a
3
abc
, M ·
b
c − a
= 1 +
2b
3
abc
.
Do đó
A = 3 +
2(a
3
+ b
3
+ c
3
)
abc
= 3 +
2(a + b + c)(a
2
+ b
2
+ c
2
− ab − bc − ca) + 6abc
abc
= 3 +
6abc
abc
= 3 + 6 = 9.
□
95/101 95/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
96
c Bài 72. Chứng minh rằng, nếu (a
2
− bc)(b − abc) = (b
2
− ac)(a − abc) và các số a, b, c, a − b khác 0 thì
1
a
+
1
b
+
1
c
= a + b + c.
Lời giải.
Từ giả thiết suy ra
a
2
b − a
3
bc − b
2
c + ab
2
c
2
= ab
2
− ab
3
c − a
2
c + a
2
bc
2
⇒ ab(a − b) + c(a
2
− b
2
) = abc
2
(a − b) + abc(a
2
− b
2
)
⇒ (a − b)(ab + ac + bc) = abc(a − b)(a + b + c).
Chia cả hai vế cho abc(a − b) = 0 ta được điều phải chứng minh. □
c Bài 73. Cho a + b + c = 0, x + y + z = 0,
a
x
+
b
y
+
c
z
= 0. Chứng minh rằng
ax
2
+ by
2
+ cz
2
= 0.
Lời giải.
Từ x + y + z = 0 suy ra x
2
= (y + z)
2
, y
2
= (z + x)
2
, z
2
= (x + y)
2
.
Do đó
ax
2
+ by
2
+ cz
2
= a(y + z)
2
+ b(z + x)
2
+ c(x + y)
2
= a(y
2
+ 2yz + z
2
) + b(z
2
+ 2zx + x
2
) + c(x
2
+ 2xy + y
2
)
= x
2
(b + c) + y
2
(a + c) + z
2
(a + b) + 2(ayz + bzx + cxy). (1)
Thay b + c = −a, a + c = −b, a + b = −c (do a + b + c = 0) và thay ayz + bzx + cxy = 0
do
a
x
+
b
y
+
c
z
= 0
vào
(1) ta được
ax
2
+ by
2
+ cz
2
= −ax
2
− by
2
− cz
2
.
Cho nên 2ax
2
+ 2by
2
+ 2cz
2
= 0 hay ax
2
+ by
2
+ cz
2
= 0. □
c Bài 74. Cho
xy + 1
y
=
yz + 1
z
=
zx + 1
x
. Chứng minh rằng x = y = z hoặc x
2
y
2
z
2
= 1.
Lời giải.
Từ giả thiết suy ra x +
1
y
= y +
1
z
= z +
1
x
. Do đó
x − y =
1
z
−
1
y
=
y − z
yz
; y − z =
1
x
−
1
z
=
z − x
xz
; z − x =
1
y
−
1
x
=
x − y
xy
.
Suy ra (x − y)(y − z)(z − x) =
(x − y)(y − z)(z − x)
x
2
y
2
z
2
.
Cho nên (x − y)(y − z)(z − x)(x
2
y
2
z
2
− 1) = 0.
Vậy x − y = 0; y − z = 0; z − x = 0; x
2
y
2
z
2
− 1 = 0 hay x = y = z; x
2
y
2
z
2
= 1. □
c Bài 75. Cho
a
b + c
+
b
c + a
+
c
a + b
= 1. Chứng minh rằng
a
2
b + c
+
b
2
c + a
+
c
2
a + b
= 0.
Lời giải.
Nhân cả hai vế của
a
b + c
+
b
c + a
+
c
a + b
= 1 với a + b + c ta được
a
2
+ a(b + c)
b + c
+
b
2
+ b(c + a)
c + a
+
c
2
+ c(a + b)
a + b
= a + b + c.
Suy ra
a
2
b + c
+ a +
b
2
c + a
+ b +
c
2
a + b
+ c = a + b + c hay
a
2
b + c
+
b
2
c + a
+
c
2
a + b
= 0. □
96/101 96/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
97
c Bài 76. Cho
a
b − c
+
b
c − a
+
c
a − b
= 0. Chứng minh rằng
a
(b − c)
2
+
b
(c − a)
2
+
c
(a − b)
2
= 0.
Lời giải.
Từ
a
b − c
+
b
c − a
+
c
a − b
= 0 suy ra
a
b − c
=
b
a − c
+
c
b − a
=
b
2
− ab + ac − c
2
(a − b)(c − a)
.
Nhân hai vế với
1
b − c
ta được
a
(b − c)
2
=
b
2
− ab + ac − c
2
(a − b)(b − c)(c − a)
.
Tương tự,
b
(c − a)
2
=
c
2
− bc + ba − a
2
(b − c)(c − a)(a − b)
;
c
(a − b)
2
=
a
2
− ca + cb − b
2
(c − a)(a − b)(b − c)
.
Cộng từng vế ba đẳng thức trên ta được điều phải chứng minh. □
c Bài 77. Cho x +
1
x
= a. Tính các biểu thức sau theo a
x
2
+
1
x
2
;a) x
3
+
1
x
3
;b) x
4
+
1
x
4
;c) x
5
+
1
x
5
.d)
Lời giải.
a) Từ x +
1
x
= a, suy ra x
2
+ 2 +
1
x
2
= a
2
hay x
2
+
1
x
2
= a
2
− 2.
b) Ta có x
3
+
1
x
3
=
Å
x +
1
x
ã
3
− 3x ·
1
x
Å
x +
1
x
ã
= a
3
− 3a.
c) Ta có x
4
+
1
x
4
=
Å
x
2
+
1
x
2
ã
2
− 2x
2
·
1
x
2
= (a
2
− 2)
2
− 2 = a
4
− 4a
2
+ 2.
d) Ta có
Å
x
2
+
1
x
2
ãÅ
x
3
+
1
x
3
ã
= x
5
+
1
x
+ x +
1
x
5
.
Suy ra
x
5
+
1
x
5
=
Å
x
2
+
1
x
2
ãÅ
x
3
+
1
x
3
ã
−
Å
x +
1
x
ã
= (a
2
− 2)(a
3
− 3a) − a = a
5
− 5a
3
+ 5a.
□
c Bài 78. Cho
Å
x
2
−
1
x
2
ã
:
Å
x
2
+
1
x
2
ã
= a. Tính giá trị của biểu thức
M =
Å
x
4
−
1
x
4
ã
:
Å
x
4
+
1
x
4
ã
theo a.
Lời giải.
Từ giả thiết suy ra a = 1 và
x
4
− 1
x
4
+ 1
= a ⇒ x
4
− 1 = ax
4
+ a ⇒ (1 − a)x
4
= a + 1 ⇒ x
4
=
a + 1
1 − a
.
Thay vào M ta được
M =
Å
a + 1
1 − a
−
1 − a
a + 1
ã
:
Å
a + 1
1 − a
+
1 − a
a + 1
ã
=
(a + 1)
2
− (1 − a)
2
(a + 1)
2
+ (1 − a)
2
=
4a
2a
2
+ 2
=
2a
a
2
+ 1
.
□
97/101 97/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
98
c Bài 79. Cho x
2
− 4x + 1 = 0. Tính giá trị của biểu thức A =
x
4
+ x
2
+ 1
x
2
.
Lời giải.
Cách 1. Ta có
x
2
− 4x + 1 = 0 ⇒ x
2
− x + 1 = 3x ⇒
x
2
− x + 1
x
= 3.
Mặt khác
A =
x
4
+ x
2
+ 1
x
2
=
x
2
− x + 1
x
·
x
2
+ x + 1
x
= 3 ·
x
2
+ x + 1
x
.
Ta thấy
x
2
+ x + 1
x
=
x
2
− x + 1
x
+
2x
x
= 3 + 2 = 5.
Vậy A = 3 · 5 = 15. Cách 2. Ta có A =
x
4
+ x
2
+ 1
x
2
=
(x
2
+ 1)
2
− x
x
2
=
(4x)
2
− x
2
x
2
= 15. □
c Bài 80. Cho
x
x
2
− x + 1
= a. Tính M =
x
2
x
4
+ x
2
+ 1
theo a.
Lời giải.
Trường hợp 1. Với x = 0 thì a = 0 và M = 0.
Trường hợp 2. Với x = 0 thì a = 0. Ta có
M =
x
2
x
4
+ x
2
+ 1
=
x
x
2
− x + 1
·
x
x
2
+ x + 1
. (1)
Lại có
x
2
+ x + 1
x
=
x
2
− x + 1
x
+
2x
x
=
1
a
+ 2 =
1 + 2a
a
. (2)
Từ (1) và (2) suy ra M = a ·
a
1 + 2a
=
a
2
1 + 2a
.
Vậy M =
a
2
1 + 2a
. □
c Bài 81. Cho x =
b
2
+ c
2
− a
2
2bc
, y =
a
2
− (b − c)
2
(b + c)
2
− a
2
. Tính giá trị của biểu thức x + y + xy.
Lời giải.
Ta xét biểu thức x + y + xy + 1 = x(y + 1) + (y + 1) = (x + 1)(y + 1).
Từ giả thiết suy ra x + 1 =
(b + c)
2
− a
2
2bc
; y + 1 =
4bc
(b + c)
2
− a
2
.
Do đó, (x + 1)(y + 1) = 2.
Vậy x + y + xy + 1 = 2, suy ra x + y + xy = 1. □
c Bài 82. Tìm hai số tự nhiên a và b sao cho a − b =
a
b
.
Lời giải.
Đặt
a − b = n, (1)
a
b
= n, (2)
trong đó a, b, n ∈ N, b = 0.
Từ (1), (2) ta có bn − b = n nên b(n − 1) = n.
98/101 98/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
99
○ Nếu n = 1 thì a = b. Khi đó, theo (1) thì n = 0, loại.
○ Với n = 1, ta có
b =
n
n − 1
= 1 +
1
n − 1
. (3)
Vì b ∈ N nên n − 1 là ước của 1, suy ra (n − 1) ∈ {−1; 1}.
◦ Với n − 1 = −1 hay n = 0, từ (3) suy ra b = 0, loại.
◦ Với n − 1 = 1 hay n = 2, từ (3), (2) suy ra b = 2, a = 4.
Thử lại ta thấy 4 − 2 =
4
2
.
Vậy a = 4, b = 2. □
c Bài 83. Tìm hai số tự nhiên a và b sao cho a − b =
a
2b
.
Lời giải.
Đặt
a − b = n, (1)
a
2b
= n, (2)
trong đó a, b, n ∈ N, b = 0.
Từ (1), (2) ta có 2bn − b = n nên b(2n − 1) = n, suy ra
b =
n
2n − 1
. (3)
○ Với n = 0, từ (3) suy ra b = 0, loại.
○ Với n ≥ 1, ta thấy n ≤ n + n − 1 = 2n − 1.
Vì b ∈ N nên
n
2n − 1
∈ N, suy ra n = 2n − 1 hay n = 1. Từ (3), (1) suy ra b = 1 và a = 2.
Thử lại ta thấy 2 − 1 =
2
2 · 1
.
Vậy a = 2, b = 1. □
c Bài 84. Cho hai số nguyên dương a và b, trong đó a > b. Tìm số nguyên dương c khác b sao cho
a
3
+ b
3
a
3
+ c
3
=
a + b
a + c
.
Lời giải.
Do a + b = 0, a + c = 0 nên từ
a
3
+ b
3
a
3
+ c
3
=
a + b
a + c
suy ra
a
3
+ b
3
a + b
=
a
3
+ c
3
a + c
⇔ a
2
− ab + b
2
= a
2
− ac + c
2
⇔ b
2
− c
2
= ab − ac
⇔ (b + c)(b − c) = a(b − c).
Do b − c = 0 nên b + c = a.
Vậy c = a − b. □
99/101 99/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
100
c Bài 85. Cho dãy số a
1
, a
2
, a
3
, . . . sao cho
a
2
=
a
1
− 1
a
1
+ 1
; a
3
=
a
2
− 1
a
2
+ 1
; . . . ; a
n
=
a
n−1
− 1
a
n−1
+ 1
.
a) Chứng minh rằng a
1
= a
5
.
b) Xác định năm số đầu của dãy, biết rằng a
101
= 3.
Lời giải.
a) Ta có
a
3
=
Å
a
1
− 1
a
1
+ 1
− 1
ã
:
Å
a
1
− 1
a
1
+ 1
+ 1
ã
=
−2
a
1
+ 1
:
2a
1
a
1
+ 1
= −
1
a
1
.
a
4
=
Å
−
1
a
1
− 1
ã
:
Å
−
1
a
1
+ 1
ã
=
−1 − a
1
a
1
:
a
1
− 1
a
1
=
1 + a
1
1 − a
1
.
a
5
=
Å
1 + a
1
1 − a
1
− 1
ã
:
Å
1 + a
1
1 − a
1
+ 1
ã
=
2a
1
1 − a
1
:
2
1 − a
1
=
2a
1
2
= a
1
.
b) Theo câu trên ta suy ra a
1
= a
5
= a
9
= ··· = a
1001
= 3.
Từ đó ta tính được a
1
= 3; a
2
=
1
2
; a
3
= −
1
3
; a
4
= −2; a
5
= 3.
□
c Bài 86. Tìm phân số
m
n
khác 0 và số tự nhiên k, biết rằng
m
n
=
m + k
nk
.
Lời giải.
Từ giả thiết suy ra mnk = mn + nk. Chia hai vế cho n, ta được mk = m + k. Do đó m = k (m − 1).
Như vậy m chia hết cho m − 1. Từ đó ta tìm được m = 0 (loại) và m = 2. Khi đó k = 2.
Vậy phân số phải tìm có dạng
2
n
và k = 2. □
c Bài 87. Cho hai số tự nhiên a và b (a < b). Tìm tổng các phân số tối giản có mẫu bằng 7, mỗi phân số
lớn hơn a nhưng nhỏ hơn b.
Lời giải.
Tổng phải tìm bằng A − B, trong đó
A =
Å
a +
1
7
ã
+
Å
a +
2
7
ã
+ ··· +
Å
b −
2
7
ã
+
Å
b −
1
7
ã
=
1
7
[(7a + 1) + (7a + 2) + ··· + (7b − 2) + (7b − 1)]
=
1
14
[(7a + 1) + (7b − 1)] [(7b − 1) − (7a + 1) + 1]
=
1
2
(a + b)(7b − 7a − 1).
B = (a + 1) + (a + 2) + ··· + (b − 2) + (b − 1)
=
1
2
[(a + 1) + (b − 1)] [(b − 1) − (a + 1) + 1]
=
1
2
(a + b)(b − a − 1).
Tính hiệu A − B ta được 3(b
2
− a
2
). □
100/101 100/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
101
c Bài 88. Mức sản xuất của một xí nghiệp năm 2001 tăng a% so với năm 2000, năm 2002 tăng b% so với
năm 2001. Mức sản xuất của xí nghiệp đó năm 2002 tăng bao nhiêu phần trăm so với năm 2000?
Lời giải.
Giả sử mức sản xuất của xí nghiệp năm 2000 là 1 thì mức sản xuất năm 2001 là 1 +
a
100
, mức sản xuất năm 2002
là
1 +
a
100
Å
1 +
b
100
ã
= 1 +
b
100
+
a
100
+
ab
10000
,
tăng so với năm 2000 là
a + b
100
+
ab
10000
hay
Å
a + b +
ab
100
ã
%. □
c Bài 89. Một số a tăng m%, sau đó lại giảm đi n% (a, m, n là các số dương) thì được số b. Tìm liên hệ
giữa m và n để b > a.
Lời giải.
Ta có b = a
1 +
m
100
1 −
n
100
nên b − a = a
h
1 +
m
100
1 −
n
100
− 1
i
.
Điều kiện để b > a là
1 +
m
100
1 −
n
100
> 1.
Rút gọn điều kiện trên ta được 100(m − n) > mn. □
c Bài 90. Chứng minh tổng sau không là số nguyên với mọi số tự nhiên n ≥ 2
A =
1
2
+
1
3
+
1
4
+ ··· +
1
n
.
Lời giải.
Gọi k là số nguyên lớn nhất sao cho 2
k
≤ n. Chọn mẫu chung là 2
k
P trong đó P là tích các số lẻ không vượt quá
n. Chỉ có duy nhất một thừa số phụ
của phân số
1
2
k
là số lẻ, còn mọi thừa số phụ khác đều chẵn.
Như vậy, sau khi quy đồng mẫu, mẫu là số chẵn, tử là số lẻ. Do đó A không là số nguyên. □
c Bài 91. Chứng minh tổng sau không là số nguyên với mọi số tự nhiên n ≥ 1
B =
1
3
+
1
5
+
1
7
+ ··· +
1
2n + 1
.
Lời giải.
Gọi k là số nguyên lớn nhất sao cho 3
k
≤ 2n + 1. Chọn mẫu chung là 3
k
P trong đó P là tích các thừa số nguyên
tố lẻ không vượt quá 2n + 1. Chỉ có duy nhất một thừa số phụ
của phân số
1
3
k
không chia hết cho 3, còn mọi
thừa số phụ khác đều chia hết cho 3.
Như vậy, sau khi quy đồng mẫu, mẫu là số chia hết cho 3, tử là số không chia hết cho 3. Do đó B không là số
nguyên. □
101/101 101/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641
| 1/101
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

1
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Chûúng 6
PHÂN THỨC ĐẠI SỐ
PHÂN THỨC ĐẠI SỐ Baâi 21
PHÂN THỨC ĐẠI SỐ A
TRỌNG TÂM KIẾN THỨC
1 Phân thức đại số A
Một phân thức đại số (hay nói gọn là phân thức) là biểu thức có dạng
, trong đó A, B là những đa thức và B
B khác đa thức 0, A được gọi là tử thức (hay tử), B được gọi là mẫu thức (hay mẫu).
Nhận xét. Mỗi đa thức cũng được coi là một phân thức với mẫu thức bằng 1. Đặc biệt, số 0 và số 1 cũng là phân thức đại số.
2 Hai phân thức bằng nhau A C Hai phân thức và
gọi là bằng nhau nếu A · D = B · C. B D A C = nếu A · D = B · C. B D
3 Điều kiện xác định và giá trị của phân thức tại một giá trị đã cho của biến
Khi thay các biến của phân thức đại số bằng các giá trị nào đó (sao cho phân thức xác định), rồi thực hiện các
phép tính thì ta nhận được giá trị của phân thức đại số đó tại các giá trị của biến.
Như vậy, để tính giá trị của phân thức tại những giá trị cho trước của biến ta thay các giá trị cho trước của
biến vào phân thức đó rồi tính giá trị của biểu thức số nhận được. A
Điều kiện xác định của phân thức
là điều kiện của biến để mẫu thức B khác 0. B
Ta chỉ cần quan tâm đến điều kiện xác định khi tính giá trị của phân thức.
Khi xét phân thức mà không nói gì thêm thì ta hiểu các biến chỉ nhận các giá trị làm cho phân thức xác định. A B CÁC DẠNG BÀI TẬP
Dạng 1. Nhận biết phân thức, xác định tử thức và mẫu thức 1/101 1/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 2 21. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Ví dụ 1. Chỉ ra các phân thức trong các biểu thức sau đây √ 2x + 1 ab √ x ; ; x2 + 2x + 1; 5; . x − 3 a + b x + 1 Lời giải. 2x + 1 ab √
Trong các biểu thức trên, ; ; x2 + 2x + 1; 5 là phân thức. x − 3 a + b √x √ Biểu thức
không phải là phân thức, vì
x không phải là đa thức. □ x + 1 c Ví dụ 2.
a) Cách viết nào sau đây không cho một phân thức? 6y3z xy + z y + z 0 ; ; ; ; x3 − xy. x2 −3 0 x + 1
b) Viết mẫu thức của mỗi phân thức trong các cách viết trên. Lời giải. y + z
a) Trong các cách viết trên, không phải là phân thức 0 6y3z xy + z 0 b) Các phân thức ; ;
; x3 − xy có mẫu lần lượt là x2; −3; x + 1; 1. x2 −3 x + 1 □
c Ví dụ 3. Trong các cặp phân thức sau, cặp phân thức nào có cùng mẫu thức? −20x 4x3 5x − 10 5x − 10 5x + 10 4 − 2x a) và ; b) và ; c) và . 3y2 5y2 x2 + 1 x2 − 1 4x − 8 4(x − 2) Lời giải. 5x + 10 4 − 2x
Cặp phân thức có cùng mẫu thức là và . □ 4x − 8 4(x − 2)
c Ví dụ 4. Trong những biểu thức sau, biểu thức nào là phân thức? 1 2x + 1 xy x2y + xy2 x2 − 2 a) . b) . x c) . d) . e) . x + 4 x + 2y x2 + 1 x − y 1 x Lời giải. 2x + 1
a) Do 2x + 1 và x + 4 là các đa thức và đa thức x + 4 khác đa thức 0 nên biểu thức là phân thức. x + 4 xy
b) Do xy và x + 2y là các đa thức và đa thức x + 2y khác đa thức 0 nên biểu thức là phân thức. x + 2y 1 1 c) Do biểu thức
không phải là đa thức nên biểu thức x
không phải là phân thức. x x2 + 1 x2y + xy2
d) Do x2y + xy2 và x − y là các đa thức và đa thức x − y khác đa thức 0 nên biểu thức là phân thức. x − y 2/101 2/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 3
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 1 x2 − 2 e) Do biểu thức
không phải là đa thức nên biểu thức
không phải là phân thức. x 1 x □
Dạng 2. Điều kiện xác định và giá trị của phân thức tại một giá trị đã cho của biến
c Ví dụ 5. Viết điều kiện xác định của mỗi phân thức sau 3x + 4 x − y x − 3 1 xy2 a) ; b) ; c) ; d) ; e) . x − 2 x + y x + 2 2a + 4 x − 2y Lời giải.
a) Phân thức xác định khi x − 2 ̸= 0 hay x ̸= 2.
b) Phân thức xác định khi x + y ̸= 0 (nghĩa là tại các giá trị của x và y thoả mãn x + y ̸= 0).
c) Điều kiện xác định của phân thức là x + 2 ̸= 0 hay x ̸= −2. 1
d) Điều kiện xác định của phân thức
là 2a + 4 ̸= 0 hay a ̸= −2. 2a + 4 xy2
e) Điều kiện xác định của phân thức
là x − 2y ̸= 0 hay x ̸= 2y. x − 2y □ x + 1
c Ví dụ 6. Viết điều kiện xác định của phân thức
và tính giá trị của phân thức tại x = 2. x − 1 Lời giải.
Điều kiện xác định của phân thức là x − 1 ̸= 0 hay x ̸= 1. 2 + 1
Giá trị của phân thức tại x = 2 là = 3. □ 2 − 1 x2 − x − 1
c Ví dụ 7. Tính giá trị của phân thức tại x = 2; x = 1. x2 + 3x Lời giải. 22 − 2 − 1 1
○ Tại x = 2, phân thức có giá trị là = . 22 + 3 · 2 10 12 − 2 − 1 −1
○ Tại x = 1, phân thức có giá trị là = . 12 + 3 · 1 4 □ x2 − 1
c Ví dụ 8. Cho phân thức P = . 2x + 1
a) Tính giá trị của phân thức tại x = 0; x = 1; x = 2. 1 b) Tại x = −
thì phân thức có xác định không? Tại sao? 2 Lời giải. 3/101 3/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 4 21. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 0 − 1 a) Tại x = 0, P = = −1. 2 · 0 + 1 12 − 1 Tại x = 1, P = = 0. 2 · 1 + 1 22 − 1 3 Tại x = 2, P = = . 2 · 2 + 1 5 1 Å 1 ã b) Với x = −
thì giá trị của mẫu thức là 2 · −
+ 1 = −1 + 1 = 0 nên phân thức không xác định. 2 2 □
c Ví dụ 9. Tìm giá trị của phân thức x2 − 2x + 1 xy − 3y2 a) tại x = −3, x = 1; b) tại x = 3, y = −1. x + 2 x + y Lời giải. a) Với x = −3, ta có (−3)2 − 2(−3) + 1 9 + 6 + 1 16 = = = −16. −3 + 2 −1 −1 Với x = 1, ta có 12 − 2 · 1 + 1 0 = = 0. 1 + 2 3
b) Với x = 3, y = −1, ta có 3 · −1 − 3 · (−1)2 3 · −1 − 3 · 1 −3 − 3 −6 = = = = −3. 3 + −1 2 2 2 □
Dạng 3. Hai phân thức bằng nhau
c Ví dụ 10. Mỗi cặp phân thức sau đây có bằng nhau không? Tại sao? xy2 xy xy − y xy − x 3x2 − 9x 3x a) và ; b) và ; c) A = và B = ; xy + y x + 1 x y x2 − 9 x + 3 x x2 − x 3 + x 1 x + y 1 d) và ; e) và ; f) và ; 5 5x − 5 3 + 2x 2 x2 − y2 x − y x 1 1 1 − x 1 + x 1 g) và ; h) = ; i) = . x2 − 1 x − 1 x2 + x + 1 1 − x3 1 − x2 1 − x Lời giải.
®(xy2) · (x + 1) = x2y2 + xy2 a) Ta có (xy + y) · xy = x2y2 + xy2.
Do đó (xy2) · (x + 1) = (xy + y) · xy. xy2 xy Vậy = ; xy + y x + 1 ®(xy − y) · y = xy2 − y2 b) Ta có . x · (xy − x) = x2y − x2.
Do đó (xy − y) · y ̸= x · (xy − x). xy − y xy − x Vậy hai phân thức và không bằng nhau. x y 4/101 4/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 5
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC ®
3x2 − 9x · (x + 3) = 3x3 + 9x2 − 9x2 − 27x = 3x3 − 27x c) Ta có x2 − 9 · 3x = 3x3 − 27x.
Vậy 3x2 − 9x · (x + 3) = x2 − 9 · 3x. 3x2 − 9x 3x Do đó = , hay A = B. x2 − 9 x + 3
d) Ta có: x · (5x − 5) = 5x2 − 5x và 5 · x2 − x = 5x2 − 5x nên x · (5x − 5) = 5 · x2 − x. x x2 − x Vậy = . 5 5x − 5 3 + x 1
e) Ta có: (3 + x) · 2 = 6 + 2x và (3 + 2x) · 1 = 3 + 2x. Do 6 + 2x ̸= 3 + 2x nên hai phân thức và không 3 + 2x 2 bằng nhau.
f) Ta có: (x + y) · (x − y) = x2 − y2 và x2 − y2 · 1 = x2 − y2 x + y 1
nên (x + y) · (x − y) = x2 − y2 · 1. Vậy = . x2 − y2 x − y
g) Ta có: x · (x − 1) = x2 − 1 và x2 − 1 · 1 = x2 − 1 x 1
nên x · (x − 1) = x2 − 1 · 1. Vậy = . x2 − 1 x − 1 1 1 − x h) Ta có =
vì 1 · (1 − x3) = (1 − x)(x2 + x + 1). x2 + x + 1 1 − x3 1 + x 1
i) Vì (1 + x)(1 − x) = (1 − x2) · 1 nên = . 1 − x2 1 − x □
c Ví dụ 11. Dùng định nghĩa hai phân thức bằng nhau, chứng tỏ rằng: 3y 6xy x + y 3x(x + y)2 x + 1 x2 + 4x + 3 a) = ; b) = ; c) = . 4 8x 3x 9x2(x + y) x + 3 x2 + 6x + 9 Lời giải. 3y 6xy
a) Ta có 3y · 8x = 4 · 6xy nên = . 4 8x x + y 3x(x + y)2
b) Ta có (x + y) · 9x2(x + y) = 3x · 3x(x + y)2 nên = . 3x 9x2(x + y) c) Ta có
(x + 1) x2 + 6x + 9 = (x + 1)(x + 3)2.
(x + 3) · x2 + 4x + 3 = (x + 3)(x + 3)(x + 1) = (x + 1)(x + 3)2.
Do đó (x + 1) x2 + 6x + 9 = (x + 3) · x2 + 4x + 3. x + 1 x2 + 4x + 3 Suy ra = . x + 3 x2 + 6x + 9 □
c Ví dụ 12. Chứng minh đẳng thức x − 2 8 − x3 = . −x x (x2 + 2x + 4) Lời giải. 5/101 5/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 6 21. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
Ta có x2 + 2x + 4 = x2 + 2x + 1 + 3 = (x + 1)2 + 3 > 0 nên x − 2 (x − 2) · x2 + 2x + 4 x3 − 8 8 − x3 = = = . −x −x · (x2 + 2x + 4) −x (x2 + 2x + 4) x (x2 + 2x + 4)
Vế trái bằng vế phải. Đẳng thức đã được chứng minh. □
c Ví dụ 13. Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong đẳng thức A x = x2 − 4 x + 2 Lời giải. Ta có (x + 2) = x · x2 − 4
A · (x + 2) = x · (x − 2) · (x + 2). Suy ra A = x · (x − 2). □
c Ví dụ 14. Dùng tính chất cơ bản của phân thức, hãy điền một đa thức thích hợp vào chỗ trống trong đẳng thức (x + 1)2 . . . = . x2 + x x Lời giải. (x + 1)2 (x + 1)2 (x + 1)2 : (x + 1) x + 1 Ta có = = = . x2 + x x(x + 1) x(x + 1) : (x + 1) x
Vậy đa thức cần tìm là x + 1. □
Dạng 4. Tìm giá trị nhỏ nhất, giá trị lớn nhất của phân thức
○ Với a > 0 (a là hằng số)
P (x) = m + a[F (x)]2 ≥ m; giá trị nhỏ nhất của P (x) bằng m khi F (x) = 0.
P (x) = m − a[F (x)]2 ≤ m; giá trị lớn nhất của P (x) bằng m khi F (x) = 0. a
○ Với a > 0 (a là hằng số), P (x) > 0 thì
nhỏ nhất (hoặc lớn nhất) khi P (x) lớn nhất (hoặc nhỏ P (x) nhất). c Ví dụ 15. x2 + 2x + 3
a) Tìm giá trị nhỏ nhất của phân thức A = . 4 4 − 4x2 + 4x
b) Tìm giá trị lớn nhất của phân thức B = . 5 Lời giải. x2 + 2x + 3 a) A =
có giá trị nhỏ nhất ⇔ x2 + 2x + 3 có giá trị nhỏ nhất. 4
Mà x2 + 2x + 3 = (x + 1)2 + 2 ≥ 2, nên giá trị nhỏ nhất của x2 + 2x + 3 là 2 khi x = −1. 2 1
Vậy giá trị nhỏ nhất của phân thức A là =
, đạt được khi x = −1. 4 2 4 − 4x2 + 4x b) B =
có giá trị lớn nhất ⇔ 4 − 4x2 + 4x có giá trị lớn nhất. 5 6/101 6/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 7
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 1
Mà 4 − 4x2 + 4x = 5 − (2x − 1)2 ≤ 5 nên giá trị lớn nhất của 4 − 4x2 + 4x là 5 khi x = . 2 5 1
Vậy giá trị lớn nhất của B là = 1, đạt được khi x = . 5 2 □ 10
c Ví dụ 16. Tìm giá trị lớn nhất của P = . x2 − 2x + 2 Lời giải.
Tử thức 10 > 0 và mẫu thức x2 − 2x + 2 = (x − 1)2 + 1 > 0 nên P lớn nhất ⇔ x2 − 2x + 2 nhỏ nhất.
Mà x2 − 2x + 2 = (x − 1)2 + 1 ≥ 1, nên giá trị nhỏ nhất của x2 − 2x + 2 là 1 khi x = 1. 10
Vậy giá trị lớn nhất của P là
= 10, đạt được khi x = 1. □ 1 Dạng 5. Vận dụng
c Ví dụ 17. Cho hình chữ nhật ABCD và M N P Q như hình vẽ (các số đo trên hình tính theo đơn vị centimét). A B M N x x + 1 Q x + 1 P D x + 3 C
a) Viết phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật M N P Q.
b) Tính giá trị của phân thức đó tại x = 2 và tại x = 5. Lời giải.
a) Diện tích của hình chữ nhật ABCD là (x + 3) · (x + 1).
Diện tích của hình chữ nhật M N P Q là (x + 1) · x. (x + 3) · (x + 1)
Do đó phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật M N P Q là . (x + 1) · x b) (2 + 3) · (2 + 1) 5
○ Với x = 2, phân thức trên có giá trị là = . (2 + 1) · 2 2 (5 + 3) · (5 + 1) 8
○ Với x = 5, phân thức trên có giá trị là = . (5 + 1) · 5 5 □
c Ví dụ 18. Giá thành trung bình của một chiếc áo sơ mi được một xí nghiệp sản xuất cho bởi biểu thức 0,0002x2 + 120x + 1000 C(x) =
, trong đó x là số áo được sản xuất và C tính bằng nghìn đồng. Tính C khi x x = 100, x = 1000. Lời giải. 7/101 7/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 8 21. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
• Khi x = 100, giá thành trung bình mỗi áo sẽ là
0,0002 · 1002 + 120 · 100 + 1000 2 + 12000 + 1000 13002 C(100) = = = = 130,02. 100 100 100
Vậy giá thành trung bình mỗi áo là 130,02 nghìn đồng.
• Khi x = 1000, giá thành trung bình mỗi áo sẽ là
0,0002 · 10002 + 120 · 1000 + 1000 200 + 120000 + 1000 121200 C(1000) = = = = 121,2. 1000 1000 1000
Vậy giá thành trung bình mỗi áo là 121,2 nghìn đồng. □
c Ví dụ 19. Chị Hà mở một xưởng thủ công với vốn đầu tư ban đầu (xây dựng nhà xưởng, mua máy móc,...)
là 80 triệu. Biết chi phí để sản xuất (tiền mua vật liệu, lương nhân công) của 1 sản phẩm là 15 nghìn đồng.
Gọi x là số sản phẩm mà xưởng của chị Hà làm được.
a) Viết phân thức biểu thị số tiền thực (đơn vị là nghìn đồng) đã bỏ ra để làm được x sản phẩm.
b) Viết phân thức biểu thị chi phí thực (đơn vị là nghìn đồng) để tạo ra 1 sản phẩm theo x.
c) Tính chi phí thực để tạo ra 1 sản phẩm nếu x = 100; x = 1 000. Nhận xét về chi phí thực để tạo ra 1
sản phẩm nếu x ngày càng tăng. Lời giải.
Đổi 80 triệu = 80 000 (nghìn đồng).
a) Phân thức biểu thị số tiền thực (đơn vị là nghìn đồng) đã bỏ ra để làm được x sản phẩm là 80 000 + 15 · x (nghìn đồng). 80 000 + 15 · x
b) Phân thức biểu thị chi phí thực (đơn vị là nghìn đồng) để tạo ra 1 sản phẩm theo x là (nghìn x đồng). c)
○ Chi phí thực để tạo ra 1 sản phẩm nếu x = 100 là
80 000 + 15 · 100 = 815 (nghìn đồng). 100
○ Chi phí thực để tạo ra 1 sản phẩm nếu x = 1 000 là
80 000 + 15 · 1000 = 95 (nghìn đồng). 1000
Vậy chi phí thực để tạo ra 1 sản phẩm sẽ ngày càng giảm nếu x ngày càng tăng. □ A C BÀI TẬP VẬN DỤNG 5x − 2
c Bài 1. Viết tử thức và mẫu thức của phân thức . 3 Lời giải. ○ Tử thức là 5x − 2. ○ Mẫu thức là 3. □ 8/101 8/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 9
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Bài 2. Trong các cặp phân thức sau, cặp phân thức nào có mẫu giống nhau? −20x 4x 3x − 1 3x − 1 x − 1 x + 1 a) và ; b) và ; c) và . 3y2 5y2 x2 + 1 x + 1 3x + 6 3(x + 2) Lời giải. x − 1 x + 1
Phân thức có mẫu giống nhau là và . □ 3x + 6 3(x + 2)
c Bài 3. Trong các biểu thức sau, biểu thức nào là phân thức? √ 3x + 1 x + x ; 2x2 − 5x + 3; . 2x − 1 3x + 2 Lời giải.
3x + 1 ; 2x2 − 5x + 3 là các phân thức. 2x − 1 √ x + x √
không phải là phân thức vì x +
x không phải là một đa thức. □ 3x + 2 0 A
c Bài 4. Cho A là một đa thức khác 0 tùy ý. Hãy giả thích vì sao = 0 và = 1. A A Lời giải. 0 A ○ Ta có = 0 vì 0 = 0 · A. ○ Ta có = 1 vì A = 1 · A. A A □
c Bài 5. Viết điều kiện xác định của các phân thức sau 4x − 1 x − 10 a) ; b) ; c) 3x2 − x + 7; 2x − 6 x + 3y y 4x x + y d) ; e) ; f) . 3y + 3 x2 + 16 x − y Lời giải.
a) Phân thức xác định khi 2x − 6 ̸= 0 hay x ̸= 3.
b) Phân thức xác định khi x + 3y ̸= 0 hay x ̸= −3y.
c) Phân thức 3x2 − x + 7 là một đa thức nên xác định với mọi x. y
d) Điều kiện để giá trị của phân thức
được xác định là 3y + 3 ̸= 0. 3y + 3 4x
e) Điều kiện để giá trị của phân thức
được xác định là x2 + 16 ̸= 0. x2 + 16 x + y
f) Điều kiện để giá trị của phân thức
được xác định là x − y ̸= 0. x − y □ x2 + x − 2
c Bài 6. Viết điều kiện xác định của phân thức
. Tính giá trị của phân thức trên lần lượt tại x3 + 2 x = 0; x = 1; x = 2. Lời giải. x2 + x − 2
Điều kiện xác định của phân thức là x3 + 2 ̸= 0. x3 + 2 9/101 9/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 10 21. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 02 + 0 − 2
○ Giá trị của phân thức tại x = 0 là = −1. 03 + 2 12 + 1 − 2
○ Giá trị của phân thức tại x = 1 là = 0. 13 + 2 22 + 2 − 2 2
○ Giá trị của phân thức tại x = 2 là = . 23 + 2 5 □
c Bài 7. Tìm giá trị của phân thức 3x2 + 3x ab − b2 a) A = tại x = −4; b) B = tại a = 4, b = −2. x2 + 2x + 1 a2 − b2 Lời giải. a) Với x = −4 ta có 3(−4)2 + 3(−4) 3 · 16 − 12 36 A = = = = 4. (−4)2 + 2(−4) + 1 16 − 8 + 1 9
b) Với a = 4 và b = −2 ta có 4 · (−2) − (−2)2 −8 − 4 −12 B = = = = −1. 42 − (−2)2 16 − 4 12 □
c Bài 8. Vì sao các kết luận sau đây đúng? −6 3y x + 3 x2 + 3x 3x(4x + 1) −3x a) = ; b) = ; c) = . −4y 2y2 5 5x 16x2 − 1 1 − 4x Lời giải. −6 3y a) Ta có =
vì −6 · 2y2 = 3y · (−4y). −4y 2y2 x + 3 x2 + 3x b) Ta có =
vì (x + 3) · 5x = (x2 + 3x) · 5. 5 5x 3x(4x + 1) −3x c) Ta có =
vì 3x(4x + 1) · (1 − 4x) = (−3x) · (16x2 − 1). 16x2 − 1 1 − 4x □
c Bài 9. Mỗi cặp phân thức sau có bằng nhau không? Tại sao? 3ac 6c 3ab − 3b2 a − b a) và ; b) và . a3b 2a2b 6b2 2b Lời giải.
a) Ta có 3ac · 2a2b = 6a3bc và a3b · 6c = 6a3bc.
Do đó 3ac · 2a2b = a3b · 6c. 3ac 6c Vậy = . a3b 2a2b
b) (3ab − 3b2) · 2b = 6ab2 − 6b3 và (a − b) · 6b2 = 6ab2 − 6b3.
Do đó (3ab − 3b2) · 2b = (a − b) · 6b2. 3ab − 3b2 a − b Vậy = . 6b2 2b □ 10/101 10/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 11
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Bài 10. Tìm đa thức thích hợp thay vào ? trong các đẳng thức sau 2x + 1 ? x2 + 2x ? a) = ; b) = . x − 1 x2 − 1 x3 + 8 x2 − 2x + 4 Lời giải. 2x + 1 (2x + 1) · (x + 1) 2x2 + 3x + 1 a) Ta có = = . x − 1 (x − 1) · (x + 1) x2 − 1 Vậy ? là 2x2 + 3x + 1. x2 + 2x x(x + 2) x b) Ta có = = . x3 + 8 (x + 2)(x2 − 2x + 4) x2 − 2x + 4 Vậy ? là x. □
c Bài 11. Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng: 3x 15xy 3x − 3y −3 x2 − x + 1 x3 + 1 a) = ; b) = ; c) = . 2 10y 2y − 2x 2 x x · (x + 1) Lời giải. 3x 15xy
a) Ta có: 3x · 10y = 30xy và 2 · 15xy = 30xy nên 3x · 10y = 2 · 15xy. Vậy = . 2 10y
b) Ta có: (3x − 3y) · 2 = 6x − 6y và (2y − 2x) · (−3) = 6x − 6y 3x − 3y −3
nên (3x − 3y) · 2 = (2y − 2x) · (−3). Vậy = . 2y − 2x 2 x2 − x + 1 x3 + 1
c) Ta có: x2 − x + 1 · x · (x + 1) = x · x3 + 1 nên = . x x · (x + 1) □ c Bài 12. A x2 + 3x + 2
a) Tìm đa thức A, cho biết = . x − 2 x2 − 4 M x2 + 3x + 2
b) Tìm đa thức M , cho biết = . x − 1 x + 1 Lời giải. Dùng định nghĩa, ta có a) A = x + 1. b) M = x2 + x − 2. □ 15
c Bài 13. Tìm giá trị lớn nhất của phân thức P , biết P = . x2 − 2x + 4 Lời giải. 15 15 15 Ta có P = = ≤ = 5. x2 − 2x + 4 (x − 1)2 + 3 3
Suy ra giá trị lớn nhất của P là 5 khi x = 1. □ 11/101 11/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 12 21. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 18
c Bài 14. Tìm giá trị nhỏ nhất của phân thức Q, biết Q = . 4x − x2 − 7 Lời giải. 18 18 Q = nhỏ nhất khi lớn nhất, mà −x2 + 4x − 7 x2 − 4x + 7 18 18 18 = ≤ = 6. x2 − 4x + 7 (x − 2)2 + 3 3
Vậy giá trị nhỏ nhất của Q là −6 khi x = 2. □ 6
c Bài 15. Tìm giá trị nguyên của x để phân thức nhận giá trị nguyên. 2x + 1 Lời giải. 6
nhận giá trị nguyên khi 2x + 1 ∈ Ư(6). 2x + 1
Mà 2x + 1 lẻ với x ∈ Z nên 2x + 1 ∈ {1; 3; −1; −3}.
Do đó x ∈ {0; 1; −1; −2}. □ n − 2
c Bài 16. Tìm số nguyên dương n nhỏ nhất sao cho
khác 0 và không tối giản. 2n + 1 Lời giải. n − 2 2n + 1
khác 0 và không tối giản khi nghịch đảo của nó
tồn tại và không tối giản. 2n + 1 n − 2 2n + 1 2(n − 2) + 5 Ta có = . n − 2 n − 2
Vì 5 là số nguyên tố nên phân số không tối giản khi n − 2 là bội của 5, do đó n − 2 = 5 hay n = 7 (vì n là số nguyên dương nhỏ nhất). □
c Bài 17. Một ô tô chạy với vận tốc trung bình là x (km/h).
a) Viết biểu thức biểu thị thời gian ô tô (tính bằng giờ) chạy hết quãng đường 120 km.
b) Tính thời gian ô tô đi được 120 km trong trường hợp vận tốc trung bình của ô tô là 60 km/h. Lời giải.
a) Biểu thức biểu thị thời gian ô tô (tính bằng giờ) chạy hết quãng đường 120 km là 120 t = (h). x
b) Thời gian ô tô đi được 120 km trong trường hợp vận tốc trung bình của ô tô là 60 km/h là 120 t = = 2 (h). 60 □
c Bài 18. Lúc 6 giờ sáng, bác Vinh lái ô tô xuất phát từ Hà Nội đi huyện Tỉnh Gia (Thanh Hoá). Khi đến
Phủ Lý (Hà Nam), cách Hà Nội khoảng 60 km, bác Vinh dừng lại ăn sáng trong 20 phút. Sau đó, bác Vinh
tiếp tục đi về Tĩnh Gia và phải tăng vận tốc thêm 10 km/h để đến nơi đúng giờ dự định.
a) Gọi x (km/h) là vận tốc ô tô đi trên quãng đường Hà Nội - Phủ Lý. Hãy viết các phân thức biểu thị thời
gian bác Vinh chạy xe trên các quãng đường Hà Nội - Phủ Lý và Phủ Lý - Tĩnh Gia, biết rằng quãng
đường Hà Nội - Tĩnh Gia có chiều dài khoảng 200 km.
b) Nếu vận tốc ô tô đi trên quãng đường Hà Nội - Phủ Lý là 60 km/h thì bác Vinh đến Tĩnh Gia lúc mấy 12/101 12/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 13
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC giờ? Lời giải. 60
a) Thời gian bác Vinh chạy xe trên quãng đường Hà Nội - Phủ Lý là (giờ). x
Quãng đường từ Phủ Lý đến Tĩnh Gia là 200 − 60 = 140 (km). 140
Thời gian bác Vinh chạy xe trên quãng đường Phủ Lý - Tĩnh Gia là (giờ). x + 10 60
b) Thời gian bác Vinh chạy xe trên quãng đường Hà Nội - Phủ Lý là = 1 (giờ). 60 140
Thời gian bác Vinh chạy xe trên quãng đường Phủ Lý - Tĩnh Gia là = 2 (giờ). 60 + 10
Vậy bác Vinh đến Tĩnh Gia vào lúc 9 giờ 20 phút. □
c Bài 19. Để loại bỏ x (tính theo %) chất gây ô nhiễm không khí từ khí thải của một nhà máy, ước tính 1,7x cần chi phí là (tỉ đồng). 100 − x
a) Nếu muốn loại bỏ 90% chất gây ô nhiễm từ khí thải nhà máy thì cần chi phí là bao nhiêu? 1,7x
b) Viết điều kiện xác định của phân thức
. Hỏi có thể loại bỏ được 100% chất gây ô nhiễm từ khí 100 − x thải nhà máy hay không? Lời giải. 1,7x · 90
a) Muốn loại bỏ 90% chất gây ô nhiễm từ khí thải nhà máy thì cần chi phí là = 15,3 (tỉ đồng). 100 − 90
b) Điều kiện xác định của phân thức là 100 − x ̸= 0 hay x ̸= 100.
Do đó, không thể loại bỏ được 100% chất thải gây ô nhiễm từ khí thải của nhà máy. □ 13/101 13/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 14 22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Baâi 22
PHÂN THỨC ĐẠI SỐ A
TRỌNG TÂM KIẾN THỨC
1 Tính chất cơ bản của phân thức ○ Tính chất cơ bản:
— Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức 0 thì được một phân
thức mới bằng phân thức đã cho A A · M =
(M là đa thức khác đa thức 0). B B · M
— Nếu chia cả tử và mẫu của một phân thức cho một nhân tử chung của chúng thì được một phân
thức mới bằng phân thức đã cho A A : N = (N là nhân tử chung). B B : N
○ Quy tắc đổi dấu: Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức bằng phân thức đã cho A −A = B −B
2 Rút gọn phân thức
Muốn rút gọn một phân thức, ta có thể:
○ Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung
○ Chia cả tử và mẫu cho nhân tử chung.
Chú ý: Có khi cần đổi dấu ở tử hoặc mẫu để nhận ra nhân tử chung của tử và mẫu (lưu ý tới tính chất A = −(−A)).
3 Quy đồng mẫu nhiều phân thức 14/101 14/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 15
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC ○ Tìm mẫu thức chung
Muốn tìm mẫu thức chung, ta có thể làm như sau:
— Phân tích mẫu thức của các phân thức đã cho thành nhân tử
— Mẫu thức chung cần tìm là một tích mà các nhân tử được chọn như sau:
+ Nhân tử bằng số của mẫu thức chung là tích các nhân tử bằng số ở các mẫu thức của các phân
thức đã cho (nếu các nhân tử bằng số ở các mẫu thức là những số nguyên dương thì nhân tử
bằng số của mẫu thức chung là BCNN của chúng)
+ Với mỗi lũy thừa của cùng một biểu thức có mặt trong các mẫu thức, ta chọn lũy thừa với số mũ cao nhất. ○ Quy đồng mẫu thức
Muốn quy đồng mẫu thức nhiều phân thức, ta có thể làm như sau:
— Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung
— Tìm nhân tử phụ của mỗi phân thức
— Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng. A B CÁC DẠNG BÀI TẬP
Dạng 1. Rút gọn phân thức
c Ví dụ 1. Rút gọn các phân thức sau: 3x2 + 6xy 2x2 − x3 x + 1 x2 − xy a) ; b) ; c) ; d) . 6x2 x2 − 4 x3 + 1 3 (xy2 − y3) Lời giải. 3x2 + 6xy 3x · (x + 2y) x + 2y 2x2 − x3 −x2 · (x − 2) −x2 a) = = . b) = = . 6x2 3x · x x x2 − 4 (x − 2)(x + 2) x + 2 x + 1 x + 1 1 x2 − xy x(x − y) x c) = = . d) = = . x3 + 1 (x + 1) · (x2 − x + 1) x2 − x + 1 3 (xy2 − y3) 3y2(x − y) 3y2 □
c Ví dụ 2. Rút gọn phân thức 2x2y5 3x(x − y)3 3x2y + 4xy2 −3x2 − 6x a) ; b) ; c) ; d) . 3x4y2 2x2(x − y)2 6x + 8y 4 − x2 Lời giải. 2x2y5 2y3 · x2y2 2y3 3x(x − y)3 3(x − y)x(x − y)2 3(x − y) a) = = . b) = = . 3x4y2 3x2 · x2y2 3x2 2x2(x − y)2 2x · x(x − y)2 2x 3x2y + 4xy2 xy · (3x + 4y) xy −3x2 − 6x 3x2 + 6x 3x(x + 2) 3x c) = = . d) = = = . 6x + 8y 2 · (3x + 4y) 2 4 − x2 x2 − 4 (x − 2)(x + 2) x − 2 □
c Ví dụ 3. Rút gọn phân thức x − y 18x2 x2 − 2xy + y2 a) A = ; b) B = ; x−y3 27 (x4 − x3y) 15/101 15/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 16 22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC x2 + 2x x2y − xy2 c) ; d) . x2 + 4x + 4 x2 − y2 Lời giải. Ta có x − y x − y 1 a) A = = = . x−y3 (x − y)(x2 + xy + y2) x2 + xy + y2 18x2 x2 − 2xy + y2 2 · 9x2(x − y)2 2(x − y) b) B = = = . 27 (x4 − x3y) 3 · 9x3(x − y) 3x x2 + 2x x · (x + 2) x c) = = . x2 + 4x + 4 (x + 2)2 x + 2 x2y − xy2 xy · (x − y) xy d) = = . x2 − y2 (x + y) · (x − y) x + y □
c Ví dụ 4. Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao có thể viết: 3 −3 x − y y − x 3x + y 3xy + y2 a) = ; b) = ; c) = . 4 − x x − 4 xy − x x − xy y y2 Lời giải. 3 3 · (x − y) −3 3 −3 a) Ta có: = = . Vậy = . 4 − x (4 − x) · (−1) x − 4 4 − x x − 4 x − y (x − y) · (−1) y − x x − y y − x b) Ta có: = = . Vậy = . xy − x (xy − x) · (−1) x − xy xy − x x − xy 3x + y (3x + y) · y 3xy + y2 c) = = . y y · y y2 □
Dạng 2. Chứng minh đẳng thức
○ Phân tích tử và mẫu của phân thức ở vế trái (vế phải) của đẳng thức đã cho rồi rút gọn phân thức.
○ So sánh kết quả ở hai vế.
c Ví dụ 5. Chứng minh các đẳng thức sau: x − y −1 2x −2x a) = ; b) = ; y2 − x2 x + y −x + 4 x − 4 −12a2bc −4ac 30xy2(x − y) 2y c) = ; d) = . 9ab3 3b2 45xy(x − y)2 3(x − y) Lời giải. x − y −(y − x) −1 2x 2x(−1) −2x a) = = . b) = = . y2 − x2 (y + x)(y − x) x + y −x + 4 (−x + 4)(−1) x − 4 −12a2bc
(−4) · 3 · a · a · b · c −4ac 30xy2(x − y) 2 · 15xyy(x − y) 2y c) = = . d) = = . 9ab3 3 · 3 · a · b · b2 3b2 45xy(x − y)2 3 · 15xy(x − y)(x − y) 3(x − y) □ 16/101 16/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 17
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Ví dụ 6. Chứng minh đẳng thức 2x − 2xy − 3 + 3y 2x − 3 = . 1 − 3y + 3y2 − y3 (1 − y)2 Lời giải. Ta có 2x − 2xy − 3 + 3y 2x(1 − y) − 3(1 − y) (1 − y) · (2x − 3) 2x − 3 = = = . 1 − 3y + 3y2 − y3 (1 − y)3 (1 − y)3 (1 − y)2
Vế trái bằng vế phải, đẳng thức được chứng minh. □ a2 − b2 a − b
c Ví dụ 7. Chứng tỏ hai phân thức và bằng nhau. a2b + ab2 ab Lời giải. a2 − b2 (a − b)(a + b) a − b Ta có = = . □ a2b + ab2 ab(a + b) ab
Dạng 3. Tính giá trị biểu thức
○ Rút gọn biểu thức đã cho.
○ Thay giá trị của biến vào biểu thức đã rút gọn, rồi thực hiện các phép tính. x3 − x
c Ví dụ 8. Cho phân thức P = với x ̸= ±1 và y ̸= ±1. (1 + xy)2 − (x + y)2 a) Rút gọn phân thức P .
b) Tìm giá trị của biểu thức P với x = −12, y = 99. Lời giải. a) Ta có x3 − x x x2 − 1 P = = (1 + xy)2 − (x + y)2
(1 + xy − x − y)(1 + xy + x + y) x(x + 1)(x − 1)
= [(1 − x) − y(1 − x)][(1 + x) + y(1 + x)] x(x + 1)(x − 1) x = =
(1 − x)(1 − y)(1 + x)(1 + y) (1 + y)(y − 1) −12 −12 −3
b) Với x = −12, y = 99, ta được P = = = . (1 + 99)(99 − 1) 100.98 2450 □ x2 − 4y2 · (x − 2y)
c Ví dụ 9. Cho phân thức Q = với x ̸= 2y. x2 − 4xy + 4y2 a) Rút gọn phân thức Q.
b) Tính giá trị của phân thức tại x = −9998 và y = −1. Lời giải. 17/101 17/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 18 22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC a) Rút gọn phân thức x2 − 4y2 · (x − 2y) (x + 2y)(x − 2y)(x − 2y) Q = = = x + 2y x2 − 4xy + 4y2 (x − 2y)2
b) Với x = −9998; y = −1; (x ̸= 2y), ta được
Q = −9998 + 2 · (−1) = −10000 □ y − x
c Ví dụ 10. Biết x > y > 0 và 3x2 + 3y2 = 10xy. Tính P = . y + x Lời giải. Cách 1:
3x2 + 3y2 = 10xy, nên 3x2 − 9xy − xy + 3y2 = 0 ⇔ (3x − y)(x − 3y) = 0.
Mà x > y > 0 nên 3x > y, do đó x = 3y. y − x y − 3y −2y 1 Suy ra P = = = = − . y + x y + 3y 4y 2 Cách 2: x2 + y2 − 2xy 10 Xét P 2 =
mà 3x2 + 3y2 = 10xy hay x2 + y2 = xy nên ta có x2 + y2 + 2xy 3 10 xy − 2xy 4 1 P 2 = 3 = = . 10 16 4 xy + 2xy 3 1
Mặt khác x > y > 0 nên P < 0, do đó p = − . 2 Nhận xét.
○ Cách 1: Phương pháp giải là phân tích đa thức thành nhân tử. Sau đó biểu diễn biến này theo biến kia rồi thay vào phân thức.
○ Cách 2: Bình phương biểu thức cần tính, rồi thay thế. Tuy nhiên phải nhận xét dấu của biểu thức để chọn
giá trị thích hợp, nếu không sẽ mắc sai lầm. □
c Ví dụ 11. Cho a, b thỏa mãn 3a − b = 5. Tính giá trị 5a − b 3b − 3a M = − với a ̸= −2,5; b ̸= 2,5. 2a + 5 2b − 5 Lời giải.
Từ 3a − b = 5, ta có b = 3a − 5. Do đó 5a − (3a − 5) 3(3a − 5) − 3a 2a + 5 6a − 15 M = − = − = 1 − 1 = 0 2a + 5 2(3a − 5) − 5 2a + 5 6a − 15
Nhận xét. Ngoài cách trên, bạn cũng có thể thay 5 = 3a − b vào biểu thức rồi rút gọn, ta cũng được kết quả như trên. □
Dạng 4. Chứng minh giá trị biểu thức không phụ thuộc vào biến
Rút gọn các phân thức đại số để phân thức đã rút gọn không còn chứa biến. 18/101 18/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 19
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Ví dụ 12. Chứng minh giá trị các biểu thức sau đây không phụ thuộc vào giá trị của x và y. x2 − 4y2 a) (x + 2y)(mx − 2my) 9x2 − 1 3xy − 3x + 2y − 2 1 b) + với x ̸= ; y ̸= 1. 1 − 3x y − 1 3 Lời giải. x2 − 4y2 (x + 2y)(x − 2y) 1 a) Ta có = = . (x + 2y)(mx − 2my) (x + 2y)(x − 2y)m m
Vậy giá trị biểu thức không phụ thuộc vào giá trị của x; y. b) Ta có 9x2 − 1 3xy − 3x + 2y − 2 (3x − 1)(3x + 1) 3x(y − 1) + 2(y − 1) + = + 1 − 3x y − 1 −(3x − 1) y − 1 3x + 1 (3x + 2)(y − 1) = + = −3x − 1 + 3x + 2 = 1 −1 y − 1
Vậy giá trị biểu thức không phụ thuộc vào giá trị của x; y. □
Dạng 5. Tìm x thỏa mãn đẳng thức cho trước
○ Đưa đẳng thức về dạng ax = b. b ○ Tìm x = (với a ̸= 0). a b ○ Rút gọn biểu thức . a
c Ví dụ 13. Tìm x, biết a2x + 3ax + 9 = a2 với a ̸= 0; a ̸= −3. Lời giải.
a2x + 3ax + 9 = a2 hay a(a + 3) · x = a2 − 9.
Vì a ̸= 0; a ̸= −3, do đó chia cả hai vế cho a(a + 3) ta được a2 − 9 (a − 3)(a + 3) a − 3 x = = = a(a + 3) a(a + 3) a □ a + b − c a − b + c −a + b + c
c Ví dụ 14. Cho a, b, c là các số thực khác 0 và = = . c b a (a + b)(b + c)(c + a) Đặt x = . Tính giá trị của x. abc Lời giải.
Cộng 2 vào các vế của đẳng thức cho, ta được a + b + c a + b + c a + b + c = = (1) c b a (−c)(−a)(−b) Nếu a + b + c = 0; x = = −1. abc 2a · 2b · 2c
Nếu a + b + c ̸= 0, từ (1) suy ra a = b = c và x = = 8 > 0. abc
Nhận xét. Sẽ là thiếu sót nếu ta chỉ có a = b = c. □ 19/101 19/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 20 22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
Dạng 6. Quy đồng mẫu thức
Xem phần trọng tâm kiến thức.
c Ví dụ 15. Quy đồng mẫu thức của các phân thức sau: −7y 11z 5x 6 11 a) , , b) , 12xz2 18x2y 6y2z 7xy2z 14x2y3z3 Lời giải.
a) Mẫu thức chung là 36x2y2z2. Ta có −7y −7y · 3xy2 −21xy3 = = 12xz2 12xz2.3xy2 36x2y2z2 11z 11z.2yz2 22yz3 = = 18x2y 18x2y.2yz2 36x2y2z2 5x 5x · 6x2z 30x3z = = 6y2z 6y2z · 6x2z 36x2y2z2
b) Mẫu thức chung là 36x2y2z2. 6 6.2xyz2 12xyz2 11 Ta có = = ; để nguyên. 7xy2z 7xy2z.2xyz2 14x2y3z3 14x2y3z3 □
c Ví dụ 16. Quy đồng mẫu thức của các phân thức sau: 5 3 x2 − x 3x + 3 2x a) ; b) ; ; 3x + 15 x2 − 25 x2 − 1 x3 + 2x2 + x x3 Lời giải.
a) 3x + 15 = 3(x + 5); x2 − 25 = (x + 5)(x − 5) MTC: 3(x + 5)(x − 5). Ta có 5 5(x − 5) = 3(x + 5) 3(x + 5)(x − 5) 3 3.3 9 = = x2 − 25 3.(x + 5)(x − 5) 3(x + 5)(x − 5)
b) Rút gọn các phân thức đã cho, ta được x 3 2 ; ; x + 1 x(x + 1) x2 MTC: x2(x + 1). x x · x2 x3 = = x + 1 (x + 1)x2 x2(x + 1) 3 3x = x(x + 1) x2(x + 1) 2 2(x + 1) = x2 x2(x + 1)
Nhận xét. Trước khi quy đồng, bạn nên rút gọn phân thức (nếu có thể). □ 20/101 20/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 21
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 3 −7
c Ví dụ 17. Quy đồng mẫu thức hai phân thức và . 5x3 + 5x2 2x3 + 4x2 + 2x Lời giải.
Ta có 5x3 + 5x2 = 5x2 · (x + 1) và 2x3 + 4x2 + 2x = 2x · x2 + 2x + 1 = 2x · (x + 1)2.
Mẫu thức chung là 10x2(x + 1)2.
Nhân tử phụ của 5x3 + 5x2 là MTC :
5x3 + 5x2 = 10x2(x + 1)2 : 5x2(x + 1) = 2(x + 1).
Nhân tử phụ của 2x3 + 4x2 + 2x là MTC :
2x3 + 4x2 + 2x = 10x2(x + 1)2 : 2x(x + 1)2 = 5x.
Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng, ta có 3 3 · 2(x + 1) 6(x + 1) −7 −7 · 5x −35x = = và = = 5x3 + 5x2 10x2(x + 1)2 10x2(x + 1)2 2x3 + 4x2 + 2x 10x2(x + 1)2 10x2(x + 1)2 □ 1 1
c Ví dụ 18. Quy đồng mẫu thức hai phân thức và . 3x2 − 3 x3 − 1 Lời giải.
Ta có 3x2 − 3 = 3(x − 1)(x + 1) và x3 − 1 = (x − 1)(x2 + x + 1).
MTC là 3(x − 1)(x + 1)(x2 + x + 1). 1 x2 + x + 1 1 3(x + 1) Khi đó, = và = . □ 3x2 − 3 3(x − 1)(x + 1)(x2 + x + 1) x3 − 1 3(x − 1)(x + 1)(x2 + x + 1) 1 2 3
c Ví dụ 19. Quy đồng mẫu thức các phân thức: , và . 3x − 6 3x + 6 4 − x2 Lời giải. 3 −3 Ta có: = ;
Chọn MTC là: 3 (x − 2) (x + 2). 4 − x2 x2 − 4 3x − 6 = 3 (x − 2) ; 3x + 6 = 3 (x + 2) ; x2 − 4 = (x − 2) (x + 2) .
Nhân tử phụ của các mẫu thức trên lần lượt là: x + 2 ; x − 2 ; 3. 1 1 x + 2 Vậy: = = ; □ 3x − 6 3 (x − 2) 3 (x − 2) (x + 2) 2 2 2 (x − 2) = = ; 3x + 6 3 (x + 2) 3 (x − 2) (x + 2) 3 −3 −3 −9 = = = . 4 − x2 x2 − 4 (x − 2) (x + 2) 3 (x − 2) (x + 2) Dạng 7. Vận dụng
c Ví dụ 20. Cho hình chữ nhật ABCD và M N P Q như hình vẽ (các số đo trên hình tính theo đơn vị centimét). 21/101 21/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 22 22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC A B M N x x + 1 Q x + 1 P D x + 3 C
a) Viết phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật M N P Q.
b) Tính giá trị của phân thức đó tại x = 2 và tại x = 5. Lời giải.
a) Diện tích của hình chữ nhật ABCD là (x + 3) · (x + 1).
Diện tích của hình chữ nhật M N P Q là (x + 1) · x. (x + 3) · (x + 1)
Do đó phân thức biểu thị tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật M N P Q là . (x + 1) · x b) (2 + 3) · (2 + 1) 5
○ Với x = 2, phân thức trên có giá trị là = . (2 + 1) · 2 2 (5 + 3) · (5 + 1) 8
○ Với x = 5, phân thức trên có giá trị là = . (5 + 1) · 5 5 □
c Ví dụ 21. Chị Hà mở một xưởng thủ công với vốn đầu tư ban đầu (xây dựng nhà xưởng, mua máy móc,...)
là 80 triệu. Biết chi phí để sản xuất (tiền mua vật liệu, lương nhân công) của 1 sản phẩm là 15 nghìn đồng.
Gọi x là số sản phẩm mà xưởng của chị Hà làm được.
a) Viết phân thức biểu thị số tiền thực (đơn vị là nghìn đồng) đã bỏ ra để làm được x sản phẩm.
b) Viết phân thức biểu thị chi phí thực (đơn vị là nghìn đồng) để tạo ra 1 sản phẩm theo x.
c) Tính chi phí thực để tạo ra 1 sản phẩm nếu x = 100; x = 1 000. Nhận xét về chi phí thực để tạo ra 1
sản phẩm nếu x ngày càng tăng. Lời giải.
Đổi 80 triệu = 80 000 (nghìn đồng).
a) Phân thức biểu thị số tiền thực (đơn vị là nghìn đồng) đã bỏ ra để làm được x sản phẩm là 80 000 + 15 · x (nghìn đồng). 80 000 + 15 · x
b) Phân thức biểu thị chi phí thực (đơn vị là nghìn đồng) để tạo ra 1 sản phẩm theo x là (nghìn x đồng). c)
○ Chi phí thực để tạo ra 1 sản phẩm nếu x = 100 là
80 000 + 15 · 100 = 815 (nghìn đồng). 100
○ Chi phí thực để tạo ra 1 sản phẩm nếu x = 1 000 là
80 000 + 15 · 1000 = 95 (nghìn đồng). 1000
Vậy chi phí thực để tạo ra 1 sản phẩm sẽ ngày càng giảm nếu x ngày càng tăng. □ 22/101 22/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 23
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC A C BÀI TẬP VẬN DỤNG
c Bài 1. Dùng tính chất cơ bản của phân thức, giải thích vì sao 2x + 2 2 −x x (x − 2)3 (x − 2)2 1 − x x − 1 a) = ; b) = ; c) = ; d) = . x2 − 1 x − 1 1 − x x − 1 x2 − 2x x −5x + 1 5x − 1 Lời giải.
Áp dụng tính chất cơ bản của phân thức, ta có 2x + 2 2(x + 1) 2 a) = = . x2 − 1 (x − 1)(x + 1) x − 1 −x x
b) Do −(−x) = x và 1 − x = −(x − 1) nên = . 1 − x x − 1 (x − 2)3 (x − 2)3 (x − 2)2 c) = = . x2 − 2x x(x − 2) x 1 − x −(x − 1) x − 1 d) = = . −5x + 1 −(5x − 1) 5x − 1 □
c Bài 2. Tìm đa thức thích hợp thay cho dấu "?". y − x ? = 4 − x x − 4 Lời giải. y − x −(x − y) x − y Ta có = = . Do đó ? = x − y. □ 4 − x −(4 − x) 4 − x
c Bài 3. Tìm a sao cho hai phân thức sau bằng nhau: 5x ax(x − 1) và x + 1 (1 − x)(x + 1) Lời giải. ax(x − 1) ax(x − 1) −ax Ta có = = . (1 − x)(x + 1) −(x − 1)(x + 1) x + 1 Do đó −a = 5 hay a = −5. □
c Bài 4. Tìm mẫu thức chung của hai phân thức 2x 3x ; x2 + 3x + 2 x2 + 4x + 3 Lời giải.
Ta có x2 + 3x + 2 = x2 + x + 2x + 2 = (x + 1)(x + 2)
x2 + 4x + 3 = x2 + x + 3x + 3 = (x + 1)(x + 3)
nên mẫu thức chung là (x + 1)(x + 2)(x + 3). □
c Bài 5. Rút gọn các phân thức sau: 5x + 10 45x(3 − x) x2 − 12 a) ; b) ; c) . 25x2 + 50 15x(x − 3)3 (x + 1) (x3 + 1) 23/101 23/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 24 22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Lời giải. 5x + 10 5(x + 2) x + 2 a) = = ; 25x2 + 50 25(x2 + 2) 5(x2 + 2) 45x(3 − x) −3 · 15x(x − 3) −3 b) = = ; 15x(x − 3)3 15x(x − 3)3 (x − 3)2 x2 − 12 (x − 1)2 (x + 1)2 (x − 1)2 c) = = . (x + 1) (x3 + 1) (x + 1) (x + 1) (x2 − x + 1) x2 − x + 1 □
c Bài 6. Rút gọn mỗi phân thức sau: 82 + 4x x3 − xy2 24x2y2 6x − 2y a) ; b) ; c) ; d) . 1 − 4x2 2x2 + 2xy 16xy3 9x2 − y2 Lời giải. 82 + 4x 4x · (2x + 1) 4x a) = = . 1 − 4x2 (1 − 2x) · (1 + 2x) 1 − 2x x3 − xy2 x · x2 − y2 x · (x − y) · (x + y) x − y b) = = = . 2x2 + 2xy 2x · (x + y) 2x · (x + y) 2 24x2y2 3x c) = . 16xy3 2y 6x − 2y 2 · (3x − y) 2 d) = = . 9x2 − y2 (3x − y) · (3x + y) 3x + y □ x + 1
c Bài 7. Cho phân thức P = . x2 − 1
a) Rút gọn phân thức đã cho, kí hiệu Q là phân thức nhận được.
b) Tính giá trị của P và Q tại x = 11. So sánh hai kết quả đó. Lời giải. x + 1 x + 1 1 a) Ta có P = = = = Q. x2 − 1 (x − 1)(x + 1) x − 1 1 1 b) P (11) = và Q(11) = . Vậy P (11) = Q(11). 10 10 □
c Bài 8. Quy đồng mẫu thức các phân thức sau: 1 3 x 1 5 3 a) và ; b) và ; c) và ; x3 − 8 4 − 2x x2 − 1 x2 + 2x + 1 2x2y3 xy4 3 2 2 3 7 13 d) và ; e) và ; f) và . 2x2 − 10x x2 − 25 x − 3y x + 3y 4x + 24 x2 − 36 Lời giải.
a) Ta có x3 − 8 = (x − 2)(x2 + 2x + 4) và 4 − 2x = −2(x − 2).
Do đó, MTC là 2(x − 2)(x2 + 2x + 4). 1 2 3 −6(x2 + 2x + 4) Ta có = và = . x3 − 8 2(x − 2)(x2 + 2x + 4) 4 − 2x 2(x − 2)(x2 + 2x + 4) 24/101 24/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 25
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
b) Ta có x2 − 1 = (x − 1)(x + 1) và x2 + 2x + 1 = (x + 1)2.
Do đó, MTC là (x − 1)(x + 1)2. x x(x + 1) 1 x − 1 Ta có = và = . x2 − 1 (x − 1)(x + 1)2 x2 + 2x + 1 (x − 1)(x + 1)2
c) Ta chọn MTC là 2x2y4. Khi đó: 5 5 · y 5y = = . 2x2y3 2x2y3 · y 2x2y4 3 3 · 2x 6x = = . xy4 xy4 · 2x 2x2y4
d) Ta có: 2x2 − 10x = 2x · (x − 5) và x2 − 25 = (x − 5) · (x + 5).
Ta chọn MTC là 2x · (x − 5) · (x + 5). Khi đó: 3 3 3 · (x + 5) 3x + 15 = = = . 2x2 − 10x 2x · (x − 5) 2x · (x − 5) · (x + 5) 2x · (x − 5) · (x + 5) 2 2 2 · 2x 4x = = = . x2 − 25 (x − 5) · (x + 5) (x − 5) · (x + 5) · 2x 2x · (x − 5) · (x + 5)
e) Ta chọn MTC là (x − 3y) · (x + 3y). Khi đó: 2 2 · (x + 3y) = . x − 3y (x − 3y) · (x + 3y) 3 3 · (x − 3y) = . x + 3y (x − 3y) · (x + 3y)
f) Ta có: 4x + 24 = 4 · (x + 6) và x2 − 36 = (x − 6) · (x + 6).
Ta chọn MTC là 4 · (x − 6) · (x + 6). Khi đó: 7 7 7 · 4 (x − 6) 28 · (x − 6) = = = . 4x + 24 4 · (x + 6) 4 · (x − 6) · (x + 6) 4 · (x − 6) · (x + 6) 13 13 13 · 4 52 = = = . x2 − 36 (x − 6) · (x + 6) 4 · (x − 6) · (x + 6) 4 · (x − 6) · (x + 6) □
c Bài 9. Quy đồng mẫu thức các phân thức sau: 1 x + 1 5 1 2x x2 − xy + y2 a) ; và . b) ; và . x + 2 x2 − 4x + 4 2 − x 3x + 3y x2 − y2 x2 − 2xy + y2 Lời giải.
a) Ta có x + 2 = x + 2; x2 − 4x + 4 = (x − 2)2 và 2 − x = −(x − 2).
Do đó, MTC là (x + 2)(x − 2)2. 1 (x − 2)2 x + 1 (x + 2)(x + 1) Ta có = ; = x + 2
(x + 2)(x − 2)2 x2 − 4x + 4 (x + 2)(x − 2)2 5 −5(x − 2)(x + 2) và = . 2 − x (x + 2)(x − 2)2
b) Ta có 3x + 3y = 3(x + y); x2 − y2 = (x + y)(x − y) và x2 − 2xy + y2 = (x − y)2.
Do đó, MTC là 3(x − y)2(x + y). 1 (x − y)2 2x 6x(x − y) Ta có = ; = 3x + 3y 3(x − y)2(x + y) x2 − y2 3(x − y)2(x + y) x2 − xy + y2 3(x + y)(x2 − xy + y2) và = . x2 − 2xy + y2 3(x − y)2(x + y) □
c Bài 10. Quy đồng mẫu thức của các phân thức sau: 2x + 1 3x 3x2 − 4x + 1 x − 3 4x a) và b) ; ; 6xy3 9x2y x2 − 25 5 − x x + 5 25/101 25/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 26 22. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Lời giải.
a) Mẫu thức chung là 18x2y3.
Nhân tử phụ tương ứng là 18x2y3 : 6xy3 = 3x . 18x2y3 : 9x2y = 2y2 2x + 1 (2x + 1) · 3x 3x(2x + 1) Ta có = = 6xy3 6xy3 · 3x 18x2y3 3x 3x · 2y2 6xy2 = = 9x2y 9x2y · 2y2 18x2y3
b) Mẫu thức chung là (x − 5)(x + 5) = x2 − 25. 3x2 − 4x + 1 Ta có để nguyên. x2 − 25 x − 3 3 − x (3 − x)(x + 5) (3 − x)(x + 5) = = = 5 − x x − 5 (x − 5)(x + 5) x2 − 25 . 4x 4x(x − 5) 4x(x − 5) = = x + 5 (x + 5)(x − 5) x2 − 25 □ 9x2 + 3x + 1 x2 − 4x
c Bài 11. Cho hai phân thức và . 27x3 − 1 16 − x2
a) Rút gọn hai phân thức đã cho.
b) Quy đồng mẫu thức hai phân thức nhận được ở câu a. Lời giải. 9x2 + 3x + 1 9x2 + 3x + 1 1 a) Ta có = = . 27x3 − 1 (3x − 1)(9x2 + 3x + 1) 3x − 1 x2 − 4x x(x − 4) −x Ta có = = . 16 − x2 (4 − x)(4 + x) x + 4
b) Ta có MTC là (3x − 1)(x + 4). 1 x + 4 −x −x(3x − 1) Ta có = = . 3x − 1 (3x − 1)(x + 4) x + 4 (3x − 1)(x + 4) □
c Bài 12. Một ô tô chạy với vận tốc trung bình là x (km/h).
a) Viết biểu thức biểu thị thời gian ô tô (tính bằng giờ) chạy hết quãng đường 120 km.
b) Tính thời gian ô tô đi được 120 km trong trường hợp vận tốc trung bình của ô tô là 60 km/h. Lời giải.
a) Biểu thức biểu thị thời gian ô tô (tính bằng giờ) chạy hết quãng đường 120 km là 120 t = (h). x
b) Thời gian ô tô đi được 120 km trong trường hợp vận tốc trung bình của ô tô là 60 km/h là 120 t = = 2 (h). 60 □ 26/101 26/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 27
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Bài 13. Lúc 6 giờ sáng, bác Vinh lái ô tô xuất phát từ Hà Nội đi huyện Tỉnh Gia (Thanh Hoá). Khi đến
Phủ Lý (Hà Nam), cách Hà Nội khoảng 60 km, bác Vinh dừng lại ăn sáng trong 20 phút. Sau đó, bác Vinh
tiếp tục đi về Tĩnh Gia và phải tăng vận tốc thêm 10 km/h để đến nơi đúng giờ dự định.
a) Gọi x (km/h) là vận tốc ô tô đi trên quãng đường Hà Nội - Phủ Lý. Hãy viết các phân thức biểu thị thời
gian bác Vinh chạy xe trên các quãng đường Hà Nội - Phủ Lý và Phủ Lý - Tĩnh Gia, biết rằng quãng
đường Hà Nội - Tĩnh Gia có chiều dài khoảng 200 km.
b) Nếu vận tốc ô tô đi trên quãng đường Hà Nội - Phủ Lý là 60 km/h thì bác Vinh đến Tĩnh Gia lúc mấy giờ? Lời giải. 60
a) Thời gian bác Vinh chạy xe trên quãng đường Hà Nội - Phủ Lý là (giờ). x
Quãng đường từ Phủ Lý đến Tĩnh Gia là 200 − 60 = 140 (km). 140
Thời gian bác Vinh chạy xe trên quãng đường Phủ Lý - Tĩnh Gia là (giờ). x + 10 60
b) Thời gian bác Vinh chạy xe trên quãng đường Hà Nội - Phủ Lý là = 1 (giờ). 60 140
Thời gian bác Vinh chạy xe trên quãng đường Phủ Lý - Tĩnh Gia là = 2 (giờ). 60 + 10
Vậy bác Vinh đến Tĩnh Gia vào lúc 9 giờ 20 phút. □
c Bài 14. Để loại bỏ x (tính theo %) chất gây ô nhiễm không khí từ khí thải của một nhà máy, ước tính 1,7x cần chi phí là (tỉ đồng). 100 − x
a) Nếu muốn loại bỏ 90% chất gây ô nhiễm từ khí thải nhà máy thì cần chi phí là bao nhiêu? 1,7x
b) Viết điều kiện xác định của phân thức
. Hỏi có thể loại bỏ được 100% chất gây ô nhiễm từ khí 100 − x thải nhà máy hay không? Lời giải. 1,7x · 90
a) Muốn loại bỏ 90% chất gây ô nhiễm từ khí thải nhà máy thì cần chi phí là = 15,3 (tỉ đồng). 100 − 90
b) Điều kiện xác định của phân thức là 100 − x ̸= 0 hay x ̸= 100.
Do đó, không thể loại bỏ được 100% chất thải gây ô nhiễm từ khí thải của nhà máy. □ 27/101 27/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 28
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Baâi 23
PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ A
TRỌNG TÂM KIẾN THỨC
1 Cộng hai phân thức cùng mẫu thức
Quy tắc: muốn cộng hai phân thức cùng mẫu thức, ta cộng các tử thức với nhau và giữ nguyên mẫu thức A B A + B + = . C C C
Kết quả của phép cộng hai phân thức được gọi là tổng của hai phân thức đó. Ta thường viết tổng dưới dạng rút gọn.
2 Cộng hai phân thức khác mẫu
Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đổng mẫu thức rổi cộng các phân thức có cùng mẫu thức vừa tìm được.
3 Trừ hai phân thức
○ Muốn trừ hai phân thức có cùng mẫu thức ta trừ các tử thức và giữ nguyên mẫu thức.
○ Muốn trừ hai phân thức có mẫu thức khác nhau, ta quy đổng mẫu thức rổi trừ các phân thức có cùng
mẫu thức vừa tìm được.
Cũng như phép trừ phân số, ta có thể chuyển phép trừ phân thức thành phép cộng phân thức như sau: A C A −C − = + . B D B D
4 Cộng, trừ nhiều phân thức đại số
Vì trừ một phân thức cũng là cộng với phân thức đối của phân thức đó nên các biểu thức gổm các phép
tính cộng, trừ phân thức cũng có thể xem là chỉ gổm các phép cộng phân thức. Chẳng hạn, biểu thức P = 2x + 1 x 1 + − có thể viết thành x + 1 x − 1 x2 − 1 2x + 1 x −1 P = + + x + 1 x − 1 x2 − 1
Cũng như phép cộng phân số, phép cộng phân thức cũng có các tính chất giao hoán, kết hợp. Vì vậy, khi làm
tính với một biểu thức chỉ gổm các phép cộng phân thức ta có thể đổi chỗ, nhóm (kết hợp) các số hạng một cách tuỳ ý.
Trong các biểu thức ta có thể đổi chỗ các số hạng kèm theo dấu của nó. Quy tắc dấu ngoặc
○ Nếu trước dấu ngoặc có dấu “+” thì bỏ dấu ngoặc và giữ nguyên các số hạng.
○ Nếu trước dấu ngoặc có dấu "-" thì bỏ dấu ngoặc và đổi dấu các số hạng trong dấu ngoặc. 28/101 28/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 29
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC A B CÁC DẠNG BÀI TẬP
Dạng 1. Cộng, trừ các phân thức cùng mẫu thức
○ Cộng,trừ các tử thức với nhau; A B A ± B ○ Giữ nguyên mẫu thức ± = . C C C
c Ví dụ 1. Thực hiện phép tính sau: x + y x − 2y x2 + 4 4x 3x + 1 x − 2 xy 2x2 a) + ; b) + ; c) − ; d) − . 3x 3x x − 2 2 − x 2xy 2xy 2x − y y − 2x Lời giải. x + y x − 2y x + y + x − 2y 2x − y a) + = = . 3x 3x 3x 3x x2 + 4 4x x2 + 4 −4x x2 + 4 − 4x (x − 2)2 b) + = + = = = x − 2. x − 2 2 − x x − 2 x − 2 x − 2 x − 2 3x + 1 x − 2 3x + 1 − x + 2 2x + 3 c) − = = . 2xy 2xy 2xy 2xy xy 2x2 xy 2x2 xy + 2x2 d) − = + = . 2x − y y − 2x 2x − y 2x − y 2x − y □
c Ví dụ 2. Thực hiện các phép cộng, trừ phân thức sau: x + y x − y x2 + 5x x − 4 3x + 2y x 5x2 5 − 10x a) + ; b) − ; c) − ; d) + . xy xy x + 2 x + 2 x2 − y2 x2 − y2 x − 1 x − 1 Lời giải. x + y x − y x + y + x − y 2x 2 a) + = = = ; xy xy xy xy y x2 + 5x x − 4 x2 + 5x − (x − 4) x2 + 5x − x + 4 b) − = = x + 2 x + 2 x + 2 x + 2 x2 + 4x + 4 (x + 2)2 (x + 2)(x + 2) = = = = x + 2; x + 2 x + 2 x + 2 3x + 2y x 3x + 2y − x 2x + 2y 2(x + y) 2 c) − = = = = . x2 − y2 x2 − y2 x2 − y2 (x + y)(x − y) (x + y)(x − y) x − y 5x2 5 − 10x 5x2 + 5 − 10x 5(x − 1)2 d) + = = = 5(x − 1). x − 1 x − 1 x − 1 x − 1 □
c Ví dụ 3. Thực hiện phép tính: x − 7 y + 7 x − 2y x + 2y 3x − 2y 2x − 3y a) + . b) + . c) − . x2y x2y x2 + xy x2 + xy x + y x + y Lời giải. 29/101 29/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 30
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC x − 7 y + 7 (x − 7) + (y + 7) x − 7 + y + 7 x + y a) Ta có + = = = . x2y x2y x2y x2y x2y x − 2y x + 2y x − 2y + x + 2y 2x 2x 2 b) Ta có + = = = = . x2 + xy x2 + xy x2 + xy x2 + xy x(x + y) x + y 3x − 2y 2x − 3y (3x − 2y) − (2x − 3y) 3x − 2y − 2x + 3y x + y c) − = = = = 1. x + y x + y x + y x + y x + y □
c Ví dụ 4. Thực hiện phép tính: x − 2y y x2 + y2 2xy 4x + 3y 3x + 4y a) − ; b) − ; c) − , x − y y − x x2 − y2 y2 − x2 x2 − y2 x2 − y2 Lời giải. x − 2y y Å y ã a) − = x−2y + − x − y y − x x−y y − x x − 2y y x − 2y + y x − y = + = = = 1. x − y x − y x − y x − y x2 + y2 2xy x2 + y2 Å 2xy ã x2 + y2 2xy b) − = + − = + x2 − y2 y2 − x2 x2 − y2 y2 − x2 x2 − y2 x2 − y2 = x2+2xy+y2 = (x+y)2 = x+y . x2−y2 (x−y)(x+y) x−y 2xy − 3y2 x 2xy − 3y2 x 3 · (2xy − 3y2) x · x c) − = − = − x2 − 3xy 3x − 9y x(x − 3y) 3(x − 3y) 3x(x − 3y) 3x(x − 3y) 6xy − 9y2 − x2 −(x − 3y)2 3y − x = = = . 3x(x − 3y) 3x(x − 3y) 3x □
c Ví dụ 5. Rút gọn biểu thức sau x4 − (x − 1)2 x2 − x2 − 12 x2(x − 1)2 − 1 A = + + (x2 + 1)2 − x2 x2(x + 1)2 − 1 x4 − (x + 1)2 Lời giải. Ta có x2 − x + 1 x2 + x − 1 x + x2 − 1 x − x2 + 1 x2 − x − 1 x2 − x + 1 A = + + (x2 + 1 − x) (x2 + 1 + x) (x2 + x − 1) (x2 + x + 1) (x2 − x − 1) (x2 + x + 1) x2 + x − 1 x − x2 + 1 x2 − x + 1 = + + x2 + x + 1 x2 + x + 1 x2 + x + 1 x2 + x + 1 = = 1 x2 + x + 1
Nhận xét. Nếu mỗi phân thức có thể rút gọn được, bạn nên rút gọn trước khi thực hiện phép tính. □
c Ví dụ 6. Cho a, b, c thõa mãn abc = 1. Tính a b c M = + + . ab + a + 1 bc + b + 1 ac + c + 1 Lời giải. 30/101 30/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 31
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
Thay 1 = abc vào biểu thức, ta có a abc · b c M = + + ab + a + 1 bc + abc · b + abc ac + c + abc a ab 1 = + + ab + a + 1 1 + ab + a a + 1 + ab ab + a + 1 = = 1 ab + a + 1 Nhận xét.
○ Lời giải trên tinh tế khi giữ nguyên một mẫu thức và thay số 1 vào vị trí hợp lí để rút gọn phân thức, đưa
các phân thức về cùng mẫu.
○ Sử dụng kỹ thuật trên, bạn có thể giải được bài toán sau
Cho a, b, c, d thỏa mãn abcd = 1. Tính giá trị của biểu thức 1 1 1 1 N = + + + . 1 + 2a + 3ab + 4abc 2 + 3b + 4bc + bcd 3 + 4c + cd + 2cda 4 + d + 2da + 3dab □
Dạng 2. Cộng, trừ các phân thức không cùng mẫu thức
○ Quy đồng mẫu thức để đưa về các phân thức có cùng mẫu.
○ Cộng, trừ tử thức với nhau và giữ nguyên mẫu thức.
c Ví dụ 7. Thực hiện phép tính: 5 3 2x + 1 y − 1 1 − x 1 1 1 a) và ; b) − ; c) + ; d) + ; x 1 − x x y xy + x2 x + y x2 + xy xy + y2 xy + 5 y 2 1 2x 1 x y e) − ; f) + ; g) − ; h) − . x2 + xy x + y a a − 3 x2 − 4 x − 2 xy − y2 x2 − xy Lời giải. 5 3 5(1 − x) 3x 5(1 − x) + 3x 5 − 2x a) + = + = = . x 1 − x x(1 − x) x(1 − x) x(1 − x) x(1 − x) 2x + 1 y − 1 (2x + 1)y x(y − 1) (2x + 1)y − x(y − 1) xy + x + y b) − = − = = . x y xy xy xy xy 1 − x 1 1 − x 1 1 − x x 1 − x + x 1 c) + = + = + = = . xy + x2 x + y x(y + x) x + y x(x + y) x(x + y) x(x + y) x(x + y) 1 1 1 1 y x x + y 1 d) + = + = + = = . x2 + xy xy + y2 x(x + y) y(x + y) xy(x + y) xy(x + y) xy(x + y) xy xy + 5 y xy + 5 y xy + 5 xy xy + 5 − xy 5 e) − = − = − = = . x2 + xy x + y x(x + y) x + y x(x + y) x(x + y) x(x + y) x(x + y) 2 1 2(a − 3) a 2a − 6 + a 3a − 6 3(a − 2) f) + = + = = = ; a a − 3 a(a − 3) a(a − 3) a(a − 3) a(a − 3) a(a − 3) 2x 1 2x (x + 2) 2x − (x + 2) x − 2 1 g) − = − = = = ; x2 − 4 x − 2 (x + 2)(x − 2) (x + 2)(x − 2) (x + 2)(x − 2) (x + 2)(x − 2) x + 2 x y x y x2 y2 x2 − y2 (x + y)(x − y) x + y h) − = − = − = = = . xy − y2 x2 − xy y(x − y) x(x − y) xy(x − y) xy(x − y) xy(x − y) xy(x − y) xy □ 31/101 31/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 32
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Ví dụ 8. Thực hiện các phép cộng, trừ phân thức sau: a 3 1 2 4 2 2xy − 3y2 x a) − ; b) + ; c) − ; d) − . a − 3 a + 3 2x x2 x2 − 1 x2 + x x2 − 3xy 3x − 9y Lời giải. a 3 a(a + 3) 3(a − 3) a2 + 3a − 3a + 9 a2 + 9 a) − = − = = ; a − 3 a + 3 (a − 3)(a + 3) (a − 3)(a + 3) a2 − 9 a2 − 9 1 2 x 2 · 2 x + 4 b) + = + = ; 2x x2 2x2 2x2 2x2 4 2 4 2 4x 2(x − 1) c) − = − = − x2 − 1 x2 + x (x − 1)(x + 1) x(x + 1) x(x − 1)(x + 1) x(x − 1)(x + 1) 4x − 2x + 2 2x + 2 2(x + 1) 2 = = = = . x(x − 1)(x + 1) x(x − 1)(x + 1) x(x − 1)(x + 1) x(x − 1) 4x + 3y 3x + 4y 4x + 3y − 3x − 4y x − y 1 d) − = = = . x2 − y2 x2 − y2 x2 − y2 (x − y)(x + y) x + y □
c Ví dụ 9. Thực hiện phép tính sau 3 5x 7 x2 3 3 a) + + ; b) + + . 4xy 2y2z 6yz2 x2 + 3x x + 3 x Lời giải. 3 5x 7 9yz2 30x2z 14xy 9yz2 + 30x2z + 14xy a) + + = + + = . 4xy 2y2z 6yz2 12xy2z2 12xy2z2 12xy2z2 12xy2z2 x2 3 3 x2 3x 3(x + 3) x2 + 3x + 3 (x + 3)2 x + 3 b) + + = + + = = = . x2 + 3x x + 3 x x(x + 3) x(x + 3) x(x + 3) x(x + 3) x(x + 3) x □
c Ví dụ 10. Thực hiện các phép tính sau 3x x 1 4 3x − 6 2a a 1 − a a) − ; b) − − ; c) + + . 5x + 5y 10x − 10y 3x − 2 3x + 2 4 − 9x2 (a + 1)2 a + 1 a2 + 2a + 1 Lời giải. 3x x 3x x a) − = − 5x + 5y 10x − 10y 5(x + y) 10(x − y) 6x(x − y) x(x + y) = − 10(x + y)(x − y) 10(x + y)(x − y) 6x2 − 6xy − x2 − xy 5x2 − 7xy = = . 10(x + y)(x − y) 10(x + y)(x − y) 1 4 3x − 6 3x + 2 4(3x − 2) 3x − 6 b) − − = − + 3x − 2 3x + 2 4 − 9x2 (3x − 2)(3x + 2) (3x − 2)(3x + 2) (3x − 2)(3x + 2) 3x + 2 − 12x + 8 + 3x − 6 −6x + 4 −2(3x − 2) = = = (3x − 2)(3x + 2) (3x − 2)(3x + 2) (3x − 2)(3x + 2) −2 = . 3x + 2 32/101 32/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 33
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 2a a 1 − a 2a 1 − a a a + 1 a c) + + = + + = + (a + 1)2 a + 1 a2 + 2a + 1 (a + 1)2 (a + 1)2 a + 1 (a + 1)2 a + 1 1 a 1 + a = + = = 1 a + 1 a + 1 a + 1 □
Dạng 3. Tìm x thõa mãn đẳng thức cho trước
Chuyển hạng tử không chứa x về một vế, ta được biểu thức của x.
Rút gọn biểu thức của x.
c Ví dụ 11. Tìm x biết 1 2 x − = (a là hằng số) a + 1 a2 − 1 Lời giải. 1 2 x − = a + 1 a2 − 1 2 1 2 + a − 1 a + 1 1 x = + = = = a2 − 1 a + 1 (a − 1)(a + 1) (a − 1)(a + 1) a − 1 □
c Ví dụ 12. Tìm x biết 1 a x + = ; (a là hằng số). a2 − a a − 1 Lời giải. a 1 a2 1 a2 − 1 (a − 1)(a + 1) a + 1 x = − = − = = = . a − 1 a2 − a a(a − 1) a(a − 1) a(a − 1) a(a − 1) a □ a2 + 2 · a 2
c Ví dụ 13. Nếu cho X + − 1 = thì X là phân thức nào? a3 − 1 a2 + a + 1 Lời giải. 2 a2 + 2 a
2(a − 1) − a3 − 2a + a3 − 1 −3 Ta có X = − + 1 = = . □ a2 + a + 1 a3 − 1 a3 − 1 a3 − 1
Dạng 4. Rút gọn và tính giá trị biểu thức
○ Sử dụng phép cộng, trừ phân thức để rút gọn biểu thức.
○ Thay giá trị của biến đã cho vào biểu thức đã rút gọn và thực hiện các phép tính. 1 1 1
c Ví dụ 14. Rút gọn biểu thức P = + − x y x Lời giải. 1 1 1 1 1 −1 1 −1 1 1 1 Ta có P = + − = + + = + + = 0 + = . □ x y x x y x x x y y y 33/101 33/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 34
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 3 ï 5 Å 5 3 ãò
c Ví dụ 15. Rút gọn biểu thức P = + − + . 2x + 1 4x − 1 4x − 1 2x + 1 Lời giải. 3 ï 5 Å 5 3 ãò Ta có P = + − + □ 2x + 1 4x − 1 4x − 1 2x + 1 3 ï 5 5 3 ò = + − − 2x + 1 4x − 1 4x − 1 2x + 1 3 5 5 3 = + − − 2x + 1 4x − 1 4x − 1 2x + 1 Å 3 3 ã Å 5 5 ã = − + − 2x + 1 2x + 1 4x − 1 4x − 1 = 0.
c Ví dụ 16. Rút gọn biểu thức x + 2 2 2x2 + 4 A = − − . x2 + x + 1 x − 1 1 − x3 Lời giải. (x + 2)(x − 1) 2 x2 + x + 1 2x2 + 4 Ta có A = − + (x − 1) (x2 + x + 1) (x − 1) (x2 + x + 1) (x − 1) (x2 + x + 1)
x2 + 2x − x − 2 − 2x2 − 2x − 2 + 2x2 + 4 = (x − 1) (x2 + x + 1) x2 − x x(x − 1) x = = = . (x − 1) (x2 + x + 1) (x − 1) (x2 + x + 1) x2 + x + 1
Nhận xét. Trong khi thực hiện phép tính cộng, trừ các phân thức đại số, nếu có hai đa thức ở mẫu đối nhau,
bạn nên áp dụng quy tắc đổi dấu một trong hai phân thức đó. □
c Ví dụ 17. Rút gọn biểu thức 20x2 + 120x + 180 5x2 − 125 (2x + 3)2 − x2 A = + − . (3x + 5)2 − 4x2 9x2 − (2x + 5)2 3 (x2 + 8x + 15) Lời giải. 20(x + 3)2 5(x − 5)(x + 5) (x + 3) · 3 · (x + 1) Ta có A = + − (x + 5).5(x + 1) 5(x + 1)(x − 5) 3(x + 3)(x + 5) 4(x + 3)2 x + 5 x + 1 = + − (x + 5) · (x + 1) x + 1 x + 5
4(x + 3)2 + (x + 5)2 − (x + 1)2 = (x + 1)(x + 5)
4x2 + 24x + 36 + x2 + 10x + 25 − x2 − 2x − 1 4(x + 3) = = . (x + 1)(x + 5) x + 1
Nhận xét. Trong khi thực hiện phép tính cộng, trừ các phân thức đại số, nếu phân thức nào rút gọn được,
bạn nên rút gọn trước khi thực hiện. □
c Ví dụ 18. Rút gọn rồi tính giá trị của biểu thức 6x2 + 8x + 7 x 6 1 P = + − với x = . x3 − 1 x2 + x + 1 x − 1 2 34/101 34/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 35
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Lời giải. Rút gọn biểu thức 6x2 + 8x + 7 x 6 P = + − x3 − 1 x2 + x + 1 x − 1 6x2 + 8x + 7 x(x − 1) 6 x2 + x + 1 = + − (x − 1) (x2 + x + 1) (x − 1) (x2 + x + 1) (x − 1) (x2 + x + 1)
6x2 + 8x + 7 + x2 − x − 6x2 − 6x − 6 = (x − 1) (x2 + x + 1) x2 + x + 1 1 = = . (x − 1) (x2 + x + 1) x − 1 1 1 Với x = , ta có P = = −2. □ 2 1 − 1 2
c Ví dụ 19. Tính giá trị của biểu thức 10 12 1 P = − − tại x = −0,75. (x + 2)(3 − x) (3 − x)(3 + x) (x + 3)(x + 2) Lời giải.
10 · (x + 3) − 12 · (x + 2) − (3 − x) 3 − x 1 Ta có P = = = . (x + 2)(3 − x)(x + 3) (x + 2)(3 − x)(x + 3) (x + 2)(x + 3) 1 16
Với x = 0,75 thì giá trị của P = = . □ (−0, 75 + 2)(−0, 75 + 3) 45
c Ví dụ 20. Rút gọn biểu thức 1 1 2a 4a3 8a7 B = + + + + . a − b a + b a2 + b2 a4 + b4 a8 + b8 Lời giải. 2a 2a 4a3 8a7 B = + + + a2 − b2 a2 + b2 a4 + b4 a8 + b8 4a3 4a3 8a7 = + + a4 − b4 a4 + b4 a8 + b8 8a7 8a7 = + a8 − b8 a8 + b8 16a15 = . a16 − b16 □
c Ví dụ 21. Cho a + b + c = 0. Rút gọn biểu thức a2 b2 c2 a) A = + + ; a2 − b2 − c2 b2 − a2 − c2 c2 − a2 − b2 1 1 1 b) B = + + . b2 + c2 − a2 c2 + a2 − b2 a2 + b2 − c2 Lời giải.
a) Ta có a = −b − c nên a2 = b2 + 2bc + c2 ⇒ a2 − b2 − c2 = 2bc. Tương tự ta có b2 − a2 − c2 = 2ac c2 − a2 − b2 = 2ab. a2 b2 c2 a3 + b3 + c3 Do đó A = + + ⇒ A = (1) 2bc 2ac 2ab 2abc 35/101 35/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 36
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
Xét a3 + b3 + c3 = a3 + b3 − (a + b)3 = −3ab(a + b) = 3abc (2) 3abc 3 Vậy từ (1) và (2) ta có A = = . 2abc 2
b) Ta có b + c = −a nên b2 + c2 + 2bc = a2 ⇒ b2 + c2 − a2 = −2bc. Tương tự ta có c2 + a2 − b2 = −2ac a2 + b2 − c2 = −2ab. 1 1 1 a + b + c Do đó ta có B = + + = = 0. −2bc −2ac −2ab −2abc Nhận xét.
○ Bài toán không quá khó, chỉ sử dụng biến đổi một cách linh hoạt các mẫu thức mà cần sử dụng giả thiết.
○ Bạn nên nhớ đẳng thức đẹp: Cho a + b + c = 0 thì ta có a3 + b3 + c3 = 3abc. □
Dạng 5. Chứng minh giá trị biểu thức không phụ thuộc vào biến. Chứng minh đẳng thức
a) Thực hiện phép cộng, trừ các phân thức để rút gọn biểu thức không còn chứa biến. b) Chứng minh đẳng thức
○ Từ đẳng thức đã cho ta biến đổi một vế bằng vế còn lại.
○ Hoặc biến đổi cả hai vế cùng bằng một biểu thức.
c Ví dụ 22. Chứng tỏ giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x. 2x x + 1 2 − x P = + + . x2 + 4x + 4 x + 2 x2 + 4x + 4 Lời giải. 2x x + 1 2 − x Å 2x 2 − x ã x + 1 P = + + = + + x2 + 4x + 4 x + 2 x2 + 4x + 4 x2 + 4x + 4 x2 + 4x + 4 x + 2 2x + 2 − x x + 1 x + 2 x + 1 1 x + 1 1 + x + 1 x + 2 = + = + = + = = = 1. x2 + 4x + 4 x + 2 (x + 2)2 x + 2 x + 2 x + 2 x + 2 x + 2 □
c Ví dụ 23. Chứng tỏ giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x, y. x2 + y2 − 1 2y 1 − 2y2 + + . x2 + 2xy + y2 x + y x2 + 2xy + y2 Lời giải. Ta có x2 + y2 − 1 2y 1 − 2y2 x2 + y2 − 1 + 1 − 2y2 2y + + = + x2 + 2xy + y2 x + y x2 + 2xy + y2 x2 + 2xy + y2 x + y x2 − y2 2y (x + y)(x − y) 2y = + = + (x + y)2 x + y (x + y)2 x + y x − y 2y x − y + 2y x + y = + = = = 1. x + y x + y x + y x + y □ 36/101 36/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 37
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Ví dụ 24. Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị biến x. x + 1 x − 1 4 A = + − với x ̸= 1; x ̸= −1. x − 1 x + 1 x2 − 1 Lời giải. (x + 1)2 (x − 1)2 4 Ta có A = + − (x − 1)(x + 1) (x − 1)(x + 1) (x − 1)(x + 1)
x2 + 2x + 1 + x2 − 2x + 1 − 4 = = 2. x2 − 1
Vậy giá trị biểu thức A đã cho không phụ thuộc vào giá trị của x. □
c Ví dụ 25. Chứng minh đẳng thức x − 5y 24xy x + 8y 2x − 3y − − = .. 2x − 3y 4x2 − 9y2 3y − 2x 2x + 3y Lời giải. x − 5y 24xy x + 8y x − 5y x + 8y 24xy − − = + − 2x − 3y 4x2 − 9y2 3y − 2x 2x − 3y 2x − 3y (2x − 3y)(2x + 3y) 2x + 3y 24xy (2x + 3y)2 − 24xy (2x − 3y)2 2x − 3y = − = = = . 2x − 3y (2x − 3y)(2x + 3y) (2x − 3y)(2x + 3y) (2x − 3y)(2x + 3y) 2x + 3y □
c Ví dụ 26. Chứng minh đẳng thức x 2xy y x2 + y2 + − = . x + y x2 − y2 x + y x2 − y2 Lời giải. x 2xy y x y 2xy x − y 2xy + − = − + = + □ x + y x2 − y2 x + y x + y x + y (x − y)(x + y) x + y (x − y)(x + y) (x − y)2 2xy x2 − 2xy + y2 + 2xy x2 + y2 = + = = . (x − y)(x + y) (x − y)(x + y) x2 − y2 x2 − y2
c Ví dụ 27. Chứng minh đẳng thức a2 + 3ab 2a2 − 5ab − 3b2 a2 + ab + ac + bc + = . a2 − 9b2 6ab − a2 − 9b2 3bc − a2 − ac + 3ab Lời giải. Biến đổi vế phải (a + b)(a + c) (a + b)(a + c) a + b V P = = = (1) 3b(c + a) − a(a + c) (a + c)(3b − a) 3b − a Biến đổi vế trái a(a + 3b) (a − 3b)(2a + b) V T = + (a − 3b)(a + 3b) −(a − 3b)2 a 2a + b −a − b a + b = − = = (2) a − 3b a − 3b a − 3b 3b − a
Từ (1) và (2) ta có vế trái bằng vế phải, suy ra điều phải chứng minh. □ 37/101 37/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 38
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Dạng 6. Vận dụng
c Ví dụ 28. Tại một cuộc đua thuyền diễn ra trên một khúc sông từ A đến B dài 3 km. Mỗi đội thực hiện
một vòng đua, xuất phát từ A đến B, rồi quay về A là đích. Một đội đua đạt tốc độ (x + 1) km/h khi xuôi
dòng từ A đến B và đạt tốc độ (x − 1) km/h khi ngược dòng từ B về A.
Viết biểu thức tính tổng thời gian đi và về, chênh lệch thời gian giữa đi và về của đội đua thuyền. Tính giá
trị của các đại lượng này khi v = 6 km/h. Lời giải. quãng đường
Quãng đường từ A đến B dài 3 km. Ta có: Thời gian = . vận tốc 3
Khi xuôi dòng, tốc độ của đội đua là (x + 1) km/h nên thời gian đi (thời gian xuôi dòng) là h. x + 1 3
Khi ngược dòng, tốc độ của đội đua là (x − 1) km/h nên thời gian về (thời gian ngược dòng) là h. x − 1 3 3
○ Tổng thời gian đi và về của đội đua thuyền là + h. x + 1 x − 1 3 3
○ Chênh lệch thời gian giữa đi và về là − h. x − 1 x + 1
○ Khi v = 6 km/h tức là x = 6. Khi đó 3 3 36
— Tổng thời gian đi và về của đội đua thuyền là + = h. 6 + 1 6 − 1 35 3 3 6
— Chênh lệch thời gian giữa đi và về là − = h. 6 − 1 6 + 1 35 6
Tức là đi khi đội đua thuyền đi về thời gian lâu hơn khi đội đi là giờ. 35 □
c Ví dụ 29. Một đoàn tàu chở khách đi một quãng đường 500 km, trong đó có 50 km đường qua thành phố
và 450 km đường qua vùng rừng núi. Biết tốc độ tàu khi chạy qua thành phố kém 30 km/h so với tốc độ tàu
khi chạy qua vùng rừng núi. Gọi x (km/h) là tốc độ tàu chạy qua vùng rừng núi. Viết phân thức biểu thị theo x:
a) Thời gian tàu chạy qua vùng rừng núi;
b) Thời gian tàu chạy qua thành phố;
c) Thời gian tàu chạy trên cả quãng đường. Lời giải. 450
a) Phân thức biểu thị thời gian tàu chạy qua vùng rừng núi là (giờ). x
b) Tốc độ tàu chạy qua thành phố là x − 30 (km/h). 50
Phân thức biểu thị thời gian tàu chạy qua thành phố là (giờ). x − 30
c) Thời gian tàu chạy trên cả quãng đường là 450 50 450(x − 30) + 50x 500x − 13500 + = = (giờ). x x − 30 x(x − 30) x(x − 30) 500x − 13500
Vậy phân thức biểu thị thời gian tàu chạy trên cả quãng đường là (giờ). x(x − 30) □ 38/101 38/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 39
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Ví dụ 30. Một tàu du lịch chạy xuôi dòng 15 km, sau đó quay ngược lại để trở về điểm xuất phát và kết
thúc chuyến du lịch. Biết rằng vận tốc của tàu khi nước yên lặng là 10 km/h và vận tốc của dòng nước là x (km/h).
a) Hãy viết các phân thức biểu thị theo x thời gian xuôi dòng, thời gian ngược dòng và tổng thời gian tàu chạy.
b) Tính tổng thời gian tàu chạy khi vận tốc dòng nước là 2 km/h. Lời giải.
a) Ta có vận tốc của tàu du lịch khi nước xuôi dòng là 10 + x (km/h) (x > 0). Suy ra thời gian xuôi dòng là 15 tx = (h). 10 + x
Tương tự vận tốc của tàu di lịch khi nước ngược dòng là 10 − x (km/h) (x > 0). Suy ra thời gian ngược 15 dòng là tn = (h). 10 − x
Vậy tổng thời gian tàu chạy là 15 15 15 · 20 300 t = + = = (h) 10 + x 10 − x 100 − x 100 − x
b) Khi vận tốc dòng nước là 2 km/h thay vào ta có 300 150 t = = (h). 100 − 2 49 □ A C BÀI TẬP VẬN DỤNG
c Bài 1. Thực hiện các phép cộng, trừ phân thức sau: a − 1 3 − a b a (a + b)2 (a − b)2 a) + ; b) + ; c) − . a + 1 a + 1 a − b b − a ab ab Lời giải. a − 1 3 − a a − 1 + 3 − a 2 a) + = = ; a + 1 a + 1 a + 1 a + 1 b a b a b − a b) + = − = = −1; a − b b − a a − b a − b a − b (a + b)2 (a − b)2
(a2 + 2ab + b2) − (a2 − 2ab + b2) 4ab c) − = = = 4. ab ab ab ab □ c Bài 2. Tính 7x + 2 2 − 2x 5x − 2 x − 2 xy x2 x + 4 1 a) − ; b) − ; c) − ; d) − . 5x − 2 5x − 2 4x2y 4x2y x2 − y2 y2 − x2 x2 − 4 x2 + 2x Lời giải. 7x + 2 2 − 2x 7x + 2 − 2 + 2x 9x a) − = = . 5x − 2 5x − 2 5x − 2 5x − 2 5x − 2 x − 2 5x − 2 − x + 2 4x 1 b) − = = = . 4x2y 4x2y 4x2y 4x2y xy 39/101 39/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 40
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC xy x2 xy x2 xy + x2 x(x + y) x c) − = + = = = . x2 − y2 y2 − x2 x2 − y2 x2 − y2 x2 − y2 (x + y)(x − y) x − y x(x + 4) − (x − 2) x + 1 d) = . x(x + 2)(x − 2) x(x − 2) □
c Bài 3. Thực hiện các phép cộng, trừ phân thức sau: 1 2 x − 1 x + 1 x + y y + z a) + ; b) − ; c) − ; 2a 3b x + 1 x − 1 xy yz 2 12 1 2 1 1 1 d) − ; e) + ; f) − + . x − 3 x2 − 9 x − 2 x2 − 4x + 4 x + 1 x3 + 1 x2 − x + 1 Lời giải. 1 2 3b 4a 4a + 3b a) + = + = ; 2a 3b 6ab 6ab 6ab x − 1 x + 1 (x − 1)2 (x + 1)2 b) − = − x + 1 x − 1 (x + 1)(x − 1) (x + 1)(x − 1)
(x2 − 2x + 1) − (x2 + 2x + 1) −4x = = ; (x + 1)(x − 1) x2 − 1 x + y y + z z(x + y) x(y + z) xz + yz − xy − xz y(z − x) z − x c) − = − = = = ; xy yz xyz xyz xyz xyz xz 2 12 2(x + 3) 12 2x + 6 − 12 d) − = − = x − 3 x2 − 9 (x − 3)(x + 3) (x − 3)(x + 3) (x − 3)(x + 3) 2(x − 3) 2 = = ; (x − 3)(x + 3) x + 3 1 2 1 2 x − 2 2 x − 2 + 2 x e) + = + = + = = . x − 2 x2 − 4x + 4 x − 2 (x − 2)2 (x − 2)2 (x − 2)2 (x − 2)2 (x − 2)2 1 1 1 x2 − x + 1 1 x + 1 x2 + 1 f) − + = − + = . x + 1 x3 + 1 x2 − x + 1 x3 + 1 x3 + 1 x3 + 1 x3 + 1 □
c Bài 4. Thực hiện các phép tính sau: x + 2 x − 3 x − 4 1 1 2x 2y2 a) − + ; b) − + ; c) x + − y. x − 1 x − 1 1 − x x + 5 x − 5 x2 − 25 x + y Lời giải. x + 2 x − 3 x − 4 (x + 2) − (x − 3) x − 4 5 − (x − 4) 9 − x a) − + = − = = ; x − 1 x − 1 1 − x x − 1 x − 1 x − 1 x − 1 1 1 2x x − 5 x + 5 2x b) − + = − + x + 5 x − 5 x2 − 25 (x + 5)(x − 5) (x + 5)(x − 5) (x + 5)(x − 5) (x − 5) − (x + 5) + 2x 2x − 10 2(x − 5) 2 = = = = ; (x + 5)(x − 5) (x + 5)(x − 5) (x + 5)(x − 5) x + 5 2y2 x(x + y) 2y2 y(x + y) x2 + xy + 2y2 − xy − y2 x2 + y2 c) x + − y = + − = = . x + y x + y x + y x + y x + y x + y □ 40/101 40/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 41
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Bài 5. Thực hiện phép tính 5x − 4 4x + 4 x2y − 6 6 − xy2 x + 1 x − 18 x + 2 a) + ; b) + ; c) + + ; 9 9 2x2y 2x2y x2 − 5x x2 − 5x x2 − 5x 7y 7y − 5 4x − 1 7x − 1 3y − 2x x − y d) − ; e) − ; f) − . 3 3 3xy2 3xy2 x − 2y 2y − x Lời giải. 5x − 4 4x + 4 5x − 4 + 4x + 4 9x a) + = = = x. 9 9 9 9 x2y − 6 6 − xy2 x2y − 6 + 6 − xy2 x2y − xy2 xy(x − y) x − y b) + = = = = . 2x2y 2x2y 2x2y 2x2y 2x2y 2x x + 1 x − 18 x + 2 x + 1 + x − 18 + x + 2 3x − 15 3(x − 5) 3 c) + + = = = = . x2 − 5x x2 − 5x x2 − 5x x2 − 5x x2 − 5x x(x − 5) x 7y 7y − 5 7y − 7y + 5 5 d) − = = . 3 3 3 3 4x − 1 7x − 1 4x − 1 − 7x + 1 −3x −1 e) − = = = . 3xy2 3xy2 3xy2 3xy2 y2 3y − 2x x − y 3y − 2x x − y 3y − 2x + x − y 2y − x −(x − 2y) f) − = + = = = = −1. x − 2y 2y − x x − 2y x − 2y x − 2y x − 2y x − 2y □
c Bài 6. Thực hiện phép tính 4x + 2 3 − 6x y 4x a) + ; b) + ; 4x − 4 6x − 6 2x2 − xy y2 − 2xy x y 2y2 x2 + 2 x 1 c) + + ; d) + + . x − y x + y x2 − y2 x3 − 1 x2 + x + 1 1 − x Lời giải. 4x + 2 3 − 6x 4x + 2 3 − 6x 12x + 6 + 6 − 12x 12 1 a) + = + = = = . 4x − 4 6x − 6 4(x − 1) 6(x − 1) 12(x − 1) 12(x − 1) x − 1 b) y 4x y 4x y2 − 4x2 + = + = 2x2 − xy y2 − 2xy x(2x − y) y(y − 2x) xy(2x − y) (y − 2x)(y + 2x) −y − 2x = = −xy(y − 2x) xy c) x y 2y2 x(x + y) + y(x − y) + 2y2 x2 + xy + xy − y2 + 2y2 + + = = x − y x + y x2 − y2 (x − y)(x + y) (x − y)(x + y) x2 + 2xy + y2 (x + y)2 x + y = = = . (x − y)(x + y) (x − y)(x + y) x − y d) x2 + 2 x 1
x2 + 2 + x(x − 1) − (x2 + x + 1) + + = x3 − 1 x2 + x + 1 1 − x (x − 1)(x2 + x + 1) x2 − 2x + 1 (x − 1)2 x − 1 = = = . (x − 1)(x2 + x + 1) (x − 1)(x2 + x + 1) x2 + x + 1 □ 41/101 41/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 42
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Bài 7. Thực hiện phép tính 1 1 12 2 a) − ; b) − ; x − 2 x + 1 x2 − 9 x − 3 1 1 2x 3 1 c) − ; d) − + . xy − x2 y2 − xy x2 − 1 2 + 2x 2 − 2x Lời giải. a) 1 1 x + 1 x − 2 − = − x − 2 x + 1 (x − 2)(x + 1) (x − 2)(x + 1) x + 1 − (x − 2) x + 1 − x + 2 3 = = = . (x − 2)(x + 1) (x − 2)(x + 1) (x − 2)(x + 1) b) 12 2 12 2 − = − x2 − 9 x − 3 (x + 3)(x − 3) x − 3 12 2(x + 3) 12 − 2(x + 3) = − = (x + 3)(x − 3) (x + 3)(x − 3) (x + 3)(x − 3) 12 − 2x − 6 6 − 2x −3(x − 3) −3 = = = = . (x + 3)(x − 3) (x + 3)(x − 3) (x + 3)(x − 3) x + 3 c) 1 1 1 1 − = − xy − x2 y2 − xy x(y − x) y(y − x) y x y − x 1 = − = = . xy(y − x) xy(y − x) xy(y − x) xy d) 2x 3 1 2x 3 1 − + = − − x2 − 1 2 + 2x 2 − 2x (x + 1)(x − 1) 2(x + 1) 2(x − 1) 4x 3(x − 1) x + 1 = − − 2(x + 1)(x − 1) 2(x + 1)(x − 1) 2(x + 1)(x − 1) (4x − 3x − x) + (3 − 1) 2 1 = = = . 2(x + 1)(x − 1) 2(x + 1)(x − 1) (x + 1)(x − 1) □
c Bài 8. Thực hiện phép tính x2 − 3x + 1 5x − 1 − x2 y x x 9 a) + . b) + . c) + . 2x2 2x2 x − y x + y 2x − 6 2x(3 − x) Lời giải. x2 − 3x + 1 5x − 1 − x2 2x 1 a) + = = . 2x2 2x2 2x2 x y x y(x + y) x(x − y) x2 + y2 b) + = + = . x − y x + y x2 − y2 x2 − y2 x2 − y2 x 9 x2 9 x2 9 (x − 3)(x + 3) x + 3 c) + = + = − = = . 2x − 6 2x(3 − x) 2x(x − 3) 2x(3 − x) 2x(x − 3) 2x(x − 3) 2x(x − 3) 2x □ 42/101 42/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 43
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Bài 9. Thực hiện phép tính 5 − 3x −2 + 5x x y 3 2 + 3x a) − . b) − . c) − . x + 1 x + 1 x − y x + y x + 1 x3 + 1 Lời giải. 5 − 3x −2 + 5x 7 − 8x a) − = . x + 1 x + 1 x + 1 x y x(x + y) y(x − y) x2 + y2 b) − = − = . x − y x + y x2 − y2 x2 − y2 x2 − y2 3 2 + 3x 3(x2 − x + 1) 2 + 3x 3x2 − 6x + 1 c) − = − = . x + 1 x3 + 1 (x + 1)(x2 − x + 1) (x + 1)(x2 − x + 1) (x + 1)(x2 − x + 1) □
c Bài 10. Thực hiện phép tính 1 2 3 1 2 3 a) + + − − − . x x + 1 x + 2 x x − 1 x + 2 2x − 1 1 − x 3 1 − 2x x − 1 3 b) + + + + − . x 2x + 1 x2 − 9 x 2x + 1 x + 3 Lời giải. 1 2 3 1 2 3 2 2 2(x − 1) − 2(x + 1) 4 a) + + − − − = − = = . x x + 1 x + 2 x x − 1 x + 2 x + 1 x − 1 (x − 1)(x + 1) (x2 − 1 2x − 1 1 − x 3 1 − 2x x − 1 3 3 3(x − 3) 12 − 3x b) + + + + − = − = . x 2x + 1 x2 − 9 x 2x + 1 x + 3 (x − 3)(x + 3) (x − 3)(x + 3) x2 − 9 □
c Bài 11. Thực hiện phép tính x2 + 4x + 4 x 4 − x a) + + . x2 − 4 2 − x 5x − 10 x Å 3 2 − x ã ï 3 Å 1 x − 2 ãò b) − + + − − . x2 + 1 x + 6 x + 4 x + 6 x2 + 1 x + 4 Lời giải. a) Ta có: x2 + 4x + 4 x 4 − x + + x2 − 4 2 − x 5x − 10 (x + 2)2 x 4 − x = − + (x − 2)(x + 2) x − 2 5(x − 2) x + 2 x 4 − x = − + x − 2 x − 2 5(x − 2) 5(x + 2) 5x 4 − x = − + 5(x − 2) 5(x − 2) 5(x − 2) 14 − x = . 5x − 10 b) Ta có: x Å 3 2 − x ã ï 3 Å 1 x − 2 ãò − + + − − x2 + 1 x + 6 x + 4 x + 6 x2 + 1 x + 4 43/101 43/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 44
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC x 3 x − 2 3 1 x − 2 = − + + − + x2 + 1 x + 6 x + 4 x + 6 x2 + 1 x + 4 Å x 1 ã Å 3 3 ã 2(x − 2) = − + − + + x2 + 1 x2 + 1 x + 6 x + 6 x + 4 x − 1 2(x − 2) = + x2 + 1 x + 4 □
c Bài 12. Thực hiện phép tính x − y y − z z − x x y a) + + . b) + . xy yz zx (x − y)2 y2 − x2 Lời giải. a) Ta có: x − y y − z z − x
z(x − y) + x(y − z) + y(z − x) + + = xy yz zx xyz
zx − zy + xy − xz + yz − yx = xyz
(zx − xz) + (−zy + yz) + (xy − yx) = xyz = 0 b) Ta có: x y x y + = + (x − y)2 y2 − x2 (x − y)2 (y − x)(x + y) x(x + y) y(x − y) = − (x − y)2(x + y) (x − y)2(x + y) x2 + xy − yx + y2 = (x − y)2(x + y) x2 + y2 = . (x + y)(x − y)2 □ c Bài 13. Tính: 5x − 2 2x + 2 2 − 2x 3 + 2y 2x − 5 x2 y2 −y2 −z2 a) + ; b) + + ; c) + + + . 15 15 6x3y 6x3y 6x3y x + y y + z x + y y + z Lời giải. 5x − 2 2x + 2 5x − 2 + 2x + 2 7x a) + = = . 15 15 15 15 2 − 2x 3 + 2y 2x − 5 2 − 2x + 3 + 2y + 2x − 5 2y 1 b) + + = = = 6x3y 6x3y 6x3y 6x3y 6x3y 3x3 x2 y2 −y2 −z2 c) + + + x + y y + z x + y y + z x2 − y2 y2 − z2 = + x + y y + z (x + y)(x − y) (y + z)(y − z) = + x + y y + z =x − y + y − z =x − z. 44/101 44/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 45
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC □ c Bài 14. Tính 4x − 2 x + 2 1 1 1 2x − 1 x + 3 a) + ; b) + + ; c) + . 7xy2 7xy2 x 2x 3x x 2 Lời giải. 4x − 2 x + 2 4x − 2 + x + 2 5x 5 a) + = = = . 7xy2 7xy2 7xy2 7xy2 7y2 1 1 1 6 3 2 11 b) + + = + + = . x 2x 3x 6x 6x 6x 6x 2x − 1 x + 3 2(2x − 1) x(x + 3) 4x − 2 + x2 + 3x x2 + 7x − 2 c) + = + = = . x 2 2x 2x 2x 2x □ 4x2 − 2x + 3
c Bài 15. Viết phân thức P =
dưới dạng tổng một đa thức và một phân thức có tử thức là 2x − 1 hằng số. Lời giải. 4x2 − 2x + 3 4x2 − 2x 3 3 P = = + = 2x + . 2x − 1 2x − 1 2x − 1 2x − 1 □ 4x2 − 2x + 7
c Bài 16. Cho phân thức P =
. Tìm giá trị nguyên của x để giá trị của phân thức P là một 2x − 1 số nguyên. Lời giải. 7 Ta có P = 2x + ; x ∈ Z. 2x − 1
Để P nhận giá trị nguyên thì 2x − 1 ∈ Ư(7). Do đó 2x − 1 = 1 ⇒ x = 1 □ 2x − 1 = 7 ⇒ x = 4 2x − 1 = −1 ⇒ x = 0 2x − 1 = −7 ⇒ x = −3 25x2 − 1 5xy − 15x + y − 3 1
c Bài 17. Cho biểu thức P = + với x ̸=
; y ̸= 3. Tính giá trị của P . 1 − 5x y − 3 5 Lời giải. (5x − 1)(5x + 1) (y − 3) · (5x + 1) Ta có P = + = −5x − 1 + 5x + 1 = 0. □ −(5x − 1) y − 3
c Bài 18. Cho (a + b + c)2 = a2 + b2 + c2. Rút gọn biểu thức a2 b2 c2 P = + + . a2 + 2bc b2 + 2ac c2 + 2ab Lời giải.
Từ (a + b + c)2 = a2 + b2 + c2, ta có
a2 + b2 + c2 + 2(ab + bc + ca) = a2 + b2 + c2 nên ab + bc + ca = 0. 45/101 45/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 46
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
Xét a2 + 2bc = a2 + 2bc − ab − bc − ca = a2 − ab − ca + bc. = (a − b)(a − c) Tương tự ta có b2 + 2ac = (b − a)(b − c) c2 + 2ab = (c − a)(c − b). a2 b2 c2 Do đó ta có P = + + (a − b)(a − c) (b − a)(b − c) (c − a)(c − b)
a2(b − c) + b2(c − a) + c2(a − b) ⇒ P = − . (a − b)(b − c)(c − a)
Phân tích tử thức thành nhân tử, ta có (a − b)(b − c)(a − c) P = − = 1. (a − b)(b − c)(c − a) □
c Bài 19. Chứng minh giá trị của biểu thức sau không phụ thuộc vào x. x + 4 x − 2 A = − . 2x + 4 x2 − 4 Lời giải. x + 4 x − 2 x + 4 1 x + 4 − 2 1 A = − = − = = . □ 2(x + 2) (x + 2)(x − 2) 2(x + 2) x + 2 2(x + 2) 2 c Bài 20. 1 1 a) Thực hiện phép tính − . x x + 1 b) Thu gọn biểu thức 1 1 1 1 A = + + + . x2 + x x2 + 3x + 2 x2 + 5x + 6 x + 3 Lời giải. 1 a) . x(x + 1)
b) Phân tích mẫu thức thành nhân tử rồi áp dụng câu a. 1 1 1 1 Ta có A = + + + x(x + 1) (x + 1)(x + 2) (x + 2)(x + 3) x + 3 1 1 1 1 1 1 1 = − + − + − + x x + 1 x + 1 x + 2 x + 2 x + 3 x + 3 1 = . x □ c Bài 21. 2x2 + 1 1 − x 1
a) Rút gọn biểu thức: A = + − ; x3 + 1 x2 − x + 1 x + 1
b) Tính giá trị của biểu thức A tại x = −3. Lời giải. 46/101 46/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 47
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
a) Rút gọn biểu thức A như sau: 2x2 + 1 1 − x 1 2x2 + 1 1 − x 1 A = + − = + − x3 + 1 x2 − x + 1 x + 1 (x + 1) (x2 − x + 1) x2 − x + 1 x + 1 2x2 + 1 (1 − x)(x + 1) x2 − x + 1 = + − (x + 1) (x2 − x + 1) (x + 1) (x2 − x + 1) (x + 1) (x2 − x + 1)
2x2 + 1 + (1 − x)(x + 1) − x2 − x + 1 = (x + 1) (x2 − x + 1)
2x2 + 1 + 1 − x2 − x2 + x − 1 x + 1 1 = = = . (x + 1) (x2 − x + 1) (x + 1) (x2 − x + 1) x2 − x + 1 1
b) Điều kiện xác định của phân thức là x2 − x + 1 ̸= 0. x2 − x + 1
Với x = −3 ta thấy x2 − x + 1 = (−3)2 − (−3) + 1 = 91 ̸= 0. 1 1
Do đó, giá trị của biểu thức A tại x = −3 là = . (−3)2 − (−3) + 1 91 □
c Bài 22. Cùng đi từ thành phố A đến thành phố B cách nhau 450 km, xe khách chạy với tốc độ x km/h;
xe tải chạy với tốc độ y km/h (x > y). Nếu xuất phát cùng lúc thì xe khách đến thành phố B sớm hơn xe tải bao nhiêu giờ? Lời giải.
Quãng đường đi từ thành phố A đến thành phố B cách nhau 450 km. 450
Xe khách chạy với tốc độ x km/h nên thời gian xe khách đi hết quãng đường AB là h. x 450
Xe tải chạy với tốc độ y km/h nên thời gian xe tải đi hết quãng đường AB là h. y 450 450 450x − 450y
Thời gian xe khách đến thành phố B sớm hơn xe tải là − = h. □ y x xy c Bài 23.
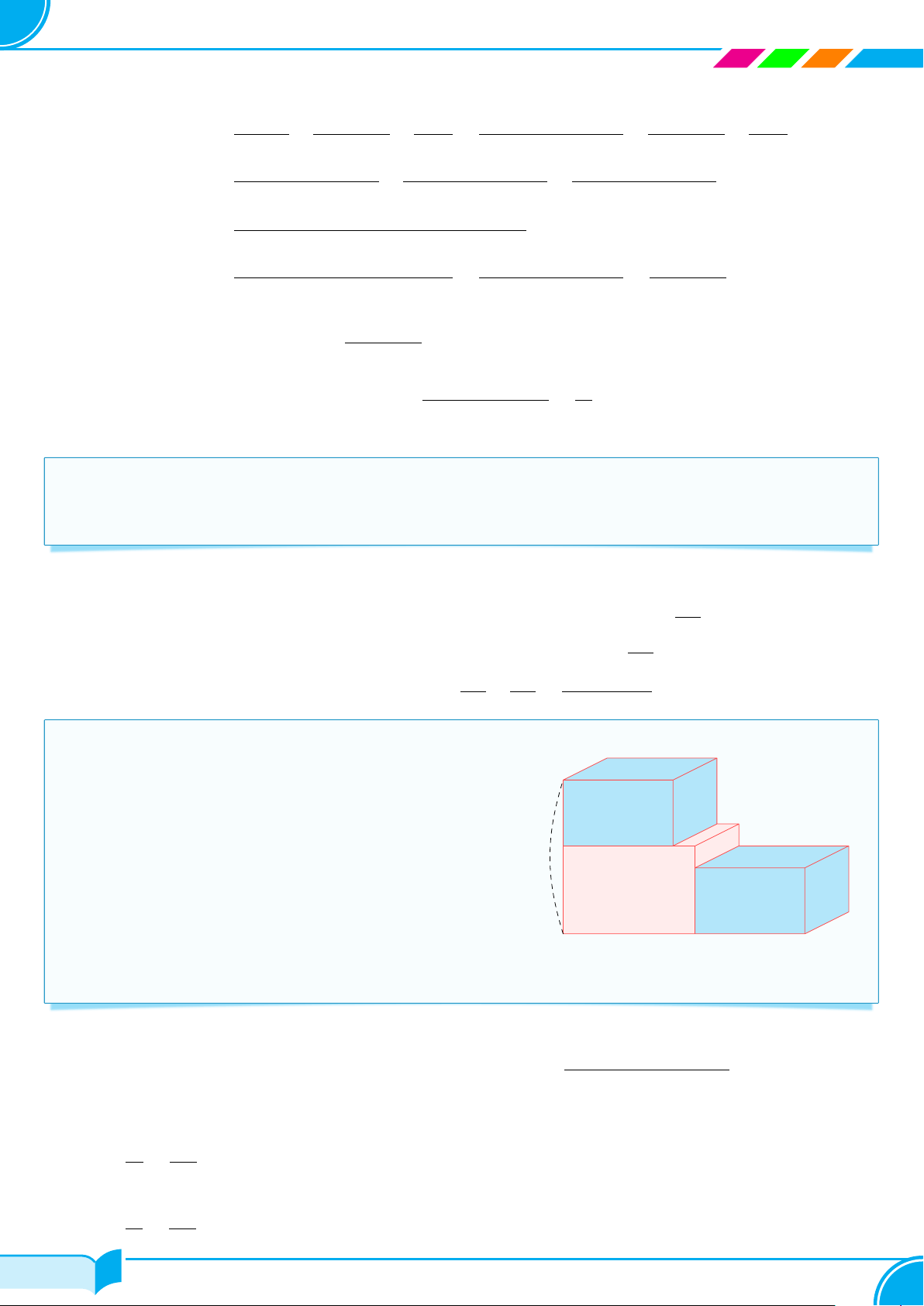
Có ba hình hộp chữ nhật A, B, C có chiều dài, chiều rộng K L
và thể tích được cho như Hình 2. Hình B và C có các kích C G C
thước giống nhau, hình A có cùng chiều rộng với B và C.
a) Tính chiều cao của các hình hộp chữ nhật. Biểu thị M N ?
chúng bằng các phân thức cùng mẫu số. ? A H D P Q A J I B
b) Tính tổng chiều cao của hình A và C, chênh lệch chiều a cm3 b cm3 cao của hình A và B. E F z cm x cm y cm Hình 2 Lời giải. V
a) Ta có V = Chiều dài · Chiều rộng · Chiều cao ⇒ Chiều cao = . Dựa vào Hình 2 ta Chiều dài · Chiều rộng thấy:
○ Khối hộp chữ nhật A có thể tích là a cm3, chiều dài là x cm và chiều rộng là z cm nên chiều cao là a ay = cm. xz xyz
○ Khối hộp chữ nhật B có thể tích là b cm3, chiều dài là y cm và chiều rộng là z cm nên chiều cao là b bx = cm. yz xyz 47/101 47/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 48
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC bx
○ Khối hộp chữ nhật C có kích thước giống khối hộp B nên chiều cao là cm. xyz ay bx ay + bx
b) Tổng chiều cao của hình A và C là + = cm. xyz xyz xyz ay bx ay − bx ay − bx Ta có − =
nên hình A cao hơn hình B là cm. xyz xyz xyz xyz □
c Bài 24. Một xí nghiệp dự định sản xuất 10 000 sản phẩm trong x ngày. Khi thực hiện, xí nghiệp đã làm
xong sớm hơn 1 ngày so với dự định và còn làm thêm được 80 sản phẩm. Viết phân thức biểu thị theo x:
a) Số sản phẩm xí nghiệp làm trong 1 ngày theo dự định;
b) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế;
c) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế nhiều hơn số sản phẩm xí nghiệp làm trong 1 ngày theo dự định. Lời giải. 10 000
a) Số sản phẩm xí nghiệp làm trong 1 ngày theo dự định là (sản phẩm). x
b) Số sản phẩm xí nghiệp đã hoàn thành trên thực tế là 10 000 + 80 = 10 080 (sản phẩm).
Số ngày xí nghiệp đã hoàn thành trên thực tế là x − 1 (ngày). 10 080
Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế là (sản phẩm) x − 1
c) Số sản phẩm xí nghiệp làm trong 1 ngày trên thực tế nhiều hơn số sản phẩm xí nghiệp làm trong 1 ngày theo dự định là 10000 10080 Å 125 126 ã Å 125(x − 1) 126x ã − = 80 − = 80 − x x − 1 x x − 1 x(x − 1) x(x − 1) 125x − 125 − 126x −80x − 10000 = 80 · = (sản phẩm). x(x − 1) x(x − 1) □
c Bài 25. Người ta mở hai vòi nước cùng chảy vào bể không chứa nước. Thời gian để vòi thứ nhất chảy một
mình đầy bể ít hơn thời gian để vòi thứ hai chảy một mình đầy bể là 2 giờ. Gọi x (giờ) là thời gian vòi thứ
nhất chảy một mình để đầy bể. Viết phân thức biểu thị theo x:
a) Thời gian vòi thứ hai chảy một mình đầy bể;
b) Phần bể mà mỗi vòi chảy được trong 1 giờ;
c) Phần bể mà cả hai vòi chảy được trong 1 giờ. Lời giải.
a) Theo đề bài, thời gian để vòi thứ nhất chảy một mình đầy bể ít hơn thời gian để vòi thứ hai chảy một mình đầy bể là 2 giờ.
Hay thời gian để vòi thứ hai chảy một mình đầy bể nhiều hơn thời gian để vòi thứ nhất chảy một mình đầy bể là 2 giờ.
Do đó, thời gian vòi thứ hai chảy một mình đầy bể là x + 2 (giờ). 1
b) Số phần bể mà vòi thứ nhất chảy được trong 1 giờ là (bể). x1
Số phần bể mà vòi thứ hai chảy được trong 1 giờ là (bể). x + 2 48/101 48/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 49
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c) Số phần bể mà cả hai vòi chảy được trong 1 giờ là 1 1 x + 2 x x + 2 + x 2x + 2 + = + = = (bể). x x + 2 x(x + 2) x(x + 2) x(x + 2) x(x + 2) □
c Bài 26. Để hưởng ứng phong trào Tết trồng cây, chi đoàn thanh niên dự định trồng 120 cây xanh. Khi
bắt đầu thực hiện, chi đoàn được tăng cường thêm 3 đoàn viên. Gọi x là số đoàn viên ban đầu của chi đoàn
và giả sử số cây mỗi đoàn viên trồng là như nhau. Viết phân thức biểu thị theo x:
a) Số cây mỗi đoàn viên trồng theo dự định;
b) Số cây mỗi đoàn viên trồng theo thực tế;
c) Số cây mỗi đoàn viên trồng theo dự định nhiều hơn số cây mỗi đoàn viên trồng theo thực tế. Lời giải.
a) Theo dự định, chi đoàn thanh niên trồng 120 cây xanh, ban đầu chi đoàn có x đoàn viên. 120
Do đó, phân thức biểu thị số cây mỗi đoàn viên trồng theo dự định là (cây). x
b) Theo thực tế, chi đoàn được tăng cường thêm 3 đoàn viên.
Khi đó, số đoàn viên của chi đoàn theo thực tế là x + 3 (đoàn viên). 120
Do đó, phân thức biểu thị số cây mỗi đoàn viên trồng theo thực tế là (cây). x + 3
c) Số cây mỗi đoàn viên trồng theo dự định nhiều hơn số cây mỗi đoàn viên trồng theo thực tế là 120 120 120(x + 3) − 120x 120x + 360 − 120x 360 − = = = (cây). x x + 3 x(x + 3) x(x + 3) x(x + 3)
Vậy phân thức biểu thị số cây mỗi đoàn viên trồng theo dự định nhiều hơn số cây mỗi đoàn viên trồng theo 360 thực tế là (cây). x(x + 3) □
c Bài 27. Gia đình cô Lương nuôi ba con lợn. Cả ba con lợn đều ăn cùng một loại thức ăn gia súc. Biểu đồ
cột ở hình dưới biểu diễn số ngày mà mỗi con lợn ăn hết một bao thức ăn. Hỏi cả ba con lợn ăn trong x ngày (x ∈ ∗
N ) thì cần bao nhiêu thức ăn? số ngày 7 6 5 4 3 2 1 O Con Con Con Con thứ nhất thứ hai thứ ba lợn 49/101 49/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 50
23. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Lời giải.
Dựa vào biểu đồ cột, ta có
○ Con lợn thứ nhất ăn 3 ngày hết 1 bao thức ăn. 1
Khi đó, mỗi ngày con lợn thứ nhất ăn hết bao thức ăn. 3 x
Do đó, con lợn thứ nhất ăn trong x ngày hết bao thức ăn. 3
○ Con lợn thứ hai ăn 6 ngày hết 1 bao thức ăn. 1
Khi đó, mỗi ngày con lợn thứ hai ăn hết bao thức ăn. 6 x
Do đó, con lợn thứ hai ăn trong x ngày hết bao thức ăn. 6
○ Con lợn thứ ba ăn 4 ngày hết 1 bao thức ăn. 1
Khi đó, mỗi ngày con lợn thứ hai ăn hết bao thức ăn. 4 x
Do đó, con lợn thứ hai ăn trong x ngày hết bao thức ăn. 4
Cả ba con lợn ăn trong x ngày (x ∈ ∗ N ) thì cần x x x 4x 2x 3x 9x 3x + + = + + = = (bao thức ăn). 3 6 4 12 12 12 12 4 3x
Vậy cả ba con lợn ăn trong x ngày (x ∈ ∗ N ) thì cần bao thức ăn. □ 4 50/101 50/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 51
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Baâi 24
PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ A
TRỌNG TÂM KIẾN THỨC
1 Phép nhân các phân thức đại số
○ Quy tắc: Muốn nhân hai phân thức, ta nhân các tử thức với nhau, các mẫu thức với nhau A C A · C · = . B D B · D
○ Phép nhân các phân thức có các tính chất: A C C A — Giao hoán: · = · . B D D B Å A C ã E A Å C E ã — Kết hợp: · · = · · ; B D F B D F A Å C E ã A C A E
— Phân phối đối với phép cộng: + = · + · B D F B D B F
2 Phân thức nghịch đảo
○ Hai phân thức được gọi là nghịch đảo của nhau nếu tích của chúng bằng 1. A A B A ○ Tổng quát, nếu là phân thức khác 0 thì · = 1, do đó
là phân thức nghịch đảo của phân thức B B A B B . A 3 Phép chia A C A C Muốn chia phân thức cho phân thức khác 0, ta nhân
với phân thức nghịch đảo của . B D B D A C A D C : = · với ̸= 0. B D B C D A B CÁC DẠNG BÀI TẬP
Dạng 1. Thực hiện phép nhân, phép chia các phân thức
c Ví dụ 1. Thực hiện các phép tính sau: 18x2y2 5z3 5x + 5y 6x − 6y Å 7z ã a) · ; b) · ; c) 3x3y4 · − . 15z 9x3y2 4x − 4y 25x + 25y 9xy5 Lời giải. 18x2y2 5z3 18x2y2 · 5z3 2z2 a) · = = . 15z 9x3y2 15z · 9x3y2 3x 51/101 51/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 52
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 5x + 5y 6x − 6y 5 · (x + y) · 6 · (x − y) 3 b) · = = . 4x − 4y 25x + 25y
4 · (x − y) · 25 · (x + y) 10 Å 7z ã 3x3y4 · (−7z) 7x2z c) 3x3y4 · − = = − . 9xy5 9xy5 3y □
c Ví dụ 2. Thực hiện phép tính sau x2 − 25 x2 + 5x 25x2y5 x3y + xy3 a) : ; b) − : 15xy2; c) (x2 + y2) : . x2 − 3x x2 − 9 3x x4y Lời giải. x2 − 25 x2 + 5x x2 − 25 x2 − 9
(x + 5)(x − 5)(x + 3)(x − 3) (x − 5)(x + 3) a) : = · = = . x2 − 3x x2 − 9 x2 − 3x x2 + 5x x(x − 3)x(x + 5) x2 25x2y5 −25x2y5 1 −5y3 b) − : 15xy2 = · = . 3x 3x 15xy2 9 x3y + xy3 x4y c) (x2 + y2) : = (x2 + y2) · = x3. x4y xy(x2 + y2) □
c Ví dụ 3. Thực hiện phép tính x + 1 x + 2 x + 3 : : . x + 2 x + 3 x + 1 Lời giải. x + 1 x + 2 x + 3 x + 1 x + 3 x + 1 (x + 1)2 : : = · · = . x + 2 x + 3 x + 1 x + 2 x + 2 x + 3 (x + 2)2 □
Dạng 2. Rút gọn biểu thức
Thực hiện phép nhân, phép chia các phân thức đại số để rút gọn biểu thức. Å x + 1 x − 1 x2 − 4x − 1 ã x + 2003 c Ví dụ 4. Cho K = − + · x − 1 x + 1 x2 − 1 x a) Rút gọn K.
b) Tìm số nguyên x để K nhận giá trị nguyên. Lời giải. a) Ta có
(x + 1)2 − (x − 1)2 + x2 − 4x − 1 x + 2003 K = · (x − 1)(x + 1) x
x2 + 2x + 1 − x2 + 2x − 1 + x2 − 4x − 1 x + 2003 K = · (x − 1)(x + 1) x x2 − 1 x + 2003 K = · . x2 − 1 x x + 2003 Vậy K = . x 52/101 52/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 53
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 2003
b) Điều kiện xác định: x ̸= 0; x ̸= 1; x ̸= −1. Ta có K = 1 + . x 2003 Để K ∈ Z thì
∈ Z ⇒ x ∈ Ư(2003) và x ̸= 1; x ̸= −1. x
Vậy x ∈ {−2003; 2003} thì K nhận giá trị nguyên. □
c Ví dụ 5. Thực hiện phép tính sau 12x + 5 4x + 3 12x + 5 6 − 3x a) P = · + · . x + 9 360x + 150 x + 9 360x + 150 x + 3y 4x − 2y x + 3y x − 3y b) P = · − · . 3x + y x − y 3x + y x − y Lời giải.
a) Dùng tính chất phân phối, ta có 12x + 5 Å 4x + 3 6 − 3x ã 12x + 5 x + 9 1 P = · + = · = . x + 9 360x + 150 360x + 150 x + 9 30(12x + 5) 30
b) Dùng tính chất phân phối, ta có x + 3y Å 4x − 2y x − 3y ã x + 3y 3x + y x + 3y P = · − = · = . 3x + y x − y x − y 3x + y x − y x − y □
c Ví dụ 6. Rút gọn biểu thức 3a2 − 2ab − b2 3a2 − 4ab + b2 R = : . 2a2 + ab − b2 3a2 + 2ab − b2 Lời giải. (a − b)(3a + b) (a − b)(3a − b) R = : (2a − b)(a + b) (3a − b)(a + b) 3a + b R = . 2a − b □
c Ví dụ 7. Cho x ̸= 0, x ̸= ±2. Rút gọn rồi tính giá trị biểu thức Å 4 3 ã x + 14 A = − : với x = −3. x − 2 x + 2 x2 Lời giải.
Rút gọn biểu thức ta có Å 4(x + 2) 3(x − 2) ã x2 A = − · (x − 2)(x + 2) (x − 2)(x + 2) x + 14 4x + 8 − 3x + 6 x2 x + 14 x2 x2 = · = · = . x2 − 4 x + 14 x2 − 4 x + 14 x2 − 4
Thay x = −3 vào biểu thức rút gọn ta được (−3)2 9 A = = . (−3)2 − 4 5 □ 53/101 53/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 54
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
Dạng 3. Tìm x thỏa mãn đẳng thức cho trước
○ Tìm x từ đẳng thức x : A = B, ta có x = A · B.
○ Tìm x từ đẳng thức A · x = B, ta có x = B : A.
○ Rút gọn biểu thức B : A dựa vào phép chia phân thức.
c Ví dụ 8. Tìm biểu thức x, biết a2 + a + 1 a + 1 x : = . 2a + 2 a3 − 1 Lời giải. a2 + a + 1 a + 1 a + 1 a2 + a + 1 x : = ⇒ x = · 2a + 2 a3 − 1 a3 − 1 2a + 2 a + 1 a2 + a + 1 x = · (a − 1)(a2 + a + 1) 2(a + 1) 1 x = . 2(a − 1) □ a + 1 a2 − 1
c Ví dụ 9. Tìm x, biết · x =
, với a là hằng số; a ̸= 1; a ̸= −1; a ̸= 0; a ̸= −2. a + 2 a2 + 2a Lời giải. a2 − 1 a + 1 (a − 1)(a + 1) a + 2 a − 1 a = : = · = . a2 + 2a a + 2 a(a + 2) a + 1 a □
Dạng 4. Chứng minh giá trị biểu thức không phụ thuộc vào giá trị của biến
Thực hiện phép tính các phân thức để rút gọn biểu thức không còn chứa biến.
c Ví dụ 10. Cho ab + bc + ca = 1. Chứng minh rằng tích sau không phụ thuộc vào biến số (a + b)2 (b + c)2 (c + a)2 A = · · . 1 + a2 1 + b2 1 + c2 Lời giải. Ta có
1 + a2 = ab + bc + ca + a2 = (a + b)(a + c). Tương tự ta có 1 + b2 = (b + a)(b + c) 1 + c2 = (c + a)(c + b). Thế vào A, ta được (a + b)2 (b + c)2 (c + a)2 A = · · = 1. (a + b)(a + c) (b + c)(b + a) (c + a)(c + b)
Vậy giá trị biểu thức A không phụ thuộc vào giá trị của biến. □ 54/101 54/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 55
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Ví dụ 11. Cho a + b + c = 0. Chứng minh rằng tích sau không phụ thuộc vào biến số 4bc − a2 4ca − b2 4ab − c2 Å ã a b c a) M = · · ; b) N = 1 + · 1 + · 1 + . bc + 2a2 ca + 2b2 ab + 2c2 b c a Lời giải. a) Ta có 4bc − a2 4bc − (b + c)2 −(b2 − 2bc + c2) −(b − c)2 = = = . bc + 2a2 bc + 2a(b + c) bc + a2 − ab − ac (a − b)(a − c) Tương tự ta có 4ca − b2 −(c − a)2 = ca + 2b2 (b − a)(b − c) 4ab − c2 −(a − b)2 = . ab + 2c2 (c − a)(c − b) Thế vào M , ta được 4bc − a2 4ca − b2 4ab − c2
−(a − b)2(b − c)2(c − a)2 M = · · = = 1. bc + 2a2 ca + 2b2 ab + 2c2
−(a − b)2(b − c)2(c − a)2
Vậy giá trị biểu thức M không phụ thuộc vào giá trị của biến. b) Ta có Å ã a b c N = 1 + · 1 + · 1 + b c a a + b b + c a + c = · · b c a (−c) · (−a) · (−b) = abc = −1.
Vậy giá trị biểu thức N không phụ thuộc vào giá trị của biến. □ Dạng 5. Vận dụng
c Ví dụ 12. Đường sắt và đường bộ đi từ thành phố A đến thành phố B có độ dài bằng nhau và bằng s
(km). Thời gian để đi từ A đến B của tàu hỏa là a (giờ), của ô tô khách là b (giờ) (a < b). Tốc độ của tàu hỏa
gấp bao nhiêu lần tốc độ của ô tô? Tính giá trị này khi s = 350, a = 5, b = 7. Lời giải. s Vận tốc tàu hỏa: (km/h). a s Vận tốc ô tô: (km/h). b s s s b b
Vận tốc tàu hỏa gấp vận tốc ô tô: : = · = (lần). a b a s a b 7 Giá trị cần tính là = . □ a 5 55/101 55/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 56
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Ví dụ 13. Máy A xát được x tấn gạo trong a giờ, máy B xát được y tấn gạo trong b giờ.
a) Viết các biểu thức biểu thị số tấn gạo mỗi máy xát được trong 1 giờ (gọi là công suất của máy).
b) Công suất của máy A gấp bao nhiêu lần máy B? Viết biểu thức biểu thị số lần này.
c) Tính giá trị biểu thức ở câu b khi x = 3, a = 5, y = 2, b = 4. Lời giải. x y a) Công suất máy A là , Công suất máy B là . a b x y x b xb
b) Công suất của máy A gấp máy B: : = · = (lần). a b a y ay
c) Tính giá trị biểu thức ở câu b khi x = 3, a = 5, y = 2, b = 4. xb 3 · 4 6 = = . ay 5 · 2 5 □
c Ví dụ 14. Một ca nô đi xuôi dòng trên một khúc sông từ A đến B dài 20 km rồi lại đi ngược dòng từ B
về A. Biết tốc độ dòng nước là 3 km/h. Gọi x( km/h) là tốc độ của ca nô. Viết phân thức biểu thị theo x:
a) Thời gian ca nô đi xuôi dòng từ A đến B;
b) Thời gian ca nô đi ngược dòng từ B về A;
c) Tỉ số của thời gian ca nô đi xuôi dòng từ A đến B và thời gian ca nô đi ngược dòng từ B về A. Lời giải.
a) Do tốc độ ca nô đi xuôi dòng là x + 3( km/h) nên phân thức biểu thị thời gian ca nô đi xuôi dòng từ A đến 20 B là (giờ). x + 3
b) Do tốc độ ca nô đi ngược dòng là x − 3( km/h) nên phân thức biểu thị thời gian ca nô đi ngược dòng từ B 20 về A là (giờ). x − 3
c) Tỉ số của thời gian ca nô đi xuôi dòng từ A đến B và thời gian ca nô đi ngược dòng từ B về A là 20 20 20 x − 3 x − 3 : = · = · x + 3 x − 3 x + 3 20 x + 3
Vậy phân thức biểu thị tỉ số thời gian ca nô đi xuôi dòng từ A đến B và thời gian ca nô đi ngược dòng từ x − 3 B về A là · x + 3 □
c Ví dụ 15. Bác Châu vay ngân hàng 1,2 tỉ đồng để mua nhà theo hình thức trả góp. Số tiền bác Châu phải
trả mỗi tháng bao gồm số tiền gốc phải trả hằng tháng (bằng số tiền gốc chia đều cho số tháng vay) và số
tiền lãi phải trả hằng tháng (bằng số tiền gốc nhân với lãi suất tháng). a) Gọi r là l¯
ai suất năm của khoản vay trả góp này. Tính số tiền x (triệu đồng) mà bác Châu phải trả mỗi
tháng theo số tháng vay y (tháng) và lãi suất năm r. Từ đó suy ra công thức tính lãi suất năm r theo x và y.
b) Tính giá trị của r tại x = 30, y = 48 rồi cho biết, nếu trả góp mỗi tháng 30 triệu đồng trong vòng 4 năm
thì lãi suất năm (tính theo %) của khoản vay này là bao nhiêu? Lời giải. 56/101 56/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 57
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 1, 2 · 103 r Å 1, 2 · 103 ã a) x = + 1, 2 · 103 · ⇒ r = x − : 102. y 12 y Å 1, 2 · 103 ã b) r = 30 − : 102 = 0, 05 = 5%. 48 □ A C BÀI TẬP TỰ LUYỆN c Bài 1. Tính 3x + 6 8 − 2x 3x2 Å −10y3 ã a) · ; b) · . 4x − 16 x + 2 5y3 9x3 Lời giải. 3x + 6 8 − 2x 3(x + 2) 2(4 − x) 3 a) · = · = − . 4x − 16 x + 2 4(x − 4) x + 2 2 3x2 Å −10y3 ã 3x2 · (−10y3) 2 b) · = = − . 5y3 9x3 5y3 · 9x3 3x □
c Bài 2. Thực hiện các phép tính sau x5 + 2x2 + 3 4x 5x3 + 5 x2 + 2x 2x − 4 a) M = · · ; b) A = · . 3x3 + 3 x2 − 4 x5 + 2x2 + 3 3x − 6 x2 + 4x + 4 Lời giải. x5 + 2x2 + 3 4x 5x3 + 5 x5 + 2x2 + 3 4x 5(x3 + 1) 20x a) M = · · = · · = . 3x3 + 3 x2 − 4 x5 + 2x2 + 3 3(x3 + 1) x2 − 4 x5 + 2x2 + 3 3(x2 − 4) x2 + 2x 2x − 4 x(x + 2) 2(x − 2) 2x b) A = · = · = . 3x − 6 x2 + 4x + 4 3(x − 2) (x + 2)2 3(x + 2) □
c Bài 3. Rút gọn rồi tính giá trị của biểu thức x2 − 1 2x + 10 P = · với x = 99. x + 5 x2 − x Lời giải. Ta có x2 − 1 2x + 10 (x + 1)(x − 1) 2(x + 5) 2(x + 1) P = · = · = . x + 5 x2 − x x + 5 x(x − 1) x 200 Thế x = 99, ta được P = . □ 99
c Bài 4. Hãy điền phân thức thích hợp vào dấu . . . trong đẳng thức sau 1 x x + 1 x + 2 x + 3 x + 4 · · · · · · . . . = 1. x x + 1 x + 2 x + 3 x + 4 x + 5 Lời giải. 57/101 57/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 58
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Ta có 1 x x + 1 x + 2 x + 3 x + 4 1 · · · · · = . x x + 1 x + 2 x + 3 x + 4 x + 5 x + 5
Vậy phân thức cần điền là x + 5. □
c Bài 5. Cho x + y + z = 1. Chứng minh rằng giá trị biểu thức sau không phụ thuộc vào giá trị của biến số (x + y)2 (y + z)2 (z + x)2 P = · · . xy + z yz + x zx + y Lời giải. Ta có
xy + z = xy + z(x + y + z) = xy + xz + yz + z2 = (z + x)(z + y). Tương tự ta có yz + x = (x + y)(x + z) zx + y = (y + x)(y + z). Thế vào P , ta được (x + y)2 (y + z)2 (z + x)2 P = · · = 1. (z + x)(z + y) (x + y)(x + z) (y + x)(y + z)
Vậy giá trị biểu thức P không phụ thuộc vào giá trị của biến. □
c Bài 6. Thực hiện các phép tính 14 + 4 54 + 4 94 + 4 174 + 4 a) A = · · · . . . · ; 34 + 4 74 + 4 114 + 4 194 + 4 1 1 1 1 14 + 34 + 54 + 294 + b) B = 4 · 4 · 4 · . . . · 4 . 1 1 1 1 24 + 44 + 64 + 304 + 4 4 4 4 Lời giải. a) Ta có
k4 + 4 = (k2 + 2)2 − 4k2 = (k2 + 2 + 2k)(k2 + 2 − 2k) = (k + 1)2 + 1 (k − 1)2 + 1 .
Áp dụng kết quả, ta được 14 + 4 54 + 4 94 + 4 174 + 4 A = · · · . . . · 34 + 4 74 + 4 114 + 4 194 + 4 (22 + 1)(02 + 1) (62 + 1)(42 + 1) (102 + 1)(82 + 1) (182 + 1)(162 + 1) = · · · . . . · (42 + 1)(22 + 1) (82 + 1)(62 + 1) (122 + 1)(102 + 1) (202 + 1)(182 + 1) 1 = 202 + 1 1 = . 401 b) Ta có 1 Å 1 ã Å 1 ã2 k4 + = k4 + k2 + − k2 = k2 + − k2 4 4 2 Å ñ ô ñ ô 1 ã Å 1 ã Å 1 ã2 1 Å 1 ã2 1 = k2 + k + k2 − k + = k + + k − + . 2 2 2 4 2 4 1
Áp dụng kết quả vào B, ta tính được B = . 1861 58/101 58/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 59
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC □
c Bài 7. Thực hiện phép tính 3x + 9 x + 3 5x2 + 10xy x + 2y a) : ; b) : . x2 − 4 x − 2 x2 + 2xy + 4y2 x3 − 8y3 Lời giải. 3x + 9 x + 3 3(x + 3) x − 2 3 a) : = · = . x2 − 4 x − 2 (x + 2)(x − 2) x + 3 x + 2 5x2 + 10xy x + 2y 5x(x + 2y) (x − 2y)(x2 + 2xy + 4y2) b) : = · = 5x(x − 2y). x2 + 2xy + 4y2 x3 − 8y3 x2 + 2xy + 4y2 x + 2y □ c Bài 8. Tính 4x2 − 1 y2 + xy a) : (1 − 2x); b) (x + y) : . x x − y Lời giải. 4x2 − 1 (2x + 1)(2x − 1) −2x − 1 a) : (1 − 2x) = = . x x(1 − 2x) x y2 + xy (x + y)(x − y) x − y b) (x + y) : = = . x − y y(x + y) y □
c Bài 9. Thực hiện phép chia x + y + z x2 + y2 − z2 + 2xy a) A = : ; (x + y)2 − (x + y)z 2x + 2y 6x − 3 4x2 − 1 b) B = : ; x 3x2 x2 − 12xy + 36y2 3x − 18y c) C = : . x2 + 12xy + 36y2 3x + 18y Lời giải. x + y + z 2(x + y) x + y + z 2(x + y) a) A = · = · . (x + y)2 − (x + y)z (x + y)2 − z2 (x + y)(x + y − z) (x + y + z)(x + y − z) 2 = (x + y − z)2 6x − 3 3x2 3(2x − 1) 3x2 9x b) B = · = · = . x 4x2 − 1 x (2x − 1)(2x + 1) 2x + 1 x2 − 12xy + 36y2 3x + 18y (x − 6y)2 3(x + 6y) x − 6y c) C = · = · = . x2 + 12xy + 36y2 3x − 18y (x + 6y)2 3(x − 6y) x + 6y □
c Bài 10. Hãy điền phân thức thích hợp vào dấu . . . trong đẳng thức sau x x + 1 x + 2 x + 3 x + 4 : : : : : . . . = 1. x + 1 x + 2 x + 3 x + 4 x + 5 59/101 59/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 60
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Lời giải.
Kết quả của 4 phép chia đầu là x x + 1 x + 2 x + 3 x + 4 x x + 2 x + 3 x + 4 x + 5 x(x + 5) : : : : = · · · · = . x + 1 x + 2 x + 3 x + 4 x + 5 x + 1 x + 1 x + 2 x + 3 x + 4 (x + 1)2 x(x + 5)
Vậy phân thức cần điền vào chỗ trống là . □ (x + 1)2
c Bài 11. Tìm x, biết 3a 4a a + 2 a2 − 4 a) · x = với a ̸= 0. b) · x = với a / ∈ {−1; 0; −2}. 4 5 a + 1 a2 + a Lời giải. 4a 3a 4a 4 16 a) x = : = · = . 5 4 5 3a 15 a2 − 4 a + 2 a2 − 4 a + 1 (a + 2)(a − 2)(a + 1) a − 2 b) x = : = · = = . a2 + a a + 1 a2 + a a + 2 a(a + 1)(a + 2) a □ 52 − 1 92 − 1 132 − 1 572 − 1 c Bài 12. Tính A = : : : . . . : . 32 − 1 72 − 1 112 − 1 552 − 1 Lời giải. Ta có 52 − 1 72 − 1 112 − 1 552 − 1 A = · · · . . . · 32 − 1 92 − 1 132 − 1 572 − 1 4 · 6 6 · 8 10 · 12 54 · 56 = · · · . . . · 2 · 4 8 · 10 12 · 14 56 · 58 6 · 6 9 = = . 2 · 58 29 □
c Bài 13. Tâm đạp xe từ nhà đến câu lạc bộ câu cá có quãng đường dài 15 km với tốc độ x (km/h). Lượt
về thuận chiều gió nên tốc độ nhanh hơn lượt đi 4 (km/h).
a) Viết biểu thức biểu thị tổng thời gian T hai lượt đi và về.
b) Viết biểu thức biểu thị hiệu thời gian t lượt đi đối với lượt về. c) Tính T và t với x = 10. Lời giải.
a) Viết biểu thức biểu thị tổng thời gian T hai lượt đi và về. 15 Thời gian đi (h). x15 Thời gian về (h). x + 4 15 15 Vậy T = + . x x + 4
b) Viết biểu thức biểu thị hiệu thời gian t lượt đi đối với lượt về: 15 15 t = − . x x + 4 60/101 60/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 61
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC c) Tính T và t với x = 10. 15 15 15 15 18 T = + = + = . x x + 4 10 14 7 15 15 15 15 3 t = − = − = . x x + 4 10 14 7 □
c Bài 14. Một xí nghiệp theo kế hoạch cần phải sản xuất 120 tấn hàng trong một số ngày quy định. Do cải
tiến kĩ thuật nên xí nghiệp đã hoàn thành kế hoạch sớm hơn thời gian quy định 1 ngày và làm thêm được 5
tấn hàng. Gọi x là số ngày xí nghiệp cần làm theo dự định. Viết phân thức biểu thị theo x:
a) Số tấn hàng xí nghiệp làm trong 1 ngày theo dự định;
b) Số tấn hàng xí nghiệp làm trong 1 ngày trên thực tế;
c) Tỉ số của số tấn hàng xí nghiệp làm trong 1 ngày trên thực tế và số tấn hàng xí nghiệp làm trong 1 ngày theo dự định. Lời giải. 120
a) Số tấn hàng xí nghiệp làm trong 1 ngày theo dự định là tấn hàng. x 120
b) Số tấn hàng xí nghiệp làm trong 1 ngày trên thực tế là + 5 tấn hàng. x − 1
c) Tỉ số của số tấn hàng xí nghiệp làm trong 1 ngày trên thực tế và số tấn hàng xí nghiệp làm trong 1 ngày theo dự định là Å 120 ã 120 5x + 115 x x(x + 23) + 5 : = · = · x − 1 x x − 1 120 24(x − 1) □
c Bài 15. Một xe ô tô chở hàng đi từ địa điểm A đến địa điểm B hết x giờ. Sau khi trả hàng tại địa điểm
B, xe quay ngược trở lại địa điểm A nhưng thời gian xe chạy về đến A chỉ là x − 1 giờ. Biết quãng đường AB
dài 160 km, viết phân thức biểu thị theo x:
a) Tốc độ xe ô tô khi chạy từ A đến B;
b) Tốc độ xe ô tô khi chạy từ B về A;
c) Tỉ số của tốc độ xe ô tô khi chạy từ A đến B và tốc độ xe ô tô khi chạy từ B về A. Lời giải. 160
a) Tốc độ xe ô tô khi chạy từ A đến B là km/h. x 160
b) Tốc độ xe ô tô khi chạy từ B về A là km/h. x − 1
c) Tỉ số của tốc độ xe ô tô khi chạy từ A đến B và tốc độ xe ô tô khi chạy từ B về A là 160 160 x − 1 : = · x x − 1 x □
c Bài 16. Bác Châu vay ngân hàng 1,2 tỉ đồng để mua nhà theo hình thức trả góp. Số tiền bác Châu phải
trả mỗi tháng bao gồm số tiền gốc phải trả hằng tháng (bằng số tiền gốc chia đều cho số tháng vay) và số
tiền lãi phải trả hằng tháng (bằng số tiền gốc nhân với lãi suất tháng).
a) Nếu mỗi tháng bác Châu trả 15 triệu đồng trong 10 năm thì lãi suất năm (tính theo %) là bao nhiêu? 61/101 61/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 62
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
Hãy cho biết tổng số tiền thực tế bác Châu phải trả chênh lệch bao nhiêu so với khoản vay 1,2 tỉ đồng.
b) Trong công thức tính lãi suất năm nói trên, hai biến x, y phải thoả mãn các điểu kiện x > 0, y > 0,
xy > 1200. Em hãy giải thích ý nghĩa thực tiễn của các điều kiện này. Lời giải. Å 1, 2 · 103 ã a) r = 15 − : 102 = 0, 05 = 5%. 120
10 năm tương đương 120 tháng.
Số tiền bác Châu phải trả hàng tháng là 15.120 = 1 800 ( triệu đồng)=1,8 (tỉ đồng).
Số tiền chêch lệch so với số tiền thực tế là 600 triệu đồng.
b) x là số tiền trả hàng tháng nên x > 0.
y là số tháng trả hết tiền nên y > 0.
1200 ở đây được hiểu hiểu là 1200 triệu hay 1,2 tỉ đồng khi trả cho ngân hàng thì ngân hàng phải có lời để
duy trì hoạt động do đó xy > 1200. □ 62/101 62/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 63
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC LUYỆN TẬP CHUNG A
TRỌNG TÂM KIẾN THỨC
○ Mỗi biểu thức là một phân thức hoặc biểu thị một dãy phép toán cộng, trừ, nhân, chia trên những phân
thức gọi là biểu thức hữu tỉ.
○ Nhờ các quy tắc của các phép toán cộng, trừ, nhân, chia các phân thức, ta có thể biến đổi biểu thức hữu
tỉ thành một phân thức.
○ Điều kiện của biến để giá trị tương ứng của mẫu thức khác 0 là điều kiện để giá trị của phân thức được xác định. A B CÁC DẠNG BÀI TẬP
Dạng 1. Tìm điều kiện của biến để phân thức xác định
Ta tìm các giá trị của biến sao cho giá trị tương ứng của mẫu thức khác 0.
c Ví dụ 1. Với giá trị nào của x thì giá trị của phân thức được xác định? 5x x − 2 x2 − 1 a) ; b) ; c) . 3x − 6 x2 + 8x 16x2 − 25 Lời giải. 5x
a) Giá trị của phân thức
được xác định khi 3x − 6 ̸= 0 hay 3x ̸= 6, suy ra x ̸= 2. 3x − 6 x − 2
b) Giá trị của phân thức
được xác định khi x2 + 8x ̸= 0 hay x(x + 8) ̸= 0, suy ra x ̸= 0 và x ̸= −8. x2 + 8x x2 − 1 25 5 5
c) Giá trị của phân thức
được xác định khi 16x2 − 25 ̸= 0 hay x2 ̸= , suy ra x ̸= và x ̸= − . 16x2 − 25 16 4 4 □
Dạng 2. Tìm giá trị của x để phân thức bằng 0
Giá trị của phân thức bằng 0 khi tử có giá trị bằng 0 và mẫu có giá trị khác 0.
A(x) = 0 khi A(x) = 0 và B(x) ̸= 0. B(x)
c Ví dụ 2. Tìm giá trị của x để giá trị phân thức sau bằng 0. x2 − 1 x2 − 5x + 6 a) ; b) . x2 + 2x + 1 x2 − 4 Lời giải.
Phân thức bằng 0 khi tử thức bằng 0, mẫu thức khác 0. ® x2 − 1 x2 − 1 = 0 a) = 0 khi suy ra x = 1. x2 + 2x + 1 (x + 1)2 ̸= 0 63/101 63/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 64
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC ® x2 − 5x + 6 (x − 2)(x − 3) (x − 2)(x − 3) = 0 b) = = 0 khi suy ra x = 3. x2 − 4 (x + 2)(x − 2) (x + 2)(x − 2) ̸= 0 □
Dạng 3. Rút gọn biểu thức
Thực hiện phép nhân và phép chia các phân thức đại số để rút gọn biểu thức.
c Ví dụ 3. Rút gọn biểu thức Å 1 1 ã Å x + 1 x + 2 ã B = − : − . x − 1 x x − 2 x − 1 Lời giải.
Điều kiện x ̸= 0; x ̸= 1; x ̸= 2. Ta có x − (x − 1)
(x − 1)(x + 1) − (x + 2)(x − 2) B = : x(x − 1) (x − 1)(x − 2) 1 x2 − 1 − x2 + 4 = : x(x − 1) (x − 1)(x − 2) 1 (x − 1)(x − 2) x − 2 = · = . x(x − 1) 3 3x □ Å x + 2 x − 2 ã x2 − 1
c Ví dụ 4. Cho biểu thức A = + · . x2 − x x2 + x x2 + 2 a) Rút gọn A.
b) Tính giá trị của A với x = 100. Lời giải.
a) Điều kiện x ̸= 0; x ̸= ±1. Ta có
(x + 2)(x + 1) + (x − 2)(x − 1) x2 − 1 A = · x(x + 1)(x − 1) x2 + 2
x2 + 2x + x + 2 + x2 − 2x − x + 2 x2 − 1 A = · x(x + 1)(x − 1) x2 + 2 2x2 + 4 x2 − 1 2 A = · = . x(x2 − 1) x2 + 2 x 2 1 b) Với x = 100, ta có A = = . 100 50 □
c Ví dụ 5. Rút gọn biểu thức a 1 + Å b2 + c2 − a2 ã b + c b2 + c2 − (b − c)2 a) A = 1 + · · . 2bc a 1 − a + b + c b + c Ü ê 2 2 + y2 − yz + z2 x2 3 y z b) B = + − · + (x + y + z)2. x y + z 1 1 1 1 1 + + + y z xy yz zx Lời giải. 64/101 64/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 65
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC a 1 + Å b2 + c2 − a2 ã b + c b2 + c2 − (b − c)2 a) A = 1 + · · 2bc a 1 − a + b + c b + c (b + c)2 − a2 b + c + a b2 + c2 − b2 + 2bc − c2 = · · 2bc b + c − a a + b + c (a + b + c)(b + c − a) b + c + a 2bc = · · 2bc b + c − a a + b + c = a + b + c. Ü ê 2 2 + y2 − yz + z2 x2 3 y z b) B = + − · + (x + y + z)2 x y + z 1 1 1 1 1 + + + y z xy yz zx 2(y + z) Å y2 − yz + z2 x2 3yz ã yz = + − · + (x + y + z)2 x y + z y + z x + y + z xyz
(y + z)(y2 − yz + z2) + x3 − 3xyz 2x(y + z) = · + (x + y + z)2 x(y + z) x + y + z x3 + y3 + z3 − 3xyz 2 = · + (x + y + z)2 1 x + y + z
2(x + y + z)(x2 + y2 + z2 − xy − yz − xz) = + (x + y + z)2 x + y + z
= 2x2 + 2y2 + 2z2 − 2xy − 2yz − 2xz + x2 + y2 + z2 + 2xy + 2yz + 2zx = 3x2 + 3y2 + 3z2. □ Dạng 4. Vận dụng
c Ví dụ 6. Hôm qua, thanh long được bán với giá a đồng mỗi kilôgam. Hôm nay, người ta đã giảm giá 1000
đồng cho mỗi kilôgam thanh long. Với cùng số tiền b đồng thì hôm nay mua được nhiều hơn bao nhiêu kilôgam thanh long so với hôm qua? Lời giải.
Gọi a − 1000 (đồng) là số tiền mỗi kilôgam thanh long ngày hôm nay. b
Số kilôgam thanh long mua được với số tiền b đồng ngày hôm qua là kilôgam. a b
Số kilôgam thanh long mua được với số tiền b đồng ngày hôm nay là kilôgam. a − 1000 b b
Số kilôgam thanh long mua được nhiều hơn so với hôm qua là − kilôgam. □ a a − 1000
c Ví dụ 7. Hai người thợ cùng sơn một bức tường. Nếu một mình sơn xong bức tường thì người thứ nhất
làm xong lâu hơn người thứ hai là 2 giờ. Gọi x là số giờ mà người thứ nhất một mình sơn xong bức tường.
Viết phân thức biểu thị tổng số phần của bức tường sơn được mà người thứ nhất sơn trong 3 giờ và người thứ hai sơn trong 4 giờ theo x. Lời giải.
Gọi x là số giờ mà người thứ nhất một mình sơn xong bức tường. 1
⇒ 1 giờ người thứ nhất sơn được bức tường. x 3
⇒ 3 giờ người thứ nhất sơn được bức tường. x 65/101 65/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 66
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
⇒ người thứ hai một mình sơn xong bức tường mất x − 2 giờ. 1
⇒ 1 giờ người thứ hai sơn được bức tường. x − 2 4
⇒ 4 giờ người thứ hai sơn được bức tường. x − 2
Do đó, số phần của bức tường sơn được mà người thứ nhất sơn trong 3 giờ và người thứ hai sơn trong 4 giờ là 3 4 3(x − 2) + 4x 7x − 6 + = = . x x − 2 x(x − 2) x(x − 2) □
c Ví dụ 8. Số tiền hằng năm A (triệu đô la Mỹ) mà người Mỹ chi cho việc mua đồ ăn, đồ uống khi ra khỏi
nhà và dân số P (triệu người) hằng năm của Mỹ từ năm 2000 đến năm 2006 lần lượt được cho bằng công thức sau −8 242,58t + 348 299,6 A = với 0 ≤ t ≤ 6. −0,06t + 1
P = 2,71t + 282,7 với 0 ≤ t ≤ 6.
Trong đó, t là số năm tính từ năm 2000, t = 0 tương ứng với năm 2000.
(Nguồn: U.S. Bureau of Economic Analysis and U.S. Census Bureau)
Viết phân thức biểu thị (theo t) số tiền bình quân hằng năm mà mỗi người Mỹ đã chi cho việc mua đồ ăn, đồ uống khi ra khỏi nhà. Lời giải.
Số tiền bình quân hằng năm mà mỗi người Mỹ đã chi cho việc mua đồ ăn, đồ uống khi ra khỏi nhà là A −8 242,58t + 348 299,6 = với 0 ≤ t ≤ 6. P (−0,06t + 1) (2,71t + 282,7) □ A C BÀI TẬP VẬN DỤNG 2x − 1
c Bài 1. Giá trị của phân thức
được xác định khi nào? x2 − 4 Lời giải. 2x − 1 Giá trị của phân thức
được xác định khi x2 − 4 ̸= 0 hay (x + 2)(x − 2) ̸= 0, suy ra x ̸= ±2. □ x2 − 4
c Bài 2. Tìm giá trị của x để giá trị của phân thức 2x2 + 10x + 12 x3 + x2 − x − 1 a) bằng 0. b) bằng 0. x3 − 4x x3 − 2x2 + x Lời giải. ® 2x2 + 10x + 12 2(x + 2)(x + 3) 2(x + 2)(x + 3) = 0 a) = = 0 khi suy ra x = −3. x3 − 4x x(x + 2)(x − 2) x(x + 2)(x − 2) ̸= 0 ® x3 + x2 − x − 1 (x + 1)2(x − 1) (x + 1)2(x − 1) = 0 b) = = 0 khi suy ra x = −1. x3 − 2x2 + x x(x − 1)2 x(x − 1)2 ̸= 0 □ 66/101 66/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 67
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Bài 3. Thực hiện các phép tính sau. 1 1 1 a) + + ; xy yz zx x y 3xy b) + + . 2x − y 2x + y y2 − 4x2 Lời giải. 1 1 1 z x y x + y + z a) + + = + + = ; xy yz zx xyz xyz xyz xyz b) x y 3xy x (2x + y) y (2x − y) 3xy + + = + − 2x − y 2x + y y2 − 4x2 (2x + y) (2x − y) (2x + y) (2x − y) (2x + y) (2x − y) 2x2 + xy + 2xy − y2 − 3xy 2x2 − y2 = = . (2x + y) (2x − y) 4x2 − y2 □
c Bài 4. Thực hiện các phép tính sau. 4x − 6 25x2 − 10x + 1 a) · ; 5x2 − x 27 − 8x3 2x + 10 (x + 5)3 b) : . (x − 3)2 x2 − 9 Lời giải. 4x − 6 25x2 − 10x + 1 2 (2x − 3) (5x − 1)2 −2 (5x − 1) a) · = · = ; 5x2 − x 27 − 8x3 x (5x − 1) (3 − 2x) (9 + 6x + 4x2) x (9 + 6x + 4x2) 2x + 10 (x + 5)3 2x + 10 x2 − 9 2 (x + 5) (x − 3) (x + 3) 2 (x + 3) b) : = · = · = . (x − 3)2 x2 − 9 (x − 3)2 (x + 5)3 (x − 3)2 (x + 5)3 (x − 3) (x + 5)2 □
c Bài 5. Thực hiện các phép tính sau. 4x2 − 1 Å 1 1 1 ã a) + + ; 16x2 − 1 2x + 1 2x − 1 1 − 4x2 Å x + y 2 ã x3y3 b) − . xy x x3 − y3 Lời giải. a) Ta có 1 1 1 2x − 1 2x + 1 1 + + = + − 2x + 1 2x − 1 1 − 4x2 (2x − 1) (2x + 1) (2x − 1) (2x + 1) (2x − 1) (2x + 1) 2x − 1 + 2x + 1 − 1 4x − 1 = = (2x − 1) (2x + 1) (2x − 1) (2x + 1) 67/101 67/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 68
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Do đó 4x2 − 1 Å 1 1 1 ã 4x2 − 1 Å 4x − 1 ã + + = 16x2 − 1 2x + 1 2x − 1 1 − 4x2 (4x2 − 1) (4x2 + 1) (2x − 1) (2x + 1) 1 Å 4x − 1 ã = 4x2 + 1 (2x − 1) (2x + 1) 1 Å 4x − 1 ã 4x − 1 = = . 4x2 + 1 (4x2 − 1) (16x2 − 1) b) Å x + y 2 ã x3y3 Å 1 1 2 ã x3y3 − = + − xy x x3 − y3 x y x x3 − y3 Å 1 1 ã x3y3 = − y x (x − y) (x2 + xy + y2) x − y x3y3 x2y2 = = . xy (x − y) (x2 + xy + y2) x2 + xy + y2 □ x2 − 6x + 9 4x + 8
c Bài 6. Cho biểu thức P = + . 9 − x2 x + 3 a) Rút gọn P .
b) Tính giá trị của P tại x = 7. 2 c) Chứng tỏ P = 3 +
. Từ đó tìm tất cả các giá trị nguyên của x sao cho biểu thức đã cho nhận giá x + 3 trị nguyên. Lời giải. x2 − 6x + 9 4x + 8 (x − 3)2 4x + 8 3 − x + 4x + 8 3x + 11 a) P = + = + = = . 9 − x2 x + 3 (3 − x) (x + 3) x + 3 x + 3 x + 3 3 · 7 + 11 32
b) Thay x = 7 vào biểu thức P ta được P = = . 7 + 3 10 3x + 11 3x + 9 + 2 2 c) P = = = 3 + . x + 3 x + 3 x + 3
Với x nguyên, P nhận giá trị nguyên khi (x + 3) ∈ Ư (2) = {±1; ±2}. ○ x + 3 = 1 ⇒ x = −2. ○ x + 3 = −1 ⇒ x = −4. ○ x + 3 = 2 ⇒ x = −1. ○ x + 3 = −2 ⇒ x = −5.
Vậy các giá trị nguyên của x để P nguyên là {−5; −4; −2; −1}. □ 2x − 10 2x 1 c Bài 7. Cho N = − + . x2 − 7x + 10 x2 − 4 2 − x a) Rút gọn N .
b) Tìm giá trị nguyên của x để N nhận giá trị nguyên. Lời giải. 68/101 68/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 69
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
a) Điều kiện x ̸= ±2; x ̸= 5. 2(x − 5) 2x 1 2 1 2x N = − − = − − (x − 2)(x − 5) x2 − 4 x − 2 x − 2 x − 2 x2 − 4 x + 2 − 2x 2 − x −1 = = = . (x − 2)(x + 2) (x − 2)(x + 2) x + 2
b) Để N nhận giá trị nguyên thì x + 2 ∈ Ư(−1).
Suy ra x + 2 ∈ {−1; 1} hay x ∈ {−3; −1}, thỏa mãn điều kiện.
Vậy với x ∈ {−3; −1} thì N nhận giá trị nguyên. □
c Bài 8. Rút gọn các biểu thức sau ï 1 1 2 Å 1 1 ãò ab a) A = + + · + · . a2 b2 a + b a b (a + b)2 ï 1 2 1 ò 4x2 + 4xy + y2 b) B = + + · . (2x − y)2 4x2 − y2 (2x + y)2 16x Lời giải. ï 1 1 2 Å 1 1 ãò ab a) A = + + · + · a2 b2 a + b a b (a + b)2 ï 1 1 2 ò ab = + + · a2 b2 ab (a + b)2 a2 + b2 + 2ab ab = · a2b2 (a + b)2 a + b)2 ab 1 = · = . a2b2 (a + b)2 ab ï 1 2 1 ò 4x2 + 4xy + y2 b) B = + + · (2x − y)2 4x2 − y2 (2x + y)2 16x ï 1 2 1 ò (2x + y)2 = + + · (2x − y)2 (2x − y)(2x + y) (2x + y)2 16x
ï (2x − y)2 + 2(2x − y)(2x + y) + (2x + y)2 ò (2x + y)2 = · (2x − y)2(2x + y)2 16x [(2x − y) + (2x + y)]2 1 = · (2x − y)2 16x 16x2 x = = . (2x − y)2 · 16x (2x − y)2 □ x y − x − y x + y
c Bài 9. Rút gọn biểu thức sau y x . + x − y x + y Lời giải. Ta có x y x − y + y x + y − x y x y x − = − = 1 + − 1 + = + . x − y x + y x − y x + y x − y x + y x − y x + y 69/101 69/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 70
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Suy ra x y − x − y x + y y x = 1. + x − y x + y □
c Bài 10. Trên một dòng sông, một con thuyền đi xuôi dòng với tốc độ (x + 3) km/h và đi ngược dòng với
tốc độ (x − 3) km/h (x > 3).
a) Xuất phát từ bến A, thuyền đi xuôi dòng trong 4 giờ, rồi đi ngược dòng trong 2 giờ. Tính quãng đường
thuyền đã đi. Lúc này thuyền cách bến A bao xa?
b) Xuất phát từ bến A, thuyền đi xuôi dòng đến bến B cách bến A 15 km, nghỉ 30 phút, rồi quay về bến
A. Sau bao lâu kể từ lúc xuất phát thì thuyền quay về đến bến A? Lời giải.
a) Quãng đường thuyền đi xuôi dòng trong 4 giờ là 4(x + 3) (km).
Quãng đường thuyền đi ngược dòng trong 2 giờ là 2(x − 3) (km).
Quãng đường thuyền đã đi là 4(x + 3) + 2(x − 3) = 4x + 12 + 2x − 6 = 6x + 6 (km).
Vì lúc đầu thuyền đi xuôi dòng và quay về đi ngược dòng nên quãng đường còn cách bến A là 4(x+3)−2(x−3) =
4x + 12 − 2x + 6 = 2x + 18 (km). 1 b) Đổi 30 (phút) bằng (h). 2 15
Thời gian thuyền đi xuôi dòng từ A đến B là (h). x + 3 15
Thời gian thuyền đi ngược dòng từ B đến A là (h). x − 3
Thời gian thuyền đi kể từ lúc xuất phát đến khi thuyền quay về đến bến A là 15 1 15 + + (h). x + 3 2 x − 3 □
c Bài 11. Một xưởng may lập kế hoạch may 80 000 bộ quần áo trong x ngày. Nhờ cải tiến kĩ thuật, xưởng
đã hoàn thành kế hoạch sớm 11 ngày và may vượt kế hoạch 100 bộ quần áo.
a) Hãy viết phân thức theo biến x biểu thị số bộ quần áo mỗi ngày xưởng may được theo kế hoạch.
b) Viết phân thức biểu thị số bộ quần áo thực tế xưởng may được mỗi ngày.
c) Viết biểu thức biểu thị số bộ quần áo mỗi ngày xưởng may được nhiều hơn so với kế hoạch.
d) Nếu theo kế hoạch, mỗi ngày xí nghiệp may 800 bộ quần áo thì nhờ cải tiến kĩ thuật, mỗi ngày xưởng
may được nhiều hơn so với kế hoạch bao nhiêu bộ quần áo. Lời giải.
a) Theo kế hoạch xưởng may 80 000 bộ quần áo trong x ngày nên số bộ quần áo mỗi ngày xưởng may được 80 000 theo kế hoạch là (bộ). x
b) Thực tế, thời gian xưởng may là x − 11 (ngày) và số bộ quần áo may được là 80 000 + 100 = 80 100 (bộ). 80 100
Do đó số bộ quần áo thực tế xưởng may được mỗi ngày là (bộ). x − 11
c) Số bộ quần áo mỗi ngày xưởng may được nhiều hơn so với kế hoạch là 80 100 80 000 80 100x − 80 000x + 880 000 100x + 880 000 − = = (bộ). x − 11 x x (x − 11) x (x − 11) 70/101 70/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 71
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 80 000
d) Theo kế hoạch, mỗi ngày xí nghiệp may 800 bộ quần áo nên = 800 suy ra x = 100. x
Khi đó, số bộ quần áo mỗi ngày xưởng may được nhiều hơn so với kế hoạch là
100 · 100 + 880 000 = 100 (bộ). 100 (100 − 11) □
c Bài 12. Một xe ô tô đi từ Hà Nội đến Vinh với vận tốc trung bình là 60 km/h và dự kiến sẽ đến Vinh sau 2
5 giờ chạy xe. Tuy nhiên, sau 2
giờ chạy với vận tốc 60 km/h, xe dừng nghỉ 20 phút. Sau khi dừng nghỉ, để 3
đến Vinh đúng thời gian dự kiến, xe phải tăng vận tốc so với chặng đầu.
a) Tính độ dài quãng dường Hà Nội - Vinh.
b) Tính độ dài quãng đường còn lại sau khi dừng nghỉ.
c) Cho biết ở chặng thứ hai xe tăng vận tốc thêm x (km/h). Hãy viết biểu thức P biểu thị thời gian (tính
bằng giờ) thực tế xe chạy hết chặng đường Hà Nội - Vinh.
d) Tính giá trị của P lần lượt tại x = 5; x = 10; x = 15, từ đó cho biết ở chặng thứ hai sau khi xe dừng nghỉ:
○ Nếu tăng vận tốc thêm 5km/h thì xe đến Vinh muộn hơn dự kiến bao nhiêu giờ?
○ Nếu tăng vận tốc thêm 10km/h thì xe đến Vinh có đúng thời gian dự kiến không?
○ Nếu tăng vận tốc thêm 15km/h thì xe đến Vinh sớm hơn dự kiến bao nhiêu giờ? Lời giải.
a) Độ dài quãng đường Hà Nội - Vinh: 60 · 5 = 300 km. 2
b) Độ dài quãng đường còn lại sau khi dừng nghỉ: 300 − 60 · 2 = 140 km 3 2 1 140 140 c) P = 2 + + = 3 + . 3 3 60 + x 60 + x 140 67 67 28
d) Thay x = 5 vào biểu thức P ta được P = 3 + =
. Như vậy xe sẽ đến Vinh muộn hơn − 5 = 65 13 13 13
giờ nếu tăng vận tốc thêm 5 km/h. 140
Thay x = 10 vào biểu thức P ta được P = 3 +
= 5. Như vậy xe sẽ đến đúng giờ dự kiến nếu tăng vận 70 tốc thêm 10km/h. 140 73 73 2
Thay x = 15 vào biểu thức P ta được P = 3 + =
. Như vậy xe sẽ đến Vinh muộn hơn 5 − = 75 15 15 15
giờ nếu tăng vận tốc thêm 15 km/h. □ 71/101 71/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 72
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC ÔN TẬP CHƯƠNG VI A BÀI TẬP RÈN LUYỆN
c Bài 1. Rút gọn phân thức 54x(x − 3)3 x2 − 3xy a) P = . b) Q = . 63(3 − x)2 21y2 − 7xy Lời giải. 54x(x − 3)3 54x(x − 3)3 6x(x − 3) a) P = = = . 63(3 − x)2 63(x − 3)2 7 x2 − 3xy −x(3y − x) −x b) Q = = = . 21y2 − 7xy 7y(3y − x) 7y □ y 4x c Bài 2. Tính tổng + . 2x2 − xy y2 − 2xy Lời giải. y 4x y 4x y2 − 4x2 (y + 2x)(y − 2x) −(2x + y) + = + = = = . 2x2 − xy y2 − 2xy x(2x − y) y(y − 2x) xy(2x − y) xy(2x − y) xy □ 2x + y 2x − y 16x
c Bài 3. Cho biểu thức P = + −
. Chứng tỏ rằng giá trị biểu thức P không phụ 2x2 − xy 2x2 + xy 4x2 − y2
thuộc giá trị của biến y. Lời giải. Ta có 2x + y 2x − y 16x P = + − x(2x − y) x(2x + y) (2x − y)(2x + y)
(2x + y)2 + (2x − y)2 − 16x2 = x(2x − y)(2x + y) −8x2 + 2y2 = x(2x − y)(2x + y) −2(4x2 − y2) −2 = = . x(4x2 − y2) x
Vậy giá trị biểu thức P không phụ thuộc vào giá trị của biến y. □ x − xy − y + y2 3 1
c Bài 4. Tính giá trị của biểu thức M = , với x = − ; y = . y3 − 3y2 + 3y − 1 4 2 Lời giải. Điều kiện y ̸= 1. x(1 − y) − y(1 − y) (x − y)(1 − y) y − x M = = = . (y − 1)3 −(1 − y)3 (1 − y)2 72/101 72/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 73
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 1 3 3 1 + Thay x = − ; y = , ta có M = 2 4 = 5. □ 4 2 Å 1 ã2 1 − 2 x − y
c Bài 5. Tính giá trị biểu thức Q =
, biết x2 − 2y2 = xy và x ̸= 0; x + y ̸= 0. x + y Lời giải.
Từ x2 − 2y2 = xy ta có x2 − xy − 2y2 = 0 ⇔ (x + y) (x − 2y) = 0.
Do x + y ̸= 0 nên x − 2y = 0 ⇔ x = 2y. x − y 2y − y 1 Vậy Q = = = . □ x + y 2y + y 3
c Bài 6. Tính giá trị biểu thức sau
20032 · 2013 + 31 · 24 − 1 (2003 · 2008 + 4) P = .
2004 · 2005 · 2006 · 2007 · 2008 Lời giải. Đặt x = 2003, ta có
x2(x + 10) + 31(x + 1) − 1 · [x(x + 5) + 4] P =
(x + 1)(x + 2)(x + 3)(x + 4)(x + 5)
x3 + 10x2 + 31x + 30 x2 + 5x + 4 = .
(x + 1)(x + 2)(x + 3)(x + 4)(x + 5)
Phân tích đa thức thành nhân tử ta được
(x + 1)(x + 2)(x + 3)(x + 4)(x + 5) P = = 1.
(x + 1)(x + 2)(x + 3)(x + 4)(x + 5)
Nhận xét. Phương pháp giải bài trên là đại số hóa bằng cách đặt x = 2003, sau đó rút gọn phân thức đại số.
Nhiều biểu thức số ta có thể giải bằng đại số như trên. □
c Bài 7. Cho a1; a2; a3; . . . ; a2007; a2008 là 2008 số thực thỏa mãn 2K + 1 aK = với K = 1; 2; 3; . . . 2008. (K2 + K)2
Tính tổng S2008 = a1 + a2 + a3 + . . . + a2007 + a2008. Lời giải. Ta có 2K + 1 (K + 1)2 − K2 1 1 aK = = = − (K2 + K)2 K2 (K + 1)2 K2 (K + 1)2 Do đó
S2008 = a1 + a2 + a3 + . . . + a2007 + a2008 1 1 1 1 1 1 1 1 = − + − + − + . . . + − 12 22 22 32 32 42 20082 20092 1 4036080 = 1 − = . 20092 4036081 □ 73/101 73/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 74
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC a b c a2 b2 c2 c Bài 8. Cho + + = 1. Chứng minh rằng + + = 0. b + c c + a a + b b + c c + a a + b Lời giải. Ta có a b c + + = 1 b + c c + a a + b Å a b c ã ⇒ + + (a + b + c) = a + b + c b + c c + a a + b a2 b2 c2 ⇒ + a + + b + + c = a + b + c b + c c + a a + b a2 b2 c2 ⇒ + + = 0. b + c c + a a + b
Nhận xét. Quan sát mẫu thức b + c; c + a; a + b ta thấy chúng không thể cùng dấu được. Do đó ta có thể
kết luận: trong ba số a, b, c có ít nhất một số âm, ít nhất một số dương. □
c Bài 9. Biết x ̸= −y, y ̸= −z, z ̸= −x, rút gọn biểu thức sau x2 − yz y2 + xz z2 + xy A = + + . (x + y)(x + z) (y + x)(y + z) (z + x)(z + y) Lời giải. Nhận xét rằng x2 − yz x2 + xy − xy − yz x y = = − . (x + y)(x + z) (x + y)(x + z) x + z x + y Tương tự ta có y2 + xz y z = − (y + x)(y + z) x + y y + z z2 + xy z x = − . (z + x)(z + y) y + z x + z Do đó ta được x y y z z x A = − + − + − = 0. x + z x + y x + y y + z y + z x + z □
c Bài 10. Biết x, y, z đôi một khác nhau, chứng minh rằng y − z z − x x − y 2 2 2 + + = + + . (x − y)(x − z) (y − z)(y − x) (z − x)(z − y) x − y y − z z − x Lời giải. Nhận xét rằng y − z x − z + y − x 1 1 = = + . (x − y)(x − z) (x − y)(x − z) x − y z − x Tương tự ta có z − x 1 1 = + ; (y − z)(y − x) y − z x − y x − y 1 1 = + . (z − x)(z − y) z − x y − z
Công vế theo vế ta được điều phải chứng minh. 74/101 74/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 75
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
Nhận xét. Kỹ thuật của bài là tách mỗi phân thức vế trái thành tổng hai phân thức mà mẫu thức giống một
mẫu thức vế phải. Ngoài ra bạn cũng có thể biến đổi từng vế bằng cách quy đồng mẫu thức, ta cũng được kết quả khá đẹp. □
c Bài 11. Chứng minh rằng x − y y − z z − x x − y y − z z − x + + = · · . 1 + xy 1 + yz 1 + zx 1 + xy 1 + yz 1 + zx Lời giải. x − y y − z z − x x − y y − x + x − z z − x + + = + + 1 + xy 1 + yz 1 + zx 1 + xy 1 + yz 1 + zx x − y x − y x − z x − z = − + − 1 + xy 1 + yz 1 + yz 1 + zx ï 1 1 ò ï 1 1 ò = (x − y) − + (x − z) − 1 + xy 1 + yz 1 + yz 1 + zx yz − xy zx − yz = (x − y) + (x − z) (1 + xy)(1 + yz) (1 + yz)(1 + zx) (x − y)(z − x) ï y z ò = − 1 + yz 1 + xy 1 + zx (x − y)(z − x) y − z = 1 + yz (1 + xy)(1 + xz) x − y y − z z − x = · · . 1 + xy 1 + yz 1 + zx □ x 10x 5
c Bài 12. Cho biểu thức A = − − . x − 5 x2 − 25 x + 5
a) Tìm tập xác định và rút gọn biểu thức A.
b) Tính giá trị của A khi x = 9. Lời giải.
a) Tập xác định x ̸= ±5. x 10x 5 A = − − x − 5 x2 − 25 x + 5
x(x + 5) − 10x − 5(x − 5) = (x + 5)(x − 5) x2 − 10x + 25 x − 5 = = . (x + 5)(x − 5) x + 5 9 − 5 4 2 b) Thay x = 9, ta được A = = = . 9 + 5 14 7 □ Å 4 1 ã 2x − 4 − x2
c Bài 13. Cho biểu thức B = + : . x3 − 4x x + 2 2x2 + 4x
a) Tìm tập xác định và rút gọn biểu thức B.
b) Tính giá trị của B tại x = 1. 75/101 75/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 76
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c) Tìm giá trị nguyên của x để biểu thức B nhận giá trị nguyên. Lời giải.
a) Tập xác định x ̸= 0; x ̸= ±2. Å 4 1 ã 2x − 4 − x2 B = + : x3 − 4x x + 2 2x2 + 4x Å 4 x(x − 2) ã 2x − 4 − x2 = + : x(x + 2)(x − 2) x(x + 2)(x − 2) 2x(x + 2) 4 + x2 − 2x 2x(x + 2) −2 2 = · = = . x(x + 2)(x − 2) −(4 + x2 − 2x) x − 2 2 − x 2 b) Thay x = 1, ta được B = = 2. 2 − 1
c) Để B nhận giá trị nguyên thì 2 − x ∈ Ư(2) ⇒ 2 − x ∈ {2; −2; 1; −1} ⇔ x ∈ {0; 4; 1; 3}.
Đối chiếu với tập xác định suy ra B nhận giá trị nguyên khi x ∈ {4; 1; 3}. □ Å 2x2 + 1 1 ã Å x2 + 4 ã
c Bài 14. Cho biểu thức P = − : 1 − . x3 − 1 x − 1 x2 + x + 1
a) Rút gọn biểu thức P .
b) Tính giá trị của P tại x = −6.
c) Tìm giá trị nguyên của x để P nhận giá trị nguyên. Lời giải. a) Tập xác định x ̸= 1. Å 2x2 + 1 1 ã Å x2 + 4 ã P = − : 1 − x3 − 1 x − 1 x2 + x + 1
Å 2x2 + 1 − (x2 + x + 1) ã Å x2 + x + 1 − x2 − 4 ã = : (x − 1)(x2 + x + 1) x2 + x + 1 Å x2 − x ã Å x − 3 ã = : (x − 1)(x2 + x + 1) x2 + x + 1 Å x(x − 1) ã Å x2 + x + 1 ã = · (x − 1)(x2 + x + 1) x − 3 x = . x − 3 −6 2
b) Thay x = −6, ta được P = = . −6 − 3 3 x 3 c) Ta có P = = 1 + . x − 3 x − 3
Do đó, P nhận giá trị nguyên khi x − 3 ∈ Ư(3) ⇒ x − 3 ∈ {3; −3; 1; −1} ⇒ x ∈ {6; 0; 4; 2}.
Vậy với x ∈ {6; 0; 4; 2} thì P nhận giá trị nguyên. □ 12x − 45 x + 5 2x + 3 c Bài 15. Cho Q = − + . x2 − 7x + 12 x − 4 3 − x 76/101 76/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 77
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
a) Rút gọn biểu thức P .
b) Tính giá trị Q tại |x| = 3.
c) Tìm giá trị nguyên của x để Q nhận giá trị nguyên. Lời giải.
a) Tập xác định x ̸= 3; x ̸= 4. 12x − 45 x + 5 2x + 3 Q = − + x2 − 7x + 12 x − 4 3 − x 12x − 45 x + 5 2x + 3 = − − (x − 3)(x − 4) x − 4 x − 3
12x − 45 − (x + 5)(x − 3) − (2x + 3)(x − 4) = (x − 3)(x − 4) −3x2 + 15x − 18 −3(x − 2)(x − 3) −3(x − 2) = = = . (x − 3)(x − 4) (x − 3)(x − 4) x − 4 ñx = 3 (loại) b) Ta có |x| = 3 ⇔ . x = −3 (nhận) −3(−3 − 2) −15
Thế x = −3, ta được Q = = . −3 − 4 7 −3(x − 2) 6 c) Ta có Q = = −3 − . x − 4 x − 4
Do đó, Q nhận giá trị nguyên khi
x − 4 ∈ Ư(6) ⇒ x − 4 ∈ {6; −6; 3; −3; 2; −2; 1; −1} ⇒ x ∈ {10; −2; 7; 1; 6; 2; 5; 3}
Đối chiếu với tập xác định suy ra Q nhận giá trị nguyên khi x ∈ {10; −2; 7; 1; 6; 2; 5}. □
c Bài 16. Cho a1; a2; . . . ; a9 được xác định bởi công thức 3k2 + 3k + 1 ak = với k ⩾ 1. (k2 + k)3
Hãy tính giá trị của tổng 1 + a1 + a2 + . . . + a9. Lời giải. Ta có 3k2 + 3k + 1 (k + 1)3 − k3 1 1 ak = = = − (k2 + k)3 k2 (k + 1)3 k3 (k + 1)3 Do đó S = 1 + a1 + a2 + . . . + a9 Å 1 1 ã Å 1 1 ã Å 1 1 ã = 1 + − + − + . . . + − 13 23 23 33 93 103 1 1999 = 2 − = . 103 1000 □ 77/101 77/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 78
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC c Bài 17. Tính
19862 − 1992 19862 + 3972 − 3 · 1987 . 1983 · 1985 · 1988 · 1989 Lời giải. Đặt x = 1986
x2 − x − 6 · x2 + 2x − 3 · (x + 1) P =
(x − 3)(x − 1)(x + 2)(x + 3)
(x − 3) (x + 2) (x − 1) (x + 3) (x + 1) =
(x − 3)(x − 1)(x + 2)(x + 3) = x + 1. Suy ra
19862 − 1992 19862 + 3972 − 3 · 1987 = 1987. 1983 · 1985 · 1988 · 1989 □
c Bài 18. Đặt a + b + c = 2p. Chứng minh rằng 1 1 1 1 abc + + − = . p − a p − b p − c p p(p − a)(p − b)(p − c) Lời giải. 1 1 1 1 p − b + p − a p − p + c c c + + − = + = + p − a p − b p − c p (p − a)(p − b) p(p − c) (p − a)(p − b) p(p − c)
c [p(p − c) + (p − a)(p − b)] c 2p2 − p(a + b + c) + ab = = p(p − a)(p − b)(p − c) p(p − a)(p − b)(p − c) abc = . p(p − a)(p − b)(p − c) □
c Bài 19. Biết a ̸= −b, b ̸= −c, c ̸= −a. Chứng minh rằng b2 − c2 c2 − a2 a2 − b2 b − c c − a a − b + + = + + . (a + b)(a + c) (b + c)(b + a) (c + a)(c + b) b + c c + a a + b Lời giải. Ta có b2 − c2 b2 − a2 a2 − c2 b − a a − c = + = + . (a + b)(a + c) (a + b)(a + c) (a + b)(a + c) a + c a + b Tương tự ta có c2 − a2 c − b b − a = + (b + c)(b + a) b + a b + c a2 − b2 a − c c − b = + . (c + a)(c + b) c + b c + a
Cộng vế theo vế ta được điều phải chứng minh. □ A B BÀI TẬP BỔ SUNG 78/101 78/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 79
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Bài 20. Cho a + b + c = 0 và a, b, c đều khác 0. Rút gọn biểu thức ab bc ca A = + + . a2 + b2 − c2 b2 + c2 − a2 c2 + a2 − b2 Lời giải.
Từ a + b + c = 0 suy ra a + b = −c.
Bình phương hai vế, ta được a2 + b2 + 2ab = c2 nên a2 + b2 − c2 = −2ab.
Tương tự, b2 + c2 − a2 = −2bc và c2 + a2 − b2 = −2ca. ab bc ca 1 1 1 3 Do đó, A = + + = − − − = − . □ −2ab −2bc −2ca 2 2 2 2
c Bài 21. Rút gọn biểu thức 1 1 2 4 8 A = + + + + . 1 − x 1 + x 1 + x2 1 + x4 1 + x8 Lời giải.
Do đặc điểm của bài toán, ta không quy đồng mẫu tất cả các phân thức mà cộng lần lượt từng phân thức. 2 2 4 8 A = + + + 1 − x2 1 + x2 1 + x4 1 + x8 4 4 8 8 8 16 = + + = + = . 1 − x4 1 + x4 1 + x8 1 − x8 1 + x8 1 − x16 □
c Bài 22. Rút gọn biểu thức 3 5 2n + 1 B = + + · · · + . (1 · 2)2 (2 · 3)2 [n(n + 1)]2 Lời giải.
Đương nhiên không thể quy đồng mẫu tất cả các phân thức. Ta tìm cách tách mỗi phân thức thành hiệu của hai
phân thức rồi dùng phương pháp khử liên tiếp. Ta có 2k + 1 (k + 1)2 − k2 1 1 = = − . k2(k + 1)2 k2(k + 1)2 k2 (k + 1)2 Do đó 1 1 1 1 1 1 B = − + − + · · · + − 12 22 22 32 n2 (n + 1)2 1 n(n + 2) = 1 − = . (n + 1)2 (n + 1)2 □
c Bài 23. Xác định các số a, b, c sao cho 1 ax + b c = + . (1) (x2 + 1)(x − 1) x2 + 1 x − 1 Lời giải.
Thực hiện phép cộng ở vế phải của (1) ta được (ax + b)(x − 1) + c(x2 + 1)
ax2 − ax + bx − b + cx2 + c = (x2 + 1)(x − 1) (x2 + 1)(x − 1)
(a + c)x2 + (b − a)x + (c − b) = . (x2 + 1)(x − 1) 79/101 79/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 80
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 1
Đồng nhất phân thức trên với phân thức , ta được (x2 + 1)(x − 1) a + c = 0  ®  c + b = 0 1 1 b − a = 0 ⇒ ⇒ c = , b = − . c − b = 1 2 2  c − b = 1 1 1 1 1 1 − x − Do đó a = − . Như vậy = 2 2 + 2 . □ 2 (x2 + 1)(x − 1) x2 + 1 x − 1 1 Å 1 1 ã c Bài 24. Cho A = − , (x + y)3 x4 y4 2 Å 1 1 ã B = − , (x + y)4 x3 y3 2 Å 1 1 ã C = − . (x + y)5 x2 y2
Thực hiện phép tính A + B + C. Lời giải. Ta có y4 − x4 (y2 + x2)(y2 − x2) (y2 + x2)(y − x) A = = = . x4y4(x + y)3 x4y4(x + y)3 x4y4(x + y)2 2 Å 1 1 1 y2 − x2 ã B + C = − + · (x + y)4 x3 y3 x + y x2y2 2 Å 1 1 y − x ã 2 y3 − x3 + xy(y − x) = − + = · (x + y)4 x3 y3 x2y2 (x + y)4 x3y3 2 (y − x)(y2 + 2yx + x2) 2(y − x) = · = . (x + y)4 x3y3 (x + y)2x3y3 Do đó, (y2 + x2)(y − x) 2(y − x) A + B + C = + x4y4(x + y)2 (x + y)2x3y3
(y2 + x2)(y − x) + 2xy(y − x) = x4y4(x + y)2 (y − x)(y2 + x2 + 2xy) = x4y4(x + y)2 y − x = . x4y4 □
c Bài 25. Thực hiện các phép tính x + 3 2x − 1 x − 3 a) − − ; x + 1 x − 1 x2 − 1 1 1 1 1 b) + + + . x(x + y) y(x + y) x(x − y) y(y − x) Lời giải. x + 3 2x − 1 x − 3
(x + 3)(x − 1) − (2x − 1)(x + 1) − (x − 3) a) − − = x + 1 x − 1 x2 − 1 x2 − 1 −x2 + 1 = = −1. x2 − 1 1 1 1 1 x + y y − x b) + + + = + x(x + y) y(x + y) x(x − y) y(y − x) xy(x + y) xy(x − y) 1 1 = − = 0. xy xy 80/101 80/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 81
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC □
c Bài 26. Thực hiện phép tính 1 1 1 a) A = + + ; (a − b)(a − c) (b − a)(b − c) (c − a)(c − b) 1 1 1 b) B = + + ; a(a − b)(a − c) b(b − a)(b − c) c(c − a)(c − b) bc ac ab c) C = + + ; (a − b)(a − c) (b − a)(b − c) (c − a)(c − b) a2 b2 c2 d) D = + + . (a − b)(a − c) (b − a)(b − c) (c − a)(c − b) Lời giải. 1 1 1 c − b + a − c + b − a a) A = + + = = 0. (a − b)(a − c) (b − a)(b − c) (c − a)(c − b) (a − b)(b − c)(c − a) b) Ta có 1 1 1 B = + + a(a − b)(a − c) b(b − a)(b − c) c(c − a)(c − b)
bc(b − c) − ac(a − c) + ab(a − b) = abc(a − b)(b − c)(a − c)
c(b2 − bc − a2 + ac) + ab(a − b) = abc(a − b)(b − c)(a − c)
c [(b − a)(b + a) − c(b − a)] + ab(a − b) = abc(a − b)(b − c)(a − c)
(a − b)(−cb − ca + c2) + ab(a − b) = abc(a − b)(b − c)(a − c)
(a − b)(−cb − ac + c2 + ab) = abc(a − b)(b − c)(a − c) (a − b)(b − c)(a − c) 1 = = . abc(a − b)(b − c)(a − c) abc c) Ta có bc ac ab C = + + (a − b)(a − c) (b − a)(b − c) (c − a)(c − b)
bc(b − c) − ac(a − c) + ab(a − b) = abc(a − b)(b − c)(a − c)
c(b2 − bc − a2 + ac) + ab(a − b) = (a − b)(b − c)(a − c)
c [(b − a)(b + a) − c(b − a)] + ab(a − b) = (a − b)(b − c)(a − c)
(a − b)(−cb − ca + c2) + ab(a − b) = (a − b)(b − c)(a − c)
(a − b)(−cb − ac + c2 + ab) = (a − b)(b − c)(a − c) (a − b)(b − c)(a − c) = = 1. (a − b)(b − c)(a − c) 81/101 81/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 82
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC d) Ta có a2 b2 c2 D = + + (a − b)(a − c) (b − a)(b − c) (c − a)(c − b)
a2(b − c) − b2(a − c) + c2(a − b) = (a − b)(b − c)(a − c)
a2(b − c) − b2a + b2c + c2a − c2b = (a − b)(b − c)(a − c)
a2(b − c) − a(b2 − c2) + bc(b − c) = (a − b)(b − c)(a − c)
(b − c)(a2 − ab − ac + cb) = (a − b)(b − c)(a − c)
(b − c) [a(a − b) − c(a − b)] = (a − b)(b − c)(a − c) (b − c)(a − b)(a − c) = = 1. (a − b)(b − c)(a − c) □
c Bài 27. Cho a, b, c là các số nguyên khác nhau đôi một. Chứng minh rằng biểu thức sau có giá trị là một số nguyên: a3 b3 c3 P = + + . (a − b)(a − c) (b − a)(b − c) (c − a)(c − b) Lời giải. Ta có a3 b3 c3 P = + + (a − b)(a − c) (b − a)(b − c) (c − a)(c − b)
a3(b − c) + b3(c − a) + c3(a − b) = . (a − b)(b − c)(a − c)
Phân tích tử thành nhân tử
a3(b − c) + b3(c − a) + c3(a − b) =
a3b − a3c + b3c − b3a + c3(a − b) =
(a3b − b3a) − (a3c − b3c) + c3(a − b) =
ab(a − b)(a + b) − c(a − b)(a2 + ab + b2) + c3(a − b) =
(a − b)(a2b + ab2 − ca2 − cb2 − abc + c3) =
(a − b) (c3 − cb2) − (abc − ab2) + (a2b − ca2) =
(a − b)(b − c)(−cb − c2 + ab + a2) =
(a − b)(b − c) (ab − cb) + (a2 − c2) =
(a − b)(b − c)(a − c)(a + b + c). Vậy P = a + b + c. □ x 2x − 3y
c Bài 28. Cho 3y − x = 6. Tính giá trị biểu thức A = + . y − 2 x − 6 Lời giải. x 2x − 3y 3y − 6 2x − x − 6 A = + = + = 3 + 1 = 4. □ y − 2 x − 6 y − 2 x − 6 x2 y2 z2 x2 + y2 + z2
c Bài 29. Tìm x, y, z biết rằng + + = . 2 3 4 5 82/101 82/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 83
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Lời giải. x2 y2 z2 x2 + y2 + z2 Å x2 x2 ã Å y2 y2 ã Å z2 z2 ã Từ + + = suy ra − + − + − = 0. 2 3 4 5 2 5 3 5 4 5 3x2 2y2 z2 Cho nên + + = 0. Do đó, x = y = z = 0. □ 10 15 20 1 1
c Bài 30. Tìm x, y biết rằng x2 + y2 + + = 4. x2 y2 Lời giải. Ta có 1 1 Å 1 ã Å 1 ã x2 + y2 + + = 4 ⇒ x2 − 2 + + y2 − 2 + = 0 x2 y2 x2 y2 Å 1 ã2 Å 1 ã2 ⇒ x − + y − = 0 x y  1 x − = 0 ®  x x2 = 1 ⇒ ⇒ 1 y2 = 1.  y − = 0 y
Có bốn đáp án như bảng sau x 1 1 −1 −1 y 1 −1 1 −1 □ 1 1 1 c Bài 31. Cho biết + + = 2, (1) a b c 1 1 1 + + = 2. (2) a2 b2 c2
Chứng minh rằng a + b + c = abc. Lời giải. 1 1 1 Å 1 1 1 ã Từ (1) suy ra + + + 2 + + = 4. a2 b2 c2 ab bc ca 1 1 1 a + b + c Do (2) nên + + = 1 suy ra = 1. ab bc ca abc Do đó a + b + c = abc. □ x y z c Bài 32. Cho + + = 0, (1) a b c a b c và + + = 2. (2) x y z a2 b2 c2 Tính giá trị biểu thức + + . x2 y2 z2 Lời giải.
Từ (1) suy ra bcx + acy + abz = 0. a2 b2 c2 Å ab bc ca ã Từ (2) suy ra + + + + + = 4. x2 y2 z2 xy yz zx a2 b2 c2 abz + acy + bcx Do đó + + = 4 − 2 = 4. □ x2 y2 z2 xyz
c Bài 33. Cho (a + b + c)2 = a2 + b2 + c2 và a, b, c khác 0. Chứng minh rằng 1 1 1 3 + + = . a3 b3 c3 abc 83/101 83/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 84
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Lời giải. bc
Từ giả thiết suy ra ab + bc + ca = 0 ⇒ b + c = − . a ab + bc + ca 1 1 1 Do đó = 0, tức là + + = 0. Suy ra abc a b c 1 Å 1 1 ã 1 Å 1 1 ã3 1 1 Å 1 1 ã = − + ⇒ = − + = − − − 3 + a b c a3 b c b3 c3 b2c bc2 1 1 1 3(b + c) 3bc 3 ⇒ + + = − = = . a3 b3 c3 b2c2 ab2c2 abc □ a b c b a c c Bài 34. Cho + + = +
+ . Chứng minh rằng trong ba số a,b,c tồn tại hai số bằng nhau. b c a a c b Lời giải. Từ giả thiết suy ra
a2c + b2a + c2b = b2c + a2b + c2a
⇒ a2(c − b) − a(c2 − b2) + bc(c − b) = 0
⇒ (c − b)(a2 − ac − ab + bc) = 0
⇒ (c − b)(a − c)(a − b) = 0.
Tồn tại một trong các thừa số c − b, a − c, a − b bằng 0. Do đó, trong ba số a, b, c tồn tại hai số bằng nhau. □
c Bài 35. Tìm các giá trị nguyên của x để phân thức sau có giá trị là số nguyên: 2x3 − 6x2 + x − 8 a) A = ; x − 3 x4 − 2x3 − 3x2 + 8x − 1 b) B = ; x2 − 2x + 1 x4 + 3x3 + 2x2 + 6x − 2 c) C = . x2 + 2 Lời giải. 2x3 − 6x2 + x − 8 5 a) A = = 2x2 + 1 − . x − 3 x − 3
A nguyên khi x nguyên, x − 3 nguyên và nó là ước của 5.
Suy ra x − 3 = 1 hoặc x − 3 = −1 hoặc x − 3 = 5 hoặc x − 3 = −5.
Hay x = 4 hoặc x = 2 hoặc x = 8 hoặc x = −2. x4 − 2x3 − 3x2 + 8x − 1 3 b) B = = x2 − 4 + . x2 − 2x + 1 (x − 1)2
B nguyên khi x nguyên, (x − 1)2 nguyên và nó là ước của 3.
Suy ra (x − 1)2 = 1 hoặc (x − 1)2 = 3.
Hay x − 1 = −1 hoặc x − 1 = 1 hay x = 0 hoặc x = 2. x4 + 3x3 + 2x2 + 6x − 2 2 c) C = = x2 + 3x − . x2 + 2 x2 + 2
C nguyên khi x nguyên, x2 + 2 nguyên và nó là ước của 2. Suy ra x2 + 2 = 2 hay x = 0. □ 84/101 84/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 85
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC a
c Bài 36. Rút gọn biểu thức sau với x = 3a + 2 x + 3a x − 3a 2a A = + − + a. 2 − x 2 + x 4 − x2 Lời giải. x + 3a x − 3a 2a 6ax + 4x − 2a 2x(3a + 2) − 2a A = + − + a = + a = + a = a. □ 2 − x 2 + x 4 − x2 4 − x2 4 − x2
c Bài 37. Rút gọn biểu thức 2 2 2
(a − b)2 + (b − c)2 + (c − a)2 A = + + + . a − b b − c c − a (a − b)(b − c)(c − a) Lời giải.
Đặt a − b = x, b − c = y, c − a = z thì x + y + z = 0. 2 2 2 x2 + y2 + z2 (x + y + z)2 Ta có A = + + + = = 0. □ x y z xyz xyz a + b − c b + c − a c + a − b c Bài 38. Cho biết − −
= 0. Chứng minh rằng trong ba phân thức ở vế trái, ab bc ca
có ít nhất một phân thức bằng 0. Lời giải. Ta có a + b − c b + c − a c + a − b − − = 0
⇔ c(a + b − c) − a(b + c − a) − b(c + a − b) = 0 ab bc ca ⇔ a2 + b2 − 2ab − c2 = 0 ⇔ (a − b)2 − c2 = 0
⇔ (a − b + c)(a − b − c) = 0.
Vậy a − b + c = 0 hoặc a − b − c = 0. □
c Bài 39. Xác định các số a, b, c sao cho: 1 a bx + c a) = + ; x(x2 + 1) x x2 + 1 1 a b b) = + ; x2 − 4 x − 2 x + 2 1 a b c c) = + + . (x + 1)2(x + 2) x + 1 (x + 1)2 x + 2 Lời giải. a bx + c a(x2 + 1) + (bx + c)x (a + b)x2 + cx + a a) Ta có + = = . x x2 + 1 x(x2 + 1) x(x2 + 1) a + b = 0 a = 1 1    
Đồng nhất với phân thức ta được c = 0 ⇒ b = −1 x(x2 + 1)   a = 1 c = 0. a b a(x + 2) + b(x − 2) (a + b)x + 2(a − b) b) Ta xó + = = . x − 2 x + 2 x2 − 4 x2 − 4 85/101 85/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 86
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC   1 a + b = 0 1 a =  
Đồng nhất với phân thức ta được 4 1 ⇒ . x2 − 4 1 a − b =  2 b = − 4 a b c
a(x + 1)(x + 2) + b(x + 2) + c(x + 1)2 c) Ta có + + = x + 1 (x + 1)2 x + 2 (x + 1)2(x + 2)
(a + c)x2 + (3a + b + 2c)x + a + 2b + c = . (x + 1)2(x + 2) a + c = 0 a = −1 1    
Đồng nhất với phân thức ta được 3a + b + 2c = 0 ⇒ b = 1 (x + 1)2(x + 2)   a + 2b + c = 1 c = 1. □
c Bài 40. Rút gọn biểu thức Å 1 1 1 ã Å 1 1 1 ã B = (ab + bc + ca) + + − abc + + . a b c a2 b2 c2 Lời giải. Å 1 1 1 ã Å 1 1 1 ã B = (ab + bc + ca) + + − abc + + a b c a2 b2 c2 bc + ca + ab b2c2 + c2a2 + a2b2 = (ab + bc + ca) − abc abc a2b2c2 □ (bc + ca + ab)2 b2c2 + c2a2 + a2b2 = − abc abc 2abc(a + b + c) = = 2(a + b + c). abc 1 1 1
c Bài 41. Cho a, b, c khác nhau đôi một và + +
= 0. Rút gọn các biểu thức: a b c 1 1 1 a) M = + + ; a2 + 2bc b2 + 2ac c2 + 2ab bc ac ab b) N = + + ; a2 + 2bc b2 + 2ac c2 + 2ab a2 b2 c2 c) P = + + . a2 + 2bc b2 + 2ac c2 + 2ab Lời giải.
Từ giả thiết suy ra ab + bc + ac = 0 nên
a2 + 2bc = a2 + bc + (−ab − ac) = a(a − b) − c(a − b) = (a − b)(a − c).
Tương tự, b2 + 2ac = (b − a)(b − c) và c2 + 2ab = (c − a)(c − b). 1 1 1 a) M = + + a2 + 2bc b2 + 2ac c2 + 2ab 1 1 1 = + + (a − b)(a − c) (b − a)(b − c) (c − a)(c − b) b − c + c − a + a − b = = 0. (a − b)(b − c)(a − c) 86/101 86/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 87
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC bc ac ab b) N = + + a2 + 2bc b2 + 2ac c2 + 2ab bc ac ab = + + (a − b)(a − c) (b − a)(b − c) (c − a)(c − b)
bc(b − c) + ac(c − a) + ab(a − b)
−c(a2 − b2) + c2(a − b) + ab(a − b) = = (a − b)(b − c)(a − c) (a − b)(b − c)(a − c)
(a − b)(−ac − cb + c2 + ab)
(a − b) [−c(a − c + b(a − c)] = = (a − b)(b − c)(a − c) (a − b)(b − c)(a − c) (a − b)(b − c(a − c)) = = 1. (a − b)(b − c)(a − c) a2 b2 c2 c) P = + + a2 + 2bc b2 + 2ac c2 + 2ab a2 b2 c2 = + + (a − b)(a − c) (b − a)(b − c) (c − a)(c − b)
a2(b − c) + b2(c − a) + c2(a − b)
ab(a − b) − c(a2 − b2) + c2(a − b) = = (a − b)(b − c)(a − c) (a − b)(b − c)(a − c)
(a − b)(ab − ac − bc + c2) (a − b)(b − c)(a − c) = = = 1. (a − b)(b − c)(a − c) (a − b)(b − c)(a − c) □ a + b b + c c + a
c Bài 42. Cho các số a, b, c khác nhau đôi một và = =
. Tính giá trị biểu thức c a b Å ã a b c M = 1 + 1 + 1 + . b c a Lời giải. a + b b + c c + a a + b + b + c + c + a 2(a + b + c) Ta có = = = = . c a b a + b + c a + b + c
Nếu a + b + c ̸= 0 thì tỉ số trên bằng 2. Suy ra a + b = 2c, b + c = 2a.
Do đó a − c = 2(c − a) nên c = a, trái với đề bài. a + b b + c c + a −c −a −b
Vậy a + b + c = 0. Ta có M = · · = · · = −1. □ b c a b c a
c Bài 43. Cho a3 + b3 + c3 = 3abc và a + b + c ̸= 0. Tính giá trị của biểu thức a2 + b2 + c2 N = . (a + b + c)2 Lời giải.
Ta có a3 + b3 + c3 − 3abc = (a + b + c)(a2 + b2 + c2 − ab − bc − ca).
Do a3 + b3 + c3 = 3abc và a + b + c ̸= 0 nên đẳng thức trên trở thành a2 + b2 + c2 − ab − bc − ca = 0. Lại có
a2 + b2 + c2 − ab − bc − ca =
(a2 − 2ab + b2) + (b2 − 2bc + c2) + (c2 − 2ca + a2) =
(a − b)2 + (b − c)2 + (c − a)2.
Như vậy từ a2 + b2 + c2 − ab − bc − ca = 0 suy ra a = b = c. 3a2 3a2 1 Do đó, N = = = . □ (3a)2 9a2 3 Å 1 ã Å 1 ã Å 1 ã Å 1 ã
c Bài 44. Rút gọn biểu thức A = 1 − 1 − 1 − · · · 1 − . 22 32 42 n2 Lời giải. 87/101 87/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 88
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC Ta có Å 1 ã Å 1 ã Å 1 ã Å 1 ã 1 · 3 2 · 4 3 · 5 (n − 1)(n + 1) A = 1 − 1 − 1 − · · · 1 − = · · · · · 22 32 42 n2 22 32 42 n2 1 · 2 · 3 · · · (n − 1) 3 · 4 · 5 · · · (n + 1) 1 n + 1 n + 1 = · = · = . 2 · 3 · 4 · · · n 2 · 3 · 4 · · · n n 2 2n □ 12 32 52 (2n + 1)2
c Bài 45. Rút gọn biểu thức B = · · · · · . 22 − 1 42 − 1 62 − 1 (2n + 2)2 − 1 Lời giải. Ta có 12 32 52 (2n + 1)2 12 32 52 (2n + 1)2 B = · · · · · = · · · · · 22 − 1 42 − 1 62 − 1 (2n + 2)2 − 1 1 · 3 3 · 5 5 · 7 (2n + 1)(2n + 3)
12 · 32 · 52 · · · (2n + 1)2 1 = = .
1 · 32 · 52 · · · (2n + 1)2 · (2n + 3) (2n + 3) □ 1 1 1 1
c Bài 46. Rút gọn biểu thức + + + · · · + . 1 · 2 2 · 3 3 · 4 (n − 1)n Lời giải. Ta có 1 1 1 1 1 1 1 1 1 1 1 1 + + + · · · + = − + − + − + · · · + − 1 · 2 2 · 3 3 · 4 (n − 1)n 1 2 2 3 3 4 n − 1 n 1 n − 1 = 1 − = . n n □ 1 1 1 1
c Bài 47. Rút gọn biểu thức + + + · · · + . 2 · 5 5 · 8 8 · 11 (3n + 2)(3n + 5) Lời giải. 1 1 Å 1 1 ã Ta có = − . (3n + 2)(3n + 5) 3 3n + 2 3n + 5 Do đó 1 1 1 1 + + + · · · + 2 · 5 5 · 8 8 · 11 (3n + 2)(3n + 5) 1 Å 1 1 1 1 1 1 1 1 ã = − + − + − + · · · + − 3 2 5 5 8 8 11 3n + 2 3n + 5 1 Å 1 1 ã 1 3n + 5 − 2 n + 1 = − = · = . 3 2 3n + 5 3 2(3n + 5) 2(3n + 5) □ 1 1 1 1
c Bài 48. Rút gọn biểu thức + + + · · · + . 1 · 2 · 3 2 · 3 · 4 3 · 4 · 5 (n − 1)n(n + 1) Lời giải. 1 1 ï 1 1 ò Ta có = − . (n − 1)n(n + 1) 2 (n − 1)n n(n + 1) Do đó 1 1 1 1 + + + · · · + 1 · 2 · 3 2 · 3 · 4 3 · 4 · 5 (n − 1)n(n + 1) 88/101 88/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 89
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 1 ï 1 1 1 1 1 1 1 1 ò = − + − + − + · · · + − 2 1 · 2 2 · 3 2 · 3 3 · 4 3 · 4 4 · 5 (n − 1)n n(n + 1) 1 ï 1 1 ò 1 n(n + 1) − 2 (n − 1)(n + 2) = − = · = . 2 2 n(n + 1) 2 2n(n + 1) 4n(n + 1) □
c Bài 49. Chứng minh rằng với mọi số tự nhiên n ≥ 1, ta luôn có 1 1 1 1 1 + + + · · · + < . 22 42 62 (2n)2 2 Lời giải. Ta có 1 1 1 1 1 Å 1 1 1 1 ã A = + + + · · · + = + + + · · · + . 22 42 62 (2n)2 4 12 22 32 n2 1 Å 1 1 1 ã Suy ra A < 1 + + + · · · + . 4 1 · 2 2 · 3 (n − 1)n 1 1 1 1 1 1 Lại có 1 + + + · · · + = 1 + − = 2 − . 1 · 2 2 · 3 (n − 1)n 1 n n 1 Å 1 ã 1 Do đó A < 2 − , suy ra A < . □ 4 n 2
c Bài 50. Chứng minh rằng với mọi số tự nhiên n ≥ 1, ta luôn có 1 1 1 1 1 + + + · · · + < . 32 52 72 (2n + 1)2 4 Lời giải. Ta có 1 1 1 1 1 1 1 1 B = + + + · · · + < + + + · · · + . 32 52 72 (2n + 1)2 32 − 1 52 − 1 72 − 1 (2n + 1)2 − 1 Lại có 1 1 1 1 + + + · · · + 32 − 1 52 − 1 72 − 1 (2n + 1)2 − 1 1 1 1 1 = + + + · · · + 2 · 4 4 · 6 6 · 8 2n(2n + 2) 1 Å 1 1 1 1 1 1 1 1 ã = − + − + − + · · · + − 2 2 4 4 6 6 8 2n 2n + 2 1 Å 1 1 ã = − . 2 2 2n + 2 1 Å 1 1 ã 1 Do đó B < − , suy ra B < . □ 2 2 2n + 2 4
c Bài 51. Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta luôn có 1 1 1 1 2 A = + + + · · · + < . 22 32 42 n2 3 Lời giải. 1 4 Å 1 1 ã
Nhận xét, với mọi số tự nhiên n ≥ 2 ta luôn có < = 2 − . n2 4n2 − 1 2n − 1 2n + 1 Khi đó Å 1 1 1 1 1 1 1 1 ã A < 2 − + − + − + · · · + − . 3 5 5 7 7 9 2n − 1 2n + 1 89/101 89/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 90
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 1 1 1 1 1 1 1 1 1 1 Lại có − + − + − + · · · + − = − . 3 5 5 7 7 9 2n − 1 2n + 1 3 2n + 1 Å 1 1 ã 2 Do đó A < 2 − , suy ra A < . □ 3 2n + 1 3
c Bài 52. Chứng minh rằng với mọi số tự nhiên n ≥ 3, ta luôn có 1 1 1 1 1 B = + + + · · · + < . 33 43 53 n3 12 Lời giải.
Với mọi số tự nhiên n ≥ 3, ta luôn có 1 1 1 1 (n + 1) − (n − 1) 1 ï 1 1 ò < = = · = − . n3 n3 − n (n − 1)n(n + 1) 2 (n − 1)n(n + 1) 2 (n − 1)n n(n + 1) Khi đó 1 ï 1 1 1 1 1 1 1 1 ò B < − + − + − + · · · + − . 2 2 · 3 3 · 4 3 · 4 4 · 5 4 · 5 5 · 6 (n − 1)n n(n + 1) 1 1 1 1 1 1 1 1 1 1 Lại có − + − + − + · · · + − = − . 2 · 3 3 · 4 3 · 4 4 · 5 4 · 5 5 · 6 (n − 1)n n(n + 1) 6 n(n + 1) 1 ï 1 1 ò 1 Do đó B < − , suy ra B < . □ 2 6 n(n + 1) 12
c Bài 53. Chứng minh rằng với mọi số tự nhiên n ≥ 1, ta luôn có Å 1 ã Å 1 ã Å 1 ã Å 1 ã A = 1 + 1 + 1 + · · · 1 + < 2. 1 · 3 2 · 4 3 · 5 n(n + 2) Lời giải. 1 n(n + 2) + 1 n2 + 2n + 1 (n + 1)2
Với mọi số tự nhiên n ≥ 1, ta có 1 + = = = . n(n + 2) n(n + 2) n(n + 2) n(n + 2) Khi đó 22 32 42 (n + 1)2 2 · 3 · 4 · · · (n + 1) 2 · 3 · 4 · · · (n + 1) A = · · · · · = · 1 · 3 2 · 4 3 · 5 n(n + 2) 1 · 2 · 3 · · · n 3 · 4 · 5 · · · (n + 2) n + 1 2 n + 2 − 1 Å 1 ã = · = 2 · = 2 1 − . 1 n + 2 n + 2 n + 2 Do đó A < 2. □
c Bài 54. Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta luôn có Å 2 ã Å 2 ã Å 2 ã Å 2 ã 1 B = 1 − 1 − 1 − · · · 1 − > . 6 12 20 n(n + 1) 3 Lời giải. 2 n(n + 1) − 2 n2 + n − 2 (n − 1)(n + 2)
Với mọi số tự nhiên n ≥ 2, ta có 1 − = = = . n(n + 1) n(n + 1) n(n + 1) n(n + 1) Khi đó Å 2 ã Å 2 ã Å 2 ã Å 2 ã 1 · 4 2 · 5 3 · 6 (n − 1)(n + 2) B = 1 − 1 − 1 − · · · 1 − = · · · · · 6 12 20 n(n + 1) 2 · 3 3 · 4 4 · 5 n(n + 1) 1 · 2 · 3 · · · (n − 1) 4 · 5 · 6 · · · (n + 2) 1 n + 2 1 Å 2 ã = · = · = 1 + . 2 · 3 · 4 · n 3 · 4 · 5 · · · (n + 1) n 3 3 n 1 Do đó B > . □ 3 90/101 90/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 91
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 32 − 1 72 − 1 112 − 1 432 − 1
c Bài 55. Rút gọn biểu thức A = · · · · · . 52 − 1 92 − 1 132 − 1 452 − 1 Lời giải. Ta có 32 − 1 72 − 1 112 − 1 432 − 1 2 · 4 6 · 8 10 · 12 42 · 44 2 1 A = · · · · · = · · · · · = = . 52 − 1 92 − 1 132 − 1 452 − 1 4 · 6 8 · 10 12 · 14 44 · 46 46 23 □ 23 + 1 33 + 1 43 + 1 93 + 1 3
c Bài 56. Chứng minh rằng A = · · · · · < . 23 − 1 33 − 1 43 − 1 93 − 1 2 Lời giải. n3 + 1 (n + 1)(n2 − n + 1) (n + 1) (n − 0,5)2 + 0,75 Ta có = = . n3 − 1 (n − 1)(n2 + n + 1) (n − 1) [(n + 0,5)2 + 0,75] Khi đó 3(1,52 + 0,75) 4(2,52 + 0, 75) 5(3,52 + 0,75) 10(8,52 + 0,75) A = · · · · · 1(2,52 + 0,75) 2(3,52 + 0,75) 3(4,52 + 0,75) 8(9,52 + 0,75) 3 · 4 · 5 · · · 10 1,52 + 0,75 9 · 10 3 3 90 = · = · = · . 1 · 2 · 3 · · · 8 9,52 + 0,75 1 · 2 91 2 91 3 Do đó A < . □ 2
c Bài 57. Chứng minh rằng với mọi số tự nhiên n ≥ 2, luôn có 23 − 1 33 − 1 43 − 1 n3 − 1 2 B = · · · · · > . 23 + 1 33 + 1 43 + 1 n3 + 1 3 Lời giải. n3 − 1 (n − 1)(n2 + n + 1) (n − 1) (n + 0,5)2 + 0,75
Với mọi số tự nhiên n ≥ 2, ta có = = . n3 + 1 (n + 1)(n2 − n + 1) (n + 1) [(n − 0,5)2 + 0,75] Khi đó 1(2,52 + 0,75) 2(3,52 + 0,75) 3(4,52 + 0,75) (n − 1) (n + 0,5)2 + 0,75 B = · · · · · 3(1,52 + 0,75) 4(2,52 + 0, 75) 5(3,52 + 0,75) (n + 1) [(n − 0,5)2 + 0,75] 1 · 2 · 3 · · · (n − 1) (n + 0,5)2 + 0,75 1 · 2 n2 + n + 1 2 n2 + n + 1 = · = · = · . 3 · 4 · 5 · · · (n + 1) 1,52 + 0,75 n · (n + 1) 3 3 n2 + n 2 Do đó B > . □ 3
14 + 4 54 + 4 94 + 4 · · · 214 + 4
c Bài 58. Rút gọn biểu thức P = .
(34 + 4) (74 + 4) (114 + 4) · · · (234 + 4) Lời giải. Ta có
n4 + 4 = (n2 + 2)2 − 4n2 = (n2 − 2n + 2)(n2 + 2n + 2) = (n − 1)2 + 1 (n + 1)2 + 1 . Khi đó (02 + 1)(22 + 1) (42 + 1)(62 + 1) (82 + 1)(102 + 1) (202 + 1)(222 + 1) P = · · · · · (22 + 1)(42 + 1) (62 + 1)(82 + 1) (102 + 1)(122 + 1) (222 + 1)(242 + 1) 02 + 1 1 = = . 242 + 1 577 □ 91/101 91/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 92
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Bài 59. Rút gọn biểu thức 1 1 1 1 M = + + + . a2 − 5a + 6 a2 − 7a + 12 a2 − 9a + 20 a2 − 11a + 30 Lời giải. Ta có 1 1 1 1 M = + + + (a − 2)(a − 3) (a − 3)(a − 4) (a − 4)(a − 5) (a − 5)(a − 6) 1 1 1 1 1 1 1 1 = − + − + − + − a − 3 a − 2 a − 4 a − 3 a − 5 a − 4 a − 6 a − 5 1 1 4 = − = . a − 6 a − 2 (a − 2)(a − 6) □
c Bài 60. Rút gọn biểu thức Å n − 1 n − 2 n − 3 2 1 ã Å 1 1 1 1 ã + + + · · · + + : + + + · · · + . 1 2 3 n − 2 n − 1 2 3 4 n Lời giải. Ta có n − 1 n − 2 n − 3 2 1 + + + · · · + + 1 2 3 n − 2 n − 1 n − 1 n − 2 n − 3 n − (n − 2) n − (n − 1) = + + + · · · + + 1 2 3 n − 2 n − 1 n n n n n = + + + · · · + +
− 1 − 1 − 1 − · · · − 1 − 1 1 2 3 n − 2 n − 1 n n n = n + + + · · · + − (n − 1) 2 3 n − 1 n n n n n = + + + · · · + + 2 3 4 n − 1 n Å 1 1 1 1 1 ã = n + + + · · · + + . 2 3 4 n − 1 n Do đó Å n − 1 n − 2 n − 3 2 1 ã Å 1 1 1 1 ã + + + · · · + + : + + + · · · + = n. 1 2 3 n − 2 n − 1 2 3 4 n □
c Bài 61. Rút gọn biểu thức 1 1 1 1 1 + + + · · · + + A 1 · (2n − 1) 3 · (2n − 3) 5 · (2n − 5) (2n − 3) · 3 (2n − 1) · 1 = . B 1 1 1 1 + + + · · · + 3 5 2n − 1 Lời giải. 1 1 Å 1 1 ã Ta có nhận xét = + . k(2n − k) 2n k 2n − k Khi đó 1 ïÅ 1 1 ã Å 1 1 ã Å 1 1 ã Å 1 1 ãò A = + + + + · · · + + + + 2n 1 2n − 1 3 2n − 3 2n − 3 3 2n − 1 1 1 Å 1 1 1 ã 1 Å 1 1 1 ã B = · 2 1 + + + · · · + = 1 + + + · · · + = . 2n 3 5 2n − 1 n 3 5 2n − 1 n 92/101 92/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 93
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC A 1 Do đó = . □ B n 1 1 1
c Bài 62. Cho abc = 1 và a + b + c = + +
. Chứng minh rằng trong ba số a, b, c tồn tại một số bằng a b c 1. Lời giải. 1 1 1 ab + bc + ca
Từ đẳng thức a + b + c = + + suy ra a + b + c = . a b c abc
Mà abc = 1 nên a + b + c = ab + bc + ca.
Để chứng minh trong ba số a, b, c tồn tại một số bằng 1, ta cần chứng minh
(a − 1)(b − 1)(c − 1) = 0. Ta có (a − 1)(b − 1)(c − 1) =
(ab − a − b + 1)(c − 1) = abc − ab − ac + a − bc + b + c − 1 =
(abc − 1) + (a + b + c) − (ab + bc + ca).
Vì abc = 1 và a + b + c = ab + bc + ca nên biểu thức trên bằng 0.
Do đó, tồn tại một trong ba thừa số a − 1, b − 1, c − 1 bằng 0.
Vậy tồn tại một trong ba số a, b, c bằng 1. □ 1 1 1 1
c Bài 63. Chứng minh rằng nếu x + y + z = a và + + =
thì tồn tại một trong ba số x, y, z bằng a. x y z a Lời giải.
Từ giả thiết suy ra a ̸= 0. Khi đó 1 1 1 1 xy + yz + zx 1 + + = hay = . x y z x + y + z xyz x + y + z
Suy ra (xy + yz + zx)(x + y + z) − xyz = 0. (1) Ta có
(xy + yz + zx)(x + y + z) − xyz =
x2y + xy2 + xyz + xyz + y2z + yz2 + x2z + xyz + xz2 − xyz =
x2y + xy2 + xyz + y2z + xyz + yz2 + x2z + xz2 =
xy(x + y) + yz(x + y) + yz(x + z) + xz(x + z) =
y(x + y)(x + z) + z(x + z)(x + y) = (x + y)(y + z)(z + x).
Từ (1) suy ra (x + y)(y + z)(z + x) = 0. Do đó x = −y hoặc y = −z hoặc z = −x. 1 1 1 1 ○ Với x = −y thì từ + + = suy ra z = a. x y z a 1 1 1 1 ○ Với y = −z thì từ + + = suy ra x = a. x y z a 1 1 1 1 ○ Với z = −x thì từ + + = suy ra y = a. x y z a
Vậy tồn tại một trong ba số x, y, z bằng a. □ 1 1 1
c Bài 64. Các biểu thức x + y + z và + +
có thể cùng có giá trị bằng 0 được hay không? x y z Lời giải. 93/101 93/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 94
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC 1 1 1 Giả sử x + y + z = 0 và + + = 0. x y z 1 1 1 xy + yz + zx 1 1 1 Ta có + + = . Mà + + = 0 nên xy + yz + zx = 0. x y z xyz x y z
Từ x + y + z = 0 suy ra (x + y + z)2 = 0 hay x2 + y2 + z2 + 2(xy + yz + zx) = 0. 1 1 1
Vì xy + yz + zx = 0 nên x2 + y2 + z2 = 0, suy ra x = y = z = 0. Điều này vô lí vì khi đó , , không xác định. x y z 1 1 1 Vậy x + y + z và + +
không thể cùng có giá trị bằng 0. □ x y z 1 1 1
c Bài 65. Tính giá trị của biểu thức M = + + , biết rằng x + 2 y + 2 z + 2
2a = by + cz; 2b = ax + cz; 2c = ax + by và a + b + c ̸= 0. Lời giải.
Cộng theo từng vế ba đẳng thức 2a = by + cz; 2b = ax + cz; 2c = ax + by ta được
a + b + c = ax + by + cz = ax + 2a = a(x + 2). 1 a Suy ra = . x + 2 a + b + c 1 b 1 c Tương tự, = , = . y + 2 a + b + c z + 2 a + b + c a + b + c Do đó M = = 1. □ a + b + c a b 2c
c Bài 66. Cho abc = 2. Rút gọn biểu thức M = + + . ab + a + 2 bc + b + 1 ac + 2c + 2 Lời giải. Với abc = 2, ta có a b 2c a ab 2c M = + + = + + ab + a + 2 bc + b + 1 ac + 2c + 2 ab + a + 2 abc + ab + a ac + 2c + abc a ab 2 a + ab + 2 = + + = = 1. a + ab + 2 a + ab + 2 a + ab + 2 a + ab + 2 □ a b c
c Bài 67. Cho abc = 1. Rút gọn biểu thức N = + + . ab + a + 1 bc + b + 1 ac + c + 1 Lời giải. Với abc = 1, ta có a b c a ab c N = + + = + + ab + a + 1 bc + b + 1 ac + c + 1 a + ab + 1 abc + ab + a ac + c + abc a ab 1 a + ab + 1 = + + = = 1. a + ab + 1 a + ab + 1 a + ab + 1 a + ab + 1 □ a a − b c Bài 68. Cho =
, a ̸= 0, c ̸= 0, a − b ̸= 0, b − c ̸= 0. Chứng minh rằng c b − c 1 1 1 1 + = − . a a − b b − c c Lời giải. 94/101 94/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 95
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
Từ giả thiết suy ra a(b − c) = c(a − b). (1) Ta có 1 1 a − b + c + = . (2) c a − b c(a − b) 1 1 a − b + c − = . (3) b − c a a(b − c)
Từ (1), (2), (3) suy ra điều phải chứng minh. □ a2 b2 c2
c Bài 69. Cho a + b + c = 0 (a ̸= 0, b ̸= 0, c ̸= 0). Rút gọn biểu thức A = + + . bc ca ab Lời giải. Ta có a2 b2 c2 a3 + b3 + c3
(a + b + c)(a2 + b2 + c2 − ab − bc − ca) + 3abc A = + + = = bc ca ab abc abc 3abc = = 3. abc □
c Bài 70. Cho a + b + c = 0 (a ̸= 0, b ̸= 0, c ̸= 0). Rút gọn biểu thức a2 b2 c2 B = + + . a2 − b2 − c2 b2 − c2 − a2 c2 − a2 − b2 Lời giải.
Từ a + b + c = 0 suy ra b + c = −a. Khi đó b2 + 2bc + c2 = a2 hay a2 − b2 − c2 = 2bc.
Tương tự, b2 − c2 − a2 = 2ca, c2 − a2 − b2 = 2ab. Do đó a2 b2 c2 a3 + b3 + c3
(a + b + c)(a2 + b2 + c2 − ab − bc − ca) + 3abc B = + + = = 2bc 2ca 2ab 2abc 2abc 3abc 3 = = . 2abc 2 □
c Bài 71. Cho biết a + b + c = 0, hãy tính giá trị của biểu thức Å a − b b − c c − a ã Å c a b ã A = + + + + . c a b a − b b − c c − a Lời giải. a − b b − c c − a Đặt M = + + , ta có c a b c c Å b − c c − a ã c b2 − bc + ac − a2 M · = 1 + + = 1 + · a − b a − b a b a − b ab c (a − b)(c − a − b) 2c2 2c3 = 1 + · = 1 + = 1 + . a − b ab ab abc a 2a3 b 2b3 Tương tự, M · = 1 + , M · = 1 + . b − c abc c − a abc Do đó 2(a3 + b3 + c3)
2(a + b + c)(a2 + b2 + c2 − ab − bc − ca) + 6abc A = 3 + = 3 + abc abc 6abc = 3 + = 3 + 6 = 9. abc □ 95/101 95/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 96
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Bài 72. Chứng minh rằng, nếu (a2 − bc)(b − abc) = (b2 − ac)(a − abc) và các số a, b, c, a − b khác 0 thì 1 1 1 + + = a + b + c. a b c Lời giải. Từ giả thiết suy ra
a2b − a3bc − b2c + ab2c2 = ab2 − ab3c − a2c + a2bc2
⇒ ab(a − b) + c(a2 − b2) = abc2(a − b) + abc(a2 − b2)
⇒ (a − b)(ab + ac + bc) = abc(a − b)(a + b + c).
Chia cả hai vế cho abc(a − b) ̸= 0 ta được điều phải chứng minh. □ a b c
c Bài 73. Cho a + b + c = 0, x + y + z = 0, + + = 0. Chứng minh rằng x y z ax2 + by2 + cz2 = 0. Lời giải.
Từ x + y + z = 0 suy ra x2 = (y + z)2, y2 = (z + x)2, z2 = (x + y)2. Do đó
ax2 + by2 + cz2 = a(y + z)2 + b(z + x)2 + c(x + y)2
= a(y2 + 2yz + z2) + b(z2 + 2zx + x2) + c(x2 + 2xy + y2)
= x2(b + c) + y2(a + c) + z2(a + b) + 2(ayz + bzx + cxy). (1) a b c
Thay b + c = −a, a + c = −b, a + b = −c (do a + b + c = 0) và thay ayz + bzx + cxy = 0 do + + = 0 vào x y z (1) ta được
ax2 + by2 + cz2 = −ax2 − by2 − cz2.
Cho nên 2ax2 + 2by2 + 2cz2 = 0 hay ax2 + by2 + cz2 = 0. □ xy + 1 yz + 1 zx + 1 c Bài 74. Cho = =
. Chứng minh rằng x = y = z hoặc x2y2z2 = 1. y z x Lời giải. 1 1 1 Từ giả thiết suy ra x + = y + = z + . Do đó y z x 1 1 y − z 1 1 z − x 1 1 x − y x − y = − = ; y − z = − = ; z − x = − = . z y yz x z xz y x xy (x − y)(y − z)(z − x)
Suy ra (x − y)(y − z)(z − x) = . x2y2z2
Cho nên (x − y)(y − z)(z − x)(x2y2z2 − 1) = 0.
Vậy x − y = 0; y − z = 0; z − x = 0; x2y2z2 − 1 = 0 hay x = y = z; x2y2z2 = 1. □ a b c a2 b2 c2 c Bài 75. Cho + + = 1. Chứng minh rằng + + = 0. b + c c + a a + b b + c c + a a + b Lời giải. a b c Nhân cả hai vế của + +
= 1 với a + b + c ta được b + c c + a a + b a2 + a(b + c) b2 + b(c + a) c2 + c(a + b) + + = a + b + c. b + c c + a a + b a2 b2 c2 a2 b2 c2 Suy ra + a + + b + + c = a + b + c hay + + = 0. □ b + c c + a a + b b + c c + a a + b 96/101 96/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 97
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC a b c c Bài 76. Cho + + = 0. Chứng minh rằng b − c c − a a − b a b c + + = 0. (b − c)2 (c − a)2 (a − b)2 Lời giải. a b c a b c b2 − ab + ac − c2 Từ + + = 0 suy ra = + = . b − c c − a a − b b − c a − c b − a (a − b)(c − a) 1 a b2 − ab + ac − c2 Nhân hai vế với ta được = . b − c (b − c)2 (a − b)(b − c)(c − a) b c2 − bc + ba − a2 c a2 − ca + cb − b2 Tương tự, = ; = . (c − a)2
(b − c)(c − a)(a − b) (a − b)2 (c − a)(a − b)(b − c)
Cộng từng vế ba đẳng thức trên ta được điều phải chứng minh. □ 1 c Bài 77. Cho x +
= a. Tính các biểu thức sau theo a x 1 1 1 1 a) x2 + ; b) x3 + ; c) x4 + ; d) x5 + . x2 x3 x4 x5 Lời giải. 1 1 1 a) Từ x + = a, suy ra x2 + 2 + = a2 hay x2 + = a2 − 2. x x2 x2 1 Å 1 ã3 1 Å 1 ã b) Ta có x3 + = x + − 3x · x + = a3 − 3a. x3 x x x 1 Å 1 ã2 1 c) Ta có x4 + = x2 + − 2x2 ·
= (a2 − 2)2 − 2 = a4 − 4a2 + 2. x4 x2 x2 Å 1 ã Å 1 ã 1 1 d) Ta có x2 + x3 + = x5 + + x + . x2 x3 x x5 Suy ra 1 Å 1 ã Å 1 ã Å 1 ã x5 + = x2 + x3 + − x +
= (a2 − 2)(a3 − 3a) − a = a5 − 5a3 + 5a. x5 x2 x3 x □ Å 1 ã Å 1 ã c Bài 78. Cho x2 − : x2 +
= a. Tính giá trị của biểu thức x2 x2 Å 1 ã Å 1 ã M = x4 − : x4 + theo a. x4 x4 Lời giải.
Từ giả thiết suy ra a ̸= 1 và x4 − 1 a + 1
= a ⇒ x4 − 1 = ax4 + a ⇒ (1 − a)x4 = a + 1 ⇒ x4 = . x4 + 1 1 − a Thay vào M ta được Å a + 1 1 − a ã Å a + 1 1 − a ã (a + 1)2 − (1 − a)2 4a 2a M = − : + = = = . 1 − a a + 1 1 − a a + 1 (a + 1)2 + (1 − a)2 2a2 + 2 a2 + 1 □ 97/101 97/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 98
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC x4 + x2 + 1
c Bài 79. Cho x2 − 4x + 1 = 0. Tính giá trị của biểu thức A = . x2 Lời giải. Cách 1. Ta có x2 − x + 1
x2 − 4x + 1 = 0 ⇒ x2 − x + 1 = 3x ⇒ = 3. x Mặt khác x4 + x2 + 1 x2 − x + 1 x2 + x + 1 x2 + x + 1 A = = · = 3 · . x2 x x x x2 + x + 1 x2 − x + 1 2x Ta thấy = + = 3 + 2 = 5. x x x x4 + x2 + 1 (x2 + 1)2 − x (4x)2 − x2
Vậy A = 3 · 5 = 15. Cách 2. Ta có A = = = = 15. □ x2 x2 x2 x x2 c Bài 80. Cho = a. Tính M = theo a. x2 − x + 1 x4 + x2 + 1 Lời giải.
Trường hợp 1. Với x = 0 thì a = 0 và M = 0.
Trường hợp 2. Với x ̸= 0 thì a ̸= 0. Ta có x2 x x M = = · . (1) x4 + x2 + 1 x2 − x + 1 x2 + x + 1 Lại có x2 + x + 1 x2 − x + 1 2x 1 1 + 2a = + = + 2 = . (2) x x x a a a a2
Từ (1) và (2) suy ra M = a · = . 1 + 2a 1 + 2a a2 Vậy M = . □ 1 + 2a b2 + c2 − a2 a2 − (b − c)2 c Bài 81. Cho x = , y =
. Tính giá trị của biểu thức x + y + xy. 2bc (b + c)2 − a2 Lời giải.
Ta xét biểu thức x + y + xy + 1 = x(y + 1) + (y + 1) = (x + 1)(y + 1). (b + c)2 − a2 4bc
Từ giả thiết suy ra x + 1 = ; y + 1 = . 2bc (b + c)2 − a2 Do đó, (x + 1)(y + 1) = 2.
Vậy x + y + xy + 1 = 2, suy ra x + y + xy = 1. □ a
c Bài 82. Tìm hai số tự nhiên a và b sao cho a − b = . b Lời giải. Đặt a − b = n, (1) a = n, (2) b
trong đó a, b, n ∈ N, b ̸= 0.
Từ (1), (2) ta có bn − b = n nên b(n − 1) = n. 98/101 98/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 99
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
○ Nếu n = 1 thì a = b. Khi đó, theo (1) thì n = 0, loại. ○ Với n ̸= 1, ta có n 1 b = = 1 + . (3) n − 1 n − 1
Vì b ∈ N nên n − 1 là ước của 1, suy ra (n − 1) ∈ {−1; 1}.
◦ Với n − 1 = −1 hay n = 0, từ (3) suy ra b = 0, loại.
◦ Với n − 1 = 1 hay n = 2, từ (3), (2) suy ra b = 2, a = 4. 4
Thử lại ta thấy 4 − 2 = . 2 Vậy a = 4, b = 2. □ a
c Bài 83. Tìm hai số tự nhiên a và b sao cho a − b = . 2b Lời giải. Đặt a − b = n, (1) a = n, (2) 2b
trong đó a, b, n ∈ N, b ̸= 0.
Từ (1), (2) ta có 2bn − b = n nên b(2n − 1) = n, suy ra n b = . (3) 2n − 1
○ Với n = 0, từ (3) suy ra b = 0, loại.
○ Với n ≥ 1, ta thấy n ≤ n + n − 1 = 2n − 1. n Vì b ∈ N nên
∈ N, suy ra n = 2n − 1 hay n = 1. Từ (3), (1) suy ra b = 1 và a = 2. 2n − 1 2
Thử lại ta thấy 2 − 1 = . 2 · 1 Vậy a = 2, b = 1. □
c Bài 84. Cho hai số nguyên dương a và b, trong đó a > b. Tìm số nguyên dương c khác b sao cho a3 + b3 a + b = . a3 + c3 a + c Lời giải. a3 + b3 a + b
Do a + b ̸= 0, a + c ̸= 0 nên từ = suy ra a3 + c3 a + c a3 + b3 a3 + c3 =
⇔ a2 − ab + b2 = a2 − ac + c2 a + b a + c ⇔ b2 − c2 = ab − ac
⇔ (b + c)(b − c) = a(b − c).
Do b − c ̸= 0 nên b + c = a. Vậy c = a − b. □ 99/101 99/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 100
24. PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Bài 85. Cho dãy số a1, a2, a3, . . . sao cho a1 − 1 a2 − 1 an−1 − 1 a2 = ; a3 = ; . . . ; an = . a1 + 1 a2 + 1 an−1 + 1
a) Chứng minh rằng a1 = a5.
b) Xác định năm số đầu của dãy, biết rằng a101 = 3. Lời giải. a) Ta có Å a ã Å ã 1 − 1 a1 − 1 −2 2a1 1 a3 = − 1 : + 1 = : = − . a1 + 1 a1 + 1 a1 + 1 a1 + 1 a1 Å 1 ã Å 1 ã −1 − a1 a1 − 1 1 + a1 a4 = − − 1 : − + 1 = : = . a1 a1 a1 a1 1 − a1 Å 1 + a ã Å ã 1 1 + a1 2a1 2 2a1 a5 = − 1 : + 1 = : = = a1. 1 − a1 1 − a1 1 − a1 1 − a1 2
b) Theo câu trên ta suy ra a1 = a5 = a9 = · · · = a1001 = 3. 1 1
Từ đó ta tính được a1 = 3; a2 =
; a3 = − ; a4 = −2; a5 = 3. 2 3 □ m m m + k
c Bài 86. Tìm phân số
khác 0 và số tự nhiên k, biết rằng = . n n nk Lời giải.
Từ giả thiết suy ra mnk = mn + nk. Chia hai vế cho n, ta được mk = m + k. Do đó m = k(m − 1).
Như vậy m chia hết cho m − 1. Từ đó ta tìm được m = 0 (loại) và m = 2. Khi đó k = 2. 2
Vậy phân số phải tìm có dạng và k = 2. □ n
c Bài 87. Cho hai số tự nhiên a và b (a < b). Tìm tổng các phân số tối giản có mẫu bằng 7, mỗi phân số
lớn hơn a nhưng nhỏ hơn b. Lời giải.
Tổng phải tìm bằng A − B, trong đó Å 1 ã Å 2 ã Å 2 ã Å 1 ã A = a + + a + + · · · + b − + b − 7 7 7 7 1 =
[(7a + 1) + (7a + 2) + · · · + (7b − 2) + (7b − 1)] 7 1 =
[(7a + 1) + (7b − 1)] [(7b − 1) − (7a + 1) + 1] 14 1 = (a + b)(7b − 7a − 1). 2 B =
(a + 1) + (a + 2) + · · · + (b − 2) + (b − 1) 1 =
[(a + 1) + (b − 1)] [(b − 1) − (a + 1) + 1] 2 1 = (a + b)(b − a − 1). 2
Tính hiệu A − B ta được 3(b2 − a2). □ 100/101 100/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641 101
Chương 6. PHÂN THỨC ĐẠI SỐ
SÁCH TOÁN 8 KẾT NỐI TRI THỨC
c Bài 88. Mức sản xuất của một xí nghiệp năm 2001 tăng a% so với năm 2000, năm 2002 tăng b% so với
năm 2001. Mức sản xuất của xí nghiệp đó năm 2002 tăng bao nhiêu phần trăm so với năm 2000? Lời giải. a
Giả sử mức sản xuất của xí nghiệp năm 2000 là 1 thì mức sản xuất năm 2001 là 1 + , mức sản xuất năm 2002 100 là Å ã a b b a ab 1 + 1 + = 1 + + + , 100 100 100 100 10000 a + b ab Å ab ã tăng so với năm 2000 là + hay a + b + %. □ 100 10000 100
c Bài 89. Một số a tăng m%, sau đó lại giảm đi n% (a, m, n là các số dương) thì được số b. Tìm liên hệ giữa m và n để b > a. Lời giải. m n h m n i Ta có b = a 1 + 1 − nên b − a = a 1 + 1 − − 1 . 100 100 100 100 m n
Điều kiện để b > a là 1 + 1 − > 1. 100 100
Rút gọn điều kiện trên ta được 100(m − n) > mn. □
c Bài 90. Chứng minh tổng sau không là số nguyên với mọi số tự nhiên n ≥ 2 1 1 1 1 A = + + + · · · + . 2 3 4 n Lời giải.
Gọi k là số nguyên lớn nhất sao cho 2k ≤ n. Chọn mẫu chung là 2kP trong đó P là tích các số lẻ không vượt quá 1
n. Chỉ có duy nhất một thừa số phụ của phân số
là số lẻ, còn mọi thừa số phụ khác đều chẵn. 2k
Như vậy, sau khi quy đồng mẫu, mẫu là số chẵn, tử là số lẻ. Do đó A không là số nguyên. □
c Bài 91. Chứng minh tổng sau không là số nguyên với mọi số tự nhiên n ≥ 1 1 1 1 1 B = + + + · · · + . 3 5 7 2n + 1 Lời giải.
Gọi k là số nguyên lớn nhất sao cho 3k ≤ 2n + 1. Chọn mẫu chung là 3kP trong đó P là tích các thừa số nguyên 1
tố lẻ không vượt quá 2n + 1. Chỉ có duy nhất một thừa số phụ của phân số
không chia hết cho 3, còn mọi 3k
thừa số phụ khác đều chia hết cho 3.
Như vậy, sau khi quy đồng mẫu, mẫu là số chia hết cho 3, tử là số không chia hết cho 3. Do đó B không là số nguyên. □ 101/101 101/101
Thầy Nguyễn Bỉnh Khôi – 0909 461 641