Phân loại và giải chi tiết các dạng bài tập Toán 8 KNTTVCS (tập 1)

Tài liệu gồm 360 trang, được biên tập bởi Toán Tiểu Học – THCS – THPT Việt Nam, phân loại và giải chi tiết các dạng bài tập môn Toán 8 bộ sách Kết Nối Tri Thức Với Cuộc Sống (tập 1). Mời bạn đọc đón xem!

14 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 8

Môn: Toán 8

Thông tin:

360 trang 1 tuần trước

Tác giả:

Profile Lê Phương
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 1.
CHƯƠNG I. ĐA THỨC
BÀI 1. ĐƠN THỨC
PHẦN A. KIẾN THỨC CẦN NHỚ
1. Đơn thức và đơn thức thu gọn
Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của các số và
biến.
Đơn thức thu gọn là đơn thức chỉ gồm một số, hoặc có dạng tích của một số với các biến, mỗi
biến chỉ xuất hiện một lần và đã được nâng lên lũy thừa với số mũ nguyên dương.
Tổng số mũ của các biến trong một đơn thức thu gọn với hệ số khác 0 gọi là bậc của đơn thức
đó.
2. Đơn thức đồng dạng
Hai đơn thức đồng dạng là hai đơn thức với hệ số khác 0 và có phần biến giống nhau.
Cộng và trừ đơn thức đồng dạng: Muốn cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay
trừ) các hệ số với nhau và giữ nguyên phần biến.
PHẦN B. PHÂN LOẠI CÁC BÀI TẬP
I. Hệ số và biến của đơn thức
Bài toán 1.
a) Cho biết phần hệ số và phần biến của đơn thức:
2 22
2,5 ;0, 25xy xy
b) Tính giá trị của mỗi đơn thức trên tại
1x =
và
1y = −
.
Bài toán 2. Hãy viết một vài đơn thức với biến
,xy
. và có giá trị bằng 9 tại
1x = −
và
1
y
=
.
Hướng dẫn: Đơn thức có dạng
mn
kx y⋅⋅
(
k
là hệ số)
Bài toán 3. Cho biết phần hệ số, phần biến và bậc của các đơn thức sau:
a)
; b)
23
aa a⋅
; c)
443
aaa−⋅⋅
Hướng dẫn: Áp dụng quy tắc nhân các lũy thừa.
Bài toán 4. Cho đơn thức
23
1
2
2
xy x

− ⋅⋅


a) Tìm bậc của đơn thức;
b) Tính giá trị của đơn thức tại
1
2;
4
xy= =
Hướng dẫn: Áp dụng quy tắc nhân các lũy thừa.
Bài toán 5. Cho đơn thức:
2
2
3
P m np= −
.
a) Tìm phần biến và bậc của đơn thức.
b) Tính giá trị của đơn thức tại
2; 6; 7mnp= = =
.
II. Đơn thức đồng dạng
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 2.
Bài toán 6. Cho các đơn thức:
2 222
1
2 ; ; 3 ;5
3
ab ab ab xy−
. Tìm đơn thức đồng dạng với
2
5ab
−
.
Hướng dẫn: Các đơn thức có cùng phần biến
2
ab
.
Bài toán khác: Tìm các đơn thức đồng dạng với nhau trong các đơn thức sau:
2 22 2 2 2 2
11
5 ;3 ; ;3 ;3 ;2 ;
35
x y xyy x y a b ab a b xy− −−
Bài toán 7. Viết ba đơn thức đồng dạng với đơn thức
32
2M xyz=
.
Bài toán 8. Cặp đơn thức sau đó đồng dạng không?
a)
22
87
P ab ab= +
và
222
357
288
Q ab ab ab
=−−
.
b)
( )( ) ( )
1
24 5
5
A m n m n mn

= − − −−


và
( )
1
4 m .3
2
B mn n

= −


Hướng dẫn: Cộng các đơn thức trước.
III. Cộng (trừ) các đơn thức
Bài toán 9. Thu gọn và cho biết bậc của đơn thức:
a)
22 2
135
246
A xy y x xy=−−
; b)
( )
( )
2
42 3
32
B xx x
= −−
Bài toán 10. Tính tổng:
( )
22
11
9 24
34
S a b a b a ab

=− ++ −


.
Bài toán khác: Tính tổng:
1.
( ) ( )
22 2 2
11
5 3; 3
Sx x x S x= + +− =
2.
222 2 2
22
1 1 1 21
5;
24 2 4
S xy xy xy xy S xy

=+++− =


3.
( )
33
5; 4S xyz xyz S xyz
=−=−
4.
2 22 2
44
13
2;
22
S x x xS x

=−− =−


.
Bài toán 11. Tìm giá trị của biểu thức:
222
11 2 3A mn mn m= −−
tại
13
;2
34
mn=−=
Bài toán khác: Tính giá trị của biểu thức:
222 2
351 3
28816
P mn mn mn mn=−+−
tại
2; 1mn= = −
Bài toán 12. Tìm đơn thức
A
, biết:
33 33
53A xyz xyz+=−
.
Bài toán khác: Tìm đơn thức
P
, biết:
1.
22
3 10P ab ab−=−
2.
23 23
35xy P xy−=−
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 3.
Bài toán 13. Cho
( )
33 2
2
2; ;
3
A x y B yx C x x y

=− =− = ⋅−


. Tính
2 3A BC+−
.
Bài toán 14. Chứng tỏ
44 4
31 1
0
2 16 32
Px x x=−+ >
với mọi
0x ≠
Bài toán 15. Viết đơn thức sau dưới dạng tổng hoặc hiệu của hai đơn thức trong đó có mặt số hạng bằng
23
3xy
.
a)
23
5xy
b)
23
3xy−
PHẦN C. BÀI TẬP
Bài 1.1. Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng.
2 2 22 2 2
2
5 1 12
; ; ;2 ; ; ; ;
3 2 45
x y xy xy x y xy x y xy
xy
−−
.
Bài 1.2. Tính tổng của ba đơn thức
a)
222
25 ; 55 ; 75xy xy xy
b)
2 22
2
5 ; ;2
3
x yz x yz x yz−
.
Bài 1.3. Thu gọn.
a)
(
)
22
33A xy xy
= −−
b)
24 24 24
372B xy xy xy=−−
.
c)
23 23 23
1
24
3
C x yz x yz x yz=+−
.
Bài 1.4. Tính giá trị biểu thức:
a)
5 55
13
24
A xy xy xy
=−+
tại
1; 1xy= = −
.
b)
( )
( )
23 2
11
4 35
22
B x x y x y xy x

=−− + −


tại
1; 2xy=−=
.
Bài 1.5. Viết ba đơn thức đồng dạng với đơn thức
2
2xy
−
rồi tính tổng của cả bốn đơn thức.
Bài 1.6. Điền đơn thức thích hợp vào ô trống
a)
22
3 .... 5xy xy+=
b)
22
.... 2 7xx−=−
c)
5
.... .... .... x
++=
Bài 1.7. Tìm đơn thức
P
sao cho
a)
33
35xy P xy+=−
b)
2 35 2 35
53P xyz xyz+=−
Bài 1.8. Chứng tỏ
( ) ( )
2
2
32x xy xy− +−
luôn nhận giá trị không âm với mọi giá trị của
;xy
.
Bài 1.9. Viết đơn thức
22
4xy z−
thành một tổng hoặc một hiệu của hai đơn thức trong đó có một đơn
thức bằng
22
2xy z−
Bài 1.10. Tìm
m
để
222 2
37 5mxy xy xy xy−+=
.
Bài 1.11. Thu gọn rồi tính giá trị của mỗi đơn thức sau
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 4.
a)
( )
2
1
2
2
A x y xy
= −
khi
1
2;
2
xy
=−=
;
b)
( )
2
0,5B xyz y z= −
khi
4x =
;
0,5y =
;
2
z
=
.
Bài 1.12. Sắp xếp các đơn thức sau thành từng nhóm, mỗi nhóm chứa tất cả các đơn thức đồng dạng với
nhau:
32 23 32 23
3
3 ; 0, 2 ; 7 ; 4 ; ; 2
4
xy xy xy y xy y−−
Bài 1.13. Rút gọn rồi tính giá trị của biểu thức
25 25
15
22
S xy xy
= −
khi
2; 1
xy=−=
.
Bài 1.14. Tính tổng của các đơn thức
23 23 23 23
38
2; ;14;
55
xy xy xy xy−−
.
Bài 1.15. Một mảnh đất có dạng như phần tô đậm trong hình bên cùng với các kích thước được ghi trên
đó. Hãy tìm đơn thức thu gọn với hai biến
x
và
y
biểu thị diện tích của mảnh đất đã cho bằng
cách:
Cách 1. Tính tổng diện tích của hai hình chữ nhật
và
.
Cách 2. Lấy diện tích của hình chữ nhật
HFGD
trừ đi diện tích của hình chữ nhật
HEBA
.
HẾT
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 5.
ĐÁP ÁN THAM KHẢO
Bài 1. ĐƠN THỨC
PHẦN B. PHÂN LOẠI CÁC BÀI TẬP
I. Hệ số và biến của đơn thức
Bài toán 1.
a) Cho biết phần hệ số và phần biến của đơn thức:
2 22
2,5 ;0, 25xy xy
b) Tính giá trị của mỗi đơn thức trên tại
1x =
và
1
y = −
.
Lời giải
a) Xét đơn thức:
2
2,5xy
ta có phần hệ số là 2,5;phần biến là
2
xy
.
Nhận xét: Đơn thức này có phần biến
2
xy
trong đó
x
là có bậc hai;
y
có bậc nhất nên bậc của
đơn thức này bằng
3
,tổng của
2
và
1:
2 1 3.+=
Phần hệ số của đơn thức
22
0, 25xy
là 0,25;phần biến là
22
.xy
.
(Bậc của đơn thức bằng
4
).
b) Thay
1x =
và
1y
= −
vào biểu thức:
2
2,5xy
, ta được:
2
2,5.1 .( 1) 2,5−=−
Thay
1
x =
và
1
y = −
vào biểu thức
22
0, 25xy
, ta được:
22
0, 25 1 ( 1) 0, 25⋅ ⋅− =
Bài toán 2. Hãy viết một vài đơn thức với biến
,xy
. và có giá trị bằng 9 tại
1
x = −
và
1
y =
.
Hướng dẫn: Đơn thức có dạng
mn
kx y⋅⋅
(
k
là hệ số)
Lời giải
Đặt đơn thức
mn
A kx y=⋅⋅
Cho
2; 1mn= =
, ta có:
( )
2
9 11 9kk
= ⋅− ⋅⇒ =
Vậy, ta có thể có:
2
9A xy=
Tương tự:
3
9 ., 9 ,..B x y C xy v v=−=−
.
Bài toán 3. Cho biết phần hệ số, phần biến và bậc của các đơn thức sau:
a)
; b)
23
aa a⋅
; c)
443
aaa−⋅⋅
Hướng dẫn: Áp dụng quy tắc nhân các lũy thừa.
Lời giải
a) Ta có:
42 6
33xx x⋅=
Phần hệ số là
3
;phần biến là
6
x
. Bậc của đơn thức là
6
.
b) Ta có:
2 3 231 6
aaa a a
++
⋅ ⋅= =
Phần hệ số là
1
;phần biến là
6
a
; bậc của đơn thức là
6
.
c) Ta có:
4 4 3 4 4 3 11
aaa a a
++
−⋅⋅ =− =−
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 6.
Phần hệ số:
1
−
;phần biến:
11
a
Bậc của đơn thức là
11
.
Bài toán 4. Cho đơn thức
23
1
2
2
xy x

− ⋅⋅


.
a) Tìm bậc của đơn thức;
b) Tính giá trị của đơn thức tại
1
2;
4
xy= =
Hướng dẫn: Áp dụng quy tắc nhân các lũy thừa.
Lời giải
a) Ta có:
2 3 42
1
2
2
x y x xy

− ⋅ ⋅⋅ =−


Đơn thức này có bậc:
426+=
(hệ số là:
1−
; phần biến:
42
xy
)
b) Thay
1
2;
4
xy= =
vào đơn thức, ta được:
( )
2
4
11
2 16 1
4 16

−⋅ =− ⋅ =−


Bài toán 5. Cho đơn thức:
2
2
3
P m np
= −
.
a) Tìm phần biến và bậc của đơn thức.
b) Tính giá trị của đơn thức tại
2; 6; 7mnp= = =
.
Lời giải
a) Ta có:
2
2
3
P m np
= −
Vậy phần biến là
2
m np
. Ta có số mũ của
,,
mn p
theo thứ tự là
2;1
và
1
.
Đơn thức có bậc là:
211 4
++=
.
b) Thay
2; 6; 7mnp= = =
vào đơn thức
P
, ta được:
2
2
2 6 7 112
3
P
=− ⋅ ⋅⋅=−
II. Đơn thức đồng dạng
Bài toán 6. Cho các đơn thức:
2 222
1
2 ; ; 3 ;5
3
ab ab ab xy−
. Tìm đơn thức đồng dạng với
2
5
ab−
.
Hướng dẫn: Các đơn thức có cùng phần biến
2
ab
.
Lời giải
Các đơn thức đồng dạng với
2
5ab−
là:
22
2 ; 3 ab ab−
Bài toán khác: Tìm các đơn thức đồng dạng với nhau trong các đơn thức sau:
2 22 2 2 2 2
11
5 ;3 ; ;3 ;3 ;2 ;
35
x y xyy x y a b ab a b xy− −−
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 7.
(
2
5
xy
và
22
1
;3
3
x y xy−
và
22
1
;3
5
xy a b
và
2
2ab
−
là các cặp đơn thức đồng dạng).
Bài toán 7. Viết ba đơn thức đồng dạng với đơn thức
32
2
M xyz=
.
Lời giải
Các đơn thức đồng dạng với
32
2M xyz=
là:
32 32 32
12 3
1
; ;5
3
M xyzM xy zM xyz
=−= =
(Bạn có thể lấy đơn thức khác nhau ở phần hệ số; còn phần biến luôn là
32
xyz
).
Bài toán 8. Cặp đơn thức sau đó đồng dạng không?
a)
22
87
P ab ab
= +
và
222
357
288
Q ab ab ab=−−
.
b)
( )
(
) ( )
1
24 5
5
A m n m n mn

= − − −−


và
( )
1
4 m .3
2
B mn n

= −


Hướng dẫn: Cộng các đơn thức trước.
Lời giải
a)
22
15 ; 0 P ab Q a b= =
. Vậy
P
và
Q
không phải là hai đơn thức đồng dạng.
b)
1 64
85
55
A mn mn mn mn
=−+ − =−
;
5
2
B mn=
. Vậy
A
và
B
là hai đơn thức đồng dạng.
Chú ý: Hệ số của các đơn thức phải khác 0.
III. Cộng (trừ) các đơn thức
Bài toán 9. Thu gọn và cho biết bậc của đơn thức:
a)
22 2
135
246
A xy y x xy=−−
; b)
( ) ( )
2
42 3
32B xx x= −−
Lời giải
a)
22
1 3 5 13
2 4 6 12
A xy xy

= −− =−


. Đơn thức
A
có bậc là
3
.
b)
66 6
34Bx x x=−=−
. Đơn thức
B
có bậc là
6
.
Bài toán 10. Tính tổng:
( )
22
11
9 24
34
S a b a b a ab

=− ++ −


Lời giải
22 2 2 2
3 6 ( 3 1 6) 8 S ab ab ab ab ab=− + − =−+− =−
Bài toán khác: Tính tổng:
1.
( ) ( )
22 2 2
11
5 3; 3
Sx x x S x= + +− =
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 8.
2.
222 2 2
22
1 1 1 21
5;
24 2 4
S xy xy xy xy S xy

=+++− =


3.
( )
33
5; 4
S xyz xyz S xyz=−=−
4.
2 22 2
44
13
2;
22
S x x xS x

=−− =−


.
Bài toán 11. Tìm giá trị của biểu thức:
222
11 2 3
A mn mn m= −−
tại
13
;2
34
mn=−=
Lời giải
Ta có:
(
)
2222
11 2 3 9 3A mn m mn m
=− −= −
.
Thay
1 3 11
;2
3 44
mn
=−==
vào biểu thức
A
, ta được:
22
1 11 1 11 1 29
93
3 4 3 4 3 12
A
 
= ⋅− ⋅ − − = − =
 
 
Bài toán khác: Tính giá trị của biểu thức:
222 2
351 3
28816
P mn mn mn mn=−+−
tại
2; 1mn= = −
Hướng dẫn
Ta có:
22
3 5 1 3 13
2 8 8 16 16
P mn mn

= −+− =


.
Thay
2; 1
mn= = −
vào biểu thức
P
ta được:
( )
2
13 13
21
16 8
P = ⋅− =
Bài toán 12. Tìm đơn thức
A
, biết:
33 33
53A xyz xyz+=−
.
Lời giải
Ta có:
33 33 33
35 8A xyz xyz xyz=−− =−
Bài toán khác: Tìm đơn thức
P
, biết:
1.
22
3 10P ab ab−=−
2.
23 23
35xy P xy−=−
Huớng dẫn
1.
22 2
3 10 7P ab ab ab=−=−
; 2.
( )
23 23 23
3 58P xy xy xy= −− =
Bài toán 13. Cho
( )
33 2
2
2; ;
3
A x y B yx C x x y

=− =− = ⋅−


. Tính
2 3A BC+−
.
Lời giải
( ) ( )
33 2
2
23 2 2 3
3
A B C x y yx x x y

+ − =− + − − ⋅ ⋅−


333 3
222 2xy xy xy xy=−− + =−
Bài toán 14. Chứng tỏ
44 4
31 1
0
2 16 32
Px x x=−+>
với mọi
0x ≠
Lời giải
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 9.
Ta có
44 4 4
3 1 1 31 11
2 16 32 2 16 32 4
Px x x x

= − + = −+−


4
39
32
Px
⇒=
vì
0x ≠
nên
4
0x >
với mọi
0x ≠
.
Bài toán 15. Viết đơn thức sau dưới dạng tổng hoặc hiệu của hai đơn thức trong đó có mặt số hạng bằng
23
3xy
.
a)
23
5xy
b)
23
3xy−
Lời giải
a)
23 23 23
532
xy xy xy
= +
b)
23 23 23
336xy xy xy−=−
PHẦN C. BÀI TẬP
Bài 1.1. Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng.
2 2 22 2 2
2
5 1 12
; ; ;2 ; ; ; ;
3 2 45
x y xy xy x y xy x y xy
xy
−−
.
Lời giải
2 22 2
51 2
; ;;
32 5
xy xyxy xy−
là các đơn thức đồng dạng;
2 22
1
;2 ;
4
xy xy xy−
là các đơn thức đồng dạng.
Bài 1.2. Tính tổng của ba đơn thức
a)
222
25 ; 55 ; 75xy xy xy
b)
2 22
2
5 ; ;2
3
x yz x yz x yz−
.
Lời giải
a)
222 2
25 55 75 155
xy xy xy xy++=
b)
2 22 2
27
52
33
x yz x yz x yz x yz
−+ + =−
c)
2 2 22
31 1
42 4
xyz xyz xyz xyz

+ +− =


(Ta cộng các hệ số của các đơn thức)
Bài 1.3. Thu gọn.
a)
( )
22
33A xy xy= −−
b)
24 24 24
372B xy xy xy
=−−
.
c)
23 23 23
1
24
3
C x yz x yz x yz=+−
.
Lời giải
a)
22 2
336A xy xy xy=+=
b)
( )
24 24
372 6B xy xy= −− =−
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 10.
c)
23
5
3
C x yz
= −
Bài 1.4. Tính giá trị biểu thức:
a)
5 55
13
24
A xy xy xy=−+
tại
1; 1xy
= = −
.
b)
( )
( )
23 2
11
4 35
22
B x x y x y xy x

=−− + −


tại
1; 2xy=−=
.
Lời giải
a)
5
3
4
A xy=
. Thay
1; 1;xy
= = −
ta có :
3
4
A
= −
b)
3
5
.
2
B xy
=
Thay
1; 2 5
xy B=− =⇒=−
.
Bài 1.5. Viết ba đơn thức đồng dạng với đơn thức
2
2xy−
rồi tính tổng của cả bốn đơn thức.
Lời giải
Ta lấy
22 2
1
3 ;6 ;
2
xy xy xy
−−
Vậy tổng của bốn đơn thức:
( )
( )
22 2 2 2
1 11
23 6 .
22
xy xy xy xy xy

−++−+− =−


Bài 1.6. Điền đơn thức thích hợp vào ô trống
a)
22
3 .... 5xy xy+=
b)
22
.... 2 7
xx−=−
c)
5
.... .... .... x++=
.
Lời giải
a)
222
3 2 5.xy xy xy+=
Cách tính :
22 2
53 2xy xy xy−=
b)
22 2
52 7xx x−−=−
c) Có nhiều cách điền vào các ô trống:
Chẳng hạn:
( )
5 5 55
33x x xx+ +− =
;
( )
5 5 55
x x xx+− + =
Bài 1.7. Tìm đơn thức
P
sao cho
a)
33
35xy P xy+=−
b)
2 35 2 35
53P xyz xyz+=−
Lời giải
a)
33 3
358P xy xy xy=+=
b)
( )
2 35 2 35 2 35
35 8P xyz xyz xyz=− −=−
Bài 1.8. Chứng tỏ
( ) ( )
2
2
32x xy xy− +−
luôn nhận giá trị không âm với mọi giá trị của
;xy
.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 11.
Lời giải
( ) (
)
2
2 22 22 22
3 2 34xxy xy xy xy xy− +− =− + =
Vì
2
0
x
≥
và
2
0
y ≥
, với mọi giá trị
,xy
nên
22
0xy
≥
, với mọi giá trị của
,xy
.
Bài 1.9. Viết đơn thức
22
4xy z−
thành một tổng hoặc một hiệu của hai đơn thức trong đó có một đơn
thức bằng
22
2xy z−
.
Lời giải
(
) ( )
23 23 23
42 2xy z xy z xy z− =− +−
23 23 23
4 6 10xy z xy z xy z−= −
.
Bài 1.10. Tìm
m
để
222 2
37 5mxy xy xy xy−+=
.
Lời giải
( )
22
37 5 375 1m xy xy m m−+ = ⇒ −+=⇒ =
Bài 1.11. Thu gọn rồi tính giá trị của mỗi đơn thức sau
a)
( )
2
1
2
2
A x y xy= −
khi
1
2;
2
xy=−=
;
b)
( )
2
0,5B xyz y z= −
khi
4x =
;
0,5y =
;
2z =
.
Lời giải
a)
( ) ( )
2 2 32
11
2 . 2. ... 3 .
22
A xyxyA xxyyA xy

=− ⇒=− ⇒=−


Thay
1
2;
2
xy=−=
vào biểu thức, ta có :
( )
2
3
11
2 . 8. 2.
24
A

=−− = =


b)
( ) ( ) ( )
2 2 32
0,5 0,5 . . . . 0,5 .B xyz y z B x y y z z B xy z= − ⇒=− ⇒=−
Thay
4; 0, 5; 2xy z= = =
vào biểu thức, ta có :
( ) ( )
3
2
0,5 .4. 0,5 .2 1B =−=−
.
Bài 1.12. Sắp xếp các đơn thức sau thành từng nhóm, mỗi nhóm chứa tất cả các đơn thức đồng dạng với
nhau:
32 23 32 23
3
3 ; 0, 2 ; 7 ; 4 ; ; 2
4
xy xy xy y xy y−−
.
Lời giải
32 32
3 ;7 .xy xy
23 23
3
0, 2 ; .
4
xy xy−
4 ; 2.yy−
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 12.
Bài 1.13. Rút gọn rồi tính giá trị của biểu thức
25 25
15
22
S xy xy= −
khi
2; 1xy=−=
.
Lời giải
25 25 25 25
1 5 15
2
2 2 22
S xy xy S xy S xy

= − ⇒= − ⇒=−


Thay
2; 1xy
=−=
vào biểu thức, ta có:
( ) ( )
2
5
2 . 2 .1 8SS=− − ⇒=−
.
Bài 1.14. Tính tổng của các đơn thức
23 23 23 23
38
2; ;14;
55
xy xy xy xy
−−
.
Lời giải
( )
23 23 23 23 23 23
3 8 38
2 14 2 14 11 .
5 5 55
xy xy xy xy xy xy

 
+− +− + = +− − + =−
 

 

Bài 1.15. Một mảnh đất có dạng như phần tô đậm trong hình bên cùng với các kích thước được ghi trên
đó. Hãy tìm đơn thức thu gọn với hai biến
x
và
y
biểu thị diện tích của mảnh đất đã cho bằng
cách:
Cách 1. Tính tổng diện tích của hai hình chữ nhật
và
.
Cách 2. Lấy diện tích của hình chữ nhật
HFGD
trừ đi diện tích của hình chữ nhật
HEBA
.
Lời giải
Cách 1:
Diện tích của hình chữ nhật
là:
2 .2 4x y xy=
(đơn vị diện tích)
Diện tích của hình chữ nhật
là:
3. 3x y xy=
(đơn vị diện tích)
Diện tích mảnh đất:
437xy xy xy+=
(đơn vị diện tích)
Cách 2:
Diện tích của hình chữ nhật
AFGD
là:
( )
3.2 3.3 9x y y x y xy+= =
(đơn vị diện tích)
Diện tích của hình chữ nhật
HEBA
là:
( )
3 2 .2 2x x y xy−=
(đơn vị diện tích)
Diện tích mảnh đất:
927xy xy xy
−=
(đơn vị diện tích)
HẾT
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 1.
BÀI 2: ĐA THỨC
PHẦN A. KIẾN THỨC CẦN NHỚ
1. Khái niệm đa thức
Đa thức là tổng của những đơn thức, mỗi đơn thức trong tổng gọi là hạng tử của đa thức đó.
2. Thu gọn đa thức
Đa thức thu gọn là đa thức không có hai hạng tử nào đồng dạng.
Chú ý:
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
Một số khác
0
tùy ý được gọi là đa thức bậc 0.
Số
0
cũng là một đa thức, gọi là đa thức
0
. Nó không có bậc xác định.
PHẦN B. PHÂN LOẠI BÀI TẬP
1. Thu gọn đa thức
Bài toán 1. Thu gọn
a)
22
11 4 4
A x xx x= +−−
b)
222 2
351 3
28816
B ab ab ab ab=−+−
c)
22
32 5
2
43 6
C xy x y xy x y
=− + −+
d)
324 34D ab bc ac ab bc ab= − + −+ +
e)
(
)
2 22
11 5
23
23 4
E x y ab a x y a b

= − ++


Hướng dẫn: Cộng trừ các đơn thức đồng dạng.
Bài toán 2. Thu gọn đa thức
a)
2 22 2
245A x yz xy z x yz xy z xyz= + − +−
b)
3 32 2
1
53
2
B x xy x xy x xy x=− + +−+ −
c)
23 2 3 2 22 4 2 22
1
33
2
C xy xy xyz z xyz= − + −−
Bài toán 3. Thu gọn và tính giá trị của đa thức
a)
22 2 2
1 11
5
3 23
A x y xy xy xy xy x y
= + −+ − −
tại
1
2
x =
và
1y =
.
b)
22
5 23B xy xy xy= +−
tại
2; 1xy
=−=
.
c)
6 25 6 25 6
C x x y xy x y xy=+++−
tại
1; 1xy=−=−
.
Bài toán 4. Chứng tỏ giá trị của đa thức
2 2 22 2 2
357 37 352M x xy x y x x y x xy y=++ −− +−+
luôn luôn
không âm với mọi giá trị
;xy
.
Hướng dẫn: Thu gọn đa thức
M
.
Bài toán khác: Chứng tỏ đa thức
22
11 4 3 4 5A x xx x= +− −+
luôn nhận giá trị dương với mọi giá trị của
x
.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 2.
Hướng dẫn:
2
85Ax= +
. Vì
22 2
0 8 0;50 8 50xx x
≥⇒ ≥ >⇒ +>
.
Bài toán 5. Cho đa thức
22
2 6 6 12
P x xx x
= −++−
. Tìm
x
để
P
nhận giá trị
0
.
Hướng dẫn: Thu gọn đa thức
P
Bài toán khác: Tìm
x
để đa thức
22
3 8 44 8 3
Px x x x
= + +− − −
nhận giá trị
3−
.
Hướng dẫn:
2
1Px
=−+
22
3 13 4Px x=− ⇒− + =− ⇒− =−
2
42xx⇒ =⇒=
hoặc
2x = −
.
Đáp số:
2x =
hoặc
2x = −
.
Bài toán 6. Chứng tỏ rằng giá trị của đa thức
22 2
3
35 2
2
P xy y xy x
=− +− +
tại
luô không âm.
Hướng dẫn: Thay giá trị
yx= −
ta tìm được
P
là đa thức của biến
x
.
Bài toán 7. Cho đa thức
2
2 35P x mx m=+ −+
. Tìm
m
biết rằng đa thức
P
nhận giá trị
0
tại
2x = −
.
Hướng dẫn: Thay
2x = −
vào đa thức
P
và tìm
m
khi
0P =
II. Bậc của đa thức
Bài toán 8. Tìm bậc của đa thức:
a)
53 2
13
3
24
P x x y xy=−− −
b)
2
1
32
2
Qx x= −+
c)
22
5 4 531T x y xyy x y= − +−+
Hướng dẫn: Bậc của đơn thức nào lớn nhất là bậc của đa thức.
Bài toán 9. Tìm bậc của mỗi đa thức sau:
a)
22
1
3 12
2
A x x xx= − ++ −
; b)
2 3332
37363Bx xxxx=+−+−
.
Hướng dẫn: Thu gọn các đa thức.
Bài toán khác: Đa thức
323 2 3
3 2 2 13
C x x x x xx= + − +− + −
thu gọn ta được:
2
1
C xx=− ++
.
Vậy
C
có bậc là 2 (ta không nên vội kết luận đa thức
C
có bậc 3).
Bài toán 10. Tìm bậc của đa thức theo biến
;xy
a)
3 22 5
32
P x m x mx m=+ −+
. b)
( )
3 22
2 2. 0Q mx xy m x y m= + + ++ ≠
.
Hướng dẫn: a) Biến của đa thức
P
là
;xm
là hệ số của mỗi đơn thức.
Bài toán khác: Tìm bậc của đa thức theo biến
x
.
1.
( )
432
.0P ax bx cx dx e a= + + ++ ≠
2.
( )
332
1. 0Qmxxx m= ++− ≠
Đáp số:
1. Bậc của
P
là
4
. 2. Bậc của
Q
là 3.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 3.
Bài toán 11. Cho đa thức
2 2 3 4 22
5 2 323
P xy xy x y xy= − +− −
a) Tìm bậc của đa thức
P
. b) Tìm các hạng tử bậc 3 trong đa thức
P
.
PHẦN C. BÀI TẬP
Bài 1.16. Tìm bậc của các đa thức sau:
a)
23323
562482
Axxxxxx=++−−+
;
b)
2 2 22 2 2 2
54 62 3 548 3B xy x y x xy x y x xy x y y=−−−+++−−
;
c)
4 2 4 23 4
63423 41C x x xx xx x
=−+−++−+
.
d)
2 22
2
D a ax x
=++
Bài 1.17. Thu gọn các đa thức:
a)
22
5 3,5 2 1,3A xy y xy y xy=− −+ −
;
b)
2 22 2 2
17 331
28 482
B ab ab a b a b ab
= − +−−
;
c)
324 34C ab bc ac ab bc ab= − + −+ +
;
d)
322 2 23
2 13P x xy x y x y xy x=−++−+−+
;
e)
22
26 13 41 16 13 4Q ax ax x x ax ax= + +−− +
.
Bài 1.18. Tính giá trị của đa thức:
a)
2 223 2
3243 24A x xy y x y x xy y= + − + −− +
, tại
1
;1
2
xy= = −
;
b)
2 2 22
235B a ab b ab a b
= + − ++−
, tại
3; 2ab=−=−
;
c)
22 3 2 2
3 263 2P x y x xy x x y xy= −−++ −−
tại
2; 1xy=−=−
;
d)
2 2 2 22 2
8 10 6 2 6Q a ab b a ab b a y= − −− + −−+
, tại
2; 2xy
=−=−
.
Bài 1.19. Chứng minh rằng:
24 3 24 3 3
3
3 5 321
2
M x y xy x y xy xy= −− +++
luôn dương với mọi
;
xy
.
Bài 1.20. Cho da thức:
22
2 6 6 12
Q x xx x
= ++−−
. Tìm
x
để
Q
nhận giá trị
0
.
HẾT
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 4.
ĐÁP ÁN THAM KHẢO
BÀI 2: ĐA THỨC
PHẦN B. PHÂN LOẠI BÀI TẬP
1. Thu gọn đa thức
Bài toán 1. Thu gọn
a)
22
11 4 4
A x xx x= +−−
b)
222 2
351 3
28816
B ab ab ab ab=−+−
c)
22
32 5
2
43 6
C xy x y xy x y=− + −+
d)
324 34D ab bc ac ab bc ab
= − + −+ +
e)
( )
2 22
11 5
23
23 4
E x y ab a x y a b

= − ++


Hướng dẫn: Cộng trừ các đơn thức đồng dạng.
Lời giải
a)
22 2
11 4 4 10
A x xx x x
= +−− =
b)
222 2 2
3 5 1 3 13
2 8 8 16 16
B ab ab ab ab ab=−+− =
c)
22 2
3 2 5 11 3
2
43 6 4 2
C xy x y xy x y xy x y=− + −+ =− +
d)
324 34 6 4D ab bc ac ab bc ab ab bc ac= − + −+ + = ++
e)
( )
2 22 2
11 5
23 2
23 4
E x y ab a xy ab xy

= − + +=


Bài toán 2. Thu gọn đa thức
a)
2 22 2
245A x yz xy z x yz xy z xyz= + − +−
b)
3 32 2
1
53
2
B x xy x xy x xy x=− + +−+ −
c)
23 23 2 22 4 2 22
1
33
2
C xy xy xyz z xyz= − + −−
Lời giải
a)
2 22 2
245A x yz xy z x yz xy z xyz= + − +−
( ) (
)
2 2 22 2 2
25 4 35x yz x yz xy z xy z xyz x yz xy z xyz= − + + −=− + −
b)
3 32 2
1
53
2
B x xy x xy x xy x=− + +−+ −
( ) ( )
3 3 22 3 2
17
35 4 2
22
x x xy xy xy x x x xy x

= + +− + + +− − = − −


c)
23 23 2 22 4 2 22
1
33
2
C xy xy xyz z xyz= − + −−
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 5.
( )
23 23 222 222 4 23 4
11
33
22
xy xy xyz xyz z xy z

= − + − −=− −


Bài toán 3. Thu gọn và tính giá trị của đa thức
a)
22 2 2
1 11
5
3 23
A x y xy xy xy xy x y= + −+ − −
tại
1
2
x =
và
1y =
.
b)
22
5 23B xy xy xy
= +−
tại
2; 1xy=−=
.
c)
6 25 6 25 6
C x x y xy x y xy=+++−
tại
1; 1
xy=−=−
.
Lời giải
a)
22 2 2
1 11
5
3 23
A x y xy xy xy xy x y= + −+ − −
( )
22 2
11 1 3
1 15 6
33 2 2
x y xy xy xy xy

= − + + +−− = −


Thay
1
2
x
=
và
1y =
vào đa thức
A
ta được:
2
31 1 3 9
. .1 6. .1 3
22 2 4 4
A = − = −=−
b)
( )
2 2 22 2
5 23 5 3 2 2 2B xy xy xy xy xy xy xy xy= +− = − += +
Thay
2; 1
xy
=−=
vào đa thức
B
ta được:
( ) ( )
2
2. 2 .1 2. 2 .1 4 4 8B = − + − =−− =−
.
c)
(
) ( )
6 25 6 25 6 6 25 25 6 6 6 25
2C x xy xy xy xy x xy xy xy xy x xy=+++−=+ + +−=+
Thay
1; 1xy=−=−
vào đa thức C ta được:
( ) ( )
( )
6 25
1 2 1. 1 12 1
C =− + − − =−=−
Bài toán 4. Chứng tỏ giá trị của đa thức
2 2 22 2 2
357 37 352M x xy x y x x y x xy y=++ −− +−+
luôn luôn
không âm với mọi giá trị
;xy
.
Hướng dẫn: Thu gọn đa thức
M
.
Lời giải
Ta có:
( )
( )
( )
222 2 2 2 2 2
333 55 7 7 2 32M x x x xy xy x y x y y x y= −+ + − + − + =+
Vì
2
0x ≥
với mọi
x
;
2
0y ≥
với mọi
y
22
32 0xy⇒+ ≥
với mọi
,
xy
.
Bài toán khác: Chứng tỏ đa thức
22
11 4 3 4 5A x xx x= +− −+
luôn nhận giá trị dương với mọi giá trị của
x
.
Hướng dẫn:
2
85
Ax= +
. Vì
22 2
0 8 0;50 8 50xx x≥⇒ ≥ >⇒ +>
.
Bài toán 5. Cho đa thức
22
2 6 6 12P x xx x= −++−
. Tìm
x
để
P
nhận giá trị
0
.
Hướng dẫn: Thu gọn đa thức
P
Lời giải
Ta có:
22 2
2 6 6 12 3 12P x xx x x= −++−= −
2
0 3 12 0Px=⇒ −=
22
3 12 4 2x xx⇒ = ⇒ =⇒=
hoặc
2x = −
.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 6.
Bài toán khác: Tìm
x
để đa thức
22
3 8 44 8 3Px x x x= + +− − −
nhận giá trị
3
−
.
Hướng dẫn:
2
1Px=−+
22
3 13 4Px x
=− ⇒− + =− ⇒− =−
2
42
xx⇒ =⇒=
hoặc
2x = −
.
Đáp số:
2x =
hoặc
2x = −
.
Bài toán 6. Chứng tỏ rằng giá trị của đa thức
22 2
3
35 2
2
P xy y xy x=− +− +
tại
luô không âm.
Hướng dẫn: Thay giá trị
yx
= −
ta tìm được
P
là đa thức của biến
x
.
Lời giải
Thay
vào biểu thức của
P
ta được:
( ) ( )
( )
22
242 224 2
3 3 17
3 5 235 23
2 22
P xx x xx x x x x x x x=−−+−− −+ = + + + = +
Vì
2
0x ≥
và
4
0x
≥
nên
42
17
30
2
xx+≥
với mọi
x
.
Bài toán 7. Cho đa thức
2
2 35P x mx m=+ −+
. Tìm
m
biết rằng đa thức
P
nhận giá trị
0
tại
2x = −
.
Hướng dẫn: Thay
2x = −
vào đa thức
P
và tìm
m
khi
0P =
Lời giải
Thay
2x = −
vào biểu thức của
P
.
Ta có:
( )
2
( 2) 2 2 3 5 9 7P mm m=− + ⋅− − + = −
.
Vì
P
nhận giá trị 0 tại
9
2 9 7 0
7
x mm=−⇒ − = ⇒ =
II. Bậc của đa thức
Bài toán 8. Tìm bậc của đa thức:
a)
53 2
13
3
24
P x x y xy=−− −
1b)
2
1
32
2
Qx x= −+
c)
22
5 4 531
T x y xyy x y= − +−+
Hướng dẫn: Bậc của đơn thức nào lớn nhất là bậc của đa thức.
Lời giải
a) Bậc của hạng tử
5
3x−
là 5 là bậc cao nhất trong các hạng tử Vậy bậc của
P
là 5.
b) Bậc của hạng tử
2
3x
là bậc 2.
Vậy bậc của
Q
là 2.
c) Bậc của các hạng tử
2
5xy
và
2
4
xy−
đều là 3. Vậy bậc của
T
là 3.
Bài toán 9. Tìm bậc của mỗi đa thức sau:
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 7.
a)
22
1
3 12
2
A x x xx= − ++ −
;
b)
2 3332
37363Bxxxxx
=+−+−
.
Hướng dẫn: Thu gọn các đa thức.
Lời giải
a)
2
3
21
2
Ax x= ++
Vậy đa thức
A
có bậc là 2.
b)
3
10Bx=
.
Vậy
B
có bậc là 3.
Bài toán khác: Đa thức
323 2 3
3 2 2 13C x x x x xx= + − +− + −
thu gọn ta được:
2
1
C xx=− ++
.
Vậy
C
có bậc là 2 (ta không nên vội kết luận đa thức
C
có bậc 3).
Bài toán 10. Tìm bậc của đa thức theo biến
;
xy
a)
3 22 5
32P x m x mx m=+ −+
. b)
( )
3 22
2 2. 0Q mx xy m x y m= + + ++ ≠
.
Hướng dẫn: a) Biến của đa thức
P
là
;xm
là hệ số của mỗi đơn thức.
Lời giải
a) Hạng tử
3
3x
có bậc 3. Vậy
P
có bậc là 3.
b) Hạng tử
3
mx
có bậc của
x
là 3. Vậy bậc của
Q
là 3.
Bài toán khác: Tìm bậc của đa thức theo biến
x
.
1.
( )
432
.0P ax bx cx dx e a
= + + ++ ≠
2.
( )
332
1. 0Qmxxx m= ++− ≠
Đáp số:
1. Bậc của
P
là
4
. 2. Bậc của
Q
là 3.
Bài toán 11. Cho đa thức
2 2 3 4 22
5 2 323P xy xy x y xy= − +− −
a) Tìm bậc của đa thức
P
. b) Tìm các hạng tử bậc 3 trong đa thức
P
.
Lời giải
a) Ta có
4
2y−
và
22
3xy−
là hai hạng tử cũng có bậc 4. Vậy
P
có bậc là 4.
b) Các hạng tử có cùng bậc 3 là:
22
5 ;2x xy−
và
3
3x
.
PHẦN C. BÀI TẬP
Bài 1.16. Tìm bậc của các đa thức sau:
a)
23323
562482Axxxxxx=++−−+
;
b)
2 2 22 2 2 2
54 62 3 548 3B xy x y x xy x y x xy x y y=−−−+++−−
;
c)
4 2 4 23 4
63423 41C x x xx xx x=−+−++−+
.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 8.
d)
2 22
2D a ax x
=++
.
Lời giải
a)
2
2
Ax x
= +
.
Bậc của
A
là
2
b)
22 22
12 9 2 3B xy x y x xy y
= − −− −
.
Bậc của
B
là
3
c)
3
41Cx x=++
.
Bậc của
C
là
3
d) Bậc của
D
là
3
(theo hai biến
a
và
x
)
Bài 1.17. Thu gọn các đa thức:
a)
22
5 3,5 2 1,3A xy y xy y xy=− −+ −
;
b)
2 22 2 2
17 331
28 482
B ab ab a b a b ab= −+−−
;
c)
324 34
C ab bc ac ab bc ab
= − + −+ +
;
d)
322 2 23
2 13P x xy x y x y xy x=−++−+−+
;
e)
22
26 13 41 16 13 4
Q ax ax x x ax ax= + +−− +
.
Lời giải
a)
( )
( )
22
5 2 1 1,3 3,5 2 2,2
A xy y xy y= −− + − = −
b)
2 2 22
171 33 7 3
282 48 8 8
B ab a b a b ab

= −− + − =− +


.
c)
( )
( )
3 1 4 2 3 4a 6a 4a
C ab bc c b bc c= −+ +−+ + = + +
.
d)
32
21P x xy=+−
là
3
e)
2
30 25Q ax x= +
Bài 1.18. Tính giá trị của đa thức:
a)
2 223 2
3243 24A x xy y x y x xy y= + − + −− +
, tại
1
;1
2
xy= = −
;
b)
2 2 22
235B a ab b ab a b
= + − ++−
, tại
3; 2ab
=−=−
;
c)
22 3 2 2
3 263 2P x y x xy x x y xy= −−++ −−
tại
2; 1
xy=−=−
;
d)
2 2 2 22 2
8 10 6 2 6Q a ab b a ab b a y= − −− + −−+
, tại
2; 2xy=−=−
.
Lời giải
a)
223
33A x xy x=+−
Thay
1
;1
2
xy= = −
vào biểu thức
A
ta được:
( )
22 3
1 1 1 331 1
3. 3. . 1
2 2 2 448 8
A
  
= + −− =−−=−
  
  
| 1/360
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 CHƯƠNG I. ĐA THỨC BÀI 1. ĐƠN THỨC
PHẦN A. KIẾN THỨC CẦN NHỚ
1. Đơn thức và đơn thức thu gọn
 Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của các số và biến.
 Đơn thức thu gọn là đơn thức chỉ gồm một số, hoặc có dạng tích của một số với các biến, mỗi
biến chỉ xuất hiện một lần và đã được nâng lên lũy thừa với số mũ nguyên dương.
 Tổng số mũ của các biến trong một đơn thức thu gọn với hệ số khác 0 gọi là bậc của đơn thức đó.
2. Đơn thức đồng dạng
 Hai đơn thức đồng dạng là hai đơn thức với hệ số khác 0 và có phần biến giống nhau.
 Cộng và trừ đơn thức đồng dạng: Muốn cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay
trừ) các hệ số với nhau và giữ nguyên phần biến.
PHẦN B. PHÂN LOẠI CÁC BÀI TẬP
I. Hệ số và biến của đơn thức Bài toán 1.
a) Cho biết phần hệ số và phần biến của đơn thức: 2 2 2 2,5x y;0,25x y
b) Tính giá trị của mỗi đơn thức trên tại x =1 và y = 1 − .
Bài toán 2. Hãy viết một vài đơn thức với biến x, y . và có giá trị bằng 9 tại x = 1 − và y =1.
Hướng dẫn: Đơn thức có dạng m n
k ⋅ x ⋅ y ( k là hệ số)
Bài toán 3. Cho biết phần hệ số, phần biến và bậc của các đơn thức sau: a) 4 2 3x ⋅ x ; b) 2 3 a a ⋅a ; c) 4 4 3
−a ⋅a ⋅a
Hướng dẫn: Áp dụng quy tắc nhân các lũy thừa.
Bài toán 4. Cho đơn thức  1  2 3 − x⋅ y ⋅   2x  2 
a) Tìm bậc của đơn thức;
b) Tính giá trị của đơn thức tại 1 x = 2; y = 4
Hướng dẫn: Áp dụng quy tắc nhân các lũy thừa.
Bài toán 5. Cho đơn thức: 2 2 P = − m np . 3
a) Tìm phần biến và bậc của đơn thức.
b) Tính giá trị của đơn thức tại m = 2;n = 6; p = 7 .
II. Đơn thức đồng dạng
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 1.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
Bài toán 6. Cho các đơn thức: 2 1 2 2 2 2a ; b ab ; 3 − a ;
b 5x y . Tìm đơn thức đồng dạng với 2 5 − a b . 3
Hướng dẫn: Các đơn thức có cùng phần biến 2 a b .
Bài toán khác: Tìm các đơn thức đồng dạng với nhau trong các đơn thức sau: 2 2 1 2 2 2 2 1 2 5x y; 3
− xyy ; x y;3a ; b 3 − ab ; 2 − a ; b xy 3 5
Bài toán 7. Viết ba đơn thức đồng dạng với đơn thức 3 2 M = 2x y z .
Bài toán 8. Cặp đơn thức sau đó đồng dạng không? a) 2 2
P = 8ab + 7ab và 3 2 5 2 7 2
Q = a b − a b − a b . 2 8 8
b) A ( m)( n)  1 2 4 m = − − (−n)−  1   
5mn và B = 4mn −  m.(3n)  5   2 
Hướng dẫn: Cộng các đơn thức trước.
III. Cộng (trừ) các đơn thức
Bài toán 9. Thu gọn và cho biết bậc của đơn thức: a) 1 2 3 2 5 2
A = xy − y x − xy ;
b) B = x (x ) −(− x )2 4 2 3 3 2 2 4 6
Bài toán 10. Tính tổng: S ( 2 a ) 1 2  1 9 b a b 24aab = − + + − . 3 4   
Bài toán khác: Tính tổng: 1. 2 2
S = x + 5x + ( 2 3 − x );( 2 S = 3x 1 1 ) 2. 2 1 2 1 2  1  2  21 2 S 5xy xy xy   xy ; S xy  = + + + − = 2 2 2 4 2 4     
3. S = xyz − 5xyz; S = 4 − xyz 3 ( 3 ) 4. 2 1 2 2  3 2 S x
x 2x ;S x  = − − = − 4 4 . 2 2   
Bài toán 11. Tìm giá trị của biểu thức: 2 2 2
A =11m n − 2m n − 3m tại 1 3 m = − ;n = 2 3 4
Bài toán khác: Tính giá trị của biểu thức: 3 2 5 2 1 2 3 2
P = mn − mn + mn −
mn tại m = 2;n = 1 − 2 8 8 16
Bài toán 12. Tìm đơn thức A , biết: 3 3 3 3 A + 5x y z = 3 − x y z .
Bài toán khác: Tìm đơn thức P , biết: 1. 2 2 P − 3ab = 10 − ab 2. 2 3 2 3 3x y − P = 5 − x y
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 2.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 Bài toán 13. Cho 3 3  2 A 2x y; B yx ;C x = − = − = ⋅( 2 −  
x y). Tính A+ 2 B − 3C .  3 
Bài toán 14. Chứng tỏ 3 4 1 4 1 4 P = x − x +
x > 0 với mọi x ≠ 0 2 16 32
Bài toán 15. Viết đơn thức sau dưới dạng tổng hoặc hiệu của hai đơn thức trong đó có mặt số hạng bằng 2 3 3x y . a) 2 3 5x y b) 2 3 3 − x y PHẦN C. BÀI TẬP
Bài 1.1. Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng. 5 2 2 1 2 2 1 2 2 2 x y; xy ; −
; − 2xy ; x y; xy ; x y; xy . 2 3 2x y 4 5
Bài 1.2. Tính tổng của ba đơn thức a) 2 2 2
25xy ; 55xy ; 75xy b) 2 2 2 2 5
− x yz; x yz; 2x yz . 3 Bài 1.3. Thu gọn. a) 2 A = xy − ( 2 3 3 − xy ) b) 2 4 2 4 2 4
B = 3x y − 7x y − 2x y . c) 2 3 1 2 3 2 3
C = 2x yz + x yz − 4x yz . 3
Bài 1.4. Tính giá trị biểu thức: a) 1 5 3 5 5
A = x y − x y + x y tại x =1; y = 1 − . 2 4
b) B ( x) 1 2  3  1 4 x y 3x y xy  = − − + −    ( 2
5x ) tại x = 1; − y = 2 .  2   2 
Bài 1.5. Viết ba đơn thức đồng dạng với đơn thức 2 2
− x y rồi tính tổng của cả bốn đơn thức.
Bài 1.6. Điền đơn thức thích hợp vào ô trống a) 2 2
3x y + .... = 5x y b) 2 2 .... − 2x = 7 − x c) 5
.... + .... + .... = x
Bài 1.7. Tìm đơn thức P sao cho a) 3 3 3x y + P = 5 − x y b) 2 3 5 2 3 5 P + 5x y z = 3 − x y z
Bài 1.8. Chứng tỏ (− x) 2 3 xy + ( 2
− xy)2 luôn nhận giá trị không âm với mọi giá trị của ; x y .
Bài 1.9. Viết đơn thức 2 2 4
− xy z thành một tổng hoặc một hiệu của hai đơn thức trong đó có một đơn thức bằng 2 2 2 − xy z
Bài 1.10. Tìm m để 2 2 2 2
mxy − 3xy + 7xy = 5xy .
Bài 1.11. Thu gọn rồi tính giá trị của mỗi đơn thức sau
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 3.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 a) A = (− ) 2 1 2 x y xy khi 1 x = 2; − y = ; 2 2
b) B = xyz (− ) 2
0,5 y z khi x = 4 ; y = 0,5; z = 2 .
Bài 1.12. Sắp xếp các đơn thức sau thành từng nhóm, mỗi nhóm chứa tất cả các đơn thức đồng dạng với nhau: 3 2 2 3 3 2 3 2 3
3x y ; − 0,2x y ; 7x y ; − 4y; x y ; y 2 4
Bài 1.13. Rút gọn rồi tính giá trị của biểu thức 1 2 5 5 2 5
S = x y − x y khi x = 2; − y =1. 2 2
Bài 1.14. Tính tổng của các đơn thức 2 3 3 2 3 2 3 8 2 3
2x y ; − x y ; −14x y ; x y . 5 5
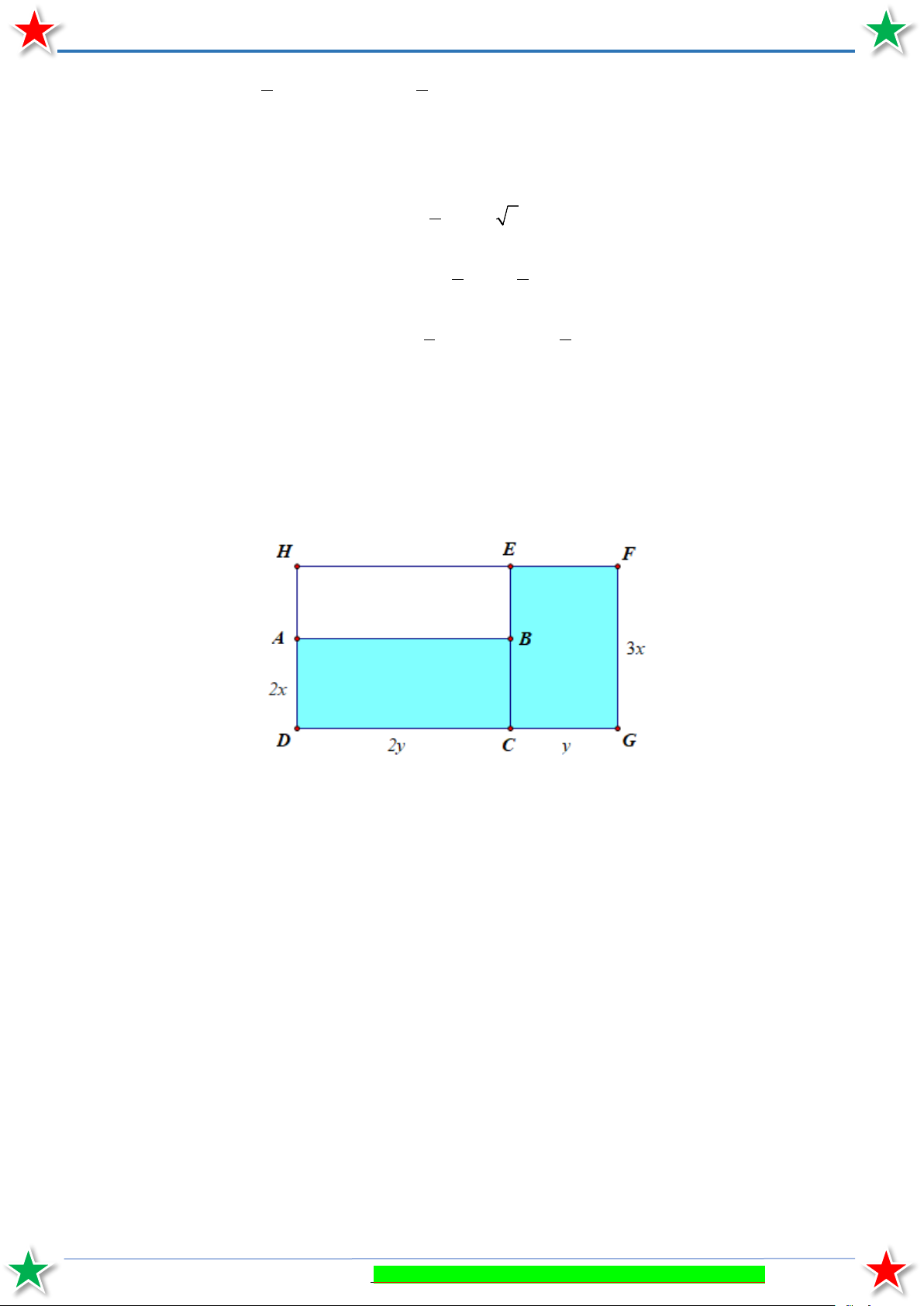
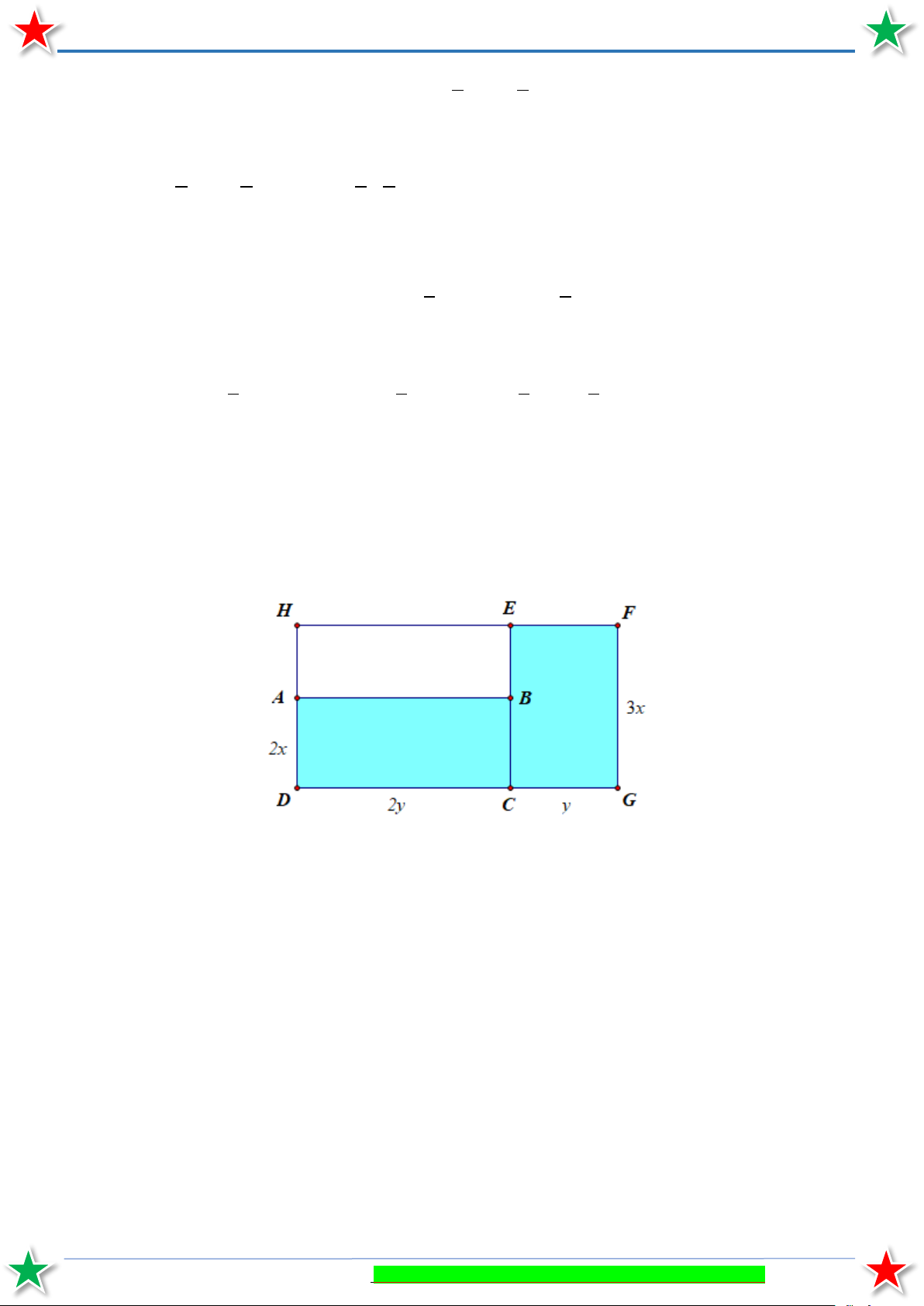
Bài 1.15. Một mảnh đất có dạng như phần tô đậm trong hình bên cùng với các kích thước được ghi trên
đó. Hãy tìm đơn thức thu gọn với hai biến x và y biểu thị diện tích của mảnh đất đã cho bằng cách:
Cách 1. Tính tổng diện tích của hai hình chữ nhật ABCD và EFGC .
Cách 2. Lấy diện tích của hình chữ nhật HFGD trừ đi diện tích của hình chữ nhật HEBA.  HẾT
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 4.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 ĐÁP ÁN THAM KHẢO Bài 1. ĐƠN THỨC
PHẦN B. PHÂN LOẠI CÁC BÀI TẬP
I. Hệ số và biến của đơn thức Bài toán 1.
a) Cho biết phần hệ số và phần biến của đơn thức: 2 2 2 2,5x y;0,25x y
b) Tính giá trị của mỗi đơn thức trên tại x =1 và y = 1 − . Lời giải a) Xét đơn thức: 2
2,5x y ta có phần hệ số là 2,5; phần biến là 2 x y .
Nhận xét: Đơn thức này có phần biến 2
x y trong đó x là có bậc hai; y có bậc nhất nên bậc của
đơn thức này bằng 3, tổng của 2 và 1: 2 +1 = 3.
Phần hệ số của đơn thức 2 2
0,25x y là 0,25; phần biến là 2 2 x .y .
(Bậc của đơn thức bằng 4 ).
b) Thay x =1 và y = 1 − vào biểu thức: 2 2,5x y , ta được: 2 2,5.1 .( 1 − ) = 2 − ,5
Thay x =1 và y = 1 − vào biểu thức 2 2 0,25x y , ta được: 2 2 0,25⋅1 ⋅( 1 − ) = 0,25
Bài toán 2. Hãy viết một vài đơn thức với biến x, y . và có giá trị bằng 9 tại x = 1 − và y =1.
Hướng dẫn: Đơn thức có dạng m n
k ⋅ x ⋅ y ( k là hệ số) Lời giải Đặt đơn thức m n
A = k ⋅ x ⋅ y
Cho m = 2;n =1, ta có: = k ⋅(− )2 9 1 ⋅1⇒ k = 9 Vậy, ta có thể có: 2 A = 9x y Tương tự: 3 B = 9
− x .y,C = 9 − xy, . v . v .
Bài toán 3. Cho biết phần hệ số, phần biến và bậc của các đơn thức sau: a) 4 2 3x ⋅ x ; b) 2 3 a a ⋅a ; c) 4 4 3
−a ⋅a ⋅a
Hướng dẫn: Áp dụng quy tắc nhân các lũy thừa. Lời giải a) Ta có: 4 2 6
3x ⋅ x = 3x
Phần hệ số là 3; phần biến là 6
x . Bậc của đơn thức là 6 . b) Ta có: 2 3 2+3 1 + 6
a ⋅a ⋅a = a = a
Phần hệ số là 1; phần biến là 6
a ; bậc của đơn thức là 6 . c) Ta có: 4 4 3 4+4+3 11
−a ⋅a ⋅a = −a = −a
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 5.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 Phần hệ số: 1 − ; phần biến: 11 a
Bậc của đơn thức là 11.
Bài toán 4. Cho đơn thức  1  2 3 − x⋅ y ⋅   2x .  2 
a) Tìm bậc của đơn thức;
b) Tính giá trị của đơn thức tại 1 x = 2; y = 4
Hướng dẫn: Áp dụng quy tắc nhân các lũy thừa. Lời giải a) Ta có:  1  2 3 4 2 −
x⋅ y ⋅2⋅ x = −   x y  2 
Đơn thức này có bậc: 4 + 2 = 6 (hệ số là: 1 − ; phần biến: 4 2 x y ) 2 b) Thay 1
x = 2; y = vào đơn thức, ta được: 4  1  − ⋅ =   (− ) 1 2 16 ⋅ = 1 − 4  4  16
Bài toán 5. Cho đơn thức: 2 2 P = − m np . 3
a) Tìm phần biến và bậc của đơn thức.
b) Tính giá trị của đơn thức tại m = 2;n = 6; p = 7 . Lời giải a) Ta có: 2 2 P = − m np 3 Vậy phần biến là 2
m np . Ta có số mũ của , m ,
n p theo thứ tự là 2;1 và 1.
Đơn thức có bậc là: 2 +1+1 = 4 . b) Thay m 2
= 2;n = 6; p = 7 vào đơn thức P , ta được: 2
P = − ⋅2 ⋅6⋅7 = 112 − 3
II. Đơn thức đồng dạng
Bài toán 6. Cho các đơn thức: 2 1 2 2 2 2a ; b ab ; 3 − a ;
b 5x y . Tìm đơn thức đồng dạng với 2 5 − a b . 3
Hướng dẫn: Các đơn thức có cùng phần biến 2 a b . Lời giải
Các đơn thức đồng dạng với 2 5 − a b là: 2 2 2a ; b 3 − a b
Bài toán khác: Tìm các đơn thức đồng dạng với nhau trong các đơn thức sau: 2 2 1 2 2 2 2 1 2 5x y; 3
− xyy ; x y;3a ; b 3 − ab ; 2 − a ; b xy 3 5
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 6.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 ( 2 5x y và 1 2 2 x y; 3 − xy và 1 2 2 xy ;3a b và 2 2
− a b là các cặp đơn thức đồng dạng). 3 5
Bài toán 7. Viết ba đơn thức đồng dạng với đơn thức 3 2 M = 2x y z . Lời giải
Các đơn thức đồng dạng với 3 2
M = 2x y z là: 3 2 1 3 2 3 2
M = −x y z;M = x y z;M = 5x y z 1 2 3 3
(Bạn có thể lấy đơn thức khác nhau ở phần hệ số; còn phần biến luôn là 3 2 x y z ).
Bài toán 8. Cặp đơn thức sau đó đồng dạng không? a) 2 2
P = 8ab + 7ab và 3 2 5 2 7 2
Q = a b − a b − a b . 2 8 8
b) A ( m)( n)  1 2 4 m = − − (−n)−  1   
5mn và B = 4mn −  m.(3n)  5   2 
Hướng dẫn: Cộng các đơn thức trước. Lời giải a) 2 2
P =15ab ;Q = 0a b . Vậy P và Q không phải là hai đơn thức đồng dạng. b) 1 64 A = 8
− mn + mn − 5mn = − mn ; 5 5 5
B = mn . Vậy A và B là hai đơn thức đồng dạng. 2
Chú ý: Hệ số của các đơn thức phải khác 0.
III. Cộng (trừ) các đơn thức
Bài toán 9. Thu gọn và cho biết bậc của đơn thức: a) 1 2 3 2 5 2
A = xy − y x − xy ;
b) B = x (x ) −(− x )2 4 2 3 3 2 2 4 6 Lời giải a)  1 3 5  2 13 2 A = − − xy = −  
xy . Đơn thức A có bậc là 3.  2 4 6  12 b) 6 6 6
B = 3x − 4x = −x . Đơn thức B có bậc là 6 .
Bài toán 10. Tính tổng: S ( 2 a ) 1 2  1 9 b a b 24aab = − + + − 3 4    Lời giải 2 2 2 2 2 S = 3
− a b + a b − 6a b = ( 3
− +1− 6)a b = 8 − a b
Bài toán khác: Tính tổng: 1. 2 2
S = x + 5x + ( 2 3 − x );( 2 S = 3x 1 1 )
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 7.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 2. 2 1 2 1 2  1  2  21 2 S 5xy xy xy   xy ; S xy  = + + + − = 2 2 2 4 2 4     
3. S = xyz − 5xyz; S = 4 − xyz 3 ( 3 ) 4. 2 1 2 2  3 2 S x
x 2x ;S x  = − − = − 4 4 . 2 2   
Bài toán 11. Tìm giá trị của biểu thức: 2 2 2
A =11m n − 2m n − 3m tại 1 3 m = − ;n = 2 3 4 Lời giải Ta có: A = ( − ) 2 2 2 2
11 2 m n − 3m = 9m n − 3m . 2 2 Thay 1 3 11 m = − ;n = 2 =
vào biểu thức A , ta được:  1  11  1  11 1 29 A = 9⋅ − ⋅ −   3 − = − = 3 4 4 3 4  3     4 3 12
Bài toán khác: Tính giá trị của biểu thức: 3 2 5 2 1 2 3 2
P = mn − mn + mn −
mn tại m = 2;n = 1 − 2 8 8 16 Hướng dẫn Ta có:  3 5 1 3  2 13 2 P = − + − mn =   mn .  2 8 8 16  16 Thay m = 2;n = 1
− vào biểu thức P ta được: 13 P = ⋅ (− )2 13 2 1 = 16 8
Bài toán 12. Tìm đơn thức A , biết: 3 3 3 3 A + 5x y z = 3 − x y z . Lời giải Ta có: 3 3 3 3 3 3 A = 3
− x y z − 5x y z = 8 − x y z
Bài toán khác: Tìm đơn thức P , biết: 1. 2 2 P − 3ab = 10 − ab 2. 2 3 2 3 3x y − P = 5 − x y Huớng dẫn 1. 2 2 2
P = 3ab −10ab = 7 − ab ; 2. 2 3 P = x y − ( 2 3 − x y ) 2 3 3 5 = 8x y Bài toán 13. Cho 3 3  2 A 2x y; B yx ;C x = − = − = ⋅( 2 −  
x y). Tính A+ 2 B − 3C .  3  Lời giải 3 A B C x y ( 3 yx )  2 2 3 2 2 3 x + − = − + − − ⋅ ⋅( 2 −   x y) 3 3 3 3 = 2
− x y − 2x y + 2x y = 2 − x y  3 
Bài toán 14. Chứng tỏ 3 4 1 4 1 4 P = x − x +
x > 0 với mọi x ≠ 0 2 16 32 Lời giải
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 8.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 Ta có 3 4 1 4 1 4  3 1 1 1  4 P = x − x + x = − + −   x 2 16 32  2 16 32 4  39 4 ⇒ P =
x vì x ≠ 0 nên 4
x > 0 với mọi x ≠ 0 . 32
Bài toán 15. Viết đơn thức sau dưới dạng tổng hoặc hiệu của hai đơn thức trong đó có mặt số hạng bằng 2 3 3x y . a) 2 3 5x y b) 2 3 3 − x y Lời giải a) 2 3 2 3 2 3
5x y = 3x y + 2x y b) 2 3 2 3 2 3 3
− x y = 3x y − 6x y PHẦN C. BÀI TẬP
Bài 1.1. Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng. 5 2 2 1 2 2 1 2 2 2 x y; xy ; −
; − 2xy ; x y; xy ; x y; xy . 2 3 2x y 4 5 Lời giải 5 2 1 2 2 2 2
x y;− x y; x y; x y là các đơn thức đồng dạng; 3 2 5 2 2 1 2 xy ; 2
− xy ; xy là các đơn thức đồng dạng. 4
Bài 1.2. Tính tổng của ba đơn thức a) 2 2 2
25xy ; 55xy ; 75xy b) 2 2 2 2 5
− x yz; x yz; 2x yz . 3 Lời giải a) 2 2 2 2
25xy + 55xy + 75xy =155xy b) 2 2 2 2 7 2 5
− x yz + x yz + 2x yz = − x yz 3 3 c) 3 2 1 2  1 2  2
xyz + xyz + − xyz =   xyz 4 2  4 
(Ta cộng các hệ số của các đơn thức) Bài 1.3. Thu gọn. a) 2 A = xy − ( 2 3 3 − xy ) b) 2 4 2 4 2 4
B = 3x y − 7x y − 2x y . c) 2 3 1 2 3 2 3
C = 2x yz + x yz − 4x yz . 3 Lời giải a) 2 2 2
A = 3xy + 3xy = 6xy b) B = ( − − ) 2 4 2 4 3 7 2 x y = 6 − x y
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 9.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 c) 5 2 3 C = − x yz 3
Bài 1.4. Tính giá trị biểu thức: a) 1 5 3 5 5
A = x y − x y + x y tại x =1; y = 1 − . 2 4
b) B ( x) 1 2  3  1 4 x y 3x y xy  = − − + −    ( 2
5x ) tại x = 1; − y = 2 .  2   2  Lời giải a) 3 5
A = x y . Thay x =1; y = 1; − ta có : 3 A = − 4 4 b) 5 3 B = x . y Thay x = 1;
− y = 2 ⇒ B = 5 − . 2
Bài 1.5. Viết ba đơn thức đồng dạng với đơn thức 2 2
− x y rồi tính tổng của cả bốn đơn thức. Lời giải Ta lấy 2 2 1 2 3x y; 6
− x y;− x y 2
Vậy tổng của bốn đơn thức: ( 2 2 − x y) 2 + 3x y + ( 2 6 − x y)  1 2  11 2 + − x y = −   x . y  2  2
Bài 1.6. Điền đơn thức thích hợp vào ô trống a) 2 2
3x y + .... = 5x y b) 2 2 .... − 2x = 7 − x c) 5
.... + .... + .... = x . Lời giải a) 2 2 2
3x y + 2x y = 5x . y Cách tính : 2 2 2
5x y − 3x y = 2x y b) 2 2 2 5 − x − 2x = 7 − x
c) Có nhiều cách điền vào các ô trống: Chẳng hạn: 5 5 x + x + ( 5 − x ) 5 3 3 = x ; 5 + ( 5 − ) 5 5 x
x + x = x
Bài 1.7. Tìm đơn thức P sao cho a) 3 3 3x y + P = 5 − x y b) 2 3 5 2 3 5 P + 5x y z = 3 − x y z Lời giải a) 3 3 3
P = 3x y + 5x y = 8x y b) P = ( 2 3 5 − x y z ) 2 3 5 2 3 5 3 − 5x y z = 8 − x y z
Bài 1.8. Chứng tỏ (− x) 2 3 xy + ( 2
− xy)2 luôn nhận giá trị không âm với mọi giá trị của ; x y .
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 10.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 Lời giải (− x) 2 xy + (− xy)2 2 2 2 2 2 2 3 2 = 3
− x y + 4x y = x y Vì 2 x ≥ 0 và 2
y ≥ 0, với mọi giá trị x, y nên 2 2
x y ≥ 0 , với mọi giá trị của x, y .
Bài 1.9. Viết đơn thức 2 2 4
− xy z thành một tổng hoặc một hiệu của hai đơn thức trong đó có một đơn thức bằng 2 2 2 − xy z . Lời giải 2 3 − xy z = ( 2 3 − xy z ) + ( 2 3 4 2 2 − xy z ) 2 3 2 3 2 3 4
− xy z = 6xy z −10xy z .
Bài 1.10. Tìm m để 2 2 2 2
mxy − 3xy + 7xy = 5xy . Lời giải (m − + ) 2 2
3 7 xy = 5xy ⇒ m − 3+ 7 = 5 ⇒ m =1
Bài 1.11. Thu gọn rồi tính giá trị của mỗi đơn thức sau a) A = (− ) 2 1 2 x y xy khi 1 x = 2; − y = ; 2 2
b) B = xyz (− ) 2
0,5 y z khi x = 4 ; y = 0,5; z = 2 . Lời giải a) A = ( 2 − ) 2 1 x . y xy ⇒ A  = ( 2 − ) 1 2 3 2 . x . .x . y y ⇒ A = 3 − x y . 2  2   2 Thay 1 x = 2;
− y = vào biểu thức, ta có : A = −(− )3  1  1 2 . = 8. =   2. 2  2  4
b) B = xyz (− ) 2
y z ⇒ B = (− ) 2
x y y z z ⇒ B = (− ) 3 2 0,5 0,5 . . . . 0,5 xy z .
Thay x = 4; y = 0,5; z = 2 vào biểu thức, ta có : B = (− ) ( )3 2 0,5 .4. 0,5 .2 = 1 − .
Bài 1.12. Sắp xếp các đơn thức sau thành từng nhóm, mỗi nhóm chứa tất cả các đơn thức đồng dạng với nhau: 3 2 2 3 3 2 3 2 3
3x y ; − 0,2x y ; 7x y ; − 4y; x y ; y 2 . 4 Lời giải 3 2 3 2 3x y ;7x y . 2 3 3 2 3 0,
− 2x y ; x y . 4 4 − y; y 2.
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 11.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
Bài 1.13. Rút gọn rồi tính giá trị của biểu thức 1 2 5 5 2 5
S = x y − x y khi x = 2; − y =1. 2 2 Lời giải 1 2 5 5 2 5  1 5  2 5 2 5
S = x y − x y ⇒ S = − x y ⇒ S = 2 −   x y 2 2  2 2  Thay x = 2;
− y =1 vào biểu thức, ta có: S = (− ) (− )2 5 2 . 2 .1 ⇒ S = 8 − .
Bài 1.14. Tính tổng của các đơn thức 2 3 3 2 3 2 3 8 2 3
2x y ; − x y ; −14x y ; x y . 5 5 Lời giải 2 3  3  2 3 2x y + − x y + ( 2 3 14
− x y ) 8 2 3   3  8 2 3 2 3
+ x y = 2 + − −14 +  x y = 11 −     x y .  5  5   5  5
Bài 1.15. Một mảnh đất có dạng như phần tô đậm trong hình bên cùng với các kích thước được ghi trên
đó. Hãy tìm đơn thức thu gọn với hai biến x và y biểu thị diện tích của mảnh đất đã cho bằng cách:
Cách 1. Tính tổng diện tích của hai hình chữ nhật ABCD và EFGC .
Cách 2. Lấy diện tích của hình chữ nhật HFGD trừ đi diện tích của hình chữ nhật HEBA. Lời giải Cách 1:
Diện tích của hình chữ nhật ABCD là: 2 .2
x y = 4xy (đơn vị diện tích)
Diện tích của hình chữ nhật EFGC là: 3 .
x y = 3xy (đơn vị diện tích)
Diện tích mảnh đất: 4xy + 3xy = 7xy (đơn vị diện tích) Cách 2:
Diện tích của hình chữ nhật AFGD là:3 .x(2y + y) = 3 .x3y = 9xy (đơn vị diện tích)
Diện tích của hình chữ nhật HEBA là: (3x − 2x).2y = 2xy (đơn vị diện tích)
Diện tích mảnh đất: 9xy − 2xy = 7xy (đơn vị diện tích)  HẾT
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/ Trang: 12.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 BÀI 2: ĐA THỨC
PHẦN A. KIẾN THỨC CẦN NHỚ
1. Khái niệm đa thức
Đa thức là tổng của những đơn thức, mỗi đơn thức trong tổng gọi là hạng tử của đa thức đó.
2. Thu gọn đa thức
Đa thức thu gọn là đa thức không có hai hạng tử nào đồng dạng. Chú ý:
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
Một số khác 0 tùy ý được gọi là đa thức bậc 0.
Số 0 cũng là một đa thức, gọi là đa thức 0 . Nó không có bậc xác định.
PHẦN B. PHÂN LOẠI BÀI TẬP 1. Thu gọn đa thức
Bài toán 1. Thu gọn a) 2 2 A 3 5 1 3
= 11x + 4x − x − 4x b) 2 2 2 2
B = a b − a b + a b − a b 2 8 8 16 c) 3 2 2 5 2
C = − xy + x y − 2xy + x y
d) D = 3ab − 2bc + 4ac − ab + 3bc + 4ab 4 3 6 e) 2  1  1 E = 2x
y − ab(3a) 5 2 2 + x y +   a b  2  3 4
Hướng dẫn: Cộng trừ các đơn thức đồng dạng.
Bài toán 2. Thu gọn đa thức a) 2 2 2 2
A = 2x yz + 4xy z − 5x yz + xy z − xyz b) 3 3 2 1 2
B = x − 5xy + 3x + xy − x + xy − x 2 c) 1 2 3 2 3 2 2 2 4 2 2 2
C = x y − x y + 3x y z − z − 3x y z 2
Bài toán 3. Thu gọn và tính giá trị của đa thức a) 1 2 2 1 2 1 2
A = x y + xy − xy + xy − 5xy − x y tại 1 x = và y =1. 3 2 3 2 b) 2 2
B = 5xy + 2xy − 3xy tại x = 2; − y =1. c) 6 2 5 6 2 5 6
C = x + x y + xy + x y − xy tại x = 1; − y = 1 − .
Bài toán 4. Chứng tỏ giá trị của đa thức 2 2 2 2 2 2
M = 3x + 5xy + 7x y − 3x − 7x y + 3x − 5xy + 2y luôn luôn
không âm với mọi giá trị ; x y .
Hướng dẫn: Thu gọn đa thức M .
Bài toán khác: Chứng tỏ đa thức 2 2
A =11x + 4x − 3x − 4x + 5 luôn nhận giá trị dương với mọi giá trị của x .
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 1.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
Hướng dẫn: 2
A = 8x + 5 . Vì 2 2 2
x ≥ 0 ⇒ 8x ≥ 0; 5 > 0 ⇒ 8x + 5 > 0 .
Bài toán 5. Cho đa thức 2 2
P = 2x − 6x + x + 6x −12 . Tìm x để P nhận giá trị 0 .
Hướng dẫn: Thu gọn đa thức P
Bài toán khác: Tìm x để đa thức 2 2
P = 3x + 8x + 4 − 4x −8x − 3 nhận giá trị 3 − .
Hướng dẫn: 2 P = −x +1 2 2 P = 3 − ⇒ −x +1 = 3 − ⇒ −x = 4 − 2
⇒ x = 4 ⇒ x = 2 hoặc x = 2 − .
Đáp số: x = 2 hoặc x = 2 − .
Bài toán 6. Chứng tỏ rằng giá trị của đa thức 2 2 3 2 P = 3
− xy + 5y − xy + 2x tại y = −x luô không âm. 2
Hướng dẫn: Thay giá trị y = −x ta tìm được P là đa thức của biến x .
Bài toán 7. Cho đa thức 2
P = x + 2mx − 3m + 5 . Tìm m biết rằng đa thức P nhận giá trị 0 tại x = 2 − .
Hướng dẫn: Thay x = 2
− vào đa thức P và tìm m khi P = 0
II. Bậc của đa thức
Bài toán 8. Tìm bậc của đa thức: a) 5 1 3 3 2 P = 3
− x − x y − xy b) 2 1
Q = 3x − x + 2 2 4 2 c) 2 2
T = 5x y − 4xyy + 5x − 3y +1
Hướng dẫn: Bậc của đơn thức nào lớn nhất là bậc của đa thức.
Bài toán 9. Tìm bậc của mỗi đa thức sau: a) 2 1 2
A = 3x − x +1+ 2x − x ; b) 2 3 3 3 2
B = 3x + 7x − 3x + 6x − 3x . 2
Hướng dẫn: Thu gọn các đa thức.
Bài toán khác: Đa thức 3 2 3 2 3
C = 3x + 2x − 2x +1− 3x + x − x thu gọn ta được: 2
C = −x + x +1.
Vậy C có bậc là 2 (ta không nên vội kết luận đa thức C có bậc 3).
Bài toán 10. Tìm bậc của đa thức theo biến ; x y a) 3 2 2 5
P = 3x + m x − 2mx + m . b) 3 2 2
Q = mx + 2xy + m x + y + 2.(m ≠ 0) .
Hướng dẫn: a) Biến của đa thức P là ;
x m là hệ số của mỗi đơn thức.
Bài toán khác: Tìm bậc của đa thức theo biến x . 1. 4 3 2
P = ax + bx + cx + dx + .e(a ≠ 0) 2. 3 3 2
Q = mx + x + x −1.(m ≠ 0) Đáp số:
1. Bậc của P là 4 .
2. Bậc của Q là 3.
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 2.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
Bài toán 11. Cho đa thức 2 2 3 4 2 2
P = 5xy − 2x y + 3x − 2y − 3x y
a) Tìm bậc của đa thức P .
b) Tìm các hạng tử bậc 3 trong đa thức P . PHẦN C. BÀI TẬP
Bài 1.16. Tìm bậc của các đa thức sau: a) 2 3 3 2 3
A = 5x + 6x + 2x − 4x −8x + 2x ; b) 2 2 2 2 2 2 2
B = 5xy − 4x y − 6x − 2xy + 3x y + 5x + 4xy −8x y − 3y ; c) 4 2 4 2 3 4
C = 6x − 3x + 4x − 2x + 3x + x − 4x +1. d) 2 2 2
D = a + 2ax + x
Bài 1.17. Thu gọn các đa thức: a) 2 2
A = 5xy − 3,5y − 2xy +1,3y − xy ; b) 1 2 7 2 3 2 3 2 1 2
B = ab − ab + a b − a b − ab ; 2 8 4 8 2
c) C = 3ab − 2bc + 4ac − ab + 3bc + 4ab ; d) 3 2 2 2 2 3 P = 2
− x + xy + x y −1+ x y − xy + 3x ; e) 2 2
Q = 26ax +13ax + 41x −16x −13ax + 4ax .
Bài 1.18. Tính giá trị của đa thức: a) 2 2 2 3 2
A = 3x + 2xy − 4y + 3x y − x − 2xy + 4y , tại 1 x = ; y = 1 − ; 2 b) 2 2 2 2
B = 2a + 3ab − 5b + ab + a − b , tại a = 3 − ;b = 2 − ; c) 2 2 3 2 2
P = 3x y − x − 2xy + 6x + 3x y − 2xy − tại x = 2; − y = 1 − ; d) 2 2 2 2 2 2
Q = 8a −10ab − b − 6a + 2ab − b − a + 6y , tại x = 2; − y = 2 − .
Bài 1.19. Chứng minh rằng: 2 4 3 3 2 4 3 3
M = 3x y − 5xy − x y + 3xy + 2xy +1 luôn dương với mọi ; x y . 2
Bài 1.20. Cho da thức: 2 2
Q = 2x + 6x + x − 6x −12 . Tìm x để Q nhận giá trị 0 .  HẾT
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 3.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 ĐÁP ÁN THAM KHẢO BÀI 2: ĐA THỨC
PHẦN B. PHÂN LOẠI BÀI TẬP 1. Thu gọn đa thức
Bài toán 1. Thu gọn a) 2 2
A =11x + 4x − x − 4x b) 3 2 5 2 1 2 3 2
B = a b − a b + a b − a b 2 8 8 16 c) 3 2 2 5 2
C = − xy + x y − 2xy + x y
d) D = 3ab − 2bc + 4ac − ab + 3bc + 4ab 4 3 6 e) 2  1  1 E = 2x
y − ab(3a) 5 2 2 + x y +   a b  2  3 4
Hướng dẫn: Cộng trừ các đơn thức đồng dạng. Lời giải a) 2 2 2
A =11x + 4x − x − 4x =10x b) 3 2 5 2 1 2 3 2 13 2
B = a b − a b + a b − a b = a b 2 8 8 16 16 c) 3 2 2 5 2 11 3 2
C = − xy + x y − 2xy + x y = − xy + x y 4 3 6 4 2
d) D = 3ab − 2bc + 4ac − ab + 3bc + 4ab = 6ab + bc + 4ac e) 2  1  1 E = 2x
y − ab(3a) 5 2 2 2 + x y + a b =   2x y  2  3 4
Bài toán 2. Thu gọn đa thức a) 2 2 2 2
A = 2x yz + 4xy z − 5x yz + xy z − xyz b) 3 3 2 1 2
B = x − 5xy + 3x + xy − x + xy − x 2 c) 1 2 3 2 3 2 2 2 4 2 2 2
C = x y − x y + 3x y z − z − 3x y z 2 Lời giải a) 2 2 2 2
A = 2x yz + 4xy z − 5x yz + xy z − xyz = ( 2 2
x yz − x yz) + ( 2 2 xy z + xy z) 2 2 2 5 4 − xyz = 3
− x yz + 5xy z − xyz b) 3 3 2 1 2
B = x − 5xy + 3x + xy − x + xy − x 2 ( 3 3 x 3x )  1 5xy xy xy  = + + − + + + ( 2 2 −x − x ) 3 7 2 = 4x − xy −   2x  2  2 c) 1 2 3 2 3 2 2 2 4 2 2 2
C = x y − x y + 3x y z − z − 3x y z 2
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 4.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1  1 2 3 2 3 x y x y  = − + ( 2 2 2 2 2 2
3x y z − 3x y z ) 4 1 2 3 4
− z = − x y −   z  2  2
Bài toán 3. Thu gọn và tính giá trị của đa thức a) 1 2 2 1 2 1 2
A = x y + xy − xy + xy − 5xy − x y tại 1 x = và y =1. 3 2 3 2 b) 2 2
B = 5xy + 2xy − 3xy tại x = 2; − y =1. c) 6 2 5 6 2 5 6
C = x + x y + xy + x y − xy tại x = 1; − y = 1 − . Lời giải a) 1 2 2 1 2 1 2
A = x y + xy − xy + xy − 5xy − x y 3 2 3  1 1  2  1  2 = − x y + 1+ xy + ( 1 − − 5) 3 2 xy = xy −     6xy  3 3   2  2 Thay 1
x = và y =1 vào đa thức A ta được: 3 1 2 1 3 9
A = . .1 − 6. .1 = − 3 = − 2 2 2 2 4 4 b) 2 2
B = xy + xy − xy = ( 2 2 xy − xy ) 2 5 2 3 5 3
+ 2xy = 2xy + 2xy Thay x = 2;
− y =1 vào đa thức B ta được: B = (− ) 2 2. 2 .1 + 2.( 2 − ).1 = 4 − − 4 = 8 − . c) 6 2 5 6 2 5 6 6
C = x + x y + xy + x y − xy = x + ( 2 5 2 5
x y + x y ) + ( 6 6 xy − xy ) 6 2 5 = x + 2x y Thay x = 1; − y = 1
− vào đa thức C ta được: C = (− )6 + (− )2 (− )5 1 2 1 . 1 =1− 2 = 1 −
Bài toán 4. Chứng tỏ giá trị của đa thức 2 2 2 2 2 2
M = 3x + 5xy + 7x y − 3x − 7x y + 3x − 5xy + 2y luôn luôn
không âm với mọi giá trị ; x y .
Hướng dẫn: Thu gọn đa thức M . Lời giải Ta có: M = ( 2 2 2
x − x + x ) + ( xy − xy) + ( 2 2 x y − x y) 2 2 2 3 3 3 5 5 7 7
+ 2y = 3x + 2y Vì 2
x ≥ 0 với mọi x ; 2
y ≥ 0 với mọi y 2 2
⇒ 3x + 2y ≥ 0 với mọi x, y .
Bài toán khác: Chứng tỏ đa thức 2 2
A =11x + 4x − 3x − 4x + 5 luôn nhận giá trị dương với mọi giá trị của x .
Hướng dẫn: 2
A = 8x + 5 . Vì 2 2 2
x ≥ 0 ⇒ 8x ≥ 0; 5 > 0 ⇒ 8x + 5 > 0 .
Bài toán 5. Cho đa thức 2 2
P = 2x − 6x + x + 6x −12 . Tìm x để P nhận giá trị 0 .
Hướng dẫn: Thu gọn đa thức P Lời giải Ta có: 2 2 2
P = 2x − 6x + x + 6x −12 = 3x −12 2
P = 0 ⇒ 3x −12 = 0 2 2
⇒ 3x =12 ⇒ x = 4 ⇒ x = 2 hoặc x = 2 − .
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 5.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1
Bài toán khác: Tìm x để đa thức 2 2
P = 3x + 8x + 4 − 4x −8x − 3 nhận giá trị 3 − .
Hướng dẫn: 2 P = −x +1 2 2 P = 3 − ⇒ −x +1 = 3 − ⇒ −x = 4 − 2
⇒ x = 4 ⇒ x = 2 hoặc x = 2 − .
Đáp số: x = 2 hoặc x = 2 − .
Bài toán 6. Chứng tỏ rằng giá trị của đa thức 2 2 3 2 P = 3
− xy + 5y − xy + 2x tại y = −x luô không âm. 2
Hướng dẫn: Thay giá trị y = −x ta tìm được P là đa thức của biến x . Lời giải
Thay y = −x vào biểu thức của P ta được: P = 3
− x(−x)2 + 5(−x)2 3 − x(−x) 2 4 2 3 2 2 4 17 2
+ 2x = 3x + 5x + x + 2x = 3x + x 2 2 2 Vì 2 x ≥ 0 và 4 x ≥ 0 nên 4 17 2 3x +
x ≥ 0 với mọi x . 2
Bài toán 7. Cho đa thức 2
P = x + 2mx − 3m + 5 . Tìm m biết rằng đa thức P nhận giá trị 0 tại x = 2 − .
Hướng dẫn: Thay x = 2
− vào đa thức P và tìm m khi P = 0 Lời giải Thay x = 2
− vào biểu thức của P . Ta có: 2 P = ( 2) − + 2m⋅( 2
− ) − 3m + 5 = 9 − 7m .
Vì P nhận giá trị 0 tại 9 x = 2 − ⇒ 9 − 7 m = 0 ⇒ m = 7
II. Bậc của đa thức
Bài toán 8. Tìm bậc của đa thức: a) 5 1 3 3 2 P = 3
− x − x y − xy 1b) 2 1
Q = 3x − x + 2 2 4 2 c) 2 2
T = 5x y − 4xyy + 5x − 3y +1
Hướng dẫn: Bậc của đơn thức nào lớn nhất là bậc của đa thức. Lời giải a) Bậc của hạng tử 5 3
− x là 5 là bậc cao nhất trong các hạng tử Vậy bậc của P là 5. b) Bậc của hạng tử 2 3x là bậc 2.
Vậy bậc của Q là 2.
c) Bậc của các hạng tử 2 5x y và 2 4
− xy đều là 3. Vậy bậc của T là 3.
Bài toán 9. Tìm bậc của mỗi đa thức sau:
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 6.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 a) 2 1 2
A = 3x − x +1+ 2x − x ; 2 b) 2 3 3 3 2
B = 3x + 7x − 3x + 6x − 3x .
Hướng dẫn: Thu gọn các đa thức. Lời giải a) 2 3
A = 2x + x +1 2
Vậy đa thức A có bậc là 2. b) 3 B =10x .
Vậy B có bậc là 3.
Bài toán khác: Đa thức 3 2 3 2 3
C = 3x + 2x − 2x +1− 3x + x − x thu gọn ta được: 2
C = −x + x +1.
Vậy C có bậc là 2 (ta không nên vội kết luận đa thức C có bậc 3).
Bài toán 10. Tìm bậc của đa thức theo biến ; x y a) 3 2 2 5
P = 3x + m x − 2mx + m . b) 3 2 2
Q = mx + 2xy + m x + y + 2.(m ≠ 0) .
Hướng dẫn: a) Biến của đa thức P là ;
x m là hệ số của mỗi đơn thức. Lời giải a) Hạng tử 3
3x có bậc 3. Vậy P có bậc là 3. b) Hạng tử 3
mx có bậc của x là 3. Vậy bậc của Q là 3.
Bài toán khác: Tìm bậc của đa thức theo biến x . 1. 4 3 2
P = ax + bx + cx + dx + .e(a ≠ 0) 2. 3 3 2
Q = mx + x + x −1.(m ≠ 0) Đáp số:
1. Bậc của P là 4 .
2. Bậc của Q là 3.
Bài toán 11. Cho đa thức 2 2 3 4 2 2
P = 5xy − 2x y + 3x − 2y − 3x y
a) Tìm bậc của đa thức P .
b) Tìm các hạng tử bậc 3 trong đa thức P . Lời giải a) Ta có 4 2 − y và 2 2 3
− x y là hai hạng tử cũng có bậc 4. Vậy P có bậc là 4.
b) Các hạng tử có cùng bậc 3 là: 2 2 5x ; 2 − x y và 3 3x . PHẦN C. BÀI TẬP
Bài 1.16. Tìm bậc của các đa thức sau: a) 2 3 3 2 3
A = 5x + 6x + 2x − 4x −8x + 2x ; b) 2 2 2 2 2 2 2
B = 5xy − 4x y − 6x − 2xy + 3x y + 5x + 4xy −8x y − 3y ; c) 4 2 4 2 3 4
C = 6x − 3x + 4x − 2x + 3x + x − 4x +1.
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 7.
PHÂN LOẠI VÀ GIẢI CHI TIẾT CÁC DẠNG BÀI TẬP TOÁN 8 SÁCH KẾT NỐI TRI THỨC CHƯƠNG 1 d) 2 2 2
D = a + 2ax + x . Lời giải a) 2
A = x + 2x . Bậc của A là 2 b) 2 2 2 2
B =12xy − 9x y − x − 2xy − 3y .Bậc của B là 3 c) 3
C = x + 4x +1. Bậc của C là 3
d) Bậc của D là 3 (theo hai biến a và x )
Bài 1.17. Thu gọn các đa thức: a) 2 2
A = 5xy − 3,5y − 2xy +1,3y − xy ; b) 1 2 7 2 3 2 3 2 1 2
B = ab − ab + a b − a b − ab ; 2 8 4 8 2
c) C = 3ab − 2bc + 4ac − ab + 3bc + 4ab ; d) 3 2 2 2 2 3 P = 2
− x + xy + x y −1+ x y − xy + 3x ; e) 2 2
Q = 26ax +13ax + 41x −16x −13ax + 4ax . Lời giải
a) A = ( − − ) xy + ( − ) 2 2 5 2 1
1,3 3,5 y = 2xy − 2,2y b)  1 7 1  2  3 3  2 7 2 3 2 B = − − ab + − a b = − a b +     ab  2 8 2   4 8  8 8 .
c) C = (3−1+ 4)ab + ( 2
− + 3)bc + 4ac = 6ab + bc + 4ac . d) 3 2
P = x + 2x y −1 là 3 e) 2
Q = 30ax + 25x
Bài 1.18. Tính giá trị của đa thức: a) 2 2 2 3 2
A = 3x + 2xy − 4y + 3x y − x − 2xy + 4y , tại 1 x = ; y = 1 − ; 2 b) 2 2 2 2
B = 2a + 3ab − 5b + ab + a − b , tại a = 3 − ;b = 2 − ; c) 2 2 3 2 2
P = 3x y − x − 2xy + 6x + 3x y − 2xy − tại x = 2; − y = 1 − ; d) 2 2 2 2 2 2
Q = 8a −10ab − b − 6a + 2ab − b − a + 6y , tại x = 2; − y = 2 − . Lời giải a) 2 2 3
A = 3x + 3x y − x Thay 1 x = ; y = 1
− vào biểu thức A 2 ta được: 2 2 3 1 1 A     = +    (− )  1  3 3 1 1 3. 3. . 1 − = − − = −  2 2  2       4 4 8 8
TOÁN TIỂU HỌC&THCS&THPT VIỆT NAM www.facebook.com/groups/ToanTieuHocTHCSTHPTVietNam/
Trang: 8.