




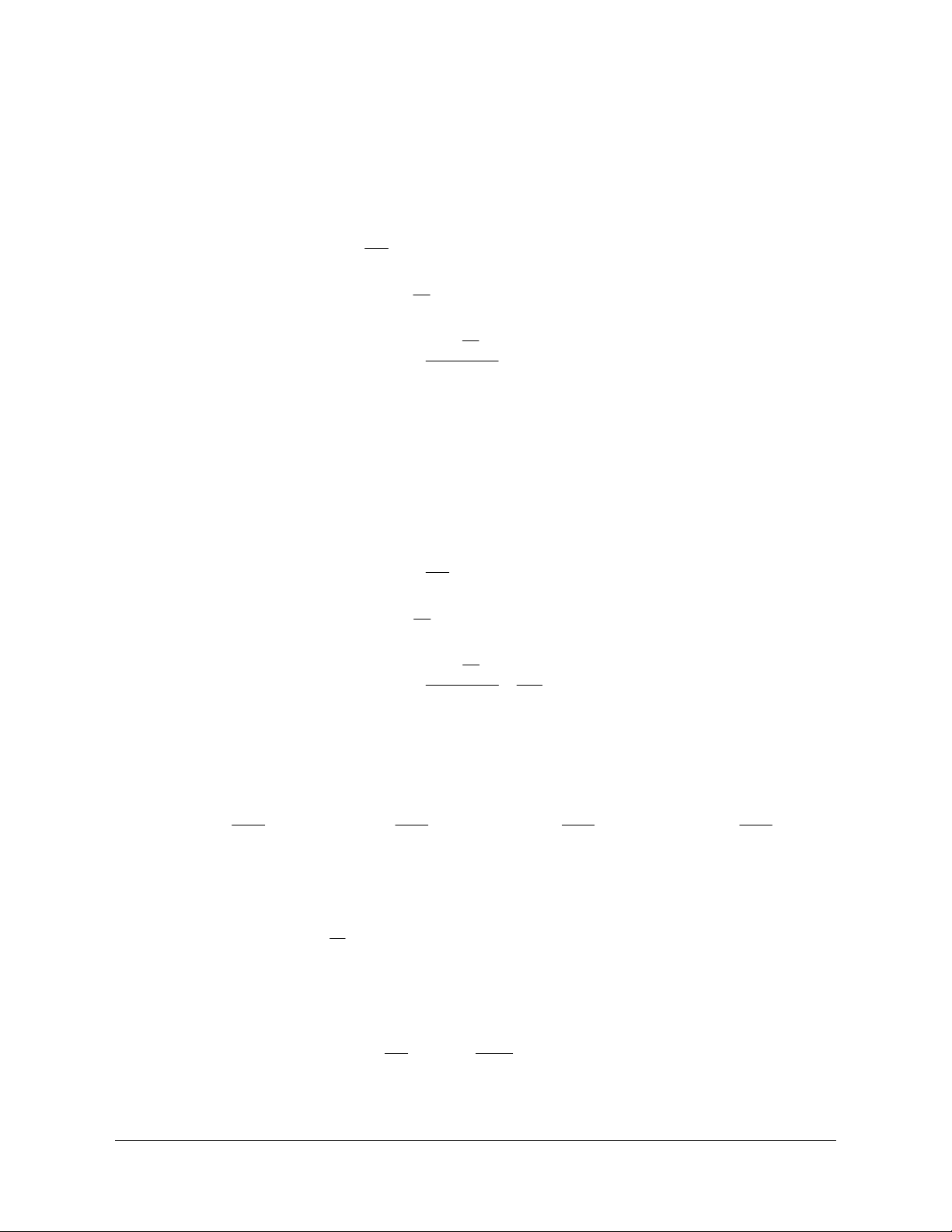






















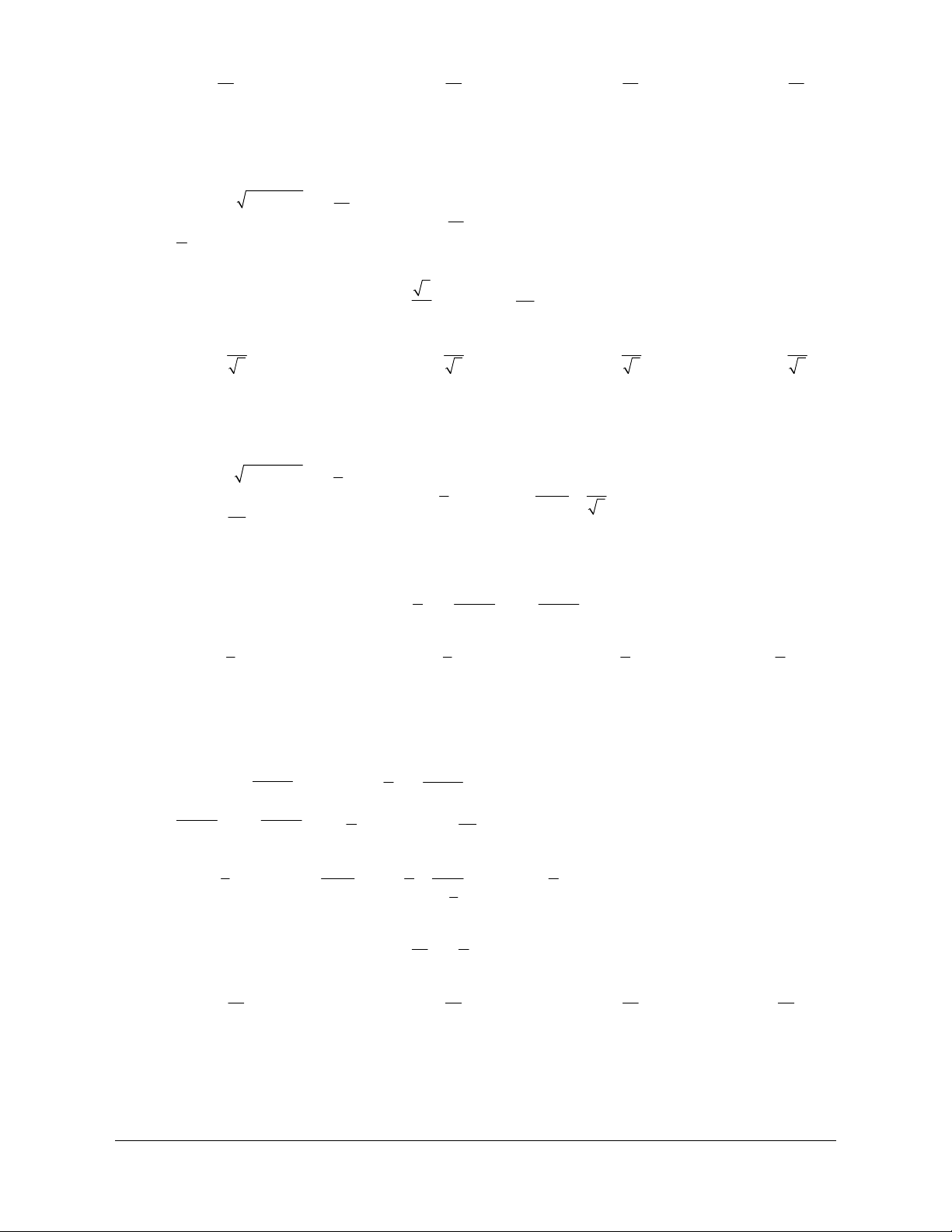
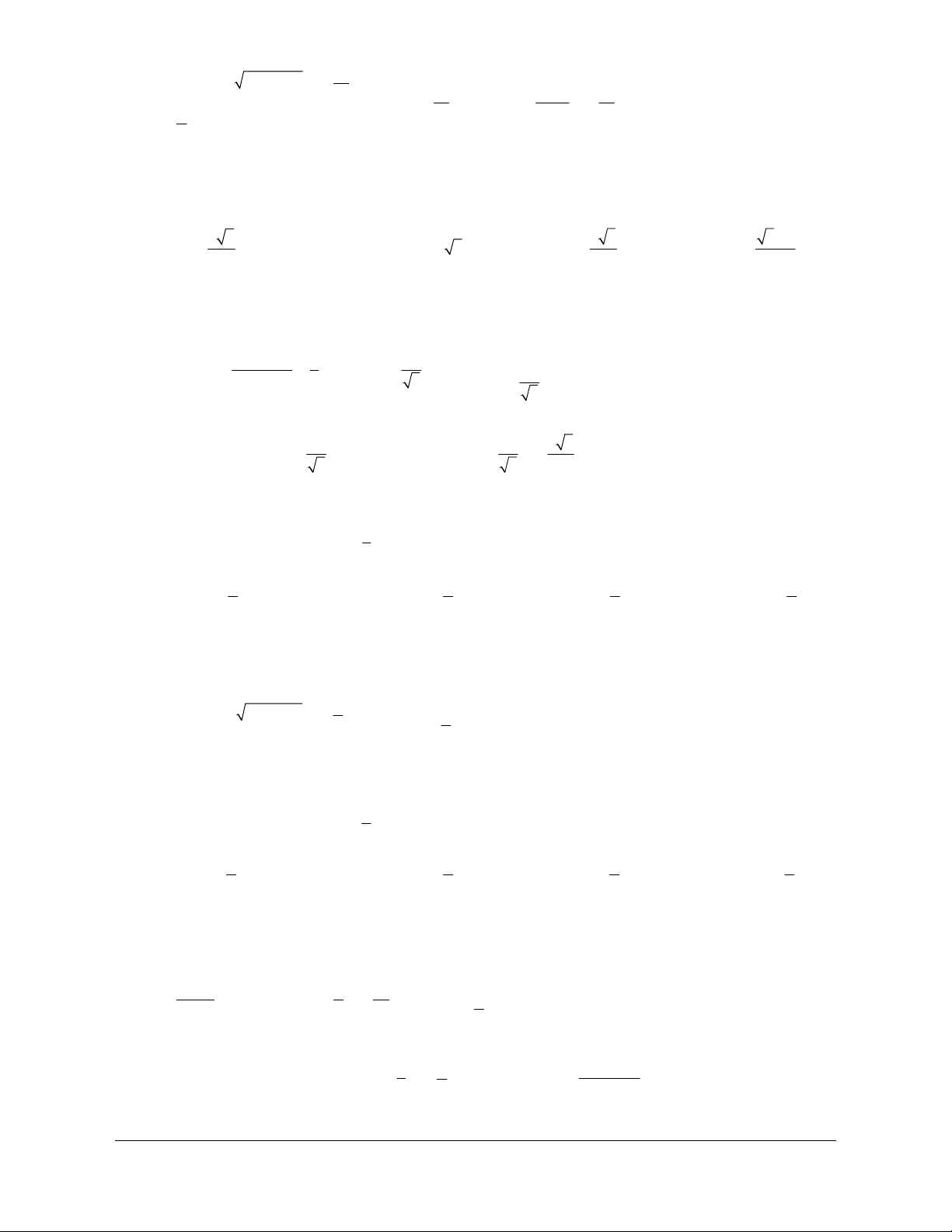

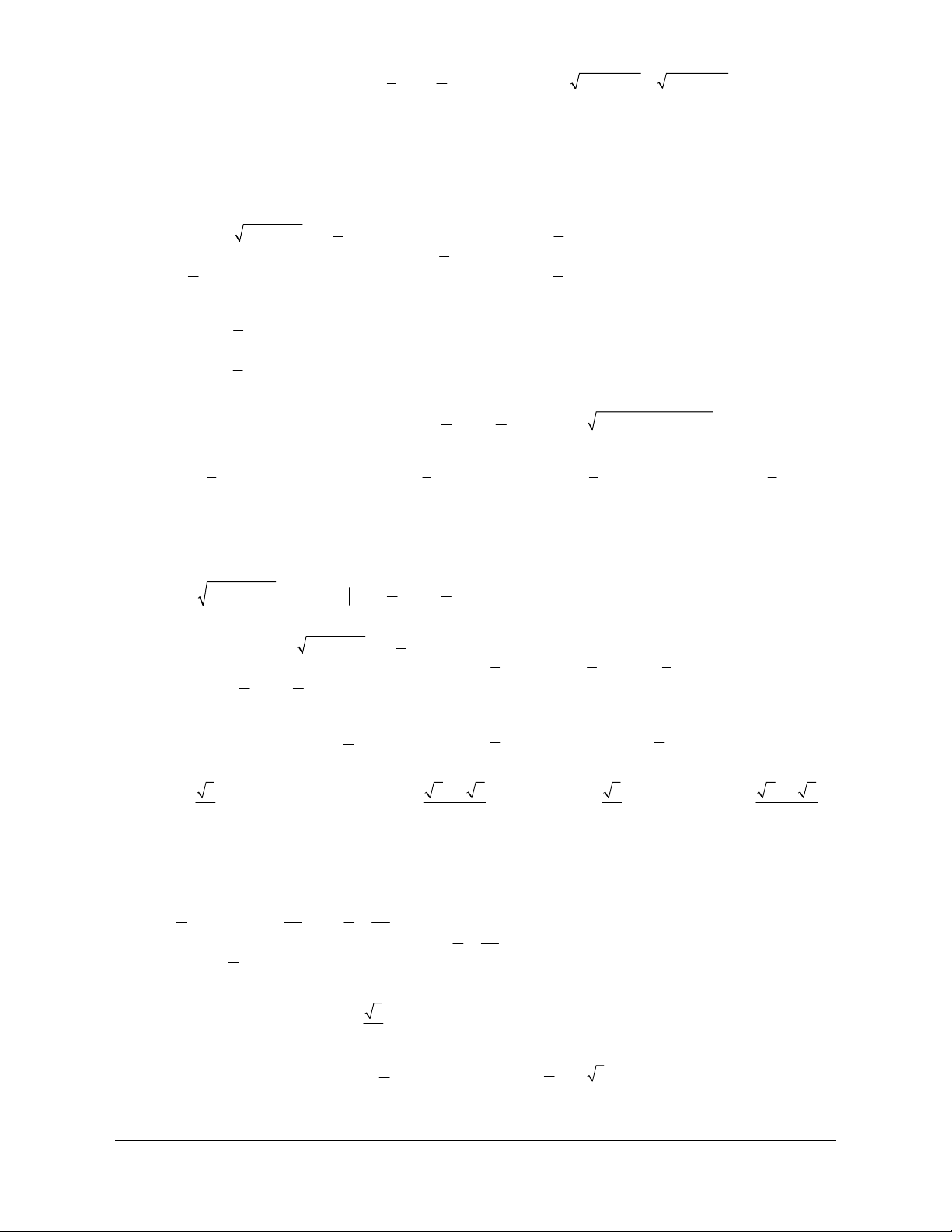
























































Preview text:
CHƯƠNG 6. CUNG LƯỢNG GIÁC VÀ CÔNG THỨC LƯƠNG GIÁC
BÀI 1. CUNG VÀ GÓC LƯỢNG GIÁC
A. KIẾN THỨC CƠ BẢN CẦN NẰM
I – KHÁI NIỆM CUNG VÀ GÓC LƯỢNG GIÁC
1. Đường tròn định hướng và cung lượng giác
Đường tròn định hướng là một đường tròn trên đó ta chọn một +
chiều chuyển động gọi là chiều dương, chiều ngược lại là chiều
âm. Ta quy ước chọn chiều ngược với chiều quay của kim đồng A hồ làm chiều dương. -
Trên đường tròn định hướng cho hai điểm A và .
B Một điểm M
di động trên đường tròn luôn theo một chiều (âm hoặc dương) từ D
A đến B tạo nên một cung lượng giác có điểm đầu A điểm cuối . B M Với hai điểm O
A, B đã cho trên đường tròn định hướng ta có vô
số cung lượng giác điểm đầu A, điểm cuối .
B Mỗi cung như vậy C
đều được kí hiệu là AB. 2. Góc lượng giác
Trên đường tròn định hướng cho một cung lượng giác CD Một điểm M chuyển động trên đường
tròn từ C tới D tạo nên cung lượng giác CD nói trên. Khi đó tia OM quay xung quanh gốc O từ vị
trí OC tới vị trí .
OD Ta nói tia OM tạo ra một góc lượng giác, có tia đầu là OC, tia cuối là . OD Kí
hiệu góc lượng giác đó là (OC, OD) .
3. Đường tròn lượng giác
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn định hướng tâm O bán kính R = 1 .
Đường tròn này cắt hai trục tọa độ tại bốn điểm +
A (1;0), A '(-1;0), B (0; ) 1 , B '(0;- ) 1 .
Ta lấy A (1;0) làm điểm gốc của đường tròn đó. O
Đường tròn xác định như trên được gọi là đường tròn lượng giác (gốc A ).
II – SỐ ĐO CỦA CUNG VÀ GÓC LƯỢNG GIÁC 1. Độ và radian a) Đơn vị radian
Trên đường tròn tùy ý, cung có độ dài bằng bán kính được gọi là cung có số đo 1 rad.
b) Quan hệ giữa độ và radian p 0 æ180ö 0 1 = rad và 1rad = ç ÷ ç ÷ . 180 çè p ÷ø
c) Độ dài của một cung tròn
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 456
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trên đường tròn bán kính R, cung nửa đường tròn có số đo là p rad và có độ dài là pR. Vậy cung
có số đo a rad của đường tròn bán kính R có độ dài = R . a
2. Số đo của một cung lượng giác
Số đo của một cung lượng giác AM ( A ¹ M ) là một số thực âm hay dương.
Kí hiệu số đo của cung AM là sđ AM . Ghi nhớ
Số đo của các cung lượng giác có cùng điểm đầu và điểm cuối sai khác nhau một bội của 2 . p Ta viết
sđ AM = a + k2 , p k Î .
trong đó a là số đo của một cung lượng giác tùy ý có điểm đầu là A , điểm cuối là M .
3. Số đo của một góc lượng giác
Số đo của góc lượng giác (OA, OC) là số đo của cung lượng giác AC tương ứng.
Chú ý Vì mỗi cung lượng giác ứng với một góc lượng giác và ngược lại, đồng thời số đo của các
cung và góc lượng giác tương ứng là trùng nhau, nên từ nay về sau khi ta nói về cung thì điều đó
cũng đúng cho góc và ngược lại.
4. Biểu diễn cung lượng giác trên đường tròn lượng giác
Chọn điểm gốc A (1;0) làm điểm đầu của tất cả các cung lượng giác trên đường tròn lượng giác. Để
biểu diễn cung lượng giác có số đo a trên đường tròn lượng giác ta cần chọn điểm cuối M của
cung này. Điểm cuối M được xác định bởi hệ thức sđ AM = . a
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng toán 1 : xác định các yếu tố liên quan đến cung và góc lượng giác. 1. Phương pháp Ngoài
việc sử dụng định nghĩa góc và cung lượng giác, công thức tính độ dài cung tròn khi
biết số đo, mối liên hệ giữa đơn vị độ, rađian và hệ thức salơ chúng ta cần lưu ý đến kết quả sau:
Nếu một góc(cung) lượng giác có số đo 0
a (hay a rad ) thì mọi góc(cung) lượng giác cùng
tia đầu(điểm đầu), tia cuối(điểm cuối) với nó có số đo dạng dạng 0 0
a + k360 (hay a + k2p rad ,
k Î Z ), mỗi góc(cung) ứng với mỗi giá trị của k . Từ đó hai góc lượng giác có cùng tia đầu và tia
cuối thì sai khác nhau một bội của 2p
2. Các ví dụ minh họa.
Ví dụ 1: a) Đổi số đo của các góc sau ra rađian: 0 0 0 72 ,600 ,- 37 45 ' 30 ' . 5p 3p
b) Đổi số đo của các góc sau ra độ: , ,- 4 . 18 5 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 457
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 p p 2p p 10p a) Vì 0 1 = rad nên 0 0 72 = 72. = , 600 = 600. = , 180 180 5 180 3 0 0 0 æ 45 ö æ 30 ö æ 4531ö 4531 p 0 0 37 - 45 ' 30 ' = -37 ç ÷ ç ÷ ç ÷ - ç ÷ - ç ÷ = ç ÷ = . » 0,6587 ç è 60 ÷ø çè60.60 ÷ø çè 120 ÷ø 120 180 0 æ180 ö 0 0 5p æ 5p 180 ö 3p æ 3p 180 ö b) Vì 1rad ç ÷ = ç ÷ ç ÷ o ç ÷ o ç nên = ç . ÷ = 50 , = ç . ÷ = 108 , è p ÷ø 18 çè 18 p ÷ø 5 çè 5 p ÷ø 0 0 æ 180 ö æ 720 ö ç ÷ ç ÷ 0 -4 = -ç4. ÷ = -ç ÷ » -2260 48 ' ç . è p ÷ø çè p ÷ø
Ví dụ 2: Một đường tròn có bán kính 36m . Tìm độ dài của cung trên đường tròn đó có số đo là 3p 1 a) b) 0 51 c) 4 3 Lời giải a p
Theo công thức tính độ dài cung tròn ta có l = Ra = .R nên 180 3p
a) Ta có l = Ra = 36.
= 27p » 84, 8m 4 a p p51 51p b) Ta có l = .R = .36 = » 32, 04m 180 180 5 1
c) Ta có l = Ra = 36. = 12m 3
Ví dụ 3: Cho hình vuông A A A A nội tiếp đường tròn tâm O (các đỉnh được sắp xếp theo chiều 0 1 2 4 þ þ
ngược chiều quay của kim đồng hồ). Tính số đo của các cung lượng giác A A , AA ( 0 i i j ,
i j = 0,1,2, 3, 4,i ¹ j ). A1 A0 Lời giải þ
Ta có AOA = 0 nên sđA A = k2p , k Î Z 0 0 0 0 O A2 A3 p þ p AOA = nên sđ A A =
+ k2p , k Î Z 0 1 2 0 1 2 þ
AOA = p nên sđ A A = p + k2p , k Î Z 0 2 0 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 458
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 p þ p 3p AOA =
nên sđ A A = 2p - + k2p =
+ k2p , k Î Z 0 3 2 0 3 2 2 þ ip Như vậy sđA A =
+ k2p , i = 0,1,2, 3 , k Î Z 0 i 2 þ þ þ p
Theo hệ thức salơ ta có sđAA =sđA A - sđA A +k2p = ( j - i ). + k2p , k Î Z . i j 0 j 0 i 2
Ví dụ 4: Tìm số đo a của góc lượng giác ( ,
Ou Ov ) với 0 £ a £ 2p , biết một góc lượng giác
cùng tia đầu, tia cuối với góc đó có số đo là: 33p 291983p a) b) - c) 30 4 3 Lời giải 33p a) Mọi góc lượng giác ( ,
Ou Ov ) có số đo là + k2 , p k Î Z 4 33p 33
Vì 0 £ a £ 2p nên 0 £ + k2p £ 2 ,
p k Î Z 0 £
+ k2 £ 2, k Î Z 4 4 33 25 - £ k £ -
, k Î Z k = -4 8 8 33p p Suy ra a = + (-4).2p = 4 4 291983p b) Mọi góc lượng giác ( ,
Ou Ov ) có số đo là - + k2 , p k Î Z 3 291983p 291983
Vì 0 £ a £ 2p nên 0 £ - + k2p £ 2 ,
p k Î Z 0 £ -
+ k2 £ 2, k Î Z 3 3 291983 291989 £ k £
, k Î Z k = 6 6 291983p p Suy ra a = - + 48664.2p = 3 3 c) Mọi góc lượng giác ( ,
Ou Ov ) có số đo là 30 + k2 , p k Î Z 15
Vì 0 £ a £ 2p nên 0 £ 30 + k2p £ 2 ,
p k Î Z 0 £
+ k £ 1, k Î Z p
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 459
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 15 p - 15 - £ k £
, k Î Z k = -4 p p Suy ra a = 30 + ( 4
- ).2p = 30 - 8p » 4,867 . p 29p 22 6p 41p
Vi dụ 5: Cho góc lượng giác ( ,
Ou Ov ) có số đo - . Trong các số - ; - ; ; , 7 7 7 7 7
những số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã cho? Lời giải
Hai góc có cùng tia đầu, tia cuối thì sai khác nhau một bội của 2p do đó 29p æ p ö 22 æ p ö 6p æ p ö Vì ç ÷ - - ç- ÷ = (-2).2p , ç ÷ - - ç- ÷ = -3p , ç ÷ - ç- ÷ = p và 7 çè 7 ÷ø 7 çè 7 ÷ø 7 çè 7 ÷ø 41p æ p ö ç ÷ 29p 41p
- ç- ÷ = 3.2p nên các số - ;
là số đo của một góc lượng giác có cùng tia đầu, tia 7 çè 7 ÷ø 7 7 cuối với góc đã cho. Ví dụ 6: Cho sđ( ,
Ou Ov ) = a và sđ(Ou ', Ov ') = b . Chứng minh rằng hai góc hình học uO ,
v u 'Ov ' bằng nhau khi và chỉ khi hoặc b - a = k2p hoặc b + a = k2p với k Î Z . Lời giải Ta có sđ( ,
Ou Ov ) = a và sđ(Ou ', Ov ') = b suy ra tồn tại a , p < a £ p , f , p < b £ p và 0 0 0 0
số nguyên k ,l sao cho a = a + k 2 ,
p b = b + l 2p . 0 0 0 0 0 0
Khi đó a là số đo của uOv và b là số đo của u 'Ov ' . 0 0 é a = b
Hai góc hình học uO ,
v u 'Ov ' bằng nhau khi và chỉ khi 0 0 a b ê = 0 0 ê a = b - ê 0 0 ë
b - a = k2p hoặc b + a = k2p với k Î Z .
C. CÂU HỎI TRẮC NGHIỆM
Câu 1: Khẳng định nào sau đây là đúng khi nói về '' đường tròn định hướng '' ?
A. Mỗi đường tròn là một đường tròn định hướng.
B. Mỗi đường tròn đã chọn một điểm là gốc đều là một đường tròn định hướng.
C. Mỗi đường tròn đã chọn một chiều chuyển động và một điểm là gốc đều là một đường tròn định hướng.
D. Mỗi đường tròn trên đó ta đã chọn một chiều chuyển động gọi là chiều dương và chiều
ngược lại được gọi là chiều âm là một đường tròn định hướng. Lời giải Chọn D
Dựa vào SGK cơ bản trang 134 ở dòng 2.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 460
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 2: Quy ước chọn chiều dương của một đường tròn định hướng là:
A. Luôn cùng chiều quay kim đồng hồ.
B. Luôn ngược chiều quay kim đồng hồ.
C. Có thể cùng chiều quay kim đồng hồ mà cũng có thể là ngược chiều quay kim đồng hồ.
D. Không cùng chiều quay kim đồng hồ và cũng không ngược chiều quay kim đồng hồ. Lời giải Chọn B
Theo SGK cơ bản trang 134 ở dòng 6, ta chọn B. þ
Câu 3: Trên đường tròn định hướng, mỗi cung lượng giác AB xác định:
A. Một góc lượng giác tia đầu OA , tia cuối OB .
B. Hai góc lượng giác tia đầu OA , tia cuối OB .
C. Bốn góc lượng giác tia đầu OA , tia cuối OB .
D. Vô số góc lượng giác tia đầu OA , tia cuối OB . Lời giải Chọn D
Theo SGK cơ bản trang 134 ở dòng cuối, ta chọn D.
Câu 4: Khẳng định nào sau đây là đúng khi nói về '' góc lượng giác '' ?
A. Trên đường tròn tâm O bán kính R = 1 , góc hình học AOB là góc lượng giác.
B. Trên đường tròn tâm O bán kính R = 1 , góc hình học AOB có phân biệt điểm đầu A
và điểm cuối B là góc lượng giác.
C. Trên đường tròn định hướng, góc hình học AOB là góc lượng giác.
D. Trên đường tròn định hướng, góc hình học AOB có phân biệt điểm đầu A và điểm
cuối B là góc lượng giác. Lời giải Chọn D
Câu 5: Khẳng định nào sau đây là đúng khi nói về '' đường tròn lượng giác '' ?
A. Mỗi đường tròn là một đường tròn lượng giác.
B. Mỗi đường tròn có bán kính R = 1 là một đường tròn lượng giác.
C. Mỗi đường tròn có bán kính R = 1 , tâm trùng với gốc tọa độ là một đường tròn lượng giác.
D. Mỗi đường tròn định hướng có bán kính R = 1 , tâm trùng với gốc tọa độ là một đường tròn lượng giác. Lời giải Chọn D
Câu 6: Trên đường tròn cung có số đo 1 rad là?
A. Cung có độ dài bằng 1. B. Cung tương ứng với góc ở tâm 0 60 .
C. Cung có độ dài bằng đường kính.
D. Cung có độ dài bằng nửa đường kính. Lời giải Chọn D
Cung có độ dài bằng bán kính (nửa đường kính) thì có số đó bằng 1 rad.
Câu 7: Khẳng định nào sau đây là đúng? A. 0 p rad = 1 . B. 0 p rad 6 = 0 . C. 0 p rad 180 = . D.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 461
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 0 æ180ö p rad = ç ÷ ç ÷ . ç è p ÷ø Lời giải Chọn C
p rad tướng ứng với 0 180 .
Câu 8: Khẳng định nào sau đây là đúng? A. 0 1 rad = 1 . B. 0 1 rad = 60 . C. 0 1 rad = 180 . D. 0 æ180ö 1 rad = ç ÷ ç ÷ . ç è p ÷ø Lời giải Chọn D
Ta có p rad tướng ứng với 0 180 .
Suy ra 1 rad tương ứng với 0 x . Vậy 180.1 x = . p
Câu 9: Nếu một cung tròn có số đo là 0
a thì số đo radian của nó là: A. p p 180p . ap a B. 180 . C. . D. . a 180 180a Lời giải Chọn C Áp dụng công thức . a p a =
với a tính bằng radian, a tính bằng độ. 180
Câu 10: Nếu một cung tròn có số đo là 0
3a thì số đo radian của nó là: A. ap . B. ap . C. 180 . D. 60 . 60 180 ap ap Lời giải Chọn A Áp dụng công thức . a p a =
với a tính bằng radian, a tính bằng độ. 180
Trong trường hợp này là 3 .p p 3 a a a ¾¾ a = = . 180 60
Câu 11: Đổi số đo của góc 0 70 sang đơn vị radian. A. 70 p . B. 7 . C. 7 . D. 7 . p 18 18 18p Lời giải Chọn C
Cách 1. Áp dụng công thức . a p a =
với a tính bằng radian, a tính bằng độ. 180 Ta có . a p 70p 7p a = = = . 180 180 18
Cách 2. Bấm máy tính:
Bước 1. Bấm shift mode 4 để chuyển về chế độ rad.
Bước 2. Bấm 70 shift DRG 1 =
Câu 12: Đổi số đo của góc 0 108 sang đơn vị radian. A. 3p p p p . B. . C. 3 . D. . 5 10 2 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 462
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn A
Tương tự như câu trên.
Câu 13: Đổi số đo của góc 0
45 32 ' sang đơn vị radian với độ chính xác đến hàng phần nghìn. A. 0,7947. B. 0,7948. C. 0,795. D. 0,794. Lời giải Chọn C Áp dụng công thức . a p a =
với a tính bằng radian, a tính bằng độ. 180 0 æ ö Trước tiên ta đổi 32 0 45 32 ' = çç45 ÷ + ÷ ç . è 60 ÷ø æ 32ö çç45 ÷ + ÷.p ç ÷
Áp dụng công thức, ta được è 60ø a = = 0,7947065861. 180
Cách 2. Bấm máy tính:
Bước 1. Bấm shift mode 4 để chuyển về chế độ rad. Bước 2. Bấm 0 0 45 32 shift DRG 1 =
Câu 14: Đổi số đo của góc 0
40 25' sang đơn vị radian với độ chính xác đến hàng phần trăm. A. 0,705. B. 0,70. C. 0,7054. D. 0,71. Lời giải Chọn D
Cách 1. Áp dụng công thức . a p a =
với a tính bằng radian, a tính bằng độ. 180 0 æ ö Trước tiên ta đổi 25 0 40 25' = çç40 ÷ + ÷ . çè 60÷ø æ 25ö çç40 ÷ + ÷.p ç ÷
Áp dụng công thức, ta được è 60ø 97p a = = = 0,705403906. 180 432
Cách 2. Bấm máy tính:
Bước 1. Bấm shift mode 4 để chuyển về chế độ rad. Bước 2. Bấm 0 0 40 25 shift DRG 1 =
Câu 15: Đổi số đo của góc 0 125 - 45¢ sang đơn vị radian. A. 503p p p p - . B. 503 . C. 251 . D. 251 - . 720 720 360 360 Lời giải Chọn A
Tương tự như câu trên. Câu 16: p
Đổi số đo của góc
rad sang đơn vị độ, phút, giây. 12 A. 0 15 . B. 0 10 . C. 0 6 . D. 0 5 . Lời giải Chọn A 0 æ ö
Cách 1. Từ công thức . a p . a 180 a = ¾¾ a = ç ÷ ç
÷ với a tính bằng radian, a tính bằng độ. 180 çè p ÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 463
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 0 æ p ö ç ÷ 0 æ ö ç .180÷ ç ÷ Ta có . a 180 = ç ÷ 12 ç ÷ = ç ÷ 0 a ÷ = 15 ç . è p ÷ ç ø è p ÷ø
Cách 2. Bấm máy tính:
Bước 1. Bấm shift mode 3 để chuyển về chế độ độ, phút, giây.
Bước 2. Bấm (shift 12 ) shift DRG 2 =
Màn hình hiện ra kết quả bất ngờ. Câu 17: p
Đổi số đo của góc 3 -
rad sang đơn vị độ, phút, giây. 16 A. 0 33 45'. B. 0 29 - 30 '. C. 0 33 - 45'. D. 0 32 - 55. Lời giải Chọn C 0 æ 3p ö ç ÷ 0 ç- .180÷ 0 æ ö ç ÷ æ ö Ta có . a 180 = ç ÷ 16 135 ç ÷ = ç ÷ 0 a ÷ = ç ÷ - ç ÷ ç ÷ ç ÷ = -33 45'. è p ø è p ø çè 4 ÷ø
Cách 2. Bấm máy tính:
Bước 1. Bấm shift mode 3 để chuyển về chế độ độ, phút, giây.
Bước 2. Bấm (shift 3 16 ) shift DRG 2 =
Câu 18: Đổi số đo của góc -5 rad sang đơn vị độ, phút, giây. A. 0 28 - 6 44 '28' . B. 0 28 - 6 28' 44 ' . C. 0 286 - . D. 0 286 28' 44 ' . Lời giải Chọn B 0 0 æ ö æ- ö Cách 1. Ta có . a 180 5.180 0 a = ç ÷ ç ÷ = ç ÷ ç ÷ = -286 28' 44 ' . ç è p ÷ø çè p ÷ø
Cách 2. Bấm máy tính:
Bước 1. Bấm shift mode 3 để chuyển về chế độ độ, phút, giây. Bước 2. Bấm 5 shift DRG 2 =
Câu 19: Đổi số đo của góc 3 rad sang đơn vị độ, phút, giây. 4 A. 0 42 97 18 ¢ ¢ . B. 0 42 58¢. C. 0 42 97 .¢ D. 0 42 58¢18¢ . Lời giải Chọn D
Tương tự như câu trên.
Câu 20: Đổi số đo của góc 2 r -
ad sang đơn vị độ, phút, giây. A. 0 11 - 4 59 1 ¢ 5¢ . B. 0 11 - 4 35¢. C. 0 11 - 4 35¢29¢ .¢ D. 0 11 - 4 59 .¢ Lời giải Chọn C
Tương tự như câu trên.
Câu 21: Mệnh đề nào sau đây là đúng?
A. Số đo của cung tròn tỉ lệ với độ dài cung đó.
B. Độ dài của cung tròn tỉ lệ với bán kính của nó.
C. Số đo của cung tròn tỉ lệ với bán kính của nó.
D. Độ dài của cung tròn tỉ lệ nghịch với số đo của cung đó. Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 464
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Từ công thức = Ra ¾¾
và a tỷ lệ nhau. Câu 22: p
Tính độ dài của cung trên đường tròn có bán kính bằng 20cm và số đo . 16
A. = 3,93cm. B. = 2, 94cm. C. = 3,39cm. D. = 1, 49cm. Lời giải Chọn A
Áp dụng công thức p = Ra = 20. » 3, 93cm. 16
Câu 23: Tính độ dài của cung trên đường tròn có số đo 1,5 và bán kính bằng 20 cm .
A. 30cm . B. 40cm . C. 20cm . D. 60cm . Lời giải Chọn A
Ta có = aR =1,5.20 = 30 cm.
Câu 24: Một đường tròn có đường kính bằng 20 cm . Tính độ dài của cung trên đường tròn có số đo 0
35 (lấy 2 chữ số thập phân).
A. 6,01cm . B. 6,11cm . C. 6, 21cm . D. 6,31cm . Lời giải Chọn B Cung có số đo p p 0
35 thì có số đó radian là ap 35 7 a = = = . 180 180 36 Bán kính đường tròn 20 R = = 10 cm. 2 Suy ra 7p = aR = .10 »6,11 cm. 36
Câu 25: Tính số đo cung có độ dài của cung bằng 40 cm trên đường tròn có bán kính 20 cm . 3
A. 1,5 rad . B. 0, 67 r ad . C. 0 80 . D. 0 88 . Lời giải Chọn B 40 Ta có 2 3 = aR a = = = » 0, 67 rad. R 20 3
Câu 26: Một cung tròn có độ dài bằng 2 lần bán kính. Số đo radian của cung tròn đó là A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn B 2R = aR a = = = 2 rad. R R 1
Câu 27: Trên đường tròn bán kính R , cung tròn có độ dài bằng độ dài nửa đường tròn thì có số 6
đo (tính bằng radian) là: A. p / 2 . B. p / 3 . C. p / 4 . D. p / 6 . Lời giải Chọn D 1 pR Ta có 6 p = aR a = = = . R R 6
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 465
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 28: Một cung có độ dài 10cm , có số đo bằng radian là 2,5 thì đường tròn của cung đó có bán kính là:
A. 2,5cm . B. 3,5cm . C. 4cm . D. 4,5cm . Lời giải Chọn C. Ta có l 10
l = Ra R = = = 4 . a 2,5
Câu 29: Bánh xe đạp của người đi xe đạp quay được 2 vòng trong 5 giây. Hỏi trong 2 giây, bánh
xe quay được 1 góc bao nhiêu? A. 8 . p B. 5 .p C. 3 .p D. 5 .p 5 8 5 3 Lời giải Chọn A.
Trong 2 giây bánh xe đạp quay được 2.2 4 =
vòng tức là quay được cung có độ dài là 5 5 4 8 l = .2pR = pR . 5 5 8 pR Ta có l 5 8
l = Ra a = = = . p R R 5
Câu 30: Một bánh xe có 72 răng. Số đo góc mà bánh xe đã quay được khi di chuyển 10 răng là: A. 0 30 . B. 0 40 . C. 0 50 . D. 0 60 . Lời giải Chọn C. p p
72 răng có chiều dài là 2p R
R nên 10 răng có chiều dài 10.2 5 l = = R . 72 18 5 5 pR 180. p Theo công thức l 5 18 180a 18
l = Ra a = = = p mà 0 a = = = 50 . R R 18 p p Cách khác: 10.360 72 răng tương ứng với 0
360 nên 10 răng tương ứng với 0 = 50 . 72
Câu 31: Cho góc lượng giác (Ox,Oy) 0 0
= 22 30 '+ k360 . Với giá trị k bằng bao nhiêu thì góc (Ox,Oy) 0 = 1822 30 ' ? A. k Î . Æ B. k = 3. C. k = –5. D. k = 5. Lời giải Chọn D.
Theo đề (Ox,Oy) 0 0 0 0 = 1822 30' ¾¾
22 30'+ k.360 = 1822 30' ¾¾ k = 5. Câu 32: p
Cho góc lượng giác a = + k2p . Tìm k để 10p < a < 11 . p 2 A. k = 4. B. k = 5. C. k = 6. D. k = 7. Lời giải Chọn B. Ta có 19p 21p
10p < a <11p ¾¾ < k2p < ¾¾ k = 5. 2 2
Câu 33: Một chiếc đồng hồ, có kim chỉ giờ OG chỉ số 9 và kim phút OP chỉ số12 . Số đo của góc
lượng giác (OG,OP) là
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 466
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
A. p + k2 , p k Î . B. 0 0
-270 + k360 , k Î . 2 C. p 0 0
270 + k360 , k Î . D.
9 +k2 ,p k Î . 10 Lời giải Chọn A.
Góc lượng giác (OG,OP) chiếm 1 đường tròn. Số đo là 1 .2p + k2p , k Î . 4 4
Câu 34: Trên đường tròn lượng giác có điểm gốc là A . Điểm M thuộc đường tròn sao cho cung
lượng giác AM có số đo 0
45 . Gọi N là điểm đối xứng với M qua trục Ox , số đo cung
lượng giác AN bằng A. 0 - 45 . B. 0 315 . C. 0 45 hoặc 0 315 . D. 0 0
- 45 + k360 , k Î . Lời giải Chọn D.
Vì số đo cung AM bằng 0 45 nên 0
AOM = 45 , N là điểm đối xứng với M qua trục Ox nên 0
AON = 45 . Do đó số đo cung AN bằng 45o nên số đo cung lượng giác AN có số đo là - 45o + 360o k , k Î .
Câu 35: Trên đường tròn với điểm gốc là A . Điểm M thuộc đường tròn sao cho cung lượng giác AM có số đo 0
60 . Gọi N là điểm đối xứng với điểm M qua trục Oy , số đo cung AN là:
A. 120o . B. 0 - 240 . C. 0 - 120 hoặc 0 240 . D. 0 0
120 + k360 , k Î . Lời giải Chọn A. Ta có 0 AOM = 60 , 0 MON = 60 Nên 0
AON = 120 . Khi đó số đo cung AN bằng 0 120 .
Câu 36: Trên đường tròn lượng giác với điểm gốc là A . Điểm M thuộc đường tròn sao cho cung
lượng giác AM có số đo 0
75 . Gọi N là điểm đối xứng với điểm M qua gốc tọa độ O , số
đo cung lượng giác AN bằng: A. 0 255 . B. 0 - 105 . C. 0 - 105 hoặc 0 255 . D. 0 0
- 105 + k360 , k Î . Lời giải Chọn D.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 467
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Ta có 0 AOM = 75 , 0 MON = 180
Nên cung lượng giác AN có số đo bằng 0 0
-105 + k360 , k Î . Câu 37: p p p p
Cho bốn cung (trên một đường tròn định hướng): 5 a = - , b = , 25 g = , 19 d = . 6 3 3 6
Các cung nào có điểm cuối trùng nhau?
A. a và b ; g và d .
B. b và g ; a và d . C. , a b, g .
D. b, g, d . Lời giải Chọn B.
Cách 1. Ta có d -a = 4p hai cung a và d có điểm cuối trùng nhau.
Và g -b = 8p hai cung b và g có điểm cuối trùng nhau.
Cách 2. Gọi A, B, C, D là điểm cuối của các cung ,
a b, g, d
Biểu diễn các cung trên đường tròn lượng giác ta có B º C, A º D.
Câu 38: Các cặp góc lượng giác sau ở trên cùng một đường tròn đơn vị, cùng tia đầu và tia cuối.
Hãy nêu kết quả SAI trong các kết quả sau đây:
A. p và 35p p p p p p p - . B. và 152 . C. - và 155 . D. và 281 . 3 3 10 5 3 3 7 7 Lời giải Chọn B.
Cặp góc lượng giác a và b ở trên cùng một đường tròn đơn vị, cùng tia đầu và tia cuối. Khi đó a - b
a = b + k 2p , k Î hay k = . 2p p 152p -
Dễ thấy, ở đáp án B vì 303 10 5 k = = - Ï . 2p 20
Câu 39: Trên đường tròn lượng giác gốc A , cung lượng giác nào có các điểm biểu diễn tạo thành tam giác đều?
A. k2p . B. kp kp kp . C. . D. . 3 2 3 Lời giải Chọn A.
Tam giác đều có góc ở đỉnh là p
60o nên góc ở tâm là 120o tương ứng k2 . 3
Câu 40: Trên đường tròn lượng giác gốc A , cung lượng giác nào có các điểm biểu diễn tạo thành hình vuông?
A. kp . B. k p kp kp . C. 2 . D. . 2 3 3 Lời giải Chọn A.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 468
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Hình vuông kp CDEF có góc
DCE là 45o nên góc ở tâm là 90o tương ứng . 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 469
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 2. GIÁ TRỊ LƯỢNG GIÁC MỘT CUNG
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I – GIÁ TRỊ LƯỢNG GIÁC CỦA CUNG a 1. Định nghĩa
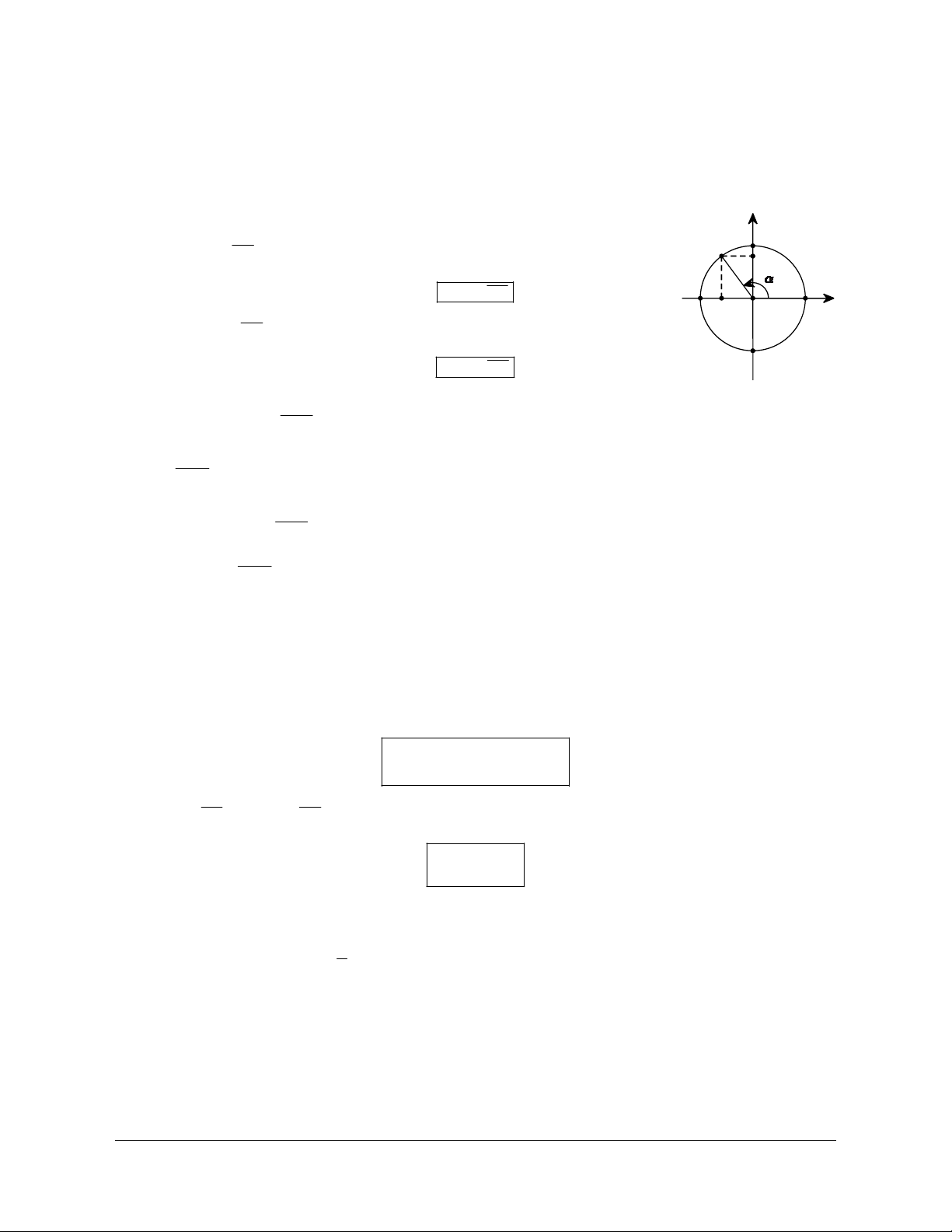
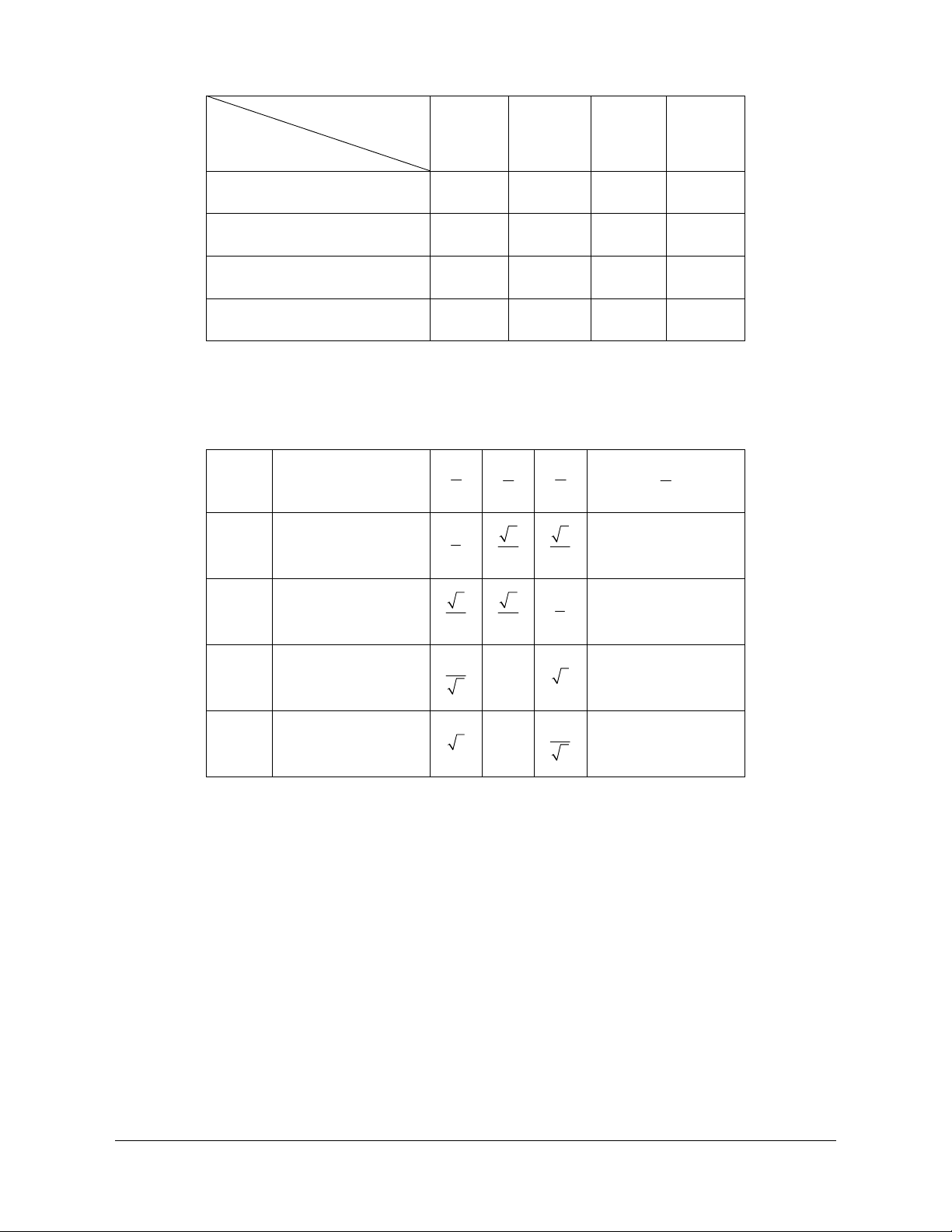
Trên đường tròn lượng giác cho cung
AM có sđ A M (còn viết A M ) y B
· Tung độ y = OK của điểm M gọi là sin của a và kí hiệu là sin . a M K sin a = OK . A' A x H O
· Hoành độ x = OH của điểm M gọi là côsin của a và kí hiệu là cos . a cosa = OH . B' a
· Nếu cosa ¹ 0, tỉ số sin
gọi là tang của a và kí hiệu là tan a (người ta còn dùng kí hiệu tga ) cosa sin a tan a = . cos a a
· Nếu sin a ¹ 0, tỉ số cos gọi là côtang của a và kí hiệu là cot a (người ta còn dùng kí hiệu cotg a sin a ) cos a cot a = . sin a Các giá trị sin , a cos , a tan ,
a cot a được gọi là các giá trị lượng giác của cung . a
Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin 2. Hệ quả
1) sin a và cosa xác định với mọi a Î . Hơn nữa, ta có
sin (a + k2p) = sin , a ; "k Î
cos(a + k2p) = cos , a . "k Î 2) Vì -1 £ OK £
1; -1 £ OH £ 1 nên ta có 1 - £ sin a £1 1 - £ cosa £1.
3) Với mọi m Î mà 1
- £m £1 đều tồn tại a và b sao cho sin a = m và cosb = m. 4) p
tan a xác định với mọi a ¹ + kp (k Î ). 2
5) cot a xác định với mọi a ¹ kp (k Î ).
6) Dấu của các giá trị lượng giác của góc
a phụ thuộc vào vị trí điểm cuối của cung AM = a trên
đường tròn lượng giác.
Bảng xác định dấu của các giá trị lượng giác
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 470
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Góc phần tư I II III IV Giá trị lượng giác cosa + - - + sin a + + - - tan a + - + - cot a + - + -
3. Giá trị lượng giác của các cung đặc biệt p p p p a 0 6 4 3 2 sin a 0 1 2 3 1 2 2 2 1 cosa 1 3 2 0 2 2 2 1 tan a 0 1 3 Không xác định 3 1 cot a Không xác định 3 1 0 3
II – Ý NGHĨA HÌNH HỌC CỦA TANG VÀ CÔTANG
1. Ý nghĩa hình học của tan a
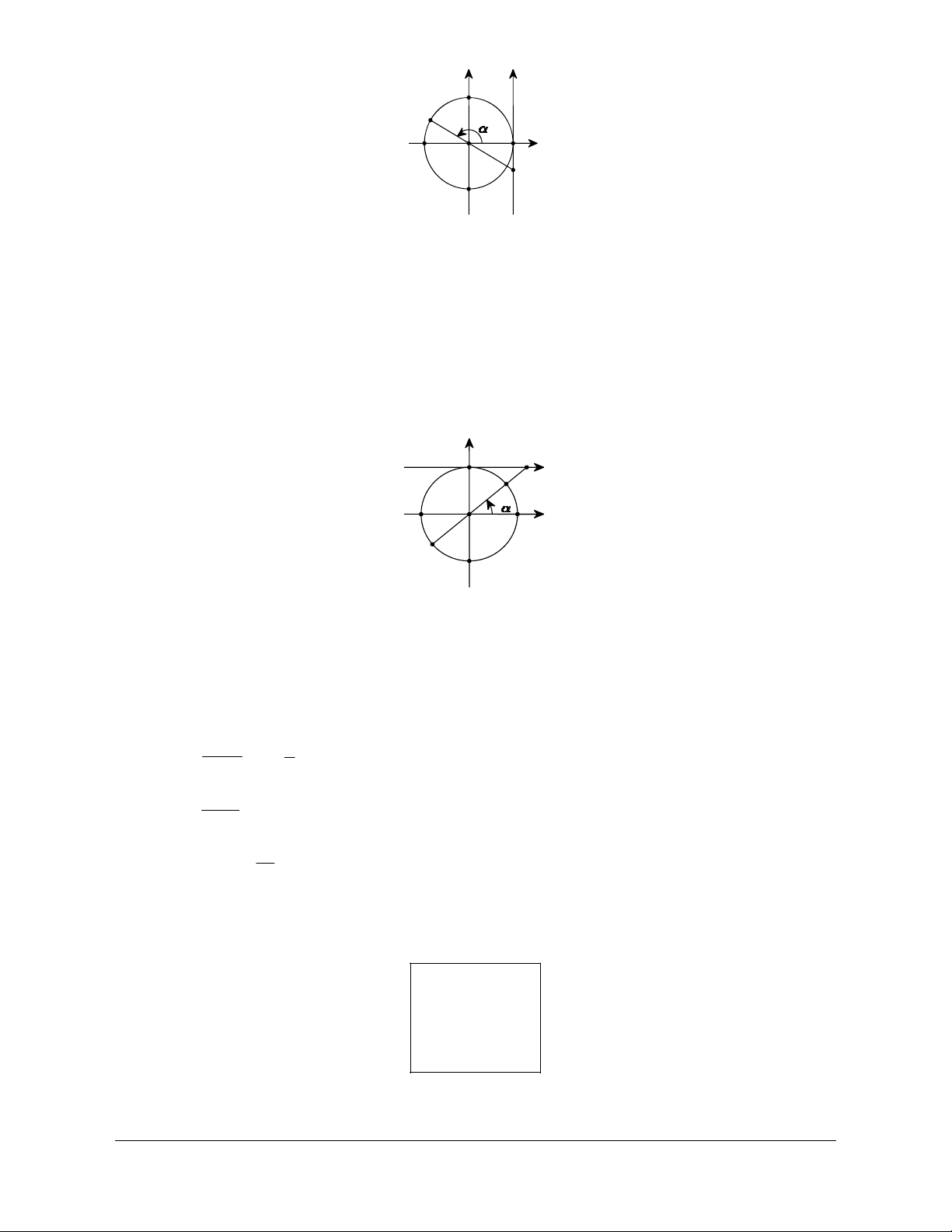
Từ A vẽ tiếp tuyến t 'At với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại A .
Gọi T là giao điểm của OM với trục t ' At.
tan a được biểu diễn bởi độ dài đại số của vectơ AT trên trục t 'At. Trục t 'At được gọi là trục tang.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 471
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 y t M A x O T t'
2. Ý nghĩa hình học của cot a
Từ B vẽ tiếp tuyến s'Bs với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại B .
Gọi S là giao điểm của OM với trục s'Bs
cot a được biểu diển bởi độ dài đại số của vectơ BS trên trục s'Bs Trục s'Bs được gọi là trục côtang. y s' B S s M x O
III – QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC
1. Công thức lượng giác cơ bản
Đối với các giá trị lượng giác, ta có các hằng đẳng thức sau 2 2 sin a+cos a =1 1 p 2 1+ tan a =
, a ¹ + kp, k Î 2 cos a 2 1 2 1+ cot a = , a ¹ k , p k Î 2 sin a tan . a cot a =1, kp a ¹ , k Î 2
2. Giá trị lượng giác của các cung có liên quan đặc biệt
1) Cung đối nhau: a và a - cos( a - ) = cosa sin ( a - ) = -sin a tan ( a - ) = -tan a cot( a - ) = -cot a
2) Cung bù nhau: a và p - a
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 472
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
sin (p -a) = sin a
cos(p -a) = -cosa
tan (p -a) = -tan a
cot(p -a) = -cot a
3) Cung hơn kém p : a và (a + p)
sin (a + p) = -sin a
cos(a + p) = -cosa
tan (a + p) = tan a
cot(a + p) = cot a æp ö
4) Cung phụ nhau: a và çç -a÷÷ ç è2 ÷ø æp ö
sin çç -a÷÷ = cosa çè2 ÷ø æp ö
cosçç -a÷÷ = sin a çè2 ÷ø æp ö
tan çç -a÷÷ = cot a çè2 ÷ø æp ö
cotçç -a÷÷ = tan a çè2 ÷ø
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng toán 1: biểu diễn góc và cung lượng giác. 1. Phương pháp giải.
Để biểu diễn các góc lượng giác trên đường tròn lượng giác ta thường sử dụng các kết quả sau
Góc a và góc a + k2 ,
p k Î Z có cùng điểm biểu diễn trên đường tròn lượng giác. k2p
Số điểm trên đường tròn lượng giác biểu diễn bởi số đo có dạng a + ( với k là số m
nguyên và m là số nguyên dương) là m. Từ đó để biểu diễn các góc lượng giác đó ta lần
lượt cho k từ 0 tới (m - 1) rồi biểu diễn các góc đó.
2. Các ví dụ minh họa.
Ví dụ 1: Biểu diễn các góc(cung) lượng giác trên đường tròn lượng giác có số đo sau: p 11p a) b) - c) 0 120 d) 0 76 - 5 4 2 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 473
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 p 1
a) Ta có 4 = . Ta chia đường tròn thành tám phần bằng nhau. 2p 8 y p B M
Khi đó điểm M là điểm biểu diễn bởi góc có số đo . 2 M 1 4 1 13p p b) Ta có -
= - + (-3).2p do đó điểm biểu diễn bởi góc 2 2 A' A O x 11p p -
trùng với góc - và là điểm B ' . 2 2 M3 B' 120 1 c) Ta có
= . Ta chia đường tròn thành ba phần bằng nhau. 360 3
Khi đó điểm M là điểm biểu diễn bởi góc có số đo 0 120 . 2 d) Ta có 0 0 - = - + (- ) 0 765 45
2 .360 do đó điểm biểu diễn bởi góc 0 76 - 5 trùng với góc 0 -45 . 45 1 =
. Ta chia đường tròn làm tám phần bằng nhau (chú ý góc âm ) 360 8
Khi đó điểm M (điểm chính giữa cung nhỏ
AB ' ) là điểm biểu diễn bởi góc có số đo 0 76 - 5 . 3
Ví dụ 2 : Trên đường tròn lượng giác gốc A . Biểu diễn các góc lượng giác có số đo sau (với k là số nguyên tùy ý). p p x = kp ; x = + kp ; x = - + kp 1 2 3 3 3
Các góc lượng giác trên có thể viết dưới dạng công thức duy nhất nào? Lời giải k2p Ta có x =
do đó có hai điểm biểu diễn bởi góc có số đo dạng x = kp 1 2 1
Với k = 0 x = 0 được biểu diễn bởi điêm A 1
k = 1 x = p được biểu diễn bởi A' 1 p 2kp x = +
do đó có hai điểm biểu diễn bởi góc có 2 3 2 p số đo dạng x = + kp y 2 3 B M4 M p 1 k = 0 x =
được biểu diễn bởi M 2 3 1 4p k = 1 x =
được biểu diễn bởi M 3 2 A' A O x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 474
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 M2 M B' 3 p k2p p x = - +
do đó có hai điểm biểu diễn bởi góc có số đo dạng x = - + kp 3 3 2 3 3 p
k = 0 x = - được biểu diễn bởi M 3 3 3 2p k = 1 x =
được biểu diễn bởi M . 6 3 4
Do các góc lượng giác x ,x ,x được biểu diễn bởi đỉnh của đa giác đều AM M A'M M 1 2 3 1 4 2 3 kp
nên các góc lượng giác đó có thể viết dưới dạng một công thức duy nhất là x = . 3
Dạng toán 2 : xác định giá trị của biểu thức chứa góc đặc biệt, góc liên quan đặc biệt và dấu
của giá trị lượng giác của góc lượng giác.
1. Phương pháp giải.
Sử dụng định nghĩa giá trị lượng giác
Sử dụng tính chất và bảng giá trị lượng giác đặc biệt
Sử dụng các hệ thức lượng giác cơ bản và giá trị lượng giác của góc liên quan đặc biệt
Để xác định dấu của các giá trị lượng giác của một cung (góc) ta xác định điểm ngọn của
cung (tia cuối của góc) thuộc góc phần tư nào và áp dụng bảng xét dấu các giá trị lượng giác.
2. Các ví dụ minh họa.
Ví dụ 1: Tính giá trị các biểu thức sau: 7p 5p 7p a) A = sin + cos 9p + tan(- ) + cot 6 4 2 1 2 sin 2550 cos(-188 ) b) B = + tan 368 2 cos 638 + cos 98 c) 2 2 2 2
C = sin 25 + sin 45 + sin 60 + sin 65 p 3p 5p d) 2 D = tan . tan .tan 8 8 8 Lời giải æ p ö æ p ö æ p ö a) Ta có A sinççp
÷÷ cos(p 4.2p) tanççp ÷÷ cotç = + + + - + + ç + 3p ÷÷ ç è 6 ÷ø çè 4 ÷ø çè 2 ÷ø p p p 1 5
A = -sin + cos p - tan + cot = - - 1 - 1 + 0 = - 6 4 2 2 2 1 2 sin( 0 30 + 7.360) 0 cos(8 + 180 ) b) Ta có B = + tan( 0 8 + 360) 2 cos( 0 0 -90 + 8 + 2.360) + cos( 0 90 + 8)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 475
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 - 1 (- ) 2. ( 0 0 0 cos 8 2 sin 30 cos 8 ) 1 2 B = + = + = 0 tan 8 2 cos( 0 0 8 - 90 ) 0 0 - sin 8 tan 8 2 cos( 0 0 90 - 8 ) 0 - sin 8 0 0 1 cos 8 1 cos 8 = - = - = 0 0 0 0 0 0 tan 8 2 sin 8 - sin 8 tan 8 sin 8 c) Vì 0 0 0 0 0
25 + 65 = 90 sin 65 = cos 25 do đó 2 2 æ ö æ ö
C = (sin 25 + cos 25)0 ç 2 ÷ 1 2 2 2 2
+ sin 45 + sin 60 = 1 + ç ÷ ç ÷ + ç ÷ ç ÷ çè 2 ÷ ç ø è 2 ÷ø 7 Suy ra C = . 4 æ p 3p ö é æ p ö 5p ù d) D ç = -çtan .tan ÷÷.êtanç ÷ ç- ÷tan ú ç è 8 8 ÷ø ê çè 8 ÷ø 8 ú ë û p 3p p p 5p p 3p p 5p æ p ö Mà + = ,- + = tan = cot , tan = cotç ÷ ç- ÷ 8 8 2 8 8 2 8 8 8 çè 8 ÷ø æ p p ö é æ p ö æ p öù Nên D ç = -çtan .cot ÷÷.ê tanç ÷ ç- ÷cotç ÷ ç- ÷ú = -1 ç . è 8 8 ÷ø ê çè 8 ÷ø çè 8 ÷øú ë û p Ví dụ 2: Cho
< a < p . Xác định dấu của các biểu thức sau: 2 æ p ö æ 3p ö a) sinçç + a÷÷ ç ÷ ç b) tanç - a÷ è 2 ÷ø çè 2 ÷ø æ p ö 14p
c) cosçç- + a÷÷.tan(p - a) ç d) sin .cot(p + a) è 2 ÷ø 9 Lời giải p p 3p æ p ö a) Ta có
< a < p p < + a <
suy ra sinçç + a÷÷ < 0 2 2 2 çè 2 ÷ø p 3p p æ 3p ö b) Ta có - > a - > p - 0 >
- a > - suy ra tançç - a ÷÷ < 0 2 2 2 çè 2 ÷ø p p p æ p ö c) Ta có
< a < p 0 < - + a <
suy ra cosçç- + a÷÷ > 0 2 2 2 çè 2 ÷ø p
Và 0 < p - a <
suy ra tan(p + a) > 0 2 æ p ö
Vậy cosçç- + a÷÷.tan(p + a) > 0 ç . è 2 ÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 476
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 3p 14p 14p d) Ta có < < 2p sin < 0 . 2 9 9 p 3p
< a < p
< p + a < 2p suy ra cot(p + a) < 0 . 2 2 14p Vậy sin
.cot(p + a) > 0 . 9
Dạng toán 3 : chứng minh đẳng thức lượng giác, chứng minh biểu thức không phụ thuộc góc
x , đơn giản biểu thức.
1. Phương pháp giải.
Sử dụng các hệ thức lượng giác cơ bản, các hằng đẳng thức đáng nhớ và sử dụng tính chất của giá
trị lượng giác để biến đổi
+ Khi chứng minh một đẳng thức ta có thể biến đổi vế này thành vế kia, biến đổi tương đương, biến
đổi hai vế cùng bằng một đại lượng khác.
+ Chứng minh biểu thức không phụ thuộc góc x hay đơn giản biểu thức ta cố gắng làm xuất hiện
nhân tử chung ở tử và mẫu để rút gọn hoặc làm xuất hiện các hạng tử trái dấu để rút gọn cho nhau.
2. Các ví dụ minh họa.
Ví dụ 1: Chứng minh các đẳng thức sau(giả sử các biểu thức sau đều có nghĩa) a) 4 2 4
cos x + 2 sin x = 1 + sin x sin x + cos x b) 3 2
= cot x + cot x + cotx + 1 3 sin x 2 2 2 2 cot x - cot y cos x - cos y c) = 2 2 2 2 cot x.cot y cos x.cos y æ p ö æ p ö d) 4 2 4 2 sin x 4 cos x cos x 4 sin x 3 tanççx ÷÷tanç + + + = + ç - x ÷÷ ç è 3 ÷ø çè 6 ÷ø Lời giải
a) Đẳng thức tương đương với x = - x + ( x )2 4 2 2 cos 1 2 sin sin x = ( - x )2 4 2 cos 1 sin (*) Mà 2 2 2 2
sin x + cos x = 1 cos x = 1 - sin x Do đó (*) x = ( x )2 4 2 cos cos (đúng) ĐPCM. sin x + cos x 1 cos x b) Ta có VT = = + 3 2 3 sin x sin x sin x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 477
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 sin x Mà 2 cot x + 1 = và tan x = nên 2 sin x cos x 2 VT = x + + x ( 2 cot 1 cot cot x + 1) 3 2
= cot x + cot x + cotx + 1 = VP ĐPCM. 2 2 cot x - cot y 1 1 c) Ta có 2 2 VT = = -
= tan y - tan x 2 2 2 2 cot x.cot y cot y cot x 2 2 æ 1 ö æ 1 ö 1 1 cos x - cos y çç 1÷ ç = - ÷ - ç - 1÷÷ = - = = VP ĐPCM. 2 ç ÷ 2 ÷ è ø ç ÷ 2 2 2 2 cos y è cos x ÷ø cos y cos x cos x.cos y d) 4 VT = x + ( 2 - x ) 4 + x + ( 2 sin 4 1 sin cos 4 1 - cos x ) = ( x )2 - x + + ( x )2 - x + = ( x - )2 + ( x - )2 2 2 2 2 2 2 sin 4 sin 4 cos 4 cos 4 sin 2 cos 2 = ( 2 - x ) + ( 2 - x ) = - ( 2 2 2 sin 2 cos 4
sin x + cos x ) = 3 æ p ö æ p ö p æ p ö æ p ö Mặt khác vì ççx ÷ ç ÷ ç x ÷÷ tançç x ÷÷ cotç + + - = - = çx ÷ + ÷ ç nên è 3 ÷ø çè 6 ÷ø 2 çè 6 ÷ø çè 3 ÷ø æ p ö æ p ö VP 3 tanççx ÷÷cotç = + çx ÷
+ ÷ = 3 VT = VP ç ĐPCM. è 3 ÷ø çè 3 ÷ø
Ví dụ 2: Cho tam giác ABC . Chứng minh rằng B B 3 3 sin cos 2 2 - = tan .
A cot(B + C )
æ A + 2B +C ö
æ A + 2B +C ö cosç ÷ ç ÷ sinç ÷ ç ÷ çè 2 ÷ø çè 2 ÷ø Lời giải
Vì A + B +C = p nên B B B B 3 3 3 3 sin cos sin cos 2 2 2 2 æ B B ö ç 2 2 VT = - = - = -çsin + cos ÷÷ = -1 æ p B ö æ p B ö B B çè 2 2 ÷ø cosç ÷ ç + ÷ sinç ÷ ç + ÷ -sin cos çè 2 2 ÷ø çè 2 2 ÷ø 2 2 VP = tan .
A cot(p - A) = tan . A (-cotA) = 1 -
Suy ra VT = VP . ĐPCM
Ví dụ 3: Đơn giản các biểu thức sau(giả sử các biểu thức sau đều có nghĩa) æ 3p ö æ 3p ö a) A cos(5p x) sinçç x ÷÷ tanç = - - + + ç ÷ ç
- x ÷÷ + cot(3p - x) è 2 ø çè 2 ÷ø
sin(900 + x) - cos(450 - x) + cot(1080 - x) + tan(630 - x) b) B =
cos(450 - x) + sin(x - 630 )
- tan(810 + x) - tan(810 - x)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 478
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 1 1 c) C = 2 - p < < p ( + với x 2 x + p ). sin 2013 1 + cos x 1 - cos x Lời giải
a) Ta có cos(5p - x) = cos(p - x + 2.2p) = cos(p - x ) = -cosx æ 3p ö æ p ö æ p ö sinçç x ÷÷ sinç ç ÷ çp x ÷÷ sinç + = + + = - è ø ç ÷
ç + x ÷÷ = -cos x 2 è 2 ø çè 2 ÷ø æ 3p ö æ p ö æ p ö tançç x ÷÷ tanç ç ÷ çp x ÷÷ tanç - = + - = è ø ç ÷
ç - x ÷÷ = cotx 2 è 2 ø çè 2 ÷ø
cot(3p - x) = cot( x - ) = -cotx
Suy ra A = -cos x - (-cosx ) + cotx + (-cotx ) = 0 b) Ta có + x = ( 0 0 + + x ) = ( 0 sin(900 ) sin 180 2.360
sin 180 + x ) = -sin x ( 0 - x ) = ( 0 0 + - x ) = ( 0 cos 450 cos 90 360
cos 90 - x ) = sin x
cot(1080 - x) = cot(3.360 - x) = cot( x - ) = -cotx 0 0
tan(630 - x) = tan(3.180 + 90 - x) = tan(90 - x) = cotx x - = ( 0 0 x - + ) = ( 0 sin( 630 ) sin 2.360 90
sin x + 90 ) = cosx 0 0
tan(810 + x) = tan(4.180 + 90 + x) = tan(90 + x) = - cotx 0
tan(810 - x) = tan(4.180 + 90 - x) = tan(90 - x) = cotx
-sin x - sin x - cotx + cotx 2 - sin x Vậy B = =
sin x + cos x - (-cotx ) - cotx sin x + cos x
c) Ta có sin(x + 2013p) = sin(x + p + 1006.2p) = sin(x + p) = -sin x nên 1
1 - cos x + 1 + cos x C = 2 + . sin x
(1 - cosx )(1 + cosx ) 1 2 1 2 æç 1 ö = 2 + . = 2 + . = 2 ç1 ÷ + ÷ ç ÷ 2 2 sin x 1 - cos x sin x sin x çè sin x sin x ÷ø
Vì p < x < 2p sin x < 0 nên æ 1 ö ç ÷ 2 C = 2 ç1 - ÷ = - 2 cot x 2 çè sin x ÷ø
Ví dụ 4: Chứng minh biểu thức sau không phụ thuộc vào x .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 479
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 6 6
sin x + cos x + 2 a) A = 4 4
sin x + cos x + 1 2 1 + cotx 2 + 2 cot x b) B = - 1 - cotx (tanx -1)( 2 tan x + 1) c) 4 2 4 4 2 4
C = sin x + 6 cos x + 3 cos x + cos x + 6 sin x + 3 sin x Lời giải a) Ta có Ta có a + a = ( a + a )2 4 4 2 2 2 2 2 2 sin cos sin cos
- 2 sin a cos a = 1 - 2 sin a cos a a + a = ( a )3 + ( a )3 6 6 2 2 = ( 2 2 a + a )( 4 4 2 2 sin cos sin cos sin cos
sin a + cos a - sin a cos a ) 4 4 2 2 2 2 2 2 2 2
= sin a + cos a - sin a cos a = 1 - 2 sin a cos a - sin a cos a = 1 - 3 sin a cos a
1 - 3 sin a cos a + 2 3( 2 2 2 2
1 - sin a cos a ) 3 Do đó A = = = 2 2
1 - 2 sin a cos a + 1 2( 2 2
1 - sin a cos a ) 2
Vậy A không phụ thuộc vào x . 2 1 2 cos x 1 + 2 + 2 b) Ta có tan x sin x B = - 1 - ( x - ) 1 1 tan 1 2 tan x sin x tan x + 1 ( 2 2
2 sin x + cos x ) tan x + 1 - 2 = - = = 1 tan x - 1 tan x - 1 tan x - 1
Vậy B không phụ thuộc vào x . 2 2 c) C = ( 2 - x ) 2 4 + x + x + ( 2 - x ) 2 4 1 cos 6 cos 3 cos 1 sin
+ 6 sin x + 3 sin x 4 2 4 2
= 4 cos x + 4 cos x + 1 + 4 sin x + 4 sin x + 1
= (2 cos x + 1)2 + (2 sin x + 1)2 2 2 2 2
= 2 cos x + 1 + 2 sin x + 1 = 3
Vậy C không phụ thuộc vào x .
Dạng toán 4 : tính giá trị của một biểu thức lượng giác khi biết một giá trị lượng giác.
1. Phương pháp giải.
Từ hệ thức lượng giác cơ bản là mối liên hệ giữa hai giá trị lượng giác, khi biết một giá trị
lượng giác ta sẽ suy ra được giá trị còn lại. Cần lưu ý tới dấu của giá trị lượng giác để chọn cho phù hợp.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 480
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Sử dụng các hằng đẳng thức đáng nhớ trong đại sô.
2. Các ví dụ minh họa.
Ví dụ 1: Tính giá trị lượng giác còn lại của góc a biết: 1 2 3p a) sin a = và 0 0 90 < a < 180 .
b) cos a = - và p < a < . 3 3 2 p 3p c) tan a = 2 -
2 và 0 < a < p d) cota = - 2 và < a < 2 2 Lời giải a) Vì 0 0
90 < a < 180 nên cos a < 0 mặt khác 2 2
sin a + cos a = 1 suy ra 1 2 2 2
cos a = - 1 - sin a = - 1 - = - 9 3 1 sin a 1 Do đó 3 tan a = = = - cos a 2 2 2 2 - 3 4 5 b) Vì 2 2
sin a + cos a = 1 nên 2
sin a = 1 - cos a = 1 - = 9 3 3p 5
Mà p < a <
sin a < 0 suy ra sin a = - 2 3 5 2 sin a - 5 cos a - 2 Ta có 3 tan a = = = và 3 cot a = = = cos a 2 2 sin a - 5 5 - 3 3 1 1 c) Vì tan a = 2 - 2 cot a = = - tan a 2 2 1 1 1 1 1 Ta có 2 2 tan a + 1 = cos a = = = cos a = . 2 2 cos a tan a + 1 (-2 2)2 9 3 + 1
Vì 0 < a < p sin a > 0 và tan a = -2 2 < 0 nên cos a < 0 1 Vì vậy cos a = - 3 sin a æ 1 ö 2 2 Ta có tan a = sin a = tan . a cos a = 2 - 2.ç ÷ ç- ÷ = . cos a çè 3÷ø 3 1 1
d) Vì cota = - 2 nên tan a = = - . cota 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 481
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 1 1 1 1 Ta có 2 2 cot a + 1 = sin a = = = sin a = 2 2 sin a cot a + 1 (- )2 3 3 2 + 1 p 3p Do < a <
cos a < 0 và cota = - 2 < 0 nên sin a > 0 2 2 3 Do đó sin a = . 3 cos a 3 6 Ta có cota = cos a = cot . a sin a = - 2. = - sin a 3 3 1
Ví dụ 2: a) Tính giá trị lượng giác còn lại của góc a biết sin a =
và tan a + cot a < 0 5 1 b) Cho 4 4
3 sin a - cos a = . Tính 4 4
A = 2 sin a - cos a . 2 Lời giải 1 1 a) Ta có 2 2 cot a + 1 = =
= 25 cot a = 24 hay cota = 2 6 2 2 sin a æ 1 ö ç ÷ ç ÷ çè 5÷ø
Vì tan a , cot a cùng dấu và tan a + cot a < 0 nên tan a < 0, cot a < 0 1 1 Do đó cota = 2 -
6 . Ta lại có tan a = = - . cota 2 6 cos a 1 2 - 6 cota =
cos a = cota sin a = 2 - 6. = sin a 5 5 1 1
b) Ta có 3 sin a - cos a =
3 sin a - (1 - sin a)2 4 4 4 2 = 2 2 4 a - ( 2 4 - a + a ) 4 2 6 sin 2 1 2 sin sin
= 1 4 sin a + 4 sin a - 3 = 0 ( 2 a - )( 2 a + ) 2 2 sin 1 2 sin
3 = 0 2 sin a - 1 = 0 (Do 2 2 sin a + 3 > 0 ) 1 Suy ra 2 sin a = . 2 1 1 Ta lại có 2 2
cos a = 1 - sin a = 1 - = 2 2 2 2 æ 1 ö æ 1 ö 1 Suy ra A = 2ç ÷ ç ÷ ç ÷ - ç ÷ = ç è 2 ÷ø çè2÷ø 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 482
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 tan a + 3 cot a
Ví dụ 3: a) Cho cos a = . Tính A = . 3 tan a + cot a sin a - cos a
b) Cho tan a = 3 . Tính B = 3 3
sin a + 3 cos a + 2 sin a
c) Cho cota = 5 . Tính 2 2
C = sin a - sin a cos a + cos a Lời giải 1 1 tan a + 3 2 + 2 a + 2 tan 3 a) Ta có tan a cos a 2 A = = = = 1 + 2 cos a 2 1 tan a + 1 1 tan a + 2 tan a cos a 4 17 Suy ra A = 1 + 2. = 9 9 sin a cos a - tan a ( 2 tan a + 1) - ( 2 3 3 tan a + 1) b) cos a cos B a = = 3 3 3 sin a 3 cos a 2 sin a
tan a + 3 + 2 tan a ( 2 tan a + 1) + + 3 3 3 cos a cos a cos a 3(9 + 1) - (9 + 1) 2 Suy ra B = = 27 + 3 + 2.3(9 + 1) 9 2 2 2
sin a - sin a cos a + cos a æ cos a cos a ö c) Ta có 2 2 C sin . a sin aç = = ç1 ÷ - + ÷ 2 2 sin a ç sin a sin a ÷ è ø 1 = ( 1 6 - 5 2
1 - cota + cot a ) = 1 - 5 + 5 = 2 2 ( ) 1 + cot a 1 + ( 5 ) 6
Ví dụ 4: Biết sin x + cos x = m
a) Tìm sin x cos x và 4 4 sin x - cos x
b) Chứng minh rằng m £ 2 Lời giải a) Ta có ( x + x )2 2 2 sin cos
= sin x + 2 sin x cos x + cos x = 1 + 2 sin x cos x (*) 2 m - 1
Mặt khác sin x + cos x = m nên 2
m = 1 + 2 sin a cos a hay sin a cos a = 2 Đặt 4 4
A = sin x - cos x . Ta có A = ( 2 2 x + x )( 2 2 sin cos
sin x - cos x ) = (sin x + cosx )(sin x - cos x )
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 483
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A = ( x + x )2 ( x - x )2 2 sin cos sin cos
= (1 + 2 sin x cosx )(1 - 2 sin x cosx ) 2 2 2 4 æ m - 1öæ m - 1ö 3 + 2m - m 2 A çç1 ÷ç = + ÷ç1 ÷ - ÷ = ç 2 ÷ç 2 ÷ è øè ø 4 2 4 3 + 2m - m Vậy A = 2 b) Ta có 2 2
2 sin x cos x £ sin x + cos x = 1 kết hợp với (*) suy ra ( x + x )2 sin cos
£ 2 sin x + cos x £ 2 Vậy m £ 2
C. CÂU HỎI TRẮC NGHIỆM
Câu 1: Cho a thuộc góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng
trong các kết quả sau đây.
A. sin a > 0. B. cosa < 0.
C. tan a < 0.
D. cot a < 0. Lời giải sin ìï a > 0 ïïco ï sa > 0
a thuộc góc phần tư thứ nhất ï í ¾¾ Chọn A. ïtan a > 0 ïïco ïï t a > 0 ïî
Câu 2: Cho a thuộc góc phần tư thứ hai của đường tròn lượng giác. Hãy chọn kết quả đúng
trong các kết quả sau đây.
A. sin a > 0; cosa > 0.
B. sin a <0; cosa <0. C. sin a >0; cosa <0. D.
sin a < 0; cosa > 0. Lời giải ìï a > ï
a thuộc góc phần tư thứ hai sin 0 í ¾¾ Chọn C. ïcosa < 0 ïî
Câu 3: Cho a thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai ?
A. sin a > 0. B. cosa < 0.
C. tan a > 0.
D. cot a > 0. Lời giải sin ìï a < 0 ïïco ï sa < 0
a thuộc góc phần tư thứ hai ï í ¾¾ Chọn A. ïtan a > 0 ïïco ïï t a > 0 ïî
Câu 4: Cho a thuộc góc phần tư thứ tư của đường tròn lượng giác. Khẳng định nào sau đây là
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 484
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 đúng ?
A. sin a > 0. B. cosa > 0.
C. tan a > 0.
D. cot a > 0. Lời giải sin ìï a < 0 ïïco ï sa > 0
a thuộc góc phần tư thứ hai ï í ¾¾ Chọn B. ïtan a < 0 ïïco ïï t a < 0 ïî Câu 5:
Điểm cuối của góc lượng giác a ở góc phần tư thứ mấy nếu sin ,
a cosa cùng dấu? A. Thứ II. B. Thứ IV. C. Thứ II hoặc IV. D. Thứ I hoặc III. Lời giải Chọn D.
Câu 6: Điểm cuối của góc lượng giác a ở góc phần tư thứ mấy nếu sin ,
a tana trái dấu? A. Thứ I. B. Thứ II hoặc IV.
C. Thứ II hoặc III. D. Thứ I hoặc IV. Lời giải Chọn C.
Câu 7: Điểm cuối của góc lượng giác a ở góc phần tư thứ mấy nếu 2
cos a = 1- sin a. A. Thứ II. B. Thứ I hoặc II.
C. Thứ II hoặc III. D. Thứ I hoặc IV. Lời giải Ta có 2 2
cosa = 1-sin a cosa = cos a cosa = cosa cos . a
Đẳng thức cosa cosa ¾¾ cos a ³ 0 ¾¾
điểm cuối của góc lượng giác a ở góc phần tư thứ I hoặc IV. Chọn D.
Câu 8: Điểm cuối của góc lượng giác a ở góc phần tư thứ mấy nếu 2 sin a = sin . a A. Thứ III. B. Thứ I hoặc III. C. Thứ I hoặc II. D. Thứ III hoặc IV. Lời giải Ta có 2
sin a = sin a sin a = sin . a
Đẳng thức sin a = sin a ¾¾ sin a ³ 0 ¾¾
điểm cuối của góc lượng giác a ở góc phần tư thứ I hoặc II. Chọn C. Câu 9: p Cho 5 2p < a <
. Khẳng định nào sau đây đúng? 2
A. tan a > 0; cot a > 0.
B. tan a <0; cot a <0.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 485
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
C. tan a > 0; cot a <0.
D. tan a <0; cot a > 0. Lời giải Ta có 5p 2p < a < ¾¾
điểm cuối cung a - p thuộc góc phần tư thứ I 2 ta ìï n a > 0 ï ¾¾ í . Chọn A. co ï t a > 0 ïî Câu 10: p
Cho 0 < a < . Khẳng định nào sau đây đúng? 2
A. sin (a -p)³ 0.
B. sin (a -p)£ 0. C.
sin (a - p) < 0. D.
sin (a - p) < 0. Lời giải Ta có p p 0 < a < p
- < a - p < - ¾¾
điểm cuối cung a - p thuộc góc phần tư thứ 2 2 III ¾¾
sin (a - p)< 0. Chọn D. Câu 11: p
Cho 0 < a < . Khẳng định nào sau đây đúng? 2 æ pö æ pö A. cot a ç ÷ ç + ÷> 0. ç ÷ ç B. cot a ç + ÷ ³ 0. C.
tan (a + p) < 0. D.
tan (a + p)> 0. è 2 ÷ø çè 2 ÷ø Lời giải ìï p p p æ p ö 0
ïï < a < < a + < p ¾¾cot a ç ÷ ç + ÷ < 0 ï ç ÷ Ta có 2 2 2 è 2 ø ïí . Chọn D. ïï p 3p 0
ï < a < p < a + p < ¾¾
tan (a + p)> 0 ïïî 2 2 Câu 12: p
Cho < a < .
p Giá trị lượng giác nào sau đây luôn dương? 2 æp ö
A. sin (p + a).
B. cot çç -a .÷÷ ç C. cos( a - ).
D. tan (p + a). è 2 ÷ø Lời giải Ta có æp ö
sin (p + a) = -sin a; cot çç -a÷÷ = sin ; a ç cos( a
- ) = cos a; tan (p + a) = tan . a è 2 ÷ø sin ìï a > 0 ï Do p ï a p co ï
< < í sa < 0 ¾¾ Chọn B. 2 ïïïtana<0 ïî Câu 13: p Cho 3 p < a <
. Khẳng định nào sau đây đúng? 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 486
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 æ p ö æ p ö A. 3 tan çç -a÷÷< 0. ç ÷ ç B. 3 tan ç -a÷> 0. è 2 ÷ø çè 2 ÷ø æ p ö æ p ö C. 3 tan çç -a÷÷£ 0. ç ÷ ç D. 3 tan ç -a÷³ 0. è 2 ÷ø çè 2 ÷ø Lời giải Chọn B. ìï æ3p ö sin ï ç ï ç -a÷÷> 0 ï ç ÷ è ø æ ö Ta có 3p 3p p 2 ï 3p p < a < 0 < -a ï < ¾¾ í ¾¾ tan çç -a÷÷> 0. 2 2 2 ï æ ï 3p ö çè 2 ÷ø co ï sçç -a÷÷> 0 ï ç ï è 2 ÷ø ïî æ p ö Câu 14: p
Cho < a < p . Xác định dấu của biểu thức M = cosç- ç +a . ÷÷ tan(p-a). 2 çè 2 ÷ø
A. M ³0. B. M > 0.
C. M £0. D. M < 0. Lời giải Chọn B. ìïp p p æ p ö
ïï < a < p 0 <- +a < ¾¾cosç- ç + a÷÷> 0 ï ç ÷ Ta có 2 2 2 è 2 ø ïí ïïp p
ï < a < p 0 < p -a < ¾¾
tan (p -a)> 0 ïïî2 2 ¾¾ M > 0. æp ö Câu 15: p Cho 3 p < a <
. Xác định dấu của biểu thức M = sin çç -a .÷÷cot(p +a). 2 çè2 ÷ø
A. M ³0. B. M > 0.
C. M £0. D. M < 0. Lời giải Chọn D. ìï 3p 3p p p æp ö p ïï < a < - < a - < p - p - < -a < - ¾¾
sin çç -a÷÷ < 0 ï ç ÷ Ta có 2 2 2 2 è 2 ø ïí ïï 3p 5p p ï < a <
2p < p + a < ¾¾
cot (p +a)> 0 ïïî 2 2 ¾¾ M < 0 . ép ù
Câu 16: Tính giá trị của cos ê +(2k + ) 1 pú. ê 4 ú ë û é ù é ù A. p p ê +( k + ) 3 cos 2 1 pú = -
. B. ê +( k + ) 2 cos 2 1 pú = - . ê 4 ú ë û 2 ê 4 ú ë û 2 ép ù é ù C. ê +( p k + ) 1 cos 2 1 pú = - . D. cos ê +(2k + ) 3 pú = ê 1 . 4 ú ë û 2 ê 4 ú ë û 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 487
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn B. é ù æ ö Ta có p ê +( p p k + ) 5 5 cos 2 1 pú = cosçç + 2kp÷÷ = cos ê 4 ú çè 4 ÷ø ë û 4 æ pö p 2 = cosççp ÷ + ÷ = -cos = - . ç è 4 ÷ø 4 2 ép ù
Câu 17: Tính giá trị của cos ê +(2k + ) 1 pú. ê 3 ú ë û é ù ép ù A. p ê +( k + ) 3 cos 2 1 pú = - . B. ê +( k + ) 1 cos 2 1 pú = . ê 3 ú ë û 2 ê 3 ú ë û 2 ép ù é ù C. ê +( p k + ) 1 cos 2 1 pú = - .
D. cos ê +(2k + ) 3 pú = ê 1 . 3 ú ë û 2 ê 3 ú ë û 2 Lời giải Chọn C. é ù æ ö æ ö Ta có p ê +( p p p k + ) 1 cos 2
1 pú = cosçç +p + k2p÷÷ = cosçç +p÷÷ = -cos = - . ê 3 ú çè3 ÷ø çè3 ÷ø ë û 3 2
Câu 18: Tính giá trị biểu thức 2 O 2 O 2 O 2 sin 10 sin 20 sin 30 ... sin 80 . O P = + + + +
A. P = 0. B. P = 2. C. P = 4. D. P = 8. Lời giải
Do 10O 80O 20O 70O 30O 60O 40O 50O 90O + = + = + = + =
nên các cung lượng giác tương ứng đôi một
phụ nhau. Áp dụng công thức sin (90O - x)= cosx , ta được P = ( 2 O 2 sin 10 + cos 10O )+( 2 O 2 sin 20 + cos 20O ) +( 2 O 2 sin 30 + cos 30O )+( 2 O 2 sin 40 + cos 40O )
=1+1+1+1= 4. Chọn C.
Câu 19: Tính giá trị biểu thức P = tan10.tan 20.tan 30.....tan 80.
A. P = 0. B. P = 1. C. P = 4. D. P = 8. Lời giải
Áp dụng công thức tan x.tan (90- x)= tan x.cot x = 1.
Do đó P =1. Chọn B.
Câu 20: Tính giá trị biểu thức 0 0 0 0
P = tan1 tan 2 tan 3 ... tan 89 .
A. P = 0. B. P = 1. C. P = 2. D. P = 3. Lời giải
Áp dụng công thức tan x.tan (90- x)= tan x.cot x = 1.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 488
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Do đó P =1. Chọn B.
Câu 21: Với góc a bất kì. Khẳng định nào sau đây đúng?
A. sin a + cosa = 1. B. 2 2
sin a +cos a =1. C. 3 3 sin a+cos a =1. D. 4 4
sin a +cos a =1. Lời giải Chọn B.
Câu 22: Với góc a bất kì. Khẳng định nào sau đây đúng? A. 2 2
sin 2a +cos 2a =1. B. ( 2 a )+ ( 2 sin cos a ) = 1. C. 2 2
sin a + cos (180-a) = 1. D. 2 2
sin a - cos (180- a) = 1. Lời giải Chọn C. Ta có ( - a) 2 = - a ¾¾ ( - a) 2 cos 180 cos cos 180 = cos . a Do đó 2 2 a + ( -a) 2 2 sin cos 180
= sin a + cos a = 1.
Câu 23: Mệnh đề nào sau đây là sai? A. a 1 - £ sin a £1 ; 1 - £ cosa £1. B. sin tan a = ( cosa ¹ 0). cos a C. cos a cot a = ( sin a ¹ 0). D. 2 ( a) 2 sin 2018 + cos (2018a) = 2018. sin a Lời giải Chọn D. Vì 2 ( a) 2 sin 2018 + cos (2018a) = 1.
Câu 24: Mệnh đề nào sau đây là sai? A. 1 1 2 1+ tan a = . B. 2 1+ cot a =
. C. tan a + cot a = 2. D. tan . a cot a = 1. 2 sin a 2 cos a Lời giải Chọn C.
Câu 25: Để tan x có nghĩa khi A. p p x = . B. x = 0.
C. x ¹ + k . p
D. x ¹ k . p 2 2 Lời giải Chọn C.
Câu 26: Điều kiện trong đẳng thức tan . a cot a = 1 là A. p p a ¹ k , k Î .
B. a ¹ + kp, k Î . 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 489
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 C. a ¹ p kp, k Î .
D. a ¹ + k2p, k Î . 2 Lời giải æ p ö p p cot ççx ÷ - ÷ ç có nghĩa khi x -
¹ kp ¬¾ x ¹ + k . p Chọn D. è 2018÷ø 2018 2018 æ pö æ pö
Câu 27: Điều kiện để biểu thức P = tan a ç ÷ ç + ÷+cot a ç ÷ ç - ÷ ç xác định là è 3÷ø çè 6 ÷ø A. p p
a ¹ + k2p, k Î . B. 2 a ¹ + kp, k Î . 6 3 C. p p a ¹ + k , p k Î . D.
a ¹ - + k2p, k Î . 6 3 Lời giải Chọn A. Ta có sin a cos a tan . a cot a = 1 . = 1 . cos a sin a ìï p ìï a ¹ ï
Đẳng thức xác định khi cos 0 a ¹ + kp ï ï p í í 2
a ¹ k , (k Î ). sin ï a ¹ 0 ï 2 ïî a ïï ¹ kp î
Câu 28: Mệnh đề nào sau đây đúng? A. 0 0 sin 60 B. 0 0 cos30 C. 0 0 tan 45 < tan 60 . D. 0 0 cot 60 > cot 240 . Lời giải Chọn C. ìï p p a ï + ¹ + kp ï
Biểu thức xác định khi ïï 3 2 p í
a ¹ + kp (k Î ). ï p 6 a ïï - ¹ kp ïïî 6
Câu 29: Mệnh đề nào sau đây đúng?
A. tan 45 > tan 46.
B. cos142 > cos143. C. sin 90 1 3¢ .¢
D. cot128 > cot126. Lời giải
Dùng MTCT kiểm tra từng đáp án. Chọn C.
Câu 30: Chọn mệnh đề đúng trong các mệnh đề sau:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 490
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 æp ö
A. cosçç -a÷÷= sin . a ç
B. sin (p +a)= sin . a è 2 ÷ø æp ö
C. cosçç +a÷÷= sin . a ç
D. tan (p + 2a)= cot(2a). è 2 ÷ø Lời giải Chọn B.
Trong khoảng giá trị từ 90 đến 180 , khi giá trị góc tăng thì giá trị cos của góc tương ứng giảm. æ p ö
Câu 31: Với mọi số thực a , ta có 9 sin çç +a÷÷ ç bằng è 2 ÷ø A. -sin . a B. cos . a C. sin . a D. -cos . a Lời giải æ ö æ ö æ ö Ta có 9p p p sin çç
+a÷÷ = sin çç4p + +a÷÷ = sin çç +a÷÷ = cos . a ç Chọn B. è 2 ÷ø çè 2 ÷ø çè2 ÷ø æ pö Câu 32: Cho 1 cos a = . Khi đó 3 sin a ç ÷ ç - ÷ bằng 3 çè 2 ÷ø A. 2 - . B. 1 - . C. 1. D. 2 . 3 3 3 3 Lời giải Chọn C. æ ö æ ö æ ö Ta có 3p p p 1 sin a ç ÷ ç - ÷ = sin a
çç + -2p÷÷= sin a ç ÷ ç + ÷ = cosa = . ç è 2 ÷ø çè 2 ÷ø çè 2 ÷ø 3
Câu 33: Với mọi a Î thì tan (2017p + a) bằng A. -tan . a B. cot . a C. tan . a D. -cot . a Lời giải Chọn C.
Ta có tan (2017p + a)= tan . a æ pö
Câu 34: Đơn giản biểu thức A = cos a ç ÷ ç - ÷+sin(a-p) ç , ta được è 2 ÷ø
A. A = cosa + sin . a B. A = 2 sin . a C.
A = sin a – cos . a D. A = 0. Lời giải Chọn D. æ ö æ ö Ta có p p A = cos a ç ÷
ç - ÷+ sin (a -p) = cosçç -a÷÷-sin (p -a) = sin a -sin a = 0. ç è 2 ÷ø çè2 ÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 491
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 æp ö æp ö
Câu 35: Rút gọn biểu thức S = cosçç -x÷÷sin(p-x)-sinçç -x÷÷cos(p-x) ç ta được è2 ÷ø çè2 ÷ø
A. S = 0. B. 2 2
S = sin x -cos x. C.
S = 2 sin x cos x. D. S = 1. Lời giải Chọn D. æ ö æ ö Ta có p p
S = cosçç - x .
÷÷ sin(p-x)-sinçç -x÷÷.cos(p-x) ç è 2 ÷ø çè2 ÷ø = x x - x (- x ) 2 2 sin . sin cos . cos
= sin x + cos x = 1. æp ö æp ö Câu 36: Cho = ç ÷ ç - ç ÷
P = sin (p + a). cos(p - a) và Q sin a . ÷ cosç +a .÷ ç
Mệnh đề nào dưới đây là đúng? è2 ÷ø çè2 ÷ø
A. P +Q = 0.
B. P +Q = 1. -
C. P +Q =1.
D. P +Q = 2. Lời giải Chọn A.
Ta có P = sin (p + a).cos(p -a)= -sin .
a (-cosa) = sin . a cos . a æ ö æ ö Và p p
Q = sin çç -a .
÷÷ cosçç +a÷÷= cos .
a (-sin a) = - sin . a cos . a ç è 2 ÷ø çè2 ÷ø
Khi đó P +Q = sin . a cosa-sin . a cosa = 0. 2 2 é æ ö ù é æ ö ù Câu 37: p 3p
Biểu thức lượng giác êsin çç - x÷÷+ sin (10p + x)ú + êcosç có giá trị bằng? ê ç ÷ ç
- x÷÷+ cos(8p - x)ú è 2 ø ú ê çè 2 ÷ø ú ë û ë û A. 1. B. 2. C. 1 . D. 3 . 2 4 Lời giải Chọn B. æ ö Ta có p
sin çç - x÷÷ = cos x; ç
sin (10p + x)= sin x. è 2 ÷ø æ ö æ ö æ ö Và 3p p p cosçç
- x÷÷ = cosçç2p- - x÷÷ = cosçç + x÷÷ = -sin x; ç
cos(8p - x) = cos x. è 2 ÷ø çè 2 ÷ø çè2 ÷ø 2 2 é æ ö ù é æ ö ù Khi đó p p ê
çç -x÷÷+ ( p + x) 3 sin sin 10 ú + êcosç ê ç ÷ ç
- x÷÷+ cos(8p - x)ú è 2 ø ú ê çè 2 ÷ø ú ë û ë û = ( x + x )2 +( x - x )2 cos sin cos sin 2 2 2 2
= cos x +2.sin x.cos x +sin x +cos x -2.sin x.cos x +sin x = 2. 2 2 é æ ùö é ù Câu 38: 17p 7p 13p
Giá trị biểu thức P = êtan + tan çç - x÷ú÷ + êcot
+ cot (7p - x)ú bằng ê 4 çè 2 ÷úø ê ë û ë 4 úû
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 492
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 1 1 2 2 . B. . C. . D. . 2 sin x 2 cos x 2 sin x 2 cos x Lời giải Chọn C. æ ö æ ö Ta có 17p p p p tan
= tan çç + 4p÷÷ = tan =1 và 7 tan çç
- x÷÷ = cot x. 4 çè4 ÷ø 4 çè 2 ÷ø æ ö Và 13p p p cot
= cot çç +3p÷÷ = cot =1; cot(7p- x)= - cot x. 4 çè4 ÷ø 4
Suy ra P = (1+ cot x)2 +(1-cot x)2 2 2 = 2 + 2 cot x = . 2 sin x æ pö p æ pö Câu 39: Biết rằng 13 sin ççx ÷ - ÷+sin = sinççx ÷ + ÷ ç
thì giá trị đúng của cos è x là 2 ÷ø 2 çè 2 ÷ø A. 1. B. 1. - C. 1 . D. 1 - . 2 2 Lời giải Chọn C. æ ö æ ö æ ö Ta có p p p sin ççx ÷
- ÷ = -sin çç - x÷÷ = -cos x ç ÷ ç
và sin çx + ÷= cos x. è 2 ÷ø çè2 ÷ø çè 2 ÷ø æ ö Kết hợp với giá trị 13p p p sin
= sin çç +6p÷÷ = sin =1. 2 çè2 ÷ø 2 æ ö æ ö Suy ra p 13p p 1 sin ççx ÷ - ÷+ sin = sin ççx ÷
+ ÷ -cos x +1 = cos x cos x = . ç è 2 ÷ø 2 çè 2 ÷ø 2 æ pö
Câu 40: Nếu cot1,25.tan(4p +1, )
25 -sin ççx + .÷÷cos(6p-x)= 0 ç thì tan è x bằng 2 ÷ø A. 1. B. 1. - C. 0. D. Một giá trị khác. Lời giải Chọn C.
Ta có tan (4p +1,25)= tan 1, 25 suy ra cot1,25.tan1,25 =1 æ ö Và p sin ççx ÷
+ ÷ = cos x; cos(6p - x) = cos(x -6p) = cos x. ç è 2 ÷ø æ ö Khi đó ( + ) p p - ççx ÷ + ÷ ( p- x) 2 cot1, 25. tan 4 1, 25 sin .cos 6
= 1-cos x = 0 sin x = 0. ç è 2 ÷ø Mặt khác sin tan x x = ¾¾ tan x = 0. cos x Câu 41: Biết , A ,
B C là các góc của tam giác ABC , mệnh đề nào sau đây đúng:
A. sin (A +C)= -sin B.
B. cos(A +C)= - cos B.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 493
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
C. tan (A +C) = tan B.
D. cot(A +C)= cot B. Lời giải Chọn B. Vì A, ,
B C là ba góc của một tam giác suy ra A +C = p - . B
Khi đó sin (A +C)= sin (p - B)= sin B; cos(A +C)= cos(p - B)= -cos B.
tan (A +C) = tan (p - B) = -tan B; cot (A +C) = cot (p - B) = -cot B. Câu 42: Biết , A ,
B C là các góc của tam giác ABC, khi đó
A. sin C = -sin (A + B).
B. cosC = cos(A + B).
C. tan C = tan (A + B).
D. cot C = cot(A+ B). Lời giải Chọn D. Vì A, ,
B C là các góc của tam giác ABC nên = 180o C
-(A + B).
Do đó C và A + B là 2 góc bù nhau sin C = sin (A + B); cosC = - cos(A + B).
Và tan C = -tan (A + B); cotC = cot(A + B).
Câu 43: Cho tam giác ABC . Khẳng định nào sau đây là sai? A. + + sin A C = cos B .
B. cos A C = sin B . 2 2 2 2
C. sin (A + B)= sin C. D.
cos(A + B) = cosC. Lời giải Chọn D.
Ta có A +B +C = p A +B = p C -
Do đó cos(A + B)= cos(p -C)= -cosC.
Câu 44: A, B, C là ba góc của một tam giác. Hãy tìm hệ thức sai: A. + + sin A B C
A = - sin (2 A + B + C ). B. 3 sin A = -cos . 2 C. A + B + 3 cos = sin C C .
D. sin C = sin (A + B + 2C). 2 Lời giải A, ,
B C là ba góc của một tam giác 0 0
A + B +C = 180 A + B = 180 -C. Ta có
(A + B + C)= ( 0 -C + C)= ( 0 sin 2 sin 180 2
sin 180 +C) = -sin C. Chọn D. Câu 45: p
Cho góc a thỏa mãn 12 sin a =
và < a < p . Tính cos . a 13 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 494
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 1 cos a = . B. 5 cos a = . C. 5 cos a = - . D. 1 cos a = - . 13 13 13 13 Lời giải Chọn D. ìï 5 2 co
ï sa = 1-sin a = ï Ta có ï 13 5 í ¾¾ cosa = - . ïp 13
ïï < a < p ïïî2 Câu 46: p
Cho góc a thỏa mãn 5 cosa = - và 3 p < a < . Tính tan . a 3 2 A. 3 tan a = - . B. 2 tan a = . C. 4 tan a = - . D. 2 tan a = - . 5 5 5 5 Lời giải Chọn B. ìï 2 2 si
ï n a = 1-cos a = ï Ta có ï 3 2 sin a 2 í ¾¾ sin a = - ¾¾ tan a = = . ï 3p 3 cosa ï 5 p ï < a < ïïî 2 Câu 47: p p
Cho góc a thỏa mãn 4 tan a = - và 2017 2019 < a < . Tính sin . a 3 2 2 A. 3 sin a = - . B. 3 sin a = . C. 4 sin a = - . D. 4 sin a = . 5 5 5 5 Lời giải Chọn D. 2 ìï 1 ìï æ ö 2 ï ï 4 1 1+ tan a = ï 1 ï +ç ÷ - ï ï ç ÷ = 2 ç ÷ 2 Ta có ï cos a ï è 3ø cos a í ¬¾í ï2017p 2019p ï ï ïp 3p ï < a <
ï +504.2p < a < + 504.2p ï 2 2 ï ïî ïî2 2 3 a a ¾¾ cosa = - . Mà sin 4 sin 4 tan a = ¬¾- = ¾¾ sin a = . 5 cos a 3 3 5 - 5 Câu 48: p
Cho góc a thỏa mãn 12 cos a = - và < a < . p Tính tan . a 13 2 A. 12 tan a = - . B. 5 tan a = . C. 5 tan a = - . D. 12 tan a = . 5 12 12 5 Lời giải Chọn C.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 495
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï 5 2 si
ï n a = 1-cos a = ï Ta có ï 13 5 sin a 5 í ¾¾ sin a = ¾¾ tan a = = - . ïp 13 cosa 12 ïï <a < . p ïïî2
Câu 49: Cho góc a thỏa mãn tan a = 2 và o o
180 <a <270 . Tính P = cosa + sin . a - A. 3 5 P = - . B. P = 1- 5. C. 3 5 P = . D. 5 1 P = . 5 2 2 Lời giải Chọn A. ìï 1 1 1 2 co ï s a = = cosa = Ta có ï 2 1 í 1+ tan a 5 5 ¾¾ cosa = - ïï 5 o o 18 ï 0 < a < 270 ïî 2 ¾¾ sin a = tan . a cosa = - . Do đó, 3 3 5 sin a + cosa = - = - . 5 5 5
Câu 50: Cho góc a thỏa 3
sin a = và 90O < <180 . O a
Khẳng định nào sau đây đúng? 5 A. 4 cot a = - . B. 4 cosa = . C. 5 tan a = . D. 4 cosa = - . 5 5 4 5 Lời giải Chọn D. ìï 4 2 ï
Ta có cosa = 1-sin a = ï 4 í 5 ¾¾ cos a = - . ï 5 90
ïï < a <180 î
Câu 51: Cho góc a thỏa 3
cota = và 0O < < 90 . O a
Khẳng định nào sau đây đúng? 4 A. 4 cosa = - . B. 4 cosa = . C. 4 sin a = . D. 4 sina = - . 5 5 5 5 Lời giải Chọn C. 2 ìï 1 æ3ö ï 25 2 ï = + = +ç ÷ Ta có 1 cot a 1 ï ç ÷ = 4 2 ísin a çè4÷ø 16 ¾¾ sin a = . ï 5 ï0
ï < a < 90 ïî Câu 52: p tan a
Cho góc a thỏa mãn 3
sin a = và < a < p . Tính P = . 5 2 2 1+ tan a
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 496
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. P = -3. B. 3 P = . C. 12 P = . D. 12 P = - . 7 25 25 Lời giải Chọn D. ìï 4 2 co
ï sa = 1-sin a = ï Ta có ï 5 4 3 í ¾¾ cosa = - ¾¾ tan a = - . ïp 5 4
ïï < a < p ïïî2 Thay 3
tan a = - vào P , ta được 12 P = - . 4 25 Câu 53: a + a +
Cho góc a thỏa 1 sin a = và 0 0
90 <a <180 . Tính 2 tan 3cot 1 P = . 3 tan a + cot a A. 19 + 2 2 - - + P = . B. 19 2 2 P = . C. 26 2 2 P = . D. 26 2 2 P = . 9 9 9 9 Lời giải Chọn C. ìï 2 2 ìï 2 ï 2 ï a = - a ï = ï a = - Ta có cos 1 sin 2 2 tan ïí 3 cos a ï ¾¾ = - ¾¾ í 4 . ï 3 ï ï 0 0 90 < a <180 co ï ï ï t a = -2 2 ïî ïî ìï 2 ïï a =- Thay tan ï - í 4 vào = . ï P , ta được 26 2 2 P 9 co ïï t a = 2 - 2 ïî æ p ö Câu 54: p
Cho góc a thỏa mãn (p +a) 1 sin
= - và < a < p . Tính 7 P = tan çç -a÷÷. 3 2 çè 2 ÷ø A. P = 2 2. B. P = -2 2. C. 2 P = . D. 2 P = - . 4 4 Lời giải Chọn B. æ ö æ ö æ ö Ta có 7p p p cosa P = tan çç -a÷÷ = tan 3
çç p + -a÷÷= tançç -a÷÷= cot a = ç . è 2 ÷ø çè 2 ÷ø çè2 ÷ø sin a Theo giả thiết: (p +a) 1 1 1 sin
= - -sin a = - sin a = . 3 3 3 ìï 2 2 ï 2 co
ï sa = 1-sin a = ï Ta có 2 2 ï 3 í ¾¾ cosa = - ¾¾ P = 2 - 2. ïïp 3 ï < a < p ïïî2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 497
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Câu 55: p
Cho góc a thỏa mãn 3 cos a =
và - < a < 0 . Tính P= 5 + 3 tan a + 6 - 4 cot a. 5 2
A. P = 4. B. P = -4. C. P = 6. D. P = -6. Lời giải Chọn A. ìï 4 ìï 4 2 sin ï
a = 1-cos a = t ï an a = - ï ï Ta có ï 5 4 ï 3 í ¾¾ sin a = - ¾¾ í . ï p 5 ï 3 ïï a 0 c ï - < < ï ot a = - ïî 2 ï ï ïî 4 ìï 4 ïtan a = - ï Thay ï 3 í vào . ï
P , ta được P = 4 3 co ïï t a = - ïïî 4 Câu 56: p p
Cho góc a thỏa mãn 3 cos a =
và < a < . Tính 2 P =
tan a - 2 tan a +1 . 5 4 2 A. 1 P = - . B. 1 P = . C. 7 P = . D. 7 P = - . 3 3 3 3 Lời giải Chọn B. Ta có p p P = ( a - )2 tan
1 = tan a -1 . Vì < a < ¾¾ tan a > 1 ¾¾
P = tan a -1. 4 2 ìï 4 2 sin ï
a = 1-cos a = ï Theo giả thiết: ï 5 4 4 1 í ¾¾ sin a = ¾¾ tan a = ¾¾ P = . ïp p 5 3 3 ïï < a < ïïî4 2 æ pö æ pö Câu 57: p
Cho góc a thỏa mãn < a < 2p và tan a ç ÷
ç + ÷ =1 . Tính P= cos a ç ÷ ç - ÷+sin a . 2 çè 4÷ø çè 6 ÷ø + - A. 3 P = . B. 6 3 2 P = . C. 3 P = - . D. 6 3 2 P = . 2 4 2 4 Lời giải Chọn C. ìïp 3p p 9p
ï < a < 2p¬¾ < a + < ïï Ta có 2 4 4 4 p 5p ïí ¾¾ a + = ¾¾ a = . p ï æ p ö 4 4 ïïtan a ç ÷ ç + ÷ = 1 ï çè 4 ÷ø ïî
Thay a = p vào P , ta được 3 P = - . 2 æ pö Câu 58: p
Cho góc a thỏa mãn < a < 2p và cot a ç ÷
ç + ÷ = - 3 . Tính giá trị của biểu thức 2 çè 3÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 498
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 æ pö P = sin a ç ÷ ç + ÷+cosa ç . è 6 ÷ø A. 3 P = . B. P = 1. C. P = -1. D. 3 P = - . 2 2 Lời giải Chọn D. ìïp 5p p 7p
ï < a < 2p¬¾ < a + < ïï Ta có 2 6 3 3 p 11p 3p ïí ¾¾ a + = ¾¾ a = . ï æ pö 3 6 2 co ïï t a ç ÷ ç + ÷ = - 3 ï çè 3 ÷ø ïî Thay 3p a = vào P , ta được 3 P = - . 2 2 2 Câu 59: p sin a - cos a
Cho góc a thỏa mãn 4
tan a = - và < a < p . Tính P = . 3 2 2 sin a - cos a A. 30 P = . B. 31 P = . C. 32 P = . D. 34 P = . 11 11 11 11 Lời giải Chọn B. ìï 1 9 3 2 co ï s a = = cosa = ï 2 Ta có ïï 1+ tan a 25 5 3 4 í ¾¾ cosa = - ¾¾ sin a = tan . a cos a = . ïp 5 ï 5 ï < a < p ïïî2 Thay 4 sin a = và 3
cos a = - vào P , ta được 31 P = . 5 5 11 Câu 60: a - a
Cho góc a thỏa mãn tan a = 2. Tính 3sin 2 cos P = . 5cosa +7 sin a A. 4 P = - . B. 4 P = . C. 4 P = - . D. 4 P = . 9 9 19 19 Lời giải Chọn D.
Chia cả tử và mẫu của a - -
P cho cosa ta được 3 tan 2 3.2 2 4 P = = = . 5 + 7 tan a 5 + 7.2 19 Câu 61: a + a
Cho góc a thỏa mãn 1 cot a = . Tính 3sin 4 cos P = . 3 2 sin a -5cosa A. 15 P = - . B. 15 P = . C. P = -13. D. P = 13. 13 13
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 499
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn D. 1 3 + 4.
Chia cả tử và mẫu của 3 + 4 cot a 3
P cho sin a ta được P = = = 13 . 2 -5 cot a 1 2 -5. 3 2 2 a + a a + a Câu 62: 2 sin 3sin .cos 4 cos
Cho góc a thỏa mãn tan a = 2. Tính P = . 2 2 5sin a +6 cos a A. 9 P = ⋅ B. 9 P = ⋅ C. 9 P = - ⋅ D. 24 P = ⋅ 13 65 65 29 Lời giải Chọn A.
Chia cả tử và mẫu của P cho 2 cos a ta được 2 2
2 tan a + 3 tan a + 4 2.2 + 3.2 + 4 9 P = = = . 2 2 5 tan a + 6 5.2 + 6 13 2 2 a + a a- a Câu 63: 2 sin 3sin .cos 4 cos
Cho góc a thỏa mãn 1
tan a = . Tính P = . 2 2 2 5cos a-sin a A. 8 P = - ⋅ B. 2 P = ⋅ C. 2 P = - ⋅ D. 8 P = - ⋅ 13 19 19 19 Lời giải Chọn D.
Chia cả tử và mẫu của P cho 2 cos a ta được 2 æ1ö 1 2.ç ÷ ç ÷ + 3. - 4 2
2 tan a + 3 tan a - 4 çè2÷ø 2 8 P = = = - . 2 2 5- tan a æ1ö 19 5-ç ÷ ç ÷ çè2÷ø
Câu 64: Cho góc a thỏa mãn tan a = 5. Tính 4 4 P = sin a -cos . a A. 9 P = ⋅ B. 10 P = ⋅ C. 11 P = ⋅ D. 12 P = ⋅ 13 13 13 13 Lời giải Chọn D. Ta có P = ( 2 2 a - a) ( 2 2 a + a) 2 2 sin cos . sin cos = sin a -cos . a (*) 2 Chia hai vế của a ( P sin *) cho 2 cos a ta được = -1 2 2 cos a cos a
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 500
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 a - - P ( tan 1 5 1 12 2 1+ tan a) 2
= tan a -1 P = = = . 2 2 1+ tan a 1+ 5 13
Câu 65: Cho góc a thỏa mãn 5
sin a + cos a = . Tính P = sin . a cos . a 4 A. 9 P = ⋅ B. 9 P = ⋅ C. 9 P = ⋅ D. 1 P = ⋅ 16 32 8 8 Lời giải Chọn B. Từ giả thiết, ta có ( 9 a + a)2 25 25 sin cos = 1+ 2 sin . a cosa = ¾¾ P = sin . a cosa = . 16 16 32
Câu 66: Cho góc a thỏa mãn 12 sin c a osa =
và sina + cosa > 0. Tính 3 3 P = sin a +cos . a 25 A. 91 P = ⋅ B. 49 P = ⋅ C. 7 P = ⋅ D. 1 P = ⋅ 125 25 5 9 Lời giải Chọn A.
Áp dụng a +b = (a +b)3 3 3
-3ab(a + b), ta có P = a + a = ( a + a)3 3 3 sin cos sin cos
-3sin a cos a(sin a + cosa).
Ta có (sin a + cosa)2 24 49 2 2
= sin a + 2 sin a cos a + cos a = 1+ = . 25 25
Vì sin a +cosa > 0 nên ta chọn 7 sin a + cos a = . 5 ìï 7 sin ï a + cosa = ï 3 æ ö Thay ïï 5 7 12 7 91 í vào P = ç ÷ ç ÷ -3. . = . ï P , ta được 12 çè5÷ø 25 5 125 sin ïï acosa = ïïî 25 Câu 67: p
Cho góc a thỏa mãn 0 < a < và 5 sin a +cosa =
. Tính P = sin a-cos . a 4 2 A. 3 P = . B. 1 P = ⋅ C. 1 P = - ⋅ D. 3 P = - . 2 2 2 2 Lời giải Chọn D. Ta có ( a - a)2 +( a + a)2 = ( 2 2 sin cos sin cos
2 sin a + cos a) = 2 . Suy ra ( a - a)2 = -( a + a)2 5 3 sin cos 2 sin cos = 2 - = . 4 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 501
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Do p 0 < a <
suy ra sin a < cosa nên sin a-cosa < 0 . Vậy 3 P = - . 4 2
Câu 68: Cho góc a thỏa mãn sin a + cosa = m. . Tính P = sin a -cosa .
A. P = 2 - m. B. 2 P = 2 -m . C. 2 P = m -2. D. 2 P = 2 - m . Lời giải Chọn D. Ta có ( a - a)2 +( a + a)2 = ( 2 2 sin cos sin cos
2 sin a + cos a) = 2 . Suy ra ( a - a)2 = -( a + a)2 2 sin cos 2 sin cos = 2 -m 2 ¾¾
P = sin a -cosa = 2 -m .
Câu 69: Cho góc a thỏa mãn tan a + cot a = 2. Tính 2 2 P = tan a +cot . a A. P = 1. B. P = 2. C. P = 3. D. P = 4. Lời giải Chọn B. Ta có P = a + a = ( a + a)2 2 2 2 tan cot tan cot - 2 tan .
a cot a = 2 - 2.1 = 2.
Câu 70: Cho góc a thỏa mãn tan a+cot a =5. Tính 3 3 P = tan a +cot . a A. P = 100. B. P = 110. C. P = 112. D. P = 115. Lời giải Chọn B. Ta có P = a + a = ( a + a)3 3 3 tan cot tan cot
-3 tan a cot a(tan a + cot a) 3 = 5 -3.5 =110 .
Câu 71: Cho góc a thỏa mãn 2 i s n a +cosa = . Tính 2 2 P = tan a +cot . a 2 A. P = 12. B. P = 14. C. P = 16. D. P = 18. Lời giải Ta có 2 sin a + a = (sin a + a)2 1 1 cos cos
= sin a cosa = - . 2 2 4 Chọn B. 2 2 2 4 4 ( 2 2 sin a + cos a) 2 2 -2 sin . a cos a 1-2(sin a cosa)2 Khi đó sin a cos a sin a + cos a P = + = = = = 14. 2 2 2 2 cos a sin a sin . a cos a 2 2 sin . a cos a (sin a cosa)2 Câu 72: p
Cho góc a thỏa mãn < a < p và tan a - cot a = 1 . Tính P = tan a +cot . a 2 A. P = 1. B. P = -1. C. P = - 5. D. P = 5. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 502
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn C. Ta có 1 1 5
tan a - cot a = 1 tan a - = 1 2
tan a -tan a -1 = 0 tan a = . tan a 2 Do p -
< a < p suy ra tan a < 0 nên 1 5 1 2 tan a = ¾¾ cot a = = . 2 2 tan a 1- 5 Thay 1- 5 - tan a = và 2 cot a = vào P , ta được 1 5 2 P = + = - 5. 2 1- 5 2 1- 5
Câu 73: Cho góc a thỏa mãn 3cosa + 2 sin a = 2 và sin a < 0 . Tính sin . a A. 5 sin a = - . B. 7 sin a = - . C. 9 sin a = - . D. 12 sin a = - . 13 13 13 13 Lời giải Chọn A. Ta có a + a = ( a + a)2 3 cos 2 sin 2 3 cos 2 sin = 4 2 2 2 9 cos a +12 cos .
a sin a + 4 sin a = 4 5cos a +12 cos . a sin a = 0 é a = a( a + a) cos 0 cos 5cos 12 sin = 0 ê .
ê5cosa +12 sin a = 0 ë
· cosa = 0 sin a =1: loại (vì sin a < 0 ). ìï 5 sin ï a = - 5c
ìï osa +12 sin a = 0 ïï ï ï 13
· 5cosa +12 sin a = 0 , ta có hệ phương trình í í . 3c
ï osa +2 sin a = 2 ï 12 ïî co ïï sa = ïïî 13 Câu 74: p
Cho góc a thỏa mãn 3 p a < <
và sin a -2 cosa = 1. Tính P = 2 tan a - cot . a 2 A. 1 P = . B. 1 P = . C. 1 P = . D. 1 P = . 2 4 6 8 Lời giải Chọn C. sin ìï a < 0 Với 3p p < a < suy ra ïí . 2 co ï sa < 0 ïî sin ìï a -2 cosa = 1 Ta có ïí (1+ 2 cosa)2 2 + cos a = 1 2 2 sin ï a + cos a = 1 ïî écosa = 0 (loaïi) ê 2
5cos a + 4 cosa = 0 ê 4 ê . cosa = - êë 5
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 503
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Từ hệ thức a 2 2
sin a +cos a =1 , suy ra 3
sin a = - (do sin a < 0 ) sin 3 ¾¾ tan a = = và 5 cos a 4 cos a 4 cot a = = . sin a 3 Thay 3 tan a = và 4 cot a = vào P , ta được 1 P = . 4 3 6
Câu 75: Rút gọn biểu thức M = ( x + x )2 +( x - x )2 sin cos sin cos . A. M = 1. B. M = 2. C. M = 4.
D. M = 4 sin x.cos x. Lời giải Chọn B. (
ìïï sin x +cosx)2 2 2
= sin x + cos x + 2 sin x.cos x = 1+ 2 sin x.cos x Ta có ïí (
ïï sin x -cos x)2 2 2
= sin x + cos x -2 sin x.cos x = 1-2 sin x.cos x ïî Suy ra M = 2.
Câu 76: Mệnh đề nào sau đây là đúng? A. 1 3 5 3 4 4 sin x + cos x = + cos 4x. B. 4 4
sin x + cos x = + cos 4x. 4 4 8 8 C. 3 1 1 1 4 4 sin x + cos x = + cos 4x. D. 4 4
sin x + cos x = + cos 4x. 4 4 2 2 Lời giải Chọn C. Ta có x + x = ( x )2 + x x +( x )2 4 4 2 2 2 2 2 2 sin cos sin 2.sin .cos cos -2.sin x.cos x ( -
= sin x + cos x )2 1
- (2.sin x.cos x )2 1 1 1 cos 4 x 3 1 2 2 2 = 1- sin 2x = 1- . = + cos 4x. 2 2 2 2 4 4
Câu 77: Mệnh đề nào sau đây là đúng? A. 4 4 2
sin x -cos x =1-2cos x. B. 4 4 2 2
sin x -cos x =1-2sin x cos . x C. 4 4 2
sin x -cos x =1-2sin x. D. 4 4 2
sin x -cos x = 2cos x 1. - Lời giải Chọn A. Ta có x - x = ( x )2 -( x )2 4 4 2 2 = ( 2 2 x - x )( 2 2 sin cos sin cos sin cos sin x +cos x) 2 2 = x - x = ( 2 - x ) 2 2 sin cos 1 cos
- cos x = 1-2 cos x.
Câu 78: Rút gọn biểu thức 6 6
M = sin x +cos x. A. 2 2
M =1+3sin x cos x. B. 2 M =1-3sin x.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 504
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 C. 3 3 2 M = 1- sin 2x. D. 2 M = 1- sin 2x. 2 4 Lời giải Chọn D. Ta có M = x + x = ( x )3 +( x )3 6 6 2 2 sin cos sin cos
= (sin x + cos x)3 3 2 2 2 2
-3 sin x cos x ( 2 2 sin x + cos x ) 2 2 2
= 1-3 sin x cos x = 1- sin 2x. 4
Câu 79: Rút gọn biểu thức 2 2
M = tan x -sin x. A. 2 M = tan x. B. 2 M = sin x. C. 2 2
M = tan x.sin x . D. M = 1. Lời giải Chọn C. 2 æ ö Ta có sin x 1 2 2 2 2 2 2
M = tan x -sin x =
-sin x = sin x çç
-1÷÷ = sin x.tan x. 2 2 cos ç ÷ x ècos x ø
Câu 80: Rút gọn biểu thức 2 2
M = cot x -cos x. A. 2 M = cot x. B. 2 M = cos x. C. M = 1. D. 2 2
M = cot x.cos x. Lời giải Chọn D. 2 æ ö Ta có cos x 1 2 2 2 2 2 2
M = cot x -cos x =
-cos x = cos x çç
-1÷÷ = cos x.cot x. 2 2 sin ç ÷ x èsin x ø
Câu 81: Rút gọn biểu thức M = ( 2 x ) 2 x +( 2 1 – sin cot 1 – cot x ). A. 2
M = sin x. B. 2
M = cos x. C. 2
M = – sin x. D. 2 M = – cos x. Lời giải Chọn A.
Ta biến đổi: M = ( 2 2 x - x )+( 2 - x ) 2 2 cot cos 1 cot
= 1-cos x = sin x.
Câu 82: Rút gọn biểu thức 2 2 2 2 2
M = sin a tan a +4 sin a-tan a +3cos . a A. 2 M =1+sin . a B. M = sin . a C. M = 2 sin . a D. M = 3. Lời giải Chọn D. Ta có 2 M = a( 2 a - ) 2 2 tan sin
1 + 4 sin a + 3 cos a 2 = a( 2 - a) 2 2 tan cos
+ 4 sin a + 3cos a
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 505
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 2 = - a + a + a = ( 2 2 sin 4 sin 3 cos
3 sin a + cos a) = 3.
Câu 83: Rút gọn biểu thức M = ( 4 4 x + x - )( 2 2 sin cos
1 tan x + cot x + 2).
A. M = -4. B. M = -2. C. M = 2. D. M = 4. Lời giải Chọn D. 2 2 æ ö Ta có = ( sin x cos 2 2 1-2 sin .cos - ) 1 x ç ÷ M x x ç + + 2÷ ç 2 2 çècos ÷ x sin x ÷ø 4 4 2 2 = (-
)æsin x +cos x +2sin x.cos ö 2 sin . cos x ç ÷ x x ç ÷ = ç ÷ (-2).( 2 2 sin x + cos x)2 2 2 = -2. 2 2 çè sin x cos x ÷ø
Câu 84: Đơn giản biểu thức 4 2 2
P = sin a + sin a cos a.
A. P = sin a . B. P = sin . a C. P = cos . a
D. P = cosa . Lời giải Chọn A. Ta có 4 2 2 2 P = a + a a = a( 2 2 a + a) 2 sin sin cos sin sin cos
= sin a = sin a . 2 + a Câu 85: 1 sin
Đơn giản biểu thức P = . 2 1-sin a A. 2 P =1+2 tan . a B. 2 P =1-2 tan . a C. 2 P = 1 - + 2 tan . a D. 2 P = 1 - - 2 tan . a Lời giải Chọn A. 2 2 Ta có 1+ sin a 1+ sin a 1 2 2 P = = = + tan a = 1+ 2 tan . a 2 2 2 1-sin a cos a cos a Câu 86: 1-cos a 1
Đơn giản biểu thức P = - . 2 sin a 1+ cos a A. 2 cos a 2 P = - . B. P = . C. 2 P = . D. P = 0. 2 sin a 2 sin a 1+ cos a Lời giải Chọn D. Ta có 1-cos a 1 1-cos a 1 P = - = - . 2 2 sin a 1+ cos a 1-cos a 1+ cos a 1-cosa 1 1 1 = - = - = 0.
(1-cosa)(1+cosa) 1+cosa 1+cosa 1+cosa
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 506
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 - a a Câu 87: 1 sin cos
Đơn giản biểu thức 2 P = -cos . a 2 cos a A. 2 P = tan . a B. P = 1. C. 2 P = -cos . a D. 2 P = cot . a Lời giải Chọn A. 2 - a a - a 1-cos a( 2 2 2 2 4 sin a + cos 1 sin cos cos a) 2 2 Ta có 1-cos a sin a P = = 2 = = = tan . a 2 2 cos a cos a 2 2 cos a cos a 2 - Câu 88: 2cos x 1
Đơn giản biểu thức P = . sin x +cos x
A. P = cos x + sin x.
B. P = cos x -sin x.
C. P = cos 2x - sin 2x.
D. P = cos 2x + sin 2x. Lời giải Chọn B. 2 x -( 2 2 x + x ) 2 2 2 cos sin cos Ta có cos x -sin x P = = = cos x -sin x. sin x + cos x sin x + cos x
(sin a + cosa)2 - Câu 89: 1
Đơn giản biểu thức P = .
cot a -sin a cos a A. 2 sin a 2 P = 2tan . a B. P = . C. 2 P = 2cot . a D. P = . 3 cos a 2 cos a Lời giải Chọn A. ( a + a)2 2 2 sin cos -1 Ta có sin a + 2 sin .
a cosa + cos a -1 P = =
cot a -sin a cosa æ 1 ö cos . a çç -sin a÷÷ çèsin a ÷ø 2 1+ 2 sin . a cos a -1 2 sin . a cos a 2 sin a 2 = = = = 2 tan . a 2 3 2 1- sin a cos a cos a cos . a sin a sin a 2 æ + ö Câu 90: sin a tan a
Đơn giản biểu thức P = ç ÷ ç ÷ +1. ç è cosa +1 ÷ø A. 1 1 P = 2. B. P = 1+ tan . a C. P = . D. P = . 2 cos a 2 sin a Lời giải Chọn C. æ 1 ö æcosa +1ö sin a 1 ç ÷ ç + ÷ sin aç ÷ ç ÷ + ç ÷ è ø ç ÷
Ta có sin a tan a cos a è cos a ø sin a = = = = tan . a . cos a +1 cos a +1 cos a +1 cos a
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 507
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Suy ra 1 2 P = tan a +1 = . 2 cos a 2 æ + ö Câu 91: 1 cos a
Đơn giản biểu thức ç ÷ P = tan aç -sin a÷. ç çè sin a ÷÷ø A. P = 2. B. P = 2 cos . a C. P = 2 tan . a D. P = 2 sin . a Lời giải Chọn B. 2 2 æ + ö æ ö Ta có 1 cos a ç ÷ sin a 1 cos a ç ÷ P = tan aç -sin a÷ = ç ÷ ç + -sin a÷. çè sin a
÷ø cosa çèsin a sin a ÷÷ø ( 2 - a) 2 2 2 2 2 1 sin + + - cos 1 sin 1 cos sin a a a a 2 cos a = + cosa - = = = = 2 cos . a cosa cos a cosa cos a cosa 2 2 - Câu 92: cot x cos x sin c x osx
Đơn giản biểu thức P = + . 2 cot x cot x
A. P = 1. B. P = -1. C. 1 P = . D. 1 P = - . 2 2 Lời giải Chọn A. 2 2 2 2
Ta có cot x -cos x cos x sin 2 x 2 = 1- = 1-cos x. = 1-sin x. 2 2 2 cot x cot x cos x Và sin x.cosx sin x 2 = sin x.cos x. = sin x . Suy ra 2 2
P = 1-sin x + sin x = 1. cot x cos x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 508
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác
BÀI 3. CÔNG THỨC LƯỢNG GIÁC
A. KIẾN THỨC CƠ BẢN CẦN NẮM I – CÔNG THỨC CỘNG
cosa b cos a cosb sin asin b
cosa b cos a cosb sin asin b
sin a b sin a cosb cos a sin b
sin a b sin a cosb cos a sin b a b tan a tan b tan
1 tanatanb a b tan a tan b tan . 1 tan a tan b
II – CÔNG THỨC NHÂN ĐÔI
sin 2a 2sin a cos a 2 2 2 2
cos 2a cos a sin a 2 cos a 1 1 2sin a 2 tan a tan 2a . 2 1 tan a
III – CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG, TỔNG THÀNH TÍCH
1. Công thức biến đổi tích thành tổng 1
cos a cosb cos
a b cosa b 2 1
sin a sin b cos
a bcosa b 2 1
sin a cos b sin
a bsina b. 2
2. Công thức biến đổi tổng thành tích u v u v
cosu cos v 2cos cos 2 2 u v u v
cosu cos v 2 sin sin 2 2 u v u v
sin u sin v 2sin cos 2 2 u v u v
sin u sin v 2cos sin 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 509
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng toán 1: tính giá trị lượng giác, biểu thức lượng giác. 1. Phương pháp giải.
Sử dụng công thức lượng giác một cách linh hoạt để biến đổi biểu thức lượng giác nhằm triệt tiêu
các giá trị lượng giác của góc không đặc biệt và đưa về giá trị lượng giác đặc biệt.
2. Các ví dụ minh họa. 7p 5p
Ví dụ 1: Tính các giá trị lượng giác sau: 0 0 cos 795 , sin18 , tan , cot . 12 8 Lời giải Vì 0 0 0 0 0 0
795 = 75 + 2.360 = 30 + 45 + 2.360 nên 3 2 1 2 6 - 2 0 0 0 0 0 0
cos 795 = cos 75 = cos 30 cos 45 - sin 30 sin 45 = . - . = 2 2 2 2 4 Vì 0 0 0 54 + 36 = 90 nên 0 0 sin 54 = cos 36 Mà 0 = ( 0 ) 2 0 cos 36 cos 2.18 = 1 - 2 sin 18 0 = ( 0 0 + ) 0 0 0 0 sin 54 sin 18 36 = sin18 cos 36 + sin 36 cos18 0 = ( 2 0 - ) 0 2 0 0 + = ( 2 0 - ) 0 + ( 2 0 sin18 . 1 2 sin 18 2 sin 18 cos 18 sin18 . 1 2 sin 18 2 sin 18 1 - sin 18 ) 0 3 0 = 3 sin 18 - 4 sin 18 Do đó 0 3 0 2 0 - = - ( 0 - )( 2 0 0 3 sin 18 4 sin 18 1 2 sin 18 sin 18 1 4 sin 18 + 2 sin18 - 1) = 0 5 - 1 5 + 1 0 sin18 = 1 hoặc 0 sin18 = hoặc 0 sin18 = 2 2 5 - 1 Vì 0 0 < sin18 < 1 nên 0 sin18 = . 2 p p tan + tan æ ö 7p p p 3 + 1 ç ÷ 3 4 tan = tanç + ÷ = = = -2 - 3 12 çè 3 4 ÷ø p p 1 - 3 1 - tan tan 3 4 æ ö 5p p p p cot = cotç ÷ ç + ÷ = -tan 8 çè 2 8 ÷ø 8
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 510
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác p 2 tan p æ p ö Ta lại có ç ÷ 8 1 = tan = tanç2. ÷ = suy ra 4 çè 8 ÷ø p 2 1 - tan 8 p p p p 2 2 1 - tan = 2 tan tan + 2 tan - 1 = 0 8 8 8 8 p p tan = -1 - 2 hoặc tan = -1 + 2 8 8 p p Do tan > 0 nên tan = 1 - + 2 8 8 5p Vậy cot = 1 - 2 8
Ví dụ 2: Tính giá trị biểu thức lượng giác sau: a) 0 0
A = sin 22 30 ' cos 202 30 ' p p b) 4 B = 4 sin + 2 cos 16 8 p 2p sin - sin c) 5 15 C = p 2p cos - cos 5 15 p 5p 7p d) D = sin - sin + sin 9 9 9 Lời giải a) Cách 1: Ta có 0 = ( 0 0 + ) 0 cos 202 30 ' cos 180 22 30 ' = - cos 22 30 ' 1 2 Do đó 0 0 0
A = -sin 22 30 ' cos 22 30 ' = - sin 45 = - 2 4 1 1 Cách 2: A = é sin( 0 0 22 30 '+ 202 30 ') + sin( 0 0 22 30 '- 202 30 ') 0 ù = ésin225 + sin( 0 -180 )ù 2 ë û 2 ë û 1 = é sin( 1 2 0 0 180 + 45 ) 0 0 - sin180 ù = - sin 45 = - 2 ë û 2 4 2 2 æ p ö p é æ p öù p b) ç 2 B = ç2 sin
÷÷ + 2cos = ê1 - cosçç2. ÷÷ú + 2cos ç è 16 ÷ø 8 ê çè 16 ÷øú 8 ë û p 2 1 cos 1 p p p + + 6 + 2 2 4 2 = 1 - 2 cos + cos + 2 cos = 1 + = 1 + = 8 8 8 2 2 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 511
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 1 æ p 2p ö 1 æ p 2 2 p p p ö 2 cos ç ÷ - ç + ÷sin ç ÷ p sin sin ç - ÷ ç ÷ è ø ç ÷ cos 2 5 15 2 è 5 15 ÷ø p c) 5 15 6 C = = = - = -cot = - 3 p 2p 1 æ p 2p ö 1 æ p 2p ö p 6 cos - cos -2 sin ç ÷ ç + ÷sin ç ÷ ç - ÷ sin 5 15 2 çè 5 15 ÷ø 2 çè 5 15 ÷ø 6 æ p 7p ö 5p 4p p 5p 4p 5p d) D ç = çsin + sin ÷÷ - sin = 2 sin .cos - sin = sin - sin = 0 ç è 9 9 ÷ø 9 9 3 9 9 9
Ví dụ 3: Tính giá trị biểu thức lượng giác sau: 1 1 a) A = + b) B = ( 0 + )( 0 1 tan 20 1 + tan 25 ) 0 0 cos 290 3 sin 250 p 2p p 2p c) 0 0 0 0
C = tan 9 - tan 27 - tan 63 + tan 81 d) 2 2 D = sin + sin + sin sin 9 9 9 9 Lời giải a) Ta có 0 = ( 0 0 0 + + ) = - ( 0 0 + ) 0 cos 290 cos 180 90 20 cos 90 20 = sin 20 0 = ( 0 0 0 + - ) = - ( 0 0 - ) 0 sin 250 sin 180 90 20 sin 90 20 = -cos 20 3 1 0 0 0 0 cos 20 - sin 20 1 1 3 sin 20 - sin 20 2 2 C = - = = 4 0 0 0 0 0 0 sin 20 3 cos 20 3 sin 20 .cos 20 3.2.sin 20 .cos 20 0 0 0 0 0 sin 60 cos 20 - cos 60 sin 20 4 sin 40 4 3 = 4 = = 0 0 3 sin 40 3 sin 40 3 0 0 0 0 0 0 æ sin 20 öæ sin 25 ö
sin 20 + cos 20 sin 25 + cos 25 b) Cách 1: Ta có B çç1 ÷ç = + ÷ç1 ÷ + ÷ = . 0 ç ÷ 0 ÷ç ÷ 0 0 cos 20 cos 25 ÷ è øè ø cos 20 cos 25 0 0 0 0 0 0 0 0 sin 20 cos 45 + cos 20 sin 45 sin 25 cos 45 + cos 25 sin 45 = 2. . 2. 0 0 cos 20 cos 25 0 0 sin 65 sin 70 = 2 = 2 0 0 cos 20 cos 25 0 0 tan 20 + tan 25 Cách 2: Ta có 0 tan 45 = tan( 0 0 20 + 50 ) = 0 0 1 - tan 20 tan 25 0 0 tan 20 + tan 25 Suy ra 0 0 0 0 1 =
tan 20 + tan 25 + tan 20 tan 25 = 1 0 0 1 - tan 20 tan 25 ( 0 + )( 0 1 tan 20 1 + tan 25 ) = 2 . Vậy B = 2 c) 0 0 C = + - ( 0 0 tan 9 tan 81 tan 27 + tan 63 )
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 512
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 0 0 0 0 0 0 0 0 sin 9 cos 81 + sin 81 cos 9 sin 27 cos 63 + sin 63 cos 27 = - 0 0 0 0 cos 9 cos 81 cos 27 cos 63 1 1 2 2 2( 0 0 sin 54 - sin18 ) = - = - = 0 0 0 0 0 0 0 0 cos 9 sin 9 cos 27 sin 27 sin18 sin 54 sin18 sin 54 0 0 4 cos 36 .sin18 = = 4 0 0 sin18 .sin 54 2 p 2p p 2p æ p 2p ö p 2p d) 2 2 D sin sin sin sin ç = + + = çsin + sin ÷÷ - sin sin 9 9 9 9 çè 9 9 ÷ø 9 9 2 æ p p ö 1 æ p p ö p 1 æ 1 p ö ç ÷ ç ÷ 2 ç2 sin cos ÷ çcos cos ÷ cos ç = + - = + ç - cos ÷÷ çè 6 18 ÷ø 2 çè 3 9 ÷ø 18 2 çè 2 9 ÷ø p 1 + cos 1 æ 1 p ö 3 9 ç = + ç - cos ÷÷ = 2 2 çè 2 9 ÷ø 4
Lưu ý: Biến đổi sau thường xuyên được sử dụng é ù 1 3 p sin x 3 cos x 2 ê sin x cos x ú = = 2 sin(x ) ê 2 2 ú 3 êë úû é ù 3 1 p 3 sin x cos x 2 ê sin x cos x ú = = 2 sin(x ) ê 2 2 ú 6 êë úû é ù 1 1 p
sin x cos x = 2 ê sin x
cos x ú = 2 sin(x ) . êë 2 2 ú 4 û
Ví dụ 4: Tính giá trị biểu thức lượng giác sau: p p p p a) A = sin cos .cos .cos b) sin10 . o sin 30 . o sin 50 . o sin 70o B = 32 32 16 8 p 3p p 2p 3p c) C = cos + cos d) 2 2 2 D = cos + cos + cos 5 5 7 7 7 Lời giải a) 1 æ p p ö p p 1 p p p 1 p p 1 p 2 A ç = ç2 sin cos
÷÷.cos .cos = sin .cos .cos = sin .cos = sin = 2 çè 32 32 ÷ø 16 8 2 16 16 8 4 8 8 8 4 16 1 b) Ta có 0 0 cos 20 cos 40 cos 80o B = do đó 2 0 0 0 0 16 sin 20 .
8 sin 20 cos 20 cos 40 cos 80o B =
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 513
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 0 0 o = 4 sin 40 cos 40 cos 80 0 0 0 = 2 sin 80 cos 80 = sin160 0 sin160 1 Suy ra B = = . 0 16 sin 20 16 p 2p p c) Ta có C = 2 cos cos . Vì sin ¹ 0 nên 5 5 5 p p p 2p 2p 2p 4p
2 sin .C = 4 sin cos cos = 2 sin cos = sin 5 5 5 5 5 5 5 1 Suy ra C = 2 2p 4p 6p 1 + cos 1 + cos 1 + cos 3 1 æ 2p 4p 6p ö c) 7 7 7 D ç = + + = + çcos + cos + cos ÷÷ 2 2 2 2 2 çè 7 7 7 ÷ø 2p 4p 6p p Xét T = cos + cos + cos , vì sin ¹ 0 nên 7 7 7 7 p p 2p p 4p p 6p 2 sin T = 2 sin cos + 2 sin cos + 2 sin cos 7 7 7 7 7 7 7 æ 3p p ö æ 5p 3p ö æ 5p ö ççsin sin ÷ ç ÷ çsin sin ÷ ç = - + - ÷ + çsin p - sin ÷÷ ç è 7 7 ÷ø çè 7 7 ÷ø çè 7 ÷ø p = -sin 7 1 Suy ra T = - . 2 3 1 æ 1 ö 5 Vậy D = + .ç ÷ ç- ÷ = . 2 2 çè 2 ÷ø 4 2 6 Ví dụ 5: Cho ,
a b thoả mãn sin a + sin b =
và cos a + cos b =
. Tính cos(a - b ) và 2 2 sin(a + b ) . Lời giải 2 1 Ta có 2 2 sin a + sin b =
sin a + sin b + 2 sin a sin b = (1) 2 2 6 3 2 2 cos a + cos b =
cos a + cos b + 2 cos a cos b = (2) 2 2
Cộng vế với vế của (1) và (2) ta được
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 514
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 2 2 2 2
sin a + sin b + cos a + cos b + 2 sin a sin b + 2 cos a cos b = 2
2 + 2(sin a sin b + cos a cos b ) = 2 2 cos(a - b ) = 0
Vậy cos(a - b ) = 0
Từ giả thiết ta có ( a + b )( a + b ) 2 6 sin sin cos cos = . 2 2 3
sin a cos a + sin a cos b + sin b cos a + sin b cos b = 2 1 ( a + b ) + (a + b ) 3 sin 2 sin 2 sin = 2 2
Mặt khác sin 2a + sin 2b = 2 sin(a + b )cos(a - b ) = 0 (Do cos(a - b ) = 0 ) Suy ra (a + b ) 3 sin = 2
Dạng toán 2: xác định giá trị của một biểu thức lượng giác có điều kiện.
1. Các ví dụ minh họa. 4 p p æ p ö æ p ö
Ví dụ 1: Cho cos 2x = - , với < x <
. Tính sin x, cos x, sinççx ÷÷, cosç + ç2x ÷ - ÷ . 5 4 2 çè 3 ÷ø çè 4 ÷ø Lời giải p p Vì < x <
nên sin x > 0, cos x > 0 . 4 2
Áp dụng công thức hạ bậc, ta có : 1 - cos 2x 9 3 2 sin x = = sin x = 2 10 10 1 + cos 2x 1 1 2 cos x = = cos x = 2 10 10
Theo công thức cộng, ta có æ p ö p p 3 1 1 3 3 + 3 sinççx ÷
+ ÷ = sin x cos + cos x sin = . + . = ç è 3 ÷ø 3 3 10 2 10 2 2 10 æ p ö p p 4 2 2 3 1 2 cosçç2x ÷
- ÷ = cos2x sin + cos sin 2x = - . + .2. . = - ç è 4 ÷ø 4 4 5 2 2 10 10 10 p Ví dụ 2: Cho 2
cos 4a + 2 = 6 sin a với
< a < p . Tính tan 2a . 2 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 515
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác Ta có 2 2
cos 4a + 2 = 6 sin a 2 cos 2a - 1 + 2 = 3(1 - cos2a) 1 2
2 cos 2a + 3 cos 2a - 2 = 0 (2 cos2a - 1)(cos2a + 2) = 0 cos2a = (Vì 2 cos 2a + 2 > 0 ) 1 1 Ta có 2 2 1 + tan 2a = tan 2a = - 1 = 3 2 2 cos 2a cos 2a p Vì
< a < p p < a < 2p nên sin 2a < 0 . Mặt khác cos2a > 0 do đó tan 2a < 0 2 Vậy tan 2a = - 3 1 1 1 1 Ví dụ 3: Cho + + + = 7 . Tính cos 4a . 2 2 2 2 tan a cot a sin a cos a Lời giải 1 1 1 1 Ta có + + + = 7 2 2 2 2 tan a cot a sin a cos a 2 2 sin a + 1 cos a + 1 + = 7 2 2 cos a sin a 2 sin a( 2 sin a + 1) 2 + cos a( 2 cos a + 1) = 7 2 2 sin a cos a 4 4 2 2
sin a + cos a + 1 = 7 sin a cos a
(sin a + cos a)2 2 2 2 2 2 2
- 2 sin a cos a + 1 = 7 sin a cos a 2 2
2 = 9 sin a cos a
8 = 9(2 sin a cos a)2 2 8 = 9 sin 2a
16 = 9(1 - cos 4a) 7 cos 4a = - 9 7 Vậy cos 4a = - 9 a æ a + 2013p ö
Ví dụ 4: Cho sin a + cos a = cot với 0 < a < p . Tính tanç ÷ ç ÷ . 2 çè 2 ÷ø Lời giải a a sin 2 tan a a a Ta có 2 2 2 sin a = 2 sin cos = 2 cos . = 2 2 2 a a 2 cos tan + 1 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 516
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác æ a ö a 2 ç ÷ 2 ç sin ÷ 1 - tan a a a ç ÷ 2 2 2 = - = ç 2 ÷ 2 cos a cos sin cos 1 - ÷ = ç 2 2 2 a ÷ ç ÷ a ç 2 ÷ 2 ç cos ÷ tan + 1 çè 2 ÷ø 2 a a 2 2 tan 1 - tan a 1 Do đó 2 2
sin a + cos a = cot + = 2 a a a 2 2 tan + 1 tan + 1 tan 2 2 2 a æ a a ö a a a a ç 2 ÷ 2 3 2 tan ç1 + 2 tan - tan ÷ = 1 + tan tan - tan - tan + 1 = 0 2 çè 2 2 ÷ø 2 2 2 2 2 æ a ö æ a ö a ççtan 1÷ ç
- ÷ çtan + 1÷÷ = 0 tan = 1 çè 2 ÷ø çè 2 ÷ø 2 a p a a a
Vì 0 < a < p 0 < < do đó tan > 0 nên tan = 1 cot = 1 2 2 2 2 2 æ a + 2013p ö æ a p ö a Ta có tanç ÷ ç ÷ tanç = ç + 2006p ÷ + ÷ = -cot = -1 ç è 2 ÷ø çè 2 2 ÷ø 2 æ a + 2013p ö Vậy tanç ÷ ç ÷ = -1 ç è 2 ÷ø a
Lưu ý: Ta có thể biểu diễn sin , a cos , a tan ,
a cota qua t = tan như sau: 2 2 2 2t 1 - t 2t 1 - t sin a = , cos a = , tan a = , cot a =
với a làm các biểu thức có nghĩa. 2 2 2 1 + t 1 + t 1 - t 2t Ví dụ 5: Cho (a + b ) 1 sin
= , tan a = -2 tan b . 3 æ 3p ö æ p ö æ 5p ö æ p ö Tính A sinçça ÷÷cosçça ÷÷ sinççb ÷÷sinç = + + + - çb ÷ - ÷ ç . è 8 ÷ø çè 8 ÷ø çè 12 ÷ø çè 12 ÷ø Lời giải Ta có (a + b ) 1 1 sin =
sin a cos b + cos a sin b = (1) 3 3
tan a = -2 tan b sin a cos b = -2 sin b cos a (2) ìï 1 ìï 1 ìï 1 2 2
ïcos a sin b = - ïcos a sin b = ï( 2 1 - sin a ) 2 sin b = ï ï ï
Từ (1) và (2) ta được ï 3 ï 9 ï 9 í í í ï 2 ï 4 ï 4 2 2 2 ïïsina cosb ïïsin a cos b ï = - = ïsin a( 2 1 - sin b ) = ïî 3 ïî 9 ïî 9
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 517
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác ìïï( 1 2 1 - sin a ) 2 sin b = ï æ 1 ö ï 1 9 ç 2 ÷ 2 í
ç1 - sin b - ÷sin b = ï 1 ç ÷ 2 2 è 3 ø 9
ïï sin a - sin b = ï î 3 2 2 1 æ 1 ö 1 4 2 ç 2 ÷ 2
sin b - sin b +
= 0 çsin b - ÷ = 0 sin b = 3 9 çè 3 ÷ø 3 1 2 Do đó 2 2 sin a = sin b + = 3 3 æ 3p ö æ p ö 1 é æ p ö p ù 1 æ ç ÷ ç ÷ ç + ÷ ç + ÷ = ê ç ÷ ç 2 ö Ta có sin a cos a
sinç2a + ÷ - sin ú = çcos2a ÷ - ÷ ç ÷ è ø ç ÷ è ø ê ç ÷ è ø ú ç ÷ 8 8 2 2 4 2 ç ë û è 2 ÷ø 1 æç 2 ö÷ 1 æç 2 2 ö÷ 2 + 3 2 2 = ç1 - 2 sin a - ÷ = ç1 - 2. - ÷ = - ç ÷ ç ÷ ç ÷ 2 è 2 ÷ø 2 çè 3 2 ÷ø 12 æ p ö æ 5p ö 1 é æ p ö p ù 1 é 3 ù sinççb ÷ - ÷cosççb ÷ - ÷ = ê sinçç2b ÷ - ÷ + sin ú ê = -cos 2b ú + ç è 12 ÷ ç ø è 12 ÷ø 2 ê çè 2 ÷ø 3 ú 2 ê 2 ú ë û êë úû 1 æ 3 ö ç ÷ 1 æ 1 3 ö ç ÷ -2 + 3 2 2 = ç-1 + 2 sin b + ÷ = ç-1 + 2. + ÷ = ç ÷ ç ÷ ç ÷ 2 è 2 ÷ø 2 çè 3 2 ÷ø 12 2 + 3 2 -2 + 3 2 1 Do đó A = - + = - 12 12 3
Dạng toán 3: chứng minh đẳng thức, đơn giản biểu thức lượng giác và chứng minh biểu thức
lượng giác không phụ thuộc vào biến. 1. Phương pháp giải.
Để chứng minh đẳng thức lượng giác ta có các cách biển đổi: vế này thành vế kia, biến đổi tương
đương, biến đổi hai vế cùng bằng một đại lương trung gian. Trong quá trình biến đổi ta cần sử dụng
linh hoạt các công thức lượng giác.
Lưu ý: Khi biến đổi cần phải hướng đích , chẳng hạn biến đổi vế phải, ta cần xem vế trái có đại
lượng nào để từ đó liên tưởng đến kiến thức đã có để làm sao xuất hiện các đại lượng ở vế trái. Và
ta thường biến đổi vế phức tạp về vế đơn giản hơn.
2. Các ví dụ minh họa.
Ví dụ 1: Chứng minh rằng với mọi góc lượng giác a làm cho biểu thức xác định thì 3 cos 4a a) 4 4 sin a + cos a = + 4 4 5 3 b) 6 6 sin a + cos a = + cos 4a 8 8
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 518
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 1 - sin 2a p c) 2 = cot ( + a) 1 + sin 2a 4 Lời giải 1
a) Ta có sin a + cos a = (sin a + cos a)2 4 4 2 2 2 2 2
- 2 sin a cos a = 1 - sin 2a 2 1 - cos 4a 3 cos 4a = 1 - = + 4 4 4 b) Ta có
sin a + cos a = (sin a)3 + (cos a)3 6 6 2 2 + 2 3 sin a 2 cos a( 2 sin a + 2 cos a ) - 2 3 sin a 2 cos a( 2 sin a + 2 cos a ) 3 3 3
= (sin a + cos a)3 - 3 sin a cos a = 1 - (2 sin a cos a)2 2 2 2 2 = 1 - 2 sin a 2 = 1 - (1 - cos 4a) 4 4 8 5 3 = + cos 4a 8 8 1 - sin 2a
sin a + cos a - 2 sin a cos a (sina - cosa)2 2 2 c) Ta có = = 2 2 1 + sin 2a
sin a + cos a + 2 sin a cos a (sina + cosa)2 2 é æ p öù æ p ö ê ç ÷ 2 2 cosça + ÷ú 2 cos çça ÷ + ÷ ê çè 4 ÷øú çè 4 ÷ø æ p ö ë û 2 cot ç = = = ça ÷ + ÷ 2 æ é æ öù p ö çè 4 ÷ p ø 2 ê ç ÷ ç + ÷ú 2 sin ç ÷ 2 sin ça a + ÷ ê ç ÷ ç ÷ è øú è 4 ÷ 4 ø ë û p
Ví dụ 2: Cho 0 < a < , p a ¹ . Chứng minh rằng: 2 æ a p ö
a) 1 + cos a + 1 - cos a = 2 sinç ÷ ç + ÷ ç è 2 4 ÷ø
1 + cos a + 1 - cos a æ a p ö b) = tanç ÷ ç + ÷ ç ÷
1 + cos a - 1 - cos a è 2 4 ÷ø Lời giải æ a p ö
a) Do 0 < a < p nên sinç ÷
ç + ÷ > 0, sin a > 0 ç è 2 4 ÷ø
Đẳng thức tương đương với ( æ a p ö
1 + cos a + 1 - cos a )2 2 = 4 sin ç ÷ ç + ÷ çè 2 4 ÷ø é æ p öù
2 + 2 1 + cos a 1 - cos a = 2 ê1 - cosçça ÷ + ÷ú ê çè 2 ÷øú ë û 2
1 - cos a = sin a
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 519
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 2 2 2 2
1 - cos a = sin a sin a + cos a = 1 (luôn đúng) ĐPCM. ( + a + - a)2 1 cos 1 cos b) VT = (
1 + cos a - 1 - cos a )( 1 + cosa + 1 - cosa ) 2
2 + 2 1 + cos a. 1 - cos a 1 + 1 - cos a 1 + sin a = = = 2 cos a cos a cos a
Vì 0 < a < p nên sin a > 0 do đó 2 æ a a a a a a ö ç ÷ 2 2 + + çsin + cos sin cos 2 sin cos ÷ 1 + sin a çè 2 2 ÷ 2 2 2 2 ø VT = = = cos a a a æ a a öæ a a ö 2 2 cos sin ççsin cos ÷ç - + ÷çcos - sin ÷÷ 2 2 çè 2 2 ÷øçè 2 2 ÷ø æ a p a a ö 2 sinç ÷ sin + cos ç + ÷ çè 2 4 ÷ 2 2 ø æ a p ö = = = tanç ÷
ç + ÷ = VP ĐPCM. a a æ a p ö çè 2 4 ÷ø cos - sin 2 cosç ÷ ç + ÷ 2 2 çè 2 4 ÷ø
Ví dụ 3: Chứng minh rằng a) 2 2
sin(a + b).sin(a - b) = sin a - sin b a b b) cot cot
= 2 với sin a + sin b = 3 sin(a + b ),a + b ¹ k2p 2 2
sin a + sin b cos(a + b ) c) = tan(a + b )
cos a - sin b sin(a + b ) Lời giải 1
a) Ta có sin(a + b).sin(a - b) =- é cos 2a - cos 2b ù 2 ë û 1 = - é( 2 1 - 2 sin a ) - ( 2 1 - 2 sin b ) 2 2
ù = sin a - sin b 2 ë û a + b a - b a + b a + b
b) Từ giả thiết ta có 2 sin cos = 6 sin cos 2 2 2 2 a + b a - b a + b
Do a + b ¹ k2p sin ¹ 0 suy ra cos = 3 cos 2 2 2 a b a b æ a b a b ö cos cos sin sin 3ç + = çcos cos - sin sin ÷÷ 2 2 2 2 çè 2 2 2 2 ÷ø a b a b 2 sin sin = cos cos 2 2 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 520
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác a b cot cot = 2 ĐPCM 2 2 1
sin a + é sin(a + 2b ) + sin( a - )ù ë û
sin a + sin(a + 2b ) c) Ta có 2 VT = = æ 1 ö a + a + b cos a ç ÷
- ç- ÷é cos(a + 2b ) - cos( a - ) cos cos( 2 ) ù çè 2 ÷ë û ø
2 sin(a + b )cos( b - ) =
= tan(a + b ) = VP ĐPCM
2 cos(a + b )cos( b - )
Ví dụ 4: Chứng minh biểu thức sau không phụ thuộc vào x . æ p 2 ö æ 2p ö a) 2 A cos a 2 ç cos ç a ÷ 2 ç = + + ÷ + cos ç - a ÷÷ ç ÷ è 3 ø ç ÷ è 3 ø æ p ö æ p ö æ p ö æ p 3 ö b) ç B cosça ÷ ç ÷ ç ÷.cosça ÷ ç ÷ è ø ç ÷ cosça ÷ ç = - + + + ÷ è ø ç ÷.cosça ÷ + ÷ è ø ç ÷ è ø 3 4 6 4 Lời giải æ p 2 ö æ p 2 ö a) Ta có: 2 A cos a 2 ç cos ç a ÷ 2 ç = + + ÷ + cos ç - a ÷÷ = ç ÷ è 3 ø ç ÷ è 3 ø 1 é æ 4p ö æ 4p öù
= ê 3 + cos 2a + cosçç + 2a ÷÷ + cosçç - 2a ÷÷ú 2 ê çè 3 ÷ø çè 3 ÷øú ë û 1 é 4p ù 3
= ê 3 + cos 2a + 2 cos cos 2a ú = 2 ê 3 ú 2 ë û p æ p ö p æ p ö æ p ö b) Vì a çça ÷÷ cosçça ÷÷ sinç + = - + + = - ça ÷ - ÷ và 6 çè 3 ÷ø 2 çè 6 ÷ø çè 3 ÷ø æ 3p ö æ p ö cosçça ÷÷ sinç + = - ça ÷ + ÷ ç nên è 4 ÷ø çè 4 ÷ø æ p ö æ p ö æ p ö æ p ö ç B cosça ÷ ç ÷ ç ÷.cosça ÷ ç ÷ è ø ç ÷ sinça ÷ ç = - + + - ÷ è ø ç ÷.sinça ÷ + ÷ è ø ç ÷ è ø 3 4 3 4 éæ p ö æ p öù æ p p ö æ p p ö = cos êçça ÷ ç - ÷ - ç ÷ ça ÷ + ÷ú ç ÷ ç ÷ = cos cos êè ø ç ÷ ç- - ÷= ç + ÷ è ø 3 4 ú ç ÷ è 3 4 ø ç ÷ è 3 4 ø ë û p p p p 1 2 3 2 2 - 6 = cos cos - sin sin = . - . = 3 4 3 4 2 2 2 2 4
Ví dụ 5: Đơn giản biểu thức sau: cos a cos a
cos a 2cos 2a cos 3a 3 3 a) A b) B
sin a sin 2a sin 3a a cot a cot 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 521
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác
c) C cos a cos(a b) cos(a 2b) ... cos(a nb) (n N) Lời giải
cosa cos3a 2cos2a 2cos2acosa 2cos2a 2cos2acosa 1 a) A a a a a a a a a cot 2a sin sin 3 2sin 2 2sin 2 cos 2sin 2 2sin 2 cos 1 b) Ta có cos a cos a
2cos a cos cos a và 3 3 3 a a a a a cos
sin cos a cos sin a sin a sin a cos a 2 2 2 2 1 2 cot a cot 2 sin a a a a a sin sin sin sin sin sin sin sin a a a a 2 2 2 2 cos a sin 2a Suy ra B
sin a cos a . 1 2 sina b b b b b
c) Ta có C.2sin 2sin cos a 2sin cos(a b) 2sin cos(a 2b) ... 2sin cos(a nb) 2 2 2 2 2 b b 3b b 5b 3b sin a sin a sin
a sin a sin a sin a 2 2 2 2 2 2 2n 1 b 2n 1 b .. . sin a sin a 2 2 b 2n 1 b nb sin a sin
a 2sinn 1 b cos a 2 2 2 nb sin n 1 b cos a 2 Suy ra C b sin 2 1 1
Ví dụ 6: Cho sin a b 2cosa b . Chứng minh rằng biểu thức M
2 sin 2a 2 sin 2b
không phụ thuộc vào a,b . Lời giải
4 sin 2a sin 2b
4 sin 2a sin 2b Ta có M
2 sin 2a2 sin 2b 4 2sin 2a sin 2b sin 2a sin 2b
Ta có sin 2a sin 2b 2sin a bcosa b Mà a b a b 2 a b 2 sin 2cos sin
4cos a b nên
cos 2a b cos 2a b 2
1 2sin a b 2
2cos a b 1 2
2 2 sin a b 2
cos a b 2
2 10cos a b
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 522
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 2
4 4 cos a b 2
4 4 cos a b 4 Suy ra M a b 1 a b 2 2 2
3 3cos a b 3 4 8cos . 2 10 cos 2
Ví dụ 7: Chứng minh rằng æ p ö æ p ö a) 3 sin 3a 3 sin a 4 sin a 4 sin . a sinçç a ÷÷.sinç = - = - ç + a ÷÷ ç è 3 ÷ø çè 3 ÷ø a a a 1 æ a ö b) 3 3 n 1 - 3 sin 3 sin ... 3 sin ç + + + = ç3n sin - sin a ÷÷. 2 3 3 3n 4 çè 3n ÷ø Lời giải
a) Ta có sin 3a = sin(2a + a) = sin2a cos a + cos2a sin a 2
= 2 sin a cos a + cos 2a sin a = 2 sin a( 2 1 - sin a ) + ( 2
1 - 2 sin a )sin a 3
= 3 sin a - 4 sin a (1) æ p ö æ p ö 1 æ 2p ö Mặt khác 4 sin . a sinçç a ÷÷.sinçç a ÷÷ 4 sin . a ç - + = - çcos - cos(-2a)÷÷ ç è 3 ÷ø çè 3 ÷ø 2 çè 3 ÷ø æ 1 ö æ 1 ö ç ÷ ç 2 = -2 sin .
a ç- - cos2a÷ = 2 sin aç + 1 - 2 sin a÷÷ çè 2 ÷ø çè2 ÷ø 3
= 3 sin a - 4 sin a (2) Từ (1) và (2) suy ra ĐPCM 3 sin a - sin 3a b) Theo câu a) ta có 3 3
sin 3a = 3 sin a - 4 sin a sin a = 4 a a a a a 3 sin - sin a 3 sin - sin 3 sin - sin a a 2 a n n 1 - Do đó 3 3 3 3 3 3 3 3 sin = , sin = , ..., sin = 2 3 4 3 4 3n 4 a a a a a 3 sin - sin a 3 sin - sin 3 sin - sin 2 n n 1 - Suy ra 3 3 3 n 1 - 3 3 VT = + 3 + ... + 3 4 4 4 a 3 sin sin a n 1 æ a ö n 1 - 3 3 ç = - + = ç3n sin
- sin a÷÷ = VP 4 4 4 çè 3n ÷ø ĐPCM.
Lưu ý: Hoàn toàn tương tự ta chứng minh được 3
cos 3a = 4 cos a - 3 cos a , 3
sin 3a = 3 sin a - 4 sin a , hai công thức này được gọi là công thức nhân ba
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 523
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác
Dạng toán 4: bất đẳng thức lượng giác và tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức lượng giác. 1. Phương pháp giải.
- Sử dụng phương pháp chứng minh đại số quen biết.
- Sử dụng các tính chất về dấu của giá trị lượng giác một góc.
- Sử dụng kết quả sin a £ 1, cos a £ 1 với mọi số thực a
2. Các ví dụ điển hình. p
Ví dụ 1: Chứng minh rằng với 0 < a < thì 2 a) 2
2 cot a ³ 1 + cos 2a
b) cota ³ 1 + cot2a Lời giải
a) Bất đẳng thức tương đương với æ 1 ö 1 ç ÷ 2 2 2ç - 1÷ ³ 2 cos a - 1 ³ 1 - sin a 2 ç ÷ 2 è sin a ÷ø sin a 1 2 4 2
+ sin a ³ 2 sin a - 2 sin a + 1 ³ 0 2 sin a ( a - )2 2 sin 1 ³ 0 (đúng) ĐPCM.
b) Bất đẳng thức tương đương với cos a sin 2a + cos 2a cos a sin 2a + cos 2a ³ ³ (*) sin a sin 2a sin a 2 sin a cos a p ìïsin a > 0 Vì 0 a ï < < í nên 2 ï cosa > 0 ïî 2 2 2
(*) 2 cos a ³ sin 2a + cos a - sin a
1 ³ sin 2a (đúng) ĐPCM. p æ 1 öæ 1 ö
Ví dụ 2: Cho 0 < a <
. Chứng minh rằng ççsin a ÷ç + ÷çcos a ÷ + ÷ ³ 2 2 çè 2 cos a ÷øçè 2 sin a ÷ø Lời giải æ 1 öæ 1 ö 1 Ta có ççsin a ÷ç + ÷çcos a ÷ +
÷ = sin a cos a + + 1 ç è 2 cos a ÷øçè 2 sin a ÷ø 4 sin a cos a p Vì 0 < a <
nên sin a cos a > 0 . 2
Áp dụng bất đẳng thức côsi ta có
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 524
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 1 1 sin a cos a + ³ 2 sin a cos . a = 1 4 sin a cos a 4 sin a cos a æ 1 öæ 1 ö Suy ra ççsin a ÷ç + ÷çcos a ÷ + ÷ ³ 2 ç ĐPCM. è 2 cos a ÷øçè 2 sin a ÷ø
Ví dụ 3: Chứng minh rằng với 0 £ a £ p thì ( æ ö a - )2 a p 2 2 cos 2 1 - 4 sin ç ÷ ç - ÷ > ç ÷
( 2sina - 2)(3 -2cos2a). è 2 4 ÷ø Lời giải
Bất đẳng thức tương đương với ( - )2 é æ p öù a - ê ç - ça ÷ - ÷ú + ( - a ) > a é - ( 2 2 cos 2 1 2 1 cos 2 3 2 cos 2 2 sin 3 2 1 - 2 sin a )ù ê çè 2 ÷øú ë û ë û 2 a - a + + a > a ( 2 4 cos 2 8 cos 2 5 2 sin 2 sin 4 sin a + 1) ( - a )2 + + a > a ( 2 4 1 cos 2 1 2 sin 2 sin 4 sin a + 1) 4 a + a + > a ( 2 16 sin 2 sin 1 2 sin 4 sin a + 1)
Đặt 2 sin a = t , vì 0 £ a £ p 0 £ t £ 2 .
Bất đẳng thức trở thành 8 2
t + t + > t ( 4 t + ) 8 5 2 1
1 t - t + t - t + 1 > 0 (*) + Nếu 0 £ t < 1: 8 2 t + t ( 3 (*)
1 - t ) + 1 - t > 0 đúng vì 3 2
1 - t > 0, 1 - t > 0,t ³ 0 và 8 t ³ 0 . + Nếu 1 £ t £ 2 : 5 t ( 3 (*)
t - 1) + t (t - 1) + 1 > 0 đúng vì 5 t ( 3
t - 1) ³ 0, t (t - 1) ³ 0 .
Vậy bất đẳng thức (*) đúng suy ra ĐPCM.
Ví dụ 4: Tìm giá trị nhỏ nhất, lớn nhất của biểu thức sau:
a) A = sin x + cos x b) 4 4
B = sin x + cos x Lời giải a) Ta có A = ( x + x )2 2 2 2 sin cos
= sin x + cos x + 2 sin x cos x = 1 + sin 2x Vì sin 2x £ 1 nên 2
A = 1 + sin 2x £ 1 + 1 = 2 suy ra - 2 £ A £ 2 . p 3p Khi x =
thì A = 2 , x = - thì A = - 2 4 4
Do đó max A = 2 và min A = - 2 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 525
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 2 2 2 2 æ1 - cos2x ö æ1 + cos2x ö
1 - 2 cos 2x + cos 2x
1 + 2 cos 2x + cos 2x b) Ta có B ç ÷ ç ÷ = ç ÷ + ç ÷ = + ç è 2 ÷ø çè 2 ÷ø 4 4 2 2 + 2 cos 2x 2 + 1 + cos 4x 3 1 = = = + .cos 4x 4 4 4 4 1 3 1 1 Vì 1
- £ cos 4x £ 1 nên £
+ .cos 4x £ 1 suy ra £ B £ 1. 2 4 4 2 1
Vậy max B = 1 khi cos 4x = 1 và min B = khi cos 4x = -1 . 2
Ví dụ 5: Tìm giá trị nhỏ nhất, lớn nhất của biểu thức A = 2 - 2 sin x - cos 2x Lời giải Ta có A = - x - ( 2 - x ) 2 2 2 sin 1 2 sin
= 2 sin x - 2 sin x + 1
Đặt t = sin x, t £ 1 khi đó biểu thức trở thành 2
A = 2t - 2t + 1 Xét hàm số 2
y = 2t - 2t + 1 với t £ 1 . Bảng biến thiên: t 1 -1 1 2 y 5 1 1 2
Từ bảng biến thiên suy ra max A = 5 khi t = -1 hay sin x = 1 . 1 1 1
min A = khi t = hay sin x = . 2 2 2
Dạng toán 5: chứng minh đẳng thức, bất đẳng thức trong tam giác.
1. Các ví dụ minh họa.
Ví dụ 1: Chứng minh trong mọi tam giác ABC ta đều có: A B C
a) sin A + sin B + sinC = 4 cos cos cos 2 2 2 b) 2 2 2
sin A + sin B + sin C = 2(1 + cos A cos B cosC )
c) sin 2A + sin 2B + sin 2C = 4 sin Asin B sinC Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 526
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác A + B A - B C C a) VT = 2 sin cos + 2 sin cos 2 2 2 2 A + B p C
Mặt khác trong tam giác ABC ta có A + B + C = p = - 2 2 2 A + B C C A + B Suy ra sin = cos , sin = cos 2 2 2 2 C A - B A + B C C æ A - B A + B ö Vậy VT 2 cos cos 2 cos cos 2 cos ç = + = çcos + cos ÷÷ 2 2 2 2 2 çè 2 2 ÷ø C A B = 4 cos cos cos = VP ĐPCM. 2 2 2 1 - cos 2A 1 - cos 2B cos 2A + cos 2B b) 2 2 VT = + + 1 - cos C = 2 - - cos C 2 2 2 = -
(A + B ) (A - B ) 2 2 cos cos - cos C
Vì A + B + C = p cos(A + B ) = -cosC nên
VT = 2 + cosC cos(A - B ) + cosC cos(A + B ) = 2 + cosC é cos(A - B ) + cos(A + B )ù ë û
= 2 + cosC.2 cos A cos B = 2(1 + cos A cos B cosC ) = VP ĐPCM.
c) VT = 2 sin(A + B )cos(A - B ) + 2 sinC cosC
Vì A + B + C = p cosC = -cos(A + B ), sin(A + B ) = sinC nên
VT = 2 sinC cos(A - B ) - 2 sinC cos(A + B ) = 2 sinC é cos(A - B ) - cos(A + B )ù ë û = 2 sinC. é 2 - sin Asin( B
- )ù = 4 sinAsinB sinC = VP ë û ĐPCM.
Ví dụ 2: Chứng minh trong mọi tam giác ABC không vuông ta đều có:
a) tan A + tan B + tanC = tan . A tan . B tanC b) cot .
A cotB + cotB.cotC + cotC.cotA = 1 Lời giải
a) Đẳng thức tương đương với tan A + tan B = tan . A tan .
B tanC - tanC
tan A + tan B = tanC (tan A tan B - 1) (*) p
Do tam giác ABC không vuông nên A + B ¹ 2 sin Asin B
sin Asin B - cos Acos B cos(A + B )
tan A tan B - 1 = - 1 = = - ¹ 0 cos Acos B cos Acos B cos Acos B Suy ra
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 527
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác ( ) tan A + tan B tan A + tan B * = tanC
= -tanC tan(A + B ) = -tanC tan A tan B - 1 1 - tan A tan B
Đẳng thức cuối đúng vì A + B + C = p ĐPCM.
b) Vì A + B + C = p cot(A + B ) = -cotC
Theo công thức cộng ta có: 1 1 - ( + ) 1 1 - tan A tan B cotA cotB - 1 cotA cot cot B A B = = = = tan(A + B ) tan A + tan B 1 1 cotA + cotB + cotA cotB cotA cotB - 1 Suy ra
= -cotC cotA cotB - 1 = -cotC (cotA + cotB ) cotA + cotB Hay cot .
A cotB + cotB.cotC + cotC.cotA = 1 ĐPCM.
Ví dụ 3: Chứng minh trong mọi tam giác ABC ta đều có: 3
a) cos A + cos B + cosC £ 2 3 3
b) sin A + sin B + sinC £ 3
c) tan A tan B tanC ³ 3 3 với ABC là tam giác nhọn. Lời giải A + B A - B
a) Ta có cos A + cos B + cosC = 2 cos cos + cosC 2 2 A + B p C A + B C Vì = - nên cos = sin 2 2 2 2 2 C Mặt khác 2 cosC = 1 - 2 sin do đó 2 C A - B C æ C C A - B 1 ö 2 ç 2
cos A + cos B + cosC = 2 sin cos + 1 - 2 sin = -2çsin - sin cos ÷ - ÷ 2 2 2 çè 2 2 2 2 ÷ø æ C C 1 A - B 1 A - B ö 1 A - B ç 2 2 ÷ 2 = -2çsin - 2 sin . cos + cos ÷ + 1 + cos ç è 2 2 2 2 4 2 ÷ø 2 2 2 æ C 1 A - B ö 1 A - B ç ÷ 2 = -2çsin + cos ÷ + 1 + cos ç è 2 2 2 ÷ø 2 2 A - B A - B Vì 2 cos £ 1 cos £ 1 nên 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 528
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 1 3
cos A + cos B + cosC £ 1 + = ĐPCM. 2 2
b) Trước tiên ta chứng minh bổ đề sau: sin x + sin y x + y Nếu 0 £ x £ ,
p 0 £ y £ p thì £ sin . 2 2 x + y x + y x - y Thật vậy, do 0 £ £ p sin > 0 và cos £ 1 nên 2 2 2 sin x + sin y x + y x - y x + y = sin cos £ sin 2 2 2 2 p p + + sin A + sin B
A + B sinC sin C Áp dụng bổ đề ta có: £ sin , 3 3 £ sin 2 2 2 2 Suy ra p p æ p ö sinC + sin ç ÷ sin + sin C A + B + 1 ç C A B + ÷ 3 3 ç A + B + £ + £ ç 3 ÷ p sin sin 2 sin ÷ + ÷ = 2 sin ç 2 2 2 2 2 2 2 ÷ ç ÷ 3 ç ÷ ç ÷ ç ÷ è ø p 3 3
Do đó sin A + sin B + sinC £ 3 sin hay sin A + sin B + sinC £ ĐPCM. 3 3
c) Vì ABC là tam giác nhọn nên tan A > 0, tan B > 0, tanC > 0 .
Áp dụng bất đẳng thức Cauchy ta có 3
tan A + tan B + tanC ³ 3 tan .
A tan B. tanC
Theo ví dụ 2 ta có tan A + tan B + tanC = tan . A tan . B tanC nên æ ö A B C ³ A B C A B C çç ( A B C )2 3 3 3 tan tan tan 3 tan . tan . tan tan .tan .tan tan tan tan - 3÷÷ ³ 0 ÷ è ø ( A B C )2 3 tan tan tan
³ 3 tan A tan B tanC ³ 3 3 ĐPCM.
Ví dụ 4: Chứng minh trong mọi tam giác ABC ta đều có: A B C
a) sin A + sin B + sinC £ cos + cos + cos 2 2 2 A B C
b) cos Acos B cosC £ sin sin sin 2 2 2 A B C
c) tan A + tan B + tanC ³ cot + cot + cot
Với tam giác ABC không vuông. 2 2 2 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 529
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác A + B C A - B a) Vì sin = cos > 0 và cos £ 1 nên 2 2 2 A + B A - B C
sin A + sin B = 2 sin cos £ 2 cos 2 2 2 A B
Hoàn toàn tương tự ta có sin B + sinC £ 2 cos , sinC + sin A £ 2 cos 2 2
Công vế với vế các bất đẳng thức trên và rút gọn ta được A B C
sin A + sin B + sinC £ cos + cos + cos . ĐPCM. 2 2 2 p p p
b) +TH1: Nếu tam giác ABC tù: không mất tính tổng quát giả sử A >
B < ,C < suy 2 2 2
ra cos A < 0, cos B > 0, cosC > 0 A B C
cosAcosB cosC < 0. Mà sin sin sin
> 0 do đó bất đẳng thức luôn đúng. 2 2 2 1
+ TH2: Nếu tam giác ABC nhọn: cos A cos B = é cos(A + B ) + cos(A - B )ù 2 ë û . 1 C
Vì cos(A + B ) = -cosC và cos(A - B ) £ 1 nên cosAcosB £ (1 - cosC ) 2 = sin . 2 2 A B
Chứng minh tương tự ta có 2 2
cos B cosC £ sin
, cosC cos A £ sin . 2 2
Do các vế đều không âm nên nhân vế với vế các bất đẳng thức trên ta được ( A B )( B C )( C A) C A B 2 2 2 cos cos cos cos cos cos £ sin sin sin 2 2 2 A B C
cos Acos B cosC £ sin sin sin ĐPCM. 2 2 2 sin (A + B ) 2 sin (A + B )
c) Ta có tan A + tan B = = cos A cos B
cos(A + B ) + cos(A - B )
Mà sin(A + B ) = sinC, cos(A + B ) = -cosC nên C C 4 sin cos 2 sinC 2 sinC 2 2 C tan A + tan B = ³ = = - C + (A - B ) 2 cot cos cos 1 - cosC C 2 2 2 sin 2 A B
Tương tự ta có tan B + tanC ³ 2 cot , tanC + tan A ³ 2 cot 2 2
Công vế với vế và rút gọn ta được
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 530
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác A B C
tan A + tan B + tanC ³ cot + cot + cot ĐPCM. 2 2 2 Nhận xét:
+ Để chứng minh x + y + z ³ a + b + c ta có thể đi chứng minh x + y ³ 2a (hoặc 2 , b 2c ) rồi
xây dựng bất đẳng thức tương tự. Cộng vế với vế suy ra đpcm.
+ Để chứng minh xyz ³ abc với x,y,z,a, ,
b c không âm ta đi chứng minh 2
xy ³ a (hoặc 2 2 b , c ) rồi
xây dựng bất đẳng thức tương tự. nhân vế với vế suy ra đpcm.
Ví dụ 5: Chứng minh trong mọi tam giác ABC ta đều có: 3
a) sin A + sin B + sinC £ 3 2 3 æ 1 ö æ 1 ö æ 1 ö æ 2 ö b) çç1 ÷÷.çç1 ÷÷.çç1 ÷ ç + + + ÷ ³ ç1 ÷ + ÷ ç è sin A ÷ø çè sin B ÷ø çè sinC ÷ø ç ÷ è 3 ø Lời giải
a) Áp dụng bất đẳng thức x + y £ ( 2 2
2 x + y ) với mọi x,y không âm ta có A + B A - B A + B
sin A + sin B £ 2(sinA + sinB ) = 2.2 sin cos £ 2 sin 2 2 2 p 1 æ p ö
Tương tự ta có sinC + sin £ 2 sin C ç ÷ ç + ÷ 3 2 çè 3 ÷ø
Công vế với vế ta được p æç A + B 1 æ p öö
sin A + sin B + sinC + sin £ 2ç sin + sin C ç ÷÷ ç + ÷÷ ç ç ç ÷÷ 3 è 2 2 è 3 ÷ø÷ø Mà A + B 1 æ p ö é A + B 1 æ p öù æ p p ö p sin + sin C ç ÷ ç + ÷ £ 2 sin ê + C ç ÷ ç + ÷ú = 2 sinç ÷ ç + ÷ = 2 sin 2 2 çè 3 ÷ø ê 2 2 çè 3 ÷øú çè 2 6 ÷ø 3 ë û p p
Suy ra sin A + sin B + sinC + sin £ 4 sin 3 3 p 3
Hay sin A + sin B + sinC £ 3 sin = 3 ĐPCM. 3 2 æ 1 ö æ 1 ö 1 1 1 b) Ta có çç1 ÷÷.ç + ç1 ÷ + ÷ = 1 + + + ç . è sin A ÷ø çè sin B ÷ø sin A sin B sin A sin B 1 1 4
Áp dụng bất đẳng thức + ³
với mọi x,y dương ta có x y x + y
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 531
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 1 1 4 4 2 + ³ = = sin A sin B sin A + sin B 2 sin Asin B sin A sin B 2 æ 1 ö æ 1 ö 2 1 æ 1 ö Do đó çç1 ÷÷.çç1 ÷÷ 1 ç + + ³ + + = ç1 ÷ + ÷ ç è sin A ÷ø çè sin B ÷ø ç ÷ sin A sin B sin A sin B è sin A sin B ø Mặt khác 1 1
sin A sin B = - é cos(A + B ) - cos(A - B )ù = é cos(A + B ) + cos(A - B )ù ë û ë û 2 2 cos(A + B ) + 1 A + B ³ = 2 sin 2 2 2 æ ö ç ÷ æ 1 ö æ 1 ö çç 1 ÷÷ Nên çç1 ÷ + ÷.çç1 ÷ + ÷ ³ ç1 ÷ + ÷ ç ÷ (1) è ø ç ÷ ç sin A è sin B ÷ø ç A + B ÷÷ çç sin ÷÷ çè 2 ÷ø 2 æ ö æ ö ç ÷ ç ÷ æ ö ç ÷ ç ÷ 1 ç 1 ÷ ç ç ÷ ç + ÷ ç ÷ ç 1 ÷÷ Tương tự ta có 1 . 1 + ÷ ³ ç1 ÷ + ç ÷ ç ÷ (2) è sinC ÷ø ç p ÷ ç ÷ ç 1 æ p ö÷÷ çç sin ÷÷ ç sin C ç ÷ ç ÷ ç ç + ÷ ÷÷ è 3 ø çè 2 çè 3 ÷÷ øø
Nhân vế với vế của (1) và (2) ta được 2 2 æ ö æ ö æ ö ç ÷ ç ÷ ç ÷ æ ö æ ö æ ö ç ÷ ç ÷ ç ÷ 1 1 1 ç 1 ÷ ç ÷ ç ÷ ç ÷ ç + ÷ ç + ÷ ç + ÷ ç ÷ ç 1 ÷ ç + ÷ ³ ç ÷ ç 1 ÷÷ 1 . 1 . 1 . 1 1 + ÷ ç1 ÷ + ç ÷ è ø ç ÷ è ø ç ÷ ç ÷ ÷ ç ÷ sin A sin B è sinC ø ç p ÷ ç A + B ÷ ç ÷ ç 1 æ p ö÷÷ çç sin ÷ ç ÷ ç ÷ ç sin ÷÷ ç sin C ç ÷ è ø ç ÷ ç ç + ÷ ÷÷ 3 è 2 ø çè 2 çè 3 ÷÷ øø Ta lại có 2 2 æ ö æ ö æ ö ç ÷ç ÷ ç ÷ æ ö ç ÷ç ÷ ç ÷ ç ÷ ç 1 ÷ç ç ÷ç 1 ÷÷ ç ÷ ç 1 ÷ ç ÷ ç 1 ÷÷ 1 + ÷ç1 + ç ÷ ³ ç1 ÷ + ÷ = ç1 ÷ + ÷ ÷ç ç + ÷ç æ ö÷ ç ÷ ç é + æ öù ÷ ç A B 1 p 1 A B 1 p ÷ ç p ÷÷ çç sin ÷÷ç sin C ç ÷ ç ÷ç ç + ÷ ÷ ç ÷ sin ê + C ç ÷ è øçè ç ÷ ç ç + ÷ú ÷ ç ÷ ç sin ÷÷ 2 2 è 3 ÷÷ øø çè 2 ê 2 2 çè 3 ÷øú ÷ çè ø 3 ÷ø ë û 4 æ ö æ ö ç ÷ ç ÷ æ 1 ö æ 1 ö æ 1 ö çç 1 ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç + ÷ ç + ÷ ç + ÷ ç ÷ ç 1 ÷÷ Suy ra 1 . 1 . 1 . 1 + ÷ ³ ç1 ÷ + ÷ ç ÷ è ø ç ÷ è ø ç ÷ ç ÷ ÷ ç sin A sin B è sinC ø ç p ÷ ç p ÷÷ çç sin ÷ ç ç ÷ ç sin ÷ ÷ ÷ è 3 ø çè 3 ÷ø 3 æ ö ç ÷ 3 æ 1 ö æ 1 ö æ 1 ö çç 1 ÷÷ æ 2 ö Hay çç1 ÷ + ÷.çç1 ÷ + ÷.çç1 ÷ + ÷ ³ ç1 ÷ ç + ÷ = ç ÷ ĐPCM. è ø ç ÷ è ø ç ÷ ç ÷ ÷ ç1 ÷ + ÷ sin A sin B è sinC ø ç p ÷ ç ÷ è ÷ 3 ø çç sin ÷ çè 3 ÷ø
Nhận xét: Cho tam giác ABC và hàm số f
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 532
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác æ ö p
Để chứng minh f (A) + f (B ) + f (C ) ³ 3f ç ÷ ç ÷ ç . Ta đi chứng minh è 3 ÷ø ( ) + ( ) æ A + B ö f A f B ³ 2f ç ÷ ç ÷ ç è 2 ÷ø æ p ö ç æ ö çC ÷ p + ÷ ç ÷ khi đó f (C ) ç ÷ + ç ÷ ³ ç 3 f 2f ÷÷ ç ÷ ç từ đó suy ra è 3 ÷ø ç 2 ÷÷ ç ÷ ç ÷ ç ÷ è ø é æ p öù ê ç æ ö æ ç ÷ ê + ö çC ÷ + ÷ú p ç ÷ æ ç ÷ + + + ç ÷ ³ ç ÷ ê ç ÷ + ç ÷ú p ö f (A) f (B ) f (C ) A B 3 f 2 f f ÷ ÷ è ø ç ÷ ç ÷ ÷ú ³ 4f ç ÷ ç ÷ 3 ê è 2 ø ç 2 ÷ ç ç ÷ú è 3 ÷ø ê ç ÷ ç ÷ú è ø ë û æ p ö
Do đó f (A) + f (B ) + f (C ) ³ 3f ç ÷ ç ÷ ç . è 3 ÷ø æ ö æ + ö p A B
Để chứng minh f (A) f (B ) f (C ) 3 ³ f ç ÷ ç ÷ ç ÷ ç
. Ta đi chứng minh f (A) f (B ) 2 ³ f ç ÷ è 3 ÷ø çè 2 ÷ø æ p ö ç æ ö çC ÷ p + ÷ ç ÷
khi đó f (C ) ç ÷ 2 ç ÷ ³ ç 3 f f ÷÷ ç ÷ ç từ đó suy ra è 3 ÷ø ç 2 ÷÷ ç ÷ ç ÷ ç ÷ è ø æ p ö ç æ ö æ + ö çC ÷ p + ÷ ç ÷ æ p ö
f (A) f (B ) f (C ) A B ç ÷ 2 ç ÷ 2 ç ÷ ³ ç ÷ ç 3 ÷ 4 f f f ÷ ³ f ç ÷ ç ÷ è ø ç ÷ ç ÷ ÷ ç ÷ 3 è 2 ø ç 2 ÷ çè 3 ÷ø ç ÷ ç ÷ ç ÷ è ø æ p ö
Do đó f (A) f (B ) f (C ) 3 ³ f ç ÷ ç ÷ ç . è 3 ÷ø A B -C
Ví dụ 6: Cho tam giác ABC thỏa mãn cos cos(B -C ) + cos A cos = 0 . 2 2
Chứng minh rằng cos 2B + cos 2C £ 1. Lời giải Từ giả thiết ta có Aæ B -C ö B -C æ A ö ç 2 ÷ ç 2 cos ç2 cos - 1÷ + cos ç2 cos - 1÷÷ = 0 2 çè 2 ÷ø 2 çè 2 ÷ø A B -C æ B -C A ö æ A B -C ö 2 cos cos ççcos cos ÷ ç + ÷ - çcos + cos ÷÷ = 0 2 2 çè 2 2 ÷ø çè 2 2 ÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 533
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác æ A B -C öæ A B -C ö ççcos cos ÷ç + ÷ç2 cos cos - 1÷÷ = 0 ç (1) è 2 2 ÷øçè 2 2 ÷ø A p A p B -C p B -C Vì 0 < < cos > 0 , - < < cos > 0 và 2 2 2 2 2 2 2 B + C p A A B + C A B -C = - cos = sin nên (1) 2 cos cos - 1 = 0 2 2 2 2 2 2 2 B + C B -C 2 sin cos
= 1 sin B + sinC = 1 2 2 (x + y )2 (sinB + sinC )2 1
Áp dụng bất đẳng thức 2 2 x + y ³ suy ra 2 2 sin B + sin C ³ = 2 2 2 1
Do đó cos 2y + cos 2z = 2 - 2( 2 2
sin y + sin z ) £ 2 - 2. = 1 ĐPCM. 2
Ví dụ 7: Chứng minh rằng trong tam giác ABC ta luôn có A B B C C A 3 3 sin cos + sin cos + sin cos £ 2 2 2 2 2 2 4 Lời giải Do , A ,
B C bình đẳng nên không mất tính tổng quát giả sử p A B C
A ³ B ³ C > ³ ³ > 0 2 2 2 2 A B C A B C Suy ra sin ³ sin ³ sin > 0, cos ³ cos ³ cos > 0 2 2 2 2 2 2 æ A B öæ B C ö ççsin sin ÷ç - ÷çcos - cos ÷÷ ³ 0 ç è 2 2 ÷øçè 2 2 ÷ø A B A C B B B C sin cos - sin cos - sin cos + sin cos ³ 0 2 2 2 2 2 2 2 2 A B B C A C B B sin cos + sin cos £ sin cos + sin cos 2 2 2 2 2 2 2 2 A B B C C A A C C A B B Do đó sin cos + sin cos + sin cos £ sin cos + sin cos + sin cos 2 2 2 2 2 2 2 2 2 2 2 2 Mà A C C A B B æ A C ö B B B B B sin cos + sin cos + sin cos = sinç ÷ ç + ÷ + sin cos = cos + sin cos 2 2 2 2 2 2 çè 2 2 ÷ø 2 2 2 2 2 (1)
Áp dụng bất đẳng thức côsi ta có:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 534
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác B 3 3 B B 2 2 cos + ³ 2 cos = 3 cos , 2 4 4 2 2 B B B B B B 2 2 2 2 3 sin + cos ³ 2 3 sin cos = 2 3 sin cos 2 2 2 2 2 2 æ B 3 ö æ B B ö B B B Suy ra ç 2 ÷ ç 2 2 2çcos + ÷ + ç3 sin + cos ÷÷ ³ 2 3 cos + 2 3 sin cos ç è 2 4 ÷ø çè 2 2 ÷ø 2 2 2 æ B B B ö 3 æ B B ö 9 Hay ç ÷ ç 2 2 2 3 çcos + sin cos ÷ £ + 3çsin + cos ÷÷ = ç è 2 2 2 ÷ø 2 çè 2 2 ÷ø 2 B B B 3 3 cos + sin cos £ (2) 2 2 2 4 A B B C C A 3 3
Từ (1) và (2) ta có sin cos + sin cos + sin cos £ ĐPCM. 2 2 2 2 2 2 4
C. CÂU HỎI TRẮC NGHIỆM
Câu 1: Rút gọn biểu thức 4 o 4 o
M cos 15 sin 15 . 3 1 A. M 1. B. M . C. M . D. M 0. 2 4 Lời giải Chọn B 2 2 Ta có 4 o 4 o M 2 o 2 o cos 15 sin 15 cos 15 sin 15 2 o 2 o 2 o 2 o cos 15 sin 15 cos 15 sin 15 3 2 o 2 o
cos 15 sin 15 cos o 2.15 o cos30 . 2
Câu 2: Tính giá trị của biểu thức 4 0 4 0 2 0 2 0
M cos 15 sin 15 cos 15 sin 15 . 1 1 A. M 3. B. M . C. M . D. M 0. 2 4 Lời giải Chọn A
Áp dụng công thức nhân đôi 2 2
cos a sin a cos 2a . Ta có M 4 o 4 o 2 o 2 o cos 15 sin 15
cos 15 sin 15 . 2 o 2 o 2 o 2 o 2 o 2 o cos 15 sin 15 cos 15 sin 15 cos 15 sin 15 . 2 o 2 o 2 o 2 o o o cos 15 sin 15 cos 15
sin 15 cos 30 cos 30 3.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 535
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác
Câu 3: Tính giá trị của biểu thức 6 o 6 o
M cos 15 sin 15 . 1 1 15 3 A. M 1. B. M . C. M . D. M . 2 4 32 Lời giải Chọn D Ta có 6 6 cos sin 2 2 cos sin 4 2 2 4
cos cos .sin sin
cos 2.cos sin 2 2 2 2 2 cos .sin 1 2 cos 2. 1 sin 2 . 4 1 3 1 1 15 3 Vậy o 2 o
M cos30 . 1 sin 30 . 1 . . 4 2 4 4 32
Câu 4: Giá trị của biểu thức cos cos sin sin là 30 5 30 5 3 3 3 1 A. . B. . C. . D. . 2 2 4 2 Lời giải Chọn A 3 Ta có cos cos sin sin cos cos . 30 5 30 5 30 5 6 2 5 5 sin cos sin cos Câu 5: 18 9 9 18
Giá trị của biểu thức P là cos cos sin sin 4 12 4 12 1 2 3 A. 1. B. . C. . D. . 2 2 2 Lời giải Chọn A sin . a cosb cos . a sin b sin a b Áp dụng công thức a b a b a b. cos .cos sin .sin cos 5 5 5 1 Khi đó sin cos sin cos sin sin . 18 9 9 18 18 9 6 2 1 1 1 Và cos cos sin sin cos cos .
Vậy P : 1. 4 12 4 12 4 12 3 2 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 536
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 0 0 0 tan 225 cot 81 .cot 69
Câu 6: Giá trị đúng của biểu thức bằng 0 0 cot 261 tan 201 1 1 A. . B. . C. 3. D. 3. 3 3 Lời giải Chọn C Ta có : tan 225 cot 81 .cot 69 tan 0 0 180 45 0 0 0 0 0 tan 9 .cot 69 . 0 0 cot 261 tan 201 cot 0 0 180 81 tan 0 0 180 21 0 0 1 tan 9 .tan 21 1 1 3. 0 0 tan 9 tan 21 tan 0 0 9 21 0 tan 30 5 7 11
Câu 7: Giá trị của biểu thức M sin sin sin sin bằng 24 24 24 24 1 1 1 1 A. . B. . C. . D. . 2 4 8 16 Lời giải Chọn D 7 5 11 Ta có sin cos và sin cos . 24 24 24 24 5 5 1 5 5 Do đó M sin sin cos cos . 2.sin .cos . 2.sin .cos 24 24 24 24 4 24 24 24 24 1 5 1 1 6 1 1 1 .sin .sin . cos cos . 0 . 4 12 12 4 2 12 3 8 2 16
Câu 8: Giá trị của biểu thức A sin .cos .cos .cos .cos là 48 48 24 12 6 1 3 3 3 A. . B. . C. . D. . 32 8 16 32 Lời giải Chọn D
Áp dụng công thức sin 2a 2.sin . a cos a, ta có 1 A sin .cos .cos .cos .cos .sin .cos .cos .cos 48 48 24 12 6 2 24 24 12 6 1 1 1 3 .sin .cos .cos .sin .cos .sin . 4 12 12 6 8 6 6 16 3 32
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 537
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác
Câu 9: Tính giá trị của biểu thức 0 0 0 0
M cos10 cos 20 cos 40 cos80 . 1 1 1 1 A. 0 M cos10 . B. 0 M cos10 . C. 0 M cos10 . D. 0 M cos10 16 2 4 8 . Lời giải Chọn D Vì 0 sin10 0 nên suy ra 0 0 0 0 0
16sin10 cos10 cos 20 cos 40 cos80 0 0 0 0 8sin 20 cos 20 cos 40 cos80 M 0 16sin10 0 16sin10 0 0 0 0 0 0 4sin 40 cos 40 cos80 2sin 80 cos80 sin160 M . 0 16sin10 0 16sin10 0 16sin10 0 0 0 sin 20 2sin10 cos10 1 M 0 cos10 . 0 16sin10 0 16sin10 8 2 4 6
Câu 10: Tính giá trị của biểu thức M cos cos cos . 7 7 7 1 A. M 0 . B. M . C. M 1. D. M 2 . 2 Lời giải Chọn B a b a b
Áp dụng công thức sin a sin b 2.cos .sin . 2 2 2 4 6
Ta có 2sin .M 2.cos .sin 2.cos .sin 2.cos .sin 7 7 7 7 7 7 7 3 5 3 7 5 sin sin sin sin sin sin 7 7 7 7 7 7
sin sin sin . 7 7 1
Vậy giá trị biểu thức M . 2
Câu 11: Công thức nào sau đây sai?
A. cosa b sin asin b cos a cos . b
B. cosa b sin asin b cos a cos . b
C. sin a b sin a cosb cos asin . b
D. sin a b sin a cosb cos asin . b Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 538
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác
Ta có cosa b cos a cosb sin asin b.
Câu 12: Khẳng định nào sau đây đúng?
A. sin 2018a 2018sin . a cos . a
B. sin 2018a 2018sin 1009a.cos1009a.
C. sin 2018a 2sin a cos . a
D. sin 2018a 2sin 1009a.cos1009a. Lời giải Chọn D
Áp dụng công thức sin 2 2sin.cos ta được
sin 2018a 2sin 1009a.cos1009a .
Câu 13: Khẳng định nào sai trong các khẳng định sau? A. 2 2
cos 6a cos 3a sin 3 . a B. 2
cos 6a 1 2sin 3 . a C. 2 cos 6a 1 6sin . a D. 2
cos 6a 2 cos 3a 1. Lời giải Chọn C Áp dụng công thức 2 2 2 2
cos 2 cos sin 2 cos 1 1 2sin , ta được 2 2 2 2
cos 6a cos 3a sin 3a 2 cos 3a 1 1 2sin 3a .
Câu 14: Khẳng định nào sai trong các khẳng định sau? 1 cos 2x 1 cos 2x A. 2 sin x . B. 2 cos x . 2 2 x x
C. sin x 2sin cos . D. 3 3
cos 3x cos x sin . x 2 2 Lời giải Chọn D Ta có 3
cos 3x 4 cos x 3cos x .
Câu 15: Khẳng định nào đúng trong các khẳng định sau?
A. sin a cos a 2 sin a . B.
sin a cos a 2 sin a . 4 4
C. sin a cos a 2 sin a . D.
sin a cos a 2 sin a . 4 4 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 539
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác Chọn B
Câu 16: Có bao nhiêu đẳng thức dưới đây là đồng nhất thức?
1) cos x sin x 2 sin x .
2) cos x sin x 2 cos x . 4 4
3) cos x sin x 2 sin x .
4) cos x sin x 2 sin x . 4 4 A. 1. B. 2. C. 3. D. 4. Lời giải Chọn B
Ta có cos x sin x 2 cos x 2 cos x 2 sin x . 4 2 4 4
Câu 17: Công thức nào sau đây đúng? A. 3
cos 3a 3cos a 4 cos . a B. 3
cos 3a 4 cos a 3cos . a C. 3
cos 3a 3cos a 4 cos . a D. 3
cos 3a 4 cos a 3cos . a Lời giải Chọn B
Câu 18: Công thức nào sau đây đúng? A. 3
sin 3a 3sin a 4sin . a B. 3
sin 3a 4sin a 3sin . a C. 3
sin 3a 3sin a 4sin . a D. 3
sin 3a 4sin a 3sin . a Lời giải Chọn A
Câu 19: Nếu cosa b 0 thì khẳng định nào sau đây đúng?
A. sin a 2b sin a .
B. sin a 2b sin b .
C. sin a 2b cos a .
D. sin a 2b cosb . Lời giải Chọn D
Ta có : cos a b 0 a b k a b k . 2 2
sin a 2b sin b
2b k cos
b k cosb . 2
Câu 20: Nếu sin a b 0 thì khẳng định nào sau đây đúng?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 540
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác
A. cos a 2b sin a .
B. cosa 2b sin b .
C. cos a 2b cos a .
D. cos a 2b cosb . Lời giải Chọn D
Ta có sin a b 0 a b k a b k .
cosa 2b cosb 2b k cosb k cosb .
Câu 21: Rút gọn M sin x ycos y cos x ysin . y A. M cos . x B. M sin . x
C. M sin x cos 2 . y D.
M cos x cos 2 . y Lời giải Chọn A
Áp dụng công thức sin a b sin a cosb sin bcos a , ta được
M sin x ycos y cos x ysin y sin x y y sin .x
Câu 22: Rút gọn M cosa bcosa b sin a bsin a b. A. 2 M 1 2 cos . a B. 2 M 1 2sin . a C. M cos 4 . a D. M sin 4 . a Lời giải Chọn B
Áp dụng công thức cos x cos y sin x sin y cos x y , ta được M
a b a b a b a b
a b a b 2 cos cos sin sin cos
cos 2a 1 2sin . a
Câu 23: Rút gọn M cosa bcosa b sin a bsin a b. A. 2 M 1 2sin . b B. 2 M 1 2sin . b C. M cos 4 . b D. M sin 4 . b Lời giải Chọn A
Áp dụng công thức cos x cos y sin x sin y cos x y , ta được
M cosa bcosa b sin a bsin a b
a b a b 2 cos (
) cos 2b 1 2sin . b
Câu 24: Giá trị nào sau đây của x thỏa mãn sin 2 .
x sin 3x cos 2 .
x cos3x ?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 541
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác A. 18 . B. 30 . C. 36 . D. 45 . Lời giải Chọn A Áp dụng công thức cos . a cosb sin .
a sin b cosa b , ta được sin 2 .
x sin 3x cos 2 .
x cos3x cos 2 .
x cos3x sin 2 . x sin 3x 0
cos5x 0 5x k x k . 2 10 5
Câu 25: Đẳng thức nào sau đây đúng:
sin b a 1
A. cot a cot b . B. 2
cos a 1 cos 2a. sin . a sin b 2 1 sin a b
C. sin a b sin 2a b.
D. tan a b . 2 cos . a cosb Lời giải Chọn B Xét các đáp án: Đáp án A. cos a cosb cos .
a sin b sin . a cosb
sin a b
Ta có cot a cot b . sin a sin b sin . a sin b sin . a sin b Đáp án B. 1 Ta có 2 2
cos 2a 2 cos a 1 cos a 1 cos 2a. 2
Câu 26: Chọn công thức đúng trong các công thức sau: 1 a b a b A. sin .
a sin b cos
a b cosa b. a b 2 B. sin sin 2sin .cos . 2 2 2 tan a C. tan 2a . D. 2 2
cos 2a sin a cos . a 1 tan a Lời giải Chọn B
Câu 27: Rút gọn M cos x cos x . 4 4 A. M 2 s n i . x
B. M 2 sin . x C. M 2 c s o . x
D. M 2 cos . x Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 542
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác Chọn B a b a b
Áp dụng công thức cos a cos b 2sin .sin , ta được 2 2 x x x x 4 4 4 4 M cos x cos x 2 sin .sin 4 4 2 2 2sin . x sin 2 sin . x 4 4 5
Câu 28: Tam giác ABC có cos A và cos B
. Khi đó cosC bằng 5 13 56 56 16 33 A. . B. . C. . D. . 65 65 65 65 Lời giải Chọn C Ta có : 4 3 cos A sin A 5 5
. Mà A B C 180 , do đó 5 12 cos B s in B 13 13 cosC cos 180
A B cos A B A B A B 4 5 3 12 16 cos .cos sin .sin . . . 5 13 5 13 65 1 1 1 Câu 29: Cho ,
A B, C là ba góc nhọn thỏa mãn tan A , tan B , tan C . Tổng A B C 2 5 8 bằng A. . B. . C. . D. . 6 5 4 3 Lời giải Chọn C 1 1 tan A tan B 7 Ta có A B 2 5 tan 1 tan . A tan B 1 1 9 1 . 2 5 7 1
A B C
tan A B tan C 9 8 tan
1 tan A B 1 .tan C 7 1 1 . 9 8
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 543
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác
A B C . 4 Câu 30: Cho ,
A B, C là các góc của tam giác ABC . Khi đó P sin A sin B sin C tương đương với: A B C A B C
A. P 4 cos cos cos .
B. P 4sin sin sin . 2 2 2 2 2 2 A B C A B C
C. P 2 cos cos cos .
D. P 2 cos cos cos . 2 2 2 2 2 2 Lời giải Chọn A
A B C A B C sin cos Do 2 2 2 2 2 . C A B C A B sin cos 2 2 2 2 2 Áp dụng, ta được A B A B C C P
sin A sin B sin C 2sin cos 2sin cos 2 2 2 2 C A B A B C 2 cos cos 2cos cos 2 2 2 2 C A B A B C A B 2 cos cos cos 4cos cos cos . 2 2 2 2 2 2 Câu 31: Cho ,
A B, C là các góc của tam giác ABC . A B B C C A Khi đó P tan .tan
tan .tan tan .tan tương đương với: 2 2 2 2 2 2 A. P 1. B. P 1. 2 A B C
C. P tan .tan .tan . D. Đáp án khác. 2 2 2 Lời giải Chọn A C B A Do A B C 2 2 2 C B tan tan C B A A 1 tan tan 2 2 cot 2 2 2 C B 2 A 1 tan tan tan 2 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 544
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác A C B C B tan tan tan tan .tan 1 2 2 2 2 2 A B B C C A
tan .tan tan .tan tan .tan 1. 2 2 2 2 2 2 sin B Câu 32: Trong A BC , nếu
2cos A thì A
BC là tam giác có tính chất nào sau đây? sin C A. Cân tại . B B. Cân tại . A
C. Cân tại C. D. Vuông tại . B Lời giải Chọn A sin B Ta có
2cos A sin B 2sin C.cos .
A sin C A sin C A sin C
Mặt khác A B C B A C sin B sin A C .
Do đó, ta được sin C A 0 A C . 2 tan A sin A Câu 33: Trong A BC , nếu thì A
BC là tam giác gì? 2 tan C sin C A. Tam giác vuông. B. Tam giác cân. C. Tam giác đều.
D. Tam giác vuông hoặc cân. Lời giải Chọn D 2 2 tan A sin A sin Acos C sin A Ta có
sin 2C sin 2A 2 2 tan C sin C cos Asin C sin C C A 2C 2A .
2C 2A A C 2 4
Câu 34: Cho góc thỏa mãn
và sin . Tính P sin 2 . 2 5 24 24 12 12 A. P . B. P . C. P . D. P . 25 25 25 25 Lời giải Chọn A
Ta có P sin 2 sin 2 2 sin 2 2sin cos . 3 Từ hệ thức 2 2
sin cos 1 , suy ra 2
cos 1 sin . 5
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 545
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 3 Do
nên ta chọn cos . 2 5 4 3 4 3 24
Thay sin và cos vào P , ta được P 2. . . 5 5 5 5 25 2 1 sin 2 cos 2
Câu 35: Cho góc thỏa mãn 0
và sin . Tính P . 2 3 sin cos 2 5 3 3 2 5 A. P . B. P . C. P . D. P . 3 2 2 3 Lời giải Chọn D 2 2sin cos 2cos
2cos sin cos Ta có P 2cos . sin cos sin cos 5 Từ hệ thức 2 2
sin cos 1 , suy ra 2
cos 1 sin . 3 5 2 5 Do 0 nên ta chọn cos P . 2 3 3 3 Câu 36: Biết 3 sin và
. Tính P sin . 5 2 6 3 3 4 3 3 4 3 3 A. P . B. P . C. P . D. P . 5 5 10 10 Lời giải Chọn C 3
Ta có sin sin . 5 4 Từ hệ thức 2 2
sin cos 1 , suy ra 2
cos 1 sin . 5 3 4 Do
nên ta chọn cos . 2 5 3 1 3 3 1 4 4 3 3
Suy ra P sin sin cos . 6 2 2 2 5 2 5 10 3
Câu 37: Cho góc thỏa mãn sin . Tính P sin sin . 5 6 6 11 11 7 10 A. P . B. P . C. P . D. P . 100 100 25 11 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 546
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác Chọn A 1 Áp dụng công thức sin .
a sin b cos
a bcosa b 2 , ta được 1 P sin sin cos cos 2 . 6 6 2 3 2 3 7 Ta có 2 cos 2 1 2sin 1 2. . 5 25 1 1 7 11
Thay vào P , ta được P . 2 2 25 100 4
Câu 38: Cho góc thỏa mãn sin . Tính P cos 4. 5 527 527 524 524 A. P . B. P . C. P . D. P . 625 625 625 625 Lời giải Chọn B 2 4 7 Ta có 2 cos 2 1 2sin 1 2. . 5 25 49 527 Suy ra 2
P cos 4 2 cos 2 1 2. 1 . 625 625 4 3
Câu 39: Cho góc thỏa mãn sin 2 và
. Tính P sin cos . 5 4 3 3 5 5 A. P . B. P . C. P . D. P . 5 5 3 3 Lời giải Chọn A 3 sin 0 Vì suy ra
nên sin cos 0 . 4 cos 0 3 Ta có 2 4 9 sin cos
1 sin 2 1 . Suy ra sin cos . 5 5 5 3 3
Do sin cos 0 nên sin cos . Vậy P . 5 5 2
Câu 40: Cho góc thỏa mãn sin 2 . Tính 4 4
P sin cos . 3 17 7 9 A. P 1. B. P . C. P . D. P . 81 9 7
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 547
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác Lời giải Chọn C
Áp dụng a b a b 2 4 4 2 2 2 2 2a b . 2 1 7 Ta có 4 4
P sin cos 2 2 sin os c 2 2 2
2sin .cos 1 sin 2 . 2 9 5 3
Câu 41: Cho góc thỏa mãn cos và
2 . Tính P tan 2 . 13 2 120 119 120 119 A. P . B. P . C. P . D. P . 119 120 119 120 Lời giải Chọn C sin 2 2sin.cos
Ta có P tan 2 . 2 cos 2 2 cos 1 12 Từ hệ thức 2 2
sin cos 1 , suy ra 2
sin 1 cos . 13 3 12 Do
2 nên ta chọn sin . 2 13 12 5 120 Thay sin và cos
vào P , ta được P . 13 13 119 2
Câu 42: Cho góc thỏa mãn cos 2 . Tính P 2 2 1 3sin 1 4 cos . 3 21 A. P 12. B. P . C. P 6. D. P 21. 2 Lời giải Chọn D 1 cos 2 1 cos 2 5 3 Ta có P 1 3. 1 4. cos 2 1 2cos 2 . 2 2 2 2 2 5 4 7
Thay cos 2 vào P , ta được P 1 1 . 3 2 3 6 3 3
Câu 43: Cho góc thỏa mãn cos và
2 . Tính P cos . 4 2 3 3 21 3 21 3 3 7 A. P . B. P . C. P . D. 8 8 8 3 3 7 P . 8
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 548
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác Lời giải Chọn B 1 3 Ta có P cos
cos cos sin sin cos sin . 3 3 3 2 2 7 Từ hệ thức 2 2
sin cos 1 , suy ra 2
sin 1 cos . 4 3 7 Do
2 nên ta chọn sin . 2 4 7 3 1 3 3 7 3 21 Thay sin
và cos vào P , ta được P . . . 4 4 2 4 2 4 8 4 3
Câu 44: Cho góc thỏa mãn cos và
. Tính P tan . 5 2 4 1 1 A. P . B. P . C. P 7. D. P 7. 7 7 Lời giải Chọn A tan 1
Ta có P tan . 4 1 tan 3 Từ hệ thức 2 2
sin cos 1 , suy ra 2
sin 1 cos . 5 3 3 sin 3 Do
nên ta chọn sin . Suy ra tan . 2 5 cos 4 3 1
Thay tan vào P , ta được P . 4 7 4
Câu 45: Cho góc thỏa mãn cos 2 và
. Tính P cos 2 . 5 4 2 4 2 2 1 1 A. P . B. P . C. P . D. P . 10 10 5 5 Lời giải Chọn B 2
Ta có P cos 2 cos2 sin 2 . 4 2 Từ hệ thức 2 2
sin 2 cos 2 1, suy ra 2 3
sin 2 1 cos 2 . 5
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 549
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 3 Do
2 nên ta chọn sin 2 . 4 2 2 5 3 4 2
Thay sin 2 và cos 2 vào P , ta được P . 5 5 10 4 3 3
Câu 46: Cho góc thỏa mãn cos và . Tính P sin .cos . 5 2 2 2 39 49 49 39 A. P . B. P . C. P . D. P . 50 50 50 50 Lời giải Chọn D 3 1 1 Ta có P sin .cos
sin 2 sin sin 2cos 1 . 2 2 2 2 Từ hệ thức 2 2
sin cos 1 , suy ra 2 3
sin 1 cos . 5 3 3 Do
nên ta chọn sin . 2 5 3 4 39
Thay sin và cos vào P , ta được P . 5 5 50 5
Câu 47: Cho góc thỏa mãn cot 2
. Tính P tan . 2 4 1 1 A. P . B. P . C. P 3. D. P 4. 2 2 Lời giải Chọn C tan tan tan 1 Ta có 4 P tan . 4 1 tan 1 tan .tan 4 5 Từ giả thiết cot
2 cot 2 2 cot 2 tan 2 . 2 2 2
Thay tan 2 vào P , ta được P 3.
Câu 48: Cho góc thỏa mãn cot 15. Tính P sin 2. 11 13 15 17 A. P . B. P . C. P . D. P . 113 113 113 113 Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 550
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác cos Ta có cot 15
15 cos 15sin. sin 30 30 30 15 Suy ra 2
P sin 2 2sin.cos 30sin . 2 2 1 1 cot 115 113 2 sin
Câu 49: Cho góc thỏa mãn cot 3
2 và . Tính P tan cot . 2 2 2 A. P 2 19. B. P 2 19. C. P 19.
D. P 19. Lời giải Chọn A 2 2 sin cos sin cos 2 Ta có 2 2 2 2 P tan cot . 2 2 sin cos sin sin cos 2 2 2 2 1 1 Từ hệ thức 2 1 cot sin . 2 sin 19 1 Do
sin 0 nên ta chọn sin P 2 19. 2 19 4 3
Câu 50: Cho góc thỏa mãn tan và ; 2 . Tính P sin cos . 3 2 2 2 5 5 A. P 5. B. P 5. C. P . D. P . 5 5 Lời giải Chọn C 3 3 Ta có 2
P 1 sin. Với ; 2 ; . 2 2 4 2 0 sin Khi đó 2 2 , suy ra P sin cos 0 . 2 2 2 1 cos 2 2 1 16 Từ hệ thức 2 2
sin cos 1 , suy ra 2 2
sin 1 cos 1 . 2 1 tan 25 3 4 Vì ; 2
nên ta chọn sin . 2 5 4 1 5 Thay sin vào 2 P , ta được 2
P . Suy ra P . 5 5 5
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 551
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác sin 2
Câu 51: Cho góc thỏa mãn tan 2 . Tính P . cos 4 1 10 9 10 9 A. P . B. P . C. P . D. P . 9 10 9 10 Lời giải Chọn C sin 2 sin 2 Ta có P . 2 cos 4 1 2cos 2 2t 2 1 t
Nhắc lại công thức: Nếu đặt t tan thì sin 2 và cos 2 . 2 1 t 2 1 t 2 tan 4 2 1 tan 3 Do đó sin 2 , cos 2 . 2 1 tan 5 2 1 tan 5 4 3 10
Thay sin 2 và cos 2 vào P , ta được P . 5 5 9 1
Câu 52: Cho góc thỏa mãn tan cot 0 và sin . Tính P sin 2 . 5 4 6 4 6 2 6 2 6 A. P . B. P . C. P . D. P . 25 25 25 25 Lời giải Chọn B
Ta có A sin 2 2sin cos . 1 Từ hệ thức 2 2 cot 1
25 cot 24 cot 2 6 . 2 sin
Vì tan , cot cùng dấu và tan cot 0 nên tan 0, cot 0 . 2 6 Do đó ta chọn cot 2
6 . Suy ra cos cot.sin . 5 1 2 6 1 2 6 4 6
Thay sin và cos
vào P , ta được P 2. . . 5 5 5 5 25
Câu 53: Cho góc thỏa mãn
và sin 2cos 1
. Tính P sin 2 . 2 24 2 6 24 2 6 A. P . B. P . C. P . D. P . 25 5 25 5 Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 552
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác sin 0 Với suy ra . 2 cos 0 sin 2cos 1 Ta có 1 2cos 2 2 cos 1 2 2 sin cos 1 cos 0 loaïi 2 5cos 4cos 0 4 . cos 5 3 Từ hệ thức 2 2
sin cos 1 , suy ra sin (do sin 0 ). 5 3 4 24
Vậy P sin 2 2sin.cos 2. . . 5 5 25 5 3
Câu 54: Biết sin a ; cos b ;
a ; 0 b . Hãy tính sin a b. 13 5 2 2 56 63 33 A. . B. . C. . D. 0. 65 65 65 Lời giải Chọn C 2 12 Ta có 2 2 5 144
cos a 1 sin a 1 mà a ; cos a . 13 169 2 13 2 4 Tương tự, ta có 2 2 3 16
sin b 1 cos b 1 mà b 0; sin b . 5 25 2 5 Khi đó a b 5 3 12 4 33 sin sin .
a cos b sin . b cos a . . . 13 5 13 5 65 5 3
Câu 55: Nếu biết rằng sin , cos 0
thì giá trị đúng của biểu 13 2 5 2
thức cos là 16 16 18 18 A. . B. . C. . D. . 65 65 65 65 Lời giải Chọn B 5 25 12 Ta có sin với
suy ra cos 1 . 13 2 169 13 3 9 4
Tương tự, có cos với 0 suy ra sin 1 . 5 2 25 5
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 553
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác Vậy 12 3 5 4 16 cos
cos.cos sin.sin . . . 13 5 13 5 65 1 1
Câu 56: Cho hai góc nhọn a ; b và biết rằng cos a ; cos b . Tính giá trị của biểu thức 3 4
P cosa b.cosa b. 113 115 117 119 A. . B. . C. . D. . 144 144 144 144 Lời giải Chọn D
Ta có P cosa b.cosa b cos . a cosb sin .
a sin bcos . a cosb sin . a sin b a b2 a b2 2 2 a b 2 a 2 cos .cos sin .sin cos .cos 1 cos . 1 cos b. 1 1 1 1 119 . 1 . 1 . 9 16 9 16 144 1 1
Câu 57: Nếu a, b là hai góc nhọn và sin a ; sin b thì cos 2a b có giá trị bằng 3 2 7 2 6 7 2 6 7 4 6 7 4 6 A. . B. . C. . D. . 18 18 18 18 Lời giải Chọn D 2 1 2 2 2
cos a 1 sin a 1 3 3 Vì a, b 0; nên suy ra . 2 2 1 3 2
cosb 1 sin b 1 2 2 Khi đó a b 2 2 3 1 1 1 2 6 cos cos .
a cos b sin . a sin b . . . 3 2 3 2 6 2 1 2 6 7 4 6
Vậy cos 2a b 2
2cos a b 1 2. 1 . 6 18 1 3
Câu 58: Cho 0 ,
và thỏa mãn tan , tan . Góc có giá trị bằng 2 7 4 A. . B. . C. . D. . 3 4 6 2 Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 554
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 1 3 tan tan Ta có 7 4 tan
1 suy ra a b . 1 tan.tan 1 3 1 . 4 7 4 3 1
Câu 59: Cho x, y là các góc nhọn và dương thỏa mãn cot x , cot y . Tổng x y bằng 4 7 3 A. . B. . C. . D. . 4 4 3 Lời giải Chọn B 3 1 . 1 cot . x cot y 1 Ta có x y 4 7 cot 1. cot x cot y 3 1 4 7 3
Mặt khác 0 x, y
suy ra 0 x y . Do đó x y . 2 4
Câu 60: Nếu , , là ba góc nhọn thỏa mãn tan .sin cos thì
A. .
B. . 4 3 3
C. .
D. . 2 4 Lời giải Chọn C
Ta có tan .sin cos sin .sin cos .cos .
cos .cos sin .sin 0 cos 0.
Vậy tổng ba góc
(vì , , là ba góc nhọn). 2 1 1
Câu 61: Biết rằng tan a 0
0 a 90 và tan b 0 0
90 b 180 thì biểu thức 2 3
cos2a b có giá trị bằng 10 10 5 5 A. . B. . C. . D. . 10 10 5 5 Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 555
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 2 1 1 2 1 tan a 2 3 4 Ta có cos 2a suy ra 2
sin 2a 1 cos 2a . 2 2 1 tan a 1 5 5 1 2 1 1 3 Lại có 2 1 tan b cosb vì 0 0 90 b 180 2 2 cos b 1 tan b 10 1 3 1
Mặt khác sin b tan . b cosb . 3 10 10 Khi đó a b 3 3 4 1 1 cos 2 cos 2 .
a cosb sin 2 .
a sin b . . . 5 10 5 10 10 1
Câu 62: Nếu sin a cos a 0 0
135 a 180 thì giá trị của biểu thức tan 2a bằng 5 20 20 24 24 A. . B. . C. . D. . 7 7 7 7 Lời giải Chọn C 1 1 1 24
Ta có sin a cos a sin a cos a2 1 sin 2a sin 2a . 5 25 25 25 2 24 7 Khi đó 2
cos 2a 1 sin 2a 1 vì 0 0 270 2a 360 . 25 25 sin 2a 24
Vậy giá trị của biểu thức tan 2a . cos 2a 7
Câu 63: Nếu tan a b 7, tan a b 4 thì giá trị đúng của tan 2a là 11 11 13 13 A. . B. . C. . D. . 27 27 27 27 Lời giải Chọn A
tan a b tan a b 7 4 11
Ta có tan 2a tan a b a b a b a b . 1 tan .tan 1 7.4 27
Câu 64: Nếu sin.cos sin với k , l , k,l thì 2 2
A. tan 2cot.
B. tan 2cot .
C. tan 2 tan . D.
tan 2 tan.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 556
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác Lời giải Chọn D
Ta có sin.cos sin sin .
sin.cos sin .cos cos .sin.
sin sin 2sin .cos sin .cos 2. 2 tan. cos cos
Câu 65: Nếu
và cot cot 2 cot thì cot.cot bằng 2 A. 3. B. 3. C. 3. D. 3. Lời giải Chọn C
Từ giả thiết, ta có
. 2 2 Suy ra tan tan cot cot 2 cot 2.cot 2.tan 2. 2 1 tan.tan 1 1 tan tan cot cot cot cot Mặt khác nên suy ra 1 tan.tan 1 1 cot.cot 1 1 . cot cot cot cot cot cot 2.
cot.cot 1 2 cot.cot 3. cot.cot 1
Câu 66: Nếu tan và tan là hai nghiệm của phương trình 2
x px q q 0 1 thì tan bằng p p 2 p 2 p A. . B. . C. . D. . q 1 q 1 1 q 1 q Lời giải Chọn A
Vì tan, tan là hai nghiệm của phương trình 2
x px q 0 nên theo định lí Viet, ta
tan tan p p có . Khi đó tan tan tan . tan.tan q 1 tan tan q 1
Câu 67: Nếu tan ; tan là hai nghiệm của phương trình 2
x px q 0 .
p q 0. Và cot ;
cot là hai nghiệm của phương trình 2
x rx s 0 thì tích P rs bằng
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 557
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác p 1 q A. p . q B. . C. . D. . 2 q pq 2 p Lời giải Chọn B
tan tan p
cot cot r
Theo định lí Viet, ta có và . tan.tan q cot.cot s
Khi đó P r s 1 1 1 1 . cot cot .cot.cot . .
tan tan tan tan tan tan p p
. Vậy P r.s . tan.tan 2 2 q 2 q
Câu 68: Nếu tan và tan là hai nghiệm của phương trình 2
x px q 0 0
q thì giá trị biểu thức 2 P
p 2 cos sin .cos
qsin bằng: p A. . p B. . q C. 1. D. . q Lời giải Chọn C
Vì tan , tan là hai nghiệm của phương trình 2
x px q 0 nên theo định lí Viet, ta
tan tan p tan tan p có tan . tan.tan q 1 tan.tan 1 q Khi đó 2 P
p 2 cos . 1 .tan .
q tan . 2 p p p q 1 . p tan 1 . . 2 . q tan 1 q 1 q 2 1 tan 2 p 1 1 q
1 q2 p 1 q .qp 1 q2 2 2 2 2 2
p p .q . q p 1.
1 q2 p 1 q2 2 2 p
Câu 69: Rút gọn biểu thức M tan x tan y .
sin x y
A. M tan x y. B. M . cos . x cos y
sin x y tan x tan y C. M . D. M . cos . x cos y 1 tan . x tan y Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 558
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác Chọn C sin x sin y
sin x cos y cos x sin y
sin x y
Ta có M tan x tan y . cos x cos y cos x cos y cos x cos y
Câu 70: Rút gọn biểu thức 2 2 M cos cos . 4 4
A. M sin 2. B.
M cos 2. C.
M cos 2. D.
M sin 2. Lời giải Chọn D Vì hai góc và phụ nhau nên cos sin . 4 4 4 4 Suy ra 2 2 2 2 M cos cos cos sin 4 4 4 4 cos 2 sin 2. 2
Câu 71: Chọn đẳng thức đúng.
a 1 sin a
a 1 sin a A. 2 cos . B. 2 cos . 4 2 2 4 2 2
a 1 cos a
a 1 cos a C. 2 cos . D. 2 cos . 4 2 2 4 2 2 Lời giải Chọn A 1 cos a a 2 1 sin a 1 sin a 2 cos . 4 2 2 2 2
sin y x
Câu 72: Gọi M thì sin . x sin y
A. M tan x tan . y
B. M cot x cot y 1 1
C. M cot y cot . x D. M . sin x sin y Lời giải Chọn B Ta có :
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 559
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác sin .
y cos x cos . y sin x sin . y cos x cos . y sin x M sin . x sin y sin . x sin y sin .s x in y . cos x cos y
cot x cot y sin x sin y
Câu 73: Gọi M cos x cos 2x cos3x thì 1
A. M 2cos 2x cos x 1 .
B. M 4 cos 2 . x cos x . 2
C. M cos 2x 2cos x 1 .
D. M cos 2x 2cos x 1 . Lời giải Chọn D
Ta có: M cos x cos 2x cos3x cos x cos3x cos 2x 2cos 2 .
x cos x cos 2x cos 2x 2cos x 1 . sin 3x sin x
Câu 74: Rút gọn biểu thức M . 2 2 cos x 1
A. tan 2x B. sin . x C. 2 tan . x D. 2sin . x Lời giải Chọn D sin 3x sin x 2 cos 2x sin x Ta có: 2sin x . 2 2 cos x 1 cos 2x
1 cos x cos 2x cos 3x
Câu 75: Rút gọn biểu thức A . 2
2 cos x cos x 1 A. cos . x B. 2cos x 1. C. 2cos . x D. cos x 1. Lời giải Chọn C
1 cos2x cos x cos3x 2
2cos x 2cos 2x cos x Ta có: A 2 2cos x 1 cos x cos x cos 2x
2cos x cos x cos 2x 2cos . x cos x cos 2x tan cot
Câu 76: Rút gọn biểu thức A cos 2 . tan cot A. 0. B. 2 2 cos . x C. 2. D. cos 2 . x Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 560
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác Ta có 2 2 sin cos sin cos 2 2 sin cos cos sin sin .cos 2 2
sin cos cos 2 . 2 2 2 2 sin cos sin cos sin cos cos sin sin.cos
Do đó A cos 2 cos 2 0. 1 sin 4 cos 4
Câu 77: Rút gọn biểu thức A . 1 sin 4 cos 4 A. sin 2 . B. cos 2 . C. tan 2 . D. cot 2 . Lời giải Chọn C Ta có : 1cos4 2 sin 4
2sin 2 2sin 2 cos 2 A 1 cos 4 2 sin 4
2cos 2 2sin 2 cos 2 .
2sin 2 (sin 2 cos 2 ) tan 2
2cos 2 (sin 2 cos 2 ) 3 4 cos 2 cos 4
Câu 78: Biểu thức A
có kết quả rút gọn bằng: 3 4 cos 2 cos 4 A. 4 tan . B. 4 tan . C. 4 cot . D. 4 cot . Lời giải Chọn B Ta có
2 2sin 2 2 2 2 cos 2 1 2sin ;cos 4 2cos 1 2 1 1. Do đó:
3 41 2sin 21 2sin 2 2 2 2 2 4 1
8sin a 8sin 8sin 4 A . tan 2 2 2 4 2 2
8cos a 8cos 8cos 3 4 2cos 1 2 2cos 1 1 2 4 2 2
sin 2 4sin 4sin .cos Câu 79: Khi
thì biểu thức A
có giá trị bằng: 6 2 2 4 sin 2 4sin 1 1 1 1 A. . B. . C. . D. . 3 6 9 12 Lời giải Chọn C Ta có 2 4 2 2 4
sin 2 4sin 4sin .cos 4sin A 2 2 2 2 2 4 sin 2 4sin
4(1 sin ) 4sin .cos
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 561
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 4 4 sin sin 4 tan . a 2 2 4 cos (1 sin ) cos 4 1 1
Do đó giá trị của biểu thức A tại là 4 tan . 6 6 3 9 sin 2 sin
Câu 80: Rút gọn biểu thức A . 1 o c s 2 cos A. tan. B. 2 tan. C.
tan 2 tan. D. tan 2. Lời giải Chọn A sin 2 sin sin 2 o c s 1 sin 2 o c s 1 Ta có A = tan . 2 1 o
c s2 cos 2 o
c s cos o c s 2 os c 1
1 sin a cos 2a
Câu 81: Rút gọn biểu thức A . sin 2a cos a 5 A. 1. B. tan. C. . D. 2 tan. 2 Lời giải Chọn B 2
1 sin a 2sin a 1
sin a 2sin a 1 sin a Ta có A a a a a a tan . a 2sin .cos cos cos 2sin 1 cos a x sin x sin
Câu 82: Rút gọn biểu thức 2 A được: x 1 cos x cos 2 x A. tan . B. cot . x C. 2 tan x . D. sin . x 2 4 Lời giải Chọn A x x x Ta có sin x sin 2. 2sin cos , 2 2 2 x x 2
1 cos x 1 cos 2. 2 o c s 2 2 x x x x x 2sin cos sin sin 2cos 1 2 2 2 2 2 x Do đó A tan . 2 x x x x 2 2cos cos cos 2cos 1 2 2 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 562
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác
Câu 83: Rút gọn biểu thức 5 5
A sin.cos sin .cos . 1 1 3 1 A. sin 2. B. sin 4. C. sin 4. D. sin 4. 2 2 4 4 Lời giải Chọn D Ta có 5 5 4 4 sin .cos sin .cos sin .cos
cos sin 1 sin 2 2 2 cos sin 2 2 cos sin 2 1 sin 2 1 1 2 2
cos sin sin 2 cos 2 sin 4. 2 2 4
Câu 84: Tìm giá trị lớn nhất M và nhỏ nhất m của biểu thức P 3sin x 2. A. M 1, 5 m . B. M 3, 1 m . C. M 2, 2 m . D. M 0, 2 m . Lời giải Chọn A Ta có 1 sin x 1 3
3sin x 3 5 3sin x 2 1 M 1 5 P 1 . m 5
Câu 85: Cho biểu thức P 2sin x 2
. Mệnh đề nào sau đây là đúng? 3 A. P 4, . x B. P 4, . x C. P 0, . x D. P 2, . x Lời giải Chọn C
Ta có 1 sin x 1 2 2 sin x 2 3 3 4 2sin x
2 0 4 P 0. 3
Câu 86: Biểu thức P sin x sin x
có tất cả bao nhiêu giá trị nguyên? 3 A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 563
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác a b a b
Áp dụng công thức sin a sin b 2cos sin , ta có 2 2 sin x
sin x 2cos x sin cos x . 3 6 6 6 Ta có 1 cos
1 1 1 P x P P 1;0; 1 . 6
Câu 87: Tìm giá trị lớn nhất M và nhỏ nhất m của biểu thức 2 2
P sin x 2 cos . x A. M 3, 0 m . B. M 2, 0 m . C. M 2, 1 m . D. M 3, 1 m . Lời giải Chọn C Ta có 2 2 P x x 2 2 x x 2 2 sin 2 cos sin cos
cos x 1 cos x M 2 Do 2 2 1
cos x 1 0 cos x 11 1 cos x 2 . m 1
Câu 88: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2
P 8sin x 3cos 2x . Tính 2
T 2M m .
A. T 1. B. T 2. C. T 112. D. T 130. Lời giải Chọn A Ta có 2 2 P x x x 2 x 2 8sin 3cos 2 8sin 3 1 2sin 2sin x 3. Mà 2 2
1 sin x 1 0 sin x 1 3 2sin x 3 5 M 5 2
3 P 5
T 2M m 1. m 3
Câu 89: Cho biểu thức 4 4
P cos x sin x . Mệnh đề nào sau đây là đúng? A. P 2, . x B. P 1, .
x C. P 2, . x D. 2 P , x . 2 Lời giải Chọn B 1
Ta có P cos x sin x sin x cos x2 4 4 2 2 2 2 2
2sin x cos x 1 sin 2x 2 1 1 cos 4x 3 1 1 . cos 4 . x 2 2 4 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 564
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Chương 6. Cung lượng giác và công thức lượng giác 1 3 1 1
Mà 1 cos 4x 1 cos 4x 1 P 1. 2 4 4 2
Câu 90: Tìm giá trị lớn nhất M và nhỏ nhất m của biểu thức 4 4
P sin x cos . x A. M 2, 2 m . B. M 2, 2 m . 1 C. M 1, 1 m . D. M 1, . m 2 Lời giải Chọn C Ta có 4 4 P x x 2 2 x x 2 2 sin cos sin cos
sin x cos x cos 2 .x M 1 Mà 1
cos 2x 1 1
cos 2x 1 1 P 1 . m 1
Câu 91: Tìm giá trị lớn nhất M và nhỏ nhất m của biểu thức P 1 2 cos3x . A. M 3, 1 m . B. M 1, 1 m . C. M 2, 2 m . D. M 0, 2 m . Lời giải Chọn B Ta có 1
cos3x 1 0 cos3x 1 0 2 cos3x 2 M 1
1 1 2 cos3x 1
1 P 1 . m 1
Câu 92: Tìm giá trị lớn nhất M của biểu thức 2
P 4sin x 2 sin 2x . 4
A. M 2. B.
M 2 1. C.
M 2 1. D. M 2 2. Lời giải Chọn D 1 cos 2x Ta có 2
P 4sin x 2 sin 2x 4
sin 2x cos 2x 4 2
sin 2x cos 2x 2 2 sin 2x 2. 4 Mà 1 sin 2x
1 2 2 2 sin 2x 2 2 2 . 4 4
Vậy giá trị lớn nhất của hàm số là 2 2.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 565
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133



