
















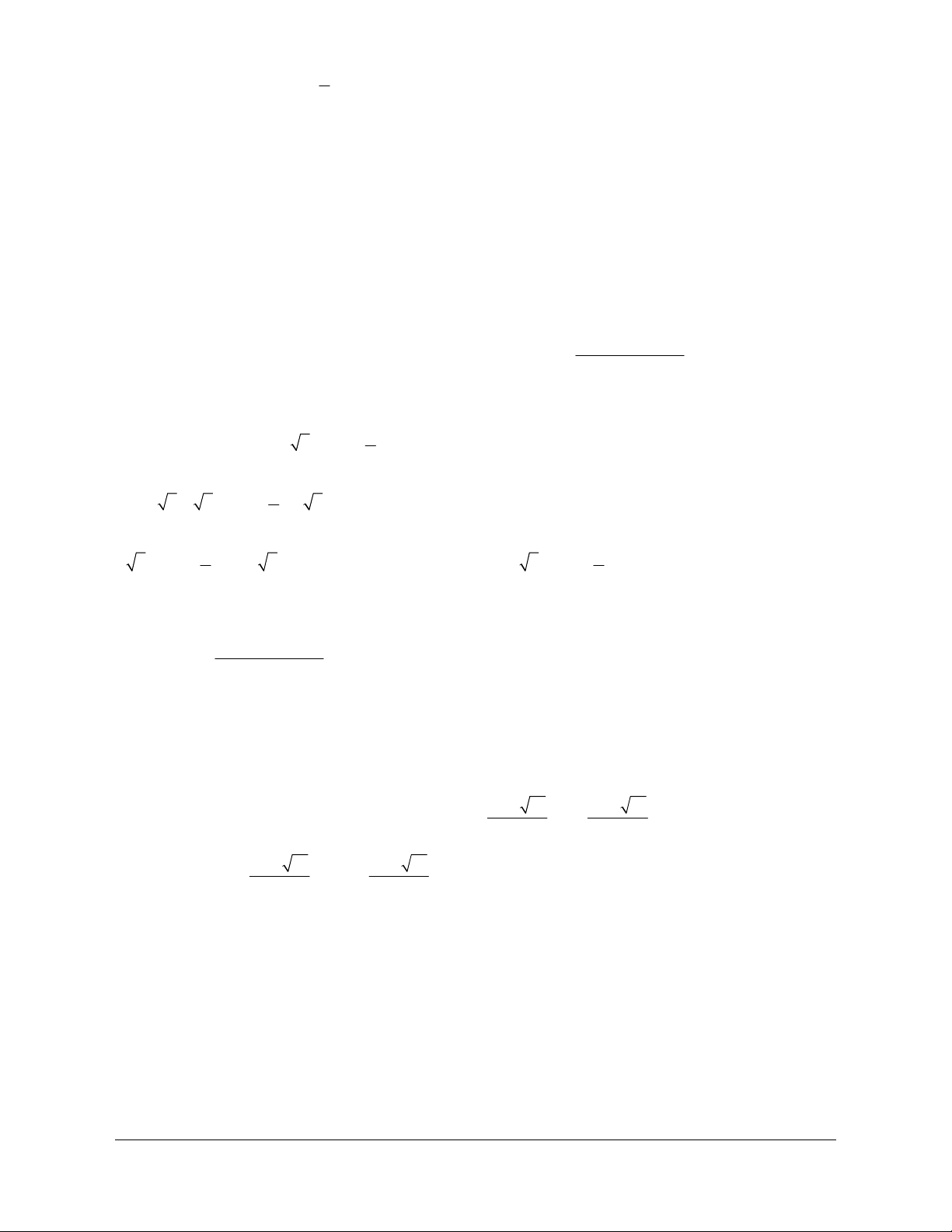

























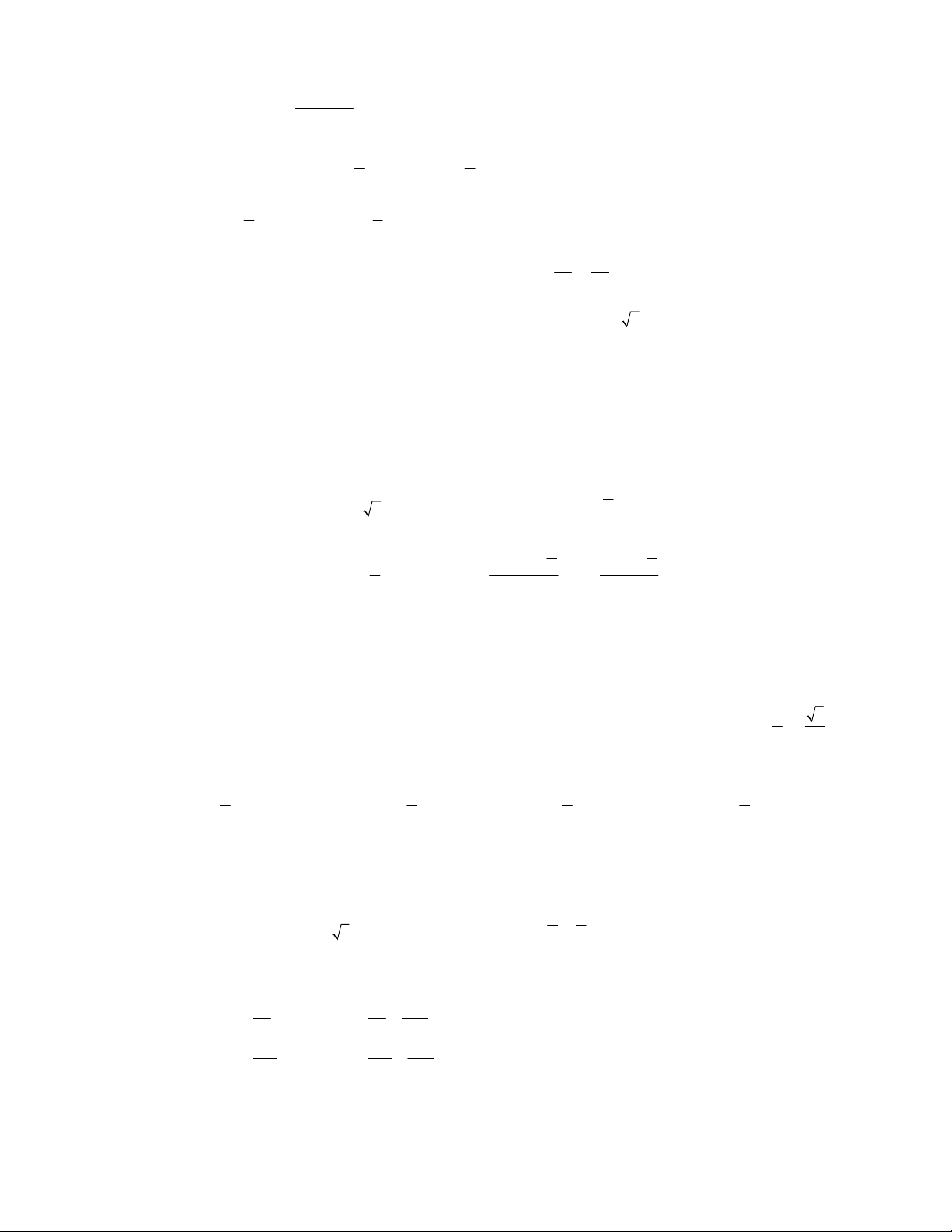
















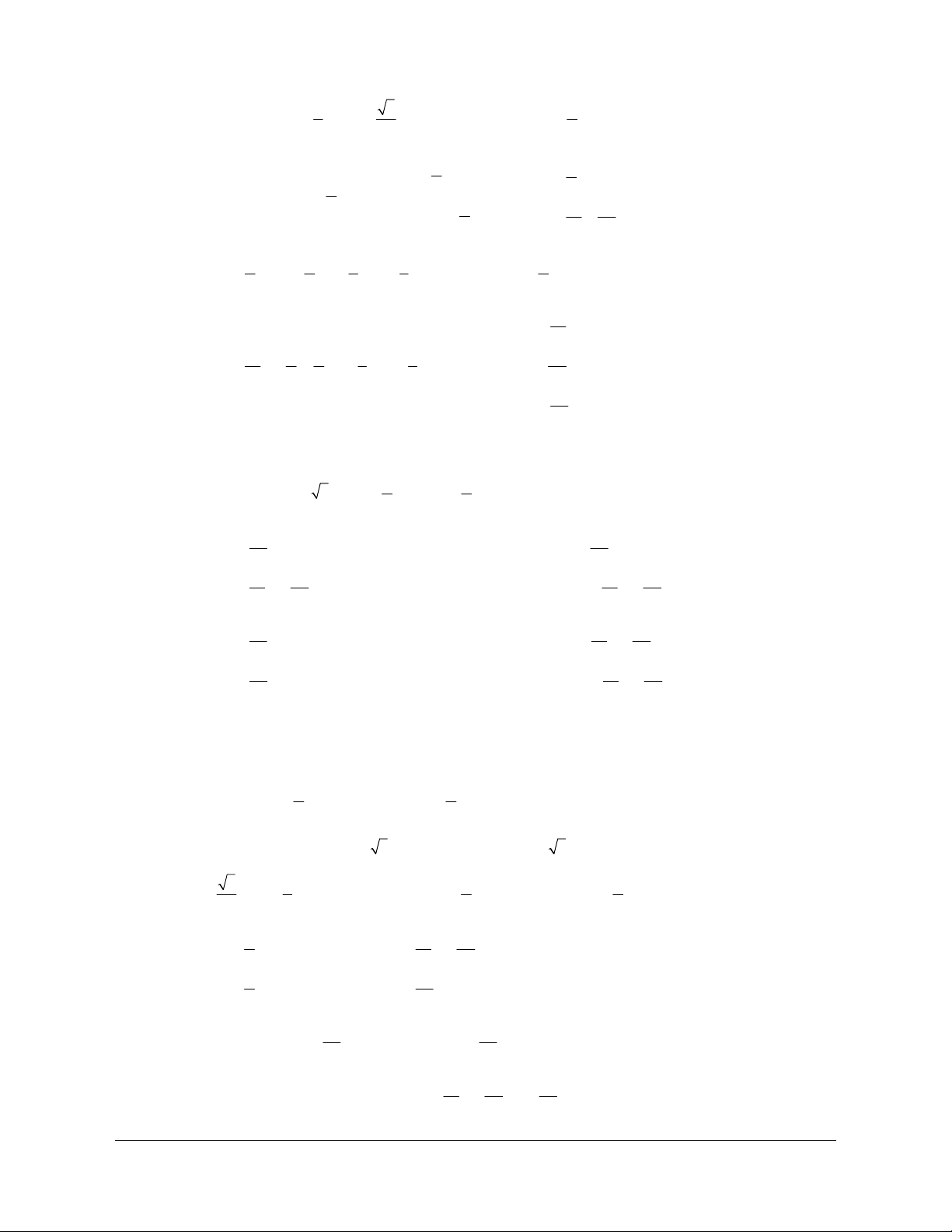
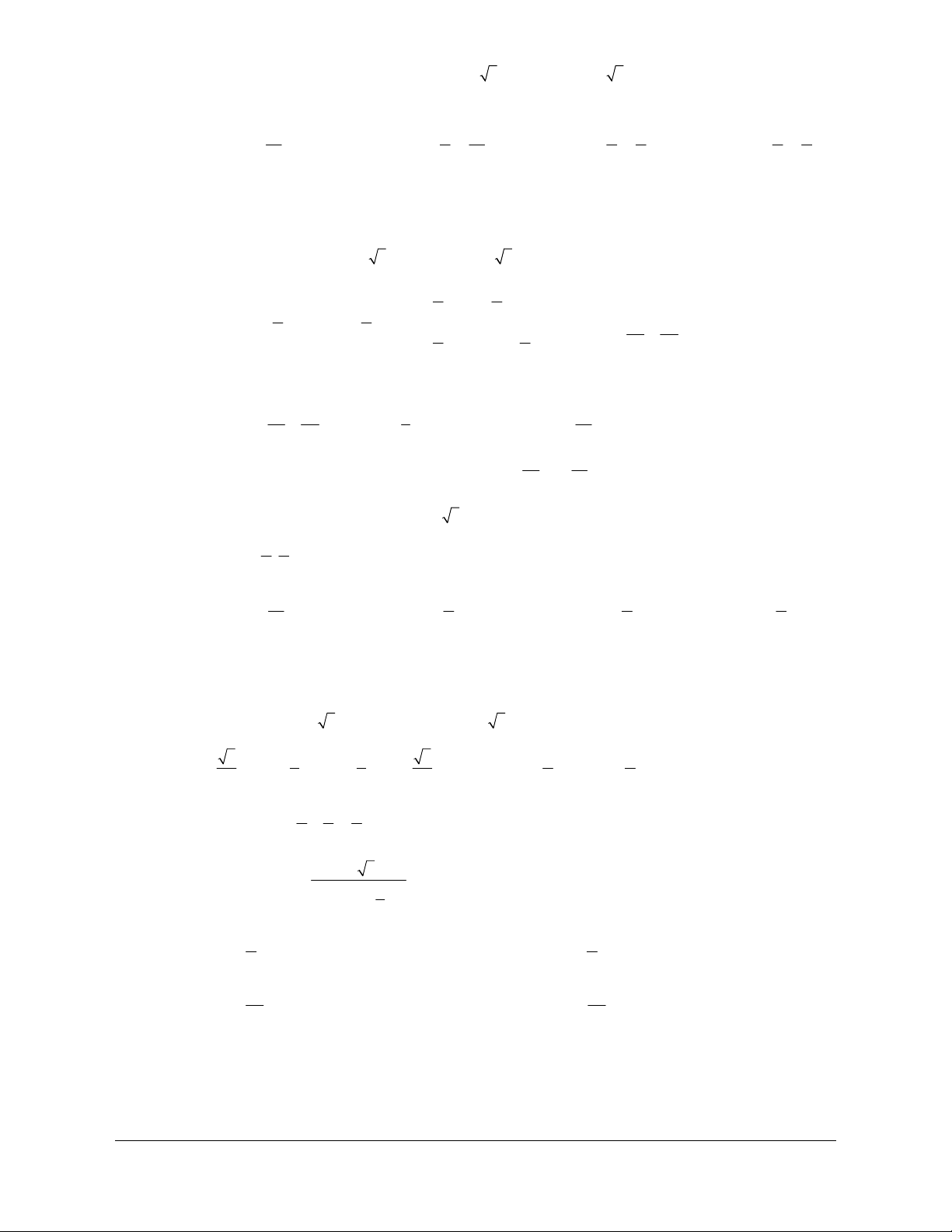





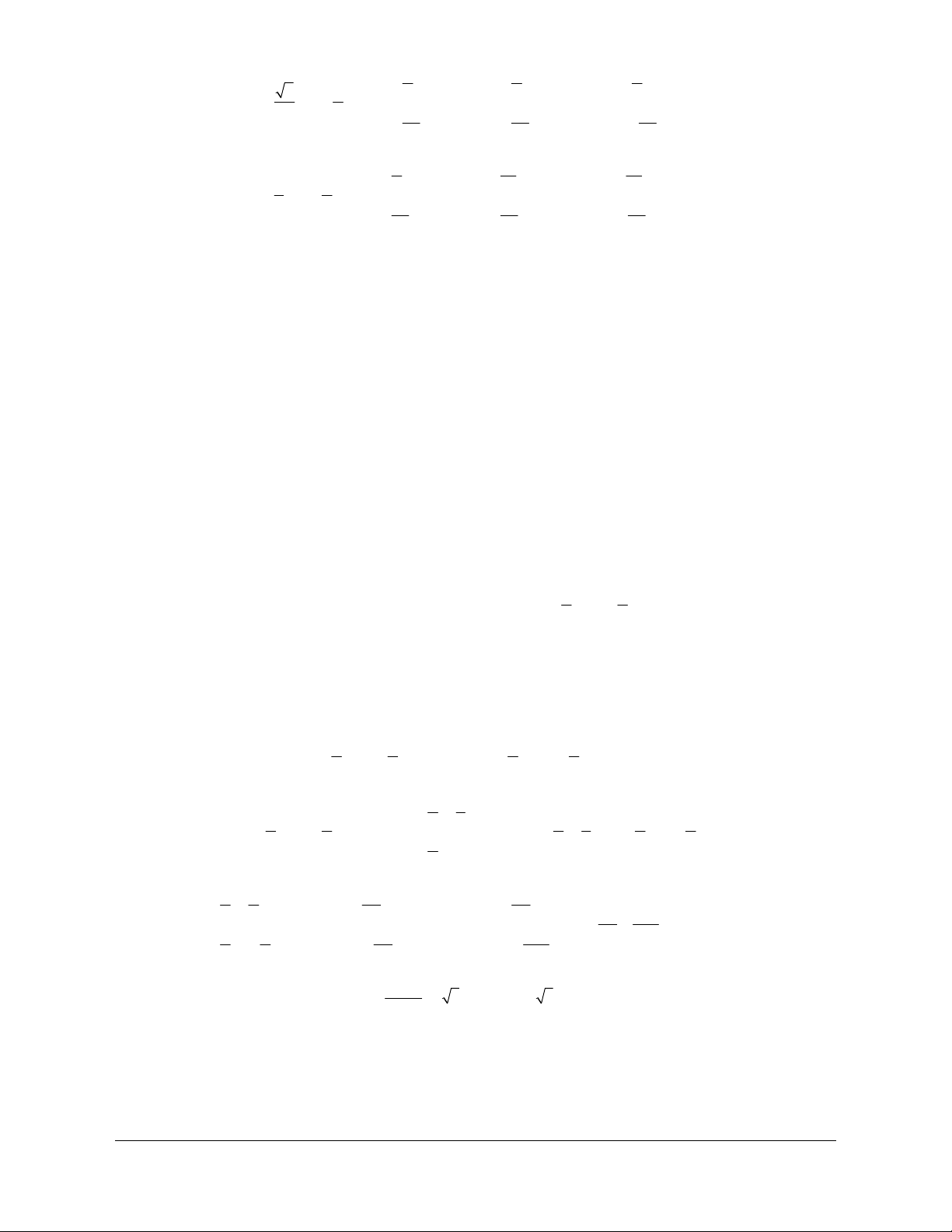

















Preview text:
CHƯƠNG I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
BÀI 1. HÀM SỐ LƯỢNG GIÁC A. LÝ THUYẾT I – ĐỊNH NGHĨA 1) Hàm số sin
Quy tắc đặt tương ứng với mỗi số thực x với số thực sin x sin x :
x y = sin x
được gọi là hàm số sin, kí hiệu là y = sin x.
Tập xác định của hàm số sin là . 2) Hàm số côsin
Quy tắc đặt tương ứng với mỗi số thực x với số thực cos x cos x :
x y = cos x
được gọi là hàm số sin, kí hiệu là y = cos x.
Tập xác định của hàm số cô sin là . 3) Hàm số tang
Hàm số tang là hàm số được xác định bởi công thức sin x y =
(cos x ¹ 0), kí hiệu là cos x y = tan x. ìï ü
Tập xác định của hàm số p ï ï y = tan x là D \ í k , p k = + Î ý . ïî2 ï ï ïþ 4) Hàm số côtang
Hàm số côtang là hàm số được xác định bởi công thức cos x y =
(sin x ¹ 0), kí hiệu là sin x y = cot x.
Tập xác định của hàm số y = cot x là D = \ {k , p k Î }.
II – TÍNH TUẦN HOÀN VÀ CHU KÌ CỦA HÀM SỐ LƯỢNG GIÁC 1) Định nghĩa
Hàm số y = f (x) có tập xác định D được gọi là hàm số tuần hoàn, nếu tồn tại một số
T ¹ 0 sao cho với mọi x Î D ta có: ● x T
- Î D và x +T Î D.
● f (x +T )= f (x).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 1
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Số dương T nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó.
Người ta chứng minh được rằng hàm số y = sin x tuần hoàn với chu kì T = 2p ; hàm số
y = cos x tuần hoàn với chu kì T = 2p ; hàm số y = tan x tuần hoàn với chu kì T = p ; hàm
số y = cot x tuần hoàn với chu kì T = . p 2) Chú ý ● Hàm số 2p
y = sin (ax + b) tuần hoàn với chu kì T = . 0 a ● Hàm số 2p
y = cos(ax +b) tuần hoàn với chu kì T = . 0 a ● Hàm số p
y = tan (ax + b) tuần hoàn với chu kì T = . 0 a ● Hàm số p
y = cot (ax + b) tuần hoàn với chu kì T = . 0 a
● Hàm số y = f x tuần hoàn với chu kì T và hàm số y = f x tuần hoàn với chu kì T 2 ( ) 1 ( ) 1 2
thì hàm số y = f x f x tuần hoàn với chu kì T là bội chung nhỏ nhất của T và T . 1 ( ) 2 ( ) 0 1 2
Lưu ý 2 số thực không xác đinh được bội chung nn, nên là T mT nT với m,n là 2 số 0 1 2
tự nhiên nguyên tố cùng nhau )
III – SỰ BIẾN THIÊN VÀ ĐỒ THỊ CỦA HÀM SỐ LƯỢNG GIÁC
1) Hàm số y = sin x
● Tập xác định D = , có nghĩa và xác định với mọi x Î ;
● Tập giá trị T = [-1; ]
1 , có nghĩa -1 £ sin x £1;
● Là hàm số tuần hoàn với chu kì 2 ,
p có nghĩa sin (x + k2p) = sin x với k Î ; æ ö
● Hàm số đồng biến trên mỗi khoảng p p ç- ç
+ k2p; + k2p÷÷ ç
và nghịch biến trên mỗi khoảng è 2 2 ÷ø æp 3p ö
çç +k2p; + k2p÷÷ ç , k Î ; è 2 2 ÷ø
● Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng.
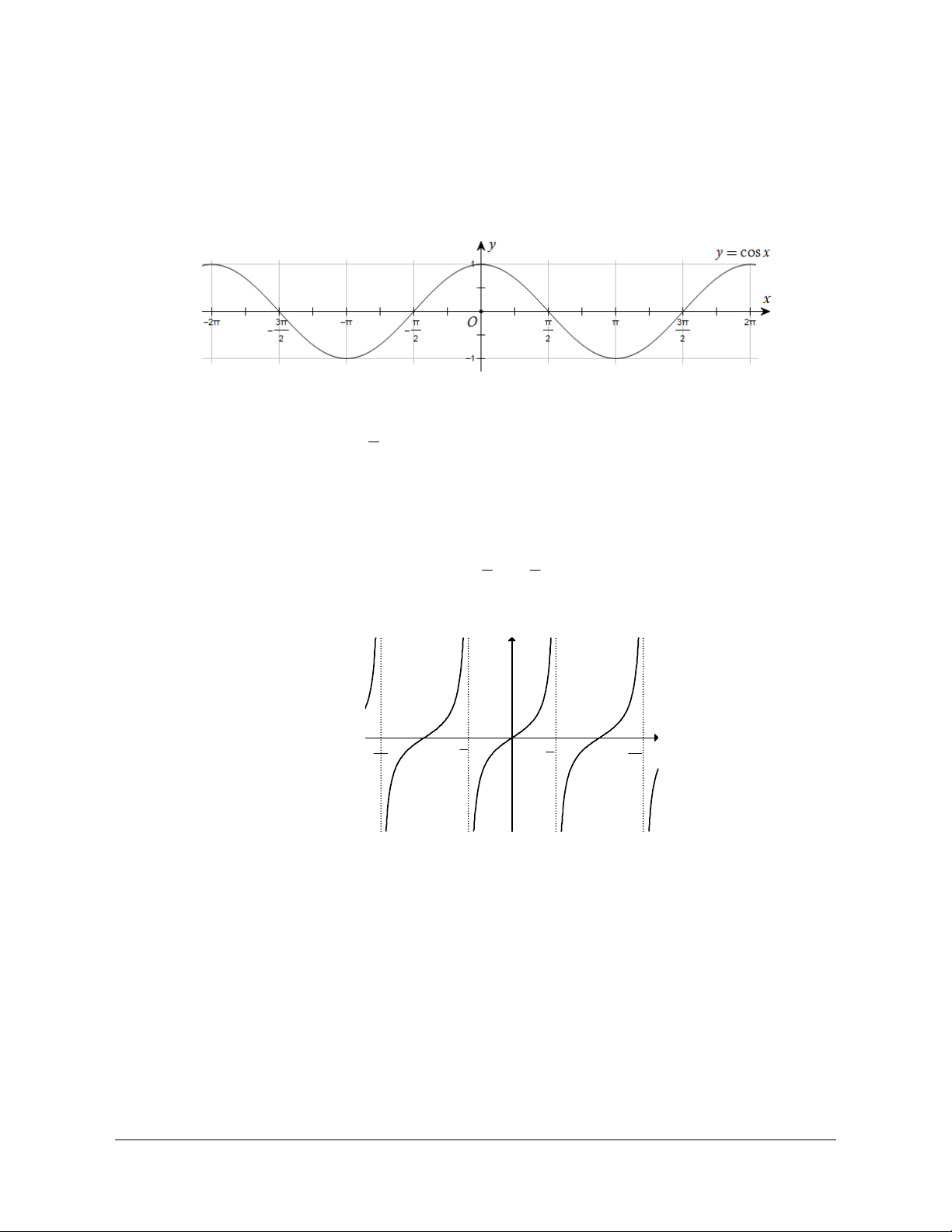
2) Hàm số y = cos x
● Tập xác định D = , có nghĩa và xác định với mọi x Î .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 2
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
● Tập giá trị T =[ 1; - ]
1 , có nghĩa -1 £ cos x £1;
● Là hàm số tuần hoàn với chu kì 2 ,
p có nghĩa cos(x + k2p) = cos x với k Î ;
● Hàm số đồng biến trên mỗi khoảng ( p
- + k2p;k2p) và nghịch biến trên mỗi khoảng
(k2p;p + k2p) , k Î ;
● Là hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng.
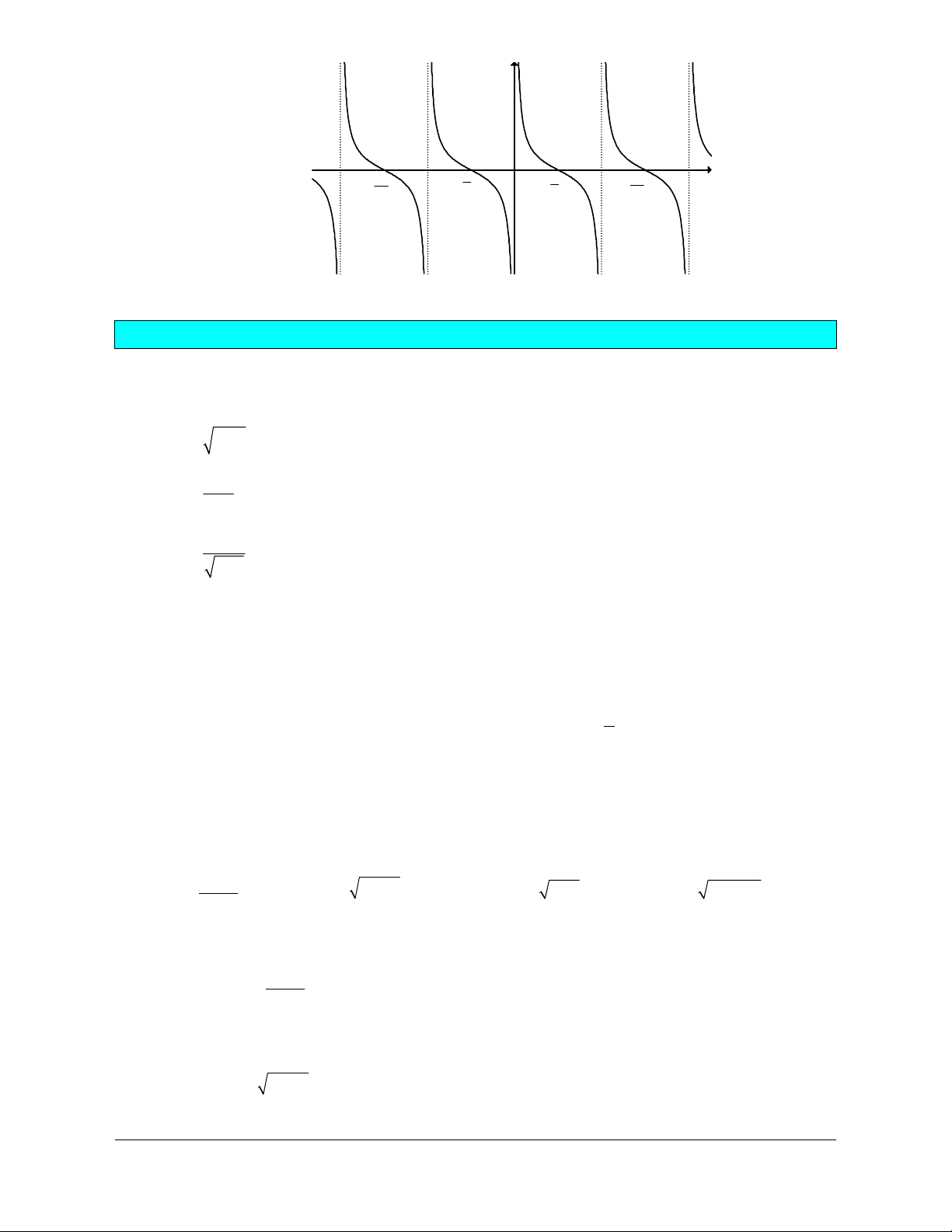
3) Hàm số y = tan x ìï ü ● Tập xác định p ï ï D \ í k , p k = + Î ý ; ïî2 ï ï ïþ
● Tập giá trị T = ;
● Là hàm số tuần hoàn với chu kì ,
p có nghĩa tan (x + kp) = tan x với k Î ; æ ö
● Hàm số đồng biến trên mỗi khoảng p p ç- ç
+ kp; + kp÷÷ , k Î ; ç è 2 2 ÷ø
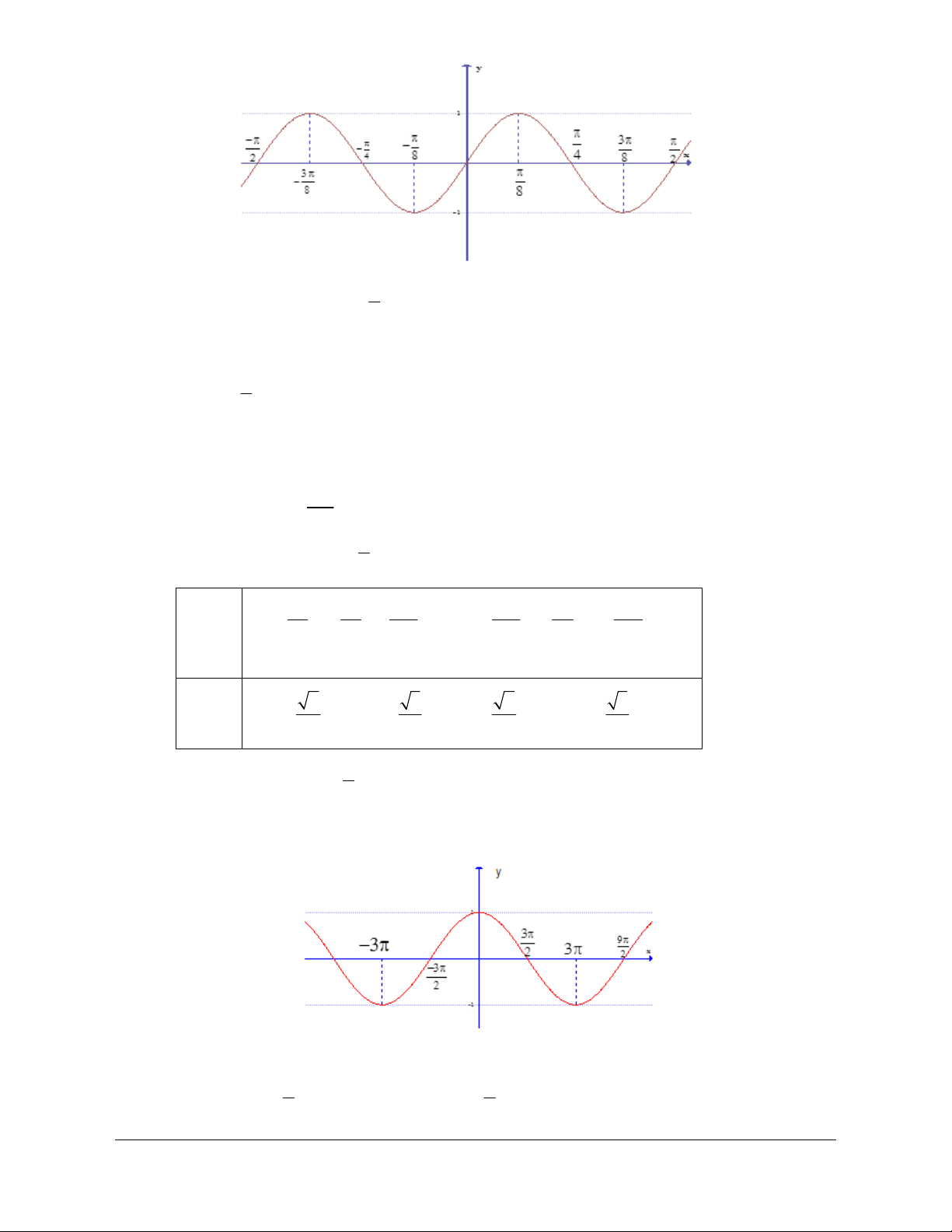
● Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng. y x p p - p 3 - O p p 3p - 2 2 2 2
4) Hàm số y = cot x
● Tập xác định D = \ {k , p k Î };
● Tập giá trị T = ;
● Là hàm số tuần hoàn với chu kì p, có nghĩa tan (x + kp) = tan x với k Î ;
● Hàm số đồng biến trên mỗi khoảng (kp;p + kp ), k Î ;
● Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 3
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 y p - p 2 - p 3p - O p p 3p 2p x - 2 2 2 2
B. PHÂN LOAIJVAF PHƯƠNG PHÁP GIẢI BAIF TÂP
Dạng 1: Tìm tập xác đinh của hàm số 1. Phương pháp
Để tìm tập xác định của hàm số ta cần lưu ý các điểm sau
y ux có nghĩa khi và chỉ khi ux xác định và u(x) 0 . u(x) y
có nghĩa khi và chỉ ux , vx xác định và v(x) 0. v(x) u(x) y
có nghĩa khi và chỉ ux , vx xác định và v(x) 0 . v(x)
Hàm số y sinx, y cosx xác định trên và tập giá trị của nó là: 1 sin x 1 ; 1 cosx 1. Như vậy, y sin u
x , y cos u
x xác định khi và chỉ khi ux xác định.
y tan ux có nghĩa khi và chỉ khi ux xác định và ux k , k 2
y cot ux có nghĩa khi và chỉ khi ux xác định và x k , k . 2. Các ví dụ mẫu
Ví dụ 1. Tìm tập xác định của các hàm số sau: 5x a) y sin ; b) 2 y cos 4 x ; c) y sin x; d) y 2 sin x . 2 x 1 Giải 5x a) Hàm số y sin xác định 2
x 1 0 x 1. 2 x 1 Vậy D \ 1 . b) Hàm số 2
y cos x 4 xác định 2 2
4 x 0 x 4 2 x 2.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 4
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Vậy D x | 2 x 2 .
c) Hàm số y sin x xác định sinx 0 k2 x k2 ,k .
Vậy D x | k2 x k2 , k . d) Ta có: 1
sinx 1 2 sinx 0 .
Do đó, hàm só luôn luôn xác định hay D .
Ví dụ 2. Tìm tập xác định của các hàm số sau: sin x 1 a) y tan x ; b) y cotx ; c) y ; d) y . 6 3 cos(x ) tan x 1 Giải 2
a) Hàm số y tan x
xác định x k x k , k . 6 6 2 3 2 Vậy D \ k,k . 3
b) Hàm số y cot x
xác định x k x k , k . 3 3 3 Vậy D \ k , k . 3 sin x c) Hàm số y xác định 3 cos x
0 x k x k , k . cos(x ) 2 2 3 Vậy D \ k , k . 2 1 d) Hàm số y
xác định tan x 1 x k,k . tan x 1 4 Vậy D \ k , k . 4
Ví dụ 3. Tìm tập xác định của các hàm số sau: 1 3cos2x a) y cos2x ; b) y . cosx sin3x cos3x Giải 1 a) Hàm số y cos2x
xác định cosx 0 x k , k . cosx 2
Vậy D \ k,k . 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 5
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 3cos2x b) Hàm số y xác định sin3x cos3x 1 k sin3x cos3x 0 sin6x 0 6x k x ,k . 2 6 k
Vậy D \ ,k . 6
Ví dụ 4. Tìm m để hàm số sau đây xác định trên : y 2m 3cosx. Giải 2m
Hàm số đã cho xác định trên R khi và chỉ khi 2m 3cosx 0 cosx 3 2m 3
Bất đẳng thức trên đúng với mọi x khi 1 m . 3 2
3. Bài tập trắc nghiệm
Câu 1. Tìm tập xác định D của hàm số 2021 y = . sin x A. D = . B. D = \ {0}. ìï ü C. p ï ï D = \ {k , p k Î }. D. D \ í k , p k = + Î ý . ïî2 ï ï ïþ Lời giải Chọn C
Hàm số xác định khi và chỉ khi sin x ¹ 0 x ¹ k , p . k Î
Vật tập xác định D = \ {k , p k Î }.
Câu 2. Tìm tập xác định + x D của hàm số 1 sin y = . cos x -1 ìï ü A. p ï ï D = . B. D \ í k , p k = + Î ý . ïî2 ï ï ïþ
C. D = \ {k , p k Î }. D.
D = \ {k2p, k Î }. Lời giải Chọn D
Hàm số xác định khi và chỉ khi cos x -1 ¹ 0 cos x ¹ 1 x ¹ k2p, . k Î
Vậy tập xác định D = \ {k2 , p k Î }.
Câu 3. Tìm tập xác định x D của hàm số cos y = . æ pö sinç ÷ çx - ÷ çè 2 ÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 6
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï ü A. p ï ï D \ ík , k = Î ý .
B. D = \ {k , p k Î }. ïî 2 ï ï ïþ ìï ü C. p ï ï D \ ( í 1 2k) , k = + Î ý . D. D = \ ( { 1+2k) , p k Î } . ïî 2 ï ï ïþ Lời giải Chọn C æ ö Hàm số xác định p p p sin ççx ÷
- ÷ ¹ 0 x - ¹ kp x ¹ + k , p . k Î ç è 2 ÷ø 2 2 ìï ü Vậy tập xác định p ï ï D \ í k , p k = + Î ý . ïî2 ï ï ïþ
Câu 4. Tìm tập xác định D của hàm số 2021 y = . sin x -cos x ìï ü A. p ï ï D = . B. D \ í k , p k = - + Î ý . ïî 4 ï ï ïþ ìï ü ìï ü C. p ï ï p ï ï D \ í k2 , p k ï = + Î ý . D. D \ í k , p k = + Î ý . ïî4 ï ï ïþ ïî4 ï ï ïþ Lời giải Chọn D Hàm số xác định p
sin x -cos x ¹ 0 tan x ¹ 1 x ¹ + k , p k Î . 4 ìï ü Vậy tập xác định p ï ï D \ í k , p k = + Î ý . ïî4 ï ï ïþ æ ö
Câu 5. Tìm tập xác định p
D của hàm số y = cot çç2x ÷ - ÷+ sin 2x. ç è 4 ÷ø ìï ü A. p ï ï D \ í k , p k = + Î ý . B. D = . Æ ïî4 ï ï ïþ ìï ü C. p p ï ï D \ í k , k = + Î ý . D. D = . ïî8 2 ï ï ïþ Lời giải Chọn C æ ö Hàm số xác định p p p kp sin çç2x ÷
- ÷ ¹ 0 2x - ¹ kp x ¹ + , . k Î ç è 4 ÷ø 4 8 2 ìï ü Vậy tập xác định p p ï ï D \ í k , k = + Î ý . ïî8 2 ï ï ïþ æ ö
Câu 6. Tìm tập xác định x p D của hàm số 2 y = 3 tan ç ÷ ç - ÷. ç è2 4 ÷ø ìï ü ìï ü A. 3p ï ï p ï ï D \ í k2 , p k ï = + Î ý . B. D \ í k2 , p k = + Î ý . ïî 2 ï ï ïþ ïî2 ï ï ïþ
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 7
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï ü ìï ü C. 3p ï ï p ï ï D \ í k , p k ï = + Î ý . D. D \ í k , p k = + Î ý . ïî 2 ï ï ïþ ïî2 ï ï ïþ Lời giải Chọn A æ ö Hàm số xác định x p x p p 3p 2 cos ç ÷
ç - ÷ ¹ 0 - ¹ + kp x ¹ + k2 , p . k Î ç è2 4 ÷ø 2 4 2 2 ìï ü Vậy tập xác định 3p ï ï D \ í k2 , p k = + Î ý . ïî 2 ï ï ïþ
Câu 7. Tìm tập xác định 3 tan x -5 D của hàm số y = . 2 1-sin x ìï ü ìï ü A. p ï ï p ï ï D \ í k2 , p k ï = + Î ý . B. D \ í k , p k = + Î ý . ïî2 ï ï ïþ ïî2 ï ï ïþ
C. D = \ {p + k , p k Î }. D. D = . Lời giải Chọn B
Hàm số xác định khi và chỉ khi 2
1-sin x ¹ 0 và tan x xác định 2 sin ìï x ¹ 1 p ï í
cos x ¹ 0 x ¹ + k , p k Î . co ï s x ¹ 0 2 ïî ìï ü Vậy tập xác định p ï ï D \ í k , p k = + Î ý . ïî2 ï ï ïþ
Câu 8. Tìm tập xác định D của hàm số y = sin x + 2. A. D = . B. D = [-2;+¥). C. D = [0;2p]. D. D = . Æ Lời giải Chọn A
Ta có -1£ sin x £1 ¾¾
1 £ sin x + 2 £ 3, "x Î .
Do đó luôn tồn tại căn bậc hai của sin x + 2 với mọi x Î . Vậy tập xác định D = .
Câu 9. Tìm tập xác định D của hàm số y = sin x -2. A. D = . B. \ {k , p k Î }. C. D =[-1; ] 1 . D. D = . Æ Lời giải Chọn D
Ta có -1£ sin x £1 ¾¾ 3
- £ sin x -2 £ -1, . "x Î
Do đó không tồn tại căn bậc hai của sin x -2. Vậy tập xác định D = . Æ
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 8
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 10. Tìm tập xác định D của hàm số 1 y = . 1-sin x ìï ü A. p ï ï D = \ {k , p k Î }. B. D \ í k , p k = + Î ý . ïî2 ï ï ïþ ìï ü C. p ï ï D \ í k2 , p k = + Î ý . D. D = . Æ ïî2 ï ï ïþ Lời giải Chọn C
Hàm số xác định khi và chỉ khi 1-sin x > 0 sin x <1. ( ) * Mà p
-1 £ sin x £1 nên ( )
* sin x ¹ 1 x ¹ + k2 , p k Î . 2 ìï ü Vậy tập xác định p ï ï D \ í k2 , p k = + Î ý . ïî2 ï ï ïþ
Câu 11. Tìm tập xác định D của hàm số y = 1-sin 2x - 1+ sin 2x. A. D = . Æ B. D = . é ù é ù C. p 5p p p D = ê + k2p;
+ k2pú , k Î . D. 5 13 D = ê + k2p;
+ k2pú , k Î . ê 6 6 ú ë û ê 6 6 ú ë û Lời giải Chọn B 1 ìï +sin 2x ³ 0 Ta có 1 sin 2x 1 ï - £ £ í , "x Î . 1 ï -sin 2x ³ 0 ïî Vậy tập xác định D = . æ ö
Câu 12. Tìm tập xác định p
D của hàm số y = tan çç cos x÷÷. ç è 2 ÷ø ìï ü ìï ü A. p ï ï p ï ï D \ í k , p k ï = + Î ý . B. D \ í k2 , p k = + Î . ï ý î2 ï ï ïþ ïî2 ï ï ïþ C. D = .
D. D = \ {k , p k Î } . Lời giải Chọn D
Hàm số xác định khi và chỉ khi p p
.cos x ¹ + kp cos x ¹ 1+ 2k . ( ) * 2 2 Do k Î nên ( )
* cos x ¹ 1 sin x ¹ 0 x ¹ k , p k Î .
Vậy tập xác định D = \ {k , p k Î }.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 9
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Dạng 2: Xét tính chẵn lẻ của hàm số 1. Phương pháp:
Giả sử ta cần xét tính chẵn, lẻ của hàm số y f(x)
Bước 1: Tìm tập xác định D của hàm số; kiểm chứng D là tập đối xứng qua số 0 tức là x ,xD xD (1)
Bước 2: Tính f(x) và so sánh f(x) với f(x)
- Nếu f(x) f(x) thì f(x) là hàm số chẵn trên D (2)
- Nếu f(x) f(x) thì f(x) là hàm số lẻ trên D (3) Chú ý:
- Nếu điều kiện (1) không nghiệm đúng thì f(x) là hàm không chẵn và không lẻ trên D;
- Nếu điều kiện (2) và (3) không nghiệm đúng, thì f(x) là hàm không chẵn và cũng không lẻ trên D .
Lúc đó, để kết luận f(x) là hàm không chẵn và không lẻ ta chỉ cần chỉ ra điểm x 0 D sao cho f(x0) f(x0) f(x 0 ) f(x0 ) 2. Các ví dụ mẫu
Ví dụ 1. Xét tính chẵn, lẻ của các hàm số sau: a) y = sin2x; b) y = tan x ; c) 4 y sin x . Giải a) TXĐ: D . Suy ra x D x D .
Ta có: f x sin2x sin2x f x .
Do đó hàm số đã cho là hàm số lẻ.
b) TXĐ: D \ k , k . Suy ra x D x D . 2
Ta có: f x tan x tan x f x .
Do đó hàm số đã cho là hàm số chẵn. c) TXĐ: D . Suy ra x D x D . Ta có: 4 4 f x sin x sin x f x .
Do đó hàm số đã cho là hàm số chẵn.
Ví dụ 2. Xét tính chẵn, lẻ của các hàm số sau: a) y = tanx + cotx; b) y = sinx.cosx.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 10
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Giải k
a) TXĐ: D \ ,k . Suy ra x D x D 2
Ta có: f x tanx cotx tanx -cot x tanx cot x f x
Do đó hàm số đã cho là hàm số lẻ. b) TXĐ: D . Suy ra x D x D
Ta có: f x sinx.cosx sinxcosx f x
Do đó hàm số đã cho là hàm số lẻ.
Ví dụ 3. Xét tính chẵn, lẻ của các hàm số sau: a) y = 2sinx + 3; b) y sinx cosx . Giải a) TXĐ: D . Suy ra x D x D Ta có: f 2sin
3 1 ; f 2sin 3 5 2 2 2 2 f f 2 2 Nhận thấy f f 2 2
Do đó hàm số không chẵn không lẻ. b) TXĐ: D . Suy ra x D x D
Ta có: y sinx cosx 2 sinx 4
f 2 sin 0; f 2 sin 2 4 4 4 4 4 4 f f 4 4 Nhận thấy f f 4 4
Do đó hàm số không chẵn không lẻ.
Ví dụ 4. Xét tính chẵn, lẻ của các hàm số sau: sinx tanx 3 cos x 1 a) y ; b) y . sinx cot x 3 sin x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 11
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Giải a) Hàm số xác định khi cosx 0 cosx 0 cosx 0 k sin x 0 s inx 0 x ,k . sin x 0 2 2 sinx cot x 0 si n x cosx 0 TXĐ: k D \ ,k Suy ra x D x D 2 sin x tan x sin x tan x sin x - tan x Ta có: f x
sinx cotx f x
sin x cot x sin x cot x
Do đó hàm số đã cho là hàm số chẵn. b) TXĐ: D \ k , k Suy ra x D x D 3 3 3 cos x 1 cos x 1 cos x 1 Ta có: f x f x 3 sin x 3 3 sin x sin x
Do đó hàm số đã cho là hàm số lẻ.
Ví dụ 5. Xác định tham số m để hàm số sau: y f x 3msin4x cos2x là hàm số chẵn. Giải TXĐ: D . Suy ra x D x D Ta có: f x 3msin 4 x cos 2 x 3m sin4x cos2x
Để hàm số đã cho là hàm số chẵn thì: f x fx, x
D 3msin4x cos2x -3msin4x cos2x, x D 6msin4x 0 m 0
3. Bài tập trắc nghiệm
Câu 1: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = sin x.
B. y = cos x.
C. y = tan x.
D. y = cot x. Lời giải Chọn B
Nhắc lại kiến thức cơ bản:
Hàm số y = sin x là hàm số lẻ.
Hàm số y = cos x là hàm số chẵn.
Hàm số y = tan x là hàm số lẻ.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 12
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Hàm số y = cot x là hàm số lẻ.
Vậy B là đáp án đúng.
Câu 2: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = - sin x. B.
y = cos x -sin x. C. 2
y = cos x + sin x. D.
y = cos x sin x. Lời giải Chọn C
Tất các các hàm số đều có TXĐ: D = . Do đó "x Î D -x Î D.
Bây giờ ta kiểm tra f (-x)= f (x) hoặc f ( x - ) = - f (x).
Với y = f (x) = - sin x . Ta có f (-x) = - sin (-x) = sin x = -(-sin x) ¾¾ f ( x
- ) = - f (x) . Suy ra hàm số y = - sin x là hàm số lẻ.
Với y = f (x) = cos x -sin x. Ta có f ( x - ) = cos( x
- )-sin (-x) = cos x + sin x ¾¾
f (-x) ¹ {- f (x), f (x)} . Suy ra hàm số y = cos x -sin x không chẵn không lẻ.
Với y = f (x) 2
= cos x + sin x . Ta có f (-x) = (-x) 2 cos + sin (-x) =
(-x)+ é (-x) 2ù = x +[- x ]2 2 cos sin cos sin = cos x + sin x ë û ¾¾ f ( x
- ) = f (x) . Suy ra hàm số 2
y = cos x + sin x là hàm số chẵn.
Với y = f (x) = cos x sin x. Ta có f (-x) = cos(-x).sin (-x) = -cos x sin x ¾¾ f ( x
- ) = - f (x) . Suy ra hàm số y = cos x sin x là hàm số lẻ.
Câu 3: Trong các hàm số sau, hàm số nào là hàm số chẵn? A. x y = sin 2x.
B. y = x cos x.
C. y = cos x.cot x. D. tan y = . sin x Lời giải Chọn D
Xét hàm số y = f (x) = sin 2x.
TXĐ: D = . Do đó "x Î D -x Î D. Ta có f ( x - ) = sin ( 2
- x) = -sin 2x = - f (x) ¾¾
f (x) là hàm số lẻ.
Xét hàm số y = f (x) = x cos x.
TXĐ: D = . Do đó "x Î D -x Î D. Ta có f ( x
- ) = (-x).cos(-x) = -x cos x = - f (x) ¾¾
f (x) là hàm số lẻ.
Xét hàm số y = f (x) = cos x cot x. TXĐ: D = \ {kp (
k Î )}. Do đó "x Î D -x Î D.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 13
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Ta có f ( x
- ) = cos(-x).cot (-x) = -cos x cot x = - f (x) ¾¾
f (x) là hàm số lẻ. x
Xét hàm số y = f (x) tan = . sin x ìï ü TXĐ: p ï ï D \ ík ( k ) = Î
ý. Do đó "x Î D -x Î D. ïî 2 ï ï ïþ tan (-x) Ta có (- ) -tan x tan x f x = = = = f (x) ¾¾
f (x) là hàm số chẵn. sin (-x) -sin x sin x
Câu 4: Trong các hàm số sau, hàm số nào là hàm số chẵn? A. x y = sin x . B. 2
y = x sin x. C. y = .
D. y = x + sin x. cos x Lời giải Chọn A
Ta kiểm tra được A là hàm số chẵn, các đáp án B, C, D là hàm số lẻ.
Câu 5: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung? æ ö A. p tan x
y = sin x cos 2x. B. 3
y = sin x.cosççx ÷ - ÷. ç C. y = . D. 3
y = cos x sin x. è 2 ÷ø 2 tan x +1 Lời giải Chọn B
Ta dễ dàng kiểm tra được A, C, D là các hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ O . æ ö Xét đáp án B, ta có p y = f (x) 3 3 4 = sin x.cosççx ÷
- ÷ = sin x.sin x = sin x ç
. Kiểm tra được đây là è 2 ÷ø
hàm số chẵn nên có đồ thị đối xứng qua trục tung.
Câu 6: Trong các hàm số sau, hàm số nào là hàm số lẻ? A. 2
y = cos x + sin x. B.
y = sin x + cos x.
C. y = -cos x. D.
y = sin x.cos3x. Lời giải Chọn D
Ta kiểm tra được đáp án A và C là các hàm số chẵn. Đáp án B là hàm số không chẵn,
không lẻ. Đáp án D là hàm số lẻ.
Câu 7: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ? A. x + y = cot 4x. B. sin 1 y = . C. 2 y = tan x.
D. y = cot x . cos x Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 14
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ta kiểm tra được đáp án A là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ.
Đáp án B là hàm số không chẵn, không lẻ. Đáp án C và D là các hàm số chẵn.
Câu 8: Trong các hàm số sau, hàm số nào là hàm số lẻ? æ ö A. p x x
y = sin çç - x÷÷. ç B. 2
y = sin x. C. cot y = . D. tan y = . è 2 ÷ø cos x sin x Lời giải Chọn C æ ö Viết lại đáp án A là p
y = sin çç - x÷÷ = cos x. ç è 2 ÷ø
Ta kiểm tra được đáp án A, B và D là các hàm số chẵn. Đáp án C là hàm số lẻ.
Câu 9: Trong các hàm số sau, hàm số nào là hàm số lẻ? A. 2
y = 1-sin x. B. 2
y = cot x . sin x. C. 2
y = x tan 2x -cot x. D.
y = 1+ cot x + tan x . Lời giải Chọn C
Ta kiểm tra được đáp án A, B và D là các hàm số chẵn. Đáp án C là hàm số lẻ.
Câu 10: Cho hàm số f (x) = sin 2x và g(x) 2
= tan x. Chọn mệnh đề đúng
A. f (x) là hàm số chẵn, g(x) là hàm số lẻ.
B. f (x) là hàm số lẻ, g(x) là hàm số chẵn.
C. f (x) là hàm số chẵn, g(x) là hàm số chẵn.
D. f (x) và g(x) đều là hàm số lẻ. Lời giải Chọn B
Xét hàm số f (x) = sin 2x.
TXĐ: D = . Do đó "x Î D -x Î D.
Ta có f (-x)= sin (-2x)= -sin 2x = - f (x) ¾¾
f (x) là hàm số lẻ.
Xét hàm số g(x) 2 = tan x. ìï ü TXĐ: p ï ï D \ í kp ( k ) = + Î
ý. Do đó "x Î D -x Î D. ïî2 ï ï ïþ Ta có g(-x)= é (-x) 2ù = (- x )2 2 tan tan
= tan x = g(x) ë û ¾¾
f (x) là hàm số chẵn. sin 2x -cos3x Câu 11: cos 2x
Cho hai hàm số f (x) = và g(x)=
. Mệnh đề nào sau đây là đúng? 2 1+ sin 3x 2 2 + tan x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 15
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
A. f (x) lẻ và g(x) chẵn.
B. f (x) và g(x) chẵn.
C. f (x) chẵn, g(x) lẻ.
D. f (x) và g(x) lẻ. Lời giải Chọn B cos 2x
Xét hàm số f (x) = . 2 1+ sin 3x
TXĐ: D = . Do đó "x Î D -x Î D. cos(-2x) Ta có (- ) cos 2x f x = = = f (x) ¾¾
f (x) là hàm số chẵn. 2 1+ sin (-3x) 2 1+ sin 3x sin 2x -cos3x
Xét hàm số g(x) = . 2 2 + tan x ìï ü TXĐ: p ï ï D \ í kp (k ) = + Î
ý . Do đó "x Î D x - Î D. ïî2 ï ï ïþ
sin (-2x) -cos(-3x) sin 2x -cos3x Ta có g(-x)= = = g(x) ¾¾
g(x) là hàm số chẵn. 2 2 + tan (-x) 2 2 + tan x
Vậy f (x) và g(x) chẵn.
Câu 12: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ? æ ö æ ö A. 1 p p y = .
B. y = sin ççx + .÷÷
C. y = 2 cosççx ÷
- ÷. D. y = sin 2x. 3 sin x çè 4 ÷ø çè 4 ÷ø Lời giải Chọn A æ ö Viết lại đáp án B là p 1 y = sin ççx ÷ + ÷ = (sin x +cos x). ç è 4 ÷ø 2 æ ö Viết lại đáp án C là p y = 2 cosççx ÷
- ÷ = sin x + cos x. ç è 4 ÷ø
Kiểm tra được đáp án A là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ.
Ta kiểm tra được đáp án B và C là các hàm số không chẵn, không lẻ. Xét đáp án D. é p ù
Hàm số xác định sin 2x ³ 0 2x Î[k2p;p + k2p] x Î êkp; + kpú ê 2 ú ë û é p ù ¾¾
D = êkp; + kpú (k Î ). ê 2 ú ë û p p
Chọn x = Î D nhưng x
- = - Ï D. Vậy y = sin 2x không chẵn, không lẻ. 4 4
Câu 13: Mệnh đề nào sau đây là sai?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 16
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
A. Đồ thị hàm số y = sin x đối xứng qua gốc tọa độ . O
B. Đồ thị hàm số y = cos x đối xứng qua trục Oy.
C. Đồ thị hàm số y = tan x đối xứng qua trục Oy.
D. Đồ thị hàm số y = tan x đối xứng qua gốc tọa độ . O Lời giải Chọn A
Ta kiểm tra được hàm số y = sin x là hàm số chẵn nên có đồ thị đối xứng qua trục Oy . Do đó đáp án A sai.
Dạng 3. Tìm giá trị lớn nhất và và giá trị nhỏ nhất của hàm số lượng giác 1. Phương pháp:
Cho hàm số y f(x) xác định trên tập D f(x) M,xD M max f(x) D x D : f(x ) 0 0 M f(x) m, x D m min f(x) D x 0 D : f(x0 ) m Lưu ý: 1
sinx 1; 1 cosx 1. 2 2
0 sin x 1; 0 cos x 1.
0 sinx 1; 0 cosx 1.
Dùng điều kiện có nghiệm của phương trình cơ bản 0 o Phương trình bậc hai: 2
ax bx c 0 có nghiệm x khi và chỉ khi a 0
o Phương trình asin x b cosx c có nghiệm x khi và chỉ khi 2 2 2 a b c a sinx b cosx c o Nếu hàm số có dạng: 1 1 1 y a2 sinx b2 cosx 2 c
Ta tìm miền xác định của hàm số rồi quy đồng mẫu số, đưa về phương trình asinx bcosx c . 2. Ví dụ mẫu
Ví dụ 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y 2sin x 1 ; b) y 2 cosx 1 3 . 4 Giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 17
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 a) Ta có: 1
sinx 1 2
2sinx 2 1
2sinx 1 3 4 4 4
Hay 1 y 3 . Suy ra: Maxy
3 khi sinx 1 x k2 , k . 4 4 Miny 3 1
khi sinx 1 x k2 , k . 4 4 b) Ta có: 1
cosx 1 0 cosx 1 2 0 cosx 1 2
0 2 cosx 1 2 2 3
2 cosx 1 3 2 2 3
Hay 3 y 2 2 3 Suy ra
Maxy 2 2 3 khi cosx 1 x k2 , k . Miny 3
khi cosx 0 x k , k . 2
Ví dụ 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: a) y sinx cosx ; b) y 3 sin2x cos2x . Giải
a) Ta có: y sinx cosx 2 sinx 2 y 2 . 4 Suy ra: Maxy
2 khi sinx 1 x k2 , k . 4 4 Miny 3
2 khi sinx 1 x k2,k . 4 4 3 1
b) Ta có: y 3 sin2x cos2x 2
sin2x cos2x 2sin2x 2 2 6
Suy ra: 2 y 2 . Do đó: Maxy
2 khi sin2x 1 2x k2 x k2 , k . 6 6 2 3 Miny 2
khi sin2x 1 2x k2 x k2,k . 6 6 2 6
Ví dụ 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 18
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 a) 2
y cos x 2sinx 2 ; b) 4 2 y sin x 2cos x 1. Giải a) Ta có:
y cos x 2sin x 2 1sin x2 2 2 2sin x 2
sin x 2sin x 3 sinx 2 2 1 4 Vì 2 1 sinx 1 2 sin x 1 0 4 sin x 1 0 2 2 4 sin x 1 0 0 sin x 1 4 4 Hay 0 y 4 Do đó: Maxy
4 khi sin x 1 x k2 , k . 2 Miny 0 khi sin x 1 x k2 , k . 2 Lưu ý:
Nếu đặt t sin x,t 1 ;1 . Ta có (P): 2
y f t t 2t 3 xác định với mọi t 1 ;1 , (P) có
hoành độ đỉnh t 1 và trên đoạn 1 ;1
hàm số đồng biến nên hàm số đạt giá trị nhỏ nhất tại t 1 hay sin x 1
và đạt giá trị lớn nhất khi t 1 hay sin x 1. b) Ta có
y sin x 2cos x 1 1 cos x2 4 2 2 2 2cos x 1
cos x 4cos x 2 cos x 22 4 2 2 2 Vì 2 2 2 2 0 cos x 1 2 cos x 2 1 4 cos x 2 1 2 2 2 cos x 2 2 1 2 y 1 Do đó: Maxy 2 khi
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 19
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 cos x 0 cosx 0 x k , k . 2 Miny 1 khi 2
cos x 1 sinx 0 x k , k . Lưu ý: Nếu đặt 2 t cos x,t 0;1 . Ta có (P): 2
y f t t 4t 2 xác định với mọi t 0;1 , (P) có hoành
độ đỉnh t 20; 1 và trên đoạn 0;1
hàm số nghịch biến nên hàm số đạt giá trị nhỏ nhất tại t 1
và đạt giá trị lớn nhất khi t 0. 2sin x cos x 1
Ví dụ 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: y sin x cos x 2 Giải Ta có: π
sin x cos x 2 2 sin x 2 4 Vì π 2 2 sin x 2, x nên 4 π 2 sin π
x 2 2 2 0, x
sin x cosx 2 2 sinx 2 0, x 4 4 Do đó: D 2sin x cos x 1 Biến đổi y sin x cos x 2
ysin x ycos x 2y 2sin x cos x 1
y 2sin x y 1 cos x 2y 1 *
Điều kiện để phương trình (*) có nghiệm x là 2 2 2 a b c
2 2 2 2 3 17 3 17 y 2 y 1
2y 1 2y 6y 4 0 y 2 2 3 17 3 17 Kết luận: max y ;min y 2 2
3. Bài tập trắc nghiệm
Câu 1: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = 3sin x -2. A. M = 1, 5 m = - . B. M = 3, 1 m = . C. M = 2, 2 m = - . D. M = 0, 2 m = - . Lời giải Chọn A
Ta có -1£ sin x £1 ¾¾
-3 £ 3sin x £ 3 ¾¾ -5 £ 3sin x -2 £1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 20
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïM = 1 5 y 1 ï ¾¾ - £ £ ¾¾ í . m ï = -5 ïî
Câu 2: Tìm tập giá trị T của hàm số y = 3cos2x +5. A. T =[ 1; - ] 1 . B. T = [-1;1 ] 1 . C. T = [2;8]. D. T = [5;8]. Lời giải Chọn C
Ta có -1£ cos2x £1 ¾¾
-3 £ 3cos 2x £ 3 ¾¾
2 £ 3cos 2x + 5 £ 8 ¾¾
2 £ y £ 8 ¾¾ T = [2;8].
Câu 3: Tìm tập giá trị T của hàm số y = 5-3sin x. A. T = [-1; ] 1 . B. T = [-3;3]. C. T = [2;8]. D. T = [5;8]. Lời giải Chọn C
Ta có -1£ sin x £1 ¾¾ 1 ³ -sin x ³ 1 - ¾¾ 3 ³ 3 - sin x ³ -3 ¾¾
8 ³ 5-3sin x ³ 2 ¾¾
2 £ y £ 8 ¾¾ T = [2;8].
Câu 4: Hàm số y = 5+ 4 sin 2x cos2x có tất cả bao nhiêu giá trị nguyên? A. 3. B. 4. C. 5. D. 6. Lời giải Chọn C
Ta có y = 5 + 4 sin 2x cos 2x = 5 + 2 sin 4x .
Mà -1£ sin 4x £1 ¾¾ 2
- £ 2 sin 4x £ 2 ¾¾
3 £ 5 + 2 sin 4x £ 7 3 7 y y Î ¾¾ £ £ ¾¾¾
y Î {3;4;5;6;7} nên y có 5 giá trị nguyên.
Câu 5: Tìm giá trị nhỏ nhất m của hàm số y = - 2 sin (2016x +2017) .
A. m = -2016 2. B. m = - 2. C. m = -1. D. m = -2017 2. Lời giải Chọn B
Ta có-1£ sin (2016x +2017)£1 ¾¾
2 ³ - 2 sin (2016x + 2017)³ - 2.
Do đó giá trị nhỏ nhất của hàm số là - 2.
Câu 6: Tìm giá trị nhỏ nhất m của hàm số 1 y = . cos x +1 A. 1 m = . B. 1 m = . C. m = 1. D. m = 2. 2 2 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 21
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A
Ta có -1£ cos x £1 . Ta có 1
nhỏ nhất khi và chỉ chi cos x lớn nhất cos x = 1 . cos x +1 Khi 1 1 cos x = 1 ¾¾ y = = . cos x +1 2
Câu 7: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sin x + cos x . Tính
P = M -m.
A. P = 4. B. P = 2 2. C. P = 2. D. P = 2. Lời giải Chọn B æ ö Ta có p
y = sin x + cos x = 2 sin ççx ÷ + ÷. ç è 4 ÷ø æ ö æ ö Mà p p -1 £ sin ççx ÷ + ÷ £1 ¾¾ - 2 £ 2 sin ç ç ÷ çx ÷ + ÷ £ 2 è 4 ø çè 4 ÷ø ìïM = 2 ï ¾¾ í
P = M -m = 2 2. m ïï = - 2 ïî
Câu 8: Tập giá trị T của hàm số y = sin 2017x -cos2017x.
A. T = [-2;2]. B.
T = [-4034;4034]. C. T é 2; 2 ù = - . ù ê D. ë úû T é = 0; 2 . êë úû Lời giải Chọn C æ ö Ta có p
y = sin 2017x -cos 2017x = 2 sin çç2017x ÷ - ÷ ç . è 4 ÷ø æ ö æ ö Mà p p -1 £ sin çç2017x ÷ - ÷ £1 ¾¾
- 2 £ 2 sin çç2017x ÷ - ÷ £ 2 ç è 4 ÷ø çè 4 ÷ø 2 y 2 T é 2; 2 ù ¾¾ - £ £ ¾¾ = - . ê ë úû æ ö Câu 9: p
Hàm số y = sin ççx ÷ + ÷-sin x ç
có tất cả bao nhiêu giá trị nguyên? è 3 ÷ø A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C Áp dụng công thức a + b a - b
sin a - sin b = 2 cos sin , ta có 2 2 æ pö æ pö p æ pö sin ççx ÷
+ ÷-sin x = 2 cosççx ÷
+ ÷sin = cosççx + .÷÷ ç è 3 ÷ø çè 6 ÷ø 6 çè 6 ÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 22
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 æ ö Ta có p -1 £ cosç ÷ ç + ÷ £1 ¾¾ -1 £ £1 y x y Î ¾¾¾ y Î {-1;0; } 1 . ç è 6 ÷ø Câu 10: Hàm số 4 4
y = sin x -cos x đạt giá trị nhỏ nhất tại x = x . Mệnh đề nào sau đây là đúng? 0
A. x = k2 , p k Î . B. x = k , p k Î . 0 0 C. p
x = p + k2 , p k Î . D. x = + k , p k Î . 0 0 2 Lời giải Chọn B Ta có 4 4 y = x - x = ( 2 2 x + x )( 2 2 sin cos sin cos
sin x - cos x) = -cos 2x. Mà -1£ cos2x £1 ¾¾
-1 ³ -cos 2x ³1 ¾¾ -1 ³ y ³1 .
Do đó giá trị nhỏ nhất của hàm số là -1 .
Đẳng thức xảy ra cos2x =1 2x = k2p x = kp (k Î ) .
Câu 11: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = 1-2 cos3x . A. M = 3, 1 m = - . B. M = 1, 1 m = - . C. M = 2, 2 m = - . D. M = 0, 2 m = - . Lời giải Chọn B
Ta có -1£ cos3x £1 ¾¾ 0 £ cos3x £1 ¾¾ 0 ³ -2 cos3x ³ -2 ìïM =1 1 1 2 cos3x 1 1 y 1 ï ¾¾ ³ - ³ - ¾¾ ³ ³ - ¾¾ í . m ï = -1 ïî æ ö Câu 12: p
Tìm giá trị lớn nhất M của hàm số 2
y = 4 sin x + 2 sin çç2x ÷ + ÷. ç è 4 ÷ø
A. M = 2. B. M = 2 -1.
C. M = 2 +1. D. M = 2 + 2. Lời giải Chọn D æ ö æ - ö Ta có p 1 cos 2x 2
y = 4 sin x + 2 sin çç2x ÷ + ÷ = 4ç ÷ ç
÷+ sin 2x + cos 2x ç è 4 ÷ø çè 2 ÷ø æ pö
= sin 2x -cos 2x + 2 = 2 sin çç2x ÷ - ÷+ 2. ç è 4 ÷ø æ ö æ ö Mà p p -1 £ sin çç2x ÷ - ÷ £1 ¾¾ - 2 + 2 £ 2 sin ç ç ÷ ç2x ÷ - ÷+ 2 £ 2 + 2 . è 4 ø çè 4 ÷ø
Vậy giá trị lớn nhất của hàm số là 2 + 2.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 23
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 13: Tìm tập giá trị T của hàm số 6 6
y = sin x + cos x. é ù é ù é ù
A. T = [0;2]. B. 1
T = ê ;1ú. C. 1
T = ê ;1ú. D. 1 T = ê0; ú. ê2 ú ë û ê 4 ú ë û ê 4 ú ë û Lời giải Chọn C Ta có y = x + x = ( x + x )2 6 6 2 2 2 2 - x x ( 2 2 sin cos sin cos 3 sin cos sin x + cos x) 3 3 1-cos 4x 5 3 2 2 2
= 1-3sin x cos x = 1- sin 2x = 1- . = + cos 4x. 4 4 2 8 8 Mà 1 5 3 1 -1 £ cos 4x £1 ¾¾
£ + cos 4x £1 ¾¾ £ y £1. 4 8 8 4
Câu 14: Tìm giá trị lớn nhất M và nhỏ nhất m của hàm số 2 2
y = sin x + 2 cos x. A. M = 3, 0 m = . B. M = 2, 0 m = . C. M = 2, 1 m = . D. M = 3, 1 m = . Lời giải Chọn C Ta có 2 2 y = x + x = ( 2 2 x + x) 2 2 sin 2 cos sin cos
+ cos x = 1+ cos x ìïM = 2 Do 2 2 1 cos x 1 0 cos x 1 1 1 cos x 2 ï - £ £ ¾¾ £ £ ¾¾ £ + £ ¾¾ í . m ï = 1 ïî Câu 15: 2
Tìm giá trị lớn nhất M của hàm số y = . 2 1+ tan x A. 1 M = . B. 2 M = . C. M = 1. D. M = 2. 2 3 Lời giải Chọn D Ta có 2 2 2 y = = = 2 cos x . 2 1+ tan x 1 2 cos x Do 2 0 £ cos x £1 ¾¾ 0 £ y £ 2 ¾¾ M = 2.
Câu 16: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y = 8 sin x + 3 cos 2x . Tính 2
P = 2M -m .
A. P =1. B. P = 2. C. P = 112. D. P = 130. Lời giải Chọn A Ta có 2 2 y = x + x = x + ( 2 - x) 2 8 sin 3 cos 2 8 sin 3 1 2 sin = 2 sin x + 3. Mà 2 2 -1 £ sin x £1 ¾¾ 0 £ sin x £1 ¾¾
3 £ 2 sin x + 3 £ 5
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 24
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïM = 5 ï 2 ¾¾ 3 £ y £ 5 ¾¾ í ¾¾
P = 2M -m = 1. m ï = 3 ïî
Câu 17: Tìm giá trị nhỏ nhất m của hàm số 2
y = 2 sin x + 3 sin 2x .
A. m = 2- 3. B. m = 1. - C. m = 1. D. m = - 3. Lời giải Chọn B Ta có 2
y = 2 sin x + 3 sin 2x = 1- cos 2x + 3 sin 2x æç 3 1 ö
= 3 sin 2x -cos 2x +1 = 2ç
sin 2x - cos 2x÷÷ ç ÷+1 çè 2 2 ÷ø æ p p ö æ pö
= 2ççsin 2x cos -sin cos2x÷÷+1 = 2 sin ç ç ÷ ç2x ÷ - ÷+1. è 6 6 ø çè 6 ÷ø æ ö æ ö Mà p p -1 £ sin çç2x ÷ - ÷ £1 ¾¾ 1 - £1+ 2 sin ç ç ÷ ç2x ÷ - ÷ £ 3 ¾¾ 1 - £ y £ 3. è 6 ø çè 6 ÷ø
Do đó giá trị nhỏ nhất của hàm số là -1.
Câu 18: Tìm tập giá trị T của hàm số y = 12 sin x -5cos x. A. T = [ 1; - ] 1 . B. T = [-7;7]. C. T = [ 13 - ;13]. D. T = [ 17 - ;17]. Lời giải Chọn C æ ö Ta có 12 5
y = 12 sin x -5 cos x = 13çç sin x - cos x . ÷÷ ç è13 13 ÷ø Đặt 12 5 = cosa ¾¾
= sin a . Khi đó y = 13(sin x cosa - sin a cos x) = 13sin (x -a) 13 13 ¾¾ 13 - £ y £13 ¾¾ T = [-13;13].
Câu 19: Tìm giá trị lớn nhất M của hàm số y = 4 sin 2x -3cos2x.
A. M = 3. B. M = 1. C. M = 5. D. M = 4. Lời giải Chọn C æ ö Ta có 4 3
y = 4 sin 2x -3cos 2x = 5çç sin 2x - cos2x÷÷ ç . è5 5 ÷ø Đặt 4 3 = cosa ¾¾
= sin a . Khi đó y = 5(cosa sin 2x -sin a cos 2x) = 5sin (2x -a) 5 5 ¾¾ -5 £ y £ 5 ¾¾ M = 5.
Câu 20: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y = sin x - 4 sin x + 5 . Tính 2
P = M -2m .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 25
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
A. P =1. B. P = 7. C. P = 8. D. P = 2. Lời giải Chọn D Ta có y = x - x + = ( x - )2 2 sin 4 sin 5 sin 2 +1. Do - £ x £ ¾¾ - £ x - £ - ¾¾ £( x - )2 1 sin 1 3 sin 2 1 1 sin 2 £ 9 ìïM = ¾¾ 2 £(sin x -2)2 10 ï 2 +1 £10 ¾¾ í
P = M -2m = 2. m ï = 2 ïî Câu 21: Hàm số 2
y = cos x -cos x có tất cả bao nhiêu giá trị nguyên? A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C 2 æ ö Ta có 1 1 2
y = cos x -cos x = ççcos x ÷ - ÷ - . ç è 2÷ø 4 2 æ ö Mà 3 1 1 1 9 -1 £ cos x £1 ¾¾ - £ cos x - £ ¾¾ 0 £ççcos x ÷ - ÷ £ 2 2 2 çè 2÷ø 4 2 1 æ 1ö 1 1 ¾¾ - £ççcos ÷ - ÷ - £ 2 ¾¾ - £ £ 2 y x y Î ¾¾¾
y Î {0;1;2} nên có 3 giá trị thỏa mãn. 4 çè 2÷ø 4 4 Câu 22: Hàm số 2
y = cos x + 2 sin x + 2 đạt giá trị nhỏ nhất tại x . Mệnh đề nào sau đây là đúng? 0 A. p p x = + k2 , p k Î . B. x = - + k2 , p k Î . 0 2 0 2
C. x = p + k2 , p k Î . D. x = k2 , p k Î . 0 0 Lời giải Chọn B Ta có 2 2
y = cos x + 2 sin x + 2 = 1-sin x + 2 sin x + 2 = - x + x + = ( - x - )2 2 sin 2 sin 3 sin 1 + 4. Mà - £ x £ ¾¾ - £ x - £ ¾¾ £( x - )2 1 sin 1 2 sin 1 0 0 sin 1 £ 4 ¾¾ ³ ( - x - )2 ³ - ¾¾ ³ -( x - )2 0 sin 1 4 4 sin 1 + 4 ³ 0 .
Suy ra giá trị nhỏ nhất của hàm số bằng 0 . Dấu p
'' = '' xảy ra sin x = 1
- x = - + k2p (k Î ) . 2
Câu 23: Tìm giá trị lớn nhất M và nhất m của hàm số 4 2
y = sin x -2 cos x +1 A. M = 2, 2 m = - . B. M = 1, 0 m = .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 26
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 C. M = 4, 1 m = - . D. M = 2, 1 m = - . Lời giải Chọn D Ta có y = x - x + = x - ( - x)+ = ( x + )2 4 2 4 2 2 sin 2 cos 1 sin 2 1 sin 1 sin 1 -2. Do £ x £ ¾¾ £ x + £ ¾¾ £ ( x + )2 2 2 2 0 sin 1 1 sin 1 2 1 sin 1 £ 4 ìïM = 1 (sin x )2 2 2 1 2 2 ï ¾¾ - £ + - £ ¾¾ í . m ï = 1 - ïî
Câu 24: Tìm giá trị nhỏ nhất m của hàm số 4
y = 4 sin x -cos 4x . A. m = 3. - B. m = 1. - C. m = 3. D. m = -5. Lời giải. Chọn B 2 æ - ö Ta có 1 cos 2x 4
y = 4 sin x -cos 4x = 4.ç ÷ ç ÷ -( 2 2 cos 2x - ) 1 ç è 2 ÷ø = - x - x + = ( - x + )2 2 cos 2 2 cos 2 2 cos 2 1 + 3 £ 3. Mà - £ x £ ¾¾ £ x + £ ¾¾ £( x + )2 1 cos 2 1 0 cos 2 1 2 0 cos 2 1 £ 4 ¾¾ - £ ( - x + )2 1 cos 2 1 + 3 £ 3 ¾¾ m = -1.
Câu 25: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 2 y = 7 -3cos x . A. M = 10, 2 m = . B. M = 7, 2 m = . C. M = 10, 7 m = . D. M = 0, 1 m = . Lời giải Chọn B Ta có 2 -1 £ cos x £1 ¾¾ 0 £ cos x £1 2 2 ¾¾
4 £ 7 -3cos x £ 7 ¾¾
2 £ 7 -3cos x £ 7 .
Câu 26: Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm 2017 được é ù cho bởi một hàm số p y = 4 sin ê
(t -60)ú +10 với t Î và 0 < t £ 365 . Vào ngày nào trong ê178 ú ë û
năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất? A. 28 tháng 5. B. 29 tháng 5. C. 30 tháng 5. D. 31 tháng 5. Lời giải Chọn B é ù é ù Vì p p sin ê (t -60)ú £1 ¾¾ y = 4 sin ê (t -60)ú +10 £14. ê178 ú ê178 ú ë û ë û
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 27
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 é ù
Ngày có ánh sáng mặt trời nhiều nhất p y = 14 sin ê (t -60)ú =1 ê178 ú ë û p ( p
t -60) = + k2p t = 149 + 356k. 178 2 Do 149 54 0 365 0 149 356 365 k t k k Î < £ ¾¾ < + £ - < £ ¾¾¾ k = 0 . 356 89 Với k = 0 ¾¾
t = 149 rơi vào ngày 29 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày,
tháng 4 có 30 ngày, riêng đối với năm 2017 thì không phải năm nhuận nên tháng 2 có 28
ngày hoặc dựa vào dữ kiện 0 < t £ 365 thì ta biết năm này tháng 2 chỉ có 28 ngày).
Câu 27: Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực
nước trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức æpt pö h = 3 cosç ÷ ç + ÷+12. ç
Mực nước của kênh cao nhất khi: è 8 4 ÷ø
A. t =13 (giờ).
B. t =14 (giờ).
C. t =15 (giờ).
D. t =16 (giờ). Lời giải . Chọn B
Mực nước của kênh cao nhất khi h lớn nhất æpt pö pt p cosç ÷ ç + ÷ = 1 + = k2p ç
với 0 < t £ 24 và k Î . è 8 4 ÷ø 8 4
Lần lượt thay các đáp án, ta được đáp án B thỏa mãn Vì với pt p t = 14 ¾¾
+ = 2p (đúng với k = 1 Î ). 8 4
Dạng 4. Chứng minh hàm số tuần hoàn và xác định chu kỳ của nó 1. Phương pháp
Muốn chứng minh hàm số tuần hoàn f(x) tuần hoàn ta thực hiện theo các bước sau:
Xét hàm số y f(x), tập xác định là D
Với mọi xD , ta có x T 0 D và x 0
T D (1) . Chỉ ra f(x 0 T ) f(x) (2)
Vậy hàm số y f(x) tuần hoàn
Chứng minh hàm tuần hoàn với chu kỳ 0 T
Tiếp tục, ta đi chứng minh 0
T là chu kỳ của hàm số tức chứng minh 0
T là số dương nhỏ nhất thỏa
(1) và (2). Giả sử có T sao cho 0 T 0
T thỏa mãn tính chất (2) ... mâu thuẫn với giả thiết 0 T 0
T . Mâu thuẫn này chứng tỏ 0
T là số dương nhỏ nhất thỏa (2). Vậy hàm số tuần hoàn với chu kỳ cơ sở 0 T
Một số nhận xét:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 28
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
- Hàm số y sin x,y cosx tuần hoàn chu kỳ 2 . Từ đó y sinax b,y cosax b có chu 2 kỳ T 0 a
- Hàm số y tanx, y cot x tuần hoàn chu kỳ . Từ đó y tanax b,y cotax b có chu kỳ 0 T a Chú ý: y 1f(x) có chu kỳ T1 ; y 2f(x) có chu kỳ T2
Thì hàm số y 1f(x) 2f(x) có chu kỳ T0 là bội chung nhỏ nhất của T1 và T2.
Các dấu hiệu nhận biết hàm số không tuần hoàn
Hàm số y f(x) không tuần hoàn khi một trong các điều kiện sau vi phạm
Tập xác định của hàm số là tập hữu hạn
Tồn tại số a sao cho hàm số không xác định với x a hoặc x a
Phương trình f(x) k có vô số nghiệm hữu hạn
Phương trình f(x) k có vô số nghiệm sắp thứ tự ... xm xm 1 . . x x 0 mà m m 1 hay 2. Ví dụ mẫu
Ví dụ 1. Chứng minh rằng các hàm số sau là những hàm số tuần hoàn với chu kỳ cơ sở 0 T a)f(x) sinx, 0 T 2 ; b)f(x) tan2x, 0 T 2 Hướng dẫn giải
a) Ta có : f(x 2) f(x), x .
Giả sử có số thực dương T 2 thỏa f(x T) f(x) sinx T sinx ,x (*)
Cho x VT(*) sin T cosT 1; VP(*) sin 1 2 2 2
(*) không xảy ra với mọi x . Vậy hàm số đã cho tuần hoàn với chu kỳ 0 T 2
b) Ta có : f(x ) f(x), x D . 2
Giả sử có số thực dương T thỏa f(x T) f(x) tan2x 2T tan2x , x D (**) 2
Cho x 0 VT(**) tan2T 0; VP(**) 0
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 29
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
B (**) không xảy ra với mọi xD . Vậy hàm số đã cho tuần hoàn với chu kỳ 0 T 2
Ví dụ 2. Xét tính tuần hoàn và tìm chu kỳ cơ sở (nếu có) của các hàm số sau 3x x a) f(x) cos cos ; b)y cosx cos( 3x); c)f(x) sin 2 x ; d)y tan x. 2 2 Hướng dẫn giải c) Hàm số 2
f(x) sin x không tuần hoàn vì khoảng cách giữa các nghiệm (không điểm) liên tiếp của nó dần tới 0 k 1 k 0 khi k k 1 k
d) Hàm số f(x) tan x không tuần hoàn vì khoảng cách giữa các nghiệm (không điểm) liên tiếp của nó dần tới 2 2 2
k 1 k khi k
3. Bài tập trắc nghiệm
Câu 1: Mệnh đề nào sau đây là sai?
A. Hàm số y = sin x tuần hoàn với chu kì 2 . p
B. Hàm số y = cos x tuần hoàn với chu kì 2 . p
C. Hàm số y = tan x tuần hoàn với chu kì 2 . p
D. Hàm số y = cot x tuần hoàn với chu kì . p Lời giải Chọn C
Vì hàm số y = tan x tuần hoàn với chu kì . p
Câu 2: Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn? A. x y = sin x
B. y = x + sin x
C. y = x cos x. D sin y = . x Lời giải Chọn A
Hàm số y = x +sin x không tuần hoàn. Thật vậy:
Tập xác định D = .
Giả sử f (x +T ) = f (x), "x Î D
(x +T )+ sin (x +T ) = x + sin x, D "x Î
T + sin (x +T ) = sin x, D "x Î . ( ) *
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 30
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 T
ìï + sin x = sin 0 = 0
Cho x = 0 và x = p , ta được ïí T
ï + sin (p +T )= sin p = 0 ïî ¾¾
2T + sinT + sin (p +T ) = 0 T = 0 . Điều này trái với định nghĩa là T > 0 .
Vậy hàm số y = x +sin x không phải là hàm số tuần hoàn.
Tương tự chứng minh cho các hàm số y = x cos x và sin x y = không tuần hoàn. x
Câu 3: Trong các hàm số sau đây, hàm số nào không tuần hoàn?
A. y = cos x.
B. y = cos2x. C. 2
y = x cos x . D. 1 y = . sin 2x Lời giải. Chọn C æ ö Câu 4: p
Tìm chu kì T của hàm số y = sin 5 çç x - .÷÷ ç è 4 ÷ø A. 2p p p p T = . B. 5 T = . C. T = . D. T = . 5 2 2 8 Lời giải Chọn A Hàm số p
y = sin (ax + b) tuần hoàn với chu kì 2 T = . a æ ö Áp dụng: Hàm số p p y = sin 5 çç x ÷ - ÷ ç tuần hoàn với chu kì 2 T = . è 4 ÷ø 5 æ ö Câu 5: x
Tìm chu kì T của hàm số y = cosçç +2016 .÷÷ ç è2 ÷ø A. T = 4 . p B. T = 2 . p C. T = -2 . p D. T = . p Lời giải Chọn A Hàm số p
y = cos(ax +b) tuần hoàn với chu kì 2 T = . a æ ö Áp dụng: Hàm số x y = cosçç + 2016÷÷ ç
tuần hoàn với chu kì T = 4 . p è2 ÷ø Câu 6: 1
Tìm chu kì T của hàm số y = - sin (100px +50p). 2 A. 1 p T = . B. 1 T = . C. T = . D. 2 T = 200p . 50 100 50 Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 31
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Hàm số 1 p
y = - sin (100px +50p) tuần hoàn với chu kì 2 1 T = = . 2 100p 50 Câu 7: x
Tìm chu kì T của hàm số y = cos2x +sin . 2 A. p T = 4 . p B. T = . p C. T = 2 . p
D. T = . 2 Lời giải Chọn A Hàm số 2p
y = cos 2x tuần hoàn với chu kì T = = . p 1 2 Hàm số x 2p y = sin
tuần hoàn với chu kì T = = 4 . p 2 2 1 2 Suy ra hàm số x y = cos 2x + sin
tuần hoàn với chu kì T = 4 . p 2
Nhận xét. T là của T và T . 1 2
Câu 8: Tìm chu kì T của hàm số y = cos3x + cos5x. A. T = . p B. T = 3 . p C. T = 2 . p D. T = 5 . p Lời giải Chọn C Hàm số 2p
y = cos3x tuần hoàn với chu kì T = . 1 3 Hàm số 2p
y = cos 5x tuần hoàn với chu kì T = . 2 5
Suy ra hàm số y = cos3x + cos5x tuần hoàn với chu kì T = 2 . p æ ö Câu 9: x
Tìm chu kì T của hàm số y = 3cos(2x + ) 1 -2 sin çç -3 .÷÷ ç è2 ÷ø A. T = 2 . p
B. T = 4p
C. T = 6p D. T = . p Lời giải Chọn B Hàm số 2p y = 3cos(2x + )
1 tuần hoàn với chu kì T = = . p 1 2 æ ö Hàm số x 2p y = -2 sin çç -3÷÷. ç
tuần hoàn với chu kì T = = 4 . p è 2 ÷ø 2 1 2 æ ö Suy ra hàm số x y = 3 cos(2x + ) 1 -2 sin çç -3÷÷ ç
tuần hoàn với chu kì T = 4 . p è 2 ÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 32
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 æ ö æ ö Câu 10: p p
Tìm chu kì T của hàm số y = sin çç2x ÷ + ÷+ 2 cos 3 ç ç ÷ ç x - . ÷÷ è 3 ø çè 4 ÷ø A. T = 2 . p B. T = . p C. T = 3 . p D. T = 4 . p Lời giải Chọn A æ ö Hàm số p 2p y = sin çç2x ÷ + ÷ ç
tuần hoàn với chu kì T = = . p è 3 ÷ø 1 2 æ ö Hàm số p 2p y = 2 cos 3 çç x ÷ - ÷ ç
tuần hoàn với chu kì T = . è 4 ÷ø 2 3 æ ö æ ö Suy ra hàm số p p y = sin çç2x ÷ + ÷+ 2 cos 3 ç ç ÷ ç x ÷
- ÷ tuần hoàn với chu kì T = 2 . p è 3 ø çè 4 ÷ø
Câu 11: Tìm chu kì T của hàm số y = tan 3px. A. p p T = . B. 4 T = . C. 2 T = . D. 1 T = . 3 3 3 3 Lời giải Chọn D Hàm số p
y = tan (ax + b) tuần hoàn với chu kì T = . a
Áp dụng: Hàm số y = tan 3px tuần hoàn với chu kì 1 T = . 3
Câu 12: Tìm chu kì T của hàm số y = tan 3x + cot x. A. p T = 4 . p B. T = . p C. T = 3 . p
D. T = . 3 Lời giải Chọn B Hàm số p
y = cot (ax + b) tuần hoàn với chu kì T = . a Áp dụng: Hàm số p
y = tan 3x tuần hoàn với chu kì T = . 1 3
Hàm số y = cot x tuần hoàn với chu kì T = . p 2
Suy ra hàm số y = tan 3x + cot x tuần hoàn với chu kì T = . p
Nhận xét. T là bội chung nhỏ nhất của T và T . 1 2 Câu 13: x
Tìm chu kì T của hàm số y = cot + sin 2x. 3 A. p T = 4 . p B. T = . p C. T = 3 . p
D. T = . 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 33
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn C Hàm số x y = cot
tuần hoàn với chu kì T = 3 . p 3 1
Hàm số y = sin 2x tuần hoàn với chu kì T = . p 2 Suy ra hàm số x
y = cot + sin 2x tuần hoàn với chu kì T = 3 . p 3 æ ö Câu 14: x p
Tìm chu kì T của hàm số y = sin - tan çç2x ÷ + ÷. 2 çè 4 ÷ø A. T = 4 . p B. T = . p C. T = 3 . p D. T = 2 . p Lời giải Chọn A Hàm số x y = sin
tuần hoàn với chu kì T = 4 . p 2 1 æ ö Hàm số p p y = -tan çç2x ÷ + ÷ ç
tuần hoàn với chu kì T = . è 4 ÷ø 2 2 æ ö Suy ra hàm số x p
y = sin - tan çç2x ÷
+ ÷ tuần hoàn với chu kì T = 4 . p 2 çè 4 ÷ø
Câu 15: Tìm chu kì T của hàm số 2
y = 2 cos x + 2017. A. T = 3 . p B. T = 2 . p C. T = . p D. T = 4 . p Lời giải Chọn C Ta có 2
y = 2 cos x + 2017 = cos 2x + 2018.
Suy ra hàm số tuần hoàn với chu kì T = . p
Câu 16: Tìm chu kì T của hàm số 2 2
y = 2 sin x + 3 cos 3x. A. p T = . p B. T = 2 . p C. T = 3 . p D. T = . 3 Lời giải Chọn A Ta có 1-cos 2x 1+ cos 6x 1 y = 2. + 3.
= (3cos 6x -2 cos 2x +5). 2 2 2 Hàm số 2p p
y = 3 cos 6x tuần hoàn với chu kì T = = . 1 6 3 Hàm số y = 2
- cos 2x tuần hoàn với chu kì T = . p 2
Suy ra hàm số đã cho tuần hoàn với chu kì T = . p
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 34
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 17: Tìm chu kì T của hàm số 2
y = tan 3x -cos 2x. A. p p T = . p B. T = . C. T = . D. T = 2 . p 3 2 Lời giải Chọn C Ta có 1+ cos 4x 1 y = tan 3x -
= (2 tan 3x -cos 4x - ) 1 . 2 2 Hàm số p
y = 2 tan 3x tuần hoàn với chu kì T = . 1 3 Hàm số 2p p
y = -cos 4x tuần hoàn với chu kì T = = . 2 4 2
Suy ra hàm số đã cho tuần hoàn với chu kì T = . p
Câu 18: Hàm số nào sau đây có chu kì khác p ? æ ö æ ö A. p p
y = sin çç -2x÷÷. = ç ÷ ç
B. y cos2çx + ÷. C. y = tan ( 2 - x + ) 1 .
D. y = cos x sin x. è 3 ÷ø çè 4 ÷ø Lời giải Chọn C Vì p p y = tan (-2x + ) 1 có chu kì T = = . -2 2 Nhận xét. Hàm số 1
y = cos x sin x = sin 2x có chu kỳ là . p 2
Câu 19: Hàm số nào sau đây có chu kì khác 2p ? A. 3 x x y = cos x. . y = sin cos . 2 2 æ ö C. x 2
y = sin (x + 2). D. 2 y = cos çç +1 .÷÷ ç è2 ÷ø Lời giải. Chọn C Hàm số 1 3
y = cos x = (cos3x +3cos x) có chu kì là 2 . p 4 Hàm số x x 1 y = sin cos
= sin x có chu kì là 2 . p 2 2 2 Hàm số 1 1 2
y = sin (x + 2) = - cos(2x + 4) có chu kì là . p 2 2 æ ö Hàm số x 1 1 2
y = cos çç +1÷÷ = + cos(x + 2) ç có chu kì là 2 . p è2 ÷ø 2 2
Câu 20: Hai hàm số nào sau đây có chu kì khác nhau?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 35
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. x
y = cos x và y = cot .
B. y = sin x và y = tan 2x. 2 C. x x y = sin và y = cos .
D. y = tan 2x và y = cot 2x. 2 2 Lời giải Chọn B Hai hàm số x
y = cos x và y = cot có cùng chu kì là 2 . p 2 Hai hàm số p
y = sin x có chu kì là 2p , hàm số y = tan 2x có chu kì là . 2 Hai hàm số x x y = sin
và y = cos có cùng chu kì là 4 . p 2 2 Hai hàm số p
y = tan 2x và y = cot 2x có cùng chu kì là . 2
Dạng 5. Đồ thị của hàm số lượng giác 1. Phương pháp
1/ Vẽ đồ thị hàm số lượng giác: - Tìm tập xác định D.
- Tìm chu kỳ T0 của hàm số.
- Xác định tính chẵn – lẻ (nếu cần).
- Lập bảng biến thiên trên một đoạn có độ dài bằng chu kỳ T0 có thể chọn: T T x 0, 0 T hoặc 0 0 x , . 2 2
- Vẽ đồ thị trên đoạn có độ dài bằng chu kỳ.
- Rồi suy ra phần đồ thị còn lại bằng phép tịnh tiến theo véc tơ v k 0
.T .i về bên trái và phải
song song với trục hoành Ox (với i là véc tơ đơn vị trên trục Ox).
2/ Một số phép biến đổi đồ thị:
a) Từ đồ thị hàm số y = f(x), suy ra đồ thị hàm số y = f(x) + a bằng cách tịnh tiến đồ thị y =
f(x) lên trên trục hoành a đơn vị nếu a > 0 và tịnh tiến xuống phía dưới trục hoành a đơn vị nếu a < 0.
b) Từ đồ thị hàm số y = f(x), suy ra đồ thị hàm số y f(x a) bằng cách tịnh tiến đồ thị y =
f(x) sang phải trục hoành a đơn vị nếu a > 0 và tịnh tiến sang trái trục hoành a đơn vị nếu a < 0.
c) Từ đồ thị y = f(x), suy ra đồ thị y = –f(x) bằng cách lấy đối xứng đồ thị y = f(x) qua trục hoành.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 36
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 f(x), neáu f(x) 0 d) Đồ thị y f(x)
nên suy ra đồ thị y = f(x) bằng cách giữ nguyên -f(x), neáu f(x) < 0
hần đồ thị y = f(x) phía trên trục hoành và lấy đối xứng y = f(x) phía dưới trục hoành qua trục hoành
Mối liên hệ đồ thị giữa các hàm số Đối xứng qua Ox y=-f(x)
Tịnh tiến theo Ox, a đơn vị y=f(x+a)
Tịnh tiến theo Oy, b đơn vị Đối xứng qua Oy Tịnh tiến theo
Đối xứng qua gốc O y=-f(-x) y=f(x+a)+b y=f(x) vec tơ v=(a;b)
Tịnh tiến theo Ox, a đơn vị Đối xứng qua Ox y=f(-x) y=f(x)+b Đối xứng qua Oy
Tịnh tiến theo Oy, b đơn vị 2. Các ví dụ mẫu
Ví dụ 1. Vẽ đồ thị các hàm số sau: y = sin 4x Hướng dẫn giải a) Haøm soá y = sin 4x. Mieàn xaùc ñònh: D=.
Ta chæ caàn veõ ñoà thò haøm soá treân mieàn 0; 2 2 (Do chu kì tuaàn hoaøn T= ) 4 2
Baûng giaù trò cuûa haøm soá y =sin 4x treân ñoaïn 0; laø: 2 x 3 5 5 3 0 16 8 16 24 4 16 8 3 2 y 2 2 3 2 3 0 1 0 - -1 - 0 2 2 2 2 2
Ta có đồ thị của hàm số y = sin4x trên đoạn 0; và sau đó tịnh tiến cho các 2 đoạn: ..., ,0 , , ,.... 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 37
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 x
Ví dụ 2: Vẽ đồ thị hàm số y = cos . 3 Hướng dẫn giải x Haøm soá y = cos . 3 Mieàn xaùc ñònh: D=.
Ta chæ caàn veõ ñoà thò haøm soá treân mieàn 0;6 2 (Do chu kì tuaàn hoaøn T= 6) 1/ 3 x
Baûng giaù trò cuûa haøm soá y = cos treân ñoaïn 0;6 laø: 3 x 3 3 21 15 9 33 0
3 4 2 6 4 2 6 6 y 2 3 2 3 1 0 - -1 - 0 1 2 2 2 2 x
Ta có đồ thị của hàm số y= cos trên đoạn 0;6và sau đó tịnh tiến cho các 3
đoạn: ...,6,0,6,12,....
Ví dụ 3. Cho đồ thị của hàm số y =sinx, (C) . Hãy vẽ các đồ thị của các hàm số sau: a) y = sin x+ b) y= sin x+ 2. 4 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 38
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Hướng dẫn giải
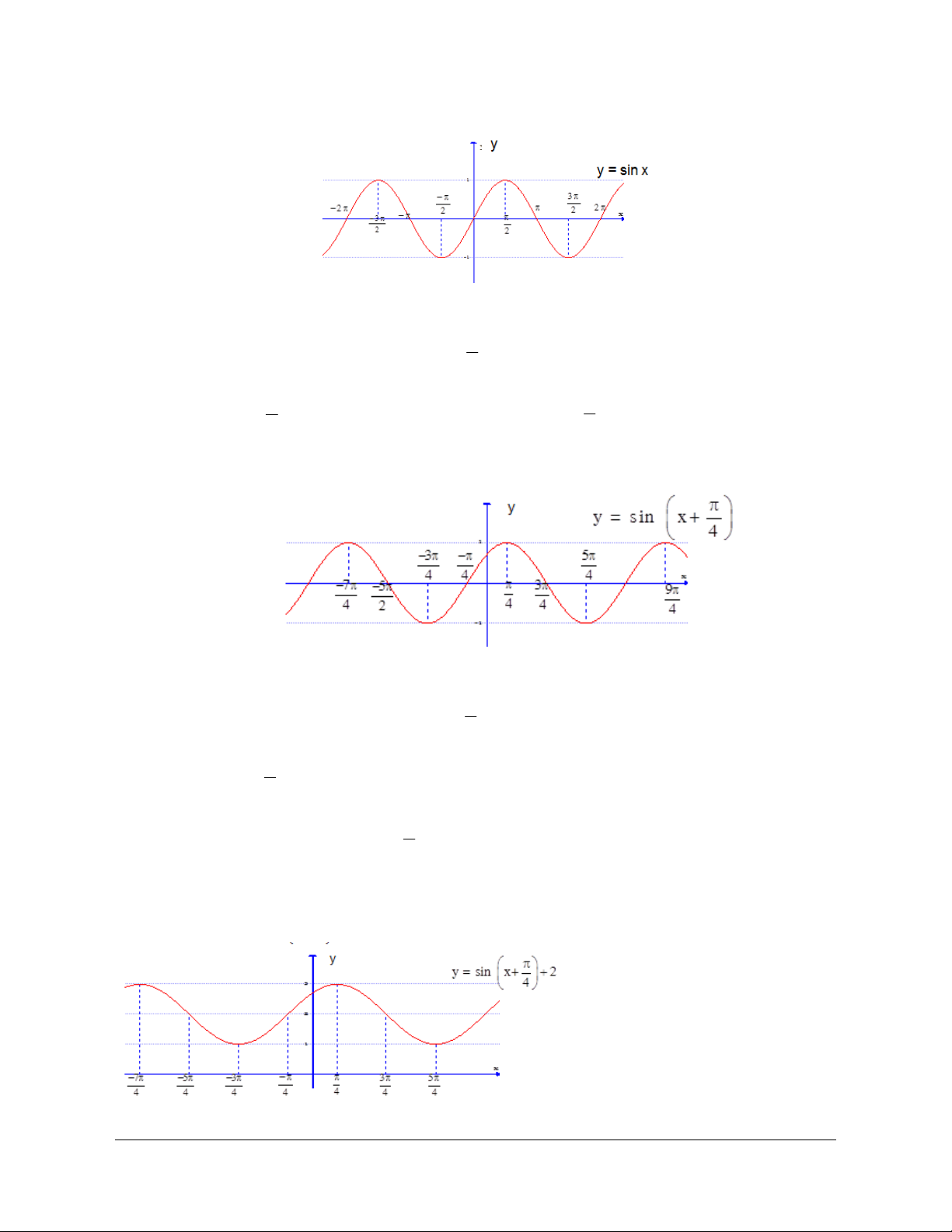
Từ đồ thị của hàm số y = sinx, (C) như sau: a)
Từ đồ thị (C), ta có đồ thị y = sin x+ bằng cách tịnh tiến (C) sang trái 4
một đoạn là đơn vị, ta được đồ thị hàm số y = sin x+
, (C') như (hình 8) 4 4 sau: b)
Từ đồ thị (C’) của hàm số y = sin x+ , ta có đồ thị hàm số 4 y = sin x+
2 bằng cách tịnh tiến (C’) lên trên một đoạn là 2 đơn vị, ta 4
được đồ thị hàm số y = sin x+ 2, (C' ) như sau: 4 y
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 39
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
3. Bài tập trắc nghiệm æ ö Câu 1: p
Đồ thị hàm số y = cosççx ÷ - ÷ ç
được suy từ đồ thị (C) của hàm số y = cos x bằng cách: è 2 ÷ø A. Tịnh tiến ( p
C) qua trái một đoạn có độ dài là . 2 B. Tịnh tiến ( p
C) qua phải một đoạn có độ dài là . 2 C. Tịnh tiến ( p
C) lên trên một đoạn có độ dài là . 2 D. Tịnh tiến ( p
C) xuống dưới một đoạn có độ dài là . 2 Lời giải Chọn B Nhắc lại lý thuyết
Cho (C) là đồ thị của hàm số y = f (x) và p > 0 , ta có:
+ Tịnh tiến (C) lên trên p đơn vị thì được đồ thị của hàm số y = f (x)+ p .
+ Tịnh tiến (C) xuống dưới p đơn vị thì được đồ thị của hàm số y = f (x)- p .
+ Tịnh tiến (C) sang trái p đơn vị thì được đồ thị của hàm số y = f (x + p).
+ Tịnh tiến (C) sang phải p đơn vị thì được đồ thị của hàm số y = f (x - p) . æ ö Vậy đồ thị hàm số p y = cosççx ÷ - ÷ ç
được suy từ đồ thị hàm số y = cos x bằng cách tịnh tiến è 2 ÷ø
sang phải p đơn vị. 2
Câu 2: Đồ thị hàm số y = sin x được suy từ đồ thị (C) của hàm số y = cos x bằng cách: A. Tịnh tiến ( p
C) qua trái một đoạn có độ dài là . 2 B. Tịnh tiến ( p
C) qua phải một đoạn có độ dài là . 2 C. Tịnh tiến ( p
C) lên trên một đoạn có độ dài là . 2 D. Tịnh tiến ( p
C) xuống dưới một đoạn có độ dài là . 2 Lời giải Chọn B æ ö æ ö Ta có p p
y = sin x = cosçç - x÷÷ = cosç ç ÷ çx - . ÷÷ è 2 ø çè 2 ÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 40
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 3: Đồ thị hàm số y = sin x được suy từ đồ thị (C) của hàm số y = cos x +1 bằng cách: A. Tịnh tiến ( p
C) qua trái một đoạn có độ dài là và lên trên 1 đơn vị. 2 B. Tịnh tiến ( p
C) qua phải một đoạn có độ dài là và lên trên 1 đơn vị. 2 C. Tịnh tiến ( p
C) qua trái một đoạn có độ dài là và xuống dưới 1 đơn vị. 2 D. Tịnh tiến ( p
C) qua phải một đoạn có độ dài là và xuống dưới 1 đơn vị. 2 Lời giải Chọn D æ ö æ ö Ta có p p
y = sin x = cosçç - x÷÷ = cosç ç ÷ çx - . ÷÷ è 2 ø çè 2 ÷ø p
Tịnh tiến đồ thị y = cos x +1 sang phải
đơn vị ta được đồ thị hàm số 2 æ pö y = cosççx ÷ - ÷+1. ç è 2 ÷ø æ pö
Tiếp theo tịnh tiến đồ thị y = cosççx ÷ - ÷+1 ç
xuống dưới 1 đơn vị ta được đồ thị hàm số è 2 ÷ø æ pö
y = cosççx - .÷÷ ç è 2 ÷ø
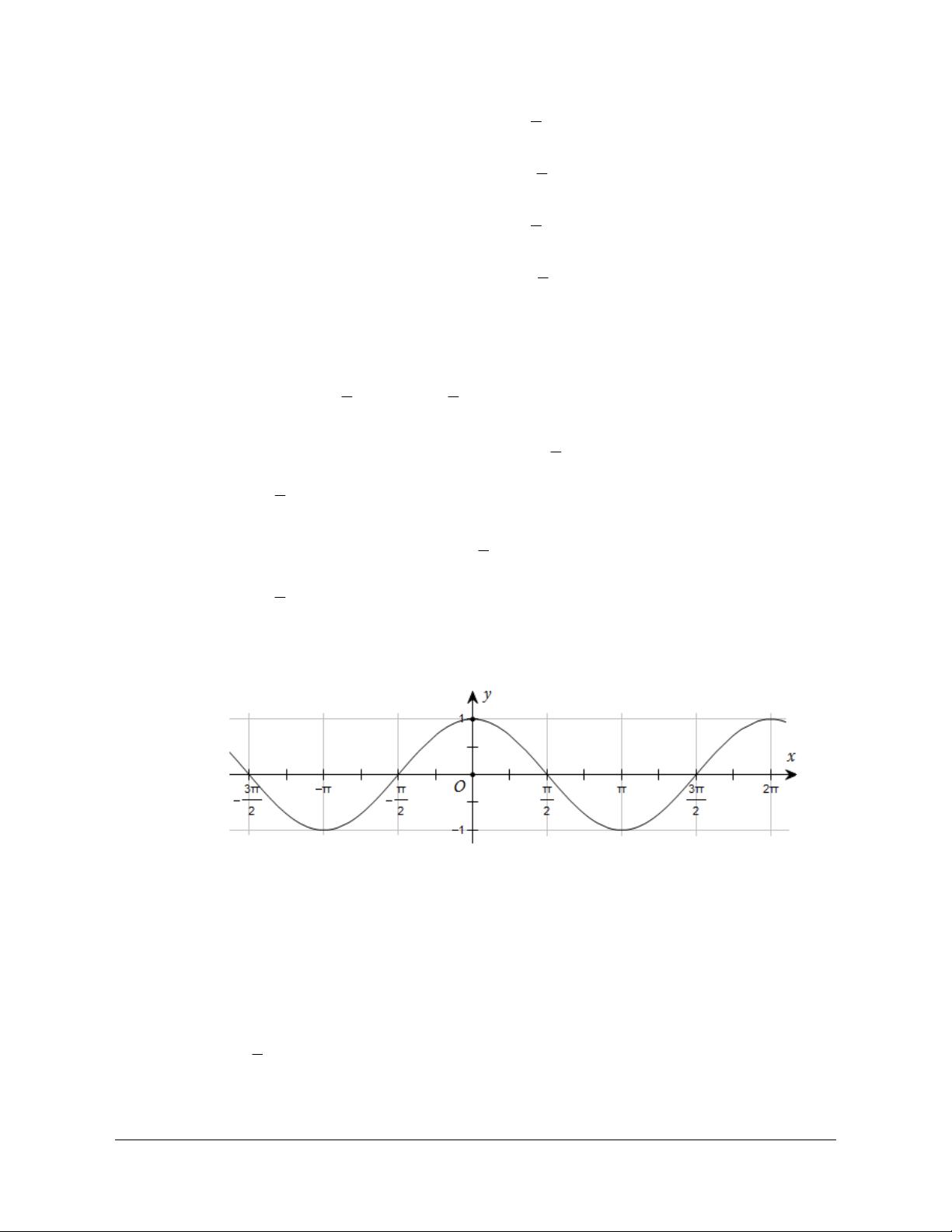
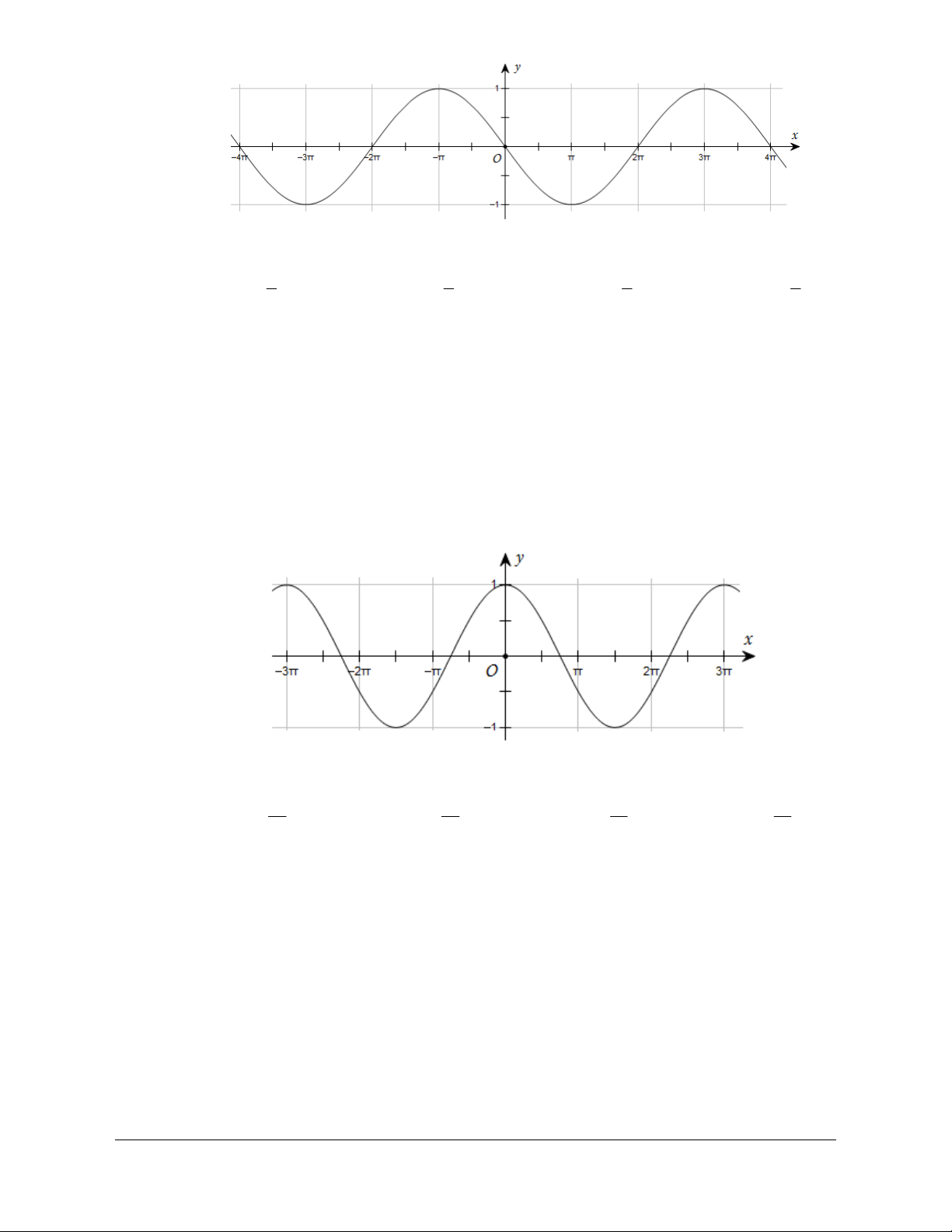
Câu 4: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C,D.
Hỏi hàm số đó là hàm số nào?
A. y = 1+ sin 2x.
B. y = cos x.
C. y = -sin x.
D. y = -cos x. Lời giải Chọn B
Ta thấy tại x = 0 thì y =1. Do đó loại đáp án C và D. Tại p x =
thì y = 0 . Do đó chỉ có đáp án B thỏa mãn. 2
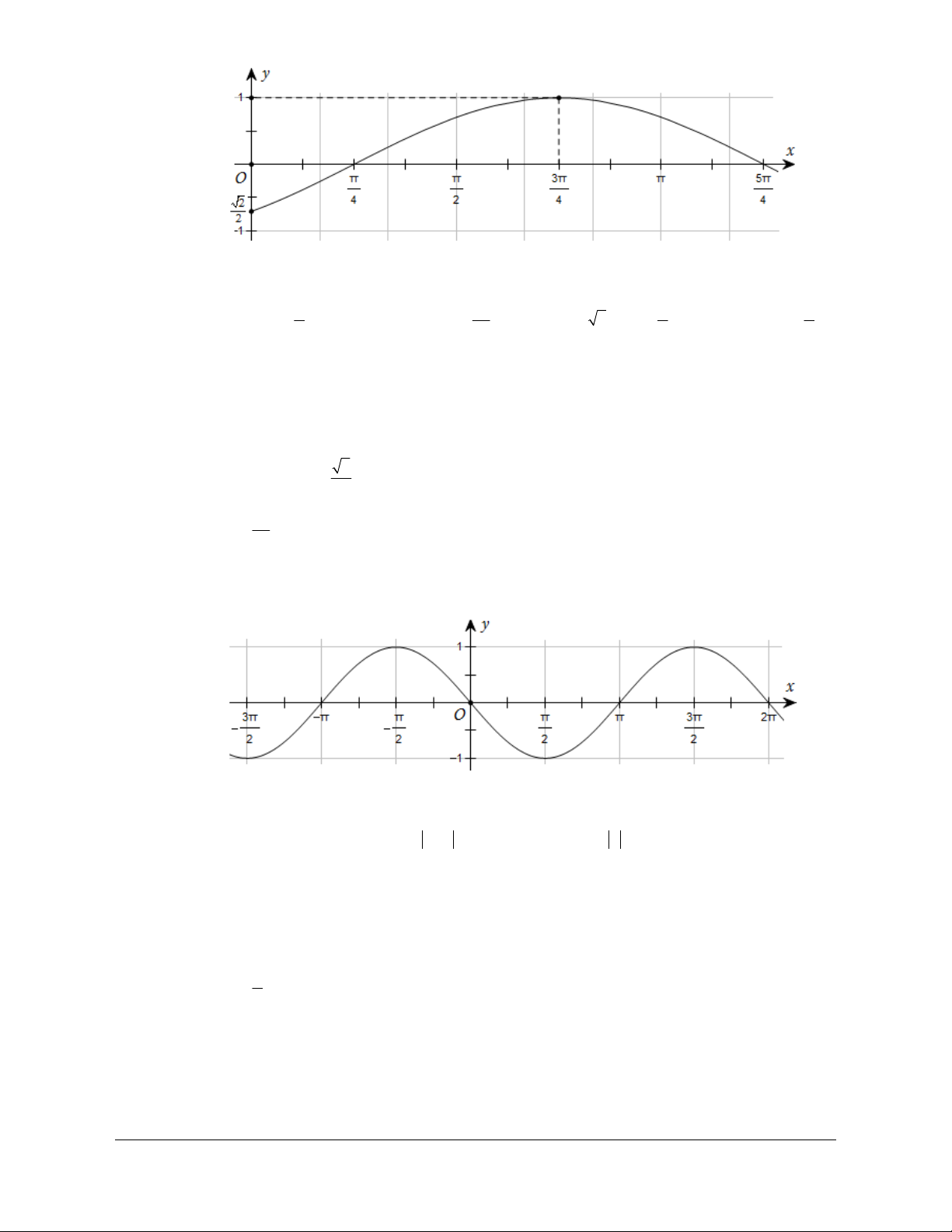
Câu 5: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C,D.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 41
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Hỏi hàm số đó là hàm số nào? æ ö A. x x x x y = sin . B. y = cos . C. y = -cos . D. y = sin ç- ç . ÷÷ 2 2 4 çè 2÷ø Lời giải Chọn D Ta thấy:
Tại x = 0 thì y = 0 . Do đó loại B và C.
Tại x = p thì y = -1. Thay vào hai đáp án còn lại chỉ có D thỏa.
Câu 6: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào? A. 2x x x x y = cos . B. 2 y = sin . C. 3 y = cos . D. 3 y = sin . 3 3 2 2 Lời giải Chọn A Ta thấy:
Tại x = 0 thì y =1. Do đó ta loại đáp án B và D.
Tại x = 3p thì y =1. Thay vào hai đáp án A và C thì chit có A thỏa mãn.
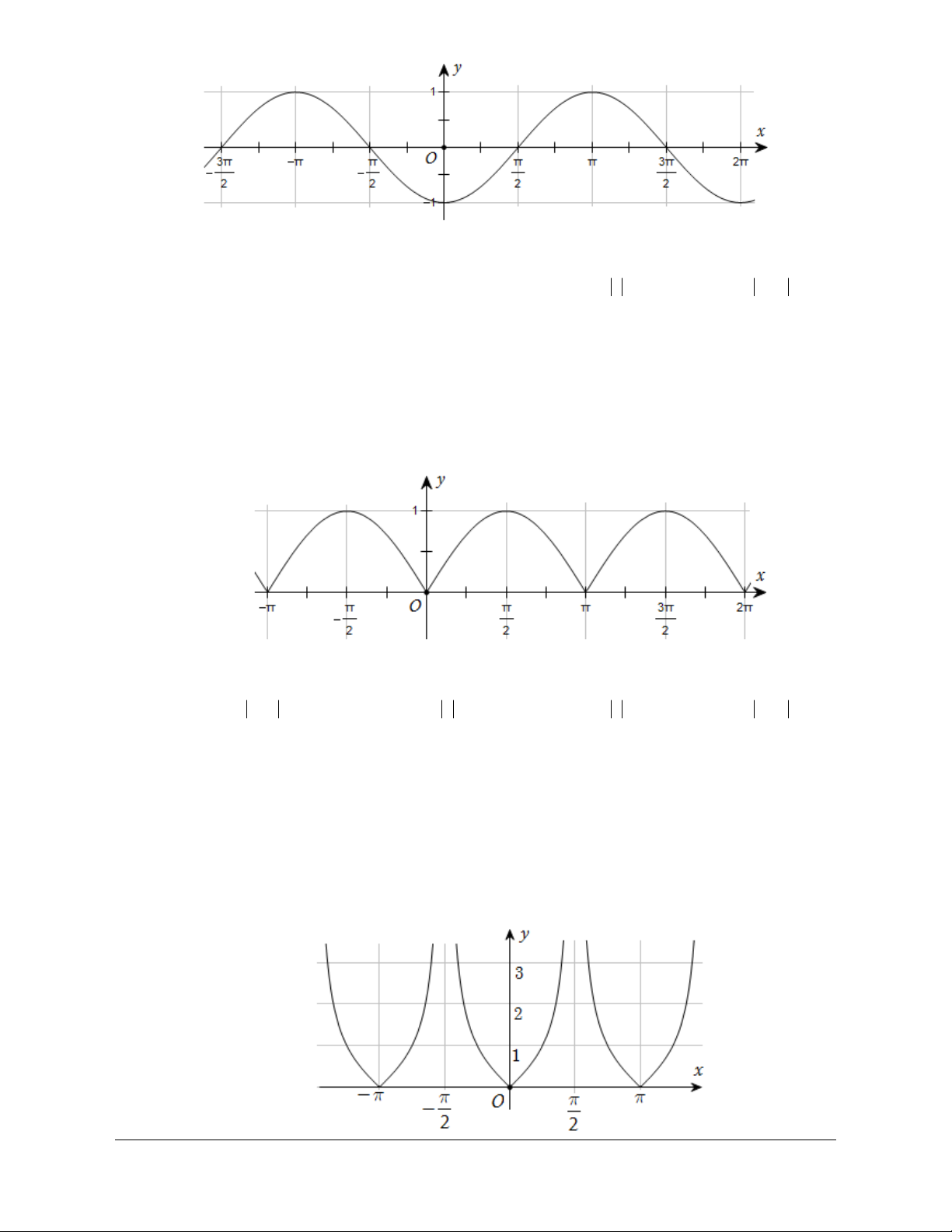
Câu 7: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C,D.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 42
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Hỏi hàm số đó là hàm số nào? æ ö æ ö æ ö æ ö A. p p p p
y = sin ççx - .÷÷ = ç ÷ = ç ÷ = ç ÷ ç B. 3 y cosçx + . ÷ C. y
2 sin çx + .÷ D. y cosçx - .÷ è 4 ÷ø çè 4 ÷ø çè 4 ÷ø çè 4 ÷ø Lời giải Chọn A
Ta thấy hàm số có GTLN bằng 1 và GTNN bằng -1 . Do đó loại đáp án C. Tại x = 0 thì 2 y = -
. Do đó loại đáp án D. 2 Tại 3p x =
thì y = 1. Thay vào hai đáp án còn lại chỉ có A thỏa mãn. 4
Câu 8: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C,D.
Hỏi hàm số đó là hàm số nào?
A. y = sin x.
B. y = sin x .
C. y = sin x .
D. y = -sin x. Lời giải Chọn D
Ta thấy tại x = 0 thì y = 0 . Cả 4 đáp án đều thỏa. Tại p x =
thì y = -1. Do đó chỉ có đáp án D thỏa mãn. 2
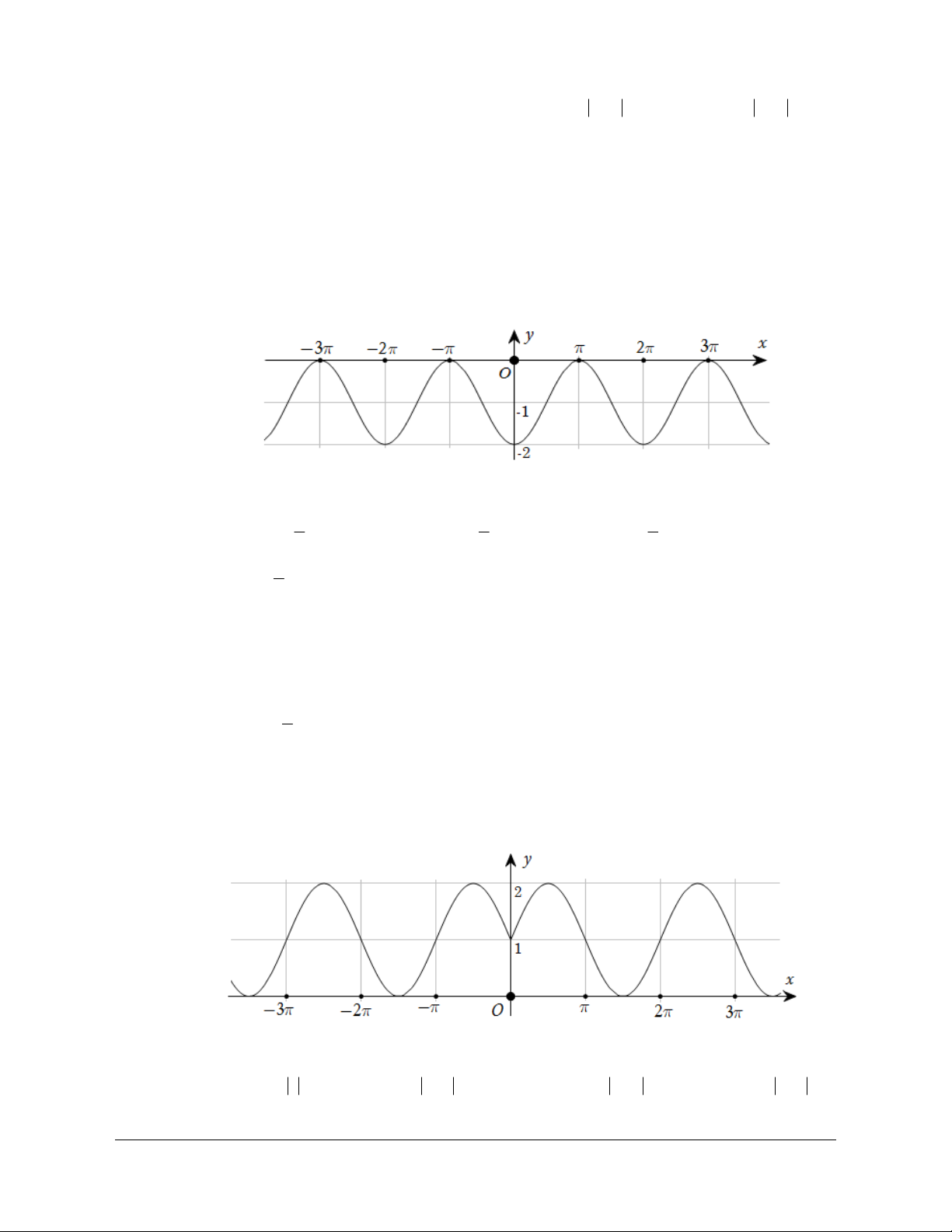
Câu 9: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 43
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Hỏi hàm số đó là hàm số nào?
A. y = cos x.
B. y = -cos x
C. y = cos x .
D. y = cos x . Lời giải Chọn B
Ta thấy tại x = 0 thì y = -1. Do đó chỉ có đáp án B thỏa mãn.
Câu 10: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B,C,D.
Hỏi hàm số đó là hàm số nào?
A. y = sin x .
B. y = sin x .
C. y = cos x .
D. y = cos x . Lời giải Chọn A
Ta thấy hàm số có GTNN bằng 0 . Do đó chỉ có A hoặc D thỏa mãn.
Ta thấy tại x = 0 thì y = 0 . Thay vào hai đáp án A và D chỉ có duy nhất A thỏa mãn.
Câu 11: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C,D.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 44
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Hỏi hàm số đó là hàm số nào?
A. y = tan x.
B. y = cot x.
C. y = tan x .
D. y = cot x . Lời giải Chọn C
Ta thấy hàm số có GTNN bằng 0 . Do đó ta loại đáp án A và B.
Hàm số xác định tại x = p và tại x = p thì y = 0 . Do đó chỉ có C thỏa mãn.
Câu 12: .Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C,D.
Hỏi hàm số đó là hàm số nào? æ ö æ ö æ ö A. p p p y = sin ççx ÷ - ÷-1. = ç ÷ = - ç ÷ ç
B. y 2 sin çx - .÷ C. y
sin çx - ÷-1. D. è 2 ÷ø çè 2 ÷ø çè 2 ÷ø æ pö y = sin ççx ÷ + ÷+1. ç è 2 ÷ø Lời giải Chọn A
Ta thấy hàm số có GTLN bằng 0 , GTNN bằng -2. Do đó ta loại đán án B vì æ pö y = 2 sin ççx ÷ - ÷ Î[ 2 - ;2]. ç è 2 ÷ø
Tại x = 0 thì y = -2 . Thử vào các đáp án còn lại chỉ có A thỏa mãn.
Câu 13: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D
Hỏi hàm số đó là hàm số nào?
A. y = 1+ sin x .
B. y = sin x .
C. y = 1+ cos x .
D. y = 1+ sin x . Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 45
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A
Ta có y = 1+ cos x ³1 và y = 1+ sin x ³1 nên loại C và D.
Ta thấy tại x = 0 thì y =1. Thay vào hai đáp án A và B thì chỉ có A thỏa mãn.
Câu 14: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào?
A. y = 1+ sin x .
B. y = sin x .
C. y = 1+ cos x .
D. y = 1+ sin x . Lời giải Chọn B
Ta có y = 1+ cos x ³1 và y = 1+ sin x ³1 nên loại C và D.
Ta thấy tại x = p thì y = 0 . Thay vào hai đáp án A và B thì chỉ có B thỏa.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 46
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 2. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1) Phương trình sin x = a
Trường hợp a >1 ¾¾
phương trình vô nghiệm, vì -1 £ sin x £1 với mọi x .
Trường hợp a £1 ¾¾
phương trình có nghiệm, cụ thể: ìï üï ▪ 1 2 3 ï ï a Î 0; í ; ; ;1ý . Khi đó ï 2 2 2 ï ïî ïþ
éx = a + k2p
sin x = a sin x = sin a ê , k Î ê .
x = p -a + k 2p ë ìï üï
éx = arcsin a + k2p ▪ 1 2 3 ï ï a Ï 0; í ; ;
;1ý . Khi đó sin x = a ê , Î . ï k 2 2 2 ï ï ê î ïþ
x = p - arcsin a + k2p ë
2) Phương trình cos x = a
Trường hợp a >1 ¾¾
phương trình vô nghiệm, vì -1 £ cos x £1 với mọi x .
Trường hợp a £1 ¾¾
phương trình có nghiệm, cụ thể: ìï üï ▪ 1 2 3 ï ï a Î 0; í ; ; ;1ý . Khi đó ï 2 2 2 ï ïî ïþ
éx = a + k2p
cos x = a cos x = cosa ê , k Î ê . x = a - + k2p ë ìï üï
éx = arc cos a + k2p ▪ 1 2 3 ï ï a Ï 0; í ; ;
;1ý . Khi đó cos x = a ê , Î . ï k 2 2 2 ï ï ê î ïþ
x = -arc cos a + k2p ë
3) Phương trình tan x = a Điều kiện: p x ¹
+ kp (k Î ). 2 ìï ü ● 1 ï ï ï a Î 0; í
;1; 3ý . Khi đó tan x = a x =
a x = a + kp tan tan , Î . ï k î 3 ï ï ïþ ìï ü ● 1 ï ï ï a Ï 0; í
;1; 3ý . Khi đó tan x = a x = arctan a + k , p Î . ï k î 3 ï ï ïþ
4) Phương trình cot x = a
Điều kiện: x ¹ p + kp (k Î ). ìï ü ● 1 ï ï ï a Î 0; í
;1; 3ý . Khi đó cot x = a cot x = cot a x = a + k , p Î . ï k î 3 ï ï ïþ ìï ü ● 1 ï ï ï a Ï 0; í ; 1
; 3ý . Khi đó cot x = a x = a + kp arccot , Î . ï k î 3 ï ï ïþ
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 47
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
B. CÁC VÍ DỤ RÈN LUYỆN KĨ NĂNG
Ví dụ 1. Giải các phương trình
a) cos2x 0 ; b) cos4x 1; c) cos x 1 ; 6 3 5 x d) sin3x 0 e) sin 1; f) sin 2x 1 ; 3 2 4 6 Hướng Dẫn Giải k
a) cos2x 0 2x k x ,k 6 6 12 2 k
b) cos 4x 1 4x k2 x ,k 3 3 12 2 4
c) cos x 1 x k2 x k2,k 5 5 5 k
d) sin3x 0 3x k x ,k 3 3 9 3 x x 3
e) sin 1 k2 x k4,k 2 4 2 4 2 2
f) sin 2x 1 2x k2 x k,k 6 6 2 3
Ví dụ 2. Giải phương trình a) 1 1 sin 3x 1 ; b) cos 2x 2 2 2 x c) tan 2 3; d) cot 2x 3 4 3 4 Giải a) Ta có: k2 3x k2 x 6 18 3 1 sin 3x sin , k 6 5 k2 3x k2 x 6 18 3
Vậy nghiệm của phương trình (1) là k2 5 k2 x ; x , k . 18 3 18 3 b) Ta có:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 48
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2x k2 x k 2 3 3 2 cos 2x cos , k 3 2 2x k2 x k 3 3
Vậy nghiệm của phương trình (*) là: x k , k 3
c) 3 x 3arctan 2 k3 , k
Vậy nghiệm của phương trình (*) là x 3arctan 2 k3,k d) Ta có: k 4 cot 2x
cot 2x k x ,k . 4 6 4 6 24 2 k
Vậy nghiệm của phương trình là: x ,k . 24 2
Lời bình: Những phương trình ch trên là nhưng phương trình lượng giác cơ bản. Sử dụng MTCT ta
có thể tìm được các giá trị đặc biệt của hàm số lượng giác 1 Ở câu a) sin3x
. Dùng MTCT (ở chế độ rad ) ta ấn SHIF sin 1 2 ta được kết quả là 2 π 1 . Do đó: π sin3x sin 6 2 6 1
Hoàn toàn tương tự cho câu b) cos2x . Ta ấn: 2 2 1 2
SHIF cos 1 2 ta được kết quả là π . Do đó: π cos2x cos 3 2 3
Ở câu c) nếu ta dùng MTCT: Thử ấn SHIFT tan 2 ta được kết quả x x
Do đó, phương trình tan 2 ta chỉ có thể ghi arctan2 kπ 3 3 1
Trên MTCT không có hàm cot, tuy nhiên ta thừa biết cot α
. Do đó, đối với câu d) tanα cot 2x 3 ta ấn máy như sau: 4 SHIT tan 1 3 π
ta được kết quả là . Do đó: cot 2x 3 cot 6 4 6
Ví dụ 3. Giải phương trình
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 49
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 a) sin 4x sin x x ; b) cot gx 0 30 cot g . 3 2 2 3 2 c) cos x ; d) sin 2x cos3x. 4 Giải a) Ta có: k2 4x x k2 x 3 9 3 sin 4x sin x , k 3 2 k2 4x x k2 x 3 15 5
Vậy nghiệm của phương trình (*) là k2 2 k2 x ; x 9 3 15 5 0 0 x 30 k.180 0 b) Điều kiện: x 30 k,n x 0 0 n.180 x n.360 2 0 x 0 x cot g x 30 cot g x 30 0 k.180 2x 0 60 x 0 k.360 2 2 x 0 60 0 k.360 , k
Vậy nghiệm của phương trình là: 0 0 x 60 k.360 , k c) Ta có 2 3 2 1 cos 2x 3 2 cos x
21 cos 2x 3 2 4 2 4 3 cos 2x
cos 2x k2 x k , k 2 6 6 12
Vậy nghiệm của phương trình (*) là x k,k 12
Nhận xét: Ngoài cách giải trên ta có thể giải theo cách sau: 3 2 3 2 x arccos k2 cos x 4 2 3 2 4 cos x ,k 4 3 2 3 2 cos x x arccos k2 4 4
Tuy nhiên không nên giải theo cách này vì mất đi cái vẻ đẹp của toán học. Lời giải ban đầu sử dụng
dụng công thức hạ bậc với các phép biến đổi hết sức đơn giản đưa về phương trình rất đẹp với đáp số. d) Ta có
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 50
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 3x 2x k2 2
sin 2x cos3x cos3x cos 2x 2 3x 2x k2 2 k2 5x k2 x 2 10 5 ;k x k2 x k2 2 2 Vậy nghiệm của (*) là k2 x
; x k2, k 10 5 2
Nhận xét: Phương trình
sin 2x cos3x được chuyển thành cos3x cos 2x , ta cũng có thể 2 chuyển thành dạng sau: sin 2x sin 3x . 2
Ví dụ 4. Giải và biện luận phương trình sinx 4m 1* Giải 1 4m 1 1 m Trường hợp 1: 4m 1 1 2 4m 1 1 m 0
Phương trình (*) vô nghiệm 1
Trường hợp 2: 4m 1 1 1
4m 11 0 m 2 x arcsin4m 1 k2
Phương trình (*) có nghiệm ,k x arcsin4m 1 k2 Tóm lại: 1 m Nếu
2 thì phương trình (*) vô nghiệm m 0 x arcsin4m 1 k2 Nếu 1
0 m thì phương trình (*) có nghiệm 2 x arcsin 4m 1 k2
Ví dụ 5. Tìm m để phương trình 2 sin x m có nghiệm x 0; 4 2 Giải 3 2 Ta có: 0 x x sin x 1 2 4 4 4 2 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 51
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Phương trình đã cho có nghiệm 2 m x 0; khi 1 1 m 2 2 2 2
Ví dụ 6. Giải phương trình
a) sin 2x sin 2x cos x 0 1 ;
b) sin x cos 2x sin 2x cos3x 2. Giải a) Ta có sin 2x 0 2x k k 1 sin 2x 1 cosx 0 x , k cosx 1 x k2 2 k
Vậy nghiệm của phương trình là x , k . 2
Lưu ý: Một số học sinh mắc sai lầm nghiệm trọng (lỗi rất cơ bản) là rút gọn phương trình ban đầu
cho sin 2x , dẫn đến thiếu nghiệm
b) Định hướng: Cả hai vế phương trình đều cho dưới dạng tích của hai hàm lượng giác. Thông
thường ta sử dụng công thức biến đổi tích thành tổng. 1
Ta nhắc lại: sinacosb sin
a bsina b 2 Ta có 1 1 2
sin 3x sinx sin 5x sinx sin 5x sin 3x 2 2 x k 5x 3x k2 k ,k 5x 3x k2 x 8 4
Vậy nghiệm của phương trình (*) là k x k ; x ,k 8 4
C. CÂU HỎI TRẮC NGHIỆM
Câu 1. Nghiệm của phương trình x 1 sin là 5 2
A. x 2k, k và 7 x 2k, k . 6 6 B. 5 x 2k, k và 35 x 2k, k . 6 6 C. 5 x 10k, k và 35 x 10k, k . 6 6
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 52
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 D. 5 o 35 x k1800 , k và o x k1800 , k . 6 6 Hướng dẫn giải CHỌN C. x 5 2k x 10k x 5 6 6 sin sin k k 5 6 x 35 2k x 10k 5 6 6
Câu 2. Nghiệm của phương trình sinx 1 là A. x k2 , k x
kk B. x k C.
D. x k2, k 2 2 2 Hướng dẫn giải CHỌN D. sin x 1 x k2, k . 2
Câu 3. Nghiệm của phương trình sinx 1 là
B. x k2, k
A. x k2, k C. 3 x k2, k D.
x k, k 2 2 2 Hướng dẫn giải CHỌN C. 3 sin x 1 x k2, k . 2
Câu 4. Nghiệm của phương trình sinx 0 là
C. x k, k D. B và C đúng
A. x k, k B.
x k, k 2 2 Hướng dẫn giải CHỌN C.
sin x 0 x k2, k .
Câu 5. Nghiệm của phương trình cosx 1 là
A. x k2, k B. x k, k
C. x k, k D. x k2, k 2 2 Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 53
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 CHỌN A.
cos x 1 x k2, k .
Câu 18. Nghiệm của phương trình cosx 1 là
A. x k, k B.
x k2, k
D. x k, k
C. x k2, k 2 Hướng dẫn giải CHỌN B. cos x 1
x k2, k .
Câu 6. Nghiệm của phương trình cosx 0 là A. o o
x 180 k360 , k B. o o
x 90 k180 , k C. o o
x 90 k360 , k D. o x k90 , k Hướng dẫn giải CHỌN B. o o
cos x 0 x 90 k180 , k .
Câu 7. Nghiệm của phương trình tanx 1 là
A. x k2, k B. x k, k C. 3 x k, k D.
x k, k 4 4 4 4 Hướng dẫn giải CHỌN B. tan x 1 x k, k . 4
Câu 8. Nghiệm của phương trình tanx 1 là
A. x k2, k B.
x k2, k 4 4
D. B và C đúng C. 2k 1 x 1 k, k 4 Hướng dẫn giải CHỌN C.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 54
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
2k1 tan x 1 x k 1 . k . 4 4
Câu 9. Phương trình tanx 0 có nghiệm là
B. x k, k C. x k2, k
A. x k, k D. 3 x k, k 2 2 Hướng dẫn giải CHỌN B.
tan x 0 x k, k .
Câu 10. Phương trình cot x 1 có nghiệm là
A. x k2, k B.
x k2, k C. x k2, k D. x k, k 4 4 6 4 Hướng dẫn giải CHỌN D. cot x 1 x k, k . 4
Câu 11. Phương trình cot x 1 có nghiệm là A. 2k 1 x 1 k, k B.
x k2, k 4 4
D. tất cả đều đúng C. 3 x k2, k 4 Hướng dẫn giải CHỌN A.
2k 1 cot x 1 x k , k 1 . k, k . 4 4
Câu 12. Phương trình cot x 0 có nghiệm là
D. tất cả đều đúng
A. x k, k B.
x k2, k C. 3 x k2, k 2 2 2 Hướng dẫn giải CHỌN A. cot x 0 x k, k . 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 55
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 13. Nghiệm của phương trình 1 cot x là 2
A. x k2, k B.
x k, k C.
x k, k D.
x k2, k 3 6 3 4 Hướng dẫn giải CHỌN A. 1 cos x
cosx cos x k2, k . 2 3 3
Câu 14. Nghiệm của phương trình 3 cos 2x là 2 A. 5 x k, k B. 5 x k, k C.
x k, k D. 5 x k, k 6 12 8 6 Hướng dẫn giải CHỌN B. Ta có: 3 5 5 5 cos 2x cos 2x k2 x k, k . 2 6 6 12
Câu 15. Nghiệm của phương trình tan 2x 3 là
A. x k, k B. x k, k C. x k , k D. k x , k 6 6 12 2 12 2 Hướng dẫn giải CHỌN D. Ta có: k tan 2x 3 tan
2x k x , k . 6 6 12 2
Câu 16. Nghiệm của phương trình cot x 3 là
A. x k, k B.
x k, k C.
x k, k D. 4 x k2, k 6 6 3 3 Hướng dẫn giải CHỌN B.
Ta có: cot x 3 cot x k, k . 6 6
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 56
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 17. Nghiệm của phương trình o tan x tan 25 là A. o o x 25 k360 và o o
x 155 k360 , k . B. o o x 25 k180 và o o
x 155 k180 , k C. o o x 25 k360 và o o x 2
5 k360 , k D. o o
x 25 k180 , k Hướng dẫn giải CHỌN D.
Câu 18. Nghiệm của phương trình tan x 5 là 12 A. o o
x 20 k180 , k B. o o
x 15 5 k180 , k C. o o
x 15 arctan5 k180 , k D. x
arctan5 k, k 12 Hướng dẫn giải CHỌN D. o
tan x 15 5 tan x arctan5 12 x arctan5 k x arctan5 k, k 12 12 æ ö
Câu 19: Giải phương trình 2 sin x p ç ÷ ç - ÷ = 0 ç . è 3 3 ÷ø A. 2p k3p
x = kp (k Î ). B. x = + (k Î ). 3 2 C. p p k3p x =
+ kp (k Î ). D. x = + (k Î ). 3 2 2 Lời giải. Chọn D æ ö Phương trình 2x p 2 p sin ç ÷ ç - ÷ = 0 x - = kp ç è 3 3 ÷ø 3 3 2x p p k3p = + kp x = + (k Î ). 3 3 2 2
Câu 20: Số nghiệm của phương trình sin ( 3 0 2x - 40 ) = với 0 0
-180 £ x £180 là? 2 A. 2. B. 4. C. 6. D. 7. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 57
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn B Phương trình sin ( 3 0 2x - 40 ) = sin ( 0 2x - 40 ) 0 = sin 60 2 0 0 0 0 0 0 0
é2x -40 = 60 + k360 é2x =100 + k360 éx = 50 + k180 ê ê ê . ê 0 0 0 0 ê 0 0 ê 0 0
ê2x - 40 = 180 -60 + k360 ë
ê2x = 160 + k360 ë êx = 80 + k180 ë Xét nghiệm 0 0
x = 50 + k180 . Vì 0 0 0 0 0 0
-180 £ x £180 ¾¾ 180 - £ 50 + k180 £180 0 23 13
ék = -1 x = -130 k k Î ê - £ £ ¾¾¾ . ê 0 18 18
êk = 0 x = 50 ë Xét nghiệm 0 0
x = 80 + k180 . Vì 0 0 0 0 0 0 -180 £ x £180 ¾¾
-180 £ 80 + k180 £180 0 13 5
ék = -1 x = -100 k k Î ê - £ £ ¾¾¾ . ê 0 9 9
êk = 0 x = 80 ë
Vậy có tất cả 4 nghiệm thỏa mãn bài toán.
Cách 2 (CASIO). Ta có 0 0 0 0 -180 £ x £180 ¾¾ -360 £ 2x £ 360 .
Chuyển máy về chế độ DEG, dùng chức năng TABLE nhập hàm f (X ) = ( X - ) 3 sin 2 40 -
với các thiết lập Start = -360, End = 360, Step = 40 . Quan sát 2
bảng giá trị của f (X ) ta suy ra phương trình đã cho có 4 nghiệm. æ ö
Câu 21: Số vị trí biểu diễn các nghiệm của phương trình p 1 sin çç2x ÷ + ÷ = ç
trên đường tròn lượng giác è 3 ÷ø 2 là? A. 1. B. 2. C. 4. D. 6. Lời giải Chọn C é p p é p
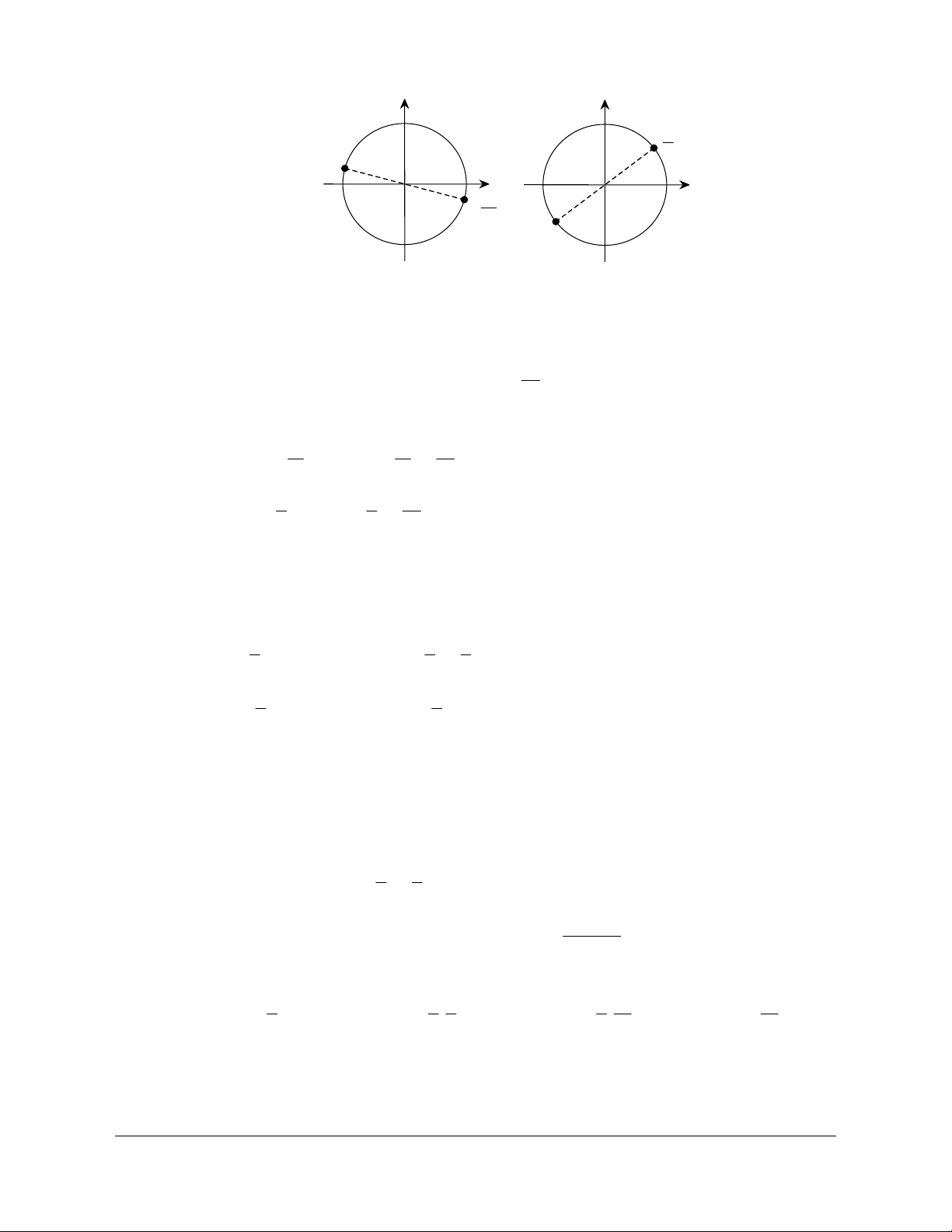
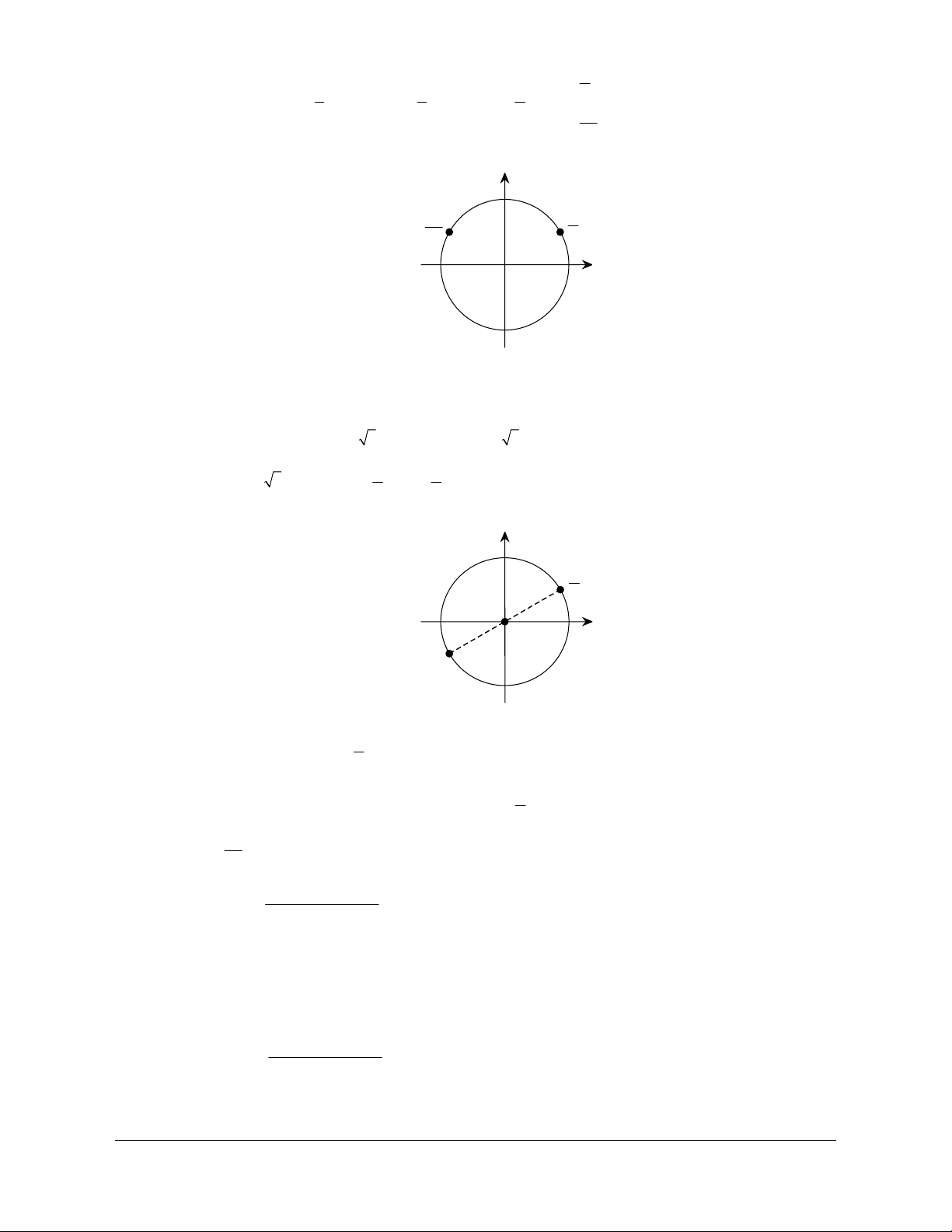
ê2x + = + k2p êx = - + kp æ ö Phương trình p p ê 3 6 ê ç ÷ 12
sin ç2x + ÷ = sin ê ê (k Î ). ç è 3 ÷ø 6 ê p p ê p
ê2x + = p - + k2p êx = + kp êë 3 6 êë 4 Biểu diễn nghiệm p x = -
+ kp trên đường tròn lượng giác ta được 2 vị trí (hình 1). 12 Biểu diễn nghiệm p x =
+ kp trên đường tròn lượng giác ta được 2 vị trí (hình 2). 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 58
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 sin sin p 4 cos O cos O p -12 Hình 1 Hình 2
Vậy có tất cả 4 vị trí biểu diễn các nghiệm các nghiệm của phương trình.
Cách trắc nghiệm. Ta đưa về dạng 2p x = a + k ¾¾
số vị trí biểu diễn trên đường tròn n lượng giác là n . p p p Xét 2 x = - + kp x = - + k ¾¾
có 2 vị trí biểu diễn. 12 12 2 p p p Xét 2 x =
+ kp x = + k ¾¾
có 2 vị trí biểu diễn. 4 4 2
Nhận xét. Cách trắc nghiệm tuy nhanh nhưng cẩn thận các vị trí có thể trùng nhau.
Câu 22: Với những giá trị nào của x thì giá trị của các hàm số y = sin 3x và y = sin x bằng nhau? éx = k2p é = p ê x k ê A. ê p
(k Î ). B. ê p p (k Î ).
êx = + k2p ê ê x = + k ë 4 êë 4 2 C. p p x = k (k Î ).
D. x = k (k Î ). 4 2 Lời giải Chọn B
Xét phương trình hoành độ giao điểm: sin 3x = sin x é = p é3 = + 2 x k x x k p ê ê ê p
p (k Î ).
ê3x = p - x + k2p êx = + k ë êë 4 2 Câu 23: Gọi x
x là nghiệm dương nhỏ nhất của phương trình 2 cos 2
= 0 . Mệnh đề nào sau đây là 0 1-sin 2x đúng? æ ö é ù æ ö é ù A. p p p p 3p 3p x Î çç0; . ÷÷
B. x Î ê ; ú. C. x Îçç ; . ÷÷ D. x Î ê ;pú. 0 çè 4÷ø 0 ê 4 2 ú ë û 0 çè2 4 ÷ø 0 ê 4 ú ë û Lời giải Chọn D
Điều kiện: 1-sin 2x ¹ 0 sin 2x ¹1.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 59
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 cos 2 ésin 2x =1 loaïi 2 2 x ( ) Phương trình
sin 2 x +cos 2 x 1 0 cos 2 ê = x = 0 = ¾¾¾¾¾¾ 1 sin 2 ê - x sin 2x = - ê ( 1 thoûa maõn) ë p p sin 2x = 1
- 2x = - + k2p x = - + kp (k Î ) . 2 4 Cho p 1 - + kp > 0 ¾¾ k > . 4 4 é ù
Do đó nghiệm dương nhỏ nhất ứng với 3p 3p k = 1 x = Î ê ;pú. 4 ê 4 ú ë û
Câu 24: Hỏi trên đoạn [-2017;2017], phương trình (sin x + )
1 (sin x - 2) = 0 có tất cả bao nhiêu nghiệm? A. 4034. B. 4035. C. 641. D. 642. Lời giải. Chọn D ésin x = -1 Phương trình p ê
sin x = -1 x = - + k2p (k Î ). ê sin x = 2 ê (vo nghiem) 2 ë p p -2017 + 2017 + Theo giả thiết p 2 2
-2017 £ - + k2p £ 2017 £ k £ 2 2p 2p xap xi 320,765 321, 265 k k Î ¾¾¾ - £ £ ¾¾¾ k Î { 320 - ;-319;...;32 } 1 .
Vậy có tất cả 642 giá trị nguyên của k tương úng với có 642 nghiệm thỏa mãn yêu cầu bài toán. æ ö
Câu 25: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình p 3 sin 3 çç x ÷ - ÷ = ç è 4 ÷ø 2 bằng:
A. p . B. p p p - . C. . D. - . 9 6 6 9 Lời giải Chọn B é p p
ê3x - = + k2p æ ö æ ö Ta có p 3 p p ê ç ÷ ç - ÷ = ç ÷ 4 3 sin 3x sin 3 ç ÷ ç x - ÷ = sin ê è 4 ø 2 çè 4 ÷ø 3 ê p p
ê3x - = p - + k2p êë 4 3 é 7p é 7p k 2p ê3x = + k2p êx = + ê 12 ê 36 3 ê ê (k Î ). ê 11p ê 11p k2p ê3x = + k2p êx = + êë 12 êë 36 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 60
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 é 7 7p
êx > 0 k > - k = 0 = min x TH1. Với 7p k2p ê Cho 24 36 x = + ¾¾¾ ê . 36 3 ê 7 17p
êx < 0 k < - k = 1 - = - max x êë 24 36 é 11 11p
êx > 0 k > - k = 0 = min x TH2. Với 11p k 2p ê Cho 24 36 x = + ¾¾¾ ê . 36 3 ê 11 13p
êx < 0 k < - k = 1 - = - max x êë 24 36
So sánh bốn nghiệm ta được nghiệm âm lớn nhất là 13p x = -
và nghiệm dương nhỏ nhất 36 là 7p p p p x =
. Khi đó tổng hai nghiệm này bằng 13 7 - + = - . 36 36 36 6
Câu 26: Tổng các nghiệm của phương trình ( 0
tan 2x -15 ) = 1 trên khoảng ( 0 0 -90 ;90 ) bằng: A. 0 0 . B. 0 -30 . C. 0 30 . D. 0 -60 . Lời giải Chọn B Ta có ( 0 x - ) 0 0 0 0 0 tan 2
15 = 1 2x -15 = 45 + k180 x = 30 + k90 (k Î ) . Do x Î( 4 2 0 0 -90 ;90 ) 0 0 0 0 ¾¾
-90 < 30 + k90 < 90 - < k < 3 3 0
ék = -1 x = -60 k Î 0 0 0 ê ¾¾¾ ¾¾ -60 + 30 = -30 . ê 0
êk = 0 x = 30 ë
Câu 27: Giải phương trình cot(3x - ) 1 = - 3. A. 1 5p p 1 p p x = +
+ k (k Î ). B. x = + + k (k Î ). 3 18 3 3 18 3 C. 5p p 1 p x =
+ k (k Î ).
D. x = - + kp (k Î ). 18 3 3 6 Lời giải Chọn A æ ö Ta có p cot (3x - ) 1 = - 3 cot (3x - ) 1 = cot ç ÷ - ç ÷ ç è 6 ÷ø p 1 p p = p
3x -1 = - + kp x = - + k (k Î ) k 1 5 1 ¾¾ x = + . 6 3 18 3 3 18 æ ö
Câu 28: Số nghiệm của phương trình 3p p tan x = tan
trên khoảng çç ;2p÷÷ là? 11 çè4 ÷ø A. 1 B. 2. C. 3. D. 4. Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 61
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Ta có 3p 3p tan x = tan x = + kp (k Î ) . 11 11 æ ö Do p p 3p CASIO
Î çç ;2p÷÷ <
+ p < 2p ¾¾¾-0, 027 < <1,72 k x k k Î ¾¾¾ k Î {0; } 1 . ç ÷ xap xi è 4 ø 4 11
Câu 29: Tổng các nghiệm của phương trình tan 5x -tan x = 0 trên nửa khoảng [0;p) bằng: A. p p p . B. 3 . C. 2p . D. 5 . 2 2 Lời giải Chọn B Ta có p
tan 5 - tan = 0 tan 5 = tan 5 k x x x x
x = x + kp x = (k Î ) . 4 Vì kp
x Î [0;p) , suy ra 0 p 0 k 4 kÎ £ < £ < ¾¾¾ k = {0;1;2; } 3 . 4 ìï ü
Suy ra các nghiệm của phương trình trên [ p p p ï ï 0;p) là 3 0; ; ; í ý. ïî 4 2 4 ï ï ïþ Suy ra p p 3p 3p 0 + + + = . 4 2 4 2
Câu 30: Giải phương trình tan 3x.cot 2x =1. A. p p p x = k (k Î ).
B. x = - + k (k Î ). 2 4 2
C. x = kp (k Î ). D. Vô nghiệm. Lời giải Chọn D ìï p p ï ¹ + co ìï s3x ¹ 0 x k ï Điều kiện: ï ï 6 3 í í (k Î ). sin ï 2x ¹ 0 ï p ïî ïïx ¹ k ïïî 2 Phương trình 1 tan 3x =
tan 3x = tan 2x 3x = 2x + kp x = kp (k Î ) . cot 2x
Đối chiếu điều kiện, ta thấy nghiệm p
x = kp không thỏa mãn x ¹ k . 2
Vậy phương trình đã cho vô nghiệm.
Câu 31: Giải phương trình cos2x tan x = 0. é p é p p ê ê A. p x = + kp x = + k x = k (k Î ). B. ê 2
(k Î ). C. ê 4
2 (k Î ). D. 2 ê ê êx = kp ë êx = kp ë p x =
+ kp (k Î ). 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 62
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn C Điều kiện: p
cos x ¹ 0 x ¹ + kp (k Î ) . 2 écos 2x = 0
Phương trình cos2x tan x = 0 ê êtan x = 0 ë é p é p p ê2x = + kp
êx = + k (thoûa maõn) ê 2 ê 4 2 (k Î ). ê ê êx = kp
êx = kp(thoûa maõn) ë ë
Câu 32: Tìm tất các các giá trị thực của tham số m để phương trình sin x = m có nghiệm.
A. m £1. B. m ³ -1. C.
-1 £ m £1. D. m £ -1. Lời giải Chọn C Với mọi x Î ,
ta luôn có -1 £ sin x £1 .
Do đó, phương trình sin x = m có nghiệm khi và chỉ khi -1£ m £1.
Câu 33: Tìm tất các các giá trị thực của tham số m để phương trình cos x -m = 0 vô nghiệm. A. m Î(- ; ¥ - ) 1 È(1;+¥).
B. m Î(1;+¥). C. m Î[-1; ] 1 . D. m Î (- ; ¥ - ) 1 . Lời giải Chọn A
Áp dụng điều kiện có nghiệm của phương trình cos x = a .
Phương trình có nghiệm khi a £1.
Phương trình vô nghiệm khi a >1.
Phương trình cos x -m = 0 cos x = m. ém < -1
Do đó, phương trình cos x = m vô nghiệm m >1 ê . êm >1 ë
Câu 34: Có bao nhiêu giá trị nguyên của tham số m để phương trình cos x = m +1 có nghiệm? A. 1. B. 2. C. 3. D. Vô số. Lời giải Chọn C
Áp dụng điều kiện có nghiệm của phương trình cos x = a .
Phương trình có nghiệm khi a £1.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 63
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Phương trình vô nghiệm khi a >1.
Do đó, phương trình cos x = m +1 có nghiệm khi và chỉ khi m +1 £1 1 1 1 2 0 m m m Î - £ + £ - £ £ ¾¾¾
m Î {-2;-1;0}.
Câu 35: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình æ pö cosçç2x ÷ - ÷-m = 2 ç
có nghiệm. Tính tổng T của các phần tử trong S. è 3 ÷ø
A. T = 6. B. T = 3. C. T = 2. - D. T = 6. - Lời giải Chọn D æ ö æ ö Phương trình p p cosçç2x ÷ - ÷-m = 2 cosç ç ÷ ç2x ÷ - ÷ = m + 2. è 3 ø çè 3 ÷ø
Phương trình có nghiệm 1
- £ m + 2 £1 -3 £ m £ 1 - mÎ ¾¾¾ S = { 3; - 2 - ;- } 1 ¾¾ T = (-3)+(-2)+(- ) 1 = 6 - .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 64
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 3. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP
A. KIẾN THỨC LÝ THUYẾT TRỌNG TÂM
1) Phương trình bậc nhất đối với một hàm số lượng giác
Định nghĩa. Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng at + b = 0 trong đó ,
a b là các hằng số (a ¹ 0) và t là một hàm số lượng giác.
Cách giải. Chuyển vế rồi chia hai vế phương trình cho a , ta đưa về phương trình lượng giác cơ bản.
2) Phương trình bậc nhất đối với sin x và cos x
Định nghĩa. Phương trình bậc nhất đối với sin x và cos x là phương trình có dạng
asin x + b cos x = c
Cách giải. Điều kiện để phương trình có nghiệm: 2 2 2
a + b ³ c .
Chia hai vế phương trình cho 2 2
a + b , ta đựợc a b c sin x + cos x = . 2 2 2 2 2 2 a + b a + b a + b 2 2 æ ö æ ö Do ç a ÷ ç b ÷ ç ÷ a b ç ÷ +ç ÷ nên đặt = cosa ¾¾ = sin . a ç ÷ ç ÷ = 1 2 2 2 2 a + b ÷ ç a +b ÷÷ è ø è ø 2 2 2 2 a + b a + b
Khi đó phương trình trở thành c c
cos a sin x + sin a cos x = s in (x +a) = . 2 2 2 2 a + b a + b
3) Phương trình bậc hai đối với một hàm số lượng giác
Định nghĩa. Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng 2
at + bt + c = 0 trong đó , a ,
b c là các hằng số (a ¹ 0) và t là một hàm số lượng giác.
Cách giải. Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có) rồi giải
phương trình theo ẩn phụ này. Cuối cùng, ta đưa về việc giải các phương trình lượng giác cơ bản.
4) Phương trình bậc hai đối với sin x và cos x
Định nghĩa. Phương trình bậc hai đối với sin x và cos x là phương trình có dạng 2 2
asin x + bsin x cos x + c cos x = 0 Cách giải.
● Kiểm tra cos x = 0 có là nghiệm của phương trình.
● Khi cos x ¹ 0 , chia hai vế phương trình cho 2
cos x ta thu được phương trình
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 65
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2
a tan x + b tan x + c = 0.
Đây là phương trình bậc hai đối với tan x mà ta đã biết cách giải.
Đặc biệt. Phương trình dạng 2 2
a sin x + b sin x cos x + c cos x = d ta làm như sau: Phương trình 2 2
a sin x + bsin x cos x + c cos x = d.1 2 2
a sin x +bsin x cos x + c cos x = d ( 2 2 sin x + cos x) (a-d) 2
sin x +b sin x cos x +(c-d) 2 cos x = 0.
5) Phương trình chứa sin x cos x và sin x.cos x
Định nghĩa. Phương trình chứa sin x cos x và sin x.cos x
a(sin x cos x)+ bsin x cos x +c = 0
Cách giải. Đặt t = sin x cos x (điều kiện - 2 £ t £ 2 )
Biểu diễn sin x.cos x theo t ta được phương trình cơ bản.
B. PHÂN LOẠI VÀ PHƯƠNG PHÁO GIẢI BÀI TẬP
Dạng 1. Phương trình bậc nhất đối với một hàm số lượng giác 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Giải phương trình 2 cos x - 3 = 0 . Lời giải é p
êx = + k2p Ta có p ê 6
2 cos x - 3 = 0 cos x = cos ê (k Î ) . 6 ê p
êx = - + k2p êë 6
Ví dụ 2: Giải phương trình 2sin x 1 0 Lời giải x k2 1 Ta có: 6
2sin x 1 0 sin x sin x sin k 2 6 5 x k2 6 æ ö
Ví dụ 3: Giải phương trình p tan çç2x ÷ - ÷+ 3 = 0 ç è 3 ÷ø Lời giải æ ö æ ö æ ö æ ö Ta có p p p p tan çç2x ÷
- ÷+ 3 = 0 tan çç2x ÷
- ÷ = - 3 tan çç2x ÷ - ÷ = tan ç ÷ - ç ÷ ç è 3 ÷ø çè 3 ÷ø çè 3 ÷ø çè 3÷ø p p kp
2x - = - + kp 2x = kp x = (k Î ). 3 3 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 66
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 sin B cos C A O D
Quá dễ để nhận ra có 4 vị trí biểu diễn nghiệm của phương trình đã cho trên đường tròn
lượng giác là A, B, C,D.
Cách trắc nghiệm. Ta có kp 2p x = = k ¾¾
có 4 vị trí biểu diễn. 2 4
Ví dụ 4: Hỏi trên đoạn [0;2018p] , phương trình 3 cot x -3 = 0 có bao nhiêu nghiệm? Lời giải Ta có p p
cot x = 3 cot x = cot
x = + kp (k Î ) . 6 6 Theo giả thiết, ta có p 1 xap xi
0 £ + kp £ 2018p ¾¾¾ - £ k £ 2017,833 6 6 3 kÎ ¾¾¾
k Î {0;1;...;2017} . Vậy có tất cả 2018 giá trị nguyên của k tương ứng với có 2018
nghiệm thỏa mãn yêu cầu bài toán.
3. Bài tập trắc nghiệm
Câu 1: Phương trình 2sin x 1 0 có nghiệm là:
x k2
x k2 A. 6 B. 6 7 7 x k2 x k2 6 6 x k2 x k C. 6 D. 6 5 7 x k2 x k 6 6 Lời giải Chọn B 1
Ta có: 2sin x 1 0 sin x sin 2 6
x k2 6 k 7 x k2 6
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 67
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 x x
Câu 2: Giải phương trình 2 cos 1 sin 2 0 2 2 2 A. x
k2 ,k B. x
k2 ,k 3 3 2 C. x
k4 ,k D. x
k4 ,k 3 3 Lời giải Chọn D x x Vì 1 sin 1, x
sin 2 0 2 2
Vậy phương trình tương đương x x 1 x 2 cos 1 0 cos k2 2 2 2 2 3 2 x
k4 ,k 3
Câu 3: Phương trình 2sin x 3 0 có tập nghiệm là:
A. k2 , k .
B. k2 , k . 6 3 5 2
C. k2 ,
k2 , k .
D. k2 ,
k2 , k . 6 6 3 3 Lời giải x k2 3 3
2sin x 3 0 sin x k . 2 2 x k2 3 2
Vậy tập nghiệm của phương trình là: S k2 ,
k2 , k 3 3 æ ö
Câu 4: Tìm nghiệm dương nhỏ nhất của phương trình p 2 sin çç4x ÷ - ÷-1 = 0. ç è 3 ÷ø A. p p p p x = . B. 7 x = . C. x = . D. x = . 4 24 8 12 Lời giải Chọn C æ ö æ ö æ ö Ta có p p 1 p p 2 sin çç4x ÷ - ÷-1 = 0 sin ç ç ÷ ç4x ÷ - ÷ = sin ç è ø ç ÷ ç4x ÷ - ÷ = sin 3 è 3 ø 2 çè 3 ÷ø 6
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 68
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 é p p é p é p kp
ê4x - = + k2p
ê4x = + k2p êx = + ê 3 6 ê 2 ê 8 2 ê ê ê (k Î ). ê p p ê 7p ê 7p kp
ê4x - = p - + k2p ê4x = + k2p êx = + êë 3 6 êë 6 êë 24 2 TH1. Với p kp > p kp 1 p Cho 0 x = + ¾¾¾ +
> 0 k > - k = 0 x = . min 8 2 8 2 4 8 TH2. Với 7p kp > 7p kp 7 7p Cho 0 x = + ¾¾¾ + > 0 k > - k = 0 x = . min 24 2 24 2 12 24
So sánh hai nghiệm ta được p x =
là nghiệm dương nhỏ nhất. 8
Câu 5: Giải phương trình 2 4 sin x = 3 . é p é p
êx = + k2p
êx = + k2p A. ê 3 ê ê , (k Î ) . B. 3 ê , (k Î ) . ê p ê 2p
êx = - + k2p êx = + k2p êë 3 êë 3 ìï p kp ì ï ï kp = + ï = C. x ï x í 3
3 (k, Î ). D. ïí
3 (k, Î ). ïï ï ïk ¹ 3 ï î ïk ¹ 3 î Lời giải Chọn D Ta có 3 3 2 2
4 sin x = 3 sin x = sin x = . 4 2 é p
êx = + k2p 3 p ê Với 3 sin x = sin x = sin ê (k Î ) . 2 3 ê 2p êx = + k2p êë 3 é p
êx = - + k2p 3 æ pö ê Với = - = ç ÷ 3 sin x sin x sin - ç ÷ ê (k Î ) . 2 çè 3÷ø ê 4p êx = + k2p êë 3
Nhận thấy chưa có đáp án nào phù hợp. Ta biểu diễn các nghiệm trên đường tròn lượng giác (hình vẽ). sin p p 2 3 3 cos B A O p 2p - - 3 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 69
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Nếu tính luôn hai điểm A, B thì có tất cả 6 điểm cách đều nhau nên ta gộp được 6 điểm
này thành một họ nghiệm, đó là p x = k . 3 ìï p ïx = k ìï kp ï ï ï =
Suy ra nghiệm của phương trình ï 3 x ï í í 3 (k, Î ). ï p ï
ïïk ¹ lp ïïk ¹ 3 3 î ïïî
Câu 6: Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 3 cos x + m -1 = 0 có nghiệm? A. 1. B. 2. C. 3. D. Vô số. Lời giải Chọn C Ta có 1-m
3 cos x + m -1 = 0 cos x = . 3 Phương trình có nghiệm 1-m -1 £
£1 1- 3 £ m £1+ 3 mÎ ¾¾¾ m Î {0;1;2}. 3
Vậy có tất cả 3 giá trị nguyên của tham số m .
Câu 7: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2108;2018] để phương trình
m cos x +1 = 0 có nghiệm? A. 2018. B. 2019. C. 4036. D. 4038. Lời giải Chọn A Ta có 1
m cos x +1 = 0 cos x = - . m Phương trình có nghiệm 1 -1 £ - £1 m ³1 mÎ ¾¾¾¾¾
m Î {1;2;3;...;2018} . m [ Î -2018;2018] m
Vậy có tất cả 2018 giá trị nguyên của tham số m .
Câu 8: Tìm giá trị thực của tham số p
m để phương trình (m -2)sin 2x = m +1 nhận x = làm 12 nghiệm. 2( 3 + ) 1
A. m ¹ 2. B. m = . C. m = -4. D. m = -1. 3 -2 Lời giải Chọn C Vì p x =
là một nghiệm của phương trình (m -2)sin 2x = m +1 nên ta có: 12 ( p - m - ) 2 m 2 2 .sin = m +1
= m +1 m -2 = 2m + 2 m = -4 . 12 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 70
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Vậy m = -4 là giá trị cần tìm.
Câu 9: Tìm tất cả các giá trị của tham số m để phương trình (m + )
1 sin x + 2 -m = 0 có nghiệm.
A. m £ -1. B. 1 m ³ . C. 1 1
- < m £ . D. m > 1. - 2 2 Lời giải Chọn B Phương trình ( - m + )
x + -m = (m + ) m 2 1 sin 2 0
1 sin x = m -2 sin x = . m +1
Để phương trình có nghiệm m -2 1 - £ £1 m +1 ìï m -2 ìï2m -1 ìïé 1 0 ï £1+ ï ³ 0 ï ï ï ïêm ³ ïï m +1 ïï m +1 ïê ï 2 1 í í íê
m ³ là giá trị cần tìm. ïm -2 ï 3 ïêm < 1 - ï ï ïë 2 ï -1 £ 0 - ï £ 0 ï ïïîm 1 ïïî m 1 m ï + + ï > 1 - î
Câu 10: Tìm tất cả các giá trị của tham số m để phương trình (m -2)sin 2x = m +1 vô nghiệm. é ù æ ö A. 1 1 m Î ê ;2ú. B. m Î ç- ç ; ÷ ¥ ÷È(2;+¥). ê 2 ú ë û çè 2÷ø æ ö æ ö C. 1
m Î çç ;2÷÷È(2;+¥). Î ç ÷ ç D. 1 m ç ;+¥÷. è2 ÷ø çè2 ÷ø Lời giải Chọn D
TH1. Với m = 2 , phương trình (m -2)sin 2x = m +1 0 = 3 : vô lý.
Suy ra m = 2 thì phương trình đã cho vô nghiệm. TH2. Với m +
m ¹ 2 , phương trình (m - ) 1
2 sin 2x = m +1 sin 2x = . m -2 é m +1 ê > 1 ém > 2 + ê - ê Để phương trình ( ) m 1 * vô nghiệm Ï [- ] m 2 1;1 ê ê1 . m -2 ê m +1 ê < m < 2 ê < 1 - êë2 êëm -2
Kết hợp hai trường hợp, ta được 1
m > là giá trị cần tìm. 2
Dạng 2. Phương trình bậc nhất đối với sin x và cos x 1. Phương pháp Cách 1
Chia hai vế phương trình cho 2 2 a b ta được:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 71
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 a b c (1) sinx cosx 2 2 2 2 2 2 a b a b a b a b Đặt: sin , cos
0, 2 phương trình trở thành: 2 2 2 2 a b a b c c sin . sin x cos . cosx cos(x ) cos 2 2 2 2 a b a b
x k2 (k Z)
Điều kiện để phương trình có nghiệm là: c 2 2 2 1 a b c . 2 2 a b Cách 2 x
Xét x k2
k có là nghiệm hay không? 2 2 x
Xét x k2 cos 0. 2 2 x 2t 1 t
Đặt: t tan , thay sin x , cosx
, ta được phương trình bậc hai theo t: 2 2 2 1 t 1 t 2
(b c)t 2at c b 0 (3) Vì
x k2 b c 0, nên (3) có nghiệm khi: 2 2 2 2 2 2
' a (c b ) 0 a b c . x
Giải (3), với mỗi nghiệm t0, ta có phương trình: tan t0. 2 Ghi chú
1/ Cách 2 thường dùng để giải và biện luận.
2/ Cho dù cách 1 hay cách 2 thì điều kiện để phương trình có nghiệm: 2 2 2 a b c . 3/ Bất đẳng thức B.C.S: 2 2 2 2 2 2
y a.sinx b.cosx a b . sin x cos x a b 2 2 2 2 sinx cosx a
min y a b vaø max y a b tan x a b b
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Giải phương trình a)sin x 2 cosx 5; b)sin x 3 cosx 1; c)5cosx 3sin x 4 2. Giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 72
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 a) Ta thấy 2 a 2 2 b
5 c 25 phương trình đã cho vô nghiệm.
b) Chia hai vế của (1) cho 2 2 a b 2 , ta được : 1 3 1 1 sin x cos x sinxcos cosxsin 2 2 2 3 3 2 x k2 x k2 3 6 2 sin x sin , k 3 6 7 x k2 x k2 3 6 6
Vậy nghiệm của phương trình (1) là 7 x k2 ; x k2 , k 2 6
b) Chia hai vế của (1) cho 2 2
a b 34 , ta được : 5 3 4 cos x sin x * 34 34 17 Đặt 5 3 cos ,sin , 0; 34 34 2 Lúc đó :
4 4 pt cos x x arccos k2,k 17 17 2 6
Ví dụ 2. Tìm nghiệm của phương trình cos7x 3sin7x 2 * thỏa mãn điều kiện x . 5 7 Giải Ta có : 1 3 2 * cos 7 x sin 7x
sin cos7x cos sin7x sin 2 2 2 6 6 4 sin 7x sin sin 7x sin 6 4 6 4 5 k2 7x k2 x 6 4 84 7 k,m 3 11 m2 7x m2 x 6 4 84 7 Do 2 5 k2 6 2 5 2k 6 5 5 84 7 7 5 84 7 7 84 2 6 k k x 5 7 2 1 1 m2 6
2 11 2m 6 11 5 84 7 7 5 84 7 7 84 m m
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 73
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 7 5 5 k 3 5 24 24 k 2 k m 1 7 11 11 m 3 m 2 5 24 24 m 52 35 59
Vậy nghiệm của phương trình (*) là x ;x ;x . 84 84 84
Ví dụ 3. Giải phương trình sin2x 1 6sinx cos2x .
Định hướng: Chuyển cos2x sang vế trái, dùng công thức nhân đôi 2
1 cos2x 2sin x . Lúc đó
phương trình đưa về phương trình tích với sự xuất hiện của nhân tử chung là sinx Giải Ta có:
sin2x 1 6sinx cos2x sin2x 6sinx 1 cos2x 0 2sin xcosx 3 2
2sin x 0 2sin xcosx 3 sinx 0 sinx 0 x π k ,k sin x cosx 3 (VN)
Vậy nghiệm của phương trình là x π k , k.
Ví dụ 4. Giải phương trình: 2sin2x cos2x 7sinx 2cosx 4 .
Định hướng: Chuyển toàn bộ vế phải của phương trình sang vế trái, nhóm
2sin2x 2cosx 2cosx2sinx 1 , sử dụng công thức 2
cos2x 1 2sin x để nhóm 2 2
2sin x 1 7sinx 4 2sin x 7sinx 3 sinx 32sinx 1
Chú ý rằng: nếu f x 2
ax bx c ax x ,x 1
x x x2 với 1 2 là nghiệm của phương trình f x 0 Giải Ta có: 2
PT 4sin x.cosx 2cosx 2sin x 1 7sin x 4 0 2cosx2sinx 2
1 2sin x 7sin x 3 0 2cosx2sinx
1 sinx 32sinx 1 0 2sinx
1 sinx 2cosx 3 0 π 1 x k2π sin x 6 2 (k ) 5π 2 2 2
sinx 2cosx 3 0 (VN vì 1 2 3 ) x k2π 6 5
Vậy nghiệm của phương trinh là: π π x k2π, x k2π, k. 6 6
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 74
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ví dụ 5. Giải phương trình: sin x2sinx 1 cosx2cosx 3.
Định hướng: Khai triển cả hai vế phương trình ta thấy vế trái xuất hiện 2 2sin x và vế phải xuất hiện 2
2cos x , như vậy nếu đặt 2 ra ngoài ta se được công thức nhân hai: 2 2
2 cos x sin x 2cos2x .
Chuyển vế, phương trình đã cho trở thành:
sinx 3 cosx 2cos2x . Giải Ta có: 2 2 PT sinx
3 cosx 2 cos x sin x sinx 3cosx 2cos2x 1 3 π π sin x
cosx cos2x sinx sin 2x 2 2 3 2 π π 5π 2π x 2x k2π x k 3 2 18 3 (k ) π π 5π x 2x k2π x k2π 3 2 6 5 2 5
Vậy phương trình có nghiệm là: π π π x k ; x k2π, k . 18 3 6
Ví dụ 6. Giải phương trình : cos7xcos5x 3 sin2x 1 sin7xsin5x*
Định hướng : Ở cả hai vế phương trình đều xuất hiện 7x,5x . Chuyển vế ta được :
cos7xcos5x sin 7xsin 5x cos7x 5x cos2x Giải Ta có :
* cos7xcos5x sin7xsin5x 3sin2x 1
cos7x 5x 3sin2x 1 cos2x 3sin2x 1 1
Chia hai vế của phương trình (1) cho 2 2 1 3 2 Ta được: 1 3 1 1 cos2x sin 2x
cos cos2x sin sin2x 2 2 2 3 3 2 x k cos 2x cos k2 3 3 3 x k 3
Vậy nghiệm của phương trình (*) là x k , x k , k 3
Ví dụ 7. Xác định m để phương trình 2 sin x m cosx m 2 * có nghiệm.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 75
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Định hướng : Phương trình asin x bcosx c có nghiệm khi 2 2 2 a b c . Giải Ta có : (*) có nghiệm 2 2 2 2 2 2 m m 2
2 m m 2 2m 2 m 0
Vậy m 0 thì phương trình đã cho có nghiệm.
Ví dụ 8. Giải và biện luận các phương trình sau theo tham số m
a)sin x m cos x 1 m 1 2 3 b) 2m 1 sin x 2m 1 cos x 2m 2 2 Giải
a) Cách 1. Thay x k ,
k hay x k2 ,
k vào (1). Ta có : 2 2 VT
1 0 m m, nên (1) không có nghiệm x k2 , k 2 Đặt x 2t 1 t t tan . Ta có (1) trở thành: m 1 m 2 2 2 1 t 1 t 2 2 2 2
2t m mt 1 t m mt t 2t 1 2m 0*
1 1 2m 2m
Nếu m 0 thì 0 * vô nghiệm 1 vô nghiệm b '
Nếu m 0 thì 0 * có nghiệm kép t t 1 1 2 a 1 có nghiệm x k hay x k2 , k 2 4 2
Nếu m 0 thì 0 * có nghiệm t 1 2m hoặc t 1 2m
1 có nghiệm là x 2arctan 1 2m k2 , k Tóm lại :
Nếu m 0 thì (1) vô nghiệm
Nếu m 0 thì có nghiệm x k2 , k 2
Nếu m 0 thì (1) có nghiệm là x 2arctan1 2m k2 ,x 2arctan1 2m k2 ,k Cách 2
(1) có dạng asinX bcosX c với a 1,b m,c 1,X x Ta có :
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 76
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 2 1 2
A a b c 1 m 1 m2 2m Nếu m 0 thì 2 2 2
A 0 a b c (1) vô nghiệm Nếu m 0 : 1 sin x 1 x k2 . k 2 Nếu m 0 thì 2 2 2
A 0 a b c 1 có nghiệm
Chia hai vế của phương trình (1) cho 2 m 1 Ta được: 1 m 1 m sin x cos x * 2 2 2 m 1 m 1 m 1 Đặt m 1 1 m cos , sin , cos . 2 2 2 m 1 m 1 m 1
* cosx cos x k2 hoặc x k2 ,k
b) (1) có dạng asinX bcosX c với 2 3
a 2m, b 2m 1,c 2m , X x . Ta có 2 2 2 b 2 2 2 a 2m 1 2m 1 8m 2 2 2 2 3 4 2 9 c 2m 4m 6m 2 4 2 (2) có nghiệm 2 2 2 4 2 1 2 1 a b c 4m 2m 0 2m 0 4 2 2 1 2 1 1
2m 0 m m 2 4 2 Với 1 m
: 2 sin x 1 x k2 , k 2 2 Với 1 m
: 2 cos x 1 x k2 .k 2
3. Bài tập trắc nghiệm
Câu 1: Gọi S là tập nghiệm của phương trình cos2x -sin 2x =1. Khẳng định nào sau đây là đúng? A. p p p p Î S. B. Î S. C. 3 Î S. D. 5 Î S. 4 2 4 4 Lời giải Chọn C æ ö æ ö Phương trình p p 1 2 cosçç2x ÷ + ÷ = 1 cosç ç ÷ ç2x ÷ + ÷ = è 4 ø çè 4 ÷ø 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 77
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 é p p
ê2x + = + k2p éx = kp æ pö p ê ç ÷ 4 4 ê
cosç2x + ÷ = cos ê ê p , k Î . ç è 4 ÷ø 4 ê p p êx = - + kp
ê2x + = - + k2p êë 4 êë 4 4 Xét nghiệm p p
x = - + kp , với k = 1 ta được 3 x = . 4 4 æ ö
Câu 2: Số nghiệm của phương trình p
sin 2x + 3 cos 2x = 3 trên khoảng çç0; ÷÷ ç là? è 2 ÷ø A. 1. B. 2. C. 3. D. 4. Lời giải Chọn A æ ö Phương trình 1 3 3 p 3 sin 2x + cos 2x = sin çç2x ÷ + ÷ = 2 2 2 çè 3 ÷ø 2 é p p
ê2x + = + k2p éx = kp æ pö p ê ç ÷ 3 3 ê
sin ç2x + ÷ = sin ê ê p , . k Î ç è 3 ÷ø 3 ê p p êx = + kp
ê2x + = p - + k2p êë 6 êë 3 3 p 1 0 p 0 k k k Î < < < < ¾¾¾
không có giá trị k thỏa mãn. 2 2 p p Î p 1 1 0 k
< + kp < - < k < ¾¾¾
k = 0 x = . 6 2 6 3 6
Câu 3: Tính tổng T các nghiệm của phương trình 2 2
cos x -sin 2x = 2 + sin x trên khoảng (0;2p). A. 7p p p p T = . B. 21 T = . C. 11 T = . D. 3 T = . 8 8 4 4 Lời giải Chọn C Phương trình 2 2
cos x -sin x -sin 2x = 2 cos 2x -sin 2x = 2 æ pö p p cosçç2x ÷
+ ÷ = 1 2x + = k2p x = - + kp (k Î ) . ç è 4 ÷ø 4 8 é 7p êk = 1 x = Do p 1 17 ê kÎ 8
0 < x < 2p ¾¾
0 < - + kp < 2p < k < ¾¾¾ ê 8 8 8 ê 15p êk = 2 x = êë 8 7p 15p 11 ¾¾ T = + = . p 8 8 4 æ ö
Câu 4: Số nghiệm của phương trình p
sin 5x + 3 cos5x = 2 sin 7x trên khoảng çç0; ÷÷ ç là? è 2 ÷ø A. 2. B. 1. C. 3. D. 4. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 78
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn D æ ö Phương trình 1 3 p sin 5x +
cos5x = sin 7x sin 5 çç x ÷ + ÷ = sin 7x 2 2 çè 3 ÷ø é p é
ê7x = 5x + + k2 p p êx = + kp æ pö ê 3 ê = ç ÷ 6 sin 7x sin 5 ç x + ÷ ê ê (k Î ) . ç è 3 ÷ø ê æ pö ê p kp ê7x = p - 5 çç x ÷ + ÷+ k2p êx = + ê çè 3 ÷ø ê ë ë 18 6 p p Î p 1 1 0 k
< + kp < - < k < ¾¾¾
k = 0 x = . 6 2 6 3 6 é p êk = 0 x = ê 18 ê p p p 1 8 ê Î p k 2 0 < + k <
- < k < ¾¾¾
êk = 1 x = . 18 6 2 3 3 ê 9 ê ê 7p êk = 2 x = êë 18
Vậy có 4 nghiệm thỏa mãn. æ ö æ ö
Câu 5: Giải phương trình p p 3 cosççx ÷ + ÷+ sin ç ç ÷ çx ÷ - ÷ = 2 sin 2x. è 2 ø çè 2 ÷ø é 5p é p ê 7 x = + k2p êx = + k2p A. ê 6 ê ê , k Î . B. 6 ê , k Î . ê p 2p ê p 2p êx = + k êx = - + k êë 18 3 êë 18 3 é 5p é p p ê 2 x = + k2p êx = + k C. ê 6 ê ê , k Î . D. 18 3 ê , k Î . ê 7p ê p 2p êx = + k2p êx = - + k êë 6 êë 18 3 Lời giải Chọn B æ ö æ ö Ta có p p cosççx ÷ + ÷ = -sin x ç ÷ ç
và sin çx - ÷= -cos x . è 2 ÷ø çè 2 ÷ø
Do đó phương trình - 3 sin x -cos x = 2 sin 2x 3 sin x + cos x = -2 sin 2x 3 1 æ pö æ pö
sin x + cos x = -sin 2x sin ççx ÷
+ ÷ = -sin 2x sin ç ç ÷ çx ÷ + ÷ = sin (-2x) 2 2 è 6 ø çè 6 ÷ø é p é p 2p
êx + = -2x + k2p êx = - + k ê 6 ê 18 3 ê ê (k Î ). ê p ê 5p
êx + = p + 2x + k2p êx = - -k2p êë 6 êë 6 Xét nghiệm 5p =- - p k k 7 1 ' x = -
-k2p ¾¾¾¾ x = + k '2p . kÎ, ' 6 k Î 6
Vậy phương trình có nghiệm p 2p 7p x = - + k , x =
+ k ' 2p (k k Î ) , ' . 18 3 6
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 79
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 6: Gọi x là nghiệm âm lớn nhất của sin 9x + 3 cos7x = sin 7x + 3 cos9x . Mệnh đề nào sau đây 0 là đúng? æ ö é ù é ö é ö A. p p p p p p p x Î ç- ç ;0÷÷.
B. x Î ê- ;- ú. C. x Î - ; ÷ ê - ÷. D. x Î - ; ÷ ê - ÷. 0 çè 12 ÷ø 0 ê 6 12 ú ë û 0 3 6 ÷ ê ø ë 0 2 3 ÷ ê ø ë Lời giải Chọn A
Phương trình sin 9x - 3 cos9x = sin 7x - 3 cos7x é p p
ê9x - = 7x - + k2p éx = kp æ pö æ pö ê 3 3 ê sin çç9x ÷ - ÷ = sin 7 ç ç ÷ ç x ÷ - ÷ ê ê 5p kp è 3 ø çè 3 ÷ø ê p æ pö êx = + ê9x - = p - 7 çç x ÷ - ÷+ k2p ê ê ç ÷ ë 48 8 3 è 3 ø ë
ékp < 0 k < 0 kÎ ¾¾¾ k = -1 x = p - max ê Cho x <0 ¾¾¾¾ ê p p
So sánh hai nghiệm ta được Î p . 5 k 5 ê + < 0 k k < - ¾¾¾ k = -1 x = - ê max ë 48 8 6 48 æ ö
nghiệm âm lớn nhất của phương trình là p p x = - Î ç- ç ;0÷÷. 48 çè 12 ÷ø
Câu 7: Biến đổi phương trình cos3x -sin x = 3(cos x -sin 3x) về dạng sin (ax +b) = sin (cx + d) với b , æ p pö d thuộc khoảng ç- ç ; ÷÷ ç
. Tính b+d . è 2 2 ÷ø A. p p p p b + d = .
B. b+d = .
C. b+d = - .
D. b+d = . 12 4 3 2 Lời giải Chọn D
Phương trình 3 sin 3x + cos3x = sin x + 3 cos x 3 1 1 3 æ pö æ pö
sin 3x + cos3x = sin x + cos x sin 3 çç x ÷ + ÷ = sin ççx ÷ + ÷. 2 2 2 2 çè 6 ÷ø çè 3 ÷ø Suy ra p p p b + d = + = . 6 3 2
Câu 8: Giải phương trình cos x - 3 sin x = 0. 1 sin x - 2 A. p p x = + k , . p k Î
B. x = + k2 , p k Î . 6 6 C. 7p p x = + k2 , p k Î . D. 7 x = + k , p k Î . 6 6 Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 80
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï p
ïx ¹ + k2p ï Điều kiện 1 1 p ï 6
sin x - ¹ 0 sin x ¹ sin x ¹ sin í (k Î ) . 2 2 6 ï 5p ïïx ¹ + k2p ïïî 6 sin 5p p 6 6 cos O Hình 1
Điều kiện bài toán tương đương với bỏ đi vị trí hai điểm trên đường tròn lượng giác (Hình 1).
Phương trình cos x - 3 sin x = 0 cos x = 3 sin x p p
cot x = 3 cot x = cot
x = + lp (l Î ) . 6 6 sin p 6 O cos Hình 2 Biểu diễn nghiệm p
x = + lp trên đường tròn lượng giác ta được 2 vị trí như Hình 2. 6
Đối chiếu điều kiện, ta loại nghiệm p
x = + k2p . Do đó phương trình có nghiệm 6 7p x = + 2lp ( l Î ). 6 Câu 9: Hàm số
2 sin 2x + cos 2x y =
có tất cả bao nhiêu giá trị nguyên?
sin 2x -cos 2x + 3 A. 1. B. 2. C. 3. D. 4. Lời giải Chọn B Ta có
2 sin 2x + cos 2x y =
(y -2)sin 2x -(y + ) 1 cos 2x = -3y.
sin 2x -cos 2x + 3
Điều kiện để phương trình có nghiệm (y - )2 +(y + )2 ³(- y)2 2 2 1 3
7 y + 2 y -5 £ 0
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 81
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 5 1 y y Î - £ £ ¾¾¾
y Î {-1;0} nên có 2 giá trị nguyên. 7
Câu 10: Gọi x là nghiệm dương nhỏ nhất của cos2x + 3 sin 2x + 3 sin x -cos x = 2. Mệnh đề nào 0 sau đây là đúng? æ ö é ù æ ù æ ù A. p p p p p p p x Î çç0; ÷÷.
B. x Î ê ; ú.
C. x Îçç ; ú.
D. x Îçç ; ú. 0 çè 12÷ø 0 ê12 6 ú ë û 0 çè6 3 úû 0 çè3 2 úû Lời giải Chọn B Phương trình 1 3 3 1 cos 2x + sin 2x +
sin x - cos x = 1 2 2 2 2 æp ö æ pö
sin çç +2x÷÷+sin ç ç ÷ çx ÷ - ÷ = 1 . è 6 ø çè 6 ÷ø Đặt p p p p p t = x - ¾¾
x = t + 2x = 2t + 2x + = 2t + . 6 6 3 6 2 æ ö Phương trình trở thành p sin çç2t ÷
+ ÷+ sin t = 1 cos2t + sin t = 1 ç è 2 ÷ø 2
2 sin t -sin t = 0 sin t (2 sin t - ) 1 = 0. p 1 Î p
sin = 0 = p ¾¾ = + p > 0 k t t k x k k > - ¾¾¾ k = 0 x = . min 6 6 6 é p p 1 Î p
êt = + k2p ¾¾
x = + k2p > 0 k k > - ¾¾¾ k = 0 x = . min 1 ê 6 3 6 3 sin t = ê 2 ê 5p 1 êt = + k2p ¾¾
x = p + k2p > 0 k k Î > - ¾¾¾ k = 0 x = . p min êë 6 2 é ù
Suy ra nghiệm dương nhỏ nhất của phương trình là p p p x = Î ê ; ú. 6 ê12 6 ú ë û
Câu 11: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10;10] để phương trình æ pö æ pö sin ççx ÷ - ÷- 3 cosç ç ÷ çx ÷
- ÷ = 2m vô nghiệm. è 3 ø çè 3 ÷ø A. 21. B. 20. C. 18. D. 9. Lời giải Chọn C ém < 1 -
Phương trình vô nghiệm 1 +(- 3)2 <(2m)2 2 2 4m -4 > 0 ê êm >1 ë mÎ ¾¾¾¾m Î { 1
- 0;-9;-8;...;-2;2;...;8;9;10} ¾¾
có 18 giá trị. m [ Î -10;10]
Câu 12: Tìm tất cả các giá trị thực của tham số m để phương trình x + x = ( 2 cos sin 2 m + ) 1 vô nghiệm.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 82
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. m Î(- ; ¥ - )
1 È(1;+¥). B. m Î[ 1; - ] 1 . C. m Î(- ; ¥ +¥) D. m Î (- ;0 ¥ )È(0;+¥). Lời giải Chọn D
Phương trình vô nghiệm é (m ) 2 2 2 2 1 1 2 1 ù + < + ê ë úû 4 2 2
m + m > m ( 2 m + ) 2 2 0
2 > 0 m > 0 m ¹ 0.
Câu 13: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10;10] để phương trình (m + )
1 sin x -m cos x = 1-m có nghiệm. A. 21. B. 20. C. 18. D. 11. Lời giải Chọn C ém ³ 0
Phương trình có nghiệm (m + )2 1 + m ³ (1-m)2 2 2
m + 4m ³ 0 ê êm £ 4 - ë mÎ ¾¾¾¾ m Î {-10; 9 - ; 8 - ;...; 4 - ;0;1;2;...;8;9;10} ¾¾
có 18 giá trị. m [ Î -10;10]
Câu 14: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2018] để phương trình (m + ) 2
1 sin x -sin 2x + cos 2x = 0 có nghiệm. A. 4037. B. 4036. C. 2019. D. 2020. Lời giải Chọn D
Phương trình ( + )1-cos2x m 1
-sin 2x + cos 2x = 0 2
-2 sin 2x +(1-m)cos 2x = m - -1.
Phương trình có nghiệm (- )2 +( -m)2 ³( m - - )2 2 1
1 4m £ 4 m £1 mÎ ¾¾¾¾¾ m Î { 2018 - ;-2017;...;0; } 1 ¾¾
có 2020 giá trị. m [ Î -2018;2018]
Dạng 3. Phương trình bậc hai đối với một hàm số lượng giác 1. Phương pháp
Phương trình bậc hai đối với phương trình lương giác là phương trình có một trong 4 dạng sau: 1. 2
asin x bsin x c 0 . Cách giải: t sinx, 1 t 1 2. 2
acos x bcosx c 0 . Cách giải: t cosx, 1 t 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 83
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 3. 2
atan x btan x c 0 . Cách giải: t tanx, x k ,k 2 4. 2
acot x bcot x c 0 . Cách giải: t cot x, x k , k
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Giải các phương trình sau a) 2
2sin x 5cosx 1 0 ; b) 2
tan x 1 3tan x 3 0 c) 2 2 tan x cot x 2 ; d) 2 cot 2x – 4cot2x 3 0 Hướng dẫn giải a) 2 2 2 2sin x 5cosx 1 0
2 1 cos x 5cosx 1 0 2
cos x 5cos x 3 0 1 cos x 1 2 2 cos x x k2,k 2 3 cos x 3
b) Điều kiện: cos x 0 x k 2 tan x 3 3 tan x 1 3 tan x 3 0 , k tan x 1 x k 4
a) Điều kiện: sin 2x 0 Đặt 2
t tan x , phương trình đã cho trở thành 1 2 2
t 2 0 t 2t 1 0 t 1 tan x 1 x k,k t 4 b) Điều kiện: sinx 0 1 k x arc cot 3 cot 2x 3 2 2 2
cot 2x – 4cot2x 3 0 , k cot 2x 1 k x 8 2
Ví dụ 2. Giải các phương trình sau a) 1 cos2x 9cosx 5 0 ; b)
3 3 tan x 3 3 0 2 cos x Hướng dẫn giải 1 a) cos x 2 2
cos2x 9cosx 5 0 2 cos x 9 cos x 4 0 2 x k2,k 3 cos x 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 84
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 b) Điều kiện: cosx 0 1 3 3 2
tan x 1 3 0 tan x 3 3 tan x 3 2 0 2 cos x tan x 1 x k 4 ,k tan x 3 2 x arctan 3 2 k
Ví dụ 3. Xác định m để phương trình
cosx 2mcosx 6m 9 0* có nghiệm x ; 2 2 Hướng dẫn giải
Đặt t cosx. Với x 0 t 1 2 2 Ta có 2
t 2m 6m 9 0 t 2m 3 hoặc t 3 1 (loại)
Phương trình (*) có nghiệm 3 x ; 0 2m 3 1 m 2. 2 2 2
Ví dụ 4. Xác định m để phương trình 2
2cos x m 2cosx m 0* có đúng hai nghiệm x 0; 2 Hướng dẫn giải Đặt
t cosx, t 1. với x 0; t 0; 1 2 t 10; 1 Ta có: 2
2t m 2 t m 0 m t 2
Để (*) có đúng hai nghiệm m x 0; thì 0;1 m 0;2 2 2
3. Bài tập trắc nghiệm é ö Câu 1: Hỏi trên p 0; ÷ ê ÷ , phương trình 2
2 sin x -3sin x +1 = 0 có bao nhiêu nghiệm? 2 ÷ ê ø ë A. 1. B. 2. C. 3. D. 4. Lời giải Chọn A é 1 ê Phương trình sin x = 2
2 sin x -3 sin x +1 = 0 ê 2 ê êsin x = 1 ë
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 85
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 é p
êx = + k2p ê 6 é p ê êsin x = sin ê 5p ê 6 êx = + k2p ( k Î ). ê ê 6 êsin x = 1 ë ê ê p
êx = + k2p êë 2 é p p é 1 1 Î p ê0 £ + k2 k p < ê- < k < ¾¾¾
k = 0 x = ê 6 2 ê 12 6 6 ê ê Theo giả thiết p ê 5p p ê 5 1 0 £ x < ê0 £ + k2 k p < - ê < k Î < - ¾¾¾ k Î Æ . 2 ê 6 2 ê 12 12 ê ê ê p p ê 1
ê0 £ + k2p < - ê < k < 0 kÎ ¾¾¾ k Î Æ êë 2 2 êë 4 é ö
Vậy phương trình có duy nhất một nghiệm trên p 0; ÷ ê ÷ . 2 ÷ ê ø ë
Câu 2: Số vị trí biểu diễn các nghiệm của phương trình 2
2 cos x + 5 cos x + 3 = 0 trên đường tròn lượng giác là? A. 1. B. 2. C. 3. D. 4. Lời giải Chọn A écos x = -1 ê Phương trình 2
2 cos x + 5cos x + 3 = 0 ê 3 êcos x = - (loaïi) êë 2
cos x = -1 x = p + k2p(k Î ).
Suy ra có duy nhất 1 vị trí biểu diễn nghiệm của phương trình trên đường tròn lượng giác.
Câu 3: Cho phương trình 2
cot 3x -3cot 3x + 2 = 0. Đặt t = cot 3x , ta được phương trình nào sau đây? A. 2
t -3t + 2 = 0. B. 2
3t -9t + 2 = 0. C. 2
t -9t + 2 = 0. D. 2
t -6t + 2 = 0. Lời giải Chọn A
Câu 4: Số nghiệm của phương trình 2
4 sin 2x -2(1+ 2)sin 2x + 2 = 0 trên (0;p) là? A. 3. B. 4. C. 2. D. 1. Lời giải Chọn B é 2 êsin 2x = ê Phương trình 2 x - ( + ) 2 4 sin 2 2 1 2 sin 2x + 2 = 0 ê . ê 1 êsin 2x = êë 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 86
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 é p é p (0;p) p
ê2x = + k2p
êx = + kp ¾¾¾ x = 2 p ê ê 4 8 8 sin 2x = = sin ê ê . 2 4 ê 3p ê 3p (0;p) 3p ê2x = + k2p êx = + kp ¾¾¾ x = êë 4 êë 8 8 é p é p (0;p) p
ê2x = + k2p êx = + kp ¾¾¾ x = 1 p ê ê 6 12 12 sin 2x = = sin ê ê . 2 6 ê 5p ê 5p (0;p) 5p ê2x = + k2p êx = + kp ¾¾¾ x = êë 6 êë 12 12
Vậy có tất cả 4 nghiệm thỏa mãn.
Câu 5: Số nghiệm của phương trình 2
sin 2x -cos 2x +1 = 0 trên đoạn [ p - ;4p] là? A. 2. B. 4. C. 6. D. 8. Lời giải Chọn C Phương trình 2 2
sin 2x -cos 2x +1 = 0 -cos 2x -cos 2x + 2 = 0 écos 2x = 1 ê
cos 2x = 1 2x = k2p x = k , p k Î . ê cos 2x = -2(loaïi) ë Do [ p;4p] p p 4p 1 4 k x k k Î Î - ¾¾ - £ £ - £ £ ¾¾¾
k Î {-1;0;1;2;3;4}.
Vậy phương trình có 6 nghiệm thỏa mãn. Câu 6: Tính tổng x x
T tất cả các nghiệm của phương trình 2 2 sin
-3cos = 0 trên đoạn [0;8p]. 4 4 A. T = 0. B. T = 8 . p C. T = 16 . p D. T = 4 . p Lời giải Chọn B æ ö Phương trình x x x x 2 2 2 sin -3cos = 0 2 1 çç -cos ÷÷-3cos = 0 4 4 çè 4 ÷ø 4 é x 1 êcos = x x ê 4 2 x 1 x p 2 -2 cos -3cos + 2 = 0 ê cos = cos = cos 4 4 ê x ê = - (loaïi) 4 2 4 3 cos 2 êë 4 é x p é 4p x [ Î 0;8p] 4p ê = + k2p êx = + k8p ¾¾¾¾ x = ê 4 3 ê 3 3 4p 20p ê ê T = + = 8 . p ê x p ê 4p x [ Î 0;8p] 20p 3 3 ê = - + k2p êx = - + k8p ¾¾¾¾ x = êë 4 3 êë 3 3
Câu 7: Số nghiệm của phương trình 1 - 3 -1 cot x - 3 +1 = 0 trên (0;p) là? 2 ( ) ( ) sin x A. 1. B. 2. C. 3. D. 4. Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 87
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Điều kiện: sin x ¹ 0 x ¹ kp (k Î ) . Phương trình ( 2 + x )-( - ) x -( + ) 2 1 cot 3 1 cot
3 1 = 0 cot x -( 3 - ) 1 cot x - 3 = 0 é æ pö é p x ê = ç ÷ ( Î 0;p) 3p cot x cot - é ç ÷
êx = - + kp ¾¾¾ x = (thoûa maõn) cot x = 1 - ê çè 4÷ø ê 4 4 ê ê ê . ê êcot x = 3 ê p ê p x ( Î 0;p) p ë êcot x = cot
êx = + kp ¾¾¾ x = (thoûa maõn) êë 6 êë 6 6
Vậy phương trình đã cho có 2 nghiệm thỏa mãn.
Câu 8: Tính tổng T tất cả các nghiệm của phương trình 2 cos2x +2 cos x - 2 = 0 trên đoạn [0;3p] . A. 17p T = . B. T = 2 . p C. T = 4 . p D. T = 6 . p 4 Lời giải Chọn A Phương trình x + x - = ( 2 2 cos 2 2 cos 2 0 2 2 cos x - ) 1 + 2 cos x - 2 = 0 é 2 êcos x = ê 2 2 2
4 cos x + 2 cos x -2 - 2 = 0 ê cos x = ê 2 +1 2 êcos x = - (loaïi) êë 2 é p x [ Î 0;3p] p 9p
êx = + k2p ¾¾¾¾ x = ; x = ê 4 4 4 p 9p 7p 17p ê ¾¾ T = + + = . ê p x [ Î 0;3p] 7p 4 4 4 4
êx = - + k2p ¾¾¾¾ x = êë 4 4
Câu 9: Số vị trí biểu diễn các nghiệm của phương trình cos2x +3sin x + 4 = 0 trên đường tròn lượng giác là? A. 1. B. 2. C. 3. D. 4. Lời giải Chọn A Phương trình ( 2 - x ) 2 1 2 sin
+ 3sin x + 4 = 0 -2 sin x +3sin x + 5 = 0 ésin x = -1 ê p ê 5
sin x = -1 x = - + k2p (k Î ) . êsin x = (loaïi) 2 êë 2
Suy ra có duy nhất 1 vị trí đường tròn lượng giác biểu diễn nghiệm.
Câu 10: Cho phương trình x x
cos x + cos +1 = 0 . Nếu đặt t = cos , ta được phương trình nào sau đây? 2 2 A. 2 2t + t = 0. B. 2 -2t + t +1 = 0. C. 2 2t + t -1 = 0. D. 2 -2t + t = 0. Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 88
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Ta có x 2 cos x = 2 cos -1. 2 æ ö Do đó phương trình x x x x 2 2 çç2 cos -1÷÷+ cos +1 = 0 2 cos + cos = 0. ç è 2 ÷ø 2 2 2 Đặt x
t = cos , phương trình trở thành 2
2t + t = 0. 2 æ ö æ ö
Câu 11: Số nghiệm của phương trình p p 5 cos 2ççx ÷ + ÷+ 4 cosç ç ÷
ç - x÷÷ = thuộc [0;2p] là? è 3 ø çè6 ÷ø 2 A. 1. B. 2. C. 3. D. 4. Lời giải Chọn B æ ö æ ö æ ö Ta có p p p 2 2 cos 2ççx ÷ + ÷ = 1-2 sin ç ç ÷ çx ÷ + ÷ = 1-2 cos ç . è ø ç ÷ ç - x÷÷ 3 è 3 ø çè6 ÷ø æ ö æ ö Do đó phương trình p p 3 2
-2 cos çç - x÷÷+ 4 cosç ç ÷ ç - x÷÷- = 0 è 6 ø çè6 ÷ø 2 é æp ö 1 é êcosçç - x÷ p ÷ = ê ê ç ÷
x = - + k2p è 6 ø 2 æp ö 1 p p ê ê ç ÷ 6
cosç - x÷ = - x = + k2p ê , k Î ê . æp ö 3 ç ÷ è ø ê p êcosç ê ç - x÷÷ = (loaïi) 6 2 6 3
êx = + k2p çè6 ÷ø 2 êë 2 ë Ta có p x [0;2p] 11p p p x k2p Î = - + ¾¾¾¾ x = ; x [0;2p] x k2p Î = + ¾¾¾¾ x = . 6 6 2 2
Vậy có hai nghiệm thỏa mãn.
Câu 12: Tìm tất cả các giá trị thực của tham số m để phương trình tan x + m cot x = 8 có nghiệm.
A. m >16. B. m <16. C. m ³16. D. m £16. Lời giải Chọn D Phương trình m 2
tan x + m cot x = 8 tan x +
= 8 tan x -8 tan x + m = 0 . tan x
Để phương trình đã cho có nghiệm khi và chỉ khi D¢ = (- )2
4 -m ³ 0 m £16 .
Câu 13: Tìm tất cả các giá trị thực của tham số m để phương trình cos2x -(2m + )
1 cos x + m +1 = 0 æ ö
có nghiệm trên khoảng p 3p çç ; ÷÷ ç . è 2 2 ÷ø
A. -1£ m £ 0 .
B. -1£ m < 0 .
C. -1< m < 0 . D. 1 1 - £ m < . 2 Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 89
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 é 1 ê Phương trình cos x = 2
2 cos x -(2m + )
1 cos x + m = 0 ê 2 . ê êcos x = m ë sin cos O 1 m 2 æ ö Nhận thấy phương trình 1 p p
cos x = không có nghiệm trên khoảng 3
çç ; ÷÷ (Hình vẽ). Do đó 2 çè2 2 ÷ø æ ö yêu cầu bài toán p p
cos x = m có nghiệm thuộc khoảng 3
çç ; ÷÷ -1£ m < 0 ç . è 2 2 ÷ø
Câu 14: Biết rằng khi m = m thì phương trình 2 x -( m + ) 2 2 sin 5
1 sin x + 2m + 2m = 0 có đúng 5 0 æ ö
nghiệm phân biệt thuộc khoảng p ç- ç ;3p÷÷ ç
. Mệnh đề nào sau đây là đúng? è 2 ÷ø æ ù æ ö A. 3 7 3 2 m = -3. B. 1 m = .
C. m Îçç ; ú. D. m Îç- ç ; ÷ - ÷. 2 0 çè5 10úû 0 çè 5 5÷ø Lời giải Chọn D
Đặt t = sin x ( 1 - £ t £ ) 1 .
Phương trình trở thành 2t -( m + ) 2 2 5
1 t + 2m + 2m = 0. ( ) * sin sin t2 cos cos O O t2 Hình 1 Hình 2
Yêu cầu bài toán tương đương với:
TH1: Phương trình ( )
* có một nghiệm t = -1 (có một nghiệm x ) và một nghiệm 1
0 < t <1 (có bốn nghiệm x ) (Hình 1). 2 c Do 2 t = -1 ¾¾ t = - = m - -m . 1 2 a
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 90
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ém = -3 ¾¾ t = -6 Ï 0;1 loaïi 2 ( )( ) ê
Thay t = -1 vào phương trình ( ) * , ta được ê . 1 1 1 êm = - ¾¾ t = Î 0;1 ê thoûa 2 ( )( ) ë 2 4
TH2: Phương trình ( )
* có một nghiệm t = 1 (có hai nghiệm x ) và một nghiệm 1
-1 < t £ 0 (có ba nghiệm x ) (Hình 2). 2 c Do 2 t = 1 ¾¾
t = = m + m . 1 2 a ém =1 ¾¾ t = 2 Ï -1;0 loaïi 2 ( ]( ) ê
Thay t = 1 vào phương trình ( ) * , ta được ê . 1 1 3 êm = ¾¾ t = Ï -1;0 ê loaïi 2 ( ]( ) ë 2 4 æ ö Vậy 1
m = - thỏa mãn yêu cầu bài toán. Do 1 3 2 m = - Î ç- ç ; ÷ - ÷. 2 2 çè 5 5÷ø
Câu 15: Tìm tất cả các giá trị thực của tham số m để phương trình æ p pö 2
2 cos 3x +(3-2m)cos3x + m -2 = 0 có đúng 3 nghiệm thuộc khoảng ç- ç ; ÷÷. ç è 6 3 ÷ø A. -1£ m £1.
B. 1< m £ 2. C. 1£ m £ 2.
D. 1£ m < 2. Lời giải Chọn B
Đặt t = cos x ( 1 - £ t £ )
1 . Phương trình trở thành 2
2t +(3-2m)t + m -2 = 0. é 1 ê Ta có t = D = ( m - )2 2
5 . Suy ra phương trình có hai nghiệm 1 ê 2 . ê êt = m -2 ë 2 sin cos O t 1 2 t = 1 2 æ ö
Ta thấy ứng với một nghiệm 1 p p
t = thì cho ta hai nghiệm x thuộc khoảng ç- ç ; ÷÷. Do đó 1 2 çè 6 3÷ø
yêu cầu bài toán -1< t £ 0 -1< m -2 £ 0 1< m £ 2. 2
Cách 2. Yêu cầu bài toán tương đươn với phương trình 2
2t +(3-2m)t + m -2 = 0 có hai ìïP £ 0 ïï
nghiệm t , t thỏa mãn 1 t 0 t 1 ï - < £ < < í . a f 1 > 0 . 2 1 ( ) 1 2 ïïïï .af (- )1>0 î
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 91
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Dạng 4. Phương trình bậc hai đối với sin x và cos x 1. Phương pháp Cách 1:
Kiểm tra cosx = 0 có thoả mãn hay không? Lưu ý: cosx = 0 2
x k sin x 1 sin x 1. 2 Khi
cosx 0 , chia hai vế phương trình (1) cho 2 cos x 0 ta được: 2 2
a.tan x b.tan x c d(1 tan x)
Đặt: t = tanx, đưa về phương trình bậc hai theo t: 2
(a d)t b.t c d 0
Cách 2: Dùng công thức hạ bậc 1 cos2x sin2x 1 cos2x (1) a. b. c. d 2 2 2
b.sin2x (c a).cos2x 2d a c
(đây là phương trình bậc nhất đối với sin2x và cos2x)
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Giải phương trình 2 sin x 2 x 3sinxcos 4cos x 0*. Giải cosx 0 Khi x k , k 2 2 sin x 1
Ta có VT * 1 VP * không có nghiệm trên 2 cos x 0 Chia hai vế của (*) cho 2 cos x, ta được: 2 tan x 3tanx 4 0 tan x 1 tan x k 4 4 , k tanx 4 x arctan 4 k
Vậy nghiệm của (*) là x k ;
x arctan4 k , k 4
Ví dụ 2. Giải phương trình 2 2
2sin x 3 3 sin xcosx cos x 2* Giải cosx 0 Khi x k , k 2 2 sin x 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 92
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ta có: VT * 2 VP* * có nghiệm x k , k 2 Khi 2 x k ,
k : cos x 0 , chia hai vế của (*) cho 2 cos x 2 1 tanx tan x k , k 3 6 6
Vậy nghiệm của phương trình (*) là x k ,
k ; x k,k . 2 6
Ví dụ 3. Giải phương trình 3 cos 2x 3 x 2sinxcos 3sin x 0*. Giải cox 0 Khi x k , k 2 2 sin x 1 Ta có: VT* 3
VP* không có nghiệm x k , k 3 cos x 0 2 Chia hai vế của (*) cho 3 cos x , ta được: 3
1 2 tanx 3tan x 0 tan x 1 2 3tan x 3tanx 1 0 0
tanx 1 tan x k , k 4 4
Vậy nghiệm của phương trình (*) là x k , k 4
Ví dụ 4. Giải phương trình 3 c s o 2
x sinx 3sin xcosx 0*. Giải cox 0 Khi x k , k 2 2 sin x 1 Ta có: VT * 1
VP * không có nghiệm trên 3 cos x 0 Chia hai vế của (*) cho 3
cos x , ta được tan x 2 1 tan 2 1 x 3tan x 0 3 2 tan 2 x 2tan x tan 1 0 tanx 1 tan x 2tanx 1 0 x tan x 1 0 tan x 1 4 2 tan x 2tanx 1 0 tan x 1 2
x arctan1 2 k
Vậy nghiệm của (*) là x ;x arctan 1 2 k ,k 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 93
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ví dụ 5. Xác định a để 2 2
asin x 2sin2x 3acos x 2* có nghiệm. Giải 1 cos2x 1 cos2x * a 2sin2x 3a 2 2 2
2sin 2x a cos2x 2 2a 1 (*) có nghiệm 1 có nghiệm 2 2
2 a 2 2a2 2 2 2 8
4 a 4 8a 4a 3a 8a 0 0 a 3 Vậy với 8 0 a
thì phương trình đã cho có nhiệm. 3
Ví dụ 6. Cho phương trình: 3 sin 2m 2 1 sin 3m 3 x xcosx 1 sin xcos x 0* .
Xác định m để phương trình có ba nghiệm phân biệt x ;0. 2 Giải cox 0 Khi x k , k 2 2 sin x 1 Ta có: VT * 1
VP * không có nghiệm trên 3 cos x 0 Chia hai vế của (*) cho 3 cos x , ta được: 3 x 2 tan 2m 1 tan x 3m 1 tanx m 1 0 Đặt
t tanx. với x ;0 t ;0 2 Ta có: 3 2 t 2m 1 t 3m 1 t m 1 0 t 1 t 1 2 t 2mt m 1 0 f t 2
t 2mt m 1 0 1
Để (*) có ba nghiệm phân biệt x ;0
khi và chỉ khi (1) có hai nghiệm phân biệt 2 2 0 m m 1 0, m t t 0 P 0 1 2 m-1 0 t , t : m 1 1 2 t , t 1 S 0 1 2 m 0 f 1 0 1 2m m 1 0
Vậy m 1 thỏa mãn đề bài.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 94
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
3. Bài tập trắc nghiệm
Câu 1: Giải phương trình 2 x -( + ) 2 sin
3 1 sin x cos x + 3 cos x = 0. A. p p x = + k2p (
k Î ). B. x = + kp (k Î ). 3 4 é p é p
êx = + k2p êx = + kp C. ê 3 ê ê (k Î ). D. 3 ê (k Î ). ê p ê p
êx = + k2p êx = + kp êë 4 êë 4 Lời giải Chọn D étan x = 1 Phương trình 2 tan x -( 3 + ) 1 tan x + 3 0 = êê êtan x = 3 ë é p êx = + kp ê 4 ê (k Î ). ê p êx = + kp êë 3
Câu 2: Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình 2
sin x + 3 sin x cos x = 1 ? æ ö é æ ö ù A. p p x ( 2 cos cot x -3) = 0 . B. sin ççx ÷ + ÷. êtan ç ç ÷ çx ÷ + ÷-2 - 3ú = 0 . è 2 ø ê çè 4 ÷ø ú ë û é æ ö ù C. p 2 êcos ççx ÷ + ÷-1ú. . D. (sin x - ) 1 (cot x - 3) = . ê ç ÷ (tan x - 3)= 0 0 è 2 ø ú ë û Lời giải Chọn B Phương trình 2 2 2
sin x + 3 sin x cos x = sin x + cos x 2
3 sin x cos x -cos x = 0 cos x ( 3 sin x -cos x) = 0. æ pö
cos x = 0 sin ççx ÷ + ÷ = 0. ç è 2 ÷ø 1
3 sin x -cos x = 0 tan x = . 3 p 1 tan x + tan +1 æ ö æ ö Ta có p ç ÷ 4 3 p tan çx + ÷ = = = 2 + 3 tan ç ç ÷ çx ÷ + ÷-2 - 3 = 0. è 4 ø p 1 çè 4 ÷ø 1- tan x. tan 1- .1 4 3 æ ö é æ ö ù
Vậy phương trình đã cho tương đương với p p sin ççx ÷ + ÷. êtan ç ç ÷ çx ÷ + ÷-2 - 3ú = 0 . è 2 ø ê çè 4 ÷ø ú ë û
Câu 3: Cho phương trình 2
cos x -3 sin x cos x +1 = 0 . Mệnh đề nào sau đây là sai?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 95
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
A. x = kp không là nghiệm của phương trình.
B. Nếu chia hai vế của phương trình cho 2
cos x thì ta được phương trình 2
tan x -3 tan x + 2 = 0 .
C. Nếu chia 2 vế của phương trình cho 2
sin x thì ta được phương trình 2
2 cot x + 3 cot x +1 = 0 .
D. Phương trình đã cho tương đương với cos2x -3sin 2x +3 = 0 . Lời giải Chọn C sin ìï x = 0 sin ìï x = 0 Với x kp ï ï = ¾¾ í í
. Thay vào phương trình ta thấy thỏa mãn. Vậy 2 co ï s x = 1 ï co ï s x =1 î ïî
A đúng. ( vì thay x = k không thỏa mãn pt) Phương trình 2 2 2
cos x -3sin x cos x + sin x + cos x = 0 2 2 2
sin x -3sin x cos x + 2 cos x = 0 tan x -3 tan x + 2 = 0 . Vậy B đúng. Phương trình 2 2 2
cos x -3sin x cos x + sin x + cos x = 0 2 2 2
2 cos x -3sin x cos x + sin x = 0 2 cot x -3cot x +1 = 0 . Vậy C sai. + x x Phương trình 1 cos 2 sin 2 -3
+1 = 0 cos 2x -3sin 2x + 3 = 0. Vậy D đúng. 2 2
Câu 4: Số vị trí biểu diễn các nghiệm phương trình 2 2
sin x - 4 sin x cos x + 4 cos x = 5 trên đường tròn lượng giác là? A. 4 . B. 3 . C. 2 . D. 1. Lời giải Chọn C Phương trình 2 2 x - x x + x = ( 2 2 sin 4 sin cos 4 cos
5 sin x + cos x) - x - x x - x = ( x + x)2 2 2 4 sin 4 sin cos cos 0 2 sin cos
= 0 2 sin x + cos x = 0 1 tan x = - ¾¾
có 2 vị trí biểu diễn nghiệm trên đường tròn lượng gác. 2
Câu 5: Số nghiệm của phương trình 2 2
cos x -3 sin x cos x + 2 sin x = 0 trên ( 2 - p;2p) ? A. 2 . B. 4 . C. 6 . D. 8 . Lời giải Chọn D é p étan x = 1 êx = + kp ê Phương trình ê 2 4
1-3 tan x + 2 tan x = 0 ê 1 ê . êtan x = ê 1 êë 2
êx = arctan + kp êë 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 96
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 p 9 7 Vì ( 2p;2p) 2p p 2 k x k p k Î Î - ¾¾ - < + < - < < ¾¾¾ k Î {-2;-1;0; } 1 . 4 4 4
Vì x Î(- p p) 1 2 ;2 ¾¾
-2p < arctan + kp < 2p 2 CASIO 28, 565 24,565 k k Î ¾¾¾- < < - ¾¾¾ k Î {-28; 2 - 7;-26;-2 } 5 . xapxi
Vậy có tất cả 8 nghiệm.
Câu 6: Nghiệm dương nhỏ nhất của phương trình 2 2
4 sin x + 3 3 sin 2x -2 cos x = 4 là: A. p . B. p . C. p . D. p . 12 6 4 3 Lời giải Chọn B Phương trình 2 2 x + x - x = ( 2 2 4 sin 3 3 sin 2 2 cos
4 sin x + cos x) écos x = 0 ê 2
3 3 sin 2x -6 cos x = 0 6 cos x ( 3 sin x -cos x)= 0 ê 1 êtan x = êë 3 é p ép 1 Î p êx = + kp ê + kp > 0 k k > - ¾¾¾ k = 0 x = min ê 2 ê Cho>0 2 2 2 ê ¾¾¾ ê . ê p êp 1 Î p êx = + kp ê + kp > 0 k k > - ¾¾¾ k = 0 x = min êë 6 êë 6 6 6
So sánh hai nghiệm ta được p x =
là nghiệm dương nhỏ nhất. 6
Câu 7: Cho phương trình ( - ) 2 x + x +( + ) 2 2 1 sin sin 2
2 1 cos x - 2 = 0 . Trong các mệnh đề sau, mệnh đề nào sai? A. 7p x =
là một nghiệm của phương trình. 8
B. Nếu chia hai vế của phương trình cho 2
cos x thì ta được phương trình 2
tan x -2 tan x -1 = 0 .
C. Nếu chia hai vế của phương trình cho 2
sin x thì ta được phương trình 2
cot x + 2 cot x -1 = 0 .
D. Phương trình đã cho tương đương với cos2x -sin 2x =1. Lời giải Chọn D
Câu 8: Nghiệm âm lớn nhất của phương trình là 2 x +( - ) x x +( - ) 2 2 sin 1 3 sin cos 1 3 cos x = 1. A. p p p p - . B. - . C. 2 - . D. - . 6 4 3 12 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 97
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn B Phương trình 2 x +( - ) x x +( - ) 2 2 2 2 sin 1 3 sin cos 1
3 cos x = sin x + cos x 2 x +( - ) 2 sin 1
3 sin x cos x - 3 cos x = 0 é p étan = -1 êx = - + k x p ê 2 tan x +(1- 3) 4 tan x - 3 = 0 ê ê ê êtan x = 3 ê p ë êx = + kp êë 3 é p 1 Î p ê- + kp < 0 k k < ¾¾¾ k = 0 x = - max ê Cho x <0 4 4 4 ¾¾¾¾ ê . êp 1 Î p k 2
ê + kp < 0 k < - ¾¾¾ k = 1 - x = - max êë 3 3 3
So sánh hai nghiệm ta được p
x = - là nghiệm âm lớn nhất. 4
Câu 9: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10;10] để phương trình 2 x +(m - ) 2 11sin
2 sin 2x + 3 cos x = 2 có nghiệm? A. 16. B. 21. C. 15. D. 6. Lời giải Chọn A Phương trình 2 x +(m - ) 2 9 sin
2 sin 2x + cos x = 0 1-cos 2x ( + + m - ) 1 cos 2x 9. 2 sin 2x +
= 0 (m -2)sin 2x -4 cos 2x = 5 - . 2 2 ém ³
Phương trình có nghiệm (m - )2 + ³ (m - )2 5 2 16 25 2 ³ 9 ê êm £ 1 - ë mÎ ¾¾¾¾ m Î { 1 - 0; 9 - ;...;-1;5;6;...;10} ¾¾
có 16 giá trị nguyên. m [ Î -10;10]
Câu 10: Có bao nhiêu giá trị nguyên của tham số m thuộc để phương trình 2 x - (m - ) x x -(m - ) 2 sin 2 1 sin cos
1 cos x = m có nghiệm? A. 2. B. 1. C. 0. D. Vô số. Lời giải Chọn A
Phương trình ( -m) 2 x - (m - ) x x -( m - ) 2 1 sin 2 1 sin cos 2 1 cos x = 0 ( - +
-m) 1 cos 2x -(m - )
x -( m - ) 1 cos 2x 1 . 1 sin 2 2 1 . = 0 2 2 2(m - )
1 sin 2x + m cos 2x = 2 -3m.
Phương trình có nghiệm (m - )2 +m ³( - m)2 2 2 4 1 2 3
4m - 4m £ 0 0 £ m £1 mÎ ¾¾¾ m Î {0; } 1 ¾¾
có 2 giá trị nguyên.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 98
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 11: Tìm điều kiện để phương trình 2 2
a sin x + a sin x cos x + bcos x = 0 với a ¹ 0 có nghiệm. A. b b a ³ 4b .
B. a £-4b . C. 4 £1 . D. 4 £1. a a Lời giải Chọn C Phương trình 2
a tan x + a tan x + b = 0 . Phương trình có nghiệm 2
D = a - 4ab ³ 0 a(a-4b)³ 0 ( - b-a) 4b a 4b a 4 £ 0 £ 0 £1. a a
Câu 12: Tìm tất cả các giá trị của tham số m để phương trình 2
2 sin x + m sin 2x = 2m vô nghiệm. A. 4 0 £ m £ . B. m < 0 , 4 m > . C. 4 0 < m < . D. 4 m < - , 3 3 3 3 m > 0 . Lời giải Chọn B Phương trình 1-cos 2x 2.
+ m sin 2x = 2m m sin 2x -cos 2x = 2m -1. 2 ém < 0 ê
Phương trình vô nghiệm m +1<(2m - )2 2 2
1 3m - 4m > 0 ê 4 . êm > êë 3
Câu 13: Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3;3] để phương trình ( 2 m + ) 2
2 cos x -2m sin 2x +1 = 0 có nghiệm. A. 3 . B. 7 . C. 6 . D. 4 . Lời giải Chọn C Phương trình ( 1+ cos 2x 2 m + 2).
-2m sin 2x +1 = 0 2 m x -( 2 m + ) 2 4 sin 2
2 cos 2x = m + 4 .
Phương trình có nghiệm m +(m + )2 ³(m + )2 2 2 2 2 2 16 2
4 12m ³12 m ³1 m ³1 mÎ ¾¾¾ ¾ m Î { 3; - 2 - ; 1 - ;1;2; } 3 ¾¾
có 6 giá trị nguyên. m [ Î -3;3]
Dạng 5. Phương trình chứa sin x cos x và sin x cos x. 1. Phương pháp
Bài toán 1: a.(sinx cosx) + b.sinx.cosx + c = 0
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 99
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Đặt: t cosx sin x 2.cosx ; t 2. 4 1 2 2
t 1 2sin x.cosx sin x.cosx (t 1). 2
Thay vào phương trình đã cho, ta được phương trình bậc hai theo t. Giải phương trình này
tìm t thỏa t 2. Suy ra x. Lưu ý dấu
cosx sin x 2 cosx 2 sin x 4 4
cosx sin x 2 cosx 2 sinx 4 4
Bài toán 2: a.|sinx cosx| + b.sinx.cosx + c = 0
Đặt: t cosx sin x 2. cos x ; Ñk : 0 t 2. 4 1 sin x.cosx 2 (t 1). 2
Tương tự dạng trên. Khi tìm x cần lưu ý phương trình chứa dấu giá trị tuyệt đối.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Giải các phương trình
a) sinx cosx 2sinxcosx 1 0 1
b) 6sinx cosx sinxcosx 6 02 Giải a) Đặt t sinx cosx 2 x , t 2 4 2
Phương trình (1) trờ thành: t 1 2 t 2
1 0 t t 2 0 2 t 1 2 sin x 1 t 2 2 4 1 sin x 1 sin 4 2 4 x k2 x k2 4 4 , k 3 x k2 x k2 2 4 4
Vậy nghiệm của phương trình (1) là x k2;x k2,k . 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 100
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 b) Đặt
t sin x cos x 2 sin x , t 2 4 2
Phương trình (2) trờ thành: 1 t 2 6t
6 0 t 12t 13 0 2 t 1 2 sin x t 1 3 2 4 1 sin x sin 4 2 4 x k2 x k2 4 4 2 , k 3 x k2 x k2 4 4
Vậy nghiệm của phương trình (2) là x k2;x k2,k . 2
Ví dụ 2. Giải phương trình: sin2x 2 2 sinx cosx 5 . Giải Đặt 2 sinx cosx t t 2 sin2x t 1. 2
PT t 2 2t 6 0 t 2 (thỏa mãn) Giải phương trình π 5π
sinx cosx 2 cosx 1 x k2π k . 4 4 5
Vậy nghiệm của phương trình là π x k2π k. 4
Ví dụ 3. Giải phương trình 3 3
sin x cos x 2sinx cosx 1 *
Định hướng: Ta sử dụng hằng đẳng thức 3 3
sin x cos x isnx cosx1 sinxcosx Giải Ta có:
* sinx cosx1 sinxcosx 2sinx cosx 1 1 Đặt
t sin x cos x 2 sin x , t 2 4 2
Phương trình (1) trở thành: t 1 t 1 2t 1 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 101
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 t 2 3 t 3
4t 2 t t 2 0 t 1 2
t t 2 0 t 1 2
do t t 2 0,t x k2 1 sin x sin , k 4 2 4 x k2 2
Vậy nghiệm của phương trình đã cho là x k2 ;x k2 , k . 2
Ví dụ 4. Giải phương trình: 2
cos3x 3cosx 4cos x 8sinx 8 0 .
Định hướng: Ta sử dụng công thức nhân 3 cho cos3x để triệt tiêu phần 3cosx phía liền kề sau đó.
Như vậy, phương trình viết thành: 3 2
4cos x 4cos x 8sin x 8 0 , nhóm các cụm 3 2 2
4cos x 4cos x 4cos xcosx
1 , 8sin x 8 81 sinx. Sử dụng hằng đẳng thức 2 2
cos x 1 sin x 1 sinx1 sinx . Đưa phương trình đã cho về phương trình tích với nhân tử chung là 1 sinx . Giải Ta có: 3 2
PT 4cos x 3cosx 3cosx 4cos x 8sinx 8 0 2 cos xcosx 1 21 sinx
1 sinx1 sinxcosx 1 21 sinx π sinx 1 x k2π 2 1 sinx cosx 1 2
sin x cosx sin x.cosx 1 * Đặt 2 t 1 sin x cosx t t 2 sin x.cosx . 2 2 * t 1 trở thành 2 t 1 t
1 t 2t 3 0 2 t 3 (loaïi) kπ
t 1 sin2x 0 x . 2 k
Vậy phương trình đã cho có một họ nghiệm là: π x (k ). 2
Ví dụ 5. Giải phương trình : 3 2 2cos x sinx 1 2sin x*
Định hướng : Biến đổi 2 2
sin x 1 cos x , chuyển vế phương trình ta được 3 x 2 2 cos
2cos x sinx 1 0 , đến đây hoàn toàn tương tự ví dụ 4. Giải Ta có :
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 102
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 3 x 2 2 x 1 0 3 2 cos x 2 * 2 cos 1 cos sinx 2cos x sinx 1 0 2 2 cos xcosx 1 1 sinx 0
21 sinx1 sinxcosx 1 1 sinx 0
1 sinx21 sinxcosx 1 1 0
1 sinx2sinx
cosx 2sin x cosx 1 0 1 sinx 0 1 2sinx
cosx 2sin x cosx 1 0 2
Ta có : 1 x k2 , k 2 Giải (2), ta đặt t sinx c osx= 2 sin x , t 2 4 (2) trở thành : 2 2t t
1 1 0 t t 2 0 t 0 2 sin x 0 x k , k 4 4
Vậy nghiệm của phương trình (*) là x k2 , x k , k 2 4
Ví dụ 6. Cho sin2x 2m 2sinx cosx 2m 2 1 0*. Xác định m để phương trình (*) có đúng hai nghiệm 5 x 0; 4 Giải Đặt
t sin x cos x 2 sin x 4 Với 5 3 0 x x 4 4 4 2
Phương trình (*) trờ thành 2
t 1 2m 2 t 2m 2 1 0 2
t 2m 2t 2m 2 0 t 2 hoặc t 2m Với t 2 sin x
1 x k2 x k2 , k 4 4 2 4 5 1 1 Mà 5 0 k2 k 0 x 4 4 8 2 k 0 4 k k
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 103
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Do đó x là một nghiệm của (*) 4
Để (*) có đúng hai nghiệm 5 x 0; khi 2 1 sin x 4 4 2 2 1 2 2m 1 m 2 2
3. Bài tập trắc nghiệm
Câu 1: Giải phương trình sin x cos x + 2(sin x + cos x)= 2 . é p é p ê ê
A. x = + kp x = + k p ê 2 , k Î . B. 2 ê 2 , k Î . ê ê êx = kp ë êx = k2p ë é p é p ê ê
C. x = - + k2p x = - + kp ê 2 , k Î . D. ê 2 , k Î . ê ê êx = k2p ë êx = kp ë Lời giải Chọn B æ ö æ ö Đặt p p
t = sin x + cos x = 2 sin ççx ÷ + ÷ ç ÷ é ù ç . Vì sin çx + ÷Î[ 1 - ] ;1 t Î - 2; 2 . è 4 ÷ø çè 4 ÷ ê ø ë úû 2 Ta có = ( t - t sin x + cos x)2 1 2 2 2
= sin x + cos x + 2 sin x cos x sin x cos x = . 2 2 t -1 ét = 1
Khi đó, phương trình đã cho trở thành 2
+ 2t = 2 t + 4t -5 = 0 ê . 2 êt = -5( ) ë loaïi æ ö æ ö Với p p p t = 1 , ta được 1
sin x + cos x = 1 sin ççx ÷ + ÷ = sin ç ç ÷ çx ÷ + ÷ = sin . è 4 ø 2 çè 4 ÷ø 4 é p p
êx + = + k2p éx = k2p ê 4 4 ê ê ê p , k Î . ê p p
êx = + k2p
êx + = p - + k2p ê ê ë 2 ë 4 4
Câu 2: Cho phương trình 3 2 (sin x +cos x)+2 sin 2x + 4 = 0 . Đặt t = sin x +cos x , ta được phương trình nào dưới đây? A. 2
2t + 3 2 t + 2 = 0. B. 2
4t + 3 2 t + 4 = 0. C. 2
2t + 3 2 t -2 = 0. D. 2
4t + 3 2 t - 4 = 0. Lời giải Chọn A Đặt 2
t = sin x + cos x ¾¾
sin 2x = t -1.
Phương trình đã cho trở thành t + ( 2 t - ) 2 3 2 2
1 + 4 = 0 2t + 3 2 t + 2 = 0.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 104
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 3: Nghiệm âm lớn nhất của phương trình 1
sin x + cos x = 1- sin 2x là: 2 A. p p - . B. - . p C. 3 - . D. -2 . p 2 2 Lời giải Chọn C æ ö Đặt p
t = sin x + cos x = 2 sin ççx ÷ + ÷ ç
. Điều kiện - 2 £ t £ 2. è 4 ÷ø Ta có t = ( x + x)2 2 2 2 2 sin cos
= sin x + cos x + 2 sin x cos x sin 2x = t -1. 2 t -1 ét = 1
Phương trình đã cho trở thành 2 t = 1-
t + 2t -3 = 0 ê . 2 êt = -3( ) ë loaïi æ ö æ ö æ ö Với p p p p t = 1 , ta được 1 2 sin ççx ÷ + ÷ = 1 sin ç ç ÷ çx ÷ + ÷ = sin ç è ø ç ÷ çx ÷ + ÷ = sin 4 è 4 ø 2 çè 4 ÷ø 4 é p p
êx + = + k2p éx = k2p ê 4 4 ê ê ê p , k Î . ê p p
êx = + k2p
êx + = p - + k2p êë 2 êë 4 4 TH1. Với 2p 0 0 k x k k Î = < < ¾¾¾ k = 1 - x = -2 . p max TH2. Với p 1 Î p k 3
x = + k2p < 0 k < - ¾¾¾ k = 1 - x = - . max 2 4 2
Vậy nghiệm âm lớn nhất của phương trình là 3p x = - . 2
Câu 4: Từ phương trình (1+ 3)(cos x +sin x)-2sin x cos x - 3 -1= 0 , nếu ta đặt t = cos x +sin x thì
giá trị của t nhận được là:
A. t =1 hoặc t = 2 .
B. t =1 hoặc t = 3 . C. t =1 . D. t = 3 . Lời giải Chọn C Đặt - = x - x (- £ t £ ) 2 1 t t sin cos 2 2 ¾¾ sin x cos x = . 2
Phương trình trở thành ( + )t -( 2 1 3 t - ) 1 - 3 -1 = 0 ét = 1 2 t (1 3)t 3 0 ê - + + = t = 1. ê t = 3 ê ( ) ë loaïi
Câu 5: Cho x thỏa mãn 2 sin 2x -3 6 sin x + cos x +8 = 0 . Tính sin 2x. A. 1 sin 2x = - . B. 2 sin 2x = - . C. 1 sin 2x = . D. 2 sin 2x = . 2 2 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 105
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn C æ ö æ ö Đặt p p
t = sin x + cos x = 2 sin ççx ÷ + ÷ ç ÷ é ù ç . Vì sin çx + ÷Î[ 1 - ] ;1 t Î 0; 2 . è 4 ÷ø çè 4 ÷ ê ø ë úû Ta có t = ( x + x)2 2 2 2 2 sin cos
= sin x + cos x + 2 sin x cos x sin 2x = t -1. é 6 êt =
Phương trình đã cho trở thành 2( 2t ) 1 3 6 t 8 0 ê - - + = 2 ê êt = 6 ê ( ) ë loaïi 1 2
sin 2x = t -1 = . 2
Câu 6: Hỏi trên đoạn [0;2018p] , phương trình sin x -cos x + 4 sin 2x = 1 có bao nhiêu nghiệm? A. 4037. B. 4036. C. 2018. D. 2019. Lời giải Chọn A æ ö æ ö Đặt p p
t = sin x -cos x = 2 sin ççx ÷ - ÷ ç ÷ é ù ç . Vì sinçx - ÷Î[ 1 - ] ;1 t Î 0; 2 . è 4 ÷ø çè 4 ÷ ê ø ë úû Ta có t = ( x - x)2 2 2 2 2 sin cos
= sin x + cos x -2 sin x cos x sin 2x = 1-t . ét = 1 ê
Phương trình đã cho trở thành t + 4( 2 1-t ) =1 ê 3 . êt = - (loaïi) êë 4 Với kp
t = 1 , ta được sin 2x = 0 2x = kp x = , k Î . 2 Theo giả thiết Î[ kp x 0;2018p] ¾¾ 0 £
£ 2018p 0 £ k £ 4046 2 kÎ ¾¾¾
k Î {0;1;2;3;...;4036} ¾¾
có 4037 giá trị của k nê có 4037 nghiệm.
Câu 7: Từ phương trình 2 (sin x +cos x) = tan x + cot x , ta tìm được cos x có giá trị bằng: A. 1. B. 2 - . C. 2 . D. 1. - 2 2 Lời giải Chọn C si ìï n x ¹ 0 Điều kiện ïí sin 2x ¹ 0 . co ï s x ¹ 0 ïî Ta có ( x + x) = x + x ( x + x) sin x cos x 2 sin cos tan cot 2 sin cos = + cos x sin x 2 2 ( + x + x) sin x cos x 2 sin cos =
2 sin x cos x. 2 (sin x + cos x) = 2. sin x cos x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 106
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Đặt - t = x + x (- £ t £ ) 2 t 1 sin cos 2 2 ¾¾ sin x cos x = . 2
Phương trình trở thành t ( 2 t - ) 3 2
1 = 2 t -t - 2 = 0 t = 2
sin x + cos x = 2 sin x = 2 -cos x. Mà x + x = x +( - x)2 2 2 2 2 sin cos 1 cos 2 cos
= 1 2 cos x -2 2 cos x +1 = 0 ( x - )2 1 2 cos 1 = 0 cos x = . 2
Câu 8: Có bao nhiêu giá trị nguyên của tham số m để phương trình sin x cos x -sin x -cos x + m = 0 có nghiệm? A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C Đặt - t = x + x (- £ t £ ) 2 t 1 sin cos 2 2 ¾¾ sin x cos x = . 2 2
Phương trình trở thành t -1-t +m = 0 -2m = t -2t -1 (t - )2 2 1 = -2m + 2 . 2 Do - £ t £ ¾¾ - - £ t - £ - ¾¾ £(t - )2 2 2 2 1 1 2 1 0 1 £ 3 + 2 2 .
Vậy để phương trình có nghiệm 1+ 2 2 0 £ 2
- m + 2 £ 3 + 2 2 - £ m £1 2 mÎ ¾¾¾ m Î { 1; - 0; } 1 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 107
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133



