







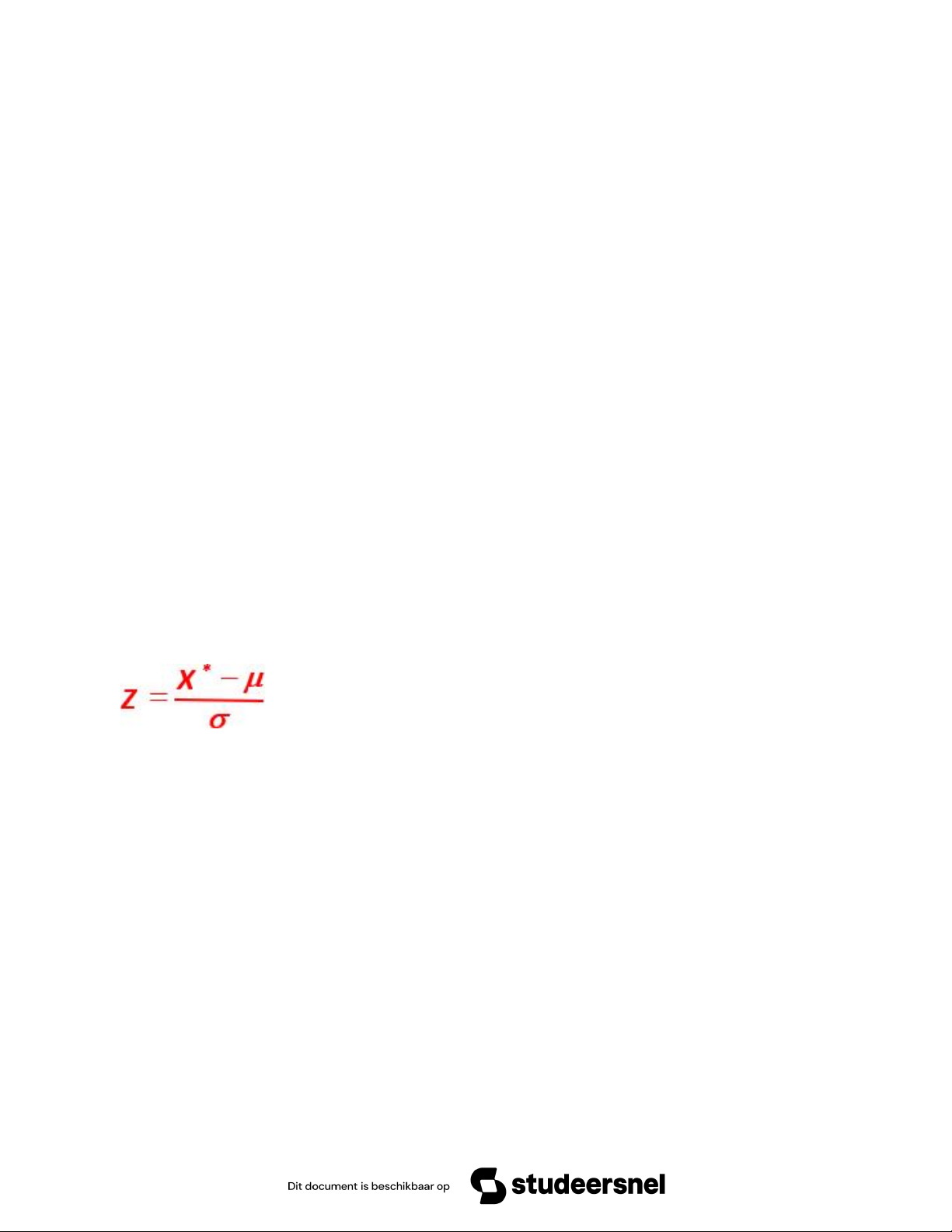

Preview text:
PHÂN TÍCH ĐỊNH LƯỢNG TRONG QUẢN TRỊ
CHƯƠNG 1: TỔNG QUAN VỀ PHÂN TÍCH ĐỊNH LƯỢNG TRONG QUẢN TRỊ
PHÂN TÍCH ĐỊNH LƯỢNG:
Là môn học nghiên cứu các phương pháp khoa học, chủ yếu là toán học ứng dụng để giải
quyết các vấn đề trong lĩnh vực quản trị.
Các thuật ngữ chuyên môn thường được dùng: • Phân tích định lượng; •
Phương pháp định lượng; • Vận trù học; • Khoa học quản lý; •
Hay khoa học ra quyết định.
CHỦ ĐỀ 2: QUI TRÌNH ỨNG DỤNG PHÂN TÍCH ĐỊNH LƯỢNG
Phương pháp phân tích định lượng bao gồm 1. Xác định vấn đề, 2. Xây dựng mô hình,
3. Thu thập dữ liệu đầu vào, 4. Tìm kiếm lời giải, 5. Kiểm tra lời giải, 6. Phân tích kết quả 7. Sử dụng kết quả.
Trong qui trình, một bước thực hiện không cần thiết phải chờ đợi bước trước đó hoàn tất.
BƯỚC 1. XÁC ĐỊNH VẤN ĐỀ
Một phát biểu rõ ràng và dễ hiểu nhằm định hướng và có ý nghĩa đối với các bước PTĐL tiếp
theo. Nó phải cụ thể và có các mục tiêu đo được.
BƯỚC 2. XÂY DỰNG MÔ HÌNH
Mô hình PTĐL: Là một phát biểu tóan học thể hiện mối quan hệ giữa các biến trong bài tóan.
Mô hình chứa 2 lọai biến (biến kiểm soát, biến không kiểm soát) và các tham số.
Có 2 loại biến: biến kiểm soát và biến không kiểm soát.
Biến kiểm soát, còn gọi là biến quyết định, là biến mà đại lượng nó biểu diễn là yếu tố chính
trong bài toán ra quyết định
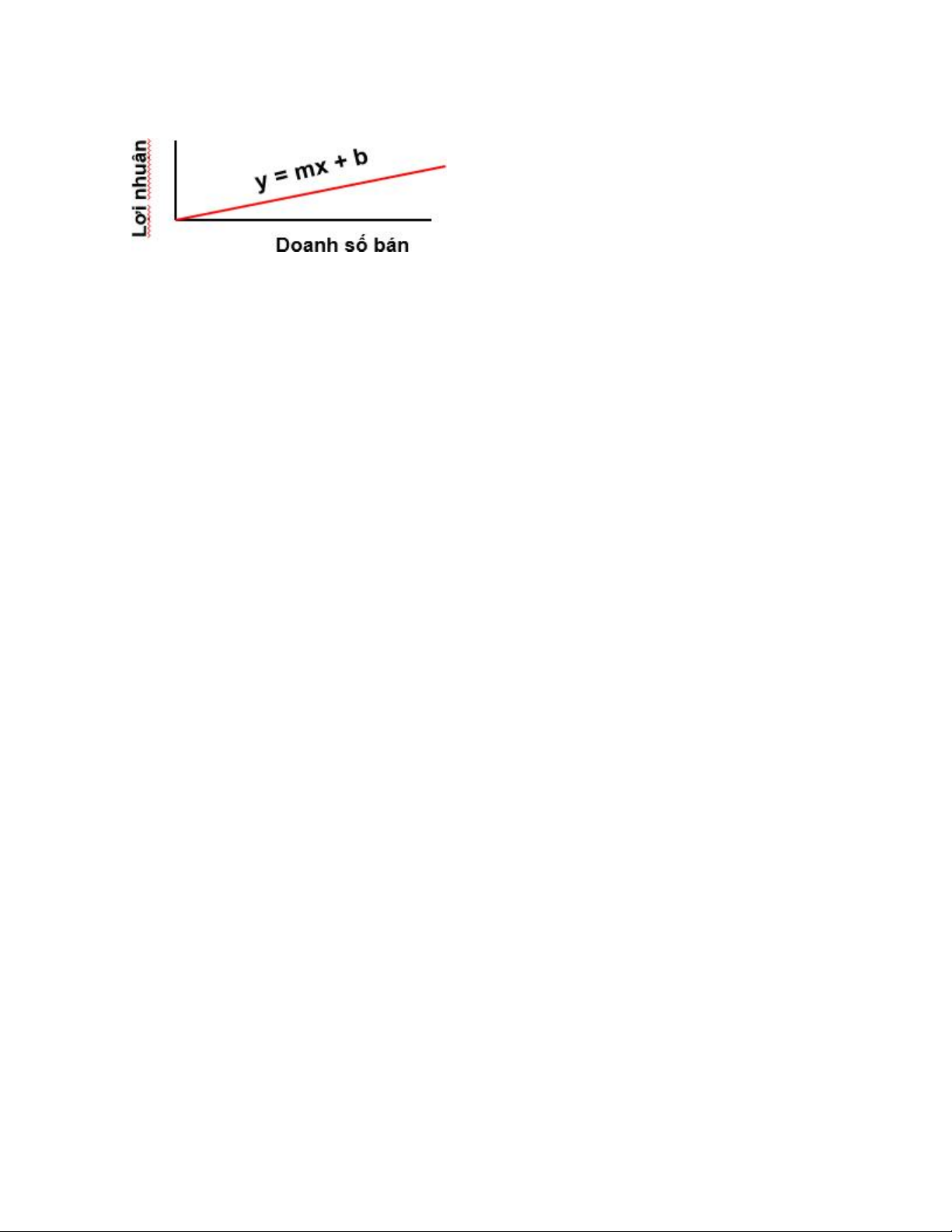
Biến không kiểm soát, thí dụ như doanh số bán
BƯỚC 3. THU THẬP DỮ LIỆU
Dữ liệu đầu vào thường có từ các nguồn như: - Các báo cáo bán hàng
- Các báo cáo kế toán, tài chính… của công ty
- Phỏng vấn, thu thập trực tiếp từ hiện trường
BƯỚC 4. TÌM LỜI GIẢI
Dựa vào các thuật tóan, các giải thuật phù hợp với mô hình.
Những cách giải thường được dùng như: - Giải hệ phương trình
- Tìm phương án tối ưu của bài tóan qui hoạch tuyến tính - Phương pháp thử và sai
- Tuần tự thử các phương án có thể dẫn đến lời giải…
BƯỚC 5. KIỂM TRA LỜI GIẢI
Kiểm tra lời giải bao gồm cả việc kiểm tra dữ liệu đầu vào và kiểm tra mô hình nhằm xác định
độ chính xác cũng như mức độ hoàn thiện của dữ liệu được sử dụng trong mô hình.
Một trong những cách phổ biến nhất là tìm cách thu thập thêm dữ liệu từ một nguồn thông tin
khác với nguồn dữ liệu ban đầu
Trong trường hợp, dữ liệu đã được kiểm tra là chính xác, nhưng các kết quả của mô hình lại
cho thấy có điểm bất hợp lý so với thực tế, lúc này mô hình cũng cần phải được kiểm tra tính
bền vững và chỉnh sửa lại sao cho nó phản ánh được đúng thực tiễn.
BƯỚC 6. PHÂN TÍCH KẾT QUẢ
Xem xét ảnh hưởng của kết quả mô hình đến thực tế
Phương pháp phân tích độ nhạy thường được sử dụng để kiểm tra kết quả thu được’
BƯỚC 7: ÁP DỤNG KẾT QUẢ
Là bước triển khai kết quả nghiên cứu vào thực tế
Cần có cơ chế giám sát để theo dõi thay đổi của điều kiện thực tế so với điều kiện lý thuyết VÍ DỤ MINH HỌA
Cửa hàng Phát Đạt chuyên kinh doanh nồi cơm điện hiệu Bông lúa.
Giả sử bạn muốn triển khai mô hình để theo dõi lợi nhuận hàng ngày và doanh thu hoà vốn (là
mức doanh thu mà ở đó, tổng chi phí bằng tổng doanh thu, tức là lợi nhuận bằng không).
Biết tổng định phí của cửa hàng là $100/ngày, biến phí bán một nồi cơm điện là $5, giá bán mỗi nồi cơm là $10. P = TR – TC •
Trong đó: P là lợi nhuận, TR là tổng doanh thu, TC là tổng chi phí. TR = p x q •
Trong đó, p là đơn giá bán một nồi cơm điện, q là số lượng nồi cơm điện bán trong ngày. TC = FC + vc x q •
Trong đó, FC là tổng định phí, vc là biến phí đơn vị và q là số lượng sản phẩm LỜI GIẢI:
Thay số vào ta có: P = 10q – 100 – 5q •
doanh thu hòa vốn: P = 0 •
Tức là: 10q – 5q – 100 = 0 hay q = 100/5=20 •
Như vậy, doanh thu hòa vốn của cửa hàng Phát Đạt là 20 nồi cơm điện/ngày
CHƯƠNG 2: PHÂN TÍCH QUYẾT ĐỊNH
CHỦ ĐỀ 1: GIỚI THIỆU LÝ THUYẾT QUYẾT ĐỊNH
LÝ THUYẾT QUYẾT ĐỊNH
Một quyết định tốt là quyết định có cơ sở logic rõ ràng, xem xét mọi dữ liệu liên quan và các
phương án khả thi, áp dụng các mô hình phân tích định lượng thích hợp cho vấn đề cần giải quyết.
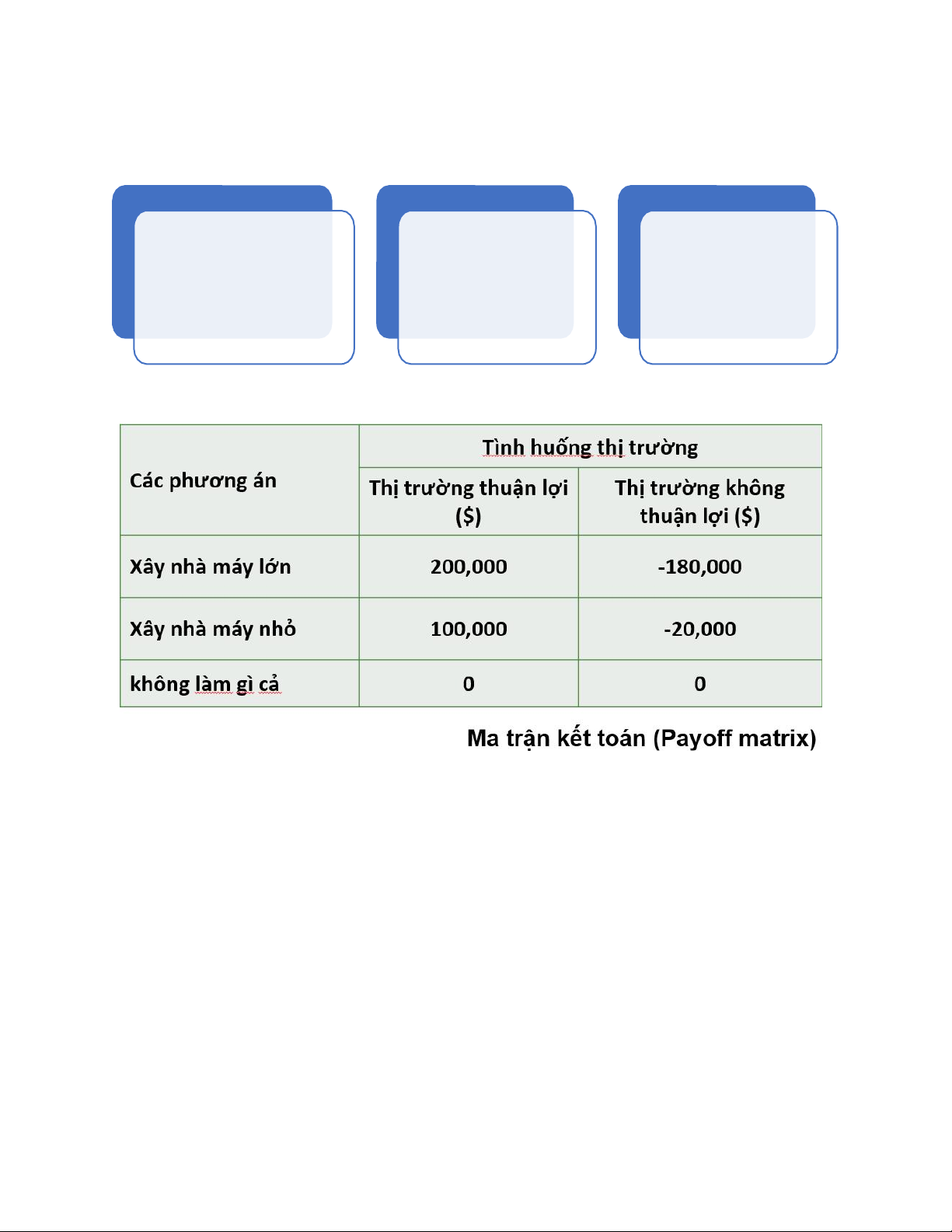
Giá trị điều kiện là giá trị thu được tại một trạng thái tự nhiên và một phương án.
CÁC BƯỚC RA QUYẾT ĐỊNH
Xác định vấn đề cần quyết định (RÕ RÀNG & D Ễ HIỂU )
Liệt kê các phư ơng án khả thi.
Xác định các biến cố có thể phát sinh ảnh hưởng đến vấn đề.
Ước tính các giá trị thu hoạch của m ỗi kết hợp giữ a phương án và biến cố.
Chọn m ột m ô hình toán trong lý thuyết ra quyết định.
Tìm lời giải của m ô hình, phân tích lời giải và ra quyết định theo lời giải đó. Ví dụ cụ thể:
CÁC LOẠI MÔI TRƯỜNG RA QUYẾT ĐỊNH: Ra quyết định Ra quyết định Ra quyết định trong môi trường trong môi trong môi chắc chắn trường không chắc chắn trường có rủi ro
PHÂN TÍCH VÍ DỤ CỤ THỂ & LẬP BẢNG QUYẾT ĐỊNH
CHƯƠNG 2: PHÂN TÍCH QUYẾT ĐỊNH
CHỦ ĐỀ 2: RA QUYẾT ĐỊNH TRONG MÔI TRƯỜNG KHÔNG CHẮC CHẮN
TIÊU CHUẨN RA QUYẾT ĐỊNH: - Tiêu chuẩn Maximax - Tiêu chuẩn Maximin
- Tiêu chuẩn khả năng như nhau (Laplace)
- Tiêu chuẩn thực tiễn (Hurwicz) - Tiêu chuẩn Minimax TIÊU CHUẨN MAXIMAX
Tiêu chuẩn Maximax được dùng để xác định phương án có giá trị kết toán tốt nhất trong số các
giá trị kết toán tốt nhất của mỗi phương án sẽ được chọn.
Theo tiêu chuẩn này, người ra quyết định có mức chấp nhận rủi ro cao, tin tưởng sẽ đạt được
thu hoạch cao nhất với phương án lựa chọn.
phù hợp với người ra quyết định có đánh giá lạc quan về vấn đề đang xem xét. TIÊU CHUẨN MAXIMIN
Tiêu chuẩn Maximin được dùng để xác định phương án có giá trị kết toán tốt nhất trong số các
giá trị kết toán xấu nhất của mỗi phương án.
Theo tiêu chuẩn này, người ra quyết định có mức mạo hiểm thấp, chấp nhận phương án sao
cho tổn thất nếu xảy ra sẽ thấp nhất
phù hợp với người ra quyết định có đánh giá bi quan về vấn đề đang xem xét.
TIÊU CHUẨN LAPLACE (tiêu chuẩn khả năng như nhau)
Khi dùng tiêu chuẩn này, người ra quyết định giả định rằng khả năng xảy ra của các biến cố là như nhau.
Chúng ta tính trung bình cộng của các thu hoạch và lấy giá trị trung bình này làm giá trị so sánh
của từng phương án, sau đó, trong số các giá trị so sánh này, chọn giá trị so sánh tốt nhất
Phù hợp với người ra quyết định có giả định bình quân về các biến cố tác động đến vấn đề đang xem xét TIÊU CHUẨN HURWICZ.
Nhà khoa học Mỹ gốc Nga – Leonid Hurwicz đã đề xuất kết hợp hai tiêu chuẩn Maximax &
maximin bằng cách đưa vào trọng số α và dùng giá trị α này để đánh giá các phương án
α được gọi là hệ số thực tiễn và có giá trị từ 0 đến 1 tùy thuộc vào mức độ lạc quan của người ra quyết định
α sẽ được gán giá trị gần với 1 nếu người ra quyết định thuộc dạng người lạc quan, trong
trường hợp ngược lại α sẽ được gán giá trị gần với 0
Dùng hệ số α (hệ số thực tiễn) để đánh giá các phương án 0 α 1
Để đánh giá các phương án, đầu tiên, chúng ta cần xác định trước giá trị của α, sau đó dùng
công thức sau để tính cho mỗi phương án:
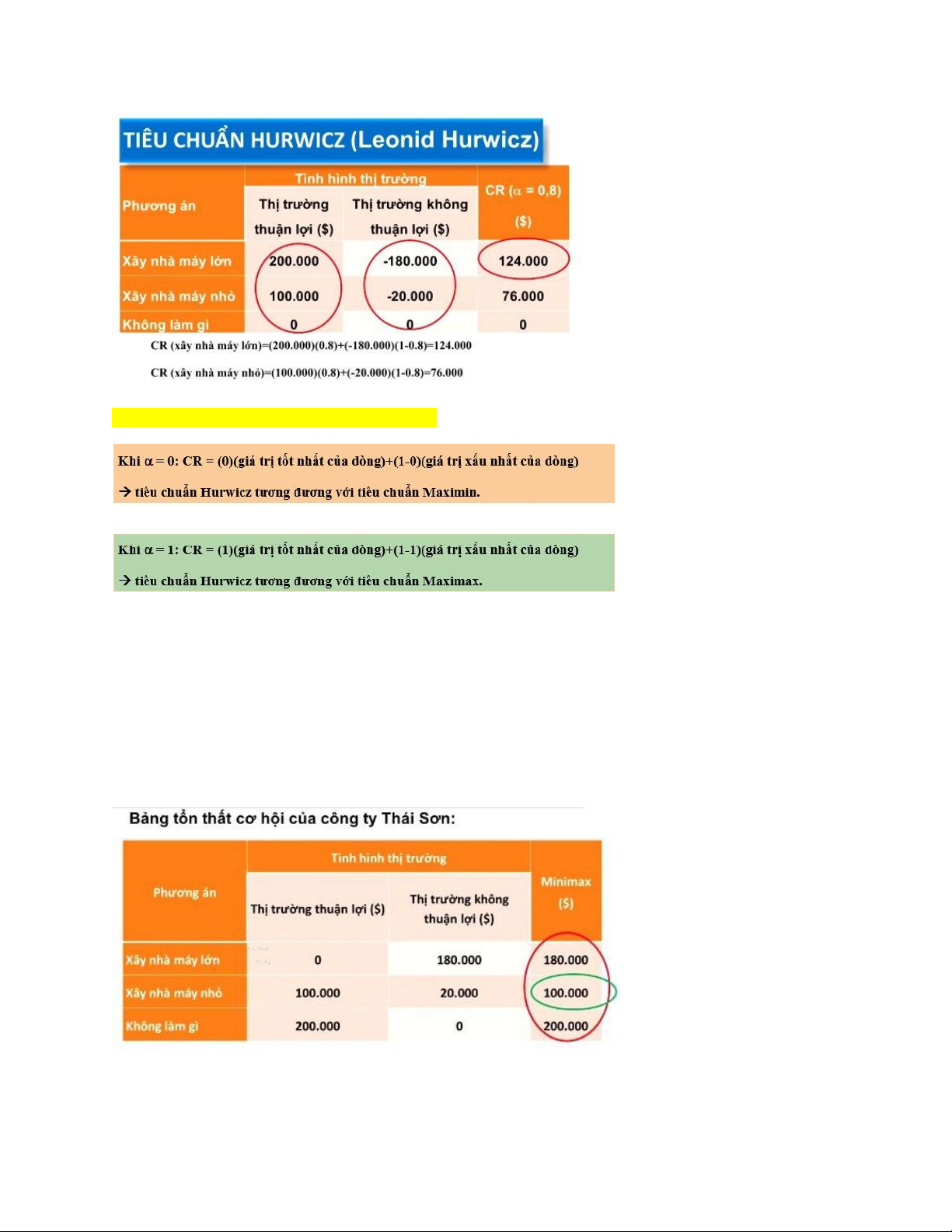
CR = α (giá trị tốt nhất của dòng) + (1-α)(giá trị xấu nhất của dòng)
Hệ số thực tiễn α = 0.8 do công ty tự đặt ra
TIÊU CHUẨN MINIMAX (MINIMAX REGRET)
Tiêu chuẩn minimax – tên đầy đủ là minimax regret – là tiêu chuẩn dựa trên việc tối thiểu hóa
sự hối tiếc (hay sự tổn thất cơ hội) lớn nhất trong từng phương án.
Để chọn lựa phương án theo tiêu chuẩn này, xác định giá trị tổn thất cơ hội của các phương án.
Giá trị này được tính bằng cách lấy hiệu số giữa giá trị kết toán tốt nhất của một biến cố và giá
trị kết toán tương ứng của mỗi phương án.
Lấy giá trị lớn nhất của dòng trừ cho các giá trị khác trong dòng để lập bảng tổn thất cơ hội.
CHƯƠNG 2: PHÂN TÍCH QUYẾT ĐỊNH
CHỦ ĐỀ 3: RA QUYẾT ĐỊNH TRONG MÔI TRƯỜNG RỦI RO
Trong môi trường này, người ra quyết định biết được các biến cố ảnh hưởng đến các phương
án của mình đồng thời cũng biết được xác suất xảy ra của các biến cố đó.
Thông tin về xác suất này có ý nghĩa lớn, nó giúp cho việc ra quyết định trở nên “khách quan” hơn.
Tổng xác suất của các biến cố = 1
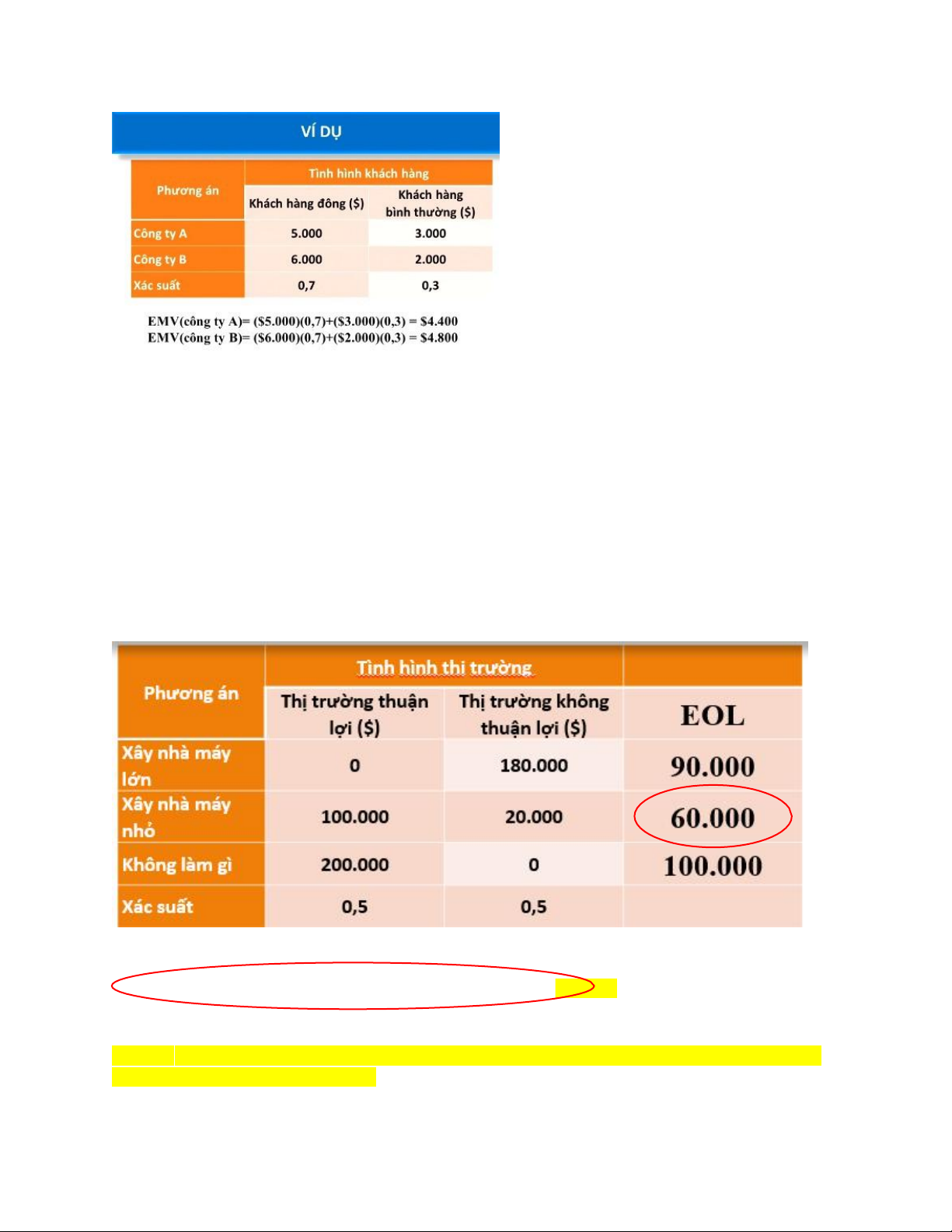
PHƯƠNG PHÁP GIÁ TRỊ KỲ VỌNG EMV (EXPECTED MONETARY VALUE)
Giá trị kỳ vọng của một phương án được tính bằng tổng có trọng số các giá trị của thu hoạch
của phương án đó, với trọng số được tính bằng xác suất xảy ra của biến cố tương ứng.
EMV (phương án i) = (giá trị kết toán của biến cố 1)(xác suất của biến cố 1) + (giá trị kết toán
của biến cố 2)(xác suất của biến cố 2) + … +(giá trị kết toán của biến cố n)(xác suất của biến cố n)
EMV(PAi)= Payoff1* P(S1) + Payoff2* P(S2) + …+ Payoffn * P(Sn)
VD: EMV1 = 200.000*0.5 + (-180.000)*0.5 = 10.000
GIÁ TRỊ THIỆT HẠI CƠ HỘI KỲ VỌNG (EXPECTED OPPORTUNITY LOSS)
Tổn thất cơ hội, đôi khi được gọi là sự hối tiếc, là một khái niệm đề cập đến sự khác biệt giữa
lợi ích tối đa thu được và lợi ích thu được thực tế
Bước 1: Lập bảng tổn thất cơ hội
Bước 2: Xác định giá trị tổn thất cơ hội EOL của các phương án
EOL (phương án i) = (giá trị tổn thất cơ hội của biến cố 1) (xác suất của biến cố 1) + (giá
trị tổn thất cơ hội của biến cố 2) (xác suất của biến cố 2) +…+(giá trị tổn thất cơ hội của
biến cố n) (xác suất của biến cố n)
Bước 3: Chọn phương án có tổn thất cơ hội kỳ vọng nhỏ nhất
EOL(Xây nhà máy lớn)=($0)(0,5)+($180.000)(0,5)=$90.000
EOL(Xây nhà máy nhỏ)=($100.000)(0,5)+($20.000)(0,5)=$60.000
EOL(không làm gì)=($200.000)(0,5)+($0)(0,5)=$100.000
Trong cùng một vấn đề, 2 phương pháp này luôn luôn cho ra kết quả giống nhau, tức là
luôn chọn cùng một phương án.
GIÁ TRỊ KỲ VỌNG KHI CÓ THÔNG TIN HOÀN HẢO (EVWPI – EXPECTED VALUE WITH PERFECT INFORMATION)
EVWPI = (giá trị kết toán tốt nhất của biến cố thứ nhất) (xác suất của biến cố thứ nhất) + (giá trị
kết toán tốt nhất của biến cố thứ hai) (xác suất của biến cố thứ hai) +…+ (giá trị kết toán tốt
nhất của biến cố thứ n)(xác suất của biến cố thứ n)
EVWPI = Payoff tốt nhất của S1 * P(S1) + Payoff tốt nhất của S2 *
P(S2) +… + Payoff tốt nhất của Sn * P(Sn)
GIÁ TRỊ KỲ VỌNG CỦA THÔNG TIN HOÀN HẢO (EVPI)
EVPI là giá cao nhất của thông tin hoàn hảo.
EVPI = EVWPI – maximum EMV
EVWPI = Giá trị kỳ vọng khi có thông tin hòan hảo
Maximun EMV = Giá trị kỳ vọng lớn nhất
EOL(Xây nhà máy lớn)=($0)(0,5)+($180.000)(0,5)=$90.000
EOL(Xây nhà máy nhỏ)=($100.000)(0,5)+($20.000)(0,5)=$60.000
EOL(không làm gì)=($200.000)(0,5)+($0)(0,5)=$100.000 PHÂN TÍCH ĐỘ NHẠY
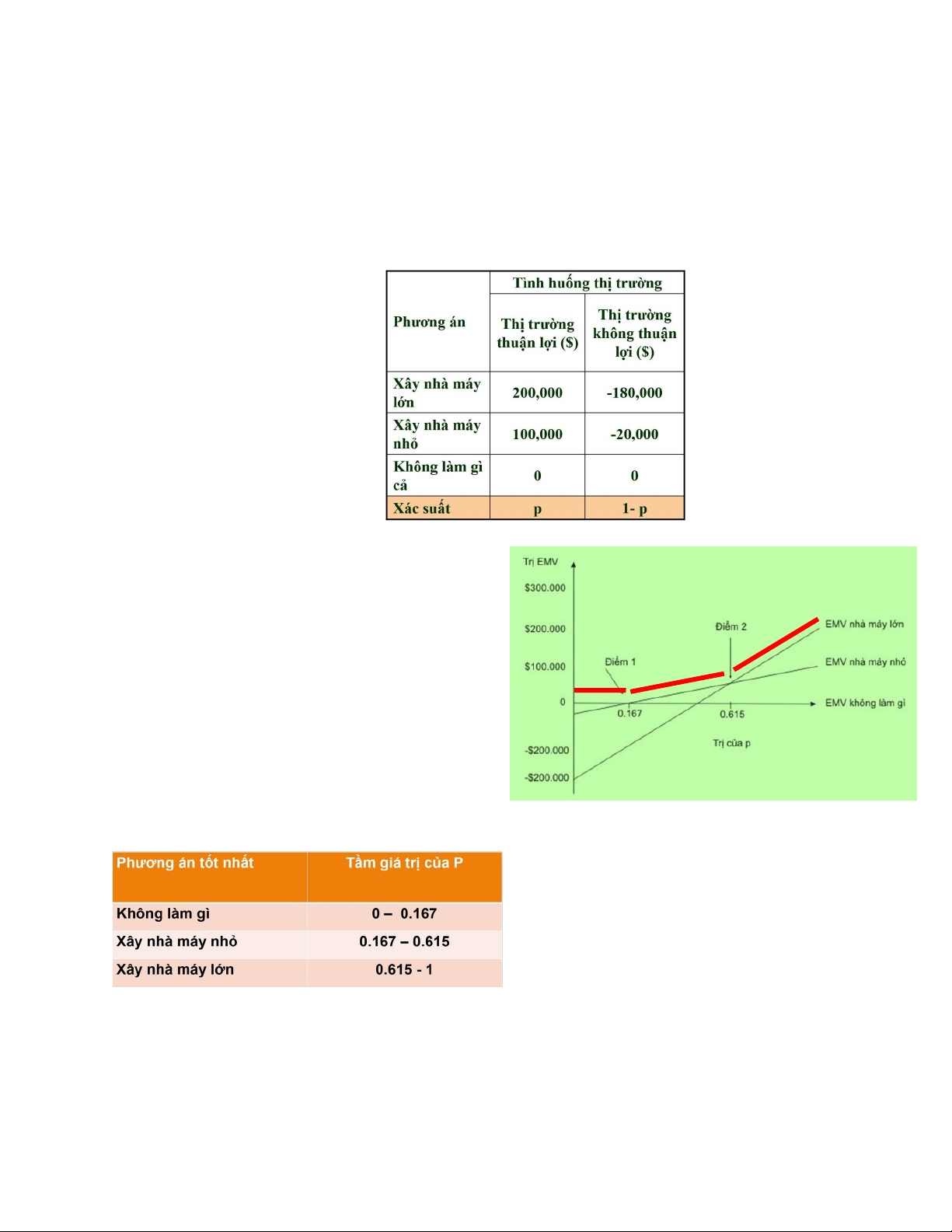
Xác xuất của biến cố thị trường thuận lợi là: P
Thì xác suất của biến cố thị trường không thuận lợi là: 1-P
Khi đó, giá trị kỳ vọng của các phương án là hàm theo P. EMV(nhà máy lớn):
= $200,000p - (1-p)$180,000 = $380.000p - $180.000 EMV(nhà máy nhỏ):
= $100,000p - $20,000(1-p) = $120.000p - $20.000
EMV(không làm gì cả):
= $0p + 0(1-p) = $0
Điểm 1: EMV (không làm gì) = EMV (xây nhà máy nhỏ) 0 = $120.000p - $20.000 P = 0.167
Điểm 2: EMV (nhà máy nhỏ) = EMV (nhà máy lớn)
$120.000p - $20.000 = $380.000p - $180.000 P = 0.615
KẾT QUẢ PHÂN TÍCH ĐỘ NHẠY
CHƯƠNG 3: PHÂN TÍCH BIÊN TẾ
CHỦ ĐỀ 1: KỸ THUẬT PHÂN TÍCH BIÊN TẾ
Để áp dụng kỹ thuật phân tích biên tế, chúng ta cần phải vận dụng 2 khái niệm: •
Lợi nhuận biên tế (Marginal Profit) •
Lỗ biên tế (Marginal Loss).
Ví dụ: Một chủ một sạp bán báo mua 1 tờ báo là 4800 đồng và bán lại với giá là 5500 đồng,
nếu như hết ngày bán hàng, báo còn dư sẽ không còn giá trị.
Lợi nhuận biên tế MP = 5.500 – 4.800 = 700 đồng
Lỗ biên tế ML (Marginal Loss) = 4.800 đồng ▪
P = xác suất mà nhu cầu D > lượng cung cho trước D0 (xác suất bán thêm được 1 đơn vị sp). ▪
1-P = xác suất mà nhu cầu D < cung D0 (xác suất bán không hết). ▪
LỢI NHUẬN BIÊN TẾ KỲ VỌNG: E(MP) = PxMP ▪
LỖ BIÊN TẾ KỲ VỌNG: E(ML) = (1-P)xML
QUI TẮC QUYẾT ĐỊNH TỐI ƯU LÀ: P*MP ? (1-P)*ML hay P ML
? MP+ML
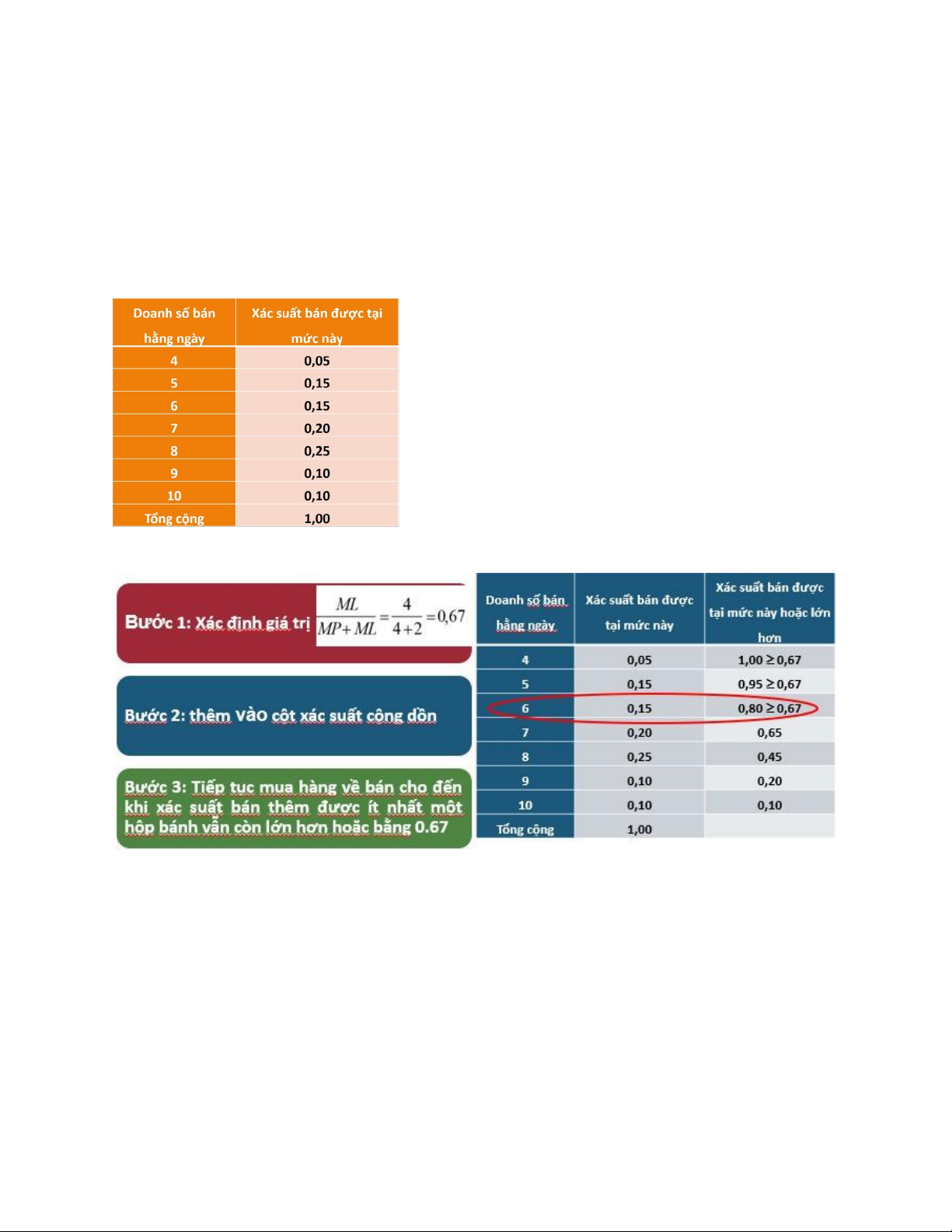
Các bước thực hiện: 1. Xác định giá trị
2. Lập bảng phân phối xác suất và thêm vào cột xác suất cộng dồn.
3. Tăng dần mức sản xuất hoặc đặt hàng để bán cho đến khi nào xác suất bán thêm
được ít nhất 1 đơn vị sản phẩm vẫn còn lớn hơn hoặc bằng
PHÂN TÍCH BIÊN TẾ VỚI PHÂN PHỐI RỜI RẠC – VÍ DỤ
Một cửa hàng bán bánh xem xét việc mua hộp bánh mì tươi về bán trong ngày. Giá mua một
hộp bánh mì tươi là $4. Bánh mì được giao hàng vào buổi sáng sớm trước giờ bán của cửa
hàng. Giá bán 1 hộp bánh mì tươi là $6. Giả sử cuối ngày bán hàng, các hộp bánh không bán
được phải bỏ và coi như cửa hàng bị thiệt hại $4 cho 1 hộp tồn kho cuối ngày bán hàng.
Cửa hàng nên mua về bao nhiêu hộp bánh mì tươi để bán để mức kỳ vọng lợi nhuận là tối ưu nhất?
Xác suất bàn được hàng P = 1,00 (100%) – xác suất bán được hàng tại mức trước đó VD: P5 = 1,00 – 0,05 = 0,95
P6 = 1,00 – 0,015 – 0,05 = 0,80
P7 = 1,00 – 0,015 – 0,05 – 0,015 = 0,65
PHÂN TÍCH BIÊN TẾ VỚI PHÂN PHỐI CHUẨN ▪
μ (Muy)= doanh số trung bình ▪
ơ (Sigma)= độ lệch chuẩn của doanh số ▪
MP = lãi biên tế (marginal profit) ▪
ML = lỗ biên tế (Marginal loss)
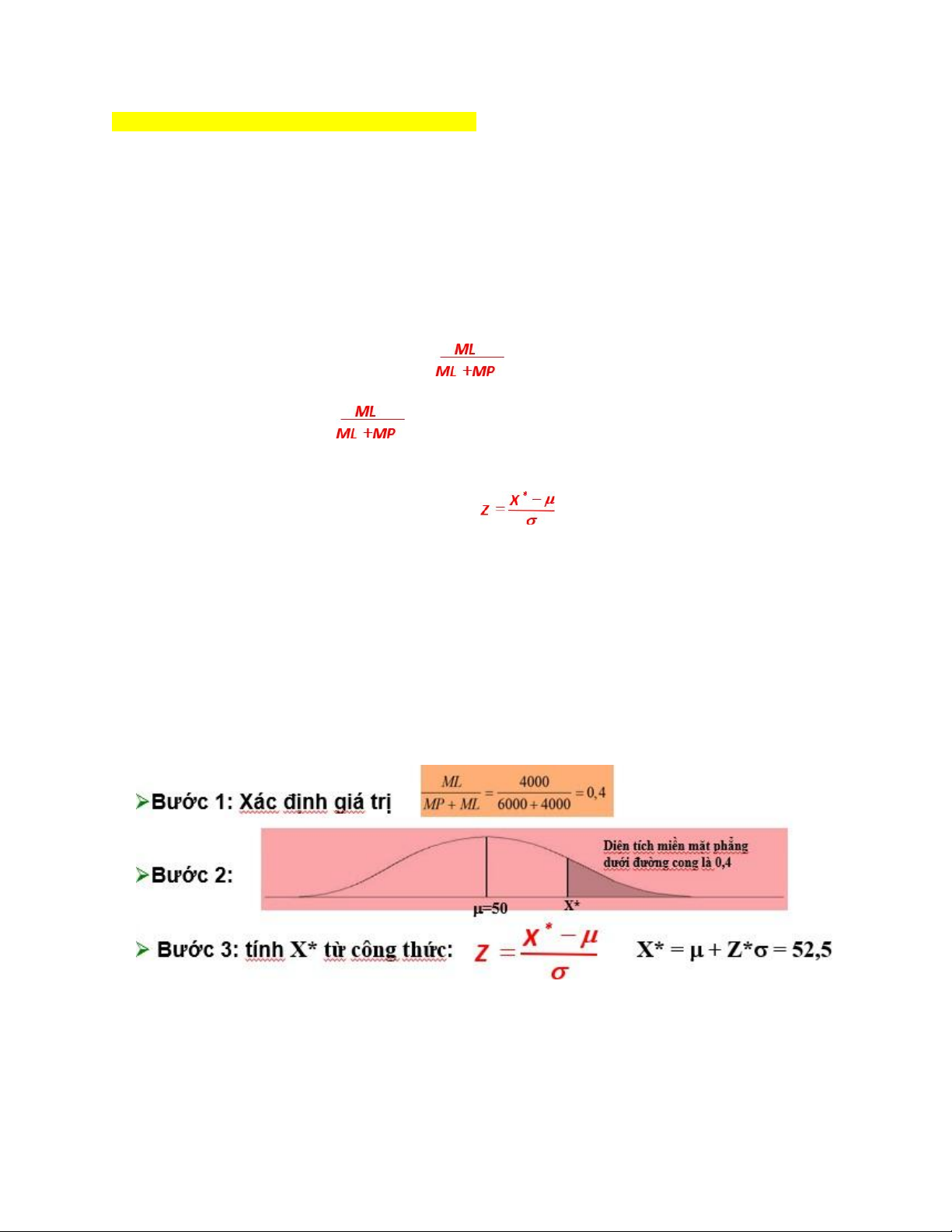
Các bước sử dụng phân phối chuẩn :
➢ Bước 1: Xác định giá trị ➢ Bước 2: Đặt
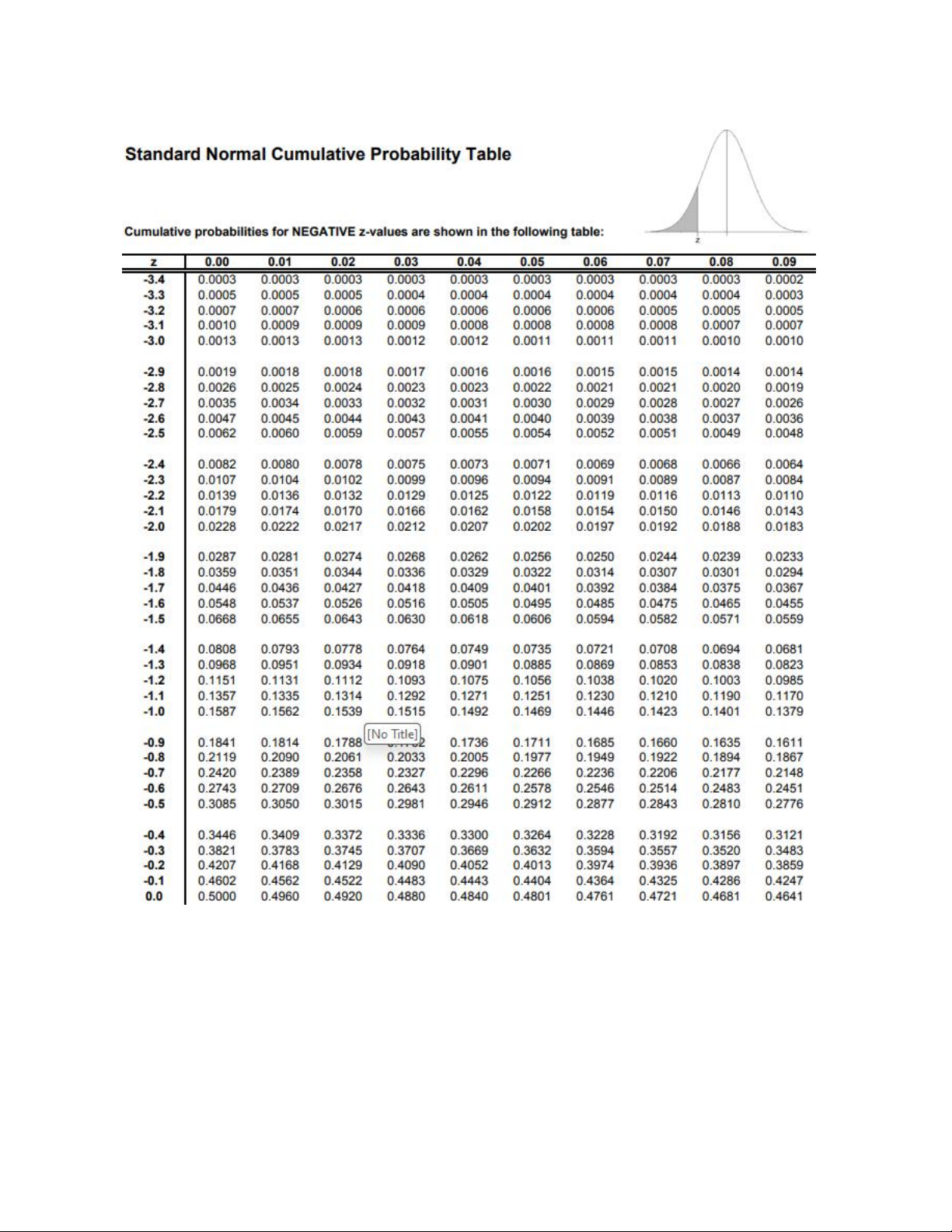
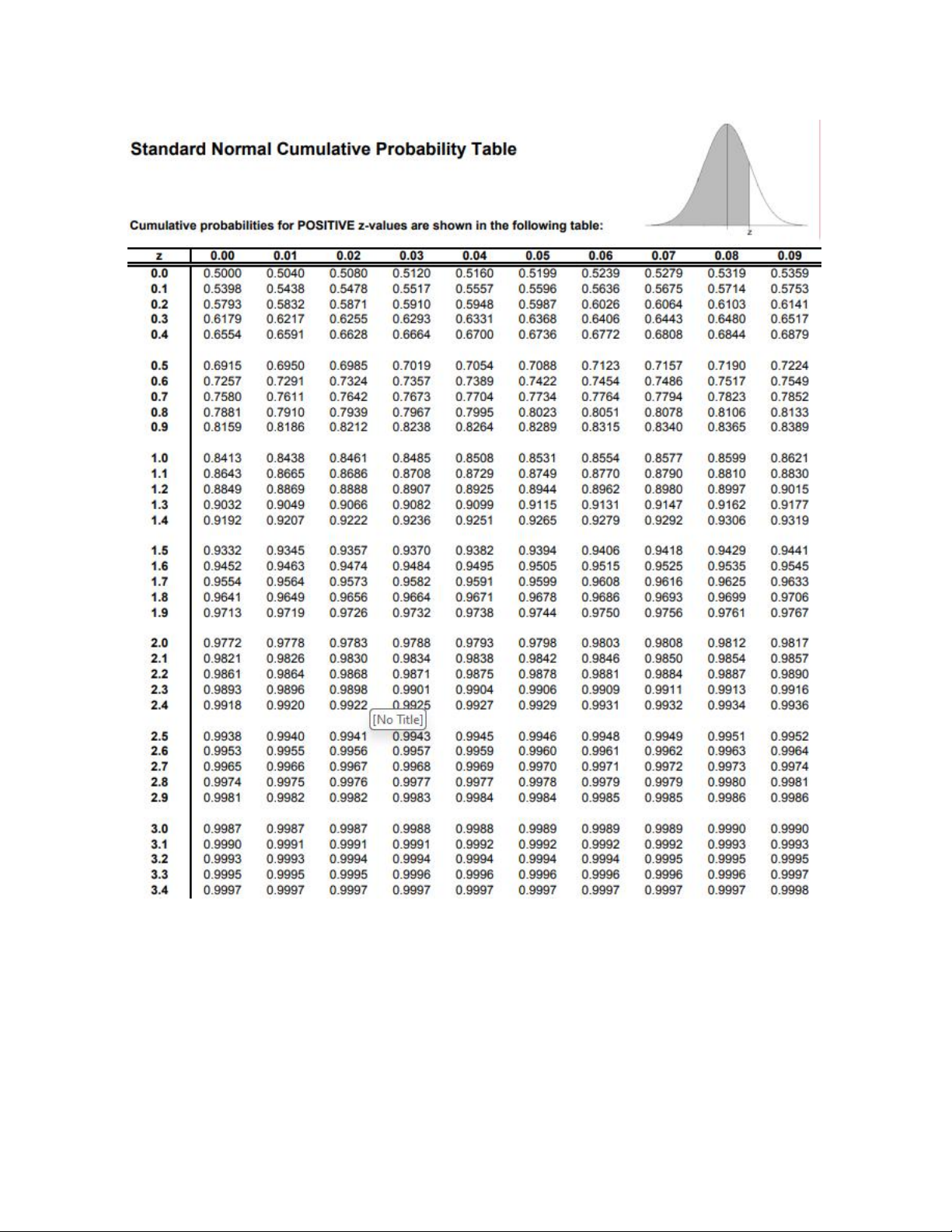
trên đường phân phối chuẩn. Ta tìm Z từ bảng phân
phối chuẩn chuẩn tắc (the standard Normal table).
➢ Bước 3: tính X* từ công thức:
Đây chính là mức mua hàng tồn kho tối ưu VÍ DỤ 1
Một tiệm bán báo có nhu cầu của khách hàng mua báo là phân phối chuẩn với doanh số trung
bình là 50 tờ mỗi ngày và độ lệch chuẩn là 10 tờ.
Với mức lỗ biên tế là 4000 đồng và lợi nhuận biên tế là 6000 đồng thì tiệm bán báo nên mua
bao nhiêu tờ để bán trong ngày. Giả sử tờ báo chỉ có giá trị trong ngày bán hàng. VÍ DỤ 2
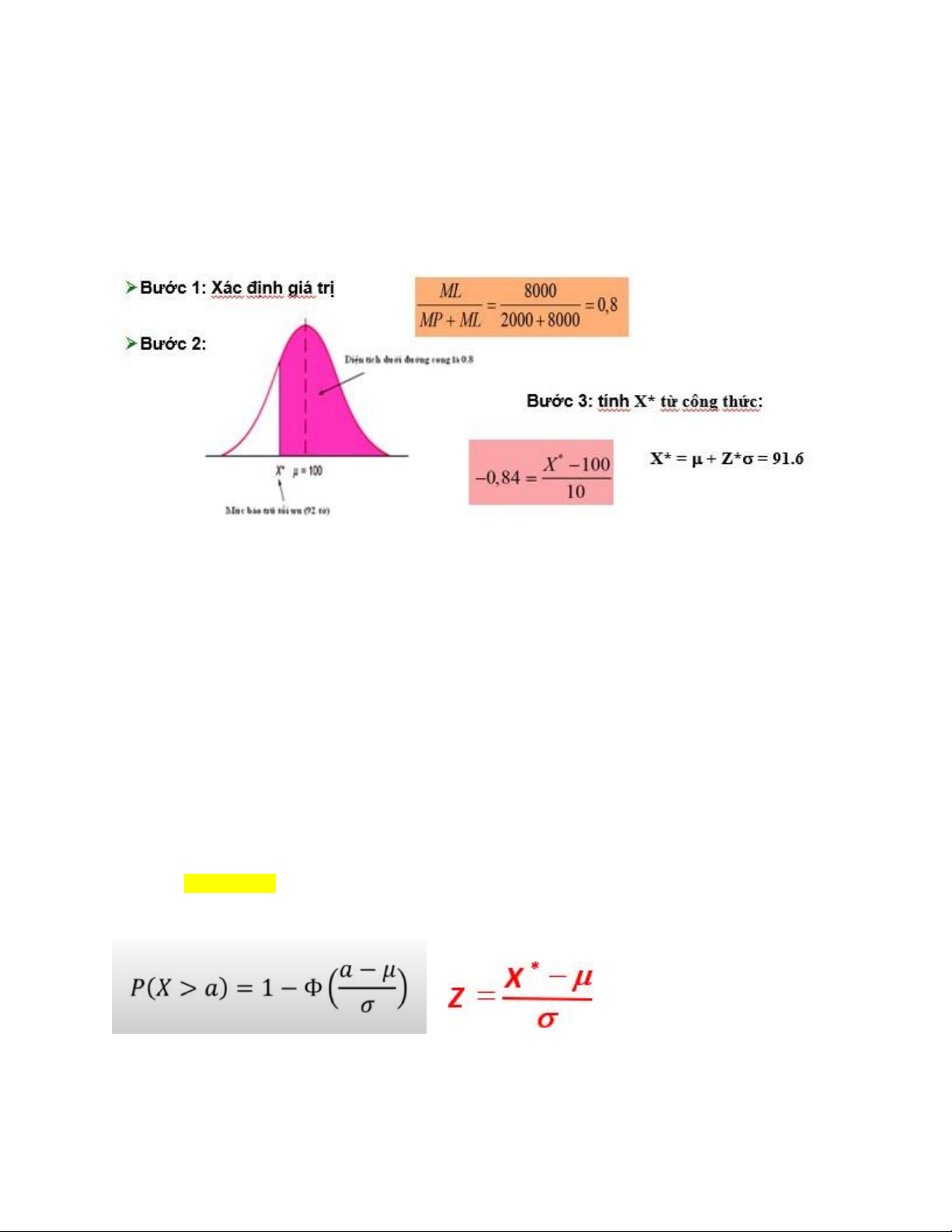
Giả sử trong tình huống mới, lỗ biên tế của tờ báo là 8.000 đồng và lợi nhuận biên tế là 2.000
đồng. Doanh số bán báo của tiệm báo cũng có dạng phân phối chuẩn với trung bình là 100 tờ
và độ lệch chuẩn là 10 tờ. Tiệm bán báo nên mua bao nhiêu tờ để bán trong ngày? VÍ DỤ 3:
Lãi suất khi đầu tư vào một công ty là biến ngẫu nhiên phân phối chuẩn.
Biết xác suất đề đạt được lãi suất trên 20% một năm là 0,2 và dưới 10% là 0,1
Tìm xác suất đề khi đầu tư vào công ty sẽ đạt được lãi ít nhất là 14%/năm ▪
X: Lãi suất khi đầu tư vào công ty (%) X~N (μ ; ơ2 )
lãi suất trên 20% một năm là 0,2 ➔ P(X>20) = 0,2
dưới 10% là 0,1 ➔ P(X<10) = 0,1
Yêu cầu: P(X>14) = ?
Một quán bún bò có lượng bán trung bình mỗi ngày là 300 tô. Từ dữ liệu cũ có khoảng
65% xác suất quán bún bò trên bán được từ 280 đến 320 tô bún bò. Chi phí trung bình
mỗi tô bún bò là 2500 đồng và giá bán trung bình là 4000 đồng/tô. Giả sử các tô bún bò
không bán được trong ngày sẽ không còn giá trị.
Hãy tính số tô bún bò tối ưu mà quán bún này cần phải nấu mỗi ngày? MP = 1500 ML = 2500 μ = 300 ơ = ? P = 2500 / 4000 = 0.625 ➔ Z = 0.32
Z = (X* - μ)/ơ ➔ 0.32 = (320-300)/ ơ ➔
CHƯƠNG 5: QUY HOẠCH TUYẾN TÍNH
CHỦ ĐỀ 1: GIỚI THIẸU BÀI TOÁN QUI HOẠCH TUYẾN TÍNH
CÁC YÊU CẦU CỦA BÀI TOÁN QUY HOẠCH TUYẾN TÍNH: •
Mỗi bài toán phải có một hàm mục tiêu. •
Các ràng buộc phải phù hợp với mục tiêu của bài toán. •
Phải có các phương án cho việc chọn lựa phương án tối ưu. •
Các quan hệ trong bài toán phải là quan hệ tuyến tính. HÀM MỤC TIÊU:
Hàm mục tiêu thường tiến đến một giá trị cực đại hay một giá trị cực tiểu. (Lợi nhuận ➔ Cực
đại, Chi phí ➔ cực tiểu).
Điều quan trọng là khi lập hàm mục tiêu, phải xác định vấn đề rõ ràng. CÁC RÀNG BUỘC:
Ràng buộc trong bài toán Qui hoạch tuyến tính thể hiện những yếu tố trong thực tế làm giới hạn
mức độ đạt được của hàm mục tiêu.
VD: số áo may được trong một ca sản xuất của một phân xưởng phụ thuộc vào số công
nhân may, số máy móc thiết bị phục vụ cho việc may áo.
Bài toán Qui hoạch tuyến tính sẽ tìm cách tối đa (hoặc tối thiểu) hóa giá trị hàm mục tiêu trong
điều kiện thỏa các ràng buộc từ điều kiện của bài toán. CÁC PHƯƠNG ÁN:
Đặc điểm của bài toán Qui hoạch tuyến tính, bản chất của tìm phương án tối ưu là trong không
gian bài toán tồn tại nhiều phương án.
Nếu bài toán mà bản chất của nó chỉ có 1 phương án hay không có tập phương án thì đó
không phải là bài toán tối ưu. QUAN HỆ TUYẾN TÍNH:
Đặc điểm quan trọng nhất của bài toán qui hoạch tuyến tính là các quan hệ toán học được thể
hiện trong bài toán là quan hệ tuyến tính, từ hàm mục tiêu cho đến các ràng buộc.
Thí dụ: ax +by = c (trong đó a, b, c là các tham số, x, y là các biến) là một quan hệ tuyến tính



