Phân Tích Dữ Liệu Thời Gian và Kiểm Định Giả Thuyết môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

I) DSTG 9 tr538)
Sử dụng phương pháp san bằng mũ giản đơn với chuỗi thời gian sau, hãy trả lời
các câu hỏi dưới đây (Chú ý: dữ liệu giống Bài tập 5.) Thời kỳ Nhu cầu 1 104 2 132 3 143 4 137 5 146 6 150 7 101 8 126 9 116 10 115
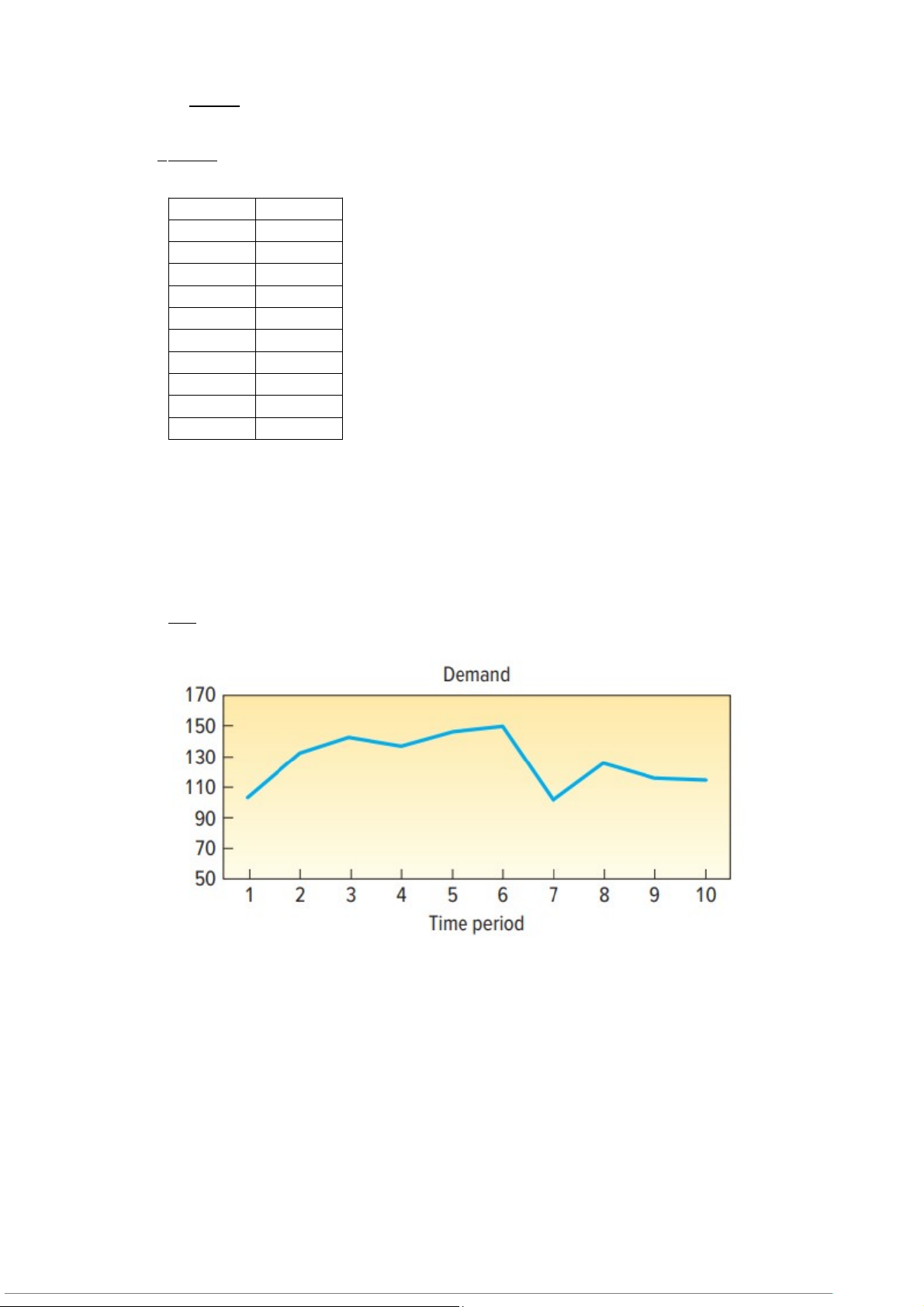
a. Vẽ đồ thị với dữ liệu trên. Bạn quan sát thấy điều gì?
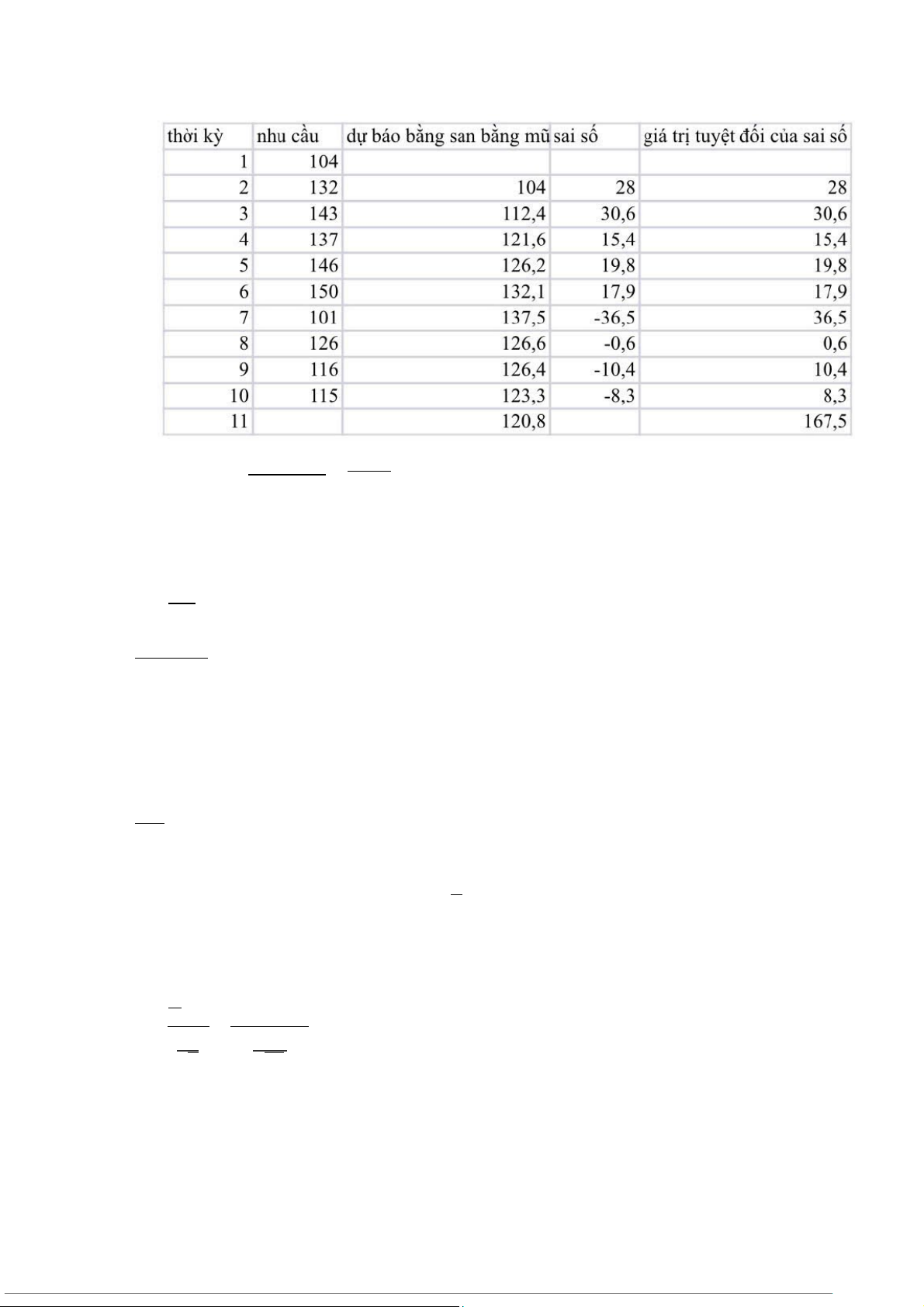
b. Tính các giá trị dự báo có thể với hệ số san bằng mũ (a) là 0.3. c. Tính MAD.
d. Hãy dự báo nhu cầu của thời kỳ thứ 11 .
e. Xác định khoảng dự báo cho nhu cầu của thời kỳ thứ 11. BL:
a) Đồ thị cho ta thấy sự thay đổi của nhu cầu qua 10 thời kì b) ∑ |saisố | 167.5 c) MAD = = ≈ 18.61 n 9
d) Dự báo nhu cầu thời kì thứ 11 = 120.8
e) Khoảng dự báo nhu cầu thời kì thứ 11 là: 120.8 ± 18.61 II) KĐ
28 tr 342) Dole Pineapple Inc. lo ngại các hộp dứa cắt lát 16 ounce bị quá trọng lượng. Giả sử
độ lệch chuẩn của tổng thể là 0.03 ounce. Bộ phận kiểm tra chất lượng lấy mẫu ngẫu nhiên 50
hộp và tính được trọng lượng trung bình là 16.05 ounce. Với mức ý nghĩa 5%, có thể kết luận
rằng trọng lượng trung bình của các hộp dứa cắt lát này lớn hơn 16 ounce không? Hãy xác định giá trị p. BL: σ=0.03 n = 50 X =16.05 α=0.05 {H0≤16 H1>16 X−μ 16.05−16 Z = σ = 0.03 ≈11.8 √n √50 Z ≈ 11.8 -> p ≈ 0
p ≈0 < α= 0.05 -> bác bỏ
H0 -> trọng lượng trung bình các hộp dứa cắt lát lớn hơn 16 ounce
47 tr 345) Một máy pha chế cola được thiết lập để rót 9.00 ounce cola vào mỗi lon với độ lệch
chuẩn là 1.00 ounce. Với mẫu gồm 36 lon, nhà sản xuất muốn đặt giới hạn sao cho 5% trung
bình mẫu lớn hơn so với giới hạn trên và 5% trung bình mẫu nhỏ hơn giới hạn dưới.
a. Hãy xác định giá trị giới hạn trên và giới hạn dưới.
b . Với giả định trung bình của tổng thể là 8.6, tìm xác suất để các giới hạn không thay đổ so với câu (a).
c. Với giả định trung bình của tổng thể là 9.6, tìm xác suất để các giới hạn không thay đổi so với câu (a). BL: μ± Z σ a)
n=9±1.645(1 36) -> giới hạn là: 8.726 và 9.274 √ √ b) μ=8.6 X−μ 8.726−8.6 Z = n=¿ ≈ 0.76 σ/ √ 1/√36 P (Z < 0.76) = 0.7764 c) μ=9.6 X−μ 9.274−9.6 Z = n=¿ = -1.956 ≈ -1.96 σ/ √ 1/ √36 P (Z > -1.96) = 0.9750