Phương pháp giải bài tập học phần vật lý Chương V: tĩnh điện môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

PHƯƠNG PHÁP GIẢI BÀI TẬP HỌC PHẦN VẬT LÝ CHƯƠNG V: TĨNH ĐIỆN
Dạng 14: Định luật Coulomb – Nguyên lý chồng chất lực
A. Một vài lưu ý khi giải toán 1. Định luật Coulomb r r = 1 q .q r 1 2 F . . π ε ε.r r 4 2
2. Nguyên lý chồng chất lực 0
“Nếu một vật có điện tích q chịu tác dụng của nhiều lực điện ur uur uur
F , F , ..., F do các điện tích q1,
q2,…, qn gây ra, thì lực điện tổng hợp tác dụng lên q được xác định bởi: 1 2 n r ur uur uur F = F + F + ... + F B. Phương pháp giải 1 2 n Các bước tiến hành:
Bước 1: Xác định chi tiết các lực tác dụng vào điện tích điểm q đang xét do các điện tích q1, q2,… gây
ra: tính các độ lớn và biểu diễn các lực đó bằng các vectơ
Bước 2: Bằng phép vẽ: xác định vectơ hợp lực rF của tất cả các lực theo quy tắc hợp lực.
Bước 3: Tính độ lớn hợp lực F theo các lực thành phần bằng phương pháp hình học.
Các trường hợp thường gặp:
1. Các lực F1, F2 cùng phương: uur + + F r -
a. Cùng chiều: Hợp lực r F
F : + Cùng chiều với 2 lực q1 q ur 2 q2 + Độ lớn: F = F1 + F2 F
b. Ngược chiều:Hợp lực r uur r ur
F:+ Cùng chiều với lực lớn 1 + F F + F + + Độ lớn F = F + F q1 2 q 1 q2 1 2 ur ^ uur r 2. Khi F
F : Hợp lực F: + Hướng theo đường chéo hình chữ nhật (cạnh F1 và F2) hợp với F1 1 2 một góc α với F tanα = 2 F + Độ lớn: 1 F = F + F 2 2 ur
uur có cùng độ lớn (F1 = F2) và hợp a 1 với nh2 3. Khi F và F au một góc ợ p lH ực r a 1 2
F: + Hướng theo đường phân giác của góc (hình thoi) α + Độ lớn: 1 F = 2.OH = 2Fcos 2 4. Tổng quát: ur uur F a ¹
và F hợp với nhau một góc và F1 F2 ur uur 1 2 r
F: + Hướng theo đường chéo của hình bình hành (2 cạnh F và F ) H ợ p + lự Đ c
ộ lớn: Áp dụng định lý hàm cosin: 1 2
F = F + F - 2FF .cos(π - α) = F + F + 2FF .coαs 2 2 2 2 2 C. Bài tập mẫu 1 2 1 2 1 2 1 2
Có hai điện tích q và -q đặt tại hai điểm A, B cách nhau một F
khoảng AB = 2d. Một điện tích dương q1 = q đặt trên đường trung trực α 1
của AB cách AB một khoảng x.
a) Xác định lực điện tác dụng lên q C + F 1.
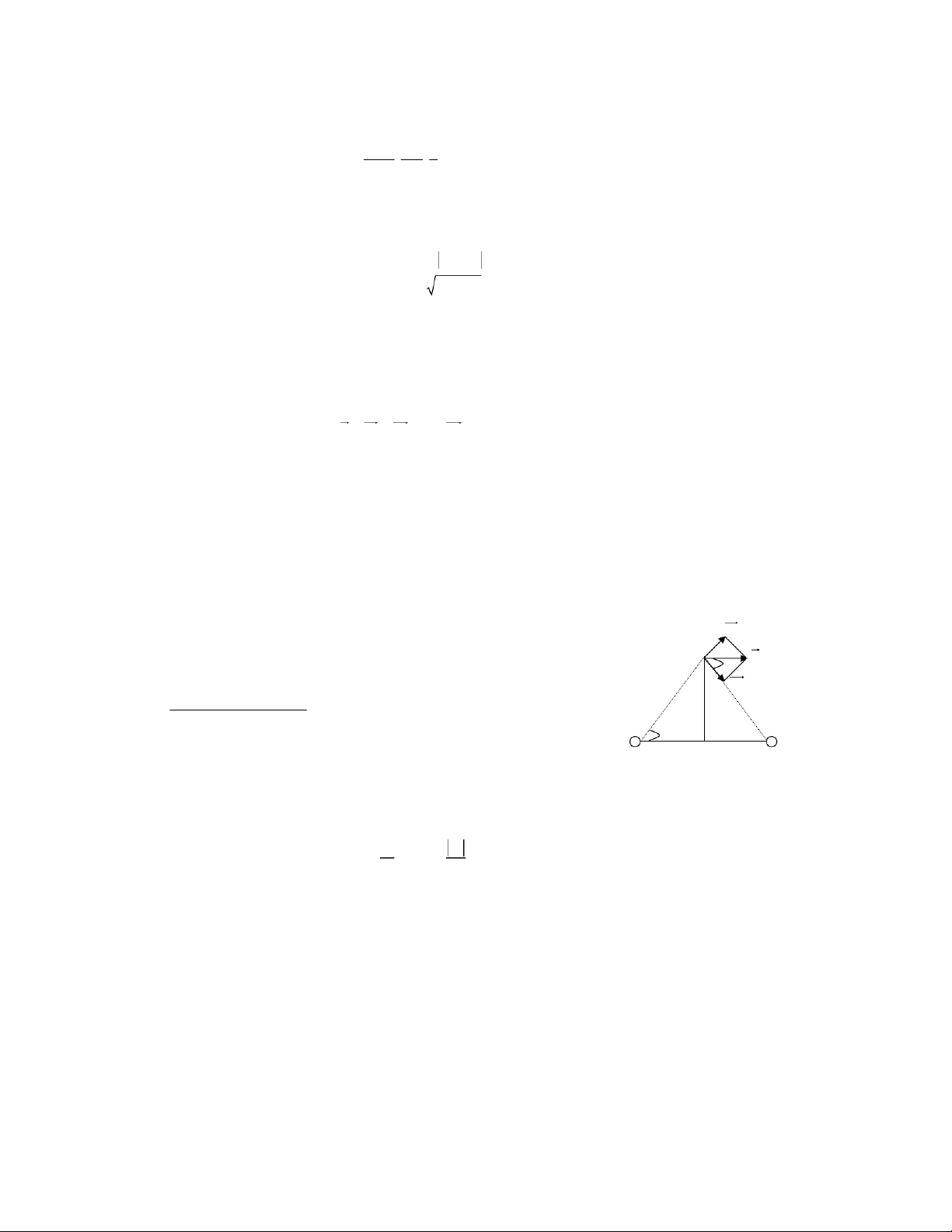
b) Áp dụng bằng số q = 4.10-6C; d = 3cm; x = 4cm. F Giải mẫu: 2 x AB = 2d; d = 3cm CO = x = 4cm q = 4.10 α -6C A + - B F ? = q d O d -q - Lực 1
F do q tác dụng lên q1 theo định luật Coulomb 2 q F 2 = k . C 2 hiều của được xác định như h ẽ 1 1 F ình v . d + x Lực 2
F do -q tác dụng lên q1 theo định luật Coulomb 2 q F 2 = k . C 2 hiều của được xác định như h ẽ 2 2 F ình v . d + x
- Áp dụng nguyên lý chồng chất lực ta có: ur ur ur F F = + F 1 2
- Vì F1 = F2 nên F có phương song song với AB và có chiều như hình vẽ. 1 F 2F = cos α - Theo hình vẽ ta có d cosα= 2 2 d +x 2 q d F = 2F cos 13/2 α = 2k » 69N ( d)22+x ì - Điểm đặt tại q ï r - V Phương AB ậy Fïí ï - Chiều A ® B ïî - Độ lớn F = 69N D. Bài tập áp dụng
Bài 1: Cho hai điện tích bằng +q (q>0) và hai điện tích bằng –q đặt tại bốn đỉnh của một hình vuông
ABCD cạnh a trong chân không, như hình vẽ. Xác định lực điện tổng hợp tác dụng lên mỗi điện tích nói trên? 2 ĐS: q F 3k = D 2 2a
Bài 2: Người ta đặt ba điện tích q1 = 8.10-9C, q2 = q3 = -8.10-9C tại ba đỉnh của một tam giác đều ABC
cạnh a = 6cm trong không khí. Xác định lực tác dụng lên điện tích q0=6.10-9C đặt tại tâm O của tam giác. ĐS: F = 72.10-5N
PHƯƠNG PHÁP GIẢI BÀI TẬP HỌC PHẦN VẬT LÝ CHƯƠNG V: TĨNH ĐIỆN
Dạng 15: Nguyên lý chồng chất điện trường
A. Một vài lưu ý khi giải toán
1. Vectơ cường độ điện trường do điện tích điểm Q gây ra tại điểm cách Q một đoạn r r r 1 Q r 2 E = . . 4π ε ε.r r 0
2. Nguyên lý chồng chất điện trường ur uur uur uur E E = E + +... + E 1 2 n uur uur E .-- EÞ = E E + E 1 2 1 2 uur uuur E -¯ EÞ = E E- E . 1 2 1 2 uur uur 2 2 E E^ E Þ = E+ E 1 2 1 2 B. Phương pháp giải Các bước tiến hành:
Bước 1: Tìm xem ở điểm đang xét có bao nhiêu cường độ điện trường. Tính độ lớn và biểu diễn các
cường độ điện trường đó bằng vectơ. ur
Bước 2: Bằng phép vẽ dựa vào nguyên lý chồng chất, tìm vectơ cường độ điện trường tổng hợ E p
theo quy tắc tổng hợp vectơ n = ... + + E + E1 E2 Eur
Bước 3: Tìm cường độ điện trường tổng hợp E theo các cường độ thành phần E1, E2,… bằng phương pháp hình học. C. Bài tập mẫu
Hai điện tích q1 = 5.10-8C và q2 = -5.10-8C đặt tại hai điểm M, N cách nhau khoảng MN = 2a = 12c trong chân không. ur
a) Xác định vectơ cường độ điện trường E tại điểm A nằm trên đường trung trực MN, cách MN một khoảng b = OA = 8cm.
b) Xác định vị trí Ao trên đường trung trực để cường độ điện trường gây bởi q1, q2 tại đó là lớn nhất. Giải mẫu: E 1 q1 = 5.10-8C A q E 2 = -5.10-8C α MN = 2a = 12cm E 2 b = OA = 8cm uuur r1 b r2 a. E = ? A M α N
b. Xác định Ao để E Max = ? + - A a a O 0 q1 q2 uur
- Tại A có hai cường độ điện trường: cường độ điện trường E do điện 1 uur
tích q1 ở M gây ra, cường độ điện trường E do điện tích q2 ở N gây ra. 2 Có độ lớn: q E q 1 = 1 k ; E2 = 2 k 2 r 2 r 1 2
- Cường độ điện trường tổng hợp tại A: ur uur uur E = E + E 1 2 ur mà E1 = E2 nên
E có phương song song MN, có chiều từ M ® N Độ lớn E = 2 E q a q a 1cos α Þ 1 1 E = 2k . = 2k 2 2 2 2 3/ a +b 2 2 a +b (a +b ) 2 a. E = q a 1 2 k(a + b ) 2 = 54000 V/m 2 2 3/ ì - Điểm đặt: tại A ï ur Vậy ï E - Phương: MN í ï - Chiều: từ M đến N
ïî - Độ lớn: E = 54000V/m b. Ta có: E = q a 1 2k
Þ Emax Û (a2 + b2)3/2 min Û b = 0 2 2 3/ (a + b ) 2 q
Vậy khi Ao Oº thì Emax = 2k 1 = 250000 V/m 2 a D. Bài tập áp dụng
Bài 1: Cho tam giác ABC có AB = 3cm, AC = 4cm, BC = 5cm. Tại B có đặt qB = 3.10-8C, tại C có đặ ur
qC = -3.10-8C. Hãy xác định vectơ cường độ điện trường
E do qB, qC gây ra tại đỉnh A của tam giác. Cho e = 1
Bài 2: Tại 3 đỉnh của một tam giác đều ABC có đặt lần lượt các điện tích qA = qB = qC = 6.10-8C. Hãy ur
xác định vectơ cường độ điện trường E do cả ba điện tích nói trên gây ra tại trọng tâm của tam giác
Cho biết cạnh của tam giác bằng 6cm v e à = 1.
Bài 3: Có hai điện tích q1 = 2.10-9C và q2 = -2.10-9C được đặt trong không khí, cách nhau một khoả
AB = 6cm. Hãy xác định vectơ cường độ điện trường do q1, q2 gây ra tại điểm nằm trên đường trung
trực của AB và nhìn AB dưới một góc vuông.
PHƯƠNG PHÁP GIẢI BÀI TẬP HỌC PHẦN VẬT LÝ CHƯƠNG V: TĨNH ĐIỆN
Dạng 16: Bài toán áp dụng định lý O - G
A. Một vài lưu ý khi giải toán
“Điện thông gửi qua một mặt kín bất kỳ bằng tổng đại số các điện tích nằm trong mặt kín đó chia cho tích ee0” å iq Fe = i os E.dS.c α ò= (S) εε o B. Phương pháp giải
Khi điện trường có tính chất đối xứng (đối xứng cầu, đối xứng trụ, đối xứng phẳng) để xác định ur
vectơ E của điện trường đó thì áp dụng định lí O - G là phương pháp đơn giản ngắn gọn hơn phương
pháp tính theo nguyên lí chồng chất điện trường. Ta thực hiện tuần tự các bước sau đây:
Bước 1: Nhận xét về sự đối xứng trong sự phân bố của hệ điện tích. ur
Bước 2: Xác định dạng đối xứng của hệ đường sức và xác định quỹ tích những điểm mà vectơ E có ur
cùng độ lớn và bằng E tại điểm ta cần khảo sát.
Bước 3: Xây dựng mặt kín S (gọi là mặt Gauss) là quỹ tích nói trên. Nếu quỹ tích đó chưa tạo thàn
mặt kín thì ta làm kín lại bằng các mặt khác tùy ý sao cho việc tính toán là đơn giản nhất.
Bước 4: Tính từng vế của biểu thức định lí O - G để rút ra đại lượng cần xác định. C. Bài tập mẫu
Xác định cường độ điện trường của một mặt phẳng vô hạn tích điện đều với mật độ điện tích mặt σ > 0 . Giải mẫu:
Mặt phẳng vô hạn tích điện đều σ> 0 E = ? ur
- Vì điện tích phân bố đối xứng phẳng nên vectơ cường độ điện trường
E tại một điểm bất kỳ trong
điện trường sẽ có phương vuông góc với mặt phẳng mang điện, hướng ra xa khỏi mặt phẳng và độ lớn ur
E chỉ có thể phụ thuộc vào khoảng cách từ điểm đang xét tới mặt phẳng. Dễ dàng nhận thấy quỹ tíc
những điểm có cùng độ lớn của cường độ điện trường là hai mặt phẳng cùng song song và cách đều mặt phẳng tích điện. ur
- Do đó, để xác định vectơ cường độ điện trường E tại một điểm M, ta vẽ mặt kín S (mặt Gauss) như
sau: Vẽ qua M một mặt trụ kín mà điểm M thuộc vào một trong hai mặt phẳng đáy có diện tích Δ l S à ,
cả hai mặt đáy cùng song song và cách đều mặt phẳng tích điện, còn các đường sinh thì vuông góc vớ ur r
mặt phẳng như hình vẽ. Chú ý là tại mọi điểm trên hai mặt đáy ta thấy
E -- n, còn ở những điểm trên ur r mặt bên thì E ^ n.
- Áp dụng định lý O - G n q å i òur r i=1 EdS = Ñ ε ε ( ) S 0
Triển khai vế trái ta được: ur r n n EdS = E dS + E dS ò Ñ ò ò (S) mat ben hai day ur r
Mọi điểm trên hai đáy n E = E = const, ta thấy E -- n, còn mọi điểm trên mặt phẳng bên thì ur r E ^ n, E =0, do đó: n ur r n EdS = E dS = E.2 ΔS ò Ñ ò (S) hai day n Khai triển vế phải, q
å là tổng điện tích có trong mặt trụ kín này, đó chính là điện tích của phần i i=1
mặt phẳng được cắt bởi mặt trên của hình trụ (là phần điện tích bị gạch trong hình). Cho nên ở đây: n q å i σΔS i=1 = ε ε ε ε 0 0
- Ghép hai vế lại, ta có: ur r σ E = n 2.ε ε o
PHƯƠNG PHÁP GIẢI BÀI TẬP HỌC PHẦN VẬT LÝ CHƯƠNG V: TĨNH ĐIỆN
Dạng 16: Bài toán áp dụng định lý O - G
A. Một vài lưu ý khi giải toán
“Điện thông gửi qua một mặt kín bất kỳ bằng tổng đại số các điện tích nằm trong mặt kín đó chia cho tích ee0” å iq Fe = i os E.dS.c α ò= (S) εε o B. Phương pháp giải
Khi điện trường có tính chất đối xứng (đối xứng cầu, đối xứng trụ, đối xứng phẳng) để xác định ur
vectơ E của điện trường đó thì áp dụng định lí O - G là phương pháp đơn giản ngắn gọn hơn phương
pháp tính theo nguyên lí chồng chất điện trường. Ta thực hiện tuần tự các bước sau đây:
Bước 1: Nhận xét về sự đối xứng trong sự phân bố của hệ điện tích. ur
Bước 2: Xác định dạng đối xứng của hệ đường sức và xác định quỹ tích những điểm mà vectơ E có ur
cùng độ lớn và bằng E tại điểm ta cần khảo sát.
Bước 3: Xây dựng mặt kín S (gọi là mặt Gauss) là quỹ tích nói trên. Nếu quỹ tích đó chưa tạo thàn
mặt kín thì ta làm kín lại bằng các mặt khác tùy ý sao cho việc tính toán là đơn giản nhất.
Bước 4: Tính từng vế của biểu thức định lí O - G để rút ra đại lượng cần xác định. C. Bài tập mẫu
Xác định cường độ điện trường của một mặt phẳng vô hạn tích điện đều với mật độ điện tích mặt σ > 0 . Giải mẫu:
Mặt phẳng vô hạn tích điện đều σ> 0 E = ? ur
- Vì điện tích phân bố đối xứng phẳng nên vectơ cường độ điện trường
E tại một điểm bất kỳ trong
điện trường sẽ có phương vuông góc với mặt phẳng mang điện, hướng ra xa khỏi mặt phẳng và độ lớn ur
E chỉ có thể phụ thuộc vào khoảng cách từ điểm đang xét tới mặt phẳng. Dễ dàng nhận thấy quỹ tíc
những điểm có cùng độ lớn của cường độ điện trường là hai mặt phẳng cùng song song và cách đều mặt phẳng tích điện. ur
- Do đó, để xác định vectơ cường độ điện trường E tại một điểm M, ta vẽ mặt kín S (mặt Gauss) như
sau: Vẽ qua M một mặt trụ kín mà điểm M thuộc vào một trong hai mặt phẳng đáy có diện tích Δ l S à ,
cả hai mặt đáy cùng song song và cách đều mặt phẳng tích điện, còn các đường sinh thì vuông góc vớ ur r
mặt phẳng như hình vẽ. Chú ý là tại mọi điểm trên hai mặt đáy ta thấy
E -- n, còn ở những điểm trên ur r mặt bên thì E ^ n.
- Áp dụng định lý O - G n q å i òur r i=1 EdS = Ñ ε ε ( ) S 0
Triển khai vế trái ta được: ur r n n EdS = E dS + E dS ò Ñ ò ò (S) mat ben hai day ur r
Mọi điểm trên hai đáy n E = E = const, ta thấy E -- n, còn mọi điểm trên mặt phẳng bên thì ur r E ^ n, E =0, do đó: n ur r n EdS = E dS = E.2 ΔS ò Ñ ò (S) hai day n Khai triển vế phải, q
å là tổng điện tích có trong mặt trụ kín này, đó chính là điện tích của phần i i=1
mặt phẳng được cắt bởi mặt trên của hình trụ (là phần điện tích bị gạch trong hình). Cho nên ở đây: n q å i σΔS i=1 = ε ε ε ε 0 0
- Ghép hai vế lại, ta có: ur r σ E = n 2.ε ε o
PHƯƠNG PHÁP GIẢI BÀI TẬP HỌC PHẦN VẬT LÝ CHƯƠNG V: TĨNH ĐIỆN
Dạng 16: Tính điện thế do hệ điện tích điểm gây ra tại một điểm
A. Một vài lưu ý khi giải toán
1. Điện thế do điện tích điểm q gây ra tại điểm M cách q một đoạn r q VM= 4π ε ε.r 0 M
2. Điện thế do hệ điện tích điểm q gây ra tại điểm M VM = V1M + V2M + ...+ VnM B. Phương pháp giải
a. Trường hợp đơn giản Q
- Nếu biết Q (gây ra V) thì dùng: V = k εr A
- Nếu biết công A và q thì dùng: V= ( B B¥ q¥vì V¥ = 0)
b. Trường hợp điện thế ở một điểm gây bởi nhiều điện tích
- Tính tổng đại số các điện thế gây bởi mỗi điện tích tại điểm đó: qi V = V = k å åi ε r i i i
- Đặc biệt: Quả cầu kim loại tích điện: vì lí do đối xứng nên coi như điện tích tập trung ở tâm quả cầu: Q
+ Điện thế trên mặt cầu: V = k (R: bán kính quả cầu). R
+ Điện thế ở một điểm M (OM = r) ngoài quả cầu trong môi trường (ε ) Q V M = k εr C. Bài tập mẫu Có 2 điện tích điểm -8 -8 q = 8.10 C , q = -3.10 C
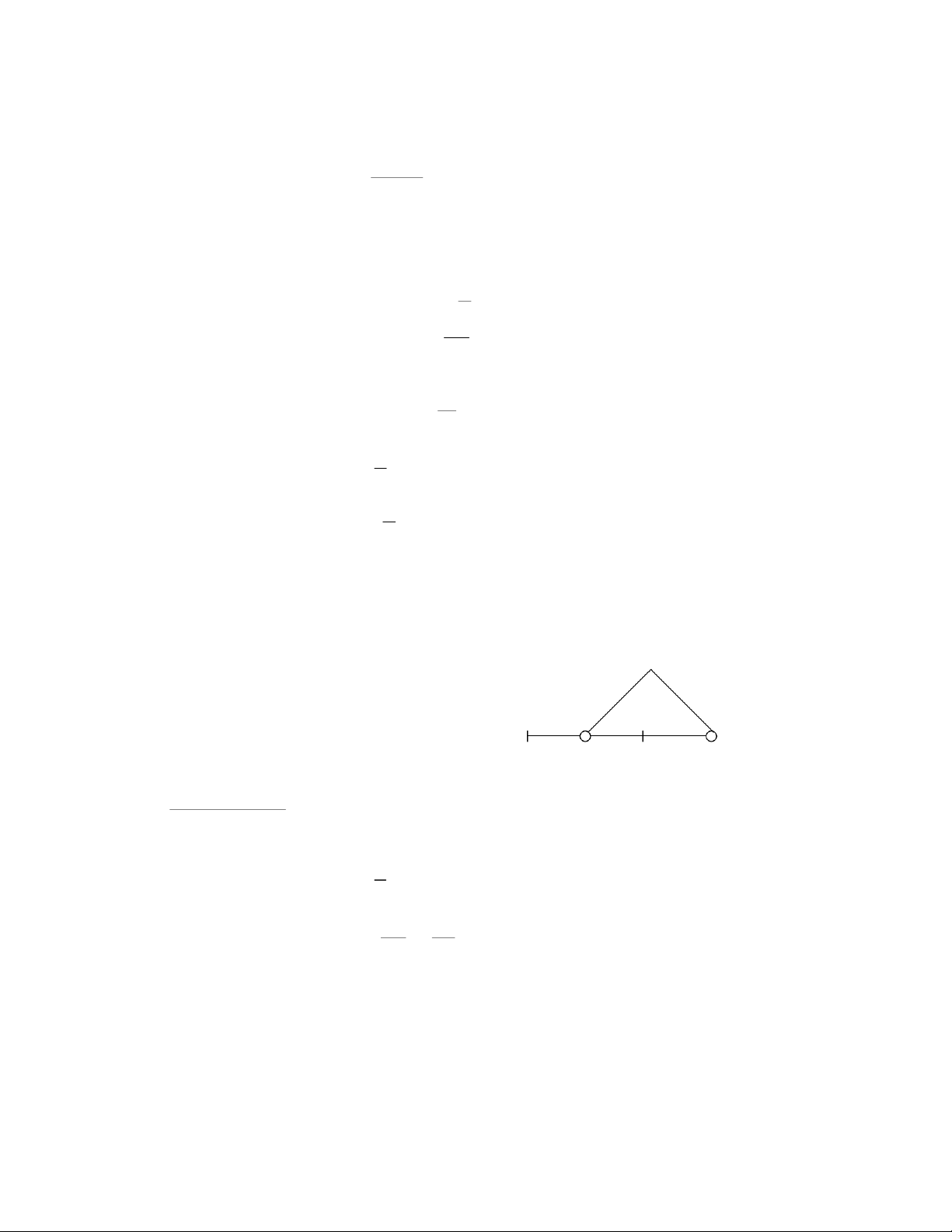
được đặt trong không khí tại hai điểm M, N cách 1 2
nhau một khoảng d = 10cm. Tính điện thế gây bởi các điện tích q , q tại các điểm A, B, C. Cho biết 1 2
MA = 4cm, MB = 5cm, MC = 9cm, NA = 6cm, NC = 7cm. Giải mẫu: q1 = 8.10-8C C q2 = -3.10-8C d = MN = 10cm MA = 4cm q MB = 5cm 1 Q2 + - MC = 9cm B M A N NA = 6cm NC = 7cm q = 5.10-10C VA; VB; VC = ?
- Điện thế gây bởi 1 điện tích điểm tại điểm cách nó một khoảng r Q V = k ( )ε = 1 r
- Điện thế gây bởi các điện tích q , q tại A: 1 2 q q 1 2 V = k + k = 13500 V A ( ) MA NA
- Điện thế gây bởi các điện tích q , q tại B: 1 2 q q 1 2 V = k + k = 12600 V B ( ) MB NB
- Điện thế gây bởi các điện tích q , q tại C : 1 2 q q 1 2 V = k + k = 4143 V C ( ) MC NC D. Bài tập áp dụng
Có một hệ điện tích điểm q1 = 12.10-9C, q2 = -6.10-9C và q3 = 5.10-9C đặt tại ba đỉnh của mộ
tam giác đều, mỗi cạnh 20cm. Xác định điện thế do hệ điện tích điểm trên gây ra tại tâm của tam giác.
PHƯƠNG PHÁP GIẢI BÀI TẬP HỌC PHẦN VẬT LÝ CHƯƠNG V: TĨNH ĐIỆN
Dạng 16: Tính hiệu điện thế giữa hai điểm
A. Một vài lưu ý khi giải toán
Hiệu điện thế giữa hai điểm M, N UMN = VM - VN B. Phương pháp giải
Hiệu điện thế giữa 2 điểm
a. Nếu biết các điện thế V , V thì U = V - V B C BC B C A
b. Nếu biết công A và q thì BC U = BC BC q ur
c. Nếu biết điện trường E và khoảng cách d giữa B,C theo phương E thì U = E.d C. Bài tập mẫu Có 2 điện tích điểm -8 -8 q = 8.10 C , q = -3.10 C
được đặt trong không khí tại hai điểm M, N cách 1 2
nhau một khoảng d = 10cm. Tính hiệu điện thế giữa hai điểm A và B; B và C. Cho biết MA = 4cm,
MB = 5cm, MC = 9cm, NA = 6cm, NC = 7cm. Giải mẫu: q1 = 8.10-8C C q2 = -3.10-8C d = MN = 10cm MA = 4cm q MB = 5cm 1 q2 + - MC = 9cm B M A N NA = 6cm NC = 7cm UAB; UBC = ?
- Điện thế gây bởi các điện tích q , q tại A: 1 2 q q 1 2 V = k + k = 13500 V A ( ) MA NA
- Điện thế gây bởi các điện tích q , q tại B: 1 2 q q 1 2 V = k + k = 12600 V B ( ) MB NB
- Điện thế gây bởi các điện tích q , q tại C : 1 2 q q 1 2 V = k + k = 4143 V C ( ) MC NC
- Hiệu điện thế giữa hai điểm A, B: U 900 = V - V = V AB A B ( )
- Hiệu điện thế giữa hai điểm B, C: U 845 = 7 V - V = V BC B C ( )
PHƯƠNG PHÁP GIẢI BÀI TẬP HỌC PHẦN VẬT LÝ
CHƯƠNG VI: TỪ TRƯỜNG VÀ SÓNG ĐIỆN TỪ
Dạng 19: Nguyên lý chồng chất từ trường
A. Một vài lưu ý khi giải toán
1. Vectơ cảm ứng từ gây ra bởi dòng điện thẳng, dài vô hạn tại một điểm cách dây dẫn một đoạn r
+ Chiều được xác định theo quy tắc nắm tay phải + Độ lớn: I 7 B 2.10- = . r
2. Nguyên lý chồng chất từ trường ur uur uur uur B B = B + +... + nB 1 2 uur uur B -- BÞ = B B + B 1 2 1 2 uur uur B -¯ BÞ = B - B B 1 2 1 2 uur uur 2 2 B B^ B Þ = B+ B 1 2 1 2 B. Phương pháp giải Các bước tiến hành:
Bước 1: Tìm xem ở điểm đang xét có bao nhiêu vectơ cảm ứng từ. Tính độ lớn và biểu diễn các cảm
ứng từ đó bằng vectơ. ur
Bước 2: Bằng phép vẽ dựa vào nguyên lý chồng chất, tìm vectơ cảm ứng từ tổng h Bợ p t heo quy tắc tổng hợp vectơ ur uur uur uur 1 2 ... B B = B + + + B n
Bước 3: Tìm cảm ứng từ tổng hợp B theo các cảm ứng từ thành phần B1, B2,… bằng phương pháp hình học. C. Bài tập mẫu
Hai dây dẫn thẳng dài vô hạn cách nhau a = 10cm trong không khí, trong đó có hai dòng điện cù
cường độ I1 = I2 = 5A chạy ngược chiều nhau. Xác định cảm ứng từ tại điểm M cách đều hai dòng điện một khoảng a = 10cm. Giải mẫu: I1 = 5A I2 = 5A M ur a = 10cm uur uuur 2 B B B = ? 1 M r uuur 1 r2 B uur M .
- Tại M có hai vectơ cảm ứng từ: cảm ứng từ
B do dòng điện I1 gây ra, 1 uur X a
cảm ứng từ B do dòng điện I I1 I2
2 gây ra. Có chiều được xác định dựa theo 2
quy tắc nắm tay phải và có độ lớn: - I 7 B B= = 2.10 . 1 2 a
- Vectơ cảm ứng từ tổng hợp tại M: ur uur uur B = B + B 1 2 ur ur ur mà B1 = B2 và ( nên 1 2 , ) 120 o B B = M
B có phương vuông góc với đoạn thẳng nối 2 dây dẫn I1I2, có
chiều từ hướng từ trên xuống. Độ lớn - 5 B = 1 B = B 2 = 10 T M ( ) ì - Điểm đặt: tại M ï ur
- Phương: vuông góc với đường thẳng Vậy ï M B í nối I1I2
ï - Chiều: từ trên xuống
ïî - Độ lớn: BM = 10-5(T) D. Bài tập áp dụng
Bài 1: Cho hai dòng điện cùng cường độ I1 = I2 = 4A chạy trong hai dây dẫn thẳng dài vô hạn, ché
nhau và vuông góc với nhau trong chân không, khoảng cách đường vuông góc chung MN = 8cm. X
định cảm ứng từ tại trung điểm của đường vuông góc chung ấy.
Bài 2: Một dòng điện cường độ I = 6A chạy trong một dây điện uống thành hình vuông có cạnh a ur
10cm. Xác định vectơ cảm ứng từ B gây ra tại tâm O của mạch điện đó.
Bài 3: Một dây dẫn được quấn thành một tam giác đều, mỗi cạnh là a = 50cm. Dòng điện chạy tron ur
dây dẫn đó có cường độ I= 3,14A. Xác định vectơ cảm ứng từ B tại tâm tam giác đó.
Bài 4: Cho hai dòng điện thẳng dài vô hạn đặt cách nhau 5cm, cường độ của hai dòng điện đó bằ ur
nhau và bằng 10A. Xác định vectơ cảm ứng từ B gây ra bởi các dòng điện đó tại một điểm A nằm
giữa hai dòng điện trong các trường hợp:
a. Các dòng điện song song với nhau, chạy cùng chiều.
b. Các dòng điện song song với nhau, chạy ngược chiều.