Phương Pháp Giải Hình 9 Dấu Hiệu Nhận Biết Tiếp Tuyến Của Đường Tròn

Bài 5. DẤU HIỆU NHẬN BIẾT TIẾP TUYẾN CỦA ĐƯỜNG TRÒN
A. KIẾN THỨC TRỌNG TÂM
▪ Dấu hiệu 1: Nếu một đường thẳng đi qua một điểm thuộc đường tròn và vuông góc với bán
kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
▪ Dấu hiệu 2: Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của
đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Chứng minh một đường thẳng là tiếp tuyến của đường tròn
▪ Để chứng minh đường thẳng a là tiếp tuyến của đường tròn (O; R) tại tiếp điểm C, ta có
thể làm theo một trong hai cách
▪ Cách 1: Chứng minh C nằm trên (O) và OC ⊥ a tại C.
▪ Cách 2: Kẻ OH ⊥ a tại H và chứng minh OH = OC = R .
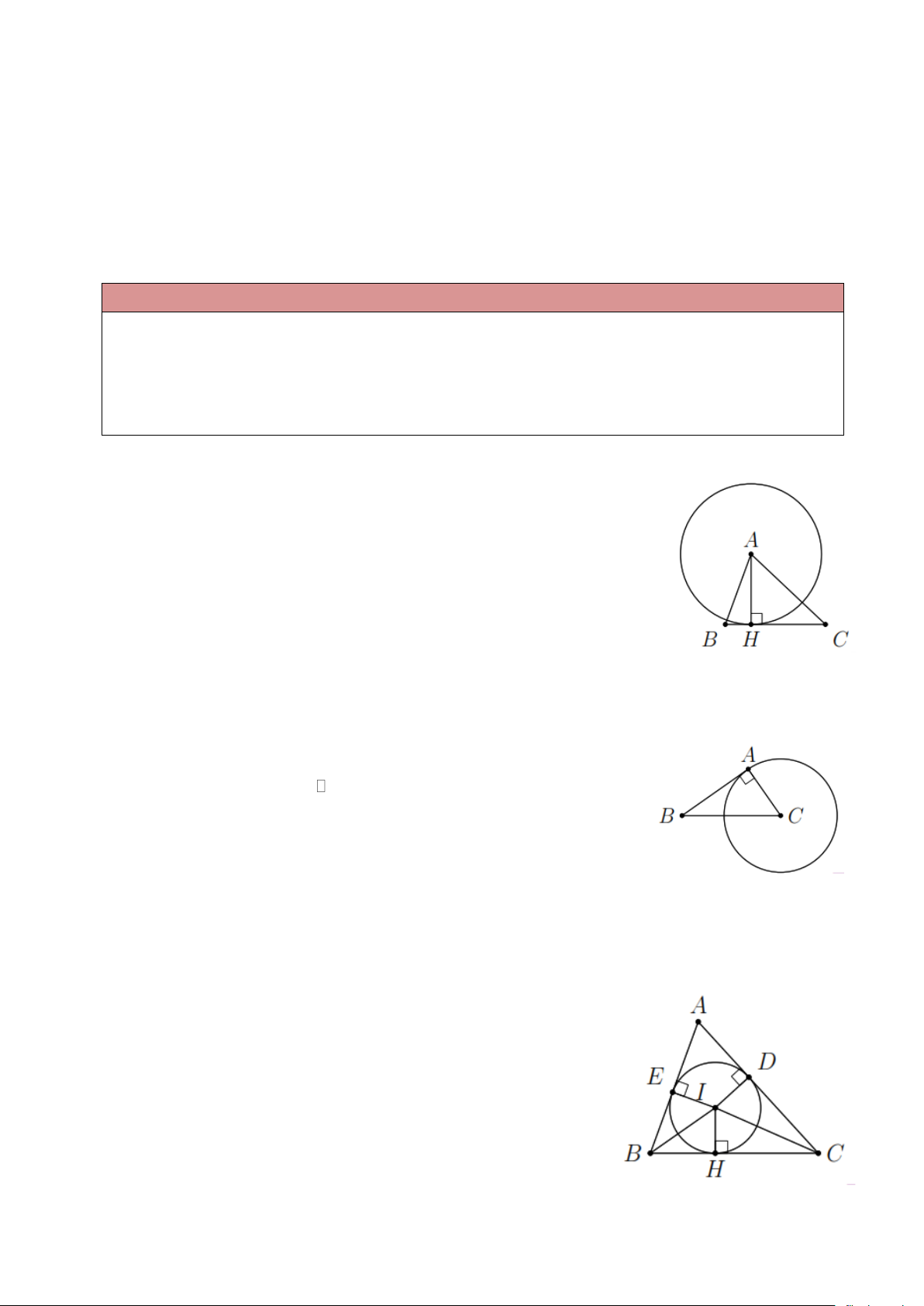
Ví dụ 1. Cho tam giác ABC có ba góc nhọn, kẻ đường cao AH , vẽ đường tròn ( ; A AH ) . Chứng
minh BC là tiếp tuyến của đường tròn ( ) A . Lời giải Do H  ( )
A và AH ⊥ BC tại H nên BC là tiếp tuyến của đường tròn ( ) A .
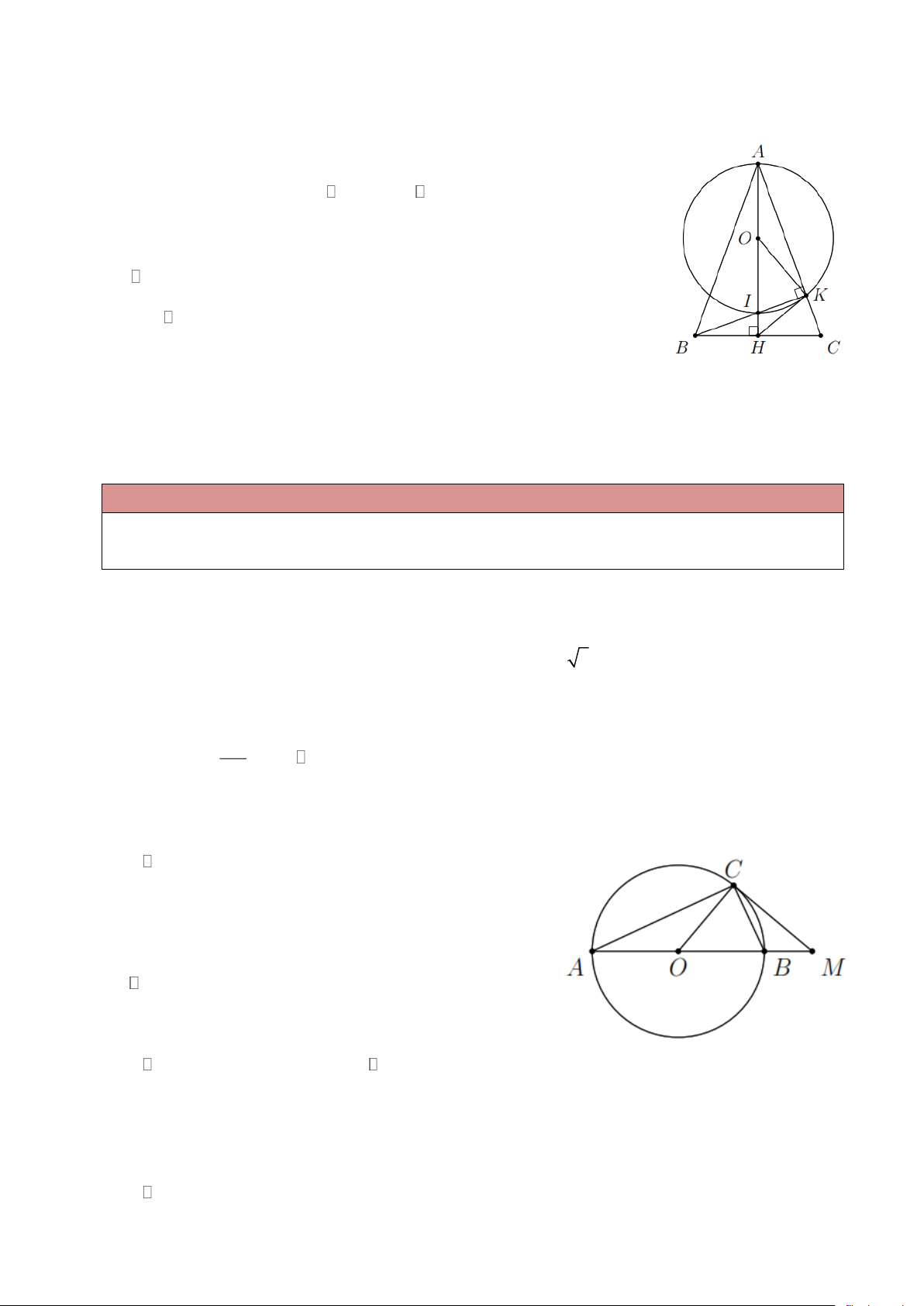
Ví dụ 2. Cho tam giác ABC có BC = 5 cm, CA = 4 cm, AB = 3 cm. Vẽ đường tròn (C;C ) A . Chứng
minh BA là tiếp tuyến của đường tròn (C) . Lời giải Do 2 2 2
BC = CA + AB nên ABC vuông tại A (theo định lí Pi-ta-go đảo).
Suy ra BA ⊥ CD mà A (C) nên BA là tiếp tuyến của đường tròn (C) .
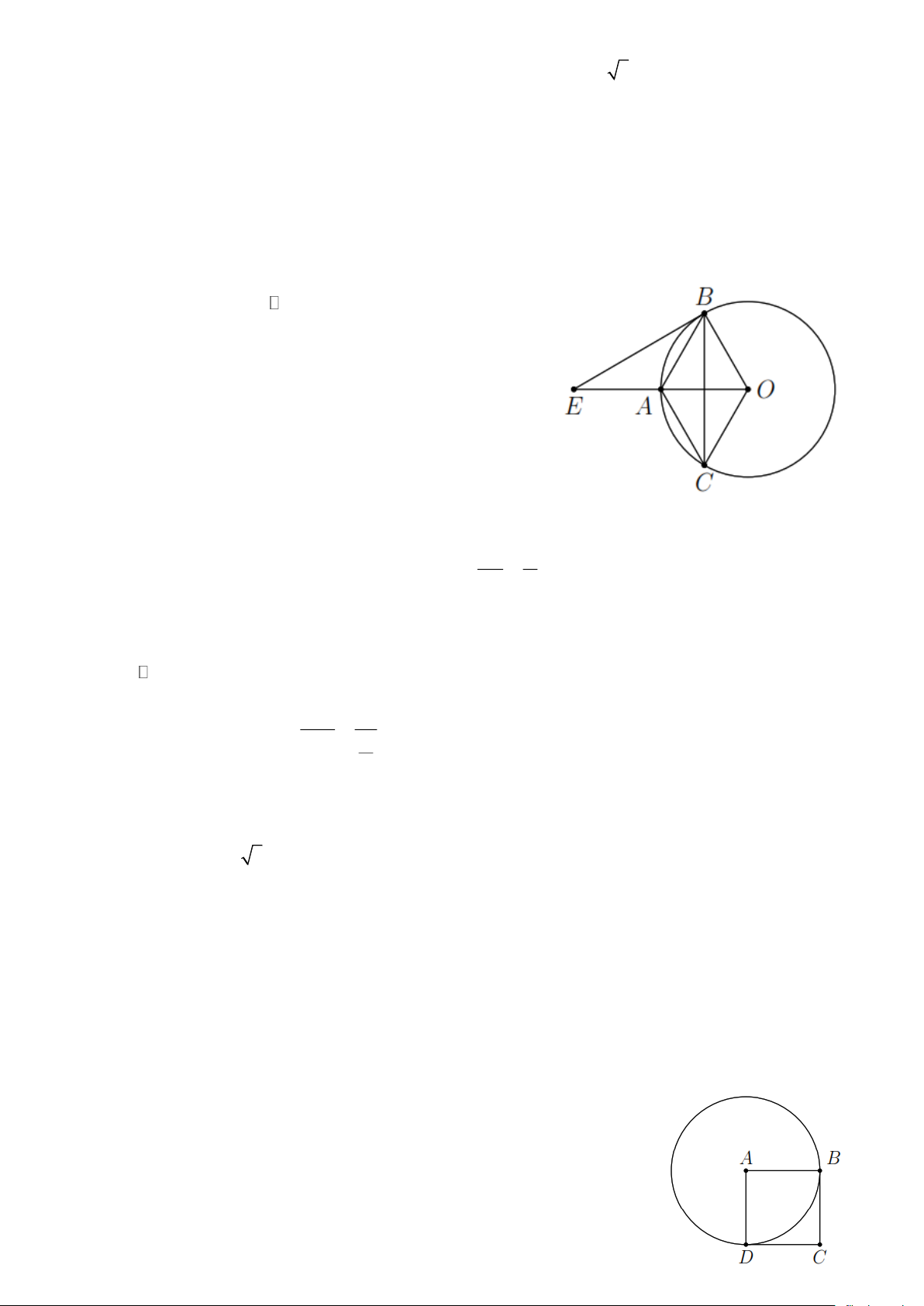
Ví dụ 3. Cho tam giác ABC , các đường phân giác trong ˆB , ˆ
C cắt nhau tại I . Gọi H là hình
chiếu của I trên BC , vẽ đường tròn tâm I , bán kính IH . Chứng minh AB , AC tiếp xúc với (I ) . Lời giải
Kẻ ID ⊥ AC tại D , IE ⊥ AB tại E thì IE = ID = IH .
Suy ra E , D  (I ) mà ID , IE lần lượt vuông góc với AC , AB
nên AC , AB là tiếp tuyến của (I ) .
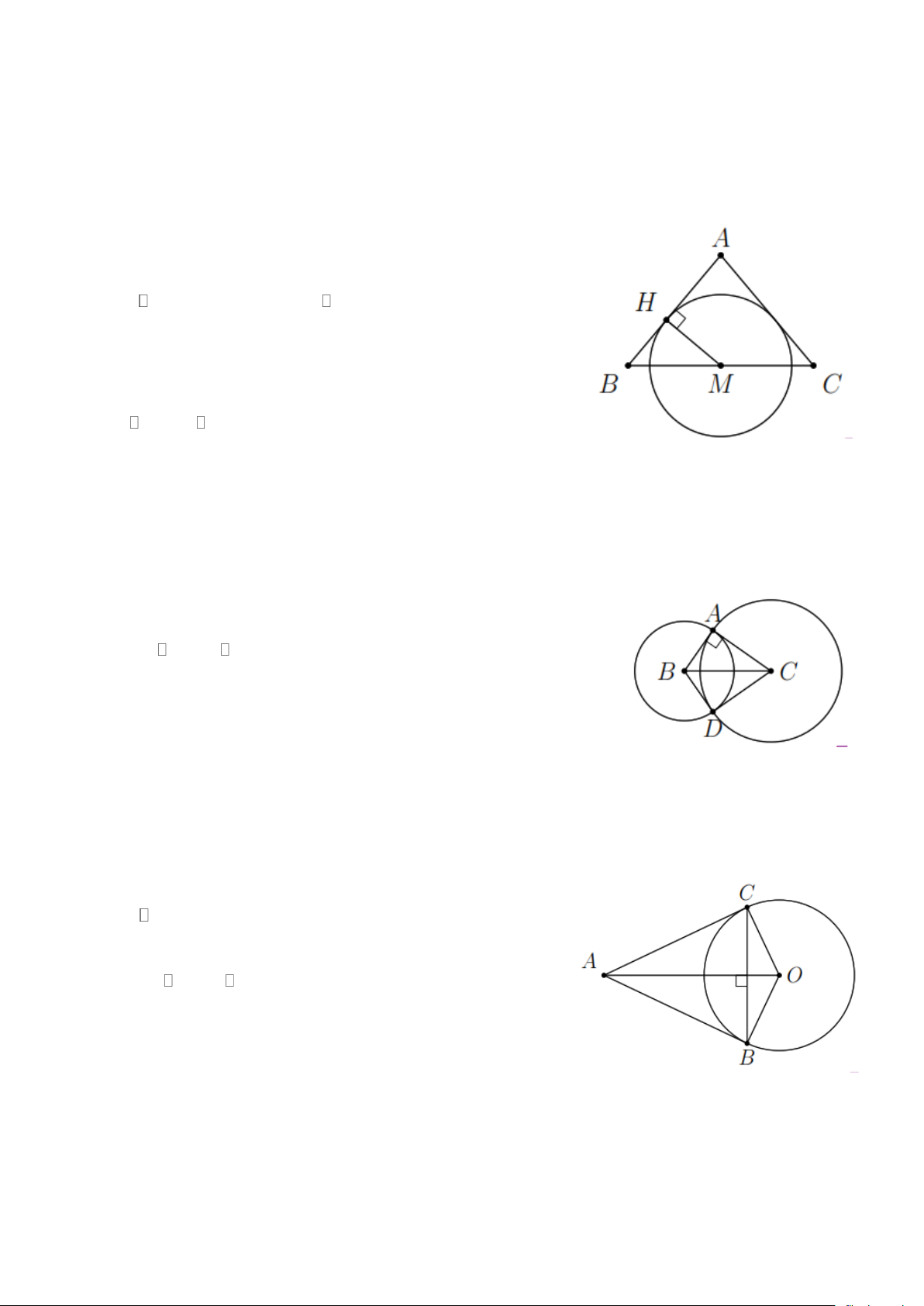
Ví dụ 4. Cho tam giác ABC cân tại A có các đường cao AH và
BK cắt nhau tại I . Chứng minh Trang 1
a) Đường tròn tâm O đường kính AI đi qua K ;
b) HK là tiếp tuyến của đường tròn (O) . Lời giải
a) Do BK là đường cao của ABC nên AKI vuông tại K .
Mà O là trung điểm của AI nên AO = IO = KO kéo theo K  (O) .
b) KBC vuông tại K có H là trung điểm BC  HK = HB = HC .
Suy ra HKC cân tại H .
Do đó OKA HKC OAK HCK 90 + = + = . Dẫn tới HKO 90 =  HK ⊥ OK .
Suy ra HK là tiếp tuyến của đường tròn (O) .
Dạng 2: Bài toán liên quan đến tính độ dài
▪ Nối tâm với tiếp điểm để vận dụng định lý về tính chất của tiếp tuyến và sử dụng các
công thức về hệ thức lượng trong tam giác vuông để tính độ dài.
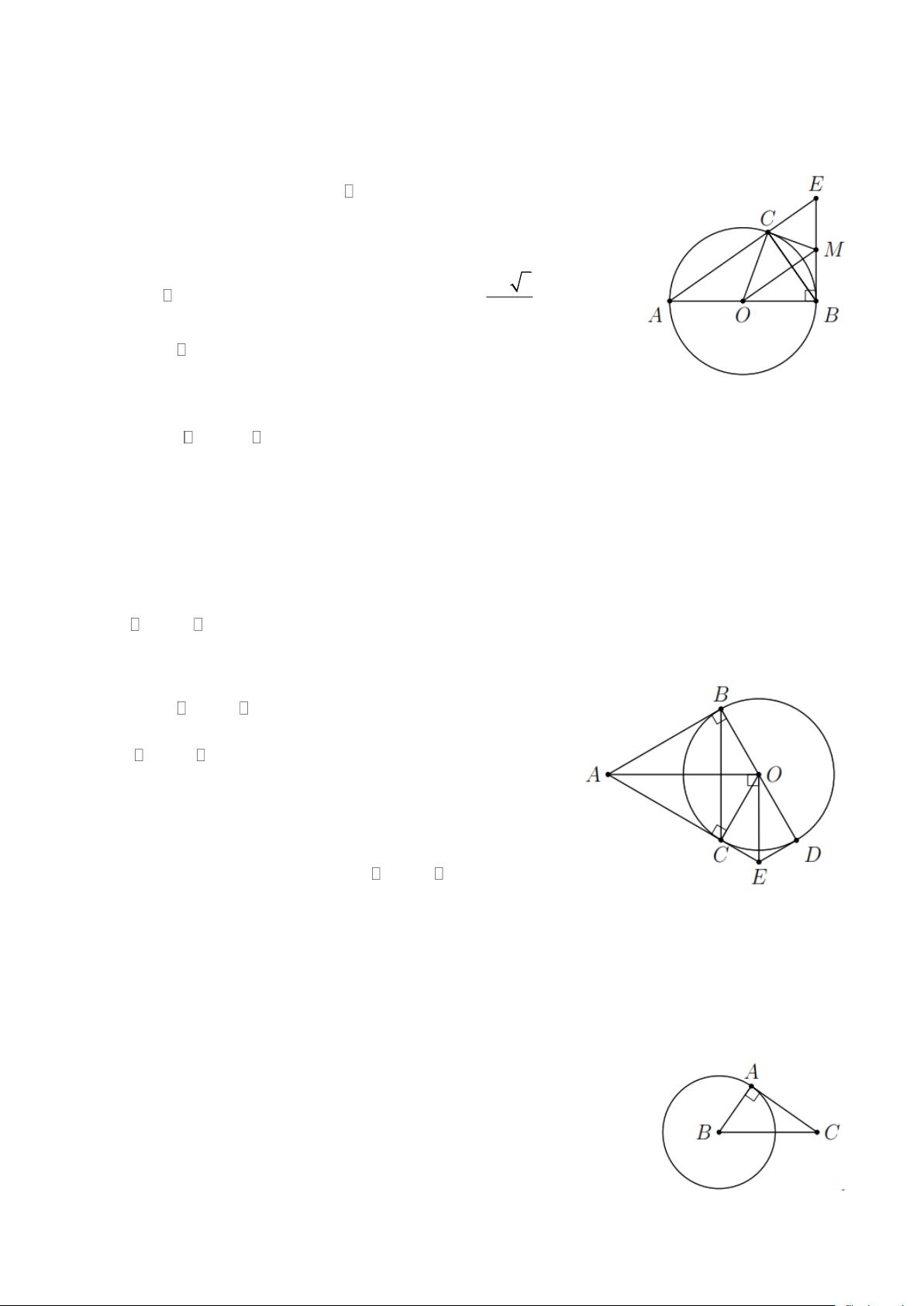
Ví dụ 5. Cho đường tròn (O; R) đường kính AB . Vẽ dây AC sao cho CAB 30 = . Trên tia đối của
tia BA lấy điểm M sao cho BM = R . Chứng minh
a) MC là tiếp tuyến của (O) ; b) MC = R 3 . Lời giải  AB  a) Do C  ; O 
 nên ABC vuông tại C  2 
Suy ra CBA 90 CAB 90 60 30 = − = − = . Xét ABC có
AB = BC = R   CA  B = 60
 ABC đều tại A .
Suy ra BC = OB = R .
Xét OMC có BC = BO = BM  OMC vuông tại C  MC ⊥ OC tại C .
Suy ra MC là tiếp tuyến của (O) .
b) Do B  OM nên OM = BM + OB = 2R .
Xét MCO vuông tại O có 2 2 2
MC + CO = OM . Trang 2 Suy ra 2 2 2 2 2 2 2
MC = OM − CO  MC = (2R) − R = 3R  MC = R 3 .
Ví dụ 6. Cho đường tròn tâm O có bán kính OA = R , dây BC vuông góc với OA tại trung điểm M của OA .
a) Tứ giác OCAB là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại B , cắt đường thẳng OA tại E . Tính độ dài BE theo R . Lời giải
a) Do OB = OC nên OBC cân tại O .
Mà OA là đường cao (do OC ⊥ AB ), suy ra OA là
đường trung trực của BC . Tứ giác OCAB có
▪ OA là đường trung trực của BC;
▪ M là trung điểm của OA.
Suy ra OCAB là hình thoi. OA R
b) Ta có M là trung điểm của OA suy ra OM = = . 2 2
Mà BE là tiếp tuyến của (O) tại B OBE 90  = .
Do OBE vuông tại B có BM là đường cao nên 2 2 OB R 2
OE OM = OB  OE = = = 2R . OM R 2 Mà 2 2 2
BE + BO = EO , suy ra 2 2 2 2 2 2
BE = EO − BO = (2R) − R = 3R .
Kéo theo BE = R 3 . C. BÀI TẬP VẬN DỤNG
Bài 1. Cho hình vuông ABCD . Vẽ đường tròn tâm A , bán kính AB . Chứng minh
a) CB là tiếp tuyến của đường tròn ( ) A ;
b) CD là tiếp tuyến của đường tròn ( ) A . Lời giải
a) Do BA là bán kính của ( ) A và CBA 90 =
nên CB là tiếp tuyến của đường tròn ( ) A .
b) Ta có AD = BA = R  D  ( ) A mà CDA 90 = . Trang 3
Suy ra CD là tiếp tuyến của đường tròn ( ) A .
Bài 2. Cho tam giác ABC cân tại A . Gọi M là trung điểm của BC và H là hình chiếu vuông góc
của M trên AB . Vẽ đường tròn (M ; MH ) . Chứng minh AC tiếp xúc với (M ) . Lời giải
Kẻ MK ⊥ AC tại K .
Do MKC vuông tại K và MHB vuông tại H nên MC = MB   KCM = HBM.
 MKC = MHB (ch gn)  MK = MH mà MK ⊥ AC tại K .
Kéo theo AC tiếp xúc với (M ; MH ) tại K .
Bài 3. Cho tam giác ABC vuông tại A . Vẽ đường tròn (B; B )
A và đường tròn (C;C ) A , chúng cắt
nhau tại điểm D ( D khác A ). Chứng minh CD là tiếp tuyến của đường tròn (B) . Lời giải
Ta có ABC = DBC (c  c c) suy ra BAC BDC 90 = = .
Kéo theo D  (B)  CD là tiếp tuyến của (B) .
Bài 4. Cho đường tròn (O) và điểm A nằm ngoài (O) . Kẻ tiếp tuyến AB với (O) ( B là tiếp
điểm). Qua B kẻ đường thẳng vuông góc với OA , cắt (O) tại C . Chứng minh AC là tiếp tuyến
của đường tròn (O) . Lời giải
Do OBC cân tại O và OA ⊥ BC nên AO là đường trung
trực của BC  AB = AC .
Suy ra OAB = OAC (c  c c). ACO ABO 90  = = ( ABO 90 =
do AB là tiếp tuyến của (O) ).
Kéo theo AC là tiếp tuyến của (O) .
Bài 5. Cho đường tròn tâm (O) , đường kính AB = 2R và d là tiếp tuyến tại B của (O) . Trên (O)
lấy điểm C sao cho BC = R , tia AC cắt d tại E .
a) Tính số đo các góc của tam giác ABC ; Trang 4
b) Tính độ dài BE theo R ;
c) Gọi M là trung điểm của BE . Chứng minh MC là tiếp tuyến của (O) . Lời giải
a) Do OC = OB = BC = R nên OBC đều.
Từ đó, ta tính được ABC 60 = , ACB 90 = , BAC 60 = .  2R 3
b) Xét ABE vuông tại B có BE = BA tan 30 = . 3
c) Ta có CBE vuông tại C có M là trung điểm BE .
Suy ra CM = BM = BE .
Kéo theo OCM = OBM (c c  c) OCM 90  = .
Dẫn tới MC là tiếp tuyến của (O) .
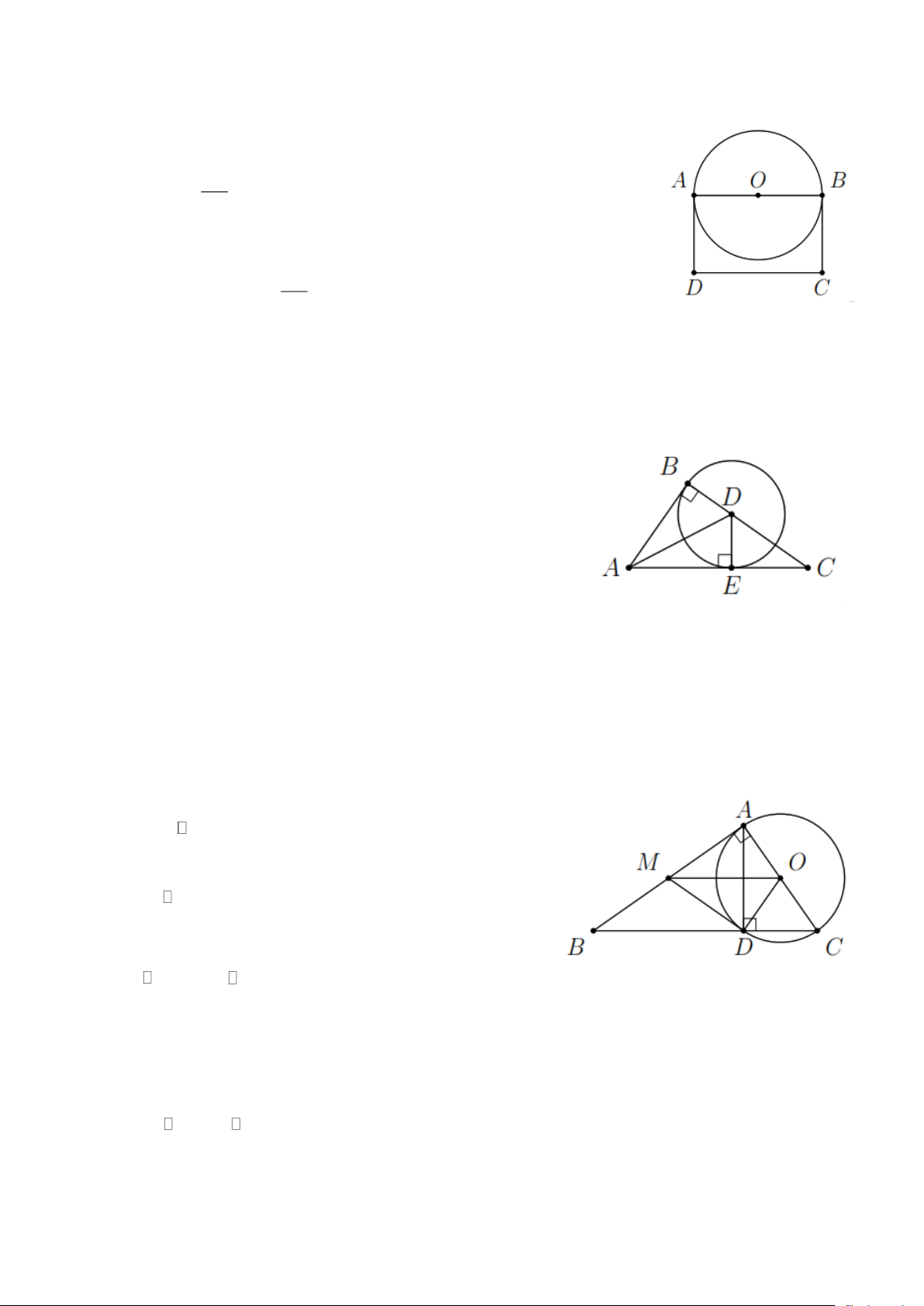
Bài 6. Cho đường tròn (O, R) và điểm A nằm ngoài (O) . Kẻ các tiếp tuyến AB , AC ( B , C là
các tiếp điểm) và đường kính BOD của (O) . Đường thẳng qua O và vuông góc với OA cắt AC tại E . Chứng minh a) ABO = ACO ;
b) OE là tia phân giác của COD ;
c) ED là tiếp tuyến của (O) . Lời giải
a) Ta có CAO = BAO (ch cgv).
b) CAO = BAO  BOA = COA nên OA là tia phân giác
của BOC , mà OE ⊥ OA
Suy ra OE là tia phân giác của COD .
c) Từ phần b) ta chứng minh được OCE = ODE (c  g c). ODE 90  =
, suy ra ED là tiếp tuyến của (O) . D. BÀI TẬP VỀ NHÀ
Bài 7. Cho tam giác ABC vuông tại A , vẽ đường tròn (B; B )
A . Chứng minh AC là tiếp tuyến của đường tròn (B) . Lời giải
Do A (B) và AC ⊥ BA tại A nên CA là tiếp tuyến của đường tròn (B) . Trang 5
Bài 8. Cho hình chữ nhật ABCD , vẽ đường tròn tâm O , đường kính AB . Chứng minh DA , BC là
các tiếp tuyến của đường tròn (O) . Lời giải  AB  Do A ; O 
 và AD ⊥ OA tại A nên AD là tiếp tuyến của đường  2  tròn (O) .  AB  Tương tự, do B  ; O 
 và BC ⊥ OB tại B nên BC là tiếp tuyến  2 
của đường tròn (O) .
Bài 9. Cho tam giác ABC vông tại B , tia phân giác góc A cắt BC tại D . Vẽ đường tròn tâm D ,
bán kính DB . Chứng minh AC tiếp xúc với đường tròn (D) . Lời giải
Kẻ DE ⊥ AC tại E , khi đó DE = DB .
Suy ra E  (D) mà DE vuông góc với AC nên AC là tiếp tuyến của (D) .
Bài 10. Cho tam giác ABC vuông tại A , kẻ đường cao AD . Gọi M là trung điểm của AB . Chứng minh
a) Đường tròn tâm O đường kính AC đi qua D ;
b) MD là tiếp tuyến của đường tròn (O) . Lời giải a) Xét
ADC vuông tại D có O là trung điểm
AC  OD = OA = OC  D  (O) .
b) Xét ADB vuông tại D có M là trung điểm AB
 MD = MA = MB .
Xét OAM và ODM có O  A = OD  AM = DM OM  laø caïnh chung. 
Suy ra OAM = ODM (c  c c) Kéo theo OAM ODM 90 = =
dẫn tới MD là tiếp tuyến của (O) . Trang 6
Bài 11. Cho đường tròn (O, R) có dây AB không là đường kính. Qua O kẻ đường thẳng vuông
góc với AB , cắt tiếp tuyến tại A của (O) ở điểm C .
a) Chứng minh CB là tiếp tuyến của (O) ;
b) Cho bán kính của (O) bằng 15 cm và dây AB = 24 cm. Tính độ dài đoạn thẳng OC . Lời giải
a) Do OA = OB nên OAB cân tại O .
Mà OC là đường cao (do OC ⊥ AB )  OC là đường
trung trực của AB .
Suy ra CA = CB .
Xét AOC và BOC có OA  = OB C  A = CB OC  laø caïnh chung. 
Suy ra AOC = BOC (c  c c) CBO CAO 90  = =
 CB ⊥ OB tại B
Kéo theo CB là tiếp tuyến của O .
b) Gọi H là giao điểm của OC và AB .
Khi đó, do OC là đường trung trực của AB nên H là trung điểm của AB . AB 24 Suy ra AH = = =12 cm. 2 2
Mà OAH vuông tại H nên 2 2 2
AH + HO = OA , suy ra 2 2
HO = OA − AH = 9 cm.
OAC vuông tại A có AH là đường cao nên 2
OC OH = AO . 2 2 AO 15 Do đó OC = = = 25 cm. CH 9
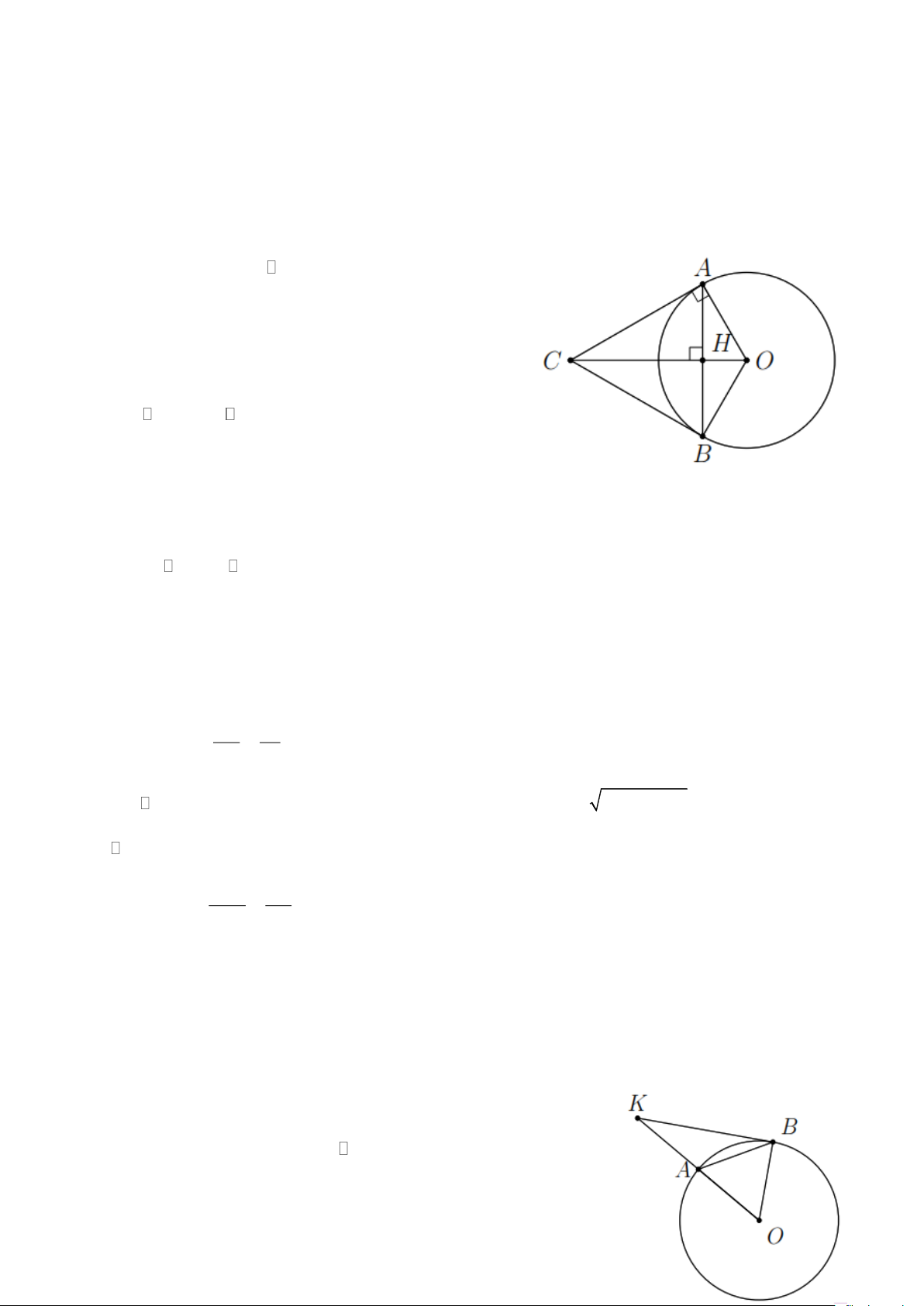
Bài 12. Cho đường tròn tâm O có bán kính OA = R , vẽ dây AB sao cho AB = R . Gọi K là điểm
đối xứng với O qua A .
a) Chứng minh KB là tiếp tuyến của (O) ;
b) Tính độ dài đoạn thẳng KB theo R . Lời giải
a) Do KA = BA = OA = R nên KBO vuông tại B .
Suy ra KB ⊥ BO tại B hay KB là tiếp tuyến của (O) . Trang 7
b) Áp dụng Định lí Pi-ta-go cho KBO vuông tại B , ta có 2 2 2 2 2 2
KB = KO − OB = (2R) − R = 3R  KB = R 3 . --- HẾT --- Trang 8