Phương Pháp Giải Hình 9 Diện Tích Hình Tròn Hình Quạt Tròn

Bài 9. DIỆN TÍCH HÌNH TRÒN – HÌNH QUẠT TRÒN
A. KIẾN THỨC TRỌNG TÂM
1. Diện tích hình tròn
▪ Diện tích S của một hình tròn bán kính R được tính theo công thức 2 S =  R .
2. Diện tích hình quạt tròn
▪ Diện tích hình quạt tròn bán kính R, cung n được tính theo công thức 2   R n l  R S = hay S = . 360 2
( l là độ dài cung n của hình quạt tròn).
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Bài 1. Lấy giá trị gần đúng của  là 3,14 , hãy điền vào ô trống trong bảng sau (đơn vị độ dài: cm, làm
tròn kết quả đến chữ số thập phân thứ hai)
Bán kính đường tròn (R) 3
Độ dài đường tròn (C) 15, 70
Diện tích hình tròn (S) 50, 24
Số đo của cung tròn ( n ) 60 80
Diện tích hình quạt tròn cung n 6, 28 Lời giải
Bán kính đường tròn (R) 3 2,5 4
Độ dài đường tròn (C) 18,84 15, 70 25,12
Diện tích hình tròn (S) 28, 26 19, 63 50, 24
Số đo của cung tròn ( n ) 60 80 45
Diện tích hình quạt tròn cung n 4, 71 4,36 6, 28
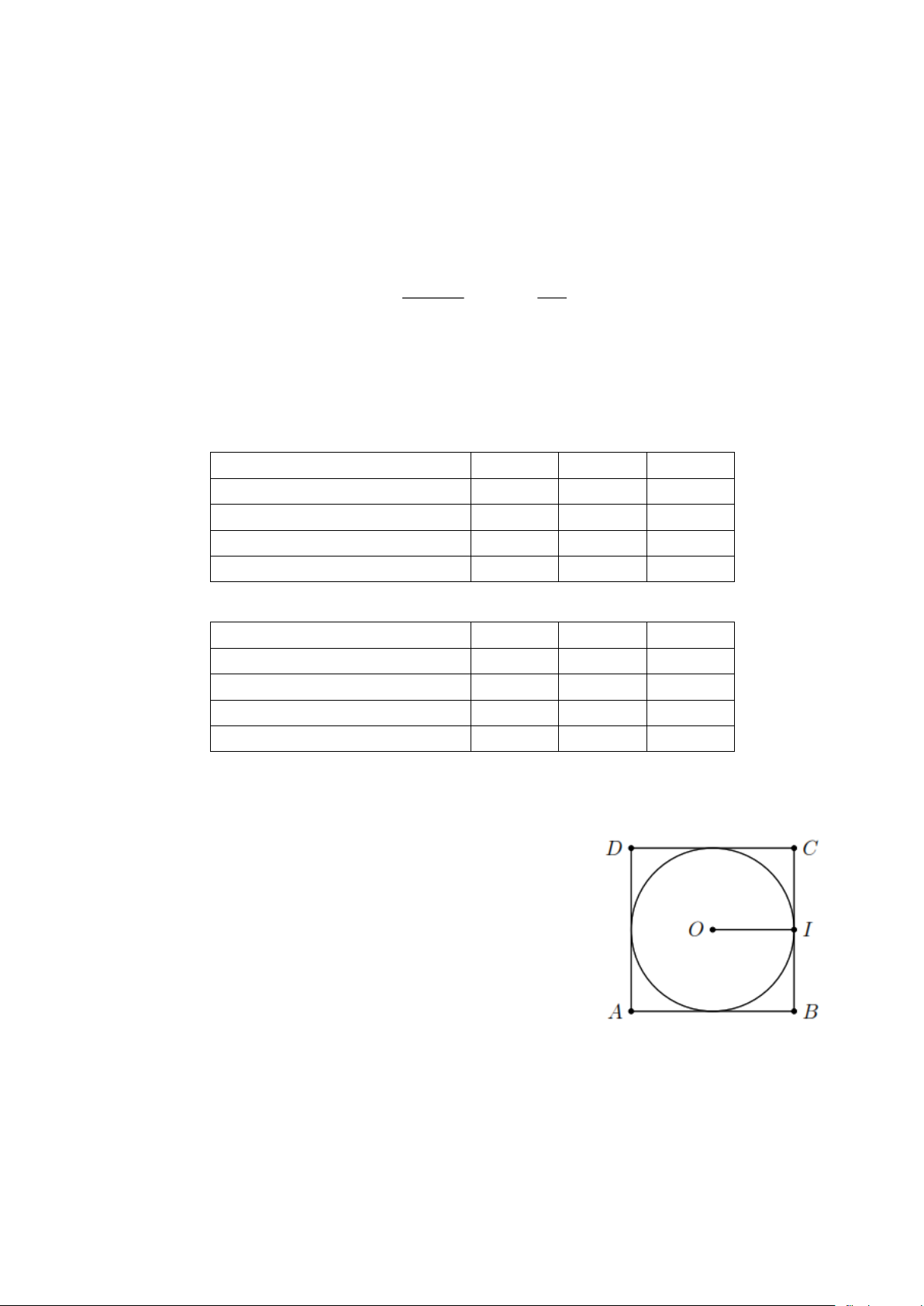
Bài 2. Tính diện tích hình tròn nội tiếp một hình vuông có cạnh bằng 8 cm. Lời giải
Do hình tròn nội tiếp hình vuông ABCD có cạnh bằng 8 cm nên
bán kình đường tròn là R = OI = 4 cm.
Vậy diện tích hình tròn cần tìm là 2 2
S =   R =   4 = 16 (cm 2 ).
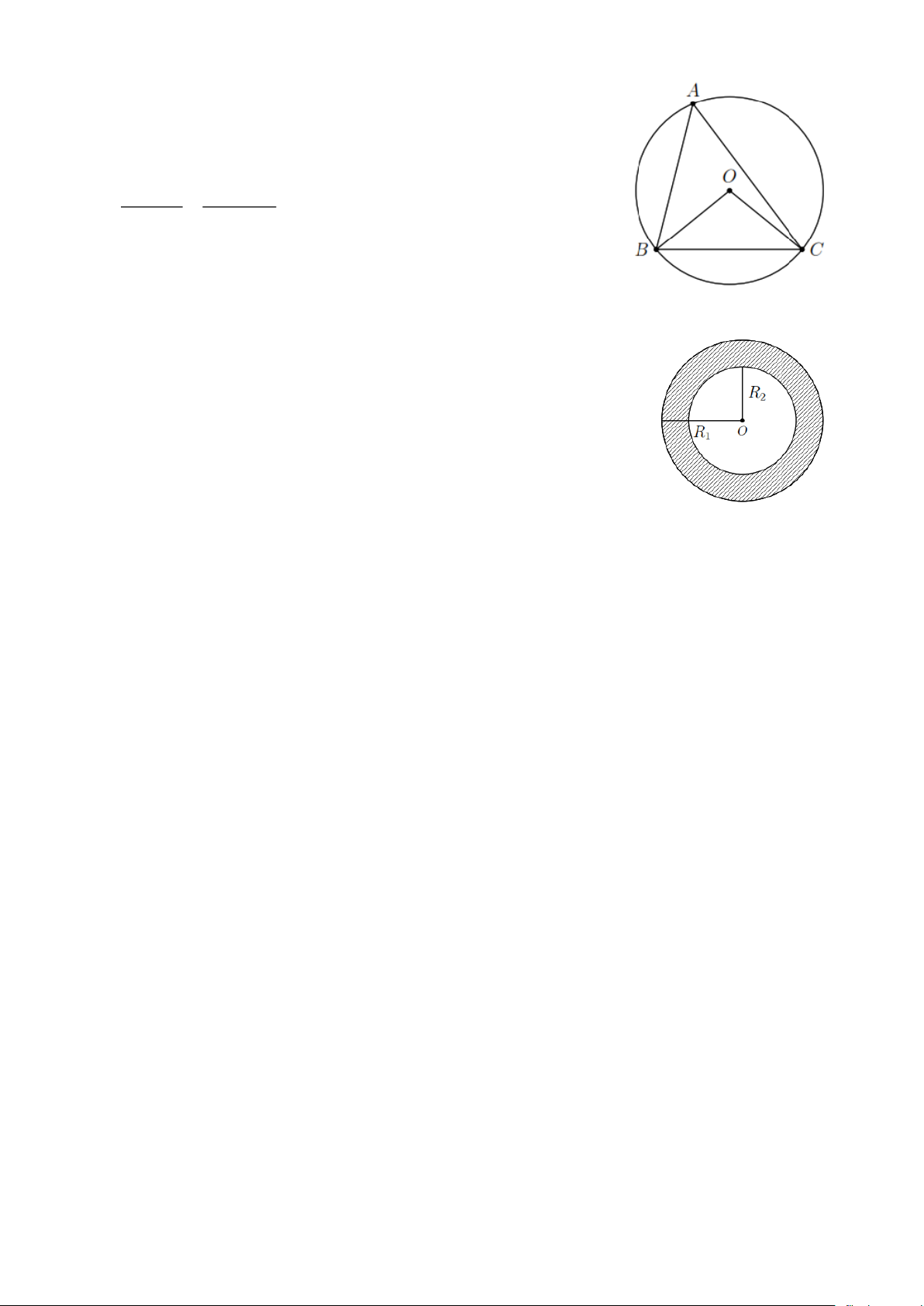
Bài 3. Cho tam giác ABC nội tiếp đường tròn tâm O , bán kính R = 3 (cm). Tính diện tích hình quạt
tròn giới hạn bởi hai bán kính OB , OC và cung nhỏ BC khi BAC 60 = . Lời giải Trang 1
Theo giả thiết BOC 2BAC 120 = = .
Vậy diện tích hình quạt tròn giới hạn bởi hai bán kính OB , OC và cung nhỏ BC là 2 2
  R n  3 120 2 S = = = 3 (cm) . 360 360
Bài 4. Hình vành khăn là phần hình tròn nằm giữa hai đường tròn đồng tâm (phân tô đậm).
a) Chứng minh diện tích S của hình vành khăn được tính theo công thức: S =  ( 2 2 R − R . 1 2 )
b) Tính diện tích hình vành khăn khi R = 4 (cm), R = 3 (cm). 1 2 Lời giải
Diện tích hình tròn tâm O , bán kính R là 2 S =   R . 1 1 1
Diện tích hình tròn tâm O , bán kính R là 2 S =   R . 2 2 2
Vậy diện tích hình vành khăn là 2 2 2 2
S = S − S =   R −  R =  (R − R ) . 1 2 1 2 1 2 Theo chứng minh trên thì 2 2 2 2
S =  (R − R ) =  (4 − 3 ) = 7 (cm 2 ). 1 2 C. BÀI TẬP VẬN DỤNG
Bài 1. Diện tích hình tròn sẽ thay đổi thế nào nếu
a) Bán kính tăng gấp đôi. b) Bán kính tăng gấp ba.
c) Bán kính tăng k lần. Lời giải
Diện tích hình tròn bán kính R là 2 S =   R .
a) Diện tích hình tròn sau khi bán kính tăng gấp đôi là 2 2
S =  (2R) = 4  R = 4S. 1
Vậy diện tích hình tròn tăng lên 4 lần.
b) Diện tích hình tròn sau khi bán kính tăng gấp ba là 2 2
S =  (3R) = 9  R = 9S. 2
Vậy diện tích hình tròn tăng lên 9 lần.
c) Diện tích hình tròn sau khi bán kính tăng gấp k là Trang 2 2 2 2 2
S =  (kR) = k   R = k S. 3
Vậy diện tích hình tròn tăng lên 2 k lần.
Bài 2. Tính diện tích một hình quạt tròn có bán kính 6 cm, số đo cung là 100 . Lời giải
Diện tích hình quạt tròn có bán kính R = 6 cm, số đo cung là n 100 = là 2 2
  R n  6 100 2 S = = =10 (cm) . 360 360
Bài 3. Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm nội tiếp đường tròn (O) . Tính
diện tích hình tròn (O) . Lời giải
Áp dụng định lý Pythago cho ABC vuông tại A , ta có 2 2 2 2 2
BC = AB + AC = 6 + 8 = 100  BC = 10(cm). BC
Do ABC nội tiếp đường tròn (O) nên đường tròn (O) có bán kính R = = 5 (cm). 2
Vậy diện tích hình tròn cần tính là 2
S =   R = 25 (cm 2 ).
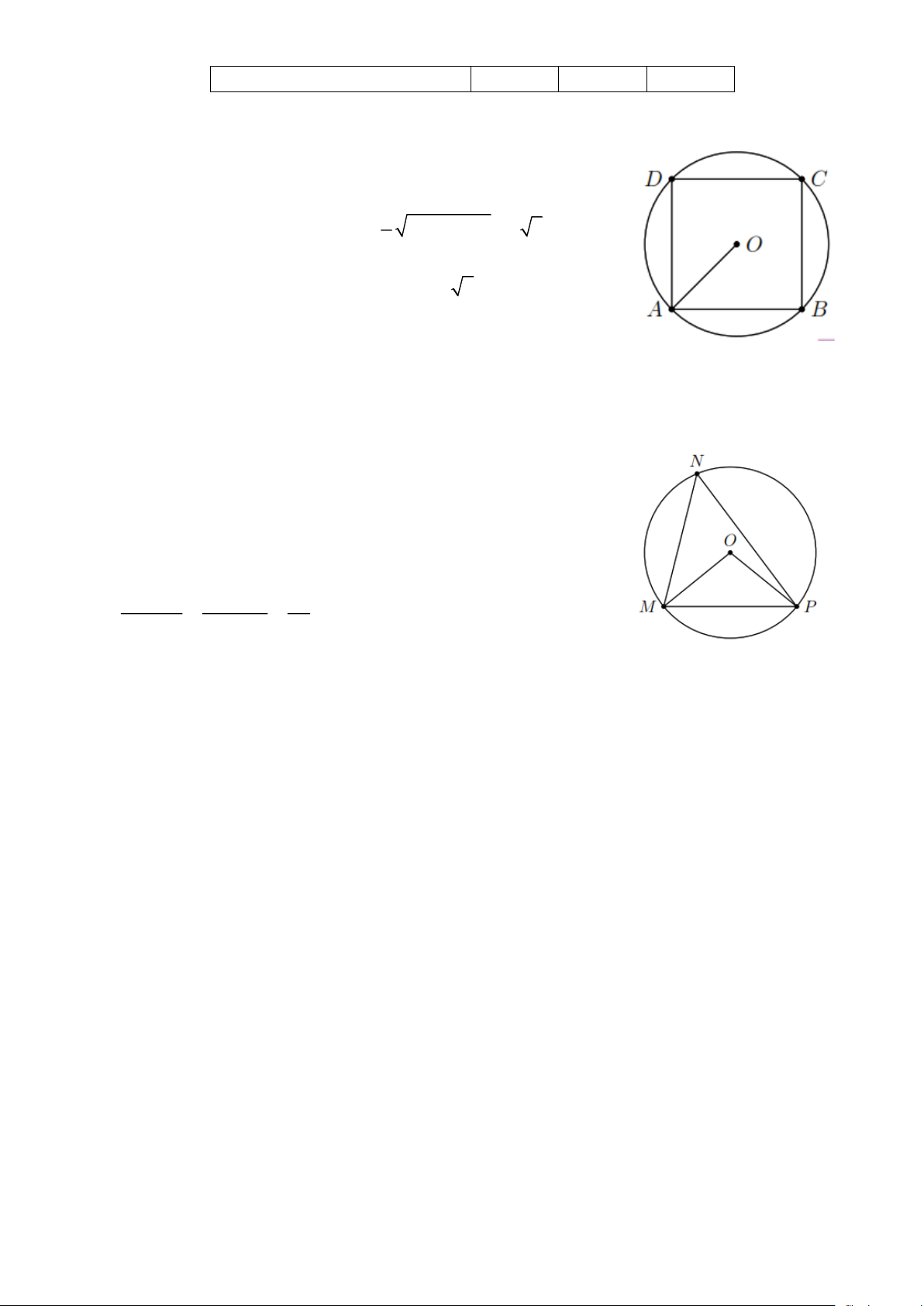
Bài 4. Cho hình vuông có cạnh 2 cm, vẽ đường tròn ngoại tiếp hình vuông đó. Tính diện tích hình tròn đó. Lời giải
Do hình vuông cạnh 2 cm nội tiếp đường tròn (O) nên đường tròn (O) có bán kính R = 2 .
Vậy diện tích của hình tròn là 2
S =   R = 2 (cm 2 ). D. BÀI TẬP VỀ NHÀ
Bài 5. Lấy giá trị gần đúng của  là 3,14 , hãy điền vào ô trống trong bảng sau (đơn vị độ dài: cm, làm
tròn kết quả đến chữ số thập phân thứ hai)
Bán kính đường tròn (R) 3,5
Độ dài đường tròn (C) 12,56
Diện tích hình tròn (S) 78,50
Số đo của cung tròn ( n ) 70 130
Diện tích hình quạt tròn cung n 15, 70 Lời giải
Bán kính đường tròn (R) 3,5 2 5
Độ dài đường tròn (C) 21,98 12,56 31, 4
Diện tích hình tròn (S) 38, 47 12,56 78,50
Số đo của cung tròn ( n ) 70 130 72 Trang 3
Diện tích hình quạt tròn cung n 7, 48 4,54 15, 70
Bài 6. Hình vuông có cạnh 4 cm nội tiếp đường tròn (O) . Tính diện tích hình tròn (O) . Lời giải
Do hình vuông ABCD có cạnh 4 cm nội tiếp đường tròn (O) nên 1
đường tròn (O) có bán kính 2 2 R = OA = AB + BC = 2 2 . 2
Vậy diện tích hình tròn (O) là 2 2
S =   R =  (2 2) = 8 (cm 2 ).
Bài 7. Cho tam giác MNP nội tiếp đường tròn tâm O , bán kính R = 3 (cm). Tính diện tích hình quạt
tròn giới hạn bởi hai bán kính OM , OP và cung nhỏ MP khi MNP 45 = . Lời giải
Theo giả thiết MOP 2MNP 90 = = .
Vậy diện tích hình quạt tròn giới hạn bởi hai bán kính OM , OP và cung nhỏ MP là 2 2
  R n  3 90 9 2 S = = = (cm) . 360 360 4
Bài 8. Tính diện tích hình vành khăn tạo bởi hai đường tròn đồng tâm có bán kính lần lượt là 7 cm và 12 cm. Lời giải Ta có 2 2
S =  (12 − 7 ) = 95 (cm 2 ). --- HẾT --- Trang 4