Phương pháp giải hình 9 sự xác định của đường tròn- tính chất đối xứng của đường tròn (có đáp án và lời giải chi tiết)

Chương 2
Bài 1. SỰ XÁC ĐỊNH CỦA ĐƯỜNG TRÒN.
TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN
A. KIẾN THỨC TRỌNG TÂM 1. Khái niệm
 Đường tròn tâm O bán kính R (R > 0) là hình gồm các điểm cách điểm O một khoảng bằng R.
2. Vị trí tương đối giữa điểm và đường tròn
 Điểm M nằm trong đường tròn (O;R ) khi OM < R .
 Điểm M nằm trên đường tròn (O;R ) khi OM = R .
 Điểm M nằm ngoài đường tròn (O;R ) khi OM > R .
3. Cách xác định đường tròn
Một đường tròn được xác định khi
 Biết tâm và bán kính đường tròn.
 Biết một đoạn thẳng là đường kính của đường tròn.
 Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.
 Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác. Khi đó tam giác
được gọi là tam giác nội tiếp đường tròn.
 Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực trong tam giác.
 Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
 Nến tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông. 4. Tâm đối xứng
 Đường tròn là hình có tâm đối xứng. Tâm đối xứng của đường tròn là tầm đối xứng của hình tròn đó.
5. Trục đối xứng
 Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Xác định tâm và bán kính của đường tròn đi qua nhiều điểm
 Dựa vào định nghĩa đường tròn: Nếu một điểm cách đều các điểm còn lại thì điểm đó
chính là tâm của đường tròn.
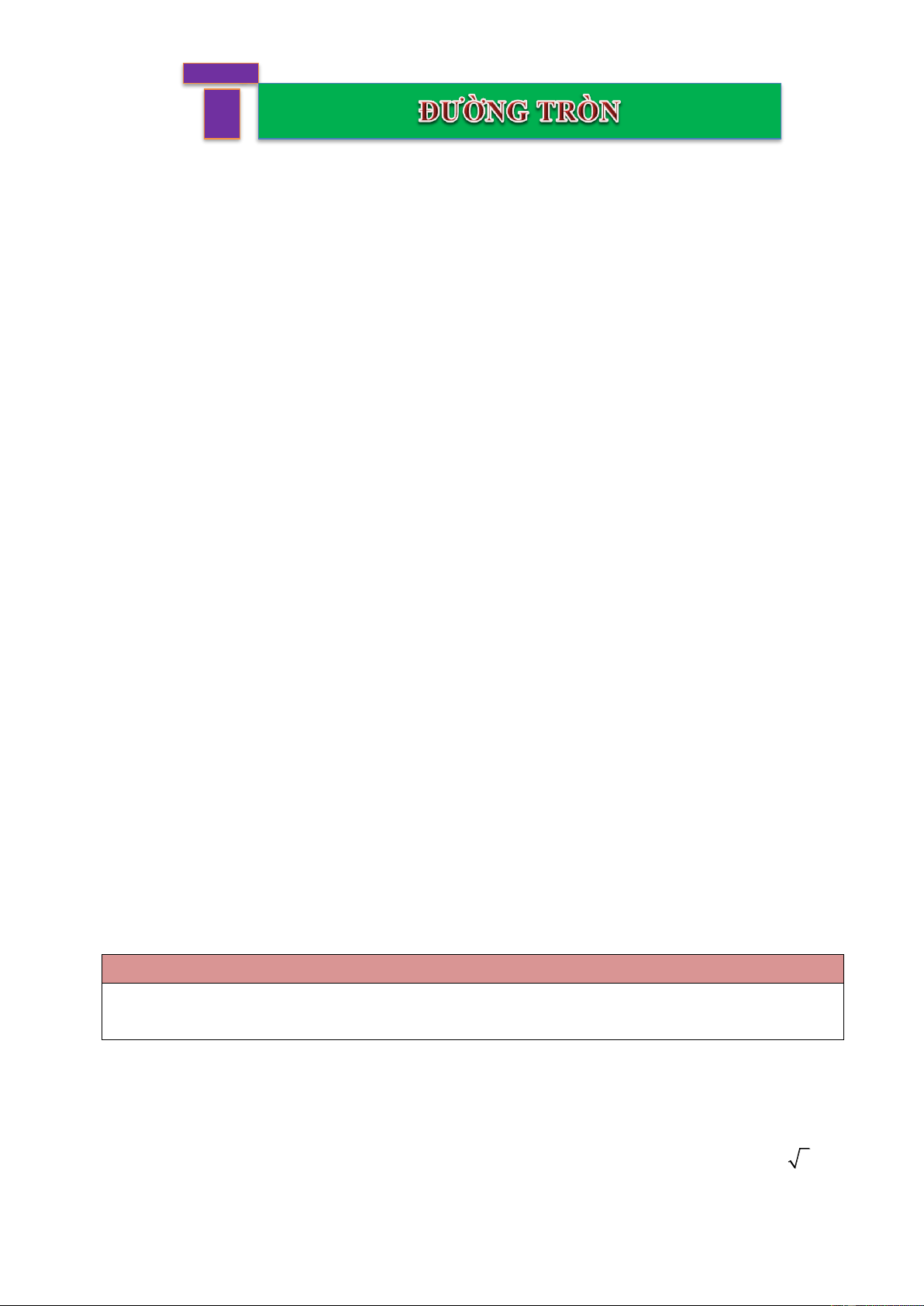
Ví dụ 1. Cho hình vuông A BCD có cạnh bằng 4 cm. Chứng minh rằng bốn điểm A , B , C , D
cùng thuộc một đường tròn. Tính bán kính của đường tròn đó. Lời giải
Gọi O = AC ÇBD Þ OA = OB = OC = OD , suy ra A , B , C , D Î (O ;OA ) với OA = 2 2 cm. Trang 1
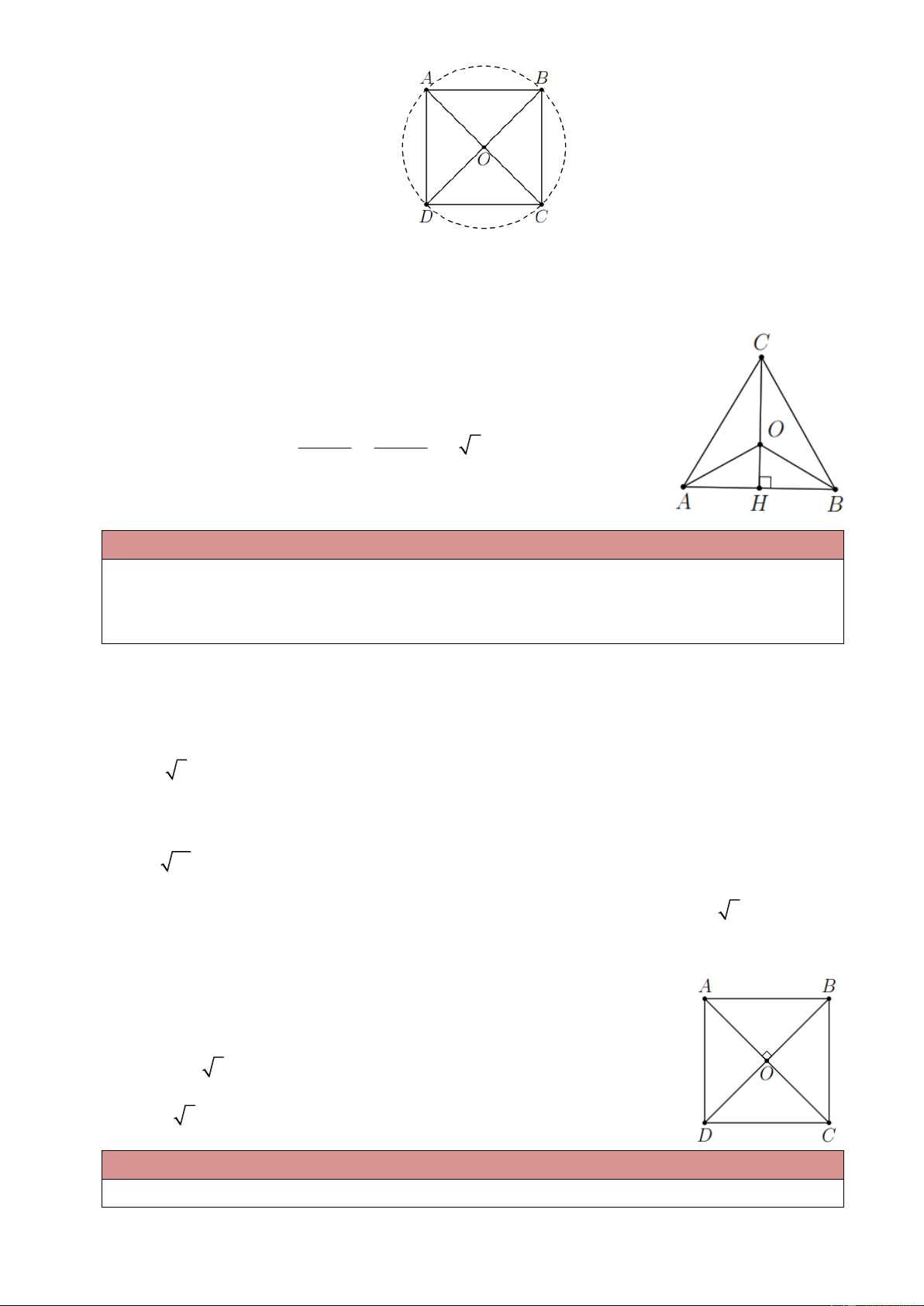
Ví dụ 2. Cho tam giác đều A BC có cạnh bằng 6 cm. Xác định tâm và bán kính của đường tròn ngoại tiếp A V B C . Lời giải
Gọi O là giao điểm của các đường trung trực của A
V B C . Suy ra O là
tâm đường tròn ngoại tiếp A V B C . A H 3 OA = = = 2 3 cm . cos 30° cos 30°
Dạng 2: Xác định vị trí của điểm và đường tròn
Muốn xác định vị trí của điểm M và đường tròn (O), ta làm như sau
 Bước 1: Xác định khoảng cách từ M đến tâm O của đường tròn.
 Bước 2: Dựa vào kết quả so sánh của OM và bán kính R của đường tròn mà kết luận.
Ví dụ 4. Trên mặt phẳng tọa độ Oxy , hãy xác định vị trí tương đối của điểm M ( ; 1 ) 1 , N ( ; 2 ) 0 , P ( ;
2 3) đối với (O ;2) . Lời giải OM =
2 < 2 nên M nằm trong đường tròn (O ;2) ;
ON = 2 Þ N Î (O ; ) 2 ; OP =
13 > 2 nên P nằm ngoài đường tròn (O ;2) .
Ví dụ 5. Cho hình vuông A BCD , O là giao điểm của hai đường chéo, OA = 2 2 cm. Vẽ đường
tròn ( A ; 4 cm). Xác định vị trí tương đối của các điểm A , B , C , D với đường tròn (O ; 4 cm). Lời giải
A B = A D = 4 cm, suy ra B , D Î (A; 4 ) cm .
Ta có A = 2 2 < 4 nên O nằm trong đường tròn (A; 4 ) cm .
A C = 4 2 > 4 nên C nằm ngoài đường tròn (A; 4 ) cm .
Dạng 3: Dựng đường tròn thỏa mãn yêu cầu cho trước
 Xem phần kiến thức trọng tâm. Trang 2
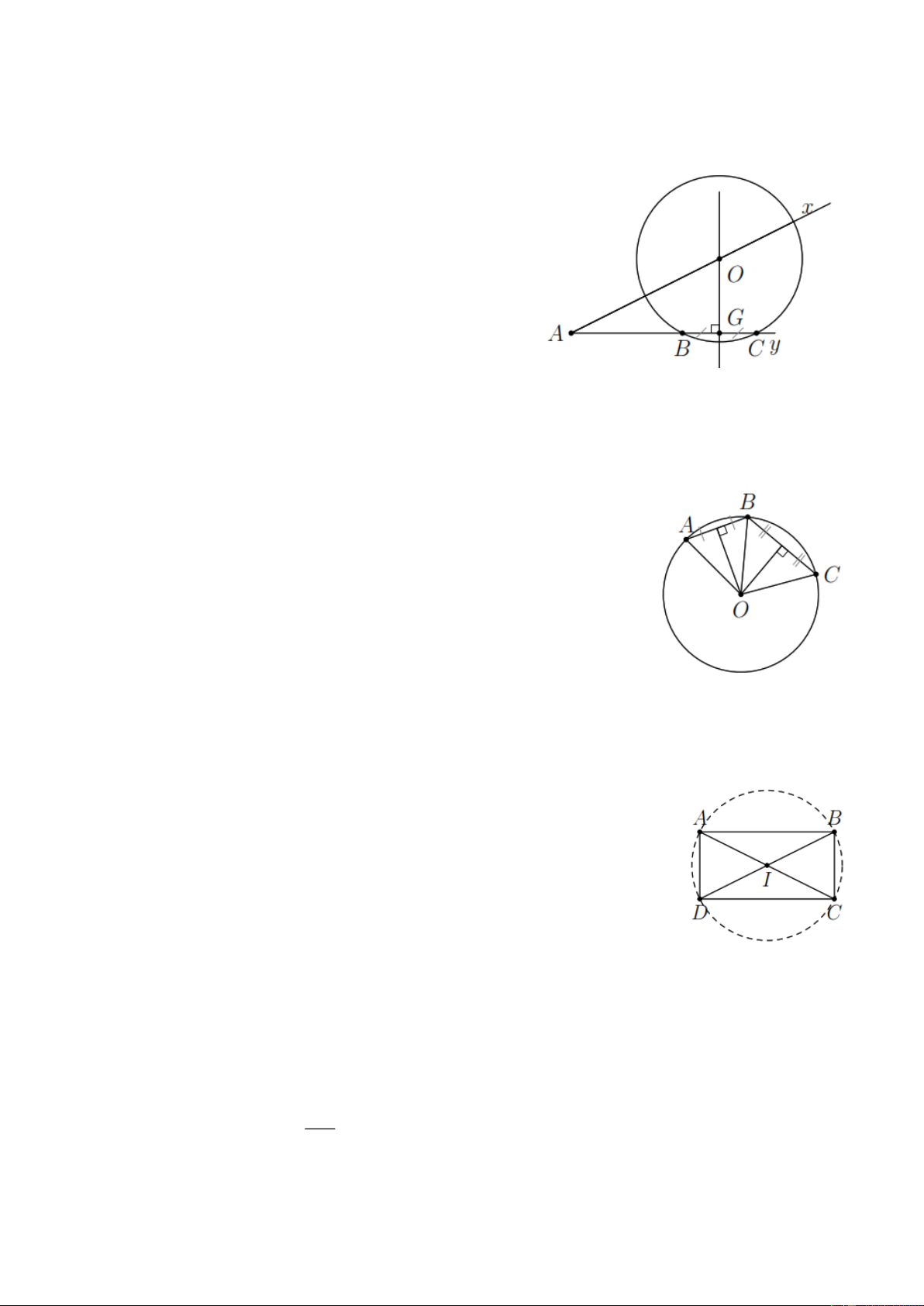
Ví dụ 6. Cho góc xA y nhọn và hai điểm B , C thuộc tia A y . Dựng đường tròn tâm O đi qua hai
điểm B , C sao cho O nằm trên tia A x . Lời giải Cách dựng:
Dựng đường trung trực d của đoạn thẳng B C cắt A y tại O .
Dựng đường tròn (O ;OB ) .
Chứng minh: Vì O thuộc trung trực của đoạn thẳng
B C nên OB = OC .
Vậy O là tâm đường tròn đi qua hai điểm B , C .
Ví dụ 7. Một tấm bìa hình tròn không còn dấu vết của tâm. Hãy xác định lại tâm và bán kính của hình tròn đó. Lời giải
Lấy ba điểm A , B , C bất kì thuộc viền hình tròn. Dựng các đường
trung trực của đoạn A B và B C , chúng cắt nhau tại O . Vậy O chính
là tâm của hình tròn và OA là bán kính của hình tròn.
C. BÀI TẬP VẬN DỤNG
Bài 1. Cho hình chữ nhật A BCD có A B = 12 cm, BC = 5 cm. Tìm tâm và bán kính của đường
tròn đi qua 4 điểm A , B , C , D . Lời giải
Gọi I = AC ÇBD Þ IA = IB = IC = ID
suy ra A , B , C , D Î (I ;IA ) .
Tính được A C = 13 cm Þ IA = , 6 5 cm. Bài 2. Cho A
V B C vuông tại A , A B = 6 cm, A C = 8 cm. Tìm tâm và bán kính của đường tròn
ngoại tiếp tam giác A BC . Lời giải
Gọi M là trung điểm của B C , suy ra M là tâm đường tròn ngoại tiếp A V B C . B C
Vậy MA = MB = MC = = 5 cm. 2 Trang 3
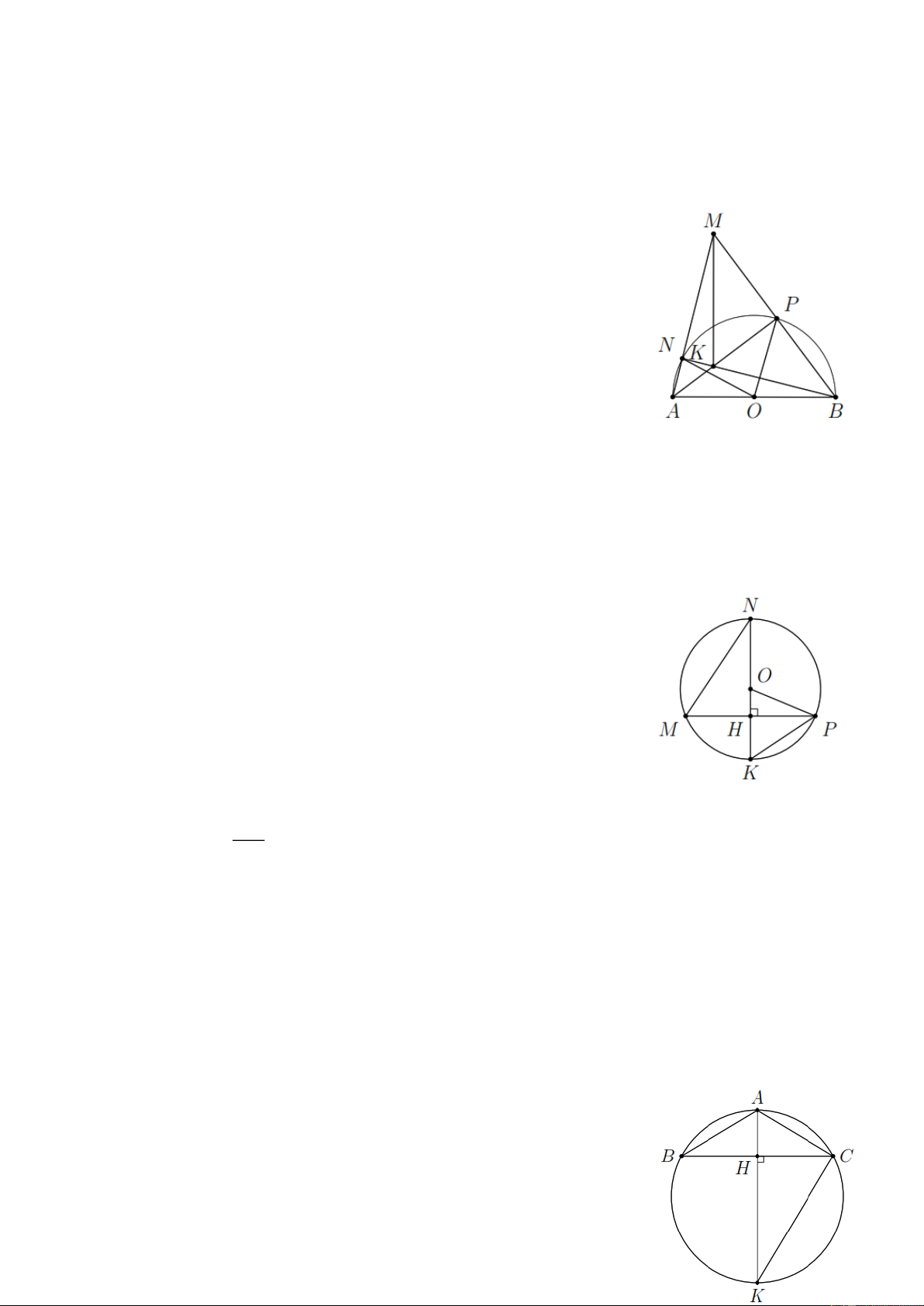
Bài 3. Cho nửa đường tròn (O ) có đường kính A B . M là điểm nằm bên ngoài đường tròn sao cho
MA , MB cắt nửa đường tròn lần lượt tại N , P .
a) Chứng minh BN ^ MA , A P ^ MB ;
b) Gọi K là giao điểm của B N và A P . Chứng minh MK ^ A B . Lời giải a) A
V NB có đường trung tuyến NO ứng với cạnh A B và bằng nửa
cạnh A B , suy ra A
V NB vuông tại N Þ BN ^ MA .
Làm tương tự, ta có A P ^ MB .
b) Từ câu trên, ta có K là trực tâm tam giác MAB Þ MK ^ AB . Bài 4. Cho M
V NP cân tại N , nội tiếp đường tròn (O ) . Đường cao NH cắt đường tròn tại K .
a) Chứng minh NK là đường kính của (O ) ; b) Tính số đo · NPK ;
c) Biết MP = 24 cm, NP = 20 cm. Tính NH và bán kính của đường tròn (O ) . Lời giải a) M
V NP cân tại N , suy ra NH là đường cao đồng thời là đường
trung trực của MP , mà O thuộc đường trung trực của MP Þ NK là
đường kính của đường tròn (O ) . · b) N
V PK nội tiếp đường tròn đường kính NK PNK 90° Þ = . MP c) Ta có HP = = 12 cm. 2
Áp dụng định lí Py-ta-go vào N
V HP vuông tại H Þ NH = 16 cm.
Áp dụng hệ thức lượng vào N
V PK vuông tại P , PH ^ NK ta tính được NK = 25 cm.
Vậy bán kính của (O ) là 25 : 2 = 1 , 2 5 cm. Bài 5. Cho A
V B C cân tại A , có BC = 36 cm, đường cao A H = 12 cm. Tính bán kính của
đường tròn ngoại tiếp A V B C . Lời giải
Gọi K = A H Ç (O ) . Trang 4 Vì A
V B C cân tại A nên A H vừa là đường cao vừa là đường trung trực của B C , mà O thuộc
trung trực của B C nên A K là đường kính của (O ) . Vì A
V CK nội tiếp (O ) có A K là đường kính nên A
V CK vuông tại C .
Theo Py-ta-go ta tính được CH = 18 cm. Áp dụng hệ thức lượng vào tam giác vuông A CK ta có
HK = 27 cm, suy ra A K = 39 cm nên R = 1 , 9 5 cm.
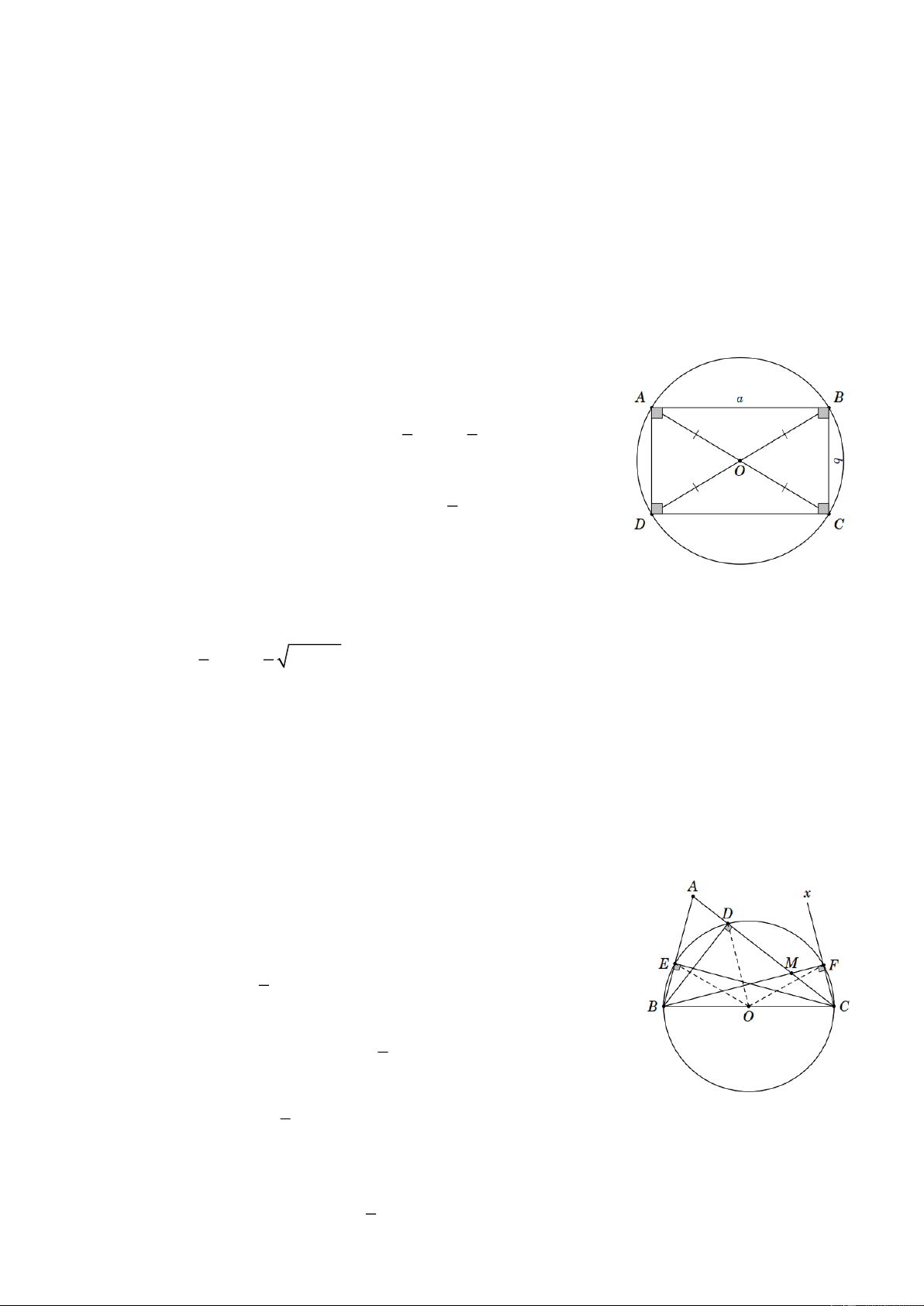
Bài 6. Cho hình chữ nhật A BCD có A B = a , BC = b . Chứng minh rằng bốn điểm A , B , C , D
cùng thuộc một đường tròn. Xác định tâm và tính bán kính của đường tròn đó. Lời giải
Gọi O là giao điểm của hai đường chéo A C và B D . Theo tính
chất hai đường chéo của hình chữ nhật, ta có æ 1 1 ö OA OB OC OD ç = = = = A C = B D . ÷ ç ÷ ç è 2 2 ÷ø æ 1 ö
Vậy bốn điểm A , B , C , D cùng thuộc O ç ; A C ÷ ç ÷ ç . è 2 ÷ø
Áp dụng định lí Py-ta-go vào tam giác vuông A BC , ta có 2 2 2 2 2
A C = A B + BC = a + b . Do đó 1 1 2 2 R = A C = a + b . 2 2
Bài 7. Cho tam giác A BC , các đường cao B D và CE . Trên cạnh A C lấy điểm M . Kẻ tia Cx
vuông góc với tia B M tại F . Chứng minh rằng năm điểm B , C , D , E , F cùng thuộc một đường tròn. Lời giải
Gọi O là trung điểm của B C . Ta có B D là đường cao nên BD ^ A C , hay tam giác BDC vuông tại D .
Trong tam giác vuông BDC có DO là trung tuyến ứng với cạnh huyền B C nên 1
OD = OB = OC = B C . (1) 2 Tương tự 1
, ta có OE = OB = OC = B C . (2) 2 1
và OF = OB = OC = B C . (3) 2 Từ ( )
1 , (2) và (3) suy ra OB = OC = OD = OE = OF . Do đó năm điểm B , C , D , E , F cùng 1
thuộc đường tròn (O;R ) với R = B C . 2 Trang 5
Bài 8. Chứng minh rằng bốn trung điểm của bốn cạnh hình thoi cùng thuộc một đường tròn. Lời giải
Gọi M , N , P , Q lần lượt là trung điểm của bốn
cạnh A B , B C , CD và DA của hình thoi A BCD .
Gọi O là giao điểm của A C và B D . Ta có
A C ^ BD . Theo tính chất đường trung tuyến ứng
với cạnh huyền của tam giác vuông, ta được 1 1 1 OM = A B ; ON = B C ; OP = CD ; 2 2 2 1 OQ = A D . 2
Mặt khác A B = BC = CD = DA nên OM = ON = OP = OQ . Do đó bốn điểm M , N , P , Q
cùng nằm trên một đường tròn.
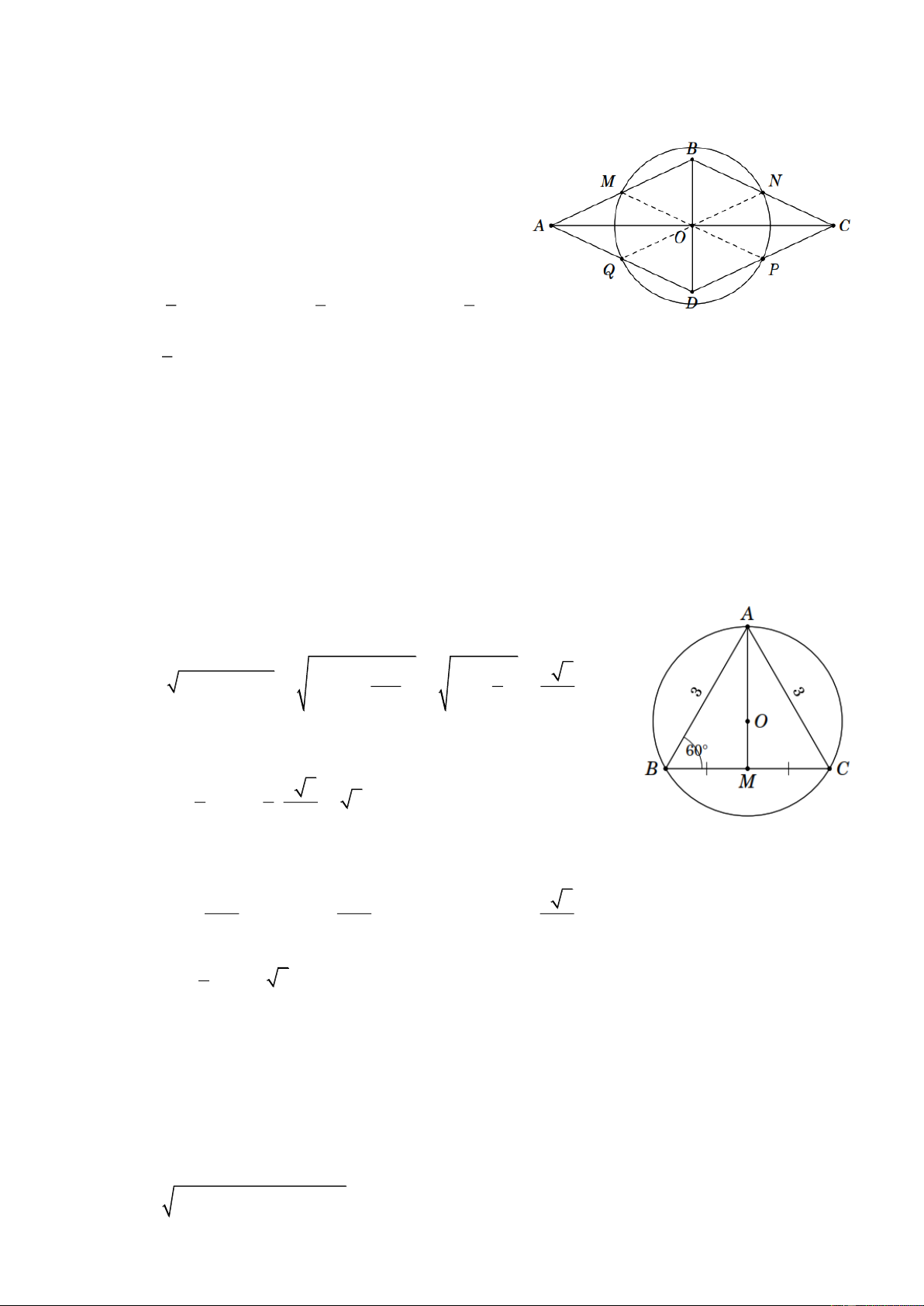
Bài 9. Tính bán kính đường tròn ngoại tiếp tam giác A BC đều, cạnh 3 cm. Lời giải
Gọi O là tâm đường tròn ngoại tiếp A
V B C . M là trung điểm của B C . Vì tam giác A BC đều
nên O cũng là trực tâm, trọng tâm của A V B C .
Áp dụng định lí Py-ta-go vào tam giác vuông A MC có 2 2 BC æ ö 3 æ ö 3 3 2 2 2 2 A M = A C - MC = A C ç ÷ - ç ÷ = 3 ç ÷ - ç ÷ = ç è 2 ÷ø çè2÷ø 2
Bán kính đường tròn ngoại tiếp tam giác A BC 2 2 3 3 R = OA = A M = × = 3 cm. 3 3 2
Nhận xét: Ta có cách giải khác như sau. Trong tam giác vuông A BM có · A M ° A M ° 3 3 sin A B M = Û sin 60 = Þ A M = 3 s × in 60 = . A B 3 2 Do đó 2 R = A M = 3 cm. . 3
Bài 10. Trong hệ trục tọa độ Oxy cho các điểm M (- ; 1 - 2) , N ( ; 1 2) và P (- ; 5 ) 0 . Tính bán kính
đường tròn ngoại tiếp tam giác MNP . Lời giải
Áp dụng công thức tính khoảng cách giữa hai điểm A (x ;y , B (x ;y ta có B B ) A A ) A B = (x - x + y - y B A )2 ( B A )2 . Trang 6
ta tính được MN = 2 5 , MP = 2 5 , NP = 2 10 . Do đó 2 2 2
MN + MP = 20 + 20 = NP Þ M
V NP vuông tại M (định lí Py-ta-go đảo). Suy ra bán kính đườ 1 ng tròn ngoại tiếp M V NP là R = NP = 10 (do trong tam giác vuông 2
đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền).
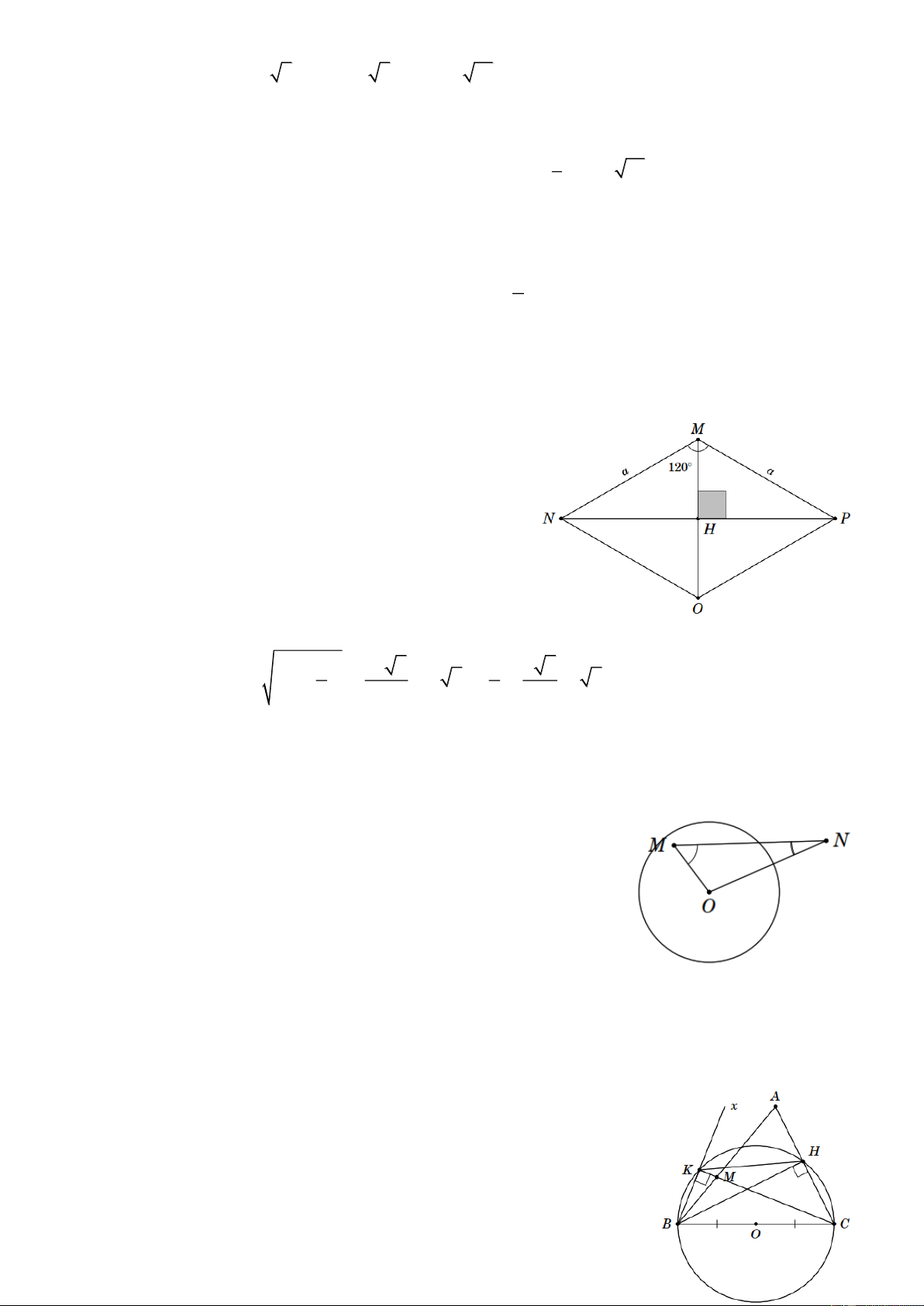
Bài 11. Cho tam giác MNP có MN = MP = a và · NMP 120° =
. Gọi O là tâm và r là bán kính d
của đường tròn ngoại tiếp tam giác MNP . Tính tỉ số với d = NP . r Lời giải
Vẽ MH ^ NP thì · · NMH HMP 60° = = (vì N
V MP cân tại M ). Trên tia MH lấy điểm O sao
cho MO = MN = MP = a .
Xét tam giác MNO có MN = MO = a ; · NMO 60° =
nên tam giác MNO đều, suy ra
ON = OM = a .
Tương tự, ta có tam giác OMP đều và OM = OP = a .
Do đó O là tâm đường tròn ngoại tiếp N V MP và bán
kính của đường tròn này bằng a ( r = a ). Ta có 2 a æ ö 2a 3 d a 3 2
d = NP = 2NH = 2 a - ç ÷ ç ÷ = = a 3 Þ = = 3. ç è2÷ø 2 r a
Bài 12. Cho đường tròn (O;R ) và hai điểm M , N sao cho M nằm trong và N nằm ngoài (O;R ) . Hãy so sánh · OMN và · ONM . Lời giải
Ta có M nằm trong (O;R ) nên OM < R , N nằm ngoài (O;R )
nên ON > R .
Trong tam giác OMN , có OM < ON (vì · ·
OM < R , ON > R ) nên OMN > ONM (trong một tam giác, góc
đối diện với cạnh lớn hơn thì lớn hơn).
D. BÀI TẬP VỀ NHÀ
Bài 13. Cho tam giác A BC , đường cao B H . Lấy một điểm M trên cạnh A B ( M ¹ A , M ¹ B ).
Qua B kẻ tia B x vuông góc với tia CM tại K . So sánh B C và HK . Lời giải Trang 7
Gọi O là trung điểm của B C . Vì tam giác BKC vuông tại K , tam giác BHC vuông tại H , nên
bốn điểm B , K , H , C cùng thuộc đường tròn tâm O đường kính B C . Do đó HK < BC .
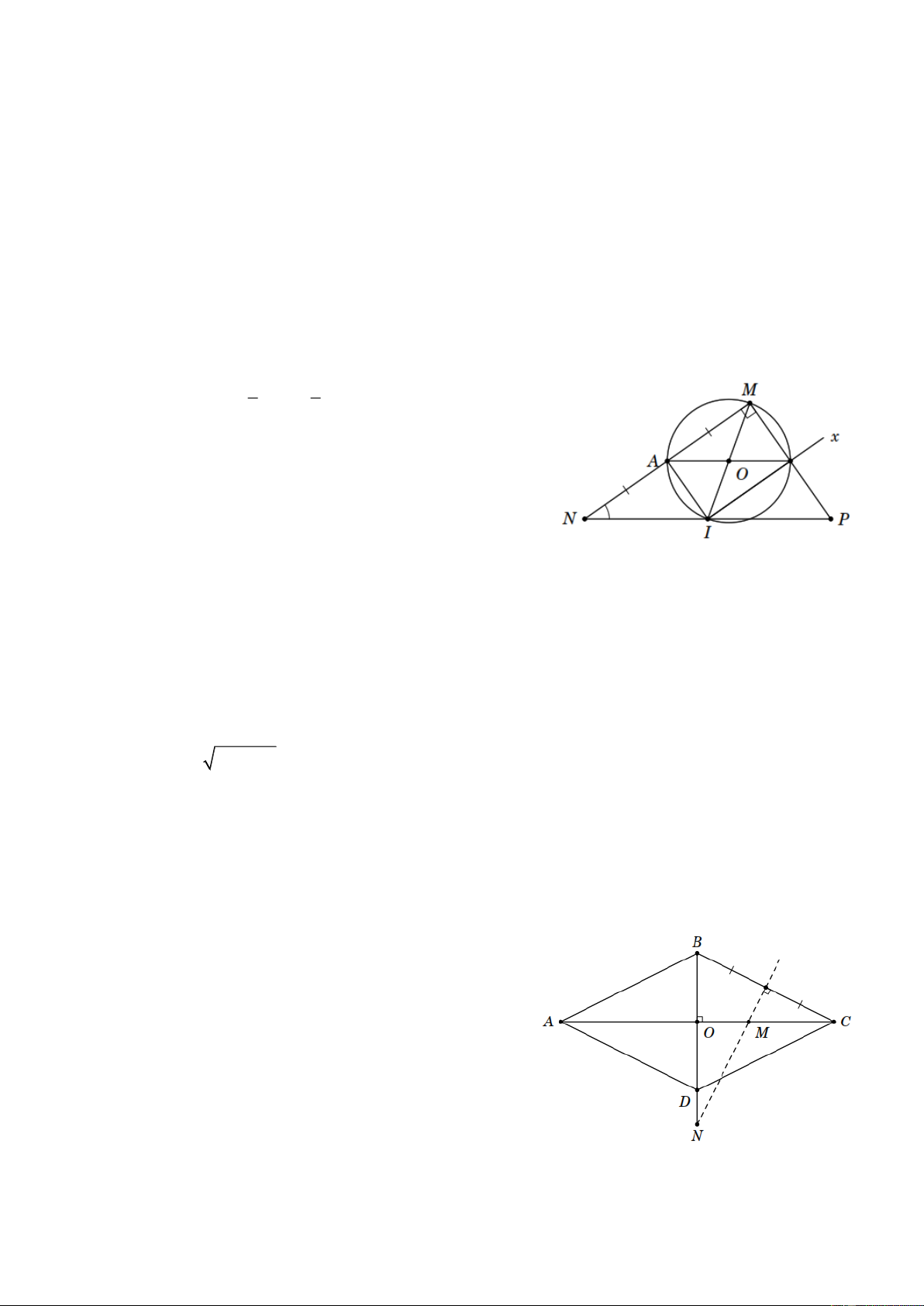
Bài 14. Cho tam giác MNP vuông tại M , NP = 2a . Trên cạnh MN lấy điểm A ( A ¹ M ,
A ¹ N ). Qua trung điểm I của NP vẽ tia Ix vuông góc với IA . Tia Ix cắt đường thẳng MP tại
B . Xác định vị trí của điểm A để độ dài đoạn A B nhỏ nhất. Lời giải
Tam giác vuông MNP có đường trung tuyến MI ứng với cạnh huyền NP nên 1 1
MI = NI = IP = NP = 2 × a = a. 2 2 Ta có · A MB 90° = , · A IB 90° =
do dó bốn điểm A , M ,
B , I cùng thuộc đường tròn đường kính A B . Suy ra
A B ³ MI hay A B ³ a . Vì vậy
minAB = a Û MI là đường kính · MA I 90° Û =
Û A I PMP Û A là trung điểm của MN (vì I là trung điểm của NP ). Vậy khi A
là trung điểm của MN thì min A B = a .
Bài 15. Bốn đỉnh của một hình chữ nhật kích thước 5´ 12 cùng nằm trên một đường tròn có bán kính bằng bao nhiêu? Lời giải Ta có 2 2 2R = 12 + 5 = 13 nên R = , 6 5 .
Bài 16. Cho hình thoi A BCD . Đường trung trực của cạnh B C cắt đường thẳng A C tại M và cắt
đường thẳng BD tại N . Chứng minh rằng M và N lần lượt là tâm của đường tròn ngoại tiếp các
tam giác BCD và A BC . Lời giải
Trong hình thoi, mỗi đường chéo là đường trung trực của đường chéo kia.
Điểm M là giao điểm hai đường trung trực của tam
giác BCD nên M là tâm đường tròn ngoại tiếp tam giác BCD .
Điểm N là giao điểm hai đường trung trực của tam
giác A BC nên N là tâm đường tròn ngoại tiếp tam giác A BC . --- HẾT --- Trang 8