




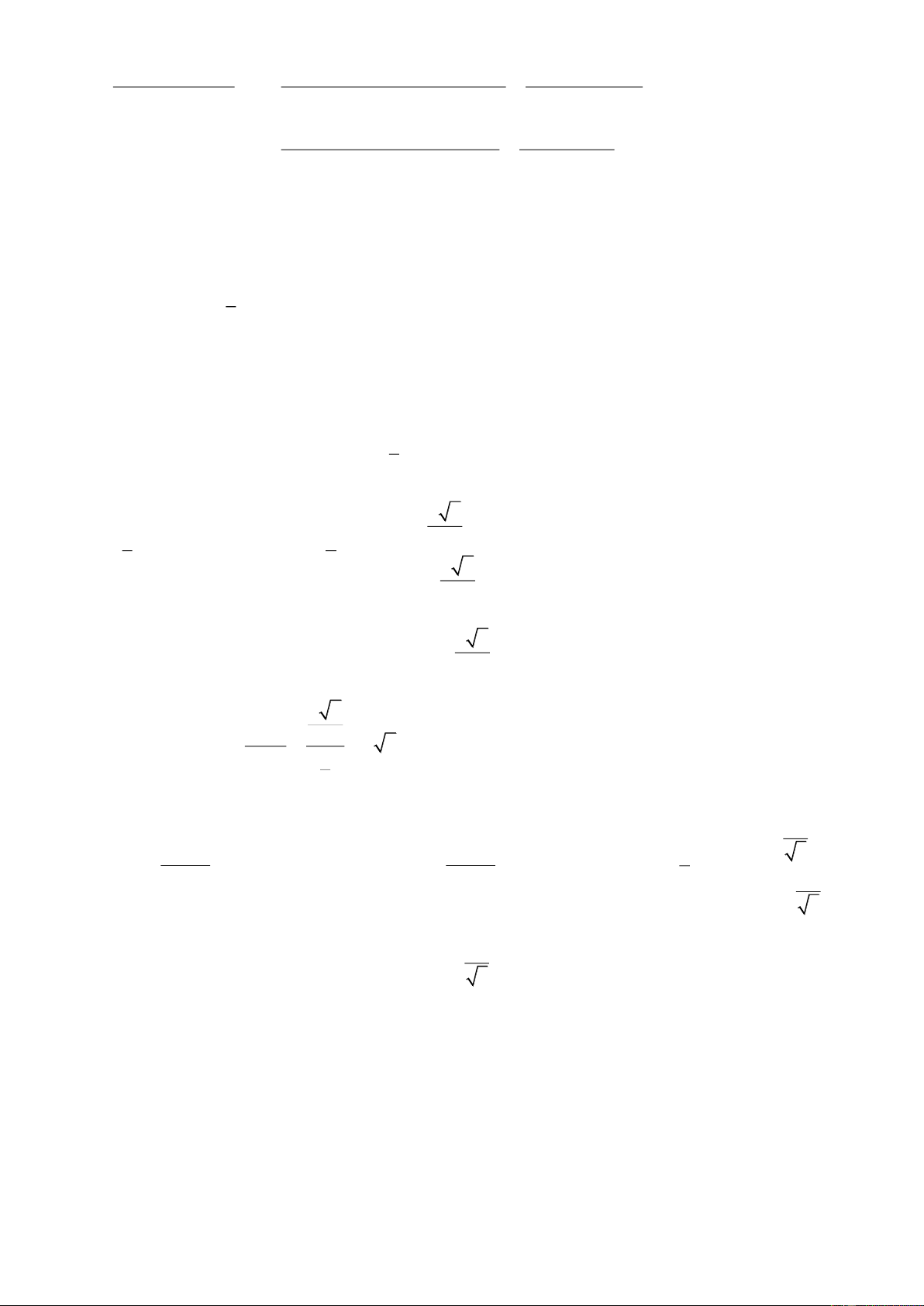
Preview text:
Bài 2. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
A. KIẾN THỨC TRỌNG TÂM 1. Định nghĩa
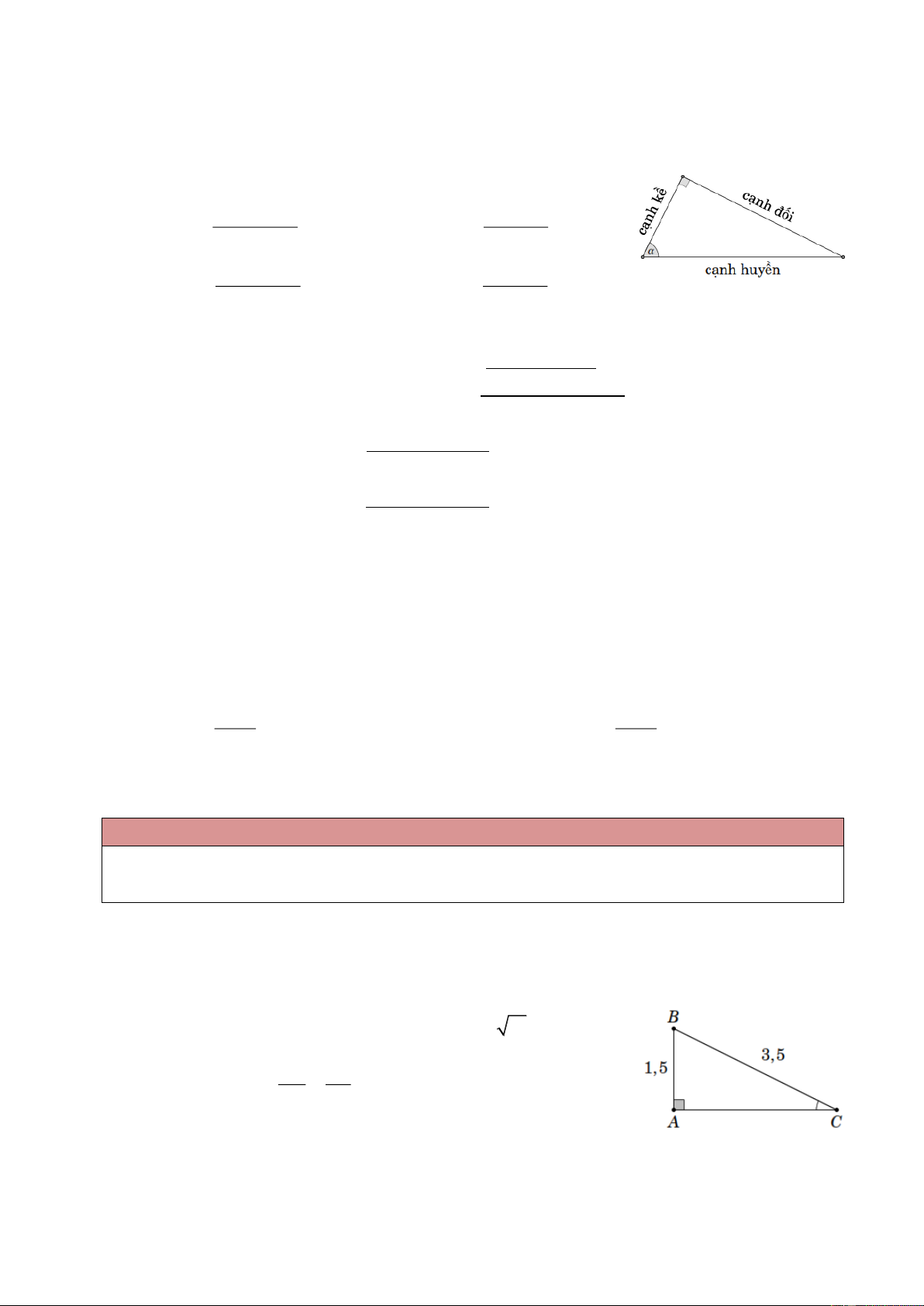
Với là góc nhọn trong tam giác vuông ta có canh doi canh doi sin ; tan ; canh huyen canh ke canh ke canh ke cos ; cot . canh huyen canh doi Cách ghi nhớ
“Tìm sin lấy đối chia huyền,
Cô-sin hai cạnh kề huyền chia nhau,
Còn tang thì phải tính sao?
Đối trên kề dưới chia nhau ra liền,
Cô-tang cũng dễ ăn tiền,
Kề trên đối dưới chia liền bạn ơi!”
2. Một số hệ thức và tính chất cơ bản
Với hai góc nhọn , và 90 thì
sin cos ; cos sin ; tan tan ; cot cot .
Với góc nhọn 0 90 , ta có
0 sin 1;0 cos 1.
Nếu tăng thì sin và tan tăng; còn cos và cot giảm. sin cos tan ; cot ; cos sin tan cot 1; 2 2 sin cos 1 .
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tính tỉ số lượng giác của góc nhọn trong tam giác vuông khi biết độ dài hai cạnh
Bước 1: Tính độ dài cạnh thứ ba theo định lý Py-ta-go (nếu cần).
Bước 2: Tính các tỉ số lượng giác của góc nhọn theo yêu cầu đề bài.
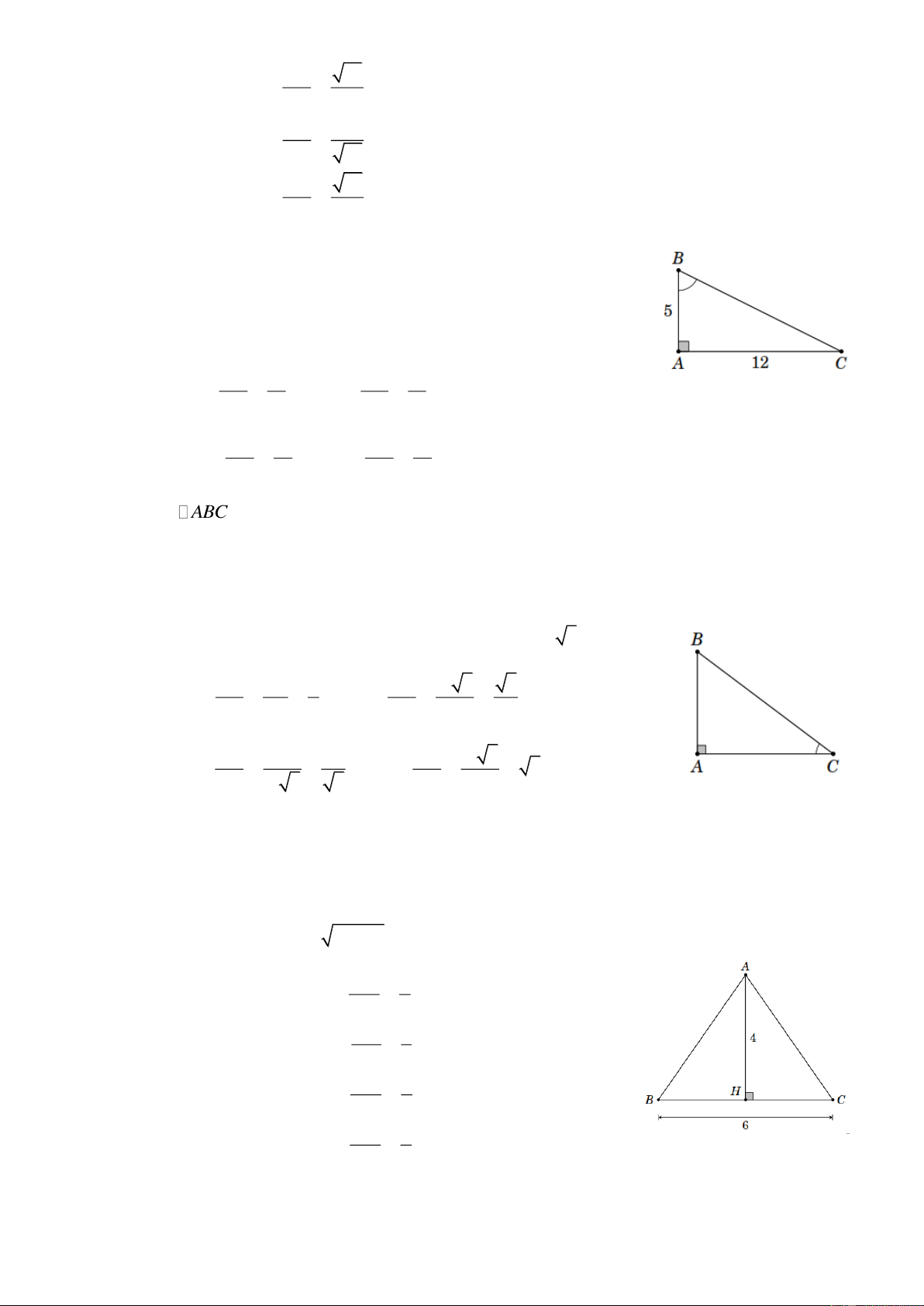
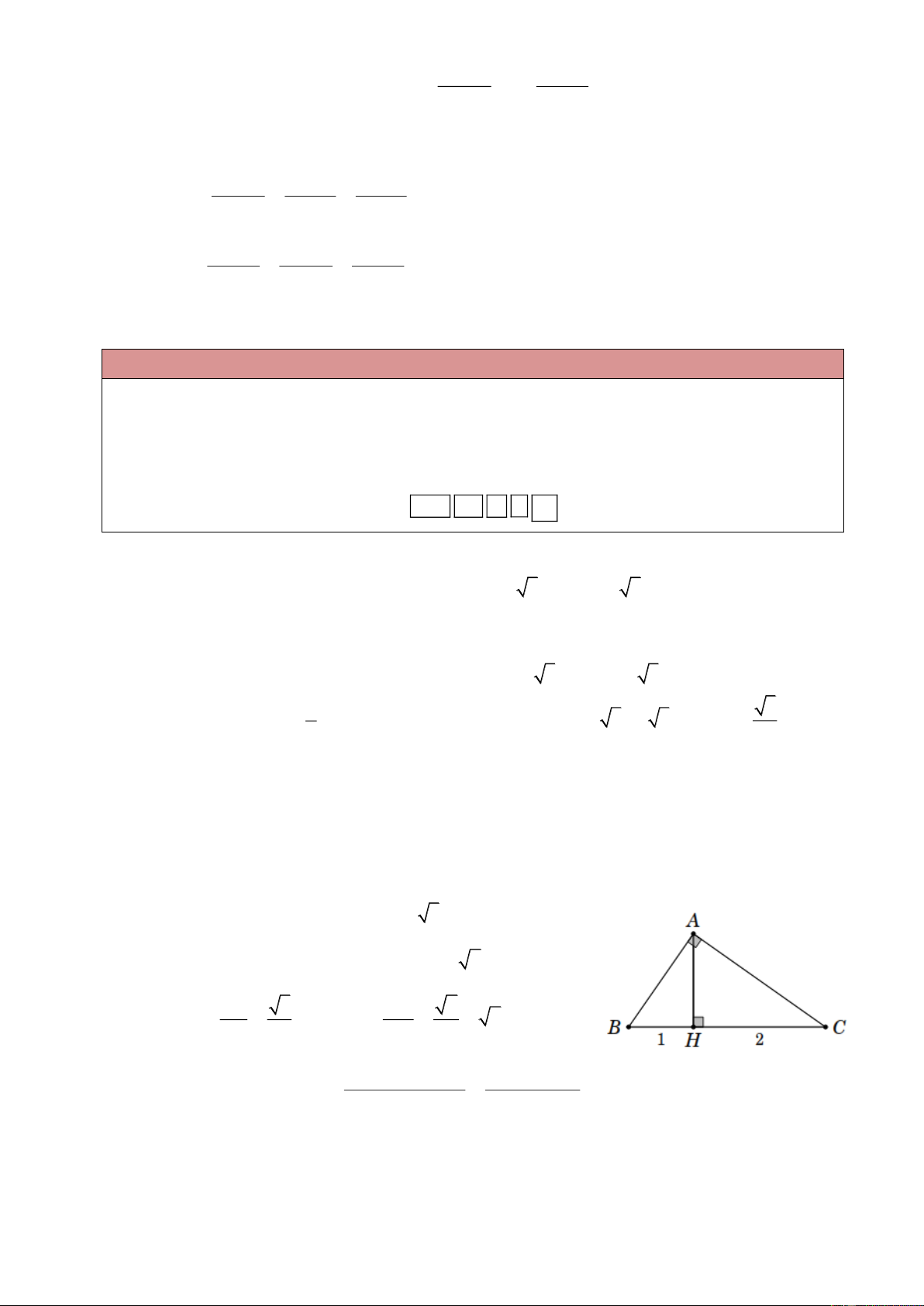
Ví dụ 1. Tam giác ABC vuông tại A , AB 1, 5 ; BC 3, 5 . Tính tỉ số lượng giác của góc C rồi
suy ra các tỉ số lượng giác của góc B . Lời giải Ta có 2 2 2 2 2
AC BC AB 3,5 1,5 10 AC 10 . Do đó AB 1, 5
cos B sin C 0, 4286 BC 3, 5 Trang 1 AC 10
sin B cos C 0,9035 BC 3, 5 AB 1, 5
cot B tan C 0, 4743 AC 10 AC 10
tan B cot C 2,1082 AB 1, 5
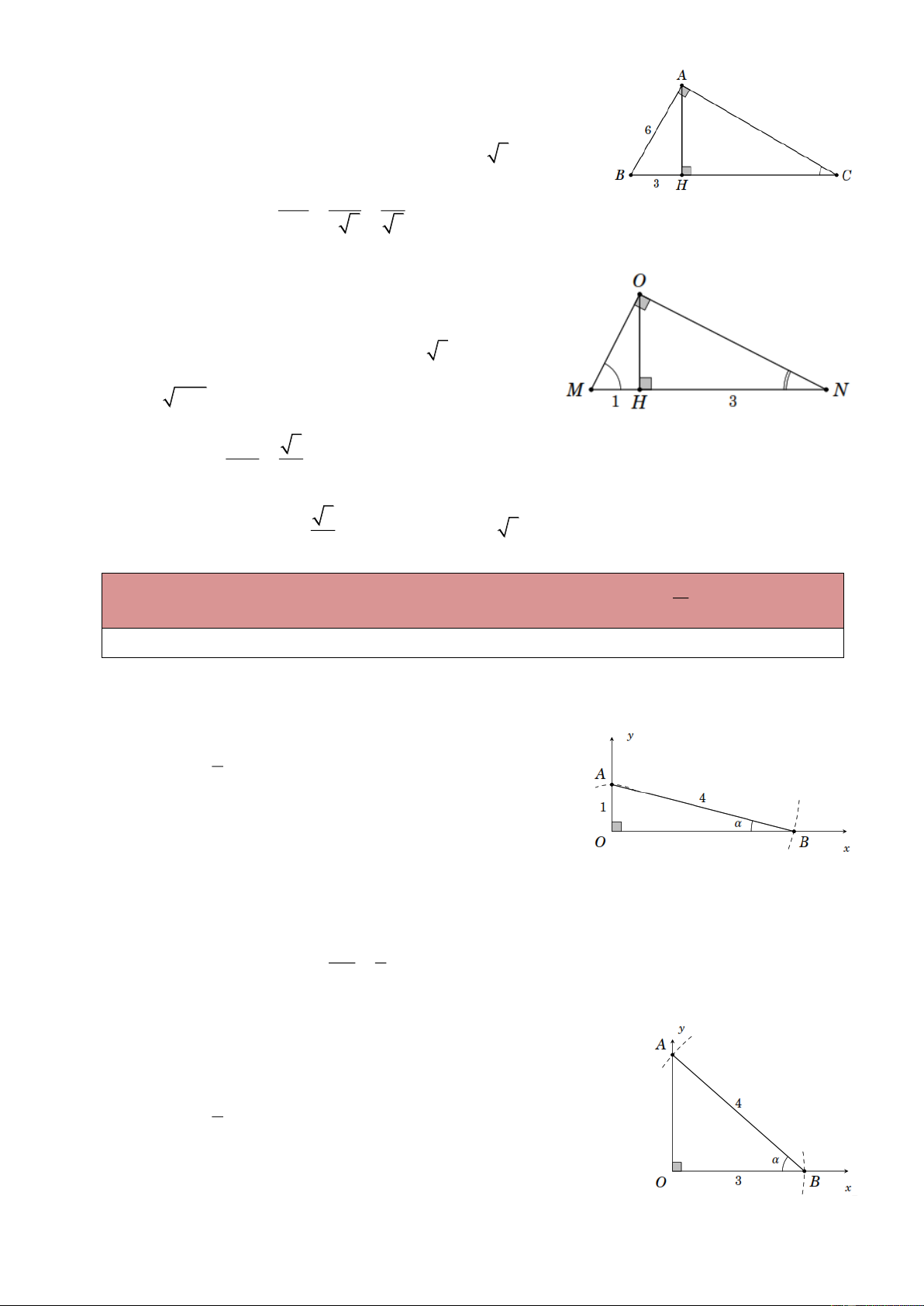
Ví dụ 2. Tính tỉ số lượng giác của góc B trong hình bên. Lời giải Ta có 2 2 2 2 2
BC AB AC 5 12 169 BC 13 . Do đó AC 12 AB 5 sin B ; cos B ; BC 13 BC 13 AC 12 AB 5 tan B ; cot B . AB 5 AC 12
Ví dụ 3. ABC vuông tại A có BC 2AB . Tính các tỉ số lượng giác của góc C . Lời giải
Ta đặt AB m thì BC 2m, suy ra 2 2 2 2 2 2
AC BC AB 4m m 3m AC m 3 . AB m 1 AC m 3 3 Ta có sin C ;cosC ; BC 2m 2 BC 2m 2 AB m 1 AC m 3 tan C ; cot C 3 . AC m 3 3 AB m
Ví dụ 4. Tam giác ABC cân tại A , có BC 6 , đường cao AH 4 . Tính các tỉ số lượng giác của góc B . Lời giải
Ta có BH 6 : 2 3 ; 2 2
AB 4 3 5 . Do đó AH 4 sin B 0,8; AB 5 BH 3 cos B 0,6; AB 5 AH 4 tan B ; AB 3 BH 3 cot B 0,75. AH 4 Trang 2
Ví dụ 5. Tính tan C trong hình bên. Lời giải Ta có 2 2 2 2 2
AH AB BH 6 3 27 AH 3 3 . Do đó BH 3 1
tan C cot B . AH 3 3 3
Ví dụ 6. Tính sin M cos N trong hình bên. Lời giải Ta có 2
OH HM HN 13 3 OH 3 ; OM 1 3 2 . Do đó OH 3 sin M . OM 2 3
Mặt khác cos N sin M
nên sin M cos N 3 . 2 m
Dạng 2: Dựng góc nhọn khi biết tỉ số lượng giác của góc nhọn đó bằng . n
Dựng một tam giác vuông có cạnh là m và n rồi vận dụng định nghĩa để nhận ra góc .
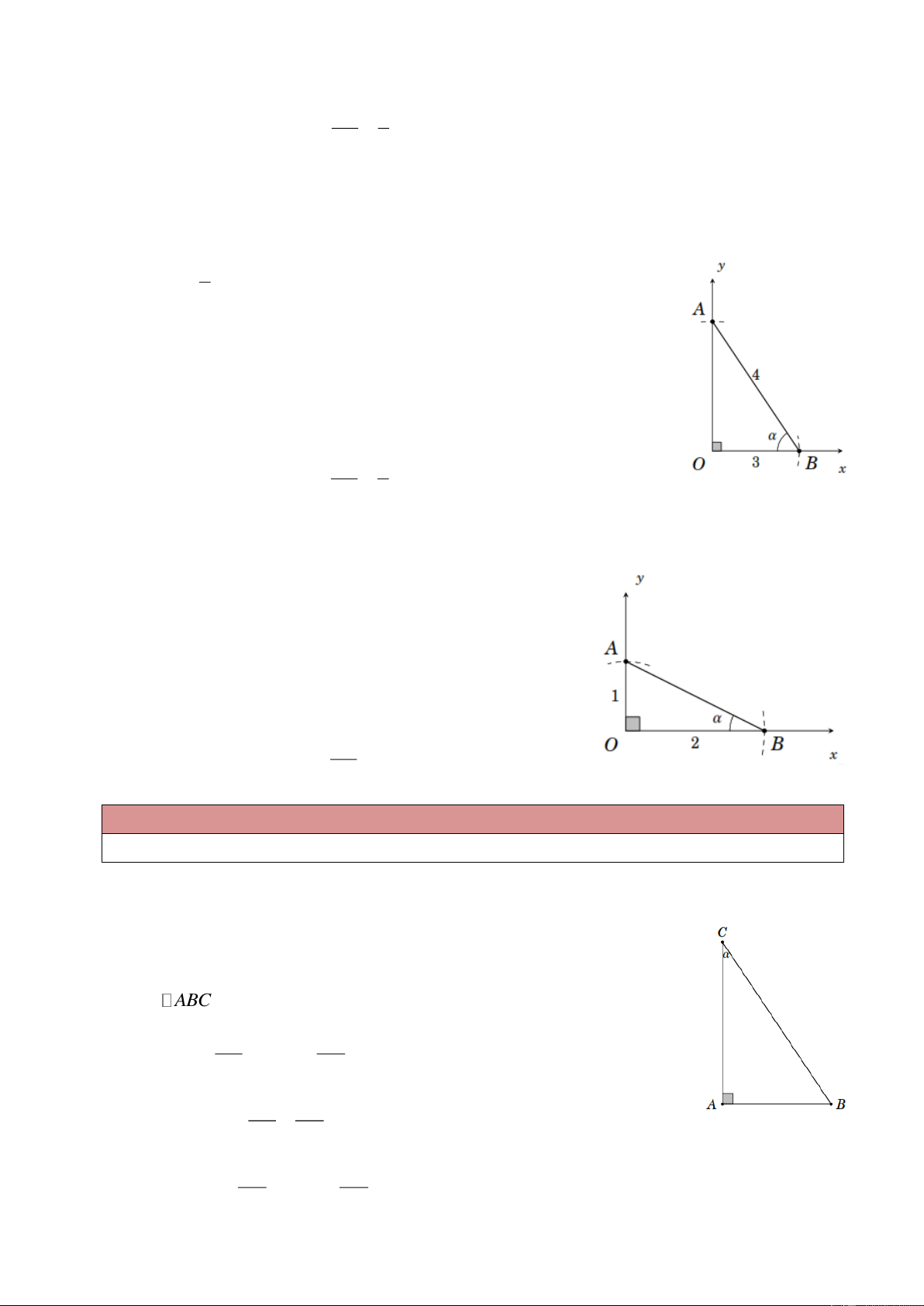
Ví dụ 7. Dựng góc , biết sin 0, 25 . Lời giải 1 Ta có 0, 25 . 4
Dựng góc vuông xOy ;
Trên cạnh Ox đặt OA 1; Dựng đường tròn ( ;
A 4) cắt cạnh Oy tại B . Khi đó OA 1
ABO vì sin . AB 4
Ví dụ 8. Dựng góc , biết cos 0, 75 . Lời giải 3 Ta có 0, 75 . 4
Dựng góc vuông xOy ;
Trên cạnh Oy đặt OB 3; Trang 3 Dựng đường tròn ( ;
B 4) cắt cạnh Ox tại A . Khi đó OB 3
ABO vì cos . AB 4
Ví dụ 9. Dựng góc , biết tan 1, 5 . Lời giải 3 Ta có 1, 5 . 2
Dựng góc vuông xOy ;
Trên cạnh Ox đặt OA 3;
Trên cạnh Oy đặt OB 2 . Khi đó OA 3
ABO vì tan . OB 2
Ví dụ 10. Dựng góc , biết cot 2 . Lời giải
Dựng góc vuông xOy ;
Trên cạnh Ox đặt OA 1;
Trên cạnh Oy đặt OB 2 . Khi đó OB
ABO vì cot 2 . OA
Dạng 3: Chứng minh hệ thức lượng giác
Sử dụng định nghĩa và một số hệ thức lượng giác cơ bản để chứng minh.
Ví dụ 11. Cho góc nhọn . Chứng minh rằng a) sin tan ; b) cos cot . Lời giải
a) Xét ABC vuông tại A , ˆ
C (hình bên). AB AB Ta có sin ; tan . BC AC AB AB
Vì BC AC nên , suy ra sin tan . BC AC AC AC b) Ta có cos ; cot . BC AB Trang 4 AC AC
Vì BC AB nên , suy ra cos cot . BC AB
Ví dụ 12. Chứng minh các hệ thức 1 1 a) 2 1 tan ; b) 2 1 cot . 2 cos 2 sin Lời giải 2 2 2 sin cos sin 1 a) 2 1 tan 1 . 2 2 cos cos cos 2 2 2 cos sin cos 1 b) 2 1 cot 1 . 2 2 sin sin sin
Ví dụ 13. Chứng minh rằng 1 cos sin tan 1 1 cot a) ; b) . sin 1 cos tan 1 1 cot Lời giải 1 cos sin a) Ta có 2
(1 cos)(1 cos) sin sin 1 cos 2 2 2 2
1 cos sin sin sin .
Đẳng thức cuối cùng đúng nên đẳng thức đã cho là đúng. tan 1 1 cot
b) Xét vế trái T ; vế phải P . tan 1 1 cot 1 1
1 cot 1 cot 1 cot T 1 : 1 : cot cot cot cot 1 cot
Rõ ràng T P .
Ví dụ 14. Chứng minh rằng 2 2 2 2
tan sin tan sin . Lời giải Ta biến đổi vế trái 2 sin 2 2 1 cos sin 2 2 sin sin 2 2 2 2 2
T tan sin sin tan sin 2 2 2 cos cos cos
Ta thấy vế trái bằng vế phải. 2 2 1 4 sin cos 2
Ví dụ 15. Chứng minh rằng sin cos . 2 sin cos Lời giải Trang 5 Xét vế trái
(1 2sin cos )(1 2sin cos ) T 2 (sin cos ) 2 2
sin cos 2sin cos 2 2
sin cos 2sin cos 2 (sin cos ) 2 2
(sin cos ) (sin cos ) 2 (sin cos ) 2 (sin cos)
Ta thấy vế trái đúng bằng vế phải.
Dạng 4: Biết một giá trị lượng giác của góc nhọn, tính các tỉ số lượng giác khác của góc đó
Vận dụng các hệ thức cơ bản đã học.
Ví dụ 16. Cho biết sin 0, 6 ; tính cos , tan , cot . Lời giải Ta có 2 2
cos 1 sin 1 (0, 6) 0,8 sin 0, 6 cos 0,8 4 tan 0,75;cot . cos 0,8 sin 0, 6 3 2
Ví dụ 17. Cho biết cos
; tính sin , tan , cot . 3 Lời giải 2 2 5 Ta có 2 sin 1 cos 1 3 3 sin 5 2 5 cos 2 5 2 tan : ; cot : . cos 3 3 2 sin 3 3 5 1
Ví dụ 18. Cho biết tan
, tính cot , sin , cos . 3 Lời giải 2 1 1 1 1 2 Ta có cot 1: 3 ; 2 1 tan 1 . tan 3 cos 3 3 2 Do đó 3 3 1 cos ; 2
sin 1 cos 1 . 2 2 2
Ví dụ 19. Cho biết cot x 2, tính tan x , sin x , cos x . Lời giải Trang 6 1 1 1 Ta có tan x ; 2 2
1 cot x 1 2 5 . cot x 2 sin x 2 Do đó 1 1 2 sin x ; 2
cos x 1 sin x 1 . 5 5 5
Dạng 5: Tính giá trị lượng giác với các góc đặc biệt (không dùng máy tính hoặc bảng số)
Căn cứ vào bảng giá trị lượng giác của các góc đặc biệt 30;45;60 .
Căn cứ vào tỉ số lượng giác của hai góc phụ nhau.
Căn cứ vào các hệ thức lượng giác cơ bản.
Ví dụ 20. Tính giá trị của biểu thức a) 2 3 M 4 cos 45 3 cot 30 16 cos 60 ; 2sin 30 sin 60 b) N . 2 cos 30 cos 60 Lời giải 2 3 2 1 a) 2 3
M 4 cos 45 3 cot 30 16 cos 60 4 3 3 16 2 3 2 3 . 2 2 1 3 3 2 1 2 sin 30 sin 60 b) 2 2 2 N 4 2 3 . 2 2 cos 30 cos 60 3 1 3 1 4 2 2 2
Ví dụ 21. Tính giá trị của biểu thức a) 2 2 2 2
P sin 30 sin 40 sin 50 sin 60 ; b) 2 2 2 2 2 Q cos 25 cos 35 cos 45 cos 55 cos 65 . Lời giải a) 2 2 2 2
P sin 30 sin 40 sin 50 sin 60 2 2
sin 30 sin 60 2 2 sin 40 sin 50 2 2
sin 30 cos 30 2 2 sin 40 cos 40 11 0 b) 2 2 2 2 2 Q cos 25 cos 35 cos 45 cos 55 cos 65 Trang 7 2 2
cos 25 cos 65 2 2 cos 35 cos 55 2 cos 45 2 2 2 2 cos 25 sin 25 2 2 cos 35 sin 35 2 1 1 11 2 2
Ví dụ 22. Tính giá trị của biểu thức sau với 0 0 90 : 2 2 2
A cos tan 60 cot 45 2sin 30 cos tan . Lời giải 2 2 2 A
cos tan 60 cot 45 2sin 30 cos tan 1 2 2 2
cos cos tan 3 1 2 2 2 cos 2
1 tan 3 11 1 2 cos 3 2 cos 1 3.
Ví dụ 23. Rút gọn các biểu thức sau với 0 90 a) 4 4 2 2
B sin cos 2sin cos ; b) 6 6 2 2
C sin cos 3sin cos . Lời giải a) B 2 4 4 2 2 2 2 sin cos 2sin cos sin cos 1. 6 6 2 2
C sin cos 3sin cos b) 6 6 2 2
sin cos 3sin cos 2 2 sin cos
sin cos 3 2 2 1 2 2 sin cos
Ví dụ 24. Cho biểu thức A . 1 2sin cos sin cos
a) Chứng minh rằng A ; sin cos 2
b) Tính giá trị của A , biết tan . 3 Lời giải 2 2 sin cos
(sin cos )(sin cos ) sin cos a) A . 2 1 2sin cos (sin cos ) sin cos Trang 8
b) Chia cả tử và mẫu của A cho cos ta được sin cos 2 1 tan 1 1 cos cos 3 A . sin cos tan 1 2 5 1 cos cos 3
Dạng 6: So sánh các tỉ số lượng giác mà không dùng máy tính hoặc bảng số
Ví dụ 25. Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần
a) sin 70, cos 30, cos 40,sin 51 ;
b) cos 34,sin 57, cot 32 . Lời giải a) Ta có cos 30 sin 60 ; cos 40 sin 50 . Vì sin 50 sin 51 sin 60 sin 70 nên cos 40 sin 51 cos 30 sin 70 . b) Ta có cos 34 sin 56 ; cot 32 tan 58 . Vì sin 56 sin 57 sin 58 tan 58 nên cos 34 sin 57 cot 32 .
Ví dụ 26. Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần
a) cot 40,sin 40, cot 43, tan 42 ;
b) tan 52, cot 63, tan 72, cot 31,sin 27 . Lời giải a) Ta có cot 40 tan 50 ; cot 43 tan 47 .
Vì sin 40 tan 40 tan 42 tan 47 tan 50 nên sin 40 tan 42 cot 43 cot 40 . b) Ta có cot 63 tan 27 ; cot 31 tan 59 .
Vì sin 27 tan 27 tan 52 tan 59 tan 72 nên sin 27 cot 63 tan 52 cot 31 tan 72 . Ví dụ 27. Cho 25 50
, hãy sắp xếp các tỉ số lượng giác sau theo thứ tự giảm dần:
sin; cos 40 ; tan 10 . Lời giải
Vì 25 50 nên 10 50 .
Mặt khác góc 50 phụ với góc a 40 .
Ta có tan 10 sin 10 sin sin 50 ,
do đó tan 10 sin cos 40 . Trang 9 sin 50 cot 70
Ví dụ 28. So sánh hai số m và n , biết m ; n . cos 65 tan 35 Lời giải sin 50 sin 50 sin 25 Ta có m 1; (1) cos 65 sin 25 sin 25 cot 70 tan 20 tan 35 n 1 . (2) tan 35 tan 35 tan 35
Từ (1) và ( 2 ) suy ra m n .
Dạng 7: Tìm góc nhọn thỏa đẳng thức cho trước
Sử dụng các hệ thức lượng giác cơ bản để biến đổi về dạng cơ bản
Dùng MTBT hoặc bảng giá trị lượng giác các góc đặc biệt để tìm.
Cách dùng MTBT tìm khi biết sin (tương tự đối với cos và tan )
Nếu sin m thì bấm các phím sau
shift sin m ' ' .
Ví dụ 29. Tìm góc nhọn x , biết a) 4sin x 1 1;
b) 2 3 3 tan x 3 . Lời giải a) 4sin x 1 1 b) 2 3 3 tan x 3 1 3
4sin x 2 sin x 3
tan x 3 2 3 tan x 2 3
sin x sin 30 x 30 . tan x tan 30 x 30 .
C. BÀI TẬP VẬN DỤNG
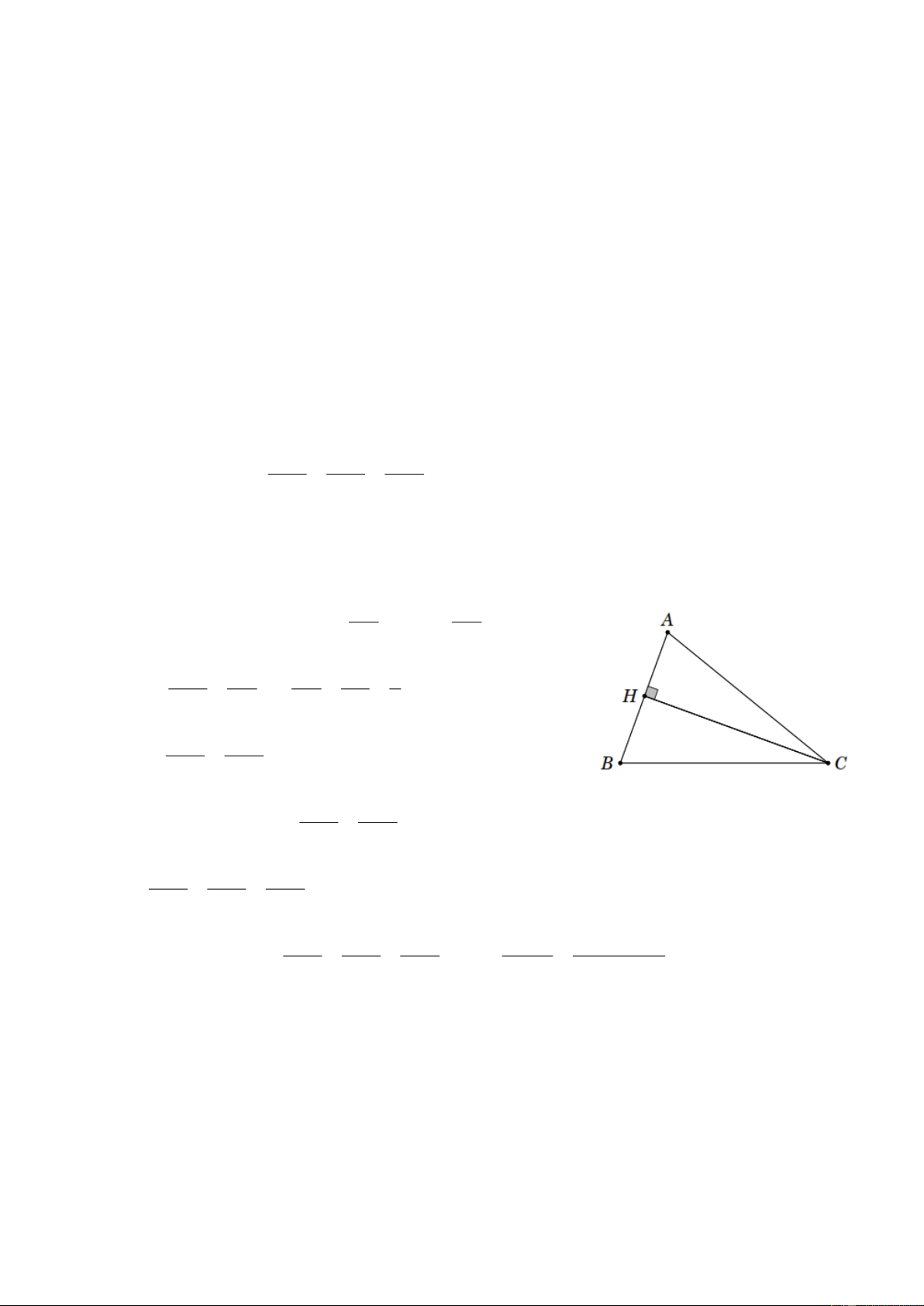
Bài 1. Cho hình bên. Tính sin C và tan B . Lời giải Ta có 2
AB BC BH 31 suy ra AB 3 . Tương tự 2
AH BH CH 1 2 suy ra AH 2 . Do đó AB 3 AH 2 sin C và tan B 2 . BC 3 BH 1 2 1 2 cos sin cos
Bài 2. Chứng minh đẳng thức . 1 2 sin cos sin cos Lời giải Ta có Trang 10 2 2 2 2 2 2 1 2 cos
cos sin 2 cos sin cos 2 2 1 2 sin cos
cos sin 2 sin cos cos sin 2
sin cos sin cos sin cos cos sin . 2 sin cos
Vậy đẳng thức được chứng minh.
Bài 3. Cho góc nhọn . 1 a) Biết cos
, hãy tính sin và tan . 3
b) Biết tan 2 , hãy tính sin và cos . Lời giải 1 a) Do 2 2
cos sin 1 mà cos nên 3 2 2 2 sin 1 8 2 2 3
sin 1 sin 3 9 2 2 sin 3
vì là góc nhọn nên sin 0 do đó 2 2 sin . 3 2 2 sin Mặt khác 3 tan 2 2 . cos 1 3 1 cos 1 1 1 5 b) Do 2
1 tan mà tan 2 nên 2 1 2 suy ra 2 cos . 2 cos 2 cos 5 1 cos 5
Vì là góc nhọn nên cos 0 do đó 1 cos . 5
Bài 4. Không dùng máy tính hoặc bảng số, hãy
a) Tính giá trị của biểu thức 2 2 2 2 2 2
M sin 20 cos 30 sin 40 sin 50 cos 60 sin 70 .
b) Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần sin 41 ; cos 58 ; cot 49 ; cos 75 ; sin 25 . Lời giải a) Ta có 2 2 2 sin 70 sin 90 20 cos 20 . Trang 11 Tương tự 2 2 2 sin 50 sin 90 40 cos 40 và 2 2 2 cos 60 cos 90 30 sin 30 . Do đó 2 2 2 2 2 2 M
sin 20 cos 30 sin 40 cos 40 sin 60 cos 20 2 2
sin 20 cos 20 2 2
cos 30 sin 30 2 2
sin 40 cos 40 111 1. b) Ta có cos 58 sin 32 , cos 49 sin 41 và cos 75 sin 25 . Mà sin 25 sin 32 sin 41 mà cos 49 cot 49 nên sin 25 cos 75 cos 58 sin 41 cos 49 cot 49 . Vậy sin 25 cos 75 cos 58 sin 41 cot 49 .
Bài 6. Cho tam giác nhọn ABC , độ dài các cạnh BC , CA , AB lần lượt bằng a , b , c . a b c a) Chứng minh rằng . sin A sin B sin C
b) Chứng minh rằng nếu a b 2c thì sin A sin B 2sin C . Lời giải CH CH
a) Kẻ CH AB . Ta có sin A ; sin B . AC BC Do đó sin A CH CH BC a và . sin B AC BC AC b a b Suy ra . sin A sin B b c b) Chứng minh tương tự . sin B sin C a b c Vậy . sin A sin B sin C a b c 2c a b Theo chứng minh trên suy ra . sin A sin B sin C 2 sin C sin A sin B
Vì a b 2c thì sin A sin B 2sin C . --- HẾT --- Trang 12




