Phương pháp giải hình 9 vị trí tương đối của hai đường tròn (có đáp án và lời giải chi tiết)
Tổng hợp Phương pháp giải hình 9 vị trí tương đối của hai đường tròn (có đáp án và lời giải chi tiết) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.
Preview text:
Bài 7. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN
A. KIẾN THỨC TRỌNG TÂM
1. Ba vị trí tương đối của hai đường tròn
Hai đường tròn có hai điểm chung gọi là hai đường tròn cắt nhau.
Hai đường tròn chỉ có một điểm chung được gọi là hai đường tròn tiếp xúc nhau. Điểm chung
đó gọi là tiếp điểm.
Hai đường tròn không có điểm chung được gọi là hai đường tròn không giao nhau.
2. Tính chất đường nối tâm
Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là
đường nối tâm là đường trung trực của dây cung ấy.
Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Chứng minh song song, vuông góc.
Vận dụng tính chất của đường nối tâm; các dấu hiệu chứng minh song song; định lí Py-
ta-go; tính chất hình hình thang; tính chất hai tiếp tuyến cắt nhau…
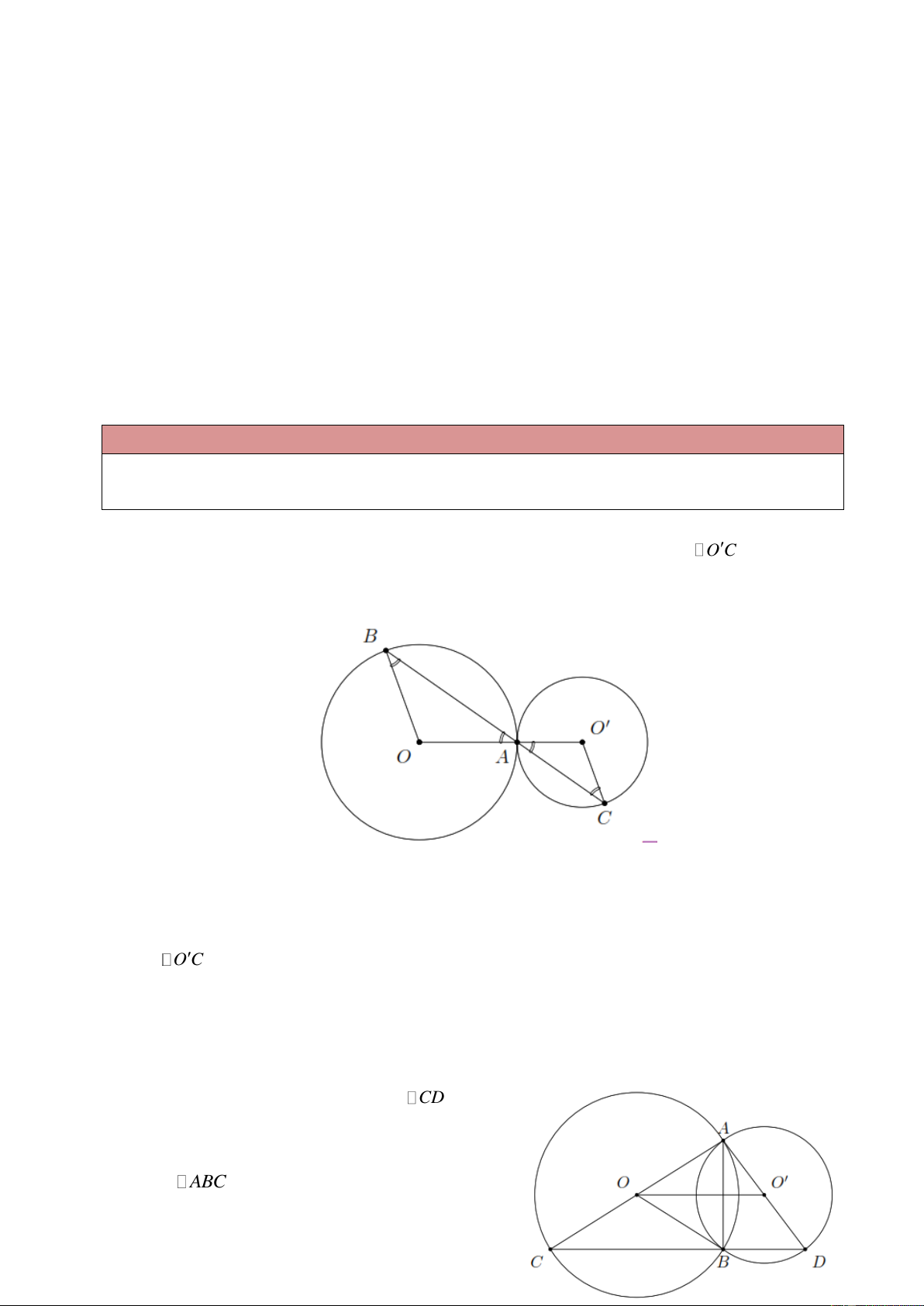
Ví dụ 1. Cho hai đường tròn ( ; O R) và (O ;
r) tiếp xúc nhau tại A ( A nằm giữa O và O ). Một
đường thẳng đi qua A cắt ( ;
O R) tại B và cắt (O ;
r) tại C . Chứng minh OB O C . Lời giải
Theo tính chất đường nối tâm thì O , A , O thẳng hàng.
OBA OAB O A C O C A . OB O C .
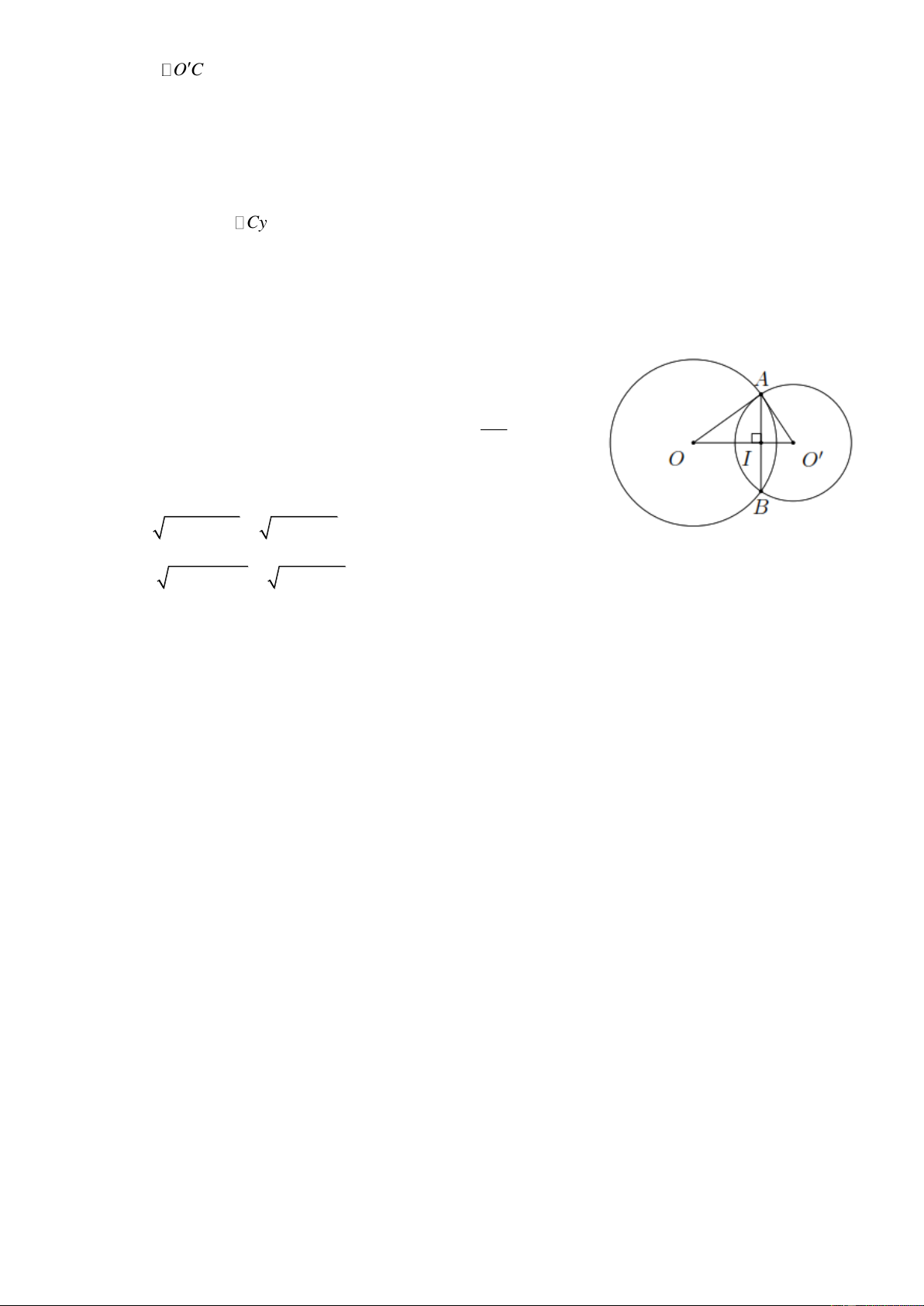
Ví dụ 2. Cho hai đường tròn (O) và (O )
cắt nhau tại hai điểm A và B . Kẻ các đường kính AOC , AO D . Chứng minh: a) AB BC .
b) C , B , D thẳng hàng. c) OO CD . Lời giải
a) Ta có ABC nội tiếp đường tròn đường kính AC Trang 1 ABC 90
AB BC .
b) Ta có ABD nội tiếp đường tròn đường kính AD ABD 90
AB BD .
Do đó CBD ABC ABD 90 90 180 .
B , C , D thẳng hàng. OO AB c) Ta có OO C . D C D AB
Dạng 2: Tính độ dài đoạn thẳng. Chứng minh đoạn thẳng bằng nhau
Vận dụng tính chất của đường nối tâm; các dấu hiệu chứng minh song song; định lí Py-
ta-go; tính chất hình hình thang; tính chất hai tiếp tuyến cắt nhau…
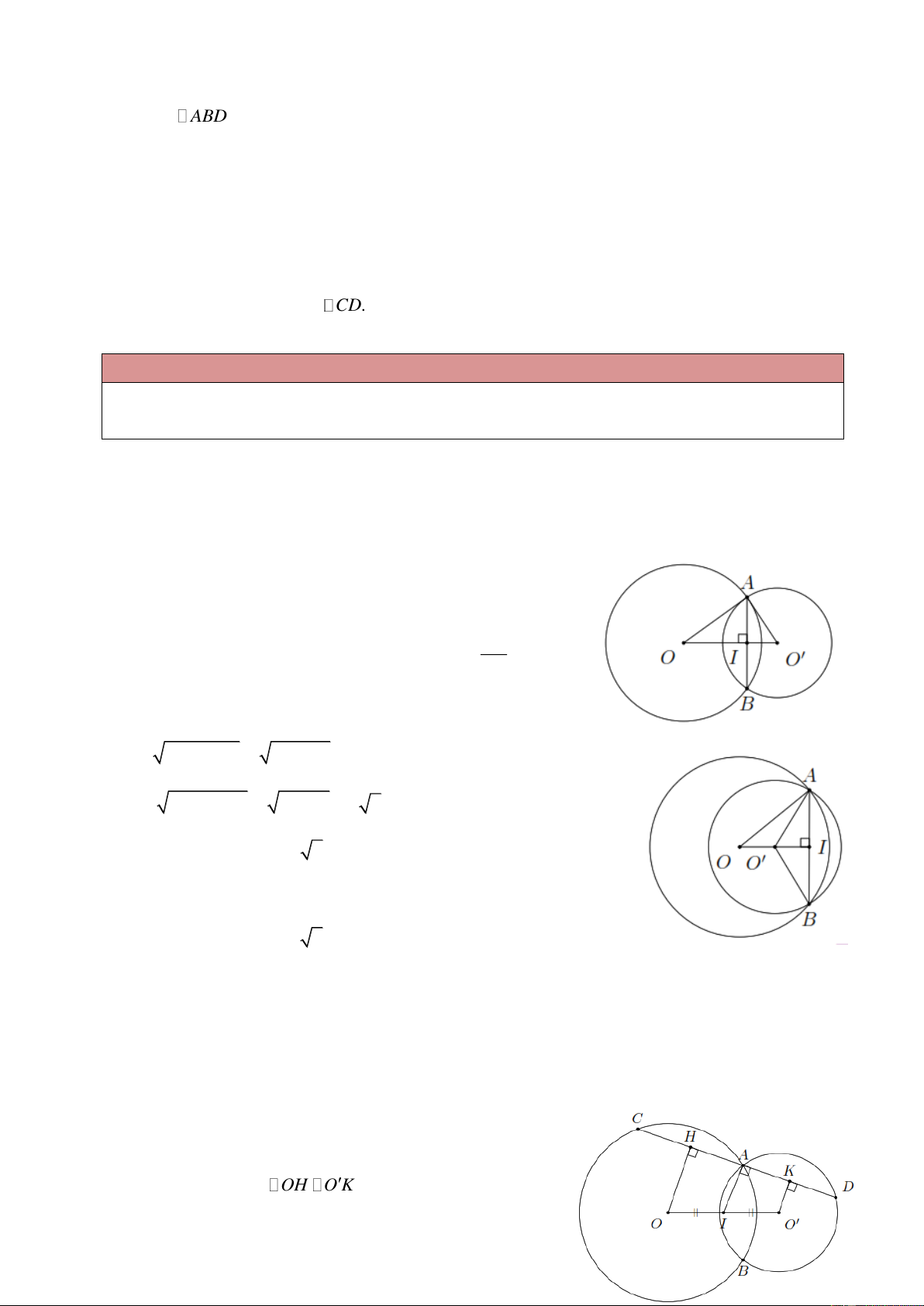
Ví dụ 3. Cho hai đường tròn ( O;10 cm) và ( O ;8
cm) cắt nhau tại hai điểm ,
A B . Biết AB 12
cm, tính đoạn nối tâm OO . Lời giải
Trường hợp 1: O và O nằm khác phía đối với AB .
Gọi I OO AB . Theo tính chất đường nối tâm AB
OO là đường trung trực của AB IA IB 6 cm. 2 Khi đó ta có 2 2 2 2
OI OA IA 10 6 8 cm. 2 2 2 2 O I O A
IA 8 6 2 7 cm.
OO OI O I 8 2 7 cm.
Trường hợp 2: O và O nằm cùng về một phía đối với AB .
OO OI O I 8 2 7 cm.
Ví dụ 4. Cho hai đường tròn (O) và (O )
cắt nhau tại A và B . Gọi I là trung điểm của OO . Qua
A vẽ đường thẳng vuông góc với AI , cắt đường tròn (O) và (O )
tại C và D (C, D A ). Chứng
minh AC AD . Lời giải
Kẻ OH AC , O K AD .
Khi đó tứ giác OHKO là hình thang vuông có I là trung
điểm của OO và IA OH O K . Trang 2 AH AK .
Mà H , K lần lượt là trung điểm của AC và AD (quan hệ vuông góc giữa đường kính và dây cung).
Do đó AC AD .
C. BÀI TẬP VẬN DỤNG
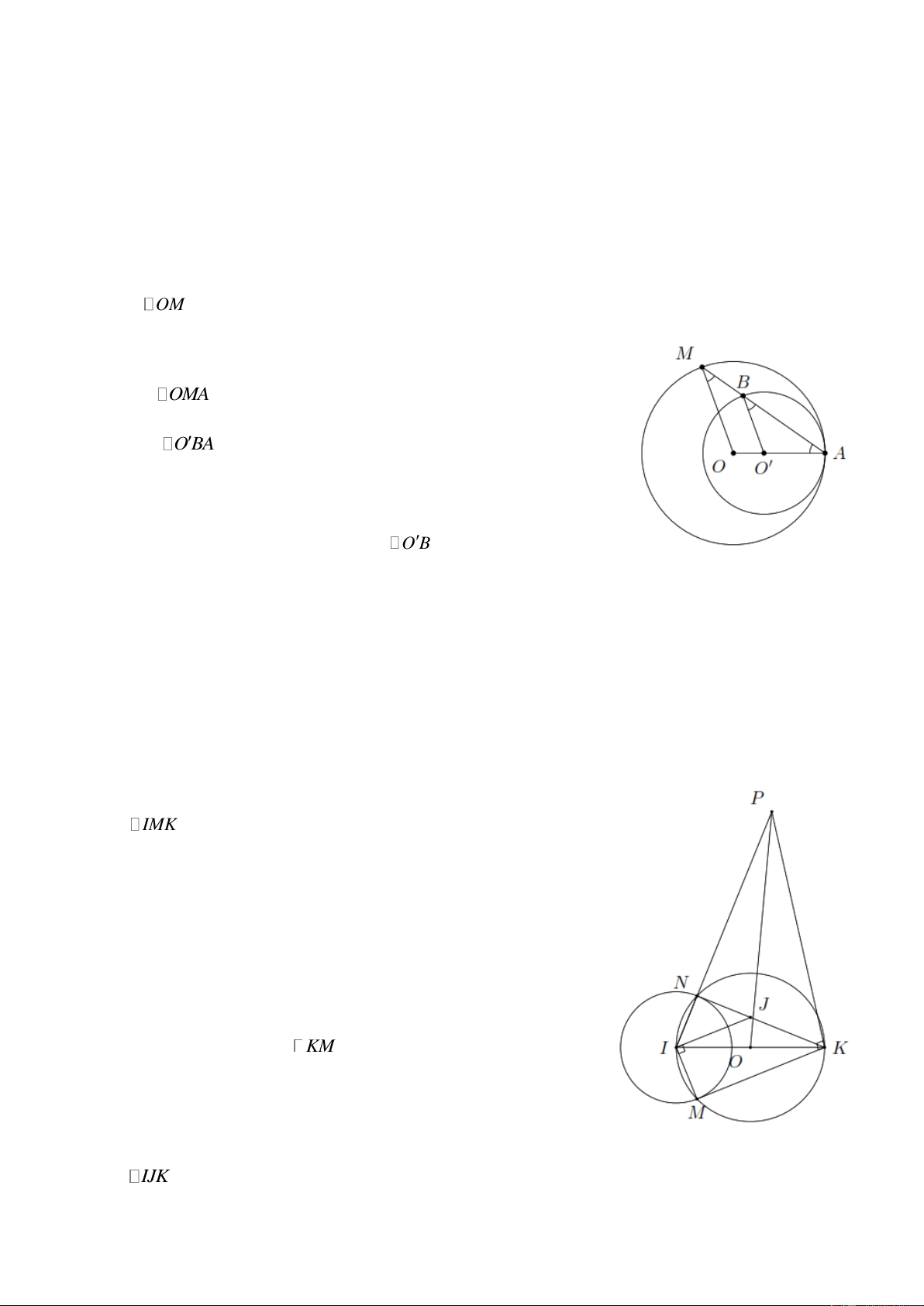
Bài 1. Cho hai đường tròn ( O ) và (O )
tiếp xúc với nhau tại điểm A sao cho O nằm giữa O và
A . Gọi M là một điểm bất kì nằm trên (O) ( M A ), AM cắt (O )
tại B . Chứng minh rằng O B OM . Lời giải
Ta có OMA cân tại O . Do đó OMA OAM (1) Lại có O B
A cân tại O . Do đó O B A OMA (2)
Từ (1) và (2) suy ra OMA O B A. Mà OMA và O B
A đồng vị nên OM O B .
Bài 2. Cho hai đường tròn ( O; R ) và ( I ; r ) cắt nhau tại M và N , trong đó I thuộc đường tròn
(O) và R r . Kẻ đường kính IOK của đường tròn (O) .
a) Chứng minh KM , KN là các tiếp tuyến của (I ) .
b) Đường vuông góc với MI tại I cắt KN tại J . Chứng minh JI JK .
c) Đường vuông góc với KM tại K cắt IN tại P . Chứng minh ba điểm O , J , P thẳng hàng. Lời giải
a) IMK nội tiếp đường tròn tâm O đường kính IK . IMK 90
KM IM .
KM là tiếp tuyến của ( I ).
Tương tự: KN là tiếp tuyến của ( I ).
b) Ta có KMI 90 KM IM .
Mà JJ IM . Do đó IJ
KM JIK IKM .
Theo tính chất của hai tiếp tuyến cắt nhau ta có
IKM JKI JIK JKI
IJK cân tại J JI JK . c) Ta có PKO IKM 90 PKO JKI 90 (1) . Trang 3 Ta lại có PIK NKI 90 (2) .
Từ (1) và ( 2 ) suy ra PIK PKI .
PIK cân tại P PI PK .
Do đó suy ra ba điểm O , P , J cùng thuộc đường trung trực của IK nên O , J , P thẳng hàng.
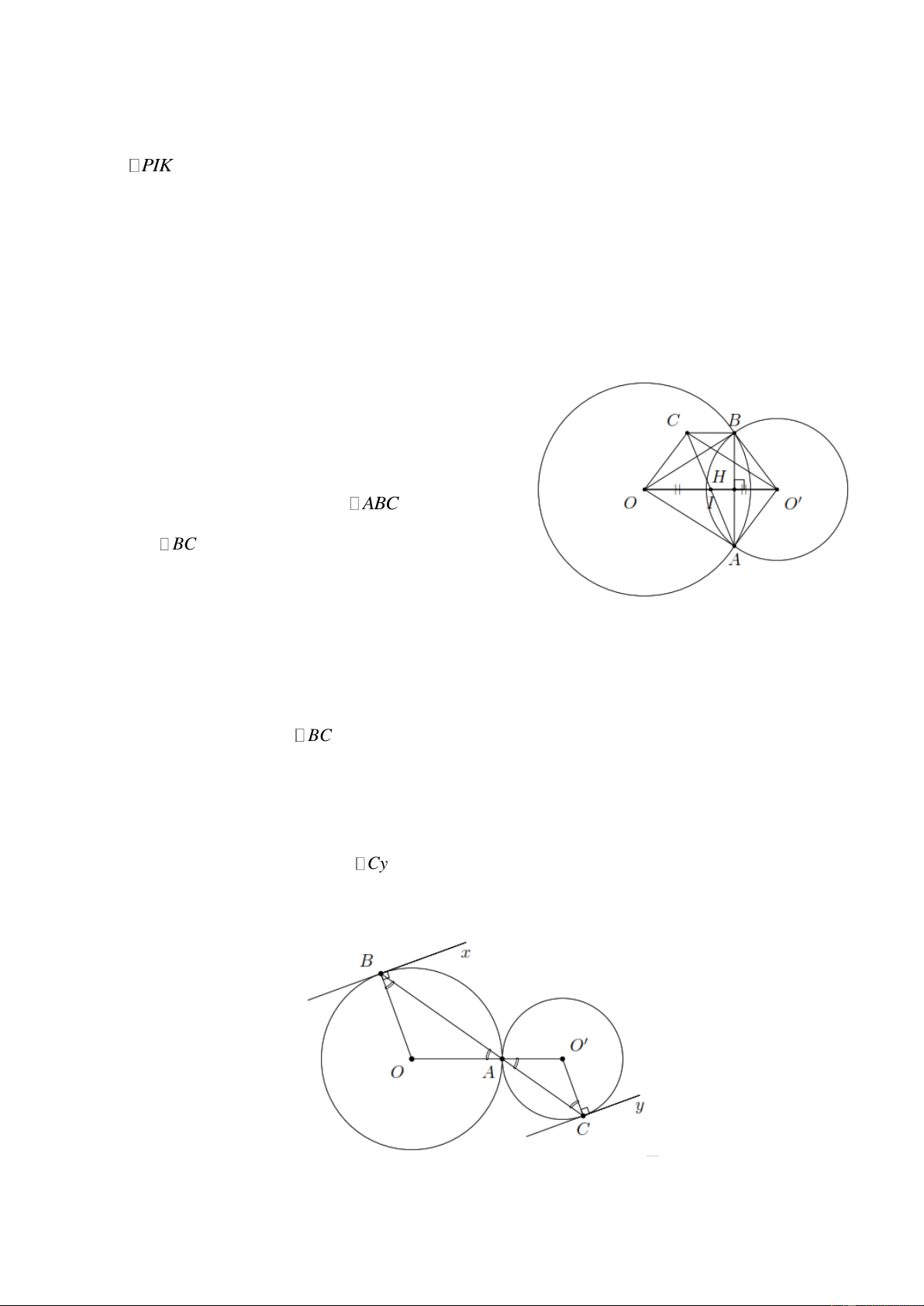
Bài 3. Cho hai đường tròn (O) và (O )
cắt nhau tại hai điểm A và B . Gọi I là trung điểm của
OO , gọi C là điểm đối xứng với A qua I . Chứng minh: a) BC AB.
b) AOCO là hình bình hành. c) OO B
C là hình thang cân. Lời giải
a) Gọi H OO AB . Theo tính chất đường nối tâm
OO là đường trung trực của AB . Do đó
OO AB và H là trung điểm của AB .
IH là đường trung bình của ABC .
IH BC mà IH AB BC AB.
b) Tứ giác AOCO có hai đường chéo cắt nhau tại
trung điểm của mỗi đường nên AOCO là hình bình hành.
c) Ta có OA O C
do AOCO là hình bình hành.
Mà OA OB OB O C . Tứ giác OO B
C có OO BC và OB O C nên OO B
C là hình thang cân.
D. BÀI TẬP VỀ NHÀ
Bài 4. Cho hai đường tròn (O) và (O )
tiếp xúc nhau tại A ( A nằm giữa O và O ). Một đường
thẳng đi qua A cắt (O) tại B , cắt (O )
tại C . Vẽ tiếp tuyến Bx tại B của (O) , vẽ tiếp tuyến Cy
tại C của (O )
. Chứng minh Bx Cy . Lời giải
Theo tính chất đường nối tâm thì O , A , O thẳng hàng.
OBA OAB O A C O C A . Trang 4 OB O C . Ta lại có
OB Bx ( Bx là tiếp tuyến của đường tròn (O));
O 'C Cy ( Cy là tiếp tuyến của đường tròn (O’)).
nên ta suy ra Bx Cy .
Bài 5. Cho hai đường tròn ( O;15 cm) và ( O ;
13 cm) cắt nhau tại hai điểm ,
A B sao cho O và O
nằm khác phía đối với AB . Biết AB 24 cm. Tính độ dài OO . Lời giải
Gọi I OO AB . Theo tính chất đường nối tâm AB
OO là đường trung trực của AB IA IB 12 cm. 2 Khi đó ta có 2 2 2 2
OI OA IA 15 12 9 cm. 2 2 2 2 O I O A
IA 13 12 5 cm.
OO OI O I 96 14 cm. --- HẾT --- Trang 5