Phương Pháp Giải Min Max Số Phức Có lời Giải

Phương pháp giải Min Max số phức được biên soạn dưới dạng file PDF gồm 53 trang. Tài liệu tổng hợp toàn bộ kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

76 38 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

53 trang 8 tháng trước

Tác giả:

Profile ha phan
Trang1
BÀI TOÁN MAX – MIN SỐ PHỨC.
Kỹ năng:
Phƣơng pháp đại số.
Phƣơng pháp hình học.
Phƣơng pháp bđt modun.
Phƣơng pháp casio.
Một số tính chất cần nhớ.
1. Môđun của số phức:
Số phức
z a bi
được biểu diễn bởi điểm M(a; b) trên mặt phẳng Oxy. Độ d|i của véctơ
OM
được gọi l| môđun của số phức z. Kí hiệu
22
z = a+ bi = a + b
Tính chất
22
z a b zz OM
0, , 0 0 z z z z
. ' . 'z z z z
, ' 0
'
'

zz
z
z
z
.,kz k z k
Chú ý:
2
2
2 2 2 2 2 2 2 2 2 2
2 ( ) 4 . z a b abi a b a b a b z z z z
.
Lưu ý:
1 2 1 2
z z z z
dấu bằng xảy ra
12
0 z kz k
1 2 1 2
z z z z
dấu bằng xảy ra
12
0 z kz k
.
1 2 1 2
z z z z
dấu bằng xảy ra
12
0 z kz k
1 2 1 2
z z z z
dấu bằng xảy ra
12
0 z kz k
2 2 2 2
1 2 1 2 1 2
2 z z z z z z
2
2
z z z z
z
2.Một số quỹ tích nên nhớ
Biểu thức liên hệ
,xy
Quỹ tích điểm M
ax 0 by c
(1)
z a bi z c di
(2)
(1)Đường thẳng
:ax 0 by c
(2) Đường trung trực đoạn AB với
, , ,A a b B c d
22
2
x a y b R
hoặc
z a bi R
Đường tròn t}m
;I a b
, bán kính
R
22
2
x a y b R
hoặc
z a bi R
Hình tròn tâm
;I a b
, bán kính
R
22
22
r x a y b R
hoặc
Hình v|nh khăn giới hạn bởi hai đường
tròn đồn t}m
;I a b
, b{n kính lần lượt l|
Trang2
r z a bi R
,rR
2
2
0
y ax bx c
c
x ay by c
Parabol
22
22
11


x a y c
bd
hoặc
1 1 2 2
2 z a b i z a b i a
1
Elip
2
Elip nếu
1 1 2 2
2 , , , ,a AB A a b B a b
Đoạn AB nếu
2 a AB
22
22
1


x a y c
bd
Hypebol
Một số dạng đặc biệt cần lƣu ý:
Dạng 1: Quỹ tích điểm biểu diễn số phức l| đường thẳng.
TQ1: Cho số phức
z
thỏa mãn
z a bi z
, tìm
Min
z
. Khi đó ta có
Quỹ tích điểm
M x; y
biểu diễn số phức
z
l| đường trung trực đoạn
OA
với
A a; b
22
0
11
22
22

Min
z z a b
ab
zi
TQ2:Cho số phức thỏa mãn điều kiện
. z a bi z c di
Tìm
min
z
. Ta có
Quỹ tích điểm
M x; y
biểu diễn số phức
z
l| đường trung trực đoạn
AB
với
A a; b ,B c;d
2 2 2 2
22
,
2

Min
a b c d
z d O AB
a c b d
Lƣu ý: Đề b|i có thể suy biến b|i to{n th|nh 1 số dạng, khi đó ta cần thực hiện biến đổi để đưa về
dạng cơ bản.
Ví dụ 1:
Cho số phức thỏa mãn điều kiện
. z a bi z c di
Khi đó ta biến đổi
. z a bi z c di z a bi z c di
Cho số phức thỏa mãn điều kiện
. iz a bi z c di
Khi đó ta biến đổi
.
a bi c di
iz a bi iz c di z z z b ai z d ci
ii
Dạng 2: Quỹ tích điểm biểu diễn số phức l| đường tròn.
Trang3
TQ: Cho số phức
z
thỏa mãn điều kiện
0
z a bi R 0 z z R
. Tìm
Max Min
z , z
. Ta có
Quỹ tích điểm
M x; y
biểu diễn số phức
z
l| đường tròn t}m
I a;b
bán kính
R
22
0
22
0
Max
Min
z OI R a b R z R
z OI R a b R z R
Lƣu ý: Đề b|i có thể cho ở dạng kh{c, ta cần thực hiện c{c phép biến đổi để đưa về dạng cơ bản.
Ví dụ 1: Cho số phức
z
thỏa mãn điều kiện
a bi R
iz a bi R z
i
i

(Chia hai vế cho
i
)
z b ai R
Ví dụ 2: Cho số phức
z
thỏa mãn điều kiện
z a bi R z a bi R
(Lấy liên hợp 2 vế)
Ví dụ 3: Cho số phức
z
thỏa mãn điều kiện
22
a bi R R
c di z a bi R z
c di
c di
cd

Hay viết gọn
1
01
0
0
z
R
z z z R z
z
z
(Chia cả hai vế cho
0
z
)
Dạng 3: Quỹ tích điểm biểu diễn số phức l| Elip.
TQ1: (Elip chính tắc). Cho số phức
z
thỏa mãn điều kiện
z c z c 2a , a c
Khi đó ta có
Quỹ tích điểm
M x; y
biểu diễn số phức
z
là Elip:
2
2
2 2 2
y
x
1
a a c

22

Max
Min
za
z a c
TQ2: (Elip không chính tắc).Cho số phức
z
thỏa mãn điều kiện
12
z z z z 2a
Thỏa mãn
12
2a z z
.
Khi đó ta thực hiện phép biến đổi để đưa Elip về dạng chính tắc (Kỹ thuật đổi hệ trục tọa độ).
Ta có
Trang4
Khi đề cho Elip dạng không chính tắc
1 2 1 2
z z z z 2a , z z 2a
và
12
z ,z c, ci
). Tìm
Max, Min của
0
P z z
.
Đặt
12
2 2 2
z z 2c
b a c


Nếu
12
0
zz
z0
2

Max
Min
Pa
Pb
(dạng chính tắc)
Nếu
12
0
0 1 0 2
zz
za
2
z z k z z

12
Max 0
12
Min 0
zz
P z a
2
zz
P z a
2
Nếu
12
0
0 1 0 2
zz
za
2
z z k z z

12
Max 0
zz
P z a
2
Nếu
0 1 0 2
z z z z
12
Min 0
zz
P z b
2
PHẦN I : BÀI TẬP CÓ HƢỚNG DẪN GIẢI CHI TIẾT.
Dạng 1: Sử dụng tính chất của modun – bđt đại số.
Phƣơng pháp : Xem hƣớng dẫn trên lớp
Dạng 2: Sử dụng tính chất hình học.
Xem hƣớng dẫn trên lớp.
Dạng 3: Tả phí lù.
Phƣơng pháp: Tin tƣởng bạn ngồi bên cạnh
Câu 1: (TRẦN HƢNG ĐẠO – NB)Trong c{c số phức thỏa mãn điều kiện
3 2 . z i z i
Tìm số
phức có môđun nhỏ nhất?
A.
12zi
. B.
12
55
zi
. C.
12
55
zi
. D.
12 zi
.
Hƣớng dẫn giải
Chọn C.
Cách 1: Phƣơng pháp tự luận
Giả sử
, z x yi x y
2 2 2
2
3 2 3 2 1 3 2 1 z i z i x y i x y i x y x y
6 9 4 4 2 1 4 8 4 0 2 1 0 2 1 y x y x y x y x y
Trang5
2
2
2 2 2 2
2 1 5
2 1 5 4 1 5
5 5 5



z x y y y y y y
Suy ra
min
5
5
z
khi
21
55
yx
Vậy
12
.
55
zi
Cách 2: Phƣơng pháp trắc nghiệm
Giả sử
, z x yi x y
2 2 2
2
3 2 3 2 1 3 2 1 z i z i x y i x y i x y x y
6 9 4 4 2 1 4 8 4 0 2 1 0 y x y x y x y
Vậy tập hợp c{c điểm biểu diễn số phức
z
thỏa điều kiện
32 z i z i
l| đường thẳng
: 2 1 0 d x y
.
Phương {n A:
12zi
có điểm biểu diễn
1; 2d
nên loại A.
Phương {n B:
12
55
zi
có điểm biểu diễn
12
;
55




d
nên loại B.
Phương {n D:
12 zi
có điểm biểu diễn
1; 2d
nên loại B.
Phương {n C:
12
55
zi
có điểm biểu diễn
12
;
55




d
(Trong trường hợp có nhiều số phức thuộc đường thẳng thì ta tiếp tục so s{nh modun, v|
nên thay luôn
z
v|o dữ kiện ban đầu chứ không nên biến đổi)
Cách 3: Tính nhanh.
Quỹ tích c{c điểm M biểu diễn số phức
z
l| đường thẳng có phương trình
: 2 1 0 xy
.
Vậy
min
22
1
5
,
5
12
z d O
Cách 4: Công thức tính nhanh.
BT1:Cho số phức thỏa mãn điều kiện
. z a bi z
Tìm
min
z
?
22
0
11
22
22

Min
z z a b
ab
zi
BT2:Cho số phức thỏa mãn điều kiện
. z a bi z c di
Tìm
min
z
?
2 2 2 2
22
2
Min
a b c d
z
a c b d
Câu 2: (LẠNG GIANG SỐ 1)Cho số phức
z
thỏa mãn
3 3 8 zz
. Gọi
M
,
m
lần lượt gi{ trị
lớn nhất v| nhỏ nhất
.z
Khi đó
Mm
bằng
A.
4 7.
B.
4 7.
C.
7.
D.
4 5.
Trang6
Hƣớng dẫn giải
Chọn B.
Cách 1 : Đại số
Gọi
z x yi
với
; xy
.
Ta có
8 3 3 3 3 2 4 z z z z z z
.
Do đó
4M max z
.
Mà
22
22
3 3 8 3 3 8 3 3 8 z z x yi x yi x y x y
.
Áp dụng bất đẳng thức Bunhiacopxki, ta có
2 2 2 2
2 2 2 2 2 2
8 1. 3 1. 3 1 1 3 3



x y x y x y x y
2 2 2 2
8 2 2 2 18 2 2 2 18 64 x y x y
2 2 2 2
7 7 7 x y x y z
.
Do đó
7M min z
.
Vậy
47 Mm
.
Cách 2: Hình học (Đọc lại lý thuyết phần Elip)
Tập hợp c{c điểm biểu diễn số phức
z
là elip
12
2
2
2 2 2 2
3;0 , 0,3
8
14
16 7 2
4 3 7







FF
y
x
a
b a c
Do vậy
4
47
7


Max
Min
za
Mm
zb
Cách 3: Tổng quát
Cho số phức
z
thỏa mãn
2, z c z c a a c
ta luôn có .
Tập hợp điểm biểu diễn
z
là Elip
2
2
2 2 2
1
y
x
a a c
22

Max
Min
za
z a c
Câu 3: (CHUYÊN PHAN BỘI CHÂU) Cho số phức
z
thỏa mãn
2 3 1 zi
. Gi{ trị lớn nhất của
1zi
là
A.
13 2
. B.
4
. C.
6
. D.
13 1
.
Hƣớng dẫn giải
Chọn D
Cách 1:Gọi
z x yi
ta có
2 3 2 3 2 3 z i x yi i x y i
.
Trang7
Theo giả thiết
22
2 3 1 xy
nên điểm
M
biểu diễn cho số phức
z
nằm trên đường
tròn tâm
2;3I
bán kính
1R
.
Ta có
22
1 1 1 1 1 1 z i x yi i x y i x y
.
Gọi
;M x y
và
1;1H
thì
2
2
11 HM x y
.
Do
M
chạy trên đường tròn,
H
cố định nên
MH
lớn nhất khi
M
l| giao của
HI
với đường
tròn.
Phương trình
23
:
32

xt
HI
yt
, giao của
HI
v| đường tròn ứng với
t
thỏa mãn:
22
1
9 4 1
13
t t t
nên
3 2 3 2
2 ; 3 , 2 ; 3
13 13 13 13
MM
.
Tính độ d|i
MH
ta lấy kết quả
13 1HM
.
Cách 2: Cho số phức
z
thỏa mãn
2 3 1 zi
. Gi{ trị lớn nhất của
w1 zi
Ta có
2 3 1 2 3 1 1 3 2 1 w 3 2 1 z i z i z i i i
(Đường tròn t}m
3, 2 , 1IR
)
Vậy
22
w 3 2 1 1 13
Max
OI R
Lƣu ý: Cho số phức
z
thỏa mãn
0 z a bi R
, khi đó ta có quỹ tích c{c điểm biểu diễn số
phức
z
l| đường tròn
, ,bk RI a b
) và
22
22
Max
Min
z OI R a b R
z OI R a b R
Ngoài ra ta luôn có công thức biến đổi
z a bi z a bi
Câu 4: (BIÊN HÒA – HÀ NAM)Cho số phức
z
thỏa mãn
1z
. Đặt
2
2
zi
A
iz
. Mệnh đề n|o sau
đ}y đúng?
A.
1A
. B.
1A
. C.
1A
. D.
1A
.
Hƣớng dẫn giải
Chọn A.
Cách 1:Đặt Có
22
, , 1 a a bi a b a b
(do
1z
)
2
2
2
2
2 2 1 4 2 1
2
22
2

a b i a b
zi
A
iz b ai
ba
Ta chứng minh
2
2
2
2
4 2 1
1
2


ab
ba
.
M1
I
H
M2
Trang8
Thật vậy ta có
2
2
22
2 2 2 2
2
2
4 2 1
1 4 2 1 2 1
2


ab
a b b a a b
ba
Dấu “=” xảy ra khi
22
1ab
.
Vậy
1A
.
Cách 2 : Trắc nghiệm
Chọn
1
1
2
1
1
2 34
2
1
2
17
z
zi
AA
iz
z
Câu 5: Cho số phức
z
thỏa mãn
1z
. Tìm gi{ trị lớn nhất của biểu thức
5
1.
i
A
z
A.
5.
B.
4.
C.
6.
D.
8.
Hƣớng dẫn giải
Cách 1:Ta có:
5 5 5
1 1 1 6.
ii
A
zz
z
Khi
6. z i A
Chọn đáp án C.
Cách 2:
5
5
15
zi
i
A z i
z
z
Theo bài
2
1 5 5 1 5 5 1 6
Max
z z i i z i
Câu 6: Cho số phức
z
thỏa mãn
1z
. Tìm gi{ trị lớn nhất
max
M
v| gi{ trị nhỏ nhất
min
M
của biểu
thức
23
1 1 . M z z z
A.
max min
5; 1.MM
B.
max min
5; 2.MM
C.
max min
4; 1.MM
D.
max min
4; 2.MM
Hƣớng dẫn giải
Ta có:
23
1 1 5 M z z z
, khi
max
1 5 5. z M M
Mặt kh{c:
3 3 3 3 3
3
1 1 1 1 1
1 1,
2 2 2
1
z z z z z
Mz
z
khi
min
1 1 1. z M M
Chọn đáp án A.
Câu 7: Cho số phức
z
thỏa
2z
. Tìm tích của gi{ trị lớn nhất v| nhỏ nhất của biểu thức
zi
P
z
.
A.
3
.
4
B.
1.
C.
2
. D.
2
.
3
Hƣớng dẫn giải
Ta có
13
1 1 .
| | 2
i
P
zz
Mặt kh{c:
11
1 1 .
| | 2
i
zz
Trang9
Vậy, gi{ trị nhỏ nhất của
P
là
1
2
, xảy ra khi
2 ; zi
gi{ trị lớn nhất của
P
bằng
3
2
xảy ra khi
2.zi
Chọn đáp án A.
Câu 8: Cho số phức
z
thỏa mãn
1 2 3 zi
. Tìm môđun lớn nhất của số phức
2.zi
A.
26 6 17 .
B.
26 6 17 .
C.
26 8 17 .
D.
26 4 17 .
Hƣớng dẫn giải
Cách 1:Gọi
; ; 2 2 z x yi x y z i x y i
. Ta có:
22
1 2 3 1 2 9 z i x y
.
Đặt
1 3sin ; 2 3cos ; 0;2 . 

x t y t t
2
22
2 1 3sin 4 3cos 26 6 sin 4cos 26 6 17 sin ; . z i t t t t t
max
26 6 17 2 26 6 17 2 26 6 17 3 17 z i z i
Chọn đáp án A.
Cách 2:Cho số phức
z
thỏa mãn
1 2 3 zi
. Tìm môđun lớn nhất của số phức
2.zi
Ta có
22
1 2 3 2 1 4 3 1 4 3 3 17
Max
z i z i i z
(đ{p {n A)
Câu 9: Cho số phức
z
thỏa mãn
1z
. Tìm gi{ trị lớn nhất của biểu thức
1 3 1 . P z z
A.
3 15
B.
65
C.
20
D.
2 20.
Hƣớng dẫn giải
Cách 1:Gọi
; ; z x yi x y
. Ta có:
2 2 2 2
1 1 1 1;1 .

z x y y x x
Ta có:
22
22
1 3 1 1 3 1 2 1 3 2 1 P z z x y x y x x
.
Xét h|m số
2 1 3 2 1 ; 1;1 .

f x x x x
H|m số liên tục trên
1;1

v| với
1;1x
ta có:
1 3 4
0 1;1 .
5
2 1 2 1

f x x
xx
Ta có:
max
4
1 2; 1 6; 2 20 2 20.
5



f f f P
Chọn đáp án D.
Cách 2: (Casio)
Từ
1z
, đặt
sin
cos

xt
z x yi
yt
Thay v|o P rồi dùng mode 7 ra đ{p {n D
Cách 3: Hình học (Xem video live của thầy)
Câu 10: Cho số phức
z
thỏa mãn
1.z
Gọi
M
và
m
lần lượt l| gi{ trị lớn nhất v| gi{ trị nhỏ nhất
của biểu thức
2
1 1 . P z z z
Tính gi{ trị của
.Mm
.
A.
13 3
.
4
B.
39
.
4
C.
3 3.
D.
13
.
4
Trang10
Hƣớng dẫn giải
Gọi
; ; z x yi x y
. Ta có:
1 . 1 z z z
Đặt
1tz
, ta có
0 1 1 1 2 0; 2 .

z z z t
Ta có
2
2
2
1 1 1 . 2 2 .
2
t
t z z z z z z x x
Suy ra
2
2 2 2
1 . 1 2 1 2 1 3 z z z z z z z z z x x t
.
Xét h|m số
2
3 , 0;2 .

f t t t t
Bằng c{ch dùng đạo h|m, suy ra
13 13 3
max ; min 3 . .
44
f t f t M n
Chọn đáp án A.
Câu 11: Cho số phức
z
thỏa mãn điều kiện
2
4 2 .zz
Khẳng định n|o sau đ}y l| đúng?
A.
3 1 3 1
.
66

z
B.
5 1 5 1. z
C.
6 1 6 1. z
D.
2 1 2 1
.
33

z
Hƣớng dẫn giải
Áp dụng bất đẳng thức
, u v u v
ta được
22
2
2 4 4 4 2 4 0 5 1. z z z z z z
22
22
2 4 4 2 4 0 5 1. z z z z z z z
Vậy,
z
nhỏ nhất l|
5 1,
khi
5 z i i
và
z
lớn nhất l|
5 1,
khi
5.z i i
Chọn đáp án B.
Câu 12: Cho số phức
z
thỏa mãn
1 2 2 zi
. Tìm môđun lớn nhất của số phức
.z
A.
9 4 5 .
B.
11 4 5
C.
6 4 5
D.
5 6 5
Hƣớng dẫn giải
Cách 1:Gọi
; ; z x yi x y
. Ta có:
22
1 2 2 1 2 4. z i x y
Đặt
1 2sin ; 2 2cos ; 0;2

x t y t t
.
Lúc đó:
2
22
22
1 2sin 2 2cos 9 4sin 8cos 9 4 8 sin ; z t t t t t
2
9 4 5 sin 9 4 5 ; 9 4 5



z t z
max
9 4 5 z
đạt được khi
5 2 5 10 4 5
.
55
zi
Chọn đáp án A.
Cách 2: Cho số phức
z
thỏa mãn
1 2 2 zi
. Tìm môđun lớn nhất của số phức
.z
Ta có
22
1 2 2 1 2 2 2 5 9 4 5
Max
z i z
Trang11
Câu 13: Cho số phức
z
thỏa mãn
1 6 2 10 i z i
. Tìm môđun lớn nhất của số phức
.z
A.
45
B.
3 5.
C.
3.
D.
35
Hƣớng dẫn giải
Cách 1:Gọi
; ; z x yi x y
.
Ta có:
22
62
1 6 2 10 1 . 10 2 4 5 2 4 5.
1

i
i z i i z z i x y
i
Đặt
2 5 sin ; 4 5 cos ; 0; 2

x t y t t
.
Lúc đó:
2 2 2 2
2
2 5 sin 4 5 cos 25 4 5 sin 8 5 cos 25 4 5 8 5 sin ; z t t t t t
2
25 20 sin 5; 3 5


z t z
max
35z
đạt được khi
3 6 .zi
Chọn đáp án B.
Cách 2:Cho số phức
z
thỏa mãn
1 6 2 10 i z i
. Tìm môđun lớn nhất của số phức
.z
Ta có
6 2 10
1 6 2 10 2 4 5
1
1

i
i z i z z i
i
i
22
2 4 5 3 5
Max
z
Câu 14: Gọi
, z x yi x y R
l| số phức thỏa mãn hai điều kiện
22
2 2 26 zz
và
33
22
zi
đạt gi{ trị lớn nhất. Tính tích
.xy
A.
9
.
4
xy
B.
13
.
2
xy
C.
16
.
9
xy
D.
9
.
2
xy
Hƣớng dẫn giải
Cách 1:Đặt
, . z x iy x y R
Thay v|o điều kiện thứ nhất, ta được
22
9.xy
Đặt
3cos , 3sin .x t y t
Thay v|o điều kiện thứ hai, ta có
33
18 18sin 6.
4
22


P z i t
Dấu bằng xảy ra khi
3 3 2 3 2
sin 1 .
4 4 2 2


t t z i
Chọn đáp án D.
Câu 15: Trong c{c số phức thỏa mãn điều kiện
2 4 2 z i z i
. Tìm môđun nhỏ nhất của số phức
2.zi
A.
5
B.
3 5.
C.
32
D.
32
Hƣớng dẫn giải
Trang12
Cách 1:Gọi
; ; z x yi x y
.
Ta có:
2 2 2
2
2 4 2 2 4 2 4 0 4 . z i z i x y x y x y y x
Ta có:
2
2 2 2
2 2 2
2 2 6 2 12 36 2 3 18 18 z i x y x x x x x
min
2 18 3 2 zi
khi
3.zi
Chọn đáp án C.
Cách 2:
2 4 2 2 2 6 2 4 w 2 6 w 4 z i z i z i i z i i i i
Trong đó
2w z i
(quay về dạng b|i to{n 1)
Câu 16: Cho số phức
z
thỏa mãn
1 2 3 zi
. Tìm môđun nhỏ nhất của số phức
1.zi
A.
4.
B.
2 2.
C.
2.
D.
2.
Hƣớng dẫn giải
Cách 1:Gọi
; ; 1 1 1 z x yi x y z i x y i
. Ta có:
22
1 2 9 1 2 9 z i x y
.
Đặt
1 3sin ; 2 3cos ; 0;2 . 

x t y t t
2
22
min
1 3sin 1 3cos 10 6cos 2 2 4 1 2 z i t t t z i z i
, khi
1.zi
Chọn đáp án C.
Cách 2: (Hình học + CT tính nhanh)
Ta có
2
1 2 3 1 3 1 1 3 2
Min
z i z i i z i
Câu 17: Biết số phức
z
thỏa mãn đồng thời hai điều kiện
3 4 5 zi
v| biểu thức
22
2 M z z i
đạt gi{ trị lớn nhất. Tính môđun của số phức
.zi
A.
2 41zi
B.
3 5.zi
C.
52zi
D.
41.zi
Hƣớng dẫn giải
Gọi
; ; z x yi x y
. Ta có:
22
3 4 5 : 3 4 5 z i C x y
: tâm
3;4I
và
5.R
Mặt kh{c:
22
22
22
2 2 1 4 2 3 : 4 2 3 0.



M z z i x y x y x y d x y M
Do số phức
z
thỏa mãn đồng thời hai điều kiện nên
d
và
C
có điểm chung
23
; 5 23 10 13 33
25
M
d I d R M M
22
max
4 2 30 0
5
33 5 4 41.
5
3 4 5



xy
x
M z i i z i
y
xy
Chọn đáp án D.
Trang13
Câu 18: Cho số phức
. Tìm môđun lớn nhất của
.z
A. 1. B. 0. C.
1
2
. D.2.
Hƣớng dẫn giải
Ta có:
2 2 2
max
1
1 1 ; 0.
12
1 1 1


m i m i
z z z z i m
m m i
m m m
Chọn đáp án A.
Câu 19: (NGUYỄN TRÃI – HD) Cho số phức
z
thỏa mãn:
2 2 1 zi
. Số phức
zi
có môđun nhỏ
nhất l|:
A.
51
B.
51
C.
52
D.
52
.
Hƣớng dẫn giải
Chọn A.
Cách 1:Gọi
z x yi
,
, xy
.
Ta có:
22
2 2 1 ( 2) ( 2) 1 ( 2) ( 2) 1 z i x y i x y
Tập hợp c{c điểm trong mặt phẳng
Oxy
biểu diễn của số phức
z
l| đường tròn
()C
tâm
(2; 2)I
và bán kính
1R
.
2
2
1 z i x y IM
, với
2; 2I
l| t}m đường tròn,
M
l| điểm chạy trên đường tròn.
Khoảng c{ch n|y ngắn nhất khi
M
l| giao điểm của đường thẳng nối hai điểm
0;1 , 2; 2N Oy I
với đường tròn (C).
min
51 IM IN R
Cách 2: Cho số phức
z
thỏa mãn:
2 2 1 zi
. Số phức
zi
có môđun nhỏ nhất
Ta có
22
2 2 1 2 1 2 1 1 5 1
Min
z i z i i z i
Câu 20: Trong mặt phẳng phức
Oxy
, c{c số phức
z
thỏa
21 z i z i
. Tìm số phức
z
được biểu
diễn bởi điểm
M
sao cho
MA
ngắn nhất với
1,3A
.
A.
3 i
. B.
13 i
. C.
23 i
. D.
23i
.
Hƣớng dẫn giải
Gọi
,M x y
l| điểm biểu diễn số phức
, z x yi x y R
y
x
1
1
O
I
M
Trang14
Gọi
1, 2E
l| điểm biểu diễn số phức
12 i
Gọi
0, 1F
l| điểm biểu diễn số phức
i
Ta có :
21 z i z i ME MF
Tập hợp điểm biểu diễn số phức
z
l| đường trung
trục
: 2 0 EF x y
.
Để
MA
ngắn nhất khi
MA EF
tại
M
3,1 3 M z i
=> Đáp án A.
Câu 21: ( CHUYÊN SƠN LA – L2) Cho số phức
z
thỏa mãn điều kiện :
1 2 5 zi
và
1 w z i
có môđun lớn nhất. Số phức
z
có môđun bằng:
A.
25
. B.
32
. C.
6
. D.
52
.
Hƣớng dẫn giải:
Chọn B.
Gọi
, 1 2 1 2 z x yi x y z i x y i
Ta có:
2 2 2 2
1 2 5 1 2 5 1 2 5 z i x y x y
Suy ra tập hợp điểm
;M x y
biểu diễn số phức
z
thuộc đường tròn
C
tâm
1; 2I
bán
kính
5R
Dễ thấy
OC
,
1; 1 NC
Theo đề ta có:
; M x y C
l| điểm biểu diễn cho số
phức
z
thỏa mãn:
1 1 1 1 w z i x yi i x y i
22
1 1 1
z i x y MN
Suy ra
1zi
đạt gi{ trị lớn nhất
MN
lớn nhất
Mà
, M N C
nên
MN
lớn nhất khi
MN
l| đường kính đường tròn
C
I
l| trung điểm
2
2
3; 3 3 3 3 3 3 2 MN M z i z
Câu 22: (CHU VĂN AN – HN) Cho số phức
z
thỏa mãn điều kiện
12z
. Tìm gi{ trị lớn
nhất của
2 T z i z i
.
A.
max 8 2T
. B.
max 4T
. C.
max 4 2T
. D.
max 8T
.
Hƣớng dẫn giải
Chọn B
2 1 1 1 1 T z i z i z i z i
.
Đặt
1wz
. Ta có
1w
và
11 T w i w i
.
Đặt
.w x y i
. Khi đó
2
22
2 w x y
.
Trang15
2 2 2 2
2 2 2 2
22
22
1 1 1 1
1. 1 1 1. 1 1
1 1 1 1 1 1
2 2 2 4 4
T x y i x y i
x y x y
x y x y
xy
Vậy
max 4T
.
Câu 23: Cho số phức
z
thỏa mãn
2 3 1 zi
. Gi{ trị lớn nhất của
1zi
là
A.
13 2
. B.
4
. C.
6
. D.
13 1
.
(THPT CHUYÊN PHAN BỘI CHÂU - NGHỆ AN)
Lời giải
Cách 1:Đặt
, z a bi a b
, ta có
2 3 1 2 3 1. z i a b i
2 2 2 2
2 3 1 2 3 1 a b a b
Đặt
2 sin
3 cos

at
bt
(vì
22
sin cos 1 tt
). Khi đó
1 1 1 . z i a b i
22
11 ab
xét biểu thức
22
1 1 . P a b
Ta có
2 2 2 2
22
1 1 sin 3 cos 2 sin 6sin 9 cos 4cos 4 a b t t t t t t
22
sin cos 13 6 sin 4 cos
14 6 sin 4 cos
t t t t
t t P
Theo bất đẳng thức Bunhiacopxki, ta được
2
2 2 2 2
6sin 4cos 6 4 sin cos t t t t
2
6sin 4cos 52 6sin 4cos 52 2 13 14 2 13. t t t t P
Vậy
2
22
1 1 1 14 2 13 13 1 13 1. z i a b
Chọn A.
Cách 2:Cho số phức
z
thỏa mãn
2 3 1 zi
. Gi{ trị lớn nhất của
1zi
Ta có
z 2 3i 1 z 2 3i 1 z 1 i 3 2i 1
22
Max
z 1 i 3 2 1 13 1
Câu 24: (THPT CHUYÊN ĐH VINH - LẦN 2)Cho c{c số phức
,zw
thỏa mãn
2 2 4 , 1z i z i w iz
. Gi{ trị nhỏ nhất của biểu thức
w
là
A.
2
2
. B.
22
. C.
2
. D.
32
2
.
Lời giải
Cách 1: Đặt
,z a bi a b
, khi đó
2 2 2 2z i a b i
và
44z i a b i
.
Nên ta có
2 2 2
2
2 2 4 2 2a b a b a b b a
Trang16
Khi đó
22
22
1 1 1 1 1w iz a bi i b ai w a b a a
.
Dễ thấy
2
2
2
1 1 1 2 2
1 2 min .
2 2 2 2 2



w
a a a w
Chọn A.
Cách 2: Chuyển về phương trình đường thẳng (dạng 1)
Câu 25: (ĐỀ THTT LẦN 5 – 2017)Cho số phức
z
thỏa mãn
4 4 10. zz
Giá trị lớn nhất và giá
trị nhỏ nhất của
z
lần lượt là
A.
10
và
4
B.
5
và
4
C.
4
và
3
. D.
5
và
3
.
Hƣớng dẫn giải.
Gọi
z x yi
,
, xy
. Theo giả thiết, ta có
4 4 10. zz
22
22
4 4 10 4 4 10 x yi x yi x y x y
Gọi
;M x y
,
1
4;0F
và
2
4;0F
.
Khi đó
12
10 MF MF
nên tập hợp c{c
điểm
Mz
l| đường elip
E
.
Ta có
4c
;
2 10 5 aa
và
2 2 2
9 b a c
.
Do đó, phương trình chính tắc của
E
là
2
2
1
25 9

y
x
.
Vậy
max ' 5 z OA OA
và
min ' 3 z OB OB
. Chọn D.
Câu 26: Trong c{c số phức
z
thỏa mãn điều kiện
2 4 2 z i z i
. Biết rằng số phức
z x yi
,
, xy
có môđun nhỏ nhất. Tính
22
P x y
.
A.
10P
. B.
8P
. C.
16P
. D.
26P
.
Hƣớng dẫn giải.
Cách 1:Gọi
z x yi
,
, xy
. Ta có
2 4 2 2 4 2 z i z i x y i x y i
2 2 2
2
2 4 2 x y x y
2 2 2 2
4 4 8 16 4 4 x x y y x y y
4 4 16 0 4 x y y x
.
Do đó
22
2 2 2 2
4 2 8 16 2 2 8 2 2 z x y x x x x x
.
Dấu
""
xảy ra
22 xy
. Vậy
22
2 2 8 P
. Chọn B.
Cách 2: Chuyển về phương trình đường thẳng (b|i tập 1)
Câu 27: Tìm gi{ trị lớn nhất của
z
biết rằng
z
thỏa mãn điều kiện
23
11
32


i
z
i
.
A.
max 1z
. B.
max 2z
. C.
max 2z
. D.
max 3z
.
Hƣớng dẫn giải.
Ta có
23
1
1 1 1 1 . 1 1
32


i
z iz i z z i
ii
.
Trang17
Vì
01 i
nên
12
max 1 1 2 z r r
. Chọn B.
Câu 28: (THPT CHUYÊN KHTN – LẦN 1)Trong c{c số phức
z
thỏa mãn điều kiện
1 1 7 2 i z i
. Tìm
max z
.
A.
max 4z
. B.
max 3z
. C.
max 7z
. D.
max 6z
.
Hƣớng dẫn giải.
Ta có
17
1 1 7 2 1 2 3 4 1
1
i
i z i i z z i
i
.
Vì
3 4 0 5 i
nên
22
12
max 1 3 4 6 z r r
. Chọn D.
Câu 29: Cho số phức
z
thỏa mãn
1z
. Đặt
2
.
2
zi
A
iz
Mệnh đề n|o sau đ}y đúng?
A.
1.A
B.
1.A
C.
1.A
D.
1.A
(THPT CHUYÊN HÀ NAM)
Lời giải
Từ giả thiết, ta có
2
2 2 2 2
2
zi
A A iz z i A Azi z i
iz
2
22
2
Ai
A i z Ai z
Ai
. Mà
2
1 1 2 2 .
2
Ai
z A i Ai
Ai
Đặt
, A x yi x y
, khi đó
2 2 1 2 x y i y xi
22
2 2 2 2 2 2 2 2
4 2 1 2 4 4 4 1 4 4 1. x y y x x y y x y y x y
Vậy môđun của
22
1. A x y
Chọn A.
Câu 30: Với hai số phức
1
z
và
2
z
thỏa mãn
12
86 z z i
và
12
2zz
. Tìm gi{ trị lớn nhất của
12
P z z
.
A.
5 3 5.P
B.
2 26.P
C.
4 6.P
D.
34 3 2.P
(THPT CHUYÊN KHOA HỌC TỰ NHIÊN - LẦN 4)
Lời giải
Bổ đề.Cho hai số phức
1
z
và
2
z
, ta luôn có
2 2 2 2
1 2 1 2 1 2
2 z z z z z z
.
Chứng minh. Sử dụng công thức
2
1 2 1 2 1 2
z z z z z z
và
2
. z z z
. Khi đó
22
1 2 1 2 1 2 1 2 1 2 1 2
1 1 1 2 1 2 2 2 1 1 1 2 1 2 2 2
22
1 1 2 2 1 2
. . . . . . . .
2 . . 2 .
z z z z z z z z z z z z
z z z z z z z z z z z z z z z z
z z z z z z đpcm
Áp dụng
, ta được
2
2 2 2
1 2 1 2 1 2 1 2
4 4 3 1 1. z z z z z z z z
Theo bất đẳng thức Bunhiacopxki, ta được
22
1 2 1 2
2 2 26. P z z z z
Chọn B.
Trang18
Câu 31: Với hai số phức
1
z
và
2
z
thỏa mãn
12
86 z z i
và
12
2zz
. Tìm gi{ trị lớn nhất của
12
P z z
.
A.
5 3 5.P
B.
2 26.P
C.
4 6.P
D.
34 3 2.P
(THPT CHUYÊN KHOA HỌC TỰ NHIÊN - LẦN 4)
Lời giải
Bổ đề.Cho hai số phức
1
z
và
2
z
, ta luôn có
2 2 2 2
1 2 1 2 1 2
2 z z z z z z
.
Chứng minh. Sử dụng công thức
2
1 2 1 2 1 2
z z z z z z
và
2
. z z z
. Khi đó
22
1 2 1 2 1 2 1 2 1 2 1 2
1 1 1 2 1 2 2 2 1 1 1 2 1 2 2 2
22
1 1 2 2 1 2
. . . . . . . .
2 . . 2 .
z z z z z z z z z z z z
z z z z z z z z z z z z z z z z
z z z z z z đpcm
Áp dụng
, ta được
2
2 2 2
1 2 1 2 1 2 1 2
4 4 3 1 1. z z z z z z z z
Theo bất đẳng thức Bunhiacopxki, ta được
22
1 2 1 2
2 2 26. P z z z z
Chọn B.
Câu 32: (THPT CHUYÊN LƢƠNG THẾ VINH - ĐỒNG NAI)Cho số phức
z
thỏa mãn
2
2 5 1 2 3 1 z z z i z i
.
Tính
min| |w
, với số phức
22 w z i
.
A.
3
min| |
2
w
. B.
min| | 2w
. C.
min| | 1w
. D.
1
min| |
2
w
.
Lời giải
Ta có
2 2 2
2
2 5 1 4 1 2 1 2 1 2 z z z z i z i z i
.
Khi đó, giả thiết
12
1 2 1 2 1 2 3 1
1 2 3 1
zi
z i z i z i z i
z i z i
TH1. Với
12zi
, ta có
2 2 1 2 2 2 1 1. w z i i i w
TH2. Với
1 2 3 1 z i z i
, đặt
, z x yi x y
, ta có
2 2 2 2
1
1 2 1 3 1 2 1 3 .
2
x y i x y i x y x y y
Do đó
2
1 3 9 3
2 2 2 2 2 2
2 2 4 2
w z i x i i x i w x
. Chọn A.
Câu 33: (TOÁN HỌC & TUỔI TRẺ LẦN 8)Cho số phức
z
thỏa mãn
1
3z
z
. Tổng của gi{ trị lớn
nhất v| gi{ trị nhỏ nhất của
z
là
A.
3.
B.
5.
C.
13.
D.
5.
Lời giải
Trang19
Ta có
2
2
1 1 1 1
a z a z z z
z z z z
42
2
2
2
2
2 2 2
21
1
.
z z z z
zz
z
z z z
Khi đó
2
2
42
2
2
4
4
. 2 1 0 ;
22





aa
aa
z z a z z z
.
Vậy
2
2
2
4
4
max ; min 4 13.
22

aa
aa
z z M m a
Chọn C.
Câu 34: (THPT NHÂN CHÍNH - HÀ NỘI)Xét số phức
z
thỏa mãn
10
1 2 2 i z i
z
. Mệnh đề
n|o sau đ}y đúng?
A.
3
2
2
z
. B.
13
22
z
.C.
2z
. D.
1
2
z
.
Lời giải
Cách 1. Từ giả thiết, ta có
10 10
1 2 2 1 2 2 i z i i z i
zz
10 10
2 2 2 2 1 z z i i z z i
zz
Lấy môđun hai vế của
, ta được
22
10
2 2 1 . zz
z
Đặt
tz
, ta có
22
2 2 4 2
10
2 2 1 5 5 10 2 0 1. t t t t t t t
t
Vậy môđun của số phức
z
bằng
13
1.
22
z
Cách 2. Sử dụng m{y tính casio ( hướng dẫn chi tiết ở câu 26) để tìm
.z
Cách 3. Đặt
, z a bi a b
và
cz
, thay v|o đẳng thức đã cho thì
2
22
10
10
1 2 2 1 2 2
10 10
2 2 1 0




a bi
Gt i c i i c i
a bi
c
ab
c i c
cc
Suy ra
2
2
2
10
10
20
2
10
10
2 1 0
12






a
a
c
c
c
c
b
b
c
c
c
c
nên
22
22
42
10
10
2 1 2
ab
cc
cc
Giải ra ta có
1c
mà
0c
nên
1c
hay
1z
. Do đó
13
.
22
z
Chọn B.
Trang20
Câu 35: (THPT CHUYÊN LÀO CAI)Xét số phức
z
v| số phức liên hợp của nó có điểm biểu diễn l|
,
MM
. Số phức
(4 3 )zi
v| số phức liên hợp của nó có điểm biểu diễn lần lượt l|
,
NN
. Biết rằng
, , ,

M M N N
l| bốn đỉnh của hình chữ nhật. Tìm gi{ trị nhỏ nhất của
45zi
A.
1
.
2
B.
2
.
5
C.
1
.
2
D.
4
.
13
Lời giải
Gọi
; ' ;M x y M x y
và
4 3 ; 3 4
4 3 4 3 3 4
' 4 3 ; 3 4

N x y x y
i z x y x y i
N x y x y
Dễ thấy
''MM NN
vì cùng vuông góc với
Ox
nên để
''MM N N
l| hình chữ nhật.
Khi v| chỉ khi
22
''
' ' 0 4 5 5 4

MM NN
MN M N x y z x xi z i x x
MN Ox
Ta có
2 2 2
min
1 1 1 1
5 4 2 9 4 5 .
2 2 2
2
x x x z i
Chọn C.
Câu 36: (THPT CHU VĂN AN - HÀ NỘI)Cho số phức
z
thỏa mãn điều kiện
1 2.z
Tìm gi{ trị
lớn nhất của biểu thức
2. T z i z i
A.
max 8 2.T
B.
max 4.T
C.
max 4 2.T
D.
max 8.T
Lời giải
Đặt
, z x yi x y
, ta có
2
2
1 2 1 2 1 2 z x yi x y
2
2 2 2 2 2
1 2 2 1 2 2 1 x y x x y x y x
Lại có
2 1 2 1 T z i z i x y i x y i
2 2 2
2 2 2 2 2
1 2 1 2 1 4 2 5 x y x y x y y x y x y
Kết hợp với
, ta được
2 2 2 6 2 2 2 2 2 2 T x y x y x y x y
Đặt
t x y
, khi đó
2 2 6 2 T f t t t
với
1;1 .

t
Ta có
max
11
' ; ' 0 1 1 4
2 2 6 2

f t f t t f t f
tt
. Chọn B.
Câu 37: (ĐHNT HN) Cho số phức
z
thỏa mãn điêu kiện
12z
. Tính giá trị lớn nhất của biểu thức
2 T z i z i
A.
max 8 2T
. B.
max 8T
. C.
max 4 2T
. D.
max 4T
.
Hướng dẫn giải
Chọn C
Đặt
, z x yi x y
, ta có:
Trang21
1 2 1 2 z x yi
2
2 2 2
1 2 2 1 * x y x y x
Lại có:
2 1 2 1 T z i z i x y i x y i
2 2 2
2
1 2 1 x y x y
2 2 2 2
2 1 4 2 5 x y y x y x y
Kết hợp với
*
, ta được:
2 2 2 6 2 2 T x y x y
Áp dụng bất đẳng thức Bunhacopxki ta được
22
22
1 1 2 2 2 6 2 2 4



T x y x y
Vậy
max 4T
.
Câu 38: Cho
w sin cos i
với
0
2
thỏa mãn
2
w 1 2 w
.
Giá trị của
2018
2
26 w 3




P
là
A.
2018
23 .P
B.
2018
23 .P
C.
2018
23 .Pi
D.
2018
29 .P
Hướng dẫn giải
Chọn A
Ta có:
2
22
w 1 sin cos 1 1 cos 2 sin2 w 1 2 2cos 2 . ii
22
2 w sin cos 2
.
Từ giả thiết:
2
w 1 2 w
cos2 0
4
vì
0
2
.
2
2 2 2 2
w w w 1
2 2 2 2
ii
.
Vậy
2018
23 .P
Câu 39: Cho các số phức
12
2 , 2 z i z i
và số phức
z
thay đổi thỏa mãn
22
12
16. z z z z
Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
z
. Giá trị biểu thức
22
Mm
bằng
A.
15
. B.
7
. C.
11
. D.
8
.
Lời giải
Chọn D.
Gọi
M
là điểm biểu diễn của
z
.
Gọi
2;1A
,
2;1B
. Gọi
0;1I
là trung điểm
AB
.
22
22
12
16 16 z z z z MA MB
2
2 2 2
2 16
2
AB
MA MB MI
2MI
Suy ra tập hợp các điểm
M
là đường tròn tâm
0;1I
bán kính
2R
.
Trang22
Ta lại có :
IM IO OM IM IO
13 OM
.
Do đó :
2
max
3 z M M
1
min
1 z M M
22
8 Mm
.
Bài tương tự
Câu 40: Cho hai số phức
12
,zz
thỏa mãn
1
12 zi
và
21
z iz
. Tìm giá trị nhỏ nhất
m
của biểu thức
12
zz
?
A.
21m
. B.
22m
. C.
2m
. D.
2 2 2m
.
Lời giải
Chọn D.
Đặt
1
; , z a bi a b
2
z b ai
12
z z a b b a i
.
Nên
22
1 2 1
2. z z a b b a z
Ta lại có
1 1 1
2 1 1 2 z i z i z
1
22 z
. Suy ra
1 2 1
2. 2 2 2 z z z
.
Dấu
""
xảy ra khi
0
11

ab
.
Vậy
12
min 2 2 2 m z z
.
Câu 41: Gọi số phức
;, z x yi x y
thỏa điều kiện
22
2 2 26 zz
và
25zi
lớn nhất.
Tính
T x y
.
A.
25 T
. B.
25T
. C.
25 T
. D.
25T
.
Lời giải
Chọn A.
Giả sử
;, z x yi x y
Ta có
22
22
2 2 2 2
2 2 26 2 2 26 9 z z x y x y x y
.
y
x
M
2
M
1
I
O
Trang23
Suy ra tập hợp các điểm biểu diễn số phức
z
là đường tròn
C
tâm là gốc tọa độ
O
, bán kính
3R
.
Ta có
2
2
2 5 2 5 z i x y
Vì
2
2
2 5 9
nên điểm
2; 5N
thuộc đường tròn
C
.
Gọi
;M x y
là điểm thuộc
C
, khi đó
2
3
2 5 2 5 z i x y MN
.
Suy ra
25zi
lớn nhất
MN
lớn nhất
MN
là đường kính của
C
2; 5 M
Vậy
25 zi
.
Câu 42: Cho
12
, zz
là hai số phức thỏa mãn phương trình
22 z i iz
, biết
12
1zz
Tính giá trị của
biểu thức:
12
P z z
.
A.
3
2
P
. B.
2P
. C.
2
2
P
. D.
3P
.
Lời giải
Chọn D.
HD: Cách 1. Ta có:
22
2 2 2 2 (2 )(2 ) (2 )(2 ) z i iz z i iz z i z i iz iz
22
4 . 2 2 4 2 2 . 3 . 3 z z iz iz i iz iz i z z z z
2
1
. 1 1 1 1 z z z z z
và
2
1z
Chú ý:
2
2
. 2 (2 )(2 ) (2 )(2 ) a a a z i z i z i z i z i
Tập hợp điểm biểu diễn số phức
12
, zz
là đường tròn tâm O
bán kính
1R
.
Gọi
1 1 2 2 1 2
( ), ( ) 1 M z M z OM OM
Ta có:
1 2 1 2 2 1 1 2
1
z z OM OM M M OM M
đều
Mà
1 2 1 2
z z O M OM OM OM
với M là điểm thỏa
mãn
12
OM MM
là hình thoi cạnh 1
33 OM P
.
Cách 2. Đặt
, , z x yi x y
, ta có
2 2 (2 1) z i x y i
và
22 iz y xi
.
Khi đó:
1
2 2 2 2 2 2
2
1
2 2 4 (2 1) ( 2) 1 1
1
z
z i iz x y y x x y z
z
Sử dụng công thức
2 2 2 2 2
1 2 1 2 1 2 1 2 1 2
2 3 3 z z z z z z z z z z
. Chọn D.
Câu 43: Cho số phức
z
thỏa mãn điều kiện
1 2 4 zi
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của
2zi
. Tính giá trị của tổng
22
S M m
.
A.
82S
. B.
34S
. C.
68S
. D.
36S
.
Lời giải
Chọn C.
y
O
x
M
2
M
1
M
Trang24
Cách 1: (Phương pháp hình học)
Đặt số phức
z x iy
,
, xy
có điểm biểu diễn hình học là
,P x y
.
Ta có
2 2 2 2
1 2 1 2 4 1 2 16 z i x y x y
.
Vậy tập hợp điểm
P
là đường tròn tâm
1; 2I
, bán kính
4R
.
Ta có
22
2 2 1 z i x y AP
, với
2; 1A
.
Vậy từ hình vẽ ta nhận thấy:
max 2
min 1
3 2 4
3 2 4
M AP AP IA R
m AP AP IA R
.
Vậy ta suy ra
22
22
3 2 4 3 2 4 68 S M m
.
Cách 2: (Phương pháp đại số)
Công cụ cơ bản:
1 2 1 2 1 2
z z z z z z
, với mọi số
phức
1
z
,
2
z
. Áp dụng, ta có:
2 1 2 3 3 1 2 3 3 4 3 2 4 3 2 z i z i i z i i M
2 1 2 3 3 1 2 3 3 3 2 4 3 2 4 z i z i i z i i m
Vậy ta có
22
22
3 2 4 3 2 4 68 S M m
.
Câu 44: [Phạm Minh Tuấn – Vted 15] Cho ba số phức
12
,,z z z
thỏa
12
6zz
và
12
62zz
. Tìm giá
trị nhỏ nhất của biểu thức
1 2 1 2
2 P z z z z z z z z z z
.
A.
30 3
. B.
36 2
. C.
50
. D.
50 2
.
Lời giải
Chọn B.
Gọi
,,A B M
là điểm biểu diễn số phức
12
,,z z z
, khi đó từ giả thiết ta suy ra tam giác
OAB
vuông
cân tại
O
và bài toán quy về tìm giá trị nhỏ nhất của
2 . . . P MA MB MO MA MO MB
.
Ta sẽ chứng minh bài toán tổng quát
Cho tam giác
ABC
, đặt
AB c
,
AC b
,
BC a
, khi đó ta có
. . .
1
MB MC MC MA MA MB
bc ca ab
Chứng minh: dùng bài toán kinh điển
222
2 2 2
. . .


xyc yza zxb
x MA y MB z MC
xyz
Đặt
;;
a b c
x y z
MA MB MC
khi đó
. . .
..

aMB MC bMC MA cMA MB
xyz
MA MB MC
và
222
..

aMA bMB cMC
xyc yza zxb abc
MA MB MC
từ đó sử dụng

suy ra hệ thức
.
Trang25
Áp dụng bài toán trên ta có
36 2P
, chọn B.
Ta có thể chứng minh bài toán
trên bằng ngôn ngữ số phức.
Gọi tọa độ các điểm
, , ,A B C M
trên mặt phẳng phức là
, , ,u v w x
khi đó
a v w
,
b w u
,
c u v
,
MA x u
,
MB x v
,
MC x w
. Khi đó bất đẳng thức
tương đương
1
x v x w x w x u x u x v
u v u w v w v u w u w v
1
x v x w x w x u x u x v
u v u w v w v u w u w v
Mặt khác :
x v x w x w x u x u x v x v x w x w x u x u x v
u v u w v w v u w u w v u v u w v w v u w u w v
Mà
1
x v x w x w x u x u x v
u v u w v w v u w u w v
nên suy ra
.
Câu 45: Cho số phức
z
thỏa mãn điều kiện
1zi
. Tìm giá trị nhỏ nhất của biểu thức:
2 2 2 3 P z i z i
A.
3
. B.
3
. C.
2
. D.
43
3
.
Lời giải
Chọn B.
Gọi điểm biểu diễn của
z
là
M
. Khi đó
M
nằm trên đường tròn tâm
0; 1 , 1.IR
Gọi tọa độ các
điểm
2; 1 , 2; 3AB
do đó:
Trang26
2 2 2 3 2 . P z i z i MA MB
Gọi
1
;1
2



K
khi đó ta có:
1
.
2

IK IM
IM IA
Vậy
IMK
và
IAM
là hai tam giác đồng dạng. Khi đó:
2MA MK
.
Vậy
2P MK MB
.
Theo bất đẳng thức tam giác:
2 2 . P MK MB BK
Vậy
2 3.Min P BK
Câu 46: Với hai số phức
1
z
và
2
z
thoả mãn
12
86 z z i
và
12
2,zz
tìm giá trị lớn nhất của
12
.P z z
A.
46P
. B.
2 26P
. C.
5 3 5P
. D.
34 3 2P
.
Lời giải
Chọn B.
Vì hai số phức
1
z
và
2
z
thoả mãn
12
86 z z i
và
12
2zz
nên
12
21
12
86
86
2

z i z
z i z
zz
1
2
12
4 3 1
4 3 1
2

zi
zi
zz
*
.
Gọi
A
,
B
lần lượt là hai điểm biểu diễn của hai số phức
1
z
và
2
z
khi đó từ
*
suy ra
,AB
nằm trên
đường tròn
C
có tâm
4;3I
, bán kính
1R
và
AB
là đường kính của đường tròn
C
.
Như vậy
12
P z z OA OB
.
Ta có
2 2 2
2 2 2 2
2 5 1 52
24
OA OB AB
OI OA OB
.
Suy ra
22
52 2 . OA OB OAOB
2
22
2 . 52 52 104 OA OB OA OB OAOB
12
104 2 26 P z z OA OB
. Dấu bằng xảy ra khi
OA OB
.
Câu 47: Giả sử
12
,zz
là hai trong số các số phức
z
thỏa mãn
21 iz i
và
12
2.zz
Giá trị lớn nhất của
12
zz
bằng
A.
4
. B.
23
. C.
32
. D.
3.
Lời giải
ChọnA.
x
y
3
4
B
O
I
1
A
Trang27
Ta có
21 iz i
2 1 1 i z i
2 1 1 zi
.
Điểm biểu diễn
z
thuộc đường tròn tâm
1; 2I
,
1R
.
Gọi
M
,
N
là điểm biểu diễn
1
z
,
2
z
nên
2MN
là đường kính. Dựng hình bình hành
OMNP
ta
có
12
23 z z OP
.
Ta có
2
22
1 2 1 2
2 z z z z
22
1 2 1 2
z z z z
16
12
4zz
. Dấu bằng xảy ra khi
12
zz
MN OI
.
Câu 48: Cho hai số phức
z
,
thỏa mãn
1 3 2 z z i
;
z m i
với
m
là tham số. Giá trị của
m
để ta
luôn có
25
là:
A.
7
3

m
m
. B.
7
3


m
m
. C.
37 m
. D.
37m
.
Lời giải
Chọn B.
Đặt
,, z a ib a b
có biểu diễn hình học là điểm
;M x y
1 3 2 z z i
1 3 2 x iy x y i
2 2 2
2
1 3 2 x y x y
2 1 6 9 4 4 xxy
2 3 0 xy
Suy ra biểu diễn của số phức
z
là đường thẳng
: 2 3 0 xy
.
Ta có:
25
25 z m i
1 2 5 x m y i
22
1 2 5 x m y
25MI
với
;1Im
.
Mà ta có
,MI d I
Nên
25MI
, 2 5 dI
24
25
5


m
2 4 10 m
Trang28
2 4 10
2 4 10
m
m
3
7
m
m
.
Câu 49: [PTNK TP HCM] Cho
z
là số phức thỏa mãn
12 zi
. Tìm giá trị lớn nhất của biểu thức
22
2 2 3 P z i z i
A.
18
. B.
14 2 10
. C.
38 8 10
. D.
16 2 10
.
Lời giải
Chọn C.
Gọi
; , ; z x yi x y M x y
là điểm biểu diễn số phức
z
.
Do
22
1 2 1 1 4 z i x y
suy ra
M
thuộc đường tròn tâm
1; 1I
, bán kính
2R
.
Đặt
2;1 , 2;3 , 0;2A B E
là trung điểm của
AB
. Khi đó
22
2 2 3 P z i z i
2 2 2 2
2 1 2 3 x y x y
22
MA MB
2
2
2
2

AB
ME
2
2 10ME
.
Do
E
nằm ngoài đường tròn, nên

Max
ME EI R
2 10 38 8 10
Max
P
.
Cách 2 :
22
2 2 3 P z i z i
2 2 2 2
2 1 2 3 x y x y
=
22
2 2 8 18 x y y
22
2 2 8 18 0 x y y P
.
Suy ra tọa độ điểm
M
thỏa mãn
22
22
2 2 8 18 0
1 1 4
x y y P
xy
22
1 1 4
: 4 12 22 0
xy
x y P
Hệ có nghiệm khi
,d I R
38 8 10 P
38 8 10 38 8 10 P
38 8 10
Max
P
.
Câu 50: (CHuyên Hạ Long-lần 2-2018-Mã đề 108)Cho các số phức
12
2 , 2z i z i
và số phức
z
thay
đổi thỏa mãn
22
12
16.z z z z
Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
z
. Giá
trị biểu thức
22
Mm
bằng
A.
15
. B.
7
. C.
11
. D.
8
Lời giải:
Trang29
Chọn D.
Cách 1:
Gọi số phức
z x yi
với
,xy
.
Ta có
22
12
16z z z z
22
2 3 0x y x
. Khi đó tập hợp các điểm
( , )M x y
biểu diễn số
phức
z
là đường tròn
()C
có tâm
( 1,0)I
và bán kính
2R
.
Ta có
min min
||z OM
,
max max
||z OM
.
Đường thẳng
OI
có phương trình
0y
.
OI
cắt
()C
tại 2 điểm phân biệt
,AB
có tọa độ là nghiệm của hệ
22
2 3 0
0
x y x
y
(1,0); ( 3,0)AB
.
Ta có
OA OM OB
nên
min
||z OA
,
max
||z OB
.
Khi đó
22
9 1 8Mm
.
Cách 2:
Gọi số phức
z x yi
với
,xy
.
Ta có
22
12
16z z z z
22
2 3 0x y x
. Khi đó tập hợp các điểm
( , )M x y
biểu diễn số
phức
z
là đường tròn
()C
có tâm
( 1,0)I
và bán kính
2R
.
12z
Ta có:
1 1 1zz
min
1z
,
1 1 3zz
max
3z
.
Cách 3:
Gọi số phức
z x yi
với
,xy
.
Ta có
22
12
16z z z z
22
2 3 0x y x
. Khi đó tập hợp các điểm
( , )M x y
biểu diễn số
phức
z
là đường tròn
()C
có tâm
( 1,0)I
và bán kính
2R
.
Ta có
min
OM OI R
,
max
OM OI R
min
1z
,
max
3z
CÂU PHÁT TRIỂN
Câu 51: Cho số phức
z
thỏa mãn điều kiện
2 4 5zi
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của
z
. Giá trị biểu thức
22
2
Mm
Mn
bằng
A.
12
. B.
1
2
. C.
4
3
. D.
8
Lời giải:
Chọn C.
Gọi số phức
z x yi
với
,xy
, khi đó
22
||z x y
.
Ta có:
2 4 5zi
2
2
2 ( 4) 5xy
22
15 4( 2 )x y x y
.
Áp dụng bđt Bu-nhi-a-cốp-xki ta có:
22
| 2 | 5( ) 5 | |x y x y z
.
Khi đó ta có bất phương trình
2
| | 15 4 5 | |zz
5 | | 3 5z
.
Do đó
22
2
Mm
Mn
4
.
3
Câu 52: Cho số phức
z
thỏa mãn điều kiện
1 | 3 2 | 5z i z i
. Gọi
M
và
m
lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của
2zi
. Giá trị biểu thức
22
Mm
bằng
Trang30
A.
25
. B.
35
. C.
15
2
. D.
20
.
Lời giải:
Chọn B.
Gọi
z x yi
(với
,xy
) có điểm
( ; )M x y
biểu diễn
z
trên mặt phẳng tọa độ.
Ta có
1 3 2 5z i z i
2 2 2 2
1 1 3 2 5x y x y
22
22
1 2 3 3 2 4 5x y x y
(1).
Số phức
22z i x y i
có điểm
;2M x y
biểu diễn
2zi
trên mặt phẳng tọa độ.
Đặt
(1;3), (3;4)AB
, từ (1) ta có
5AM BM


.
Mặt khác
5AB
nên
M
thuộc đoạn
AB
. Khi đó
max
2M z i
5OB
,
min
2m z i
10OA
.
Vậy
22
35Mm
.
Nhận xét:
- GTLN, GTNN ở câu dạng này chỉ có thể đạt được tại 2 đầu
,AB
.
- Một sai lầm thường gặp là đánh giá
min
;z d O AB
nhưng do góc
OAB
là góc tù nên không
tồn tại điểm
M
trên đoạn
AB
sao cho
OM AB
.
Câu 53: (Chuyên Hạ Long-lần 2-2018-Mã đề 123) Cho số phức
z
thỏa mãn
3 4 5 zi
. Gọi
,Mm
lần
lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
22
2 P z z i
. Khi đó modun của số phức
w M mi
A.
2 314
. B.
1258
. C.
3 137
. D.
2 309
.
Lơ
igia
i
Chọn B.
Cách 1:Giả sử
, z x yi x y R
ta có
3 4 5 zi
22
3 4 5 xy
Ta có
4 2 3 P x y
4 3 2 4 23 x y P
Ta có
2
22
4 3 2 4 20 3 4 100





x y x y
Suy ra
10 23 10 P
13 33 P
suy ra
33, 13Mm
do đó ta được
33 13wi
vậy
w 1258
.
Cách 2:Gọi
z x yi
với
, xy
.
Ta có:
22
3 4 5 3 4 5 z i x y
. Suy ra, tập hợp điểm
;M x y
biểu diễn cho số
phức
z
trên hệ tọa độ
Oxy
là đường tròn
C
tâm
3;4I
và bán kính
5R
.
Lại có:
22
22
22
2 2 1 0 4 2 3 0 P z z i x y x y P x y P
, đây là
phương trình của đường thẳng
: 4 2 3 0 x y P
.
Ta thấy
MC
.
Trang31
Điều kiện để
cắt
C
là:
23
, 5 10 23 10 13 33
25
P
d I R P P
.
Suy ra:
13, 33mM
và
33 13 1258 w i w
.
Cách 3:
Gọi
z x yi
với
, xy
.
Ta có
22
22
2 1 4 2 3 P x y x y x y
suy ra
43
2

Px
y
.
Từ
2
2 2 2
43
3 4 5 3 4 5 3 4 5 0
2


Px
z i x y f x x
.
Ta có
4 11
2 3 4 2 10 16
2


Px
f x x P x
.
0 0,2 1,6
f x x P
. Suy ra
0,1 1,7yP
.
Thay
,xy
vừa tìm được vào
fx
ta được
22
0,2 1,6 3 0,1 1,7 4 5 0 PP
.
Ta giải được
33P
hoặc
13P
. Đây tương ứng là GTLN và GTNN của
P
.
Vậy
33, 13Mm
. Khi đó,
1258
.
Câu 54: Biết số phức
z x yi
,
, xy
thỏa mãn đồng thời hai điều kiện
43 z z i
và biểu thức
1 2 3 P z i z i
đạt giá trị nhỏ nhất. Tính
2P x y
.
A.
61
10
P
. B.
253
50
P
. C.
41
5
P
. D.
18
5
P
.
Lời giải
Chọn A .
Theo giả thiết
43 z z i
43 x yi x y i
22
22
43 x y x y
2 2 2 2
8 16 6 9 x y x x y y
8 6 25 0 xy
.
Ta có
2 2 2 2
1 1 2 3 P x y x y
Xét điểm
1;1E
;
2; 3F
và
;M x y
. Khi đó,
P ME MF
.
Bài toán trở thành tìm điểm
: 8 6 25 0 M x y
sao cho
ME MF
đạt giá trị nhỏ nhất.
Vì
8 8 25 . 8 8 25 0
E E F F
x y x y
nên hai điểm
,EF
nằm cùng phía đối với đường thẳng
.
Gọi
E
là điểm đối xứng với
E
qua
Đường thẳng
EE
đi qua điểm
1; 1E
và có VTPT
3; 4

EE
nu
nên có phương trình
3 1 4 1 0 xy
3 4 7 0 xy
Trang32
Gọi
H
là giao điểm của
EE
và
. Tọa độ điểm
H
là nghiệm của hệ phương trình
3 4 7
8 6 25
xy
xy
71
25
19
50


x
y
suy ra
71 19
;
25 50




H
E
đối xứng với
E
qua
H
nên
117
25
44
25


E
E
x
y
.
Ta có

ME+MF = ME +MF E F
.
Dấu bằng xảy ra
M
là giao điểm của
EF
và đường thẳng
Đường thẳng
EF
đi qua điểm
2; 3F
và có VTPT
31;167
EE
n
có phương trình
31 2 167 3 0 xy
31 +167 + 439 = 0xy
Tọa độ điểm
M
là nghiệm của hệ phương trình
31 167 439
8 6 25
xy
xy
67
50
119
50


x
y
Vậy
61
2
10
P x y
.
Câu 55: Gọi
12
,zz
là 2 nghiệm của phương trình
1 2 1 2 z i z i
thỏa mãn
12
2zz
. Biết rằng
w
là số phức thỏa mãn
w 3 2 2 i
. Tìm GTNN của biểu thức
12
ww P z z
.
A.
13
B.
23
C.
2
D.
6
.
Lời giải.
Chọn D .
Giả sử
, z x yi x y R
ta có
1 2 1 2 z i z i
0x
suy ra tập hợp điểm biểu diễn
12
,zz
là trục tung.
Giả sử
,AB
lần lượt là 2 điểm biểu diễn cho
12
,zz
, ta có
12
2zz
2AB
.
Giả sử
w, a bi a b R
và
M
là điểm biểu diễn cho số phức
w
, ta có
w 3 2 2 i
22
( 3) ( 2) 4 ab
suy ra tập hợp
điểm biểu diễn
M
cho số phức
w
là đường tròn tâm
3;2I
bán
kính
2R
.
Ta có
P MA MB
, gọi
E
là hình chiếu vuông góc của
I
lên
trục tung, ta thấy
P
nhỏ nhất khi
E
là trung điểm
AB
suy ra
6
2
MA MB
, vậy
6
2. 6
2
MinP
Câu 56: Cho
z
là số phức thỏa
12 zi
. Tìm giá trị lớn nhất của biểu thức
Trang33
22
2 2 3 P z i z i
A.
18
. B.
38 8 10
. C.
18 2 10
. D.
16 2 10
.
Hướng dẫn giải
Chọn B
Gọi
, z x yi x y
Ta có:
22
1 2 1 2 1 1 4 z i x yi i x y
2 2 2 2
2 2 2 0 2 2 2 x y x y x y x y
(*)
Theo bài ra:
2 2 2 2
2 2 3 2 2 3 P z i z i x yi i x yi i
2 2 2 2
22
2 1 2 3 2 8 18 x y x y x y y
Thay (*) vào
P
ta được:
4 12 22 4 1 12 1 38 P x y x y
Áp dụng bđt Bunhiacopxki ta được
22
2 2 2 2
4 1 12 1 38 4 12 1 1 38 4 12 .4 38 8 10 38



x y x y
Vậy
max
8 10 38P
.
Câu 57: Giả sử
12
,zz
là hai trong số các số phức
z
thỏa mãn
21 iz i
và
12
2.zz
Giá trị lớn nhất của
12
zz
bằng
A.
4
. B.
23
. C.
32
. D.
3.
Lời giải
ChọnA.
Ta có
21 iz i
2 1 1 i z i
2 1 1 zi
.
Điểm biểu diễn
z
thuộc đường tròn tâm
1; 2I
,
1R
.
Trang34
Gọi
M
,
N
là điểm biểu diễn
1
z
,
2
z
nên
2MN
là đường kính. Dựng hình bình hành
OMNP
ta
có
12
23 z z OP
.
Ta có
2
22
1 2 1 2
2 z z z z
22
1 2 1 2
z z z z
16
12
4zz
. Dấu bằng xảy ra khi
12
zz
MN OI
.
Câu 58: Xét các số phức
z a bi
, ab
thỏa mãn
2 3 2 2 zi
. Tính
2P a b
khi
1 6 7 2 z i z i
đạt giá trị lớn nhất.
A.
1P
. B.
3P
. C.
3P
. D.
7P
.
Lời giải
Chọn B
Gọi
z x yi
với
, xy
.
Ta có:
22
2 3 2 2 2 3 8 z i x y
. Suy ra, tập hợp điểm
;M x y
biểu diễn cho số
phức
z
trên hệ tọa độ
Oxy
là đường tròn
C
tâm
2;3I
và bán kính
8R
.
Gọi
1; 6A
,
7; 2B
và
3; 2J
là trung điểm của
AB
.
Đặt
1 6 7 2 P z i z i
suy ra
22
2 P MA MB MA MB
. (BĐT Bunhiacopxki).
Phương trình đường trung trực
của
AB
là:
3
2
xt
yt
.
Ta co
:
2
2 2 2
2
2
AB
MA MB MJ
vơ
i
J
là trung điểm của
AB
.
Vì
M
chạy trên đường tròn ,
J
cô đi
nh nên
IJ .MJ R
Do vâ
y
2
22
4 IJ P R AB
nên
2
2
ax
4 IJ .
m
P R AB
Dâu « = » xa
y ra khi
MA MB
và ba điểm
,,M I J
thẳng hàng. Điêu na
y tho
a ma
n nhơ
IA IB
.
Do đó:
MC
, tọa độ của
M
là nghiệm hệ:
2 2 2 2
3 3 0 4
2 2 1 5
37
2 3 8 5 5 8
x t x t x x
y t y t y y
tt
x y t t







Mặt khác :
4; 5 2 130 M P MA MB
và
0;1 2 50M P MA MB
.
Vậy để
Max
P
thì
4; 5M
Suy ra
23 ab
.
Câu 59: (SGD – HÀ TĨNH )Trong các số phức z thoả mãn
2 4 2 zi
, gọi
1
z
và
2
z
là số phức có mô-
đun lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức
1
z
và
2
z
bằng.
A.
8i
. B.
4
. C.
8
. D.
8
.
Lời giải
Chọn D.
Trang35
Gọi
,, z x yi x y
và
;M x y
là điểm biểu diễn số phức
z
.
Theo giả thiết
2 4 2 zi
2 4 2 x yi i
22
2 4 4 xy
.
Suy ra
22
: 2 4 4 M C x y
Suy ra tập hợp các điểm biểu diễn số phức
z
thỏa mãn
2 4 2 zi
là đường tròn
C
có tâm
2; 4I
bán kính
2R
.
Đường
OI
có phương trình
2yx
cắt đường tròn
C
tại hai điểm
10 2 5 20 4 5
;
55





A
,
10 2 5 20 4 5
;
55





B
. Do
OA OB
nên điểm
A
biểu diễn số phức có môđun lớn nhất, và điểm
B
biểu diễn số phức có môđun nhỏ nhất.
Câu 60: [HKII-SỞ BẠC LIÊU-2017-2018] Xét số phức
z a bi
(
, ab
và
0b
) thỏa mãn
1z
.
Tính
2
24P a b
khi
3
2zz
đạt giá trị lớn nhất.
A.
4P
. B.
22P
. C.
2P
. D.
22P
.
Lời giải
ChọnC.
Cách 1:
Từ giả thiết có
22
1ab
22
10 ba
với
1;1a
và
.1zz
.
Ta có
3
2zz
2
2
12
. zz
z
z
2
2. z z z
22
2 2 2 bi a b abi
22
22 a b b ab i
2
2
22
22 a b b ab
2
2
2 2 2
2 1 2 a b b a
2
2
22
2 2 1 1 2 1 a a a
32
2 4 4 2 a a a
Xét
32
4 4 2 f a a a a
, với
11 a
.
2
12 2 4
f a a a
;
2
0 12 2 4 0
f a a a
1
1;1
2
2
1;1
3
a
a
Bảng biến thiên:
Trang36
Suy ra
1;1
1 13
max
24




a
f a f
, đạt được khi
1
2
a
,
2
3
4
b
.
Vậy
2
1
2 4 2 3 2
2



P a b
.
Cách 2:
Ta có
3
cos sin cos3 sin3 z x i x z x i x
. Vì
0b
nên
sin 0x
,
cos 1;1x
.
Khi đó
3
2zz
cos3 sin3 cos sin 2 x i x x i x
cos3 cos 2 sin3 sin x x x x i
22
cos3 cos 2 sin 3 sin x x x x
22
2 2sin 2 .sin 2cos2 .sin x x x x
2 2 2 2
4 8sin 2 sin 4sin sin 2 4cos 2 sin x x x x x x
22
4 16sin cos 4sin x x x
22
4 16 1 4 1 t t t
32
16 4 16 8 t t t
với
cos 1;1 tx
.
Đặt
32
16 4 16 8 f t t t t
,
1;1 t
.
2
48 8 16 0
f t t t
1
1;1
2
2
1;1
3
t
t
Bảng biến thiên:
1;1
1
max 13
2




t
f t f
1
cos
2
tx
.
Khi đó:
2
22
1 1 3
2 2 4
a
ab
ab
.
Vậy
2
1
2 4 2 3 2
2



P a b
.
t
1
1
2
2
3
1
ft
0
0
ft
13
1
a
1
1
2
2
3
1
fa
0
0
fa
13
4
1
Trang37
Nhận xét: có thể đổi câu hỏi thành tìm Min
Câu 61: Cho
1
z
,
2
z
là hai số phức thỏa mãn
22 z i iz
, biết
12
1zz
. Tính giá trị của biểu thức
12
P z z
A.
3
2
P
. B.
2P
. C.
2
2
P
. D.
3P
.
Lời giải
Chọn D.
Cách 1.
+ Đặt
z x yi
,
, xy
, ta có
2 2 2 2 1 2 z i iz x y i y xi
22
2 2 2 2 2 2
4 2 1 2 4 4 4 1 4 4 x y y x x y y y y x
22
12
1 1 1 x y z z z
+ Sử dụng công thức:
12
,zz
ta có
2 2 2 2
1 2 1 2 1 2
2 z z z z z z
Suy ra
3P
.
Cách 2.
+ Biến đổi:
2 2 2 iz i iz z i
Ta có
22
12
2 2 2 2 1 1 z i z i z i z i z z z
.
+ Sử dụng công thức bình phương mô đun
2
2 2 2 2
1 2 1 1 2 1 2 2
2, mz nz m z mnz z cos z z n z
Trong đó
12
,zz
là góc
MON
với M, N lần lượt là các điểm biểu diễn số phức
12
,zz
trên mặt
phẳng phức
2 2 2
1 2 1 2 1 2 1 2 1 2 1 2
1
1 1 2 . . , 1 ,
2
z z z z z z z z cos z z cos z z
.
Vậy
2 2 2
2
1 2 1 2 1 2 1 2
1 2 . . , 3 3 P z z z z z z cos z z P
.
Câu 62: Cho số phức
z
thỏa mãn điều kiện
12z
. Tìm giá trị lớn nhất của biểu thức:
2 T z i zi
.
A.
max 8 2T
. B.
max 4T
. C.
max 4 2T
. D.
max 8T
Lời giải
Chọn B.
Đặt
, z x yi x y R
, ta có
22
1 2 1 2 ( 1) 2 z x yi x y
2
2 2 2
1 2 2 1 x y x y x
(*)
Lại có
2 ( 1) 2 ( 1) T z i z i x y i x y i
2 2 2 2 2 2 2 2
( 1) ( 2) ( 1) 2 1 4 2 5 x y x y x y y x y x y
Kết hợp với (*), ta được
2 2 2 6 2 2 2( ) 2 6 2( ) T x y x y x y x y
Áp dụng BĐT Cauchy schwarz ta có
Trang38
2( ) 2 6 2( ) 2(2( ) 2 6 2( )) 4 T x y x y x y x y
.
Câu 63: Cho số phức
z
thỏa mãn điều kiện
5 1 3 3 1 z i z i z i
. Tìm giá trị lớn nhất M của biểu
thức:
23zi
?
A.
10
3
M
. B.
1 13M
. C.
45M
. D.
9M
Lời giải
Chọn C.
2 2 2 2 2 2
5 ( 1) ( 1) ( 3) 3 ( 1) ( 1) x y x y x y
2 2 2 2 2 2
5 ( 1) 10. ( 1) ( 3) ( 1) ( 1) x y x y x y
2 2 2 2 2 2
25 ( 1) 10 ( 1) ( 3) ( 1) ( 1) 0
x y x y x y
22
( 1) 20 2 5 x y z i
2 3 (4 2) 4 2 2 5 2 5 4 5 P z i z i i z i i
Câu 64: Cho hai số phức
,z
thỏa mãn
1 3 2 z z i
;
z m i
với
m
là tham số. Giá trị của
m
để ta luôn có
25
là:
A.
7
3

m
m
. B.
7
3


m
m
. C.
37 m
. D.
37m
.
Lời giải
Chọn B.
Đặt
,, z a ib a b
có biểu diễn hình học là điểm
;M x y
1 3 2 z z i
1 3 2 x iy x y i
2 2 2
2
1 3 2 x y x y
2 1 6 9 4 4 xxy
2 3 0 xy
Suy ra biểu diễn của số phức
z
là đường thẳng
: 2 3 0 xy
.
Ta có:
25
25 z m i
1 2 5 x m y i
22
1 2 5 x m y
25MI
với
;1Im
.
Mà ta có
,MI d I
Nên
25MI
, 2 5 dI
24
25
5


m
2 4 10 m
2 4 10
2 4 10
m
m
3
7
m
m
.
Câu 65: Cho số phức
z
thỏa mãn
11
3
2
z
zi
. Tìm giá trị lớn nhất của biểu thức
2 4 7 P z i z i
A.
20
. B.
10
. C.
12 5
. D.
45
.
Trang39
Lời giải
Chọn A.
Gọi
z x yi
,
, xy
.
Ta có
11
3
2
z
zi
2 1 3 z z i
22
22
2 1 3 x y x y
22
4 6 7 0 x y x y
.
Lại có
2 4 7 P z i z i
2 2 2
2
1 2 4 7 x y x y
4 8 8 2 4 8 72 x y x y
.
Mặt khác
2
4 8 8 2 4 8 72 5.80 x y x y
4 8 8 2 4 8 72 20 x y x y
Suy ra
20P
.
Câu 66: Cho số phức
z a bi
(
a
,
b
là các số thực) thỏa mãn
34 z z i
và có môđun nhỏ nhất. giá trị
của
.P a b
là?
A.
3
4
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn D.
Ta có:
34 a bi a bi i
22
22
34 a b a b
6 8 25 0 ab
25 8
6

b
a
Mô đun của số phức
z
là:
22
z a b
2
2
25 8
6



b
b
2
100 2 225
36

b
15
6
Số phức
min
2zb
3
2
a
3P
Câu 67: Trong các số phức
z
thỏa mãn điều kiện
2 4 2 z i z i
. Tìm số phức
z
có môđun nhỏ nhất.
A.
1 zi
. B.
22 zi
. C.
22zi
. D.
32 i
.
Lời giải
Chọn C.
Gọi số phức
z
có dạng
z a bi
.
z
thỏa mãn
2 4 2 z i z i
Trang40
2 2 2
2
2 2 2 2
2 4 2
2 4 2
4 4 8 16 4 4
4 4 16
4


a b i a b i
a b a b
a a b b a b b
ab
ab
Theo bất đẳng thức Bunhiacopxki.
2
2
2 2 2 2 2 2
16 1 1 8 a b a b z a b
22z
Dấu
xảy ra
2 2 2
11
4

ab
a b z i
ab
Câu 68: Trong các số phức
z
thỏa mãn điều kiện
2 4 2 z i z i
. Số phức
z
có mô đun bé nhất bằng
A.
32
B.
2
. C.
22
. D.
4
.
Lời giải
Chọn C
Đặt
, z x yi x y
. Khi đó
2 4 2 z i z i
2 4 2 x yi i x yi i
2 2 2
2
2 4 2 x y x y
4 4 16 0 xy
40 xy
.
Số phức có mô đun nhỏ nhất bằng khoảng cách từ
O
đến đường thẳng
: 4 0 xy
.
min
4
; 2 2
2
z d O
.
Trang41
Câu 69: (Đề Star Education) Cho hai số phức
12
;zz
thỏa mãn
12
5zz
và
12
1zz
. Giá trị lớn nhất của
biểu thức
12
P z z
là:
A.
26.
B.
26
.
2
C.
9.
D.
1
.
2
Lời giải
Chọn A.
Ta gọi
,MN
lần lượt là các điểm biểu diễn của các số phức
12
;zz
.
Từ giả thiết :
12
5zz
5OM ON
5
2
OI
với
I
là trung điểm của đoạn thẳng
MN
.
12
1zz
1OM ON
1MN
.
Ta có
2 2 2
2
24
OM ON MN
OI

2
2
22
2O
2
MN
IOM ON 
13
12
P z z
OM ON
2 2 2 2 2
11P OM ON
26
. Vậy
max
26.P
Câu 70: Cho hai số phức
12
;zz
thỏa mãn
12
5zz
và
12
1zz
. Gọi
,Mm
lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của biểu thức
12
P z z
. Khi đó mô đun của số phức
.M mi
là :
A.
76
. B.
76
. C.
2 10
. D.
2 11
.
Lời giải
Chọn A.
Ta gọi
,MN
lần lượt là các điểm biểu diễn của các số phức
12
;zz
.
Từ giả thiết :
12
6zz
6OM ON
3OI
với
I
là trung điểm của đoạn thẳng
MN
.
12
2zz
2OM ON
2MN
.
Ta có
2 2 2
2
24
OM ON MN
OI

2
2
22
2O
2
MN
IOM ON 
20.
12
P z z
OM ON
2 2 2 2 2
11P OM ON
40.
Vậy
ax 2 0 .m 1PM
12
P z z
OM ON
OM ON
6
.
Vậy
min 6Pm
.
Suy ra
.M mi
40 36 76.
Câu 71: Cho số phức
z
thỏa mãn
5
.3
2
iz
. Giá trị lớn nhất của biểu thức
425z 11 iP z i 
là:
A.
25
. B.3. C.
35
. D.
5
2
.
Lời giải
Chọn C.
Ta gọi
( ; )M x y
là điểm biểu diễn số phức
z
.
Trang42
5
.3
2
iz
2
2
5
3
2
xy
. Suy ra
5
( ; ) (0;3);
2
M x y C I R





Khi đó:
425z 11 iP z i 
22 z 5
1
2
1i zi
2 MA MB
,
với
1
;2 ; 1;5
2
AB



Ta có:
1
;1
2
IA



; 1;2IB
suy ra
2.IB IA
.
Theo định lý Stewart ta có:
2 2 2
5 3 5 5
5 . 5
2 2 2
MA MB MI




22
2 15MA MB
(Hoặc có thể chứng minh theo phương pháp véc tơ
MI MA AB
1
3
MA AB
1
3
MA MB MA
21
33
MA MB
Suy ra:
2 2 2
4 1 4
. .cos ,
9 9 9
MI MA MB MA MB MA MB
22
4 1 4
. .cosAMB
9 9 9
MA MB MA MB
2 2 2
22
4 1 4
.
9 9 9 2. .
MA MB AB
MA MB MA MB
MAMB




2 2 2
2 1 2
3 3 9
MA MB AB
22
2MA MB
22
2
3
3
MI AB
15
)
Vậy
2P MA MB
2. 2.MA MB
2
2 2 2
2 1 2MA MB
45
3 5.
Câu 72: Cho hai số phức
12
1 3 1 3
,
2 2 2 2
ii
zz
. Gọi
z
là số phức thỏa mãn
3 3 3zi
. Đặt
,Mn
lần lượt là giá trị lớn nhât, giá trị nhỏ nhất của biểu thức
12
T z z z z z
. Tính modun của số
phức
w M ni
A.
2 21
3
B.
13
C.
43
3
D.
4
Lời giải
Giả sử
,, z x yi x y R
. Ta có
2
2
3
3 3 3 1( )
3




z i x y C
Gọi
1 3 1 3
; , ; , ;
2 2 2 2
K x y A B
lần lượt là các điểm biểu diễn số phức
12
,,z z z
Ta tìm Max – Min của
T OK OA OB
Ta có
,,A B O
thuộc đường tròn
()C
và
ABO
đều
22
Min
T OA
.
Gọi
K
thuộc cung
OB
. Ta có
. . . KAOB OA BK ABOK KA KB OK
43
2 2.2
3
Max
T KA R T
Trang43
2
2
4 3 2 21
w2
33




Câu 73: Cho số phức
z
thỏa mãn
5 1 3 3 1 z i z i z i
. Tìm giá trị lớn nhất
M
của
23zi
?
A.
10
3
M
. B.
1 13M
. C.
45M
. D.
9M
.
Lờigiải
ChọnD
Gọi
1; 3 , 1; 1 , 0;1 A B C C
là trung điểm
AB
Suy ra
2 2 2
2 2 2 2
2 10
24
MA MB AB
MC MA MB MC
.
Mặt khác
22
5 1 3 3 1 5 3 10 z i z i z i MC MA MB MA MB
22
25 10 2 10 2 5 MC MC MC
.
Mà
2 3 2 4 2 4 2 5 4 5 z i z i i z i i MC
.
Dấu “ = “ xẩy ra khi và chỉ khi
25 zi
.
Câu 74: [ Phạm Minh Tuấn, lần 3, năm 2018- Câu 46]
Cho số phức
z
thỏa mãn
3
1 2 1 2
2
z i z i
zi
. Tìm giá trị nhỏ nhất của biểu thức
2P z i
.
A.
1
2
P
. B.
2P
. C.
3
. D.
1
3
.
Lời giải
Chọn A
Áp dụng tính chất:
2 2 2 2
1 1 1
22 z z z z z z
Ta có:
2 2 2
3
1 2 1 2 2 2 1 2 1 2 2 1
2



z i z i z i z i z i
zi
42
1
4 2 4 2 3 0 2
2
z i z i P z i
Câu 75: [2D4-4] [THPT Chuyên LQĐ, LAI CHÂU, lần 1, 2018]Cho hai số phức
12
,zz
thỏa mãn điều kiện
1 1 1
22 z i z z i
và
2
10 1 zi
. Tìm giá trị nhỏ nhất của biểu thức
12
zz
?
A.
10 1
. B.
3 5 1
. C.
101 1
. D.
101 1
.
Lời giải
Trang44
Chọn B.
+) Gọi
1
;, z a bi a b
.
Nên
2
22
2
1 1 1
2 2 2. 1 2 2
4
a
z i z z i a b b b
.
Do đó tập hợp điểm biểu diễn số phức
1
z
là Parabol
2
4
x
y
.
+) Gọi
2
,, z a bi a b
.
Khi đó
22
2
10 1 10 1 1 z i a b
Nên tập hợp điểm biểu diễn số phức
2
z
là đường tròn
22
10 1 1 C x y
tâm
10;1I
bamns kính
1r
.
12
zz
nhỏ nhất khi và chỉ khi
MN
nhỏ nhất.
Ta có:
1 MN IN IM MN IM IN IM
.
Nên
MN
nhỏ nhất khi
IM
nhỏ nhất.
Ta có:
22
22
22
2
5
10 1 4 4 45
4 4 2
xx
IM x x
.
45 3 5 IM
.
Do đó
3 5 1MN
.
Vậy
1 2 1 2
min
3 5 1 3 5 1 z z MN z z
.
Câu 76: [2D4-4]Cho hai số phức
12
,zz
thỏa mãn
1
12 zi
và
21
z iz
. Tìm giá trị lớn nhất
m
của biểu thức
12
zz
A.
2 2 2m
. B.
21m
. C.
22m
. D.
2m
.
Lời giải
Chọn A.
Ta có
1 2 1 1 1 1
1 . 2. z z z iz i z z
Đặt
1
z a bi
với (
, ab
) theo đề bài ta có
22
1 1 4 ab
(*). Ta cần tìm GTLN của
22
2m a b
x
y
N
I
1
M
Trang45
Đặt
22
t a b
. Ta có:
22
(*) 4 2 1 2 1 2( ) 2 a a b b a b t
.
Mà
2
2 2 2 2
1 ( 1) . a b a b
(**) nên
2
2
2 4( ) 8 t a b t
2
12 4 0 tt
6 4 2 6 4 2 t
Kết hợp với
22
0t a b
suy ra
0 6 4 2 t
Suy ra
2 12 8 2 2 2 2 mt
Dấu "=" xảy ra khi (**) xảy ra khi
11
ab
ab
. Kết hợp (*) ta được
1
1 2 1 zi
Vậy giá trị lớn nhất của
m
bằng
2 2 2
.
Câu 77: [Chuyên Ngoại Ngữ - Hà Nội - 2018] Cho hai số phức
1
z
;
2
z
thỏa mãn
1
3 5 2 zi
và
2
1 2 4 iz i
. Tìm giá trị lớn nhất của biểu thức
12
23T iz z
.
A.
313 16
. B.
313
. C.
313 8
. D.
313 2 5
Lời giải.
Chọn A
Ta có
1
3 5 2 zi
1
2 6 10 4 iz i
.
Suy ra điểm
M
biểu diễn số phức
1
2iz
nằm trên đường tròn
1
T
có tâm
1
6; 10I
và có bán kính
là
1
4R
.
Mặt khác,
2
1 2 4 iz i
2
3 6 3 12 zi
nên điểm biểu diễn số phức
2
3 z
là điểm
N
nằm
trên đường tròn
2
T
có tâm
2
6;3I
và có bán kính là
2
12R
.
Ta thấy
12
23iz z
12
23iz z
MN
.
T
lớn nhất khi và chỉ khi
MN
lớn nhất, khi đó bốn điểm
M
,
1
I
,
2
I
,
N
theo thứ tự thẳng hàng.
Vậy giá trị lớn nhất của
1 2 1 2
MN I I R R
313 16
.
Câu 78: Cho hai số phức
,zw
thỏa mãn
3 2 1
1 2 2
zi
w i w i
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
P z w
.
I
2
I
1
N
M
Trang46
A.
min
3 2 2
2
P
. B.
min
21P
. C.
min
5 2 2
2
P
. D.
min
3 2 2
2
P
.
Lời giải
Chọn C.
Cách 1 :
Giả sử
z a bi
, ab
,
w x yi
, xy
.
3 2 1 zi
22
3 2 1 ab
(1)
1 2 2 w i w i
2 2 2 2
1 2 2 1 x y x y
.
Suy ra
0xy
.
2 2 2 2
P z w a x b y a x b x
.
Từ (1) ta có
3;2I
, bán kính
1r
. Gọi
H
là hình chiếu của
I
trên
: d y x
.
Đường thẳng
HI
có PTTS
3
2

xt
yt
.
3 ; 2 M HI M t t
2
21 M C t
1
2
1
2

t
t
11
2 3 ; 2
22



tM
,
52
2
MH
11
3 3 ; 2
22



tM
,
52
2
MH
Vậy
min
5 2 2
2
P
.
Cách 2 :
3 2 1 zi
điều này cho thấy
Mz
đang nằm trên hình tròn tâm
3;2I
bán kính bằng 1.
1 2 2 w i w i
điều này cho thấy
Nw
đang thuộc nửa mặt phẳng tạo bởi đường thẳng
là
trung trực của đoạn
AB
với
1; 2 , 2;1 .AB
: 0. xy
(Minh hoạ như hình vẽ)
Trang47
. P z w MN
min
32
5 2 2
, 1 .
2
2
P d I R
Câu 79: [Nguyễn Khuyến, Bình Dương, 18/3,2018] Cho
1
z a bi
và
2
z c di
là
2
số phức thỏa mãn:
2
1
4z
và
1
10z c d
. Gọi
M
là giá trị lớn nhất của biểu thức
T ac bd cd
. Hãy chọn khẳng định
đúng về
M
.
A.
11;15M
. B.
15;17M
.
C.
11;12M
. D.Không tồn tại
M
.
Lời giải
Chọn A.
Ta có
2
1
1
4
10

z
z c d
22
4
5


ab
cd
.
Khi đó:
T ac bd cd
2 2 2 2
(5 ) a b c d c c
.
Đặt
22
( ) 2 2 10 25 5 f c c c c c
.
Ta có
2
4 10
52
2 10 25

c
f c c
cc
2
2
2 2 10 25
25
2 10 25






cc
c
cc
5
2
c
Bảng biến thiên:
O
y
x
2
1
2
3
-2
-1
B
A
I
M
N
Δ
O
y
x
2
1
2
3
-2
-1
N
M
I
Trang48
Dựa vào bảng biến thiên ta
có
25
5 2 13,3
4
M
.
Dấu bằng xảy ra khi
2
5
2


ab
cd
.
Câu 80: Cho số phức
z
thỏa mãn
3
3
1
2z
z
và
1
axM m z
z
. Khẳng định nào sau đây đúng?
A.
1; 2M
. B.
7
2;
2



M
.
C.
5
1;
2



M
. D.
2
5MM
.
Lời giải
Chọn C.
Ta có
3
3
3
1 1 1
3
z z z
zz
z
3
3
3
1 1 1
3
z z z
zz
z
3
3
3
1 1 1
3
z z z
zz
z
3
11
32
zz
zz
.
Mặt khác:
33
1 1 1 1
33
z z z z
z z z z
.
Suy ra:
3
11
32 zz
zz
. Đặt
1
0 tz
z
ta được:
3
3 2 0 tt
2
2 1 0 tt
2t
.
Vậy
2M
.
Câu 81: Cho số phức
z x yi
với
,xy
là các số thực không âm thỏa mãn
3
1
12

z
zi
và biểu thức
2
22
22
11





P z z i z z z i z i
. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
. Môđun của
M mi
là
A.
3
. B.
1
. C.4. D.
2
.
c

5
2

fc
0
fc

25
52
4

Trang49
Lời giải
Chọn B.
Ta có
3
1
12

z
zi
3 1 2 z z i
1 xy
.
2
22
22
11





P z z i z z z i z i
22
16 8 ( ) x y xy x y
22
16 8x y xy
.
Đặt
t xy
ta có
2
1
0
44
xy
t
.
Tính giá trị lớn nhất và nhỏ nhất của
2
16 8P t t
, với
1
0;
4



t
ta được
max
0P
;
min
1P
Vậy
1M mi
.
Câu 82: (THPT Nguyễn Đăng Đạo – Bắc Ninh lần 3-2018) Cho hai số phức
12
1 3 1 3
,
2 2 2 2
z i z i
.
Gọi
z
là số phức thỏa mãn
3 3 3zi
. Đặt
,Mm
lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức
12
T z z z z z
. Tính mô đun của số phức
w M mi
.
A.
2 21
3
. B.
13
. C.
43
3
. D.
4
Lời giải
Chọn A.
Giả sử
,,M A B
lần lượt biểu diễn số phức
12
,,z x yi z z
.
Từ giả thiết
3 3 3zi
ta có:
22
11
()
3
3
xy
.
Nên
M
thuộc đường tròn tâm
11
0; ,
33



IR
.
Ta có
T MO MA MB
.
Để
min
T
thì
M
trùng
,,O A B
nên
2
2
min
13
2 2 2
22







T OA
.
Để
max
T
thì
max
OM
và
()
max
MA MB
nên
2OM R
và
M
nằm
chính giữa cung nhỏ
AB
và
2
0;
3



M
. Do vậy
2
2
2 1 3 2 4
22
22
3 3 3







max
T OM MA
.
Vậy
2
2 2 2
4 2 21
w2
3
3



Mm
.
x
y
3
2
-
1
2
1
2
M
O
1
I
A
B
Trang50
Câu 83: Cho hai số phức
z
và
w
thỏa mãn các điều kiện sau:
2 2 1
max 2 2 , 2
iz i z
w i w
.
Tìm giá trị nhỏ nhất của
zw
.
A.
9
25
. B.
13
25
. C.
5
2
. D.
1
25
.
Lời giải
Chọn B.
Gọi
,MN
lần lượt làđiểm biểu diễn của
,zw
với
;M x y
.
Ta có
2 2 1 2 2 1 iz i z z i z
2 2 2
2
2 2 1 2 4 7 0 x y x y x y
.
Do đó,
M
thuộc nửa mặt phẳng bờ
: 2 4 7 0 xy
không chứa
O
, kể cả
bờ.
Ta có
max 2 2 , 2 w i w
suy ra
2 2 2
2 , 2; 2
2
2




wi
NI I
w
NO
.
Do đó,
N
thuộc phần chung của hai hình
tròn
;2I
và
;2O
.
Dễ thấy hai hình tròn này tiếp xúc ngoài tại
điểm
1; 1E
. Do đó,
1; 1N
.
Ta thấy
z w MN
nên
zw
nhỏ nhất khi
MN
ngắn nhất, khi đó
M
là hình chiếu của
N
trên
.
Ta có
2
2
2 1 4.1 7
13
,
25
24

dN
.
Vậy
13
min
25
zw
.
Câu 84: [CHUYÊN NGỮ LẦN 1-2018] Cho hai số phức
12
; zz
thỏa mãn
1
3 5 2 zi
và
2
1 2 4 iz i
.
Tìm giá trị lớn nhất của biểu thức
12
23T iz z
.
A.
313 16
. B.
313
. C.
313 8
. D.
313 2 5
.
Lời giải
Chọn A.
Trang51
Đặt
12
2 , 3 ; ; ; iz a bi z c di a b c d
, gọi
; , ;A a b B c d
.
Có
1
3 5 2 zi
3 5 2
2
a bi
i
i
6 10 4 a b i
22
6 10 16 ab
nên
AI
có tâm
6; 10I
bán kính
4R
.
Có
2
1 2 4 iz i
. 1 2 4
3
c di
ii
3 6 12 d c i
22
2
6 3 12 cd
nên
BJ
có tâm
6; 3J
, bán kính
12
R
.
Có
12
23T iz z
22
a c b d a c b d
AB
.
Do
AI
,
BJ
,
313 16
IJ R R
nên
Max
AB R R IJ
16 313
.
Câu 85: Xét các số phức
,( , ) z a bi a b
thỏa mãn
3 2 2. zi
Tính
ab
biết biểu thức
1 2 2 2 5 S z i z i
đạt giá trị nhỏ nhất.
A.
43
. B.
23
. C.
43
. D. 3.
Lời giải:
Chọn A
Giả thiết
22
3 2 2 ( ) :( 3) ( 2) 4 z i T a b
Gọi
( 1;2), (2; 5), ( ; )A B M a b
lần lượt là các điểm biểu diễn của
các số phức
1 2 3
1 2 , 2 5 , z i z i z a bi
Bài toán trở thành: Tìm
()MT
sao cho biểu thức
2S MA MB
nhỏ nhất
Ta có
2 2 2 2
( 1) ( 2) 2 4 5 MA a b a b a b
22
2 4 4 8 a b a b
22
2 ( 2) ( 2) 2 a b MC
với
(2; 2)C
O
I
J
A
B
M
-1
2
5
Trang52
Ta có
2 2( ) 2 MA MB MB MC BC
dấu “=”xảy ra khi và chỉ khi
,,B M C
theo thứ tự đó thẳng
hàng.
Phương trình đường thẳng
:2BC x
M
là giao của của BC và
( ) (2;2 3) a b 4 3 TM
.
Câu 86: Cho các số phức
1 2 3
,,z z z
thỏa mãn
1 2 1 2
2 2 6 2 z z z z
. Tìm giá trị nhỏ nhất của biểu thức
12
P z z z z z
.
A.
6 2 2P
B.
3 2 3P
. C.
6 2 3P
. D.
9
23
2
P
.
Lời giải
Chọn C.
Chọn
,,A B M
lần lượt là các điểm biểu diễn số phức
12
,,z z z
,
Dựa vào điều kiện
1 2 1 2
2 2 6 2 z z z z
6OA OB
,
62AB
.
Suy ra ta có tam giác
OAB
vuông cân tại
O
.
Phép quay tâm
B
góc quay
0
60
ta có:
0
, 60
:
B
Q A A
MM
Do tam giác
BMM
đều

AM A M
,
BM MM
Suy ra
12
P z z z z z
OM AM BM OM MM A M OA
.
Dấu
""
xảy ra khi
, , ,

O M M A
thẳng hàng.
Khi đó tam giác
OBA
có
6OB
,
62
BA BA
và
0
105
OBA
.
Từ đó suy ra
2 2 0
2 . .cos105 6 2 3
OA OB BA OB BA
.
Vậy
min 6 2 3P
.
Câu 87: Cho hai số phức
,z
thỏa mãn
1 3 2 z z i
;
z m i
với
m
là tham số. Giá trị của
m
để ta luôn có
25
là:
6
6
6
2
6
0
0
6
0
0
M'
A'
A
O
B
M
Trang53
A.
7
3

m
m
. B.
7
3


m
m
. C.
37 m
. D.
37m
.
Lời giải
Chọn B.
Đặt
,, z a ib a b
có biểu diễn hình học là điểm
;M x y
1 3 2 z z i
1 3 2 x iy x y i
2 2 2
2
1 3 2 x y x y
2 1 6 9 4 4 xxy
2 3 0 xy
Suy ra biểu diễn của số phức
z
là đường thẳng
: 2 3 0 xy
.
Ta có:
25
25 z m i
1 2 5 x m y i
22
1 2 5 x m y
25MI
với
;1Im
.
Mà ta có
,MI d I
Nên
25MI
, 2 5 dI
24
25
5


m
2 4 10 m
2 4 10
2 4 10
m
m
3
7
m
m
.
Câu 88: Cho số phức
z
thỏa mãn
11
3
2
z
zi
. Tìm giá trị lớn nhất của biểu thức
2 4 7 P z i z i
A.
20
. B.
10
. C.
12 5
. D.
45
.
Lời giải
Chọn A.
Gọi
z x yi
,
, xy
.
Ta có
11
3
2
z
zi
2 1 3 z z i
22
22
2 1 3 x y x y
22
4 6 7 0 x y x y
.
Lại có
2 4 7 P z i z i
2 2 2
2
1 2 4 7 x y x y
4 8 8 2 4 8 72 x y x y
.
Mặt khác
2
4 8 8 2 4 8 72 5.80 x y x y
4 8 8 2 4 8 72 20 x y x y
Suy ra
20P
.
| 1/53
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI TOÁN MAX – MIN SỐ PHỨC. Kỹ năng:
Phƣơng pháp đại số.
Phƣơng pháp hình học.
Phƣơng pháp bđt modun.
Phƣơng pháp casio.
Một số tính chất cần nhớ.
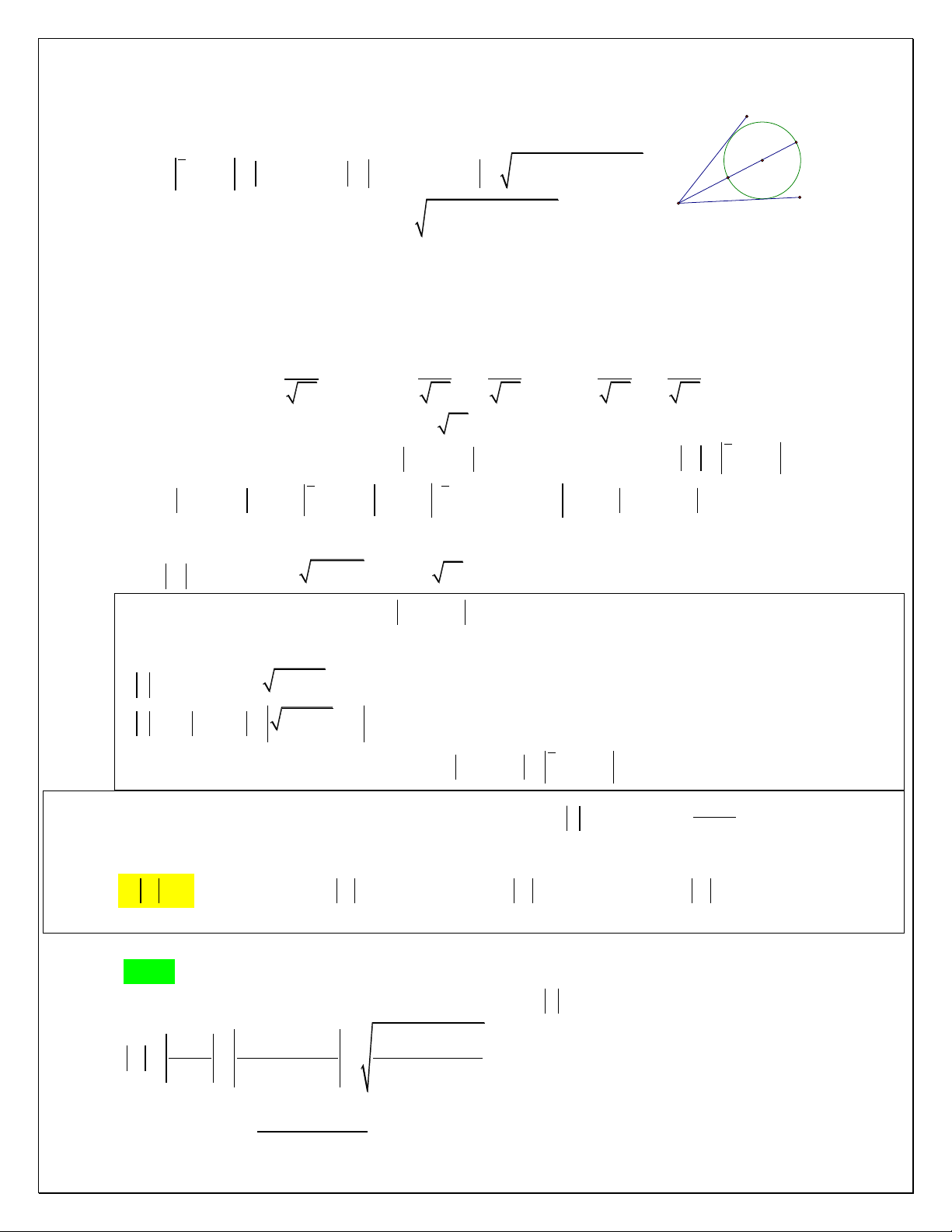
1. Môđun của số phức: 
 Số phức z a bi được biểu diễn bởi điểm M(a; b) trên mặt phẳng Oxy. Độ d|i của véctơ OM
được gọi l| môđun của số phức z. Kí hiệu 2 2
z = a + bi = a + b  Tính chất   2 2
z a b zz OM z  0, z  , z  0  z  0 z z  .
z z'  z . z '  
,z'  0  z z'  z z'  z z' z' z'
kz k . z ,k  2  2 Chú ý: 2 2 2 2 2 2 2 2 2 2
z a b  2abi  (a b )  4a b a b z z  . z z . Lưu ý:
z z z z dấu bằng xảy ra  z kz k  0 1 2   1 2 1 2
z z z z dấu bằng xảy ra  z kz k  0 . 1 2   1 2 1 2
z z z z dấu bằng xảy ra  z kz k  0 1 2   1 2 1 2
z z z z dấu bằng xảy ra  z kz k  0 1 2   1 2 1 2  2 2 2 2 z z
z z  2 z z 1 2 1 2  1 2  2  2
z z z zz
2.Một số quỹ tích nên nhớ
Biểu thức liên hệ x, y Quỹ tích điểm M
ax  by c  0 (1) (1)Đường thẳng :
 ax  by c  0
z a bi z c di (2)
(2) Đường trung trực đoạn AB với
Aa,b,Bc,d
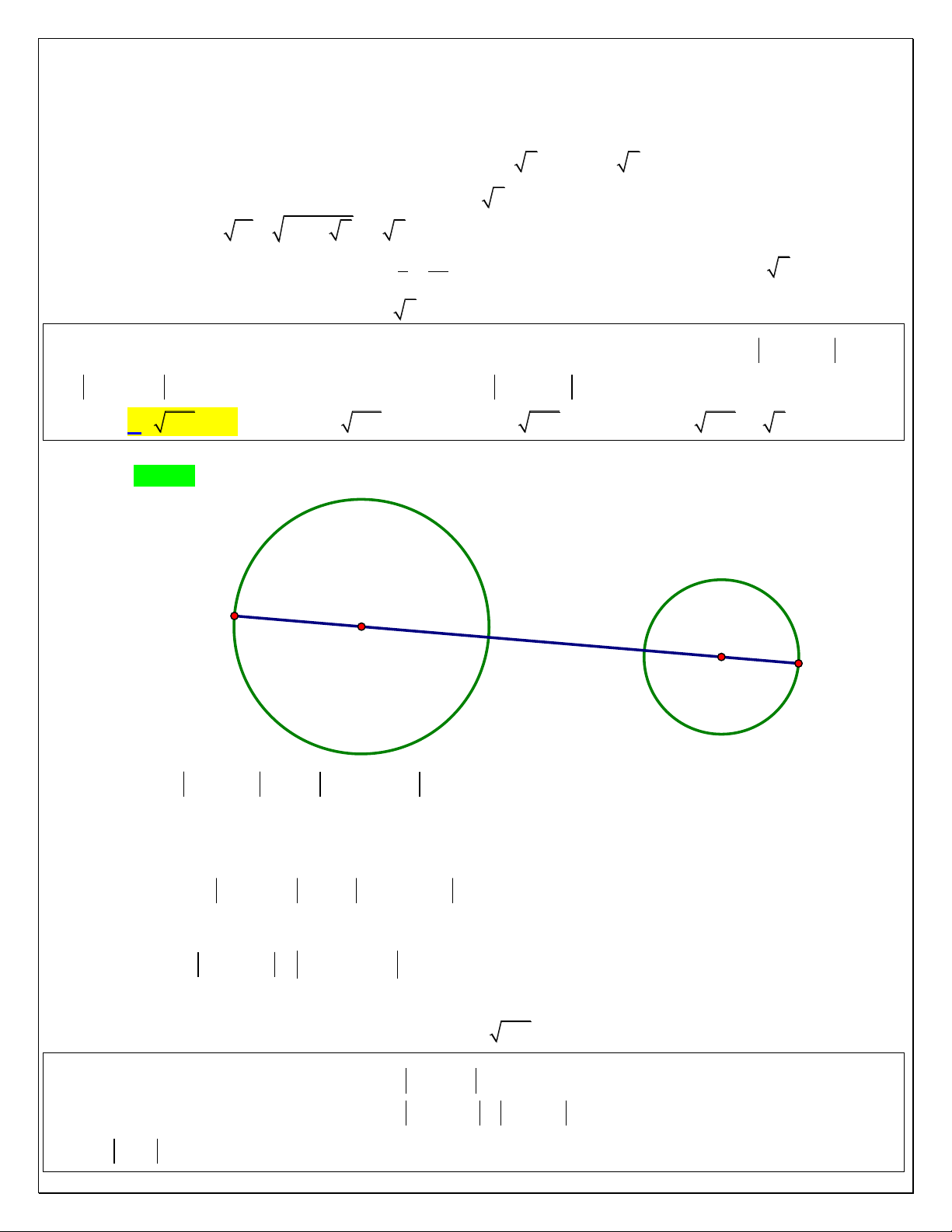
x a2 y b2 2     R hoặc
Đường tròn t}m I a;b , bán kính R
z a bi R
x a2 y b2 2     R hoặc
Hình tròn tâm I a;b , bán kính R
z a bi R r
x a2 y b2 2 2      R hoặc
Hình v|nh khăn giới hạn bởi hai đường
tròn đồn t}m I a;b , b{n kính lần lượt l| Trang1
r z a bi R r, R 2
y ax bx c Parabol  c  0 2
x ay by   c
xa2 y c2  1 Elip   1 1 hoặc 2 2   b d
z a b i z a b i  2a
2 Elip nếu 2a AB ,Aa ,b ,B a ,b 1 1   2 2 1 1 2 2
Đoạn AB nếu 2a AB
xa2 y c2 Hypebol   1 2 2 b d
Một số dạng đặc biệt cần lƣu ý:
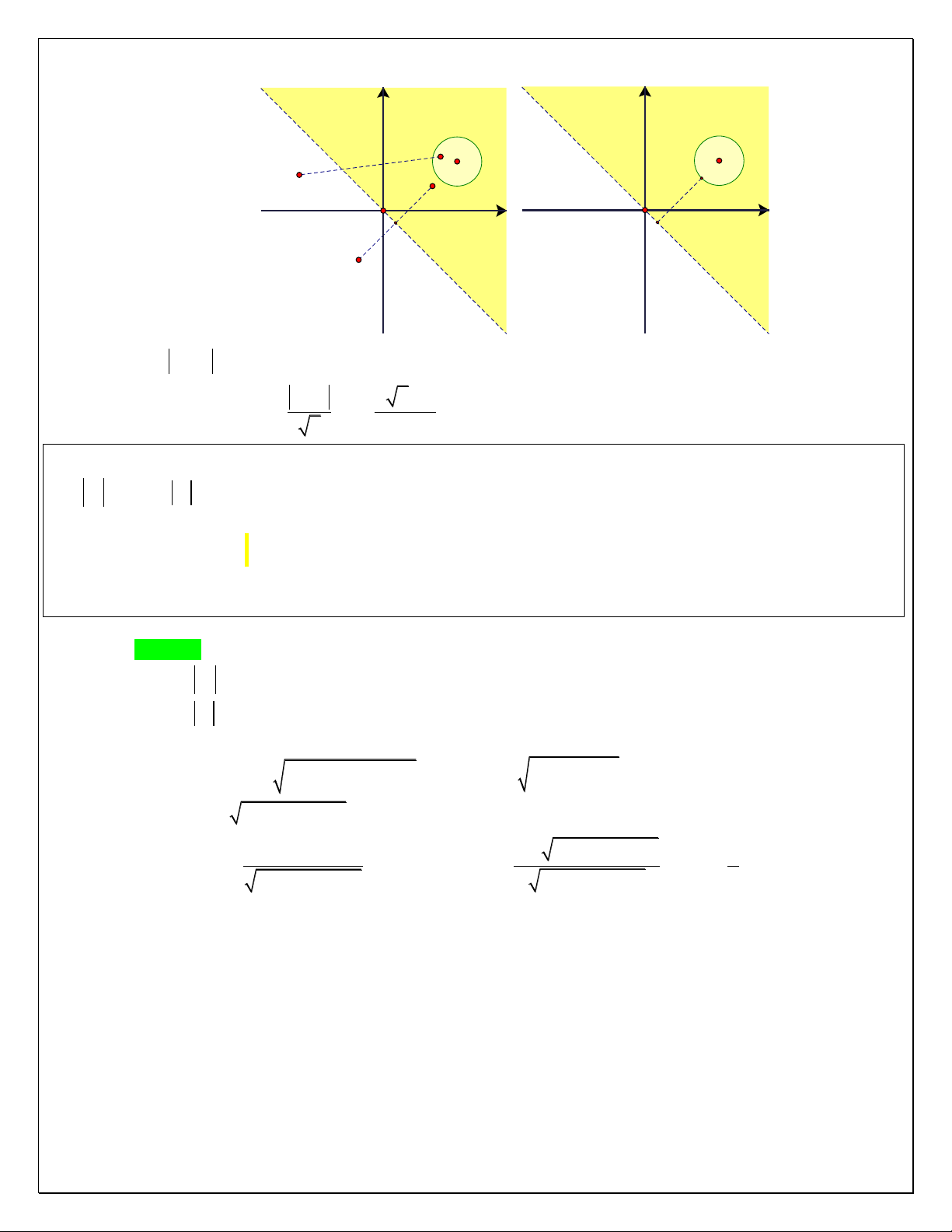
Dạng 1: Quỹ tích điểm biểu diễn số phức l| đường thẳng.
TQ1: Cho số phức z thỏa mãn z  a  bi  z , tìm z . Khi đó ta có Min
 Quỹ tích điểm Mx; y biểu diễn số phức z l| đường trung trực đoạn OA với Aa; b  1 1 2 2 zz a   b 0   Min 2 2 
z a b  i 2 2
TQ2:Cho số phức thỏa mãn điều kiện z a bi z c di . Tìm z . Ta có min
 Quỹ tích điểm Mx; y biểu diễn số phức z l| đường trung trực đoạn AB với Aa; b,Bc;d 2 2 2 2
a b c dz
dO, AB  Min
2 a c2  b d2
Lƣu ý: Đề b|i có thể suy biến b|i to{n th|nh 1 số dạng, khi đó ta cần thực hiện biến đổi để đưa về dạng cơ bản. Ví dụ 1:
 Cho số phức thỏa mãn điều kiện z a bi z c di . Khi đó ta biến đổi
z a bi z c di z a bi z c di .
 Cho số phức thỏa mãn điều kiện iz a bi z c di . Khi đó ta biến đổi a bic           di iz a bi iz c di z z
z b ai z d ci . i i
Dạng 2: Quỹ tích điểm biểu diễn số phức l| đường tròn. Trang2
TQ: Cho số phức z thỏa mãn điều kiện z  a  bi  R  0 z  z  R . Tìm z , z . Ta có 0  Max Min
 Quỹ tích điểm Mx; y biểu diễn số phức z l| đường tròn t}m Ia; b bán kính R  2 2 z
OI R a b R z   R  0 Max 2 2  z
OI R a b R z R 0  Min
Lƣu ý: Đề b|i có thể cho ở dạng kh{c, ta cần thực hiện c{c phép biến đổi để đưa về dạng cơ bản. a   bi R
Ví dụ 1: Cho số phức z thỏa mãn điều kiện iz  a  bi  R  z   (Chia hai vế cho i ) i i  z  b  ai  R
Ví dụ 2: Cho số phức z thỏa mãn điều kiện z  a  bi  R  z  a  bi  R (Lấy liên hợp 2 vế)
Ví dụ 3: Cho số phức z thỏa mãn điều kiện    a   bi R R
c di z  a  bi  R  z    2 2 c  di c  di c  d z R Hay viết gọn 1 z z  z  R  z   (Chia cả hai vế cho z ) 0 1 z z 0 0 0
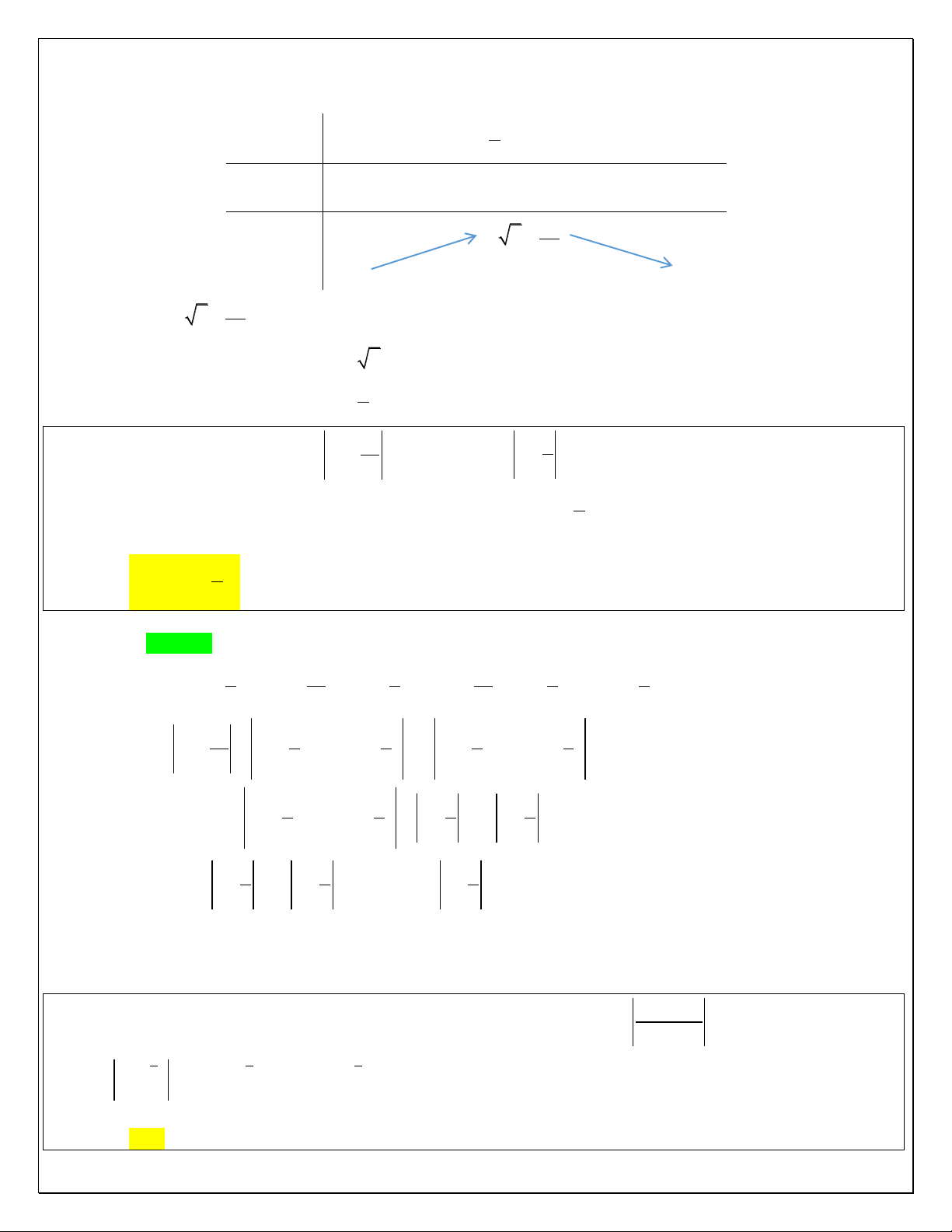
Dạng 3: Quỹ tích điểm biểu diễn số phức l| Elip.
TQ1: (Elip chính tắc). Cho số phức z thỏa mãn điều kiện z  c  z  c  2a ,a  c Khi đó ta có 2 2 x y
 Quỹ tích điểm Mx; y biểu diễn số phức z là Elip:   1 2 2 2 a a  c  z   a   Max 2 2  za   c Min
TQ2: (Elip không chính tắc).Cho số phức z thỏa mãn điều kiện z  z  z  z  2a 1 2 Thỏa mãn 2a  z  z . 1 2
Khi đó ta thực hiện phép biến đổi để đưa Elip về dạng chính tắc (Kỹ thuật đổi hệ trục tọa độ). Ta có Trang3
Khi đề cho Elip dạng không chính tắc z  z  z  z  2a , z  z  2a và z ,z  c  , c  i ). Tìm 1 2  1 2  1 2
Max, Min của P  z  z . 0  z  z  2c Đặt 1 2  2 2 2 b  a  c z  z P  a Nếu 1 2 z   0 Max  0 (dạng chính tắc) 2 P  b  Min  z  z  z  z 1 2  z   a 1 2 P  z   a Nếu 0  2 Max 0  2   z  z  k z  z  z   z 0 1  0 2 1 2 P  z   a Min 0  2   z  z z  z 1 2  z   a 1 2 P  z   a Max 0 Nếu 0  2 2 z  z  k z  z  0 1  0 2 Nếu z  z  z  z  0 1 0 2 z z 1 2 P  z   b Min 0 2
PHẦN I : BÀI TẬP CÓ HƢỚNG DẪN GIẢI CHI TIẾT.
Dạng 1: Sử dụng tính chất của modun – bđt đại số.
Phƣơng pháp : Xem hƣớng dẫn trên lớp
Dạng 2: Sử dụng tính chất hình học.
Xem hƣớng dẫn trên lớp.
Dạng 3: Tả phí lù.
Phƣơng pháp: Tin tƣởng bạn ngồi bên cạnh Câu 1:
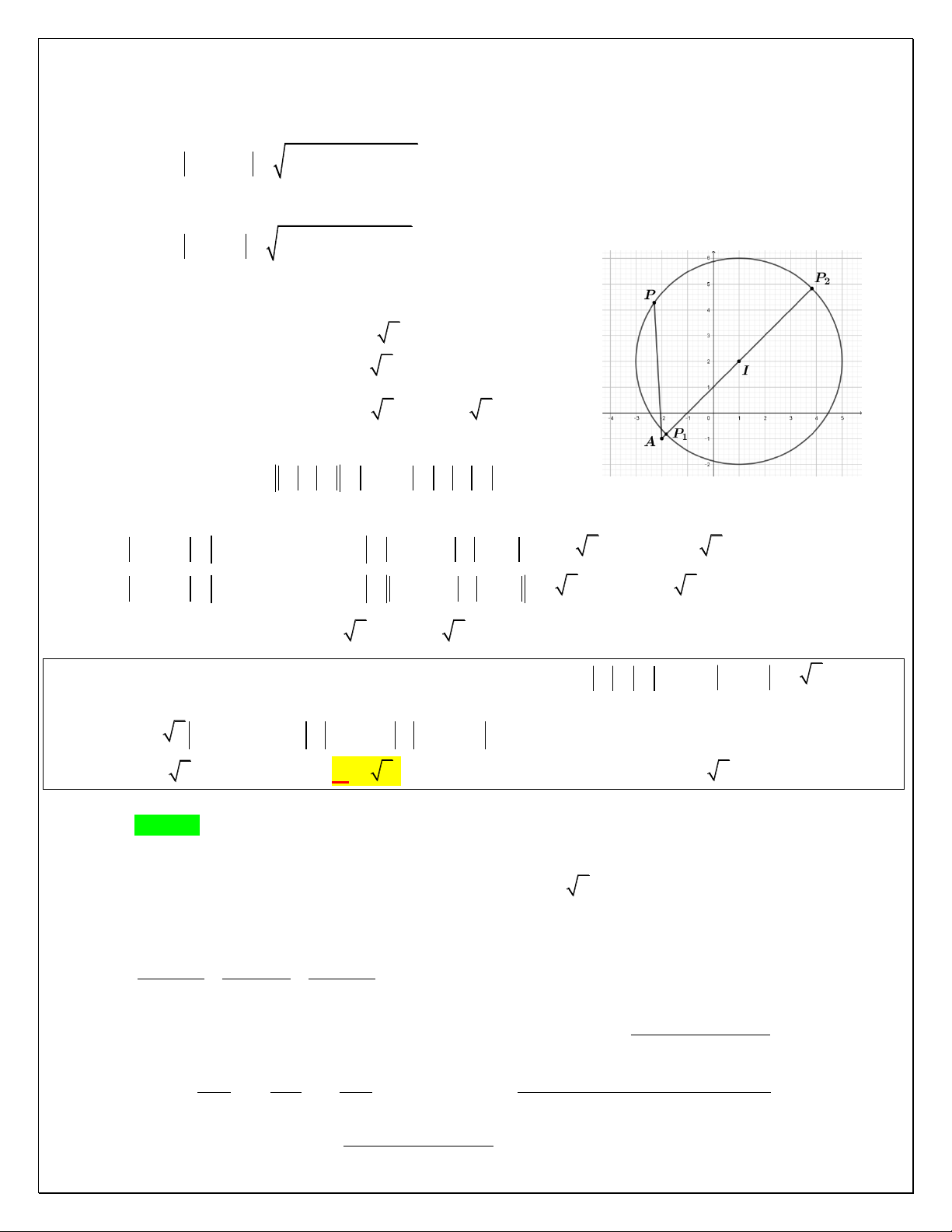
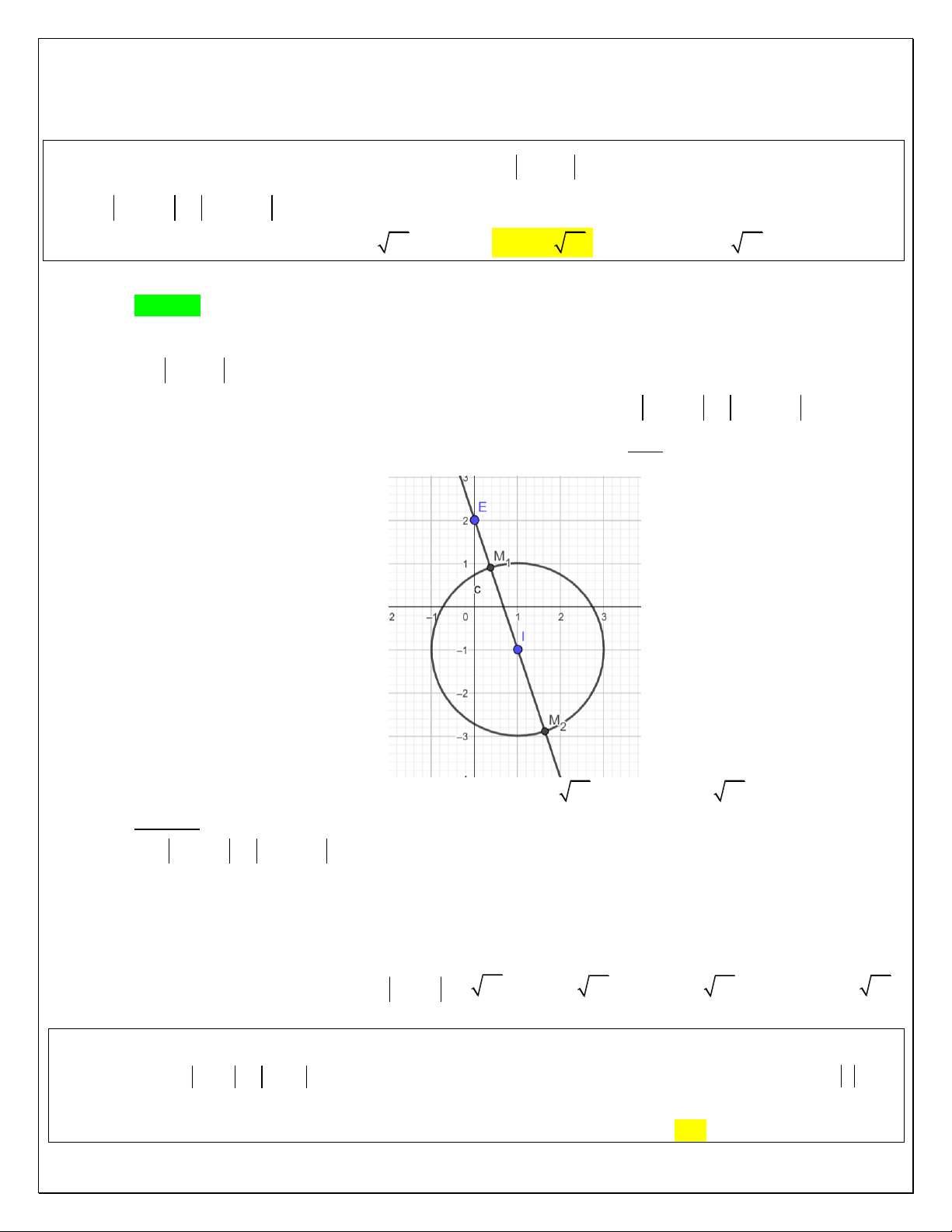
(TRẦN HƢNG ĐẠO – NB)Trong c{c số phức thỏa mãn điều kiện z  3i z  2  i . Tìm số
phức có môđun nhỏ nhất? 1 2 1 2
A. z  1 2i .
B. z    i . C. z   i . D. z  1   2i . 5 5 5 5 Hƣớng dẫn giải Chọn C.
Cách 1: Phƣơng pháp tự luận
Giả sử z x yi x, y  
z i z   i x  y  i  x    y  i x  y  2  x  2  y  2 2 3 2 3 2 1 3 2 1
 6y  9  4x  4  2y 1  4x 8y  4  0  x  2y 1  0  x  2y 1 Trang4 2
z x y   y  2   2 2 2 2 2 1 5 2
1  y  5y  4y  1  5 y       5  5 5 5 2 1 Suy ra z
khi y    x  min 5 5 5 1 2 Vậy z   .i 5 5
Cách 2: Phƣơng pháp trắc nghiệm
Giả sử z x yi x, y  
z i z   i x  y  i  x    y  i x  y  2  x  2  y  2 2 3 2 3 2 1 3 2 1
 6y  9  4x  4  2y 1  4x 8y  4  0  x  2y 1  0
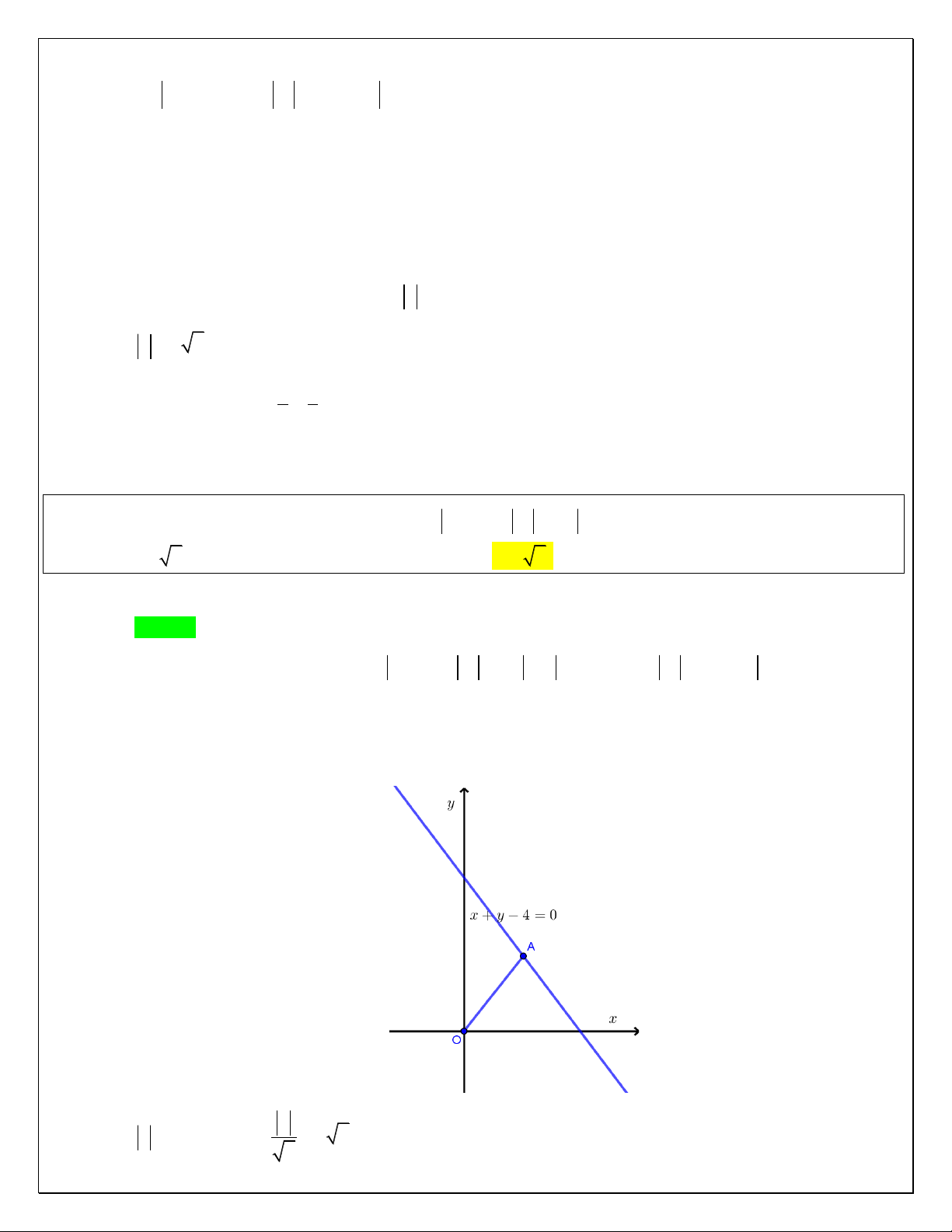
Vậy tập hợp c{c điểm biểu diễn số phức z thỏa điều kiện z  3i z  2  i l| đường thẳng
d : x  2y 1  0 .
Phương {n A: z  1 2i có điểm biểu diễn 1;  2d nên loại A. 1 2  1 2 
Phương {n B: z    i có điểm biểu diễn  ;    d nên loại B. 5 5  5 5  Phương {n D: z  1
  2i có điểm biểu diễn  1
 ; 2d nên loại B. 1 2  1 2  Phương {n C: z
i có điểm biểu diễn ;     d 5 5  5 5 
(Trong trường hợp có nhiều số phức thuộc đường thẳng thì ta tiếp tục so s{nh modun, v|
nên thay luôn z v|o dữ kiện ban đầu chứ không nên biến đổi) Cách 3: Tính nhanh.
Quỹ tích c{c điểm M biểu diễn số phức z l| đường thẳng có phương trình  : x  2y 1  0 . 1  5 Vậy z
dO,   min 2 2  5 1 2
Cách 4: Công thức tính nhanh.
BT1:Cho số phức thỏa mãn điều kiện z a bi z . Tìm z ? min  1 1 2 2 zz a   b 0  Min 2 2 
z a b  i 2 2
BT2:Cho số phức thỏa mãn điều kiện z a bi z c di . Tìm z ? min 2 2 2 2
a b c d zMin
ac2 bd2 2 Câu 2:
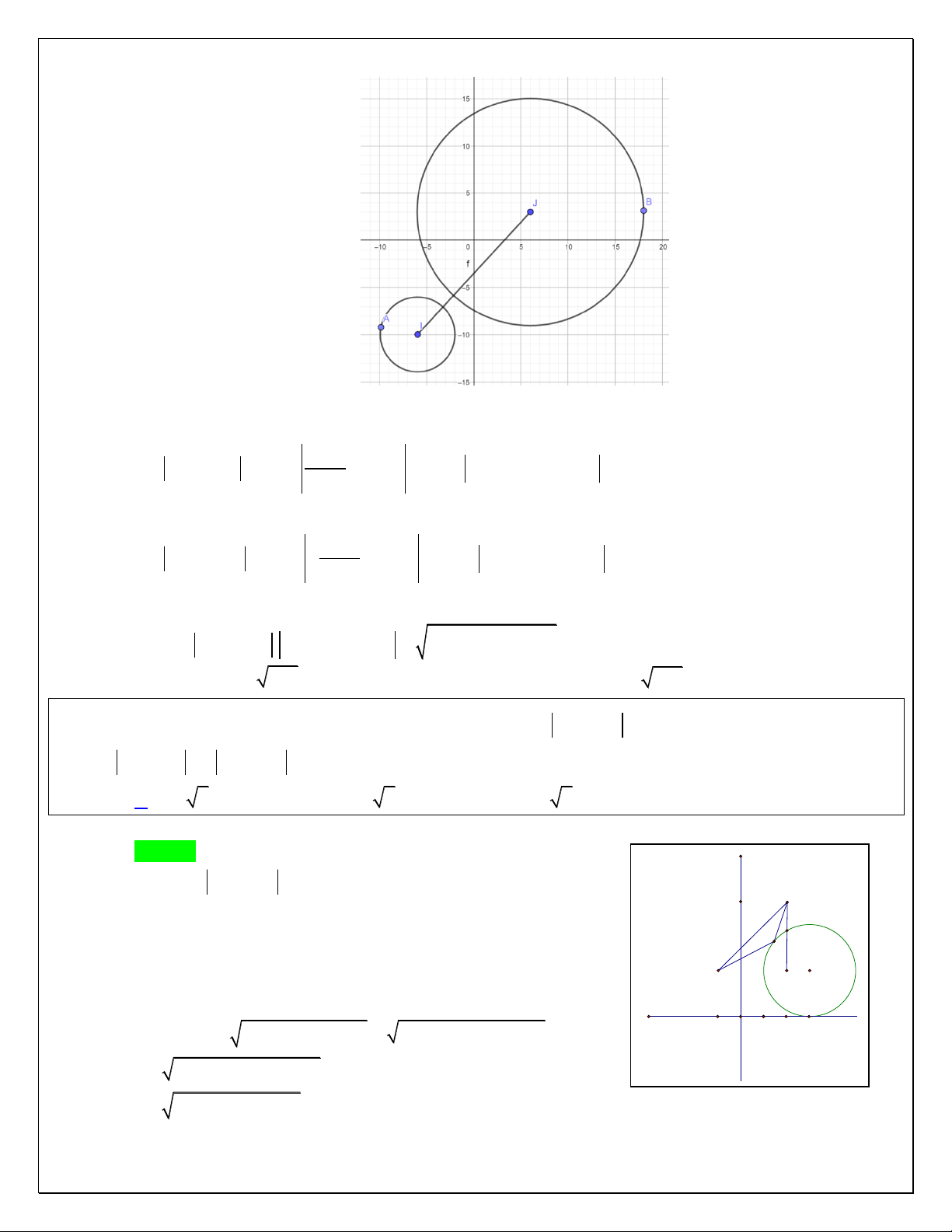
(LẠNG GIANG SỐ 1)Cho số phức z thỏa mãn z  3  z  3  8 . Gọi M , m lần lượt gi{ trị
lớn nhất v| nhỏ nhất z . Khi đó M m bằng A. 4  7. B. 4  7. C. 7. D. 4  5. Trang5 Hƣớng dẫn giải Chọn B. Cách 1 : Đại số
Gọi z x yi với x; y   .
Ta có 8  z  3  z  3  z  3  z  3  2z z  4 .
Do đó M max z  4 . 2 2
Mà z   z
  x   yi x   yi   x   2
y  x   2 3 3 8 3 3 8 3 3  y  8 .
Áp dụng bất đẳng thức Bunhiacopxki, ta có x 2 yx 2 y
x 2 y x 2 2 2 2 2 2 2 8 1. 3 1. 3 1 1 3 3                y     2 2 x y     2 2 8 2 2 2 18
2 2x  2y  18  64 2 2 2 2
x y  7  x y  7  z  7 .
Do đó M min z  7 .
Vậy M m  4  7 .
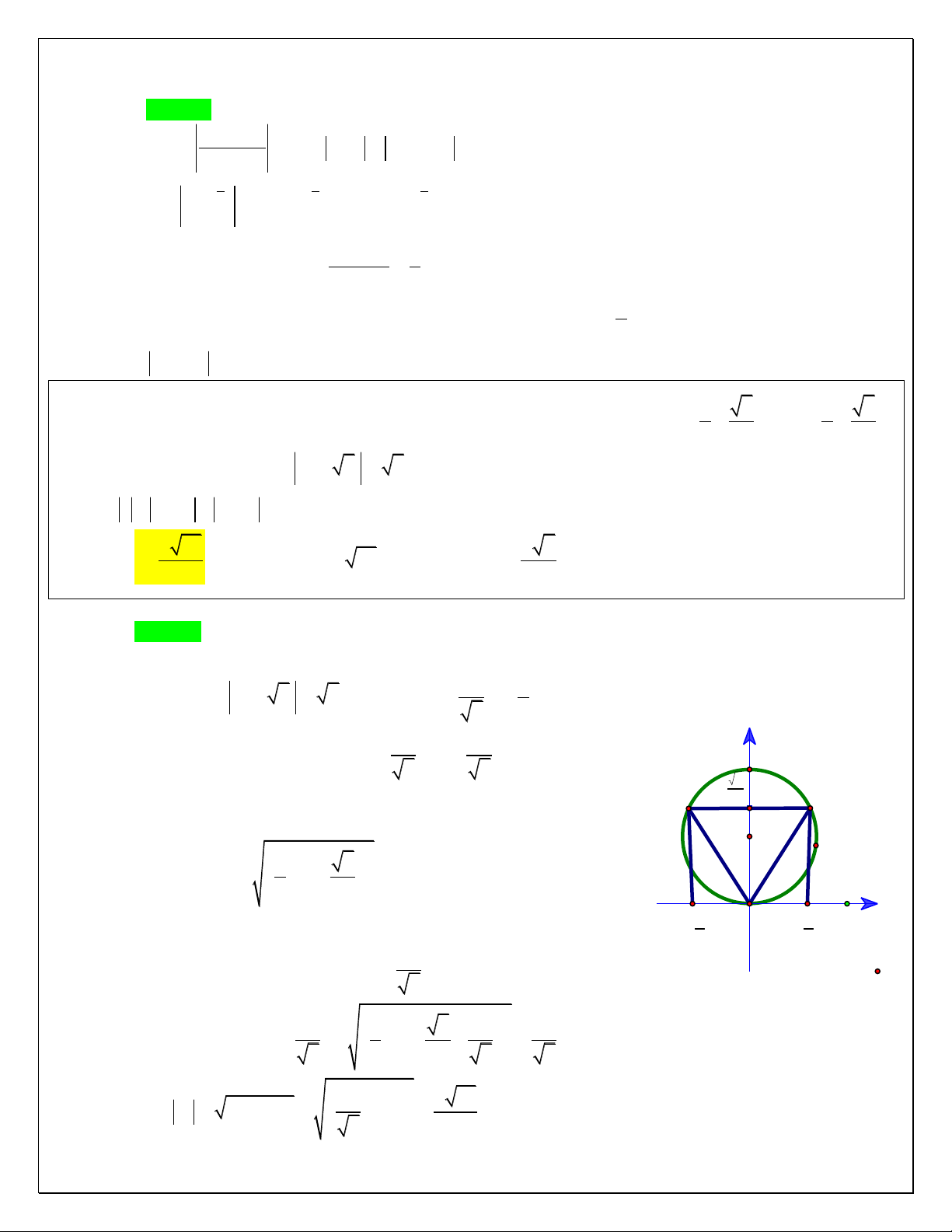
Cách 2: Hình học (Đọc lại lý thuyết phần Elip)  F 3;  0 ,F 0,3  1   2      2 2 x y   8 
Tập hợp c{c điểm biểu diễn số phức z là elip   1 a   4   16 7 2    2 2 2 2
 b a c  4  3  7      za  4  Do vậy Max
M m  4  7 zb  7  Min Cách 3: Tổng quát
Cho số phức z thỏa mãn z c z c  2a,a c ta luôn có . 2 2  x y
Tập hợp điểm biểu diễn z là Elip   1 2 2 2 a a cz   a Max 2 2  za   c Min Câu 3:
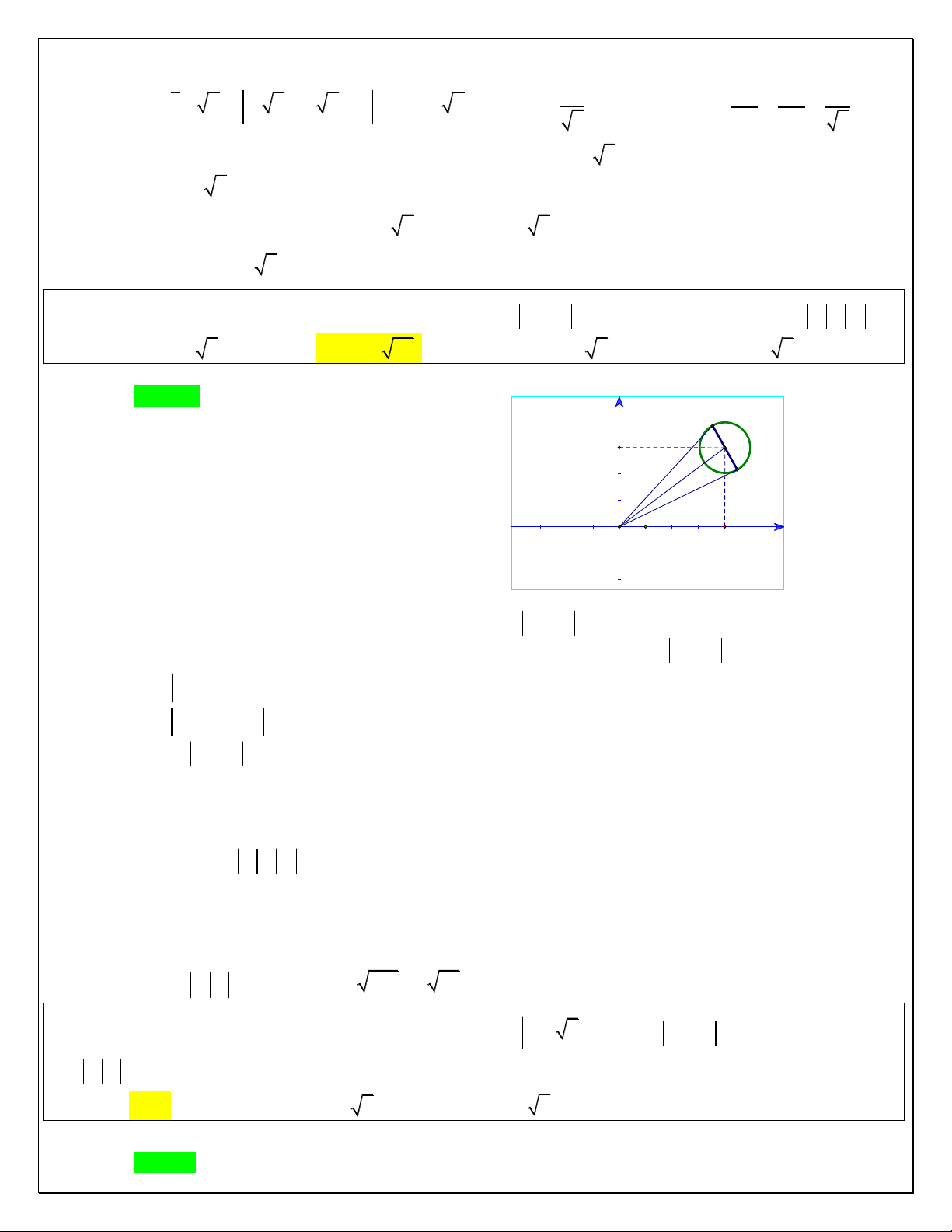
(CHUYÊN PHAN BỘI CHÂU) Cho số phức z thỏa mãn z  2  3i  1. Gi{ trị lớn nhất của
z  1  i là A. 13  2 . B. 4 . C. 6 . D. 13  1 . Hƣớng dẫn giải Chọn D
Cách 1:Gọi z x yi ta có z  2  3i x yi  2  3i x  2  y  3i . Trang6 2 2
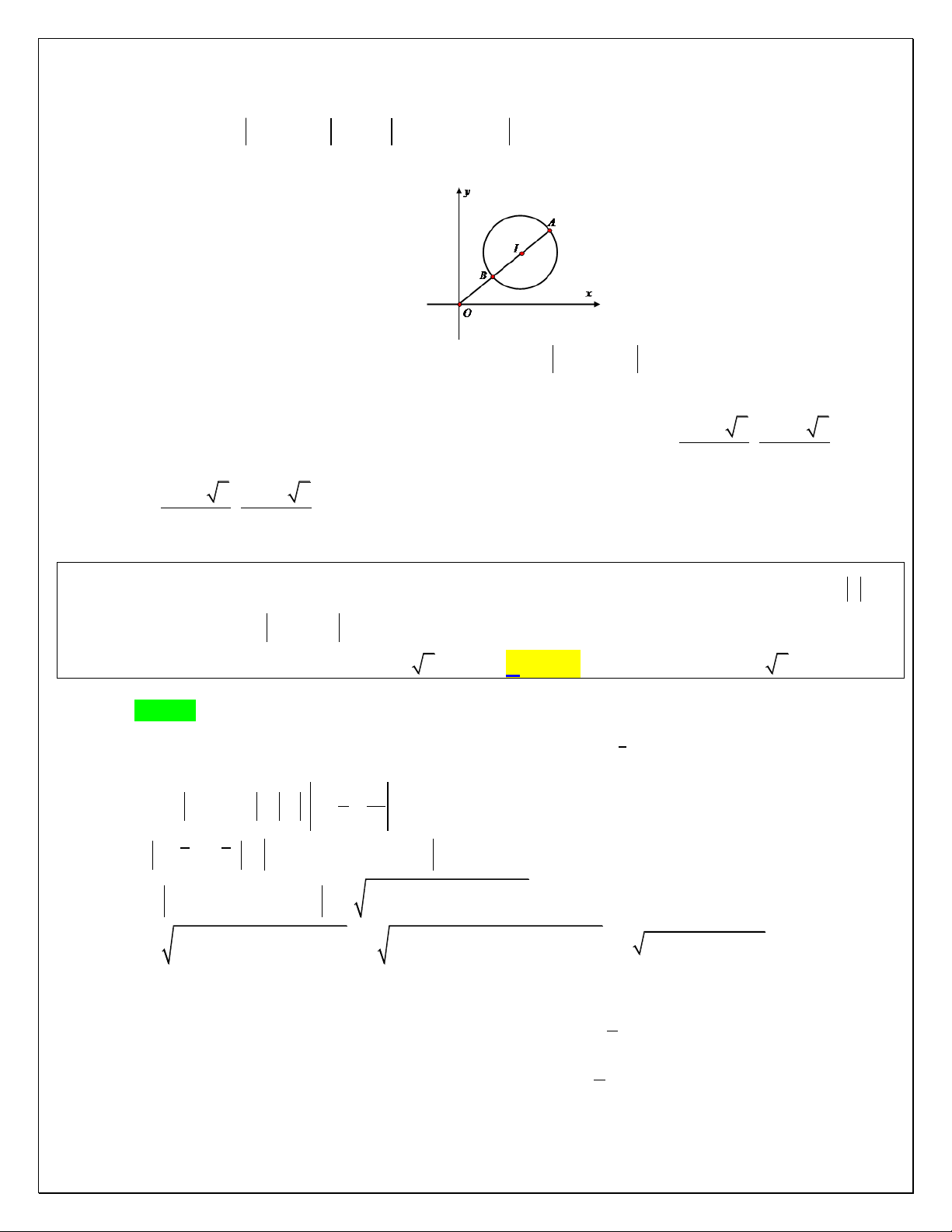
Theo giả thiết x  2  y  3  1 nên điểm M biểu diễn cho số phức z nằm trên đường
tròn tâm I 2; 3 bán kính R  1. M2 2 2
Ta có z  1 i x yi  1 i x  1 1 yi  x   1  y   1 . M1 I H
Gọi M x; y và H  1  ; 
1 thì HM  x    y  2 2 1 1 .
Do M chạy trên đường tròn, H cố định nên MH lớn nhất khi M l| giao của HI với đường tròn.
x  2  3t
Phương trình HI : 
, giao của HI v| đường tròn ứng với t thỏa mãn: y  3   2t     2 2 1 3 2 3 2
9t  4t  1  t   nên M  2  ; 3   , M  2  ; 3   . 13  13 13   13 13 
Tính độ d|i MH ta lấy kết quả HM  13  1.
Cách 2: Cho số phức z thỏa mãn z  2  3i  1. Gi{ trị lớn nhất của w  z  1  i
Ta có z  2  3i  1  z  2  3i  1  z  1 i  3  2i  1  w  3  2i  1 (Đường tròn t}m I 3, 2  ,R  1 ) Vậy 2 2 w
OI R  3  2 1  1 13 Max
Lƣu ý: Cho số phức z thỏa mãn z a bi R  0 , khi đó ta có quỹ tích c{c điểm biểu diễn số
phức z l| đường tròn I a,b ,bk  R ) và  2 2 z
OI R a b   RMax 2 2  z
OI R a b   R Min
Ngoài ra ta luôn có công thức biến đổi z a bi z a bi 2z i Câu 4:
(BIÊN HÒA – HÀ NAM)Cho số phức z thỏa mãn z  1. Đặt A  . Mệnh đề n|o sau 2  iz đ}y đúng? A. A  1 . B. A  1 . C. A  1 . D. A  1. Hƣớng dẫn giải Chọn A.
Cách 1:Đặt Có a a bi a b  2 2 , ,
a b  1 (do z  1) 2z i
2a  2b 1i
4a  2b  12 2 A    2  iz 2  b ai 2b2 2  a
4a  2b  2 2 1 Ta chứng minh   . 2  b 1 2 2  a Trang7
4a  2b  2 2 1 2 2 Thật vậy ta có 2
 1  4a  2b 1  2  b a a b  1 2     2 2 2 2b 2  a Dấu “=” xảy ra khi 2 2 a b  1 . Vậy A  1 .
Cách 2 : Trắc nghiệm z  1 1 2z i Chọn A    A  1 1 2 34 z  2  iz  1 2 17 5 Câu 5:
Cho số phức z thỏa mãn z  1. Tìm gi{ trị lớn nhất của biểu thức  1 i A . z A. 5. B. 4. C. 6. D. 8. Hƣớng dẫn giải 5i 5i 5
Cách 1:Ta có: A  1   1   1
 6. Khi z i A  6. z z z
Chọn đáp án C. 5i z  5i
Cách 2: A  1   z  5i z z Theo bài 2
z  1  z  5i  5i  1  z  5i  5 1  6 Max Câu 6:
Cho số phức z thỏa mãn z  1. Tìm gi{ trị lớn nhất M
v| gi{ trị nhỏ nhất M của biểu max min thức 2 3
M z z  1  z  1 . A. M  5; M  1. B. M  5; M  2. max min max min C. M  4; M  1. D. M  4; M  2. max min max min Hƣớng dẫn giải 2 3
Ta có: M z z  1 z  1  5 , khi z  1  M  5  M  5. max 3 3 3 3 3 1 z 1 z 1 z
1 z  1 z Mặt kh{c: 3 M   1 z     1, khi 1 z 2 2 2 z  1
  M  1 M  1. min
Chọn đáp án A.  Câu 7:
Cho số phức z thỏa z  2 . Tìm tích của gi{ trị lớn nhất v| nhỏ nhất của biểu thức  z i P . z 3 2 A. . B. 1. C. 2 . D. . 4 3 Hƣớng dẫn giải i 1 3 i 1 1 Ta có P  1  1
 . Mặt kh{c: 1  1  . z |z| 2 z |z| 2 Trang8 1 3
Vậy, gi{ trị nhỏ nhất của P là , xảy ra khi z  2
i; gi{ trị lớn nhất của P bằng xảy ra khi 2 2 z  2 . i
Chọn đáp án A. Câu 8:
Cho số phức z thỏa mãn z  1 2i  3. Tìm môđun lớn nhất của số phức z  2 . i A. 26  6 17 . B. 26  6 17 . C. 26  8 17 . D. 26  4 17 . Hƣớng dẫn giải
Cách 1:Gọi z x yi; x ; y    z  2i x  y  2i . Ta có:
z   i   x  2  y  2 1 2 3 1 2  9 .
Đặt x  1 3sint; y  2
  3cost; t 0; 2.   2
z i    t2    t2 2 1 3sin 4 3cos
 26  6sint 4cost  26 6 17 sint ;  .
 26  6 17  z  2i  26  6 17  z  2i  26  6 17  3  17 max
Chọn đáp án A.
Cách 2:Cho số phức z thỏa mãn z  1 2i  3. Tìm môđun lớn nhất của số phức z  2 . i
Ta có z   i   z i 2 2 1 2 3
2 1 4i  3  z
 1  4  3  3 17 (đ{p {n A) Max Câu 9:
Cho số phức z thỏa mãn z  1. Tìm gi{ trị lớn nhất của biểu thức P  1 z  3 1 z . A. 3 15 B. 6 5 C. 20 D. 2 20. Hƣớng dẫn giải
Cách 1:Gọi z x yi; x ; y   . Ta có: 2 2 2 2
z  1  x y  1  y  1 x x  1  ;1.   2 2
Ta có: P   z
z    x 2  y   x 2 1 3 1 1 3 1
y  21 x  3 21 x .
Xét h|m số f x  21 x  3 21 x; x 1  ;1. 
 H|m số liên tục trên  1  ;1   v| với 1 3 4 x  1  ; 
1 ta có: f x  
 0  x    1  ;    x  x 1 . 5 2 1 2 1  4  Ta có: f   1  2; f   1  6; f   2 20  P    2 20. max  5 
Chọn đáp án D. Cách 2: (Casio) x  sint
Từ z  1, đặt z x yi  
Thay v|o P rồi dùng mode 7 ra đ{p {n D y   cos t
Cách 3: Hình học (Xem video live của thầy)
Câu 10: Cho số phức z thỏa mãn z  1. Gọi M và m lần lượt l| gi{ trị lớn nhất v| gi{ trị nhỏ nhất của biểu thức 2
P z  1  z z  1 . Tính gi{ trị của . M m . 13 3 39 13 A. . B. . C. 3 3. D. . 4 4 4 Trang9 Hƣớng dẫn giải
Gọi z x yi; x ; y   . Ta có: z  1  . z z  1
Đặt t z  1 , ta có 0  z 1  z  1  z  1  2  t  0; 2 .    Ta có       2 2 2 1 1
 1 .    2  2   t t z z z z z z x x . 2
Suy ra z z   z z z z z z   z   x  2 2 2 2 1 . 1 2 1
 2x 1  t  3 .
Xét h|m số f t 2
t t  3 ,t 0;2. 
 Bằng c{ch dùng đạo h|m, suy ra f t 13  f t 13 3 max ; min
 3  M.n  . 4 4
Chọn đáp án A.
Câu 11: Cho số phức z thỏa mãn điều kiện 2
z  4  2 z . Khẳng định n|o sau đ}y l| đúng? 3  1 3  1 A.  z  .
B. 5  1  z  5  1. 6 6 2  1 2  1
C. 6  1  z  6  1. D.  z  . 3 3 Hƣớng dẫn giải
Áp dụng bất đẳng thức u v u v , ta được 2 2 2 2 z  4   z  4  4
  z z  2 z  4  0  z  5  1. 2 2 2 2
2 z z z  4  z  4  z  2 z  4  0  z  5  1.
Vậy, z nhỏ nhất l| 5 1, khi z  i i 5 và z lớn nhất l| 5  1, khi z i i 5.
Chọn đáp án B.
Câu 12: Cho số phức z thỏa mãn z  1 2i  2 . Tìm môđun lớn nhất của số phức z. A. 9  4 5 . B. 11  4 5 C. 6  4 5 D. 5  6 5 Hƣớng dẫn giải 2 2
Cách 1:Gọi z x yi; x ; y   . Ta có: z 1 2i  2  x  
1  y  2  4.
Đặt x  1 2 sint; y  2
  2cost; t 0; 2   . 2 2 2
Lúc đó: z    t    t    t t 2 2 1 2sin 2 2cos 9 4sin 8cos
 9  4  8 sint ;   2  
z  9  4 5 sint    z  9  4 5; 9  4 5         5 2 5 10 4 5 z
 9  4 5 đạt được khi z   i. max 5 5
Chọn đáp án A.
Cách 2: Cho số phức z thỏa mãn z  1 2i  2 . Tìm môđun lớn nhất của số phức z. Ta có 2 2
z  1  2i  2  z
 1  2  2  2  5  9  4 5 Max Trang10
Câu 13: Cho số phức z thỏa mãn 1 iz  6  2i  10 . Tìm môđun lớn nhất của số phức z. A. 4 5 B. 3 5. C. 3. D. 3  5 Hƣớng dẫn giải
Cách 1:Gọi z x yi; x ; y   . Ta có:
 iz  i    i 6   2i 1 6 2 10 1 . z
 10  z  2  4i  5  x  22  y  42  5.Đặt 1 i
x  2  5 sin t; y  4  5 cos t; t  0; 2   . Lúc đó: z    t2    t2    t t    2  2 2 2 5 sin 4 5 cos 25 4 5 sin 8 5 cos 25 4 5 8 5
sin t  ;     2
z  25  20sint    z  5;3 5    z
 3 5 đạt được khi z  36 .i max
Chọn đáp án B.
Cách 2:Cho số phức z thỏa mãn 1 iz  6  2i  10 . Tìm môđun lớn nhất của số phức z.   i Ta có   i 6 2 10 1
z  6  2i  10  z  
z  2  4i  5 1  i 1  i 2 2  z  2  4  5  3 5 Max 2 2
Câu 14: Gọi z x yi x, y R l| số phức thỏa mãn hai điều kiện z  2  z  2  26 và 3 3 z  
i đạt gi{ trị lớn nhất. Tính tích . xy 2 2 9 13 16 9 A. xy  . B. xy  . C. xy  . D. xy  . 4 2 9 2 Hƣớng dẫn giải
Cách 1:Đặt z x iyx, y R. Thay v|o điều kiện thứ nhất, ta được 2 2 x y  9.
Đặt x  3cost, y  3sin .
t Thay v|o điều kiện thứ hai, ta có 3 3    P z  
i  18  18 sin t     6. 2 2  4     3 3 2 3 2
Dấu bằng xảy ra khi sin t   1   t    z      i.  4  4 2 2
Chọn đáp án D.
Câu 15: Trong c{c số phức thỏa mãn điều kiện z  2  4i z  2i . Tìm môđun nhỏ nhất của số phức z  2 . i A. 5 B. 3 5. C. 3 2 D. 3  2 Hƣớng dẫn giải Trang11
Cách 1:Gọi z x yi; x ; y   . 2 2 2
Ta có: z   i z i  x    y   2 2 4 2 2 4
x  y  2  x y  4  0  y  4  . x 2 2 2 2 Ta có: 2
z i x  y   2
x    x 2 2 2 6
 2x 12x  36  2x 3 18  18  z  2i
 18  3 2 khi z  3 .i min
Chọn đáp án C.
Cách 2: z  2  4i z  2i  z  2i  2  6i  z  2i  4i  w  2  6i  w  4i
Trong đó w z  2i (quay về dạng b|i to{n 1)
Câu 16: Cho số phức z thỏa mãn z  1 2i  3. Tìm môđun nhỏ nhất của số phức z 1 . i A. 4. B. 2 2. C. 2. D. 2. Hƣớng dẫn giải
Cách 1:Gọi z x yi; x ; y    z 1 i  x   1  y   1 i . Ta có:
z   i   x  2  y  2 1 2 9 1 2  9 .
Đặt x  1 3sint; y  2
  3cost; t 0; 2.   2
z 1 i  3sint2  1
  3cost2  10 6cost  2  z 2i  4  z 1 i  2, khi min z  1 . i
Chọn đáp án C.
Cách 2: (Hình học + CT tính nhanh)
Ta có z   i   z   i 2 1 2 3 1
i  3  z 1 i  1  3  2 Min
Câu 17: Biết số phức z thỏa mãn đồng thời hai điều kiện z  3  4i  5 v| biểu thức 2 2
M z  2  z i đạt gi{ trị lớn nhất. Tính môđun của số phức z  . i
A. z i  2 41
B. z i  3 5.
C. z i  5 2
D. z i  41. Hƣớng dẫn giải 2 2
Gọi z x yi; x ; y   . Ta có: z  3  4i  5  C : x  3  y  4  5 : tâm I 3; 4 và R  5. Mặt kh{c: 2 2 M z z ix 2  y x  y 2 2 2 2 2 1           
 4x  2y  3  d : 4x  2y  3  M  0.  
Do số phức z thỏa mãn đồng thời hai điều kiện nên d và C có điểm chung d I d 23  M  ;  R
 5  23  M  10  13  M  33 2 5
4x  2y  30  0  x  5  M  33    
z i  5  4i z i  41. max x  3 
2 y42  5 y   5 
Chọn đáp án D. Trang12m i
Câu 18: Cho số phức z
m  . Tìm môđun lớn nhất của z.
mm i ,  1 2 1 A. 1. B. 0. C. . D.2. 2 Hƣớng dẫn giải m i m i 1 Ta có: z     z    z
  z i m
1  mm  2i 1 1 ; 0. 2 2 2 max m  1 m  1 m  1
Chọn đáp án A.
Câu 19: (NGUYỄN TRÃI – HD) Cho số phức z thỏa mãn: z  2  2i  1. Số phức z i có môđun nhỏ nhất l|: A. 5  1 B. 5  1 C. 5  2 D. 5  2 . Hƣớng dẫn giải Chọn A. y I 1 M O 1 x
Cách 1:Gọi z x yi , x, y   . Ta có: 2 2
z  2  2i  1  (x  2)  (y  2)i  1  (x  2)  (y  2)  1
Tập hợp c{c điểm trong mặt phẳng Oxy biểu diễn của số phức z l| đường tròn (C) tâm
I(2; 2) và bán kính R  1 .
z i x  y  2 2 1
IM , với I 2;2 l| t}m đường tròn, M l| điểm chạy trên đường tròn.
Khoảng c{ch n|y ngắn nhất khi M l| giao điểm của đường thẳng nối hai điểm N 0; 
1 Oy, I 2; 2 với đường tròn (C). IM
IN R  5 1 min
Cách 2: Cho số phức z thỏa mãn: z  2  2i  1. Số phức z i có môđun nhỏ nhất
Ta có z   i   z i 2 2 2 2 1
 2  i  1  z i
 2  1 1  5 1 Min
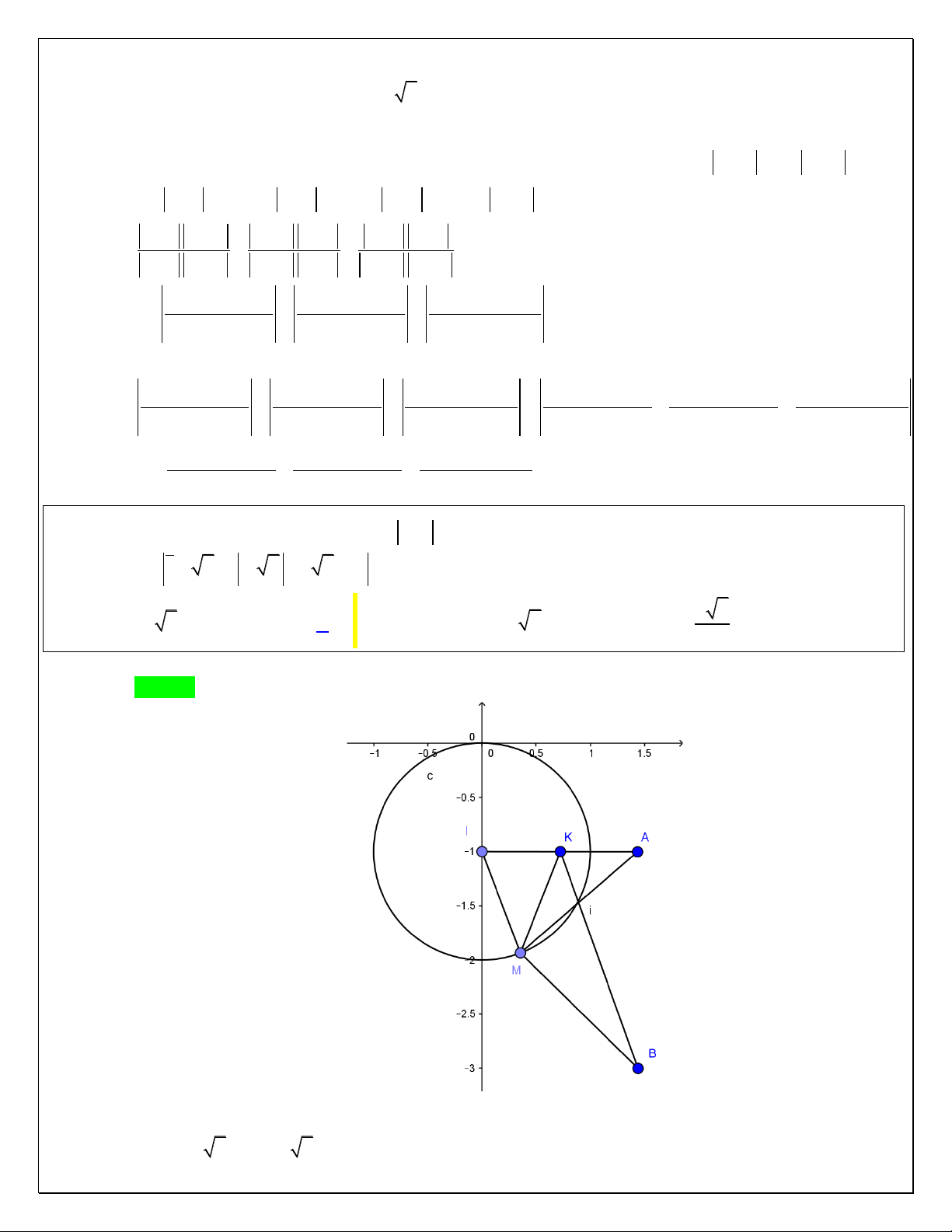
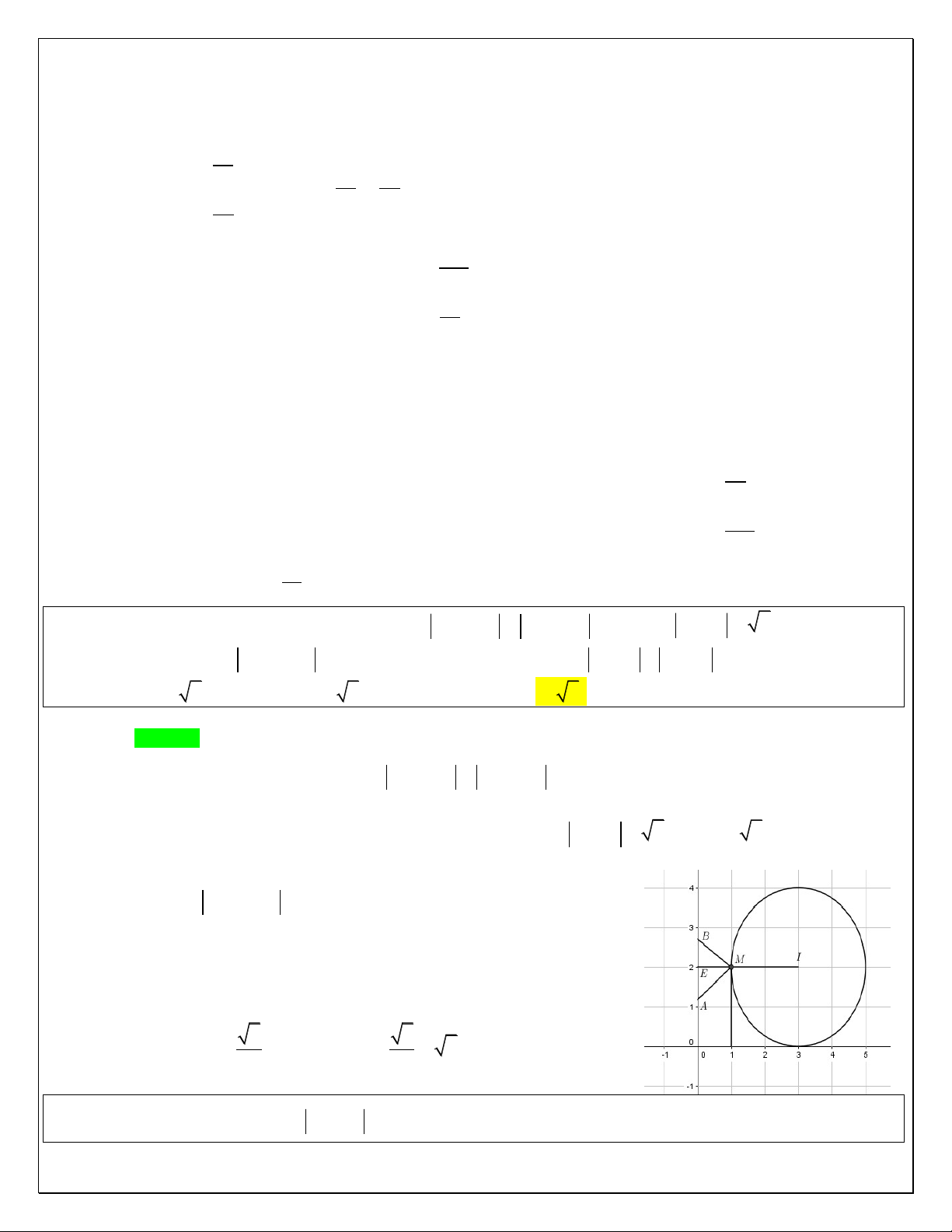
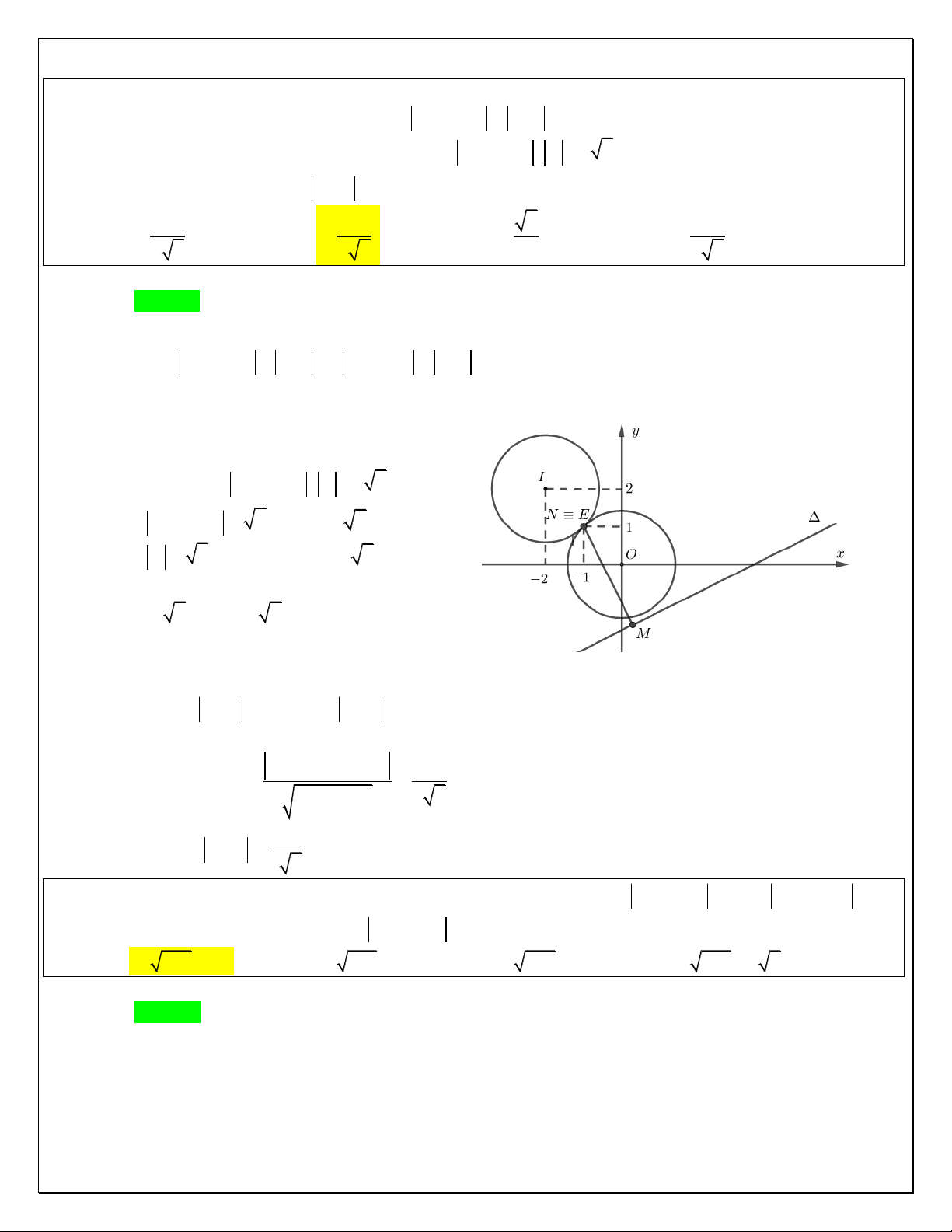
Câu 20: Trong mặt phẳng phức Oxy , c{c số phức z thỏa z  2i  1  z i . Tìm số phức z được biểu
diễn bởi điểm M sao cho MA ngắn nhất với A1,3. A. 3  i . B. 1 3i . C. 2  3i . D. 2   3i . Hƣớng dẫn giải
Gọi M x, y l| điểm biểu diễn số phức z x yi x, y R Trang13 Gọi E1, 2
  l| điểm biểu diễn số phức 1 2i Gọi F 0,  1
 l| điểm biểu diễn số phức i
Ta có : z  2i 1  z i ME MF  Tập hợp điểm biểu diễn số phức z l| đường trung
trục EF : x y  2  0 .
Để MA ngắn nhất khi MA EF tại M M 3, 
1  z  3  i => Đáp án A.
Câu 21: ( CHUYÊN SƠN LA – L2) Cho số phức z thỏa mãn điều kiện : z  1 2i  5 và
w z 1 i có môđun lớn nhất. Số phức z có môđun bằng: A. 2 5 . B. 3 2 . C. 6 . D. 5 2 . Hƣớng dẫn giải: Chọn B.
Gọi z x yi x, y    z 1 2i  x  
1  y  2i 2 2 2 2
Ta có: z  1 2i  5  x  
1  y  2  5  x  
1  y  2  5
Suy ra tập hợp điểm M x; y biểu diễn số phức z thuộc đường tròn C tâm I 1; 2   bán kính R  5
Dễ thấy OC , N  1  ;   1 C Theo đề ta có: M  ;
x yC l| điểm biểu diễn cho số phức z thỏa mãn:
w z  1 i x yi  1 i  x   1  y   1 i 
z   i  x  2 y  2 1 1 1  MN
Suy ra z  1 i đạt gi{ trị lớn nhất  MN lớn nhất
Mà M, N C nên MN lớn nhất khi MN l| đường kính đường tròn C
I l| trung điểm MN M    z   i z    2 2 3; 3 3 3 3 3  3 2 Câu 22:
(CHU VĂN AN – HN) Cho số phức z thỏa mãn điều kiện z  1  2 . Tìm gi{ trị lớn
nhất của T z i z  2  i .
A. maxT  8 2 . B. maxT  4 .
C. maxT  4 2 . D. maxT  8 . Hƣớng dẫn giải Chọn B
T z i z  2  i  z  
1  1 i  z   1  1 i .
Đặt w z 1 . Ta có w  1 và T w  1 i  w  1 i . 2
Đặt w x  . y i . Khi đó 2 2
w  2  x y . Trang14
T  x  1  y  1i  x  1  y  1i
 1. x 12  y 12 1. x 12  y 12
 1 1  x12 y 12 x12 y 12 2 2   2 2 2
2x  2y  4  4 Vậy maxT  4 .
Câu 23: Cho số phức z thỏa mãn z  2  3i  1. Gi{ trị lớn nhất của z 1 i là A. 13  2 . B. 4 . C. 6 . D. 13 1 .
(THPT CHUYÊN PHAN BỘI CHÂU - NGHỆ AN) Lời giải
Cách 1:Đặt z a bi a,b  , ta có z  2  3i  1  a  2  b  3i  1.
 a  2 b  2   a  2 b 2 2 3 1 2 3  1 
a  2  sint Đặt  (vì  2 2
 sin t  cos t  1). Khi đó z 1 i  a  
1  1 bi . b  3   cos t   2 2
a  2    b2 1 1
 xét biểu thức P  a   1  1 b . 2 2 2 2
Ta có a      b   t     t   2 2 1 1 sin 3 cos
2  sin t  6sint  9  cos t  4cost  4   2 2
sin t  cos t  13  6sint  4cost
 14  6sint  4cost P 2
Theo bất đẳng thức Bunhiacopxki, ta được  t t   2 2   2 2 6 sin 4 cos 6 4
sin t  cos t   t t2 6sin 4cos
 52  6sint  4cost  52  2 13  P  14  2 13.
Vậy z   i  a      b      2 2 2 1 1 1 14 2 13 13 1  13 1.Chọn A.
Cách 2:Cho số phức z thỏa mãn z  2  3i  1. Gi{ trị lớn nhất của z 1 i
Ta có z  2  3i  1  z  2  3i  1  z  1 i  3  2i  1 2 2  z  1 i
 3  2  1  13  1 Max
Câu 24: (THPT CHUYÊN ĐH VINH - LẦN 2)Cho c{c số phức
z, w thỏa mãn
z  2  2i z  4i , w iz 1. Gi{ trị nhỏ nhất của biểu thức w là 2 3 2 A. . B. 2 2 . C. 2 . D. . 2 2 Lời giải
Cách 1: Đặt z a bi a,b    , khi đó z  2  2i a  2  b  2i và z  4i a  b  4i .
Nên ta có a  2  b  2  a  b  2 2 2 2 4
a b  2  b  2  a Trang15 2 2
Khi đó w iz   a bi 2
i    b ai w
a  b   2 1 1 1 1
a  a   1 . 2  
Dễ thấy a  a  2 2 1 1 1 2 2 1  2 a     w   min    . Chọn A.  2  2 2 2 w 2
Cách 2: Chuyển về phương trình đường thẳng (dạng 1) Câu 25:
(ĐỀ THTT LẦN 5 – 2017)Cho số phức z thỏa mãn z  4  z  4  10. Giá trị lớn nhất và giá
trị nhỏ nhất của z lần lượt là A. 10 và 4 B. 5 và 4 C. 4 và 3 . D. 5 và 3 . Hƣớng dẫn giải.
Gọi z x yi , x, y   . Theo giả thiết, ta có z  4  z  4  10.
 x   yi  x   yi   x  2  y  x  2 2 2 4 4 10 4
4  y  10 
Gọi M x; y , F  4; 0 và F 4; 0 . 2   1  
Khi đó   MF MF  10 nên tập hợp c{c 1 2
điểm M z l| đường elip E .
Ta có c  4 ; 2a  10  a  5 và 2 2 2
b a c  9 . 2 2 x y
Do đó, phương trình chính tắc của E là   1. 25 9
Vậy max z OA OA'  5 và min z OB OB'  3 . Chọn D.
Câu 26: Trong c{c số phức z thỏa mãn điều kiện z  2  4i z  2i . Biết rằng số phức z x yi ,
x,y  có môđun nhỏ nhất. Tính 2 2
P x y . A. P  10 . B. P  8 . C. P  16 . D. P  26 . Hƣớng dẫn giải.
Cách 1:Gọi z x yi , x, y   . Ta có z  2  4i z  2i  x  2  y  4i x  y  2i
 x  2 y  2  x y  2 2 2 4 2 2 2 2 2
x  4x  4  y  8y 16  x y  4y  4
 4x  4y 16  0  y  4  x. 2 2 Do đó 2 2 2
z x y x    x 2 4
 2x  8x 16  2x  2  8  2 2 .
Dấu "  " xảy ra  x  2  y  2 . Vậy 2 2
P  2  2  8 . Chọn B.
Cách 2: Chuyển về phương trình đường thẳng (b|i tập 1)  2  3i
Câu 27: Tìm gi{ trị lớn nhất của z biết rằng z thỏa mãn điều kiện z  1  1 . 3  2i
A. max z  1 .
B. max z  2 . C. max z  2 .
D. max z  3 . Hƣớng dẫn giải.  2  3i 1 Ta có
z  1  1   iz  1  1   i . z
 1  z  i  1 . 3  2ii Trang16
Vì i  0  1 nên max z r r  1 1  2 . Chọn B. 1 2
Câu 28: (THPT CHUYÊN KHTN – LẦN 1)Trong c{c số phức z thỏa mãn điều kiện
1iz17i  2 . Tìm max z .
A. max z  4 .
B. max z  3 .
C. max z  7 .
D. max z  6 . Hƣớng dẫn giải. 1 7i
Ta có 1 iz 17i  2  1 i z
 2  z 3 4i  1. 1 i
Vì 3  4i  0  5 nên 2 2
max z r r  1 3  4  6 . Chọn D. 1 2 2z i
Câu 29: Cho số phức z thỏa mãn z  1. Đặt A
. Mệnh đề n|o sau đ}y đúng? 2  iz A. A  1. B. A  1. C. A  1. D. A  1. (THPT CHUYÊN HÀ NAM) Lời giải 2z i
Từ giả thiết, ta có A
A2  iz  2z i  2A Azi  2z i 2  iz 2A i
A i z Ai   2A   i 2 2  z  . Mà z  1 
 1  2A i Ai  2 . Ai  2 Ai  2
Đặt A x yi x, y   , khi đó   2x  2y  
1 i   y  2  xi
x   y  2  y  2 2 2 2 2 2 2 2 2 4 2 1
2  x  4x  4y  4y  1  x y  4y  4  x y  1. Vậy môđun của 2 2
A x y  1. Chọn A. Câu 30:
Với hai số phức z và z thỏa mãn z z  8  6i và z z  2 . Tìm gi{ trị lớn nhất của 1 2 1 2 1 2
P z z . 1 2
A. P  5  3 5. B. P  2 26. C. P  4 6.
D. P  34  3 2.
(THPT CHUYÊN KHOA HỌC TỰ NHIÊN - LẦN 4) Lời giải  2 2 2 2
Bổ đề.Cho hai số phức z và z , ta luôn có z z
z z  2 z z  . 1 2 1 2  1 2    1 2 2 2
Chứng minh. Sử dụng công thức z zz z z z và .
z z z . Khi đó 1 2  1 2 1 2 2 2 z z
z z z z
z z z z z z 1 2 1 2
 1 2 1 2  1 2 1 2
z .z z .z z .z z .z z .z z .z z .z z .z 1 1 1 2 1 2 2 2 1 1 1 2 1 2 2 2
 2z .z z .z   2 2 2 zz  . đpcm 1 1 2 2 1 2 
Áp dụng  , ta được z z z z  4  z z  4  32 2 2 2
 1 z z  1. 1 2 1 2 1 2 1 2 2 2
Theo bất đẳng thức Bunhiacopxki, ta được P z z  2 zz  2 26. Chọn B. 1 2  1 2  Trang17 Câu 31:
Với hai số phức z và z thỏa mãn z z  8  6i và z z  2 . Tìm gi{ trị lớn nhất của 1 2 1 2 1 2
P z z . 1 2
A. P  5  3 5. B. P  2 26. C. P  4 6.
D. P  34  3 2.
(THPT CHUYÊN KHOA HỌC TỰ NHIÊN - LẦN 4) Lời giải  2 2 2 2
Bổ đề.Cho hai số phức z và z , ta luôn có z z
z z  2 z z  . 1 2 1 2  1 2    1 2 2 2
Chứng minh. Sử dụng công thức z zz z z z và .
z z z . Khi đó 1 2  1 2 1 2 2 2 z z
z z z z
z z z z z z 1 2 1 2
 1 2 1 2  1 2 1 2
z .z z .z z .z z .z z .z z .z z .z z .z 1 1 1 2 1 2 2 2 1 1 1 2 1 2 2 2
 2z .z z .z   2 2 2 zz  . đpcm 1 1 2 2 1 2 
Áp dụng  , ta được z z z z  4  z z  4  32 2 2 2
 1 z z  1. 1 2 1 2 1 2 1 2 2 2
Theo bất đẳng thức Bunhiacopxki, ta được P z z  2 zz  2 26. Chọn B. 1 2  1 2 
Câu 32: (THPT CHUYÊN LƢƠNG THẾ VINH - ĐỒNG NAI)Cho số phức z thỏa mãn 2
z  2z  5  z 1 2iz  3i   1 . Tính min| |
w , với số phức w z  2  2i . 3 1 A. min|w| . B. min| | w  2 . C. min| | w  1 . D. min|w| . 2 2 Lời giải 2 2 2 Ta có 2
z  2z  5  z  
1  4  z  
1  2i  z 1 2iz 1 2i. z   i
Khi đó, giả thiết  z   iz   i  z   iz i   1 2 1 2 1 2 1 2 3 1  
z  1  2i z  3i   1 
TH1. Với z  1 2i , ta có w z  2  2i  1 2i  2  2i  1  w  1.
TH2. Với z 1 2i z  3i 1  , đặt z x yi x, y   , ta có
  x y i x y i  x 2 y 2  x 2 y 2 1 1 2 1 3 1 2 1 3  y   . 2 1 3 9 3
Do đó w z  2  2i x i  2  2i x  2  i w  x  22   . Chọn A. 2 2 4 2 1
Câu 33: (TOÁN HỌC & TUỔI TRẺ LẦN 8)Cho số phức z thỏa mãn z
 3 . Tổng của gi{ trị lớn z
nhất v| gi{ trị nhỏ nhất của z là A. 3. B. 5. C. 13. D. 5. Lời giải Trang18 2 1 1  1  1  Ta có 2 a z   a z   z z     z zz  z  2 z z
z z zz  2  2 4 1  2 2 2 1  z    . 2 2 2 z z za a 4     a a  4
Khi đó z z .a  2 1  z z  2 2 4 2 2 2  0  z   ;  .  2 2    2 2 a a  4 a a  4 Vậy 2 max z  ; min z
M m a  4  13. Chọn C. 2 2
Câu 34: (THPT NHÂN CHÍNH - HÀ NỘI)Xét số phức z thỏa mãn   i 10 1 2 z
 2  i . Mệnh đề z n|o sau đ}y đúng? 3 1 3 1 A.
z  2 . B. z  .C. z  2 . D. z  . 2 2 2 2 Lời giải 10 10
Cách 1. Từ giả thiết, ta có 1 2iz
 2  i  1 2iz  2  i z z 10
z z i   i
z    z   10 2 2 2 2 1 i   z z 2 2 10
Lấy môđun hai vế của  , ta được    z  2  2 z 1  . z 2 2 10
Đặt t z , ta có t  2  2t   2 1   t  2 5t  5 4 2
 10  t t  2  0  t  1. t 1 3
Vậy môđun của số phức z bằng 1   z  . 2 2
Cách 2. Sử dụng m{y tính casio ( hướng dẫn chi tiết ở câu 26) để tìm z .
Cách 3. Đặt z a bi a,b  và c z , thay v|o đẳng thức đã cho thì  a bi Gti 10   1 2 c
 2  i  1 2i   10 c   2  i 2 a bi c a 10  b 10   c
 2  i 2c   1  0 2 2   cc   a 10  a 10 c   2  0 c  2  10  2 2 a b 2 2  2 2  c  10 Suy ra    c
nên c  2  1 2c    4 2 b 10  b 10 c c 2c  1  0 1  2c   2   cc 1 3
Giải ra ta có c  1 mà c  0 nên c  1 hay z  1. Do đó  z  . Chọn B. 2 2 Trang19
Câu 35: (THPT CHUYÊN LÀO CAI)Xét số phức z v| số phức liên hợp của nó có điểm biểu diễn l|
M, M . Số phức z(4  3i) v| số phức liên hợp của nó có điểm biểu diễn lần lượt l| N, N . Biết rằng
M, M, N, N l| bốn đỉnh của hình chữ nhật. Tìm gi{ trị nhỏ nhất của z  4i  5 1 2 1 4 A. . B. . C. . D. . 2 5 2 13 Lời giải
N 4x  3y;3x   4y
Gọi M x; y  M'x;  y và 4  3iz  4x  3y  3x  4y   i   N ' 
4x3y;3x  4y
Dễ thấy MM '  NN ' vì cùng vuông góc với Ox nên để MM' N' N l| hình chữ nhật. MM '  NN '  2 2
Khi v| chỉ khi MN M ' N '  x y  0  z x xi z  4i  5  x  5  x  4  MN Ox 2 2 1 2 1 1 1
Ta có x  5  x  4  2x  9    z  4i  5  . Chọn C. min 2 2 2 2
Câu 36: (THPT CHU VĂN AN - HÀ NỘI)Cho số phức z thỏa mãn điều kiện z  1  2. Tìm gi{ trị
lớn nhất của biểu thức
T z i z  2  i .
A. maxT  8 2. B. maxT  4.
C. maxT  4 2. D. maxT  8. Lời giải
Đặt z x yi x, y   , ta có z  
x   yi   x  2 2 1 2 1 2 1  y  2  x  2 2 2 2 2 2
1  y  2  x  2x  1 y  2  x y  2x  1 
Lại có T z i z  2  i x  y  
1 i x  2  y   1 i
x  y  2  x  2  y  2 2 2 2 2 2 1 2 1
x y  2y 1  x y  4x  2y  5
Kết hợp với  , ta được T  2x  2y  2  6  2x  2y  2x y  2  2  2x y
Đặt t x y , khi đó T f t  2t  2  6  2t với t  1;1.   1 1
Ta có f 't  
; f 't  0  t  1  f t  f   1  4 . Chọn B. max 2t  2 6  2t
Câu 37: (ĐHNT HN) Cho số phức z thỏa mãn điêu kiện z  1  2 . Tính giá trị lớn nhất của biểu thức
T z i z  2  i
A. maxT  8 2 .
B. maxT  8 .
C. maxT  4 2 . D. maxT  4 . Hướng dẫn giải Chọn C
Đặt z x yix,y  , ta có: Trang20
z  1  2  x  1 yi  2  x  2 2 2 2
1  y  2  x y  2x  1*
Lại có: T z i z  2  i x  y  
1 i x  2  y   1 i
x  y  2  x  2  y  2 2 1 2 1 2 2 2 2
x y  2y  1  x y  4x  2y  5
Kết hợp với * , ta được:
T  2x  2y  2  6  2x  2y
Áp dụng bất đẳng thức Bunhacopxki ta được
T      x y  2  
x y 2 2 2 1 1 2 2 2 6 2 2  4   
Vậy maxT  4.
Câu 38: Cho w  sin  i cos với 0    thỏa mãn 2 w  1  2 w . 2 2018 2  
Giá trị của P   26 w  3 là   A. 2018 P  23 . B. 2018 P  2  3 . C. 2018 P  23 . i D. 2018 P  29 . Hướng dẫn giải Chọn A Ta có:      i 2 2 2 w 1 sin cos
 1  1 cos 2  i sin 2  w 1  2  2cos 2. 2 2
2 w  sin   cos   2 .   Từ giả thiết: 2
w  1  2 w  cos 2  0    vì 0    . 4 2 2 2 2 2 2  w   i  w   i  w  1 . 2 2 2 2 Vậy 2018 P  23 .
Câu 39: Cho các số phức z  2
  i,z  2  i và số phức z thay đổi thỏa mãn 2 2 z z
z z  16. Gọi M 1 2 1 2
và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z . Giá trị biểu thức 2 2 M m bằng A. 15 . B. 7 . C. 11 . D. 8 . Lời giải Chọn D.
Gọi M là điểm biểu diễn của z . Gọi A 2  ;  1 , B2;  1 . Gọi I 0; 
1 là trung điểm AB . 2 2 2 2 z z
z z  16  MA MB  16 1 2 2 2 2 2   AB MA MB 2MI   16  MI  2 2
Suy ra tập hợp các điểm M là đường tròn tâm I 0;  1 bán kính R  2 . Trang21 y M2 I O x M1
Ta lại có : IM IO OM IM IO  1 OM  3 . Do đó : z
 3  M M 2 max z
 1  M M 1 min 2 2
M m  8 . Bài tương tự
Câu 40: Cho hai số phức z , z thỏa mãn z  1 i  2 và z iz . Tìm giá trị nhỏ nhất m của biểu thức 1 2 1 2 1
z z ? 1 2 A. m  2  1 . B. m  2 2 . C. m  2 . D. m  2 2  2 . Lời giải Chọn D.
Đặt z a bi; a,b  z  b ai 1 2
z z a b b a i . 1 2     2 2 Nên z z
a b b a  2. z 1 2     1
Ta lại có 2  z  1 i z  1 i z  2 1 1 1
z  2  2 . Suy ra z z  2. z  2 2  2 . 1 1 2 1 Dấu a b "  " xảy ra khi   0 . 1 1 
Vậy m  min z z  2 2  2 . 1 2
Câu 41: Gọi số phức z x yi; x, y   thỏa điều kiện 2 2
z  2  z  2  26 và z  2  5i lớn nhất.
Tính T x y . A. T  2   5 .
B. T  2  5 . C. T  2   5 .
D. T  2  5 . Lời giải Chọn A.
Giả sử z x yi; x, y  2 2 2 2 Ta có z   z    x   2
y  x   2 2 2 2 2 26 2
2  y  26  x y  9 . Trang22
Suy ra tập hợp các điểm biểu diễn số phức z là đường tròn C tâm là gốc tọa độ O , bán kính R  3 . Ta có z   
i  x    y  2 2 2 5 2 5 Vì   2 2 2 5
 9 nên điểm N 2; 5 thuộc đường tròn C .
Gọi M x; y là điểm thuộc C , khi đó z    i  x    y  2 3 2 5 2 5  MN .
Suy ra z  2  5i lớn nhất  MN lớn nhất  MN là đường kính của C  M 2;  5  Vậy z  2   5i . Câu 42:
Cho z , z là hai số phức thỏa mãn phương trình 2z i  2  iz , biết z z  1 Tính giá trị của 1 2 1 2
biểu thức: P z z . 1 2 3 2 A. P  . B. P  2 . C. P  . D. P  3 . 2 2 Lời giải Chọn D. 2 2
HD: Cách 1. Ta có: 2z i  2  iz  2z i  2  iz  (2z i)(2z i)  (2  iz)(2  iz) y 2 2  4 .
z z  2iz  2iz i  4  2iz  2iz i . z z  3 . z z  3 2  .
z z  1  z  1  z  1  z  1 và z  1 M 1 2 M 2 2 Chú ý: 2 .
a a a  2z i  (2z i)(2z i)  (2z i)(2z i)
Tập hợp điểm biểu diễn số phức z , z là đường tròn tâm O 1 2 M bán kính R  1 . 1
Gọi M (z ), M (z )  OM OM  1 O x 1 1 2 2 1 2
  
Ta có: z z OM OM M M  1  OM M đều 1 2 1 2 2 1 1 2
  
Mà z z OM OM OM OM với M là điểm thỏa 1 2 1 2
mãn OM MM là hình thoi cạnh 1  OM  3  P  3 . 1 2
Cách 2. Đặt z x yi, x, y   , ta có 2z i  2x (2y 1)i và 2  iz  2  y xi .  z   1 Khi đó: 2 2 2 2 2 2 1
2z i  2  iz  4x  (2y  1)  (y  2)  x x y  1  z  1   z   1  2 Sử dụng công thức 2 2 z z
z z  2 2 2 zz  2
z z  3  z z  3 . Chọn D. 1 2 1 2 1 2 1 2 1 2
Câu 43: Cho số phức z thỏa mãn điều kiện z  1 2i  4 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của z  2  i . Tính giá trị của tổng 2 2
S M m . A. S  82 . B. S  34 . C. S  68 . D. S  36 . Lời giải Chọn C. Trang23
Cách 1: (Phương pháp hình học)
Đặt số phức z x iy , x, y  có điểm biểu diễn hình học là Px,y . 2 2 2 2
Ta có z  1 2i  x  
1  y  2  4  x  
1  y  2  16 .
Vậy tập hợp điểm P là đường tròn tâm I 1; 2 , bán kính R  4 . 2 2
Ta có z  2  i  x  2  y   1
AP, với A 2;    1 . Vậy từ hình vẽ ta nhận thấy:
M AP AP IAR  3 2  4 max 2  .
m AP AP IA R   3 2  4 min 1 2 2 Vậy ta suy ra 2 2
S M m  3 2  4 3 2  4  68 .
Cách 2: (Phương pháp đại số)
Công cụ cơ bản: z z z z z z , với mọi số 1 2 1 2 1 2
phức z , z . Áp dụng, ta có: 1 2
z  2  i  z 1 2i  3  3i  z 1 2i  3  3i  4  3 2  M  4  3 2
z  2  i  z 1 2i  3  3i  z 1 2i  3  3i  3 2  4  m  3 2  4 2 2 Vậy ta có 2 2
S M m  3 2  4 3 2  4  68 .
Câu 44: [Phạm Minh Tuấn – Vted 15] Cho ba số phức z, z , z thỏa z z  6 và z z  6 2 . Tìm giá 1 2 1 2 1 2
trị nhỏ nhất của biểu thức
P  2 z z z z
z z z z z z . 1   2   1   2  A. 30 3 . B. 36 2 . C. 50 . D. 50 2 . Lời giải Chọn B.
Gọi A, B, M là điểm biểu diễn số phức z ,z ,z, khi đó từ giả thiết ta suy ra tam giác OAB vuông 1 2
cân tại O và bài toán quy về tìm giá trị nhỏ nhất của P  2M . A MB M . O MA M . O MB .
Ta sẽ chứng minh bài toán tổng quát
Cho tam giác ABC , đặt AB c , AC b , BC a , khi đó ta có M . B MC MC.MA M . 
A MB  1  bc ca ab 2 2 2 xyc yza
Chứng minh: dùng bài toán kinh điển zxb 2 2 2 . x MA  . y MB  . z MC  
x y z   Đặt  a b c x ; y  ; z  khi đó . . .
   aMB MC bMC MA cMA MB x y z MA MB MC M . A M . B MC   và 2 2 2    aMA bMB cMC xyc yza zxb abc
từ đó sử dụng  suy ra hệ thức  . M . A M . B MC Trang24
Áp dụng bài toán trên ta có P  36 2 , chọn B.
Ta có thể chứng minh bài toán  trên bằng ngôn ngữ số phức.
Gọi tọa độ các điểm A, B,C, M trên mặt phẳng phức là ,
u v,w, x khi đó a v w , b w u ,
c u v , MA x u , MB x v , MC x w . Khi đó bất đẳng thức  tương đương
x v x w
x w x u
x u x v    1
u v u w
v w v u
w u w v
xvxw xwxu xuxv  
u vu w  v wv u  w uw v  1 Mặt khác :
xvxw xwxu xuxv xvxw x wx u x ux v
u vu w  v wv u  w uw v  u vu w  v wv u           
w uw v
xvxw xwxu xuxv Mà  nên suy ra  .
u vu w  v wv u  w uw v  1
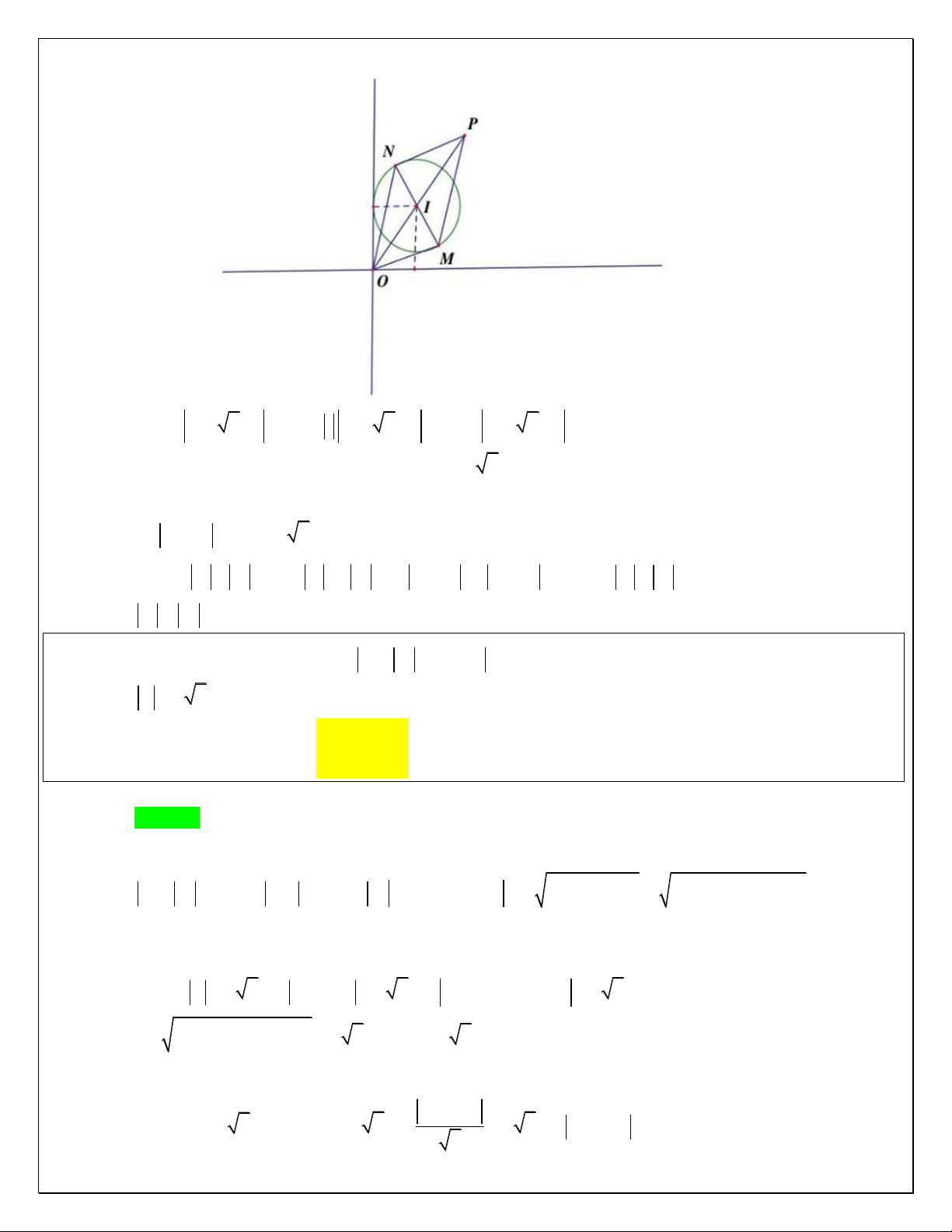
Câu 45: Cho số phức z thỏa mãn điều kiện z i  1 . Tìm giá trị nhỏ nhất của biểu thức:
P z  2  i  2 z  2  3i 4 3 A. 3 . B. 3 . C. 2 . D. . 3 Lời giải Chọn B.
Gọi điểm biểu diễn của z là M . Khi đó M nằm trên đường tròn tâm I 0; 
1 , R  1. Gọi tọa độ các
điểm A 2;1,B 2; 3   do đó: Trang25   IK IM
P z  2  i  2 z  2  3i MA  2M . B Gọi 1 K  ; 1   khi đó ta có: 1   . Vậy  2  IM IA 2
IMK và IAM là hai tam giác đồng dạng. Khi đó: MA  2MK .
Vậy P  2 MK MB.
Theo bất đẳng thức tam giác: P  2 MK MB  2BK.
Vậy MinP  2BK  3.
Câu 46: Với hai số phức z và z thoả mãn z z  8  6i và z z  2, tìm giá trị lớn nhất của P z z . 1 2 1 2 1 2 1 2 A. P  4 6 . B. P  2 26 .
C. P  5  3 5 .
D. P  34  3 2 . Lời giải Chọn B. y A I 3 B O x 1 4
z  8  6i z 1 2 
Vì hai số phức z và z thoả mãn z z  8  6i và z z  2 nên z  8  6i z 1 2 1 2 1 2 2 1
z z  2  1 2
z  4  3i  1 1   
  z  4  3i  1 * . 2    z z  2  1 2 
Gọi A , B lần lượt là hai điểm biểu diễn của hai số phức z và z khi đó từ * suy ra A,B nằm trên 1 2
đường tròn C có tâm I 4;3 , bán kính R  1 và AB là đường kính của đường tròn C .
Như vậy P z z OA OB. 1 2 2 2 2 OA OB AB Ta có 2 2 2 
OI OA OB   2 2 5  1  52 . 2 4 Suy ra 2 2
52  OA OB  2O .
A OB  OA OB2 2 2
OA OB  2O .
A OB  52  52  104
P z z OA OB  104  2 26 . Dấu bằng xảy ra khi OA OB. 1 2
Câu 47: Giả sử z , z là hai trong số các số phức z thỏa mãn iz  2  i  1 và z z  2. Giá trị lớn nhất của 1 2 1 2
z z bằng 1 2 A. 4 . B. 2 3 . C. 3 2 . D. 3. Lời giải ChọnA. Trang26
Ta có iz  2  i  1  i z i 2  1  1  z i 2  1  1 .
Điểm biểu diễn z thuộc đường tròn tâm I 1; 2 , R  1.
Gọi M , N là điểm biểu diễn z , z nên MN  2 là đường kính. Dựng hình bình hành OMNP ta 1 2
có z z OP  2 3 . 1 2 2 2 2 2 2
Ta có  z z  2 z z
z z z z  16  z z  4 . Dấu bằng xảy ra khi 1 2   1 2  1 2 1 2 1 2
z z MN OI . 1 2
Câu 48: Cho hai số phức z ,  thỏa mãn z  1  z  3  2i ;   z m i với m  là tham số. Giá trị của m để ta luôn có   2 5 là: m  7 m  7 A.  . B.  . C. 3   m  7.
D. 3  m  7 . m   3 m  3   Lời giải Chọn B.
Đặt z a ib,a,b  có biểu diễn hình học là điểm Mx; y 2 2 2
z  1  z  3  2i x  1 iy x  3  y  2i  x   2
1  y  x  3  y  2  2
x 1  6x  9  4y  4  2x y  3  0
Suy ra biểu diễn của số phức z là đường thẳng  : 2x y  3  0 .
Ta có:   2 5  z m i  2 5  x m    y  1i  2 5
 x m2 y  2 1
 2 5  MI  2 5 với I  ; m   1 .
Mà ta có MI dI, 2  m  4
Nên MI  2 5  d I,  2 5   2 5  2  m 4  10 5 Trang27 2m  4  10 m    3    . 2  m  4  10   m   7
Câu 49: [PTNK TP HCM] Cho z là số phức thỏa mãn z 1 i  2 . Tìm giá trị lớn nhất của biểu thức 2 2
P z  2  i z  2  3i A. 18 . B. 14  2 10 . C. 38  8 10 . D. 16  2 10 . Lời giải Chọn C.
Gọi z x yi x; y ,Mx; y là điểm biểu diễn số phức z . 2 2
Do z 1 i  2  x   1  y  
1  4 suy ra M thuộc đường tròn tâm I 1; 1
 , bán kính R  2 . Đặt A 2  ; 
1 , B2; 3 , E0; 2 là trung điểm của AB . Khi đó 2 2
P z  2  i z  2  3i 2
 x  2 y  2 x  2 y  2 2 1 2 3 2 2  MA MB 2  2  AB ME 2  2ME 10 . 2
Do E nằm ngoài đường tròn, nên ME
EI R  2  10  P  38  8 10 . Max Max Cách 2 : 2 2 2 2 2 2
P z  2  i z  2  3i  x  2  y  
1  x  2  y  3 = 2 2
2x  2y  8y  18 2 2
 2x  2y  8y 18  P  0 . 2 2
2x  2y  8y 18  P  0 
x 2 y 2 1 1  4
Suy ra tọa độ điểm M thỏa mãn     x   2 1  y  2 1  4 
  : 4x 12y  22  P  0
Hệ có nghiệm khi dI,  R P  38  8 10  38 8 10  P  38  8 10  P  38  8 10 Max .
Câu 50: (CHuyên Hạ Long-lần 2-2018-Mã đề 108)Cho các số phức z  2
  i, z  2  i và số phức z thay 1 2 đổi thỏa mãn 2 2 z z
z z 16. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z . Giá 1 2 trị biểu thức 2 2 M m bằng A.15 . B. 7 . C.11 . D. 8 Lời giải: Trang28 Chọn D. Cách 1:
Gọi số phức z x yi với x, y   . 2 2 Ta có z z
z z 16 2 2
x y  2x  3  0 . Khi đó tập hợp các điểm M (x, y) biểu diễn số 1 2
phức z là đường tròn (C) có tâm I (1,0) và bán kính R  2 . Ta có | z |
OM , | z |  OM . min min max max
Đường thẳng OI có phương trình y  0 . 2 2
x y  2x  3  0
OI cắt (C) tại 2 điểm phân biệt ,
A B có tọa độ là nghiệm của hệ y  0  ( A 1, 0); B( 3  ,0) .
Ta có OA OM OB nên | z |
OA ,| z |  OB . min max Khi đó 2 2
M m  9 1  8 . Cách 2:
Gọi số phức z x yi với x, y   . 2 2 Ta có z z
z z 16 2 2
x y  2x  3  0 . Khi đó tập hợp các điểm M (x, y) biểu diễn số 1 2
phức z là đường tròn (C) có tâm I (1,0) và bán kính R  2 .  z 1  2
Ta có: z z 1 1  1  z
1 , z z 1  1   3  z  3 . min max Cách 3:
Gọi số phức z x yi với x, y   . 2 2 Ta có z z
z z 16 2 2
x y  2x  3  0 . Khi đó tập hợp các điểm M (x, y) biểu diễn số 1 2
phức z là đường tròn (C) có tâm I (1,0) và bán kính R  2 . Ta có OM
OI R , OM
OI R z 1, z  3 min max min max CÂU PHÁT TRIỂN
Câu 51: Cho số phức z thỏa mãn điều kiện z  2  4i  5 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị 2 2 M m
nhỏ nhất của z . Giá trị biểu thức bằng 2Mn 1 4 A.12 . B. . C. . D. 8 2 3 Lời giải: Chọn C.
Gọi số phức z x yi với x, y   , khi đó 2 2 | z | x y .
Ta có: z  2  4i  5   x  2 2 2  (y  4)  5 2 2
x y 15  4(x  2y) .
Áp dụng bđt Bu-nhi-a-cốp-xki ta có: 2 2
| x  2y | 5(x y )  5 | z | .
Khi đó ta có bất phương trình 2 | z | 1
 5  4 5 | z |  5 |  z | 3 5 . 2 2 M m Do đó 4  . 2Mn 3
Câu 52: Cho số phức z thỏa mãn điều kiện z 1 i  | z  3  2i | 5 . Gọi M và m lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của z  2i . Giá trị biểu thức 2 2 M m bằng Trang29 15 A. 25 . B. 35 . C. . D. 20 . 2 Lời giải: Chọn B.
Gọi z x yi (với x, y   ) có điểm M (x; y) biểu diễn z trên mặt phẳng tọa độ.
Ta có z 1 i z  3  2i  5
 x  2   y  2  x  2   y  2 1 1 3 2  5
 x  2   y   2     x  2 1 2 3 3
  y  2 2  4  5  (1).
Số phức z  2i x   y  2i có điểm M  ;
x y  2 biểu diễn z  2i trên mặt phẳng tọa độ. Đặt (
A 1;3), B(3; 4) , từ (1) ta có AM   BM   5 .
Mặt khác AB  5 nên M  thuộc đoạn AB . Khi đó M z  2i
OB  5 , m z  2i max min  OA  10 . Vậy 2 2
M m  35 . Nhận xét:
- GTLN, GTNN ở câu dạng này chỉ có thể đạt được tại 2 đầu , A B .
- Một sai lầm thường gặp là đánh giá zd  ;
O AB nhưng do góc OAB là góc tù nên không min
tồn tại điểm M trên đoạn AB sao cho OM AB .
Câu 53: (Chuyên Hạ Long-lần 2-2018-Mã đề 123) Cho số phức z thỏa mãn z  3  4i  5 . Gọi M, m lần
lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2 2
P z  2  z i . Khi đó modun của số phức w  M mi A. 2 314 . B. 1258 . C. 3 137 . D. 2 309 . Lờigiải Chọn B. 2 2
Cách 1:Giả sử z x yi x, y R ta có z  3  4i  5  x  3  y  4  5
Ta có P  4x  2y  3  4x  3  2y  4  P  23 2 2 2   Ta có 4
 x  3  2y  4  20 
x3 y 4  100   Suy ra 1
 0  P23  10 13  P  33 suy ra M  33,m  13 do đó ta được w  3313i vậy w  1258 .
Cách 2:Gọi z x yi với x, y   . 2 2
Ta có: z  3  4i  5  x  3  y  4  5 . Suy ra, tập hợp điểm M x; y biểu diễn cho số
phức z trên hệ tọa độ Oxy là đường tròn C tâm I 3;4 và bán kính R  5 . Lại có: 2 2 P z
z i  x  2  y x y  2 2 2 2 2
1  P  0  4x  2y  3  P  0 , đây là
phương trình của đường thẳng  : 4x  2y  3  P  0 .
Ta thấy M   C . Trang30P
Điều kiện để  cắt C là: dI  23 ,  R   5  1
 0  23  P  10  13  P  33 . 2 5
Suy ra: m  13, M  33 và w  33  13i w  1258 . Cách 3:
Gọi z x yi với x, y  . 2 2  4  3
Ta có P  x   2 2
2  y x  y  
1  4x  2y  3 suy ra  P x y . 2 2  P x  
Từ z   i
 x  2 y  2   f x  x  2 4 3 3 4 5 3 4 5 3   4  5    0 .  2 
P x  
Ta có f x  x   4 11 2 3  4  2  P 10x    16 .  2 
f x  0  x  0,2P 1,6 . Suy ra y  0,1P 1,7 . 2 2
Thay x, y vừa tìm được vào f x ta được 0,2P 1,6  3  0,1P 1,7  4  5  0 .
Ta giải được P  33 hoặc P  13. Đây tương ứng là GTLN và GTNN của P .
Vậy M  33, m  13 . Khi đó,   1258 .
Câu 54: Biết số phức z x yi , x, y   thỏa mãn đồng thời hai điều kiện z z  4  3i và biểu thức
P z  1 i z  2  3i đạt giá trị nhỏ nhất. Tính P x  2y . 61 253 41 18 A. P   . B. P   . C. P   . D. P   . 10 50 5 5 Lời giải Chọn A .
Theo giả thiết z z  4  3i x yi  x  4 y  3i
x y  x  2 y  2 2 2 4 3 2 2 2 2
x y x  8x 16  y  6y  9
 8x  6y  25  0 . 2 2 2 2
Ta có P  x   1  y  
1  x  2  y  3 Xét điểm E 1  ;  1 ; F 2; 3
  và Mx; y . Khi đó, P MEMF .
Bài toán trở thành tìm điểm M  : 8x  6y  25  0 sao cho MEMF đạt giá trị nhỏ nhất.
Vì 8x  8y  25 x y
nên hai điểm E, F nằm cùng phía đối với đường thẳng  . E E .8 8 25 F F   0
Gọi E là điểm đối xứng với E qua    Đường thẳng 
EE đi qua điểm E1; 1
 và có VTPT n u    nên có phương trình EE  3; 4 3x   1  4y  
1  0  3x  4y  7  0 Trang31
3x  4y  7 
Gọi H là giao điểm của 
EE và  . Tọa độ điểm H là nghiệm của hệ phương trình 8x6y  25    71 x    25    71 19  suy ra H  ;    19   25 50  y    50  117 x      E
E đối xứng với E qua H nên 25  . 44 y     E 25
Ta có ME + MF = ME+ MF EF .
Dấu bằng xảy ra  M là giao điểm của 
E F và đường thẳng   Đường thẳng 
E F đi qua điểm F 2; 3
  và có VTPT n   có phương trình EE 31;167
31x  2  167 y  3  0  31x +167 y + 439 = 0  67  x  
31x  167y  43  9 
Tọa độ điểm M là nghiệm của hệ phương trình  50   8x  6y  25   119 y    50 Vậy 61
P x  2y   . 10
Câu 55: Gọi z , z là 2 nghiệm của phương trình z  1 2i z  1 2i thỏa mãn z z  2 . Biết rằng w 1 2 1 2
là số phức thỏa mãn w  3  2i  2 . Tìm GTNN của biểu thức P  w  z  w  z . 1 2
A. 1 3 B. 2 3 C. 2 D. 6 . Lời giải. Chọn D .
Giả sử z x yi x,yR ta có z 1 2i z 1 2i x  0 suy ra tập hợp điểm biểu diễn z ,z 1 2 là trục tung.
Giả sử A, B lần lượt là 2 điểm biểu diễn cho z ,z , ta có z z  2  AB  2 . 1 2 1 2
Giả sử w  a bi a,bR và M là điểm biểu diễn cho số phức
w , ta có w  3  2i  2 2 2
 (a  3) (b  2)  4suy ra tập hợp
điểm biểu diễn M cho số phức w là đường tròn tâm I 3;2 bán kính R  2 .
Ta có P MA MB , gọi E là hình chiếu vuông góc của I lên
trục tung, ta thấy P nhỏ nhất khi E là trung điểm AB suy ra 6 MA MB  , vậy 6 MinP  2.  6 2 2
Câu 56: Cho z là số phức thỏa z  1 i  2 . Tìm giá trị lớn nhất của biểu thức Trang32 2 2
P z  2  i z  2  3i A. 18 . B. 38  8 10 . C. 18  2 10 . D. 16  2 10 . Hướng dẫn giải Chọn B
Gọi z x yix,y  2 2
Ta có: z 1 i  2  x yi 1 i  2  x   1  y   1  4 2 2 2 2
x y  2x  2y  2  0  x y  2x  2y  2 (*) Theo bài ra: 2 2 2 2
P z  2  i z  2  3i x yi  2  i x yi  2  3i
 x  2 y  2  x  2  y  2   2 2 2 1 2 3
2 x y   8y  18
Thay (*) vào P ta được:
P  4x  12y  22  4x   1  12y   1  38
Áp dụng bđt Bunhiacopxki ta được x  y  
x 2 y 2 2 2                2 2 4 1 12 1 38 4 12 1 1 38
4  12 .4  38  8 10  38  Vậy P  8 10  38 . max
Câu 57: Giả sử z , z là hai trong số các số phức z thỏa mãn iz  2  i  1 và z z  2. Giá trị lớn nhất của 1 2 1 2
z z bằng 1 2 A. 4 . B. 2 3 . C. 3 2 . D. 3. Lời giải ChọnA.
Ta có iz  2  i  1  i z i 2  1  1  z i 2  1  1 .
Điểm biểu diễn z thuộc đường tròn tâm I 1; 2 , R  1. Trang33
Gọi M , N là điểm biểu diễn z , z nên MN  2 là đường kính. Dựng hình bình hành OMNP ta 1 2
có z z OP  2 3 . 1 2 2 2 2 2 2
Ta có  z z  2 z z
z z z z  16  z z  4 . Dấu bằng xảy ra khi 1 2   1 2  1 2 1 2 1 2
z z MN OI . 1 2
Câu 58: Xét các số phức z a bi a,b   thỏa mãn z  2  3i  2 2 . Tính P  2a b khi
z  1 6i z  7  2i đạt giá trị lớn nhất. A. P  1. B. P  3  . C. P  3 .
D. P  7 . Lời giải Chọn B
Gọi z x yi với x,y  . 2 2
Ta có: z  2  3i  2 2  x  2  y  3  8. Suy ra, tập hợp điểm M x; y biểu diễn cho số
phức z trên hệ tọa độ Oxy là đường tròn C tâm I  2;
 3 và bán kính R  8 . Gọi A 1  ; 6
 , B7;2 và J3; 2
 là trung điểm của AB .
Đặt P z 1 6i z  7  2i suy ra P MA MB   2 2
2 MA MB  . (BĐT Bunhiacopxki). x  3  t
Phương trình đường trung trực  của AB là:  . y  2    t 2 Ta có: 2 2 2   2  AB MA MB MJ
với J là trung điểm của AB . 2
Vì M chạy trên đường tròn , J cố đi ̣nh nên MJ  IJ  . R
Do vâ ̣y P    R2 2 2 4 IJ
AB nên P  4 R AB m IJ 2 2  . ax
Dấu « = » xảy ra khi MA MB và ba điểm M,I, J thẳng hàng. Điều này thỏa mãn nhờ IA IB .
Do đó: M   C , tọa độ của M là nghiệm hệ: x 3 t    x  3  t
x  0 x  4      y  2   t  y  2   t
 y 1  y  5       x  
2  y  2    t   2 t  2 t  3 t  7 2 3 8 5 5  8   Mặt khác : M 0; 
1  P MA MB  2 50 M  4
 ; 5  P MA MB  2 130 và .
Vậy để P thì M  4;
 5 Suy ra 2ab  3  . Max
Câu 59: (SGD – HÀ TĨNH )Trong các số phức z thoả mãn z  2  4i  2 , gọi z và z là số phức có mô- 1 2
đun lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức z và z bằng. 1 2 A. 8i . B. 4 . C. 8  . D. 8 . Lời giải Chọn D. Trang34
Gọi z x yi,x,y  và Mx; y là điểm biểu diễn số phức z . Theo giả thiết 2 2
z  2  4i  2  x yi  2  4i  2  x  2  y  4  4 . 2 2
Suy ra M C : x  2  y  4  4
Suy ra tập hợp các điểm biểu diễn số phức z thỏa mãn z 2  4i  2 là đường tròn C có tâm
I 2; 4 bán kính R  2 .    
Đường OI có phương trình y  2x cắt đường tròn C tại hai điểm 10 2 5 20 4 5 A ;   , 5 5     10  2 5 20  4 5  B ;  
. Do OA OB nên điểm A biểu diễn số phức có môđun lớn nhất, và điểm 5 5   
B biểu diễn số phức có môđun nhỏ nhất.
Câu 60: [HKII-SỞ BẠC LIÊU-2017-2018] Xét số phức z a bi ( a, b   và b  0 ) thỏa mãn z  1. Tính 2
P  2a  4b khi 3
z z  2 đạt giá trị lớn nhất. A. P  4 .
B. P  2  2 . C. P  2 .
D. P  2  2 . Lời giải ChọnC. Cách 1: Từ giả thiết có 2 2 a b  1 2 2
b  1 a  0 với a 1  ;  1 và . z z  1 . 1 2 Ta có 3 z z  2 2
z . z   2 z z 2
z z  2.z bi   2 2 2
2 a b  2abi   2 2 2 2
2 a b   b  2abi   2 2 2
a b   b  2ab   2 2
a b 2  b   a2 2 2 2 2 1 2   2a    2 2 2 1
1 a 2a 1 3 2
 2 4a a  4a  2 Xét f a 3 2
 4a a  4a  2 , với 1   a  1.  1 a      1  ;  1 f a 2
 12a  2a  4 ; f a 2
 0  12a  2a  4  0 2    2 a   1  ;  1  3 Bảng biến thiên: Trang35 1 2 a 1  1 2 3
f a  0  0  13 1
f a 4  1  13
Suy ra max f a  f   , đạt được khi 1 a   , 2 3 b  . a     1  ;  1  2  4 2 4   Vậy 2 1
P  2a  4b  2   3    2 .  2  Cách 2: Ta có 3
z  cos x i sin x z  cos 3x i sin 3x . Vì b  0 nên sin x  0 , cos x 1  ;  1 . Khi đó 3
z z  2  cos 3x i sin 3x  cos x i sin x  2
 cos3x cosx  2sin3x sin xi   x x  2   x x2 cos 3 cos 2 sin 3 sin    x x2   x x2 2 2 sin 2 .sin 2 cos 2 .sin 2 2 2 2
 4  8sin 2xsin x  4sin xsin 2x  4cos 2xsin x 2 2
 4 16sin xcos x  4sin x    2
t t   2 4 16 1 4 1 t  3 2
 16t  4t 16t  8 với t  cos x 1  ;  1 . Đặt f t 3 2
 16t  4t 16t  8 , t  1  ;  1 .  1 t      1  ;  1 f t 2
 48t  8t 16  0 2    2 t   1  ;  1  3 Bảng biến thiên: 1 2 t 1  1 2 3
f t  0  0  13 1
f t 1 f t  1   max  f   
 13  t    cos x . t   1;  1  2  2 Khi đó: a 1 1 2 3
   a    b  . 2 2 a  2 2 4 b   Vậy 2 1
P  2a  4b  2   3    2 .  2  Trang36
Nhận xét: có thể đổi câu hỏi thành tìm Min
Câu 61: Cho z , z là hai số phức thỏa mãn 2z i  2  iz , biết z z  1 . Tính giá trị của biểu thức 1 2 1 2
P z z 1 2 3 2 A. P  . B. P  2 . C. P  . D. P  3 . 2 2 Lời giải Chọn D. Cách 1.
+ Đặt z x yi , x, y  , ta có 2z i  2  iz  2x  2y  
1 i  2  y  xi
x   y  2    y2 2 2 2 2 2 2 4 2 1 2
x  4x  4y  4y 1  4  4y y x 2 2
x y  1 z  1 z z  1 1 2
+ Sử dụng công thức:  2 2 2 2
z , z  ta có z z
z z  2 z z 1 2 1 2  1 2  1 2 Suy ra P  3 . Cách 2.
+ Biến đổi: iz  2  iiz  2  z  2i 2 2
Ta có 2z i z  2i  2z i z  2i z  1  z z  1 . 1 2
+ Sử dụng công thức bình phương mô đun 2 2 2 mz nz
m z  2mnz z cosz ,z  2 2  n z 1 2 1 1 2 1 2 2
Trong đó z , z là góc MON với M, N lần lượt là các điểm biểu diễn số phức z ,z trên mặt 1 2  1 2 phẳng phức 2 2 2 1
z z  1  z z
 1 z z  2 z . z .cos z ,z  1 cos z ,z  . 1 2 1 2 1 2 1 2  1 2  1 2 2 Vậy 2 2 2 2
P z z
 1 z z  2 z . z .cos z ,z  3  P  3 . 1 2 1 2 1 2  1 2
Câu 62: Cho số phức z thỏa mãn điều kiện z  1  2 . Tìm giá trị lớn nhất của biểu thức: T z i z  2  i .
A. maxT  8 2 . B. maxT  4 .
C. maxT  4 2 . D. maxT  8 Lời giải Chọn B.
Đặt z x yi x,yR , ta có 2 2
z 1  2  x 1 yi  2  (x 1)  y  2  x  2 2 2 2
1  y  2  x y  2x  1 (*)
Lại có T z i z  2  i x  (y  1)i x  2  (y 1)i 2 2 2 2 2 2 2 2
x  (y  1)  (x  2)  (y 1)  x y  2y  1  x y  4x  2y  5
Kết hợp với (*), ta được T  2x  2y  2  6  2x  2y  2(x y)  2  6  2(x y)
Áp dụng BĐT Cauchy schwarz ta có Trang37
T  2(x y)  2  6  2(x y)  2(2(x y)  2  6  2(x y))  4 .
Câu 63: Cho số phức z thỏa mãn điều kiện 5 z i z  1 3i  3 z  1 i . Tìm giá trị lớn nhất M của biểu
thức: z  2  3i ? 10 A. M  .
B. M  1 13 . C. M  4 5 . D. M  9 3 Lời giải Chọn C. 2 2 2 2 2 2
5 x  (y  1)  (x  1)  (y  3)  3 (x  1)  (y  1) 2 2 2 2 2 2
 5 x  (y 1)  10. (x 1) (y  3) (x 1) (y 1) 2 2 2 2 2 2
 25x (y 1)  10 (
x 1) (y 3) (x 1) (y 1)   0     2 2
x  (y 1)  20  z i  2 5
P z  2  3i z i  (4i  2)  z i  4i  2  2 5  2 5  4 5
Câu 64: Cho hai số phức z, thỏa mãn z  1  z  3  2i ;   z m i với m là tham số. Giá trị của
m để ta luôn có   2 5 là: m  7 m  7 A.  . B.  . C. 3   m  7.
D. 3  m  7 . m   3 m  3   Lời giải Chọn B.
Đặt z a ib,a,b  có biểu diễn hình học là điểm Mx; y 2 2 2
z  1  z  3  2i x  1 iy x  3  y  2i  x   2
1  y  x  3  y  2  2
x 1  6x  9  4y  4  2x y  3  0
Suy ra biểu diễn của số phức z là đường thẳng  : 2x y  3  0 .
Ta có:   2 5  z m i  2 5  x m    y  1i  2 5
 x m2 y  2 1
 2 5  MI  2 5 với I  ; m   1 .
Mà ta có MI dI, 2  m  4
Nên MI  2 5  d I,  2 5   2 5  2  m 4  10 5 2m  4  10 m    3    . 2  m  4  10   m   7 z
Câu 65: Cho số phức z thỏa mãn 1 1 
. Tìm giá trị lớn nhất của biểu thức P z i  2 z  4  7i z  3i 2 A. 20 . B. 10 . C. 12 5 . D. 4 5 . Trang38 Lời giải Chọn A.
Gọi z x yi , x,y  . z  1 1 2 2 Ta có 
 2 z 1  z  3i  x  2 2 2
1  y x  y  3 z  3i 2 2 2
x y  4x  6y 7  0 . Lại có 2 2 2
P z i  2 z  4  7i 2
x  y  
1  2 x  4  y  7
 4x  8y  8  2 4
x  8y  72 .
Mặt khác  xy    xy  2 4 8 8 2 4 8 72
 5.80  4x  8y  8  2 4
x  8y  72  20 Suy ra P  20 .
Câu 66: Cho số phức z a bi ( a , b là các số thực) thỏa mãn z z  3  4i và có môđun nhỏ nhất. giá trị của P  . a b là? 3 A. . B. 4 . C. 2 . D. 3 . 4 Lời giải Chọn D. Ta có: 2 2 25  8
a bi a bi  3  4i 2 2
a b  a  3 b 4  6a8b25  0   b a 6
Mô đun của số phức z là: 2   b  b 2 100 2  225 15 2 2 25 8
z a b 2     b    6  36 6 Số phức 3 z
b  2  a   P  3 min 2
Câu 67: Trong các số phức z thỏa mãn điều kiện z  2  4i z  2i . Tìm số phức z có môđun nhỏ nhất. A. z  1   i . B. z  2   2i .
C. z  2  2i . D. 3  2i . Lời giải Chọn C.
Gọi số phức z có dạng z a bi . z thỏa mãn z  2  4i z  2i Trang39
a  2  b  4i a  b  2i
 a  22  b  42  a  b  22 2 2 2 2 2
a  4a  4  b  8b  16  a b  4b  4
 4a  4b  16
a b  4
Theo bất đẳng thức Bunhiacopxki.
 a b2   2 2   2 2 a b  2 2 2 16 1 1
z a b  8 z  2 2  a b Dấu  xảy ra  1 1
a b  2  z  2  2i a b   4
Câu 68: Trong các số phức z thỏa mãn điều kiện z  2  4i z  2i . Số phức z có mô đun bé nhất bằng A. 3 2 B. 2 . C. 2 2 . D. 4 . Lời giải Chọn C
Đặt z x yix,y  . Khi đó z  2  4i z  2i x yi  2  4i x yi  2i
 x  2 y  2  x y  2 2 2 4 2  4
x  4y 16  0  x y  4  0 .
Số phức có mô đun nhỏ nhất bằng khoảng cách từ O đến đường thẳng  : x y  4  0 . zdO  4 ;   2 2 . min 2 Trang40
Câu 69: (Đề Star Education) Cho hai số phức z ; z thỏa mãn z z  5 và z z  1. Giá trị lớn nhất của 1 2 1 2 1 2
biểu thức P z z là: 1 2 26 1 A. 26. B. . C. 9. D.  . 2 2 Lời giải Chọn A.
Ta gọi M , N lần lượt là các điểm biểu diễn của các số phức z ; z . 1 2   Từ giả thiết 
: z z  5    5   1 2 OM ON 5 OI 2
với I là trung điểm của đoạn thẳng MN .  
z z  1  OM ON  1  MN 1. 1 2 2 2 2 OM ON MN Ta có 2 OI   2 4 2 MN 2 2 2
OM ON  2OI  13 2
P z z OM ON 2  P   2 2   2 2 1 1
OM ON   26. Vậy P  26. 1 2 max Câu 70:
Cho hai số phức z ; z thỏa mãn z z  5 và z z 1 . Gọi M , m lần lượt là giá trị lớn nhất và 1 2 1 2 1 2
giá trị nhỏ nhất của biểu thức P z z . Khi đó mô đun của số phức 1 2 M  . mi là : A. 76 . B. 76 . C. 2 10 . D. 2 11 . Lời giải Chọn A.
Ta gọi M , N lần lượt là các điểm biểu diễn của các số phức z ; z . 1 2   Từ giả thiết 
: z z  6    
 với I là trung điểm của đoạn thẳng MN . 1 2 OM ON 6 OI 3  
z z  2  OM ON  2  MN  2 . 1 2 2 2 2 OM ON MN 2 MN Ta có 2 OI   2 2 2
OM ON  2OI   20. 2 4 2
P z z OM ON 2  P   2 2   2 2 1 1 OM ON   40. 1 2 Vậy a m x P  2 0 1  M .    
P z z OM ON OM ON  6 . 1 2
Vậy min P  6  m . Suy ra M  .
m i  40  36  76. Câu 71:
Cho số phức z thỏa mãn 5 . i z  3 
. Giá trị lớn nhất của biểu thức P  2z 1 4i z 1 5i là: 2 5 A. 2 5 . B.3. C. 3 5 . D. . 2 Lời giải Chọn C.
Ta gọi M (x; y) là điểm biểu diễn số phức z . Trang41 5 5  5  . i z  3 
x   y  32 2  . Suy ra M ( ;
x y)  C I (0;3); R     2 2 2   Khi đó: 1  
P  2z 1 4i z 1 5i  2 z 
 2i z 15i  2 MA MB , 2   với 1 A  ; 2 ; B   1;5  2    1     Ta có: IA   ; 1  
 ; IB  1;2 suy ra IB  2.  IA.  2  5 3 5  5 
Theo định lý Stewart ta có: 2 2 2 5MA MB   MI  . 5  2 2
 2MA MB  15 2 2  2   
(Hoặc có thể chứng minh theo phương pháp véc tơ   
 1   1   2  1 
MI MA AB MA
AB MA  MB MA  MA MB 3 3 3 3 Suy ra: 4 1 4   4 1 4 2 2 2 MI MA MB M . A M . B cos M , A MB 2 2 
MA MB M . A M . B cos AMB 9 9 9 9 9 9 2 2 2 4 1 4
MA MB AB  2 2  2 1 2 MA MB M . A MB   2 2 2
MA MB AB 9 9 9 2.M . A MB   3 3 9 2 2  2 2MA MB 2 2
 3MI AB 15 ) 3   Vậy 2
P  2 MA MB   2. 2.MAMB   2   2 2 2 1
2MA MB   45  3 5. 1 3i 1 3i Câu 72:
Cho hai số phức z   , z   
. Gọi z là số phức thỏa mãn 3z  3i  3 . Đặt 1 2 2 2 2 2
M,n lần lượt là giá trị lớn nhât, giá trị nhỏ nhất của biểu thức T z z z z z . Tính modun của số 1 2
phức w  M ni 2 21 4 3 A. B. 13 C. D. 4 3 3 Lời giải 2  
Giả sử z x yi,x, y R . Ta có 2 3
3z  3i  3  x   y    1(C)  3       
Gọi K x y 1 3 1 3 ; , A ;  ,B  ;  
lần lượt là các điểm biểu diễn số phức z, z , z 2 2   2 2      1 2
Ta tìm Max – Min của T OK OA OB
Ta có A, B,O thuộc đường tròn (C) và ABO đều  T  2OA  2 . Min
Gọi K thuộc cung  OB . Ta có K . AOB O . A BK A .
BOK KA KBOK 4 3
T  2KA  2.2R   T 3 Max Trang42 2  4 3  2 21 2  w     2   3  3  
Câu 73: Cho số phức z thỏa mãn 5 z i z  1 3i  3 z  1 i . Tìm giá trị lớn nhất M của z  2  3i ? 10 A. M  . B. M  1 13 . C. M  4 5 . D. M  9 . 3 Lờigiải ChọnD Gọi A 1
 ; 3,B1;  1 ,C 0; 
1  C là trung điểm AB 2 2 2 MA MB AB Suy ra 2 2 2 2 MC  
MA MB  2MC  10 . 2 4 Mặt khác 2 2
5 z i z  1 3i  3 z 1 i  5MC MA  3MB  10 MA MB 2  MC   2 25
10 2MC  10  MC  2 5 .
Mà z  2  3i z i   2
  4i  z i  2
  4i MC  2 5  4 5 .
Dấu “ = “ xẩy ra khi và chỉ khi z  2   5i .
Câu 74: [ Phạm Minh Tuấn, lần 3, năm 2018- Câu 46]
Cho số phức z thỏa mãn 3
z  1  2i z  1  2i
. Tìm giá trị nhỏ nhất của biểu thức z  2i
P z  2i . 1 1 A. P  . B. P  2 . C. 3 . D. . 2 3 Lời giải Chọn A Áp dụng tính chất: 2 2 2 2 z z
z z  2 z  2 z 1 1 1 3 2 2 2   Ta có:
z  1 2i z 1 2i  2 z  2i  1  z  2i 1
 2 z  2i 1 z  2  i   4 2 1
 4 z  2i  4 z  2i  3  0  P z  2i  2
Câu 75: [2D4-4] [THPT Chuyên LQĐ, LAI CHÂU, lần 1, 2018]Cho hai số phức z , z thỏa mãn điều kiện 1 2
2 z i z z  2i và z i 10  1. Tìm giá trị nhỏ nhất của biểu thức z z ? 1 1 1 2 1 2 A. 10  1 . B. 3 5 1. C. 101  1 . D. 101  1 . Lời giải Trang43 Chọn B.
+) Gọi z a bi; a,b . 1   Nên 2     2  2.
  1  2  2 2 2 2 2   a z i z z i a b b b . 1 1 1 4 2
Do đó tập hợp điểm biểu diễn số phức z là Parabol  x y . 1 4
+) Gọi z a bi, a,b . 2  
Khi đó z i 10  1  a 102  b  2 1  1 2
Nên tập hợp điểm biểu diễn số phức 2 2
z là đường tròn C x 10  y  
1  1 tâm I 10;  1 2 bamns kính r  1 . y M I N 1 x
z z nhỏ nhất khi và chỉ khi MN nhỏ nhất. 1 2
Ta có: MN IN IM MN IM IN IM 1.
Nên MN nhỏ nhất khi IM nhỏ nhất. 2 2 2 2  x   x  2 5 2 Ta có: 2
IM  x 10  
1    4  x  4  45.  4   4  2
IM  45  3 5 .
Do đó MN  3 5 1.
Vậy z z MN  3 5  1  z z  3 5 1. 1 2 1 2 min
Câu 76: [2D4-4]Cho hai số phức z , z thỏa mãn z  1 i  2 và z iz . Tìm giá trị lớn nhất m của biểu thức 1 2 1 2 1 z z 1 2
A. m  2 2  2 .
B. m  2  1 . C. m  2 2 . D. m  2 . Lời giải Chọn A.
Ta có z z z iz  1  i . z  2. z 1 2 1 1 1 1 Đặt 2 2
z a bi với ( a,b   ) theo đề bài ta có a   1  b  
1  4 (*). Ta cần tìm GTLN của 1 2 2
m  2 a b Trang44 Đặt 2 2
t a b . Ta có: 2 2
(*)  4  a  2a  1 b  2b  1  2(a  ) b  2  t . 2
Mà a b   2 2     2 2 1
( 1) . a b (**) nên  t2 2 2  4(a  ) b  8t 2
t 12t  4  0  6  4 2  t  6  4 2 Kết hợp với 2 2
t a b  0 suy ra 0  t  6  4 2
Suy ra m  2t  12  8 2  2 2  2
Dấu "=" xảy ra khi (**) xảy ra khi a b a  b . Kết hợp (*) ta được z  1 2 1 i 1    1 1 
Vậy giá trị lớn nhất của m bằng 2 2  2 .
Câu 77: [Chuyên Ngoại Ngữ - Hà Nội - 2018] Cho hai số phức z ; z thỏa mãn z  3i  5  2 và 1 2 1
iz  1 2i  4 . Tìm giá trị lớn nhất của biểu thức T  2iz  3z . 2 1 2 A. 313  16 . B. 313 . C. 313  8 . D. 313  2 5 Lời giải. Chọn A M I N 1 I2
Ta có z  3i  5  2  2iz  6  10i  4 . 1 1
Suy ra điểm M biểu diễn số phức 2iz nằm trên đường tròn T có tâm I 6;  1  0 và có bán kính 1   1  1 là R  4 . 1
Mặt khác, iz 1 2i  4  3
z  6  3i  12 nên điểm biểu diễn số phức 3
z là điểm N nằm 2 2 2
trên đường tròn T có tâm I 6;3 và có bán kính là R  12 . 2   2  2
Ta thấy 2iz  3z  2iz  3  z MN . 1  2 1 2
T lớn nhất khi và chỉ khi MN lớn nhất, khi đó bốn điểm M , I , I , N theo thứ tự thẳng hàng. 1 2
Vậy giá trị lớn nhất của MN I I R R  313 16 . 1 2 1 2
z  3  2i   1
Câu 78: Cho hai số phức z,w thỏa mãn 
. Tìm giá trị nhỏ nhất P của biểu thức
w  1 2i w  2   min  i
P z w . Trang45 3 2  2 5 2  2 3 2  2 A. P  . B. P  2  1. C. P  . D. P  . min 2 min min 2 min 2 Lời giải Chọn C. Cách 1 :
Giả sử z a bi a,b  , w x yi x,y  . 2 2
z  3  2i  1  a  3  b  2  1 (1) 2 2 2 2
w  1 2i w  2  i  x  
1  y  2  x  2  y   1 .
Suy ra x y  0 . P z w
a x2 b y2
a x2 b x2           .
Từ (1) ta có I 3;2 , bán kính r  1. Gọi H là hình chiếu của I trên d : y  x. x  3  t
Đường thẳng HI có PTTS  . y  2   t
M HI M 3  t; 2  t  1 t   2 M C 2  2t  1    1 t     2  1 1  5  2
t  2  M  3  ; 2   , MH   2 2  2  1 1  5  2
t  3  M  3  ; 2   , MH   2 2  2  Vậy 5 2 2 P  . min 2 Cách 2 :
z  3  2i  1 điều này cho thấy M z đang nằm trên hình tròn tâm I 3; 2 bán kính bằng 1.
w  1 2i w  2  i điều này cho thấy N w đang thuộc nửa mặt phẳng tạo bởi đường thẳng  là
trung trực của đoạn AB với A 1  ; 2  ,B2;  1 .
 : x y  0. (Minh hoạ như hình vẽ) Trang46 y y M 2 I 2 M I N B 1 1 -1 x -1 x O 2 3 O 2 3 N A -2 -2 Δ
P z w MN. 3  2 5 2  2 P
d I,  R   1  . min   2 2
Câu 79: [Nguyễn Khuyến, Bình Dương, 18/3,2018] Cho z a bi và z c di là 2 số phức thỏa mãn: 1 2 2
z  4 và z c d  10 . Gọi M là giá trị lớn nhất của biểu thức T ac bd cd . Hãy chọn khẳng định 1   1 đúng về M .
A. M 11;15 .
B. M 15;17 .
C. M 11;12 .
D.Không tồn tại M . Lời giải Chọn A. 2  z   4 2 2
a b  4 Ta có 1    .
z c d  10  c d   5 1   Khi đó:
T ac bd cd   2 2 a b  2 2
c d   ( c 5  c) 
c    c2 2 2 2 5  5c c . Đặt 2 2
f (c)  2 2c 10c  25  5c c . 4c 10
 2 2c 10c 25     5
Ta có f c 
 5  2c  2c  5 2    c  2   2c 10c  25 2 2c  10c   25  2 Bảng biến thiên: Trang47
c  5  2
f c 0 
f c 25 5 2 Dựa vào 4 bảng biến thiên ta   có 25 M  5 2   13,3 . 4 a b  2  Dấu bằng xảy ra khi  5 . c d   2 1 1
Câu 80: Cho số phức z thỏa mãn 3 z
 2 và M max z  . Khẳng định nào sau đây đúng? 3 z z  7  A. M  1  ; 2 .
B. M  2;  .  2   5 
C. M  1;  . D. 2 M M  5 .  2  Lời giải Chọn C. 3  3 1  1  1  1  1   1  Ta có 3 z   z   3 z      3  z   z   3 z      3  z zz  3 zz   z  3     3     3 1 1 1  1 1 z   z   3 z       z   3 z       2 . 3 zz   z   z   z  3 3     Mặt khác: 1 1 1 1 z   3 z   z   3 z      .  z   z z z 3 1 1 Suy ra: z
 3 z   2 . Đặt 1 t z   0 ta được: z z z 3
t  3t  2  0  t  t  2 2 1  0  t  2 . Vậy M  2. z
Câu 81: Cho số phức z x yi với x, y là các số thực không âm thỏa mãn 3  1và biểu thức z  1  2i 2 2 2 2  2 
P z ziz  
z z 1 i  z 1 i . Gọi    
M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P . Môđun của M mi là A. 3 . B. 1 . C.4. D. 2 . Trang48 Lời giải Chọn B. z  3 Ta có
 1  z  3  z 1 2i x y  1 . z  1  2i 2 2 2 2  2 
P z ziz  
z z 1 i  z 1 i 2 2
x y xy x  2 2  x y      16 8 ( y) 16 8xy . xy2 Đặt 1
t xy ta có 0  t   . 4 4  
Tính giá trị lớn nhất và nhỏ nhất của 2
P  16t  8t , với 1 t  0;   ta được P  0; P  1  Vậy  4  max min
M mi  1 . 1 3 1 3
Câu 82: (THPT Nguyễn Đăng Đạo – Bắc Ninh lần 3-2018) Cho hai số phức z   i, z    i . 1 2 2 2 2 2
Gọi z là số phức thỏa mãn 3z  3i  3 . Đặt M,m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức
T z z z z z . Tính mô đun của số phức w  M mi . 1 2 2 21 4 3 A. . B. 13 . C. . D. 4 3 3 Lời giải Chọn A.
Giả sử M, A,Blần lượt biểu diễn số phức z x yi,z ,z . 1 2 Từ giả thiết 1 1
3z  3i  3 ta có: 2 2 x  (y  )  . 3 3   y
Nên M thuộc đường tròn tâm 1 1 I  0;  , R  . M  3  3 3
Ta có T MO MA MB. 2 A B
Để T thì M trùng O, A,B nên min I 2 2  1   3  T  2OA  2       2 . min 2  2      Để 1 1 x T thì OM và (MA M ) B
nên OM  2R và M nằm O 1 max max max -   2 2 chính giữa cung nhỏ  2 AB và M  0;  . Do vậy  3  2 2 2  1   3 2  4 T
OM  2MA   2  . max         3  2  2  3  3 2   Vậy 2 2 4 2 2 21
w  M m     2  .  3  3 Trang49
Câu 83: Cho hai số phức z và w thỏa mãn các điều kiện sau:
iz  2i  2  z 1   . max 
w22i , w  2
Tìm giá trị nhỏ nhất của z w . 9 13 5 1 A. . B. . C. . D. . 2 5 2 5 2 2 5 Lời giải Chọn B.
Gọi M, N lần lượt làđiểm biểu diễn của z, w với M x; y .
Ta có iz  2i  2  z  1  z  2  2i z  1
 x  2 y  2  x  2 2 2 2 1  y  2
x  4y  7  0 .
Do đó, M thuộc nửa mặt phẳng bờ  : 2
x  4y 7  0 không chứaO , kể cả bờ.
Ta có max w  2  2i , w  2 suy ra  w   2  2i  2
NI  2 , I 2;  2    .  w  2 NO    2
Do đó, N thuộc phần chung của hai hình tròn
I; 2 và O; 2.
Dễ thấy hai hình tròn này tiếp xúc ngoài tại điểm E 1  ;  1 . Do đó, N  1  ;  1 .
Ta thấy z w MN nên z w nhỏ nhất khi MN ngắn nhất, khi đó M là hình chiếu của N trên  . 2  1   4.1 7 13
Ta có d N,      .  2 2 2 5 2  4 Vậy 13 min z w  . 2 5
Câu 84: [CHUYÊN NGỮ LẦN 1-2018] Cho hai số phức z ; z thỏa mãn z  3i  5  2 và iz  1 2i  4 . 1 2 1 2
Tìm giá trị lớn nhất của biểu thức T  2iz  3z . 1 2 A. 313  16 . B. 313 . C. 313  8 . D. 313  2 5 . Lời giải Chọn A. Trang50
Đặt 2iz a bi, 3
z c di ; a ;
b c; d   , gọi A ;
a b , Bc; d . 1 2   a bi 2 2
Có z  3i  5  2 
 3i  5  2  a  610  bi  4  a 6 b10  16 nên 1 2i
A I  có tâm I  6
 ; 10 bán kính R  4 . c di 2 2
Có iz  1 2i  4  . i
1 2i  4  3dc 6i  12  c   d  2 6 3  12 nên 2 3 
B J có tâm J 6; 3 , bán kính  R  12 . 2 2
Có T  2iz  3z
acbd  ac bd  AB . 1 2
Do A I  , B J , IJ  313  R   R  16 nên ABR 
R IJ  16  313 . Max
Câu 85: Xét các số phức z a bi,(a,b   ) thỏa mãn z  3  2i  2. Tính a b biết biểu thức
S z  1 2i  2 z  2  5i đạt giá trị nhỏ nhất. A. 4  3 . B. 2  3 . C. 4  3 . D. 3. Lời giải: Chọn A Giả thiết 2 2
z  3  2i  2  (T) : (a  3)  (b  2)  4 B 5 Gọi ( A 1  ; 2), (
B 2; 5), M(a; b) lần lượt là các điểm biểu diễn của các số phức M z  1
  2i,z  2  5i,z a bi 1 2 3 Bài toán trở thành: Tìm I
M (T) sao cho biểu thức A J
S MA  2MB nhỏ nhất -1 O Ta có 2 2 2 2
MA  (a  1)  (b  2)  a b  2a  4b  5 2 2 2
 2 a b  4a  4b  8 2 2
 2 (a  2) (b  2)  2MC với C(2; 2) Trang51
Ta có MA  2MB  2(MB MC)  2BC dấu “=”xảy ra khi và chỉ khi ,
B M, C theo thứ tự đó thẳng hàng.
Phương trình đường thẳng BC : x  2
M là giao của của BC và (T)  (
M 2; 2  3)  a b  4  3 .
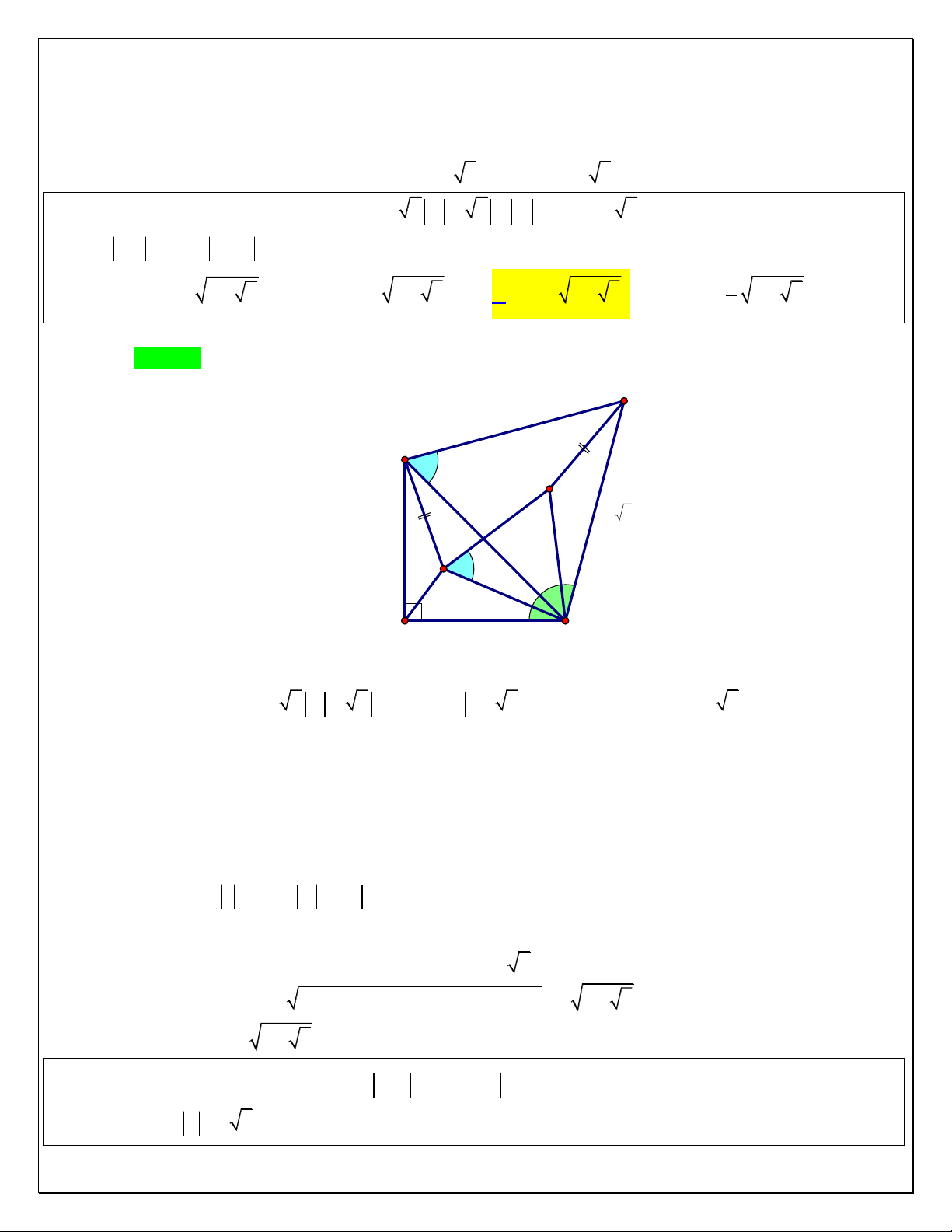
Câu 86: Cho các số phức z , z , z thỏa mãn 2 z  2 z z z  6 2 . Tìm giá trị nhỏ nhất của biểu thức 1 2 3 1 2 1 2
P z z z z z . 1 2 9
A. P  6 2  2
B. P  3 2  3 .
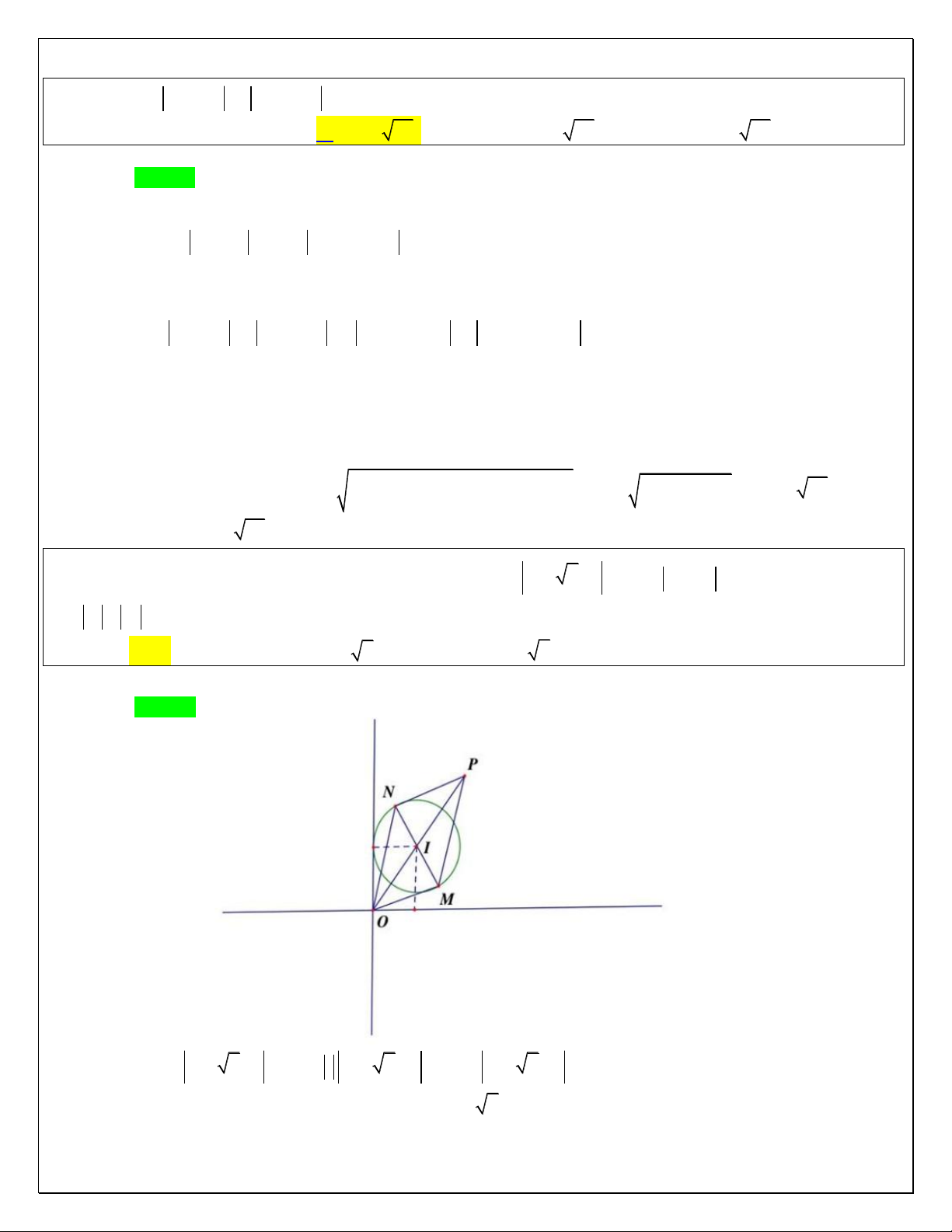
C. P  6 2  3 . D. P  2  3 . 2 Lời giải Chọn C. A ' A 600 M ' 6 2 6 M 600 O 6 B
Chọn A, B, M lần lượt là các điểm biểu diễn số phức z ,z ,z, 1 2
Dựa vào điều kiện 2 z  2 z z z  6 2  OA OB  6, AB  6 2 . 1 2 1 2
Suy ra ta có tam giác OAB vuông cân tại O .
Phép quay tâm B góc quay 0 60  ta có:  Q : A   A 0 B, 60   M   M Do tam giác  BM
M đều  AM   A
M , BM M M
Suy ra P z z z z z OM AM BM OM M M   AM O A . 1 2
Dấu "  " xảy ra khi O, M,  M ,  A thẳng hàng.
Khi đó tam giác OB A
có OB  6 , B
A BA  6 2 và 0 OB A  105 . Từ đó suy ra 2 2 0 O
A OB B A  2O .
B BA .cos105  6 2  3 .
Vậy min P  6 2  3 .
Câu 87: Cho hai số phức z, thỏa mãn z  1  z  3  2i ;   z m i với m là tham số. Giá trị của m
để ta luôn có   2 5 là: Trang52m  7 m  7 A.  . B.  . C. 3   m  7.
D. 3  m  7 . m   3 m  3   Lời giải Chọn B.
Đặt z a ib,a,b  có biểu diễn hình học là điểm Mx; y 2 2 2
z  1  z  3  2i x  1 iy x  3  y  2i  x   2
1  y  x  3  y  2  2
x 1  6x  9  4y  4  2x y  3  0
Suy ra biểu diễn của số phức z là đường thẳng  : 2x y  3  0 .
Ta có:   2 5  z m i  2 5  x m    y  1i  2 5
 x m2 y  2 1
 2 5  MI  2 5 với I  ; m   1 .
Mà ta có MI dI, 2  m  4
Nên MI  2 5  d I,  2 5   2 5  2  m 4  10 5 2m  4  10 m    3    . 2  m  4  10   m   7 z
Câu 88: Cho số phức z thỏa mãn 1 1 
. Tìm giá trị lớn nhất của biểu thức P z i  2 z  4  7i z  3i 2 A. 20 . B. 10 . C. 12 5 . D. 4 5 . Lời giải Chọn A.
Gọi z x yi , x,y  . z  1 1 2 2 Ta có 
 2 z 1  z  3i  x  2 2 2
1  y x  y  3 z  3i 2 2 2
x y  4x  6y 7  0 . Lại có 2 2 2
P z i  2 z  4  7i 2
x  y  
1  2 x  4  y  7
 4x  8y  8  2 4
x  8y  72 .
Mặt khác  xy    xy  2 4 8 8 2 4 8 72
 5.80  4x  8y  8  2 4
x  8y  72  20 Suy ra P  20 . Trang53