


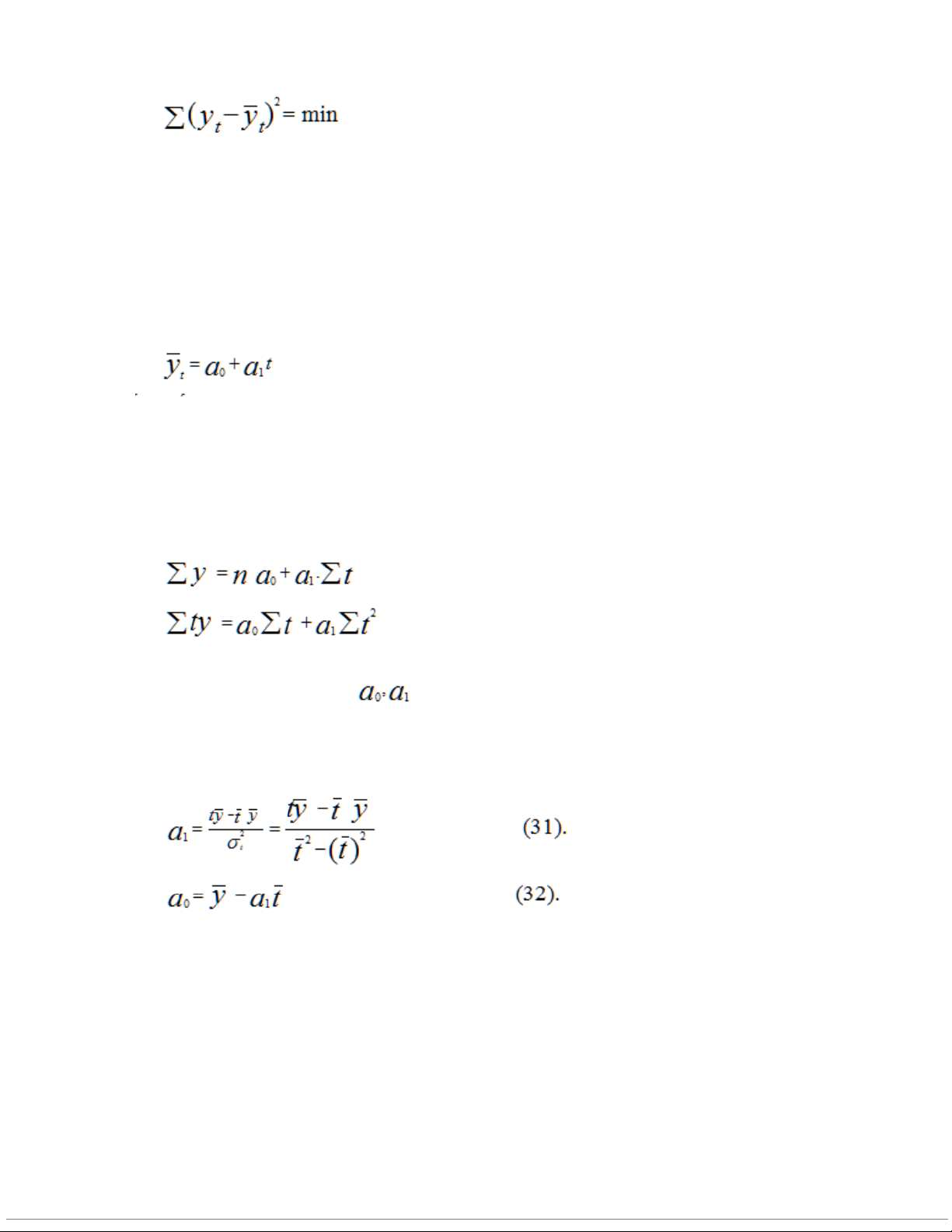
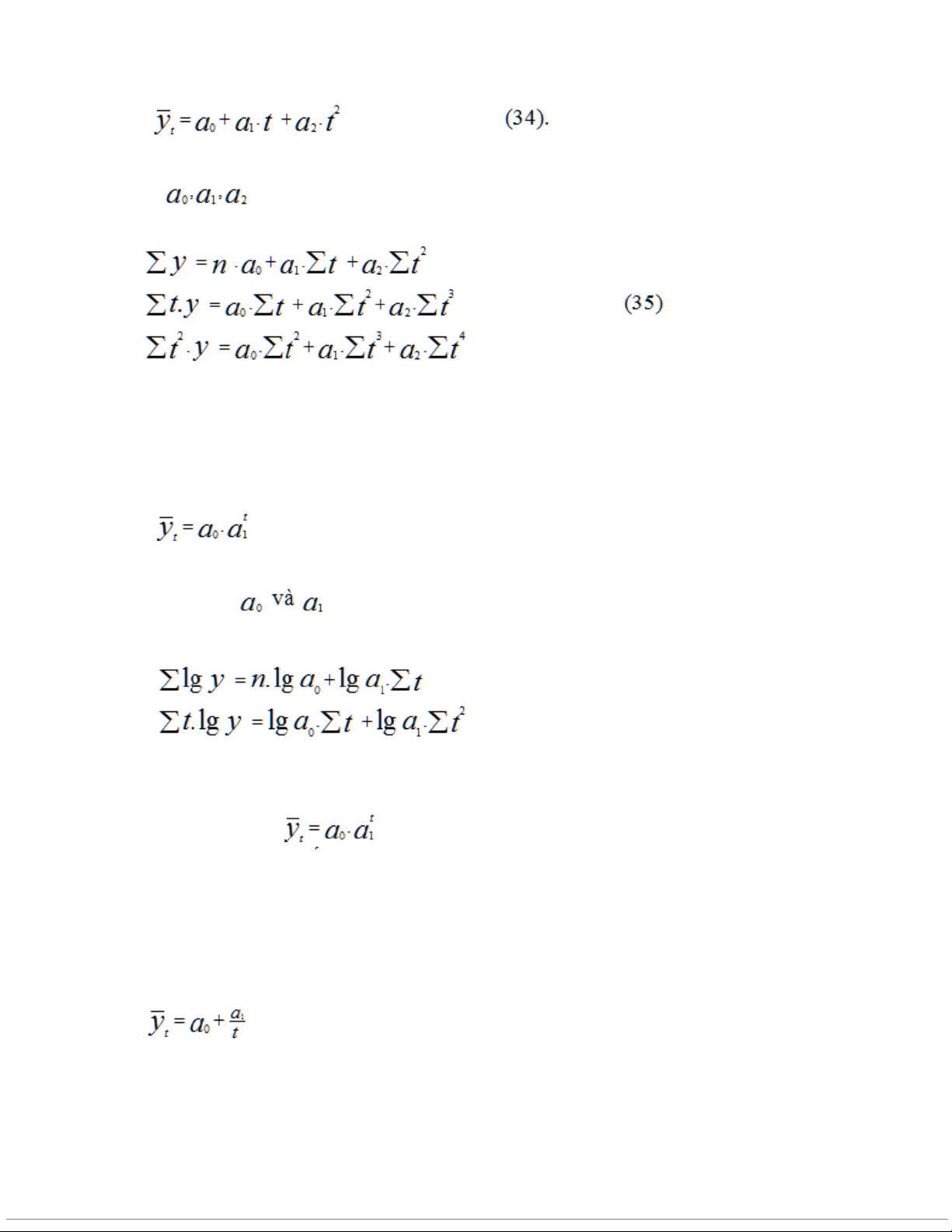
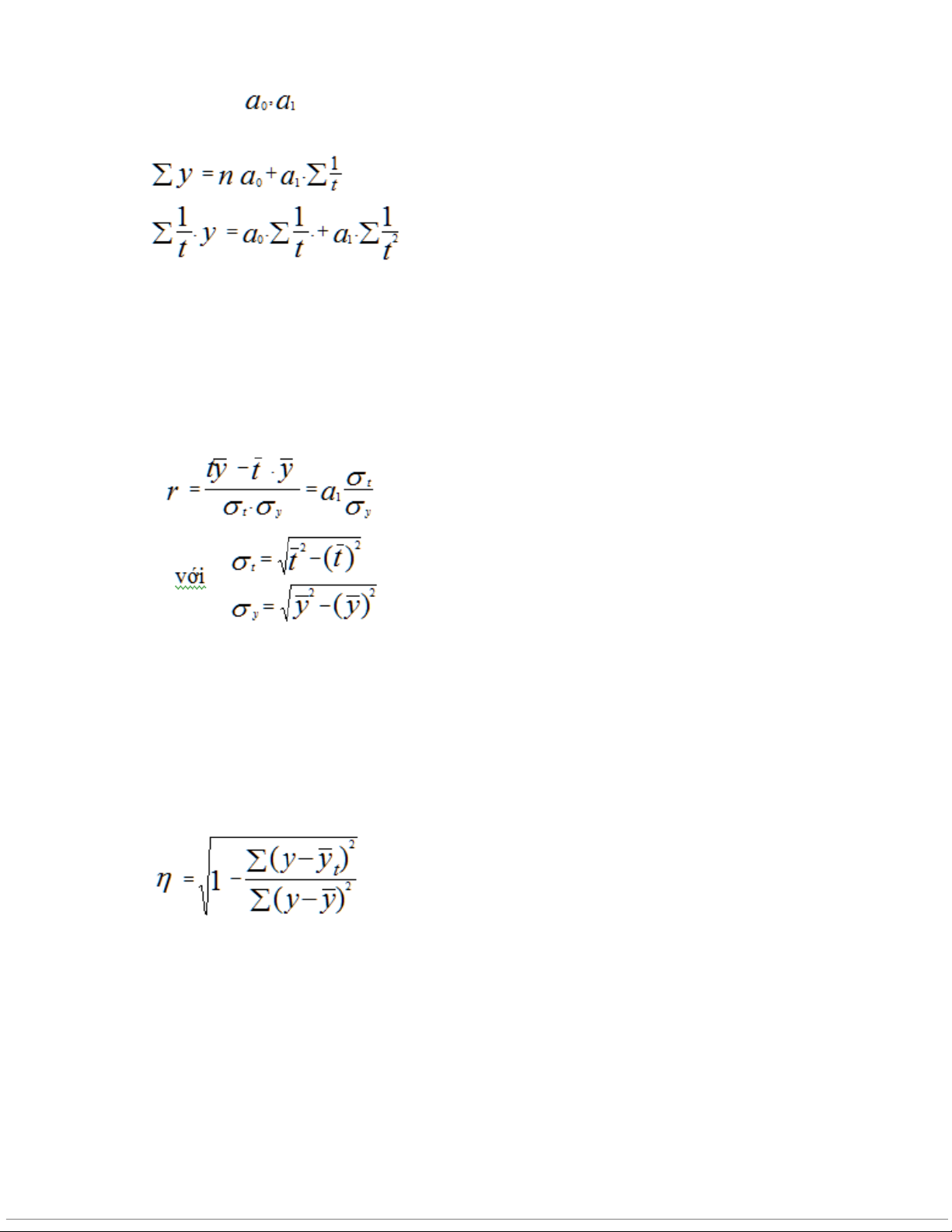


Preview text:
Một số phương pháp biểu
ột số p ươ g p áp b ểu ệ u ướ g b ế độ g của ệ tượ g
hiện xu hướng biến động của hiện tượng Bởi: hanh phamminh
Phương pháp mở rộng khoảng cách thời gian
Mở rộng khoảng cách thời gian là ghép một số khoảng thời gian gần nhau lại thành một
khoảng thời gian dài hơn với mức độ lớn hơn.Trước khi ghép, các mưc độ trong dãy số
chưa phản ánh được mức biến động cơ bản của hiện tượng hoặc biểu hiện chưa rõ rệt.
Sau khi ghép, ảnh hưởng của các nhân tố ngẫu nhiên triệt tiêu lẫn nhau do ảnh hưởng
của các chiều hướng trái ngược nhau và các mức độ mới bộc lộ rõ xu hướng biến động
cơ bản của hiện tượng.
Tuy nhiên, phương pháp mở rộng khoảng cách thời gian còn có một số nhược điểm nhất định .
• Thứ nhất, phương pháp này chỉ áp dụng đối với dãy số thời kì vì nếu áp dụng
cho dãy số thời điểm, các mức độ mới trở lên vô nghĩa.
• Thứ hai, chỉ nên áp dụng cho dãy số tương đối dài và chưa bộc lộ rõ xu hường
biến động của hiện tượng vì sau khi mở rộng khoảng cách thời gian,số lượng
các mức độ trong dãy số giảm đi nhiều .
Phương pháp bình quân trượt
Số bình quân trượt (còn gọi là số bình quân di động) là số bình quân cộng của một nhóm
nhất định các mức độ của dãy số được tính bằng cách lần lượt loại dần các mức độ đầu
và thêm dần các mức độ tiếp theo sao cho tổng số lượng các mức độ tham gia tính số
lần bình quân không đổi.
Có hai phương pháp số bình quân trượt cơ bản. 1/7
Một số phương pháp biểu hiện xu hướng biến động của hiện tượng
Số bình quân trươt đơn giản
Phương pháp này coi vai trò của các mức độ tham gia tính số bình quân trượt là như
nhau.Thông thường,số mức độ tham gia trượt là lẻ (VD:3,5,7,…,2n+1) để giá trị bình
quân nằm giữ khoảng trượt. Công thức tổng quát:
Trong đó : yt:Số bình quân trượt tại thời gian t.
yi:Mức độ tại thời gian i.
m:Số mức độ tham gia trượt.
t:Thời gian có mức độ tính bình quân trượt.
Giả sử có dãy số thời gian: y1, y2,..., yn-1 , yn(gồm m mức độ).
Nếu tính bình quân trượt cho nhóm ba mức độ, chúng ta triển khai công thức như sau:
Số bình quân trượt gia quyền
Cơ sở của phương pháp là gắn hệ số vai trò cho các mức độ tham gia tính bình quân
trượt. Các mức độ này càng gần mức độ tính thì hệ số càng cao và càng xa thì hệ số càng
nhỏ. Các hệ số vai trò được lấy từ các hệ số của tam giác Pascal. 2/7
Một số phương pháp biểu hiện xu hướng biến động của hiện tượng
Tuỳ theo mức độ tham gia tính bình quân trượt, chúng ta chọn dòng hê số tương ứng.
Chẳng hạn, số mức độ tham gia là 3, công thức là: Phương pháp này cho
chúng ta hiệu quả cao hơn phương pháp trên.Tuy nhiên cách tính phức tạp hơn nên ít được sử dụng. Phương pháp hồi quy
Hồi quy là phương pháp của toán học được vận dụng trong thống kê để biểu hiện xu
hướng biến động cơ bản của hiện tượng theo thời gian. Những biến động này có nhiều
giao động ngẫu nhiên và mức độ tăng (giảm) thất thường.
Hàm xu thế tổng quát có dạng: Trong đó: : Hàm xu thế lí thuyết .
t: Thứ tự thời gian tương ứng với một mức độ trong dãy số.
:Các tham số của hàm xu thế ,các tham số này thường được xác định
bằng phương pháp bình phương nhỏ nhất. 3/7
Một số phương pháp biểu hiện xu hướng biến động của hiện tượng
Do sự biến động của hiện tượng là vô cùng đa dạng nên có hàm xu thế tương ứng sao
cho sự mô tả là gần đúng nhất so với xu hướng biến động thực tế của hiện tượng.
Một số dạng hàm xu thế thường gặp là: Hàm xu thế tuyến tính
Hàm xu thế tuyến tính được sử dụng khi dãy số thời gian có các lượng tăng (giảm) liên
hoàn tuyệt đối xấp xỉ nhau.Theo phương pháp bình phương nhỏ nhất, chúng ta biến đổi được hệ phương trình:
Từ đó, chúng ta tíng được .
Ngoài ra, tham số có thể tính trực tiếp theo công thức :
Hàm xu thế dạng Parabol bậc hai
Hàm Parabol được sử dụng khi các sai phân bậc hai(tức là sai phân của sai phân bậc một) xấp xỉ nhau. Dạng hàm : 4/7
Một số phương pháp biểu hiện xu hướng biến động của hiện tượng với
là các nghiệm của phương trình: Hàm mũ
Phương trình hàm mũ có dạng: Hai tham số
là nghiệm của phương trình: Hàm xu thế dạng
được vận dụng khi dãy số thời gian có các tốc độ phát
triển liên hoàn xấp xỉ nhau. Hàm Hypecpol
Phương trình hàm xu thế Hypecpol có dạng:
Hàm xu thế này được sử dụng khi dãy số thời gian có các mức độ ngày càng giảm chậm dần. 5/7
Một số phương pháp biểu hiện xu hướng biến động của hiện tượng Các tham số
được xác định theo hệphương trình:
Trên đây là một số hàm xu hướng thường gặp. Sau khi xây dựng xong hàm xu thế, chúng
ta cần thiết phải đánh giá xem mức độ phù hợp của dạng hàm có chấp nhận được hay
không, hay mối liên hệ tương quan có chặt chẽ hay không.
Đói với hàm xu thế dạng tuyến tính, người ta sử dụng hệ số tương quan r :
Khi /r/ càng gần 1 thì mối liên hệ tương quan càng chặt chẽ. r mang dấu (-) khi y và t có
mối liên hệ tương quan nghịch, còn r mang dấu (+) khi y và t có mối liên hệ tương quan
thuận. Thông thường /r/ > 0.9 thì chúng ta có thể chấp nhận được.
Ngoài ra, để đánh giá trình độ chặt chẽ của mối liên hệ tương quan giữa y và t trong các
hàm xu thế phi tuyến người ta sử dụng tỉ số tương quan ?.
Nếu ? càng gần 1 thì mối liên hệ tương quan càng chặt chẽ.
Phương pháp biểu hiện biến động thời vụ
Để xác định được tính chất và mức độ của biến động thời vụ, chúng ta phải sử dụng số
liệu trong nhiều năm theo nhiều phương pháp khác nhau. Phương pháp thông dụng nhất
là sử dụng chỉ số thời vụ. 6/7
Một số phương pháp biểu hiện xu hướng biến động của hiện tượng
Có 2 loại chỉ số thời vụ:
+Chỉ số thời vụ đối với dãy số thời gian có các mật độ tương đối ổn định.
+Chỉ số thời vụ đối với dãy số thời gian có xu hướng biến động rõ rệt.
*. Chỉ số thời vụ đối với dãy số thời gian có các mật độ tương đối ổn định nghĩa là trong
cùng một kì, năm này qua năm khác không có sự thay đổi rõ rệt, các mức độ xấp xỉ
nhau, khi đó chỉ số thời vụ được tính theo công thức sau: Trong đó:
:Chỉ số thời vụ của kì thứ i trong năm.
:Số bình quân cộng của các mức độ cùng kì thứ i .
:Số bình quân cộng của tất cả các mức độ trong dãy số .
*.Chỉ số thời vụ đối với dãy số thời gian có xu hướng biến động rõ rệt.
Trong trường hợp này, chúng ta phả đIều chỉnh bằng phương trình hồi quy để tính các
mức độ lí thuyết.Sau đó dùng các mức độ này để làm căn cứ so sánh:
Trong đó: yij : Mức độ thực tế của kì thứ i năm j .
: Mức độ lí thuyết của kì thứ i năm j . 7/7




