





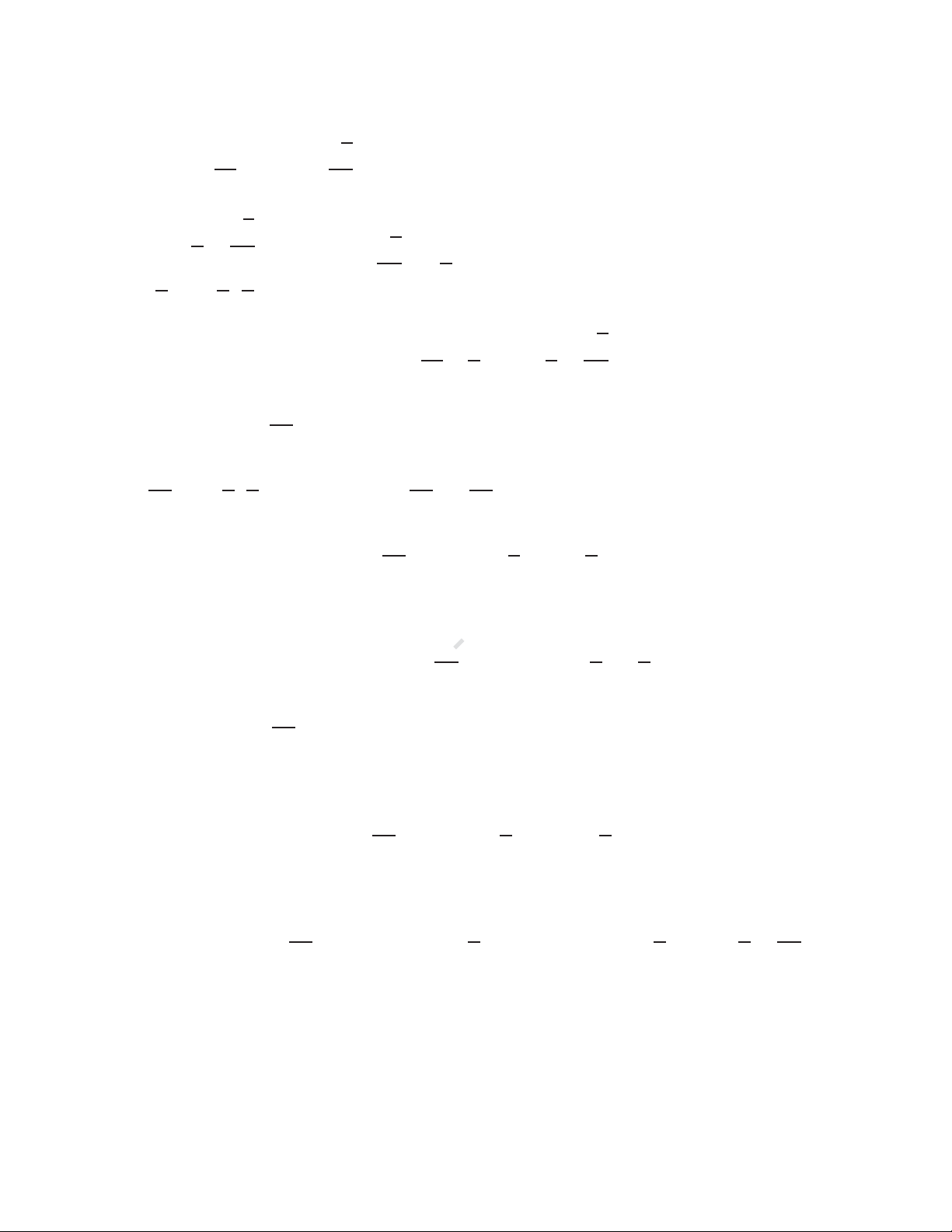













































































































































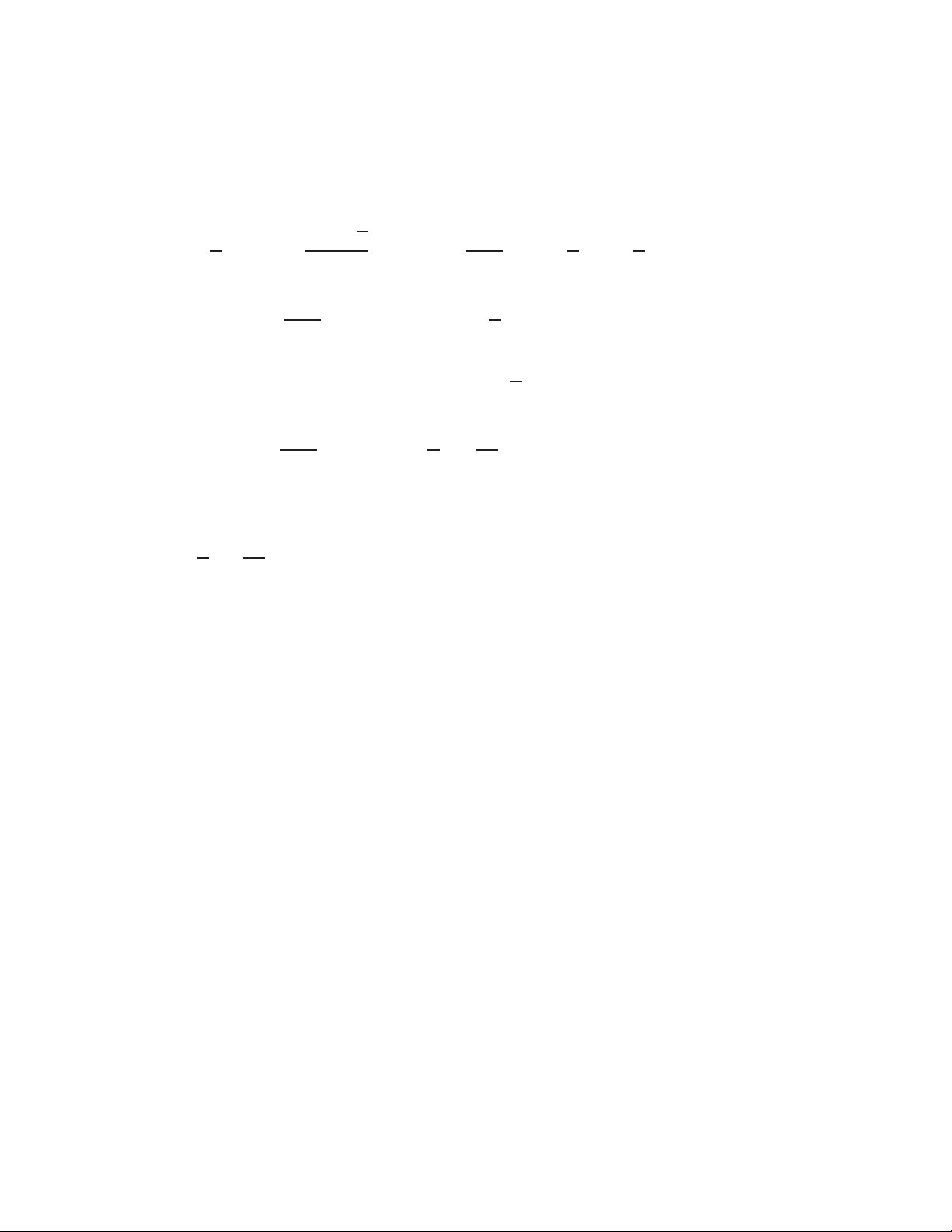

































Preview text:
LƯỢNG GIÁC
MỘT SỐ CHUYÊN ĐỀ VÀ ỨNG DỤNG
TẬP 2 : PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH,
BẤT PHƯƠNG TRÌNH LƯỢNG GIÁC
VÕ ANH KHOA – HOÀNG BÁ MINH
VÕ ANH KHOA – HOÀNG BÁ MINH LƯỢNG GIÁC
MỘT SỐ CHUYÊN ĐỀ VÀ ỨNG DỤNG
TẬP 2 : PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH,
BẤT PHƯƠNG TRÌNH LƯỢNG GIÁC TP. HỒ CHÍ MINH TOANMATH.com LỜI NÓI ĐẦU
Cuốn sách “LƯỢNG GIÁC – MỘT SỐ CHUYÊN ĐỀ VÀ ỨNG DỤNG” này được biên
soạn với mục đích cung cấp, bổ sung kiến thức cho học sinh THPT và một số bạn đọc
quan tâm đến mảng kiến thức này trong quá trình học tập và làm việc. Trong tập 2
“PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH LƯỢNG GIÁC”
này, chúng tôi sẽ xoáy vào trọng tâm là “PHƯƠNG TRÌNH LƯỢNG GIÁC”, một dạng
toán quen thuộc trong các đề thi THPT, đặc biệt là đề thi tuyển sinh Đại Học.
Ở các chương chính, chúng tôi chia làm 3 phần : -
Phần I : Nêu lý thuyết cùng ví dụ minh họa ngay sau đó, giúp bạn đọc hiểu và biết
cách trình bày bài. Đồng thời đưa ra các dạng toán cơ bản, thường gặp trong quá trình
làm bài trên lớp của học sinh THPT. Ở phần này, chúng tôi sẽ trình bày một số bài để bạn
đọc có thể nắm vững hơn, tránh sai sót. -
Phần II : Trong quá trình tham khảo và tổng hợp tài liệu, chúng tôi sẽ đưa vào
phần này các dạng toán khó nhằm giúp cho các học sinh bồi dưỡng, rèn luyện kĩ năng
giải LƯỢNG GIÁC thành thạo hơn khi gặp phải những dạng toán này. -
Phần III : Chúng tôi sẽ đưa ra lời giải gợi ý cho một số bài, qua đó bạn đọc kiểm
tra lại đáp số, lời giải hoặc cũng có thể tham khảo thêm.
Trong quá trình biên soạn, mặc dù chúng tôi đã cố gắng bằng việc tham khảo một lượng
rất lớn các tài liệu có sẵn và tiếp thu có chọn lọc ý kiến từ các bạn đồng nghiệp để dần
hoàn thiện cuốn sách này, nhưng khó tránh khỏi những thiếu sót bởi tầm hiểu biết và kinh
nghiệm còn hạn chế, chúng tôi rất mong nhận được ý kiến đóng góp quý báu của bạn đọc gần xa.
Chi tiết liên hệ tại : anhkhoavo1210@gmail.com minh.9a1.dt@gmail.com CÁC TÁC GIẢ
VÕ ANH KHOA – HOÀNG BÁ MINH. TOANMATH.com LỜI CẢM ƠN
Trong quá trình biên soạn, chúng tôi xin cám ơn đến những bạn đã cung cấp tài liệu tham
khảo và vui lòng nhận kiểm tra lại từng phần của bản thảo hoặc bản đánh máy, tạo điều
kiện hoàn thành cuốn sách này :
- Ngô Minh Nhựt (ĐH Kinh Tế Tp.HCM)
- Mai Ngọc Thắng (ĐH Kinh Tế Tp.HCM)
- Nguyễn Thị Thanh Huyền (THPT Chuyên Lương Thế Vinh Đồng Nai)
- Nguyễn Huy Hoàng (THPT Chuyên Lê Hồng Phong Tp.HCM)
- Trần Lam Ngọc (THPT Chuyên Trần Đại Nghĩa Tp.HCM)
- Vương Tuấn Phong (THPT Chuyên Trần Đại Nghĩa Tp.HCM)
- Lê Quang Hiếu (THPT Chuyên Lương Thế Vinh Đồng Nai)
- Hoàng Minh Quân (ĐH Khoa Học Tự Nhiên Hà Nội)
và một số thành viên diễn đàn MathScope. TOANMATH.com MỤC LỤC
TẬP 2 : PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH,
BẤT PHƯƠNG TRÌNH LƯỢNG GIÁC
CHƯƠNG 4 : SƠ LƯỢC VỀ HÀM LƯỢNG GIÁC NGƯỢC I.
MỘT SỐ TÍNH CHẤT CƠ BẢN
VỀ HÀM LƯỢNG GIÁC NGƯỢC ........................................................... 1 II.
BÀI TẬP VÍ DỤ VỀ HÀM LƯỢNG GIÁC NGƯỢC ............................... 2
CHƯƠNG 5 : PHƯƠNG TRÌNH LƯỢNG GIÁC I.
PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN ............................................ 3
BÀI TẬP TỰ LUYỆN ................................................................................ 13 II.
CÁC DẠNG PHƯƠNG TRÌNH LƯỢNG GIÁC ĐƯA VỀ
PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN ........................................... 20 1.
PHƯƠNG TRÌNH BẬC HAI ...................................................................... 20
BÀI TẬP TỰ LUYỆN ................................................................................ 35 2.
PHƯƠNG TRÌNH BẬC NHẤT THEO ݔ VÀ ݔ .............................. 41
BÀI TẬP TỰ LUYỆN ................................................................................. 50 3.
PHƯƠNG TRÌNH ĐỐI XỨNG THEO ݔ VÀ ݔ ............................... 53
BÀI TẬP TỰ LUYỆN ................................................................................. 60 4.
PHƯƠNG TRÌNH BẬC HAI THUẦN NHẤT ĐỐI VỚI ݔ ǡ ݔ ......... 61
BÀI TẬP TỰ LUYỆN ................................................................................ 67 5.
CÁC DẠNG PHƯƠNG TRÌNH LƯỢNG GIÁC KHÁC ............................ 73 a.
TỔNG HỢP ................................................................................................ 73
BÀI TẬP TỰ LUYỆN ................................................................................ 95 TOANMATH.com b.
PHƯƠNG TRÌNH CHỨA CĂN THỨC.................................................... 100
BÀI TẬP TỰ LUYỆN ............................................................................... 103 c.
PHƯƠNG TRÌNH KHÔNG MẪU MỰC .................................................. 107
BÀI TẬP TỰ LUYỆN ............................................................................... 127 d.
PHƯƠNG TRÌNH CÓ CHỨA THAM SỐ ................................................ 131
BÀI TẬP TỰ LUYỆN ............................................................................... 148
CHƯƠNG 6 : HỆ PHƯƠNG TRÌNH LƯỢNG GIÁC ........................................... 154 I.
TÓM TẮT MỘT SỐ PHƯƠNG PHÁP THƯỜNG GẶP ....................... 154 II.
CÁC BÀI TẬP MINH HỌA .................................................................... 155
BÀI TẬP TỰ LUYỆN ............................................................................... 171
CHƯƠNG 7 : BẤT PHƯƠNG TRÌNH LƯỢNG GIÁC ......................................... 175 I.
TÓM TẮT MỘT SỐ PHƯƠNG PHÁP THƯỜNG GẶP ....................... 175 II.
CÁC BÀI TẬP MINH HỌA .................................................................... 176
BÀI TẬP TỰ LUYỆN ............................................................................... 186 ĐỌC THÊM :
TẢN MẠN VỀ SỐ PI ............................................................................... 189
TÀI LIỆU THAM KHẢO .......................................................................................... 194 TOANMATH.com
Chương 4 : Sơ lược về hàm lượng giác ngược CHƯƠNG 4
SƠ LƯỢC VỀ HÀM LƯỢNG GIÁC NGƯỢC I.
MỘT SỐ TÍNH CHẤT CƠ BẢN VỀ HÀM LƯỢNG GIÁC NGƯỢC -
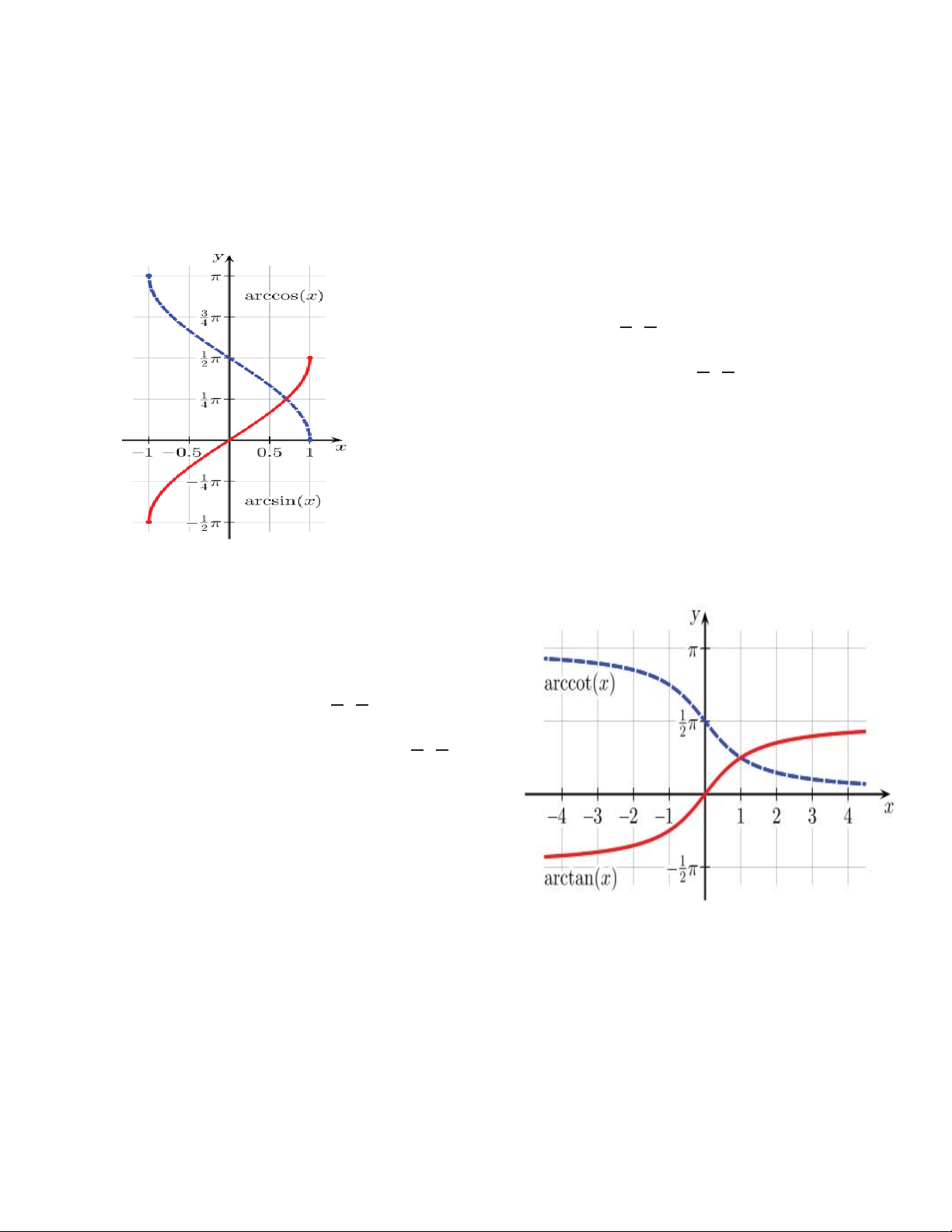
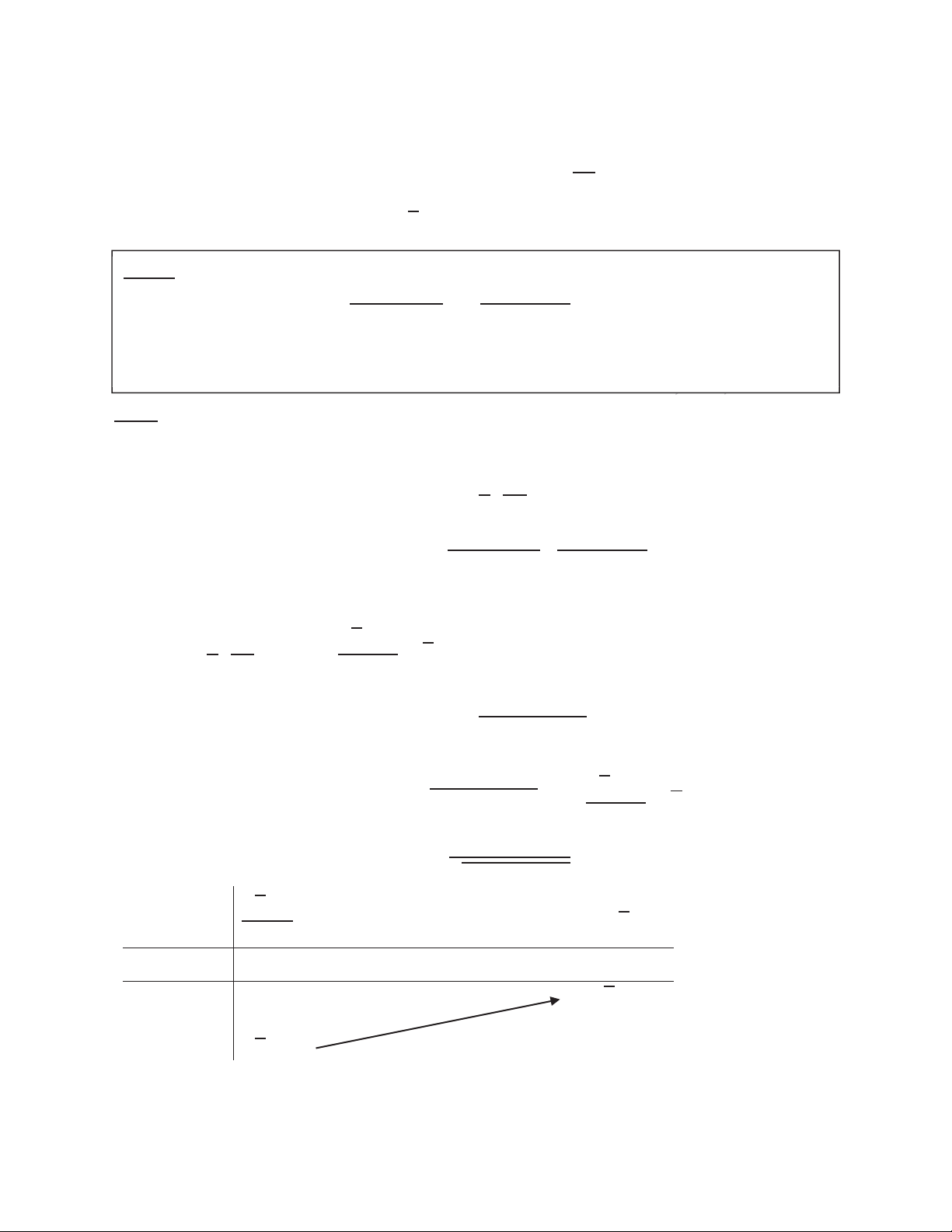
Hàm số ݕ ൌ ݔ là hàm lượng giác ngược của
hàm số ݔ ൌ ݕ, có một số tính chất cơ bản sau ߨ ߨ ۓ ݕ א ቂെ Ǣ ቃ ۖ ʹ ʹ ߨ ߨ
ሺ ݔሻ ൌ ݔǡ ݔ א ቂെ Ǣ ቃ ۔ ʹ ʹ
ۖ ሺ ݔሻ ൌ ݔǡ ݔ א ሾെͳǢ ͳሿ ە ሺെݔሻ ൌ െ ݔ -
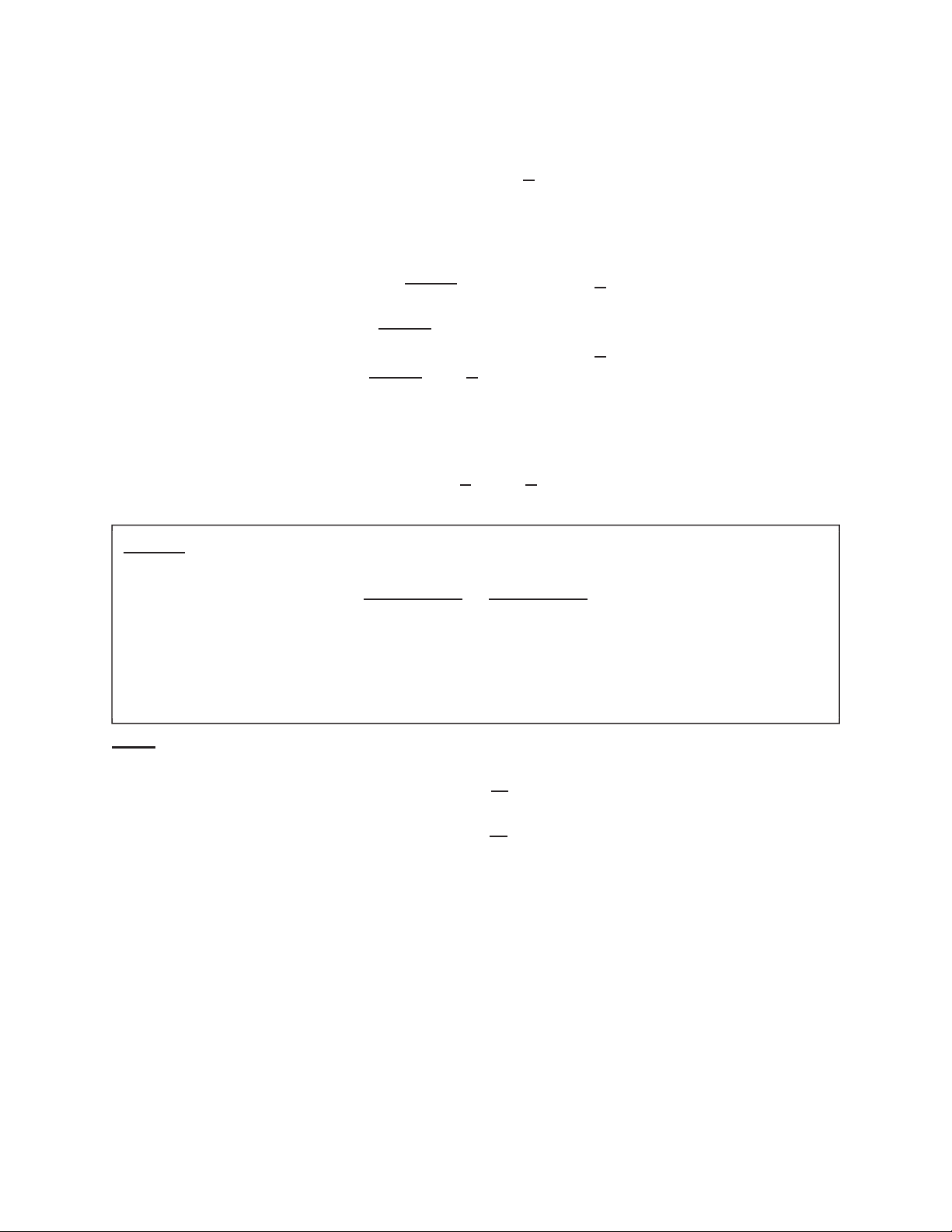
Hàm số ݕ ൌ ݔ là hàm lượng giác ngược
của hàm số ݔ ൌ ݕ, có một số tính chất cơ bản sau ݕ א ሾͲǢ ߨሿ
ሺ ݔሻ ൌ ݔǡ ݔ א ሾͲǢ ߨሿ
൞ሺ ݔሻ ൌ ݔǡݔ א ሾെͳǢͳሿ ሺെݔሻ ൌ ߨ െ ݔ -
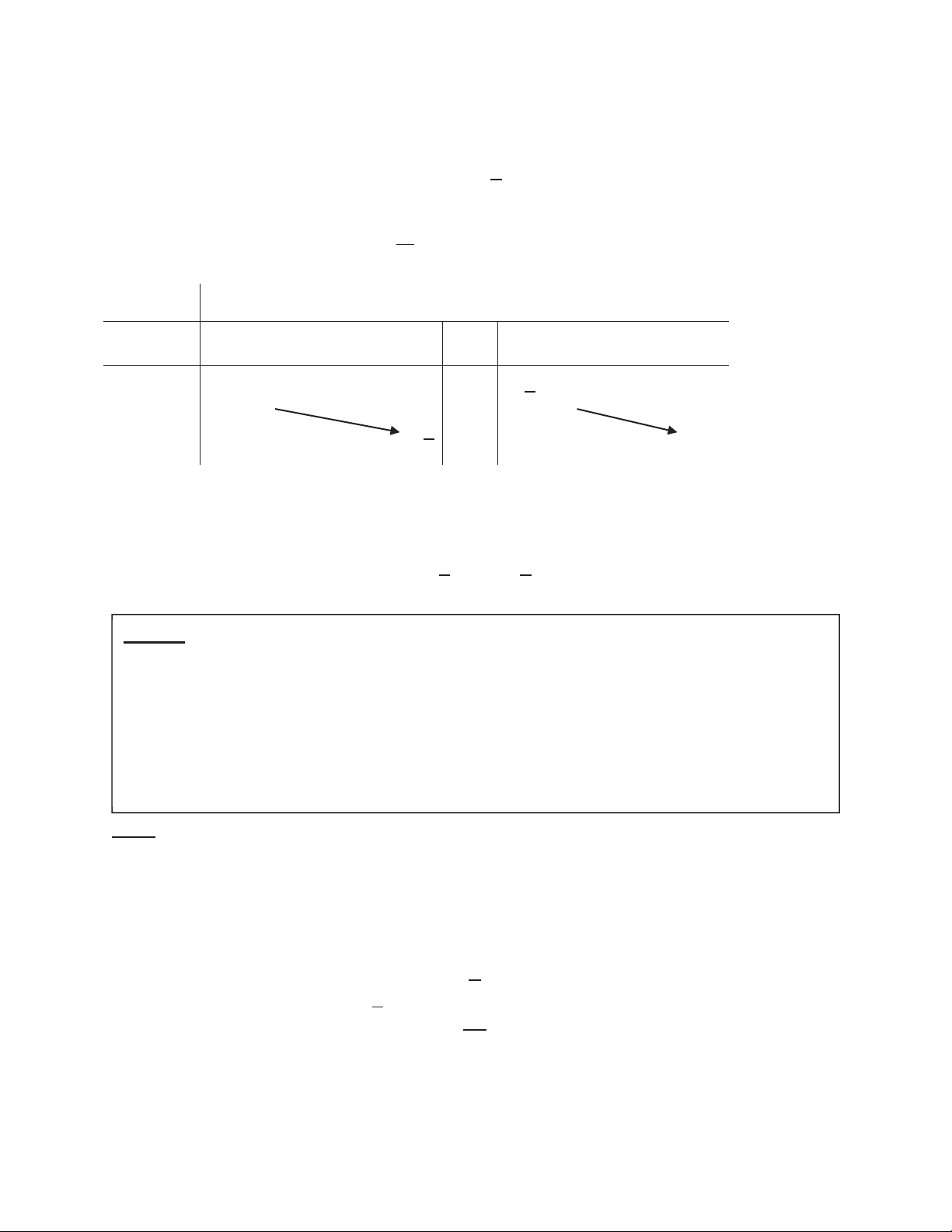
Hàm số ݕ ൌ ݔ là hàm lượng giác
ngược của hàm số ݔ ൌ ݕ, có một số tính chất cơ bản sau ߨ ߨ ۓ ݕ א ቀെ Ǣ ቁ ۖ ʹ ʹ ߨ ߨ
ሺ ݔሻ ൌ ݔǡ ݔ א ቀെ Ǣ ቁ ۔ ʹ ʹ ۖ ሺ ݔሻ ൌ ݔǡ ݔ א Թ ە ሺെݔሻ ൌ െ ݔ -
Hàm số ݕ ൌ ݔ là hàm lượng giác
ngược của hàm số ݔ ൌ ݕ, có một số tính chất cơ bản sau ݕ א ሺͲǢ ߨሻ
ሺ ݔሻ ൌ ݔǡ ݔ א ሺͲǢ ߨሻ ൞ ሺ ݔሻ ൌ ݔǡݔ א Թ ሺെݔሻ ൌ ߨ െ ݔ 1 TOANMATH.com
Chương 4 : Sơ lược về hàm lượng giác ngược II.
BÀI TẬP VÍ DỤ VỀ HÀM LƯỢNG GIÁC NGƯỢC ߨ ξʹ Ǥ ൌ ቆ ቆ ቇቇ ͳʹ ʹ ߨ ξʹ ൌ ξʹ ߨ ¿ ൞ Ͷ ʹ ߨ ߨ ߨ ² ቆ ቇ ൌ Ǥ¯×ǡ ʹ Ͷ א ቂെ Ǣ ቃ Ͷ ʹ ʹ ߨ ߨ ߨ ξ͵ ൌ ቀ ቁ ൌ ൌ ͳʹ Ͷ ͵ ʹ ʹߨ Ǥ ൌ ൬ ൰ ͵ ʹߨ ߨ ߨ ʹߨ ʹߨ ב ቂെ Ǣ ቃ ² ൬ ൰ ് Ǥậ ͵ ʹ ʹ ͵ ͵ ʹߨ ߨ ߨ ൌ ቀߨ െ ቁ ൌ ͵ ͵ ͵ Do đó, ʹߨ ߨ ߨ ൌ ൬ ൰ ൌ ቀ ቁ ൌ ͵ ͵ ͵ Ͷߨ Ǥ ൌ ൬ ൰ ͵ Ta thấy : Ͷߨ ߨ ߨ ൌ ቀߨ ቁ ൌ െ ͵ ͵ ͵ Do đó, Ͷߨ ߨ ߨ ߨ ʹߨ ൌ ൬
൰ ൌ ቀെ ቁ ൌ ߨ െ ቀ ቁ ൌ ߨ െ ൌ ͵ ͵ ͵ ͵ ͵ 2 TOANMATH.com
Chương 5 : Phương trình lượng giác CHƯƠNG 5
PHƯƠNG TRÌNH LƯỢNG GIÁC I.
PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN -
CÁC DẠNG PHƯƠNG TRÌNH CƠ BẢN
Ǥ ݑ ൌ ݒ ቂ ݑ ൌ ݒ ݇ʹߨ ሺ݇ א Ժሻ ݑ ൌ ߨ െ ݒ ݇ʹߨ
Ǥ ݑ ൌ ݒ ቂ ݑ ൌ ݒ ݇ʹߨ ሺ݇ א Ժሻ ݑ ൌ െݒ ݇ʹߨ ݑ ൌ ݒ ݇ߨ Ǥ ݑ ൌ ݒ ቊ ߨ ݑ ് ݇ߨሺ݇ א Ժሻ ʹ
Ǥ ݑ ൌ ݒ ቄݑ ൌ ݒ ݇ߨሺ݇ א Ժሻ ݑ ് ݇ߨ -
CÁC DẠNG PHƯƠNG TRÌNH CƠ BẢN ĐẶC BIỆT
ͳǤ ݑ ൌ Ͳ ݑ ൌ ݇ߨሺ݇ א Ժሻ ߨ
ʹǤ ݑ ൌ Ͳ ݑ ൌ ݇ߨሺ݇ א Ժሻ ʹ ߨ
͵Ǥ ݑ ൌ ͳ ݑ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ
ͶǤ ݑ ൌ ͳ ݑ ൌ ݇ʹߨሺ݇ א Ժሻ ߨ
ͷǤ ݑ ൌ െͳ ݑ ൌ െ ݇ʹߨሺ݇ א Ժሻ ʹ
Ǥ ݑ ൌ െͳ ݑ ൌ ߨ ݇ʹߨሺ݇ א Ժሻ ߨ ͳ ݑ ൌ ݇ʹߨ Ǥ ݑ ൌ ൦ ሺ݇ א Ժሻ ʹ ͷߨ ݑ ൌ ݇ʹߨ ͳ ߨ
ͺǤ ݑ ൌ ݑ ൌ േ ݇ʹߨሺ݇ א Ժሻ ʹ ͵ 3 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ξ͵ ݑ ൌ ݇ʹߨ ͻǤ ݑ ൌ ൦ ͵ ሺ݇ א Ժሻ ʹ ʹߨ ݑ ൌ ݇ʹߨ ͵ ξ͵ ߨ ͳͲǤ ݑ ൌ
ݑ ൌ േ ݇ʹߨሺ݇ א Ժሻ ʹ ߨ ͳ ݑ ൌ െ ݇ʹߨ ͳͳǤ ݑ ൌ െ ൦ ሺ݇ א Ժሻ ʹ ߨ ݑ ൌ ݇ʹߨ ͳ ʹߨ
ͳʹǤ ݑ ൌ െ ݑ ൌ േ ݇ʹߨሺ݇ א Ժሻ ʹ ͵ ߨ ξ͵ ݑ ൌ െ ݇ʹߨ ͳ͵Ǥ ݑ ൌ െ ൦ ͵ ሺ݇ א Ժሻ ʹ Ͷߨ ݑ ൌ ݇ʹߨ ͵ ξ͵ ͷߨ ͳͶǤ ݑ ൌ െ ݑ ൌ േ ݇ʹߨሺ݇ א Ժሻ ʹ Chú ý rằng: ߨ ߨ
ͳሻươ¿ ݔ ൌ ݉ሺ݉ א ሾെͳǢ ͳሿሻׯïộệộ ቂെ Ǣ ቃǤ ʹ ʹ Àệệ¯× ݉Ǥ
ʹሻươ¿ ݔ ൌ ݉ሺ݉ א ሾെͳǢ ͳሿሻ ׯïộệộሾͲǢ ߨሿǤ Àệệ¯× ݉Ǥ ߨ ߨ
͵ሻươ¿ ݔ ൌ ݉ሺ݉ א Թሻׯïộệộ ቀെ Ǣ ቁǤ ʹ ʹ Àệệ¯× ݉Ǥ
Ͷሻươ¿ ݔ ൌ ݉ሺ݉ א ԹሻׯïộệộሺͲǢ ߨሻǤ Àệệ¯× ݉Ǥ
Chúng ta sử dụng các công thức biến đổi lượng giác đã nêu trong Chương 2, phân tích
phương trình thành các nhân tử để xuất hiện các dạng phương trình trên. 4 TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 1: Giải các phương trình sau ξ͵ Ǥ ʹݔ ൌ ͳǤ ݔ ൌ െ ͵ ͳ Ǥ ͵ݔ ൌ Ǥ ʹݔ ൌ ͳ ʹ Giải: a. Ta có: ߨ ߨ
ʹݔ ൌ ͳ ʹݔ ൌ ݇ʹߨ ݔ ൌ ݇ߨሺ݇ א Ժሻ ʹ Ͷ b. Ta có: ͳ ߨ ߨ ݇ʹߨ
͵ݔ ൌ ͵ݔ ൌ േ ݇ʹߨ ݔ ൌ േ ሺ݇ א Ժሻ ʹ ͵ ͻ ͵ c. Ta có: ߨ ξ͵ ݔ ൌ െ ݇ߨ ߨ ݔ ൌ െ ൞
ݔ ൌ െ ݇ߨሺ݇ א Ժሻ ͵ ߨ ݔ ് ݇ߨ ʹ d. Ta có: ߨ ݇ߨ ݔ ൌ ͺ ʹ ߨ ݇ߨ ʹݔ ൌ ͳ ൞ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ ͺ ʹ ݔ ് ʹ
Bài 2: Giải các phương trình sau ͳ
Ǥ ሺݔ ʹሻ ൌ Ǥ ሺʹݔ െ ͳሻ ൌ ξ͵ ʹ
Ǥ ሺߨ െ ݔሻ ൌ ͳ Ǥ ሺ͵ݔ െ ͳሻ ൌ െξ͵ 5 TOANMATH.com
Chương 5 : Phương trình lượng giác Giải: a. Ta có: ߨ ߨ ͳ ݔ ʹ ൌ ݇ʹߨ ݔ ൌ ݇ʹߨ െ ʹ ሺݔ ʹሻ ൌ ൦ ൦ ሺ݇ א Ժሻ ʹ ͷߨ ͷߨ ݔ ʹ ൌ ݇ʹߨ ݔ ൌ ݇ʹߨ െ ʹ b. Ta có:
ሺߨ െ ݔሻ ൌ ͳ ߨ െ ݔ ൌ ݇ʹߨ ݔ ൌ ߨ ݇ʹߨሺ݇ א Ժሻ c. Ta có: ߨ ߨ ݇ߨ ͳ ʹݔ െ ͳ ൌ ݇ߨ ݔ ൌ
ሺʹݔ െ ͳሻ ൌ ξ͵ ൞ ͵ ʹ ʹ ߨ ൞ ʹݔ െ ͳ ് ݇ߨ ߨ ݇ߨ ͳ ʹ ݔ ് Ͷ ʹ ʹ ߨ ݇ߨ ͳ ݔ ൌ ሺ݇ א Ժሻ ʹ ʹ d. Ta có: ߨ ݇ߨ ͳ ߨ ݔ ൌ െ
ሺ͵ݔ െ ͳሻ ൌ െξ͵ ൞͵ݔ െ ͳ ൌ െ ݇ߨ ͳͺ ͵ ͵ ൞ ݇ߨ ͳ ͵ݔ െ ͳ ് ݇ߨ ݔ ് ͵ ͵ ߨ ݇ߨ ͳ ݔ ൌ െ ሺ݇ א Ժሻ ͳͺ ͵ ͵
Bài 3: Giải các phương trình sau ߨ ߨ
Ǥ ቀݔ ቁ ൌ ቀʹݔ ቁ Ͷ ͵ ߨ ߨ
Ǥ ቀݔ ቁ ൌ െ ቀʹݔ െ ቁ Ͷ ͵ Ǥ ݔ ൌ ሺݔ ߨሻ Giải: a. Ta có: ߨ ߨ ߨ ߨ ߨ ʹݔ ൌ ݔ ݇ߨ ݔ ൌ െ ݇ߨ
ቀݔ ቁ ൌ ቀʹݔ ቁ ൞ ͵ Ͷ ൞ Ͷ ͵ ߨ ߨ ߨ ݇ߨ ʹݔ ് ݇ߨ ͵ ʹ ݔ ് ͳʹ ʹ ߨ
ݔ ൌ െ ݇ߨሺ݇ א Ժሻ b. Ta có: ߨ ߨ ߨ ߨ
ቀݔ ቁ ൌ െ ቀʹݔ െ ቁ ቀݔ ቁ ൌ ሺʹݔ ሻ Ͷ ͵ Ͷ 6 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ߨ ߨ ʹݔ ൌ ݔ ݇ߨ ݔ ൌ ݇ߨ ߨ ൞ Ͷ ͳʹ ߨ ߨ ൞ ߨ ݇ߨ ݔ ൌ ݇ߨሺ݇ א Ժሻ ʹݔ ് ݇ߨ ͳʹ ʹ ݔ ് ʹ c. Ta có: ߨ ߨ ݔ ൌ െݔ െ ݇ʹߨ
ݔ ൌ ሺݔ ߨሻ ݔ ൌ ቀെݔ െ ቁ ൦ ʹ ʹ ߨ
ݔ ൌ ߨ ݔ ݇ʹߨ ʹ ߨ ݔ ൌ െ ݇ߨ ߨ ൦ Ͷ ͵ߨ
ݔ ൌ െ ݇ߨሺ݇ א Ժሻ Ͳݔ ൌ ݇ʹߨሺØýሻ Ͷ ʹ
Bài 4: Giải các phương trình sau ʹ Ǥ ݔ ݔ ൌ െ ݔ ݔ ݔ Ǥ െ ൌ Ͳ ͷݔ ͷݔ
Ǥ ሺʹ ݔ െ ͳሻሺʹ ݔ ݔሻ ൌ ʹݔ െ ݔ (Tuyển sinh khối D 2004) Giải: a. Điều kiện : ݇ߨ ݔ ് ሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với ͳ ʹ ൌ െ ݔ ݔ ݔ ߨ ͳ ݔ ൌ െ ݇ʹߨ ݔ ൌ െ ൦ ሺ݇ א Ժሻ ʹ ߨ ݔ ൌ ݇ʹߨ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. Ǥ Điều kiện : ݇ߨ
൜ ʹݔ ് Ͳ Ͷݔ ് Ͳ ֞ ݔ ് ሺ݇ א Ժሻሺכሻ ʹݔ ് Ͳ Ͷ
Phương trình tương đương với
ݔ ʹݔ െ ݔ ʹݔ ൌ Ͳ ݔ ൌ Ͳ ݔ ൌ ݇ߨ ሺ݇ א Ժሻ ʹݔ ʹݔ 7 TOANMATH.com
Chương 5 : Phương trình lượng giác
Kết hợp với ሺכሻ ta được nghiệm là ݔ ൌ ߨ ݉ʹߨሺ݉ א Ժሻ c. Ta có:
ሺʹ ݔ െ ͳሻሺʹ ݔ ݔሻ ൌ ʹݔ െ ݔ
ሺʹ ݔ െ ͳሻሺʹ ݔ ݔሻ ൌ ݔሺʹ ݔ െ ͳሻ
ሺʹ ݔ െ ͳሻሺ ݔ ݔሻ ൌ Ͳ ߨ
ξʹሺʹ ݔ െ ͳሻ ቀݔ ቁ ൌ Ͳ Ͷ ͳ ݔ ൌ ൦ ʹ ߨ ቀݔ ቁ ൌ Ͳ Ͷ ߨ ݔ ൌ േ ݇ʹߨ ൦ ͵ߨ ሺ݇ א Ժሻ ݔ ൌ െ ݇ߨ Ͷ
Bài 5: Giải các phương trình sau
Ǥξ͵ ሺʹݔ െ ͵ሻ െ ͳ ൌ Ͳ ǡ ݔ א ሾͻͲǢ ͳͺͲሿ
Ǥ ሺ͵ݔ ͳሻ ሺ͵ݔ െ ͳሻ ൌ Ͳ ǡ ݔ א ሾെߨǢ ߨሿ
Ǥ ͵ݔ െ Ͷ ʹݔ ͵ ݔ െ Ͷ ൌ Ͳ ǡ ݔ א ሾͲǢ ͳͶሿ (Tuyển sinh khối D 2002) Giải: a. Ta có:
ξ͵ ሺʹݔ െ ͵ሻ െ ͳ ൌ Ͳ (với ݔ א ሾͻͲǢ ͳͺͲሿ) ξ͵ ሺʹݔ െ ͵ሻ ൌ
൜ʹݔ െ ͵ ൌ ͵Ͳ ݇ͳͺͲ ͵
ʹݔ െ ͵ ് ͻͲ ݇ͳͺͲ
൜ݔ ൌ ͵͵ ݇ͻͲ ݔ ൌ ͵͵ ݇ͻͲሺ݇ א Ժሻ ݔ ് ͵ ݇ͻͲ Lại có:
ݔ א ሾͻͲǢ ͳͺͲሿ ቄͻͲ ͵͵ ݇ͻͲ ͳͺͲ ݇ א Ժ ͳͻ Ͷͻ ൝ ݇ ͵Ͳ ͵Ͳ ݇ א ሼͳሽ ݇ א Ժ
Vậy nghiệm của phương trình là ݔ ൌ ͳʹ͵ b. Ta có:
ሺ͵ݔ ͳሻ ሺ͵ݔ െ ͳሻ ൌ Ͳ (với ݔ א ሾെߨǢ ߨሿ) 8 TOANMATH.com
Chương 5 : Phương trình lượng giác ݇ߨ
ʹ ͵ݔ ͳ ൌ Ͳ ͵ݔ ൌ Ͳ ݔ ൌ ሺ݇ א Ժሻ ͵ Lại có: ݇ߨ
ݔ א ሾെߨǢ ߨሿ ൝െߨ ߨ ͵
ቄെ͵ ݇ ͵ ݇ א ሼͲǢ േͳǢ േʹǢ േ͵ሽ ݇ א Ժ ݇ א Ժ ߨ ʹߨ
ậệዚዛዓ¿ݔ א ൜ͲǢ േ Ǣ േ Ǣ േߨൠ ͵ ͵ c. Ta có:
͵ݔ െ Ͷ ʹݔ ͵ ݔ െ Ͷ ൌ Ͳ (với ݔ א ሾͲǢ ͳͶሿ)
Ͷ ଷ ݔ െ ͵ ݔ െ Ͷሺʹ ଶ ݔ െ ͳሻ ͵ ݔ െ Ͷ ൌ Ͳ
Ͷ ଶ ݔሺ ݔ െ ʹሻ ൌ Ͳ ݔ ൌ Ͳ
ݔ ൌ ʹ ͳሺạ¿ݔ ͳሻ ߨ
ݔ ൌ ݇ߨሺ݇ א Ժሻ ʹ Lại có: ߨ ͳ ͳͶ ͳ
ݔ א ሾͲǢ ͳͶሿ ቊͲ ݇ߨ ͳͶ ݇ െ ʹ ൝െ ʹ ߨ
ʹ ݇ א ሼͲǢ ͳǢ ʹǢ ͵ሽ ݇ א Ժ ݇ א Ժ ߨ ͵ߨ ͷߨ ߨ ậệủươ¿ݔ א ൜ Ǣ Ǣ Ǣ ൠ ʹ ʹ ʹ ʹ
Bài 6: Giải các phương trình sau ͷߨ ߨ ߨ Ǥ ൬ʹݔ ൰ െ ͵ ൬ݔ െ
൰ ൌ ͳ ʹ ݔ ǡ ݔ א ቂ ǡ ͵ߨቃ ʹ ʹ ʹ ͵ݔ െ ݔ Ǥ
ൌ ʹݔ ʹݔ ǡ ݔ א ሺͲǡʹߨሻ ξͳ െ ʹݔ Giải: a. Ta có : ͷߨ ߨ ൬ʹݔ
൰ ൌ ቀʹݔ ቁ ൌ ʹݔ ʹ ʹ ߨ ߨ ൬ݔ െ
൰ ൌ ቀݔ െ Ͷߨቁ ൌ െ ݔ ʹ ʹ
Như vậy, phương trình viết lại thành
ʹݔ ͵ ݔ ൌ ͳ ʹ ݔ ͳ
ʹ ʹݔ ൬ ݔ െ ൰ ൌ Ͳ ʹ 9 TOANMATH.com
Chương 5 : Phương trình lượng giác ݔ ൌ ݇ߨ ۍ ߨ ێ ݔ ൌ ݇ʹߨ ێ ሺ݇ א Ժሻ ێ ͷߨ ۏݔ ൌ ݇ʹߨ ߨ ߨ ͷߨ ͳߨ
¿ݔ א ቂ ǡ ͵ߨቃ ²ệủươ¿ݔ א ൜ߨǢ ʹߨǢ ͵ߨǢ Ǣ Ǣ ൠ ʹ ʹ b.
Phương trình tương đương với ʹ ʹݔ ݔ ߨ ൌ ξʹ ቀʹݔ െ ቁ ξʹȁ ݔȁ Ͷ
Nếu ݔ א ሺͲǡ ߨሻ thì ݔ Ͳ nên ߨ ߨ ݇ߨ
ʹݔ ൌ ቀʹݔ െ ቁ ݔ ൌ ሺ݇ א Ժሻ Ͷ ͳ ʹ Khi đó, ߨ ͻߨ ݔ א ൜ Ǣ ൠ ͳ ͳ
Nếu ݔ א ሺߨǡ ʹߨሻ thì ݔ ൏ Ͳ nên ߨ ͷߨ ݇ߨ
ʹݔ ൌ െ ቀʹݔ െ ቁ ݔ ൌ ሺ݇ א Ժሻ Ͷ ͳ ʹ Khi đó, ʹͳߨ ʹͻߨ ݔ א ൜ Ǣ ൠ ͳ ͳ ߨ ͻߨ ʹͳߨ ʹͻߨ ኼệủươ¿ݔ א ൜ Ǣ Ǣ Ǣ ൠ ͳ ͳ ͳ ͳ
Bài 7: Giải các phương trình sau
Ǥሺʹ ݔ െ ͳሻሺʹ ݔ ݔሻ ൌ ʹݔ െ ݔ (Tuyển sinh khối D 2004)
Ǥ ݔ ݔ ͳ ʹݔ ʹݔ ൌ Ͳ (Tuyển sinh khối B 2005) ݔ
Ǥ ݔ ݔ ቀͳ ݔ ቁ ൌ Ͷ ሺểnốʹͲͲሻ ʹ ͳ ͳ ߨ Ǥ ൌ Ͷ ൬
െ ݔ൰ሺểnốʹͲͲͺሻ ݔ ͵ߨ ቀݔ െ Ͷ ʹ ቁ Giải: a.
Phương trình tương đương với
ሺʹ ݔ െ ͳሻሺʹ ݔ ݔሻ ൌ ݔ ሺʹ ݔ െ ͳሻ
ሺʹ ݔ െ ͳሻሺ ݔ ݔሻ ൌ Ͳ 10 TOANMATH.com
Chương 5 : Phương trình lượng giác ͳ ݔ ൌ ൦ ʹ ߨ ξʹ ቀݔ ቁ ൌ Ͳ Ͷ ߨ ݔ ൌ േ ݇ʹߨ ൦ ͵ߨ ሺ݇ א Ժሻ ݔ ൌ െ ݇ߨ Ͷ b.
Phương trình tương đương với
ʹ ଶ ݔ ʹ ݔ ݔ ݔ ݔ ൌ Ͳ
ሺʹ ݔ ͳሻሺ ݔ ݔሻ ൌ Ͳ ʹߨ ݔ ൌ േ ݇ʹߨ ൦ ͵ߨ ሺ݇ א Ժሻ ݔ ൌ െ ݇ߨ Ͷ c. 0ều kiệnǣ ݔ ് Ͳ ݇ߨ ቐ ݔ ് Ͳ ݔ ʹݔ ് Ͳ ݔ ് ሺ݇ א Ժሻሺכሻ ് Ͳ Ͷ ʹ Ta thấy : ݔ ݔ ݔ ݔ ݔ ݔ ͳ ͳ ݔ ൌ ͳ ʹ ൌ ʹ ݔ ʹ ൌ ʹ ݔ ݔ ݔ ݔ ʹ ݔ ʹ
Do đó, phương trình tương đương với ߨ ͳ ݔ ൌ ݇ߨ
ݔ ݔ ൌ Ͷ ʹݔ ൌ ൦ ͳʹ ሺ݇ א Ժሻ ʹ ͷߨ ݔ ൌ ݇ߨ ͳʹ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. d. Điều kiện : ݔ ് Ͳ ൝ ͵ߨ ሺכሻ ൬ݔ െ ൰ ് Ͳ ʹ
Phương trình tương đương với ͳ ͳ ൌ െʹξʹሺ ݔ ݔሻ ݔ ݔ 11 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ۍݔ ൌ െ ݇ߨ ͺ ߨ ͳ ێ ͷߨ ቀݔ ቁ ൬ ξʹ൰ ൌ Ͳ ێ ሺ݇ א Ժሻ Ͷ ʹݔ ݔ ൌ ݇ߨ ێ ͺ ێ ߨ ۏݔ ൌ െ ݇ߨ Ͷ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình.
Bài 8: Tìm tất cả các giá trị nguyên của ݔ thỏa mãn ߨ
ቀ͵ݔ െ ඥͻݔଶ െ ͳݔ െ ͺͲቁ ൌ ͳ Ͷ
Giải: Phương trình tương đương với
ߨ ቀ͵ݔ െ ඥͻݔଶ െ ͳݔ െ ͺͲቁ ൌ ݇ʹߨሺ݇ א Ժሻ Ͷ
ඥͻݔଶ െ ͳݔ െ ͺͲ ൌ ͵ݔ െ ͺ݇ ͵ݔ െ ͺ݇ Ͳ
൜ͻݔଶ െ ͳݔ െ ͺͲ ൌ ሺ͵ݔ െ ͺ݇ሻଶ ͵ݔ െ ͺ݇ Ͳ ൝ Ͷͻ ሺכሻ
ͻݔ ൌ ͳʹ݇ Ͷ ͵݇ െ ͳ
Do đó, ͵݇ െ ͳ là ước nguyên của 49. Ta được : ͵݇ െ ͳ ൌ േͳǡ േǡ േͶͻ
Vì ݇ א Ժ nên ݇ ൌ Ͳǡ െʹǡ െͳ. Thay vào ሺכሻ, ta được ݔ ൌ െ͵ǡ െʹͳ 12 TOANMATH.com
Chương 5 : Phương trình lượng giác - BÀI TẬP TỰ LUYỆN
5.1.1. Giải các phương trình sau: ξ͵ Ǥ ʹݔ ൌ ͵ Ǥ ͳͲݔ ൌ ͳ ǤͶ ଶ ݔ െ ͵ ൌ Ͳ Ǥ͵ ݔ െ ʹ ൌ Ͳ
Ǥ ͳ ʹݔ ൌ ଶ ݔ ଶ ݔ
5.1.2. Giải các phương trình sau: ʹݔ ߨ Ǥ ൬ െ ൰ ൌ Ͳ ͵ ͵ ߨ
Ǥ ͳ ቀʹݔ െ ቁ ൌ Ͳ ݔ ߨ ξ͵ Ǥ ቀ ቁ ൌ ʹ ͵ ͵ Ǥ ଶሺݔ ͳሻ ൌ ͳ ߨ ξʹ Ǥ ʹ ቈ ቆ ݔ െ ͳ ቇ ൌ ξ͵ ʹ
5.1.3. Giải các phương trình sau: Ͷݔ Ǥ ݔ ൌ ൬ ͵ߨ൰ ͷ
Ǥ ሺʹݔ ߨሻ ൌ െ ݔ Ǥ ݔ ൌ െ ʹݔ ߨ
Ǥ ݔ ቀʹݔ ቁ ൌ Ͳ ͵
Ǥ ͷݔ െ ሺ͵ݔ Ɏሻ ൌ Ͳ
5.1.4. Giải các phương trình sau: ǤͶ ݔ ݔ ʹݔ ൌ ͳ ͳ
Ǥ ݔ ʹݔ Ͷݔ ͺݔ ͳݔ ͵ʹݔ ൌ Ͷݔ ݔ Ǥ ݔ ൌ ͳ ͳ ݔ
Ǥ ͵ݔ െ ʹݔ െ ݔ ൌ ʹݔ െ ݔ െ ͳ
Ǥ ሺͳ െ ݔሻሺͳ ʹݔሻ ൌ ͳ ݔ 13 TOANMATH.com
Chương 5 : Phương trình lượng giác
Ǥ ͳͲݔ ʹ ଶ Ͷݔ ͵ݔ ݔ ൌ ݔ ͺ ݔ ଷ ͵ݔ
ǤͶ ଷ ݔ ͵ ଶ ݔ െ ͵ ݔ െ ଶ ݔ ݔ ൌ Ͳ
Ǥ ݔ ݔ ൌ ʹሺ଼ ݔ ଼ ݔሻ Ǥ ଶ ݔ െ ݔ ͵ݔ ൌ ʹ
5.1.5. Giải các phương trình sau: ߨ ߨ
Ǥ ʹݔ ൌ ͳǡ ݔ א ቂെ Ǣ ቃ ʹ ʹ ߨ
Ǥ ݔ ͵ݔ ൌ Ͳǡ ݔ א ቂͲǢ ቃ ʹ
5.1.6. Giải các phương trình sau: ݔ
Ǥ ʹ ͵ ݔ ൌ ʹ ሺọcệnͳͻͻͺሻ ʹ ݔ െ ʹ ݔ ݔ Ǥ
ൌ ξ͵ሺ0ạiữͳͻͻͺሻ ʹ ଶ ݔ ݔ െ ͳ
Ǥ ݔ ʹݔ ͵ݔ ൌ ݔ ʹݔ ͵ݔ (ĐH Ngoại Thương 1999)
Ǥ ଶ ͵ݔ െ ଶ Ͷݔ ൌ ଶ ͷݔ െ ଶ ݔሺểnốʹͲͲʹሻ ݔ ߨ ݔ
Ǥ ଶ ቀ െ ቁ ଶ ݔ െ ଶ ൌ ͲሺểnốʹͲͲ͵ሻ ʹ Ͷ ʹ -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN
5.1.1.Nghiệm của phương trình là : ߨ ݇ߨ Ǥ ݔ ൌ ሺ݇ א Ժሻ ͳʹ ʹ ߨ ݇ߨ Ǥ ݔ ൌ ሺ݇ א Ժሻ ʹͲ ͷ ߨ ݔ ൌ േ ݇ʹߨ Ǥ ൦ ሺ݇ א Ժሻ ͷߨ ݔ ൌ േ ݇ʹߨ ʹ ݔ ൌ ݇ʹߨ Ǥ ൦ ͵ ʹ ሺ݇ א Ժሻ ݔ ൌ ߨ െ ݇ʹߨ ͵ ݇ߨ Ǥ ݔ ൌ ሺ݇ א Ժሻ ʹ 14 TOANMATH.com
Chương 5 : Phương trình lượng giác
5.1.2. Nghiệm của phương trình là : ߨ ͵݇ߨ Ǥ ݔ ൌ ሺ݇ א Ժሻ ʹ ʹ ߨ Ǥ ݔ ൌ ݇ߨሺ݇ א Ժሻ ͳʹ ߨ
Ǥݔ ൌ െ ݇ʹߨሺ݇ א Ժሻ ͵ ߨ ݔ ൌ ݇ʹߨ െ ͳ Ǥ ൦ ʹߨ ሺ݇ א Ժሻ ݔ ൌ െ ʹߨ െ ͳ ʹ ߨ
Ǥ ݔ ൌ ݇ߨ ሺെͳሻାଵǤ Ͷ
5.1.3. Nghiệm của phương trình là : ݔ ൌ ͳͷߨ ݇ͳͲߨ Ǥ ͳͲߨ ݇ͳͲߨ ሺ݇ א Ժሻ ݔ ൌ െ ͻ ͻ ߨ ݇ʹߨ ݔ ൌ Ǥ ൦ ͵ ߨ ሺ݇ א Ժሻ ݔ ൌ െ ݇ʹߨ ʹ ߨ ݔ ൌ ݇ʹߨ Ǥ ൦ ʹߨ ݇ʹߨሺ݇ א Ժሻ ݔ ൌ െ ͵ ߨ ݇ߨ Ǥݔ ൌ െ ሺ݇ א Ժሻ ͻ ͵ ߨ ݔ ൌ ݇ߨ Ǥ ൦ Ͷߨ ݇ߨሺ݇ א Ժሻ ݔ ൌ െ ͳ Ͷ 15 TOANMATH.com
Chương 5 : Phương trình lượng giác 5.1.4. a.
ử dụng công thức nhân đôi ʹܽ ൌ ʹ ܽ ܽ sẽ đưa phương trình trở thành : ߨ ݇ߨ Ͷݔ ൌ ͳ ֞ ݔ ൌ ሺ݇ א Ժሻ ͺ ʹ b.
Tương tự câu a, ta cũng sử dụng công thức nhân đôi ʹܽ ൌ ʹ ܽ ܽ sẽ đưa phương trình trở thành : ߨ ݇ߨ Ͷݔ ൌ ͳ ݔ ൌ ሺ݇ א Ժሻ ͳʹͺ ͵ʹ c. Điều kiện : ߨ
ቄ ݔ ് Ͳ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ ݔ ് െͳ ʹ
Phương trình tương đương với ߨ
ሺ ݔ ͳሻሺ ݔ െ ͳሻ ൌ Ͳ ቂ ݔ ൌ െͳ ݇ʹߨ ቈݔ ൌ െ ʹ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ݔ ൌ ͳ ݔ ൌ ݇ʹߨ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. d.
ệm của phương trình là : ߨ ۍݔ ൌ െ ݇ʹߨ ێ ߨ ێ ݔ ൌ ݇ʹߨ ێ ሺ݇ א Ժሻ ێ ݔ ൌ ݇ʹߨ ێ ߨ ݇ʹߨ ݔ ൌ ۏ ͵ ͵ e. Điều kiện : ߨ ݔ ് ݇ߨሺ݇ א Ժሻ ʹ ʹݐ 0ặݐ ൌ ݔ ฺ ʹݔ ൌ ͳ ݐଶ
Thay vào phương trình, ta được 16 TOANMATH.com
Chương 5 : Phương trình lượng giác ݔ ൌ ݇ʹߨ
ቂ ݐ ൌ Ͳ ቂ ݔ ൌ Ͳ ቈ ߨ ݐ ൌ െͳ ݔ ൌ െͳ
ݔ ൌ െ ݇ߨሺ݇ א Ժሻ Ͷ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. f.
Để ý : ʹ ଶ Ͷݔ ൌ ͳ ͺݔ và Ͷ ଷ ͵ݔ ൌ ͵ ͵ݔ െ ͻݔ
Phương trình có nghiệm ݔ ൌ ݇ʹߨሺ݇ א Ժሻ g.
Phương trình tương đương với
ሺͶ ଶ ݔ െ ͵ሻሺ ݔ െ ݔሻ ൌ Ͳ ߨ ݔ ൌ േ ݇ߨ ൦ ͵ ߨ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ Ͷ h.
Phương trình tương đương với :
ݔ ʹݔ െ ݔ ʹݔ ൌ Ͳ
ʹݔ ሺ ݔ െ ݔሻ ൌ Ͳ ߨ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ Ͷ ʹ i. Điều kiện :
ቄ ݔ ് Ͳ ֞ ͵ݔ ് Ͳሺכሻ ͵ݔ ് Ͳ
Phương trình tương đương với ݔ ݔ ͵ݔ ൬ െ ൰ ൌ ʹ ݔ ݔ ͵ݔ
ݔ ሺ ݔ ͵ݔ െ ͵ݔ ݔሻ ൌ ʹ ଶ ݔ ͵ݔ
െ ʹ ݔ ʹݔ ൌ ʹଶ ݔ ͵ݔ
െ ଶ ݔ ൌ ݔ ͵ݔሺ ݔ ് Ͳሻ
ʹݔ െ ͳ ൌ Ͷݔ ʹݔ 17 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ݇ߨ
Ͷݔ ൌ െͳ ֞ ݔ ൌ ሺ݇ א Ժሻ Ͷ ʹ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. 5.1.5. a. Ta có: ͳ ߨ ߨ ߨ
ʹݔ ൌ ቀݔ א ቂെ Ǣ ቃቁ ݔ ൌ ݇ߨሺ݇ א Ժሻ ʹ ʹ ʹ Ͷ ại có: ߨ ߨ ߨ ߨ ߨ
ݔ א ቂെ Ǣ ቃ ቊെ ݇ߨ ֞ ݇ א ሼͲሽ ʹ ʹ ʹ Ͷ Ͷ ݇ א Ժ ߨ ኼệủươ¿ݔ ൌ Ͷ Ǥ Ta có: ߨ ߨ ݔ ൌ ݉ߨ
ݔ ͵ݔ ൌ Ͳ ቀݔ א ቂͲǢ ʹ
ቃቁ ʹ ʹݔ ݔ ൌ Ͳ ൦ ሺ݉ǡ ݊ א Ժሻ ʹ ߨ ݊ߨ ݔ ൌ Ͷ ʹ ại có: ߨ ߨ ۍቊͲ ݉ߨ ʹ ʹ ߨ ێ ݉ א ሼͲሽ ݔ א ቂͲǢ ቃ ݉ א Ժ ʹ ێ ߨ ݊ߨ ߨ ݊ א ሼͲሽ ێ ቊͲ Ͷ ʹ ʹ ۏ ݊ א Ժ ߨ ߨ
ኼዉዚዛዓ¿ݔ א ቄ Ǣ ቅ Ͷ ʹ 5.1.6. a. Gợi ý : ݔ ͳ െ ݐଶ 0ặݐ ൌ ฺ ݔ ൌ ʹ ͳ ݐଶ ߨ
ệủươ¿ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ 18 TOANMATH.com
Chương 5 : Phương trình lượng giác b. Điều kiện: ݔ ് ͳ ൝ ͳሺכሻ ݔ ് െ ʹ
ương trình tương đương với
ݔ െ ʹݔ ൌ ξ͵ሺെʹ ଶ ݔ ݔ ͳሻ
ݔ െ ʹݔ ൌ ξ͵ ʹݔ ξ͵ ݔ ߨ ߨ
ቀݔ ቁ ൌ ቀʹݔ െ ቁ ͵ ߨ ݔ ൌ ݇ʹߨ ൦ ʹߨ ݇ʹߨሺ݇ א Ժሻ ݔ ൌ െ ͳͺ ͵
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. c.
Phương trình tương đương với
ʹ ʹݔ ݔ ʹݔ ൌ ʹ ʹݔ ݔ ʹݔ
ሺʹ ݔ ͳሻሺ ʹݔ െ ʹݔሻ ൌ Ͳ ʹߨ ݔ ൌ േ ݇ʹߨ ൦ ͵ ߨ ݇ߨ ሺ݇ א Ժሻ ݔ ൌ ͺ ʹ d.
Phương trình tương đương với ͳ ͳ ͳ ͳ
ሺͳ െ ݔሻ െ ሺͳ ͺݔሻ ൌ ሺͳ െ ͳͲݔሻ െ ሺͳ ͳʹݔሻ ʹ ʹ ʹ ʹ
ͺݔ െ ݔ ൌ ͳʹݔ െ ͳͲݔ
ݔ ሺ ͳͳݔ െ ݔሻ ൌ Ͳ ߨ ۍݔ ൌ ݇ߨ ʹ ێ ݇ߨ ێ ݔ ൌ െ ሺ݇ א Ժሻ ێ ʹ ێ ݇ߨ ۏ ݔ ൌ ͻ 19 TOANMATH.com
Chương 5 : Phương trình lượng giác e. Điều kiện : ߨ
ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với
ሺͳ െ ݔሻሺͳ െ ݔሻሺͳ ݔሻ െ ሺͳ ݔሻ ൌ Ͳ ሺͳ െ ݔሻሺͳ ݔሻ
ሺ ݔ ͳሻሺ ݔ ݔሻ ൌ Ͳ ݔ ൌ ߨ ݇ʹߨ ቈ ߨ
ݔ ൌ െ ݇ߨሺ݇ א Ժሻ Ͷ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. II.
CÁC DẠNG PHƯƠNG TRÌNH LƯỢNG GIÁC ĐƯA VỀ PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN 1.
PHƯƠNG TRÌNH BẬC HAI
- Phương trình bậc hai theo các hàm số lượng giác là những phương trình có dạng sau: x ܽ ଶ ݔ ܾ ݔ ൌ ܿ x ܽ ଶ ݔ ܾ ݔ ൌ ܿ x ܽ ଶ ݔ ܾ ݔ ൌ ܿ x ܽ ଶ ݔ ܾ ݔ ൌ ܿ
- Cách giải phương trình này thì ta sẽ coi các ẩn ݔǡ ݔ ǡ ݔ ǡ ݔ là các
nghiệm của phương trình ܽݐଶ ܾݐ ܿ ൌ Ͳሺܽ ് Ͳሻ, đồng thời lưu ý đến các điều kiện của ݐ.
- Chúng ta cũng sử dụng những phép biến đổi lượng giác để đưa phương trình ban
đầu về các phương trình loại này.
Lưu ý các công thức lượng giác sau: x ଶ ݔ ଶ ݔ ൌ ͳ
x ସ ݔ ସ ݔ ൌ ͳ െ ʹ ଶ ݔ ଶ ݔ
x ݔ ݔ ൌ ͳ െ ͵ ଶ ݔ ଶ ݔ 20 TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 1: Giải các phương trình sau
Ǥʹ ଶ ݔ ͵ ݔ െ ͷ ൌ ͲǤʹ ଶ ʹݔ ͵ ʹݔ ͳ ൌ Ͳ
Ǥ ସ ݔ െ ʹ ଶ ݔ ͳ ൌ ͲǤ ଶ ݔ ʹ ݔ െ ͵ ൌ Ͳ Giải: a.
Phương trình tương đương với ݔ ൌ ͳ ߨ ͷ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ݔ ൌ െ ൏ െͳሺ ạ¿ ݔ െͳሻ ʹ ʹ b. Ta có: ߨ ʹݔ ൌ െͳ ݔ ൌ ݇ߨ
ʹ ଶ ʹݔ ͵ ʹݔ ͳ ൌ Ͳ ൦ ʹ ͳ ൦ ሺ݇ א Ժሻ ʹݔ ൌ െ ߨ ʹ ݔ ൌ േ ݇ߨ ͵ c. Điều kiện: ߨ
ݔ ് Ͳ ֞ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với ߨ ݔ ൌ ݇ߨ
ሺଶ ݔ െ ͳሻଶ ൌ Ͳ ൦ ݔ ൌ ͳ ൦ Ͷ ሺ݇ א Ժሻ ݔ ൌ െͳ ߨ ݔ ൌ െ ݇ߨ Ͷ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. d. Điều kiện:
ݔ ് Ͳ ֞ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ
Phương trình tương đương với ߨ ݔ ൌ ݇ߨ ݔ ൌ ͳ ሺ݇ א Ժሻ ݔ ൌ െ͵ Ͷ ݔ ൌ ሺെ͵ሻ ݇ߨ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. 21 TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 2: Giải các phương trình sau ͳ ͳ
Ǥ ସ ݔ ସ ݔ ൌ ʹݔ െ Ǥ ସ ݔ ସ ݔ ൌ െ ʹݔ ʹ ʹ ସ ݔ ସ ݔ ͳ ͳͳ Ǥ
ൌ െ ʹݔ Ǥ ସ ݔ ସ ݔ ൌ െ ʹݔ ଶ ݔ െ ଶ ݔ ʹ ͺ Giải: a.
Phương trình tương đương với ͳ
ͳ െ ʹ ଶ ݔ ଶ ݔ ൌ ʹݔ െ ʹ
ଶ ʹݔ ʹ ʹݔ െ ͵ ൌ Ͳ ݔ ൌ ͳ
ݔ ൌ െ͵ ൏ െͳሺạሻ ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ b.
Phương trình tương đương với ͳ
ͳ െ ʹ ଶ ݔ ଶ ݔ ൌ െ ʹݔ ʹ ଶ ʹݔ ͳ ͳ െ ൌ െ ʹݔ ʹ ʹ
ଶ ʹݔ ʹݔ െ ʹ ൌ Ͳ ݔ ൌ ͳ
ݔ ൌ െʹ ൏ െͳሺሻ ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ c. Điều kiện: ߨ ݇ߨ
൜ଶ ݔ െ ଶ ݔ ് Ͳ ʹݔ ് Ͳ ݔ ് ሺ݇ א Ժሻሺכሻ ʹݔ ് Ͳ Ͷ ʹ
Phương trình tương đương với 22 TOANMATH.com
Chương 5 : Phương trình lượng giác ସ ݔ ସ ݔ ʹݔ ͳ ൌ െ
ସ ݔ ସ ݔ ൌ െ ʹݔ ʹݔ ʹ ʹݔ ʹ
Đây chính là câu b của bài này.
Nghiệm của phương trình là: ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. d.
Phương trình tương đương với ͳͳ ͳ െ ʹ ଶ ݔ ଶ ݔ ൌ െ ʹݔ ͺ ଶ ʹݔ ͳͳ ͳ െ ൌ െ ʹݔ ʹ ͺ
Ͷଶ ʹݔ െ ͺ ʹݔ ͵ ൌ Ͳ ͳ ʹݔ ൌ ൦ ʹ ͵ ʹݔ ൌ ͳሺạሻ ʹ ߨ ݔ ൌ ݇ߨ ͳʹ ൦ ͷߨ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ ͳʹ
Bài 3: Giải các phương trình sau: ߨ ߨ
Ǥ ଶ ቀݔ ቁ ʹ ቀെݔ ቁ ൌ ͵ ͵
Ǥ ସ ʹݔ ସ ʹݔ ൌ ʹݔ ʹݔ ͳ Ǥ ଼ ݔ ଼ ݔ ൌ ଶ ʹݔ ͳ
Ǥ ݔ ݔ െ ʹݔ ൌ Ͳ ݔ ݔ Ǥ ସ ଶ ൌ ͳ ͷ ͷ 23 TOANMATH.com
Chương 5 : Phương trình lượng giác Giải: a.
Phương trình tương đương với ߨ ߨ
ଶ ቀݔ ቁ ʹ ቀݔ ቁ െ ͵ ൌ Ͳ ͵ ͵ ߨ ቀݔ ቁ ൌ ͳ ൦ ͵ ߨ
ቀݔ ቁ ൌ െ͵ ൏ െͳሺạሻ ͵ ߨ
ݔ ൌ െ ݇ʹߨሺ݇ א Ժሻ ͵ b.
Phương trình tương đương với
ͳ െ ʹ ଶ ʹݔ ଶ ʹݔ ൌ ʹݔ ʹݔ
ʹ െ ሺʹ ʹݔ ʹݔሻଶ ൌ ʹ ʹݔ ʹݔ
ଶ Ͷݔ Ͷݔ െ ʹ ൌ Ͳ Ͷݔ ൌ ͳ
Ͷݔ ൌ െʹ ൏ െͳሺạሻ ߨ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ ͺ ʹ c. Ta có:
଼ ݔ ଼ ݔ ൌ ሺସ ݔ ସ ݔሻଶ െ ʹ ସ ݔ ସ ݔ
ൌ ሺͳ െ ʹ ଶ ݔ ଶ ݔሻଶ െ ʹ ସ ݔ ସ ݔ ଶ ʹݔ ଶ ͳ ൌ ቆͳ െ ቇ െ ସ ʹݔ ʹ ͺ
Khi đó, phương trình tương đương: ଶ ʹݔ ଶ ͳ ͳ ͳ ቆͳ െ ቇ െ ସ ʹݔ ൌ െ ଶ ʹݔ ʹ ͺ ͳ ͳ
ʹ ସ ʹݔ ଶ ʹݔ െ ͳ ൌ Ͳ 24 TOANMATH.com
Chương 5 : Phương trình lượng giác ଶ ʹݔ ൌ െͳሺạሻ ͳ ଶ ʹݔ ൌ ʹ ͳ
ଶ ʹݔ ൌ ֞ Ͷݔ ൌ Ͳ ʹ ߨ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ ͺ Ͷ d.
Phương trình tương đương với
ͳ െ ͵ ଶ ଶ ݔ െ ʹݔ ൌ Ͳ
͵ ଶ ʹݔ Ͷ ʹݔ െ Ͷ ൌ Ͳ ʹ ʹݔ ൌ ͵
ʹݔ ൌ െʹ ൏ െͳሺạሻ ʹ ۍ ቀ ێ ݔ ൌ ͵ቁ ݇ߨ ێ ʹ ሺ݇ א Ժሻ ێ ʹ ێ ߨ െ ቀ͵ቁ ۏݔ ൌ ݇ߨ ʹ e.
Phương trình tương đương với ݔ ݔ ସ ͳ െ ଶ ൌ ͳ ͷ ͷ ݔ ݔ ସ െ ଶ ൌ Ͳ ͷ ͷ ݔ ଶ ൌ Ͳ ͷ ൦ ݔ ଶ ൌ ͳ ͷ ݔ ൌ Ͳ ൦ ͷ ݔ ൌ Ͳ ͷ 25 TOANMATH.com
Chương 5 : Phương trình lượng giác ͷߨ ݔ ൌ ݇ͳͲߨ ʹ ሺ݇ א Ժሻ ݔ ൌ ݇ͷߨ
Bài 4: Giải các phương trình sau:
ݔ ൫ʹ ݔ ͵ξʹ൯ െ ʹ ଶ ݔ െ ͳ Ǥ ൌ ͳ ͳ ʹݔ Ɏ Ɏ
Ǥ ቀʹݔ ቁ ቀʹݔ െ ቁ Ͷ ݔ ൌ ʹ ξʹሺͳ െ ݔሻ Ͷ Ͷ
Ǥ͵ ଶ ݔ ʹξʹ ଶ ݔ ൌ ൫ʹ ξʹ൯ ݔ
Ͷ ଶ ʹݔ ଶ ݔ െ ͻ െ ͵ ʹݔ Ǥ ൌ Ͳ ݔ
Ǥ ʹݔ ሺ ݔ ʹݔሻ ൌ Ͷ ଶ ݔ Giải: a. Điều kiện: ߨ
ʹݔ ് െͳ ֞ ݔ ് െ ݇ߨሺ݇ א Ժሻሺכሻ Ͷ
Phương trình tương đương với
ʹ ݔ ݔ ͵ξʹ ݔ െ ʹ ଶ ݔ െ ͳ ൌ ͳ ʹݔ
ʹ ଶ ݔ െ ͵ξʹ ݔ ʹ ൌ Ͳ ξʹ ݔ ൌ ʹ ݔ ൌ ξʹ ͳሺạሻ ߨ
ݔ ൌ േ ݇ʹߨሺ݇ א Ժሻ Ͷ
Kết hợp với ሺכሻ, ta nhận nghiệm ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ Ͷ 26 TOANMATH.com
Chương 5 : Phương trình lượng giác b.
Phương trình tương đương với ߨ ߨ ߨ ߨ ʹݔ ʹݔ ʹ ቌ Ͷ ʹݔ െ Ͷቍ ቌ
Ͷ െ ʹݔ Ͷቍ Ͷ ݔ ൌ ʹ ξʹሺͳ െ ݔሻ ʹ ʹ ߨ
ʹ ʹݔ Ͷ ݔ െ ʹ െ ξʹ ξʹ ݔ ൌ Ͳ Ͷ
ξʹ ʹݔ ൫Ͷ ξʹ൯ ݔ െ ʹ െ ξʹ ൌ Ͳ
ʹξʹ ଶ ݔ െ ൫Ͷ ξʹ൯ ݔ ʹ ൌ Ͳ ͳ ݔ ൌ ʹ ݔ ൌ ξʹ ͳሺạሻ ߨ ݔ ൌ ݇ʹߨ ൦ ͷߨ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ c. Điều kiện:
ݔ ് Ͳ ֞ ݔ ് ݇ߨሺכሻ
Phương trình tương đương với ଶ ݔ ͵
ʹξʹ ଶ ݔ ൌ ൫ʹ ξʹ൯ ݔ ଶ ݔ ଶ ݔ ൫ʹ ξʹ൯ ݔ ͵ െ ʹξʹ ൌ Ͳ ସ ݔ ଶ ݔ ݔ 0ặݐ ൌ Ǥ ươ¿ở ଶ ݔ ݐ ൌ ξʹ
͵ݐଶ െ ൫ʹ ξʹ൯ݐ ʹξʹ ൌ Ͳ ʹ ݐ ൌ ͵ Khi ݐ ൌ ξʹ, ta có:
ξʹ ଶ ݔ ݔ െ ξʹ ൌ Ͳ 27 TOANMATH.com
Chương 5 : Phương trình lượng giác ξʹ ݔ ൌ ʹ ݔ ൌ ξʹ ͳሺạሻ ߨ
ݔ ൌ േ ݇ʹߨሺ݇ א Ժሻ Ͷ ʹ ݐ ൌ ǡ ×ǣ ͵ ݔ ʹ ݔ ʹ ൌ ൌ ଶ ݔ ͵ ͳ െ ଶ ݔ ͵
ʹ ଶ ݔ ͵ ݔ െ ʹ ൌ Ͳ ͳ ݔ ൌ ʹ
ݔ ൌ െʹ ൏ െͳሺạሻ ߨ
ݔ ൌ േ ݇ʹߨሺ݇ א Ժሻ ͵
Kết hợp với ሺכሻ, ta nhận các nghiệm trên là nghiệm của phương trình. d. Điều kiện:
ݔ ് Ͳ ଶ ݔ ് Ͳ ʹݔ ് െͳሺכሻ
Phương trình tương đương với
Ͷሺͳ െ ଶ ʹݔሻ ͵ሺͳ െ ʹݔሻ െ ͻ െ ͵ ʹݔ ൌ Ͳ
ʹ ଶ ʹݔ ͵ ʹݔ ͳ ൌ Ͳ
ʹݔ ൌ െͳ൫ạሺכሻ൯ ͳ ʹݔ ൌ െ ʹ ߨ
ݔ ൌ േ ݇ߨሺ݇ א Ժሻ ͵
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. 28 TOANMATH.com
Chương 5 : Phương trình lượng giác e. Điều kiện:
ቄ ݔ ് Ͳ ቄ ʹݔ ് ͳሺכሻ ʹݔ ് Ͳ ʹݔ ് Ͳ
Phương trình tương đương với ଶ ʹݔ ʹ ଶ ݔ ൌ Ͷ ଶ ݔ ʹݔ ͳ െ ଶ ʹݔ ൌ ʹ ଶ ݔ ʹݔ
ͳ െ ଶ ʹݔ ൌ ʹݔ ሺ ʹݔ ͳሻ
ʹ ଶ ʹݔ ʹݔ െ ͳ ൌ Ͳ ʹݔ ൌ െͳ ͳ ʹݔ ൌ ʹ ݔ ൌ ߨ ݇ʹߨ ߨ
ݔ ൌ േ ݇ʹߨሺ݇ א Ժሻ ͵
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình.
Bài 5: Giải các phương trình sau: ߨ ߨ
Ǥ ସ ݔ ସ ݔ ൌ ቀݔ ቁ ቀ െ ݔቁሺ0ộͳͻͻͻሻ ͺ ͵
Ǥͷ ݔ െ ʹ ൌ ͵ሺͳ െ ݔሻ ଶ ݔ ൫ểnốʹͲͲͶ൯
Ǥ ଶ ͵ݔ ʹݔ െ ଶ ݔ ൌ Ͳ൫ểnốʹͲͲͷ൯ ߨ ߨ ͵
Ǥ ସ ݔ ସ ݔ ቀݔ െ ቁ ቀ͵ݔ െ ቁ െ ൌ Ͳ൫ểnốʹͲͲͷ൯ Ͷ Ͷ ʹ
ʹሺ ݔ ݔሻ െ ݔ ݔ Ǥ ൌ Ͳ ൫ểnốʹͲͲ൯ ξʹ െ ʹ ݔ 29 TOANMATH.com
Chương 5 : Phương trình lượng giác Giải: a. Điều kiện : ߨ ߨ ቀݔ ቁ ് Ͳ ݔ ് െ ݇ߨ ൞ ͵ ͵ ߨ ൞ ߨ ሺ݇ א Ժሻሺכሻ ቀ െ ݔቁ ് Ͳ ݔ ് ݇ߨ
Phương trình tương đương với ͳ െ ʹ ଶ ݔ ଶ ݔ ൌ ͺ ଶ ʹݔ ͳ െ ൌ ʹ ͺ ۍ ξʹ ʹݔ ൌ ێ ʹ ێ ێ ξʹ ۏ ʹݔ ൌ െ ʹ ߨ ۍ ݔ ൌ ݇ߨ ͺ ێ ͵ߨ ێ ݔ ൌ ݇ߨ ێ ͺ ሺ݇ א Ժሻ ێ ߨ ݔ ൌ െ ݇ߨ ێ ͺ ێ ͷߨ ۏ ݔ ൌ ݇ߨ ͺ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. b. Điều kiện : ߨ
ݔ ് Ͳ ֞ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với ͵ሺͳ െ ݔሻ ଶ ݔ ͷ ݔ െ ʹ ൌ ଶ ݔ ͵ሺͳ െ ݔሻ ଶ ݔ ͷ ݔ െ ʹ ൌ ሺͳ െ ݔሻሺͳ ݔሻ 30 TOANMATH.com
Chương 5 : Phương trình lượng giác ͵ ଶ ݔ ͷ ݔ െ ʹ ൌ ͳ ݔ
ʹ ଶ ݔ ͵ ݔ െ ʹ ൌ Ͳ ͳ ݔ ൌ ʹ
ݔ ൌ െʹ ൏ െͳሺạሻ ߨ ݔ ൌ ݇ʹߨ ൦ ͷߨ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. c.
Phương trình tương đương với
ʹ ଶ ͵ݔ ʹݔ െ ʹ ଶ ݔ ൌ Ͳ
ሺ ݔ ͳሻ ʹݔ െ ʹݔ െ ͳ ൌ Ͳ ݔ ʹݔ െ ͳ ൌ Ͳ
Ͷ ସ ʹݔ െ ͵ ଶ ʹݔ െ ͳ ൌ Ͳ ଶ ʹݔ ൌ ͳ ͳ ଶ ʹݔ ൌ െ ሺØýሻ Ͷ ʹݔ ൌ Ͳ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ Ͷ d.
Phương trình tương đương với ߨ ߨ
ʹሺͳ െ ʹ ଶ ݔ ଶ ݔሻ ʹ ቀݔ െ ቁ ݏ݅݊ ቀ͵ݔ െ ቁ െ ͵ ൌ Ͳ Ͷ Ͷ ߨ
െ ଶ ʹݔ ቀͶݔ െ ቁ ሺʹݔሻ െ ͳ ൌ Ͳ ʹ
െ ଶ ʹݔ െ Ͷݔ ʹݔ െ ͳ ൌ Ͳ
ଶ ʹݔ ʹݔ െ ʹ ൌ Ͳ 31 TOANMATH.com
Chương 5 : Phương trình lượng giác ʹݔ ൌ ͳ
ʹݔ ൌ െʹ ൏ െͳሺạሻ ߨ
ݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ e. Điều kiện : ξʹ
ξʹ െ ʹ ݔ ് Ͳ ֞ ݔ ് ሺכሻ ʹ
Phương trình tương đương với
ʹ െ ଶ ݔ ଶ ݔ െ ݔ ݔ ൌ Ͳ ͵ ଶ ʹݔ ʹݔ ʹ െ െ ൌ Ͳ ʹ ʹ ݔ ൌ ͳ Ͷ
ݔ ൌ െ ൏ െͳሺạሻ ͵ ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. - BÀI TẬP TỰ LUYỆN
5.2.1. Giải các phương trình sau:
Ǥ ଶ ݔ െ ൫ξ͵ െ ͳ൯ ݔ െ ξ͵ ൌ Ͳ
Ǥ ଶ ݔ Ͷ ݔ െ Ͷ ൌ Ͳ Ǥͳ Ͷݔ ൌ ʹݔ Ǥʹ ʹݔ ݔ ൌ ͳ
Ǥ ʹ ଶ ʹݔ െ ʹ൫ʹ ξʹ൯ ݔ ݔ ξʹ ൌ Ͳ
Ǥ ʹݔ ൫ͳͲ െ ξ͵൯ ݔ ͷξ͵ െ ͳ ൌ Ͳ ߨ ߨ
Ǥ ଶ ቀ ʹݔቁ െ ଶ ʹݔ െ ͵ ቀ െ ʹݔቁ ʹ ൌ Ͳ ʹ ʹ 32 TOANMATH.com
Chương 5 : Phương trình lượng giác
5.2.2. Giải các phương trình sau:
Ǥ ͷሺͳ ݔሻ ൌ ʹ ସ ݔ െ ସ ݔ ʹ ߨ ͳ
Ǥ ସ ݔ ସ ݔ ൌ ଶ ቀݔ ቁ ͵ Ͷ ͵ ସ ݔ ସ ݔ ͳ ͳ Ǥ ൌ ʹݔ െ ͷ ʹݔ ʹ ͺ ʹݔ ͷ ߨ ߨ ʹͳ Ǥ ସ ݔ ସ ݔ ൌ െ
ቀݔ െ ቁ ቀ͵ݔ െ ቁ ͳʹ Ͷ Ͷ ʹͶ
5.2.3. Giải các phương trình sau: ͳ ʹ Ǥ Ͷͺ െ െ ሺͳ ʹݔ ݔሻ ൌ Ͳ ସ ݔ ଶ ݔ ସ ʹݔ ସ ʹݔ Ǥ ߨ ߨ ൌ ସ Ͷݔ
ቀͶ െ ݔቁ ቀͶ ݔቁ ߨ
Ǥ ଷ ቀݔ െ ቁ ൌ ݔ െ ͳ Ͷ ʹ Ͷ Ǥ ݔ ൌ ݔ ʹݔ ͳ
Ǥ ସ ݔ ସ ݔ ൌ ʹ ݔ ݔ െ ଶ ʹݔ ʹ ͷ ͷ
Ǥ ସ ݔ ସ ݔ ൌ ʹݔ െ ʹ ͺ
ʹሺସ ݔ ସ ݔሻ െ Ͷ ݔ ݔ ͳ Ǥ ൌ Ͳ ξʹ െ ʹ ݔ 33 TOANMATH.com
Chương 5 : Phương trình lượng giác -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN
5.2.1. Nghiệm của phương trình là : ߨ ݔ ൌ െ ݇ߨ Ǥ ൦ Ͷ ߨ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ ͵ Ǥ ݔ ൌ ݇ߨሺ݇ א Ժሻ ߨ ݇ߨ ݔ ൌ Ǥ ൦ Ͷ ʹ ߨ ሺ݇ א Ժሻ ݔ ൌ േ ݇ߨ ݔ ൌ ߨ ݇ʹߨ Ǥ ͵ ሺ݇ א Ժሻ ݔ ൌ േ ൬ ൰ ݇ʹߨ Ͷ ߨ ۍ ݔ ൌ ݇ߨ ێ Ͷ ߨ
Ǥ ێ ݔ ൌ ݇ߨ ሺ݇ א Ժሻ ێ ͺ ێ ͵ߨ ۏݔ ൌ ݇ߨ ͺ ߨ ݔ ൌ െ ݇ʹߨ Ǥ ൦ ͵ Ͷߨ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ ͵ ߨ ۍ ݔ ൌ ݇ߨ ێ Ͷ ߨ
Ǥ ێ ݔ ൌ ݇ʹߨ ሺ݇ א Ժሻ ێ ێ ͷߨ ۏݔ ൌ ݇ʹߨ 5.2.2. a.
Phương trình tương đương với
ͷሺͳ ݔሻ ൌ ʹ ሺଶ െ ଶ ݔሻሺଶ ݔ ଶ ݔሻ
ͷ ͷ ݔ ൌ ʹ ͳ െ ଶ ݔ െ ଶ ݔ 34 TOANMATH.com
Chương 5 : Phương trình lượng giác
ʹ ଶ ݔ ͷ ݔ ͵ ൌ Ͳ ݔ ൌ െͳ ͵
ݔ ൌ െ ൏ െͳሺạሻ ʹ
ݔ ൌ ߨ ݇ʹߨሺ݇ א Ժሻ b.
Phương trình tương đương với ͳ ߨ ͳ
ͳ െ ʹ ଶ ݔ ଶ ݔ ൌ ቂͳ െ ቀʹݔ ቁቃ ͵ ʹ ͵ ଶ ʹݔ ͳ ͳ ͳ ͳ െ ൌ െ ʹݔ ʹ ͵ ͵ ͵
͵ ଶ ʹݔ െ ʹ ʹݔ െ ʹ ൌ Ͳ ۍ ͳ െ ξ ݔ ൌ ێ ʹ ێ ێ ͳ ξ ۏ ݔ ൌ ͳሺạሻ ʹ ۍ ͳ െ ξ ݔ ൌ ቆ ቇ ݇ʹߨ ێ ʹ ێ ሺ݇ א Ժሻ ێ ͳ െ ξ ݔ ൌ ߨ െ ቆ ቇ ݇ʹߨ ۏ ʹ c. Điều kiện : ݇ߨ ʹݔ ് Ͳ ֞ ݔ ് ሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với ͳ െ ʹ ଶ ݔ ଶ ݔ ʹݔ ͳ ൌ െ ͷ ʹݔ ʹ ʹݔ ͺ ʹݔ
ͺ െ ͳ ଶ ݔ ଶ ݔ ൌ ʹͲ ʹݔ െ ͷ
Ͷ ଶ ʹݔ ʹͲ ʹݔ െ ͳ͵ ൌ Ͳ ֞ െͶ ଶ ʹݔ ʹͲ ʹݔ െ ͻ ൌ Ͳ 35 TOANMATH.com
Chương 5 : Phương trình lượng giác ͳ ʹݔ ൌ ൦ ʹ ͻ ʹݔ ൌ ͳሺạሻ ʹ ߨ
ݔ ൌ േ ݇ߨሺ݇ א Ժሻ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. d.
Phương trình tương đương với ͷ ߨ ʹͳ
ͳ െ ʹ ଶ ݔ ଶ ݔ ൌ െ
ቂ ቀͶݔ െ ቁ ʹݔቃ ʹͶ ʹ ʹͶ ଶ ʹݔ ͷ ʹͳ ͳ െ ൌ െ ሺെ Ͷݔ ʹݔሻ ʹ ʹͶ ʹͶ
ʹͶ െ ͳʹ ଶ ʹݔ ൌ െͷሺെͳ ʹ ଶ ʹݔ ʹݔሻ ʹͳ
ʹ ଶ ʹݔ െ ͷ ʹݔ ʹ ൌ Ͳ ͳ ʹݔ ൌ ʹ ʹݔ ൌ ʹ ͳሺạሻ ߨ ݔ ൌ ݇ߨ ൦ ͳʹ ͷߨ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ ͳʹ 5.2.3. a. Điều kiện : ସ ݔ ് Ͳ
൞ଶ ݔ ് Ͳ ʹݔ ് Ͳሺכሻ ʹݔ ് Ͳ ݔ ് Ͳ
Phương trình tương đương với ͳ ʹ ʹݔ ݔ Ͷͺ െ െ ൬ͳ ൰ ൌ Ͳ ସ ݔ ଶ ݔ ʹݔ ݔ 36 TOANMATH.com
Chương 5 : Phương trình lượng giác ͳ ͳ Ͷͺ െ െ ൌ Ͳ ସ ݔ ସ ݔ
Ͷͺ ସ ݔ ସ ݔ െ ሺସ ݔ ସ ݔሻ ൌ Ͳ ͳ
͵ ସ ʹݔ ଶ ʹݔ െ ͳ ൌ Ͳ ʹ ͳ ଶ ʹݔ ൌ ൦ ʹ ʹ ଶ ʹݔ ൌ െ ሺØýሻ ͵ ߨ ݇ߨ ֞ Ͷݔ ൌ Ͳ ݔ ൌ ሺ݇ א Ժሻ ͺ Ͷ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. b. Điều kiện : ߨ ۓ ቀ െ ݔቁ ് Ͳ Ͷ ۖ ۖ ߨ ߨ ቀ ݔቁ ് Ͳ ቀ െ ʹݔቁ ് Ͳ Ͷ ൞ ʹ
ʹݔ ് Ͳ ʹݔ ് േͳሺכሻ ۔ ߨ ߨ ቀ െ ݔቁ ് Ͳ ቀ ʹݔቁ ് Ͳ ۖ Ͷ ʹ ۖ ߨ ە ቀ ݔቁ ് Ͳ Ͷ Ta có: ߨ ߨ ͳ െ ݔ ͳ ݔ
ቀ െ ݔቁ ቀ ݔቁ ൌ Ǥ ൌ ͳ Ͷ Ͷ ͳ ݔ ͳ െ ݔ
Khi đó, phương trình tương đương với
ସ ʹݔ ସ ʹݔ ൌ ସ Ͷݔ ଶ Ͷݔ ͳ െ ൌ ସ Ͷݔ ʹ
ʹ ସ Ͷݔ െ ଶ Ͷݔ െ ͳ ൌ Ͳ ଶ Ͷݔ ൌ ͳ ͳ ଶ Ͷݔ ൌ െ ሺØýሻ ʹ 37 TOANMATH.com
Chương 5 : Phương trình lượng giác Ͷݔ ൌ Ͳ ቂ ʹݔ ൌ Ͳ ʹݔ ൌ Ͳ
Kết hợp với ሺכሻ, ta nhận nghiệm ݇ߨ ݔ ൌ ሺ݇ א Ժሻ Ͷ c. Điều kiện : ߨ ቊ ቀݔ െ ቁ ് Ͳ Ͷ ሺכሻ ݔ ് Ͳ ߨ ߨ
0ặݐ ൌ ݔ െ ֞ ݔ ൌ ݐ Ͷ Ͷ ߨ
ớሺכሻ¿×ǣ ് Ͳ ቀݐ ቁ ് Ͳ Ͷ
¯×ǡương trình tương đương với ߨ
ଷ ݐ ൌ ቀݐ ቁ െ ͳ Ͷ ͳ ݐ ଷ ݐ ൌ െ ͳ ͳ െ ݐ
ሺଶ ݐ ݐሻሺଶ ݐ െ ʹ ݐ ʹሻ ൌ Ͳ ቂ ݐ ൌ Ͳ ݐ ൌ െͳ ݐ ൌ ݇ߨ ቈ ߨ
ݐ ൌ െ ݇ߨሺ݇ א Ժሻ Ͷ ߨ ቈݔ ൌ ݇ߨ Ͷ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. 38 TOANMATH.com
Chương 5 : Phương trình lượng giác d. Điều kiện : ݔ ് Ͳ
൝ ݔ ് Ͳ ʹݔ ് Ͳሺכሻ ʹݔ ് Ͳ
Phương trình tương đương với ݔ ݔ ʹ Ͷݔ ൌ ݔ ݔ ʹ ݔ ݔ ଶ ݔ ൌ ଶ ݔ Ͷݔ
ʹ ଶ ʹݔ െ ʹݔ െ ͳ ൌ Ͳ ʹݔ ൌ ͳ ͳ ʹݔ ൌ െ ʹ ߨ ݔ ൌ േ ݇ߨ ൦ ʹ ʹߨ ሺ݇ א Ժሻ ݔ ൌ േ ݇ߨ ͵
Kết hợp với ሺכሻ, ta nhận nghiệm ʹߨ ݔ ൌ േ ݇ߨሺ݇ א Ժሻ ͵ e.
Phương trình tương đương với ͳ
ͳ െ ʹ ଶ ݔ ଶ ݔ ൌ ʹݔ െ ሺͳ െ ଶ ʹݔሻ ʹ ଶ ʹݔ ͳ ͳ െ
ൌ ʹݔ െ ሺͳ െ ଶ ʹݔሻ ʹ ʹ
ଶ ʹݔ ʹ ʹݔ െ ͵ ൌ Ͳ ʹݔ ൌ ͳ
ʹݔ ൌ െ͵ ൏ െͳሺạሻ ߨ
ݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ f.
Phương trình tương đương với 39 TOANMATH.com
Chương 5 : Phương trình lượng giác ͷ ͷ
ͳ െ ʹ ଶ ݔ ଶ ݔ ൌ ʹݔ െ ʹ ͺ
െͶ ଶ ʹݔ െ ʹͲ ʹݔ ʹͳ ൌ Ͳ
ʹ ଶ ʹݔ െ ͳͲ ʹݔ ͳ͵ ൌ Ͳ ሺØệ¿ȟԢ ൌ െͳ ൏ Ͳሻ g. Điều kiện : ξʹ
ξʹ െ ʹ ݔ ് Ͳ ݔ ് ሺכሻ ʹ
Phương trình tương đương với
ʹሺͳ െ ʹ ଶ ݔ ଶ ݔሻ െ Ͷ ݔ ݔ ͳ ൌ Ͳ
െ ଶ ʹݔ െ ʹ ʹݔ ͵ ൌ Ͳ ʹݔ ൌ ͳ
ʹݔ ൌ െ͵ ൏ െͳሺạሻ ߨ
ݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. 40 TOANMATH.com
Chương 5 : Phương trình lượng giác 2.
PHƯƠNG TRÌNH BẬC NHẤT THEO ܛܑܖ ࢞ VÀ ܋ܗܛ ࢞
- Phương trình bậc nhất theo ݔ và ݔ là những phương trình có dạng tổng quát :
ܽ ݔ ܾ ݔ ൌ ܿሺܽଶ ܾଶ ് Ͳሻሺכሻ
Những trường hợp đặc biệt :
x ܽ ൌ Ͳǡ ܾ ് Ͳ;ሺכሻ có dạng : ܿ ݔ ൌ ܾ
x ܽ ് Ͳǡ ܾ ൌ Ͳ; ሺכሻ có dạng : ܿ ݔ ൌ ܽ
x ܽ ് Ͳǡ ܾ ് Ͳǡ ܿ ൌ Ͳ; do ݔ ൌ Ͳ không là nghiệm nên ሺכሻ có dạng : ܽ ݔ ൌ െ ܾ
Phương pháp giải : (trường hợp ܽ ് Ͳǡ ܾ ് Ͳǡ ܿ ് Ͳ)
Chia 2 vế phương trình cho ξܽଶ ܾଶ ta sẽ được phương trình: ܽ ܾ ܿ ݔ ݔ ൌ ξܽଶ ܾଶ ξܽଶ ܾଶ ξܽଶ ܾଶ Ta thấy : ܽ ଶ ܾ ଶ ൬ ൰ ൬ ൰ ൌ ͳ ξܽଶ ܾଶ ξܽଶ ܾଶ
Nên có góc ݑ thỏa mãn : ܽ ۓ ݑ ൌ ξܽଶ ܾଶ ۔ ܾ ݑ ൌ ە ξܽଶ ܾଶ 41 TOANMATH.com
Chương 5 : Phương trình lượng giác
¯×ương trình trở thành : ܿ ܿ ݑ ݔ ݑ ݔ ൌ ሺݔ ݑሻ ൌ ξܽଶ ܾଶ ξܽଶ ܾଶ
Phương trình ሺכሻ có nghiệm khi và chỉ khi ܿଶ ܽଶ ܾଶ Khi đó, ta đặt ܿ ߙ ൌ ξܽଶ ܾଶ
Phương trình trở thành :
ሺݔ ݑሻ ൌ ߙ ቂ ݔ ൌ ߙ െ ݑ ݇ʹߨ ሺ݇ א Ժሻ
ݔ ൌ ߨ െ ߙ െ ݑ ݇ʹߨ Cách khác :
x Chia 2 vế phương trình cho ܽ, phương trình trở thành : ܾ ܿ ܿ ܾ
ݔ ݔ ൌ ሺݔ െ ߙሻ ൌ ߙǡ ߙ ൌ ܽ ܽ ܽ ܽ
x Chia 2 vế phương trình cho ܾ, phương trình trở thành : ܽ ܿ ܿ ܽ
ݔ ݔ ൌ ሺݔ ߙሻ ൌ ߙǡ ߙ ൌ ܾ ܾ ܾ ܾ
x Với ݔ ് ߨ ݇ʹߨሺ݇ א Ժሻ thì ta đặt ݔ ݐ ൌ ʹ Khi đó, ʹݐ ͳ െ ݐଶ ሺכሻ ܽ ܾ ൌ ܿ ͳ ݐଶ ͳ ݐଶ
ሺܾ ܿሻݐଶ െ ʹܽݐ ܿ െ ܾ ൌ Ͳ ሺܾ ܿ ് Ͳሻ Giải ݐ rồi suy ra ݔ. 42 TOANMATH.com
Chương 5 : Phương trình lượng giác
Một số công thức cần lưu ý : ߨ
ܽ േ ܽ ൌ ξʹ ቀܽ േ ቁ Ͷߨ
ܽ േ ܽ ൌ ξʹ ቀܽ ט ቁ Ͷߨ ߨ
ξ͵ ܽ േ ܽ ൌ ʹ ቀܽ േ ቁ ൌ ʹ ቀܽ ט ቁ ͵ ߨ ߨ
ܽ േ ξ͵ ܽ ൌ ʹ ቀܽ േ ቁ ൌ ʹ ቀܽ ט ቁ ͵
Bài 1: Giải các phương trình sau:
Ǥ ݔ െ ξ͵ ݔ ൌ െξʹ Ǥ ͵ݔ ൌ ξʹ ͵ݔ Ǥ͵ ݔ ݔ ൌ ͳ Ǥ ݔ ͷ ݔ ൌ ͳ ͳ ξ͵ ͳ െ ξ͵ ͳ Ǥ ݔ ݔ ൌ ʹξʹ ʹξʹ ξʹ Giải: a. Ta có:
ݔ െ ξ͵ ݔ ൌ െξʹ ߨ ξʹ ቀݔ െ ቁ ൌ ʹ ͷߨ ݇ʹߨ ݔ ൌ ൦ ͺͶ ͳͳߨ ݇ʹߨሺ݇ א Ժሻ ݔ ൌ ͺͶ b. Ta có: ͵ݔ ൌ ξʹ ͵ݔ ߨ ቀ͵ݔ െ ቁ ൌ ͳ Ͷ ߨ ݇ʹߨ ݔ ൌ ሺ݇ א Ժሻ Ͷ ͵ c.
Ta thấy ݔ ൌ ߨ ݇ʹߨሺ݇ א Ժሻ không là nghiệm của phương trình. 43 TOANMATH.com
Chương 5 : Phương trình lượng giác ݔ ݔ
് Ͳ ݔ ് ߨ ݇ʹߨሺ݇ א Ժሻ ሺכሻǤ ¯ặݐ ൌ ʹ ʹ ương trình trở thành: ݐ ͳ െ ݐଶ ൌ ͳ ͳ ݐଶ ͳ ݐଶ ݔ ൌ Ͳ
ʹݐଶ െ ݐ ൌ Ͳ ቂݐ ൌ Ͳ ൦ ʹ ݐ ൌ ͵ ݔ ൌ ͵ ʹ ቂ ݔ ൌ ݇ߨ ൫ỏሺכሻ൯ ݔ ൌ ʹ ͵ ݇ʹߨ d.
Ta thấy ݔ ൌ ߨ ݇ʹߨሺ݇ א Ժሻ không là nghiệm của phương trình. ݔ ݔ
് Ͳ ݔ ് ߨ ݇ʹߨሺ݇ א ԺሻǤ ¯ặݐ ൌ ʹ ʹ Phương trình trở thành: ʹݐ ͷሺͳ െ ݐଶሻ ൌ ͳ ͳ ݐଶ ͳ ݐଶ
͵ݐଶ െ ݐ െ ʹ ൌ Ͳ ݐ ൌ ͳ ʹ ݐ ൌ െ ͵ ݔ ൌ ͳ ൦ ʹ ݔ ʹ ൌ െ ʹ ͵ߨ ݔ ൌ ݇ʹߨ ൦ ʹ ʹ ሺ݇ א Ժሻ
ݔ ൌ ʹ ൬െ ൰ ݇ʹߨ ͵ e. Ta có:
൫ͳ ξ͵൯ ݔ ൫ͳ െ ξ͵൯ ݔ ൌ ʹሺכሻ ݔ
¿Ȃ ൫ͳ െ ξ͵൯ ് ʹ² ൌ ͲØệủươ¿ ʹ ݔ ݔ
് Ͳ ݔ ് ߨ ݇ʹߨሺ݇ א ԺሻǤ ¯ặݐ ൌ ʹ ʹ
ương trình ሺכሻ trở thành: 44 TOANMATH.com
Chương 5 : Phương trình lượng giác ൫ͳ ξ͵൯ʹݐ
൫ͳ െ ξ͵൯ሺͳ െ ݐଶሻ ൌ ʹ ሺͳ ݐଶሻ ሺͳ ݐଶሻ
൫͵ ξ͵൯ݐଶ െ ʹ൫ͳ ξ͵൯ݐ ͳ ξ͵ ൌ Ͳ ۍ ξ͵ ݐ ൌ ێ ͵ ێ ێ ͳ ξ͵ ݐ ൌ ۏ ͳ െ ξ͵ ۍ ݔ ξ͵ ൌ ێ ʹ ͵ ێ ێ ݔ ͳ ξ͵ ൌ ۏ ʹ ͳ െ ξ͵ ߨ ݔ ൌ ݇ʹߨ ൦ ͵ ͷߨ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ
Bài 2: Giải các phương trình sau: ξ͵ ͳ Ǥͺ ݔ ൌ ݔ ݔ ଶ Ɏ
Ǥ൫ ʹݔ ξ͵ ʹݔ൯ െ ͷ ൌ ቀʹݔ െ ቁ
Ǥʹξʹሺ ݔ ݔሻ ݔ ൌ ͵ ʹݔ Giải: a. Điều kiện: ݇ߨ ʹݔ ് Ͳ ֞ ݔ ് ሺ݇ א Ժሻሺכሻ ʹ
Với điều kiện ሺכሻ, phương trình tương đương với :
ͺ ଶ ݔ ݔ ൌ ξ͵ ݔ ݔ
Ͷሺͳ െ ʹݔሻ ݔ ൌ ξ͵ ݔ ݔ 45 TOANMATH.com
Chương 5 : Phương trình lượng giác
െͶ ʹݔ ݔ ൌ ξ͵ ݔ െ ͵ ݔ
െʹ ͵ݔ െ ʹ ݔ ൌ ξ͵ ݔ െ ͵ ݔ ߨ ͵ݔ ൌ ቀݔ ቁ ͵ ߨ ݔ ൌ ݇ߨ ൦ ߨ ݇ߨሺ݇ א Ժሻ ݔ ൌ െ ͳʹ ʹ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. b. Ta có: ଶ Ɏ
൫ ʹݔ ξ͵ ʹݔ൯ െ ͷ ൌ ቀʹݔ െ ቁ ߨ ߨ
Ͷ ଶ ቀʹݔ െ ቁ െ ቀʹݔ െ ቁ െ ͷ ൌ Ͳ ߨ ቀʹݔ െ ቁ ൌ െͳ ൦ ߨ ͷ
ቀʹݔ െ ቁ ൌ ͳሺạሻ Ͷ ߨ
ݔ ൌ െ ݇ߨሺ݇ א Ժሻ c. Ta có:
ʹξʹሺ ݔ ݔሻ ݔ ൌ ͵ ʹݔ
ξʹ ʹݔ ξʹሺͳ ʹݔሻ ൌ ͵ ͵ ʹݔ
ξʹ ʹݔ ൫ξʹ െ ͳ൯ ʹݔ ൌ ͵ െ ξʹ ଶ ଶ ଶ
Vì ൫ξʹ൯ ൫ξʹ െ ͳ൯ ൏ ൫͵ െ ξʹ൯ nên phương trình vô nghiệm. 46 TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 3: Giải các phương trình sau:
Ǥ ݔ ሺͳ െ ʹ ݔሻ ൌ ሺ ݔ െ ͳሻሺʹ ݔ ͳሻ
ǤͶ ଷ ݔ Ͷ ݔ ଶ ݔ ʹ ݔ ൌ Ͳ
Ǥ͵ െ Ͷ ଶ ݔ ൌ Ͷ ݔ ଶ ݔ െ ͵ ݔ Giải: a.
Phương trình tương đương với
ݔ െ ʹݔ ൌ ʹ ଶ ݔ െ ݔ െ ͳ
ݔ ݔ ൌ ʹݔ ʹݔ ߨ ߨ
ቀݔ ቁ ൌ ቀʹݔ ቁ Ͷ Ͷ ݔ ൌ ݇ʹߨ ߨ ݇ʹߨ ሺ݇ א Ժሻ ݔ ൌ ͵ b.
Phương trình tương đương với
ʹ ݔ െ Ͷ ଷ ݔ Ͷ ଷ ݔ െ ʹ ݔ ൌ Ͳ
͵ ݔ െ Ͷ ଷ ݔ Ͷ ଷ ݔ െ ͵ ݔ ൌ ݔ െ ݔ
͵ݔ ͵ݔ ൌ ݔ െ ݔ ߨ ߨ
ቀ͵ݔ ቁ ൌ ቀݔ െ ቁ Ͷ Ͷ ߨ ݔ ൌ െ ݇ߨ Ͷ ൦ ݇ߨ ሺ݇ א Ժሻ ݔ ൌ ʹ c. Điều kiện :
ݔ ് Ͳ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ
Phương trình tương đương với ͵ݔ െ ͵ݔ ൌ ͳ 47 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ξʹ ቀ͵ݔ െ ቁ ൌ Ͷ ʹ ߨ ݇ʹߨ ݔ ൌ ൦ ͵ ߨ ݇ʹߨሺ݇ א Ժሻ ݔ ൌ ͵ ͵
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình.
Bài 4: Giải các phương trình sau:
Ǥ ଷ ݔ െ ξ͵ ଷ ݔ ൌ ݔ ଶ ݔ െ ξ͵ ଶ ݔ ݔ൫ốʹͲͲͺ൯ ሺͳ െ ʹ ݔሻ ݔ Ǥ ൌ ξ͵ ൫ốʹͲͲͻ൯
ሺͳ ʹ ݔሻሺͳ െ ݔሻ
Ǥ ݔ ݔ ʹݔ ξ͵ ͵ݔ ൌ ʹሺ Ͷݔ ଷ ݔሻ൫ốʹͲͲͻ൯ Giải: a.
Phương trình tương đương với
ݔ ሺଶ ݔ െ ଶ ݔሻ ൌ ξ͵ ݔ ሺଶ ݔ െ ଶ ݔሻ
ሺ ݔ െ ݔሻሺ ݔ ݔሻ൫ ݔ െ ξ͵ ݔ൯ ൌ Ͳ ݔ െ ݔ ൌ Ͳ ݔ ݔ ൌ Ͳ ݔ െ ξ͵ ݔ ൌ Ͳ ߨ ۍ ቀݔ െ ቁ ൌ Ͳ ێ Ͷ ߨ ێ ቀݔ ቁ ൌ Ͳ ێ Ͷ ێ ߨ ۏ ቀݔ െ ቁ ൌ Ͳ ߨ ۍ ݔ ൌ ݇ߨ ێ Ͷߨ
ێݔ ൌ െ ݇ߨሺ݇ א Ժሻ ێ Ͷ ێ ߨ ۏ ݔ ൌ ݇ߨ 48 TOANMATH.com
Chương 5 : Phương trình lượng giác b. Điều kiện : ͳ ൝ ݔ ് െ ʹሺכሻ ݔ ് ͳ
Phương trình tương đương với
ݔ െ ʹ ݔ ݔ ൌ ξ͵ െ ξ͵ ݔ ʹξ͵ ݔ െ ʹξ͵ ଶ ݔ
ݔ െ ʹݔ ൌ ξ͵ ʹݔ ξ͵ ݔ
ݔ െ ξ͵ ݔ ൌ ξ͵ ʹݔ ʹݔ ߨ ߨ
ቀݔ ቁ ൌ ቀʹݔ െ ቁ ͵ ߨ ݔ ൌ ݇ʹߨ ൦ ʹߨ ݇ʹߨሺ݇ א Ժሻ ݔ ൌ െ ͳͺ ͵
Thay nghiệm vào ሺכሻ ta sẽ có nghiệm của phương trình là: ߨ ݇ʹߨ ݔ ൌ െ ሺ݇ א Ժሻ ͳͺ ͵ c.
Phương trình tương đương với
ʹ ݔ ʹ ݔ ʹݔ ʹξ͵ ͵ݔ ൌ Ͷ Ͷݔ Ͷ ଷ ݔ
ʹ ݔ ͵ݔ ݔ ʹξ͵ ͵ݔ ൌ Ͷ Ͷݔ ͵ ݔ െ ͵ݔ
ʹ ͵ݔ െ Ͷ Ͷݔ ʹξ͵ ͵ݔ ൌ Ͳ ߨ ቀ͵ݔ െ ቁ ൌ Ͷݔ ߨ ݔ ൌ െ ݇ʹߨ ൦ ߨ ݇ʹߨ ሺ݇ א Ժሻ ݔ ൌ Ͷʹ 49 TOANMATH.com
Chương 5 : Phương trình lượng giác - BÀI TẬP TỰ LUYỆN
5.2.4. Giải các phương trình sau: Ǥ ͷݔ ͷݔ ൌ ξʹ Ǥ ξ͵ ͵ݔ ͵ݔ ൌ ξʹ Ǥʹ ݔ െ ͷ ݔ ൌ ͷ ߨ
Ǥ ቀݔ ቁ ξ͵ ሺെݔሻ ൌ ξ͵ ʹ
5.2.5. Giải các phương trình sau:
Ǥ Ͷ ݔ ͵ݔ ʹ ʹݔ ൌ ξ͵ ݔ ݔ ͳ ξ͵ ݔ Ǥ ʹξ͵ ݔ െ ൌ ͳ െ ଶ ݔ ݔ ݔ
Ǥ ʹݔ െ ͵ ݔ ݔ െ ʹ ൌ Ͳ
5.2.6. Giải các phương trình sau: ݔ ߨ
൫ʹ െ ξ͵൯ ݔ െ ʹ ଶ ቀ ቁ Ǥ ʹ െ Ͷ ൌ ͳ ʹ ݔ െ ͳ
Ǥ ͺ ଶ ʹݔ ʹݔ ൌ ξ͵ ʹݔ ʹݔሺ ዎʹͲͲሻ ݔ ݔ ଶ
Ǥ ቀ ቁ ξ͵ ݔ ൌ ʹ ൫ốʹͲͲ൯ ʹ ʹ -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN
5.2.4. Nghiệm của phương trình : ߨ ݇ʹߨ Ǥ ݔ ൌ ሺ݇ א Ժሻ ʹͲ ͷ ߨ ݇ʹߨ ݔ ൌ െ Ǥ ൦ ͵ ͵ ߨ ݇ʹߨሺ݇ א Ժሻ ݔ ൌ െ ͵ ͵ 50 TOANMATH.com
Chương 5 : Phương trình lượng giác ͷ
Ǥ ݔ ൌ ʹ ݇ʹߨሺ݇ א Ժሻ ʹ ݔ ൌ ݇ʹߨ Ǥ ͷߨ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ ͵ 5.2.5. a.
Phương trình tương đương với ߨ
ʹ ݔ ͵ݔ ʹ ݔ ݔ ൌ ቀݔ ቁ ߨ
ʹ ݔ ሺ ͵ݔ ݔሻ ൌ ቀݔ ቁ ߨ
Ͷ ݔ ݔ ሺʹ ଶ ݔ െ ͳሻ ൌ ቀݔ ቁ ߨ Ͷݔ ൌ ቀݔ ቁ ߨ ݇ʹߨ ݔ ൌ ൦ ͳͺ ͵ ߨ ݇ʹߨ ሺ݇ א Ժሻ ݔ ൌ ͷ b. Điều kiện :
ݔ ് Ͳ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ
Phương trình tương đương với
ξ͵ ʹݔ െ ݔ ൌ ʹ ଶ ݔ ξ͵ ݔ െ ͳ
ξ͵ ʹݔ ʹݔ ൌ ݔ ξ͵ ݔ ߨ ߨ
ቀʹݔ ቁ ൌ ቀݔ ቁ ͵ ߨ ݔ ൌ ݇ʹߨ ൦ ߨ ݇ʹߨ ሺ݇ א Ժሻ ݔ ൌ ͵
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. 51 TOANMATH.com
Chương 5 : Phương trình lượng giác c.
Phương trình tương đương với
ଶ ݔ െ ଶ ݔ ͵ ݔ െ ݔ ʹ ൌ Ͳ
ሺ ݔ െ ݔ ͳሻሺ ݔ ݔ ʹሻ ൌ Ͳ ߨ ξʹ ቀݔ െ ቁ ൌ െ ൦ Ͷ ʹ ߨ
ቀݔ ቁ ൌ െξʹ ൏ െͳሺሻ Ͷ ݔ ൌ ݇ʹߨ ͵ߨ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ ʹ 5.2.6. a. Điều kiện : ͳ ߨ
ݔ ് ݔ ് േ ݇ʹߨሺ݇ א Ժሻሺכሻ ʹ ͵
Phương trình tương đương với ݔ െ ξ͵ ݔ ൌ Ͳ ߨ ቀݔ െ ቁ ൌ Ͳ ͵ ߨ ݔ ൌ ݇ʹߨ ൦ ͵ ʹߨ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ ͵
Kết hợp với ሺכሻ, ta nhận nghiệm ʹߨ ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ͵ b.
Phương trình tương đương với
Ͷ ʹݔ Ͷݔ ൌ ξ͵ ʹݔ ʹݔ
ʹ ʹݔ െ ʹ ݔ ൌ ξ͵ ʹݔ ʹݔ
െʹ ݔ ൌ ξ͵ ʹݔ െ ʹݔ 52 TOANMATH.com
Chương 5 : Phương trình lượng giác ʹߨ ሺߨ ݔሻ ൌ ൬ െ ʹݔ൰ ͵ ߨ ݇ʹߨ ݔ ൌ െ ൦ ʹͶ ͷߨ ݇ߨ ሺ݇ א Ժሻ ݔ ൌ െ ͳʹ ʹ c.
Phương trình tương đương với ݔ ݔ ͳ ʹ ξ͵ ݔ ൌ ʹ ʹ ʹ ݔ ξ͵ ݔ ൌ ͳ ߨ ͳ ቀݔ ቁ ൌ ͵ ʹ ߨ ݔ ൌ െ ݇ʹߨ ൦ ߨ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ ʹ 3.
PHƯƠNG TRÌNH ĐỐI XỨNG THEO ܛܑܖ ࢞ VÀ ܋ܗܛ ࢞
Phương trình đối xứng theo ݔ và ݔ là phương trình có dạng sau :
ܽሺ ݔ ݔሻ ܾ ݔ ݔ ൌ ܿ Phương pháp giải : ߨ
0ặݐ ൌ ݔ ݔ ൌ ξʹ ቀݔ ቁ ሺכሻǡ ݐ א ൣെξʹǢ ξʹ൧ Ͷ Khi đó, ݐଶ െ ͳ ݔ ݔ ൌ ʹ 53 TOANMATH.com
Chương 5 : Phương trình lượng giác
Thay vào phương trình, ta được : ܾሺݐଶ െ ͳሻ ܽݐ ൌ ܿ ʹ
ܾݐଶ ʹܽݐ െ ܾ െ ʹܿ ൌ Ͳሺככሻ
Ta giải ሺככሻ tính ra ݐ so điều kiện và thay ݐ vào ሺכሻ để tính ݔ.
Ngoài ra, chúng ta còn một dạng có họ hàng với dạng ở trên :
ܽሺ ݔ െ ݔሻ ܾ ݔ ݔ ൌ ܿ Phương pháp giải : ߨ
0ặݐ ൌ ݔ െ ݔ ൌ ξʹ ቀݔ െ ቁ ሺכሻǡ ݐ א ൣെξʹǢ ξʹ൧ Ͷ Khi đó, ͳ െ ݐଶ ݔ ݔ ൌ ʹ
Thay vào phương trình rồi làm tương tự như dạng trên.
Bài 1: Giải các phương trình sau:
Ǥξʹሺ ݔ ݔሻ െ ݔ ݔ ൌ ͳ
Ǥ൫ͳ ξʹ൯ሺ ݔ ݔሻ െ ʹݔ െ ͳ െ ξʹ ൌ Ͳ
Ǥͷ ʹݔ െ ͳʹሺ ݔ െ ݔሻ ͳʹ ൌ Ͳ
Ǥ ݔ ݔ ൌ ሺ ݔ െ ݔ െ ͳሻ Giải: a. ߨ
0ặݐ ൌ ݔ ݔ ൌ ξʹ ቀݔ ቁ ǡ ݐ א ൣെξʹǢ ξʹ൧ሺכሻ Ͷ 54 TOANMATH.com
Chương 5 : Phương trình lượng giác
Khi đó, phương trình trở thành ݐଶ െ ͳ ݐ െ
ൌ ͳ ֞ ݐ ൌ ͳ൫ỏሺכሻ൯ ʹ ߨ ξʹ ݔ ൌ ݇ʹߨ ቀݔ ቁ ൌ ቈ ߨ Ͷ ʹ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ b. ߨ
0ặݐ ൌ ݔ ݔ ൌ ξʹ ቀݔ ቁ ǡ ݐ א ൣെξʹǢ ξʹ൧ሺכሻ Ͷ
Khi đó, phương trình trở thành
൫ͳ ξʹ൯ݐ െ ሺݐଶ െ ͳሻ െ ͳ െ ξʹ ൌ Ͳ
ݐଶ െ ൫ͳ ξʹ൯ݐ ξʹ ൌ Ͳ ݐ ൌ ͳ ൫ỏሺכሻ൯ ݐ ൌ ξʹ ߨ ξʹ ቀݔ ቁ ൌ ൦ Ͷ ʹ ߨ ቀݔ ቁ ൌ ͳ Ͷ ݔ ൌ ݇ʹߨ ۍ ߨ ێ ݔ ൌ ݇ʹߨ ێ ʹ ሺ݇ א Ժሻ ێ ߨ ۏݔ ൌ െ ݇ߨ Ͷ c. ߨ
0ặݐ ൌ ݔ െ ݔ ൌ ξʹ ቀݔ െ ቁ ǡ ݐ א ൣെξʹǢ ξʹ൧ሺכሻ Ͷ
Khi đó, phương trình trở thành
ͷሺͳ െ ݐଶሻ െ ͳʹݐ ͳʹ ൌ Ͳ
ͷݐଶ ͳʹݐ െ ͳ ൌ Ͳ 55 TOANMATH.com
Chương 5 : Phương trình lượng giác ݐ ൌ ͳ ͳ ݐ ൌ െ ൏ െξʹሺạሻ ͷ ߨ ξʹ ቀݔ ቁ ൌ Ͷ ʹ ݔ ൌ ݇ʹߨ ቈ ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ d. ߨ
0ặݐ ൌ ݔ െ ݔ ൌ ξʹ ቀݔ െ ቁ ǡ ݐ א ൣെξʹǢ ξʹ൧ሺכሻ Ͷ
Khi đó, phương trình trở thành
ͳ െ ݐଶ ൌ ሺݐ െ ͳሻ ʹ
ݐଶ ͳʹݐ െ ͳ͵ ൌ Ͳ ݐ ൌ ͳ
ݐ ൌ െͳ͵ ൏ െξʹሺạሻ ߨ ξʹ ቀݔ ቁ ൌ Ͷ ʹ ݔ ൌ ݇ʹߨ ߨ ݔ
ቈ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ
Bài 2: Giải các phương trình sau:
Ǥ ݔ ݔ ݔ ݔ െ ͳ ൌ Ͳ
Ǥ ʹݔ ͷ ൌ ሺͶ െ ʹ ݔሻሺ ݔ െ ݔሻ
Ǥξʹሺ ݔ ݔሻ ൌ ݔ ݔ
Ǥ ଷ ݔ ଷ ݔ ൌ ʹݔ ݔ ݔ
Ǥʹ ଷ ݔ െ ʹݔ ݔ ൌ Ͳ 56 TOANMATH.com
Chương 5 : Phương trình lượng giác Giải: a. ߨ
0ặݐ ൌ ݔ ݔ ൌ ξʹ ቀݔ ቁ ǡ ݐ א ൣെξʹǢ ξʹ൧ሺכሻ Ͷ
Khi đó, phương trình trở thành ݐଶ െ ͳ ݐ െ ͳ ൌ Ͳ ʹ
ݐଶ ʹݐ െ ͵ ൌ Ͳ ݐ ൌ ͳ
ݐ ൌ െ͵ ൏ െξʹሺạሻ ߨ ξʹ ቀݔ ቁ ൌ Ͷ ʹ ݔ ൌ ݇ʹߨ ቈ ߨ ݔ ൌ ݇ʹߨ ሺ݇ א Ժሻ ʹ Ǥ
Phương trình tương đương với
ଶ ݔ െ ଶ ݔ ͷ ൌ Ͷ ݔ െ Ͷ ݔ െ ʹ ݔ ݔ ʹ ଶ ݔ
ʹሺ ݔ െ ݔሻ െ ݔ ݔ െ ʹ ൌ Ͳሺͳሻ ߨ
0ặݐ ൌ ݔ െ ݔ ൌ ξʹ ቀݔ െ ቁ ǡ ݐ א ൣെξʹǢ ξʹ൧ Ͷ
Khi đó, phương trình ሺͳሻ trở thành: ͳ െ ݐଶ ʹݐ െ െ ʹ ൌ Ͳ ʹ
ݐଶ Ͷݐ െ ͷ ൌ Ͳ ݐ ൌ ͳ
ݐ ൌ െͷ ൏ െξʹሺạሻ ߨ ξʹ ቀݔ െ ቁ ൌ Ͷ ʹ 57 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ቈݔ ൌ ݇ʹߨ ʹ ሺ݇ א Ժሻ ݔ ൌ ߨ ݇ʹߨ c. Điều kiện :
ቄ ݔ ് Ͳ ʹݔ ് Ͳሺכሻ ݔ ് Ͳ
Ta biến đổi phương trình thành ͳ ξʹሺ ݔ ݔሻ ൌ ሺͳሻ ݔ ݔ ߨ
0ặݐ ൌ ݔ ݔ ൌ ξʹ ቀݔ ቁ ǡ ݐ א ൣെξʹǢ ξʹ൧ Ͷ
ương trình ሺͳሻ trở thành: ʹ ξʹݐ ൌ ݐଶ െ ͳ
ݐଷ െ ݐ െ ξʹ ൌ Ͳ ݐ ൌ ξʹ
ቈݐଶ ξʹݐ ͳ ൌ ͲሺØệሻ ߨ ቀݔ ቁ ൌ ͳ Ͷ ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ Ͷ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. d.
Phương trình tương đương với
ሺ ݔ ݔሻሺͳ െ ݔ ݔሻ െ ʹ ݔ ݔ െ ሺ ݔ ݔሻ ൌ Ͳሺͳሻ ߨ
0ặݐ ൌ ݔ ݔ ൌ ξʹ ቀݔ ቁ ǡ ݐ א ൣെξʹǢ ξʹ൧ Ͷ
Khi đó, phương trình ሺͳሻ trở thành: ݐଶ െ ͳ ݐ ቆͳ െ
ቇ െ ሺݐଶ െ ͳሻ െ ݐ ൌ Ͳ ʹ 58 TOANMATH.com
Chương 5 : Phương trình lượng giác
ݐଷ ʹݐଶ െ ݐ െ ʹ ൌ Ͳ ݐ ൌ ͳ ݐ ൌ െͳ
ݐ ൌ െʹ ൏ െξʹሺạሻ ۍ ߨ ξʹ ቀݔ ቁ ൌ ێ Ͷ ʹ ێ ێ ߨ ξʹ ۏ ቀݔ ቁ ൌ െ Ͷ ʹ ݔ ൌ ݇ʹߨ ۍ ߨ ێ ݔ ൌ ݇ʹߨ ێ ʹ ߨ
ێݔ ൌ െ ݇ʹߨሺ݇ א Ժሻ ێ ʹ ێ ͷߨ ۏ ݔ ൌ ݇ʹߨ Ͷ e.
Phương trình tương đương với
ʹ ଷ ݔ ʹ ଶ ݔ ݔ െ ͳ ൌ Ͳ
ʹሺͳ െ ଶ ݔሻሺ ݔ ͳሻ ݔ െ ͳ ൌ Ͳ
ሺͳ െ ݔሻሾʹሺͳ ݔሻሺͳ ݔሻ െ ͳሿ ൌ Ͳ ݔ ൌ ͳሺͳሻ
ʹሺݔ ݔሻ ʹݔ ݔ ͳ ൌ Ͳሺʹሻ
Với phương trình ሺͳሻ ta có nghiệm ݔ ൌ ݇ʹߨሺ݇ א Ժሻ
Với phương trình ሺʹሻ, ta đặt ߨ
ݐ ൌ ݔ ݔ ൌ ξʹ ቀݔ ቁ ǡ ݐ א ൣെξʹǢ ξʹ൧ Ͷ
Khi đó, phương trình trở thành ݐ ൌ Ͳ
ݐଶ ʹݐ ൌ Ͳ ݐ ൌ െʹሺሻ Với ݐ ൌ Ͳ thì ߨ ߨ
ቀݔ ቁ ൌ Ͳ ݔ ൌ െ ݇ߨሺ݇ א Ժሻ Ͷ Ͷ 59 TOANMATH.com
Chương 5 : Phương trình lượng giác - BÀI TẬP TỰ LUYỆN
5.2.7. Giải các phương trình sau: ͵
Ǥ െ ͳ ଷ ݔ ଷ ݔ ൌ ʹݔ ʹ Ǥ ͳ ݔ ൌ ʹξʹ ݔ
Ǥ ݔ ݔ ȁ ݔ ݔȁ ൌ ͳ
5.2.8. Giải các phương trình sau:
Ǥ ଷ ݔ ଷ ݔ ൌ ʹݔ ݔ ݔ
Ǥ ଷ ݔ െ ଷ ݔ ൌ െͳ
Ǥͳ ଷ ݔ െ ଷ ݔ ൌ ʹݔ ߨ
Ǥ ʹݔ ξʹ ቀݔ െ ቁ ൌ ͳ Ͷ
Ǥ ʹ ʹݔ ଶ ݔ ݔ ݔ ଶ ݔ ൌ ʹሺ ݔ ݔሻ -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN
5.2.7. Nghiệm của phương trình là : ݔ ൌ ݇ʹߨ ۍ ߨ ێ ݔ ൌ ݇ʹߨ ێ ʹ Ǥ ێ െʹ ξ͵ ߨ ሺ݇ א Ժሻ ێ ݔ ൌ െ ݇ʹߨ ξʹ Ͷ ێ ێ ͵ߨ െʹ ξ͵ ݔ ൌ െ ݇ʹߨ ۏ Ͷ ξʹ ߨ ۍ ݔ ൌ ݇ʹߨ ێ Ͷߨ Ǥ ێݔ ൌ െ ݇ʹߨሺ݇ א Ժሻ ێ ͳʹ ێ ߨ ۏ ݔ ൌ ݇ʹߨ ͳʹ ݇ߨ Ǥݔ ൌ ሺ݇ א Ժሻ ʹ 60 TOANMATH.com
Chương 5 : Phương trình lượng giác
5.2.8. Nghiệm của phương trình là :
Ǥ ݔ ൌ ߨ ݇ߨሺ݇ א Ժሻ ߨ Ǥ ቈݔ ൌ ݇ʹߨ ʹ ሺ݇ א Ժሻ ݔ ൌ ߨ ݇ʹߨ ߨ
Ǥݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ ߨ ۍ ݔ ൌ ݇ߨ Ͷ Ǥ ێێ ߨ ሺ݇ א Ժሻ ێݔ ൌ ݇ʹߨ ʹ ۏݔ ൌ ߨ ݇ʹߨ ߨ
Ǥ ݔ ൌ െ ݇ߨሺ݇ א Ժሻ Ͷ 4.
PHƯƠNG TRÌNH BẬC HAI THUẦN NHẤT ĐỐI VỚI ܛܑܖ ࢞ VÀ ܋ܗܛ ࢞
Phương trình bậc hai thuần nhất đối với ݔ và ݔ là phương trình có dạng :
ܽ ଶ ݔ ܾ ݔ ݔ ܿ ଶ ݔ ൌ ݀ Phương pháp giải :
Cách 1: Ta sử dụng công thức ͳ െ ʹݔ ۓଶ ݔ ൌ ۖ ʹ ͳ ʹݔ ଶ ݔ ൌ ۔ ʹ ۖ ʹݔ ە ݔ ݔ ൌ ʹ
¯ó đưa phương trình về dạng: ܿ െ ܽ ܾ ܽ ܿ ʹݔ ʹݔ ൌ ݀ െ ʹ ʹ ʹ 61 TOANMATH.com
Chương 5 : Phương trình lượng giác
Cách 2: Thay ݀ ൌ ݀ሺଶ ݔ ଶ ݔሻ; ta biến đổi đưa phương trình về dạng :
ଶ ݔ ݔ ݔ ଶ ݔ ൌ Ͳ
- Nếu ൌ Ͳ (hoặc ൌ Ͳ) : ta đặt ݔ (hoặc ݔ) làm nhân tử chung, ta sẽ có phương trình tích.
- Nếu ് Ͳ, xét thấy ݔ ൌ Ͳ không là nghiệm của phương trình, ta tiến hành
chia 2 vế cho ଶ ݔ thì đưa phương trình về dạng
ଶ ݔ ݔ ൌ Ͳሺכሻ
Giải phương trình ሺכሻ rồi so với điều kiện.
Ngoài ra chúng ta cũng có một dạng phương trình tương tự :
ܽ ଷ ݔ ܾ ଷ ݔ ܿ ଶ ݔ ݔ ݀ ݔ ଶ ݔ ݁ ݔ ݂ ݔ ൌ Ͳ
Phương pháp giải : Chúng ta sử dụng cách 2 đã nêu ở trên (chia 2 vế cho ଷ ݔ).
Bài 1: Giải các phương trình sau:
Ǥ ଶ ʹݔ െ ξ͵ Ͷݔ ൌ ͳ ଶ ʹݔ
Ǥ ݔ െ Ͷ ଷ ݔ ݔ ൌ Ͳ
Ǥ ଶ ݔ െ ξ͵ ʹݔ ൌ ͳ ଶ ݔ
Ǥ ଷ ݔ െ Ͷ ଷ ݔ െ ͵ ݔ ଶ ݔ ݔ ൌ Ͳ Giải: a.
Vì ݔ ൌ Ͳ không là nghiệm của phương trình nên chia 2 vế cho ଶ ݔ. Khi đó, phương trình trở thành:
ʹ ଶ ݔ ʹξ͵ ݔ ൌ Ͳ ݔ ൌ Ͳ ݔ ൌ ݇ߨ ቈ ߨ ݔ ൌ െξ͵
ݔ ൌ െ ݇ߨሺ݇ א Ժሻ ͵
(thỏa điều kiện ݔ ് Ͳ) 62 TOANMATH.com
Chương 5 : Phương trình lượng giác b.
Vì ݔ ൌ Ͳ không là nghiệm của phương trình nên chia 2 vế cho ଷ ݔǤ Khi đó, phương trình trở thành:
ݔ ሺͳ ଶ ݔሻ െ Ͷ ଷ ݔ ͳ ଶ ݔ ൌ Ͳ
͵ ଷ ݔ െ ଶ ݔ െ ݔ െ ͳ ൌ Ͳ
ሺ ݔ െ ͳሻሺ͵ ଶ ݔ ʹ ݔ ͳሻ ൌ Ͳ ݔ ൌ ͳ ߨ
ݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ
(thỏa điều kiện ݔ ് Ͳ) c.
Phương trình tương đương với :
ଶ ݔ ͳ ʹξ͵ ݔ ݔ െ ଶ ݔ ൌ Ͳ
Vì ݔ ൌ Ͳ không là nghiệm của phương trình nên chia 2 vế cho ଶ ݔ. Khi đó, phương trình trở thành:
ଶ ݔ ͳ ଶ ݔ ʹξ͵ ݔ െ ͳ ൌ Ͳ ଶ ݔ ξ͵ ݔ ൌ Ͳ ݔ ൌ Ͳ ݔ ൌ െξ͵ ݔ ൌ ݇ߨ ቈ ߨ
ݔ ൌ െ ݇ߨሺ݇ א Ժሻ ͵
(thỏa điều kiện ݔ ് Ͳ) d.
Vì ݔ ൌ Ͳ không là nghiệm của phương trình nên chia 2 vế cho ଷ ݔ. Khi đó, phương trình trở thành:
ͳ െ Ͷ ଷ ݔ െ ͵ ଶ ݔ ݔ ሺͳ ଶ ݔሻ ൌ Ͳ
ሺ ݔ ͳሻሺ͵ ଶ ݔ െ ͳሻ ൌ Ͳ 63 TOANMATH.com
Chương 5 : Phương trình lượng giác ݔ ൌ െͳ ۍ ێ ξ͵ ݔ ൌ ێ ͵ ێ ξ͵ ۏ ݔ ൌ െ ͵ ߨ ۍݔ ൌ െ ݇ߨ ێ Ͷ ߨ
ێ ݔ ൌ ݇ߨ ሺ݇ א Ժሻ ێ ێ ߨ ۏݔ ൌ െ ݇ߨ
(thỏa điều kiện ݔ ് Ͳ)
Bài 2: Giải các phương trình sau:
Ǥ ଶ ݔ ሺ ݔ െ ʹሻ ൌ ͵ሺ ʹݔ ݔ ݔሻ
Ǥ ݔ ʹݔ ͵ݔ ൌ ଷ ݔ
Ǥ͵ ସ ݔ െ ଶ ʹݔ ସ ݔ ൌ Ͳ
Ǥ ͵ݔ ͵ݔ ʹ ݔ ൌ Ͳ Giải: a. Điều kiện: ߨ
ݔ ് Ͳ ֞ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với
ݔ ݔ െ ʹ ଶ ݔ ൌ ͵ െ ଶ ݔ ͵ ݔ ݔ
Ͷ ଶ ݔ െ ʹ ݔ െ ͵ሺͳ ଶ ݔሻ ൌ Ͳ
ଶ ݔ െ ʹ ݔ െ ͵ ൌ Ͳ ቂ ݔ ൌ െͳ ݔ ൌ ͵ ߨ ቈ ݔ ൌ െ ݇ߨ Ͷ ሺ݇ א Ժሻ ݔ ൌ ͵ ݇ߨ 64 TOANMATH.com
Chương 5 : Phương trình lượng giác
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. b.
Phương trình tương đương với
ʹ ݔ ʹݔ ʹ ͵ݔ ൌ ͳʹ ଷ ݔ
ݔ െ ͵ݔ ݔ െ ͺ ଷ ݔ ൌ ͳʹ ଷ ݔ
ͳ ଷ ݔ ͺ ଷ ݔ െ Ͷ ݔ െ ݔ ൌ Ͳ
Vì ݔ ൌ Ͳ không là nghiệm của phương trình nên chia 2 vế phương trình cho ଷ ݔ.
Khi đó, phương trình trở thành:
ͳ ͺ ଷ ݔ െ Ͷሺͳ ଶ ݔሻ െ ݔ ሺͳ ଶ ݔሻ ൌ Ͳ
ଷ ݔ െ ʹ ଶ ݔ െ ͵ ݔ ൌ Ͳ
ሺଶ ݔ െ ͵ሻሺ ݔ െ ʹሻ ൌ Ͳ ݔ ൌ ξ͵ ݔ ൌ െξ͵ ݔ ൌ ʹ ߨ ۍ ݔ ൌ ݇ߨ ͵ ێێ ߨ
ݔ ൌ െ ݇ߨ ሺ݇ א Ժሻ ێ ͵ ۏݔ ൌ ʹ ݇ߨ
(thỏa điều kiện ݔ ് Ͳ) c.
Ta đưa phương trình về dạng
͵ ସ ݔ െ Ͷ ଶ ݔ ଶ ݔ ସ ݔ ൌ Ͳ
Vì ݔ ൌ Ͳ không là nghiệm của phương trình nên chia 2 vế phương trình cho ସ ݔ
Khi đó, phương trình trở thành:
͵ െ Ͷ ଶ ݔ ସ ݔ ൌ Ͳ ቂଶ ݔ ൌ ͳ ଶ ݔ ൌ ͵ 65 TOANMATH.com
Chương 5 : Phương trình lượng giác ݔ ൌ ͳ ݔ ൌ െͳ ൦ ݔ ൌ ξ͵ ݔ ൌ െξ͵ ߨ ݔ ൌ േ ݇ߨ ൦ Ͷ ߨ ሺ݇ א Ժሻ ݔ ൌ േ ݇ߨ ͵
(thỏa điều kiện ݔ ് Ͳ) d.
Ta đưa phương trình về dạng
Ͷ ଷ ݔ െ Ͷ ଷ ݔ െ ͵ ݔ ݔ ൌ Ͳ
Vì ݔ ൌ Ͳ không là nghiệm của phương trình nên chia 2 vế phương trình cho ଷ ݔ.
Khi đó, phương trình trở thành:
Ͷ ଷ ݔ െ Ͷ െ ͵ ሺͳ ଶ ݔሻ ͳ ଶ ݔ ൌ Ͳ
ଷ ݔ ଶ ݔ െ ͵ ݔ െ ͵ ൌ Ͳ
ሺ ݔ ͳሻሺଶ ݔ െ ͵ሻ ൌ Ͳ ݔ ൌ െͳ ݔ ൌ ξ͵ ݔ ൌ െξ͵ ߨ ݔ ൌ െ ݇ߨ ൦ Ͷ ߨ
ሺ݇ א Ժሻሺỏ¯ềệ ݔ ് Ͳሻ ݔ ൌ േ ݇ߨ ͵ 66 TOANMATH.com
Chương 5 : Phương trình lượng giác - BÀI TẬP TỰ LUYỆN
5.2.9. Giải các phương trình sau:
Ǥ ଶ ݔ െ ξ͵ ʹݔ ൌ ͳ ଶ ݔ Ǥ ʹݔ ʹ ݔ ൌ ͵ ͵ ξʹ
Ǥ ଶ ݔ ξ͵ ݔ ݔ ʹ ଶ ݔ ൌ ʹ
Ǥʹ ଶ ݔ ʹݔ ݔ ൌ Ͳ
Ǥ Ͷሺଷ ݔ ଷ ݔሻ ൌ ݔ ͵ ݔ ͷ
ǤͶξ͵ ݔ ݔ Ͷ ଶ ݔ ൌ ʹ ଶ ݔ ʹ
Ǥ ଶ ݔ െ ͵ ݔ ݔ ͳ ൌ Ͳ
5.2.10. Giải các phương trình sau: ͳ
Ǥ ସ ݔ ସ ݔ ൌ ʹ ʹݔ ʹݔ െ ଶ ʹݔ ʹ ͷ ͳ ͵
Ǥ ସ ݔ ସ ݔ ൌ െ ʹݔ ʹݔ െ ଶ ʹݔ Ͷ Ͷ ʹ ͷ Ͷݔ ݔ Ǥ ݔ െ ʹ ଷ ݔ ൌ ʹ ʹݔ
Ǥ ݔ ଶ ݔ െ ʹ ଶ ݔ ൌ ͵ሺ ʹݔ ݔ ݔሻ ߨ
Ǥ ʹξʹ ଷ ቀݔ െ ቁ െ ͵ ݔ െ ݔ ൌ Ͳ Ͷ ߨ
Ǥξʹ ଷ ቀݔ ቁ ൌ ʹ ݔ Ͷ ߨ
Ǥͺ ଷ ቀݔ ቁ ൌ ͵ݔ ͵ 67 TOANMATH.com
Chương 5 : Phương trình lượng giác -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN
5.2.9. Nghiệm của phương trình là : ݔ ൌ ݇ߨ Ǥ ቈ ߨ
ݔ ൌ െ ݇ߨሺ݇ א Ժሻ ͵ ߨ
Ǥ ݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ ۍ ξ͵ ξʹ ݔ ൌ ݇ߨ ێ Ǥ ͳ ξʹ ێ ሺ݇ א Ժሻ ێ ξ͵ െ ξʹ ݔ ൌ ݇ߨ ۏ ͳ ξʹ ߨ Ǥ ݔ ൌ െ ݇ߨ Ͷͷ ሺ݇ א Ժሻ ݔ ൌ ͵ ݇ߨ ߨ ݔ ൌ ݇ߨ Ǥ ൦ Ͷߨ ሺ݇ א Ժሻ ݔ ൌ േ ݇ߨ ͵ ߨ Ǥ ቈݔ ൌ ݇ߨ Ͷ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ ߨ ݔ ൌ ݇ߨ Ǥ ൦ Ͷ ͳ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ ʹ 5.2.10. a.
Phương trình tương đương với ͳ ͳ
ͳ െ ଶ ʹݔ ൌ ʹ ʹݔ ʹݔ െ ଶ ʹݔ ʹ ʹ
ଶ ʹݔ Ͷ ʹݔ ʹݔ െ ଶ ʹݔ െ ʹ ൌ Ͳ
Vì ʹݔ ൌ Ͳ không là nghiệm của phương trình nên chia 2 vế phương trình cho ଶ ʹݔ
Khi đó, phương trình trở thành: 68 TOANMATH.com
Chương 5 : Phương trình lượng giác
ଶ ʹݔ Ͷ ʹݔ െ ͳ െ ʹሺͳ ଶ ʹݔሻ ൌ Ͳ
ଶ ʹݔ െ Ͷ ʹݔ ͵ ൌ Ͳ ቂ ʹݔ ൌ ͳ ʹݔ ൌ െ͵ ߨ ݇ߨ ݔ ൌ ൦ ͺ ʹ ͳ ݇ߨሺ݇ א Ժሻ ݔ ൌ ሺെ͵ሻ ʹ ʹ
(thỏa điều kiện ʹݔ ് Ͳ) b.
Phương trình tương đương với ͳ ͷ ͳ ͵
ͳ െ ଶ ʹݔ ൌ െ ʹݔ ʹݔ െ ଶ ʹݔ ʹ Ͷ Ͷ ʹ
Ͷ ଶ ʹݔ െ ͷ ʹݔ ʹݔ ଶ ʹݔ ൌ Ͳ
Vì ʹݔ ൌ Ͳ không là nghiệm của phương trình nên chia 2 vế phương trình cho ଶ ʹݔ
Khi đó, phương trình trở thành:
Ͷ ଶ ʹݔ െ ͷ ݔ ͳ ൌ Ͳ ʹݔ ൌ ͳ ͳ ʹݔ ൌ ͷ ߨ ݇ߨ ݔ ൌ ͺ ʹ ൦ ͳ ͳ ݇ߨሺ݇ א Ժሻ ݔ ൌ ʹ ͷ ʹ
(thỏa điều kiện ʹݔ ് Ͳ) c. Điều kiện:
ʹݔ ് Ͳ ଶ ݔ െ ଶ ݔ ് Ͳ ݔ ് േͳ
Phương trình tương đương với ͳͲ ʹݔ ʹݔ ݔ ݔ െ ʹ ଷ ݔ ൌ ʹ ʹݔ 69 TOANMATH.com
Chương 5 : Phương trình lượng giác
ݔ െ ʹ ଷ ݔ ൌ ͷ ʹݔ ݔ
ͳͲ ݔ ଶ ݔ ʹ ଷ ݔ െ ݔ ൌ Ͳ
Vì ݔ ൌ Ͳ không là nghiệm của phương trình nên chia 2 vế phương trình cho ଷ ݔ
Khi đó, phương trình trở thành:
ͳͲ ݔ ʹ െ ݔ ሺͳ ଶ ݔሻ ൌ Ͳ
͵ ଶ ݔ െ ʹ ݔ െ ͳ ൌ Ͳ
ሺ ݔ െ ͳሻሺ͵ ଶ ݔ ͵ ݔ ͳሻ ൌ Ͳ
ݔ ൌ ͳ (loại vì ݔ ് ͳ)
Vậy phương trình vô nghiệm. d. Điều kiện: ߨ ݔ ് Ͳ ݔ ്
݇ߨሺ݇ א Ժሻሺכሻ ʹ
Do ݔ ് Ͳ nên chia 2 vế phương trình cho ଶ ݔ. Khi đó, phương trình trở thành:
ଷ ݔ െ ʹ ଶ ݔ ൌ ͵ሺͳ െ ଶ ݔ ݔሻ
ଷ ݔ ଶ ݔ െ ͵ ݔ െ ͵ ൌ Ͳ
ሺ ݔ ͳሻሺଶ ݔ െ ͵ሻ ൌ Ͳ ݔ ൌ െͳ ݔ ൌ ξ͵ ݔ ൌ െξ͵ ߨ ݔ ൌ െ ݇ߨ Ͷ ൦ ߨ ሺ݇ א Ժሻ ݔ ൌ േ ݇ߨ ͵
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. e.
Phương trình tương đương với
ଷ ݔ ଷ ݔ ͵ ଶ ݔ ݔ ͵ ݔ ଶ ݔ െ ͵ ݔ െ ݔ ൌ Ͳ 70 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ
ͳǣ ݔ ൌ Ͳ ݔ ൌ ݇ߨሺ݇ א Ժሻ ฺ ݔ ൌ േͳ ʹ
Thay vào phương trình ta có:
ሺേͳሻଷ Ͳ ͵ሺേͳሻଶǤ Ͳ ͵ሺേͳሻǤ Ͳ െ ͵ǤͲ െ ሺേͳሻ ൌ Ͳ (đúng) ߨ
ậݔ ൌ ݇ߨሺ݇ א Ժሻệủươ¿ ʹ ߨ
ʹǣ ݔ ് Ͳ ݔ ് ݇ߨሺ݇ א Ժሻ ʹ
Khi đó phương trình trở thành:
ଷ ݔ ͳ ͵ ଶ ݔ ͵ ݔ െ ͵ሺͳ ଶ ݔሻ െ ሺͳ ଶ ݔሻ ൌ Ͳ ߨ ݔ ൌ ͳ ݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ
(thỏa điều kiện ݔ ് Ͳ)
Vậy nghiệm của phương trình là: ߨ ݔ ൌ ݇ߨ ൦ ʹ ሺ݇ א Ժሻ ߨ ݔ ൌ ݇ߨ Ͷ f.
Phương trình tương đương với
ଷ ݔ ଷ ݔ ͵ ଶ ݔ ݔ ͵ ݔ ଶ ݔ െ Ͷ ݔ ൌ Ͳ
Vì ݔ ൌ Ͳ không là nghiệm của phương trình nên chia 2 vế phương trình cho ଷ ݔ
Khi đó, phương trình trở thành:
ଷ ݔ ͳ ͵ ଶ ݔ ͵ ݔ െ Ͷ ሺͳ ଶ ݔሻ ൌ Ͳ
͵ ଷ ݔ െ ͵ ଶ ݔ ݔ െ ͳ ൌ Ͳ
ሺ ݔ െ ͳሻሺ͵ ଶ ݔ ͳሻ ൌ Ͳ ߨ
֞ ݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ
(thỏa điều kiện ݔ ് Ͳ) 71 TOANMATH.com
Chương 5 : Phương trình lượng giác g.
Phương trình tương đương với ଷ
ͺ൫ ݔ െ ξ͵ ݔ൯ ൌ Ͷଷ ݔ െ ͵ݔ ͺ
ଷ ݔ െ ͵ξ͵ ଶ ݔ ݔ ͻ ݔ ଶ ݔ െ ͵ξ͵ ଷ ݔ ൌ Ͷ ଷ ݔ െ ͵ ݔ
Vì ݔ ൌ Ͳ không là nghiệm của phương trình nên chia 2 vế phương trình cho ଷ ݔ
Khi đó, phương trình trở thành:
ͳ െ ͵ξ͵ ݔ ͻ ଶ ݔ െ ͵ξ͵ ଷ ݔ ൌ Ͷ െ ͵ሺͳ ଶ ݔሻ
͵ξ͵ ଷ ݔ െ ͳʹ ଶ ݔ ͵ξ͵ ݔ ൌ Ͳ ݔ ൌ Ͳ ۍ ݔ ൌ ξ͵ ێ ێ ξ͵ ۏ ݔ ൌ ͵ ݔ ൌ ݇ߨ ۍ ߨ ݔ ൌ ݇ߨ ێێ ͵ ሺ݇ א Ժሻ ێ ߨ ۏݔ ൌ ݇ߨ
(thỏa điều kiện ݔ ് Ͳ) 72 TOANMATH.com
Chương 5 : Phương trình lượng giác 5.
CÁC DẠNG PHƯƠNG TRÌNH LƯỢNG GIÁC KHÁC a. TỔNG HỢP
- Phương trình tổng hợp là những phương trình đưa về phương trình tích mà trong
đó, các nhân tử là các dạng phương trình đã nêu ở trên.
Bài 1: Giải các phương trình sau:
Ǥ ሺ ݔ ͵ݔሻ ʹݔ ൌ ሺ ݔ ͵ݔሻ ʹݔ
ǤͶ ଷ ݔ ͵ ଷ ݔ െ ͵ ݔ െ ଶ ݔ ݔ ൌ Ͳ
Ǥ ଶ ݔ ଶ ʹݔ ͵ݔ ൌ ଶ ݔ െ ଶ ʹݔ ͵ݔ
ሺͳ െ ݔሻଶ ሺͳ ݔሻଶ ͳ Ǥ
െ ଶ ݔ ݔ ൌ ሺͳ ݔሻ ଶ ݔ Ͷሺͳ െ ݔሻ ʹ Giải: a.
Phương trình tương đương với
ʹ ʹݔ ݔ ʹݔ ൌ ʹ ʹݔ ݔ ʹݔ
ʹݔ ሺʹ ݔ ͳሻ ൌ ʹݔ ሺʹ ݔ ͳሻ
ሺʹ ݔ ͳሻሺ ʹݔ െ ʹݔሻ ൌ Ͳ ቂ ʹ ݔ ͳ ൌ Ͳ ʹݔ െ ʹݔ ൌ Ͳ ͳ ݔ ൌ െ ൦ ʹ ߨ ቀʹݔ െ ቁ ൌ Ͳ Ͷ ʹߨ ݔ ൌ േ ݇ʹߨ ൦ ͵ ߨ ݇ߨ ሺ݇ א Ժሻ ݔ ൌ ͺ ʹ b.
Phương trình tương đương với
Ͷ ଷ ݔ ͵ ଷ ݔ െ ͵ ݔ െ ଶ ݔ ݔ ൌ Ͳ
ݔ ሺͶ ଶ ݔ െ ͵ሻ ݔ ሺ͵ ଶ ݔ െ ଶ ݔሻ ൌ Ͳ 73 TOANMATH.com
Chương 5 : Phương trình lượng giác
ሺͶ ଶ ݔ െ ͵ሻሺ ݔ െ ݔሻ ൌ Ͳ
ቂ Ͷ ଶ ݔ െ ͵ ൌ Ͳ ݔ െ ݔ ൌ Ͳ ۍ ξ͵ ݔ ൌ ێ ʹ ێ ξ͵ ێ ݔ ൌ െ ێ ʹ ێ ߨ ۏ ቀݔ െ ቁ ൌ Ͳ Ͷ ߨ ʹߨ ۍ ݔ ൌ ݇ʹߨ ש ݔ ൌ ݇ʹߨ ێ ͵ ͵ ێ ߨ Ͷߨ
ݔ ൌ െ ݇ʹߨ ש ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ێ ͵ ͵ ێ ߨ ۏ ݔ ൌ ݇ߨ Ͷ ߨ ݔ ൌ േ ݇ߨ ൦ ͵ ߨ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ Ͷ c. Điều kiện: ݔ ് Ͳ
൝ ʹݔ ് Ͳ ቄ ʹݔ ് Ͳሺכሻ ͵ݔ ് Ͳ ͵ݔ ് Ͳ
Phương trình tương đương với
͵ݔ ሺଶ ݔ ଶ ʹݔ െ ͳሻ ൌ ଶ ݔ െ ଶ ʹݔ
ሺͳ െ ʹݔሻሺͳ Ͷݔሻ ͳ െ ʹݔ ͳ Ͷݔ ͵ݔ ቈ െ ͳ ൌ െ
ሺͳ ʹݔሻሺͳ െ Ͷݔሻ ͳ ʹݔ ͳ െ Ͷݔ
͵ݔ ሾሺͳ െ ʹݔሻሺͳ Ͷݔሻ െ ሺͳ ʹݔሻሺͳ െ Ͷݔሻሿ
ൌ ሺͳ െ ʹݔሻሺͳ െ Ͷݔሻ െ ሺͳ Ͷݔሻሺͳ ʹݔሻ
͵ݔ ሺʹ Ͷݔ െ ʹ ʹݔሻ ൌ െʹሺ Ͷݔ ʹݔሻ ͵ݔ ͵ݔ ݔ ൌ ͵ݔ ݔ ͵ݔ 74 TOANMATH.com
Chương 5 : Phương trình lượng giác
͵ݔ ሺ ݔ െ ݔሻ ൌ Ͳ ቂ ͵ݔ ൌ Ͳ ݔ െ ݔ ൌ Ͳ ߨ ݇ߨ ݔ ൌ ൦ ͵ ߨ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ Ͷ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. d. Điều kiện:
ቄ ݔ ് Ͳ ݔ ് Ͳ ݔ ് േͳሺכሻ ݔ ് ͳ
Phương trình tương đương với ʹሺͳ ଶ ݔሻ ଷ ݔ ͳ ଶ ݔ െ ൌ ሺͳ ݔሻ Ͷሺͳ െ ݔሻ ͳ െ ଶ ݔ ʹ ͳ െ ଶ ݔ
ሺͳ ݔሻሺͳ ଶ ݔሻ െ ሺͳ ݔሻ ଶ ݔ െ ʹ ଶ ݔ ሺͳ ݔሻ ൌ Ͳ
ሺͳ ݔሻሺͳ െ ʹ ଶ ݔሻ ൌ Ͳ ቂ ݔ ͳ ൌ Ͳ ଶ ʹ ݔ െ ͳ ൌ Ͳ ݔ ൌ െͳሺạሻ ۍ ێ ξʹ ێ ݔ ൌ ʹ ێ ێ ξʹ ۏ ݔ ൌ െ ʹ ߨ ͵ߨ ݔ ൌ ݇ʹߨ ש ݔ ൌ ݇ʹߨ ൦ Ͷ Ͷ ሺ ߨ ͷߨ ݇ א Ժሻ
ݔ ൌ െ ݇ʹߨ ש ݔ ൌ ݇ʹߨ Ͷ Ͷ ߨ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ Ͷ ʹ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. 75 TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 2: Giải các phương trình sau:
ǤͶ ଷ ݔ ͵ξʹ ʹݔ ൌ ͺ ݔ ͳ ͳ Ǥʹ ͵ݔ െ ൌ ʹ ͵ݔ ݔ ݔ ݔ ͵ݔ ݔ ͵ݔ ͳ Ǥ ݔ െ ݔ ൌ ʹ ʹ ʹ ʹ ʹ
Ǥ ݔ ͵ݔ ʹ ͷݔ ൌ Ͳ Giải: a.
Phương trình tương đương với
ݔ ൫ʹ ଶ ݔ ͵ξʹ ݔ െ Ͷ൯ ൌ Ͳ
ݔ ൫ʹ ଶ ݔ െ ͵ξʹ ݔ ʹ൯ ൌ Ͳ ݔ ൌ Ͳ
ʹ ଶ ݔ െ ͵ξʹ ݔ ʹ ൌ Ͳ ݔ ൌ Ͳ ۍ ξʹ ێ ݔ ൌ ێ ʹ ۏ ݔ ൌ ξʹ ͳሺạሻ ߨ ۍ ݔ ൌ ݇ߨ ێ ʹ ߨ ێ ݔ ൌ ݇ʹߨ ێ Ͷ ሺ݇ א Ժሻ ێ ͵ߨ ݔ ൌ ݇ʹߨ ۏ Ͷ b. Điều kiện:
ቄ ݔ ് Ͳ ʹݔ ് Ͳሺכሻ ݔ ് Ͳ
Phương trình tương đương với ͳ ͳ ʹሺ ͵ݔ െ ͵ݔሻ െ െ ൌ Ͳ ݔ ݔ 76 TOANMATH.com
Chương 5 : Phương trình lượng giác ݔ ݔ
ʹሺ͵ ݔ െ Ͷ ଷ ݔ െ Ͷ ଷ ݔ ͵ ݔሻ െ ൌ Ͳ ݔ ݔ ݔ ݔ
ʹሺ ݔ ݔሻሾ͵ െ Ͷሺଶ ݔ െ ݔ ݔ ଶ ݔሻሿ െ ൌ Ͳ ݔ ݔ ͳ
ሺ ݔ ݔሻ െʹ ͺ ݔ ݔ െ ൨ ൌ Ͳ ݔ ݔ
ሺ ݔ ݔሻሺʹ ଶ ʹݔ െ ʹݔ െ ͳሻ ൌ Ͳ ቂ ݔ ݔ ൌ Ͳ
ʹ ଶ ʹݔ െ ʹݔ െ ͳ ൌ Ͳ ߨ ۍ ቀݔ ቁ ൌ Ͳ Ͷ ێێ ʹݔ ൌ ͳ ێ ͳ ۏ ʹݔ ൌ െ ʹ ߨ ۍ ݔ ൌ േ ݇ߨ ێ Ͷ ߨ ێݔ ൌ െ ݇ߨሺ݇ א Ժሻ ێ ͳʹ ێ ߨ ۏ ݔ ൌ ݇ߨ ͳʹ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. c.
Phương trình tương đương với ͳ ͳ ͳ
ݔ ሺ ʹݔ ݔሻ ݔ ሺ ʹݔ െ ݔሻ ൌ ʹ ʹ ʹ
ʹݔ ሺ ݔ ݔሻ ଶ ݔ െ ͳ െ ݔ ݔ ൌ Ͳ
ʹݔ ሺ ݔ ݔሻ െ ݔ ሺ ݔ ݔሻ ൌ Ͳ
ሺ ݔ ݔሻሺͳ െ ݔ െ ʹ ଶ ݔሻ ൌ Ͳ ቂ ݔ ݔ ൌ Ͳ ʹ ଶ ݔ ݔ െ ͳ ൌ Ͳ 77 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ۍ ቀݔ ቁ ൌ Ͳ Ͷ ێێ ݔ ൌ െͳ ێ ͳ ۏ ݔ ൌ ʹ ߨ ۍ ݔ ൌ െ ݇ߨ Ͷ ێ ߨ ێݔ ൌ െ ݇ʹߨ ێ ʹ ߨ ሺ݇ א Ժሻ ێ ݔ ൌ ݇ʹߨ ێ ێ ͷߨ ۏ ݔ ൌ ݇ʹߨ d.
Phương trình tương đương với
ݔ ͷݔ ͵ݔ ͷݔ ൌ Ͳ
͵ݔ ʹݔ Ͷݔ ݔ ൌ Ͳ
ሺͶ ଷ ݔ െ ͵ ݔሻ ʹݔ ሺʹ ଶ ʹݔ െ ͳሻ ݔ ൌ Ͳ
ݔ ሾሺͶ ଶ ݔ െ ͵ሻ ʹݔ ʹ ଶ ʹݔ െ ͳሿ ൌ Ͳ
ݔ ሾሺʹ ʹݔ െ ͳሻ ʹݔ ʹ ଶ ʹݔ െ ͳሿ ൌ Ͳ
ݔ ሺͶ ଶ ʹݔ െ ʹݔ െ ͳሻ ൌ Ͳ ቂ ݔ ൌ Ͳ
Ͷ ଶ ʹݔ െ ʹݔ െ ͳ ൌ Ͳ ݔ ൌ Ͳ ۍ ͳ ێ ξͳ ʹݔ ൌ ێ ͺ ێ ͳ െ ξͳ ۏ ʹݔ ൌ ͺ ߨ ۍ ݔ ൌ ݇ߨ ʹ ێ ێ ͳ ͳ ξͳ ݔ ൌ േ ቆ ݇ʹߨቇ ێ ʹ ͺ ሺ݇ א Ժሻ ێ ێ ͳ ͳ െ ξͳ ݔ ൌ േ ቆ ݇ʹߨቇ ۏ ʹ ͺ 78 TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 3: Giải các phương trình sau: ͷݔ ݔ Ǥ ൌ ͷ ଷ ݔ ʹ ʹ ͷ
Ǥ ଼ ݔ ଼ ݔ ൌ ʹሺଵ ݔ ଵ ݔሻ ʹݔ Ͷ ݔ ͺݔ Ǥʹ ଶ ͳ ൌ ͵ ͷ ͷ
Ǥ ʹݔ ʹ ݔ ൌ ͵ Giải: a. ݔ ݔ
ወấ ൌ ͲØệủươ¿²ʹếʹ ʹ ʹ
¯×ǡương trình trở thành: ͷݔ ݔ ݔ ݔ ʹ ൌ ͳͲ ଷ ݔ ʹ ʹ ʹ ʹ
͵ݔ ʹݔ ൌ ͷ ଷ ݔ ݔ
͵ ݔ െ Ͷ ଷ ݔ ʹ ݔ ݔ ൌ ͷ ଷ ݔ ݔ ቂ ݔ ൌ Ͳ
͵ െ Ͷ ଶ ݔ ʹ ݔ ൌ ͷ ଷ ݔ ݔ ۍ ൌ Ͳ ʹ ێ ݔ ێ ൌ Ͳሺạሻ ێ ʹ
ۏͷ ଷ ݔ െ Ͷ ଶ ݔ െ ʹ ݔ ͳ ൌ Ͳ ݔ ۍ ൌ Ͳ ʹ ێ ݔ ൌ ͳ ێ െͳ ێ ξʹͳ ݔ ൌ ێ ͳͲ ێ െͳ െ ξʹͳ ۏ ݔ ൌ ͳͲ 79 TOANMATH.com
Chương 5 : Phương trình lượng giác ݔ ൌ ʹ݇ߨ ۍ ێ െͳ ξʹͳ ݔ ൌ േ ݇ʹߨ ێ ͳͲ ሺ݇ א Ժሻ ێ െͳ െ ξʹͳ ۏݔ ൌ േ ݇ʹߨ ͳͲ b.
Phương trình tương đương với ͷ
଼ ݔ ሺͳ െ ʹ ଶ ݔሻ ଼ ݔ ሺͳ െ ʹ ଶ ݔሻ ൌ ʹݔ Ͷ ͷ
଼ ݔ ʹݔ െ ଼ ݔ ʹݔ ൌ ʹݔ Ͷ
Ͷ ʹݔ ሺ଼ ݔ െ ଼ ݔሻ ൌ ͷ ʹݔ ʹݔ ൌ Ͳ
Ͷሺ଼ ݔ െ ଼ ݔሻ ൌ ͷ ʹݔ ൌ Ͳ
Ͷሺସ ݔ െ ସ ݔሻሺସ ݔ ସ ݔሻ ൌ ͷ ʹݔ ൌ Ͳ ͳ
Ͷሺଶ ݔ െ ଶ ݔሻ ൬ͳ െ ଶ ʹݔ൰ ൌ ͷ ʹ ʹݔ ൌ Ͳ ͳ
Ͷ ൬ͳ െ ଶ ʹݔ൰ ൌ ͷ ʹ ʹݔ ൌ Ͳ ͳ ଶ ʹݔ ൌ െ ሺØệሻ ʹ ߨ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ Ͷ ʹ c.
Phương trình tương đương với ͳʹݔ Ͷݔ ͳ ͳ ൌ ͵ ൬ʹ ଶ െ ͳ൰ ͷ ͷ Ͷݔ Ͷݔ Ͷݔ Ͷ ଷ െ ଶ െ ͵ ͷ ൌ Ͳ ͷ ͷ ͷ 80 TOANMATH.com
Chương 5 : Phương trình lượng giác Ͷݔ Ͷݔ Ͷݔ ൬ െ ͳ൰ ൬Ͷ ଶ െ ʹ െ ͷ൰ ൌ Ͳ ͷ ͷ ͷ Ͷݔ െ ͳ ൌ Ͳ ൦ ͷ Ͷݔ Ͷݔ Ͷ ଶ െ ʹ െ ͷ ൌ Ͳ ͷ ͷ Ͷݔ ۍ ൌ ͳ ێ ͷ ێ Ͷݔ ͳ െ ξʹͳ ێ ൌ ێ ͷ Ͷ ێ Ͷݔ ͳ ξʹͳ ۏ ൌ ͳሺạሻ ͷ Ͷ ͷ݇ߨ ۍ ݔ ൌ ێ ʹ ሺ݇ א Ժሻ ێ ͷ ͳ െ ξʹͳ ͳͷߨ ۏݔ ൌ േ Ͷ Ͷ ʹ d. Điều kiện: ߨ
ݔ ് Ͳ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ ʹ
Khi đó, phương trình tương đương với ʹ ݔ ʹ ݔ ൌ ͵ ͳ ଶ ݔ
ʹ ଷ ݔ െ ͵ ଶ ݔ Ͷ ݔ െ ͵ ൌ Ͳ
ሺ ݔ െ ͳሻሺʹ ଶ ݔ െ ݔ ͵ሻ ൌ Ͳ ݔ െ ͳ ൌ Ͳ ʹ
ଶ ݔ െ ݔ ͵ ൌ ͲሺØệሻ ߨ
ݔ ൌ ͳ ֞ ݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. 81 TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 4: Giải các phương trình sau:
Ǥʹሺͳ െ ݔሻሺͳ ʹݔሻ ൌ ͳ ݔ ͳ ʹݔ ߨ Ǥ ݔ ൌ ʹ ቀݔ ቁ ξʹ ݔ ݔ ʹ
Ǥͺሺ ݔ ݔሻ ͵ξ͵ Ͷݔ ൌ ͵ξ͵ ʹݔ െ ͳͳ ʹݔ ͳͳ
Ǥξ͵ ʹݔ ሺʹ ݔ ͳሻ ʹ ൌ ͵ݔ ʹݔ െ ͵ ݔ Giải: a. Điều kiện: ߨ
ݔ ് Ͳ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với ʹ ݔ ʹሺͳ െ ݔሻ ൬ͳ ൰ ൌ ͳ ݔ ͳ ଶ ݔ
ʹሺͳ െ ݔሻሺͳ ݔሻଶ ൌ ͳ ݔ ͳ ଶ ݔ ʹ െ ʹ ଶ ݔ ሺͳ ݔሻ ቆ െ ͳቇ ൌ Ͳ ͳ ଶ ݔ
ሺͳ ݔሻሺ͵ ଶ ݔ െ ͳሻ ൌ Ͳ ቂ ݔ ͳ ൌ Ͳ ଶ ͵ ݔ െ ͳ ൌ Ͳ ݔ ൌ െͳ ۍ ێ ξ͵ ݔ ൌ ێ ͵ ێ ξ͵ ۏ ݔ ൌ െ ͵ ߨ ݔ ൌ െ ݇ߨ ൦ Ͷ ߨ ሺ݇ א Ժሻ ݔ ൌ േ ݇ߨ 82 TOANMATH.com
Chương 5 : Phương trình lượng giác
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. b. Điều kiện: ݔ ് ݇ߨ ቊ ݔ ് Ͳ ቊ ߨ ݔ ݔ ് Ͳ
ݔ ് െ ݇ߨሺ݇ א Ժሻሺכሻ Ͷ
Phương trình tương đương với ݔ ʹ ݔ ݔ ൌ ʹ ݔ ξʹ ݔ ݔ ݔ ͳ ʹ ݔ ݔ ൬ െ ʹ൰ ൌ Ͳ ξʹ ݔ ݔ ݔ
ݔ ൣ ݔ ݔ ʹξʹ ଶ ݔ െ ʹξʹ ݔ ሺ ݔ ݔሻ൧ ൌ Ͳ
ݔ ൫ ݔ ݔ െ ξʹ ݔ ݔ൯ ൌ Ͳ ݔ ൌ Ͳሺͳሻ
ݔ ݔ െ ξʹݔ ݔ ൌ Ͳሺʹሻ
Với phương trình ሺͳሻ, ta có: ߨ
ݔ ൌ ݇ߨሺ݇ א Ժሻ൫ỏሺכሻ൯ ʹ
Với phương trình ሺʹሻ, ta có: ߨ ݐଶ െ ͳ
0ặݐ ൌ ݔ ݔ ൌ ξʹ ቀݔ ቁ ǡ ݐ א ൣെξʹǢ ξʹ൧Ǥ ¯×ǡ ݔ ݔ ൌ Ͷ ʹ
ương trình ሺʹሻ trở thành: ݐଶ െ ͳ ݐ െ ൌ Ͳ ξʹ ۍ ͳ െ ξ͵ ݐ ൌ ێ ξʹ ێ ێ ͳ ξ͵ ۏݐ ൌ ͳሺạሻ ʹ 83 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ͳ െ ξ͵ ቀݔ ቁ ൌ Ͷ ʹ ۍ ͳ െ ξ͵ ߨ ݔ ൌ െ ݇ʹߨ ێ ʹ Ͷ ێ ሺ݇ א Ժሻ ێ ͳ െ ξ͵ ۏݔ ൌ ߨ െ ݇ʹߨ ʹ
Vậy nghiệm của phương trình là: ۍ ͳ െ ξ͵ ߨ ݔ ൌ െ ݇ʹߨ ێ ʹ Ͷ ێ ͳ െ ξ͵ ێݔ ൌ ߨ െ ݇ʹߨሺ݇ א Ժሻ ێ ʹ ێ ߨ ۏ ݔ ൌ ݇ߨ ʹ c.
Phương trình tương đương với
ሺʹ ଶ ݔሻଷ ሺʹ ଶ ݔሻଷ ͵ξ͵ Ͷݔ ൌ ͵ξ͵ ʹݔ െ ͻ ʹݔ ͳͳ
ሺʹ ʹݔ ͳሻଷ ሺͳ െ ʹ ʹݔሻଷ ͵ξ͵ Ͷݔ ൌ ͵ξ͵ ʹݔ െ ͻ ʹݔ ͳͳ
ʹ ଶ ʹݔ ʹξ͵ ʹݔ ʹݔ ൌ ͵ξ͵ ʹݔ െ ͻ ʹݔ ͳͳ
െʹ ଶ ʹݔ ʹξ͵ ʹݔ ʹݔ ൌ ͵ξ͵ ʹݔ െ ͻ ʹݔ ͳͳ
ሺʹ ݔ െ ͳሻ൫ξ͵ ʹݔ െ ʹݔ ͳ൯ ൌ Ͳ ʹ ݔ െ ͳ ൌ Ͳ
ξ͵ ʹݔ െ ʹݔ ͳ ൌ Ͳ ͳ ݔ ൌ ൦ ʹ ߨ ͳ ቀʹݔ ቁ ൌ ͵ ʹ ߨ ቈݔ ൌ േ ݇ʹߨ ͵ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ 84 TOANMATH.com
Chương 5 : Phương trình lượng giác d.
Phương trình tương đương với
ξ͵ ʹݔ ሺʹ ݔ ͳሻ ൌ Ͷ ଷ ݔ ʹ ଶ ݔ െ ݔ െ ͵
ξ͵ ʹݔ ሺʹ ݔ ͳሻ ൌ ሺʹ ݔ ͳሻሺʹ ଶ ݔ െ ͵ሻ
ሺʹ ݔ ͳሻ൫ξ͵ ʹݔ െ ʹ ଶ ݔ ͵൯ ൌ Ͳ
ሺʹ ݔ ͳሻ൫ξ͵ ʹݔ െ ʹݔ ʹ൯ ൌ Ͳ ʹ ݔ ͳ ൌ Ͳ
ξ͵ ʹݔ െ ʹݔ ʹ ൌ Ͳ ͳ ݔ ൌ െ ൦ ʹ ߨ ቀʹݔ െ ቁ ൌ െͳ ʹߨ ݔ ൌ േ ݇ʹߨ ൦ ͵ߨ ሺ݇ א Ժሻ ݔ ൌ െ ݇ߨ
Bài 5: Giải các phương trình sau:
Ǥ ݔ Ͷݔ ʹݔ ͵ݔ ൌ Ͳ
Ǥ ȁ ݔ ʹ ʹݔ െ ͵ݔȁ ൌ ͳ ʹ ݔ െ ʹݔ
Ǥʹ ଷ ݔ ʹݔ ݔ ൌ Ͳ ͳ
Ǥͳ ଷ ʹݔ ଷ ʹݔ ൌ Ͷݔ ʹ Giải: a.
Phương trình tương đương với
ݔ ሺʹ ଶ ʹݔ െ ͳሻ ʹݔ ሺ ʹݔ ݔ െ ʹݔ ݔሻ ൌ Ͳ
ݔ ሺ͵ ଶ ʹݔ െ ʹ ଶ ݔ ʹݔ െ ͳሻ ൌ Ͳ
ݔ ሺͶ ଶ ʹݔ െ ʹݔ െ ͳሻ ൌ Ͳ ݔ ൌ Ͳ ͳ േ ξͳ ʹݔ ൌ ͺ 85 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ۍ ݔ ൌ ݇ߨ ێ ʹ ێ ͳ ͳ ξͳ ێݔ ൌ േ ሺ݇ א Ժሻ ێ ʹ ͺ ێ ͳ ͳ െ ξͳ ۏݔ ൌ േ ʹ ͺ b. Ta thấy :
ȁ ݔ ʹ ʹݔ െ ͵ݔȁ ൌ ȁͶ ݔ ଶ ݔ ʹ ʹݔȁ ൌ ʹሺͳ ݔሻȁ ʹݔȁ
Và ͳ ʹ ݔ െ ʹݔ ൌ ʹ ݔ ሺͳ ݔሻ. Nên phương trình đã cho viết thành
ʹሺͳ ݔሻȁ ʹݔȁ ൌ ʹ ݔ ሺͳ ݔሻ ͳ ݔ ൌ Ͳሺͳሻ
ȁ ʹݔȁ ൌ ݔሺʹሻ
Với phương trình ሺͳሻ có nghiệm là ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ
Với phương trình ሺʹሻ chỉ thỏa mãn ݔ Ͳ. Trong điều kiện này, phương trình ሺʹሻ tương đương với ݔ ൌ Ͳ ݔ ൌ ݇ߨ ͳ ߨ ȁ ቈ ݔȁ ൌ ݔ ൌ ݇ߨሺ݇ א Ժሻ ʹ ͵ c.
Phương trình tương đương với
ʹ ଷ ݔ ʹ ଶ ݔ െ ͳ ݔ ൌ Ͳ
ʹሺͳ െ ݔሻሺͳ ݔሻሺ ݔ ͳሻ െ ሺͳ െ ݔሻ ൌ Ͳ
ሺͳ െ ݔሻሾʹሺͳ ݔሻሺ ݔ ͳሻ െ ͳሿ ൌ Ͳ
ሺͳ െ ݔሻሾͳ ʹ ݔ ݔ ʹሺ ݔ ݔሻሿ ൌ Ͳ
Nghiệm của phương trình là: ߨ ݔ ൌ ݇ʹߨ ൦ ʹߨ ሺ݇ א Ժሻ ݔ ൌ െ ݇ʹߨ Ͷ d.
Phương trình tương đương với
ͳ ሺ ʹݔ ʹݔሻሺͳ െ ʹݔ ʹݔሻ ൌ ʹݔ ʹݔ
ሺͳ െ ʹݔ ʹݔሻሺ ʹݔ ʹݔ ͳሻ ൌ Ͳ 86 TOANMATH.com
Chương 5 : Phương trình lượng giác
Nghiệm của phương trình là: ߨ ݔ ൌ െ ݇ߨ ൦ Ͷ ߨ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ ʹ
Bài 6: Giải các phương trình sau:
Ǥ ଶ ͵ݔ ʹݔ െ ଶ ݔ ൌ Ͳ (Tuyển sinh khối A 2005)
Ǥͳ ݔ ݔ ʹݔ ʹݔ ൌ Ͳ (Tuyển sinh khối B 2005)
Ǥ ͵ݔ ʹݔ െ ݔ ͳ ൌ Ͳ (Tuyển sinh khối D 2006) ሺ ߨ
ͳ ݔ ʹݔሻ ቀݔ ͳ Ǥ Ͷቁ ൌ ݔሺዎʹͲͳͲሻ ͳ ݔ ξʹ Giải: a.
Phương trình tương đương với
ሺͶ ଷ ݔ െ ͵ ݔሻଶ ʹݔ െ ଶ ݔ ൌ Ͳ
ଶ ݔ ሺͶ ଶ ݔ െ ͵ሻଶ ʹݔ െ ଶ ݔ ൌ Ͳ
ଶ ݔ ሾሺͶ ଶ ݔ െ ͵ሻଶ ʹݔ െ ͳሿ ൌ Ͳ
ଶ ݔ ሾሺͳ ସ ݔ െ ʹͶ ݔ ͻሻሺʹ ଶ ݔ െ ͳሻ െ ͳሿ ൌ Ͳ
ଶ ݔ ሺ͵ʹ ݔ െ Ͷ ସ ݔ Ͷʹ ଶ ݔ െ ͳͲሻ ൌ Ͳ
ଶ ݔ ሺଶ ݔ െ ͳሻሺ͵ʹ ସ ݔ െ ͵ʹ ଶ ݔ ͳͲሻ ൌ Ͳ ݔ ൌ Ͳ ቂݔ ൌ േͳ
Nghiệm của phương trình là: ݇ߨ ݔ ൌ ሺ݇ א Ժሻ ʹ b.
Phương trình tương đương với
ͳ ݔ ݔ ʹ ݔ ݔ ʹ ଶ ݔ െ ͳ ൌ Ͳ 87 TOANMATH.com
Chương 5 : Phương trình lượng giác
ݔ ሺʹ ݔ ͳሻ ݔ ሺʹ ݔ ͳሻ ൌ Ͳ
ሺʹ ݔ ͳሻሺ ݔ ݔሻ ൌ Ͳ ͳ ݔ ൌ െ ൦ ʹ ߨ ቀݔ ቁ ൌ Ͳ Ͷ
Nghiệm của phương trình là: ʹߨ ݔ ൌ േ ݇ʹߨ ൦ ͵ ߨ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ Ͷ c.
Phương trình tương đương với
Ͷ ଷ ݔ െ ͵ ݔ ʹ ଶ ݔ െ ͳ െ ݔ ͳ ൌ Ͳ
ʹ ଷ ݔ ଶ ݔ െ ʹ ݔ ൌ Ͳ
ݔ ሺʹ ଶ ݔ ݔ െ ʹሻ ൌ Ͳ ቂ ݔ ൌ Ͳ ଶ ʹ ݔ ݔ െ ʹ ൌ Ͳ
Nghiệm của phương trình là: ߨ ݔ ൌ ݇ߨ ʹ ൦ െͳ ሺ݇ א Ժሻ ξͳ ݔ ൌ േ ݇ʹߨ Ͷ d. Điều kiện: ߨ ݔ ് ݇ߨ ൞ ݔ ് Ͳ ൞ ʹ ሺ݇ א Ժሻሺכሻ ݔ ് െͳ ߨ ݔ ് െ ݇ߨ Ͷ
Phương trình tương đương với
ሺͳ ݔ ʹ ଶ ݔ െ ͳሻሺ ݔ ݔሻ ͳ ݔ ݔ ൌ ݔ ξʹǤ ξʹ ݔ 88 TOANMATH.com
Chương 5 : Phương trình lượng giác
ሺ ݔ ʹ ଶ ݔሻ ݔ ൌ ݔ
ݔ ሺʹ ଶ ݔ ݔ െ ͳሻ ൌ Ͳ
ݔ ሺͳ ݔ െ ʹ ଶ ݔሻ ൌ Ͳ ቂ ݔ ൌ Ͳ ʹ ଶ ݔ െ ݔ െ ͳ ൌ Ͳ
Kết hợp với ሺכሻ, ta nhận nghiệm ߨ ݔ ൌ െ ݇ʹߨ ൦ ߨ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ - BÀI TẬP TỰ LUYỆN
5.2.11. Giải các phương trình sau:
Ǥʹ ʹݔ െ ʹݔ ൌ ݔ ʹ ݔ െ Ͷ
Ǥ ͻ ݔ ݔ െ ͵ ʹݔ ʹݔ ൌ ͺ
Ǥ ʹݔ െ ʹݔ ൌ ͵ ݔ ݔ െ ʹ ͳ
Ǥ ݔ െ ʹݔ െ ʹݔ ʹ ൬ʹ ݔ െ ൰ ൌ Ͳ ݔ
Ǥ ଷ ݔ ଷ ݔ ൌ ݔ െ ݔ
5.2.12. Giải các phương trình sau:
Ǥ ݔ ଶ ݔ ଷ ݔ ସ ݔ ൌ ݔ ଶ ݔ ଷ ݔ ସ ݔ ͵ሺͳ ݔሻ ߨ ݔ Ǥ ͵ ଷ ݔ െ ݔ ൌ ͺ ଶ ቀ െ ቁ ଶ ݔ Ͷ ʹ
Ǥ͵ሺ ݔ െ ݔሻ െ ͷሺ ݔ െ ݔሻ ൌ ʹ
Ǥ ଶ ݔ ሺͳ െ ଷ ݔሻ ଷ ݔ െ ͳ ൌ Ͳ 89 TOANMATH.com
Chương 5 : Phương trình lượng giác
5.2.13. Giải các phương trình sau:
Ǥ ʹ ଷ ݔ െ ݔ ൌ ʹ ଷ ݔ െ ݔ ʹݔ
Ǥ ݔ ሺ Ͷݔ ʹሻ ʹݔ ͵ݔ ൌ Ͳ ͳ െ ʹݔ Ǥͳ ʹݔ ൌ ଶ ʹݔ
Ǥ ଷ ݔ ଶ ݔ ʹ ݔ െ ʹ ൌ Ͳ
Ǥ Ͷ ଶ ݔ െ ͵ݔ ൌ ݔ ʹሺͳ ʹݔሻ
Ǥͳ ݔ ͵ݔ ൌ ݔ ʹݔ ʹݔ
5.2.14. Giải các phương trình sau: ͳ ͳ Ǥ ʹݔ ݔ െ െ ൌ ʹ ʹݔ ʹ ݔ ʹݔ ߨ ݔ ߨ ͵ݔ
Ǥ ቀͷݔ െ ቁ െ ቀ െ ቁ ൌ ξʹ Ͷ ʹ Ͷ ʹ
Ǥ ʹݔ ʹݔ ͵ ݔ െ ݔ െ ʹ ൌ Ͳ ሺʹ െ ଶ ʹݔሻ ͵ݔ Ǥ ସ ݔ ͳ ൌ ସ ݔ
Ǥ͵ ସ ݔ െ Ͷ ଶ ݔ ଶ ݔ ସ ݔ ൌ Ͳ
Ǥ ʹݔ ൌ ͳ ξʹ ݔ ʹݔ -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN 5.2.11. a.
Phương trình tương đương với
Ͷ ݔ ݔ െ ሺͳ െ ʹ ଶ ݔሻ ൌ ݔ ʹ ݔ െ Ͷ
Ͷ ݔ ݔ െ ݔ െ ʹ ݔ ʹ ଶ ݔ െ ͷ ൌ Ͳ
ʹ ݔ ሺʹ ݔ െ ͳሻ ሺʹ ݔ െ ͳሻሺ ݔ െ ͵ሻ ൌ Ͳ
ሺʹ ݔ െ ͳሻሺʹ ݔ ݔ െ ͵ሻ ൌ Ͳ 90 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ݔ ൌ ݇ʹߨ ൦ ͷߨ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ b.
Phương trình tương đương với
ͻ ݔ ݔ െ ݔ ݔ ͳ െ ʹ ଶ ݔ ൌ ͺ
ݔ ሺͳ െ ݔሻ ሺͳ െ ݔሻሺʹ ݔ െ ሻ ൌ Ͳ
ሺͳ െ ݔሻሺ ݔ ʹ ݔ െ ሻ ൌ Ͳ ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ c.
Phương trình tương đương với
ʹ ݔ ݔ െ ͳ ʹ ଶ ݔ ൌ ͵ ݔ ݔ െ ʹ
ݔ ሺʹ ݔ െ ͳሻ ሺʹ ݔ െ ͳሻሺ ݔ െ ͳሻ ൌ Ͳ
ሺʹ ݔ െ ͳሻሺ ݔ ݔ െ ͳሻ ൌ Ͳ ߨ ۍ ݔ ൌ ݇ʹߨ ێ ێ ͷߨ ݔ ൌ ݇ʹߨ ێ ሺ݇ א Ժሻ ێ ߨ ێ ݔ ൌ ݇ʹߨ ʹ ۏ ݔ ൌ ݇ʹߨ
Qua các bài a, b và c thì ta thấy có cùng dạng phương trình là:
ܽ ʹݔ ܾ ʹݔ ܿ ݔ ݀ ݔ ݁ ൌ Ͳሺכሻ
Nguyên gốc phương trình trên là xuất phát từ phương trình này:
ሺܽଵ ݔ ܽଶ ݔ ܽଷሻሺܽସ ݔ ܽହ ݔ ܽሻ ൌ Ͳሺככሻ
Từ phương trình ሺככሻ người ta khai triển ra và thêm bớt vào để đưa về phương trình ሺכሻ.
Cách giải thông thường là chúng ta sử dụng công thức ʹݔ ൌ ʹ ݔ ݔ và công
thức ʹݔ ൌ ʹ ଶ ݔ െ ͳ hay ʹݔ ൌ ͳ െ ʹ ଶ ݔ xem cái nào có thể đưa phương
trình ሺכሻ phương trình ሺככሻ. 91 TOANMATH.com
Chương 5 : Phương trình lượng giác d. Điều kiện: ߨ
ݔ ് Ͳ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với ݔ ʹ
െ ʹݔ െ ʹݔ Ͷ ݔ െ ൌ Ͳ ݔ ݔ
ݔ െ ݔ ʹݔ െ ʹݔ ݔ Ͷ ଶ ݔ െ ʹ ൌ Ͳ
ݔ ሺͳ െ ʹ ଶ ݔሻ െ ʹݔ ݔ ʹ ʹݔ ൌ Ͳ
െ ݔ ʹݔ െ ʹݔ ݔ ʹ ʹݔ ൌ Ͳ
ʹݔ ሺ ݔ ݔ െ ʹሻ ൌ Ͳ
Kết hợp với ሺכሻ, ta nhận nghiệm ߨ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ Ͷ ʹ e.
Phương trình tương đương với
ݔ ሺଶ ݔ െ ͳሻ ଷ ݔ ݔ ൌ Ͳ
െ ݔ ଶ ݔ ଷ ݔ ݔ ൌ Ͳ
ݔ ሺ ʹݔ െ ʹݔ െ ͵ሻ ൌ Ͳ
Nghiệm của phương trình là: ߨ ݔ ൌ ݇ߨሺ݇ א Ժሻ ʹ 5.2.12. a.
Phương trình tương đương với
ݔ െ ݔ ଶ ݔ െ ଶ ݔ ଷ ݔ െ ଷ ݔ ସ ݔ െ ସ ݔ ൌ Ͳ
ሺ ݔ െ ݔሻሺͳ ݔ ݔ ͳ ݔ ݔ ݔ ݔሻ ൌ Ͳ
Nghiệm của phương trình là: 92 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ۍ ݔ ൌ ݇ߨ ێ Ͷ
ێ ݔ ൌ ߨ ݇ʹߨ ሺ݇ א Ժሻ ێ ߨ ۏݔ ൌ െ ݇ʹߨ ʹ b. Điều kiện: ߨ
ݔ ് Ͳ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với : ߨ
͵ ଷ ݔ െ ݔ ͵ሺͳ ݔሻሺͳ ଶ ݔሻ ൌ Ͷ ቂͳ ቀ െ ݔቁቃ ʹ
ݔ ሺ͵ ଶ ݔ െ ͳሻ ͵ሺͳ ݔሻሺͳ ଶ ݔሻ ൌ Ͷሺͳ ݔሻ
ݔ ሺ͵ ଶ ݔ െ ͳሻ ሺͳ ݔሻሺ͵ ͵ ଶ ݔ െ Ͷሻ ൌ Ͳ
ݔ ሺ͵ ଶ ݔ െ ͳሻ ሺͳ ݔሻሺ͵ ଶ ݔ െ ͳሻ ൌ Ͳ
ሺ͵ ଶ ݔ െ ͳሻሺ ݔ ͳ ݔሻ ൌ Ͳ
ሺ͵ ଶ ݔ െ ͳሻሺ ݔ ݔ ݔ ݔሻ ൌ Ͳ
Kết hợp với ሺכሻ, ta nhận nghiệm ߨ ۍ ݔ ൌ േ ݇ߨ ێ ξʹ െ ͳ ߨ ێ ݔ ൌ െ ݇ʹߨ ሺ݇ א Ժሻ ێ ξʹ Ͷ ێ ͵ߨ ξʹ െ ͳ ێݔ ൌ െ ݇ʹߨ ۏ Ͷ ξʹ c. Điều kiện: ݇ߨ
൜ ݔ ് Ͳ ʹݔ ് Ͳ ݔ ് ሺ݇ א Ժሻሺכሻ ݔ ് Ͳ ʹ
Phương trình tương đương với :
͵ ଶ ݔ ሺͳ െ ݔሻ െ ͷ ଶ ݔ ሺͳ െ ݔሻ ൌ ʹ ݔ ݔ
͵ ݔ ሺ ݔ െ ݔ ݔ ݔሻ െ ͷ ݔ ሺ ݔ െ ݔ ݔ ݔሻ ൌ Ͳ 93 TOANMATH.com
Chương 5 : Phương trình lượng giác
ሺ ݔ ݔ െ ݔ ݔሻሺ͵ ݔ െ ͷ ݔሻ ൌ Ͳ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. ۍ ͳ െ ξʹ ߨ ݔ ൌ െ ݇ʹߨ ێ ʹ Ͷ ێ ͵ߨ ͳ െ ξʹ ێݔ ൌ െ ݇ʹߨሺ݇ א Ժሻ ێ Ͷ ʹ ێ ͵ ۏ ݔ ൌ ݇ߨ ͷ d. Điều kiện: ߨ ݔ ് Ͳ ݔ ്
݇ߨሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với
ଶ ݔ ሺͳ െ ଷ ݔሻ ሺଷ ݔ െ ͳሻ ଶ ݔ ൌ Ͳ
ሺͳ െ ଶ ݔሻሺͳ െ ଷ ݔሻ ሺଷ ݔ െ ͳሻሺͳ െ ଶ ݔሻ ൌ Ͳ
ሺͳ െ ݔሻሺͳ െ ݔሻሺଶ ݔ ଶ ݔ ݔ െ ଶ ݔ െ ݔ ଶ ݔሻ ൌ Ͳ
ሺͳ െ ݔሻሺͳ െ ݔሻሺ ݔ െ ݔሻሺ ݔ ݔ ݔ ݔሻ ൌ Ͳ
Kết hợp với ሺכሻ, ta nhận nghiệm ݔ ൌ ݇ʹߨ ۍ ߨ ݔ ൌ ݇ߨ ێ Ͷ ሺ݇ א Ժሻ ێ ξʹ െ ͳ ߨ ێݔ ൌ േ ݇ʹߨ ۏ ξʹ Ͷ 5.2.13. a.
Phương trình tương đương với
ݔ ሺʹ ଶ ݔ െ ͳሻ ൌ ሺͳ െ ݔሻሺʹ ଶ ݔ െ ͳሻ
ሺʹ ଶ ݔ െ ͳሻሺ ݔ ݔ ͳሻ ൌ Ͳ
Nghiệm của phương trình là: 94 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ۍ ݔ ൌ േ ݇ʹߨ Ͷ ێ ͵ߨ ێݔ ൌ േ ݇ʹߨ ێ Ͷ ሺ݇ א Ժሻ ێ ݔ ൌ ݇ʹߨ ێ ͵ߨ ۏ ݔ ൌ ݇ʹߨ Ͷ b.
Phương trình tương đương với
ݔ ሺ Ͷݔ ʹሻ ʹݔ ሺͶ ଷ ݔ െ ͵ ݔሻ ൌ Ͳ
ݔ ሾ Ͷݔ ʹ ʹݔ ሺͶ ଶ ݔ െ ͵ሻሿ ൌ Ͳ
ݔ ሾʹ ଶ ʹݔ െ ͳ ʹ ʹݔ ሺʹ ʹݔ ʹ െ ͵ሻሿ ൌ Ͳ
ݔ ሺͶ ଶ ʹݔ െ ʹݔ ͳሻ ൌ Ͳ
Nghiệm của phương trình là: ߨ ݔ ൌ ݇ߨ ሺ݇ א Ժሻ ʹ c. Điều kiện: ݇ߨ ʹݔ ് Ͳ ݔ ് ሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với
ଶ ʹݔ ʹݔ ʹݔ ൌ ͳ െ ʹݔ
ͳ െ ଶ ʹݔ ʹݔ ʹݔ ൌ ͳ െ ʹݔ
ʹݔ ሺ ʹݔ െ ʹݔ െ ͳሻ ൌ Ͳ
Kết hợp với ሺכሻ, ta nhận nghiệm ߨ ݇ߨ ݔ ൌ െ Ͷ ʹ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ d.
Phương trình tương đương với
ଶ ݔ ሺ ݔ ͳሻ ʹሺ ݔ െ ͳሻ ൌ Ͳ 95 TOANMATH.com
Chương 5 : Phương trình lượng giác
ሺͳ െ ݔሻሺͳ ݔሻሺ ݔ ͳሻ െ ʹሺͳ െ ݔሻ ൌ Ͳ
ሺͳ െ ݔሻሾሺͳ ݔሻሺ ݔ ͳሻ െ ʹሿ ൌ Ͳ
ሺͳ െ ݔሻሺ ݔ ݔ ݔ ݔ െ ͳሻ ൌ Ͳ
Nghiệm của phương trình là: ߨ ቈݔ ൌ ݇ʹߨ ʹ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ e.
Phương trình tương đương với
Ͷ ଶ ݔ ͵ ݔ െ Ͷ ଷ ݔ ൌ ݔ ʹሺʹ ଶ ݔሻ
Ͷ ଷ ݔ െ ͵ ݔ ൌ Ͳ
ݔ ሺͶ ଶ ݔ െ ͵ሻ ൌ Ͳ
Nghiệm của phương trình là: ݔ ൌ ߨ ݇ߨ ۍ ߨ ێ ݔ ൌ േ ݇ʹߨ ێ ͵ ሺ݇ א Ժሻ ێ ʹߨ ۏݔ ൌ േ ݇ʹߨ ͵ f.
Phương trình tương đương với
ͳ ݔ ͵ݔ െ ݔ െ ʹݔ െ ͳ ʹ ଶ ݔ ൌ Ͳ
ݔ െ ʹ ʹݔ ݔ െ ʹ ݔ ݔ ʹ ଶ ݔ ൌ Ͳ
ݔ ሺͳ െ ʹ ʹݔ െ ʹ ݔ ʹ ݔሻ ൌ Ͳ
ݔ ሾሺ ݔ െ ݔሻଶ ʹሺ ݔ െ ݔሻሿ ൌ Ͳ
ݔ ሺ ݔ െ ݔሻሺ ݔ െ ݔ ʹሻ ൌ Ͳ
Nghiệm của phương trình là: ݔ ൌ ݇ߨ ቈ ߨ ݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ 96 TOANMATH.com
Chương 5 : Phương trình lượng giác 5.2.14. a. Điều kiện: ݇ߨ ൜ ݔ ് Ͳ ݔ ് ሺ݇ א Ժሻሺכሻ ʹݔ ് Ͳ ʹ
Phương trình tương đương với ଶ ʹݔ െ ͳ ʹ ଶ ݔ െ ͳ ʹ ʹݔ ൌ ʹݔ ݔ ʹݔ െ ଶ ʹݔ ʹݔ ʹ ʹݔ െ ൌ ʹݔ ݔ ʹݔ ʹݔ ͳ ʹ ʹݔ ൬ െ ൰ ൌ Ͳ ʹݔ ݔ ʹݔ
ʹݔ ሺ ʹݔ ݔ െ ʹሻ ൌ Ͳ
ʹݔ ሺʹ ଶ ݔ ݔ ͳሻ ൌ Ͳ
Kết hợp với ሺכሻ, ta nhận nghiệm ߨ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ Ͷ ʹ b.
Phương trình tương đương với ξʹ ͷݔ ͷݔ ξʹ ݔ ݔ ͵ݔ ൬ െ ൰ െ ቀ ቁ ൌ ξʹ ʹ ʹ ʹ ʹ ʹ ʹ ʹ ͵ݔ ͵ݔ ͵ݔ ʹ ʹݔ െ ʹ ʹݔ ൌ ʹ ʹ ʹ ʹ ͵ݔ ʹ
ሺ ʹݔ െ ʹݔ െ ͳሻ ൌ Ͳ ʹ
Nghiệm của phương trình là: ߨ ʹ݇ߨ ۍ ݔ ൌ ێ ͵ ͵ ێ ߨ
ݔ ൌ ݇ߨ ሺ݇ א Ժሻ ێ Ͷ ێ ߨ ۏ ݔ ൌ ݇ߨ ʹ 97 TOANMATH.com
Chương 5 : Phương trình lượng giác c.
Phương trình tương đương với
ʹ ݔ ݔ െ ݔ െ ʹ ଶ ݔ ͵ ݔ െ ͳ ൌ Ͳ
ݔ ሺʹ ݔ െ ͳሻ െ ሺ ݔ െ ͳሻሺʹ ݔ െ ͳሻ ൌ Ͳ
ሺʹ ݔ െ ͳሻሺ ݔ െ ݔ ͳሻ ൌ Ͳ
Nghiệm của phương trình là: ߨ ۍ ݔ ൌ ݇ʹߨ ێ ێ ͷߨ ݔ ൌ ݇ʹߨ ێ ሺ݇ א Ժሻ ێ ߨ ێ ݔ ൌ ݇ʹߨ ʹ ۏ ݔ ൌ െߨ ݇ʹߨ d. Điều kiện: ߨ ቄ ݔ ് Ͳ ݔ ്
݇ߨሺ݇ א Ժሻሺכሻ ସ ݔ ് Ͳ ʹ
Phương trình tương đương với ସ ݔ ସ ݔ ሺʹ െ ଶ ʹݔሻ ͵ݔ ൌ ସ ݔ ସ ݔ
ସ ݔ ସ ݔ ൌ ʹ ͵ݔ െ ଶ ʹݔ ͵ݔ
ͳ െ ʹ ଶ ݔ ଶ ݔ ൌ ʹ ͵ݔ െ ଶ ʹݔ ͵ݔ
ʹ െ ଶ ʹݔ ൌ Ͷ ͵ݔ െ ʹ ଶ ʹݔ ʹݔ
ଶ ʹݔ ሺʹ ͵ݔ െ ͳሻ ൌ ʹሺʹ ͵ݔ െ ͳሻ
ሺʹ ͵ݔ െ ͳሻሺଶ ʹݔ െ ʹሻ ൌ Ͳ
Kết hợp với ሺכሻ, ta nhận nghiệm ߨ ݇ʹߨ ݔ ൌ ൦ ͳͺ ͵ ͳߨ ݇ʹߨሺ݇ א Ժሻ ݔ ൌ ͳͺ ͵ 98 TOANMATH.com
Chương 5 : Phương trình lượng giác e.
Phương trình tương đương với
͵ ଶ ݔ ሺଶ ݔ െ ଶ ݔሻ െ ଶ ݔ ሺଶ ݔ െ ଶ ݔሻ ൌ Ͳ
ʹݔ ሺ͵ ଶ ݔ െ ଶ ݔሻ ൌ Ͳ
ʹݔ ሺͶ ଶ ݔ െ ͳሻ ൌ Ͳ
Nghiệm của phương trình là: ߨ ۍ ݔ ൌ ݇ߨ ێ Ͷߨ
ێ ݔ ൌ േ ݇ʹߨ ሺ݇ א Ժሻ ێ ͵ ێ ʹߨ ۏݔ ൌ േ ݇ʹߨ ͵ f.
Phương trình tương đương với
ʹ ݔ ݔ ൌ ͳ ξʹ ݔ ʹ ଶ ݔ െ ͳ
ʹ ݔ ݔ ൌ ʹ ଶ ݔ ξʹ ݔ
ξʹ ݔ ൫ξʹ ݔ െ ξʹ ݔ െ ͳ൯ ൌ Ͳ
Nghiệm của phương trình là: ߨ ۍ ݔ ൌ ݇ߨ ʹ ێ ͷߨ ێ ݔ ൌ ݇ʹߨ ሺ݇ א Ժሻ ێ ͳʹ ێ ͳ͵ߨ ۏݔ ൌ ݇ʹߨ ͳʹ 99 TOANMATH.com
Chương 5 : Phương trình lượng giác b.
PHƯƠNG TRÌNH CHỨA CĂN THỨC
- Ở dạng phương trình chứa căn thức này, chúng ta thường áp dụng các công thức
bên dưới. Sau khi giải đến phần so điều kiện thì chúng ta sẽ thử nghiệm trực tiếp. x ξ ൌ ξ ֞ ൌ Ͳ x ξ ൌ ֞ ቄ Ͳ ൌ ଶ Ͳ x ξ ξ ൌ ξ ൝ Ͳ ʹξ ൌ
x ξ ൌ ቊ ξǤ ξǡ Ͳ Ͳ ξെǤ ξെǡ Ͳ Ͳ
Bài 1: Giải phương trình sau:
ଷ ݔ ଷ ݔ ଷ ݔ ݔ ଷ ݔ ݔ ൌ ξʹ ʹݔ
Giải: Điều kiện: ݔ ് Ͳ
൝ ݔ ് Ͳ ቄ ʹݔ ് Ͳ
ʹݔ Ͳ ʹݔ Ͳሺכሻ ʹݔ Ͳ
Phương trình tương đương với
ଷ ݔ ଷ ݔ ଶ ݔ ݔ ݔ ଶ ݔ ൌ ξʹ ʹݔ
ଶ ݔ ሺ ݔ ݔሻ ଶ ݔ ሺ ݔ ݔሻ ൌ ξʹ ʹݔ
ሺ ݔ ݔሻሺଶ ݔ ଶ ݔሻ ൌ ξʹ ʹݔ ݔ ݔ ൌ ξʹ ʹݔ ߨ ቊ ቀݔ ቁ Ͳ Ͷ ͳ ʹ ݔ ݔ ൌ ʹ ʹݔ ߨ ቀݔ ቁ Ͳ ൝ Ͷ ʹݔ ൌ ͳሺỏሺכሻሻ 100 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ۓ ቀݔ ቁ Ͳ ۖ Ͷ ߨ ݔ ൌ ݇ʹߨ ۔൦ Ͷ ሺ݇ǡ ݈ א Ժሻ ۖ ͷߨ ە ݔ ൌ ݈ʹߨ Ͷ ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ Ͷ
Bài 2: Giải phương trình sau:
ξͷ ݔ െ ʹݔ ʹ ݔ ൌ Ͳ
Giải: Phương trình tương đương với ξͷ ݔ െ ʹݔ ൌ െʹ ݔ ቄ ݔ Ͳ ͷ ݔ െ ʹݔ ൌ Ͷ ଶ ݔ ቄ ݔ Ͳ
ʹ ଶ ݔ ͷ ݔ െ ͵ ൌ Ͳ ݔ Ͳͳ ൞ ݔ ൌ ʹ
ݔ ൌ െ͵ ൏ െͳሺạሻ ݔ Ͳ ߨ
ቊݔ ൌ േ ݇ʹߨሺ݇ א Ժሻ ͵ ߨ
ݔ ൌ െ ݇ʹߨሺ݇ א Ժሻ ͵
Bài 3: Giải phương trình sau: ߨ
ʹ ቀ͵ݔ ቁ ൌ ඥͳ ͺ ʹݔ ଶ ʹݔ Ͷ
(ĐH Kinh Tế Quốc Dân 2000) 101 TOANMATH.com
Chương 5 : Phương trình lượng giác
Giải: Phương trình tương đương với ߨ
ቀ͵ݔ ቁ Ͳሺכሻ ൞ Ͷ ߨ
Ͷ ଶ ቀ͵ݔ ቁ ൌ ͳ ͺ ʹݔ ଶ ʹݔሺͳሻ Ͷ
Ta giải phương trình ሺʹሻ : ߨ
ʹ ቂͳ െ ቀݔ ቁቃ ൌ ͳ Ͷ Ͷݔ ʹݔ ʹ
ʹሺͳ ݔሻ ൌ ͳ ʹሺ ݔ ʹݔሻ ߨ ͳ ݔ ൌ ݇ߨ ʹݔ ൌ ൦ ͳʹ ሺ݇ א Ժሻ ʹ ͷߨ ݔ ൌ ݇ߨ ͳʹ
Kiểm tra điều kiện ሺכሻ, ta nhận nghiệm của phương trình là ߨ ݔ ൌ ݉ʹߨ ൦ ͳʹ ͳߨ ሺ݉ א Ժሻ ݔ ൌ ݉ʹߨ ͳʹ
Bài 4: Giải phương trình sau:
ξ ʹݔ ξͳ ʹݔ ൌ ʹξ ݔ ݔ
Giải: Điều kiện : ቄ ʹݔ Ͳ ቄ ݔ െ ݔ Ͳ ݔ ݔ Ͳ ݔ ݔ Ͳ
Phương trình tương đương với
ඥሺ ݔ െ ݔሻሺ ݔ ݔሻ ඥሺ ݔ ݔሻଶ ൌ ʹξ ݔ ݔ
Với ݔ ݔ ൌ Ͳ, ta được ߨ
ݔ ൌ െͳ ݔ ൌ െ ݇ߨሺ݇ א Ժሻ Ͷ
Với ݔ ݔ Ͳ và ݔ െ ݔ Ͳ thì 102 TOANMATH.com
Chương 5 : Phương trình lượng giác
ξ ݔ ݔ ൫ξ ݔ െ ݔ ξ ݔ ݔ൯ ൌ ʹξ ݔ ݔ
ξ ݔ െ ݔ ξ ݔ ݔ ൌ ʹ
ʹ ݔ ʹඥଶ ݔ െ ଶ ݔ ൌ Ͷ
ଶ ݔ െ ଶ ݔ ൌ ሺʹ െ ݔሻଶ
ଶ ݔ Ͷ ݔ െ ͷ ൌ Ͳ ݔ ൌ ͳ
ݔ ൌ െͷሺሻ ݔ ൌ ݇ʹߨሺ݇ א Ժሻ
Vậy nghiệm của phương trình là ߨ ቈݔ ൌ െ ݇ߨ Ͷ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ - BÀI TẬP TỰ LUYỆN
5.2.15. Giải phương trình sau: Ǥ ξͳ ݔ ݔ ൌ Ͳ ͳ
Ǥ ൫ξͳ െ ݔ ξ ݔ൯ ʹݔ ൌ Ͷݔ ʹ
ξͳ െ ʹݔ ξͳ ʹݔ Ǥ ൌ Ͷ ݔ ݔ
Ǥ ݔ ξ͵ ݔ ට ݔ ξ͵ ݔ ൌ ʹ 103 TOANMATH.com
Chương 5 : Phương trình lượng giác -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN 5.2.15. a.
Phương trình tương đương với ξͳ ݔ ൌ െ ݔ ቄ ݔ Ͳ ͳ ݔ ൌ ଶ ݔ ቄ ݔ Ͳ ଶ ݔ ݔ ൌ Ͳ ݔ Ͳ ቊቂ ݔ ൌ Ͳ ݔ ൌ െͳ ݔ Ͳ ቐ ݔ ൌ ݇ߨ ቈ ߨ
ݔ ൌ െ ݇ʹߨሺ݇ א Ժሻ ʹ ݔ ൌ ߨ ݇ʹߨ ቈ ߨ
ݔ ൌ െ ݇ʹߨ ሺ݇ א Ժሻ ʹ b. Điều kiện : ݔ Ͳሺכሻ
Phương trình tương đương với
൫ξͳ െ ݔ ξ ݔ൯ ʹݔ ൌ ʹݔ ʹݔ
ξͳ െ ݔ ξ ݔ ൌ ʹݔሺͳሻ ʹݔ ൌ Ͳሺʹሻ
Với phương trình ሺͳሻ ta có ʹݔ Ͳ
൜ͳ ʹඥݔ ሺͳ െ ݔሻ ൌ ଶ ʹݔ ʹݔ Ͳ ൜ ሺ ሺ Øዉሻ
ʹ ଶ ݔ െ ͳሻଶ ʹඥ ݔ ሺͳ െ ݔሻ ൌ Ͳ
Với phương trình ሺʹሻ ta có ߨ
ݔ ൌ േ ݇ߨሺ݇ א Ժሻ Ͷ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. 104 TOANMATH.com
Chương 5 : Phương trình lượng giác c. Điều kiện : ʹݔ ͳ
൝ ʹݔ ͳ ݔ ് Ͳ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ ݔ ് Ͳ
Phương trình tương đương với
ξͳ െ ʹݔ ξͳ ʹݔ ൌ ʹ ʹݔ ʹݔ Ͳ ൜
ͳ െ ʹݔ ͳ ʹݔ ʹඥͳ െ ଶ ʹݔ ൌ Ͷ ଶ ʹݔ ʹݔ Ͳ ൜ඥ
ͳ െ ଶ ʹݔ ൌ ʹ ଶ ʹݔ െ ͳ ʹݔ Ͳͳ ൞ ଶ ʹݔ ʹ
ͳ െ ଶ ʹݔ ൌ Ͷ ସ ʹݔ െ Ͷ ଶ ʹݔ ͳ ξʹ ቐ ʹݔ ʹ
Ͷ ସ ʹݔ െ ͵ ଶ ʹݔ ൌ Ͳ ۓ ξʹ ۖ ʹݔ ʹ ଶ ʹݔ ൌ Ͳ ۔ ۖ ͵ ە ଶ ʹݔ ൌ Ͷ ξʹ ۓ ʹݔ ۖ ʹ ۖ ۍ ξ͵ ʹݔ ൌ ێ ۔ ʹ ێ ێ ۖ ۖ ξ͵ ۏ ʹݔ ൌ െ ە ʹ ξ͵ ʹݔ ൌ ʹ 105 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ݔ ൌ ݇ߨ ൦ ߨ ሺ݇ א Ժሻ ݔ ൌ ݇ߨ ͵
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. d. ߨ
0ặݐ ൌ ݔ ξ͵ ݔ ൌ ʹ ቀݔ ቁ ǡ ݐ Ͳሺכሻ ͵
Khi đó, phương trình trở thành ξݐ ൌ ʹ െ ݐ
ቊͲ ݐ ʹ ቀếợሺכሻቁ ݐ ൌ ݐଶ െ Ͷݐ Ͷ ቄ Ͳ ݐ ʹ ଶ ݐ െ ͷݐ Ͷ ൌ Ͳ Ͳ ݐ ʹ ቊ ቂݐ ൌ ͳ ݐ ൌ Ͷ ݐ ൌ ͳ Do đó, ߨ ߨ ͳ ݔ ൌ െ ݇ʹߨ ቀݔ ቁ ൌ ൦ ሺ݇ א Ժሻ ͵ ʹ ߨ ݔ ൌ ݇ʹߨ ʹ 106 TOANMATH.com
Chương 5 : Phương trình lượng giác c.
PHƯƠNG TRÌNH KHÔNG MẪU MỰC
- Các phương trình không mẫu mực là các phương trình không có một cách giải cụ
thể nào, thường là sử dụng các bất đẳng thức hoặc đạo hàm hàm số để đánh giá và tìm ra nghiệm.
- Chúng thường sử dụng các bất đẳng thức sau: x െͳ ݔ ͳ x െͳ ݔ ͳ x ቄ ฺ ൌ Ͳ x ൝ Ͳ ฺ ൌ ൌ Ͳ ൌ Ͳ x ቄ ฺ ൌ ൌ x ቄ ฺ ൌ ൌ ൌ
Bài 1: Giải các phương trình sau:
Ǥ ଵଷ ݔ ଵସ ݔ ൌ ͳ Ǥ ହ ݔ ହ ݔ ൌ ͳ Giải: a.
Phương trình tương đương với
ଵଷ ݔ ଵସ ݔ ൌ ଶ ݔ ଶ ݔ
ଶ ݔ ሺଵଵ ݔ െ ͳሻ ଶ ݔ ሺଵଶ ݔ െ ͳሻ ൌ Ͳ Ta có:
ቄ ݔ ͳ ฺ ଶ ݔ ሺଵଵ ݔ െ ͳሻ Ͳ ൞ ଶ ݔ Ͳ
ቄ ݔ ͳ ฺ ଶ ݔ ሺଵଶ ݔ െ ͳሻ Ͳ ଶ ݔ Ͳ
ฺ ଶ ݔ ሺଵଵ ݔ െ ͳሻ ଶ ݔ ሺଵଶ ݔ െ ͳሻ Ͳ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi: 107 TOANMATH.com
Chương 5 : Phương trình lượng giác ۍ ቄ ݔ ൌ Ͳ ݔ ൌ Ͳ ێ ێቄ ݔ ൌ ͳ ߨ
ێ ଶ ݔ ൌ ͳ ቈݔ ൌ ݇ߨ ʹ ሺ݇ א Ժሻ ێ ቄ ݔ ൌ ͳ ێ ݔ ൌ Ͳ ݔ ൌ ݇ʹߨ ێ ۏቄ ݔ ൌ ͳ ଶ ݔ ൌ ͳ b.
Phương trình tương đương với
ହ ݔ ହ ݔ ൌ ଶ ݔ ଶ ݔ
ଶ ݔ ሺଷ ݔ െ ͳሻ ଶ ݔ ሺଷ ݔ െ ͳሻ ൌ Ͳ Ta có:
ቄ ݔ ͳ ฺ ଶ ݔ ሺଷ ݔ െ ͳሻ Ͳ ൞ ଶ ݔ Ͳ ቄ ݔ ͳ
ଶ ݔ Ͳ ฺ ଶ ݔ ሺଷ ݔ െ ͳሻ Ͳ
ฺ ଶ ݔ ሺଷ ݔ െ ͳሻ ଶ ݔ ሺଷ ݔ െ ͳሻ Ͳ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi: ۍቄ ݔ ൌ Ͳ ݔ ൌ Ͳ ێ ێ ߨ ቄ ݔ ൌ Ͳ
ێ ݔ ൌ ͳ ቈݔ ൌ ݇ʹߨ ʹ ሺ݇ א Ժሻ ێቄ ݔ ൌ ͳ ێ ݔ ൌ Ͳ ݔ ൌ ݇ʹߨ ێ ۏቄ ݔ ൌ ͳ ݔ ൌ ͳ 108 TOANMATH.com
Chương 5 : Phương trình lượng giác
Qua 2 bài trên chúng ta thấy rằng với ܽǡ ܾ không đồng thời bằng 2, dạng phương trình:
ݔ ݔ ൌ ͳሺכሻ
Chúng ta thường giải như sau:
ሺכሻ ݔ ݔ ൌ ଶ ݔ ଶ ݔ
ଶ ݔ ሺିଶ ݔ െ ͳሻ ଶ ݔ ሺିଶ ݔ െ ͳሻ ൌ Ͳ
Khi đó, chúng ta sử dụng các đánh giá:
ቄ ݔ ͳ ֜ ଶ ݔ ሺିଶ ݔ െ ͳሻ Ͳ ൞ ଶ ݔ Ͳ
ቄ ݔ ͳ ֜ ଶ ݔ ሺିଶ ݔ െ ͳሻ Ͳ ଶ ݔ Ͳ
ฺ ଶ ݔ ሺିଶ ݔ െ ͳሻ ଶ ݔ ሺିଶ ݔ െ ͳሻ Ͳ
Đến đây, ta xét dấu ̶ ൌ ̶ xảy ra khi và chỉ khi: ۍ ቄ ݔ ൌ Ͳ ݔ ൌ Ͳ ێ ێቄ ݔ ൌ Ͳ ێ ିଶ ݔ ൌ ͳ ێቄିଶ ݔ ൌ ͳ ێ ݔ ൌ Ͳ ێ ۏቄିଶ ݔ ൌ ͳ ିଶ ݔ ൌ ͳ
Ngoài ra, chúng ta cũng có thể làm như sau :
൜ ݔ ଶ ݔ ฺ ݔ ݔ ଶ ݔ ଶ ݔ ൌ ͳ ݔ ଶ ݔ
Đến đây, chúng ta cũng xét dấu ̶ ൌ ̶ xảy ra đối với phương trình ሺכሻ. 109 TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 2: Giải các phương trình sau:
ǤͶ ଶ ݔ ͵ ଶ ݔ െ Ͷξ͵ ݔ ʹξ͵ ݔ Ͷ ൌ Ͳ ଵ ݔ ଵ ݔ ݔ ݔ Ǥ ൌ Ͷ Ͷ ଶ ʹݔ ଶ ʹݔ ͳ
Ǥ ହ ݔ ݔ ሺଷ ݔ ହ ݔሻ ʹݔ ൌ ݔ ݔ ʹ Giải: a. Điều kiện: ߨ
ݔ ് Ͳ ݔ ് ݇ߨሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với ଶ ଶ
൫ʹ ݔ െ ξ͵൯ ൫ξ͵ ݔ ͳ൯ ൌ Ͳ ൜ʹ ݔ െ ξ͵ ൌ Ͳ ξ͵ ݔ ͳ ൌ Ͳ ۓ ξ͵ ۖ ݔ ൌ ʹ ۔ ξ͵ ۖ ݔ ൌ െ ە ͵ ߨ ۓ ݔ ൌ ݇ʹߨ ൦ ۖ ߨ
ݔ ൌ െ ݇ʹߨሺ݇ א Ժሻ ۔ ߨ ۖ ݔ ൌ െ ݇ߨ ە ߨ
ݔ ൌ െ ݇ߨሺ݇ א Ժሻ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. 110 TOANMATH.com
Chương 5 : Phương trình lượng giác b. Điều kiện: ͵ ʹ
Ͷ ଶ ʹݔ ଶ ʹݔ ് Ͳ Ͷ ൬ͳ െ ଶ ʹݔ൰ ് Ͳ ଶ ʹݔ ് ሺכሻ ʹ ͵
Phương trình tương đương với ଵ ݔ ଵ ݔ ͳ െ ͵ ଶ ݔ ଶ ݔ ൌ Ͷ Ͷ ଶ ʹݔ ଶ ʹݔ ͵ ଵ ݔ ଵ ݔ ͳ െ ൌ ʹ ଶ ʹݔ Ͷ ͵ Ͷ ቀͳ െ ʹଶ ʹݔቁ
ଵ ݔ ଵ ݔ ൌ ͳ
ଶሺ଼ ݔ െ ͳሻ ଶ ݔ ሺ଼ ݔ െ ͳሻ ൌ Ͳ Ta có:
ቄ ݔ ͳ ֜ ଶ ݔ ሺ଼ ݔ െ ͳሻ Ͳ ൞ ଶ ݔ Ͳ
ቄ ݔ ͳ ֜ ଶ ݔ ሺ଼ ݔ െ ͳሻ Ͳ ଶ ݔ Ͳ
ฺ ଶሺ଼ ݔ െ ͳሻ ଶ ݔ ሺ଼ ݔ െ ͳሻ Ͳ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ۍ ቄ ݔ ൌ Ͳ ݔ ൌ Ͳ ێ ݔ ൌ Ͳ ێቄ ଼ ݇ߨ ێ ݔ ൌ ͳ ݔ ൌ ሺ݇ א Ժሻ ێቄ଼ ݔ ൌ ͳ ʹ ێ ݔ ൌ Ͳ ێ ۏቄ଼ ݔ ൌ ͳ ଼ ݔ ൌ ͳ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. c.
Phương trình tương đương với
ହ ݔ ସ ݔ ݔ ݔ ݔ ݔ ൌ ݔ ݔ
ସ ݔ ሺ ݔ ݔሻ ݔ ሺ ݔ ݔሻ ൌ ݔ ݔ
ሺ ݔ ݔሻሺସ ݔ ݔ െ ͳሻ ൌ Ͳ 111 TOANMATH.com
Chương 5 : Phương trình lượng giác ݔ ݔ ൌ Ͳሺͳሻ
ସ ݔ ݔ ൌ ͳሺʹሻ
Với phương trình ሺͳሻ ta có nghiệm ߨ
ݔ ൌ െ ݇ߨሺ݇ א Ժሻ Ͷ
Với phương trình ሺʹሻ, ta thấy
൜ ݔ ଶ ݔ ฺ ସ ݔ ݔ ͳ ସ ݔ ଶ ݔ Do đó, ቄଶ ݔ ൌ ͳ ݇ߨ
ସ ݔ ݔ ൌ ͳ ൦ ଶ ݔ ൌ Ͳ ݔ ൌ ሺ݇ א Ժሻ ቄଶ ݔ ൌ Ͳ ʹ ଶ ݔ ൌ ͳ
Vậy nghiệm của phương trình là ߨ ݔ ൌ െ ݇ߨ ൦ Ͷ݇ߨ ሺ݇ א Ժሻ ݔ ൌ ʹ
Bài 3: Giải các phương trình sau:
Ǥͺ Ͷݔ ଶ ʹݔ ξͳ െ ͵ݔ ͳ ൌ Ͳ
Ǥ ሺ ʹݔ െ Ͷݔሻଶ ൌ ʹ ͵ݔ
Ǥξ ݔ ଶ ݔ ݔ ݔ ൌ ͳ Giải: a.
Phương trình tương đương với
Ͷ Ͷݔ ሺͳ Ͷݔሻ ξͳ െ ͵ݔ ͳ ൌ Ͳ
ሺʹ Ͷݔ ͳሻଶ ξͳ െ ͵ݔ ൌ Ͳ ቄʹ Ͷݔ ͳ ൌ Ͳ ͳ െ ͵ݔ ൌ Ͳ ͳ ൝ Ͷݔ ൌ െ ʹ ͵ݔ ൌ ͳ 112 TOANMATH.com
Chương 5 : Phương trình lượng giác ʹߨ ݔ ൌ േ ݇ʹߨ ൞ ͵݊ʹߨ ሺ݇ǡ݊ א Ժሻ ݔ ൌ ͵ ʹߨ ݔ ൌ േ ݇ʹߨሺ݇ א Ժሻ ͵ b.
Phương trình tương đương với
Ͷ ଶ ͵ݔ ଶ ݔ ൌ ʹ ͵ݔ Ta có :
ʹ ͵ݔ Ͷሺ ͵ݔ െͳሻ ൝ ͵ݔ ͳ
Ͷ ଶ ͵ݔ ଶ ݔ Ͷ ൬ ൜ଶ ൰ ଶ ݔ ͳ Suy ra
Ͷ ଶ ͵ݔ ଶ ݔ Ͷ ʹ ͵ݔ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ͵ݔ ൌ െͳ ߨ
൝ ଶ ͵ݔ ൌ ͳ ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ ଶ ݔ ൌ ͳ
Vậy nghiệm của phương trình là: ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ c. Điều kiện : ݔ Ͳሺכሻ
Phương trình đã cho có thể viết lại thành ͳ ͳ
ݔ ξ ݔ െ ൬ଶ ݔ െ ݔ ൰ ൌ Ͳ Ͷ Ͷ ͳ ଶ ͳ ଶ
൬ξ ݔ ൰ െ ൬ ݔ െ ൰ ൌ Ͳ ʹ ʹ
൫ξ ݔ ݔ൯൫ξ ݔ െ ݔ ͳ൯ ൌ Ͳ ξ ݔ ݔ ൌ Ͳሺͳሻ
ቈξݔ െ ݔ ͳ ൌ Ͳሺʹሻ
Với phương trình ሺͳሻ, ta có : 113 TOANMATH.com
Chương 5 : Phương trình lượng giác െͳ ξͷ ቄ ݔ Ͳ ݔ ൌ ݔ ൌ ͳ െ ଶ ݔ ʹ ۍ െͳ ξͷ ݔ ൌ ቆ
ቇ ݇ʹߨሺ¿ ݔ Ͳሻ ێ ʹ ێ ሺ݇ א Ժሻ ێ െͳ ξͷ ݔ ൌ ߨ െ ቆ ቇ ݇ʹߨ ۏ ʹ
Với phương trình ሺʹሻ, ta có : ξ ݔ ൌ ݔ െ ͳ
Mà với mọi ݔ, ta đều có ൜ξ ݔ Ͳ ݔ ͳ Do đó,
ξ ݔ ൌ ݔ െ ͳ ቄ ݔ ൌ Ͳ ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ݔ ൌ ͳ
Kết hợp với ሺכሻ, ta nhận nghiệm của phương trình là െͳ ξͷ ݔ ൌ ߨ െ ቆ ቇ ݇ʹߨ ʹ ሺ݇ א Ժሻ ݔ ൌ ݇ʹߨ
Bài 4: Giải các phương trình sau:
Ǥ ʹݔ െ ξ͵ ʹݔ െ ξ͵ ݔ െ ݔ Ͷ ൌ Ͳ ͵ݔ Ǥ ʹݔ െ ʹ ൌ Ͳ Ͷ
Ǥʹ ݔ ξʹ ͳͲݔ ൌ ͵ξʹ ʹ ʹͺݔ ݔ Giải: a.
Ta biến đổi phương trình trở thành ߨ ߨ
ቀʹݔ െ ቁ ቀݔ ቁ ൌ ʹ Ta thấy : ߨ ቀʹݔ െ ቁ ͳ ߨ ߨ ൞ ߨ
ฺ ቀʹݔ െ ቁ ቀݔ ቁ ʹ ቀݔ ቁ ͳ 114 TOANMATH.com
Chương 5 : Phương trình lượng giác
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ߨ ቀʹݔ െ ቁ ൌ ͳ ൞ ߨ ቀݔ ቁ ൌ ͳ ߨ ݔ ൌ ݉ߨ ൞ ͵ ߨ ሺ݉ǡ ݊ א Ժሻ ݔ ൌ ݊ʹߨ ͵ ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ͵
Vậy nghiệm của phương trình là: ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ͵ b.
Ta biến đổi phương trình trở thành ͵ݔ ʹݔ ൌ ʹ Ͷ Ta thấy : ʹݔ ͳ ͵ݔ ൝ ͵ݔ ฺ ʹݔ ʹ ͳ Ͷ Ͷ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ʹݔ ൌ ͳ ൝ ͵ݔ ൌ ͳ Ͷ ݔ ൌ ݉ߨ ቊ ͺ݊ߨ ݔ ൌ ሺ݉ǡ ݊ א Ժሻ ͵
ݔ ൌ ͺ݇ߨሺ݇ א Ժሻ
Vậy nghiệm của phương trình là: ݔ ൌ ͺ݇ߨሺ݇ א Ժሻ 115 TOANMATH.com
Chương 5 : Phương trình lượng giác c.
Phương trình tương đương với
ʹሺ ݔ െ ʹͺݔ ݔሻ ൌ ͵ξʹ െ ξʹ ͳͲݔ
Áp dụng bất đẳng thức Bunyakovsky, ta có
ൌ ݔ െ ʹͺݔ ݔ ඥͳ ଶ ʹͺݔ ξʹ Mặt khác :
ൌ ͵ξʹ െ ξʹ ͳͲݔ ͵ξʹ െ ξʹ ൌ ʹξʹ
Do đó, phương trình trở thành ଶ ʹͺݔ ൌ ͳሺͳሻ
ቐ ݔ ʹͺݔ ൌ െ ݔሺʹሻ ͳͲݔ ൌ ͳሺ͵ሻ
Phương trình ሺͳሻ cho nghiệm ݇ߨ ݔ ൌ ሺ݇ א Ժሻ ʹͺ
Phương trình ሺ͵ሻ cho nghiệm ߨ ݊ߨ ݔ ൌ ሺ݊ א Ժሻ ʹͲ ͷ Suy ra ݇ߨ ߨ ݊ߨ ൌ
ͷሺ݇ െ ሻ ൌ ʹͺሺ݊ െ ͳሻ ʹͺ ʹͲ ͷ Khi đó,
ቄ݇ െ ൌ ʹͺݐሺݐ א Ժሻ ݊ െ ͳ ൌ ͷݐ Suy ra ሺʹͺݐ ሻߨ ߨ ݔ ൌ ൌ ݐߨሺݐ א Ժሻ ʹͺ Ͷ
Nghiệm này chỉ thỏa mãn phương trình ሺʹሻ nếu ݐ chẵn. Do đó, nghiệm của phương trình ߨ
ݔ ൌ ݉ʹߨሺ݉ א Ժሻ Ͷ
Bài 5: Giải các phương trình sau: ͷ Ǥ െ Ͷݔ െ ݔଶ ൌ ݕ ݕ ቚ ݔ ݔቚ
Ǥ ସ ݔ ସ ݕ ʹ ଶ ݔ ଶ ݕ ൌ ͵ ଶሺݔ ݕሻ
Ǥ ଶ ݔ ଶ ݕ ଶሺݔ ݕሻ ൌ ͳ ͳ ଶ ͳ ଶ ͳ Ǥ ൬ଶ ݔ ൰ ൬ଶ ݔ ൰ ൌ ͳʹ ݕ ଶ ݔ ଶ ݔ ʹ 116 TOANMATH.com
Chương 5 : Phương trình lượng giác Giải: a. Điều kiện : ݔ ് Ͳ ൝ ʹݕ ሺכሻ ് Ͳ ݔ Ta có :
െ Ͷݔ െ ݔଶ ൌ ͳͲ െ ሺʹ ݔሻଶ ͳͲ ൞ ͷ ͳͲ ݕ ݕ ൌ ͳͲ ቚ ʹݕ ݔ ݔቚ ቚ ݔ ቚ
Vậy phương trình chỉ thỏa khi và chỉ khi െ Ͷݔ െ ݔଶ ൌ ͳͲ ݔ ൌ െʹ ൝ ʹݕ ቊ ߨ ฬ ฬ ൌ ͳ
ݕ ൌ െ ݇ʹߨሺ݇ א Ժሻ ݔ ʹ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. b. Điều kiện : ʹݔ ് Ͳ ൜ʹݕ ് Ͳሺכሻ
Theo bất đẳng thức Cauchy, ta có :
ସ ݔ ସ ݕ ʹ ଶ ݔ ଶ ݕ Suy ra
ʹሺଶ ݔ ଶ ݕ ଶ ݔ ଶ ݕሻ
Lại theo bất đẳng thức Cauchy, ta được :
ଶ ݔ ଶ ݕ ଶ ݔ ଶ ݕ ʹ
Nên Ͷ. Mặt khác, ta thấy
ൌ ͵ ଶሺݔ ݕሻ Ͷ
Do đó, phương trình chỉ thỏa khi và chỉ khi ସ ݔ ൌ ସ ݕሺͳሻ
ቐଶ ݔ ଶ ݕ ൌ ଶ ݔ ଶ ݕሺʹሻ
ଶሺݔ ݕሻ ൌ ͳሺ͵ሻ
Từ ሺͳሻ và ሺʹሻ ta có ଶ ݔ ൌ ଶ ݕ ൌ ͳ
Kết hợp với ሺ͵ሻ ta được ߨ ߨ ݔ ൌ ݇ߨ ݔ ൌ െ ݇ߨ ൞ Ͷ Ͷ ߨ ሺ݇ǡ ݉ א Ժሻ ש൞ ߨ ሺ݇ǡ ݉ א Ժሻ ݕ ൌ ݉ߨ ݕ ൌ െ ݉ߨ Ͷ Ͷ
Thử lại với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. 117 TOANMATH.com
Chương 5 : Phương trình lượng giác c. Điều kiện : ݔ ് Ͳ ൝ ݕ ് Ͳ ሺכሻ ሺݔ ݕሻ ് Ͳ Ta có : ͳ െ ݔ ݕ ሺݔ ݕሻ ൌ
ฺ ݔ ሺݔ ݕሻ ሺݔ ݕሻ ݕ ݔ ݕ ൌ ͳ ݔ ݕ Ta thấy :
ݔ ሺݔ ݕሻ ሺݔ ݕሻ ݕ ݔ ݕ
ଶ ݔ ଶሺݔ ݕሻ ଶሺݔ ݕሻ ଶ ݕ ଶ ݕ ଶ ݔ ʹ Nên
ͳ ൌ ݔ ሺݔ ݕሻ ሺݔ ݕሻ ݕ ݔ ݕ ଶ ݔ ଶ ݕ ଶሺݔ ݕሻ
Vậy phương trình chỉ thỏa khi và chỉ khi ߨ ۍ ݔ ൌ ݇ߨ ݔ ൌ ሺݔ ݕሻ ێ ൞ ߨ
ۓሺݔ ݕሻ ൌ ݕ ێ ݕ ൌ ݉ߨ ێ ሺ݇ǡ ݉ א Ժሻ ۔ ξ͵ ێ ߨ ݔ ൌ െ ݇ߨ ە ݔ ൌ േ ͵ ێ ێ൞ ߨ ۏ ݕ ൌ െ ݉ߨ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. d. Điều kiện : ʹݔ ് Ͳሺכሻ Ta có : ͳ ͳ ͳ
ൌ ሺସ ݔ ସ ݔሻ ൬ͳ
൰ Ͷ ൌ ൬ͳ െ ଶ ʹݔ൰ ൬ͳ ൰ Ͷ ସ ݔ ସ ݔ ʹ ସ ʹݔ ͳ ʹͷ
൬ͳ െ ൰ ሺͳ ͳሻ Ͷ ൌ ʹ ʹ Mặt khác, ͳ ʹͷ ൌ ͳʹ ݕ ʹ ʹ
Do đó, phương trình chỉ thỏa khi và chỉ khi ߨ ݇ߨ ݔ ൌ ൜ଶ ʹݔ ൌ ͳ ൞ Ͷ ʹ ሺ݇ǡ ݉ א Ժሻ ݕ ൌ ͳ ߨ ݕ ൌ ݉ʹߨ ʹ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. 118 TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 6: Giải các phương trình sau: ʹݔ ସ Ǥ͵ ൬ͳ ൰ Ͷ ݔ ൌ ଶ ݔ
(Đề nghị Olympic 30-4, 2006) ͳ ͳ
Ǥ ଵଽହ ݔ െ ଵଽହ ݔ ൌ െ ଶ ݔ ଶ ݔ
(Đề nghị Olympic 30-4, 2007)
Ǥ ͷݔ ݔ ൌ ͵ݔ െ ͵ݔ
(Đề nghị Olympic 30-4, 2008) Giải: a. Điều kiện: ߨ ݔ ് ݇ߨሺכሻ ʹ Ta đặt : ʹݔ ͳ ൝ݑ ൌ ଶ ݔ ݒ ൌ ଶ ݔ
Phương trình đưa về dạng
͵ݑସ Ͷݒଷ ൌ ሺͳሻ Mà ta có : ʹݔ ʹݔ ͳ ʹ ଶ ݔ ݑ ݒ ൌ ሺͳ ଶ ݔሻ ൌ ൌ ൌ ʹ ଶ ݔ ଶ ݔ ଶ ݔ Do đó,
ሺͳሻ ͵ݑସ Ͷሺʹ െ ݑሻଷ ൌ
ሺݑ െ ͳሻଶ ሺᇣ͵ݑ ᇧᇧଶᇧᇧ ʹ ᇤݑᇧᇧ ᇧʹᇧͷᇥሻ ൌ Ͳ வ ݑ ൌ ͳ
Thay vào ሺͳሻ, ta được : ߨ
ݔ ൌ േͳ ݔ ൌ േ ݇ߨሺ݇ א Ժሻ Ͷ
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. b.
Nhận xét ݔ ൌ േͳ không là nghiệm của phương trình vì nếu ݔ ൌ േ thì
phương trình không thỏa mãn. Tương tự, ݔ ൌ േͳ không là nghiệm của phương trình. 119 TOANMATH.com
Chương 5 : Phương trình lượng giác ͳ
ảốǣ݂ሺݐሻ ൌ ݐଵଽହ െ
²ݐ א ሺെͳǢ Ͳሻ ሺͲǢ ͳሻ ݐଶ ʹͲͲ
݂ᇱሺݐሻ ൌ ͳͻͷݐଵଽସ
Ͳớݐ א ሺെͳǢ Ͳሻ ሺͲǢ ͳሻ ݐଶ଼
Nên hàmố tăng trên mỗi khoảng xác định. Ngoài ra hàm số này với ݐ א ሺͲǢ ͳሻ sẽ chỉ
nhận giá trị âm và với ݐ א ሺͲǢ ͳሻ chỉ nhận giá trị dương. Cho nên mỗi giá trị ݂ሺݐሻ trên
khoảng này không thể ứng với giá trị của ݂ሺݐሻ trên khoảng kia.
Cho nên phương trình ݂ሺ ݔሻ ൌ ݂ሺ ݔሻ tương đương với ݔ ൌ ݔ ሺכሻ. ߨ ảሺכሻ¿¯ượệݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ c.
Nếu ݔ ൌ ݇ߨሺ݇ א Ժሻ
ቄ ൌ ͷ݇ߨ ݇ߨ ൌ േʹ
ൌ ͵݇ߨ െ ͵݇ߨ ൌ േͳ
Do đó, phương trình không có nghiệm ݔ ൌ ݇ߨ.
Nếu ݔ ് ݇ߨሺ݇ א Ժሻ. Ta nhân 2 vế phương trình cho ʹ ݔ, ta được
ݔ െ Ͷݔ ʹݔ ൌ െ Ͷݔ ʹݔ െ Ͷݔ ʹݔ
ʹ ͵ݔ ሺ ͵ݔ െ ݔሻ ൌ Ͳ ͵ݔ ൌ Ͳ ቈ ߨ
͵ݔ ൌ ݔ ൌ ቀ െ ݔቁ ʹ ݇ߨ ۍ ݔ ൌ ሺ݇ ് ͵݄ǡ ݄ א Ժሻ ͵ ێ ߨ ݉ߨ ێ ݔ ൌ ێ൦ ͺ ʹ ߨ ሺ݉ǡ ݊ א Ժሻ ێ ݔ ൌ െ ݊ߨ ۏ Ͷ 120 TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 7: Giải các phương trình sau:
Ǥ ሺʹ ͵ݔ ݔ ͳሻଷ ൌ ͳʹ ݔ െ ʹ
(Đề nghị Olympic 30-4, 2008)
Ǥ͵ଶଽ௫ାଷୡ୭ୱ௫ െ ͵ଶଽ௫ାସୡ୭ୱయ ௫ െ ͵ ͵ݔ ൌ Ͳ
(Đề nghị Olympic 30-4, 2009) Ǥ ݔ ඥ
మబబఴ ଶ ݔ ʹͲͲͺ െ ሺ ݔ ͳሻ ඥ
మబబఴ ଶ ݔ ʹ ݔ ʹͲͲͻ ൌ ݔ െ ݔ ͳ
(Đề nghị Olympic 30-4, 2009) ͷߨ ͷߨ ͷߨ Ǥ ݔ ൌ ଶ ൬ʹݔ ൰ ଶ ൬ݔ ൰ ݔ ൬͵ݔ ൰ ͳʹ ͳʹ
(Đề nghị Olympic 30-4, 2010) Giải: a. య
Đặt ݐ ൌ ʹ ݔ ǡ ȁݐȁ ʹ. Ta có : ݐଷ ͳ ൌ ͵ ξ͵ݐ െ ͳ Lại đặt ݑ ൌ ξ య ͵ݐ െ ͳ. Ta có hệ ቄݐଷ ൌ ͵ݑ െ ͳ ݑଷ ൌ ͵ݐ െ ͳ
Trừ 2 phương trình theo từng về, ta được
ݐଷ െ ݑଷ ൌ ͵ሺݑ െ ݐሻ
ሺݐ െ ݑሻ ሺᇣݐଶᇧᇧᇧ ݐᇧᇧ ݑᇤ ᇧݑᇧଶᇧᇧ ͵ ᇧᇥሻ ൌ Ͳ வ
Từ đó suy ra ݐ ൌ ݑ ݐଷ െ ͵ݐ ͳ ൌ Ͳ Vậy
ͺ ଷ ݔ െ ݔ ͳ ൌ Ͳ ʹ ͵ݔ ͳ ൌ Ͳ ͳ ͵ݔ ൌ െ ʹ ʹߨ ݇ʹߨ ݔ ൌ േ ሺ݇ א Ժሻ ͻ ͵ b.
Phương trình tương đương với
͵ଶଽ௫ାଷୡ୭ୱ௫ െ ͵ଶଽ௫ାସୡ୭ୱయ ௫ ൌ ͵ሺͶ ଷ ݔ െ ͵ ݔሻ
͵ଶଽ௫ାଷୡ୭ୱ௫ ͵ሺʹͲͲͻݔ ͵ ݔሻ ൌ ͵ଶଽ௫ାସୡ୭ୱయ ௫ ͵ሺʹͲͲͻݔ Ͷ ଷ ݔሻ 121 TOANMATH.com
Chương 5 : Phương trình lượng giác Xét hàm số
݂ሺݐሻ ൌ ͵௧ ͵ݐǡ ݐ א Թ
݂ᇱሺݐሻ ൌ ͵௧ ͵ ͵ Ͳ
Do đó, ݂ሺݐሻ đồng biến. Vậy ta suy ra
ʹͲͲͻݔ ͵ ݔ ൌ ʹͲͲͻݔ Ͷ ଷ ݔ ͵ݔ ൌ Ͳ ߨ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ ͵ c.
Phương trình tương đương với ݔ ඥ
మబబఴ ଶ ݔ ʹͲͲͺ మబబఴ
ݔ ൌ ሺ ݔ ͳሻ ඥሺ ݔ ͳሻଶ ʹͲͲͺ ݔ ͳ Xét hàm số
݂ሺݐሻ ൌ ݐ ݐమబబඥ
ఴ ݐଶ ʹͲͲͺǡ ݐ א Թ ݐଶ ͳ ݂ᇱሺݐሻ ൌ ͳ ඥ
మబబఴ ݐଶ ʹͲͲͺ Ǥ Ͳ
ͳͲͲͶ మబబఴඥሺݐଶ ʹͲͲͺሻଶ
Do đó, ݂ሺݐሻ đồng biến. Khi đó, phương trình tương đương với ߨ
ݔ ൌ ݔ ͳ ቈݔ ൌ ݇ʹߨ ʹ ሺ݇ א Ժሻ ݔ ൌ ߨ ݇ʹߨ d. Ta có:
ሺܽ ܾሻ ሺܽ െ ܾሻ ൌ ଶ ܽ ଶ ܾ െ ଶ ܽ ଶ ܾ
ൌ ሺͳ െ ଶ ܽሻሺͳ െ ଶ ܾሻ െ ଶ ܽ ଶ ܾ Suy ra
ଶ ܽ ଶ ܾ ሺܽ ܾሻ ሺܽ െ ܾሻ ൌ ͳሺͳሻ ͷߨ ͷߨ 0ặܽ ൌ ʹݔ Ǣ ܾ ൌ ݔ ͳʹ ͳʹ
ương trình ሺͳሻ trở thành: ͷߨ ͷߨ ͷߨ ଶ ൬ʹݔ ൰ ଶ ൬ݔ ൰ ݔ ൬͵ݔ ൰ ൌ ͳ ͳʹ ͳʹ
Do đó, phương trình đã cho trở thành ߨ
ݔ ൌ ͳ ݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ 122 TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 8: Giải các phương trình sau: ୡ୭ୱ ଶ௫ ୱ୧୬మ ௫ ୡ୭ୱమ ௫ ୡ୭ୱ ଶ௫ ξʹ Ǥ൫ʹ ξʹ൯ െ ൫ʹ ξʹ൯ ൫ʹ െ ξʹ൯ ൌ ቆͳ ቇ ʹ ͳ
Ǥ ൬ ݔ ݔ൰ ൌ ݔ ݔ ǡ ݊ א Գǡ ݊ ʹ Ͷ ͵ ݔ ݔ
Ǥ ݔ ݔ െ ݔ ݔ ൌ ͳ െ Ͷ ݔ ݔ Giải: a. Ta xét các trường hợp :
- ʹݔ Ͳ thì ଶ ݔ ଶ ݔ. Suy ra ୡ୭ୱమ ௫ ୱ୧୬మ ௫ ൫ʹ ξʹ൯ ൫ʹ ξʹ൯ ୱ୧୬మ ௫ ୡ୭ୱమ ௫ ୡ୭ୱ ଶ௫ ୡ୭ୱ ଶ௫ ฺ ൫ʹ ξʹ൯ െ ൫ʹ ξʹ൯ ൫ʹ െ ξʹ൯ ൏ ൫ʹ െ ξʹ൯ ൏ ͳ Mặt khác : ୡ୭ୱ ଶ௫ ξʹ ቆͳ ቇ ͳ ʹ
Do đó, phương trình vô nghiệm.
- ʹݔ ൏ Ͳ, chứng minh tương tự, ta được : ୡ୭ୱ ଶ௫ ୱ୧୬మ ௫ ୡ୭ୱమ ௫ ୡ୭ୱ ଶ௫ ξʹ ൫ʹ ξʹ൯ െ ൫ʹ ξʹ൯ ൫ʹ െ ξʹ൯ ͳ ቆͳ ቇ ʹ
Do đó, phương trình vô nghiệm.
- ʹݔ ൌ Ͳ, ta thấy họ nghiệm thỏa mãn phương trình đã cho.
Vậy phương trình có nghiệm ߨ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ Ͷ ʹ 123 TOANMATH.com
Chương 5 : Phương trình lượng giác b. Điều kiện : ʹݔ ് Ͳሺכሻ
- ݊ ൌ ʹ, phương trình đã cho trở thành ͳ ଶ ൬ ݔ ݔ൰ ൌ ͳ Ͷ
Theo bất đẳng thức Cauchy, ta có : ͳ ͳ ଶ ݔ ଶ ݔ ͳ ͳ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ͳ ͳ
ݔ ൌ േ ݔ ൌ േ ݇ߨሺ݇ א Ժሻ ʹ ʹ
- ݊ ʹ, theo bất đẳng thức Cauchy, ta có : ͳ ͳ
ฬ ݔ ݔฬ ൌ ൬ȁ ݔȁ ȁ ݔȁ൰ ͳ Ͷ Ͷ Mặt khác : ȁ ݔȁ ଶ ݔ ൜
ฺ ȁ ݔȁ ȁ ݔȁ ͳ ȁ ݔȁ ଶ ݔ Nên ͳ
ȁ ݔ ݔȁ ȁ ݔȁ ȁ ݔȁ ͳ ฬ ݔ ݔฬ Ͷ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ݔ ൌ ݉ߨ ȁ ݔȁ ൌ ଶ ݔ ۓ ߨ
ۖቈݔ ൌ ݉ߨሺ݉ א Ժሻ ൞ ȁ ݔȁ ൌ ଶ ݔ ʹ ͳ ȁ ݔȁ ൌ ȁ ݔȁ ۔ ͳ Ͷ ۖ ȁ ݔȁ ൌ ȁ ݔȁ ە Ͷ
Ta thấy hệ trên vô nghiệm. Do đó, kết hợp với ሺכሻ, ta có nghiệm của phương trình : ͳ
ݔ ൌ േ ݇ߨሺ݇ א Ժሻ ʹ 124 TOANMATH.com
Chương 5 : Phương trình lượng giác c. Ta có : ߨ
͵ ݔ ݔ ൌ ͵ ξʹ ቀݔ ቁ Ͳǡ ݔ Ͷ ͳ
Ͷ ݔ ݔ ൌ Ͷ ʹݔ Ͳǡ ݔ ʹ
Do đó, phương trình luôn xác định. Khi đó, ta đưa phương trình trở thành
ሺͶ ݔ ݔሻ Ͷ ݔ ݔ ൌ ሺ͵ ݔ ݔሻ ͵ ݔ ݔ Ta đặt
ቄ ݑ ൌ Ͷ ݔ ݔ Ͳ ݒ ൌ ͵ ݔ ݔ Ͳ
Phương trình đưa về dạng ݑ ݑ ൌ ݒ ݒ Ta xét hàm số :
݂ሺݐሻ ൌ ݐ ݐǡ ݐ Ͳ ͳ
݂ᇱሺݐሻ ൌ ͳ Ͳ ݐ
Do đó, hàm số đồng biến trên ሺͲǡ λሻ. Khi đó,
݂ሺݑሻ ൌ ݂ሺݒሻ ݑ ൌ ݒ
Ͷ ݔ ݔ ൌ ͵ ݔ ݔ ሺ ݔ െ ͳሻሺͳ െ ݔሻ ൌ Ͳ ߨ
ቂ ݔ ൌ ͳ ቈݔ ൌ ݇ʹߨሺ݇ א Ժሻ ݔ ൌ ͳ ʹ ݔ ൌ ݇ʹߨ
Bài 9: Giải các phương trình sau: ͷ Ǥ ݔ ʹݔ ͵ݔ ൌ ʹ
Ǥ ଶ ݔ ଶ ʹݔ ଶ ͵ݔ ൌ ͳ Ǥʹ ଷ ݔ ൌ ଶ ݔ Giải: a.
Theo bất đẳng thức Bunyakovsky, ta có :
ݔ ͵ݔ ʹݔ ൌ ʹ ݔ ʹݔ ʹ ݔ ݔ
ʹඥሺଶ ݔ ଶ ݔሻሺଶ ʹݔ ଶ ݔሻ ൌ ʹඥଶ ʹݔ ଶ ݔ ͳ ଶ ͷ ͷ
ൌ ʹඨʹͷ െ ൬ ʹݔ െ ൰ ʹǤ ൌ ͳ Ͷ Ͷ ʹ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi 125 TOANMATH.com
Chương 5 : Phương trình lượng giác ͳ ͷ ʹݔ ൌ ʹ ଶ ݔ ൌ ൞ Ͷ Ͷ ݔ ݔ ൞ ͵ ൌ ݔ ൌ ʹݔ ݔ Ͷ
Ta thấy, hệ này vô nghiệm. Do đó, phương trình vô nghiệm. b. Điều kiện : ݔ ് Ͳ ൝ ʹݔ ് Ͳሺכሻ ͵ݔ ് Ͳ Ta có : ͳ ʹݔ ݔ ൌ ሺʹݔ ݔሻ ൌ ͵ݔ ͳ െ ʹݔ ݔ
ݔ ʹݔ ʹݔ ͵ݔ ͵ݔ ݔ ൌ ͳ
Theo bất đẳng thức Bunyakovsky, ta có :
ͳ ൌ ݔ ʹݔ ʹݔ ͵ݔ ͵ݔ ݔ ଶ ݔ ଶ ʹݔ ଶ ͵ݔ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi ʹ ݔ ݔ ൌ ʹݔ ൌ ͵ݔ ൝
ൌ ݔ ቄ ݔ ൌ ݇ߨ ሺ݇ א Ժሻ ͳ െ ଶ ݔ ͵ݔ ൌ Ͳ ͵ݔ ൌ ݔ
Ta thấy, hệ trên vô nghiệm. Do đó, phương trình vô nghiệm. c. Điều kiện : ቄ ݔ Ͳሺכሻ ݔ Ͳ
Phương trình tương đương với ଶ ݔ ൌ
ଷ ଶ ݔ ൌ ଶ ݔ ଷ ͳ െ ଶ ݔ ଶ ݔ
Ta đặt ݐ ൌ ଶ ݔ thì ݔ ൌ ʹ௧. Khi đó, Ͷ௧ Ͷ ௧
ൌ ݐ ൬ ൰ Ͷ௧ ൌ ͳሺͳሻ ଷ ͳ െ Ͷ௧ ͵ Ta xét hàm số : Ͷ ௧
݂ሺݐሻ ൌ ൬ ൰ Ͷ௧ ͵ Ͷ ௧ Ͷ
݂ᇱሺݐሻ ൌ ൬ ൰ Ͷ௧ Ͷ Ͳ ͵ ͵
Do đó, hàm số đồng biến trên Թ. Mà ta thấy ݂ሺെͳሻ ൌ ͳ nên ݐ ൌ െͳ là nghiệm duy nhất
của phương trình ሺͳሻ. Với ݐ ൌ െͳ thì 126 TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ͳ ݔ ൌ ݇ʹߨ ݔ ൌ ൦ ሺ݇ א Ժሻ ʹ ͷߨ ݔ ൌ ݇ʹߨ
Kết hợp với ሺכሻ, nghiệm của phương trình là : ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ - BÀI TẬP TỰ LUYỆN
5.2.16. Giải các phương trình sau:
Ǥ ͵ ହ ݔ ͷ ହ ݔ ൌ ͷ Ǥ ݔ ʹݔ ൌ ʹ ͷݔ Ǥ ͵ݔ െ ʹ ൌ Ͳ Ͷ
Ǥ ݔ ݔ ൌ ξʹሺʹ െ ͵ݔሻ
Ǥ ݔ ݔ ൌ ξʹሺʹ െ ݔሻ
5.2.17. Giải các phương trình sau:
Ǥ ξ͵ െ ݔ െ ξ ݔ ͳ ൌ ʹ
Ǥ ͵ݔ ඥʹ െ ଶ ͵ݔ ൌ ʹሺͳ ଶ ʹݔሻ
Ǥ ʹݔ Ͷݔ ݔ ൌ ݔ ʹݔ ͵ݔ ʹ ͳ Ǥ ʹݔ ͵ݔ ൌ Ͳ ݔ ʹݔ ͵ݔ
Ǥ ଶ ͵ݔ ʹݔ െ ଶ ݔ ൌ Ͳ 127 TOANMATH.com
Chương 5 : Phương trình lượng giác -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN 5.2.17. a. Điều kiện: ቄ ݔ ͵ ݔ א Թ ݔ െͳ
Khi đó, phương trình tương đương:
ξ͵ െ ݔ ൌ ʹ ξ ݔ ͳ
͵ െ ݔ ൌ ͷ ݔ Ͷξ ݔ ͳ
െʹሺ ݔ ͳሻ ൌ Ͷξ ݔ ͳሺͳሻ Lại có: ൜ Ͷξ ݔ ͳ Ͳ െʹሺ ݔ ͳሻ Ͳ Khi đó,
ሺͳሻ ൜ Ͷξ ݔ ͳ ൌ Ͳ െʹሺ ݔ ͳሻ ൌ Ͳ ݔ ൌ െͳ
ݔ ൌ ߨ ݇ʹߨሺ݇ א Ժሻ b. Điều kiện: ଶ ͵ݔ ʹ ݔ א Թ
Áp dụng bất đẳng thức Bunyakovsky, ta có: ଶ
ቀͳǤ ͵ݔ ͳǤ ඥʹ െ ଶ ͵ݔቁ ʹሺଶ ͵ݔ ʹ െ ଶ ͵ݔሻ ൌ Ͷ
ฺ ͵ݔ ඥʹ െ ଶ ͵ݔ ʹ Lại có:
ʹሺͳ ଶ ʹݔሻ ʹ 128 TOANMATH.com
Chương 5 : Phương trình lượng giác
Khi đó, phương trình tương đương với
ቊ ͵ݔ ൌ ඥʹ െ ଶ ͵ݔ ଶ ʹݔ ൌ Ͳ ͵ݔ Ͳ ൝ ͵ݔ ൌ േͳ ʹݔ ൌ Ͳ ͵ݔ ൌ ͳ ൝ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ Ͷ
ݔ ൌ ݉ʹߨሺ݉ א Ժሻ
Vậy nghiệm của phương trình là: ݔ ൌ ݉ʹߨሺ݉ א Ժሻ c.
Phương trình tương đương với
ʹݔ Ͷݔ ݔ ൌ ݔ ʹݔ ͵ݔ ʹ ͳ
ʹݔ Ͷݔ ݔ ൌ ሺ ͵ݔ ݔሻ ͵ݔ ʹ ʹ ͳ
ʹݔ Ͷݔ ݔ ൌ ሺ ʹݔ Ͷݔ ݔ ͳሻ ʹ Ͷ
ʹݔ Ͷݔ ݔ ൌ ͵ Ta có: ʹݔ ͳ
൝ Ͷݔ ͳ ฺ ʹݔ Ͷݔ ݔ ͵ ݔ ͳ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi: ʹݔ ൌ ͳ
൝ Ͷݔ ൌ ͳ ݔ ൌ ݇ߨሺ݇ א Ժሻ ݔ ൌ ͳ
Vậy nghiệm của phương trình là: ݔ ൌ ݇ߨሺ݇ א Ժሻ 129 TOANMATH.com
Chương 5 : Phương trình lượng giác d. Điều kiện:
ʹݔ ʹݔ ͵ݔ ് Ͳሺכሻ
Khi đó, phương trình tương đương với: ʹݔ ͵ݔ ͳ ൌ Ͳ ʹݔ ͵ݔ ݔ ʹݔ ͵ݔ
ݔ ሺ ʹݔ ͵ݔ ͵ݔ ʹݔሻ ͳ ൌ Ͳ ݔ ͷݔ ൌ െͳ ቄ ݔ ൌ ͳ ͷݔ ൌ െͳ ቄ ݔ ൌ െͳ ͷݔ ൌ ͳ ݔ א
Vậy phương trình vô nghiệm. e.
Phương trình tương đương với
ሺͳ ݔሻ ʹݔ െ ʹ ଶ ݔ ൌ Ͳ
ʹݔ ݔ ʹݔ െ ʹ ଶ ݔ ൌ Ͳ ݔ ʹݔ ൌ ͳ ͺݔ Ͷݔ ൌ ʹ Ta có:
ቄ ͺݔ ͳ ฺ ͺݔ Ͷݔ ʹ Ͷݔ ͳ
Dấu ̶ ൌ ̶ xảy ra khi và chỉ khi: ݇ߨ ቄ ͺݔ ൌ ͳ ݔ ൌ ሺ݇ א Ժሻ Ͷݔ ൌ ͳ ʹ
Vậy nghiệm của phương trình là: ݇ߨ ݔ ൌ ሺ݇ א Ժሻ ʹ 130 TOANMATH.com
Chương 5 : Phương trình lượng giác d.
PHƯƠNG TRÌNH CÓ CHỨA THAM SỐ
- Ở những phương trình này, chúng ta có một số phương pháp thông dụng thường gặp như sau :
x Phương pháp lượng giác :
Phương trình có dạng ݂ሺݔሻ ൌ ݉ǡ ݂ሺݔሻ ൌ ݉ǡ ݂ሺݔሻ א Թ có
nghiệm khi và chỉ khi ȁ݉ȁ ͳ.
Phương trình có dạng ܽ ݂ሺݔሻ ܾ ݂ሺݔሻ ൌ ܿǡ ݂ሺݔሻ א Թ có
nghiệm khi và chỉ khi ܽଶ ܾଶ ܿଶ.
Chú ý : Nếu miền giá trị của ݂ሺݔሻ không phải Թ thì điều kiện trên chỉ là điều kiện cần.
x Phương pháp đại số : Cho phương trình lượng giác ሺͳሻ có chứa tham số, sơ
đồ giải và biện luận có thể theo các thứ tự sau :
Biến đổi ሺͳሻ thành phương trình ሺʹሻ có thể đặt ẩn phụ, ở đây có thể
xuất hiện điều kiện ሺሻ. Nghiệm của phương trình ሺͳሻ cũng là nghiệm
của phương trình ሺʹሻ với điều kiện ሺሻ.
Xét phương trình ሺʹሻ, đặt ẩn phụ để trở thành phương trình đại số ሺ͵ሻ
kèm điều kiện của ẩn phụ là ሺሻ.
Nếu điều kiện ሺሻ có thể biến đổi thành điều kiện ሺሻ tương đương
trong ẩn phụ thì ta kết luận : Điều kiện cần và đủ để ሺͳሻ có nghiệm là
ሺ͵ሻǡ ሺሻǡ ሺሻ có nghiệm.
Trong trường hợp ሺሻ không thể biến đổi thành điều kiện mới trong ẩn
phụ, ta phải kiểm tra trực tiếp nghiệm của ሺͳሻ khi cần phải đối chiếu điều kiện ሺሻ.
Bài toán sẽ ít phức tạp hơn nếu ta có không có điều kiện ሺሻ, nghĩa là
ሺͳሻ tương đương ሺʹሻ.
x Phương pháp dùng miền giá trị :
Phương pháp này chỉ dùng được sau khi biến đổi phương trình lượng
giác thành phương trình đại số chỉ có bậc nhất hoặc bậc hai. Bằng
phương pháp đạo hàm hay phương pháp bất đẳng thức, ta không cần vẽ
đồ thị hàm số mà chỉ cần miền giá trị khi cần tìm điều kiện để phương trình có nghiệm.
- Nhắc lại công thức so sánh nghiệm : Cho phương trình bậc hai ܽݔଶ ܾݔ ܿ ൌ Ͳ,
với ܽ ് Ͳ, kí hiệu là ݂ሺݔሻ, có hai nghiệm ݔଵ ൏ ݔଶ và hai số ߙ ൏ ߚ. Ta có
x ݔଵ ൏ ߙ ൏ ݔଶ khi và chỉ khi ݂ܽሺߙሻ ൏ Ͳ 131 TOANMATH.com
Chương 5 : Phương trình lượng giác
x ݔଵ ൏ ݔଶ ൏ ߙ khi và chỉ khi ȟ Ͳ ݂ܽሺߙሻ Ͳ ൞ܵ െߙ ൏ Ͳ ʹ
x ߙ ൏ ݔଵ ൏ ݔଶ khi và chỉ khi ȟ Ͳ ݂ܽሺߙሻ Ͳ ൞ܵ െߙ Ͳ ʹ
x ߙ ൏ ݔଵ ൏ ߚ ൏ ݔଶ khi và chỉ khi ݂ܽሺߙሻ Ͳ ൜ ݂ܽሺߚሻ ൏ Ͳ
x ݔଵ ൏ ߙ ൏ ݔଶ ൏ ߚ khi và chỉ khi ݂ܽሺߙሻ ൏ Ͳ ൜ ݂ܽሺߚሻ Ͳ
x ݔଵ ൏ ߙ ൏ ߚ ൏ ݔଶ khi và chỉ khi ݂ܽሺߙሻ ൏ Ͳ ൜ ݂ܽሺߚሻ ൏ Ͳ
x ߙ ൏ ݔଵ ൏ ݔଶ ൏ ߚ khi và chỉ khi ȟ Ͳ ۓ ݂ۖܽሺߙሻ Ͳ ݂ܽሺߚሻ Ͳ ۔ ܵ ߙ ۖ ൏ ൏ ߚ ە ʹ
Bài 1: Định m để phương trình sau có nghiệm:
Ǥ ሺ݉ െ ͳሻ ݔ ሺʹ െ ݉ሻ ൌ Ͳ
Ǥ ݉ ݔ െ ͳ ൌ ሺʹ݉ ͵ሻ ݔ
Ǥʹ ଶ ݔ െ ݔ ݔ െ ଶ ݔ ൌ ݉ 132 TOANMATH.com
Chương 5 : Phương trình lượng giác Giải: a. Ta xét 2 trường hợp
Khi ݉ ൌ ͳ thì Ͳ ݔ ൌ െͳሺØýሻ. Khi ݉ ് ͳ thì ݉ െ ʹ ݔ ൌ ݉ െ ͳ
Phương trình có nghiệm khi và chỉ khi ݉ െ ʹ ͵ െͳ ͳ ֞ ݉ ݉ െ ͳ ʹ b.
Đưa phương trình về dạng ሺ݉ ͵ሻ ݔ ൌ െͳ
Khi ݉ ൌ െ͵ thì Ͳ ݔ ൌ െͳሺØýሻ Khi ݉ ് െ͵ thì െͳ ݔ ൌ ݉ ͵
Phương trình có nghiệm khi và chỉ khi െͳ െͳ ͳ ቂ ݉ ͵ ݉ ͵ ݉ െͶ c.
Ta biến đổi phương trình trở thành
ʹݔ ͵ ʹݔ ൌ െʹ݉ ͳ
Khi đó, để phương trình có nghiệm thì
ͳ ͻ ሺെʹ݉ ͳሻଶ
Ͷ݉ଶ െ Ͷ݉ െ ͻ Ͳ ͳ െ ξͳͲ ͳ ξͳͲ ݉ ʹ ʹ 133 TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 2: Cho phương trình ʹݔ െ ሺʹ݉ ͳሻ ݔ ݉ ͳ ൌ Ͳ ͵ Ǥảươ¿݉ ൌ ʹ ߨ ͵ߨ
Ǥ¿݉¯ểươ¿×ệả ൬ Ǣ ൰ ʹ ʹ
Giải: Ta biến đổi phương trình trở thành ͳ
ʹ ଶ ݔ െ ሺʹ݉ ͳሻ ݔ ݉ ൌ Ͳ ቈ ݔ ൌ ʹ ሺכሻ ݔ ൌ ݉ a. ͵ ݉ ൌ ǡ ዛዓ¿ở ʹ ͳ ݔ ൌ ߨ ሺכሻ ൦ ʹ ͵
ݔ ൌ േ ݇ʹߨሺ݇ א Ժሻ ͵ ݔ ൌ ͳሺạሻ ʹ b. ߨ ͵ߨ ݔ א ൬ Ǣ ൰ ¿ ݔ א ሾെͳǢ Ͳሻ ʹ ʹ Khi đó, ͳב ሾെͳǢͲሻሺạሻ ሺכሻ ቈ ݔ ൌ ݔ ൌ ݉ ʹ ݔ ൌ ݉ Ta có :
ݔ א ሾെͳǢ Ͳሻ ݉ א ሾെͳǢ Ͳሻ 134 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 3: Cho phương trình sau: ʹ ሺͳ െ ܽሻ ଶ ݔ െ ͳ ͵ܽ ൌ Ͳ ݔ ͳ Ǥảዛዓ¿ܽ ൌ ʹ ߨ
Ǥ¿ܽ¯ểዛዓ¿×ềơộệ² ቀͲǢ ቁ ʹ
Giải: Điều kiện: ݇ߨ ݔ ് Ͳ ݔ ്
݇ߨሺ݇ א Ժሻሺכሻ ʹ
Phương trình tương đương với
ሺͳ െ ܽሻ ଶ ݔ െ ʹ ݔ ሺͳ ͵ܽሻ ଶ ݔ ൌ Ͳ
Ͷܽ ଶ ݔ െ ʹ ݔ ͳ െ ܽ ൌ Ͳ
ሺʹ ݔ െ ͳሻሾܽሺʹ ݔ ͳሻ െ ͳሿ ൌ Ͳ ͳ ݔ ൌ ʹ ሺͳሻ
ܽሺʹ ݔ ͳሻ െ ͳ ൌ Ͳ a. ͳ ܽ ൌ ¿ ʹ ͳ ߨ
ݔ ൌ ݔ ൌ േ ݇ʹߨሺ݇ א Ժሻ ʹ ͵
Kết hợp với ሺכሻ, ta nhận nghiệm trên là nghiệm của phương trình. b. ߨ
ݔ א ቀͲǢ ቁ ¿ ݔ א ሺͲǢ ͳሻ ʹ Ta có: 135 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác ͳ
ሺͳሻ ݔ ൌ א ሺͲǢ ͳሻ ʹ ʹܽ ݔ ൌ ͳ െ ܽ
Khi đó, yêu cầu bài toán tương đương với ܽ ് Ͳ ۓ ͳ ۖ ͳ െ ܽ Ͳ ൏ ൏ ͳ ൏ ܽ ൏ ͳ ʹܽ ൞͵ ۔ ͳ ۖ ͳ െ ܽ ܽ ് ە ് Ͳ ʹܽ ʹ
Bài 4: Cho phương trình Ͷݔ ݔ ݔ ൌ ݉ Ǥảዛዓ¿݉ ൌ ͳ ߨ
Ǥ¿݉¯ểዛዓ¿×ʹệệ² ቂͲǢ ቃ Ͷ
Giải:Phương trình đưa về dạng
ʹ ଶ ʹݔ െ ͵ ʹݔ ݉ െ ͳ ൌ Ͳ a.
Khi ݉ ൌ ͳ, phương trình trở thành
ʹ ଶ ʹݔ െ ͵ ʹݔ ൌ Ͳ ʹݔ ൌ Ͳ ͵
ʹݔ ൌ െ ൏ െͳሺạሻ ʹ ݇ߨ ݔ ൌ ሺ݇ א Ժሻ ʹ b. ߨ
ݔ א ቂͲǢ ቃ ¿ ʹݔ א ሾͲǢ ͳሿ Ͷ
Đặt ݂ሺݔሻ ൌ ʹ ଶ ʹݔ െ ͵ ʹݔ ݉ െ ͳ
Khi đó, yêu cầu bài toán tương đương với 136 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác ȟ Ͳ ۓ ۖ ݂ሺͲሻ Ͳ ͳ
݂ሺͳሻ Ͳ ʹ ݉ ۔ ͺ ۖ ܵ ەͲ ͳ ʹ
Bài 5: Tìm ݉ để phương trình sau có nghiệm
ξͳ ʹ ݔ ξͳ ʹ ݔ ൌ ݉
(Đề nghị Olympic 30-4, 2008)
Giải: Không mất tính tổng quát, ta chỉ cần xét nghiệm trên ൣȂ ߨǡ ߨ൧ Điều kiện: ߨ ʹߨ ݔ א െ Ǣ ൨ ͵ Ta có :
൜ʹ ʹሺ ݔ ݔሻ ʹξͳ ʹ ݔ ξͳ ʹ ݔ ൌ ݉ଶሺכሻ ݉ Ͳ Đặt ݐ ൌ ݔ ݔ. ߨ ʹߨ ξ͵ െ ͳ ớݔ א െ Ǣ ൨ ¿ݐ א ቈ Ǣ ξʹ ͵ ʹ
Mặt khác, ta lại có : ݐଶ ൌ ͳ ʹ ݔ ݔ. Do đó,
ሺכሻ ʹ ʹݐ ʹඥʹݐଶ ʹݐ െ ͳ ൌ ݉ଶ Xét hàm số ξ͵ െ ͳ
݂ሺݐሻ ൌ ʹݐ ʹ ʹඥʹݐଶ ʹݐ െ ͳǡ ݐ א ቈ Ǣ ξʹ ʹ Ͷݐ ʹ ݂ᇱሺݐሻ ൌ ʹ Ͳ ξʹݐଶ ʹݐ െ ͳ ݐ ξଷିଵ ξʹ ଶ ݂Ԣሺݐሻ Ͷ൫ξʹ ͳ൯ ݂ሺݐሻ ξ͵ ͳ 137 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác
Từ bảng biến thiên, ta kết luận rằng phương trình có nghiệm khi và chỉ khi
൜ξ͵ ͳ ݉ଶ Ͷ൫ξʹ ͳ൯ ටξ͵ ͳ ݉ ʹටξʹ ͳ ݉ Ͳ
Bài 6: Xác định ݉ để phương trình
͵ݔ െ ʹݔ ݉ ݔ െ ͳ ൌ Ͳ ߨ
ׯïዉዒ ቀെ Ǣ ʹߨቁ ʹ (ĐH Y Dược Tp.HCM 1999)
Giải: Phương trình tương đương với
Ͷ ଷ ݔ െ ͵ ݔ െ ሺʹ ଶ ݔ െ ͳሻ ݉ ݔ െ ͳ ൌ Ͳ
ݔ ሺͶ ଶ ݔ െ ʹ ݔ ݉ െ ͵ሻ ൌ Ͳ ݔ ൌ Ͳሺͳሻ
Ͷ ଶ ݔ െ ʹ ݔ ݉ െ ͵ ൌ Ͳሺʹሻ
Với phương trình ሺͳሻ, ta có nghiệm ߨ ݔ ൌ ݇ߨሺ݇ א Ժሻ ʹ ߨ ݔ א ቀെ Ǣ ʹߨቁ ² ʹ ߨ ͵ߨ ݔ ൌ ש ݔ ൌ ʹ ʹ
Với phương trình ሺʹሻ, ta đặt ݐ ൌ ݔ ǡ ȁݐȁ ͳ. Khi đó :
݂ሺݐሻ ൌ Ͷݐଶ െ ʹݐ ݉ െ ͵ ൌ Ͳሺ͵ሻ
Do phương trình ሺͳሻ có 2 nghiệm phân biệt với mọi ݔ, nên ta cần xác định ݉ để phương ߨ ߨ ͵ߨ
¿ሺʹሻ×ͷዉዉዒ ቀെ Ǣ ʹߨቁ ̳ ൜ Ǣ ൠ ʹ ʹ ʹ
Khi đó, phương trình ሺ͵ሻ có 2 nghiệm ݐଵǡ ݐଶ thỏa điều kiện
െͳ ൏ ݐଵ ൏ Ͳ ൏ ݐଶ ൏ ͳ 138 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác ͶǤ ݂ሺͲሻ ൏ Ͳ ݉ ൏ ͵
ቐͶǤ ݂ሺെͳሻ Ͳ ൝݉ െ͵ ͳ ൏ ݉ ൏ ͵ ͶǤ ݂ሺͳሻ Ͳ ݉ ͳ
Bài 7: Cho phương trình tham số ݉
ʹ ʹݔ ଶ ݔ ݔ ଶ ݔ ݔ ൌ ݉ሺ ݔ ݔሻ Ǥዛዓ¿݉ ൌ ʹ ߨ
Ǥ¿݉¯ዛዓ¿×Àኸͳዉዒ ቂͲǢ ቃ ʹ (ĐH Sư Phạm Tp.HCM 2001)
Giải: Phương trình tương đương với
ʹሺଶ ݔ െ ଶ ݔሻ ݔ ݔ ሺ ݔ ݔሻ ൌ ݉ሺ ݔ ݔሻ
ሺ ݔ ݔሻሾʹሺ ݔ െ ݔሻ ݔ ݔ െ ݉ሿ ൌ Ͳ ݔ ݔ ൌ Ͳሺͳሻ
ʹሺݔ െ ݔሻ ݔ ݔ െ ݉ ൌ Ͳሺʹሻ
Với phương trình ሺͳሻ, ta có nghiệm ߨ
ݔ ൌ െ ݇ߨሺ݇ א Ժሻ Ͷ
Với phương trình ሺʹሻ, ta đặt ݐ ൌ ݔ െ ݔ ǡ ȁݐȁ ξʹ. Khi đó, phương trình ሺʹሻ trở thành
െݐଶ Ͷݐ ͳ ൌ ʹ݉ሺ͵ሻ a. Khi ݉ ൌ ʹ thì ሺ ݐ ൌ ͳ
͵ሻ ݐଶ െ Ͷݐ ͵ ൌ Ͳ ݐ ൌ ͵ሺሻ ߨ ξʹ ݔ ൌ ݇ʹߨ ቀݔ ቁ ൌ ቈ ߨ Ͷ ʹ
ݔ ൌ െ ݇ʹߨሺ݇ א Ժሻ ʹ
Vậy phương trình có nghiệm 139 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác ݔ ൌ ݇ʹߨ ۍ ߨ ێݔ ൌ െ ݇ʹߨ ێ ʹ ሺ݇ א Ժሻ ێ ߨ ۏ ݔ ൌ െ ݇ߨ Ͷ b. Ta có : ߨ ߨ Ͳ ݔ
ฺ െͳ ξʹ ቀݔ ቁ ͳ ฺ ݐ א ሾെͳǢ ͳሿ ʹ Ͷ
Do đó, ta cần xác định ݉ để phương trình ሺ͵ሻ có nghiệm ݐ א ሾെͳǢ ͳሿ. Xét hàm số :
݂ሺݐሻ ൌ െݐଶ Ͷݐ ͳǡ ݐ א ሾെͳǢ ͳሿ
݂ᇱሺݐሻ ൌ െʹݐ Ͷ Ͳ
Hàm số đồng biến trên ሾെͳǢ ͳሿ. Ta có : ݂ሺെͳሻ ൌ െͶ ൜ ݂ሺͳሻ ൌ Ͷ
Khi đó, yêu cầu bài toán tương đương với
െͶ ʹ݉ Ͷ െʹ ݉ ʹ
Bài 8: Giải và biện luận phương trình theo tham số ݉ ݉ଶ ଶ ݔ ݉ଶ െ ʹ ൌ ͳ െ ଶ ݔ ʹݔ
Giải: Điều kiện : ݔ ് Ͳ ൝ ݔ ് േͳሺכሻ ʹݔ ് Ͳ
Phương trình tương đương với
݉ଶ ଶ ݔ ൌ ଶ ݔ ݉ଶ െ ʹ
Khi đó, ta đặt ݐ ൌ ଶ ݔ ǡ ݐ א ሾͲǡͳሿ. Ta đưa phương trình về dạng ݉ଶ െ ͳ
ሺ݉ଶ ͳሻݐ ൌ ݉ଶ െ ͳ ݐ ൌ ሺͳሻ ݉ଶ ͳ 140 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác
Tuy nhiên, do điều kiện ሺכሻ ta được ͳ ݐ א ሺͲǡͳሿ̳ ൜ ൠ ʹ
Do đó, để phương trình đã cho có nghiệm thì ݉ଶ െ ͳ ۓͲ ൏ ͳ ݉ଶ ͳ ȁ݉ȁ ͳ ൜ ۔ ݉ଶ െ ͳ ͳ ȁ݉ȁ ് ξ͵ ە ് ݉ଶ ͳ ʹ
Ta thấy, từ phương trình ሺͳሻ, ta có thể suy ra nghiệm của phương trình là ݉ଶ െ ͵ ݔ ൌ േ ݇ߨሺ݇ א Ժሻ ݉ଶ ͳ
Bài 9: Định ݉ để phương trình sau có nghiệm ݉ ݔ ݉ ݔ ൌ ʹ ʹݔ െ ͳ ሺଶ ݔ െ ͵ ଶ ݔሻ ݔ Giải: Ta có :
ʹ ʹݔ െ ͳ ൌ ଶ ݔ െ ͵ ଶ ݔ ൌ ͳ െ Ͷ ଶ ݔ
Nên ta có điều kiện của bài toán là ͳ ൝ଶ ݔ ് ሺכሻ Ͷ ʹݔ ് Ͳ
Phương trình đưa về dạng ݉ ݔ ൌ ݉ ݔሺͳሻ
Đặt ݐ ൌ ݔ ǡ ȁݐȁ ͳ, phương trình ሺͳሻ trở thành
ሺ݉ െ ͳሻݐ ൌ ݉ሺʹሻ
Ta thấy, ݉ ൌ ͳ không là nghiệm của phương trình ሺʹሻ nên ݉ ݐ ൌ ݉ െ ͳ 141 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác
Tuy nhiên, do điều kiện ሺכሻ ta được ͳ
ݐ ് ൜Ͳǡ േͳǡ േ ൠ ʹ
Khi đó, điều kiện cần và đủ để phương trình có nghiệm là ݉ ͳ ۓെͳ ൏ ൏ ͳ ۓ ݉ ൏ ۖ ݉ െ ͳ ݉ ۖ ʹ ് Ͳ ݉ ് Ͳ ۔ ݉ െ ͳ ۔ ͳ ۖ ݉ ͳ ۖ ݉ ് ͵ ە ് േ ݉ െ ͳ ʹ ە݉ ് െͳ
Do đó, ta tìm được giá trị của ݉ thỏa yêu cầu bài toán là ͳ ͳ
݉ א ൬െλǡ ൰ ̳ ൜ͲǢ Ǣ േͳൠ ʹ ͵
Bài 10: Cho phương trình chứa tham số ݉ ݉ ݔ െ ʹ ݉ ݔ െ ʹ ൌ ݉ െ ʹ ݔ ݉ െ ʹ ݔ
Khi ݉ ് Ͳ phương trình có bao nhiêu nghiệm nằm trong đoạn ሾʹͲߨǢ ʹͷߨሿ (ĐH Cần Thơ 1998)
Giải: Điều kiện : ݉ ݔ ് ൞ ʹ ݉ ሺכሻ ݔ ് ʹ
Phương trình tương đương với
ሺ݉ ݔ െ ʹሻሺ݉ െ ʹ ݔሻ ൌ ሺ݉ ݔ െ ʹሻሺ݉ െ ʹ ݔሻ
െʹ݉ ଶ ݔ ሺ݉ଶ Ͷሻ ݔ െ ʹ݉ ൌ െʹ݉ ଶ ݔ ሺ݉ଶ Ͷሻ ݔ െ ʹ݉
ʹ݉ሺଶ ݔ െ ଶ ݔሻ ሺ݉ଶ Ͷሻሺ ݔ െ ݔሻ ൌ Ͳ
ሺ ݔ െ ݔሻሾʹ݉ሺ ݔ ݔሻ െ ሺ݉ଶ Ͷሻሿ ൌ Ͳ 142 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác ݔ ൌ ݔሺͳሻ ߨ ݉ଶ Ͷ ቀݔ ቁ ൌ ሺʹሻ Ͷ ʹξʹ݉
Với phương trình ሺͳሻ, ta có nghiệm ߨ ݔ ൌ ݇ߨሺ݇ א Ժሻ Ͷ
Với phương trình ሺʹሻ, phương trình có nghiệm khi và chỉ khi ݉ଶ Ͷ ଶ
ͳ ൫ȁ݉ȁ െ ξʹ൯ ʹ Ͳ ʹξʹȁ݉ȁ
Do đó, phương trình ሺʹሻ vô nghiệm. Mặt khác, ta thấy nghiệm của phương trình ሺͳሻ thỏa
mãn điều kiện ሺכሻ khi ݉ ് Ͳ, ta xét : ߨ
ቊʹͲߨ ݇ߨ ʹͷߨ Ͷ
݇ ൌ ሼʹͲǢ ʹͳǢ ʹʹǢ ʹ͵Ǣ ʹͶሽ ݇ א Ժ
Như vậy, phương trình đã cho có 5 nghiệm nằm trong đoạn ሾʹͲߨǢ ʹͷߨሿ.
Bài 11: Cho phương trình chứa tham số ݉ ͳ
ଶ ݔ ݉ሺ ݔ ݔሻ ʹ ൌ Ͳ ଶ ݔ
Xác định ݉ để phương trình vô nghiệm.
(ĐH Giao Thông Vận Tải 1995)
Giải: Điều kiện : ʹݔ ് Ͳሺכሻ
Phương trình tương đương với
ଶ ݔ ଶ ݔ ݉ሺ ݔ ݔሻ ͵ ൌ Ͳ
Đặt ݐ ൌ ݔ ݔ ǡ ȁݐȁ ʹ. Khi đó, phương trình trở thành ͳ
ݐଶ ݉ݐ ͳ ൌ Ͳ ݉ ൌ െݐ െ ݐ 143 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác Xét hàm số ͳ
݂ሺݐሻ ൌ െݐ െ ǡ ȁݐȁ ʹ ݐ ͳ ݂ᇱሺݐሻ ൌ െͳ
൏ Ͳǡ ݐ א ሺെλǡ െʹሿ ሾʹǡ λሻ ݐଶ ݐ െλ െʹ ʹ λ ݂Ԣሺݐሻ െ λ ͷ െ ݂ሺݐሻ ʹ ͷ ʹ െλ
Dựa vào bảng biến thiên, giá trị của ݉ thỏa yêu cầu bài toán là : ͷ ͷ െ ൏ ݉ ൏ ʹ ʹ Bài 12: a. Giải phương trình :
͵ݔ ʹݔ ൌ ͳ ʹ ݔ ʹݔሺͳሻ b.
Tìm tất cả các giá trị của ݉ để phương trình ሺͳሻ tương đương với phương trình
͵ݔ െ ݉ ݔ ൌ ሺͶ െ ʹȁ݉ȁሻ ଶ ݔሺʹሻ (ĐH Thái Nguyên 2000) Giải: a.
Phương trình tương đương với
͵ݔ ͳ െ ʹ ଶ ݔ ൌ ͳ ͵ݔ െ ݔ
ሺʹ ݔ െ ͳሻ ݔ ൌ Ͳ ݔ ൌ ݇ߨ ݔ ൌ Ͳ ۍ ߨ ێ ݔ ൌ ݇ʹߨ ͳ ሺ݇ א Ժሻ ݔ ൌ ێ ʹ ێ ͷߨ ۏݔ ൌ ݇ʹߨ b.
Phương trình ሺʹሻ tương đương với
͵ ݔ െ Ͷ ଷ ݔ െ ݉ ݔ ൌ ሺͶ െ ʹȁ݉ȁሻ ଶ ݔ 144 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác
ݔ ሾͶ ଶ ݔ ʹሺʹ െ ȁ݉ȁሻ ݔ ݉ െ ͵ሿ ൌ Ͳ ݔ ൌ Ͳ
Ͷଶ ݔ ʹሺʹ െ ȁ݉ȁሻ ݔ ݉ െ ͵ ൌ Ͳሺכሻ
- Điều kiện cần :
Phương trình ሺͳሻ và ሺʹሻ tương đương thì phương trình ሺכሻ phải được thỏa bởi phương trình ͳ ݔ ൌ ʹ
Điều này tương đương với ͳ ͳ
ͶǤ ʹሺʹ െ ȁ݉ȁሻǤ ݉ െ ͵ ൌ Ͳ Ͷ ʹ
ȁ݉ȁ ൌ ݉ ݉ Ͳ
- Điều kiện đủ : Với ݉ Ͳ thì ሺ ݔ ൌ Ͳ
ʹሻ Ͷଶ ݔ െ ʹሺ݉ െ ʹሻ ݔ ݉ െ ͵ ൌ Ͳ ݔ ൌ Ͳ ۍ ͳ ێ ݔ ൌ ێ ʹ ێ ݉ െ ͵ ۏ ݔ ൌ ʹ
Như vậy, phương trình ሺͳሻ và ሺʹሻ tương đương với nhau khi và chỉ khi ݉ Ͳ ۓ ݉ െ ͵ ۖ ۖۍ ൌ Ͳ ݉ ൌ ͵ ێ ʹ ݉ െ ͵ ͳ ൦ ݉ ൌ Ͷ ۔ێ ൌ Ͳ ݉ ൏ ͳ ێ ʹ ʹ ۖ ۖ ݉ ͷ ێ ݉ െ ͵ ەۏฬ ฬ ͳ ʹ 145 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 13: Xác định ݉ để hai phương trình sau tương đương
͵ݔ ൌ Ͷ ሺ͵ߨ ݔሻሺͳሻ ߨ
݉ ଶ ݔ ሺͳ െ ݉ሻ ቀ ݔቁ ൌ Ͳሺʹሻ ʹ
Giải: Phương trình ሺͳሻ tương đương với
Ͷ ଷ ݔ െ ͵ ݔ ൌ െͶ ݔ
ሺͶ ଶ ݔ ͳሻ ݔ ൌ Ͳ ݔ ൌ Ͳ
Phương trình ሺʹሻ tương đương với
݉ ଶ ݔ ሺͳ െ ݉ሻ ݔ ൌ Ͳ
ݔ ሺ݉ ݔ ͳ െ ݉ሻ ൌ Ͳ ቂ ݔ ൌ Ͳ ݉ ݔ ͳ െ ݉ ൌ Ͳ
Với ݉ ൌ Ͳ thì phương trình ሺͳሻ và ሺʹሻ tương đương với nhau.
Với ݉ ് Ͳ thì phương trình ሺʹሻ tương đương ݔ ൌ Ͳ ݉ െ ͳ ݔ ൌ ݉
Do đó, phương trình ሺͳሻ và ሺʹሻ tương đương khi và chỉ khi ݉ ് Ͳ ۓ ݉ ് Ͳ ۖ ݉ െ ͳ ൌ Ͳ ݉ ൌ ͳ ݉ ൞ ۔൦ ͳ ۖ ݉ െ ͳ ݉ ൏ ە ฬ ฬ ͳ ʹ ݉
Từ các giá trị trên, ta có giá trị ݉ thỏa yêu cầu bài toán là ͳ ݉ ൏ ש ݉ ൌ ͳ ʹ 146 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác
Bài 14: Cho phương trình chứa tham số ݉
Ͷ ହ ݔ ݔ െ Ͷ ହ ݔ ݔ ൌ ଶ Ͷݔ ݉
Tìm tất cả các nghiệm của phương trình thỏa mãn bất phương trình ݔସ െ ͵ݔଶ ʹ Ͳ ߨ
ዅኾݔ ൌ െ ዒዉዚዛዓ¿ ͺ
Giải: Phương trình tương đương với
Ͷ ݔ ݔ ሺଶ ݔ െ ଶ ݔሻሺଶ ݔ ଶ ݔሻ ൌ ଶ Ͷݔ ݉
ʹ ʹݔ ʹݔ ൌ ଶ Ͷݔ ݉
Ͷݔ ൌ ଶ Ͷݔ ݉ሺͳሻ ߨ
ዅݔ ൌ െ ሺͳሻ¿݉ ൌ െʹ ͺ
Với ݉ ൌ െʹ thì ሺͳሻ trở thành
ଶ Ͷݔ െ Ͷݔ െ ʹ ൌ Ͳ Ͷݔ ൌ െͳ Ͷݔ ൌ ʹሺሻ ߨ ݇ߨ ݔ ൌ െ ሺ݇ א Ժሻ ͺ ʹ
Bất phương trình tương đương với
ቈെξʹ ݔ െͳሺכሻ ͳ ݔ ξʹሺככሻ
Họ nghiệm vừa tìm được thỏa mãn ሺכሻ khi ߨ ݇ߨ ൝െξʹ െ െͳ ͺ ʹ ฺ ݔ א ݇ א Ժ
Họ nghiệm vừa tìm được thỏa mãn ሺככሻ khi 147 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác ߨ ݇ߨ ൝ͳ െ ξʹ ͺ ʹ ฺ ݇ ൌ ͳ ݇ א Ժ
Do đó, ta có được nghiệm của phương trình thỏa yêu cầu bài toán là ͵ߨ ݔ ൌ ͺ - BÀI TẬP TỰ LUYỆN
5.2.18. Cho phương trình: ͵ߨ ͷ Ͷ ቀ ʹ െ ݔቁ ܽ ൌ ݔ ͳ ଶ ܽ ߨ Ǥ ảươ¿ܽ ൌ െ Ͷ Ǥ¿ܽ¯ểươ¿×ệ
5.2.19. Cho 2 phương trình sau:
ʹ ݔ ʹݔ ൌ ͳ ʹݔ ͵ݔ
Ͷ ଶ ݔ െ ͵ݔ ൌ ܽ ݔ ሺͶ െ ܽሻሺͳ ʹݔሻ
Tìm ܽ để 2 phương trình tương đương. (ĐH Y Dược Tp.HCM 1998)
5.2.20. Cho phương trình sau:
ଶ ݔ ሺʹ݉ െ ʹሻ ݔ ݔ െ ሺ݉ ͳሻ ଶ ݔ ൌ ݉ a.
Giải phương trình khi ݉ ൌ െʹ. b.
Tìm ݉ để phương trình có nghiệm.
5.2.21. Cho phương trình sau:
ʹݔ Ͷሺ ݔ െ ݔሻ ൌ ݉
Tìm ݉ để phương trình có nghiệm. 148 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác
5.2.22. Tìm ݉ để hai phương trình sau tương đương
ʹ ݔ ሺ݉ െ ͳሻ ଷ ݔ ሺʹ݉ଷ െ ʹ݉ െ ͳሻ ݔ ൌ Ͳ
ʹ ݔ ሺʹ െ ݉ሻ ଶ ݔ ʹ݉ଷ െ ݉ െ ʹ ൌ Ͳ
ሺĐề nghị Olympic 30-4, 2007ሻ
5.2.23. Tìm tất cả các giá trị ݉ để phương trình ݉ݔଶ ʹ ݔ ൌ ʹ có đúng 2 nghiệm ߨ ệ ቂͲǢ ቃ ʹ
(Đề nghị Olympic 30-4, 2007) -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN 5.2.18. Điều kiện: ቄ ݔ ് Ͳ ሺכሻ ܽ ് Ͳ Phương trình trở thành
͵ ʹܽ ݔ Ͷ ݔ ൌ ͷሺͳሻ a. ߨ ܽ ൌ െ ¿ሺͳሻở Ͷ ͵ Ͷ െ ݔ ݔ ൌ ͳ ͷ ͷ Ta đặt ͵ ݕ ൌ െ ൞ ͷ Ͷ ݕ ൌ ͷ
Khi đó, phương trình trở thành: 149 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác ݕ ݔ ݕ ݔ ൌ ͳ ሺݔ ݕሻ ൌ ͳ
ݔ ൌ െݕ ݇ߨሺ݇ א Ժሻ െ͵ ݔ ൌ െ
݇ߨሺ݇ א Ժሻ൫ውሺכሻ൯ ͷ b.
Yêu cầu bài toán tương đương với
ሺ͵ ʹܽሻଶ ሺͶሻଶ ሺͷሻଶ ቄ ܽ ് Ͳ ଶ ʹܽ ͳ ቄ ܽ ് Ͳ ଶ ʹܽ ൌ ͳ ቄ ܽ ് Ͳ ʹܽ ൌ Ͳ ߨ ݇ߨ ܽ ൌ ሺ݇ א Ժሻ Ͷ ʹ 5.2.19. Ta đặt
ʹ ݔ ʹݔ ൌ ͳ ʹݔ ͵ݔሺͳሻ
൜Ͷଶ ݔ െ ͵ݔ ൌ ܽ ݔ ሺͶ െ ܽሻሺͳ ʹݔሻሺʹሻ Ta có:
ሺͳሻ ͵ݔ ݔ ൌ ͳ ʹݔ ͵ݔ ʹ ଶ ݔ െ ݔ ൌ Ͳ ݔ ൌ Ͳ ͳ ݔ ൌ ʹ Lại có:
ሺʹሻ Ͷ ଶ ݔ െ ሺͶ ଷ ݔ െ ͵ ݔሻ ൌ ܽ ݔ ʹሺͶ െ ܽሻ ଶ ݔ
Ͷ ଷ ݔ ሺͶ െ ʹܽሻ ଶ ݔ ሺܽ െ ͵ሻ ݔ ൌ Ͳ
ݔ ሾͶଶ ݔ ʹሺʹ െ ܽሻ ݔ ܽ െ ͵ሿ ൌ Ͳ 150 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác ͳ
ݔ ൬ ݔ െ ൰ ሺʹ ݔ ͵ െ ܽሻ ൌ Ͳ ʹ ݔ ൌ Ͳ ۍ ͳ ێ ݔ ൌ ێ ʹ ێ ܽ െ ͵ ۏ ݔ ൌ ʹ
Yêu cầu bài toán tương đương với ܽ െ ͵ ۍ ൌ Ͳ ێ ʹ ێ ܽ െ ͵ ͳ ܽ ൌ ͵ ൌ ێ ʹ ʹ ൦ܽ ൌ Ͷ ێ ܽ െ ͵ ܽ ൏ ͳ ͳ ێ ʹ ܽ ͷ ێܽ െ ͵ ۏ ൏ െͳ ʹ
5.2.20. Khi ݔ ൌ Ͳ ta có: ݉ ൌ ͳ
ቄ ݔ ൌ Ͳ ቄ ଶ ݔ ൌ ͳ ቄ ݉ ൌ ͳ ቊ ߨ ଶ ݔ ൌ ݉ ଶ ݔ ൌ ݉ ݔ ൌ ͳ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ
Vậy khi ݉ ് ͳ thì ݔ ൌ Ͳ không là nghiệm của phương trình. Khi ấy, ta chia 2 vế phương trình cho ଶ ݔ.
Khi đó, phương trình trở thành:
ሺ݉ െ ͳሻ ଶ ݔ െ ʹሺ݉ െ ͳሻ ݔ ʹ݉ ͳ ൌ Ͳ a.
Khi ݉ ൌ െʹ ് ͳ thì ta có ߨ
ݔ ൌ ͳ ݔ ൌ ݇ߨሺ݇ א Ժሻሺው ݔ ് Ͳሻ Ͷ b.
Phương trình có nghiệm khi và chỉ khi ݉ ൌ ͳ ݉ ൌ ͳ ቈቄ݉ ് ͳ ቈቄ ݉ ് ͳ െʹ ݉ ͳ ȟᇱ Ͳ െ݉ଶ െ ݉ ʹ Ͳ 151 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác 5.2.21. ߨ
0ặݐ ൌ ݔ െ ݔ ൌ ξʹ ቀ െ ݔቁ ǡ ݐ א ൣെξʹǡ ξʹ൧ Ͷ ương trình trở thành
െݐଶ Ͷݐ ͳ ൌ ݉
Đặt ݂ሺݐሻ ൌ െݐଶ Ͷݐ ͳ ൌ ݉ với ݐ א ൣെξʹǢ ξʹ൧
Suy ra ݂ᇱሺݐሻ ൌ Ͷ െ ʹݐ Ͳ với ݐ א ൣെξʹǢ ξʹ൧
Nên ݂ሺݐሻ đồng biến trên khoảng ൣെξʹǢ ξʹ൧
Khi đó tập giá trị của ݂ሺݐሻ là ൣ݂൫െξʹ൯Ǣ ݂൫ξʹ൯൧ ൌ ൣെͶξʹ െ ͳǢ Ͷξʹ ͳ൧
Vậy phương trình có nghiệm khi và chỉ khi ݂ሺݐሻ ൌ ݉ có nghiệm ݐ א ൣെξʹǢ ξʹ൧
݉ א ൣെͶξʹ െ ͳǢ Ͷξʹ ͳ൧ 5.2.22. Ta đặt
൜ʹ ݔ ሺ݉ െ ͳሻ ଷ ݔ ሺʹ݉ଷ െ ʹ݉ െ ͳሻ ݔ ൌ Ͳሺͳሻ
ʹ ݔ ሺʹ െ ݉ሻ ଶ ݔ ʹ݉ଷ െ ݉ െ ʹ ൌ Ͳሺʹሻ
Phương trình ሺͳሻ luôn có nghiệm là ݔ ൌ Ͳ ݔ ൌ ݇ߨሺ݇ א Ժሻ
Vậy phương trình ሺͳሻ tương đương với phương trình ሺʹሻ thì điều kiện cần là phương
trình ሺʹሻ phải có nghiệm ݔ ൌ ݇ߨሺ݇ א Ժሻ Khi đó:
ሺʹሻ ʹ ሺ݇ߨሻ ሺʹ െ ݉ሻ ଶሺ݇ߨሻ ʹ݉ଷ െ ݉ െ ʹ ൌ Ͳ ݉ ൌ Ͳ ݉ ൌ ͳ ݉ ൌ െͳ
Khi ݉ ൌ ͳ thay vào 2 phương trình và giải ra 2 tập nghiệm không trùng nhau nên loại ݉ ൌ ͳ.
Khi ݉ ൌ െͳ và ݉ ൌ Ͳ thay vào 2 phương trình và giải ra 2 tập nghiệm trùng nhau nên nhận ݉ ൌ െͳ. 152 --------------------- TOANMATH.com
Chương 5 : Phương trình lượng giác
Vậy ቂ ݉ ൌ Ͳ thỏa yêu cầu bài toán. ݉ ൌ െͳ
5.2.23. Chứng minh được ݔ ൌ Ͳ là một nghiệm của phương trình. ߨ Ͷ ଶ ݔ ݐ ଶ ݔ ߨ ớݔ א ቀͲǢ ቃ ¿݉ ൌ ʹ ݉ ൌ ൬ ൰ ǡ ݐ ൌ א ቀͲǢ ቃ ʹ ݔଶ ݐ ʹ Ͷ ݐ ଶ ߨ ±ố݂ሺݐሻ ൌ ൬ ൰ ²ả ቀͲǢ ቃ ݐ Ͷ ߨ
ứ¯ượ݂ሺݐሻịế² ቀͲǢ ቃ Ͷ ݐ ଶ ߨ ͺ ݂ሺݐሻ ൌ ൬ ൰ ൌ ͳ݂ ቀ ቁ ൌ ௧՜ ௧՜ ݐ Ͷ ߨଶ
ế nên điều kiện cần và đủ để thỏa yêu cầu bài toán là ݂ሺݐሻ ൌ ݉ có đúng một nghiệm ߨ ͺ ቀͲǢ ቃ ݉ ͳ Ͷ ߨଶ 153 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác CHƯƠNG 6
HỆ PHƯƠNG TRÌNH LƯỢNG GIÁC I.
TÓM TẮT MỘT SỐ PHƯƠNG PHÁP THƯỜNG GẶP 1. PHƯƠNG PHÁP THẾ
- Phương pháp thế là một phương pháp cơ bản trong việc giải hệ phương trình
lượng giác. Thông thường, ta có ba cách sử dụng ở phương pháp này : thế trực
tiếp, biến đổi rồi thế sau, giải tìm nghiệm của một phương trình rồi thế vào phương trình còn lại. 2.
PHƯƠNG PHÁP CỘNG ĐẠI SỐ
- Trong phương pháp này ta sẽ có một số loại cơ bản cần nắm : ߙݔ ߚݔ ൌ ܽ i.
Loại 1 : ൜ߙݔ ߚݔ ൌ ܾ ߙݔ ߚݔ ൌ ܽ ii.
Loại 2 : ൜݉ ߙݔ ൌ ݊ ߚݔ ߙݔ ߚݔ ൌ ܽ iii.
Loại 3 : ൜݉ ߙݔ ൌ ݊ ߚݔ ߙ ݔ ߚݔ ൌ ܽ iv.
Loại 4 : ൜ ߙݔ ߚݔ ൌ ܾ ߙݔ ߚݔ ൌ ܽ v.
Loại 5 : ൜ ߚݔ ߙݔ ൌ ܾ
- Ở những loại này ta thường có ba bước giải : đổi ߙݔ ǡ ߚݔ thành
ߙݔ ǡ ߚݔ; cộng và trừ hai phương trình của hệ để được một hệ phương
trình mới cơ bản hơn; giải hệ vừa có để tìm nghiệm. 3.
PHƯƠNG PHÁP KHỬ SAU KHI BÌNH PHƯƠNG
- Có hai dạng đặc trưng trong phương pháp này : ݂ሺݔሻ ൌ ߙ ܽݕ ݂ሺݕሻ ൌ ߙ ܾݔ ൜ ặ ൜ ݃ሺݔሻ ൌ ߙ ܽݕ ݃ሺݕሻ ൌ ߙ ܾݔ
- Phương pháp này cũng thường gồm ba bước giải : bình phương hai vế hai
phương trình của hệ; cộng lại thì được một phương trình một ẩn số; giải
phương trình vừa tìm được rồi thế nghiệm vào hai phương trình ban đầu để kiểm tra. 4.
MỘT SỐ PHƯƠNG PHÁP KHÁC
- Ngoài ra, ta còn có nhiều phương pháp khác, chẳng hạn như : đặt ẩn phụ; sử
dụng bất đẳng thức cổ điển, dùng đạo hàm… 154 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác II.
CÁC BÀI TẬP MINH HỌA
Bài 1: Giải hệ phương trình sau: ݔ ݕ ൌ ͳ ሺכሻ ൝ ߨ ݔ ݕ ൌ ͵ Giải: Ta có ݔ ݕ ݔ െ ݕ ʹ ൌ ͳ ሺכሻ ൞ ʹ ʹ ߨ ݔ ݕ ൌ ͵ ݔ െ ݕ ൌ ͳ ൞ ʹ ߨ ݔ ݕ ൌ ͵ ݔ െ ݕ ൌ ݇ʹߨ ൝ ߨ ሺ݇ א Ժሻ ݔ ݕ ൌ ͵ ߨ ݔ ൌ ݇ʹߨ ൞ ߨ ሺ݇ א Ժሻ ݕ ൌ െ ݇ʹߨ
Bài 2: Giải hệ phương trình sau : ߨ ʹݔ െ ͵ݕ ൌ ͵ ሺכሻ ൞ ξ͵ ʹݔ ͵ݕ ൌ Ͷ Giải: Ta có ߨ ʹݔ െ ͵ݕ ൌ ͵ ሺכሻ ൞ͳ ξ͵
ሾሺʹݔ ͵ݕሻ ሺʹݔ െ ͵ݕሻሿ ൌ ʹ Ͷ 155 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác ߨ ʹݔ െ ͵ݕ ൌ ͵ ൞ ߨ ξ͵ ሺʹݔ ͵ݕሻ ൌ ͵ ʹ ߨ ʹݔ െ ͵ݕ ൌ ൝ ͵ ሺ݇ א Ժሻ ʹݔ ͵ݕ ൌ ݇ߨ ߨ ݇ߨ ݔ ൌ ൞ ͳʹ Ͷ ߨ ݇ߨሺ݇ א Ժሻ ݕ ൌ െ ͳͺ
Bài 3: Giải hệ phương trình sau: ݔ ݕ ൌ ξʹ ሺכሻ ቊݔ ݕ ൌ ξʹ (ĐH Y Dược Tp.HCM 1997) Giải: Ta có
ݔ െ ݔ ݕ െ ݔ ൌ Ͳ
ሺכሻ ൜ݔ ݔ ݕ െ ݔ ൌ ʹξʹ ߨ ߨ
ቀݔ െ ቁ ቀݕ െ ቁ ൌ Ͳ ൞ Ͷ Ͷ ߨ ߨ
ቀݔ ቁ ቀݕ ቁ ൌ ʹ Ͷ Ͷ ߨ ߨ
ۓ ቀݔ െ ቁ ቀݕ െ ቁ ൌ Ͳ Ͷ Ͷ ۖ ߨ ቀݔ ቁ ൌ ͳ ۔ Ͷ ߨ ۖ ቀݕ ቁ ൌ ͳ ە Ͷ ߨ ߨ
ۓ ቀݔ െ ቁ ቀݕ െ ቁ ൌ Ͳ ۖ Ͷ Ͷ ߨ ݔ ൌ ݇ʹߨ ሺ݇ǡ ݈ א Ժሻ ۔ Ͷ ۖ ߨ ە ݕ ൌ ݈ʹߨ Ͷ 156 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác ߨ ݔ ൌ ݇ʹߨ ൞ Ͷߨ ሺ݇ǡ ݈ א Ժሻ ݕ ൌ ݈ʹߨ Ͷ
Bài 4: Giải hệ phương trình sau: ͳ ሺכሻ ൝ ݔ ݕ ൌ െ ʹ ݔ ݕ ൌ ͳ
Giải: Điều kiện: ݔ ݕ ് Ͳ Ta có:
ሺݔ ݕሻ ሺݔ െ ݕሻ ൌ െͳ ሺכሻ ቐ ݔ ݕ െ ͳ ൌ Ͳ ݔ ݕ
ሺݔ ݕሻ ሺݔ െ ݕሻ ൌ െͳ ൜ ݔ ݕ െ ݔ ݕ ൌ Ͳ ሺݔ ݕሻ ൌ െͳ ൜ ሺݔ െ ݕሻ ൌ Ͳ ߨ ݔ ݕ ൌ െ ݇ʹߨ ൝ ʹ ሺ݇ǡ ݈ א Ժሻ ݔ െ ݕ ൌ ݈ߨ ߨ ሺʹ݇ ݈ሻߨ ݔ ൌ െ Ͷ ʹ ൞ ሺ݇ǡ ݈ א Ժሻ ߨ ሺʹ݇ െ ݈ሻߨ ݕ ൌ െ Ͷ ʹ
Bài 5: Giải hệ phương trình sau :
ଷ ݔ െ ݔ ݕ ൌ Ͳሺͳሻ ൜
ଷ ݕ െ ݕ ݔ ൌ Ͳሺʹሻ
(ĐH Ngoại Ngữ Tin Học Tp.HCM 1997) 157 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác
Giải: Lấy ሺͳሻ ሺʹሻ theo từng vế, ta có :
ଷ ݔ ଷ ݕ ൌ Ͳ ݕ ൌ െ ݔሺ͵ሻ
Thế ሺ͵ሻ vào ሺͳሻ, ta được
ݔ ሺଶ ݔ െ ʹሻ ൌ Ͳ ݔ ൌ Ͳ
Với ݔ ൌ Ͳ thì ݕ ൌ Ͳ, khi đó ߨ ݔ ൌ ݇ߨ ൝ ʹ ሺ݇ǡ ݈ א Ժሻ ݕ ൌ ݈ߨ
Bài 6: Giải hệ phương trình sau : ξʹ ݔ ൌ ͳ ݕ ሺכሻ ቊ ξʹݔ ൌ ݕ (ĐH Sư Phạm Vinh 1997) Giải:
ʹ ଶ ݔ ൌ ͳ ʹ ݕ ଶ ݕሺͳሻ ሺכሻ ൜ ʹ ଶ ݔ ൌ ଶ ݕሺʹሻ
Lấy ሺͳሻ ሺʹሻ theo từng vế, ta có :
ʹሺଶ ݔ ଶ ݔሻ ൌ ଶ ݕ ଶ ݕ ʹ ݕ ͳ ߨ
ݕ ൌ Ͳ ݕ ൌ ݇ߨሺ݇ א Ժሻ ʹ
- Nếu ݇ ൌ ʹ݈ǡ ݈ א Ժ thì ξʹ ߨ ሺכሻ ݔ ൌ ݔ ൌ
ݔ ൌ ݉ʹߨሺ݉ א Ժሻ ʹ Ͷ
Vậy nghiệm của hệ là : ߨ ݔ ൌ ݉ʹߨ ൞ Ͷߨ ሺ݉ǡ ݈ א Ժሻ ݕ ൌ ݈ʹߨ ʹ 158 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác
- Nếu ݇ ൌ ʹ݈ ͳǡ ݈ א Ժ thì ۓ ξʹ ۖ ݔ ൌ ߨ ሺכሻ
ʹ ݔ ൌ െ ݉ʹߨሺ݉ א Ժሻ ۔ ξʹ Ͷ ۖ ݔ ൌ െ ە ʹ
Vậy nghiệm của hệ là : ߨ ݔ ൌ െ ݉ʹߨ ൞ Ͷ ߨ ሺ݉ǡ ݈ א Ժሻ ݕ ൌ ሺʹ݈ ͳሻߨ ʹ
Bài 7: Giải hệ phương trình sau : ݔ െ ݕ ൌ Ͳ
ሺכሻ ൜ͷݕ െ ݔ ൌ Giải: ଶ ݔ ൌ Ͷͻ ଶ ݕሺͳሻ
ሺכሻ ൜ଶ ݔ ൌ ʹͷଶ ݕ െ Ͳݕ ͵ሺʹሻ
Lấy ሺͳሻ ሺʹሻ theo từng vế, ta có :
ʹͷ ଶ ݕ Ͷͻ ଶ ݕ െ Ͳ ݕ ͵ ൌ ͳ
ʹ ଶ ݕ ͷ ݕ െ ൌ Ͳ ݕ ൌ ͳ ߨ
ݕ ൌ ݇ʹߨሺ݇ א Ժሻ ݕ ൌ െ ሺạሻ ʹ ʹ Khi đó,
ሺכሻ ቄ ݔ ൌ Ͳ ݔ ൌ ߨ ݈ʹߨሺ݈ א Ժሻ ݔ ൌ െͳ
Thử lại, ta nhận nghiệm của hệ là : ݔ ൌ ߨ ݈ʹߨ ቊ ߨ
ݕ ൌ ݇ʹߨሺ݈ǡ ݇ א Ժሻ ʹ 159 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác
Bài 8: Giải hệ phương trình sau : ݔ ʹݕ ൌ ʹݔ
ሺכሻ ൜ʹݕሺݔ െ ݕሻ ൌ ݔ
Giải: Điều kiện : ߨ ݔ ് ݊ߨሺ݊ א Ժሻ ʹ Ta có : ݔ ʹݕ ൌ ʹݔ ሺכሻ ൜ ሺʹݕ െ ݔሻ ൌ Ͳ
ሺʹݕ െ ݇ߨሻ ʹݕ ൌ ሺͶݕ ݇ʹߨሻ ൜ ሺ݇ א Ժሻ ݔ ൌ ʹݕ െ ݇ߨ Suy ra ʹݕ ʹݕ ൌ Ͷݕ ͳ ʹݕ ൬ ͳ െ ʹ ʹݕ൰ ൌ Ͳ ʹݕ ʹݕ ൌ Ͳ
ʹଶ ʹݕ െ ʹݕ െ ͳ ൌ Ͳ ݉ߨ ʹݕ ൌ Ͳ ۍ ݕ ൌ ʹݕ ൌ Ͳ ێ ʹ ʹݕ ൌ ͳ ߨ ൦ ͳ ێ ͳ
ݕ ൌ െ ݉ߨሺ݉ א Ժሻ ʹݕ ൌ െ ێ ͵ ʹݕ ൌ െ ʹ ʹ ێ ߨ ۏ ݕ ൌ ݉ߨ ͵
Ứng với ݔ ൌ ʹݕ െ ݇ߨ và điều kiện bài toán, ta có nghiệm của hệ là : ʹߨ ݔ ൌ ሺ݉ െ ݇ሻߨ ݔ ൌ േ ሺʹ݉ െ ݇ሻߨ ൝ ݉ߨ ש ൞ ͵ ሺ݉ǡ ݇ א Ժሻ ݕ ൌ ߨ ʹ ݕ ൌ േ ݉ߨ ͵ 160 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác
Bài 9: Giải hệ phương trình sau : ͳ ߨݔ ߨݕ ൌ ሺכሻ ൞ Ͷ ͵ ߨݔ ൌ ߨݕ Ͳ ൏ ݔ ݕ ൏ ʹ
Giải: Điều kiện : ͳ ݔ ് ݉ ൞ ʹͳ ሺ݉ǡ݊ א Ժሻ ݕ ് ݊ ʹ Ta có : ͳ ሺכሻ ൝ ߨݔ ߨݕ ൌ Ͷ ͵ ߨݔ ߨݕ ൌ ߨݕ ߨݔ ͳ ߨݔ ߨݕ ൌ ൞ Ͷ ͵ ߨݕ ߨݔ ൌ Ͷ ߨሺݔ ݕሻ ൌ ͳ ൝ ͳ ߨሺݔ െ ݕሻ ൌ െ ʹ ߨ
ۓ ߨሺݔ ݕሻ ൌ ݇ʹߨ ۖ ʹ ߨ
ߨሺݔ െ ݕሻ ൌ െ ݈ʹߨሺ݇ǡ ݈ א Ժሻ ۔൦ ۖ ߨ ە ߨሺݔ െ ݕሻ ൌ ݈ʹߨ 161 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác ͳ ۍ ݔ ൌ ݇ ݈ ێ ൞ ێ ͳ ݕ ൌ ݇ െ ݈ ێ ͵ ሺ݇ǡ ݈ א Ժሻ ێ ͷ ݔ ൌ ݇ ݈ ێ൞ ێ ͳ ۏ ݕ ൌ െ ݇ െ ݈ ͵
Với Ͳ ൏ ݔ ݕ ൏ ʹ thì ݇ ൌ Ͳ. Do đó, kết hợp với điều kiện bài toán, nghiệm của hệ là ͳ ͷ ݔ ൌ ݈ ݔ ൌ ݈ ൞ ͳ ש൞ ͳ ሺ݈ א Ժሻ ݕ ൌ െ ݈ ݕ ൌ െ െ ݈ ͵ ͵
Bài 10: Giải hệ phương trình sau : ͳ ݔ ݔ ൌ ݕ െ ݕ ൞ ʹ͵ ʹ ʹݔ ൌ ʹݕ ʹ Giải: Ta đặt ߨ
ݑ ൌ ݔ ݔ ൌ ξʹ ቀݔ ቁ Ͷ ൞
ߨ ൫ݑǡ ݒ א ൣെξʹǢ ξʹ൧൯ሺכሻ
ݒ ൌ ݕ െ ݕ ൌ ξʹ ቀݕ െ ቁ Ͷ
Khi đó, hệ phương trình tương đương với ͳ ݑ ൌ ݒ ൞ ʹ͵
ʹሺݑଶ െ ͳሻ ൌ ሺͳ െ ݒଶሻ ʹ ͳ ݑ ൌ ݒ ൞ ʹ ͳ ͻ
ʹ ൬ ݒ ݒଶ൰ ݒଶ ൌ Ͷ ʹ 162 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác ͳ ൝ ݑ ൌ ݒ ʹ ͵ݒଶ ʹݒ െ Ͷ ൌ Ͳ ۓ ͳ ʹξͳ͵ ۖݑ ൌ ൫ውሺכሻ൯ ۔ െͳ ξͳ͵ ۖݒ ൌ ە ͵ ۓ ߨ ͳ ʹξͳ͵ ۖ ቀݔ ቁ ൌ ൌ ߙ Ͷ ξʹ ۔ ߨ െͳ ξͳ͵ ۖ ቀݕ െ ቁ ൌ ൌ ߚ ە Ͷ ͵ξʹ ߨ ۓ ݔ ൌ ߙ െ ݇ʹߨ Ͷ ۖ൦ ۖ ͵ߨ ݔ ൌ െ ߙ ݇ʹߨ Ͷ ሺ݇ǡ ݈ א Ժሻ ۔ ߨ ݕ ൌ ߚ ݈ʹߨ ۖ Ͷ ۖ൦ ͷߨ ە ݕ ൌ െ ߚ ݈ʹߨ Ͷ
Bài 11: Giải hệ phương trình sau :
ݔ െ ʹݕ ൌ ݔ െ ʹݕሺͳሻ ൜ ݔ ൌ ͵ ݕሺʹሻ
Giải: Điều kiện : ߨ ݔ ് ݉ߨ ൞ ʹߨ ሺ݉ǡ ݊ א Ժሻሺכሻ ݕ ് ݊ߨ ʹ
Ở phương trình ሺͳሻ ta có : ݔ െ ݔ ൌ ʹݕ െ ʹݕ
Do đó, ta sẽ khảo sát hàm số
݂ሺݐሻ ൌ ݐ െ ݐǡ ݐ א Թ 163 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác
݂ᇱሺݐሻ ൌ െ ݐ െ ͳ Ͳ
Vậy hàm số nghịch biến. Do đó, ݔ ൌ ʹݕ
Thay vào ሺʹሻ ta được : ʹݕ ൌ ͵ ݕ
ݕ ሺͳ െ ͵ ଶ ݕሻ ൌ Ͳ ݕ ൌ Ͳ ͳ ଶ ݕ ൌ ͵ ݕ ൌ ݇ߨ ߨ ሺ݇ א Ժሻ ݕ ൌ േ ݇ߨ
Từ đó, kết hợp với điều kiện ሺכሻ, ta nhận được nghiệm của hệ là : ߨ ߨ ݔ ൌ ʹ݇ߨ ݔ ൌ ݇ߨ ݔ ൌ െ ݇ߨ ൜ ͵ ͵ ݕ ൌ ݇ߨ ש൞ ߨ ש൞ ߨ ሺ݇ א Ժሻ ݕ ൌ ݇ߨ ݕ ൌ െ ݇ߨ
Bài 12: Giải hệ phương trình sau : ߨ
ݔ ݔ ൌ ʹ ቀݕ ቁሺͳሻ ൞ Ͷ ߨ
ݕ ݕ ൌ ʹ ቀݔ െ ቁሺʹሻ Ͷ Giải: Điều kiện ݇ߨ ݔ ് ൞ ʹ
݈ߨ ሺ݇ǡ ݈ א Ժሻሺכሻ ݕ ് ʹ Ta có :
ȁ ݔ ݔȁ ൌ ȁ ݔȁ ȁ ݔȁ ʹ ൝ ߨ ʹ ቚ ቀݕ ቁቚ ʹ Ͷ 164 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác
Nên ሺͳሻ tương đương với ݔ ݔ ൌ ʹ ݔ ݔ ൌ െʹ ሺሻ ቊ ߨ ߨ
ቀݕ ቁ ൌ ͳ ש ሺሻ ቊ ቀݕ ቁ ൌ െͳ Ͷ Ͷ Giải ሺሻ : ݔ ൌ ͳ ቊ ߨ ቀݕ ቁ ൌ ͳ Ͷ ߨ ݔ ൌ ߨ ൞ Ͷ ߨ ሺǡ ݍ א Ժሻ ݕ ൌ ݍʹߨ Ͷ
Nghiệm trên thỏa điều kiện của hệ, ta thế vào ሺʹሻ: ߨ ߨ
ൌ ݕ ݕ ൌ ቀ ݍʹߨቁ ቀ ݍʹߨቁ ൌ ʹ Ͷ Ͷ ߨ
ൌ ʹ ቀݔ െ ቁ ൌ ʹ ߨ ൌ Ͳ Ͷ
Do đó, nghiệm trên không là nghiệm của hệ. Giải ሺሻ : ݔ ൌ െͳ ߨ ቊ ቀݕ ቁ ൌ െͳ Ͷ ߨ ݔ ൌ െ ߨ ൞ Ͷ ͵ߨ ሺǡ ݍ א Ժሻ ݕ ൌ െ ݍʹߨ Ͷ
Nghiệm trên thỏa điều kiện của hệ, ta thế vào ሺʹሻ: ͵ߨ ͵ߨ ൌ ݕ ݕ ൌ ൬െ ݍʹߨ൰ ൬െ ݍʹߨ൰ ൌ ʹ Ͷ Ͷ ߨ ߨ െʹǢ ếẵ
ൌ ʹ ቀݔ െ ቁ ൌ ʹ ቀെ ߨቁ ൌ ቊ Ͷ ʹ ʹǢ ếẻ
Do đó, kết hợp với điều kiện ሺכሻ, ta nhận được nghiệm của hệ là 165 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác ߨ
ݔ ൌ െ ሺʹ݉ ͳሻߨ ൞ Ͷ ͵ߨ ሺ݉ǡ ݍ א Ժሻ ݕ ൌ െ ݍʹߨ Ͷ
Bài 13: Giải hệ phương trình sau : ݔ ݕ ൌ ሺݔ ݕሻ ሺכሻ ൜ ȁݔȁ ȁݕȁ ൌ ͳ Giải: ݔ ݕ ݔ െ ݕ ݔ ݕ ݔ ݕ ሺכሻ ൝ʹ ൌ ʹ ʹ ʹ ʹ ʹ ȁݔȁ ȁݕȁ ൌ ͳ ݔ ݕ ݔ െ ݕ ݔ ݕ ሺͳሻ ൝ ൌ Ͳ ൌ ʹ ặሺʹሻ ൝ ʹ ʹ ȁݔȁ ȁݕȁ ൌ ͳ ȁݔȁ ȁݕȁ ൌ ͳ Giải ሺͳሻ : ݔ ݕ ൌ ݇ʹߨ ൜ȁ ሺ݇ א Ժሻ ݔȁ ȁݕȁ ൌ ͳ
Vì ȁ݇ʹߨȁ ൌ ȁݔ ݕȁ ȁݔȁ ȁݕȁ ൌ ͳ nên ݇ ൌ Ͳ. Suy ra ݔ ݕ ൌ Ͳ ൜ȁݔȁ ȁݕȁ ൌ ͳ
Do đó, nghiệm của hệ là : ͳ ͳ ͳ ͳ
ሺݔǢ ݕሻ א ൜൬ Ǣ െ ൰ ǡ ൬െ Ǣ ൰ൠ ʹ ʹ ʹ ʹ Giải ሺʹሻ : ݔ െ ݕ ݔ ݕ ൝ ൌ േ ݇ʹߨ ʹ ʹ ሺ݇ א Ժሻ ȁݔȁ ȁݕȁ ൌ ͳ ȁݔȁ ȁݕȁ ൌ ͳ ൜ ሺ݇ א Ժሻ ݕ ൌ െ݇ʹߨ ൦ ݔ ൌ ݇ʹߨ
൜ȁݔȁ ȁݕȁ ൌ ͳሺ݇ א Ժሻ 166 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác
Đánh giá tương tự như trên, ta có nghiệm của hệ là :
ሺݔǢ ݕሻ א ሼሺͳǢ Ͳሻǡ ሺെͳǢ Ͳሻǡ ሺͲǢ ͳሻǡ ሺͲǢ െͳሻሽ
Bài 14: Giải hệ phương trình sau : ۓ͵ξ͵ݔଵ ൌ ߨݔଶ ۖ͵ξ͵ݔଶ ൌ ߨݔଷ ۔͵ξ͵ݔ ۖ ଷ ൌ ߨݔସ ە͵ξ͵ݔସ ൌ ߨݔଵ
Giải: Vì hàm số ݐ có chu kỳ tuần hoàn ʹߨ và ta thấy ͲǢ ʹߨ đều không là nghiệm của
hệ nên ta xét hệ trên ሺͲǢ ʹߨሻ. Đặt ݐ ൌ ߨ
ݔ ǡ ݅ ൌ തͳǢതതതͶത. Khi đó ݐ א ሺͲǢ ʹߨሻ và hệ tương đương với ۓ͵ξ͵ ݐ ۖ ߨ ଵ ൌ ݐଶ ሺͳሻ ۖ ۖ͵ξ͵ ݐ ߨ ଶ ൌ ݐଷ ሺʹሻ ۔͵ξ͵ ۖ ݐଷ ൌ ݐସሺ͵ሻ ۖ ߨ ۖ͵ξ͵ ە ݐ ߨ ସ ൌ ݐଵ ሺͶሻ
Cộng theo vế các phương trình của hệ, ta được ସ ସ ͵ξ͵ ݐ ൌ ݐ ߨ ୀଵ ୀଵ ସ ͵ξ͵ ቆ ݐ െ ݐ ൌ Ͳ ߨ ቇ ୀଵ ߨ ξ͵
ếݐଵ ൏ ìởươìሺͳሻđượ ݐ ଶ ൏ ʹ ߨ
ìݐଵà ݐଶ ùấǢ ݐଵ א ሺͲǢ ʹߨሻêݐଶ ൏ 167 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác ߨ
ươựậǡ đượݐ ൏ ሺכሻ
Mặt khác, ta xét hàm số : ͵ξ͵ ݂ሺݑሻ ൌ ݑ െ ݑǡ ݑ א Թ ߨ ͵ξ͵ ݂ᇱሺݑሻ ൌ െ ݑ െ ൏ Ͳ ߨ
Do đó, hàm số nghịch biến. Kết hợp với ሺכሻ, suy ra : ସ ͵ξ͵ ቆ ݐ െ ݐ ͲሺǨሻ ߨ ቇ ୀଵ ߨ
ươựớườợݐଵ ǡ đượ ߨ ۓ ݐ ۖ ସ ۔ ͵ξ͵ ۖ ቆ ݐ െ ݐቇ ൏ ͲሺǨሻ ە ߨ ୀଵ ߨ ߨ
ݐ ൌ ỏ ệươ¿ǡ ²ậݐ ệ ൌ Khi đó, ͳ
ݔଵ ൌ ݔଶ ൌ ݔଷ ൌ ݔସ ൌ
Bài 15: Giải hệ phương trình sau : ͳ
ቐ ݔ ݕ ሺݔ ݕሻ ൌ Ͳሺͳሻ ͺ ݔ ൌ ݕ ݖሺʹሻ Giải: Ta có : ͳ ͳ
ሺͳሻ ሾሺݔ ݕሻ ሺݔ െ ݕሻሿ ሺݔ ݕሻ ൌ Ͳ ʹ ͺ 168 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác ͳ ଶ ͳ ͳ
ሺݔ ݕሻ ሺݔ െ ݕሻ൨ െ ଶሺݔ െ ݕሻ ൌ Ͳ ʹ Ͷ Ͷ ͳ ଶ ͳ
ሺݔ ݕሻ ሺݔ െ ݕሻ൨ ଶሺݔ െ ݕሻ ൌ Ͳ ʹ Ͷ ͳ
൝ሺݔ ݕሻ ൌ െ ሺݔ െ ݕሻ ʹ ሺݔ െ ݕሻ ൌ Ͳ ͳ ͳ
൝ሺݔ ݕሻ ൌ െ ʹש൝ ሺݔ ݕሻ ൌ ʹ ሺݔ െ ݕሻ ൌ ͳ ሺݔ െ ݕሻ ൌ െͳ ߨ ߨ
ۍ ݔ ݕ ൌ െ ݇ʹߨ ۍ ݔ ݕ ൌ ݇ʹߨ ێ൞ ߨ ێ൞ ߨ ێ ݔ െ ݕ ൌ ݈ʹߨ
ێ ݔ െ ݕ ൌ െ ݈ʹߨ ێ ʹ שێ ʹ ሺ݇ǡ ݈ א Ժሻ ێ ߨ ێ ͷߨ ێ ݔ ݕ ൌ ݇ʹߨ ݔ ݕ ൌ ݇ʹߨ ێ ێ ൞ ߨ ێ൞ ߨ ۏ ݔ െ ݕ ൌ ݈ʹߨ ݔ െ ݕ ൌ െ ݈ʹߨ ʹ ۏ ʹ ߨ ߨ
ۍۓ ݔ ൌ ሺ݇ ݈ሻߨ ሺ݇ ݈ሻߨ ۍۓݔ ൌ െ ێۖ ߨ ێۖ ߨ
ێ ݕ ൌ െ ሺ݇ െ ݈ሻߨ
ێ ݕ ൌ ሺ݇ െ ݈ሻߨ ێ۔ ͵ ͵ ߨ ێ۔ ߨ ێۖ ۖ ە ݖ ൌ ݈ʹߨ ێە ݖ ൌ െ ݈ʹߨ ێ ʹ שێ ʹ ͷߨ ߨ ሺ݇ǡ ݈ א Ժሻ ێ ۓݔ ൌ ሺ݇ ݈ሻߨ
ێ ۓ ݔ ൌ ሺ݇ ݈ሻߨ ێ ێ ۖ ۖ ێ ߨ ێ ʹߨ
ێ ݕ ൌ ሺ݇ െ ݈ሻߨ ݕ ൌ ሺ݇ െ ݈ሻߨ ۔ ͵ ێ ۔ ͵ ێ ߨ ۖ ێ ۖ ߨ ۏ ݖ ൌ ݈ʹߨ ݖ ൌ െ ݈ʹߨ ە ʹ ۏ ە ʹ
Bài 16: Giải hệ phương trình sau : ݔ ݕ ݔ െ ݕ ሺ ଶ ݔ െ ʹ ݔ ʹݕ ൌ െ ʹ כሻ ൝ ʹ ʹ
ݔ ݕ െ ʹ ଶ ʹݕ ൌ Ͳ 169 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác Giải: ݔ ݕ
ଶ ݔ െ ʹ ݔ ʹݕ ൌ ʹ െ ʹሺͳሻ ሺכሻ ൞ ʹ ʹ ݔ ݕ
ʹ ଶ ʹݕ ଶ ଶ െ ʹ ൌ Ͳሺʹሻ ʹ ʹ
Lấy ሺͳሻ ሺʹሻ theo từng vế, ta được ݔ ݕ ଶ
ሺ ݔ െ ʹݕሻଶ ቀ െ ቁ ൌ Ͳ ʹ ʹ ݔ ൌ ʹݕሺ͵ሻ ൝ ݔ ݕ ൌ ሺͶሻ ʹ ʹ Giải ሺͶሻ : ݔ ൌ ݕ ݇Ͷߨ
ݔ ൌ െݕ ݇Ͷߨሺ݇ א Ժሻ
Với ݔ ൌ ݕ ݇Ͷߨ, ta thay vào ሺ͵ሻ : ሺݕ ݇Ͷߨሻ ൌ ʹݕ ߨ ʹݕ ൌ ቀ െ ݕቁ ʹ ߨ ʹݕ ൌ െ ݕ ݈ʹߨ ʹ ൦ ߨ ሺ݈ א Ժሻ ʹݕ ൌ ݕ െ ݈ʹߨ ʹ ߨ ݈ʹߨ ݕ ൌ ൦ ͵ ߨ ሺ݈ א Ժሻ ݕ ൌ െ ݈ʹߨ ʹ Do đó, ta có : ߨ ݈ʹߨ ߨ ݔ ൌ ݇Ͷߨ
ݔ ൌ െ ሺ݈ ʹ݇ሻʹߨ ሺሻ ൞ ͵ ʹ ߨ ݈ʹߨ ש ሺሻ ൞ ߨ ሺ݇ǡ ݈ א Ժሻ ݕ ൌ ݕ ൌ െ ݈ʹߨ ͵ ʹ
Lần lượt thay ሺሻǡ ሺሻ vào ሺכሻ ta nhận ሺሻ là nghiệm của hệ. 170 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác
Với ݔ ൌ െݕ ݇Ͷߨ thay vào ሺ͵ሻ, ta được :
ʹݕ ൌ ሺെݕ ݇Ͷߨሻ ߨ ʹݕ ൌ ቀ ݕቁ ʹ ߨ ݕ ൌ ݈ʹߨ ൦ ʹߨ ݈ʹߨሺ݈ א Ժሻ ݕ ൌ െ ͵ Do đó, ta có : ߨ ߨ ݈ʹߨ
ݔ ൌ െ ሺʹ݇ െ ݈ሻʹߨ ݔ ൌ െ ݇Ͷߨ ሺሻ ൞ ʹ ͵ ߨ ש ሺሻ ൞ ݕ ൌ ݈ʹߨ ߨ ݈ʹߨ ʹ ݕ ൌ െ ͵
Lần lượt thay ሺሻǡ ሺሻ vào ሺכሻ ta nhận ሺሻ là nghiệm của hệ. - BÀI TẬP TỰ LUYỆN
6.1.1. Giải các hệ phương trình sau ۓ ʹξ͵ ۖ ݔ ݕ ൌ Ǥ ͵ ۔ ʹξ͵ ۖ ݔ ݕ ൌ െ ە ͵ ݔ ͳ ൌ Ǥ ൞ ݕ ʹߨ ݔ ݕ ൌ ͵ ͳ ଶ ݔ ଶ ݕ ൌ Ǥ ൞ ʹ ߨ ݔ െ ݕ ൌ ͵ 171 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác ߨ ݔ െ ݕ ൌ ͵ Ǥ ൞ ξʹ
ଶ ݔ ଶ ݕ ൌ ͳ Ͷ
6.1.2. Giải các hệ phương trình sau ݔ െ ݕ െ ݔ ݕ ൌ ͳ Ǥ ൜ ʹݕ ξ͵ ʹݔ ൌ െͳ ͳ Ǥ ൝ െ ݕ ൌ ʹ ݔ ݔ ݕ ൌ െͳ ۓ ξ͵ ݔ െ ʹݕ ൌ Ǥ ʹ ۔ ͳ ە ݔ ʹݕ ൌ ʹ ݔ ൌ ʹݕ ۓ ۖ ݔ ൌ ξʹ ݕ Ǥ ݔ א ሾͲǢ ߨሿ ۔ ۖ ߨ ߨ ە ݕ א ቂെ Ǣ ቃ Ͷ Ͷ
6.1.3. Giải các hệ phương trình sau ݔ െ ݕ ൌ ݔ െ ݕ Ǥ ൝ ͷݔ ͺݕ ൌ ʹߨ Ͳ ൏ ݔǡ ݕ ൏ ߨ
ሺݔ ݕሻ ൌ ʹ ሺݔ െ ݕሻ Ǥ ൝ ͵ ݔ ݕ ൌ Ͷ ͵ߨ ݔ ݔ ൌ ʹ ൬ݕ െ ൰ Ǥ ൞ Ͷ ߨ
ݕ ݕ ൌ ʹ ቀݔ ቁ Ͷ 172 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác ݔ ۓ ݁௫ି௬ ൌ ۖ ݕ
Ǥ ͳͲඥݔ ͳ ൌ ͵ሺݕସ ʹሻ ۔ ۖ ͷߨ ە ݔǡ ݕ א ൬ߨǢ ൰ Ͷ ܽ ܾ ܿ ് Ͳ
6.1.4. Cho ൜ ܽ ǡ ܾ ǡ ܿ ừ¯Øộ
Giải hệ phương trình sau :
ݔ ܽ ݕ ʹܽ ݖ ͵ܽ ൌ Ͷܽ
൝ ݔ ܾ ݕ ʹܾ ݖ ͵ܾ ൌ Ͷܾ
ݔ ܿ ݕ ʹܿ ݖ ͵ܿ ൌ Ͷܿ -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN
6.1.1. Nghiệm của hệ phương trình là: ݔ ൌ ݇ߨ Ǥ ൝ ʹߨ ሺ݇ǡ ݉ א Ժሻ ݕ ൌ െ ݉ߨ ͵ ߨ ݔ ൌ ݇ߨ Ǥ ൝ ͵ ሺ݇ א Ժሻ ݕ ൌ െ݇ߨ ߨ ݔ ൌ ݇ߨ Ǥ ൞ ߨ ሺ݇ א Ժሻ ݕ ൌ െ ݇ߨ ߨ ߨ ݔ ൌ ݇ߨ ݔ ൌ ݇ߨ Ǥ ൞ ʹͶ ʹͶ ߨ ש ൞ ߨ ሺ݇ א Ժሻ ݕ ൌ െ ݇ߨ ݕ ൌ െ ݇ߨ ʹͶ ʹͶ 173 --------------------- TOANMATH.com
Chương 6 : Hệ phương trình lượng giác
6.1.2. Nghiệm của hệ phương trình là: ͷߨ ݔ ൌ ሺ݉ ݊ሻߨ Ǥ ൞ ߨ ሺ݉ǡ ݊ א Ժሻ ݕ ൌ ݊ߨ ߨ ݔ ൌ ݉ʹߨ Ǥ ൝ ʹ ሺ݉ǡ ݊ א Ժሻ ݕ ൌ ߨ ݊ʹߨ ʹߨ ݔ ൌ ݉ʹߨ Ǥ ൝ݔ ൌ ݉ʹߨ ͵ ש൝ ʹߨ ሺ݉ǡ ݊ א Ժሻ ݕ ൌ ݊ߨ ݕ ൌ ݊ߨ ͵ ǤØệ
6.1.3.Nghiệm của hệ phương trình là: ʹߨ ݔ ൌ Ǥ ൞ ͳ͵ ʹߨ ݕ ൌ ͳ͵ ߨ ߨ ݔ ൌ ሺ݉ ݊ሻߨ
ݔ ൌ െ ሺ݉ ݊ሻߨ Ǥ ൞ ߨ ש൞ ሺ݉ǡ ݊ א Ժሻ ߨ
ݕ ൌ െ ሺ݉ െ ݊ሻߨ ݕ ൌ ሺ݉ െ ݊ሻߨ ߨ ݔ ൌ ݇ߨ Ǥ ൞ Ͷ ͷߨ ሺ݇ǡ ݈ א Ժሻ ݕ ൌ ݈ʹߨ Ͷ
Ǥݔ ൌ ݕ ൌ ටͷ ξ͵͵
6.1.4. Nghiệm của hệ phương trình là:
ݔ ൌ െͺ ܽ ܾ ܿ ʹሺ ܽ ܾ ܿሻ
ቐݕ ൌ െͶሺ ܽ ܾ ܾ ܿ ܿ ܽሻ െ ʹ
ݖ ൌ ʹሺ ܽ ܾ ܿሻ 174 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác CHƯƠNG 7
BẤT PHƯƠNG TRÌNH LƯỢNG GIÁC I.
TÓM TẮT MỘT SỐ PHƯƠNG PHÁP THƯỜNG GẶP
- Để giải một bất phương trình lượng giác, ta thường dùng hai phương pháp sau :
1. Phương pháp 1 : Đưa bất phương trình về các dạng cơ bản như : ݔ
ܽǢ ݔ ܽǢ ݔ ܽǢ ݔ ܽ ǥ Thông thường ta dùng đường tròn lượng giác
để tìm các họ nghiệm tương ứng.
2. Phương pháp 2 : Viết bất phương trình về tích hoặc thương các hàm số lượng
giác dạng cơ bản. Xét dấu các thừa số từ đó chọn nghiệm thích hợp.
CÁC BẤT PHƯƠNG TRÌNH CẦN NẮM - ݔ ܽ
x Nếu ܽ ͳ, bất phương trình vô nghiệm.
x Nếu ܽ ൌ ͳ, bất phương trình có nghiệm là : ݔ ൌ ݇ʹߨሺ݇ א Ժሻ
x Nếu െͳ ൏ ܽ ൏ ͳ, bất phương trình có nghiệm là :
െ ܽ ݇ʹߨ ݔ ܽ ݇ʹߨሺ݇ א Ժሻ
x Nếu ܽ െͳ, bất phương trình có vô số nghiệm. - ݔ ܽ
x Nếu ܽ ͳ, bất phương trình vô nghiệm.
x Nếu ܽ ൌ ͳ, bất phương trình có nghiệm là : ߨ
ݔ ൌ ݇ʹߨሺ݇ א Ժሻ ʹ
x Nếu െͳ ൏ ܽ ൏ ͳ, bất phương trình có nghiệm là :
െ ܽ ݇ʹߨ ݔ ܽ ݇ʹߨሺ݇ א Ժሻ
x Nếu ܽ െͳ, bất phương trình có vô số nghiệm. 175 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác - ݔ ܽ có nghiệm là : ߨ
ܽ ݇ߨ ݔ ൏ ݇ߨሺ݇ א Ժሻ ʹ - ݔ ܽ có nghiệm là :
݇ߨ ൏ ܽ ܽ ݇ߨሺ݇ א Ժሻ II.
CÁC BÀI TẬP MINH HỌA
Bài 1: Giải bất phương trình sau : ݔ െ ݔ ͳ Ͳ ݔ ݔ െ ͳ
Giải: Bất phương trình tương đương với
ሺ ݔ െ ݔ ͳሻሺ ݔ ݔ െ ͳሻ Ͳ
ଶ ݔ െ ሺͳ െ ݔሻଶ Ͳ
ͳ െ ଶ ݔ െ ሺͳ െ ʹ ݔ ଶ ݔሻ Ͳ
ʹ ଶ ݔ െ ʹ ݔ ൏ Ͳ Ͳ ൏ ݔ ൏ ͳ ߨ ߨ
݇ʹߨ ൏ ݔ ൏ ݇ʹߨ ቊെ ʹ ʹ ሺ݇ א Ժሻ ݔ ് ݇ʹߨ
Bài 2: Giải bất phương trình sau :
ͷ ʹ ʹݔ ͵ȁʹ ݔ െ ͳȁ
Giải: Ta đặt : ݐ ൌ ݔ ǡ ݐ א ሾെͳǢ ͳሿ
Bất phương trình tương đương với
ͷ ʹሺͳ െ ʹݐଶሻ ͵ȁʹݐ െ ͳȁ
െ Ͷݐଶ ͵ȁʹݐ െ ͳȁ 176 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác െ Ͷݐଶ ݐ െ ͵ ۍ൝ ͳ ێ ݐ ێ ʹ
ێ െ Ͷݐଶ ͵ െ ݐ ێ൝ ͳ ۏ ݐ ʹ ݐ ͳ ۍۓ ͷ ێۖ ݐ െ ێ ʹ ۔ ێۖ ͳ ە ݐ ێ ʹ ێ ݐ ʹ ۓ ێۖ ͳ ݐ െ ێ ʹ ێ۔ ۖ ͳ ۏە ݐ ʹ ݐ ൌ ͳ ͳ ݐ െ ʹ ݔ ൌ ͳ ͳ ݔ െ ʹ ߨ ݔ ൌ ݇ʹߨ ൦ ʹ ͷߨ ͳͳߨ ሺ݇ א Ժሻ ݇ʹߨ ݔ ݇ʹߨ
Bài 3: Giải bất phương trình sau : ͺξ͵
ݔ െ ݔ െ ʹ ʹݔ െ Ͷ Ͷݔ ൏ ͵
Giải: Điều kiện : ݔ ് Ͳ ݈ߨ
൞ ݔ ് Ͳ ͺݔ ് Ͳ ݔ ് ሺ݈ א Ժሻሺכሻ ʹݔ ് Ͳ ͺ Ͷݔ ് Ͳ 177 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác
Bất phương trình tương đương với ͺξ͵
ʹ ʹݔ െ ʹ ʹݔ െ Ͷ Ͷݔ ൏ ͵ ͺξ͵
ʹሺ ʹݔ െ ʹݔሻ െ Ͷ Ͷݔ ൏ ͵ ͺξ͵
Ͷሺ Ͷݔ െ Ͷݔሻ ൏ ͵ ξ͵ ͺݔ ൏ ͵ ߨ
݇ߨ ൏ ͺݔ ൏ ߨ ݇ߨሺ݇ א Ժሻ ͵ ߨ ݇ߨ ߨ ݇ߨ ൏ ݔ ൏
ሺ݇ א Ժሻ൫ỏሺכሻ൯ ʹͶ ͺ ͺ ͺ
Bài 4: Giải bất phương trình sau :
ݔ െ ݔ െ ʹ ʹݔ െ Ͷ Ͷݔ െ ͺ ͺݔ ͳξ͵
Giải: Điều kiện : ݈ߨ ͳݔ ് Ͳ ݔ ് ሺ݈ א Ժሻሺכሻ ͳ
Bất phương trình tương đương với
ͳ െ ଶ ݔ െ ʹʹݔ െ ͶͶݔ െ ͺͺݔ ͳξ͵ ݔ ͳ ʹ ൬
െ ʹݔ൰ െ Ͷ Ͷݔ െ ͺ ͺݔ ͳξ͵ ʹݔ ͳ Ͷ ൬
െ Ͷݔ൰ െ ͺ ͺݔ ͳξ͵ Ͷݔ ͳ ͺ ൬ െ ͺݔ൰ ͳξ͵ ͺݔ ͳݔ ξ͵ 178 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác ߨ ݇ߨ ݇ߨ ൏ ݔ
ሺ݇ א Ժሻ൫ỏሺכሻ൯ ͻ
Bài 5: Giải bất phương trình sau : ͵ݔ ͵ݔ ͳ ͳ ʹ ʹݔ
Giải: Điều kiện : ߨ ݔ ് ݈ߨ ൦ ͳʹߨ ሺ݈ א Ժሻሺכሻ ݔ ് െ ݈ߨ ͳʹ
Bất phương trình tương đương với
͵ሺ ݔ െ ݔሻ െ Ͷሺ ݔ െ ݔሻሺͳ ݔ ݔሻ ͳ ͳ ʹ ʹݔ ሺ ͳ
ݔ െ ݔሻ ቂ͵ െ Ͷ ቀͳ ʹ ʹݔቁቃ ͳ ͳ ʹ ʹݔ ݔ െ ݔ ͳ ߨ ͳ ቀݔ ቁ Ͷ ξʹ ͵ߨ ݇ʹߨ ݔ ݇ʹߨሺ݇ א Ժሻ ʹ
Kết hợp với ሺכሻ ta có nghiệm của bất phương trình là ͵ߨ ۓ݇ʹߨ ݔ ݇ʹߨ ۖ ʹ ߨ ݔ ് ݈ߨ ሺ݇ǡ ݈ א Ժሻ ۔ ͳʹ ۖ ߨ ە ݔ ് െ ݈ߨ ͳʹ 179 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác
Bài 6: Giải bất phương trình sau : ξ͵ ʹ ݔ െ ݔ ʹ ʹݔ ͵
Giải: Điều kiện : ݈ߨ ʹݔ ് Ͳ ݔ ് ሺ݈ א Ժሻሺכሻ ʹ
Bất phương trình tương đương với ξ͵ ݔ ሺ ݔ െ ݔሻ ʹ ʹݔ ͵ ξ͵ ݔ ʹ ʹݔ ʹ ʹݔ ͵ ξ͵ ݔ ͵ ߨ
݇ߨ ݔ ൏ ߨ ݇ߨሺ݇ א Ժሻ ͵
Kết hợp với ሺכሻ ta có nghiệm của bất phương trình là
ߨ ݇ߨ ݔ ൏ ߨ ݇ߨሺ݇ ് Ͷ݈ ͳǢ݈ א Ժሻ ͵
Bài 7: Tìm nghiệm của bất phương trình ͳ
ξ͵ ଶ ݔ ʹݔ ξ͵ሺͳሻ ʹ
Thỏa mãn bất phương trình ሺݔଶ ݔ Ͷሻ ൏ ͳሺʹሻ
Giải: Bất phương trình ሺͳሻ tương đương với ξ͵ ͳ
ሺͳ ʹݔሻ ʹݔ ξ͵ ʹ ʹ
ξ͵ ʹݔ ʹݔ ξ͵ 180 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác ߨ ξ͵ ቀʹݔ ቁ ͵ ʹ ߨ
݇ߨ ݔ ݇ߨሺ݇ א Ժሻ
Bất phương trình ሺʹሻ tương đương với
ݔଶ ݔ െ ൏ Ͳ െ͵ ൏ ݔ ൏ ʹ
Do đó, nghiệm của bất phương trình đã cho là ߨ Ͳ ݔ
Bài 8: Giải bất phương trình sau : ʹ ʹݔ ʹݔ ݔ
Giải: Điều kiện : ߨ
ݔ ് Ͳ ݔ ് ݈ߨሺ݈ א Ժሻሺכሻ ʹ
Đặt ൌ ݔ ǡ ݐ א Թ . Khi đó, bất phương trình tương đương với ͳ െ ݐଶ ʹݐ ʹǤ ݐ ͳ ݐଶ ͳ ݐଶ
ݐଷ ʹݐଶ െ ݐ െ ʹ Ͳ ቂ ݐ ͳ െʹ ݐ െͳ
Với െʹ ݐ െͳ thì ߨ
െߙ ݇ߨ ݔ െ ݇ߨሺ݇ א ԺǢ ߙ ൌ ʹሻ Ͷ Với ݐ ͳ thì ߨ ߨ
݇ߨ ݔ ൏ ݇ߨሺ݇ א Ժሻ Ͷ ʹ
So với điều kiện ሺכሻ, ta nhận 2 nghiệm trên là nghiệm của bất phương trình. 181 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác
Bài 9: Giải bất phương trình sau :
ʹ ʹݔ ଶ ݔ ݔ ݔ ଶ ݔ ʹሺ ݔ ݔሻ (ĐH Kinh Tế Tp.HCM 1997)
Giải: Bất phương trình tương đương với
ሺ ݔ ݔሻሾʹሺ ݔ െ ݔሻ ݔ ݔ െ ʹሿ Ͳ
Đặt ݂ሺݔሻ ൌ ሺ ݔ ݔሻሾʹሺ ݔ െ ݔሻ ݔ ݔ െ ʹሿ
Do hàm số tuần hoàn có chu kỳ ʹߨ nên ta chỉ cần xét dấu của ݂ሺݔሻ trên ሾͲǢ ʹߨሿ. Ta có : ݔ ݔ ൌ Ͳሺͳሻ
݂ሺݔሻ ൌ Ͳ ʹሺݔ െ ݔሻ ݔ ݔ െ ʹ ൌ Ͳሺʹሻ Với ሺͳሻ : ߨ ݔ ൌ ߨ ξʹ ቀݔ Ͷ ቁ ൌ Ͳ ൦ Ͷ ͵ߨ ݔ ൌ Ͷ
Với ሺʹሻ, ta đặt ݐ ൌ ݔ െ ݔ ǡ ȁݐȁ ξʹ : ͳ െ ݐଶ ʹݐ െ ʹ ൌ Ͳ ʹ ݐ ൌ ͳ ݐ ൌ ͵ሺạሻ Suy ra ߨ ͳ ݔ ൌ Ͳ ቀݔ ቁ ൌ ͵ߨ Ͷ ξʹ ݔ ൌ ʹ
Lập bảng xét dấu của ݂ሺݔሻ trên ሾͲǢ ʹߨሿ ta thấy 182 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác ଷగ గ ݔ ଷగ 0 ʹߨ ସ ଶ ସ ݂ሺݔሻ 0 Ȃ 0 0 Ȃ 0 0
Như vậy, ta có trong 1 chu kỳ nghiệm của bất phương trình là ͵ߨ ͵ߨ ൏ ݔ ൏ ൦ Ͷ ʹ ߨ ൏ ݔ ൏ ʹߨ Ͷ
Do đó, nghiệm của bất phương trình là ͵ߨ ͵ߨ ݇ʹߨ ൏ ݔ ൏ ݇ʹߨ ൦ Ͷ ʹ ߨ ሺ݇ א Ժሻ
݇ʹߨ ൏ ݔ ൏ ʹߨ ݇ʹߨ Ͷ
Bài 10: Giải bất phương trình sau :
ʹݔ Ͷݔ ݔ ͵ݔ
Giải: Đặt ݂ሺݔሻ ൌ െ ݔ െ ͵ݔ ʹݔ Ͷݔ
Do hàm số tuần hoàn có chu kỳ ʹߨ nên ta chỉ cần xét dấu của ݂ሺݔሻ trên ሾͲǢ ʹߨሿ.
Ta có, bất phương trình tương đương với
ʹ ͵ݔ ݔ െ ʹ ʹݔ ݔ Ͳ ͷݔ ݔ ݔ Ͳ ʹ ʹ ͷݔ ൝ ݔ Ͳ ʹ Ͳ ൏ ݔ ൏ ʹߨ
Lập bảng xét dấu trên ሾͲǢ ʹߨሿ ta thấy 183 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác గ గ ଷగ గ ଷగ ଽగ ݔ 0 ߨ ʹߨ ହ ଶ ହ ହ ଶ ହ ݔ 0 െ െ െ െ 0 ͷݔ 0 െ െ 0 Ͳ െ 0 0 െ ʹ ͷݔ ݔ
0 െ 0 0 െ 0 0 െ 0 0 െ ʹ
Suy ra nghiệm của bất phương trình là ߨ ۍ ݇ʹߨ ൏ ݔ ൏ ݇ʹߨ ͷ ێ ߨ ͵ߨ ێ ݇ʹߨ ൏ ݔ ൏ ݇ʹߨ ێ ʹ ʹ ሺ݇ א Ժሻ ێ ߨ ߨ ݇ʹߨ ൏ ݔ ൏ ݇ʹߨ ێ ͷ ێ͵ߨ ͻߨ ۏ ݇ʹߨ ൏ ݔ ൏ ݇ʹߨ ʹ ͷ
Bài 11: Giải bất phương trình sau : ݔ ʹ ݔ ͵ξ ݔ ͳǤ ʹଵିξ୲ୟ୬௫ ݔ ͵ ݔ
Giải: Điều kiện : ቄ ݔ Ͳሺכሻ ݔ ് Ͳ
Bất phương trình tương đương với ݔ ʹ ͵ξ ݔ ͳǤ ʹଵିξ୲ୟ୬௫ ݔ ͵
Đặt ݐ ൌ ݔ ǡ ݐ Ͳ, ta đưa bất phương trình trở thành ݐ ʹ ͵ξݐ ͳǤ ʹଵିξ௧ ݐ ͵ Ta xét hàm số ݐ ʹ ݂ሺݐሻ ൌ ͵ξݐ ͳǤ ǡ ݐ Ͳ ݐ ͵ 184 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác ͳ ݐ ʹ ͳ ݂ᇱሺݐሻ ൌ ͵ Ǥ ξݐ ͳǤ ൨ Ͳ ʹξݐ ͳ ݐ ͵ ሺݐ ͵ሻଶ
Do đó, ݂ሺݐሻ đồng biến trên ሾͲǡ λሻ Ta xét thêm hàm số
݃ሺݐሻ ൌ ʹଵିξ௧ǡ ݐ Ͳ ͳ
݃ᇱሺݐሻ ൌ െʹଵିξ௧Ǥ ൏ Ͳ ʹξݐ
Do đó, ݃ሺݐሻ nghịch biến trên ሾͲǡ λሻ
Suy ra với mọi ݐ א ሾͲǡ λሻ
݂ሺݐሻ ݂ሺͲሻ ൌ ʹ ൜
݃ሺݐሻ ݃ሺͲሻ ൌ ʹ
ฺ ݂ሺݐሻ ʹ ݃ሺݐሻǡ ݐ א ሾͲǡ λሻ Như vậy, ta có :
݂ሺݐሻ ൌ ݃ሺݐሻ ൌ ʹ ݐ ൌ Ͳ Khi đó,
ݔ ൌ Ͳ ݔ ൌ ݇ߨሺ݇ א Ժሻ൫ỏሺכሻ൯
Bài 12: Giải bất phương trình sau :
ξ ݔ ሺଶ ݔ ͵ ଶ ݔሻ ξ
ర ͵ሺଶ ݔ Ͷ ଶ ݔሻ
(Đề nghị Olympic 30-4, 2006)
Giải: Điều kiện : ቄ ݔ Ͳሺכሻ ݔ ് Ͳ
Bất phương trình tương đương với ଶ ݔ ͵ ξ ݔ Ǥ ξ ర ͵ ଶ ݔ Ͷ 185 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác
Đặt ݐ ൌ ݔ ǡ ݐ Ͳ. Ta đưa bất phương trình trở thành ݐଶ ͵ ξݐǤ ξ ర ͵ ݐଶ Ͷ Ta xét hàm số ݐଶ ͵ ݂ሺݐሻ ൌ ξݐǤ ǡ ݐ Ͳ ݐଶ Ͷ ͳ ݐଶ ͵ ʹݐ ݂ᇱሺݐሻ ൌ ቈ Ǥ ξݐǤ Ͳ ʹξݐ ݐଶ Ͷ ሺݐଶ Ͷሻଶ
Do đó, ݂ሺݐሻ đồng biến trên ሾͲǡ λሻ. Suy ra : ݂ሺݐሻ ξ ర ͵ ݐ ξ͵ Như vậy, ߨ
Ͳ ݔ ξ͵ ݇ߨ ݔ ݇ߨሺ݇ א Ժሻ൫ỏሺכሻ൯ ͵ - BÀI TẬP TỰ LUYỆN
7.1.1. Giải các bất phương trình sau :
Ǥ ଶ ݔ ξ͵ ݔ ݔ ൏ ͳ ͳ Ǥ ሺ ݔሻ ʹ ݔ െ ݔ Ǥ Ͳ ݔ ݔ
7.1.2. Giải các bất phương trình sau : Ǥ ͵ݔ ݔ ൏ ʹݔ ͳ
Ǥ ଷ ݔ ͵ݔ െ ଷ ݔ ͵ݔ ʹ ͳ ͷ Ǥ ݔ ݔ ʹ 186 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác
7.1.3. Giải các bất phương trình sau :
Ǥ ξ͵ ݔ െ ݔ ξ͵ െ ͳ ʹ
Ǥ ʹ ݔ ݔ ξ͵ ʹݔ ʹ ݔ െ ͳ Ǥ ʹ ʹݔ ݔ
7.1.4. Giải các bất phương trình sau : Ǥ ݔ െ ݔ െ ʹݔ Ͳ
Ǥ ݔ ʹݔ ͵ݔ ͳ ݔ െ ݔ ݔ Ǥ ξ͵ ݔ ݔ ʹ -
GỢI Ý GIẢI BÀI TẬP TỰ LUYỆN
7.1.1. Nghiệm của bất phương trình là : ߨ Ǥ
݇ߨ ൏ ݔ ൏ ߨ ݇ߨሺ݇ א Ժሻ ͵ ߨ ߨ
Ǥߙ ݇ʹߨ ݔ ʹߨ െ ߙ ݇ʹߨǡ ߙ א ቀͲǢ ቁǡ ߙ ൌ ǡ ݇ א Ժ ʹ ߨ ͵ߨ Ǥ ݇ߨ ൏ ݔ ൏ ݇ߨሺ݇ א Ժሻ ʹ Ͷ
7.1.2. Nghiệm của bất phương trình là : ͵ߨ ۍߨ ݇ʹߨ ൏ ݔ ൏ ݇ʹߨ ێ ʹ ߨ ߨ
Ǥ ێ ݇ʹߨ ൏ ݔ ൏ ݇ʹߨ ሺ݇ א Ժሻ ێ ͵ ʹ ێ ߨ
ۏ െ ݇ʹߨ ൏ ݔ ൏ ݇ʹߨ ͵ ǤØốệ ߨ ߨ
݇ʹߨ ൏ ݔ ݇ʹߨ Ǥ ൦ ʹ ͵ ͵ߨ ͷߨ ሺ݇ א Ժሻ ݇ʹߨ ൏ ݔ ݇ʹߨ ʹ ͵ 187 --------------------- TOANMATH.com
Chương 7 : Bất phương trình lượng giác
7.1.3. Nghiệm của bất phương trình là : ߨ ߨ
െ ݇ߨ ൏ ݔ ൏ െ ݇ߨ Ǥ ൦ ʹ ͵ ߨ ሺ݇ א Ժሻ ݇ߨ ൏ ݔ ൏ ݇ߨ Ͷ ߨ ߨ Ǥ
݇ߨ ݔ ൏ ݇ߨሺ݇ א Ժሻ ͵ ʹ ʹߨ Ͷߨ Ǥ ݇ʹߨ ݔ ݇ʹߨሺ݇ א Ժሻ ͵ ͵
7.1.4. Nghiệm của bất phương trình là : ߨ ߨ
݇ʹߨ ൏ ݔ ൏ ݇ʹߨ Ǥ ൦ Ͷ ʹ ͷߨ ሺ݇ א Ժሻ
݇ʹߨ ൏ ݔ ൏ ʹߨ ݇ʹߨ Ͷ ݔ ൌ ߨ ݇ʹߨ Ǥ ߨ ߨ
െ ݇ʹߨ ݔ ݇ʹߨሺ݇ א Ժሻ ͵ ͵ ʹߨ ݇ʹߨ ൏ ݔ ݇ʹߨ Ǥ ൞ ͵ ݇ߨ ሺ݇ א Ժሻ ݔ ് ʹ 188 --------------------- TOANMATH.com
Đọc thêm : Tản mạn về số pi Đọc Thêm TẢN MẠN VỀ SỐ PI
Số ߨ là một trong những hằng số độc đáo và đặc biệt nhất của Toán học, và luôn hấp
dẫn các nhà khoa học nói chung và nhà Toán học nói riêng bởi ở hầu hết các lĩnh vực đều
thấy sự xuất hiện của số ߨ. Cụ thể như số ߨ đóng vai trò là tỉ lệ của đường kính và chu vi
đường tròn, hay là một số siêu việt, tức là số không là nghiệm của bất kì phương trình đại
số với hệ số nguyên nào…
Đã hàng nghìn năm nay, con người luôn cố gắng tính toán nhiều hơn nữa các chữ số
sau dấu phẩy thập phân của số ߨ. Chẳng hạn như Archimedes đã tính giá trị ߨ bằng đánh
giá xuất phát từ cách tăng số cạnh của đa giác nội tiếp vòng tròn ͳ ͳͲ ͵ ൏ ݔ ൏ ͵ ͳ
Cách xấp xỉ trên của Archimedes có độ chính xác đến 3 chữ số sau dấu phẩy. Còn
Ptomely vào năm 150 sau Công Nguyên đã tính ߨ xấp xỉ bằng ͵ǡͳͶͳ. Và cuộc đua này 189 --------------------- TOANMATH.com
kết thúc bởi kết quả của Ludolf van Ceulen (1540-1610), người đã tốn 10 năm, tính cạnh
của ʹଶ- giác đều để tìm được số ߨ với độ chính xác 35 chữ số sau dấu phẩy.
Về mặt lý thuyết, phương pháp xấp xỉ của Archimedes có thể kéo dài vô hạn, nhưng
với phát minh về phép tính vi phân, phương pháp của người Hy Lạp không được dùng
đến nữa. Thay vào đó, các chuỗi tích và liên phân số vô hạn hội tụ đã được sử dụng để xấp xỉ số ߨ. Ͷ ͳ ൌ ͳ ߨ Ͷ ͵ ͻ ͷ ͳ ʹͷ ͻ ͵ ͳͳ ͳ͵ ڮ
Từ cuối thế kỷ 17, các dãy vô hạn và chuỗi trở thành những đối tượng chủ yếu trong
nghiên cứu của các nhà Toán học. Một trong những kết quả đầu tiên theo hướng này là
chuỗi Leibnitz được Gottfried Wilhelm Leibnitz (1646-1716) tìm ra vào năm 1673. ߨ ͳ ͳ ͳ ͳ ͳ ൌ ͳ െ െ െ ڮ Ͷ ͵ ͷ ͻ ͳͳ
Chuỗi Leibnitz là một trường hợp riêng của một chuỗi tổng quát hơn, được tìm ra bởi
James Gregory (1638-1675) vào năm 1670. ݔଷ ݔହ ݔ ݔଽ ݔଵଵ ሺݔሻ ൌ ݔ െ െ െ ڮ ሺȁݔȁ ͳሻ ͵ ͷ ͻ ͳͳ
Nếu như trong chuỗi Gregory, ngoài việc thay ݔ ൌ ͳ để được chuỗi Leibnitz thì ta có
thể thay ݔ với các giá trị khác nhỏ hơn, để được một chuỗi khác có tốc độ hội tụ cao hơn
rất nhiều. Abraham Sharp (1651-1742) đã sử dụng kết quả trên để đạt được kết quả kỷ lục
vào năm 1699 với 71 chữ số sau dấu phẩy. ߨ ξ͵ ͳ ͳ ͳ ͳ ͳ ൌ ൬ͳ െ െ െ ڮ ൰ ͵ ͻ Ͷͷ ͳͺͻ ʹͻ ʹ͵
Tiếp theo đó, các nhà Toán học đã thông qua việc tìm nhưng tổ hợp các ሺݔሻ
mà mỗi trong chúng được biểu diễn bởi các chuỗi hội tụ nhanh hơn chuỗi Leibnitz. ͳ ͳ ͳ ൌ Ͷ െ ͷ ʹ͵ͻ ͳ ͳ ͳ ൌ ʹ ͵ ͳ ͳ ͳ ͳ ൌ Ͷ െ ͷ Ͳ ͻͻ 190 --------------------- TOANMATH.com
Đọc thêm : Tản mạn về số pi ͳ ͳ ͳ ͳ ൌ ʹ ͷ ͺ
Chúng ta có thể kiểm tra dễ dàng các đẳng thức này bẳng cách sử dụng các hằng đẳng thức lượng giác : ݔ ݕ ݔ ݕ ൌ ሺݔݕ ൏ ͳሻ ͳ െ ݔݕ ݔ െ ݕ ݔ െ ݕ ൌ ሺݔݕ െͳሻ ͳ ݔݕ ʹݔ ʹ ݔ ൌ ሺȁݔȁ ൏ ͳሻ ͳ െ ݔଶ
Việc khai triển này cho ta được một chuỗi thuận tiện hơn rất nhiều cho việc tính toán.
Và giúp John Machin (1680-1751) tính được 100 chữ số sau dấu phẩy vào năm 1706.
Thành công của John Machin đã khởi lên cho các nhà Toán học khác tiếp tục tham gia
cuộc chạy đua mà nó đã bắt đầu từ thời Archimedes.
Sử dụng phương pháp của Abraham Sharp, De Lagny (1660-1734) đã tính được 127
chữ số sau dấu phẩy vào năm 1719. Không lâu sau đó, Leonard Euler (1707-1783) bằng
một phương pháp khác kiểm tra kết quả của De Lagny và tìm ra sai sót ở chữ số thứ 113.
Năm 1841, William Reserford (không rõ năm sinh, năm mất) đã tìm ra 208 chữ số sau
dấu phẩy và được kiểm tra lại bởi Johan Martin Zacharias Dase (1824-1861) sai ở chữ số
153. Năm 1847, Thomas Clausen (1801-1885) tiến thêm đến 250 chữ số sau dấu phẩy,
trong đó có 248 chữ số tính đúng.
Năm 1853, William Reserford tăng thành tích của mình lên 440 chữ số sau dấu phẩy.
Và kỷ lục của thời kỳ này được thiết lập bởi William Shanks (1812-1882) với 530 chữ số
(trong đó 527 chữ số tính đúng). Về sau, William Shanks đã phải làm việc cật lực để tính
tiếp các chữ số tiếp theo, đưa kỷ lục lên đến 707 chữ số tính đúng.
Đến thế kỷ 20, cuộc cách mạng máy tính đánh dấu những thành tựu vĩ đại của trí tuệ
con người. Những kiểm tra đầu tiên trên máy tính điện tử vào năm 1945 đã phát hiện
William Shanks đã sai ngay từ chữ số thứ 528. Điều này khiến nhà Toán học Harold
Scott MacDonald Coxeter (1907-2003) phải thốt lên rằng : “Không thể không buồn khi
nghĩ rằng, những tính toán mà Shanks tội nghiệp đã phải bỏ ra một phần lớn của cuộc đời
để tính, thì máy tính điện tử hiện đại có thể thực hiện trong vài giây như là để khởi động
vậy”. Và như vậy, sự xuất hiện của máy tính điện tử làm cho tốc độ cuộc đua tìm những
chữ số sau dấu phẩy càng tăng nhanh. 191 --------------------- TOANMATH.com
Năm 1949, John Von Neumann (1903-1957) cùng các cộng sự đã tính được 2037 chữ
số sau dấu phẩy trên một trong những máy tính điện tử đầu tiên ENIAC. Ngưỡng 10000
chữ số đạt được vào năm 1958 bởi Fredrick Jenuine (1908-1973) với sự trợ giúp của máy
tính IBM 704. Và 100.000 chữ số sau dấu phẩy của số ߨ được tính vào năm 1961 bởi
Daniel Shanks (1917-1996) cùng với máy tính IBM 7079. Năm 1973, Jan Gyiu và M.
Buet (không rõ năm sinh, năm mất) đã lập kỷ lục với mức 1 triệu chữ số sau dấu phẩy, sử
dụng gần một ngày làm việc của máy CDC-7600.
Đến cuối thế kỷ 20, người ta đã tính được số ߨ với độ chính xác đến chữ số thứ 200 tỉ.
Và cho tới hiện tại, mới đây nhất là kỷ lục của Fabrice Bellard (1972) khi tính chính xác
đến chữ số thứ 2.7 tỉ tỉ của số ߨ. Mất đến 131 ngày để tính toán, nhưng đây là một kết
quả cực kỳ ấn tượng vì Fabrice Bellard chỉ sử dụng máy tính để bàn thông thường để xử
lý số liệu cùng với việc phát triển một phần mềm xử lý thuật toán mạnh hơn 20 lần so với
những sản phẩm tương tự trước đó.
Tưởng như là kỷ nguyên của máy tính điện tử đã loại bỏ con người ra khỏi cuộc chơi
một cách dứt khoát, máy tính nào có tốc độ xử lý nhanh hơn thì máy đó thắng. Nhưng sự
thực thì không như vậy, chính con người đã khởi xướng cuộc chạy đua không tiền khoán
hậu này và tạo nên nhiều thuật toán nhân nhanh giúp máy tính điện tử xử lý hiệu quả hơn.
Trở lại con số 200 tỉ đã được thiết lập vào cuối thế kỷ 20…
Năm 1987, Jonathan và Peter Borwein (1953) đã tìm ra một chuỗi đáng ngạc nhiên : ஶ ߨ ሺെͳሻሺ݊ሻǨ ൌ
ൣʹͳʹͳͷͳͲͻͳʹξͳ ͳʹ ଷାଷ
ୀ ሺ݊Ǩሻଷሺ͵݊ሻǨ ൣͷʹͺͲ൫ʹ͵Ͷ ͵Ͳ͵Ͳ͵ξͳ൯൧ ଶ
ͳͷͳͶͷʹ͵ͷ ݊൫ͳ͵͵ͻͻͲͺͻʹʹξͳ ͳͲͷͺʹʹͻͺͲʹͷͲ൯൧
Dãy các số hạng dưới dấu tính tổng với ݊ ൌ Ͳǡͳǡʹǡ͵ ǥ bổ sung thêm khoảng 25 chữ
số sau dấu phẩy cho số ߨ ứng với mỗi số hạng. Chỉ riêng số hạng đầu tiên ሺ݊ ൌ Ͳሻ cho
giá trị gần đúng đến 24 chữ số sau dấu phẩy.
Thậm chí, Jonathan và Peter Borwein còn đưa ra thuật toán giúp tính toán các chữ số
sau dấu phẩy của số ߨ, có hiệu quả thần kỳ. Mỗi một bước tính của thuật toán này làm
tăng thêm độ dài các chữ số sau dấu phẩy được tính đúng lên 4 lần. Dưới đây là mô tả của thuật toán này :
Ta đặt ݕ ൌ ξʹ െ ͳ và ܽ ൌ െ Ͷξʹ, các số hạng tiếp theo ݕାଵ được tính theo số
hạng trước đó bởi công thức 192 --------------------- TOANMATH.com
Đọc thêm : Tản mạn về số pi ͳ െ ඥ ర ͳ െ ݕସ ݕ
ାଵ ൌ ͳ ඥరͳ ݕସ
Dãy số ሼܽሽ được xây dựng bởi công thức ܽ ଶ
ାଵ ൌ ሺͳ ݕାଵሻସܽ െ ʹଶାଷݕାଵሺͳ ݕାଵ ݕାଵሻ
Khi ݊ càng tăng thì ta có đánh giá ͳ
Ͳ ൏ ܽ െ ൏ ʹଶାଷǤ ݁ିଶమశభగ ߨ Nói cách khác, ՜ஶ ͳ ܽ ሱۛሮ ߨ
Cơ sở của phát minh ra thuật toán này là những nghiên cứu trong lĩnh vực tích phân
elliptic và hàm theta. Thuật toán kỳ diệu này lấy ý tưởng của nhà Toán học thiên tài
người Ấn Độ Srinivasa Ramanujan (1887-1920). Và con số 200 tỉ đã xuất hiện từ đó…
Có thể nói thêm rằng, một trong những phương pháp gây tò mò nhất để tính số ߨ là
của Count Buffon vào thế kỷ 18 cùng với Bài toán chiếc kim của ông. Trên một mặt
phẳng, ta kẻ các đường thẳng song song cách đều nhau ݀ đơn vị chiều dài. Thả chiếc kim
có độ dài nhỏ hơn ݀ lên mặt phẳng đó. Nếu chiếc kim rơi lên trên đường kẻ thì lần thả đó
được coi là thành công. Khám phá đầy bất ngờ của Buffon là tỉ lệ số lần thả thành công
so với không thành công là một biểu thức chứa số ߨ.
Nếu chiều dài kim bằng ݀ đơn vị thì xác suất thả thành công là ʹ ͲǤ͵ͻͶͳͺ ൎ ߨ
Số lần thả càng nhiều thì xấp xỉ cho số ߨ càng chính xác. Trong một phương pháp xác
suất khác để tính số ߨ là vào năm 1904, R. Chartes đã tìm ra xác suất để hai số nguyên
được viết ngẫu nhiên nguyên tố cùng nhau và xác suất để một số nguyên được chọn ngẫu
nhiên mà nó không chia hết cho số chính phương đều mang chung giá trị tuyệt vời là ߨଶ 193 --------------------- TOANMATH.com TÀI LIỆU THAM KHẢO
[1] Nguyễn Văn Nho, Nguyễn Văn Thổ, Chuyên đề Lượng giác, NXB Tổng hợp Tp.HCM, 2007.
[2] Võ Giang Giai, Tuyển tập 400 bài toán lượng giác, NXB Đại học Sư Phạm, 2007.
[3] Phạm Tấn Phước, Các chuyên đề Lượng giác, NXB Tp.HCM, 1999.
[4] Huỳnh Công Thái, Đào Khải, Phương pháp giải toán Lượng giác THPT, NXB Đại học Sư Phạm, 2004.
[5] Trần Văn Toàn, Võ Hữu Phước, Luyện Thi Cấp Tốc Toán Học, NXB ĐHQG Tp.HCM, 2009.
[6] Doãn Minh Cường, Giới thiệu Đề Thi Tuyển Sinh Vào Đại Học môn Toán (từ
1997-1998 đến 2004-2005), NXB ĐHQG Hà Nội, 2004.
[7] Huỳnh Công Thái, Các dạng toán điển hình : Phương Trình, Hệ Phương Trình
Lượng Giác, NXB ĐHQG Hà Nội, 2006.
[8] Theoni Pappas, Niềm vui Toán Học, NXB Kim Đồng, 2009.
[9] Tuyển tập đề thi Olympic 30 tháng 4, Lần XII – 2006, Toán học, NXBGD, 2006.
Tuyển tập đề thi Olympic 30 tháng 4, Lần XIII – 2007, Toán học, NXBGD, 2007.
Tuyển tập đề thi Olympic 30 tháng 4, Lần XIV – 2008, Toán học, NXBGD, 2008.
Tuyển tập đề thi Olympic 30 tháng 4, Lần XV – 2009, Toán học, NXBGD, 2009. 194 --------------------- TOANMATH.com




