Phương trình lượng giác trong đề thi Đại học – Huỳnh Đức Khánh

Các nội dung chính của tài liệu:

+ Phần 1: Các công thức cơ bản
+ Phần 2: Các công thức liên hệ
+ Phần 3: 5 Dạng phương trình lượng giác cơ bản

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

50 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
HÀ NAM 8-2014
GIAÛI PHÖÔNG TRÌNH
BÍ QUYEÁT
LÖÔÏNG
GIAÙC
THAÏC SÓ. TRAÀN MAÏNH HAÂN
- CÁC KĨ THUẬT GIẢI PHƯƠNG TRÌNH ĐẶC SẮC
- CÁC MẸO LOẠI NGHIỆM NHANH, CHÍNH XÁC
- CÁCH BẤM MÁY TÍNH TÌM HƯỚNG GIẢI.
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
1
I. CÁC HỆ THỨC LƯỢNG GIÁC CƠ BẢN
2 2
2 2
2 2
sin 1 cos
sin cos 1
cos 1 sin
x x
x x
2 2
2 2
1 1
1 tan tan 1
cos cos
x x
x x
2 2
2 2
1 1
1 cot cot 1
sin sin
x x
x x
1
tan .cot 1 cot
tan
x x x
x
4 4 2 2
6 6 2 2
sin cos 1 2 sin cos ;
sin cos 1 3 sin cos
x x x x
x x x x
3 3
3 3
sin cos (sin cos )(1 sin cos )
sin cos (sin cos )(1 sin cos )
x x x x x x
x x x x x x
II. DẤU CỦA CÁC HÀM SỐ LƯỢNG GIÁC
Góc I Góc II Góc III Góc IV
sin
x
cos
x
tan
x
cot
x
III. MỐI QUAN HỆ CỦA CÁC CUNG LƯỢNG GIÁC ĐẶC BIỆT
Hai cung đối nhau
cos( ) cos
x x
sin( ) sin
x x
tan( ) tan
x x
cot( ) cot
x x
Hai cung bù nhau
sin( ) sin
x x
cos( ) cos
x x
tan( ) tan
x x
cot( ) cot
x x
Hai cung phụ nhau
sin( ) cos
2
x x
cos( ) sin
2
x x
tan( ) cot
2
x x
cot( ) tan
2
x x
Hai cung hơn nhau
sin( ) sin
x x
cos( ) cos
x x
tan( ) tan
x x
cot( ) cot
x x
Hai cung hơn nhau
2
CÔNG TH
ỨC L
Ư
ỢNG GIÁC CẦN NẮM VỮNG
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
2
sin( ) cos
2
x x
cos( ) sin
2
x x
tan( ) cot
2
x x
cot( ) cot
2
x x
Với
k
là số nguyên thì ta có:
sin( 2 ) sin
x k x
cos( 2 ) cos
x k x
tan( ) tan
x k x
cot( ) cot
x k x
IV. CÔNG THỨC CỘNG
sin( ) sin cos cos sin
cos( ) cos cos sin sin
tan tan
tan( )
1 tan tan
x y x y x y
x y x y x y
x y
x y
x y
sin( ) sin cos cos sin
cos( ) cos cos sin sin
tan tan
tan( )
1 tan tan
x y x y x y
x y x y x y
x y
x y
x y
Đặc biệt:
TH1: Công thức góc nhân đôi:
2 2 2 2
2
sin 2 2 sin cos
cos2 cos sin 2 cos 1 1 2 sin
2 tan
tan 2
1 tan
x x x
x x x x x
x
x
x
Hệ quả: Công thức hạ bậc 2:
2 2
1 cos2 1 cos2
sin ;cos
2 2
x x
x x
TH2: Công thức góc nhân ba:
3
3
sin 3 3 sin 4 sin
cos 3 4 cos 3 cos
x x x
x x x
V. CÔNG THỨC BIẾN ĐỔI TỔNG SANG TÍCH VÀ TÍCH SANG TỔNG
cos cos 2 cos cos
2 2
x y x y
x y
cos cos 2 sin cos
2 2
x y x y
x y
sin sin 2 sin cos
2 2
x y x y
x y
sin sin 2 cos sin
2 2
x y x y
x y
1
cos cos cos( ) cos( )
2
x y x y x y
1
sin sin cos( ) cos( )
2
x y x y x y
1
sin cos sin( ) sin( )
2
x y x y x y
1
cos sin sin( ) sin( )
2
x y x y x y
Chú ý:
sin cos 2 sin 2 cos
4 4
x x x x
sin cos 2 sin 2 cos
4 4
x x x x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
3
2
sin sin
2
u v k
u v
u v k
2
cos cos
2
u v k
u v
u v k
tan tan
2
u v k
u v
u k
cot cot
u v k
u v
u k
Đặc biệt:
sin 0
sin 1 2
2
sin 1 2
2
x x k
x x k
x x k
cos 0
2
cos 1 2
cos 1 2
x x k
x x k
x x k
Chú ý:
Điều kiện có nghiệm của phương trình
sin
x m
và
cos
x m
là:
1 1
m
.
Sử dụng thành thạo câu thần chú " Cos đối - Sin bù - Phụ chéo" để đưa các phương trình dạng sau
về phương trình cơ bản:
sin cos sin sin
2
u v u v
cos sin cos cos
2
u v u v
sin sin sin sin( )
u v u v
cos cos cos cos( )
u v u v
Đối với phương trình
2
2
cos 1 cos 1
sin 1
sin 1
x x
x
x
không nên giải trực tiếp vì khi đó phải giải 4
phương trình cơ bản thành phần, khi đó việc kết hợp nghiệm sẽ rất khó khăn. Ta nên dựa vào công
thức
2 2
sin cos 1
x x
để biến đổi như sau:
2
2
cos 1 sin 0
sin 2 0
cos 0
sin 1
x x
x
x
x
.
Tương tự đối với phương trình
2
2
2
2
1
cos
2 cos 1 0
2
cos2 0
1
1 2 sin 0
sin
2
x
x
x
x
x
.
Bài 1. Giải các phương trình sau
2
cos
4 2
x
2 sin 2 3 0
6
x
2 cos 2 0
3
x
3 tan 3
3
x
Hướng dẫn giải:
2 3
cos cos cos
4 2 4 4
x x
PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
4
Ta xác định ở phương trình này
3
,
4 4
u x v
, nên dựa vào công thức nghiệm ta có
3
2
4 4
x k
hoặc
3
2
4 4
x k
.
Vậy nghiệm của phương trình là:
2
x k
;
2
2
x k
,
( )
k
.
2 sin 2 3 0
6
x
3
sin 2 sin 2 sin
6 2 6 3
x x
2 2
6 3 12
4 3
2 2
6 3 4
x k x k
x k x k
( )
k
.
2 cos 2 0
3
x
2
cos cos cos
3 2 3 4
x x
2
3 4
2
3 4
x k
x k
2
12
7
2
12
x k
x k
( )
k
.
3 tan 3
3
x
3
tan tan tan
3 3 3 6
x x
3 6
x k
6
x k
,
( )
k
.
Chú ý: Đối với phương trình
tan
x m
(
tan
x m
), trong đó
m
là hằng số thì điều kiện
cos 0
x
(
sin 0
x
) là không cần thiết.
Bài 2. Giải các phương trình sau
sin sin 2
4
x x
sin cos 2
6 4
x x
tan 3 tan
4 6
x x
cot 2 tan 0
4 6
x x
Hướng dẫn giải:
sin sin 2
4
x x
2 2
4
2 2
4
x x k
x x k
2
4
2
4 3
x k
x k
,
( )
k
.
PT
2
cos 2 cos
4 3
x x
2
2 2
4 3
2
2 2
4 3
x x k
x x k
5 2
36 3
11
2
12
x k
x k
.
Do PT có dạng
tan tan
u v
nên ta chỉ cần một điều kiện
cos 0
u
hoặc
cos 0
v
. Để đơn
giản ta chọn điều kiện:
cos 0
6 6 2 3
x x k x k
. Khi đó:
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
5
5
tan 3 tan 3
4 6 4 6 24 2
x x x x k x k
,
( )
k
.
Kết hợp nghiệm trên đường tròn lượng giác thu được nghiệm của PT:
5
24 2
x k
,
( )
k
.
Do có thể biến đổi PT về dạng
tan tan
u v
nên ta chỉ cần một điều kiện
cos 0
u
hoặc
cos 0
v
. Để đơn giản ta chọn điều kiện:
cos 0
6 6 2 3
x x k x k
.
PT
cot 2 tan
4 6
x x
3
tan tan 2
6 4
x x
3
2
6 4
x x k
11
36 3
x k
( )
k
.
Kết hợp nghiệm trên đường tròn lượng giác thu được nghiệm của PT:
11
36 3
x k
,
( )
k
.
Bài 3. Giải các phương trình sau
2
4 cos 2( 3 1)cos 3 0
x x
2
2 cos 5 sin 4 0
x x
2
3 tan (1 3) tan 1 0
x x
2 2
sin cos
4
x x
Hướng dẫn giải:
PT
1
cos
2
2
3
3
2
cos
6
2
x
x k
x k
x
( ).
k
PT
2
2(1 sin ) 5 sin 4 0
x x
(lo¹i)
(t/m)
2
sin 2
2 sin 5 sin 2 0
1
sin
2
x
x x
x
Vậy phương trình có nghiệm:
2
6
x k
và
5
2
6
x k
,
( )
k
.
PT
tan 1
1
tan
3
x
x
(lo¹i)
2
sin 2
2 sin 5 sin 2 0
1
sin
2
x
x x
x
Vậy phương trình có nghiệm:
2
6
x k
và
5
2
6
x k
,
( )
k
.
PT
1 cos 2
2
1 cos2
2 2
x
x
sin 2 cos 2
x x
tan 2 1
x
.
8 2
x k
Bài 4. Giải các phương trình sau
4 4
1
sin cos sin 2
2
x x x
4 4
sin cos 1 2 sin
2 2
x x
x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
6
4 4
2(sin cos ) cos 2 0
2
x x x
6 6
sin cos cos 4
x x x
Hướng dẫn giải:
PT
2 2 2
1 1 1
1 2 sin cos sin 2 1 sin 2 sin 2
2 2 2
x x x x x
2
sin 2 2 sin 2 3 0
x x
(lo¹i)
sin 2 1
sin 2 3
x
x
2 2
2
x k
,( ).
4
x k k
PT
2
1
1 sin 1 2 sin
2
x x
(lo¹i)
2
sin 0
sin 4 sin 0
sin 4
x
x x
x
( ).
x k k
PT
2
1
2 1 sin 2 sin2 0
2
x x
2
sin 2 sin 2 2 0
x x
(lo¹i)
sin 2 1
sin 2 2
x
x
2 2
2
x k
,( ).
4
x k k
PT
2 2 2
1 3 sin cos 1 2 sin 2
x x x
2 2
3
1 sin 2 1 2 sin 2
4
x x
sin 2 0 2 ,( ).
2
x x k x k k
Bài 5. Giải các phương trình sau
4 4
sin cos sin cos 0
x x x x
6 6
2(sin cos ) sin cos
0
2 2 sin
x x x x
x
(A06)
4 2
1
cos sin
4
x x
2
(2 3)cos 2 sin ( )
2 4
1
2 cos 1
x
x
x
Hướng dẫn giải:
PT
2
1 1
1 sin 2 sin 2 0
2 2
x x
2
sin 2 sin 2 2 0
x x
(lo¹i)
sin 2 1
sin 2 2
x
x
,( ).
4
x k k
(A-2006) Điều kiện:
2
4
2 2 sin 0 sin
3
2
2
4
x k
x x
x k
PT
6 6
2(sin cos ) sin cos 0
x x x x
2
3 1
2 1 sin 2 sin 2 0
4 2
x x
(lo¹i)
2
sin 2 1
3 sin 2 sin 2 4 0
4
sin 2
3
x
x x
x
4
x k
,
( ).
k
Kết hợp nghiệm ta thu được nghiệm của phương trình
5
2 .
4
x k
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
7
PT
4 2 4 2
1
cos 1 cos 4 cos 4 cos 3 0
4
x x x x
(lo¹i)
2
2
1
cos
2
3
cos
4
x
x
2
2 cos 1 0 cos 2 0 2
2 4 2
x x x k x k
,
( )
k
.
Điều kiện:
2 cos 1 2 .
3
x x k
PT
2
(2 3)cos 2 sin ( ) 2 cos 1
2 4
x
x x
3 cos 1 cos 1
2
x x
3 cos cos 0
2
x x
3 cos sin 0
x x
tan 3 ,( ).
3
x x k k
Bài 6. Giải các phương trình sau
sin 3 cos 2 sin 0
x x x
(D-2013)
2
sin 5 2 cos 1
x x
(B-2013)
sin 4 cos 2 sin 2
x x x
(A-2014)
cos 3 cos 2 cos 1 0
x x x
(D-2006)
Hướng dẫn giải:
PT
sin 3 sin cos 2 0
x x x
2 cos 2 sin cos 2 0
x x x
cos 2 (2 sin 1) 0
x x
4 2
cos2 0
2
1
6
sin
2
7
2
6
x k
x
x k
x
x k
.
PT
sin 5 1 cos 2 1
x x
cos 2 sin 5 cos 2 sin 5
x x x x
2 5 2
2
cos2 cos 5
2
2 5 2
2
x x k
x x
x x k
2
6 3
( ).
2
14 7
x k
k
x k
PT
sin 4 cos 2 2 sin cos
x x x x
sin (1 2 cos ) 2(2 cos 1) 0
x x x
(sin 2)(1 2 cos ) 0
x x
(lo¹i)sin 2
2 .
1
3
cos
2
x
x k
x
PT
2
cos 3 cos cos 2 1 0 2 sin 2 sin 2 sin 0
x x x x x x
sin (sin 2 sin ) 0
x x x
sin 0 sin 0
sin 2 sin 0 2 cos 1 0
x x
x x x
2
2
3
x k
x k
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
8
DẠNG 1. PHƯƠNG TRÌNH BẬC NHẤT VỚI SINX VÀ COSX
Dạng phương trình:
sin cos
a x b x c
Cách giải: Chia hai vế phương trình cho
2 2
a b
2 2 2 2 2 2
sin cos
a b c
x x
a b a b a b
C1: Đặt
2 2 2 2
cos , sin .
a b
a b a b
Khi đó
2 2
PT sin( ) ?
c
x x
a b
C2: Đặt
2 2 2 2
sin , cos .
a b
a b a b
Khi đó
2 2
PT cos( ) ?
c
x x
a b
Điều kiện có nghiệm của phương trình:
2 2 2
a b c
Chú ý: Khi phương trình có
a c
hoặc
b c
thì dùng công thức góc nhân đôi và sử dụng
phép nhóm nhân tử chung.
Bài 1. Giải các phương trình sau
cos 3 sin 2
x x
2 sin 2 cos 6
x x
3 cos 3 sin 3 2
x x
sin cos 2 sin 5
x x x
Hướng dẫn giải:
Nhận xét: Trong PT này ta xác định các hệ số
1, 3, 2
a b c
thỏa mãn điều kiện
2 2 2
a b c
do đó phương trình này có nghiệm. Để giải PT ta cần chia cả hai vế cho
2 2 2 2
1 ( 3) 2
a b
.
PT
1 3 2
cos sin
2 2 2
x x
2
sin
6 2
x
2
12
7
2
12
x k
x k
PT
1 1 3
cos sin
2
2 2
x x
3
sin
4 2
x
2
12
5
2
12
x k
x k
PT
3 1 2
cos 3 sin 3
2 2 2
x x
2
sin 3
3 2
x
3
3 4
3
3 2
3 4
x k
x k
36 3
5 2
.
36 3
x k
x k
,
( )
k
.
PT
1 1
sin cos sin 5
2 2
x x x
sin sin 5
4
x x
MỘT SỐ DẠNG PHƯƠNG TRÌNH LƯỢNG GIÁC
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
9
5 2
4 16 2
3
5 2
4 8 3
x x k x k
x x k x k
.
Bài 2. Giải các phương trình sau
3 sin 2 sin 2 1
2
x x
( 3 1)sin ( 3 1)cos 3 1 0
x x
3
3 sin 3 cos 3 1 4 sin
x x x
2 6
cos 7 3 sin 7 2 0, ;
5 7
x x x
Hướng dẫn giải:
PT
3 1 1
3 sin 2 cos 2 1 sin 2 cos 2
2 2 2
x x x x
1
sin 2
6 2
x
2 2
6 6
5
2 2
6 6
x k
x k
3
x k
x k
( )
k
.
PT
3 1 3 1 1 3
sin cos
8 8 8
x x
Nhận xét: Sử dụng máy tính 570ES PLUS ta bấm SHIFT SIN của
3 1
8
thu được
5
12
, tức là
5 3 1
sin
12
8
. Vậy ta có nên đưa phương trình về dạng
5 5 1 3
cos sin sin cos
12 12
8
x x
ngay lập tức hay chưa? Câu trả lời là chưa. Bởi vì kết quả
5
12
không phải giá trị cung lượng giác đặc
biệt có mặt trong SGK?Vì vậy ta nên làm như sau cho thuyết phục:
Ta có
5 2 3 2 1 3 1
sin sin sin cos cos sin . .
12 4 6 4 6 4 6 2 2 2 2
8
.
Nên PT
5 5 3 1
cos sin sin cos
12 12
8
x x
5 5
sin cos
12 12
x
5 7
sin cos
12 12
x
5
sin sin
12 12
x
5
2
12 12
5 13
2
12 12
x k
x k
Vậy phương trình có nghiệm:
2
2
x k
và
2
2
3
x k
,
( )
k
.
PT
sin 3 3 cos 3 1
x x
1 3 1
sin 3 cos 3
2 2 2
x x
1
sin 3
3 2
x
3 2
3 6
5
3 2
3 6
x k
x k
2
18 3
2
6 3
x k
x k
.
ThS. Trần Mạnh Hân (0974514498) thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
10
PT
3 1 2
sin 7 cos 7
2 2 2
x x
2
sin 7
6 2
x
7 2
6 4
3
7 2
6 4
x k
x k
5
7 2
12
11
7 2
12
x k
x k
5 2
84 7
11 2
84 7
x k
x k
( )
k
.
Nhận xét: Để tìm nghiệm
2 6
;
5 7
x
thực chất là ta phải chọn số nguyên
k
thỏa mãn
2 5 2 6
5 84 7 7
k
hoặc
2 11 2 6
5 84 7 7
k
tức là ta phải giải các bất phương trình
2 5 2 6
5 84 7 7
k
;
2 11 2 6
5 84 7 7
k
để tìm các miền giá trị của
k
rồi sau đó chọn
k
là số
nguyên.
KL: Vậy phương trình có các nghiệm thỏa mãn điều kiện là:
53
84
x
,
5
12
x
và
59
84
x
.
Ngoài ra, ta có thể không cần giải các BPT nghiệm nguyên ở trên bằng cách sử dụng 570ES PLUS
như sau:
- Trước tiên ta tìm khoảng gần đúng của
2 6
;
5 7
là
0,4; 0, 857...
- Nhập biểu thức thứ nhất
5 2
84 7
X
vào máy tính (vì máy tính không có
k
nên ta coi
X
là
k
) rồi
CALC với các giá trị
0; 1; 2; 3...
X
để kiểm tra xem có thỏa mãn hay không. Khi đó ta tìm
được
2
k
, ứng với nghiệm là
53
84
x
.
- Tương tự cho biểu thức thứ 2 thu được
1; 2
k k
, tương ứng với nghiệm
5
12
x
và
59
84
x
.
Bài 3. Giải các phương trình sau
cos 7 sin 5 3(cos 5 sin 7 )
x x x x
tan 3 cot 4(sin 3 cos )
x x x x
3(1 cos 2 )
cos
2 sin
x
x
x
sin sin 2
3
cos cos 2
x x
x x
(CĐ2004)
Hướng dẫn giải:
Nhận xét: Đối với PT dạng
sin cos
a x b x c
thì chúng ta có thể giải một cách dễ dàng bằng
cách chia cho
2 2
a b
. Nhưng nếu gặp dạng
sin cos sin cos
a mx b mx c nx d nx
trong
đó
2 2 2 2
a b c d
thì làm thế nào? Cứ bình tĩnh quan sát nhé! Chúng ta nhận thấy mỗi vế của
phương trình đều có dạng bậc nhất của sin và cos, ta thử chia mỗi vế cho
2 2
a b
, rất may
2 2 2 2
a b c d
. Nhưng lưu ý rằng, ta phải chuyển vế sao cho mỗi vế có cùng một cung. Từ đó
ta có lời giải như sau:
PT
cos 7 3 sin 7 sin 5 3 cos 5
x x x x
1 3 1 3
cos7 sin7 sin5 cos5
2 2 2 2
x x x x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
11
sin 7 sin 5
6 3
x x
7 5 2
6 3
2
7 5 2
6 3
x x k
x x k
12
24 6
x k
x k
Điều kiện:
sin 0
sin 2 0 .
cos 0
2
x
x x k
x
PT
2 2
sin 3 cos
4(sin 3 cos )
sin cos
x x
x x
x x
sin 3 cos
(sin 3 cos ) 4 0
sin cos
x x
x x
x x
sin 3 cos 0
sin 3 cos 2 sin 2
x x
x x x
tan 3
sin sin2
3
x
x x
Giải và kết hợp nghiệm trên đường tròn lượng giác ta thu được:
; 2 ;
3 3
x k x k
2 2
9 3
x k
,
( )
k
.
Điều kiện:
sin 0
x x k
PT
sin 2 3 cos2 3
x x
3
sin 2
3 2
x
2 2
3 3
2
2 2
3 3
x k
x k
(lo¹i)
6
x k
x k
. Vậy phương trình có nghiệm:
,( )
6
x k k
.
Điều kiện:
2
cos cos 2 0 2 2
3
x x x x k x k
PT
sin sin 2 3(cos cos 2 )
x x x x
sin 3 cos sin 2 3 cos2
x x x x
1 3 1 3
sin cos sin 2 cos 2
2 2 2 2
x x x x
sin sin 2
3 3
x x
2
5 2
9 3
x k
x k
( )
k
.
Vậy phương trình có nghiệm:
5 2
2 ;
9 3
x k x k
.
Bài 4. Giải các phương trình sau
1
cos 3 sin
cos
x x
x
1 tan 2 2 sin
4
x x
(A2013)
3 cos 5 2sin 3 cos2 sin 0
x x x x
(D09)
6
4 sin 3 cos 6
4 sin 3 cos 1
x x
x x
Hướng dẫn giải:
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
12
Điều kiện:
cos 0 .
2
x x k
PT
2
cos 3 sin cos 1
x x x
cos 2 3 sin 2 1
x x
1 3 1
cos2 sin 2
2 2 2
x x
2 2
1
6 6
sin 2
5
6 2
2 2
6 6
x k
x
x k
(t/m)
(t/m)
3
x k
x k
( )
k
.
Vậy phương trình có nghiệm:
;
3
x k x k
.
Điều kiện:
cos 0 .
2
x x k
PT
sin
1 2(sin cos )
cos
x
x x
x
1
(sin cos ) 2 0
cos
x x
x
tan 1
1
cos
2
x
x
Kết hợp với điều kiện thu được nghiệm của PT:
; 2
4 3
x k x k
,
( )
k
.
PT
3 cos5 (sin5 sin ) sin 0
x x x x
3 cos5 sin 5 2 sin
x x x
sin 5 sin
3
x x
5 2
3
5 2
3
x x k
x x k
18 3
6 4
x k
x k
,
( )
k
.
Vậy phương trình có nghiệm:
;
18 3 6 4
x k x k
.
Đặt
4 sin 3 cos 1
t x x
,
( 0)
t
PT
6
1 6
t
t
2
1
7 6 0
6
t
t t
t
+ Với
1
t
ta có
4 sin 3 cos 0
x x
4 3
sin cos 0
5 5
x x
cos sin sin cos 0
x x
sin 0
x
x k
.
+ Với
6
t
ta có
4 sin 3 cos 5
x x
4 3
sin cos 1
5 5
x x
cos sin sin cos 1
x x
sin 1
x
2
2
x k
.
Vậy phương trình có nghiệm:
2 ; 2
2
x k x k
trong đó
3
sin
5
và
cos
5
.
DẠNG 2. PHƯƠNG TRÌNH THUẦN BẬC HAI VỚI SINX VÀ COSX
Dạng phương trình:
2 2
sin sin cos .cos 0
a x b x x c x d
Cách giải:
Cách 1: + Xét
cos 0
x
có là nghiệm phương trình không?
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
13
+ Xét
cos 0
x
, chia hai vế phương trình cho
2
cos
x
ta được:
2 2
tan tan (1 tan ) 0 tan
a x b x c d x x x
Cách 2: Dùng công thức hạ bậc đưa về phương trình bậc nhất với
sin 2
x
và
cos2
x
(dạng 1).
Bài 1. Giải các phương trình sau
2 2
2 sin sin cos 3 cos 0
x x x x
2 2
2 sin 3 sin cos cos 0
x x x x
2 2
sin 10 sin cos 21 cos 0
x x x x
2 2
2 sin 5 sin cos 3 cos 0
x x x x
Hướng dẫn giải:
2 2
2 sin sin cos 3 cos 0
x x x x
+ Xét
cos 0
x
(tức
2
sin 1
x
): Khi đó PT trở thành
2 0
nên
cos 0
x
không thỏa mãn.
+ Xét
cos 0
x
, chia hai vế phương trình cho
2
cos
x
ta được:
2
tan 1
2 tan tan 3 0
3
tan
2
x
x x
x
4
3
arctan
2
x k
x k
( )
k
.
Cách 2: PT
2(1 cos 2 ) sin 2 3(1 cos2 ) 0
x x x
sin 2 5 cos 2 1
x x
Đặt
tan
t x
khi đó
2
2 2
2 1
sin 2 ; cos2
1 1
t t
x x
t t
. Phương trình trở thành
2
2 3 0
t t
1
3
2
t
t
.
2 2
2 sin 3 sin cos cos 0
x x x x
+ Xét
cos 0
x
(tức
2
sin 1
x
): Khi đó PT trở thành
2 0
nên
cos 0
x
không thỏa mãn.
+ Xét
cos 0
x
, chia hai vế phương trình cho
2
cos
x
ta được:
2
tan 1
2 tan 3 tan 1 0
1
tan
2
x
x x
x
4
1
arctan
2
x k
x k
( )
k
.
2 2
sin 10 sin cos 21 cos 0
x x x x
+ Xét
cos 0
x
(tức
2
sin 1
x
): Khi đó phương trình trở thành
1 0
nên
cos 0
x
không t/m.
+ Xét
cos 0
x
, chia hai vế phương trình cho
2
cos
x
ta được:
2
tan 3
tan 10 tan 21 0
tan 7
x
x x
x
arctan 3
arctan 7
x k
x k
( )
k
.
2 2
2 sin 5 sin cos 3 cos 0
x x x x
+ Xét
cos 0
x
(tức
2
sin 1
x
): Khi đó phương trình trở thành
2 0
nên
cos 0
x
không t/m.
+ Xét
cos 0
x
, chia hai vế phương trình cho
2
cos
x
ta được:
2
tan 1
2 tan 5 tan 3 0
3
tan
2
x
x x
x
4
3
arctan
2
x k
x k
( )
k
.
Bài 2. Giải các phương trình sau
2 2
sin (1 3)sin cos 3 cos 0
x x x x
2 2
3 sin 4 sin 2 4 cos 0
x x x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
14
2 2
3 sin 4 sin cos 5 cos 2
x x x x
2 2
3 sin 4 sin 2 (8 3 3)cos 3
x x x
Hướng dẫn giải:
2 2
sin (1 3)sin cos 3 cos 0
x x x x
+ Xét
cos 0
x
(tức
2
sin 1
x
): Khi đó phương trình trở thành
1 0
nên
cos 0
x
không t/m.
+ Xét
cos 0
x
, chia hai vế phương trình cho
2
cos
x
ta được:
2
tan 1
tan (1 3) tan 3 0
tan 3
x
x x
x
4
3
x k
x k
( )
k
.
PT
2 2
3 sin 8 sin cos 4 cos 0
x x x x
+ Xét
cos 0
x
(tức
2
sin 1
x
): Khi đó phương trình trở thành
3 0
nên
cos 0
x
không t/m.
+ Xét
cos 0
x
, chia hai vế phương trình cho
2
cos
x
ta được:
2
tan 2
3 tan 8 tan 4 0
2
tan
3
x
x x
x
arctan( 2)
2
arctan
3
x k
x k
( )
k
.
2 2
3 sin 4 sin cos 5 cos 2
x x x x
+ Xét
cos 0
x
(tức
2
sin 1
x
): Khi đó phương trình trở thành
3 2
nên
cos 0
x
không t/m.
+ Xét
cos 0
x
, chia hai vế phương trình cho
2
cos
x
ta được:
2 2
tan 1
3 tan 4 tan 5 2(1 tan )
tan 3
x
x x x
x
4
arctan 3
x k
x k
( )
k
.
PT
2 2
3 sin 8 sin cos (8 3 3)cos 3
x x x x
+ Xét
cos 0
x
(tức
2
sin 1
x
): Khi đó phương trình trở thành
3 3
nên
cos 0
x
thỏa mãn.
Tức là
2
x k
là nghiệm của phương trình.
+ Xét
cos 0
x
, chia hai vế phương trình cho
2
cos
x
ta được:
2 2
3 tan 8 tan 8 3 3 3(1 tan ) tan 3
x x x x
3
x k
( )
k
.
Vậy phương trình có nghiệm:
, .
2 3
x k x k
DẠNG 3. PHƯƠNG TRÌNH BẬC BA VỚI SINX VÀ COSX
Dạng phương trình:
3 3 2 2
a sin cos sin cos cos sin sin cos 0
x b x c x x d x x e x f x
Cách giải:
+ Xét
cos 0
x
có là nghiệm phương trình không?
+ Xét
cos 0
x
, chia hai vế phương trình cho
3
cos
x
với chú ý:
2
2
1
1 tan
cos
x
x
.
Bài 1. Giải các phương trình sau
3
sin 4 sin cos 0
x x x
3
2 sin cos
x x
3
2 cos sin 3
x x
3 3
4 cos 2 sin 3 sin 0
x x x
Hướng dẫn giải:
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
15
3
sin 4 sin cos 0
x x x
+ Xét
cos 0
x
(tức
sin 1
x
): Khi đó PT trở thành
3 0
nên
cos 0
x
không thỏa mãn.
+ Xét
cos 0
x
, chia hai vế phương trình cho
3
cos
x
ta được:
2 3 2
tan (1 tan ) 4 tan (1 tan ) 0
x x x x
3 2
3 tan tan tan 1 0
x x x
2
(tan 1)(3 tan 2 tan 1) 0
x x x
tan 1
x
4
x k
( )
k
.
Nhận xét: Khi giải phương trình bậc 3 các em thường bấm máy tính để ra nghiệm ngay, nên các em
biến đổi phương trình
3 2
3 1 0
t t t
1
t
. Như thế liệu đã đầy đủ chưa? Câu trả lời là
chưa đủ vì chúng ta không hề học công thức nghiệm phương trình bậc 3. Các em cần phải phân tích
thành nhân tử trước khi đưa ra nghiệm. Vậy làm thế nào để phân tích nhanh nhất?
Bước 1: Dùng máy tính 570ES PLUS thu được nghiệm như sau
1
t
,
1
0,47
3
t i
(1 nghiệm
thực và 2 nghiệm phức). Chú ý đến số
1
3
nhé!
Bước 2: Viết nhân tử: do PT có nghiệm
1
t
nên có một nhân tử
( 1)
t
, vậy nhân tử còn lại là gì?
Dựa vào hệ số đầu tiên và cuối cùng trong phương trình bậc 3 ta thu được hệ số đầu tiên và cuối cùng
của nhân tử còn lại, tức là có nhân tử nữa
2
(3 1)
t Bt
. Để tìm
B
ta dựa vào phần thực của
nghiệm phức còn lại
1
3 2
B
A
từ đó suy ra
2
B
. Vậy ta lập tức phân tích phương trình thành
2
( 1)(3 2 1) 1
t t t t
.
3
2 sin cos
x x
+ Xét
cos 0
x
(tức
sin 1
x
): Khi đó PT trở thành
2 0
nên
cos 0
x
không thỏa mãn.
+ Xét
cos 0
x
, chia hai vế phương trình cho
3
cos
x
ta được:
3 2
2 tan 1 tan
x x
3 2
2 tan tan 1 0
x x
2
(tan 1)(2 tan tan 1) 0
x x x
tan 1
x
4
x k
( )
k
.
3 3 3
2 cos sin 3 2 cos 3 sin 4 sin
x x x x x
+ Xét
cos 0
x
(tức
sin 1
x
): Khi đó PT trở thành
0 1
nên
cos 0
x
không thỏa mãn.
+ Xét
cos 0
x
, chia hai vế phương trình cho
3
cos
x
ta được:
2 3
2 3 tan (1 tan ) 4 tan
x x x
3
tan 3 tan 2 0
x x
2
(tan 1) (tan 2) 0
x x
tan 1
tan 2
x
x
4
arctan( 2) .
x k
x k
( )
k
.
Nhận xét: Khi bấm máy tính giải phương trình
3
3 2 0
t t
, chúng ta thu được 2 nghiệm
1, 2
t t
. Khi đó phân tích phương trình thành
3
3 2 ( 1)( 2)
t t t t
. Như thế liệu đầy
đủ chưa? Các em hãy để ý bậc ở hai vế để tự đưa ra câu trả lời nhé. Như vậy là đa thức này còn có 1
nhân tử nữa, theo các em nhân tử này là
1
t
hay
2
t
. Câu trả lời là
1
t
, vì sao lại như vậy?
Rất dễ dàng thôi nhân tử thứ ba này là
2
t
thì số hạng tự do của đa thức ban đầu phải là
4
,
không ổn rồi. Vậy kết quả là
3 2
3 2 ( 1)( 2)(t 1) (t 1) ( 2)
t t t t t
.
3 3
4 cos 2 sin 3 sin 0
x x x
+ Xét
cos 0
x
(tức
sin 1
x
): Khi đó PT trở thành
1 0
nên
cos 0
x
không thỏa mãn.
+ Xét
cos 0
x
, chia hai vế phương trình cho
3
cos
x
ta được:
3 2
4 2 tan 3 tan (1 tan ) 0
x x x
3
tan 3 tan 4 0
x x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
16
2
(tan 1)(tan tan 4) 0
x x x
tan 1
x
4
x k
( )
k
.
Bài 2. Giải các phương trình sau
3
sin sin 2 sin 3 6 cos
x x x x
3 3
cos sin sin cos
x x x x
3
6 sin 2 cos 5 sin 2 cos
x x x x
3 2
cos sin 3 sin cos 0
x x x x
Hướng dẫn giải:
3 2 3 3
sin sin 2 sin 3 6 cos 2 sin cos 3 sin 4 sin 6 cos
x x x x x x x x x
+ Xét
cos 0
x
(tức
sin 1
x
): Khi đó PT trở thành
1 0
nên
cos 0
x
không thỏa mãn.
+ Xét
cos 0
x
, chia hai vế phương trình cho
3
cos
x
ta được:
2 2 3
2 tan 3 tan (1 tan ) 4 tan 6
x x x x
3 2
tan 2 tan 3 tan 6 0
x x x
2
(tan 2)(tan 3) 0
x x
tan 1
tan 3
tan 3
x
x
x
4
3
3
x k
x k
x k
( )
k
.
PT
3 3
cos sin sin cos 0
x x x x
+ Xét
cos 0
x
(tức
sin 1
x
): Khi đó PT trở thành
2 0
nên
cos 0
x
không thỏa mãn.
+ Xét
cos 0
x
, chia hai vế phương trình cho
3
cos
x
ta được:
3 2
1 tan (tan 1)(1 tan ) 0
x x x
3 3 2
1 tan (tan tan tan 1) 0
x x x x
2
tan tan 0
x x
tan 0
tan 1
x
x
4
x k
x k
( )
k
.
3
6 sin 2 cos 5 sin 2 cos
x x x x
3 2
6 sin 2 cos 10 sin cos
x x x x
+ Xét
cos 0
x
(tức
sin 1
x
): Khi đó PT trở thành
6 0
nên
cos 0
x
không thỏa mãn.
+ Xét
cos 0
x
, chia hai vế phương trình cho
3
cos
x
ta được:
2
6 tan (1 tan ) 2 10 tan
x x x
3
6 tan 4 tan 2 0
x x
2
(tan 1)(6 tan 6 tan 2) 0
x x x
tan 1
x
4
x k
( )
k
.
3 2
cos sin 3 sin cos 0
x x x x
+ Xét
cos 0
x
(tức
sin 1
x
): Khi đó PT trở thành
1 0
nên
cos 0
x
không thỏa mãn.
+ Xét
cos 0
x
, chia hai vế phương trình cho
3
cos
x
ta được:
2 2
1 tan (1 tan ) 3 tan 0
x x x
3
2 tan tan 1 0
x x
2
(tan 1)(2 tan 2 tan 1) 0
x x x
tan 1
x
4
x k
( )
k
.
Bài 3. Giải các phương trình sau
3 3 2
cos 4 sin 3 cos sin sin 0
x x x x x
1 3 tan 2 sin 2
x x
3 1
2 sin 2 3 cos
cos sin
x x
x x
2 2
tan sin 2sin 3(cos2 sin cos )
x x x x x x
Hướng dẫn giải:
3 3 2
cos 4 sin 3 cos sin sin 0
x x x x x
+ Xét
cos 0
x
(tức
sin 1
x
): Khi đó PT trở thành
1 0
nên
cos 0
x
không thỏa mãn.
+ Xét
cos 0
x
, chia hai vế phương trình cho
3
cos
x
ta được:
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
17
3 2 2
1 4 tan 3 tan tan (1 tan ) 0
x x x x
3 2
3 tan 3 tan tan 1 0
x x x
2
(tan 1)(3 tan 1) 0
x x
tan 1
3
tan
3
3
tan
3
x
x
x
4
6
6
x k
x k
x k
( )
k
.
Điều kiện:
cos 0
x
. Khi đó phương trình trở thành:
2
cos 3 sin 4 sin cos
x x x x
Chia hai vế phương trình cho
3
cos
x
ta được:
2
(1 3 tan )(1 tan ) 4 tan
x x x
3 2
3 tan tan tan 1 0
x x x
2
(tan 1)(3 tan 2 tan 1) 0
x x x
tan 1
4
x x
(t/m),
( )
k
.
Điều kiện:
cos 0
x
. PT trở thành:
2 2
2 sin cos 2 3 cos sin 3 sin cos
x x x x x x
Chia hai vế phương trình cho
3
cos
x
ta được:
2 2
2 tan 2 3 tan ( 3 tan 1)(tan 1)
x x x x
3 2
3 tan tan 3 tan 1 0
x x x
2
(tan 1)( 3 tan 1) 0
x x
tan 1
tan 1
3
tan
3
x
x
x
4
4
6
x k
x k
x k
(t/m),
( )
k
.
Điều kiện:
cos 0
x
. PT trở thành:
3 2 3 2
sin 2 sin cos 3(2 cos sin cos cos )
x x x x x x x
Chia hai vế phương trình cho
3
cos
x
ta được:
3 2 2
tan 2 tan 3(2 tan 1 tan )
x x x x
3 2
tan tan 3 tan 3 0
x x x
2
(tan 1)(tan 3) 0
x x
tan 1
tan 3
tan 3
x
x
x
4
3
3
x k
x k
x k
(t/m),
( )
k
.
Bài 4. Giải các phương trình sau
3 3 2 2
cos sin cos sin
x x x x
3 3
cos sin cos 2
x x x
6 6 2
13
cos sin cos 2
8
x x x
4 4
7
sin cos cot cot
8 3 6
x x x x
Hướng dẫn giải:
PT
3 3 2 2
cos sin cos sin
x x x x
(cos sin )(1 sin cos cos sin ) 0
x x x x x x
cos sin (1)
1 sin cos sin cos 0 (2)
x x
x x x x
Giải (1):
cos cos 2
2 2 4
x x x x k x k
.
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
18
Giải (2): Đặt
sin cos
t x x
2
1
sin cos
2
t
x x
. Khi đó (2)
2
2 ( 1) 2 0
t t
2
2 1 0 1
t t t
1
sin cos 1 sin
4
2
x x x
2
2
4 4
3
2
2
2
4 4
x k
x k
x k
x k
( )
k
.
Vậy phương trình có nghiệm:
; 2 ; 2 ( ).
4 2
x k x k x k k
PT
2 2
(cos sin )(1 sin cos ) cos sin
x x x x x x
(cos sin )(1 sin cos sin cos ) 0
x x x x x x
sin cos 0 tan 1
4
x x x x k
1 sin cos sin cos 0
x x x x
Đặt
sin cos
t x x
2
1
sin cos
2
t
x x
ta có:
2
2 1 2 0 1
t t t
1
sin cos 1 sin
4
2
x x x
2
2
4 4
3
5
2
2
2
4 4
x k
x k
x k
x k
Vậy phương trình có nghiệm:
3
; 2 ; 2 ( ).
4 2
x k x k x k k
PT
2 2 4 4 2 2 2
13
(cos sin )(cos sin sin cos ) cos 2
8
x x x x x x x
2 2 2
13
cos 2 (1 sin cos ) cos 2
8
x x x x
2
1 13
cos 2 1 sin 2 cos 2 0
4 8
x x x
cos 2 0 2
2 4 2
x x k x k
2
8 2 sin 2 13 cos2 0
x x
2
2 cos 2 13 cos 2 6 0
x x
1
cos 2
2
x
,
cos2 6
x
(loại)
6
x k
.
Vậy phương trình có nghiệm:
; ( ).
4 2 6
x k x k k
Điều kiện:
2
sin sin 0 sin cos 0 sin 2 0
3 6 3 3 3
x x x x x
2 2
7
1 2 sin cos
8
x x
2 2
1 7 1
1 sin 2 sin 2
2 8 4
x x
1
sin 2
2
x
Vậy phương trình có nghiệm:
5 7
; ; ; ( ).
12 12 12 12
x k x k x k x k k
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
19
DẠNG 4. PHƯƠNG TRÌNH ĐỐI XỨNG VỚI SINX VÀ COSX
Dạng phương trình:
(sin cos , sin cos ) 0
f x x x x
Cách giải:
+ Đặt
2
1
sin cos sin cos
2
t
t x x x x
+ Đặt
2
1
sin cos sin cos
2
t
t x x x x
. Đưa về phương trình ẩn
t
.
Chú ý
: Nếu
sin cos 2 sin
4
t x x x
thì
2 2
t
.
Bài 1. Giải các phương trình sau
2(sin cos ) sin 2 1 0
x x x
sin cos 6(sin cos 1)
x x x x
sin 2 2 sin( ) 1
4
x x
tan 2 2 sin 1
x x
Hướng dẫn giải:
2(sin cos ) sin 2 1 0
x x x
2(sin cos ) 2 sin cos 1 0
x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
Phương trình trở thành:
2
2 ( 1) 1 0
t t
(t/m)
(lo¹i)
2
0
2 0
2
t
t t
t
Khi đó
sin cos 0 sin 0
4 4
x x x x k
Vậy phương trình có nghiệm:
sin cos 6(sin cos 1)
x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
Phương trình trở thành:
(t/m)
(lo¹i)
2 2
1
1 12( 1) 12 13 0
13
t
t t t t
t
Vì vậy
1
sin cos 1 sin
4
2
x x x
Vậy phương trình có nghiệm:
; 2 ( ).
2
x k x k k
sin 2 2 sin( ) 1 2 sin cos sin cos 1
4
x x x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
Phương trình trở thành:
(t/m)
(t/m)
2 2
0
1 1 0
1
t
t t t t
t
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
20
sin cos 0 sin 0
4 4
x x x x k
2
1
sin cos 1 sin
2
4
2
2
x k
x x x
x k
Vậy phương trình có nghiệm:
; 2 ; 2 ( ).
4 2
x k x k x k k
tan 2 2 sin 1 sin cos 2 2 sin cos 0
x x x x x x
(
cos 0
x
)
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
PT trở thành:
(t/m)
(t/m)
2 2
2
2(1 ) 0 2 2 0
2
2
t
t t t t
t
5
2
2 1
12
sin cos sin
13
2 4 2
2
12
x k
x x x
x k
sin cos 2 sin 1 2
4 4
x x x x k
Kết hợp với điều kiện, PT có nghiệm:
5 13
2 ; 2 ; 2 ( ).
12 12 4
x k x k x k k
Bài 2. Giải các phương trình sau
1
1 tan 2 sin
cos
x x
x
2 2
sin cos
tan cot
x x
x x
1 1 10
sin cos
sin cos 3
x x
x x
2 sin cot 2 sin 2 1
x x x
Hướng dẫn giải:
1
1 tan 2 sin cos sin 2 sin cos 1
cos
x x x x x x
x
,
cos 0
x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
PT trở thành:
(t/m)
(t/m)
2 2
1
( 1) 1
0
t
t t t t
t
sin cos 0 sin 0
4 4
x x x x k
2
1
sin cos 1 sin
4
2
2
2
x k
x x x
x k
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
21
Vậy phương trình có nghiệm:
; 2 ; 2 ( ).
4 2
x k x k x k k
Điều kiện:
sin 0
cos 0
x
x
. Khi đó:
PT
2 2
cos sin
sin cos 2 (sin cos )(sin cos 2 sin 2 cos ) 0
sin cos
x x
x x x x x x x x
x x
sin cos 0 sin 0
4 4
x x x x k
(t/m)
sin cos 2 sin 2 cos 0
x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
PT trở thành:
(lo¹i)
(lo¹i)
2 2
2 5
(1 ) 4 0 4 1 0
2 5
t
t t t t
t
Vậy phương trình có nghiệm:
( ).
4
x k k
Điều kiện:
sin 0
cos 0
x
x
.
PT
sin cos 10
sin cos
sin cos 3
x x
x x
x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
PT trở thành:
3 2
3 10 3 10 0
t t t
2
2 19
( 2)(3 4 5) 0
3
t t t t
Khi đó
2 19
sin cos
3
x x
2 19
sin sin
4
3 2
x
Kết hợp điều kiện, phương trình có nghiệm là:
3
2 ; 2 ( ).
4 4
x k x k k
Điều kiện:
sin 0
x
PT
2 2
2 sin cos 4 sin cos sin
x x x x x
2
sin (2 sin 1) cos (4 sin 1)
x x x x
(2 sin 1) cos (2 sin 1) sin 0
x x x x
t/m
2
1
6
sin
5
2
2
6
x k
x
x k
2 sin cos (sin cos ) 0
x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
22
PT trở thành:
(t/m)
(lo¹i)
2 2
1 5
2
(1 ) 0 1 0
1 5
2
t
t t t t
t
Khi đó
1 5
sin cos
2
x x
1 5
sin sin
4
2 2
x
Kết hợp điều kiện, phương trình có nghiệm là:
5
2 ; 2
6 6
x k x k
;
2 ;
4
x k
5
2 ( ).
4
x k k
Bài 3. Giải các phương trình sau
3 3
sin cos 2 sin cos sin cos
x x x x x x
3 3
1 sin cos sin 2
x x x
2 sin cos tan cot
x x x x
(1 sin )(1 cos ) 2
x x
Hướng dẫn giải:
PT
(sin cos )(1 sin cos ) 2sin cos sin cos
x x x x x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
PT trở thành:
2 2
(2 1) 2( 1) 2
t t t t
(t/m)
(t/m)
(lo¹i)
1
( 1)( 1)( 2) 0 1
2
t
t t t t
t
2
1
sin cos 1 sin
4
2
2
2
x k
x x x
x k
2
1
sin cos 1 sin
2
4
2
2
x k
x x x
x k
Kết hợp nghiệm ta thu được:
; ( ).
2
x k x k k
Chú ý: Ở đây hai họ nghiệm
2
x k
và
2
x k
được gộp thành họ nghiệm
x k
. Còn
hai họ nghiệm
2
2
x k
và
2
2
x k
được gộp thành họ nghiệm
2
x k
.
PT
1 (sin cos )(1 sin cos ) 2 sin cos
x x x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
PT trở thành:
2 2
2 (2 1 ) 2(1 )
t t t
(t/m)
(t/m)
(lo¹i)
1
( 1)( 3) 0 0
3
t
t t t t
t
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
23
2
1
sin cos 1 sin
2
4
2
2
x k
x x x
x k
sin cos 0 sin 0
4 4
x x x x k
Vậy phương trình có nghiệm là:
2 ; 2 ; ( ).
2 4
x k x k x k k
Điều kiện:
sin 0
cos 0
x
x
. Phương trình
1
2(sin cos )
sin cos
x x
x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
PT trở thành:
2
2
2
1
t
t
3
2 2 2 0
t t
2
( 2 2)( 2 1) 0 2
t t t t
Khi đó
sin cos 2
x x
sin 1 2
4 4
x x k
Kết hợp điều kiện, phương trình có nghiệm là:
2 ( ).
4
x k k
(1 sin )(1 cos ) 2
x x
sin cos sin cos 1
x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
PT trở thành:
2
1 2 2
t t
2
2 3 0
t t
(t/m)
(lo¹i)
1
3
t
t
Khi đó
2
1
sin cos 1 sin
4
2
2
2
x k
x x x
x k
Vậy phương trình có nghiệm là:
2 ; 2 ( ).
2
x k x k k
Bài 4. Giải các phương trình sau
sin cos sin cos 1
x x x x
2 2
(1 sin )cos (1 cos )sin 1 sin2
x x x x x
2 sin 2 (sin cos ) 2
x x x
sin cos 4 sin 2 1
x x x
2 sin 2 3 6 sin cos 8 0
x x x
Hướng dẫn giải:
sin cos sin cos 1
x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
0 2
t
PT trở thành:
2
1 2 2
t t
2
2 3 0
t t
(t/m)
(lo¹i)
1
3
t
t
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
24
2
1
sin cos 1 sin
4
2
2
2
x k
x x x
x k
2
1
sin cos 1 sin
2
4
2
2
x k
x x x
x k
Kết hợp nghiệm ta thu được:
; ( ).
2
x k x k k
PT
sin cos sin cos (sin cos ) 1 2 sin cos
x x x x x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
PT trở thành:
2 2
2 ( 1) 2 2( 1)
t t t t
3 2
2 0
t t t
2
0
( 1) 0
1
t
t t
t
2
1
sin cos 1 sin
4
2
2
2
x k
x x x
x k
sin cos 0 sin 0
4 4
x x x x k
Vậy phương trình có nghiệm:
2 ; 2 ; ( ).
2 4
x k x k x k k
PT
2 2 sin cos (sin cos ) 2
x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
2 2
t
PT trở thành:
2
2 1 2
t t
3
2 2 2 0
t t
2
( 2 2)( 2 1) 0 2
t t t t
Khi đó
sin cos 2
x x
sin 1 2
4 4
x x k
Vậy phương trình có nghiệm là:
2 ( ).
4
x k k
PT
sin cos 8 sin cos 1
x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
0 2
t
PT trở thành:
2
4(1 ) 1
t t
2
4 3 0
t t
(t/m)
(lo¹i)
1
3
4
t
t
2
1
sin cos 1 sin
2
4
2
2
x k
x x x
x k
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
25
2
1
sin cos 1 sin
3
4
2
2
2
x k
x x x
x k
Kết hợp nghiệm ta thu được:
; ( ).
2
x k x k k
PT
4 sin cos 3 6 sin cos 8 0
x x x x
Đặt
sin cos 2 sin
4
t x x x
2
1
sin cos
2
t
x x
0 2
t
PT trở thành:
2
2( 1) 3 6 8 0
t t
2
2 3 6 6 0
t t
(t/m)
(lo¹i)
6
2
6
t
t
2
6 3
12
sin cos sin
5
2 4 2
2
12
x k
x x x
x k
7
2
6 3
12
sin cos sin
13
2 4 2
2
12
x k
x x x
x k
Vậy PT có nghiệm:
5 7 13
2 ; 2 ; 2 ; 2 ( ).
12 12 12 12
x k x k x k x k k
DẠNG 5. PHƯƠNG TRÌNH DẠNG THUẬN NGHỊCH
Dạng phương trình:
2
2
2
( ) ( ) 0
( )
( )
k k
A f x B f x C
f x
f x
, với
( ) sin , cos
f x x x
(1)
hoặc
2 2 2 2
tan cot tan cot 0
A a x b x B a x b x C
(2)
Cách giải: Đối với phương trình (1): Đặt
( )
( )
k
t f x
f x
Đối với phương trình (2): Đặt
tan cot
t a x b x
Bài 1. Giải các phương trình sau
2
2
1 1
4 sin 4 sin 7 0
sin
sin
x x
x
x
2
2
2
2 tan 5(tan cot ) 4 0
sin
x x x
x
2
2
3
3 cot 4(tan cot ) 1 0
cos
x x x
x
Hướng dẫn giải:
Điều kiện:
sin 0
x
.
Đặt
1
sin
sin
t x
x
2 2
2
1
sin 2
sin
t x
x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
26
PT trở thành:
2
4( 2) 4 7 0
t t
2
3 5
4 4 15 0 ;
2 2
t t t t
2
1 3
sin 2 sin 3 sin 2 0
sin 2
x x x
x
(vô nghiệm)
2
1 5
sin 2 sin 5 sin 2 0
sin 2
x x x
x
(t/m)
(lo¹i)
1
sin
2
sin 2
x
x
2
6
7
2
6
x k
x k
Vậy phương trình có nghiệm:
7
2 ; 2 ( )
6 6
x k x k k
.
Nhận xét: Dùng bất đẳng thức Cô si cho 2 số dương nghịch đảo, ta có thể đánh giá
t
như sau:
1 1 1
sin sin 2 sin . 2
sin
sin sin
t x x x
x
x x
để đưa ra điều kiện
2
t
.
Điều kiện:
sin 0
cos 0
x
x
. PT
2 2
2(cot tan ) 5(tan cot ) 6 0
x x x x
Đặt
tan cot
t x x
2 2 2
tan cot 2
t x x
2 2 2
tan cot 2
x x t
PT trở thành:
2
2( 2) 5 6 0
t t
2
1
2 5 2 0
2
2
t
t t
t
2
1
tan cot 2 tan tan 2 0
2
x x x x
(vô nghiệm)
2
tan cot 2 tan 2 tan 1 0
x x x x
tan 1
x
.
4
x k
Kết hợp với điều kiện, phương trình có nghiệm:
( )
4
x k k
.
Nhận xét: Dùng bất đẳng thức Cô si cho 2 số dương nghịch đảo, ta có thể đánh giá
t
như sau:
tan cot tan cot 2 tan . cot 2
t x x x x x x
để đưa ra điều kiện
2
t
.
Điều kiện:
sin 0
cos 0
x
x
. PT
2 2
3(tan cot ) 4(tan cot ) 2 0
x x x x
Đặt
tan cot
t x x
2 2 2
tan cot 2
t x x
,
2
t
.
PT trở thành:
2
3( 2) 4 2 0
t t
(lo¹i)
2
2
3 4 4 0
3
2
t
t t
t
Khi đó
2
tan cot 2 tan 2 tan 1 0
x x x x
tan 1
x
.
4
x k
Kết hợp với điều kiện, phương trình có nghiệm:
( )
4
x k k
.
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
27
KĨ THUẬT 1: LỰA CHỌN CÔNG THỨC LƯỢNG GIÁC
1. Sử dụng các phép biến đổi góc lượng giác
Khi việc giải phương trình lượng giác cần xem xét mối quan hệ giữa các góc (cung) để từ đó kết hợp
với các phép biến đổi góc đặc biệt, công thức cộng lượng giác để đưa về dạng góc cơ bản là một vấn
đề rất then chốt trong việc giải phương trình lượng giác...
Bài 1. Giải các phương trình sau
1 1 7
4 sin
sin 4
3
sin
2
x
x
x
(A08)
4 4
7
sin cos cot cot
8 3 6
x x x x
4 4
4
sin 2 cos 2
cos 4
tan tan
4 4
x x
x
x x
5 7
sin 2 3 cos 1 2 sin
2 2
x x x
Hướng dẫn giải
Nhận xét: Từ sự xuất hiện hai cung
2
x
và
4
x
mà chúng ta liên tưởng đến việc đưa 2
cung này về cùng một cung
x
. Để làm được điều đó ta có thể sử dụng công thức cộng cung hoặc công
thức về các góc đặc biệt.
Điều kiện:
sin 0, cos 0 sin 2 0 ,
2
x x x x k k
1 1
(1) 2 2(cos sin ) (sin cos )( 2 sin 2 1) 0
sin cos
x x x x x
x x
Kết hợp với điều kiện ta được nghiệm pt là:
5
; ;
4 8 8
x k x k x k
( )
k
.
Điều kiện:
sin .sin 0 cos 2 cos 0
3 6 6 2
x x x
Do
3 6 2
x x
nên (2)
4 4 2
7 1 7
sin cos 1 sin 2
8 2 8
x x x
1
sin 2
2
x
. Kết hợp với điều kiện ta được:
12 2
x k
( )
k
Nhận xét: Từ tổng hai cung
4 4 2
x x
nên
tan tan 1
4 4
x x
Điều kiện 1:
cos cos 0 cos 2 cos 0 cos 2 0
4 4 2 2
x x x x
Điều kiện 2:
sin sin 0 cos2 cos 0 cos 2 0
4 4 2 2
x x x x
4 4 4
(3) sin 2 cos 2 cos 4
x x x
2 4
1
1 sin 4 cos 4
2
x x
MỘT SỐ KĨ THUẬT GIẢI PT LƯỢNG GIÁC
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
28
(lo¹i)
2
4 2
2
cos 4 1
2 cos 4 cos 4 1 0
1
cos 4
2
x
x x
x
(lo¹i)
sin 2 0
sin 4 0
cos2 0
x
x
x
Vậy phương trình có nghiệm
.
2
x k
Chú ý:
Chắc hẳn các em sẽ ngạc nhiên bởi cách giải ngắn gọn này, nếu không có sự nhận xét về tổng hai
cung mà quy đồng và biến đổi thì ... ra không?
Việc giải điều kiện và đối chiếu với điều kiện đặc biệt là những phương trình có dạng phân thức như
trên nếu không khôn khéo thì rất ... phức tạp.
2. Sử dụng công thức biến đổi tổng sang tích và ngược lại
Khi giải pt mà gặp dạng tổng (hoặc hiệu) của sin (hoặc cos) với nhiều cung khác nhau ta cần để ý đến
các cung có tổng (hiệu) các góc bằng nhau để áp dụng công thức tổng sang tích.
Bài 2. Giải các phương trình sau
sin sin 2 sin 3 sin 4 sin 5 sin 6 0
x x x x x x
3 3
2 3 2
cos 3 cos sin 3 sin
8
x x x x
1 sin cos 3 cos sin2 cos2
x x x x x
3 3
cos sin sin 2 sin cos
x x x x x
Hướng dẫn giải
Nhận xét: Bài toán có các cung khác nhau biểu diễn dưới dạng tổng (hiệu) của các hàm số sin (hàm
số cos) ta nên ghép các số hạng này thành cặp sao cho tổng (hiệu) các cung của chúng bằng nhau, cụ
thể trong trường hợp này ta để ý
6 2 5 3 4
x x x x x x
. Tại sao lại cần phải ghép như vậy?
Lý do là chúng ta cần xuất hiện thừa số chung để nhóm ra ngoài, đưa bài toán về dạng tích.
PT
(sin 6 sin ) (sin 5 sin 2 ) (sin 4 sin 3 ) 0
x x x x x x
7 5 3 7 3
2 sin cos cos cos 0 4 sin cos (2 cos 1) 0
2 2 2 2 2 2
x x x x x x
x
Vậy phương trình có nghiệm
2 2 2
, , 2 , .
7 3 3 3
k k
x x x k k
Đối với bài này mà sử dụng công thức nhân ba của sin và cos thì cũng ra nhưng phức tạp hơn.
Chính vì thế mà ta khéo léo phân tích để áp dụng công thức tích sang tổng.
2 2
1 1 2 3 2
(2) cos 4 cos 2 cos (cos 4 cos 2 )sin
2 2 8
x x x x x x
2 2 2 2 2
2 3 2 2 3 2
cos 4 sin cos cos2 cos sin cos 4 cos 2
4 4
x x x x x x x x
2 3
cos 4 .
2 16 2
x x k
(ĐHNT HCM 2000) PT
1 cos2 sin sin 2 cos 3 cos 0
x x x x x
2
2 sin sin 2 sin cos 2 sin 2 sin 0
x x x x x x
sin (2 sin 2 cos 2 sin 2 1) 0
x x x x
sin 0
2(sin cos ) 4 sin cos 1 0
x
x x x x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
29
ĐS:
7
, 2 , 2 , 2 .
3 6 6
x k x k x k x k
(ĐHCS 2000) PT
3 3
2 sin cos sin sin cos cos 0
x x x x x x
2 2
2 sin cos sin cos cos sin 0
x x x x x x
sin cos (2 sin cos ) 0
x x x x
ĐS:
2
x k
.
Bài 3. Giải các phương trình sau
sin2 sin 5 sin 3 sin 4
x x x x
4 4
3
cos sin cos sin 3 0
4 4 2
x x x x
(D2005)
3 cos 5 2 sin 3 cos2 sin 0
x x x x
(D2009)
3
sin cos sin 2 3 cos 3 2(cos 4 sin )
x x x x x x
(B2009)
Hướng dẫn giải
1 1
(cos7 cos3 ) (cos 7 cos )
2 2
x x x x
cos 3 cos
x x
3 2
2
x x k x k
.
PT
2
1 1 3
1 sin 2 sin 4 sin 2 0
2 2 2 2
x x x
2
sin 2 sin 2 2 0
x x
(loai)
sin 2 1
,( ).
sin 2 2
4
x
x k k
x
Nhận xét: Từ sự xuất hiện các cung
5 , 3 ,2 ,
x x x x
và
3 2 5
x x x
ta nghĩ ngay đến việc áp dụng
công thức tích sang tổng để đưa về cung
5
x
. Còn cung
x
thì xử lí thế nào, ta quan sát lời giải sau:
PT
3 1
3 cos 5 sin 5 sin sin 0 cos 5 sin 5 sin
2 2
x x x x x x x
sin 5 sin
3
x x
12 3
6 2
x k
x k
Vậy phương trình có nghiệm: ;
12 3 6 2
x k x k
.
Chú ý: Đối với dạng phương trình
sin cos ' sin 'cos , 0,1
a x b x a kx b kx k
ta coi như 2 về
của phương trình là 2 phương trình bậc nhất với sin và cos. Do đó ta có cách làm tương tự.
PT
2
sin (1 2 sin ) cos sin 2 3 cos 3 2 cos 4
x x x x x x
1 3
sin 3 3 cos 3 2 cos 4 sin 3 cos 3 cos 4
2 2
x x x x x x
2
6
cos 4 cos 3 4 3 2
6 6
42 7
x k
x x x x k
x k
( )
k
.
3. Sử dụng công thức hạ bậc
Khi giải các phương trình lượng giác mà bậc của sin và cos là bậc chẵn ta thường hạ bậc từ đó đưa về
phương trình cơ bản.
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
30
Bài 4. Giải các phương trình sau
2 2 2
3
sin sin 2 sin 3
2
x x x
2 2 2 2
sin 3 cos 4 sin 5 cos 6
x x x x
(B02)
2 2 2
sin tan cos 0
2 4 2
x x
x
(D03)
2 2
cos 3 cos 2 cos 0
x x x
(A05)
Hướng dẫn giải
(ĐHAG2000) Từ sự xuất hiện bậc chẵn của hàm số sin và tổng hai cung
6 2
4
2
x x
x
mà ta
nghĩ đến việc hạ bậc và sử dụng công thức biến tổng sang tích sau đó nhóm các hạng tử để đưa về
phương trình tích.
PT
cos 2 cos 4 cos 6 0 cos 4 (2 cos 2 1) 0
x x x x x
cos 4 0
1
cos2
2
x
x
Vậy phương trình có nghiệm:
, .
8 4 3
k
x x k
PT
1 cos 6 1 cos 8 1 cos10 1 cos12
2 2 2 2
x x x x
(cos12 cos10 ) (cos 8 cos 6 ) 0 2 cos11 cos 2 cos 7 cos
0
x x x x x x x x
cos (cos11 cos 7 ) 0 cos sin 9 sin 2 0
x x x x x x
.
Vậy phương trình có nghiệm:
; ,( ).
9 2
x k x k k
Điều kiện:
cos 0.
x
PT
2
2 2
2
1 sin 1
1 cos 1 cos (1 sin )sin (1 cos ) cos
2 2 2
cos
x
x x x x x x
x
(1 sin )(1 cos )(sin cos ) 0
x x x x
ĐS: Kết hợp với điều kiện ta được
2 , .
4
x k x k
PT
1 cos 6 1 cos 2
cos2 0 cos 6 . cos2 1 0
2 2
x x
x x x
cos 8 cos 4 2 0
x x
2
2 cos 4 cos 4 3 0 cos 4 1 .
2
x x x x k
Bài 5. Giải các phương trình sau
2
2 sin 2 sin 7 1 sin
x x x
(B07)
4 4
cos sin 1
4
x x
2
(2 3)cos 2 sin 2 cos 1
2 4
x
x x
3 2
2
3(1 sin )
3tan tan 8cos 0
4 2
cos
x x
x x
x
Hướng dẫn giải
PT
2
sin 7 sin (1 2 sin 2 ) 0 2 cos 4 .sin 3 cos 4 0
x x x x x x
cos 4 (2 sin 3 1) 0
x x
.
Vậy PT có nghiệm:
2 5 2
, , .
8 4 18 3 18 3
x k x k x k
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
31
(ĐHL1995)
2 2
(1 cos 2 ) (1 sin 2 ) 1 sin 2 cos2 1
x x x x
2 cos 2 1
2
x
,( ).
2 4
x k x k k
(DB03)
1 3
3 cos sin 0 sin cos 0 sin 0
2 2 3
x x x x x
.
3
x k
(KT1999)
3
2
3(1 sin )
3 tan tan 4(1 sin ) 0
cos
x
x x x
x
2 2
tan (3 tan 1) (1 sin )(3 tan 1) 0
x x x x
2
(3 tan 1)(tan 1 sin ) 0
x x x
TH1:
1
tan , .
6
3
x x k k
TH2:
1 sin tan 0 sin cos sin cos 0
x x x x x x
(pt đối xứng với sin và cos)
Giải phương trình này được
2 1
arccos 2 , .
4 2
x k k
4. Sử dụng các đẳng thức lượng giác quan trọng (hằng đẳng thức)
Bài 6. Giải các phương trình sau
2
sin cos 3 cos 2
2 2
x x
x
(D07)
2
cot tan 4 sin 2
sin 2
x x x
x
(B03)
3
tan cot 2 cot 2
x x x
tan cot 2(sin 2 cos2 )
x x x x
Hướng dẫn giải
1 2 sin cos 3 cos 2
2 2
x x
x
sin 3 cos 2
x x
1 3
sin cos 1
2 2
x x
2
1
6
sin
3 2
2
2
x k
x
x k
( ).
k
Nhận xét: Từ sự xuất hiện của
cot tan
x x
và
sin 2
x
ta xem chúng có mối quan hệ nào?
Ta có
2 2
cos sin cos2
cot tan 2
sin cos sin 2
x x x
x x
x x x
. Từ đó ta định hướng giải cho bài toán như sau:
Điều kiện:
sin 2 0
2
x x k
PT
cos 2 2
2 4 sin 2
sin 2 sin 2
x
x
x x
2 2
cos 2 2 sin 2 1 2 cos 2 cos 2 1 0
x x x x
(lo¹i)
(t/m)
2
cos 2 1 sin 2 0
.
1 3
3
cos 2 sin 2
2 4
x x
x k
x x
Chú ý: Ta có thể đặt
2
1 2
tan cot , sin 2
1
t
t x x x
t
t
đưa phương trình về ẩn
t
để giải.
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
32
(ĐHQGHN1996) Điều kiện
sin 2 0
2
x x k
PT
3 3
sin cos cos2
2 cot 2 2 2 cot 2
cos sin sin 2
x x x
x x
x x x
3
cot2 cot 2 0
x x
(t/m).
cot2 0
4 2
x x k
(GTVT1998) Điều kiện:
sin 2 0
2
x x k
PT
sin cos
2(sin 2 cos 2 )
cos sin
x x
x x
x x
2
2(sin 2 cos 2 )
sin 2
x x
x
2
1 sin 2 sin 2 cos2
x x x
2
cos 2 sin 2 cos 2
x x x
cos2 0
4 2
,( ).
tan 2 1
8 2
x k
x
k
x
x k
Bài 7. Giải các phương trình sau
6 6 2
13
cos sin cos 2
8
x x x
6 6
2(cos sin ) sin cos
0
2 2 sin
x x x x
x
(A06)
4 4
cos sin 1 1
cot2
5 sin 2 2 8 sin 2
x x
x
x x
2 cos 4
cot tan
sin 2
x
x x
x
Hướng dẫn giải
Nhận xét: Xuất hiện
6 6
cos sin
x x
ta nghĩ đến việc sử dụng hằng đẳng thức
3 3
a b
.
PT
2 2 4 4 2 2 2
13
(cos sin )(cos sin sin cos ) cos 2
8
x x x x x x x
2 2 2
1 1 13
cos 2 (1 sin 2 sin 2 ) cos 2
2 4 8
x x x x
2
cos 2 (8 2 sin 2 13 cos 2 ) 0
x x x
2
cos 2 0
cos2 0
4 2
1
2 cos 2 13 cos2 6 0
cos 2
2
6
x
x k
x
x x
x
x k
( ).
k
Điều kiện:
2
1
4
sin
3
2
2
4
x k
x
x k
PT
4 4 2 2
2(cos sin sin cos ) sin cos 0
x x x x x x
2 2
2 6 sin cos sin cos 0
x x x x
2
3 sin 2 sin 2 4 0 sin 2 1
4
x x x x k
.
Kết hợp với điều kiện ta được nghiệm của phương trình là
5
2 , .
4
x k k
(DB2002) Điều kiện:
sin 2 0
2
x x k
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
33
PT
2
1
1 sin 2
1 cos 2 1
2
5 sin 2 2 sin 2 8 sin 2
x
x
x x x
2
9
cos 2 5 cos 2 0
4
x x
1
cos2 .
2 6
x x k
Điều kiện:
sin 2 0
2
x x k
PT
2
2 cos 2 2 cos 4
2 cos 2 cos 2 1 0
sin 2 sin 2
x x
x x
x x
1 2
cos 2 .
2 3
x x k
Bài 8. Giải các phương trình sau
(1 tan )(1 sin 2 ) 1 tan
x x x
cot sin (1 tan tan ) 4
2
x
x x x
(B06)
(1 sin cos 2 )sin
4
1
cos
1 tan
2
x x x
x
x
(1 2 sin )cos
3
(1 2 sin )(1 sin )
x x
x x
(A09)
Hướng dẫn giải
Điều kiện:
cos 0
2
x x k
PT
2
(cos sin )(sin cos ) sin cos
x x x x x x
2 2
(sin cos )(cos sin 1) 0
x x x x
2 2
sin cos 0
tan 1
cos 2 1
cos sin 1
x x
x
x
x x
(t/m)
(t/m)
4
x k
x k
.
Chú ý: Ta có thể đặt
2
2
tan sin 2
1
t
t x x
t
để đưa phương trình về dạng đại số ẩn
t
.
Điều kiện:
sin 0, cos 0, cos 0 ,
2 2
x
x x x k k
PT
cos cos sin sin
2 2
cot sin 4
cos cos
2
x x
x x
x x
x
x
cot tan 4 1 4 sin cos
x x x x
Giải
1
sin 2
2
x
và kết hợp với điều kiện, thu được nghiệm:
5
,
12 12
x k x k
( )
k
.
(A2010) Điều kiện:
cos 0
tan 1
x
x
PT
2 sin (1 sin cos 2 ) (1 tan ) cos
4
x x x x x
(sin cos )(1 sin cos 2 ) sin cos
x x x x x x
sin cos 2 0
x x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
34
2
2 sin sin 1 0
x x
1
sin
2
x
Kết hợp với điều kiện, thu được nghiệm của phương trình là:
7
2 , 2 .
6 6
x k x k
Điều kiện:
1
sin 1, sin
2
x x
PT
(1 2 sin )cos 3(1 2 sin )(1 sin )
x x x x
2
cos 3 sin sin2 3(1 2 sin )
x x x x
1 3 1 3
cos sin sin 2 cos 2
2 2 2 2
x x x x
cos cos 2
3 6
x x
2 .
2 18 3
x k x k
Kết hợp với điều kiện ta được nghiệm của phương trình là
2
( ).
18 3
x k k
Chú ý: Có thể sử dụng đẳng thức
2
cos cos 1 sin
1 sin cos (1 sin ) cos
x x x
x x x x
đưa phương trình về
dạng
sin cos 2
3 sin sin 2
cos sin 2 3 6
x x
x x
x x
.
KĨ THUẬT 2: ĐƯA VỀ PHƯƠNG TRÌNH TÍCH
Xu hướng trong đề thi đại học những năm gần đây việc giải phương trình lượng giác thường đưa về
phương trình tích bằng cách sử dụng các công thức lượng giác, các phép biến đổi lượng giác, các kĩ
năng tách, nhóm các số hạng hợp lý để tạo ra nhân tử chung...
Bài 1. Giải các phương trình sau
1 sin cos sin 2 cos 2 0
x x x x
(2cos 1)(2sin cos ) sin2 sin
x x x x x
cos 2 3 sin 2 5 sin 3 cos 3
x x x x
2 sin (1 cos 2 ) sin 2 1 2 cos
x x x x
sin 2 cos 2 3 sin cos 1 0
x x x x
(sin2 cos2 )cos 2cos2 sin 0
x x x x x
Hướng dẫn giải
(B-2005)
2
sin cos 2 sin cos 2 cos 0
x x x x x
sin cos (1 2 cos ) 0
x x x
(D2004) PT
(2 cos 1)(2 sin cos ) sin (2 cos 1)
x x x x x
(2 cos 1)(sin cos ) 0
x x x
PT
2
1 2 sin 6 sin cos 5 sin 3 cos 3
x x x x x
2
3 cos (2 sin 1) (2 sin 5 sin 2) 0
x x x x
(2 sin 1)(3 cos sin 2) 0
x x x
(D2008)
2
4 sin cos 2 sin cos 1 2 cos
x x x x x
(2 cos 1)(2 sin cos 1) 0
x x x
(D2010) PT
2
2 sin cos (1 2 sin ) 3 sin cos 1 0
x x x x x
2
cos (2 sin 1) 2 sin 3 sin 2 0
x x x x
cos (2 sin 1) (2 sin 1)(sin 2) 0
x x x x
(2 sin 1)(cos sin 2) 0
x x x
(B2010) PT
2
2 sin cos cos 2 cos 2 cos 2 sin 0
x x x x x x
2
sin (2 cos 1) cos 2 (cos 2) 0
x x x x
sin cos 2 cos 2 (cos 2) 0
x x x x
cos 2 (sin cos 2) 0
x x x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
35
Bài 2. Giải các phương trình sau
1 1
2 2 sin
4 sin cos
x
x x
2
tan 2 cot 8 cos
x x x
2
2 tan cot 3
sin 2
x x
x
2
cos 2 cos (2 tan 1) 2
x x x
1 2(cos sin )
tan cot2 cot 1
x x
x x x
2
cos2 1
cot 1 sin sin 2
1 tan 2
x
x x x
x
Hướng dẫn giải
(ĐHQGHN1997) Điều kiện:
sin 2 0
2
x x k
PT
sin cos
2(sin cos )
sin cos
x x
x x
x x
sin cos 0 tan 1
sin 2 1 sin2 1
x x x
x x
Giải và kết hợp với điều kiện thu được:
,
4 4
x k x k
hay
.
4 2
x k
Điều kiện:
cos 2 0, sin 0
x x
PT
2
sin 2 sin
8 cos
cos2 cos
x x
x
x x
2
sin 2 sin cos 2 cos
8 cos
cos 2 sin
x x x x
x
x x
cos (1 8 cos cos2 sin ) 0
x x x x
cos 0
1
sin 4
2
x
x
ĐS:
5
.
2 24 2 24 2
x k x k x k
(ĐHNT1997) Điều kiện:
sin 0, cos 0
x x
2 sin cos 1
3
cos sin sin cos
x x
x x x x
2 2
2 sin cos 3 sin cos 1
x x x x
2
1 sin 3 sin cos 1 sin (sin 3 cos ) 0
x x x x x x
(lo¹i)
sin 0
sin 3 cos
x
x x
tan 3
x
.
3
x k
(DB2003) Điều kiện:
cos 0
x
2
sin
cos 2 2 cos 2
cos
x
x x
x
2
sin
2 cos 2 1 1 cos
cos
x
x x
x
2
1
2 sin 1 1 cos
cos
x x
x
2
(1 cos ) 2(1 cos ) cos 0
x x x
ĐS:
2 , 2 .
3
x k x k
Điều kiện:
cos .sin 2 .sin (tan cot2 ) 0
cot 1
x x x x x
x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
36
PT
1 2(cos sin ) cos sin 2
2 sin
sin cos2 cos cos
1
cos sin 2 sin
x x x x
x
x x x x
x x x
sin (2 cos 2) 0
x x
Kết hợp với điều kiện thu được nghiệm của phương trình là:
2 ,( ).
4
x k k
(A2003) Điều kiện:
cos 0, sin 0, tan 1
x x x
2 2
2
cos sin cos (cos sin )
sin sin cos
sin cos sin
x x x x x
x x x
x x x
1
(cos sin ) cos sin 0
sin
x x x x
x
2
cos sin 0
sin sin cos 1 0
x x
x x x
t/m)
2
tan 1
(
2 tan tan 1 0
4
x
x k
x x
Bài 3. Giải các phương trình sau
3 3 5 5
sin cos 2(sin cos )
x x x x
6 6 8 8
sin cos 2(sin cos )
x x x x
8 8 10 10
5
sin cos 2(sin cos ) cos 2
4
x x x x x
(ĐHNT HCM2000)
Hướng dẫn giải
3 2 3 2
sin (1 2 sin ) cos (2 cos 1)
x x x x
3 3
cos 2 (sin cos ) 0
x x x
cos 2 0
tan 1
x
x
.
(QGHN99) PT
6 2 6 2
sin (1 2 sin ) cos (2 cos 1) 0
x x x x
6 6
cos 2 (sin cos ) 0
x x x
cos 2 0
tan 1
x
x
.
PT
8 2 8 2
5
sin (1 2 sin ) cos (1 2 cos ) cos 2 0
4
x x x x x
8 8
5
cos2 cos sin 0
4
x x x
.
Bài 4. Giải các phương trình sau
3 tan (tan 2 sin ) 6 cos 0
x x x x
(DB2003)
2
3 tan 3 cot2 2 tan
sin 4
x x x
x
3 2
2
4 cos 2 cos (2 sin 1) sin 2 2(sin cos )
0
2 sin 1
x x x x x x
x
3
sin 2 cos 3 2 3 cos 3 3 cos 2 8( 3 cos sin ) 3 3 0
x x x x x x
6 3 4
8 2 cos 2 2 sin sin 3 6 2 cos 1 0
x x x x
3(cot cos ) 5(tan sin ) 2
x x x x
Hướng dẫn giải
(DB2003) Điều kiện:
cos 0
x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
37
PT
sin sin 2 sin cos
3 6 cos 0
cos cos
x x x x
x
x x
2 2 3
3 cos sin (1 2 cos ) 6 cos 0
x x x x
2 2
3 cos (1 2 cos ) sin (1 2 cos ) 0
x x x x
2 2
(1 2 cos )(3 cos sin ) 0
x x x
ĐS:
,( ).
3
x k k
* Điều kiện:
cos 3 0
cos 0
sin 4 0
sin 2 0
x
x
x
x
,
6 3 4
x k x k
PT
2
2(tan 3 tan ) (tan 3 cot2 )
sin 4
x x x x
x
2 sin 2 cos 2
cos 3 cos cos 3 sin 2 sin 4
x x
x x x x x
4 sin 4 sin 2 cos 2 cos 2 cos 3
x x x x x
4 sin 4 sin cos 3 cos 2 cos 3
x x x x x
4 sin 4 sin cos 3 cos 8 sin 2 cos 2 sin 2 sin 2 sin
x x x x x x x x x
sin 2 sin (4 cos 1) 0
x x x
(t/m)
1
cos 2
4
x
Cách 2 (Bạn Hồng& Thanh Tùng A1) Điều kiện:
,
6 3 4
x k x k
.
PT
3 tan 3 cot 2 2 tan tan 2 cot2
x x x x x
3 tan 3 2 tan tan 2 0
x x x
2(tan 3 tan ) tan 3 tan2 0
x x x x
2 sin 2 sin
0
cos 3 cos cos 3 cos 2
x x
x x x x
2 sin 2 cos 2 sin cos
0
cos 3 cos cos 2
x x x x
x x x
sin 2 4 cos 2 1 0
x x
(lo¹i)
sin 2 0
4 cos 2 1 0
x
x
(t/m)
1
cos 2
4
x
.
Vậy phương trình có nghiệm
1 1
arccos
2 4
x k
.
Điều kiện:
2
2 sin 1 0 cos 2 0
4 2
x x x k
PT
2 2
4 cos (cos sin ) 2 cos (cos sin ) 2(sin cos ) 0
x x x x x x x x
2(sin cos )(cos 1)(2 cos 1)
x x x x
Kết hợp với điều kiện thu được nghiệm của phương trình:
2
, .
3
x k k
PT
2 3 2
2 sin cos 6 sin cos 2 3 cos 6 3 cos 8( 3 cos sin ) 0
x x x x x x x x
2
2 cos (sin 3 cos ) 6 cos (sin 3 cos ) 8( 3 cos sin ) 0
x x x x x x x x
2
(sin 3 cos )(2 cos 6 cos 8) 0
x x x x
PT
3 3 3
2 2 cos (4 cos 3 cos ) 2 2 sin sin 3 1 0
x x x x x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
38
2 2
2 cos 2 cos cos 3 2 sin (2 sin sin 3 ) 2
x x x x x x
(1 cos 2 )(cos 2 cos 4 ) (1 cos2 )(cos 2 cos 4 ) 2
x x x x x x
2
2
2(cos 2 cos 2 cos 4 ) 2 cos 2 cos 2
4
x x x x x
2
cos2 .
2 8
x x k
Điều kiện:
sin 0, cos 0
x x
.
PT
3(cot cos 1) 5(tan sin 1) 0
x x x x
cos sin cos sin sin sin cos cos
3 5 0
sin cos
x x x x x x x x
x x
cos sin cos sin 0
3 5
sin cos
x x x x
x x
víi
2
2 1 0 ( sin cos 2 cos( ))
4
5
tan
3
t t t x x x
x
Đối chiếu với điều kiện thu được:
1 2
arccos 2
4
2
x k
,
3
arctan .
5
x k
KĨ THUẬT 3: ĐẶT ẨN PHỤ
1. Chọn góc để đặt ẩn phụ
Bài 1. Giải các phương trình sau
3 1
sin sin
10 2 2 10 2
x x
3
cos 2 sin 3
2 2
x
x
sin 3 sin 2 .sin
4 4
x x x
5 3
sin cos 2 cos
2 4 2 4 2
x x x
Hướng dẫn giải
Nhận xét: Nhìn vào phương trình này ta nghĩ dùng công thức biến đổi sin của một tổng ... nhưng
đừng vội làm như thế khó ra lắm, ta xem mối quan hệ giữa hai cung
3
10 2
x
và
3
10 2
x
có
quan hệ với nhau như thế nào?
Thật vậy nếu ta đặt
3 9 3 3
3
10 2 10 2 10 2
x x x
t t
thì khi đó sử dụng công thức
góc nhân ba là biến đổi dễ dàng.
PT
3 2
sin 0
1 1
sin sin 3 sin 3 sin 4 sin sin (1 sin ) 0
cos 0
2 2
t
t t t t t t t
t
Vậy nghiệm của phương trình là:
3 3
2 , 4 , .
5 5 6
x k x k k
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
39
Chú ý: Nếu không quen với cách biến đổi trên, ta có thể làm như sau:
3 3 3
2
10 2 5 10 2
x x
t x t t
.
Đặt
3
3 2
2 2
x
t x t
. PT
2
cos(3 2 ) 2 sin 3 sin sin 2 0
t t t t
.
Đặt
4
t x
. ĐS:
4 2
k
x
Đặt
3 3 5
3 , 5
2 4 2 4 2 4
x x x
t t t
.
PT
3
sin(5 t ) cos 2 cos 3
4
t t
sin 5 cos cos 3 sin 3
t t t t
sin 5 sin 3 cos 3 cos
t t t t
2 sin (cos 4 sin 2 ) 0
t t t
.
Chú ý: Có thể chuyển
3
cos sin
2 4 4 2
x x
rồi áp dụng công thức tổng sang tích cho vế trái.
Bài 2. Giải các phương trình sau
3
8 cos cos 3
3
x x
3
tan tan 1
4
x x
2 3
2 cos 6 sin 2 sin 2 sin
5 12 5 12 5 3 5 6
x x x x
Hướng dẫn giải
Đặt
3
t x
. ĐS:
2
, ,
6 3
x k x k x k
Đặt
4
t x
. PT
3 3
1 tan
tan 1 (1 tan ) tan 2 tan
1 tan
t
t t t t
t
.
(ĐHYTB1997) ĐS:
5 5 5
5 , 5 , 5 .
4 12 3
x k x k x k
2. Chọn biểu thức để đặt ẩn phụ
Bài 3. Giải các phương trình sau
6
3 sin 4 cos 6
3 sin 4 cos 1
x x
x x
sin 3 cos sin 3 cos 2
x x x x
2
2
1 1
cos cos
cos
cos
x x
x
x
2 2 2
2 cos 2 cos 2 4 sin 2 cos
x x x x
1 3 tan 2 sin 2
x x
2 2
3 cot 2 2 sin (3 2 2)cos
x x x
Hướng dẫn giải
Đặt
3 sin 4 cos 1
t x x
(
0
t
). Từ phương trình ta có
2
1
7 6 0
6
t
t t
t
.
Đặt
sin 3 cos ,( 0)
t x x t
. Từ phương trình ta có
1, 2
t t
(loại).
Vậy
sin 3 cos 1 sin sin
3 6
x x x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
40
Đặt
2 2
2
1 1
cos cos 2
cos
cos
t x x t
x
x
. Từ phương trình ta có
1, 2
t t
.
2 2
2 cos 2 cos2 2(1 cos 2 )(1 cos2 )
x x x x
. Do đó ta đặt
cos 2 , 1
t x t
.
Đặt
2
2
tan sin 2
1
t
t x x
t
.
Ngoài ra ta có thể khai triển đưa về phương trình đẳng cấp bậc 3 theo sin và cos.
2
2
2
(1 cos )
3 2 2(1 cos ) (3 2 2)cos
cos
x
x x
x
. Do đó đặt
cos , 1
t x t
Chú ý: Có thể đưa phương trình về dạng tích
2 2
(sin cos )(3 cos 2 2 sin ) 0
x x x x
.
KĨ THUẬT 4: NHÓM BÌNH PHƯƠNG
1. Biến đổi phương trình về dạng A
2
+ B
2
= 0
Bài 1. Giải các phương trình sau
2 2
4 cos 3 tan 4 3 cos 2 3 tan 4 0
x x x x
2
3 sin 2 2 sin 2 cos 2 2 2 sin
x x x x
2
4 cos 2 2 cos 2 6 4 3 sin
x x x
Hướng dẫn giải
PT
2 2
(4 cos 4 3 cos 1) (3 tan 2 3 tan 1) 0
x x x x
2 2
2 cos 3 3 tan 1 0
x x
2 cos 3 0
3 tan 1 0
x
x
2 .
6
x k
Nhận xét: Vì xuất hiện
2
sin 2
x
và
2 sin 2
x
ta nghĩ đến việc đưa về
2
(sin 2 1)
x
do đó ta biến
đổi như sau:
PT
2
sin 2 2 sin 2 1 (1 cos2 ) 2 2 sin 1 0
x x x x
2
2
sin 2 1 2 sin 1 0
x x
2
1
4
sin
3
2
2
4
x k
x
x k
.
Nhận xét: Vì xuất hiện
2
4 cos 2
x
và
cos2
x
ta nghĩ đến việc đưa về
2
(2 cos 2 1)
x
, phần còn lại
ta biến đổi về
2
sin
x
.
PT
2 2
4 cos 2 4 cos 2 1 4 sin 4 3 sin 3 0
x x x x
2
2
2 cos 2 1 2 sin 3 0
x x
3
sin
2
1
cos 2
2
x
x
2
3
3
sin
2
2
2
3
x k
x
x k
.
2. Biến đổi phương trình về dạng A
2
= B
2
Bài 2. Giải các phương trình sau
2
sin 2 2 tan tan
x x x
2 2 2
tan sin 2 4 cos
x x x
2
2
1
4 tan 4 tan 2
sin
x x
x
2
2 cos 2
4 cot 4 cot
1 cos 2
x
x x
x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
41
2
sin 2 cos 2 cos 3 cos
x x x x
2 2 2
cos 3 cos 3 cos 2 cos 2 2
x x x x
6
32 cos sin 3 3 sin
2
x
x x
Hướng dẫn giải
PT
2
1 2 sin cos 1 2 tan tan
x x x x
2 2
(sin cos ) (1 tan )
x x x
Nhận xét: Ta nhận thấy
2
tan sin 2 2 sin
x x x
do đó ta cộng vào 2 vế 1 lượng
2
4 sin
x
.
PT
2 2 2 2
tan 2 tan sin 2 sin 2 4 cos 4 sin
x x x x x x
2
(tan sin 2 ) 4
x x
Nhận xét: Vì chúng ta nhận thấy xuất hiện
2
4 tan
x
và
4 tan
x
nên ta chuyển vế để đưa về dạng
hằng đẳng thức
2
(2 tan 1)
x
.
PT
2
2
1
1 4 tan 4 tan 1
sin
x x
x
2 2
cot (2 tan 1) 2 tan 1 cot
x x x x
Nhận xét: Vì nhìn thấy xuất hiện
2
4 cot
x
và
4 cot
x
nên ta chuyển vế để xuất hiện
2
(2 cot 1)
x
.
PT
2
cos2 1
4 cot 4 cot 1 0
1 cos 2
x
x x
x
2
2
2
sin
2 cot 1 0
cos
x
x
x
2
2
2 cot 1 tan
x x
2 cot 1 tan
x x
.
Nhận xét: Do xuất hiện nhiều góc khác nhau nên ta biến đổi
cos 3 cos 2 sin 2 sin
x x x x
,
sau đó do vế trái có
2
sin 2
x
nên ta đưa về
2
(sin 2 sin )
x x
.
PT
2
sin 2 cos 2 2 sin 2 sin
x x x x
2 2
(sin 2 sin ) cos2 sin
x x x x
2 2
(sin 2 sin ) cos
x x x
Nhận xét: Do xuất hiện
2 2
cos 3 cos
x x
nên ta nghĩ đến hằng đẳng thức
2
(cos 3 cos )
x x
. Vì
thế ta cộng thêm cả hai vế với
2 cos 3 cos
x x
và ở vế phải ta dùng công thức biến đổi tích sang tổng
2 cos 3 cos cos 4 cos2
x x x x
.
PT
2 2 2
cos 3 2 cos 3 cos cos 2 3 cos 2 cos 2 2 cos 3 cos
x x x x x x x x
2 2
(cos 3 cos ) 2 3 cos 2 cos 4
x x x x
2 2
(cos 3 cos ) sin 2
x x x
6
32 cos sin 3 3 sin
2
x
x x
6
32 cos 3 sin sin 3
2
x
x x
3
2 3
4 2 cos 4 sin
2
x
x
1 cos sin
x x
2 sin 1
4
x
.
KĨ THUẬT 5: XỬ LÍ PHƯƠNG TRÌNH CÓ ĐIỀU KIỆN
1. Biểu diễn nghiệm và điều kiện qua cùng một hàm số lượng giác
Trong phần này cần sử dụng tốt các kết quả sau:
2
sin 0 cos 1;
x x
cos 0 sin 1
x x
sin 0 cos 1
sin 2 0
cos 0 sin 1
x x
x
x x
2
cos 1 sin 0;
x x
sin 1 cos 0
x x
cos 1 sin 0
sin 2 0
sin 1 cos 0
x x
x
x x
Bài 1. Giải các phương trình sau
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
42
1 1 2
cos sin 2 sin 4
x x x
(THTT09)
2 4
sin 2 cos 2 1
0
sin cos
x x
x x
cot sin 1 tan tan 4
2
x
x x x
(B06)
(1 sin cos2 )sin
4
1
cos
1 tan
2
x x x
x
x
4 4
4
sin 2 cos 2
cos 4
tan tan
4 4
x x
x
x x
Hướng dẫn giải
(THTT09) Điều kiện:
cos 0, sin 1,
sin 2 0, sin 0,
sin 4 0
2
sin
2
x x
x x
x
x
Khi đó PT
2
4 sin cos 2 2 cos 2 2 sin 2 sin sin 1 0
x x x x x x
Giải các nghiệm
sin
x
và kết hợp điều kiện ta được:
2
1
6
sin
5
2
2
6
x k
x
x k
.
Điều kiện:
sin 2 0
x
. Khi đó phương trình đã cho trở thành
2
2 4 4 2
2
cos 2 0 sin2 1
sin 2 cos 2 1 0 cos 2 cos 2 0
sin 2 0
cos 2 1
x x
x x x x
x
x
Đối chiếu với điều kiện ta được:
sin 2 1 .
4
x x k
(B2006) Điều kiện:
sin 0, cos 0, cos 0 sin 2 0
2
x
x x x
PT
cos sin
cos cos sin sin 4
sin 2 2
cos cos
2
x x x x
x x
x x
x
cos sin
4
sin cos
x x
x x
2
4
sin 2
x
(t/m)
1
sin 2
2
x
2 ,
12
5
12
x k
x k
( )
k
.
(A2010) Điều kiện:
cos 0 sin 1
tan 1 tan 1
x x
x x
Khi đó PT
(1 sin cos 2 ) sin cos cos
1
cos
2(cos sin ) 2
x x x x x
x
x x
1 sin cos 2 1
x x
2
sin 1 2 sin 0
x x
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
43
(lo¹i)
(t/m)
sin 1
1
sin
2
x
x
2
6
7
2
6
x k
x k
.
Điều kiện:
sin 0, cos 0, sin 0, cos 0.
4 4 4 4
x x x x
sin 2 0, cos 2 0 cos2 0 sin 2 1.
2 2
x x x x
Nhận thấy
tan tan 1
4 4
x x
, do đó phương trình đã cho trở thành
4 4 4 4 4
1
sin 2 cos 2 cos 4 1 sin 4 cos 4
2
x x x x x
4 2
2 cos 4 cos 4 1 0
x x
2
sin 2 0
cos 4 1 sin 4 0
cos 2 0
x
x x
x
.
Đối chiếu với điều kiện ta được
sin 2 0 ,( ).
2
x x k k
2. Biểu diễn trên đường tròn lượng giác
Mỗi cung (hoặc góc) lượng giác được biểu diễn bởi các điểm trên đường tròn lượng giác:
2
x k
được biểu diễn trên ĐTLG bởi 1 điểm xác định bởi cung
.
x k
được biểu diễn trên ĐTLG bởi 2 điểm đối xứng nhau qua tâm
O
.
2
3
x k
được biểu diễn trên ĐTLG bởi 3 điểm cách đều nhau, tạo thành 3 đỉnh một tam giác đều.
2
x k
n
được biểu diễn trên ĐTLG bởi
n
điểm cách đều nhau, tạo thành đa giác đều nội tiếp
đường tròn lượng giác.
Ta biểu diễn trên ĐTLG những điểm không thỏa mãn điều kiện (đánh dấu
) và những điểm
nghiệm tìm được (đánh dấu
). Những điểm đánh dấu "
" mà không trùng với những điểm đánh
dấu "
" chính là những điểm thỏa mãn điều kiện.
Bài 2. Giải các phương trình sau
sin 2 2 cos sin 1
0
tan 3
x x x
x
(D2011)
6 6
2(sin cos ) sin cos
0
2 2 sin
x x x x
x
(A06)
sin sin 2
1
sin 3
x x
x
(1 2 sin )cos
3
(1 2 sin )(1 sin )
x x
x x
(A2009)
Hướng dẫn giải
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
44
Điều kiện:
tan 3
cos 0
x
x
3
2
x k
x k
Khi đó phương trình đã cho trở thành:
sin2 2 cos sin 1 0
x x x
2cos (sin 1) (sin 1) 0
x x x
(sin 1)(2 cos 1) 0
x x
sin 1
2
2
1
cos
2
2
3
x
x k
x
x k
Kết hợp với điều kiện trên đường tròn lượng giác ta được nghiệm của PT là
2 , ( ).
3
x k k
Điều kiện:
2
2
4
sin
3
2
2
4
x k
x
x k
. Khi đó phương trình trở thành:
6 6
2(sin cos ) sin cos 0
x x x x
2
3 1
2 1 sin 2 sin 2 0
4 2
x x
2
3 sin 2 sin 2 4 0
x x
sin 2 1
x
4
x k
.
Kết hợp với điều kiện trên đường tròn LG ta được nghiệm của PT là:
5
2
4
x k
(
k
).
Điều kiện:
sin 3 0 .
3
x x k
Khi đó phương trình trở thành
sin sin 2 sin 3 0 sin 2 (2 cos 1) 0
x x x x x
sin 2 0
2
1
2
cos
2
2
3
x
x k
x
x k
Kết hợp với điều kiện trên đường tròn lượng giác, ta có nghiệm của PT là:
2
x k
.
Điều kiện:
sin 1
x
và
1
sin
2
x
(*)
Với điều kiện trên phương trình đã cho tương đương:
(1 2 sin ) cos 3(1 2 sin )(1 sin )
x x x x
cos 3 sin sin 2 3 cos 2
x x x x
cos cos 2
3 6
x x
2
2
x k
hoặc
2
18 3
x k
.
Kết hợp điều kiện (*) ta được nghiệm:
2
( ).
18 3
x k k
3. Thử trực tiếp (dùng mệnh đề phủ định)
Chúng ta cần lưu ý các kết quả về tính chu kì của hàm số lượng giác sau đây:
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
45
sin( 2 ) sin ,
x k x x
cos( 2 ) cos ,
x k x x
tan( ) tan ,
2
x k x x k
cot( ) cot ,
x k x x k
Bài 3. Giải các phương trình sau
2
1 sin 2 cos2
2 sin sin 2
1 cot
x x
x x
x
1
3 sin 2 cos 3(1 tan )
cos
x x x
x
cos 3 . tan 5 sin 7
x x x
tan 5 tan 2 1
x x
Hướng dẫn giải
Điều kiện:
sin 0 cos 1.
x x
Khi đó phương trình đã cho trở thành
2 2
sin (1 sin 2 cos 2 ) 2 2 sin cos
x x x x x
2
1 2 sin cos 2 cos 1 2 2 cos
x x x x
(t/m) cos 0
2 cos (sin cos 2) 0
2
sin cos 0 (*)
x x k
x x x
x x
Dùng mệnh đề phủ định: Giả sử
sin 0 cos 1
x x
, khi đó
(*) 0 1 2
(vô lí). Tức
là các nghiệm của (*) đều thỏa mãn. Giải (*) ta được:
cos 1
4
x
2
4
x k
.
Vậy phương trình có nghiệm:
, 2 .
2 4
x k x k
Điều kiện:
cos 0 sin 1.
x x
Khi đó phương trình đã cho trở thành
cos (3 sin 2 cos ) 3(sin cos ) 1
x x x x x
cos (3 sin 2 cos ) cos 3 sin 2 cos 1
x x x x x x
(t/m)
cos 1 2
(3 sin 2 cos 1)(cos 1) 0
3 sin 2 cos 1 (*)
x x k
x x x
x x
Xét (*): Giả sử
cos 0 sin 1.
x x
, khi đó
(*) 3 1 0
(vô lí). Tức là các nghiệm
của (*) đều thỏa mãn. Giải (*) ta được:
arccos 2
13
x k
(với
2 3
cos ;sin
13 13
).
Vậy phương trình có nghiệm:
1
2 , arccos .
13
x k x k
Điều kiện:
cos 5 0 , ( )
10 5
x x m m
. Khi đó phương trình trở thành
2 sin 5 cos 3 2 sin 7 cos 5 sin 8 sin12
x x x x x x
2
( )
20 10
x k
k
x k
+ Giả sử
5 1 2
2 10 5
k m k m
(*). Suy ra
1
2
2
k
m k
.
Mặt khác, do
,
k m
nên tồn tại
s
sao cho:
1
2 1
2
k
s k s
(tức
k
là số lẻ).
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
46
Suy ra
2
x k
là nghiệm PT khi
2 1
k s
. Chọn
2
k s
thu được nghiệm là
x s
( )
s
.
+ Giả sử
1
2 4 1 2
20 10 10 5 2
k m k m k m
(**).
Ta nhận thấy
2
k m
,
1
2
nên không tồn tại
,
k m
thỏa mãn (**).
Do đó
20 10
x k
là nghiệm của PT với mọi
k
.
Vậy phương trình có nghiệm:
x s
và
20 10
x k
( , )
k s
.
Điều kiện:
(1)
cos 5 0
10 5
cos2 0
(2)
4 2
x m
x
x
x n
(
,
m n
).
PT
1
tan 5 tan 5 cot2 tan 5 tan 2
tan 2 2
x x x x x
x
.
14 7
x k
+ Đối chiếu điều kiện (1):
Giả sử
1 2
14 7 10 5 5
m
k m k m
(*)
Do
,
k m
nên tồn tại
t
sao cho:
1 2 1
2
5 2
m t
t m t
Mặt khác, do
,
t m
nên tồn tại
s
sao cho:
1
2 1
2
t
s t s
.
Thay vào (*) ta được:
7 3
k s
. Do đó
14 7
x k
thỏa mãn điều kiện (*) với
7 3.
k s
+ Đối chiếu điều kiện (2):
Giả sử
4 14 5
14 7 4 2
k n k n
(**).
Ta nhận thấy vế trái (**) là số chẵn, vế phải (**) là số lẻ nên không tồn tại
,
k n
thỏa mãn điều
kiện (**). Do đó
14 7
x k
luôn thỏa mãn điều kiện (**).
Vậy phương trình có nghiệm:
14 7
x k
với
7 3.
k s
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
47
Bài 1 (ĐH A2002) Tìm nghiệm thuộc khoảng (0; 2
) của phương trình :
cos 3 sin 3
5 sin cos 2 3
1 2 sin 2
x x
x x
x
. ĐS :
5
;
3 3
x x
Bài 2 (ĐH B2002) Giải phương trình :
2 2 2 2
sin 3 cos 4 sin 5 cos 6
x x x x
ĐS : ;
9 2
k k
x x
(
k
)
Bài 3 (ĐH D2002)Tìm
x
thuộc đoạn
0;14
nghiệm đũng của phương trình :
4
cos 3 4 cos 2 3 cos 0
x x x
ĐS :
3 5 7
; ; ;
2 2 2 2
x x x x
Bài 4 (ĐH A2003) Giải phương trình :
2
cos2 1
cot 1 sin sin 2
1 tan 2
x
x x x
x
ĐS :
4
x k
(
k
)
Bài 5 (ĐH B2003) Giải phương trình :
2
cot tan 4 sin 2
sin 2
x x x
x
ĐS :
3
x k
(
k
)
Bài 6 (ĐH D2003) Giải phương trình:
2 2 2
sin tan cot 0.
2 4 2
x x
x
ĐS :
2 ;
4
x k x k
Bài 7 (ĐH A2004) Cho tam giác ABC không tù, thỏa mãn điều kiện
cos 2 2 2 cos 2 2 cos 3.
A B C
Tính ba góc của tam giác ABC. ĐS :
0 0
90 ; 45
A B C
Bài 8 (ĐH B2004) Giải phương trình:
2
5 sin 2 3(1 sin ) tan
x x x
ĐS :
5
2 ; 2
6 6
x k x k
Bài 9 (ĐH D2004) Giải phương trình:
(2 cos 1)(2 sin cos ) sin 2 sin
x x x x x
ĐS :
2 ;
3 4
x k x k
Bài 10 (ĐH A2005) Giải phương trình:
2 2
cos 3 cos 2 cos 0
x x x
ĐS :
2
k
x
(
k
)
Bài 11 (ĐH B2005) Giải phương trình:
1 sin cos sin 2 cos 2 0
x x x x
ĐS :
2
2 ;
3 4
x k x k
Bài 12 (ĐH D2005) Giải phương trình:
4 4
3
cos sin cos sin 3 0
4 4 2
x x x x
ĐS :
4
x k
(
k
)
Bài 13 (ĐH A2006) Giải phương trình:
6 6
2(cos sin ) sin cos
0
2 2 sin
x x x x
x
ĐS :
5
2
4
x k
(
k
)
LƯ
ỢNG GIÁC TRONG ĐỀ THI 2002
-
2014
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
48
Bài 14 (ĐH B2006) Giải phương trình:
cot sin 1 tan tan 4
2
x
x x x
ĐS :
5
;
12 12
x k x k
Bài 15 (ĐH D2006) Giải phương trình:
cos 3 cos 2 cos 1 0
x x x
ĐS :
2
; 2
3
x k x k
Bài 16 (ĐH A2007) Giải phương trình:
2 2
1 sin cos 1 cos sin 1 sin2
x x x x x
ĐS:
2 ; 2 ;
2 4
x k x k x k
Bài 17 (ĐH B2007) Giải phương trình
2
2 sin 2 sin 7 1 sin
x x x
ĐS :
2 5 2
; ;
8 4 18 3 18 3
k k k
x x x
Bài 18 (ĐH D2007) Giải phương trình :
2
sin cos 3 cos 2
2 2
x x
x
ĐS :
2 ; 2
2 6
x k x k
Bài 19 (ĐH A2008) Giải hệ phương trình:
1 1 7
4 sin
sin 4
3
sin
2
x
x
x
ĐS:
5
; ;
4 8 8
x k x k x k
Bài 20 (ĐH B2008) Giải phương trình:
3 3 2 2
sin 3 cos sin cos 3 sin cos
x x x x x x
ĐS:
;
4 2 3
k
x x k
Bài 21 (ĐH D2008) Giải phương trình:
2sin 1 cos2 sin2 1 2cos
x x x x
ĐS:
2
2 ;
3 4
x k x k
Bài 22 (ĐH A2009) Giải phương trình:
1 2 sin cos
3
1 2 sin 1 sin
x x
x x
ĐS:
2
18 3
k
x
(
k
)
Bài 23 (ĐH B2009) Giải phương trình:
3
sin cos sin 2 3 cos 3 2 cos 4 sin
x x x x x x
ĐS:
2
2 ;
6 42 7
k
x k x
Bài 24 (ĐH D2009) Giải phương trình:
3 cos 5 2 sin 3 cos 2 sin 0
x x x x
ĐS:
;
18 3 6 2
k k
x x
Bài 25 (ĐH A2010) Giải phương trình :
(1 sin cos 2 ) in( )
1
4
cos
1 tan
2
x x s x
x
x
ĐS:
7
2 ; 2
6 6
x k x k
Bài 26 (ĐH B2010) Giải phương trình:
2
(sin 2 cos )cos cos 2 sin 0
x x x x x
ĐS :
4 2
k
x
(
k
)
Bài 27 (ĐH D2010) Giải phương trình:
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam
49
sin 2 cos 2 3 sin cos 1 0
x x x x
ĐS:
5
2 ; 2
6 6
x k x k
Bài 28 (ĐH A2011) Giải phương trình:
2
1 sin 2 cos2
2 sin sin 2
1 cot
x x
x x
x
ĐS:
; 2
2 4
x k x k
Bài 29 (ĐH B2011) Giải phương trình:
sin 2 cos sin cos cos 2 sin cos
x x x x x x x
ĐS :
2
2 ;
2 3 3
k
x k x
Bài 30 (ĐH D2011) Giải phương trình :
sin 2 2 cos in 1
0
3 tan
x x s x
x
ĐS:
2
3
x k
(
k
)
Bài 31 (ĐH A2012) Giải phương trình :
3 sin 2 cos 2 2 cos 1
x x x
ĐS:
2
; 2 ; 2
2 3
x k x k x k
Bài 32 (ĐH B2012) Giải phương trình:
2(cos 3 sin )cos cos 3 sin 1
x x x x x
ĐS:
2 2
2 ;
3 3
k
x k x
(
k
)
Bài 33 (ĐH D2012) Giải phương trình:
sin 3 cos 3 sin cos 2 cos2
x x x x x
ĐS:
7
; 2 ; 2
4 2 12 12
k
x x k x k
Bài 34 (ĐH A2013) Giải phương trình:
1 tan 2 2 sin
4
x x
ĐS:
; 2
4 3
x k x k
Bài 35 (ĐH B2013) Giải phương trình:
2
sin 5 2 cos 1
x x
ĐS:
2 2
;
6 3 14 7
k k
x x
Bài 36 (ĐH D2013) Giải phương trình
sin 3 cos2 sin 0
x x x
ĐS:
7
; 2 ; 2
4 2 6 6
k
x x k x k
Bài 37 (ĐH A2014) Giải phương trình
sin 4 cos 2 sin 2
x x x
ĐS :
2
3
x k
(
k
)
Bài 38 (ĐH B2014) Giải phương trình
2(sin 2 cos ) 2 sin 2
x x x
ĐS :
3
2
4
x k
(
k
)
-----------------------------------------Hết-----------------------------------------
| 1/50
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


THAÏC SÓ. TRAÀN MAÏNH HAÂN BÍ QUYEÁT GIAÛI PHÖÔNG TRÌNH LÖÔÏNG GIAÙC
- CÁC KĨ THUẬT GIẢI PHƯƠNG TRÌNH ĐẶC SẮC
- CÁC MẸO LOẠI NGHIỆM NHANH, CHÍNH XÁC
- CÁCH BẤM MÁY TÍNH TÌM HƯỚNG GIẢI. HÀ NAM 8-2014
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
CÔNG THỨC LƯỢNG GIÁC CẦN NẮM VỮNG
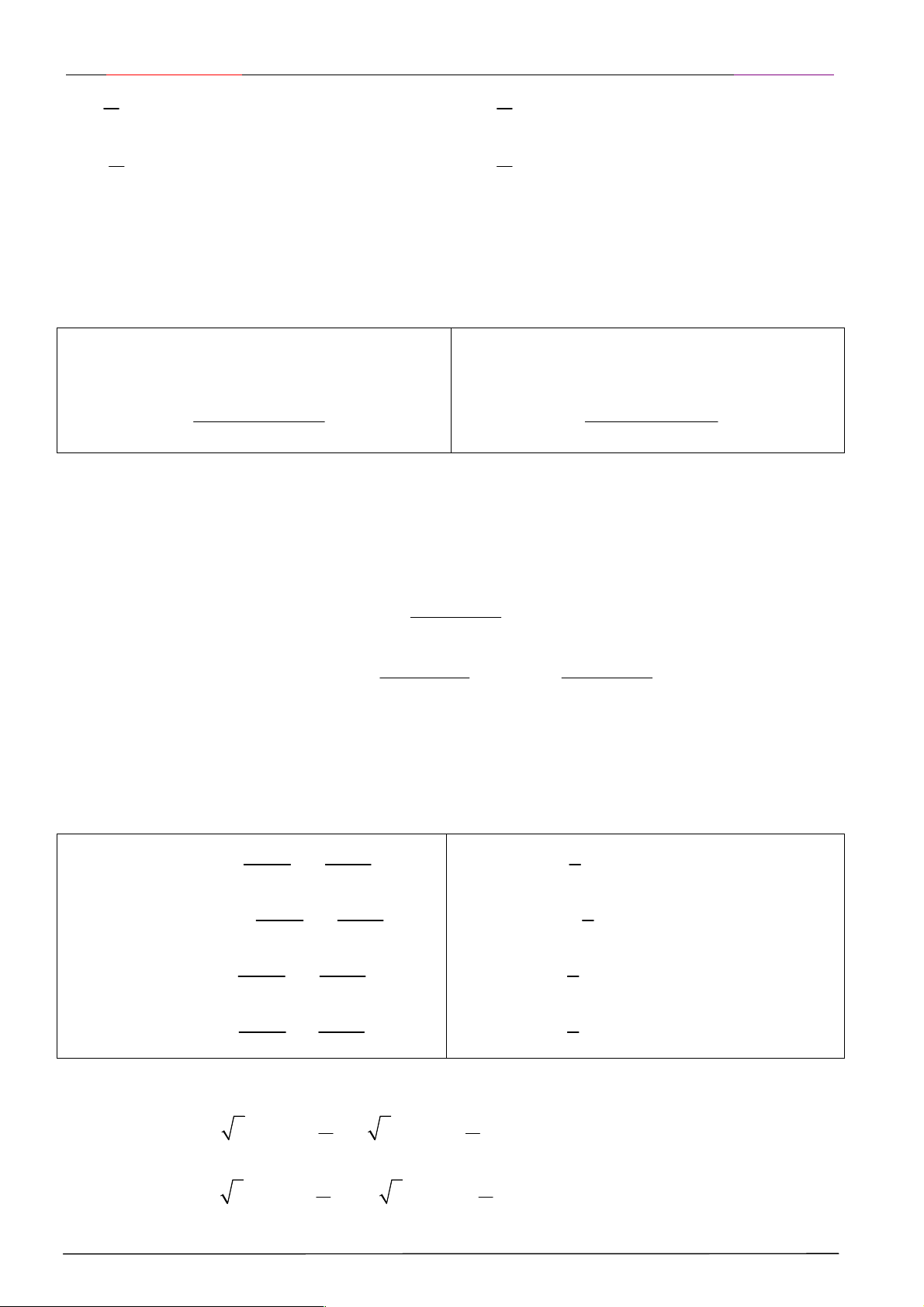
I. CÁC HỆ THỨC LƯỢNG GIÁC CƠ BẢN  2 2 sin 
x  1  cos x   2 2
sin x  cos x  1   2 2 c
 os x  1  sin x  1 1  2 2
 1  tan x  tan x   1 2 2 cos x cos x 1 1  2 2
 1  cot x  cot x   1 2 2 sin x sin x 1
 tan x. cot x  1  cot x  tan x  4 4 2 2 sin 
x  cos x  1  2 sin x cos x;    6 6 2 2 sin 
x  cos x  1  3 sin x cos x   3 3 si
 n x  cos x  (sin x  cosx)(1 sin x cosx)    3 3 si
 n x  cos x  (sin x  cosx)(1  sin x cosx) 
II. DẤU CỦA CÁC HÀM SỐ LƯỢNG GIÁC Góc I Góc II Góc III Góc IV sin x     cos x     tan x     cotx    
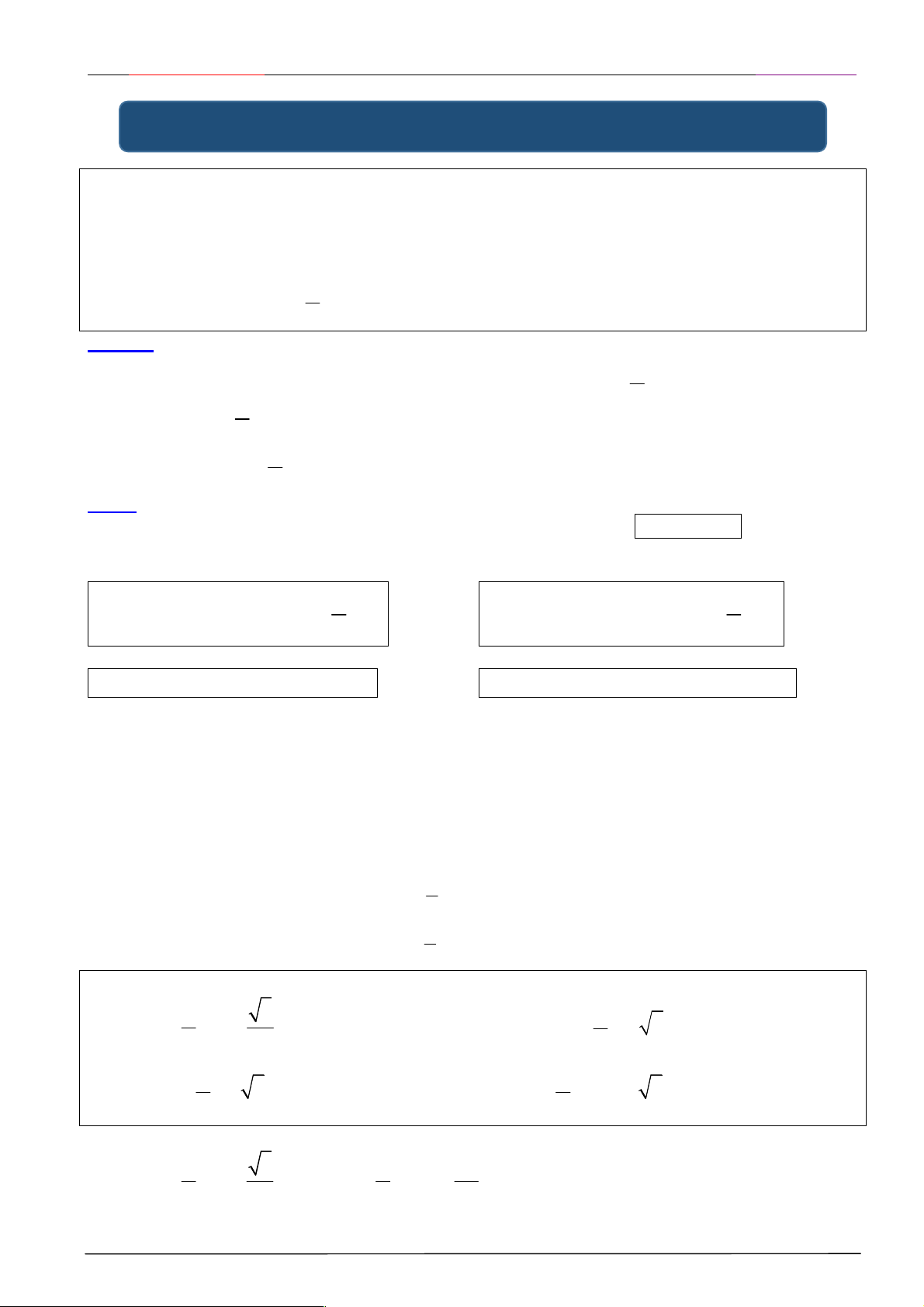
III. MỐI QUAN HỆ CỦA CÁC CUNG LƯỢNG GIÁC ĐẶC BIỆT  Hai cung đối nhau cos( x  )  cos x sin( x  )  sin x tan( x  )   tan x cot( x  )  cotx  Hai cung bù nhau
sin(x)  sin x
cos(x)  cos x
tan(x)   tan x
cot(x)  cotx  Hai cung phụ nhau
sin(  x)  cos x
cos(  x)  sin x 2 2
tan(  x)  cotx
cot(  x)  tan x 2 2
 Hai cung hơn nhau
sin(x)  sin x
cos(x)  cos x
tan(x)  tan x
cot(x)  cotx  Hai cung hơn nhau 2
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 1
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
sin(  x)  cosx
cos(  x)  sin x 2 2
tan(  x)  cotx
cot(  x)  cotx 2 2
 Với k là số nguyên thì ta có: sin(x k2 )  sin x
cos(x k2)  cos x
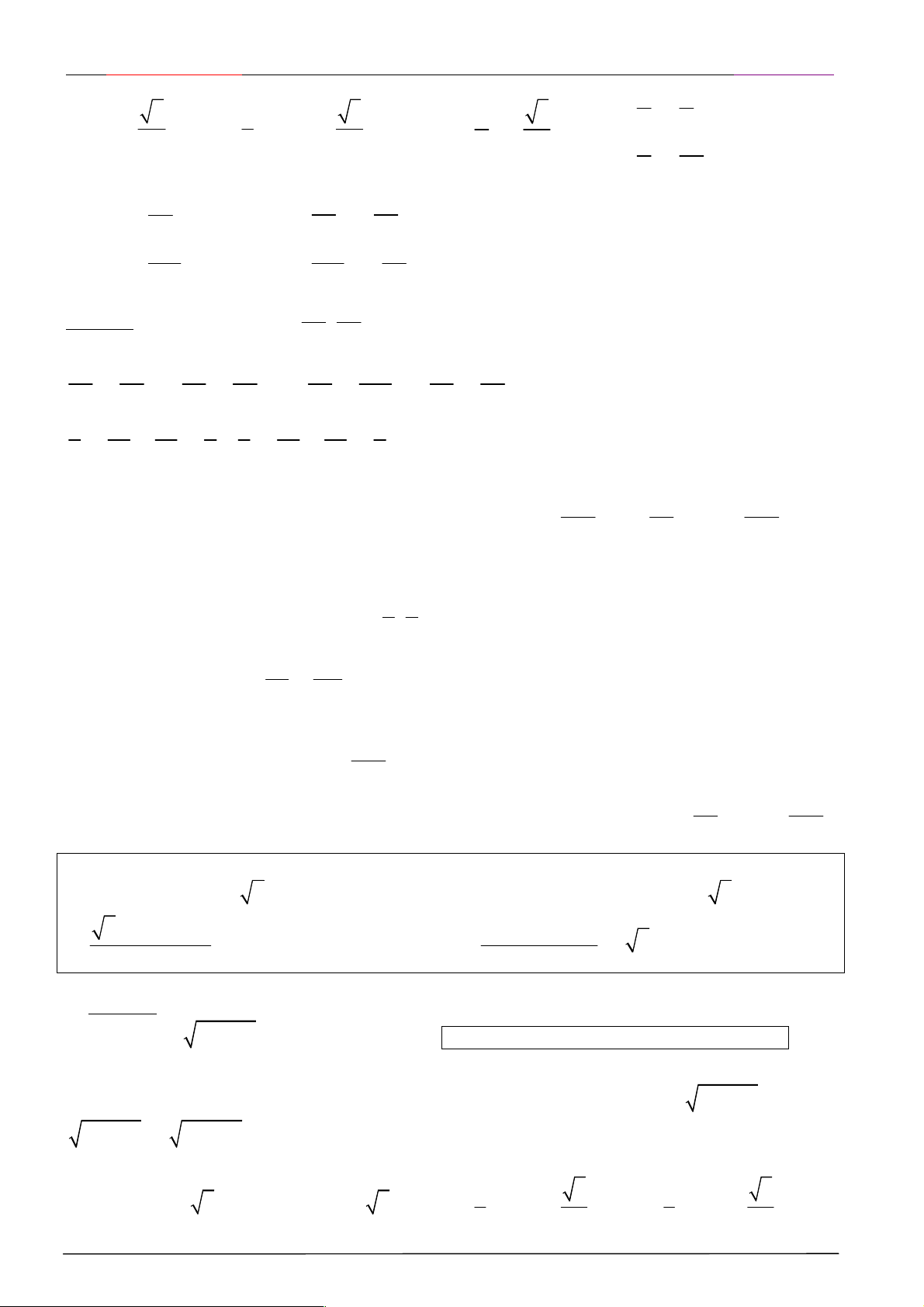
tan(x k)  tan x cot(x k )  cotx IV. CÔNG THỨC CỘNG
sin(x y)  sin x cosy  cos x sin y
sin(x y)  sin x cosy  cos x sin y
cos(x y)  cos x cosy  sin x sin y
cos(x y)  cosx cosy  sin x sin y tan x  tan y tan x  tan y tan(x y)  tan(x y) 
1  tan x tan y
1  tan x tan y Đặc biệt:
sin2x  2sinx cosx  2 2 2 2
TH1: Công thức góc nhân đôi: cos 
2x  cos x  sin x  2 cos x 1  1  2 sin x   2 tan x tan  2x   2  1  tan x 1  cos 2x 1  cos 2x 2 2
Hệ quả: Công thức hạ bậc 2: sin x  ;cos x  2 2  3 si
 n 3x  3 sin x  4 sin x
TH2: Công thức góc nhân ba:  3 cos 
3x  4 cos x  3 cos x 
V. CÔNG THỨC BIẾN ĐỔI TỔNG SANG TÍCH VÀ TÍCH SANG TỔNG x y x y 1
cos x  cos y  2 cos cos cos x cos y
cos(x y) cos(x y)     2 2 2   x y x y 1
cos x  cos y  2  sin cos sin x sin y
cos(x y) cos(x y)      2 2 2   x y x y 1
sin x  sin y  2 sin cos sin x cos y
sin(x y) sin(x y)     2 2 2   x y x y 1
sin x  sin y  2 cos sin cos x sin y
sin(x y) sin(x y)     2 2 2   Chú ý:        
 sin x  cos x  2 sin x     2 cos x      4     4         
 sin x  cos x  2 sin x
     2 cos x      4     4 
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 2
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN u
  v k2 u
  v k2   
sin u  sin v
 cos u  cos v u
  v k2      u v k2  u
  v k    u
  v k
 tan u  tan v  
 cot u  cotv   u   k u   k    2  Đặc biệt:
sin x  0  x k
cos x  0  x   k 2
sin x  1  x   k2
cos x  1  x k2 2 cos x  1
  x k2 sin x  1
  x    k2 2 Chú ý:
 Điều kiện có nghiệm của phương trình sin x m và cos x m là: 1   m  1.
 Sử dụng thành thạo câu thần chú " Cos đối - Sin bù - Phụ chéo" để đưa các phương trình dạng sau
về phương trình cơ bản:   
sin u  cos v  sin u  sin  v    u v u   v  cos sin cos cos  2  2 
sin u  sin v  sin u  sin( v  )
cos u  cos v  cos u  cos(v) 2 cos x 1   cos x  1    Đối với phương trình  
không nên giải trực tiếp vì khi đó phải giải 4 2 sin x  1 sinx  1    
phương trình cơ bản thành phần, khi đó việc kết hợp nghiệm sẽ rất khó khăn. Ta nên dựa vào công 2 cos x 1   sin x  0 2 2  
thức sin x  cos x  1 để biến đổi như sau:   sin 2x  0  . 2 sin x  1 cosx  0      1 2    2 cos x 2 cos x 1  0  
 Tương tự đối với phương trình 2    cos 2x  0  . 2  1 2 1  2 sin x  0 sin x     2
Bài 1. Giải các phương trình sau     2      cos x        x       2 sin 2 3 0  4  2  6           2 cos x     2  0    x    3 tan 3  3 3  Hướng dẫn giải:   2       3  cos x       cos x     cos   4  2  4  4
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 3
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 3
Ta xác định ở phương trình này u x  ,v
, nên dựa vào công thức nghiệm ta có 4 4 3 3 x  
k2 hoặc x     k2. 4 4 4 4
Vậy nghiệm của phương trình là: x k2; x  
k2, (k  )  . 2       3            2 sin 2
x    3  0   sin 2  x      sin 2
x    sin      6   6  2  6     3  
2x     k2x    k  6 3  12    k   ( ). 4    3 2x    k2 x   k  6 3    4       2        2 cos x     2  0   cos x      cos x     cos   3  3  2  3  4  x
    k2   x    k2 3 4    12   (k  )  .   7 x
   k2x    k2  3 4  12       3      
 3 tan   x  3   tan  x 
 tan  x  tan   3  3  3 3  6   x
k x
k , (k  )  . 3 6 6
Chú ý: Đối với phương trình tan x m ( tan x m ), trong đó m là hằng số thì điều kiện
cos x  0 ( sin x  0 ) là không cần thiết.
Bài 2. Giải các phương trình sau              sin x  sin 2  x    x      x     sin cos 2  4   6     4                   tan 3
x    tan x      x      x    cot 2 tan 0  4     6   4     6  Hướng dẫn giải:     x  2x   k2
x    k2      sin x  sin 2  x   4 4    k      , ( ).  4   2
x  2x   k2x   k  4  4 3  2  5 2     2  2x  
x k2 x   k        PT  cos 2
x    cos  x 4 3 36 3       .  4     3   2  11 2x   
x k2x    k2  4 3  12
 Do PT có dạng tan u  tan v nên ta chỉ cần một điều kiện cos u  0 hoặc cos v  0 . Để đơn    
giản ta chọn điều kiện: cos x
    0  x  
k x   k  . Khi đó:  6  6 2 3
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 4
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1         5 tan 3
x    tan x     3x   x
k x   kk    , ( ).  4     6  4 6 24 2 5
Kết hợp nghiệm trên đường tròn lượng giác thu được nghiệm của PT: x   k ,(k  )  . 24 2
 Do có thể biến đổi PT về dạng tan u  tan v nên ta chỉ cần một điều kiện cos u  0 hoặc
cos v  0 . Để đơn giản ta chọn điều kiện:    
cos  x  0   x
k x    k  .  6  6 2 3           3      PT  cot 2
x    tan x      tan x     tan  2x   4     6   6     4  3 11 x  
 2x k x   k (k  )  . 6 4 36 3 11
Kết hợp nghiệm trên đường tròn lượng giác thu được nghiệm của PT: x   k ,(k  )  . 36 3
Bài 3. Giải các phương trình sau  2 2
4 cos x  2( 3  1) cos x  3  0
 2 cos x  5 sin x  4  0      2 2 2 3 tan x  (1  3) tan x  1  0  sin x     cos x   4  Hướng dẫn giải:  1  cos x x
    k2  2   3 PT     (k  ).   3  cos x x    k2   2  6 sinx  2 (lo¹i)   2 2
PT  2(1  sin x )  5 sin x  4  0  2 sin x  5 sin x  2  0   1  sin x  (t/m)  2 5
Vậy phương trình có nghiệm: x
k2 và x
k2, (k  )  . 6 6 tan x  1  sin x  2 (lo¹i)   2 PT   1 
 2 sin x  5 sin x  2  0   tan x  1   sin x   3  2 5
Vậy phương trình có nghiệm: x
k2 và x
k2, (k  )  . 6 6   1  cos 2  x     2  1  cos 2x  PT  
 sin 2x  cos 2x  tan 2x  1  x   k . 2 2 8 2
Bài 4. Giải các phương trình sau 1 x x  4 4 4 4
sin x  cos x  sin 2x   sin  cos  1  2 sin x 2 2 2
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 5
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1      4 4 6 6
2(sin x  cos x)  cos   2x  0 
sin x  cos x  cos 4x   2  Hướng dẫn giải: 1 1 1  2 2 2
PT  1  2 sin x cos x  sin 2x
 1  sin 2x  sin 2x  2 2 2 sin2x  1  2
 sin 2x  2 sin 2x  3  0   
 2x   k2x   k , (k  )  . sin 2x  3 (lo¹i)  2 4 1 sinx  0  2 2  PT  1 
sin x  1 2 sin x  sin x  4 sinx  0 
x k (k  ).  2 sinx  4 (lo¹i)    1     sin 2x  1  2 2  PT  2 1
  sin 2x  sin 2x  0 
 sin 2x  sin 2x  2  0    2  sin2x  2  (lo¹i)   2x
k2x   k , (k  ).  2 4 3  2 2 2 2 2
PT  1  3 sin x cos x  1  2 sin 2x  1 
sin 2x  1  2 sin 2x 4
 sin 2x  0  2x k x k ,(k  )  . 2
Bài 5. Giải các phương trình sau 6 6
2(sin x  cos x) sin x cos x  4 4
sin x  cos x  sin x cos x  0   0 (A06) 2  2 sin x 2 x 1
(2  3) cos x  2 sin (  ) 2 4  4 2
cos x  sin x    1 4 2 cos x 1 Hướng dẫn giải: 1 1 sin2x  1   2 2  PT  1 
sin 2x  sin 2x  0  sin 2x  sin 2x  2  0  2 2 sin2x  2 (lo¹i)  
x    k , (k  )  . 4   2 x   k   (A-2006) Điều kiện: 4
2  2 sin x  0  sin x    2  3 x   k2  4   6 6 3   1 2
PT  2(sin x  cos x )  sin x cos x  0  2 1
  sin 2x  sin 2x  0   4  2 sin2x  1  2
 3 sin 2x  sin 2x  4  0   4  x   k k    , ( ). sin 2x   (lo¹i)  4  3 5
Kết hợp nghiệm ta thu được nghiệm của phương trình x   k2 . 4
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 6
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1  1 2  1 cos x    4 2 4 2
PT  cos x  1  cos x
 4 cos x  4 cos x  3  0 2   4  3 2 cos x   (lo¹i)  4 2
 2 cos x 1  0  cos 2x  0  2x
k x   k , (k  )  . 2 4 2
 Điều kiện: 2 cos x  1  x    k2 . 3 x      2    PT  (2 
3)cos x  2 sin (  )  2 cos x 1   3 cos x  1   cos x      1 2 4     2    
 3 cos x  cos  x  0 
 3 cos x  sin x  0  tanx  3  x  k , (k  )  .   2  3
Bài 6. Giải các phương trình sau  2
sin 3x  cos 2x  sin x  0
 sin 5x  2 cos x  1 (D-2013) (B-2013)
 sin x  4 cos x  2  sin 2x (A-2014)
 cos 3x  cos 2x  cos x  1  0 (D-2006) Hướng dẫn giải:
 PT  sin 3x  sin x  cos 2x  0  2 cos 2x sin x  cos 2x  0  cos 2x(2 sin x  1)  0  x    k   4 2 cos 2x  0     
x    k2 1   . sin x    6  2  7 x    k2  6 
 PT  sin 5x  1  cos 2x  1  cos 2x   sin 5x  cos 2x  sin  5  x   2   2
x   5x k2 x    k    2  
cos 2x  cos  5x  6 3      (k  ).    2   2
2x    5x k2x    k   2  14 7
 PT  sin x  4 cos x  2  2 sin x cos x  sin x(1  2 cos x)  2(2 cos x  1)  0 sinx  2 (lo¹i) 
 (sin x  2)(1 2 cos x)  0  
x    k2 . 1  cos x  3  2  2
PT  cos 3x  cos x  cos 2x  1  0  2
 sin 2x sin x  2 sin x  0   sin x 0   sin x  0 x k
 sin x(sin 2x  sin x)  0        sin 2x sin x 0    2 cos x  1  0 2     x    k2  3
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 7
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
MỘT SỐ DẠNG PHƯƠNG TRÌNH LƯỢNG GIÁC
DẠNG 1. PHƯƠNG TRÌNH BẬC NHẤT VỚI SINX VÀ COSX
 Dạng phương trình: a sin x b cos x c  2 2
Cách giải: Chia hai vế phương trình cho a b a b c  sin x  cos x  2 2 2 2 2 2 a b a b a b a b c C1: Đặt  cos ,  sin .
Khi đó PT  sin(x )   x  ? 2 2 2 2 a b a b 2 2 a b a b c C2: Đặt  sin ,
 cos . Khi đó PT  cos(x )   x  ? 2 2 2 2 a b a b 2 2 a b  2 2 2
Điều kiện có nghiệm của phương trình: a b c
 Chú ý: Khi phương trình có a c hoặc b c thì dùng công thức góc nhân đôi và sử dụng phép nhóm nhân tử chung.
Bài 1. Giải các phương trình sau
 cos x  3 sin x  2  x x  2 sin 2 cos 6
 3 cos 3x  sin 3x  2
 sin x  cos x  2 sin 5x Hướng dẫn giải:
 Nhận xét: Trong PT này ta xác định các hệ số a  1,b
3,c  2 thỏa mãn điều kiện 2 2 2
a b c do đó phương trình này có nghiệm. Để giải PT ta cần chia cả hai vế cho 2 2 2 2
a b  1  ( 3)  2.  1 3 2  x   k2   2  PT  cos x  sin x   sin x     12   2 2 2  6  2  7 x   k2  12   1 1 3  x   k2   3   PT  cos x  sin x   sin x     12     2 2 2  4  2  5 x   k2  12   3 1 2    3x   k     2   PT 
cos 3x  sin 3x
 sin  3x  3 4   2 2 2 3  2  3  3x   k2  3 4   x   k  36 3   , (k  )  .  5 2 x   k .  36 3 1 1      PT  sin x
cos x  sin 5x  sin x     sin 5x   2 2  4 
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 8
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 
5x x   k2x   k   4 16 2    . 3    5x
x k2 x   k  4    8 3
Bài 2. Giải các phương trình sau    
 3 sin 2x  sin   2x   1   x   x      ( 3 1)sin ( 3 1)cos 3 1 0  2  26    3 3 sin x
3 cos 3x  1  4 sin x
 cos 7x  3 sin 7x  2  0, x   ;   5 7  Hướng dẫn giải: 3 1 1     1  PT 
3 sin 2x  cos 2x  1 
sin 2x  cos 2x   sin 2  x    2 2 2  6  2 
2x    k2 x   k  6 6      (k  )  .  5  2x    k2 x   k    6 6  3 3 1 3  1 1  3  PT  sin x  cos x  8 8 8 3  1 5
Nhận xét: Sử dụng máy tính 570ES PLUS ta bấm SHIFT SIN của thu được , tức là 8 12 5 3  1 5 5 1 3 sin 
. Vậy ta có nên đưa phương trình về dạng cos sin x  sin cos x 12 8 12 12 8 5
ngay lập tức hay chưa? Câu trả lời là chưa. Bởi vì kết quả
không phải giá trị cung lượng giác đặc 12
biệt có mặt trong SGK?Vì vậy ta nên làm như sau cho thuyết phục: 5    2 3 2 1 3  1 Ta có sin
 sin    sin cos  cos sin  .  .  . 12 4 6 4 6 4 6 2 2 2 2 8 5 5 3 1  5 5     Nên PT  cos sin x  sin cos x    sin x      cos  12 12       8  12  12   5   5  x     k2   7  5      sin x      cos      12 12   sin x     sin        12     12   12     12  5 13 x    k2  12 12 2
Vậy phương trình có nghiệm: x  
k2 và x
k2, (k  )  . 2 3 1 3 1
 PT  sin 3x  3 cos 3x  1  sin 3x  cos 3x  2 2 2  2     3x    k2 x    k   1  sin   3x    3 6 18 3       .  3  2  5 2 3x    k2x   k  3 6  6 3
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 9
ThS. Trần Mạnh Hân (0974514498) thayHanSP1   3 1 2   7x    k2   2   PT 
sin 7x  cos 7x   sin 7  x    6 4   2 2 2  6  2  3 7x    k2  6 4  5   5 2 7x   k2   x   k 12    84 7   (k  )  .  11  11 2 7x   k2x   k   12  84 7 26  
Nhận xét: Để tìm nghiệm x   ;  
thực chất là ta phải chọn số nguyên k thỏa mãn  5 7  2 5 2 6 2 11 2 6   k hoặc   k
tức là ta phải giải các bất phương trình 5 84 7 7 5 84 7 7 2 5 2k 6 2 11 2k 6    ;  
để tìm các miền giá trị của k rồi sau đó chọn k là số 5 84 7 7 5 84 7 7 nguyên. 53 5 59
KL: Vậy phương trình có các nghiệm thỏa mãn điều kiện là: x  , x và x . 84 12 84
Ngoài ra, ta có thể không cần giải các BPT nghiệm nguyên ở trên bằng cách sử dụng 570ES PLUS như sau: 2 6  
- Trước tiên ta tìm khoảng gần đúng của  ;   0, 4; 0, 857...  là   5 7 5 2X
- Nhập biểu thức thứ nhất
vào máy tính (vì máy tính không có k nên ta coi X là k ) rồi 84 7
CALC với các giá trị X  0; 1  ; 2  ; 3..
 . để kiểm tra xem có thỏa mãn hay không. Khi đó ta tìm 53
được k  2 , ứng với nghiệm là x . 84 5 59
- Tương tự cho biểu thức thứ 2 thu được k  1; k  2 , tương ứng với nghiệm x và x . 12 84
Bài 3. Giải các phương trình sau
 cos 7x  sin 5x
3(cos 5x  sin 7x)  x x x x tan 3 cot 4(sin 3 cos ) 3(1  cos 2x) sin x  sin 2x   cos x   3 (CĐ2004) 2 sin x cos x  cos 2x Hướng dẫn giải:
 Nhận xét: Đối với PT dạng a sin x b cos x c thì chúng ta có thể giải một cách dễ dàng bằng 2 2 cách chia cho
a b . Nhưng nếu gặp dạng a sin mx b cos mx c sin nx d cos nx trong 2 2 2 2
đó a b c d thì làm thế nào? Cứ bình tĩnh quan sát nhé! Chúng ta nhận thấy mỗi vế của 2 2
phương trình đều có dạng bậc nhất của sin và cos, ta thử chia mỗi vế cho
a b , rất may 2 2 2 2
a b c d . Nhưng lưu ý rằng, ta phải chuyển vế sao cho mỗi vế có cùng một cung. Từ đó
ta có lời giải như sau: 1 3 1 3 PT  cos 7x
3 sin 7x  sin 5x  3 cos 5x  cos 7x
sin7x  sin5x  cos 5x 2 2 2 2
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 10
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1       7x   5x   k2 x   k     sin 7    x   sin 5    x    6 3 12        6     3  2 7x  
 5x k2x   k  6 3  24 6 sin  x  0   Điều kiện: 
 sin 2x  0  x k . c  os x  0 2  2 2
sin x  3 cos x sinx 3 cos x    PT 
 4(sin x  3 cos x)  (sin x  3 cos x)  4    0 sin x cos x  sin x cos x     tanx   3
sin x  3 cos x  0        
sin x  3 cosx  2 sin 2x sin x       sin 2x     3  
Giải và kết hợp nghiệm trên đường tròn lượng giác ta thu được: x    k ;  x   k2 ; 3 3 2 2 x   k , (k  )  . 9 3
 Điều kiện: sin x  0  x k    2x    k2   3  PT  sin 2x
3 cos 2x  3  sin 2  x    3 3      3  2  2 2x    k2  3 3 x   k (lo¹i)   
. Vậy phương trình có nghiệm: x   k , (k  )  . x    k  6  6 2
 Điều kiện: cos x  cos 2x  0  2x x
  k2x k 3
PT  sin x  sin 2x
3(cos x  cos 2x)  sin x  3 cos x  sin 2x  3 cos 2x 1 3 1 3        sin x
cos x  sin 2x  cos 2x    sin x     sin 2  x   2 2 2 2  3    3  x k  2    5 2 k    ( ). x   k  9 3 5 2
Vậy phương trình có nghiệm: x k  2 ;  x   k . 9 3
Bài 4. Giải các phương trình sau 1    
 cos x  3 sin x
 1  tan x  2 2 sin x    (A2013) cos x  4  6
 3 cos 5x  2 sin 3x cos 2x  sin x  0 (D09)
 4 sin x  3 cos x   6
4 sin x  3 cos x 1 Hướng dẫn giải:
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 11
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
 Điều kiện: cos x  0  x   k . 2 1 3 1 2 PT  cos x
3 sin x cos x  1  cos 2x  3 sin 2x  1  cos 2x  sin 2x  2 2 2     2
x    k2 x k (t/m)   1  6 6   sin 2  x          k    ( ).  6  2  5  2x    k2 x   k (t/m)    6 6  3
Vậy phương trình có nghiệm: x k ;  x   k . 3
 Điều kiện: cos x  0  x   k . 2 tan x  1 sin x  1     PT  1 
 2(sin x  cos x)  (sin x  cos x)  2  0   cos x  1 cos x  cosx   2
Kết hợp với điều kiện thu được nghiệm của PT: x    k ;
 x    k2, (k  )  . 4 3
 PT  3 cos 5x (sin 5x  sin x)  sin x  0 
3 cos 5x  sin 5x  2 sin x   
 5x x k2 x    k  sin  
  5x  sin x 3 18 3    k      , ( ).  3  
 5x x k2x   k  3  6 4
Vậy phương trình có nghiệm: x  
k ;x   k . 18 3 6 4
 Đặt t  4 sin x  3 cos x  1 , (t  0) 6 t  1 2  PT  t  1 
 6  t  7t  6  0  t t  6  4 3
+ Với t  1 ta có 4 sin x  3 cos x  0 
sin x  cos x  0 5 5
 cos sin x  sin cos x  0  sinx   0  x k . 4 3
+ Với t  6 ta có 4 sin x  3 cos x  5 
sin x  cos x  1 5 5
 cos sin x  sin cos x  1  sinx   1  x   k2. 2 3 
Vậy phương trình có nghiệm: x k2 ;
 x
k2 trong đó sin  và cos  . 2 5 5
DẠNG 2. PHƯƠNG TRÌNH THUẦN BẬC HAI VỚI SINX VÀ COSX  2 2
Dạng phương trình: a sin x b sin x cos x c. cos x d  0  Cách giải:
Cách 1: + Xét cos x  0 có là nghiệm phương trình không?
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 12
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 2
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được: 2 2
a tan x b tan x c d(1  tan x)  0  tan x x
Cách 2: Dùng công thức hạ bậc đưa về phương trình bậc nhất với sin 2x và cos 2x (dạng 1).
Bài 1. Giải các phương trình sau  2 2 2 2
2 sin x  sin x cos x  3 cos x  0
 2 sin x  3 sin x cos x  cos x  0  2 2 2 2
sin x  10 sin x cos x  21 cos x  0
 2 sin x  5 sin x cos x  3 cos x  0 Hướng dẫn giải:  2 2
2 sin x  sin x cos x  3 cos x  0 2
+ Xét cos x  0 (tức sin x  1): Khi đó PT trở thành 2  0 nên cos x  0 không thỏa mãn. 2
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được:   tan x  1   x   k  2
2 tan x  tan x  3  0   4 3   k      ( ). tan x    3     2 x  arctan     k    2 
Cách 2: PT  2(1  cos 2x )  sin 2x  3(1  cos 2x )  0  sin 2x  5 cos 2x  1 2 2t 1  t
Đặt t  tan x khi đó sin 2x  ; cos 2x
. Phương trình trở thành 2 2 1  t 1  t t  1  2
2t t  3  0   3 . t    2  2 2
2 sin x  3 sin x cos x  cos x  0 2
+ Xét cos x  0 (tức sin x  1): Khi đó PT trở thành 2  0 nên cos x  0 không thỏa mãn. 2
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được:   tan x  1   x   k  2
2 tan x  3 tan x  1  0   4 1   k      ( ). tan x   1     2
x  arctan   k   2   2 2
sin x  10 sin x cos x  21 cos x  0 2
+ Xét cos x  0 (tức sin x  1): Khi đó phương trình trở thành 1  0 nên cos x  0 không t/m. 2
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được: tan x  3
x  arctan 3  k 2 tan x 10 tan x 21 0         (k  )  . tan x  7     x arctan 7 k   2 2
2 sin x  5 sin x cos x  3 cos x  0 2
+ Xét cos x  0 (tức sin x  1): Khi đó phương trình trở thành 2  0 nên cos x  0 không t/m. 2
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được:   tan x  1   x   k  2
2 tan x  5 tan x  3  0   4 3   k      ( ). tan x   3     2
x  arctan    k   2 
Bài 2. Giải các phương trình sau  2 2 2 2
sin x  (1  3)sin x cos x  3 cos x  0
 3 sin x  4 sin 2x  4 cos x  0
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 13
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1  2 2 2 2
3 sin x  4 sin x cos x  5 cos x  2
 3 sin x  4 sin 2x  (8 3  3) cos x  3 Hướng dẫn giải:  2 2
sin x  (1  3)sin x cos x  3 cos x  0 2
+ Xét cos x  0 (tức sin x  1): Khi đó phương trình trở thành 1  0 nên cos x  0 không t/m. 2
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được:   tan x  1  x     k 2  tan x (1 3) tan x 3 0        4   (k  )  . tan x  3  x   k  3  2 2
PT  3 sin x  8 sin x cos x  4 cos x  0 2
+ Xét cos x  0 (tức sin x  1): Khi đó phương trình trở thành 3  0 nên cos x  0 không t/m. 2
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được: tan x  2  x  arctan( 2  )  k   2
3 tan x  8 tan x  4  0   2     k    2    ( ). tan x        x arctan k     3    3   2 2
3 sin x  4 sin x cos x  5 cos x  2 2
+ Xét cos x  0 (tức sin x  1): Khi đó phương trình trở thành 3  2 nên cos x  0 không t/m. 2
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được:   tan x  1    2 2 x k 3 tan x 4 tan x 5 2(1 tan x)          (k  )  . tan x  3 4   
x  arctan 3  k   2 2
PT  3 sin x  8 sin x cos x  (8 3  3) cos x  3 2
+ Xét cos x  0 (tức sin x  1): Khi đó phương trình trở thành 3  3 nên cos x  0 thỏa mãn. Tức là x
k là nghiệm của phương trình. 2 2
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được: 2 x x    2 3 tan 8 tan 8 3
3  3(1  tan x)  tan x  3  x
k (k  )  . 3
Vậy phương trình có nghiệm: x   k ,  x   k . 2 3
DẠNG 3. PHƯƠNG TRÌNH BẬC BA VỚI SINX VÀ COSX  Dạng phương trình: 3 3 2 2
a sin x b cos x c sin x cos x d cos x sin x e sin x f cos x  0  Cách giải:
+ Xét cos x  0 có là nghiệm phương trình không? 3 1 2
+ Xét cos x  0 , chia hai vế phương trình cho cos x với chú ý:  1  tan x . 2 cos x
Bài 1. Giải các phương trình sau  3 3
sin x  4 sin x  cos x  0
 2 sin x  cos x  3 3 3
2 cos x  sin 3x
 4 cos x  2 sin x  3 sin x  0 Hướng dẫn giải:
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 14
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1  3
sin x  4 sin x  cos x  0
+ Xét cos x  0 (tức sin x  1
 ): Khi đó PT trở thành 3
  0 nên cos x  0 không thỏa mãn. 3
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được: 2 3 2
tan x(1  tan x)  4 tan x  (1  tan x)  0 3 2
 3 tan x  tan x  tan x 1  0 2
 (tan x 1)(3 tan x  2 tan x  1)  0  tan x  1  x
k (k  )  . 4
Nhận xét: Khi giải phương trình bậc 3 các em thường bấm máy tính để ra nghiệm ngay, nên các em 3 2
biến đổi phương trình 3t t t  1  0  t  1 . Như thế liệu đã đầy đủ chưa? Câu trả lời là
chưa đủ vì chúng ta không hề học công thức nghiệm phương trình bậc 3. Các em cần phải phân tích
thành nhân tử trước khi đưa ra nghiệm. Vậy làm thế nào để phân tích nhanh nhất? 1
Bước 1: Dùng máy tính 570ES PLUS thu được nghiệm như sau t  1, t    0, 47i (1 nghiệm 3 1
thực và 2 nghiệm phức). Chú ý đến số nhé! 3
Bước 2: Viết nhân tử: do PT có nghiệm t  1 nên có một nhân tử (t  1) , vậy nhân tử còn lại là gì?
Dựa vào hệ số đầu tiên và cuối cùng trong phương trình bậc 3 ta thu được hệ số đầu tiên và cuối cùng 2
của nhân tử còn lại, tức là có nhân tử nữa (3t Bt  1) . Để tìm B ta dựa vào phần thực của 1 B
nghiệm phức còn lại   
từ đó suy ra B  2 . Vậy ta lập tức phân tích phương trình thành 3 2A 2
(t 1)(3t  2t  1)  t  1.  3
2 sin x  cos x
+ Xét cos x  0 (tức sin x  1
 ): Khi đó PT trở thành 2
  0 nên cos x  0 không thỏa mãn. 3
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được: 3 2
2 tan x  1  tan x 3 2
 2 tan x  tan x 1  0 2
 (tan x 1)(2 tan x  tan x  1)  0  tan x  1  x
k (k  )  . 4  3 3 3
2 cos x  sin 3x  2 cos x  3 sin x  4 sin x
+ Xét cos x  0 (tức sin x  1
 ): Khi đó PT trở thành 0  1 nên cos x  0 không thỏa mãn. 3
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được: 2 3
2  3 tan x(1  tan x) 4 tan x 3
 tan x  3 tan x  2  0   tan x  1    2 x k
 (tan x 1) (tan x  2)  0      (k  )  . tan x  2 4    x   arctan( 2  )  k .  3
Nhận xét: Khi bấm máy tính giải phương trình t  3t  2  0 , chúng ta thu được 2 nghiệm t  1,t  2  3
. Khi đó phân tích phương trình thành t  3t  2  (t  1)(t  2). Như thế liệu đầy
đủ chưa? Các em hãy để ý bậc ở hai vế để tự đưa ra câu trả lời nhé. Như vậy là đa thức này còn có 1
nhân tử nữa, theo các em nhân tử này là t  1 hay t  2 . Câu trả lời là t  1 , vì sao lại như vậy?
Rất dễ dàng thôi nhân tử thứ ba này là t  2 thì số hạng tự do của đa thức ban đầu phải là 4 , 3 2
không ổn rồi. Vậy kết quả là t  3t  2  (t  1)(t  2)(t 1)  (t 1) (t  2).  3 3
4 cos x  2 sin x  3 sin x  0
+ Xét cos x  0 (tức sin x  1
 ): Khi đó PT trở thành 1
  0 nên cos x  0 không thỏa mãn. 3
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được: 3 2
4  2 tan x  3 tan x(1  tan x)  0 3
 tan x  3 tan x  4  0
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 15
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 2
 (tan x 1)(tan x  tan x  4)  0  tan x  1  x
k (k  )  . 4
Bài 2. Giải các phương trình sau  3 3 3
sin x sin 2x  sin 3x  6 cos x
 cos x  sin x  sin x  cos x  3 3 2
6 sin x  2 cos x  5 sin 2x cos x
 cos x  sin x  3 sin x cos x  0 Hướng dẫn giải:  3 2 3 3
sin x sin 2x  sin 3x  6 cos x  2 sin x cos x  3 sin x  4 sin x  6 cos x
+ Xét cos x  0 (tức sin x  1
 ): Khi đó PT trở thành 1
  0 nên cos x  0 không thỏa mãn. 3
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được: 2 2 3
2 tan x  3 tan x(1  tan x)  4 tan x  6 3 2
 tan x  2 tan x  3 tan x  6  0  x    k tan x  1   4    2
 (tan x  2)(tan x  3)  0  tan x  3  x
k (k  )  .    3 tan x   3    x     k  3   3 3
PT  cos x  sin x  sin x  cos x  0
+ Xét cos x  0 (tức sin x  1
 ): Khi đó PT trở thành 2
  0 nên cos x  0 không thỏa mãn. 3
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được: 3 2
1  tan x (tan x  1)(1  tan x)  0 3 3 2
 1  tan x (tan x  tan x  tan x  1)  0   tan x  0 x k  2
 tan x  tan x  0      (k  )  . tan x  1   
x    k  4  3 3 2
6 sin x  2 cos x  5 sin 2x cos x  6 sin x  2 cos x  10 sin x cos x
+ Xét cos x  0 (tức sin x  1
 ): Khi đó PT trở thành 6
  0 nên cos x  0 không thỏa mãn. 3
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được: 2
6 tan x(1  tan x) 2  10 tan x 3
 6 tan x  4 tan x  2  0 2
 (tan x 1)(6 tan x  6 tan x  2)  0  tan x  1  x
k (k  )  . 4  3 2
cos x  sin x  3 sin x cos x  0
+ Xét cos x  0 (tức sin x  1
 ): Khi đó PT trở thành 1
  0 nên cos x  0 không thỏa mãn. 3
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được: 2 2
1  tan x(1  tan x) 3 tan x  0 3
 2 tan x  tan x 1  0 2
 (tan x 1)(2 tan x  2 tan x  1)  0  tan x  1  x
k (k  )  . 4
Bài 3. Giải các phương trình sau  3 3 2
cos x  4 sin x  3 cos x sin x  sin x  0   x x 1 3 tan 2 sin 2 3 1  2 2
2 sin x  2 3 cos x  
 tanx sin x 2 sin x  3(cos2x  sinx cosx) cos x sin x Hướng dẫn giải:  3 3 2
cos x  4 sin x  3 cos x sin x  sin x  0
+ Xét cos x  0 (tức sin x  1
 ): Khi đó PT trở thành 1
  0 nên cos x  0 không thỏa mãn. 3
+ Xét cos x  0 , chia hai vế phương trình cho cos x ta được:
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 16
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 3 2 2
1  4 tan x  3 tan x  tan x(1  tan x)  0 3 2
 3 tan x  3 tan x  tan x 1  0    tan x  1  x     k    4   2 3
 (tan x  1)(3 tan x 1)  0   tan x    x
k (k  )  . 3    6  3  tan x   x     k  3  6   2
Điều kiện: cos x  0 . Khi đó phương trình trở thành: cos x  3 sin x  4 sin x cos x 3
Chia hai vế phương trình cho cos x ta được: 2
(1  3 tan x)(1  tan x)  4 tan x 3 2
 3 tan x  tan x  tan x  1  0 2
 (tan x  1)(3 tan x  2 tan x  1)  0  tan x  1
  x   (t/m),(k  )  . 4  2 2
Điều kiện: cos x  0 . PT trở thành: 2 sin x cos x  2 3 cos x sin x
3 sin x  cos x 3
Chia hai vế phương trình cho cos x ta được: 2 2
2 tan x  2 3 tan x  ( 3 tan x 1)(tan x  1) 3 2
 3 tan x  tan x  3 tan x  1  0   x    k tan x  1  4    2
 (tan x 1)( 3 tan x 1)  0  tan x  1      x k  (t/m),(k  )  .   4 3   tan x   x    k  3  6   3 2 3 2
Điều kiện: cos x  0 . PT trở thành: sin x  2 sin x cos x  3(2 cos x  sin x cos x  cos x ) 3
Chia hai vế phương trình cho cos x ta được: 3 2 2
tan x  2 tan x  3(2  tan x 1 tan x) 3 2
 tan x  tan x  3 tan x  3  0  x    k tan x  1   4    2
 (tan x  1)(tan x  3)  0  tan x  3  x
k (t/m),(k  )  .    3 tan x   3    x     k  3 
Bài 4. Giải các phương trình sau  3 3 2 2 3 3
cos x  sin x  cos x  sin x
 cos x  sin x  cos 2x 13          6 6 2 4 4 7
cos x  sin x  cos 2x
 sin x  cos x  cot x
  cot  x 8 8  3     6  Hướng dẫn giải:  3 3 2 2
PT  cos x  sin x  cos x  sin x
 (cos x  sin x)(1  sin x cos x  cos x  sin x)  0
cosx  sinx (1)   1
  sinx cosx  sinx  cosx  0 (2)     
Giải (1): cos x  cos 
x  x
x k2x   k  .  2  2 4
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 17
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 2 t 1 2
Giải (2): Đặt t  sin x  cos x  sin x cos x
. Khi đó (2)  2  (t  1)  2t  0 2     1 2
t  2t  1  0  t  1  sin x  cos x  1  sin x       4  2 
x    k2 x   k2 4 4       (k  )  .  3 x    k2 x    k2    2  4 4
Vậy phương trình có nghiệm: x   k ;  x k2 ;  x
k2(k  ).  4 2  2 2
PT  (cos x  sin x )(1  sin x cos x)  cos x  sin x
 (cos x  sin x)(1  sin x cos x  sin x  cos x)  0
 sin x  cos x  0  tan x  1
  x    k 4
 1  sin x cos x  sin x  cos x  0 2 1 t 2
Đặt t  sin x  cos x  sin x cos x
ta có: 2  t  1  2t  0  t  1  2   
x     k2
x k2    1 
 sin x  cos x  1   sin x       4 4      3  4  2  5 x    k2 x    k2    2  4 4 3
Vậy phương trình có nghiệm: x    k ;  x k2 ;  x
k2(k  ).  4 2 13  2 2 4 4 2 2 2
PT  (cos x  sin x)(cos x  sin x  sin x cos x )  cos 2x 8 13  1 13  2 2 2
 cos 2x(1  sin x cos x)  cos 2x  2  cos 2x 1   sin 2x  cos 2x  0 8  4 8 
 cos 2x  0  2x
k x   k 2 4 2  2 2
8  2 sin 2x  13 cos 2x  0  2 cos 2x  13 cos 2x  6  0 1
 cos 2x  , cos 2x  6 (loại)  x    k . 2 6
Vậy phương trình có nghiệm: x
k ;x    k (k  ).  4 2 6          2          
 Điều kiện: sin x
  sin  x  0  sin x   cos x     0  sin 2  x    0   3     6     3     3     3  7 1 7 1 1 2 2
 1  2 sin x cos x  2 2  1  sin 2x   sin 2x   sin 2x   8 2 8 4 2
Vậy phương trình có nghiệm: 5 7 x   k ;  x   k ;  x    k ;  x
k (k  ).  12 12 12 12
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 18
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
DẠNG 4. PHƯƠNG TRÌNH ĐỐI XỨNG VỚI SINX VÀ COSX  Dạng phương trình:
f (sin x  cos x, sin x cos x)  0  Cách giải: 2 t 1
+ Đặt t  sin x  cos x  sin x cos x  2 2 1t
+ Đặt t  sin x  cos x  sin x cos x
. Đưa về phương trình ẩn t . 2    
Chú ý: Nếu t  sin x  cos x  2 sin x       t   thì 2 2 .  4 
Bài 1. Giải các phương trình sau
 2(sin x  cos x)  sin 2x  1  0  x x x x  sin cos 6(sin cos 1)
 sin 2x  2 sin(x  )  1
 tan x  2 2 sin x  1 4 Hướng dẫn giải:
 2(sin x  cos x)  sin 2x  1  0  2(sin x  cos x)  2 sin x cos x  1  0   2   t 1
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2 t  0 (t/m) 2 2 
Phương trình trở thành: 2t  (t  1)  1  0  t  2t  0  t  2  (lo¹i)     
Khi đó sin x  cos x  0  sin x
    0  x    k   4  4
Vậy phương trình có nghiệm:
 sin x cos x  6(sin x  cos x  1)   2   1 t
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2 t  (t/ 1 m) 2 2 
Phương trình trở thành: 1  t  12(t  1)  t  12t  13  0  t  13  (lo¹i)      1
Vì vậy sin x  cos x  1  sin x       4  2
Vậy phương trình có nghiệm: x   k ;
 x k2(k  ).  2
 sin 2x  2 sin(x
)  1  2 sin x cos x  sin x  cos x  1 4   2   1 t
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2 t  0 (t/m) 2 2 
Phương trình trở thành: 1  t t  1  t t  0  t  1 (t/m) 
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 19
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1    
 sin x  cos x  0  sin x
    0  x   k   4  4     1 x
   k2
 sin x  cos x  1  sin x         2   4  2 x
  k2
Vậy phương trình có nghiệm: x   k ;  x   k2 ;
 x k2(k  ).  4 2
 tan x  2 2 sin x  1  sin x  cos x  2 2 sin x cos x  0 ( cos x  0 )   2   1 t
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2  2   2 2 t (t/m) 
PT trở thành: t  2(1  t )  0 
2t t  2  0  2  t   2 (t/m)   5    x   k2 2   1   12
sin x  cos x   sin x         2  4  2  13 x   k2  12    
 sin x  cos x   2  sin x     1
  x    k2   4  4 5 13
Kết hợp với điều kiện, PT có nghiệm: x   k2 ;  x   k2 ;
 x    k2(k  )  . 12 12 4
Bài 2. Giải các phương trình sau 1 2 2
 1  tan x  2 sin x
 sin x  cos x   cos x tan x cotx 1 1 10  sin x   cos x  
 2 sin x  cot x  2 sin 2x  1 sin x cos x 3 Hướng dẫn giải: 1
 1  tan x  2 sin x
 cos x  sin x  2 sin x cos x  1, cos x   0 cos x 2   t 1
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2 t  (t/m) 1 2 2 
PT trở thành: t  (t  1)  1  t t t  0 (t/m)     
 sin x  cos x  0  sin x
    0  x    k   4  4
x k2 1   
 sin x  cos x  1  sin x           4  2
x   k2  2
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 20
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Vậy phương trình có nghiệm: x    k ;  x   k2 ;
 x k2(k  ).  4 2 sin  x  0   Điều kiện:  . Khi đó: c  os x  0  2 2 cos x  sin x
PT  sin x  cos x  2
 (sin x  cos x)(sin x cos x  2 sin x  2 cos x)  0 sin x cos x  
 sin x  cos x  0  sin x
    0  x    k  (t/m)  4  4
 sin x cos x  2 sin x  2 cos x  0   2   1 t
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2 t  2  5  (lo¹i) 2 2
PT trở thành: (1  t )  4t  0  t  4t  1  0  
t  2  5 (lo¹i) 
Vậy phương trình có nghiệm: x  
k (k  ).  4 sin  x  0   Điều kiện:  . c  os x  0  sin x  cos x 10
PT  sin x  cos x   sin x cos x 3   2   t 1
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2 2  19 3 2 2
PT trở thành: 3t  10t  3t  10  0  (t  2)(3t  4t  5)  0  t  3 2  19     2  19
Khi đó sin x  cos x   sin x      sin 3  4  3 2 3
Kết hợp điều kiện, phương trình có nghiệm là: x    k2 ;  x
k2(k  )  . 4 4
 Điều kiện: sin x  0 2 2
PT  2 sin x  cos x  4 sin x cos x  sin x 2
 sin x(2 sin x 1)  cos x(4 sin x 1) (2 sin x
1) cos x(2 sin x 1) sin x      0    x    k2 1   x  t/m 6 sin   2  5 x   k2  6
 2 sin x cos x  (sin x  cos x)  0   2   1 t
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 21
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1  1  5 t  (t/m)  2 2 PT trở thành: 2
(1 t )t  0  t t  1  0   1 5 t  (lo¹i)  2 1   5     1   5
Khi đó sin x  cos x   sin x      sin 2  4  2 2 5
Kết hợp điều kiện, phương trình có nghiệm là: x   k2 ;  x
k2; x   k2 ; 6 6 4 5 x
k2(k  ).  4
Bài 3. Giải các phương trình sau  3 3 3 3
sin x  cos x  2 sin x cos x  sin x  cos x  1  sin x  cos x  sin 2x
 2 sin x  cos x  tan x  cotx
 (1  sin x)(1  cos x)  2 Hướng dẫn giải:
 PT  (sin x  cos x)(1 sin x cos x)  2 sin x cos x  sin x  cos x  2   t 1
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2 t  1 (t/m)  2 2 
PT trở thành: t(2  t  1)  2(t  1)  2t  (t  1)(t  1)(t  2)  0  t   1 (t/m) 
t  2 (lo¹i) 
x k2 1   
 sin x  cos x  1  sin x           4  2
x   k2  2     1 x
    k2
 sin x  cos x  1   sin x          2   4  2 x
  k2
Kết hợp nghiệm ta thu được: x k ;  x
k (k  ).  2
Chú ý: Ở đây hai họ nghiệm x k2 và x k2 được gộp thành họ nghiệm x k . Còn hai họ nghiệm x
k2 và x    k2 được gộp thành họ nghiệm x   k . 2 2 2
 PT  1  (sin x  cos x)(1  sin x cos x)  2 sin x cos x  2   t   1
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2 t  1 (t/m)  2 2 
PT trở thành: 2  t(2  1  t )  2(1  t )  t(t  1)(t  3)  0  t  0 (t/m) 
t  3 (lo¹i) 
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 22
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1     1 x
   k2
 sin x  cos x  1  sin x         2   4  2 x
  k2     
 sin x  cos x  0  sin x
    0  x   k   4  4
Vậy phương trình có nghiệm là: x   k2 ;
 x k2 ;  x
k (k  ).  2 4 sin  x  0  1  Điều kiện:  . Phương trình 
2(sin x  cos x)  c  os x  0  sin x cos x 2   t 1
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2 2 3 2 PT trở thành: 2t  
2t  2t  2  0  ( 2t  2)(t  2t  1)  0  t  2 2 t 1    
Khi đó sin x  cos x  2  sin x
    1  x   k2   4  4
Kết hợp điều kiện, phương trình có nghiệm là: x
k2(k  ).  4
 (1  sin x)(1  cos x)  2  sin x cos x  sin x  cos x  1   2   t 1
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2 t  (t/ 1 m) 2 2 
PT trở thành: t  1  2t  2  t  2t  3  0  t  3  (lo¹i) 
x k2 1   
Khi đó sin x  cos x  1  sin x           4  2
x   k2  2
Vậy phương trình có nghiệm là: x k2 ;  x
k2(k  ).  2
Bài 4. Giải các phương trình sau  2 2
sin x cos x  sin x  cos x  1
 (1sin x)cosx (
 1cos x)sinx 1sin2x
 2 sin 2x(sin x  cos x)  2
 sin x  cos x  4 sin 2x  1
 2 sin 2x  3 6 sin x  cos x  8  0 Hướng dẫn giải:
 sin x cos x  sin x  cos x  1   2   t 1
Đặt t  sin x  cos x  2 sin x    
 sin x cos x  0  t  2     4  2 t  (t/ 1 m) 2 2 
PT trở thành: t  1  2t  2  t  2t  3  0  t  3  (lo¹i) 
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 23
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
x k2 1   
 sin x  cos x  1  sin x           4  2
x   k2  2     1 x
    k2
 sin x  cos x  1   sin x          2   4  2 x
  k2
Kết hợp nghiệm ta thu được: x k ;  x
k (k  ).  2
 PT  sin x  cos x  sin x cos x(sin x  cos x)  1  2 sin x cos x  2   t 1
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2 t  0 2 2 3 2 2 
PT trở thành: 2t  (t  1)t  2  2(t  1)  t  2t t  0  t(t  1)  0  t  1 
x k2 1   
 sin x  cos x  1  sin x           4  2
x   k2  2    
 sin x  cos x  0  sin x
    0  x    k   4  4
Vậy phương trình có nghiệm: x k2 ;  x   k2 ;
 x    k (k  ).  2 4
 PT  2 2 sin x cos x(sin x  cos x)  2   2   t 1
Đặt t  sin x  cos x  2 sin x    
 sin x cos x   2  t  2     4  2 2 3 2
PT trở thành: 2 t  
1 t  2  2t  2t 2  0  ( 2t 2)(t  2t 1)  0  t  2    
Khi đó sin x  cos x  2  sin x
    1  x   k2   4  4
Vậy phương trình có nghiệm là: x
k2(k  ).  4
 PT  sin x  cos x  8 sin x cos x  1   2   1 t
Đặt t  sin x  cos x  2 sin x    
 sin x cos x  0  t  2     4  2 t  (t/ 1 m)  2 2
PT trở thành: t  4(1  t )  1  4t t  3  0   3 t   (lo¹i)  4     1 x
   k2
 sin x  cos x  1  sin x         2   4  2 x
  k2
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 24
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
x k2 1   
 sin x  cos x  1  sin x          3   4  2 x   k2  2
Kết hợp nghiệm ta thu được: x k ;  x
k (k  ).  2
 PT  4 sin x cos x  3 6 sin x  cos x  8  0   2   t 1
Đặt t  sin x  cos x  2 sin x    
 sin x cos x  0  t  2     4  2  6   2 2 t (t/m) 
PT trở thành: 2(t  1)  3 6t  8  0  2t  3 6t  6  0  2  t  6 (lo¹i)      x   k2 6   3   12
sin x  cos x   sin x         2  4  2  5 x   k2  12  7    x    k2 6   3   12
sin x  cos x    sin x          2  4  2  13 x   k2  12 5 7 13
Vậy PT có nghiệm: x   k2 ;  x   k2 ;  x    k2 ;  x
k2(k  ).  12 12 12 12
DẠNG 5. PHƯƠNG TRÌNH DẠNG THUẬN NGHỊCH  Dạng phương trình:  2 k     k  2
Af (x)   B     f (x)  
 C  0, với f (x)  sin x, cos x (1) 2  f (x)    f (x) 2 2 2 2
hoặc Aa tan x b cot x  B a tan x b cotx  C  0 (2) k
 Cách giải:  Đối với phương trình (1): Đặt t f (x)  f (x)
 Đối với phương trình (2): Đặt t a tan x b cot x
Bài 1. Giải các phương trình sau  1   1       2 4 sin x    4 si  n x   7  0  2  sin x     sin x  2  2
 2 tan x  5(tan x  cotx)  4  0 2 sin x 3  2
 3 cot x  4(tan x  cotx) 1  0 2 cos x Hướng dẫn giải:
 Điều kiện: sin x  0 . 1 1
Đặt t  sin x  2 2
t  sin x   2 sin x 2 sin x
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 25
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1  2 3 5 2
PT trở thành: 4(t  2)  4t  7  0  4t  4t  15  0  t   ;t    2 2  1 3  2 sin x  
 2 sin x  3 sin x  2  0 (vô nghiệm) sin x 2 1 5  2 sin x
   2 sin x  5 sin x  2  0 sin x 2   1   sin x  
x    k2 (t/m)    2 6     7 sin x  2  (lo¹i)  x   k2  6 7
Vậy phương trình có nghiệm: x    k2 ;  x
k2(k  )  . 6 6
Nhận xét: Dùng bất đẳng thức Cô si cho 2 số dương nghịch đảo, ta có thể đánh giá t như sau: 1 1 1 t  sin x   sin x   2 sin x .
 2 để đưa ra điều kiện t  2 . sin x sin x sin x sin  x  0   2 2 Điều kiện: 
. PT  2(cot x  tan x)  5(tan x  cot x)  6  0 c  os x  0  2 2 2 2 2 2
Đặt t  tan x  cot x t  tan x  cot x  2  tan x  cot x t  2  1    2 2 t
PT trở thành: 2(t  2)  5t  6  0  2t  5t  2  0   2 t  2   1  2
tan x  cot x  
 2 tan x  tan x  2  0 (vô nghiệm) 2  2
tan x  cot x  2
  tan x  2 tan x  1  0  tan x  1  x    k . 4
Kết hợp với điều kiện, phương trình có nghiệm: x  
k (k  )  . 4
Nhận xét: Dùng bất đẳng thức Cô si cho 2 số dương nghịch đảo, ta có thể đánh giá t như sau:
t  tan x  cotx  tan x  cotx  2 tan x . cotx  2 để đưa ra điều kiện t  2 . sin  x  0   2 2 Điều kiện: 
. PT  3(tan x  cot x )  4(tan x  cot x )  2  0 c  os x  0  2 2 2
Đặt t  tan x  cot x t  tan x  cot x  2 , t   2 .  2   2 2 t (lo¹i)
PT trở thành: 3(t  2)  4t  2  0  3t  4t  4  0   3 t  2   2
Khi đó tan x  cot x  2
  tan x  2 tan x  1  0  tan x  1  x    k . 4
Kết hợp với điều kiện, phương trình có nghiệm: x  
k (k  )  . 4
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 26
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
MỘT SỐ KĨ THUẬT GIẢI PT LƯỢNG GIÁC
KĨ THUẬT 1: LỰA CHỌN CÔNG THỨC LƯỢNG GIÁC
1. Sử dụng các phép biến đổi góc lượng giác
Khi việc giải phương trình lượng giác cần xem xét mối quan hệ giữa các góc (cung) để từ đó kết hợp
với các phép biến đổi góc đặc biệt, công thức cộng lượng giác để đưa về dạng góc cơ bản là một vấn
đề rất then chốt trong việc giải phương trình lượng giác...
Bài 1. Giải các phương trình sau 1 1 7             4 4 7   4 sin
x(A08)  sin x  cos x  cot x
  cot x sin x     3           4  8  3  6  sin x     2  4 4
sin 2x  cos 2x  5  7      4  cos 4x           sin 2x 3 cos x 1 2 sin x             2   2  tan  x tan    x 4     4  Hướng dẫn giải  
 Nhận xét: Từ sự xuất hiện hai cung x và
x mà chúng ta liên tưởng đến việc đưa 2 2 4
cung này về cùng một cung x . Để làm được điều đó ta có thể sử dụng công thức cộng cung hoặc công
thức về các góc đặc biệt.
Điều kiện: sin x  0, cos x  0  sin 2x  0  x k , k   2 1 1 (1)    2 
2(cos x  sin x)  (sin x  cos x)( 2 sin 2x  1)  0 sin x cos x 5
Kết hợp với điều kiện ta được nghiệm pt là: x    k ;
 x    k ;  x
k (k  )  . 4 8 8            
 Điều kiện: sin x
  .sin  x  0  cos 2  x    cos  0   3     6     6  2         7 1 7 4 4 2 Do x
      x  
 sin x  cos x   1  sin 2x   nên (2)  3     6  2 8 2 8 1
 sin 2x   . Kết hợp với điều kiện ta được: x    k (k  )  2 12 2               
 Nhận xét: Từ tổng hai cung   x    x     x   x   nên tan tan 1  4     4  2 4     4               Điều kiện 1: cos 
xcos  x  0  cos 
2x  cos   0  cos 2x  0   4     4  2  2               Điều kiện 2: sin 
xsin   x  0  cos 
2x  cos   0  cos 2x  0   4     4  2  2  4 4 4 1
(3)  sin 2x  cos 2x  cos 4x 2 4
 1  sin 4x  cos 4x 2
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 27
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 2 cos 4x  1  sin2x  0 4 2 
 2 cos 4x  cos 4x  1  0   1  sin 4x  0  2   cos 4x   (lo¹i) cos 2x  0  (lo¹i)   2 
Vậy phương trình có nghiệm x k . 2 Chú ý:
Chắc hẳn các em sẽ ngạc nhiên bởi cách giải ngắn gọn này, nếu không có sự nhận xét về tổng hai
cung mà quy đồng và biến đổi thì ... ra không?
Việc giải điều kiện và đối chiếu với điều kiện đặc biệt là những phương trình có dạng phân thức như
trên nếu không khôn khéo thì rất ... phức tạp.
2. Sử dụng công thức biến đổi tổng sang tích và ngược lại
Khi giải pt mà gặp dạng tổng (hoặc hiệu) của sin (hoặc cos) với nhiều cung khác nhau ta cần để ý đến
các cung có tổng (hiệu) các góc bằng nhau để áp dụng công thức tổng sang tích.
Bài 2. Giải các phương trình sau
 sin x  sin 2x  sin 3x  sin 4x  sin 5x  sin 6x  0 2  3 2  3 3
cos 3x cos x  sin 3x sin x  8
 1  sin x  cos 3x  cos x  sin 2x  cos 2x  3 3
cos x  sin x  sin 2x  sin x  cos x Hướng dẫn giải
 Nhận xét: Bài toán có các cung khác nhau biểu diễn dưới dạng tổng (hiệu) của các hàm số sin (hàm
số cos) ta nên ghép các số hạng này thành cặp sao cho tổng (hiệu) các cung của chúng bằng nhau, cụ
thể trong trường hợp này ta để ý x  6x  2x  5x  3x  4x . Tại sao lại cần phải ghép như vậy?
Lý do là chúng ta cần xuất hiện thừa số chung để nhóm ra ngoài, đưa bài toán về dạng tích.
PT  (sin 6x  sin x )  (sin 5x  sin 2x )  (sin 4x  sin 3x )  0 7x  5x x 3x    7x 3x  2 sin cos  cos  cos   0  4 sin cos (2 cos x  1)  0 2  2 2 2  2 2 k2 k2 2
Vậy phương trình có nghiệm x  , x   ,x    k2 ,
k  . 7 3 3 3
Đối với bài này mà sử dụng công thức nhân ba của sin và cos thì cũng ra nhưng phức tạp hơn.
Chính vì thế mà ta khéo léo phân tích để áp dụng công thức tích sang tổng. 1 
(2)  cos 4x  cos 2x 1 2 3 2 2 2
cos x  (cos 4x  cos 2x) sin x  2 2 8    x  2 2 x x  x  2 2 x x 2 3 2 2 2 3 2 cos 4 sin cos cos2 cos sin 
 cos 4x  cos 2x  4 4 2 3  cos 4x    x    k . 2 16 2
 (ĐHNT HCM 2000) PT  1  cos 2x  sin x  sin 2x  cos 3x  cos x  0 2
 2 sin x  sin x  2 sin x cos x  2 sin 2x sin x  0
 sin x(2 sinx  2 cosx  2 sin 2x  1)  0 sinx  0   2
 (sinx  cosx) 4 sinx cosx 1  0 
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 28
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 7 ĐS: x k ,
 x    k2 ,
 x    k2 ,  x   k2 . 3 6 6  3 3
(ĐHCS 2000) PT  2 sin x cos x  sin x  sin x  cos x  cos x  0 2 2
 2 sin x cos x  sin x cos x  cos x sin x  0  sin x cos x(2  sin x  cos x)  0 ĐS: x k . 2
Bài 3. Giải các phương trình sau
 sin 2x sin 5x  sin 3x sin 4x        4 4 3
cos x  sin x  cos x   sin 3  x    0  (D2005)  4    4 2
 3 cos 5x  2 sin 3x cos 2x  sin x  0 (D2009)  3
sin x  cos x sin 2x
3 cos 3x  2(cos 4x  sin x) (B2009) Hướng dẫn giải 1 1  
(cos 7x  cos 3x)  (cos 7x  cos x)  cos 3x  cos x  3x x
 k2x k . 2 2 2 1 1         3  2 PT  1  sin 2x  si  n 4
x    sin 2x   0 2 2     2       2 sin2x  1 2
 sin 2x  sin 2x  2  0    x   k , (k  ).   sin 2x  2  (loai) 4 
 Nhận xét: Từ sự xuất hiện các cung 5x, 3x, 2x, x và 3x  2x  5x ta nghĩ ngay đến việc áp dụng
công thức tích sang tổng để đưa về cung 5x . Còn cung x thì xử lí thế nào, ta quan sát lời giải sau: 3 1 PT 
3 cos 5x  sin 5x  sin x  sin x  0 
cos 5x  sin 5x  sin x 2 2    x   k  sin 
  5x  sin x 12 3      3   x    k  6 2
Vậy phương trình có nghiệm: x
k ;x    k . 12 3 6 2
Chú ý: Đối với dạng phương trình a sin x b cos x a ' sin kx b 'cos kx, k  0,1 ta coi như 2 về
của phương trình là 2 phương trình bậc nhất với sin và cos. Do đó ta có cách làm tương tự.  2
PT  sin x(1  2 sin x)  cos x sin 2x
3 cos 3x  2 cos 4x 1 3
 sin 3x  3 cos 3x  2 cos 4x  sin 3x
cos 3x  cos 4x 2 2      x
    k2      6  cos 4x  cos 3
x    4x   3
x    k2   k        ( ).  6   6   x   k   42 7
3. Sử dụng công thức hạ bậc
Khi giải các phương trình lượng giác mà bậc của sin và cos là bậc chẵn ta thường hạ bậc từ đó đưa về
phương trình cơ bản.
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 29
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Bài 4. Giải các phương trình sau  2 2 2 3 2 2 2 2
sin x  sin 2x  sin 3x
 sin 3x  cos 4x  sin 5x  cos 6x (B02) 2 x    x  2 2 2
sin    tan x  cos  0  x x x  2 4  2 (D03)  2 2 cos 3 cos 2 cos 0 (A05) Hướng dẫn giải 6x  2x
 (ĐHAG2000) Từ sự xuất hiện bậc chẵn của hàm số sin và tổng hai cung  4x mà ta 2
nghĩ đến việc hạ bậc và sử dụng công thức biến tổng sang tích sau đó nhóm các hạng tử để đưa về phương trình tích. cos 4x  0 
PT  cos 2x  cos 4x  cos 6x  0  cos 4x(2 cos 2x  1)  0   1  cos 2x    2 k
Vậy phương trình có nghiệm: x   ,x    k . 8 4 3 1 cos 6x 1  cos 8x 1 cos10x 1  cos12x  PT     2 2 2 2
 (cos12x  cos10x) (cos 8x  cos 6x)  0  2 cos11x cos x  2 cos 7x cos x  0
 cos x(cos11x  cos 7x)  0  cos x sin 9x sin 2x  0 .
Vậy phương trình có nghiệm: x k
;x k ,(k  )  . 9 2
 Điều kiện: cos x  0.    2 1     sin x 1 2 2 PT  1  cos x     
1  cos x  (1  sin x) sin x  (1  cos x) cos x      2   2   2    cos x 2 
 (1  sin x)(1  cos x)(sin x  cos x)  0
ĐS: Kết hợp với điều kiện ta được x k2 ,
 x    k . 4 1  cos 6x 1  cos 2x  PT  cos 2x
 0  cos 6x.cos 2x 1  0 2 2
 cos 8x  cos 4x  2  0 2
 2 cos 4x  cos 4x  3  0  cos 4x  1  x k . 2
Bài 5. Giải các phương trình sau      2 4 4
2 sin 2x  sin 7x 1  sin x (B07)
 cos x  sin x     1   4 x    3(1 sinx)  x     2
(2  3)cos x 2 sin     2 cosx 1 
3tan x tanx  8cos     0  2 4   3 2 2 cos x 4 2 Hướng dẫn giải  2
PT  sin 7x  sin x  (1  2 sin 2x)  0  2 cos 4x. sin 3x  cos 4x  0
 cos 4x(2 sin 3x 1)  0 . 2 5 2
Vậy PT có nghiệm: x   k ,x   k , x   k . 8 4 18 3 18 3
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 30
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1  2 2
(ĐHL1995) (1  cos 2x )  (1  sin 2x )  1  sin 2x  cos 2x  1    2 cos 2  x     1    x
k x    k , (k  ).    2  2 4 1 3    
 (DB03)   3 cos x  sin x  0  sin x
cos x  0  sin x     0 2 2  3  x   k . 3 3(1  sin x)  3
(KT1999)  3 tan x  tan x
 4(1  sin x)  0 2 cos x 2 2
 tan x(3 tan x 1) (1 sinx)(3 tan x 1)  0 2
 (3 tan x 1)(tan x  1  sin x)  0 1 TH1: tan x  
x    k ,  k  .  3 6
TH2: 1  sin x  tan x  0  sin x  cos x  sin x cos x  0 (pt đối xứng với sin và cos)  2 1  
Giải phương trình này được x   arccos     k2 ,  k  .  4  2   
4. Sử dụng các đẳng thức lượng giác quan trọng (hằng đẳng thức)
Bài 6. Giải các phương trình sau 2  x x    2  sin
 cos   3 cos x  2 
cotx  tan x  4 sin 2x   (D07)  (B03)  2 2  sin 2x  3
tan x  cot x  2 cot 2x x x x x  tan cot 2(sin 2 cos 2 ) Hướng dẫn giải x x   1  2 sin
cos  3 cos x  2  sin x  3 cos x  2 2 2   1 3   x    k2   1  sin x  cos x  1  6  sin x         (k  ).  2 2  3  2  x   k2  2
 Nhận xét: Từ sự xuất hiện của cot x  tan x và sin 2x ta xem chúng có mối quan hệ nào? 2 2 cos x  sin x cos 2x
Ta có cot x  tan x   2
. Từ đó ta định hướng giải cho bài toán như sau: sin x cos x sin 2x
Điều kiện: sin 2x  0  x k 2 cos 2x 2 2 2 PT  2  4 sin 2x
cos 2x  2 sin 2x  1  2 cos 2x  cos 2x  1  0 sin 2x sin 2x
cos2x  1  sin2x  0 (lo¹i)   
x    k . 1 3 2
cos2x    sin 2x  (t/m) 3  2 4 1 2t
Chú ý: Ta có thể đặt t  tan x  cot x  , sin 2x
đưa phương trình về ẩn t để giải. 2 t 1 t
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 31
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
 (ĐHQGHN1996) Điều kiện sin 2x  0  x k 2 sin x cos x cos 2x 3 3 3 PT    2 cot 2x  2
 2 cot 2x  cot2x  cot 2x  0 cos x sin x sin 2x
 cot2x  0  x   k (t/m). 4 2
 (GTVT1998) Điều kiện: sin 2x  0  x k 2 sin x cos x 2 PT  
 2(sin 2x  cos 2x) 
 2(sin 2x  cos 2x) cos x sin x sin 2x 2
 1  sin 2x  sin 2x cos 2x 2
 cos 2x  sin 2x cos 2x cos 2  0 x   k x   4 2     ,(k  ).  tan 2x  1   x   k  8 2
Bài 7. Giải các phương trình sau 13 6 6
2(cos x  sin x) sin x cos x  6 6 2
cos x  sin x  cos 2x   0 (A06) 8 2  2 sin x 4 4 cos x  sin x 1 1 2 cos 4x   cot2x
cotx  tan x  5 sin 2x 2 8 sin 2x  sin 2x Hướng dẫn giải  6 6 3 3
Nhận xét: Xuất hiện cos x  sin x ta nghĩ đến việc sử dụng hằng đẳng thức a b . 13 2 2 4 4 2 2 2
PT  (cos x  sin x)(cos x  sin x  sin x cos x )  cos 2x 8 1 1 13 2 2 2
 cos 2x(1  sin 2x  sin 2x)  cos 2x 2
 cos 2x(8  2 sin 2x  13 cos 2x )  0 2 4 8    cos 2x  0 cos 2  0 x   k x       4 2   k   2 1  ( ).
2 cos 2x 13 cos 2x  6  0   cos 2x     2 x    k  6  x   k2 1   Điều kiện: 4 sin x    3 2 x    k2  4 4 4 2 2
PT  2(cos x  sin x  sin x cos x )  sin x cos x  0 2 2
 2  6 sin x cos x  sin x cos x  0 2
 3 sin 2x  sin 2x  4  0  sin 2x  1  x   k . 4 5
Kết hợp với điều kiện ta được nghiệm của phương trình là x   k2 ,  k  .  4
 (DB2002) Điều kiện: sin 2x  0  x k 2
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 32
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 1 2 1  sin 2x 1 cos 2x 1 2 9 2 PT   
 cos 2x  5 cos 2x   0 5 sin 2x 2 sin 2x 8 sin 2x 4 1  cos 2x
x    k . 2 6
Điều kiện: sin 2x  0  x k 2 2 cos 2x 2 cos 4x 1 2 PT  2 
 2 cos 2x  cos 2x 1  0  cos 2x    x    k . sin 2x sin 2x 2 3
Bài 8. Giải các phương trình sau x
 (1  tan x)(1  sin 2x)  1  tan x
 cot x  sin x(1  tan x tan )  4 (B06) 2 
(1  sin x  cos 2x)sin x       4  1
(1  2 sin x)cos x   cos x   3 (A09) 1  tan x 2
(1  2 sin x)(1  sin x) Hướng dẫn giải
 Điều kiện: cos x  0  x   k 2 2
PT  (cos x  sin x)(sin x  cos x )  sin x  cos x
sinx  cosx  0 tan x  1  2 2
 (sin x  cos x)(cos x  sin x 1)  0      2 2
cos x  sin x  1 cos2x  1     
x    k (t/m)   4  .
x k (t/m)  2t
Chú ý: Ta có thể đặt t  tan x  sin 2x
để đưa phương trình về dạng đại số ẩn t . 2 1  t x
 Điều kiện: sin x  0, cos x  0, cos
 0  x k ,k   2 2 x x
cos x cos  sin x sin 2 2
PT  cot x  sin x
 4  cotx  tan x  4  1  4 sin x cos x x cos x cos 2 1 5 Giải sin 2x
và kết hợp với điều kiện, thu được nghiệm: x   k ,  x
k (k  )  . 2 12 12 c  osx  0 
 (A2010) Điều kiện:  tan x  1       PT  2 sin x
  (1  sin x  cos 2x)  (1  tan x)cos x   4 
 (sin x  cos x)(1  sin x  cos 2x)  sin x  cos x  sin x  cos 2x  0
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 33
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 1 2
 2 sin x  sin x 1  0  sin x   2 7
Kết hợp với điều kiện, thu được nghiệm của phương trình là: x    k2 ,  x   k2 . 6 6 1
 Điều kiện: sin x  1, sin x   2
PT  (1  2 sin x) cos x
3(1  2 sin x)(1 sin x) 2
 cos x  3 sin x  sin 2x  3(1  2 sin x) 1 3 1 3  cos x
sin x  sin 2x  cos 2x 2 2 2 2        cos x    cos 2    x      x
k2x    k .   3     6  2 18 3 2
Kết hợp với điều kiện ta được nghiệm của phương trình là x    k (k  ).  18 3 2 cos x cos x 1  sin x
Chú ý: Có thể sử dụng đẳng thức  
đưa phương trình về 1 sin x
cos x(1 sin x) cos x sin x cos 2x         dạng  3  sin x
    sin  2x. cos x  sin 2x  3    6 
KĨ THUẬT 2: ĐƯA VỀ PHƯƠNG TRÌNH TÍCH
Xu hướng trong đề thi đại học những năm gần đây việc giải phương trình lượng giác thường đưa về
phương trình tích bằng cách sử dụng các công thức lượng giác, các phép biến đổi lượng giác, các kĩ
năng tách, nhóm các số hạng hợp lý để tạo ra nhân tử chung...
Bài 1. Giải các phương trình sau
 1  sin x  cos x  sin 2x  cos 2x  0
 (2 cos x 1)(2 sin x  cos x)  sin 2x  sin x
 cos 2x  3 sin 2x  5 sin x  3 cos x  3
 2 sin x(1  cos 2x)  sin 2x  1  2 cos x
 sin 2x  cos 2x  3 sin x  cos x  1  0 x x x x x   (sin 2 cos2 )cos 2 cos 2 sin 0 Hướng dẫn giải  2
(B-2005)  sin x  cos x  2 sin x cos x  2 cos x  0  sin x  cos x (1  2 cos x)  0
 (D2004) PT  (2 cos x  1)(2 sin x  cos x)  sin x(2 cos x  1)
 (2 cos x 1)(sin x  cos x)  0  2
PT  1  2 sin x  6 sin x cos x  5 sin x  3 cos x  3 2
 3 cosx(2 sin x 1) (2 sin x  5 sin x  2)  0  (2 sin x 1)(3 cos x  sin x  2)  0  2
(D2008)  4 sin x cos x  2 sin x cos x  1  2 cos x  (2 cos x  1)(2 sin x cos x  1)  0  2
(D2010) PT  2 sin x cos x  (1  2 sin x )  3 sin x  cos x  1  0 2
 cos x(2 sin x 1)  2 sin x  3 sin x  2  0
 cos x(2 sin x 1)  (2 sin x 1)(sin x  2)  0  (2 sin x 1)(cos x  sin x  2)  0  2
(B2010) PT  2 sin x cos x  cos 2x cos x  2 cos 2x  sin x  0 2
 sin x(2 cos x 1)  cos 2x(cos x  2)  0  sin x cos 2x  cos 2x(cos x  2)  0
 cos 2x(sin x  cos x  2)  0
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 34
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Bài 2. Giải các phương trình sau     1 1  2 2 2 sin x      
tan 2x  cotx  8 cos x    4  sin x cos x 2  2
2 tan x  cot x  3 
 cos 2x  cos x(2 tan x 1)  2 sin 2x 1
2(cos x  sin x) cos 2x 1  2  cotx 1 
 sin x  sin 2x tan x  cot2x cotx 1  1  tan x 2 Hướng dẫn giải
 (ĐHQGHN1997) Điều kiện: sin 2x  0  x k 2 sin x  cos x sinx cosx 0    tan x  1   
PT  2(sin x  cos x )    sin x cos x sin2x 1   sin 2x  1  
Giải và kết hợp với điều kiện thu được: x    k ,  x
k hay x   k . 4 4 4 2
 Điều kiện: cos 2x  0, sin x  0 sin 2x sin x
sin 2x sin x  cos 2x cos x 2 2 PT    8 cos x   8 cos x cos 2x cos x cos 2x sin x cosx  0 
 cos x(1  8 cos x cos 2x sin x)  0   1  sin 4x   2 5 ĐS: x
k x   kx   k . 2 24 2 24 2
 (ĐHNT1997) Điều kiện: sin x  0, cos x  0 2 sin x cos x 1    3  2 2
 2 sin x  cos x
3 sin x cos x  1 cos x sin x sin x cos x sin x  0 (lo¹i) 2
 1  sin x  3 sin x cos x  1  sin x(sin x  3 cos x)  0   
sin x  3 cos x
 tan x  3 x   k . 3
 (DB2003) Điều kiện: cos x  0 2 sin x 2 sin x  cos 2x  2  cos x  2  2
 cos 2x 1  1  cos x cos x cos x  1  2  2 sin x 
1  1  cos x 2   
 (1  cos x) 2(1  cos x)  cos x  0 cos x   
ĐS: x k2 ,
 x    k2 . 3 c
 osx.sin2x.sinx(tanx  cot2x)  0   Điều kiện:  c  otx  1 
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 35
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 1
2(cos x  sin x) cos x sin 2x PT     2 sin x sin x cos 2x cos x cos x  1 cos x sin 2x sin x
 sin x(2 cos x  2)  0
Kết hợp với điều kiện thu được nghiệm của phương trình là: x    k2 , (k  ).  4
 (A2003) Điều kiện: cos x  0, sin x  0, tan x  1  2 2 cos x  sin x
cos x(cos x  sin x) 2  
 sin x  sin x cos x sin x cos x  sin x  1 
cosx  sinx  0
 (cos x  sin x)
 cos x  sin x  0     sin x   2
sin x  sin x cos x 1  0  tan x  1    x   k t ( /m)  2
2 tan x  tan x  1  0 4 
Bài 3. Giải các phương trình sau  3 3 5 5 6 6 8 8
sin x  cos x  2(sin x  cos x )
 sin x  cos x  2(sin x  cos x) 5  8 8 10 10
sin x  cos x  2(sin x  cos x ) 
cos 2x (ĐHNT HCM2000) 4 Hướng dẫn giải cos2x  0  3 2 3 2 3 3 
 sin x(1  2 sin x )  cos x(2 cos x  1)  cos 2x(sin x  cos x )  0   . tan x  1   6 2 6 2
(QGHN99) PT  sin x(1  2 sin x )  cos x(2 cos x  1)  0 cos2x  0 6 6
 cos 2x(sin x  cos x)  0    . tan x  1   5  8 2 8 2
PT  sin x(1  2 sin x )  cos x(1  2 cos x )  cos 2x  0 4  5  8 8  cos 2x cos  x  sin x     0  .  4
Bài 4. Giải các phương trình sau
 3  tan x(tan x  2 sin x)  6 cos x  0 (DB2003) 2
 3 tan 3x  cot2x  2 tan x  sin 4x 3 2
4 cos x  2 cos x(2 sin x 1) sin 2x  2(sin x  cos x)   0 2 2 sin x 1  x x   3 sin 2 cos
3  2 3 cos x  3 3 cos 2x  8( 3 cos x  sin x)  3 3  0  6 3 4
8 2 cos x  2 2 sin x sin 3x  6 2 cos x  1  0
 3(cot x  cos x)  5(tan x  sin x)  2 Hướng dẫn giải
 (DB2003) Điều kiện: cos x  0
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 36
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 sin x sin x
2 sin x cos x     PT  3     6 cos x  0 cos x  cos x  2 2 3
 3 cos x  sin x(1  2 cos x)  6 cos x  0 2 2
 3 cos x(1  2 cos x)  sin x(1  2 cosx)  0 2 2
 (1  2 cos x )(3 cos x  sin x )  0 ĐS: x    k , (k  ).  3 c  os 3x  0 cosx  0  * Điều kiện:   x
k ,x k sin  4x  0  6 3 4 sin  2x  0  2
PT  2(tan 3x  tan x )  (tan 3x  cot 2x )  sin 4x 2 sin 2x cos x 2    cos 3x cos x cos 3x sin 2x sin 4x
 4 sin 4x sin x  2 cos 2x cos x  2 cos 3x  4 sin 4x sin x  cos 3x  cos x  2 cos 3x
 4 sin 4x sin x  cos 3x  cos x  8 sin 2x cos 2x sin x  2 sin 2x sin x 1
 sin 2x sin x(4 cos x  1)  0  cos 2x   (t/m) 4
Cách 2 (Bạn Hồng& Thanh Tùng A1) Điều kiện: x
k ,x k . 6 3 4
PT  3 tan 3x  cot 2x  2 tan x  tan 2x  cot 2x  3 tan 3x  2 tan x  tan 2x  0 2 sin 2x sin x
 2(tan 3x  tan x)  tan 3x  tan 2x  0    0 cos 3x cos x cos 3x cos 2x
2 sin 2x cos 2x  sin x cos x sin2x  0 (lo¹i) 
 0  sin 2x 4 cos 2x   1  0  
cos 3x cos x cos 2x 4 cos2x 1  0  1
 cos 2x   (t/m) . 4 1  1  
Vậy phương trình có nghiệm x   arccos     k . 2  4  2
Điều kiện: 2 sin x  1  0  cos 2x  0  x   k 4 2 2 2
PT  4 cos x(cos x  sin x )  2 cos x(cos x  sin x)  2(sin x  cos x )  0
 2(sin x  cos x)(cos x 1)(2 cos x 1) 2
Kết hợp với điều kiện thu được nghiệm của phương trình: x k ,k  . 3  2 3 2
PT  2 sin x cos x  6 sin x cos x  2 3 cos x  6 3 cos x  8( 3 cos x  sin x )  0 2
 2 cos x(sin x  3 cos x)  6 cos x(sin x  3 cos x)  8( 3 cos x  sin x)  0 2
 (sin x  3 cos x)(2 cos x  6 cos x  8)  0  3 3 3
PT  2 2 cos x(4 cos x  3 cos x)  2 2 sin x sin 3x  1  0
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 37
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 2  x x x  2 2 cos
2 cos cos 3  2 sin x(2 sin x sin 3x)  2
 (1  cos 2x)(cos2x  cos 4x)  (1 cos 2x)(cos 2x  cos 4x)  2 2 2
 2(cos 2x  cos 2x cos 4x)  2  cos 2x cos 2x  4 2  cos 2x
x    k . 2 8
 Điều kiện: sin x  0, cos x  0 .
PT  3(cot x  cos x  1)  5(tan x  sin x  1)  0
cosx sinx cosx sinx     sin x sin x cos x cos x       3  5     0   sin x     cos x 
cosx  sinx cosx  sinx  0    3 5   sinx cos x 2
t  2t 1  0 v
( íi t  sin x  cos x  2 cos(x  ))  4    5 tan x   3 1  2 3
Đối chiếu với điều kiện thu được: x   arccos
k2, x  arctan  k . 4 2 5
KĨ THUẬT 3: ĐẶT ẨN PHỤ
1. Chọn góc để đặt ẩn phụ
Bài 1. Giải các phương trình sau 3 x    1  x     3 x     sin     sin    cos x  2 sin     3   10 2 2 10 2   2 2         5x  x      3x
 sin 3x    sin 2x. sin x     sin
   cos    2 cos    4     4   2 4    2 4  2 Hướng dẫn giải
 Nhận xét: Nhìn vào phương trình này ta nghĩ dùng công thức biến đổi sin của một tổng ... nhưng 3 x     3x   
đừng vội làm như thế khó ra lắm, ta xem mối quan hệ giữa hai cung         và có 10 2 10 2 
quan hệ với nhau như thế nào? 3 x 9 3x 3x   
Thật vậy nếu ta đặt t    3t     
thì khi đó sử dụng công thức 10 2 10 2 10 2 
góc nhân ba là biến đổi dễ dàng. 1 1 sint  0 3 2  PT  sin t
sin 3t  sint  3 sint  4 sin t  sint(1 sin t)  0  2 2 cost  0  3 3
Vậy nghiệm của phương trình là: x   k2 ,  x    k4 ,
k  . 5 5 6
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 38
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Chú ý: Nếu không quen với cách biến đổi trên, ta có thể làm như sau: 3 x 3 3x t    x   2t    t . 10 2 5 10 2 3 x  2 Đặt t
  x  3 2t . PT cos(3 2t)  2 sint  3  sin t  sin t  2  0 . 2 2 k
 Đặt t x  . ĐS: x    4 4 2 x 3x 35x  Đặt t     3t  , 
 5t . 2 4 2 4 2 4  3  
PT  sin(5 t )  cos t  2 cos 3  t   
 sin 5t  cost  cos 3t  sin 3t   4 
 sin 5t  sin 3t  cos 3t  cost  2 sint(cos 4t  sin 2t)  0 . x  3 x     
Chú ý: Có thể chuyển cos     sin    
rồi áp dụng công thức tổng sang tích cho vế trái. 2 4     4 2
Bài 2. Giải các phương trình sau          3 3 8 cos x     cos 3x  tan x
    tan x 1    3   4  x  x  x 2 3x           2 cos  
  6 sin    2 sin    2 sin    5 12   5 12   5 3     5 6  Hướng dẫn giải 2
 Đặt t x  . ĐS: x   k ,  x    k ,  x k 3 6 3 1  tant  3 3
Đặt t x  . PT  tan t
1  (1  tant) tan t  2 tant . 4 1 tan t 5 5 5
 (ĐHYTB1997) ĐS: x   k5 ,  x    k5 ,  x    k5 . 4 12 3
2. Chọn biểu thức để đặt ẩn phụ
Bài 3. Giải các phương trình sau 6
 3 sin x  4 cos x
 6  sin x  3 cos x  sin x  3 cos x  2
3 sin x  4 cos x  1 1 1  2 2 2 2 cos x   cos x
 2 cos 2x  cos 2x  4 sin 2x cos x 2 cos x cos x
1  3 tan x  2 sin 2x 2 2
 3 cot x  2 2 sin x  (3  2 2) cos x Hướng dẫn giải t  1  2 
Đặt t  3 sin x  4 cos x  1 (t  0 ). Từ phương trình ta có t  7t  6  0  . t  6   Đặt t
sin x  3 cos x ,(t  0). Từ phương trình ta có t  1,t  2  (loại).     Vậy sin x
3 cos x  1  sin x     sin   3 6
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 39
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 1 1  2 2
Đặt t  cos x   cos x
t  2 . Từ phương trình ta có t  1  ,t  2. 2 cos x cos x  2 2
 2 cos 2x  cos 2x  2(1  cos 2x )(1  cos 2x). Do đó ta đặt t  cos 2x, t  1 . 2t
 Đặt t  tan x  sin 2x  . 2 1  t
Ngoài ra ta có thể khai triển đưa về phương trình đẳng cấp bậc 3 theo sin và cos. 2 (1 cos x)  2  3
 2 2(1 cos x)  (3  2 2)cos x . Do đó đặt t  cos x, t  1 2 cos x 2 2
Chú ý: Có thể đưa phương trình về dạng tích (sin x  cos x)(3 cos x  2 2 sin x )  0 .
KĨ THUẬT 4: NHÓM BÌNH PHƯƠNG
1. Biến đổi phương trình về dạng A2 + B2 = 0
Bài 1. Giải các phương trình sau  2 2
4 cos x  3 tan x  4 3 cos x  2 3 tan x  4  0  2
3  sin 2x  2 sin 2x  cos 2x  2 2 sin x  2
4 cos 2x  2 cos 2x  6  4 3 sin x Hướng dẫn giải  2 2
PT  (4 cos x  4 3 cos x  1)  (3 tan x  2 3 tan x  1)  0 2
 cosx  3  0   x  2  x  2 2 cos 3 3 tan 1  0   
x    k2 .   3 tan x  1  0 6  2 2
 Nhận xét: Vì xuất hiện sin 2x và 2 sin 2x ta nghĩ đến việc đưa về (sin 2x  1) do đó ta biến đổi như sau: 2
PT  sin 2x  2 sin 2x  1  (1  cos 2x)  2 2 sin x  1  0  x    k2 1   x     x  2 2 sin 2 1 2 sin 1  0  4  sin x    .  3 2 x   k2  4  2 2
Nhận xét: Vì xuất hiện 4 cos 2x và cos 2x ta nghĩ đến việc đưa về (2 cos 2x  1) , phần còn lại 2
ta biến đổi về sin x . 2 2
PT  4 cos 2x  4 cos 2x  1  4 sin x  4 3 sin x  3  0  3  sin  x    x   k2 3   x    x  2 2 2 cos 2 1 2 sin 3  0   2   3  sin x     . 1 2  2 c  os2x   x   k2    2  3
2. Biến đổi phương trình về dạng A2 = B2
Bài 2. Giải các phương trình sau  2 2 2 2
sin 2x  2 tan x  tan x
 tan x  sin 2x  4 cos x 1 x  2 2 2 cos 2
 4 tan x  4 tan x  2
 4 cot x  4 cot x  2 sin x 1  cos 2x
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 40
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1  2 2 2 2
sin 2x  cos 2x  cos 3x  cos x
 cos 3x  cos x  3 cos 2x  cos 2x  2 x  6 32 cos
 sin 3x  3 sin x 2 Hướng dẫn giải  2 2 2
PT  1  2 sin x cos x  1  2 tan x  tan x  (sin x  cos x )  (1  tan x )  2 2
Nhận xét: Ta nhận thấy tan x sin 2x  2 sin x do đó ta cộng vào 2 vế 1 lượng 4 sin x . 2 2 2 2 2
PT  tan x  2 tan x sin 2x  sin 2x  4 cos x  4 sin x  (tan x  sin 2x)  4  2
Nhận xét: Vì chúng ta nhận thấy xuất hiện 4 tan x và 4 tan x nên ta chuyển vế để đưa về dạng 2
hằng đẳng thức (2 tan x  1) . 1 2 2 2 PT 
1  4 tan x  4 tan x  1  cot x  (2 tan x 1)  2 tan x 1   cotx 2 sin x  2 2
Nhận xét: Vì nhìn thấy xuất hiện 4 cot x và 4 cot x nên ta chuyển vế để xuất hiện (2 cot x  1) .  2 cos 2x 1 sin x
PT  4 cot x  4 cot x  1 
 0  2 cotx   2 2 1   0 1  cos 2x 2 cos x   x  2 2 2 cot
1  tan x  2 cot x  1   tan x .
 Nhận xét: Do xuất hiện nhiều góc khác nhau nên ta biến đổi cos 3x  cos x  2
 sin 2x sin x , 2 2
sau đó do vế trái có sin 2x nên ta đưa về (sin 2x  sin x ) . 2 2 2
PT  sin 2x  cos 2x  2 sin 2x sin x  (sin 2x  sin x )  cos 2x  sin x 2 2
 (sin 2x  sin x)  cos x  2 2 2
Nhận xét: Do xuất hiện cos 3x  cos x nên ta nghĩ đến hằng đẳng thức (cos 3x  cos x) . Vì
thế ta cộng thêm cả hai vế với 2 cos 3x cos x và ở vế phải ta dùng công thức biến đổi tích sang tổng
2 cos 3x cos x  cos 4x  cos 2x . 2 2 2
PT  cos 3x  2 cos 3x cos x  cos x  2  3 cos 2x  cos 2x  2 cos 3x cos x 2 2
 (cos 3x  cos x)  2  3 cos 2x  cos 4x 2 2
 (cos 3x  cos x)  sin 2x 3 x xx     6 6 2 3 32 cos
 sin 3x  3 sin x  32 cos
 3 sin x  sin 3x  4 2  cos   4 sin x 2 2  2  
 1  cos x  sin x  2 sin x       1  .  4 
KĨ THUẬT 5: XỬ LÍ PHƯƠNG TRÌNH CÓ ĐIỀU KIỆN
1. Biểu diễn nghiệm và điều kiện qua cùng một hàm số lượng giác
Trong phần này cần sử dụng tốt các kết quả sau: 2
sin x  0  cos x  1; 2
cos x  1  sin x  0;
cos x  0  sin x  1
sin x  1  cos x  0 sin  x  0 cos  x  1 cosx 1    sin x  0 sin 2x 0            sin 2x  0  c  os x  0 s  in x  1          sin x 1 cos x 0  
Bài 1. Giải các phương trình sau
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 41
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 1 1 2 2 4
sin 2x  cos 2x 1    (THTT09)   0 cos x sin 2x sin 4x sin x cos x
(1  sin x  cos 2x)sin x       x       4 1
 cot x  sin x 1
  tan x tan   4   cos x  (B06)   2 1  tan x 2 4 4
sin 2x  cos 2x  4  cos 4x      tan  x tan    x 4     4  Hướng dẫn giải  c  osx  0, sin  x  1  ,      
 (THTT09) Điều kiện: sin  2x  0,  sin  x  0,   sin  4x 0    2  sin  x    2 2
Khi đó PT  4 sin x cos 2x  2 cos 2x  2  sin x 2 sin x  sin x   1  0  x   k2 1
Giải các nghiệm sin x và kết hợp điều kiện ta được: 6 sin x    . 2  5 x   k2  6
 Điều kiện: sin 2x  0 . Khi đó phương trình đã cho trở thành 2 cos 2x 0   sin 2x  1 2 4 4 2 sin 2x cos 2x 1 0 cos 2x cos 2x 0            2 cos 2x  1 sin2x  0    
Đối chiếu với điều kiện ta được: sin 2x  1  x   k . 4  x
 (B2006) Điều kiện: sin 
x  0, cos x  0, cos  0  sin 2x  0  2  cos x sin xx x    cos x sin x PT  
cos x cos  sin x sin   4    4 sin x x  2 2  sin x cos x cos x cos  2   2 1 x   k2 ,   4  sin 2x   (t/m) 12   (k  )  . sin 2x 2  5 x   k  12 c  osx  0 sin  x  1   
 (A2010) Điều kiện:     tan x  1 tan  x  1   
(1  sin x  cos 2x)sin x  cos xcos x 1 Khi đó PT   cos x
2(cos x  sin x) 2
 1  sin x  cos 2x  1 2
 sin x  1  2 sin x  0
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 42
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1   sin x (lo¹i) 1  x
    k2    1 6    . sin x   (t/m)  7  2 x   k2  6                    Điều kiện: sin 
  x  0, cos  x  0, sin  x  0, cos  x  0.    4     4     4     4            sin 
  2x  0, cos 
  2x  0  cos 2x  0  sin 2x  1.    2    2           Nhận thấy tan 
x tan  x  1 
, do đó phương trình đã cho trở thành  4     4  1 4 4 4 4 4
sin 2x  cos 2x  cos 4x  1  sin 4x  cos 4x 4 2
 2 cos 4x  cos 4x 1  0 2 sin2x  0 2 cos 4x 1 sin 4x 0        . cos 2x  0 
Đối chiếu với điều kiện ta được sin 2x  0  x k ,(k  ).  2
2. Biểu diễn trên đường tròn lượng giác
Mỗi cung (hoặc góc) lượng giác được biểu diễn bởi các điểm trên đường tròn lượng giác:
x k2 được biểu diễn trên ĐTLG bởi 1 điểm xác định bởi cung  .
x k được biểu diễn trên ĐTLG bởi 2 điểm đối xứng nhau qua tâm O . 2
x k
được biểu diễn trên ĐTLG bởi 3 điểm cách đều nhau, tạo thành 3 đỉnh một tam giác đều. 3 2
x k
được biểu diễn trên ĐTLG bởi n điểm cách đều nhau, tạo thành đa giác đều nội tiếp n
đường tròn lượng giác.
Ta biểu diễn trên ĐTLG những điểm không thỏa mãn điều kiện (đánh dấu ) và những điểm
nghiệm tìm được (đánh dấu ). Những điểm đánh dấu " " mà không trùng với những điểm đánh
dấu "" chính là những điểm thỏa mãn điều kiện.
Bài 2. Giải các phương trình sau
sin 2x  2 cos x  sin x 1 6 6
2(sin x  cos x) sin x cos x   0 (D2011)   0 (A06) tan x  3 2  2 sin x sin x  sin 2x
(1  2 sin x)cos x   1  3 (A2009) sin 3x
 (12sinx)(1sinx) Hướng dẫn giải
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 43
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1     tan x   3 x     k    Điều kiện:  3   c  os x  0    x   k  2
Khi đó phương trình đã cho trở thành:
sin2x  2 cosx  sinx 1  0  2cosx(sin x 1)(sinx 1)  0  sinx  1
x    k2
 (sin x  1)(2 cos x 1)  0    2 1    cos x   x    k2  2  3
Kết hợp với điều kiện trên đường tròn lượng giác ta được nghiệm của PT là x   k2 , (k  ).  3  x   k2 2   Điều kiện: 4 sin x   
. Khi đó phương trình trở thành: 2  3 x    k2  4   6 6 3   1
2(sin x  cos x)  sin x cos x  0 2  2 1
  sin 2x  sin 2x  0   4  2 2
 3 sin 2x  sin 2x  4  0  sin 2x  1 x   k . 4 5
Kết hợp với điều kiện trên đường tròn LG ta được nghiệm của PT là: x
k2 (k   ). 4
 Điều kiện: sin 3x  0  x k
. Khi đó phương trình trở thành 3  sin2x  0 x k
sin x  sin 2x  sin 3x  0  sin 2x(2 cos x  1)  0    2 1    cos x    2x    k2  2  3
Kết hợp với điều kiện trên đường tròn lượng giác, ta có nghiệm của PT là: x   k . 2 1
 Điều kiện: sin x  1 và sin x   (*) 2
Với điều kiện trên phương trình đã cho tương đương:
(1  2 sin x)cos x  3(1  2 sin x)(1  sin x)     
 cos x  3 sin x  sin 2x  3 cos 2x  cos x    cos 2    x      3     6  2x
k2 hoặc x    k . 2 18 3 2
Kết hợp điều kiện (*) ta được nghiệm: x    k (k  ).  18 3
3. Thử trực tiếp (dùng mệnh đề phủ định)
Chúng ta cần lưu ý các kết quả về tính chu kì của hàm số lượng giác sau đây:
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 44
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
sin(x k2)  sin x, x  
cos(x k2)  cos x, x  
tan(x k)  tan x, x   k
cot(x k)  cotx, x   k 2
Bài 3. Giải các phương trình sau
1  sin 2x  cos 2x 1 
 2 sin x sin 2x
 3 sin x  2 cos x  3(1  tan x)  2 1  cot x cos x
 cos 3x. tan 5x  sin 7x
 tan 5x tan 2x  1 Hướng dẫn giải
 Điều kiện: sin x  0  cos x  1. Khi đó phương trình đã cho trở thành 2 2
sin x(1  sin 2x  cos 2x)  2 2 sin x cos x 2
 1  2 sin x cosx  2 cos x 1  2 2 cos x
cosx  0 (t/m)  x   k
 2 cos x(sin x  cos x  2)  0   2 
sin x  cos x  0 (*) 
Dùng mệnh đề phủ định: Giả sử sin x  0  cos x  1 , khi đó (*)  0  1  2 (vô lí). Tức    
là các nghiệm của (*) đều thỏa mãn. Giải (*) ta được: cos x     1   x   k2  .  4  4
Vậy phương trình có nghiệm: x   k ,  x   k2 . 2 4
 Điều kiện: cos x  0  sin x  1. Khi đó phương trình đã cho trở thành
 cos x(3 sin x  2 cos x)  3(sin x  cos x) 1
 cos x(3 sin x  2 cos x)  cos x  3 sin x  2 cos x 1 cosx  (
1 t/m)  x k2 (3 sin x 2 cos x 1)(cos x 1) 0        
3 sin x  2 cos x  1 (*) 
Xét (*): Giả sử cos x  0  sin x  1. , khi đó (*)  3
 1  0 (vô lí). Tức là các nghiệm 
của (*) đều thỏa mãn. Giải (*) ta được: x  arccos
k2 (với 13 2 3 cos  ;sin  ). 13 13 1
Vậy phương trình có nghiệm: x k2 ,
 x  arccos  k . 13
 Điều kiện: cos 5x  0  x   m , (m  )
 . Khi đó phương trình trở thành 10 5  x k
2 sin 5x cos 3x  2 sin 7x cos 5x  sin 8x  sin 12x 2   (k  )   x   k  20 10 k 1 + Giả sử k   m
 5k  1  2m (*). Suy ra m  2k  . 2 10 5 2 k 1
Mặt khác, do k, m   nên tồn tại s   sao cho: s
k  2s  1 (tức k là số lẻ). 2
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 45
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 Suy ra x k
là nghiệm PT khi k  2s  1. Chọn k  2s thu được nghiệm là x s (s  )  . 2 1 + Giả sử  k   m
 2k  4m  1  k  2m  (**). 20 10 10 5 2 1
Ta nhận thấy k  2m   ,
  nên không tồn tại k,m   thỏa mãn (**). 2 Do đó x   k
là nghiệm của PT với mọi k   . 20 10
Vậy phương trình có nghiệm: x s và x   k (k, s  )  . 20 10   x      m (1) cos 5x 0    Điều kiện: 10 5    ( , m n   ). c  os 2x  0   x    n (2)  4 2 1     PT  tan 5x
 tan 5x  cot2x  tan 5x  tan  2x  x   k . tan 2x 2  14 7
+ Đối chiếu điều kiện (1): 1  2m Giả sử  k   mk m  (*) 14 7 10 5 5 1  2m t 1
Do k, m   nên tồn tại t   sao cho: t   m  2t  5 2 t 1
Mặt khác, do t, m   nên tồn tại s   sao cho: s
t  2s  1. 2
Thay vào (*) ta được: k  7s  3 . Do đó x
k thỏa mãn điều kiện (*) với k  7s  3. 14 7
+ Đối chiếu điều kiện (2): Giả sử  k   n
 4k 14n  5 (**). 14 7 4 2
Ta nhận thấy vế trái (**) là số chẵn, vế phải (**) là số lẻ nên không tồn tại k, n   thỏa mãn điều
kiện (**). Do đó x
k luôn thỏa mãn điều kiện (**). 14 7
Vậy phương trình có nghiệm: x
k với k  7s  3. 14 7
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 46
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
LƯỢNG GIÁC TRONG ĐỀ THI 2002 - 2014
Bài 1 (ĐH A2002) Tìm nghiệm thuộc khoảng (0; 2) của phương trình :  cos 3x sin 3x     5 5 si  n x    cos 2x  3  x  ;x   . ĐS : 
1  2 sin 2x  3 3
Bài 2 (ĐH B2002) Giải phương trình : k k 2 2 2 2
sin 3x  cos 4x  sin 5x  cos 6x ĐS : x  ;x  (k   ) 9 2
Bài 3 (ĐH D2002)Tìm x thuộc đoạn 0;14 
 nghiệm đũng của phương trình : 3 5 7
cos 3x  4 cos 2x  3 cos x  4  0 ĐS : x  ;x  ;x  ;x  2 2 2 2
Bài 4 (ĐH A2003) Giải phương trình : cos 2x 2 1 cotx 1 
 sin x  sin 2x ĐS : x
k (k   ) 1  tan x 2 4
Bài 5 (ĐH B2003) Giải phương trình : 2
cotx  tan x  4 sin 2x  ĐS : x  
k (k   ) sin 2x 3
Bài 6 (ĐH D2003) Giải phương trình: x    x 2 2 2
sin    tan x  cot  0. 
x k  x    k  ĐS : 2 ; 2 4  2 4
Bài 7 (ĐH A2004) Cho tam giác ABC không tù, thỏa mãn điều kiện
cos 2A  2 2 cos B  2 2 cosC  3. 0 0
Tính ba góc của tam giác ABC. ĐS : A  90 ; B C  45
Bài 8 (ĐH B2004) Giải phương trình: 2 5
5 sin x  2  3(1  sin x ) tan x ĐS : x   k2 ;  x   k2 6 6
Bài 9 (ĐH D2004) Giải phương trình:
(2 cos x 1)(2 sin x  cos x)  sin 2x  sin x x  
k  x    k ĐS : 2 ; 3 4
Bài 10 (ĐH A2005) Giải phương trình: 2 2 k
cos 3x cos 2x  cos x  0 ĐS : x  (k   ) 2
Bài 11 (ĐH B2005) Giải phương trình: 2
1  sin x  cos x  sin 2x  cos 2x  0 ĐS : x    k2 ;
 x    k 3 4
Bài 12 (ĐH D2005) Giải phương trình:     3 4 4    
cos x  sin x  cos x   sin 3  x    0  x   k  ĐS : (k   )  4    4 2 4
Bài 13 (ĐH A2006) Giải phương trình: 6 6
2(cos x  sin x) sin x cos x 5  0 ĐS : x
k2 (k   ) 2  2 sin x 4
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 47
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1
Bài 14 (ĐH B2006) Giải phương trình:  x    5
cot x  sin x 1
  tan x tan   4  x   k ;  x   k  ĐS :  2 12 12
Bài 15 (ĐH D2006) Giải phương trình: 2
cos 3x  cos 2x  cos x  1  0 ĐS : x k ;  x    k2 3
Bài 16 (ĐH A2007) Giải phương trình: 2 2
1 sin x cosx 1 cos x sinx  1 sin2x ĐS: x k2 ;
 x  k2 ;
 x   k 2 4
Bài 17 (ĐH B2007) Giải phương trình k k2 5 k2 2
2 sin 2x  sin 7x  1  sin x ĐS :x   ;x   ;x   8 4 18 3 18 3
Bài 18 (ĐH D2007) Giải phương trình : 2  x x    sin
 cos   3 cos x  2  x
k  x    k   ĐS : 2 ; 2  2 2  2 6
Bài 19 (ĐH A2008) Giải hệ phương trình: 1 1 7    5   4 sin  x ĐS: x    k ;
 x    k ;  x   k sin x     3     4  4 8 8 sin x     2 
Bài 20 (ĐH B2008) Giải phương trình: k 3 3 2 2
sin x  3 cos x  sin x cos x  3 sin x cos x ĐS: x  
;x    k 4 2 3
Bài 21 (ĐH D2008) Giải phương trình: 2
2sinx 1  cos2x   sin2x  1  2cosx ĐS: x    k2 ;  x   k 3 4
Bài 22 (ĐH A2009) Giải phương trình:
12sinxcosx k2   ĐS: x    (k   )  x   x  3 1 2 sin 1 sin 18 3
Bài 23 (ĐH B2009) Giải phương trình: k2 x x x x   3 sin cos sin 2 3 cos 3
2 cos 4x  sin x ĐS: x    k2 ;  x   6 42 7
Bài 24 (ĐH D2009) Giải phương trình: k k
3 cos 5x  2 sin 3x cos 2x  sin x  0 ĐS: x   ;x    18 3 6 2
Bài 25 (ĐH A2010) Giải phương trình :
(1  sin x  cos 2x)s in(x  ) 1 4 7  cos x ĐS: x    k2 ;  x   k2 1  tan x 2 6 6
Bài 26 (ĐH B2010) Giải phương trình: k
(sin 2x  cos 2x ) cos x  cos 2x  sin x  0 ĐS : x   (k   ) 4 2
Bài 27 (ĐH D2010) Giải phương trình:
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 48
ThS. Trần Mạnh Hân (0974514498) FB: thayHanSP1 5
sin 2x  cos 2x  3 sin x  cos x  1  0 ĐS: x   k2 ;  x   k2 6 6
Bài 28 (ĐH A2011) Giải phương trình:
1  sin 2x  cos 2x
 2 sin x sin 2x ĐS: x   k ;  x   k2 2 1  cot x 2 4
Bài 29 (ĐH B2011) Giải phương trình: k2
sin 2x cos x  sin x cos x  cos 2x  sin x  cos x ĐS : x   k2 ;  x   2 3 3
Bài 30 (ĐH D2011) Giải phương trình :
sin 2x  2 cos x s in x 1  0 ĐS: x
k2 (k   ) 3  tan x 3
Bài 31 (ĐH A2012) Giải phương trình : 2
3 sin 2x  cos 2x  2 cos x  1 ĐS: x  k ;  x k2 ;  x  k2 2 3
Bài 32 (ĐH B2012) Giải phương trình: 2 k2
2(cos x  3 sin x)cos x  cos x  3 sin x  1 ĐS: x   k2 ;  x  (k   ) 3 3
Bài 33 (ĐH D2012) Giải phương trình: k 7
sin 3x  cos 3x  sin x  cos x  2 cos 2x ĐS: x   ;x   k2 ;  x    k2 4 2 12 12
Bài 34 (ĐH A2013) Giải phương trình:    
1  tan x  2 2 sin x    
x    k x    k   ĐS: ; 2  4  4 3
Bài 35 (ĐH B2013) Giải phương trình: k2 k2 2
sin 5x  2 cos x  1 ĐS: x    ;x    6 3 14 7
Bài 36 (ĐH D2013) Giải phương trình k 7
sin 3x  cos 2x  sin x  0 ĐS: x  
;x    k2 ;  x   k2 4 2 6 6
Bài 37 (ĐH A2014) Giải phương trình
sin x  4 cos x  2  sin 2x ĐS : x  
k2(k   ) 3
Bài 38 (ĐH B2014) Giải phương trình 3
2(sin x  2 cos x)  2  sin 2x ĐS : x  
k2(k   ) 4
-----------------------------------------Hết-----------------------------------------
Trường THPT Nguyễn Hữu Tiến - Duy Tiên - Hà Nam 49