Phương Trình Trạng Thái và Quá Trình Nhiệt Động Cơ Bản Chất Khí môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Chương 1:
phương trình trạng thái
và các quá trình nhiệt động cơ bản của chất khí 1. Bài tập giải mẫu: Bài 1:
Xác định thể tích riêng và khối lượng riêng của khí N2 ở điều kiện tiêu chuẩn
vật lý và điều kiện áp suất dư p d= 0,2bar với nhiệt độ t = 127 C. 0 Biết áp suất khí quyển 750mmHg. Lời giải:
Điều kiện tiêu chuẩn vật lý: p0 = 760 mmHg; t = 0 0 0C.
* ở điều kiện tiêu chuẩn vật lý thể tích riêng v0 và
khối lượng riêng ρ0 của N 2được
xác định từ phương trình trạng thái: p0. v0 = R.T 0 = R T . v p 0 0 = 8314 = 0 8314 R µ J / kg K 28 0 N T0 = t + 273 = 0 + 273 = 273 0 K 0 2 p 760 0 = 750 10 . 5 N / m2 273 . 8314 Do đó: v0 = 760 = 0,8 m . 28 10 . 3/kg ρ = = 0= 750 5 13 1 , 1 25 m / kg v 8 , 0
* ở điều kiện p d= 0,2bar nhiệt độ t = 127 C 0
thể tích riêng v và khối lượng riêng ρ 0
của N cũng được xác định tương tự: 2 v= R T . p
T = t + 273 = 127 + 273 = 400 K 0 = + = + = p p p 10 . 1 10 . 2 , 0 10 . 2 , 1 N / m 5 5 5 2 = 400 . 8318 = 0 d v 98 , 0 m / kg 28 10 . 2 , 1 . 3 5 ρ = 1 = 1 = 02 , 1 kg / m v 98 , 0 3
Truờng đại học công nghiệp hà nội
bài tập kỹ thuật nhiệt 2 Bài 2:
Một bình có thể tích 0,5m 3chứa không khí ở áp xuất dư 2bar, nhiệt độ 20 C. 0
Lượng không khí cần thoát ra khỏi bình là bao nhiêu để áp suất trong bình có độ
chân không 420mmHg trong điều kiện nhiệt độ trong bình coi như không đổi. Biết
áp suất khí quyển 768mmHg. Lời giải:
Lượng không khí thoát ra khỏi bình G: G = G - G 1 2 ở đây: G1, G là 2
lượng không khí có trong bình lúc đầu và sau khi lấy không khí ra
khỏi bình, được xác định từ phương trình trạng thái: p1. V1 = G R. T 1. 1 p2. V2 = G2. R.T2 p V . 1 1 G= 1 R T . 1 p V . 2 2 G=2 R T.2 = V = = V = V 5 , 0 m3 1 2 8314 8314 R = = 287 J / kg0K µ 29
T = T = T = 273+ t = 273+ 20 = 293 0 K 1 2 p V p V V = − 1 = G2 1 − 2 (p p ) RT RT RT 768 5 5 2 = + 10 ). = + 10 . 024 , 3 N 1/ p m = pd1 p0 (2 750 (768 − ) 420 5 5 2 p = p −p = 10 . = . 464 , 0 10 N / m 2 0 ck2 750 5 , 0 = − G5= ( 024 , 3 464 , 0 10 ). 52 , 1 . kg 293 . 287 Bài 3:
Một bình thể tích 200lít chứa 0,2kg khí N2 áp suất khí quyển là 1 bar. Xác định
chỉ số áp kế gắn trên nắp bình nếu:
a, Nhiệt độ trong bình là 7 C? 0
b, Nhiệt độ trong bình là 127 C? 0 Lời giải:
a, Khi nhiệt độ trong bình là 70C áp suất tuyệt đối trong bình p1: GRT1 p= 1V 1 280 . 8314 . 2 , 0 5 = p21= 10 . 8314 , 0 N / m 8314 , 0 bar 2 , 0 . 28
Truờng đại học công nghiệp hà nội
bài tập kỹ thuật nhiệt 3 Trong đó: G = 2 , 0 Kg 8314 0 R = J / kg K 28 0 = + = T+= 273 = = t = 273 7 280 K 1 1 3 V V V 2 , 0 m 1 2
Chỉ số áp kế gắn trên nắp bình: = − = − p 31 ck = p0 p1 1 8 , 0 4 1686 , 0 bar.
b, áp suất tuyệt đối trong bình p khi nhiệt độ trong bình là 127 2 0C: GRT2 p= 2V 2 28314 , 0 127 .( ) 273 = + 5 p2== 10 . 1877 , 1 N / m 1877 , 1 bar 2 , 0 . 28
Chỉ áp kế gắn trên nắp bình: − = − d = 2 p 0 p p 1877 , 1 1 1877 , 0 bar. Bài 4:
Tìm nhiệt dung riêng khối lượng đẳng áp trung bình và nhiệt dung riêng thể
tích đẳng tích trung bình của khí N từ nhiệt độ 200 2 C đến 800 0 0C. Lời giải:
Theo công thức tổng quát tính nhiệt dung riêng trung bình: t 1 t t 1 t C . tC tC .− = 2 0 1 0 2 t − t [ ] 2 1 2 1
* Từ bảng nhiệt dung riêng khối lượng đẳng áp trung bình phụ thuộc nhiệt độ đối với khí N ta có: 2 = C 0p0+ 024 , 1 t. 00008855 , 0 kJ / . kg K Với t = 800 2 C, t 0 1= 200 C sẽ là: 0 = + C t 0 p 20= 024 , 1 800 . 00008855 , 0 09484 , 1 kJ / kg K = + C t 0 p 10= 024 , 1 0000 , 0 8855 200 . kJ 04171 , 1 / kg K Vậy ta có: − t 1 C0p 2t1== 800 . 09484 , 1 [ ] 200 . 04171 , 1 11255 , 1 kJ / kg K 800 − 200
Ta có thể tính nhiệt dung riêng trung bình theo cách sau: t C = 024 , 1 + . 00008855 , 0 t = a + t. b p 0 t t = + C 2 = + a t. b ; C 1 a t. b p 0 2 p 0 1
Truờng đại học công nghiệp hà nội
bài tập kỹ thuật nhiệt 4
Khi thế các giá trị này vào biểu thức tổng quát ta rút ra được: t = 1+ C 2p2t1+ a b(t t ) Với t = 800 2 C và t 0 1 = 200 0C ta có: = + + C t0 p 2t1= 024 , 1 , 0 ( 00008855 800 200) 11255 , 1 kJ / . kg K
* Từ bảng nhiệt dung riêng thể tích đẳng tích trung bình N , ta có: 2 C ' t= 9 , 0 089 + 000 , 0 . 107 t kJ / m3 0 K v 0 tc
áp dụng quy tắc trên ta có: = + + C' t 3 0 v2 1= 9089 , 0 ( 000107 , 0 800 ) 200 , 1 0196 KJ / m . K t tc Bài 5:
Xác định các thông số: entanpi, thể tích riêng, nội năng của 1 kg và 300 kg/h
hơi nước ở áp suất p =10 bar với độ khô x = 0,9. Lời giải:
Với 1 kg hơi nước bão hoà ẩm ta có: ix = i’ + x.(i’’- i’) vx = v’ + x.(v’’- v’) ux = i - p.v x x
Từ bảng hơi nước bão hoà trong phần phụ lục với p = 10bar ta tra được: i’ = 762,7 kJ/kg i’’ = 2728 kJ/kg v’ = 0,0011273 m /kg 3 v’’= 0,1946 m3/kg
Entanpi và thể thích riêng của 1kg hơi nước:
ix = 762,7 + 0,9.(2728 - 762,7) = 2576,5 kJ/kg
vx = 0,0011273 + 0,9.(0,1946 - 0,0011273) = 0,17525 m /kg 3 Với 300 kg/h ta có:
Ix = G.i = 300.2576,5 = 772950 kJ/h = 215 KW x
Vx = G.v = 300.0,17525 = 52,6 m x /h = 0,0 3 146 m3/s Nội năng của 1kg hơi: ux = i – p.v x x ux = 2576,5.10 - 10 3 .10 .0,17525 = 2,4.10 5 J/kg = 2400 kJ/kg 6
Nội năng của 300 kg/h hơi nước: Ux = G.u = 300 x .2400 = 720000 kJ/h = 200KW.
Truờng đại học công nghiệp hà nội
bài tập kỹ thuật nhiệt 5 Bài 6:
Xác định entanpi, thể tích, entrôpi, nội năng của 10kg hơi nước có áp suất
p = 10 bar với nhiệt độ t = 3000C bằng bảng và đồ thị i - s. Lời giải:
Từ bảng nước chưa sôi và hơi quá nhiệt ở p = 10 bar và t = 300 C ta có: 0 v = 0,2578 m /kg 3 i = 3058 kJ/kg s = 7,116 kJ/kg K 0 Với 10 kg hơi nước: I = G.i = 10.3058 = 30580 kJ
S = G.s = 10.7,116 = 71,16 kJ/ K 0
Nội năng của 1 kg hơi nước: u = i – p.v u = 3058.10 - 10.10 3 .0,2578 = 2,8.10 5 J/kg = 2800 kJ/kg. 6
Nội năng của 10 kg hơi nước: U = G.u = 10.2800 = 28000 kJ Bài 7:
1kg hơi bão hoà khô môi chấ
(s = const) đến áp suất 0,4 MPa. X
entanpi ban đầu và cuối, nhiệt độ c Lời giải:
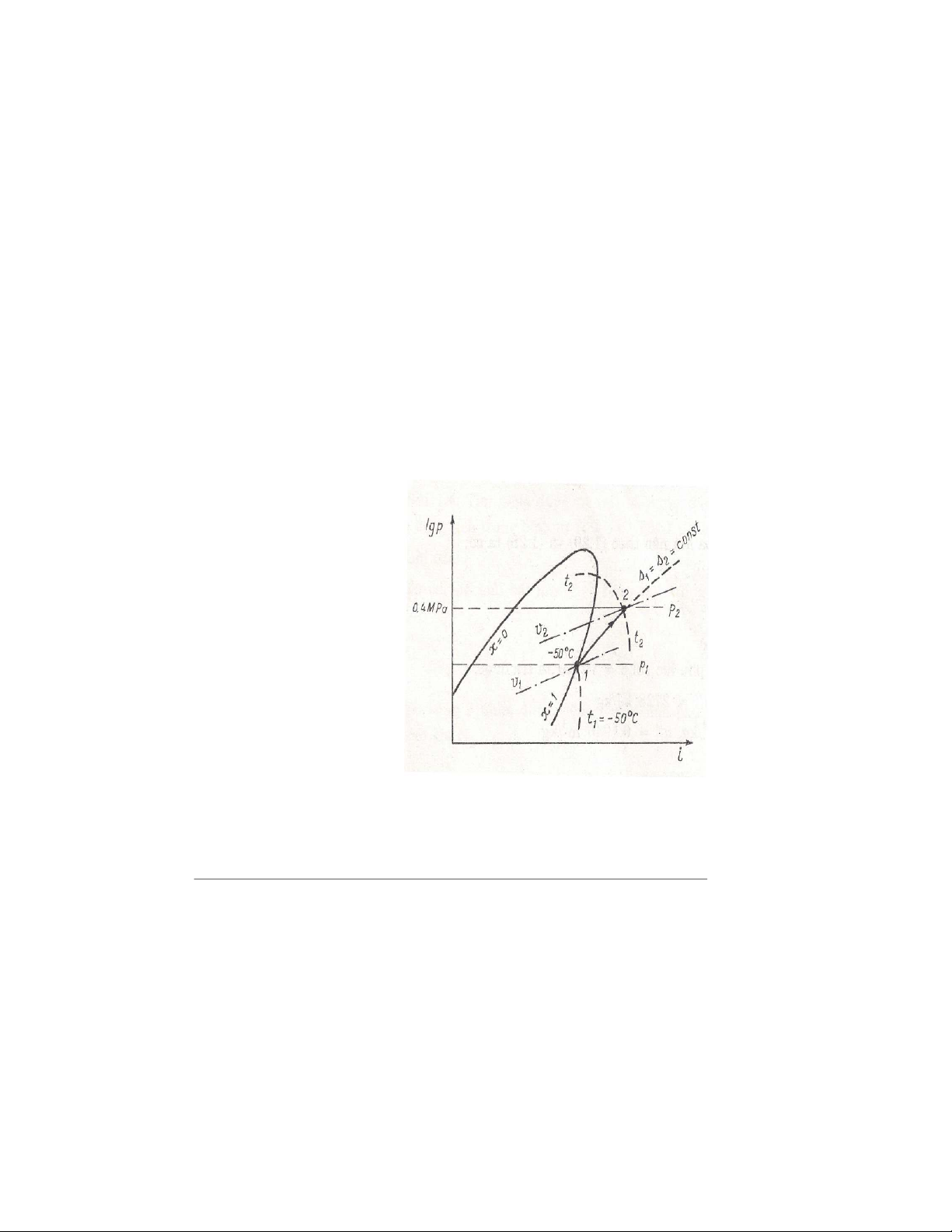
Sử dụng đồ thị lgp-i của R12
hình 1. Từ đồ thị ta tìm được áp su p1 = 0,04 Mpa = 0,4 bar Thể tích ban đầu v : 1 v1= 0,4 m /kg. 3 Entanpi ban đầu i : 1 i1 = 630 kJ/kg
Từ điểm 1 là giao điểm của đường
và x = 1, vì là hơi bão hoà khô, vạc 1
s1 = const cắt đường áp suất p = 0,4 Mpa tại 2 điểm 2. Hình 1
Từ đó ta tìm được thể tích cuối v , nhiệt độ cuối t 2 , entanpi c 2 uối của quá trình i : 2 v2 = 0,05 m /kg 3 t2 = 30 C 0 i2 = 670 kJ/kg.
Truờng đại học công nghiệp hà nội
bài tập kỹ thuật nhiệt 6 Bài 8
10 kg không khí ở nhiệt độ 27 C 0
được đốt nóng đến 127 C 0 ở áp suất không
đổi. Xác định nhiệt lượng, biến đổi entanpi, biến đổi nội năng, công thay đổi thể tích của quá trình. Lời giải:
Không khí là hỗn hợp của nhiều khí nhưng chủ yếu là N và 2 O 2nên coi không
khí là khí lý tưởng hai nguyên tử và khi tính toán lấy µ = 29 kg. Vì đây là quá trình
đẳng áp nên nhiệt lượng tính theo nhiệt dung riêng: Q = G.Cp. (t - t 2 ) 1 Nhiệt dung riêng C : p C P 3 , 29 C = µ = = 01 , 1 kJ / . kg 0K p µ 29
Vậy: Q = 10.1,01(127 - 27) = 1010 kJ Biến đổi entanpi ∆I: ∆I = G.C (t p - t 2 ) = Q = 1010 kJ 1
Biến đổi nội năng ∆U: ∆U = G.Cv (t - t 2 ) 1 Nhiệt dung riêng C : v C v 9 , 20 = C0v==µ 72 , 0 kJ / . kg K µ 29
∆U = 10. 0,72 (127 - 27) = 720 kJ
Công thay đổi thể tích của quá trình đẳng áp tính theo phương trình định luật I: Q = ∆U + L12
L12 = Q - ∆U = 1010 – 720 = 290 kJ. Bài 9:
1kg nước ở áp suất 1 bar, nhiệt độ 20 0C được đốt nóng đến 200 C 0 trong điều
kiện áp suất không đổi. Xác định nhiệt lượng q đốt nón 1
g nước ban đầu đến nhiệt độ
sôi, nhiệt lượng q2 biến
nước sôi thành hơi bão hoà khô, nhiệt lượng q3 biến hơi bão
hoà khô thành hơi quá nhiệt và nhiệt lượng q biến nước ban đầu thành hơi ở trạng thái cuối. Lời giải:
Nhiệt lượng đốt nóng q với nhiệt dung riêng nước C 1 = 4,18 kJ/kg n K 0 q1 = C .(t n
2 - t ) = 4,18 (100 - 20) = 334,4 kJ/kg 1
Nhiệt lượng biến nước sôi thành hơi bão hoà khô q : 2 q2 = i’’ - i’ = r
Truờng đại học công nghiệp hà nội
bài tập kỹ thuật nhiệt 7
Từ bảng hơi nước bão hoà theo p = 1 bar ta có: r = 2258 kJ/kg
Truờng đại học công nghiệp hà nội
bài tập kỹ thuật nhiệt 8
Nhiệt lượng biến hơi bão hoà khô thành hơi quá nhiệt q : 3 q3 = i - i’’
Từ bảng hơi nước bão hoà theo p = 1 bar ta có: i’’= 2675 kJ/kg.
Từ bảng hơi quá nhiệt với p = 1 bar, t = 200 C ta có: 0 i = 2875.
Vậy: q3 = 2875 – 2675 = 200 kJ/kg.
Nhiệt lượng tổng cộng biến nước ban đầu thành hơi quá nhiệt ở trạng thái cuối: q = q + q 1
2 + q3 = 334,4 + 2258 + 200 = 2792,4 kJ/kg. Bài 10:
Xylanh có đường kính d = 400 mm chứa không khí có thể tích 0,08 m , áp suất 3 3,06 at, nhiệt độ 15 C. 0
Nếu không khí nhận nhiệt trong điều kiện pistông chưa kịp
dịch chuyển và nhiệt độ không khí tăng tới 398 C. 0
Xác định lực tác dụng lên mặt
pistông, khối lượng không khí có trong xylanh, nhiệt lượng cung cấp, lượng biến đổi entanpi. Lời giải:
Lực tác dụng lên mặt pistông sau khi nhận nhiệt: F = p S 2. . Trong đó:
p - áp suất không khí sau quá trình nhận nhiệt, N/m 2 2
S - diện tích bề mặt pistông, m2 2 1256 , 0 πd m , 0 . 14 , 3 2 4 2 = S= 4 4
Không khí nhận nhiệt trong điều kiện pistông không dịch chuyển có nghĩa đây là quá trình đẳng tích: T2 398 + 273 p2 = p1 = 06 , 3 129 , 7 at T 15+ 273 1
F = 7,129.0,98.10 .0,1256 = 0,877.10 5 N 5
Khối lượng không khí được xác định từ phương trình trạng thái: p1 V1 = G.R.T1 G5 p V 10 . 98 , 0 . 06 , 3 08 , 0 . = 1 1 = = 29 , 0 kg RT 287 15 .( + ) 273 1
Nhiệt lượng trong quá trình đẳng tích:
Q = G.Cv (t2 - t ) = 0,29. 0,72 (398 - 15) = 79,97 kJ 1 Biến đổi entrôpi ∆S:
Truờng đại học công nghiệp hà nội
bài tập kỹ thuật nhiệt 9 T2 398 + 273 ∆S 0= C . G v.ln = = 72 , 0 . 29 , 0 .ln 177 , 0 kJ / . K T 15 + 273 1
Truờng đại học công nghiệp hà nội
10 bài tập kỹ thuật nhiệt Bài 11:
Đốt nóng 1 kg không khí trong điều kiện áp suất không đổi p = 2bar từ nhiệt độ 20 C 0
đến 1100C. Tính thể tích cuối, nhiệt lượng, công thay đổi thể tích, lượng
thay đổi nội năng và entrôpi. Lời giải:
Không khí coi là khí lý tưởng và đây là quá trình đẳng áp cho 1 kg không khí. Thể tích cuối: T2 v = v . 2 T 1 1 RT1 287.(20 ) 273 v31= + = = 42 , 0 m / . kg p 10 . 2 5 1 110 + 273 v 32== . 42 , 0 549 , 0 m / kg 20 + 273
Nhiệt lượng của quá trình đẳng áp: q = Cp(t - t 2 ). 1
Nhiệt dung riêng đẳng áp C của không khí với p µ = 29 kg: C 3 , 29 C = Ρ µ = = 01 , 1 kJ / . kg 0K p µ 29
q = 1,01(110 - 20) = 20,9 kJ/kg Công thay đổi thể tích: l12 = p.(v - v 2 ) = 2.10 1 (0 5 ,549 - 0,42) = 25,8.10 J/kg 3 l12 = 25,8 kJ/kg
Biến đổi nội năng tính cách thứ nhất tính theo nhiệt dung riêng: ∆u = Cv (t - t 2 ) 1 C v 9 , 20 = C0v==µ , 0 72 kJ / . kg K µ 29
∆u = 0,72.(120 - 20) = 64,8 kJ/kg.
Cách thứ hai tính từ ∆u từ phương trình định luật I:
∆u = q - l = 90,9 - 25,8 = 65,1 kJ/kg 12
(Sai số khi tính ∆u bằng hai phương pháp là do khi tính ta đã lấy gần đúng một số
giá trị như R ≈ 287 kJ/kg .K, 0 µ ≈ 29 kg…)
Biến đổi entrôpi của quá trình đẳng áp: T ∆s = C ln 2 p T1110 ( + ) 273 ∆s = . 01 , 1 ln = , 0 27 kJ / kg0 . K (20 + ) 273
Truờng đại học công nghiệp hà nội
11 bài tập kỹ thuật nhiệt Bài 12:
Khi nén đẳng nhiệt 4 kg chất khí có hằng số khí R = 189 J/kg. K 0 từ áp suất 2
at đến 5,4 at, cần thải một lượng nhiệt 378 kJ (coi là khí lý tưởng). Xác định nhiệt
độ của quá trình, thể tích cuối cùng của chất khí đó. Lời giải:
Trong quá trình đẳng nhiệt của khí lý tưởng: p2 Q = GRTln p1
Từ đó nhiệt độ của quá trình: Q 10 . 378 3 T0= 1= − = 500 K p 2 GR ln . 189 . 4 ln p , 5 4 2 t = 500 – 273 = 227 0C. Thể tích cuối: p1 2 = = V23= V1. . 93 , 1 72 , 0 m . p 4 , 5 2 Bài 13:
Không khí có thể tích 2,48 m ,3 nhiệt độ 15 C, 0
áp suất 1 bar, khi bị nén đoạn
nhiệt không khí nhận công thay đổi thể tích 471kJ. Xác định nhiệt độ cuối, sự thay
đổi nội năng và entanpi. Lời giải:
Không khí ở đây coi là khí lý tưởng và quá trình là quá trình đoạn nhiệt. Biến
đổi nội năng được tính theo phương trình định luật I: Q = ∆U + L12 = 0
∆U = -L = - (-471) kJ = 471 kJ 12
Nhiệt độ cuối của quá trình tính theo biểu thức tổng quát tính lượng thay đổi nội năng: ∆U = G.Cv (t2 - t )1 U t2t + ∆ = 1 C . G v
Khối lượng không khí xác định được từ phương trình trạng thái ban đầu: p1. v1 = G.R.T1 G5 p v 10 . 1 . , 2 48 = 1 1 = = 3 kg RT 15 .( 287 + ) 273 1 471 Vậy: = + t02= 15 233 C 72 , 0 . 3
Biến đổi entanpi được xác định:
Truờng đại học công nghiệp hà nội
12 bài tập kỹ thuật nhiệt ∆I = G.Cp (t - t 2
) = 3. 1,01.(233 - 15) = 661 kJ. 1
Truờng đại học công nghiệp hà nội
13 bài tập kỹ thuật nhiệt Bài 14:
2 kg khí O 2thực hiện quá trình đa biến với chỉ số mũ đa biến n = 1,2 từ nhiệt độ t1 = 27 C 0 đến t2 = 537 C. 0
Xác định biến đổi entrôpi, lượng nhiệt của quá trình,
biến đổi nội năng, công thay đổi thể tích và công kỹ thuật của quá trình. Lời giải:
Nhiệt dung riêng của quá trình đa biến: +
Nhiệt dung riêng đẳng tích C : v C v 9 , 20 = C0v==µ 65 , 0 kJ / kg K µ 32 , 1 2 − 4 , 1 C 0n = −= . 65 , 0 65 , 0 kJ / Kg K 2 , 1 − 1
Biến đổi entrôpi của quá trình: ∆S = G.Cnln(T / T 2 ) 1
∆S = 2.(-0,65).ln [(537 + 273) / (27 + 273)]= -1,3 kJ/ K 0
Nhiệt lượng của quá trình: Q = G.Cn(t - t 2
) = 2(-0,65).(537 - 27) = - 663 kJ 1
Biến đổi nội năng của quá trình: ∆U = G.Cv(t - t 2
) = 2. 0,65. (537 - 27) = 663 kJ 1 Công thay đổi thể tích:
L12 = Q - ∆U = - 663 – 663 = -1326 kJ
Công kỹ thuật của quá trình
Lkt12 = n.L = 1,2.(-1326) = -1591 kJ. 12 Bài 15:
Xác định số mũ đa biến khi quá trình đa biến thay đổi từ áp suất 0,001at, nhiệt
độ –73 C đến áp suất 1000 at, nhiệt độ 172 0 0C. Lời giải:
Từ quan hệ giữa nhiệt độ và áp suất của quá trình đa biến: n 1 T− p2 n 2) = ( T p 1 1 T2 172 (− + + ) 273 ln ln n − 1 T1 ( 73 ) 273 Ta có: = = = 166 , 0 n p2 1000 ln ln p1 001 , 0 n - 1 = n. 0,166
Truờng đại học công nghiệp hà nội
14 bài tập kỹ thuật nhiệt 1 Vậy: n= , 1 2 1− 166 , 0 .
Truờng đại học công nghiệp hà nội
15 bài tập kỹ thuật nhiệt Bài 16:
Hơi nước bão hoà ẩm ở áp suất p = 2 bar, độ khô x = 0,9. Hãy xác định các giá
trị thể tích riêng v ,x entanpi i ,x entrôpi s ,x nội năng u .x bằng bảng số và sử dụng đồ thị i-s của hơi nước. Lời giải:
Từ đồ thị i-s của hơi nước trong phần
phụ lục, qua hình 2 điểm A là trạng thái
của hơi nước bão hoà ẩm (giao điểm của
đường p = 2 bar và x = 0,9). Từ điểm A
ta tìm được các giá trị v , i x x, sx
Mặt khác từ bảng nước và hơi nước bão hoà
với p = 2 bar ta tra được: Hình 2 v, = 0,0010605 m /kg v 3 = 0,8854 m ,, /kg 3
i, = 504,8 kJ/kg i’’ = 2707 kJ/kg s, = 1,5320 kJ/kg K s 0 = 7,127 kJ/kg ,, K 0 Từ đó ta tính được: vx = v + x.(v , ,, - v ) ,
vx = 0,0010605 + 0,9(0,8854 - 0,0010605) = 0,797 m /kg 3 ix = i + x.(i , - i ,, ,)
ix = 504,8 + 0,9(2707 - 504,8) = 2486,8 kJ/kg sx = s’ + x.(i’’+ i’)
sx = 15320 + 0,9.(7.127 + 504,8) = 6,567 kJ/kg K 0 ux = i – p.v x = 2486,8.10 x - 2.10 5 .0 5 ,797
ux = 2,3266.106 J/kg = 2326,6 kJ/kg. Bài 17:
Một bình thể tích V=0,035m3 chứa
5kg hơi nước bão hoà ẩm. Nhiệt độ trong
bình 3100C. Xác định độ khô của hơi nước trong bình. Lời giải:
Thể tích riêng của hơi nước bão hoà ẩm trong bình: V 035 , 0 = = v3x= ; 007 , 0 m / kg G 5 Mặt khác ta có: vx = v’ + x.(v’’ - v’)
Từ đó độ khô x của hơi:
Truờng đại học công nghiệp hà nội
16 bài tập kỹ thuật nhiệt v − v' x = x− v'' v'
Truờng đại học công nghiệp hà nội
17 bài tập kỹ thuật nhiệt
Từ bảng hơi nước bão hoà trong phần phụ lục với nhiệt độ t = 310 C ta tìm được: 0 v’ = 0,001447 m /kg 3 v’’ = 0,01832 m3/kg 007 , 0 − 001447 , 0 Vậy: x= . 33 , 0 0 , 0 1832− 001447 , 0 Bài 18:
Bao hơi của hơi lò hơi có thể tích V = 9 m3. Một phần ba thể tích đó chứa đầy
hơi bão hoà khô, phần còn lại chứa nước sôi. áp suất trong bao hơi p = 100 bar. Xác
định lượng nước sôi, lượng hơi bão hoà và độ khô. Lời giải:
Từ bảng hơi nước bão hoà trong phần phụ lục với p = 100 bar:
Ta có thể tích riêng của nước sôi: v’= 0,0014521 m /kg 3
Của hơi bão hoà khô: v’’= 0,01803 m /kg 3
Thể tích của nước sôi V’ và của hơi bão hoà khô V’’: 2 2 = 9 .= 6 ' V m = V 3 3 3 1 1 = 9 = 3V' m = V 3 3 3
Từ đó lượng nước sôi G : n V' V' 6 ⇒ = = vn'= ; G 4130kg G v' 0014521 , 0 n
Lượng hơi bão hoà khô G : k V' V" 3 ⇒ = = vk'= ; G 166 kg G v" 01803 , 0 k
Độ khô của hơi bão hoà ẩm x: G 166 x = k= = 0386 , 0 G + G 4130 + 166 k n Bài 19:
Lượng hơi nước bão hoà ẩm G =1,4 kg/s ở áp suất p =100 bar, độ khô x = 0,96
chuyển động trong ống với tốc độ ω = 40 m/s. Xác định đường kính trong của ống. Lời giải:
Từ phương trình liên tục của dòng chảy trong ống ta có: G ω . f. f . = ωρ = v Trong đó: ω-tốc độ m/s
ρ-khối lượng riêng, kg/m3
f- tiết diện của ống, m2
Truờng đại học công nghiệp hà nội
18 bài tập kỹ thuật nhiệt f2 . G v πd . Ta có: = = ω 4
Truờng đại học công nghiệp hà nội
19 bài tập kỹ thuật nhiệt Đường kính của ống d: d = . G 4 v . π ω
Từ bảng hơi nước hơi bão hoà với p =100bar, ta có: v”= 0,01803 m3/kg
Do đó có thể tính gần đúng thể tích riêng của hơi bão hoà ẩm:
v = v’ + x.(v” - v’) ≈ x.v”
v = 0,96. 0,01803 = 0,0173 m kg 3
Vậy đường kính trong của ống: 4 , 1 . 0173 , 0 . 4 = d= 028 , 0 m 28 . mm 40 . 14 , 3 Bài 20
Một lượng hơi nước bão hoà ẩm từ tuabin đi vào bình ngưng G=200kg/s ở độ
khô x = 0,872. Xác định lưu lượng thể tích của hơi bão hoà ẩm vào bình ngưng, nếu
biết áp kế của bình ngưng chỉ 720 tor và áp suất khí quyển chọn 1bar Lời giải:
áp suất tuyệt đối trong bình ngưng: 720 = − = − 0 = p ck p p 1 04 , 0 bar 750
Từ bảng hơi nước bão hoà với p = 0,04 bar: Ta có: v” = 34,81 m /kg. 3
Thể tích riêng của hơi bão hoà ẩm vào bình ngưng:
vx = v’ + x.(v” - v’) ≈ x.v” = 0,872. 34,81 = 30,35 m /kg. 3
Lưu lượng thể tích của hơi bão hoà ẩm vào bình ngưng: V = v .G = 30,35. 200 = 6070 m x 3/s. Bài 21:
Bao hơi của lò hơi có thể tích V=12m 3 chứa lượng nước sôi và hơi có khối
lượng G =1800 kg ở áp suất p =110 bar. Xác định lượng nước sôi và lượng hơi bão hoà khô trong bao hơi. Lời giải:
Thể tích của nước sôi: Vn = Gnv’
Thể tích của hơi bão hoà khô: Vh = Ghv’’ Ta có: V = V + V n = G h v’ + G n .v” h G = G + G n h
Truờng đại học công nghiệp hà nội
20 bài tập kỹ thuật nhiệt Gn = G - Gh
Truờng đại học công nghiệp hà nội
21 bài tập kỹ thuật nhiệt