Sec x là gì? Cách tính đạo hàm của sin cos tan cot sec csc
Đạo hàm của sin cos tan cot sec csc là gì? Đây đều là các ký tự toán học được sử dụng trong các công
thức lượng giác và vi phân. Nếu như ban vẫn chưa nắm được Sec (x) Csc Cot trong toán học là gì thì có
thể tham khảo bài viết dưới đây của Luật Minh Khuê. Trong bài viết này chúng tôi xin chia sẻ một số
kiến thức về các hàm lượng giác đồng biến cosecant, secant và cotang. Mời bạn đọc cùng tham khảo
bài viết dưới đây để hiểu rõ về vấn đề này nhé.
Mục lục bài viết
1. Hàm Sec x, Csc x là gì? 1.1 Hàm Sec x
Sec x là một hàm toán học trong đại số và giải tích, được định nghĩa như là lấy giá trị nghịch đảo của
hàm lượng giác Cos x. Cụ thể, sec x = 1/cos x. Hàm sec x có thể được sử dụng trong các bài toán liên
quan đến các hình học và lượng giác, ví dụ như tính toán độ dài đường chéo của một hình chữ nhật,
hoặc trong các phép tính liên quan đến phương trình sóng và sóng âm.
Hàm toán học Sec x có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm: Trong hình học:
- Sec x được sử dụng để tính toán độ dài đường chéo của một hình chữ nhật. Khi ta biết chiều dài và
chiều rộng của hình chữ nhật, ta có thể tính toán đường chéo bằng cách sử dụng công thức d =
sqrt(a^2 + b^2), trong đó a và b là chiều dài và chiều rộng, và d là đường chéo. Khi thay a và b bằng cos
x và sin x, ta có thể viết lại công thức thành d = sec x * sqrt(cos^2x + sin^2x), hay d = sec x.
- Trong lượng giác: Sec x cũng được sử dụng để tính toán các giá trị lượng giác khác, bao gồm cả
cosecant (csc), tangent (tan) và cotangent (cot). Các hàm này có thể được biểu diễn dưới dạng của hàm Sec x.
- Trong vật lý: Sec x được sử dụng trong các phép tính liên quan đến phương trình sóng và sóng âm.
Các sóng âm có thể được biểu diễn dưới dạng của hàm Sec x và các hàm lượng giác khác.
- Trong kỹ thuật: Sec x cũng được sử dụng trong các phép tính liên quan đến các mạch điện và điện tử.
Ví dụ, hàm Sec x có thể được sử dụng để tính toán các thông số của các bộ lọc tín hiệu và các mạch điện khác.
- Trong khoa học máy tính: Sec x cũng có ứng dụng trong khoa học máy tính và kỹ thuật phần mềm. Ví
dụ, hàm Sec x có thể được sử dụng để giải quyết các bài toán liên quan đến xử lý ảnh, xử lý âm thanh,
mã hóa tín hiệu và xác định định dạng file. 1.2 Hàm Csc x
Hàm Csc x là một hàm toán học trong đại số và giải tích, được định nghĩa như là lấy giá trị nghịch đảo
của hàm lượng giác Sin x. Cụ thể, Csc x = 1/Sin x. Hàm Csc x cũng có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:
- Trong hình học: Csc x được sử dụng để tính toán các góc trong các hình học không gian, ví dụ như
trong các bài toán liên quan đến hình cầu, hình nón và các hình khác.
- Trong lượng giác: Csc x cũng được sử dụng để tính toán các giá trị lượng giác khác, bao gồm cả
secant (sec), tangent (tan) và cotangent (cot). Các hàm này có thể được biểu diễn dưới dạng của hàm Csc x.
- Trong vật lý: Csc x được sử dụng trong các phép tính liên quan đến sóng âm và các loại sóng khác, ví
dụ như sóng ánh sáng. Các hàm sóng này có thể được biểu diễn dưới dạng của hàm Csc x và các hàm lượng giác khác.
- Trong kỹ thuật: Csc x cũng được sử dụng trong các phép tính liên quan đến các mạch điện và điện tử.
Ví dụ, hàm Csc x có thể được sử dụng để tính toán các thông số của các bộ lọc tín hiệu và các mạch điện khác.
- Trong khoa học máy tính: Csc x cũng có ứng dụng trong khoa học máy tính và kỹ thuật phần mềm. Ví
dụ, hàm Csc x có thể được sử dụng để giải quyết các bài toán liên quan đến xử lý ảnh, xử lý âm thanh,
mã hóa tín hiệu và xác định định dạng file.
2. Cách tính csc cot và sec?
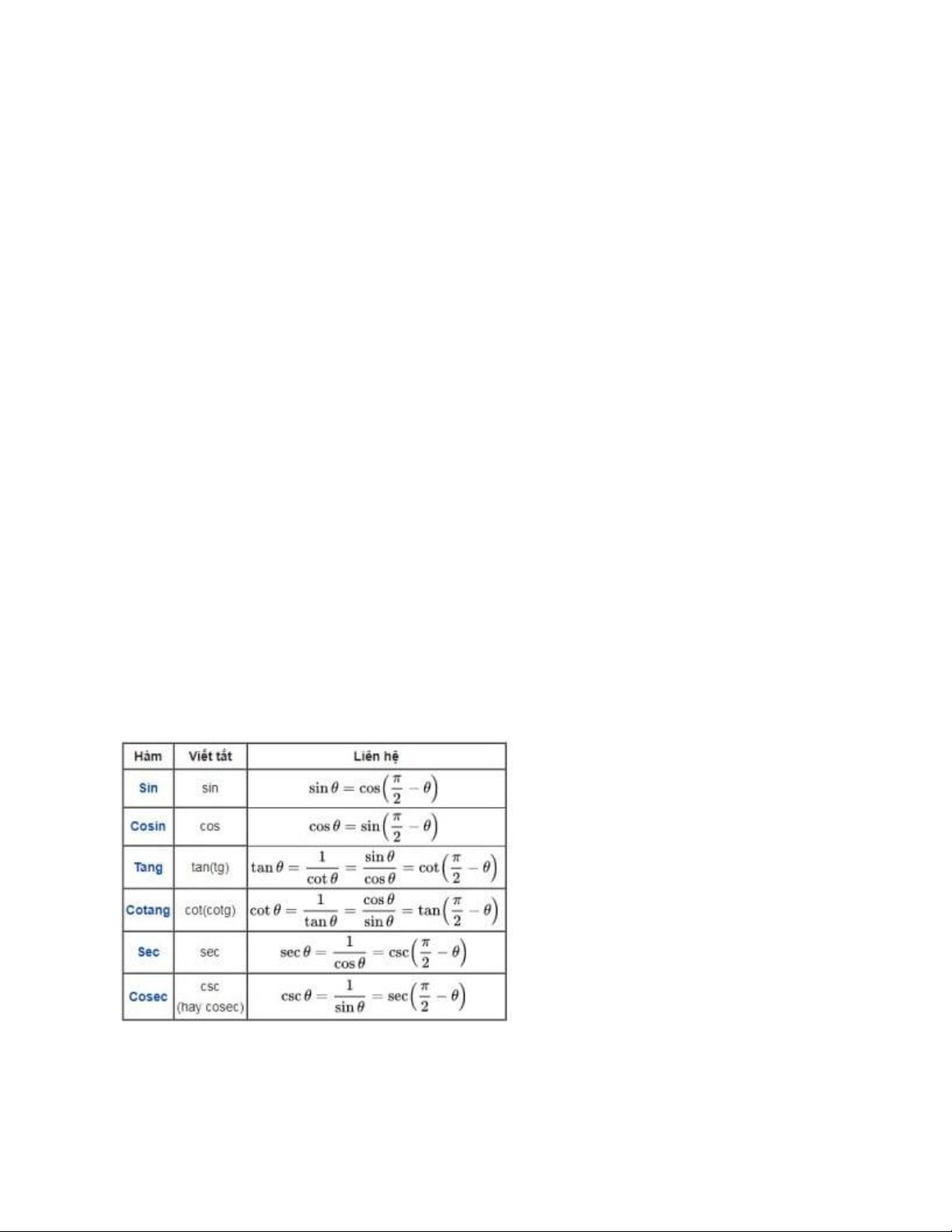
Csc sec cot lần lượt là ba hàm lượng giác cosecant, secant và cotang. Các hàm này còn được gọi là các
hàm lượng giác đồng biến vì chúng lần lượt là nghịch đảo của hàm sin, hàm cosin và tangent.
Cotang của x được định nghĩa là cosin của x chia cho sin của x: cot x = cos x sin x. Secant của x là 1 chia
cho cosin của x: sec x = 1 cos x, và cosec của x được định nghĩa là 1 chia cho sin của x: csc x = 1 sin x. = tan 5π 4.
Ví dụ, csc A = 1 / sin A, sec A = 1 / cos A, cot A = 1 / tan A và tan A = sin A / cos A.
Trong lượng giác, cot hay cotang là một trong sáu tỷ số lượng giác. Trong một tam giác vuông, cot của
một góc bằng tỉ số cạnh kề và cạnh đối của góc. Cot x cũng bằng nghịch đảo của tan x.
Cotangent được sử dụng giống như cách sử dụng các hàm sin, cosine và tangent . Bạn có thể sử dụng
chúng dựa trên một tam giác vuông, sử dụng các cạnh đối diện và liền kề của tam giác hoặc bạn có thể
sử dụng nó dựa trên vòng tròn đơn vị, biểu thị các góc tính bằng radian.
Secant của góc 0 độ được viết là trong hệ thống Sexagesimal và giá trị chính xác của secant của góc 0
độ bằng một. Trong một tam giác vuông, tích của một góc là: Độ dài cạnh huyền chia cho độ dài cạnh
kề. Viết tắt là sec. sec (θ) = cạnh huyền / liền kề.
Giá trị của một góc trong tam giác vuông là giá trị được tìm thấy bằng cách chia độ dài cạnh huyền cho
độ dài cạnh kề với góc đã cho. Tỷ lệ secant là nghịch đảo của tỷ số cosin.
3. Công thức tính các góc sin cos tan cot sec csc
Các hàm sin, cos, tan và cot là các hàm lượng giác trong toán học, được sử dụng rộng rãi trong đại số,
hình học và giải tích. Chúng được định nghĩa dựa trên các góc trong tam giác vuông, và giá trị của
chúng phụ thuộc vào giá trị của góc đó. Sin, cos, tan, cot, sec, csc là các ký tự toán học được sử dụng
trong các công thức tính lượng giác và đạo hàm. Các hàm lượng giác này được định nghĩa như sau:
+ sin: là tỷ số giữa cạnh đối và cạnh huyền của góc
+ cos: là tỷ số giữa cạnh kề và cạnh huyền của góc
+ tan: là tỷ số giữa cạnh đối và cạnh kề của góc
+ cot: là tỷ số giữa cạnh kề và cạnh đối của góc Sin= đối/ huyền Cos= kề/ huyền Tan= đối/ kề Cot= kề/ huyền Sec= 1/cos Csc= 1/sin
Mẹo nhớ nhanh thần thánh độc đáo của người Việt, đây có thể là một cách học thuộc vẹt cực hay và
dễ nhớ qua câu tựa vè: Sin đi học, Cos không hư, Tan đoàn kết, Cot kết đoàn
Để quá trình giải các bài toán đạo hàm được đơn giản và nhanh chóng hơn. Sau đây là các đạo hàm
của sáu hàm số lượng giác bạn nhất định phải nhớ
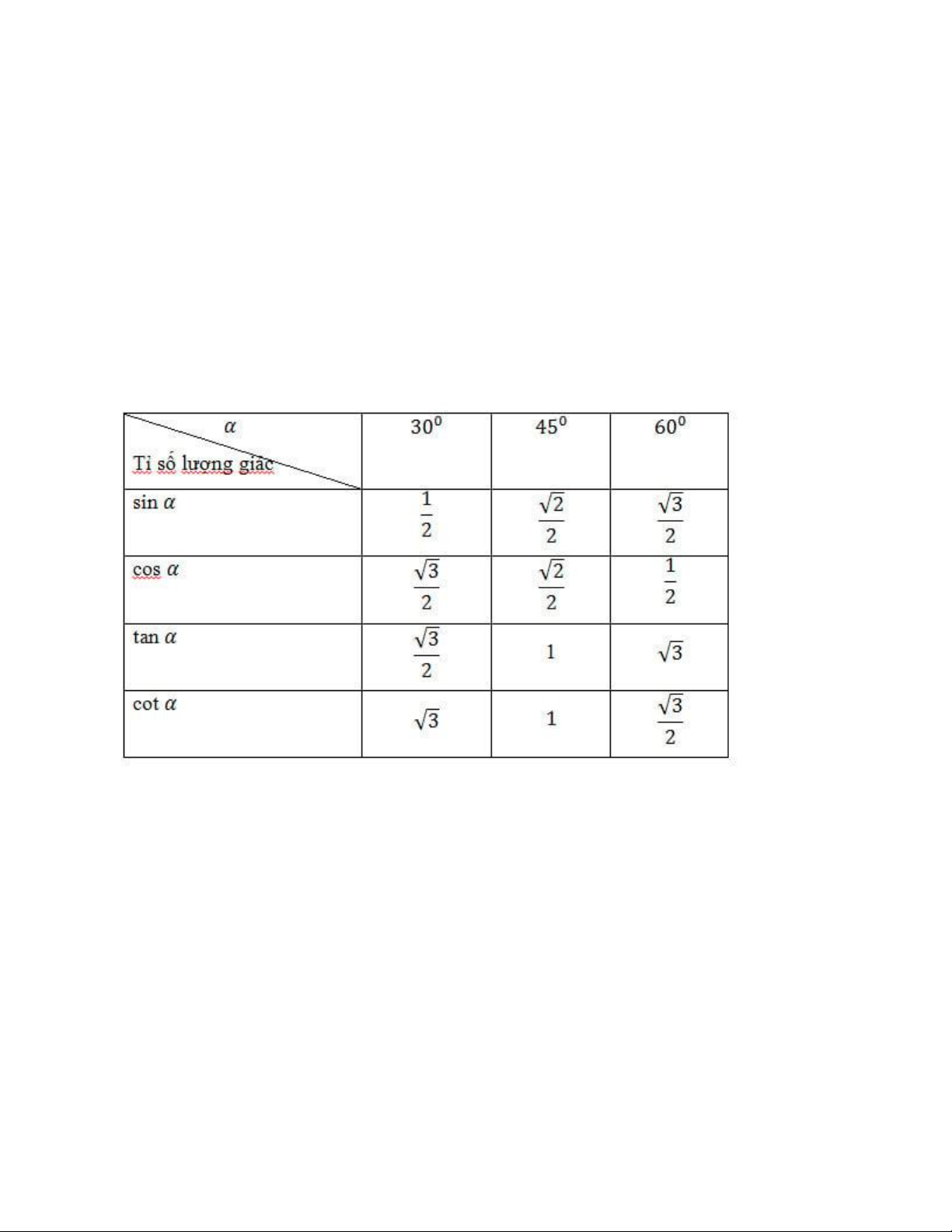
Tỉ số lượng giác của 2 góc phụ nhau ( α + β = 90° )
sin α = cos β, cos α = sin β,
tan α = cot β, cot α = tan β
Bảng tỉ số của các góc đặc biệt.
Các hàm lượng giác này có thể được tính toán sử dụng máy tính hoặc các bảng giá trị lượng giác.
Chúng có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm trong vật lý, khoa học máy tính, kỹ
thuật và các lĩnh vực khác. Các hàm sin, cos, tan và cot có rất nhiều ứng dụng trong các lĩnh vực khác
nhau của khoa học và kỹ thuật. Dưới đây là một số ứng dụng phổ biến của các hàm này:
- Vật lý: Các hàm lượng giác được sử dụng trong các công thức và phương trình của vật lý, bao gồm
trong lĩnh vực cơ học, điện tử, sóng học, quang học,...Ví dụ, các hàm lượng giác được sử dụng trong
các phương trình sóng âm và sóng ánh sáng.
- Khoa học máy tính: Các hàm lượng giác được sử dụng rộng rãi trong các thuật toán xử lý ảnh và âm
thanh, và trong các thuật toán tối ưu hóa và truy vấn cơ sở dữ liệu.
- Kỹ thuật: Các hàm lượng giác được sử dụng trong thiết kế và phân tích các mạch điện tử, các hệ
thống điều khiển tự động, và các hệ thống thông tin và viễn thông. Chúng cũng được sử dụng trong
các ứng dụng liên quan đến tín hiệu và xử lý tín hiệu, bao gồm trong các hệ thống âm thanh, video và giao tiếp.
- Toán học: Các hàm lượng giác được sử dụng rộng rãi trong các phép tính và công thức trong toán
học, bao gồm trong đại số, hình học và giải tích. Chúng cũng được sử dụng trong các nghiên cứu và
ứng dụng của toán học, bao gồm trong các lĩnh vực như thống kê, lý thuyết số, lý thuyết trò chơi,...
- Thiết kế và nghiên cứu trong các lĩnh vực kỹ thuật và khoa học: Các hàm lượng giác được sử dụng để
mô hình hóa và phân tích các vấn đề trong các lĩnh vực như cơ khí, vật liệu, kỹ thuật hóa học, khoa học môi trường,...
- Thực tiễn cuộc sống: Các hàm lượng giác được sử dụng trong các ứng dụng hàng ngày của chúng ta,
bao gồm trong các thiết bị đo và định vị, như GPS, la bàn, máy tính cầm tay,... Chúng cũng được sử
dụng trong các ứng dụng như mô phỏng,...
4. Đạo hàm của các hàm số lượng giác cơ bản bạn cần nhớ
sin(x): Đạo hàm của hàm số sin(x) là cos(x). Các ứng dụng của đạo hàm của sin(x) bao gồm tính tốc độ
và gia tốc trong các vấn đề về chuyển động và dao động cơ học.
cos(x): Đạo hàm của hàm số cos(x) là -sin(x). Các ứng dụng của đạo hàm của cos(x) bao gồm tính tốc
độ và gia tốc trong các vấn đề về chuyển động và dao động cơ học.
tan(x): Đạo hàm của hàm số tan(x) là sec^2(x). Các ứng dụng của đạo hàm của tan(x) bao gồm tính tốc
độ và gia tốc trong các vấn đề về chuyển động và dao động cơ học, cũng như tính các đường tiếp
tuyến và tiếp diễn cho các đồ thị hàm số.
cot(x): Đạo hàm của hàm số cot(x) là -csc^2(x). Các ứng dụng của đạo hàm của cot(x) bao gồm tính tốc
độ và gia tốc trong các vấn đề về chuyển động và dao động cơ học, cũng như tính các đường tiếp
tuyến và tiếp diễn cho các đồ thị hàm số.
sec(x): Đạo hàm của hàm số sec(x) là sec(x)tan(x). Các ứng dụng của đạo hàm của sec(x) bao gồm tính
các đường tiếp tuyến và tiếp diễn cho các đồ thị hàm số.
csc(x): Đạo hàm của hàm số csc(x) là -csc(x)cot(x). Các ứng dụng của đạo hàm của csc(x) bao gồm tính
các đường tiếp tuyến và tiếp diễn cho các đồ thị hàm số.
Dưới đây bảng tổng hợp đạo hàm lượng giác cơ bản: Hàm số Đạo hàm sin(x) cos(x) cos(x) -sin(x) tan(x) sec2(x) cot(x) -csc2(x) sec(x) sec(x)tan(x) csc(x) -csc(x).cot(x)
Trên đây Luật Minh Khuê chia sẻ tới các bạn về hàm Sec x và cách tính đạo hàm hàm sin, cos, tan, cot,
sec, csc một cách chọn lọc chi tiết đầy đủ nhất. Hy vọng tài liệu này giúp ích các em học sinh học tập
tốt. Cảm ơn các bạn đã quan tâm theo dõi bài viết!