Simulation-Based Optimization for Yard Design at M - Tài liệu tham khảo | Đại học Hoa Sen

Hindawi Publishing Corporation
Mathematical Problems in Engineering
Volume 2016, Article ID 7467498, 13 pages
http://dx.doi.org/10.1155/2016/7467498 Research Article
Simulation-Based Optimization for Yard Design at Mega
Container Terminal under Uncertainty
Yong Zhou, Wenyuan Wang, Xiangqun Song, and Zijian Guo
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian, China
Correspondence should be addressed to Wenyuan Wang; wangwenyuan@dlut.edu.cn
Received 19 May 2016; Accepted 30 August 2016
Academic Editor: Ricardo Aguilar o-L pe´z
Copyright © 2016 Yong Zhou et al. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
The conventional approach of designing a container yard should be reexamined in the context of sustainable port development.
Considering the uncertain future throughput, a simulation-based optimization framework is proposed to obtain a cost-effective
and reliable design solution to the physical layout and equipment deployment strategy of the yard at a mega container terminal. In
this framework, a two-stage stochastic programming model is presented aided with a simulation procedure of terminal operations.
Finally, an application is given and the results show that the proposed integrated decision framework is effective and helpful for
optimizing container yard design in the context of sustainable development of container terminals. 1. Introduction
which may not be reliable during the future operation stage.
In China, yard design in engineering practice addresses
Worldwide container throughput has been steadily growinguncertainties through the introduction of an unbalance fac-
over the past decades. Between 1990 and 2014, the world’s tor, the value of which is driven by experience. Yard block size
container trade expanded at an average annual rate of 8.4%
and equipment deployment are also empirically determined
[1]. Many ports, especially those in the countries with fast- [9, 10]. This design approach easily gives rise to either an over-
growing economy such as China, have gone through or allocation of yard resources or a low efficiency of terminal
are currently undergoing expansion of existing facilities or
operation which is usually hard to be adjusted in the future.
build-out of new terminals to cope with the increasing For example, the second phase of Yantian International
container traffic and ship size. However, the global maritime
Container Terminals (YICT) borrows part of the adjacent
logistics market contains various uncertainties, such as world
yard and rents off-dock yard in the peak period, which raises
economy, trade policies, and freight rates, which results in athe difficulty in port traffic management and increases the
fluctuation of the demand for freight transportation [2, 3].operating cost. The cost resulting from the increment of
For example, container trade volume fell sharply by 9.0% itn
rucks going back and forth between the terminal and off-
2009 due to the global economy crisis [4], and the volume dock yard and venue rental for YICT reaches 25∼35 million
of containers exported from China to US dropped by about China Yuan (CNY) per year [11]. Therefore, a question arises
20% following 911 terrorist attacks [5]. Port infrastructure,
naturally in an uncertain decision environment: how can we
especially the mega container terminal, is capital intense antd
ake into account future uncertainties in early stage of yard
serves long-term societal needs and thus should be reliable
d sign, so that it is easier to adjust to random events in
and adaptive to future uncertainties.
operation stage later on? This question is especially relevant
With the advancements of quay side technologies, the to developing countries, where most terminals are not in
bottleneck of terminal operations has moved from quay sideplace yet, thus presenting an opportunity to incorporate risks
to yard side [6, 7]. The design of container yard is a factor thatdirectly into the strategic planning of future infrastructure.
affects terminal productivity and competitiveness. However,
For designing a container yard, some researches focused
yard design is determined during the initial planning stage,
on yard storage capacity estimation by advanced simulation
when the available information and details are lacking [8],
models or analytical formula [12–15]. Other studies have 2
Mathematical Problems in Engineering
sought to calculate the space requirement for planning [16–
of the techniques in a unique model framework, which is
18]. Once the main decisions about storage capacity and powerful for decision-making.
equipment choice have been made, the next step for plan-
The remainder of the paper is organized as follows.
ners involves the yard and block layout. Several studies on
Section 2 describes the procedures and their limitations
container terminal design have been conducted to comparewhen optimizing yard designs as well as yard design under
parallel and perpendicular yard layouts using simulatio
u nscertainty. Section 3 focuses on the modeling and solution
[19, 20]. Simulation and analytical techniques have also beenmethod, including the proposed formulation and the solution
used on yard design problem. For example, Petering [21]framework for yard optimization. A numerical example and
and Petering and Murty [22] developed a fully integrated
its computational results are given in Section 4, followed by
simulation model to analyze the influence of the width anddiscussions on advantages, limitations, and possible future
length of yard block on terminal performance. Kim et al.
extensions of this research in Section 5.
[23] proposed an analytical method to get the optimal yard
layout. Kemme [24] examined the design of strategic yard2. Problem Description
crane systems and block layouts and their effects on terminal
performance. Lee and Kim [25] attempted to determine 2.1. Quantitative and Qualitative Design Guidelines. The most
the optimal size of a single block by taking into accountcommonly used layout format of a parallel yard with trans-
the throughput requirements of yard cranes and the blockfer lanes at manually operated terminals in China will be
storage requirements. They provided detailed formulae for
studied in this paper, as depicted in Figure 1. It is noted
the expected cycle times and variances of all yard crane
that container terminal operation generally consists of four
operations. Lee and Kim [26] provided more detail on the components: seaside operation, horizontal transport, yard
expression of expectation of the yard crane cycle time foroperation, and landside operation. At the seaside, containers
yard with different block layouts, useful for estimating yard
are discharged from and loaded into containerships by quay
crane operating costs. Lee and Kim [27] later determinedcranes deployed along the coastline. Internal trucks are
the optimal layout of a whole container yard, as specifieddispatched for transporting containers between quay cranes
by the dimensions of a block and the number of aisles. and certain storage stacks in the yard. Container yard can
However, none of these studies attempted to analyticallyusually be divided into large zones and each zone is further
determine storage space requirements by considering thecomposed of rectangular shaped blocks. Each block contains
stochastic properties of the storage yard. In view of this, several lanes of space for storing containers in stacks and
Zhen [2] focused on the yard template planning problemone lane for trucks to pick up and deliver containers. For
under uncertainty. It considered the number of containersthe convenience of vehicular traffic, blocks are laid out in
loaded onto (and unloaded from) each vessel within a cyclethe unit of module, which combines two blocks with transfer
time as a stochastic parameter. Alcalde et al. [8] used an
lanes in back to back form [23]. Yard cranes, standing over a
analytical model based on a stochastic approach (random
storage block space, can be transferred from block to block,
variables and probabilistic functions) to forecast storage
to stack and shuffle containers. The landside operation is
space requirements over an extended period. However, thethe task of receiving or delivering containers undertaken
optimized yard dimensions were not considered as optimal, by external trucks. According to the MTPRC and several
because yard depth and block length were not optimized withpractical handbooks, input variables and the procedures to
the number of handling equipment deployed simultaneously.determine yard layout are as follows.
Therefore, this paper will propose an optimization frame-
work to obtain a cost-effective and reliable yard design
(1) The yard capacity 𝐸𝑦 and the number of ground slots
solution that hedges well against uncertain future terminal 𝑁𝑠 are calculated as
throughput. This framework is composed of a simulation
model for terminal operations and an optimization program
𝐸𝑦 = 𝑄ℎ𝑡𝑑𝑐𝐾𝐵𝐾,
with yard depth, yard block length, the quantity of handling 𝑇𝑦𝑘
equipment deployed, and the number of containers handled (1) 𝐸
in the design yard as decision variables. The optimization 𝑁 𝑦 𝑠 = ,
program evaluates the capital costs and benefits of various 𝑁𝑙𝐴𝑠
yard layouts, while the simulation model emulates truck
traffic and equipment moving at the terminal and calculates
where 𝑄ℎ is the annual throughput of the container
terminal efficiency indicators. The main contribution of this
terminal; 𝑡𝑑𝑐 is the average cluration of the containers,
paper is simultaneously optimizing yard physical layout,
determined by the statistical material; 𝐾𝐵𝐾 is the
equipment deployment, and storage schemes covering both
unbalance factor of containers stacked in the yard,
planning and operation stages under uncertain environ-
determined by the statistical material; 𝑇𝑦𝑘 is the
ment, which would be more practical for yard design and
annual working days of the container yard; 𝑁𝑙 is the
management in developing countries, where the availability
stacking height of the containers, determined by the
of data is often limited and the economic background is
yard equipment; 𝐴𝑠 is the capacity utilization of the
usually volatile. Although the analytical techniques used container yard.
are not new (two-stage stochastic programming and system
(2) The length of the yard 𝐵 generally is equivalent to the
simulation), another contribution is essentially an integration
length of the container terminal, and it is determined
Mathematical Problems in Engineering 3 Berth e Horizontal transport Zone Seasid v Transfer lane Driving lane e ard Y Module w h e sid Outer lane Block d an Gate L B
Figure 1: Typical layout of a parallel container terminal.
mainly by the coastline, the total amount of the
Therefore, selections of the number of rows of blocks, the
berths, and the tonnage of the containerships.
number of columns of blocks, and the number of yard cranes
(3) The depth of the yard 𝐴 should be determined by deployed are the key to determining the yard layout. These
the design container traffic volume and the han- three decisions interact with each other and cause several
dling technology of the container terminal, and it istrade-offs in the system. For example, a large number of expressed as
rows of blocks bring higher capital investment but result in a
lower number of relocations during retrieval operations due 𝐴 = 1
to the reduced stacking height. Similarly, a larger number of 2𝑀 (2𝑒 + ℎ) + 2V, (2)
columns of blocks (equivalently, a larger number of driving
lanes) bring a shorter travel distance for trucks but reduce
where 𝑀 is the number of rows of blocks in the yard the ground space for stacking containers, which then increase
layout; 𝑒 is the width of a block, determined by the the stacking height. In this paper, systems approach is nec-
yard equipment; ℎ and V are the width of a transfer essary to capture the interactions of various design variables
lane and driving lane, respectively. simultaneously.
(4) The length of yard block 𝑙 is selected taking into
account rational service radius of the handling equip-
ment. Based on the layout of berth and yard, 𝑙 is
suitable between 200 and 300 meters, and it can be 2.2. Yard Design under Uncertainty. The global maritime expressed as
logistics market contains various uncertainties that inherit
from the fluctuation of the demand for freight transportation. 𝑙 = 𝐵 − (𝑁 + 1) V
Influenced by terminal scale, freight organization, truck and 𝑁 , (3)
ship operation, natural conditions, and production man-
agement, terminal production shows unbalance response,
where 𝑁 is the number of columns of blocks in the evident by collected real data of a variety of ports in China yard layout.
[9]. The monthly throughput of the container terminal
(5) There are no detailed procedures to determine thegenerally has a long-term variation trend and seasonal
quantity of yard cranes deployed at the terminal. Itfluctuations [28, 29]. Therefore, the randomness contained
can be found from several engineering projects inin the container terminal logistics system has brought new
operation and under construction that the number of challenges for making a cost-effective and reliable yard design
deployed yard cranes is generally 2∼4 times of quayso as to support sustainable development of the terminal cranes. infrastructure. 4
Mathematical Problems in Engineering
There are three basic programming methods dealing 3. Methodologies
with uncertainty, that is, stochastic, fuzzy, and interval
programming. The main difference lies in the modeling3.1. Optimization Model. The yard design optimization prob-
method of uncertainty. Uncertainty is described by dis- lem is stated as follows: which yard layout is chosen under
crete or continuous probability distribution function in given investment budget constraints to minimize the sum
stochastic programming. In fuzzy programming, uncertaintyof capital cost and operation losses considering uncertain
and constraint are treated as fuzzy number and fuzzy set,terminal throughput? In this model, the number of rows
respectively. A certain extent of constraint being not sat- of blocks 𝑀, the number of columns of blocks 𝑁, and
isfied is allowed, and the satisfaction degree is defined asthe number of yard cranes per row of blocks 𝑛 are first-
membership function of the constraint. In interval program-stage decision variables, while the throughput of containers
ming, value range of uncertainty is denoted in the formthat will be stacked in or out of the designed yard 𝑦(𝜉)
of interval numbers. Interval programming is a relativel a y
nd 𝜔(𝜉) are second-stage decision variables. The proposed
new research field and direction, and there are still a lot
model addressing the yard design optimization problem is
of issues to be resolved. The research on fuzzy linear pro-formulated as
gramming is mature but that on fuzzy nonlinear program- min 𝐶 + 𝐸 ,
ming needs further study. The theory and application of 𝑀,𝑁,𝑛 = 𝐶cap 𝜉𝐶ope (4)
stochastic programming are mature though it is difficultsubject to
to get the precise probability distribution from the actual problem. 𝑀
The monthly container throughput 𝜉 (TEU/month) is 2 , 𝑁, 𝑛 ∈ 𝑍+, (5)
considered as an uncertain parameter in this study. With
historical data and the projection for future economy, a long- 𝐶 ≤ 𝐵 , cap cap (6)
term variation trend and seasonal fluctuation of 𝜉 can be
obtained (see [28, 29] for details). Since this is a complex 𝑦 ≤ 𝑉, (7)
process and not the main issue of this paper, we assume such
information as given; that is, discrete 𝜉 is described by a 𝑦 + 𝜔 = 𝜉, (8)
set of scenarios and their associated probabilities. With this 𝑦, 𝜔 ≥ 0,
information and in view of the nonlinear characteristics, we (9)
choose stochastic programming, the mature and convenient where 𝐶
programming method, to deal with uncertain throughput.
cap is the capital cost of the proposed container yard; 𝐸
Two-stage stochastic programming separates the a pri- 𝜉 denotes mathematical expectation with respect to 𝜉; 𝐵cap
is the expected investment budget and 𝐶
ori planning decisions, taken under uncertainty before the ope is the operation
losses of trucks travelling and yard cranes moving during the
activity cycle starts, and the adjustments performed at eachprocess of achieving the throughput 𝜉. Constraint (5) simply
period of operations once information becomes available.restricts 𝑀/2, 𝑁, and 𝑛 to be positive integer. Constraint
The former makes up the first stage of the model, while(6) represents the investment budget constraint. Constraint
the recourse actions, defining the admissible adjustments(7) sets the capacity restriction, where 𝑉 is a predefined
to the plan, make up the second stage. The lead time of maximum capacity which is determined by 𝑀, 𝑁, and the
container yard is not short. In the process of yard design maximum stacking height. Constraint (8) requires that all
under uncertain environment, planning decisions, such ascontainers must be stored, whether at the designed yard area
yard size and the equipment deployment, need to be made or its neighboring yards or off-dock yards. Constraint (9)
in the planning stage before the uncertain throughput issimply restricts 𝑦, 𝜔 to be nonnegative.
revealed. These decisions are usually capital intensive and
cannot be easily adjusted once implemented. For a designed
container yard with certain capacity, the required space is3.1.1. Capital Cost 𝐶cap. Initial investment is used for the cost
sometimes higher than the provided space during the realof yard space and the purchasing of yard cranes. The total
operation. In such a situation, extra space will be required
capital cost is written as follows:
(e.g., stacking surplus containers in an adjacent yard or rental
space from an off-dock yard), resulting in a recourse cost due 𝐶 = 𝑐 cap 𝑎𝑎 + 𝑐𝑓𝑛𝑀, (10)
to overcapacity. Operational decisions, such as the amount
of containers stacked in and out of the designed yard, can where 𝑐𝑎 is the capital cost for unit area of yard per
be adjusted (with a recourse cost) depending on the actualmonth, including the land fee and construction cost
realization of uncertain future throughput. To distinguish(CNY/m2/month); 𝑎 is the required area of the container
different natures of planning and operational decisions, weyard; for given 𝑀, 𝑎 can be calculated by 𝑎 = (𝑒𝑀 + 0.5ℎ𝑀 +
choose to develop a two-stage stochastic programming with 2ℎ)𝐵 (see Figure 1); 𝑐𝑓 is the fixed cost of a yard crane per
recourse model [30], which has been successfully used inmonth (CNY/month).
logistics planning [31]. This model can well describe the plan-
ning and operation stages of container yard and recognize3.1.2. Operation Losses 𝐶ope. If the space of the yard or the
the nonanticipativity of planning decisions while allowingquantity of yard cranes deployed is not adequate, the opera-
recourse for operational decisions.
tional cost of containers stacked in and out of the designed
Mathematical Problems in Engineering 5
yard area (denoted by 𝑐in and 𝑐out, resp.) will be increased.where 𝑇 is the average stacking height, which can be calcu-
The operation losses can be considered as the recourse costlated as follows:
quantifying the effectiveness of the first-stage decision. Three
categories of containers, namely, the import, export, and 𝑇 = 𝑦𝑡𝑑𝑐 ,
transit containers, are considered. Import containers flow 𝑡𝑦𝑘𝐺𝐴𝑠
from containerships to the storage yard by internal trucks for (13)
temporary storage and then are picked up by external trucks
𝐺 = 𝑒𝑀𝐵 − 𝑒𝑀V (𝑁 + 1)
to the customers. Export process is opposite from import 𝑠 ,
process. Transit containers flow from one containership to thewhere 𝑡
yard and will be loaded into another ship later on. Internal
𝑦𝑘 is the monthly operational days of container yard
(day); 𝐺 is the number of ground slots for stacking containers;
trucks are designated for single berth instead of the whole𝐴
terminal. They deliver containers in a single-cycle mode, in𝑠 is the capacity utilization of the container yard, which
is between 0 and 1 because of some unused space for the
which they repeat a loaded-then-empty travel, alternately,
requirement of relocations; 𝑠 is the space required for a TEU,
between transfer positions under quay cranes and storageincluding the allowance between containers (m2).
sites in the yard. Therefore, the losses are formulated as
In the optimization model, the average travel distance
of the yard crane between moves (𝑑) and the average travel 𝐶 =
{𝑐 𝛾𝑦 + 𝑐 𝛾𝜔} ,
distance between berth and yard (𝑑𝑏) and between gate ope min 𝑦,𝜔 in out
and yard (𝑑𝑔) are the key to calculating the values of the
objective function. However, since the container terminal 𝑐 = 2𝑐 𝑡 𝑑 (11)
logistics system is a stochastic dynamic service system with in
𝑟𝑡𝑡𝑑 + 2𝑐𝑟𝑡ℎ + 𝑐𝑟𝑡𝑟𝑅 + 𝛽 (2𝑐it it 𝑏)
multiple random factors and complex dynamic relations [33], + (1 − 𝛽) (𝑐 𝑡 𝑑 𝑡 𝑑
these indicators are hard to be derived from the conventional it it 𝑏 + 𝑐et et 𝑔) ,
analytical method and thus they will be computed by the
incorporation of simulation models descried in the following section.
where 𝛾 is the factor that converts TEUs into a number of
containers; 𝑐𝑟𝑡𝑡𝑑 denotes the travel time cost of the yard
crane per move (𝑐𝑟 is the variable cost of a yard crane per3.2. Model Framework. Figure 2 presents the proposed
second (CNY/s); 𝑡𝑡 is the travel time of yard crane per metersimulation-based optimization framework to optimize con-
(s/m); 𝑑 is the average travel distance of the yard cranetainer yard design concerning throughput uncertainty. It can
between moves); 𝑐𝑟𝑡ℎ is the cycle time cost of the yard crane be seen that the framework is composed of a two-stage
handling a container (𝑡ℎ is the cycle time required for thestochastic programming (TSSP) model and a simulation
handling of a container (s)); 𝑐𝑟𝑡𝑟𝑅 means the relocation costmodel of terminal operations (SMTO). In the framework, the
of the yard crane (𝑡𝑟 is the time required for the relocationTSSP generates feasible yard design schemes, transfers it to
of a container (s); 𝑅 is the average number of rehandlesthe SMTO, and evaluates the total cost. The SMTO emulates
for picking up an arbitrary container out of a bay); 𝛽 isthe container flow at mega terminal, outputs the values of 𝑑,
the proportion of transit containers among all containers;𝑑𝑏, and 𝑑𝑔, and returns the simulation results to the TSSP. 2𝑐 𝑡 𝑑
Therefore, the core of this framework is the TSSP aided with
it it 𝑏 represents the transport cost for a transit container,
which is transported by internal trucks twice during its staythe SMTO.
at the terminal (𝑐it is the cost of an internal truck per second,
including the overhead cost and the operating cost (costs 3.2.1. Optimization Program. As illustrated in Figure 2, the
for labour, fuel, and maintenance) (CNY/s); 𝑡it is the travelsolution procedure of the TSSP consists of the following steps
time of internal trucks per meter (s/m); 𝑑𝑏 is the averagein sequence.
travel distance between the berth and yard); similarly, 𝑐 𝑡 𝑑 it it 𝑏+ 𝑐 𝑡 𝑑
et et 𝑔 is the transport cost for each import/export container(1) Input Data Generation. Inputs include uncertain container
(𝑐et is the cost of an external truck per second, including thethroughput, terminal handling technology, terminal opera-
overhead cost and the operating cost (costs for labour, fuel,tional parameters, and cost coefficients.
and maintenance) (CNY/s); 𝑡et is the travel time of external
Uncertain container throughput is expressed by the ran-
trucks per meter (s/m); 𝑑𝑔 is the average travel distancedom vector 𝜉(𝑠) depending on the scenario 𝑠 (𝑠 = 1, 2, . . . , 𝑆) between the gate and yard).
with associated probabilities 𝑝(𝑠) (𝑝(1)+𝑝(2)+⋅ ⋅ ⋅+𝑝(𝑆) = 1).
For a bay of 6 stacking lanes of containers, suppose thatInformation about 𝜉(𝑠) and 𝑝(𝑠) can be drawn based on the
the relocation of containers is restricted to a single bay and
historical data and the projection for future economy, which
that pre-schedule for reducing relocations is ignored; the
is not the main concern in this paper.
expected number of relocations 𝑅 then can be evaluated by
Yard handling technology includes the type and span the following formula [32]:
width of the yard crane and the width of a transfer lane and
a driving lane, which can be determined by the MTPRC and practical design handbooks. 𝑅 = 2𝑇 − 1
Yard operational parameters include monthly operational 4 + 𝑇 + 1 48 , (12)
days, the average cluration of containers, the maximum 6
Mathematical Problems in Engineering
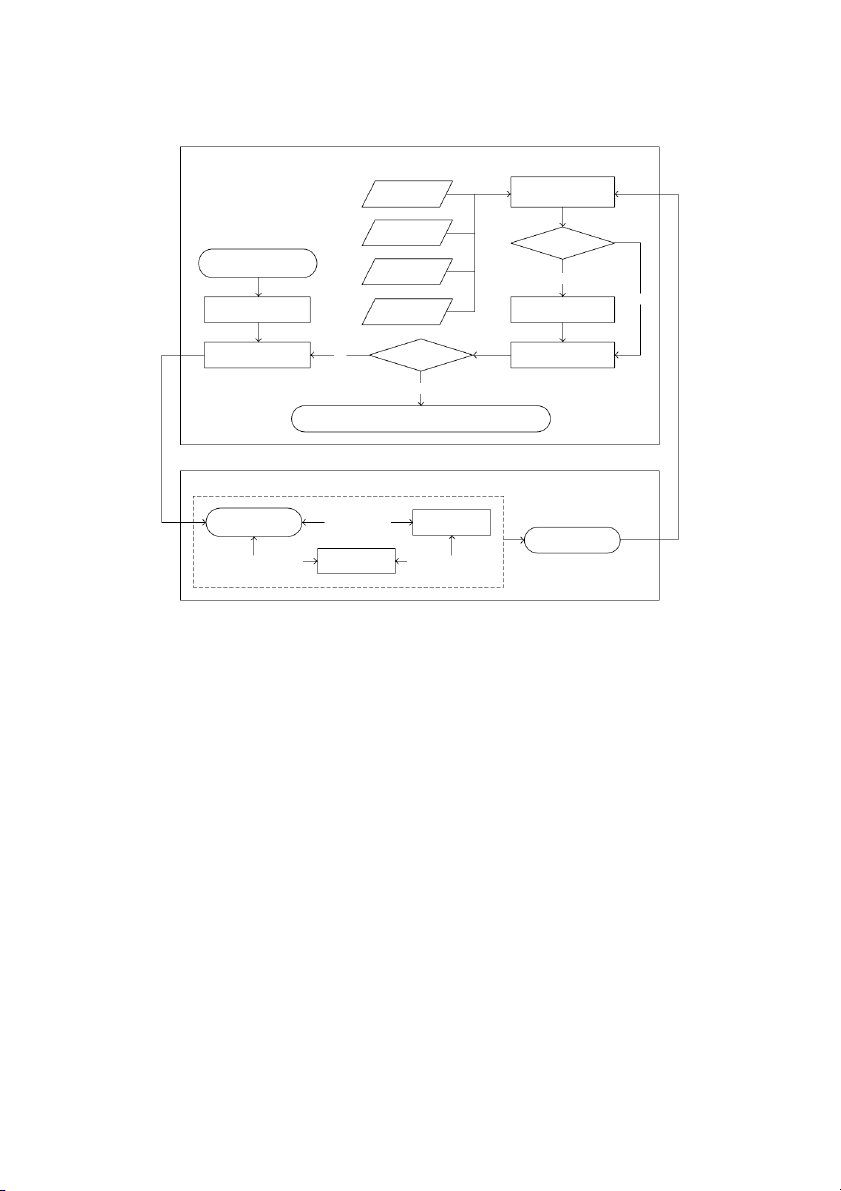
Two-stage stochastic programming (TSSP) Uncertain Optimize Q𝜉 and then throughput evaluate C k total Handling technology C k total < Cmin? Generate Operational
Xk ∈ X󳰀 = {X1, X2, . . . , XK} parameters Yes No Initialization: k = 1, Cost Set C k, p = k C min = Ctotal min = +∞ and p = 1 coefficient Search Xk = (Mk k , N , nk) No k = K + 1? Update k = k + 1 Yes
Output the optimal solution and the minimum cost {Xp, Cmin}
Simulation model of terminal operation (SMTO) Ship/external truck Berth operating Container flows arriving system system (d, db, d ) g Data statistics system Yard operating Container flows system Container flows
Figure 2: The simulation-based optimization framework for yard design at mega container terminal.
stacking height, the average moving speed of yard crane, andand obtain the optimal 𝑄 as well as the corresponding
the average running speed of trucks.
decision variables 𝑦 and 𝜔 under uncertain throughput 𝜉.
Cost coefficients involve the unit space cost, the capital Evaluate the objective function 𝐶 𝑘
total , that is, the sum of the
cost for the yard crane, and variable operational costs asso-
first-stage and expected second-stage costs.
ciated with the yard crane and trucks. These cost coefficients
generally can be provided by the potential terminal operato ( r
5) Optimization and Decision. If 𝐶 𝑘 < 𝐶 total min, set 𝐶min =
or through field investigation. 𝐶 𝑘 total
and 𝑝 = 𝑘. Update 𝑘 = 𝑘 + 1. If the termination
criterion is satisfied, that is, 𝑘 = 𝐾 + 1, stop and output the
(2) Feasible Solution Set Delimitation. The possible yard
optimal design scheme and its corresponding minimum cost
design schemes 𝑋󸀠 are enumerated by calculating all com-
{𝑋𝑝, 𝐶min}; otherwise go to step (4).
binations of possible block quantities (measured in 𝑀 and
𝑁) and yard crane amount 𝑛, and all feasible solutions are
3.2.2. Simulation Model. A process interaction-based dis-
numbered in order for searching; that is, 𝑋𝑘 = (𝑀𝑘, 𝑁𝑘, 𝑛𝑘) crete event simulation model is developed for terminal
belongs to 𝑋󸀠 = {𝑋1, 𝑋2, . . . , 𝑋𝐾}.
operations via commercial software Arena 10.0, and it is
verified and validated before running productive simulations
(3) Initialization. Set 𝑘 = 1; the minimum total costs 𝐶min = +∞
[34]. According to the operational processes as outlined in
and the corresponding index of solution in the set 𝑝 = 1. Figure 3, the simulation model consists of five systems as
(4) Simulation Activation and Objective Function Evaluation. follows.
Search the feasible solution 𝑋𝑘. Transfer 𝑋𝑘 to the SMTO, run
(1) Ship/external truck arriving system: ships are cre-
the simulation model to get 𝑑, 𝑑𝑏, and 𝑑𝑔, and return them
ated and initialized in accordance with the shipping
to the TSSP. Optimize the second-stage model of the TSSP,
schedule and the handling plan. The processes of
Mathematical Problems in Engineering 7 Ship arrivals Data initialization External trucks arrivals Berth available? No Ship waits in queue Export? Yes Yes Ship berths at an available berth Storage yard assignment for Unloading Storage yard Loading plan and export containers Assigning quay cranes and and stowage assignment for storage site of internal trucks to ship plan of ship import and transit export containers containers Transporting export containers to assigned Unloading containers from ship by quay cranes blocks by external trucks Transporting import and Unloading process Requesting internal trucks transit containers to No Stacking containers by finished? for quay cranes assigned blocks by yard cranes internal trucks No Internal trucks request rules Yes Import or transit? Yes Storage site of Requesting internal trucks Dispatching containers by import containers for yard cranes yard cranes in the yard No Transporting import External trucks exit Export or transit? No containers to gate by from the terminal external trucks Yes Transporting export and transit containers to assigned berths by internal trucks No Loading Loading containers to and stowage ship by quay cranes plan of ship Loading process Ship unberths and Yes finished? leaves the terminal
Figure 3: The logic flowchart of container terminal operation.
berth allocation and external trucks picking up and
corresponding ship. The operations of quay cranes
delivering containers are triggered, respectively.
coordinating with internal trucks are simulated.
(2) Berth operating system: ships begin to receive
(3) Yard operating system: import, export, and transit
unloading and loading service after berthing and
containers realize stockpiling and extracting by han-
preparatory work. Internal trucks are designated
dling equipment in designate section of the yard
equally among the quay cranes assigned to the
according to the stacking plan. Yard cranes are 8
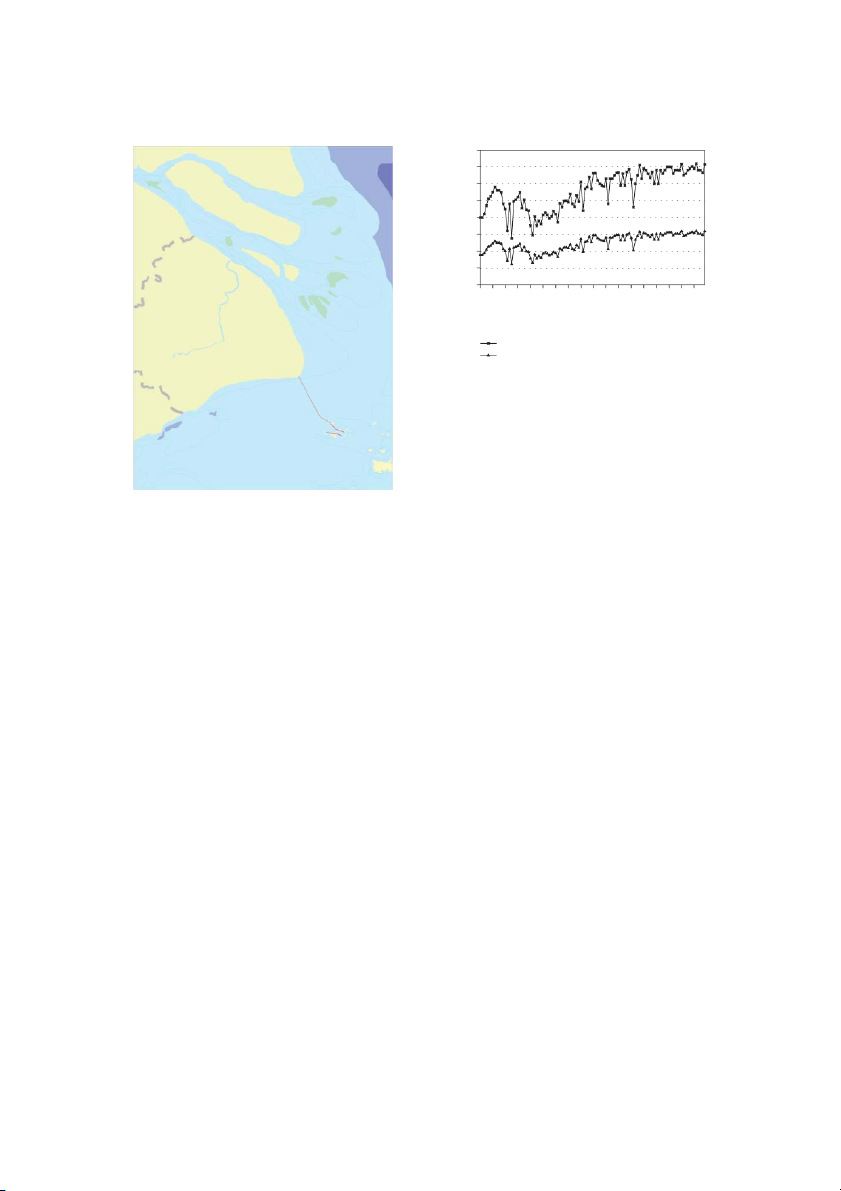
Mathematical Problems in Engineering 80 ) U Jiangsu E 70 T Province 4 60 Ch 10 on × gm t ( 50 ing u Is p Jiangsu lan 40 d gh Province rou 30 ly th 20 Yangtze Estuary th 10 on M 0 /07 /08 /09 /10 l/07 l/10 /11 /12 l/08 l/09 l/11 l/12 /13 /14 l/13 l/14 /15 l/15 Ju Ju Jan Jan Ju Jan Ju Jan Ju Ju Jan Jan Ju Ju Jan Jan Ju Jan Months (Jan/2007~Dec/2015) City of Shanghai Phases I and II Phase II Do n
Figure 5: Monthly throughput of Phase I and Phase II Terminals. ghai B Zhejiang ridg Province e
at the terminal is reclaimed from the sea and not easy to Yangshan Port Area
be adjusted during the operational period. Therefore, due Hangzhou Bay
to the huge investment, economic and sustainable pressures
have acknowledged the need not only to minimize the initial
investment but also to ensure the terminal efficiency and
reliability when determining the yard design.
Figure 4: Sketch of location of Yangshan Port Area.
4.1. Model Input. The monthly throughput data of Phase I
and Phase II Terminal (two terminals have been merged in
assigned to each zone of the container yard, prevent- real operation since Phase II Terminal went into operation)
ing the gantry move of yard crane in different zones. from 2007 to 2015 are provided by China Ports and Harbours
Internal and external truck streamlines converge here,
Association, as plotted in Figure 5. The monthly throughput
and the next station of trucks will be the gate or berthof Phase II Terminal is estimated assuming it is proportional
corresponding to their different tasks.
to the length of the terminal. 108 monthly throughputs are
used to construct a set of discrete scenarios with equal
(4) Assignment generating system: both the loading and probabilities in this case study.
unloading plan of each ship and the storage yard
Input data of the proposed optimization framework for
assignment for corresponding import, export, and this container terminal are provided as shown in Table 1 [9,
transit containers are generated. 35].
(5) Data statistics system: the above four systems work
This study evaluates 6 options for the initial monthly
independently and interact with each other by con- investment budgets, including 5 MCNY (Million CNY), 5.5
tainer flows. Yard crane and truck information isMCNY, 6 MCNY, 6.5 MCNY, 7 MCNY, and 7.5 MCNY, to be
recorded and the average travel distance of yard crane investigated.
between moves and the average travel distances of
Based on the geographical location of Phase II Terminal
internal trucks and external trucks can be calculated
and field investigation, we set a relatively high recourse cost:
and transferred to the optimization program.
the operation cost of storing a container out of the designed
yard is 10 times the value of a container stacked in the designed yard area. 4. Case Study
The framework is applied to the second phase terminal4.2. Results and Discussions. Table 2 shows the optimal yard
(hereafter referred to as Phase II Terminal) of Shanghai
design schemes under various investment budget constraints
Yangshan Port Area in China as a case study. With an aimby the proposed optimization framework. As listed in Table 2,
to become an international shipping center, Shanghai Citythe optimal decision with the initial monthly investment
has selected Yangshan as the site for its deep-water terminals;
budget of at least 7 MCNY (in fact, the investment cost
see Figure 4. The construction of container terminals incalculated is 6.57 MCNY) is 14 rows and 6 columns of
this port area is implemented in four phases. Phase IIblocks and 3 yard cranes deployed in each zone of blocks.
Terminal, possessing a total of 1,400 meters coastline, isThe corresponding yard design scheme of yard depth, block
equipped with four container berths which can accommodate length, and amount of yard cranes are 413 m, 210 m, and 42,
containerships over 8,000 TEUs. The land area of the yardrespectively.
Mathematical Problems in Engineering 9
Table 1: Input data of the proposed optimization framework for this container terminal. Items Unit Data input (1) Simulation time Hour 30 × 24 (2) Uncertain throughput
(i) Random vector with associated probability, 𝜉(𝑠), 𝑝(𝑠) See Figure 5 (3) Yard handling technology
(i) Maximum span width of yard crane Meter 23.47 (ii) Block width, 𝑒 Meter 16.63
(iii) Width of transfer lane and driving lane, ℎ, V Meter 20
(iv) Space required for a TEU, 𝑠 Square meter 17.63
(4) Yard operational parameters
(i) Monthly operational days, 𝑡𝑦𝑘 Day 30
(ii) Capacity utilization, 𝐴𝑠 0.7
(iii) Average cluration of containers, 𝑡 Day 5.5 dc (iv) Maximum stacking tiers 5
(v) Travel time of yard crane per meter, 𝑡𝑡 Second/meter 0.45
(vi) Cycle time required for handling a container, 𝑡ℎ Second 77.1
(vii) Average relocation time, 𝑡𝑟 Second 74.2
(viii) Travel time of trucks per meter, 𝑡 , 𝑡 Second/meter 0.18 it et (5) Cost coefficients
(i) Capital cost for yard space, 𝑐𝑎 CNY/square meter/month 8.33
(ii) Capital cost for yard crane, 𝑐𝑓 MCNY/month 0.042
(iii) Variable cost for yard crane, 𝑐𝑟 CNY/second 0.053
(iv) Variable cost for truck, 𝑐 , 𝑐 CNY/second 0.023 it et (6) Investment budgets (i) Options, 𝐵 MCNY 5, 5.5, 6, 6.5, 7, 7.5 cap
Moreover, from an engineering perspective, the following 18 observations are made. 16 )
(1) Optimal yard design schemes change as the invest- th n 14
ment budget varies. For example, if the monthly o
budget is less than 6 MCNY, 360 m yard depth with /m 12 Y N
higher block length and less yard cranes deployed is C 10
preferred. However, the optimal yard design scheme
will not change when the monthly budget is between sts (M 8 o
6 MCNY and 6.5 MCNY or greater than 7 MCNY, as C 6
shown in Table 2. It is noted that more budgets would
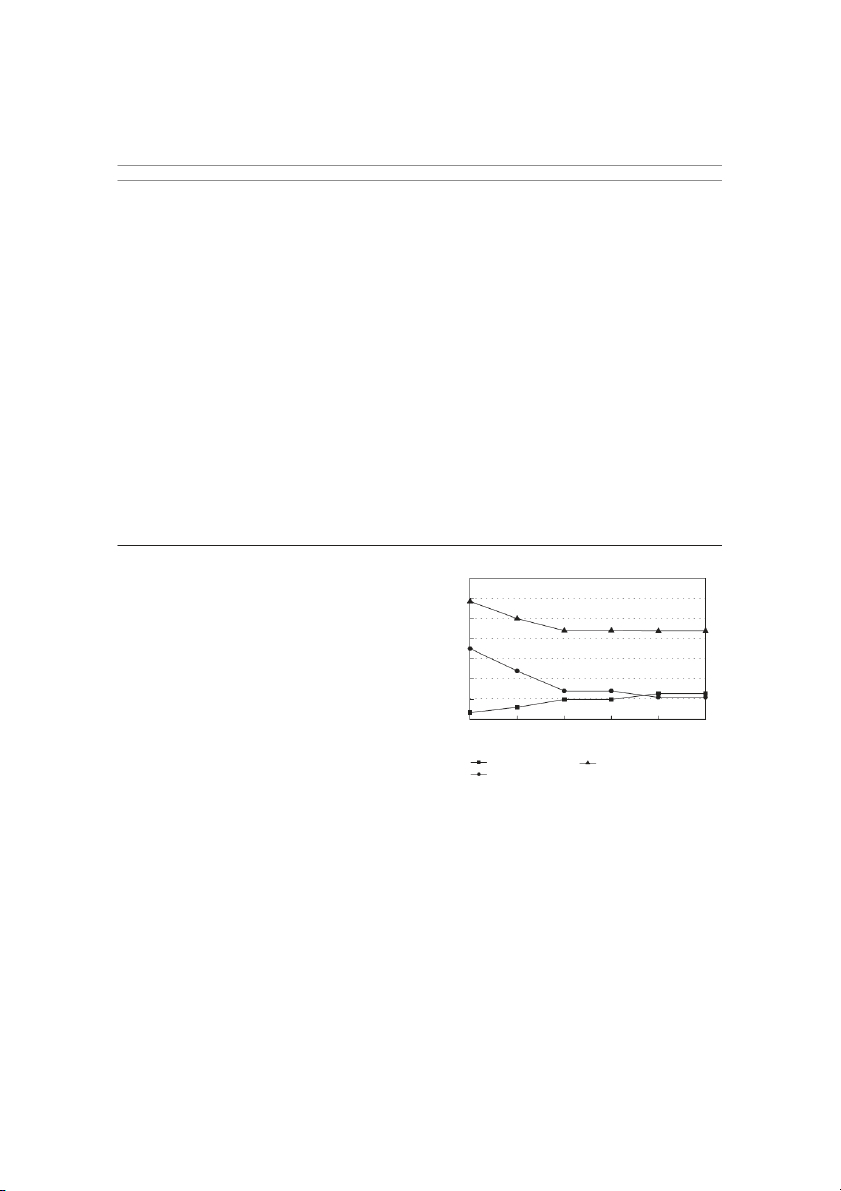
not always obtain extra profits; therefore, investors 45 5.5 6 6.5 7 7.5
should pay more attention to these situations to avoid
Investment budgets (MCNY/month) unnecessary investment. Investment cost
(2) The investment budget has a negative correlation with Total costs Operation losses
the losses from yard operation in a certain scope.
As shown in Figure 6, when the initial monthly Figure 6: The costs of optimal yard design scheme for various
investment budget increases from 5 MCNY to 7 investment budgets.
MCNY, the operation losses will decrease from 11.01
MCNY to 6.19 MCNY, and the gained benefit is
the yard (with given yard depth and block length), the
about 44% equivalently. Therefore, if the investment
variations of yard cranes deployed may not affect the
budget is adequate, larger depth yard with less block
total costs significantly. As shown in Table 2, for a yard
length and more yard cranes deployed is favourable
layout with 413 m depth and 210 m block length, the
for improving operation efficiency and reducing oper-
number of yard cranes deployed increases from 28 to ation losses.
42, resulting in the investment cost increasing from
(3) Large quantity of yard cranes deployed at the con-
5.98 MCNY to 6.57 MCNY, but the operation losses
tainer terminal results in a higher investment cost but
decreasing from 6.82 MCNY to 6.19 MCNY, and the
lower operation losses. However, for certain layout of
total costs being stable at about 12.8 MCNY. In this 10
Mathematical Problems in Engineering sts co 0 l 70 .0 ta o 15. 14 12.80 12.80 12.76 12.76 T ) th n o n /m Y tio 1 N a sses 82 82 19 19 C er 11.0 8.81 6. 6. 6. 6. p lo (M O sts o C t ets. g en d 8 8 u st 19 9 9 57 57 b co .69 5. 5. 6. t 4 5. 6. en Investm investm d s r u es ya n 8 2 2 io f a 12 24 28 2 4 4 r o cr va # es er d n em u sch th g es n ) 0 0 em len 4 esig ck (m 67 4 210 210 210 210 sch d n d lo r B a Y esig d d th r ep ya d ) 0 13 13 l d 13 13 4 4 4 4 a r (m 36 360 a tim Y op d n a bles 𝑛 1 2 2 2 3 3 ia r va n les b ia r ecisio d va e n 𝑁 2 3 6 6 6 6 h 2:T ecisio le D b a T 𝑀 12 12 14 14 14 14 ) nth ets o g d /m 5 5 6 5 7 u Y 5. 6. 7.5 B N C (M er b m u N 1 2 3 4 5 6