























Preview text:
lOMoARcPSD|36403279 CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ Khoa Toán Tin
Trường Đại học Sư phạm Hà Nội
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 1 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Nội dung của chương 1
Đặt bài toán kiểm định giả thuyết. 2
Bài toán kiểm định giả thuyết cho giá trị trung bình một mẫu. 3
Bài toán kiểm định giả thuyết cho tỉ lệ một mẫu. 4
Bài toán kiểm định giả thuyết cho giá trị trung bình hai mẫu. 5
Bài toán kiểm định giả thuyết cho tỉ lệ hai mẫu.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 2 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Mục tiêu của chương 1
Hiểu được cách đặt bài toán và các khái niệm: giả thuyết, đối thuyết, sai lầm
loại 1, sai lầm loại 2, mức ý nghĩa, nguyên lý xây dựng tiêu chuẩn kiểm định. 2
Nhận biết được tình huống
so sánh trung bình một mẫu, hai mẫu;
so sánh tỉ lệ một mẫu, hai mẫu. 3
Sử dụng quy trình 6 bước để giải bài toán kiểm định trung bình, tỉ lệ và diễn
giải chính xác kết quả thu được.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 3 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
4.1 Bài toán kiểm định giả thuyết
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 4 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Tình huống thực tế
Một chuỗi cửa hàng cà phê X sau khi ra mắt sản phẩm đầu tiên rất thành
công với 70% phản hồi tích cực từ tất cả khách hàng. Ông chủ muốn tiếp
tục cho ra mắt công thức pha chế tiếp theo và hy vọng cũng nhận được sự
thành công như lần trước.
Ông chủ đã ngầm khẳng định giả thuyết rằng 70% tất cả khách hàng sẽ yêu
thích sản phẩm mới này và tiến hành khảo sát để kiểm chứng.
Ông cho bán miễn phí trên 100 khách hàng bất kỳ và ghi nhận được 67
người cho kết quả tích cực. Với kết quả như trên, ông chủ hơi nghi ngờ về giả thuyết của mình.
Nếu kết quả càng xa con số 70%, sự nghi ngờ của ông chủ càng lớn và đến
một ngưỡng nào đó ông chủ sẽ phải bác bỏ giả thuyết của mình. Liệu có
cách nào để cụ thể hóa mối tương quan giữa kết quả khảo sát và kết luận
của ông chủ về giả thuyết hay không?
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 5 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
Bài toán kiểm định giả thuyết (Hypothesis Testing)
Giả thuyết thống kê là một phát biểu nào đó về tính chất của quần thể.
Bài toán kiểm định giả thuyết thống kê thường xuất hiện khi ta cần phải đưa
ra kết luận về hai giả thuyết trái ngược nhau thông qua việc khảo sát.
Cụ thể, kiểm định giả thuyết thống kê là một quy trình để xác minh xem có
thể chấp nhận giả thuyết thống kê hay không dựa trên mẫu số liệu quan sát được từ quần thể.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 6 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Mô hình hoá
Với tình huống thực tế trên, ta có hai giả thuyết như sau:
- Giả thuyết H0: tỉ lệ khách hàng thích sản phẩm mới bằng 70% (được giả sử là đúng)
- Đối thuyết H1: tỉ lệ khách hàng thích sản phẩm mới không bằng 70% (được giả sử là sai)
Dựa trên mẫu số liệu thu được, ta cần phải lựa chọn một trong hai quyết định:
- Bác bỏ giả thuyết H0 để ủng hộ đối thuyết H1;
- Không bác bỏ giả thuyết H0 để ủng hộ đối thuyết H1. Tức là chấp nhận H0 và không ủng hộ H1.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 7 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Miền tiêu chuẩn
Một miền S được gọi là miền tiêu chuẩn (hay còn gọi là miền bác bỏ) cho
bài toán kiểm định giả thuyết H0 với đối thuyết H1 nếu:
kết quả khảo sát nằm trong miền S, ta sẽ bác bỏ H0 để ủng hộ H1.
kết quả khảo sát nằm ngoài miền S, ta sẽ chấp nhận H0 và không ủng hộ H1.
Ví dụ, trong tình huống thực tế trên, nếu kết quả khảo sát nằm trong
khoảng 65% đến 75% thì ta bác bỏ H0, ngược lại ta sẽ chấp nhận H0.
Việc xác định miền tiêu chuẩn rất giống với quá trình tìm Khoảng tin cậy
và vì thế cũng sẽ tồn tại sự không chắc chắn. Do ta đưa ra quyết định dựa
trên một mẫu số liệu nên có thể mắc phải sai lầm.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 8 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Hai loại sai lầm Quy tắc quyết định Quyết định H0 đúng H1 đúng Bác bỏ giả thuyết H0 Sai lầm loại 1 Quyết định đúng
Chấp nhận giả thuyết H0 Quyết định đúng Sai lầm loại 2 Nhận xét
Nếu ta luôn chấp nhận H0 thì không mắc phải sai lầm loại 1 nhưng sẽ làm
xác suất mắc sai lầm loại 2 đạt cao nhất.
Ngược lại, nếu ta luôn bác bỏ H0 thì không mắc phải sai lầm loại 2 nhưng sẽ
làm xác suất mắc sai lầm loại 1 đạt cao nhất.
Như vậy, Không thể làm triệt tiêu đồng thời cả hai loại sai lầm!
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 9 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
Nguyên lý chung để tìm miền tiêu chuẩn
Ta cần tìm miền S sao cho xác suất mắc hai loại sai lầm là nhỏ nhất.
Trong thực tế, người ta thường kiểm soát xác suất xảy ra sai lầm loại 1 theo
ý muốn (thông qua cách thiết kế thí nghiệm, điều chỉnh các thông số,...). Cụ
thể, người ta sẽ khống chế xác suất mắc sai lầm loại 1 không vượt quá
α ∈ (0, 1) và từ đó sẽ chọn miền tiêu chuẩn S sao cho xác suất mắc sai lầm loại 2 nhỏ nhất.
Khi đó, α được gọi là mức ý nghĩa của bài toán kiểm định.
Ta thường chọn mức ý nghĩa α = 0, 05 = 5%.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 10 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
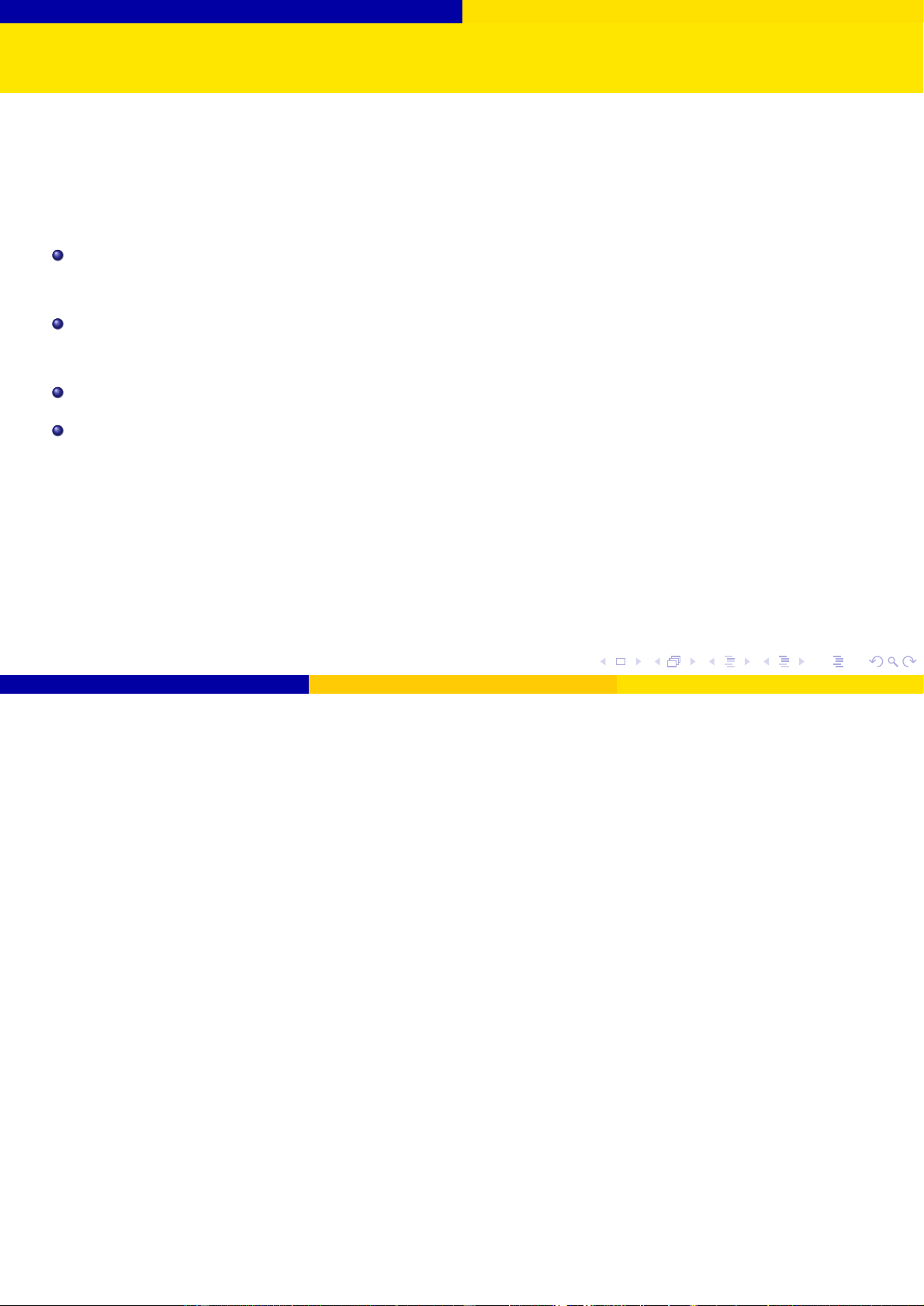
Bài toán kiểm định giả thuyết cho tham số
Giả sử θ là một tham số chưa biết của quần thể (Ví dụ: giá trị trung bình, tỉ lệ,...) Giả thuyết H0 : θ = θ0. Đối thuyết 1
H1 : θ 6= θ0 Kiểm định hai phía 2
H1 : θ > θ0 Kiểm định một phía 3
H1 : θ < θ0 Kiểm định một phía
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 11 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
4.2 Bài toán kiểm định giả thuyết
cho giá trị trung bình một mẫu
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 12 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
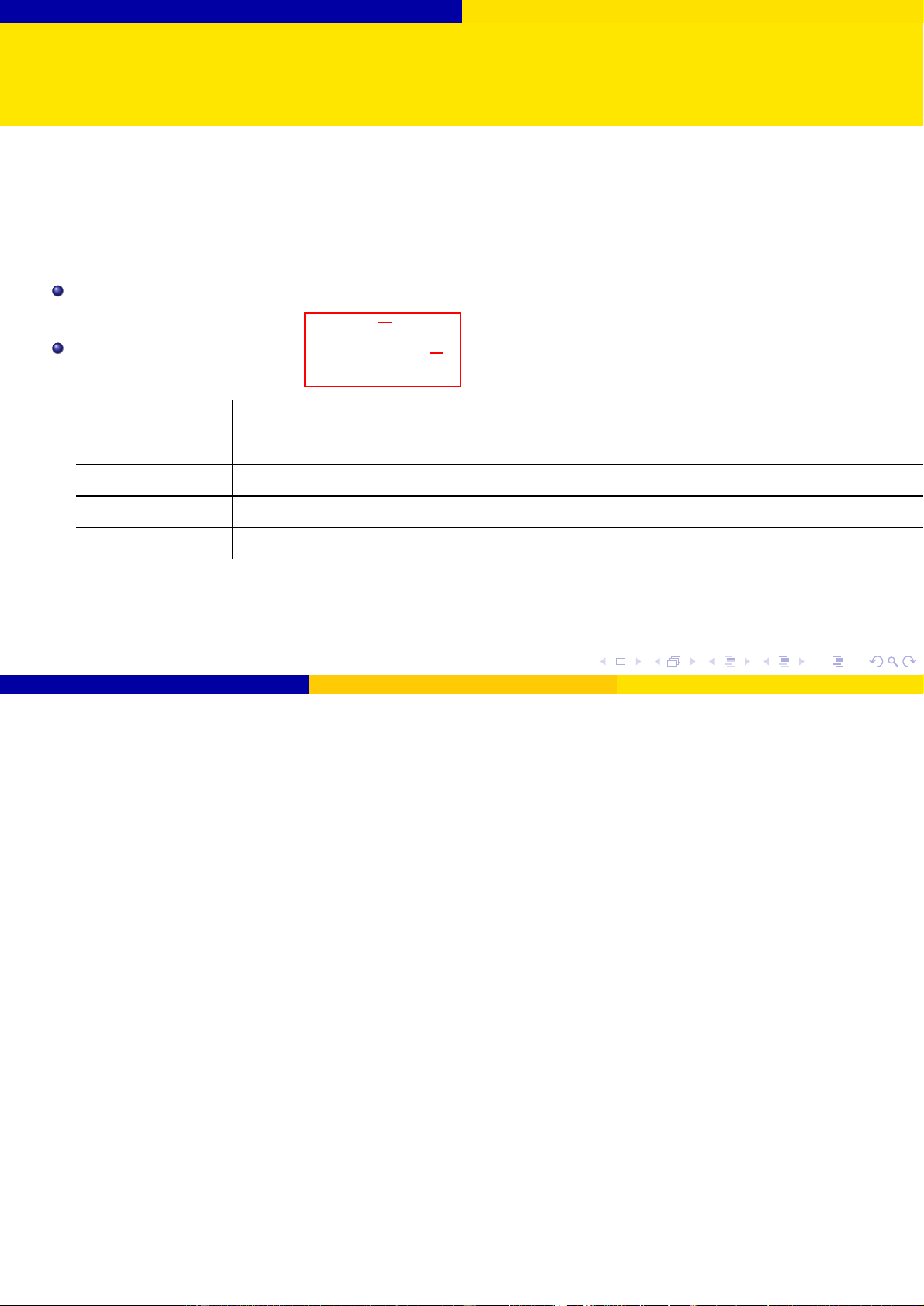
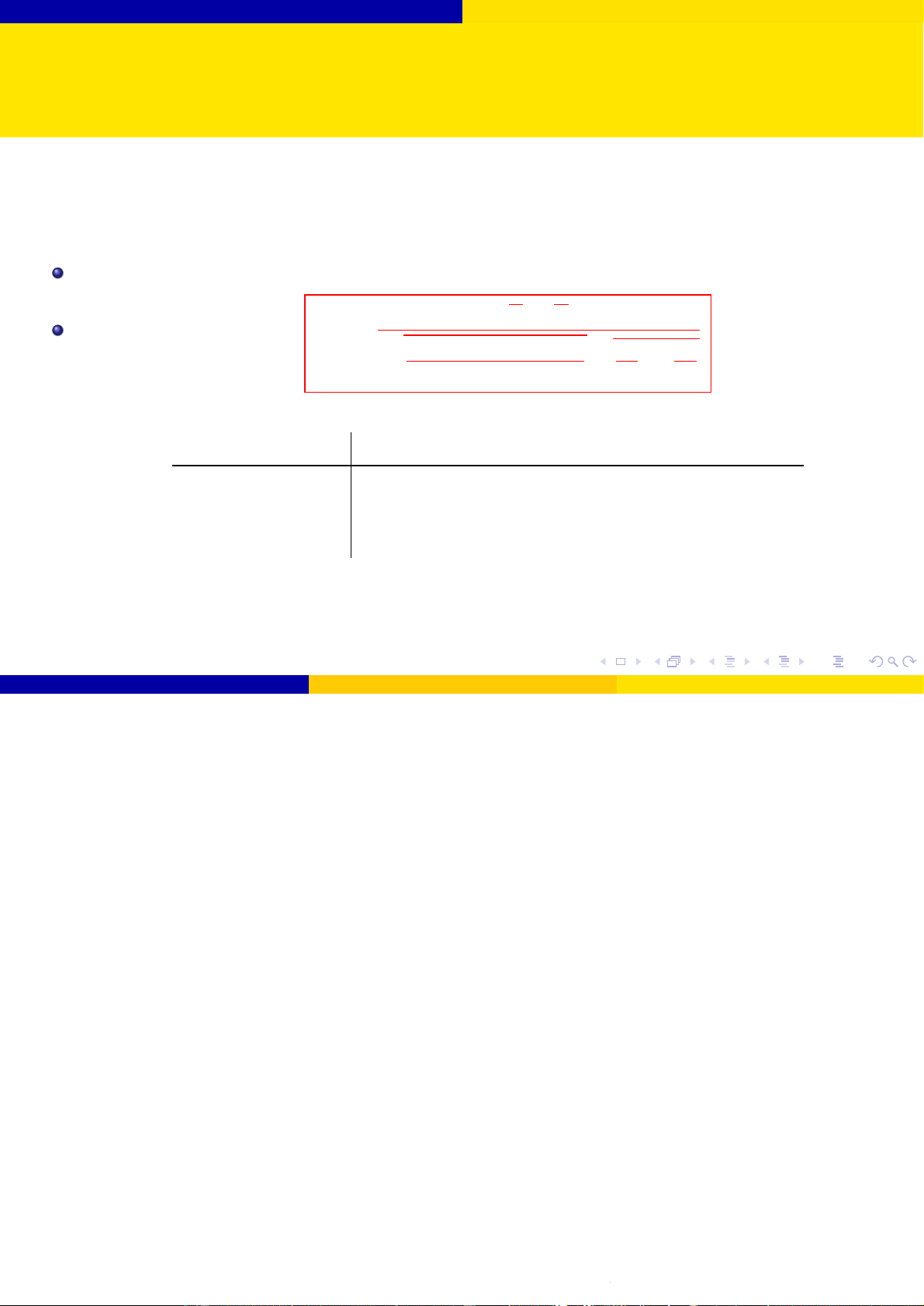
Bài toán 1: Kiểm định giả thuyết cho giá trị trung bình với phương sai 2 σ đã biết
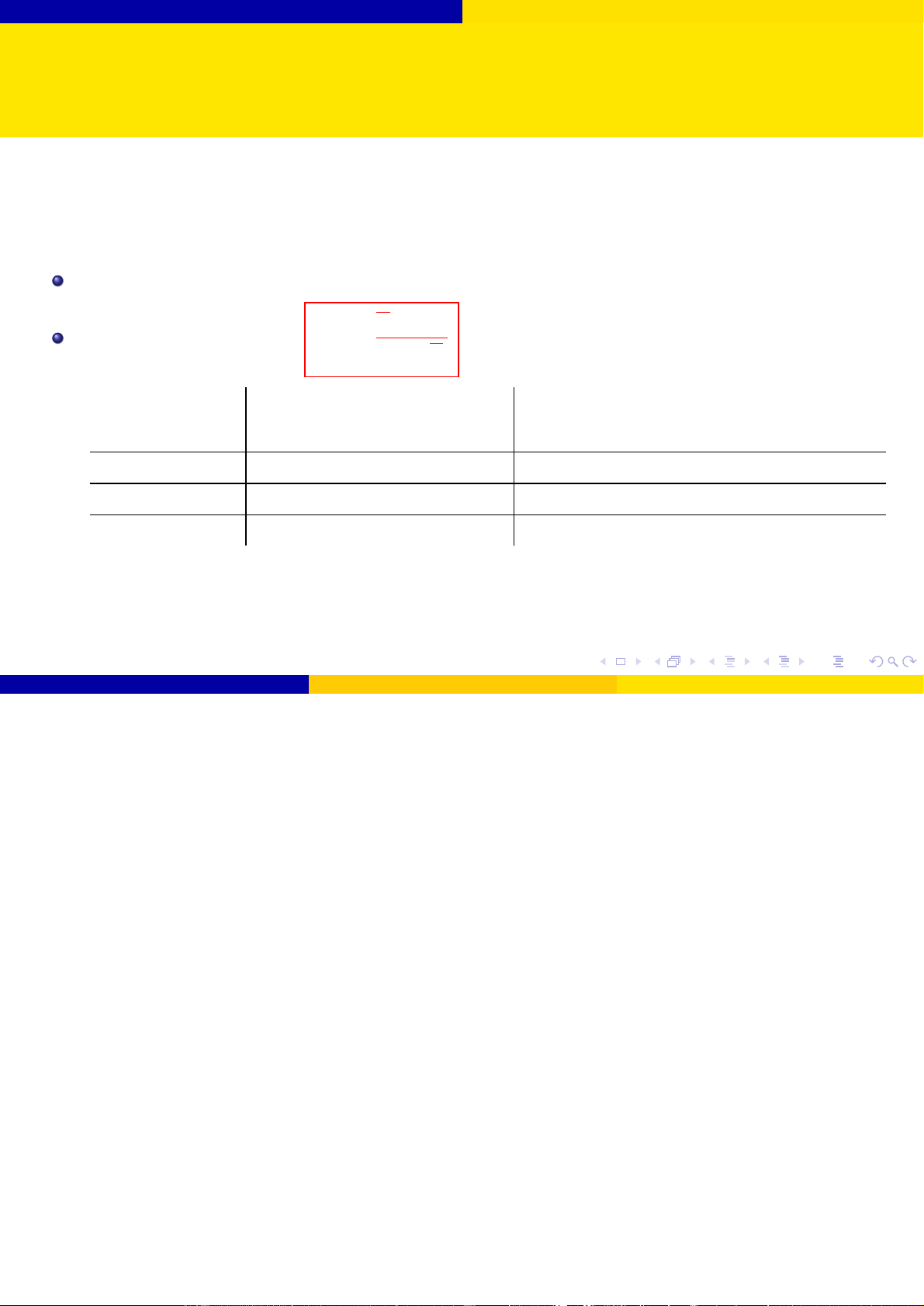
Giả sử quần thể X có phân phối chuẩn N (µ, σ2) với σ2 đã biết. Giả thuyết H0 : µ = µ0. Thống kê kiểm định: x − µ0 Z0 = √ σ/ n Đối thuyết Tiêu chuẩn bác bỏ H0 Miền tiêu chuẩn ở mức ý nghĩa α H1 : µ 6= µ0 |Z0| > zα/2
S = (−∞; −zα/2) ∪ (zα/2; +∞) H1 : µ > µ0 Z0 > zα S = (zα; +∞) H1 : µ < µ0 Z0 < −zα S = (−∞; −zα)
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 13 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Ví dụ 1
Thống kê năm 2015 ta có năng suất lúa trung bình của tỉnh Thái Bình là 66 tạ/ha.
Khảo sát ngẫu nhiên 10 thửa ruộng ở huyện Đông Hưng thấy năng suất
trung bình của 10 thửa ruộng này là 68 tạ/ha.
Biết rằng năng suất của mỗi thửa ruộng có phân phối chuẩn với độ lệch chuẩn σ = 4 tạ/ha.
Hãy kiểm định xem năng suất lúa ở Đông Hưng có cao hơn năng suất trung
bình của tỉnh Thái Bình được hay không, cho mức ý nghĩa α = 5%?
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 14 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
Lời giải - Quy trình 6 bước 1
Tham số cần kiểm định là năng suất lúa trung bình của huyện Đông Hưng, kí hiệu là µ tạ/ha. 2
Ta cần kiểm định xem năng suất lúa ở Đông Hưng có cao hơn năng suất
trung bình của tỉnh Thái Bình được hay không, do đó ta có bài toán kiểm định H0 : µ = 66 với H1 : µ > 66. 3
Cỡ mẫu n = 10; trung bình mẫu ¯x = 68 và độ lệch chuẩn σ = 4. 68 − 66 4
Thống kê kiểm định Z0 = √ = 1, 581. 4/ 10 5
Mức ý nghĩa α = 5% nên α = 0, 05 ⇒ zα = 1, 645. 6
Do Z0 < zα nên ta không bác bỏ H0 : µ = 66 để ủng hộ H1 : µ > 68 ở mức ý nghĩa α = 5%.
Vậy, ta không có đủ căn cứ để kết luận năng suất lúa của huyện Đông Hưng
cao hơn của tỉnh Thái Bình dựa trên mẫu gồm 10 số liệu đã thu được.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 15 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
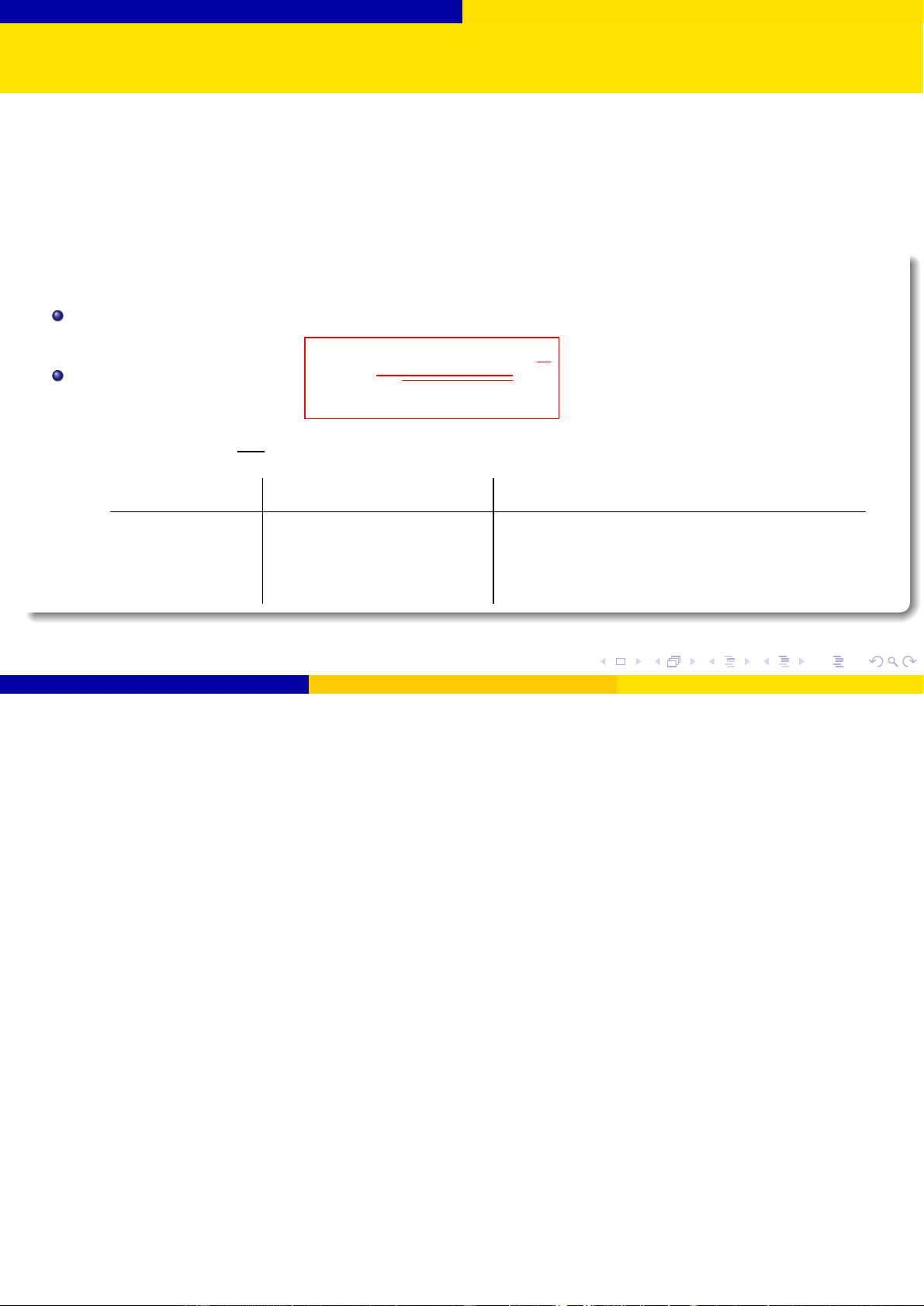
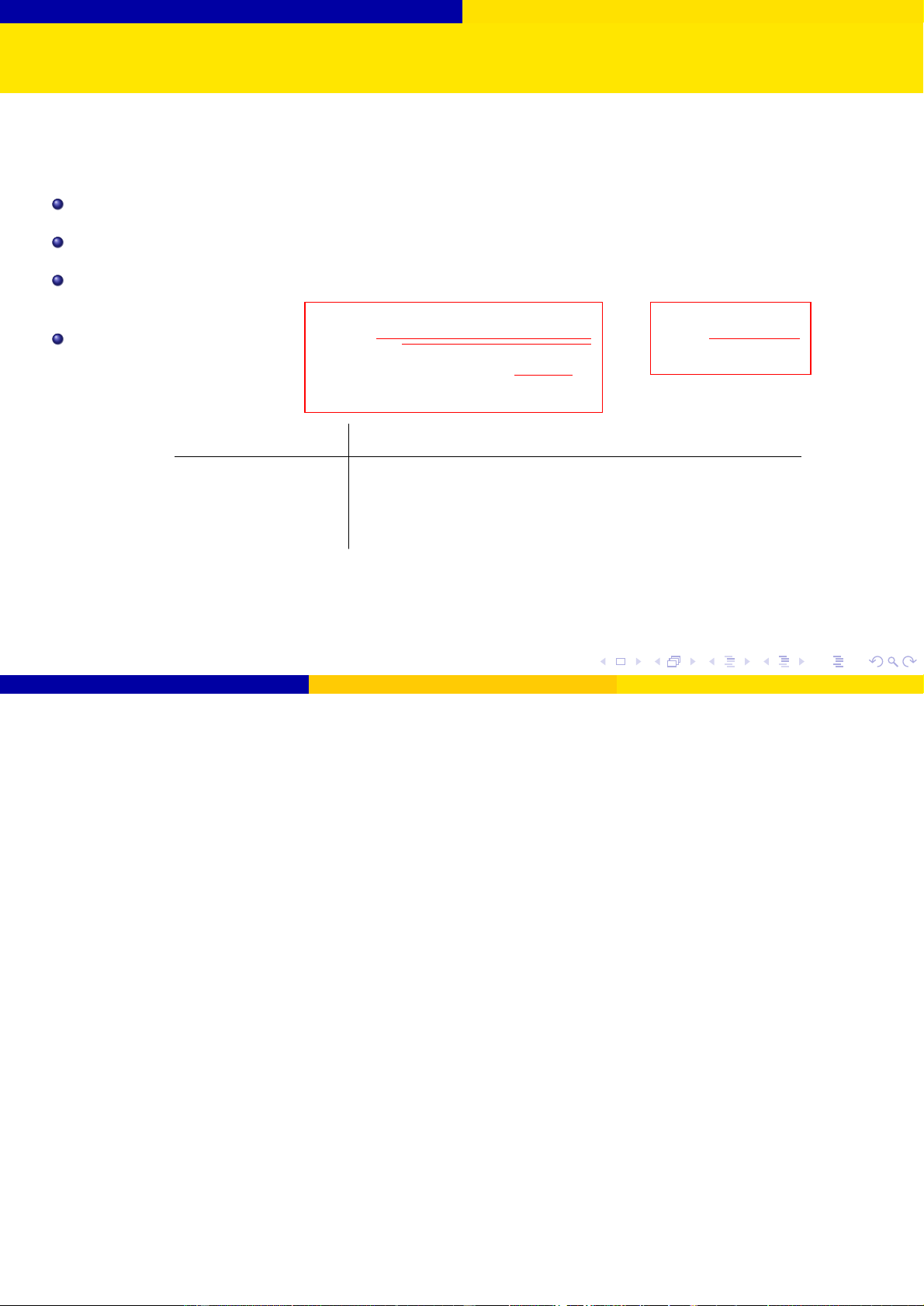
Bài toán 2: Kiểm định giả thuyết cho giá trị trung bình với mẫu cỡ lớn
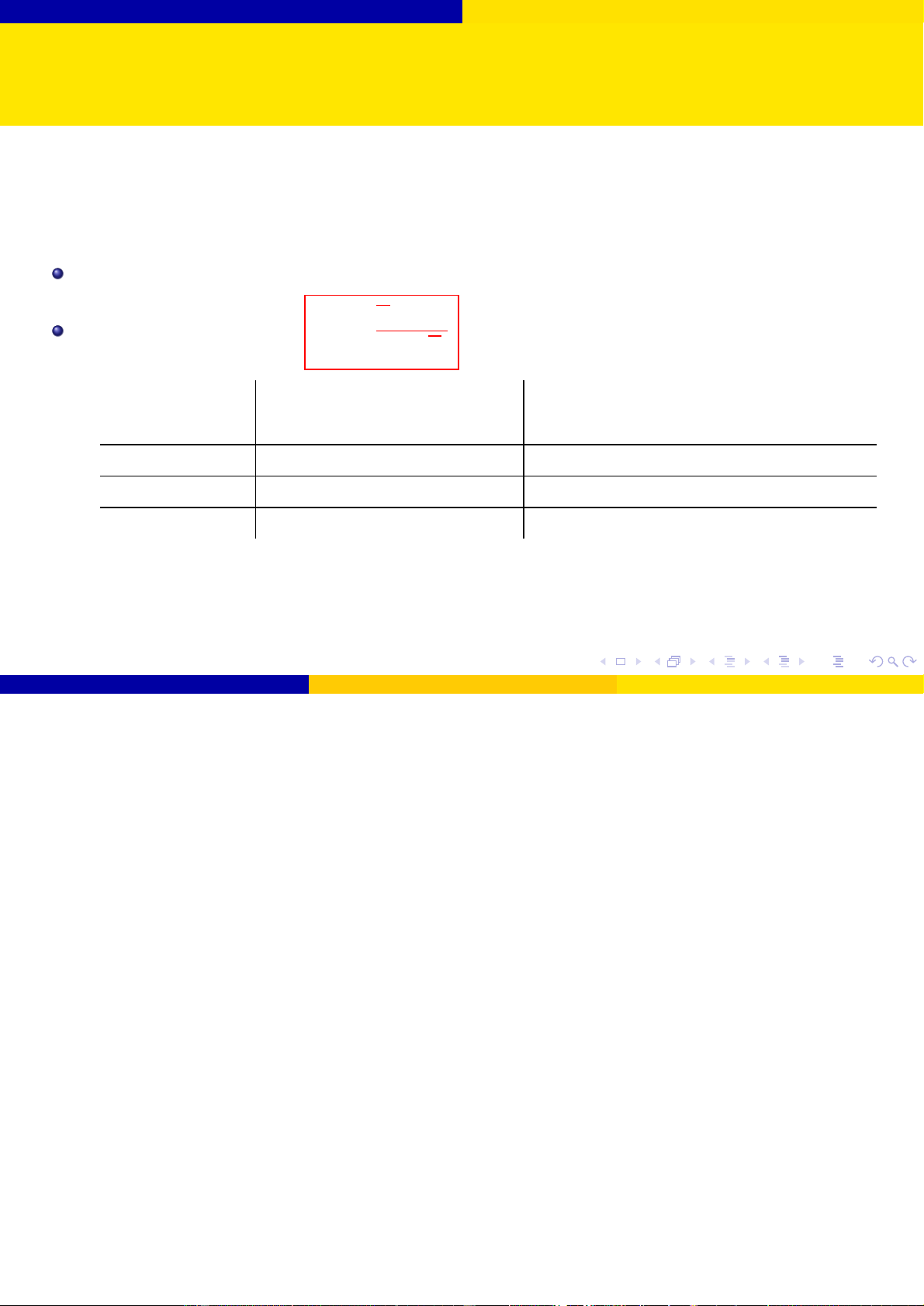
Giả sử mẫu ngẫu nhiên có cỡ mẫu n ≥ 30. Giả thuyết H0 : µ = µ0. Thống kê kiểm định: x − µ0 Z0 = √ s/ n Đối thuyết Tiêu chuẩn bác bỏ H0 Miền tiêu chuẩn ở mức ý nghĩa α H1 : µ 6= µ0 |Z0| > zα/2
S = (−∞; zα/2) ∪ (zα/2; +∞) H1 : µ > µ0 Z0 > zα S = (zα; +∞) H1 : µ < µ0 Z0 < −zα S = (−∞; −zα)
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 16 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Ví dụ 2
Một nhà máy sản xuất mì chính ghi trọng lượng của mỗi gói mì chính trên bao bì
là 2kg. Để kiểm tra thông tin này, người ta lấy mẫu ngẫu nhiên gồm 100 gói thì
thấy trọng lượng trung bình của 100 gói này là 2002g và độ lệch mẫu s = 5g. Với
mức ý nghĩa α = 0, 05, hãy cho biết trọng lượng các gói mì chính liệu có đúng
như ghi trên bao bì hay không?
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 17 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Lời giải 1
Tham số cần kiểm định là trọng lượng trung bình của các gói mì chính, kí hiệu là µ g. 2
Ta cần kiểm định xem trọng lượng các gói mì chính có đúng như công bố hay
không, do đó ta có bài toán kiểm định H0 : µ = 2000 với H1 : µ 6= 2000. 3
Cỡ mẫu n = 100; trung bình mẫu ¯x = 2002; độ lệch mẫu s = 5. 2002 − 2000 4
Thống kê kiểm định: Z0 = √ = 4. 5/ 100 5
Mức ý nghĩa α = 0, 05 nên α/2 = 0, 025 ⇒ zα/2 = 1, 96. 6
Do |Z0| > zα/2 nên ta bác bỏ H0 : µ = 2000 để ủng hộ H1 : µ 6= 2000 ở mức ý nghĩa α = 0, 05.
Vậy, ta có đủ căn cứ để kết luận rằng trọng lượng của mỗi gói mì chính
không giống như trong công bố của nhà sản xuất dựa trên mẫu 100 số liệu đã thu được.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 18 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
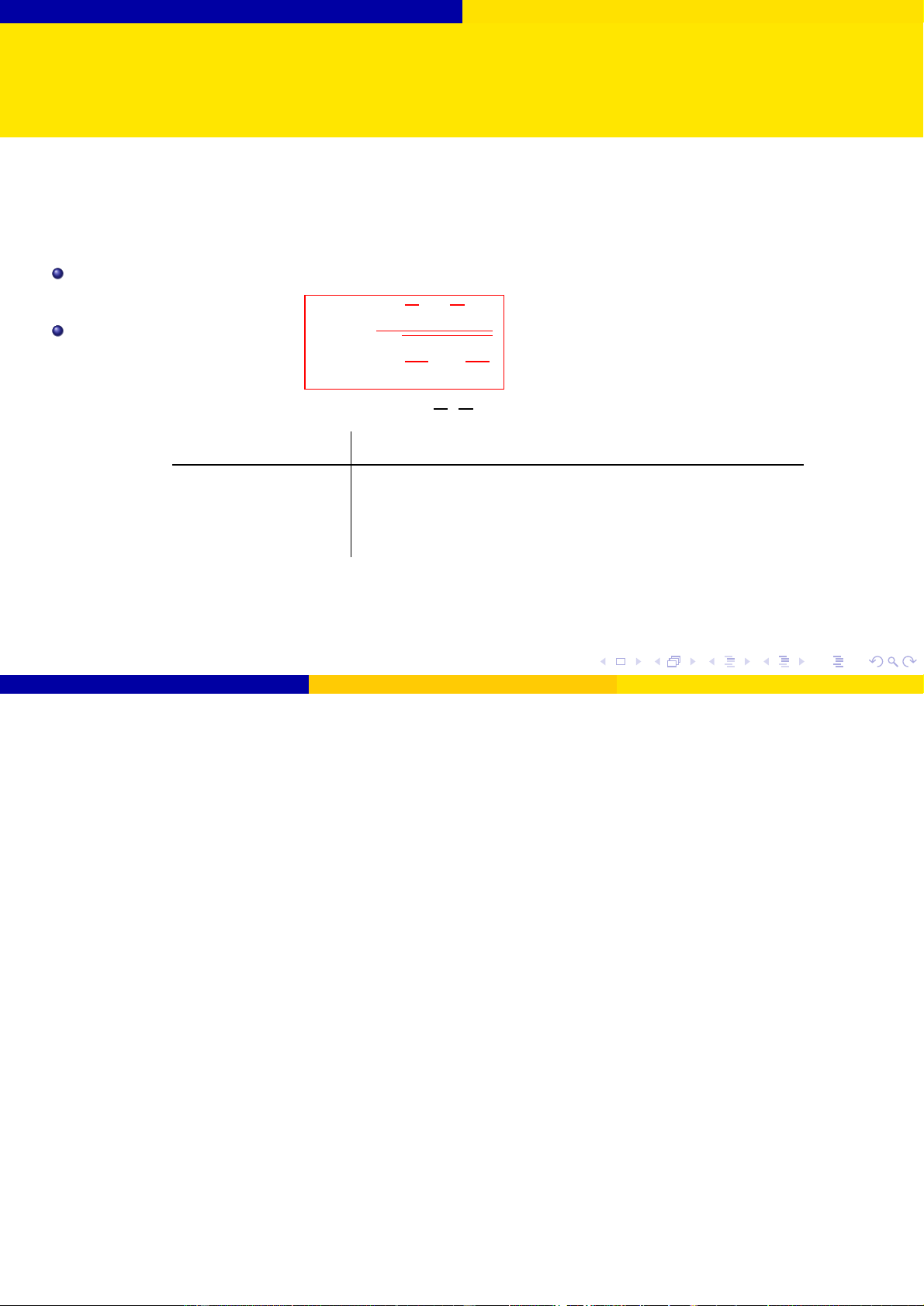
Bài toán 3: Kiểm định giả thuyết cho giá trị trung bình với mẫu cỡ nhỏ
Giả sử quần thể X có phân phối chuẩn N (µ, σ2) với σ2 chưa biết. Mẫu số liệu mà
ta thu được có cỡ nhỏ (n ≤ 30). Giả thuyết H0 : µ = µ0. Thống kê kiểm định: x − µ0 T0 = √ s/ n Đối thuyết Tiêu chuẩn bác bỏ H0 Miền tiêu chuẩn S ở mức ý nghĩa α H1 : µ 6= µ0 |T0| > tα/2;n 1 S = (−∞; −t 1) ∪ (t 1; +∞ − α/2;n− α/2;n− H1 : µ > µ0 T0 > tα;n 1 S (t 1; +∞) − α;n− H1 : µ < µ0 T0 < −tα;n 1 S = (−∞; −t 1) − α;n−
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 19 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Ví dụ 3
Thống kê được năng suất lúa trung bình của tỉnh Thái Bình năm 2015 là 66 tạ/ha.
Khảo sát ngẫu nhiên 10 thửa ruộng ở huyện Đông Hưng thấy năng suất
trung bình của 10 thửa ruộng này là 68 tạ/ha và độ lệch mẫu s = 4 tạ/ha.
Biết rằng năng suất của mỗi thửa ruộng có phân phối chuẩn.
Hãy kiểm định xem năng suất lúa ở Đông Hưng có cao hơn năng suất trung
bình của tỉnh Thái Bình được hay không, cho mức ý nghĩa α = 5%?
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 20 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Lời giải 1
Tham số cần kiểm định là năng suất lúa trung bình của huyện Đông Hưng, kí hiệu là µ tạ/ha. 2
Ta cần kiểm định xem năng suất lúa ở Đông Hưng có cao hơn năng suất
trung bình của tỉnh Thái Bình được hay không, do đó ta có bài toán kiểm định H0 : µ = 66 với H1 : µ > 66. 3
Cỡ mẫu n = 10; trung bình mẫu ¯x = 68; độ lệch mẫu s = 4. 68 − 66 4
Thống kê kiểm định T0 = √ = 1, 581. 4/ 10 5
Mức ý nghĩa α = 5% nên tα;n 1 = t0 − ,05;9 = 1, 833. 6
Do T0 < tα;n 1 nên ta không bác bỏ H0 : µ = 66 để ủng hộ H1 : µ > 68 ở − mức ý nghĩa α = 5%.
Vậy, ta không có đủ căn cứ để kết luận năng suất lúa của huyện Đông Hưng
cao hơn của tỉnh Thái Bình dựa trên mẫu gồm 10 số liệu đã thu được.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 21 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
4.3 Bài toán kiểm định giả thuyết cho tỉ lệ
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 22 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Tình huống thực tế
Trở lại tình huống thực tế ở phần 4.1, ta có hai giả thuyết như sau:
Giả thuyết H0: tỉ lệ khách hàng thích sản phẩm mới bằng 70%.
Đối thuyết H1: tỉ lệ khách hàng thích sản phẩm mới không bằng 70%.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 23 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
Bài toán kiểm định giả thuyết cho tỉ lệ
Giả sử ta cần quan tâm đến p là tỉ lệ số phần tử có cùng tính chất A nào đó của quần thể X .
Cụ thể, ta cần so sánh p với số p0 cho trước.
Các bài toán kiểm định giả thuyết cho p như sau: Giả thuyết H0 : p = p0. √ Thống kê kiểm định: (fn − p0) Z0 = n pp0(1 − p0) trong đó, nA f
là tần suất của số phần tử có cùng tính chất A trong mẫu. n = n Đối thuyết Tiêu chuẩn bác bỏ Miền tiêu chuẩn S H1 : p 6= p0 |Z0| > zα/2
S = (−∞; −zα/2) ∪ (zα/2; +∞) H1 : p > p0 Z0 > zα S = (zα; +∞) H1 : p < p0 Z0 < −zα S = (−∞; −zα)
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 24 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Ví dụ
Những năm trước nhà máy áp dụng công nghệ A sản xuất thì có tỷ lệ phế phẩm là 6%.
Năm nay nhà máy nhập công nghệ B để sản xuất, hy vọng sẽ giảm được tỷ lệ phế phẩm.
Lấy ngẫu nhiên 100 sản phẩm để kiểm tra thì thấy có 5 phế phẩm. Với mức ý
nghĩa 5%, có thể cho rằng tỷ lệ phế phẩm của công nghệ B nhỏ hơn công nghệ A hay không.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 25 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
Lời giải- Quy trình 6 bước 1
Tham số cần kiểm định là tỉ lệ phế phẩm của nhà máy khi sản xuất theo
công nghệ B, kí hiệu là p. 2
Ta cần quan tâm xem tỷ lệ phế phẩm của công nghệ B có nhỏ hơn công
nghệ A hay không nên ta có bài toán kiểm định một phía.
H0 : p = 0, 06 với H1 : p < 0, 06. 5 3
Theo đề bài, ta có: n = 100, nA = 5 ⇒ fn = 100 = 0,05. 4 Thống kê kiểm định (f √ n − p0) √ (0, 05 − 0, 06) Z0 = n = 100 = −0, 421. pp p 0(1 − p0) 0, 06(1 − 0, 06) 5
Mức ý nghĩa α = 5% nên zα = z0,05 = 1, 65. 6
Vì Z0 > −zα nên ta không bác bỏ giả thuyết H0 : p = 0, 06 để ủng hộ giả
thuyết H1 : p < 0, 06 ở mức ý nghĩa α = 5%.
Vậy ta không đủ căn cứ để kết luận công nghệ B làm giảm được tỷ lệ phế
phẩm dựa trên mẫu gồm 100 dữ liệu quan sát được.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 26 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
4.4 Bài toán so sánh hai giá trị trung bình
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 27 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Tình huống thực tế
Trong một trại chăn nuôi, để so sánh sự hiệu quả của hai loại thức ăn A và
B, người ta chọn một giống gà để nuôi thử nghiệm. Sau một thời gian, người ta chọn ngẫu nhiên:
50 con gà được nuôi bằng thức ăn A thì thấy khối lượng trung bình là ¯
x = 2, 2 kg, độ lệch mẫu là sX = 1, 25 kg.
40 con gà được nuôi bằng thức ăn B thì thấy khối lượng trung bình là ¯
y = 1, 2 kg, độ lệch mẫu là sY = 1, 02 kg.
? Hãy đánh giá hiệu quả của hai loại thức ăn?
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 28 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
Bài toán 1: So sánh giá trị trung bình của hai mẫu có phân
phối chuẩn với phương sai đã biết
Giả sử hai độ lệch chuẩn σ là đã biết. X , σY Giả thiết H0 : µ . X = µY Thống kê kiểm định: x − y Z0 = q σ2X + σ2Y nX nY trong đó n là hai cỡ mẫu và X , nY
x, y là hai trung bình mẫu của hai quần thể. Đối thuyết
Tiêu chuẩn bác bỏ H0 ở mức ý nghĩa α H1 : µX 6= µY |Z0| > zα/2 H1 : µX > µY Z0 > zα H1 : µX < µY Z0 < −zα
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 30 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Ví dụ 1
Để so sánh điểm thi môn Toán của học sinh hai trường A và B, người ta
khảo sát kết quả thi hết môn của một số học sinh của hai trường và thu được kết quả như sau: Trường A: nX = 64 ¯ x = 7 32. , , Trường B: nY = 68 ¯ y = 7 66. , ,
Biết rằng điểm thi môn Toán của học sinh của hai trường là biến ngẫu nhiên
có phân phối chuẩn với độ lệch chuẩn tương ứng là σX = 1, 09; σY = 1, 12.
Với mức ý nghĩa 1% có thể cho rằng kết quả thi của trường B cao hơn trường A hay không?
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 31 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
Lời giải-Quy trình 6 bước 1
Gọi X , Y là kết quả thi môn Toán của học sinh hai trường A và B tương
ứng. Ta có X ∼ N (µX , σ2 ), Y ). X ∼ N (µY , σ2Y 2
Ta cần kiểm định xem kết quả thi của học sinh trường B cao hơn trường A
hay không nên ta có bài toán kiểm định một phía.
H0 : µX = µY , với H1 : µX < µY 3 Theo đề bài, ta có: nX = 64, ¯
x = 7, 32, σX = 1, 09; nY = 68, ¯ y = 7, 66, σY = 1, 12. 7, 32 − 7, 66 4 Thống kê Z0 = = −1, 767. r 1, 092 1, 122 64 + 68 5
Mức ý nghĩa α = 1% nên zα = z0,01 = 2, 33. 6
Vì Z0 > −zα nên ta không bác bỏ giả thuyết H0 : µ1 = µ2 để ủng hộ đối
thuyết H1 : µ1 < µ2 ở mức ý nghĩa α = 1%.
Vậy ta không có đủ căn cứ để kết luận kết quả thi của học sinh trường B
cao hơn trường A dựa trên hai mẫu số liệu thu được.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 32 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
Bài toán 2: So sánh hai giá trị trung bình của hai mẫu có
phân phối chuẩn với phương sai chưa biết
Giả sử hai độ lệch chuẩn σ chưa biết. X = σY Giả thiết H0 : µ . X = µY Thống kê kiểm định: x − y T0 = q (n 1 1 q X − )s 2 +(n )s2 1 X Y − Y + 1 n 2 X +nY n n − X Y trong đó: s
là hai độ lệch mẫu của X , sY X , Y tương ứng. Đối thuyết
Tiêu chuẩn bác bỏ H0 ở mức ý nghĩa α H1 : µX 6= µY |T0| > tα/2,n 2 X +nY − H1 : µX > µY T0 > tα,n 2 X +nY − H1 : µX < µY T0 < −tα,n 2 X +nY −
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 33 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Ví dụ 2
Điều tra thu nhập (đơn vị tính $) trong một tháng của công nhân ở hai nhà máy
sản xuất thiết bị điện tử A và B ta thu được số liệu sau:
Nhà máy A: 91, 50; 94, 18; 92, 18; 95, 39; 91, 79.
Nhà máy B: 90, 46; 93, 21; 97, 19; 97, 04; 91, 07; 92, 75.
Với mức ý nghĩa 5%, có thể cho rằng thu nhập trung bình của công nhân trong
hai nhà máy trên là như nhau hay không, biết rằng thu nhập trong hai nhà máy có phân phối chuẩn.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 34 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
Lời giải-Quy trình 6 bước 1
Gọi X , Y lần lượt có phân phối chuẩn N (µX , σ2 ), ) là thu nhập X N (µY , σ2Y
của nhà máy A và B tương ứng. Ta cần so sánh µ và . X µY 2
Ta cần kiểm tra xem thu nhập trung bình của công nhân trong hai nhà máy
trên là như nhau hay không nên ta có bài toán kiểm định hai phía H0 : µ , với . X = µY H1 : µX 6= µY 3
Theo đề bài, ta có: nX = 5; x = 93, 008; s2 = 2, 873 và X
nY = 6; y = 93, 62; s2 = 8, 371. Y 93, 008 − 93, 62 4 Thống kê T0 = = −0, 415. r 4.2, 873 + 5.8, 371 q 1 5 + 6 − 2 5 + 16 5
Mức ý nghĩa α = 5% nên tα/2,n 2 = t0 X +nY ,025;9 = 2, 262. − 6 Ta có |T0| < t để ủng hộ α/2,n
2 nên ta không bác bỏ H0 : µX = µY X +nY − H1 : µ ở mức ý nghĩa X 6= µY α = 5%.
Vậy ta không có đủ căn cứ để kết luận thu nhập của công nhân hai nhà máy
là khác nhau dựa trên hai mẫu đã thu được.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 35 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
4.5 Bài toán so sánh hai tỉ lệ
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 36 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Tình huống thực tế
Để so sánh chất lượng của một loại sản phẩm do hai công ty X và Y sản xuất,
người ta lấy hai mẫu dữ liệu sau:
Trong 30 sản phẩm do công ty X sản xuất thấy có 12 sản phẩm đạt loại A.
Trong 40 sản phẩm do công ty Y sản xuất thấy có 14 sản phẩm đạt loại A.
? Hỏi chất lượng loại sản phẩm này của hai công ty có như nhau không?
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 37 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
Bài toán so sánh hai tỉ lệ
Dựa trên hai mẫu số liệu quan sát được từ hai quần thể X và Y , ta muốn so sánh p
là hai tỉ lệ của số phần tử có cùng tính chất X , pY
A nào đó của hai quần thể.
Bài toán so sánh hai tỉ lệ Giả thuyết H0 : p . X = pY Đối thuyết 1 H1 : p Kiểm định hai phía X 6= pY 2 H1 : p Kiểm định một phía X > pY 3 H1 : p Kiểm định một phía X < pY
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 38 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Tiêu chuẩn kiểm định n
là kích thước hai mẫu quan sát được từ hai quần thể X , nY X , Y tương ứng. k
là số phần tử có cùng tính chất X , kY
A trong hai mẫu tương ứng. f
là tần suất các phần tử có cùng tính chất X , fY
A trong hai mẫu tương ứng. Thống kê kiểm định: fX − fY kX + kY Z0 = với f = . r nX + nY f (1 − f ) nX +nY nX nY Đối thuyết
Tiêu chuẩn bác bỏ H0 ở mức ý nghĩa α H1 : pX 6= pY |Z0| > zα/2 H1 : pX > pY Z0 > zα H1 : pX < pY Z0 < −zα
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 39 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279 Ví dụ
Điều tra hiện tượng học sinh bỏ học ở hai vùng nông thôn A và B ta thu được số liệu sau:
Vùng A: Điều tra 1900 em có 175 em bỏ học.
Vùng B: Điều tra 2600 em có 325 em bỏ học.
Có ý kiến cho rằng tình trạng học sinh bỏ học ở vùng A là ít phổ biến hơn vùng
B. Với mức ý nghĩa 5%, hãy cho biết ý kiến đó đúng hay sai?
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 40 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com) lOMoARcPSD|36403279
Lời giải - Quy trình 6 bước Gọi p
là tỷ lệ học sinh bỏ học ở hai vùng A, B tương ứng. A , pB
Ta cần kiểm định tình trạng học sinh bỏ học ở vùng A là ít phổ biến hơn
vùng B nên ta có bài toán kiểm định một phía: H0 : p với A = pB H1 : pA < pB . k 175 325 A kB fA = = = n 1900 = 0, 092 và fB = 2600 = 0, 125; A nB 175 + 325 ⇒ f = 1900 + 2600 = 0,111 0 Thống kê kiểm định: , 092 − 0, 125 Z0 = = −3, 48. s 1900 0 + 2600 , 111(1 − 0, 111) 1900.2600
Vì mức ý nghĩa α = 5% nên zα = z0,05 = 1, 65.
Ta có Z0 < −zα nên ta bác bỏ H0 : p để ủng hộ ở mức A = pB H1 : pA < pB ý nghĩa α = 5%.
Vậy có đủ căn cứ để kết luận tỉ lệ học sinh bỏ học ở vùng A là ít phổ biến
hơn vùng B dựa trên hai mẫu thu được.
Khoa Toán Tin Trường Đại học Sư phạm Hà Nội CHƯƠNG 4: KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 41 / 41
Downloaded by ti?n v?n lê (vanletien573@gmail.com)




