Tài liệu chủ đề hàm số lượng giác

Tài liệu gồm 40 trang, bao gồm kiến thức trọng tâm, hệ thống ví dụ minh họa và bài tập trắc nghiệm tự luyện chủ đề hàm số lượng giác, có đáp án và lời giải chi tiết

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

40 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1
CHỦ ĐỀ HÀM SỐ LƯỢNG GIÁC
I. KIẾN THỨC TRỌNG TÂM
1) Các hệ thức lượng giác cơ bản
* Hàm số
sin
y x D R
* Hàm số
cos
y x D R
* Hàm số
tan \
2
y x D R k
* Hàm số
cot \
y x D R k
* Hàm số
u x
y
v x
điều kiện xác định là
0
v x
* Hàm số
u x
y
v x
điều kiện xác định là
0
v x
2) Tính tuần hoàn của hàm số lượng giác
- Định nghĩa
Hàm số
y f x
có tập xác định D được gọi là hàm số tuần hoàn, nếu tồn tại một số
0
T
sao cho với
mọi
x D
ta có:
*
x T D
và
x T D
*
f x T f x
Số dương T nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó.
Người ta chứng minh được rằng hàm số
sin
y x
tuần hoàn với chu kì
2
T
; hàm số
cos
y x
tuần
hoàn với chu kì
2
T
; hàm số
tan
y x
tuần hoàn với chu kì
T
; hàm số
cot
y x
tuần hoàn với
chu kì T
.
- Chú ý
* Hàm số
sin
y ax b
tuần hoàn với chu kì
0
2
T
a
* Hàm số
cos
y ax b
tuần hoàn với chu kì
0
2
T
a
* Hàm số
tan
y ax b
tuần hoàn với chu kì
0
T
a
* Hàm số
cot
y ax b
tuần hoàn với chu kì
0
T
a
Trang 2
* Hàm số
1
y f x
tuần hoàn với chu kì
1
T
và hàm số
2
y f x
tuần hoàn với chu kì
2
T
thì hàm số
1 2
y f x f x
tuần hoàn với chu kì
0
T
là bội chung nhỏ nhất của
1
T
và
2
T
.
3) Tính chẵn lẻ của hàm số lượng giác
- Định nghĩa
* Hàm số
y f x
có tập xác định D được gọi là hàm số chẵn nếu nó thỏa mãn đồng thời hai điều kiện
sau:
x D x D
f x f x
* Hàm số
y f x
có tập xác định D được gọi là hàm số lẻ nếu nó thỏa mãn đồng thời hai điều kiện
sau:
x D x D
f x f x
- Chú ý
* Các hàm số chẵn thường gặp:
2 2 2
cos ; cos ; sin ; sin ; cos
x kx x kx kx
* Các hàm số lẻ thường gặp:
3 3
sin ; tan ; cot ; sin ; tan ...
x x x x x
* Hàm số
f x
chẵn và
g x
lẻ thì hàm
.
f x g x
và
f x
g x
đều là hàm số lẻ.
* Hàm số
f x
và
g x
đều là hàm lẻ thì hàm
.
f x g x
và
f x
g x
đều là hàm số chẵn.
4) Sự biến thiên và đồ thị các hàm số lượng giác
a) Hàm số y = sinx
* Tập xác định:
D R
* Tập giá trị
1; 1
T , có nghĩa là
1 sin 1
x
* Là hàm số tuần hoàn chu kì
2
, có nghĩa
2 sin
x k x
với k
* Hàm số đồng biến trên mỗi khoảng
2 ; 2
2 2
k k
và nghịch biến trên mỗi khoảng
3
2 ; 2 ,
2 2
k k k
* Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng. Đồ thị hàm số như hình vẽ bên
dưới.
Trang 3
b) Hàm số y = cosx
* Tập xác định:
D R
* Tập giá trị
1; 1
T , có nghĩa
1 sin 1
x
* Là hàm số tuần hoàn với chu kì
2
, có nghĩa
cos 2 cos
x k x
với
k
* Hàm số đồng biến trên mỗi khoảng
2 ; 2
k k
và nghịch biến trên mỗi khoảng
2 ; 2 ,k k k
* Là hàm số chẵn nên đồ thị hàm số nhận trục Oy làm trục đối xứng. Đồ thị hàm số như hình vẽ bên dưới
c) Hàm số y = tanx
* Tập xác định
\ ,
2
D k k
* Tập giá trị
T
* Là hàm số tuần hoàn với chu kì
, có nghĩa
tan tan
x k x
với
k
* Hàm số đồng biến trên mỗi khoảng
; ,
2 2
k k k
* Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng
Trang 4
d) Hàm số y = cotx
* Tập xác định
\ ,D k k
* Tập giá trị
T
* Là hàm số tuần hoàn với chu kì
, có nghĩa
tan tan
x k x
với
k
* Hàm số đồng biến trên mỗi khoảng
; ,k k k
* Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng.
II. HỆ THỐNG VÍ DỤ MINH HỌA
- Dạng 1: Tập xác định và Tập giá trị của hàm số lượng giác
Ví dụ 1. Tìm tập xác định của các hàm số sau:
a)
2
sin
1
x
y
x
b)
sin
y x
Lời giải:
a) ĐK xác định:
1
x
TXĐ:
\ 1
D
Trang 5
b) ĐK xác định:
sin 0 2 2 1
x k x k
Suy ra TXĐ:
2 ; 2 1D k k
Ví dụ 2. Tìm tập xác định và tập giá trị của các hàm số sau:
a)
2
1 cos
y x
b)
1
sin 1
y
x
Lời giải:
a) ĐK xác định:
2
1 cos 0
x
(luôn đúng)
TXĐ:
Lại có:
2 2
0 cos 1 0 1 cos 1 0 1
x x y
Tập giá trị là
0, 1
T
b) ĐK xác định:
sin 1 0 sin 1 sin 2 \ 2
2 2
x x x k D R k
Ta có:
1
0 sin 1 2
2
x y
Tập giá trị là
1
,
2
T
Ví dụ 3. Tìm tập xác định D của hàm số
1 sin
cos 1
x
y
x
a)
D
. b)
\ ,
2
D k k
.
c)
\ ,D k k
. d)
\ 2 ,D k k
.
Lời giải:
Hàm số xác định khi và chỉ khi
cos 1 0 cos 1 2 ,x x x k k
Vậy tập xác định
\ 2 ,D k k
. Chọn D
Ví dụ 4. Tìm tập xác định D của hàm số
1
sin
2
y
x
a)
\ ,
2
D k k
. b)
\ ,D k k
.
c)
\ 1 2 ,
2
D k k
. d)
\ 1 2 ,D k k
.
Lời giải:
Hàm số xác định
sin 0 ,
2 2 2
x x k x k k
Vậy tập xác định
\ ,
2
D k k
. Chọn C
Ví dụ 5. Tìm tập xác định D của hàm số
1
sin cos
y
x x
a)
D
. b)
\ ,
4
D k k
.
Trang 6
c)
\ 2 ,
4
D k k
. d)
\ ,
4
D k k
.
Lời giải:
Hàm số xác định
sin cos 0 tan 1 ,
4
x x x x k k
Vậy tập xác định
\ ,
4
D k k
. Chọn D
Ví dụ 6. Tìm tập xác định D của hàm số
cot 2 sin 2
4
y x x
a)
\ ,
4
D k k
. b) D
Ø
.
c)
\ ,
8 2
D k k
. d)
D
.
Lời giải:
Hàm số xác định
sin 2 0 2 ,
4 4 8 2
k
x x k x k
Vậy tập xác định
\ ,
8 2
D k k
. Chọn C
Ví dụ 7. Tìm tập xác định D của hàm số
2
3tan
2 4
x
y
a)
3
\ 2 ,
2
D k k
. b)
\ 2 ,
2
D k k
.
c)
3
\ ,
2
D k k
. d)
\ ,
2
D k k
.
Lời giải:
Hàm số xác định
2
3
cos 0 2 ,
2 4 2 4 2 2
x x
k x k k
Vậy tập xác định
3
\ 2 ,
2
D k k
. Chọn A
Ví dụ 8. Tìm tập xác định D của hàm số
1 sin 2 1 sin 2
y x x
a) D
Ø
. b)
D
.
c)
5
2 ; 2 ,
6 6
D k k k
. d)
5 13
2 ; 2 ,
6 6
D k k k
.
Lời giải:
Ta có:
1 sin 2 0
1 sin 2 1 ,
1 sin 2 0
x
x x
x
.
Vậy tập xác định
D
. Chọn B
Trang 7
Ví dụ 9. Tìm tập xác định D của hàm số
2
5 2cot sin cot
2
y x x x
a)
\ ,
2
k
D k
. b)
\ ,
2
D k k
.
c)
D
. d)
\ ,D k k
.
Lời giải:
Hàm số xác định khi và chỉ khi các điều kiện sau thỏa mãn đồng thời
2
5 2cot sin 0, cot
2
x x x
xác định và
cot
x
xác định.
Ta có:
2
2
2cot 0
5 2cot sin 0,
1 sin 1 5 sin 0
x
x x x
x x
*
cot
2
x
xác định
sin 0 ,
2 2 2
x x k x k k
*
cot
x
xác định
sin 0 ,x x k k
Do đó hàm số xác định ,
2
2
x k
k
x k
x k
Vậy tập xác định
\ ,
2
k
D k
. Chọn A
Ví dụ 10. Hàm số
1 1
tan cot
sin cos
y x x
x x
không xác định trong khoảng nào trong các khoảng
sau đây?
a)
2 , 2
2
k k
với k
. b)
3
2 , 2
2
k k
với k
.
c)
2 , 2
2
k k
với
k
. d)
2 , 2 2
k k
với
k
.
Lời giải:
Hàm số xác định
sin 0
sin 2 0 2 ,
cos 0
2
x
k
x x k x k
x
.
Ta chọn
3
3
2
k x
nhưng điểm
3
2
thuộc khoảng
2 ; 2 2
k k
.
Vậy hàm số không xác định trong khoảng
2 ; 2 2
k k
. Chọn D
Dạng 2: Tính chẵn lẻ của hàm số lượng giác
Ví dụ 1. Xét tính chẵn – lẻ của hàm số sau
a)
sin 2
y x
b)
2sin 3
y x
Trang 8
Lời giải:
a)
sin 2 sin 2
f x x x f x
. Suy ra hàm số đã cho là hàm lẻ.
b) Ta có
2sin 3 2sin 3 2sin 3 9 9
f x x x x f x
Suy ra hàm số đã cho không phải là hàm chẵn (lẻ)
Ví dụ 2. Xét tính chẵn – lẻ của hàm số sau
a)
sin cos
y x
b)
tan cot
y x x
Lời giải:
a)
sin cos sin cos sin cos 2cos 2cos
f x x x x x x x x f x x
Suy ra hàm số đã cho không phải là hàm chẵn (lẻ)
b)
sin cos
sin cos
tan cot
cos sin cos sin
x x
x x
f x x x
x x x
tan cot tan cot
x x x x f x
Vậy hàm số đã cho là hàm lẻ .
Ví dụ 3. Xét tính chẵn – lẻ của hàm số sau
a)
sin tan
sin cot
x x
y
x x
b)
3
3
cos 1
sin
x
y
x
Lời giải:
a) Ta có
sin tan
sin tan sin tan
sin cot sin cot sin cot
x x
x x x x
f x f x
x x x x x x
Suy ra hàm số đã cho là hàm chẵn.
b) Ta có
3
3
3 3
cos 1
cos 1
sin sin
x
x
f x f x
x x
. Suy ra hàm số đã cho là hàm lẻ.
Ví dụ 4. Trong các hàm số sau, hàm số nào là hàm số chẵn
a)
sin
y x
b)
cos sin
y x x
c)
2
cos sin
y x x
d)
cos sin
y x x
Lời giải:
Tất cả các hàm số đề có TXĐ:
D
. Do đó
x D x D
.
Bây giờ ta kiểm tra
f x f x
hoặc
f x f x
* Với
sin
y f x x
. Ta có
sin sin sin
f x x x x
f x f x
. Suy ra hàm số
sin
y x
là hàm số lẻ.
* Với
cos sin
y f x x x
. Ta có:..
,
f x f x f x
. Suy ra hàm số
cos sin
f x x x
không chẵn không lẻ.
* Với
2
cos sin
y f x x x
. Ta có
2
cos sin
f x x x
Trang 9
2
2
2
cos sin cos sin cos sin
x x x x x x
f x f x
. Suy ra hàm số
2
cos sin
y x x
là hàm chẵn. Chọn C.
* Với
cos sin
y f x x x
. Ta có
cos .sin cos sin
f x x x x x
f x f x
. Suy ra hàm số
cos sin
y x x
là hàm số lẻ.
Ví dụ 5. Trong các hàm số sau, hàm số nào là hàm số chẵn?
a)
sin 2
y x
b)
cos
y x x
c)
cos .cot
y x x
d)
tan
sin
x
y
x
Lời giải:
* Xét hàm số
sin 2
y f x x
.
TXĐ:
D
. Do đó
x D x D
.
Ta có
sin 2 sin 2
f x x x f x f x
là hàm số lẻ.
* Xét hàm số
cos
y f x x x
.
TXĐ:
D
. Do đó
x D x D
.
Ta có:
.cos cos
f x x x x x f x f x
là hàm số lẻ.
* Xét hàm số
cos cot
y f x x x
TXĐ:
\
D k k
. Do đó
x D x D
.
Ta có
cos .cot cos cot
f x x x x x f x f x
là hàm số lẻ.
* Xét hàm số
tan
sin
x
y f x
x
TXĐ:
\
2
D k k
. Do đó
x D x D
.
Ta có
tan
tan tan
sin sin sin
x
x x
f x f x f x
x x x
là hàm số chẵn. Chọn D.
Ví dụ 6. Trong các hàm số sau, hàm số nào là hàm số chẵn?
a)
sin
y x
b)
2
sin
y x x
c)
cos
x
y
x
d)
sin
y x x
Lời giải:
Dựa vào các dấu hiệu nhận biết hàm chẵn lẻ ở phần lí thuyết ta dễ dàng thấy rằng ở phương án A là hàm
số chẵn, các đáp án B, C, D là hàm số lẻ. Chọn A.
Ví dụ 7. Trong các hàm số sau, hàm số nào là hàm số lẻ?
Trang 10
a)
2
cos sin
y x x
. b)
sin cos
y x x
.
c)
cos
y x
. d)
sin .cos3
y x x
.
Lời giải:
Dựa vào các dấu hiệu nhận biết hàm chẵn lẻ ở phần lí thuyết ta dễ dàng thấy rằng ở phương án A và C là
các hàm số chẵn. Đáp án B là hàm số không chẵn, không lẻ. Đáp án D là hàm số lẻ. Chọn D.
Ví dụ 8. Cho hàm số
sin 2
f x x
và
2
tan
g x x
. Chọn mệnh đề đúng
a)
f x
là hàm số chẵn,
g x
là hàm số lẻ. b)
f x
là hàm số lẻ,
g x
là hàm số chẵn.
c)
f x
là hàm số chẵn,
g x
là hàm số chẵn. d)
f x
và
g x
đều là hàm số lẻ.
Lời giải:
* Xét hàm số
sin 2
f x x
.
TXĐ:
D
. Do đó
x D x D
.
Ta có
sin 2 sin 2
f x x x f x f x
là hàm số lẻ.
* Xét hàm số
2
tan
g x x
TXĐ:
\
2
D k k
. Do đó
x D x D
.
Ta có
2
2
2
tan tan tan
g x x x x g x f x
là hàm số chẵn. Chọn B.
Ví dụ 9. Cho hai hàm số
2
cos 2
1 sin 3
x
f x
x
và
2
sin 2 cos3
2 tan
x x
g x
x
.
Mệnh đề nào sau đây là đúng?
a)
f x
lẻ và
g x
chẵn. b)
f x
và
g x
chẵn.
c)
f x
chẵn,
g x
lẻ. d)
f x
và
g x
lẻ.
Lời giải:
* Xét hàm số
2
cos 2
1 sin 3
x
f x
x
TXĐ:
D
. Do đó
x D x D
.
Ta có
2 2
cos 2
cos2
1 sin 3 1 sin 3
x
x
f x f x f x
x x
là hàm số chẵn.
* Xét hàm số
2
sin 2 cos3
2 tan
x x
g x
x
.
TXĐ:
\
2
D k k
. Do đó
x D x D
.
Ta có
2 2
sin 2 cos 3
sin 2 cos3
2 tan 2 tan
x x
x x
g x g x g x
x x
là hàm số chẵn.
Vậy
f x
và
g x
chẵn. Chọn B.
Trang 11
Dạng 3: Chu kì của hàm số lượng giác
Ví dụ 1. Mệnh đề nào sau đây là sai?
a) Hàm số
sin
y x
tuần hoàn với chu kì
2
.
b) Hàm số
cos
y x
tuần hoàn với chu kì
2
.
c) Hàm số
tan
y x
tuần hoàn với chu kì
2
.
d) Hàm số
cot
y x
tuần hoàn với chu kì
.
Lời giải:
Vì hàm số
tan
y x
tuần hoàn với chu kì
. Chọn C.
Ví dụ 2. Trong các hàm số sau đây, hàm số nào không tuần hoàn?
a)
cos
y x
. b)
cos2
y x
.
c)
2
cos
y x x
. d)
1
sin 2
y
x
.
Lời giải:
* Hàm số
cos
y x
tuần hoàn với chu kì
2
T
.
* Hàm số
cos2
y x
tuần hoàn với chu kì
T
.
* Hàm số
1
sin 2
y
x
tuần hoàn với chu kì
T
.
* Hàm số
2
cos
y x x
không phải là hàm tuần hoàn. Chọn C.
Ví dụ 3. Tìm chu kì T của hàm số
sin 5
4
y x
a)
2
5
T
b)
5
2
T
c)
2
T
d)
8
T
Lời giải:
Hàm số
sin
y ax b
tuần hoàn với chu kì
2
T
a
.
Áp dụng: Hàm số
sin 5
4
y x
tuần hoàn với chu kì
2
5
T
. Chọn A.
Ví dụ 4. Tìm chu kì T của hàm số
cos 2016
2
x
y
a)
4
T
b)
2
T
c)
2
T
d)
T
Lời giải:
Trang 12
Hàm số
cos
y ax b
tuần hoàn với chu kì
2
T
a
Áp dụng: Hàm số
cos 2016
2
x
y
tuần hoàn với chu kì
4
T
. Chọn A.
Ví dụ 5. Tìm chu kì T của hàm số
cos 2 sin
2
x
y x
.
a)
4
T
. b)
T
.
c)
2
T
. d)
2
T
.
Lời giải:
Hàm số
cos 2
y x
tuần hoàn với chu kì
1
2
2
T
.
Hàm số
sin
2
x
y
tuần hoàn với chu kì
2
2
4
1
2
T
Suy ra hàm số
cos 2 sin
2
x
y x tuần hoàn với chu kì
4
T
. Chọn A.
Nhận xét. T là bội chung nhỏ nhất của
1
T
và
2
T
.
Ví dụ 6. Tìm chu kì T của hàm số
cos3 cos 5
y x x
.
a)
T
b)
3
T
c)
2
T
d)
5
T
Lời giải:
Hàm số
cos3
y x
tuần hoàn với chu kì
1
2
3
T
.
Hàm số
cos5
y x
tuần hoàn với chu kì
2
2
5
T
.
Suy ra hàm số
cos3 cos 5
y x x
tuần hoàn với chu kì
2
T
. Chọn C.
Ví dụ 7. Tìm chu kì T của hàm số
sin 2 2cos 3
3 4
y x x
.
a)
2
T
. b)
T
.
c)
3
T
. d)
4
T
.
Lời giải:
Hàm số
sin 2
3
y x
tuần hoàn với chu kì
1
2
2
T
.
Hàm số
2cos 3
4
y x
tuần hoàn với chu kì
2
2
3
T
.
Suy ra hàm số
sin 2 2cos 3
3 4
y x x
tuần hoàn với chu kì
2
T
. Chọn A
Trang 13
Ví dụ 8. Tìm chu kì T của hàm số
tan 3 cot
y x x
.
a)
4
T
. b)
T
.
c)
3
T
. d)
3
T
.
Lời giải:
Hàm số
cot
y ax b
tuần hoàn với chu kì
T
a
Áp dụng: Hàm số
tan 3
y x
tuần hoàn với chu kì
1
3
T
.
Hàm số
cot
y x
tuần hoàn với chu kì
2
T
.
Suy ra hàm số
tan 3 cot
y x x
tuần hoàn với chu kì
T
. Chọn B.
Nhận xét. T là bội chung nhỏ nhất của
1
T
và
2
T
.
Ví dụ 9. Tìm chu kì T của hàm số
cot sin 2
3
x
y x
a)
4
T
. b)
T
.
c)
3
T
. d)
3
T
.
Lời giải:
Hàm số
cot
3
x
y tuần hoàn với chu kì
1
3
T
.
Hàm số
sin 2
y x
tuần hoàn với chu kì
2
T
.
Suy ra hàm số
cot sin 2
3
x
y x
tuần hoàn với chu kì
3
T
. Chọn C.
Ví dụ 10. Tìm chu kì T của hàm số
2 2
2sin 3cos 3
y x x
a)
T
. b)
2
T
.
c)
3
T
. d)
3
T
.
Lời giải:
Ta có
1 cos 2 1 cos6 1
2. 3. 3cos 6 2cos 2 5
2 2 2
x x
y x x
Hàm số
3cos6
y x
tuần hoàn với chu kì
1
2
6 3
T
.
Hàm số
2cos 2
y x
tuần hoàn với chu kì
2
T
.
Suy ra hàm số đã cho tuần hoàn với chu kì
T
. Chọn A.
Ví dụ 11. Tìm chu kì T của hàm số
2
tan 3 cos 2
y x x
Trang 14
a)
T
. b)
3
T
.
c)
2
T
. d)
2
T
.
Lời giải:
Ta có
1 cos 4 1
tan 3 2 tan3 cos 4 1
2 2
x
y x x x
.
Hàm số
2 tan3
y x
tuần hoàn với chu kì
1
3
T
.
Hàm số
cos 4
y x
tuần hoàn với chu kì
2
2
4 2
T
.
Suy ra hàm số đã cho tuần hoàn với chu kì
T
. Chọn C.
Ví dụ 12. Hàm số nào sau đây có chu kì khác
2
?
a)
3
cos
y x
. b)
sin cos
2 2
x x
y
.
c)
2
sin 2
y x . d)
2
cos 1
2
x
y
.
Lời giải:
Hàm số
3
1
cos cos3 3cos
4
y x x x
có chu kì là
2
.
Hàm số
1
sin cos sin
2 2 2
x x
y x
có chu kì là
2
.
Hàm số
2
1 1
sin 2 cos 2 4
2 2
y x x có chu kì là
.
Hàm số
2
1 1
cos 1 cos 2
2 2 2
x
y x
có chu kì là
2
. Chọn C.
Ví dụ 13. Hai hàm số nào sau đây có chu kì khác nhau?
a)
cos
y x
và
cot
2
x
y
. b)
sin
y x
và
tan 2
y x
.
c)
sin
2
x
y và
cos
2
x
y . d)
tan 2
y x
và
cot 2
y x
.
Lời giải:
Hàm số
cos
y x
và
cot
2
x
y có cùng chu kì là
2
.
Hàm số
sin
y x
có chu kì là
2
, hàm số
tan 2
y x
có chu kì là
2
.
Hàm số
sin
2
y
và
cos
2
x
y có cùng chu kì là
4
.
Trang 15
Hàm số
tan 2
y x
và
cot 2
y x
có cùng chu kì là
2
. Chọn B.
Dạng 4: Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác
* Miền giá trị:
2 2
1 sin 1; 1 cos 1; 0 sin 1; 0 cos 1
kx kx kx kx
* Với hàm số
2 2 2 2
.sin .cos
y a x b x a b y a b
* Với hàm số
.sin .cos
.sin .cos
a x b x c
y
m x n x p
nhân chéo và đưa về trường hợp trên để tìm miền giá trị.
Ví dụ 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a)
2
4sin 4sin 3
y x
b)
2
cos 2sin 2
y x x
Lời giải:
a)
2
2
4sin 4sin 3 2sin 1 2
y x x x
Ta có:
2
1 sin 1 3 2sin 1 1 0 2sin 1 9 2 9
x x x y
max 9 sin 1 2
2
,
1 5
min 2 sin 2 , 2
2 6 6
y x x k
k l
y x x l x l
b)
2
2 2
cos 2sin 2 sin 2sin 3 4 sin 1
y x x x x x
Ta có:
2
1 sin 1 2 sin 1 0 0 2sin 1 4 0 4
x x x y
max 4 sin 1 2
2
,
min 0 sin 1 2
2
y x x k
k l
y x x l
Ví dụ 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a)
4 2
sin 2cos 1
y x x
b)
3 sin 2 cos 2
y x x
Lời giải:
a)
2
4 2 4 2 2
sin 2cos 1 sin 2sin 1 sin 1 2
y x x x x x
Ta có:
2
2 2 2
0 sin 1 1 sin 1 2 1 sin 1 2 1 2
x x x y
2
2
max 2 sin 1 2
,
2
min 1 sin 0
y x x k
k l
y x x l
b) Áp dụng bất đẳng thức Bunhiacopxki ta có:
Trang 16
2 2
2
2 2 2
3 sin 2 cos 2 3 1 sin cos 4 2 2
y x x x x y
sin 2 cos 2
max 2 0
1 6
3
,
sin 2 cos 2
min 2 0
1 6
3
x x
y x k
k l
x x
y x k
Ví dụ 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
sin 3 cos 3
y x x
Lời giải:
Áp dụng bất đẳng thức Bunhiacopxki ta có
2 2
2
2 2
sin 3 cos 1 3 sin cos 4 2 sin 3 cos 2 1 5
x x x x x x y
sin cos
max 5 0 2
1 6
3
,
sin cos 5
min 1 0 2
1 6
3
x x
y x k
k l
x x
y x k
Ví dụ 4. Cho hàm số
2sin 2
3
y x
. Mệnh đề nào sau đây là đúng?
a)
4,
y x
. b)
4,
y x
.
c)
0,
y x
. d)
2,
y x
.
Lời giải:
Ta có:
1 sin 1 2 2sin 2
3 3
x x
4 2sin 2 0 4 0
3
x y
. Chọn C.
Ví dụ 5. Hàm số
5 4sin 2 cos 2
y x x
có tất cả bao nhiêu giá trị nguyên?
a) 3. b) 4.
c) 5. d) 6.
Lời giải:
Ta có
5 4sin 2 cos 2 5 2sin 4
y x x x
.
Mà
1 sin 4 1 2 2sin 4 2 3 5 2sin 4 7
x x x
3 7 3; 4; 5; 6; 7

y
y y nên y có 5 giá trị nguyên. Chọn C
Ví dụ 6. Hàm số
sin sin
3
y x x
có tất cả bao nhiêu giá trị nguyên?
a) 1. b) 2.
c) 3. d) 4.
Lời giải:
Trang 17
Áp dụng công thức
sin sin 2cos sin
2 2
a b a b
a b
, ta có
sin sin 2cos sin cos
3 6 6 6
x x x x
Ta có
1 cos 1 1 1 1; 0; 1
6

y
x y
. Chọn C
Ví dụ 7. Hàm số
4 4
sin cos
y x x
đạt giá trị nhỏ nhất tại
0
x x
. Mệnh đề nào sau đây là đúng?
a)
0
2 ,
x k k
. b)
0
,
x k k
.
c)
0
2 ,
x k k
. d)
0
,
2
x k k
.
Lời giải:
Ta có
4 4 2 2 2 2
sin cos sin cos sin cos cos 2
y x x x x x x x
.
Mà
1 cos 2 1 1 cos 2 1 1 1
x x y
Do đó giá trị nhỏ nhất của hàm số là -1.
Đẳng thức xảy ra
cos2 1 2 2
x x k x k k
. Chọn B
Ví dụ 8. Tìm giá trị lớn nhất M của hàm số
2
4sin 2 sin 2
4
y x x
.
a)
2
M . b)
2 1
M .
c)
2 1
M
. d)
2 2
M
.
Lời giải:
Ta có
2
1 cos2
4sin 2 sin 2 4 sin 2 cos2
4 2
x
y x x x x
sin 2 cos2 2 2 sin 2 2
4
x x x
.
Mà
1 sin 2 1 2 2 2 sin 2 2 2 2
4 4
x x
.
Vậy giá trị lớn nhất của hàm số là
2 2
. Chọn D.
Ví dụ 9. Tìm tập giá trị T của hàm số
6 6
sin cos
y x x
a)
0; 2
T . b)
1
; 1
2
T
.
c)
1
; 1
4
T
. d)
1
0;
4
T
.
Lời giải:
Ta có
2
6 6 2 2 2 2 2 2
sin cos sin cos 3sin cos sin cos
y x x x x x x x x
Trang 18
2 2 2
3 3 1 cos 4 5 3
1 3sin cos 1 sin 2 1 . cos 4
4 4 2 8 8
x
x x x x
.
Mà
1 5 3 1
1 cos 4 1 cos 4 1 1
4 8 8 4
x x y . Chọn C
Ví dụ 10. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
8sin 3cos 2
y x x
. Tính
2
2
P M m
.
a)
1
P
. b)
2
P
.
c)
112
P
. d)
130
P
.
Lời giải:
Ta có
2 2 2 2
8sin 3cos 2 8sin 3 1 2sin 2sin 3
y x x x x x
.
Mà
2 2
1 sin 1 0 sin 1 3 2sin 3 5
x x
2
5
3 5 2 1
3
M
y P M m
m
. Chọn A.
Ví dụ 11. Tìm giá trị nhỏ nhất m của hàm số
2
2sin 3 sin 2
y x x
.
a)
2 3
m . b)
1
m .
c)
1
m
. d)
3
m
.
Lời giải:
Ta có
2
2sin 3 sin 2 1 cos 2 3 sin 2
y x x x x
3 1
3 sin 2 cos 2 1 2 sin 2 cos2 1
2 2
x x x x
2 sin 2 cos sin cos 2 1 2sin 2 1
6 6 6
x x x
Mà
1 sin 2 1 1 1 2sin 2 3 1 3
6 6
x x y
.
Do đó giá trị nhỏ nhất của hàm số là -1. Chọn B.
Trang 19
BÀI TẬP TỰ LUYỆN
Câu 1. Tìm tập xác định D của hàm số
1 sin
cos 1
x
y
x
A.
D
. B.
\ ,
2
D k k
.
C.
\ ,D k k
. D.
\ 2 ,D k k
.
Câu 2. Tìm tập xác định D của hàm số
1
sin
2
y
x
A.
\ ,
2
D k k
. B.
\ ,D k k
.
C.
\ 1 2 ,
2
D k k
. D.
\ 1 2 ,D k k
.
Câu 3. Tìm tập xác định D của hàm số
cot 2 sin 2
4
y x x
.
A.
\ ,
4
D k k
. B. D
Ø
.
C.
\ ,
8 2
D k k
. D.
D
.
Câu 4. Tìm tập xác định D của hàm số
2
3tan
2 4
x
y
.
A.
3
\ 2 ,
2
D k k
. B.
\ 2 ,
2
D k k
.
C.
3
\ ,
2
D k k
. D.
\ ,
2
D k k
.
Câu 5. Tìm tập xác định D của hàm số
2
3tan 5
1 sin
x
y
x
.
A.
\ 2 ,
2
D k k
. B.
\ ,
2
D k k
.
C.
\ ,D k k
. D.
cos 1 sin 0 ,x x x k k
.
Câu 6. Tìm tập xác định D của hàm số
sin 2
y x
A.
D
. B.
2;D
. C.
0; 2
D
. D. D
Ø
.
Câu 7. Tìm tập xác định D của hàm số
1
1 sin
y
x
Trang 20
A.
\ ,D k k
. B.
\ ,
2
D k k
.
C.
\ 2 ,
2
D k k
. D. D
Ø
.
Câu 8. Tập xác định của hàm số
1 cos
sin 1
x
y
x
là
A.
\
2
k k
. B.
\ k k
.
C.
\ 2k k
. D.
\ 2
2
k k
.
Câu 9. Tập xác định của hàm số
cot
cos 1
x
y
x
là
A.
\ ,
2
k
D k
. B.
\ ,
2
k
D k k
.
C.
\ ,D k k
. D.
\ 2 ,D k k
.
Câu 10. Tập xác định của hàm số
1
1 cos
f x
x
là
A.
\ 2 1 ,
2
D k k
. B.
\ 2 1 ,D k k
.
C.
\ ,D k k
. D.
\ 2 ,D k k
.
Câu 11. Tìm tập xác định D của hàm số
cot sin 5 cos
y x x x
.
A.
\
2
k k
. B.
\ 2
2
k k
.
C.
\ k k
. D.
\ 2k k
.
Câu 12. Tìm tập giá trị của hàm số
2cos3 1
y x
.
A.
3; 1
. B.
3; 1
. C.
1; 3
. D.
1; 3
.
Câu 13. Tìm tập xác định D của hàm số
3sin
2cos 1
x
y
x
A.
4
\ 2 , 2 ,
3 3
D k k k
. B.
2
\ 2 ,
3
D k k
.
C.
5
\ 2 ,
6
D k k
. D.
\ 2 ,
3
D k k
.
Câu 14. Tìm điều kiện xác định của hàm số
tan
cos 1
x
y
x
Trang 21
A.
2
x k
. B.
2
3
x k
. C.
2
2
x k
x k
. D.
2
3
x k
x k
.
Câu 15. Tìm điều kiện để hàm số
2cos
sin 1
x
y
x
có nghĩa.
A.
2
x k k
. B.
2x k k
.
C.
2
2
x k k
. D.
x k k
.
Câu 16. Tìm tập xác định của hàm số
sin 1
sin 2
x
y
x
là
A.
2;
. B.
. C.
2;
. D.
\ 2
.
Câu 17. Trong các hàm số sau đây, hàm số nào có tập xác định là
?
A.
1 sin 2
y x
. B.
2
tan
cos 1
x
y
x
. C.
sin cot 2
y x x
. D.
sin
y x
.
Câu 18. Tìm tập giá trị của hàm số
cos 2 1
y x
là
A.
1; 1
. B.
1; 1
. C.
. D.
2; 2
.
Câu 19. Tìm tập xác định của hàm số
2
cot
sin 3
1 sin
x
y x
x
.
A.
\ ,
2
k
k
. B.
\ ,k k
.
C.
\ 2 ,
2
k k
. D.
\ 2 ,
2
k k
Câu 20. Tìm tập xác định của hàm số
2cos3 1
cos 1
x
y
x
là
A.
\D k k
. B.
\ 2D k k
.
C. \
2
D k k
. D.
\ 2D k k
.
Câu 21. Tìm tập xác định của hàm số
sin 2 2
1 cos
x
f x
x
A.
D
. B.
\ 2 ,D k k
.
C.
2 ,D k k
. D.
\ ,D k k
.
Câu 22. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin
y x
. B.
cos
y x
. C.
tan
y x
. D.
cot
y x
.
Câu 23. Trong các hàm số sau, hàm số nào là hàm số chẵn?
Trang 22
A.
sin
y x
. B.
cos sin
y x x
. C.
2
cos sin
y x x
. D.
cos sin
y x x
.
Câu 24. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin 2
y x
. B.
cos
y x x
. C.
cos cot
y x x
. D.
tan
sin
x
y
x
.
Câu 25. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?
A.
sin cos2
y x x
. B.
3
sin cos
2
y x x
.
C.
2
tan
tan 1
x
y
x
. D.
3
cos sin
y x x
.
Câu 26. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
2
cos sin
y x x
. B.
sin cos
y x x
. C.
cos
y x
. D.
sin cos3
y x x
.
Câu 27. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
sin
2
y x
. B.
2
sin
y x
. C.
cot
cos
x
y
x
. D.
tan
sin
x
y
x
.
Câu 28. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
2
1 sin
y x
. B.
2
cot .sin
y x x
.
C.
2
tan 2 cot
y x x x
. D.
1 cot tan
y x x
.
Câu 29. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A.
3
1
sin
y
x
. B.
sin
4
y x
.
C.
2 cos
4
y x
. D.
sin 2
y x
.
Câu 30. Mệnh đề nào sau đây là sai?
A. Đồ thị hàm số
sin
y x
đối xứng qua gốc tọa độ O.
B. Đồ thị hàm số
cos
y x
đối xứng qua trục Oy.
C. Đồ thị hàm số
tan
y x
đối xứng qua truc Oy.
D. Đồ thị hàm số
tan
y x
đối xứng qua gốc tọa độ O.
Câu 31. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
4
cos
3
y x x
. B.
2017
cos
2
y x x
.
C.
2018
2015 cos sin
y x x
. D.
2017 2018
tan sin
y x x
.
Câu 32. Mệnh đề nào sau đây là sai?
A. Hàm số
sin
y x
tuần hoàn với chu kì
2
.
B. Hàm số
cos
y x
tuần hoàn với chu kì
2
.
Trang 23
C. Hàm số
tan
y x
tuần hoàn với chu kì
2
.
D. Hàm số
cot
y x
tuần hoàn với chu kì
.
Câu 33. Trong các hàm số sau, hàm số nào là hàm số tuần hoàn?
A.
sin
y x
. B.
sin
y x x
. C.
cos
y x x
. D.
sin
x
y
x
.
Câu 34. Tìm chu kì T của hàm số
cos 2016
2
x
y
A.
4
T
. B.
2
T
. C.
2
T
. D.
T
.
Câu 35. Tìm chu kì T của hàm số
1
sin 100 50
2
y x
.
A.
1
50
T . B.
1
100
T . C.
50
T
. D.
2
200
T
.
Câu 36. Tìm chu kì T của hàm số
sin 2 2cos 3
3 4
y x x
A.
2
T
. B.
T
. C.
3
T
. D.
4
T
.
Câu 37. Tìm chu kì T của hàm số
sin tan 2
2 4
x
y x
.
A.
4
T
. B.
T
. C.
3
T
. D.
2
T
.
Câu 38. Tìm chu kì T của hàm số
2
2cos 2017
y x
.
A.
3
T
. B.
2
T
C. T
. D.
4
T
.
Câu 39. Hàm số nào sau đây có chu kì khác
?
A.
sin 2
3
y x
. B.
cos 2
4
y x
. C.
tan 2 1
y x
. D.
cos .sin
y x x
.
Câu 40. Với
0;
4
x
, mệnh đề nào sau đây là đúng?
A. Cả hai hàm số
sin 2
y x
và
1 cos 2
y x
đều nghịch biến.
B. Cả hai hàm số
sin 2
y x
và
1 cos 2
y x
đều đồng biến.
C. Hàm số
sin 2
y x
nghịch biến, hàm số
1 cos 2
y x
đồng biến.
D. Hàm số
sin 2
y x
đồng biến, hàm số
1 cos 2
y x
nghịch biến.
Câu 41. Hàm số
sin 2
y x
đồng biến trên khoảng nào trong các khoảng sau?
A.
0;
4
. B.
;
2
. C.
3
;
2
. D.
3
; 2
2
.
Câu 42. Trong các hàm số sau, hàm số nào đồng biến trên khoảng
;
3 6
A.
tan 2
6
y x
. B.
cot 2
6
y x
. C.
sin 2
6
y x
. D.
cos 2
6
y x
.
Trang 24
Câu 43. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số
3sin 2
y x
A.
1; 5
M m
. B.
3; 1
M m
. C.
2; 2
M m
. D.
0; 2
M m
.
Câu 44. Tìm tập giá trị T của hàm số
3cos 2 5
y x
.
A.
1; 1
T . B.
1; 11
T . C.
2; 8
T . D.
5; 8
T .
Câu 45. Tìm tập giá trị T của hàm số
5 3sin
y x
.
A.
1; 1
T . B.
3; 3
T . C.
2; 8
T . D.
5; 8
T .
Câu 46. Cho hàm số
2sin 2
3
y x
. Mệnh đề nào sau đây đúng?
A.
4,y x
B.
4,y x
C.
0,y x
D.
2,y x
Câu 47. Tìm giá trị nhỏ nhất m của hàm số
1
cos 1
y
x
A.
1
2
m
. B.
1
2
m . C.
1
m
. D.
2
m .
Câu 48. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
sin cos
y x x
. Tính
P M m
.
A.
4
P
. B.
2 2
P . C.
2
P . D.
2
P
.
Câu 49. Tập giá trị T của hàm số
sin 2017 cos2017
y x x
.
A.
2; 2
T . B.
4034; 4034
T . C.
2; 2
T
. D.
0; 2
T
.
Câu 50. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số
1 2 cos3
y x
A.
3; 1
M m
. B.
1; 1
M m
. C.
2; 2
M m
. D.
0; 2
M m
.
Câu 51. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
8sin 3cos 2
y x x
. Tính
2
2
M m
A. 1. B. 2. C. 112. D. 130.
Câu 52. Tìm giá trị nhỏ nhất m của hàm số
2
2sin 3 sin 2
y x x
A.
2 3
. B. -1. C. 1. D.
3
.
Câu 53. Tìm giá trị nhỏ nhất m của hàm số
12sin 5cos
y x x
A.
1; 1
. B.
7; 7
. C.
13; 13
. D.
17; 17
.
Câu 54. Tìm giá trị lớn nhất của hàm số
4sin 2 3cos 2
y x x
A. 3. B. 1. C. 5. D. 4.
Câu 55. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
sin 4sin 5
y x x
. Tính
2
2
M m
A. 1. B. 7. C. 8. D. 2.
Trang 25
Câu 56. Hàm số
2
cos cos
y x x
có tất cả bao nhiêu giá trị nguyên?
A. 1. B. 2. C. 3. D. 4.
Câu 57. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số
4 2
sin 2cos 1
y x x
A.
2, 2
M m
. B.
1, 0
M m
. C.
4, 1
M m
. D.
2, 1
M m
.
Câu 58. Tìm giá trị nhỏ nhất của hàm số
4
4sin cos 4
y x x
A. -3 B. -1 C. 3 D. -5
Câu 59. Cho hàm số
cos 2 cos 1
f x x x
. Giá trị nhỏ nhất của hàm số trên
là
A.
1
min
8
f x
. B.
1
min
4
f x
. C.
1
min
8
f x
. D.
1
min
4
f x
.
Câu 60. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 sin
cos 2
x
y
x
. Tính M. m.
A. 2. B. 0. C. -2. D. -1.
Câu 61. Tìm giá trị nhỏ nhất của hàm số
sin cos 1
sin cos 2
x x
y
x x
.
A.
3 5
2
. B. 1. C.
1
3
. D.
2 6
2
.
Câu 62. Tìm giá trị lớn nhất của biểu thức
sin 2cos 3
2sin cos 4
x x
P
x x
.
A. 2. B. 3. C.
9
11
. D.
2
11
.
Câu 63. Tìm giá trị nhỏ nhất và lớn nhất của hàm số
sin cos
2sin cos 3
x x
y
x x
lần lượt là
A.
1
1;
2
m M
. B.
1; 2
m M
. C.
1
; 1
2
m M
. D.
1; 2
m M
.
Câu 64. Tìm giá trị lớn nhất M của hàm số
sin 2cos 1
sin cos 2
x x
y
x x
.
A.
2
M
. B.
3
M
. C.
3
M
. D.
1
M
.
Câu 65. Gọi T là tập giá trị của hàm số
2
1 3
sin cos2 3
2 4
y x x
. Tìm tổng các giá trị nguyên của T
A. 4. B. 6. C. 7. D. 3.
Câu 66. Tập giá trị của hàm số
cos 1
sin 1
x
y
x
trên
0;
2
A.
1
; 2
2
B.
0; 2
C.
1
; 2
2
D.
1
; 2
2
Câu 67. Tìm giá trị lớn nhất của hàm số
2 2
1 1
1 cos 5 2sin
2 2
y x x
Trang 26
A.
11
2
B.
1 5
C.
5
1
2
D.
22
2
Câu 68. Cho hàm số
1 sin
cos 2
m x
y
x
. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn
0; 10
để
giá trị nhỏ nhất của hàm số nhỏ hơn -2?
A. 1. B. 9. C. 3. D. 6.
Câu 69. Có bao nhiêu giá trị nguyên của m để phương trình
3sin 1 0
x m
có nghiệm?
A. 7. B. 6. C. 3. D. 5.
Câu 70. Có bao nhiêu giá trị nguyên của tham số m để hàm số
5 sin 1 cos
y m x m x
xác định
trên
?
A. 5. B. 8. C. 7. D. 6.
Câu 71. Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm 2017 được cho bởi
một hàm số
4sin 60 10,
178
y t t
và
0 365
t
. Vào ngày nào trong năm thành phố A có
nhiều giờ có ánh sáng mặt trời nhất?
A. 28 tháng 5 B. 29 tháng 5 C. 30 tháng 5 D. 31 tháng 5
Câu 72. Hàng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h(m) của mực nước trong
kênh tính theo thời gian t(h) được cho bởi công thức
3cos 12
8 4
t
h
. Mực nước của kênh cao
nhất khi
A.
13
t h
B.
14
t h
C.
15
t h
D.
16
t h
Câu 73. Hàng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h(m) của mực nước trong
kênh tính theo thời gian t(h) được cho bởi công thức
3cos 12
6 3
t
h
. Khi nào mực nước của
kênh là cao nhất với thời gian ngắn nhất?
A.
22
t h
. B.
15
t h
. C.
14
t h
. D.
10
t h
.
Câu 74. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
sin
2
x
y
B.
cos
2
x
y
C.
cos
4
x
y
D.
sin
2
x
y
Câu 75. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?
Trang 27
A.
2
cos
3
x
y
B.
2
sin
3
x
y
C.
3
cos
2
x
y
D.
3
sin
2
x
y
Câu 76. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
sin
4
y x
B.
3
cos
4
y x
C.
2 sin
4
y x
D.
cos
4
y x
Câu 77. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
sin
4
y x
B.
cos
4
y x
C.
2 sin
4
y x
D.
2 cos
4
y x
Câu 78. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
sin
y x
B.
sin
y x
C.
sin
y x
D.
sin
y x
Câu 79. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?
Trang 28
A.
cos
y x
B.
cos
y x
C.
cos
y x
D.
cos
y x
Câu 80. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
sin 1
2
y x
B.
2sin
2
y x
C.
sin 1
2
y x
D.
sin 1
2
y x
Câu 81. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
1 sin
y x
B.
sin
y x
C.
1 cos
y x
D.
1 sin
y x
Câu 82. Cho hàm số
y f x
xác định trên
\ ,
2
k k
và có đồ thị như hình vẽ bên. Hỏi hàm
số
y f x
là hàm số nào trong các hàm số sau đây?
A.
tan
y x
B.
cos
y x
C.
sin
y x
D.
cot
y x
Trang 29
Câu 83. Hãy nêu tất cả các hàm số trong các hàm số
sin , cos , tan , cot
y x y x y x y x
thỏa mãn
điều kiện đồng biến và nhận giá trị âm trong khoảng
; 0
2
A.
tan
y x
B.
cos , cot
y x y x
C.
tan , sin
y x y x
D.
cos , tan
y x y x
Câu 84. Hình chữ nhật ABCD có hai đỉnh A, B thuộc trục Ox, hai đỉnh C, D thuộc đồ thị hàm số
cos
y x
(như hình vẽ). Biết rằng
2
3
AB
. Diện tích hình chữ nhật ABCD bằng bao nhiêu?
A.
2
3
B.
2
3
C.
3
D.
2
2
3
Câu 85. Cho hai điểm A, B thuộc đồ thị hàm số
sin
y x
trên đoạn
0;
, các điểm C, D thuộc trục Ox
thỏa mãn ABCD là hình chữ nhật và
2
3
CD
. Tính độ dài đoạn BC
A.
2
2
B.
1
2
C. 1 D.
3
2
Trang 30
ĐÁP ÁN VÀ LỜI GIẢI BÀI TẬP TỰ LUYỆN
1-D 2-C 3-C 4-A 5-B 6-A 7-C 8-D 9-D 10-D
11-C 12-C 13-B 14-C 15-C 16-B 17-A 18-A 19-A 20-D
21-B 22-B 23-C 24-D 25-B 26-D 27-C 28-C 29-A 30-A
31-B 32-C 33-A 34-A 35-A 36-A 37-A 38-C 39-C 40-A
41-A 42-C 43-A 44-C 45-C 46-C 47-A 48-B 49-C 50-B
51-A 52-B 53-C 54-C 55-D 56-C 57-D 58-B 59-A 60-D
61-D 62-A 63-A 64-D 65-C 66-A 67-D 68-D 69-A 70-B
71-B 72-B 73-D 74-D 75-A 76-A 77-D 78-D 79-B 80-A
81-D 82-A 83-C 84-C 85-B
Câu 1: Hàm số xác định khi
cos 1 2
x x k
. Vậy
\ 2 ,D k k
. Chọn D
Câu 2: Hàm số xác định khi
sin 0
2 2
x x k
.
Vậy
\ ,
2
D k k
. Chọn C.
Câu 3: Hàm số xác định
sin 2 0 2 ,
4 4 8 2
k
x x k x k
.
Vậy tập xác định
\ ,
8 2
D k k
. Chọn C.
Câu 4: Hàm số xác định khi
2
3
cos 0 2 ,
2 4 2 4 2 2
x x
k x k k
.
Vậy tập xác định
3
\ 2 ,
2
D k k
. Chọn A
Câu 5: Hàm số xác định khi
2
1 sin 0
x
và
tan
x
xác định
2
sin 1
cos 0 ,
2
cos 0
x
x x k k
x
.
Vậy tập xác định
\ ,
2
D k k
. Chọn B.
Câu 6: Ta có 1 sin 1 1 sin 2 3,x x
Do đó luôn tồn tại căn bậc hai của
sin 2
x
với mọi
x
.
Vậy tập xác định
D
. Chọn A
Câu 7: Hàm số xác định khi và chỉ khi
1 sin 0 sin 1
x x
(*)
Mà
1 sin 1
x
nên
* sin 1 2 ,
2
x x k k
.
Trang 31
Vậy tập xác định
\ 2 ,
2
D k k
. Chọn C.
Câu 8: Hàm số xác định khi
sin 1 ,
2
x x k k
. Chọn D.
Câu 9: Hàm số xác định khi
sin 0
cos 1 2 ,
cos 1 0
x
x x k k
x
. Chọn D.
Câu 10: Hàm số xác định khi
cos 1 2 ,x x k k
. Chọn D.
Câu 11: Hàm số xác định khi
sin 0 ,x x k k
Chọn C.
Câu 12: Ta có
1 cos3 1 2 2cos3 2 1 3
x x y
. Vậy
1; 3
T . Chọn C.
Câu 13: Hàm số xác định khi
1 2
cos ,
2 3
x x k k
. Chọn B.
Câu 14: Hàm số xác định khi
cos 0
2
cos 1
2
x
x k
x
x k
. Chọn C.
Câu 15: Hàm số xác định khi
sin 1 2 ,
2
x x k k
. Chọn C.
Câu 16: Hàm số xác định khi
sin 2
x
(luôn đúng). Vậy
D
. Chọn B.
Câu 17: Ta có
sin 2 1; 1 1 sin 2 0;x x x
nên
1 sin 2
y x
có
D
. Chọn A.
Câu 18: Ta có
1 cos 2 1 1 1; 1
x T . Chọn A.
Câu 19: Hàm số xác định khi
2
sin 0
sin 0
sin 2 0
cos 0
2
1 sin 0
x
x
k
x x
x
x
. Chọn A.
Câu 20: Hàm số xác định khi
cos 1 2
x x k
Vậy
\ 2 ,D k k
. Chọn D.
Câu 21: Hàm số xác định khi
sin 2 2
0
1 cos
x
x
mà
sin 2 1; 1 sin 2 2 1; 3
x x
Do đó
1 cos 0 cos 1 cos 1
x x x
(vì
cos 1
x
)
2
x k
. Chọn B.
Câu 22: Nhắc lại kiến thức cơ bản:
* Hàm số
sin
y x
là hàm số lẻ.
* Hàm số
cos
y x
là hàm số chẵn.
* Hàm số
tan
y x
là hàm số lẻ.
* Hàm số
cot
y x
là hàm số lẻ.
Vậy B là đáp án đúng. Chọn B.
Câu 23: Kiểm tra
f x f x
hoặc
f x f x
.
* Với
sin
y f x x
. Ta có
sin sin sin
f x x x x
Trang 32
f x f x
. Suy ra hàm số
sin
y x
là hàm số lẻ.
* Với
cos sin
y f x x x
. Ta có
cos sin cos sin
f x x x x x
,
f x f x f x
. Suy ra hàm số
cos sin
y x x
không chẵn không lẻ.
* Với
2
cos sin
y f x x x
. Ta có
2
cos sin
f x x x
2
2
2
cos sin cos sin cos sin
x x x x x x
f x f x
. Suy ra hàm số
2
cos sin
y x x
là hàm số chẵn. Chọn C
* Với
cos sin
y f x x x
. Ta có
cos .sin cos sin
f x x x x x
f x f x
. Suy ra hàm số
cos sin
y x x
là hàm số lẻ.
Câu 24:
* Xét hàm số
sin 2
y f x x
.
Ta có
sin 2 sin 2
f x x x f x f x
là hàm số lẻ.
* Xét hàm số
cos
y f x x x
Ta có
.cos cos
f x x x x x f x f x
là hàm số lẻ.
* Xét hàm số
cos cot
y f x x x
.
Ta có
cos .cot cos cot
f x x x x x f x f x
là hàm số lẻ.
* Xét hàm số
tan
sin
x
y f x
x
Ta có
tan
tan tan
sin sin sin
x
x x
f x f x f x
x x x
là hàm số chẵn. Chọn D.
Câu 25: Ta dễ dàng kiểm tra được A, C, D là các hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ O.
Xét đáp án B, ta có
3 3 4
sin .cos sin .sin sin
2
y f x x x x x x
Kiểm tra được đây là hàm số chẵn nên có đồ thị đối xứng qua trục tung. Chọn B.
Câu 26:
Hàm số
2 2
cos sin cos sin cos sin
y x x y x x x x x y x
Hàm số
sin cos sin cos sin cos
y x x y x x x x x
Hàm số
cos cos cos
y x y x x x
Hàm số
sin cos3 sin .cos 3 sin cos3
y x x y x x x x x y x
Do đó hàm số
sin cos3
y x x
là hàm số lẻ. Chọn D.
Trang 33
Câu 27: Ta có
sin cos
2
y x x y x y x
Hàm số
2
2 2
sin sin sin
y x y x x x
Hàm số
tan
tan tan tan
sin sin sin sin
x
x x x
y y x
x x x x
Hàm số
cot
cot cot
cos cos cos
x
x x
y y x y x
x x x
hàm số là hàm số lẻ. Chọn C.
Câu 28: Hàm số
2
tan 2 cot
f x x x x
có
2
2
tan 2 cot tan 2 cot
f x x x x x x x
Suy ra
f x f x
nên hàm số
2
tan 2 cot
f x x x x
là hàm số lẻ. Chọn C.
Câu 29: Hàm số lẻ có đồ thị đối xứng qua gốc tọa độ.
Ta có:
3 3 3 3
1 1 1 1
sin sin
sin
sin
f x f x
x x
x
x
Suy ra hàm số
3
1
sin
y
x
là hàm số lẻ. Chọn A.
Câu 30: Hàm số chẵn có đồ thị đối xứng qua trục Oy. Hàm số lẻ có đồ thị đối xứng qua gốc tọa độ O.
Hàm số
sin
y x
có
sin sin
y x x x
là hàm số chẵn nên có đồ thị đối xứng qua trục Oy.Vậy
khẳn định sai là A. Chọn A.
Câu 31: Hàm số
4
4 4
cos cos cos
3 3 3
y x x y x x x x x
Suy ra hàm số không là hàm lẻ.
Hàm số
2017 2017 2017
cos cos sin
2 2
y x x x x x x
Suy ra
2017
2017
sin sin
y x x x x x y x
nên hàm số ở ý B là hàm số lẻ.
Chọn B
Câu 32: Hàm số
sin
y x
và
cos
y x
tuần hoàn với chu kì
2
.
Hàm số
tan
y x
và
cot
y x
tuần hoàn với chu kì
.
Khẳng định sai là C. Chọn C
Câu 33: Ta có
sin 2 sin
x k x
nên hàm số
sin
y x
tuần hoàn với chu kì
2
. Chọn A.
Câu 34: Hàm số
cos 2016
2
x
y
tuần hoàn với chu kì
2
4
1
2
T
. Chọn A.
Trang 34
Câu 35: Hàm số
1
sin 100 50
2
y x
tuần hoàn với chu kì
2 1
100 50
T
. Chọn A.
Câu 36: Hàm số
sin 2
3
y x
tuần hoàn với chu kì
1
T
.
Hàm số
2cos 3
4
y x
tuần hoàn với chu kì
2
2
3
T
Bội số chung nhỏ nhất của
1
T
và
2
T
là
2
Chu kì tuần hoàn của hàm số đã cho là
2
T
. Chọn A
Câu 37: Hàm số
sin
2
x
y tuần hoàn với chu kì
1
2
4
1
2
T
.
Hàm số
tan 2
4
y x
tuần hoàn với chu kì
2
2
T
.
Bội số chung nhỏ nhất của
1
T
và
2
T
là 4
Chu kì tuần hoàn của hàm số đã cho là
4
T
. Chọn A.
Câu 38: Ta có
2
2cos 2017 1 cos 2 2017 2018 cos 2
y x x x
Do đó hàm số đã cho tuần hoàn với chu kì
2
2
T
. Chọn C.
Câu 39: Hàm số
sin 2
3
y x
tuần hoàn với chu kì
2
2
T
.
Hàm số
cos 2 cos 2
4 2
y x x
tuần hoàn với chu kì
2
2
T
Hàm số
tan 2 1
y x
tuần hoàn với chu kì
2
T
.
Hàm số
1
cos .sin sin 2
2
y x x x
tuần hoàn với chu kì
2
2
T
. Chọn C.
Câu 40: Trên khoảng
0; 2 0;
4 2
x x
nên hàm số
sin 2
y x
đồng biến, hàm số
cos 2
y x
nghịch biến.
Do đó hàm số
sin 2
y x
nghịch biến và hàm số
1 cos 2
y x
cũng nghịch biến trên khoảng
0;
4
x
. Chọn A.
Câu 41: Hàm số
sin 2
y x
đồng biến khi
2 ; ;
2 2 4 4
x x
Do đó hàm số
sin 2
y x
đồng biến trên khoảng
0;
4
. Chọn A.
Câu 42: Do
;
3 6
x
nên
2 ;
6 2 2
x
Trang 35
Mặt khác trên khoảng
;
2 2
thì hàm
sin
x
là hàm đồng biến.
Vậy trên khoảng
;
3 6
thì hàm số
sin 2
6
y x
là hàm đồng biến. Chọn C.
Câu 43: Do
sin 1; 1
x nên
3. 1 2 3sin 2 3 2 5 1
x y
.
Vậy giá trị lớn nhất và giá trị nhỏ nhất của hàm số là
1, 5
M m
. Chọn A.
Câu 44: Do
1 cos 2 1
x
suy ra
3 5 3cos 2 5 3 5 2 8
x y
.
Vậy tập giá trị của hàm số là
2; 8
T . Chọn C.
Câu 45: Do
sin 1; 1
x nên
5 3.1 5 3sin 5 3 1 2 8
x y
Vậy tập giá trị của hàm số là
2; 8
T . Chọn C.
Câu 46: Ta có
1 sin 1 2 2sin 2
3 3
x x
Do đó
4 2sin 2 0 0; 4
3
x y
. Chọn C.
Câu 47: Ta có
2
1 1
cos 1
2cos
2
y
x
x
, điều kiện
cos 0
2
x
Mặt khác
2
2
1 1 1
0 cos 1
2 2.1 2
2cos
2
x
x
Vậy giá trị nhỏ nhất m của hàm số là
min
1
2
y
. Chọn A.
Câu 48: Ta có
sin cos 2 sin
4
y x x x
Suy ra
2
2 2 2 2
2
M
y M m
m
. Chọn B.
Câu 49:
sin 2017 cos 2017 2 sin 2017
4
y x x x
Suy ra
2 2
y
nên tập giá trị của hàm số đã cho là
2; 2
T
. Chọn C.
Câu 50: Ta có
0 cos3 1
x
Suy ra
1 2.1 1 2 cos3 1 2.0 1 1
x y
Do đó
1; 1
M m
. Chọn B.
Câu 51: Ta có
1 cos 2
8. 3cos 2 4 cos2
2
x
y x x
mà
cos2 1; 1
x
Trang 36
Suy ra
3 4 cos 2 5 5; 3
x M m
nên
2 2
2 2.5 3 1
M m
. Chọn A.
Câu 52: Ta có
1 cos 2
2. 3 sin 2 3 sin 2 cos 2 1
2
x
y x x x
Lại có
2 2
2
2 2
3 sin 2 cos 2 3 1 . sin 2 cos 2 4
x x x x
Suy ra
2
2
1 4 2 3 0 1; 3
y y y y . Chọn B.
Câu 53:
2 2
2 2 2 2 2
12sin 5cos 12 5 . sin cos 13 13; 13
y x x x x y
. Chọn C.
Câu 54:
2 2
2 2 2 2 2
4sin 2 3cos 2 4 3 . sin 2 cos 2 5 5; 5
y x x x x y
. Chọn C.
Câu 55: Đặt
sin 1; 1
t x nên hàm số trở thành:
2
4 5
f t t t
Ta có
2 1; 1
2
b
t
a
. Tính
1 10; 1 2 10; 2
f f M m
Vậy
2 2
2 10 2.2 2
M m
. Chọn D.
Câu 56: Đặt
cos 1; 1
t x nên hàm số trở thành:
2
f t t t
Ta có
1
1; 1
2 2
b
t
a
. Tính
1 1
1 2; 1 0;
2 4
f f f
Suy ra
1
2
4
f t
nên có tất cả 3 giá trị nguyên:
0; 1; 2
f t . Chọn C.
Câu 57: Ta có
4 2 4 2
sin 2. 1 sin 1 sin 2sin 1
y x x x x
Đặt
2
sin 0; 1
t x nên hàm số trở thành:
2
2 1
f t t t
Lại có
1 0; 1
2
b
t
a
. Tính
0 1; 1 2 2, 1
f f M m
. Chọn D.
Câu 58: Ta có
2
4 2 4 2
4sin 2cos 2 1 4sin 2. 1 2sin 1
y x x x x
4 4 2 4 2
4sin 2. 4sin 4sin 1 1 4sin 8sin 1
x x x x x
Đặt
2
sin 0; 1
t x nên hàm số trở thành:
2
4 8 1
f t t t
Lại có
1 0; 1
2
b
t
a
. Tính
0 1; 1 3
f f
min 1
y
. Chọn B
Câu 59: Ta có
2 2
2cos 1 cos 1 2cos cos
y x x x x
Đặt
cos 1; 1
t x nên hàm số trở thành:
2
2
f t t t
Lại có
1
1; 1
2 4
b
t
a
. Tính
1 1
1 3, 1 1,
4 8
f f f
Vậy giá trị nhỏ nhất cần tìm là
1
min
8
f x
. Chọn A.
Trang 37
Câu 60: Ta có
. cos 2 3 sin 3 sin .cos 2
y x x x y x y
Phương trình có nghiệm khi
2
2 2
2
3 2 1 1; 1
y y y y . Chọn D.
Câu 61: Ta có
. sin cos 2 sin cos 1 1 sin 1 cos 2 1
y x x x x y x y x y
Phương trình có nghiệm khi:
2 2 2
2
2 6
1 1 2 1 2 4 1 0
2
y y y y y y
.
Chọn D.
Câu 62: Ta có
sin 2cos 3
. 2sin cos 4 sin 2cos 3
2sin cos 4
x x
P P x x x x
x x
2 .sin .cos 4 sin 2cos 3 2 1 .sin 2 .cos 4 3
P x P x P x x P x P x P
Phương trình có nghiệm khi:
2 2 2
2
2 1 2 4 3 2
11
P P P P
. Chọn A.
Câu 63: Ta có
2sin cos 3 0x x x
Khi đó
sin cos
sin cos 2sin cos 3
2sin cos 3
x x
y x x y x x
x x
2 1 sin 1 cos 3 *
y x y x y
Phương trình (*) có nghiệm khi và chỉ khi
2 2 2
2 1 1 3
y y y
2 2 2
1
5 2 2 9 4 2 2 0 1
2
y y y y y y
Vậy
1
1;
2
m M
. Chọn A.
Câu 64: Ta có
sin cos 2 0x x x
Khi đó:
sin 2cos 1
sin cos 2 sin 2cos 1
sin cos 2
x x
y y x y x y x x
x x
1 sin 2 cos 1 2 *
y x y x y
Phương trình (*) có nghiệm khi và chỉ khi
2 2 2
1 2 1 2
y y y
2 2 2
2 6 5 4 4 1 2 2 4 0 2 1
y y y y y y y
. Vậy
1
M
. Chọn D.
Câu 65: Ta có
1 cos 2 3 7 5 14 5cos 2
cos 2 3 cos 2
2 4 2 4 4
x x
y x x
Vì
1 cos 2 1
x
nên
9 14 5cos 2 19
3; 4
4 4 4
x
y y
Do đó tổng các giá trị nguyên của T là 7. Chọn C.
Câu 66: Ta có
0 cos 1
0;
0 sin 1
2
x
x
x
nên
0 1 cos 1 1 1 1
2
1 1 sin 1 0 1 2
x
y
x
. Chọn A.
Trang 38
Câu 67: Ta có
2 2 2 2
1 1 1 5 1
1 cos 5 2sin 1 cos sin
2 2 2 4 2
y x x x x
Áp dụng bất đẳng thức
2
2 2
2
a b a b
Do đó
2 2 2 2
1 5 1 9 1 11 22
2 1 cos sin 2.
2 4 2 4 2 2 2
x x y y y
Dấu bằng xảy ra
2 2
1 5 1 1 1 1
1 cos sin cos 2 cos 2
2 4 2 2 4 2
x x x x
. Chọn D.
Câu 68: Ta có
. cos 2 1 .sin .sin .cos 1 2
y x m x m x y x y
Phương trình có nghiệm khi:
2
2 2 2 2
2 1 3 4 1 0
m y y y y m
Nghiệm của phương trình
2 2
3 4 1 0
y y m
là
2
2 3 1
3
m
x
Suy ra
2 2 2
2 3 1 2 3 1 2 3 1
min
3 3 3
m m m
y y
Yêu cầu bài toán
2
2
21
2 3 1
2 3 1 8
3
21
m
m
m
m
Kết hợp với
0; 10 5; 6; 7; 8; 9; 10
m m . Chọn D.
Câu 69: Ta có
1
sin 1; 1 3 1 3 2 4
3
m
x m m
Kết hợp với
m
có
4 2 1 7
giá trị nguyên m. Chọn A.
Câu 70: Hàm số đã cho xác định khi:
5 sin 1 cos 0;m x m x x
.
2
2 2
5 max .sin 1 .cos 5 1 12 0 4; 3
m x m x m m m m m
Kết hợp với
4; 3; 2; 1; 0; 1; 2; 3
m m
. Chọn B.
Câu 71: Ta có
4sin 60 10 4.1 10 14
178
y t
Như vậy thành phố A có nhiều giờ có ánh sáng mặt trời nhất khi
sin 60 1
178
t
60 60 89 178 149 178
178 2
t k t k t k
Do
0 365
t
Vào ngày thứ 149 tức là ngày 29 tháng 5 thì thành phố A có nhiều giờ ánh sáng mặt
trời nhất. Chọn B.
Câu 72: Ta có
3cos 12 3 12 15 cos 1
8 4 8 4
t t
h
Trang 39
Do đó mực nước của kênh cao nhất khi
cos 1 2 16 2
8 4 8 4
t t
k t k
Vì
0 24 1 14
t k t
Vậy mực nước của kênh cao nhất khi
14
t h
. Chọn B.
Câu 73: Ta có
cos 1
6 3
t
nên
3.1 12 15
h
Dấu bằng xảy ra khi
cos 1 2 12 2
6 3 6 3
t t
k t k
Để
min
12 2 0
t k
và
min
12 2
k nên
1 10
k t h
. Chọn D.
Câu 74: Dựa vào đồ thị hàm số
y f x
như hình vẽ ta thấy:
0 0
f
nên ta loại đáp án B và C.
Mặt khác dựa vào đồ thị suy ra
0
f
nên loại đáp án A. Chọn D.
Câu 75: Dựa vào đồ thị hàm số
y f x
như hình vẽ ta thấy:
0 0
f
nên ta loại các đáp án B và D.
Mặt khác hàm số đã cho tuần hoàn với chu kì
3
, trong 2 hàm số ở ý A và C thì hàm số
2
cos
3
x
y thỏa
mãn điều kiện trên. Chọn A.
Câu 76: Dựa vào đồ thị hàm số
y f x
như hình vẽ ta thấy:
3
1
4
f
nên ta loại các đáp án B, C và D. Chọn A.
Câu 77: Dựa vào đồ thị hàm số
y f x
như hình vẽ ta thấy:
3
2
4
f
nên ta loại các đáp án A,
B, và C. Chọn D.
Trang 40
Câu 78: Dựa vào đồ thị hàm số ta thấy: Hàm số nhận giá trị âm trên khoảng
0;
nên ta loại các đáp án
A, B, và C. Chọn D.
Câu 79: Dựa vào đồ thị hàm số ta thấy: Hàm số nhận giá trị âm trên khoảng
0;
2
nên ta loại các đáp
án A, C và D. Chọn B.
Câu 80: Dựa vào đồ thị hàm số ta thấy: Hàm số
y f x
trong hình vẽ luôn thỏa mãn
0
f x
nên ta
loại đáp án B.
Lại có:
0 0
f
nên ta loại đáp án D và
0
f
nên ta loại đáp án C. Chọn A
Câu 81: Dựa vào đồ thị hàm số ta thấy: Hàm số
y f x
trong hình vẽ có tập giá trị là
0; 2
T ta
loại đáp án A và B.
Ta có:
0 1
f
nên loại đáp án C. Chọn D.
Câu 82: Dựa vào đồ thị hàm số ta thấy, hàm số đã cho xác định và đồng biến trên khoảng
;
2 2
do
đó hàm số cần chọn là hàm số
tan
y x
. Chọn A.
Câu 83: Hàm số
tan
y x
đồng biến và nhận giá trị âm trên khoảng
; 0
2
(loại đáp án B).
Trên khoảng
; 0
2
hàm số
sin
y x
đồng biến và nhận giá trị âm. Chọn C
Câu 84: Gọi
2 2
; cos ; cos
3 3
C a a D a a
Do ABCD là hình chữ nhật nên
2
/ / cos cos
3
C D
AB CD y y a a
2 1
cos
3 3 3 2
a a a AD
Diện tích hình chữ nhật ABCD bằng
.
3
AB BC
. Chọn C.
Câu 85: Gọi
2
3
; sin
2
sin
3
B
B
x a
A a a
y a
Mặt khác
2 2
sin sin
3 3 6
A B
y y a a a a a
Do đó
1
sin
6 2
BC AD
. Chọn B.
| 1/40
| | Tải xuống

Có thể bạn quan tâm:

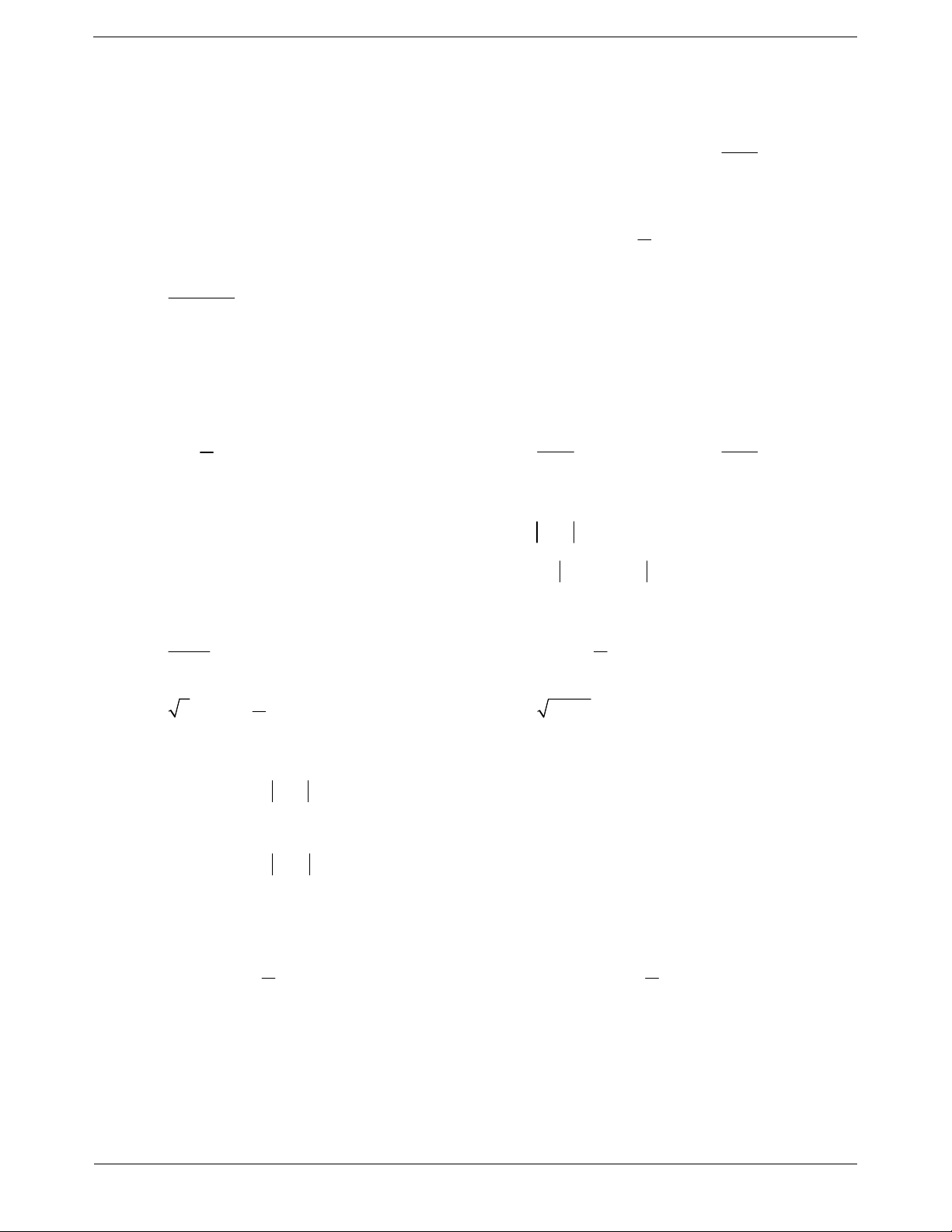
Preview text:

CHỦ ĐỀ HÀM SỐ LƯỢNG GIÁC I. KIẾN THỨC TRỌNG TÂM
1) Các hệ thức lượng giác cơ bản
* Hàm số y  sin x  D  R
* Hàm số y  cos x  D  R  
* Hàm số y  tan x  D  R \   k   2 
* Hàm số y  cot x  D  R \ k u  x * Hàm số y 
 điều kiện xác định là vx  0 v  x u x * Hàm số y 
 điều kiện xác định là vx  0 v  x
2) Tính tuần hoàn của hàm số lượng giác - Định nghĩa
Hàm số y  f  x có tập xác định D được gọi là hàm số tuần hoàn, nếu tồn tại một số T  0 sao cho với mọi x  D ta có:
* x  T  D và x  T  D
* f  x  T   f  x
Số dương T nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó.
Người ta chứng minh được rằng hàm số y  sin x tuần hoàn với chu kì T  2 ; hàm số y  cos x tuần
hoàn với chu kì T  2 ; hàm số y  tan x tuần hoàn với chu kì T   ; hàm số y  cot x tuần hoàn với chu kì T   . - Chú ý 2
* Hàm số y  sin ax  b tuần hoàn với chu kì T  0 a 2
* Hàm số y  cos ax  b tuần hoàn với chu kì T  0 a 
* Hàm số y  tan ax  b tuần hoàn với chu kì T  0 a 
* Hàm số y  cot ax  b tuần hoàn với chu kì T  0 a Trang 1
* Hàm số y  f x tuần hoàn với chu kì T và hàm số y  f x tuần hoàn với chu kì T thì hàm số 2   1   1 2
y  f x  f x tuần hoàn với chu kì T là bội chung nhỏ nhất của T và T . 1   2   0 1 2
3) Tính chẵn lẻ của hàm số lượng giác - Định nghĩa
* Hàm số y  f  x có tập xác định D được gọi là hàm số chẵn nếu nó thỏa mãn đồng thời hai điều kiện x   D  x  D sau:   f  x  f  x
* Hàm số y  f  x có tập xác định D được gọi là hàm số lẻ nếu nó thỏa mãn đồng thời hai điều kiện x   D  x  D sau:   f
 x   f  x - Chú ý
* Các hàm số chẵn thường gặp: 2 2 x kx x kx 2 cos ; cos ; sin ; sin ; cos kx
* Các hàm số lẻ thường gặp: 3 3 sin ; x tan ; x cot ; x sin ; x tan . x .. f  x
* Hàm số f  x chẵn và g  x lẻ thì hàm f  x.g  x và đều là hàm số lẻ. g x f  x
* Hàm số f  x và g  x đều là hàm lẻ thì hàm f  x.g  x và đều là hàm số chẵn. g  x
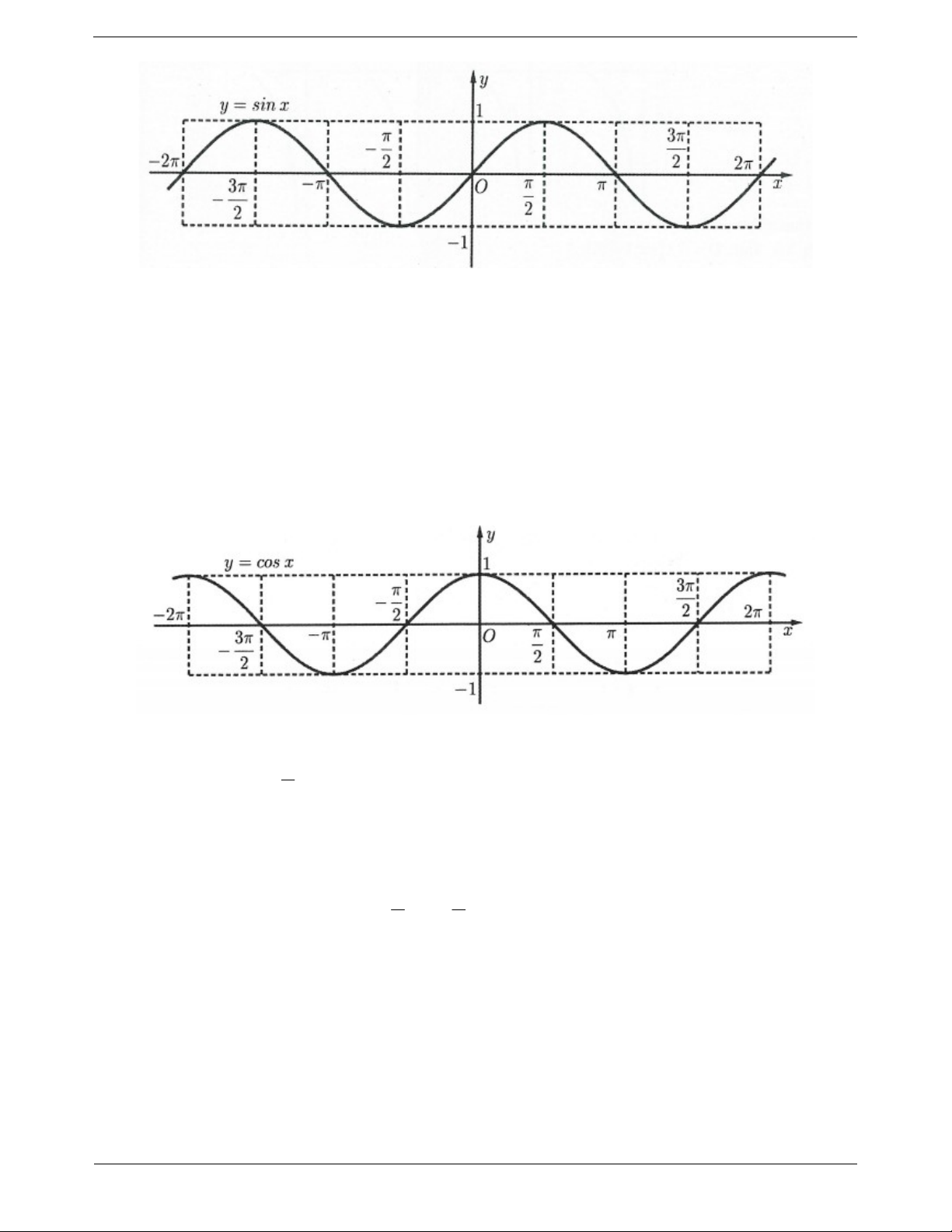
4) Sự biến thiên và đồ thị các hàm số lượng giác a) Hàm số y = sinx * Tập xác định: D  R * Tập giá trị T   1  ; 
1 , có nghĩa là 1  sin x  1
* Là hàm số tuần hoàn chu kì 2 , có nghĩa  x  k2   sin x với k      
* Hàm số đồng biến trên mỗi khoảng   k2 ;  k2 
 và nghịch biến trên mỗi khoảng  2 2    3   k2 ;  k2 , k      2 2 
* Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng. Đồ thị hàm số như hình vẽ bên dưới. Trang 2 b) Hàm số y = cosx * Tập xác định: D  R * Tập giá trị T   1  ; 
1 , có nghĩa 1  sin x  1
* Là hàm số tuần hoàn với chu kì 2 , có nghĩa cos x  k2   cos x với k  
* Hàm số đồng biến trên mỗi khoảng  
  k2; k2  và nghịch biến trên mỗi khoảng
k2;   k2 , k 
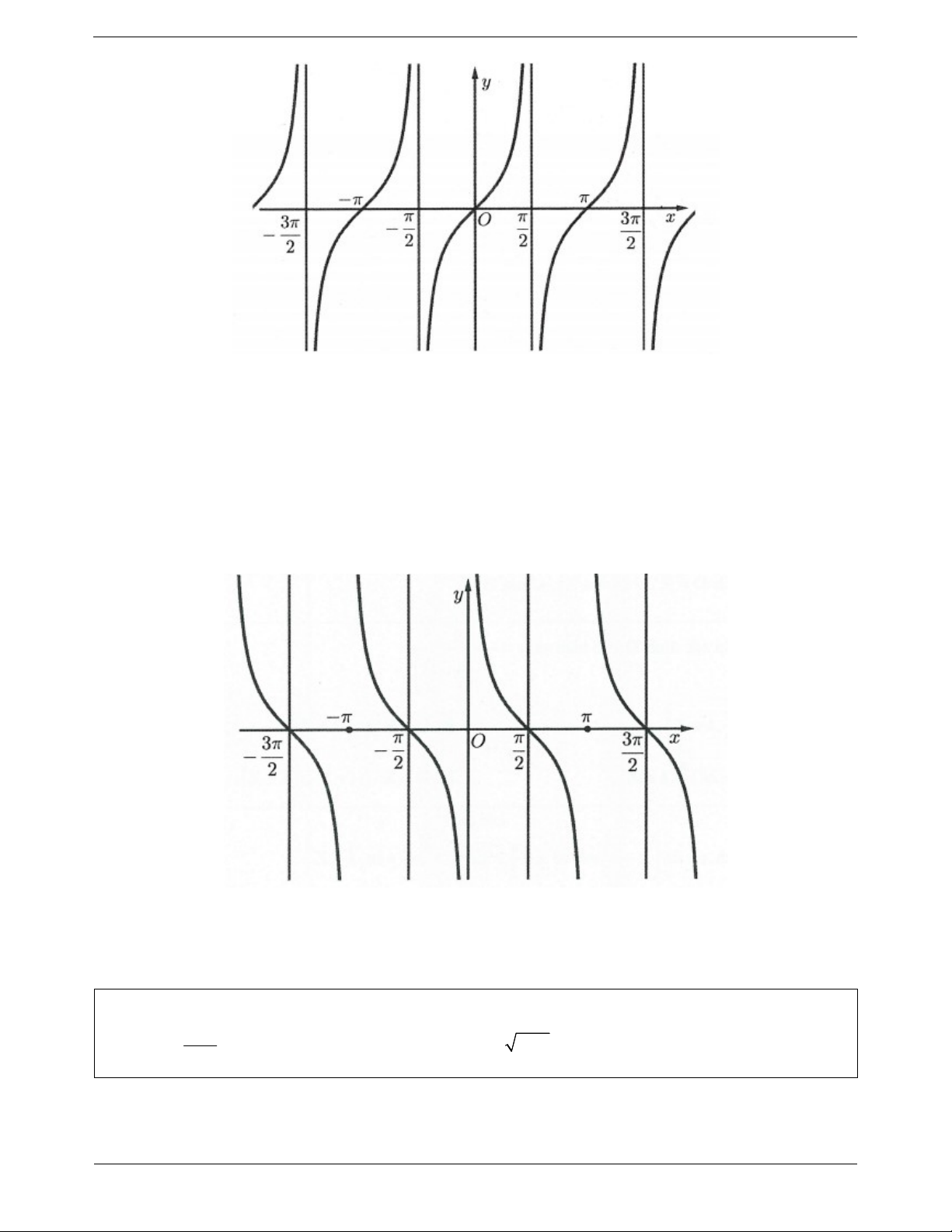
* Là hàm số chẵn nên đồ thị hàm số nhận trục Oy làm trục đối xứng. Đồ thị hàm số như hình vẽ bên dưới c) Hàm số y = tanx  
* Tập xác định D   \   k , k    2  * Tập giá trị T  
* Là hàm số tuần hoàn với chu kì  , có nghĩa tan  x  k   tan x với k      
* Hàm số đồng biến trên mỗi khoảng   k ;  k , k      2 2 
* Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng Trang 3 d) Hàm số y = cotx
* Tập xác định D   \ k , k    * Tập giá trị T  
* Là hàm số tuần hoàn với chu kì  , có nghĩa tan  x  k   tan x với k  
* Hàm số đồng biến trên mỗi khoảng k ;   k , k  
* Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng.
II. HỆ THỐNG VÍ DỤ MINH HỌA
- Dạng 1: Tập xác định và Tập giá trị của hàm số lượng giác
Ví dụ 1. Tìm tập xác định của các hàm số sau:  2x  a) y  sin   b) y  sin x  x 1 Lời giải:
a) ĐK xác định: x  1  TXĐ: D   \   1 Trang 4
b) ĐK xác định: sin x  0  2k  x  2k   1 
Suy ra TXĐ: D  2k ; 2k   1    
Ví dụ 2. Tìm tập xác định và tập giá trị của các hàm số sau: 1 a) 2 y  1 cos x b) y  sin x 1 Lời giải: a) ĐK xác định: 2
1 cos x  0 (luôn đúng)  TXĐ:  Lại có: 2 2
0  cos x  1  0  1  cos x  1  0  y  1  Tập giá trị là T  0,  1    
b) ĐK xác định: sin x 1  0  sin x  1
  sin x    2k  D  R \   2k  2  2  1 1 
Ta có: 0  sin x  1  2  y   Tập giá trị là T  ,     2 2  1  sin x
Ví dụ 3. Tìm tập xác định D của hàm số y  cos x 1   a) D   .
b) D   \   k , k   .  2 
c) D   \ k , k    .
d) D   \ k2, k    . Lời giải:
Hàm số xác định khi và chỉ khi cos x 1  0  cos x  1  x  k2 , k  
Vậy tập xác định D   \ k2 , k    . Chọn D 1
Ví dụ 4. Tìm tập xác định D của hàm số y     sin x     2    
a) D   \ k , k   .
b) D   \ k , k    .  2     c) D   \ 
 1 2k  , k  . d) D   \   1 2k, k    .  2  Lời giải:     
Hàm số xác định  sin x 
 0  x   k  x   k , k      2  2 2  
Vậy tập xác định D   \   k , k   . Chọn C  2  1
Ví dụ 5. Tìm tập xác định D của hàm số y  sin x  cos x    a) D   .
b) D   \   k, k  .  4  Trang 5    
c) D   \   k2 , k  .
d) D   \   k , k  .  4   4  Lời giải: 
Hàm số xác định  sin x  cos x  0  tan x  1  x   k , k   4  
Vậy tập xác định D   \   k , k   . Chọn D  4    
Ví dụ 6. Tìm tập xác định D của hàm số y  cot 2x   sin 2x    4   
a) D   \   k , k   . b) D  Ø .  4    
c) D   \   k , k   . d) D   .  8 2  Lời giải:      k
Hàm số xác định sin 2x   0  2x   k  x   , k      4  4 8 2   
Vậy tập xác định D   \   k , k   . Chọn C  8 2   x  
Ví dụ 7. Tìm tập xác định D của hàm số 2 y  3tan     2 4  3    a) D   \   k2 , k   .
b) D   \   k2 , k  .  2   2  3    c) D   \   k , k  .
d) D   \   k, k   .  2   2  Lời giải:  x   x   3 Hàm số xác định 2  cos 
 0     k  x   k2 , k      2 4  2 4 2 2 3 
Vậy tập xác định D   \ 
 k2 , k   . Chọn A  2 
Ví dụ 8. Tìm tập xác định D của hàm số y  1  sin 2x  1  sin 2x a) D  Ø . b) D   .  5  5 13  c) D   k2 ;  k2 , k    . d) D   k2 ;  k2 , k   . 6 6     6 6    Lời giải: 1   sin 2x  0
Ta có: 1  sin 2x  1   , x    . 1   sin 2x  0
Vậy tập xác định D   . Chọn B Trang 6   
Ví dụ 9. Tìm tập xác định D của hàm số 2
y  5  2cot x  sin x  cot  x    2  k     a) D   \  , k   .
b) D   \   k , k  .  2   2  c) D   .
d) D   \ k , k    . Lời giải:
Hàm số xác định khi và chỉ khi các điều kiện sau thỏa mãn đồng thời   2 
5  2cot x  sin x  0, cot  x 
 xác định và cot x xác định.  2  2 2cot x  0 Ta có: 2 
 5  2cot x  sin x  0, x   
1  sin x  1  5  sin x  0          * cot  x   xác định  sin  x  0 
 x  k  x    k , k      2   2  2 2
* cot x xác định  sin x  0  x  k , k     x    k k
Do đó hàm số xác định   2  x  , k   2 x  k k 
Vậy tập xác định D   \  , k   . Chọn A  2  1 1
Ví dụ 10. Hàm số y  tan x  cot x  
không xác định trong khoảng nào trong các khoảng sin x cos x sau đây?     3  a) k2 ,  k2   với k   . b)   k2 ,  k2   với k   .  2   2     c)  k2 ,   k2   với k   .
d)   k2 , 2  k2  với k   .  2  Lời giải: s  in x  0 k Hàm số xác định  
 sin 2x  0  2x  k  x  , k   . cos x  0 2 3 3 Ta chọn k  3  x  nhưng điểm
thuộc khoảng   k2; 2  k2  . 2 2
Vậy hàm số không xác định trong khoảng   k2; 2  k2  . Chọn D
Dạng 2: Tính chẵn lẻ của hàm số lượng giác
Ví dụ 1. Xét tính chẵn – lẻ của hàm số sau a) y  sin 2x b) y  2sin x  3 Trang 7 Lời giải:
a) f x  sin 2x  sin 2x   f  x . Suy ra hàm số đã cho là hàm lẻ.
b) Ta có f x  2sin x  3  2sin x  3  2sin x  3  9   f  x  9
Suy ra hàm số đã cho không phải là hàm chẵn (lẻ)
Ví dụ 2. Xét tính chẵn – lẻ của hàm số sau a) y  sin x  cos b) y  tan x  cot x Lời giải:
a) f x  sin x  cosx  sin x  cos x  sin x  cos x  2cos x   f  x  2cos x
Suy ra hàm số đã cho không phải là hàm chẵn (lẻ) sin x cos x sin x cos x
b) f x  tan x  cot x       cos x sin x cos sin x
  tan x  cot x  tan x  cot x   f  x
Vậy hàm số đã cho là hàm lẻ .
Ví dụ 3. Xét tính chẵn – lẻ của hàm số sau sin x  tan x 3 cos 1 a) y  b)  x y sin x  cot x 3 sin x Lời giải: sin x  tan x
sin x  tan x sin x  tan x a) Ta có f x         f x
sin x  cot x   sin x  cot x sin x  cot x
Suy ra hàm số đã cho là hàm chẵn. 3 3 cos x 1 cos x 1 b) Ta có f x     
  f x . Suy ra hàm số đã cho là hàm lẻ. 3 sin x 3   sin x
Ví dụ 4. Trong các hàm số sau, hàm số nào là hàm số chẵn a) y  sin x b) y  cos x  sin x c) 2 y  cos x  sin x d) y  cos x sin x Lời giải:
Tất cả các hàm số đề có TXĐ: D   . Do đó x  D  x  D .
Bây giờ ta kiểm tra f x  f  x hoặc f x   f  x
* Với y  f  x  sin x . Ta có f x  sin x  sin x  sin x
 f x   f  x . Suy ra hàm số y  sin x là hàm số lẻ.
* Với y  f  x  cos x  sin x . Ta có:..
 f x   f x, f x. Suy ra hàm số f x  cos x  sin x không chẵn không lẻ. * Với y  f  x 2
 cos x  sin x . Ta có f x  x 2 cos  sin x Trang 8 
x   x 2  x    x2 2 cos sin cos sin  cos x  sin x
 f x  f x . Suy ra hàm số 2
y  cos x  sin x là hàm chẵn. Chọn C.
* Với y  f  x  cos xsin x . Ta có f x  cosx.sin x   cos xsin x
 f x   f x . Suy ra hàm số y  cos xsin x là hàm số lẻ.
Ví dụ 5. Trong các hàm số sau, hàm số nào là hàm số chẵn? a) y  sin 2x b) y  x cos x tan c) y  cos . x cot x d)  x y sin x Lời giải:
* Xét hàm số y  f  x  sin 2x .
TXĐ: D   . Do đó x  D  x  D .
Ta có f x  sin 2x  sin 2x   f  x  f x là hàm số lẻ.
* Xét hàm số y  f  x  x cos x .
TXĐ: D   . Do đó x  D  x  D .
Ta có: f x  x.cosx  x cos x   f x  f  x là hàm số lẻ.
* Xét hàm số y  f  x  cos x cot x
TXĐ: D   \ k k  . Do đó x  D  x  D .
Ta có f x  cosx.cot x  cos xcot x   f  x  f  x là hàm số lẻ.
* Xét hàm số    tan  x y f x sin x   
TXĐ: D   \ k k   . Do đó x  D  x  D .  2  tan x  tan x tan x Ta có f x     
 f x  f x là hàm số chẵn. Chọn D. sin x     sin x sin x
Ví dụ 6. Trong các hàm số sau, hàm số nào là hàm số chẵn? a) y  sin x b) 2 y  x sin x c)  x y d) y  x  sin x cos x Lời giải:
Dựa vào các dấu hiệu nhận biết hàm chẵn lẻ ở phần lí thuyết ta dễ dàng thấy rằng ở phương án A là hàm
số chẵn, các đáp án B, C, D là hàm số lẻ. Chọn A.
Ví dụ 7. Trong các hàm số sau, hàm số nào là hàm số lẻ? Trang 9 a) 2 y  cos x  sin x . b) y  sin x  cos x . c) y   cos x . d) y  sin . x cos 3x . Lời giải:
Dựa vào các dấu hiệu nhận biết hàm chẵn lẻ ở phần lí thuyết ta dễ dàng thấy rằng ở phương án A và C là
các hàm số chẵn. Đáp án B là hàm số không chẵn, không lẻ. Đáp án D là hàm số lẻ. Chọn D.
Ví dụ 8. Cho hàm số f  x  sin 2x và g  x 2
 tan x . Chọn mệnh đề đúng
a) f  x là hàm số chẵn, g  x là hàm số lẻ.
b) f  x là hàm số lẻ, g  x là hàm số chẵn.
c) f  x là hàm số chẵn, g  x là hàm số chẵn. d) f  x và g  x đều là hàm số lẻ. Lời giải:
* Xét hàm số f  x  sin 2x .
TXĐ: D   . Do đó x  D  x  D .
Ta có f x  sin 2x  sin 2x   f  x  f x là hàm số lẻ. * Xét hàm số g  x 2  tan x  
TXĐ: D   \   k k  . Do đó x  D  x  D .  2 
Ta có g x   x 2     x2 2 tan tan
 tan x  g x  f x là hàm số chẵn. Chọn B. cos 2x sin 2x  cos 3x
Ví dụ 9. Cho hai hàm số f  x  và g  x  . 2 1 sin 3x 2 2  tan x
Mệnh đề nào sau đây là đúng?
a) f  x lẻ và g  x chẵn.
b) f  x và g  x chẵn.
c) f  x chẵn, g  x lẻ.
d) f  x và g  x lẻ. Lời giải: cos 2x
* Xét hàm số f  x  2 1  sin 3x
TXĐ: D   . Do đó x  D  x  D . cos 2  x cos 2x Ta có f x    
 f x  f x là hàm số chẵn. 2 1 sin  3  x 2     1 sin 3x sin 2x  cos3x
* Xét hàm số g  x  . 2 2  tan x  
TXĐ: D   \   k k  . Do đó x  D  x  D .  2  sin 2x  cos 3  x sin 2x  cos3x Ta có g x  
 g x  g x là hàm số chẵn. 2 2  tan x 2     2  tan x
Vậy f  x và g  x chẵn. Chọn B. Trang 10
Dạng 3: Chu kì của hàm số lượng giác
Ví dụ 1. Mệnh đề nào sau đây là sai?
a) Hàm số y  sin x tuần hoàn với chu kì 2 .
b) Hàm số y  cos x tuần hoàn với chu kì 2 .
c) Hàm số y  tan x tuần hoàn với chu kì 2 .
d) Hàm số y  cot x tuần hoàn với chu kì  . Lời giải:
Vì hàm số y  tan x tuần hoàn với chu kì  . Chọn C.
Ví dụ 2. Trong các hàm số sau đây, hàm số nào không tuần hoàn? a) y  cos x . b) y  cos 2x . 1 c) 2 y  x cos x . d) y  . sin 2x Lời giải:
* Hàm số y  cos x tuần hoàn với chu kì T  2 .
* Hàm số y  cos 2x tuần hoàn với chu kì T   . 1 * Hàm số y 
tuần hoàn với chu kì T   . sin 2x * Hàm số 2
y  x cos x không phải là hàm tuần hoàn. Chọn C.   
Ví dụ 3. Tìm chu kì T của hàm số y  sin 5x     4  2 5 a) T  b) T  5 2   c) T  d) T  2 8 Lời giải: 2
Hàm số y  sin ax  b tuần hoàn với chu kì T  . a    2
Áp dụng: Hàm số y  sin 5x  
 tuần hoàn với chu kì T  . Chọn A.  4  5  x 
Ví dụ 4. Tìm chu kì T của hàm số y  cos  2016    2  a) T  4 b) T  2 c) T  2 d) T   Lời giải: Trang 11 2
Hàm số y  cos ax  b tuần hoàn với chu kì T  a  x 
Áp dụng: Hàm số y  cos  2016 
 tuần hoàn với chu kì T  4 . Chọn A.  2 
Ví dụ 5. Tìm chu kì T của hàm số  cos 2  x y x sin . 2 a) T  4 . b) T   .  c) T  2 . d) T  . 2 Lời giải: 2
Hàm số y  cos 2x tuần hoàn với chu kì T    . 1 2 2 Hàm số  x
y sin tuần hoàn với chu kì T   4 2 2 1 2 Suy ra hàm số  cos 2  x y
x sin tuần hoàn với chu kì T  4 . Chọn A. 2
Nhận xét. T là bội chung nhỏ nhất của T và T . 1 2
Ví dụ 6. Tìm chu kì T của hàm số y  cos3x  cos 5x . a) T   b) T  3 c) T  2 d) T  5 Lời giải: 2
Hàm số y  cos3x tuần hoàn với chu kì T  . 1 3 2
Hàm số y  cos5x tuần hoàn với chu kì T  . 2 5
Suy ra hàm số y  cos3x  cos 5x tuần hoàn với chu kì T  2 . Chọn C.      
Ví dụ 7. Tìm chu kì T của hàm số y  sin 2x   2cos 3x      .  3   4  a) T  2 . b) T   . c) T  3 . d) T  4 . Lời giải:    2 Hàm số y  sin 2x  
 tuần hoàn với chu kì T    .  3  1 2    2 Hàm số y  2cos 3x  
 tuần hoàn với chu kì T  .  4  2 3      
Suy ra hàm số y  sin 2x   2cos 3x    
 tuần hoàn với chu kì T  2 . Chọn A  3   4  Trang 12
Ví dụ 8. Tìm chu kì T của hàm số y  tan 3x  cot x . a) T  4 . b) T   .  c) T  3 . d) T  . 3 Lời giải: 
Hàm số y  cot ax  b tuần hoàn với chu kì T  a 
Áp dụng: Hàm số y  tan 3x tuần hoàn với chu kì T  . 1 3
Hàm số y  cot x tuần hoàn với chu kì T   . 2
Suy ra hàm số y  tan 3x  cot x tuần hoàn với chu kì T   . Chọn B.
Nhận xét. T là bội chung nhỏ nhất của T và T . 1 2 x
Ví dụ 9. Tìm chu kì T của hàm số y  cot  sin 2x 3 a) T  4 . b) T   .  c) T  3 . d) T  . 3 Lời giải: Hàm số  x
y cot tuần hoàn với chu kì T  3 . 3 1
Hàm số y  sin 2x tuần hoàn với chu kì T   . 2 x
Suy ra hàm số y  cot  sin 2x tuần hoàn với chu kì T  3 . Chọn C. 3
Ví dụ 10. Tìm chu kì T của hàm số 2 2 y  2sin x  3cos 3x a) T   . b) T  2 .  c) T  3 . d) T  . 3 Lời giải: 1 cos 2x 1  cos 6x 1 Ta có y  2.  3.
 3cos6x  2cos 2x  5 2 2 2 2 
Hàm số y  3cos6x tuần hoàn với chu kì T   . 1 6 3 Hàm số y  2
 cos 2x tuần hoàn với chu kì T   . 2
Suy ra hàm số đã cho tuần hoàn với chu kì T   . Chọn A.
Ví dụ 11. Tìm chu kì T của hàm số 2 y  tan 3x  cos 2x Trang 13  a) T   . b) T  . 3  c) T  . d) T  2 . 2 Lời giải: 1 cos 4x 1 Ta có y  tan 3x 
 2 tan 3x  cos 4x   1 . 2 2 
Hàm số y  2 tan 3x tuần hoàn với chu kì T  . 1 3 2 
Hàm số y   cos 4x tuần hoàn với chu kì T   . 2 4 2
Suy ra hàm số đã cho tuần hoàn với chu kì T   . Chọn C.
Ví dụ 12. Hàm số nào sau đây có chu kì khác 2 ? a) 3 y  cos x . b)  x x y sin cos . 2 2  x  c) 2 y  sin  x  2 . d) 2 y  cos 1   .  2  Lời giải: 1 Hàm số 3
y  cos x  cos3x  3cos x có chu kì là 2 . 4 x x 1
Hàm số y  sin cos  sin x có chu kì là 2 . 2 2 2 1 1 Hàm số 2
y  sin  x  2   cos2x  4 có chu kì là  . 2 2  x  1 1 Hàm số 2 y  cos 1   cos  
x  2 có chu kì là 2 . Chọn C.  2  2 2
Ví dụ 13. Hai hàm số nào sau đây có chu kì khác nhau? a) y  cos x và  x y cot .
b) y  sin x và y  tan 2x . 2 c)  x y sin và  x y cos .
d) y  tan 2x và y  cot 2x . 2 2 Lời giải: Hàm số y  cos x và  x
y cot có cùng chu kì là 2 . 2 
Hàm số y  sin x có chu kì là 2 , hàm số y  tan 2x có chu kì là . 2  Hàm số y  sin và  x
y cos có cùng chu kì là 4 . 2 2 Trang 14 
Hàm số y  tan 2x và y  cot 2x có cùng chu kì là . Chọn B. 2
Dạng 4: Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác * Miền giá trị:  kx   kx 2   kx 2 1 sin 1; 1 cos 1; 0 sin
 1; 0  cos kx  1 * Với hàm số 2 2 2 2 y  . a sin x  .
b cos x   a  b  y  a  b . a sin x  . b cos x  c * Với hàm số y 
 nhân chéo và đưa về trường hợp trên để tìm miền giá trị. . m sin x  . n cos x  p
Ví dụ 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: a) 2 y  4sin  4sin x  3 b) 2 y  cos x  2sin x  2 Lời giải: a) y  x  x    x  2 2 4sin 4sin 3 2sin 1  2 Ta có:   x     x      x  2 1 sin 1 3 2sin 1 1 0 2sin 1  9  2  y  9   max y  9  sin x  1   x    2  k  2   k,l  1  5   min y  2  sin x   x   2l , x   2   l  2 6 6 b) y  x  x    x  x     x  2 2 2 cos 2sin 2 sin 2sin 3 4 sin 1 Ta có:   x     x      x  2 1 sin 1 2 sin 1 0 0 2sin 1  4  0  y  4  
max y  4  sin x  1  x   2  k  2   k,l    min y  0  sin x  1   x    2   l  2
Ví dụ 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: a) 4 2 y  sin x  2 cos x 1 b) y  3 sin 2x  cos 2x Lời giải: a) y  x  x   x  x    x  2 4 2 4 2 2 sin 2cos 1 sin 2sin 1 sin 1  2 Ta có:  x    x       x  2 2 2 2 0 sin 1 1 sin 1 2 1 sin 1  2  1  y  2   2
max y  2  sin x  1  x    2k   2 k,l  2
min y  1 sin x  0  x  l
b) Áp dụng bất đẳng thức Bunhiacopxki ta có: Trang 15 y   x 
x2   2   2 2  2 2 3 sin 2 cos 2 3 1 sin x  cos x  4  2   y  2  sin 2x cos 2x  max y  2    0  x   k  3 1 6   k,l  sin 2x cos 2x  min y  2     0  x    k  3 1 6
Ví dụ 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  sin x  3 cos x  3 Lời giải:
Áp dụng bất đẳng thức Bunhiacopxki ta có  x
x2      2 2  2 2 sin 3 cos 1 3
sin x  cos x  4  2  sin x  3 cos x  2  1  y  5  sin x cos x  max y  5    0  x   2  k  1 3 6   k,l  sin x cos x 5   min y  1    0  x    2k  1 3 6   
Ví dụ 4. Cho hàm số y  2  sin x   2  
. Mệnh đề nào sau đây là đúng?  3  a) y  4, x   . b) y  4, x   . c) y  0, x   . d) y  2, x   . Lời giải:       Ta có: 1  sin x   1  2  2  sin x   2      3   3      4  2  sin x   2  0  4  y  0   . Chọn C.  3 
Ví dụ 5. Hàm số y  5  4sin 2x cos 2x có tất cả bao nhiêu giá trị nguyên? a) 3. b) 4. c) 5. d) 6. Lời giải:
Ta có y  5  4sin 2x cos 2x  5  2sin 4x .
Mà 1  sin 4x  1  2
  2sin 4x  2  3  5  2sin 4x  7 3 7      y y   y 3; 4; 5; 6; 
7 nên y có 5 giá trị nguyên. Chọn C   
Ví dụ 6. Hàm số y  sin x   sin  
x có tất cả bao nhiêu giá trị nguyên?  3  a) 1. b) 2. c) 3. d) 4. Lời giải: Trang 16  
Áp dụng công thức sin  sin  a b a b a b 2 cos sin , ta có 2 2           sin x   sin x  2cos x  sin  cos x         3   6  6  6     Ta có 1  cos   1  1    1   y x y     1; 0;  1 . Chọn C  6  Ví dụ 7. Hàm số 4 4
y  sin x  cos x đạt giá trị nhỏ nhất tại x  x . Mệnh đề nào sau đây là đúng? 0 a) x  k2 , k   . b) x  k , k   . 0 0 
c) x    k2 , k   . d) x   k , k   . 0 0 2 Lời giải: Ta có 4 4 y  x  x   2 2 x  x 2 2 sin cos sin cos
sin x  cos x  cos 2x .
Mà 1  cos 2x  1  1
   cos 2x  1  1  y  1
Do đó giá trị nhỏ nhất của hàm số là -1.
Đẳng thức xảy ra  cos 2x  1  2x  k2  x  k k   . Chọn B   
Ví dụ 8. Tìm giá trị lớn nhất M của hàm số 2 y  4sin x  2 sin 2x    .  4  a) M  2 . b) M  2 1. c) M  2  1. d) M  2  2 . Lời giải:    1 cos 2x  Ta có 2 y  4sin x  2 sin 2x   4  sin 2x  cos 2     x  4   2    
 sin 2x  cos 2x  2  2 sin 2x   2   .  4        Mà 1  sin 2x 
 1   2  2  2 sin 2x   2  2  2     .  4   4 
Vậy giá trị lớn nhất của hàm số là 2  2 . Chọn D.
Ví dụ 9. Tìm tập giá trị T của hàm số 6 6 y  sin x  cos x 1  a) T  0; 2. b) T  ; 1  . 2    1   1  c) T  ; 1  . d) T  0; . 4     4   Lời giải: 2 Ta có 6 6 y  x  x   2 2 x  x 2 2  x x  2 2 sin cos sin cos 3sin cos sin x  cos x Trang 17 3 3 1 cos 4x 5 3 2 2 2
 1 3sin x cos x  1 sin 2x  1 .   cos 4x . 4 4 2 8 8 1 5 3 1 Mà 1  cos 4x  1 
  cos 4x  1   y  1. Chọn C 4 8 8 4
Ví dụ 10. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  8sin x  3cos 2x . Tính 2 P  2M  m . a) P  1. b) P  2 . c) P  112 . d) P  130 . Lời giải: Ta có 2 2 y  x  x  x   2  x 2 8sin 3cos 2 8sin 3 1 2sin  2sin x  3 . Mà 2 2
1  sin  1  0  sin x  1  3  2sin x  3  5 M  5 2  3  y  5  
 P  2M  m  1. Chọn A. m  3
Ví dụ 11. Tìm giá trị nhỏ nhất m của hàm số 2 y  2sin x  3 sin 2x . a) m  2  3 . b) m  1. c) m  1. d) m   3 . Lời giải: Ta có 2
y  2sin x  3 sin 2x  1  cos 2x  3 sin 2x  3 1 
 3 sin 2x  cos 2x 1  2 sin 2x  cos 2x  1  2 2          
 2 sin 2x cos  sin cos 2x 1  2sin 2x  1      6 6   6        Mà 1  sin 2x   1  1   1  2sin 2x   3  1   y  3     .  6   6 
Do đó giá trị nhỏ nhất của hàm số là -1. Chọn B. Trang 18 BÀI TẬP TỰ LUYỆN 1  sin x
Câu 1. Tìm tập xác định D của hàm số y  cos x 1   A. D   .
B. D   \   k , k  .  2 
C. D   \k , k    .
D. D   \ k2 , k    . 1
Câu 2. Tìm tập xác định D của hàm số y     sin x     2    
A. D   \ k , k   .
B. D   \ k , k    .  2     C. D   \ 
 1 2k  , k   . D. D   \   1 2k, k    .  2    
Câu 3. Tìm tập xác định D của hàm số y  cot 2x   sin 2x   .  4   
A. D   \   k , k   . B. D  Ø .  4    
C. D   \   k , k   . D. D   .  8 2   x  
Câu 4. Tìm tập xác định D của hàm số 2 y  3tan    .  2 4  3    A. D   \   k2 , k   .
B. D   \   k2 , k  .  2   2  3    C. D   \   k , k  .
D. D   \   k, k   .  2   2  3 tan x  5
Câu 5. Tìm tập xác định D của hàm số y  . 2 1 sin x    
A. D   \   k2 , k  .
B. D   \   k , k   .  2   2 
C. D   \   k , k    .
D. cos x  1  sin x  0  x  k , k   .
Câu 6. Tìm tập xác định D của hàm số y  sin x  2 A. D   .
B. D  2;   . C. D  0; 2  . D. D  Ø . 1
Câu 7. Tìm tập xác định D của hàm số y  1 sin x Trang 19  
A. D   \ k , k    .
B. D   \   k , k   .  2   
C. D   \   k2 , k  . D. D  Ø .  2  1  cos x
Câu 8. Tập xác định của hàm số y  là sin x 1  
A.  \   k k   . B.  \ k k    .  2    C.  \ k2 k    .
D.  \   k2 k  .  2  cot x
Câu 9. Tập xác định của hàm số y  là cos x 1 k  k  A. D   \  , k  . B. D   \   k , k  .  2   2 
C. D   \ k , k    .
D. D   \ k2 , k    .
Câu 10. Tập xác định của hàm số f  x 1  là 1 cos x    A. D   \   2k   1 , k   . B. D   \   2k  1 , k    .  2 
C. D   \ k , k    .
D. D   \ k2 , k    .
Câu 11. Tìm tập xác định D của hàm số y  cot x  sin 5x  cos x .    
A.  \   k k   .
B.  \   k2 k   .  2   2  C.  \ k k    . D.  \ k2 k    .
Câu 12. Tìm tập giá trị của hàm số y  2cos 3x  1. A. 3;  1 . B. 3;   1 . C. 1;  3 . D. 1;  3 . 3sin x
Câu 13. Tìm tập xác định D của hàm số y  2cos x  1   4   2 
A. D   \   k2 ,  k2 , k   . B. D   \   k2 , k  .  3 3   3   5     C. D   \   k2 , k  .
D. D   \   k2 , k   .  6   3  tan x
Câu 14. Tìm điều kiện xác định của hàm số y  cos x 1 Trang 20         x k x   k  A. x  k 2 . B. x   k2 . C.  2 . D. 2  . 3   x  k2 x   k  3 2 cos x
Câu 15. Tìm điều kiện để hàm số y  có nghĩa. sin x 1  A. x   k k  .
B. x  k2 k   . 2  C. x   k2 k   .
D. x  k k  . 2 sin x  1
Câu 16. Tìm tập xác định của hàm số y  là sin x  2 A. 2;   . B.  . C. 2;   . D.  \   2 .
Câu 17. Trong các hàm số sau đây, hàm số nào có tập xác định là  ? tan x A. y  1 sin 2x . B. y  . C. y  sin x  cot 2x . D. y  sin x . 2 cos x  1
Câu 18. Tìm tập giá trị của hàm số y  cos2x   1 là A. 1;  1 . B. 1;  1 . C.  . D. 2; 2 . cot x
Câu 19. Tìm tập xác định của hàm số y   sin 3x . 2 1 sin x k  A.  \  , k   .
B.  \ k, k   .  2      
C.  \   k2 , k  .
D.  \   k2 , k    2   2  2 cos 3x 1
Câu 20. Tìm tập xác định của hàm số y  là cos x  1
A. D   \   k k    .
B. D   \k2 k    .  
C. D   \   k k  .
D. D   \  k2 k    .  2  x 
Câu 21. Tìm tập xác định của hàm số f  x sin 2 2  1 cos x A. D   .
B. D   \ k2, k   .
C. D  k2, k  .
D. D   \k, k  .
Câu 22. Trong các hàm số sau, hàm số nào là hàm số chẵn? A. y  sin x . B. y  cos x . C. y  tan x . D. y  cot x .
Câu 23. Trong các hàm số sau, hàm số nào là hàm số chẵn? Trang 21 A. y   sin x . B. y  cos x  sin x . C. 2 y  cos x  sin x . D. y  cos x sin x .
Câu 24. Trong các hàm số sau, hàm số nào là hàm số chẵn? tan x A. y  sin 2x . B. y  x cos x . C. y  cos x cot x . D. y  . sin x
Câu 25. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?    A. y  sin x cos 2x . B. 3 y  sin x cos x    .  2  tan x C. y  . D. 3 y  cos x sin x . 2 tan x  1
Câu 26. Trong các hàm số sau, hàm số nào là hàm số lẻ? A. 2 y  cos x  sin x . B. y  sin x  cos x . C. y   cos x . D. y  sin x cos 3x .
Câu 27. Trong các hàm số sau, hàm số nào là hàm số lẻ?    cot x tan x A. y  sin  x   . B. 2 y  sin x . C. y  . D. y  .  2  cos x sin x
Câu 28. Trong các hàm số sau, hàm số nào là hàm số lẻ? A. 2 y  1  sin x . B. 2 y  cot x .sin x . C. 2 y  x tan 2x  cot x .
D. y  1  cot x  tan x .
Câu 29. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ? 1    A. y  . B. y  sin x  . 3   sin x  4     C. y  2 cos x    . D. y  sin 2x .  4 
Câu 30. Mệnh đề nào sau đây là sai?
A. Đồ thị hàm số y  sin x đối xứng qua gốc tọa độ O.
B. Đồ thị hàm số y  cos x đối xứng qua trục Oy.
C. Đồ thị hàm số y  tan x đối xứng qua truc Oy.
D. Đồ thị hàm số y  tan x đối xứng qua gốc tọa độ O.
Câu 31. Trong các hàm số sau, hàm số nào là hàm số lẻ?       A. 4 y  x  cos x    . B. 2017 y  x  cos x    .  3   2  C. 2018 y  2015  cos x  sin x . D. 2017 2018 y  tan x  sin x .
Câu 32. Mệnh đề nào sau đây là sai?
A. Hàm số y  sin x tuần hoàn với chu kì 2 .
B. Hàm số y  cos x tuần hoàn với chu kì 2 . Trang 22
C. Hàm số y  tan x tuần hoàn với chu kì 2 .
D. Hàm số y  cot x tuần hoàn với chu kì  .
Câu 33. Trong các hàm số sau, hàm số nào là hàm số tuần hoàn? sin x A. y  sin x . B. y  x  sin x . C. y  x cos x . D. y  . x  x 
Câu 34. Tìm chu kì T của hàm số y  cos  2016    2  A. T  4 . B. T  2 . C. T  2 . D. T   . 1
Câu 35. Tìm chu kì T của hàm số y   sin 100 x  50  . 2 1 1  A. T  . B. T  . C. T  . D. 2 T  200 . 50 100 50      
Câu 36. Tìm chu kì T của hàm số y  sin 2x   2cos 3x       3   4  A. T  2 . B. T   . C. T  3 . D. T  4 . x   
Câu 37. Tìm chu kì T của hàm số y  sin  tan 2x    . 2  4  A. T  4 . B. T   . C. T  3 . D. T  2 .
Câu 38. Tìm chu kì T của hàm số 2 y  2cos x  2017 . A. T  3 . B. T  2 C. T   . D. T  4 .
Câu 39. Hàm số nào sau đây có chu kì khác  ?       A. y  sin  2x   . B. y  cos 2 x    . C. y  tan 2x   1 . D. y  cos . x sin x .  3   4     Câu 40. Với x  0; 
 , mệnh đề nào sau đây là đúng?  4 
A. Cả hai hàm số y   sin 2x và y  1
  cos 2x đều nghịch biến.
B. Cả hai hàm số y   sin 2x và y  1
  cos 2x đều đồng biến.
C. Hàm số y   sin 2x nghịch biến, hàm số y  1
  cos 2x đồng biến.
D. Hàm số y   sin 2x đồng biến, hàm số y  1
  cos 2x nghịch biến.
Câu 41. Hàm số y  sin 2x đồng biến trên khoảng nào trong các khoảng sau?        3   3  A. 0;   . B. ;    . C.  ;   . D. ; 2   .  4   2   2   2     
Câu 42. Trong các hàm số sau, hàm số nào đồng biến trên khoảng  ;    3 6              A. y  tan 2x    . B. y  cot 2x    . C. y  sin 2x    . D. y  cos 2x    .  6   6   6   6  Trang 23
Câu 43. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y  3sin x  2 A. M  1; m  5 . B. M  3; m  1. C. M  2; m  2 . D. M  0; m  2  .
Câu 44. Tìm tập giá trị T của hàm số y  3cos 2x  5 . A. T  1;  1 . B. T  1; 1  1 . C. T  2; 8. D. T  5;  8 .
Câu 45. Tìm tập giá trị T của hàm số y  5  3sin x . A. T  1;  1 . B. T   3  ;  3 . C. T  2; 8. D. T  5;  8 .    Câu 46. Cho hàm số y  2  sin x   2  
. Mệnh đề nào sau đây đúng?  3  A. y  4  , x   B. y  4, x   C. y  0, x    D. y  2, x    1
Câu 47. Tìm giá trị nhỏ nhất m của hàm số y  cos x  1 1 1 A. m  . B. m  . C. m  1. D. m  2 . 2 2
Câu 48. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  sin x  cos x . Tính P  M  m . A. P  4 . B. P  2 2 . C. P  2 . D. P  2 .
Câu 49. Tập giá trị T của hàm số y  sin 2017x  cos 2017x . A. T   2  ; 2 .
B. T  4034; 4034 . C. T   2; 2     . D. T 0; 2   .
Câu 50. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y  1  2 cos 3x A. M  3; m  1. B. M  1; m  1. C. M  2; m  2 . D. M  0; m  2  .
Câu 51. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  8sin x  3cos 2x . Tính 2 2M  m A. 1. B. 2. C. 112. D. 130.
Câu 52. Tìm giá trị nhỏ nhất m của hàm số 2 y  2sin x  3 sin 2x A. 2  3 . B. -1. C. 1. D.  3 .
Câu 53. Tìm giá trị nhỏ nhất m của hàm số y  12sin x  5cos x A. 1;  1 . B. 7; 7 . C. 13; 1  3 . D. 17; 17 .
Câu 54. Tìm giá trị lớn nhất của hàm số y  4sin 2x  3cos 2x A. 3. B. 1. C. 5. D. 4.
Câu 55. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  sin x  4sin x  5. Tính 2 M  2m A. 1. B. 7. C. 8. D. 2. Trang 24 Câu 56. Hàm số 2
y  cos x  cos x có tất cả bao nhiêu giá trị nguyên? A. 1. B. 2. C. 3. D. 4.
Câu 57. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 4 2 y  sin x  2cos x  1 A. M  2, m  2  . B. M  1, m  0 . C. M  4, m  1  . D. M  2, m  1  .
Câu 58. Tìm giá trị nhỏ nhất của hàm số 4 y  4sin x  cos 4x A. -3 B. -1 C. 3 D. -5
Câu 59. Cho hàm số f  x  cos 2x  cos x 1. Giá trị nhỏ nhất của hàm số trên  là A. f  x 1 min   . B. f  x 1 min   . C. f  x 1 min  . D. f  x 1 min  . 8 4 8 4 3 sin x
Câu 60. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  . Tính M. m. cos x  2 A. 2. B. 0. C. -2. D. -1. sin x  cos x 1
Câu 61. Tìm giá trị nhỏ nhất của hàm số y  . sin x  cos x  2 3   5 1 2  6 A. . B. 1. C.  . D. . 2 3 2 sin x  2 cos x  3
Câu 62. Tìm giá trị lớn nhất của biểu thức P  . 2sin x  cos x  4 9 2 A. 2. B. 3. C. . D. . 11 11 sin x  cos x
Câu 63. Tìm giá trị nhỏ nhất và lớn nhất của hàm số y  lần lượt là 2sin x  cos x  3 1 1 A. m  1; M  . B. m  1  ; M  2 . C. m   ; M  1. D. m  1; M  2 . 2 2 sin x  2cos x 1
Câu 64. Tìm giá trị lớn nhất M của hàm số y  . sin x  cos x  2 A. M  2 . B. M  3 . C. M  3 . D. M  1. 1 3
Câu 65. Gọi T là tập giá trị của hàm số 2
y  sin x  cos 2x  3. Tìm tổng các giá trị nguyên của T 2 4 A. 4. B. 6. C. 7. D. 3. cos x  1   
Câu 66. Tập giá trị của hàm số y  trên 0; sin x  1  2    1  1   1  A. ; 2  B. 0; 2 C. ; 2   D. ; 2   2    2   2  1 1
Câu 67. Tìm giá trị lớn nhất của hàm số 2 2 y  1  cos x  5  2sin x 2 2 Trang 25 11 5 22 A. B. 1 5 C. 1 D. 2 2 2 1 msin x Câu 68. Cho hàm số y 
. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 0; 10 để cos x  2
giá trị nhỏ nhất của hàm số nhỏ hơn -2? A. 1. B. 9. C. 3. D. 6.
Câu 69. Có bao nhiêu giá trị nguyên của m để phương trình 3sin x  m 1  0 có nghiệm? A. 7. B. 6. C. 3. D. 5.
Câu 70. Có bao nhiêu giá trị nguyên của tham số m để hàm số y  5  msin x  m   1 cos x xác định trên  ? A. 5. B. 8. C. 7. D. 6.
Câu 71. Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm 2017 được cho bởi    một hàm số y  4sin t  60 10, t  
 và 0  t  365 . Vào ngày nào trong năm thành phố A có 178   
nhiều giờ có ánh sáng mặt trời nhất? A. 28 tháng 5 B. 29 tháng 5 C. 30 tháng 5 D. 31 tháng 5
Câu 72. Hàng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h(m) của mực nước trong  t  
kênh tính theo thời gian t(h) được cho bởi công thức h  3cos  12  
. Mực nước của kênh cao  8 4  nhất khi A. t  13h B. t  14h C. t  15h D. t  16h
Câu 73. Hàng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h(m) của mực nước trong  t  
kênh tính theo thời gian t(h) được cho bởi công thức h  3cos  12  
. Khi nào mực nước của  6 3 
kênh là cao nhất với thời gian ngắn nhất? A. t  22h . B. t  15h . C. t  14h . D. t  10h .
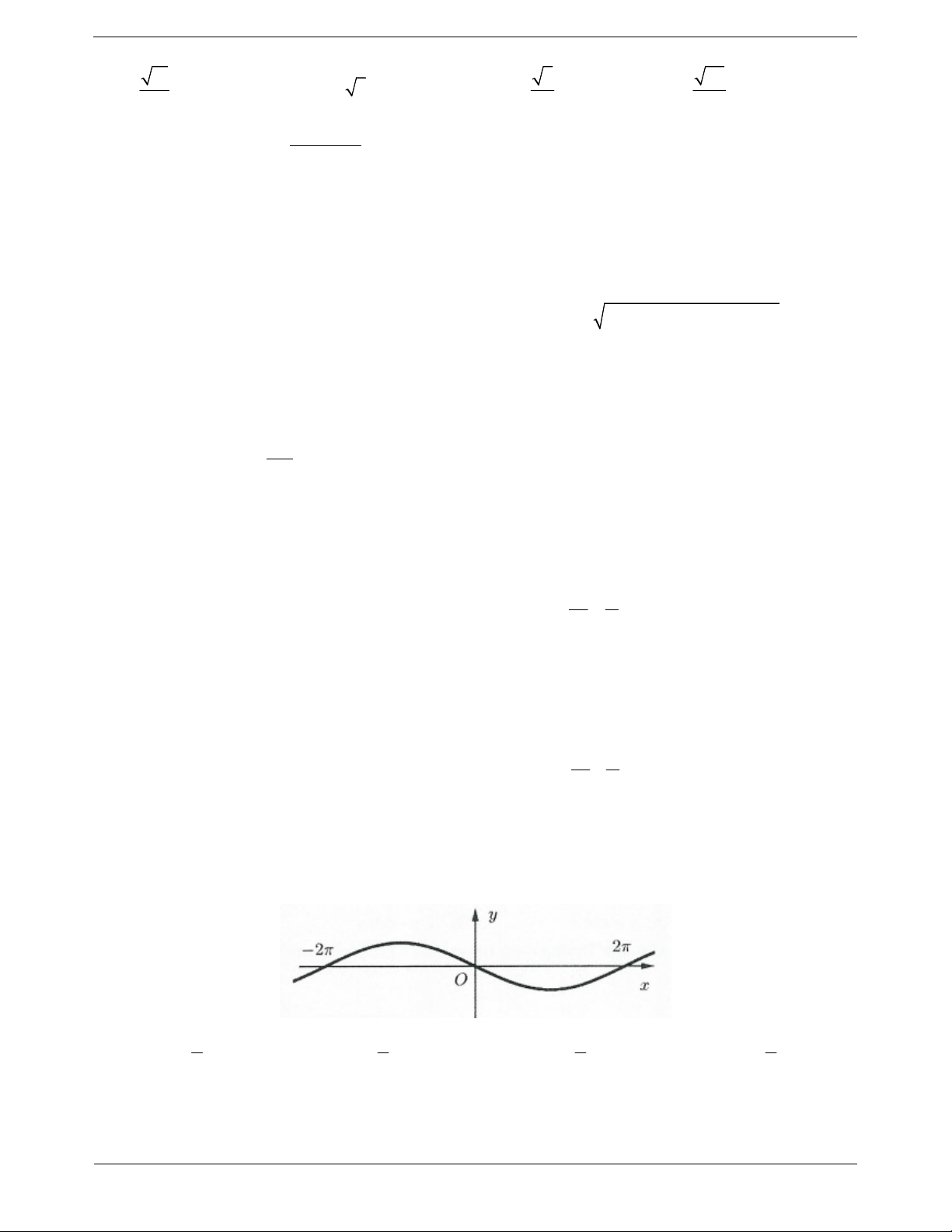
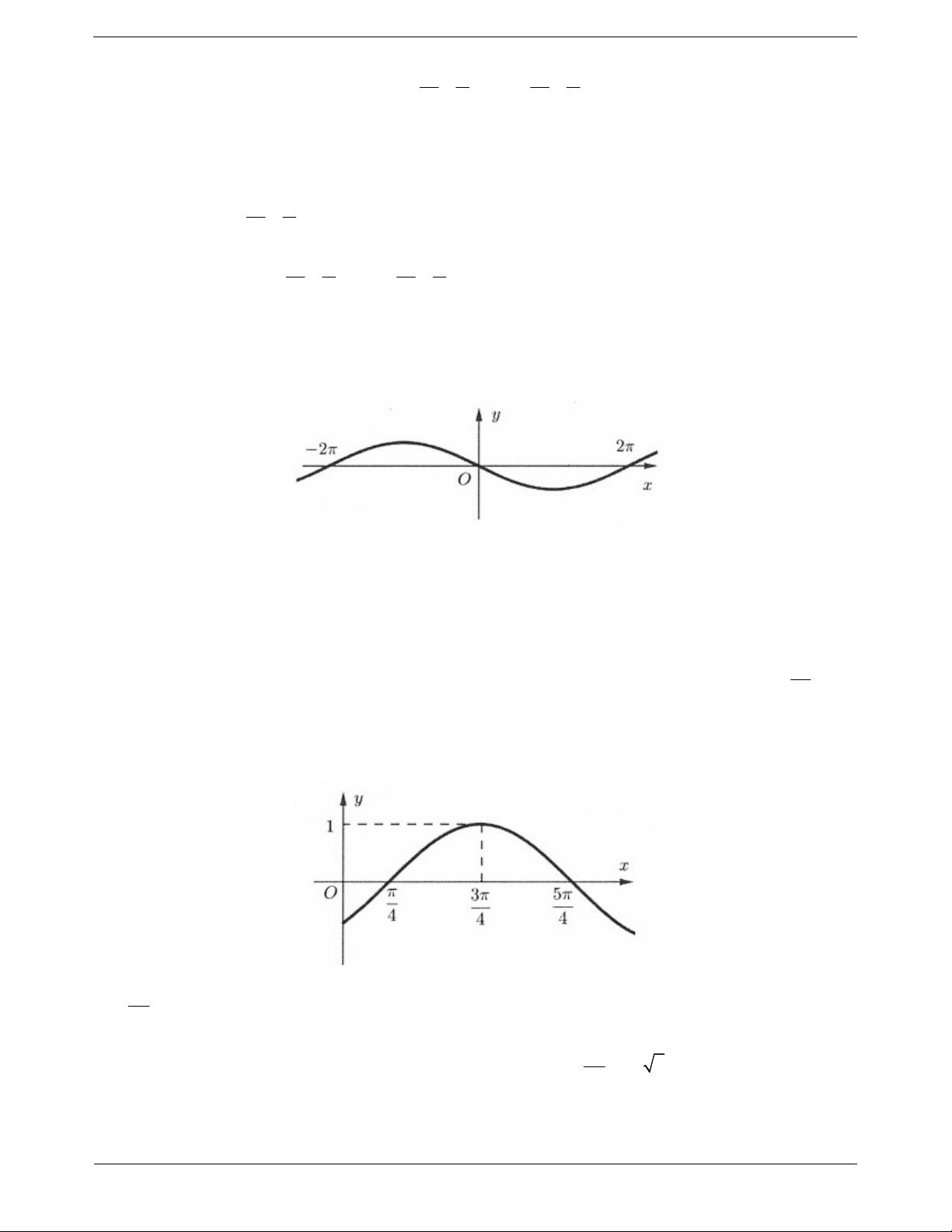
Câu 74. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây? x x x  x  A. y  sin B. y  cos C. y   cos D. y  sin    2 2 4  2 
Câu 75. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây? Trang 26 2x 2x 3x 3x A. y  cos B. y  sin C. y  cos D. y  sin 3 3 2 2
Câu 76. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?     3        A. y  sin x    B. y  cos x    C. y  2 sin x    D. y  cos x     4   4   4   4 
Câu 77. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?             A. y  sin x    B. y  cos x    C. y  2 sin x    D. y  2 cos x     4   4   4   4 
Câu 78. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây? A. y  sin x B. y  sin x C. y  sin x D. y  sin x
Câu 79. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây? Trang 27 A. y  cos x B. y   cos x C. y  cos x D. y  cos x
Câu 80. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây?       A. y  sin x  1   B. y  2sin x     2   2        C. y  sin x  1   D. y  sin x  1    2   2 
Câu 81. Đường cong trong hình vẽ là đồ thị của hàm số nào trong các hàm số dưới đây? A. y  1  sin x B. y  sin x C. y  1  cos x D. y  1 sin x  
Câu 82. Cho hàm số y  f  x xác định trên  \   k , k   và có đồ thị như hình vẽ bên. Hỏi hàm  2 
số y  f  x là hàm số nào trong các hàm số sau đây? A. y  tan x B. y  cos x C. y  sin x D. y  cot x Trang 28
Câu 83. Hãy nêu tất cả các hàm số trong các hàm số y  sin x, y  cos x, y  tan x, y  cot x thỏa mãn   
điều kiện đồng biến và nhận giá trị âm trong khoảng  ; 0    2  A. y  tan x B. y  cos x, y  cot x C. y  tan x, y  sin x D. y  cos x, y  tan x
Câu 84. Hình chữ nhật ABCD có hai đỉnh A, B thuộc trục Ox, hai đỉnh C, D thuộc đồ thị hàm số 2
y  cos x (như hình vẽ). Biết rằng AB 
. Diện tích hình chữ nhật ABCD bằng bao nhiêu? 3 2  2  2 2 A. B. C. D. 3 3 3 3
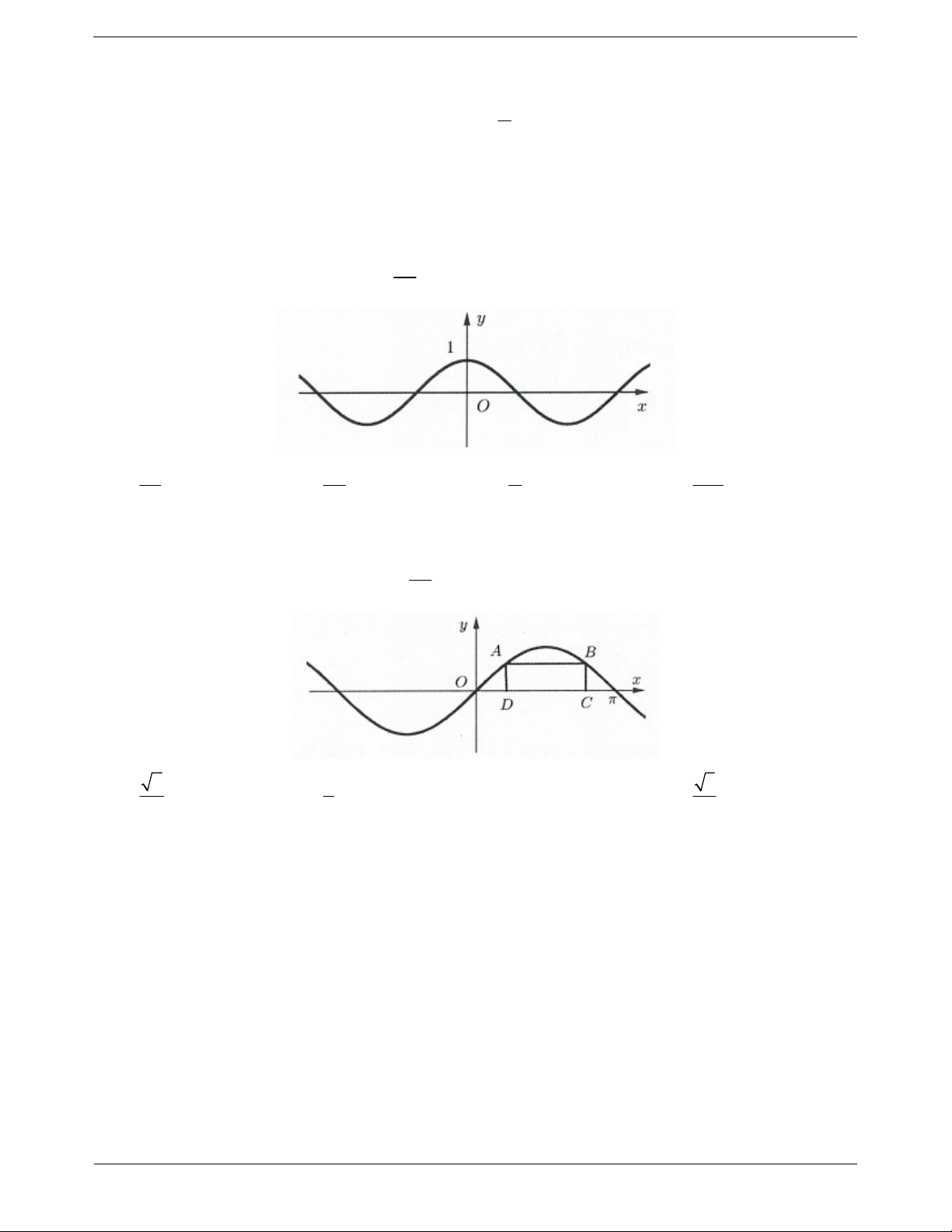
Câu 85. Cho hai điểm A, B thuộc đồ thị hàm số y  sin x trên đoạn 0;  , các điểm C, D thuộc trục Ox 2
thỏa mãn ABCD là hình chữ nhật và CD  . Tính độ dài đoạn BC 3 2 1 3 A. B. C. 1 D. 2 2 2 Trang 29
ĐÁP ÁN VÀ LỜI GIẢI BÀI TẬP TỰ LUYỆN 1-D 2-C 3-C 4-A 5-B 6-A 7-C 8-D 9-D 10-D 11-C 12-C 13-B 14-C 15-C 16-B 17-A 18-A 19-A 20-D 21-B 22-B 23-C 24-D 25-B 26-D 27-C 28-C 29-A 30-A 31-B 32-C 33-A 34-A 35-A 36-A 37-A 38-C 39-C 40-A 41-A 42-C 43-A 44-C 45-C 46-C 47-A 48-B 49-C 50-B 51-A 52-B 53-C 54-C 55-D 56-C 57-D 58-B 59-A 60-D 61-D 62-A 63-A 64-D 65-C 66-A 67-D 68-D 69-A 70-B 71-B 72-B 73-D 74-D 75-A 76-A 77-D 78-D 79-B 80-A 81-D 82-A 83-C 84-C 85-B
Câu 1: Hàm số xác định khi cos x  1  x  k 2 . Vậy D   \ k2 , k    . Chọn D    
Câu 2: Hàm số xác định khi sin x   0  x   k   .  2  2  
Vậy D   \   k , k   . Chọn C.  2       k
Câu 3: Hàm số xác định sin 2x   0  2x   k  x   , k     .  4  4 8 2   
Vậy tập xác định D   \   k , k   . Chọn C.  8 2   x   x   3
Câu 4: Hàm số xác định khi 2 cos   0     k  x   k2 , k     .  2 4  2 4 2 2 3 
Vậy tập xác định D   \ 
 k2 , k   . Chọn A  2 
Câu 5: Hàm số xác định khi 2
1 sin x  0 và tan x xác định 2 s  in x  1     cos x  0  x   k , k   . cos x  0 2  
Vậy tập xác định D   \   k , k   . Chọn B.  2 
Câu 6: Ta có 1  sin  1  1  sin x  2  3, x   
Do đó luôn tồn tại căn bậc hai của sin x  2 với mọi x   .
Vậy tập xác định D   . Chọn A
Câu 7: Hàm số xác định khi và chỉ khi 1 sin x  0  sin x  1 (*) 
Mà 1  sin x  1 nên *  sin x  1  x   k2 , k   . 2 Trang 30  
Vậy tập xác định D   \   k2 , k  . Chọn C.  2  
Câu 8: Hàm số xác định khi sin x  1  x 
 k , k  . Chọn D. 2 s  in x  0
Câu 9: Hàm số xác định khi 
 cos x  1  x  k2 , k  . Chọn D. cos x 1  0
Câu 10: Hàm số xác định khi cos x  1  x  k2 , k   . Chọn D.
Câu 11: Hàm số xác định khi sin x  0  x  k , k   Chọn C.
Câu 12: Ta có 1  cos3x  1  2   2cos3x  2  1
  y  3. Vậy T  1;  3 . Chọn C. 1 2
Câu 13: Hàm số xác định khi cos x    x    k   , k   . Chọn B. 2 3   cos x  0 x   k
Câu 14: Hàm số xác định khi    2 . Chọn C. cos x  1 x  k2 
Câu 15: Hàm số xác định khi sin x  1  x 
 k2 , k   . Chọn C. 2
Câu 16: Hàm số xác định khi sin x  2 (luôn đúng). Vậy D   . Chọn B.
Câu 17: Ta có sin 2x 1;  1  1  sin 2x  0; x
   nên y  1 sin 2x có D   . Chọn A.
Câu 18: Ta có 1  cos2x   1  1  T   1  ;  1 . Chọn A. s  in x  0 s  in x  0 k
Câu 19: Hàm số xác định khi     sin 2x  0  x  . Chọn A. 2 1 sin x  0  cos x  0 2
Câu 20: Hàm số xác định khi cos x  1  x    k2
Vậy D   \   k2 , k    . Chọn D. sin 2x  2
Câu 21: Hàm số xác định khi
 0 mà sin 2x 1; 
1  sin 2x  2 1;  3 1 cos x
Do đó 1 cos x  0  cos x  1  cos x  1 (vì cos x  1 )  x  k 2 . Chọn B.
Câu 22: Nhắc lại kiến thức cơ bản:
* Hàm số y  sin x là hàm số lẻ.
* Hàm số y  cos x là hàm số chẵn.
* Hàm số y  tan x là hàm số lẻ.
* Hàm số y  cot x là hàm số lẻ.
Vậy B là đáp án đúng. Chọn B.
Câu 23: Kiểm tra f x  f  x hoặc f x   f  x .
* Với y  f  x  sin x . Ta có f x  sin x  sin x  sin x Trang 31
 f x   f x . Suy ra hàm số y  sin x là hàm số lẻ.
* Với y  f  x  cos x  sin x . Ta có f x  cosx  sin x  cos x  sin x
 f x   f x, f x. Suy ra hàm số y  cos x  sin x không chẵn không lẻ. * Với y  f  x 2
 cos x  sin x . Ta có f x  x 2 cos  sin x 
x   x 2  x    x2 2 cos sin cos sin  cos x  sin x
 f x  f x . Suy ra hàm số 2
y  cos x  sin x là hàm số chẵn. Chọn C
* Với y  f  x  cos xsin x . Ta có f x  cosx.sin x   cos xsin x
 f x   f  x . Suy ra hàm số y  cos xsin x là hàm số lẻ. Câu 24:
* Xét hàm số y  f  x  sin 2x .
Ta có f x  sin 2x  sin 2x   f  x  f x là hàm số lẻ.
* Xét hàm số y  f  x  x cos x
Ta có f x  x.cosx  x cos x   f x  f  x là hàm số lẻ.
* Xét hàm số y  f  x  cos x cot x .
Ta có f x  cosx.cot x  cos x cot x   f  x  f  x là hàm số lẻ. x
* Xét hàm số y  f  x tan  sin x tan x  tan x tan x Ta có f x     
 f x  f x là hàm số chẵn. Chọn D. sin x     sin x sin x
Câu 25: Ta dễ dàng kiểm tra được A, C, D là các hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ O.   
Xét đáp án B, ta có y  f  x 3 3 4  sin . x cos x   sin . x sin x  sin x    2 
Kiểm tra được đây là hàm số chẵn nên có đồ thị đối xứng qua trục tung. Chọn B. Câu 26:  Hàm số 2 y  x  x  y x 
x   x   x 2 cos sin cos sin cos  sin x  y x
Hàm số y  sin x  cos x  y x  sin x  cosx  sin x  cos x
Hàm số y   cos x  y x  cosx  cos x
Hàm số y  sin x cos 3x  y x  sin x.cos 3
 x  sin xcos3x   y x
Do đó hàm số y  sin x cos 3x là hàm số lẻ. Chọn D. Trang 32    Câu 27: Ta có y  sin  x  cos x  y   x  yx  2  Hàm số y 
x  y x   x 2 2 2 sin sin   sin x  tan x tan x  tan x tan x Hàm số y   y x      sin x sin x sin x sin x cot x cot x cot x Hàm số y   y x    
 y x  hàm số là hàm số lẻ. Chọn C. cos x cos x   cos x Câu 28: Hàm số f  x 2  x tan 2x  cot x có f x  x2  x  x 2 tan 2 cot  x tan 2x  cot x
Suy ra f x   f  x nên hàm số f  x 2
 x tan 2x  cot x là hàm số lẻ. Chọn C.
Câu 29: Hàm số lẻ có đồ thị đối xứng qua gốc tọa độ. 1 1 1 1 Ta có: f  x   f x     3   sin x
sinx3 sin x3 3 sin x 1 Suy ra hàm số y 
là hàm số lẻ. Chọn A. 3 sin x
Câu 30: Hàm số chẵn có đồ thị đối xứng qua trục Oy. Hàm số lẻ có đồ thị đối xứng qua gốc tọa độ O.
Hàm số y  sin x có y x  sin x  sin x là hàm số chẵn nên có đồ thị đối xứng qua trục Oy.Vậy
khẳn định sai là A. Chọn A.          Câu 31: Hàm số y  x  x 
 y x  x4 4 4 cos  cos x   x  cos x         3   3   3 
Suy ra hàm số không là hàm lẻ.       Hàm số 2017 2017 2017 y  x  cos x   x  cos  x  x  sin x      2   2 
Suy ra y x  x2017  x 2017 sin  x
 sin x   y x nên hàm số ở ý B là hàm số lẻ. Chọn B
Câu 32: Hàm số y  sin x và y  cos x tuần hoàn với chu kì 2 .
Hàm số y  tan x và y  cot x tuần hoàn với chu kì  .
Khẳng định sai là C. Chọn C
Câu 33: Ta có sin  x  k2   sin x nên hàm số y  sin x tuần hoàn với chu kì 2 . Chọn A.  x  2 Câu 34: Hàm số y  cos  2016 
 tuần hoàn với chu kì T   4 . Chọn A.  2  1 2 Trang 33 1 2 1
Câu 35: Hàm số y   sin 100 x  50  tuần hoàn với chu kì T   . Chọn A. 2 100 50   
Câu 36: Hàm số y  sin 2x  
 tuần hoàn với chu kì T   .  3  1    2 Hàm số y  2cos 3x  
 tuần hoàn với chu kì T   4  2 3
Bội số chung nhỏ nhất của T và T là 2  Chu kì tuần hoàn của hàm số đã cho là T  2 . Chọn A 1 2 x 2
Câu 37: Hàm số y  sin tuần hoàn với chu kì T   4 . 2 1 1 2     Hàm số y  tan 2x  
 tuần hoàn với chu kì T  .  4  2 2
Bội số chung nhỏ nhất của T và T là 4  Chu kì tuần hoàn của hàm số đã cho là T  4 . Chọn A. 1 2 Câu 38: Ta có 2
y  2cos x  2017  1  cos 2x  2017  2018  cos 2x 2
Do đó hàm số đã cho tuần hoàn với chu kì T    . Chọn C. 2    2 Câu 39: Hàm số y  sin  2x 
 tuần hoàn với chu kì T    .  3  2       2 Hàm số y  cos 2 x   cos 2x    
 tuần hoàn với chu kì T     4   2  2  Hàm số y  tan  2  x  
1 tuần hoàn với chu kì T  . 2 1 2 Hàm số y  cos .
x sin x  sin 2x tuần hoàn với chu kìT    . Chọn C. 2 2      
Câu 40: Trên khoảng x  0;  2x  0;   
 nên hàm số y  sin 2x đồng biến, hàm số y  cos 2x  4   2  nghịch biến.
Do đó hàm số y   sin 2x nghịch biến và hàm số y  1
  cos 2x cũng nghịch biến trên khoảng    x  0;   . Chọn A.  4         
Câu 41: Hàm số y  sin 2x đồng biến khi 2x   ;  x   ;      2 2   4 4    
Do đó hàm số y  sin 2x đồng biến trên khoảng 0;   . Chọn A.  4           Câu 42: Do x   ;   nên 2x    ;    3 6  6  2 2  Trang 34    
Mặt khác trên khoảng  ; 
 thì hàm sin x là hàm đồng biến.  2 2         Vậy trên khoảng  ; 
 thì hàm số y  sin 2x  
 là hàm đồng biến. Chọn C.  3 6   6 
Câu 43: Do sin x 1;  1 nên 3. 
1  2  3sin x  2  3  2  5   y  1.
Vậy giá trị lớn nhất và giá trị nhỏ nhất của hàm số là M  1, m  5 . Chọn A.
Câu 44: Do 1  cos 2x  1 suy ra 3  5  3cos 2x  5  3  5  2  y  8 .
Vậy tập giá trị của hàm số là T  2; 8. Chọn C.
Câu 45: Do sin x 1; 
1 nên 5  3.1  5  3sin x  5  3  1  2  y  8
Vậy tập giá trị của hàm số là T  2; 8. Chọn C.      
Câu 46: Ta có 1  sin x   1   2  2sin x   2      3   3     Do đó 4  2  sin x   2  0  y    0; 4. Chọn C.  3  1 1 x Câu 47: Ta có y   , điều kiện cos  0 cos x  1 x 2 2 cos 2 2 x 1 1 1 Mặt khác 2 0  cos  1    2 x 2 2.1 2 2cos 2 1
Vậy giá trị nhỏ nhất m của hàm số là y  . Chọn A. min 2   
Câu 48: Ta có y  sin x  cos x  2 sin x     4  M  2
Suy ra  2  y  2  
 M  m  2 2 . Chọn B. m   2   
Câu 49: y  sin 2017x  cos 2017x  2 sin 2017x     4 
Suy ra  2  y  2 nên tập giá trị của hàm số đã cho là T   2; 2    . Chọn C.
Câu 50: Ta có 0  cos 3x  1
Suy ra 1 2.1  1 2 cos 3x  1  2.0  1   y  1
Do đó M  1; m  1. Chọn B. 1  cos 2x Câu 51: Ta có y  8.
 3cos 2x  4  cos 2x mà cos 2x 1;  1 2 Trang 35
Suy ra 3  4  cos 2x  5  M  5; m  3 nên 2 2
2M  m  2.5  3  1. Chọn A. 1 cos 2x Câu 52: Ta có y  2.
 3 sin 2x  3 sin 2x  cos 2x 1 2 2 2 Lại có  x x     2      2 2 3 sin 2 cos 2 3 1 . sin 2x  cos 2x  4    Suy ra  y  2 2
1  4  y  2y  3  0  y 1;  3 . Chọn B. Câu 53: y   x  x2     2 2 2   2 2 x  x 2 12sin 5cos 12 5 . sin cos  13  y  1  3; 1  3   . Chọn C. Câu 54: y   x  x2     2 2 2   2 2 x  x 2 4sin 2 3cos 2 4 3 . sin 2 cos 2  5  y  5  ; 5   . Chọn C.
Câu 55: Đặt t  sin x  1  ; 
1 nên hàm số trở thành: f t  2  t  4t  5 b Ta có t    2 1;  1 . Tính f   1  10; f   1  2  M  10; m  2 2a Vậy 2 2
M  2m  10  2.2  2 . Chọn D.
Câu 56: Đặt t  cos x 1; 
1 nên hàm số trở thành:   2 f t  t  t b 1   Ta có t    1;  1 . Tính f    f   1 1 1 2; 1  0; f     2a 2  2  4 1
Suy ra   f t  2 nên có tất cả 3 giá trị nguyên: f t   0; 1;  2 . Chọn C. 4 Câu 57: Ta có 4 y  x   2  x 4 2 sin 2. 1 sin
1  sin x  2sin x 1 Đặt 2 t  sin x 0; 
1 nên hàm số trở thành: f t  2  t  2t 1 b Lại có t    1  0; 
1 . Tính f 0  1; f  
1  2  M  2, m  1. Chọn D. 2a Câu 58: Ta có y  x   x    x    x2 4 2 4 2 4sin 2 cos 2 1 4sin 2. 1 2sin 1 4  x   4 2 x  x   4 2 4sin 2. 4sin 4sin 1  1  4  sin x  8sin x 1 Đặt 2 t  sin x 0; 
1 nên hàm số trở thành: f t  2  4  t  8t 1 b Lại có t    10;  1 . Tính f 0  1  ; f  
1  3  min y  1. Chọn B 2a Câu 59: Ta có 2 2
y  2cos x 1  cos x 1  2cos x  cos x
Đặt t  cos x 1; 
1 nên hàm số trở thành: f t  2  2t  t b 1   Lại có t    1;  1 . Tính f    f   1 1 1 3, 1  1, f     2a 4  4  8
Vậy giá trị nhỏ nhất cần tìm là f  x 1 min   . Chọn A. 8 Trang 36 Câu 60: Ta có .
y cos x  2  3 sin x  3 sin x  . y cos x  2 y 2
Phương trình có nghiệm khi    y2   y2 2 3 2  y  1  y  1  ;  1 . Chọn D. Câu 61: Ta có .
y sin x  cos x  2  sin x  cos x 1  1 ysin x  1 ycos x  2y 1 2  6
Phương trình có nghiệm khi: 1 y2  1 y2  2y  2 2
1  2 y  4 y  1  0  y  . 2 Chọn D. sin x  2 cos x  3 Câu 62: Ta có P   .
P 2sin x  cos x  4  sin x  2cos x  3 2sin x  cos x  4  2 . P sin x  .
P cos x  4P  sin x  2cos x  3  2P  
1 .sin x  P  2.cos x  4P  3
Phương trình có nghiệm khi:  P  2  P  2   P  2 2 2 1 2 4 3   P  2 . Chọn A. 11
Câu 63: Ta có 2sin x  cos x  3  0 x    sin x  cos x Khi đó y 
 sin x  cos x  y 2sin x  cos x  3 2sin x  cos x  3  2y   1 sin x   y   1 cos x  3y *
Phương trình (*) có nghiệm khi và chỉ khi  y  2  y  2   y2 2 1 1 3 1 2 2 2
 5y  2y  2  9y  4y  2y  2  0  1   y  2 1
Vậy m  1; M  . Chọn A. 2
Câu 64: Ta có sin x  cos x  2  0  x    sin x  2cos x 1 Khi đó: y 
 y sin x  y cos x  2y  sin x  2cos x 1 sin x  cos x  2   y  
1 sin x   y  2cos x  1 2y *
Phương trình (*) có nghiệm khi và chỉ khi  y  2   y  2    y2 1 2 1 2 2 2 2
 2y  6y  5  4y  4y 1  2y  2y  4  0  2  y 1. Vậy M  1. Chọn D. 1 cos 2x 3 7 5 14  5cos 2x Câu 65: Ta có y 
 cos 2x  3   cos 2x  2 4 2 4 4 9 14  5cos 2x 19
Vì 1  cos 2x  1 nên  
 y    y  3;  4 4 4 4
Do đó tổng các giá trị nguyên của T là 7. Chọn C. 0  cos x  1     0 1 cos x 1 1 1 1 Câu 66: Ta có  x   0; nên     y  2 . Chọn A. 0  sin x  1       2   1  1 sin x  1 0 1 2 Trang 37 1 1 1 5 1 Câu 67: Ta có 2 2 2 2 y  1  cos x 
5  2sin x  1  cos x   sin x 2 2 2 4 2
Áp dụng bất đẳng thức       2 2 2 2 a b a b  1   5 1   9 1  11 22 Do đó 2 2 2 2 2 1 cos x   sin x  y  y  2.    y         2   4 2   4 2  2 2 1 5 1 1 1 1 Dấu bằng xảy ra 2 2
 1 cos x   sin x  cos 2x   cos 2x  . Chọn D. 2 4 2 2 4 2 Câu 68: Ta có . y cos x  2  1 . m sin x  . m sin x  . y cos x  1 2y
Phương trình có nghiệm khi: m  y   y  2 2 2 2 2 2
1  3y  4y 1  m  0 2 2  3m 1
Nghiệm của phương trình 2 2
3y  4y 1 m  0 là x  3 2 2 2 2  3m  1 2  3m  1 2  3m 1 Suy ra  y   min y  3 3 3 2 2  3m  1 m  21 Yêu cầu bài toán 2   2   3m 1  8   3 m    21
Kết hợp với m 0; 10  m  5; 6; 7; 8; 9; 1  0 . Chọn D. 1 m Câu 69: Ta có sin x  1;  1  3
  1 m  3  2  m  4 3
Kết hợp với m    có 4   2
  1  7 giá trị nguyên m. Chọn A.
Câu 70: Hàm số đã cho xác định khi: 5  msin x  m   1 cos x  0; x    .   m x  m    x   m  m  2 2 2 5 max .sin 1 .cos 5
1  m  m 12  0  m  4  ;  3
Kết hợp với m    m   4
 ;  3;  2; 1; 0; 1; 2;  3 . Chọn B.    Câu 71: Ta có y  4sin
t  60 10  4.110 14  178      
Như vậy thành phố A có nhiều giờ có ánh sáng mặt trời nhất khi sin t  60  1  178        t  60 
 k  t  60  89 178k  t  149 178k 178 2
Do 0  t  365  Vào ngày thứ 149 tức là ngày 29 tháng 5 thì thành phố A có nhiều giờ ánh sáng mặt trời nhất. Chọn B.  t    t   Câu 72: Ta có h  3cos 
12  3 12  15  cos   1      8 4   8 4  Trang 38   t   t 
Do đó mực nước của kênh cao nhất khi cos   1    k2  t  16k  2    8 4  8 4
Vì 0  t  24  k  1  t  14
Vậy mực nước của kênh cao nhất khi t  14h . Chọn B.   t   Câu 73: Ta có cos   1   nên h  3.1  12  15  6 3    t   t  Dấu bằng xảy ra khi cos   1    k2  t  12k  2    6 3  6 3 Để t
 12k  2  0 và 12k   2
nên k  1  t  10h . Chọn D. min min
Câu 74: Dựa vào đồ thị hàm số y  f  x như hình vẽ ta thấy:
f 0  0 nên ta loại đáp án B và C.
Mặt khác dựa vào đồ thị suy ra f    0 nên loại đáp án A. Chọn D.
Câu 75: Dựa vào đồ thị hàm số y  f  x như hình vẽ ta thấy: f 0  0 nên ta loại các đáp án B và D. 2x
Mặt khác hàm số đã cho tuần hoàn với chu kì 3 , trong 2 hàm số ở ý A và C thì hàm số y  cos thỏa 3
mãn điều kiện trên. Chọn A.
Câu 76: Dựa vào đồ thị hàm số y  f  x như hình vẽ ta thấy:  3  f  1  
nên ta loại các đáp án B, C và D. Chọn A.  4   3 
Câu 77: Dựa vào đồ thị hàm số y  f  x như hình vẽ ta thấy: f   2  
nên ta loại các đáp án A,  4  B, và C. Chọn D. Trang 39
Câu 78: Dựa vào đồ thị hàm số ta thấy: Hàm số nhận giá trị âm trên khoảng 0;   nên ta loại các đáp án A, B, và C. Chọn D.   
Câu 79: Dựa vào đồ thị hàm số ta thấy: Hàm số nhận giá trị âm trên khoảng 0;   nên ta loại các đáp  2  án A, C và D. Chọn B.
Câu 80: Dựa vào đồ thị hàm số ta thấy: Hàm số y  f  x trong hình vẽ luôn thỏa mãn f x  0 nên ta loại đáp án B.
Lại có: f 0  0 nên ta loại đáp án D và f    0 nên ta loại đáp án C. Chọn A
Câu 81: Dựa vào đồ thị hàm số ta thấy: Hàm số y  f  x trong hình vẽ có tập giá trị là T  0; 2 ta loại đáp án A và B.
Ta có: f 0  1 nên loại đáp án C. Chọn D.    
Câu 82: Dựa vào đồ thị hàm số ta thấy, hàm số đã cho xác định và đồng biến trên khoảng  ;   do  2 2 
đó hàm số cần chọn là hàm số y  tan x . Chọn A.   
Câu 83: Hàm số y  tan x đồng biến và nhận giá trị âm trên khoảng  ; 0   (loại đáp án B).  2     Trên khoảng  ; 0 
 hàm số y  sin x đồng biến và nhận giá trị âm. Chọn C  2       Câu 84: Gọi C a a 2 2 ; cos  D a  ; cos a      3  3   2 
Do ABCD là hình chữ nhật nên AB / /CD  y  y  cos a  cos a  C D    3  2     1  a  a 
 a    AD  cos     3 3  3  2 
Diện tích hình chữ nhật ABCD bằng A . B BC  . Chọn C. 3  2 x  a   B  3 Câu 85: Gọi A ; a sin a    2   y  sin a  B     3   2  2 
Mặt khác y  y  sin a  sin a   a    a   a  A B    3  3 6  1 Do đó BC  AD  sin  . Chọn B. 6 2 Trang 40