Tài liệu chủ đề phương trình lượng giác cơ bản

Tài liệu gồm 20 trang, bao gồm kiến thức trọng tâm, hệ thống ví dụ minh họa và bài tập trắc nghiệm tự luyện chủ đề phương trình lượng giác cơ bản, có đáp án và lời giải chi tiết; giúp học sinh lớp 11 tham khảo khi học chương trình Đại số 

38 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

20 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1
CHỦ ĐỀ PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
I. KIẾN THỨC TRỌNG TÂM
Loại 1: Phương trình bậc hai, bậc ba theo một hàm số lượng giác
Với phương trình
2
.sin .sin 0
a kx b kx c thì ta đặt
sin
với
1 1
t
, quy về phương trình
bậc hai:
2
. . 0 sin
a t b t c t kx x
Với phương trình
2
.cos .cos 0
a kx b kx c thì ta đặt
cos
t kx
với
1 1
t
, quy về phương
trình bậc hai:
2
. . 0 cos
a t b t c t kx x
Với phương trình
2
.tan .tan 0
a kx b kx c thì ta đặt
tan
t kx
quy về phương trình bậc hai:
2
. . 0 tan
a t b t c t kx x
. Tương tự cho phương trình ẩn
cot
t kx
Chú ý: Với phương trình bậc ba theo một hàm số lượng giác thì cách giải tương tự!
Loại 2: Phương trình nhóm nhân tử chung
Với phương trình
0
f x , bằng các kĩ thuật phân tích, các công thức lượng giác đã học ta nhóm được
nhân tử chung và quy về dạng
0
. 0
0
g x
g x h x
h x
II. HỆ THỐNG VÍ DỤ MINH HỌA
Ví dụ 1. Giải các phương trình sau
a)
2
3 tan 1 3 tan 1 0
x x b)
2
4 2 3 1 cos 3 0
cos x x
Lời giải:
a)
2
3 tan 1 3 tan 1 0 tan 1 3 tan 1 0
x x x x
tan 1
4
1
tan
3
6
x
x k
x
x k
Vây phương trình có họ nghiệm
,
4 6
x k x k
,
b)
2
4 2 3 1 cos 3 0 2cos 3 2cos 1 0
cos x x x x
3
2
cos
6
2
1
2
cos
3
2
x k
x
x k
x
Vây phương trình có họ nghiệm
2
3
x k
,
2
6
x k
,
Trang 2
Ví dụ 2. Giải các phương trình sau
a)
4 4
2 sin 2 0
2
x cos x cos x
b)
6 6
sin 4
x cos x cos x
Lời giải:
a)
2
4 4 2 2 2 2
2 sin 2 0 2 sin 2sin sin 2 0
2
x cos x cos x x cos x xcos x x
2
1
2
sin
6
2
2 sin sin 2 0 sin 2 1 sin 2 2 0
5
sin 2
2
6
x k
x
x x x x
x loai
x k
Vây phương trình có họ nghiệm
5
2
6
x k
,
2
6
x k
,
b)
2
2 2 2 2 2 2 2
3
sin 3sin 2sin 2 1 0 sin 2 2sin 2 0
4
x cos x xcos x x x x
sin 2 0
2
x x k
Vây phương trình có họ nghiệm
2
k
x ,
Ví dụ 3. Giải các phương trình sau
a)
4 4
1
sin sin 2
2
x cos x x b)
4 4
sin cos 1 2sin
2 2
x x
x
Lời giải:
a)
2
4 4 2 2 2 2
1 1
sin sin 2 sin 2sin sin 2 0
2 2
x cos x x x cos x xcos x x
2
sin 2 3 1
sin 2 0 sin 2 1 sin 2 3 0
2 2 2
x
x x x
sin 1
2
sin 3
2
x
x k
x loai
,
Vây phương trình có họ nghiệm
2
2
x k
,
b)
2
4 4 2 2 2 2
sin cos 1 2sin sin 2sin 1 2sin 0
2 2 2 2 2 2
x x x x x x
x cos cos x
2
sin 0
sin 1
sin 0 sin sin 2 0
sin 2
2 2
x
x
x x x x k
x loai
,
Vậy phương trình có họ nghiệm
2
k
x
,
Ví dụ 4. Giải các phương trình sau
Trang 3
a)
6 6
2 sin cos sin .cos
0
2 2sin
x x x x
x
b)
4 4
sin cos sin .cos 0
x x x x
Lời giải:
a) Điều kiện:
3
2 , 2
4 4
x k k
6 6
6 6
2 sin cos sin .cos
0 2 sin cos sin .cos 0
2 2sin
x x x x
PT x x x x
x
2
2 2 2 2 2 2
2 sin sin 3sin sin 0
x cos x x cos x xcos x xcosx
2
6 sin sin 2 0 3sin 2 2sin 1 0
xcosx xcosx xcosx xcosx
2
4
sin
sin 2
3
3
1 4
sin 2 1
sin
2
xcosx
x loai
x k
x
xcosx
,
Kết hợp với điều kiện suy ra nghiệm của phương trình là
2 1
4
x m
b)
2
2
4 4 2 2
sin cos sin .cos 0 sin 2 sin sin 0
x x x x x cos x xcosx xcosx
2
2 sin sin 1 0 sin 1 2sin 1 0
xcosx xcosx xcosx xcosx
sin 1
sin 2 2
1
4
sin
sin 2 1
2
xcosx
x loai
x k
xcosx
x
,
Vây phương trình có họ nghiệm
4
x k
,
Ví dụ 5. Giải các phương trình sau
a) b)
4 2
1
sin
4
cos x
Lời giải:
a) ĐKXĐ:
2
3
x k
sinx 3 cos 0 2 0
6 6 2 3
x cos x x k x k
,
Kết hợp với ĐKXĐ suy ra phương trình có họ nghiệm
3
x k
với k lẻ
b)
Trang 4
Vây phương trình có họ nghiệm
4 2
x k
,
Ví dụ 6. Giải các phương trình sau
a)
6 6
2 2
sin 1
tan 2
sin 4
x cos x
x
cos x x
b)
4 4
5
sin
3 3 8
x x
cos
Lời giải:
a) Với
2 0
cos x
, phương trình đã cho tương đương
3
2 2 2 2 2 2
6 6
2 2
sin 3sin sin
sin 1 sin 2
tan 2
sin 4 2 4 2
x cos x xcos x x cos x
x cos x x
x
cos x x cos x cos x
sin 2 1
sin 2 1
4
4
sin 2 1
3
x
x x k
x
,
b) Phương trình đã cho tương đương với
2
4
1
2 3 3 4 1 4 2 3
3
sin 2
3 4 2 4 3 2 3 3 2 2
x
cos
x x x k
cos k x
,
Ví dụ 7. Giải các phương trình sau
a)
2 2 2
sin tan 0
2 4 2
x x
x cos
b)
3 2 cos 1 0
cos x cos x x
Lời giải:
a) Với điều kiện
cos 0
x
phương trình đã cho tương đương với
2
2 2
2
1 sin 1 cos
1 1 sin sin 1 cos
2 2 2
x x
cos x x x x cos x
cos x
1 sin 1 cos 1 cos 1 cos 1 sin 1 sin
x x x x x x
1 sin 1 cos sin cos 0
x x x x
2
0
2
1
1
tan 1
2
tanx 1
4
cos x
x k
cosx
cosx
x
x k
,
b) Phương trình đã cho tương đương với
3 2 3 2
4 3cos 2 1 cos 1 0 4 2 4cos 2 0
cos x x cos x x cos x cos x x
2 2
2cos 2cos 1 2 2cos 1 0 2 cos 1 2cos 1 0
x x x x x
Trang 5
2
sinx 0
2
1
2
cosx
3
2
x k
x k
,
k
Ví dụ 8. Giải các phương trình sau
a)
2
tan cos cos sin 1 tan .tan
2
x
x x x x x
b)
cos sin 21
c 0
i 2s sn ox xx x
Lời giải:
a) Điều kiện:
cos cos 0
2
x
x
Phương trình đã cho tương đương
2
sin
sin
2
cosx cos sin 1 .
cos co
o
sin
s
c s
2
x
x
x x
x
x x
x
b) Phương trình đã cho tương đương với cos sin 21
c 0
i 2s sn ox xx x
2
cos cos 2 0 sin 2sin cosin s 1 cos 2cossin 2 11
0
xx x x x x x x x
cos cos 1 2cos 0 1 2cos sin cn s1
o 0
si 2 x xx x x x x
1
2
2
3
4
cos
2
tan 1
x
x
x k
x k
,
Ví dụ 9. Giải các phương trình sau
a)
2 2 2 2
sin sin 3 2 4
x x cos x cos x
b)
6 6
sin cos 4
x cos x x
Lời giải:
a) Phương trình đã cho tương đương
2 2 2 2
sin sin 3 2 4
x x cos x cos x
2cos5 cos3 2cos5 cos 0 cos5 cos cos3 0
x x x x x x x
10 5
cos5 0
cos5 cos cos 2 0 cos 0
2
cos2 0
4 2
k
x
x
x x x x x k
x
k
x
,
b) Phương trình đã cho tương đương với
Trang 6
3
6 6 2 2 2 2 2 2
sin cos 4 sin 3sin sin cos 4
x cos x x x cos x xcos x x cos x x
2
3 3
1 sin 2 cos 4 1 1 cos 4 cos 4 cos 4 1
4 8 2
k
x x x x x x
,
Ví dụ 10. Giải các phương trình sau
a)
2
1
3 3 tan 3 3 0
cos
x
x
b)
2
3
tan 9
cos
x
x
Lời giải:
a) Với điều kiện
cos 0
x
phương trình đã cho tương đương với
2
2
1
3 3 tan 3 3 0 1 tan 3 3 tan 3 3 0
cos
x x x
x
2
tan 3 3 tan 3 2 0
x x
3 3 20 2 3
tan tan
2
3 3 20 2 3
tan tan
2
x m
x m k
x n k
x n
,
b) Với điều kiện
cos 0
x
phương trình đã cho tương đương
2
2 2 2
2
3 3 1
tan 9 9 3cos 1 9
cos cos
cos x
x x cos x cos x
x x cos x
2
1
cos
2
2
10 3cos 1 0
3
1
2
cos
5
x
x k
cos x x
x m k
x
,
Ví dụ 11. Giải các phương trình sau
a)
2
4
9 13cos 0
1 tan
x
x
b)
2
1
cot 3
sin
x
x
Lời giải:
a) Với điều kiện
cos 0
x
phương trình đã cho tương đương
2
2
4
9 13cos 0 9 13cos 4 0
1 tan
x x cos x
x
cos 1
cos 1 2
9
cos 1
4
x
x x k
x
,
b) Với điều kiện
sin 0
x
phương trình đã cho tương đương
2 2
2
1
cot 3 1 cot cot 3 cot cot 2 0
sin
x x x x x
x
cot 1
4
cot 2
x
x k
x
x m k
,
Trang 7
Ví dụ 12. Giải các phương trình sau
a)
2
2 3cos 4
2
x
cos x x cos
b)
Lời giải:
a) Phương trình đã cho tương đương với
2 2
2 3cos 4 2 1 3cos 2 1 cos
2
x
cos x x cos cos x x x
2
cos 3 1
2cos 5cos 3 0 2
1
cos
3
2
x
x x x k
x
b) Với điều kiện
sin 2 0
x
phương trình đã cho tương đương với
tan 1
tan 1
tan 2 1
4
tan 2 3 tan 3
3
tan 3
x
x k
x
x
x x
x k
x
,
Ví dụ 13. Giải phương trình
2sin 1 cos 2 sin 2 1 2cos
x x x x
Lời giải:
2
4sin 2sin cos 1 2cos sin 2 2cos 1 1 2cos
PT xcos x x x x x x x
2
1
2
cos
3
1 2cos sin 2 1 0
2
sin 2 1
4
x k
x
x x
x
x k
Vậy phương trình có 3 họ nghiệm:
2
2 ;
3 4
x k k
,
Ví dụ 14. Giải phương trình
cot sin 1 tan tan 4
2
x
x x x
Lời giải:
Điều kiện:
sin 0
sin 2 0
cos 0
2
2
2
cos 0
2
x
k
x
x
x
x k
x
x k
Phương trình tương đương:
sin .sin cos .cos cos
cos cos cos sin
2 2 2
sin . 4 sin . 4
sin sin sin cos
cos .cos cos .cos
2 2
x x x
x x
x x x x
x x
x x
x x x x
x x
Trang 8
2 2
1
12
sin 4sinxcosx 2sin 2 x sinx
5
2
12
x k
cos x x
x k
Vậy phương trình có 2 họ nghiệm:
5
;
12 12
x k k
,
Ví dụ 15. Giải phương trình
3 3 2
sin 2sin 1
cos x x x
Lời giải:
sin cos 1 sin cos sin cos sin cos 0
PT x x x x x x x x
sin cos 0 1
sin cos 1 sin cos sin cos 0
1 sin cos sin cos 0 2
x x
x x x x x x
x x x x
Giải
1 sin 0
4 4 4
x x k x k
Giải (2): Đặt
sin cos
x x t
,
2
1
2; 2 sin cos
2
t
t x x ta có:
2
2
2
1
2 1 0 1 0 1 2 1
3
2
2 4
2
x k
t
t t t sin x
x k
Vậy phương trình có 3 họ nghiệm:
3
2 ; k ; 2
2 4
x k k
,
Ví dụ 16. Giải phương trình
2cos 4
cot tan
sin 2
x
x x
x
Lời giải:
Điều kiện: sin 2 0
2
k
x x
2 2
cos sinx cos4
cos sin cos 4 cos 2 cos 4
sinx cos sinx cos
x x
PT x x x x x
x x
2
2
cos 1
cos2 2cos 2 1 cos 1 2cos 1 0
2
1
2
cos
3
2
x k
x
x x x x
x k
x
Vậy phương trình có 3 họ nghiệm:
2
; 2
3
x k k
,
Ví dụ 17. Giải phương trình
sin 2 2cos sin 1
0
tan 3
x x x
x
Lời giải:
Trang 9
Điều kiện:
cos 0
2
tan 3
3
x k
x
x
x k
Ta có phương trình
sin 2 2cos sin 1 0 sin 1 2cos 1 0
x x x x x
Kết hợp điều kiện, vậy phương trình có 2 họ nghiệm:
2 ; 2
3 2
x k k
,
Ví dụ 18. Giải phương trình
3 sin
tan 2
2 1 cos
x
x
x
Lời giải:
Điều kiện:
sin 0
cos 1 2
x x k
x x k
. Ta có phương trình tương đương:
2 2
sin cos sin
cot 2 2 cos cos sin 2sin 2sin cos
1 cos sin 1 cos
x x x
x x x x x x x
x x x
2
1
6
cos 1 2sin 1 sin
5
2
2
6
x k
x x x
x k
Vậy phương trình có hai họ nghiệm:
5
2 ; 2
6 6
x k k
,
Ví dụ 19. Giải phương trình
2
2 3 cos 2sin
2 4
1
2cos 1
x
x
x
Lời giải:
Điều kiện:
1
cos 2
2 3
x x k
. Phương trình đã cho tương đương
2 2
2 3 cos 2sin 2cos 1 1 2sin 3 cos 0
2 4 2 4
x x
x x x
cos 3 cosx 0 sin 3 cos 0 sin 0
2 3 3
x x x x x k
Kết hợp điều kiện, suy ra nghiệm của phương trình là:
2
2
3
x k
,
Ví dụ 20. Giải phương trình
2
2sin 3 2 sin sin 2 1
1 0
sin 2 1
x x x
x
Lời giải:
Trang 10
Điều kiện:
sin 2 1
4
x x k
. Phương trình tương đương
2 2
2sin 3 2 sin sin 2 1 sin 2 1 0 2sin 3 2 sin 2 0
x x x x x x
2
2
4
2sin 2 sin 2 0 sin
5
2
2
4
x k
x x x
x k
Kết hợp điều kiện, suy ra nghiệm của phương trình là:
3
2
4
x k
,
Ví dụ 21. Giải phương trình
4 4
sin 1 1
cot 2
5sin 2 2 8sin 2
x cos x
x
x x
Lời giải:
Điều kiện:
sin 2 0
2
k
x x
. Phương trình tương đương:
2 2
4 4 2 20 2 5 4 2 20 2 9 0 2cos 1 2cos 9 0
cos x cos x cos x cos x x x
1
cos 2
2 3
x x k
. Vậy phương trình có hai họ nghiệm là:
2
3
x k
,
Ví dụ 22. Giải phương trình
2
4
4
2 sin 2 sin 3
tan 1
x x
x
cos x
Lời giải:
Điều kiện:
cos 0
2
x x k
. Phương trình tương đương:
4 4 2 2 2
1
sin 2 sin 2 sin3 1 sin 2 2 sin 2 sin 3
2
x cos x x x x x x
Vậy phương trình có hai họ nghiệm là:
2 17 2
;
18 3 18 3
k k
x
,
Ví dụ 23. Giải phương trình
3 2sin
2cos 1 cot
sin cos 1
x
x x
x x
Lời giải:
Điều kiện:
sin 0
cos 1
x
x
. Phương trình tương đương:
2 3 2
2cos 1 cos 1 cos 3 cos 1 2 1 cos 2cos cos 2cos 1 0
x x x x x x x x
Trang 11
2
1
2cos 1 cos 1 0 cos 2
2 3
x x x x k
Vậy phương trình có hai họ nghiệm :
2
3
x k
,
Ví dụ 24. Giải phương trình
sin 2 cos2
tan cot
cos sin
x x
x x
x x
Lời giải:
Điều kiện:
sin 2 0
2
k
x x
. Phương trình tương đương:
2 2 2 2
sin 2 .sin 2 .cos sin 1 2 cos 1 2
x x cos x x x cos x cos x x cos x
1
cos 1 2cos 1 0 cos 2
2 3
x x x x k
Vậy phương trình có hai họ nghiệm :
2
3
x k
,
Ví dụ 25. Giải phương trình
2
1 sin 2 cos 2
2 sin sin 2
1 cot
x x
x x
x
Lời giải:
Điều kiện: sin 0
x x k
. Phương trình tương đương:
2
2
1
1 sin 2 cos 2 2 sin sin 2 1 cot 2 sin sin 2 . 2 2 cos
sin
x x x x x x x x
x
2
sin 2 2 2 2 cos 1 0 sin cos cos 2 cos 0
x cos x x x x x x
cos 0
cos sin cos 2
sin cos 2
x
x x x
x x
Với
cos 0
2
x x k
Với
sin cos 2 sin 1 2
4 4
x x x x k
Vậy phương trình có hai họ nghiệm :
; 2
2 4
x k k
,
Ví dụ 26. Giải phương trình
cos cos5
8sin sin3
cos3 cos
x x
x x
x x
Lời giải:
Điều kiện:
cos 0
cos3 0
x
x
. Phương trình tương đương:
2 2
cos cos5 .cos3 8sin .cos .sin 3 . 3 cos cos3 .cos5 2
sin 2 .sin 6
x x x x x x cos x x x x x x
1 cos 2 cos8 cos2 2 cos4 cos8 cos8 2cos 4 1 0
x x x x x x x
Trang 12
2
cos4 0
4
8 4
cos 4 cos4 0
2
cos4 1
4 2
2
k
x
x
x k
x x
x
k
x k
x
Vậy phương trình có hai họ nghiệm :
;
2 8 4
k k
x
,
BÀI TẬP TỰ LUYỆN
Câu 1. Tìm nghiệm của phương trình sau
4 4
sin 0
x cos x
A.
4 2
x k
, B.
4
x k
,
C.
2
4
x k
, D.
2
x k
,
Câu 2. Phương trình
2 1
3
cos x
có số nghiệm thuộc đoạn
0;2
là
A. 1 B. 2 C. 0 D. 3
Câu 3. Số nghiệm của phương trình
sin 1
4
x
,
5
x
là
A. 0 B. 2 C. 3 D. 1
Câu 4. Phương trình
3
sin 3
3 2
x
có bao nhiêu nghiệm thuộc khoảng
0;
2
?
A. 3 B. 4 C. 1 D. 2
Câu 5. Cho phương trình
3
sin 2
2
x
. Gọi n là số các nghiệm của phương trình trong đoạn
0;3
thì
giá trị của n là
A. 2 B. 5 C. 6 D. 8
Câu 6. Số nghiệm của phương trình
2 sin 3 0
cos x x
thuộc
0;2
là
A. 6 B. 4 C. 3 D. 5
Câu 7. Tính tổng tất cả các nghiệm của phương trình
sin sin 2 0
x x
trên đoạn
0;2
.
A.
4
B.
5
C.
3
D.
2
Câu 8. Cho phương trình
sin 2 2cos 0
x x , nghiệm của phương trình là
A.
2
x k
, B.
8
x k
,
C.
3
2
4
x k
, D.
6
x k
,
Câu 9. Nghiệm dương nhỏ nhất của phương trình
2sin 2 2 sin cos 0
x x x là
A.
B.
4
C. D.
3
4
Trang 13
Câu 10. Phương trình
sin5 sin 0
x x
có bao nhiêu nghiệm thuộc đoạn
2018 ; 2018
?
A. 16145 B. 20181 C. 16144 D. 20179
Câu 11. Phương trình
cos 2 3 1 0
x cos x cos x
có mấy nghiệm thuộc nửa khoảng
;0
?
A. 3 B. 1 C. 4 D. 2
Câu 12. Phương trình
3
sin 2 sin
4 4
x x
có tổng các nghiệm thuộc khoảng
0;
bằng
A.
7
2
B.
C.
3
2
D.
4
Câu 13. Tìm số nghiệm thuộc khoảng
;
của phương trình
cos sin 2 0
x x
A. 4 B. 3 C. 1 D. 2
Câu 14. Tìm số nghiệm của phương trình
sin cos 0
x trên đoạn
0;2
x
A. 0 B. 1 C. 2 D. Vô số.
Câu 15. Tìm tổng tất cả các nghiệm của phương trình
cos sin 1
x thuộc đoạn
0;2
A.
2
B. 0 C.
D.
3
Câu 16. Tổng các nghiệm của phương trình
2 2
sin sin 2 0
x x cos x
trên đoạn
0;2018
là
A.
4071315
2
B. C.
4075351
2
D.
8142627
2
Câu 17. Cho hai điểm A, B thuộc đồ thị hàm số
sin
y x
trên đoạn
0;
, các điểm C, D thuộc trục Ox
thỏa mãn ABCD là hình chữ nhật và
2
3
CD
. Tính độ dài đoạn BC
A.
2
2
B.
1
2
C. 1 D.
3
2
Câu 18. Nghiệm âm lớn nhất của phương trình
2
3
3cot 3
sin
x
x
là
A.
6
B.
5
6
C.
2
D.
2
3
Câu 19. Nghiệm của phương trình lượng giác
2
cos 0
cos x x thỏa mãn điều kiện 0
x
là
Trang 14
A.
0
x
B.
3
4
x
C.
2
x
D.
2
x
Câu 20. Phương trình
2 2cos 3 0
cos x x có bao nhiêu nghiệm trong khoảng
0;2019
?
A. 320 B. 1009 C. 1010 D. 321
Câu 21. Tổng tất cả các nghiệm của phương trình
cos5 cos 2 2sin 3 .sin 2 0
x x x x
trên đoạn
0;3
là
A.
16
3
B.
11
3
C.
25
3
D.
37
3
Câu 22. Cho phương trình
2
sin
0
cos 3cos 2
x
x x
. Tính tổng tất cả các nghiệm trong đoạn
0;2018
của phương trình trên.
A.
1018018
B.
1018080
C.
1018081
D.
1020100
Câu 23. Cho phương trình
2 2
2 1 3sin cos sin cos
0
2 2sin
x x x x
x
có
0
x
là nghiệm dương lớn nhất
trên khoảng
0;100
và có dạng
0
x a
b
, . Tính tổng
a b
A. 100 B. 101 C. 102 D. 103
Câu 24. Số nghiệm của phương trình
2
3sin 2 2 1 0
x cos x
trên nửa khoảng
0;4
là
A. 8 B. 2 C. 4 D. 12
Câu 25. Gọi
0
x
là một nghiệm của phương trình
sin 2 cos
x x
trên
;
2
. Tính giá trị của biểu thức
0 0 0 0
sin sin 2 sin 3 .. sin 2018
S x x x x
A.
1 3
2
S
B.
1
2
S
C.
0
S
D.
1 3
2
S
Câu 26. Tính tổng các nghiệm của phương trình
4 4
2 2 5 sin 3 0
cos x x cos x
trong khoảng
0;2018
A.
2010.2018
B.
1010.2018
C.
2
2018
D.
2016.2018
ĐÁP ÁN VÀ LỜI GIẢI BÀI TẬP TỰ LUYỆN
1-A 2-B 3-B 4-D 5-C 6-A 7-B 8-A 9-D 10-B
11-D 12-B 13-A 14-C 15-D 16-A 17-B 18-C 19-C 20-D
21-D 22-C 23-D 24-D 25-D 26-C 27- 28- 29- 30-
Câu 1:
4 4 2 2 2 2
sin 0 sin . sin 0
x cos x x cos x x cos x
Trang 15
2 2
sin 0 2 0 2
2 4 2
k
x cos x cos x x k x
. Chọn A.
Câu 2:
2
2
2
3 4
12
7
3 2
2 2
3 4 12
x k
x k
cos x
x k x k
TH1. Với
1 25
0 2 0 2 2 1
12 24 24
k
x k k k
TH2. Với
7 7 31
0 2 0 2 2 1
12 24 24
k
x k k k
Vậy phương trình đã cho có hai nghiệm. Chọn B.
Câu 3:
sin 1 2 2
4 4 2 4
x x k x k
Mà
3 19
5 2 5 1;2
4 8 8
x k k k

. Chọn B.
Câu 4:
2 2
3 2
3
3 3 9 3
sin 3
2
3 2
3 2
3 3 3 3
k
x k x
x
k
x k x
Mà
2 2
0
4
9 3 2
0 ;
2
2 3 9
0
3 3 2
k
x x
k
. Chọn D.
Câu 5:
2 2
3
3 6
sin 2
2
2 2
3 3
x k x k
x
x k x k
Mà
7 13 4 7
0 3 ; ; ; ; ;
6 3 6 6 3 3
x x

. Chọn C.
Câu 6:
2 sin 3 sin 3 3
2
cos x x x cos x
2
3 2 2
22
2
3 2 2
10 5
2
x k
x x k
k
x
x x k
Mà
3 3 7 11 3 19
0;2 ; ; ; ; ;
2 10 10 10 2 10
x x
. Chọn A.
Câu 7: Phương trình
sin 0
sin 2sin cos 0 sin 1 2cos 0
1
cos
2
x
x x x x x
x
Trang 16
2
2
3
x k
x k
TH1: Với
0
0;2
2
x
x k
x
x
x
TH2: Với
2
2
3
x k
ta giải
2
2
3
0 2 2
4
3
3
x
k
x
Vậy tổng các nghiệm của phương trình trên đoạn
0;2
là
5
. Chọn B.
Câu 8:
0
sin 2 2cos 0 2sin cos 2cos 0 2cos sin 1 0
sin 1
cosx
x x x x x x x
x
0
2
cosx x k
, . Chọn A.
Câu 9:
sin 0
2sin 2 2 sin cos 0 2sin 1 2 cos 0
1 2 cos 0
x
x x x x x
x
1
3
cos
2
2 4
x k
x k
x
x k
Vậy nghiệm dương nhỏ nhất của phương trình đã cho là
3
4
. Chọn D.
Câu 10:
5 2
2
sin 5 sin
5 2
6 3
k
x
x x k
x x
k
x x k
x
TH1: Với
2
k
x
mà
2018 ;2018 2018 2018
2
k
x
có
4036 4036 1 8073
nghiệm k.
TH2: Với
6 3
k
x
mà
12109 12107 12109 12107
6 3 6 2 2
k
k
k

k

có
6053 6054 1 12108
nghiệm k.
Vậy phương trình đã cho có
8073 12108 20181
nghiêm. Chọn B.
Câu 11:
2 3
cos 2 3 1 0 cos 2cos 1 4cos 3cos 1 0
x cos x cos x x x x x
Trang 17
3 2 2
sinx 0
4cos 2cos 4cos 2 0 cos 1 2cos 1 0
1
cos
2
x x x x x
x
2
2
3
x k
x k
mà . Chọn D.
Câu 12:
3
2
2 2
3
4 4
sin 2 sin
2
3
4 4
2 2
6 3
4 4
x k
x x k
x x
k
x
x x k
TH1. Với
2
x k
mà
0; 0 2x k
1
2 0 0
2
k
k k k

TH2. Với
2
6 3
k
x
mà
2
0; 0
6 3
k
x
2 5 1 15 5
0;1 ;
6 3 6 4 12 6 6
k
k
k k x
Vậy tổng các nghiệm của phương trình đã cho là
. Chọn B.
Câu 13:
cos sin 2 sin 2 2
2
x x x cos x
2
2 2
2
2
2
2 2
6 3
2
x k
x x k
k
xx x k
k
TH1. Với
2
2
x k
mà
; 2
2
x k
3 1 3
2 0
2 2 4 4 2
k
k k k x

TH2. Với
2
6 3
k
x
mà
2
;
6 3
k
x
5 2 7 5 21
1;0;1
6 3 6 12 12
k
k
k k
Vậy phương trình đã cho có tất cả 4 nghiệm. Chọn A.
Câu 14:
sin cos 0 cos
x x k
mà
cos 1;1
x
Suy ra
1 1
1 1 0
k
k k k

Do đó
cos 0 .
2
x x n
mà
3
0;2 ;
2 2
x x
. Chọn C.
Trang 18
Câu 15:
cos sin 1 sin 2
x x k
mà
sin 1;1
x
Suy ra
1 1
1 2 1 0
2 2
k
k k k
Do đó
sin 0 .
x x n
mà
0;2 0; ;2
x x
 . Chọn D.
Câu 16: sin 2 1 2 2
2 4
x x k x k
k
Mà
1 8071
0 2018 0 2018
4 4 4
x k k

Suy ra
4071315
0;1;2;...;2017
2
k x
. Chọn A.
Câu 17: Vì
2
;0
3 2 6 6 6
D
CD
CD OD x D
Do đó
1 1 1
sin ;
6 6 2 6 2 2
A A
x y A BC AD
. Chọn B.
Câu 18: Phương trình
2 2
3 1 cot 3cot 3 cot 3 cot 0
x x x x
. Chọn C.
Câu 19: Phương trình
2
cos 0
cos 0
2
cos 1
2
x
x k
cos x x
x
x k
k
Với
2
x k
mà
1 1
0 0
2 2 2
x k k x

Với
2
x k
mà
1
0 9
2
x k k

. Chọn C.
Câu 20: Phương trình
2 2
2 1 2cos 3 0 cos cos 2 0
cos x x x x
cos 1
cos 1 2
cos 2
x
x x k
x l
mà
2019
0;2019 0
2
x k
Mặt khác
k
1;2;...;321
k nên có 321 nghiệm cần tìm. Chọn D.
Câu 21: Phương trình
cos5 cos2 cos cos5 0 cos 2 cos
x x x x x x
2
2 2
2
2 2
3 3
x k
x x k
k
x x k
x
mà
0;3
x
5 7 37
;3 ; ; ; ;3
3 3 3 3
x x

. Chọn D.
Trang 19
Câu 22: Phương trình
2
sin 0
sin 0
cos 1
cos 1
cos 3cos 2 0
x
x
x
x
x x
Do đó
cos 1 2
x x k
mà
1 2017
0;2018
2 2
x k
Mặt khác
1008
0
0;1;2;...;1008 2 1018081
k
k k k

. Chọn C.
Câu 23: Điều kiện:
2
2 2sin 0 sin
2
x x
Phương trình trở thành:
2 2 2
2 6sin cos sin cos 0 4 3sin 2 sin 2 0
x x x x x x
k
Với
1 399
0;100 0 100
4 4 4
x k k
Mà
99 99
4
max
k k x
(thỏa mãn)
99 4 103
a b
. Chọn D.
Câu 24: Phương trình
2 2
3 1 2 2 1 0 3 2 2 2 0
cos x cos x cos x cos x
2 2
2 1
2 1 2
2
2 2
2
3 2 3
3
x k x k
cos x
x arccos k x arccos k
cos x
TH1. Với
0;4 0 4 0;1;2;3
x k k k
 nên có 4 nghiệm.
TH2. Với
1 2
0;4 0,116 3,883
2 3
x arccos k k
0;1;2;3
k nên có 4 nghiệm.
TH3. Với
1 2
0;4 0,116 4,116
2 3
x arccos k k
nên có 4 nghiệm. Vậy phương trình có tổng 12 nghiệm. Chọn D.
Câu 25: Phương trình
2
2 2
6 3
2
sin 2 sin
2
2 2
2
2
2
k
x
x x k
x x
x x k
x k
Với
0
; sin sin 2. .. sin 2018.
2 6 6 6 6
x x S
Ta có
1
sin
2
sin sin 2 sin 3 ... sin .sin
2
sin
2
n
x
nx
x x x nx
x
Trang 20
Với
2019
sin . 2018.
1 3 1 1 3
2 6 6
; 2018 .sin :
6 2 2
2 2 2 2
sin
12
x n S
. Chọn D.
Câu 26: Phương trình
2 2 2 2
2 2 5 sin sin 3 0
cos x x cos x x cos x
2
2 . 2 2 5 3 0 2 2 5 2 3 0
cos x cos x cos x cos x
1
2 2
2
3 6
2
2 3
2 2
3 6
x k x k
cos x
cos x
x k x k
TH1. Với
1 12107
0;2018 0 2018
6 6 6 6
x k k k
Mà
k
nên
2017
0
0;1;2;...;2017 2018. 2035153
6 6
k
k k

TH2. Với
1 12109
0;2018 0 2018
6 6 6 6
x k k k
Mà k
nên
2018
0
0;1;2;...;2017;2018 2018. 2037171
6 6
k
k k
Vậy tổng các nghiệm cần tính là
2
4072324 2018
. Chọn C.
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHỦ ĐỀ PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN I. KIẾN THỨC TRỌNG TÂM
Loại 1: Phương trình bậc hai, bậc ba theo một hàm số lượng giác Với phương trình 2 . a sin kx  .
b sin kx  c  0 thì ta đặt t  sin kx với 1  t  1 , quy về phương trình bậc hai: 2 . a t  .
b t  c  0  t  sin kx  x Với phương trình 2 . a cos kx  .
b coskx  c  0 thì ta đặt t  coskx với 1 t 1 , quy về phương trình bậc hai: 2 . a t  .
b t  c  0  t  coskx  x Với phương trình 2 . a tan kx  .
b tan kx  c  0 thì ta đặt t  tan kx quy về phương trình bậc hai: 2 . a t  .
b t  c  0  t  tan kx  x . Tương tự cho phương trình ẩn t  cot kx
Chú ý: Với phương trình bậc ba theo một hàm số lượng giác thì cách giải tương tự!
Loại 2: Phương trình nhóm nhân tử chung
Với phương trình f  x  0 , bằng các kĩ thuật phân tích, các công thức lượng giác đã học ta nhóm được g x  0
nhân tử chung và quy về dạng g  x.h x  0   hx  0
II. HỆ THỐNG VÍ DỤ MINH HỌA
Ví dụ 1. Giải các phương trình sau a) 2
3 tan x  1 3tan x 1 0 b) 2 4cos x  2 3   1 cos x  3  0 Lời giải: a) 2
3 tan x  1 3tan x 1  0  tan x   1  3 tan x   1  0   tan x 1   x    k  4  1    tan x     3 x   k  6  
Vây phương trình có họ nghiệm x   k , x   k , 4 6 b) 2 4cos x  2 3  
1 cos x  3  0  2cos x  32cos x   1  0  3   cos x  x    k2   2 6      1  cos  x  x    k2    2  3  
Vây phương trình có họ nghiệm x  
 k2 , x    k2 , 3 6 Trang 1
Ví dụ 2. Giải các phương trình sau    a)  4 4 2 sin x  cos x  cos  2x  0   b) 6 6 sin x  cos x  cos4x  2  Lời giải:    a)  x cos x  cos  x   x cos x2 4 4 2 2 2 2 2 sin 2 0 2 sin 2sin         xcos x  sin 2x  0  2      1   x   k2 sin x   2
 2  sin x  sin 2x  0  sin 2x   1 sin 2x  2  6  0  2      x loai 5 sin 2    x   k2    6 5 
Vây phương trình có họ nghiệm x   k2 , x   k2 , 6 6 b)  sin x  cos x2 3 2 2 2 2 2 2 2
 3sin xcos x  2sin 2x 1  0   sin 2x  2sin 2x  0 4   sin 2x  0  x  k 2 k
Vây phương trình có họ nghiệm x  , 2
Ví dụ 3. Giải các phương trình sau 1 x x a) 4 4
sin x  cos x  sin 2x  b) 4 4 sin  cos 1 2sin x 2 2 2 Lời giải: 1 1
a) sin x  cos x  sin 2x   sin x  cos x2 4 4 2 2 2 2
 2sin xcos x  sin 2x   0 2 2 2 sin 2x 3 1  
 sin 2x   0   sin 2x   1 sin 2x  3  0 2 2 2 sin x  1    x k  , x    loai    2 sin 3 2 
Vây phương trình có họ nghiệm x   k2 , 2 2 x x  x x  x x b) 4 4 2 2 2 2 sin  cos 1 2sin x  sin  cos  2sin cos 1 2sin x  0   2 2  2 2  2 2 2 sin x 1  x   
 sin x  0   sin xsin x  2 sin 0  0    x  k , 2 2 sin x  2  loai k
Vậy phương trình có họ nghiệm x  , 2
Ví dụ 4. Giải các phương trình sau Trang 2  6 6
2 sin x  cos x  sin .xcos x a)  0 b) 4 4 sin x  cos x  sin . x cos x  0 2  2sin x Lời giải:  3 
a) Điều kiện: x    k2 ,  k2   4 4  2 6 6
sin x  cos x  sin .xcos x PT   0  2 6 6
sin x  cos x sin .xcos x  0 2  2sin x
 x cos x x cos x2 2 2 2 2 2 2 2 sin sin 3sin      xcos x  sin xcosx  0       xcosx2 6 sin
 sin xcosx  2  0  3sin xcosx  22sin xcosx   1  0  2 sin xcosx    4  3 sin 2x   loai      3  x   k , 1  4 sin xcosx  sin 2x 1  2 
Kết hợp với điều kiện suy ra nghiệm của phương trình là x   2m   1  4 2 b) x  x  x x    x  cos x   xcosx2 4 4 2 2 sin cos sin .cos 0 sin 2 sin  sin xcosx  0   xcosx2 2 sin
 sin xcosx 1  0  sin xcosx   1 2sin xcosx   1  0 sin xcosx  1 sin 2x  2loai    1    x     k , sin xcosx   sin 2x  1 4  2 
Vây phương trình có họ nghiệm x     k , 4
Ví dụ 5. Giải các phương trình sau 1 a) b) 4 2 cos  sin x  4 Lời giải:  a) ĐKXĐ: x    k2 3      
 sinx 3 cos x  0  2cos x 
 0  x    k  x     k ,  6  6 2 3 
Kết hợp với ĐKXĐ suy ra phương trình có họ nghiệm x   k với k lẻ 3 b) Trang 3  
Vây phương trình có họ nghiệm x   k , 4 2
Ví dụ 6. Giải các phương trình sau 6 6 sin x  cos x 1 x x 5 a)  tan 2x b) 4 4 sin  cos  2 2 cos x  sin x 4 3 3 8 Lời giải:
a) Với cos2x  0 , phương trình đã cho tương đương  sin xcos x3 2 2 2 2  3sin xcos x  2 2 6 6 sin sin 1 x  cos x x cos x  sin2  x tan 2x   2 2 cos x  sin x 4 cos2x 4cos2x sin 2x  1    4
 sin 2x 1  x   k , sin 2x    1  4  3
b) Phương trình đã cho tương đương với 4x 1 2 3 cos x 3 4x 1 4x 2  k3 2 3  sin     cos      k2  x   , 3 4 2 4 3 2 3 3 2 2
Ví dụ 7. Giải các phương trình sau  x   x a) 2 2 2 sin  tan x  cos  0  
b) cos3x  cos2x  cos x 1  0  2 4  2 Lời giải:
a) Với điều kiện cos x  0 phương trình đã cho tương đương với 2 1     sin x 1 cos x 1 cos x       1sin x 2 sin x  1 cos x 2 cos x 2 2   2  cos x 2
 1sin x1 cos x1 cos x  1 cos x1 sin x1 sin x
 1sin x1 cos xsin x  cos x  0 2 cos x  0 x    k2  cosx  1 cosx 1          , tan x  1 x    k2   tanx  1   4 
b) Phương trình đã cho tương đương với 3 2 3 2
4cos x  3cos x  2cos x 1 cos x 1  0  4cos x  2cos x  4cos x  2  0 2  x  x     x      2 2 cos 2 cos 1 2 2 cos 1 0 2 cos x   1 2cos x   1  0 Trang 4 sinx  0 x  k2   1   2 , k    cosx   x    k2  2  3
Ví dụ 8. Giải các phương trình sau  x  a) 2
tan x  cos x  cos x  sin x 1 tan . x tan   b) 1 i
s n x  cos x  sin 2x  cos 2x  0  2  Lời giải: x
a) Điều kiện: cos x cos  0 2  x  sin sin x  sin x 
Phương trình đã cho tương đương 2 2
 cosx cos x  sin x1 .  cos x cos x x  cos   2 
b) Phương trình đã cho tương đương với 1 i
s n x  cos x  sin 2x  cos 2x  0 2
 sin x  sin 2x 1 cos x  cos 2x  0  sin x  2sin x cos x 1 cos x  2cos x 1  0
 sin x1 2cos x  cos x1 2cos x  0  1 2cos xsin x  c s o x  0  2  1 x    k2 cos x     3  2   ,   tan x  1 x    k  4
Ví dụ 9. Giải các phương trình sau a) 2 2 2 2
sin x  sin 3x  cos 2x  cos 4x b) 6 6 sin x  cos x  cos 4x Lời giải:
a) Phương trình đã cho tương đương 2 2 2 2
sin x  sin 3x  cos 2x  cos 4x
 2cos5x cos3x  2cos5x cos x  0  cos5xcos x  cos3x  0   k x    10 5 cos5x  0    
 cos5x cos x cos 2x  0  cos x  0  x   k   , 2 cos 2x  0    k x    4 2
b) Phương trình đã cho tương đương với Trang 5 x  cos x  x   x  cos x3 6 6 2 2 2 2  xcos x  2 2 sin cos 4 sin 3sin sin x  cos x  cos 4x 3 3 k 2
 1 sin 2x  cos 4x  1 1 cos 4x  cos 4x  cos 4x 1  x  , 4 8 2
Ví dụ 10. Giải các phương trình sau 1 3 a)
 3  3 tan x  3  3  0 b) 2  tan x  9 2   cos x cos x Lời giải:
a) Với điều kiện cos x  0 phương trình đã cho tương đương với 1  3 3 2
tan x  3  3  0  1 tan x  3  3 tan x  3  3  0 2   cos x 2
 tan x  3 3tan x  3  2  0  3  3  20  2 3 tan x   tan m  2 x  m  k     , 3  3  20  2 3 x  n  k tan x   tan n  2
b) Với điều kiện cos x  0 phương trình đã cho tương đương 2 3 3 1 cos x 2 2 2  tan x  9  
 9  3cos x 1 cos x  9cos x 2 cos x cos x cos x  1 cos x     2 x    2k 2 10cos x 3cos x 1 0         3 , 1  cos x   x  m  k2  5
Ví dụ 11. Giải các phương trình sau 4 1 a) 9 13cos x   0 b)  cot x  3 2 1 tan x 2 sin x Lời giải:
a) Với điều kiện cos x  0 phương trình đã cho tương đương 4 2 9 13cos x 
 0  9 13cos x  4cos x  0 2 1 tan x cos x 1   9
 cos x 1  x  k2 , cos x  1  4
b) Với điều kiện sin x  0 phương trình đã cho tương đương 1 2 2
 cot x  3  1 cot x  cot x  3  cot x  cot x  2  0 2 sin x   cot x  1 x    k     4 , cot x  2  x  m  k Trang 6
Ví dụ 12. Giải các phương trình sau x a) 2 cos2x  3cos x  4cos b) 2 Lời giải:
a) Phương trình đã cho tương đương với x 2 2 cos2x  3cos x  4cos
 2cos x 1 3cos x  21 cos x 2 cos x  3 1  2
 2cos x  5cos x  3  0   1  x    k2 cos x   3  2
b) Với điều kiện sin 2x  0 phương trình đã cho tương đương với tan x  1    x      k tan 2x  1 tan x  1  4      , tan 2x  3 tan x  3     x    k tan x   3  3
Ví dụ 13. Giải phương trình 2sin x 1 cos 2x  sin 2x 1 2cos x Lời giải: 2
PT  4sin xcos x  2sin x cos x  1 2cos x  sin 2x 2cos x   1 1 2cos x  2  1 x    k2    x x   cos x       3 1 2cos sin 2 1 0 2     sin 2x 1 x   k  4  2  
Vậy phương trình có 3 họ nghiệm: x    k2 ;  k ,  3 4   x 
Ví dụ 14. Giải phương trình cot x  sin x 1 tan x tan  4    2  Lời giải: sinx  0    k sin 2x  0 x 
Điều kiện: cos x  0     2 x    2  k x x    2k cos  0  2
Phương trình tương đương:  x x   x  sin . x sin  cos . x cos cos cos x   cos x   cos x sin 2 2 2   x sin . x    4   sin . x      4 sin x x sin x x sin x cos  cos .cos   cos .cos  x x x  2   2  Trang 7   x    1  k 2 2 12
 cos x  sin x  4sinxcosx  2sin 2 x  sinx    2 5   x   k  12   5 
Vậy phương trình có 2 họ nghiệm: x    k;  k  , 1  2 12 
Ví dụ 15. Giải phương trình 3 3 2
cos x  sin x  2sin x  1 Lời giải:
PT  sin x  cos x1 sin x cos x  sin x  cos xsin x  cos x  0 x x   x  x  x x  x  x sin  cos  0  1 sin cos 1 sin cos sin cos  0  1
 sin xcos x sin x cos x  0  2      Giải   1  sin x 
 0  x   k  x      k  4  4 4  t
Giải (2): Đặt sin x  cos x  t , t   2 1 2; 2  sin x cos x    ta có: 2 2 x  k2   1 t    2  1  t  0  t  2 1  0  t  1   2sin x   1     3 2  4  x   k2  2 3  
Vậy phương trình có 3 họ nghiệm: x  
 k2 ;  k ;k2 ,  2 4  2cos 4
Ví dụ 16. Giải phương trình cot  tan  x x x sin 2x Lời giải: 
Điều kiện: sin 2  0   k x x 2 cos x sinx cos 4x 2 2 PT   
 cos x  sin x  cos 4x  cos 2x  cos 4x sinx cos x sinx cos x cos x  1 x  k2 2
 cos 2x  2cos 2x 1  cos x   1 2cos x   1  0   1   2 cos x   x    k2  2  3  2 
Vậy phương trình có 3 họ nghiệm: x  k;  k2 ,  3 
sin 2x  2cos x  sin x 1
Ví dụ 17. Giải phương trình  0 tan x  3 Lời giải: Trang 8   cos  0 x    k x  Điều kiện: 2    tan x   3   x    k  3
Ta có phương trình  sin 2x  2cos x  sin x 1  0  sin x   1 2cos x   1  0   
Kết hợp điều kiện, vậy phương trình có 2 họ nghiệm: x    k2;  k2  ,  3 2   3  sin x
Ví dụ 18. Giải phương trình tan  x   2    2  1 cos x Lời giải: sin x  0 x  k Điều kiện:   cos x  1
xk2 . Ta có phương trình tương đương: sin x cos x sin x 2 2 cot x   2  
 2  cos x  cos x  sin x  2sin x  2sin x cos x 1 cos x sin x 1 cos x   x   k2   x   x   1  6 cos 1 2sin 1  sin x    2 5   x   k2  6  5 
Vậy phương trình có hai họ nghiệm: x    k2;  k2  ,  6 6      2  x  2 3 cos x  2sin     2 4
Ví dụ 19. Giải phương trình  1 2cos x 1 Lời giải: 1  Điều kiện: cos x 
 x    k2 . Phương trình đã cho tương đương 2 3      x x 2   2    2 3 cos x  2sin   2cos x 1  1 2sin   3 cos x  0      2 4   2 4          cos x 
 3 cosx  0  sin x  3 cos x  0  sin x   0  x       k  2   3  3 2
Kết hợp điều kiện, suy ra nghiệm của phương trình là: x    k2 , 3 2
2sin x  3 2 sin x  sin 2x 1
Ví dụ 20. Giải phương trình 1  0 sin 2x 1 Lời giải: Trang 9 
Điều kiện: sin 2x  1  x    k . Phương trình tương đương 4 2  x  x  x    x   2 2sin 3 2 sin sin 2 1 sin 2
1  0  2sin x  3 2 sin x  2  0   x k    x   x     2 2  4 2sin 2 sin 2  0  sin x     2 5   x   k2  4 3
Kết hợp điều kiện, suy ra nghiệm của phương trình là: x    k2 , 4 4 4 sin x  cos x 1 1
Ví dụ 21. Giải phương trình  cot 2x  5sin 2x 2 8sin 2x Lời giải: 
Điều kiện: sin 2  0   k x x
. Phương trình tương đương: 2 2 2
 4  4cos 2x  20cos2x  5  4cos 2x  20cos2x  9  0  2cos x   1 2cos x 9  0 1  
 cos x   x    k2 . Vậy phương trình có hai họ nghiệm là: x    k2 , 2 3 3  2 2  sin 2x sin 3x 4 
Ví dụ 22. Giải phương trình tan x 1  4 cos x Lời giải: 
Điều kiện: cos x  0  x 
 k . Phương trình tương đương: 2 1 4 4 sin x  cos x   2 2  sin 2x 2 sin 3x  1 sin 2x   2 2  sin 2xsin 3x 2   k 2 17 k2 
Vậy phương trình có hai họ nghiệm là: x    ;   , 1  8 3 18 3  x
Ví dụ 23. Giải phương trình  x   3 2sin 2 cos 1 cot x   sin x cos x 1 Lời giải: x  Điều kiện: sin 0
cos x  . Phương trình tương đương: 1   x   x   x   x     2  x 3 2 2 cos 1 cos 1 cos 3 cos 1 2 1 cos
 2cos x  cos x  2cos x 1  0 Trang 10   2cos x   1  1 2 cos x   1  0  cos x   x    k2 2 3 
Vậy phương trình có hai họ nghiệm : x    k2 , 3 sin 2x cos 2x
Ví dụ 24. Giải phương trình   tan x  cot x cos x sin x Lời giải: 
Điều kiện: sin 2  0   k x x
. Phương trình tương đương: 2 2 2 2 2  sin 2 . x sin x  cos2 .
x cos x  sin x  cos x  1 2cos x  cos x  1 2cos x    x   x   1 cos 1 2cos 1  0  cos x   x    k2 2 3 
Vậy phương trình có hai họ nghiệm : x    k2 , 3 1 sin 2x  cos 2x
Ví dụ 25. Giải phương trình  2 sin xsin 2x 2 1 cot x Lời giải:
Điều kiện: sin x  0  x  k . Phương trình tương đương:
 1 sin 2x  cos 2x  2 sin x sin 2x 1 2
1 cot x  2 sin xsin 2 .x  2 2 cos x 2 sin x 2
 sin 2x  cos2x  2 2 cos x 1  0  sin x cos x  cos x  2 cos x  0 x  x  x  x   cos 0 cos sin cos 2   sin x  cos x  2 
 Với cos x  0  x   k 2     
Với sin x  cos x  2  sin x   1  x   k2     4  4   
Vậy phương trình có hai họ nghiệm : x    k ;  k2  ,  2 4  cos x cos 5x
Ví dụ 26. Giải phương trình   8sin x sin 3x cos 3x cos x Lời giải: x 
Điều kiện: cos 0 . Phương trình tương đương: cos 3x  0 2 2  cos x  cos5 . x cos 3x  8sin . x cos . x sin 3 . x cos3x  cos x  cos 3 . x cos 5x  2sin 2 . x sin 6x
 1 cos 2x  cos8x  cos 2x  2cos 4x  cos8x  cos8x  2cos 4x 1  0 Trang 11   k   x    x  x   k  2 cos 4 0 4  x  x     8 4 cos 4 cos 4 0  2  cos 4x  1   k 4x  k2 x   2 k  k 
Vậy phương trình có hai họ nghiệm : x   ;   ,  2 8 4  BÀI TẬP TỰ LUYỆN
Câu 1. Tìm nghiệm của phương trình sau 4 4 sin x  cos x  0    A. x   k , B. x   k , 4 2 4   C. x    k2 , D. x  k , 4 2   
Câu 2. Phương trình 2cos x   1  
có số nghiệm thuộc đoạn 0;2  là  3  A. 1 B. 2 C. 0 D. 3   
Câu 3. Số nghiệm của phương trình sin x   1   ,   x  5 là  4  A. 0 B. 2 C. 3 D. 1    3   
Câu 4. Phương trình sin 3x     
có bao nhiêu nghiệm thuộc khoảng 0;   ?  3  2  2  A. 3 B. 4 C. 1 D. 2 3
Câu 5. Cho phương trình sin 2x 
. Gọi n là số các nghiệm của phương trình trong đoạn 0;3  thì 2 giá trị của n là A. 2 B. 5 C. 6 D. 8
Câu 6. Số nghiệm của phương trình cos2x  sin 3x  0 thuộc 0;2  là A. 6 B. 4 C. 3 D. 5
Câu 7. Tính tổng tất cả các nghiệm của phương trình sin x  sin 2x  0 trên đoạn 0;2 . A. 4 B. 5 C. 3 D. 2
Câu 8. Cho phương trình sin 2x  2 cos x  0 , nghiệm của phương trình là   A. x   k , B. x   k , 2 8 3  C. x   k2 , D. x    k , 4 6
Câu 9. Nghiệm dương nhỏ nhất của phương trình 2sin x  2 2 sin x cos x  0 là  3 A.  B. C. D. 4 4 Trang 12
Câu 10. Phương trình sin 5x  sin x  0 có bao nhiêu nghiệm thuộc đoạn 2018;2018  ? A. 16145 B. 20181 C. 16144 D. 20179
Câu 11. Phương trình cos x  cos2x  cos3x 1  0 có mấy nghiệm thuộc nửa khoảng ;0 ? A. 3 B. 1 C. 4 D. 2     3 
Câu 12. Phương trình sin 2x   sin x    
 có tổng các nghiệm thuộc khoảng 0;  bằng  4   4  7 3  A. B.  C. D. 2 2 4
Câu 13. Tìm số nghiệm thuộc khoảng ;  của phương trình cos x  sin 2x  0 A. 4 B. 3 C. 1 D. 2
Câu 14. Tìm số nghiệm của phương trình sin cos x  0 trên đoạn x 0;2  A. 0 B. 1 C. 2 D. Vô số.
Câu 15. Tìm tổng tất cả các nghiệm của phương trình cos sin x  1 thuộc đoạn 0;2  A. 2 B. 0 C.  D. 3
Câu 16. Tổng các nghiệm của phương trình 2 2
sin x  sin 2x  cos x  0 trên đoạn 0;2018  là 4071315 4075351 8142627 A. B. C. D. 2 2 2
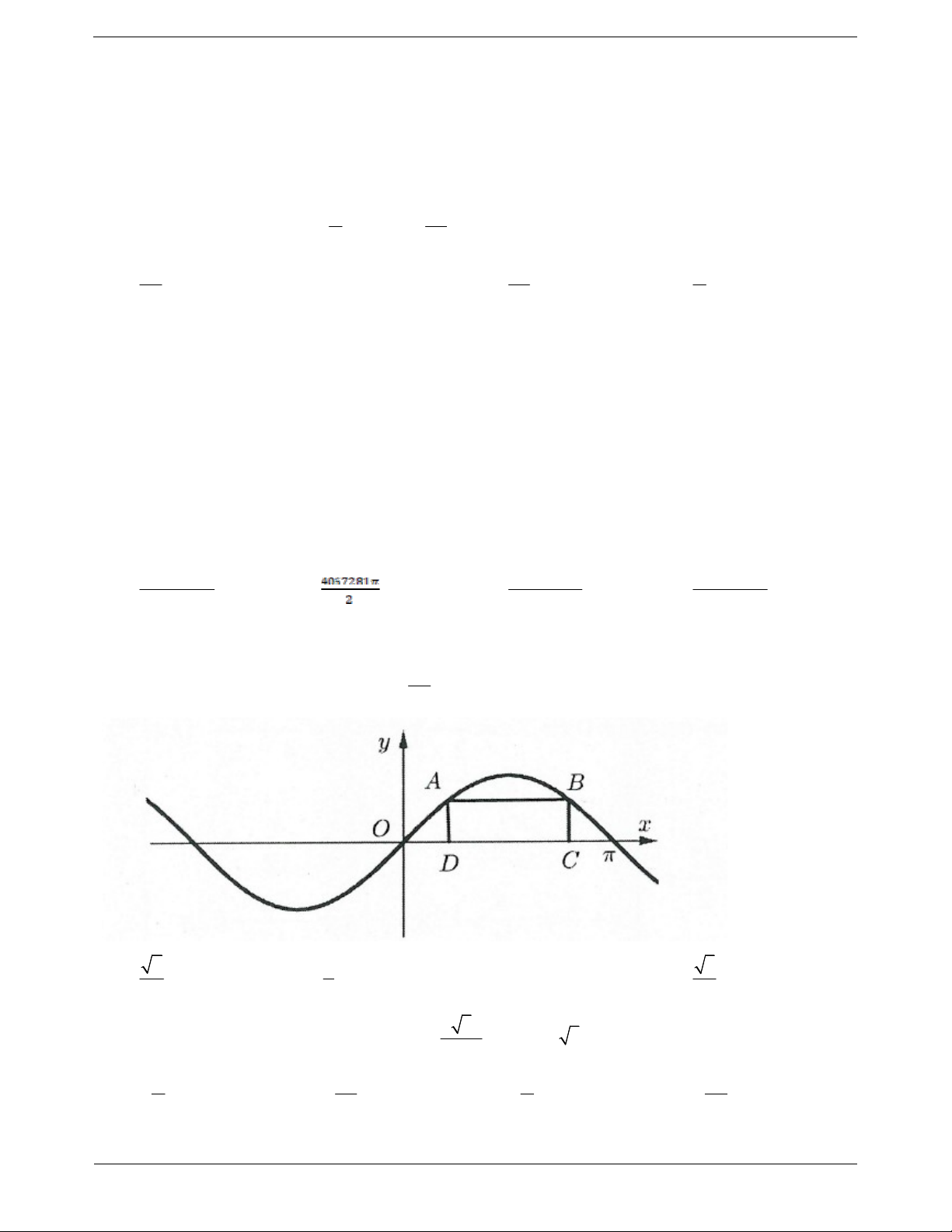
Câu 17. Cho hai điểm A, B thuộc đồ thị hàm số y  sin x trên đoạn 0; , các điểm C, D thuộc trục Ox 2
thỏa mãn ABCD là hình chữ nhật và CD  . Tính độ dài đoạn BC 3 2 1 3 A. B. C. 1 D. 2 2 2 3
Câu 18. Nghiệm âm lớn nhất của phương trình  3cot x  3 là 2 sin x  5  2 A.  B.  C.  D.  6 6 2 3
Câu 19. Nghiệm của phương trình lượng giác 2
cos x  cos x  0 thỏa mãn điều kiện 0  x   là Trang 13 3   A. x  0 B. x  C. x  D. x   4 2 2
Câu 20. Phương trình cos2x  2 cos x  3  0 có bao nhiêu nghiệm trong khoảng 0;2019 ? A. 320 B. 1009 C. 1010 D. 321
Câu 21. Tổng tất cả các nghiệm của phương trình cos5x  cos 2x  2sin 3 .
x sin 2x  0 trên đoạn 0;3  là 16 11 25 37 A. B. C. D. 3 3 3 3 sin x Câu 22. Cho phương trình
 0 . Tính tổng tất cả các nghiệm trong đoạn 0;2018  2 cos x  3cos x  2 của phương trình trên. A. 1018018 B. 1018080 C. 1018081 D. 1020100  2 2
2 1 3sin x cos x sin xcos x Câu 23. Cho phương trình
 0 có x là nghiệm dương lớn nhất 2  2sin x 0 
trên khoảng 0;100  và có dạng x  a  , . Tính tổng a  b 0 b A. 100 B. 101 C. 102 D. 103
Câu 24. Số nghiệm của phương trình 2
3sin 2x  cos2x 1  0 trên nửa khoảng 0;4  là A. 8 B. 2 C. 4 D. 12   
Câu 25. Gọi x là một nghiệm của phương trình sin 2x  cos x trên
; . Tính giá trị của biểu thức 0    2 
S  sin x  sin 2x  sin 3x  ..  sin 2018x 0 0 0 0 1 3 1 1 3 A. S  B. S  C. S  0 D. S  2 2 2
Câu 26. Tính tổng các nghiệm của phương trình  cos x   4 4 2 2
5 sin x  cos x  3  0 trong khoảng 0;2018  A. 2010.2018 B. 1010.2018 C. 2 2018  D. 2016.2018
ĐÁP ÁN VÀ LỜI GIẢI BÀI TẬP TỰ LUYỆN 1-A 2-B 3-B 4-D 5-C 6-A 7-B 8-A 9-D 10-B 11-D 12-B 13-A 14-C 15-D 16-A 17-B 18-C 19-C 20-D 21-D 22-C 23-D 24-D 25-D 26-C 27- 28- 29- 30- Câu 1: 4 4 x  cos x    2 2 x  cos x  2 2 sin 0 sin . sin x  cos x  0 Trang 14   k 2 2
 sin x  cos x  0  cos2x  0  2x   k  x   . Chọn A. 2 4 2      x    k2 x    k2    2   Câu 2: 3 4 12 cos x          3  2   7 x     k2 x    k2  3 4  12  1 25 TH1. Với 0 2 0 2 2 k x k  k             k 1 12 24 24 7 7 31 TH2. Với 0 2 0 2 2 k x k  k              k  1 12 24 24
Vậy phương trình đã cho có hai nghiệm. Chọn B.       Câu 3: sin x 
 1  x    k2  x   k2    4  4 2 4  3 19 Mà   x  5 
   k2  5   k    k  1;  2 . Chọn B. 4 8 8     2 k2 3x     k2       3 x   Câu 4: 3 3 9 3 sin 3x           3  2    k2
3x      k2 x    3 3  3 3  2 k2  0       9 3 2  4  Mà 0  x      x   ; . Chọn D. 2   k2   3 9  0     3 3 2     2x   k2    3 x k   Câu 5: 3 6 sin 2x      2   2x     k2 x   k  3  3   7 13 4 7 Mà 0 x 3       x   ; ; ; ; ;  . Chọn C.  6 3 6 6 3 3    
Câu 6: cos2x  sin 3x  sin  3  x  cos 3x     2      3x   2x  k2 x    k2  2  2       k2 3x   2x  k2 x     2  10 5         Mà x    3 3 7 11 3 19 0; 2  x   ; ; ; ; ;  . Chọn A.  2 10 10 10 2 10  sin x  0
Câu 7: Phương trình  sin x  2sin x cos x  0  sin x 1 2cos x  0   1 cos x    2 Trang 15 x  k   2 x    k2  3 x  0 x  k   TH1: Với      x   x 0; 2    x  2   2 x  2 2  TH2: Với x    k2 ta giải 3 0    k2  2   3 3 4   x   3
Vậy tổng các nghiệm của phương trình trên đoạn 0;2  là 5 . Chọn B. cosx  Câu 8: x  x   x x  x   x  x   0 sin 2 2cos 0 2sin cos 2 cos 0 2cos sin 1  0   sin x  1 
 cosx  0  x   k , . Chọn A. 2  x  Câu 9: x  x x   x   x sin 0 2sin 2 2 sin cos 0 2sin 1 2 cos  0  1    2 cos x  0 x  k x  k  1    3  cos x   x   k2  2  4 3
Vậy nghiệm dương nhỏ nhất của phương trình đã cho là . Chọn D. 4  k  5   2 x x x k   Câu 10: 2 sin 5x  sin x    5x    x  k2   k x    6 3 k k TH1: Với x  mà x  2  018;2018   2  018   2018 2 2 có 4036   4
 036 1 8073 nghiệm k.  k TH2: Với x   mà 6 3 12109 k 12107 k 12109 12107        k  6 3 6 2 2 k   có 6053  6
 054 112108 nghiệm k.
Vậy phương trình đã cho có 8073 12108  20181 nghiêm. Chọn B. Câu 11: 2 3
cos x  cos2x  cos3x 1  0  cos x  2 cos x 1 4 cos x  3cos x 1  0 Trang 16 sinx  0 3 2 4 cos x 2cos x 4cos x 2 0  2 cos x 12cosx 1 0            1 cos x    2 x  k   2 mà . Chọn D. x    k2  3   3 2x   x   k2 x    k2     3   Câu 12: 4 4 sin 2x   sin x           k2  4   4  3  x   2x     x   k2  6 3  4 4
TH1. Với x    k 2 mà x 0;   0    k2   1  2 0 0 k k k            k   2  k2  k  TH2. Với x   mà x    2 0;  0     6 3 6 3  k 2 5 1 15    k         k    k    5 0;1  x   ;  6 3 6 4 12  6 6 
Vậy tổng các nghiệm của phương trình đã cho là  . Chọn B.   
Câu 13: cos x   sin 2x  sin 2x  cos 2x     2      2x   x  k2 x    k2  2  2       k  k2 2x   x  k2 x     2  6 3  
TH1. Với x    k 2 mà x    ;        k2   2 2  3 1 3      2 k k      k   k  0  x   2 2 4 4 2  k2  k  TH2. Với x    mà x      2 ;         6 3 6 3 5 k2 7 5 21 k k           k   1  ;0;  1 6 3 6 12 12
Vậy phương trình đã cho có tất cả 4 nghiệm. Chọn A.
Câu 14: sin cos x  0  cos x  k mà cos x  1  ;  1 1 1 Suy ra 1  1 k k k          k  0       Do đó cos x  0  x   . n  mà x    3 0; 2 
 x   ; . Chọn C. 2  2 2  Trang 17
Câu 15: cos sin x 1  sin x  k2 mà sin x 1;  1 1 1 Suy ra 1 2 1 k k k           k  0 2 2
Do đó sin x  0  x  .
n  mà x 0;2  
 x  0;;2. Chọn D.  
Câu 16: sin 2x  1  2x 
 k2  x   k k  2 4  1 8071 Mà 0  x  2018 
0   k  2018    k  4 4 4  Suy ra k    4071315 0;1; 2;...; 2017   x  . Chọn A. 2 2   CD      Câu 17: Vì CD   OD    x   D ;0   3 2 6 D 6  6    1   1  1 Do đó x   y  sin   A ;  BC  AD  . Chọn B. A   6 A 6 2  6 2  2 Câu 18: Phương trình   2  x 2 3 1 cot
 3cot x  3  cot x  3 cot x  0 . Chọn C.    x     Câu 19: Phương trình 2 cos 0   cos  0 x k cos x x     2 k  cos x  1 x   k2  1 1  Với x 
 k mà 0  x   
   k   k  0  x  2 2 2 2 1
Với x  k 2 mà 0  x   
9  k   k   . Chọn C. 2 Câu 20: Phương trình 2 2
 2cos x 1 2cos x  3  0  cos x  cos x  2  0 cos x 1        mà x   2019 0; 2019  0  k  x    l cos x 1 x k2 cos 2 2
Mặt khác k   k  1;2;...;32 
1 nên có 321 nghiệm cần tìm. Chọn D.
Câu 21: Phương trình  cos 5x  cos 2x  cos x  cos 5x  0  cos 2x  cos   x x    k2 2x  x   k2     k2  mà x 0;3 
2x  x   k2 x     3 3   5 7  37  x    ;3 ; ; ; ;3    x  . Chọn D.  3 3 3  3 Trang 18 sin x  0 sin x  0
Câu 22: Phương trình     cos x  1  2
cos x  3cos x  2  0 cosx1 Do đó cos x  1
  x    k2 mà x    1 2017 0; 2018    k  2 2 1008 Mặt khác k     k  0;1;2;...;100 
8    k2  1018081 . Chọn C. k 0 2
Câu 23: Điều kiện: 2  2sin x  0  sin x  2 Phương trình trở thành: 2 2 2
2  6sin x cos x  sin x cos x  0  4  3sin 2x  sin 2x  0 k   Với x    1 399 0;100 
0   k  100    k  4 4 4  Mà k     k
 99  x   99 (thỏa mãn)  a  b  99  4  103. Chọn D. max 4 Câu 24: Phương trình  2  cos x 2 3 1 2  cos2x 1  0  3
 cos 2x  cos2x  2  0 cos2x  1 2x  k2 x  k   2    2    1  2  cos2x   2x  arccos   k2   x   arccos   k    3   3   2  3 
TH1. Với x  k 0;4   0  k  4   k  0;1;2;  3 nên có 4 nghiệm. 1  2  TH2. Với x  arccos   k   
0;4   0,116  k  3,883 2  3    k  0;1;2;  3 nên có 4 nghiệm. 1  2 
TH3. Với x   arccos   k   
0;4   0,116  k  4,116 2  3 
nên có 4 nghiệm. Vậy phương trình có tổng 12 nghiệm. Chọn D.     k2 2x   x  k2 x        Câu 25: Phương trình 2 6 3  sin 2x  sin  x        2   
2x     x  k2 x   k2  2  2            Với x  ; 
 x   S  sin  sin 2.  .. sin 2018.   0      2  6 6  6   6  n 1 sin x nx Ta có 2
sin x  sin 2x  sin 3x  ... sin nx  .sin x 2 sin 2 Trang 19 2019   sin . 2018.  1 3 1 1 3 Với 2 6 6 x  ; n  2018   S  .sin  :  . Chọn D. 6  2 2 2 2 2 2 sin 12
Câu 26: Phương trình   cos x   2 2 x  cos x 2 2 2 2 5 sin
sin x  cos x  3  0  cos x  cos x   2 2 . 2 2
5  3  0  2cos 2x  5cos2x  3  0      1 2x   k2 x   k cos2x     3  6 2        cos2x  3  2x    k2 x    k  3  6   TH1. Với x   k    1 12107 0; 2018
 0   k  2018    k  6 6 6 6    
Mà k   nên k  0;1;2;...;201  2017 7   
 k  2018.  2035153   k 0  6  6  
TH2. Với x    k    1 12109 0; 2018
 0    k  2018   k  6 6 6 6    
Mà k   nên k  0;1;2;...;2017;201  2018 8      k  2  018.  2037171   k 0  6  6
Vậy tổng các nghiệm cần tính là 2
4072324  2018  . Chọn C. Trang 20