


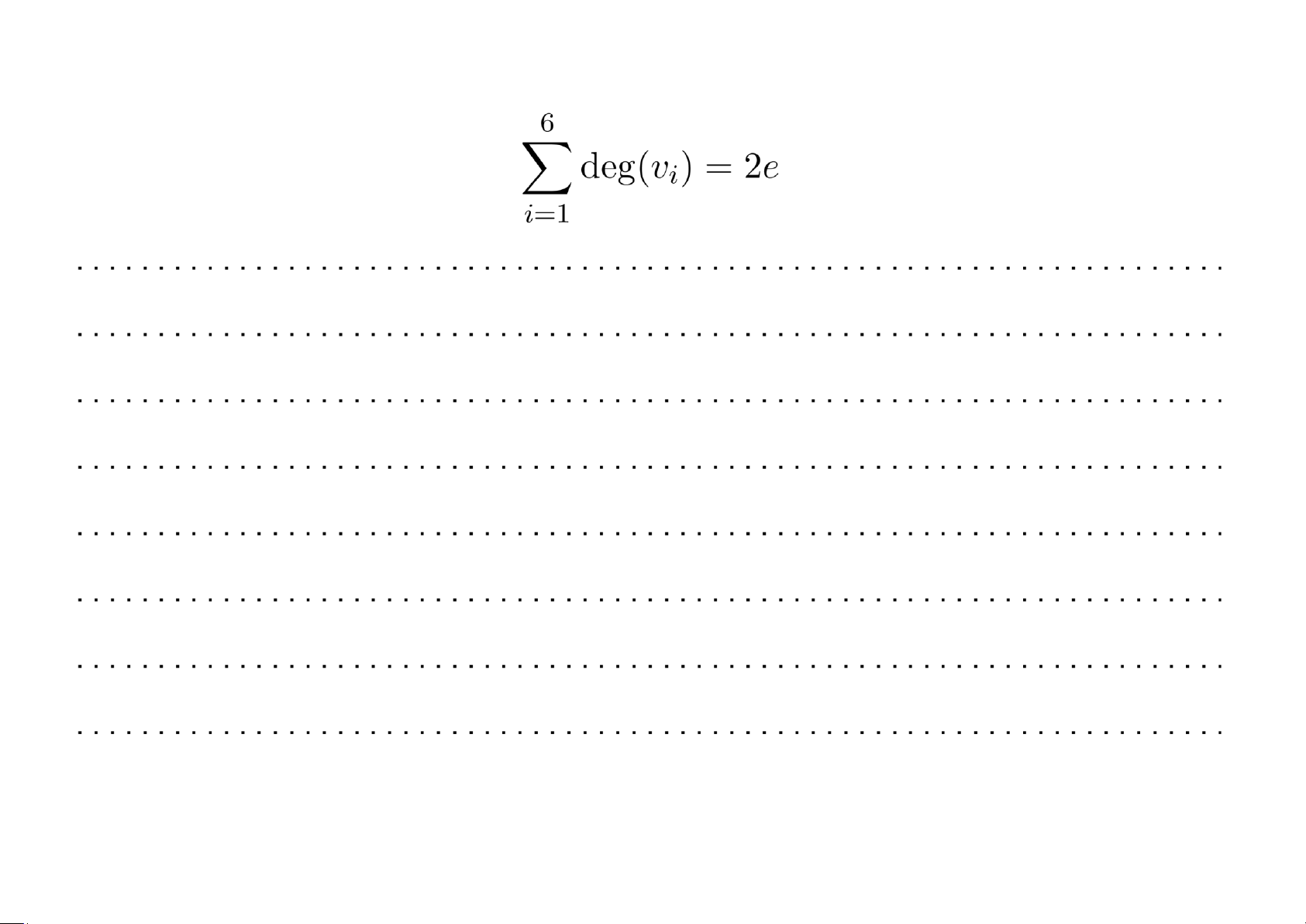










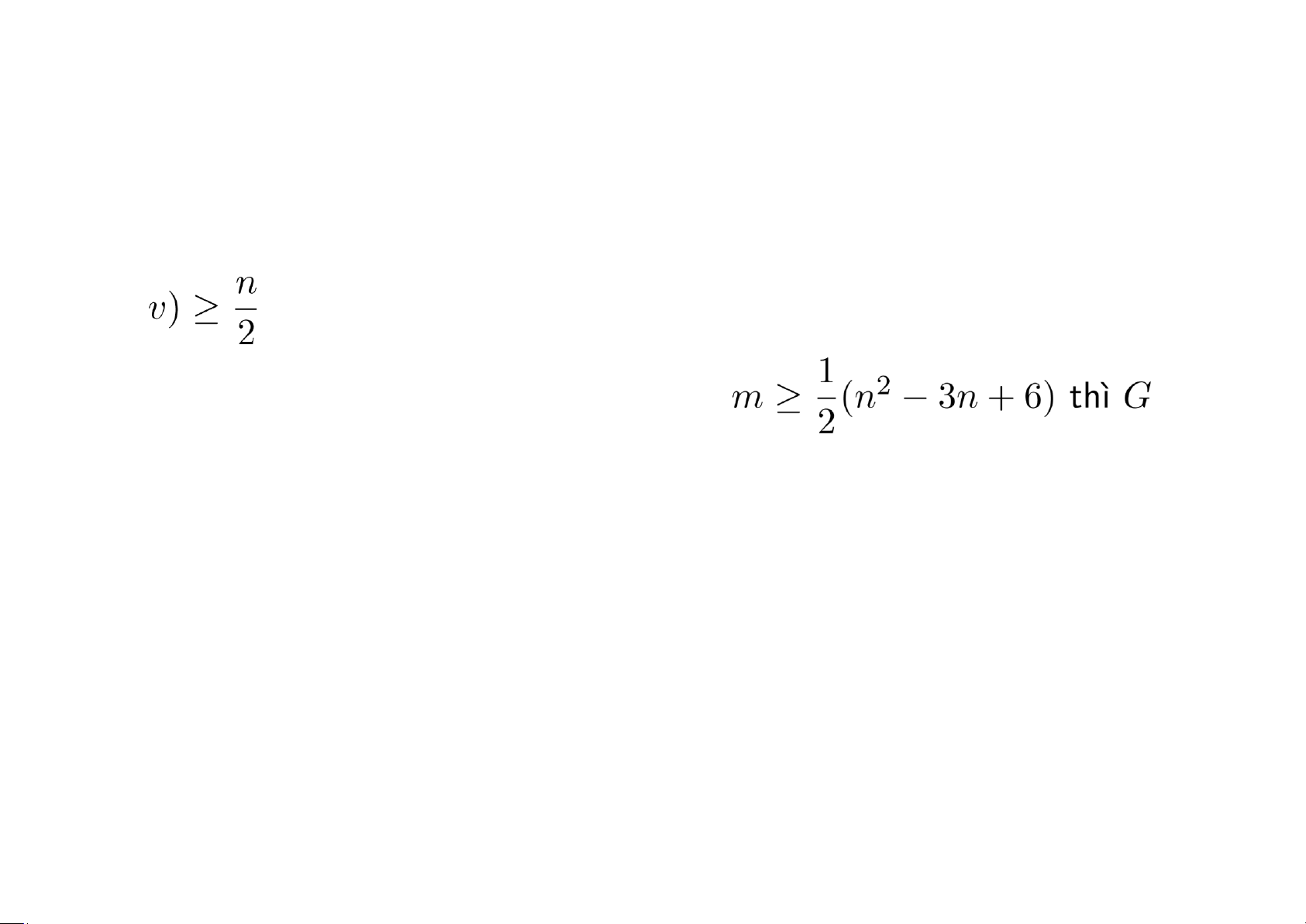




Preview text:
lOMoAR cPSD| 40425501
Chương 5: Lý thuyết đồ thị Các khái niệm cơ bản Biểu diễn đồ thị Đồ thị có hướng
Chu trình và đường đi Euler
Chu trình và đường đi Hamilton
Bài toán đường đi ngắn nhất lOMoAR cPSD| 40425501
5.1 Các khái niệm cơ bản
Định nghĩa 5.1 Một đồ thị (graph) (vô hướng) G = (V,E) là một bộ gồm 2 tập
hợp: V được gọi là tập các đỉnh (vertex) và E được gọi là tập các cạnh (edge).
• Mỗi cạnh e ∈ E nối tương ứng một cặp đỉnh u,v ∈ V, kí hiệu e = uv •
Nếu e = uv thì ta nói u,v là hai đỉnh kề nhau (liên kết nhau) (adjacent),
e liên thuộc với u và v. Các đỉnh u,v được gọi là đầu mút của cạnh e.
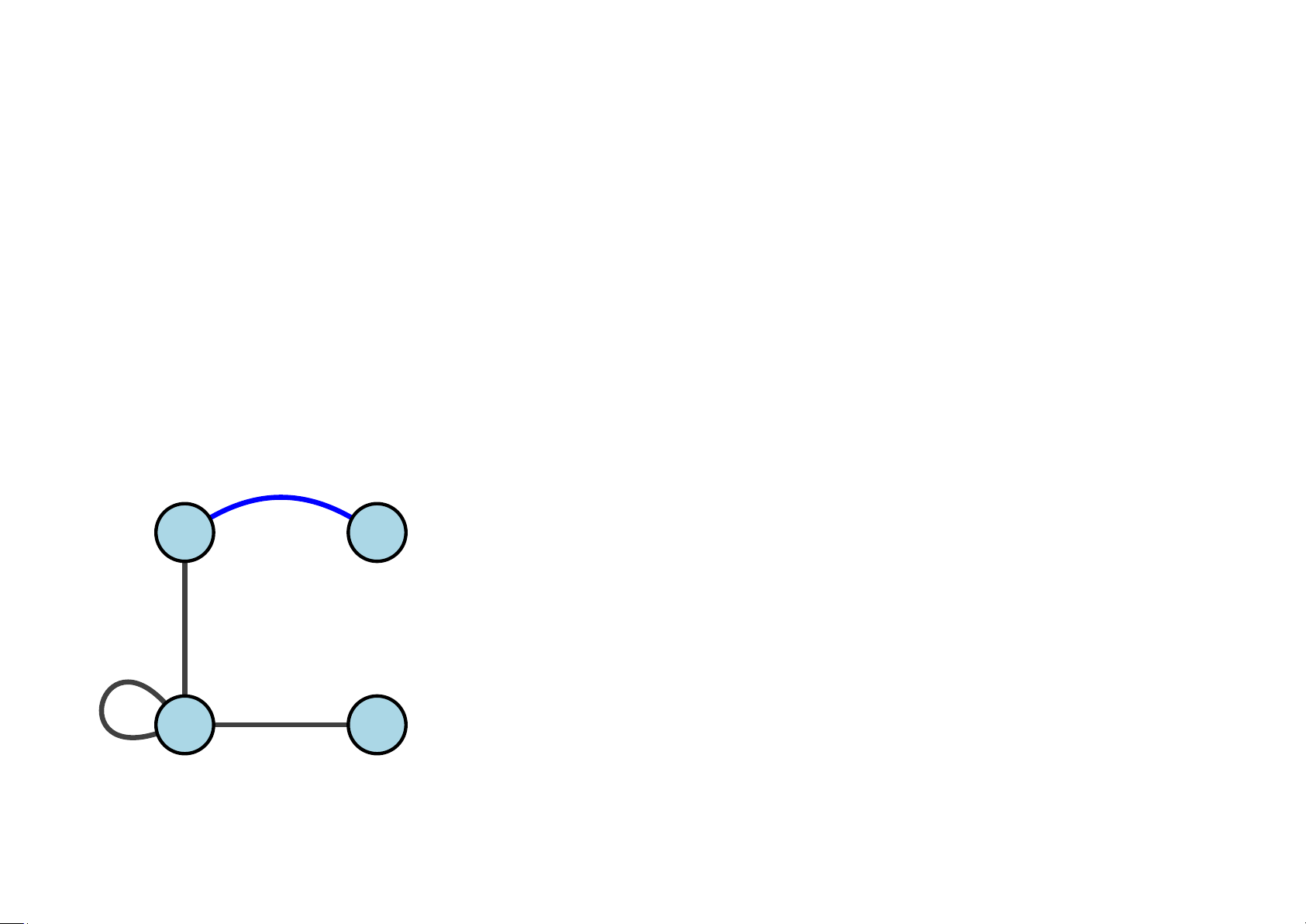
• Nếu u ≡ v thì cạnh uu được gọi là một vòng (khuyên) (loop) tại u. Ví dụ 5.2 v 3 v 4 •
Đồ thị G = (V,E)
• Tập các đỉnh V = {v1,v2,v3,v4}
• Tập các cạnh E = {v1v1,v1v2,v1v3,v3v4} v 1 v 2
• Hai cạnh được gọi là song song nếu chúng cùng
nối tương ứng một cặp đỉnh. lOMoAR cPSD| 40425501
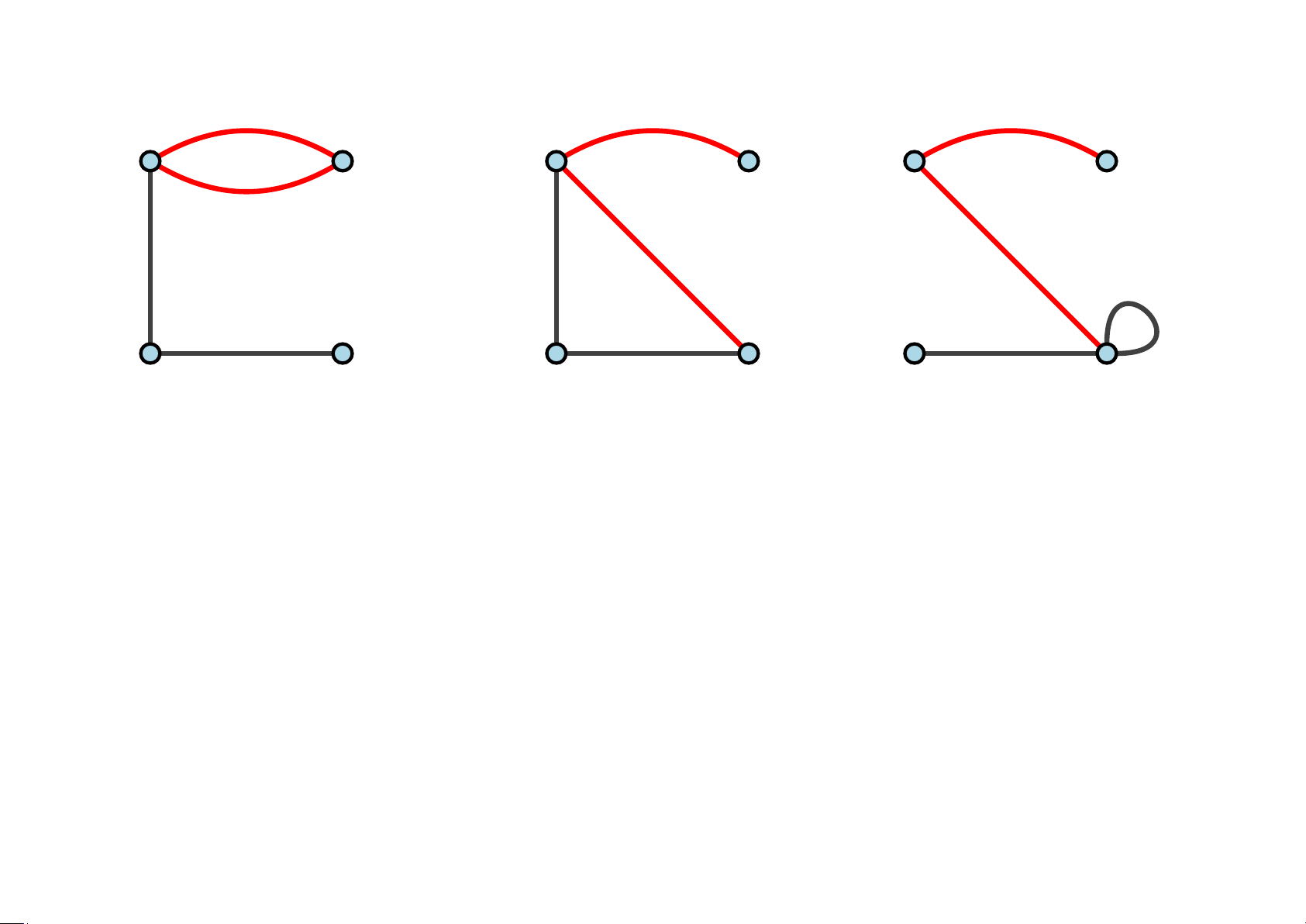
• Một đồ thị được gọi là đơn đồ thị (simple graph) nếu nó không có cạnh
song song và cũng không có vòng. Ngược lại, ta gọi là đa đồ thị. Đồ thị có cạnh song Đơn đồ thị Đa đồ thị song
• Một đồ thị G′ = (V ′,E′) được gọi là đồ thị con của đồ thị
G = (V,E) nếu V ′ ⊆ V và E′ ⊆ E.
• Một đồ thị G = (V,E) được gọi là hữu hạn nếu V,E là các tập hữu hạn.
Ngược lại, ta gọi là đồ thị vô hạn.
• Bậc của đỉnh v trong đồ thị G = (V,E), ký hiệu deg(v), là số đỉnh kề với
nó, riêng vòng (khuyên) tại một đỉnh được tính hai lần cho bậc của nó. lOMoAR cPSD| 40425501
• Đỉnh v gọi là đỉnh treo nếu deg(v) = 1 và gọi là đỉnh cô lập nếu deg(v) = 0.
• Cạnh treo là cạnh có đầu mút là đỉnh treo.
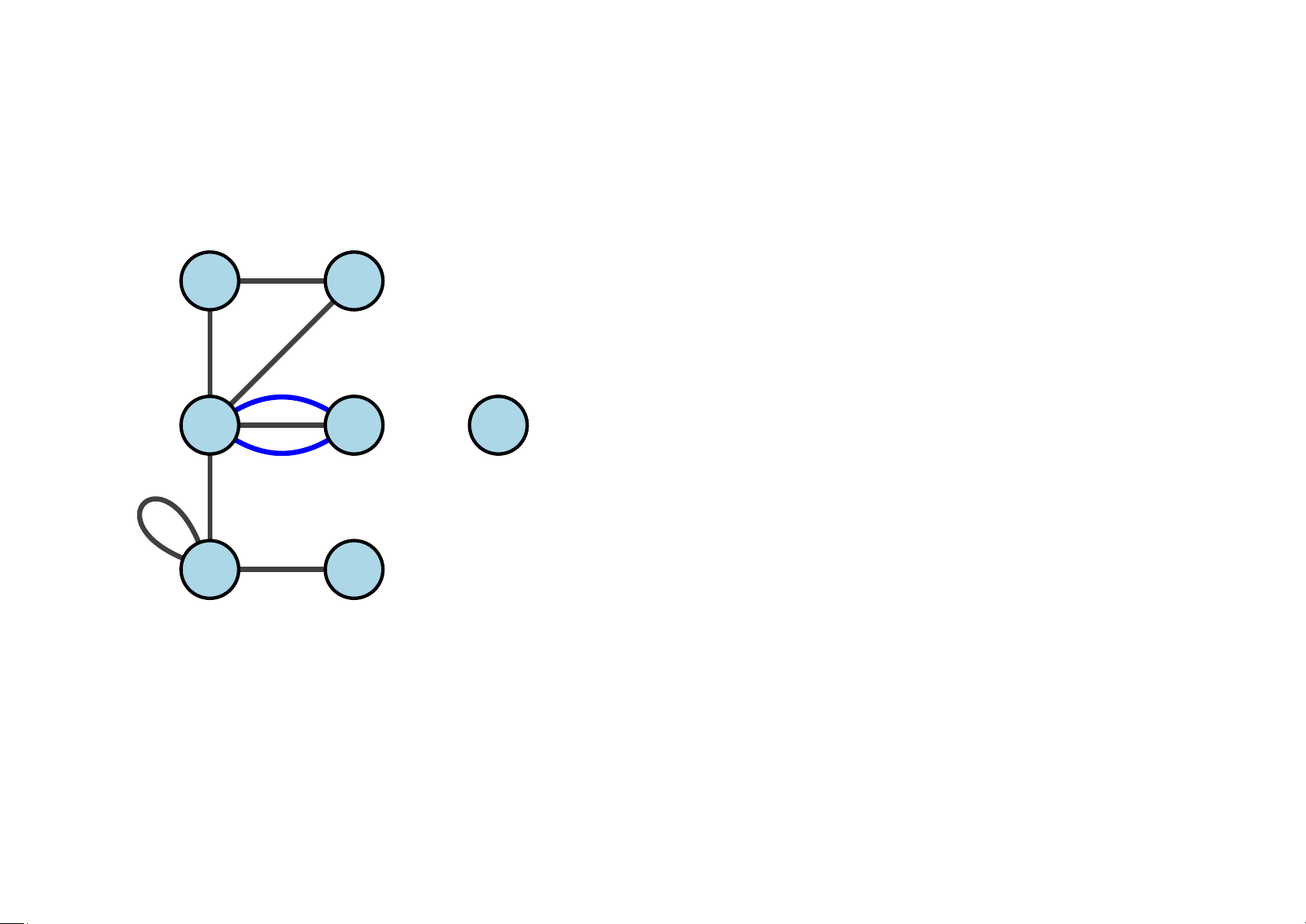
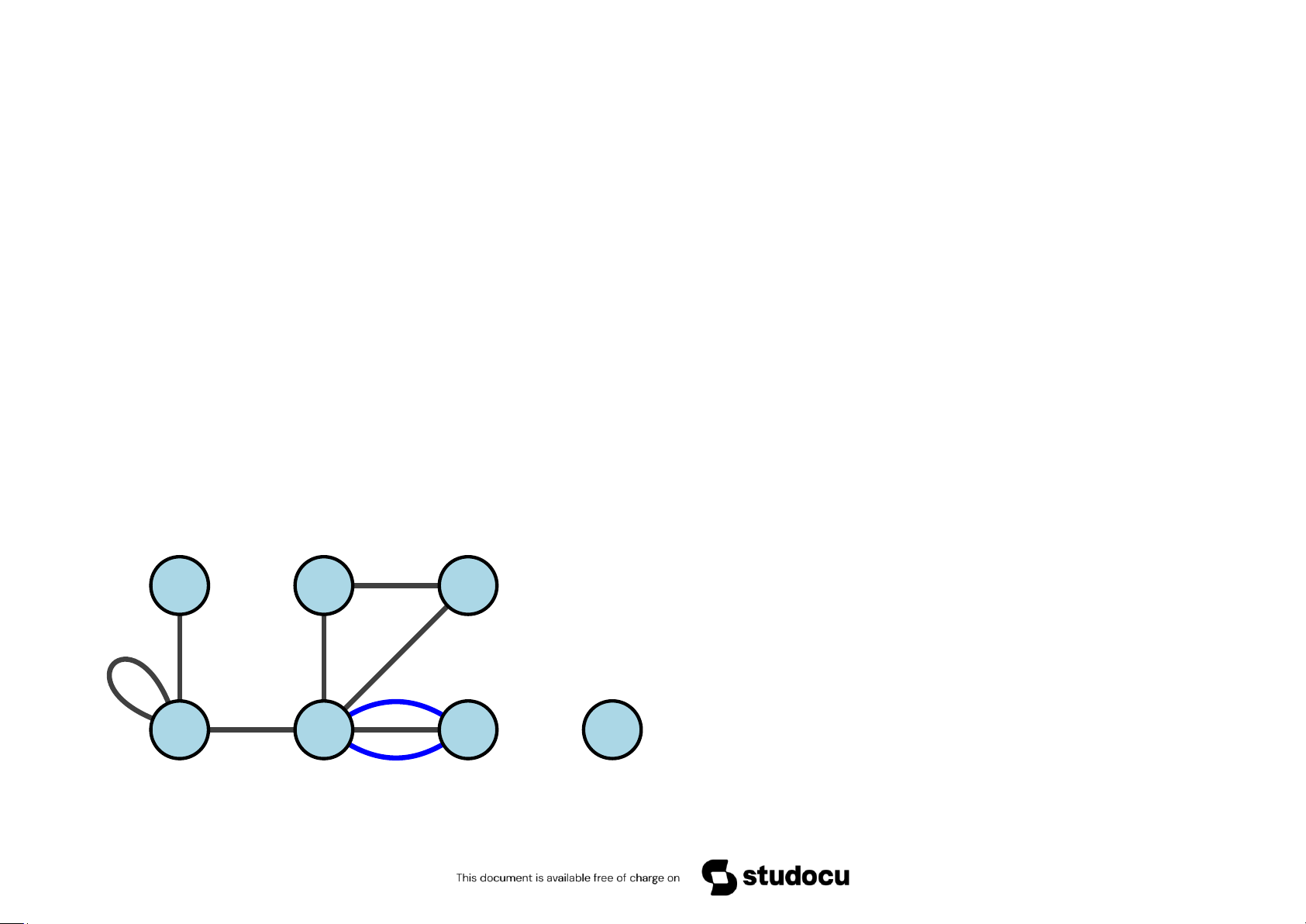
• deg(v1) = 4,deg(v2) = 1, deg(v3) = v 6 v 5
6;deg(v4) = 3, deg(v5) = 2,deg(v6) = 2, deg(v7) = 0 v 3 v 4
v 7 • Đỉnh treo là v2.
• Đỉnh cô lập là v7.
Định lý 5.3 Tổng số bậc của các đỉnh của một v 1 v 2
đồ thị bằng 2 lần số cạnh của nó.
Nhận xét. Cho một đồ thị G. Khi đó
1. Số đỉnh bậc lẻ là một số chẵn
2. Tổng bậc của các đỉnh bậc lẻ là một số chẵn lOMoAR cPSD| 40425501 Định lý 5.4
1. Nếu số đỉnh của một đơn đồ thị nhiều hơn 1 thì tồn tại ít nhất 2 đỉnh có bậc bằng nhau.
2. Cho đồ thị G. Nếu số đỉnh n > 2 và có đúng 2 đỉnh cùng bậc thì bậc của
hai đỉnh này không đồng thời bằng 0 hoặc n − 1.
Ví dụ 5.5 Chứng minh rằng, trong một bàn tròn có 6 người nào, có ba người
đều biết nhau hoặc ba người không biết ai trong số hai người còn lại.
Giải. Ta vẽ một đồ thị trong đó mỗi người được biểu diễn bằng một đỉnh và
nối hai đỉnh bằng một cạnh liền nếu những người tương ứng biết nhau và
bằng một cạnh chấm nếu hai người không biết nhau. Ta sẽ chỉ ra rằng luôn
tồn tại một tam giác gồm các cạnh liền hoặc tam giác chấm.
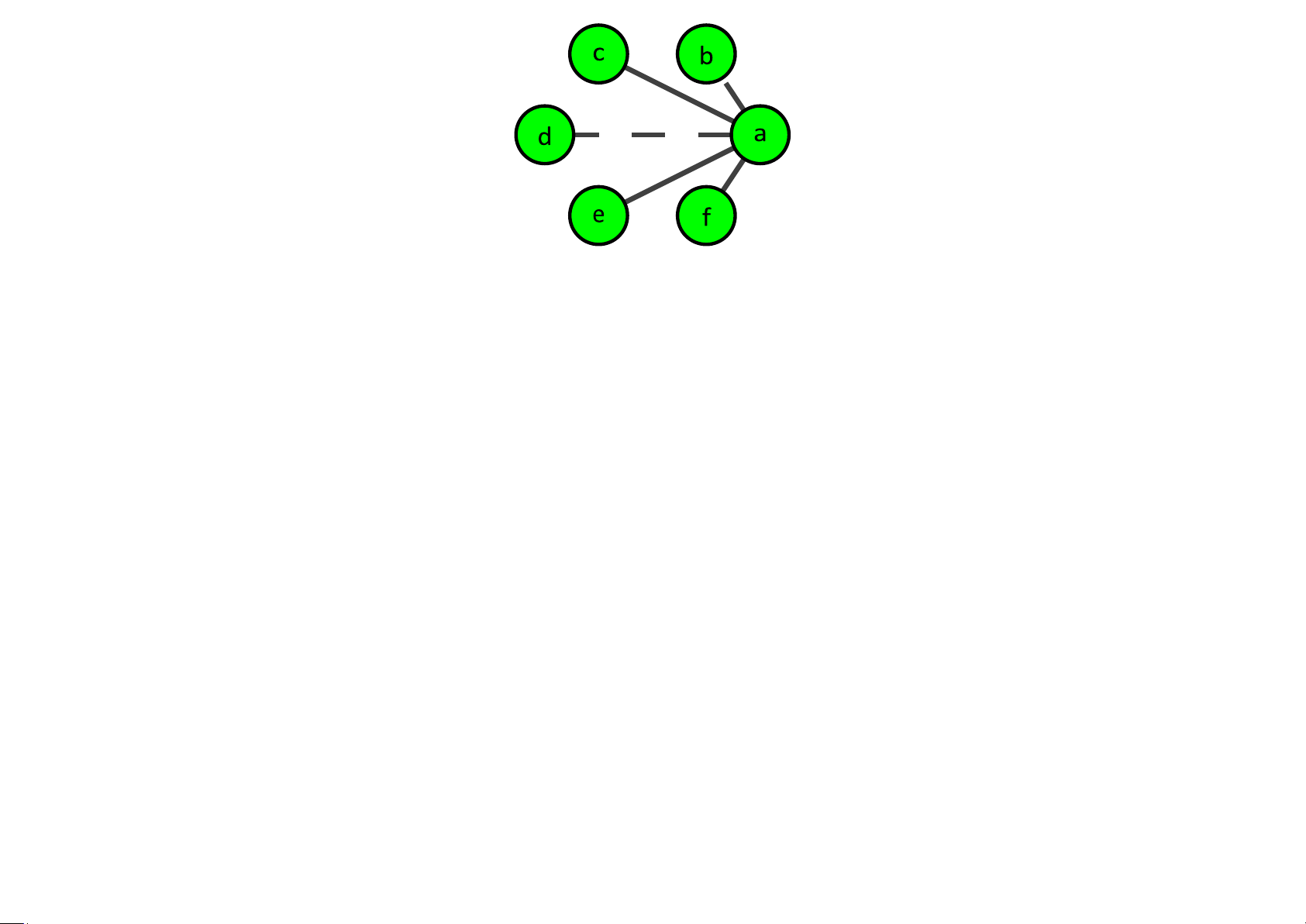
• Cho a là một đỉnh bất kỳ. Khi đó phải có chính xác năm cạnh kề với a,
nét liền hoặc nét đứt, và do đó ít nhất ba trong số các cạnh này phải cùng loại.
• Ta giả sử rằng có ba cạnh liền nét (xem hình); trường hợp có ít nhất ba
nét đứt cũng tương tự. lOMoAR cPSD| 40425501
• Nếu những người tương ứng với các đỉnh c và e biết nhau thì a, c và e
tạo thành một tam giác liền theo yêu cầu.
• Tương tự, nếu những người tương ứng với các đỉnh c và f, hoặc các
đỉnh e và f biết nhau thì chúng ta lại thu được một tam giác liền.
• Nếu không có hai người tương ứng với các đỉnh c, e và f biết nhau thì c,
e và f từ một tam giác nét đứt theo yêu cầu. lOMoAR cPSD| 40425501 Ví dụ 5.6
Cho các đồ thị dưới đây. Xác định tập đỉnh và tập cạnh d c d c t z a b a b Tập đỉnh Tập đỉnh
V = {.......................} ....................... Tập đỉnh
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Ví dụ 5.7 Tập cạnh Tập cạnh .......................
E = {........................} ....................... Tập cạnh .......................
Determine the number of edges in a graph with 6 vertices, 2 of
degree 4 and 4 of degree 2. Draw two such graphs. Giải. Giả sử đồ thị có 6
đỉnh và e cạnh, theo Định lý 5.3
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Ví dụ 5.8
Show that there exists no simple graph corresponds to the following degree sequence : a. 0, 2, 2, 3, 4 b. 1, 1, 2, 3 c. 2, 2, 3, 4, 5, 5 d. 2, 2, 4, 6
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Ví dụ 5.9 Giải.
.......................................................................
.......................................................................
.......................................................................
.......................................................................
Ví dụ 5.9 Show that the sequence 6, 6, 6, 6, 4, 3, 3, 0 is not graphical.
Giải. Giả sử tồn tại một đồ thị có dãy các bậc của các đỉnh là 6, 6, 6, 6, 4, 3, 3, 0
Sau khi xóa 1 đỉnh có bậc 6, ta có một đồ thị có dãy các đỉnh là 5, 5, 5, 3, 2, 2, 0
Xóa tiếp 1 đỉnh bậc 5, ta có một đồ thị có dãy các đỉnh là ....................... Xóa
tiếp 1 đỉnh bậc ...., ta có một đồ thị có dãy các đỉnh là .......................
.......................................................................
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Ví dụ 5.10
.......................................................................
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Ví dụ 5.10 Show that the following sequence is graphical. Also find a graph
corresponding to the sequence 6, 5, 5, 4, 3, 3, 2, 2, 2. Giải.
- Xóa đỉnh bậc 6 (trừ 1 bậc của 6 đỉnh tiếp theo) : 4, 4, 3, 2, 2, 1, 2, 2
- Sắp xếp lại dãy các bậc : 4, 4, 3, 2, 2, 2, 2, 1
- Xóa 1 đỉnh bậc 4 (trừ 1 bậc của 4 đỉnh kế tiếp) : 3, 2, 1, 1, 2, 2, 1
- Sắp xếp lại dãy các bậc : 3, 2, 2, 2, 1, 1, 1
- Xóa 1 đỉnh bậc 3 (trừ 1 bậc của 3 đỉnh tiếp theo) : 1, 1, 1, 1, 1, 1
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
5.2 Một số đồ thị đặc biệt
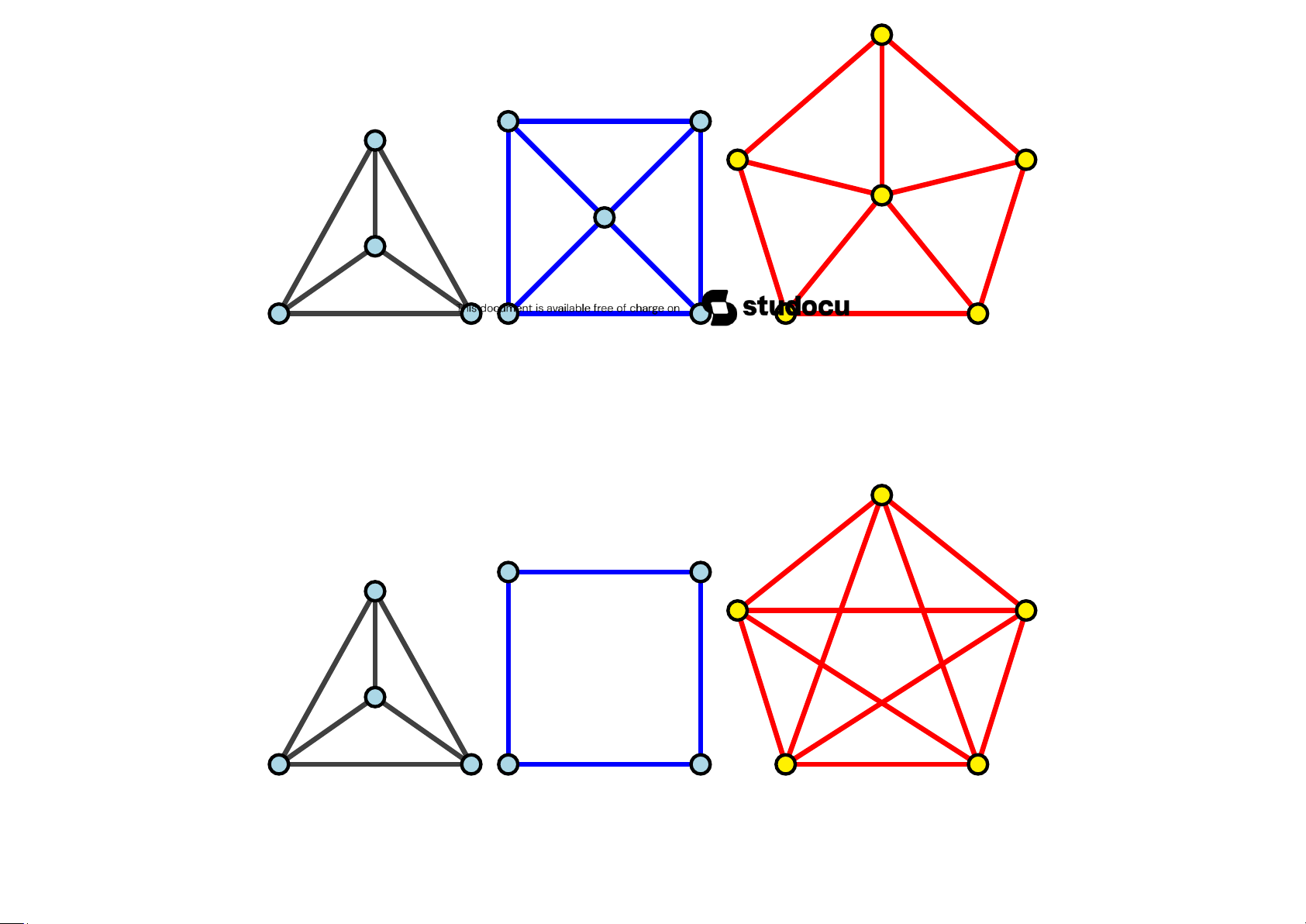
5.2.1 Đồ thị đầy đủ • Đồ thị G = (V,E) có n đỉnh được gọi là đầy đủ, ký hiệu
là Kn, là đơn đồ thị mà hai đỉnh phân biệt bất kỳ của nó luôn liền kề.
• deg(v) = n − 1 với mọi v ∈ V. • Số cạnh . 5.2.2 Đồ thị vòng
• Đồ thị G = (V,E) có n > 2 đỉnh v1,v2,...,vn và n cạnh
v1v2,v2v3,v3v4,...,vn−1vn,vnv1 được gọi là đồ thị vòng, ký hiệu Cn.
• deg(v) = 2 với mọi v ∈ V.
• Số cạnh |E| = n.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 5.2.3 Đồ thị bánh xe
• Đồ thị G = (V,E) có n + 1 đỉnh được gọi là bánh xe, ký hiệu là Wn+1, là
đồ thị vòng Cn và đỉnh vn+1 nối với tất cả các đỉnh của Cn.
• deg(vi) = 3 với mọi vi ∈ V \ {vn+1}.
• deg(vn+1) = n
• Số cạnh |E| = 2n.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 5.2.4 Đồ thị đều
• Đồ thị G được gọi là đồ thị đều bậc k nếu các đỉnh của G đều có bậc bằng k.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
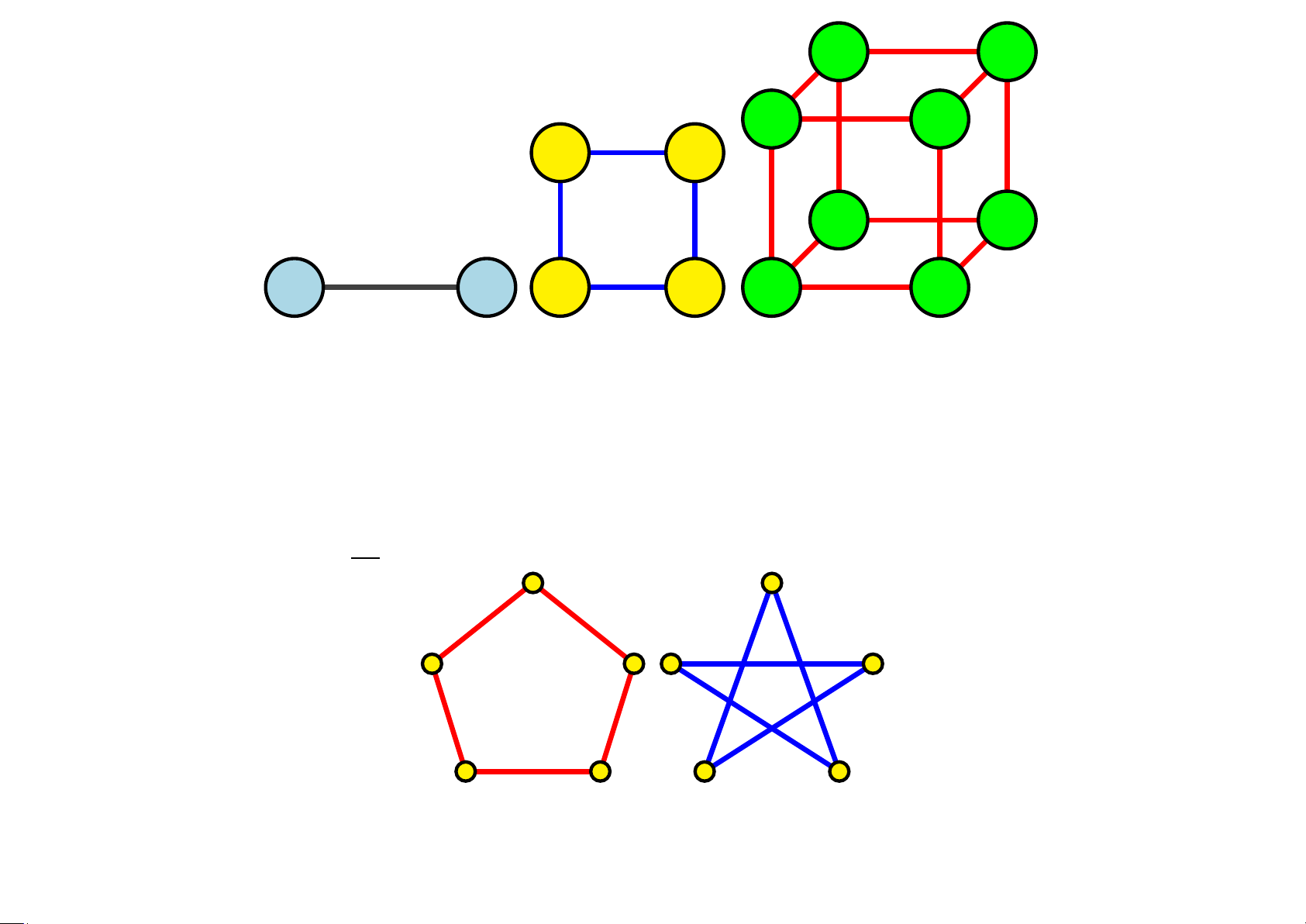
5.2.5 Đồ thị khối • Đồ thị khối n chiều (n ≥ 1), kí hiệu Qn, là đồ thị có 2n
đỉnh, mỗi đỉnh được biểu diễn bằng xâu nhị phân có độ dài n.
• Hai đỉnh là liền kề khi và chỉ khi các xâu nhị phân biểu diễn chúng khác nhau đúng một bit.
• Bậc của mỗi đỉnh trong Qn là n.
• Số cạnh của Qn là n.2n−1
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 110 111 010 011 10 11 100 101 0 1 00 01 000 001 5.2.6 Đồ thị bù
• Hai đơn đồ thị G và G′ được gọi là bù nhau nếu chúng có chung các đỉnh
và cạnh nào thuộc G thì không thuộc G′.
• Kí hiệu G′ = G.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
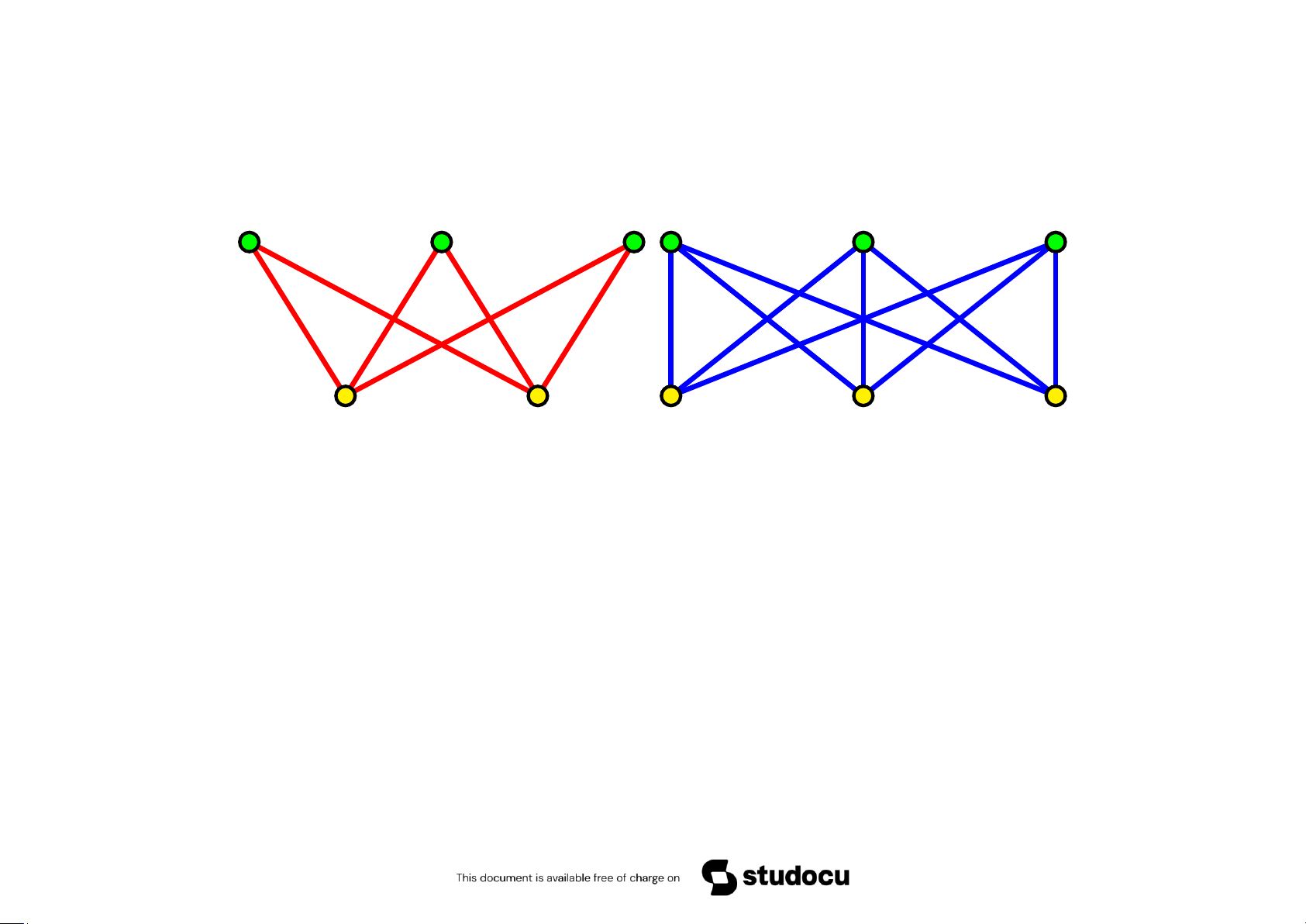
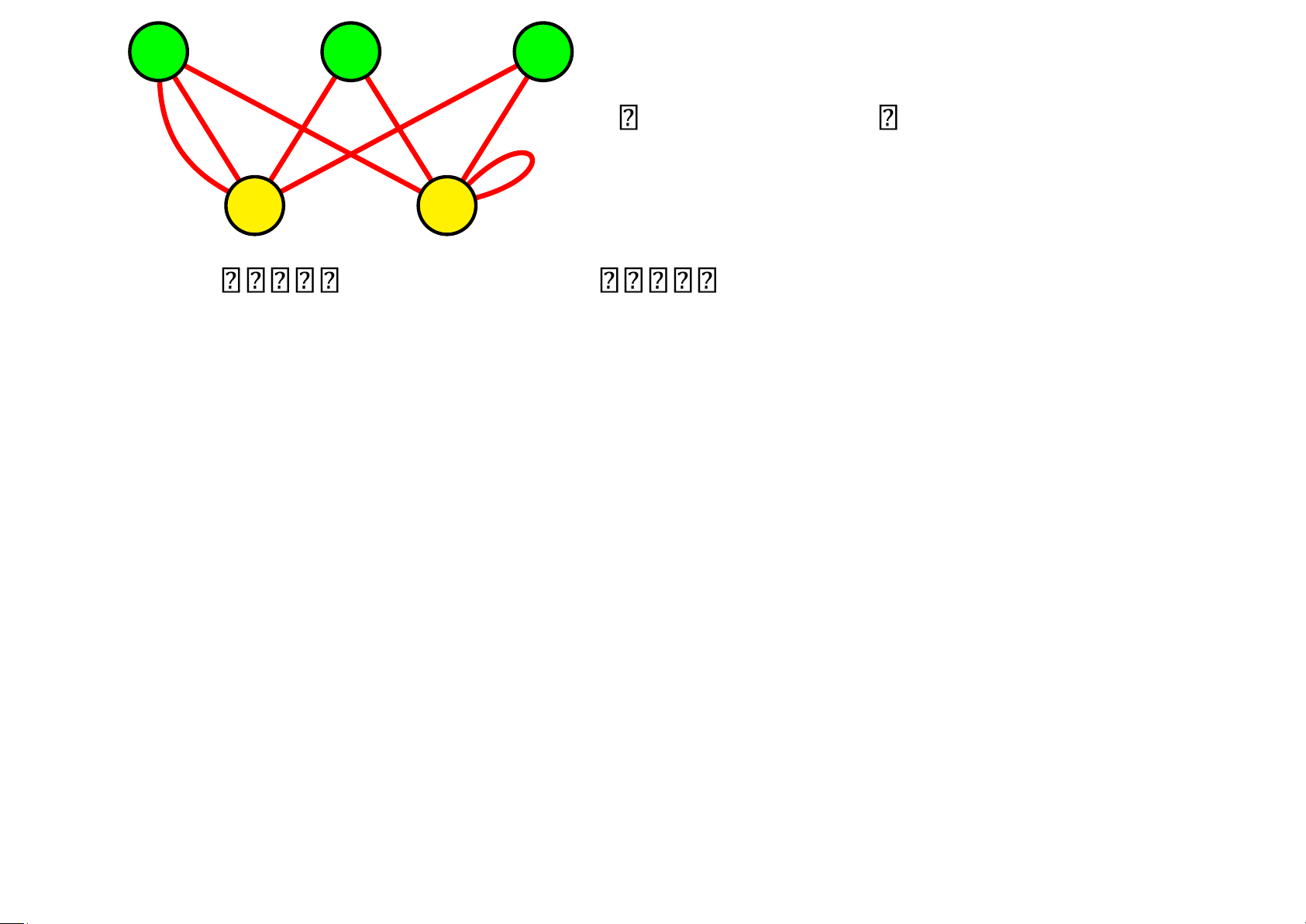
5.2.7 Đồ thị lưỡng phân • Một đồ thị G được gọi là đồ thị lưỡng phân nếu tập
các đỉnh của G có thể phân thành 2 tập hợp không rỗng, rời nhau sao cho
mỗi cạnh của G nối một đỉnh thuộc tập này đến một đỉnh thuộc tập kia. • Kí hiệu Km,n 5.3 Biểu diễn đồ thị
Định nghĩa 5.11 Cho đồ thị G = (V,E) có n đỉnh. Ma trận liền kề của G là A =
[aij]n trong đó
aij = số cạnh nối đỉnh i và đỉnh j.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 v 5 v 4 v 3
v1 v2 v3 v4 v5
v1 0 0 1 1 2 v2 0 1 1 1 1 v 1 v 2 A = v3 1 1 0 0 0
v4 1 1 0 0 0 v5 2 1 0 0 0
Định nghĩa 5.12 Hai đồ thị G = (V,E) và G′ = (V ′,E′) được gọi là đẳng cấu, kí
hiệu G ∼= G′, nếu
1. tồn tại một đẳng cấu f : V → V ′ và
2. cạnh uv ∈ E khi và chỉ khi cạnh f(u)f(v) ∈ E′. Ví dụ 5.13
Ta có G ∼= G′ vì có song ánh
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 u 4 u 3 v 4
v 3 f : V → V ′ u1 7→ v1 u2 7→ v2 u3 7→ v4
G = (V,E)G
′ = (V ′,E′) u 1 u 2 v 1 v 2 u4 →7 v3
Định lý 5.14 Nếu G ∼= G′ thì |V | = |V ′|,|E| = |E′| và deg(v) =
deg(f(v)) với mọi v ∈ V.
Định nghĩa 5.15 Đồ thị G được gọi là tự bù nếu G đẳng cấu với phần bù của nó. Ví dụ 5.16
Ta có G ∼= G với đẳng cấu v 4 v 4 v 5 v
v1 7→ v1 v2 7→ v3 v3 7→ v 5 v 3 3
v5 v4 7→ v2 v 1 v 2 v 1 v 2 G G
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) → lOMoAR cPSD| 40425501
Định lý 5.17 Hai đồ thị có ma trận liền kề (theo một thứ tự nào đó của các
đỉnh) bằng nhau thì đẳng cấu với nhau. v 4 u 4 v 5 v 3 u 5 u 3 G G ′ v 1 v 2 u 1 u 2
có các ma trận liền kề v1
v2 v3 v4 v5
u1 u3 u5 u2 u4 v 1 0 0 1 0 0 1 1 0 v2 1 0 1 0 10 uu13 0 1 0 v 0 345 1 0 1 01 1 0 1 0 v 0 v 1 0 1 0 0 1 0 0 0 0 1 0 0 1 1 0
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 0 = uuu524 001 1 0 5.4 Đồ thị có hướng
Định nghĩa 5.19 Một đồ thị có hướng G = (V,E) gồm một tập khác rỗng V mà
các phần tử của nó gọi là các đỉnh và một tập E mà các phần tử của nó gọi là
các cung, đó là các cặp có thứ tự của các phần tử thuộc V. Ví dụ 5.20 v 3 v 4
Đồ thị G = (V,E) •
• Tập các đỉnh V = {v1,v2,v3,v4}
• Tập các cạnh E = v 1 v 2
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
{(v1,v1),(v1,v2),(v2,v1),(v1,v3),(v4,v3)}
Cho G = (V,E) là một đồ thị có hướng.
• Nếu e = (u,v) ∈ E thì ta kí hiệu e = −uv→
• e có hướng từ u đến v
• u là đỉnh đầu, v là đỉnh cuối
• e là khuyên (vòng) khi và chỉ khi u ≡ v
• Bậc vào tại u ∈ V, kí hiệu deg−(u), là số cung đi vào nó.
• Bậc ra tại u ∈ V, kí hiệu deg+(u), là số cung đi ra khỏi nó. Ví dụ 5.21 v 3 v 4
• deg−(v1) = 2,deg+(v1) = 3
• deg−(v2) = 1,deg+(v2) = 1
• deg−(v3) = 2,deg+(v3) = 0 v 1 v 2
• deg−(v4) = 0,deg+(v4) = 1
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Định lý 5.22 Tổng bậc vào của các đỉnh bằng tổng bậc ra và bằng số cạnh của đồ thị
X deg−(v) = X deg+(v) = |E|. v∈V v∈V
Định nghĩa 5.23 Cho một đồ thị G = (V,E). Một đường đi có độ dài k là một
dãy k cạnh liên tiếp. Kí hiệu v1v2,v2v3,...,vk−1vk hoặc v1v2 ...vk trong đó v1 được
gọi là đỉnh đầu, vk được gọi là đỉnh cuối.
• Đường đi v1v3v4v6v3v4 v 2 v 6
v 5 • Đường đi v2v1v3v1v1v2 • Đường đi
v3v5v6v3. v 1 v 3 v 4
v 7 • Đường đi đơn (giản) là đường đi
không qua cạnh nào quá một lần.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
• Đường đi sơ cấp là đường đi không qua đỉnh nào quá một lần.
• Mọi đường đi sơ cấp đều là đường đi đơn. Ví dụ 5.24 v 6 v 5 v 4 u 6 u 5 u 4 v 1 v 2 v 3 u 1 u 2 u 3
• Đường đi đơn: v1v2v3v4v2v5v6;u1u2u5u4u3u6u5 (không là đường đi sơ cấp)
• Đường đi sơ cấp: v1v5v2v4v3;u1u2u5u4u3u6
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
• Chu trình là một đường đi có điểm đầu và cuối trùng nhau.
• Chu trình đơn giản là chu trình không chứa cạnh nào quá 1 lần.
• Chu trình sơ cấp là chu trình chứa đỉnh nào quá 1 lần. Ví dụ 5.25 v 6 v 5 v 4 u 6 u 5 u 4 v 1 v 2 v 3 u 1 u 2 u 3
• Chu trình đơn v1v2v3v4v2v5v6v1 (không là chu trình sơ cấp)
• Chu trình sơ cấp: v1v5v4v4v3v2v1;u6u5u4u3u6 Định lý 5.26
1. Cho G = (V,E) là một đồ thị vô hướng có số đỉnh lớn hơn hoặc bằng 3 và
bậc của mọi đỉnh đều lớn hơn hoặc bằng 2. Khi đó G luôn tồn tại một chu trình sơ cấp.
2. Cho G = (V,E) là một đồ thị vô hướng có số đỉnh lớn hơn hoặc bằng 4 và
bậc của mọi đỉnh đều lớn hơn hoặc bằng 3. Khi đó G luôn tồn tại một chu
trình sơ cấp có độ dài chẵn.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Định nghĩa 5.27
• Hai đỉnh v,u trong đồ thị G được gọi là liên thông nếu tồn tại một đường đi nối chúng với nhau.
• Một đồ thị (vô hướng) được gọi là liên thông nếu có đường đi giữa mọi
cặp đỉnh phân biệt của đồ thị. Ví dụ 5.28
G là đồ thị liên thông, G′ là v 6 v 5 v 4 u 6 u 5
u 4 đồ thị không liên thông. v 1 v 2 v 3 u 1 u 2 u 3 G G′
• Một đồ thị không liên thông là hợp của hai hay nhiều đồ thị con liên
thông, mỗi cặp các đồ thị con này không có đỉnh chung.
• Các đồ thị con liên thông rời nhau như vậy được gọi là các thành phần
liên thông của đồ thị đang xét.
• Một đồ thị là liên thông khi và chỉ khi nó chỉ có một thành phần liên thông.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Định nghĩa 5.29
• Đỉnh u là một đỉnh cắt nếu số thành phần liên thông tăng lên khi bỏ u và
các cạnh liên thuộc với nó.
• Cạnh e là một cầu nếu số thành phần liên thông tăng lên khi bỏ cạnh e. Ví dụ 5.30 v 10 v 11 v 12 v 13 v 14 v 9 v 2 v 5 v 6 v 1 v 3 v 4 v 7 v 8
• Các đỉnh cắt: v2,v5,v6
• Cầu v5v6.
Định lý 5.31 Mọi đơn đồ thị n đỉnh (n ≥ 2) có tổng bậc của hai đỉnh tuỳ ý
không nhỏ hơn n đều là đồ thị liên thông.
Nhận xét. Đơn đồ thị mà bậc của mỗi đỉnh của nó không nhỏ hơn một nửa số đỉnh là đồ thị liên thông.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Định lý 5.32 Nếu một đồ thị có đúng hai đỉnh bậc lẻ thì hai đỉnh này phải liên
thông, tức là có một đường đi nối chúng. Định nghĩa 5.33
• Đồ thị có hướng được gọi là liên thông mạnh nếu luôn tồn tại đường đi
giữa hai đỉnh phân biệt bất kỳ.
• Đồ thị có hướng được gọi là liên thông yếu nếu đồ thị vô hướng tương
ứng của nó là liên thông. Ví dụ 5.34 u v w u v w x x y s t y s t liên thông liên thông yếu Định lý 5.35
1. Nếu một đồ thị có đúng 2 đỉnh bậc lẻ thì 2 đỉnh này liên thông với nhau.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
2. Một đồ thị là lưỡng phân khi và chỉ khi mọi chu trình của nó đều có độ dài chẵn.
Định nghĩa 5.36 Hợp của hai đồ thị G = (V,E) và G′ = (V ′,E′) là một đồ thị G′′ =
(V ′′,E′′) trong đó
V ′′ = V ∪ V ′;E′′ = E ∪ E′. Ví dụ 5.37 G G ′
G ′′ = G ∪ G ′ Định nghĩa 5.38
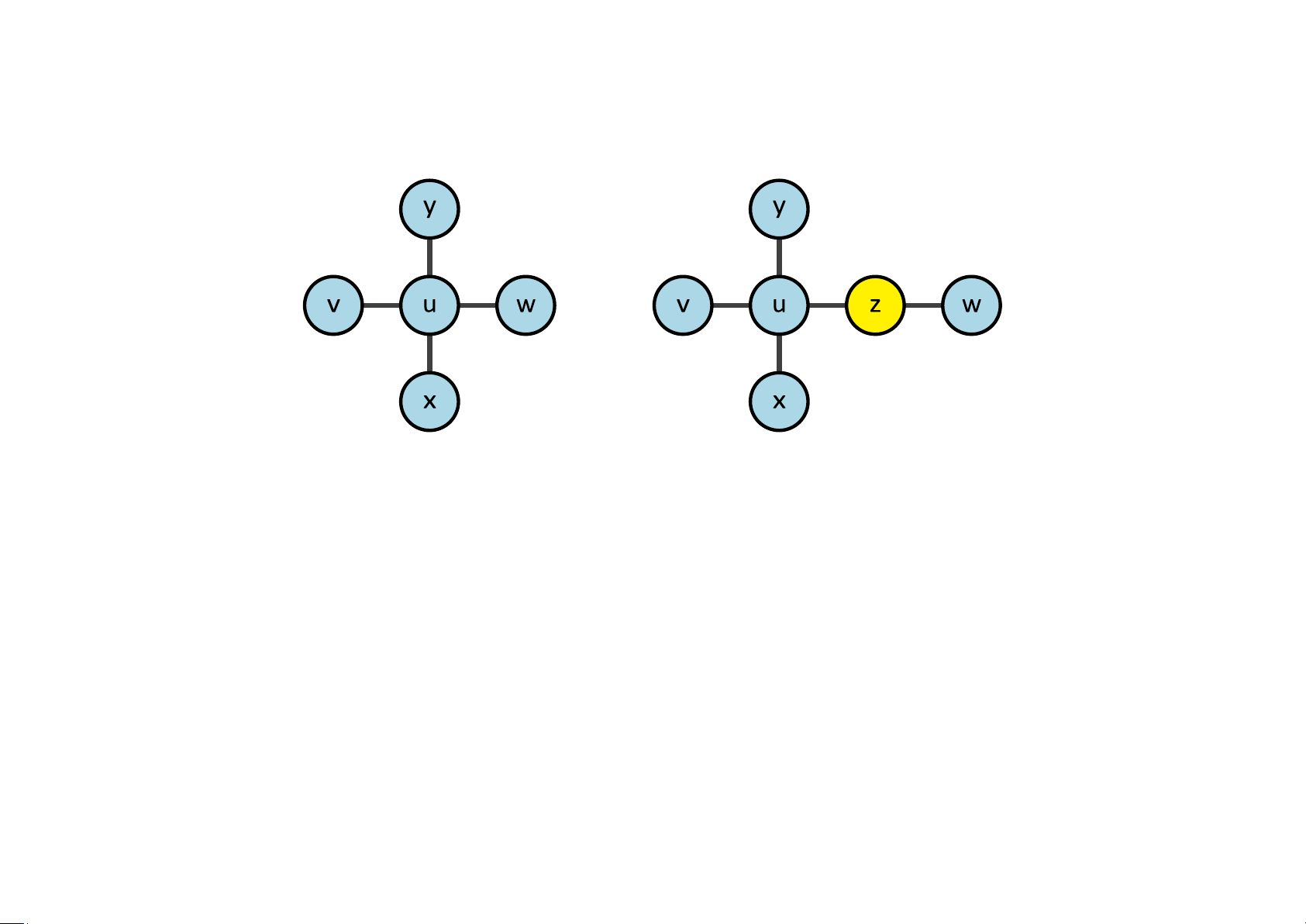
• Phép phân chia sơ cấp là phép thay thế cạnh uv của đồ thị G bởi một đỉnh mới w cùng
với 2 cạnh uw và vw.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
• Hai đồ thị G và G′ được gọi là đồng phôi nếu chúng có thể nhận được từ
cùng một đồ thị bằng một dãy các phép phân chia sơ cấp. Ví dụ 5.39
5.4 Chu trình và đường đi Euler
Thành phố Konigsberg thuộc Phổ (nay gọi là Kaliningrad thuộc Nga) được
chia thành bốn vùng bằng các nhánh sông Pregel, các vùng này gồm hai
vùng bên bờ sông, đảo Kneiphof và một miền nằm giữa hai nhánh của sông
Pregel. Vào thế kỷ 18, người ta xây bảy chiếc cầu nối các vùng này với nhau.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
• Bài toán. Có thể xuất phát tại một điểm nào đó trong thành phố, đi qua
tất cả 7 cây cầu, mỗi cây một lần, rồi trở về điểm xuất phát được không?
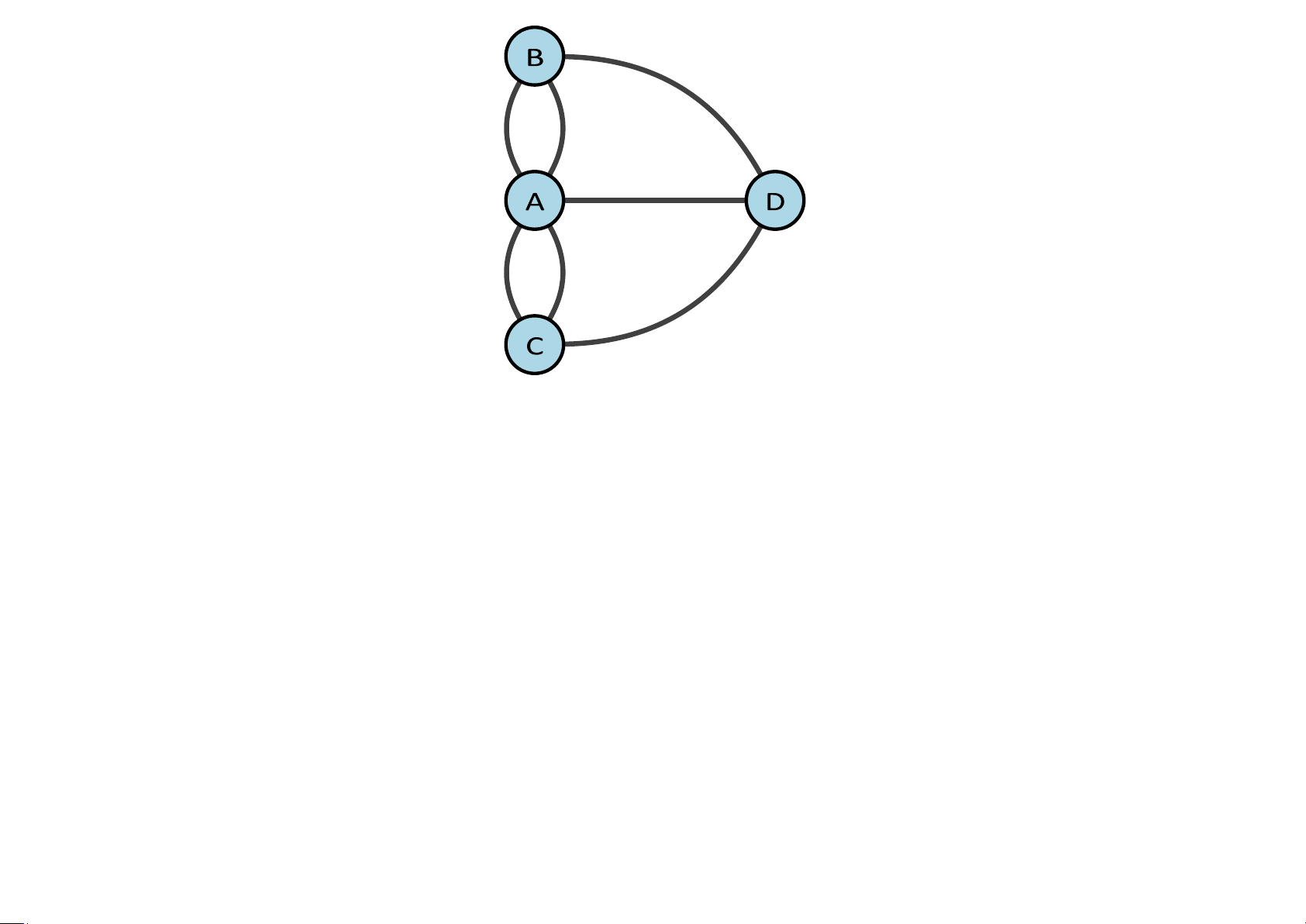
• Nếu ta coi mỗi khu vực A, B, C, D như một đỉnh và mỗi cầu qua lại hai
khu vực là một cạnh nối hai đỉnh thì ta có sơ đồ của Konigsberg là một
đa đồ thị G như hình dưới
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
• Bài toán tìm đường đi qua tất cả các cầu, mỗi cầu chỉ qua một lần có
thể được phát biểu lại bằng mô hình này như sau: Có tồn tại chu trình
đơn trong đa đồ thị G chứa tất cả các cạnh?
• Leonhard Euler (1707-1783) đã tìm ra lời giải cho bài toán vào năm 1736.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Định nghĩa 5.40
• Đường đi Euler (Euler path) trong đồ thị là đường đi của đồ thị đi qua
mỗi cạnh của đồ thị đúng một lần.
• Chu trình Euler (Euler circuit) trong đồ thị là một chu trình đi qua mỗi
cạnh của đồ thị đúng một lần và có đỉnh đầu trùng với đỉnh cuối.
• Đồ thị Euler là đồ thị có chứa ít nhất một chu trình Euler.
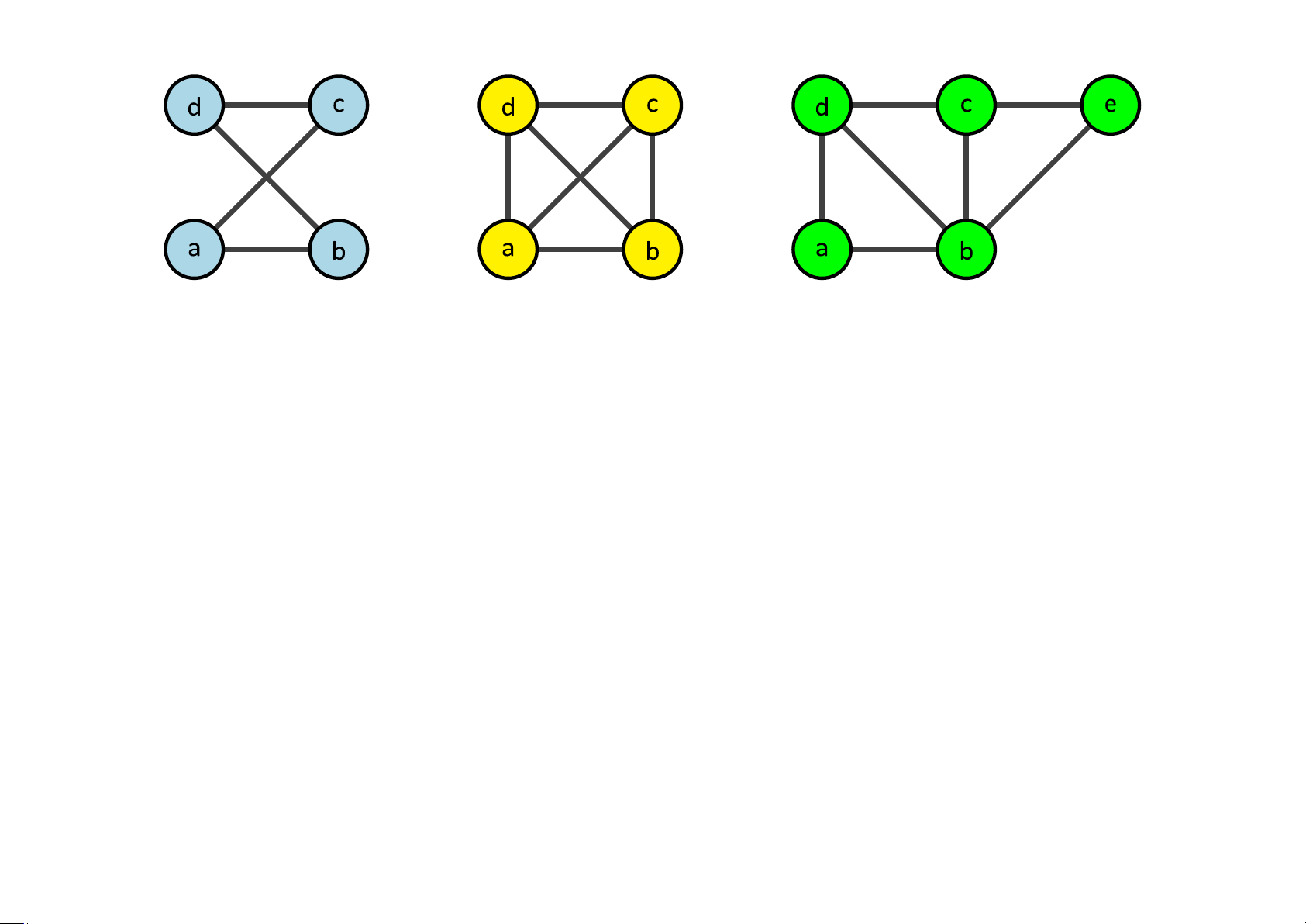
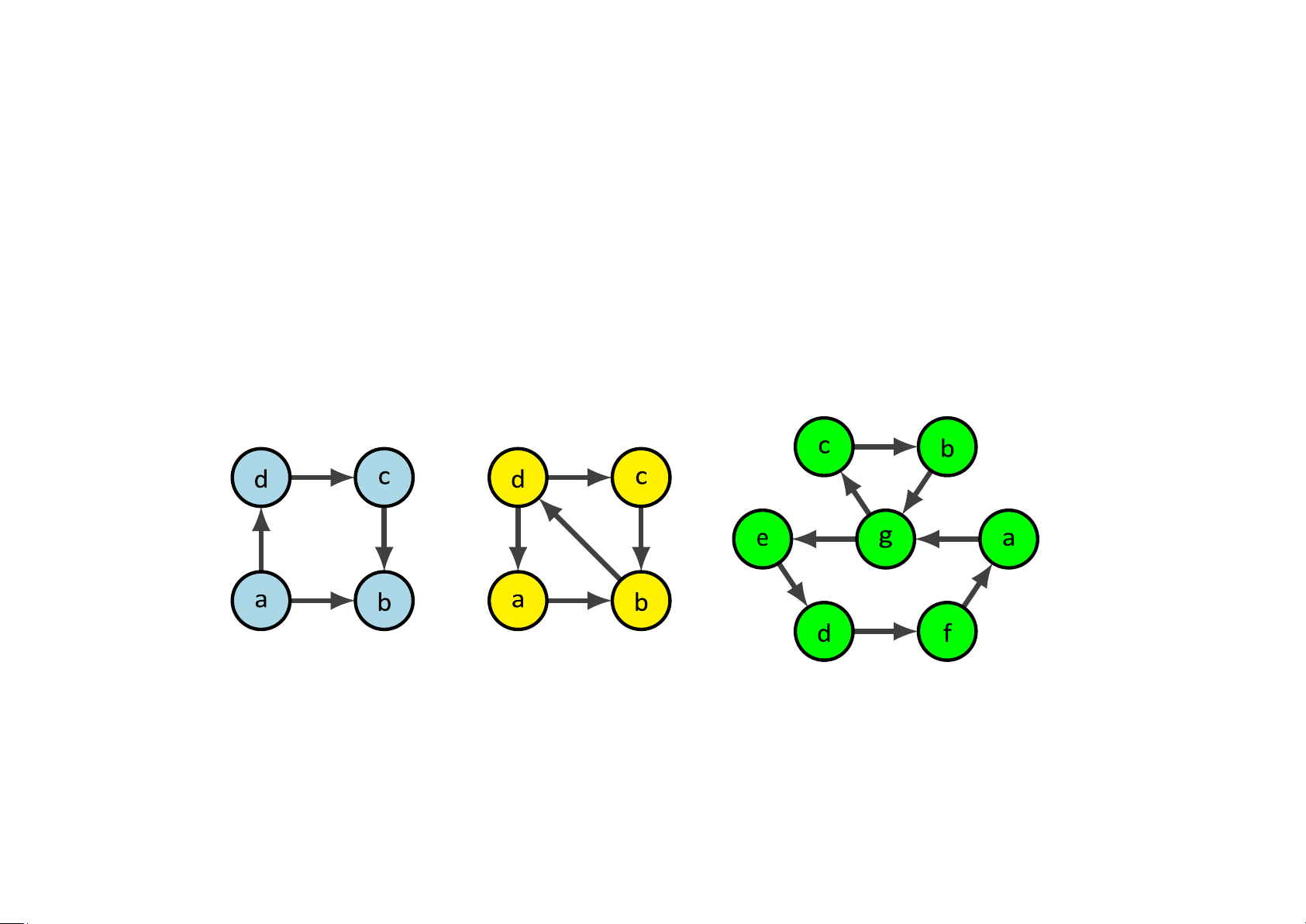
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Ví dụ 5.41 G 1 G2 G3
Đồ thị G1 là đồ thị Euler vì nó có chu trình Euler abdca. Đồ thị G2 không có chu
trình và đường đi Euler. Đồ thị G3 không có chu trình Euler nhưng có đường đi Euler dabdcbec.
Chú ý: Sự tồn tại của đường đi (chu trình) Euler tùy thuộc vào bậc của các
đỉnh. Để xác định đường đi (chu trình) Euler, ta chú ý các đặc điểm:
1. Liệt kê bậc của tất cả các đỉnh
2. Nếu có đỉnh bậc 0 thì đồ thị không liên thông và do đó không có đường đi và chu trình Euler.
3. Nếu tất cả các đỉnh có bậc chẵn thì đồ thị có đường đi và chu trình Euler.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
4. Nếu chỉ có 2 đỉnh bậc lẻ thì đồ thị có đường đi Euler nhưng không có chu trình Euler.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Định lý 5.42 Cho G là một đồ thị liên thông. Các điều sau là tương đương
1. G là đồ thị Euler
2. Các đỉnh của G đều có bậc chẵn.
3. Tập tất cả các cạnh của G phân hoạch thành các chu trình rời nhau. Định
lý 5.43 Đồ thị liên thông có đường đi Euler, không có chu trình Euler khi và chỉ
khi nó có đúng 2 đỉnh bậc lẻ.
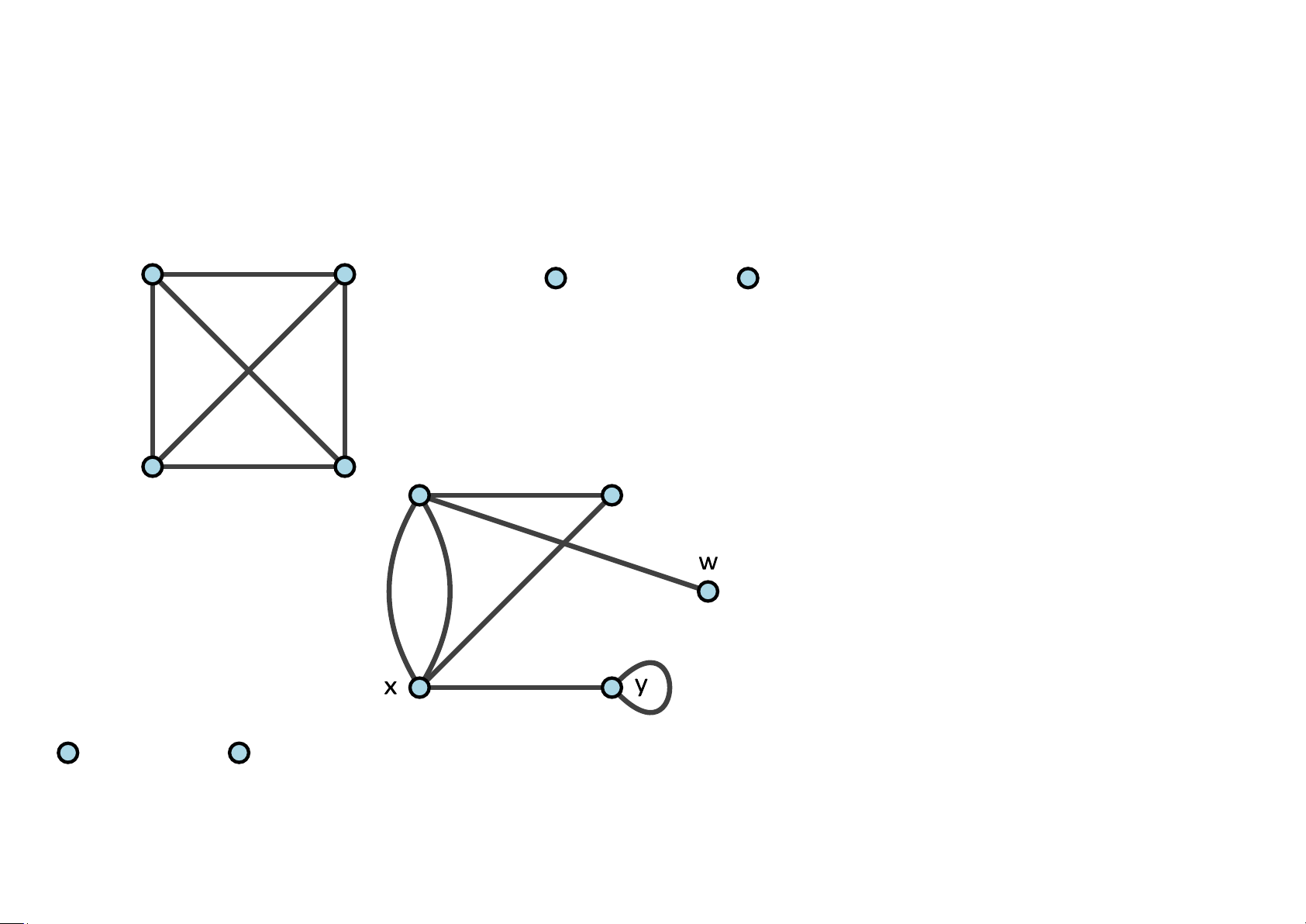
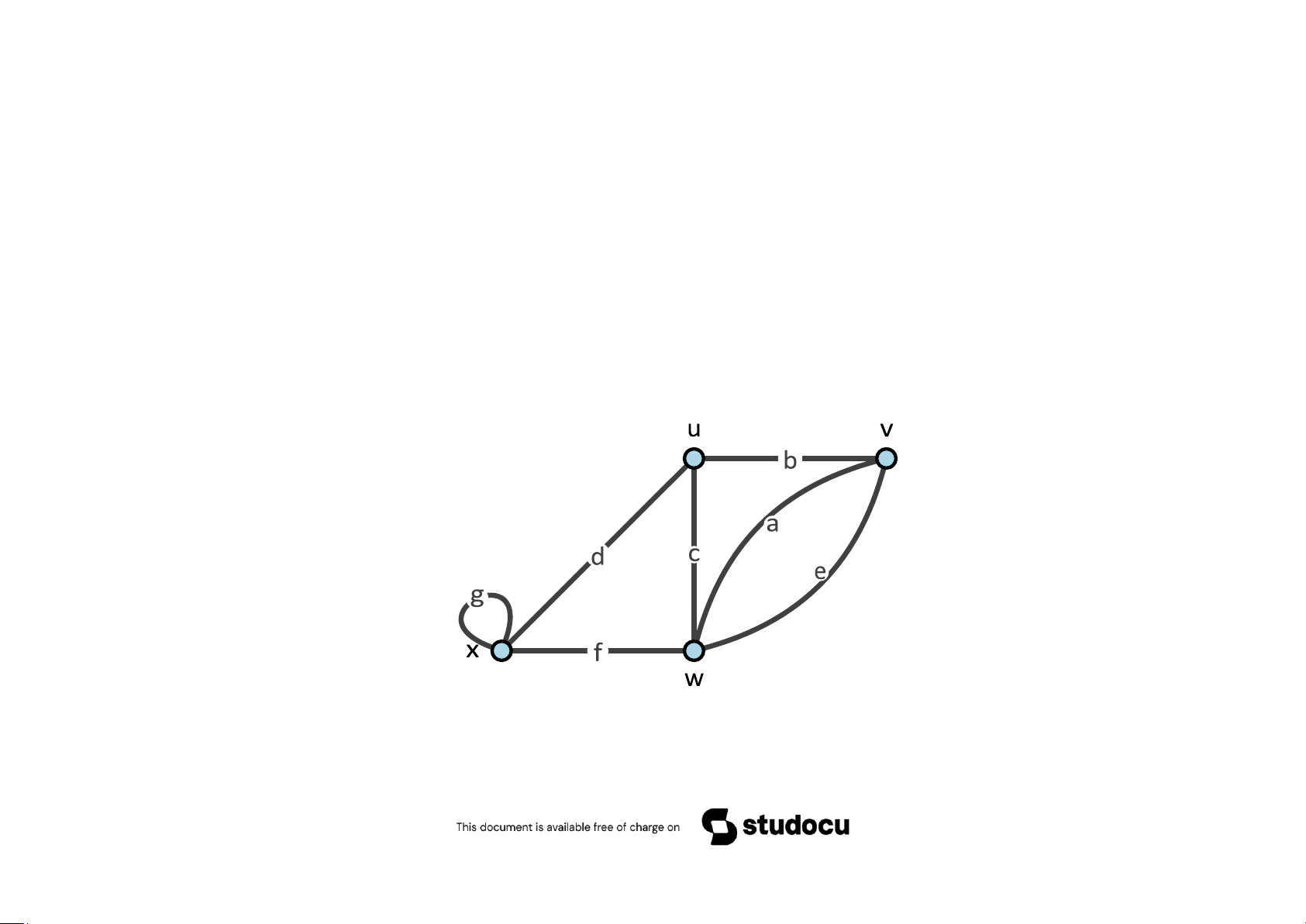
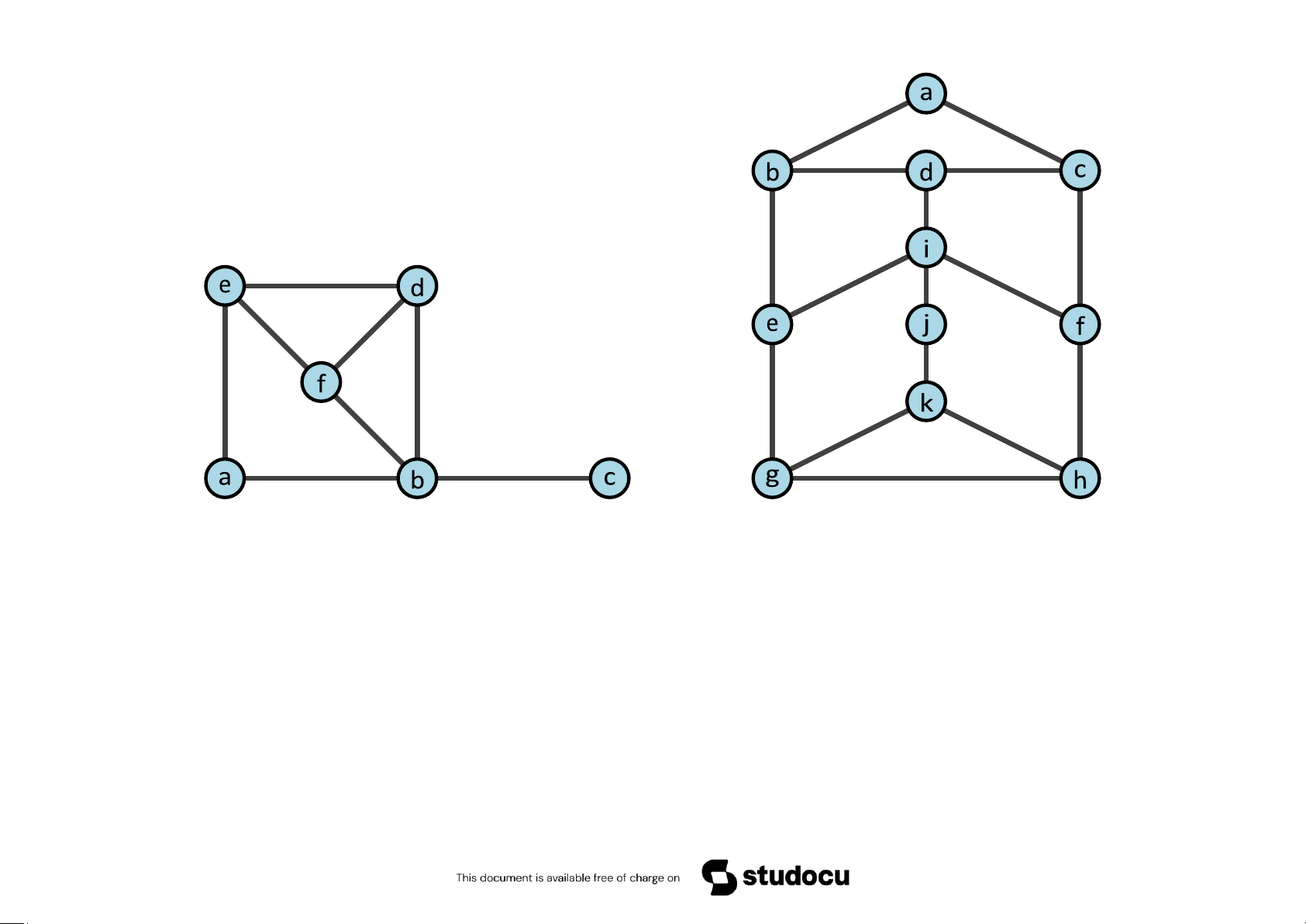
Ví dụ 5.44 Chứng minh rằng đồ thị dưới đây có đường đi Euler nhưng không có chu trình Euler
Giải. Ta có deg(u) = deg(v) = 3 và deg(x) = deg(w) = 4. Vì đồ thị chỉ có 2
đỉnh bậc lẻ nên nó có một đường đi Euler và không có chu trình Euler. Đường
đi Euler cần tìm là b-a-c-d-g-f-e.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
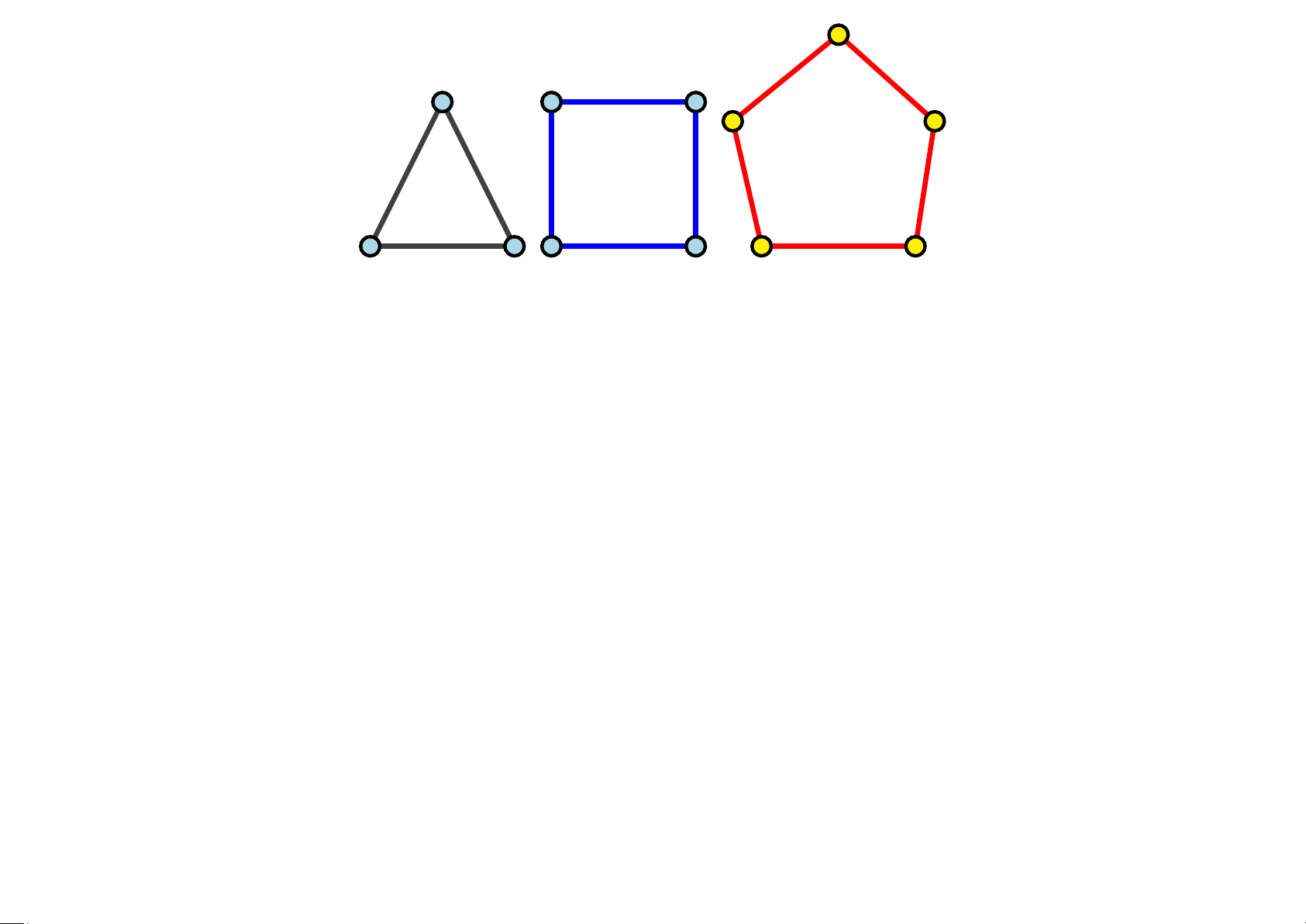
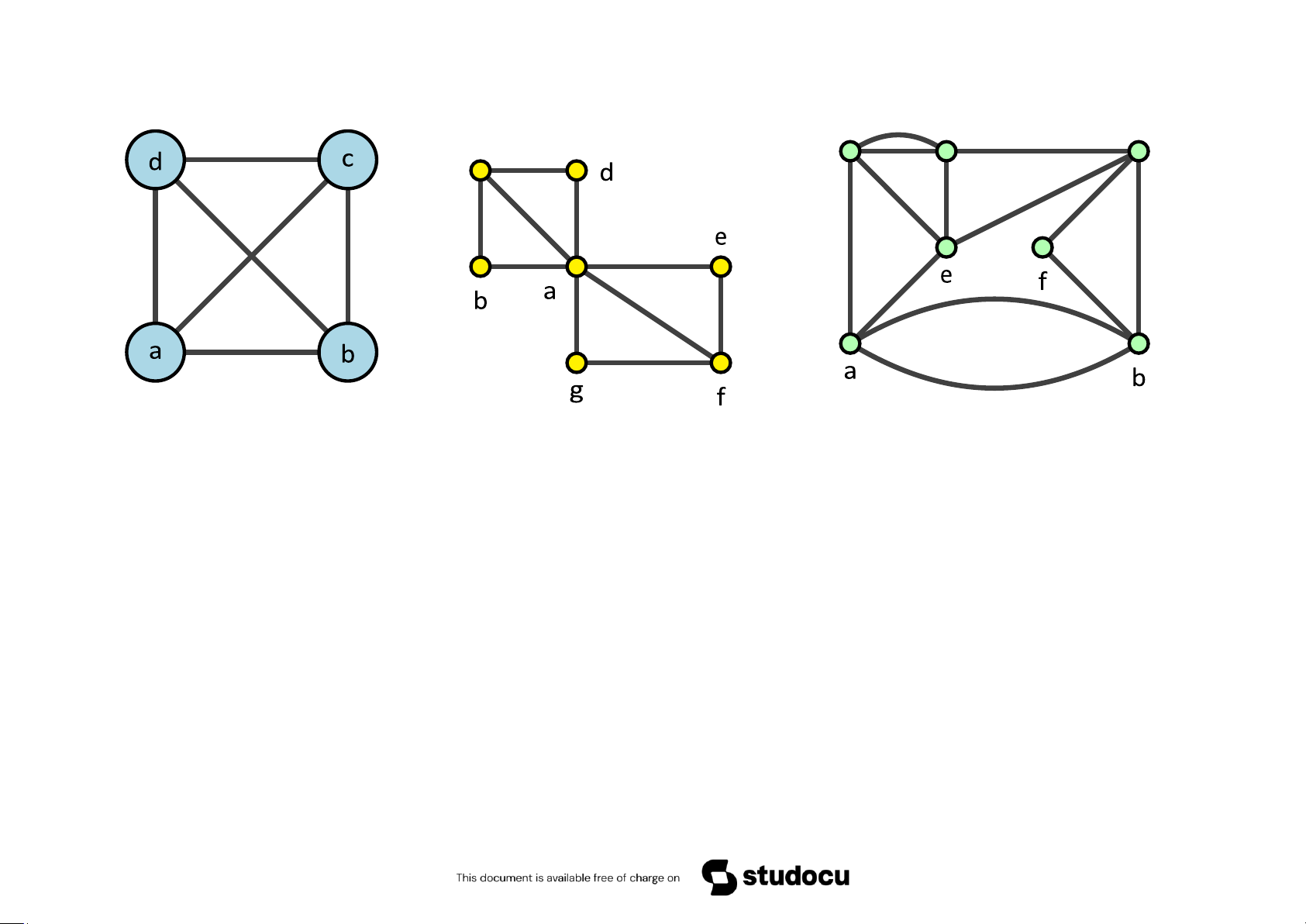
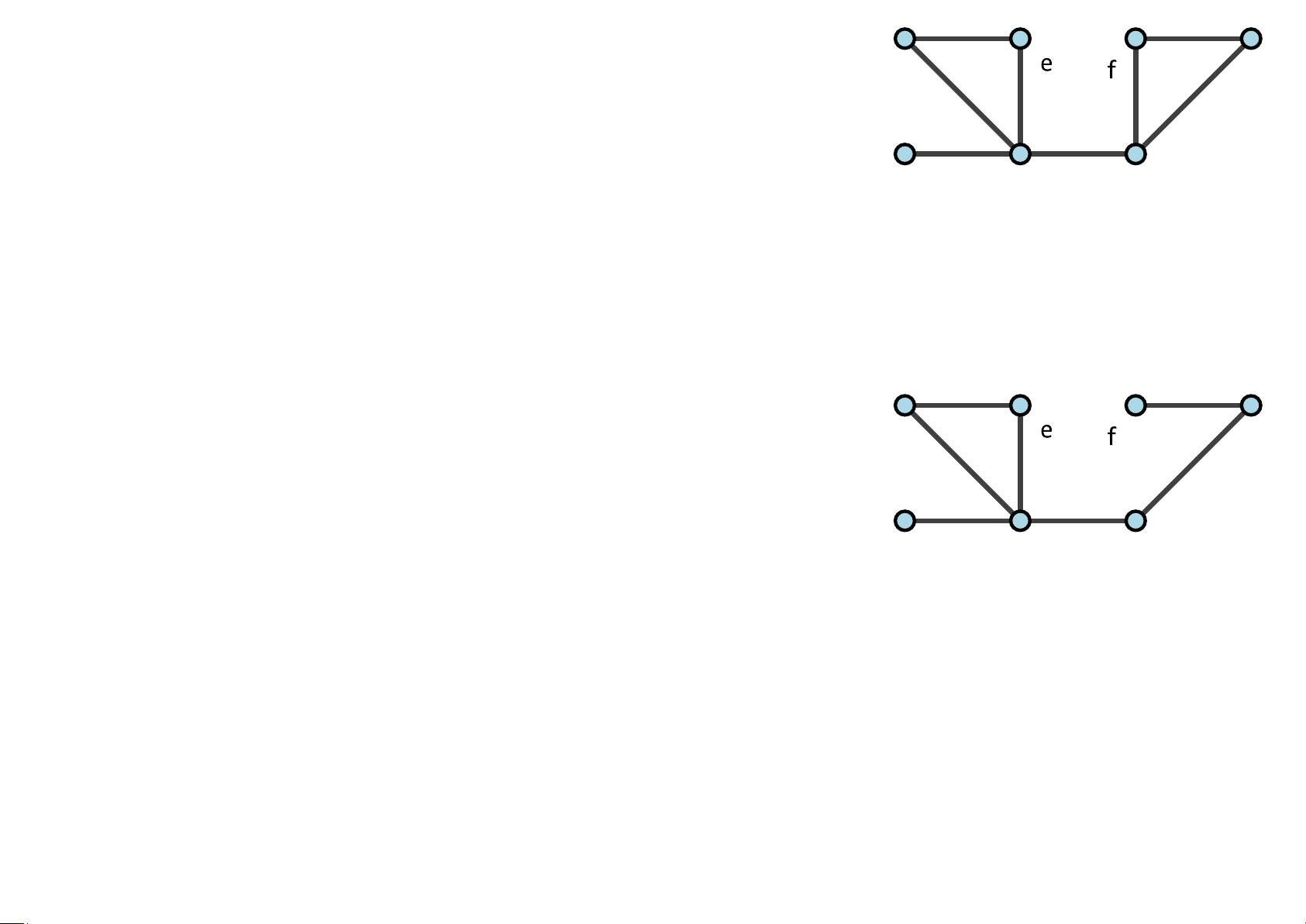
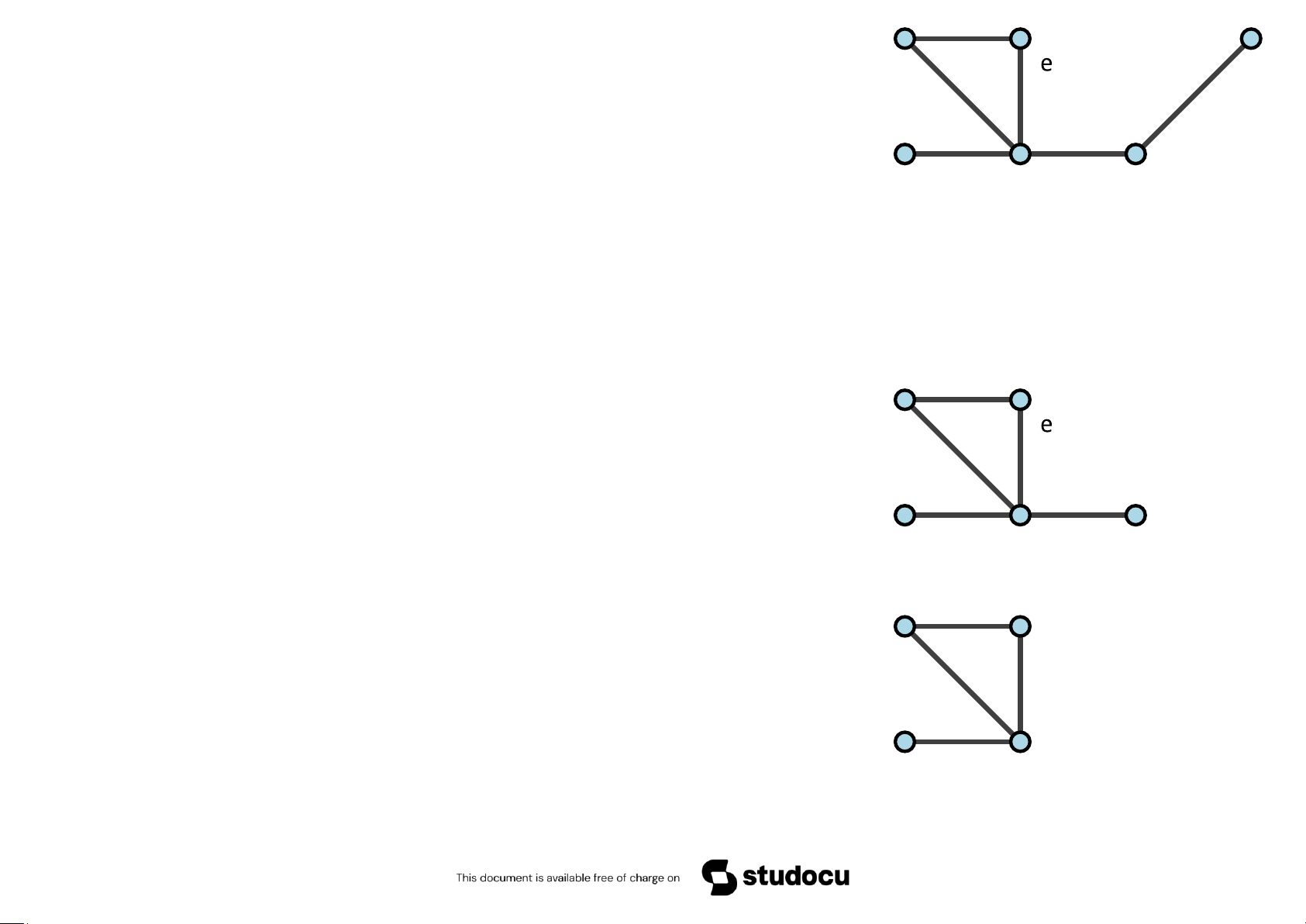
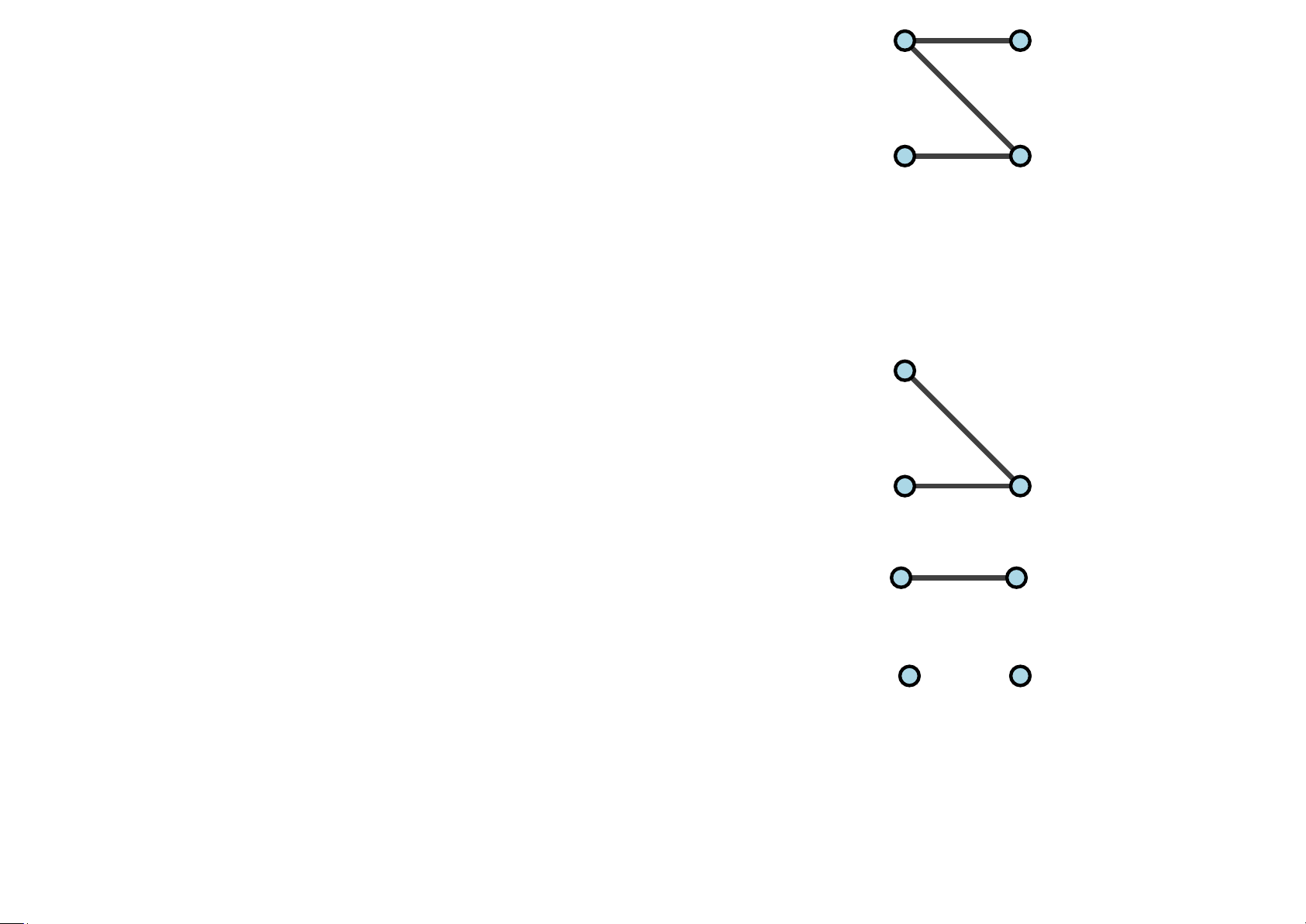
Ví dụ 5.45 Đồ thị nào sau đây có đường đi (chu trình) Euler? g c d c H 1 H2 H3
Giải. Đồ thị H1 : mỗi đỉnh đều có bậc .... do đó ........................
.......................................................................
Đồ thị H2 : ...........................................................
.......................................................................
Đồ thị H3 : ...........................................................
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
.......................................................................
Thuật toán Fleury (trong đồ thị vô hướng)
Bước 1. Kiểm tra xem đồ thị G là liên thông và hoặc (1) không có đỉnh bậc lẻ hoặc (2)
chỉ có 2 đỉnh bậc lẻ.
Bước 2. Chọn đỉnh v bất kì của G đối với (1), chọn đỉnh có bậc lẻ đối với (2).
Bước 3. Chọn bất kỳ cạnh nào nối với đỉnh hiện tại. Nếu có nhiều cạnh nối với đỉnh
đó thì chọn cạnh không phải là cầu. Chỉ đi theo một cạnh là cầu nếu
không có sự lựa chọn nào khác.
Bước 4. Thêm cạnh đó vào chu trình. Mỗi khi đi qua một cạnh nào thì xóa cạnh
vừa đi qua và xóa đỉnh cô lập (nếu có).
Bước 5. Tiếp tục quá trình đến khi tìm được đường đi (chu trình) Euler. Ví dụ
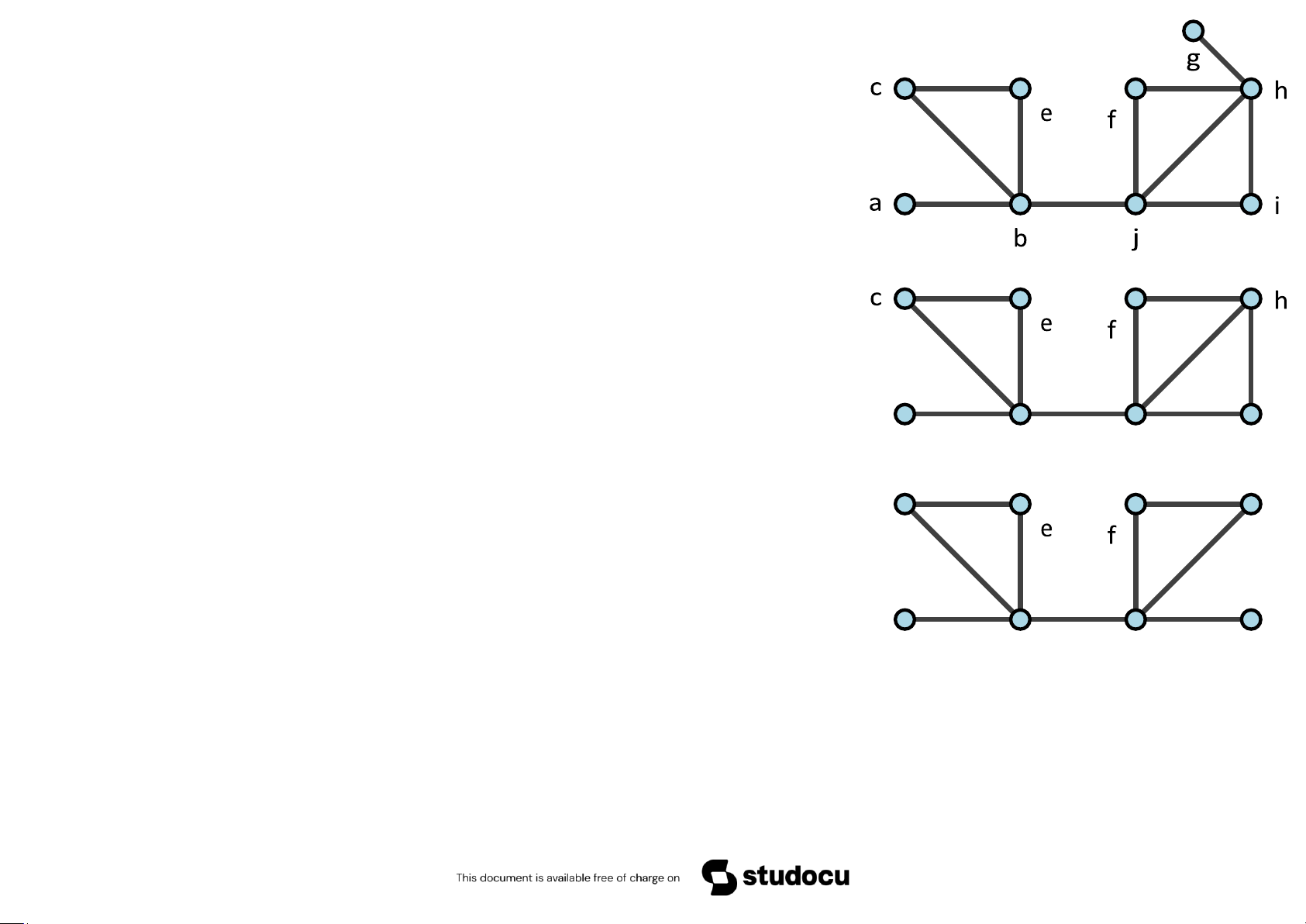
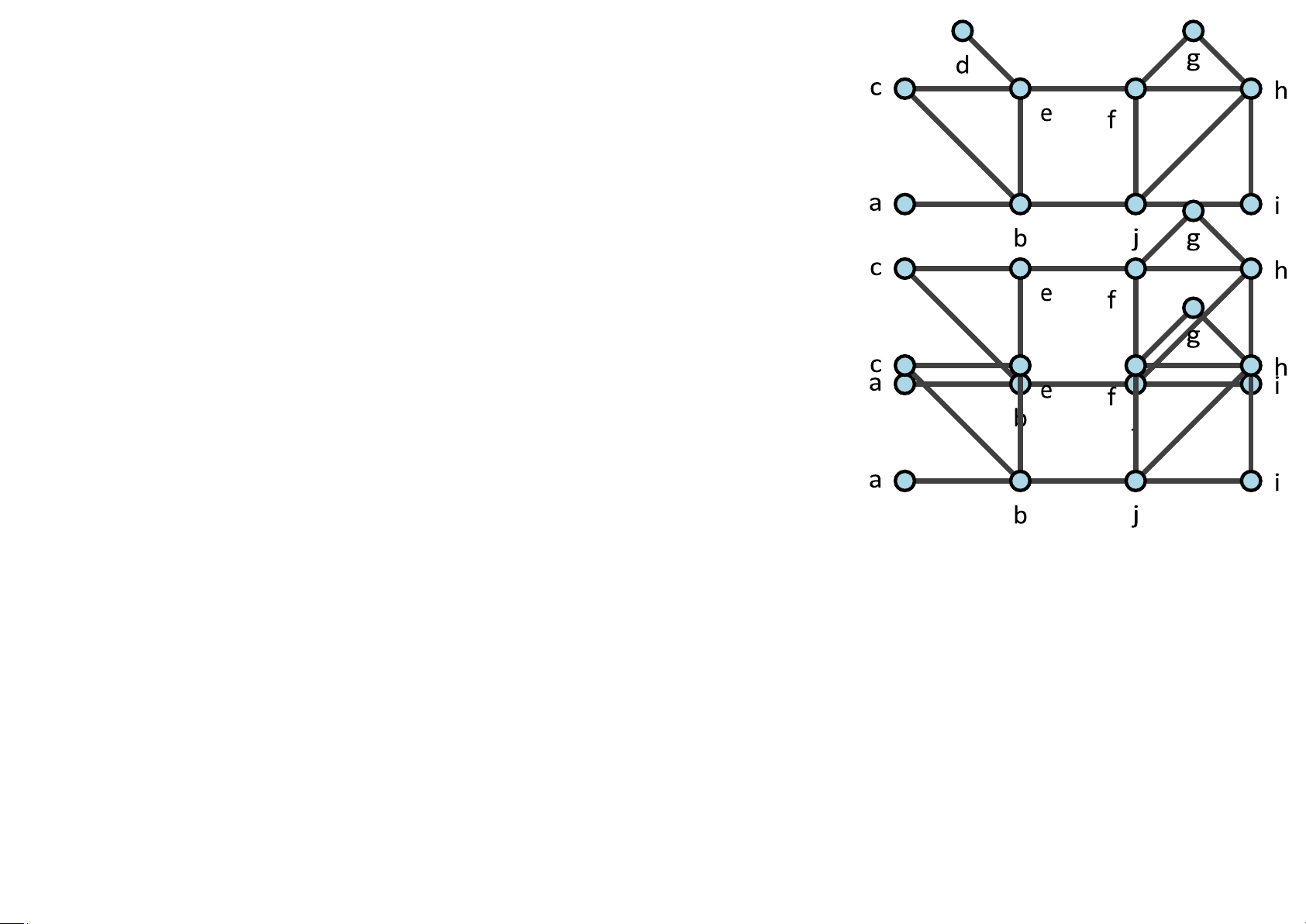
5.46 Dùng thuật toán Fleury, tìm chu trình Euler của đồ thị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 b j
Giải. Các đỉnh đều có bậc chẵn nên đồ thị có chu trình Euler.
Chọn đỉnh a. Chọn cạnh ac (có thể chọn ab). Ta có đường đi ac
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chọn cạnh cd (có thể chọn cd hoặc cb). Ta có đường đi acd Chọn cạnh de. Ta có đường đi acde
Chọn cạnh ef (có thể chọn ec, eb). Ta có đường đi acdef
Chọn cạnh fg (có thể chọn fh, fj, fg). Ta có đường đi acdefg Chọn cạnh gh.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Ta có đường đi acdefgh ai b j ch
Chọn cạnh hi (hoặc hf, hj). Ta có đường đi acdefghi ai b j
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 ch Chọn cạnh ij.
Ta có đường đi acdefghij a b j ch
Chọn cạnh jf (hoặc jh, không chọn jb).
Ta có đường đi acdefghijf a b j
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 ch Chọn cạnh fh.
Ta có đường đi acdefghijfh a b j c Chọn cạnh hj.
Ta có đường đi acdefghijfhj a b j c e Chọn cạnh jb.
Ta có đường đi acdefghijfhjb a b
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 c e
Chọn cạnh be (hoặc bc, không chọn ba).
Ta có đường đi acdefghijfhjbe a b c Chọn cạnh ec.
Ta có đường đi acdefghijfhjbec a b Chọn cạnh cb. a
Ta có đường đi acdefghijfhjbecb b Chọn cạnh ba. a
Ta có chu trình Euler acdefghijfhjbecba b Ví dụ 5.47 Tìm chu trình Euler của đồ thị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
.......................................................................
.......................................................................
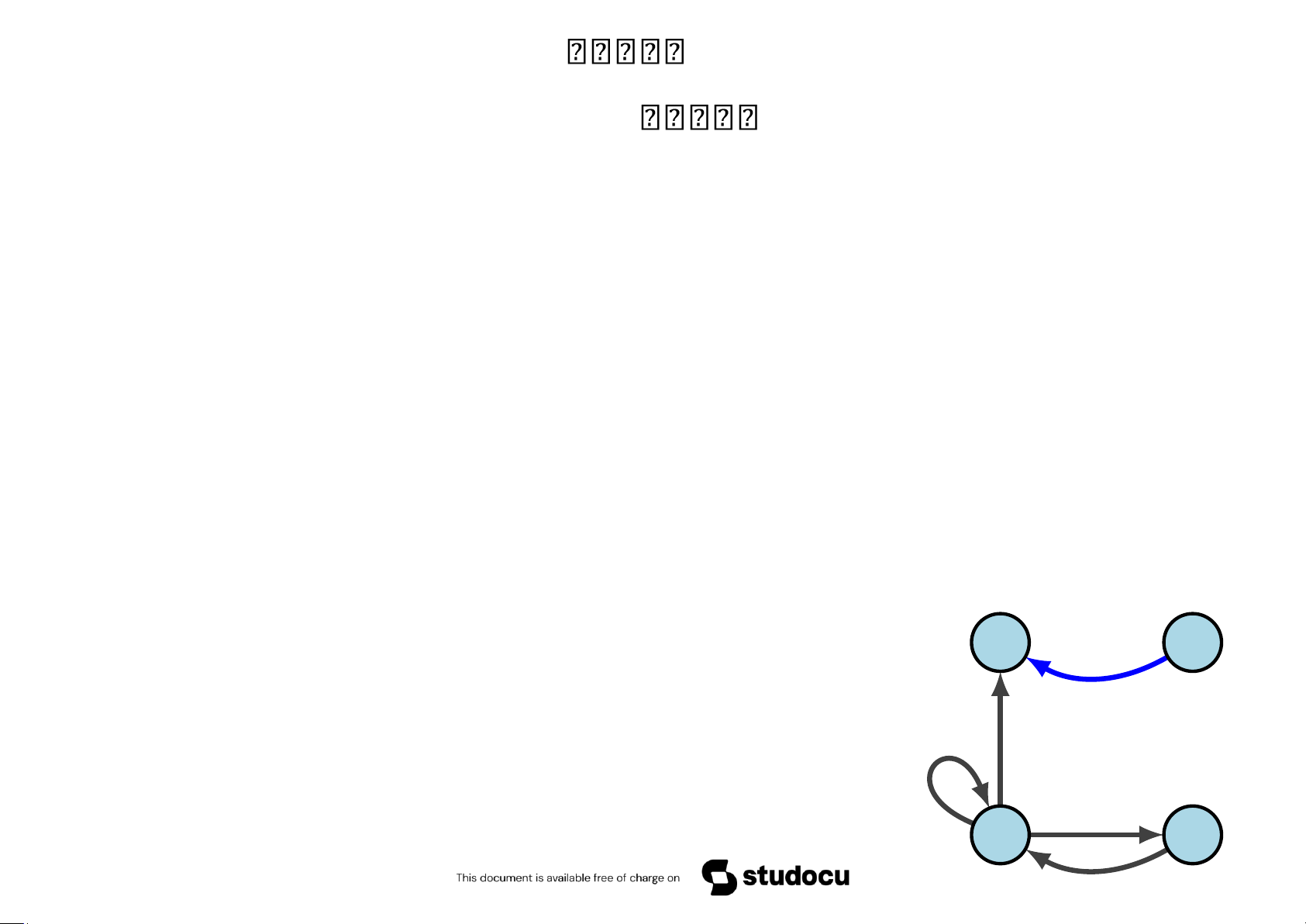
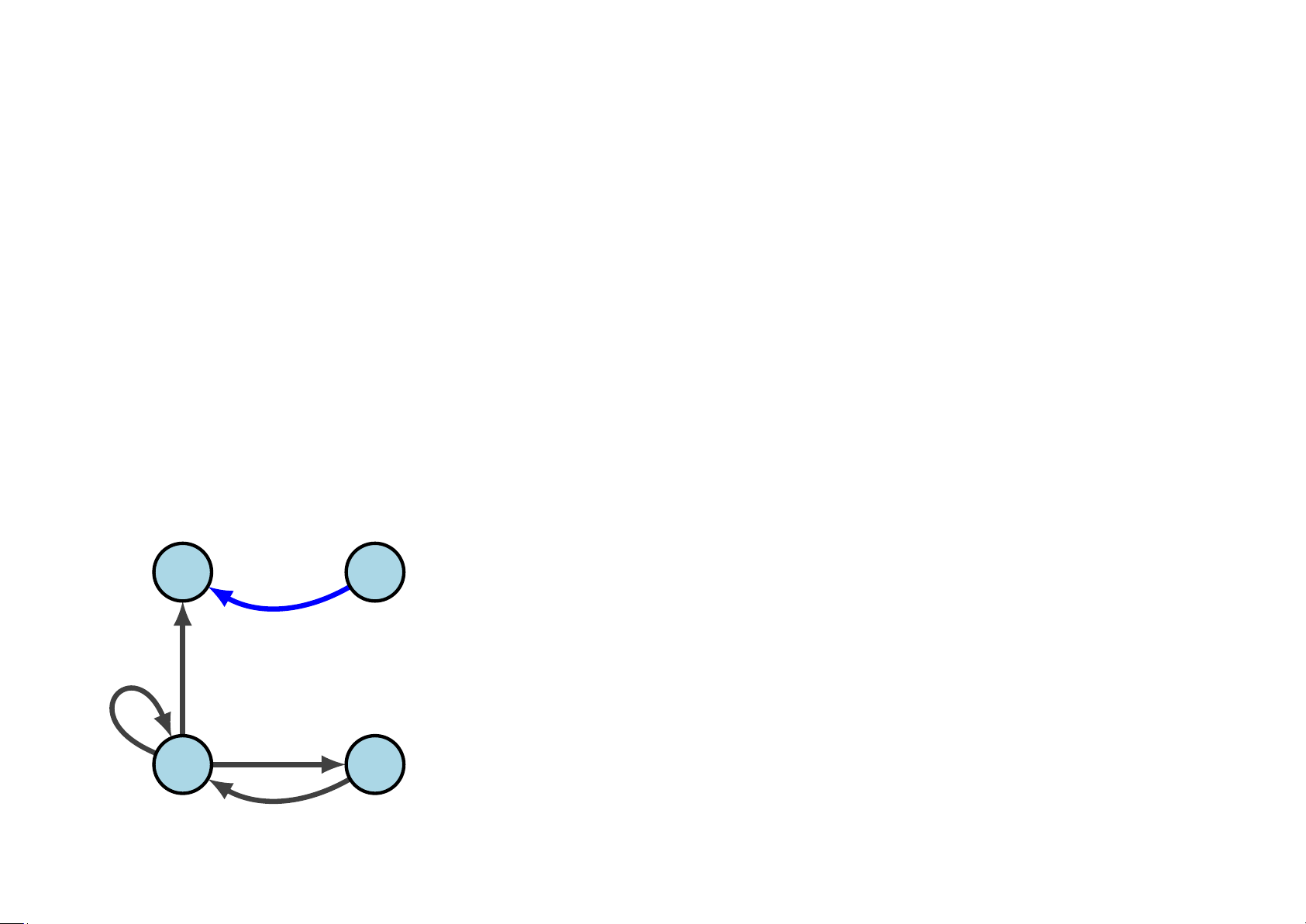
Định lý 5.48 Đồ thị có hướng G = (V,E) có chu trình Euler khi và chỉ khi G
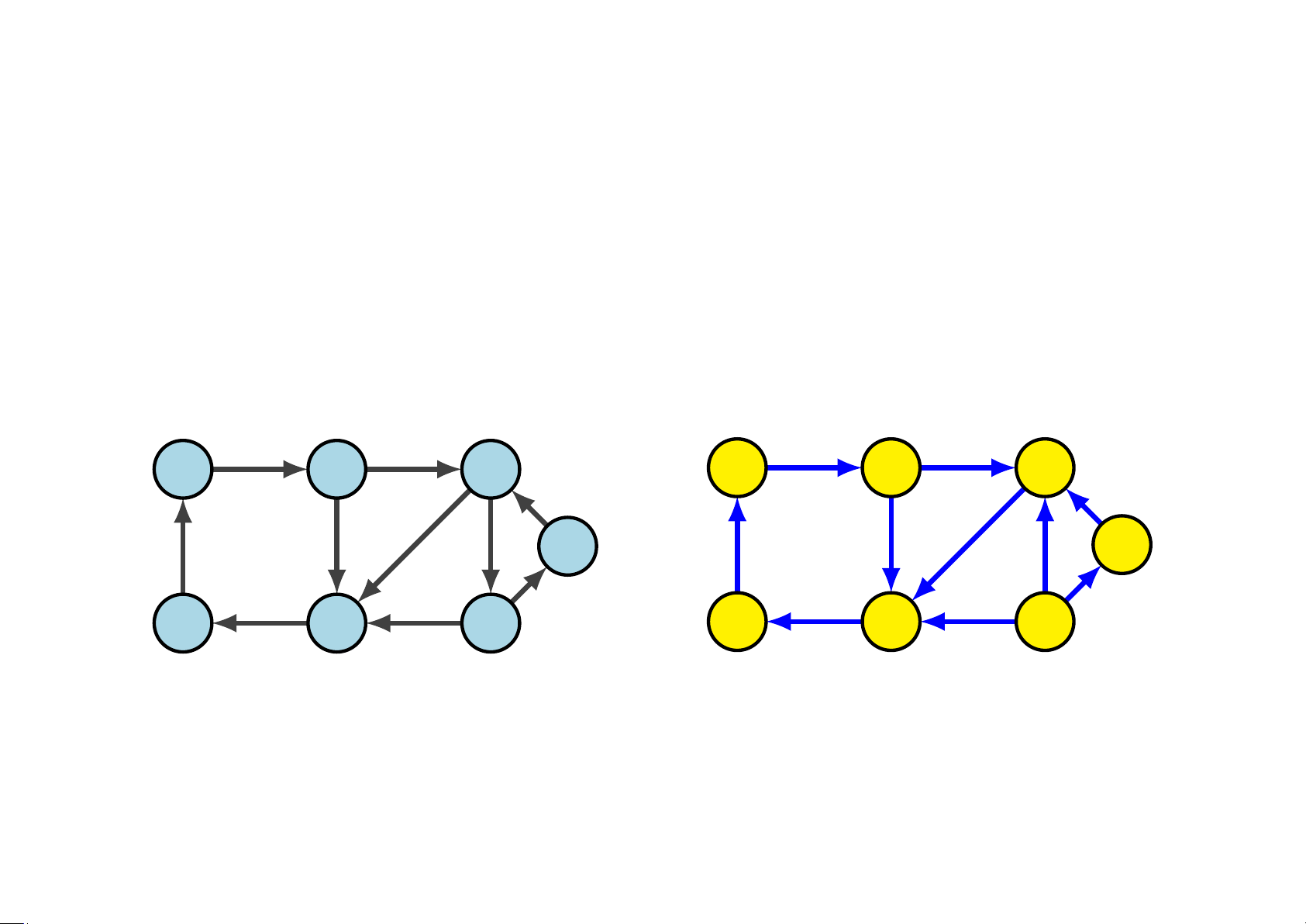
là liên thông mạnh và deg+(v) = deg−(v) với mọi v ∈ V. Ví dụ 5.49 Đồ thị nào có chu trình Euler? G 1 G2 G3
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Định lý 5.50 Đồ thị có hướng G = (V,E) có đường đi Euler nhưng không có chu
trình Euler khi và chỉ khi G thỏa các điều kiện sau
1. G liên thông yếu
2. Tồn tại duy nhất v ∈ V sao cho deg+(v) = deg−(v) + 1 3. Tồn tại duy
nhất u ∈ V sao cho deg+(u) = deg−(u) − 1
4. deg+(x) = deg−(x) với mọi x ∈ V \ {u,v}.
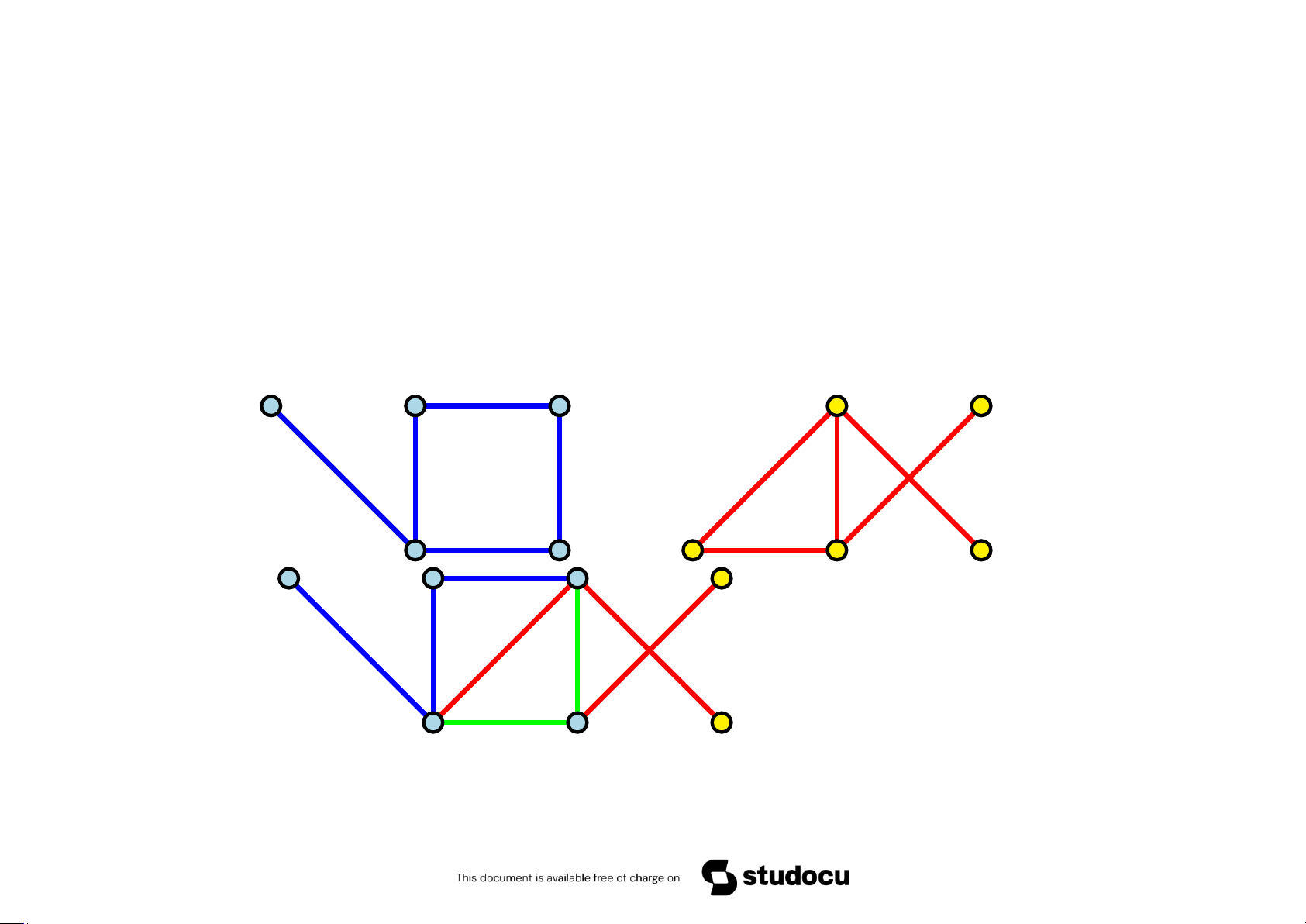
Ví dụ 5.51 Đồ thị nào có đường đi Euler? G 1 G2 G3
5.5 Chu trình và đường đi Hamilton
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Định nghĩa 5.52
• Đường đi Hamilton là đường đi sơ cấp đi qua tất cả các đỉnh của đồ thị
(đi qua mỗi đỉnh đúng một lần).
• Chu trình bắt đầu từ một đỉnh v nào đó qua tất cả các đỉnh còn lại mỗi
đỉnh đúng một lần rồi quay trở về v được gọi là chu trình Hamilton.
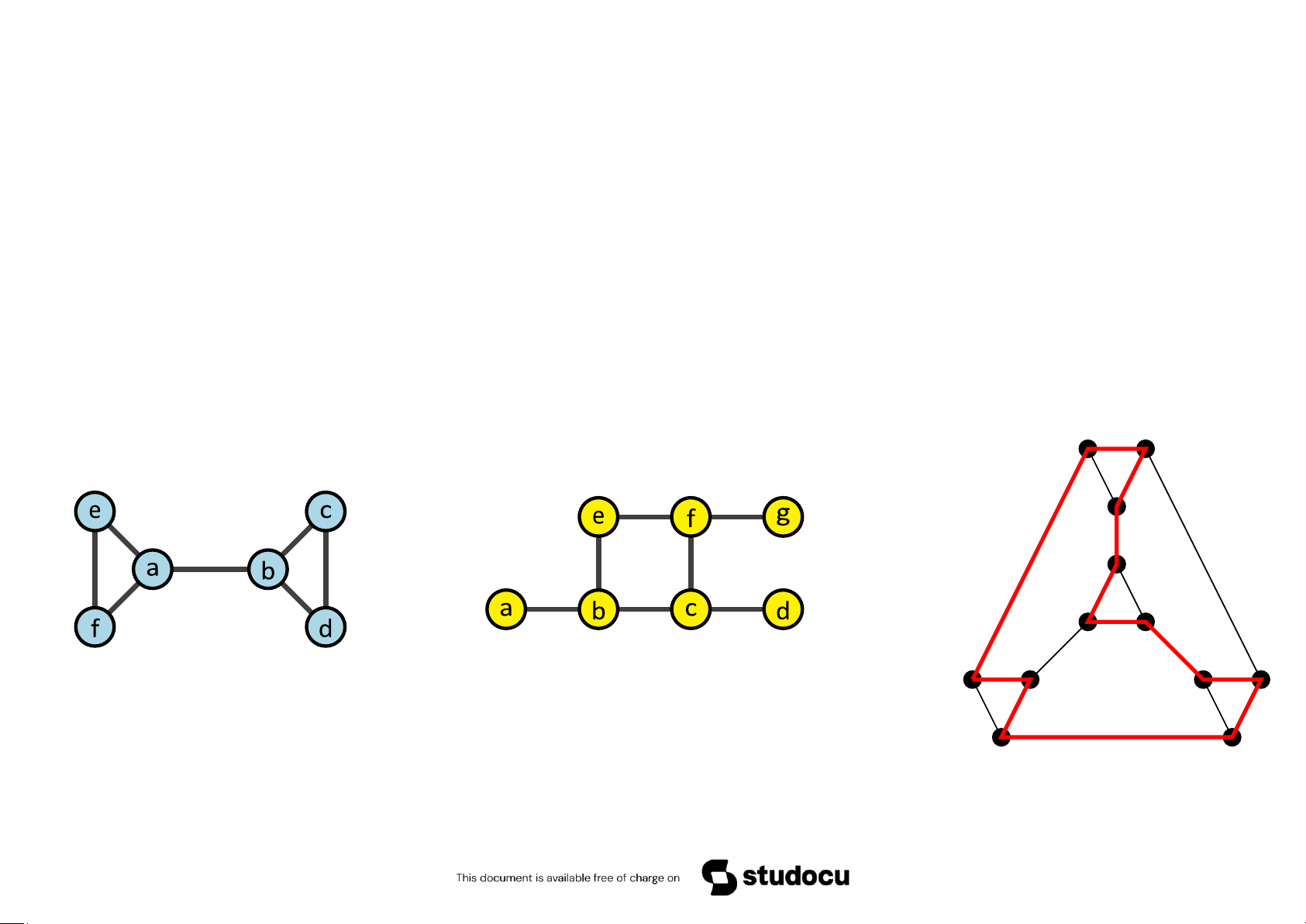
• Đồ thị Hamilton là đồ thị có chứa chu trình Hamilton. Ví dụ 5.53
efabdc Không có đường đi Hamilton
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Định lý 5.54
• (Định lý Ore) Cho G = (V,E) là một đơn đồ thị liên thông có n ≥ 3 đỉnh và
deg(v) + deg(w) ≥ n với mọi cặp đỉnh không liền kề v,w. Khi đó G có chu trình Hamilton.
• (Định lý Dirac) Cho G = (V,E) là một đơn đồ thị có n ≥ 3 đỉnh và deg(
với mọi v ∈ V. Khi đó G có chu trình Hamilton.
• Cho đồ thị G có m cạnh và n đỉnh. Nếu có chu trình Hamilton.
Các quy tắc tìm chu trình Hamilton
QT 1. Nếu tồn tại một đỉnh v của G có deg(v) ≤ 1 thì đồ thị G không có chu trình Hamilton.
QT 2. Nếu deg(v) = 2 thì cả 2 cạnh tới v đều phải thuộc chu trình Hamilton.
QT 3. Chu trình Hamilton không chứa bất kỳ chu trình con thực sự nào.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
QT 4. Trong quá trình xây dựng chu trình Hamilton, sau khi đã lấy 2 cạnh tới
một đỉnh v đặt vào chu trình Hamilton thì không thể lấy thêm cạnh nào
tới v nữa, do đó có thể xóa mọi cạnh còn lại tới v.
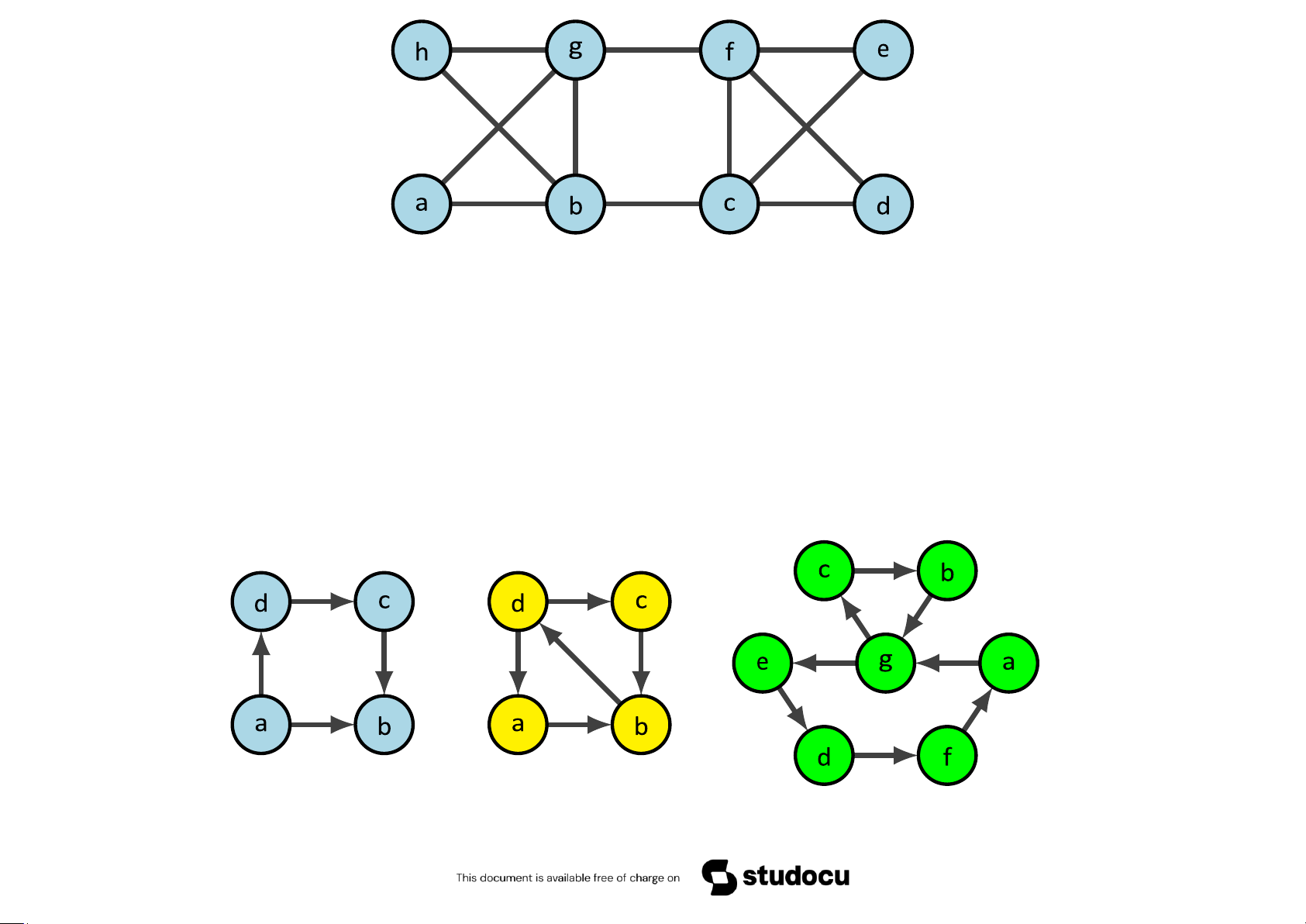
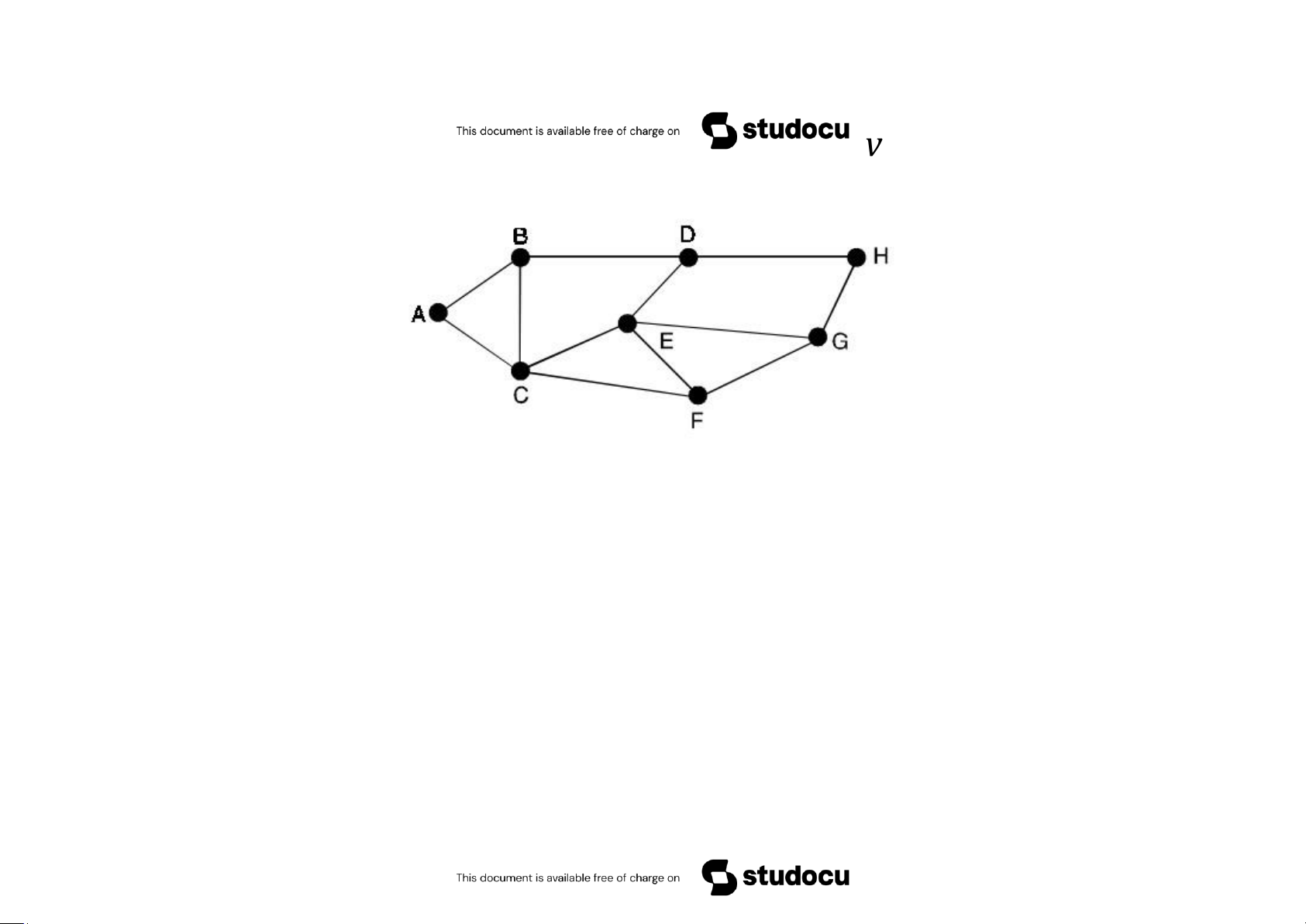
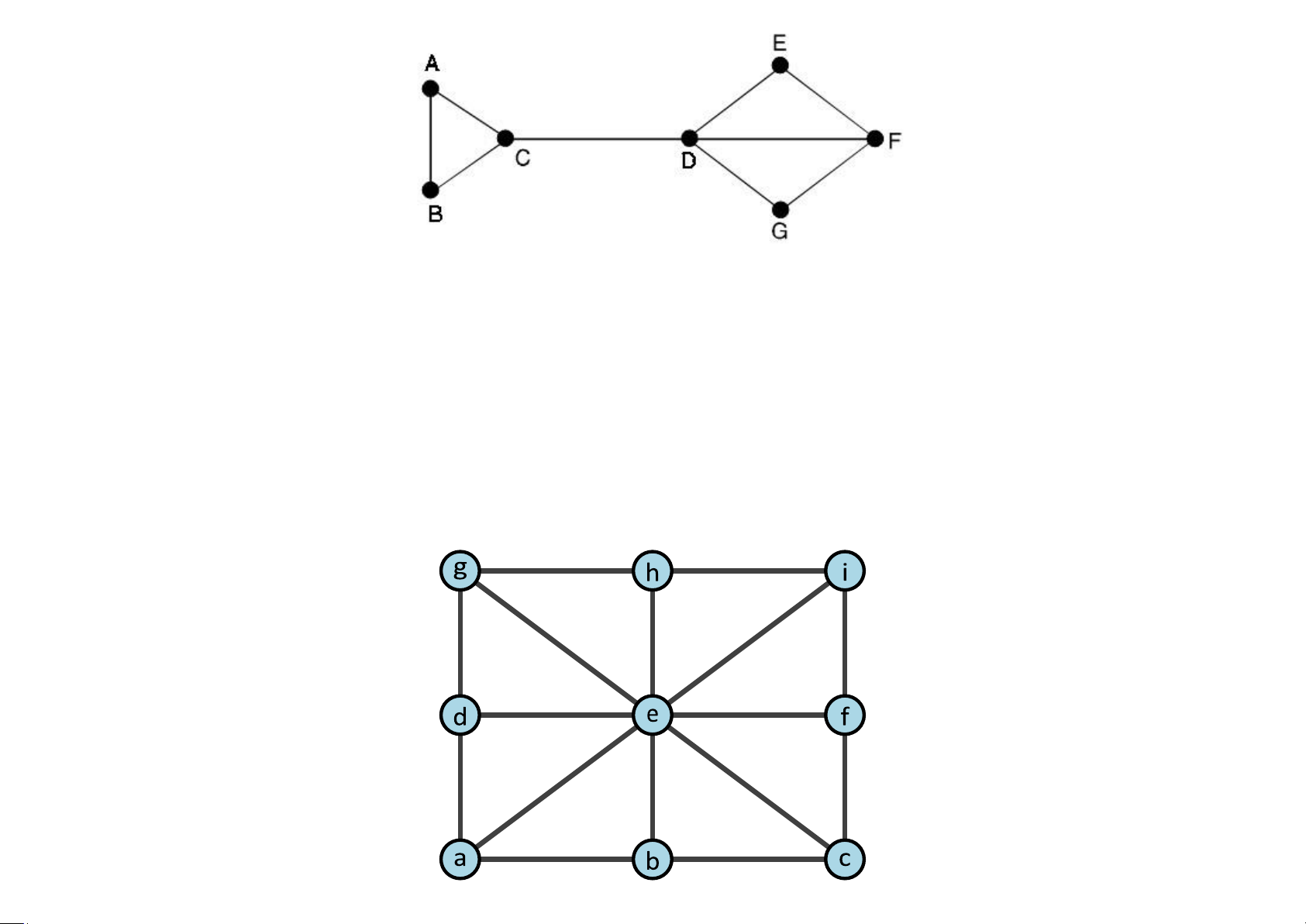
Ví dụ 5.55 Tìm một chu trình Hamilton
Giải. Chọn đỉnh A để bắt đầu. Tiếp theo, đi đến B hoặc C, chọn B. Tiếp tục đi
đến D (không đi đến C vì nếu đi đến C sẽ có một chu trình). Xóa đỉnh B và các
cạnh AB, BD, BC. Đi đến H (hoặc E). Xóa đỉnh D và cạnh DH, DE. Tiếp đến, đi
đến G, xóa cạnh GH, đỉnh H. Sau đó đến F (hoặc E), xóa cạnh GF và đỉnh G.
Tiếp tục đi đến F. Cuối cùng đi đến C và về
A. Như vậy chu trình Hamilton là ABDHGEFCA.
Ví dụ 5.56 Tìm chu trình (đường đi) Hamilton của đồ thị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Giải. Bắt đầu từ đỉnh A. Không nên đi đến C vì bước tiếp theo không thể đến B hoặc D.
Do đó, đi đến B. Tiếp theo, đi đến C và đi đến D. Ta có một phần đường đi
ABCD. Tiếp theo, đi đến E (hoặc G, không đến F). Các bước tiếp theo đi đến F
và G. Như vậy, ta có đường đi Hamilton ABCDEFG.
Ví dụ 5.57 Tìm một chu trình Hamilton
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Ví dụ 5.58 Đồ thị sau có chu trình Hamilton không?
Định lý 5.59 (Định lý K¨onig) Mọi đồ thị có hướng đầy đủ (đồ thị vô hướng
tương ứng là đầy đủ) đều có đường đi Hamilton.
5.5 Bài toán đường đi ngắn nhất
Mở đầu. Nhiều bài toán không chỉ quan tâm tồn tại hay không đường đi giữa
2 đỉnh mà còn lựa chọn đường đi ngắn nhất (với chi phí ít nhất).
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Có thể coi sơ đồ của đường đi từ A đến B trong thành phố là một đồ thị, với
đỉnh là các giao lộ (A và B coi như giao lộ), cạnh là đoạn đường nối hai giao
lộ. Trên mỗi cạnh của đồ thị này, ta gán một số dương, ứng với chiều dài của
đoạn đường, thời gian đi đoạn đường hoặc cước phí vận chuyển trên đoạn đường đó, ...
Định nghĩa 5.60 Đồ thị có trọng số là đồ thị G = (V,E) mà mỗi cạnh (hoặc
cung) e ∈ E được gán bởi một số thực w(e), gọi là trọng số của cạnh (hoặc cung) e.
• Trọng số của mỗi cạnh được xét là một số dương và còn gọi là chiều dài của cạnh đó.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
• Mỗi đường đi từ đỉnh u đến đỉnh v, có chiều dài là w(u,v), bằng tổng
chiều dài các cạnh mà nó đi qua.
• Khoảng cách d(u,v) giữa hai đỉnh u và v là chiều dài đường đi ngắn nhất
(theo nghĩa w(u,v) nhỏ nhất) trong các đường đi từ u đến v.
• Độ dài đường đi abec là 1 + 8 + 6 = 15. •
Độ dài đường đi afec là 2 + 5 + 6 = 13.
• Độ dài đường đi aec là 3 + 6 = 9. Thuật toán Dijkstra
Bài toán. Cho đơn đồ thị liên thông, có trọng số G = (V,E). Tìm khoảng cách
d(a,v) từ một đỉnh a cho trước đến một đỉnh v bất kỳ của G và tìm đường đi
ngắn nhất từ a đến v. Kí hiệu:
• L(v) := d(a,v)
• S là tập các đỉnh mà đường đi ngắn nhất từ a đến chúng đã xác định.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Thuật toán tìm đường đi ngắn nhất từ a đến v
Bước 1. Khởi tạo các nhãn
L(a) := 0,L(v) := ∞(v ̸= a),S;= ∅
Bước 2. Nếu v ∈ S thì kết thúc. Bước 3. Chọn đỉnh
- Chọn đỉnh u sao cho L(u) = min{L(x) | x ̸∈ S}
- Đăt S := S ∪ {u}
Bước 4. Sửa nhãn: Với mỗi đỉnh v ̸∈ S kề với u
L(v) = min{L(v),L(u) + w(u,v)} Bước 5. Quay lại Bước 2.
Định lý 5.61 Thuật toán Dijkstra tìm được đường đi ngắn nhất giữa 2 đỉnh
trong đơn đồ thị liên thông, có trọng số. Nhận xét.
• Chỉ đúng cho đồ thị có trọng số không âm.
• Nhãn sau cùng của mỗi đỉnh là độ dài đường đi ngắn nhất từ đỉnh xuất phát đến nó.
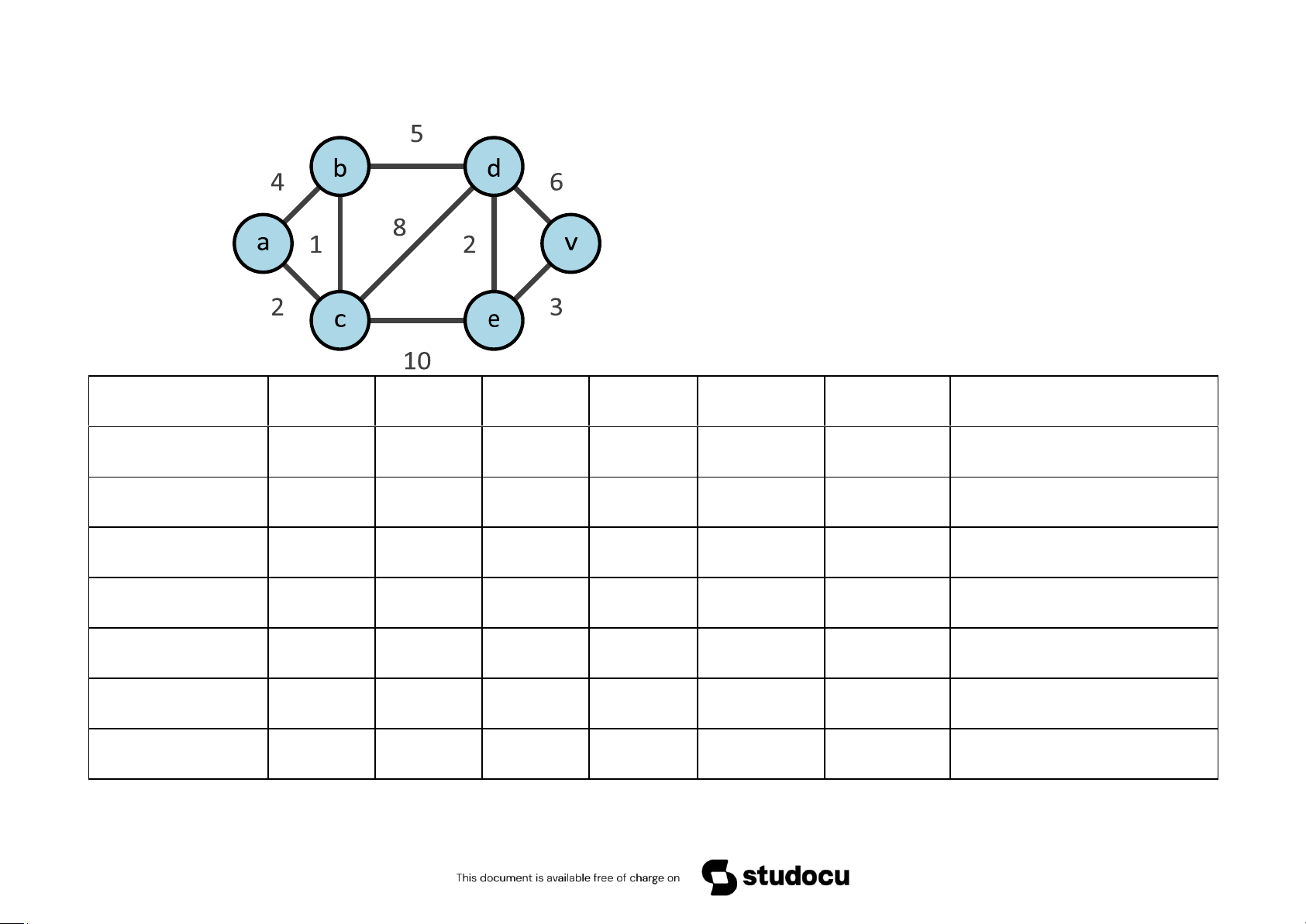
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Ví dụ 5.62 Tìm
đường đi ngắn nhất từ a đến v - Cặp
L(x),a là đường đi ngắn nhất từ a
đến x - Đánh dấu * vào đỉnh có
đường đi ngắn nhất từ a. Bước lặp a b c d e v S Khởi tạo 0,a* ∞,a ∞,a ∞,a ∞,a ∞,a ∅ 1 - 4,a 2,a* ∞,a ∞,a ∞,a {a} 2 - 3,c* - 10,c 12,c ∞,a {a,c} 3 - - - 8,b* 12,c ∞,a {a,c,b} 4 - - - - 10,d* 14,d {a,c,b,d} 5 - - - - - 13,e* {a,c,b,d,e} 6 0,a 3,c 2,a 8,b 10,d 13,e {a,c,b,d,e,v}
Đường đi ngắn nhất từ a đến v là acbdev.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
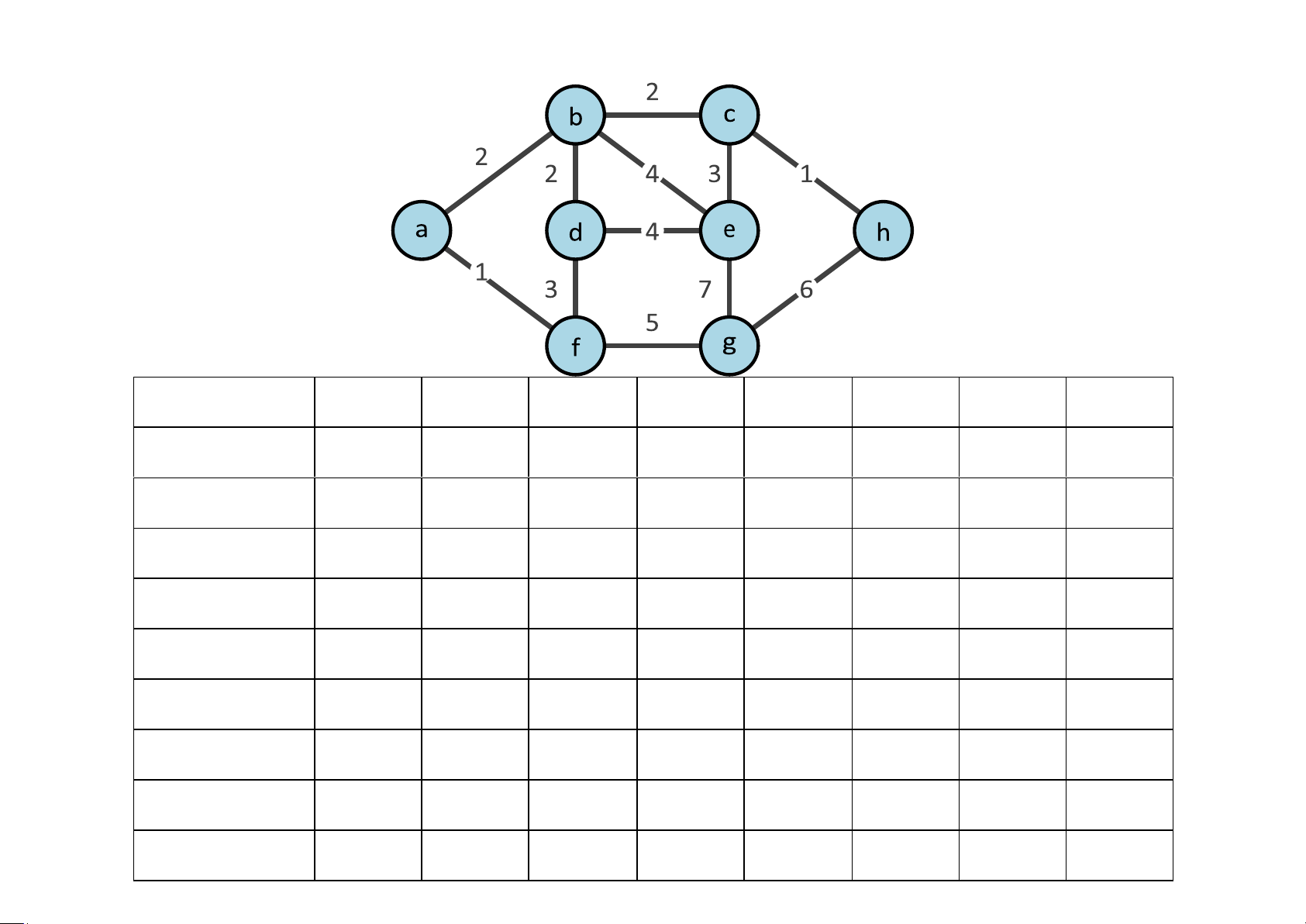
Ví dụ 5.63 Tìm đường đi ngắn nhất từ a đến các đỉnh còn lại. Bước lặp a b c d e f g h Khởi tạo 0,a* ∞,a
∞,a ∞,a ∞,a ∞,a ∞,a ∞,a 1 - 2,a
∞,a ∞,a ∞,a 1,a* ∞,a ∞,a 2 - 2,a* ∞,a 4,f ∞,a - 6,f ∞,a 3 - - 4,b* 4,f 6,b - 6,f ∞,a 4 - - - 4,f* 6,b - 6,f 5,c 5 - - - - 6,b - 6,f 5,c* 6 - - - - 6,b* - 6,f - 7 - - - - - - 6,f* - 8 0,a 2,a 4,b 4,f 6,b 1,a 6,f 5,c
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Đường đi ngắn nhất • a đến b là ab
độ dài bằng 2 • a đến c là abc độ dài bằng 4
• a đến d là afd độ dài bằng 4
• a đến e là abe độ dài bằng 6
• a đến f là af độ dài bằng 1
• a đến g là afg độ dài bằng 6
• a đến h là abch độ dài bằng 5 BÀI TẬP
Bài 5.1 Xác định tập các đỉnh và các cạnh của các đồ thị sau G2 G1 G3
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
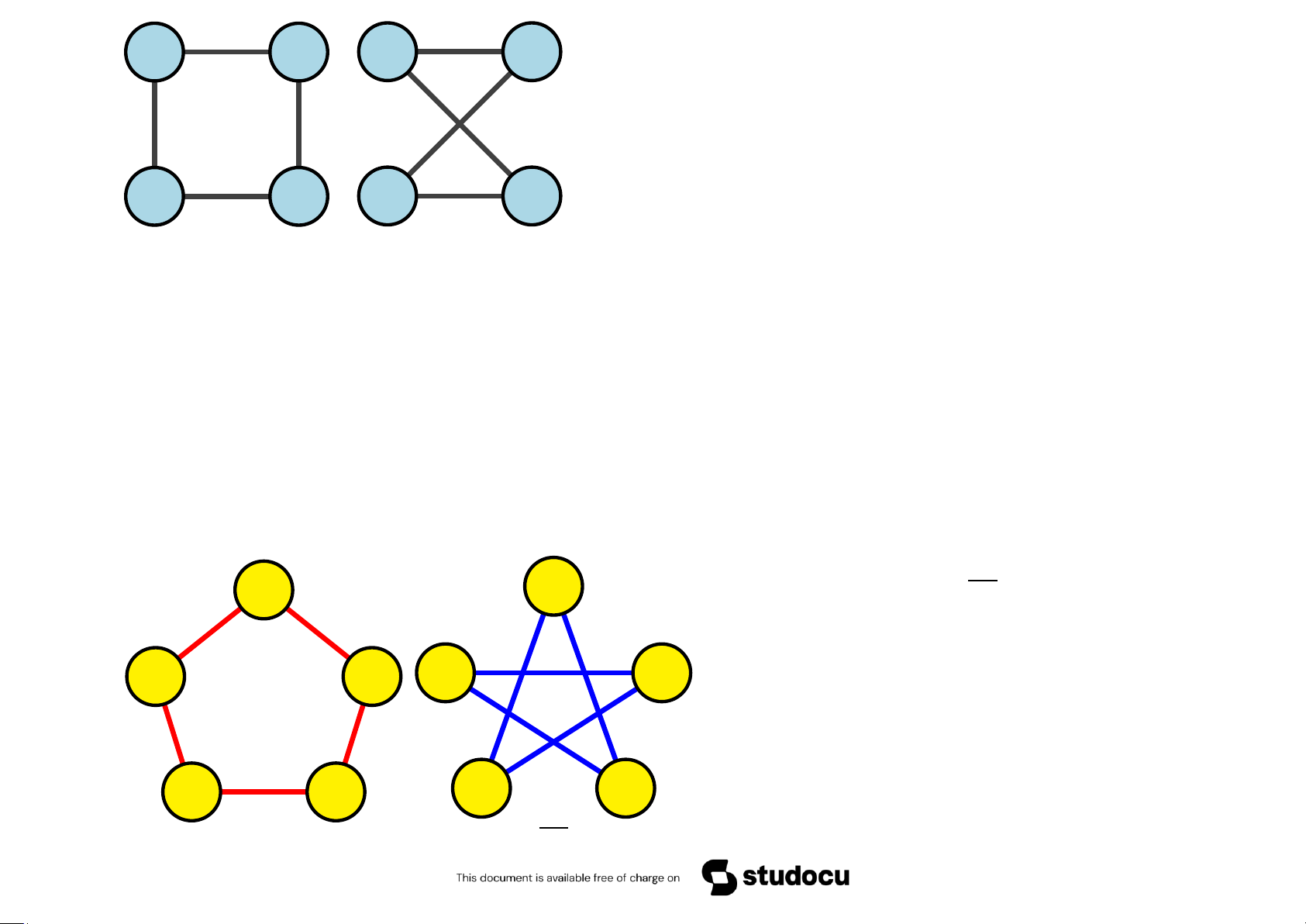
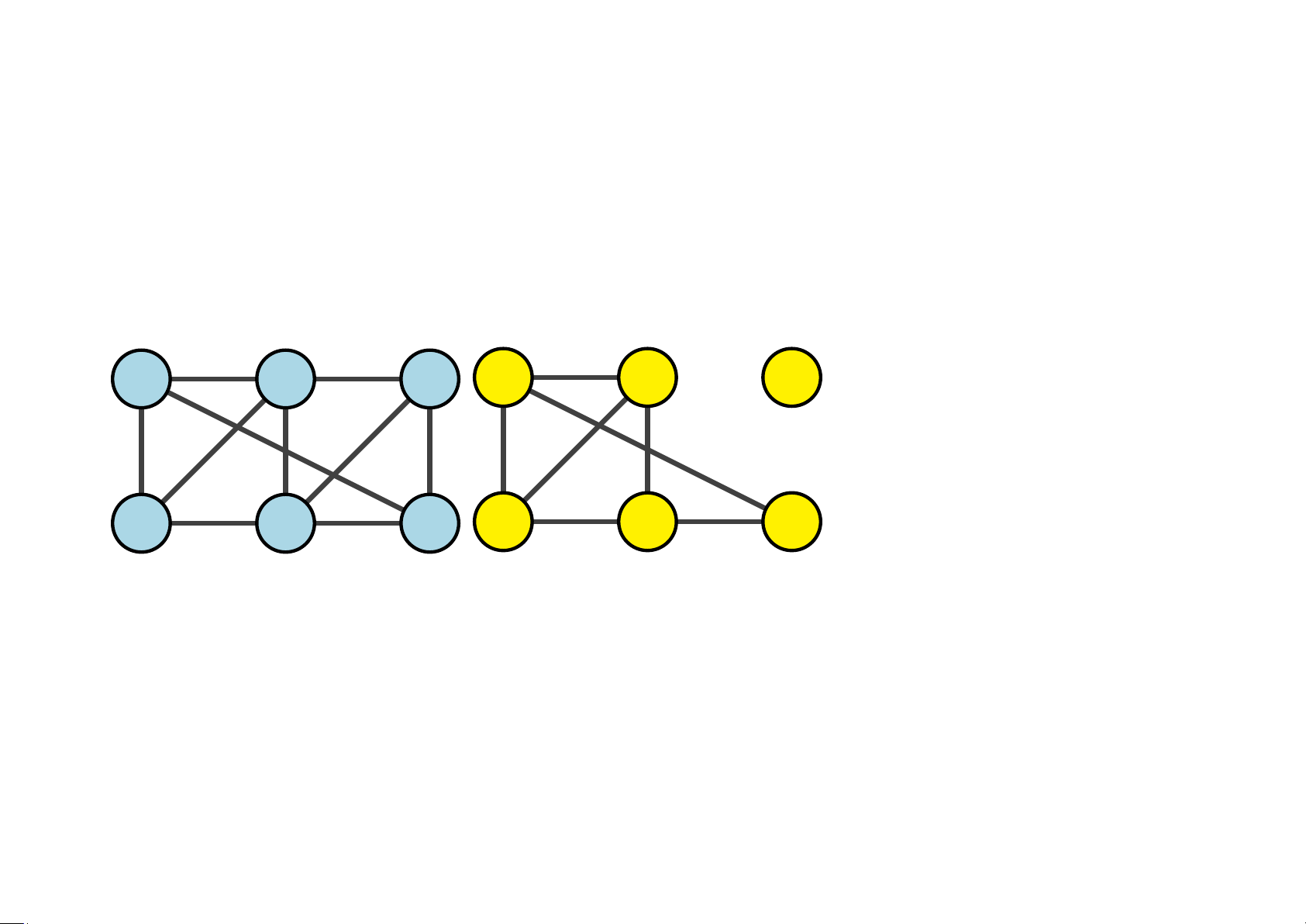
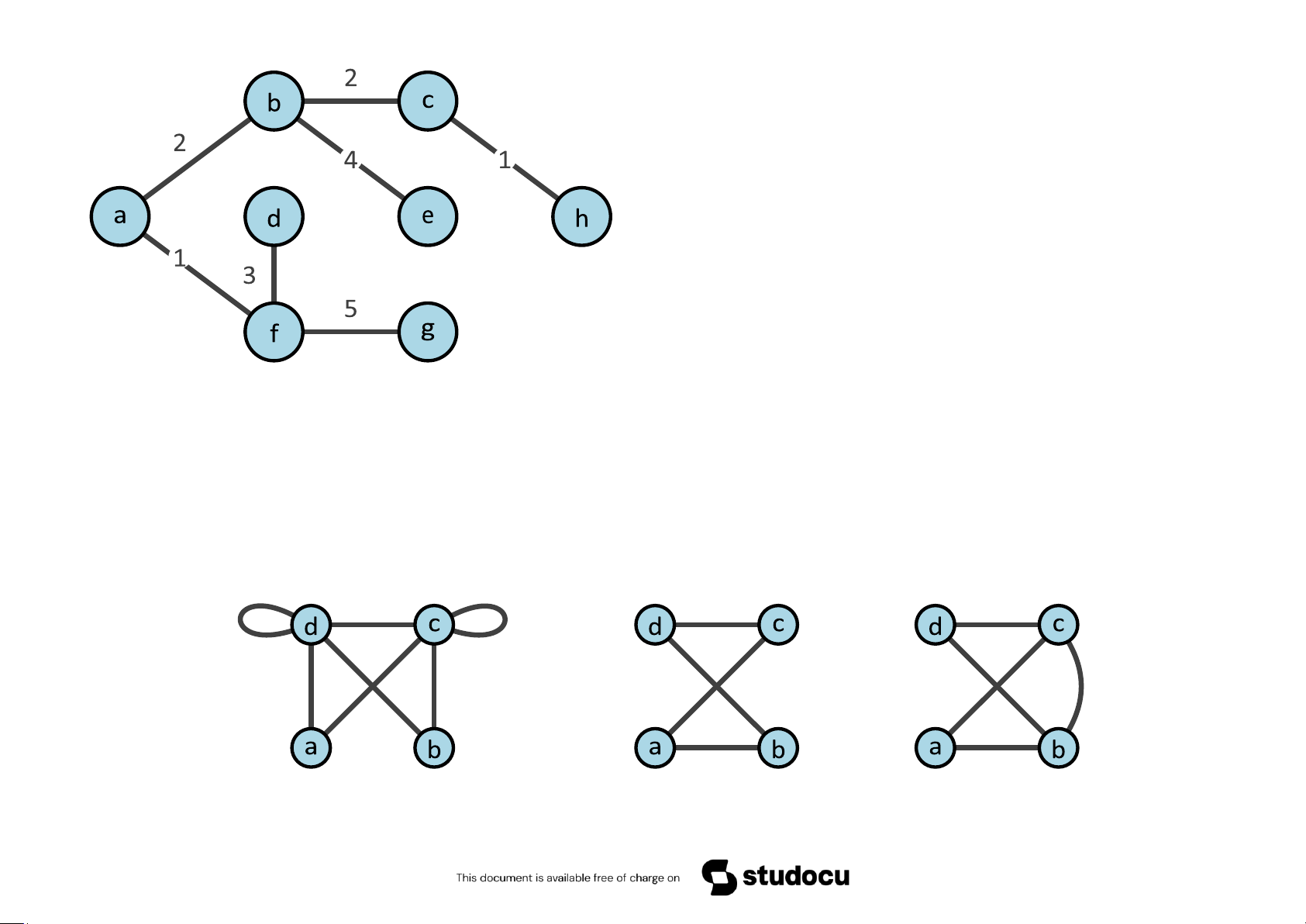
Bài 5.2 Tìm 3 đồ thị con có cùng số đỉnh và không đẳng cấu với nhau của đồ thị
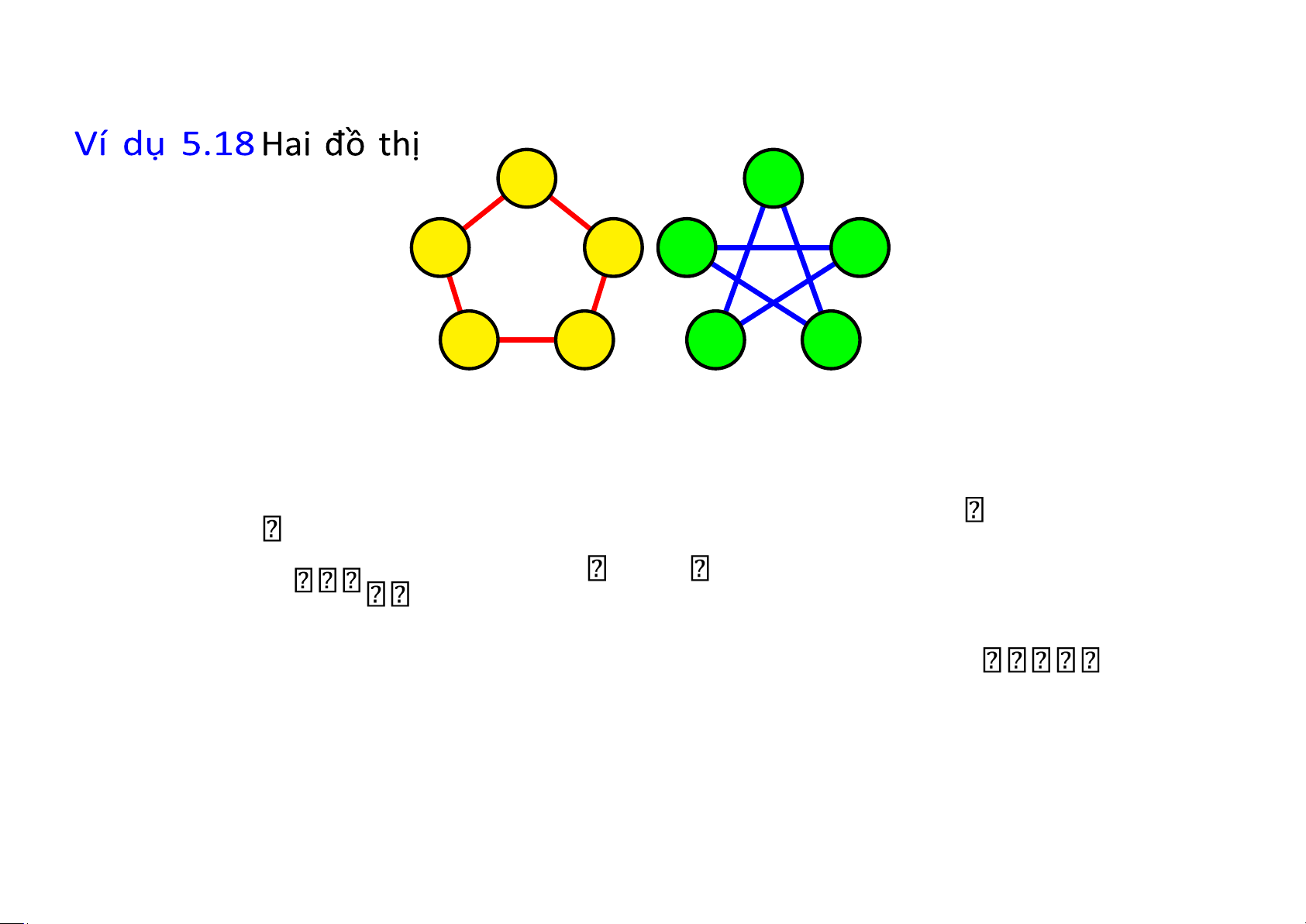
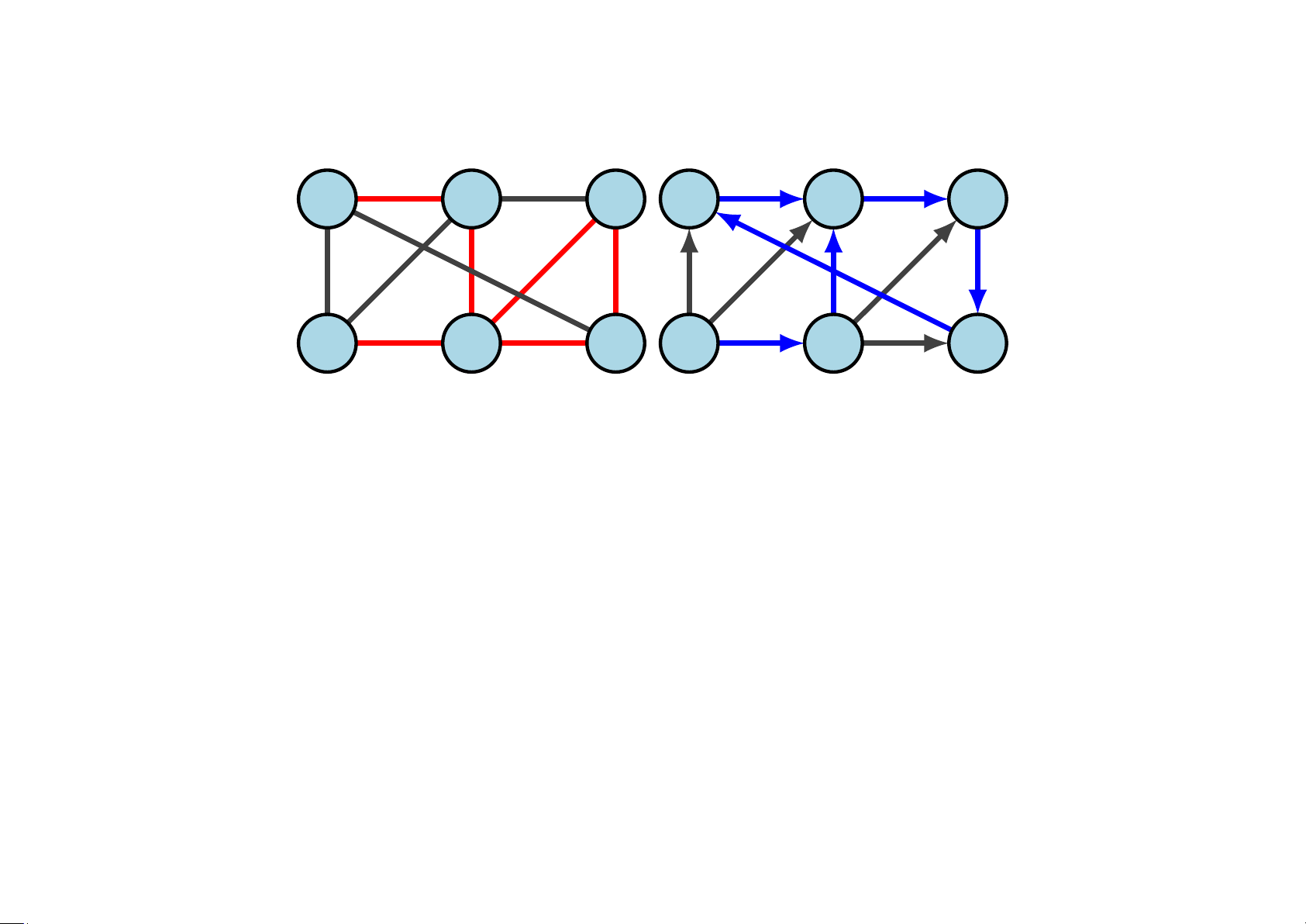
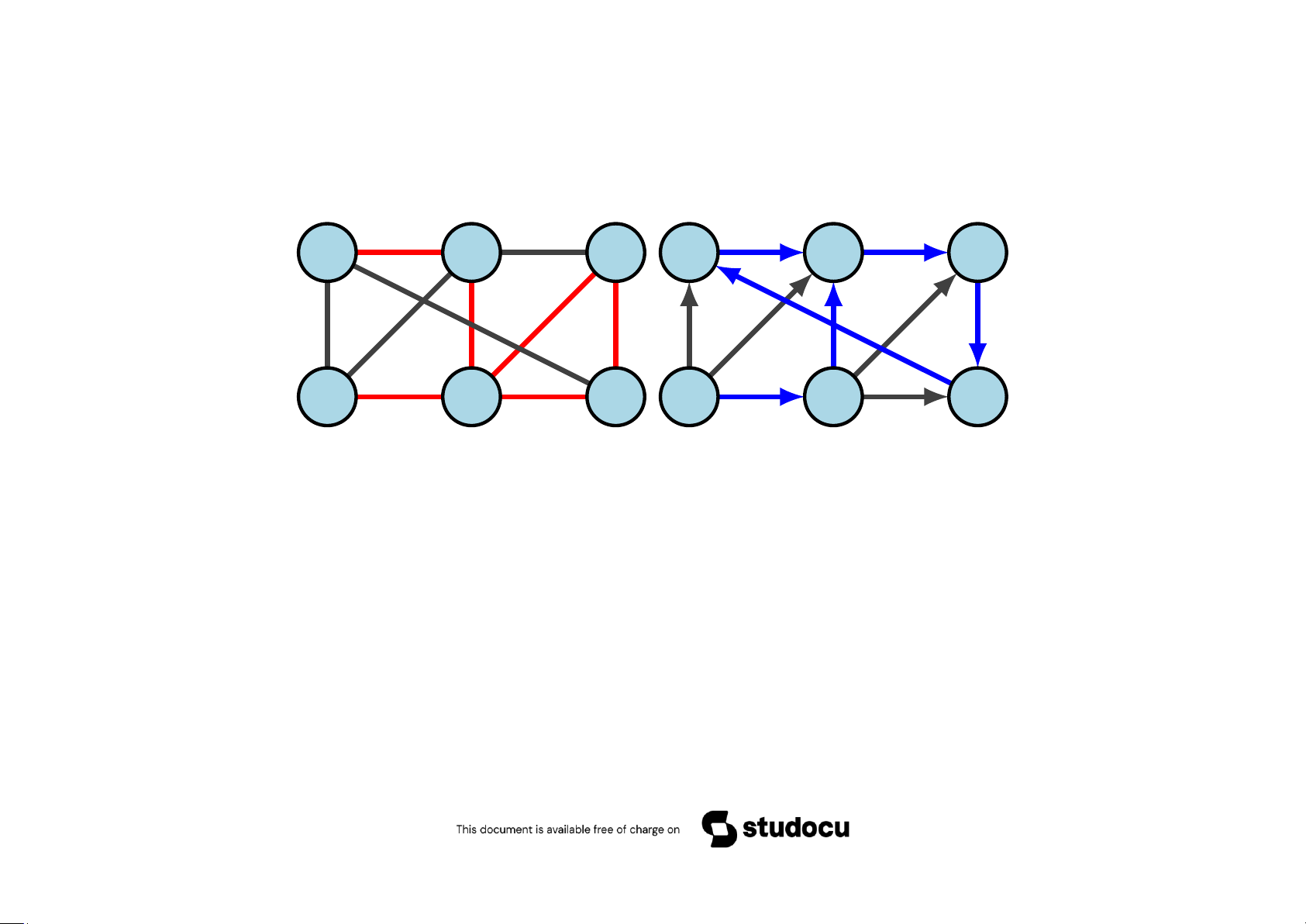
Bài 5.3 Chứng minh rằng hai đồ thị sau đẳng cấu
Bài 5.4 Một nước có 10 thành phố. Hãy thiết lập một mạng đường hàng không thỏa 2 điều kiện:
• Mỗi thành phố có đường hàng không nối trực tiếp với đúng 3 thành phố khác
• Từ mỗi thành phố có đường hàng không đi tới một thành phố tùy ý sao cho trên đường hành trình
tới đích có thể đi qua các thành phố khác, mỗi thành phố đi qua đúng một lần.
Bài 5.5 Cho đồ thị liên thông G có 6 đỉnh với bậc lần lượt là 2, 2, 3, 4, 4, 5. Hãy vẽ phác họa G trong các
trường hợp: a. G là đơn đồ thị.
b. G là đa đồ thị không có vòng.
c. G là đa đồ thị không có cạnh bội.
d. G là đa đồ thị có vòng và có cạnh bội.
Bài 5.6 Cho G là một đồ thị liên thông vô hướng có 6 đỉnh với bậc lần lượt là 1, 2, 2, 3, 3, 3.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Hãy vẽ phác họa đồ thị G (1 trường hợp đơn đồ thị, 1 trường hợp đa đồ thị). Bài 5.7
Hãy vẽ các đồ thị vô hướng (nếu có) trong các trường hợp a. Đồ thị đơn có 6 đỉnh và
bậc các đỉnh là 1, 2, 3, 3, 4, 5
b. Có 6 đỉnh và bậc các đỉnh là 1, 2, 3, 3, 4, 5
c. Đồ thị đơn, có 6 đỉnh và bậc các đỉnh là 1,2, 2, 3, 3, 5
d. Đa đồ thị có 6 đỉnh và bậc các đỉnh là 2, 2, 4, 4, 6,6
Bài 5.8 Xác định số đỉnh của các đồ thị vô hướng trong các trường hợp sau
a. Tổng số bậc là 28, có 2 đỉnh bậc 5, 1 đỉnh bậc 7, các đỉnh còn lại có bậc lớn hơn 1.
b. Tổng số bậc là 54, có ít nhất 6 đỉnh bậc 7, còn lại là các đỉnh có bậc lớn hơn 1.
c. Tổng số bậc là 20, có ít nhất 2 đỉnh bậc 5, các đỉnh còn lại có bậc lẻ
Bài 5.9 Có thể tồn tại một nhóm gồm 9 người trong đó mỗi người đều chỉ quen biết đúng 5 người khác trong nhóm hay không?
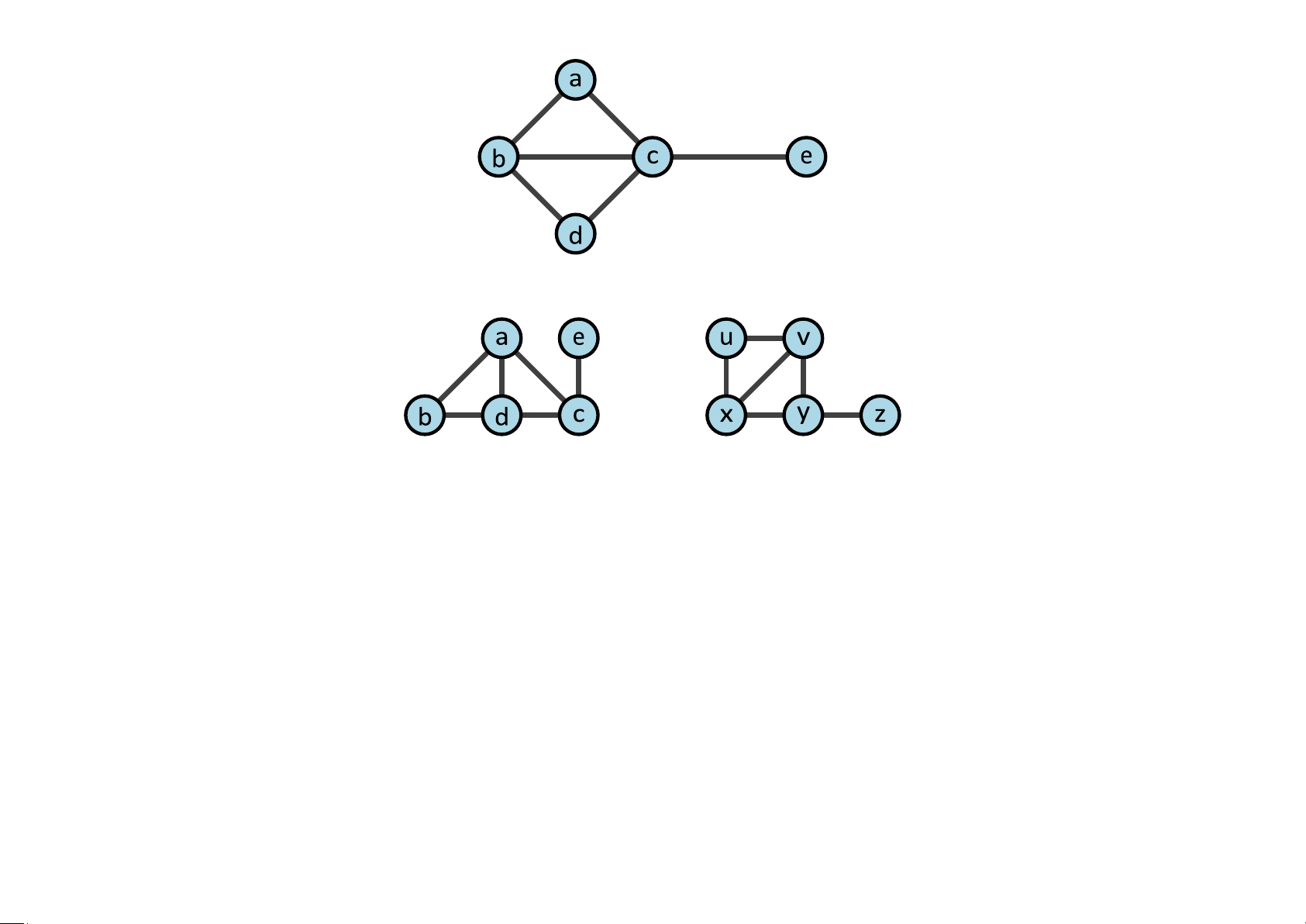
Bài 5.10 Đồ thị nào có đường đi (chu trình) Euler? Vì sao? G1 G2 G3
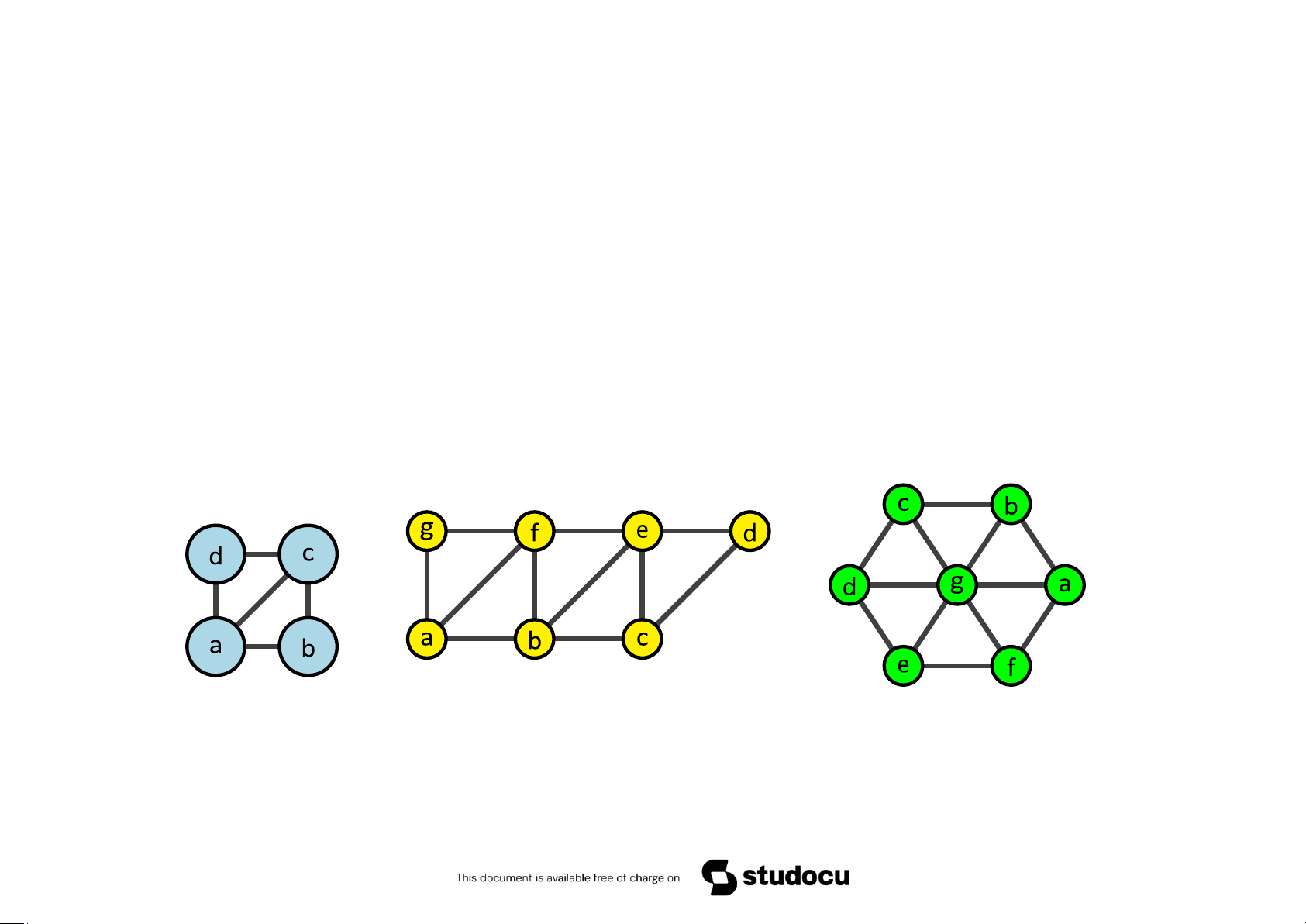
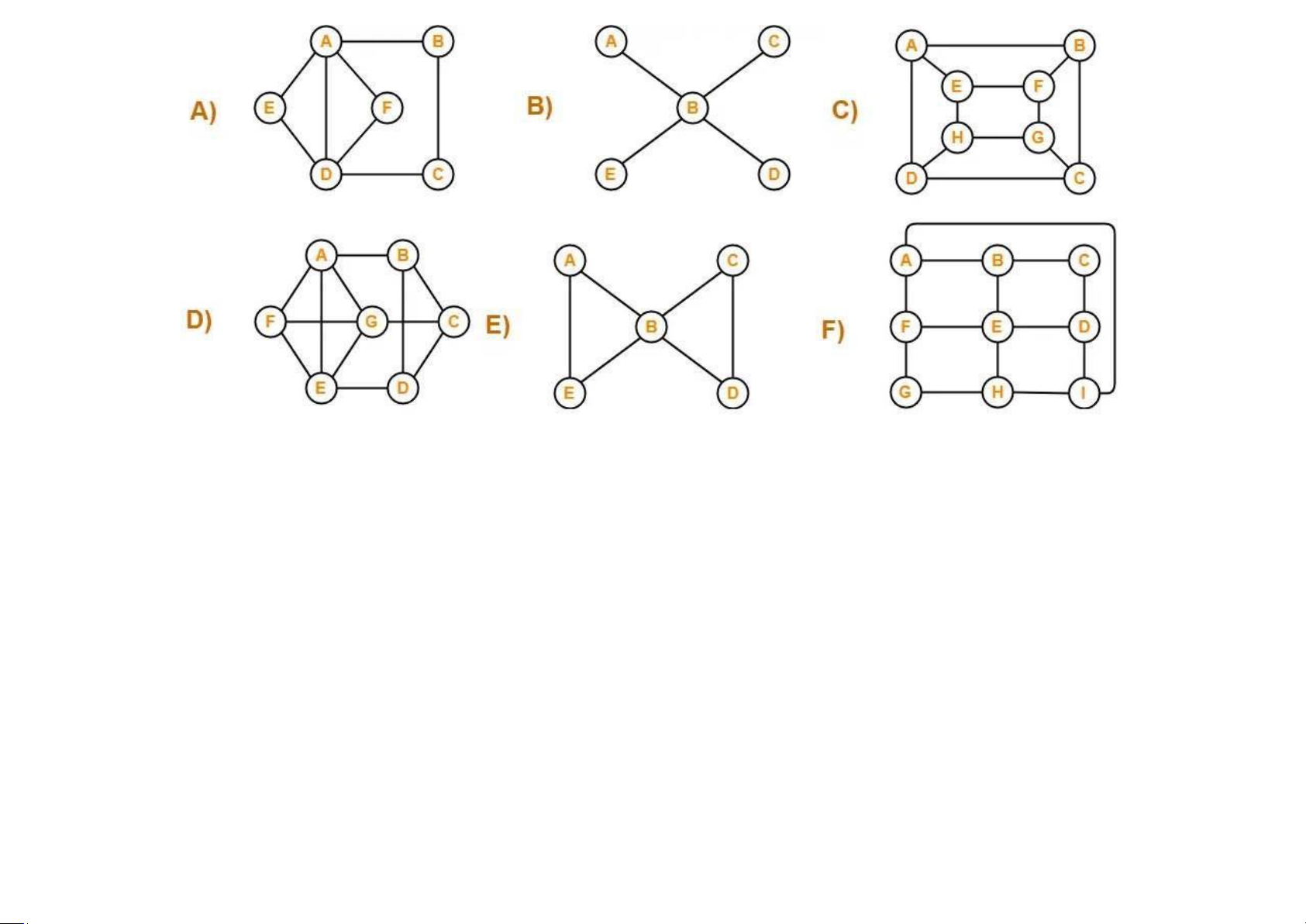
Bài 5.11 Tìm chu trình (đường đi) Hamilton/Euler của các đồ thị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Bài 5.12 Dùng thuật toán Dijkstra để tìm đường đi ngắn nhất từ A đến các đỉnh khác của đồ thị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
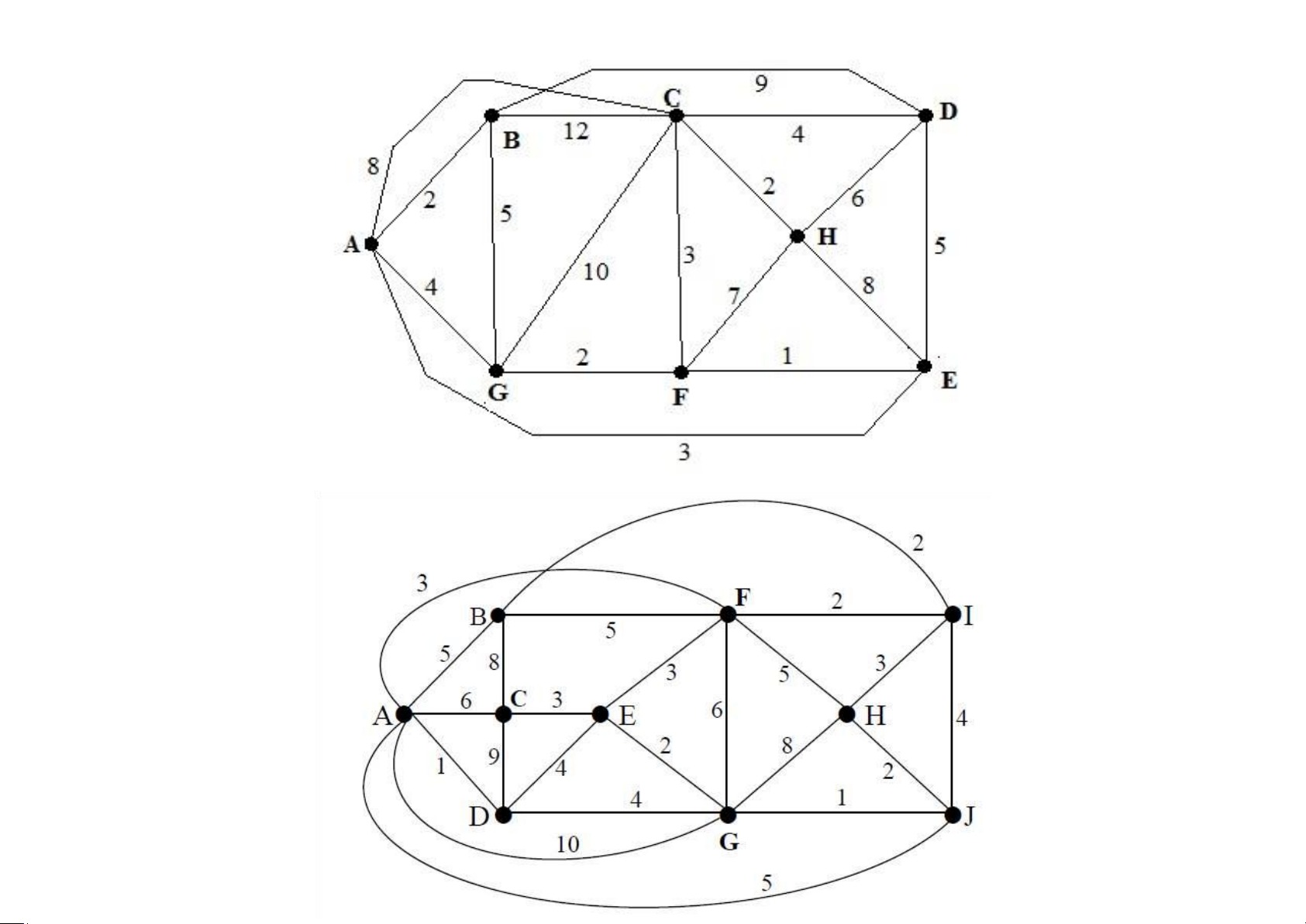
Bài 5.13 Cho G là một đồ thị vô hướng, có trọng số như sau:
a. Đồ thị có chu trình (đường đi) Euler không? Tại sao? Nếu có, hãy chỉ ra một chu trình(đường đi) Euler của đồ thị.
b. Hãy chỉ ra một chu trình (đường đi) Hamilton của đồ thị (nếu có).
c. Tìm đường đi ngắn nhất từ đỉnh F đến các đỉnh còn lại của đồ thị (chỉ rõ thuật toán).
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
C. Vasudev (2006), Graph theory with applications, New Age
International (P) Ltd., Publishers
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com)