









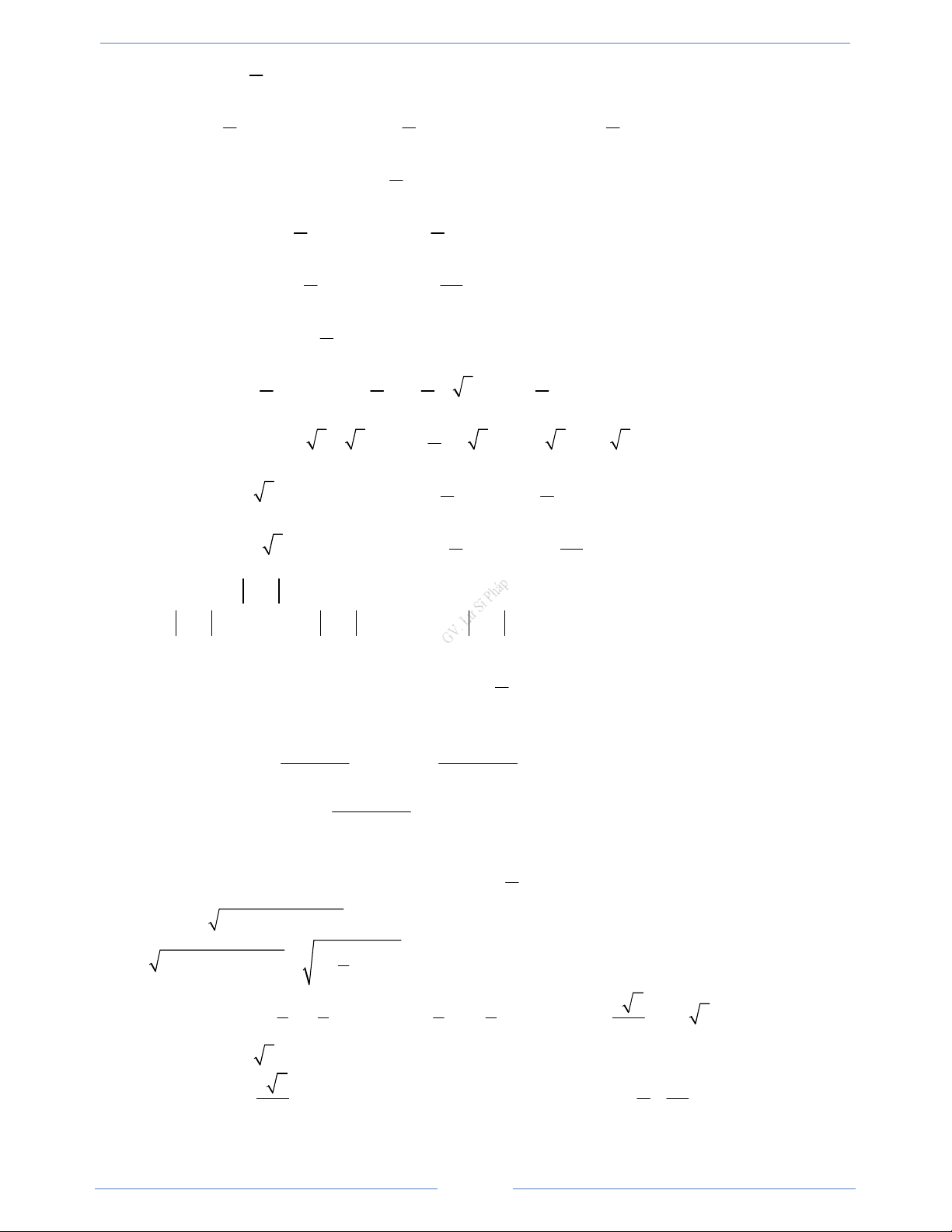


































Preview text:
Giáo Viên Trường THPT Tuy Phong TOAÙN 11 CHƯƠNG I
HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC LỜI NÓI ĐẦU
Quý đọc giả, quý thầy cô và các em học sinh thân mến!
Nhằm giúp các em học sinh có tài liệu tự học môn Toán,
tôi biên soạn cuốn giải toán trọng tâm của lớp 11.
Nội dung của cuốn tài liệu bám sát chương trình chuẩn và
chương trình nâng cao về môn Toán đã được Bộ Giáo dục và Đào tạo quy định. Nội dung gồm 4 phần
Phần 1. Kiến thức cần nắm
Phần 2. Dạng bài tập có hướng dẫn giải và bài tập đề nghị
Phần 3. Phần trắc nghiệm có đáp án.
Cuốn tài liệu được xây dựng sẽ còn có những khiếm
khuyết. Rất mong nhận được sự góp ý, đóng góp của quý
đồng nghiệp và các em học sinh.
Mọi góp ý xin gọi về số 0355334679 – 0916.620.899 Email: lsp02071980@gmail.com Chân thành cảm ơn. Lư Sĩ Pháp Gv_Trường THPT Tuy Phong MỤC LỤC
CHƯƠNG I. HÀM SỐ LƯỢNG GIÁC VÀ
PHƯƠNG TRÌNH LƯỢNG GIÁC
ÔN TẬP CÔNG THỨC LƯỢNG GIÁC 1 – 2
§1. HÀM SỐ LƯỢNG GIÁC 3 – 11
§2. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN 11 – 17
§3. PHƯƠNG TRÌNH LƯỢNG GIÁC ĐƠN GIẢN THƯỜNG GẶP 18 – 27 ÔN TẬP CHƯƠNG I 28 – 41
TRẮC NGHIỆM CHƯƠNG I 41 – 58 ĐÁP ÁN 59 – 60
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp CHƯƠNG I ---0o0---
HÀM SỐ LƯỢNG GIÁC & PHƯƠNG TRÌNH LƯỢNG GIÁC ---0O0---
ÔN TẬP CÔNG THỨC LƯỢNG GIÁC
1. Hằng đẳng thức lượng giác cơ bản sinα π 2 2 sin α + cos α =1 tanα =
;α ≠ + kπ,k ∈ℤ cosα 2 cosα kπ cotα =
;α ≠ kπ,k ∈ℤ tanα.cotα = 1;α ≠ ,k ∈ℤ sinα 2 1 π 1 2 1+ tan α =
;α ≠ + kπ ,k ∈ℤ 2 1+ cot α =
;α ≠ kπ ,k ∈ℤ 2 cos α 2 2 sin α
2. Các công thức lượng giác 2.1. Công thức cộng
cos(α ± β ) = cosα cosβ ∓ sinα sin β
sin (α ± β ) = sinα cosβ ± cosα sin β α ± β (α ± β) tan tan tan =
, với mọi α,β làm cho các biểu thức có nghĩa. 1∓ tanα tan β 2.2. Công thức nhân đôi sin 2α = 2sinα cosα 2 2 2 2
cos2α = cos α − sin α = 2cos α −1 = 1− 2sin α 2 tanα π tan 2α =
;α,2α ≠ + kπ ,k ∈ℤ 2 1− tan α 2 2.3. Công thức nhân ba 3 cos3α = 4cos α − 3cosα 3 sin3α = 3sinα − 4sin α 2.4. Công thức hạ bậc 1 cos2α 1 cos2α 2 cos α + = 2 sin α − = 2 2 1− cos2α 2 tan α =
, với α làm cho biểu thức có nghĩa. 1+ cos2α
2.6. Công thức biến đổi tổng thành tích α + β α − β α + β α − β cosα + cos β = 2 cos .cos cosα − cos β = −2sin .sin 2 2 2 2 α + β α − β α + β α − β sinα + sin β = 2sin .cos sinα − sin β = 2 cos .sin 2 2 2 2
, với mọi α,β làm cho các biểu thức có nghĩa.
2.7. Công thức biến đổi tích thành tổng 1 cosα.cos β cos (α β) cos(α β) = + + − 2 1 sinα.sin β cos (α β) cos(α β) = − + − − 2 1 sinα.cos β sin (α β) sin(α β) = + + − 2 2.8. Công thức rút gọn 1
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp π π
sinα + cosα = 2 sinα + = 2 cosα − 4 4 π π
sinα − cosα = 2 sinα − = − 2 cosα + 4 4 2 tanα + cotα =
, với α làm cho biểu thức có nghĩa sin 2α
3. Giá trị lượng giác của các góc (cung) có liên quan đặt biệt
3.1. Hai góc đối nhau ( cung đối) (α làm cho các biểu thức có nghĩa) cos( α − ) = cosα sin( α − ) = −sinα tan( α − ) = − tanα cot( α − ) = − cotα
3.2. Hai góc bù nhau( cung bù)(α làm cho các biểu thức có nghĩa) sin(π −α ) = sinα cos(π −α) = − cosα tan(π −α) = − tanα cot(π −α ) = − cotα
3.3. Hai góc phụ nhau ( cung phụ)(α làm cho các biểu thức có nghĩa) π π sin −α = cosα cos −α = sinα 2 2 π π tan −α = cotα cot −α = tanα 2 2
3.4. Hai góc hơn kém π (cung hơn kém π ),(α làm cho các biểu thức có nghĩa) sin(π +α ) = −sinα cos(π +α ) = − cosα tan(π +α ) = tanα cot(π +α) = cotα π π
3.5. Hai góc hơn kém (cung hơn kém ),(α làm cho các biểu thức có nghĩa) 2 2 π π sin +α = cosα cos +α = −sinα 2 2 π π tan +α = − cotα cot +α = − tanα 2 2
3.6. Cung bội. ( k ∈ ℤ , α làm cho các biểu thức có nghĩa)
sin(α + k2π ) = sinα
cos(α + k2π ) = cosα
tan(α + kπ ) = tanα
cot(α + kπ ) = cotα
4. Bảng giá trị lượng giác các góc (cung) đặt biệt α 00 300 450 600 900 1200 1350 1500 1800 π π π π 2π 3π 5π π 0 HSLG 6 4 3 2 3 4 6 sinα 1 2 3 3 2 1 0 2 2 2 1 2 2 2 0 cosα 3 2 1 1 2 3 1 − − − 2 2 2 0 2 2 2 - 1 tanα 3 3 − 3 3 0 − 3 1 | - 1 3 0 cotα 3 3 3 − 3 | 1 − 3 0 3 - 1 | | : Không xác định 2
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
§1. HÀM SỐ LƯỢNG GIÁC
A. KIẾN THỨC CẦN NẮM
Hàm số y = sin x
Hàm số y = cos x
• Có tập xác định là ℝ
• Có tập xác định là ℝ
• Có tập giá trị là −1;1
• Có tập giá trị là 1 − ;1 • Là hàm số lẻ • Là hàm số chẵn
• Là hàm số tuần hoàn với chu kì T = 2π
• Là hàm số tuần hoàn với chu kì T = 2π
• Đồng biến trên mỗi khoảng
• Đồng biến trên mỗi khoảng π π ( π
− + k2π;k2π ) và nghịch biến trên mỗi −
+ k2π; + k2π và nghịch biến trên 2 2
khoảng (k2π;π + k2π ),k ∈ℤ π 3π
mỗi khoảng + k2π;
+ k2π ,k ∈ℤ 2 2
• Có đồ thị là một đường hình sin
• Có đồ thị là một đường hình sin
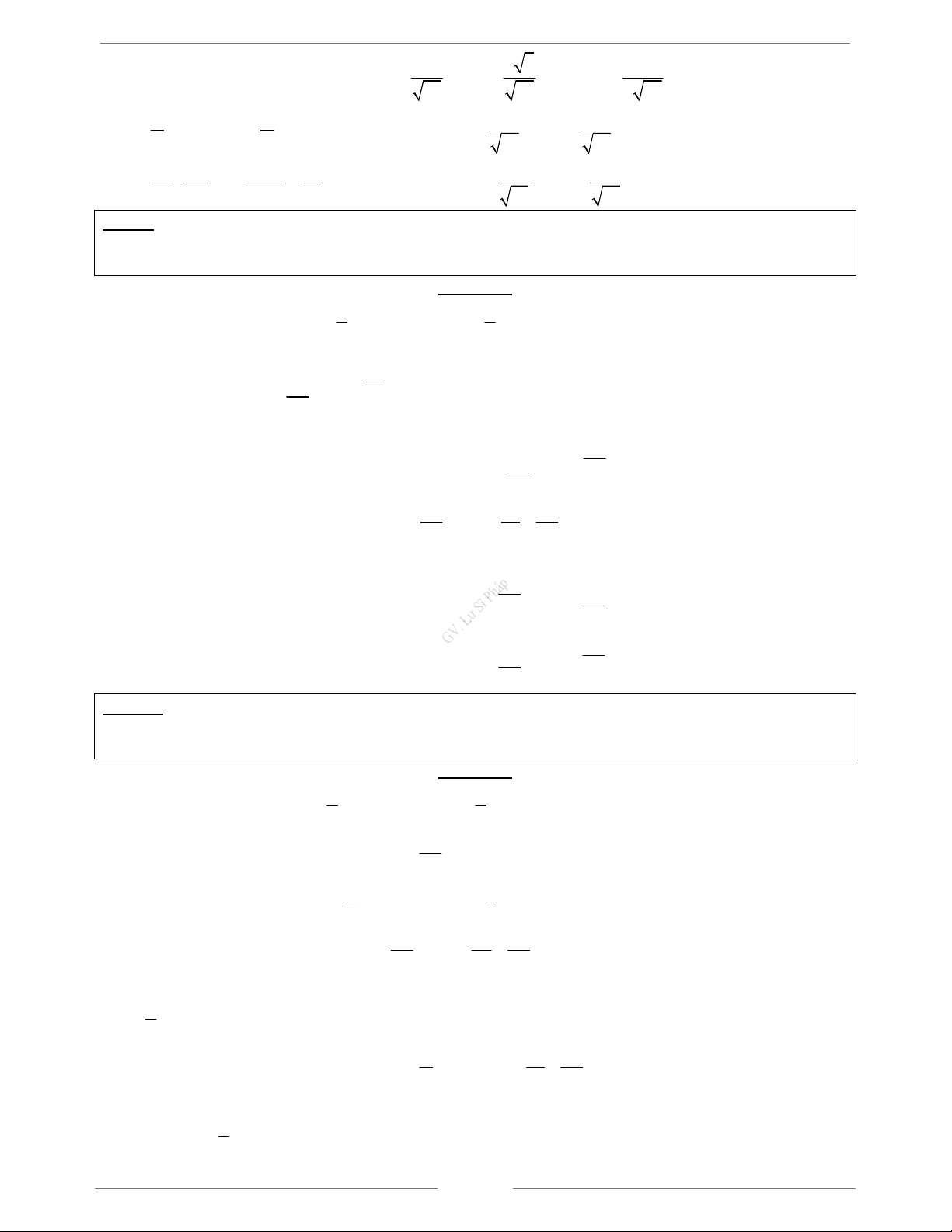
Hàm số y = tan x
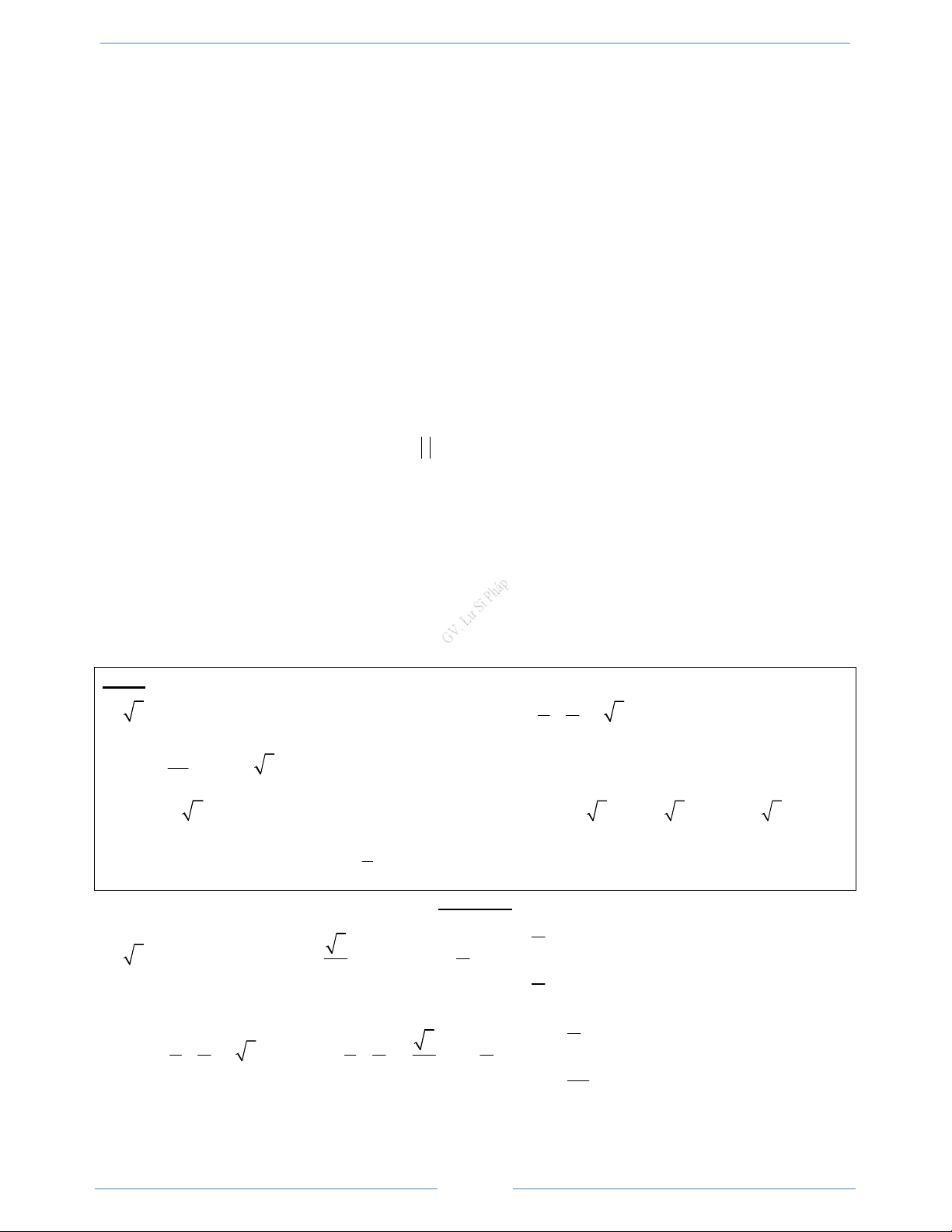
Hàm số y = cot x D = ℝ \ kπ , • π • ∈ Có tập xác định là Có tập xác định là k ℤ 2 { }
D = ℝ \ + kπ ,k ∈ 1 ℤ 2
• Có tập giá trị là ℝ
• Có tập giá trị là ℝ • Là hàm số lẻ • Là hàm số lẻ
• Là hàm số tuần hoàn với chu kì là π
• Là hàm số tuần hoàn với chu kì là π
• Đồng biến trên mỗi khoảng
• Nghịch biến trên mỗi khoảng π π
(kπ;π +kπ );k∈ℤ −
+ kπ; + kπ ;k ∈ℤ 2 2
• Có đồ thị nhận mỗi đường thẳng
• Có đồ thị nhận mỗi đường thẳng π
x = kπ ; k ∈ ℤ làm một đường tiệm cận x =
+ kπ;k ∈ℤ làm một đường tiệm cận 2 B. BÀI TẬP
ạng 1. Tập xác định của hàm số
D- Hàm số xác định với một điều kiện
- Hàm số xác định bởi hai hay nhiều điều kiện - Hàm số y = sin ;
x y = cos x có tập xác định là ℝ
- Hàm số y = tan x xác định khi và chỉ khi cos x ≠ 0; Hàm số y = cot x xác định khi và chỉ khisin x ≠ 0 3
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp Lưu ý: 1 π π
sin u = 1 ⇔ u = + k2π sin u = 1
− ⇔ u = − + k2π
sin u = 0 ⇔ u = kπ 2 2 2 π
cos u = 1 ⇔ u = k2π
cos u = −1 ⇔ u = π + k2π cosu = 0 ⇔ u = + kπ 2 3 π π
tan u = 1 ⇔ u = + kπ tan u = 1
− ⇔ u = − + kπ
tan u = 0 ⇔ u = kπ 4 4 4 π π π
cot u = 1 ⇔ u = + kπ
cot u = −1 ⇔ u = − + kπ
cot u = 0 ⇔ u = + kπ 4 4 2 1 - Hàm số y =
xác định khi và chỉ khi A ≠ 0 A
- Hàm số y = A xác định khi và chỉ khi A ≥ 0 1 - Hàm số y =
xác định khi và chỉ khi A > 0 A
Bài 1.1. Tìm tập xác định các hàm số sau: 1+ cos x 1+ sin x 1+ cos x a) y = b) y = c) y =
d) y = 3 − sin x sin x cos x 1− cos x HD Giải
a) Hàm số xác định khi và chỉ khi sin x ≠ 0 ⇔ x ≠ kπ ,k ∈ℤ . Vậy D = ℝ \ {kπ,k ∈ } ℤ π π
b) Hàm số xác định khi và chỉ khi cos x ≠ 0 ⇔ x ≠
+ kπ ,k ∈ℤ . Vậy D = ℝ \ + kπ ,k ∈ℤ 2 2 1+ cos x
c) Hàm số xác định khi và chỉ khi
≥ 0 . Vì 1+ cos x ≥ 0 nên điều kiện là 1− cos x > 0 hay 1− cos x
1− cos x ≠ 0 ⇔ cos x ≠ 1 ⇔ x ≠ k2π ,k ∈ℤ . Vậy D = ℝ \ {k π 2 ,k ∈ } ℤ
d) Vì −1 ≤ sin x ≤ 1 nên 3 − sin x ≥ 0, x
∀ ∈ ℝ . Vậy D = ℝ
Bài 1.2. Tìm tập xác định các hàm số sau: π π π
a) y = tan x −
b) y = cot x +
c) y = tan 2x +
d) y = tan x + cot x 3 6 3 HD Giải π π π 5π
a) Hàm số xác định khi và chỉ khi cos x − ≠ 0 ⇔ x − ≠ + kπ ⇔ x ≠
+ kπ ,k ∈ℤ . 3 3 2 6 5π Vậy D = ℝ \ + kπ ,k ∈ℤ 6 π π π
b) Hàm số xác định khi và chỉ khi sin x + ≠ 0 ⇔ x + ≠ kπ ⇔ x ≠ − + kπ ,k ∈ℤ . 6 6 6 π
Vậy D = ℝ \ − + kπ ,k ∈ℤ 6 π π π π kπ
c) Hàm số xác định khi và chỉ khi cos2x + ≠ 0 ⇔ x + ≠ + kπ ⇔ x ≠ + ,k ∈ℤ . 3 3 2 12 2 π kπ Vậy D = ℝ \ + ,k ∈ℤ 12 2 cos x ≠ 0 kπ
d) Hàm số xác định khi và chỉ khi
⇔ sin2x ≠ 0 ⇔ x ≠ ,k ∈ℤ . s in x ≠ 0 2 4
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp kπ Vậy D = ℝ \ ,k ∈ℤ 2
Bài 1.3. Tìm tập xác định các hàm số sau: 2x x a) y = cos b) y = tan c) y = cot2x x −1 3 1 2 d) y = sin e) y = cos x +1 f) y = 2 x −1 cos x − cos3x 3 1− sin x 3sin x − 7 g) y = h) y = i) y = 2 2 sin x − cos x 1+ cos x 2 cos x − 5 HD Giải 2x 2x a) Ta có y = cos
xác định trên ℝ khi và chỉ khi
∈ ℝ ⇔ x −1 ≠ 0 ⇔ x ≠ 1. x −1 x −1 2x
Vậy tập xác định của hàm số y = cos là D = ℝ \ { } 1 x −1 x x x π 3π
b) Hàm số y = tan xác định khi và chỉ khi cos ≠ 0 ⇔ ≠ + kπ ⇔ x ≠
+ k3π,k ∈ℤ. 3 3 3 2 2 3π
Vậy tập xác định của hàm số D = ℝ \
+ k3π ,k ∈ℤ 2 kπ
c) Tập xác định của hàm số D = ℝ \ ,k ∈ℤ 2
d) Tập xác định của hàm số D = ℝ \ {−1; } 1
e) Ta có cos x +1 ≥ 0, x
∀ ∈ ℝ . Vậy tập xác định của hàm số D = ℝ f) Ta có 2
cos x − cos3x = −2sin2x sin(−x) = 4sin x cos x . kπ
Vậy tập xác định của hàm số D = ℝ \ ,k ∈ℤ 2 π kπ g) Ta có 2 2
sin x − cos x = −cos2x . Vậy tập xác định của hàm số D = ℝ \ + ,k ∈ℤ 4 2
h) Ta có 1− sin x ≥ 0,1+ cos x ≥ 0 . Do đó hàm số xác định x
∀ ∈ ℝ khi cos x ≠ −1. Vậy tập xác định của
hàm số D = ℝ \ {π + k2π,k ∈ } ℤ 3sin x − 7
i) Ta có 3sin x − 7 < 0, 2 cos x − 5 < 0 nên > 0, x
∀ ∈ ℝ . Vậy tập xác định của hàm số D = ℝ 2 cos x − 5
Bài 1.4. Tìm tập xác định các hàm số sau: 1+ x 1− cos2x a) y = cos x b) y = sin c) y = 1− x 2 1+ cos 2x cot x 2 − cos x tan x + cot x d) y = e) y = f) y = cos x −1 1−sin 2 1+ tan π x x − 3 HD Giải
a) Ta có y = cos x xác định trên ℝ khi và chỉ khi x ∈ ℝ ⇔ x ≥ 0 .
Vậy tập xác định của hàm số D = [0;+∞) 1+ x 1+ x 1+ x b) Ta có y = sin
xác định trên ℝ khi và chỉ khi ∈ ℝ ⇔ ≥ 0 ⇔ 1 − ≤ x < 1. 1− x 1− x 1− x
Vậy tập xác định của hàm số D = [ 1 − ;1) 5
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp c) Ta có 2
1− cos2x ≥ 0,1+ cos 2x ≥ 0, x
∀ ∈ ℝ . Vậy tập xác định của hàm số D = ℝ cot x s in x ≠ 0 x ≠ kπ d) Hàm số y = xác định ⇔ ⇔
⇔ x ≠ kπ;k ∈ℤ . cos x −1 cos x ≠ 1 x ≠ k2π
Vậy tập xác định của hàm số D = ℝ \ {kπ,k ∈ } ℤ π 5 cos x − ≠ 0 π 2 − cos x ≠ + kπ x 3 e) Hàm số 6 y = xác định ⇔ ⇔ ;k ∈ℤ . 1+ tan π π π x − tan x − ≠ 0 ≠ + π 3 x k 3 12 5π π
Vậy tập xác định của hàm số D = ℝ \
+ kπ ∪ + kπ ;k ∈ℤ 6 12 cos ≠ 0 k x π tan x ≠ x + cot x f) Hàm số 2 y = xác định ⇔ s in x ≠ 0 ⇔ ;k ∈ℤ. 1−sin 2x π sin 2x ≠ 1 x ≠ + kπ 4 kπ π
Vậy tập xác định của hàm số D = ℝ \
∪ + kπ ;k ∈ ℤ 2 4
ạng 2. Xét tính chẵn, lẻ của hàm số
DNhắc lại kiến thức: Về tính chẵn, lẻ của hàm số y= f(x)
Tìm tập xác định D của hàm số, kiểm chứng D là tập đối xứng hay không, tức là x
∀ , x ∈ D ⇒ −x ∈ D (1)
Tính f (−x) và so sánh f (−x) với f (x) :
Nếu f (−x) = f (x) thì f (x) là hàm số chẵn (2)
Nếu f (−x) = − f (x) thì f (x) là hàm số lẻ (3) Do vậy
Nếu điều kiện (1) không nghiệm đúng thì f (x) là hàm số không chẵn, không lẻ trên D
Nếu điều kiện (2) và (3) không nghiệm đúng thì f (x) là hàm số không chẵn, không lẻ trên D
Để kết luận f (x) là hàm số không chẵn, không lẻ trên D, ta chỉ cần tìm một điểm x sao 0
cho f (−x ) ≠ f (x ) và f (−x ) ≠ − f (x ) 0 0 0 0
Lưu ý: vận dụng hai góc (cung) đối nhau của HSLG
Bài 1.5. Xác định tính chẵn, lẻ của các hàm số sau: cos x a) y =
b) y = x – sinx
c) y = 1− cos x x 3π
d) y = 1+ cos x.sin − 2x e) y = sin 2
x.cos2x + tanx
f) y = sinx – cosx tan x + cot x g) 3
y = sin x − tan x h) y = sin x HD Giải cos a) Hàm số = ( ) x y f x =
có tập xác định D = ℝ \ { } 0 . Ta có x
∀ , x ∈ D ⇒ −x ∈ D và x cos(−x) cos cos (− ) x f x = = −
= − f (x) . Vậy hàm số = ( ) x y f x = là hàm số lẻ. (−x) x x b) Hàm số lẻ c) Là hàm số chẵn d) Là hàm số chẵn e) Là hàm số lẻ
f) Hàm số y = f (x) = sin x − cos x có tập xác định D = ℝ . 6
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp π π 1 3 π 1 3 π π Lấy x =
ta có : f = −
; f − = − −
. Suy ra f ≠ f − 6 6 2 2 6 2 2 6 6
Vậy hàm số y = f (x) = sin x − cos x là hàm số không chẵn, không lẻ g) Là hàm số lẻ h) Là hàm số lẻ
ạng 3. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
DĐịnh nghĩa: Cho hàm số y= f(x) có tập xác định là D và hai hằng số M và m. Nếu x
∀ ∈ D, f (x) ≤ M và x
∃ sao cho f (x ) = M thì
y = f x trên D và 0 0
M gọi là GTLN của hàm số ( )
kí hiệu Max y = M D Nếu x
∀ ∈ D, f (x) ≥ m và x
∃ sao cho f (x ) = m thì = trên D và kí 0 0
m gọi là GTNN của hàm số y f (x)
hiệu Min y = m D Chú ý:
−1 ≤ sin x ≤ 1,∀x ∈ 2 ℝ
0 ≤ sin x ≤ 1,∀x ∈ ℝ
0 ≤ sin x ≤ 1,∀x ∈ ℝ
−1 ≤ cos x ≤ 1,∀x ∈ 2 ℝ
0 ≤ cos x ≤ 1,∀x ∈ ℝ
0 ≤ cos x ≤ 1,∀x ∈ℝ
Bài 1.6. Tìm giá trị lớn nhất và nhỏ nhất của mỗi hàm số sau π
a) y = 2 cos x +1
b) y = 3 − 2sin x
c) y = 2(1+ cos x) +1
d) y = 3sin x − − 2 6 HD Giải cos x ≥ 0
a) y = 2 cos x +1. Điều kiện:
⇔ 0 ≤ cos x ≤1, x ∀ ∈ ℝ −1 ≤ cos x ≤ 1
Ta có: 0 ≤ cos x ≤ 1 ⇔ 0 ≤ 2 cos x ≤ 2 ⇔ 1 ≤ 2 cos x ≤ 3 hay 1 ≤ y ≤ 3
Vậy: Max y = 3 ⇔ cos x = 1 ⇔ x = k2π , k ∈ℤ ℝ π
Min y = 1 ⇔ cos x = 0 ⇔ x = + kπ ,k ∈ℤ ℝ 2
b) y = 3 − 2sin x . Tập xác định: D = ℝ
Ta có: −1 ≤ sin x ≤ 1 ⇔ 2 ≥ −2sin x ≥ −2 ⇔ 2 + 3 ≥ 3 − 2sin x ≥ −2 + 3 ⇔ 5 ≥ 3 − 2sin x ≥ 1hay 5 ≥ y ≥ 1 π
Vậy: Max y = 5 ⇔ sin x = 1
− ⇔ x = − + k2π ,k ∈ℤ ℝ 2 π
Min y = 1 ⇔ sin x = 1 ⇔ x =
+ k2π ,k ∈ℤ ℝ 2
c) y = 2(1+ cos x) +1. Tập xác định: D = ℝ
Ta có: −1 ≤ cos x ≤ 1 ⇔ 0 ≤ 1+ cos x ≤ 2 ⇔ 0 ≤ 2(1+ cos x) ≤ 4
⇔ 0 ≤ 2(1+ cos x) ≤ 2 ⇔ 1≤ 2(1+ cos x) +1≤ 3
Vậy: Max y = 3 ⇔ cos x = 1 ⇔ x = k2π , k ∈ℤ ℝ
Min y = 1 ⇔ cos x = 1
− ⇔ x = π + k2π , k ∈ℤ ℝ
Bài 1.7. Tìm giá trị lớn nhất và nhỏ nhất của mỗi hàm số sau π π
a) y = 2 cos + x + 3
b) y = cos x + cos x −
c) y = 3 − 2 sin x 3 3 d) 2
y = cos x + 2 cos 2x e) 2 2
y = 5 − 2 cos x.sin x f) 2
2sin x − cos 2x HD Giải 7
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp π
a) Hàm số y = 2 cos + x + 3 có tập xác định là D = ℝ . 3 π π π
Ta có: −1 ≤ cos + x ≤ 1 ⇔ −2 ≤ 2 cos + x ≤ 2 ⇔ −1+ 3 ≤ 2 cos + x + 3 ≤ 2 + 3 3 3 3 π
⇔ 1 ≤ 2 cos + x + 3 ≤ 5 hay 1 ≤ y ≤ 5 3 π π
Vậy: Max y = 5khi cos + x = 1 ⇔ x = − + k2π ,k ∈ℤ ℝ 3 3 π 2π Min y = 1
− khi cos + x = −1 ⇔ x =
+ k2π ,k ∈ℤ ℝ 3 3 π
b) Hàm số y = cos x + cos x −
có tập xác định là D = ℝ . 3 π π π π
Ta có cos x + cos x − = 2 cos x − cos = 3 cos x − . 3 6 6 6 π
Với mọi x ∈ ℝ ta luôn có: − 3 ≤ 3 cos x − ≤ 3 hay − 3 ≤ y ≤ 3 6 π π
Vậy: GTLN của y là 3 , đạt đựơc khi cos x − = 1 ⇔ x = + k2π;k ∈ℤ 6 6 π 7π
GTNN của y là − 3 , đạt được khi cos x − = −1 ⇔ x = + k2π;k ∈ℤ 6 6
c) Hàm số y = 3 − 2 sin x có tập xác định là D = ℝ .
Ta có 0 ≤ sin x ≤ 1 ⇔ −2 ≤ 2
− sin x ≤ 0 ⇔ 1 ≤ 3 − 2 sin x ≤ 3 hay 1 ≤ y ≤ 3
Vậy: GTLN của y là 3, đạt được khi sin x = 0 ⇔ x = kπ ,k ∈ ℤ π
GTNN của y là 1, đạt được khi sin x = 1
± ⇔ x = ± + kπ ,k ∈ℤ 2 d) Hàm số 2
y = cos x + 2 cos2x có tập xác định là D = ℝ . 1+ cos2x 1+ 5cos2x Ta có 2 cos x + 2cos2x = + 2 cos2x = . 2 2 1+ 5cos2x
Với mọi x ∈ ℝ ta luôn có: −2 ≤ ≤ 3 . 2
Vậy: GTLN của y là 3, đạt được khi cos2x = 1 ⇔ x = kπ ,k ∈ℤ π
GTNN của y là -2, đạt được khi cos2x = 1
− ⇔ x = + kπ ,k ∈ℤ 2 e) Hàm số 2 2
y = 5 − 2 cos x.sin x có tập xác định là D = ℝ . 1 Ta có 2 2 2
5 − 2cos x.sin x = 5− sin 2x . 2 1 1 9 1 3 2 Vì 2
0 ≤ sin 2x ≤ 1 nên 2 2
− ≤ − sin 2x ≤ 0 ⇔ ≤ 5− sin 2x ≤ 5 hay ≤ y ≤ 5 . 2 2 2 2 2
Vậy: GTLN của y là 5 , đạt được khi 2
sin 2x = 0 ⇔ sin 2x = 0 ⇔ x = kπ,k ∈ℤ 3 2 π kπ GTNN của y là , đạt được khi 2
sin 2x = 1 ⇔ sin2x = 1 ± ⇔ x = ± + ,k ∈ℤ 2 4 2 f) Hàm số 2
y = 2sin x − cos2x = 1− 2 cos2x có tập xác định là D = ℝ . 8
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
Ta có −1 ≤ 1− 2 cos2x ≤ 3 π
Vậy: GTLN của y là 3, đạt được khi cos2x = 1
− ⇔ x = + kπ ,k ∈ℤ 2
GTNN của y là -1, đạt được khi cos2x = 1 ⇔ x = kπ ,k ∈ℤ
Bài 1.8. Tìm giá trị lớn nhất và nhỏ nhất của mỗi hàm số sau: 2
a) y = 3 + sin x cos x b) 2
y = 4 − 2 cos x c) y = 3 + cos x 3 d) y = e) y = − ( 2 1 sin x ) −1 f) y = 4sin x 2 5 − sin x HD Giải 7 π
a) GTLN của y là , đạt được khi x = + kπ ,k ∈ℤ 2 4 5 π
GTNN của y là , đạt được khi x = − + kπ ,k ∈ℤ 2 4 π
b) GTLN của y là 4, đạt được khi x = + kπ ,k ∈ℤ 2
GTNN của y là 2, đạt được khi x = k2π ∨ x = π + k2π ,k ∈ℤ 2 c) Hàm số y =
có tập xác định là D = ℝ . 3 + cos x 1 1 1 1 2
Ta có −1 ≤ cos x ≤ 1 ⇔ 2 ≤ 3 + cos x ≤ 4 ⇔ ≤ ≤ ⇔ ≤ ≤ 1 4 3 + cos x 2 2 3 + cos x
GTLN của y là 1, đạt được khi x = π + k2π ,k ∈ℤ 1
GTNN của y là , đạt được khi x = k2π ,k ∈ℤ 2 3 π
d) GTLN của y là , đạt được khi x = + kπ ,k ∈ℤ 4 2 3
GTNN của y là , đạt đươc khi x = kπ ,k ∈ℤ 5 e) Hàm số y = − ( 2
1 sin x ) −1 có tập xác định là D = ℝ . Với mọi x ∈ 2
ℝ ta luôn có: −1 ≤ 1− sin ( x ) −1≤ 2 −1. Vậy π
GTLN của y là 2 −1, đạt được khi 2 x = − + k2π ,k ≥ 1 2 π GTNN của y là 1 − , đạt được khi 2 x =
+ k2π ,k > 0 2
f) Hàm số y = 4sin x có tập xác định là D = 0;
+∞) . Trên D ta có: −4 ≤ 4sin x ≤ 4 . π
Vậy: GTLN của y là 4, đạt được khi x = + k2π ,k ≥ 0 2 π GTNN của y là 4
− , đạt được khi x = − + k2π ,k ≥ 1 2
Bài 1.9. Tìm giá trị lớn nhất và nhỏ nhất của mỗi hàm số sau: a) 4 4
y = sin x − cos x b) 4 4
y = sin x + cos x c) 2
y = sin x + 2 sin x + 6 d) 4 2
y = cos x + 4 cos x + 5 HD Giải 9
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp a) 4 4 y = x − x = ( 2 2 x − x)( 2 2 sin cos sin cos
sin x + cos x) = −cos2x .
Mặt khác: −1 ≤ cos2x ≤ 1 π
GTLN của y là 1, đạt được khi x = + kπ ,k ∈ℤ 2 GTNN của y là 1
− , đạt được khi x = kπ,k ∈ℤ 1
b) y = sin x + cos x = (sin x + cos x)2 4 4 2 2 2 2 2
− 2sin x cos x = 1− sin 2x . 2 1 1 Mặt khác 2 ≤ 1− sin 2x ≤1 2 2 kπ
GTLN của y là 1, đạt được khi x = ,k ∈ℤ 2 1 π kπ
GTNN của y là , đạt được khi x = + ,k ∈ℤ 2 4 2 c) Ta có y = x + x + = ( x + )2 2 sin 2sin 6 sin
1 + 5 . Mặt khác: ≤ ( x + )2 5 sin 1 + 5 ≤ 9 π
GTLN của y là 9, đạt được khi x = + k2π ,k ∈ℤ 2 π
GTNN của y là 5, đạt được khi x = − + k2π ,k ∈ℤ 2 d) Ta có y = x + x + = ( x + )2 4 2 2 cos 4 cos 5 cos 2 +1. Mặt khác: ≤ ( x + )2 2 5 cos 2 +1≤ 10
GTLN của y là 10, đạt được khi x = kπ ,k ∈ℤ π
GTNN của y là 5, đạt được khi x = + kπ ,k ∈ℤ 2
ạng 4. Chu kì tuần hoàn của hàm số
DĐịnh nghĩa: Hàm số y= f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại một số
T ≠ 0 sao cho với mọi x ∈ D ta có:
i) x −T ∈ D và x + T ∈ D
ii) f (x + T ) = f (x).
Số T dương nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó. Định lí: 2π
1. Hai hàm số y = sin(ax + b) và y = cos(ax + b) với a ≠ 0 là hai hàm số tuần hoàn với chu kì T = . a π
2. Hai hàm số y = tan(ax + b) và y = cot(ax + b) với a ≠ 0 là hai hàm số tuần hoàn với chu kì T = . a 3. Hàm số y = + với T , y , 1 y y2 1 2
T lần lượt là chu kì tuần hoàn của hàm số 1 y . Chu kì tuần hoàn của hàm 2
số y là T = BCNN (T ,T ) . 1 2 MTCT: Nhập hàm số đã cho
Calc cho x = 1 và ghi nhớ kết quả nhận được.
Calc cho x + T so sánh với kết quả nhận được ở trên, đưa ra đáp án đúng. T là chu kì ở
bốn đáp án mà câu trắc nghiệm cho.
C. BÀI TẬP ĐỀ NGHỊ
Bài 1.10. Tìm tập xác định của các hàm số sau tan x 1 3sin x +1 sin x a) y = b) y = c) y = d) y = 1+ tan x 3 cot 2 π π x +1 3 − 3cos x + 1− cos x + 6 4 10
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 1+cos9 sin e) x x tan 2x −1 2 − cot3x y = +cot9x f) y = g) y = h) y = 1+cos9x 2 cos x + 2 1+ sin x +1 1− 1+ sin3x
Bài 1.11. Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau
a) y = 1+ cos2x − 5 π 3 b) y = 4+5cos y = − + x 3x + c) 2 4 2sin 5 d) y = +1 3 2 cot x +1 π f) 2 = − e) y 1 8sin 2x g) y = 9 − 9 sin 9
h) y = sin 2x − 5 y = 1− 3sin x 2x − 3
§2. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
A. KIẾN THỨC CẦN NẮM
1. Phương trình sin x = m (1)
Nếu m > 1: phương trình (1) vô nghiệm
Nếu m ≤ 1 : Nếu α là một nghiệm của phương trình (1), nghĩa là sinα = m x = α + k2π
sin x = m ⇔ ;k ∈ℤ
x = π −α + k2π 0 x = α + k360
Nếu số đo của α được cho bằng độ thì: sin x = m ⇔ ;k ∈ℤ 0 0
x = 180 −α + k360
Nhận thấy, trong một công thức nghiệm của phương trình lượng giác không được dùng đồng thời hai đơn vị độ và radian. Chú ý: π π − ≤ α ≤
i) Nếu số thực α thoả mãn điều kiện: 2
2 thì ta viết α = arcsin m . s inα = m
x = arcsin m + k π 2
Khi đó: sin x = m ⇔ ,k ∈ℤ
x = π − arcsin m + k π 2
ii) Các trường hợp đặc biệt • π
m = −1 , phương trình sin x = −1 có nghiệm là x = − + k π 2 ,k ∈ℤ 2
• m = 0 , phương trình sin x = 0 có nghiệm là x = kπ;k ∈ℤ • π
m =1 , phương trình sin x = 1 có nghiệm là x = + k2π;k ∈ℤ 2
u = v + k π 2
iii) Tổng quát: sin u = sin v ⇔ ,k ∈ℤ
u = π − v + k π 2
2. Phương trình cos x = m (2)
Nếu m > 1: phương trình (2) vô nghiệm
Nếu m ≤ 1 : Nếu α là một nghiệm của phương trình (2), nghĩa là cosα = m x = α + k π 2
cos x = m ⇔ ,k ∈ℤ x = α − + k π 2 x = α + 0 k360
Nếu số đo của α được cho bằng độ thì: cos x = m ⇔ ,k ∈ℤ 0 x = α − + k360 11
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp Chú ý:
i) Nếu α thoả điều kiện 0 ≤ α ≤ π và cosα = m thì ta viết α = arccosm.
Khi đó pt (2) có nghiệm là : x = ± arccosm + k2π;k ∈ℤ
ii) Các trường hợp đặc biệt khi m ∈{0;± } 1 • π
cos x = 0 ⇔ x = + kπ , k ∈ 2 ℤ
• cos x = −1 ⇔ x = π + k2π , k ∈ℤ
• cos x = 1 ⇔ x = k2π , k ∈ℤ
u = v + k π 2
iii) Tổng quát: cosu = cos v ⇔ ,k ∈ℤ
u = −v + k π 2 π
3. Phương trình tan x = m (3) Điều kiện: x ≠ + kπ ,k ∈ℤ 2
• Nếu α là một nghiệm của phương trình (3), nghĩa là tanα = m thì tan x = m ⇔ x = α + kπ;k ∈ℤ
• Nếu số đo của α được cho bằng độ thì 0
tan x = m ⇔ x = α + 1
k 80 ; k ∈ ℤ • π π
Nếu α thảo mãn điều kiện − < α < và tanα = m thì ta viết α = arctanm. Lúc đó nghiệm 2 2
của phương trình (3) là: x = arctan m + kπ ,k ∈ℤ
• Các trường hợp đặc biệt biệt khi m ∈{0;± } 1
tan x = 0 ⇔ x = kπ,k ∈ℤ tan π
x = −1 ⇔ x = −
+ kπ , k ∈ℤ 4 tan π x = 1 ⇔ x = + kπ , k ∈ 4 ℤ
• Tổng quát : tanu = tan v có nghiệm: u = v + π k ,k ∈ ℤ
4. Phương trình cot x = m (4) Điều kiện: x ≠ kπ ,k ∈ℤ
• Nếu α là một nghiệm của phương trình (4), nghĩa là cotα = m thì cot x = m ⇔ x = α + π k ,k ∈ ℤ
• Nếu số đo của α được cho bằng độ thì 0
cot x = m ⇔ x = α + 1
k 80 ; k ∈ ℤ
• Nếu α thảo mãn điều kiện 0 < α < π và cotα = m thì ta viết α = arc cot m . Lúc đó nghiệm của
phương trình (4) là: x = arccot m + kπ ,k ∈ℤ
• Tổng quát : cot u = cot v có nghiệm: u = v + π k ,k ∈ ℤ
Chú ý: Kể từ đây, ta qui ước rằng nếu trong một biểu thức nghiệm của phương trình lương giác có
chứa k mà không giải thích gì thêm thì ta hiểu rằng k nhận mọi giá trị thuộc ℤ
Ghi nhớ công thức nghiệm của phương trình lượng giác cơ bản Với u = (
u x), v = v(x) và ,
u v làm cho biểu thức có nghĩa, k ∈ ℤ
u = v + k2π
u = v + k2π
1/ sin u = sin v ⇔
2 / cosu = cosv ⇔
u = π − v + k2π
u = −v + k2π
3 / tan u = tan v ⇔ u = v + kπ
4 / cot u = cot v ⇔ u = v + kπ B. BÀI TẬP
ạng 1. Giải phương trình lượng giác cơ bản
D- Các công thức nghiệm của bốn phương trình lượng giác cơ bản - Cung đối và cung bù
Bài 2.1. Giải các phương trình sau: 1 3 2 π π a) sin x = b) sin x = − c) sin x =
d) sin 2x − = sin + x 2 2 3 5 5 12
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp x 1 π 1 2x π π 1 e) 0
sin +10 = − f) sin2x + = − g) sin
− = 0 h) sin 9x − = 2 2 6 2 3 3 3 2 HD Giải π a) Ta có: 0 1
sin 30 = = sin . Phương trình đã cho tương đương với: 2 6 π π x = + k2π x = + k2π π 6 6 sin x = sin ⇔ ⇔ , k ∈ ℤ 6 π 5π x = π − + k2π x = + k2π 6 6 π 5π
Vậy phương trình có các nghiệm là: x = + k2π; x =
+ k2π ,k ∈ℤ 6 6 3 π π b) Ta có: −
= −sin = sin − (áp dụng cung đối đưa dấu trừ vào trong _ sin( α − ) = −sinα ) 2 3 3 π x = − + k π 2 π 3
Phương trình đã cho tương đương: ⇔ sin x = sin − ⇔ ,k ∈ℤ 3 π 4 x = + k π 2 3 2 2 2
c) Vì < 1 nên có số α để sinα = ⇒ α = arcsin . Do đó: 3 3 3 2 2
x = arcsin + k2 π x = α + k2π sin 3 x = ⇔ sin x = sinα ⇔ hay ,k ∈ℤ 3
x = π −α + k2π 2
x = π − arcsin + k2π 3 π π π 2 2x − = + x + k π 2 x = + k π 2 π π 5 5 5 d) sin 2x − = sin + x ⇔ ⇔ ,k ∈ℤ 5 5 π π π k π 2 2x −
= π − + x + k π 2 x = + 5 5 3 3 e) 0 0
x = −80 + k720 và 0 0
x = 400 + k720 ; k ∈ ℤ π π
f) x = − + kπ và x = + kπ;k ∈ 6 2 ℤ π k3π g) x = + ;k ∈ℤ 2 2 π k2π 7π k 2π h) x = + ; x = + , k ∈ℤ 18 9 54 9
Bài 2.2. Giải các phương trình sau: 2 1 4 π π a) cos x = b) cos x = − c) cos x =
d) cos3x − = cos + x 2 2 5 6 3 3 3x π 1 3x π π 3 e) cos( 0 3x − 45 ) = f) cos − = − g) cos
− = −1 h) cos 2 − = 2 x 2 4 2 2 6 3 2 HD Giải π x = + k2π 2 π π a) Ta có:
= cos . Phương trình đã cho tương đương với: 4 cos x = cos ⇔ , k ∈ ℤ 2 4 4 π x = − + k2π 4 13
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp π
Vậy phương trình có nghiệm là x = ± + k2π , k ∈ℤ 4 1 π π 2π
b) Ta có: − = − cos = cosπ − = cos
(Áp dụng cung bù_ cos(π −α ) = − cosα ) 2 3 3 3 π 2 π 2
Phương trình đã cho tương đương với: cos x = cos ⇔ x = ± + k π 2 ,k ∈ℤ 3 3 4 4 4
c) Vì < 1 nên có số α để cosα = ⇒ α = arccos . Do đó: 5 5 5 4 4 x arccos k2 = + π x = α + k π 2 cos 5 x =
⇔ cos x = cosα ⇔ hay ,k ∈ℤ 5 x = α − + k π 2 4
x = − arcc os + k π 2 5 π π π 3x − = + x + k π 2 x = + π π π 6 3 k d) 3x − = cos + x ⇔ ⇔ 12 cos ,k ∈ℤ 6 3 π π π 3x −
= − + x + k π 2 x = − + π k 6 3 24 0 0 0 0 0 3 3x 45 30 k360 x 25 1 k 20 e) cos( 0 3x 45 ) cos( 0 3x 45 ) 0 − = + = + − = ⇔ − = cos30 ⇔ ⇔ ,k ∈ℤ 2 3x − 0 45 = − 0 30 + 0 k360 x = 0 5 + 0 1 k 20 3x π π 2 1 π 1 k π 4 − = + k π 2 3x π 1 3x π π x = + 2 f) − = − ⇔ cos − = cos ⇔ 2 4 3 ⇔ 18 3 cos ,k ∈ℤ 2 4 2 2 4 3 3x π π 2 π 5 k π 4 − = − + k π 2 x = − + 2 4 3 18 3 3x π 3x π π 7 g) cos − = −1 ⇔ − = π + k π 2 ⇔ x = + k π 4 ,k ∈ℤ 2 6 2 6 9 3
h) Vì > 1 nên phương trình đã cho vô nghiệm. 2
Bài 2.3. Giải các phương trình sau: 3 π 3 1
a) tan x = 3 b) tan x = −
c) tan − x = tan 2x d) tan ( 0 x −15 ) = e) tan 2x = 3 4 3 2 HD Giải π π
a) tan x = 3 ⇔ tan x = tan
⇔ x = + kπ ,k ∈ℤ 3 3 3 π π b) tan x = −
⇔ tan x = tan − ⇔ x = − + kπ ,k ∈ℤ 3 6 6 π π π π
c) tan − = tan 2 ⇔ − = 2 k x x x
x + kπ ⇔ x = − , k ∈ ℤ 4 4 12 3 3 d) tan ( 0 x −15 ) = ⇔ tan ( 0 x −15 ) 0 0 0 0 0 0
= tan 30 ⇔ x −15 = 30 + 1
k 80 ⇔ x = 45 + 1
k 80 , k ∈ ℤ 3 1 1 1 1 π
e) tan 2 = ⇔ 2 = arctan + π ⇔ = arctan k x x k x + , k ∈ℤ 2 2 2 2 2
Bài 2.4. Giải các phương trình sau: 3 π 3 a) cot x =
b) cot x = − 3 c) cot − x = cot 2x d) ( 0
cot x −15 ) = 3 e) cot 3x = 3 4 5 HD Giải 14
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 3 π π a) cot x =
⇔ cot x = cot ⇔ x = + kπ ,k ∈ℤ 3 3 3 π π
b) cot x = − 3 ⇔ cot x = cot − ⇔ x = − + kπ ,k ∈ℤ 6 6 π π π π
c) cot − = cot 2 ⇔ − = 2 k x x x
x + kπ ⇔ x = − , k ∈ ℤ 4 4 12 3 d) ( 0 x − ) = ⇔ ( 0 x − ) 0 0 0 0 0 0 cot 15 3 cot
15 = cot 30 ⇔ x −15 = 30 + k180 ⇔ x = 45 + 1
k 80 , k ∈ ℤ 3 3 1 3 π
e) cot 3 = ⇔ 3 = arc cot + π ⇔ = arc cot k x x k x + , k ∈ ℤ 5 5 3 5 3
Bài 2.5. Giải các phương trình sau: sin3x 2π a) = 0 b) cot 3x = tan c) (sin x + ) 1 (2cos2x − 2) = 0 cos3x −1 5 π 2π x d) tan 0 0 +12x = − 3 e) sin x +
= cos3x f) tan (2x + 45 )tan180 − = 1 12 3 2 HD Giải
a) Điều kiện : cos3x ≠ 1. Ta có sin3x = 0 ⇔ 3x = kπ . π
Do điều kiện, các giá trị k = 2m,m ∈ℤ bị loại, nên 3x = (2m +1)π ⇔ x = (2m +1) ,m ∈ 3 ℤ π
Vậy nghiệm của phương trình là x = (2m +1) ,m ∈ 3 ℤ π π
b) Nghiệm của phương trình là: x = + k ,k ∈ℤ 30 3 π π
c) Nghiệm của phương trình là: x = − + k2π và x = ± + kπ ,k ∈ 2 8 ℤ 5π kπ
d) Nghiệm của phương trình là: x = − + ,k ∈ℤ 144 12 2π π e) sin x +
= cos3x ⇔ cos3x − cos x +
= 0 . Vậy nghiệm của phương trình: 3 6 π kπ π x = − + ; x = + kπ,k ∈ 24 2 12 ℤ x x
f) Với ĐKXĐ của phương trình, ta có ( 0 x + ) = ( 0 tan 2 45 cot 45 − x) và 0 tan180 − = tan− nên 2 2 ( 0 ) x 0 0 tan 2 45 tan x x 180 1 cot (45 2x) + − = ⇔ − .tan− = 1 2 2 x ⇔ 0 0 0
tan− = tan(45 −2x) ⇔ x = 30 + 1 k 20 ,k ∈ ℤ 2
ạng 2. Tìm nghiệm của phương trình trên một khoảng, đoạn.
D- Giải phương trình và tìm nghiệm thỏa khoảng đề bài cho.
Bài 2.6. Giải các phương trình sau trong khoảng đã cho: 1 3
a) sin 2x = − với 0 < x < π b) cos(x − 5) = với π − < x < π 2 2 1 π c) ( 0 tan 2 0 0
x −15 ) =1 với −180 < x < 90 d) cot 3x = −
với − < x < 0 3 2 HD Giải 15
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 2 π π x = − + k2 1 π x = − + kπ a) 6 12 sin 2x = − ⇔ ⇔ ,k ∈ℤ 2 7π 7 2 π x = + k2π x = + kπ 6 12
Xét điều kiện 0 < x < π , ta có π 1 1 11 • π 0 < − + kπ < π ⇔ < k <
+1⇒ k = 1 ( Do k ∈ℤ ). Vì vậy : x = 12 12 12 12 7 7 • π π 0 <
+ kπ < π ⇒ k = 0 . Vì vậy: x = 12 12 11π 7π Vậy: x = và x = 12 12 π π x − 5 = + k2π x = + 5 + k2 3 π 6 6 b) cos(x − 5) = ⇔ ⇔ ,k ∈ℤ 2 π π x − 5 = − + k2π x = − + 5+ k2π 6 6 Xét điều kiện π
− < x < π , ta có: 11 • π π π
− < + 5+ k2π < π ⇒ k = −1. Do vậy, có x = 5− 6 6 13 • π π π
− < − + 5+ k2π < π ⇒ k = −1. Do vậy, có x = 5− 6 6 11π 13π Vậy: x = 5 − và x = 5 − 6 6 c) ( 0 x − ) 0 0 0 0 0 tan 2
15 = 1 ⇔ 2x =15 + 45 + 1
k 80 ⇔ x = 30 + k90 ,k ∈ ℤ Xét điều kiện 0 0
−180 < x < 90 , ta có 1 • 0 0 0 0
−180 < 30 + k90 < 90 ⇔ 2
− < + k <1 ⇔ k ∈{−2,−1, } 0 3
Vậy các nghiệm của phương trình là: 0 0 x = 1 − 50 , x = −60 và 0 x = 30 1 π kπ π d) cot 3x = − ⇔ x = − +
,k ∈ℤ . Xét điều kiện − < x < 0 , ta có: 3 9 3 2 • π π π k − < − +
< 0 ⇔ k ∈{−1; } 0 2 9 3 4π π
Vậy các nghiệm của phương trình là: x = − và x = − 9 9
Bài 2.7. Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 400 bắc trong một ngày thứ t của một π
năm không nhuận được cho bởi hàm số: d(t) = 3sin
(t − 80) +12 với t ∈ℤ và 0 < t < 365. 182
a) Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm ?
b) Vào ngày nào trong năm thì thành phố A có it giờ có ánh sáng mặt trời nhất ?
c) Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất ? HD Giải π
a) Ta phải giải phương trình: 3sin
(t − 80) +12 =12 với t ∈ℤ và 0 < t < 365. 182 π π
Phương trình dẫn đến sin (t −80) = 0 ⇔
(t −80) = kπ ⇔ t =182k + 80,(k ∈ℤ) 182 182
Mặt khác 0 < 182k + 80 < 365 ⇔ k ∈{0; } 1 16
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
Vậy thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 80 ( ứng với k = 0) và ngày thứ 262(
ứng với k = 1) trong năm.
b) Do sin x ≥ −1 với mọi x, nên thành phố A có ít giờ có ánh sáng mặt trời nhất khi và chỉ khi: π sin
(t −80) = −1 với t ∈ℤ và 0 < t < 365. Từ đó suy ra t = 364k −11,k ∈ℤ 182
Mặt khác: 0 < 364k −11 < 365 ⇔ k = 1
Vậy: Thành phố A có ít giờ ánh sáng mặt trời nhất (9 giờ) vào ngày thứ 353 trong năm. π
a) Tương tự, ta giải phương trình sin
(t −80) =1 với t ∈ℤ và 0 < t < 365. 182
Vậy: Thành phố A có nhiếu giờ ánh sáng mặt trời nhất (15 giờ) vào ngày thứ 171 trong năm.
C. BÀI TẬP ĐỀ NGHỊ
Bài 2.7. Giải các phương trình sau: 2 π 2x π 1 1. sin ( 0 2x − 30 ) = − 2. sin 3x + = 1 − 3. sin − = 2 6 3 4 2 2 π π 4. sin 3 2 π 3 x =
5. sin 2x − = sin − 3x − = − 3 6. sin 2x 4 3 6 2 1 π 7. cos( 0 60 − 3 x 2 x) = − 8. 0 1 cos +10 = − 9. cos 2x − = 1 2 2 2 3 π 3 π 0 10. ( cos 4x +125 = 1 − x − ) 3 cos 2 5 = 11. cos3x − = cos x + 12. ( ) 4 4 3 13. ( 0 tan 2x + 60 ) = − 3 π 3 3 14. cot 0 5x − = − 15. cos(3x −135 ) = 9 3 2 π
17. sin(9o − 9x) = 0 π 2 16. cot 2x − = −2
18. sin 3x − = − 3 3 2
Bài 2.8. Giải các phương trình sau: 3 3 π 3 π π 1. sin x =
với 0 ≤ x ≤ 2π 2. cos x =
với 0 ≤ x ≤ 2π 3. cos x + = với − ≤ x ≤ 2 2 3 2 2 2 π 0 π 1 4. −2cos
5. 2cos(45 − x) + 2 = 0 x + + 3 = 0
6. sin x + = với π − ≤ x ≤ π 3 với 0 0 2 2 x ∈ 1 80 ;340 π π với − ≤ x ≤ 2 2 π 3 7π π 7. 3 3 + cos x + = với
−x=0,x∈ ;30 8. 3 sin 5 3 0
9. 2 sin 3x + +1 = 0 trên đoạn 4 4 x ∈(−90 ; ° 180°] 6 [−2π;π ]
Bài 2.9. Giải các phương trình sau:
1. sin 3x − cos5x = 0
2. tan 3x.tan x = 1 cos3x 3. = 0 sin3x −1
4. sin 3x + sin 5x = 0
5. cot 2x.cot 3x = 1 π
6. sin 2x.tan x − = 0 4 π
8. cos(50° + 4x) + sin 3x = 0 9. sin 5x + cos x = 0
7. cot 9x = − tan + 9x 9 17
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
§3. MỘT SỐ DẠNG PHƯƠNG TRÌNH LƯỢNG GIÁC ĐƠN GIẢN THƯỜNG GẶP
A. KIẾN THỨC CẦN NẮM Phương trình Cách giải
Đặt ẩn phụ t = f (x) và đặt điều kiện cho ẩn phụ
(nếu có) rồi giải phương trình theo ẩn phụ này và
1. Phương trình bậc nhất, bậc hai đối với một
từ đó suy ngược lại nghiệm x.
hàm số lượng giác, trong đó f (x) là một biểu
Khi đặt t = sinx hay t = cosx, điều kiện là t ≤ 1
thức lượng giác nào đó.
Khi đặt t = tanx, t = cotx, cần lưu ý điều kiện xác
định của tanx và cotx.
Thực hiện các bước sau: B1: Kiểm tra
2. Phương trình bậc nhất đối với sinx và cosx có • Nếu 2 2 2
a + b < c thì phương trình (2) vô dạng: 2 2
a sin x + b cos x = ,
c (a + b ≠ 0) ( 2 ) nghiệm • Nếu 2 2 2
a + b ≥ c , ta thực hiện tiếp B2
B2. Chia hai vế phương trình (2) cho 2 2 a + b .
Từ đó áp dụng công thức cộng đưa phương trình
(2) về phương trình lượng giác cơ bản dạng:
sin u = sin v hay cosu = cosv .
Cách 1. Thực hiện các bước sau π
B1. Xét cos x = 0 ⇔ x = + kπ ( nghĩa là 2
3. Phương trình thuần nhất bậc hai đối với sinx sin x = 1
± ) có phải là nghiệm của phương trình và cosx , có dạng: (3) hay không ? 2 2
a sin x + bsin x cos x + c cos x = 0 (3) π 2 2 2 (
B2. Xét cos x ≠ 0 ⇔ x ≠ + kπ , chia hai vế
a + b + c ≠ 0) 2 phương trình cho 2
cos x ta sẽ có được phương
trình bậc hai theo một hàm số lượng giác tanx Cách 2.
Áp dụng công thức hạ bậc, ta đưa phương trình
(3) về dạng phương trình bậc nhất đối với sin 2x và cos2x . Phương trình dạng Viết 2 2
d = d(sin x + cos x) rồi đưa về dạng 2 2
a sin x + bsin x cos x + c cos x = d (4)
phương trình thuần nhất bậc hai đối với sinx và 2 2 2
(a + b + c ≠ 0)
cosx ( đưa về dạng phương trình (3) ) B. BÀI TẬP
ạng 1. Giải phương trình bậc nhất đối với một hàm số lượng giác
- Phương trình dạng at + b = 0, a ≠ 0
D- Một số phương trình biến đổi đưa về phương trình bậc nhất
- Từ phương trình đã cho đưa về phương trình lượng giác cơ bản và giải
Bài 3.1. Giải các phương trình sau: π a) ( x− 0 2 cos 3 60 )+1= 0
b) 2sin 2x − + 3 = 0 6 x π c) 0 3 tan + 20 +1 = 0
d) 3 cot x − + 3 = 0 4 3 HD Giải 18
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 1 a) 2 cos(3x − 0
60 )+1= 0 ⇔ cos(3x − 0
60 ) = − ⇔ cos(3x − 0 60 ) = 0 cos120 2 0 0 0 0 0
3x − 60 =120 + k360 x = 90 + 1 k 20 ⇔ ⇔ , k ∈ ℤ 0 0 0 0 0 3x − 60 = 1 − 20 + k360 x = 20 + 1 k 20 π π 3 π π
b) 2sin 2x − + 3 = 0 ⇔ sin 2x − = −
⇔ sin2x − = sin − 6 6 2 6 3 π π π 2x − = − + k2π x = − + kπ 6 3 12 ⇔ ⇔ , k ∈ ℤ π π 3π 2x − = π + + k2π x = + kπ 6 3 4 x x 1 x c) 0 0 3 tan 0 0
+ 20 +1 = 0 ⇔ tan + 20 = −
⇔ tan + 20 = tan(−30 ) 4 4 3 4 x ⇔ + 0 = − 0 + 0 k ⇔ x = − 0 + 0 20 30 180 200 k720 ,k ∈ ℤ 4 π π π π
d) 3 cot x − + 3 = 0 ⇔ cot x − = − 3 ⇔ cot x − = cot − 3 3 3 6 π π π ⇔ x − = − + π k ⇔ x = + π k , k ∈ ℤ 3 6 6
Bài 3.2. Giải các phương trình sau: a) 3 tan 2x + 3 = 0 b) ( 0 x + ) 2 0 cos 30 + 2 cos 15 = 1 c) 2 cos x − 3 = 0
d) 8cos2x sin 2x cos 4x = 2 HD Giải π π kπ
a) 3 tan 2x + 3 = 0 ⇔ tan 2x = − 3 ⇔ tan 2x = tan − ⇔ x = − + 3 6 2 π kπ
(lưu ý ĐK: cos2x ≠ 0 ). Vậy, nghiệm của phương trình là: x = − + ,k ∈ℤ 6 2 b) ( 0 x + ) 2 0 + = ⇔ ( 0 x + ) 2 0 = − ⇔ ( 0 x + ) 0 cos 30 2 cos 15 1 cos 30 1 2 cos 15 cos 30 = −cos30 cos( = + ⇔ x + 30 ) 0 0 x 120 k360 0 0 = cos150 ⇔ ;k ∈ℤ 0 0 x = 1 − 80 + k360
Vậy, nghiệm của phương trình là: 0 0
x = 120 + k360 và 0 0 x = 1
− 80 + k360 , k ∈ℤ 3 π
c) 2 cos x − 3 = 0 ⇔ cos x =
⇔ x = ± + k2π 2 6 π kπ 2 x = + 32 4
d) 8cos2x sin 2x cos 4x = 2 ⇔ sin 8x = ⇔ ,k ∈ℤ 2 3π kπ x = + 32 4 π kπ 3π kπ
Vậy, nghiệm của phương trình là x = + và x = + , k ∈ 32 4 32 4 ℤ
Bài 3.3. Giải các phương trình sau:
a) cos2x – sinx – 1 = 0
b) cosx.cos2x = 1 + sin2x.sinx
c) 4sin x cos x cos2x = −1 d) tanx = 3cotx HD Giải a) x − x − = ⇔ − 2 cos2 sin 1 0
1 2sin x −sin x −1 = 0 19
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp x = π k sin x = 0 π
⇔ sin x(2sin x +1) = 0 ⇔
1 ⇔ x = − + k π 2 ,k ∈ ℤ sin x = 6 2 π 7 x = + k π 2 6 π 7π
Vậy, phương trình có các nghiệm là x = kπ , x = − + k2π và x =
+ k2π với k ∈ℤ 6 6
b) cos x cos2x = 1+ sin x sin 2x ⇔ cos x cos2x − sin x sin 2x = 1 k2 k2 cos3 π ⇔ π x = 1 ⇔ x = ,k ∈ x = ,k ∈ 3
ℤ . Vậy, phương trình có nghiệm là 3 ℤ π kπ
c) 4sin x cos x cos2x = 1 − ⇔ sin 4x = 1 − ⇔ x = − + ,k ∈ℤ 8 2 π k
d) tan x = 3cot x . Điều kiện sin 2x ≠ 0 ⇔ x ≠ ,k ∈ℤ 2 3 π Ta có 2 tan x =
⇔ tan x = 3 ⇔ tan x = ± 3 ⇔ x = ± + kπ ,k ∈ℤ tan x 3 π
So với điều kiện, phương trình có nghiệm là x = ± + kπ ,k ∈ 3 ℤ
ạng 2. Giải phương trình bậc hai đối với một hàm số lượng giác - Phương trình dạng 2 D
at + bt + c = 0, a ≠ 0
- Một số phương trình biến đổi đưa về phương trình bậc hai
- Từ phương trình đã cho đưa về phương trình lượng giác cơ bản và giải
- Lưu ý điều kiện của bài toán (nếu có)
Bài 3.4. Giải các phương trình sau: a) 2
2sin x + 5sin x −3 = 0 b) 2
cot 3x − cot3x − 2 = 0 c) 2
4 cos x − 2(1+ 2)cosx + 2 = 0
d) 5tan x − 2 cot x − 3 = 0 HD Giải 1
a) Đặt sinx = t ( với t ≤ 1(*)), ta được phương trình 2
2t + 5t −3 = 0 ⇔ t = ,t = 3 − (không thỏa (*)) 1 2 2 π x = + k π 2 1 1 Với: t = ⇒ x = ⇔ 6 sin ,k ∈ℤ . 2 2 π 5 x = + k π 2 6 π 5π
Vậy, phương trình đã cho có các nghiệm là: x = + k2π và x = + k2π , k ∈ 6 6 ℤ
b) Điều kiện: sin 3x ≠ 0(*) Đặt t = cot3x, ta được phương trình 2
t − t − 2 = 0 ⇔ t = −1,t = 2 π π k
Với t = −1⇒ cot 3x = −1 ⇔ x = + ,k ∈ℤ 4 3 1 π k
Với t = 2 ⇒ cot 3x = 2 ⇔ x = arc cot 2 +
,k ∈ℤ , k ∈ℤ 3 3 π kπ 1 kπ
So với (*),vậy phương trình đã cho cáo các nghiệm x = +
và x = arc cot 2 + , k ∈ 4 3 3 3 ℤ 1 2 c) Đặt 2
t = cosx, ( với t ≤ 1), ta được phương trình 4t − 2 (1+ 2)t + 2 = 0 ⇔ t = ,t = 1 2 2 2 20
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 1 cos π x = x = ± + k2 2 π Do đó: 2 x ( ) 3 4 cos 2 1 2 cos x 2 0 − + + = ⇔ ⇔ , k ∈ℤ 2 π cos x = x = ± + k2π 2 4 π π
Vậy, phương trình đã cho có các nghiệm là x = ± + k2π và x = ± + k2π , k ∈ℤ 3 4
d) Điều kiện sin 2x ≠ 0, khi đó ta có tan x ≠ 0 1 2
5tan x − 2cot x − 3 = 0 ⇔ 5tan x − 2
− 3 = 0 ⇔ 5tan x − 3tan x − 2 = 0 tan x π tan x = 1 x = + kπ 4 2 ⇔ ⇔ , k ∈ ℤ tan x 2 = − x = arctan 5 − + kπ 5 π 2
So với ĐK, phương trình đã cho có các nghiệm x =
+ kπ và x = arctan − + kπ , k ∈ℤ 4 5
Bài 3.5. Giải các phương trình sau: a) 2
2 cos x − 3cos x +1= 0 b) 2
cos x + sin x +1 = 0 c) 2
3 tan x − (1+ 3)tan x +1= 0 d) ( 0 x + )− ( 0 cos 4 60 5cos 2x + 30 )+ 4 = 0 HD Giải π
a) Phương trình đã cho có các nghiệm là x = k2π và x = ± + k2π , k ∈ 3 ℤ π
b) Phương trình đã cho có nghiệm là x = − + k2π , k ∈ℤ 2 π π
c) Phương trình đã cho có các nghiệm là x = + kπ và x = + kπ , k ∈ 4 6 ℤ d) ( 0 x + )− ( 0 x + ) 2 + = ⇔ ( 0 x + )− ( 0 cos 4 60 5cos 2 30 4 0 2 cos 2 30 5cos 2x + 30 )+3 = 0 cos ( 0 2x + 30 ) =1 0 0 0 0 ⇔ ⇔ x + = k ⇔ x = − + k , k ∈ℤ cos ( 2 30 360 15 180 3 0 2x + 30 ) = 2
ạng 3. Phương trình bậc nhất đối với sin và cos
- Phương trình có dạng 2 2
a sin x + b cos x = c,(a + b ≠ 0) D- B1: Kiểm tra • Nếu 2 2 2
a + b < c thì phương trình vô nghiệm • Nếu 2 2 2
a + b ≥ c , ta thực hiện tiếp B2
- B2. Chia hai vế phương trình cho 2 2
a + b . Từ đó áp dụng công thức cộng đưa phương trình về phương
trình lượng giác cơ bản dạng: sin u = sin v hay cosu = cos v .
Bài 3.6. Giải các phương trình sau:
a) 3 sin x − cos x = 1
b) 2sin3x + 5 cos3x = 3 −
c) 3cos x + 4sin x = −5 1 d) 2
5sin 2x − 6cos x =13
e) 2sin 2x − 2 cos2x = 2 f) 2
sin 2x + sin x = 2 HD Giải π π 1 π x = + k2π
a) 3 sin x − cos x = 1 ⇔ 2sin x − = 1 ⇔ sin x − = ⇔ 3 , k ∈ℤ 6 6 2
x = π + k2π 21
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 2 5
b) 2sin 3x + 5 cos3x = 3 − ⇔ 3 sin3x + cos3x = −3 ⇔ 3 . Trong
(sinα sin3x+cosα cos3x) = −3 3 3 2 5 α +π kπ đó sinα = ;cosα =
. Dó đó: cos(3x −α ) = −1⇔ x = + , k ∈ 3 3 ℤ 3 3 3 4
c) x = π +α + k2π , k ∈ℤ trong đó α là số thoả mãn cosα = và sinα = 5 5 d) 2
5sin 2x − 6cos x = 13 ⇔ 5sin2x −3cos2x =16, phương trình vô nghiệm. 5π 13π e) x = + kπ và x = + kπ , k ∈ 24 24 ℤ 1 1 1 1 f) 2
sin 2x + sin x = ⇔ 2sin2x − cos2x = 0 , với cos2x ≠ 0 , ta có tan 2x = ⇔ x = arctan + kπ , 2 2 2 2 k ∈ ℤ
Bài 3.7. Giải các phương trình sau: 1 1 2
a) sin x = 2 sin 5x − cos x b) + =
sin 2x cos2x sin 4x
c) sin 5x + 3 cos5x = 2sin 7x
d) 3 cos5x − 2 cos3x + sin 5x = 0 HD Giải
a)sin x = 2 sin 5x − cos x ⇔ sin x + cos x = 2 sin 5x π kπ x π = + 16 2 ⇔ sin x + = sin5x ⇔ ;k ∈ℤ 4 π kπ x = + 8 3
b) ĐKXĐ: sin 4x ≠ 0 , 1 1 2 x = kπ ta có: sin 2x cos2x 1 + = ⇔ + = ⇔ , k ∈ℤ sin 2 π x cos2x sin 4x x = + kπ 4
Cả hai nghiệm đều không thoả điều kiện bài toán. Vậy, phương trình đã cho vô nghiệm. π x = + kπ π c) 16
sin 5x + 3 cos5x = 2sin 7x ⇔ sin 5x + = sin 7x ⇔ ;k ∈ℤ 3 π kπ x = + 18 6
d) 3 cos 5x − 2 cos3x + sin 5x = 0 ⇔ 3 cos5x + sin 5x = 2 cos3x π x = + kπ π 12 ⇔ cos 5x − = cos3x ⇔ ,k ∈ℤ 6 π kπ x = + 48 4
Bài 3.8. Giải các phương trình sau: 9
a) 4sin x − 3cos x = 5
b) 3cos x + 2 3 sin x = 2
c) 3sin 2x + 2 cos2x = 3
d) 2sin 2x + 3cos2x = 13 sin14x HD Giải π 3 4
a) x = α + + k2π , k ∈ sinα = ;cosα = 2 ℤ với α thoả mãn 5 5 22
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 3 2 3 9
b) x = α ± β + k2π , k ∈ℤ trong đó cosα = ,sinα = và cos β = 21 21 2 21 π π 3 2 c) x =
−α + kπ , x = + kπ , k ∈ℤ trong đó cosα = ,sinα = 2 4 13 13 α kπ π −α kπ 2 3 d) x = + , x = +
, k ∈ℤ trong đó cosα = ,sinα = 12 6 16 8 13 13
Bài 3.9. Giải các phương trình sau:
a) sin 2x sin 5x = sin3x sin 4x
b) cos x sin 5x = cos2x cos4x
c) cos5x sin 4x = cos3x sin 2x
d) sin 2x + sin 4x = sin 6x HD Giải 1 1
a) sin 2x sin 5x = sin3x sin 4x ⇔ (cos3x − cos7x) = (cos x − cos7x) 2 2 x = kπ ⇔ cos3 = cos kπ x x ⇔ ⇔ x = ,k kπ ∈ ℤ x = 2 2 x = kπ kπ
b) cos x sin 5x = cos2x cos4x ⇔ cos 4x = cos2x ⇔ ⇔ x kπ = , k ∈ ℤ x = 3 3 kπ π kπ
c) Phương trình đã cho có các nghiệm là x = và x = + , k ∈ℤ 2 14 7
d) sin 2x + sin 4x = sin 6x ⇔ 2 sin 3x cos x = 2sin 3x cos3x kπ x = 3 kπ = sin3 = 0 x x 3 ⇔ sin3
x(cos x − cos3x) = 0 ⇔
⇔ x = kπ ⇔ ,k ∈ℤ cos x = cos3x kπ kπ x = x = 2 2
Bài 3.10. Giải các phương trình sau:
a) sin x sin 7x = sin3x sin 5x
b) sin 5x cos3x = sin 9x cos 7x
c) cos x cos3x − sin 2x sin 6x − sin 4x sin 6x = 0
d) sin 4x sin 5 + sin 4x sin3x − sin 2x sin x = 0 HD Giải 1 1
a) sin x sin 7x = sin3x sin 5x ⇔ (cos6x − cos8x) = (cos2x − cos8x) ⇔ cos6x = cos2x 2 2 kπ
Vậy, nghiệm của phương trình đã cho là x = , k ∈ℤ 4 1 1
b) sin 5x cos3x = sin 9x cos 7x ⇔ (sin8x + sin2x) = (sin16x + sin2x) ⇔ sin8x = sin16x 2 2 kπ π kπ
Vậy, nghiệm phương trình đã cho là x = và x = + , k ∈ℤ 4 24 12
c) cos x cos3x − sin 2x sin 6x − sin 4x sin 6x = 0 1
⇔ (cos4x + cos2x − cos4x + cos8x − cos2x + cos10x) = 0 2 π π kπ
Vậy, nghiệm của phương trình đã cho là x = + kπ và x = + , k ∈ℤ 2 18 9
d) sin 4x sin 5 + sin 4x sin3x − sin 2x sin x = 0 1
⇔ sin 4x sin 5+ (cos x − cos7x + cos3x − cos x) = 0 2 23
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
⇔ sin 4x sin5x + sin5x sin 2x = 0 ⇔ sin5x(sin 4x + sin2x) = 0 kπ kπ π
Vậy, phương trình đã cho có các nghiệm x = , x =
và x = ± + k2π , k ∈ℤ 2 5 3
Bài 3.11. Giải các phương trình sau: 3 a) 2 2 2
sin x + sin 2x + sin 3x = b) 2 2 2 2
sin 3x + sin 4x = sin 5x + sin 6x 2 3 c) 2 2 2 2
cos x + cos 2x + cos 3x + cos 4x = 2 d) 2 2 2
cos 3x + cos 4x + cos 5x = 2 e) 4
8cos x = 1+ cos4x f) 2 2 2
3cos 2x −3sin x + cos x = 0 HD Giải 3 1 a) Ta có 2 2 2
sin x + sin 2x + sin 3x = − (cos2x + cos4x + cos6x). Do đó phương trình đã cho tương 2 2
đương với cos2x + cos 4x + cos6x = 0 ⇔ cos4x + 2 cos4x cos2x = 0 ⇔ cos 4x(1+ 2 cos2) = 0 π kπ π
Vậy, phương trình đã cho có các nghiệm x = +
và x = ± + kπ , k ∈ 8 4 3 ℤ
b) Dùng công thức hạ bậc, rút gọn ta được:
cos6x + cos8x = cos10x + cos12x ⇔ 2 cos7x cos x = 2cos11x cos x kπ kπ
Vậy, phương trình đã cho có các nghiệm x = , x = , k ∈ℤ 2 9 π π kπ π kπ
c) Phương trình đã cho có các nghiệm x = + kπ , x = + và x = + , k ∈ 2 4 2 10 5 ℤ π kπ π
d) Phương trình đã cho có các nghiệm x = +
và x = ± + kπ , k ∈ℤ 16 8 3 e) Sử dụng công thức 2
2 cos x =1+ cos2x và 2
1+ cos4x = 2cos 2x để biến đổi đưa về phương trình bậc π
hai đối cos2x. Vậy, phương trình đã cho có nghiệm x = ± + kπ , k ∈ℤ 3 π 1
f) Phương trình đã cho có các nghiệm x = + kπ và x = α ± + kπ , k ∈ cos2α = 2 ℤ , trong đó 3
Bài 3.12. Giải các phương trình sau:
a) 1+ sin x − cos x − sin 2x + 2 cos2x = 0
b) cos x tan3x = sin 5x 1 1 3 1 c) 2 sin x − = sin x − d) + = 8sin x 2 sin x sin x cos x sin x HD Giải a) Ta có: 2 − x = x − x x = ( 2 2 1 sin 2 (sin cos ) ;2 cos2
2 cos x − sin x) = −2(sin x −cosx)(sin x + cosx)
1+ sin x − cos x − sin2x + 2cos2x = 0 ⇔ (sin x − cos x)(1− sin x −3cos x) = 0 sin x = cos x ⇔
3cos x + sin x = 1 π 1
Vậy, phương trình đã cho có các nghiệm x = + kπ và x = α ± arccos
+ k2π , k ∈ℤ 4 10 3 1 Trong đó cosα = ,sinα = 10 10
b) Điều kiện cos3x ≠ 0 24
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
cos x tan3x = sin5x ⇔ cos x sin3x = cos3x sin5x kπ 1 x = ⇔ ( , k ∈ℤ x + x ) 1 = ( x + x ) 2 sin 4 sin 2 sin8
sin 2 ⇔ sin8x = sin 4x ⇔ 2 2 π kπ x = + 12 6 kπ π kπ
So với điều kiện, nghịêm của phương trình đã cho: x = và x = + , k ∈ℤ 2 12 6
c) Điều kiện sin x ≠ 0 1 1 1 1 2 sin x − = sin x − ⇔ ( 2
sin x − sin x + − = 0 2 ) 2 sin x sin x sin x sin x 1− sin sin x = 1 π ⇔ sin (1− sin ) x x x + = 0 ⇔ (1− sin x)( 3 sin x + )1 = 0 ⇔
⇔ x = ± + k2π , k ∈ℤ 2 sin x sin x = 1 − 2 π
So với điều kiện, nghiệm của phương trình đã cho: x = ± + k2π , k ∈ℤ 2
d) Điều kiện sin 2x ≠ 0 3 1 1 cos2 2 − +
= 8sin ⇔ 3 sin + cos = 8sin cos ⇔ 3 sin + cos = 8. x x x x x x x x cos x cos x sin x 2
⇔ 3 sin x + cos x = 4cos x − 4cos2x cos x ⇔ 3 sin x − 3cos x = −2(cos x + cos3x) 1 3 π
⇔ cos x − 3 sin x = 2cos3x ⇔ cos3x = cos x −
sin x ⇔ cos3x = cos x + 2 2 3 π x = + kπ 6 ⇔
;k ∈ℤ ( thoả điều kiện sin2x ≠ 0) π kπ x = − + 12 2
ạng 4. Phương trình bậc nhất bậc hai đối với sin và cos
- Nắm phương pháp giải
D- Kiểm tra điều kiện của phương trình.
Bài 3.13. Giải các phương trình sau: a) 2 2
4sin x − 5sin x cos x − 6cos x = 0 b) 2 2
sin x − 3 sin x cos x + 2cos x =1 c) 2 2
2sin x + 3 3 sin x cos x − cos x = 4 d) 2 x + x + ( − ) 2 3sin 4sin 2 8 3 9 cos x = 0 HD Giải a) 2 2
4sin x − 5sin x cos x − 6cos x = 0 . Khi cos x = 0 thì sin x = 1
± , vế trái bằng 4, còn vế phải bằng 0.
Nên cosx = 0 không phải là nghiệm của phương trình.. Với cos x ≠ 0, chia hai vế phương trình cho tan x = 2
x = arctan 2 + kπ 2 cos x , ta được: 2
4 tan x − 5tan x − 6 = 0 3 ⇔ 3 , k ∈ ℤ tan x = −
x = arctan − + kπ 4 4 2 2 2 2 2 2
b) sin x − 3 sin x cos x + 2 cos x = 1 ⇔ sin x − 3 sin x cos x + 2 cos x = sin x + cos x 2
⇔ − 3 sin x cos x + cos x = 0 ⇔ cos x (− 3sin x +cosx) = 0 π x = + kπ ⇔ 2 ,k ∈ℤ π x = + kπ 6
c) Phương trình vô nghiệm 25
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp π 8
d) Phương trình đã cho có nghiệm là x = − + kπ và x = arctan − + 3 + kπ , k ∈ℤ 3 3
Bài 3.14. Giải các phương trình sau: 1 a) 2 2
sin x + sin2x − 2 cos x = b)
2 x + ( + ) x x +( − ) 2 2sin 3 3 sin cos 3 1 cos x = 1 − 2 c) 2 2
3sin 2x − sin2x cos2x − 4 cos 2x = 2 d) 2 2
3sin x −sin2x − cos x = 0 HD Giải π
a) Phương trình đã cho có các nghịêm là x =
+ kπ và x = arctan( 5
− )+ kπ , k ∈ℤ 4 π π
b) Phương trình đã cho có các nghịêm là x = − + kπ và x = − + kπ , k ∈ℤ 4 6 1 kπ 1 kπ
c) Phương trình đã cho có các nghiệm là x = arctan (−2) + và x = arctan 3 + , k ∈ℤ 2 2 2 2 π 1
d) Phương trình đã cho có các nghịêm là x = + kπ và x = arctan − + kπ , k ∈ℤ 4 3
C. BÀI TẬP ĐỀ NGHỊ
Bài 3.13. Giải các phương trình sau 1. 3 cot 2x + 3 = 0 π 2. tan x + x = +12x + 3 = 0 3. 2sin 3 2 sin 6 0 12 4. ( 0
2sin 3x −120 ) + 3 = 0 0 5. 2 cos x π 3 tan 3x − 45 +1 = 0 + −1 = 0 6. ( ) 2 5
Bài 3.14. Giải các phương trình sau 1. 2
2 cos x −3cos x = 1 − 2. 2
4sin 4x + 3sin 4x −1 = 0 3. 2 6sin 2x ( − 8+3 )3sin2x+4 3=0 π π π π 6. 2 − − = 4. 2
2 cos 4x 7 cos 4x 4 0 2cos 2x− c − os2x− 3 − =0 5. 2
2sin x− −3sinx− +2=0 3 3 4 4 7. 2
2sin 4x + 9sin 4x − 5 = 0 π π 2 8. 2 tan
3tan x − 1+ 3 tan x+1= 0
x + −4tan x + +3 = 0 9. ( ) 3 3 10. 2
4cos x−2(1+ 2)cosx+ 2 =0 11. 2
2sin x + 7 sin x − 4 = 0 12. 2
3cos 2x − 7 cos 2x + 4 = 0
Bài 3.15. Giải các phương trình sau
1. cos2x + 2 sin x −1 = 0
2. cos x = 2 sin 7x − sin x
3. 3 cos5x + sin 5x = 2 cos3x 4. ( 0 x+ )− ( 0 2sin 10 12cos x 1 + 0 ) =3 5. 2 2 3cos8x 2 − sin4 c x os4x= s − in x c − os x x x 6. 3sin − 3 cos = − 3 2 2 7. 3
4cos x + 3 2 sin 2x = 8cos x 8. 3 3 sin x x − x = − − 3cos x = 3 2 9. 3 sin 7 cos 7 2 2 2
10. 3 cos 5x − sin 5x = 2 π π π π
11. 3sin −2x− 3cos −2x= 6 12. 6cos 3 − x+ 2sin 3 − x= 2 − 3 3 6 6
13. 3 sin 2x − cos 2x = 3
14. sin 2x − 3 cos 2x = 3
15. 3 sin 4x − cos 4x = − 3
Bài 3.16. Giải các phương trình sau 1. ( 2 + )x x ( 2 1 sin
cos + 1+cos )xsinx
3. cos3x + 2cos 2x = cos x + 2 3 2 3 sinx c + os x 3 − sin c x osx 4 − sin x 2. 1 = =0 1+2sinxcosx 2sinx 1 − 26
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
(2cos x − )1sin 4x 1 1
cos x(cos x + sin x) −1 4. = 2sin 2x 5. 2 sin4x + cos x = 6. = 0 cos 2 x − sin x 2 2 cos x − cos x
7. 2sin 2x + 2 cos x = 0 2
sin2x+4sin x+2sin ( x 1 c − os ) 9. 2 5sin8x−2sin .
x sin3x−2sin x 1 + =0 8. x =0 2cosx− 3 3 12. cos3 2 + sin2 .cos 8 − sin2 c − os s + in x x x x x x 2 2 2 9
cos 2x+6sin x−cos x− 10. 2 1 = 2 2 4sin6x−8sin5 .
x cos x −2cos x +1= 0 3 11. =0 sin x cos3x 1 + 2 13. 2 2 2 2
cos 3x+cos 5x=sin 4x s + in 6x (cosx s − in )x(1 s + in2 )x c − osx s − in (sinx c − os )x(1 s + in2 ) x c + osx s + in 14. x 0 = 15. x 0 = tanx 1 + cotx 1 + 27
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp ÔN TẬP CHƯƠNG I
I. Hàm số lượng giác: Cần nắm các dạng toán cơ bản
1. Tập xác định của hàm số lượng giác
2. Tập giá trị: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3. Xét tính chẵn lẻ của hàm số
4. Xét sự đồng biến, nghịc biến của hàm số 5. Chu kì tuần hoàn
II. Phương trình lượng giác
1. Phương trình lượng giác cơ bản
- Nắm được cách giải từng phương trình cụ thể Với u = (
u x), v = v(x) và ,
u v làm cho biểu thức có nghĩa, k ∈ ℤ
u = v + k2π
u = v + k2π
1/ sin u = sin v ⇔
2 / cosu = cosv ⇔
u = π − v + k2π
u = −v + k2π
3 / tan u = tan v ⇔ u = v + kπ
4 / cot u = cot v ⇔ u = v + kπ
2. Một số phương trình đưa về phương trình lượng giác cơ bản
a/ Phương trình bậc nhất, bậc hai đối với một hàm số lượng giác: Phương trình có dạng: 2
at + b = 0; at + bt + c = 0 , t = {sin u,cosu, tan u,cot } u .
Lưu ý: Khi đặt t = {sin u,cos }
u điều kiện là t ≤ 1.Phương trình bậc 2 cùng một góc u .
b/ Phương trình bậc nhất đối với sin u,cos u
Phương trình có dạng: a sin u + b cosu = c hay a sin u + b cosu = c sin v(hay = c cos v)
Lưu ý: - Kiểm tra phương trình cùng một góc u
- Điều kiện có nghiệm của phương trình: 2 2 2
a + b ≥ c .
c/ Phương trình không mẫu mực
Lưu ý: - Nắm vững các công thức lượng giác
- Biến đổi đưa về các dạng phương trình đã biết cách giải A = 0 - Phương trình tích: . A B = 0 ⇔ B = 0
Bài 1. Giải các phương trình sau x π a) 3 − 2sin 2x = 0 b) 2 cos + − 3 = 0 3 4 2x c) 0 2 tan − 20 + 3 = 0
d) 4sin x.cos x.cos2x = 1 3
e) 2sin x − 2 sin 2x = 0
f) tan 2x.sin x + 3 (sin x − 3tan2x)−3 3 = 0 2 3 g) (2sin x + ) 1 − (2sin x + ) 1 sin x − = 0 h) 3 8cos x −1 = 0 2 HD Giải π 3 x = + kπ π 6
a) 3 − 2sin 2x = 0 ⇔ sin 2x =
⇔ sin 2x = sin ⇔ ;k ∈ℤ 2 3 π x = + kπ 3 π x = − + k6π x π x π 3 π b) 4 2 cos + − 3 = 0 ⇔ cos + = = cos ⇔ ;k ∈ℤ 3 4 3 4 2 6 5π x = − + k6π 4 c) Điều kiện : 0 0
x ≠ 135 + k270 28
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 2x 2x 3 0 0 0 0 0 2 tan − 20 + 3 = 0 ⇔ tan − 20 = − = tan( 3 − 0 ) ⇔ x = 1
− 5 + k270 ,k ∈ℤ 3 3 2 π kπ
d) 4sin x.cos x.cos2x = 1 ⇔ sin 4x = 1 ⇔ x = + ,k ∈ℤ 8 4 sin π x = 0 x = + k2π e) 2
2sin x − 2 sin2x = 0 ⇔ ⇔ , 2 k ∈ ℤ cos x = π x = ± + k2 2 π 4 π kπ f) Điều kiện x ≠ + . 4 2
tan 2x.sin x + 3 (sin x − 3tan2x)−3 3 = 0 ⇔ (sin x −3)(tan2x + 3) = 0 ⇔ tan 2 = − 3 π kπ x ⇔ x = − + 6 2 2sin π x +1 = 0 x = − + k2π 2 3 1 g) (2sin 6 x + ) 1 − (2sin x + )
1 sin x − = 0 ⇔ 5 ⇔ sin x = − ⇔ ;k ∈ℤ 2 sin x + = 0 2 7π 2 x = + k2π 6 2 cos x −1 = 0 1 π h) 3 8cos x −1 = 0 ⇔
⇔ cos x = ⇔ x = ± + k2π ,k ∈ℤ 2
cos x + cos x +1 = 0 2 3
Bài 2. Giải các phương trình sau
a) cos x.cos3x = cos5x.cos 7x
b) sin 3x.cos 7x = sin13x.cos17x
c) cos2x.cos5x = cos7x
d) sin 4x.sin 3x = cos x 1
e) sin 3x sin 5x = sin11x.sin13x
f) sin x.sin 2x.sin 3x = sin 4x 4 HD Giải
Dùng công thức biến đối tích thành tổng và tìm ra nghiệm của phương trình. kπ x = a) 4
cos x.cos3x = cos5x.cos7x ⇔ cos4x = cos12x ⇔ ,k ∈ℤ kπ x = 8 kπ x = b) 10
sin3x.cos 7x = sin13x.cos17x ⇔ sin10x = sin30x ⇔ ,k ∈ℤ π kπ x = + 40 20 kπ x = c) 2
cos2x.cos5x = cos7x ⇔ cos3x = cos7x ⇔ ,k ∈ℤ kπ x = 5 π kπ x = + d) 8 4
sin 4x.sin3x = cos x ⇔ cos(π − 7x) = cos x ⇔ ;k ∈ℤ π kπ x = + 6 3 29
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp kπ x = e) 8
sin3x sin 5x = sin11x.sin13x ⇔ cos8x = cos24x ⇔ ,k ∈ℤ kπ x = 16 π kπ 1 x = + f) 8 2
sin x.sin 2x.sin3x = sin 4x ⇔ sin 2x.cos4x = 0 ⇔ ;k ∈ℤ 4 kπ x = 2
Bài 3. Giải các phương trình sau:
a) 1+ 2 cos x + cos2x = 0
b) cos x + cos2x + cos3x + cos 4x = 0
c) sin x + sin 2x + sin 3x + sin 4x = 0
d) sin x + sin 2x + sin 3x = 1+ cos x + cos2x e) 2 2 2 2
cos x + cos 2x + cos 3x + cos 4x = 2
f) 1+ sin x + cos3x = cos x + sin 2x + cos2x HD Giải cos π x = 0 x = + kπ
a)1+ 2 cos x + cos2x = 0 ⇔ 2 cos x(cos x +1) = 0 ⇔ ⇔ 2 ,k ∈ℤ cos x 1 = −
x = π + k2π
b) cos x + cos2x + cos3x + cos4x = 0 ⇔ 2 cos2x.cos x + 2 cos3x cos x = 0 π = + π cos = 0 x k x 2 5x x 5x π k2π
⇔ 2 cos x(cos2x + cos3x) = 0 ⇔ 2 cos x.cos .cos = 0 ⇔ cos = 0 ⇔ x = + , ∈ℤ 2 2 k 2 5 5 x x = π + k 2π cos = 0 2 k2π x = 5 π
c) Phương trình có nghiệm là x = + kπ ,k ∈ ℤ 2 x = π − + k2π 2
d)sin x + sin 2x + sin 3x = 1+ cos x + cos2x ⇔ 2sin 2x cos x + sin 2x = 2 cos x + cos x = 0
⇔ cos x(2 cos x +1)(2sin x −1) = 0 π 2π π 5π
Vậy, nghiệm của phương trình x = + kπ , x = ±
+ k2π , x = + k2π , x =
+ k2π ,k ∈ℤ 2 3 6 6 e) 2 2 2 2
cos x + cos 2x + cos 3x + cos 4x = 2 ⇔ cos2x + cos4x + cos6x + cos8x = 0 π π kπ π kπ
Vậy, nghiệm của phương trình x = + kπ , x = + , x = + ,k ∈ℤ 2 4 2 10 5
f) 1+ sin x + cos3x = cos x + sin 2x + cos2x ⇔ (2sin x +1)(sin x − sin 2x) = 0 π 7π π k2π
Vậy, nghiệm của phương trình x = − + k2π , x =
+ k2π, x = k2π , x = + ,k ∈ℤ 6 6 3 3
Bài 4. Giải các phương trình sau: a) 3 3
sin x + cos x = cos x b) 3 3 3
sin x cos3x + cos xsin3x = sin 4x 1 c) 3 3
sin x cos x − cos x sin x = d) 3
2 cos x + sin x cos x +1 = 2(sin x + cos x) 4 e) 3 3
cos x − sin x = sin x − cos x f) ( x + )( x + x − ) 2 2sin 1 3cos4 2sin 4 + 4cos x = 3 HD Giải 3 3 3 3 3 2
a) sin x + cos x = cos x ⇔ sin x + cos x − cos x = 0 ⇔ sin x + cos x(cos x −1) = 0 30
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp sin = π x = 0 x k 3 2
sin x sin x cos x 0 ⇔ − = ⇔ ⇔ ;k ∈ℤ sin π x − cos x = 0 x = + kπ 4 1 b) Ta cần chú ý: 3 3
sin3α = 3sinα − 4sin α ⇒ sin α = (3sinα −sin3α ) 4 1 3 3
cos3α = 4cos α − 3cosα ⇒ cos α = (cos3α −3cosα ) 4 3 Từ đó 3 3 3 3
sin x cos3x + cos x sin3x = sin 4x ⇔ sin 4x = sin 4x 4 3
3sin 4 − 4sin 4 = 0 ⇔ sin12 = 0 kπ ⇔ x x x ⇔ x = 12 1 1 1 1 3 3
c) sin x cos x − cos x sin x =
⇔ sin x cos x ( 2 2
sin x − cos x) = ⇔ − sin4x = 4 4 4 4 ⇔ sin 4 = −1 π kπ x ⇔ x = − + ;k ∈ℤ 8 2 3 3
d) 2 cos x + sin x cos x +1 = 2(sin x + cos x) ⇔ 2 cos x − 2 cos x + sin x cos x +1− 2sin x = 0 2 2
⇔ 2cos x(cos x −1) + sin x cos x +1− 2sin x = 0 ⇔ −2cos x sin x + sin x cos x +1− 2sin x = 0
⇔ sin x cos x(1− 2sin x) +1− 2sin x = 0 ⇔ (1− 2sin x)(sin x cos x +1) = 0 π x = + k2 1 − 2sin π x = 0 1 6 ⇔ ⇔ sin x = ⇔
;k ∈ℤ ( vì sin x cos x +1 = 0 vô nghiệm )
sin x cos x +1 = 0 2 5π x = + k2π 6 1 π 1 e) 3 3
cos x − sin x = sin x − cos x ⇔ sin 2x + 2(sin x − cos x) = 0 ⇔ x = + kπ (Vì sin2x + 2 = 0 vô 2 4 2 nghiệm) f ) (2sin x + )
1 (3cos4x + 2sin x − 4) 2 + 4cos x = 3 ⇔ (2sin x + )
1 (3cos4x + 2sin x − 4) 2
+ 4(1− sin x) − 3 = 0 ⇔ (2sin x + )
1 (3cos4x + 2sin x − 4) 2 +1− 4sin x = 0 ⇔ (2sin x + )
1 (3cos4x + 2sin x − 4)+(1−2sin x)(1+ 2sin x) = 0 ⇔ (2sin x + ) 1 3cos 4x
+ 2sin x − 4 +1− 2sin x = 0 ⇔ (2sin x + ) 1 (3cos4x −3) = 0 π x = − + k2π 6 1 sin x = − 7π ⇔ 2 ⇔ x = + k2π ;k ∈ ℤ 6 cos4x = 1 k π x = 2
Bài 5. Giải các phương trình sau:
a) 2sin x + cot x = 2sin 2x +1 b) 2 x ( 3 − x ) 3 tan 1 sin + cos x −1 = 0 1− cos2x 5sin 4x cos x c) 1+ cot 2x = d) 3
6sin x − 2cos x = 2 sin x 2 cos2x 1+ cos x 3 e) 2 tan x = f) 2 2 tan x + 3 = 1+ sin x cos x HD Giải 31
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
a) Với đều kiện sin x ≠ 0 , ta có 2 2
2sin x + cot x = 2sin 2x +1 ⇔ 2sin x + cos x = 4sin x cos x + sin x ( − = ⇔ x − )( x − x − x x ) 2sin x 1 0 (1) 2sin 1 sin cos 2sin cos = 0 ⇔
sin x − cos x − 2 sin x cos x = 0 (2) π x = + k2π 6
Giải (1): 2sin x −1 = 0 ⇔ ;k ∈ℤ 5π x = + k2π 6
Giải (2): sin x − cos x − 2sin x cos x = 0 , đăt 2
t = sin x − cos x ⇒ 2
− sin x cos x = t −1với t ≤ 2 1 − + 5 2
sin x − cos x − 2sin x cos x = 0 ⇔ t + t −1 = 0 ⇔ t =
( thoả điều kiện t ≤ 2 ) 2 1 − + 5 π 1− 5 π 1− 5
Suy ra: sin x − cos x = ⇔ cos x + =
⇔ x = − ± arccos
+ k2π , k ∈ℤ 2 4 2 2 4 2 2
b) Với điều kiện cos x ≠ 0 , ta có 2 x ( 3 − x ) 3 2 + x − = ⇔ x ( 3 − x ) 2 + x ( 3 tan 1 sin cos 1 0 sin 1 sin cos cos x − )1 = 0 ⇔ ( 2 1− cos x)( 3 1−sin x)−( 2 1− sin x)( 3 1− cos x) = 0
(1 sin x)(1 cos x)(1 cosx)( 2
1 sin x sin x) (1 sin x)( 3
1 cos x cos x) ⇔ − − + + + − + + + = 0
(1 sin x)(1 cos x)(sin x cos x)(sin x cos x) sin x cos x(sin x cos x) ⇔ − − + − + − = 0
⇔ (1− sin x)(1− cos x)(sin x − cos x)(sin x + cos x + sin x cos x) = 0 1 − sin x = 0 (1) 1 − cos x = 0 (2) ⇔
sin x − cos x = 0 (3)
sin x + cos x + sin x cos x = 0 (4)
Phương trình (1) không thoả điều kiện cos x ≠ 0
Giải phương trình (4), ta đặt t = sin x + cos x với t ≤ 2 π π 2 1
Vậy, nghiệm của phương trình: x =
+ kπ , x = k2π , x = ±α + m2π;k,m∈ℤ với cosα − = 4 4 2 1− cos2x
c) Với điều kiện sin 2x ≠ 0 , ta có 2 1+ cot 2x =
⇔ sin 2x + sin2x cos2x = 1− cos2x 2 sin x 2 2
⇔ 1− sin 2x − cos2x − sin2x cos2x = 0 ⇔ cos 2x − cos2x − sin 2x cos2x = 0
⇔ cos2x (cos2x −sin2x − ) 1 = 0 π kπ π
Vậy, nghiệm của phương trình x = +
, x = − + lπ;k,l∈ℤ (Chú ý loại nghiệm không thoả điều 4 2 4 kiện) 5sin 4x cos x
d) Với điều kiện cos2x ≠ 0 , ta có 3 3
6sin x − 2cos x =
⇔ 6sin x − 2 cos x = 5sin2x cos x 2 cos2x 3 2 3 2
⇔ 6sin x − 2cos x = 10sin x cos x ⇔ 3sin x − cos x − 5sin x cos x = 0
Với cos x ≠ 0 , chia hai vế cho 2
cos x ta được một phuơng trình đối với tanx. Nhưng các nghiệm của
phương trình này đều không thoả điều kiện cos2x ≠ 0 .
Vậy, phương trình đã cho vô nghiệm π 2 1− cos x
e) Các nghiệm của phương trình x = π + k2π , x = + kπ;k ∈ 2 ℤ ( viết tan x = ) 4 2 1−sin x 32
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 1
f) Với điều kiện cos x ≠ 0 , đặt t = , ta có 2
2t − 3t +1 = 0 . Vậy, nghiệm của phương trình cos x
x = kπ ,k ∈ ℤ
Bài 6. Giải các phương trình sau: 1 3 a) 3
3sin3x − 3 cos9x =1+ 4sin 3x b) + = 8sin x sin x cos x
c) tan x − 3cot x = 4(sin x + 3 cosx)
d) 2 2 (sin x + cos x)cos x = 3+ cos2x π 1 1 e) 2 2 sin x + = + f) 3 3
sin x + cos x = sin x − cos x
4 sin x cos x HD Giải a) x − x = + 3 x ⇔ ( x − 3 3sin3 3 cos9 1 4sin 3 3sin3
4sin 3x)− 3 cos9x =1 π k2π 1 3 1 π 1 x = + ⇔ sin 9 18 9
x − 3 cos9x = 1 ⇔ sin 9x −
cos9x = ⇔ sin 9x − = ⇔ ;k ∈ℤ 2 2 2 3 2 7π k2π x = + 54 9 1 3
b) Điều kiện sin 2x ≠ 0 , ta có 2 +
= 8sin x ⇔ 3 sin x + cos x = 8sin x cos x sin x cos x 1− cos2 ⇔ 3 sin + cos = 8. x x x
cos x ⇔ 3 sin x + cos x = 4cos x − 4cos2x cos x 2
⇔ 3 sin x − 3cos x = −2(cos x + cos3x) ⇔ cos x − 3 sin x = 2 cos3x π x = + kπ π 6
⇔ cos3x = cos x + ⇔ ;k ∈ℤ 3 π kπ x = − + 12 2
c) Điều kiện sin 2x ≠ 0 , x − x = ( x + x ) 2 2 tan 3cot 4 sin 3 cos
⇔ sin x − 3cos x = 4sin x cos x (sin x + 3cosx) ( + = ⇔ x + x )( x − x − x ) sin x 3 cos x 0 (1) sin 3 cos sin 3 cos 2sin 2 = 0 ⇔
sin x − 3 cos x − 2sin 2x = 0 (2) π 4π k2π
Giải (1) và (2), các nghiệm của phương trình đã cho x = − + kπ , x = + 3 9 3
d) 2 2 (sin x + cos x)cos x = 3+ cos2x ⇔ 2 sin2x + ( 2 − )1cos2x = 3−2 2 2 2 2
Phương trình này vô nghiệm vì ( 2) +( 2 − )1 < (3−2 ) π 1 1
e) Điều kiện sin 2x ≠ 0 , ta có 2 2 sin x + = +
⇔ 2(sin x + cos x)sin x cos x = sin x + cos x
4 sin x cos x π sin + cos = 0 x = − + kπ x x 4
⇔ (sin x + cos x)(2sin x cos x −1) = 0 ⇔ ⇔
;k ∈ℤ (thoả điều kiện) 2sin 2x = 1 π x = − + kπ 4 f) 3 3 2 3
sin x + cos x = sin x − cos x ⇔ sin x(1−sin x) − cos x − cos x = 0 2
⇔ cos x(sin x cos x −1− cos x) = 0 33
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp cos x = 0 (1) ⇔ . 2
sin x cos x −1− cos x = 0 (2) π
Giải (1) và (2), phương trình (2) vô nghiệm. Nghiệm của phương trình là x = + kπ ,k ∈ℤ 2
Bài 7. Giải các phương trình sau: (Đại học – cao đẳng năm 2006 - 2007) 2 x x
a) sin + cos + 3 cos x = 2 b) 2
2sin 2x + sin 7x −1 = sin x 2 2 ( 6 6
2 cos x + sin x)−sin x cosx c) ( 2 + x) x + ( 2 1 sin cos
1+ cos x)sin x =1+sin2x d) = 0 2 − 2sin x x
e) cot x + sin x 1+ tan x tan = 4
f) cos3x + cos2x − cos x −1 = 0 2 HD Giải π 1
a) Phương trình đã cho tương đương với: 1+ sin x + 3 cos x = 2 ⇔ cos x − = 6 2 π π
Vậy, nghiệm của phương trình: x =
+ k2π , x = − + k2π ,k ∈ℤ 2 6
b) Phương trình đã cho tưong đương với 2
sin 7x −sin x + 2sin 2x −1 = 0 ⇔ cos4x (2sin3x − ) 1 = 0 π kπ π k2π 5π k2π
Vậy, nghiệm của phương trình: x = + , x = + , x = + ,k ∈ℤ 8 4 18 3 18 3
c) Phươngt trình đã cho tương đương với 2
(sin x + cos x)(1+ sin x cos x) = (sin x + cos x) ⇔ (sin x + cos x)(1− sin x)(1− cos x) = 0 π π
Vậy, nghiệm của phương trình: x = − + kπ , x = + k2π , x = k2π ,k ∈ℤ 4 2 2
d) Điều kiện: sin x ≠
(*) phương trình đã cho tương đương với: 2 2( 3 1 6 6 sin x + cos x) 2
− sin x cos x = 0 ⇔ 21− sin 2x − sin 2x = 0 4 2 2 ⇔ 3sin 2 π
x + sin 2x − 4 = 0 ⇔ sin 2x = 1 ⇔ x = + kπ ,k ∈ℤ 4 5π
Do điều kiện (*) nên nghiệm của phương trình: x =
+ 2mπ ,m ∈ℤ 4 x
e) Điều kiện: sin x ≠ 0,cos x ≠ 0,cos ≠ 0 (*) phương trình đã cho tương đương với: 2
cos x cos x + sin x sin x cos x cos x sin x 1 2 2 + sin x = 4 ⇔ + = 4 ⇔ sin2x = sin x x sin x cos x 2 cos x cos 2 π 5π
So với (*), nghiệm của phương trình: x = + kπ , x = + kπ,k ∈ℤ 12 12
f) Phương trình đã cho tương đương với 2 2
−2sin2x sin x − 2sin x = 0 ⇔ sin x(sin2x + sin x) = 0 ⇔ sin x(2 cos x +1) = 0 2π
Vậy, nghiệm của phương trình: x = ±
+ k2π , x = kπ ,k ∈ℤ 3
Bài 8. Giải các phương trình sau: (Đại học – cao đẳng năm 2008) 34
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 1 1 7π a) + = 4sin − x b) 3 3 2 2
sin x − 3 cos x = sin x cos x − 3 sin x cos x sin x 3π 4 sin x − 2
c) 2sin x (1+ cos2x) + sin2x =1+ 2cos x d) sin3x − 3 cos3x = 2sin2x HD Giải 3π
a) Điều kiện sin x ≠ 0 và sin x − ≠ 0 . 2
Phương trình đã cho tương đương với: 1 1 ( + = − x + x ) ⇔ ( x + x ) 1 2 2 sin cos sin cos + 2 2 = 0 sin x cos x sin x cos x π π 5π
So với điều kiện, nghiệm của phương trình là: x = − + kπ , x = − + kπ và x = + kπ ,k ∈ℤ 4 8 8
b) Phương trình đã cho tương đương với: x ( 2 2 x − x ) + x ( 2 2 sin cos sin
3 cos cos x −sin x) = 0 ⇔ cos2x(sin x + 3cosx) = 0 π kπ π
Vậy, nghiệm của phương trình là: x = +
, x = − + kπ ,k ∈ℤ 4 2 3
c) Phương trình đã cho tương đương với: 2
4sin x cos x + sin2x = 1+ 2cos x ⇔ (2cos x +1)(sin 2x −1) = 0 2π π
Vậy, nghiệm của phương trình: x = ±
+ k2π , x = + kπ ,k ∈ℤ 3 4 1 3 π
d) Phương trình đã cho tương dương với: sin 3x −
cos3x = sin2x ⇔ sin3x − = sin 2x 2 2 3 2π 4π k2π
Vậy, nghiệm của phương trình là: x = + k2π , x = + ,k ∈ℤ 3 15 5
Bài 9. Giải các phương trình sau: (Đại học – cao đẳng năm 2009)
(1− 2sin x)cos x a) = 3 b) 3
sin x + cos x sin2x + 3 cos3x = 2(cos4x + sin x)
(1+ 2sin x)(1− sin x) c) 2
(1+ 2sin x) cos x =1+ sin x + cos x
d) 3 cos5x − 2sin3x cos2x − sin x = 0 HD Giải 1
a) Điều kiện sin x ≠ 1,sin x ≠ − (*) 2
(1− 2sin x)cos x = 3 ⇔ (1−2sinx)cosx = 3(1+2sinx)(1−sinx)
(1+ 2sin x)(1−sin x) π x = + k π 2 π π ⇔ x − x = x + x ⇔ x + = cos 2x − ⇔ 2 cos 3 sin sin 2 3 cos2 cos ,k ∈ℤ 3 6 π k π 2 x = − + 18 3 π k2π
So với (*), nghiệm của phương trình là x = − + ,k ∈ℤ 18 3
b) Phương trình đã cho tương đương với 35
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 2
(1− 2sin x)sin x + cos x sin2x + 3 cos3x = 2cos4x
⇔ sin x cos2x + cos x sin 2x + 3 cos3x = 2 cos4x π x = − + k2π π 6
⇔ sin3x + 3 cos3x = 2 cos4x ⇔ cos 3x − = cos4x ⇔ ,k ∈ℤ 6 π k2π x = + 42 7
c) Phương trình tương đương với (sin x +1)(2sin 2x −1) = 0 π π 5π
Vậy, nghiệm của phương trình: x = − + k2π , x = + kπ , x = + kπ ,k ∈ℤ 2 12 12
d) Phương trình đã cho tương đương với 3 1
3 cos5x − (sin 5x + sin x) − sin x = 0 ⇔
cos5x − sin5x = sin x 2 2 π π k π x = + ⇔
− 5x = sin x ⇔ 18 3 sin ,k ∈ℤ 3 π π x = − + k 6 2
Bài 10. Giải các phương trình sau: (Đại học – cao đẳng năm 2010) ( 1+ sin π
x + cos2x)sin x + 4 1 a) = cos x
b) (sin2x + cos2x)cos x + 2cos2x −sin x = 0 1+ tan x 2 5x 3x
c) sin 2x − cos2x + 3sin x − cos x −1 = 0 d) 4 cos cos + 2(8sin x − ) 1 cos x = 5 2 2 HD Giải
a) Điều kiện cos x ≠ 0 và 1+ tan x ≠ 0 ( 1+ sin π
x + cos2x)sin x + 4 1 π =
cos x ⇔ 2 sin x + (1+sin x + cos2x) = (1+ tan x)cos x 1+ tan x 2 4 ⇔ ( + )( + + ) sinx +cos sin cos 1 sin cos2 x x x x x =
cos x ⇔ sin x + cos2x = 0 cos x 1 2
⇔ 2sin x − sin x −1 = 0 ⇔ sin x = 1(loại) hoặc sin x = − 2 π 7 ⇔ π
x = − + k2π hoặc x = + k2π;k ∈ℤ 6 6 b) ( x + x ) 2 sin 2
cos2 cos x + 2 cos2x −sin x = 0 ⇔ 2sin x cos x − sin x + cos2x cos x + 2cos2x = 0
⇔ cos2x sin x + (cos x + 2)cos2x = 0 ⇔ cos2x(sin x + cos x + 2) = 0 π π
⇔ cos2x = 0 ⇔ x = + k ;k ∈ℤ ( vì sin x + cos x + 2 = 0 (vô nghiệm)) 4 2 c) x − x + x − x − = ⇔ x x − x − ( − 2 sin 2 cos2 3sin cos 1 0 2sin cos cos
1 2sin x)+3sin x −1= 0
⇔ (2sin x −1)(cos x + sin x + 2) = 0 2sin x −1 = 0 ⇔
cos x + sin x + 2 = 0
Phương trình: sin x + cos x + 2 = 0 vô nghiệm 1 π 5π
Phương trình: 2sin x −1 = 0 ⇔ sin x = ⇔ x = + k π 2 hoặc x = + k2π;k ∈ℤ 2 6 6 36
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 5x 3x d) 4 cos cos + 2(8sin x − ) 1 cos x = 5 2 2 2
⇔ 2cos4x + 8sin2x − 5 = 0 ⇔ 4sin 2x − 8sin2x + 3 = 0 3 1 π 5π
⇔ sin 2x = ( vô nghiệm) hoặc sin 2x = ⇔ x = + kπ hoặc x = + kπ;k ∈ℤ 2 2 12 12
Bài 11. Giải các phương trình sau: (Đại học – cao đẳng năm 2011) 1+ sin2x + cos2x a)
= 2 sin x sin 2x
b) sin 2x cos x + sin x cos x = cos2x + sin x + cos x 2 1+ cot x
sin 2x + 2cos x − sin x −1 c) = 0 d) 2
cos 4x +12sin x −1 = 0 tan x + 3 HD Giải
a) Điều kiện sin x ≠ 0 (*). Phương trình đã cho tương đương với: ( + x + x ) 2 2 1 sin 2
cos2 sin x = 2 2 sin x cos x
⇔ 1+ sin 2x + cos2x = 2 2 cos x = ⇔
x ( x + x − ) cos x 0 (1) cos cos sin
2 = 0 ⇔ cosx+sinx− 2 =0 (2) π
Giải (1): cos x = 0 ⇔ x = + kπ ,k ∈ℤ (thoả mãn (*)) 2 π π
Giải (2): cos x + sin x = 2 ⇔ sin x + = 1 ⇔ x = + k2π ,k ∈ℤ (thoả mãn (*)) 4 4 π π
Vậy, phương trình có nghiệm: x = + kπ ; x = + k2π ,k ∈ℤ 2 4
b) sin 2x cos x + sin x cos x = cos2x + sin x + cos x
⇔ sin x (1+ cos2x) +sin x cos x = cos2x +sin x + cos x
⇔ cos2x (sin x − )
1 + cos x (sin x − ) 1 = 0 ( − = ⇔ x − )( x + x ) sin x 1 0 (1) sin 1 cos2 cos
= 0 ⇔ cos2x+cosx = 0 (2) π
Giải (1): sin x = 1 ⇔ x = + k2π ,k ∈ℤ 2 π π Giải (2): x = − x = (π − x) 2 cos2 cos cos ⇔ x = + k ,k ∈ℤ 3 3 π π 2π
Vậy, phương trình có nghiệm: x = + k2π ; x = + k ,k ∈ℤ 2 3 3
c) Điều kiện cos x ≠ 0,tan x ≠ 3 (*).
sin 2x + 2cos x −sin x −1 = 0 ⇔ sin2x +2cosx −sinx −1= 0 tan x + 3
⇔ 2 cos x (sin x + ) 1 − (sin x + ) 1 = 0 ⇔ (sin x + ) 1 (2cos x − ) 1 = 0 π sin x = −1 x = − + k π 2 ⇔ 1 ⇔ 2 ;k ∈ ℤ cos x = π 2 x = ± + k π 2 3 π
So với (*). Vậy, nghiệm của phương trình: x = + k2π ,k ∈ℤ 3 37
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp d) 2
cos 4x +12sin x −1 = 0 2 ⇔ x − + ( − x ) 2 2 cos 2
1 6 1 cos2 −1 = 0 ⇔ cos 2x −3cos2x + 2 = 0
⇔ cos2x = 2 (vô nghiệm) hoặc cos2x = 1 ⇔ x = kπ,k ∈ℤ
Vậy, nghiệm của phương trình: x = kπ ,k ∈ℤ
Bài 12. Giải các phương trình sau: (Đại học – cao đẳng năm 2012)
a) 3 sin 2x + cos2x = 2 cos x −1
b) 2(cosx + 3sin x)cosx = cosx − 3sin x +1
c) sin 3x + cos3x − sin x + cos x = 2 cos2x
d) 2 cos2x + sin x = sin3x HD Giải
a) 3 sin 2x + cos2x = 2 cos x −1 ⇔ ( 3sin x + cosx − )1cosx = 0 π x = + kπ 2 cos x = 0 ⇔ ⇔ x = kπ ;k ∈ℤ
3 sin x + cos x −1 = 0 2π x = + k2π 3 π 2π
Vậy nghiệm của phương trình đã cho là x = + kπ , x = kπ và x =
+ k2π ( k ∈ℤ ) 2 3
b) 2(cosx + 3sin x)cosx = cosx − 3sin x +1⇔ cos2x + 3sin2x = cosx − 3sin x 2π x = + k2π π π 3 ⇔ cos 2x − = cos x + ⇔ ;k ∈ℤ 3 3 2π x = k 3 2π 2π
Vậy nghiệm của phương trình đã cho là x =
+ k2π và x = k ( k ∈ ℤ ) 3 3
c) sin 3x + cos3x − sin x + cos x = 2 cos2x ⇔ (2sin x +2cosx − 2)cos2x = 0 π π cos2 = 0 k x ⇔ x = + (k ∈ℤ) 4 2 π 1 7π π
2sin x + 2cos x − 2 = 0 ⇔ cos x − = ⇔ x =
+ k2π hoaëc x = −
+ k2π (k ∈ℤ). 4 2 12 12 π kπ 7π π
Vậy nghiệm của phương trình đã cho là x = + , x =
+ k2π và x = −
+ k2π (k ∈ℤ) 4 2 12 12
d) 2 cos2x + sin x = sin3x ⇔ 2 cos2x + sin x − sin3x = 0 ⇔ 2 cos2x − 2 cos2x.sin x = 0 π π cos2 = 0 x = + k x 4 2
⇔ 2cos2x(sin x −1) = 0 ⇔ ⇔ (k ∈ℤ) sin x = 1 π x = + k2π 2 π π π
Vậy nghiệm của phương trình đã cho là x = + k và x = + k2π (k ∈ℤ) 4 2 2
Bài 13. Giải các phương trình sau: (Đại học – cao đẳng năm 2013) π
a) 1+ tan x = 2 2 sin x + b) 2
sin 5x + 2cos x = 1 4 π
c) sin 3x + cos2x − sin x = 0
d) cos − x + sin 2x = 0 2 38
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp HD Giải
a) Điều kiện cos x ≠ 0 . Phương trình đã cho tương đương với: sin 1 x 2(sin + = + =
x + cos x) ⇔ (sin x + cos x)(2 cos x −1 = 0) sin x cos x 0 ⇔ cos x 2 cos x −1 = 0 π
sin x + cos x = 0 ⇔ x = − + kπ ,k ∈ℤ 4 π
2 cos x −1 = 0 ⇔ x = ± + k2π ,k ∈ℤ 3 π π
So với điều kiện, vậy nghiệm của phương trình là: x = − + kπ và x = ± + k2π ,k ∈ℤ . 4 3 π b) 2
sin 5x + 2cos x = 1 ⇔ sin5x = cos2x ⇔ cos5x + = cos2x 2 π π 2 5 π x + = 2x + k2π x = − + k 2 6 3 ⇔ ⇔ ,k ∈ℤ π π 2 5 π x + = −2x + k2π x = − + k 2 14 7 π 2π π 2π
Vậy nghiệm của phương trình là: x = − + k và x = − + k ,k ∈ℤ . 6 3 14 7 x = c) x + x − x = ⇔ x x + x = ⇔ x ( x + ) cos2 0 sin3 cos2 sin 0 2 cos2 sin cos2 0 cos2 2sin 1 = 0 ⇔ 2sin x +1 = 0 π kπ
cos2x = 0 ⇔ x = + ,k ∈ℤ 4 2 π x = − + k2π 6 2sin x +1 = 0 ⇔ ,k ∈ℤ 7π x = + k2π 6 π kπ π 7π
Vậy nghiệm của phương trình là: x = +
, x = − + k2π và x =
+ k2π ,k ∈ℤ . 4 2 6 6 2π π x = k
d) cos − x + sin 2x = 0 ⇔ sin 2x = −sin x ⇔ sin 2x = sin(−x) ⇔ 3 ,k ∈ℤ 2
x = π + k2π k2π
Vậy nghiệm của phương trình là: x =
và x = π + k2π ,k ∈ℤ . 3
Bài 14. Giải các phương trình sau: (Đại học – cao đẳng năm 2014)
a) sin x + 4 cos x = 2 + sin 2x
b) 2 (sin x − 2cos x) = 2 −sin2x HD Giải
a) sin x + 4 cos x = 2 + sin 2x ⇔ sin x + 4 cos x = 2 + 2sin x cos x ⇔ (sin x − 2)(2cos x − ) 1 = 0
sin x − 2 = 0 ⇔ sin x = 2 : Phương trình vô nghiệm 1 π
2 cos x −1 = 0 ⇔ cos x = ⇔ x = ± + k2π ,k ∈ℤ 2 3 π
Vậy nghiệm của phương trình đã cho: x = ± + k2π ,k ∈ℤ 3
b) 2 (sin x −2cosx) = 2−sin2x ⇔ 2sin xcosx −2 2 cosx + 2 sin x −2 = 0 = (sinx − 2)(2cosx + 2) = 0 39
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
sin x − 2 = 0 : Phương trình vô nghiệm 2 3π
2 cos x + 2 = 0 ⇔ cos x = − ⇔ x = ± + k2π,k ∈ℤ 2 4 3π
Vậy nghiệm của phương trình đã cho là x = ± + k2π ,k ∈ℤ 4
Bài 15. Giải các phương trình sau: (THPTQG 2015, 2016) π 3 tanα
a) Cho góc α thỏa mãn < α < π và sinα = . Tính = 2 A 5 2 1+ tan α 2
b) Tính giá trị của biểu thức P = (1− 3cos 2α )(2 + 3cos 2α ), biết sinα = 3 c) Giải phương trình: 2
2sin x + 7sin x − 4 = 0 HD Giải 2 π 4 a) Ta có: 2 2 3 16 cos α 1 sin α = − =1− = . Vì
< α < π nên cosα = − 5 25 2 5 3 3 tanα − 12
Khi đó suy ra: tanα = − . Vậy: 4 A = = = − 4 2 2 1+ tan α 3 25 1+ − 4 2 b) Ta có: 2 2 1 cos 2α 1 2sin α = − =1− 2. = 3 9 Vậy: P = ( − α )( + α ) 1 1 14 1 3cos 2 2 3cos 2
= 1− 3. 2 + 3. = 9 9 9 sin x = −4 c) 2 2sin
x + 7 sin x − 4 = 0 ⇔ 1 sin x = 2 Với sin x = 4
− ⇒ phương trình vô nghiệm π x = + k2π 1 Với 6 sin x = ⇔ , k ∈ ℤ 2 5π x = + k2π 6
Giải các phương trình Bài Giải phương trình Bài Giải phương trình 1 π 2 cos3
3 sin 2x + cos 2x = sin x + 3 cos x
x − sin 2x − = 0 4 3 π π 4 2 + = sin
1 sin 2x 2cos x x + + 3 sin − x =1 3 6 5
2(2 − cos x)cos x = 3 sin 2x 6 sin 3 .
x cos 3x = sin 2x 7 2 8 π
1− sin 3 = sin x − cos x x
sin 3x − cos 2x − = 0 2 2 4 9 π 10
2sin x − sin 2x = 2sin 2x.cos x
sin 2x + + cos x − sin x = 0 2 11
sin 2x + cos(π − x) = 0 12
sin 5x + sin 3x = sin 4x 40
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 13 2 14 sin π 3 π x − + cos3x = 0
2 cos 4x cos x − cos + 3x = sin5x 3 2 15 16
sin 7x cos3x − cos2x = cos7x sin3x cos π
+ 3x − sin2x = 0 2 17 2
sin x + 2sin 2x = sin 7x +1 18 2 cos 4 π
x cos x − cos + 3x = sin 5x 2 19
sin x + 4 cos x = 2 + sin 2x 20
2 (sin x −2cos x) = 2−sin2x 21 2
sin5x + 2cos x = 1 22
sin 3x + cos2x − sin x = 0 23 24 cos π π
− x + sin2x = 0
1+ tan x = 2 2 sin x + 2 4 25
3 sin 2x + cos2x = 2 cos x −1 26
2(cosx + 3sinx)cosx = cosx − 3sinx +1 27 sin3 + =
x + cos3x −sin x + cos x = 2 cos2x 28
2 cos2x sin x sin 3x 29 2
cos4x +12sin x −1= 0 30
(sin2x +cos2x)cosx +2cos2x −sinx = 0 31 5x 3 32
sin 2x − cos2x + 3sin x − cos x −1 = 0 4cos
cos x +2(8sinx− )1cosx =5 2 2 33
sin2xcosx+sinxcosx = cos2x+sinx+cosx 34
3 cos5x − 2sin3x cos2x − sin x = 0 35 2
(1+ 2sin x) cos x = 1+ sin x + cos x 36
sin3x − 3 cos3x = 2sin2x 37
2sin x (1+ cos2x)+sin2x =1+ 2cos x 38
cos3x + cos2x − cos x −1 = 0 39 2 40 2
2sin 2x + sin 7x −1 = sin x
sin x + cos x + 3 cos x = 2 2 2 41
cos3x + cos2x − cos x −1 = 0 42
cos x + cos2x + cos3x + cos4x = 0 43
sin x + sin 2x + sin3x + sin 4x = 0 44 3
3sin3x − 3 cos9x =1+ 4sin 3x 45
2 2 (sin x + cos x)cos x = 3+ cos2x 46 1 3 + = 8sin x sin x cos x 47 3 3
sin x + cos x = sin x − cos x 48 9π 15 sin 2 π x + − 3 cos x − = 1+ 2 sin x 2 2 49 2sin + + =
x − 2 sin 2x = 0 50
1 2 cos x cos2x 0 51 π 52 2 cos 5 .
x cos 3x + sin x = cos 8x
3 sin 3x + cos3x = 2sin 2x + 3 53
sin 2x − 3 cos x = 0 54
cos x + sin x = 1+ sin 2x + cos 2x 41
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
BÀI TẬP TRẮC NGHIỆM π
Câu 1: Tìm tập xác định D của hàm số y = tan2x + . 3 π A. k D = . ℝ B. D = ℝ \ ,k ∈ℤ. 2 π π π C. k
D = ℝ \ + kπ ,k ∈ ℤ.
D. D = ℝ \ + ,k ∈ℤ. 6 12 2
Câu 2: Tìm tất cả giá trị của x để hàm số 4 2
y = cos x + 4 cos x + 5 có giá trị lớn nhất bằng 10. π A. k
x = kπ ,k ∈ . ℤ B. x = ,k ∈ . 2 ℤ π π
C. x = + kπ ,k ∈ . x = − + k π k ∈ 2 ℤ D. 2 , . 2 ℤ
Câu 3: Tìm hàm số lẻ trong các hàm số dưới đây. sin x
A. f (x) = sin 3 . x sin 4 . x
B. f (x) = . 2 3 + cot x 4 π C. tan x f (x) = .
D. f (x) = 2cos x + + sin(π − 2x). 2 + cos 2x 2
Câu 4: Giải phương trình 3 cos5x − 2cos3x + sin5x = 0. π π π π π π A. k k x = + k2π x = + k ∈ x = + kπ x = − + k ∈ 8 hoặc , . 48 2 ℤ B. 6 hoặc , . 48 4 ℤ π π π π π π C. k k x = + kπ x = + k ∈ x = + k π x = + k ∈ 12 hoặc , . 48 4 ℤ D. 2 12 hoặc , . 48 8 ℤ
Câu 5: Giải phương trình tan x = 3. π π π π
A. x = + kπ ,k ∈ . x = + kπ k ∈ x = + k π k ∈ x = − + kπ k ∈ 6 ℤ B. , . 3 ℤ C. 2 , . 3 ℤ D. , . 3 ℤ π
Câu 6: Số nghiệm của phương trình 2 cos x + = 1 với 0 ≤ x ≤ 2π là 3 A. 3. B. 2. C. 0. D. 1.
Câu 7: Cho phương trình: 3cosx + cos2x − cos3x +1 = 2sin .
x sin 2x . Gọi α là nghiệm lớn nhất thuộc π
khoảng (0;2π ) của phương trình. Giá trị của sin α − bằng 4 A. 2 − . B. 3 . C. 0. D. 1. 2 2
Câu 8: Tìm chu kì tuần hoàn T của hàm số y = tan3π x. π 1 A. T = . T = . T = π T = π 3 B. 3 C. 3 . D. . Câu 9: x x
Tìm chu kì tuần hoàn T của hàm số y = cos + cos . 2 3 A. T = 12π. B. T = 8π. C. T = 4π. D. T = 6π.
Câu 10: Kí hiệu M là giá trị lớn nhất của hàm số: 2
y = cos x − sin x. Tìm M. 3 1 A. M = . M = . M = M = 4 B. 4 C. 5 . D. 4 . 4 5
Câu 11: Giải phương trình sin3x = sin x. 42
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp π π π A. k x = + kπ
x = k π k ∈ = x = + k ∈ 2 hoặc 2 , . ℤ B. x kπ hoặc , . 4 2 ℤ π π π
C. x = + k2π ,k ∈ . x = + kπ x = + k π k ∈ 4 ℤ D. 8 hoặc 2 , . 4 ℤ
Câu 12: Giải phương trình 2
sin 5x + 2cos x =1. π π π k2π π 2π π 2π A. k x = + x = − + ,k ∈ . x = − + k x = − + k ,k ∈ . 6 3 hoặc 7 7 ℤ B. 6 3 hoặc 14 7 ℤ π π π π π 2π π 2π C. k k x = + x = − + k ∈ x = + k x = + k ,k ∈ . 3 3 hoặc , . 3 3 ℤ D. 6 3 hoặc 14 7 ℤ 3sin x − 7
Câu 13: Tìm tập xác định D của hàm số y = . 2 cos x − 5 5 A. D = . ℝ
B. D = ℝ \ . 2 π C. k
D = ℝ \ {kπ ,k ∈ } ℤ . D. D = ℝ \ ,k ∈ℤ. 2 π
Câu 14: Tìm số nghiệm của phương trình sin 2x + = 1 − thuộc đoạn 0; π . 4 A. 2. B. 3. C. 0. D. 1.
Câu 15: Mệnh đề nào dưới đây sai ? π
A. Hàm số y = sin x đồng biến trên khoảng 0; . 2 π π
B. Hàm số y = tan x nghịch biến trên khoảng − ; . 2 2
C. Hàm số y = cos x đồng biến trên khoảng ( π − ;0).
D. Hàm số y = cot x nghịch biến trên khoảng (0;π ).
Câu 16: Tìm tập nghiệm S của phương trình sin x + cos x = 2. π π
A. S = − + kπ , k ∈ℤ.
B. S = + kπ , k ∈ ℤ. 4 4 π π C. 3 S = −
+ k2π ,k ∈ℤ. D. 5 S =
+ kπ ,k ∈ℤ. 4 4
Câu 17: Tìm tất cả giá trị của x để hàm số 2
y = 3 + cos x có giá trị lớn nhất bằng 2. π A. k x = ,k ∈ .
x = kπ k ∈ 2 ℤ B. , . ℤ π
C. x = − + k2π ,k ∈ .
x = k π k ∈ 2 ℤ D. 2 , . ℤ π
Câu 18: Số nghiệm của phương trình sin x + =1 thỏa mãnπ ≤ x ≤ 3π là : 4 A. 1. B. 3. C. 2. D. 0. sin3 Câu 19: x
Tìm số nghiệm của phương trình = 0 π π cos
có số nghiệm thuộc đoạn 2 ; 4 . x +1 A. 2. B. 5. C. 4. D. 6.
Câu 20: Gọi m và M là giá trị nhỏ nhất và giá trị lớn nhất của hàm số 2
y = sin x + 2sin x + 6 . Tính
S = m + M. 43
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp A. S =14. B. S = 3 − . C. S = 9. D. S = 5.
Câu 21: Giải phương trình 2sin x (1+ cos2x) + sin2x =1+ 2cos x. π π 2π π
A. x = ± + k2π , x = + kπ ,k ∈ . x = ±
+ kπ , x = + k2π ,k ∈ . 3 2 ℤ B. 3 4 ℤ 2π π 2π π C. x = ±
+ k2π , x = + kπ ,k ∈ . x =
+ k2π , x = − + kπ,k ∈ . 3 4 ℤ D. 3 4 ℤ 2 Câu 22: x Giải phương trình 0 2 tan − 20 + 3 = 0. 3 A. 0 0 x = 3
− 5 + k270 ,k ∈ . ℤ B. 0 0 x = 1
− 5 + k270 ,k ∈ . ℤ C. 0 0 x = 4
− 5 + k270 ,k ∈ . ℤ D. 0 0
x = 15 + k270 ,k ∈ . ℤ
Câu 23: Tìm tập xác định D của hàm số y = 6 tan 3x − 4 cot 3x. π A. k D = (0;+∞). B. D = ℝ \ ,k ∈ℤ. 6
C. D = ℝ \ {kπ,k ∈ } ℤ . D. D = . ℝ π
Câu 24: Giải phương trình cos − x + sin 2x = 0. 2 π π 2π A. k x =
x = k π k ∈ x = + kπ x = − + kπ ,k ∈ . 3 hoặc 2 , . ℤ B. 3 hoặc 3 ℤ π k2π C. k x =
x = π + kπ k ∈ x =
x = π + k π k ∈ 3 hoặc , . ℤ D. 3 hoặc 2 , . ℤ
Câu 25: Kí hiệu m là giá trị nhỏ nhất của hàm số: y = sin x + 3 cos x . Tìm m. A. m = − 3. B. m = 1. C. m = 2 − . D. m = − 2.
Câu 26: Phương trình 3sin x + mcos x = 5 vô nghiệm khi và chỉ khi m ≤ 4 − A. m < 4 − . B. . C. m > 4. D. 4 − < m < 4. m ≥ 4 3 + x x − Câu 27: 1 cos sin x
Cho các hàm số f (x) = , g(x) =
. Mệnh đề nào dưới đây đúng ? 1− cos x cos 2x
A. f (x) và g(x) là các hàm số lẻ.
B. f (x) là hàm số lẻ và g(x) là hàm số chẵn.
C. f (x) và g(x) là các hàm số chẵn.
D. f (x) là hàm số chẵn và g(x) là hàm số lẻ.
Câu 28: Tìm chu kì tuần hoàn T của hàm số y = cos x + cos3x. 2π A. T = 2π. B. T = . T = π T = π 3 C. 4 . D. . 2 + tan 2 Câu 29: x Cho hàm số y = . sin 2
Tìm điều kiện xác định của hàm số đã cho. x sin x ≠ 0 s in 2x ≠ 0 A. .
B. sin 2x ≠ 0.
C. sin 4x ≠ 0. D. . cos x ≠ 0 cos x ≠ 0 π π Câu 30: x x
Tìm chu kì tuần hoàn T của hàm số y = tan − + cot − . 2 4 4 3 A. T = 8π B. T = 6π C. T = 2π D. T = 4π π
Câu 31: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = 2 sin x − +1. 4 44
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
A. M = 2,m = − 2.
B. M = 1,m = 1 − .
C. M = 1+ 2,m = 1− 2.
D. M = 1− 2,m = 1 − − 2. Câu 32: x x Giải hương trình 4 4 1 sin − cos = . 4 4 2 π π A. 4 x = ± + k4π ,k ∈ . ℤ B. 4 x = ± + k2π ,k ∈ . ℤ 3 3 π π π C. 4 x = ± + kπ ,k ∈ . ℤ D. 4 x = ± + k , k ∈ . ℤ 3 3 2 cos Câu 33: x Cho hàm số y =
. Mệnh đề nào dưới đây đúng ? x
A. Hàm số đã cho không chẵn, không lẻ.
B. Hàm số đã cho vừa chẵn, vừa lẻ.
C. Hàm số đã cho là hàm số chẵn.
D. Hàm số đã cho là hàm số lẻ. tan x + cot Câu 34: x
Tìm tập xác định D của hàm số y = . 1 − sin 2x 5π π kπ π
A. D = ℝ \
+ kπ ∪ + kπ ;k ∈ℤ.
B. D = ℝ \
∪ + kπ ; k ∈ ℤ . 6 12 2 4 π π C. k
D = ℝ \ + kπ ,k ∈ ℤ. D. D = ℝ \ ,k ∈ℤ. 4 2
Câu 35: Giải phương trình 8cos2x sin 2x cos 4x = 2. π π 3π π π π 3π π A. k k k k x = − + x = + ,k ∈ . x = + x = + ,k ∈ . 32 4 hoặc 32 2 ℤ B. 32 4 hoặc 32 4 ℤ π 3π π π 3π C. k x = + k2π x = + k2π ,k ∈ . x = + x = + kπ ,k ∈ . 32 hoặc 32 ℤ D. 32 2 hoặc 32 ℤ 2
Câu 36: Giải phương trình sin x = . 2 π 5π π 3π
A. x = − + k2π x = + k2π ,k ∈ . x = + kπ x = + kπ ,k ∈ . 4 hoặc 4 ℤ B. 4 hoặc 4 ℤ π 3π π 3π
C. x = + k2π x = + k2π ,k ∈ . x = + k π x = − + k2π ,k ∈ . 4 hoặc 4 ℤ D. 2 4 hoặc 4 ℤ
Câu 37: Giải phương trình sin x + 3 cos x = 2sin 2x. π 2π k2π π π
A. x = − k2π x = + ,k ∈ . x = + kπ x = + kπ k ∈ 3 hoặc 9 3 ℤ B. 3 hoặc , . 6 ℤ π π k2π π 2π π C. k x = − − k2π x = + ,k ∈ . x = − k π x = + ,k ∈ . 3 hoặc 9 3 ℤ D. 2 6 hoặc 3 3 ℤ 2π
Câu 38: Giải phương trình sin x + = cos3x. 3 π π π π π π A. k k x = − + x = + kπ k ∈ x = + x = − + kπ k ∈ 24 2 hoặc , . 12 ℤ B. 24 2 hoặc , . 12 ℤ π π π π π C. k x = − + kπ x = + k ∈ x = + kπ
x = − + kπ k ∈ 24 hoặc , . 12 2 ℤ D. 12 hoặc , . 4 ℤ
Câu 39: Cho phương trình cos5x = 3m − 5. Gọi đoạn [ ;
a b] là tập hợp tất cả các giá trị của m để phương
trình có nghiệm. Giá trị 3a + b bằng 45
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp A. 6. B. 2 − . C. 19 . D. 5. 3
Câu 40: Kí hiệu M là giá trị lớn nhất của hàm số: 4 4
y = sin x + cos x. Tìm M. 1 A. M = 2. B. M = . M = M = 2 C. 1. D. 0. π 1
Câu 41: Giải phương trình sin 2x + = . 6 2 π π
A. x = + kπ ,k ∈ . x = + k π k ∈ 6 ℤ B. 2 , . 2 ℤ π π π
C. x = + kπ x = − + kπ k ∈ = x = + kπ k ∈ 3 hoặc , . 2 ℤ D. x kπ hoặc , . 2 ℤ
Câu 42: Giải phương trình 2
2sin x + 5sin x −3 = 0. π 5π π 4π
A. x = − + k2π x = − + k2π,k ∈ . x = + k π x = + k2π ,k ∈ . 6 hoặc 6 ℤ B. 2 3 hoặc 3 ℤ π 5π π 5π
C. x = + k2π x = + k2π ,k ∈ . x = + kπ x = + kπ ,k ∈ . 6 hoặc 6 ℤ D. 6 hoặc 6 ℤ 1
Câu 43: Tìm tập xác định D của hàm số y = . sin 2 x − cos3x π k π 2 π π k π 2 π A. D = ℝ \ + ;− + k π 2 ,k ∈ℤ.
B. D = ℝ \ + ; + π
k , k ∈ ℤ. 10 5 2 10 3 2 π π 3 k π 2 π
C. D = ℝ \ + k π 2 ;− + k π 2 ,k ∈ℤ. D. D = ℝ \ ;− + k π 2 ,k ∈ℤ. 10 2 5 2
Câu 44: Giải phương trình 2 cos2x + sin x = sin3x. π π π π π π A. k k x = + x = + k π k ∈ x = + x = + kπ k ∈ 4 2 hoặc 2 , . 2 ℤ B. 4 4 hoặc , . 2 ℤ π π π π π C. k x = − + x = + k π k ∈ x = + k π x = + kπ k ∈ 4 2 hoặc 2 , . 3 ℤ D. 2 4 hoặc , . 2 ℤ 2 cos x + cot Câu 45: x Cho hai hàm số 3
f (x) = sin x − tan x và ( g x) = sin
. Mệnh đề nào dưới đây đúng ? x
A. f (x) là hàm số lẻ, g(x) là hàm số chẵn.
B. f (x) và (
g x) là hàm số chẵn.
C. f (x) là hàm số lẻ, g(x) là hàm số lẻ.
D. f (x) và g(x) là hàm số lẻ.
Câu 46: Tìm tất cả giá trị của x để hàm số 4 2
y = cos x + 4 cos x + 5 có giá trị nhỏ nhất bằng 5. π π
A. x = − + k2π ,k ∈ . x = − + kπ k ∈ 2 ℤ B. , . 2 ℤ π π
C. x = + k2π ,k ∈ . x = + kπ k ∈ 2 ℤ D. , . 2 ℤ 3
Câu 47: Giải phương trình cot x = − . 3 π π π π
A. x = + k2π ,k ∈ .
x = − + kπ k ∈ x = + kπ k ∈
x = − + kπ k ∈ 3 ℤ B. , . 3 ℤ C. , . 6 ℤ D. , . 6 ℤ
sin 2x + 2cos x − sin x −1
Câu 48: Giải phương trình = 0. tan x + 3 46
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 2π π A. x = + k2π ,k ∈ . x = + k π k ∈ 3 ℤ B. 2 , . 3 ℤ π π
C. x = + kπ ,k ∈ . x = − + k π k ∈ 3 ℤ D. 2 , . 3 ℤ
Câu 49: Tìm nghiệm âm lớn nhất của phương trình 2
2tan x + 5tan x + 3 = 0. 3π π 5π π A. x = − . x = − x = − . x = − 4 B. . 3 C. 6 D. . 4
Câu 50: Tìm số nghiệm của phương trình sin x = cos x có số nghiệm thuộc đoạn π − ;π . A. 2. B. 4. C. 5. D. 6. 2
Câu 51: Tìm tập xác định D của hàm số y = . cos x − cos3x π π
A. D = ℝ \ + kπ ,k ∈ℤ.
B. D = ℝ \ + kπ ,k ∈ℤ. 2 4 π π C. = k ℝ \ k D ,k ∈ℤ. D. D = ℝ \ ,k ∈ℤ. 3 2
Câu 52: Tìm tập nghiệm S của phương trình sin x + cos x = − 2. π π
A. S = − + kπ ,k ∈ℤ.
B. S = + kπ ,k ∈ℤ. 4 4 π π C. 3 S = −
+ k2π ,k ∈ℤ. D. 5 S =
+ k2π ,k ∈ℤ. 4 4 3
Câu 53: Gọi m và M là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y =
. Tính P = m.M 2 5 − sin x A. P = 20. B. 9 P = . C. 3 P = . D. P = 4. 20 4
Câu 54: Tìm chu kì tuần hoàn T của hàm số y = sin 3x.cos 4x. A. T = π . B. T = 3π. C. T = 2π. D. T = 4π.
Câu 55: Tìm tập nghiệm S của phương trình sin x − cos x = − 2. π π
A. S = − + kπ ,k ∈ℤ. B. 3 S = −
+ k2π ,k ∈ℤ. 4 4 π π C. 5 S =
+ k2π ,k ∈ℤ.
D. S = + k2π ,k ∈ℤ. 4 4 π
Câu 56: Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 3sin x − − 2. 6
A. Min y = 1 và Max y = 5.
B. Min y = −1 và Max y = 1. ℝ ℝ ℝ ℝ
C. Min y = −5 và Max y = 1.
D. Min y = −5 và Max y = 2. ℝ ℝ ℝ ℝ 2 + cos Câu 57: x
Tìm tập xác định D của hàm số y = . 1 + sin x
A. D = ℝ \ {kπ,k ∈ } ℤ .
B. D = (0;+∞). π
C. D = ℝ \ − + k2π ,k ∈ℤ. D. D = . ℝ 2
Câu 58: Giải phương trình sin x + 4 cos x = 2 + sin 2x. 47
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 2π π A. x = ± + k2π,k ∈ . x = ± + k π k ∈ 3 ℤ B. 2 , . 4 ℤ π π
C. x = ± + k2π ,k ∈ . x = ± + k π k ∈ 6 ℤ D. 2 , . 3 ℤ 1
Câu 59: Giải phương trình cos x = − . 2 π 2π
A. x = ± + kπ ,k ∈ . x = ± + kπ,k ∈ . 3 ℤ B. 3 ℤ π 2π
C. x = ± + k2π ,k ∈ . x = ± + k2π ,k ∈ . 3 ℤ D. 3 ℤ
Câu 60: Hàm số y = sin x đồng biến trên khoảng nào sau đây? π π π π π π π A. 7 9 ; . B. 9 11 ; . C. 7 ;3π . D. 5 7 ; . 4 4 4 4 4 4 4
Câu 61: Phương trình cos x − m = 0 vô nghiệm khi và chỉ khi m < −1 A. . B. m < 1 − . C. 1 − ≤ m ≤1. D. m > 1. m > 1 π Câu 62: k
Biết phương trình sin 3x + sin 5x = sin 4x có nghiệm x =
; x = α + k 2π ; x = β + k 2π , k ∈ . ℤ 4 Tính S = α + β. π A. 2 S = . B. S = π. C. S = 1 − . D. S = 0. 3
Câu 63: Giải phương trình 2
cos4x +12sin x −1 = 0. π π A. k x = + kπ ,k ∈ .
x = k π k ∈ x = k ∈
x = kπ k ∈ 2 ℤ B. 2 , . ℤ C. , . 3 ℤ D. , . ℤ 3 + 4cot 2 Câu 64: x
Tìm tập xác định D của hàm số y = . cos2 x −1 π A. k D = ℝ \ { } 1 . B. D = ℝ \ ,k ∈ℤ. 2 1
C. D = ℝ \ {kπ,k ∈ } ℤ .
D. D = ℝ \ . 2 π π
Câu 65: Kí hiệu m là giá trị nhỏ nhất của hàm số: y = cos 2x + − cos2x − . Tìm m. 4 4 A. m = − 2. B. m = 3 2. C. m = 2 − . D. m = 4 − .
Câu 66: Giải phương trình sin3x = cos x. π π π π π A. k x = + kπ x = + k π k ∈ x = + x = + kπ k ∈ 8 hoặc 2 , . 4 ℤ B. 8 2 hoặc , . 4 ℤ π π π
C. x = + k2π ,k ∈ . x = + k π x = − + kπ k ∈ 4 ℤ D. 2 8 hoặc , . 4 ℤ sin x + 3 cos Câu 67: x Giải phương trình = 0. sin π x − cos 4 π π
A. x = − + kπ ,k ∈ . x = + kπ k ∈ 3 ℤ B. , . 3 ℤ 48
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 2π π C. x = + k2π ,k ∈ .
x = − + k π k ∈ 3 ℤ D. 2 , . 3 ℤ π
Câu 68: Tìm tất cả giá trị của x để hàm số y = 2 cos + x + 3 có giá trị nhỏ nhất bằng 1 − . 3 2π π A. x = − + k2π ,k ∈ .
x = − + k π k ∈ 3 ℤ B. 2 , . 3 ℤ π 2π
C. x = + k2π ,k ∈ . x = + k2π ,k ∈ . 3 ℤ D. 3 ℤ
Câu 69: Cho hai hàm số f (x) = tan x và g(x) = cot x. Mệnh đề nào dưới đây đúng ?
A. g(x) là hàm số lẻ và là f (x) hàm số chẵn.
B. f (x) − g(x) là hàm số chẵn.
C. f (x) là hàm số lẻ và g(x) là hàm số chẵn.
D. f (x).g(x) là hàm số chẵn. cos4 π Câu 70: x
Tìm số nghiệm của phương trình = tan2x cos2
có số nghiệm thuộc khoảng 0; . x 2 A. 5. B. 3. C. 4. D. 2.
Câu 71: Cặp hàm số nào sau đây có cùng tập xác định ?
A. y = cos x và y = cot x.
B. y = tan x và y = sin x. + C. 2 sin
y = tan x và y = cot x.
D. y = tan x và = x y . cos x π
Câu 72: Trên khoảng − ;π x − x − = 2 . Phương trình 2 tan 2cot 3 0 có bao nhiêu nghiệm ? A. 3. B. 1. C. 2. D. 4.
Câu 73: Cho hàm số f (x) = tan x + sin .
x Mệnh đề nào dưới đây đúng ?
A. f (x) xác định khi và chỉ khi x ≠ kπ , k ∈ . ℤ
B. f (x) là hàm số lẻ.
C. f (x) tuần hoàn với chu kì T = π.
D. f (x) là hàm số chẵn.
Câu 74: Tìm số nghiệm của phương trình ( x+ 0 2 cos 3 15 ) = 3 thuộc khoảng ( 0 0 90 ;360 ). A. 3. B. 4. C. 0. D. 5.
Câu 75: Giải phương trình sin 2x − 3 cos2x = 2sin3x. π 4π π 4π k2π
A. x = − + kπ x = + k2π ,k ∈ . x = − k π x = + ,k ∈ . 3 hoặc 15 ℤ B. 2 3 hoặc 5 5 ℤ π 4π k2π π 4π k2π
C. x = − k2π x = + ,k ∈ . x = − − k π x = + ,k ∈ . 6 hoặc 15 3 ℤ D. 2 3 hoặc 15 5 ℤ
Câu 76: Giải phương trình 2
2 sin x + 7 sin x − 4 = 0. π 7π π 5π A. x = + k2π x = + k2π ,k ∈ . x = + k π x = + k2π ,k ∈ . 12 hoặc 6 ℤ B. 2 hoặc ℤ 6 6 π 5π π 5π
C. x = + kπ x = + kπ,k ∈ . x = − + k π x = − + k2π ,k ∈ . 6 hoặc 6 ℤ D. 2 6 hoặc 6 ℤ
Câu 77: Giải phương trình 3 8cos x −1= 0. 2π π π A. k x = ± + kπ ,k ∈ . x = ± + k ∈ 3 ℤ B. , . 3 2 ℤ π π
C. x = + kπ ,k ∈ . x = ± + k π k ∈ 3 ℤ D. 2 , . 3 ℤ
Câu 78: Giải phương trình 3 sin x + cos x = 2. 49
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp π π
A. x = + k2π ,k ∈ .
x = − + k π k ∈ 6 ℤ B. 2 , . 6 ℤ π π
C. x = + k2π ,k ∈ . x = + kπ k ∈ 3 ℤ D. , . 3 ℤ
Câu 79: Mệnh đề nào dưới đây đúng ? π
A. Hàm số y = 2cos x + cos x + là hàm số chẵn. 3
B. Hàm số y = cos x + x sin x có đồ thị nhận gốc tọa độ O làm tâm đối xứng. π
C. Hàm số y = 2sin x + tan x là hàm số lẻ trên khoảng 0; . 2 D. cos x Hàm số y =
có đồ thị nhận trục tung làm trục đối xứng. 4 + cos 2x
Câu 80: Tìm tập xác định D của hàm số y = 1− sin x + 1+ sin x. π
A. D = ℝ \ + kπ ,k ∈ℤ.
B. D = −1;1. 2 π C. = ℝ \ k D ,k ∈ℤ. D. D = . ℝ 2 1+ Câu 81: x
Tìm tập xác định D của hàm số y = sin . 1 − x A. D = ℝ \ { } 1 .
B. D = −1;1.
C. D = −1; ) 1 . D. D = . ℝ 3sin x − 5
Câu 82: Tìm tập xác định D của hàm số y = . cos x A. D = ℝ \ { } 0 .
B. D = ℝ \ {k2π,k ∈ } ℤ . π
C. D = ℝ \ + kπ ,k ∈ℤ.
D. D = ℝ \ {π + kπ,k ∈ } ℤ . 2
Câu 83: Trong các hàm số sau đây, hàm số nào là hàm số lẻ?
A. y = cot | x | . B. y | = tan x | . C. y = tan 2 . x D. 2 y = cot . x
Câu 84: Giải phương trình 3 3
sin x + cos x = cos x. π kπ 3π
A. x = k2π , x = − + kπ ,k ∈ . x = , x = + kπ ,k ∈ . 4 ℤ B. 2 4 ℤ π π
C. x = k2π , x = + k2π ,k ∈ .
x = kπ x = + kπ k ∈ 4 ℤ D. , , . 4 ℤ
Câu 85: Giải phương trình 3 sin 2x + cos2x = 2 cos x −1. π 2π π 2π
A. x = + kπ x = kπ , x = + k2π ,k ∈ . x =
+ k π x = k2π, x = + kπ ,k ∈ . 2 , 3 ℤ B. 2 2 , 3 ℤ π π π 2π
C. x = − + k2π x = kπ x = + k π k ∈ x =
+ kπ x = k2π , x = − + kπ ,k ∈ . 2 , , 2 , . 3 ℤ D. 2 , 3 ℤ
Câu 86: Hàm số nào sau đây là hàm số không chẵn, không lẻ ?
A. y = sin x + 2.
B. y = 2cos x +1. C. 2
y = 2 cos x − 2x .
D. y = 2sin x + . x
Câu 87: Phương trình m cos x m
= −1 có nghiệm khi và chỉ khi 1
A. m > 0. B. m ∈(−∞;0) ∪ ;+∞. C. m < 0. D. m ≥ 1 . 2 2
Câu 88: Giải phương trình cos3x + cos2x − cos x −1 = 0. 50
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp π 2π π A. k x =
+ k2π, x = k2π ,k ∈ . x = + kπ , x = ,k ∈ . 3 ℤ B. 3 2 ℤ 2π 2π C. x = ±
+ k2π , x = kπ ,k ∈ . x =
+ k2π , x = k2π ,k ∈ . 3 ℤ D. 3 ℤ
Câu 89: Giải phương trình sin3x − 3 cos3x = 2sin 2x. π 4π k2π 2π π k2π
A. x = + k2π , x = + ,k ∈ . x = − + k2π , x = + ,k ∈ . 3 5 5 ℤ B. 3 15 5 ℤ 2π 4π k2π 2π 4π π C. k x = + k2π , x = + ,k ∈ . x = + kπ , x = + ,k ∈ . 3 15 5 ℤ D. 3 15 5 ℤ π
Câu 90: Cho hai hàm số f (x) = tan 4x và (
g x) = sin x + 2 . Mệnh đề nào dưới đây đúng ?
A. f (x) là hàm số chẵn, (
g x) là hàm số lẻ.
B. f (x) và (
g x) là hàm số chẵn.
C. f (x) là hàm số lẻ, g(x) là hàm số chẵn.
D. f (x) và g(x) là hàm số lẻ. 1+ sin 2x + cos2 Câu 91: x Giải phương trình
= 2 sin x sin 2x. 2 1+ cot x π π π π
A. x = + kπ , x = + k2π ,k ∈ . x =
+ k π x = + kπ k ∈ 2 4 ℤ B. 2 , , . 2 4 ℤ 3π 3π π π C. x = + kπ, x = + k2π ,k ∈ . x = −
+ k π x = + kπ k ∈ 2 4 ℤ D. 2 , , . 2 3 ℤ
Câu 92: Cho hai hàm số f (x) = sin 2x và (
g x) = cos3x . Mệnh đề nào dưới đây đúng ?
A. f (x) và (
g x) là hàm số chẵn.
B. f (x) là hàm số chẵn, (
g x) là hàm số lẻ.
C. f (x) và (
g x) là hàm số lẻ.
D. f (x) là hàm số lẻ, g(x) là hàm số chẵn. 2 Câu 93: x x
Giải phương trình sin + cos + 3 cos x = 2. 2 2 π π π π
A. x = + k2π , x = − + k2π ,k ∈ . x =
+ kπ x = − + kπ k ∈ 2 6 ℤ B. , , . 2 6 ℤ π π π π
C. x = − + kπ , x = + kπ ,k ∈ . x =
+ k π x = − + k π k ∈ 2 6 ℤ D. 2 , 2 , . 4 3 ℤ
Câu 94: Phương trình 5cos x − msin x = m +1 có nghiệm khi và chỉ khi A. m ≤ 24. B. m ≤12. C. m ≥ 24. D. m ≤ 1 − 3.
Câu 95: Nếu xét trên khoảng (0;2π ) . Trên những khoảng nào thì hàm y = sin x và y = cos x cùng đồng biến ? π 3π 3π A. ;π . B. ;2π . C. 0; . D. (π;2π ). 2 2 2
Câu 96: Nghiệm của phương trình 2sin x +1 = 0 được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào? y
A. Điểm E , điểm . D B B. D C
Điểm D , điểm C. ′ A A
C. Điểm C , điểm F. x O E F
D. Điểm E , điểm F. ′ B 51
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
Câu 97: Kí hiệu m là giá trị nhỏ nhất của hàm số: 4 4
y = sin x − cos x. Tìm m. A. m = 2 − . B. m = 1 − . C. m = 3 − . D. m = 4.
Câu 98: Tìm chu kì tuần hoàn T của hàm số y = sin (ax + b). π 2π 2π A. T = . B. T = 2π. C. T = . D. T = . a a a π Câu 99: x
Tìm tất cả giá trị của x để hàm số y = 2sin + − 3 có giá trị nhỏ nhất bằng 5 − . 2 5 13π π A. x = − + k4π ,k ∈ . x = + k π k ∈ 5 ℤ B. 4 , . 5 ℤ 13π 13π C. x = + k4π,k ∈ . x = + k2π,k ∈ . 5 ℤ D. 5 ℤ
Câu 100: Với giá trị nào của hằng số A và của hằng số α thì hàm số y = Asin(x +α) là 1 hàm số lẻ. π kπ
A. A ≠ 0,α = + kπ ,k ∈ . ℤ B. A > 0,α = , k ∈ . ℤ 2 2 kπ
C. A ≠ 0,α = kπ , k ∈ . ℤ D. A ≠ 0,α = , k ∈ . ℤ 2 2π
Câu 101: Kí hiệu m là giá trị nhỏ nhất của hàm số: y = sin x + sin x + . Tìm m. 3 3 A. m = 1 − . B. m = 2 − . C. m = . m = 2 D. 0.
Câu 102: Tìm nghiệm dương nhỏ nhất của phương trình 2
sin x + sin2x = cos x + 2cos x. π π π π A. x = . x = x = x = 4 B. . 6 C. . 3 D. . 2
Câu 103: Số giá trị nguyên dương của tham số m để phương trình 4 3 cos x + sin x + 2m −1 = 0 có nghiệm là A. 3. B. 5. C. 4. D. 6. π
Câu 104: Tìm tập xác định D của hàm số y = tan2x + . 5 π π 3π A. = ℝ \ k D − + ,k ∈ℤ. B. D = ℝ \
+ kπ ,k ∈ℤ. 20 2 5 3π π 3π C. = ℝ \ k D + ,k ∈ℤ. D. D = ℝ \
+ k2π ,k ∈ ℤ. 20 2 2
Câu 105: Cho phương trình: cos 2x + sin x −1 = 0 (*) . Bằng cách đặt t = sin x ( 1 − ≤ t ≤ ) 1 thì phương
trình (*) trở thành phương trình nào sau đây? A. 2 −2t + t = 0. B. 2
t + t − 2 = 0. C. 2
−2t + t − 2 = 0. D. 2 −t + t = 0. 3tan x − 2
Câu 106: Tìm tập xác định D của hàm số y = . 1+ sin x π π
A. D = ℝ \ − + k2π ,k ∈ℤ.
B. D = ℝ \ + kπ ,k ∈ℤ. 2 2
C. D = ℝ \ {π + kπ,k ∈ } ℤ .
D. D = ℝ \ {kπ,k ∈ } ℤ . π
Câu 107: Tìm số nghiệm của phương trình sin x + = 1 thuộc đoạn π ;2 π . 4 52
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp A. 1 B. 0 C. 2 D. 3 Câu 108: 1
Tập xác định D của hàm số y = là sin x − cos x π
A. D = ℝ \{kπ | k ∈ } Z .
B. D = ℝ \ + kπ | k ∈Z. 2 π
C. D = ℝ \ + kπ | k ∈Z.
D. D = ℝ \{k2π | k ∈ } Z . 4
Câu 109: Mệnh đề nào dưới đây sai ?
A. Hàm số y = sin x và y = tan x là các hàm số lẻ.
B. Hàm số y = tan x và y = cot x có cung chu kì là π.
C. Hàm số y = sin x và y = cos x có cùng tập xác định.
D. Hàm số y = cos x và y = cot x là các hàm số chẵn.
Câu 110: Hàm số y = sin x đồng biến trên khoảng nào dưới đây ? 15π 7π 19π A. 7π; . B. − ; 3 − π . C. ;10π . D. (−6π;−5π ). 2 2 2
Câu 111: Hàm số y = cos x nghịch biến trên khoảng nào dưới đây ? 11π 19π 3π π 11π A. − ; 5 − π . B. ;10π . C. − ; . D. ;7π . 2 2 2 2 2 Câu 112: sin 3x
Số nghiệm của phương trình
= 0 thuộc đoạn [2π;4π ] là cos x +1 A. 6. B. 4. C. 5. D. 6. π
Câu 113: Tìm chu kì tuần hoàn T của hàm số y = cos5x − . 4 π 2π A. T = . T = π T = . T = π 5 B. 5 . C. 5 D. 10 .
Câu 114: Nếu xét trên khoảng (0;2π ) . Trên những khoảng nào thì hàm y = sin x và y = cos x cùng nghịch biến ? 3π 3π π A. 0; . B. ;2π . C. (π;2π ). D. ;π . 2 2 2 1
Câu 115: Giải phương trình sin x = . 2 π π 5π 5π
A. x = − + k2π x = + k π k ∈ x = + kπ x = − + k2π ,k ∈ . 6 hoặc 2 , . 6 ℤ B. 6 hoặc 6 ℤ π 5π π 5π
C. x = + kπ x = + kπ ,k ∈ . x = + k π x = + k2π ,k ∈ . 6 hoặc 6 ℤ D. 2 6 hoặc 6 ℤ π π
Câu 116: Số nghiệm nằm trong đoạn − ; của phương trình sin5x + sin3x = sin 4x là 2 2 A. 9. B. 7. C. 5. D. 3.
Câu 117: Mệnh đề nào dưới đây sai ?
A. Hàm số y = cot x nghịch biến trên khoảng (0;π ). π
B. Hàm số y = sin x đồng biến trên khoảng 0; . 2
C. Hàm số y = cos x đồng biến trên khoảng( π − ;0). 53
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp π π
D. Hàm số y = tan x nghịch biến trên khoảng − ; . 2 2 Câu 118: x
Tìm chu kì tuần hoàn T của hàm số 2 y = cos . 2 π A. T = 8π. B. T = 4π. C. T = 2π. D. T = . 2 sin3 Câu 119: x
Tìm tập xác định D của hàm số y = . cot x π k A. D = ℝ \ ,k ∈ℤ.
B. D = ℝ \ {k π 2 ,k ∈ } ℤ . 2 π
C. D = ℝ \ + π
k , k ∈ ℤ.
D. D = ℝ \ { π k , k ∈ } ℤ . 2 tan Câu 120: x
Tìm tập xác định D của hàm số y = . 1 − cos2x π k A. D = ℝ \ ,k ∈ℤ.
B. D = ℝ \ {k π 2 ,k ∈ } ℤ . 2 π k
C. D = ℝ \ {π + k π 2 ,k ∈ } ℤ . D. D = ℝ \ ,k ∈ℤ. 4
Câu 121: Chu kì tuần hoàn T của hàm số y = sin 3x.cos3x. π A. T = 6π. B. T = 3π. C. T = . T = π 3 D. 2 . π
Câu 122: Xét trên khoảng 0; , hàm số nào dưới đây đồng biến ? 2
A. y = 3− 2sin . x
B. y = sin x + 3. C. 2 y = 2 − sin . x
D. y = tan x + 2. π
Câu 123: Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số y = 2 sin x − +1. Tính 4 P = M . . m A. P = 1 − . B. P = 2. C. P = 2 − . D. 1 P = . 2 5x 3 Câu 124: x Giải phương trình 4 cos cos + 2(8sin x − ) 1 cos x = 5. 2 2 5π k2π 5π π π 5π A. k x = + x = + ,k ∈ . x = − + k π x = + k2π ,k ∈ . 6 3 hoặc 12 3 ℤ B. 2 12 hoặc 12 ℤ π 5π π 5π C. x = + kπ x = + kπ;k ∈ . x = + k π x = + k2π ,k ∈ . 12 hoặc 12 ℤ D. 2 12 hoặc 12 ℤ tan x + cot Câu 125: x
Tìm tập xác định D của hàm số y = . 1 − sin 2x 1
A. D = ℝ \ . B. D = ℝ \ { } 1 2 kπ π π
C. D = ℝ \
∪ + kπ ; k ∈ ℤ .
D. D = ℝ \ + kπ ,k ∈ℤ. 2 4 4 1
Câu 126: Tìm tập xác định D của hàm số y = + cot x. sin x 54
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp π k A. D = ℝ \ ,k ∈ℤ.
B. D = ℝ \ { π k , k ∈ } ℤ . 2 π k π 2
C. D = ℝ \ + π
k , k ∈ ℤ. D. D = ℝ \ ,k ∈ℤ. 2 3 π Câu 127: cos 4x
Số nghiệm của phương trình
= tan 2x thuộc khoảng 0; là cos 2x 2 A. 3. B. 2. C. 4. D. 5. π
Câu 128: Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 3sin x + − 2. Tìm 3
S = M + m. A. S = 4 − . B. S = 5 − . C. S = 1. D. S = 6. 1 1
Câu 129: Tìm tập xác định D của hàm số y = + . sin x cos x A. D = ℝ \ { } 0 .
B. D = ℝ \ {kπ,k ∈ } ℤ . π π C. k
D = ℝ \ + kπ ,k ∈ ℤ. D. D = ℝ \ ,k ∈ℤ. 2 2
Câu 130: Giải phương trình 2
3 tan x − (1+ 3)tan x +1= 0. π π π π
A. x = + kπ x = + kπ k ∈ x = + kπ x = + kπ k ∈ 3 hoặc , . 6 ℤ B. 4 hoặc , . 6 ℤ π π π π
C. x = + k2π x = + k π k ∈ x = − + kπ
x = − + kπ k ∈ 4 hoặc 2 , . 6 ℤ D. 4 hoặc , . 6 ℤ
Câu 131: Số vị trí biểu diễn các nghiệm của phương trình 2
4 cos x − 4 cos x − 3 = 0 trên đường tròn lượng giác là A. 1. B. 0. C. 2. D. 4.
Câu 132: Số nghiệm của phương trình 2
2sin x + 5sin x − 3 = 0 thuộc khoảng (0; 2018π ) là A. 4035. B. 2018. C. 4036. D. 4034. 3
Câu 133: Giải phương trình cos x = − . 2 π 5π
A. x = ± + kπ ,k ∈ . x = ± + k2π ,k ∈ . 6 ℤ B. 6 ℤ 5π π C. x = ± + kπ ,k ∈ . x = ± + k π k ∈ 6 ℤ D. 2 , . 6 ℤ
Câu 134: Kí hiệu M là giá trị lớn nhất của hàm số: 4 4
y = sin x − cos x. Tìm M. A. M = 2. B. M = 2. C. M = 1 − . D. M = 1.
Câu 135: Số nghiệm của phương trình tan x = − 3 thuộc khoảng ( 2 − 017π; 2017π ) là A. 4034. B. 2017. C. 4033. D. 4035.
Câu 136: Phương trình sin x − m =1 có nghiệm khi và chỉ khi A. m ≤ 0. B. 2 − ≤ m ≤ 0. C. m ≥1.
D. 0 ≤ m ≤1.
Câu 137: Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 2(1+ cos x) +1.
A. Min y = 2 và Max y = 3.
B. Min y = 1 và Max y = 3. ℝ ℝ ℝ ℝ
C. Min y = −3 và Max y = 1.
D. Min y = −1 và Max y = 3. ℝ ℝ ℝ ℝ 55
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp cos2 sin x − cos3x Câu 138: x
Cho hai hàm số f (x) = và g(x) =
. Mệnh đề nào dưới đây đúng ? 2 1+ sin 3x 2 2 + tan x
A. f (x) là hàm số chẵn, (
g x) là hàm số lẻ.
B. f (x) và (
g x) là hàm số chẵn.
C. f (x) là hàm số lẻ, g(x) là hàm số chẵn.
D. f (x) và g(x) là hàm số lẻ.
Câu 139: Cho phương trình 2 2
sin x = m − 4 . Gọi [a;b]∪[ ;
c d ] (a < b < c < d ) là tập hợp tất cả các giá trị
của m để phương trình có nghiệm. Giá trị 2 2
a + b + c + d bằng A. 12. B. 10. C. 8. D. 14. Câu 140: Gọi ( ;
a b) là tập hợp tất cả các giá trị của của m để phương trình msin 2x − 4cos 2x = 6 − vô nghiệm. Giá trị . a b bằng A. 52. B. 2 − 0. C. 20. D. 52. Câu 141: Gọi [ ;
a b] là tập hợp tất cả các giá trị của của m để phương trình msin 4x − 2cos 4x = 2m −1 có nghiệm. Giá trị của 2 2 a + b bằng A. 34 . B. 43 . C. 22 . D. 14 . 9 18 9 9 2 − cos Câu 142: x
Tìm tập xác định D của hàm số y = . 1+ tan π x − 3 5π π A. D = ℝ \
+ kπ ,k ∈ ℤ. B. D = ℝ \
+ kπ ,k ∈ℤ. 6 12 5π π
C. D = ℝ \
+ kπ ∪ + kπ ;k ∈ℤ.
D. D = ℝ \ {− } 1 . 6 12
Câu 143: Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình ( π 3π 2
2 m +1− sin x) − (4m + )
1 cos x = 0 có nghiệm thuộc khoảng ; . 2 2 A. 1 − ;0 . B. 1 − ; ∞ − . C. 1 − ;0 . D. (0;+∞). 2 2 2
Câu 144: Số giá trị nguyên của tham số m để phương trình 4 3 cos x + sin x + 2m −1 = 0 có nghiệm là A. 6. B. 8. C. 9. D. 7.
Câu 145: Hàm số nào dưới đây có tập xác định là . ℝ 1 2 cos x − 5
A. y = sin x + .
B. y = cot x + 2x.
C. y = tan x + cot x. D. y = . x 3sin x − 4
Câu 146: Kí hiệu M là giá trị lớn nhất của hàm số y = sin x + cos x. Tìm M. A. M = 2 2. B. M = 1. C. M = − 2. D. M = 2.
Câu 147: Tìm tập nghiệm S của phương trình sin x − cos x = 2. π π
A. S = − + kπ ,k ∈ℤ. B. 3 S =
+ kπ ,k ∈ℤ. 4 4 π π
C. S = + k2π ,k ∈ℤ. D. 3 S = −
+ k2π ,k ∈ℤ. 4 4 Câu 148: Gọi + − = . Khẳng 0
x là nghiệm dương nhỏ nhất của phương trình 2 2
3sin x 2sin x cos x cos x 0
định nào dưới đây đúng? π π π π A. 3 3 x ∈ ; 2π .
B. x ∈ ; π .
C. x ∈ 0; . D. x ∈π; . 0 2 0 2 0 2 0 2 56
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp
Câu 149: Giá trị nhỏ nhất của hàm số của hàm số 2
y = 1+ 2 sin x cos x − cos 2x là: A. 1 − . B. 5 − . C. 1 − . D. 0. 4 4
Câu 150: Cho x là nghiệm của phương trình sin x cos x + 2(sin x + cos x) = 2 thì giá trị của 0 π P = sin x + là 0 4 A. P =1. B. 2 P = . C. 1 P = . D. 2 P = − . 2 2 2 2
Câu 151: Giải phương trình cos( 0 3x − 60 ) = . 2 A. 0 0 x = 35 + 1 k 80 hoặc 0 0 x = 5 + 1 k 80 , k ∈ . ℤ B. 0 0
x = 35 + k360 hoặc 0 0
x = 5 + k360 ,k ∈ . ℤ C. 0 0 x = 35 + 1 k 20 hoặc 0 0 x = 5 + 1 k 20 , k ∈ . ℤ D. 0 0
x = 35 + k60 hoặc 0 0
x = 5 + k60 ,k ∈ . ℤ
Câu 152: Giải phương trình 3 3
sin x + cos x = sin x − cos x. π 3π
A. x = − + kπ ,k ∈ . x = + k2π ,k ∈ . 2 ℤ B. 2 ℤ π π
C. x = + k2π ,k ∈ . x = + kπ k ∈ 2 ℤ D. , . 2 ℤ 2π
Câu 153: Giải phương trình tan 4x − = 3. 3 A. 0 0 x = 45 + 1 k 80 , k ∈ . ℤ B. 0 0 x = 180 + 1 k 80 , k ∈ . ℤ C. 0 0
x = 45 + k45 ,k ∈ . ℤ D. 0 0
x = 60 + k180 ,k ∈ . ℤ
Câu 154: Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 2 cos x +1.
A. Min y = 1 và Max y = 3.
B. Min y = −1 và Max y = 3. ℝ ℝ ℝ ℝ
C. Min y = −3 và Max y = 1.
D. Min y = −3 và Max y = 3. ℝ ℝ ℝ ℝ
Câu 155: Tổng tất cả các giá trị nguyên của m để phương trình 4sin x + (m − 4)cos x − 2m + 5 = 0 có nghiệm là A. 10. B. 5. C. 6. D. 3. Câu 156: x
Gọi X là tập nghiệm của phương trình 0
cos +15 = sin x . Mệnh đề nào dưới đây đúng? 2 A. 0 220 ∈ X. B. 0 200 ∈ X. C. 0 240 ∈ X. D. 0 290 ∈ X.
Câu 157: Giải phương trình 2 (sin x − 2cos x) = 2 −sin2x. 5π π A. x = ± + k2π ,k ∈ . x = ± + kπ k ∈ 4 ℤ B. , . 4 ℤ 3π 3π C. x = ± + k2π ,k ∈ . x = ± + kπ,k ∈ . 4 ℤ D. 4 ℤ
Câu 158: Giải phương trình sin x + 3 cos x = 2 − . π 5π
A. x = − + k2π ,k ∈ . x = − + k2π,k ∈ . 6 ℤ B. 6 ℤ π 5π
C. x = + k2π ,k ∈ . x = + kπ ,k ∈ . 6 ℤ D. 6 ℤ 57
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp π
Câu 159: Tìm tất cả giá trị của x để hàm số y = 2 cos + x + 3 có giá trị lớn nhất bằng 5. 3 π 2π
A. x = + k2π ,k ∈ . x = − + k2π,k ∈ . 3 ℤ B. 3 ℤ π 2π
C. x = − + k2π ,k ∈ . x = + k2π ,k ∈ . 3 ℤ D. 3 ℤ 3π
Câu 160: Cho hai hàm số f (x) = x − sin x và g(x) = 1+ cos x.sin − 2x 2
.Mệnh đề nào dưới đây đúng?
A. f (x) là hàm số chẵn, (
g x) là hàm số lẻ.
B. f (x) và (
g x) là hàm số chẵn.
C. f (x) và (
g x) là hàm số lẻ.
D. f (x) là hàm số lẻ, g(x) là hàm số chẵn.
Câu 161: Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 3 − 2sin x.
A. Min y = −5 và Max y = 1.
B. Min y = −1 và Max y = 5. ℝ ℝ ℝ ℝ
C. Min y = −5 và Max y = −1.
D. Min y = 1 và Max y = 5. ℝ ℝ ℝ ℝ
Câu 162: Trong bốn hàm số: (1) y = cos2x , (2) y = sin x ; (3) y = tan 2x ; (4) y = cot 4x có mấy hàm số
tuần hoàn với chu kỳ π ? A. 1. B. 0 . C. 2 . D. 3 . π Câu 163: 5
Hàm số nào dưới đây đồng biến trên khoảng 0; ? 6 π π
A. y = sin x − . B. y = cos . x C. y = sin . x
D. y = sin x + . 3 3
Câu 164: Đường cong trong hình dưới đây là đồ thị của một hàm số nào dưới đây? A. y = cos . x B. y =1− sin . x C. y = sin . x D. y = 1+ cos . x 2 cos x − 5
Câu 165: Tìm tập xác định D của hàm số y = . 3sin x − 4 π A. = ℝ \ k D ,k ∈ℤ. B. D = . ℝ 2 4
C. D = ℝ \ {kπ,k ∈ } ℤ .
D. D = ℝ \ 3 Câu 166: x π
Trên khoảng (π;8π ) . Phương trình cos + = 0 có bao nhiêu nghiệm ? 2 4 A. 3. B. 1. C. 2. D. 4. 58
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 A B C D
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 A B C D
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 A B C D
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 A B C D 1 1 1 1 1 1 1 1 1 1 1
112 113 114 115 116 117 118 119 120 0 0 0 0 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 1 A B C D 1 1 1 1 1 1 1 1 1 1 1
132 133 134 135 136 137 138 139 140 2 2 2 2 2 2 2 2 2 3 3 1 2 3 4 5 6 7 8 9 0 1 A B C D 59
Chương I. HSLG & PTLG Phần Tự Luận
Tài liệu học tập Toán 11 GV. Lư Sĩ Pháp 1 1 1 1 1 1 1 1 1 1 1
152 153 154 155 156 157 158 159 160 4 4 4 4 4 4 4 4 4 5 5 1 2 3 4 5 6 7 8 9 0 1 A B C D
161 162 163 164 165 166 A B C D 60
Chương I. HSLG & PTLG Phần Tự Luận




