Tài liệu Ôn thi Định luật Coulomb và Điện trường môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Câu 1: Nêu nội dung định luật Coulomb. Định nghĩa điện trường. Nêu đặc
điểm của véc tơ cường độ điện trường. Phát biểu nguyên lí chồng chất điện trường.
* Nội dung định luật Coulomb:
Lực tương tác tĩnh điện giữa hai điện tích điểm q1 và q2 đặt cách nhau một khoảng r:
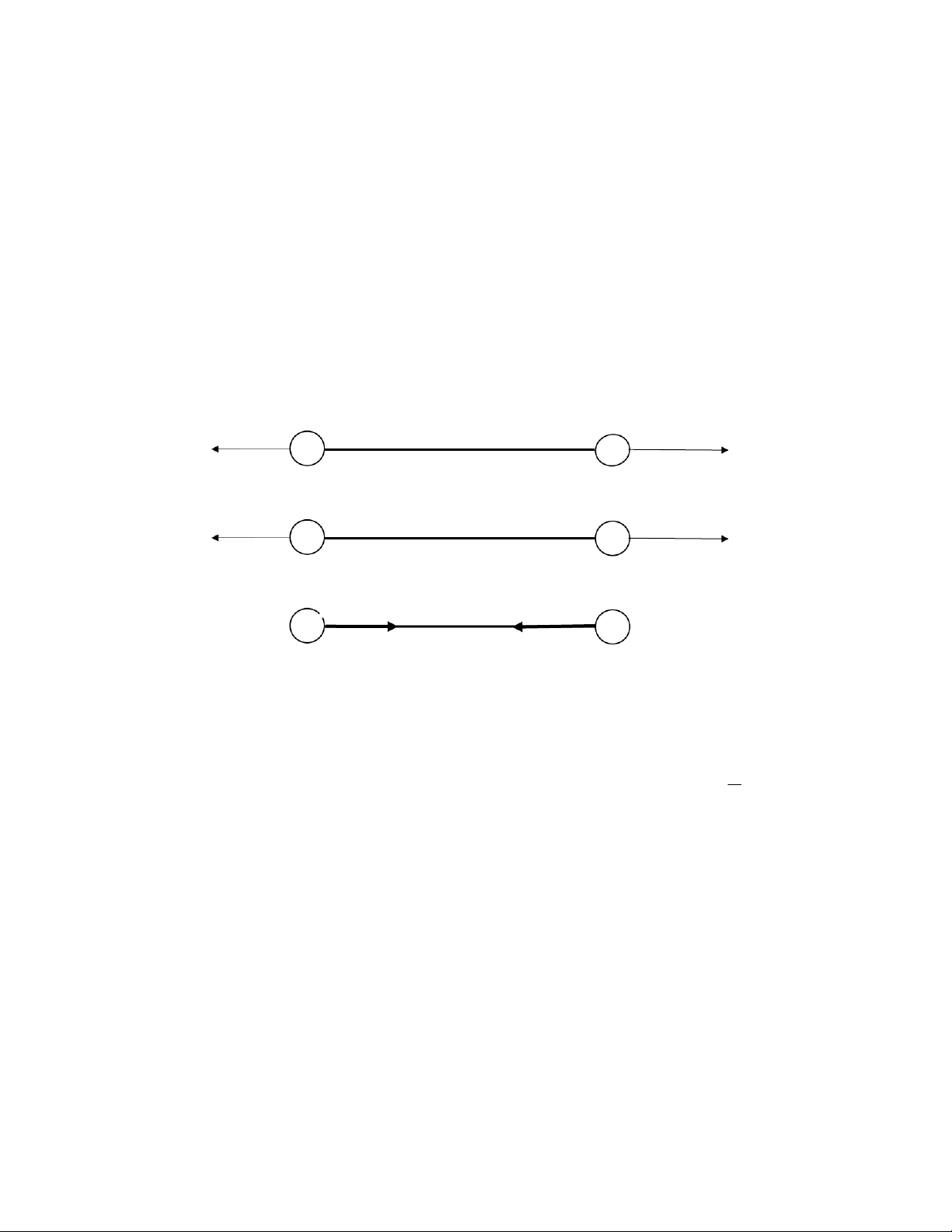
- Có phương nằm trên đường thẳng nối q1 và q2
- Có chiều như hình 1a khi q1, q2 cùng dấu, hoặc có chiều như hình 1b khi q1, q2 trái dấu
- Có độ lớn tỉ lệ thuận với tích các độ lớn của hai điện tích và tỉ lệ nghịch với bình phương khoảng cách r
- Phụ thuộc vào môi trường xung quanh. a)   F1 + + F2 r   F1 - - F2 r b) +   F F 1 2 - r Hình 1
* Định nghĩa điện trường
- Đặt một điện tích điểm q0 tại một điểm M trong khoảng không gian có điện
trường. Trên q0 xuất hiện lực điện  tác dụng. Thực nghiệm chứng tỏ rằng, tỉ số F F q0
là một đại lượng không phụ thuộc q0 mà chỉ phụ thuộc vào các điện tích gây ra
điện trường và vị trí điểm M. Theo định nghĩa, đại lượng này được gọi là véc tơ
điện trường tại M, ký hiệu là:   (V/m) E= F q0
* Đặc điểm của véc tơ cường độ điện trường
- Phương: cùng phương với lực tĩnh điện F
- Chiều : +Hướng ra xa điện tích nếu q0 > 0
+Hướng lại gần điện tích nếu q0 < 0 E=1 - Độ lớn: | | q r2 4π ε0ε
* Nguyên lí chồng chất điện trường:
- Véc tơ điện trường tại điểm M do một hệ n điện tích điểm gây ra bằng tổng hợp
các véc tơ điện trường do từng điện tích điểm gây ra tại M E=∑  n Ei i=1
Câu 2: Phát biểu và chứng minh định lý Ostrogradski – Gauss (Định luật Gauss)
* Phát biểu định lí Ostrogradski-Gauss:
Điện thông qua một mặt kín S bằng tổng đại số các điện tích chứa bên trong mặt
kín S đó( với quy ước chọn chiều pháp tuyến dương hướng ra ngoài S)
* Chứng minh định lý Gauss
a) Điện thông xuất phát từ một điện tích điểm q
- Cho một điện tích điểm q đặt tại vị trí O cố định: trong khoảng không gian xung
quanh q tồn tại điện trường của q
Xét một diện tích vi phân dS và gọi là véc tơ pháp tuyến dương (độ dài đơn vị) n
của dS, có chiều hướng ra ngoài O. Tại một điểm M của dS (OM=r) véc tơ điện
cảm D có phương nằm theo OM= r, có chiều từ O đi ra nếu q>0, đi vào O nếu q<0 và có độ lớn: D= | 1 q| 4π r2
Điện thông qua diện tích vi phân dS cho bởi:
|q| dScosα
dϕe=DdScosα= 4π r2
hay theo định nghĩa góc khối: |q| dϕe= 4πdΩ
dΩ là góc khối từ O nhìn dS, ta có thể viết:
dϕe=q4πdΩ
b) Bây giờ ta tính điện thông đi qua một mặt kín S bao quanh q: điện
thông ấy tính bằng tích phân dϕe=q ϕ dΩ e=∫ 4π∫ tích phân theo toàn mặt S S
kín S bao quanh O với quy ước pháp tuyến dương hướng ra ngoài S,
trong điều kiện ấy ta có: ∫ dΩ=4π S
Vậy điện thông qua mặt kín S (với quy ước pháp tuyến dương hướng ra
ngoài S) do điện tích q chứa trong S gây ra có giá trị: ϕe=q
c) Trong trường hợp điện tích q nằm ngoài mặt kín S, điện thông qua S cho bởi:
ϕe=q4π∫ dΩ S
Ta dựng mặt nón đỉnh O tiếp xúc với mặt kín S, đường tiếp xúc của mặt
nón ấy với S chia S thành 2 phần S1 và S2. Khi đó tích phân góc khối đối
với S tách tổng thành 2 tích phân:
∫dΩ=∫ dΩ+∫dΩ S S1 S2
với quy ước chọn chiều pháp tuyến dương tại một điểm trên S luôn hướng ra ngoài S. Ta có:
∫dΩ=+ΔΣ;∫ dΩ=−ΔΣ S1 S2
Với ΔΣ là phần diện tích của mặt cầu (tâm O, bán kính r=1) nằm trong
hình nón tiếp xúc nói trên. Cuối cùng ta được điện thông ϕequa S: q ϕe=¿ (ΔΣ−ΔΣ )=0 4π
d) Kết luận: điện thông qua một điện tích q gây ra qua mặt kín S có giá
trị bằng q nếu q ở trong mặt kín S và bằng 0 nếu q ở ngoài mặt kín S
(với quy ước chọn chiều pháp tuyến dương hướng ra ngoài S).
Câu 3: Chứng minh tính chất thế của điện trường tĩnh. Trình bày mối liên hệ
giữa cường độ điện trường và điện thế.
* Chứng minh tính chất thế của điện trường tĩnh:
a) Công của lực tĩnh điện
- Giả sử điện tích điểm q0 dịch chuyển trong điện trường của một điện tích điểm q.
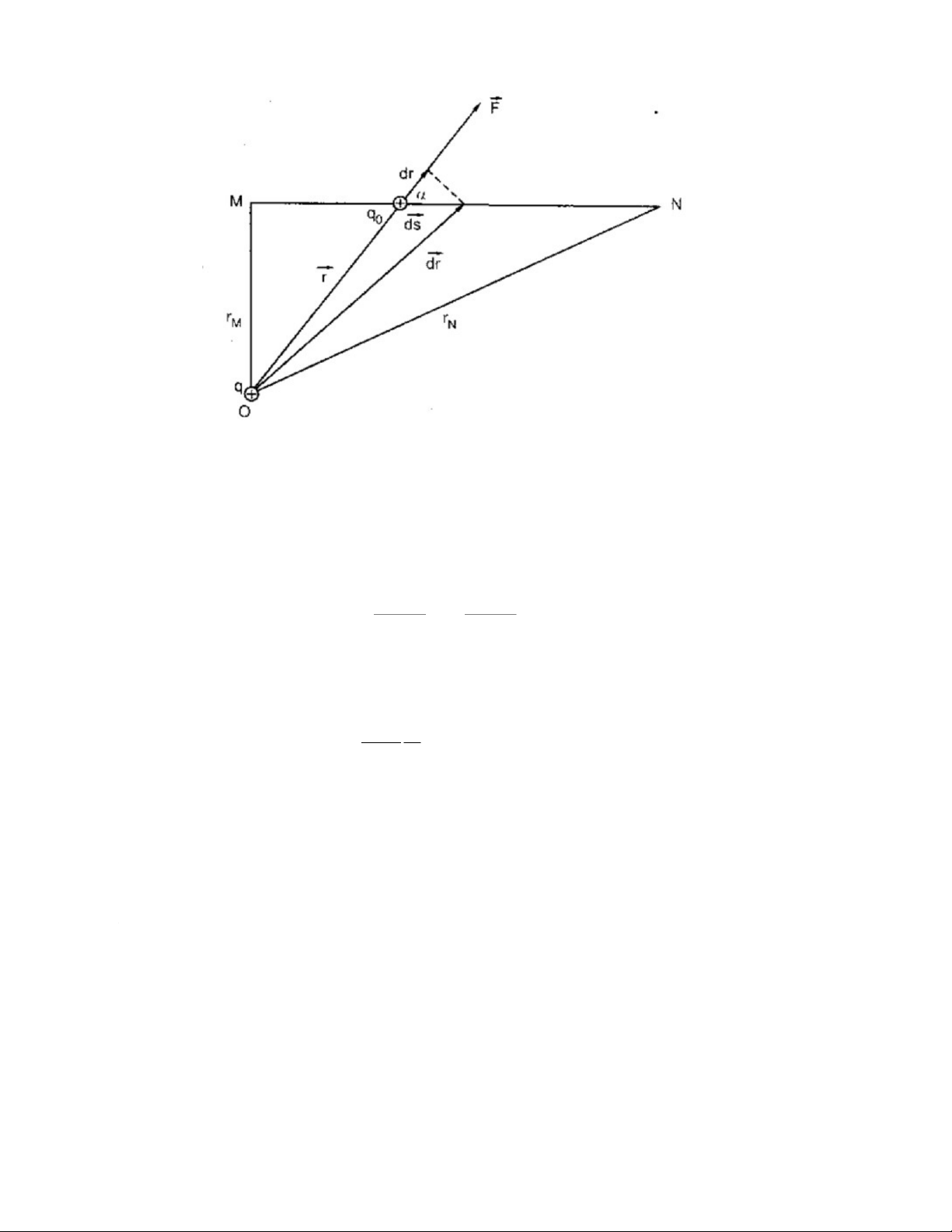
Ta sẽ tính công của lực tĩnh điện trong sự dịch chuyển điện tích q0 từ điểm M đến
điểm N trên một đường cong bất kì (hình vẽ) ứng với trường hợp q và q0 là điện tích dương
Ta có công thức lực tác dụng lên điện tích q  
0 bằng: F=q0 E
Công của lực tĩnh điện trong chuyển dời vô cùng nhỏ ds bằng: d A=  Fd  s=q  0 Ed  s q
hay: dA=q0
rd s=q0q
4πε 0ε r 2dscosα 4πε0εr3
trong đó α là góc giữa véc tơ bán kính r và ds. Từ hình vẽ ta thấy rằng ds
cosα = hình chiếu của ds lên véc tơ bán kính r. Có độ lớn xấp xỉ bằng dr ~ ds cosα: d  r
d A=q0q 4πε r 0ε 2
Vậy công của lực tĩnh điện trong sự chuyển dời điện tích q0 từ M đến N là: N rNq0q  d  r A q0 Ed  MN=∫
s=∫ 4πε0ε r2 M rM r rN A Nd MN=q0q r  r 2=q0q 4πε [−1] 0ε∫ 4πε0ε r rM rM A q0q MN=q0q - (*) 4πε0εrM 4πε0εr N
Công thức (*) chứng tỏ rằng: công của lực tĩnh điện trong sự dịch
chuyển điện tích q0 trong điện trường của một điện tích điểm không phụ
thuộc vào dạng của đường cong dịch chuyển mà chỉ phụ thuộc vào vị trí
điểm đầu và điểm cuối của chuyển dời.
Dễ dàng thấy (*) vẫn đúng khi q0 và q có dấu bất kì
b) Tính chất thế của trường tĩnh điện
Theo kết quả trên, nếu ta dịch chuyển q0 theo một đường cong kín bất kì
thì công của lực tĩnh điện trong dịch chuyển đó sẽ bằng 0 (vì khi đó
điểm cuối trùng với điểm đầu). Vậy trường tĩnh điện là một trường thế
* Mối liên hệ giữa cường độ điện trường và điện thế
Điện thế tại một điểm M trong điện trường bất kỳ có biểu thức: ∞ V Ed s M=∫M
Câu 4: Nêu định nghĩa và các tính chất của mặt đẳng thế. Trình bày mối liên
hệ giữa cường độ điện trường và hiệu điện thế.
*) Định nghĩa mặt đẳng thế:
Mặt đẳng thế là quỹ tích những điểm có cùng điện thế
*) Tính chất của mặt đẳng thế
- Các mặt đẳng thế không cắt nhau, vì tại mỗi điểm có một giá trị xác định của điện thế
- Công của lực điện trong sự dịch chuyển điện tích q0 trên một mặt đẳng thế bằng 0
- Véc tơ điện trường tại một điểm luôn trực giao với mặt đẳng thế đi qua điểm ấy,
có chiều là chiều giảm điện thế và có độ lớn bằng độ giảm điện thế trên đơn vị độ
dài dọc theo đường sức.
*) Mối liên hệ giữa cường độ điện trường và hiệu điện thế
Như ta đã biết, công của lực tác dụng lên điện tích điểm q0 khi điện tích
này chuyển dời từ điểm A đến điểm B trong điện trường cho bởi: B B B A Fd  q0  Ed  ∫ Ed s AB=∫ s=∫ s=q0 A A A Mặt khác:
AAB=q0(VA−VB) B Vậy: q0 (V 
A−VB )=q ∫ Ed  s 0 A
Từ đó suy ra công thức tính hiệu điện thế theo véc tơ điện trường: B V Ed s
A−VB=∫A
Câu 5: Nêu điều kiện cân bằng tĩnh điện và tính chất của vật dẫn tích điện.
Nêu định nghĩa và công thức tính điện dung của vật dẫn cô lập.
*) Điều kiện cân bằng tĩnh điện của vật dẫn tích điện:
Một vật dẫn tích điện được gọi là (ở trạng thái) cân bằng (về điện) khi các điện tích
trong vật dẫn ấy không chuyển động (để tạo thành dòng điện). Để cho một vật dẫn
tích điện cân bằng, điều kiện cần là điện trường bên trong vật dẫn ấy phải bằng 0: Etrong= 0
*) Tính chất của vật dẫn tích điện:
- Vật dẫn tích điện cân bằng là một khối đẳng thế
- Khi vật dẫn tích điện cân bằng, điện tích chỉ phân bố trên bề mặt vật dẫn
- Nếu trong vật dẫn tích điện cân bằng có những lỗ rỗng thì ta kết luận rằng:
+ Điện trường trong lỗ rỗng và ở thành lỗ rỗng bằng 0
+ Không có điện tích ở trong lỗ rỗng và trên thành lỗ rỗng
- Một vật dẫn rỗng hay đặc nếu được giữ ở trạng thái có điện thế luôn không đổi
(chẳng hạn bằng cách nối vật ấy với đất) thì cũng có thể coi là ở trạng thái tích điện
cân bằng cân bằng, và khi đó: Etrong=−grad V= 0
à Hệ quả: Một vật dẫn rỗng nếu được nối đất thì điện trường bên trong lỗ rỗng
luôn bằng 0. Một vật dẫn khác nằm trong lỗ rỗng sẽ không bị ảnh hưởng bởi điện trường ngoài.
à Như vậy: Vật dẫn nối đất có tác dụng triệt tiêu ảnh hưởng của điện trường ngoài
đối với các vật dẫn bên trong.Các vật rỗng như vậy được gọi là màn điện
*) Định nghĩa và công thức tính điện dung của vật dẫn cô lập
Khi một vật dẫn ở xa các vật dẫn khác ta gọi vật dẫn đó là vật dẫn cô lập.
- Định nghĩa điện dung của vật dẫn cô lập: Tỷ số không đổi giữa điện tích và điện
thế của một vật dẫn cô lập được gọi là điện dung của vật dẫn ấy. - Công thức: C=q V