Thông tin
Quiz

Tài liệu tự học hàm số lượng giác và phương trình lượng giác

Tài liệu gồm 110 trang phân dạng và tuyển chọn 119 câu hỏi và bài toán trắc nghiệm hàm số lượng giác và phương trình lượng giác, có đáp án và lời giải chi tiết, giúp học sinh tự học chương trình Đại số và Giải tích 11 chương 1.

Chủ đề:

Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT) 134 tài liệu

Môn:

Toán 11 3.3 K tài liệu

Thông tin:

110 trang 1 năm trước

Tác giả:

Kim Oanh

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Tài liệu tự học hàm số lượng giác và phương trình lượng giác

51 26 lượt tải Tải xuống

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

MỤC LỤC

PHẦN 1 – ĐỀ BÀI .............................................................................................................. 2

DẠNG 1. XÁC ĐỊNH ĐỒ THỊ HÀM SỐ LƯỢNG GIÁC. ............................................................ 2

DẠNG 2. XÁC ĐỊNH CHU KỲ HÀM SỐ LƯỢNG GIÁC. ........................................................... 7

DẠNG 3. TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ LƯỢNG GIÁC. .................... 8

DẠNG 4: XÁC ĐỊNH SỐ ĐIỂM BIỂU DIỄN CỦA PHƯƠNG TRÌNH LƯỢNG GIÁC CHO

TRƯỚC TRÊN ĐƯỜNG TRÒN LƯỢNG GIÁC........................................................................... 12

DẠNG 5. BIỆN LUẬN NGHIỆM PHƯƠNG TRÌNH LƯỢNG GIÁC KHÔNG CHỨA

THAM SỐ ............................................................................................................................................. 19

5.1. Tìm số nghiệm của phương trình lượng giác trên tập

................................................................... 19

5.2. Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình lượng giác:. ................... 21

5.3. Tính tổng tất cả các nghiệm của phương trình lượng giác trên tập

. ........................................... 23

DẠNG 6. TÌM ĐIỀU KIỆN CỦA THAM SỐ

ĐỂ PHƯƠNG TRÌNH LƯỢNG GIÁC CHO

TRƯỚC CÓ NGHIỆM. ....................................................................................................................... 35

DẠNG 7. TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ LƯỢNG GIÁC ............ 40

7.1. Tìm GTLN, GTNN sử dụng điều kiện

1 sin ,cos 1xx  

. ............................................................... 40

7.2. Tìm GTLN, GTNN dạng

sin cosy a x b x c  

. ............................................................................... 43

7.3. Tìm GTLN, GTNN sử dụng bất đẳng thức cổ điển. ............................................................................ 47

PHẦN 2: BẢNG ĐÁP ÁN .............................................................................................. 50

PHẦN 3: ĐÁP ÁN CHI TIẾT ........................................................................................ 51

DẠNG 1. XÁC ĐỊNH ĐỒ THỊ HÀM SỐ LƯỢNG GIÁC. .......................................................... 51

DẠNG 2. XÁC ĐỊNH CHU KỲ HÀM SỐ LƯỢNG GIÁC. ......................................................... 56

DẠNG 3. TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ LƯỢNG GIÁC. .................. 58

DẠNG 4: XÁC ĐỊNH SỐ ĐIỂM BIỂU DIỄN CỦA PHƯƠNG TRÌNH LƯỢNG GIÁC CHO

TRƯỚC TRÊN ĐƯỜNG TRÒN LƯỢNG GIÁC........................................................................... 62

DẠNG 5. BIỆN LUẬN NGHIỆM PHƯƠNG TRÌNH LƯỢNG GIÁC KHÔNG CHỨA

THAM SỐ ............................................................................................................................................. 70

5.1. Tìm số nghiệm của phương trình lượng giác trên tập

................................................................... 70

5.2. Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình lượng giác:. ................... 73

5.3. Tính tổng tất cả các nghiệm của phương trình lượng giác trên tập

. ........................................... 76

DẠNG 6. TÌM ĐIỀU KIỆN CỦA THAM SỐ

ĐỂ PHƯƠNG TRÌNH LƯỢNG GIÁC CHO

TRƯỚC CÓ NGHIỆM. ....................................................................................................................... 93

DẠNG 7. TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ LƯỢNG GIÁC ............ 97

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

7.1. Tìm GTLN, GTNN sử dụng điều kiện

1 sin ,cos 1xx  

. ............................................................... 97

7.2. Tìm GTLN, GTNN dạng

sin cosy a x b x c  

. ............................................................................. 101

7.3. Tìm GTLN, GTNN sử dụng bất đẳng thức cổ điển. .......................................................................... 105

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

PHẦN 1 – ĐỀ BÀI

DẠNG 1. XÁC ĐỊNH ĐỒ THỊ HÀM SỐ LƯỢNG GIÁC.

Câu 1: Hình nào dưới đây biểu diễn đồ thị hàm số

 

2sin2y f x x

A. . B. .

C. . D. .

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 2: Hình vẽ nào sau đây biểu diễn đồ thị hàm số

cos

y 

A. . B. .

C. . D. .

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

..........................................................................................................................................................................

Câu 3: Cho đồ thị hàm số

cosyx

như hình vẽ:

Hình vẽ nào sau đây là đồ thị hàm số

cos 2yx

A. . B. .

C. . D. .

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 4: Cho đồ thị hàm số

sinyx

như hình vẽ:

Hình nào sau đây là đồ thị hàm số

sinyx

A. . B. .

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

C. . D. .

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 5: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt

kê ở bốn phương án

, , ,A B C D

Hỏi hàm số đó là hàm số nào?

tanyx

. B.

cotyx

. C.

tanyx

. D.

cotyx

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 6: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt

kê ở bốn phương án

, , ,A B C D

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Hỏi hàm số đó là hàm số nào?

sin 1





  





. B.

2sin











sin 1





   





. D.

sin 1





  





Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 7: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt

kê ở bốn phương án

, , ,A B C D

Hỏi hàm số đó là hàm số nào?

1 sinyx

. B.

sinyx

. C.

1 cosyx

. D.

1 sinyx

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 8: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt

kê ở bốn phương án

, , ,A B C D

Hỏi hàm số đó là hàm số nào?

1 sinyx

. B.

sinyx

. C.

1 cosyx

. D.

1 sinyx

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 9: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt

kê ở bốn phương án A, B, C,. D. Hỏi hàm số đó là hàm số nào?

sin











. B.

cos











sin 1





   





. D.

cos 1yx  

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

..........................................................................................................................................................................

DẠNG 2. XÁC ĐỊNH CHU KỲ HÀM SỐ LƯỢNG GIÁC.

Câu 10: Chu kỳ tuần hoàn của hàm số

sin cos cos2 cos4y x x x x

là



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 11: Tìm chu kỳ tuần hoàn của hàm số

 

3sin4 4 sin cos 2y x x x   



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 12: Tìm chu kỳ tuần hoàn của hàm số

 

3 3 3

sin 4 sin cos3 cos sin3f x x x x x x  



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 13: Tìm chu kỳ tuần hoàn của hàm số

 

cos .cos3 sin .sin3f x x x x x



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

DẠNG 3. TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ LƯỢNG GIÁC.

Câu 14: Tìm mệnh đề đúng trong các mệnh đề sau?

A. Hàm số

y cot x

đồng biến trên khoảng

 



B. Hàm số

y sin x

nghịch biến trên khoảng

 

3 ;4



C. Hàm số

y sin x

đồng biến trên khoảng

;











 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

D. Hàm số

y cosx

đồng biến trên khoảng

;











Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 15: Cho các hàm số

sinyx

;

cosyx

;

tanyx

;

cotyx

. Có bao nhiêu hàm số nghịch

biến trên











. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 16: Cho hàm số

tanyx

. Khẳng định nào dưới đây sai?

A. Hàm số đã cho là hàm lẻ.

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

B. Hàm số đã cho có tập giá trị là

 

1;1

C. Hàm số đã cho đồng biến trên











D. Hàm số đã cho có tập xác định











Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 17: Khẳng định nào sau đây đúng?

sinyx

là hàm số nghịch biến trên

;











cosyx

là hàm số nghịch biến trên

;









sinyx

là hàm số nghịch biến trên









tanyx

là hàm số nghịch biến trên

;









Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 18: Hàm số

cosyx

nghịch biến trên khoảng nào sau đây?

;10









. B.

;











. C.









. D.











Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 19: Để hàm số

sin cosy x x

tăng, ta chọn

thuộc khoảng nào?

2 ; 2





  





. B.

;





  





2 ; 2





  





. D.

 

2 ;2 2kk

   



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 20: Xét hai mệnh đề sau:

(I):

;





  





:Hàm số

tanyx

tăng.

(II):

;





  





:Hàm số

sinyx

tăng.

Chọn câu đúng?

A. Chỉ (I) đúng. B. Chỉ (II) đúng. C. Cả hai đúng. D. Cả hai sai.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

DẠNG 4: XÁC ĐỊNH SỐ ĐIỂM BIỂU DIỄN CỦA PHƯƠNG TRÌNH LƯỢNG GIÁC

CHO TRƯỚC TRÊN ĐƯỜNG TRÒN LƯỢNG GIÁC.

Câu 21: Biểu diễn các nghiệm của phương trình

cos 0x 

trên đường tròn lượng giác được bao

nhiêu điểm?

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 22: Nghiệm của phương trình

cos 1x 

là:

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 23: Cho phương trình

2cos 3 0x 

. Số điểm biểu diễn tất cả các nghiệm của phương trình

trên đường tròn lượng giác là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 24: Số điểm biểu diễn các nghiệm của phương trình

cos

x 

trên đường tròn lượng giác là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 25: Biểu diễn tất cả các nghiệm của phương trình

3cos 1 0x

trên đường tròn lượng giác,

số điểm biểu diễn là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 26: Biểu diễn nghiệm của phương trình

cos3 cosxx

trên đường tròn lượng giác. Số điểm

biểu diễn là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 27: Biểu diễn nghiệm của phương trình

cos cos 0xx

trên đường tròn lượng giác. Số

điểm biểu diễn là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 28: Số điểm biểu diễn nghiệm của phương trình

cos

x 

trên đường tròn lượng giác là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 29: Biểu diễn tập nghiệm của phương trình

cos cos2 cos3 0x x x

trên đường tròn lượng

giác ta được số điểm cuối là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

..........................................................................................................................................................................

Câu 30: Biểu diễn các nghiệm của phương trình

 

cos sin 1x 

trên đường tròn lượng giác là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 31: Biểu diễn tất cả các nghiệm của phương trình

cos5 .cos cos4x x x

trên đường tròn lượng

giác. Số điểm biểu diễn là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 32: Số vị trí biểu diễn các nghiệm của phương trình

4cos 4cos 3 0xx  

trên đường tròn

lượng giác là?

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 33: Số điểm biểu diễn các họ nghiệm của phương trình

sin2 3cos2 3xx

trên đường

tròn lượng giác là:

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 34: Số điểm biểu diễn các họ nghiệm của phương trình

sin5 3cos5 2sin7x x x

trên

đường tròn lượng giác là:

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 35: Số điểm biểu diễn của phương trình

   

sin cos sin2 12 cos sin 12cos2 0x x x x x x    

là:

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 36: Nghiệm của phương trình

 

sin sin cos cos 2sin2 sin 1 1x x x x x x    

thoả điều kiện





  

có số điểm biểu diễn là:

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 37: Số điểm biểu diễn các nghiệm của phương trình

cos sin2 2 cos

2sin 1

x x x





   















trên đường tròn lượng giác là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 38: Số điểm biểu diễn các nghiệm của phương trình

sin sin2 2sin cos sin cos

3cos2

sin cos

x x x x x x

  





trên đường tròn lượng giác là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

..........................................................................................................................................................................

DẠNG 5. BIỆN LUẬN NGHIỆM PHƯƠNG TRÌNH LƯỢNG GIÁC KHÔNG CHỨA

THAM SỐ

5.1. Tìm số nghiệm của phương trình lượng giác trên tập

Câu 39: Tìm số nghiệm của phương trình

cos5 .cos cos4x x x

trên

 

0;10



là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 40: Số nghiệm thuộc khoảng

 

0;100



của phương trình

sin cos 3cos 3



  





là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 41: Số nghiệm của phương trình

cos sin2 2 cos

x x x





   





trên khoảng

 

0;3



là

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 42: Gọi

là số nghiệm thuộc khoảng

 

0;2023

của phương trình lượng giác

 

3 1 cos2 sin2 4cos 8 4 3 1 sinx x x x     

. Tìm

là

322

. B.

320

. C.

300

. D.

321

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 43: Số nghiệm của phương trình

2cos 3sin2 3xx

trên





0;2020



là:

1010

. B.

2019

. C.

2020

. D.

2021

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 44: Huyết áp là đại lượng để đo độ lớn của lực tác dụng lên thành mạch máu. Nó được đo

bằng hai chỉ số: huyết áp tâm thu (lúc tim đập) và huyết áp tâm trương (lúc tim nghỉ).

Huyết áp của mỗi người thường khác nhau, nhưng huyết áp tiêu chuẩn là

120/80

, nó

có nghĩa là huyết áp tâm thu là 120mmHg và huyết áp tâm trương là 80 mmHg. Giả sử

rằng trái tim của một người đập

lần một phút, huyết áp

giây có thể được

mô tả bằng hàm số

 

100 20sin

P t t











. Với

 

0;60t 

, có bao nhiêu lần huyết áp

người đó bằng

100

mmHg?

139

. B.

140

. C.

141

. D.

142

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

..........................................................................................................................................................................

Câu 45: Năm 1893, George Ferris chế tạo vòng đu quay. Nó có đường kính

250

foot. Nếu với

mỗi

giây vòng đu quay quay

vòng thì chiều cao

(foot) của một chỗ ngồi trên

vòng đu quay là một hàm số của thời gian

(giây) được xác định như sau

 

125sin 0,157 125

h t t





  





Vòng quay bắt đầu tính từ thời điểm

0.t 

Trong

giây đầu tiên của chuyến đi, tại thời điểm

nào sau đây (làm tròn đến hàng đơn vị) thì người ngồi trên ghế đu quay đó cách mặt đất

125

foot? (Chú thích:

foot xấp xỉ

30,48

cm).

giây. B.

giây. C.

giây. D.

giây.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

5.2. Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình lượng giác:.

Câu 46: Nghiệm lớn nhất của phương trình

2cos2 1 0x

trong đoạn

 



là:





. B.





. C.





. D.





Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 47: Phương trình

cos2 2cos 3 0xx  

có nghiệm lớn nhất trong khoảng

 

0;2019

644



. B.



. C.

640



. D.

642



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 48: Nghiệm dương nhỏ nhất của phương trình

 

sin cos2 0x 

là



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 49: Gọi

là nghiệm dương nhỏ nhất của phương trình

3sin 2sin cos cos 0x x x x  

Chọn khẳng định đúng?

;











. B.

;











. C.











. D.











Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 50: Cho phương trình

sin .tan cos .cot 2sin cos

x x x x x x  

. Tính hiệu nghiệm âm lớn

nhất và nghiệm dương nhỏ nhất của phương trình.





. B.



. C.





. D.



 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 51: Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu

 

của mực

nước trong kênh tính theo thời gian

 

được cho bởi công thức

3cos 12





  





Khi nào mực nước của

kênh là cao nhất với thời gian ngắn nhất?

 

22 ht 

. B.

 

15 ht 

. C.

 

14 ht 

. D.

 

10 ht 

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

5.3. Tính tổng tất cả các nghiệm của phương trình lượng giác trên tập

Câu 52: Tính tổng tất cả các nghiệm của phương trình

sin sin2 0xx

trên đoạn

 

0;2



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 53: Tính tổng các nghiệm trong đoạn

 

0;30

của phương trình:

tan tan3xx

(1)

55 .



. B.

171



. C.

45 .



. D.

190



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 54: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình

sin 3











bằng



. B.



. C.





. D.





Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 55: Tổng tất cả các nghiệm của phương trình

cos2 cos 0xx

trong khoảng

 

0;2



bằng

. Vậy

bằng bao nhiêu?





. B.





. C.





. D.





Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 56: Tổng các nghiệm của phương trình

sin2 3 6sin cosx x x  

trong khoảng









là



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 57: Tổng tất cả các nghiệm thuộc

 

0;10π

của phương trình

2sin 5sin 3 0xx  

là



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 58: Tổng các nghiệm trong đoạn

 

0;2



của phương trình

sin cos 1xx

bằng



. B.



. C.

2

. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 59: Phương trình

6sin 7 3sin2 8cos 6x x x  

có tổng hai nghiệm dương nhỏ nhất bằng



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 60: Gọi

là tổng các nghiệm của phương trình

sin

cos 1





trên đoạn

 

0;2017



. Tính

2035153S





. B.

1001000S





. C.

1017072S





. D.

2000200S





Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 61: Tìm tổng các nghiệm của phương trình

sin3 cos 0xx

trên

 



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

..........................................................................................................................................................................

Câu 62: Tìm tổng tất cả các nghiệm thuộc đoạn

 

0;30

của phương trình

cos3 4cos2 3cos 4 0x x x   

là



. B.

121



. C.



. D.



Lời gii

Chọn D

cos3 4cos2 3cos 4 0x x x   

 

4cos 3cos 4 2cos 1 3cos 4 0x x x x     

4cos 8cos 0xx  













cos 0

cos 2 (vn)

+ Với

cos 0

x x k



   

.Theo giải thiết,

 

1 30

0;30 0



    

1 30 1



    

mà

 

0;1;2;3; ;9k Z k   

Vậy tổng các nghiệm thỏa mãn yêu cầu bài toán là

 

2 9 5 1 2 9 5 45 50

2 2 2 2

   

       

     

            

     

     

Câu 63: Tính tổng

tất cả các nghiệm của phương trình

 

2cos2 5 sin cos 3 0x x x   

trên

khoảng

 

0;2





. B.





. C.





. D.





Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 64: Cho phương trình

 

2sin 1 3tan 2sin 3 4cos   x x x x

. Gọi

là tập hợp các

nghiệm thuộc đoạn

 

0;20



của phương trình trên. Tính tổng các phần tử của

570



. B.

875



. C.

880



. D.

1150



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 65: Tính tổng tất cả các nghiệm của phương trình

cos cos 1

cos2 tan

cos





trên đoạn

[1;70]

188



. B.

263



. C.

363



. D.

365



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

..........................................................................................................................................................................

Câu 66: Tổng các nghiệm của phương trình

4 4 4

sin sin sin

4 4 4

x x x



   

    

   

   

trong khoảng

 

0;2



bằng



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 67: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình

1 tan tan sin cot 4

x x x



  





là





. B.



. C.



. D.





Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 68: Tính tổng các nghiệm thuộc

 



của phương trình:

sin2

cos 1





 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 69: Tính tổng

các nghiệm của phương trình

cos sin cos 2sin cos 2x x x x x   

trên

khoảng

;5 .













. B.





. C.





. D.





Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 70: Tính tổng các nghiệm trên

 

44 ;





của phương trình

sin 3 3sin 2 2 0xx   



. B.





. C.





. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

..........................................................................................................................................................................

Câu 71: Phương trình

1 1 1

cos sin2 sin4x x x



có tổng các nghiệm trên

(0; )



là:



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 72: Phương trình

sin2 2cos sin 1

tan 3

x x x

  





có bao nhiêu nghiệm trên

(0;3 )



A. 1. B. 2. C. 3. D. 4

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 73: Gọi

là tổng tất cả các nghiệm thuộc

 

0;20



của phương trình

2cos sin 1 0xx  

Khi đó giá trị của

bằng:

570S





. B.

295S





. C.

590S





. D.

200





Lời giải: ........................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 74: Tính tổng

các nghiệm của phương trình

cos sin2 2 cos

x x x





   





trên khoảng

 

0;2





. B.





. C.





. D.





Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 75: Tính tổng tất cả các nghiệm của phương trình

3cos sin 1xx

trên

 

0;2



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 76: Gọi

là tập hợp các nghiệm thuộc khoảng

 

0;100



của phương trình

sin cos 3cos 3



  





. Tổng các phần tử của

là

7400



. B.

7525



. C.

7375



. D.

7550



 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 77: Gọi

là tập hợp tất cả các nghiệm thuộc khoảng

 

0;2018

của phương trình sau:

 

3 1 cos2 sin2 4cos 8 4 3 1 sinx x x x     

. Tính tổng tất cả các phần tử của

103255



. B.

310408



. C.

312341



. D.

102827



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 78: Tính tổng tất cả các nghiệm của phương trình

sin2 4sin 2cos 4 0   x x x

trong đoạn

 

0;100



của phương trình.

100



. B.

2476



. C.



. D.

2475



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 79: Tổng tất cả các nghiệm của phương trình

 

cos sin 1x 

trên

 

0;2



bằng

. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 80: Tính tổng

các nghiệm của phương trình

 

2cos2 5 sin cos 3 0x x x   

trong

khoảng

 

0;2





. B.





. C.





. D.





Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 81: Cho phương trình

 

2018 2018 2020 2020

sin cos 2 sin cosx x x x  

. Tính tổng các nghiệm của

phương trình trong khoảng

 

0;2018

1285









. B.

 

643



. C.

 

642



. D.

1285









Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

..........................................................................................................................................................................

Câu 82: Phương trình lượng giác:

cos3 cos2 9sin 4 0x x x   

trên khoảng

 

0;3



. Tổng số

nghiệm của phương trình trên là:



. B.



. C. Kết quả khác. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

DẠNG 6. TÌM ĐIỀU KIỆN CỦA THAM SỐ

ĐỂ PHƯƠNG TRÌNH LƯỢNG GIÁC

CHO TRƯỚC CÓ NGHIỆM.

Câu 83: Tính tổng

tất cả các giá trị nguyên của tham số

để phương trình

2cos 2 5





  





có nghiệm thuộc khoảng

;









25S 

. B.

22S 

. C.

22S 

. D.

25S 

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 84: Tìm

để phương trình

  

3cos 4 3cos 1 3 0x x m   

có số nghiệm trên đoạn









là lớn nhất.

m  

. B.

m  

. C.

m  

. D.

m  

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 85: Tìm điều kiện của tham số

để phương trình

   

sin 2 1 sin 3 2 0x m x m m    

có

nghiệm



  







. B.



  







. C.

   









. D.

  









Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

..........................................................................................................................................................................

Câu 86: Tìm điều kiện của tham số

để phương trình

 

cc oos s2 2 1 1 0xx m m    

có đúng

hai nghiệm trên đoạn

;











10m  

. B.

01m

. C.

01m

. D.

11m  

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 87: Cho phương trình

   

2sin 1 sin2 6 cos 1x m x m x    

. Có bao nhiêu giá trị nguyên

của tham số

để phương trình vô nghiệm?

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 88: Tìm tất cả các giá trị của tham số

để phương trình

2cos 4 sin cosx m x x m

có

nghiệm:

m 

. B.

m 

hoặc

m  

. D.

0m 

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 89: Số các giá trị nguyên m để phương trình

4 4.sin .cos 2.cos2 3 9m x x m x m    

có nghiệm là

A. 7. B. 6. C. 5. D. 4

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 90: Có tất cả bao nhiêu giá trị nguyên của tham số

để phương trình

3cos 1 0xm  

có

nghiệm?

. B.

. C.

. D. Vô số.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 91: Tìm tất cả các giá trị của tham số

để phương trình

 

1 sin 2 0m x m   

có nghiệm.

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

1.m 

. B.

m 

. C.

m  

. D.

1.m 

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 92: Có tất cả bao nhiêu giá trị nguyên của tham số

để phương trình

3cos 1 0xm  

có

nghiệm?

. B.

. C.

. D. Vô số.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 93: Tìm tất cả các giá trị của tham số

để phương trình

 

1 sin 2 0m x m   

có nghiệm.

1.m 

. B.

m 

. C.

m  

. D.

1.m 

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

DẠNG 7. TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ LƯỢNG GIÁC

7.1. Tìm GTLN, GTNN sử dụng điều kiện

1 sin ,cos 1xx  

Câu 94: Tìm giá trị nhỏ nhất của biểu thức

sin sin

A x x







  







1

. B.

. C.

2

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 95: Tìm giá trị lớn nhất của biểu thức

sin cosA x x

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 96: Tập giá trị của hàm số

sin2 3cos2 1y x x  

là đoạn

 

;.ab

Tính tổng

.T a b

1T 

. B.

2T 

. C.

0T 

. D.

1T 

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 97: Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu

 

của mực

nước trong kênh tính theo thời gian

 

được cho bởi công thức

3cos 12







  







Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?

 

22 ht 

. B.

 

15 ht 

. C.

 

14 ht 

. D.

 

10 ht 

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 98: Gọi

và

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

 

1 2cos 2 3 sin cosy x x x



    



trên . Biểu thức

2MN

có giá trị bằng

. B.

4 2 3

. C.

. D.

2 3 2

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 99: Số giờ có ánh sáng của một thành phố X ở vĩ độ

40

bắc trong ngày thứ

của một năm

không nhuận được cho bởi hàm số:

   

3sin 80 12

182

d t t





  





t 

và

0 365t

Vào ngày nào trong năm thì thành phố X có nhiều giờ ánh sáng nhất?

262

. B.

353

. C.

. D.

171

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 100: Hàm số

2cos3 3sin3 2y x x  

có tất cả bao nhiêu giá trị nguyên?

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 101: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau

2sin cos 2y x x

max 4y 

min

y 

. B.

max 3y 

min 2y 

max 4y 

min 2y 

. D.

max 3y 

min

y 

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 102: Gọi

và

lần lượt là GTLN và GTNN của hàm số

sin cos sin2y x x x  

. Tổng

Mm

là



. B.



. C.

. D.

Lời giải: ........................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

..........................................................................................................................................................................

7.2. Tìm GTLN, GTNN dạng

sin cosy a x b x c  

Câu 103: Cho hàm số

sin 2cos

sin cos 3







. Gọi

lần lượt là giá trị nhỏ nhất và giá trị lớn nhất

của hàm số đã cho. Tính

75mM

bằng?

. B.

. C.

. D.

10

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 104: Hàm số

 

3sin4 4 sin cos

2cos 2 sin4 2

x x x







có giá trị lớn nhất

và giá trị nhỏ nhất

. Khi

đó tổng

Mm

bằng?

. B.



. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 105: Giá trị lớn nhất

, giá trị nhỏ nhất

của hàm số:

2cos 2 3sin cos 1y x x x  

là

4; 0Mm

. B.

3; 0Mm

. C.

3; 1Mm

. D.

M 4; 1m

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 106: Cho hàm số

sin 2cos 1

sin cos 2







. Gọi

;

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất

của hàm số. Tổng

Mm

bằng

. B.

2

. C.

1

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 107: Giá trị lớn nhất của hàm số

cos 2sin 3

2cos sin 4







là

3 2 3

. B.

. C.

1

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

..........................................................................................................................................................................

Câu 108: Có bao nhiêu giá trị nguyên của tham số

để giá trị lớn nhất của hàm số

sin 1

cos 2







nhỏ hơn

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 109: Giả sử

là giá trị lớn nhất và

là giá trị nhỏ nhất của hàm số

sin 2cos 1

sin cos 2







trên . Tìm

23Mm

12

. B.

. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 110: Gọi

tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

2sin 2

cos 2







Khẳng định nào sau đây đúng?

38mM

. B.

38mM  

. C.

30mM

. D.

mM  

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 111: Tập giá trị của hàm số

sin2 3cos2 1y x x  

là đoạn

 

;.ab

Tính tổng

.T a b

0T 

. B.

1T 

. C.

1T 

. D.

2.T 

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 112: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

3sin 4cos 1y x x  

max 6y 

min 4y 

. B.

max 8y 

min 6y 

max 4y 

min 6y 

. D.

max 6y 

min 8y 

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

7.3. Tìm GTLN, GTNN sử dụng bất đẳng thức cổ điển.

Câu 113: Cho hàm số

1 2sin 1 2cos 1.y x x    

Gọi

, mM

lần lượt là giá trị nhỏ nhất và

giá trị lớn nhất của hàm số. Khi đó giá trị của

Mm

bằng

3 2 2

. B.

3 2 1

. C.

3 2 2 1

. D.

3 3 2 1  

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 114: Tìm giá trị lớn nhất của hàm số

2sin 3cos 1

sin cos 2







3 33



. B.

3 33



. C.

. D.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 115: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số

 

2018 2018

sin cosf x x x

lần lượt là

1008

và

. B.

1009

và

. C.

và

. D.

1008

và

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

..........................................................................................................................................................................

Câu 116: Cho

là các số thực thỏa mãn

cos2 cos2 1.xy

Giá trị nhỏ nhất của biểu thức

tan tanP x y

bằng

. B.

. D.

. C.

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 117: Cho hai số thực

, xy

thuộc













và thỏa mãn

 

cos2 cos2 2sin 2.x y x y   

Giá trị

nhỏ nhất của

cos cosxy



bằng



. B.



. C.



. D.



Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 118: Cho

, , a b c

là các số thực thỏa mãn

2 2 2

4.a b c  

Tìm giá trị lớn nhất

trong tất cả

các hàm số

sin cosy a b x c x  

với

0; .













12M 

. B.

12M 

. C.

2 1 2M 

. D.

 

2 1 2 .M 

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

Câu 119: Tập giá trị của hàm số

sin2 3cos2 1y x x  

là đoạn

 

;.ab

Tính tổng

.T a b

1T 

. B.

2T 

. C.

0T 

. D.

1T 

Lời giải: ........................................................................................................................................

..........................................................................................................................................................................

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

PHẦN 2: BẢNG ĐÁP ÁN

1.C

2.D

3.A

4.C

5.C

6.A

7.A

8.B

9.D

10.C

11.B

12.A

13.D

14.C

15.B

16.B

17.B

18.D

19.A

20.D

21.B

22.A

23.B

24.D

25.C

26.D

27.A

28.C

29.C

30.D

31.B

32.D

33.C

34.C

35.B

36.B

37.A

38.B

39.A

40.B

41.B

42.A

43.C

44.C

45.C

46.D

47.D

48.C

49.C

50.C

51.D

52.B

53.C

54.C

55.D

56.D

57.B

58.D

59.B

60.C

61.D

62.D

63.C

64.B

65.D

66.B

67.D

68.A

69.C

70.B

71.D

72.B

73.B

74.C

75.A

76.C

77.B

78.D

79.B

80.B

81.D

82.B

83.C

84.D

85.B

86.B

87.A

88.B

89.D

90.C

91.B

92.C

93.B

94.A

95.A

96.B

97.D

98.C

99.D

100.A

101.D

102.D

103

104.C

105.A

106.C

107.B

108.C

109.D

110.B

111.D

112.C

113.C

114.A

115.D

116.B

117.C

118.C

119.B

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

PHẦN 3: ĐÁP ÁN CHI TIẾT

DẠNG 1. XÁC ĐỊNH ĐỒ THỊ HÀM SỐ LƯỢNG GIÁC.

Câu 1: Hình nào dưới đây biểu diễn đồ thị hàm số

 

2sin2y f x x

A. . B. .

C. . D. .

Lời gii

Chọn C

Ta thấy

2 2sin2 2x  

nên ta có loại Hình 2 và Hình 3.

Tiếp theo với Hình 1 và Hình 4 ta có:

Từ phần lý thuyết ở trên ta có hàm số tuần hoàn với chu kỳ





Ta thấy

0x 

thì

0y 

nên đồ thị hàm số đi qua gốc tọa độ. Từ đây ta chọn đáp án Hình 1.

Câu 2: Hình vẽ nào sau đây biểu diễn đồ thị hàm số

cos

y 

A. . B. .

C. . D. .

Lời gii

Chọn D

Ta thấy

1 cos 1

  

nên ta có loại Hình 2.

Tiếp theo ta có hàm số

y cos

có chu kỳ tuần hoàn là





 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ta thấy

0x 

thì

cos cos0 1

y   

nên ta chọn Hình 4.

Câu 3: Cho đồ thị hàm số

cosyx

như hình vẽ:

Hình vẽ nào sau đây là đồ thị hàm số

cos 2yx

A. . B. .

C. . D. .

Lời gii

Chọn A

Ta thực hiện phép tịnh tiến đồ thị hàm số

cosyx

trên trục

lên trên 2 đơn vị.

Câu 4: Cho đồ thị hàm số

sinyx

như hình vẽ:

Hình nào sau đây là đồ thị hàm số

sinyx

A. . B. .

C. . D. .

Lời gii

Chọn C

Suy diện đồ thị hàm số

sinyx

từ đồ thị hàm số

sinyx

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Giữ nguyên phần đồ thị của hàm số

sinyx

nằm bên phải trục

Lấy đối xứng phần đồ thị trên qua trục

Dưới đây là đồ thị ta thu được sau khi thực hiện các bước suy diễn ở trên. Phần đồ thị nét đứt là

phần bỏ đi của hàm số

sinyx

Câu 5: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt

kê ở bốn phương án

, , ,A B C D

Hỏi hàm số đó là hàm số nào?

tanyx

. B.

cotyx

. C.

tanyx

. D.

cotyx

Lời gii

Chọn C

Ta thấy hàm số có GTNN bằng 0.

Hàm số xác định tại





và tại





thì

0y 

Câu 6: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt

kê ở bốn phương án

, , ,A B C D

Hỏi hàm số đó là hàm số nào?

sin 1





  





. B.

2sin











sin 1





   





. D.

sin 1





  





 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Lời gii

Chọn A

Ta thấy hàm số có GTLN bằng 0, GTNN bằng

2

. Do đó ta loại đáp án

2sin











. Vì

 

2sin 2;2





   





Tại

0x 

thì

2y 

. Thử vào các đáp án còn lại chỉ có

sin 1





  





thỏa mãn.

Câu 7: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt

kê ở bốn phương án

, , ,A B C D

Hỏi hàm số đó là hàm số nào?

1 sinyx

. B.

sinyx

. C.

1 cosyx

. D.

1 sinyx

Lời gii

Chọn A

Ta có:

1 cos 1yx  

và

1 sin 1yx  

nên loại

1 cosyx

và

1 sinyx

Ta thấy tại

0x 

thì

1y 

. Thay vào hai đáp án:

1 sinyx

và

sinyx

thì chỉ có

1 sinyx

thỏa.

Câu 8: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt

kê ở bốn phương án

, , ,A B C D

Hỏi hàm số đó là hàm số nào?

1 sinyx

. B.

sinyx

. C.

1 cosyx

. D.

1 sinyx

Lời gii

Chọn B

Ta có:

1 cos 1yx  

và

1 sin 1yx  

nên loại

1 cosyx

và

1 sinyx

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Ta thấy tại





thì

0y 

. Thay vào hai đáp án còn lại thì chỉ có

sinyx

thỏa mãn.

Câu 9: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt

kê ở bốn phương án A, B, C,. D. Hỏi hàm số đó là hàm số nào?

sin











. B.

cos











sin 1





   





. D.

cos 1yx  

Lời gii

Chọn D

Lấy đối xứng qua trục hoành đồ thị hàm số

cosyx

ta được đồ thị hàm số

cosyx

. Sau đó

tịnh tiến đồ thị hàm số

cosyx

lên trên ta được đồ thị hàm số

cos 1yx  

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

DẠNG 2. XÁC ĐỊNH CHU KỲ HÀM SỐ LƯỢNG GIÁC.

Câu 10: Chu kỳ tuần hoàn của hàm số

sin cos cos2 cos4y x x x x

là



. B.



. C.



. D.



Lời gii

Chọn C

Ta có

1 1 1

sin cos cos2 cos4 sin2 cos2 cos4 sin4 cos4 sin8

2 4 8

y x x x x x x x x x x   

Do đó chu kỳ của hàm số là





Câu 11: Tìm chu kỳ tuần hoàn của hàm số

 

3sin4 4 sin cos 2y x x x   



. B.



. C.



. D.



Lời gii

Chọn B

Ta có

 

4 4 2 2 2

1 1 3 1

sin cos 1 2sin cos 1 sin 2 1 1 cos2 cos4

2 4 4 4

x x x x x x x         

Do đó

3sin4 3 cos4 2 2sin 4 5

y x x x





      





Vậy chu kỳ tuần hoàn của hàm số là





Câu 12: Tìm chu kỳ tuần hoàn của hàm số

 

3 3 3

sin 4 sin cos3 cos sin3f x x x x x x  



. B.



. C.



. D.



Lời gii

Chọn A

Ta có:

   

3 3 3 3 3 3

sin cos3 cos sin3 sin . 4cos 3cos cos . 3sin 4sinx x x x x x x x x x    

 

3 3 3 3 3 3 2 2

4sin .cos 3sin cos 3cos sin 4sin .cos 3sin cos cos sinx x x x x x x x x x x x     

sin2 cos2 sin4

x x x

Do đó

 

3 1 1

sin 4 sin4 3sin4 4sin 4 sin12

4 4 4

f x x x x x x      

Vậy chu kỳ tuần hoàn của hàm số là

12 6





 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 13: Tìm chu kỳ tuần hoàn của hàm số

 

cos .cos3 sin .sin3f x x x x x



. B.



. C.



. D.



Lời gii

Chọn D

Ta có:

     

cos3 .cos .cos sin3 .sin .sinf x x x x x x x

   

cos4 cos2 .cos cos2 cos4 .sin

x x x x x x   

2 2 2 2

cos4 .cos cos2 .cos cos2 .sin cos4 .sin

x x x x x x x x



   



 

1 1 1 1 3

cos4 cos 2 cos4 1 cos4 cos4

2 2 2 4 4

x x x x x



      







Vậy chu kỳ tuần hoàn của hàm số là





 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

DẠNG 3. TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ LƯỢNG GIÁC.

Câu 14: Tìm mệnh đề đúng trong các mệnh đề sau?

A. Hàm số

y cot x

đồng biến trên khoảng

 



B. Hàm số

y sin x

nghịch biến trên khoảng

 

3 ;4



C. Hàm số

y sin x

đồng biến trên khoảng

;











D. Hàm số

y cosx

đồng biến trên khoảng

;











Lời gii

Chọn C

* Hàm số

y cot x

nghịch biến trên mỗi khoảng mà nó xác định.

* Hàm số

y sin x

đồng biến trên mỗi khoảng

2 ; 2





  





và nghịch biến trên mỗi

khoảng

2 ; 2











* Hàm số

y cosx

đồng biến trên mỗi khoảng

 

2 ; 2kk

  



và nghịch biến trên mỗi khoảng

 

2 ; 2kk

  



Vậy đáp án đúng là C.

Câu 15: Cho các hàm số

sinyx

;

cosyx

;

tanyx

;

cotyx

. Có bao nhiêu hàm số nghịch

biến trên











. B.

. C.

. D.

Lời gii

Chọn B

Hàm số

sinyx

nghịch biến trên mỗi khoảng

k2 ; k2











nên nghịch biến trên khoảng











Hàm số

cosyx

nghịch biến trên mỗi khoảng

 

2 ; 2kk

  



nên nghịch biến trên khoảng











Hàm số

tanyx

đồng biến trên mỗi khoảng xác định của nó.

Hàm số

cotyx

trên mỗi khoảng

 

;kk

  



nên nghịch biến trên khoảng











 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Vậy có

hàm số nghịch biến trên











Câu 16: Cho hàm số

tanyx

. Khẳng định nào dưới đây sai?

A. Hàm số đã cho là hàm lẻ.

B. Hàm số đã cho có tập giá trị là

 

1;1

C. Hàm số đã cho đồng biến trên











D. Hàm số đã cho có tập xác định











Lời gii

Chọn B

• Hàm số

tanyx

có tập xác định:











nên D đúng.

• Hàm số

tanyx

có tập giá trị:

T 

Ta có:

x D x D    

. Mà

     

tan tanf x x x f x      

Do đó hàm số

 

tany f x x

là hàm lẻ. Suy ra A đúng.

• Hàm số

tanyx

đồng biến trên khoảng

;











và nghịch biến trên

;









. Do đó C đúng.

Vậy đáp án B sai.

Câu 17: Khẳng định nào sau đây đúng?

sinyx

là hàm số nghịch biến trên

;











cosyx

là hàm số nghịch biến trên

;









sinyx

là hàm số nghịch biến trên









tanyx

là hàm số nghịch biến trên

;









Lời gii

Chọn B

Dựa vào đường tròn lượng giác ta thấy

cosyx

là hàm số nghịch biến trên

 



nên

cosyx

là hàm số nghịch biến trên

;









 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 18: Hàm số

cosyx

nghịch biến trên khoảng nào sau đây?

;10









. B.

;











. C.









. D.











Lời gii

Chọn D

Dựa vào đường tròn lượng giác ta thấy

cosyx

là hàm số nghịch biến trên mỗi khoảng

 

2 ; 2kk

  



nên

cosyx

là hàm số nghịch biến trên











Câu 19: Để hàm số

sin cosy x x

tăng, ta chọn

thuộc khoảng nào?

2 ; 2





  





. B.

;





  





2 ; 2





  





. D.

 

2 ;2 2kk

   



Lời gii

Chọn A

Ta có

sin cos 2 sin

y x x x





   





. Để hàm số

sin cosy x x

tăng thì

2 2 ,

2 4 2

k x k k

  



      

2 2 ,

k x k k



      

Câu 20: Xét hai mệnh đề sau:

(I):

;





  





:Hàm số

tanyx

tăng.

(II):

;





  





:Hàm số

sinyx

tăng.

Chọn câu đúng?

A. Chỉ (I) đúng. B. Chỉ (II) đúng. C. Cả hai đúng. D. Cả hai sai.

Lời gii

Chọn D

Ta có

;











.Hàm số

tanyx

có bảng biến thiên:

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Suy ra trên











hàm số

tanyx

giảm.

Xét bảng biến thiên:

Suy ra trên











hàm số

sinyx

giảm.

Vậy cả hai kết luận trên đều sai.

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

DẠNG 4: XÁC ĐỊNH SỐ ĐIỂM BIỂU DIỄN CỦA PHƯƠNG TRÌNH LƯỢNG GIÁC

CHO TRƯỚC TRÊN ĐƯỜNG TRÒN LƯỢNG GIÁC.

Câu 21: Biểu diễn các nghiệm của phương trình

cos 0x 

trên đường tròn lượng giác được bao

nhiêu điểm?

. B.

. C.

. D.

Lời gii

Chọn B

Ta có

 

cos 0 cos 0

x x x k k



      

Biểu diễn họ nghiệm trên đường tròn lượng giác ta được

điểm.

Câu 22: Nghiệm của phương trình

cos 1x 

là:

. B.

. C.

. D.

Lời gii

Chọn A

Ta có

cos 1 2 , x x k k



     

Biểu diễn họ nghiệm trên đường tròn lượng giác được

điểm.

Câu 23: Cho phương trình

2cos 3 0x 

. Số điểm biểu diễn tất cả các nghiệm của phương trình

trên đường tròn lượng giác là

. B.

. C.

. D.

Lời gii

Chọn B

Ta có

 

2cos 3 0 cos cos

x x k









     



  





Mỗi họ nghiệm







  

biểu diễn được

điểm trên đường tròn lượng giác,

do đó số điểm biểu diễn của tất cả các nghiệm của phương trình là

Câu 24: Số điểm biểu diễn các nghiệm của phương trình

cos

x 

trên đường tròn lượng giác là

. B.

. C.

. D.

Lời gii

Chọn D

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Ta có

cos

x 











  





k 

Mỗi họ nghiệm







  

biểu diễn được

điểm trên đường tròn lượng giác,

do đó số điểm biểu diễn của tất cả các nghiệm của phương trình là

Câu 25: Biểu diễn tất cả các nghiệm của phương trình

3cos 1 0x

trên đường tròn lượng giác,

số điểm biểu diễn là

. B.

. C.

. D.

Lời gii

Chọn C

Ta có:

3cos 1 0x

cos

x

arccos 2



   xk

k

Mỗi họ nghiệm trên biểu diễn được

điểm trên đường tròn lượng giác, do đó số điểm biểu

diễn trên đường tròn lượng giác của phương trình là

Câu 26: Biểu diễn nghiệm của phương trình

cos3 cosxx

trên đường tròn lượng giác. Số điểm

biểu diễn là

. B.

. C.

. D.

Lời gii

Chọn D

 

3 2 2 2

cos3 cos

3 2 4 2

x x k x k

x x x k k

x x k x k













  





      





   







. Biểu diễn họ nghiệm

trên đường tròn lượng giác được

điểm.

Câu 27: Biểu diễn nghiệm của phương trình

cos cos 0xx

trên đường tròn lượng giác. Số

điểm biểu diễn là

. B.

. C.

. D.

Lời gii

Chọn A

cos cos 0xx

 

cos 0

cos 1















  











Họ nghiệm





biểu diễn trên đường tròn lượng giác được

điểm, họ nghiệm

2xk





biểu diễn trên đường tròn lượng giac được

điểm, do đó số điểm biểu diễn là

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 28: Số điểm biểu diễn nghiệm của phương trình

cos

x 

trên đường tròn lượng giác là

. B.

. C.

. D.

Lời gii

Chọn C

1 1 cos2 1

cos cos2 0 2 ,

2 2 2 2 4 2

x x x k x k

  





           

Biểu diễn họ nghiệm trên đường tròn lượng giác được

điểm.

Câu 29: Biểu diễn tập nghiệm của phương trình

cos cos2 cos3 0x x x

trên đường tròn lượng

giác ta được số điểm cuối là

. B.

. C.

. D.

Lời gii

Chọn C

Ta có

 

cos cos2 cos3 0 cos3 cos cos2 0x x x x x x      

 

2cos2 .cos cos2 0 cos2 2cos 1 0x x x x x     

 

2 4 2

cos2 0

2 2 ,

cos

x k x k

x k x k k

x k x k

  



    















         















       





Vậy biểu diễn tập nghiệm của phương trình

cos cos2 cos3 0x x x

trên đường tròn lượng giác

ta được số điểm cuối là

Câu 30: Biểu diễn các nghiệm của phương trình

 

cos sin 1x 

trên đường tròn lượng giác là

. B.

. C.

. D.

Lời gii

Chọn D

Ta có

 

0;2x





 

sin 1;1x  

Khi đó:

 

cos sin 1 sin 2x x k



  

 

k 

với

1 2 1 0kk



    

Phương trình trở thành

sin 0

x x m







   







 

m

Vậy số điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác là

Câu 31: Biểu diễn tất cả các nghiệm của phương trình

cos5 .cos cos4x x x

trên đường tròn lượng

giác. Số điểm biểu diễn là

. B.

. C.

. D.

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Lời gii

Chọn B

Ta có

cos5 .cos cos4x x x

 

cos4 cos6 cos4

x x x  

cos6 cos4xx

6 4 2

x x k











  























Vậy số điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác là

Câu 32: Số vị trí biểu diễn các nghiệm của phương trình

4cos 4cos 3 0xx  

trên đường tròn

lượng giác là?

. B.

. C.

. D.

Lời gii

Chọn D

Ta có

4cos 4cos 3 0xx  

 

cos L

cos N

















Với

cos

x 

cos cos









  

 

k 

Vậy số vị trí biểu diễn các nghiệm của phương trình trên đường tròn lượng giác là

Câu 33: Số điểm biểu diễn các họ nghiệm của phương trình

sin2 3cos2 3xx

trên đường

tròn lượng giác là:

. B.

. C.

. D.

Lời gii

Chọn C

Ta có

1 3 3 3

sin2 3cos2 3 sin2 cos2 sin 2

2 2 2 3 2

x x x x x





       

















  













  







;

k 

Họ nghiệm





được biểu diễn bởi

điểm trên đường tròn lượng giác.

Họ nghiệm





được biểu diễn bởi

điểm trên đường tròn lượng giác không trùng với

các điểm biểu diễn của họ nghiệm thứ nhất.

Vậy nghiệm của phương trình được biểu diễn bởi

điểm trên đường tròn lượng giác.

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 34: Số điểm biểu diễn các họ nghiệm của phương trình

sin5 3cos5 2sin7x x x

trên

đường tròn lượng giác là:

. B.

. C.

. D.

Lời gii

Chọn C

Ta có:

sin5 3cos5 2sin7 sin5 cos5 sin7 sin 5 sin7

2 2 3

x x x x x x x x





       





7 5 2

;

7 5 2

18 6

x x k







  





  







   













Họ nghiệm





được biểu diễn bởi

điểm trên đường tròn lượng giác.

Họ nghiệm

18 6





được biểu diễn bởi

điểm trên đường tròn lượng giác không trùng với

các điểm biểu diễn của họ nghiệm thứ nhất.

Vậy nghiệm của phương trình được biểu diễn bởi

điểm trên đường tròn lượng giác.

Câu 35: Số điểm biểu diễn của phương trình

   

sin cos sin2 12 cos sin 12cos2 0x x x x x x    

là:

. B.

. C.

. D.

Lời gii

Chọn B

Ta có:

   

sin cos sin2 12 cos sin 12cos2 0x x x x x x    

   

 

sin cos sin2 12 cos sin 12 cos sin 0x x x x x x x      

   

 

sin cos sin2 12 sin cos 12 0x x x x x     

 

   

sin cos 0 1

sin2 12 sin cos 12 0 2

x x x









   





 

1 sin cos 0xx

2sin 0





  







  



  

 

k 

nên phương trình có

điểm biểu diễn.

   

2 sin2 12 sin cos 12 0x x x   

Đặt

sin cost x x

(điều kiện

2t 

)

sin cos





 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

 

2 12 13 0tt   













Đối chiếu điều kiện ta có

sin cos 1xx  

sin





   











  











 

k 

nên

phương trình có

điểm biểu diễn.

Vậy phương trình có

điểm biểu diễn nghiệm.

Câu 36: Nghiệm của phương trình

 

sin sin cos cos 2sin2 sin 1 1x x x x x x    

thoả điều kiện





  

có số điểm biểu diễn là:

. B.

. C.

. D.

Lời gii

Chọn B

Ta có:





  



























   





















  















  































  













 

sin sin cos cos 2sin2 sin 1 1x x x x x x    

 

   

sin 1 cos sin 1 2sin2 sin 1 0x x x x x      

  

sin 1 sin 1 cos 2sin2 0x x x x     

 

sin 1 0 1

sin cos 2sin 2 1 0 2

x x x









   





 

sin 1 0x 

sin 1x



  

 

k 

 

sin cos 2sin2 1 0x x x   

Đặt

sin cost x x

(điều kiện

2t 

)

sin cos





 

2 1 1 0tt   

2 3 0tt    















Đối chiếu điều kiện của

ta có:

sin cos 1xx  

sin





   





















 

k 

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Đối chiếu điều kiện

 

ta có





nên có

điểm biểu diễn.

Câu 37: Số điểm biểu diễn các nghiệm của phương trình

cos sin2 2 cos

2sin 1

x x x





   















trên đường tròn lượng giác là

. B.

. C.

. D.

Lời gii

Chọn A

Điều kiện:

 

sin

24 2





  





   















Phương trình trở thành

cos sin2 2 sin 0x x x   

cos2 sin2 2xx  

2 cos 2 2





  





cos 2 1





  







  



   

 

k 

So với điều kiện, ta được

 

x k k



  

Vậy có một điểm biểu diễn trên đường tròn lượng giác.

Câu 38: Số điểm biểu diễn các nghiệm của phương trình

sin sin2 2sin cos sin cos

3cos2

sin cos

x x x x x x

  





trên đường tròn lượng giác là

. B.

. C.

. D.

Lời gii

Chọn B

Điều kiện

sin cos 0xx

sin 0





  







  

 

x k k



    

Ta có:

sin sin2 2sin cos sin cos

3cos2

sin cos

x x x x x x

  





 

sin2 sin cos sin cos

3cos2

sin cos

x x x x x

  





  

sin2 1 sin cos

3cos2

sin cos

x x x







 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

sin2 3cos2 1xx   

sin 2 sin



   

   

   

   









   







   





 



















Vì mỗi họ nghiệm biểu diễn hai điểm trên đường tròn lượng giác nên các nghiệm phương trình

có bốn điểm biểu diễn trên đường tròn lượng giác.

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

DẠNG 5. BIỆN LUẬN NGHIỆM PHƯƠNG TRÌNH LƯỢNG GIÁC KHÔNG CHỨA

THAM SỐ

5.1. Tìm số nghiệm của phương trình lượng giác trên tập

Câu 39: Tìm số nghiệm của phương trình

cos5 .cos cos4x x x

trên

 

0;10



là

. B.

. C.

. D.

Lời gii

Chọn A

Ta có

cos5 .cos cos4x x x

 

cos4 cos6 cos4

x x x  

cos6 cos4xx

6 4 2

x x k











  



















x k Z



  

0 10x





0 10 0 50



     

.Vây có 49 nghiệm thỏa điều kiện.

Câu 40: Số nghiệm thuộc khoảng

 

0;100



của phương trình

sin cos 3cos 3



  





là

. B.

. C.

. D.

Lời gii

Chọn B

Ta có

sin cos 3cos 3



  





1 sin 3cos 3xx   

sin 3cos 2xx  

sin cos 1

xx  

sin 1





  





x k k



   

Theo đề bài cho ta có

0 100x





0 2 100





   

1 599

12 12

k   

Mà

 

0;1;2;3;4,....;48;49kk  

Câu 41: Số nghiệm của phương trình

cos sin2 2 cos

x x x





   





trên khoảng

 

0;3



là

. B.

. C.

. D.

Lời gii

Chọn B

cos sin2 2 cos

x x x





   





cos sin2 2 sinx x x   

cos2 sin2 2xx  

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

2 cos 2 2





  





cos 2 1





  







  



   

 

k 

Trên

 

0;3













Câu 42: Gọi

là số nghiệm thuộc khoảng

 

0;2023

của phương trình lượng giác

 

3 1 cos2 sin2 4cos 8 4 3 1 sinx x x x     

. Tìm

là

322

. B.

320

. C.

300

. D.

321

Lời gii

Chọn A

Ta có

 

3 1 cos2 sin2 4cos 8 4 3 1 sinx x x x     

 

2 3sin 2sin cos 4cos 8 4 3 1 sinx x x x x     

     

2 3sin sin 2 2cos sin 2 4 sin 2x x x x x     

2 3sin 2cos 4xx  

(vì

sin 1 2x 

)

3sin cos 2xx  

sin cos cos sin 1



  

sin 1





  







    



   

 

k 

Theo đề bài

 

0;2023x

 

2 0;2023



  

1 2023

2 0;



  









 

0;1;...;321k 

Vậy

322n 

Câu 43: Số nghiệm của phương trình

2cos 3sin2 3xx

trên





0;2020



là:

1010

. B.

2019

. C.

2020

. D.

2021

Lời gii

Chọn C

Ta có:

2cos 3sin2 3xx

cos2 3sin2 2xx  

cos 2 1





  







  



  

 

k 

Xét

0 2020x





0 2020





   

2020



   



 

0;1;...;2019k 

Vậy số nghiệm là

2020

Câu 44: Huyết áp là đại lượng để đo độ lớn của lực tác dụng lên thành mạch máu. Nó được đo

bằng hai chỉ số: huyết áp tâm thu (lúc tim đập) và huyết áp tâm trương (lúc tim nghỉ).

Huyết áp của mỗi người thường khác nhau, nhưng huyết áp tiêu chuẩn là

120/80

, nó

có nghĩa là huyết áp tâm thu là 120mmHg và huyết áp tâm trương là 80 mmHg. Giả sử

rằng trái tim của một người đập

lần một phút, huyết áp

giây có thể được

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

mô tả bằng hàm số

 

100 20sin

P t t











. Với

 

0;60t 

, có bao nhiêu lần huyết áp

người đó bằng

100

mmHg?

139

. B.

140

. C.

141

. D.

142

Lời gii

Chọn C

Với

 

100 100 20sin 100

P t t





   





sin 0















 

k 

t

 

k 

Với

 

0;60 0 60

t    

0 140k  

k 

nên có tất cả

141

giá trị

thỏa mãn.

Vậy với

 

0;60t 

có

141

lần huyết áp người đó bằng

100

mmHg.

Câu 45: Năm 1893, George Ferris chế tạo vòng đu quay. Nó có đường kính

250

foot. Nếu với

mỗi

giây vòng đu quay quay

vòng thì chiều cao

(foot) của một chỗ ngồi trên

vòng đu quay là một hàm số của thời gian

(giây) được xác định như sau

 

125sin 0,157 125

h t t





  





Vòng quay bắt đầu tính từ thời điểm

0.t 

Trong

giây đầu tiên của chuyến đi, tại thời điểm

nào sau đây (làm tròn đến hàng đơn vị) thì người ngồi trên ghế đu quay đó cách mặt đất

125

foot? (Chú thích:

foot xấp xỉ

30,48

cm).

giây. B.

giây. C.

giây. D.

giây.

Lời gii

Chọn C

Ta có:

 

125 125sin 0,157 125 125 sin 0,157 0

h t t t



   

       

   

   

0,157



  

0,157 2





  





k 

1 1 6,28 1

0 40 0 40 0,5 1,499

0,157 2 2 2

t k k k





              





 

0;1kk  

Với

0 . 10

0,157 2



   

giây.

Với

1 . 30

0,157 2



   

giây.

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

 Trong

giây đầu tiên của chuyến đi, có

thời điểm người ngồi trên ghế đu quay đó cách

mặt đất

125

foot, đó là lúc khoảng

giây và khoảng

giây.

5.2. Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình lượng giác:.

Câu 46: Nghiệm lớn nhất của phương trình

2cos2 1 0x

trong đoạn

 



là:





. B.





. C.





. D.





Lời gii

Chọn D

Phương trình

2cos2 1 0x

cos2

x













  

















  





Xét

 

0;x















  







   























mà

k 

suy ra





























Vậy nghiệm lớn nhất của phương trình

2cos2 1 0x

trong đoạn

 



là





Câu 47: Phương trình

cos2 2cos 3 0xx  

có nghiệm lớn nhất trong khoảng

 

0;2019

644



. B.



. C.

640



. D.

642



Lời gii

Chọn D

cos2 2cos 3 0xx  

2cos 2cos 4 0xx   

cos 1x

hay

cos 2x 

(loại)

Với

cos 1 2 ;x x k k



   

Với

0 2019 0 2 2019 0 321.49x k k



       

max

321k

Vậy nghiệm lớn nhất thuộc khoảng

 

0;2019

là

642x





Câu 48: Nghiệm dương nhỏ nhất của phương trình

 

sin cos2 0x 

là



. B.



. C.



. D.



Lời gii

Chọn C

Ta có

 

sin 2 0 2cos x cos x k



  

 

k 

Vì

 

 

1 1 1

2 1;1 0 2 0 2 .

2 4 2

cos x k cos x x k x k k

  



            

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

min





Vậy phương trình có nghiệm dương nhỏ nhất là



Câu 49: Gọi

là nghiệm dương nhỏ nhất của phương trình

3sin 2sin cos cos 0x x x x  

Chọn khẳng định đúng?

;











. B.

;











. C.











. D.











Lời gii

Chọn C

3sin 2sin cos cos 0x x x x  

3sin 3sin cos sin cos cos 0x x x x x x    

(3sin cos )(sin cos ) 0x x x x   

3sin cos 0

sin cos 0













3sin

cos

sin

cos

















tan

tan 1















arctan













  





 

k 

là nghiệm dương nhỏ nhất của phương trình

3sin 2sin cos cos 0x x x x  

nên

arctan

x 

Câu 50: Cho phương trình

sin .tan cos .cot 2sin cos

x x x x x x  

. Tính hiệu nghiệm âm lớn

nhất và nghiệm dương nhỏ nhất của phương trình.





. B.



. C.





. D.



Lời gii

Chọn C

Điều kiện:

sin2 0



  

Phương trình

sin cos 4 3

2sin cos

cos sin 3

   

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

4 4 2 2

sin cos 2sin cos sin cos

x x x x x x   

 

sin cos sin2

x x x  

sin2

x

 



















Suy ra nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình lần lượt là





và



Ta có:

3 6 6

  

   

Câu 51: Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu

 

của mực

nước trong kênh tính theo thời gian

 

được cho bởi công thức

3cos 12





  





Khi nào mực nước của

kênh là cao nhất với thời gian ngắn nhất?

 

22 ht 

. B.

 

15 ht 

. C.

 

14 ht 

. D.

 

10 ht 

Lời gii

Chọn D

Ta có:

1 cos 1





   





9 15h  

. Do đó mực nước cao nhất của kênh là

15m

đạt được khi

cos 1















  

2 12tk   

Vì

0t 

2 12 0k   

k

Chọn số

nguyên dương nhỏ nhất thoả

k 

là

1 10kt  

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

5.3. Tính tổng tất cả các nghiệm của phương trình lượng giác trên tập

Câu 52: Tính tổng tất cả các nghiệm của phương trình

sin sin2 0xx

trên đoạn

 

0;2



. B.



. C.



. D.



Lời gii

Chọn B

Ta có

   

sin sin2 0 sin2 sin , ,

x x k

x x x x k l

x x l







  







       



  







Vì

 

0;2x





nên

02x





+ Với





. Ta có

0 2 0 3



    

. Suy ra



  





  



  



  



+ Với

2xl





. Tương tự

0 2 2

  

      

. Suy ra

0lx



  

Vậy tổng tất cả các nghiệm của phương trình đã cho trên

 

0;2



là



Câu 53: Tính tổng các nghiệm trong đoạn

 

0;30

của phương trình:

tan tan3xx

(1)

55 .



. B.

171



. C.

45 .



. D.

190



Lời gii

Chọn C

Điều kiện để phương trình (1) có nghĩa

 

cos 0

cos3 0

































Khi đó, phương trình (1)

x k x



   

so sánh với đk (*)

 

   

, 0;30 0;...;4 0; ;2 ;....;9

x k x



  







    







Vậy, tổng các nghiệm trong đoạn

 

0;30

của phương trình (1) là:



Câu 54: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình

sin 3











bằng

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold



. B.



. C.





. D.





Lời gii

Chọn C

sin 3





























  





36 3

11 2

36 3



















;

;kl

TH1:

0x 

;

lớn nhất

Chọn





   



   







  

(nhận)

TH2:

0x 

;

nhỏ nhất

Chọn



















(nhận)

Khi đó tổng cần tìm là:

13 7

36 36 6

  

   

Câu 55: Tổng tất cả các nghiệm của phương trình

cos2 cos 0xx

trong khoảng

 

0;2



bằng

. Vậy

bằng bao nhiêu?





. B.





. C.





. D.





Lời gii

Chọn D

cos2 cos 0 cos2 cos

x x k

x x x x x k

x x k













       



  





Với

 

0;2 ;

x x x





   

Vậy





  

Câu 56: Tổng các nghiệm của phương trình

sin2 3 6sin cosx x x  

trong khoảng









là



. B.



. C.



. D.



 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Lời gii

Chọn D

Ta có:

sin2 3 6sin cosx x x  

2sin cos cos 6sin 3x x x x   

   

cos 2sin 1 3 2sin 1x x x   

2sin 1 0

cos 3( )













sin

x



















k 











suy ra













Suy ra tổng các nghiệm là



Câu 57: Tổng tất cả các nghiệm thuộc

 

0;10π

của phương trình

2sin 5sin 3 0xx  

là



. B.



. C.



. D.



Lời gii

Chọn B

Ta có:

 

sin 3

2sin 5sin 3 0

sin

x VN

x x k









  



     

















 Xét

1 61

0 2 10

6 12 12





      

mà

k 

nên

 

1;2;3;4;5k 

11 23 35 47 59

; ; ; ;

6 6 6 6 6

    









Xét

7 7 53

0 2 10

6 12 12





      

mà

k 

nên

 

0;1;2;3;4k 

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

7 19 31 43 55

; ; ; ;

6 6 6 6 6

    









Vậy tổng tất cả các nghiệm thuộc

 

0;10



của phương trình là



Câu 58: Tổng các nghiệm trong đoạn

 

0;2



của phương trình

sin cos 1xx

bằng



. B.



. C.

2

. D.



Lời gii

Chọn D

sin cos 1xx

  

sin cos 1 sin cos 1x x x x   

 

Đặt

sin cos 2 sin

t x x x





   





22t  

Có

1 2sin cost x x

 

sin cos 1

x x t  

 

trở thành:

 

1 1 1



  





3 2 0tt   

 

1 2 0t t t    

 















2 sin 1





  





sin





  









   











   









  







   





Có

0;2x







nên ta có các nghiệm

x 

;





Vậy tổng các nghiệm

0;2x







của phương trình đã cho là



Câu 59: Phương trình

6sin 7 3sin2 8cos 6x x x  

có tổng hai nghiệm dương nhỏ nhất bằng



. B.



. C.



. D.



Lời gii

Chọn B

Ta có:

1 cos2 1 cos2

6sin 7 3sin2 8cos 6 6 7 3sin2 8 6

x x x x



   

      

   

   

   

3 1 cos2 7 3sin2 4 1 cos2 6 3sin2 cos2 1x x x x x        

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

3 1 1 1

sin2 cos2 sin 2 sin 2 sin

2 2 2 6 2 6 6

x x x x

  

   

        

   

   

























   







 

k 

+ Trường hợp





, do

x k k



      

. Lại có

k 

nên nghiệm dương nhỏ

nhất của phương trình trong trường hợp này là nghiệm





ứng với

0k 

+ Trường hợp





, do

x k k



      

. Lại có

k 

nên nghiệm dương nhỏ

nhất của phương trình trong trường hợp này là nghiệm





ứng với

0k 

Vậy hai nghiệm dương nhỏ nhất của phương trình là:





;





và tổng của chúng là



Câu 60: Gọi

là tổng các nghiệm của phương trình

sin

cos 1





trên đoạn

 

0;2017



. Tính

2035153S





. B.

1001000S





. C.

1017072S





. D.

2000200S





Lời gii

Chọn C

sin 0

sin

0 cos 1 2

cos 1

x x k







     









Suy ra tập nghiệm là

 

0;2 ;4 ;....2 ,..n

  

Vậy

   

0 2 4 ... 2016 2 1 2 ... 1008 1017072S

  

         

Câu 61: Tìm tổng các nghiệm của phương trình

sin3 cos 0xx

trên

 



. B.



. C.



. D.



Lời gii

Chọn D

Ta có:

sin3 cos 0 sin3 sin

x x k

x x x x

x x l





  





     









  





 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

 







  













Mà

 

0;x





nên









   



  





. Do











nên















3 3 3 7

8 4 8 8



   









      









Câu 62: Tìm tổng tất cả các nghiệm thuộc đoạn

 

0;30

của phương trình

cos3 4cos2 3cos 4 0x x x   

là



. B.

121



. C.



. D.



Lời gii

Chọn D

cos3 4cos2 3cos 4 0x x x   

 

4cos 3cos 4 2cos 1 3cos 4 0x x x x     

4cos 8cos 0xx  













cos 0

cos 2 (vn)

+ Với

cos 0

x x k



   

.Theo giải thiết,

 

1 30

0;30 0



    

1 30 1



    

mà

 

0;1;2;3; ;9k Z k   

Vậy tổng các nghiệm thỏa mãn yêu cầu bài toán là

 

2 9 5 1 2 9 5 45 50

2 2 2 2

   

       

     

            

     

     

Câu 63: Tính tổng

tất cả các nghiệm của phương trình

 

2cos2 5 sin cos 3 0x x x   

trên

khoảng

 

0;2





. B.





. C.





. D.





Lời gii

Chọn C

Ta có:

 

4 4 2 2

2cos2 5 sin cos 3 0 2cos2 5 sin cos 3 0x x x x x x        

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

 

2cos2 5 cos2 3 0 2cos 2 5cos2 3 0x x x x        

cos2 3

cos2 2 2

2 3 3

cos2

x x k x k











        







 Với





 

1 5 4

0;2 0 2 , {0;1} ;

3 3 3 3 3

x k k k k x

  





            





 Với







 

0;2 0 2 ,

3 3 3

x k k k



  



        

{1;2} ;





   





Vậy tổng





Câu 64: Cho phương trình

 

2sin 1 3tan 2sin 3 4cos   x x x x

. Gọi

là tập hợp các

nghiệm thuộc đoạn

 

0;20



của phương trình trên. Tính tổng các phần tử của

570



. B.

875



. C.

880



. D.

1150



Lời gii

Chọn B

Điều kiện:



  x k k Z

Phương trình đã cho tương đương với

 

2sin 1 3tan 2sin 4sin 1   x x x x

 

2sin 1 3tan 1 0   xx

sin

tan

























  



























 

k

(thỏa mãn điều kiện).

*Trường hợp 1: Với



xk

 

k

 

 

0;20 0 2 20



  

    xk

5 115

12 12



  k

. Mà

k

nên

 

0; 1; 2....; 9k



Tổng tất cả các nghiệm thuộc đoạn

 

0;20



của họ nghiệm

 

là:















295





*Trường hợp 2: Với



xk

 

k

 

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

 

0;20 0 20



  

    xk

1 119



  k

. Mà

k

nên

 

0;1; 2....;19k



Tổng tất cả các nghiệm thuộc đoạn

 

0;20



của họ nghiệm

 

là:

580









  







Vậy tổng các phần tử của

là

875





Câu 65: Tính tổng tất cả các nghiệm của phương trình

cos cos 1

cos2 tan

cos





trên đoạn

[1;70]

188



. B.

263



. C.

363



. D.

365



Lời gii

Chọn D

Ta có điều kiện

cos 0 ,

x x k k



    

Phương trình đã cho trở thành:

cos cos 1

2cos 1 tan

cos



  

1 cos cos 1

2cos

cos cos



  

4 3 2

2cos cos cos 0x x x   

cos (2cos cos 1) 0x x x   

cos 0

cos 1

cos









  









So sánh điều kiện ta có

 

2 1;70 0;1;2;3;4;5;6;7;8;9;10

cos 1

2 1;70 0;1;2;3;4;5;6;7;8;9;10

cos

2 1;70 1;2;3;4;5;6;7;8;9;10;11

x k k









    







      













    



Tổng các nghiệm trên đoạn đã cho của họ thứ nhất là:

11( 2.10 )

121









Tổng các nghiệm trên đoạn đã cho của họ thứ hai là:

11( 2.10 )

341









 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Tổng các nghiệm trên đoạn đã cho của họ thứ ba là:

11( 2 2.11 )

385







  



Vậy tổng các nghiệm trên đoạn đã cho của phương trình là:

1 2 3

363S S S S



   

Câu 66: Tổng các nghiệm của phương trình

4 4 4

sin sin sin

4 4 4

x x x



   

    

   

   

trong khoảng

 

0;2



bằng



. B.



. C.



. D.



Lời gii

Chọn B

Ta có

4 4 4

sin sin sin

4 4 4

x x x



   

    

   

   

1 cos 2 1 cos 2

1 cos2 5

2 2 2 4



   

   

   





   

   

   





   

   

     

2 2 2

1 cos2 1 sin2 1 sin2 5x x x      

1 2cos2 cos 2 2 2sin 2 5x x x     

2cos2 sin 2 1xx   

2cos2 1 sin 2 cos 2 2cos2 0x x x x      

 

cos2 0

;

cos2 2







    







voâ nghieäm

Theo bài ra ta có

4 2 2 2





      

, vì

nên

 

0;1;2;3k 

Tổng các nghiệm là

4 4 2 4 4 2

     



      

Câu 67: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình

1 tan tan sin cot 4

x x x



  





là





. B.



. C.



. D.





Lời gii

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Chọn D

Điều kiện

cos 0

sin2 0 ,

sin 0

x x k k







    







sin sin cos cos

1 tan tan sin cot 4 sin cot 4

cos cos

x x x x x





     





cos

sin cot 4

cos cos

  

tan cot 4xx  

tan 4tan 1 0xx   

tan 2 3











  

























Với hai họ nghiệm trên dễ thấy nghiệm dương nhỏ nhất là



; để

được

nghiệm âm lớn nhất ta

đều cho

1kl  

được nghiệm âm

7 11

;

12 12





khi đó nghiệm âm lớn nhất là





Ta có

12 12 2

  



  

Câu 68: Tính tổng các nghiệm thuộc

 



của phương trình:

sin2

cos 1







. B.



. C.



. D.



Lời gii

Chọn A

ĐK:

cos 1 0 cos 1 2x x x k



     

k 



sin2 0 2

x x k x



    

k 

Kết hợp với ĐK ta được





2xk





k 

Với





, mà

 

 

;3 1;2

2 2 2



  





    



    









suy ra

;











 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Với

2xk





, mà

 

 

;3 0;1

   





  







    













suy ra

 

;3x





Vậy tổng các nghiệm bằng



Câu 69: Tính tổng

các nghiệm của phương trình

cos sin cos 2sin cos 2x x x x x   

trên

khoảng

;5 .













. B.





. C.





. D.





Lời gii

Chọn C

cos sin cos 2sin cos 2x x x x x   

sin 2sin 3 cos sin cos 0x x x x x      

    

1 sin sin 3 cos 1 sin 0x x x x     

  

1 sin sin cos 3 0x x x    

 

sin 1 1

sin cos 3 0 2









  





   

1 2 .

x k k



   

Vì











nên phương trình có các nghiệm:





và





 

2 sin cos 3xx   

vô nghiệm vì

 

1 1 3 .  

Vậy tổng tất cả các nghiệm của phương trình là:

T x x





    

Câu 70: Tính tổng các nghiệm trên

 

44 ;





của phương trình

sin 3 3sin 2 2 0xx   



. B.





. C.





. D.

Lời gii

Chọn B

 

sin 3 3sin 2 2 0 1   xx

sin 3sin 3sin 2 3 3sin 2     x x x x

Đặt

3sin 2tx

, phương trình trở thành

 

sin 3 sin 0x t x t   

 

sin sin .sin 3 0x t x t x t     

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Dễ chứng minh

sin .sin 3 0t t x t   

nên

sin xt

sin 3sin 2xx  

sin 3sin 2 0   xx

sin 1

sin 2 ( )













sin 1x

 

 xkk



Ta có:

4 24 k



  

k

Vậy tổng các nghiệm trên

 

44 ;





của

 









  







Câu 71: Phương trình

1 1 1

cos sin2 sin4x x x



có tổng các nghiệm trên

(0; )



là:



. B.



. C.



. D.



Lời gii

Chọn D

Điều kiện:

cos 0 cos 0 cos 0 sin 1

sin2 0 sin 0 sin 0 sin 0

sin4 0 cos2 0

sin sin

x x x x





    





   

      

   

   







   





 

1 1 1

cos 2sin cos 4sin cos cos2

2sin cos2 cos2 1 0

2sin (1 2sin ) 1 2sin 1 0

2sin (1 2sin sin ) 0

sin 1

sin 0

sin

1 2sin sin 0

x x x x x x

x x x



  

   

     

   















   





  















Suy ra phương trình có 2 nghiệm trên

(0; )



là





và





Vậy tổng các nghiệm trên

(0; )



là:







 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Câu 72: Phương trình

sin2 2cos sin 1

tan 3

x x x

  





có bao nhiêu nghiệm trên

(0;3 )



A. 1. B. 2. C. 3. D. 4

Lời gii

Chọn B

Điều kiện:

cos 0

tan 3



























  





 

sin2 2cos sin 1 0 2sin cos sin 2cos 1 0

sin 1

(2cos 1)(sin 1) 0

cos

Pt x x x x x x x

x x k



         





  





      







  







Kết hợp điều kiện xác định ta được nghiệm của phương trình là





Vậy phương trình có hai nghiệm thuộc

(0;3 )



là





và





Câu 73: Gọi

là tổng tất cả các nghiệm thuộc

 

0;20



của phương trình

2cos sin 1 0xx  

Khi đó giá trị của

bằng:

570S





. B.

295S





. C.

590S





. D.

200





Lời gii

Chọn B

2cos sin 1 0xx  

2sin sin 1 0xx    

sin 1

sin



















  



  









 

1 2 3

,,k k k 

 

0;20x





nên:

0 2 20















   



  





  





1 41

1 119

12 12

5 115

12 12







   





  





 

1;2;3;...;10

0;1;2;...;9

















Ta thấy tất cả các nghiệm này không có hai nghiệm nào giống nhau nên tổng các nghiệm của

phương trình trong đoạn

 

0;20



là:

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold







   



































295





Câu 74: Tính tổng

các nghiệm của phương trình

cos sin2 2 cos

x x x





   





trên khoảng

 

0;2





. B.





. C.





. D.





Lời gii

Chọn C

Ta có

cos sin2 2 cos

x x x





   







cos sin2 2 sinx x x  



cos2 sin2 2xx



cos 2 1

















k 





  

k 

Vì

02x











   



1 17

k

Vì

k 

nên

 

1;2k 



7 15

;





Vậy





Câu 75: Tính tổng tất cả các nghiệm của phương trình

3cos sin 1xx

trên

 

0;2



. B.



. C.



. D.



Lời gii

Chọn A

Ta có

3cos sin 1 cos

x x x





    





 













  





Do đó các nghiệm trên

 

0;2



của phương trình là









Vậy tổng tất cả các nghiệm của phương trình trên

 

0;2



bằng

6 2 3

  



Câu 76: Gọi

là tập hợp các nghiệm thuộc khoảng

 

0;100



của phương trình

sin cos 3cos 3



  





. Tổng các phần tử của

là

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

7400



. B.

7525



. C.

7375



. D.

7550



Lời gii

Chọn C

Ta có

sin cos 3cos 3



  





1 sin 3cos 3xx   

sin 3cos 2xx  

sin cos 1

xx  

sin 1





  





x k k



   

Theo đề bài cho ta có

0 100x





0 2 100





   

1 599

12 12

k   

Mà

 

0;1;2;3;4,....;48;49kk  

Vậy

2 2 2 ...... 49 2

6 6 6 6

   

  

         

 

2 1 2 3 4 ..... 49



      

 

49 49 1

50 7375

6 2 3







  

Câu 77: Gọi

là tập hợp tất cả các nghiệm thuộc khoảng

 

0;2018

của phương trình sau:

 

3 1 cos2 sin2 4cos 8 4 3 1 sinx x x x     

. Tính tổng tất cả các phần tử của

103255



. B.

310408



. C.

312341



. D.

102827



Lời gii

Chọn B

Ta có

 

3 1 cos2 sin2 4cos 8 4 3 1 sinx x x x     

2 3sin 2sin cos 4cos 4 3sin 4sin 8 0x x x x x x      

   

2sin 3sin cos 2 4 3sin cos 2 0x x x x x      

 

2 sin 2 3sin cos 2 0x x x    

3sin cos 2 0xx   

sin 1



  







  

k 

Vì

 

0;2018x

nên

0 2 2018



  

1 1009 1

6 π6

k    





 

0;1;2;...;321

Suy ra

; 2 ; 2.2 ;...; 321.2

3 3 3 3

   

  



   





Vậy tổng tất cả các phần tử của

là

 

322. 2 1 2 3 ... 321



     

310408





 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 78: Tính tổng tất cả các nghiệm của phương trình

sin2 4sin 2cos 4 0   x x x

trong đoạn

 

0;100



của phương trình.

100



. B.

2476



. C.



. D.

2475



Lời gii

Chọn D

Ta có

sin2 4sin 2cos 4 0 2sin cos 4sin 2cos 4 0        x x x x x x x

      

2sin cos 2 2 cos 2 0 cos 2 sin 1 0        x x x x x

 

sin 1

cos 2







    







x k k

x VN

Cách 1: Trong đoạn

 

0;100



, phương trình có các nghiệm

; 2 ; 4 ; 6 ;...; 98

2 2 2 2 2

    

   

   

Tổng các nghiệm bằng

 

2 4 6 ... 98 50. 2 4 6 ... 98 .

2 2 2 2 2 2

     

    

               S

 

2 98 .49

25 . 2475

  



  S

Cách 2: Tìm

thỏa mãn

0 2 100 0 49





     

Bấm máy

2 2475









  







Câu 79: Tổng tất cả các nghiệm của phương trình

 

cos sin 1x 

trên

 

0;2



bằng

. B.



. C.



. D.



Lời gii

Chọn B

Ta có

 

0;2x





 

sin 1;1x  

Khi đó:

 

cos sin 1 sin 2x x k



  

 

k 

với

1 2 1 0kk



    

Phương trình trở thành

sin 0

x x m







   







 

m

Vậy tổng tất cả các nghiệm của phương trình

 

cos sin 1x 

trên

 

0;2



bằng



Câu 80: Tính tổng

các nghiệm của phương trình

 

2cos2 5 sin cos 3 0x x x   

trong

khoảng

 

0;2



 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn





. B.





. C.





. D.





Lời gii

Chọn B

Ta có:

 

4 4 2 2

2cos2 5 sin cos 3 0 2cos2 5 sin cos 3 0x x x x x x        

 

2cos2 5 cos2 3 0 2cos (2 ) 5cos2 3 0 cos2

x x x x x           

 

1 5 7 11

cos2 ; ; ;

2 6 6 6 6 6

x x k k x

    





       





Do đó:

5 7 11

6 6 6 6

   



    

Câu 81: Cho phương trình

 

2018 2018 2020 2020

sin cos 2 sin cosx x x x  

. Tính tổng các nghiệm của

phương trình trong khoảng

 

0;2018

1285









. B.

 

643



. C.

 

642



. D.

1285









Lời gii

Chọn D

 

2018 2018 2020 2020

sin cos 2 sin cosx x x x  

   

2018 2 2018 2

sin 1 2sin cos 1 2cos 0x x x x    

2018 2018

sin .cos2 cos cos2 0x x x x  

2018 2018

cos2 0

sin cos













cos2 0x 



  

 



   

 

2018 2018

sin cosxx

2018

tan 1x

(





không là nghiệm)

tan 1x  

 

x k k



    

 

. Từ

 

và

 

ta có

 



  

là nghiệm của pt.

 

0;2018x

0 2018



   

0 1284,kk   

Vậy tổng các nghiệm của phương trình trong khoảng

 

0;2018

bằng

 

.1285 1 2 ... 1284



   

1284.1285

.1285





1285











Câu 82: Phương trình lượng giác:

cos3 cos2 9sin 4 0x x x   

trên khoảng

 

0;3



. Tổng số

nghiệm của phương trình trên là:

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold



. B.



. C. Kết quả khác. D.



Lời gii

Chọn B

Ta có

cos3 cos2 9sin 4 0x x x   

4cos 3cos 2sin 9sin 5 0x x x x     

 

  

cos 1 4sin 2sin 1 sin 5 0x x x x     

  

2sin 1 cos 2sin cos sin 5 0x x x x x      

 

2sin 1 0 1

sin cos 2sin cos 5 0 2

x x x x









   



Giải

 

, ta có

 

1 sin









  









Với

 

0;3x





nên

 

có các nghiệm thoả bài toán là:

















Giải

 

, đặt

sin cos 2 sin

t x x x





   





với

2t 

Khi đó

1 2sin cos 2sin cos 1t x x x x t    

;

Phương trình

 

trở thành

1 5 0 4 0t t t t       

phương trình vô nghiệm.

Vậy tổng các nghiệm là:

13 5 17

6 6 6 6

   



   

DẠNG 6. TÌM ĐIỀU KIỆN CỦA THAM SỐ

ĐỂ PHƯƠNG TRÌNH LƯỢNG GIÁC

CHO TRƯỚC CÓ NGHIỆM.

Câu 83: Tính tổng

tất cả các giá trị nguyên của tham số

để phương trình

2cos 2 5





  





có nghiệm thuộc khoảng

;









25S 

. B.

22S 

. C.

22S 

. D.

25S 

Lời gii

Chọn C

Theo giả thiết, ta có

; 2 0;

6 4 3 6

   

   

   

   

   

Phương trình

2cos 2 5 cos 2

3 3 2

x m x





   

     

   

   

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Với

2 0; 1 cos 2 1

3 6 3

  

   

      

   

   

1 1 2 5 2



        

7 3 3 7mm        

Vì

m

nên

 

4;5;6;7m

. Khi đó

4 5 6 7 22S     

Câu 84: Tìm

để phương trình

  

3cos 4 3cos 1 3 0x x m   

có số nghiệm trên đoạn









là lớn nhất.

m  

. B.

m  

. C.

m  

. D.

m  

Lời gii

Chọn D

Ta có:

  

 

cos

3cos 4 3cos 1 3 0

cos *

x x m







    













 

k 

Vì phương trình

cos

x 

vô nghiệm nên thỏa mãn yêu cầu bài toán khi

 

có số nghiệm trên

đoạn









nhiều nhất.

Khi đó

m 

  

3 3 1 0



       

Câu 85: Tìm điều kiện của tham số

để phương trình

   

sin 2 1 sin 3 2 0x m x m m    

có

nghiệm



  







. B.



  







. C.

   









. D.

  









Lời gii

Chọn B

Đặt

sintx

11t  

Phương trình trở thành

   

2 1 3 2 0t m t m m    













Phương trình có nghiệm

1 3 1

1 2 1

   







   





  











Câu 86: Tìm điều kiện của tham số

để phương trình

 

cc oos s2 2 1 1 0xx m m    

có đúng

hai nghiệm trên đoạn

;











 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

10m  

. B.

01m

. C.

01m

. D.

11m  

Lời gii

Chọn B

Ta có

 

cc oos s2 2 1 1 0xx m m    

 

2cos 2 1 cos 0x m x m    

cos















Với

;











thì

0 cos 1x

Suy ra

cos

x 

không thỏa bài toán.

Phương trình đã cho có 2 nghiệm trên đoạn

;











0 cos 1x  

01m  

Câu 87: Cho phương trình

   

2sin 1 sin2 6 cos 1x m x m x    

. Có bao nhiêu giá trị nguyên

của tham số

để phương trình vô nghiệm?

. B.

. C.

. D.

Lời gii

Chọn A

       

1 cos2

2sin 1 sin2 6 cos 1 1 cos2 1 sin2 6 1

x m x m x x m x m



           

    

2 2cos2 2 1 sin2 6 1 cos2 2x m x m x       

     

4 cos2 2 1 sin2 6m x m x m      

Phương trình vô nghiệm

       

2 2 2

4 4 1 6 4 12 16 0 1;4m m m m m m            

Vậy có 4 giá trị nguyên của tham số

để phương trình vô nghiệm.

Câu 88: Tìm tất cả các giá trị của tham số

để phương trình

2cos 4 sin cosx m x x m

có

nghiệm:

m 

. B.

m 

hoặc

m  

. D.

0m 

Lời gii

Chọn B

Ta có

2cos 4 sin cosx m x x m

1 cos2 2 sin2 cos2 2 sin2 1x m x m x m x m       

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Phương trình

cos2 2 sin2 1x m x m

có nghiệm

 

1 4 1mm   

3 2 0

m m m     

hoặc

0m 

Câu 89: Số các giá trị nguyên m để phương trình

4 4.sin .cos 2.cos2 3 9m x x m x m    

có nghiệm là

A. 7. B. 6. C. 5. D. 4

Lời gii

Chọn D

Điều kiện xác định:

4 4 0 1

2 0 2 3.

3 9 0 3

  





     





  



m m m

4 4.sin .cos 2.cos2 3 9m x x m x m    

 

1. 2sin .cos 2.cos2 3 9m x x m x m     

1.sin2 2.cos2 3 9m x m x m     

Phương trình có nghiệm khi

     

2 2 2

1 2 3 9m m m    

1 2 3 9m m m     

6.m

Kết hợp điều kiện ta được

3 6.m

Mà

m

nên

 

3;4;5;6m

Vậy có 4 giá trị nguyên của m thỏa mãn yêu cầu đề bài.

Câu 90: Có tất cả bao nhiêu giá trị nguyên của tham số

để phương trình

3cos 1 0xm  

có

nghiệm?

. B.

. C.

. D. Vô số.

Lời gii

Chọn C

Ta có

3cos 1 0 cos

x m x



    

Phương trình có nghiệm

m

   

1 3 1 3m    

Vì

m

nên

 

0;1;2 .m

Vậy có tất cả 3 giá trị nguyên của tham số

Câu 91: Tìm tất cả các giá trị của tham số

để phương trình

 

1 sin 2 0m x m   

có nghiệm.

1.m 

. B.

m 

. C.

m  

. D.

1.m 

Lời gii

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Chọn B

Phương trình

 

1 sin 2 0m x m   

 

1 sin 2m x m   

sin .







Để phương trình có nghiệm



   

















































































m

Câu 92: Có tất cả bao nhiêu giá trị nguyên của tham số

để phương trình

3cos 1 0xm  

có

nghiệm?

. B.

. C.

. D. Vô số.

Lời gii

Chọn C

Ta có

3cos 1 0 cos

x m x



    

Phương trình có nghiệm

m

   

1 3 1 3m    

Vì

m

nên

 

0;1;2 .m

Vậy có tất cả 3 giá trị nguyên của tham số

Câu 93: Tìm tất cả các giá trị của tham số

để phương trình

 

1 sin 2 0m x m   

có nghiệm.

1.m 

. B.

m 

. C.

m  

. D.

1.m 

Lời gii

Chọn B

Phương trình

 

1 sin 2 0m x m   

 

1 sin 2m x m   

sin .







Để phương trình có nghiệm



   

















































































m

DẠNG 7. TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ LƯỢNG GIÁC

7.1. Tìm GTLN, GTNN sử dụng điều kiện

1 sin ,cos 1xx  

Câu 94: Tìm giá trị nhỏ nhất của biểu thức

sin sin

A x x







  







1

. B.

. C.

2

. D.

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Lời gii

Chọn A

Ta có

sin sin 2sin cos sin

3 3 3 3

A x x x x

   

  

  

      

     

  

  

1 sin 1 1 1,

x A x







         







Vậy

min 1 khi sin 1 2 ,

x x k k











         







Câu 95: Tìm giá trị lớn nhất của biểu thức

sin cosA x x

. B.

. C.

. D.

Lời gii

Chọn A

Ta có

4 4 2

sin cos 1 sin 2

A x x x   

0 sin 2 1 1 sin 2 1,

x x x       

Vậy

max 1 khi sin 1 cos 0 ,

x x x k k





       

Câu 96: Tập giá trị của hàm số

sin2 3cos2 1y x x  

là đoạn

 

;.ab

Tính tổng

.T a b

1T 

. B.

2T 

. C.

0T 

. D.

1T 

Lời gii

Chọn B

Cách 1:

sin2 3cos2 1 sin2 3cos2 1y x x x x y      

Để phương trình trên có nghiệm thì

 

1 3 1 2 3 0 1 3y y y y          

Suy ra

 

1;3y

. Vậy

1 3 2.T    

Cách 2:

sin2 3cos2 1 2sin 2 1

y x x x







     







 

sin 2 1;1







  







nên

 

2sin 2 1 1;3







   







Vậy

13y  

.( Ta thấy

1y 

khi

sin 2 1







  







3y 

khi

sin 2 1















 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 97: Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu

 

của mực

nước trong kênh tính theo thời gian

 

được cho bởi công thức

3cos 12







  







Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?

 

22 ht 

. B.

 

15 ht 

. C.

 

14 ht 

. D.

 

10 ht 

Lời gii

Chọn D

Ta có:

1 cos 1







   







9 15h  

. Do đó mực nước cao nhất của kênh là

15m

đạt được khi

cos 1



















  

2 12tk   

Vì

0t 

2 12 0k   

k

. Chọn số

nguyên dương nhỏ nhất thoả

k 

là

1 10kt  

Câu 98: Gọi

và

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

 

1 2cos 2 3 sin cosy x x x



    



trên . Biểu thức

2MN

có giá trị bằng

. B.

4 2 3

. C.

. D.

2 3 2

Lời gii

Chọn C

Ta có

 

1 2cos 2 3 sin cosy x x x



    



 

1 2 2 3 sin cos 2cosx x x    

 

2 3 sin2 2cos 1xx   

 

2 3 sin2 cos2xx  

 

6 2 1

6 2 sin2 cos2





  







 

6 2 sin 2x



  

(với

cos







;

sin







)

Suy ra

6 2 6 2y    

. Do đó

max 6 2yM  

;

min 6 2yN   

Vậy

22MN  

Câu 99: Số giờ có ánh sáng của một thành phố X ở vĩ độ

40

bắc trong ngày thứ

của một năm

không nhuận được cho bởi hàm số:

   

3sin 80 12

182

d t t





  





t 

và

0 365t

Vào ngày nào trong năm thì thành phố X có nhiều giờ ánh sáng nhất?

262

. B.

353

. C.

. D.

171

Lời gii

Chọn D

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

100

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ta có:

   

3sin 80 12

182

d t t





  





3 12 15  

Dấu bằng xảy ra khi

 

sin 80 1

182











   

80 2

182 2

t k k





    

tk  

Mặt khác





0;365t 

nên

365k   

171 194

364 364

k   

Mà

k 

nên

0k 

Vậy

171t 

Câu 100: Hàm số

2cos3 3sin3 2y x x  

có tất cả bao nhiêu giá trị nguyên?

. B.

. C.

. D.

Lời gii

Chọn A

TXD:

D 

2cos3 3sin3 2y x x  

13 cos3 sin3 2

13 13





  







13sin 3 arccos 2





   







Để hàm số

có giá trị nguyên

13sin 3 arccos













nguyên

sin 3 arccos

13 13





  







(với

là một số nguyên)

Mà:

 

sin 3 arccos 1;1





  







1 1 13 13

n       

Mà:

n

 

0; 1; 2 3n    



có

giá trị nguyên.

Câu 101: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau

2sin cos 2y x x

max 4y 

min

y 

. B.

max 3y 

min 2y 

max 4y 

min 2y 

. D.

max 3y 

min

y 

Lời gii

Chọn D

Đặt

sin , 0 1 cos2 1 2t x t x t     

 

2 1 2 4 2 1 2

y t t t t t





         







 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

101

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Cách 1: Do

1 1 3 1 9

0 1 2 0 2

2 2 2 2 4

t t t





          







y  

Cách 2: Có

82yt





 

0 0;1



    

Ta có:

 

01y 

;













;

 

13y 

Vậy

max 3y 

đạt được khi





min

y 

đạt được khi

1 1 cos2 1 1

sin cos2

4 2 4 2



    



   



   

Câu 102: Gọi

và

lần lượt là GTLN và GTNN của hàm số

sin cos sin2y x x x  

. Tổng

Mm

là



. B.



. C.

. D.

Lời gii

Chọn D

Ta có:

4 4 2 2

sin cos sin2 1 sin 2 sin2 sin 2 sin2 1

y x x x x x x x         

Đặt

 

sin2 1 1t x t   

y t t   

 

11t  

là parabol có đỉnh

;

2a 2a

























 

1; 1 1;1





    







 

y   

;

 

y 

. Suy ra

;





Vậy

1Mm

7.2. Tìm GTLN, GTNN dạng

sin cosy a x b x c  

Câu 103: Cho hàm số

sin 2cos

sin cos 3







. Gọi

lần lượt là giá trị nhỏ nhất và giá trị lớn nhất

của hàm số đã cho. Tính

75mM

bằng?

. B.

. C.

. D.

10

Lời gii

Chọn D

TXĐ:

D 

Ta có:

sin 2cos

sin cos 3







     

1 sin 2 cos 3 1y x y x y    

Phương trình

 

có nghiệm

   

1 2 9y y y    

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

102

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

7 2 5 0 1 ; 1

y y y m M           

Vậy

7 5 5 5 10mM     

Câu 104: Hàm số

 

3sin4 4 sin cos

2cos 2 sin4 2

x x x







có giá trị lớn nhất

và giá trị nhỏ nhất

. Khi

đó tổng

Mm

bằng?

. B.



. D.

Lời gii

Chọn C

TXĐ:

D 

Ta có:

   

4 4 2 2 2

3sin4 4 sin cos 3sin4 4 1 2sin cos 2sin 2x 3sin4 4x x x x x x x       

3sin4x cos4x 3  

Xét mẫu thưc:

2cos 2 sin4 2 cos4x sin4 3x x x    

Suy ra

 

3sin4 4 sin cos

3sin4x cos4x 3

2cos 2 sin4 2 cos4 sin4x 3

x x x







   

     

3 sin 1 cos 3 3 2y x y x y     

Phương trình

 

có nghiệm

     

2 2 2

3 1 3 3y y y     

5 4 2 5 4 2

7 10 1 0

y y y

   

      

mM   

Câu 105: Giá trị lớn nhất

, giá trị nhỏ nhất

của hàm số:

2cos 2 3sin cos 1y x x x  

là

4; 0Mm

. B.

3; 0Mm

. C.

3; 1Mm

. D.

M 4; 1m

Lời gii

Chọn A

Tập xác định

D 

Ta có

2cos 2 3sin cos 1y x x x  

 

cos2 3sin2 2 *xx  

2 cos2 sin2 2





  











2cos 2 2







  







Mặt khác

0 2cos 2 2 4,







     







0 4, xy    

Vậy giá trị lớn nhất của hàm số là

4M 

khi







 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

103

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Và giá trị nhỏ nhất của hàm số là

0m 

khi





Câu 106: Cho hàm số

sin 2cos 1

sin cos 2







. Gọi

;

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất

của hàm số. Tổng

Mm

bằng

. B.

2

. C.

1

. D.

Lời gii

Chọn C

Tập xác định

D 

(do

sin cos 2 0; x x x    

Xét phương trình:

sin 2cos 1

sin cos 2







     

1 sin 2 cos 1 2 0 *y x y x y      

Phương trình

 

có nghiệm

     

2 2 2

1 2 1 2y y y     

2 0 2 1y y y       

Vậy

1; 2 1M m M m      

Câu 107: Giá trị lớn nhất của hàm số

cos 2sin 3

2cos sin 4







là

3 2 3

. B.

. C.

1

. D.

Lời gii

Chọn B

Xét phương trình:

2cos sin 4 0xx  

 

Ta có :

 

2 1 4  

nên phương trình

 

vô nghiệm, hay

2cos sin 4 0,x x x    

Do đó, hàm số đã cho có tập xác định

D 

cos 2sin 3

2cos sin 4







   

2 1 cos 2 sin 3 4y x y x y     

 

Để tồn tại giá trị lớn nhất của hàm số ban đầu thì phương trình

 

phải có nghiệm

     

2 2 2

2 1 2 4 3 11 24 4 0 2

y y y y y y            

Vậy GTLN của hàm số đã cho là

Câu 108: Có bao nhiêu giá trị nguyên của tham số

để giá trị lớn nhất của hàm số

sin 1

cos 2







nhỏ hơn

. B.

. C.

. D.

Lời gii

Chọn C

Dễ thấy

cos 2,xx   

nên hàm số có tập xác định là

D 

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

104

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

Ta có

sin 1

cos 2 sin 1 sin cos 2 1

cos 2

y y x y m x m x y x y



        



 

có nghiệm khi

 

2 2 2 2

2 1 3 4 1 0m y y y y m       

2 1 3 2 1 3

   

  

max

2 1 3

2 1 3 4 5

y m m



       

m

 

2; 1;0;2;1m   

. Vậy có

giá trị của

thỏa ycbt.

Câu 109: Giả sử

là giá trị lớn nhất và

là giá trị nhỏ nhất của hàm số

sin 2cos 1

sin cos 2







trên . Tìm

23Mm

12

. B.

. C.

. D.

Lời gii

Chọn D

Ta có:

0 2sinsin cos 2n

2 si 2

xxxx







        

   







(vô nghiệm).

Do đó, hàm số đã cho có tập xác định

D 

Ta có

sin 2cos 1

sin cos 2







   

1 sin 2 cos 1 2y x y x y     

 

Hàm số đạt giá trị lớn nhất, nhỏ nhất khi

 

có nghiệm

     

2 2 2

1 2 1 2y y y     

2 2 4 0yy   

21y   

. Do đó

2m 

1M 

. Vậy

2 3 8Mm

Câu 110: Gọi

tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

2sin 2

cos 2







Khẳng định nào sau đây đúng?

38mM

. B.

38mM  

. C.

30mM

. D.

mM  

Lời gii

Chọn B

Dễ thấy

cos 2,xx  

nên hàm số có tập xác định là

D 

Ta có

2sin 2

.cos 2sin 2 2

cos 2

y y x x y



    



 

Để tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số ban đầu thì phương trình

 

phải có

nghiệm

 

4 2 2 3 8 0 0

y y y y y          

. Do đó















Vậy

38mM  

Câu 111: Tập giá trị của hàm số

sin2 3cos2 1y x x  

là đoạn

 

;.ab

Tính tổng

.T a b

0T 

. B.

1T 

. C.

1T 

. D.

2.T 

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

105

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Lời gii

Chọn D

Cách 1:

sin2 3cos2 1 sin2 3cos2 1y x x x x y      

 

Để tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số ban đầu thì phương trình

 

phải có

nghiệm thì

 

1 3 1 2 3 0 1 3y y y y          

Suy ra

 

1;3y

. Vậy

1 3 2.T    

Cách 2: Ta có

1 sin2 3cos2 .y x x  

Mặt khác áp dụng bất đẳng thức Bunhiacopskii ta có

 

1 sin2 3 os2 1 3 sin 2 os 2 4 2 1 2 1 3.y x c x x c x y y               

Vậy

1 3 2.T    

Cách 3:

sin2 3cos2 1 2sin 2 1

y x x x







     







 

sin 2 1;1







  







nên

 

2sin 2 1 1;3







   







Vậy

13y  

Câu 112: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

3sin 4cos 1y x x  

max 6y 

min 4y 

. B.

max 8y 

min 6y 

max 4y 

min 6y 

. D.

max 6y 

min 8y 

Lời gii

Chọn C

Ta có

3sin 4cos 1 3sin 4cos 1y x x x x y      

 

Ta coi

 

như là phương trình cổ điển với

3a 

4b 

1cy

Phương trình

 

có nghiệm khi và chỉ khi

 

2 2 2

9 16 1 6 4a b c y y         

Vậy

max 4y 

min 6y 

Chú ý:

Ta có thể áp dụng bất đẳng thức BCS như sau:

  

2 2 2 2

1 3sin 4cos 3 4 sin cos 5y x x x x      

7.3. Tìm GTLN, GTNN sử dụng bất đẳng thức cổ điển.

Câu 113: Cho hàm số

1 2sin 1 2cos 1.y x x    

Gọi

, mM

lần lượt là giá trị nhỏ nhất và

giá trị lớn nhất của hàm số. Khi đó giá trị của

Mm

bằng

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

106

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

3 2 2

. B.

3 2 1

. C.

3 2 2 1

. D.

3 3 2 1  

Lời gii

Chọn C

Đặt

1 2sin 1 2cost x x   

      

2 2 2 2 2 2

1 2sin 1 2cos 2 1 2sin 1 2cos 4 2 3 sin 2t x x x x x          

4 2 3 sin 2 4 2 3 1 3tx       

1 2sin 1 2cos 1 3y x x      

Dấu

'' ''

xảy ra khi

sin2 0



  

. Khi đó

3m 

Mặt khác, áp dụng bất đẳng thức Cauchy – Schwarz, ta có

  

2 2 2 2 2 2

1 2sin 1 2cos 1 1 1 2sin 1 2cos 2 2x x x x        

1 2sin 1 2cos 1 2 2 1.y x x       

Dấu

'' ''

xảy ra khi

sin cos

x x k





  



  









. Khi đó

2 2 1M 

Vậy

3 2 2 1Mm   

Câu 114: Tìm giá trị lớn nhất của hàm số

2sin 3cos 1

sin cos 2







3 33



. B.

3 33



. C.

. D.

Lời gii

Chọn A

Ta có

   

2sin 3cos 1

2 sin 3 cos 1 2

sin cos 2

y y x y x y



      



         

 

2 2 2

1 2 2 sin 3 cos 2 3 sin cosy y x y x y y x x



         





2 6 12 0yy   

3 33 3 33



  

Câu 115: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số

 

2018 2018

sin cosf x x x

lần lượt là

1008

và

. B.

1009

và

. C.

và

. D.

1008

và

 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

107

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Lời gii

Chọn D

Đặt

sin , cos .a x b x

Ta có

2018 2018 2 2

sin cos sin cos 1.x x x x   

Dấu

""

xảy ra





1009

1009 1009

2018 2018

1008

sin cos 2. 2 .

2 2 2

a b a b











   















Dấu

""

xảy ra



  

Vậy giá trị nhỏ nhất bằng

1008

;

giá trị lớn nhất bằng

Câu 116: Cho

là các số thực thỏa mãn

cos2 cos2 1.xy

Giá trị nhỏ nhất của biểu thức

tan tanP x y

bằng

. B.

. D.

. C.

Lời gii

Chọn B

Ta có

1 1 1 1

1 1 2 2.

cos cos 1 cos2 1 cos2

x y x y









      

















Áp dụng BĐT cộng mẫu, ta được

 

2 2 2. 2 .

2 cos2 cos2 2 1 3







    







  





Câu 117: Cho hai số thực

, xy

thuộc













và thỏa mãn

 

cos2 cos2 2sin 2.x y x y   

Giá trị

nhỏ nhất của

cos cosxy



bằng



. B.



. C.



. D.



Lời gii

Chọn C

Ta có

   

cos2 cos2 2sin 2 sin sin sin .x y x y x y x y       

Suy ra





Áp dụng BĐT cộng mẫu

 

m n m n







ta được

 Quảng Thuận – Ba Đồn – QB Hàm số lượng giác và phương trình lượng giác

108

https://www.facebook.com/vietgold

https://luyenthitracnghiem.vn

 

cos cos

cos sin

cos cos

x y x y x y























   

   

  

Dấu

'' ''

xảy ra



  

Nhận xét. Việc suy ra





được chứng minh như sau:

Với

, 0;















suy ra





cùng thuộc

0; .













Trên đoạn

0; ,









hàm

sinyx

đồng biến.

Nếu

sin sin cos

x y x y y

y x y x x













     









  









     











 

sin sin sin .sin sin .sin sin .cos sin .cos sin :x y x x y y x y y x x y       

mâu thuẫn.

Tương tự cho





Trường hợp





thỏa mãn.

Câu 118: Cho

, , a b c

là các số thực thỏa mãn

2 2 2

4.a b c  

Tìm giá trị lớn nhất

trong tất cả

các hàm số

sin cosy a b x c x  

với

0; .













12M 

. B.

12M 

. C.

2 1 2M 

. D.

 

2 1 2 .M 

Lời gii

Chọn C

Ta có

 

2 2 2

sin cos 1 sin cosa b x c x a b c x x      

 

4 1 2sin 4 1 2 .









    











Suy ra

sin cos 2 1 2.a b x c x   

Dấu

'' ''

xảy ra

2 2 2

sin cos

sin 1, 0;

a b c









   







  



  

  





  





2 2 2

;

2 2 2 2

a b c





  

















 Quảng Thuận – Ba Đồn – QB “Thành công là nói không với lười biếng”

109

https://luyenthitracnghiem.vn

https://www.facebook.com/vietgold

Câu 119: Tập giá trị của hàm số

sin2 3cos2 1y x x  

là đoạn

 

;.ab

Tính tổng

.T a b

1T 

. B.

2T 

. C.

0T 

. D.

1T 

Lời gii

Chọn B

Ta có

1 sin2 3cos2 .y x x  

Mặt khác áp dụng bất đẳng thức Bunhiacopskii ta có

 

1 sin2 3 os2 1 3 sin 2 os 2 4 2 1 2 1 3y x c x x c x y y               

Vậy

1 3 2.T    

Bấm Tải xuống để xem toàn bộ.

| 1/110

| | Tải xuống

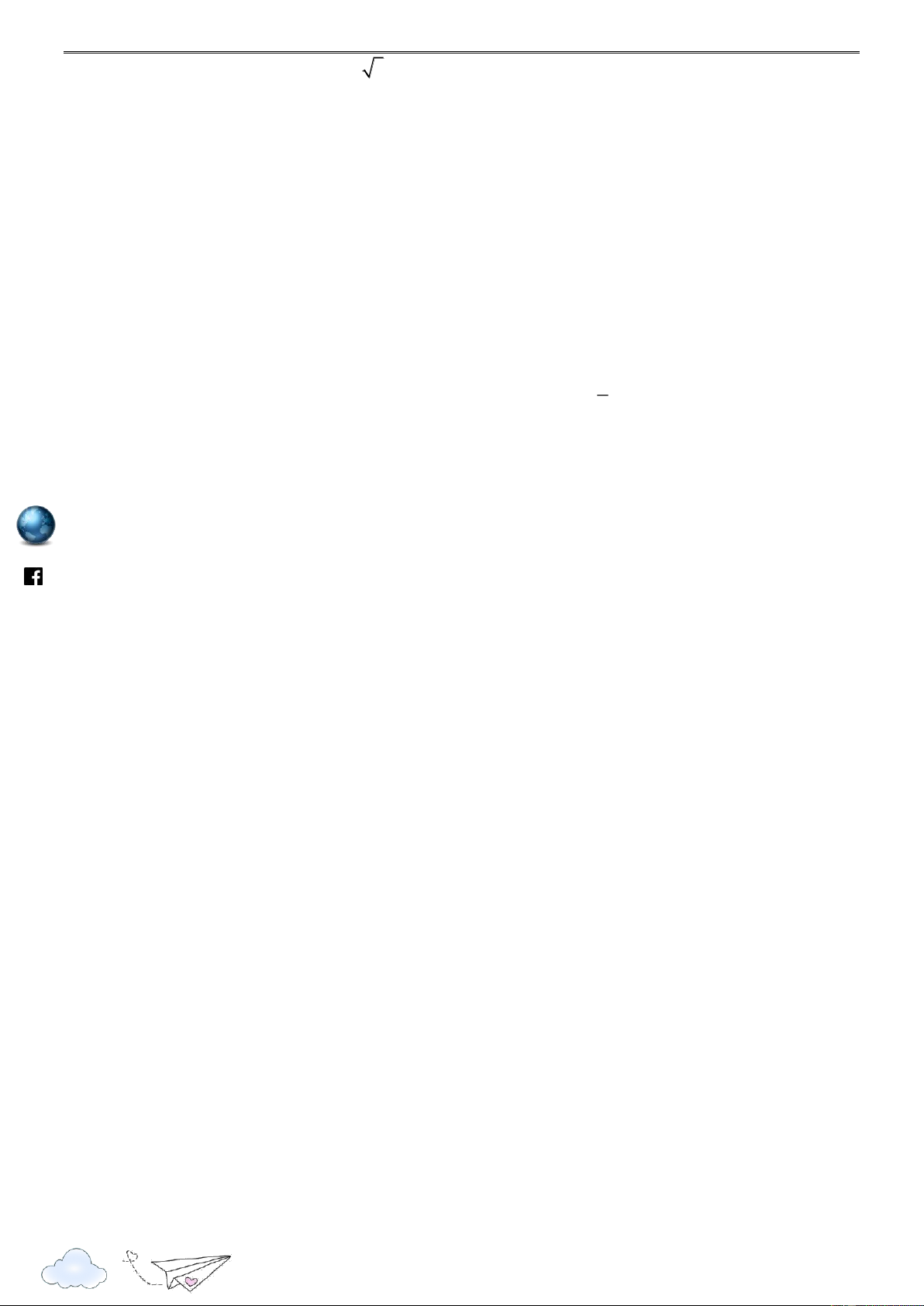
Preview text:

 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác MỤC LỤC
PHẦN 1 – ĐỀ BÀI .............................................................................................................. 2
DẠNG 1. XÁC ĐỊNH ĐỒ THỊ HÀM SỐ LƯỢNG GIÁC. ............................................................ 2 h
DẠNG 2. XÁC ĐỊNH CHU KỲ HÀM SỐ LƯỢNG GIÁC. ........................................................... 7 ttp
DẠNG 3. TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ LƯỢNG GIÁC. .................... 8 s:// lu
DẠNG 4: XÁC ĐỊNH SỐ ĐIỂM BIỂU DIỄN CỦA PHƯƠNG TRÌNH LƯỢNG GIÁC CHO ye
TRƯỚC TRÊN ĐƯỜNG TRÒN LƯỢNG GIÁC........................................................................... 12 n th
DẠNG 5. BIỆN LUẬN NGHIỆM PHƯƠNG TRÌNH LƯỢNG GIÁC KHÔNG CHỨA it r
THAM SỐ ............................................................................................................................................. 19 acn
5.1. Tìm số nghiệm của phương trình lượng giác trên tập K ................................................................... 19 gh ie
5.2. Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình lượng giác:. ................... 21 m.vn
5.3. Tính tổng tất cả các nghiệm của phương trình lượng giác trên tập K . ........................................... 23
DẠNG 6. TÌM ĐIỀU KIỆN CỦA THAM SỐ m ĐỂ PHƯƠNG TRÌNH LƯỢNG GIÁC CHO
TRƯỚC CÓ NGHIỆM. ....................................................................................................................... 35
DẠNG 7. TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ LƯỢNG GIÁC ............ 40
7.1. Tìm GTLN, GTNN sử dụng điều kiện 1   sin ,
x cos x  1. ............................................................... 40
7.2. Tìm GTLN, GTNN dạng y  asin x  bcos x  c . ............................................................................... 43
7.3. Tìm GTLN, GTNN sử dụng bất đẳng thức cổ điển. ............................................................................ 47 http
PHẦN 2: BẢNG ĐÁP ÁN .............................................................................................. 50 s://www
PHẦN 3: ĐÁP ÁN CHI TIẾT ........................................................................................ 51
DẠNG 1. XÁC ĐỊNH ĐỒ THỊ HÀM SỐ LƯỢNG GIÁC. .......................................................... 51 .fa ceboo
DẠNG 2. XÁC ĐỊNH CHU KỲ HÀM SỐ LƯỢNG GIÁC. ......................................................... 56
DẠNG 3. TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ LƯỢNG GIÁC. .................. 58 k.com
DẠNG 4: XÁC ĐỊNH SỐ ĐIỂM BIỂU DIỄN CỦA PHƯƠNG TRÌNH LƯỢNG GIÁC CHO /v
TRƯỚC TRÊN ĐƯỜNG TRÒN LƯỢNG GIÁC........................................................................... 62 ietgold
DẠNG 5. BIỆN LUẬN NGHIỆM PHƯƠNG TRÌNH LƯỢNG GIÁC KHÔNG CHỨA
THAM SỐ ............................................................................................................................................. 70
5.1. Tìm số nghiệm của phương trình lượng giác trên tập K ................................................................... 70
5.2. Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình lượng giác:. ................... 73
5.3. Tính tổng tất cả các nghiệm của phương trình lượng giác trên tập K . ........................................... 76
DẠNG 6. TÌM ĐIỀU KIỆN CỦA THAM SỐ m ĐỂ PHƯƠNG TRÌNH LƯỢNG GIÁC CHO
TRƯỚC CÓ NGHIỆM. ....................................................................................................................... 93
DẠNG 7. TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ LƯỢNG GIÁC ............ 97 0
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
7.1. Tìm GTLN, GTNN sử dụng điều kiện 1   sin ,
x cos x  1. ............................................................... 97
7.2. Tìm GTLN, GTNN dạng y  asin x  bcos x  c . ............................................................................. 101
7.3. Tìm GTLN, GTNN sử dụng bất đẳng thức cổ điển. .......................................................................... 105 m.vn ie gh racn it th n ye lu s:// ttp h /vietgold k.com ceboo .fa https://www 1
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác PHẦN 1 – ĐỀ BÀI
DẠNG 1. XÁC ĐỊNH ĐỒ THỊ HÀM SỐ LƯỢNG GIÁC.
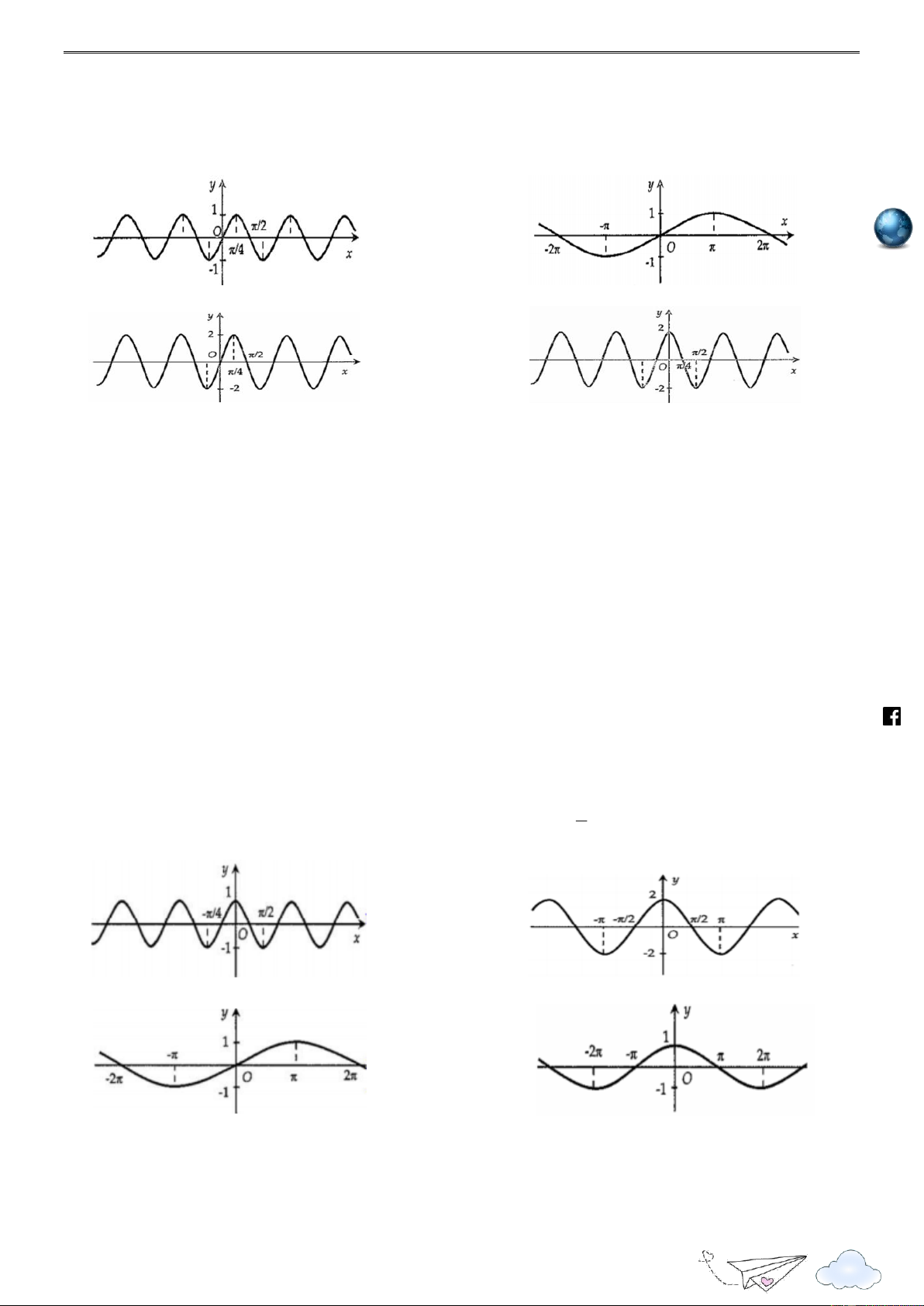
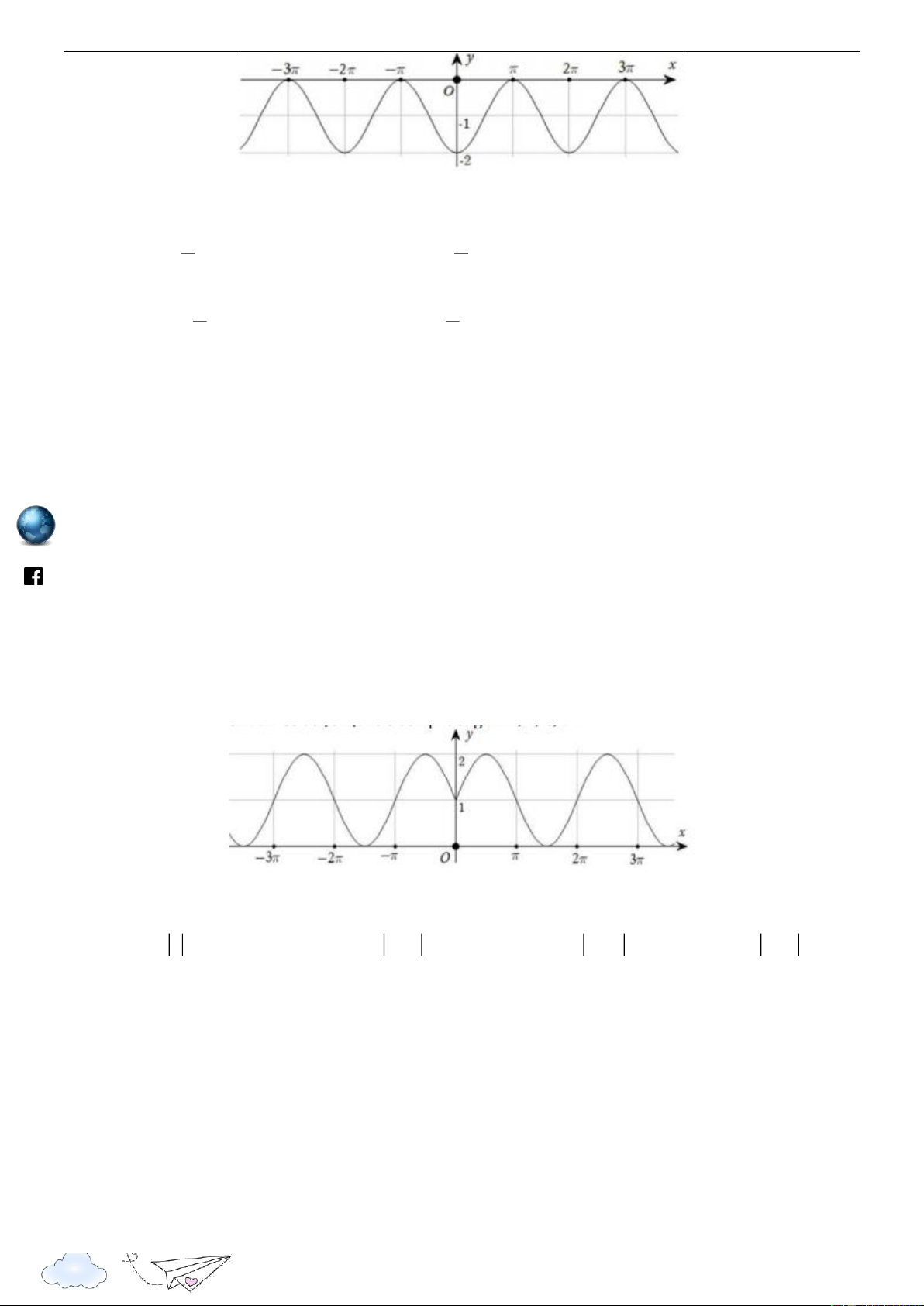
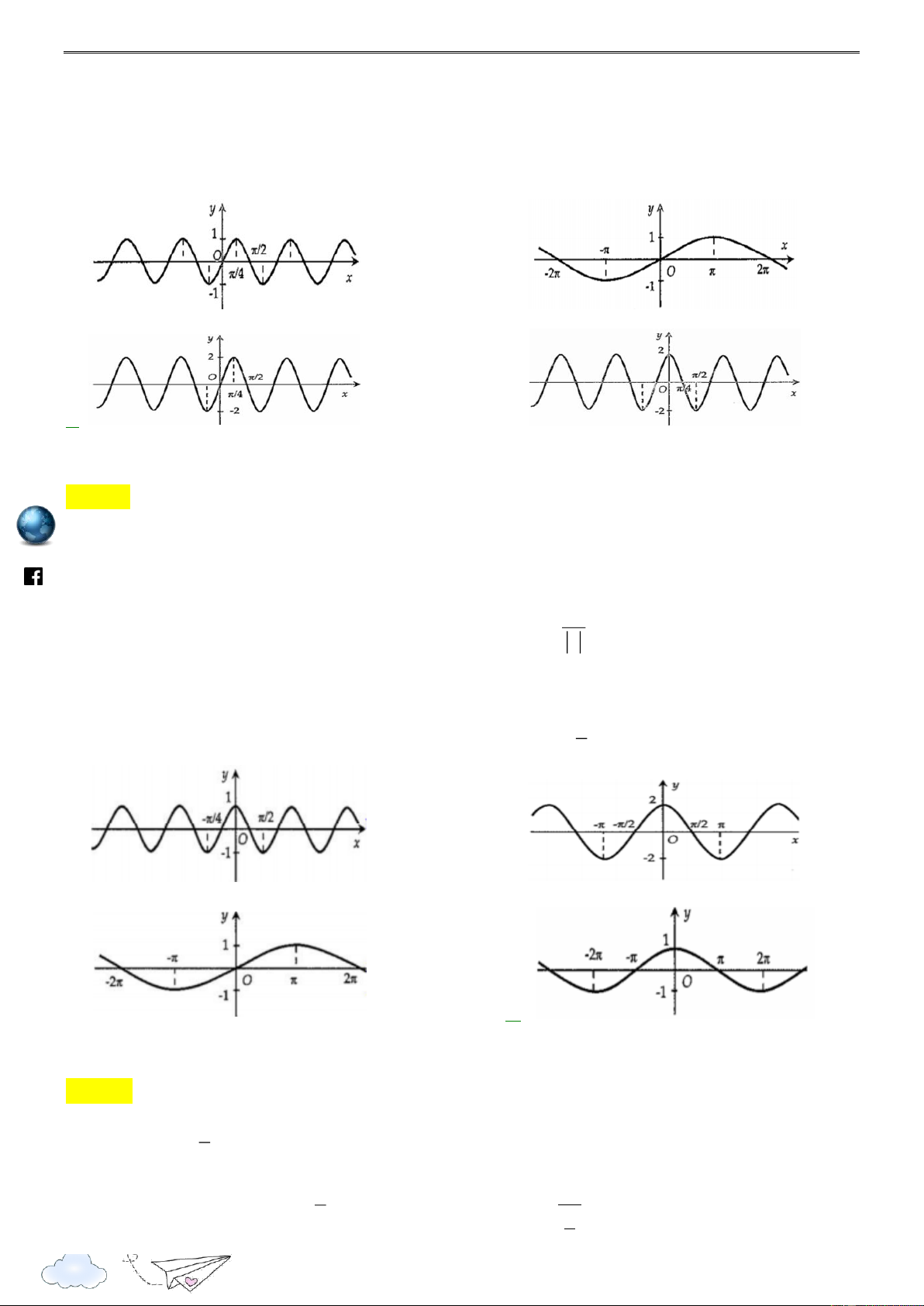
Câu 1: Hình nào dưới đây biểu diễn đồ thị hàm số y  f  x  2sin 2x ? h ttp A. . B. . s:// lu ye n th C. . D. . it rac
Lời giải: ........................................................................................................................................ n gh
.......................................................................................................................................................................... ie m.vn
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... https://www
.......................................................................................................................................................................... x
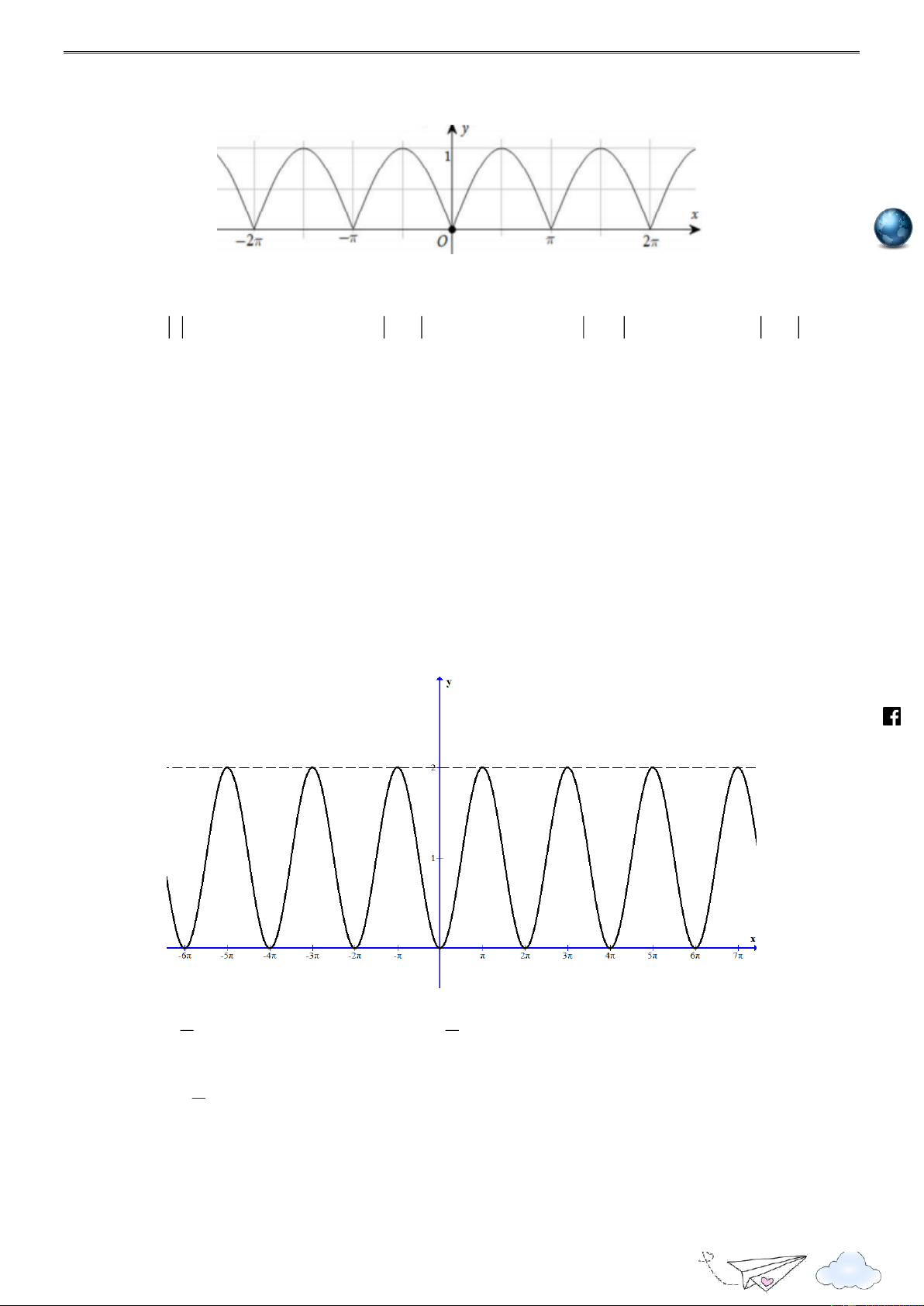
Câu 2: Hình vẽ nào sau đây biểu diễn đồ thị hàm số y  cos ? 2 .fa ceboo k.com /v A. . B. . ietgold C. . D. .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 2
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
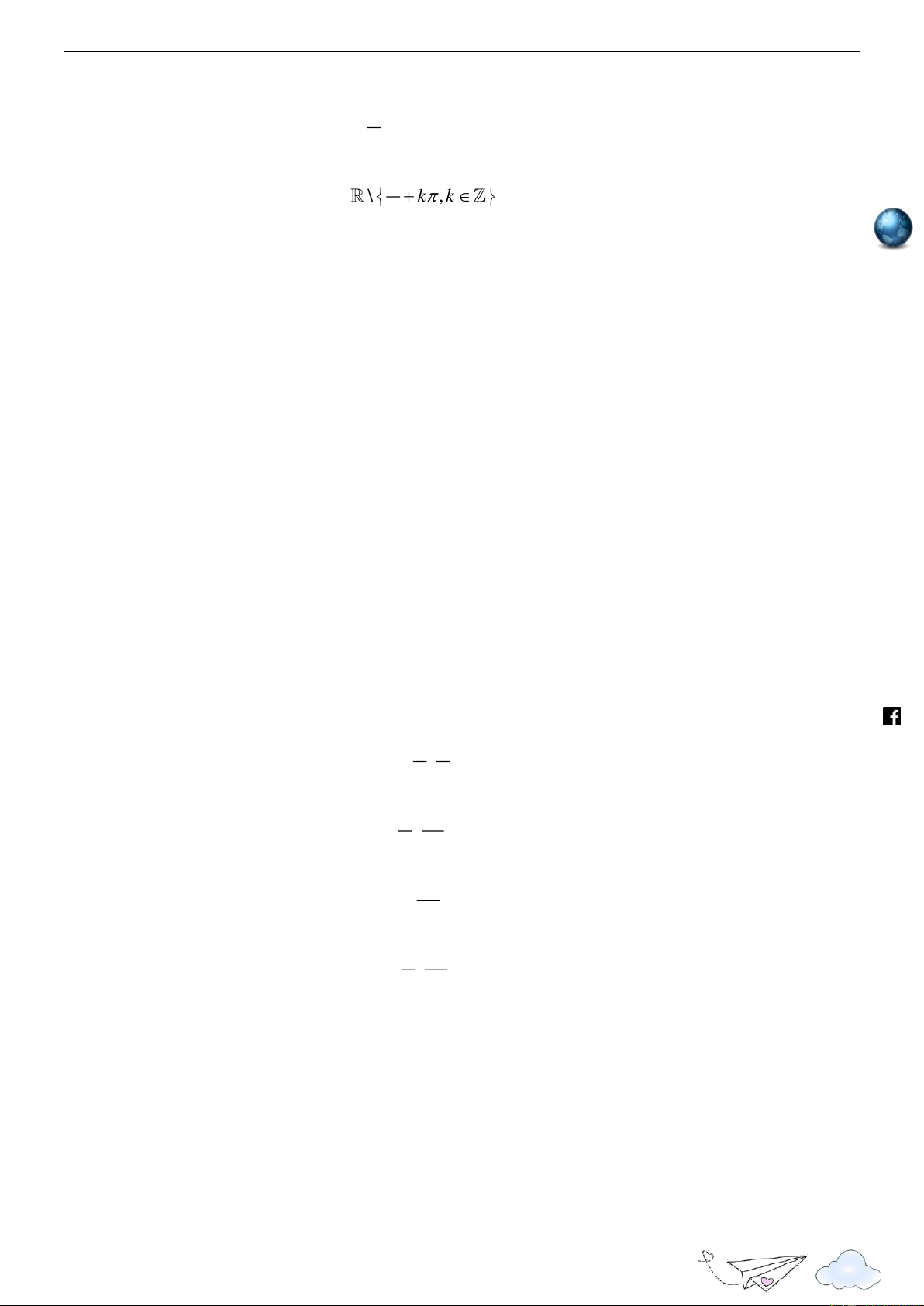
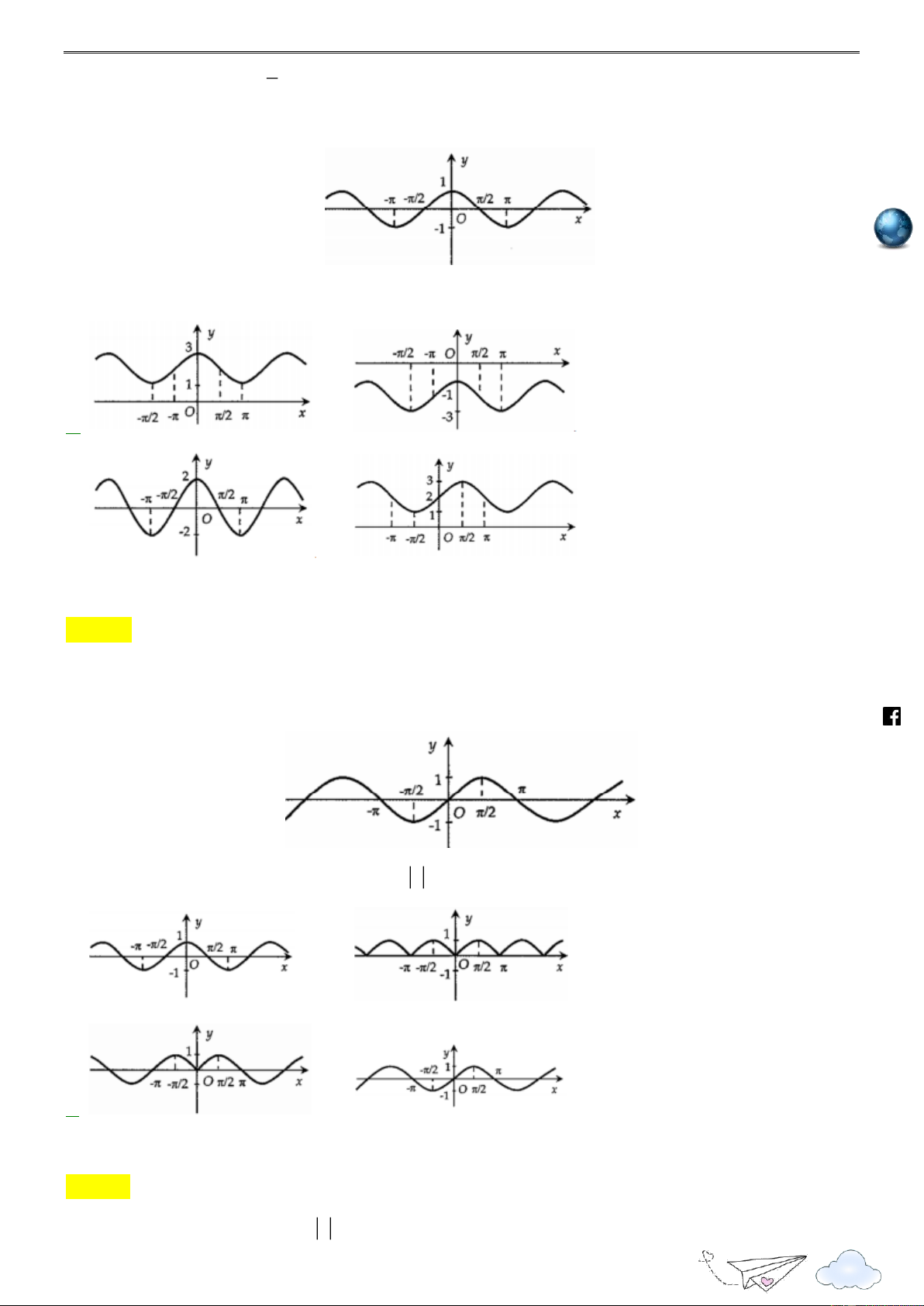
Câu 3: Cho đồ thị hàm số y  cos x như hình vẽ: m.vn ie gh racn it th n ye
Hình vẽ nào sau đây là đồ thị hàm số y  cos x  2 ? lu s:// ttp h A. . B. . C. . D. .
Lời giải: ........................................................................................................................................
/vietgold ..........................................................................................................................................................................
k.com .......................................................................................................................................................................... ceboo
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 4: Cho đồ thị hàm số y  sin x như hình vẽ: https://www
Hình nào sau đây là đồ thị hàm số y  sin x ? A. . B. . 3
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác C. . D. .
Lời giải: ........................................................................................................................................
.......................................................................................................................................................................... h
.......................................................................................................................................................................... ttp s://
.......................................................................................................................................................................... lu ye
.......................................................................................................................................................................... n th
.......................................................................................................................................................................... it ra
.......................................................................................................................................................................... cngh
.......................................................................................................................................................................... ie m.vn
..........................................................................................................................................................................
..........................................................................................................................................................................
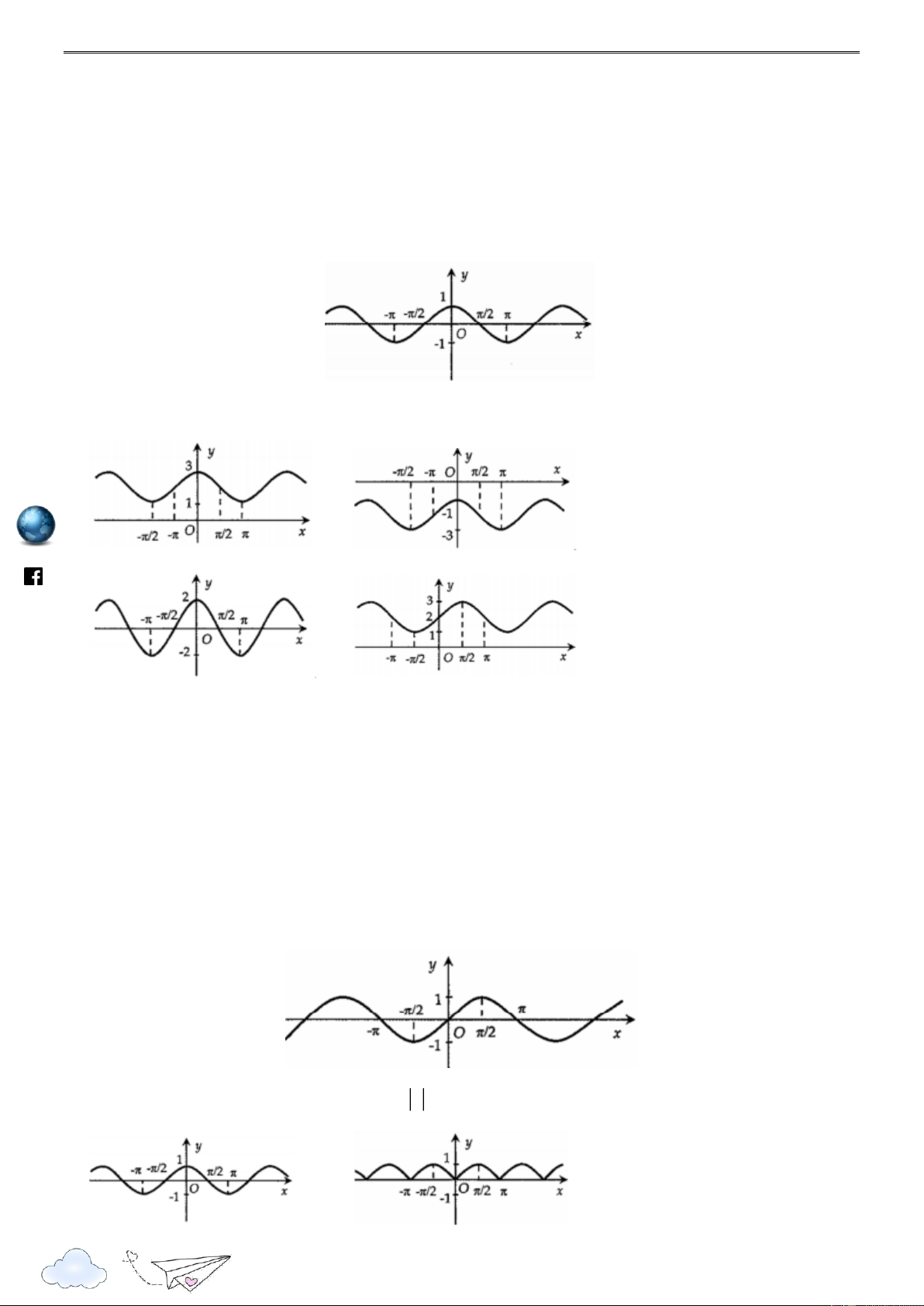
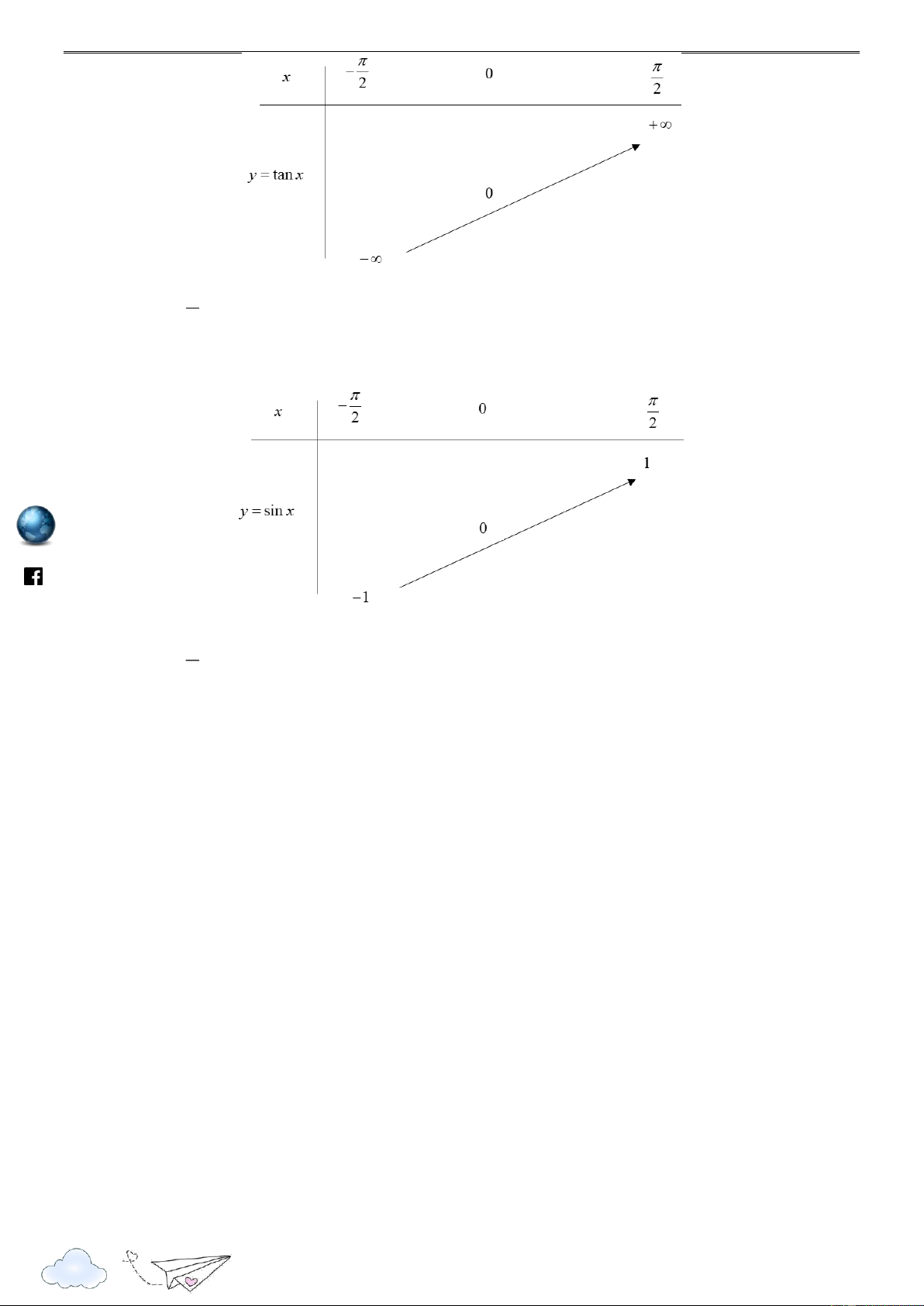
Câu 5: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án , A , B C , D . https://www .fa
Hỏi hàm số đó là hàm số nào? ceboo
A. y  tan x .
B. y  cot x .
C. y  tan x .
D. y  cot x . k.com
Lời giải: ........................................................................................................................................ /viet
.......................................................................................................................................................................... gold
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
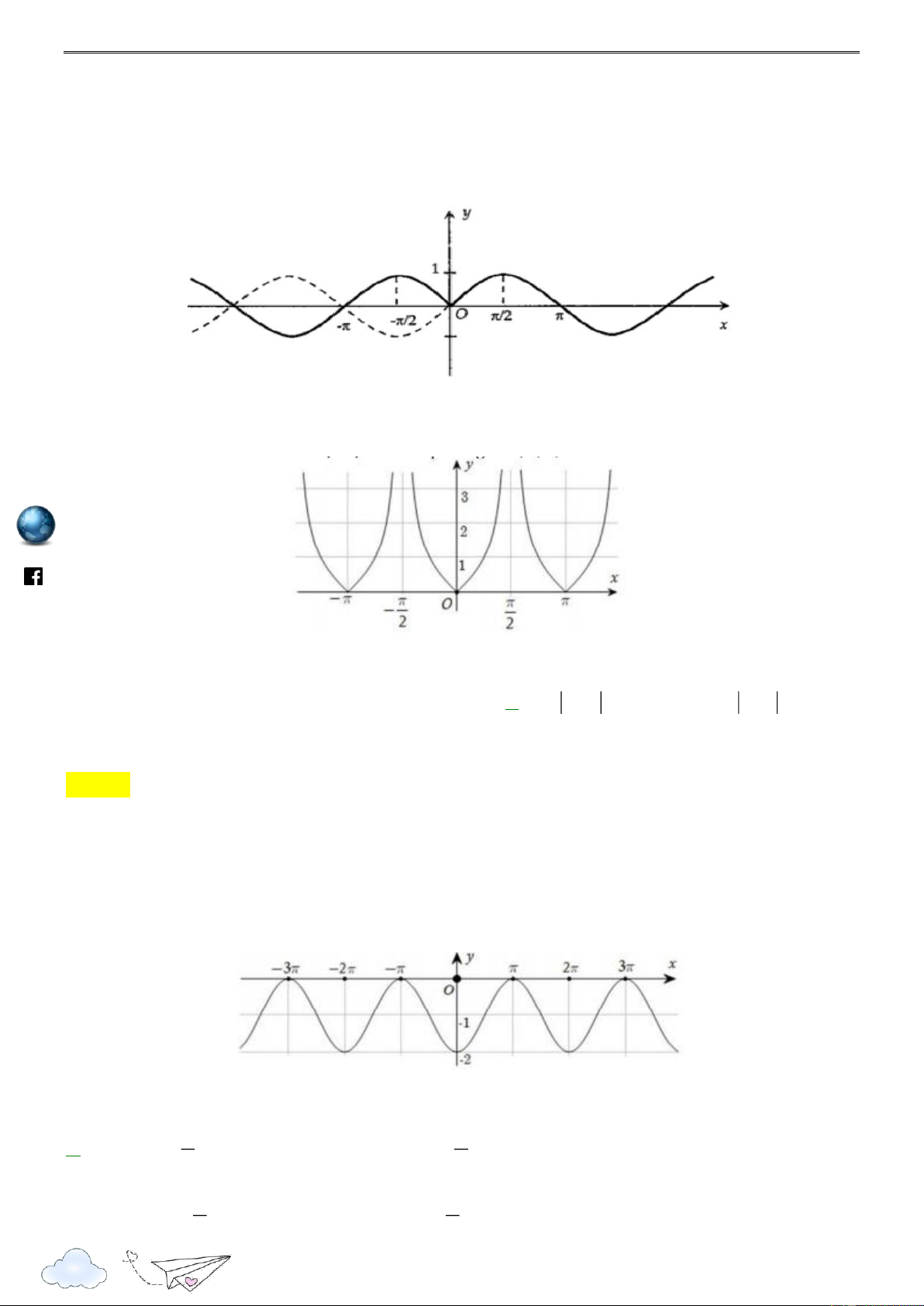
Câu 6: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án , A , B C, D . 4
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Hỏi hàm số đó là hàm số nào? m.vn            ie
A. y sin x 1   . B. y 2sin x   .  2   2  gh              racn C. y sin x 1   .
D. y sin x 1   . it  2   2  th n
Lời giải: ........................................................................................................................................ ye lu
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... ttp h
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 7: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án , A , B C, D . /vietgold k.com ceboo .fa
Hỏi hàm số đó là hàm số nào?
A. y  1 sin x .
B. y  sin x .
C. y  1 cos x .
D. y  1 sin x . https://www
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 5
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
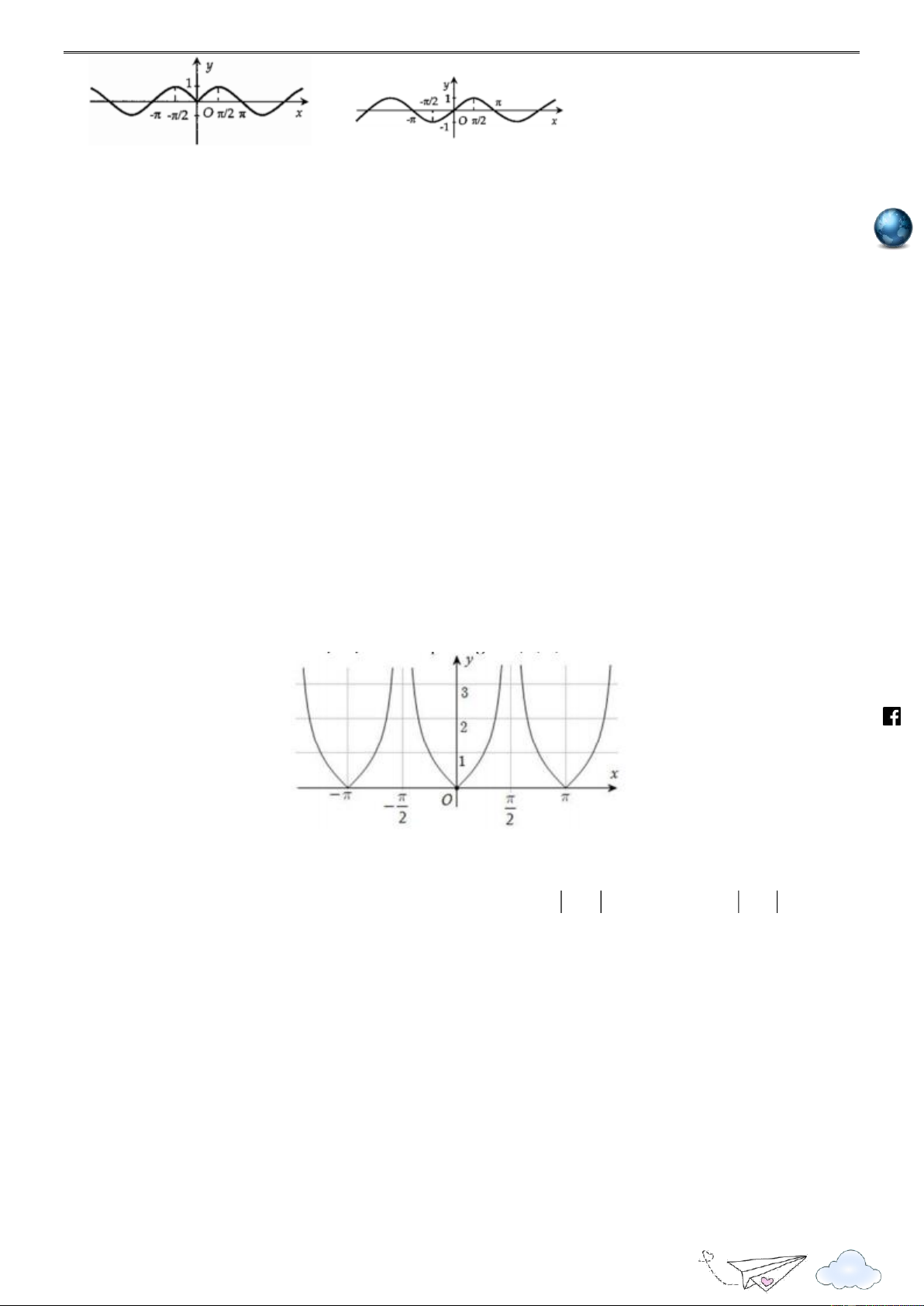
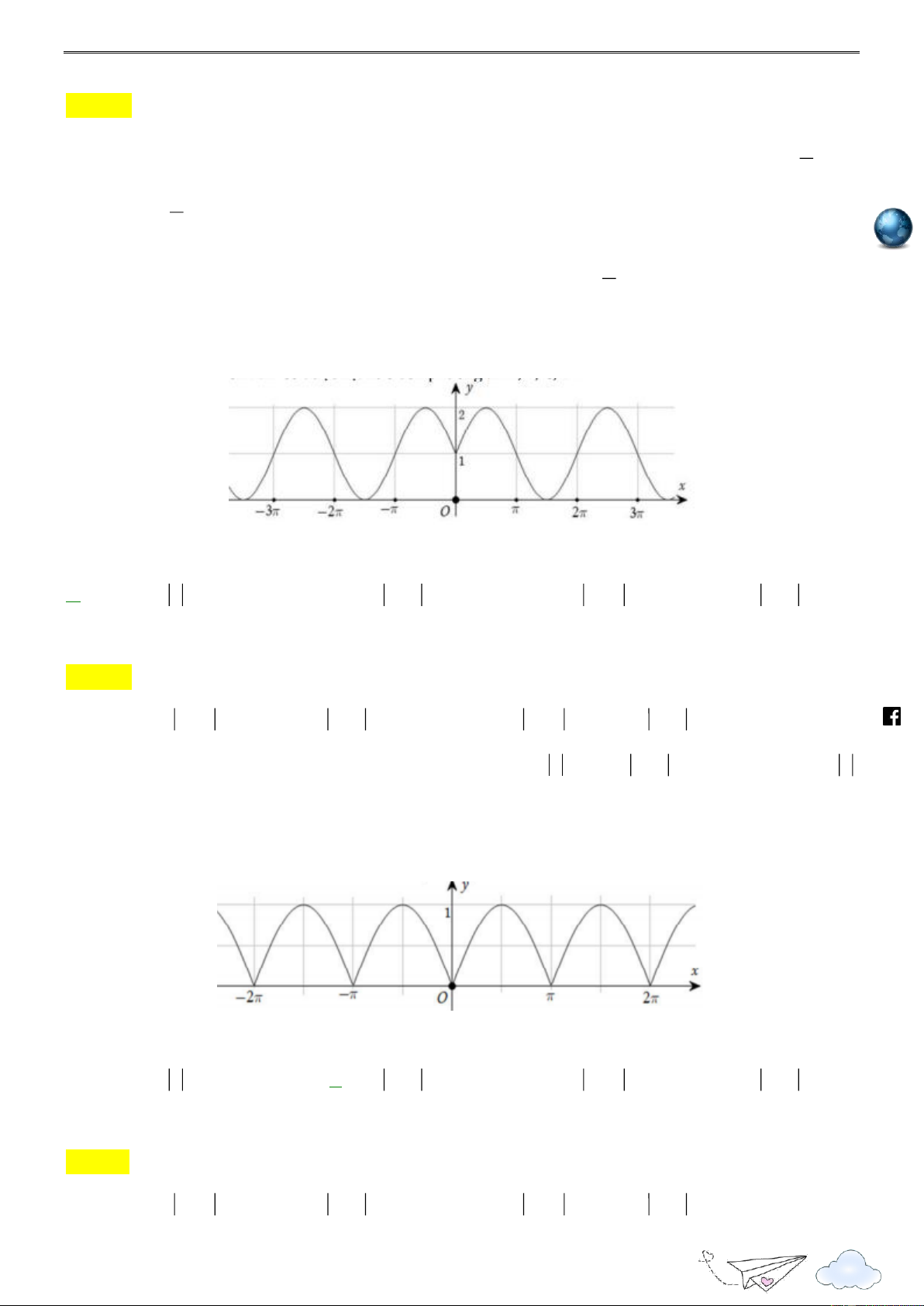
Câu 8: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án , A , B C, D . h ttp
Hỏi hàm số đó là hàm số nào? s://        lu
A. y 1 sin x . B. y sin x .
C. y 1 cos x .
D. y 1 sin x . ye n
Lời giải: ........................................................................................................................................ th it
.......................................................................................................................................................................... racn
.......................................................................................................................................................................... gh ie
.......................................................................................................................................................................... m.vn
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 9: Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt
kê ở bốn phương án A, B, C,.
D. Hỏi hàm số đó là hàm số nào? https://www .fa ceboo k.com /viet gold      
A. y  sin x    .
B. y  cos x   .  2   2    
C. y  sin x  1   .
D. y  cos x 1.  2 
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 6
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... m.vn ie
DẠNG 2. XÁC ĐỊNH CHU KỲ HÀM SỐ LƯỢNG GIÁC. gh
Câu 10: Chu kỳ tuần hoàn của hàm số y  sin x cos x cos 2x cos 4x là racn it   th n A. 2 . B. 4 . C. . D. . 4 8 ye lu
Lời giải: ........................................................................................................................................ s://
.......................................................................................................................................................................... ttp h
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 11: Tìm chu kỳ tuần hoàn của hàm số y  x   4 4 3 sin 4
4 sin x  cos x  2 .   /vietgold A. 2 . B. . C. . D.  . 2 4 k.com
Lời giải: ........................................................................................................................................
ceboo ..........................................................................................................................................................................
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................
https://www ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 12: Tìm chu kỳ tuần hoàn của hàm số f  x 3 3 3
 sin 4x sin xcos3x cos xsin3x .   2 A. . B. . C. . D. 2 . 6 12 3
Lời giải: ........................................................................................................................................
.......................................................................................................................................................................... 7
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... h ttp
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... lu ye
.......................................................................................................................................................................... n th
Câu 13: Tìm chu kỳ tuần hoàn của hàm số f  x 3 3  cos . x cos 3x  sin . x sin 3x . it rac   n A. . B. 2 . C.  . D. . gh 6 2 ie m.vn
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... http
.......................................................................................................................................................................... s://www
..........................................................................................................................................................................
.......................................................................................................................................................................... .fa ceboo
.......................................................................................................................................................................... k.com
.......................................................................................................................................................................... /v
.......................................................................................................................................................................... ietgold
DẠNG 3. TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ LƯỢNG GIÁC.
Câu 14: Tìm mệnh đề đúng trong các mệnh đề sau?
A. Hàm số y  cot x đồng biến trên khoảng 0;  .
B. Hàm số y  sin x nghịch biến trên khoảng 3 ;4  .  5 3 
C. Hàm số y  sin x đồng biến trên khoảng  ;    .  2 2  8
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”    
D. Hàm số y  cos x đồng biến trên khoảng  ;   .  2 2 
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... m.vn ie
.......................................................................................................................................................................... gh
.......................................................................................................................................................................... racn it
.......................................................................................................................................................................... th n
.......................................................................................................................................................................... ye lu
.......................................................................................................................................................................... s:// ttp
.......................................................................................................................................................................... h
..........................................................................................................................................................................
Câu 15: Cho các hàm số y  sin x ; y  cos x ; y  tan x ; y  cot x . Có bao nhiêu hàm số nghịch  5  biến trên 3  ;   ?  2  A. 1. B. 3 . C. 0 . D. 2 .
Lời giải: ........................................................................................................................................
/vietgold ..........................................................................................................................................................................
k.com ..........................................................................................................................................................................
ceboo ..........................................................................................................................................................................
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
https://www ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 16: Cho hàm số y  tan x . Khẳng định nào dưới đây sai?
A. Hàm số đã cho là hàm lẻ. 9
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
B. Hàm số đã cho có tập giá trị là  1   ;1 .   
C. Hàm số đã cho đồng biến trên  ;0   .  2   
D. Hàm số đã cho có tập xác định
\   k , k   .  2 
Lời giải: ........................................................................................................................................ h ttp
.......................................................................................................................................................................... s:// lu
.......................................................................................................................................................................... ye n
.......................................................................................................................................................................... th it r
.......................................................................................................................................................................... acngh
.......................................................................................................................................................................... ie
.......................................................................................................................................................................... m.vn
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 17: Khẳng định nào sau đây đúng? ht     tp
A. y  sin x là hàm số nghịch biến trên  ;  . s://www  4 4    3 
B. y  cos x là hàm số nghịch biến trên ;   . .fa  4 4  ceboo  2 
C. y  sin x là hàm số nghịch biến trên 0;   . k.com  3  /v   3 
D. y  tan x là hàm số nghịch biến trên ; . iet    4 4  gold
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 10
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Câu 18: Hàm số y  cos x nghịch biến trên khoảng nào sau đây? 19   3   11   11  A. ;10   . B.  ;   . C. ; 7   . D.  ;  5   .  2   2 2   2   2 
Lời giải: ........................................................................................................................................
.......................................................................................................................................................................... m.vn ie
.......................................................................................................................................................................... gh
.......................................................................................................................................................................... racn it
.......................................................................................................................................................................... th n
.......................................................................................................................................................................... ye lu
Câu 19: Để hàm số y  sin x  cos x tăng, ta chọn x thuộc khoảng nào? s:// ttp  3    3   h A. 
 k2;  k2   . B. 
 k;  k   .  4 4   4 4      C. 
 k2;  k2   .
D.   k2;2  k2  .  2 2 
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
k.com ..........................................................................................................................................................................
ceboo ..........................................................................................................................................................................
.fa Câu 20: Xét hai mệnh đề sau:     (I): x    ;   :Hàm số 2
y  tan x tăng.  2 2  https://www     (II): x    ;   :Hàm số 2
y  sin x tăng.  2 2  Chọn câu đúng? A. Chỉ (I) đúng. B. Chỉ (II) đúng. C. Cả hai đúng. D. Cả hai sai.
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 11
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... h ttp
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... lu ye
.......................................................................................................................................................................... n th
.......................................................................................................................................................................... it rac
.......................................................................................................................................................................... n gh
.......................................................................................................................................................................... ie m.vn
DẠNG 4: XÁC ĐỊNH SỐ ĐIỂM BIỂU DIỄN CỦA PHƯƠNG TRÌNH LƯỢNG GIÁC
CHO TRƯỚC TRÊN ĐƯỜNG TRÒN LƯỢNG GIÁC.
Câu 21: Biểu diễn các nghiệm của phương trình 2
cos x  0 trên đường tròn lượng giác được bao nhiêu điểm? A. 1 . B. 2 . C. 0 . D. 4 .
Lời giải: ........................................................................................................................................ ht
.......................................................................................................................................................................... tps://www
..........................................................................................................................................................................
.......................................................................................................................................................................... .fa ceboo
.......................................................................................................................................................................... k.com
..........................................................................................................................................................................
Câu 22: Nghiệm của phương trình cos x  1  là: /vietgold A. 1 . B. 2 . C. 0 . D. 4 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 12
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Câu 23: Cho phương trình 2cos x  3  0. Số điểm biểu diễn tất cả các nghiệm của phương trình
trên đường tròn lượng giác là A. 1 . B. 2 . C. 3 . D. 4 .
Lời giải: ........................................................................................................................................
.......................................................................................................................................................................... m.vn
.......................................................................................................................................................................... ie
.......................................................................................................................................................................... gh
.......................................................................................................................................................................... racn
.......................................................................................................................................................................... it th
.......................................................................................................................................................................... n 1 ye
Câu 24: Số điểm biểu diễn các nghiệm của phương trình cos x 
trên đường tròn lượng giác là 2 lu A. 3 . B. 1. C. 4 . D. 2 . s:// ttp
Lời giải: ........................................................................................................................................ h
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 25: Biểu diễn tất cả các nghiệm của phương trình 3cos x 1  0 trên đường tròn lượng giác, /vietgold
số điểm biểu diễn là A. 3 . B. 0 . C. 2 . D. 4 . k.com
Lời giải: ........................................................................................................................................ ceboo
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
https://www ..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 26: Biểu diễn nghiệm của phương trình cos3x  cos x trên đường tròn lượng giác. Số điểm biểu diễn là A. 3 . B. 0 . C. 2 . D. 4 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 13
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 27: Biểu diễn nghiệm của phương trình 2
cos x  cos x  0 trên đường tròn lượng giác. Số
điểm biểu diễn là A. 3 . B. 5 . C. 2 . D. 4 . h
Lời giải: ........................................................................................................................................ ttp s://
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... ye n th
.......................................................................................................................................................................... it ra
.......................................................................................................................................................................... cngh
.......................................................................................................................................................................... ie m.vn
..........................................................................................................................................................................
.......................................................................................................................................................................... 1
Câu 28: Số điểm biểu diễn nghiệm của phương trình 2 cos x 
trên đường tròn lượng giác là 2 A. 8 . B. 2 . C. 4 . D. 6 .
Lời giải: ........................................................................................................................................ ht
.......................................................................................................................................................................... tps://www
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... .fa
.......................................................................................................................................................................... ceboo
Câu 29: Biểu diễn tập nghiệm của phương trình cos x  cos 2x  cos3x  0 trên đường tròn lượng k.com
giác ta được số điểm cuối là A. 4 . B. 2 . C. 6 . D. 5 /viet
Lời giải: ........................................................................................................................................ gold
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 14
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 30: Biểu diễn các nghiệm của phương trình cossin x 1 trên đường tròn lượng giác là A. 3. B. 1 . C. 0 . D. 2 . m.vn
Lời giải: ........................................................................................................................................ ie
.......................................................................................................................................................................... gh
.......................................................................................................................................................................... racn it
.......................................................................................................................................................................... th n ye
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... s:// ttp
.......................................................................................................................................................................... h
..........................................................................................................................................................................
Câu 31: Biểu diễn tất cả các nghiệm của phương trình cos5 .
x cos x  cos 4x trên đường tròn lượng
giác. Số điểm biểu diễn là A. 8 . B. 10 . C. 4 . D. 15 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
k.com ..........................................................................................................................................................................
ceboo ..........................................................................................................................................................................
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 32: Số vị trí biểu diễn các nghiệm của phương trình 2
4cos x  4cos x  3  0 trên đường tròn
https://www lượng giác là? A. 4 . B. 0 . C. 1. D. 2 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 15
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 33: Số điểm biểu diễn các họ nghiệm của phương trình sin 2x  3 cos 2x  3 trên đường
tròn lượng giác là: A. 2 . B. 3 . C. 4 . D. 1. h
Lời giải: ........................................................................................................................................ ttp
.......................................................................................................................................................................... s:// lu
.......................................................................................................................................................................... ye n
.......................................................................................................................................................................... th it r
.......................................................................................................................................................................... acngh
.......................................................................................................................................................................... ie
.......................................................................................................................................................................... m.vn
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 34: Số điểm biểu diễn các họ nghiệm của phương trình sin 5x  3 cos5x  2sin 7x trên
đường tròn lượng giác là: ht A. 12 . B. 8 . C. 14 . D. 7 . tps://www
Lời giải: ........................................................................................................................................
.......................................................................................................................................................................... .fa
.......................................................................................................................................................................... ceboo
.......................................................................................................................................................................... k.com
.......................................................................................................................................................................... /viet
.......................................................................................................................................................................... gold
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 16
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Câu 35: Số điểm biểu diễn của phương trình sin x  cos xsin 2x 12cos x  sin x 12cos 2x  0 là: A. 3 . B. 4 . C. 5 . D. 6 .
Lời giải: ........................................................................................................................................
.......................................................................................................................................................................... m.vn ie
.......................................................................................................................................................................... gh
.......................................................................................................................................................................... racn it
.......................................................................................................................................................................... th n
.......................................................................................................................................................................... ye lu
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... ttp h
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
k.com .......................................................................................................................................................................... ceboo
.fa ..........................................................................................................................................................................
Câu 36: Nghiệm của phương trình 2
sin x  sin x cos x  cos x  2sin 2x sin x   1  1 thoả điều kiện    3x 
  có số điểm biểu diễn là: 2 2 https://www A. 0. B. 1. C. 2 . D. 3 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 17
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... h ttp
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... lu    2 2
cos x  sin 2x  2  cos  x   ye  2 
Câu 37: Số điểm biểu diễn các nghiệm của phương trình  0 n  7  th 2sin x  1    24 it  ra
trên đường tròn lượng giác là cngh A. 1. B. 2 . C. 3 . D. 4. ie m.vn
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... http Câu 38: Số điểm biểu diễn các nghiệm của phương trình s://www 2
sin x sin 2x  2sin x cos x  sin x  cos x  3cos2x trên đường tròn lượng giác là sin x  cos x .fa A. 2 . B. 4 . C. 3 . D. 5 . ceboo
Lời giải: ........................................................................................................................................ k.com
..........................................................................................................................................................................
.......................................................................................................................................................................... /viet
.......................................................................................................................................................................... gold
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 18
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
DẠNG 5. BIỆN LUẬN NGHIỆM PHƯƠNG TRÌNH LƯỢNG GIÁC KHÔNG CHỨA THAM SỐ m.vn ie
5.1. Tìm số nghiệm của phương trình lượng giác trên tập K . gh
Câu 39: Tìm số nghiệm của phương trình cos5 .
x cos x  cos 4x trên 0;10  là racn it A. 49 . B. 50 . C. 52 . D. 48 . th n
Lời giải: ........................................................................................................................................ ye
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... ttp h
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 2  x x 
Câu 40: Số nghiệm thuộc khoảng 0;100  của phương trình sin  cos  3 cos x  3   là  2 2  A. 49 . B. 50 . C. 52 . D. 48 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
k.com ..........................................................................................................................................................................
..........................................................................................................................................................................
ceboo ..........................................................................................................................................................................
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................   
Câu 41: Số nghiệm của phương trình 2 2
cos x  sin 2x  2  cos  x 
 trên khoảng 0;3  là  2  https://www A. 2. B. 3 . C. 4. . D. 1.
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 19
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
Câu 42: Gọi n là số nghiệm thuộc khoảng 0;2023 của phương trình lượng giác
3 1 cos 2x  sin 2x  4cos x  8  4 3  
1 sin x . Tìm n là A. 322 . B. 320 . C. 300 . D. 321.
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... h ttp
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... ye
.......................................................................................................................................................................... n th
.......................................................................................................................................................................... it
.......................................................................................................................................................................... rac
.......................................................................................................................................................................... n gh
.......................................................................................................................................................................... ie
.......................................................................................................................................................................... m.vn
Câu 43: Số nghiệm của phương trình 2
2cos x  3 sin 2x  3 trên 0;2020  là: A. 1010 . B. 2019 . C. 2020 . D. 2021.
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... http
.......................................................................................................................................................................... s://www
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 44: Huyết áp là đại lượng để đo độ lớn của lực tác dụng lên thành mạch máu. Nó được đo .fa ceboo
bằng hai chỉ số: huyết áp tâm thu (lúc tim đập) và huyết áp tâm trương (lúc tim nghỉ).
Huyết áp của mỗi người thường khác nhau, nhưng huyết áp tiêu chuẩn là 120 / 80 , nó k.com
có nghĩa là huyết áp tâm thu là 120mmHg và huyết áp tâm trương là 80 mmHg. Giả sử /v
rằng trái tim của một người đập 70 lần một phút, huyết áp P sau t giây có thể được iet    gold
mô tả bằng hàm số P t  7 100  20sin t 
 . Với t 0;60 , có bao nhiêu lần huyết áp  3 
người đó bằng 100 mmHg? A. 139 . B. 140 . C. 141. D. 142 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 20
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 45: Năm 1893, George Ferris chế tạo vòng đu quay. Nó có đường kính 250 foot. Nếu với
mỗi 40 giây vòng đu quay quay 1 vòng thì chiều cao h (foot) của một chỗ ngồi trên m.vn
vòng đu quay là một hàm số của thời gian t (giây) được xác định như sau ie    gh
h t   125sin 0,157t  125   .  2  racn it
Vòng quay bắt đầu tính từ thời điểm t  0. Trong 40 giây đầu tiên của chuyến đi, tại thời điểm th
nào sau đây (làm tròn đến hàng đơn vị) thì người ngồi trên ghế đu quay đó cách mặt đất 125 n ye
foot? (Chú thích: 1 foot xấp xỉ 30, 48 cm). lu A. 20 giây. B. 25 giây. C. 30 giây. D. 35 giây. s:// ttp
Lời giải: ........................................................................................................................................ h
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
..........................................................................................................................................................................
k.com ..........................................................................................................................................................................
.......................................................................................................................................................................... ceboo
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................
5.2. Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình lượng giác:.
Câu 46: Nghiệm lớn nhất của phương trình 2cos 2x 1  0 trong đoạn 0;  là: https://www 11 2 5 A. x   . B. x  . C. x  . D. x  . 12 3 6
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 21
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
Câu 47: Phương trình cos 2x  2cos x  3  0 có nghiệm lớn nhất trong khoảng 0;2019 ? A. 644 . B. 2 . C. 640 . D. 642 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... h ttp
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... ye
.......................................................................................................................................................................... n th
Câu 48: Nghiệm dương nhỏ nhất của phương trình sin cos 2x  0 là it r   3 a A.  . B. . C. . D. . cn 2 4 4 gh ie
Lời giải: ........................................................................................................................................ m.vn
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 49: Gọi x là nghiệm dương nhỏ nhất của phương trình 2 2
3sin x  2sin x cos x  cos x  0 . ht 0 tp
Chọn khẳng định đúng? s://www  3         3  A. x   ; . B. x  ; . C. x  0; . D. x  ;2 . 0          2  0  2  0  2  0  2  .fa ceboo
Lời giải: ........................................................................................................................................
.......................................................................................................................................................................... k.com
.......................................................................................................................................................................... /v
.......................................................................................................................................................................... ietgold
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 4 3
Câu 50: Cho phương trình 2 2 sin . x tan x  cos .
x cot x  2sin x cos x 
. Tính hiệu nghiệm âm lớn 3
nhất và nghiệm dương nhỏ nhất của phương trình. 3 5 5 A.  . B. . C.  . D.  . 2 6 6 22
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... m.vn ie
.......................................................................................................................................................................... gh
..........................................................................................................................................................................
.......................................................................................................................................................................... racn it
.......................................................................................................................................................................... th n
.......................................................................................................................................................................... ye
Câu 51: Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h m của mực lu  t   s://
nước trong kênh tính theo thời gian t h được cho bởi công thức h  3cos  12   .  6 3  ttp h Khi nào mực nước của
kênh là cao nhất với thời gian ngắn nhất?
A. t  22h .
B. t  15h .
C. t  14h .
D. t  10h .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
k.com ..........................................................................................................................................................................
..........................................................................................................................................................................
ceboo ..........................................................................................................................................................................
.fa ..........................................................................................................................................................................
5.3. Tính tổng tất cả các nghiệm của phương trình lượng giác trên tập K .
Câu 52: Tính tổng tất cả các nghiệm của phương trình sin x  sin 2x  0 trên đoạn 0;2 . https://www A. 4 . B. 5 . C. 3 . D. 2 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 23
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
Câu 53: Tính tổng các nghiệm trong đoạn 0;30của phương trình: tan x  tan3x (1) 171 190 A. 55. . B. . . C. 45 .. D. . 2 2
Lời giải: ........................................................................................................................................
.......................................................................................................................................................................... h
.......................................................................................................................................................................... ttp
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... lu ye
.......................................................................................................................................................................... n th
.......................................................................................................................................................................... it
.......................................................................................................................................................................... rac
Câu 54: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình n gh   3 sin 3x    ie  4  bằng   2 m.vn     A. . B. . C.  . D.  . 9 6 6 9
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... http
.......................................................................................................................................................................... s://www
..........................................................................................................................................................................
.......................................................................................................................................................................... .fa
.......................................................................................................................................................................... ceboo
..........................................................................................................................................................................
Câu 55: Tổng tất cả các nghiệm của phương trình cos 2x  cos x  0 trong khoảng 0;2  bằng T k.com
. Vậy T bằng bao nhiêu? /v    7  4    iet A. T  . B. T . C. T . D. T 2 . 6 3 gold
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 24
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”  5 
Câu 56: Tổng các nghiệm của phương trình sin 2x  3  6sin x  cos x trong khoảng 0;   là  2  2 5 19 A.  . B. . C. . D. . 3 6 6
Lời giải: ........................................................................................................................................
.......................................................................................................................................................................... m.vn ie
.......................................................................................................................................................................... gh
..........................................................................................................................................................................
.......................................................................................................................................................................... racn it
.......................................................................................................................................................................... th n
.......................................................................................................................................................................... ye
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... ttp h
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 57: Tổng tất cả các nghiệm thuộc 0;10π của phương trình 2
2sin x  5sin x  3  0 là A. 50 . B. 55 . C. 45 . D. 60 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
..........................................................................................................................................................................
k.com ..........................................................................................................................................................................
ceboo ..........................................................................................................................................................................
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 58: Tổng các nghiệm trong đoạn 0;2  của phương trình 3 3
sin x  cos x  1 bằng https://www 5 7 3 A. 2 . B. 2 . C. 2 . D. 2 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 25
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 59: Phương trình 2 2
6sin x  7 3 sin 2x  8cos x  6 có tổng hai nghiệm dương nhỏ nhất bằng 17 2 5 7 A. . B. . C. . D. . 12 3 24 12 h ttp
Lời giải: ........................................................................................................................................ s://
.......................................................................................................................................................................... lu ye
.......................................................................................................................................................................... n
.......................................................................................................................................................................... th it
.......................................................................................................................................................................... rac
.......................................................................................................................................................................... n gh
.......................................................................................................................................................................... ie
.......................................................................................................................................................................... m.vn
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... http sin x
Câu 60: Gọi S là tổng các nghiệm của phương trình
 0 trên đoạn 0;2017  . Tính S . s://www cos x 1
A. S  2035153 .
B. S 1001000 .
C. S  1017072 .
D. S  2000200 . .fa
Lời giải: ........................................................................................................................................ ceboo
.......................................................................................................................................................................... k.com
..........................................................................................................................................................................
.......................................................................................................................................................................... /viet
.......................................................................................................................................................................... gold
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 61: Tìm tổng các nghiệm của phương trình sin 3x  cos x  0 trên 0;  . 5  A. . B. . C.  . D. 2 . 8 3
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 26
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 62: Tìm tổng tất cả các nghiệm thuộc đoạn 0;30 của phương trình m.vn
cos3x  4cos 2x  3cos x  4  0 là ie 121 99 gh A. 45 . B.  . C.  . D. 50 . 2 2 racn it Lời giải th n Chọn D ye lu
PT cos3x  4cos2x  3cos x  4  0 s:// cos x  0 ttp 3  x  x   2 4 cos
3cos 4 2 cos x      3 2     h 1 3cos x 4 0 4cos x 8cos x 0  cos x  2 (vn)  1 30 1
+ Với cos x  0  x 
 k .Theo giải thiết, x  1 30 0;30  0   k     k   mà 2 2  2  2
k  Z  k 0;1;2;3; ;   9 .
Vậy tổng các nghiệm thỏa mãn yêu cầu bài toán là              2   9  5       
1 2  9  5  45  50 . 2  2   2   2 
/vietgold Câu 63: Tính tổng S tất cả các nghiệm của phương trình  x   4 4 2cos 2
5 sin x  cos x  3  0 trên k.com khoảng 0;2  . ceboo 7   11      .fa A. S . B. S . C. S 4 . D. S 5 . 6 6
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
https://www ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 27
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
Câu 64: Cho phương trình  x   x  x 2 2sin 1 3 tan 2sin
 3 4cos x . Gọi T là tập hợp các
nghiệm thuộc đoạn 0;20  của phương trình trên. Tính tổng các phần tử của T . 570 875 880 1150 A.  . B.  . C.  . D.  . 3 3 3 3
Lời giải: ........................................................................................................................................
.......................................................................................................................................................................... h ttp
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... ye
.......................................................................................................................................................................... n th
.......................................................................................................................................................................... it r
.......................................................................................................................................................................... acn
.......................................................................................................................................................................... gh
.......................................................................................................................................................................... ie m.vn
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 2 3
cos x  cos x 1
Câu 65: Tính tổng tất cả các nghiệm của phương trình 2
cos 2x  tan x  trên đoạn 2 ht cos x tp [1;70] s://www A. 188 . B. 263 . C. 363 . D. 365
Lời giải: ........................................................................................................................................ .fa ceboo
..........................................................................................................................................................................
.......................................................................................................................................................................... k.com
.......................................................................................................................................................................... /v
.......................................................................................................................................................................... ietgold
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 28
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................       5
Câu 66: Tổng các nghiệm của phương trình 4 4 4 sin x  sin x   sin x       trong khoảng  4   4  4 m.vn 0;2  bằng ie A. 2 . B. 4 . C.  . D. 3 . gh
Lời giải: ........................................................................................................................................ racn it th
.......................................................................................................................................................................... n
.......................................................................................................................................................................... ye lu
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... ttp
.......................................................................................................................................................................... h
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 67: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình /vietgold  x  1 tan x tan
sin x  cot x  4   là  2  k.com     A.  . B. . C. . D.  . ceboo 6 2 6 2 .fa
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
https://www ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... sin 2x
Câu 68: Tính tổng các nghiệm thuộc  ;3  của phương trình:  0 . cos x 1 29
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác 3 A. 8 . B. 9 . C. 10 . D. . 2
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... h
.......................................................................................................................................................................... ttp
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... lu ye
.......................................................................................................................................................................... n
.......................................................................................................................................................................... th it
.......................................................................................................................................................................... ra
.......................................................................................................................................................................... cngh
.......................................................................................................................................................................... ie
Câu 69: Tính tổng T các nghiệm của phương trình 2
cos x  sin x cos x  2sin x  cos x  2 trên m.vn    khoảng ;5 .    2  15 21 3 A. T  . B. T  . C. T  7 . D. T  . 2 8 4
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... ht
.......................................................................................................................................................................... tps://www
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... .fa
.......................................................................................................................................................................... ceboo
.......................................................................................................................................................................... k.com
..........................................................................................................................................................................
.......................................................................................................................................................................... /v
.......................................................................................................................................................................... ietgold
..........................................................................................................................................................................
Câu 70: Tính tổng các nghiệm trên  4
 ;4  của phương trình 3 3
sin x  3 3sin x  2  2  0 A.  . B. 2   . C.   . D. 0 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 30
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... m.vn
.......................................................................................................................................................................... ie
.......................................................................................................................................................................... gh
.......................................................................................................................................................................... racn
.......................................................................................................................................................................... it th
.......................................................................................................................................................................... n 1 1 1 ye
Câu 71: Phương trình  
có tổng các nghiệm trên (0; ) là: lu cos x sin 2x sin 4x   2 s:// A. . B. . C. . D.  6 6 3 ttp h
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
/vietgold .......................................................................................................................................................................... k.com
sin 2x  2 cos x  sin x 1
Câu 72: Phương trình
 0 có bao nhiêu nghiệm trên (0;3 ) ? tan x  3 ceboo A. 1. B. 2. C. 3. D. 4 .fa
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
https://www ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 73: Gọi S là tổng tất cả các nghiệm thuộc 0;20  của phương trình 2
2cos x  sin x 1  0 .
Khi đó giá trị của S bằng: 200
A. S  570 .
B. S  295 .
C. S  590 . D. S   . 3
Lời giải: ........................................................................................................................................ 31
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... h ttp
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... ye   
Câu 74: Tính tổng T các nghiệm của phương trình 2 2
cos x  sin 2x  2  cos
 x trên khoảng n    2  th it 0;2  . rac 7 21 11 3 n A. T  . B. T  . C. T  . D. T  . gh 8 8 4 4 ie m.vn
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... http
.......................................................................................................................................................................... s://www
..........................................................................................................................................................................
Câu 75: Tính tổng tất cả các nghiệm của phương trình 3 cos x  sin x 1 trên 0;2 . .fa 5 11  3 A. . B. . C. . D. . ceboo 3 6 6 2
Lời giải: ........................................................................................................................................ k.com
.......................................................................................................................................................................... /viet
.......................................................................................................................................................................... gold
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 76: Gọi S là tập hợp các nghiệm thuộc khoảng 0;100  của phương trình 2  x x  sin  cos  3cos x  3  
. Tổng các phần tử của S là  2 2  7400 7525 7375 7550 A. . B. . C. . D. . 3 3 3 3 32
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... m.vn ie
.......................................................................................................................................................................... gh
..........................................................................................................................................................................
.......................................................................................................................................................................... racn it
.......................................................................................................................................................................... th n
Câu 77: Gọi S là tập hợp tất cả các nghiệm thuộc khoảng 0;2018 của phương trình sau: ye
3 1 cos 2x  sin 2x  4cos x  8  4 3  
1 sin x . Tính tổng tất cả các phần tử của S . lu   s:// 310408 312341 A. 103255 . B. . C. . D. 102827 . ttp 3 3 h
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
..........................................................................................................................................................................
k.com ..........................................................................................................................................................................
.......................................................................................................................................................................... ceboo
.fa ..........................................................................................................................................................................
Câu 78: Tính tổng tất cả các nghiệm của phương trình sin 2x  4sin x  2cos x  4  0 trong đoạn
0;100  của phương trình. A. 100 . B. 2476 . C. 25 . D. 2475 . https://www
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 33
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 79: Tổng tất cả các nghiệm của phương trình cossin x 1 trên 0;2  bằng A. 0 . B.  . C. 2 . D. 3 . h
Lời giải: ........................................................................................................................................ ttp s://
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... ye
.......................................................................................................................................................................... n th
.......................................................................................................................................................................... it
.......................................................................................................................................................................... rac
.......................................................................................................................................................................... n gh
.......................................................................................................................................................................... ie 4 4     m.vn
Câu 80: Tính tổng S các nghiệm của phương trình 2cos 2x 5sin x cos x 3 0 trong khoảng 0;2  . 11 7 A. S  . B. S  4 . C. S  5 . D. S  . 6 6
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... ht
.......................................................................................................................................................................... tps://www
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... .fa
.......................................................................................................................................................................... ceboo
Câu 81: Cho phương trình 2018 2018 x  x   2020 2020 sin cos 2 sin x  cos
x . Tính tổng các nghiệm của k.com
phương trình trong khoảng 0;2018 2 2 /v 1285  1285  A.  . B.  2 643  . C.  2 642  . D.  . iet      4   2  gold
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 34
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 82: Phương trình lượng giác: cos3x cos2x 9sin x 4  0 trên khoảng 0;3 . Tổng số
nghiệm của phương trình trên là: m.vn 25 11 ie A. . B. 6 . C. Kết quả khác. D. . 6 3 gh
Lời giải: ........................................................................................................................................ racn it
.......................................................................................................................................................................... th n
.......................................................................................................................................................................... ye lu
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... ttp h
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
k.com .......................................................................................................................................................................... ceboo
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
https://www ..........................................................................................................................................................................
..........................................................................................................................................................................
DẠNG 6. TÌM ĐIỀU KIỆN CỦA THAM SỐ m ĐỂ PHƯƠNG TRÌNH LƯỢNG GIÁC
CHO TRƯỚC CÓ NGHIỆM.
Câu 83: Tính tổng S tất cả các giá trị nguyên của tham số m để phương trình      3  2 cos 2x   5  m  
có nghiệm thuộc khoảng ; .    3   6 4  A. S  25  . B. S  22  . C. S  22 . D. S  25 . 35
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... h ttp
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... lu ye
.......................................................................................................................................................................... n th
.......................................................................................................................................................................... it rac  3  n
Câu 84: Tìm m để phương trình 3cos x  43cos x 1 3m  0 có số nghiệm trên đoạn 0;   gh  2  ie là lớn nhất. m.vn 2 1 2 4 2 1 2 1
A.   m  . B.   m  .
C.   m  .
D.   m  . 3 3 3 3 3 3 3 3
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... http
.......................................................................................................................................................................... s://www
.......................................................................................................................................................................... .fa
.......................................................................................................................................................................... ceboo
.......................................................................................................................................................................... k.com
Câu 85: Tìm điều kiện của tham số m để phương trình 2
sin x  2m  
1 sin x  3m m  2  0 có /v nghiệm ietgold  1 1    1 1 m     m    2   m  1   1   m  1 A. 2 2  . B. 3 3  . C.  . D.  . 0  m  1 3  m  4 1   m  2 1   m  3
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 36
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 86: Tìm điều kiện của tham số m để phương trình cos2x 2m 
1 cos x  m 1  0 có đúng     m.vn hai nghiệm trên đoạn  ;   .  2 2  ie gh A. 1   m  0 .
B. 0  m 1.
C. 0  m 1. D. 1   m 1. racn it
Lời giải: ........................................................................................................................................ th n
.......................................................................................................................................................................... ye
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... ttp h
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 87: Cho phương trình
2 x  m  
x  m   2 2sin 1 sin 2
6 cos x  1. Có bao nhiêu giá trị nguyên
của tham số m để phương trình vô nghiệm? A. 4 . B. 6 . C. 5 . D. 2 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
..........................................................................................................................................................................
k.com ..........................................................................................................................................................................
ceboo ..........................................................................................................................................................................
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
https://www Câu 88: Tìm tất cả các giá trị của tham số m để phương trình 2
2cos x  4msin x cos x  m có nghiệm: 2 2 A. m   .
B. m   hoặc m 0 . 3 3 2
C.   m  0 . D. m  0 . 3
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 37
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 89: Số các giá trị nguyên m để phương trình 4m  4.sin .
x cos x  m  2.cos 2x  3m  9 có nghiệm là h A. 7. B. 6. C. 5. D. 4 ttp s://
Lời giải: ........................................................................................................................................ lu
.......................................................................................................................................................................... ye n
.......................................................................................................................................................................... th it r
.......................................................................................................................................................................... acngh
.......................................................................................................................................................................... ie
.......................................................................................................................................................................... m.vn
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... ht
.......................................................................................................................................................................... tps://www
..........................................................................................................................................................................
Câu 90: Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 3 cos x  m 1  0 có .fa ceboo nghiệm? A. 1. . B. 2.. C. 3. . D. Vô số. k.com
Lời giải: ........................................................................................................................................ /viet
.......................................................................................................................................................................... gold
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 91: Tìm tất cả các giá trị của tham số m để phương trình m  
1 sin x  2  m  0 có nghiệm. 38
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” 1 1 A. m  1.  . B. m  .. C. 1   m  .. D. m  1.  2 2
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... m.vn ie
.......................................................................................................................................................................... gh
.......................................................................................................................................................................... racn it
.......................................................................................................................................................................... th n
.......................................................................................................................................................................... ye lu
Câu 92: Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 3 cos x  m 1  0 có s:// nghiệm? ttp h A. 1. . B. 2.. C. 3. . D. Vô số.
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
k.com ..........................................................................................................................................................................
ceboo Câu 93: Tìm tất cả các giá trị của tham số m để phương trình m 1sinx2m0 có nghiệm. .fa 1 1 A. m  1.  . B. m  .. C. 1   m  .. D. m  1.  2 2
Lời giải: ........................................................................................................................................
https://www ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 39
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
DẠNG 7. TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ LƯỢNG GIÁC
7.1. Tìm GTLN, GTNN sử dụng điều kiện 1   sin ,
x cos x  1.  2 
Câu 94: Tìm giá trị nhỏ nhất của biểu thức A  sin x  sin x     3  3 A. 1  . B. 0 . C. 2  . D. . 2 h ttp
Lời giải: ........................................................................................................................................ s://
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... ye n
.......................................................................................................................................................................... th
.......................................................................................................................................................................... it ra
.......................................................................................................................................................................... cngh
.......................................................................................................................................................................... ie
Câu 95: Tìm giá trị lớn nhất của biểu thức 4 4
A  sin x  cos x m.vn 1 A. 1 . B. 0 . C. 2 . D. . 2
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... ht
.......................................................................................................................................................................... tp
.......................................................................................................................................................................... s://www
Câu 96: Tập giá trị của hàm số y  sin 2x  3 cos2x 1 là đoạn  ;
a b. Tính tổng T  a  . b A. T  1. B. T  2 . C. T  0 . D. T  1  . .fa ceboo
Lời giải: ........................................................................................................................................ k.com
..........................................................................................................................................................................
.......................................................................................................................................................................... /v
.......................................................................................................................................................................... ietgold
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 40
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Câu 97: Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu hm của mực  t  
nước trong kênh tính theo thời gian t h được cho bởi công thức h  3cos  12   .  6 3 
Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
A. t  22h.
B. t  15h .
C. t  14h .
D. t  10h . m.vn
Lời giải: ........................................................................................................................................ ie
.......................................................................................................................................................................... gh
.......................................................................................................................................................................... racn it
.......................................................................................................................................................................... th
.......................................................................................................................................................................... n ye
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... ttp
Câu 98: Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số h y  1
  2cos x 2 3sinx  cosx trên . Biểu thức M  N  2 có giá trị bằng A. 0 . B. 4 2  3 . C. 2 . D. 2  3  2 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
..........................................................................................................................................................................
k.com ..........................................................................................................................................................................
ceboo ..........................................................................................................................................................................
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 99: Số giờ có ánh sáng của một thành phố X ở vĩ độ 40 bắc trong ngày thứ t của một năm   
không nhuận được cho bởi hàm số: d t   3sin t  80 12  
, t  và 0  t  365. https://www 182 
Vào ngày nào trong năm thì thành phố X có nhiều giờ ánh sáng nhất? A. 262 . B. 353 . C. 80 . D. 171 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 41
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 100: Hàm số y  2cos3x  3sin3x  2 có tất cả bao nhiêu giá trị nguyên? A. 7 . B. 3 . C. 5 . D. 6 .
Lời giải: ........................................................................................................................................
.......................................................................................................................................................................... h ttp
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... ye
.......................................................................................................................................................................... n th
.......................................................................................................................................................................... it
.......................................................................................................................................................................... rac
.......................................................................................................................................................................... n gh
.......................................................................................................................................................................... ie m.vn
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 101: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau 2 2
y  2sin x  cos 2x . 3
A. max y  4 , min y  .
B. max y  3, min y  2 . 4 3
C. max y  4 , min y  2 .
D. max y  3, min y  . 4
Lời giải: ........................................................................................................................................ http
.......................................................................................................................................................................... s://www
..........................................................................................................................................................................
.......................................................................................................................................................................... .fa
.......................................................................................................................................................................... ceboo
.......................................................................................................................................................................... k.com
..........................................................................................................................................................................
.......................................................................................................................................................................... /v
.......................................................................................................................................................................... ietgold
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 102: Gọi M và m lần lượt là GTLN và GTNN của hàm số 4 4
y  sin x  cos x  sin 2x . Tổng
M  m là 3 1 3 A. . B.  . C. . D. 1 . 2 2 2
Lời giải: ........................................................................................................................................ 42
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... m.vn
.......................................................................................................................................................................... ie
.......................................................................................................................................................................... gh
.......................................................................................................................................................................... racn it
7.2. Tìm GTLN, GTNN dạng y  asin x  bcos x  c . th n sin x  2cos x  ye
Câu 103: Cho hàm số y
. Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất
sin x  cos x  3 lu
của hàm số đã cho. Tính 7m  5M bằng? s:// A. 10 . B. 1 . C. 0 . D. 10  . ttp h
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
/vietgold .......................................................................................................................................................................... k.com 3sin 4x  4 4 4
sin x  cos x
Câu 104: Hàm số y 
có giá trị lớn nhất M và giá trị nhỏ nhất m . Khi 2
2cos 2x  sin 4x  2 ceboo .fa
đó tổng M  m bằng? 5 10 3 A. 0 . B.  .  . D. . 7 C. 7 7
Lời giải: ........................................................................................................................................
https://www ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 43
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
Câu 105: Giá trị lớn nhất M , giá trị nhỏ nhất m của hàm số: 2
y  2cos x  2 3sin x cos x  1 là
A. M  4;m  0 .
B. M  3;m  0 .
C. M  3;m  1.
D. M  4;m  1.
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... h ttp
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... ye
.......................................................................................................................................................................... n th
.......................................................................................................................................................................... it
.......................................................................................................................................................................... rac
.......................................................................................................................................................................... n gh
.......................................................................................................................................................................... ie
sin x  2 cos x  1 m.vn
Câu 106: Cho hàm số y  . Gọi M ; m
sin x  cos x  2
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
của hàm số. Tổng M  m bằng A. 1 . B. 2  . C. 1  . D. 2 .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... http
.......................................................................................................................................................................... s://www
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... .fa ceboo
..........................................................................................................................................................................
cos x  2sin x  3
Câu 107: Giá trị lớn nhất của hàm số y  là k.com
2cos x  sin x  4 A. 3  2 3 . B. 2 . C. 1  . D. 0 . /vietgold
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 44
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... msin x  1
Câu 108: Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số y   cos x 2 nhỏ hơn 2 . m.vn A. 4 . B. 6 . C. 5 . D. 3 . ie
Lời giải: ........................................................................................................................................ gh
.......................................................................................................................................................................... racn it
.......................................................................................................................................................................... th n
.......................................................................................................................................................................... ye
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... ttp h
..........................................................................................................................................................................
..........................................................................................................................................................................
sin x  2cos x  1
Câu 109: Giả sử M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số y 
sin x  cos x  2 trên
. Tìm 2M  3m A. 1 2 . B. 0 . C. 1 . D. 8
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
/vietgold ..........................................................................................................................................................................
k.com ..........................................................................................................................................................................
..........................................................................................................................................................................
ceboo ..........................................................................................................................................................................
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... https://www 2sin x  2
Câu 110: Gọi M , m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  . cos x  2
Khẳng định nào sau đây đúng? 8
A. 3m  M  8.
B. 3m  M  8  .
C. 3m  M  0 .
D. 3m  M   3
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 45
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 111: Tập giá trị của hàm số y  sin 2x  3 cos2x 1 là đoạn  ;
a b. Tính tổng T  a  . b A. T  0. B. T  1  . C. T  1. D. T  2. h
Lời giải: ........................................................................................................................................ ttp s://
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... ye
.......................................................................................................................................................................... n th
.......................................................................................................................................................................... it
.......................................................................................................................................................................... rac
.......................................................................................................................................................................... n gh
.......................................................................................................................................................................... ie
.......................................................................................................................................................................... m.vn
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 112: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  3sin x  4cos x 1.
A. max y  6, min y  4  .
B. max y  8 , min y  6  . https://www
C. max y  4 , min y  6  .
D. max y  6, min y  8  .
Lời giải: ........................................................................................................................................ .fa ceboo
..........................................................................................................................................................................
.......................................................................................................................................................................... k.com
..........................................................................................................................................................................
.......................................................................................................................................................................... /viet
.......................................................................................................................................................................... gold
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 46
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
7.3. Tìm GTLN, GTNN sử dụng bất đẳng thức cổ điển.
Câu 113: Cho hàm số 2 2
y  1 2sin x  1 2cos x  1. Gọi ,
m M lần lượt là giá trị nhỏ nhất và
giá trị lớn nhất của hàm số. Khi đó giá trị của M  m bằng A. 3  2 2 . B. 3  2 1. C. 3  2 2 1. D.  3  3 2 1.
Lời giải: ........................................................................................................................................ m.vn ie
.......................................................................................................................................................................... gh
..........................................................................................................................................................................
.......................................................................................................................................................................... racn it
.......................................................................................................................................................................... th n
.......................................................................................................................................................................... ye
.......................................................................................................................................................................... lu
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... ttp h
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
2sin x  3cos x  1
Câu 114: Tìm giá trị lớn nhất của hàm số y 
sin x  cos x  2 3  33 3  33 1 A. . B. . C. 3 . D. . 2 2 2 /vietgold
Lời giải: ........................................................................................................................................
k.com ..........................................................................................................................................................................
ceboo ..........................................................................................................................................................................
.fa ..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
https://www ..........................................................................................................................................................................
Câu 115: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số f  x 2018 2018  sin x  cos
x lần lượt là 1 1 1 A. và 2 . B. và 1 . C. 0 và 1 . D. và 1. 1008 2 1009 2 1008 2
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... 47
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
Câu 116: Cho x ,  
y là các số thực thỏa mãn cos2x cos2y 1. Giá trị nhỏ nhất của biểu thức 2 2
P  tan x  tan y bằng 1 2 8 A. . B. . D. . C. 3. 3 3 3 h ttp
Lời giải: ........................................................................................................................................ s://
.......................................................................................................................................................................... lu ye
.......................................................................................................................................................................... n
.......................................................................................................................................................................... th it
.......................................................................................................................................................................... rac
.......................................................................................................................................................................... n gh   
Câu 117: Cho hai số thực x, y thuộc 0; 
 và thỏa mãn cos2x  cos2y  2sinx  y  2. Giá trị ie  2  m.vn 4 4 cos x cos y P   y x nhỏ nhất của bằng 2 3 2 5 A. 3 . B.  . C.  . D.  .
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... http
.......................................................................................................................................................................... s://www
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... .fa ceboo
..........................................................................................................................................................................
.......................................................................................................................................................................... k.com
..........................................................................................................................................................................
.......................................................................................................................................................................... /viet
.......................................................................................................................................................................... gold
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... Câu 118: Cho , a ,
b c là các số thực thỏa mãn 2 2 2
a  b  c  4. Tìm giá trị lớn nhất M trong tất cả   
các hàm số y  a  b sin x  c cos x với x  0; .    4 
A. M  1 2 .
B. M  1 2 .
C. M  2 1 2 .
D. M  21 2. 48
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Lời giải: ........................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
.......................................................................................................................................................................... m.vn ie
.......................................................................................................................................................................... gh
..........................................................................................................................................................................
Câu 119: Tập giá trị của hàm số y  sin 2x  3 cos2x 1 là đoạn  ;
a b. Tính tổng T  a  . b racn it A. T  1. B. T  2 . C. T  0 . D. T  1  . th n
Lời giải: ........................................................................................................................................ ye lu
.......................................................................................................................................................................... s://
.......................................................................................................................................................................... ttp
.......................................................................................................................................................................... h
..........................................................................................................................................................................
.......................................................................................................................................................................... /vietgold k.com ceboo .fa https://www 49
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
PHẦN 2: BẢNG ĐÁP ÁN 1.C 2.D 3.A 4.C 5.C 6.A 7.A 8.B 9.D 10.C 11.B 12.A 13.D 14.C 15.B 16.B 17.B 18.D 19.A 20.D 21.B 22.A 23.B 24.D 25.C 26.D 27.A 28.C 29.C 30.D 31.B 32.D 33.C 34.C 35.B 36.B 37.A 38.B 39.A 40.B h 41.B 42.A 43.C 44.C 45.C 46.D 47.D 48.C 49.C 50.C ttp s:// 51.D 52.B 53.C 54.C 55.D 56.D 57.B 58.D 59.B 60.C lu 61.D 62.D 63.C 64.B 65.D 66.B 67.D 68.A 69.C 70.B ye n th 71.D 72.B 73.B 74.C 75.A 76.C 77.B 78.D 79.B 80.B it r 81.D 82.B 83.C 84.D 85.B 86.B 87.A 88.B 89.D 90.C acngh 91.B 92.C 93.B 94.A 95.A 96.B 97.D 98.C 99.D 100.A ie m.vn 101.D 102.D 103 104.C 105.A 106.C 107.B 108.C 109.D 110.B 111.D 112.C 113.C 114.A 115.D 116.B 117.C 118.C 119.B https://www .fa ceboo k.com /vietgold 50
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
PHẦN 3: ĐÁP ÁN CHI TIẾT
DẠNG 1. XÁC ĐỊNH ĐỒ THỊ HÀM SỐ LƯỢNG GIÁC.
Câu 1: Hình nào dưới đây biểu diễn đồ thị hàm số y  f x  2sin 2x ? m.vn ie gh A. . B. . racn it th n ye lu C. . D. . s:// Lời giải ttp h Chọn C Ta thấy 2
  2sin 2x  2 nên ta có loại Hình 2 và Hình 3.
Tiếp theo với Hình 1 và Hình 4 ta có: 2
Từ phần lý thuyết ở trên ta có hàm số tuần hoàn với chu kỳ   . 2
Ta thấy x0 thì y0 nên đồ thị hàm số đi qua gốc tọa độ. Từ đây ta chọn đáp án Hình 1. /vietgold x Câu 2:
Hình vẽ nào sau đây biểu diễn đồ thị hàm số y  cos ? 2 k.com ceboo .fa A. . B. . https://www C. . D. . Lời giải Chọn D x Ta thấy 1
  cos 1 nên ta có loại Hình 2. 2 x 2
Tiếp theo ta có hàm số y  cos có chu kỳ tuần hoàn là T   4 . 2 1 2 51
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác x
Ta thấy x  0 thì y  cos
 cos0 1 nên ta chọn Hình 4. 2 Câu 3:
Cho đồ thị hàm số y  cos x như hình vẽ: h ttp
Hình vẽ nào sau đây là đồ thị hàm số y  cos x  2 ? s:// lu ye n th it ra A. . B. . cngh ie m.vn C. . D. . Lời giải Chọn A
Ta thực hiện phép tịnh tiến đồ thị hàm số y  cos x trên trục Oy lên trên 2 đơn vị. Câu 4:
Cho đồ thị hàm số y  sin x như hình vẽ: https://www .fa ceboo
Hình nào sau đây là đồ thị hàm số y  sin x ? k.com /vietgold A. . B. . C. . D. . Lời giải Chọn C
Suy diện đồ thị hàm số y  sin x từ đồ thị hàm số y  sin x 52
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Giữ nguyên phần đồ thị của hàm số y  sin x nằm bên phải trục Oy .
Lấy đối xứng phần đồ thị trên qua trục Oy .
Dưới đây là đồ thị ta thu được sau khi thực hiện các bước suy diễn ở trên. Phần đồ thị nét đứt là 
phần bỏ đi của hàm số y sin x . m.vn ie gh racn it th n . ye lu Câu 5:
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt s:// kê ở bốn phương án , A , B C , D . ttp h
Hỏi hàm số đó là hàm số nào?
A. y  tan x .
B. y  cot x .
C. y  tan x .
D. y  cot x . /vietgold Lời giải k.com Chọn C
ceboo Ta thấy hàm số có GTNN bằng 0.
.fa Hàm số xác định tại x và tại x thì y 0. Câu 6:
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án , A , B C, D . https://www
Hỏi hàm số đó là hàm số nào?      
A. y  sin x  1   .
B. y  2sin x    .  2   2       
C. y  sin x  1   .
D. y  sin x  1   .  2   2  53
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác Lời giải Chọn A   
Ta thấy hàm số có GTLN bằng 0, GTNN bằng 2
 . Do đó ta loại đáp án y  2sin x    . Vì  2     y  2sin x      2  ;2.  2  h    ttp
Tại x  0 thì y  2
 . Thử vào các đáp án còn lại chỉ có y  sin x  1   thỏa mãn.  2  s:// lu Câu 7:
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt ye kê ở bốn phương án , A , B C, D . n th it racngh ie m.vn
Hỏi hàm số đó là hàm số nào?
A. y  1 sin x .
B. y  sin x .
C. y  1 cos x .
D. y  1 sin x . Lời giải Chọn A
Ta có: y  1 cos x  1 và y  1 sin x  1 nên loại y  1 cos x và y  1 sin x . http
Ta thấy tại x  0 thì y  1. Thay vào hai đáp án: y  1 sin x và y  sin x thì chỉ có y  1 sin x s://www thỏa. Câu 8:
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt .fa ceboo kê ở bốn phương án , A , B C, D . k.com /vietgold
Hỏi hàm số đó là hàm số nào?
A. y  1 sin x .
B. y  sin x .
C. y  1 cos x .
D. y  1 sin x . Lời giải Chọn B
Ta có: y  1 cos x  1 và y  1 sin x  1 nên loại y  1 cos x và y  1 sin x . 54
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Ta thấy tại x   thì y  0. Thay vào hai đáp án còn lại thì chỉ có y  sin x thỏa mãn. Câu 9:
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt
kê ở bốn phương án A, B, C,. D. Hỏi hàm số đó là hàm số nào? m.vn ie gh racn it th n ye lu s:// ttp h      
A. y  sin x    .
B. y  cos x   .  2   2    
C. y  sin x  1   .
D. y  cos x 1.  2  Lời giải Chọn D
Lấy đối xứng qua trục hoành đồ thị hàm số y  cos x ta được đồ thị hàm số y  cos x . Sau đó
/vietgold tịnh tiến đồ thị hàm số y cosx   
lên trên ta được đồ thị hàm số y cos x 1. k.com ceboo .fa https://www 55
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
DẠNG 2. XÁC ĐỊNH CHU KỲ HÀM SỐ LƯỢNG GIÁC.
Câu 10: Chu kỳ tuần hoàn của hàm số y  sin x cos x cos 2x cos 4x là   A. 2 . B. 4 . C. . D. . 4 8 Lời giải Chọn C h ttp 1 1 1
Ta có y  sin x cos x cos 2x cos 4x  sin 2x cos 2x cos 4x  sin 4x cos 4x  sin 8x . s:// 2 4 8 lu 2  ye
Do đó chu kỳ của hàm số là T   . 8 4 n th 4 4 it
Câu 11: Tìm chu kỳ tuần hoàn của hàm số y  3 sin 4x  4sin x  cos x  2 . rac   n A. 2 . B. . C. . D.  . gh 2 4 ie m.vn Lời giải Chọn B 1 1 3 1 Ta có 4 4 2 2 2
sin x  cos x  1 2sin x cos x  1 sin 2x  1
1cos2x   cos4x . 2 4 4 4   
Do đó y  3 sin 4x  3  cos 4x  2  2sin 4x   5   .  6  2 
Vậy chu kỳ tuần hoàn của hàm số là T   . ht 4 2 tps://www
Câu 12: Tìm chu kỳ tuần hoàn của hàm số f  x 3 3 3
 sin 4x sin xcos3x cos xsin3x .   2 A. . B. . C. . D. 2 . 6 12 3 .fa ceboo Lời giải k.com Chọn A Ta có: /viet 3 3 3 3 3 3 gold
sin x cos 3x  cos x sin 3x  sin .
x 4cos x 3cos x  cos .
x 3sin x  4sin x 3 3 3 3 3 3  x x  x x  x x  x x  x x  2 2 4sin .cos 3sin cos 3cos sin 4sin .cos 3sin cos
cos x  sin x 3 3
 sin 2x cos 2x  sin 4x . 2 4 3 1 1
Do đó f  x 3
 sin 4x  sin 4x    3
3sin 4x  4sin 4x   sin12x . 4 4 4 2 
Vậy chu kỳ tuần hoàn của hàm số là T   . 12 6 56
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Câu 13: Tìm chu kỳ tuần hoàn của hàm số f  x 3 3  cos . x cos 3x  sin . x sin 3x .   A. . B. 2 . C.  . D. . 6 2 Lời giải Chọn D m.vn Ta có: ie gh
f  x   x x 2 x   x x 2 cos 3 .cos .cos sin 3 .sin .sin x racn 1 1 2 2 it
 cos4x  cos2x.cos x  cos2x cos4x.sin x 2 2 th n 1 ye 2 2 2 2  cos 4 .
x cos x  cos 2 .
x cos x  cos 2 .
x sin x  cos 4 . x sin x   lu 2 s:// 1 1  1  1 3 2
 cos 4x  cos 2x  cos 4x 
1cos4x   cos4x ttp       h 2 2 2 4 4 2 
Vậy chu kỳ tuần hoàn của hàm số là T   . 4 2 /vietgold k.com ceboo .fa https://www 57
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
DẠNG 3. TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ LƯỢNG GIÁC.
Câu 14: Tìm mệnh đề đúng trong các mệnh đề sau?
A. Hàm số y  cot x đồng biến trên khoảng 0;  .
B. Hàm số y  sin x nghịch biến trên khoảng 3 ;4  .  5 3 
C. Hàm số y  sin x đồng biến trên khoảng  ;    .  2 2  h ttp     s://
D. Hàm số y  cos x đồng biến trên khoảng  ;   .  2 2  lu ye Lời giải n th Chọn C it rac
* Hàm số y  cot x nghịch biến trên mỗi khoảng mà nó xác định. n gh     ie
* Hàm số y  sin x đồng biến trên mỗi khoảng 
 k2;  k2 
 và nghịch biến trên mỗi m.vn  2 2    3  khoảng  k2;  k2 .    2 2 
* Hàm số y  cos x đồng biến trên mỗi khoảng  
  k2;k2  và nghịch biến trên mỗi khoảng
k2;  k2 .
Vậy đáp án đúng là C.
Câu 15: Cho các hàm số y  sin x ; y  cos x ; y  tan x ; y  cot x . Có bao nhiêu hàm số nghịch http  5  biến trên 3  ; ? s://www    2  A. 1. B. 3 . C. 0 . D. 2 . .fa Lời giải ceboo Chọn B k.com   3 
Hàm số y  sin x nghịch biến trên mỗi khoảng  k 2;  k 2 
 nên nghịch biến trên khoảng /v  2 2  iet  5  gold 3  ;   .  2 
Hàm số y  cos x nghịch biến trên mỗi khoảng k2;  k2  nên nghịch biến trên khoảng  5  3  ;   .  2 
Hàm số y  tan x đồng biến trên mỗi khoảng xác định của nó.  5 
Hàm số y  cot x trên mỗi khoảng k;  k  nên nghịch biến trên khoảng 3  ;   .  2  58
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”  5 
Vậy có 3 hàm số nghịch biến trên 3  ;   .  2 
Câu 16: Cho hàm số y  tan x . Khẳng định nào dưới đây sai?
A. Hàm số đã cho là hàm lẻ.
B. Hàm số đã cho có tập giá trị là  1 ;1. m.vn    ie
C. Hàm số đã cho đồng biến trên  ;0   .   gh 2   racn
D. Hàm số đã cho có tập xác định
\   k , k   . it  2  th n Lời giải ye lu Chọn B s://   ttp
• Hàm số y  tan x có tập xác định:
\   k , k   nên D đúng. h  2 
• Hàm số y  tan x có tập giá trị: T  . Ta có: x
 D  xD . Mà f x  tanx  tan x   f x.
Do đó hàm số y  f  x  tan x là hàm lẻ. Suy ra A đúng.       3 
• Hàm số y  tan x đồng biến trên khoảng  ;   và nghịch biến trên ;   . Do đó C đúng.  2 2   2 2 
/vietgold Vậy đáp án B sai.
k.com Câu 17: Khẳng định nào sau đây đúng?      
ceboo A. y sinx là hàm số nghịch biến trên ;  .  4 4  .fa   3 
B. y  cos x là hàm số nghịch biến trên ;   .  4 4    2 
https://www C. y sinx là hàm số nghịch biến trên 0;   .  3    3 
D. y  tan x là hàm số nghịch biến trên ;   .  4 4  Lời giải Chọn B
Dựa vào đường tròn lượng giác ta thấy y  cos x là hàm số nghịch biến trên 0;  nên y  cos x   3 
là hàm số nghịch biến trên ;   .  4 4  59
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
Câu 18: Hàm số y  cos x nghịch biến trên khoảng nào sau đây? 19   3   11   11  A. ;10   . B.  ;   . C. ; 7   . D.  ;  5   .  2   2 2   2   2  Lời giải Chọn D
Dựa vào đường tròn lượng giác ta thấy y  cos x là hàm số nghịch biến trên mỗi khoảng h ttp   11 
k2 ;  k2  nên y  cos x là hàm số nghịch biến trên  ;  5   . s://  2  lu
Câu 19: Để hàm số y  sin x  cos x tăng, ta chọn x thuộc khoảng nào? ye n  3    3   th A. 
 k2;  k2   . B. 
 k;  k   .  4 4   4 4  it rac     n C. 
 k2;  k2   .
D.   k2;2  k2  . gh  2 2  ie m.vn Lời giải Chọn A   
Ta có y  sin x  cos x  2 sin x  
 . Để hàm số y  sin x  cos x tăng thì  4         3 k2  x 
  k2,k   
 k2  x   k2,k  . 2 4 2 4 4
Câu 20: Xét hai mệnh đề sau: ht     tp (I): x    ;   :Hàm số 2
y  tan x tăng. s://www  2 2      (II): x    ;   :Hàm số 2
y  sin x tăng. .fa  2 2  ceboo Chọn câu đúng? k.com A. Chỉ (I) đúng. B. Chỉ (II) đúng. C. Cả hai đúng. D. Cả hai sai. /v Lời giải ietgold Chọn D     Ta có x   ; 
 .Hàm số y  tan x có bảng biến thiên:  2 2  60
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” m.vn ie gh    Suy ra trên  ;0   hàm số 2
y  tan x giảm. racn  2  it th Xét bảng biến thiên: n ye lu s:// ttp h    Suy ra trên  ;0   hàm số 2
y  sin x giảm.  2 
Vậy cả hai kết luận trên đều sai. /vietgold k.com ceboo .fa https://www 61
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
DẠNG 4: XÁC ĐỊNH SỐ ĐIỂM BIỂU DIỄN CỦA PHƯƠNG TRÌNH LƯỢNG GIÁC
CHO TRƯỚC TRÊN ĐƯỜNG TRÒN LƯỢNG GIÁC.
Câu 21: Biểu diễn các nghiệm của phương trình 2
cos x  0 trên đường tròn lượng giác được bao nhiêu điểm? A. 1 . B. 2 . C. 0 . D. 4 . Lời giải h ttp Chọn B s://  Ta có 2
cos x  0  cos x  0  x 
 k k   . lu 2 ye n
Biểu diễn họ nghiệm trên đường tròn lượng giác ta được 2 điểm. th it
Câu 22: Nghiệm của phương trình cos x  1  là: rac A. 1 . B. 2 . C. 0 . D. 4 . n gh Lời giải ie m.vn Chọn A Ta có cos x  1
  x    k2, k  .
Biểu diễn họ nghiệm trên đường tròn lượng giác được 1 điểm.
Câu 23: Cho phương trình 2cos x  3  0. Số điểm biểu diễn tất cả các nghiệm của phương trình
trên đường tròn lượng giác là A. 1 . B. 2 . C. 3 . D. 4 . ht Lời giải tps://www Chọn B   x   k2 .fa   6
Ta có 2 cos x  3  0  cos x  cos   k   . ceboo 6 
x    k2  6 k.com  
Mỗi họ nghiệm x 
 k2 , x    k2 biểu diễn được 1 điểm trên đường tròn lượng giác, /v 6 6 ietgold
do đó số điểm biểu diễn của tất cả các nghiệm của phương trình là 2 . 1
Câu 24: Số điểm biểu diễn các nghiệm của phương trình cos x 
trên đường tròn lượng giác là 2 A. 3 . B. 1. C. 4 . D. 2 . Lời giải Chọn D 62
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”   x   k2 1  3 Ta có cos x    , k  . 2 
x    k2  3  
Mỗi họ nghiệm x 
 k2 , x    k2 biểu diễn được 1 điểm trên đường tròn lượng giác, 6 6 m.vn
do đó số điểm biểu diễn của tất cả các nghiệm của phương trình là 2 . ie
Câu 25: Biểu diễn tất cả các nghiệm của phương trình 3cos x 1  0 trên đường tròn lượng giác, gh
số điểm biểu diễn là racn A. 3 . B. 0 . C. 2 . D. 4 . it th n Lời giải ye lu Chọn C s:// 1
Ta có: 3cos x 1  0  cos x  1
 x   arccos  k2 , k  . ttp 3 3 h
Mỗi họ nghiệm trên biểu diễn được 1 điểm trên đường tròn lượng giác, do đó số điểm biểu
diễn trên đường tròn lượng giác của phương trình là 2 .
Câu 26: Biểu diễn nghiệm của phương trình cos3x  cos x trên đường tròn lượng giác. Số điểm biểu diễn là A. 3 . B. 0 . C. 2 . D. 4 . Lời giải Chọn D /vietgold x  k         k.com 3x x k 2 2x k 2 cos 3x cos x     
  x  k k   
 . Biểu diễn họ nghiệm
3x  x  k2 4x  k2 x  k 2  2 ceboo
.fa trên đường tròn lượng giác được 4 điểm.
Câu 27: Biểu diễn nghiệm của phương trình 2
cos x  cos x  0 trên đường tròn lượng giác. Số
điểm biểu diễn là A. 3 . B. 5 . C. 2 . D. 4 . https://www Lời giải Chọn A   cos x  0 x   k 2 
cos x  cos x  0   2 k   . cos x  1  
x    k2  Họ nghiệm x 
 k biểu diễn trên đường tròn lượng giác được 2 điểm, họ nghiệm 2
x    k2 biểu diễn trên đường tròn lượng giac được 1 điểm, do đó số điểm biểu diễn là 3 . 63
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác 1
Câu 28: Số điểm biểu diễn nghiệm của phương trình 2 cos x 
trên đường tròn lượng giác là 2 A. 8 . B. 2 . C. 4 . D. 6 . Lời giải Chọn C 1 1 cos 2x 1   k 2 cos x  
  cos 2x  0  2x   k  x   , k  . h 2 2 2 2 4 2 ttp s://
Biểu diễn họ nghiệm trên đường tròn lượng giác được 4 điểm. lu
Câu 29: Biểu diễn tập nghiệm của phương trình cos x  cos 2x  cos3x  0 trên đường tròn lượng ye n
giác ta được số điểm cuối là th A. 4 . B. 2 . C. 6 . D. 5 it rac Lời giải n gh Chọn C ie        m.vn
Ta có cos x cos 2x cos3x 0
cos3x cos x cos2x 0  2cos2 .
x cos x  cos 2x  0  cos 2x 2cos x   1  0      2x   k x   k   2 4 2 cos 2x  0   2 2     1  x 
 k2  x 
 k2 ,k    . cos x    3  3  2   2 2 x    k2 x    k2  3  3 ht
Vậy biểu diễn tập nghiệm của phương trình cos x  cos 2x  cos3x  0 trên đường tròn lượng giác tps://www
ta được số điểm cuối là 6 .
Câu 30: Biểu diễn các nghiệm của phương trình cossin x 1 trên đường tròn lượng giác là .fa A. 3 . B. 1 . C. 0 . D. 2 . ceboo Lời giải k.com Chọn D /v
Ta có x 0;2   sin x  1  ;  1 ietgold
Khi đó: cossin x 1  sin x  k2 k   với 1
  k2 1 k  0 . x  0
Phương trình trở thành sin x  0  x  m   m  . x  
Vậy số điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác là 2 .
Câu 31: Biểu diễn tất cả các nghiệm của phương trình cos5 .
x cos x  cos 4x trên đường tròn lượng
giác. Số điểm biểu diễn là A. 8 . B. 10 . C. 4 . D. 15 . 64
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” Lời giải Chọn B 1 Ta có cos5 .
x cos x  cos 4x 
cos4x cos6x  cos4x  cos6x  cos4x 2     x k
6x  4x  k 2   k    k  x  .       m.vn 6x 4x k 2 x  5  5 ie gh
Vậy số điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác là 10 . racn
Câu 32: Số vị trí biểu diễn các nghiệm của phương trình 2
4cos x  4cos x  3  0 trên đường tròn it th lượng giác là? n A. 4 . B. 0 . C. 1. D. 2 . ye lu Lời giải s:// Chọn D ttp h  3 cos x  L  Ta có 2 2
4cos x  4cos x  3  0   . 1
cos x   N  2 1   Với cos x   2  cos x  cos  2 x  
 k2 k   . 2 3 3
Vậy số vị trí biểu diễn các nghiệm của phương trình trên đường tròn lượng giác là 2.
Câu 33: Số điểm biểu diễn các họ nghiệm của phương trình sin 2x  3 cos 2x  3 trên đường /vietgold
tròn lượng giác là: k.com A. 2. B. 3 . C. 4 . D. 1. ceboo Lời giải .fa Chọn C 1 3 3    3
Ta có sin 2x  3 cos 2x  3  sin 2x  cos 2x   sin 2x     2 2 2  3  2    https://www 2x    k2 x  k  3 3       ; k  . 2   x   k 2x    k2  6  3 3
Họ nghiệm x  k được biểu diễn bởi 2 điểm trên đường tròn lượng giác.  Họ nghiệm x 
 k được biểu diễn bởi 2 điểm trên đường tròn lượng giác không trùng với 6
các điểm biểu diễn của họ nghiệm thứ nhất.
Vậy nghiệm của phương trình được biểu diễn bởi 4 điểm trên đường tròn lượng giác. 65
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
Câu 34: Số điểm biểu diễn các họ nghiệm của phương trình sin 5x  3 cos5x  2sin 7x trên
đường tròn lượng giác là: A. 12 . B. 8 . C. 14 . D. 7 . Lời giải Chọn C Ta có: h ttp 1 3   
sin 5x  3 cos 5x  2sin 7x  sin 5x 
cos 5x  sin 7x  sin 5x   sin 7x   s:// 2 2  3  lu     ye 7x  5x   k2 x   k   n 3 6     ; k  th      k  it
7x    5x   k2    x   r   3    18 6 acngh  Họ nghiệm x 
 k được biểu diễn bởi 2 điểm trên đường tròn lượng giác. ie 6 m.vn  k Họ nghiệm x  
được biểu diễn bởi 12 điểm trên đường tròn lượng giác không trùng với 18 6
các điểm biểu diễn của họ nghiệm thứ nhất.
Vậy nghiệm của phương trình được biểu diễn bởi 14 điểm trên đường tròn lượng giác.
Câu 35: Số điểm biểu diễn của phương trình sin x  cos xsin 2x 12cos x  sin x 12cos 2x  0 là: A. 3 . B. 4 . C. 5 . D. 6 . http Lời giải s://www Chọn B
Ta có: sin x  cos xsin 2x 12cos x  sin x 12cos 2x  0 .fa ceboo   x  x x 
 x  x   2 2 sin cos sin 2 12 cos sin
12 cos x  sin x  0 k.com
 sin x  cos xsin 2x 12sin x  cos x 12  0 /v
sin x  cos x  0   1 iet   . gold sin 2x 12 
sin x  cos x 12  0 2       
1 sin x  cos x  0  2 sin x   0    x 
 k  x 
 k k   nên phương trình có  4  4 4 2 điểm biểu diễn.
2sin2x 12sin x  cos x 12  0 . 2 t 1
Đặt t  sin x  cos x (điều kiện t  2 )  sin x cos x  . 2 66
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”   t   2
2  t 12t 13  1 0   . t  13      x    k2
Đối chiếu điều kiện ta có sin x  cos x  1  2   sin x       2 k   nên    4 2
x    k2
phương trình có 2 điểm biểu diễn. m.vn ie
Vậy phương trình có 4 điểm biểu diễn nghiệm. gh
Câu 36: Nghiệm của phương trình 2
sin x  sin x cos x  cos x  2sin 2x sin x   1  1 thoả điều kiện racn   it  3x 
  có số điểm biểu diễn là: th 2 2 n A. 0 . B. 1. C. 2 . D. 3 . ye lu Lời giải s:// Chọn B ttp h           3x       x    3x    2         6 2  x 0 2      6 Ta có:  3x       3x         * . 2 2    2 2  x      3x       3 x  2 2       3 2 3x        x 0  2 2 2
sin x  sin x cos x  cos x  2sin 2x sin x   1  1   2 sin x  
1  cos x sin x  
1  2sin 2x sin x   1  0
/vietgold sinx 1sinx1cosx2sin2x0 k.com sin x 1  0   1 ceboo   .
sin x  cos x  2sin 2x 1  0  2 .fa   
1 sin x 1  0  sin x  1  x 
 k2 k   . 2
2 sin x cos x  2sin2x 1 0. https://www 2 1  t
Đặt t  sin x  cos x (điều kiện t  2 )  sin x cos x  . 2 t  1   t   2
2 1  t  1  0 2  2
 t  t  3  0  3  . t   2 x  k2   
Đối chiếu điều kiện của 
t ta có: sin x  cos x  1  2  sin x        k   .  3 4  2 x   k2  2 67
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác 
Đối chiếu điều kiện * ta có x 
nên có 1 điểm biểu diễn. 2    2 2
cos x  sin 2x  2  cos  x    2 
Câu 37: Số điểm biểu diễn các nghiệm của phương trình  0  7  2sin x  1    24 
trên đường tròn lượng giác là h A. 1. B. 2 . C. 3 . D. 4. ttp s:// Lời giải lu Chọn A ye n th   x    k2  it  7  1  8 r
Điều kiện: sin x       k  . a  24  2 13 c     n x k 2  gh  24 ie x  x   x 
 cos 2x sin 2x  2 m.vn Phương trình trở thành 2 2 cos sin 2 2 sin 0               
        2 cos 2x 2   cos 2x 1   2x k 2 x k k    4   4  4 8 7
So với điều kiện, ta được x 
 k2 k  . 8
Vậy có một điểm biểu diễn trên đường tròn lượng giác. Câu 38: Số điểm biểu diễn các nghiệm của phương trình 2 ht
sin x sin 2x  2sin x cos x  sin x  cos x  tp
3 cos 2x trên đường tròn lượng giác là sin x  cos x s://www A. 2 . B. 4 . C. 3 . D. 5 . Lời giải .fa ceboo Chọn B k.com Điều kiện      /v
sin x  cos x  0  sin x   0  
 x   k  x    k ,k  . iet  4  4 4 gold Ta có: 2
sin x sin 2x  2sin x cos x  sin x  cos x  3cos2x sin x  cos x
sin 2x sin x  cos x  sin x  cos x   3 cos 2x sin x  cos x sin 2x  
1 sin x  cos x   3 cos 2x sin x  cos x 68
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”       
sin 2x  3 cos 2x  1   sin 2x   sin       3   6       2x     k2  x   k  3 6   12   k   .    3  2x      k2  x   k  3 6  4 m.vn
Vì mỗi họ nghiệm biểu diễn hai điểm trên đường tròn lượng giác nên các nghiệm phương trình ie gh
có bốn điểm biểu diễn trên đường tròn lượng giác. racn it th n ye lu s:// ttp h /vietgold k.com ceboo .fa https://www 69
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
DẠNG 5. BIỆN LUẬN NGHIỆM PHƯƠNG TRÌNH LƯỢNG GIÁC KHÔNG CHỨA THAM SỐ
5.1. Tìm số nghiệm của phương trình lượng giác trên tập K .
Câu 39: Tìm số nghiệm của phương trình cos5 .
x cos x  cos 4x trên 0;10  là A. 49 . B. 50 . C. 52 . D. 48 . Lời giải h ttp Chọn A s:// 1 lu Ta có cos5 .
x cos x  cos 4x 
cos4x cos6x  cos4x  cos6x  cos4x ye 2 n th     x k
6x  4x  k 2  it  k     x  , k  Z r  k a 6x  4  x  k2 x  5 c  5 n gh k ie
Do 0  x 10  0 
10  0  k  50 .Vây có 49 nghiệm thỏa điều kiện. m.vn 5 2  x x 
Câu 40: Số nghiệm thuộc khoảng 0;100  của phương trình sin  cos  3 cos x  3   là  2 2  A. 49 . B. 50 . C. 52 . D. 48 . Lời giải Chọn B 2  x x  ht sin  cos  3 cos x  3   tp Ta có  2 2 
1 sin x  3cos x  3  sin x  3cos x  2 s://www 1 3      sin x 
cos x  1  sin x   1  
 x   k  k  2 2  3  2 , 6 . .fa ceboo     1 599 k       k 
Theo đề bài cho ta có 0  x  0 2 100 100 6 12 12 k.com k 
 k 0;1;2;3;4,....;48;4  9 /v Mà . ietgold   
Câu 41: Số nghiệm của phương trình 2 2
cos x  sin 2x  2  cos  x 
 trên khoảng 0;3  là  2  A. 2 . B. 3 . C. 4. . D. 1. Lời giải Chọn B    2 2
cos x  sin 2x  2  cos  x   2 2
 cos x sin 2x  2 sin x  cos2x sin 2x  2  2  70
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”          2 cos 2x   2    cos 2x  1    2x 
 k2  x    k k    4   4  4 8 7 15 23
Trên 0;3   x  , x  , x  . 8 8 8
Câu 42: Gọi n là số nghiệm thuộc khoảng 0;2023 của phương trình lượng giác
3 1 cos 2x  sin 2x  4cos x  8  4 3   m.vn
1 sin x . Tìm n là ie A. 322 . B. 320 . C. 300 . D. 321. gh Lời giải racn it Chọn A th       n
Ta có 3 1 cos 2x sin 2x 4cos x 8 4 3  1 sin x ye 2
 2 3 sin x  2sin xcos x  4cos x 8  4 3   1 sin x lu s://
 2 3sin xsin x  2  2cos xsin x  2  4sin x  2 ttp
 2 3 sin x  2cos x  4 (vì sin x 1 2) h  
 3 sin x  cos x  2  sin x cos  cos xsin 1 6 6        sin x  1  
 x    k2  x   k2 k   .  6  6 2 3  1  2023 
Theo đề bài x 0;2023 
 k20;2023  2k   0; 
  k 0;1;...;32  1 . 3 3    Vậy n  322 .
Câu 43: Số nghiệm của phương trình 2
2cos x  3 sin 2x  3 trên 0;2020  là: /vietgold A. 1010. B. 2019 . C. 2020 . D. 2021. k.com Lời giải Chọn C ceboo .fa    Ta có: 2
2cos x  3 sin 2x  3  cos 2x  3 sin 2x  2  cos 2x  1    3   
 2x   k2  x   k k   . 3 6 https://www  
Xét 0  x  2020  0   k  1 1 2020 
 k  2020   k 0;1;...;201  9 . 6 6 6
Vậy số nghiệm là 2020 .
Câu 44: Huyết áp là đại lượng để đo độ lớn của lực tác dụng lên thành mạch máu. Nó được đo
bằng hai chỉ số: huyết áp tâm thu (lúc tim đập) và huyết áp tâm trương (lúc tim nghỉ).
Huyết áp của mỗi người thường khác nhau, nhưng huyết áp tiêu chuẩn là 120 / 80 , nó
có nghĩa là huyết áp tâm thu là 120mmHg và huyết áp tâm trương là 80 mmHg. Giả sử
rằng trái tim của một người đập 70 lần một phút, huyết áp P sau t giây có thể được 71
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác   
mô tả bằng hàm số P t  7 100  20sin t 
 . Với t 0;60 , có bao nhiêu lần huyết áp  3 
người đó bằng 100 mmHg? A. 139 . B. 140 . C. 141. D. 142 . Lời giải Chọn C           7    7  t  k k  h Với P t  7 100 100 20sin t 100   sin t 0     ttp  3   3  3 s:// 3k  t  k   . 7 lu ye k Với t   3 0;60  0 
 60  0  k 140 . n 7 th
Do k  nên có tất cả 141 giá trị k thỏa mãn. it ra
Vậy với t 0;60 có 141 lần huyết áp người đó bằng 100 mmHg. cngh
Câu 45: Năm 1893, George Ferris chế tạo vòng đu quay. Nó có đường kính 250 foot. Nếu với ie
mỗi 40 giây vòng đu quay quay 1 vòng thì chiều cao h (foot) của một chỗ ngồi trên m.vn
vòng đu quay là một hàm số của thời gian t (giây) được xác định như sau   
h t   125sin 0,157t  125   .  2 
Vòng quay bắt đầu tính từ thời điểm t  0. Trong 40 giây đầu tiên của chuyến đi, tại thời điểm
nào sau đây (làm tròn đến hàng đơn vị) thì người ngồi trên ghế đu quay đó cách mặt đất 125
foot? (Chú thích: 1 foot xấp xỉ 30, 48 cm). A. 20 giây. B. 25 giây. C. 30 giây. D. 35 giây. http Lời giải s://www Chọn C       .fa
h t   125 125sin 0,157t 
125 125  sin 0,157t   0      2   2  ceboo Ta có: .   1  k.com 
 0,157t   k  t   k   2 0,157  2  , k  . /viet   1  1 6, 28 1
Do 0  t  40  0 
 k  40    k    0
 ,5  k 1,499 . gold   0,157  2  2  2
Do k   k 0;  1 .  1
Với k  0  t  . 10 giây. 0,157 2  3
Với k  1 t  .  30 giây. 0,157 2 72
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
 Trong 40 giây đầu tiên của chuyến đi, có 2 thời điểm người ngồi trên ghế đu quay đó cách
mặt đất 125 foot, đó là lúc khoảng 10 giây và khoảng 30 giây.
5.2. Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình lượng giác:.
Câu 46: Nghiệm lớn nhất của phương trình 2cos 2x 1  0 trong đoạn 0;  là: 11 2 5 A. x   . B. x  . C. x  . D. x  . 12 3 6 m.vn ie Lời giải gh Chọn D racn it     th 2x   k2  x   k  n 3 6
Phương trình 2cos 2x 1  1 0  cos 2x      . ye 2     2x    k2 x    k lu  3  6 s://    1  5   ttp 0   k     k      x  h 6 6 6 k 0 6
Xét x 0;         mà k  suy ra  .  1 7  k  1 5  0    k       k x  6 6 6  6 5
Vậy nghiệm lớn nhất của phương trình 2cos 2x 1  0 trong đoạn 0;  là x  . 6
Câu 47: Phương trình cos 2x  2cos x  3  0 có nghiệm lớn nhất trong khoảng 0;2019 ? A. 644 . B. 2 . C. 640 . D. 642 . Lời giải /vietgold Chọn D
k.com cos2x2cosx30 2
 2cos x  2cos x  4  0  cos x 1hay cos x  2  (loại)
ceboo Với cosx1 xk2;k .
.fa Với 0 x20190k2 20190k 321.49 k 321. max
Vậy nghiệm lớn nhất thuộc khoảng 0;2019 là x  642 . 
https://www Câu 48: Nghiệm dương nhỏ nhất của phương trình sincos2x 0 là   3 A.  . B. . C. . D. . 2 4 4 Lời giải Chọn C
Ta có sin cos2x  0  cos2x  k k     
Vì cos2x  1  ; 
1  k  0  cos2x  0  2x 
 k   x   k k  . 1 1  1  2 4 2 73
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác   x  min 4 
Vậy phương trình có nghiệm dương nhỏ nhất là . 4
Câu 49: Gọi x là nghiệm dương nhỏ nhất của phương trình 2 2
3sin x  2sin x cos x  cos x  0 . 0
Chọn khẳng định đúng?  3         3  h A. x   ; . B. x  ; . C. x  0; . D. x  ;2 . 0   0   0   0   ttp  2   2   2   2  s:// Lời giải lu ye Chọn C n th 2 2
3sin x  2sin x cos x  cos x  0 2 2
 3sin x 3sin xcos x sin xcos x cos x  0 it rac 3sin x n  1   1 gh      x x tan x (3sin x  cos )
x (sin x  cos ) x  3sin cos 0 0  cos x      3 ie
sin x  cos x  0 sin x    1  tan x  1  m.vn cos x  1 x  arctan  k  3   k    .
x    k  4
Do x là nghiệm dương nhỏ nhất của phương trình 2 2
3sin x  2sin x cos x  cos x  0 nên 0 1 x  arctan 0 . 3 http 4 3 s://www
Câu 50: Cho phương trình 2 2 sin . x tan x  cos .
x cot x  2sin x cos x 
. Tính hiệu nghiệm âm lớn 3
nhất và nghiệm dương nhỏ nhất của phương trình. 3 5 5 .fa A.  . B. . C.  . D.  . ceboo 2 6 6 Lời giải k.com Chọn C /viet k gold
Điều kiện: sin 2x  0  x  . 2 3 3 sin x cos x 4 3 Phương trình  
 2sin x cos x  cos x sin x 3 74
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” 4 3 2 3 4 4 2 2
 sin x  cos x  2sin xcos x 
sin x cos x  sin x  cos x2 2 2  3
sin 2x  sin 2x  3 3 2   x   k  6   k    .  x   k  3   m.vn 2
Suy ra nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình lần lượt là  và ie 3 6 gh 2  5 Ta có:     . racn 3 6 6 it th
Câu 51: Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h m của mực n ye  t  
nước trong kênh tính theo thời gian t h được cho bởi công thức h  3cos  12 . lu    6 3  s:// Khi nào mực nước của ttp
kênh là cao nhất với thời gian ngắn nhất? h
A. t  22h .
B. t  15h .
C. t  14h .
D. t  10h . Lời giải Chọn D     Ta có: 1   cos t  1  
 9  h 15. Do đó mực nước cao nhất của kênh là 15m đạt được khi  6 3        cos t  1  
 t   k2  t  2  12k  6 3  6 3
/vietgold Vì t 0  212k  1 0  k  k.com 6 1
ceboo Chọn số k nguyên dương nhỏ nhất thoả k  là k 1t 10. .fa 6 https://www 75
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
5.3. Tính tổng tất cả các nghiệm của phương trình lượng giác trên tập K .
Câu 52: Tính tổng tất cả các nghiệm của phương trình sin x  sin 2x  0 trên đoạn 0;2 . A. 4 . B. 5 . C. 3 . D. 2 . Lời giải Chọn B  2k h
2x  x  k2 x  ttp Ta có 
sin x  sin 2x  0  sin 2x  sin x   3 , k,l    .
2x    x  l2  s://
x    2l lu ye
Vì x 0;2  nên 0  x  2 . n th
k  0  x  0 it  r 2 a
k 1 x  cn 2k 2k  3 gh + Với x  . Ta có 0 
 2  0  k  3. Suy ra  . 3 3 4 ie
k  2  x   3 m.vn
k  3 x  2 1 1
+ Với x    2l . Tương tự 0    2l  2    l  . Suy ra l  0  x   . 2 2
Vậy tổng tất cả các nghiệm của phương trình đã cho trên 0;2  là 5 .
Câu 53: Tính tổng các nghiệm trong đoạn 0;30của phương trình: tan x  tan3x (1) 171 190 A. 55. . B. . . C. 45 .. D. . ht 2 2 tps://www Lời giải Chọn C .fa   ceboo x   k  cos x  0  2
Điều kiện để phương trình (1) có nghĩa    * cos3x  0  k k.com x    6 3 /v k iet
Khi đó, phương trình (1) 3x  x  k  x  so sánh với đk (*) gold 2 x  k2
, x 0;30  k  0;...;  4  x   0;;2;....;9
x    k2
Vậy, tổng các nghiệm trong đoạn 0;30của phương trình (1) là: 45 .
Câu 54: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình   3 sin 3x     4  bằng   2 76
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”     A.   9 . B. 6 . C. 6 . D. 9 . Lời giải Chọn C     7 k2   3
3x    k2  x    m.vn sin 3x    4 3 36 3       ; k;l  ie  4  2   2 3x   11 l2    l2 x   gh  4 3  36 3 racn
TH1: x  0 ; x lớn nhất it th  17 n k  1;  x    13 ye 36 Chọn  x     (nhận) lu  13 36 l  1;  x     s://  36 ttp h
TH2: x  0; x nhỏ nhất  7 k  0; x    36 7 Chọn  x    (nhận)  11 36 l  0; x    36 13 7 
Khi đó tổng cần tìm là:    36 36 6 .
Câu 55: Tổng tất cả các nghiệm của phương trình cos 2x  cos x  0 trong khoảng 0;2  bằng T /vietgold
. Vậy T bằng bao nhiêu?   k.com 7 4 A. T   . B. T  . C. T  . D. T  2 . 6 3 ceboo Lời giải .fa Chọn D x  k2
2x  x  k2 2 
cos 2x  cos x  0  cos 2x  cos x    2  x  k . https://www
2x  x  k2 x  k 3  3   Với x    2 4 0; 2  x  ; x  . 3 3 2 4 Vậy T    2 . 3 3  5 
Câu 56: Tổng các nghiệm của phương trình sin 2x  3  6sin x  cos x trong khoảng 0;   là  2  2 5 19 A.  . B. . C. . D. . 3 6 6 77
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác Lời giải Lời giải Chọn D h 5π ttp π 6 6 s:// lu ye n th it ra cngh
Ta có: sin 2x  3  6sin x  cos x  2sin xcos x  cos x  6sin x 3 ie m.vn
 2sin xcos x cos x  6sin x 3  cos x2sin x  
1  32sin x   1       x k 2 2sin x 1  0   1 6   sin x    , k  .
cos x  3(L) 2 5 x   k2  6  5   5 13 Do x  0; 
 suy ra x  , x  , x  .  2  6 6 6 19 ht
Suy ra tổng các nghiệm là . tp 6 s://www
Câu 57: Tổng tất cả các nghiệm thuộc 0;10π của phương trình 2
2sin x  5sin x  3  0 là A. 50 . B. 55 . C. 45 . D. 60 . .fa ceboo Lời giải k.com Chọn B /v  
sin x  3 VN  x    k2 iet  2  6 gold
Ta có: 2sin x  5sin x  3  0  1   k    . sin x   7   x   k2  2  6  1 61
 Xét 0    k2 10   k 
mà k  nên k 1;2;3;4;  5 6 12 12
11 23 35 47 59   x  ; ; ; ;  .  6 6 6 6 6  7 7 53 Xét 0 
 k2 10    k 
mà k  nên k 0;1;2;3;  4 6 12 12 78
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
7 19 31 43 55   x  ; ; ; ;  .  6 6 6 6 6 
Vậy tổng tất cả các nghiệm thuộc 0;10  của phương trình là 55 .
Câu 58: Tổng các nghiệm trong đoạn 0;2  của phương trình 3 3
sin x  cos x  1 bằng 5 7 3 A. . B. . C. 2 . D. . m.vn 2 2 2 ie gh Lời giải Chọn D racn it 3 3 th
sin x  cos x 1  sin x cosx1sin xcosx 1   1 . n ye    lu
Đặt t  sin x  cos x  2 sin x     t  4  , 2 2 .   s:// ttp 1 h Có 2
t 12sin x cos x  sin x cos x   2 1 t  2 .    1  1 trở thành: t 1   2 1 t  1 3
 t 3t  2  0  t   2
1 t  t  2  0 2  .   t  1       1    2 sin x   1  sin x   t  2      .  L  4  4   2 x      k2  x    k2 /vietgold 4 4     2 k,l  .   3  x     l2 
x    l2 k.com  4 4
ceboo Có x0;2 
 nên ta có các nghiệm x   ; x   . .fa 2 3
Vậy tổng các nghiệm x  0;2 
 của phương trình đã cho là 2 . x  x  x 
https://www Câu 59: Phương trình 2 2 6sin 7 3 sin 2 8cos
6 có tổng hai nghiệm dương nhỏ nhất bằng 17 2 5 7 A. . B. . C. . D. . 12 3 24 12 Lời giải Chọn B 1 cos 2x  1 cos 2x  Ta có: 2 2
6sin x  7 3 sin 2x  8cos x  6  6  7 3 sin 2x 8  6     .  2   2 
 31cos2x  7 3sin 2x  41 cos2x  6  3sin 2x cos2x 1. 79
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác 3 1 1    1     
sin 2x  cos 2x   sin 2x    sin 2x   sin     . 2 2 2  6  2  6  6      2x    k2 x   k   6 6 6       k   .    2x      k2 x   k  6 6  2   1 h + Trường hợp x 
 k , do x  0   k  0  k   . Lại có k  nên nghiệm dương nhỏ ttp 6 6 6 s:// 
nhất của phương trình trong trường hợp này là nghiệm x  ứng với k  0 . lu 6 ye   1 n + Trường hợp x 
 k , do x  0   k  0  k   . Lại có k  nên nghiệm dương nhỏ th 2 2 2 it  ra
nhất của phương trình trong trường hợp này là nghiệm x  ứng với k  0 . c 2 n gh   2 ie
Vậy hai nghiệm dương nhỏ nhất của phương trình là: x  ; x  và tổng của chúng là . m.vn 6 2 3 sin x
Câu 60: Gọi S là tổng các nghiệm của phương trình
 0 trên đoạn 0;2017  . Tính S . cos x 1
A. S  2035153 .
B. S 1001000 .
C. S  1017072 .
D. S  2000200 . Lời giải Chọn C sin x s  in x  0         0 cos x 1 x k2 . ht cos x 1 cos x  1  tps://www
Suy ra tập nghiệm là 0;2;4;....2n ,.  . .
Vậy S  0  2  4 ... 2016  2 1 2 ...1008 1017072 . .fa ceboo
Câu 61: Tìm tổng các nghiệm của phương trình sin 3x  cos x  0 trên 0;  . k.com 5  A. . B. . C.  . D. 2 . 8 3 /viet Lời giải gold Chọn D   3x  x   k2     2
Ta có: sin 3x  cos x  0  sin 3x  sin x       2  3 3x   x  l2  2 80
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”   x    k  4  
k,l   . 3  x   l  8 2   0    k    k  1 4 k  
Mà x 0;  nên     . Do  nên l 0    m.vn 3  l 0   l   l  1  ie  8 2 gh  3 x   racn 4 it  3 3 3 7  th  x   T     2 . n  8 4 8 8  ye 7   lu x  8 s:// ttp
Câu 62: Tìm tổng tất cả các nghiệm thuộc đoạn 0;30 của phương trình h
cos3x  4cos 2x  3cos x  4  0 là 121 99 A. 45 . B.  . C.  . D. 50 . 2 2 Lời giải Chọn D
PT cos3x4cos2x3cosx40 cos x  0 /vietgold 3  x  x   2 4 cos 3cos 4 2 cos x  
1  3cos x  4  0 3 2
 4cos x 8cos x  0  cosx  2 (vn) k.com  1 30 1
+ Với cos x  0  x 
 k .Theo giải thiết, x  1 30 0;30  0   k        k  mà ceboo 2 2 2 2
.fa kZ k0;1;2;3; ;   9 .
Vậy tổng các nghiệm thỏa mãn yêu cầu bài toán là               2   9  5       
1 2  9  5  45  50 . https://www 2  2   2   2 
Câu 63: Tính tổng S tất cả các nghiệm của phương trình  x   4 4 2cos 2
5 sin x  cos x  3  0 trên khoảng 0;2  . 7 11 A. S  . B. S  . C. S  4 . D. S  5 . 6 6 Lời giải Chọn C Ta có:  x   4 4 x  x     x   2 2 2cos 2 5 sin cos 3 0 2cos 2
5 sin x  cos x  3  0 81
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác   x   2 2cos 2
5 cos 2x  3  0  2cos 2x  5cos 2x  3  0 cos 2x  3  1 2       1  cos 2x   2x 
 k2  x   k  . cos 2x  2 3 3  2    
 Với x   k : x    1 5 4 0; 2 0 k 2         
 k  ,k   k {0;1} x  ;  . 3 3 3 3  3 3  h     ttp     2 5  Với x 
 k : x   1 7 0;2  0 
 k  2   k  , k   k {1;2} x ; . s:// 3 3 3 3  3 3  lu
Vậy tổng S  4 . ye n
Câu 64: Cho phương trình  x   x  x  
x . Gọi T là tập hợp các th   2 2sin 1 3 tan 2sin 3 4 cos it r
nghiệm thuộc đoạn 0;20  của phương trình trên. Tính tổng các phần tử của T . acn 570 875 880 1150 gh A.  . B.  . C.  . D.  . 3 3 3 3 ie m.vn Lời giải Chọn B  Điều kiện: x 
 k , k  Z . 2
Phương trình đã cho tương đương với  x   x  x 2 2sin 1 3 tan 2sin  4sin x 1.  2sin x   1  3 tan x   1  0 . http   s://www x   k2   1 6  5 sin x    x   k2  2    5   6 x   k2  
, k   (thỏa mãn điều kiện). 1   6   .fa tan x    x   k  3   6 ceboo
x   k  6 k.com 5
*Trường hợp 1: Với x 
 k2 , k   .   1 6 /viet  5  115 gold x    5 0; 20  0   k2  20   k 
. Mà k  nên k 0; 1; 2....;  9 . 6 12 12
 Tổng tất cả các nghiệm thuộc đoạn 0;20  của họ nghiệm   1 là: 9  5  295 S    k2  . 1   3 k   6  0 
*Trường hợp 2: Với x 
 k , k   . 2 6 82
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” 1  119 x   0; 20   0    k  20   k 
. Mà k  nên k 0;1; 2....;1  9 . 6 6 6
 Tổng tất cả các nghiệm thuộc đoạn 0;20  của họ nghiệm 2 là: 19    580 S     k  . 2   k   6  3 0 m.vn 875 ie
Vậy tổng các phần tử của T là S  S   . 1 2 3 gh 2 3
cos x  cos x 1 2   racn
Câu 65: Tính tổng tất cả các nghiệm của phương trình cos 2x tan x trên đoạn 2 it cos x th [1;70] n ye A. 188 . B. 263 . C. 363 . D. 365 lu Lời giải s:// ttp Chọn D h 
Ta có điều kiện cos x  0  x 
 k,k  . 2 2 3
cos x  cos x 1
Phương trình đã cho trở thành: 2 2
2cos x 1  tan x  . 2 cos x 2 3 1
cos x  cos x 1 2    4 3 2     2 2     2cos x
2cos x cos x cos x 0 cos x(2cos x cos x 1) 0 2 2 cos x cos x   cos x  0 /vietgold   cos x  1   k.com 1  cos x   2 ceboo
.fa So sánh điều kiện ta có 
 x    k2 1;70  k  0;1;2;3;4;5;6;7;8;9;10 cos x  1       1  x 
 k2 1;70  k  0;1;2;3;4;5;6;7;8;9;10  cos x   3 https://www  2    x 
 k2 1;70  k 1;2;3;4;5;6;7;8;9;10;11  3
Tổng các nghiệm trên đoạn đã cho của họ thứ nhất là: 11(  2.10 ) S  121 1 2
Tổng các nghiệm trên đoạn đã cho của họ thứ hai là:   11(   2.10 ) 341 3 3  S   2 2 3 83
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
Tổng các nghiệm trên đoạn đã cho của họ thứ ba là:     11(  2   2.11 ) 385 3 3  S   3 2 3
Vậy tổng các nghiệm trên đoạn đã cho của phương trình là:
S  S  S  S  363 1 2 3 . h ttp       5 s://
Câu 66: Tổng các nghiệm của phương trình 4 4 4 sin x  sin x   sin x       trong khoảng  4   4  4 lu ye 0;2  bằng n A. 2 . B. 4 . C.  . D. 3 . th it r Lời giải acngh Chọn B ie       5 m.vn Ta có 4 4 4 sin x  sin x   sin x        4   4  4 2 2               2 1 cos 2x 1 cos 2x         1 cos2x   2   2  5            2   2   2  4            x2    x2    x2 1 cos2 1 sin 2 1 sin 2  5 2 2 ht
1 2cos2x  cos 2x  2  2sin 2x  5 tps://www 2  2
 cos2x  sin 2x 1 2 2  2
 cos2x 1 sin 2x  cos 2x  2cos2x  0 .fa cos2x  0 ceboo  k       . x    voâ nghieäm x ; k cos 2 2 4 2 k.com  k 1 7 Theo bài ra ta có 0  
 2    k  , vì k nên k  0;1;2;  3 . /v 4 2 2 2 ietgold      3 Tổng các nghiệm là        4 . 4 4 2 4 4 2
Câu 67: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình  x  1 tan x tan
sin x  cot x  4   là  2      A.  . B. . C. . D.  . 6 2 6 2 Lời giải 84
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” Chọn D cos x  0  Điều kiện 
 sin 2x  0  x  k ,k  s  in x  0 2 x x sin x sin  cos x cos  x  2 2 1 tan x tan
sin x  cot x  4 
sin x  cot x  4    2 x  cos x cos m.vn 2 ie gh x cos 2 
sin x  cot x  4  tan x  cot x  4 2
 tan x  4tan x 1 0 racn x it cos x cos 2 th n   ye  5 tan x  2  3 x   k  lu   12 1       . s:// tan x 2 3    2  3  x   l  ttp 12 h 
Với hai họ nghiệm trên dễ thấy nghiệm dương nhỏ nhất là ; để nghiệm âm lớn nhất ta 12 được 7   1  1 7
đều cho k  l  1  được nghiệm âm ;
khi đó nghiệm âm lớn nhất là . 12 12 12 7     Ta có    . 12 12 2 sin 2x
Câu 68: Tính tổng các nghiệm thuộc  ;3  của phương trình:  0 . cos x 1 /vietgold 3 A. 8 . B. 9 . C. 10 . D. . k.com 2 Lời giải ceboo .fa Chọn A
ĐK: cos x 1  0  cos x  1  x  k2 , k  . k
PT  sin 2x  0  2x  k  x  , k  . https://www 2 
Kết hợp với ĐK ta được x 
 k , x    k2 , k  . 2    1 5 
   k  3   k  Với x 
 k , mà x ;3    2  2 2  k 1;  2 2 k  k  3 5  suy ra x   ;  .  2 2  85
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác  3 
    k2  3 0  k 
Với x    k2 , mà x  ;3      2  k 0  ;1 k  k 
suy ra x  ;3.
Vậy tổng các nghiệm bằng 8 .
Câu 69: Tính tổng T các nghiệm của phương trình 2
cos x  sin x cos x  2sin x  cos x  2 trên h ttp    khoảng ;5 .   s://  2  lu 15 21 3 A. T  . B. T  . C. T  7 . D. T  . ye 2 8 4 n th Lời giải it ra Chọn C cngh 2
cos x  sin x cos x  2sin x  cos x  2 ie m.vn 2
 sin x  2sin x  3 cos x sin xcos x  0
 1 sin xsin x  
3  cos x 1 sin x  0
 1 sin xsin x  cos x   3  0 sin x 1   1   .
sin x  cos x  3  0  2    1  x 
 k2 k  . ht 2 tp s://www    5 9 Vì x  ;5 
 nên phương trình có các nghiệm: x  và x  .  2  1 2 2 2 .fa
2  sin x  cos x  3
 vô nghiệm vì    2 2 2 1 1 3 . ceboo 5 9
Vậy tổng tất cả các nghiệm của phương trình là: T  x  x    7 . k.com 1 2 2 2 /v
Câu 70: Tính tổng các nghiệm trên  4
 ;4  của phương trình 3 3
sin x  3 3sin x  2  2  0 ietgold A.  . B. 2   . C.   . D. 0 . Lời giải Chọn B 3 3
sin x  3 3sin x  2  2  0   1 3 3
 sin x  3sin x  3sin x  2  3 3sin x  2 Đặt 3
t  3sin x  2 , phương trình trở thành 3 3
sin x  t  3sin x  t   0   x  t  2 2 sin
sin x  t.sin x  t  3  0 86
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” Dễ chứng minh 2 2
sin t  t.sin x  t  3  0 nên sin x  t 3
 sin x  3sin x  2 3
 sin x 3sin x  2  0 sin x  1   sin x  2  (L) m.vn ie  sin x 1 gh 
 x   k2 , k   racn 2 it th  9 n Ta có: 4
    k2  4 7    k  2 4 4 ye lu 1   
Vậy tổng các nghiệm trên  4  ;4  của   1   k2  2     . s://   k  2 2 ttp h 1 1 1
Câu 71: Phương trình  
có tổng các nghiệm trên (0; ) là: cos x sin 2x sin 4x   2 A. . B. . C. . D.  6 6 3 Lời giải Chọn D Chọn D /vietgold     cos x  0 cos x  0 cos x  0 sin x  1        k.com Điều kiện: sin  2x  0  sin  x  0  sin  x  0  sin  x  0     sin 4x  0 cos 2x  0   ceboo 2 2 sin  x sin    x     .fa 2  2 1 1 1 Pt    cos x 2 sin x cos x
4 sin x cos x cos 2x
 2sin x cos 2x  cos 2x 1  0 https://www 2 2
 2sin x(1 2sin x) 1 2sin x 1  0 2
 2sin x(1 2sin x  sin x)  0          x  l  sin x 1l  x k 2 sin 0   6    1   k  2  1
  2sin x sin x  0 sin x  5   x   k2  2  6  5
Suy ra phương trình có 2 nghiệm trên (0; ) là x  và x  6 6  5
Vậy tổng các nghiệm trên (0; ) là:    . 6 6 87
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác
sin 2x  2 cos x  sin x 1
Câu 72: Phương trình
 0 có bao nhiêu nghiệm trên (0;3 ) ? tan x  3 A. 1. B. 2. C. 3. D. 4 Lời giải Chọn B   x   k h cos x  0    2 ttp Điều kiện:    . tan x   3   s:// x    k  3 lu ye
Pt  sin 2x  2 cos x  sin x 1  0  2sin x cos x  sin x  2 cos x 1  0 n   th sin x  1  x    k2  it  2         r
(2 cos x 1)(sin x 1) 0 1 k  a cos x    c  x    k2 n 2  3 gh ie  m.vn
Kết hợp điều kiện xác định ta được nghiệm của phương trình là x   k2 3  7
Vậy phương trình có hai nghiệm thuộc (0;3 ) là x  và x  . 3 3
Câu 73: Gọi S là tổng tất cả các nghiệm thuộc 0;20  của phương trình 2
2cos x  sin x 1  0 .
Khi đó giá trị của S bằng: 200
A. S  570 .
B. S  295 .
C. S  590 . D. S   . 3 ht Lời giải tps://www Chọn B   x    k 2  1 .fa  2 sin x  1   ceboo  2 
2cos x  sin x 1  0 2  2
 sin x sin x 1 0   1   
 k ,k ,k  1 2 3   x k 2 2 sin x   6   k.com 2 5 x   k 2 3  6 /viet
Do x 0;20  nên: gold   1 41 0    k 2  20   k  1  2 1  4 4  k  1;2;3;...;10 1        1 119 0 
 k 2  20    k 
 k  0;1;2;...;9 2   2 6  2 12 12    k  0;1; 2;...;9  3   5  5 115 0   k 2  20    k  3   6 3  12 12
Ta thấy tất cả các nghiệm này không có hai nghiệm nào giống nhau nên tổng các nghiệm của
phương trình trong đoạn 0;20  là: 88
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” 10    9    9  5 
S     k 2    k 2 
 k 2  295 . 1        2   3   k  6 k  6 k  2 1 0 0 1 2 2   
Câu 74: Tính tổng T các nghiệm của phương trình 2 2
cos x  sin 2x  2  cos  x   trên khoảng  2  0;2  . 7 21 11 3 m.vn A. T  . B. T  . C. T  . D. T  . ie 8 8 4 4 gh Lời giải racn Chọn C it th   n  Ta có 2 2
cos x  sin 2x  2  cos  x    2 2
cos x  sin 2x  2  sin x ye  2  lu     s://
 cos2x sin 2x  2  cos 2x  1  
 2x   k2 , k   4  4 ttp h 
 x    k , k  8  1 17
Vì 0  x  2  0  
 k  2   k  8 8 8 7 15
Vì k  nên k 1;  2  x  ; x  1 2 8 8 11
Vậy x  x  . 1 2 /vietgold 4
Câu 75: Tính tổng tất cả các nghiệm của phương trình 3 cos x  sin x 1 trên 0;2 . k.com 5 11  3 A. . B. . C. . D. . ceboo 3 6 6 2 .fa Lời giải Chọn A   x   k2  https://www    1 6
Ta có 3 cos x  sin x  1  cos x       k  .  6  2 
x    k2  2  3
Do đó các nghiệm trên 0;2  của phương trình là x  , x  . 6 2  3 5
Vậy tổng tất cả các nghiệm của phương trình trên 0;2  bằng   . 6 2 3
Câu 76: Gọi S là tập hợp các nghiệm thuộc khoảng 0;100  của phương trình 2  x x  sin  cos  3cos x  3  
. Tổng các phần tử của S là  2 2  89
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác 7400 7525 7375 7550 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn C 2  x x  Ta có sin  cos  3cos x  3  
1 sin x  3cos x  3  sin x  3cos x  2  2 2  h ttp 1 3      sin x 
cos x  1  sin x   1  x 
 k2 ,k  . s://   2 2  3  6 lu ye 
Theo đề bài cho ta có 0  x 100  0   k2  1 599 100    k  n 6 12 12 th it
Mà k   k 0;1;2;3;4,....;48;4  9 racn      gh 50 Vậy S 
  2   2 2  ......   49 2 
 2 1 2  3 4  ..... 49 ie 6 6 6 6 6 m.vn 50 4949   1 7375   2  . 6 2 3
Câu 77: Gọi S là tập hợp tất cả các nghiệm thuộc khoảng 0;2018 của phương trình sau:
3 1 cos 2x  sin 2x  4cos x  8  4 3  
1 sin x . Tính tổng tất cả các phần tử của S . 310408 312341 A. 103255 . B. . C. . D. 102827 . 3 3 Lời giải http Chọn B s://www
Ta có 3 1 cos 2x  sin 2x  4cos x 8  4 3   1 sin x .fa 2
 2 3sin x  2sin xcos x  4cos x  4 3sin x  4sin x 8  0 ceboo
 2sin x 3sin x cos x 24 3sin x cos x 2  0 k.com
 2sin x  2 3sin x cos x 2  0 /vietgold    
3 sin x  cos x  2  π 0  sin x  1  
 x   k2 , k  .  6  3 
Vì x 0;2018 nên 0   k2  1 1009 1 2018    k 
  k  0;1;2;...;32  1 . 3 6 π 6     
Suy ra S   ;  2;  2.2;...;  321.2   3 3 3 3   
Vậy tổng tất cả các phần tử của S là T  322.
 2 1 2 3... 310408 32  1  . 3 3 90
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Câu 78: Tính tổng tất cả các nghiệm của phương trình sin 2x  4sin x  2cos x  4  0 trong đoạn
0;100  của phương trình. A. 100 . B. 2476 . C. 25 . D. 2475 . Lời giải Chọn D m.vn
Ta có sin 2x  4sin x  2cos x  4  0  2sin xcos x  4sin x  2cos x  4  0 ie gh
 2sin xcos x  2  2cos x  2  0  cos x  2sin x   1  0 racn  sin x  1  it   x   k2   k  . th cos x  2   VN   2 n ye
Cách 1: Trong đoạn 0;100  , phương trình có các nghiệm lu s://      ;
 2;  4;  6;...;  98 ttp 2 2 2 2 2 h Tổng các nghiệm bằng       S 
  2   4   6 ...  98  50.  2 4 6...98. 2 2 2 2 2 2 298.49 S  25  .  2475 . 2 
Cách 2: Tìm k thỏa mãn 0 
 k2 100  0  k  49 2 /vietgold 49    Bấm máy S    k2  2475   . k.com   k  2 0
ceboo Câu 79: Tổng tất cả các nghiệm của phương trình cossinx1 trên 0;2 bằng .fa A. 0 . B.  . C. 2 . D. 3 . Lời giải Chọn B
https://www Ta có x0;2 sinx 1; 1
Khi đó: cossin x 1  sin x  k2 k   với 1
  k2 1 k  0 . x  0
Phương trình trở thành sin x  0  x  m   m  . x  
Vậy tổng tất cả các nghiệm của phương trình cossin x 1 trên 0;2  bằng  .
Câu 80: Tính tổng S các nghiệm của phương trình  x   4 4 2cos 2
5 sin x  cos x  3  0 trong khoảng 0;2  . 91
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác 11 7 A. S  . B. S  4 . C. S  5 . D. S  . 6 6 Lời giải Chọn B Ta có:  x   4 4 x  x     x   2 2 2cos 2 5 sin cos 3 0 2cos 2
5 sin x  cos x  3  0 h
 2cos2x 5 1 2
cos 2x  3  0  2
 cos (2x) 5cos 2x  3  0  cos 2x  ttp . 2 s:// 1   5 7 11  lu cos 2x 
 x    k k    x ; ; ;  . ye 2 6  6 6 6 6  n th  5 7 11 Do đó: S      4.. it 6 6 6 6 rac 2018 2018 2020 2020 n
Câu 81: Cho phương trình sin x  cos x  2sin x  cos
x . Tính tổng các nghiệm của gh ie
phương trình trong khoảng 0;2018 m.vn 2  2 1285  1285  A.    . B.  2 643  . C.  2 642  . D.    .  4   2  Lời giải Chọn D 2018 2018 x  x   2020 2020 sin cos 2 sin x  cos x 2018  x  2  x 2018  x  2 sin 1 2sin cos 1 2cos x  0 cos 2x  0 2018 2018 ht  sin . x cos 2x  cos
x cos 2x  0   . 2018 2018   tp sin x cos x s://www   k
+ cos 2x  0  2x 
 k  x   k    1 2 4 2 .fa  2018 ceboo + 2018 2018 sin x  cos x  tan x  1 ( x 
 k không là nghiệm)  tan x  1  2 k.com     k x  
 k k   2 . Từ  
1 và 2 ta có x  
k  là nghiệm của pt. 4 4 2 /viet  k gold
Do x 0;2018  0  
 2018  0  k 1284,k  . 4 2
Vậy tổng các nghiệm của phương trình trong khoảng 0;2018 bằng    2 1285  .1285  1 2  ... 1284.1285 1284  .1285       . 4 2 4 4  2 
Câu 82: Phương trình lượng giác: cos3x  cos 2x  9sin x  4  0 trên khoảng 0;3  . Tổng số
nghiệm của phương trình trên là: 92
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” 25 11 A. . B. 6 . C. Kết quả khác. D. . 6 3 Lời giải Chọn B
Ta có cos3xcos2x9sin x4  0 3 2 m.vn
 4cos x 3cos x  2sin x 9sin x 5  0 ie  x  2 cos
1 4sin x  2sin x   1 sin x  5  gh 0 racn  2sin x  
1 cos x  2sin x cos x  sin x  5  0 it th n 2sin x 1  0   1   ye
sin x  cos x  2sin x cos x  5  0  2 lu s://   x   k2  ttp 1 6 h Giải   1 , ta có   1  sin x    . 2 5 x   k2  6  13 5 17
Với x 0;3  nên  
1 có các nghiệm thoả bài toán là: x  , x  , x  , x  . 6 6 6 6   
Giải 2 , đặt t  sin x  cos x  2 sin x    với t  2 .  4  Khi đó 2 2
t 1 2sin x cos x  2sin x cos x 1 t ;
/vietgold Phương trình 2 trở thành 2 2
t 1 t  5  0  t  t  4  0 phương trình vô nghiệm. k.com  13 5 17
Vậy tổng các nghiệm là:     6 . 6 6 6 6 ceboo
.fa DẠNG 6. TÌM ĐIỀU KIỆN CỦA THAM SỐ m ĐỂ PHƯƠNG TRÌNH LƯỢNG GIÁC
CHO TRƯỚC CÓ NGHIỆM.
Câu 83: Tính tổng S tất cả các giá trị nguyên của tham số m để phương trình      3  https://www 2 cos 2x   5  m  
có nghiệm thuộc khoảng ; .    3   6 4  A. S  25  . B. S  22  . C. S  22 . D. S  25 . Lời giải Chọn C   3    7 
Theo giả thiết, ta có x  ;  2x   0;     .  6 4  3  6        5 m
Phương trình 2cos 2x 
 5  m  cos 2x       .  3   3  2 93
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác   7     5  m Với 2x   0;  1   cos 2x  1      1   1  2   5  m  2 3  6   3  2  7   m   3   3  m  7.
Vì m nên m4;5;6; 
7 . Khi đó S  4  5  6  7  22.  3 
Câu 84: Tìm m để phương trình 3cos x  43cos x 1 3m  0 có số nghiệm trên đoạn 0;    2  h ttp là lớn nhất. s:// 2 1 2 4 2 1 2 1
A.   m  . B.   m  .
C.   m  .
D.   m  . lu 3 3 3 3 3 3 3 3 ye Lời giải n th it Chọn D rac  4 n cos x   gh  3
Ta có: 3cos x  43cos x 1 3m  0   , k   . ie 3m 1  m.vn cos x    *  3 4
Vì phương trình cos x   vô nghiệm nên thỏa mãn yêu cầu bài toán khi * có số nghiệm trên 3  3  đoạn 0;   nhiều nhất.  2  3m 1  Khi đó 1    2 1 0  3
  3m 1 0   m  . 3 3 3 2 ht
Câu 85: Tìm điều kiện của tham số m để phương trình sin x  2m  
1 sin x  3m m  2  0 có tps://www nghiệm  1 1    1 1 m    m   2   m  1   1   m  1 A.   2 2 . B. 3 3 . C.  . D.  . .fa   0  m  1 3  m  4 1   m  2 1   m  3 ceboo Lời giải k.com Chọn B /viet
Đặt t  sin x , 1   t 1. gold t   m 2
Phương trình trở thành t  2m  
1 t  3mm  2  3 0   . t  m  2   1 1 1   3  m 1   m 
Phương trình có nghiệm     3 3 .  1   m  2 1 1 m3
Câu 86: Tìm điều kiện của tham số m để phương trình cos2x  2m  
1 cos x  m 1  0 có đúng     hai nghiệm trên đoạn  ;   .  2 2  94
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” A. 1   m  0 .
B. 0  m 1.
C. 0  m 1. D. 1   m 1. Lời giải Chọn B  1 cos x  
Ta có cos2x  2m  
1 cos x  m 1  0 2
 2cos x 2m  
1 cos x  m  0   2  .   m.vn cos x m ie     gh Với x   ; 
 thì 0  cos x 1.  2 2  racn it 1 th
Suy ra cos x   không thỏa bài toán. n 2 ye     lu
Phương trình đã cho có 2 nghiệm trên đoạn  ; 
  0  cos x 1  0  m 1.  2 2  s:// ttp
Câu 87: Cho phương trình
2 x  m  
x  m   2 2sin 1 sin 2
6 cos x  1. Có bao nhiêu giá trị nguyên h
của tham số m để phương trình vô nghiệm? A. 4 . B. 6 . C. 5 . D. 2 . Lời giải Chọn A 1 cos 2x 2 2
2sin xm 1sin2xm6cos x 11cos2xm 1sin2xm6 1 2
 2  2cos2x  2m 
1 sin 2x  m  61 cos 2x  2
/vietgold m4cos2x2m 1sin2xm6.
k.com Phương trình vô nghiệm ceboo 2 2 2
.fa m   m  m  2 4 4 1 6
 4m 12m 16  0  m 1  ;4 .
Vậy có 4 giá trị nguyên của tham số m để phương trình vô nghiệm.
Câu 88: Tìm tất cả các giá trị của tham số m để phương trình 2
2cos x  4msin x cos x  m có https://www nghiệm: 2 2 A. m   .
B. m   hoặc m 0 . 3 3 2
C.   m  0 . D. m  0 . 3 Lời giải Chọn B Ta có 2
2cos x  4msin x cos x  m 1 cos 2x  2msin 2x  m  cos 2x  2msin 2x  m 1 95
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác 2 Phương trình cos 2x 2msin 2x
m 1 có nghiệm   m  m  2 2 1 4 1 2
 3m  2m  0  m   3 hoặc m  0 .
Câu 89: Số các giá trị nguyên m để phương trình 4m  4.sin .
x cos x  m  2.cos 2x  3m  9 có nghiệm là A. 7. B. 6. C. 5. D. 4 h Lời giải ttp s:// Chọn D lu 4m  4  0 m 1 ye   m  
 m   m  n Điều kiện xác định: 2 0 2 3. th   3m  9  0 m  3   it rac 4m  4.sin .
x cos x  m  2.cos 2x  3m  9 n gh ie
 m 1.2sin .xcos x  m  2.cos2x  3m 9 m.vn
 m 1.sin 2x  m  2.cos2x  3m 9 2 2 2
Phương trình có nghiệm khi  m 1   m  2   3m 9  m1 m 2  3m9  m  6.
Kết hợp điều kiện ta được 3  m  6.
Mà m nên m3;4;5;  6 .
Vậy có 4 giá trị nguyên của m thỏa mãn yêu cầu đề bài. http
Câu 90: Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 3 cos x  m 1  0 có s://www nghiệm? A. 1. . B. 2.. C. 3. . D. Vô số. .fa Lời giải ceboo Chọn C k.com 1 m
Ta có 3 cos x  m 1  0  cos x  . /v 3 ietgold 1 m
Phương trình có nghiệm  1  
1 1 3  m 1 3 . 3
Vì m nên m0;1; 
2 . Vậy có tất cả 3 giá trị nguyên của tham số m .
Câu 91: Tìm tất cả các giá trị của tham số m để phương trình m  
1 sin x  2  m  0 có nghiệm. 1 1 A. m  1.  . B. m  .. C. 1   m  .. D. m  1.  2 2 Lời giải 96
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” Chọn B m 
Phương trình m  
1 sin x  2  m  0  m  
1 sin x  m  2 2  sin x  . m 1  m  2 2m 1  1 0  1  0 m   m  2   m 1  m 1  2 1
Để phương trình có nghiệm  1  1         m  m 1 m  2       3   m 1  2 m.vn 1 0  0  m 1  m 1 m  1 ie gh .    racn
Câu 92: Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 3 cos x m 1 0 có it nghiệm? th n A. 1. . B. 2.. C. 3. . D. Vô số. ye lu Lời giải s:// Chọn C ttp h 1 m
Ta có 3 cos x  m 1  0  cos x  . 3 1 m
Phương trình có nghiệm  1  
1 1 3  m 1 3 . 3
Vì m nên m0;1; 
2 . Vậy có tất cả 3 giá trị nguyên của tham số m .
Câu 93: Tìm tất cả các giá trị của tham số m để phương trình m 1sinx2m0 có nghiệm. 1 1 A. m  1.  . B. m  .. C. 1   m  .. D. m  1.  /vietgold 2 2 k.com Lời giải ceboo Chọn B .fa m 
Phương trình m  
1 sin x  2  m  0  m  
1 sin x  m  2 2  sin x  . m 1  m  2 2m 1  1 0  1  0 m   m  2   m 1  m 1  2 1
https://www Để phương trình có nghiệm  1 1         m  m 1 m  2      3 m 1 2 1  0     0  m 1  m 1 m  1 .
DẠNG 7. TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ LƯỢNG GIÁC
7.1. Tìm GTLN, GTNN sử dụng điều kiện 1   sin ,
x cos x  1.  2 
Câu 94: Tìm giá trị nhỏ nhất của biểu thức A  sin x  sin x     3  3 A. 1  . B. 0 . C. 2  . D. . 2 97
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác Lời giải Chọn A  2        
Ta có A  sin x  sin x   2sin x  cos  sin x         3   3  3  3     1   sin x   1  1
  A  1, x      3  h ttp    5 Vậy min  1  khi sin x   1   x    k2, k    . s:// x  3  6 lu   ye
Câu 95: Tìm giá trị lớn nhất của biểu thức 4 4 A sin x cos x n 1 th A. 1 . B. 0 . C. 2 . D. . it 2 rac Lời giải n gh Chọn A ie m.vn 1 Ta có 4 4 2
A  sin x  cos x  1 sin 2x 2 1 1 2 2 0  sin 2x  1 
 1 sin 2x  1, x   2 2  Vậy 2
max  1 khi sin x  1  cos x  0  x 
 k, k  . x 2
Câu 96: Tập giá trị của hàm số y  sin 2x  3 cos2x 1 là đoạn  ;
a b. Tính tổng T  a  . b  ht A. T  1. B. T  2 . C. T  0 . D. T  1. tps://www Lời giải Chọn B .fa
Cách 1: y  sin 2x  3 cos2x 1  sin 2x  3 cos2x  y 1 ceboo 2
Để phương trình trên có nghiệm thì
     y  2 2 2 1 3 1
 y  2y  3  0  1   y  3. k.com Suy ra y  1  ;  3 . Vậy T  1   3  2. /vietgold   
Cách 2: y  sin 2x  3 cos2x 1  2sin 2x  1    3        Do sin 2x      1  ;  1 nên 2sin 2x  1    1  ;  3 .  3   3        Vậy 1
  y  3.( Ta thấy y  1  khi sin 2x   1   
, y  3 khi sin 2x   1   ).  3   3  98
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Câu 97: Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu hm của mực  t  
nước trong kênh tính theo thời gian t h được cho bởi công thức h  3cos  12   .  6 3 
Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
A. t  22h.
B. t  15h .
C. t  14h .
D. t  10h . Lời giải m.vn ie Chọn D gh        racn Ta có: 1   cos t   1   9
h 15 . Do đó mực nước cao nhất của kênh là 15m đạt được khi it  6 3  th       n cos t   1  
 t   k2  t  2  12k  ye 6 3  6 3 lu     1 1    s:// Vì t  0 2 12k 0  k 
. Chọn số k nguyên dương nhỏ nhất thoả k  là k 1 t 10 . 6 6 ttp h
Câu 98: Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  1
  2cos x 2 3sinx  cosx trên . Biểu thức M  N  2 có giá trị bằng A. 0 . B. 4 2  3 . C. 2 . D. 2  3  2 . Lời giải Chọn C Ta có y  1   2cos x   1   22  3 2
2  3sin x  cos x
sin x cos x  2cos x
/vietgold    x 2 2 3 sin 2 2cos x  
1  2  3sin2x  cos2x k.com    6 2 1  6 2  sin 2x 
cos 2x   6  2sin2x    ceboo 4 6  2   .fa 6  2 1 (với  cos ;  sin ) 4 6  2
Suy ra  6  2  y  6  2 . Do đó max y  6  2  M ; min y   6  2  N .
https://www Vậy M N 22.
Câu 99: Số giờ có ánh sáng của một thành phố X ở vĩ độ 40 bắc trong ngày thứ t của một năm   
không nhuận được cho bởi hàm số: d t   3sin t  80 12  
, t  và 0  t  365. 182 
Vào ngày nào trong năm thì thành phố X có nhiều giờ ánh sáng nhất? A. 262 . B. 353 . C. 80 . D. 171 . Lời giải Chọn D 99
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác   
Ta có: d t   3sin t  80 12    312  15 182       Dấu bằng xảy ra khi sin t  80 1   
t 80   k2 k   182  182 2
t  k .
Mặt khác t 0;36 
5 nên    k  171 194 365    k  . 364 364
Mà k  nên k  0 . h ttp Vậy t  171. s://
Câu 100: Hàm số y  2cos3x  3sin3x  2 có tất cả bao nhiêu giá trị nguyên? lu A. 7 . B. 3 . C. 5 . D. 6 . ye Lời giải n th Chọn A it ra TXD: D  cngh   ie
y  2cos3x  3sin3x  2 3 2  13 cos3x  sin 3x  2    13 13  m.vn  3 
 y  13sin 3x  arccos  2    13   3 
Để hàm số y có giá trị nguyên  13sin 3x  arccos   nguyên  13   3  n +  sin 3x  arccos   
(với n là một số nguyên)  13  13 http  3  n Mà: sin 3x  arccos     1  ;  1  1  
 1   13  n  13 s://www  13  13
Mà: n   n  0; 1  ; 2    3 .fa ceboo
 y có 7 giá trị nguyên. k.com
Câu 101: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau 2 2
y  2sin x  cos 2x . 3
A. max y  4 , min y  .
B. max y  3, min y  2 . /v 4 ietgold 3
C. max y  4 , min y  2 .
D. max y  3, min y  . 4 Lời giải Chọn D Đặt 2 t  sin ,
x 0  t  1  cos2x  1 2t . 2  
 y  2t  1 2t2 1 3 2
 4t  2t 1  2t     .  2  4 100
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” 2 1 1 3  1  9 3
Cách 1: Do 0  t  1    2t    0  2t       y  3 . 2 2 2  2  4 4 1
Cách 2: Có y  8t  2  y  0  t  0;  1 . 4  1  3
Ta có: y 0  1; y    ; y   1  3 .  4  4 m.vn ie     gh
Vậy max y  3 đạt được khi x k . 2 racn 3 1 1  cos 2x 1 1   it min y  đạt được khi 2 sin x  
  cos2x   2x    k2  x    k . th 4 4 2 4 2 3 6 n ye
Câu 102: Gọi M và m lần lượt là GTLN và GTNN của hàm số 4 4
y  sin x  cos x  sin 2x . Tổng lu
M  m là s:// 3 1 3 A. . B.  . C. . D. 1 . ttp 2 2 2 h Lời giải Chọn D 1 1 Ta có: 4 4 2 2
y  sin x  cos x  sin 2x  1
sin 2x  sin 2x   sin 2x  sin 2x  1 2 2
Đặt t sin2x  1t  1. 1  b  b    2 3
y   t  t  1  1   t  
1 là parabol có đỉnh I  ; y    .  I 1;  t  1    1  ;  1 /vietgold 2  2a  2a   2  k.com 3 1  y   1 1   ; y   3 1 
. Suy ra M  ;m  . 2 2 2 2 ceboo
.fa Vậy M m1.
7.2. Tìm GTLN, GTNN dạng y  asin x  bcos x  c . sin x  2cos x
Câu 103: Cho hàm số y 
. Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất
sin x  cos x  3 https://www
của hàm số đã cho. Tính 7m  5M bằng? A. 10 . B. 1 . C. 0 . D. 10  . Lời giải Chọn D TXĐ: D  sin x  2cos x Ta có: y 
 1 ysin x   y  2cos x  3y  1
sin x  cos x  3 Phương trình   2 2
1 có nghiệm    y   y   2 1 2  9y 101
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác 5 5 2
 7y  2y  5  0    y  1 m   ;M  1 7 7
Vậy 7m  5M  5   5  1  0 . 3sin 4x  4 4 4
sin x  cos x
Câu 104: Hàm số y 
có giá trị lớn nhất M và giá trị nhỏ nhất m . Khi 2
2cos 2x  sin 4x  2
đó tổng M  m bằng? 5 10 3 h A. 0 . B.  .  . D. . ttp 7 C. 7 7 s:// Lời giải lu ye Chọn C n th TXĐ: D  it ra 4 4 2 2 2 c
Ta có: 3sin 4x  4sin x  cos x  3sin4x  41 2sin xcos x  2sin 2x  3sin4x  4 n gh ie  3sin4x  cos4x  3. m.vn Xét mẫu thưc: 2
2cos 2x  sin 4x  2  cos4x  sin 4x  3 3sin 4x  4 4 4
sin x  cos x 3sin 4x  cos 4x  3 Suy ra y   2
2cos 2x  sin 4x  2 cos 4x  sin 4x  3
 3 ysin x   y  
1 cos x  3y  32 Phương trình  2 2 2
2 có nghiệm  3  y   y   1  3y   3 5   4 2 5   4 2 2 ht
 7y 10y 1  0   y  10
 m  M   . tp 7 7 7 s://www
Câu 105: Giá trị lớn nhất M , giá trị nhỏ nhất m của hàm số: 2
y  2cos x  2 3sin x cos x  1 là
A. M  4;m  0 .
B. M  3;m  0 .
C. M  3;m  1.
D. M  4;m  1. .fa ceboo Lời giải k.com Chọn A
Tập xác định D  . /viet   gold Ta có 2
y  2cos x  2 3sin x cos x  1  cos 2x  3 sin 2x  1 3
2*  2 cos2x  sin 2x   2  2 2       2cos 2x   2   .  3    
Mặt khác 0  2cos 2x   2  4, x    
 0  y  4,x  .  3   
Vậy giá trị lớn nhất của hàm số là M  4 khi x   k . 6 102
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” 
Và giá trị nhỏ nhất của hàm số là m  0 khi x   k . 3
sin x  2 cos x  1
Câu 106: Cho hàm số y 
. Gọi M ; m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
sin x  cos x  2
của hàm số. Tổng M  m bằng A. 1 . B. 2  . C. 1  . D. 2 . m.vn Lời giải ie gh Chọn C racn
Tập xác định D 
(do sin x  cos x  2  0; x   ). it th   n sin x 2 cos x 1
Xét phương trình: y 
 1 ysin x  2  ycos x 1 2y  0* . ye
sin x  cos x  2 lu Phương trình  2 2 2
* có nghiệm  1 y  2  y  1 2y 2
 y  y  2  0  2   y  1. s:// ttp        h Vậy M 1;m 2 M m 1.
cos x  2sin x  3
Câu 107: Giá trị lớn nhất của hàm số y  là
2cos x  sin x  4 A. 3  2 3 . B. 2 . C. 1  . D. 0 . Lời giải Chọn B
Xét phương trình: 2cos x  sin x  4  0 * .
/vietgold Ta có :  2 2 2 2 1
 4 nên phương trình * vô nghiệm, hay 2cos x  sin x  4  0, x   .
k.com Do đó, hàm số đã cho có tập xác định D . ceboo
cos x  2sin x  3 .fa y   2y  
1 cos x   y  2sin x  3  4y ** .
2cos x  sin x  4
Để tồn tại giá trị lớn nhất của hàm số ban đầu thì phương trình ** phải có nghiệm  2y  2
1   y  22  4 y  32 2 2
 11y  24y  4  0   y  2. https://www 11
Vậy GTLN của hàm số đã cho là 2 . msin x  1
Câu 108: Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số y  cos x  2 nhỏ hơn 2 . A. 4 . B. 6 . C. 5 . D. 3 . Lời giải Chọn C Dễ thấy cos x  2  , x
  nên hàm số có tập xác định là D  103
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác msin x  1 Ta có y 
 y cos x  2y  msin x 1  msin x  y cos x  2y 1 * cos x  2
* có nghiệm khi m  y   y  2 2 2 2 2 2 1
 3y  4y 1 m  0 2 2 2  1  3m 2  1  3m 2     2 1 3m y  2 2  y 
 2  1 3m  4  m  5 3 3 max 3 Do m  m 2  ; 1  ;0;2; 
1 . Vậy có 5 giá trị của m thỏa ycbt. h ttp
sin x  2cos x  1 s://
Câu 109: Giả sử M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số y 
sin x  cos x  2 lu trên
. Tìm 2M  3m ye n A. 1 2 . B. 0 . C. 1 . D. 8 th it Lời giải racn Chọn D gh ie       m.vn
Ta có: sin x  cos x  2  0  2 sin x   2   s n i x    2     (vô nghiệm).  4   4 
Do đó, hàm số đã cho có tập xác định D  .
sin x  2cos x  1 Ta có y    y  
1 sin x   y  2cos x  1 2y * .
sin x  cos x  2
Hàm số đạt giá trị lớn nhất, nhỏ nhất khi  2 2 2
* có nghiệm  1 2y   y   1   y  2 2
 2y  2y  4  0  2
  y  1. Do đó m  2
 , M  1. Vậy 2M  3m  8. ht 2sin x  2 y  tp
Câu 110: Gọi M , m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số . cos x  2 s://www
Khẳng định nào sau đây đúng? 8
A. 3m  M  8.
B. 3m  M  8  .
C. 3m  M  0 .
D. 3m  M   .fa 3 ceboo Lời giải Chọn B k.com
Dễ thấy cos x  2, x
  nên hàm số có tập xác định là D  /viet 2sin x  2 y   .
y cos x  2sin x  2  2 y * gold Ta có   . cos x  2
Để tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số ban đầu thì phương trình * phải có M  0 8 
nghiệm  y  4  2  2 y2 2 2
 3y  8y  0    y  0 . Do đó  8 . 3 m    3
Vậy 3m  M  8  .
Câu 111: Tập giá trị của hàm số y  sin 2x  3 cos2x 1 là đoạn  ;
a b. Tính tổng T  a  . b A. T  0. B. T  1  . C. T  1. D. T  2. 104
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” Lời giải Chọn D
Cách 1: y  sin 2x  3 cos2x 1  sin 2x  3 cos2x  y 1 *
Để tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số ban đầu thì phương trình * phải có 2 2 2 2            m.vn nghiệm thì 1
 3 y 1 y 2y 3 0 1 y 3. ie gh Suy ra y  1  ;  3 . Vậy T  1   3  2. racn
Cách 2: Ta có y 1  sin 2x  3 cos2 .
x Mặt khác áp dụng bất đẳng thức Bunhiacopskii ta có it th 2 2 n  y     x  c x     2 2 1 sin 2 3 os2 1 3 sin 2x  o
c s 2x  4  2
  y 1 2  1
  y  3. ye lu Vậy T  1   3  2. s://    ttp
Cách 3: y  sin 2x  3 cos2x 1  2sin 2x  1   h  3        Do sin 2x      1  ;  1 nên 2sin 2x  1    1  ;  3 .  3   3  Vậy 1   y  3.
Câu 112: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  3sin x  4cos x 1.
A. maxy 6, miny  4.
B. max y  8 , min y  6  .
C. max y  4 , min y  6  .
D. max y  6, min y  8  . /vietgold Lời giải k.com Chọn C
ceboo Ta có y 3sinx4cosx13sinx4cosx  y1 *
.fa Ta coi * như là phương trình cổ điển với a3, b4, c y1.
Phương trình * có nghiệm khi và chỉ khi a  b  c     y  2 2 2 2 9 16 1  6   y  4 .
https://www Vậy maxy  4, miny  6. Chú ý:
Ta có thể áp dụng bất đẳng thức BCS như sau: y   x  x   2 2   2 2 1 3sin 4cos 3 4
sin x  cos x  5 .
7.3. Tìm GTLN, GTNN sử dụng bất đẳng thức cổ điển.
Câu 113: Cho hàm số 2 2
y  1 2sin x  1 2cos x  1. Gọi ,
m M lần lượt là giá trị nhỏ nhất và
giá trị lớn nhất của hàm số. Khi đó giá trị của M  m bằng 105
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác A. 3  2 2 . B. 3  2 1. C. 3  2 2 1. D.  3  3 2 1. Lời giải Chọn C Đặt 2 2
t  1 2sin x  1 2cos x 2  t   2  x   2  x   2  x 2  x 2 1 2sin 1 2cos 2 1 2sin 1 2cos
 4  2 3  sin 2x h ttp 2
 t  4  2 3  sin 2x  4  2 3  1 3 s:// lu 2 2
 y  1 2sin x  1 2cos x 1 3 . ye n  th k
Dấu ''  '' xảy ra khi sin 2x  0  x  . Khi đó m  3 . it 2 racn
Mặt khác, áp dụng bất đẳng thức Cauchy – Schwarz, ta có gh ie 2 2  x   x   2 2   2 2 1 2sin 1 2cos 1 1
1 2sin x  1 2cos x  2 2 m.vn 2 2
 y  1 2sin x  1 2cos x 1 2 2 1.   x    k  Dấu ''  '' xảy ra khi 2 2 4
sin x  cos x   k   
. Khi đó M  2 2 1.
x   k  4
Vậy M  m  3  2 2 1. ht
2sin x  3cos x  1 tp
Câu 114: Tìm giá trị lớn nhất của hàm số y  s://www
sin x  cos x  2 3  33 3  33 1 A. . B. . C. 3 . D. . 2 2 2 .fa ceboo Lời giải Chọn A k.com
2sin x  3cos x  1 Ta có y 
  y  2sin x   y  3cos x  1 2y . /v
sin x  cos x  2 ietgold
  y2  y   x y   2 x   
 y  2   y  2 2 2 1 2 2 sin 3 cos 2 3
sin x  cos x   2
 2y  6y 12  0 3  33 3  33   y  . 2 2
Câu 115: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số f  x 2018 2018  sin x  cos
x lần lượt là 1 1 1 A. và 2 . B. và 1 . C. 0 và 1 . D. và 1. 1008 2 1009 2 1008 2 106
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng” Lời giải Chọn D Đặt 2 2 a  sin , x b  cos . x Ta có  2018 2018 2 2 sin x  cos
x  sin x  cos x  1. Dấu "  " xảy ra  x  k . 2 m.vn 1009 1009 1009    ie a b  a  b  1   2018 2018 sin x  cos x  2.   2  .  
Dấu "  " xảy ra  x   k . 1008 gh  2   2  2 4 2 racn 1 it
Vậy giá trị nhỏ nhất bằng
; giá trị lớn nhất bằng 1 . 1008 2 th n
Câu 116: Cho x , x  y 
Giá trị nhỏ nhất của biểu thức ye
y là các số thực thỏa mãn cos2 cos 2 1. lu 2 2
P  tan x  tan y bằng s:// 1 2 8 A. . B. . D. . C. 3. ttp 3 3 3 h Lời giải Chọn B  1   1   1 1  Ta có P  1  1  2   2.       2 2  cos x   cos y 
1 cos2x 1 cos2y     2 1 1  4 2
Áp dụng BĐT cộng mẫu, ta được P  2   2  2.  2  .  .
2  cos 2x  cos 2 y  2  1 3   /vietgold   
Câu 117: Cho hai số thực x, y thuộc 0; 
 và thỏa mãn cos2x  cos2y  2sinx  y  2. Giá trị k.com  2  4 4 cos x cos y ceboo P   y x .fa nhỏ nhất của bằng 2 3 2 5 A. 3 . B.  . C.  . D.  . Lời giải https://www Chọn C Ta có x  y  x  y 2 2 cos 2 cos 2 2sin
 2  sin x  sin y  sinx  y. 
Suy ra x  y  . 2 a b a  b2 2 2 Áp dụng BĐT cộng mẫu   , ta được m n m  n 107
 Quảng Thuận – Ba Đồn – QB
Hàm số lượng giác và phương trình lượng giác 2        2 2 x x     cos x cos y 2 2 2 2 cos cos 2 2  cos x  sin   2 x    2 P     . x  y x  y x  y  
Dấu ''  '' xảy ra  x  y  . 4 
Nhận xét. Việc suy ra x  y 
được chứng minh như sau: 2 h ttp         s://
Với x, y  0; 
 suy ra  x,  y cùng thuộc 0; .    2  2 2  2  lu ye    Trên đoạn 0;
, hàm y  sin x đồng biến. n   th  2  it r      a       c x y sin x sin y cos y    n   2  2  gh
Nếu x  y    2      ie y 
 x  sin y  sin  x  cos x    m.vn  2  2  2 2
 sin x  sin y  sin .
x sin x  sin .
y sin y  sin .
x cos y  sin .
y cos x  sin  x  y : mâu thuẫn. 
Tương tự cho x  y  . 2 
Trường hợp x  y  : thỏa mãn. 2 Câu 118: Cho , a ,
b c là các số thực thỏa mãn 2 2 2
a  b  c  4. Tìm giá trị lớn nhất M trong tất cả ht    tp
các hàm số y  a  b sin x  c cos x với x  0; .  s://www   4 
A. M  1 2 .
B. M  1 2 .
C. M  2 1 2 .
D. M  21 2. .fa Lời giải ceboo Chọn C k.com 2
Ta có a  b x  c x    2 2 2 sin cos
a  b  c 1 sin x  cos x /vietgold      4 1 2 sin x   4    1 2.   4 
Suy ra a  b sin x  c cos x  2 1 2.  b c a    4  2 2 2 sin x cos x  a  ;b  c      Dấu ''  '' xảy ra 2 2 2
 a  b  c  4 2 2 2 2   . .           x  sin x   1, x  0;          4 4   4  108
 Quảng Thuận – Ba Đồn – QB
“Thành công là nói không với lười biếng”
Câu 119: Tập giá trị của hàm số y  sin 2x  3 cos2x 1 là đoạn  ;
a b. Tính tổng T  a  . b A. T  1. B. T  2 . C. T  0 . D. T  1  . Lời giải Chọn B
Ta có y 1  sin 2x  3 cos2 .
x Mặt khác áp dụng bất đẳng thức Bunhiacopskii ta có m.vn ie  y     x  c x2 2     2 2 1 sin 2 3 os2 1 3 sin 2x  o
c s 2x  4  2
  y 1 2  1   y  3 . gh Vậy T  1   3  2. racn it th n ye lu s:// ttp h /vietgold k.com ceboo .fa https://www 109
Document Outline

PHẦN 1 – ĐỀ BÀI
- DẠNG 1. XÁC ĐỊNH ĐỒ THỊ HÀM SỐ LƯỢNG GIÁC.
- DẠNG 2. XÁC ĐỊNH CHU KỲ HÀM SỐ LƯỢNG GIÁC.
- DẠNG 3. TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ LƯỢNG GIÁC.
- DẠNG 4: XÁC ĐỊNH SỐ ĐIỂM BIỂU DIỄN CỦA PHƯƠNG TRÌNH LƯỢNG GIÁC CHO TRƯỚC TRÊN ĐƯỜNG TRÒN LƯỢNG GIÁC.
- DẠNG 5. BIỆN LUẬN NGHIỆM PHƯƠNG TRÌNH LƯỢNG GIÁC KHÔNG CHỨA THAM SỐ
  - 5.1. Tìm số nghiệm của phương trình lượng giác trên tập .
  - 5.2. Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình lượng giác:.
  - 5.3. Tính tổng tất cả các nghiệm của phương trình lượng giác trên tập .
- DẠNG 6. TÌM ĐIỀU KIỆN CỦA THAM SỐ ĐỂ PHƯƠNG TRÌNH LƯỢNG GIÁC CHO TRƯỚC CÓ NGHIỆM.
- DẠNG 7. TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ LƯỢNG GIÁC
  - 7.1. Tìm GTLN, GTNN sử dụng điều kiện .
  - 7.2. Tìm GTLN, GTNN dạng .
  - 7.3. Tìm GTLN, GTNN sử dụng bất đẳng thức cổ điển.
PHẦN 2: BẢNG ĐÁP ÁN
PHẦN 3: ĐÁP ÁN CHI TIẾT
- DẠNG 1. XÁC ĐỊNH ĐỒ THỊ HÀM SỐ LƯỢNG GIÁC.
- DẠNG 2. XÁC ĐỊNH CHU KỲ HÀM SỐ LƯỢNG GIÁC.
- DẠNG 3. TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ LƯỢNG GIÁC.
- DẠNG 4: XÁC ĐỊNH SỐ ĐIỂM BIỂU DIỄN CỦA PHƯƠNG TRÌNH LƯỢNG GIÁC CHO TRƯỚC TRÊN ĐƯỜNG TRÒN LƯỢNG GIÁC.
- DẠNG 5. BIỆN LUẬN NGHIỆM PHƯƠNG TRÌNH LƯỢNG GIÁC KHÔNG CHỨA THAM SỐ
  - 5.1. Tìm số nghiệm của phương trình lượng giác trên tập .
  - 5.2. Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình lượng giác:.
  - 5.3. Tính tổng tất cả các nghiệm của phương trình lượng giác trên tập .
- DẠNG 6. TÌM ĐIỀU KIỆN CỦA THAM SỐ ĐỂ PHƯƠNG TRÌNH LƯỢNG GIÁC CHO TRƯỚC CÓ NGHIỆM.
- DẠNG 7. TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ LƯỢNG GIÁC
  - 7.1. Tìm GTLN, GTNN sử dụng điều kiện .
  - 7.2. Tìm GTLN, GTNN dạng .
  - 7.3. Tìm GTLN, GTNN sử dụng bất đẳng thức cổ điển.