Tập giá trị và GTLN – GTLN của hàm số lượng giác

Tài liệu gồm 23 trang, được biên soạn bởi quý thầy, cô giáo nhóm Nhóm Word – Biên Soạn Tài Liệu, hướng dẫn phương pháp giải bài toán trắc nghiệm tìm tập giá trị và giá trị lớn nhất – giá trị nhỏ nhất (GTLN – GTLN / max – min) 

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

23 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 1
PHƯƠNG PHÁP
1. Các kiến thức về giá trị lớn nhất, giá trị nhỏ nhất
Cho hàm số
y f x
xác định trên miền
D R
.
a. Số thực M được gọi là giá trị lớn nhất của hàm số
y f x
trên
D
nếu
0 0
,
,
f x M x D
x D f x M
b. Số thực N được gọi là giá trị nhỏ nhất của hàm số
y f x
trên D nếu
0 0
m,
,
f x x D
x D f x m
2. Một số kiến thức ta sử dụng trong các bài toán này
a) Dựa vào tập giá trị của hàm số lượng giác, chẳng hạn :
2
2
1 sin 1
0 sin 1
1 cos 1
0 cos 1
x
x
x
x
b) Bảng biến thiên của hàm số lượng giác.
c) Kỹ thuật sử dụng máy tính cầm tay.
MỨC ĐỘ 1
BÀI TẬP TỰ LUẬN
Bài 1. Tìm giá trị lớn nhất và nhỏ nhất của đồ thị hàm số
3 siny x
Lời giải
Tập xác định
D
.
Ta có:
1 sin 1x x
1 sin 1x x
3 1 3 sin 3 1x x
4 2y x
Ta có:
4
y
khi
sin 1
x
và
2
y
khi
sin 1x
Vậy
min 2
y
và
max 4
y
.
Bài 2. Tìm tập giá trị
T
của hàm số
3cos 2 5y x
TẬP GIÁ TRỊ VÀ MAX - MIN CỦA HÀM SỐ LƯỢNG GIÁC
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 2
Lời giải
Tập xác định
D
.
Ta có:
1 cos 2 1 3 3cos2 3 3 5 3cos 2 5 3 5 8 2
x x x y
Vậy tập giá trị của hàm số
3cos 2 5y x
là
8; 2
T
Bài 3. Tìm tập giá trị
T
của hàm số
2 2
sin 2cos 1y x x
trên khoảng
Lời giải
Ta có:
2 2 2 2 2
sin 2 cos 1 sin 2 1 sin 1 3 siny x x x x x
Với
x
thì
2 2
0 sin 1 0 sin 1
x x
2
3 3 sin 3 1 2
x
Vậy tập giá trị của hàm số
2 2
sin 2cos 1y x x
trên
là
2 ; 3
T
Bài 4. Tìm giá trị nhỏ nhất
m
của hàm số
1
cos 1
y
x
Lời giải
ĐKXĐ:
cosx -1 x k2
. TXĐ:
/ 2
D k
Ta có:
1 1
: 1 cos 1 0 1 cos 2
1 cos 2
x D x x
x
Ta có:
1
2
y
khi
cos x 1
.
Vậy,
1
min
2
y
.
Bài 5. Tìm giá trị nhỏ nhất của biểu thức
2sin 1
3
P x
Lời giải
Ta có:
sin 1 2sin 2 2sin 1 1
3 3 3
x x x
Dấu " = " xảy ra khi và chỉ khi
sin 1
3
x
.
Vậy giá trị nhỏ nhất của biểu thức
P
là
1
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 3
BÀI TẬP TRẮC NGHIỆM
Câu 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
10
2017cos8 2016
2017
y x
A.
min 1; maxy 4033
y
B.
min 1; maxy 4033
y
C.
min 1; maxy 4022
y
D.
min 1; max 4022
y y
Lời giải
Chọn B
Hàm số xác định trên
Ta có
10
1 cos8 1,
2017
x x
10
2017 2016 2017 cos8 2016 2017 2016,
2017
x x
.
10
1 2017cos8 2016 4033,
2017
x x
Ta có
1
y
khi
10
cos8 1
2017
x
;
4033
y
khi
10
cos8 1
2017
x
.
Vậy
min 1; maxy 4033
y
.
Câu 2. Giá trị nhỏ nhất và lớn nhất của hàm số
4cosy x
là:
A. 0 và 4. B.
4 và 4. C. 0 và 1. D.
1 và 1.
Lời giải
Chọn B
Tập xác định:
0 ;D
.
Ta có:
1 cos 1, 0 ;x x
4 4co 4 ; s , 0x x
Ta có
4
y
khi
cos 1
x
và
4
y
khi
cos 1
x
.
Vậy
min 4 ; max 4
y y
Câu 3. Cho hàm số
sin .
4
y x
Giá trị lớn nhất của hàm số là:
A.
1
. B.
0
. C.
1
. D.
4
.
Lời giải
Chọn C
Ta có:
1 sin 1
4
x
. Suy ra giá trị lớn nhất của hàm số
sin
4
y x
là 1.
Câu 4. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
2
1 cos 2
y x
là:
A.
0
và
2 1
. B.
1
và
2 1
. C.
2
và
1
D.
1
và
1
Lời giải
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 4
Chọn C
Ta có
2 2
1 cos 2 sin 2 sin 2
y x x x
Mặt khác
0 sin 1 2 sin 2 1
x x
2 1
y
Ta có:
2
y
khi
sin 0
x
và
1
y
khi
sin 1
x
Vậy giá trị lớn nhất và nhỏ nhất của hàm số là
2
và
1
.
Câu 5. Cho hàm số
2sin 2
3
y x
. Mệnh đề nào sau đây là đúng?
A.
4 ,y x
B.
4 ,y x
C.
0 ,y x
D.
2 ,y x
Lời giải
Chọn C
Ta có
1 sin 1,
3
x x
2 2sin 2 ,
3
x x
4 2sin 2 0 ,
3
x x
Ta có:
4
y
khi
sin 1
3
x
và
0
y
khi
sin 0
3
x
Suy ra chọn đáp án C.
MỨC ĐỘ 2
BÀI TẬP TỰ LUẬN
Bài 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
10
2017 cos 8 2016
2017
y x
.
Lời giải
Cách 1: Hàm số xác định trên
.
Ta có :
10
1 cos 8 1
2017
x
,
x
10
2017 2017cos 8 2017
2017
x
,
x
10
1 2017cos 8 2016 4033
2017
x
,
x
Ta có
1
y
khi
10
cos 8 1
2017
x
;
4033
y
khi
10
cos 8 1
2017
x
.
Vậy
min 1;maxy 4033
y
.
Bài 2. Tìm giá trị nhỏ nhất của hàm số:
2
2cos sin 2 5y x x
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 5
Lời giải
Ta có
2
2cos sin 2 5y x x
cos 2 sin 2 6
x x
2 cos 2 6
4
x
.
Do
2 2 cos 2 2
4
x
nên
2 6 2 cos 2 6 2 6
4
x
.
Vậy giá trị nhỏ nhất của hàm số
2
2cos sin 2 5y x x
là
6 2
.
Bài 3. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
sin cosy x x
. Tính
P M m
.
Lời giải
Ta có
in cos 2 si
4
s nx x xy
.
Mà
2
1 sin 1 2 sin 2 2 2
4 4
2
2
M
x x P
m
.
Vậy
2 2
P
.
Bài 4. Tìm giá trị nhỏ nhất của hàm số
sin 1
cos 2
x
y
x
.
Lời giải
Cách 1 :
cos 2 0
x
,
x
. Vậy
sin 1
sin 1 cos 2
cos 2
x
y x y x
x
sin cos 1 2 0
x y x y
.
Ta có
2 2
2 2 2 2
4
1 1 2 1 4 4 1 3 4 0 0
3
y y y y y y y y
.
Vậy
min 0
y
min.
Cách 2 : Ta có
sin 1 0
0 min 0 sin 1
cos 2 0
x
y y x
x
.
Bài 5. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
2
2cos 2 3 sin cos 1y x x x
.
Lời giải
Cách 1:
2
2cos 2 3 sin cos 1y x x x
2
2cos 1 3 sin 2 2
x x
cos 2 3 sin 2 2
x x
1 3
2 cos 2 sin 2 2
2 2
x x
2cos 2 2
3
x
.
Mặt khác
0 2cos 2 2 4
3
x
,
x
0 4
y
,
x
.
Cách 2:
2
2cos 2 3 sin cos 1y x x x
2
2cos 1 3 sin 2 2
x x
cos 2 3 sin 2 2
x x
*
Ta có
1 3 2 1 3 2
y
0 4
y
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 6
BÀI TẬP TRẮC NGHIỆM
Câu 1. Tìm giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
2 2
sin 2cosy x x
.
A.
2M
,
0
m
. B.
2M
,
1
m
. C.
3
M
,
1
m
. D.
3
M
,
0.
m
Lời giải
Chọn B
Ta có:
2 2 2 2 2 2
sin 2 cos sin cos cos 1 cosy x x x x x x
.
Do
2 2
1 cosx 1 0 cos x 1 1 cos x 2
. Suy ra
2
1
M
m
.
Câu 2. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
8sin 3cos2y x x
. Tính
Tính
2
2
P M m
.
A.
1P
. B.
2P
. C.
112
. D.
130
P
.
Lời giải
Chọn A
Ta có:
2 2 2 2
8sin 3cos 2 8sin 3 1 2sin 2sin 3y x x x x x
.
Mà
1 sinx 1
2 2
0 sin 1 3 2sin 3 5
x x
3 5
y
. Suy ra:
5
3
M
m
.
Do đó:
2
2 1
P M m
.
Câu 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3sin 4cos 1y x x
.
A.
max 8
y
,
min 6
y
. B.
max 4
y
,
min 6
y
.
C.
max 6
y
,
min 8
y
. D.
max 6
y
,
min 4
y
.
Lời giải
Chọn B
Ta có
3sin 4cos 1 3sin 4cos 1y x x x x y
*
Ta coi
*
như là phương trình cổ điển với
3
a
,
4
b
,
1c y
.
Phương trình
*
có nghiệm khi và chỉ khi
2
2 2 2
9 16 1 6 4
a b c y y
.
Vậy
max 4
y
,
min 6
y
.
Chú ý:
Ta có thể áp dụng bất đẳng thức BCS như sau:
2 2 2 2
1 3sin 4cos 3 4 sin cos 5
y x x x x
.
Câu 4. Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số
2
sin sin 2
y x x
.
A.
7
min ;max 4
4
y y
. B.
7
min ;max 2
4
y y
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 7
C.
min 1; max 1y y
. D.
1
min ;max 2
2
y y
.
Lời giải
Chọn A
Đặt
sin
x u
;
1;1
u
.
Xét hàm số:
2
2
y u u
trên
1;1
.
Ta có:
1
1;1
2 2
b
a
. Từ đây có bảng biến thiên
Ta kết luận:
1;1
7
min
4
f u
và
1;1
max 4 1
y u
.
Hay
7 1
min sin
4 2
y x
và
max 4 sin 1
y x
.
Câu 5. Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số
sin 2cos 3
2 cos
x x
y
x
A.
2
min
3
y
;
max 2
y
B.
2
min
3
y
;
max 2
y
.
B.
1
min
2
y
;
3
max
2
y
. D.
1
min
2
y
;
3
max
2
y
.
Lời giải
Chọn B
Cách 1: Ta có
cos 2 0
x
,
x
.
sin 2cos 3
2 cos
x x
y
x
sin 2cos 3 2 cosx x y y x
sin 2 cos 3 2 0
x y x y
.
Ta có:
2 2
2
1 2 3 2y y
2 2
4 12 9 4 4 1 0
y y y y
2
3 8 4 0
y y
2
2
3
y
.
Cách 2 : sử dụng máy tính cầm tay
Tương tự như ở ví dụ 1 thì ta có thể sử dụng SHIFT SOLVE:
sin x 2cos x 3
2
2 cos x
thì phương trình
có nghiệm. Do 2 là số lớn nhất trong các phương án A; B; C; D nên ta không cần thử trường hợp
3
max
2
.
Lúc này chỉ còn A và B. Thử với
2
min y
3
thì không có nghiệm.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 8
MỨC ĐỘ 1
BÀI TẬP TỰ LUẬN
Bài 1. Tìm tập giá trị của các hàm số sau:
3cos 2
3
y x
Lời giải
Vì
1 cos 1
3
x
nên
3 3cos 3 3 2 3 2 1 5
2
x y y
.
Vậy tập gái trị của hàm số là
1;5
.
Bài 2. Tìm tập giá trị của các hàm số sau:
3 2sin 2y x
.
Lời giải
Ta có:
1 sin 2 1 2 2sin 2 2 1 3 2sin 2 5 1 3 2sin 2 5
x x x x
.
Vậy tập giá trị của hàm số là
1; 5
.
Bài 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau:
4sin cos 1y x x
.
Lời giải
Ta có
2sin 2 1y x
.
Do
1 sin 2 1 2 2sin 2 2 1 2sin 2 1 3
x x x
1 3
y
.
*
1 sin 2 1 2 2
2 4
y x x k x k
.
*
3 sin 2 1
4
y x x k
.
Vậy giá trị lớn nhất của hàm số bằng
3
, đạt được khi
4
x k
.
giá trị nhỏ nhất bằng
1
, đạt được khi
4
x k
.
Bài 4. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau:
2
4 3sin 2y x
.
Lời giải
Ta có:
2 2
0 sin 1 1 4 3sin 4
x x
.
*
2
1 sin 1 cos 0
2
y x x x k
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 9
*
2
4 sin 0
y x x k
.
Vậy giá trị lớn nhất của hàm số bằng
4
, đạt được khi
x k
.
giá trị nhỏ nhất bằng
1
, đạt được khi
2
x k
.
Bài 5. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
2sin 3
y x
.
Lời giải
Ta có
1 2sin 3 5 1 5
x y
.
Vậy giá trị lớn nhất của hàm số bằng
max 5
y
, đạt được khi
sin 1 2
2
x x k
.
Giá trị nhỏ nhất bằng
min 1y
, đạt được khi
1 2
2
x x k
.
BÀI TẬP TRẮC NGHIỆM
Câu 1. Tìm tập giá trị hàm số sau
1 3sin 2
4
y x
.
A.
2;4
. B.
2;2
. C.
1;4
. D.
2;3
.
Lời giải
Chọn A
Ta có:
1 sin 2 1 3 3sin 2 3 2 1 3sin 2 4
4 4 4
x x x
.
2 4
y
.
Vậy tập giá trị của hàm số là
2;4
.
Câu 2. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
2cos 3 3
3
y x
A.
min 2
y
,
max 5
y
. B.
min 1y
,
max 4
y
.
C.
min 1y
,
max 5
y
. D.
min 1y
,
max 3
y
.
Lời giải
Chọn C
Ta có:
1 cos 3 1 2 2cos 3 2 1 2cos 3 3 5 1 5
3 3 3
x x x y
.
min 1y
đạt được khi
4 2
9 3
x k
.
max 5
y
đạt được khi
2
9 3
x k
.
Câu 3. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
2
1 2cos 1y x
A.
max 1y
,
min 1 3
y
. B.
max 3
y
,
min 1 3
y
.
C.
max 2
y
,
min 1 3
y
. D.
max 0
y
,
min 1 3
y
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 10
Lời giải
Chọn D
Ta có
2
1 2cos 1 3 1 3 0
x y
.
Vậy giá trị nhỏ nhất của hàm số bằng
max 0
y
, đạt được khi
2
x k
.
Giá trị nhỏ nhất của hàm số bằng
min 1 3
y
, đạt được khi
x k
.
Câu 4. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
1 3sin 2
4
y x
.
A.
min 2
y
,
max 4
y
. B.
min 2
y
,
max 4
y
.
C.
min 2
y
,
max 3
y
. D.
min 1
y
,
max 4
y
.
Lời giải
Chọn A
Ta có:
1 sin 2 1 2 4
4
x y
2 sin 2 1
4 8
y x x k
min 2
y
3
4 sin 2 1
4 8
y x x k
max 4
y
Câu 5. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
2
3 2cos 3y x
A.
min 1y
,
max 2
y
. B.
min 1y
,
max 3
y
.
C.
min 2
y
,
max 3
y
. D.
min 1
y
,
max 3
y
.
Lời giải
Chọn C
Ta có:
2
0 cos 3 1 1 3
x y
.
2
1 cos 3 1
3
k
y x x
min 1y
.
2
3 cos 3 0
6 3
k
y x x
max 3
y
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 11
MỨC ĐỘ 2
BÀI TẬP TỰ LUẬN
Bài 1. Tìm giá trị lớn nhất của hàm số
2
3sin 4
12
y x
Lời giải
Ta có
2 2 2
sin 1 3sin 3 3sin 4 7
12 12 12
x x x
.
Vậy giá trị lớn nhất của hàm số bằng
7
.
Bài 2. Tìm giá trị lớn nhất của hàm số
2
2sin sin 2 10
f x x x
.
Lời giải
Ta có
2
2sin sin 2 10
f x x x
11 sin 2 cos 2x x
11 2 sin 2
4
x
.
Do
1 sin 2 1
4
x
2 2 sin 2 2
4
x
nên
11 2 sin 2 11 2
4
x
.
Dấu
" ''
xảy ra khi
3
sin 2 1
4 8
x x k
,
k
. Vậy
max 11 2
f x .
Bài 3.
Tìm giá trị nhỏ nhất của hàm số
2
2cos sin 2 5y x x
.
Lời giải
Ta có
2
2cos sin 2 5y x x
cos 2 sin 2 6x x
2 cos 2 6
4
x
.
Do
2 2 cos 2 2
4
x
nên
2 6 2 cos 2 6 2 6
4
x
.
Vậy giá trị nhỏ nhất của hàm số
2
2cos sin 2 5y x x
là
6 2
.
Bài 4. Giả sử
M
là giá trị lớn nhất và
m
là giá trị nhỏ nhất của hàm số
2 3 sin cosy x x
. Tính
M m
.
Lời giải
Ta có:
2 2
2 3 1 2 3 sin cos 2 3 1
x x
.
Vậy
0
M m
.
Bài 5. Cho hàm số
12
7 4sin
y
x
có giá trị lớn nhất
M
và giá trị nhỏ nhất
m
trên đoạn
5
;
6 6
. Tìm
,M m
.
Lời giải
Ta có:
5
6 6
x
1
sin 1
2
x
1
1 sin
2
x
4 4sin 2
x
3 7 4sin 9
x
4 12
4
3 7 4sin x
. Hay
4
4
3
y
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 12
Vậy
4M
,
4
3
m
.
Bài 6. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2siny x
trên đoạn
5
;
6 6
.
Lời giải
2cos 0
2
y x x k
,
k
.
Với
5
;
6 6
x
suy ra:
2
x
.
1
6
y
,
2
2
y
,
5
1
6
y
.
Vậy giá trị lớn nhất của hàm số là 2 và giá trị nhỏ nhất của hàm số là
1
.
BÀI TẬP TRẮC NGHIỆM
MỨC ĐỘ 2
Câu 1. Tìm tập giá trị của hàm số
3sin cos 2
y x x
.
A.
2; 3
. B.
3 3; 3 1
. C.
4;0
. D.
2;0
.
Lời giải
Chọn C
Xét
3sin cos 2
y x x
2 sin .cos cos .sin 2
6 6
x x
2sin 2
6
x
.
Ta có
1 sin 1
6
x
4 2sin 2 0
6
x
4 0
y
với mọi
x
.
Vậy tập giá trị của hàm số là
4;0
.
Câu 2. Giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của hàm số
sin 2cos 1
sin cos 2
x x
y
x x
là
A.
1
2
m
;
1M
. B.
1
m
;
2M
. C.
2
m
;
1M
. D.
1
m
;
2M
.
Lời giải
Chọn C
Ta có
sin 2cos 1
1 sin 2 cos 1 2
sin cos 2
x x
y y x y x y
x x
*
.
Phương trình
*
có nghiệm
2 2 2
2
1 2 1 2 2 0 2 1y y y y y y
.
Vậy
2
m
;
1M
.
Câu 3. Giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
12
7 4sin
y
x
trên đoạn
5
;
6 6
là
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 13
A.
12
5
M
;
4
3
m
. B.
4M
;
4
3
m
. C.
12
5
M
;
12
7
m
. D.
4M
;
12
11
m
.
Lời giải
Chọn B
Do
5 1 12
; sin ;1 0
6 6 2 7 4sin
x x y
x
;
12 7 12 1 4
7 4 sin 12 sin ;1 ;4
7 4sin 4 2 3
y
y y y x x y
x y
.
Do đó
1
;1
2
max 1 4
M f t f
và
1
;1
2
1 4
min
2 3
m f t f
.
Câu 4. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
siny x
trên đoạn
;
2 3
lần lượt là
A.
1
2
;
3
2
. B.
3
2
;
1
. C.
3
2
;
2
. D.
2
2
;
3
2
.
Lời giải
Chọn B
Ta có:
2 3
x
sin sin sin
2 3
x
3
1 sin
2
x
.
Vậy
;
2 3
3
max sin
3 2
y
;
;
2 3
min sin 1
2
y
.
Câu 5. Gọi
M
,
m
tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2cos 1
cos 2
x
y
x
. Khẳng định
nào sau đây đúng?
A.
9 0
M m
. B.
9 0
M m
. C.
9 0
M m
. D.
0
M m
.
Lời giải
Chọn C
Ta có
2cos 1 5
2
cos 2 cos 2
x
y
x x
.
Mà
1 cos 1x
3 cos 2 1
x
5 5
5
3 cos 2x
1 5
2 3
3 cos 2x
1
3
3
y
.
Vậy
1
3
M
và
1 cos 1x
9 0
M m
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 14
MỨC ĐỘ 3
BÀI TẬP TỰ LUẬN
Bài 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
10
2020cos 8 2021
2019
y x
.
Lời giải
Ta có
10
1 cos 8 1,
2019
x x
.
Nên
10
2020 2020cos 8 2020
2019
x
10
1 2020cos 8 2021 4041
2019
x
.
Vậy
min 1y
đạt được khi
10
cos 8 1
2019
x
,
max 4041
y
đạt được khi
10
cos 8 1
2019
x
.
Bài 2. Tìm GTNN của hàm số
2
cos 2 cosy x x
.
Lời giải
Ta có
cos 1
x
, dấu “
” xảy ra khi
cos 1
x
. (1)
Mặt khác
2 2 2
0 cos 1 1 cos 0 1 2 cos 2
x x x
.
2
2 cos 1
x
, dấu “
” xảy ra khi
cos 1
x
. (2)
Từ (1) và (2) ta có
2
cos 2 cos 0
x x
.
Suy ra
min 0
y
, đạt được khi
cos 1 2x x k k
.
Bài 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
cos 2 3 sin 2 2
y x x
.
Lời giải
Ta có
1 3
cos2 3sin 2 2 2 cos2 sin 2 2
2 2
y x x x x
2 cos cos 2 sin sin 2 2 2cos 2 2
3 3 3
x x x
.
Mặt khác
1 cos 2 1 2 2cos 2 2 0 2cos 2 2 4
3 3 3
x x x
.
Vậy
min 0
y
đạt được khi
cos 2 1
3
x
,
max 4
y
đạt được khi
cos 2 1
3
x
.
Bài 4. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
2cos 2 3 sin .cos 1y x x x
trên đoạn
7
0;
12
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 15
Lời giải
Ta có
cos 2 3 sin 2 2 2cos 2 2
3
y x x x
.
Đặt
2
3
t x
. Theo giả thiết
7 3
0; ;
12 3 2
x t
.
Ta lập BBT của hàm số
2cos 2f t t
trên
3
;
3 2
.
Từ bảng biến thiên ta có
7 3
0; ;
12 3 2
min min 0
y f t
, đạt được khi
3
t x
7 3
0; ;
12 3 2
max max 3
y f t
,
đạt được khi
0
3
t x
Bài 5. Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số
2
cos cos 2y x x
.
Lời giải
Đặt
cos x t
;
1;1
t
Xét hàm số bậc hai:
2
2f t t t
trên
1;1
.
Ta có:
1
1;1
2 2
b
a
. Từ đây có bảng biến thiên
Ta kết luận:
1;1
7
min min
4
y f t
, đạt được khi
1
cos
2
x
;
1;1
max max 4
y f t
, đạt được khi
cos 1
x
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 16
BÀI TẬP TRẮC NGHIỆM
Câu 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
2 2
2sin cos 2y x x
.
A.
max 4
y
,
3
min
4
y
. B.
max 3
y
,
min 2
y
.
C.
max 4
y
,
min 2
y
. D.
max 3
y
,
3
min
4
y
.
Lời giải
Chọn D
Đặt
2
sin , 0 1 cos2 1 2t x t x t
.
2
2
2
1 3
2 1 2 4 2 1 2
2 4
y t t t t t
.
Cách 1: Do
2
1 1 3 1 9
0 1 2 0 2
2 2 2 2 4
t t t
3
3
4
y
.
Cách 2: Có
' 8 2y t
1
0 0;1
4
y t
.
Ta có:
0 1
y
;
1 3
4 4
y
;
1 3
y
.
Vậy
max 3
y
đạt được khi
2
x k
.
3
min
4
y
đạt được khi
2
1 1 cos 2 1
sin
4 2 4
x
x
.
1
cos 2 2 2
2 3 6
x x k x k
.
Câu 2. Tìm giá trị nhỏ nhất của hàm số sau
2 2
tan cot 3 tan cot 1
y x x x x
.
A.
min 2
y
. B.
min 4
y
. C.
min 5
y
. D.
min 1
y
.
Lời giải
Chọn C
Ta có:
2
tan cot 3 tan cot 3
y x x x x
.
Đặt
2
tan cot 2
sin 2
t x x t
x
.
Suy ra
2
3 3
y t t f t
.
Bảng biến thiên
Vậy
min 5
y
đạt được khi
4
x k
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 17
Câu 3. Gọi giá trị lớn nhất và nhỏ nhất của hàm số
2
sin 2 siny x x
là
M
,
m
. Tính
M m
.
A.
3
. B.
4
. C.
6
. D.
2
.
Lời giải
Chọn D
Ta có
1 sin 0 ,y x x
và
2 2
2 2sin 2 siny x x
.
Mà
2 2 2
2 sin 2 sin sin 2 sin 2
x x x x
.
Suy ra
2
0 4 0 2
y y
.
Vậy
min 0
y
đạt được khi
2
2
x k
.
max 2
y
đạt được khi
2
2
x k
.
Vậy
2, 0
M m
hay
2
M m
.
Câu 4. Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số
sin 2cos 3
2 cos
x x
y
x
.
A.
2
min ; max 2
3
y y
. B.
2
min ; max 2
3
y y
.
C.
1 3
min ; max
2 2
y y
. D.
1 3
min ; max
2 2
y y
.
Lời giải
Chọn B
Cách 1: Ta có
cos 2 0
x
,
x
.
sin 2cos 3
2 cos
x x
y
x
sin 2cos 3 2 cosx x y y x
sin 2 cos 2 3x y x y
Ta có
2
2 2
2 2 2
2 3 sin 2 cos 1 2 sin cos 5 4
y x y x y x x y y
2 2
4 12 9 4 5 0
y y y y
2
3 8 4 0
y y
2
2
3
y
Cách 2: (dùng sau khi học xong bài phương trình bậc nhất theo sin và cos).
Ta có
cos 2 0
x
,
x
.
sin 2cos 3
2 cos
x x
y
x
sin 2cos 3 2 cosx x y y x
sin 2 cos 3 2 0
x y x y
Ta có
2 2
2
1 2 3 2y y
2 2
4 12 9 4 4 1 0
y y y y
2
3 8 4 0
y y
2
2
3
y
.
Cách 3: sử dụng máy tính cầm tay.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 18
Tương tự như ở ví dụ 1 thì ta có thể sử dụng SHIFT SOLVE:
sin 2cos 3
2
2 cos
x x
x
thì phương trình
có nghiệm. Do 2 là số lớn nhất trong các phương án A; B; C; D nên ta không cần thử trường hợp
3
max
2
.
Lúc này chỉ còn A và B Thử với
2
min
3
y
thì không có nghiệm.
Từ đây chọn B.
Câu 5. Cho hàm số
4 4
sin cos 2 sin .cosh x x x m x x
. Tất cả các giá trị của tham số
m
để hàm số xác
định với mọi số thực
x
(trên toàn trục số) là
A.
1 1
2 2
m
. B.
1
0
2
m
. C.
1
0
2
m
. D.
1
2
m
.
Lời giải
Chọn A
Xét hàm số
2 2
2 2
sin cos sin 2g x x x m x
2
2 2 2 2
sin cos 2sin cos sin 2x x x x m x
2
1
1 sin 2 sin 2
2
x m x
.
Đặt
sin 2t x
1;1
t
.
Hàm số
h x
xác định với mọi
x
0,g x x
2
1
1 0, 1;1
2
t mt t
2
2 2 0, 1;1
t mt t
.
Đặt
2
2 2f t t mt
trên
1;1
.
Đồ thị hàm số có thể là một trong ba đồ thị trên.
Ta thấy
1;1
max 1f t f
hoặc
1;1
max 1
f t f
.
Ycbt
2
2 2 0
f t t mt
,
1;1
t
1;1
max 0
f t
1 0
1 0
f
f
1 2 0
1 2 0
m
m
1 1
2 2
m
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 19
MỨC ĐỘ 4
BÀI TẬP TỰ LUẬN
Bài 1. Tìm giá trị nhỏ nhất của hàm số
sin cos cos siny x x x x
.
Lời giải
Điều kiện xác định:
sin 0
cos 0
x
x
.
Áp dụng bất đẳng thức Cô-si cho 2 số không âm
sin cosx x
và
cos sinx x
ta có :
sin cos cos sin 2 sin cos sin cosx x x x x x x x
1 1
2 sin 2 sin 2 0
2 2
y x x
.
Dấu bằng xảy ra khi và chỉ khi
sin 2 0 2 , ,
2
k
x x k k x k
.
Bài 2. Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số
sinx 2cos 3
2 cos
x
y
x
.
Lời giải
Ta có:
cos 2 0,
x x R
.
Khi đó:
sinx 2cos 3
2 cos
x
y
x
sinx 2 cos 3 2 cosx y y x
sinx 2 cos 3 2 0 *
y x y
Phương trình
*
có nghiệm
2 2
2
1 2 3 2y y
2 2
4 12 9 4 4 1 0
y y y y
2
3 8 4 0
y y
2
2
3
y
.
Vậy
2
min ;max 2
3
y y
.
Bài 3. Tìm giá trị nhỏ nhất của biểu thức
4 4 2 2
cot cot 2 tan .tan 2
P a b a b
.
Lời giải
Ta có:
2
2 2 2 2 2 2
2
2 2 2 2 2 2
2
2 2 2 2 2 2
2
2
2 2
cot cot 2cot .cot 2 tan .tan 2
cot cot 2 cot .cot tan .tan 2 6
cot cot 2 cot .cot tan .tan 2cot .cotb.tan .tan 6
cot cot 2 cot .cot tan .tan 6 6
P a b a b a b
a b a b a b
a b a b a b a a b
a b a b a b
Vậy
min 6
y
, đạt được khi
2
2 2
2
cot 1
cot cot
cot .cot tan .tan
cot 1
a
a b
a b a b
b
,( )
4 2
k
a b k
.
Bài 4. Tìm giá trị nhỏ nhất của hàm số
2 2
1 1
1 os 5 2sin
2 2
y c x x
.
Lời giải
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 20
Ta có
2 2 2 2
1 1 1 5 1
1 os 5 2sin 1 os sin
2 2 2 4 2
y c x x y c x x
Áp dụng bất đẳng thức Bunyakopvsky cho
4
số: 1; 1;
2
1
1 os
2
c x
;
2
5 1
sin
4 2
x
ta có:
2 2 2 2 2 2
1 5 1 1 5 1 9 1 22
1. 1 os 1. sin 1 1 . 1 os sin 2.
2 4 2 2 4 2 4 2.1 2
c x x c x x
.
Vậy
22
min
2
y
, xảy ra khi
2 2
1 5 1
1 os sin ,
2 4 2 6
c x x x k k
.
Bài 5. Tìm giá trị lớn nhất của hàm số
4 4
sin cos sin cosy x x x x
.
Lời giải
Ta có
4 4
sin cos sin cosy x x x x
2 2
1 2sin cos sin cosy x x x x
2
1 1
1 sin 2 sin 2
2 2
y x x
2 2
1 1 1 9 1 1 9
1 sin 2 sin 2
2 2 4 8 2 2 8
y x y x
.
Vậy
9
max
8
y
,
đạt được khi
1
sin 2
2
x
.
BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho
, , 0
x y z
và
2
x y z
. Tìm giá trị lớn nhất của
1 tan .tan 1 tan .tan 1 tan .tany x y y z z x
A.
max
1 2 2
y
. B.
max
3 3
y
. C.
max
4
y
. D.
max
2 3
y
.
Lời giải
Chọn D
Ta có
tan tan
2 2 2
x y z x y z x y z
tan tan 1
1 tan .tan tan
x y
x y z
tan .tan tan .tan 1 tan .tanx z y z x y
tan .tan tan .tan tan .tan 1x z y z x y
Ta thấy
tan .tan ; tan .tan ; tan .tanx z y z x y
lần lượt xuất hiện trong hàm số đề bài cho.
Khi đó, áp dụng bất đẳng thức Bunyakovsky cho 6 số ta có:
1. 1 tan .tan 1. 1 tan .tan 1. 1 tan .tan
x y y z z x
2 2 2
1 tan .tan 1 tan .tan 1 tan .ta1 1 1 .
nx z y z x y
tan .tan tan .tan tan .ta
2
n
3 3 3
x z y z x y
.
Vậy
max
2 3
y
.
Câu 2: Hàm số
2
2
3 1 tan
3cot 2
tan
x
y x
x
đạt giá trị nhỏ nhất là
A.
1
. B.
3 2 3
. C.
2 2 2
. D.
0
.
Lời giải
Chọn A
Ta có
2
1 tan
cot 2
2tan
x
x
x
.
Từ đó suy ra
2
2 2
2 3 1 tan
3cot 2 3cot 2 2 3 cot 2
2 tan
x
y x x x
x
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 21
2
3 cot 2 1 1 1,x x
.
Vậy
min 1 cot 2
y x
.
Câu 3: Hàm số
2cos sin
4
y x x
đạt giá trị lớn nhất là
A.
5 2 2
. B.
5 2 2
. C.
5 2 2
. D.
5 2 2
.
Lời giải
Chọn C
Ta có:
1
2cos sin 2cos 2 sin
4 4
2
y x x x x
1
2cos sin cos
2
x x x
1 1
2 cos sin
2 2
x x
.
Áp dụng bất đẳng thức Bunyakovsky ta có:
2 2
2 2
1 1
2 5 2 2
2 2
y y
.
Do đó
5 2 2 5 2 2
y
.
Vậy giá trị lớn nhất của hàm số là
5 2 2
.
Câu 4: Có bao nhiêu giá trị nguyên của tham số
m
để giá trị lớn nhất của hàm số
sin 1
cos 2
m x
y
x
nhỏ hơn
2
.
A.
3
. B.
5
. C.
4
. D.
6
.
Lời giải
Chọn B
Ta có:
sin 1
cos 2 sin 1 sin cos 2 1
cos 2
m x
y y x y m x m x y x y
x
*
*
có nghiệm khi
2
2 2 2 2
2 1 3 4 1 0
m y y y y m
2 2
2 1 3 2 1 3
3 3
m m
y
2
2 2
max
2 1 3
2 1 3 4 5
3
m
y m m
.
Do
m
2; 1;0;2;1
m
. Vậy có
5
giá trị của
m
thỏa ycbt.
Câu 5: Số giờ có ánh sáng của một thành phố
A
trong ngày thứ
t
của năm
2020
được cho bởi một hàm số
4sin 60 10
178
y t
, với
t Z
và
0 366
t
. Vào ngày nào trong năm thì thành phố
A
có
nhiều giờ ánh sáng mặt trời nhất ?.
A.
28
tháng
5
. B.
29
tháng
5
. C.
30
tháng
5
. D.
31
tháng
5
.
Lời giải
Chọn A
Vì
sin 60 1 4sin 60 10 14
178 178
t y t
.
Khi đó, ngày có ánh nắng mặt trời chiếu nhiều nhất là
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 22
14 sin 60 1 60 2 149 356
178 178 2
y t t k t k
.
Mà
149 217
0 366 0 149 356 366
356 356
t k k
.
Vì
k
nên
0
k
.
Với
0 149
k t
tức rơi vào ngày
28
tháng
5
(vì ta đã biết tháng
1
và
3
có
31
ngày, tháng
4
có
30
ngày, riêng đối với năm
2020
là năm nhuận nên tháng
2
có
29
ngày hoặc dựa vào dữ kiện
0 366
t
thì ta biết năm này tháng
2
có
29
ngày).
NHÓM WORD – BIÊN SOẠN TÀI LIỆU TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM:
https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/
Trang 23
| 1/23
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11
TẬP GIÁ TRỊ VÀ MAX - MIN CỦA HÀM SỐ LƯỢNG GIÁC PHƯƠNG PHÁP
1. Các kiến thức về giá trị lớn nhất, giá trị nhỏ nhất
Cho hàm số y f x xác định trên miền D R .  f
  x  M , x   D
a. Số thực M được gọi là giá trị lớn nhất của hàm số y f x trên D nếu  x   D, f xM   0  0   f
  x  m, x   D
b. Số thực N được gọi là giá trị nhỏ nhất của hàm số y f x trên D nếu  x   D, f xm   0  0 
2. Một số kiến thức ta sử dụng trong các bài toán này 2 1  sin x  1  0  sin x  1
a) Dựa vào tập giá trị của hàm số lượng giác, chẳng hạn :    2 1  cos x  1  0  cos x  1 
b) Bảng biến thiên của hàm số lượng giác.
c) Kỹ thuật sử dụng máy tính cầm tay.  MỨC ĐỘ 1 BÀI TẬP TỰ LUẬN
Bài 1. Tìm giá trị lớn nhất và nhỏ nhất của đồ thị hàm số y  3  sin x Lời giải
Tập xác định D   .
Ta có: 1  sin x  1 x   
 1   sin x  1 x   
 3 1  3  sin x  3    1 x     4  y  2 x   
Ta có: y  4 khi sin x  1
 và y  2 khi sin x  1
Vậy min y  2 và max y  4 .
Bài 2. Tìm tập giá trị T của hàm số y  3cos 2x  5
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 1
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11 Lời giải
Tập xác định D   .
Ta có: 1  cos 2x  1  3  3cos 2x  3  3
  5  3cos 2x  5  3  5  8   y  2 
Vậy tập giá trị của hàm số y  3cos 2x  5 là T   8  ; 2  
Bài 3. Tìm tập giá trị T của hàm số 2 2
y  sin x  2 cos x 1 trên khoảng  Lời giải Ta có: 2 2 2 y x x   x   2  x 2 sin 2 cos 1 sin 2 1 sin 1  3  sin x Với x   thì 2 2
0  sin x  1  0   sin x  1 2
 3  3  sin x  3 1  2
Vậy tập giá trị của hàm số 2 2
y  sin x  2 cos x 1 trên  là T  2 ;  3 1
Bài 4. Tìm giá trị nhỏ nhất m của hàm số y  cos x 1 Lời giải
ĐKXĐ: cos x  -1  x   k2 . TXĐ: D   / k2 1 1 Ta có: x   D : 1
  cos x  1  0  1 cos x  2   1 cos x 2 1 Ta có: y  khi cos x  1 . 2 1 Vậy, min y  . 2   
Bài 5. Tìm giá trị nhỏ nhất của biểu thức P  2 sin x  1    3  Lời giải          Ta có: sin x   1   2 sin x   2   2 sin x  1  1        3   3   3    
Dấu " = " xảy ra khi và chỉ khi sin x   1    .  3 
Vậy giá trị nhỏ nhất của biểu thức P là 1.
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 2
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11
BÀI TẬP TRẮC NGHIỆM  10 
Câu 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y  2017 cos 8 x   2016    2017 
A. min y  1 ; maxy  4033
B. min y  1 ; maxy  4033
C. min y  1 ; maxy  4022
D. min y  1 ; max y  4022 Lời giải Chọn B
Hàm số xác định trên   10 
Ta có 1  cos 8 x   1, x       2017   10 
 2017  2016  2017 cos 8 x
 2016  2017  2016, x      .  2017   10   1
  2017 cos 8 x   2016  4033, x       2017   10   10  Ta có y  1  khi cos 8 x   1  
; y  4033 khi cos 8 x   1   .  2017   2017 
Vậy min y  1 ; maxy  4033 .
Câu 2. Giá trị nhỏ nhất và lớn nhất của hàm số y  4 cos x là: A. 0 và 4. B.  4 và 4. C. 0 và 1. D.  1 và 1. Lời giải Chọn B
Tập xác định: D  0 ;   .
Ta có: 1  cos x  1 , x  0 ;  
 4  4 cos x  4 , x  0 ;  
Ta có y  4 khi cos x  1
 và y  4 khi cos x  1.
Vậy min y  4 ; max y  4   
Câu 3. Cho hàm số y  sin x  . 
 Giá trị lớn nhất của hàm số là:  4   A. 1. B. 0 . C. 1. D. . 4 Lời giải Chọn C      
Ta có: 1  sin x   1  
. Suy ra giá trị lớn nhất của hàm số y  sin x    là 1.  4   4 
Câu 4. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số 2
y  1  cos x  2 là: A. 0 và 2 1. B. 1 và 2 1.
C. 2 và 1 D. 1 và 1 Lời giải
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 3
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11 Chọn C Ta có 2 2
y  1 cos x  2  sin x  2  sin x  2
Mặt khác 0  sin x  1  2
  sin x  2  1   2   y  1 
Ta có: y  2 khi sin x  0 và y  1  khi sin x  1
Vậy giá trị lớn nhất và nhỏ nhất của hàm số là 2 và 1.   
Câu 5. Cho hàm số y  2 sin x   2  
. Mệnh đề nào sau đây là đúng?  3  A. y  4  , x    B. y  4 , x    C. y  0 , x    D. y  2 , x    Lời giải Chọn C   
Ta có 1  sin x   1 , x       3    
 2  2 sin x   2  , x       3    
 4  2 sin x   2  0 , x       3       
Ta có: y  4 khi sin x   1   
và y  0 khi sin x   0    3   3 
Suy ra chọn đáp án C. MỨC ĐỘ 2 BÀI TẬP TỰ LUẬN  10 
Bài 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y  2017 cos 8x   2016   .  2017  Lời giải
Cách 1: Hàm số xác định trên  .  10 
Ta có : 1  cos 8x   1   , x     2017   10   2
 017  2017 cos 8x   2017   , x     2017   10 
 1  2017 cos 8x   2016  4033   , x     2017   10   10 
Ta có y  1 khi cos 8x   1  
; y  4033 khi cos 8x   1   .  2017   2017 
Vậy min y  1; maxy  4033 .
Bài 2. Tìm giá trị nhỏ nhất của hàm số: 2
y  2 cos x  sin 2x  5 .
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 4
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11 Lời giải    Ta có 2
y  2 cos x  sin 2x  5  cos 2x  sin 2x  6  2 cos 2x   6   .  4        Do  2  2 cos 2x   2   nên  2  6  2 cos 2x   6  2  6   .  4   4 
Vậy giá trị nhỏ nhất của hàm số 2
y  2 cos x  sin 2x  5 là 6  2 .
Bài 3. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  sin x  cos x . Tính P M m . Lời giải   
Ta có y  sin x  cos x  2 sin x    .  4         M  2 Mà 1  sin x
 1   2  2 sin x   2        P  2 2 .  4   4  m   2  Vậy P  2 2 . sin x  1
Bài 4. Tìm giá trị nhỏ nhất của hàm số y  . cos x  2 Lời giải sin x 1
Cách 1 : cos x  2  0 , x
   . Vậy y
 sin x 1  y cos x  2 cos x  2
 sin x y cos x 1 2 y  0 . 2 2 4 Ta có 2
1   y  1 2 y 2 2 2
y 1  4 y  4 y 1  3y  4 y  0  0  y  . 3 Vậy min y  0 min. sin  x 1  0
Cách 2 : Ta có 
y  0  min y  0  sin x  1  . cos x  2  0 
Bài 5. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: 2
y  2 cos x  2 3 sin x cos x  1 . Lời giải Cách 1: 2
y  2 cos x  2 3 sin x cos x  1 2
 2 cos x 1 3 sin 2x  2  cos 2x  3 sin 2x  2  1 3      2  cos 2x
sin 2x   2  2 cos 2x   2 .    2 2     3    
Mặt khác 0  2 cos 2x   2  4   , x
    0  y  4 , x    .  3  Cách 2: 2
y  2 cos x  2 3 sin x cos x  1 2
 2 cos x 1 3 sin 2x  2  cos 2x  3 sin 2x  2   *
Ta có  1 3  2  y  1  3  2  0  y  4 .
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 5
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11
BÀI TẬP TRẮC NGHIỆM Câu 1.
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 2 2
y  sin x  2 cos x .
A. M  2 , m  0 .
B. M  2 , m  1.
C. M  3 , m  1.
D. M  3 , m  0. Lời giải Chọn B Ta có: 2 2 y x x   2 2 x x 2 2 sin 2 cos sin cos
 cos x  1 cos x . M  2 Do 2 2 1
  cosx  1 0  cos x  1  1  cos x  2 . Suy ra  . m  1  Câu 2.
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  8sin x  3cos 2x . Tính Tính 2
P  2M m .
A. P  1 .
B. P  2 . C. 112 .
D. P  130 . Lời giải Chọn A Ta có: 2 2 y x x x   2  x 2 8sin 3cos 2 8sin 3 1 2 sin  2 sin x  3 . M  5 Mà 1   sinx  1 2 2
 0  sin x  1  3  2sin x  3  5  3  y  5 . Suy ra:  . m  3  Do đó: 2
P  2M m  1. Câu 3.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  3sin x  4 cos x 1.
A. max y  8 , min y  6 .
B. max y  4 , min y  6 .
C. max y  6 , min y  8 .
D. max y  6 , min y  4 . Lời giải Chọn B
Ta có y  3sin x  4 cos x 1  3sin x  4 cos x y 1   * Ta coi  
* như là phương trình cổ điển với a  3, b  4 , c y 1 . Phương trình  
* có nghiệm khi và chỉ khi a b c     y  2 2 2 2 9 16 1  6  y  4 .
Vậy max y  4 , min y  6 . Chú ý:
Ta có thể áp dụng bất đẳng thức BCS như sau: y   x x   2 2   2 2 1 3sin 4 cos 3 4
sin x  cos x  5 . Câu 4.
Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số 2
y  sin x  sin x  2 . 7 7 A. min y  ; max y  4 . B. min y  ; max y  2 . 4 4
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 6
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11 1
C. min y  1; max y  1. D. min y  ; max y  2 . 2 Lời giải Chọn A
Đặt sin x u ; u  1   ;1 . Xét hàm số: 2
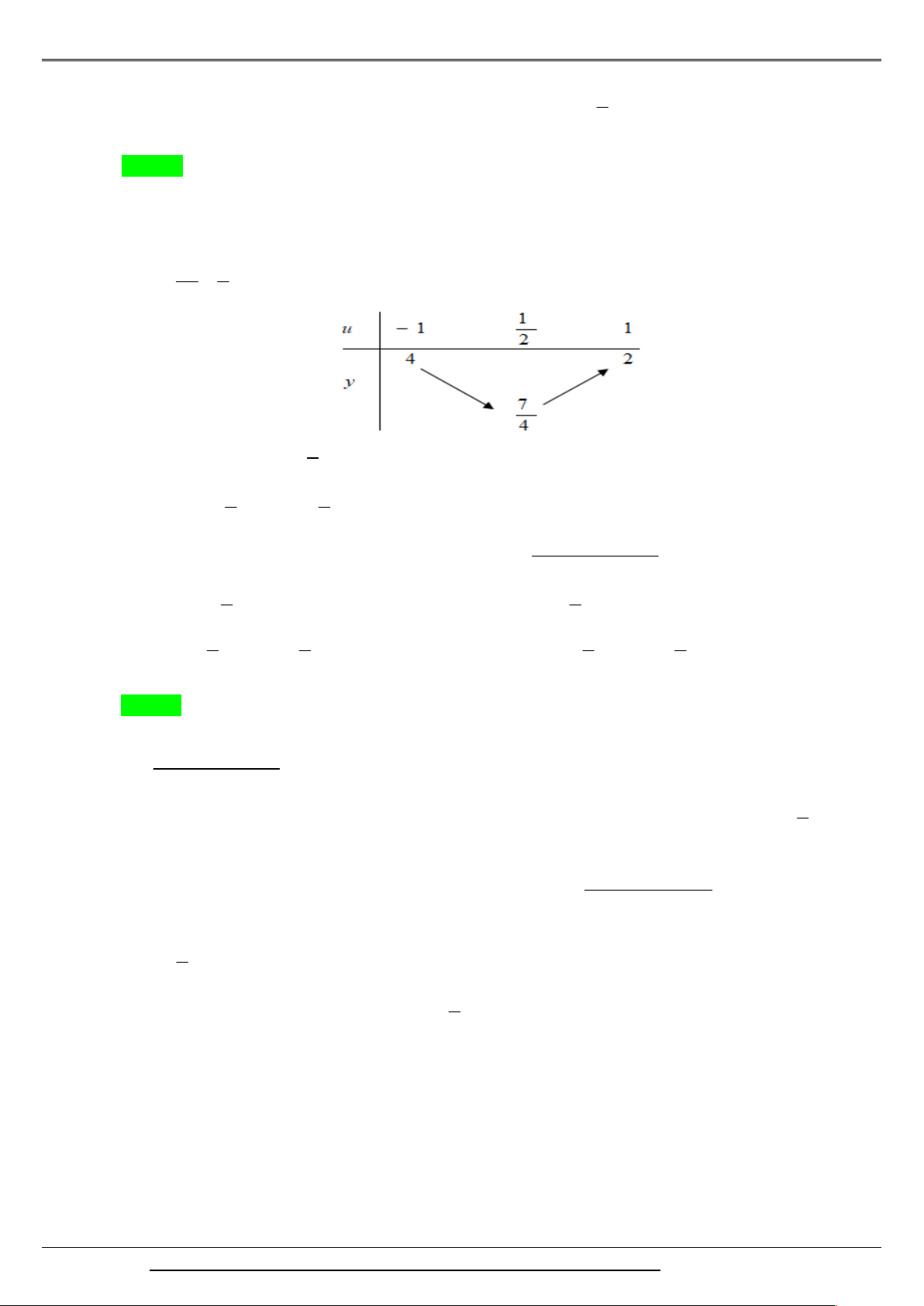
y u u  2 trên  1   ;1 . b 1 Ta có:  1; 
1 . Từ đây có bảng biến thiên 2a 2 7
Ta kết luận: min f u 
và max y  4  u  1  .  1  ;  1 4  1  ;  1 7 1 Hay min y   sin x
và max y  4  sin x  1. 4 2
sin x  2 cos x  3 Câu 5.
Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y 2  cos x 2 2 A. min y   ; max y  2 B. min y  ; max y  2 . 3 3 1 3 1 3 B. min y  ; max y  . D. min y   ; max y  . 2 2 2 2 Lời giải Chọn B
Cách 1: Ta có cos x  2  0 , x    .
sin x  2 cos x  3 y
 sin x  2 cos x  3  2 y y cos x  sin x  2  y cos x  3  2y  0 . 2  cos x 2 2 2 Ta có: 2
1  2  y   3  2 y  2 2
 4 y 12 y  9  y  4 y  4 1  0 2
 3y  8 y  4  0   y  2 . 3
Cách 2 : sử dụng máy tính cầm tay sin x  2 cos x  3
Tương tự như ở ví dụ 1 thì ta có thể sử dụng SHIFT SOLVE:  2 thì phương trình 2  cos x
có nghiệm. Do 2 là số lớn nhất trong các phương án A; B; C; D nên ta không cần thử trường hợp 3 max  . 2 2
Lúc này chỉ còn A và B. Thử với min y   thì không có nghiệm. 3
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 7
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11  MỨC ĐỘ 1 BÀI TẬP TỰ LUẬN   
Bài 1. Tìm tập giá trị của các hàm số sau: y  3cos x   2    3  Lời giải       Vì 1  cos x   1  
nên 3  3cos x   3  3
  2  y  3  2  1  y  5   .  3   2 
Vậy tập gái trị của hàm số là  1  ;  5 .
Bài 2. Tìm tập giá trị của các hàm số sau: y  3  2 sin 2x . Lời giải
Ta có: 1  sin 2x  1  2  2 sin 2x  2  1  3  2 sin 2x  5  1  3  2 sin 2x  5 .
Vậy tập giá trị của hàm số là 1  ; 5 .  
Bài 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau: y  4 sin x cos x 1 . Lời giải
Ta có y  2 sin 2x 1 . Do 1
  sin 2x  1  2
  2 sin 2x  2  1
  2sin 2x 1  3  1  y  3 .  
* y  1  sin 2x  1   2x  
k 2  x    k . 2 4 
* y  3  sin 2x  1  x   k . 4 
Vậy giá trị lớn nhất của hàm số bằng 3 , đạt được khi x   k . 4 
giá trị nhỏ nhất bằng 1
 , đạt được khi x    k . 4
Bài 4. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau: 2
y  4  3sin 2x . Lời giải Ta có: 2 2
0  sin x  1  1  4  3sin x  4 .  * 2
y  1  sin x  1  cos x  0  x   k . 2
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 8
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11 * 2
y  4  sin x  0  x k .
Vậy giá trị lớn nhất của hàm số bằng 4 , đạt được khi x k . 
giá trị nhỏ nhất bằng 1, đạt được khi x   k . 2
Bài 5. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y  2 sin x  3 . Lời giải
Ta có 1  2 sin x  3  5  1  y  5 . 
Vậy giá trị lớn nhất của hàm số bằng max y  5 , đạt được khi sin x  1  x   k 2 . 2 
Giá trị nhỏ nhất bằng min y  1, đạt được khi x  1  x    k 2 . 2
BÀI TẬP TRẮC NGHIỆM   
Câu 1. Tìm tập giá trị hàm số sau y  1 3sin 2x    .  4  A.  2  ; 4 . B.  2  ; 2 . C.  1  ; 4 . D.  2  ;  3 . Lời giải Chọn A         
Ta có: 1  sin 2x
 1  3  3sin 2x   3  2
  1 3sin 2x   4       .  4   4   4   2  y  4 .
Vậy tập giá trị của hàm số là  2  ; 4 .   
Câu 2. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y  2 cos 3x   3    3 
A. min y  2 , max y  5 .
B. min y  1, max y  4 .
C. min y  1, max y  5 .
D. min y  1, max y  3 . Lời giải Chọn C         
Ta có: 1  cos 3x
 1  2  2 cos 3x
 2  1  2 cos 3x
 3  5  1  y  5       .  3   3   3  4 2
min y  1 đạt được khi x   k . 9 3  2
max y  5 đạt được khi x   k . 9 3
Câu 3. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau 2
y  1 2 cos x 1
A. max y  1 , min y  1  3 .
B. max y  3 , min y  1  3 .
C. max y  2 , min y  1  3 .
D. max y  0 , min y  1  3 .
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 9
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11 Lời giải Chọn D Ta có 2
1  2 cos x 1  3  1 3  y  0 . 
Vậy giá trị nhỏ nhất của hàm số bằng max y  0 , đạt được khi x   k . 2
Giá trị nhỏ nhất của hàm số bằng min y  1  3 , đạt được khi x k .   
Câu 4. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y  1 3sin 2x    .  4 
A. min y  2 , max y  4 .
B. min y  2 , max y  4 .
C. min y  2 , max y  3 . D. min y  1  , max y  4 . Lời giải Chọn A   
Ta có: 1  sin 2x
 1  2  y  4    4     
y  2  sin 2x   1   x    k    min y  2   4  8    3
y  4  sin 2x   1  x   k    max y  4  4  8
Câu 5. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau 2
y  3  2 cos 3x
A. min y  1, max y  2 .
B. min y  1, max y  3 .
C. min y  2 , max y  3 . D. min y  1  , max y  3 . Lời giải Chọn C Ta có: 2
0  cos 3x  1  1  y  3 . k  2
y  1  cos 3x  1  x   min y  1. 3  k  2
y  3  cos 3x  0  x  
 max y  3 . 6 3
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 10
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11  MỨC ĐỘ 2 BÀI TẬP TỰ LUẬN    Bài 1.
Tìm giá trị lớn nhất của hàm số 2 y  3sin x   4    12  Lời giải          Ta có 2 2 2 sin x   1  3sin x   3  3sin x   4  7       .  12   12   12 
Vậy giá trị lớn nhất của hàm số bằng 7 . Bài 2.
Tìm giá trị lớn nhất của hàm số f x 2
 2sin x  sin 2x 10 . Lời giải   
Ta có f x 2
 2sin x  sin 2x 10  11  sin 2x  cos 2x  11 2 sin 2x    .  4           Do 1  sin 2x   1     2  2 sin 2x   2  
nên 11 2 sin 2x   11 2   .  4   4   4     3
Dấu "  ' xảy ra khi sin 2x   1   x    k  
, k  . Vậy max f x  11 2 .  4  8 Bài 3.
Tìm giá trị nhỏ nhất của hàm số 2
y  2 cos x  sin 2x  5 . Lời giải    Ta có 2
y  2 cos x  sin 2x  5  cos 2x  sin 2x  6  2 cos 2x   6   .  4       
Do  2  2 cos 2x   2  
nên  2  6  2 cos 2x   6  2  6   .  4   4 
Vậy giá trị nhỏ nhất của hàm số 2
y  2 cos x  sin 2x  5 là 6  2 . Bài 4.
Giả sử M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số y  2  3sin x  cos x . Tính
M m . Lời giải 2 2
Ta có:  2  3 1  2  3sin x  cos x  2  3 1.
Vậy M m  0 . 12   5  Bài 5. Cho hàm số y
có giá trị lớn nhất M và giá trị nhỏ nhất m trên đoạn  ; . Tìm 7  4 sin x  6 6    M , m . Lời giải Ta có:  5 1 1   x   
 sin x  1  1   sin x
 4  4 sin x  2  3  7  4 sin x  9 6 6 2 2 4 12 4    4 . Hay  y  4 . 3 7  4 sin x 3
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 11
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11 4
Vậy M  4 , m  . 3   5  Bài 6.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2 sin x trên đoạn  ;  . 6 6    Lời giải
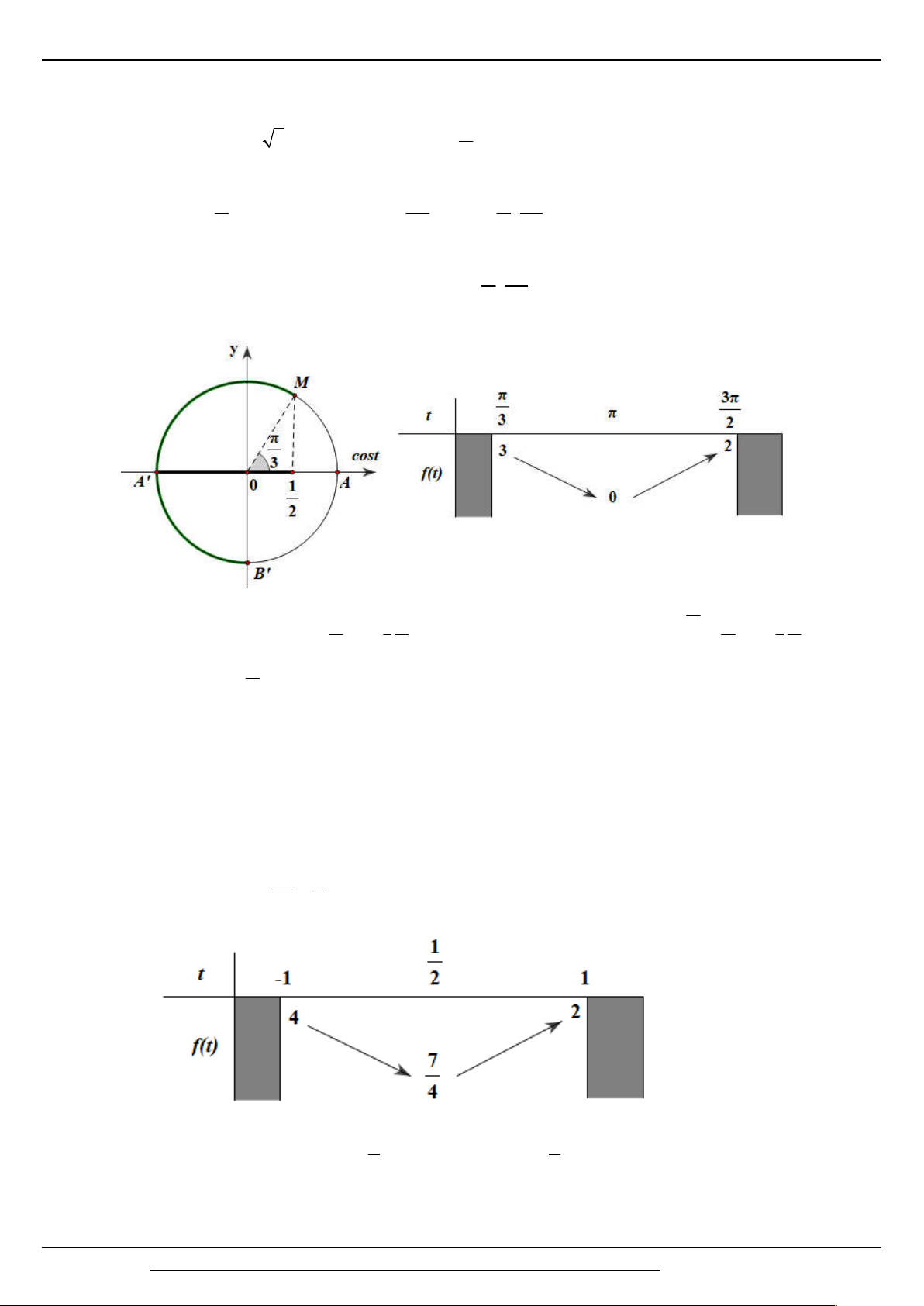
y  2 cos x  0  x
k , k . 2   5   Với x   ;  suy ra: x  . 6 6    2        5  y   1   , y  2   , y  1   .  6   2   6 
Vậy giá trị lớn nhất của hàm số là 2 và giá trị nhỏ nhất của hàm số là 1.
BÀI TẬP TRẮC NGHIỆM MỨC ĐỘ 2
Câu 1. Tìm tập giá trị của hàm số y  3 sin x  cos x  2 . A.  2  ; 3 .
B.  3  3; 3 1 . C.  4  ;0 . D.  2  ;0 .     Lời giải Chọn C       
Xét y  3 sin x  cos x  2  2 sin . x cos  cos . x sin  2    2 sin x   2   .  6 6   6       
Ta có 1  sin x   1  
 4  2 sin x   2  0    4
  y  0 với mọi x   .  6   6 
Vậy tập giá trị của hàm số là  4  ;  0 .
sin x  2 cos x 1
Câu 2. Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y  là
sin x  cos x  2 1 A. m   ; M  1 .
B. m  1 ; M  2 .
C. m  2 ; M  1 .
D. m  1 ; M  2 . 2 Lời giải Chọn C
sin x  2 cos x 1 Ta có y    y  
1 sin x   y  2 cos x  1 2 y * .
sin x  cos x  2 2 2 2
Phương trình * có nghiệm   y     y      y 2 1 2 1 2
y y  2  0  2   y  1 .
Vậy m  2 ; M  1 . 12   5 
Câu 3. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y  trên đoạn  ; là 7  4 sin x  6 6   
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 12
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11 12 4 4 12 12 12 A. M  ; m  .
B. M  4 ; m  . C. M  ; m
. D. M  4 ; m  . 5 3 3 5 7 11 Lời giải Chọn B   5   1  12 Do x   ;
 sin x   ;1  y   0  ;  6 6     2   7  4 sin x 12 7 y 12  1   4  y
 7 y  4 y sin x  12  sin x    ;1  y  ; 4 . 7 4 sin x 4 y  2   3        1  4
Do đó M  max f t   f  
1  4 và m  min f t   f     .  1   1   ;1   2  3  ;1 2       2     
Câu 4. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  sin x trên đoạn  ;   lần lượt là 2 3    1 3 3 3 2 3 A.  ;  . B.  ; 1. C.  ; 2 . D.  ;  . 2 2 2 2 2 2 Lời giải Chọn B         3 Ta có:   x    sin   sin x  sin    
  1  sin x   . 2 3  2   3  2    3    Vậy max y  sin      ; min y  sin   1   .          ;  3  2    2   ; 2 3       2 3  2 cos x 1
Câu 5. Gọi M , m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  . Khẳng định cos x  2 nào sau đây đúng?
A. M  9m  0 .
B. 9M m  0 .
C. 9M m  0 .
D. M m  0 . Lời giải Chọn C 2 cos x 1 5 Ta có y   2  . cos x  2 cos x  2 5 5 1 5 Mà
1  cos x  1  3  cos x  2  1     5   2   3  3 cos x  2 3 cos x  2 1  y  3 . 3 1 Vậy M
và 1  cos x  1  9M m  0 . 3
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 13
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11  MỨC ĐỘ 3 BÀI TẬP TỰ LUẬN  10  Bài 1.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y  2020 cos 8x   2021   .  2019  Lời giải  10 
Ta có 1  cos 8x   1, x      .  2019   10   10  Nên 20  20  2020 cos 8x   2020  
 1  2020 cos 8x   2021  4041   .  2019   2019   10 
Vậy min y  1 đạt được khi cos 8x   1   ,  2019   10 
max y  4041 đạt được khi cos 8x   1   .  2019  Bài 2. Tìm GTNN của hàm số 2
y  cos x  2  cos x . Lời giải Ta có cos x  1
 , dấu “  ” xảy ra khi cos x  1. (1) Mặt khác 2 2 2 0  cos x  1  1
   cos x  0  1  2  cos x  2 . 2
 2  cos x  1, dấu “  ” xảy ra khi cos x  1. (2) Từ (1) và (2) ta có 2
cos x  2  cos x  0 .
Suy ra min y  0 , đạt được khi cos x  1
  x    k 2 k  . Bài 3.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: y  cos 2x  3 sin 2x  2 . Lời giải Ta có  1 3 
y  cos 2x  3 sin 2x  2  2 cos 2x  sin 2x   2  2 2            2 cos cos 2x  sin
sin 2x  2  2 cos 2x   2     .  3 3   3          
Mặt khác 1  cos 2x   1  2   2 cos 2x
 2  0  2 cos 2x   2  4       .  3   3   3       
Vậy min y  0 đạt được khi cos 2x   1  
, max y  4 đạt được khi cos 2x   1   .  3   3   7  Bài 4.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
y  2 cos x  2 3 sin .
x cos x  1 trên đoạn 0;  . 12   
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 14
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11 Lời giải   
Ta có y  cos 2x  3 sin 2x  2  2 cos 2x   2   .  3    7   3 
Đặt t  2x
. Theo giả thiết x  0;  t  ; . 3  12   3 2       3 
Ta lập BBT của hàm số f t   2cost  2 trên ;  . 3 2    
Từ bảng biến thiên ta có min y  min f t   0 , đạt được khi t    x
max y  max f t   3 ,  7   3   7   3  0; ; 3  0; ; 12   3 2           12   3 2  
đạt được khi t   x  0 3 Bài 5.
Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số 2
y  cos x  cos x  2 . Lời giải
Đặt cos x t ; t  1   ;1
Xét hàm số bậc hai: f t  2
t t  2 trên  1  ;  1 . b 1 Ta có:   1;  1 . Từ đây có bảng biến thiên 2a 2 7 1
Ta kết luận: min y  min f t  
, đạt được khi cos x  ; 1;  1 4 2
max y  max f t   4 , đạt được khi cos x  1  . 1;  1
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 15
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11
BÀI TẬP TRẮC NGHIỆM Câu 1.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau 2 2
y  2 sin x  cos 2x . 3
A. max y  4 , min y  .
B. max y  3 , min y  2 . 4 3
C. max y  4 , min y  2 .
D. max y  3 , min y  . 4 Lời giải Chọn D Đặt 2
t  sin x, 0  t  1  cos 2x  1 2t . 2  1  3
y  2t  1 2t 2 2
 4t  2t 1  2t     .  2  4 2 1 1 3  1  9 3
Cách 1: Do 0  t  1    2t    0  2t       y  3 . 2 2 2  2  4 4 1
Cách 2: Có y '  8t  2  y  0  t  0;  1 . 4  1  3
Ta có: y 0  1; y    ; y   1  3.  4  4 
Vậy max y  3 đạt được khi x   k . 2 3 1 1  cos 2x 1 min y  đạt được khi 2 sin x    . 4 4 2 4 1    cos 2x   2x  
k 2  x    k . 2 3 6 Câu 2.
Tìm giá trị nhỏ nhất của hàm số sau 2 2
y  tan x  cot x  3tan x  cot x 1.
A. min y  2 .
B. min y  4 .
C. min y  5 . D. min y  1  . Lời giải Chọn C 2
Ta có: y  tan x  cot x  3tan x  cot x  3 . 2
Đặt t  tan x  cot x   t  2 . sin 2x Suy ra 2
y t  3t  3  f t . Bảng biến thiên 
Vậy min y  5 đạt được khi x    k . 4
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 16
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11 Câu 3.
Gọi giá trị lớn nhất và nhỏ nhất của hàm số 2
y  sin x  2  sin x là M , m . Tính M m . A. 3. B. 4 . C. 6 . D. 2 . Lời giải Chọn D
Ta có y  1 sin x  0 , x  và 2 2
y  2  2sin x 2  sin x . Mà 2 2 2
2 sin x 2  sin x  sin x  2  sin x  2 . Suy ra 2
0  y  4  0  y  2 . 
Vậy min y  0 đạt được khi x    k 2 . 2 
max y  2 đạt được khi x   k 2 . 2
Vậy M  2, m  0 hay M m  2 .
sin x  2 cos x  3 Câu 4.
Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y  . 2  cos x 2 2
A. min y   ; max y  2 . B. min y  ; max y  2 . 3 3 1 3 1 3 C. min y  ; max y  .
D. min y   ; max y  . 2 2 2 2 Lời giải Chọn B
Cách 1: Ta có cos x  2  0 , x    .
sin x  2 cos x  3 y
 sin x  2 cos x  3  2 y y cos x  s in x  2  y cos x  2y  3 2  cos x Ta có  y  2  
x    y
x2      y2  2 2 x x 2 2 3 s in 2 cos 1 2 s in cos
 5  4 y y 2 2 2
 4 y 12 y  9  y  4 y  5  0 2
 3y  8 y  4  0   y  2 3
Cách 2: (dùng sau khi học xong bài phương trình bậc nhất theo sin và cos).
Ta có cos x  2  0 , x    .
sin x  2 cos x  3 y
 sin x  2 cos x  3  2 y y cos x  sin x  2  y cos x  3  2y  0 2  cos x 2 2 2 Ta có 2
1  2  y   3  2 y  2 2
 4 y 12 y  9  y  4 y  4 1  0 2
 3y  8 y  4  0   y  2 3 .
Cách 3: sử dụng máy tính cầm tay.
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 17
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11
sin x  2 cos x  3
Tương tự như ở ví dụ 1 thì ta có thể sử dụng SHIFT SOLVE:  2 thì phương trình 2  cos x
có nghiệm. Do 2 là số lớn nhất trong các phương án A; B; C; D nên ta không cần thử trường hợp 3 max  . 2 2
Lúc này chỉ còn A và B Thử với min y   thì không có nghiệm. 3 Từ đây chọn B. Câu 5.
Cho hàm số h x 4 4
 sin x  cos x  2m sin .
x cos x . Tất cả các giá trị của tham số m để hàm số xác
định với mọi số thực x (trên toàn trục số) là 1 1 1 1 1 A.   m  . B. 0  m  . C.   m  0 . D. m  . 2 2 2 2 2 Lời giải Chọn A 2 2
Xét hàm số g x   2 x   2 sin
cos x  msin 2x   x x2 2 2 2 2 sin cos
 2sin x cos x m sin 2x 1 2  1
sin 2x m sin 2x . 2
Đặt t  sin 2x t  1   ;1 . 1
Hàm số hx xác định với mọi x    g x  0, x    2
  t mt 1  0, t   1  ;  1 2 2
t  2mt  2  0, t   1   ;1 .
Đặt f t  2
t  2mt  2 trên  1  ;  1 .
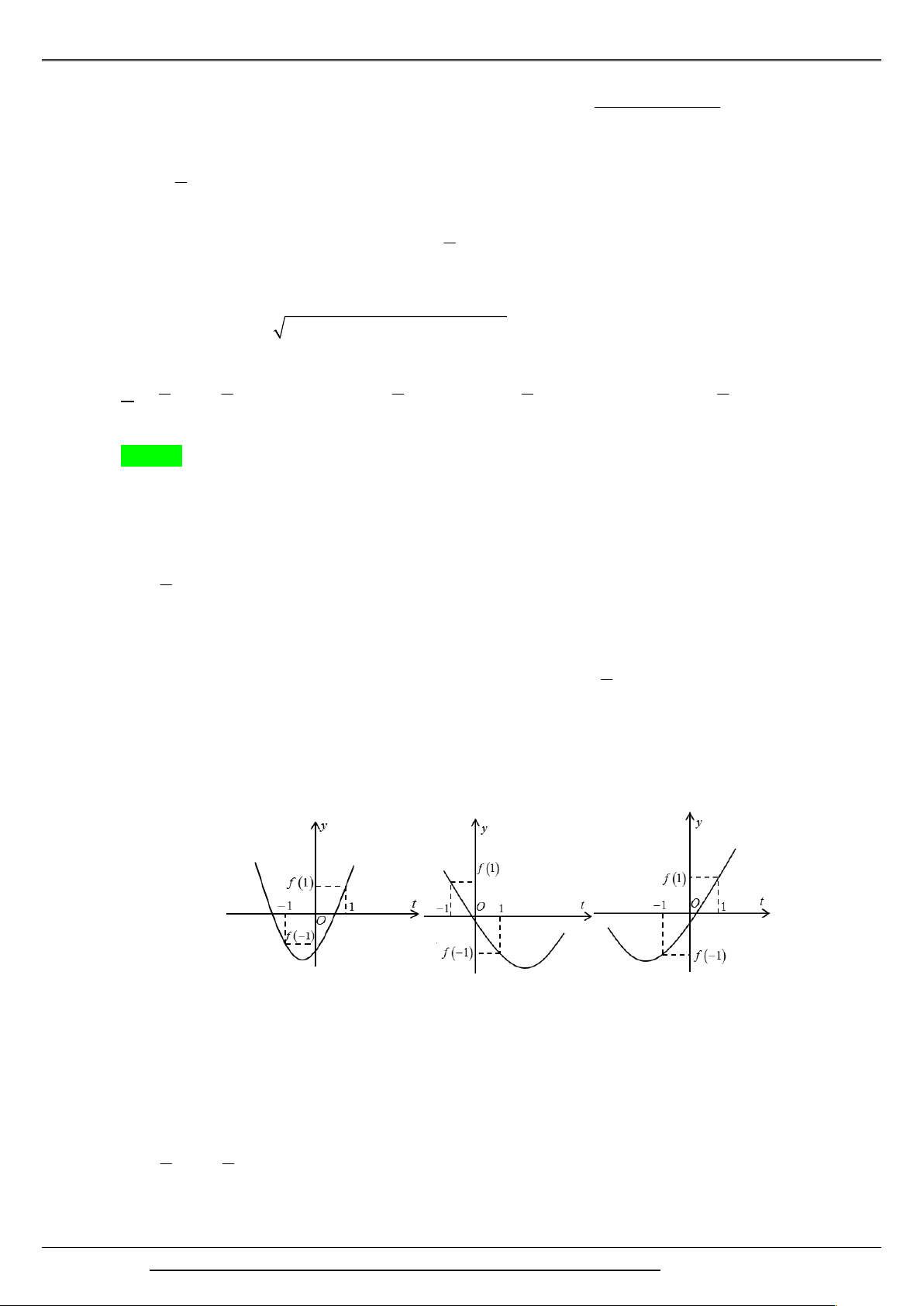
Đồ thị hàm số có thể là một trong ba đồ thị trên.
Ta thấy max f t   f  
1 hoặc max f t   f   1 . 1;  1 1;  1  f   1  0  1   2m  0 Ycbt f t  2
t  2mt  2  0 , t   1   ;1
 max f t   0     1;  1  f   1  0  1   2m  0  1 1    m  . 2 2
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 18
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11  MỨC ĐỘ 4 BÀI TẬP TỰ LUẬN
Bài 1. Tìm giá trị nhỏ nhất của hàm số y  sin x cos x  cos x sin x . Lời giải sin  x  0 
Điều kiện xác định:  . c  os x  0 
Áp dụng bất đẳng thức Cô-si cho 2 số không âm sin x cos x và cos x sin x ta có : 1 1
sin x cos x  cos x sin x  2 sin x cos x sin x cos x y  2 sin 2x sin 2x  0 . 2 2 k
Dấu bằng xảy ra khi và chỉ khi sin 2x  0  2x k , k    x  , k   . 2 s inx  2 cos x  3
Bài 2. Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y  . 2  cos x Lời giải
Ta có: cos x  2  0, x R . s inx  2 cos x  3 Khi đó: y
 s inx  2 cos x  3  2 y y cos x  s inx  2  y cos x  3  2y  0   * 2  cos x 2 2 Phương trình   * có nghiệm 2
 1  2  y  3  2 y 2 2 2
 4 y 12 y  9  y  4 y  4 1  0 2
 3y  8y  4  0   y  2 . 3 2 Vậy min y  ; max y  2 . 3
Bài 3. Tìm giá trị nhỏ nhất của biểu thức 4 4 2 2
P  cot a  cot b  2 tan .
a tan b  2 . Lời giải Ta có:
P  cot a  cot b2 2 2 2 2 2 2  2 cot .
a cot b  2 tan . a tan b  2
 cot a  cot b2 2 2  2 2 2 2 2 cot . a cot b  tan .
a tan b  2  6
 cot a  cot b2 2 2  2 2 2 2 2 cot . a cot b  tan .
a tan b  2 cot . a cotb.tan . a tan b  6
 cot a  cot b2  2cot .
a cot b  tan . a tan b2 2 2  6  6 2 2 2
cot a  cot b c   ot a  1  k
Vậy min y  6 , đạt được khi     a b   , (k ) . 2 cot .
a cot b  tan . a tan b  c  ot b  1  4 2 1 1
Bài 4. Tìm giá trị nhỏ nhất của hàm số 2 2 y  1 os c x  5  2 sin x . 2 2 Lời giải
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 19
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11 1 1 1 5 1 Ta có 2 2 2 2 y  1 os c x
5  2sin x y  1 os c x   sin x 2 2 2 4 2 1 5 1
Áp dụng bất đẳng thức Bunyakopvsky cho 4 số: 1; 1; 2 1 os c x ; 2  sin x ta có: 2 4 2 1 5 1 1 5 1 9 1 22 2 2 2 2 2 2 1. 1 os c x 1.  sin x  1 1 . 1 os c x   sin x  2.   . 2 4 2 2 4 2 4 2.1 2 22 1 5 1  Vậy min y  , xảy ra khi 2 2 1 os c x  
sin x x  
k , k   . 2 2 4 2 6
Bài 5. Tìm giá trị lớn nhất của hàm số 4 4
y  sin x  cos x  sin x cos x . Lời giải 1 1 Ta có 4 4
y  sin x  cos x  sin x cos x 2 2
y  1 2sin x cos x  sin x cos x 2  y  1 sin 2x  sin 2x 2 2 2 2 1  1 1    9 1  1  9  y  1  sin 2x       y   sin 2x     . 2  2  4 8 2    2  8  9 1 Vậy max y
, đạt được khi sin 2x  . 8 2
BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho x, y, z  0 và x y z
. Tìm giá trị lớn nhất của 2 y  1 tan .
x tan y  1 tan .
y tan z  1 tan . z tan x A. y  1 2 2 . B. y  3 3 . C. y  4 . D. y  2 3 . max max max max Lời giải Chọn D      tan x  tan y 1
Ta có x y z   x y
z  tan  x y  tan  z     2 2  2  1 tan . x tan y tan z  tan .
x tan z  tan y. tan z  1  tan .
x tan y  tan .
x tan z  tan y. tan z  tan . x tan y  1 Ta thấy tan . x tan z; tan . y tan z; tan .
x tan y lần lượt xuất hiện trong hàm số đề bài cho.
Khi đó, áp dụng bất đẳng thức Bunyakovsky cho 6 số ta có: 1. 1 tan .
x tan y 1. 1 tan .
y tan z 1. 1 tan . z tan x  2 2 2
 1 1 1 . 1 tan .
x tan z   1 tan .
y tan z   1 tan . x tan y  3 3  tan .
x tan z  tan .
y tan z  tan .
x tan y   2 3 . Vậy y  2 3 . max 3  2 1 tan x 2  Câu 2:
Hàm số y  3cot 2x
đạt giá trị nhỏ nhất là tan x A. 1  . B. 3  2 3 . C. 2  2 2 . D. 0 . Lời giải Chọn A 2 1 tan x Ta có cot 2x  . 2 tan x 2 3  2 1 tan x 2  Từ đó suy ra 2
y  3cot 2x
 3cot 2x  2 3 cot 2x 2 tan x
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 20
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11   x  2 3 cot 2 1 1  1  , x    . 1 Vậy min y  1   cot 2x  . 3    Câu 3:
Hàm số y  2 cos x  sin x  
 đạt giá trị lớn nhất là  4  A. 5  2 2 . B. 5  2 2 . C. 5  2 2 . D. 5  2 2 . Lời giải Chọn C Ta có:    1    1
y  2 cos x  sin x   2 cos x  2 sin x       2 cos x
sin x  cos x  4  2  4  2  1  1  2  cos x  sin x   .  2  2 2 2  1   1 
Áp dụng bất đẳng thức Bunyakovsky ta có: 2 2 y  2    y  5  2 2     .  2   2 
Do đó  5  2 2  y  5  2 2 .
Vậy giá trị lớn nhất của hàm số là 5  2 2 . m sin x 1 Câu 4:
Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số y  nhỏ hơn 2 . cos x  2 A. 3 . B. 5. C. 4 . D. 6 . Lời giải Chọn B m sin x 1 Ta có: y
y cos x  2 y m sin x 1  m sin x y cos x  2 y 1 * cos x  2
* có nghiệm khi m y   y  2 2 2 2 2 2 1
 3 y  4 y  1 m  0 2 2 2  1 3m 2  1 3m   y  3 3 2 2  1 3m 2 2  y
 2  1 3m  4  m  5 . max 3
Do m    m  2  ; 1  ;0; 2 
;1 . Vậy có 5 giá trị của m thỏa ycbt. Câu 5:
Số giờ có ánh sáng của một thành phố A trong ngày thứ t của năm 2020 được cho bởi một hàm số  y  4 sin
t  60 10 , với t Z và 0  t  366 . Vào ngày nào trong năm thì thành phố A có 178
nhiều giờ ánh sáng mặt trời nhất ?.
A. 28 tháng 5. B. 29 tháng 5. C. 30 tháng 5. D. 31 tháng 5. Lời giải Chọn A   Vì sin
t  60  1 y  4sin
t  60 10  14 . 178 178
Khi đó, ngày có ánh nắng mặt trời chiếu nhiều nhất là
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 21
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11    y  14  sin
t  60  1  t  60 
k 2  t  149  356k . 178 178 2 149 217
Mà 0  t  366  0  149  356k  366    k  . 356 356
Vì k  nên k  0 .
Với k  0  t 149 tức rơi vào ngày 28 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày, tháng 4 có
30 ngày, riêng đối với năm 2020 là năm nhuận nên tháng 2 có 29 ngày hoặc dựa vào dữ kiện
0  t  366 thì ta biết năm này tháng 2 có 29 ngày).
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 22
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
TÀI LIỆU TỰ HỌC TOÁN 11
LINK NHÓM: https://www.facebook.com/groups/nhomwordvabiensoantailieutoan/ Trang 23