TCC1 Bài Tập Số Phức và Toán Cao Cấp - Chương 1 | Đại học Điện lực

lOMoARcPSD| 59149108 Bài tập Toán cao cấp 1 lOMoARcPSD| 59149108
Số phức và các phép toán về số phức
Bài 1. Tìm căn bậc 3 của các số phức sau: a) z = 4
4i√3b) z = 4+4i√3 −−
c) z = 2+2i√3 d) z = 2 2i√3 − − e) z = √3 i f) z = √3+ i 1+ i√ − 3 − 1+ i√ 3 z = z 1 = − 2 2 g)h) √ − i i 3+ − √ − i 3 i z = − z − 1 = − i)h) − i 1+ i
Bài 2. Tìm mô đun và argument của các số phức sau: a) b) c) d)
Bài 3. Chuyển các số phức sau về dạng lượng giác: a) b) c) d) e) f) g) f) − −
Bài 4. Tính z100, biết: a) b) c) d)
Bài 5. Giải phương trình: 1 2 lOMoARcPSD| 59149108
a) z3 +√3 i = 0 −
b) z5 (1+ i√3)2 = 0 −
c) z3(1+ i) = (1+ i√3)3(1 i)5 d) z3(1
i) = ( 1+ i√3)3(1+ i)5 − − −
e) z3( 1+ i) = (√3 i)3(1+ i)5 f) z3( 1
i) = (√3+ i)3( 1+ i)5 − − − − − Bài 6.
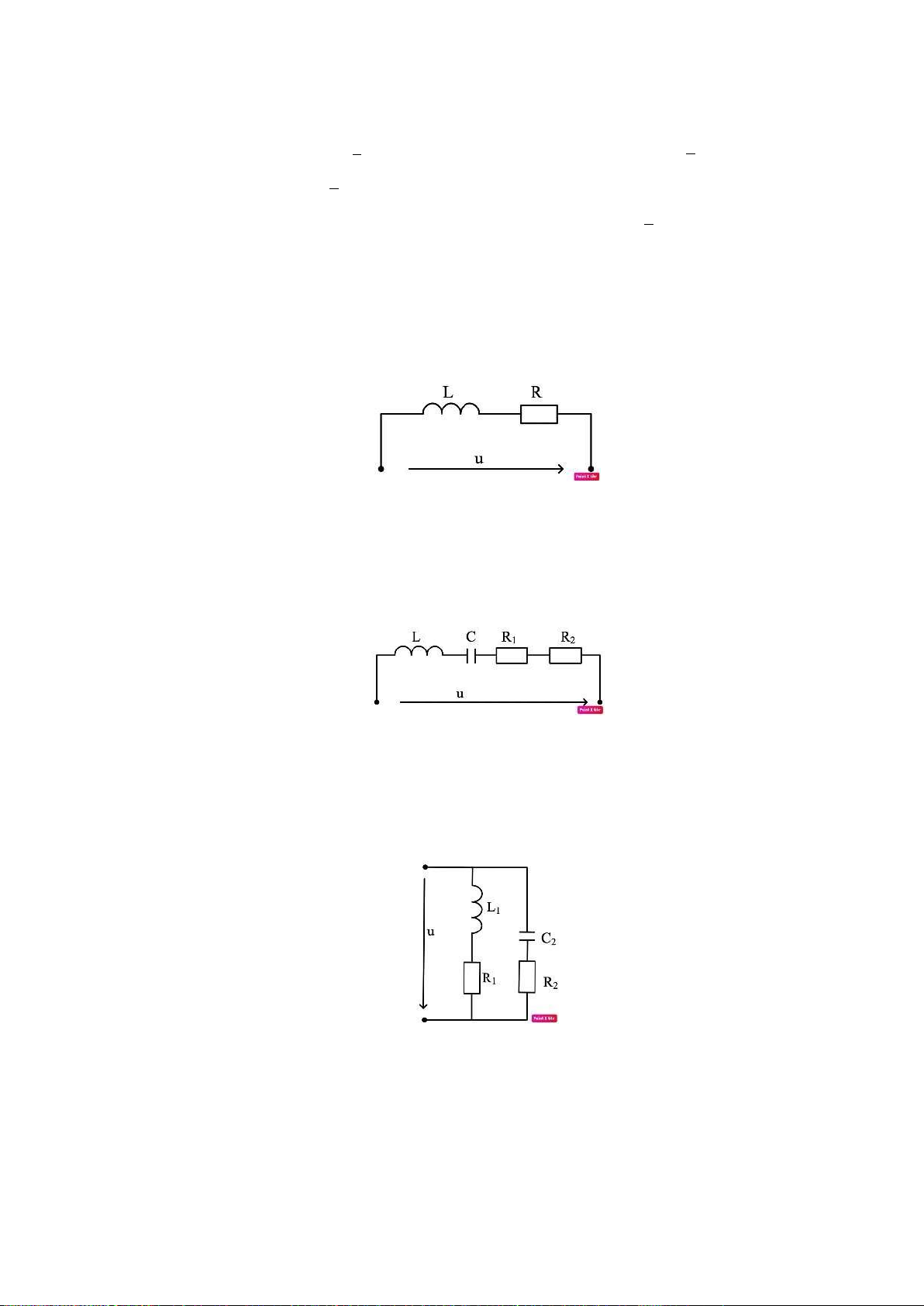
Cho mạch điện như hình vẽ. Xác định tổng trở phức của mạch, biết R = 12Ω,L = 15mH,f = 100Hz Bài 7.
Cho mạch điện như hình vẽ. Xác định tổng trở phức của mạch, biết R1 = 10Ω,R2 = 12Ω,L
= 20mH,C = 120µF,f = 200Hz. Bài 8.
Cho mạch điện như hình vẽ. Xác định tổng trở phức tương đương của mạch biết R1 =
12Ω,L1 = 100mH,R2 = 10Ω,C = 200µF,f = 100Hz. lOMoARcPSD| 59149108 Tài liệu tham khảo
[1] Nguyễn Đình Trí, Toán cao cấp 1, Nhà xuất bản giáo dục.
[2] Nguyễn Đình Trí, Bài tập Toán cao cấp 1, Nhà xuất bản giáo dục.
[3] Steven J. Leon, Linear Algebra with Applications, Prentice Hall, 1998.
[4] Lê Tuấn Hoa, Đại số tuyến tính qua các ví dụ và bài tập, Viện toán học. Ha Huong Giang
Faculty of Fundamental Sciences Electric Power University
235-Hoang Quoc Viet, Cau Giay, Ha Noi, Vietnam E-mail: gianghh@epu.edu.vn 3