Thí Nghiệm Mô Men Quán Tính Vật Rắn Đối Xứng môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Mẫu xử lý số liệu báo cáo Thí nghiệm Vật lý đại cương I BÀI SỐ 2
XÁC ĐỊNH MÔ MEN QUÁN TÍNH CỦA VẬT RẮN ĐỐI XỨNG
NGHIỆM LẠI ĐỊNH LÝ STEINER - HUYGHENS
Xác nhận của giáo viên hướng dẫn
Trường …………………………………………
Lớp ……………………Nhóm……………..
Họ tên …………………………………………
I. MỤC ĐÍCH THÍ NGHIỆM
Xác định mô men quán tính của vật rắn đối xứng. Nghiệm lại định lý S-H
II. KẾT QUẢ THÍ NGHIỆM
1. Xác định mô men quán tính I0 của vật rắn đối xứng Bả - ng M ô 1
men quán tính của đĩa đỡ khối trụ: 𝐼Đ= 0.00011 ± 0.00001 (𝑘𝑔. 𝑚2)
- Độ chính xác của bộ đếm thời gian: (Δ𝑇)𝑑𝑐 = 0.001 (𝑠) 𝑇𝑇𝐻(𝑠) Δ𝑇 (𝑠) 𝑇ĐĐ(𝑠) Δ𝑇 (𝑠) 𝑇𝑇𝑅+Đ(𝑠) Δ𝑇 (𝑠) 𝑇𝐶(𝑠) Δ𝑇 (𝑠) r ng Khối cầu Lần đo 2.6 T 1 h 4 anh dà 0.i Đĩa đặc Trụ ỗ 0008 2.070 0.0016 1.142 0.0012 2.105 0.0008 2.615 0.0002 2.069 0.0004 1.144 0.0008 2.104 0.0002 1 2.614 0.0008 2.068 0.0006 1.142 0.0012 2.105 0.0008 2 2.616 0.0012 2.069 0.0004 1.145 0.0018 2.103 0.0012 3 2.615 0.0002 2.067 0.0013 1.143 0.0002 2.104 0.0002 4 2.6148 0.0006 2.0686 0.0009 1.1432 0.0010 2.1042 0.0006 5 2𝜋)2(𝑘𝑔. 𝑚2) TB
2. Nghiệm lại định lý Steiner - Huygens 𝐼 = 𝐷𝑧(𝑇
Bảng 2 𝑑(×10−3𝑚) 𝑇(𝑠) 𝑥 = 𝑑2(× 10−6𝑚2) 2.620 0 0.0077 2.741 900 0.0084 0 3.019 3600 0.0102 30 3.446 8100 0.0132 60 3.921 14400 0.0171 90 120
III. XỬ LÝ SỐ LIỆU
1. Tính mô men quán tính của các vật rắn đối xứng a-. T S h ai a n s h ố td u à y i ệ (t Lđ = ối 6c2ủ0a m p m hé , pM đ = o 2 c 4 h 0
u kgỳ) 𝑇𝑇𝐻 (đo trực tiếp) Δ𝑇 2𝜋 )2= 0.044. ( 2.6148
𝑇𝐻 =(Δ𝑇)𝑑𝑐 + Δ𝑇  𝑇  𝐻   =2 0. ×00 3. 1 + 42 0 ) .20 0 = 0 6 0= .0 0 0 .0 7 0 6 1 2 6 ( 𝑘(𝑠 𝑔. ) 𝑚2)
𝐼𝑇𝐻 = 𝐷𝑧(𝑇
- Mô men quán tính trung bình của  t𝑇h𝐻anh dài:
𝐼𝑇𝐻 = Δ𝐷𝑧+2Δ𝑇𝑇𝐻 
0.044 +2 ×20..60104186 +2Δ𝜋 𝜋 = 0.024 +2 × 0.001 𝑇𝐻 +2Δ𝜋 𝜋 = 0.001 𝛿 = Δ𝐼𝑇𝐻 3.142 = 0.025 = 2.5 (%)
- Sai số tương đối trung bình của phép đo mô men quán tính của thanh dài: 𝑇
Vũ Tiến Lâm – Viện Vật lý kỹ thuật, ĐHBK Hà Nội CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Mẫu xử lý số liệu báo cáo Thí nghiệm Vật lý đại cương I
Cách lấy số 𝝅 và sai số của nó: Sai số tương đối của 𝝅 không lớn hơn 1/10 tổng sai số tương đối
của các đại lượng còn lại, tương tự cho các số 𝝅 bên dưới.
- Sai số tuyệt đối của mô men quán tính Δ𝐼𝑇𝐻:
Δ𝐼𝑇𝐻 = 𝛿. 𝐼𝑇𝐻 =2.5100×0.00762 = 0.00019 (𝑘𝑔.𝑚2)
- Kết quả đo mô men quán tính của thanh dài:
𝐼𝑇𝐻 = 𝐼𝑇𝐻 ± Δ𝐼𝑇𝐻 = 0.00762 ± 0.00019 (𝑘𝑔.𝑚2)
- Mô men quán tính của thanh dài tính theo lý thuyết (𝐼𝑇𝐻)𝐿𝑇:
(𝐼𝑇𝐻)𝐿𝑇 =112𝑀𝐿2=112 .24 1 0 0 0. ( 6 1 2 0 0
0 )2= 0.00769 (𝑘𝑔.𝑚2)
- Sai số tỷ đối: 𝛿∗=|(𝐼𝑇𝐻)𝐿(𝑇𝐼−𝐻𝐼𝑇 )𝐿𝐻𝑇| = |0.00769−0 0..0 0 0 0 7 7 6 6 2 9 | = 0.0091 = 0.91 (%)
b. Đĩa đặc (D = 220 mm, M = 795 g)
- Sai số tuyệt đối của phép đo chu kỳ 𝑇ĐĐ (đo trực tiếp)
Δ𝑇ĐĐ =(Δ𝑇)𝑑𝑐 + Δ𝑇Đ
Đ = 0.001 + 0.0009 = 0.0019 (𝑠)
- Mô men quán tính trung bình của đĩa đặc:
𝐼ĐĐ = 𝐷𝑧(𝑇Đ 2 Đ 𝜋 )2= 0.044.( 2.0 2 6 ×86
3.142)2 = 0.00477 (𝑘𝑔. 𝑚2)
- Sai số tương đối trung bình của phép đo mô men quán tính của đĩa đặc: 𝛿 = Δ𝐼Đ Đ Đ Đ = Δ𝐷𝑧 𝐷𝑧+2Δ𝑇ĐĐ ĐĐ +2Δ𝜋𝜋 = 0.00 . 1 044 +2 ×2.0.0 6 0 8 1
6 9+2Δ𝜋𝜋 = 0.025 +2 × 0.001 𝑇 3.142 = 0.026 = 2.6 (%)
- Sai số tuyệt đối của mô men quán tính Δ𝐼ĐĐ:
Δ𝐼ĐĐ = 𝛿. 𝐼ĐĐ =2.6100×0.00477 = 0.00012 (𝑘𝑔.𝑚2)
- Kết quả đo mô men quán tính của đĩa đặc:
𝐼ĐĐ = 𝐼ĐĐ ± Δ𝐼ĐĐ = 0.00477 ± 0.00012 (𝑘𝑔. 𝑚2)
- Mô men quán tính của đĩa đặc tính theo lý thuyết (𝐼ĐĐ)𝐿𝑇:
(𝐼ĐĐ)𝐿𝑇 =18𝑀𝐷2=18.7915000. ( 2 1 2 0 0
0 )2= 0.00481 (𝑘𝑔.𝑚2)
- Sai số tỷ đối: 𝛿∗=|(𝐼ĐĐ)𝐿(𝑇𝐼− ĐĐ 𝐼Đ
)𝐿Đ𝑇| = |0.00481−0.00477| 0.00481 = 0.0083 = 0.83 (%)
c. Trụ rỗng (D = 89 mm, M = 789 g)
- Sai số tuyệt đối của phép đo chu kỳ 𝑇𝑇𝑅+Đ (đo trực tiếp)
Δ𝑇𝑇𝑅+Đ =(Δ𝑇)𝑑𝑐 + Δ𝑇 𝑇𝑅 +
Đ = 0.001 + 0.0010 = 0.0020 (𝑠)
- Mô men quán tính trung bình của trụ rỗng và đĩa đỡ:
𝐼𝑇𝑅+Đ = 𝐷𝑧(𝑇𝑇𝑅 2 + 𝜋 Đ)2= 0.044. ( 1.1243
× 23.142)2 = 0.00146 (𝑘𝑔. 𝑚2)
- Sai số tương đối trung bình của phép đo mô men quán tính của trụ rỗng và đĩa đỡ:
Vũ Tiến Lâm – Viện Vật lý kỹ thuật, ĐHBK Hà Nội
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Mẫu xử lý số liệu báo cáo Thí nghiệm Vật lý đại cương I 𝛿 = Δ𝐼𝑇 𝑇 𝑅 𝑅 + + Đ Đ = Δ𝐷𝑧 𝐷 +2Δ𝑇𝑇𝑅𝑇+ 𝑅 Đ + +2Δ𝜋𝜋 = 0.00 . 1 044 +2 × 0 1. .0 1 0 4 2 3 0
2 +2Δ𝜋𝜋 = 0.026 +2 × 0.001 𝑇 3.142 = 0.027 = 2.7 (%)
- Sai số tuyệt đối của mô men quán tính của trụ rỗng và đĩa đỡ Δ𝐼𝑇𝑅+Đ:
Δ𝐼𝑇𝑅+Đ = 𝛿. 𝐼𝑇𝑅+Đ =2.7
100 × 0.00146 = 0.00004 (𝑘𝑔. 𝑚2)
- Mô men quán tính trung bình của trụ rỗng 𝐼𝑇𝑅:
𝐼𝑇𝑅 = 𝐼𝑇𝑅+Đ − 𝐼Đ= 0.00146 − 0.00011 = 0.00135 (𝑘𝑔. 𝑚2)
- Sai số tuyệt đối của mô men quán tính trụ rỗng Δ𝐼𝑇𝑅:
Δ𝐼𝑇𝑅 = Δ𝐼𝑇𝑅+Đ + Δ𝐼Đ = 0.0004 + 0.0001 = 0.0005 (𝑘𝑔. 𝑚2)
- Kết quả đo mô men quán tính của trụ rỗng:
𝐼𝑇𝑅 = 𝐼𝑇𝑅 ± Δ𝐼𝑇𝑅 = 0.00135 ± 0.00005 (𝑘𝑔.𝑚2)
- Mô men quán tính của đĩa đặc tính theo lý thuyết (𝐼𝑇𝑅)𝐿𝑇:
(𝐼𝑇𝑅)𝐿𝑇 =14𝑀𝐷2=14.7819000 .( 8 1 9
000)2= 0.00156 (𝑘𝑔.𝑚2)
- Sai số tỷ đối: 𝛿∗=|(𝐼𝑇𝑅)𝐿(𝑇𝐼− 𝑇𝑅 𝐼𝑇
)𝐿𝑅𝑇| = |0.00156−0.00135| 0.00156 = 0.14 =14 (%)
d. Khối cầu đặc (D = 146 mm, M = 2290 g)
- Sai số tuyệt đối của phép đo chu kỳ 𝑇𝐶 (đo trực tiếp)
Δ𝑇𝐶=(Δ𝑇)𝑑𝑐 + Δ𝑇𝐶  = 0.001 + 0.0006 = 0.0016 (𝑠)
- Mô men quán tính trung bình của khối cầu đặc:
𝐼𝐶= 𝐷𝑧(𝑇 2𝐶𝜋)2= 0.044.( 2.210
× 432.142)2 = 0.00494 (𝑘𝑔. 𝑚2)
- Sai số tương đối trung bình của phép đo mô men quán tính của đĩa đặc:
𝛿 = Δ𝐼𝐶𝐶= Δ𝐷𝑧𝐷𝑧+2Δ𝑇𝐶𝐶+2Δ𝜋𝜋 = 0.00.1 044 +2 ×2.01.0 0 0 4 1 2 6 6 +2Δ𝜋 = 0.024 +2 × 0.001 𝑇 3.142 = 0.025 = 2.5 (%)
- Sai số tuyệt đối của mô men quán tính Δ𝐼𝐶:
Δ𝐼𝐶= 𝛿. 𝐼𝐶=2.5100×0.00494 = 0.00012 (𝑘𝑔.𝑚2)
- Kết quả đo mô men quán tính của khối cầu đặc:
𝐼𝐶= 𝐼𝐶± Δ𝐼𝐶 = 0.00494 ± 0.00012 (𝑘𝑔.𝑚2)
- Mô men quán tính của khối cầu đặc tính theo lý thuyết (𝐼ĐĐ)𝐿𝑇:
(𝐼𝐶)𝐿𝑇 =110 𝑀𝐷2=110 .22 1 9 0 0 0 . ( 1 1 4 0 6
00)2= 0.00488 (𝑘𝑔.𝑚2)
- Sai số tỷ đối: 𝛿∗=|(𝐼𝐶)𝐿(𝑇𝐼− 𝐶 𝐼 ) 𝐶 𝐿 | 𝑇 = |0.00488−0.00494| 0.00488 = 0.012 = 1.2 (%)
3. Kiểm nghiệm định lý Steiner - Huygens
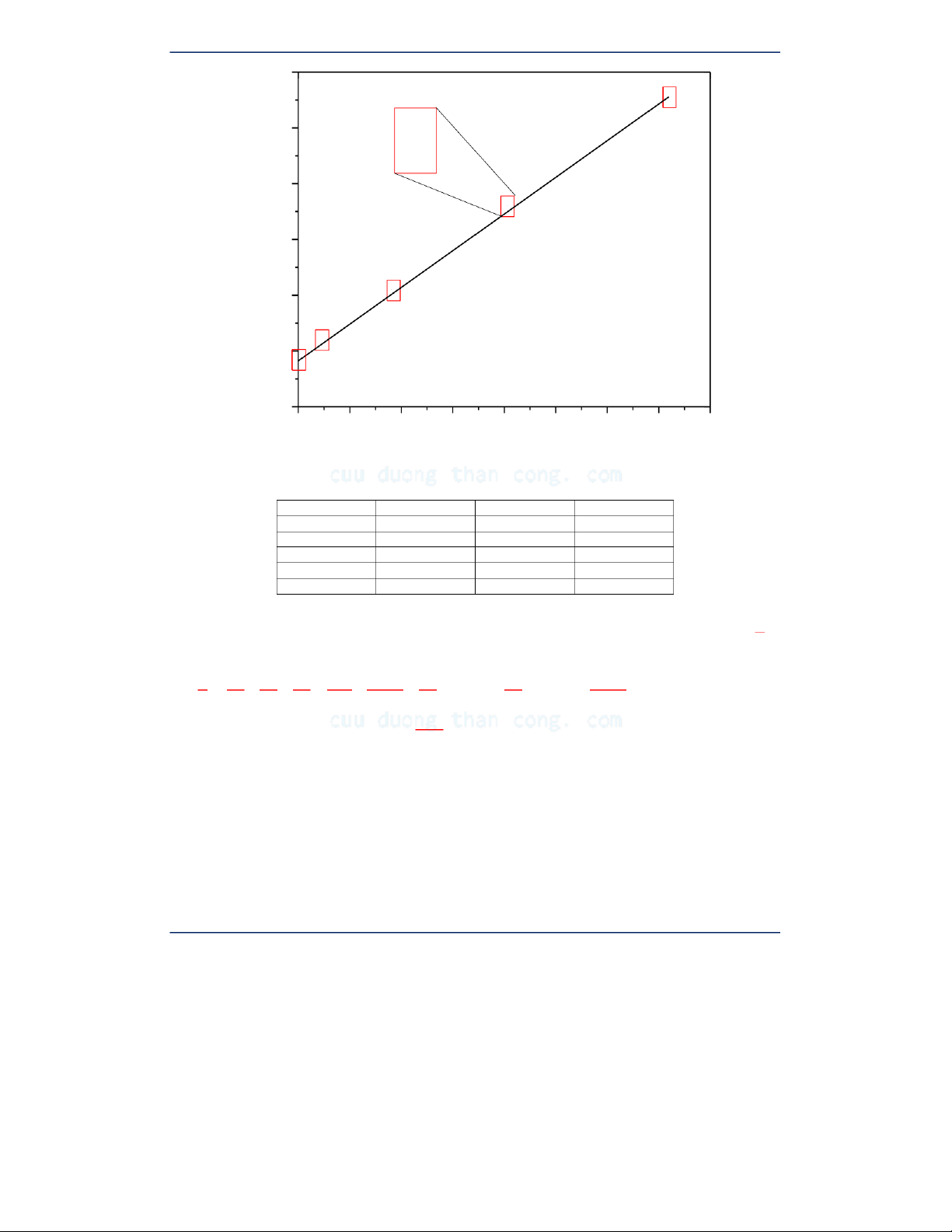
Đồ thị 𝐼 = 𝑀𝑥 + 𝐼𝑜 (𝑥 = 𝑑2)
Vũ Tiến Lâm – Viện Vật lý kỹ thuật, ĐHBK Hà Nội
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Mẫu xử lý số liệu báo cáo Thí nghiệm Vật lý đại cương I 0.018 2x=0.0004 (m) 0.016 0.014 2I=0.0008 (kg.m2) 0.012 I(kg.m2) 0.010 0.008 0.006 0.000 0.002 0.004 0.006 0.008 0.010 0.012 0.014 0.016 x(m)
Bảng 3. Nghiệm lại định lý Steiner - Huygens (Kẻ ra mặt sau tờ báo cáo) 𝐼 Δ𝐼 𝑥 Δ𝑥 0.0077 0.0002 0 0 0.0084 0.0002 0.0009 0.00006 0.0102 0.0003 0.0036 0.00012 0.0130 0.0003 0.0081 0.00018 0.0171 0.0004 0.0144 0.00024
Cách xác định 𝚫𝑰 và 𝚫𝒙:
- Sai số tuyệt đối 𝚫𝑰 được xác định dựa vào giá trị 𝑰 và sai số tương đối 𝜹 của 𝑰 tương ứng (𝜹 = 𝚫𝑰 𝑰)
Ví dụ tính cho 𝑰 = 𝟎. 𝟎𝟎𝟕𝟕, Ta có:
𝜹 = 𝚫𝑰𝑰= 𝚫𝑫𝒛𝑫𝒛+𝟐𝚫𝐓𝑻+𝟐𝚫𝛑𝝅=𝟎.𝟎𝟎𝟏 𝟎.𝟎𝟒𝟒 +𝟐×𝟎. 𝟐. 𝟎𝟎𝟏
𝟐𝟔𝟐𝟎 +𝟐𝚫𝝅𝝅= 𝟎. 𝟎𝟐𝟒 +𝟐𝚫𝝅𝝅= 𝟎. 𝟎𝟐𝟒 +𝟐×𝟎.𝟎𝟎𝟏
𝟑.𝟏𝟒𝟐 = 𝟎. 𝟎𝟐𝟓 = 𝟎. 𝟐𝟓 (%)
→ 𝚫𝑰 = 𝜹.𝑰 = 𝟎.𝟐𝟓
𝟏𝟎𝟎 × 𝟎. 𝟎𝟎𝟕𝟕 = 𝟎.𝟎𝟎𝟎𝟐 (𝒌𝒈.𝒎𝟐)
- Sai số tuyệt đối 𝚫𝒙 = 𝟐𝒅. 𝚫𝒅 (do 𝒙 = 𝒅𝟐), với 𝚫𝒅 = 𝟎. 𝟎𝟎𝟏 (𝒎)
Ví dụ tính cho 𝒙 = 𝟎. 𝟎𝟎𝟎𝟗 𝒎𝟐, Ta có: 𝚫𝐱 = 𝟐 × 𝟑𝟎 × 𝟏𝟎−𝟑 × 𝟎. 𝟎𝟎𝟏 = 𝟎. 𝟎𝟎𝟎𝟎𝟔 (𝒎𝟐)
Cách xác định ô sai số: Thực tế đối với đồ thị này, ứng với mỗi điểm giá trị sẽ có một ô sai số với
kích thước khác nhau (như bảng 3). Tuy nhiên, để đơn giản hóa thì ta có thể coi sai số tuyệt đối của
từng giá trị I và x chính bằng sai số tuyệt đối lớn nhất của nó. Tức là 𝚫𝒙 = 𝟎. 𝟎𝟎𝟎𝟒 và 𝚫𝑰 = 𝟎. 𝟎𝟎𝟎𝟖.
- Đánh giá kết quả thu được từ thực nghiệm: Dựa vào đồ thị thu được, ta thấy dạng đồ thị thỏa mãn
đúng cho phương trình 𝑰 = 𝑴𝒙 + 𝑰𝒐 (𝒙 = 𝒅𝟐) là đồ thị của hàm số bậc nhất. Như vậy, định lý Steiner
- Huygens được nghiệm đúng.
Vũ Tiến Lâm – Viện Vật lý kỹ thuật, ĐHBK Hà Nội
CuuDuongThanCong.com https://fb.com/tailieudientucntt