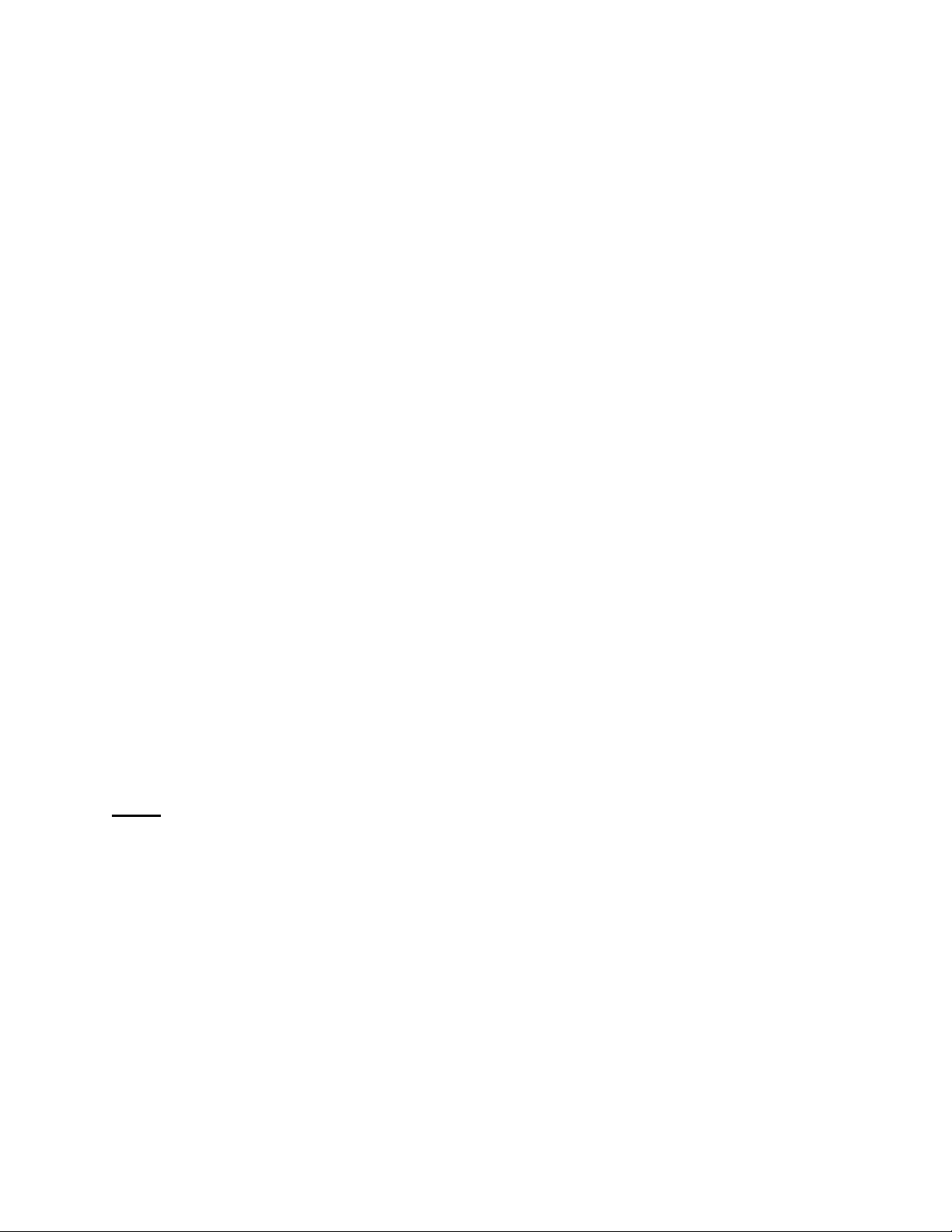



Preview text:
Tia phân giác là gì? Đường phân giác là gì? Tính chất đường
phân giác của tam giác
1. Tia phân giác là gì?
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.
- Mỗi góc (không phải là góc bẹt) chỉ có một tia phân giác
* Định lý thuận:
Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
* Định lí đảo:
- Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
- Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó.
2. Đường phân giác là gì?
- Đường phân giác của một góc chia góc đó thành hai góc có độ lớn bằng nhau.
- Mọi điểm trên một đường phân giác cách đều hai cạnh của góc đó và ngược lại.
3. Tính chất đường phân giác trong tam giác
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ
với hai cạnh kề hai đoạn ấy.
* Lưu ý: Định lí vẫn đúng với tia phân giác của góc ngoài của tam giác.
Ví dụ: Cho tam giác ABC có AD và AE lần lượt là đường phân giác trong và góc ngoài tại đỉnh A.
Khi đó, ta có: DB/DC = AB/AC và EB/EC = AB/AC
4. Dạng bài tập về tia phân giác
4.1. Dạng 1. Chứng minh một tia phân giác của một góc cho trước
Phương pháp giải: Chứng minh tia Oy là tia phân giác của góc xOz
- Cách 1. Chứng minh tia Oy nằm giữa hai tia Ox và Oz
Chứng minh góc xOy = góc yOz
- Cách 2: Chứng minh góc xOy = góc yOz = 1/2 góc xOz
- Cách 3: Dùng tính chất đường trung tuyến trong tam giác cân đồng thời là đường phân giác
Bài 1. Cho tam giác ABC, hai đường phân giác của hai góc ngoài đỉnh B và đỉnh C cắt nhau
tại E. Chứng minh E thuộc phân giác trong của BAC.
Hướng dẫn giải
Từ E hạ EH vuông góc BC, EF vuông góc AB, EG vuông góc AC với H thuộc BC, F thuộc AB, G thuộc AC. Ta có:
EF = EH (E thuộc phân giác ngoài của góc B) (1)
và EH = EG (E thuộc phân giác ngoài của góc C) (2)
Từ (1) và (2) ta có: EF = EG => E thuộc tia phân giác trong của góc BAC (tính chất tia phân giác của một góc)
Bài 2. Cho tam giác ABC vuông tại A . Từ một điểm K bất kì trên cạnh BC, kẻ KH vuông
góc AC (H thuộc AC). Trên tia đối của tuan HK lấy điểm I sao cho HI = HK. Chứng minh: a. AB // HK b. góc KAH = góc IAH c. tam giác AKI cân
Hướng dẫn giải
a. Ta có: AB vuông góc AC (tam giác ABC vuông tại A),
KH vuông góc AC (giả thiết)
=> AB // KH (từ vuông góc đến song song)
b. Xét tam giác AHK và tam giác AHI, có: Hk = HI (giả thiết)
góc AHK = góc AHI = 90 (giả thiết) AH chung
Do đó, tam giác AHK = tam giác AHI (hai cạnh góc vuông)
=> góc KAH = góc IAh (hai góc tương ứng)
c. Theo câu b, ta có: tam giác AHK = tam giác AHI => AK = AI (hai cạnh tương ứng)
=> tam giác AKI cân tại A.
Bài 3. Cho góc xOy. Lấy các điểm A, B thuộc tia Ix sao cho OA > OB. Lấy các điểm C, D
thuộc Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng: a. AD = BC
b. tam giác ABE = tam giác CDE
c. OE là tia phân giác của góc xOy
Hướng dẫn giải
a. Xét tam giác OAD và tam giác OCB, có OA = OC (giả thiết) góc O chung OD = OB (giả thiết)
Do đó, tam giác OAD = tam giác OCB (cgc)
=> AD = CB (hai cạnh tương ứng)
b. Do OA = OC và OB = OD nên AB = CD
Lại có: tam giác OAD = tam giác OCB (chứng minh trên)
=> góc OBC = góc ODA; OAD = OCB (hai góc tương ứng)
Mặt khác, góc ABE + góc OBC = góc CDE + góc ODA = 180 => góc ABE = góc CDE
Xét tam giác ABE và tam giác CDE, có:
góc OAD = góc OCB (chứng minh trên) AB = CD (chứng minh trên)
góc ABE = góc CDE (chứng minh trên)
Do đó, tam giác ABE = tam giác CDE (gcg)
c. Vì tam giác ABE = tam giác CDE (chứng minh trên) nên AE = CE (hai cạnh tương ứng)
Xét tam giác AEO và tam giác CEO có: AE = CE (chứng minh trên) OE cạnh chung OA = OC (giả thiết)
Do đo, tam giác AEO = tam giác CEO (ccc)
=> góc AOE = góc COE (hai góc tương ứng)
=> OE là tia phân giác của góc xOy
4.2. Dạng 2. Tính số đo góc
Bài 1. Cho hai góc xOy và góc yOz là hai góc kề bù, biết góc xOy = 120 a. Tính góc yOz
b. Gọi Om là tia phân giác của góc xOy. Tính góc zOm
Hướng dẫn giải
a. Vì góc xOy và góc yOz là hai góc kề bù nên ta có góc xOy + góc yOz = 180 hay góc yOz = 180 - góc xOy = 60
b. Tia Om là tia phân giác của góc xOy nên góc xOm = mOy = góc xOy / 2 = 120/2 = 60
Hai góc xOm và zOm kề bù nên góc xOm + góc zOm = 180 => góc zOm = 120
Bài 2. Cho hai góc kề nhau góc AOB và góc BOC sao cho góc AOB = 50, góc BOC = 80. Gọi
OD là tia đối của tia OC. a. Tính số đo góc AOC
b. chứng tỏ tia OA nằm giữa hai tia OB và OD
c. Tia OA có phải là tia phân giác của BOD không? Vì sao?
Hướng dẫn giải
a. Ta có: góc AOC = góc AOB + góc BOC = 50 + 80 = 130
b. Ta có: góc AOC < COD (130<180) và góc COB < góc AOC (80 < 130) do đó, tia OA nằm giữa tia OB và OD
c. Tia OA nằm giữa hai tia OC và OD nên góc COD = góc COA + góc AOD => góc AOD = 50
Như vậy góc AOD = góc AOB = 50 kết hợp với câu b, OA nằm giữa hai tia OB và OD nên OA là
tia phân giác của góc BOD.
4.3. Dạng 3. Vận dụng tính chất của một góc để chứng minh các đoạn thẳng bằng nhau
Phương pháp giải: Áp dụng định lí thuận: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Bài 1. Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt đường thẳng vuông góc
với BC tại trung điểm của BC ở D. Gọi H và K là chân các đường vuông góc kẻ từ D đến các
đường thẳng AB, AC. Chứng minh: BH = CK.
Hướng dẫn giải
TA có: D thuộc phân giác của góc A
DH vuông góc với AB, DK vuông góc với AC
=> DH = DK (tính chất tia phân giác của một góc)
Gọi G là trung điểm của BC
Xét tam giác BGD và tam giác CGD, ta có:
góc BGD = góc CGD = 90° (DG là đường trung trực của BC) BG = CG (giả thiết) DG là cạnh chung
Do đó, tam giác BGD = tam giác CGD (hai cạnh góc vuông)
=> BD = CD (hai cạnh tương ứng)
Xét tam giác BHD và tam giác CKD có: góc BHD = CKD = 90° DH = DK (chứng minh trên) BD = CD (chứng minh trên)
Do đó, tam giác BHD = tam giác CKD (cạnh huyền - cạnh góc vuông)
=> BH = CK (hai cạnh tương ứng)
Bài 2. Cho tam giác ABC có góc A = 120°. Tia phân giác của góc A cắt BC tại D. Tia phân
giác của góc ADC cắt AC tại I. Gọi H và K lần lượt là hình chiếu của I trên đường thẳng AB,
BC. Chứng minh: IH = IK
Hướng dẫn giải
Kẻ IE vuông góc Ad (E thuộc AD). Gọi Ax là tia đối của tia AB.
Vì góc BAC và góc CAx là hai hóc kề bù mà góc BAC = 120 nên góc CAx = 60 (1)
Ta có: AD là phân giác của BAC => góc DAC = 1/2 góc BAC = 60 (2)
Từ (1) và (2) suy ra AC là tia phân giac của góc DAx
=> IH = IE (tính chất phân giác của một góc) (3)
Vì DI là phân giác của góc ADC nên IK = IE (tính chất phân giác của một góc) (4)
Từ (3) và (4) suy ra: IH = IK
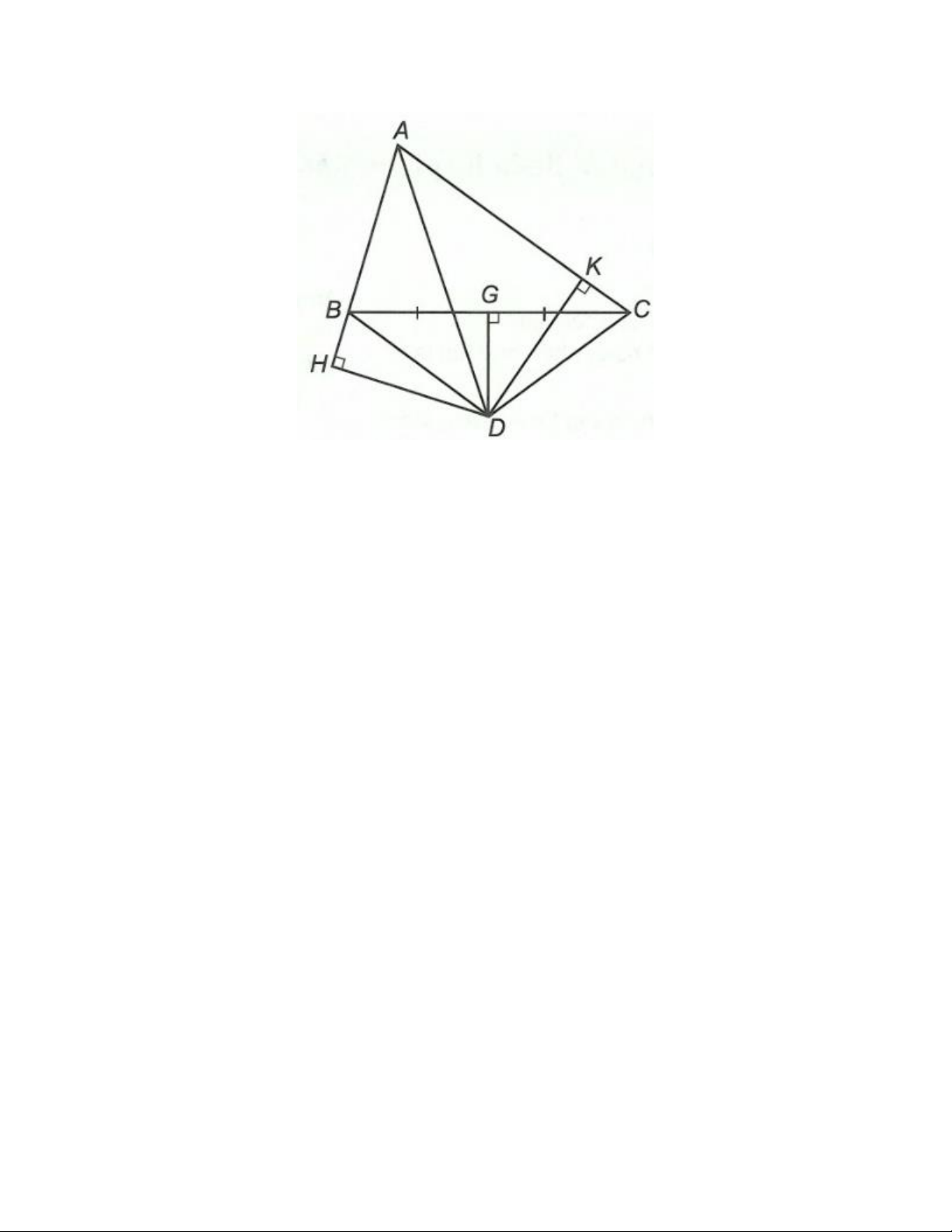
Bài 3. Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 6 cm. Gọi E là trung điểm AC, tia
phân giác của góc A cắt BC tại D. a. Tính BC?
b. Chứng minh: tam giác BAD = tam giác EAD
c. Gọi H và K lần lượt là hình chiếu của G trên Ab, AC. Chứng minh rằng: điểm D cách đều AB và AC.
Hướng dẫn giải
a. Xét tam giác ABC vuông tại A, ta có:
AB^2 + AC^2 = BC^2 (định lý pytago)
=> BC = căn bậc hai của 45 (cm)
b. Vì E là trung điểm của AC nên:
AE = 1/2 AC = 3cm => AE = AB
Xét tam giác BAD và tam giác EAD có:
góc BAd = góc EAD (AD là phân giác) AD chung AB = AE (chứng minh tên)
Do đó, tam giác BAD = tam giác EAD (cgc)
c. Vì D nằm trên tia phân giác của góc BAC nên DH = DK (tính chất tia phân giác của một góc)
Vậy điểm D cách đều AB và AC.




