Tích phân kép - Giải tích 2 | Trường đại học Bách Khoa, Đại học Đà Nẵng
Tích phân kép - Giải tích 2 | Trường đại học Bách Khoa, Đại học Đà Nẵng được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Giải tích 2(GT2101) 6 tài liệu
Trường: Trường Đại học Bách khoa, Đại học Đà Nẵng 410 tài liệu
Tác giả:
Preview text:
Tích phân kép (Tích phân 2 lớp) Chử Văn Tiệp
Giải tích II- 2023-2024, ĐHBKĐN 1 Tóm tắt lý thuyết 1. Đặt bài toán:
• Tích phân xác định (Tích phân một lớp) xuất phát từ bài toán tính DIỆN TÍCH hình thang cong.
Bài toán: Hãy tính diện tích hình phẳng nằm bên dưới đồ thị của hàm số
y = f (x) trên đoạn [a, b] như hình vẽ bên dưới. y A y = f (x) B x a b
Chia đoạn [a, b] thành các đoạn nhỏ bởi n + 1 điểm chia x0 = a < x1 < · · · < x tùy ý và lập tổng
n−1 < xn = b, trên mỗi đoạn nhỏ đó lấy một điểm ξ∗ i n X S ≈ f (ξ∗i)∆xi i=1 y A y = f (x) B x ξ∗ ξ∗ ξ∗ ξ∗ ξ∗ ξ∗ ξ∗ ξ∗ x 0 1 2 3 4 5 6 7 0 x1 x2 x3 x4 x5 x6 x7 x8 Z b n X S = f (x)dx = lim f (ξ∗i)∆xi. a |∆xi|→0 i=1 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 1 / 29
• Tích phân kép (Tích phân hai lớp) xuất phát từ bài toán tính THỂ TÍCH hình trụ cong.
Bài toán: Hãy ước lượng thể tích một nhà kho có mái vòm là mặt cong z =
f (x, y) như hình vẽ bên dưới. Hình 1: Thể tích ?
Ước lượng thô cận dưới
Hình 2: (m, n) = (2, 2) và (m, n) = (4, 4)
Để tăng độ chính xác, ta giảm kích thước hình chữ nhật đáy. m n Hình 3: X X V = lim f (x∗ m,n→∞ i , y∗ j )∆xi∆yj i=1 j=1 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 2 / 29
2. Định nghĩa: Tích phân kép của hàm f trên hình chữ nhật D là Z Z Z Z n X f (x, y)dxdy = f (x, y)dA = lim f (x∗i, y∗i)∆Ai D D |∆Ai|→0 i=1
nếu giới hạn trên tồn tại.
Nếu D là một miền bị chặn bất kỳ trong mặt phẳng R2. Khi đó tồn tại một hình
chữ nhật R sao cho D ⊂ R. Đặt hàm mới f (x, y), nếu (x, y) ∈ D F (x, y) = 0 nếu (x, y) ∈ R \ D Khi đó ta định nghĩa Z Z Z Z f (x, y)dxdy = F (x, y)dxdy. D R
3. Công thức tính tích phân kép trong tọa độ Decartes
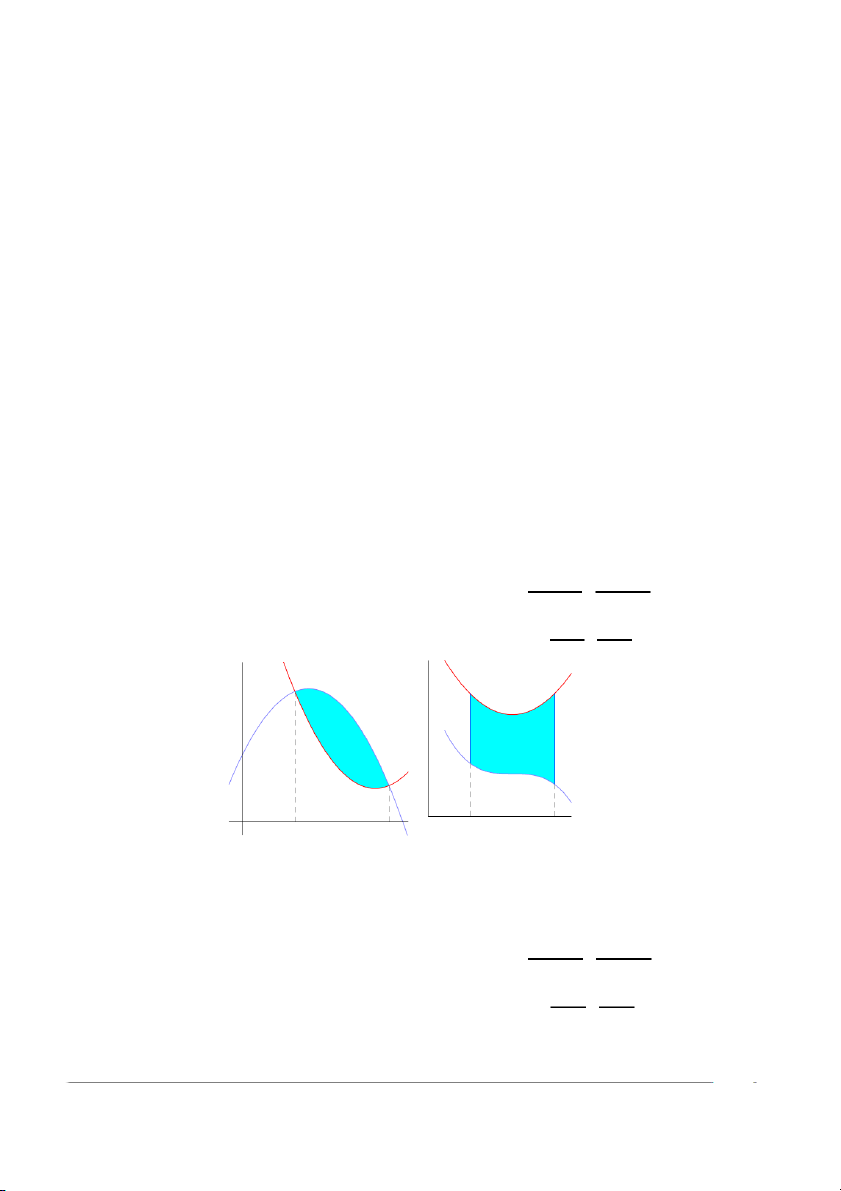
(a) Nếu f : D → R liên tục trên miền D có dạng
D = {(x, y) ∈ R2 : a ≤ x ≤ b, g1(x) ≤ y ≤ g2(x)} thì z }| { Z Z Z b Z g2(x) Z b Z g2(x) f (x, y)dxdy = dx f (x, y)dy = f (x, y)dy dx . D a g1(x) a g1(x) | {z } y = g2(x) y = g2(x) y = g1(x) y = g1(x) a b a b
(b) Nếu f : D → R liên tục trên miền D có dạng
D = {(x, y) ∈ R2 : c ≤ y ≤ d, h1(y) ≤ x ≤ h2(y)} thì z }| { Z Z Z d Z h2(y) Z d Z h2(y) f (x, y)dxdy = dy f (x, y)dx = f (x, y)dx dy . D c h1(y) c h1(y) | {z } Chử Văn Tiệp (BKĐN) Giải tích 2-2023 3 / 29 y y d d x x x x = = = = h h h h 1 2 ( ( 1 2 y y ( ( y y ) ) ) ) c c x x
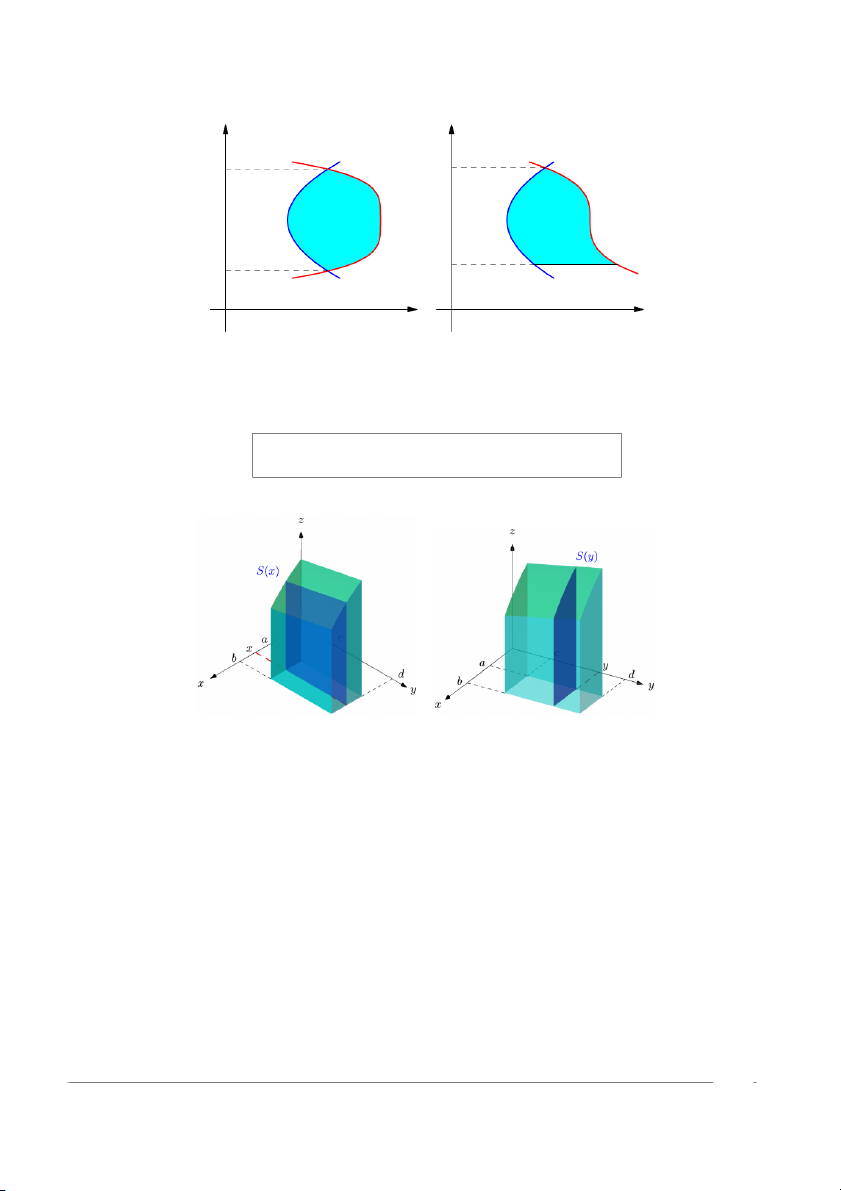
Định lý 1 (Định lý Fubini). Nếu hàm f liên tục trên hình chữ nhật
R = {(x, y) : a ≤ x ≤ b, c ≤ y ≤ d}, thì Z Z Z dZ b Z b Z d f (x, y)dA = f (x, y) dx dy = f (x, y) dy dx R c a a c
Hình 4: Minh họa công thức Fubini
4. Tích phân kép trong tọa độ cực.
Nếu miền D trong hệ tọa độ cực có dạng
{(r, θ) : α ≤ θ ≤ β, r1(θ) ≤ r ≤ r2(θ)} thì Z Z Z β Z r2(θ) f (x, y)dxdy = dθ f (r cos θ, r sin θ)rdr. D α r1(θ) 5. Công thức đổi biến Z Z Z Z f (x, y)dxdy = f (x(u, v), y(u, v))|J|dudv D Duv Chử Văn Tiệp (BKĐN) Giải tích 2-2023 4 / 29
trong đó Jacobian J được tính như sau: ∂(x, y) x0 x0 J = = u v = x0 ∂(x, y) uy0v − x0vy0u. y0 y0 u v
6. Ứng dụng (Xem trong Giáo trình)
• Tính diện tích hình phẳng
• Tính thể tích khối trụ cong • Diện tích mặt cong
• Khối lượng bản phẳng không thuần nhất • Tọa độ trọng tâm • Moment 2 Matlab Z Z
Ví dụ 1 (Tính tích phân dùng Matlab). Tính (|x| + |y|)dxdy |x|+|y|≤1
Lời giải. Chia miền thành 4 phần y D2 D1 x D3 D4 Z Z I = (|x| + |y|)dxdy |x|+|y|≤1 Z Z Z Z Z Z Z Z = (|x| + |y|)dxdy + (|x| + |y|)dxdy + (|x| + |y|)dxdy + (|x| + |y|)dxdy. D1 D2 D3 D4 Ta có Z Z Z 1 Z 1−x Z 1 Z 1−x (|x| + |y|)dxdy = dx (|x| + |y|)dy = dx (x + y)dy D1 0 0 0 0 Z 1 y2 1−x Z 1 (1 − x)2 = xy + dx = x(1 − x) + dx 0 2 0 0 2 x2 x3 1 x3 1 1 = − + x − x2 + = . 2 3 2 3 3 0 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 5 / 29
Tính toán tương tự ta cũng có 3 tích phân còn lại bằng 1. Vậy 4 I = . 3 3 Cách 2. Z Z Z 1 Z 1−|x| I = (|x| + |y|)dxdy = dx (|x| + |y|)dy D −1 −(1−|x|) Z 1 Z 1−|x| Z 1 Z 1−|x| = 2 dx (|x| + |y|)dy = 2 dx (|x| + y)dy −1 0 −1 0 Z 1 y2 1−|x| Z 1 (1 − |x|)2 = 2 |x|y + dx = 2 |x|(1 − |x|) + dx 2 −1 2 0 −1 Z 1 (1 − |x|)2 Z 1 (1 − x)2 4 = 4 |x|(1 − |x|) + dx = 4 x(1 − x) + dx = . 3 0 2 0 2 Matlab code
syms x y; f(x,y)=abs(x)+abs(y);
I=int(int(f,y,-(1-abs(x)),1-abs(x)),x,-1,1) Matlab code
syms x y; f(x,y)=abs(x)+abs(y);
I=int(int(f,y,-(1-abs(x)),1-abs(x)),x,-1,1) 3 Ví dụ mẫu
Ví dụ 2 (Minh họa định lý Fubini). Tính tích phân kép sau Z Z 1 dxdy D (1 + x + y)2
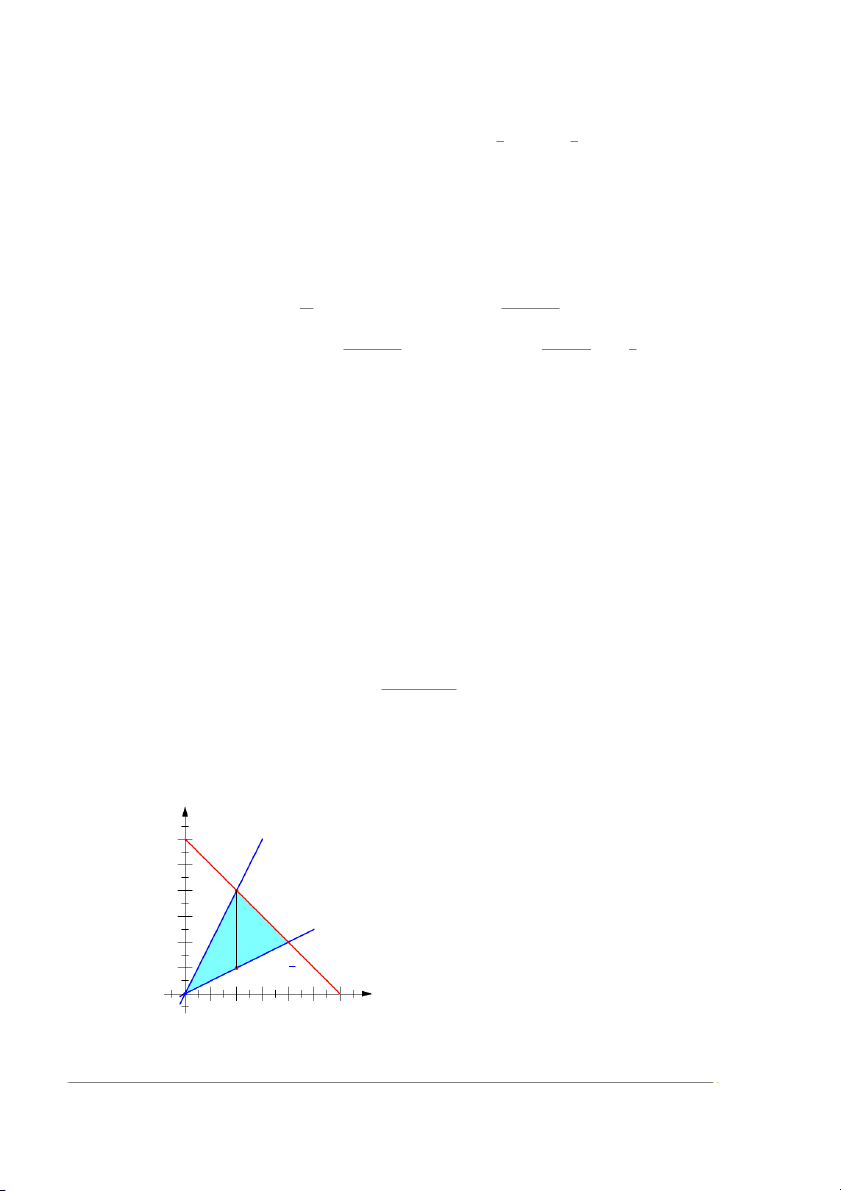
trong đó D là miền giới hạn bởi các đường x = 2y, y = 2x, x + y = 6.
Lời giải. Chia D thành hai miền D1, D2 như hình vẽ. y 6 5 y = 2x 4 3 x + y = 6 2 D2 D1 1 y = x2 O 1 2 3 4 5 6 x Chử Văn Tiệp (BKĐN) Giải tích 2-2023 6 / 29 Z Z 1 Z Z 1 Z Z 1 I = dxdy = dxdy + dxdy D (1 + x + y)2 D (1 + x + y)2 (1 + x + y)2 1 D2 Z 2 Z 2x 1 Z 4 Z 6−x 1 = dx dy + dx dy 0 x/2 (1 + x + y)2 2 x/2 (1 + x + y)2 Z 2 Z 2x 1 Z 4 Z 6−x 1 = dx d(1 + x + y) + dx d(1 + x + y) 0 x/2 (1 + x + y)2 2 x/2 (1 + x + y)2 Z 2x 6 2 −x 1 Z 4 1 = − dx dx + − 0 1 + x + y 2 1 + x + y x/2 x/2 Z 2 1 1 Z 4 1 1 = − + dx + − + dx 0 1 + 3x 1 + 3x/2 2 7 1 + 3x/2 2 4 ln |1 + 3x| 2 ln |1 + 3x/2| 1 2 ln |1 + 3x/2| = − + + − x + 3 3 7 3 0 2 ln 7 2 ln 4 4 2 ln 7 2 2 ln 4 2 ln 7 = − + − + + − = − + . 3 3 7 3 7 3 7 3
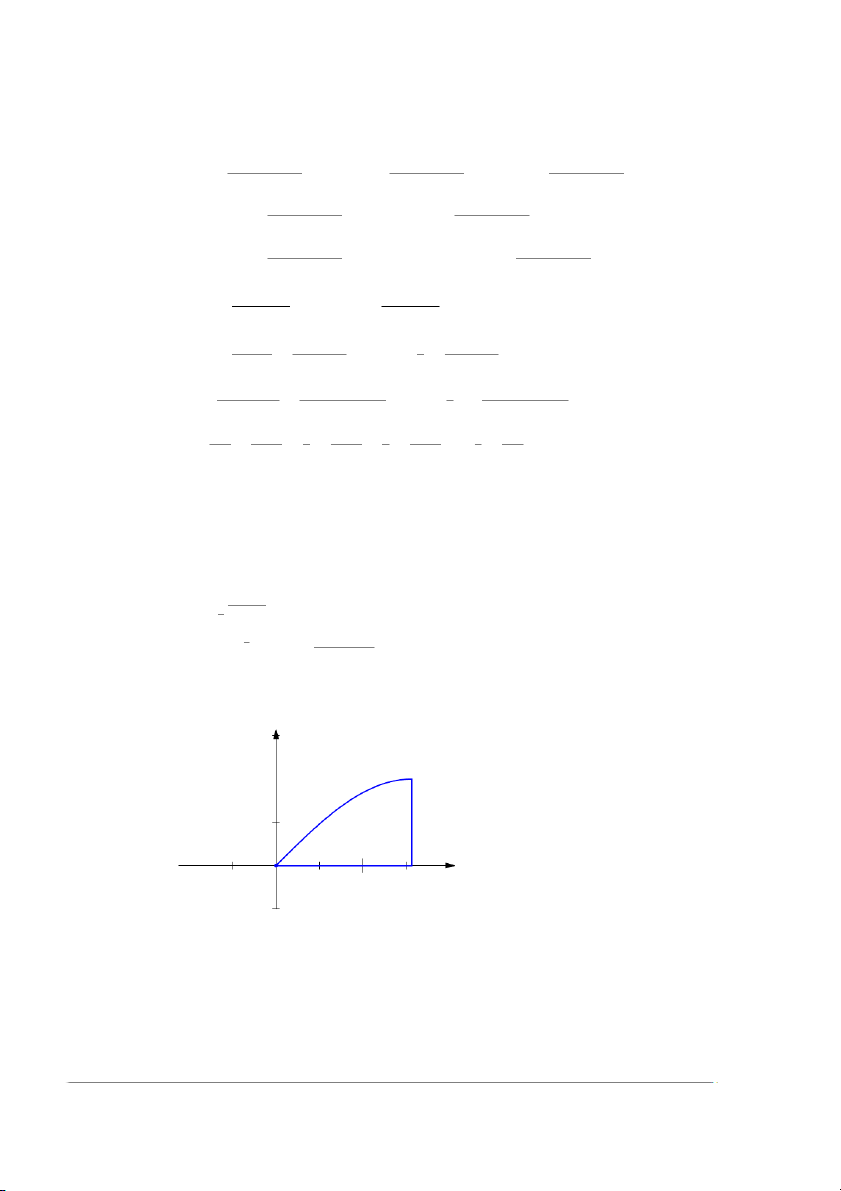
Ví dụ 3. Tính các tích phân sau bằng cách đổi thứ tự lấy tích phân Z 1 Z 3 1. ex2dxdy 0 3y Z 4 Z 2 2. 1 dydx √ 0 y3 + 1 x Z 1 Z π √ 3. 2 I = cos x 1 + cos2 xdxdy 0 arcsin y
D = {(x, y) ∈ R2 : 0 ≤ y ≤ 1, arcsin y ≤ x ≤ π/2} y x = arcsin(y) 1 −1 O 1 π/2 x
D = {(x, y) ∈ R2 : 0 ≤ x ≤ π/2, 0 ≤ y ≤ sin x} Chử Văn Tiệp (BKĐN) Giải tích 2-2023 7 / 29 Z π/2 Z sin x √ I = cos x 1 + cos2 xdydx 0 0 Z π/2 √ sin x = y cos x 1 + cos2 x dx 0 0 Z π/2 √ =
sin x cos x 1 + cos2 xdx (Đổi biến t = 1 + cos2 x) 0 Z 1 dt = − t1/2 2 2 √ 1 Z 2 t3/2 2 8 − 1 = t1/2dt = = . 2 3 1 3 1 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 8 / 29
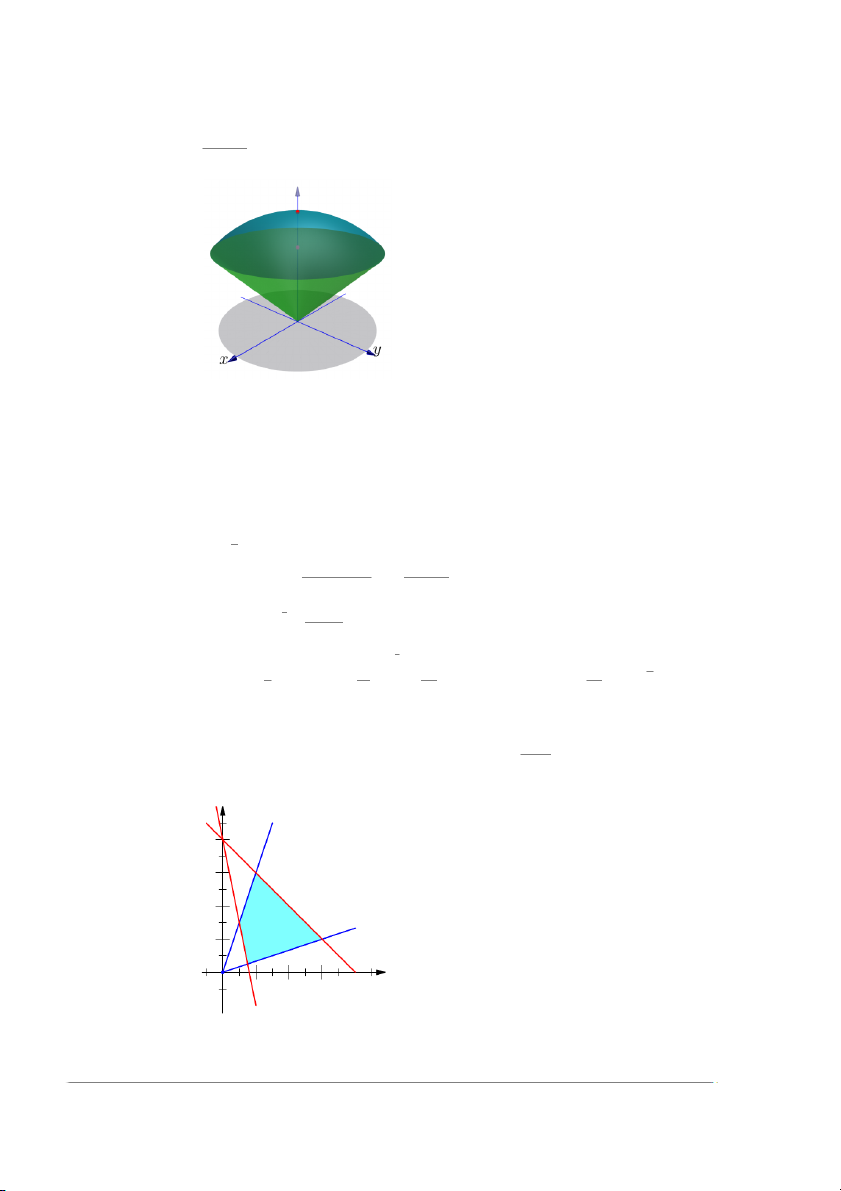
Ví dụ 4 (Đổi biến tọa tọa độ cực). Tính thể tích miền V bị chặn bởi x2 +y2 +z2 ≤ 4 và p z ≥ x2 + y2. Lời giải.
Trước hết ta xác định hình chiếu xuống mặt phẳng xoy
D = {(x, y) ∈ R2 : x2 + y2 ≤ 2}.
đổi biến tọa độ cực x = r cos ϕ J = r ⇒ |J| = r y = r sin ϕ, với √
0 ≤ r ≤ 2, 0 ≤ ϕ < 2π. Khi đó ta có công thức tính thể tích như sau: Z Z p p V = ( 4 − x2 − y2 − x2 + y2)dxdy {x2+y2≤2}√ Z 2π Z 2 √ = dϕ ( 4 − r2 − r)rdr 0 0 √ 2 1 r3 2π 8π √ = 2π × − (4 − r2)3/2 − = (−23/2 − 23/2 + 43/2) = (2 − 2) 3 3 3 3 0 Z Z dxdy
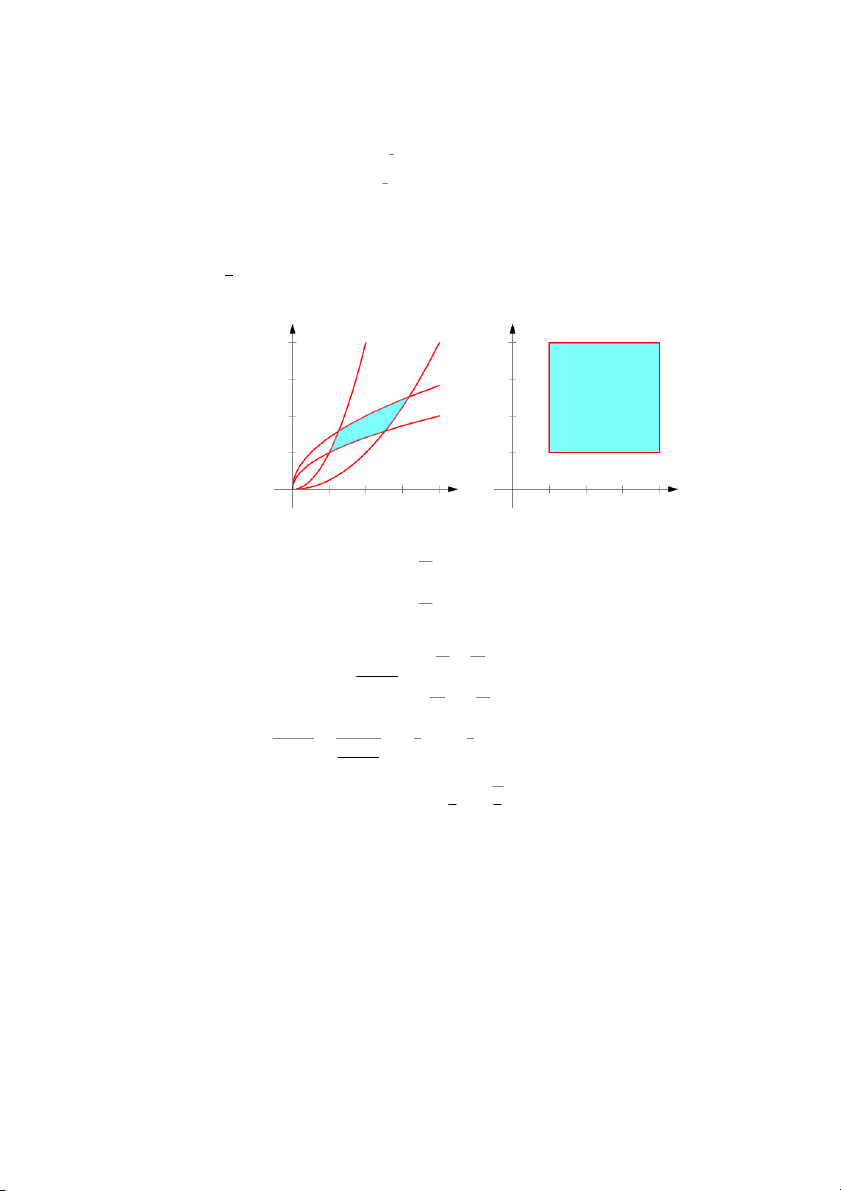
Ví dụ 5 (Đổi biến tổng quát). Tính tích phân sau , S : 3y = x, y = x2y2 S 3x, y = 4 − 5x, y = 4 − x; y y = 3x 3 2 y = 4 − x S 1 y = x/3 O 1 2 3 x Lời giải. y = 4 − 5x Chử Văn Tiệp (BKĐN) Giải tích 2-2023 9 / 29 Đặt x 4u u = x = y 1 − uv y − 4 ⇒ 4
, (u, v) ∈ [1/3, 3] × [−5, −1]. v = y = x 1 − uv 4u2 4u2 4(1 − uv) + 4uv 4 x0 x0 J = u v (1 − uv)2 (1 − uv)2 (1 − uv)2 (1 − uv)2 = 4v 4u = 4v 4u y0 y0 u v (1 − uv)2 (1 − uv)2 (1 − uv)2 (1 − uv)2) 16u − 16u2v 16u = =
> 0, ∀(u, v) ∈ [1/3, 3] × [−5, −1]. (1 − uv)4 (1 − uv)3
Theo công thức đổi biến ta có Z Z dxdy Z Z (1 − uv)4 16u = × dvdu x2y2 [1/3,3]×[−5,−1] 256u2 (1 − uv)3 S Z Z 1 − uv Z Z 1 v = dvdu = − dvdu 16u 16 [1/3,3]×[−5,−1] 16u [1/3,3]×[−5,−1] Z Z 1 Z Z v = dvdu − dvdu 16 [1/3,3]×[−5,−1] 16u [1/3,3] 1 3 −1 3 v2−1 ln 3 = ln u v − u = + 4 16 1/3 −5 1/316 −5 2 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 10 / 29 Z Z
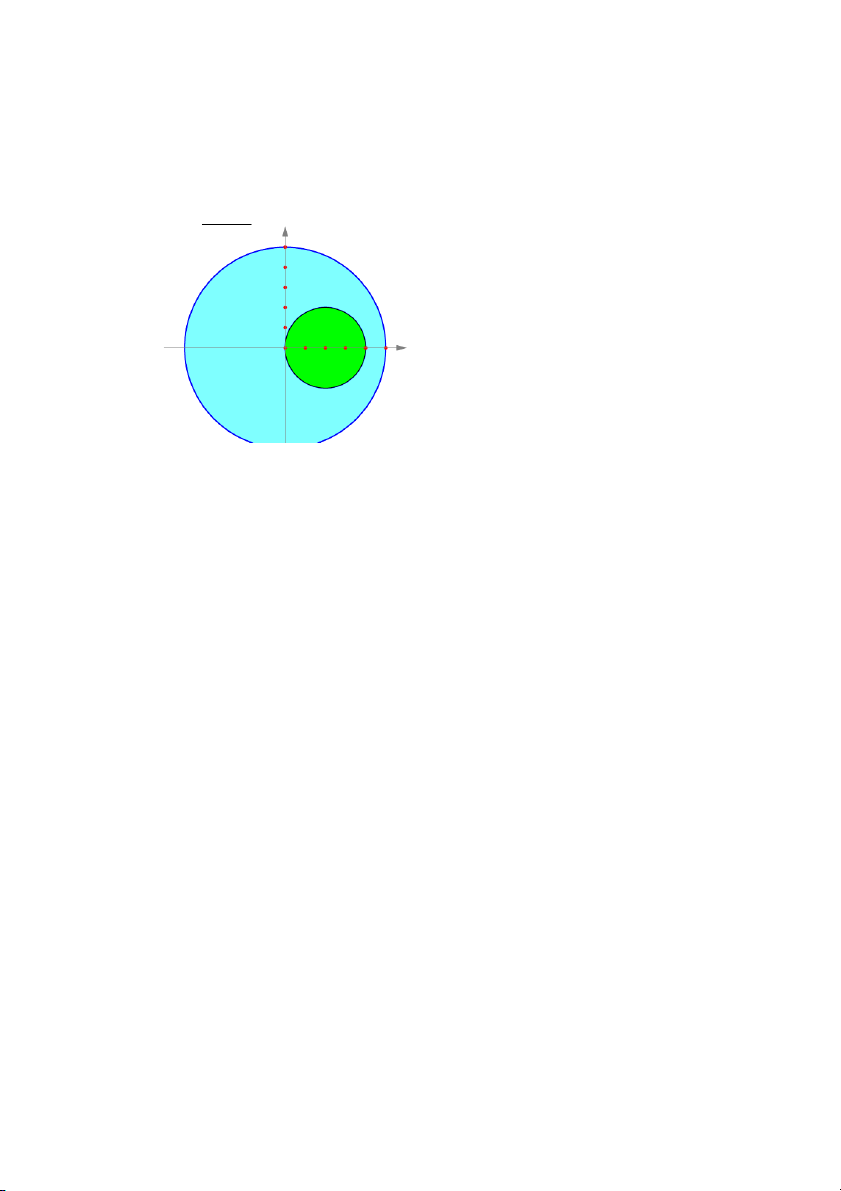
Ví dụ 6 (Ví dụ tổng hợp). Tính tích phân kép sau xdxdy trong đó D là miền D 4x ≤ x2 + y2 ≤ 25. Lời giải. Cách 1 y D1 D D2 x Do D1 = D ∪ D2
và hai miền trên ko đè lên nhau nên Z Z Z Z Z Z xdxdy = xdxdy − xdxdy. D D1 D2 | {z } | {z } I1 I2
Để tính I1 ta có thể dùng đổi biến tọa độ cực x = r cos ϕ J = r ⇒ |J| = r y = r sin ϕ,
với 0 ≤ r ≤ 5, 0 ≤ ϕ < 2π. Từ đó ta có Z Z Z 2π Z 5 Z 2π Z 5 xdxdy = dϕ r cos ϕrdr = cos ϕdϕ × r2dr D1 0 0 0 0 2π r35 = sin ϕ × = 0. 0 3 0
Phương trình đường tròn nhỏ có thể viết dưới dạng (x − 2)2 + y2 = 4.
Để tính I2 ta có thể dùng đổi biến tọa độ cực (suy rộng) x − 2 = r cos ϕ x = 2 + r cos ϕ ⇔ y = r sin ϕ, y = r sin ϕ, Chử Văn Tiệp (BKĐN) Giải tích 2-2023 11 / 29
với 0 ≤ r ≤ 2, 0 ≤ ϕ < 2π. Jacobiên của phép đổi biến x0 x0 cos ϕ −r sin ϕ J = r ϕ = = r ⇒ |J| = r y0 y0 r ϕ sin ϕ r cos ϕ Từ đó ta có Z Z Z 2π Z 2 Z 2π Z 2 I2 = xdxdy = dϕ (2 + r cos ϕ)rdr = dϕ (2r + r2 cos ϕ)dr D2 0 0 0 0 Z 2 2π 2π r3 Z 2π 8 8 = r2 + cos ϕ dϕ = 4 + cos ϕ dϕ = 4ϕ + sin ϕ = 8π. 3 3 3 0 0 0 0 Vậy Z Z Z Z Z Z xdxdy = xdxdy − xdxdy = 0 − 8π = −8π. D D1 D2
Cách 2 Tách D thành hai nửa trái và phải D = Dt ∪ Dp
hai miền trên ko đè lên nhau nên Z Z Z Z Z Z xdxdy = xdxdy + xdxdy. D Dt Dp | {z } | {z } K1 K2 y D Dp Dt x
Để tính K1 ta dùng đổi biến tọa độ cực x = r cos ϕ J = r ⇒ |J| = r y = r sin ϕ, Chử Văn Tiệp (BKĐN) Giải tích 2-2023 12 / 29 với π 3π 0 ≤ r ≤ 5, ≤ ϕ ≤ . Từ đó ta có 2 2 ! Z Z Z 3π/2 Z 5 Z 3π/2 Z 5 xdxdy = dϕ r cos ϕrdr = cos ϕdϕ × r2dr Dt π/2 0 π/2 0 3π/2 r3 5 125 250 = sin ϕ × = −2 · = − . π/2 3 0 3 3
Để tính K2 ta cũng dùng đổi biến tọa độ cực x = r cos ϕ J = r ⇒ |J| = r. y = r sin ϕ, với π π
− ≤ ϕ ≤ . Để xác định cận cho r ta để ý rằng r chạy từ đường tròn nhỏ có phương 2 2
trình tọa độ cực dạng r = 4 cos ϕ đến đường tròn lớn có phương trình r = 5. Vậy 4 cos ϕ ≤ r ≤ 5. Từ đó Z Z Z π/2 Z 5 Z π/2 Z 5 K2 = xdxdy = dϕ r cos ϕrdr = dϕ r2 cos ϕdr Dp −π/2 4 cos ϕ −π/2 4 cos ϕ Z π/2 r3 5 Z π/2 125 64 = cos ϕdϕ = − cos3 ϕ cos ϕdϕ −π/2 3 4 cos ϕ −π/2 3 3 125 Z π/2 64 Z π/2 = cos ϕdϕ − cos4 ϕdϕ. 3 −π/2 3 −π/2 Ta có Z π/2 π/2 cos ϕdϕ = sin ϕ = 2. −π/2 −π/2
Sử dụng công thức hạ bậc 1 + cos 2ϕ cos2 ϕ = 2 ta được 2 2 1 + cos 2ϕ 1 cos 2ϕ cos2 2ϕ cos4 ϕ = cos2 ϕ = = + + 2 4 2 4 1 cos 2ϕ 1 + cos 4ϕ 3 cos 2ϕ cos 4ϕ = + + = + + . 4 2 8 8 2 8 Từ đó Z π/2 3 sin 2ϕ sin 4ϕ π/2 3π cos4 ϕdϕ = ϕ + + = . 8 4 32 −π/2 −π/2 8 Vậy 125 64 3π 250 K2 = · 2 − · = − 8π. 3 3 8 3 Vậy Z Z 250 250 xdxdy = − + − 8π = −8π. D 3 3 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 13 / 29 y D1 D D2 x
Cách 3 Ta sẽ tính trực tiếp bằng cách sử dụng tọa độ Descartes (xem hình vẽ ở cách 1) Z Z Z Z Z Z xdxdy = xdxdy − xdxdy. D D1 D2 | {z } | {z } I1 I2
Ta xem D như miền loại II như sau 1 p p
D1 = {(x, y) ∈ R2 : −5 ≤ y ≤ 5, − 25 − y2 ≤ x ≤ 25 − y2}. Khi đó √ Z Z Z 5 Z 25−y2 I1 = xdxdy = dy √ xdx = 0 D1 −5 − 25−y2 √ Z 25−y2 vì với mỗi y tích phân √
xdx là tích phân của hàm lẻ trên cận đối xứng nên bằng − 25−y2 0.
Tương tự, ta cũng xem D2 là miền loại II như sau p p
D2 = {(x, y) ∈ R2 : −2 ≤ y ≤ 2, 2 − 4 − y2 ≤ x ≤ 2 + 4 − y2}. Khi đó √ Z Z Z 2 Z 2+ 4−y2 I2 = xdxdy = dy √ xdx D2 −2 2− 4−y2 √ Z 2 p p x2 2+ 4−y2
Z 2 (2 + 4 − y2)2 (2 − 4 − y2)2 = dy = √ − dy −2 2 2− 4−y2 −2 2 2 Z 2 Z p π/2 = 4 4 − y2dy = 4 4 cos2 tdt (Đổi biến y = 2 sin t) −2 −π/2 Z π/2 Z π/2 π/2 = 8 (1 + cos 2t)dt = 16
(1 + cos 2t)dt = 16t + 8 sin 2t = 8π. −π/2 0 0 Vậy I = I1 − I2 = −8π. Chử Văn Tiệp (BKĐN) Giải tích 2-2023 14 / 29
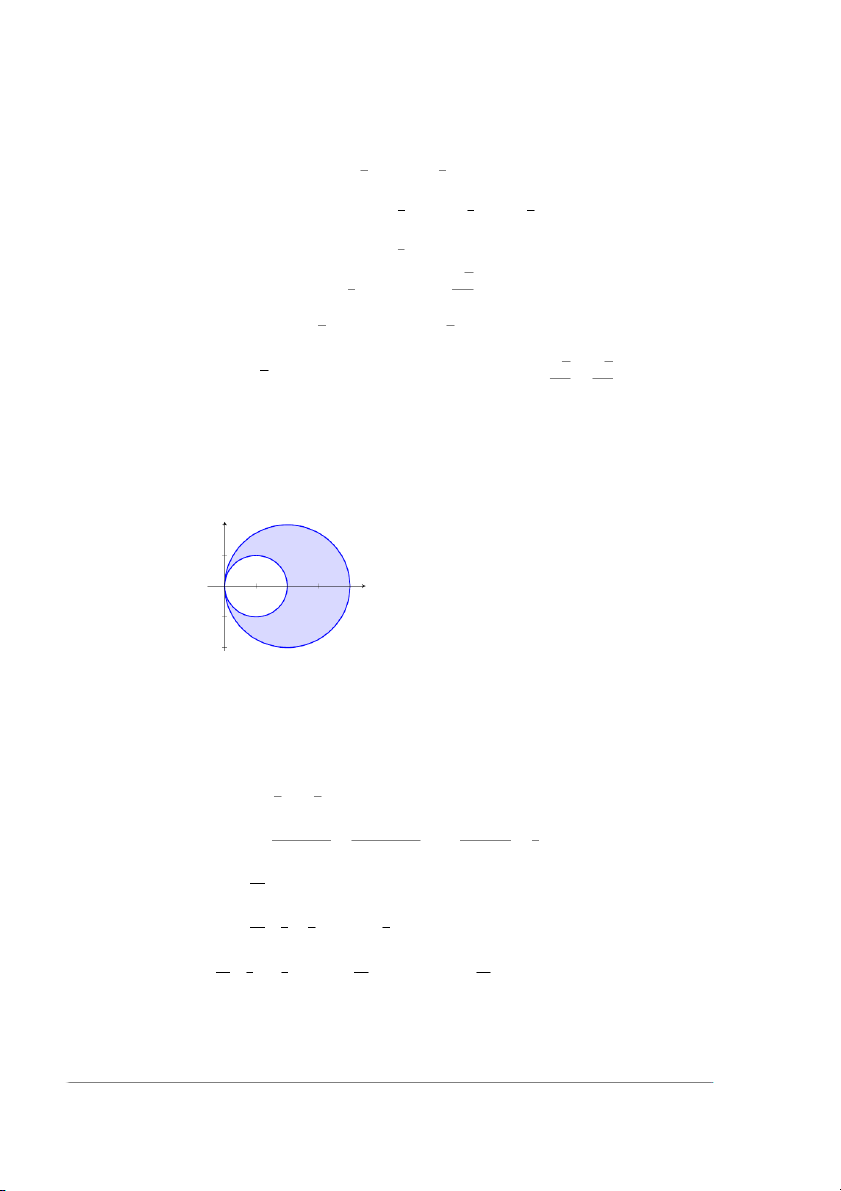
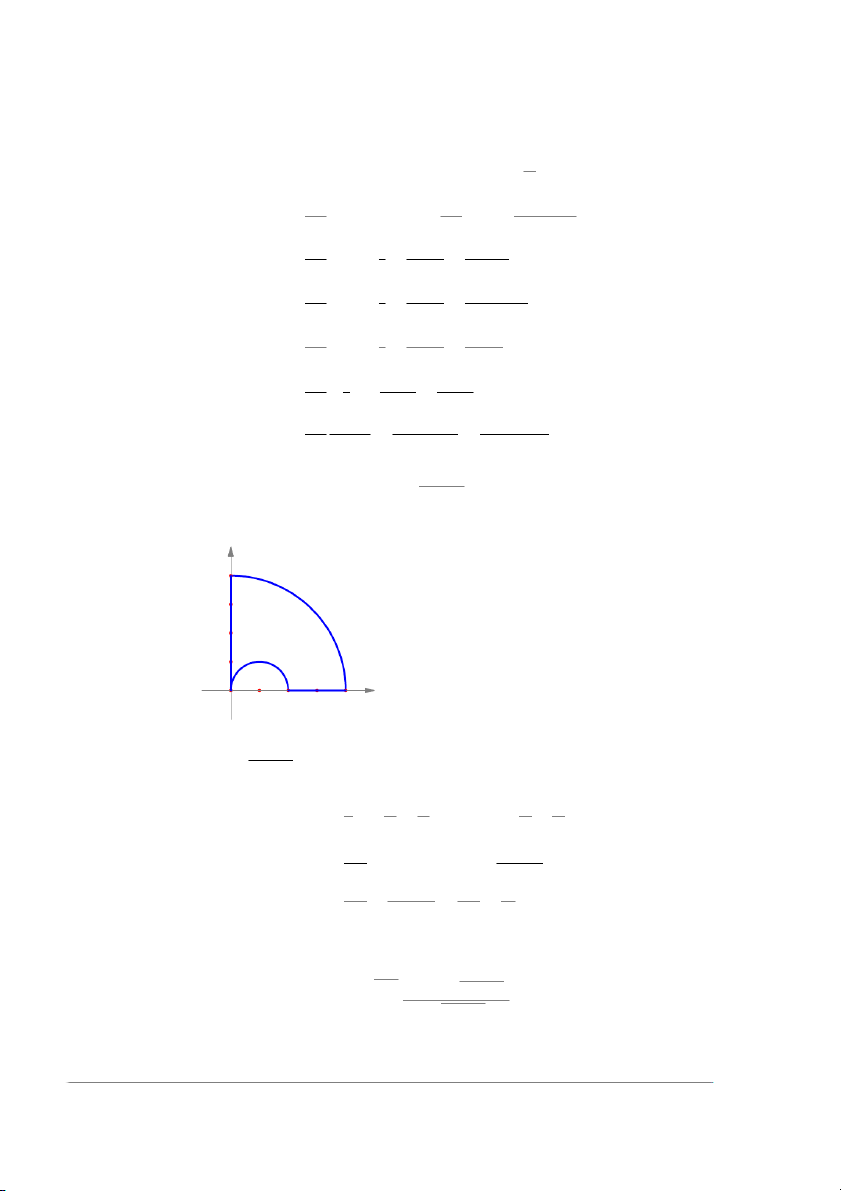
Ví dụ 7 (Ứng dụng tính diện tích). Tính diện tích miền tô màu dưới đây y r = 1 + cos(θ) r = 1 x
Lời giải. Gọi D là phần miền cần tính diện tích. Sử dụng tọa độ cực ta có: Z Z Z π/2 Z 1+cos θ S = dxdy = dθ rdr D 0 1 Z 1+cos θ π/2 r2 Z π/2 1 = dθ = (1 + cos θ)2 − 1 dθ 0 2 0 2 1 1 Z π/2 Z π/2 1 1 + cos 2θ = 2 cos θ − cos2 θ dθ = 2 cos θ + dθ 2 0 2 0 2 π/2 1 1 sin 2θ π = θ + 2 sin θ + = + 1. 2 2 4 8 0
Ví dụ 8 (Cách tính tích phân liên quan đến phân phối chuẩn tắc trong xác Z ∞ suất thống kê). Tính I = e−x2dx 0 Lời giải. Z ∞ Z ∞ I2 = e−x2dx e−y2dy 0 0 Z ∞ Z ∞ = e−x2−y2dxdy x=0 y=0 Z π/2 Z ∞ π Z ∞ = e−r2rdrdθ = e−r2rdr θ=0 r=0 2 0 π 1 ∞ π 1 1 = − e−r2 = lim − e−c2 + e−02 2 2 2 2 2 0 c→∞ π 1 π = 0 + = , (5) 2 2 4 √ Vậy I = π. 2 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 15 / 29
Chú ý sử dụng tích phân từng phần ta có Z ∞ 1 ∞ Z 1 ∞ x2e−x2dx = − xe−x2 + e−x2 dx 0 2 0 2 0 1 1 1 Z ∞ = lim − ce−c2 + 0e−02 + e−x2 dx c→∞ 2 2 2 0 1 Z ∞ = 0 + 0 + e−x2 dx 2 0 √ 1 Z ∞ π = e−x2 dx = . 2 4 0 Z ∞ Đối với tích phân √ √ xe−xdx ta đặt t = x suy ra 0 Z √ ∞ √ √ Z ∞ Z ∞ π π xe−xdx = 2t2e−t2dt = 2 t2e−t2dt = 2 · = . 4 2 0 0 0
Ví dụ 9 (Ứng dụng tính thể tích). Tính thể tích của miền nằm bên dưới paraboloid
z = 4 − (x − 2)2 − y2 bị chặn bởi mặt phẳng xoy và bị giới hạn bởi (x − 1)2 + y2 = 1 và (x − 2)2 + y2 = 4. y 2 1 x 1 2 3 4 −1 Lời giải. −2 Z Z Z π/2 Z 4 cos θ 2 2 f (x, y) dxdy =
4 − r cos θ − 2 − r sin θ r dr dθ R −π/2 2 cos θ Z π/2 Z 4 cos θ = − r3 + 4r2 cos θ dr dθ −π/2 2 cos θ Z π/2 1 4 4 cos θ = − r4 + r3 cos θ dθ −π/2 4 3 2 cos θ Z π/2 256 cos4 θ 4(64 cos4 θ) 16 cos4 θ 4 = − + − − + (8 cos4 θ) dθ −π/2 4 3 4 3 Z π/2 44 = cos4 θ dθ −π/2 3 Z π/2 44 3 1 1 = + cos(2θ) + cos(4θ) dθ 8 2 −π/2 3 8 44 3 1 1 π/2 11 = θ + sin(2θ) + sin(4θ) = π. 3 8 4 32 2 −π/2 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 16 / 29
Ví dụ 10 (Ứng dụng trong vật lý). Cho một chiếc hoa tai tạo thành từ một đĩa
kinh loại mỏng phẳng, đồng chất bán kính R bằng việc khoét đi một hình tròn bán kính r như hình vẽ P
1. Tìm tọa độ trong tâm của chiếc hoa tai theo r và R.
2. CMR khi trọng tâm của chiếc hoa tai là tại điểm P thì tỉ số √ R 1 + 5 = . r 2
Ví dụ 11. Tính tọa độ trọng tâm của các hình sau: A B 1 1 x = 1 + y2 1 1 y = −x2 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 17 / 29 4 Luyện tập
CÂU 1. Tính tích phân RR y sin(xy)dA trong đó R = [1, 2] × [0, π] bằng 2 cách. R
CÂU 2. Tìm thể tích của vật rắn S bị chặn bởi elliptic paraboloit x2 + 2y2 + z = 16, các
mặt phẳng x = 2, y = 2 và ba mặt phẳng tọa độ.
CÂU 3. Tính RR x + 2ydA, trong đó D là bị chặn bởi hai parabol y = 2x2 và y = 1 + x2. D
CÂU 4. Tính thể tích vật rắn nằm phía dưới paraboloid z = x2 + y2 và phía trên miền
D trong mặt phẳng xy bị chặn bởi đường thẳng y = 2x và parabol y = x2.
CÂU 5. Tính thể tích của tứ diện sau tạo bởi bốn mặt phẳng sau:x + 2y + z = 2, x = 2y, x = 0, z = 0.
CÂU 6. Tính tích phân sau: R 1 R 1 sin(y2)dydx. 0 x
CÂU 7. Tính các tích phân sau:
(a) RR y2dA, D = {(x, y)| − 1 ≤ y ≤ 1, −y − 2 ≤ x ≤ y} D
(b) RR xdA, D = {(x, y)|0 ≤ x ≤ π, 0 ≤ y ≤ sin x} D
(c) RR y2exydA, D = {(x, y)|0 ≤ y ≤ 4, 0 ≤ x ≤ y} D
(d) RR x cos ydA, D bị chặn bởi y = 0, y = x2, x = 1. D
(e) RR (2x − y)dA, D bị chặn bởi hình tròn tâm tại gốc tọa độ và bán kính D bằng 2
CÂU 8. Tính thể tích của vật rắn sau:
(a) Bên dưới mặt phẳng x + 2y − z = 0 và bên trên miền bị chặn bởi y = x và y = x4
(b) Nằm dưới mặt z = xy và trên tam giác có ba đỉnh (1, 1), (4, 1) và (1,2)
(c) Bị chặn bởi các mặt phẳng tọa độ và mặt phẳng 3x + 2y + z = 6
(d) Bị chặn bởi z = x2, y = x2 và các mặt phẳng z = 0, y = 4
(e) Bị chặn bởi y = 1 − x2, y = x2 − 1 và các mặt phẳng x + y + z = 2, 2x + 2y − z + 10 = 0
CÂU 9. Vẽ miền lấy tích phân và đổi thứ tự lấy tích phân sau: Z 4 Z √x (a) f (x, y)dydx 0 0 √ Z 3 Z 9−y2 (b) √ f (x, y)dxdy 0 − 9−y2 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 18 / 29 Z 2 Z ln x (c) f (x, y)dydx 1 0
CÂU 10. Tính các tích phân sau bằng cách đổi thứ tự lấy tích phân Z 1 Z 3 (a) ex2dxdy 0 3y Z 4 Z 2 (b) 1 dydx √ 0 y3 + 1 x Z 1 Z π (c) 2 √ cos x 1 + cos2 xdxdy 0 arcsin y
CÂU 11. Tính tích phân sau bằng cách chuyển sang tọa độ cực. (a) RR (3x + 4y2)dA,
D là miền thuộc nửa mặt phẳng trên bị chặn bởi hai D
đường tròn x2 + y2 = 1 và x2 + y2 = 4 √ Z 1 Z 1−y2 (b) √ (x2 + y2)dxdy −1 − 1−y2 √ Z a Z a−x2 (c) dydx √ −a − a2−x2 Z 0 Z 0 (d) 2 dydx √ p −1 − 1−x2 1 + x2 + y2 Z 1 Z 0 p (e) 4 x2 + y2 √ dydx −1 1 + x2 + y2 − 1−y2 √ Z 2 Z 1−(x−1)2 (f) x + y dxdy x2 0 + y2 0
CÂU 12. Dùng tích phân hai lớp tính diện tích các miền sau:
(a) Tính diện tích của miền nằm bên trong đường cardioid r = 1 + cos 2θ và
bên ngoài đường tròn r = 1
(b) Tính diện tích của một nhánh cách hoa hồng cho bởi r = 12 cos 3θ
(c) Tính diện tích của miền nằm trong 2 đường cardioid r = 1 + cos θ và r = 1 − cos θ
CÂU 13. Sử dụng tọa độ cực tính thể tích của các vật sau:
(a) Tính thể tích của vật thể bị chặn bởi mặt phẳng z = 0 và paraboloid z = 1 − x2 − y2.
(b) Tính thể tích của vật thể nằm bên dưới paraboloid z = x2 + y2, bên trên
mặt phẳng xy và bên trong của hình trụ x2 + y2 = 2x.
CÂU 14. Tính các tích phân kép sau Chử Văn Tiệp (BKĐN) Giải tích 2-2023 19 / 29 Z Z (a) √ (12x2y2 + 16x3y3)dxdy, S : x = 1, y = x2, y = − x; S Z Z (b) √ (9x2y2 + 48x3y3)dxdy, S : x = 1, y = x, y = −x2; S Z Z (c) √ (36x2y2 − 96x3y3)dxdy, S : x = 1, y = 3 x, y = −x3; S Z Z (d) √ (18x2y2 + 32x3y3)dxdy,
S : x = 1, y = x3, y = − 3 x; S Z Z (e) √ (27x2y2 + 48x3y3)dxdy,
S : x = 1, y = x2, y = − 3 x; S Z Z (f) √ (18x2y2 + 32x3y3)dxdy, S : x = 1, y = 3 x, y = −x2; S Z Z (g) √ (18x2y2 + 32x3y3)dxdy, S : x = 1, y = x3, y = − x; S Z Z (h) √ (27x2y2 + 48x3y3)dxdy, S : x = 1, y = x, y = −x3; S Z Z (i) √ (4xy + 3x2y2)dxdy, S : x = 1, y = x2, y = − x; S Z Z (j) √ (12xy + 9x2y2)dxdy, S : x = 1, y = x, y = −x2. S Z Z CÂU 15. xdxdy,
S : y = x2, 8y = x2, x = y2, 8x = y2; y S Z Z CÂU 16. (x + y)dxdy,
S : xy = 1, xy = 3, y = x, y = x − 2; S Z Z CÂU 17. dxdy ,
S : 2y = x, y = 2x, y = 1 − x, y = 1 − 3x; x2y2 S Z Z CÂU 18. x2dxdy,
S : xy = 2, xy = 4, y = x, y = 3x(x > 0, y > 0); S Z Z CÂU 19. (2x + y)dxdy, S : xy = 1, xy = 2, x + y = 3; S Chử Văn Tiệp (BKĐN) Giải tích 2-2023 20 / 29 y v 3 x = u + v 3 x + y = u − v y 2 = 2 3 xy x S = 1 y 2 1 = 1 D √ 1 2 3 1 2 2 3 x u Lời giải. Đổi biến x = u + v y = u − v. Jacobian 1 1 J = = −2, |J| = 2. 1 −1 Ta có xy = 1 ⇔ u2 − v2 = 1. xy = 2 ⇔ u2 − v2 = 2. x + y = 3 ⇔ u = 1.5. Ta có Z Z Z Z Z Z (2x + y)dxdy = (3u + v)2dudv = 6u + 2vdudv S D D √ √ Z 1.5 Z u2−1 Z 1.5 Z u2−2 = du 6u + 2vdv − du 6u + 2vdv √ √ √ 1 − u2−1 2 − u2−2 √ √ Z 1.5 Z u2−1 Z 1.5 Z u2−2 = 2 du 6udv − 2 du 6udv √ 1 0 2 0
(tính chất tích phân hàm chẵn, lẻ trên cận đối xứng) Z 1.5 √ √ u2−1 Z 1.5 u2−2 = 2 6uv du du − 2 6uv √ 1 0 2 0 Z 1.5 √ Z 1.5 √ = 12 u u2 − 1du − 12 u u2 − 2du √ 1 2 Z 1.5 Z 1.5 = 6 (u2 − 1)1/2d(u2 − 1) − 6 (u2 − 2)1/2d(u2 − 2) √ 1 2 1.5 1.5 √ 2 2 5 5 1
= 6 × (u2 − 1)3/2 − 6 × (u2 − 2)3/2 = − . 3 3 √ 2 2 1 2 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 21 / 29
Chú ý, ta vẫn có thể làm trực tiếp như sau: √ Z Z Z (3+ 5)/2 Z 3−x Z 2 Z 3−x (2x + y)dxdy = 2x + ydydx − 2x + ydydx. √ S (3− 5)/2 1/x 1 1/x
Tính toán một cách tỉ mỉ ta vẫn thu được kết quả trên. Có điều các bước tính
có hơi cồng kềnh hơn cách đổi biến một chút. Z Z CÂU 20. xdxdy,
S : x = y2, 4x = y2, y = x2, 4y = x2; y S y v 4 4 3 y = x2 3 4x = y2 D 2 2 S x = y2 1 1 4y = x2 Lời giải. 1 2 3 4 1 2 3 4 x u y2 u = , u ∈ [1, 4] x x2 v = , v ∈ [1, 4] y Jacobian y2 2y − ∂(u, v) x2 x = = −5. ∂(x, y) 2x x2 − y y2 Suy ra ∂(x, y) 1 1 1 J = = = − , |J| = và ∂(u, v) ∂(u, v) 5 5 ∂(x, y) r x v f (x, y) = = 3 . y u Từ đó Z Z r r x Z Z v 1 1 Z 4 Z 4 v dxdy = 3 · dudv = 3 dudv y D u 5 5 1 u 1 S 1 Z 4 Z 4 = u1/3du v−1/3dv 5 1 1 4 4 1 3 3 = u4/3 × u2/3 = · · · 54 2 1 1 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 22 / 29 Z Z CÂU 21. xydxdy,
S : |x + 2y| ≤ 3, |x − y| ≤ 3. S Z Z
Câu 24. Tính tích phân kép sau x2 + y2dxdy trong đó D
D = {(x, y) ∈ R2 : 0 ≤ x ≤ 2, x2 ≤ y ≤ 2x}. Lời giải. ĐS: 216. 35 Z Z
Câu 25. Tính tích phân kép
(x − 2y)dxdy trong đó D là miền giới hạn bởi các đường D 1 x = 0, y = 7 − x, y = x + 1. 2 Lời giải. Gợi ý: Z Z Z 4 Z 7−x (x − 2y)dxdy = dx (x − 2y)dy = ... = −72 D 0 x 2 +1 Z Z
Câu 26. Tính tích phân kép sau
xdxdy trong đó D là miền giới hạn bởi D
2x ≤ x2 + y2 ≤ 6x, y ≤ x. y D x Lời giải. Chử Văn Tiệp (BKĐN) Giải tích 2-2023 23 / 29
Sử dụng tọa độ cực ta có (viết hơi tắt) Z Z Z π/4 Z 6 cos ϕ Z π/4 r3 6 cos ϕ xdxdy = dϕ r cos ϕrdr = cos ϕ dϕ 3 D −π/2 2 cos ϕ −π/2 2 cos ϕ 208 Z π/4 208 Z π/4 1 + cos 2ϕ2 = cos4 ϕdϕ = dϕ 3 3 −π/2 −π/2 2 208 Z π/4 1 cos 2ϕ cos2 2ϕ = + + dϕ 3 −π/2 4 2 4 208 Z π/4 1 cos 2ϕ 1 + cos 4ϕ = + + dϕ 3 −π/2 4 2 8 208 Z π/4 3 cos 2ϕ cos 4ϕ = + + dϕ 3 −π/2 8 2 8 208 π/4 3 sin 2ϕ sin 4ϕ = ϕ + + 3 8 4 32 −π/2 2089π + 8 13(9π + 8) 117π + 104 = = = 3 32 6 6 Z Z
Câu 27. Tính tích phân kép sau p 1 +
x2 + y2dxdy trong đó D là miền giới hạn bởi D
2x ≤ x2 + y2 ≤ 16, x ≥ 0, y ≥ 0. y D x Lời giải. Z Z Z π/2 Z 4 Z π/2 Z 2 cos ϕ p 1 + x2 + y2dxdy = dϕ (1 + r)rdr − dϕ (1 + r)rdr D 0 0 0 0 4 2 cos ϕ π r2 r3 Z π/2 r2 r3 = × + − + dϕ 2 2 3 0 2 3 0 0 44π Z π/2 8 cos3 ϕ = − 2 cos2 ϕ + dϕ 3 3 0 44π 9π + 32 85π 16 = − = − 3 18 6 9
Câu 28. Tính tích phân kép sau √ Z 0 Z 1−x2 p ln(1 + x2 + y2) dx p dy. −1 0 x2 + y2 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 24 / 29
Lời giải. ĐS: π(2 ln 2 − 1). 2 Z Z 1 Câu 29. Tính tích phân
cos πx2dxdy trong đó D là miền giới hạn bởi các đường D 2 sau y = 0, x = 1, y = x. Lời giải. ĐS: 1 π
Câu 30. Tính thể tích của vật thể bị chặn trên bởi nón p z = 2 − x2 + y2 và bị chặn
dưới bởi hình tròn (x − 1)2 + y2 ≤ 1. Lời giải. Z Z 1
Câu 31. Tính tích phân kép sau
dxdy trong đó D là tam giác OAB D (1 + x + y)3/2
với đỉnh O = (0, 0), A = (1, 0) và B = (1, 1).
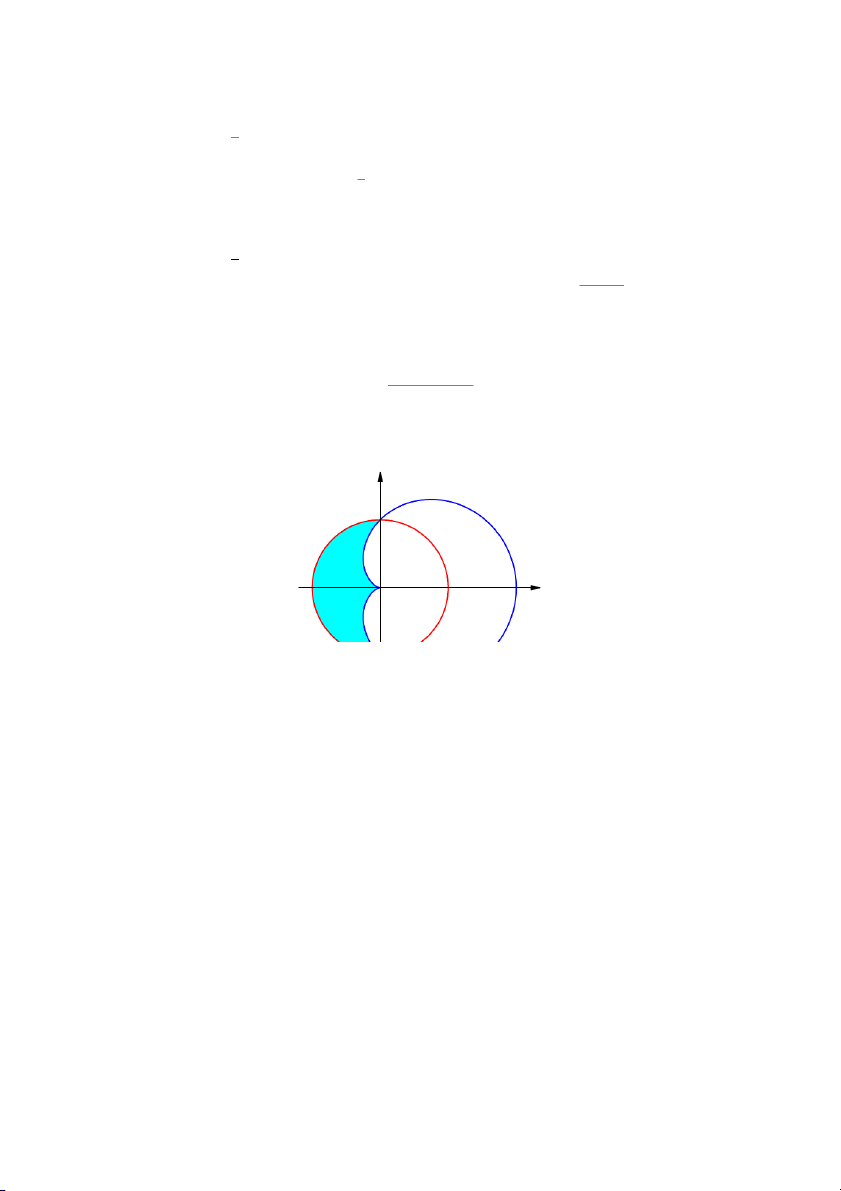
Câu 32. Tính diện tích miền tô màu dưới đây y r = 1 + cos(θ) r = 1 x Lời giải.
Câu 33. Tính diện tích miền tô màu dưới đây y r = 1 + cos θ r = 3 cos θ x √ Z √ 4 Z 2 z Z 4z−x2 Câu 34. Tính dydxdz. 0 0 0 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 25 / 29 Lời giải. ĐS: 8π. √ √ Z a Z a2−x2 Z a2−x2−y2 dzdydx Câu 35. Tính p . 0 0 0 a2 − x2 − y2 − z2 Lời giải. ĐS: π2a2. 8
Câu 36. Tính thể tích của miền bị chặn bởi mặt cầu x2 + y2 + z2 = a2 nằm trong mặt trụ x2 + y2 = ay.
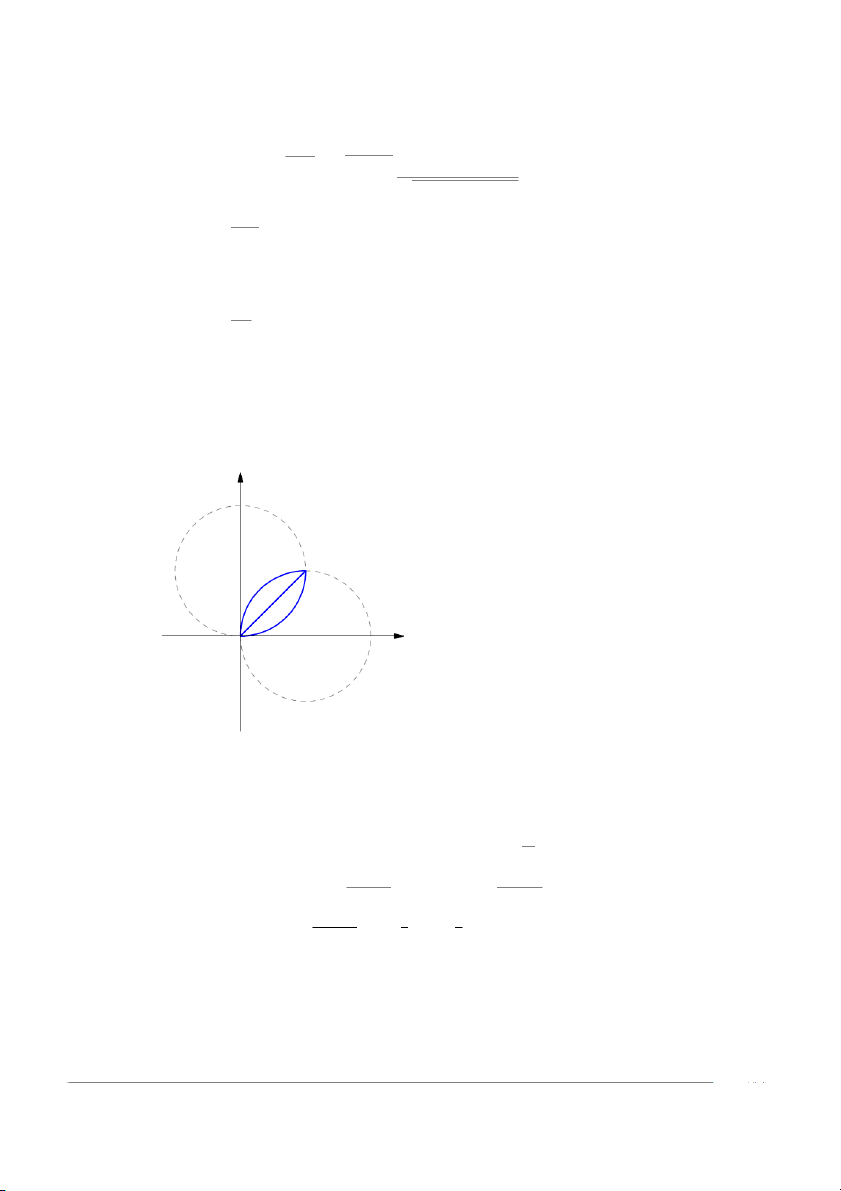
Lời giải. ĐS: 2a3(3π − 4). 9 Câu 37. Tính tích phân Z Z xdxdy D
trong đó D là miền bị chặn bởi hai đường tròn x2 + y2 = 2x, x2 + y2 = 2y y x2 + y2 = 2y D2D1 x x2 + y2 = 2x Lời giải. Z Z Z π/4 Z 2 sin ϕ xdxdy = r cos ϕrdrdϕ D1 0 0 Z π/4 Z 2 sin ϕ Z π/4 r3 2 sin ϕ = r2 cos ϕdrdϕ = cos ϕ dϕ 0 0 0 3 0 Z π/4 8 sin3 ϕ Z π/4 8 sin3 ϕ = cos ϕdϕ = d(sin ϕ) 0 3 0 3 2 sin4 ϕ π/4 1 1 = = − 0 = . 3 0 6 6 Chử Văn Tiệp (BKĐN) Giải tích 2-2023 26 / 29 Z Z Z π/2 Z 2 cos ϕ xdxdy = r cos ϕrdrdϕ D2 π/4 0 Z π/2 Z 2 cos ϕ Z π/2 r3 2 cos ϕ = r2 cos ϕdrdϕ = cos ϕ dϕ π/4 0 π/4 3 0 Z π/2 8 8 Z π/2 3 cos 2ϕ cos 4ϕ = cos4 ϕdϕ = + + dϕ π/4 3 3 π/4 8 2 8 π/2 Z π/2 4 cos 2ϕ cos 4ϕ 2 sin 2ϕ sin 4ϕ π 2 = 1 + + dϕ = ϕ + + = − 3 π/4 3 3 3 12 4 π/4 Do đó Z Z Z Z Z Z 1 π 2 π 1 xdxdy = xdxdy + xdxdy = + − = − . D 6 4 3 4 D 2 1 D2
Cách 2 sử dụng tọa độ Decartes. Phương trình đường tròn x2 + y2 = 2y có thể viết lại
dưới dạng x2 + (y − 1)2 = 1. Từ đó trong góc phần tư thứ nhất ta suy ra √
y = 1 − 1 − x2, x ∈ [0, 1].
Trong góc phần tư thứ nhất phương trình x2 + y2 = 2x có dạng √ y = 2x − x2, x ∈ [0, 1]. Do đó √ √ 2x Z Z Z −x2 1 Z 2x−x2 Z 1 xdxdy = xdydx = xy dx √ D 0 1− 1−x2 0 √ 1− 1−x2 Z 1 √ √ =
x 2x − x2 − x + x 1 − x2dx 0 Z 1 √ Z 1 Z 1 √ = x 2x − x2dx − xdx + x 1 − x2dx 0 0 0 = I1 − I2 + I3. Chử Văn Tiệp (BKĐN) Giải tích 2-2023 27 / 29 Dễ thấy 1 I2 = . Ta có 2 Z 1 √ Z 1 p I 2 1 = x 2x − x dx = x
1 − (1 − x)2dx, (t = 1 − x, dt = −dx) 0 0 Z 0 √ Z 1 √ = − (1 − t) 1 − t2dt = (1 − t) 1 − t2dt 1 0 Z 1 √ = 1 − x2dx − I3. 0 1 Z 1 √ ⇒ I1 − I2 + I3 = − + 1 − x2dx (x = sin t, dx = cos tdt) 2 0 1 Z π/2 1 Z π/2 1 + cos 2t = − + cos2 tdt = + dt 2 2 0 2 0 π/2 1 t sin 2t 1 π = − + + = − + 2 2 4 2 4 0
Cách 3. Xem D là miền loại II. Phương trình đường tròn x2 + y2 = 2y có thể viết lại dưới
dạng x2 + (y − 1)2 = 1. Từ đó trong góc phần tư thứ nhất ta suy ra p x = 2y − y2, y ∈ [0, 1].
Trong góc phần tư thứ nhất phương trình x2 + y2 = 2x có dạng p x = 1 − 2y − y2, y ∈ [0, 1]. √ Z Z Z 1 Z 2y−y2 xdxdy = √ xdxdy D 0 1− 1−y2 √ Z 1 p x2 2y−y2
Z 1 2y − y2 (1 − 1 − y2)2 = dy = √ − dy 0 2 1− 1−y2 0 2 2 1 Z 1 Z p y2 1 p = y − 1 + 1 − y2dy = − y + 1 − y2dy 2 0 0 0 1 Z 1 p = − + 1 − y2dy (y = sin t, dy = cos tdt) 2 0 1 Z π/2 1 Z π/2 1 + cos 2t = − + cos2 tdt = + dt 2 0 2 0 2 π/2 1 t sin 2t 1 π = − + + = − + 2 2 4 2 4 0
Câu 38. Tính diện tích hình phẳng bị chặn bởi đường cong phương trình x2/3 + y2/3 = 1. Chử Văn Tiệp (BKĐN) Giải tích 2-2023 28 / 29 y D2 D1 x D3 D4
Bản phác thảo (còn lỗi sai) Lưu hành nội bộ. Làm hoàn thiện một ý nhỏ được tính một điểm. Chử Văn Tiệp (BKĐN) Giải tích 2-2023 29 / 29