lOMoARcPSD|46958826 lOMoARcPSD|46958826
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP. HCM
KHOA LÝ LUẬN CHÍNH TRỊ
MÔN HỌC: NHẬP MÔN LOGIC HỌC TIỂU LUẬN
CẤU TRÚC, LOẠI HÌNH VÀ CÁC QUY
TẮC CỦA TAM ĐOẠN LUẬN ĐƠN
GVHD: Thầy Đoàn Đức Hiếu SVTH: MSSV Nguyễn Hoài Phong 16142178 Trần Viết Phi 16142174 Trần Ngọc Vũ Kha 16142127 Tống Quang Khải 16142130
Lớp thứ 3 – Tiết 10-11 INLO220405 - 01CLC
Tp. Hồ Chí Minh, tháng 04 năm 2018 lOMoARcPSD|46958826 ĐIỂM SỐ
TIÊU CHÍ NỘI DUNG BỐ CỤC TRÌNH BÀY TỔNG ĐIỂM NHẬN XÉT
.........................................................................................................................................
.........................................................................................................................................
.........................................................................................................................................
.........................................................................................................................................
.........................................................................................................................................
.........................................................................................................................................
.........................................................................................................................................
.........................................................................................................................................
.........................................................................................................................................
.........................................................................................................................................
.........................................................................................................................................
.........................................................................................................................................
......................................................................................................................................... Ký tên
Thầy Đoàn Đức Hiếu lOMoARcPSD|46958826 MỤC LỤC
MỞ ĐẦU...........................................................................................................................1
1. Đặt vấn đề:.................................................................................................................1
2. Mục tiêu nghiên cứu:................................................................................................2
3. Các phương pháp nghiên cứu được áp dụng:.........................................................2
NỘI DUNG.......................................................................................................................3
CHƯƠNG 1. CẤU TRÚC, CÁC LOẠI HÌNH VÀ KIỂU CỦA TAM ĐOẠN LUẬN
ĐƠN................................................................................................................................... 3
1.1. Định nghĩa và cấu trúc của tam đoạn luận đơn:..................................................3
1.1.1. Định nghĩa:.......................................................................................................3
1.1.2. Cấu trúc của tam đoạn luận đơn:.....................................................................3
1.2. Hình và kiểu của tam đoạn luận đơn:...................................................................5
1.2.1. Hình của tam đoạn luận đơn:..........................................................................5
1.2.2. Kiểu của tam đoạn luận đơn:...........................................................................6
CHƯƠNG 2: SƠ ĐỒ VENN VÀ CÁC QUY TẮC TAM ĐOẠN LUẬN......................8
2.1 Phép tam đoạn luận với các tiền đề có dạng A, I, E, O.........................................8
2.2 Biểu diễn phán đoán A, I, E, O bằng sơ đồ Venn.................................................9
2.3 Khảo sát các phép tam đoạn luận bằng sơ đồ Venn...........................................11
2.4 Các quy tắc tam đoạn luận...................................................................................15
KẾT LUẬN.....................................................................................................................18
CÁC TÀI LIỆU THAM KHẢO....................................................................................19 lOMoARcPSD|46958826 MỞ ĐẦU 1. Đặt vấn đề:
Trong cuộc sống thường ngày, mọi hoạt động của con người từ đơn giản đến phức
tạp đều thông qua tư duy. Cùng với sự phát triển của thực tiễn và của nhận thức, con
người càng ngày càng có sự hiểu biết đầy đủ hơn, sâu sắc hơn, chính xác hơn về bản thân tư duy đang nhận thức.
Nói về tư duy, phải nhắc đến các hình thức cơ bản của tư duy: khái niệm, phán đoán,
suy luận, chứng minh, bác bỏ, ngụy biện. Trong đó, suy luận chính là một trong những
hình thức quan trọng nhất của tư duy. Nếu như khái niệm hay phán đoán là các hình thức
biểu thị tư tưởng thì suy luận lại được xem là một loại hình thức sản sinh ra tư tưởng mới
từ các tư tưởng đã có, rút ra các tri thức mới từ tri thức đã biết. Suy luận có vai trò vô
cùng to lớn trong nhận thức và trong đời sống. Nghiên cứu suy luận chính là vấn đề trọng
tâm của logic học. Suy luận có hai hình thức chính là suy luận quy nạp và suy luận diễn
dịch, và trong suy luận diễn dịch, ta có hai dạng suy luận trực tiếp và gián tiếp.
Dạng suy luận diễn dịch gián tiếp (tam đoạn luận) được nhà triết học cổ đại Hy Lạp
Aristote nghiên cứu kỹ lưỡng từ thế kỷ thứ IV trước công nguyên. Ngày nay trong logic
học người ta đã dùng những phương pháp hiện đại để nghiên cứu loại suy luận này, và
đưa ra những hệ thống chuẩn hóa khác nhau về nó. Đặc biệt, đã có nhiều chương trình về
tam đoạn luận đơn được viết cho máy tính. Có thể nói rằng, thái độ hoài nghi hay thậm
chí là phủ nhận đối với tam đoạn luận đơn đã từng có lúc ngự trị trong logic học đã vĩnh
viễn lùi vào dĩ vãng. Trong tư duy hàng ngày, tam đoạn luận đơn vẫn có một giá trị không gì có thể thay thế.
Nhằm tìm hiểu về tính quan trọng của dạng suy luận diễn dịch gián tiếp (tam đoạn
luận) trong tư duy, nhóm đã lựa chọn đề tài: “Cấu trúc, loại hình và các quy tắc của tam đoạn luận đơn”. - 1 - lOMoARcPSD|46958826
2. Mục tiêu nghiên cứu:
Đề tài sẽ nghiên cứu làm rõ các vấn đề về:
+ Định nghĩa và các thành phần cấu trúc chính của tam đoạn luận đơn.
+ Các loại hình và kiểu của tam đoạn luận đơn.
+ Tiên đề và các quy tắc của tam đoạn luận đơn.
3. Các phương pháp nghiên cứu được áp dụng:
+ Phương pháp thu thập phân tích tài liệu: thông qua các giáo trình, sách tham khảo,
các bài báo khoa học để làm rõ nội dung của mục tiêu nghiên cứu.
+ Phương pháp phân loại hệ thống hóa kiến thức: thông qua các tài liệu thu thập
được nhằm hệ thống và sắp xếp các tài liệu khoa học theo chủ đề, theo đơn vị kiến thức
để nội dung của bài tiểu luận dễ nhận biết và nghiên cứu. - 2 - lOMoARcPSD|46958826 NỘI DUNG
CHƯƠNG 1. CẤU TRÚC, CÁC LOẠI HÌNH VÀ KIỂU CỦA TAM ĐOẠN LUẬN ĐƠN
1.1. Định nghĩa và cấu trúc của tam đoạn luận đơn:
1.1.1. Định nghĩa:
Tam đoạn luận được hiểu là một cách suy luận trong suy luận diễn dịch, trong đó kết
luận được rút ra từ hai tiền đề. Tam đoạn luận là hệ thống suy diễn tiền đề cổ xưa nhất do
Aristote xây dựng. Trong tam đoạn luận các tiền đề và kết luậnđều là những phán đoán
đơn, thuộc các dạng: A, I, E, O, với đúng ba thuật ngữ khác nhau.
Tam đoạn luận là một phát minh lớn của Aristote. Trong học thuyết lôgíc học của
mình, ông đã xây dựng tam đoạn luận làm cơ sở cho chứng minh: “Cần phải nói về tam
đoạn luận trước khi nói về chứng minh, bởi tam đoạn luận là một cái gì đó chung hơn và
chứng minh là một loại tam đoạn luận nào đó, nhưng không phải bất kỳ tam đoạn luận
nào cũng là chứng minh”.
1.1.2. Cấu trúc của tam đoạn luận đơn:
1.1.2.1. Các loại thuật ngữ:
Như đã nhắc trong phần định nghĩa, ta dễ dàng thấy rằng, một tam đoạn luận đơn có
cấu trúc bao gồm hai tiền đề và một kết luận, và chúng đều là những phán đoán đơn,
thuộc các dạng: A, E, I, O.
Ví dụ 1: (1) Mọi động vật đều sinh sản.
(2) Rùa là động vật. (3) Rùa sinh sản.
Ta có, hai tiền đề là (1) và (2), kết luận là (3), cả tiền đề và kết luận đều ở dạng các phán đoán đơn. - 3 - lOMoARcPSD|46958826
Trong mỗi một tam đoạn luận, ta chỉ có ba khái niệm là ba thuật ngữ, ký hiệu là: S,
P, M. Trong đó, S được gọi là tiểu thuật ngữ, M là thuật ngữ giữa hay trung gian và P là
đại thuật ngữ. Thuật ngữ trung gian (M) có mặt trong cả hai tiền đề nhưng lại không có mặt trong kết luận.
Như ví dụ tam đoạn luận ở trên, ta có “động vật” là thuật ngữ trung gian (M), “sinh
sản” là đại thuật ngữ (P) và “rùa” là tiểu thuật ngữ (S). Tiền đề lớn là: Mọi động vật đều
sinh sản, tiên đề nhỏ: Rùa là động vật, và kết luận: Rùa sinh sản.
Như vậy ta có thể viết tam đoạn luận trên dưới dạng:
1.1.2.2. Các loại tiền đề:
Ở ví dụ phía trên, ta thấy phán đoán (1) chứa đại thuật ngữ P, nên nó được gọi là đại
tiền đề, còn phán đoán (2) chứa tiểu thuật ngữ S nên là tiểu tiền đề.
Trong tam đoạn luận đơn, ta không nhất thiết phải viết đại tiền đề trước và tiểu tiền
đề sau. Nên để xác định một tiền đề là đại tiền đề hay tiểu tiền đề thì ta không thể dựa vào
vị trí của nó trong tam đoạn luận đơn, mà ta phải xét xem tiền đề đó chứa đại thuật ngữ hay là tiểu thuật ngữ.
1.2. Hình và kiểu của tam đoạn luận đơn:
1.2.1. Hình của tam đoạn luận đơn:
Thuật ngữ trung gian (M) – hay còn gọi là trung từ – có thể chiếm các vị trí khác
nhau trong các tiền đề, trung từ có thể là chủ từ hoặc thuộc từ trong đại tiền đề và tiểu tiền
đề. Mỗi vị trí của trung từ trong các tiền đề sẽ cho ra một hình của tam đoạn luận đơn. Và - 4 - lOMoARcPSD|46958826
theo Aristote, hình 1 được xem là quan trọng nhất. Ở đây, ta có chính xác bốn hình khác
nhau của tam đoạn luận dựa theo đặc điểm trên:
* Hình 1: Trung từ là chủ từ trong đại tiền đề và là thuộc từ trong tiểu tiền
đề. Ví dụ 2: Mọi sinh viên đều phải thi. Nam là sinh viên. Vậy Nam phải thi.
* Hình 2: Trung từ là thuộc từ trong cả hai tiền đề.
Ví dụ 3: Tháng 6 rất nóng.
Tháng này không nóng.
Vậy tháng này không phải là tháng 6.
* Hình 3: Trung từ là chủ từ trong cả hai tiền
đề. Ví dụ 4: Con người có thể tư duy.
Con người là động vật. Vậy
động vật có thể tư duy.
* Hình 4: Trung từ là thuộc từ trong đại tiền đề và là chủ từ trong tiểu tiền
đề. Ví dụ 5: Thuốc trừ sâu là chất độc.
Độc là chất nguy hiểm đối với con người.
Vậy có chất nguy hiểm với con người là thuốc trừ sâu.
1.2.2. Kiểu của tam đoạn luận đơn:
Như đã nói ở phần cấu trúc của tam đoạn luận, các phán đoán tiền đề và kết luận có
thể là các phán đoán đơn dạng A, E, I, hoặc O. “Kiểu của một tam đoạn luận đơn là khái
niệm cho biết các phán đoán tiền đề và kết luận của nó có dạng nào. Vì có 4 dạng phán - 5 - lOMoARcPSD|46958826
đoán đơn, nên có tất cả 43 kiểu tam đoạn luận đơn. Nếu phân biệt kiểu tam đoạn luận đơn
theo các hình khác nhau thì có thể nói đến 64×4 = 256 kiểu tam đoạn luận đơn tất cả”2.
Nghĩa là chỉ cần với ba khái niệm M, S, P ta có thể xây dựng 256 kiểu tam đoạn luận khác
nhau. Điều này giúp ta hiểu rằng: với một vấn đề được đưa ra ta có thể suy nghĩ ở 256
khía cạnh khác nhau. Vậy nên mới có câu “Lưỡi không xương trăm đường lắt léo”, trước
khi nói gì đó phải “Uốn lưỡi bảy lần”, xem xét sự đúng sai của vấn đề. Ta có 256 kiểu của
tam đoạn luận, nhưng không phải tất cả các kiểu đều đúng, để xác định được các kiểu
đúng của tam đoạn luận, phải dựa vào các quy tắc chung của tam đoạn luận để loại bỏ các kiểu sai.
Một suy luận được xem là đúng đắn khi thỏa mãn đồng thời hai yêu cầu: hợp logic
và xuất phát từ tiền đề đúng.
Theo nghiên cứu của các nhà logic học, chỉ có 19 trong tổng số 256 kiểu của tam
đoạn luận là đúng. Các kiểu đúng tương ứng với các hình như sau:
+ Hình thứ nhất: AAA, EAE, AII, EIO
+ Hình thứ hai: EAE, AEE, EIO, AOO
+ Hình thứ ba: AAI, IAI, AII, EAO, OAO, EIO
+ Hình thứ tư: AAI, AEE, IAI, EAO, EIO3
Như vậy, để xác định được các kiểu đúng trên, ta sẽ dựa trên các quy tắc của tam
đoạn luận bao gồm các quy tắc đối với khái niệm và các quy tắc đối với mệnh đề sẽ được
trình bày và làm rõ trong chương 2. - 6 - lOMoARcPSD|46958826
CHƯƠNG 2: SƠ ĐỒ VENN VÀ CÁC QUY
TẮC TAM ĐOẠN LUẬN
2.1 Phép tam đoạn luận với các tiền đề có dạng A, I, E, O
Trong logic truyền thống của Aristote, người ta xét kĩ các phép tam đoạn luận (suy
luận ba đoạn) mà hai tiền đề cũng như kết luận đều có dạng A, E, I hoặc O.
Thí dụ: Xét suy luận từ hai tiền đề :
(1) Mọi người yêu nước đều hòa bình.
(2) Mọi người Việt Nam đều yêu nước.
Gọi : M là tập hợp người yêu nước.
P là tập hợp người yêu hòa bình
S là tập hợp người Việt Nam - 7 - lOMoARcPSD|46958826 Các tiền đề có dạng :
(1) Mọi M đều là P (MaP). (Mọi phần tử thuộc M đều thuộc P)
(2) Mọi S đều là M (SaM). (Mọi phần tử thuộc S đều thuộc
M) Theo (1) thì M là bộ phận của P,
Theo (2) thì S là bộ phận của M.
Từ đó suy ra S là bộ phận của P,
Tức là : Mọi S đều là P (SaP). (Mọi phần tử thuộc S đều thuộc P)
(Mọi người Việt Nam đều yêu hòa bình) Ta có quy tắc suy diễn : M a P S a M ——— S a P
Trong mọi phép tam đoạn luận, đều có ba thuật ngữ (khái niệm), ứng với ba tập
hợp. Một thuật ngữ, được gọi là thuật ngữ giữa (trong thí dụ trên là M), có mặt trong cả
hai tiền đề, và không có mặt trong kết luận; kết luận nêu lên quan hệ (nếu có) giữa hai thuật ngữ kia (S và P).
Có nhiều phương pháp xem xét một phép tam đoạn luận dạng này có hợp logic hay
không. Sau đây là một phương pháp tương đối đơn giản, dùng sơ đồ Venn để biểu diễn
các phán đoán dạng A, E, I, O.
2.2 Biểu diễn phán đoán A, I, E, O bằng sơ đồ Venn Xét các phán đoán
(1) Mọi sinh viên đều mê bóng đá.
(2) Một số sinh viên mê bóng đá. - 8 - lOMoARcPSD|46958826
(3) Mọi sinh viên đều không mê bóng đá.
(4) Một số sinh viên đều không mê bóng đá
Gọi: S là tập hợp sinh viên
M là tập hợp những người mê bóng đá.
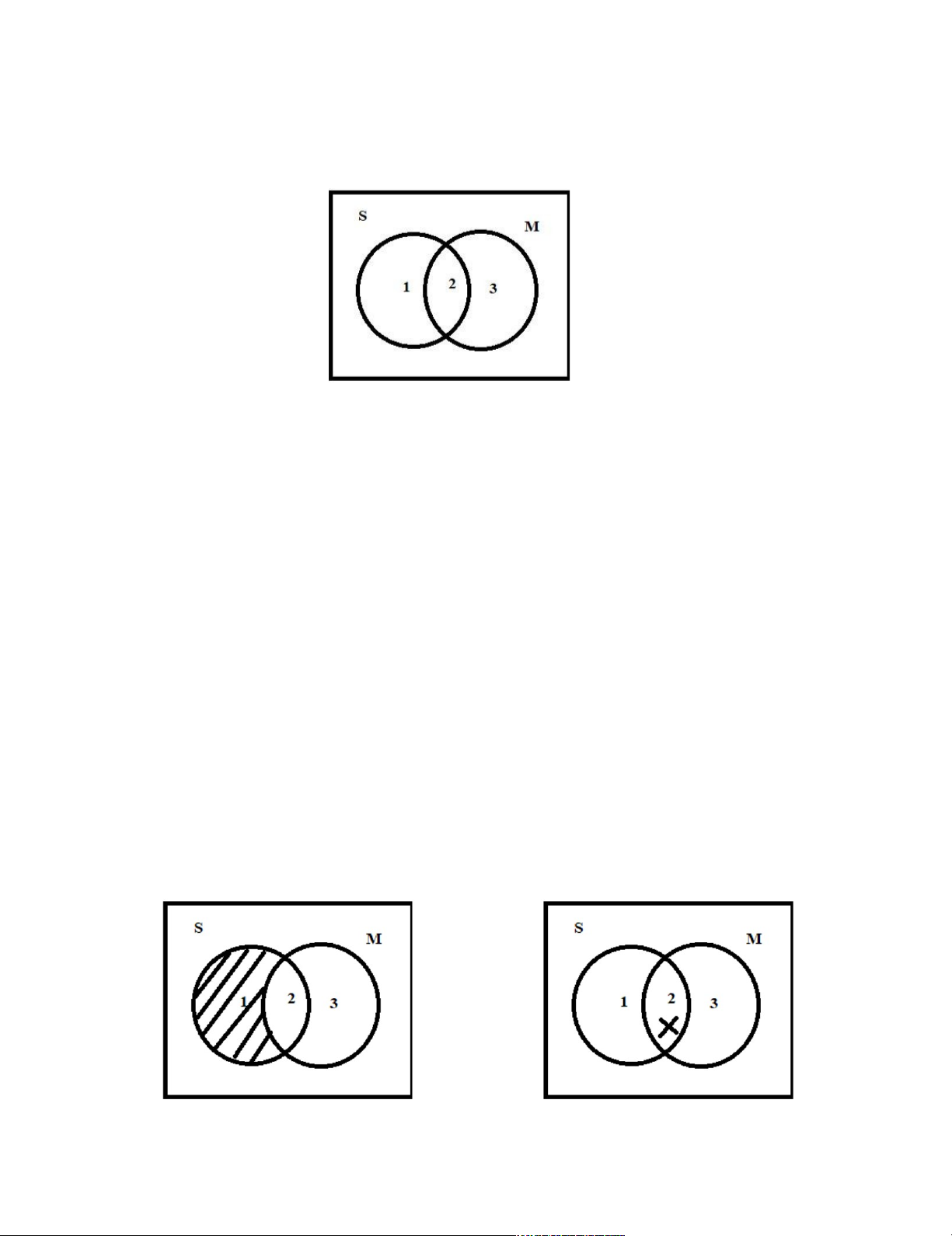
Ta hình dung hai vòng tròn giao nhau như hình. Vòng tròn S chứa tất cả sinh viên
và vòng tròn M chứa tất cả những người mê bóng đá.
Phần bên trong của vòng tròn S và M là gồm ba vùng: vùng 1 thuộc S nhưng ở
ngoài M (chứa tất cả những sinh viên không mê bóng đá), vùng 2 vừa thuộc S vừa thuộc
M (chứa tất cả sinh viên mê bóng đá) và vùng 3 thuộc M nhưng không thuộc S (chứa tất
cả những người mê bóng đá mà không phải sinh viên). Nếu phán đoán
(1) Mọi sinh viên đều mê bóng đá (SaM)
là đúng thì không thể có sinh viên nào ở trong vùng 1 được, vùng 1 là rỗng
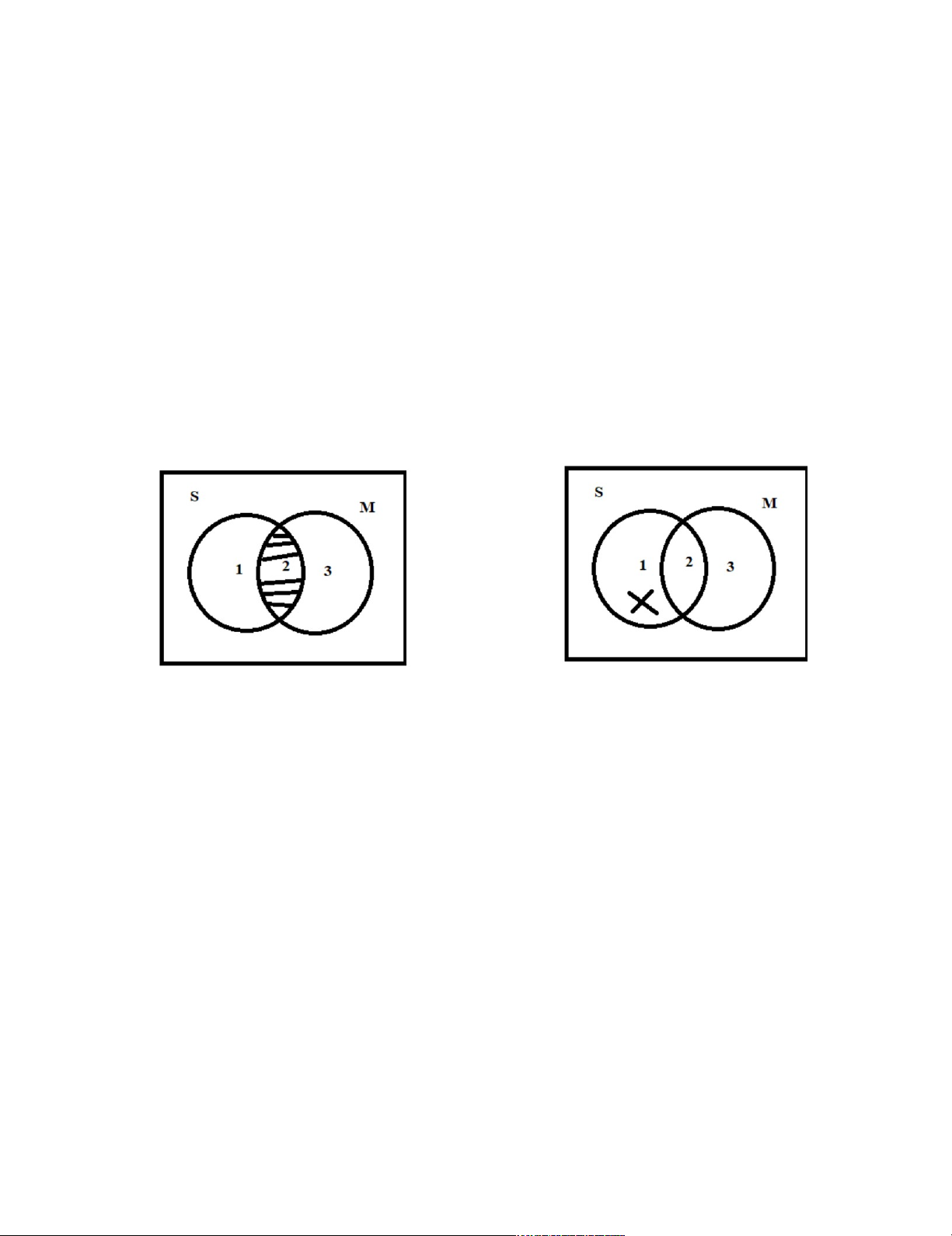
(không chứa phần tử nào), ta gạch chéo vùng này như hình Mọi S đều là M (SaM) Một số S là M. (SiM) - 9 - lOMoARcPSD|46958826
(Mọi phần tử thuộc S đều thuộc M)
(Một số phần tử thuộc S là thuộc M.)
Vùng 1 là rỗng, được gạch chéo.
Trong vùng 2 có một dấu x Nếu phán đoán
(2) Một số sinh viên mê bóng đá (SiM) là đúng thì có (ít nhất một) sinh viên ở vùng
2, ta ghi điều này bằng một dấu x trong vùng 2 Nếu phán đoán
(3) Mọi sinh viên điều không mê bóng đá (SeM) là đúng thì không thể có sinh viên
nào trong vùng 2 được, vùng 2 là rỗng và ta gạch chéo vùng này như hình
Mọi S không là M (SeM)
Một số S không là M. (SoM)
(Mọi phần tử thuộc S không thuộc M)
(Một số phần tử thuộc S không thuộc M.)
Vùng 2 là rỗng được gạch chéo
Trong vùng 1 có một dấu x Nếu phán đoán
(4) Một số sinh viên không mê bóng đá (SoM) là đúng thì có (ít nhất một) sinh viên
ở vùng 1, ta ghi điều này bằng một dấu x trong vùng 1
Chú ý: Các hình vẽ trên chính là cách biễu diễn quan hệ giữa hai tập hợp S và M,
khác với cách biểu diễn thường được dùng trong sách giáo khoa về toán ( Xem chẳng hạn
Đại số 10, NXB Giáo dục, 1993). Cách biểu diễn này đặc biệt thuận lợi khi cần xem xét -10- lOMoARcPSD|46958826
các quan hệ từng đôi một giữa ba tập hợp, có mặt trong tiền đề có dạng A, E, I, O của một
phép tam đoạn luận, giúp thấy được phép tam đoạn luận đó có hợp logic hay không.
2.3 Khảo sát các phép tam đoạn luận bằng sơ đồ Venn
Thí dụ 1: Trở lại phép tam đoạn luận từ hai tiền đề đã xét
(1) Mọi người yêu nước đều yêu hòa bình (MaP)
(2) Mọi người Việt Nam đều yêu nước (SaM)
Ta vẽ ba vòng tròn, tương ứng với ba tập hợp S,M,P như trong hình . Trong các
vòng tròn này, ta có tất cả 7 vùng đánh số từ 1 đến 7. Theo tiền đề (1) , ta gạch chéo các
vùng 1 và 4. Theo tiền đề (2) ta gạch chéo các vùng 6 và 7. Kết luận cho ta quan hệ giữa
S và P. Các vùng 4 và 7 bị gạch chéo, chứng tỏ rằng SaP. Vậy từ hai tiền đề (1) và (2), ta có kết luận logic là :
Mọi người Việt Nam đều yêu hòa bình (SaP)
Thí dụ 2: Xét xem phép tam đoạn luận sau đây có hợp logic không :
Không một kẻ xu nịnh nào là có lòng tự trọng
Một số người xung quanh ta là kẻ xu nịnh
Một số người xung quanh ta không có lòng tự trọng
Gọi : M là tập hợp những kẻ xu nịnh -11- lOMoARcPSD|46958826
P là tập hợp những người có lòng tự trọng
S là tập hợp những người xung quanh ta
Vẽ ba vòng tròn M, P, S ứng với ba tập hợp trên như trong hình. Tiền đề thứ nhất là
MeP, do đó ta gạch chéo các vùng 2 và 5. Tiền đề thứ hai là SiM, do đó ta đánh dấu x
trong vùng 4 (không đánh dấu x trong vùng 5 được vì vùng này đã bị gạch chéo)
Trong vùng 4 có dấu x chứng tỏ rằng giữa S và P có quan hệ SoP (Một số người xung
quanh ta không có lòng tự trọng)
Suy luận là hợp logic , theo quy tắc M e P S i M ——— S o P
Thí dụ 3: Xét xem phép tam đoạn luận sau đây có hợp logic không :
Mọi người mê bóng đá đều không thích học logic học
Mọi người mê bóng đá đều ham hoạt động
Một số người ham hoạt động không thích học logic học
Gọi: M là tập hợp tất cả những người mê bóng đá -12- lOMoARcPSD|46958826
P là tập hợp tất cả những người thích học logic học
S là tập hợp tất cả những người ham hoạt động
Vẽ ba vòng tròn S,P,M ứng với ba tập hợp trên
Theo tiên đề thứ nhất (MeP), các vùng 2 và 5 bị gạch chéo.
Theo tiên đề thứ hai (MaS), các vùng 1 và 2 bị gạch chéo.
Kết luận có dạng SoP, tức là có dấu x trong vùng 4 hoặc 7. Điều này có thể thực
hiện được, vì từ hai tiên đề đã cho, hai vùng này không bị gạch chéo. Suy luận là hợp logic, quy tắc suy luận M s P M a S ———— S o P
Thí dụ 4: Suy luận sau đây có hợp logic không
(1) Mọi sinh viên đều yêu nước
(2) Một số người yêu nước là người ham
học Một số người ham học là sinh viên
Để dễ nhớ, ta có thể gọi: -13- lOMoARcPSD|46958826
Tập hợp những sinh viên là S,
Tập hợp những người yêu nước là Y
Tập hợp những người ham học là H.
Ta vẽ ba vòng tròn S, Y, H ứng với ba tập hợp trên
Tiên đề (1) có dạng SaY, do đó các vùng 1 và 4 bị gạch chéo. Tiên đề (2) có dạng
YiH, ta đánh dấu x vào vùng 5 hoặc 6. Kết luận cho ta quan hệ giữa S và H.
Nếu đặt dấu x ở vùng 5 thì ta có:
a) Một số người ham học là sinh viên
Nếu đặt dấu x ở vùng 6 thì ta có
b) Một số người ham học không phải là sinh viên
Như vậy, khi cả hai tiền đề (1) và (2) đều đúng, thì không nhất thiết (a) đúng. Suy luận không hợp logic
Qua các ví dụ trên ta thấy rằng:
Để xem xét một phép tam đoạn luận có hợp logic không ta biểu diễn hai tiền đề trên
cùng một sơ đồ Venn với ba vòng tròn. Nếu kết luận biểu diễn được trên sơ đồ này thì suy
luận là hợp logic. Nếu kết luận không biểu diễn được trên sơ đồ này thì không hợp logic. -14- lOMoARcPSD|46958826
2.4 Các quy tắc tam đoạn luận
Người ta chứng minh rằng có tất cả 19 quy tắc tam đoạn luận từ các tiền đề có dạng A,E,I,O
Nếu quy ước gọi ba thuật ngữ trong hai tiền đề luôn là M, P, S thì ta có 4 loại hình tam đoạn luận: Loại hình 1: M – P S – M ——— S – P Loại hình 2: P – M S – M ——— S – P Loại hình 3: M – P M – S ——— S – P Loại hình 4: P – M M – S ——— S – P
Trong mỗi loại hình, có 64 cách đặt các chữ a, e, i, o vào các gạch ngang, vì vậy có tất cả
256 khả năng, nhưng chỉ có 19 quy tắc suy diễn, các quy tắc này được gọi tên như sau:
Loại hình 1: b A r b A r A c E t A r E n t d A r I I -15- lOMoARcPSD|46958826 f E r I O
Loại hình 2: c E s A r E c A m E s t r E s c E s t I n O b A r O c O
Loại hình 3: d A t I s I f E r I s O d I s A m I s b O c A d O d A r I p t I f E l A p t O n
Loại hình 4: c A b E m E s f r E s I s O n d I m A t I s b A m A t I p b E s A p O
Thí dụ: Barbara là quy tắc có được bằng cách thay a, a, a vào loại hình 1 và đó là
quy tắc ta gặp ở ví dụ 1 trong mục 3) M a P S a M ——— S a P
Ta đã gặp quy tắc ferio ở thí dụ 2 và quy tắc felapton ở thí dụ 3. -16- lOMoARcPSD|46958826 -17-