lOMoARcPSD| 37054152
BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP.HCM
KHOA LÝ LUẬN CHÍNH TRỊ
MÔN HỌC: NHẬP MÔN LOGIC HỌC
TIỂU LUẬN CUỐI KỲ
DDỀ : VAI TRÒ CỦA HÌNH VUÔNG LOGIC TRONG XÁC
Đ TÀI Đ
ỊNH GIÁ TRỊ CHÂN LÝ CỦA PHÁN ĐOÁN ĐƠN VÀ XÂY
DỰNG CÁC KIỂU SUY LUẬN TRỰC TIẾP
TỪ HÌNH VUÔNG LOGIC
Giảng viên hướng dẫn : PGS.TS. ĐOÀN ĐỨC HIẾU
Sinh viên thực hiện : MSSV
1 . Nguyễn Việt An 21110118
2 . Trần Viết Trung 21110859
3 . Đặng Hoàng Toàn 21110322
4 . Trình Học Tuấn 21110340
5. Phạm Tuấn Minh 21110840
6 . Bùi Hoàng Hưng 21110832
Mã môn học : INLO220405_22_1_11CLC
Lớp : Thứ 4, tiết 13-14
Tp.Hồ Chí Minh, tháng 11, năm 2022 lOMoARcPSD| 37054152
………………………………………………………………………………………………
MỞ ĐẦU .............................................................................................................................. 1
1. Lý do chọn đề tài ......................................................................................................... 1
2. Mục đích nghiên cứu .................................................................................................. 1
3. Nhiệm vụ nghiên cứu .................................................................................................. 1
4. Cơ sở lí luận và phương pháp nghiên cứu ................................................................ 1
CHƯƠNG 1: VAI TRÒ CỦA HÌNH VUÔNG LOGIC TRONG XÁC ĐỊNH GIÁ
TRỊCHÂN LÝ CỦA PHÁN ĐOÁN ĐƠN ........................................................................ 2
1.1. Khái niệm phán đoán, phán đoán đơn .................................................................. 2
1.1.1. Phán đoán .................................................................................................................. 2
1.1.2. Phán đoán đơn .......................................................................................................... 4
1.2. Quan hệ về giá trị chân lí của các phán đoán ....................................................... 6
1.3. Hình vuông logic và vai trò ..................................................................................... 7
CHƯƠNG 2: XÂY DỰNG CÁC KIỂU SUY LUẬN TRỰC TIẾP TỪ HÌNH
VUÔNGLOGIC .................................................................................................................. 8
2.1. Định nghĩa suy luận trực tiếp ................................................................................. 8
2.2 Xây dựng các kiểu suy luận dựa vào hình vuông logic ......................................... 9
2.2.1 Dựa vào quan hệ mâu thuẫn ..................................................................................... 9
2.2.2. Dựa vào quan hệ thứ bậc ....................................................................................... 10
2.2.3. Dựa vào quan hệ đối chọi ....................................................................................... 10
KẾT LUẬN ........................................................................................................................ 12
TÀI LIỆU THAM KHẢO ................................................................................................ 13
……………………………………………………………………………………………… lOMoARcPSD| 37054152 MỞ ĐẦU
1. Lý do chọn đề tài
Thế giới hiện nay phát triển theo hướng công nghiệp hóa, hiện đại hóa, hầu hết mọi
người trong xã hội đã thích nghi với lối sống – thời đại công nghệ 4.0. Mọi người càng ngày
càng nâng cao nhu cầu bản than lên trong cuộc sống, công việc. Để đạt được mục tiêu đó
thì bắt buộc ai cũng phải cố gắng phấn đấu. Trình độ phát triển của giới trẻ ngày nay là vô
cùng rộng mở, vì vậy mỗi chúng ta cần nhìn nhận vấn đề một cách khách quan, từ đó có
những hiểu biết đúng đắn để hoàn thiện bản thân. Trong đó, phán đoán có vai trò quan trọng
như một hình thức tư duy và là công cụ thiết yếu để hoàn thiện quá trình nhận thức. Chúng
ta không chỉ liên kết kiến thức của mình thành những tổ hợp hợp lý mà còn phát triển, làm
phong phú thêm kiến thức đó. Phần lớn kiến thức do các thế hệ trước để lại cũng bắt nguồn
từ những phán đoán và giá trị chân lý của nó. Phán đoán ngày càng có vai trò quan trọng
trong việc hình thành lý luận, giúp ý thức khám phá sâu sắc hơn bản chất bên trong của hiện
thực khách quan và giúp phản ánh đúng hiện thực.
Trong chương trình môn học logic học, chúng ta thấy rằng, tư duy đúng, nhận thức
đúng, suy luận đúng là cơ sở để có những hành động đúng đắn, phục vụ nhu cầu đời sống
con người. Xây dựng lối tư duy khoa học, lập luận chặt chẽ, làm rõ giá trị sự thật của bản
án. Phán đoán ảnh hưởng đến suy luận hay suy luận ảnh hưởng đến phán đoán, và giá trị
chân lý của phán đoán ảnh hưởng đến cuộc sống của con người ngày nay như thế nào? Đây
là lý do nhóm chúng em lựa chọn đề tài : “Vai trò của hình vuông logic trong xác định giá
trị chân lý của phán đoán đơn và xây dựng các kiểu suy luận trực tiếp từ hình vuông logic”
2. Mục đích nghiên cứu
Xem xét các giá trị chân lý của phán đoán đơn từ đó xây dựng các kiểu suy luận trực
tiếp, nhằm định vị lại tính đúng đắn của các hiện thực khách quan. Cần có những tác động
từ bên ngoài để hình thành các suy luận đúng từ bên trong mỗi chúng ta. Đáp ứng đúng nhu
cầu của chúng ta khi thế giới đang phát triển, những suy nghĩ, tư duy lệch lạc để có hiệu
suất tốt hơn trong học tập cũng như công việc.
3. Nhiệm vụ nghiên cứu
Làm rõ các giá trị chân lý giữa các phán đoán thông qua hình vuông logic. Hình
thành các kiểu suy luận trực tiếp
4. Cơ sở lí luận và phương pháp nghiên cứu
Cơ sở lí luận: Giáo trình nhập môn Logic học.
Phương pháp nghiên cứu: Tìm dữ liệu, tổng hợp, chọn lọc và phân tích, so sánh. lOMoARcPSD| 37054152
CHƯƠNG 1: VAI TRÒ CỦA HÌNH VUÔNG LOGIC TRONG XÁC ĐỊNH GIÁ
TRỊ CHÂN LÝ CỦA PHÁN ĐOÁN ĐƠN
1.1. Khái niệm phán đoán, phán đoán đơn 1.1.1. Phán đoán a. Khái niệm
Phân đoán là hình thức cơ bản của tư duy trừu tượng.
Phân đoán là cách thức liên hệ giữa các khái niệm, phản ánh mối liên hệ giữa các sự vật,
hiện tượng trong ý thức của con người.
Phán đoán là sự phản ánh những thuộc tính, những mối liên hệ của sự vật, hiện tượng
của thế giới khách quan, sự phản ánh đó có thể hợp hoặc không phù hợp với bản thân thế
giới khách quan. Vì vậy, không phải tất cả mọi phán đoán đều đúng, mỗi phán đoán có thể
đúng hoặc sai. Không có phán đoán nào không đúng lại không sai, cũng không có phán
đoán nào vừa đúng lại vừa sai. Khác với khái niệm phản ánh những thuộc tính chung, bản
chất của sự vật, hiện tượng, phán đoán phản ánh những mối liên hệ giữa các sự vật, hiện
tượng và giữa các mặt của chúng. Do đó, phán đoán là hình thức biểu đạt các quy luật khách quan.
Phán đoán được diễn đạt dưới dạng ngôn ngữ thành một câu nhưng không phải câu
nào cũng là một phán đoán. Ví dụ các câu sau đây không phải là câu phán đoán: -
Cuối tuần này tụi mình đi về quê cùng tớ không? -
Bức tranh màu này đẹp thật!
Những câu cảm thán, câu hỏi, mệnh lệnh thường không diễn đạt một phán đoán. Vì
nội dung không truyền tải được tính đúng hay sai một thực tế. Tuy nhiên những câu hỏi tu
từ lại diễn đạt một phán đoán. -
Ví dụ câu “Ớt nào mà ớt chẳng cay” đây là một phán đoán đúng, vì
nội dung củanó nói lên tính chất cay của ớt.
b. Cấu trúc của phán đoán
Mỗi phán đoán gồm 02 thành phần cơ bản: Chủ từ và vị từ.
-Chủ từ của phán đoán chỉ đối tượng của tư tưởng
Chủ từ của phán đoán ký hiệu là S
- Vị từ của phán đoán là những thuộc tính ta gắn cho đối tượng lOMoAR cPSD| 37054152
Vị từ của phán đoán ký hiệu là P
Chủ từ và vị từ của phán đoán là các thuật ngữ của phán đoán. Giữa chủ từ và vị từ
là một liên từ làm nhiệm vụ liên kết hai thành phần của phán đoán. Các liên từ thường gặp
trong các phán đoán: Là, không phải là, không một, nào là,…
- Ví dụ: Nếu tôi không nhầm người vừa làm rơi cuốn sách kia (S) là (liên từ) anhtrai của bạn (P)
c. Phân loại phán đoán
Thứ nhất: Phân loại phán đoán theo chất -
Phán đoán khẳng định: Là phán đoán xác nhận S cùng lớp với P
Ví dụ: Đồng là kim loại
Thông thường phán đoán khẳng định có liên từ logic “là”. Tuy vậy, nhiều trường
hợp không có liên từ logic “là” vẫn là phán đoán khẳng định
Ví dụ: Trái đất quay xung quanh mặt trời -
Phán đoán phủ định: Là phán đoán xác nhận S không cùng lớp với P
Ví dụ: Sông Tô Lịch không phải là con sông dài nhất Việt Nam - Công thức: S không là P
→ Phán đoán phủ định thường có liên từ logic không là, không phải là.
Thứ hai: Phán đoán theo lượng
Lượng của phán đoán biểu hiện ở chủ từ (S), nó cho biết có bao nhiêu đối tượng của
S thuộc P hay không thuộc P -
Phán đoán chung (hay còn gọi là phán đoán toàn thể): Là phán đoán cho biết
mọiđối tượng đều thuộc hoặc không thuộc về vị từ. Ví dụ:
+ Mọi món ăn trên bàn là do cô ấy chuẩn bị
+ Tất cả mọi quả trứng này đều không phải là trứng gà
→ Phán đoán chung thường được bắt đầu bằng các lượng từ phổ biến như: mọi, tất cả, toàn thể,.. -
Phán đoán riêng (phán đoán bộ phận): Là phán đoán chỉ có 01 đối tượng của
chủtừ thuộc hoặc không thuộc về vị từ
Ví dụ: Một số bông hoa không phải hoa hồng lOMoARcPSD| 37054152
→ Phán đoán riêng thường được bắt đầu bằng các lượng từ bộ phận: Một số, một vài,.. -
Phán đoán đơn nhất: Là phán đoán cho biết một đối tượng cụ thể, duy nhất
tronghiện thực thuộc hoặc không thuộc về P
Ví dụ: Bắc Kinh là thủ đô của Trung Quốc
Lưu ý: Cũng có thể coi phán đoán đơn nhất cũng là một loại phán đoán chung, bởi vì cho
dù phán đoán chỉ phản ảnh một đối tượng, nhưng đối tượng đó là cái duy nhất, trong hiện
thực không có cái thứ hai. Vì thế, nói một cái duy nhất cũng là nói đến toàn thể cái duy nhất
đó, do vậy mà ngoại diên của chủ từ trong phán đoán này luôn luôn đầy đủ.
Thứ ba: Phân loại phán đoán theo chất và lượng -
Phán đoán khẳng định chung Công thức: Mọi S là P
Ví dụ: Mọi quyển sách trong tủ sách này đều rất hay
Trong nhiều trường hợp, phán đoán không có dạng mọi S là P mà vẫn là phán đoán
khẳng định chung. Ví dụ: Ớt nào mà ớt chẳng cay -
Phán đoán khẳng định riêngCông thức: Một số S là P
Ví dụ: Một số quyển sách rất nặng -
Phán đoán phủ định chungCông thức: Mọi S không là P
Ví dụ: Mọi cốc nước trên bàn đều không nóng
Trong nhiều trường hợp, phán đoán phủ định chung nhiều lúc không bắt đầu bằng
lượng từ phổ biến: Mọi, tất cả, toàn thể, thậm chí còn không có liên từ phủ định
Ví dụ: Mấy đời bánh đúc có xương,
Mấy đời địa chủ mà thương dân cày -
Phán đoán phủ định riêng
Công thức: Một số S không là P
Ví dụ: Một số quyển sách không phải là quyển sách của tôi
1.1.2. Phán đoán đơn
a. Cấu trúc logic hình thức của phán đoán đơn
Cấu tạo của phán đoán đơn gồm 4 bộ phận:
Chủ từ: là bô phận chỉ đối tượng hay lớp đối tượng mà phán đoán phản ánh. Ký hiệu bằng chữ S. lOMoAR cPSD| 37054152
Vị từ: là bô phân chỉ nôi dung (thuôc tính) mà phán đoán phản ánh. Ký hiệu bằng chữ P.
Chủ từ và vị từ trong phán đoán đơn được gọi chung là “thuật ngữ”.
Lượng từ: là bộ phận dùng để chỉ số lượng các đối tượng thuôc ngoại diên của chủ
từ có tham gia vào phán đoán; số lượng này có thể là toàn bô (mọi, tất cả, ký hiệu V); có
thể là môt phần (môt số, đa số ký hiệu ∀). Lượng từ đặc trưng cho phán đoán đơn về mặt
lượng, theo đó có hai loại: phán đoán toàn thể (∀S — P) và phán đoán bô phân (∃S — P).
Hệ từ: là bô phân nằm giữa chủ từ âf vị từ, dùng để nối kết hoặc tách rời các đối
tượng của chủ từ với vị từ. Thường nó biểu hiện quan hệ khẳng định (là) hay phủ định
(không là) giữa chủ từ và vị từ. Hệ từ đặc trưng cho phán đoán đơn về mặt chất, theo đó có
hai loại phán đoán: khẳng định (S là P) và phủ định (S không là P).
Như vậy, dạng tổng quát của phán đoán đơn thuôc tính là: ∀(∃) S □ P
Phân loại phán đoán đơn. Mọi phán đoán đơn nhất thiết đều phải có 4 bô phân nêu trên.
Tuy nhiên, việc phân loại chúng phải dựa cùng lúc vào cả hai tiêu chí là lượng và chất.
Nếu vây thi sẽ có 4 kiểu như sau:
+ Phán đoán toàn thể khẳng định: ∀S là P, ký hiệu A
+ Phán đoán toàn thể phủ định: ∀S không là P, ký hiệu E
+ Phán đoán bô phân khẳng định: ∃S là P, ký hiệu I
+ Phán đoán bô phân phủ định: ∃S không là P, ký hiệu O
Ngoài ra, có thể còn có phán đoán gọi là đơn nhất (khẳng định hoặc phủ định) do
chủ từ của chúng là khái niệm đơn nhất như: “Hà Nôi là thành phố anh hùng”, hay “trời
không mưa”, nhưng căn cứ vào định nghĩa về lượng từ đã nêu ở trên chúng ta sẽ đều coi
chúng là phán đoán toàn thể, điều này sẽ thuận tiện hơn cho việc xác định chu diên của các thuật ngữ.
b. Tính chu diên của thuật ngữ trong phán đoán đơn
Các thuật ngữ S và P trong phán đoán đơn biểu thị các khái niệm. Nếu ngoại diên
của khái niệm được bao quát dầv đủ thì người ta gọi thuật ngữ tương ứng là chu diên; trong
trường hợp ngược lại, được gọi là không chu diên.
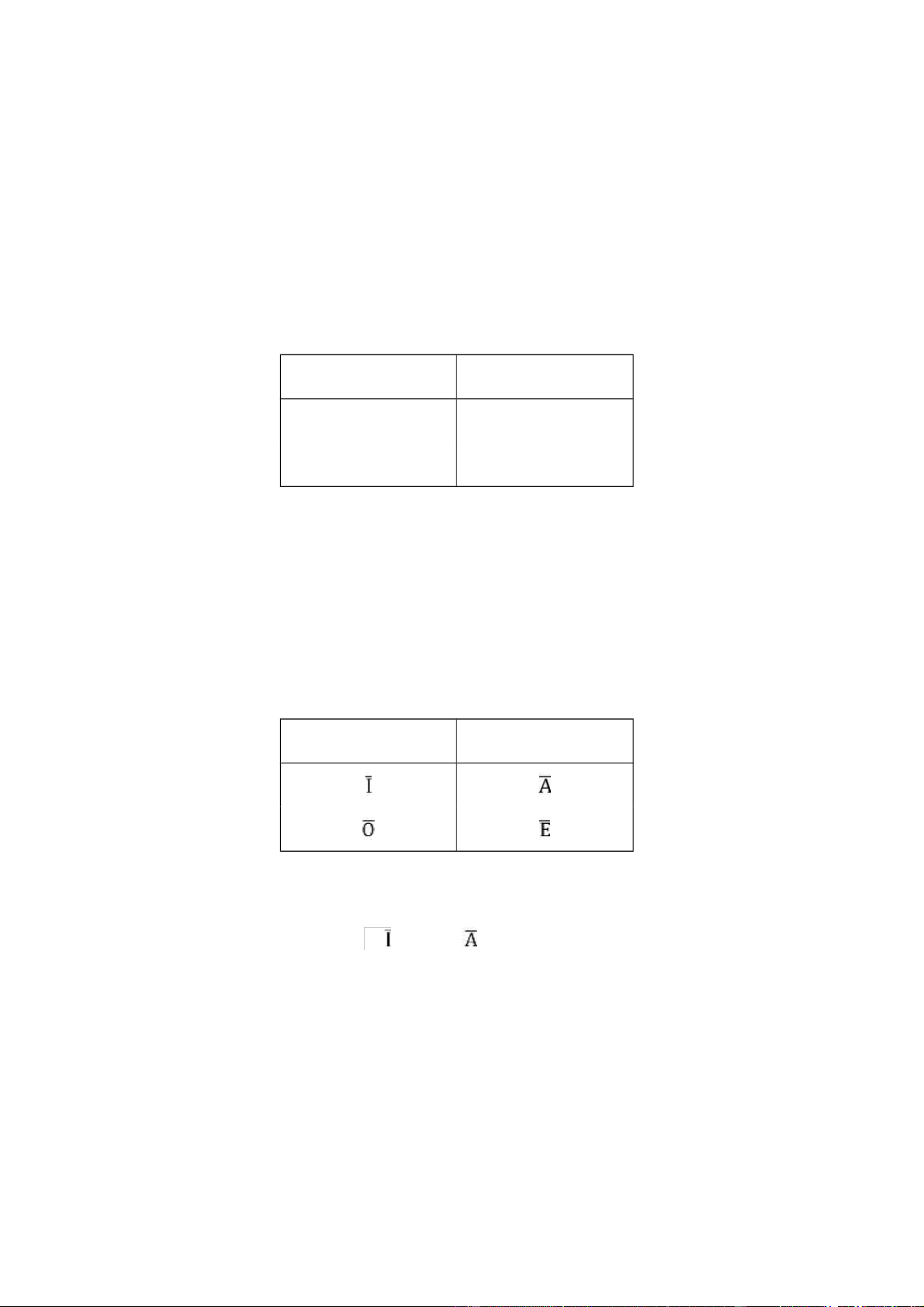
Ta hãy xét tình hình chu diên của các thuật ngữ trong các loại phán đoán A, E, O, I. Ta sẽ
sử dụng hai loại ký hiệu biểu trưng. lOMoARcPSD| 37054152
Loại thứ nhất: Ký hiệu thuật ngữ chu diên bằng dấu (+) đi kèm sau thuật ngữ đó;
trường hợp ngược lại, không chu diên, sẽ ký hiệu bằng dấu (-) đi kèm sau thuật ngữ tương ứng.
Loại thứ hai: sử dụng sơ đồ Gi. Ven (J.Venn), biểu thị ngoại diên khái niệm, tức là
tập hợp đối tượng được khái niệm bao quát bằng đường cong khép kín: nếu chu diên thì
biểu thị bằng đường liền nét, ngược lại thì biểu thị bằng đường không liền nét.
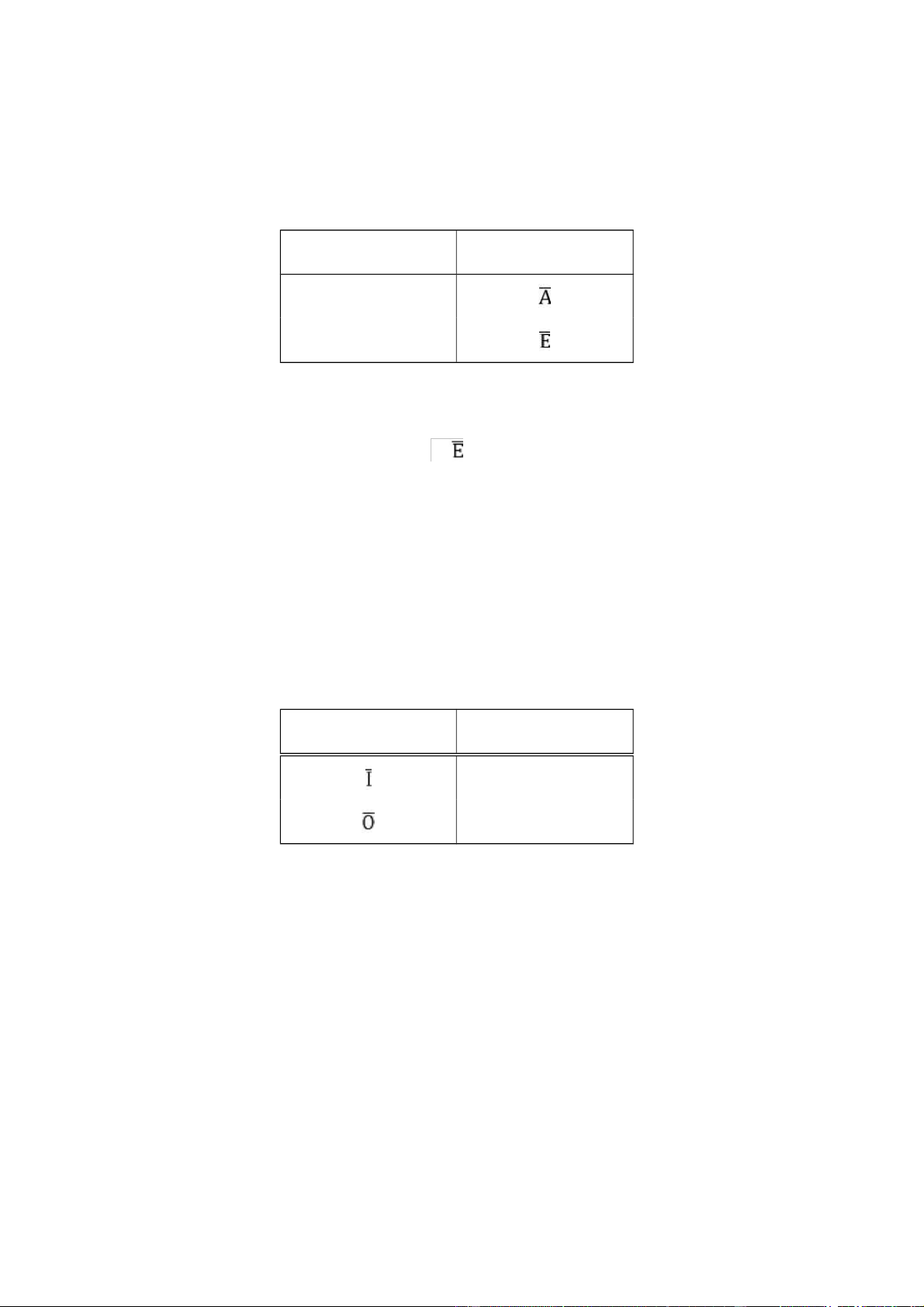
1.2. Quan hệ về giá trị chân lí của các phán đoán. A Đối lập trên F Lệ thuộc Mâu thuẫn Lệ thuộc I Đối lập dưới O
Các đỉnh của hình vuông là các phán đoán đơn A, E, I, O còn các cạnh và đường
chéo biểu thị quan hệ giữa chúng:
A và E tương phản, chúng cùng sai hoặc cùng đúng.
I và O tương phản với nhau, chúng có thể cùng đúng nhưng không thể cùng sai, có thể một
phán đoán đúng một phán đoán sai.
Phán đoán I phụ thuộc A, nếu A đúng thì I đúng, nếu A sai thì I có thể đúng hoặc sai. Nếu
I đúng thì A đúng, hoặc có thể sai. Nhưng nếu I sai thì chắc chắn A sai. Ví dụ:
Hai phán đoán A và E không thể đồng thời đúng, nhưng có thể đồng thời sai.
Tất cả các dòng sông đều chảy (A) : đúng.
Tất cả các dòng sông đều không chảy (E) : sai.
-> Hai phán đoán trên không đồng thời đúng. lOMoARcPSD| 37054152
Mọi sinh viên đều giỏi tiếng Nga (A) : sai.
Mọi sinh viên đều không giỏi tiếng Nga (E) : sai.
-> Hai phán đoán trên không đồng thời sai. Ví dụ :
Một số nhà bác học được nhận giải thưởng Nobel (I) : đúng.
Một số nhà bác học không được nhận giải thưởng Nobel (O) : đúng.
-> Hai phán đoán trên đồng thời đúng. Nhưng :
Một số kim loại không dẫn diện (O) : sai.
Một số kim loại dẫn điện (I) : đúng.
-> Hai phán đoán trên không đồng thời sai
1.3. Hình vuông logic và vai trò
Hình vuông logic là hình vuông thể hiện giữa các phán đoán thuộc tính so sánh được
và có dạng A, E, I hoặc O
Loại A (viết tắt của chữ Latinh Affirmo), đó là phán đoán khẳng định chung. Thí dụ:
Mọi kim loại đều dẫn điện.
Loại E (viết tắt của chữ Latinh nEgo), là phán đoán phủ định chung. Thí dụ: Không
có á kim nào dẫn điện cả.
Loại O (viết tắt của chữ Latinh negO), là phán đoán phủ định riêng.
Loại I (viết tắt của chữ Latinh aiELrmo), là phán đoán khẳng định riêng. Thí dụ:
Một số thiên nga không có long màu trắng. Thí dụ: Một số sinh viên là coder. Ví dụ:
+ Mọi người trong trường ĐH Sư Phạm Kỹ Thuật Tp.HCM đều tốt.
+ Những dụng cụ trên sàn đều do anh ấy cất.
Phán đoán chung thường bắt đầu bằng các lượng từ phổ biến như: mọi, tất cả, toàn thể,.. lOMoARcPSD| 37054152
- Phán đoán riêng (phán đoán bộ phận): Là phán đoán chỉ có 01 đối tượng của chủ từ
thuộc hoặc không thuộc về vị từ.
Ví dụ: Một vài bạn trong số đó không phải là sinh viên của trường ĐH Sư Phạm Kỹ Thuật Tp.HCM
Phán đoán riêng thường được bắt đầu bằng các lượng từ bộ phận: Một số, một vài,..
- Phán đoán đơn nhất: Là phán đoán cho biết một đối tượng cụ thể, duy nhất trong
thực thuộc hoặc không thuộc về P.
Ví dụ: Pari là thủ đô nước Pháp.
Lưu ý: Cùng có thể coi phán đoán đơn nhất cùng là một loại phán đoán chung,
bởi vì dù cho phán đoán là phản ánh một đối tượng , nhưng dối tượng đó là duy nhất,
trong hiện thực không có cái thứ 2. Vì thế, nói một cái duy nhất cùng nói đến toàn
thể cái duy nhất đó, do vậy mà ngoại diên của chủ từ trong phán đoán này luôn luôn đầy đủ.
Thứ ba: Phân loại phán đoán theo chất và lượng
- Phán đoán khẳng định chung Công thức: Mọi S là P
Ví dụ: Mọi đồ dung trong giá bếp đều phục vụ cho nấu ăn.
Trong nhiều trường hợp, phán đoán không có dạnh mọi S là P mà vânx là phán đoán khẳng định chung.
Ví dụ: Chanh nào cả chanh chẳng chua.
- Phán đoán khẳng định riêng
Công thức: Một số S là P
Ví dụ: Một số thực phẩm rất dể bị hỏng.
- Phán đoán phủ định chung.
CHƯƠNG 2: XÂY DỰNG CÁC KIỂU SUY LUẬN TRỰC TIẾP TỪ HÌNH VUÔNG LOGIC
2.1. Định nghĩa suy luận trực tiếp
Suy luận trực tiếp là loại suy luận diễn dịch, gồm có một tiền đề và một kết luận. Ta
xét suyu luận trực tiếp với các tiền đề và kết luận là phán đoán đơn . lOMoARcPSD| 37054152
Ví dụ 1 : Từ tiền đề “Cơ lưu chất là một trong những môn học khó” từ đây ta kết luận
“Trong những môn học khó có môn Cơ lưu chất”
Trong ví dụ trenem cả tiền đề và kết luận đều là phán đoán đơn.
Ví dụ 2 : Từ tiền đề “Một số sinh viên điều khiển phương tiện giao thông thường vi phạm
an toàn giao thông” từ đây ta có kết luận “Một số người điều khiển phương tiện giao thông
để vi phạm an toàn giao thông là sinh viên”
Từ đây, ta rút ra kết luận là cả tiền đề và kết luận đều là phán đoán đơn.
Về sau chúng ta sẽ thấy trong các suy luận trực tiếp thông thường tiền đề và kết luận
là các phán đoán tương đương với nhau (trừ trường ợp đảo ngược phán đoạn hạng A)
Trong cuộc sống, suy luận trực tiếp là dạng suy luận được phổ biến Lý do của việc này là :
- Thứ nhất, khi cần nhắc lại một tư tưởng, một câu hỏi nào đó, người ta thường
không muốn nhắc lại nguyên văn, mà chỉ nhắc lại nội dung tương đương, còn lời văn khác đi để tránh nhàm chán
-Thứ hai, mặc dù phán đoán ban đầu(tiền đề) và phán đoán thu được (kết luận) tương
đương nhau về mặt logic, nhưng hiệu quả ngôn ngữ, tâm lý đối với người nghe thì khác
nhau, nên có thể sử dụng suy luận trực tiếp để nhấn mạnh ý nào đó, hay lưu ý gì đó…
2.2 Xây dựng các kiểu suy luận dựa vào hình vuông logic
2.2.1 Dựa vào quan hệ mâu thuẫn
Quan hệ mâu thuẫn: là quan hệ giữa những phán đoán khác nhau về cả chất, lẫn
lượng. Mối quan hệ này thể hiện trên hai đường chéo của hình vuông, đó là quan hệ giữa
hai cặp phán đoán: A và O; E và I. Chúng không thể cùng chân thực hoặc cùng giả dối, mà
nhất thiết phải có một phán đoán là chân thực, còn phán đoán kia phair là giả dối Giá trị
Logic của các phán đoán đơn trong quan hệ mâu thuẫn như sau : A = 1 => O = 0 O = 1 => A = 0 E = 1 => I = 0 I = 1 => E= 0
Ví dụ: Cho tiền đề “Mọi tội phạm đều bị trừng phạt”, ta rút ra kết luận “Một số tội
phạm không bị trừng phạt” Cấu trúc:
Ví dụ: Tiền đề “Mọi con đường ở TP Hồ Chí Minh đều không bị hư hỏng” suy ra
kết luận “Một số con đường ở TP Hồ Chí Minh đã bị hư hỏng” Cấu trúc : lOMoARcPSD| 37054152
2.2.2. Dựa vào quan hệ thứ bậc
Quan hệ thứ bậc là quan hệ giữa các phán đoán đơn có cùng các khái niệm S, P cùng hệ
từ, nhưng trái ngược nhau về lượng từ. Đó là quan hệ phán đoán A và I, giữa E và O. Trong quan hệ thứ bậc: -
Nếu phán đoán toàn xưng là đúng thì phán đoán đặc xưng cũng đúng. Nếu phán
đoántoàn xưng là sai thì không xác định được giá trị của phán đoán đặc xưng. -
Nếu phán đoán đặc xưng là sai thì phán đoán toàn xưng cũng sai. Nếu phán đoán
đặcxưng là đúng thì không xác định được giá trị của phán đoán toàn xưng.
Nếu tiền đề là phán đoán bậc trên thì kết luận là phán đoán bậc dưới. Tiền đề Kết luận A I E O
Ví dụ: Cho tiền đề “Mọi sinh viên đều phải học ngoại ngữ” ta rút ra kết luận “Một số
sinh viên học ngoại ngữ”. Cấu trúc: SAP → SIP.
Ví dụ: Cho tiền đề “Cây nhãn không phải là cây công nghiệp” rút ra kết luận “Một số
cây nhãn không phải là cây công nghiệp”. Cấu trúc: SEP → SOP.
Nếu tiền đề là phủ định phán đoán bậc dưới thì kết luận sẽ là phủ định phán đoán bậc trên. Tiền đề Kết luận
Ví dụ: Cho tiền đề “Một số sinh vật sống không có cấu tạo từ tế bào” rút ra kết luận “Mọi
sinh vật sống đều không có cấu tạo từ tế bào”. Cấu trúc: S P → S P.
2.2.3. Dựa vào quan hệ đối chọi
Quan hệ đối chọi là quan hệ giữa các phán đoán có cùng các khái niệm S, P cùng lượng
từ, nhưng trái ngược nhau về hệ từ.
• Quan hệ đối chọi trên (giữa A và E): lOMoARcPSD| 37054152
Hai phán đoán quan hệ đối chọi trên có thể cùng sai nhưng không thể cũng đúng. Nếu
biết 1 trong 2 phán đoán đúng thì phán đoán còn lại là sai. Nếu biết trong 2 phán đoán là sai
thì không xác định được giá trị của phán đoán còn lại.
Nếu tiền đề là phán đoán toàn xưng thì kết luận sẽ là phủ định phán đoán đối chọi với nó. Tiền đề Kết luận E A
Ví dụ: Cho tiền đề “Mọi loài cá đều biết bơi” rút ra kết luận “Không phải một số loài cá không biết bơi”. Cấu trúc: SAP → S P.
• Quan hệ đối chọi dưới (giữa I và O):
Hai phán đoán quan hệ đối chọi dưới có thể cùng đúng nhưng không thể cùng sai. Nếu
biết 1 trong 2 phán đoán là sai thì phán đoán còn lại là đúng. Nếu biết trong 2 phán đoán là
đúng thì không xác định được giá trị của phán đoán còn lại.
Nếu tiền đề là phủ định phán đoán đặc xưng thì kết luận sẽ là phán đoán đối chọi với
phán đoán đặc xưng ấy. Tiền đề Kết luận O I
Ví dụ: Cho tiền đề “Không phải một số quốc gia bị dịch bệnh hoành hành” rút ra kết luận
“Một số quốc gia không bị dịch bệnh hoành hành”. Cấu trúc: SIP → SOP lOMoARcPSD| 37054152 KẾT LUẬN
Nghiên cứu vai trò của hình vuông logic trong việc định giá trị chân lý của các câu
lệnh đơn giản và xây dựng các kiểu suy luận trực tiếp từ hình vuông logic giúp chúng ta
nhận thức đúng giá trị chân lý của các câu lệnh đơn giản và suy ra loại trực tiếp từ hình
vuông logic. Đánh giá thác triệt để sức mạnh nội dung của hình vuông logic trong việc xác
định giá trị của một câu lệnh, chúng ta cần tìm ra giá trị chân lý của câu lệnh đó là gì, từ đó
chúng ta có thể mở rộng và khám phá ý nghĩa sâu sắc hơn của nó. Đồng thời, khi tiền đề là
một phán đoán thuộc tính đơn lẻ, chúng ta có thể rút ra những kết luận nhất định theo mối
quan hệ được xác định bởi khối logic. lOMoARcPSD| 37054152
TÀI LIỆU THAM KHẢO
[1] Phạm Đình Nghiệm (2009), Nhâp môn Logic học, Nhà xuất bản Đại học Quốc gia Thành phố Hồ Chí Minh
[2] Trần Hoàng (2003), Logic học nhập môn, Nhà xuất bản Đại học Quốc gia Thành phố Hồ Chí Minh
[3] htttps://www.elib.vn/huong-dan/bai-2-phan-doan-don-28982.html
[4] https://hoc247.net/logic-hoc/bai-2-phan-doan-don-18198.html
[5] https://luathoangphi.vn/phan-doan-la-gi-vi-du-ve-phan-doan/
[6] https://ybox.vn/ky-nang/phan-doan-don-phan-doan-logic-hinh-thuc- 5ca497a60674cc13fe41b73f
[7] https://voer.edu.vn/m/quan-he-giua-cac-phan-doan-hinh-vuong-logic/20cc9b8a