Tọa Độ Cầu và Tọa Độ Trụ trong Lý Thuyết | Lý thuyết Độ đo và tích phân | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội
Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF với mục đích hỗ trợ học tập và tham khảo. Nội dung tài liệu được trình bày rõ ràng, dễ tiếp cận, phù hợp cho việc ôn tập và củng cố kiến thức trong quá trình học đại học. Đây sẽ là nguồn tư liệu hữu ích giúp các bạn sinh viên chuẩn bị tốt hơn cho các buổi học, đồng thời mở rộng thêm hiểu biết về môn học. Hy vọng tài liệu này sẽ mang lại nhiều giá trị và hỗ trợ các bạn trong hành trình học tập. Mời bạn đọc cùng tham khảo!
Môn: Lý thuyết Độ đo và tích phân 10 tài liệu
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội 867 tài liệu
Tác giả:
Preview text:
HCMUT CNCP GIẢI TÍCH 2 NGUYỄN QUỐC VƯƠNG
Tọa độ cầu và tọa độ trụ trong tích phân bội 3 Nội dung: - Tọa độ cầu - Tọa độ trụ 1. Tọa độ cầu
Áp dụng cho vật thể được tạo thành bởi 1 phần hình cầu b d f 2 f (x ,y ,z ) dxdydz d d sin( p ) (f ,x ,y )z a c e
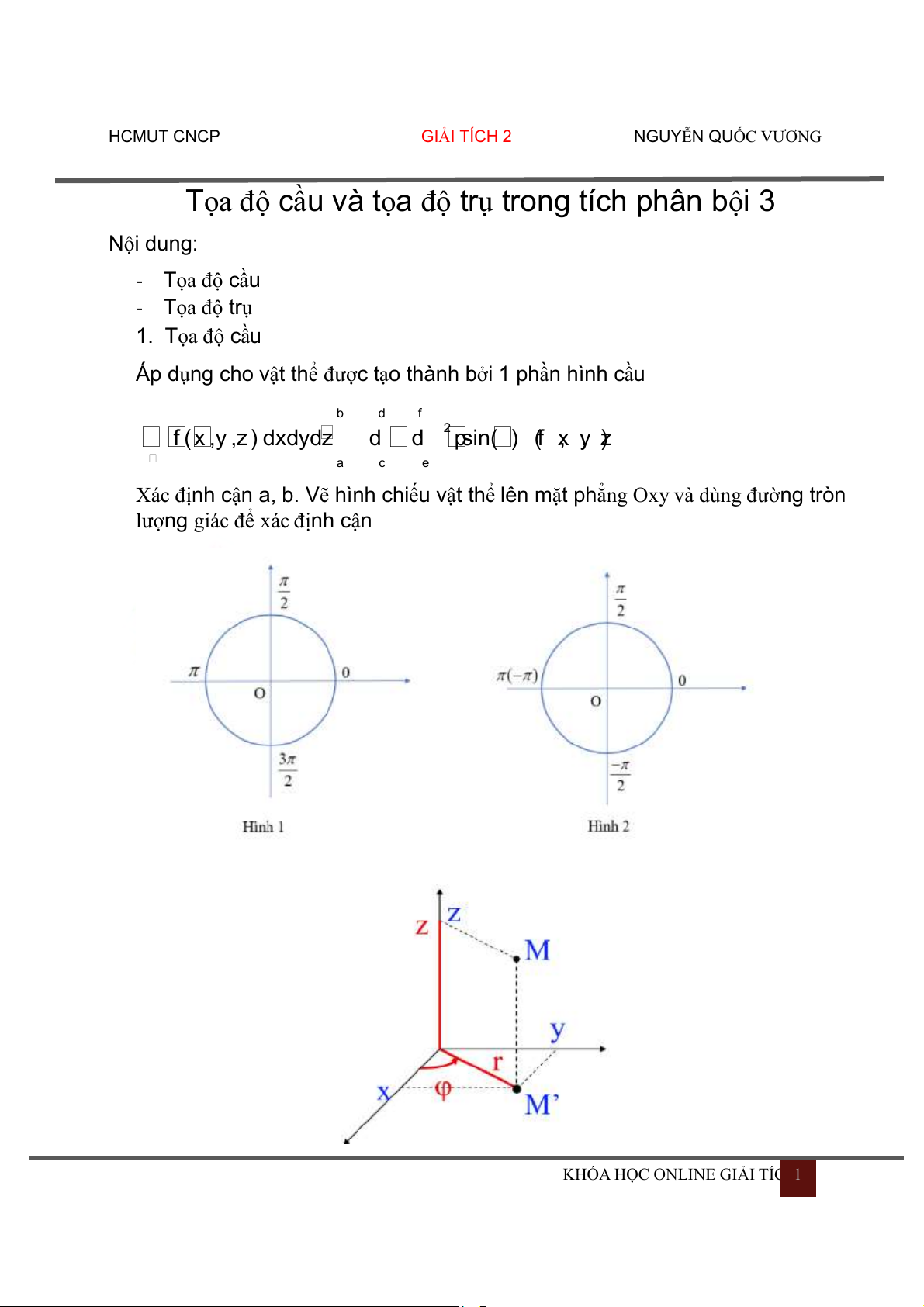
Xác định cận a, b. Vẽ hình chiếu vật thể lên mặt phẳng Oxy và dùng đường tròn
lượng giác để xác định cận
KHÓA HỌC ONLINE GIẢI TÍC 1 HCMUT CNCP GIẢI TÍCH 2 NGUYỄN QUỐC VƯƠNG
Xác định cận c, d góc quét từ trụ Oz đến phần xa nhất của vật thể Xác định cận e,f
- Tìm e ta thế x,y,z vào phương trình mặt cong biên của vật thể gần gốc tọa độ nhất
- Tìm f ta thế x,y,z vào phương trình mặt cong biên của vật thể xa gốc tọa độ nhất
Các lý thuyết trên khá cứng, nên theo dõi livestream để có cái nhìn tổng quan hơn
Một số phương trình nên nhớ để tìm nhanh cận dP 2 2 2 2 x y z R p R 2 2 2 x y z 2 Rz 2 p cos R ( 2 2 2 R x y R p sin( ) 2. Tọa độ trụ Đặt x r cos( y r sin( ) b d 2 z f ( , x , y z ) dxdydz d dr ( rf cros( ), s r in( ), z ) a c 1 z
KHÓA HỌC ONLINE GIẢI TÍC 2 HCMUT CNCP GIẢI TÍCH 2 NGUYỄN QUỐC VƯƠNG
Xác định cận a, b. Vẽ hình chiếu vật thể lên mặt phẳng Oxy và dùng đường tròn
lượng giác để xác định cận
Xác định cận c,d. Xác định hình chiếu vật thể lên mặt phẳng Oxy
- Tìm c bằng cách thế x, y vô phương trình gần gốc tọa độ nhất
- Tìm d bằng cách thế x, y vô phương trình xa gốc tọa độ nhất
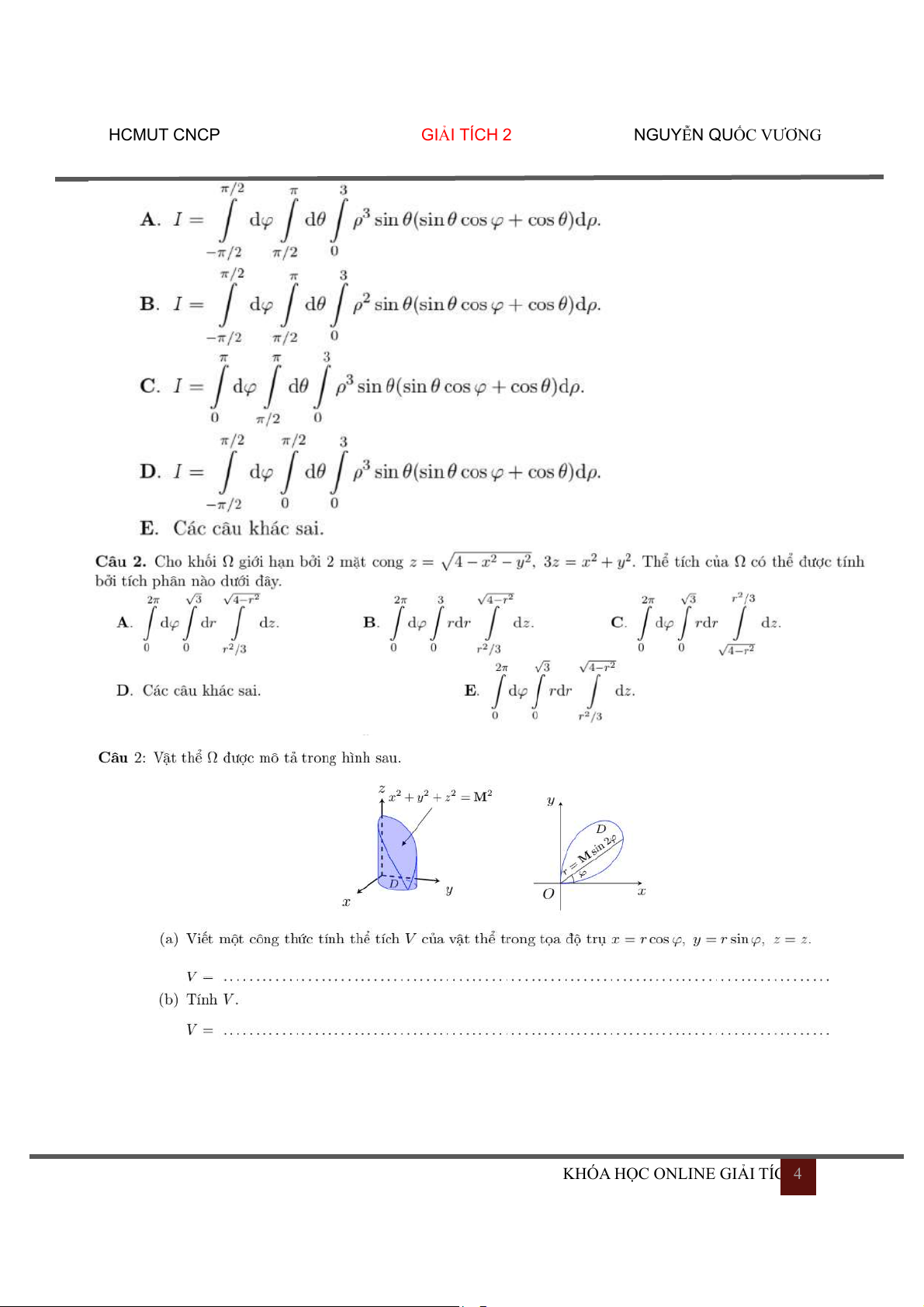
MỘT SỐ CÂU TRONG ĐỀ THI
KHÓA HỌC ONLINE GIẢI TÍC 3 HCMUT CNCP GIẢI TÍCH 2 NGUYỄN QUỐC VƯƠNG
KHÓA HỌC ONLINE GIẢI TÍC 4 HCMUT CNCP GIẢI TÍCH 2 NGUYỄN QUỐC VƯƠNG
KHÓA HỌC ONLINE GIẢI TÍC 5 HCMUT CNCP GIẢI TÍCH 2 NGUYỄN QUỐC VƯƠNG
KHÓA HỌC ONLINE GIẢI TÍC 6