Chương 1: Phân Tích Đồ Thị và Độ Bậc | Lý thuyết Độ đo và tích phân | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội

Problem 1 What are the degrees and what are the neighborhoods of the vertices in the graph G and H Hinh G Deg(a) = 2 Deg(b) = 4 Deg(c) = 4 Deg(d) = 1 Deg(e) = 3 Deg(f) = 4 Deg(g) = 0
Problem 2 How many edges are there in the graph with 10 vertices each of degree six?
 Định lý Handshaking phát biểu rằng tổng của tất cả các bậc của các đỉnh
trong đồ thị bằng 2 lần số cạnh. Tức là: ∑deg(v)=2m
trong đó m là số cạnh của đồ thị.
 Đồ thị của bạn có 10 đỉnh, và mỗi đỉnh có bậc 6.
Tổng bậc của các đỉnh là: ∑deg(v)=10×6=60
 Theo định lý Handshaking, tổng bậc của các đỉnh bằng 2 lần số cạnh, do đó: 2m=60 60
 Giải phương trình này để tìm số cạnh m: m= =30 2
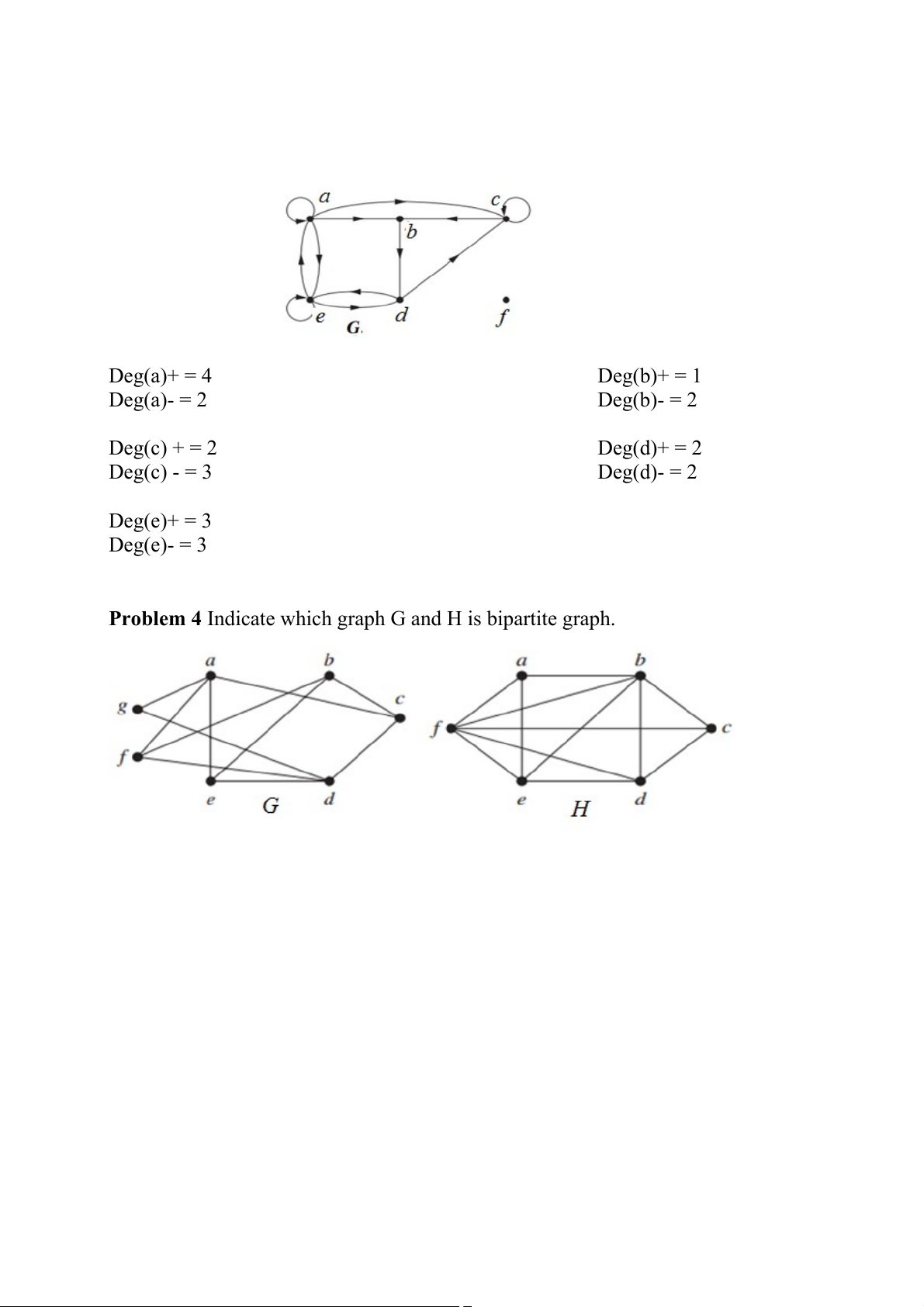
Problem 3 Find the in-degree and out-degree of each vertex in the graph G Deg(a)+ = 4 Deg(b)+ = 1 Deg(a)- = 2 Deg(b)- = 2 Deg(c) + = 2 Deg(d)+ = 2 Deg(c) - = 3 Deg(d)- = 2 Deg(e)+ = 3 Deg(e)- = 3
Problem 4 Indicate which graph G and H is bipartite graph. Problem 5
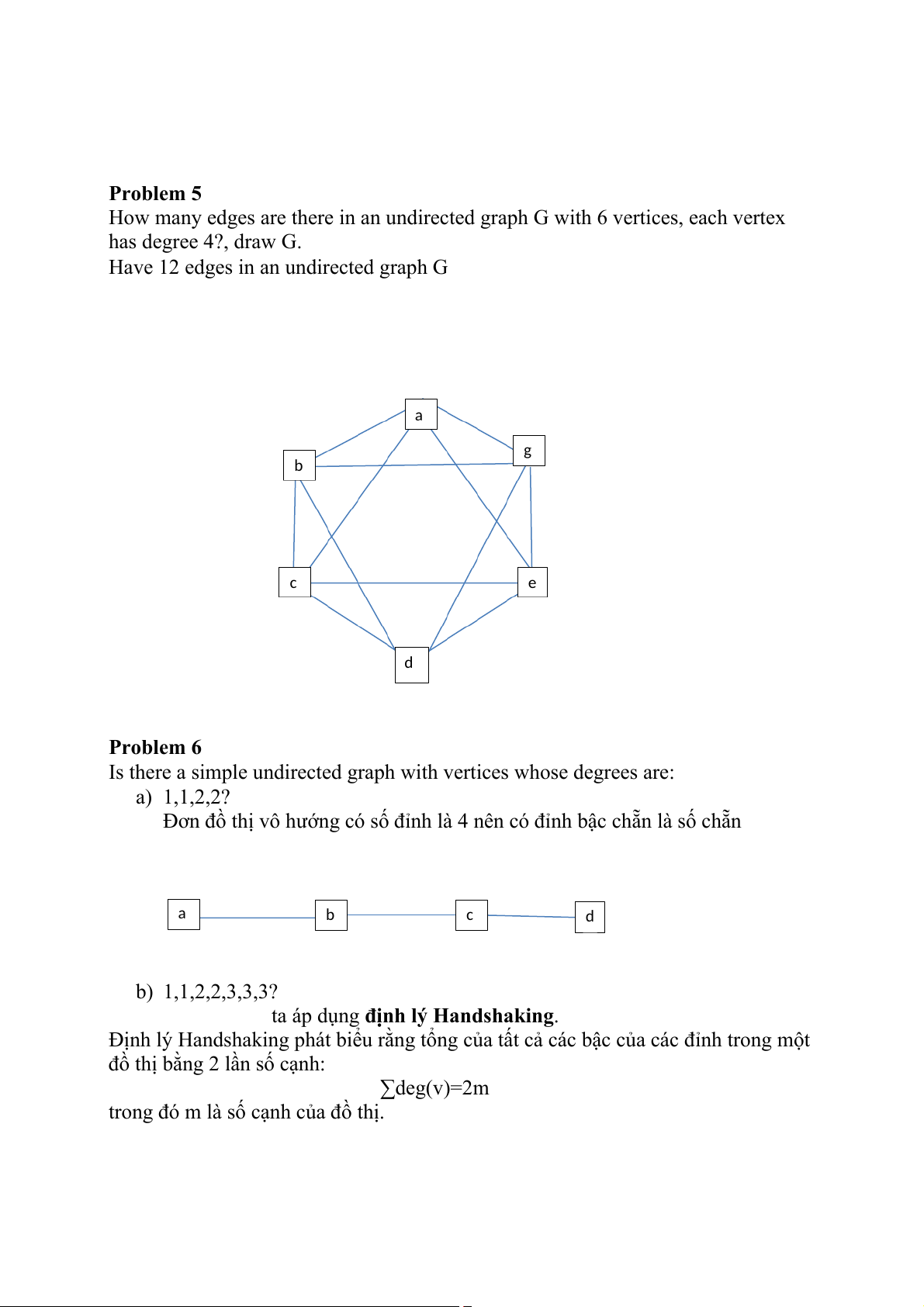
How many edges are there in an undirected graph G with 6 vertices, each vertex has degree 4?, draw G.
Have 12 edges in an undirected graph G a g b c e d Problem 6
Is there a simple undirected graph with vertices whose degrees are: a) 1,1,2,2?
Đơn đồ thị vô hướng có số đỉnh là 4 nên có đỉnh bậc chẵn là số chẵn a b c d b) 1,1,2,2,3,3,3?
ta áp dụng định lý Handshaking.
Định lý Handshaking phát biểu rằng tổng của tất cả các bậc của các đỉnh trong một
đồ thị bằng 2 lần số cạnh: ∑deg(v)=2m
trong đó m là số cạnh của đồ thị.
Ở đây, đồ thị của bạn có 7 đỉnh với các bậc là 1, 1, 2, 2, 3, 3, 3.
Tổng bậc của các đỉnh là: ∑deg(v)=1+1+2+2+3+3+3=15
Theo định lý Handshaking, tổng bậc của các đỉnh phải bằng 2 lần số cạnh, tức là: 2m=15
Tuy nhiên, 15 là một số lẻ. Không có số nguyên nào khi nhân với 2 lại cho ra một
số lẻ. Điều này cho thấy rằng tổng bậc của các đỉnh không thể là một số lẻ nếu tồn
tại một đồ thị đơn vô hướng. c) 1,2,3,4?
ta áp dụng định lý Handshaking.
 Định lý Handshaking phát biểu rằng tổng của tất cả các bậc của các đỉnh
trong một đồ thị bằng 2 lần số cạnh: ∑deg(v)=2m
trong đó m là số cạnh của đồ thị.
Ở đây, đồ thị của bạn có 7 đỉnh với các bậc là 1, 2, 3,4. Tổng bậc của các đỉnh là: ∑deg(v)=1+2+3+4=10
Theo định lý Handshaking, tổng bậc của các đỉnh phải bằng 2 lần số cạnh, tức là: 2m=10
Một đỉnh có bậc 4 nghĩa là nó phải được kết nối với 4 đỉnh khác. Nhưng nếu đồ thị
chỉ có 4 đỉnh, thì đỉnh có bậc 4 không thể tồn tại vì không có đủ đỉnh để kết nối. d) 3,3,3,3? a b c d e) 1,2,3,4,5,6,7?
Không tồn tại do có số đỉnh là 7 mà bậc bằng 7 If so, draw the graph. Problem 7
How many edges are there in an undirected graph with 8 vertices, each vertex has degree 4? Draw this graph.
1 đỉnh có bậc bằng 4 - tổng bậc bằng 32 do có 8 đỉnh Theo định lý bắt tay, đặt m là số cạnh ta có: -
2m = 32 m = 16 ⇨ Có 16 cạnh. Problem 8
What is the maximum number of edges possible in a simple undirected graph of 10
vertices? What about multigraphs and pseudographs?
 Đồ thị đầy đủ là đồ thị trong đó mỗi đỉnh được kết nối với tất cả các đỉnh khác.
 Nếu có n đỉnh, mỗi đỉnh sẽ có n−1 cạnh (kết nối với n−1 đỉnh còn lại).
 Với 10 đỉnh (n=10), số cạnh tối đa sẽ là 10 ×(10−1) 10 × 9 E = = =45 max 2 2