




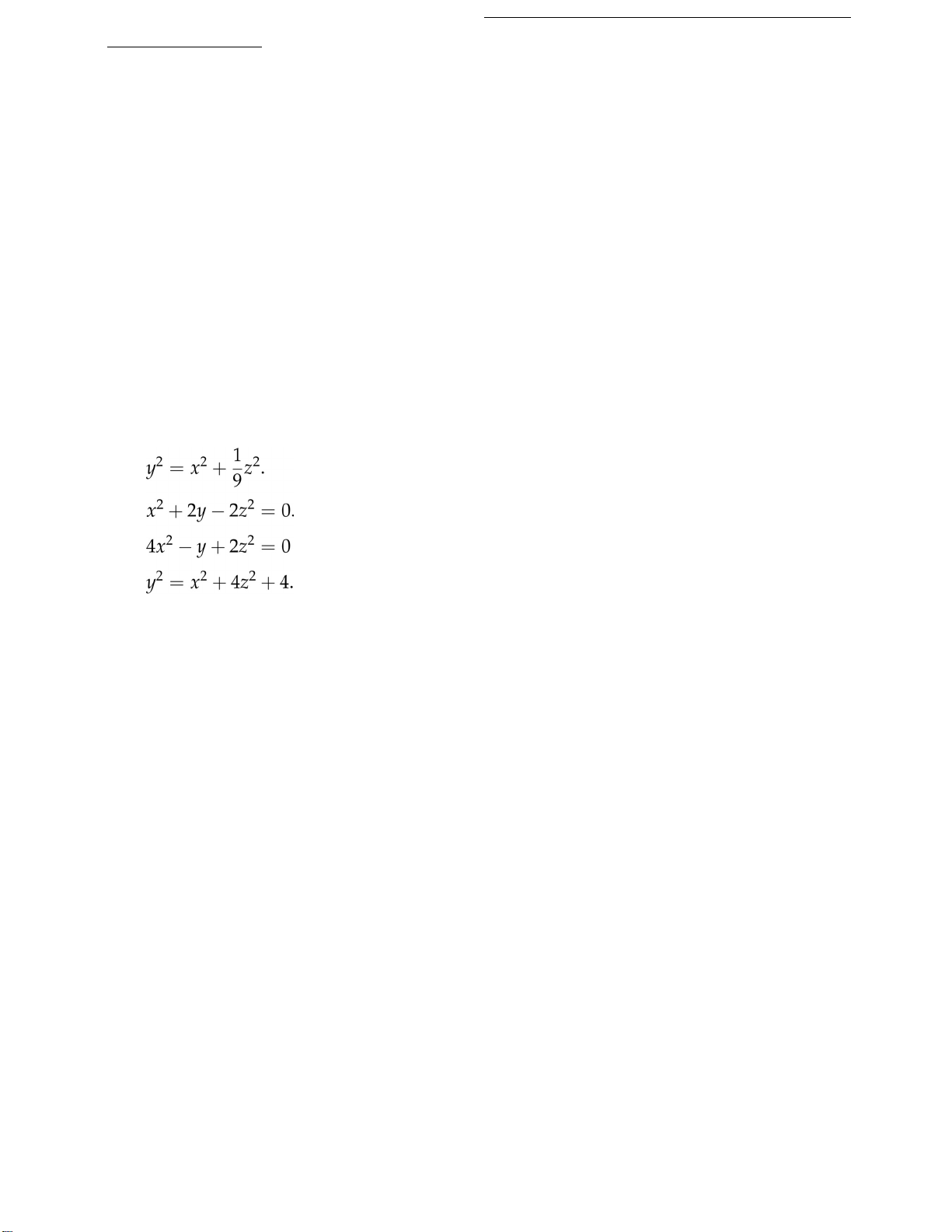




Preview text:
lOMoAR cPSD| 59256994 BÙITHANHDUY KHOAKHOAHỌCCƠBẢN
Trường Đại học Kiến trúc Tp. Hồ Chí Minh PHẠMMINHTRÍ
Trường Đại học Sư Phạm Kỹ Thuật Tp. Vĩnh Long Thành phố Hồ Chí Minh Ngày 12 tháng 9 năm 2024 lOMoAR cPSD| 59256994 Mục lục
1 HÌNH HỌC GIẢI TÍCH.... .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. ... 1
1.1 MẶT TRỤ VÀ CÁC MẶT BẬC HAI ..... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... . 1
1.2 BÀI TẬP .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... . 6
1.3 ĐƯỜNG CONG THAM SỐ .. .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .. 7
1.4 MẶT CONG THAM SỐ ..... .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... 9
1.5 BÀI TẬP .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... . 9
1.6 TỌA ĐỘ CỰC ..... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .. 11
1.7 BÀI TẬP .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... 13
1.8 TỌA ĐỘ TRỤ .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... 14
1.9 BÀI TẬP .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... 15
1.10 TỌA ĐỘ CẦU .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... . 15
1.11 BÀI TẬP .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .. 16
2 TÍCH PHÂN BỘI HAI .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. 18
2.1 BÀI TOÁN TÍNH THỂ TÍCH .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ... 18
2.2 TÍCH PHÂN BỘI HAI TRÊN MIỀN HÌNH CHỮ NHẬT ..... .. .... .... .. .... .... .. .... .... .. .... .... .. 20
2.3 TÍCH PHÂN BỘI HAI TRÊN MIỀN BẤT KỲ .... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .. 21
2.4 CÁC TÍNH CHẤT CƠ BẢN ..... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... 22
2.5 CÁCH TÍNH TÍCH PHÂN BỘI HAI THEO MIỀN D ... ..... .... .... .... .. .... .... .. .... .... .. .... .... .. 22
2.6 BÀI TẬP .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... 25
2.7 CÔNG THỨC ĐỔI BIẾN SỐ ... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. 31
2.8 BÀI TẬP TÍNH TÍCH PHÂN BỘI HAI BẰNG TỌA ĐỘ CỰC .... .... .... .... .. .... .... .. .... .... .. ... 35
2.9 BÀI TẬP TÍNH TÍCH PHÂN BỘI HAI BẰNG ĐỔI BIẾN TỔNG QUÁT ..... .... .. .... .... .. .... .... 41
2.10 ỨNG DỤNG CỦA TÍCH PHÂN BỘI HAI ..... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... 42
2.11 BÀI TẬP VỀ ỨNG DỤNG CỦA TÍCH PHÂN BỘI HAI ..... .. .... .... .. .... .... .. .... .... .. .... .... . 47
3 TÍCH PHÂN BỘI BA .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... 49
3.1 BÀI TOÁN TÍNH KHỐI LƯỢNG ..... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... ... 49 lOMoAR cPSD| 59256994
3.2 TÍCH PHÂN BỘI BA TRÊN MIỀN HÌNH HỘP CHỮ NHẬT ... ..... .... .... .... .. .... .... .. .... .... .. 50
3.3 TÍCH PHÂN BỘI BA TRÊN MIỀN BẤT KỲ .... .... .... .... .. .... .... .. .... .... .. .... .... .. .... .... .. .... 51
3.4 CÁC TÍNH CHẤT CƠ BẢN ..... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... 52
3.5 CÁCH TÍNH TÍCH PHÂN BỘI BA THEO MIỀN E .... .... .... .... .. .... .... .. .... .... .. .... .... .. .... . 52
3.6 BÀI TẬP .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... 58
3.7 ỨNG DỤNG CỦA TÍCH PHÂN BỘI BA ... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. . 62
3.8 CÔNG THỨC ĐỔI BIẾN SỐ ... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. 68
3.9 BÀI TẬP ĐỔI BIẾN SANG TỌA ĐỘ TRỤ .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... 70
3.10 BÀI TẬP TÍNH TÍCH PHÂN BẰNG TỌA ĐỘ CẦU .... .. .... .... .. .... .... ..... .... .... .... .. .... .... 74
4 TÍCH PHÂN ĐƯỜNG.... .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .. 78
4.1 TÍCH PHÂN ĐƯỜNG LOẠI 1 .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... 78
4.2 GIỚI THIỆU BÀI TOÁN ... .... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... 78
4.3 PHƯƠNG PHÁP TÍNH ...... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... . 79
4.4 CÁC TÍNH CHẤT CƠ BẢN ..... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... 82
4.5 ỨNG DỤNG .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... 82
4.6 BÀI TẬP TÍCH PHÂN ĐƯỜNG LOẠI 1 ..... .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... ..... .. 84
4.7 TRƯỜNG VECTƠ ...... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... ..... ... 87
4.8 TÍCH PHÂN ĐƯỜNG LOẠI 2 .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... 90
4.9 CÁC TÍNH CHẤT CƠ BẢN ..... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... 92
4.10 ỨNG DỤNG .. .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ... 96
4.11 BÀI TẬP TÍCH PHÂN ĐƯỜNG LOẠI 2 ... .... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... 97
5 TÍCH PHÂN MẶT ... .... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .. 103
5.1 TÍCH PHÂN MẶT LOẠI 1 ... .... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. 103
5.2 GIỚI THIỆU BÀI TOÁN ... .... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. ... 103
5.3 CÁC TÍNH CHẤT CƠ BẢN ..... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .. 104
5.4 PHƯƠNG PHÁP TÍNH ...... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... 105
5.5 ỨNG DỤNG CỦA TÍCH PHÂN MẶT LOẠI 1 ..... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... 108
5.6 BÀI TẬP TÍCH PHÂN MẶT LOẠI 1 ..... .... .... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... 108
5.7 TÍCH PHÂN MẶT LOẠI 2 ... .... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. 109 lOMoAR cPSD| 59256994
5.8 ĐỊNH NGHĨA .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. .. 110
5.9 TÍNH LƯU LƯỢNG CỦA DÒNG CHẢY QUA MỘT MẶT CONG ĐỊNH HƯỚNG ..... .... .... 111
5.10 PHƯƠNG PHÁP TÍNH .... .... .. .... .... .. .... .... ..... .... .... .... .. .... .... .. .... .... .. .... .... ..... ... 113
5.11 BÀI TẬP VỀ ĐỊNH LÝ DIVERGENCE .. .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... .. 118
5.12 BÀI TẬP VỀ ĐỊNH LÝ STOKES ..... .... .... .... .. .... .... .. .... .... .. .... .... .. .... .... ..... .... .... .... 121 lOMoAR cPSD| 59256994 Chương1 HÌNH HỌC GIẢI TÍCH 1.1
MẶT TRỤ VÀ CÁC MẶT BẬC HAI Vết.
Vết của một mặt cong S : f(x, y, z) = 0 là phần giao của S lần lượt với các mặt x = k, y = k, z = k. Bằng
cách m vết của một mặt cong S khi k thay đổi ta có thể phác họa hình ảnh của nó trong không gian.
Ví dụ. Xét mặt sau đây z = y2 − x2. Mặt này là mặt bậc hai (ta sẽ giới thiệu sau). Bằng cách xác định vết của
nó như hình bên dưới, ta có thể phác họa được mặt này.
Vết của mặt là các đường hyperbolic và parabol nên mặt này còn có tên hyperbolic paraboloid. Mặt trụ.
Là tập hợp tất cả những đường thẳng song song với một đường cố định (gọi
là đường sinh) và tựa trên một đường cong phẳng.
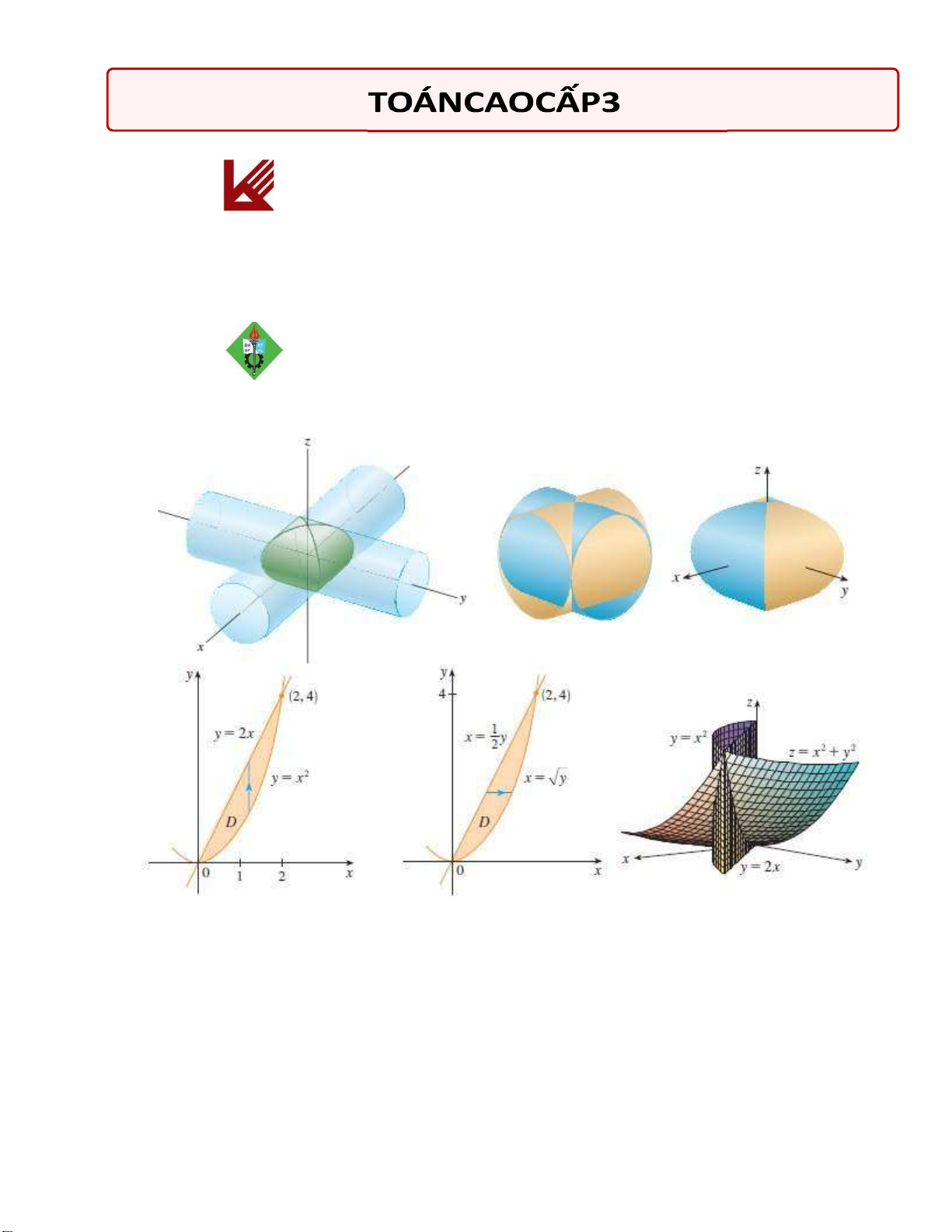
Ví dụ. Xét mặt trụ z = x2.
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3
Phương trình z = x2 không có biến y nghĩa là y tự do hay y = k. Vết trên Oxz
là (giao giữa mặt z = x2 và y = 0) một parabol khi k thay đổi parabol quét
theo phương Oy được mặt trụ.
Ví dụ. Ta xem thêm hai mặt trụ sau đây
• Vết của mặt x2 + y2 = 1 trên Oxy (giao giữa mặt x2 + y2 = 1 và z = 0) là đường tròn tâm O, bán kính 1.
Khi cho z = k thay đổi thì nghĩa là ta đang quét đường tròn theo phương Oz và được một mặt trụ.
• Vết của mặt y2 + z2 = 1 trên Oyz (giao giữa mặt y2 + z2 = 1 và x = 0) là đường tròn tâm O, bán kính 1,
kéo đường tròn theo phương Ox được mặt trụ. ( ) + + + + + + + + + = ··· + + =
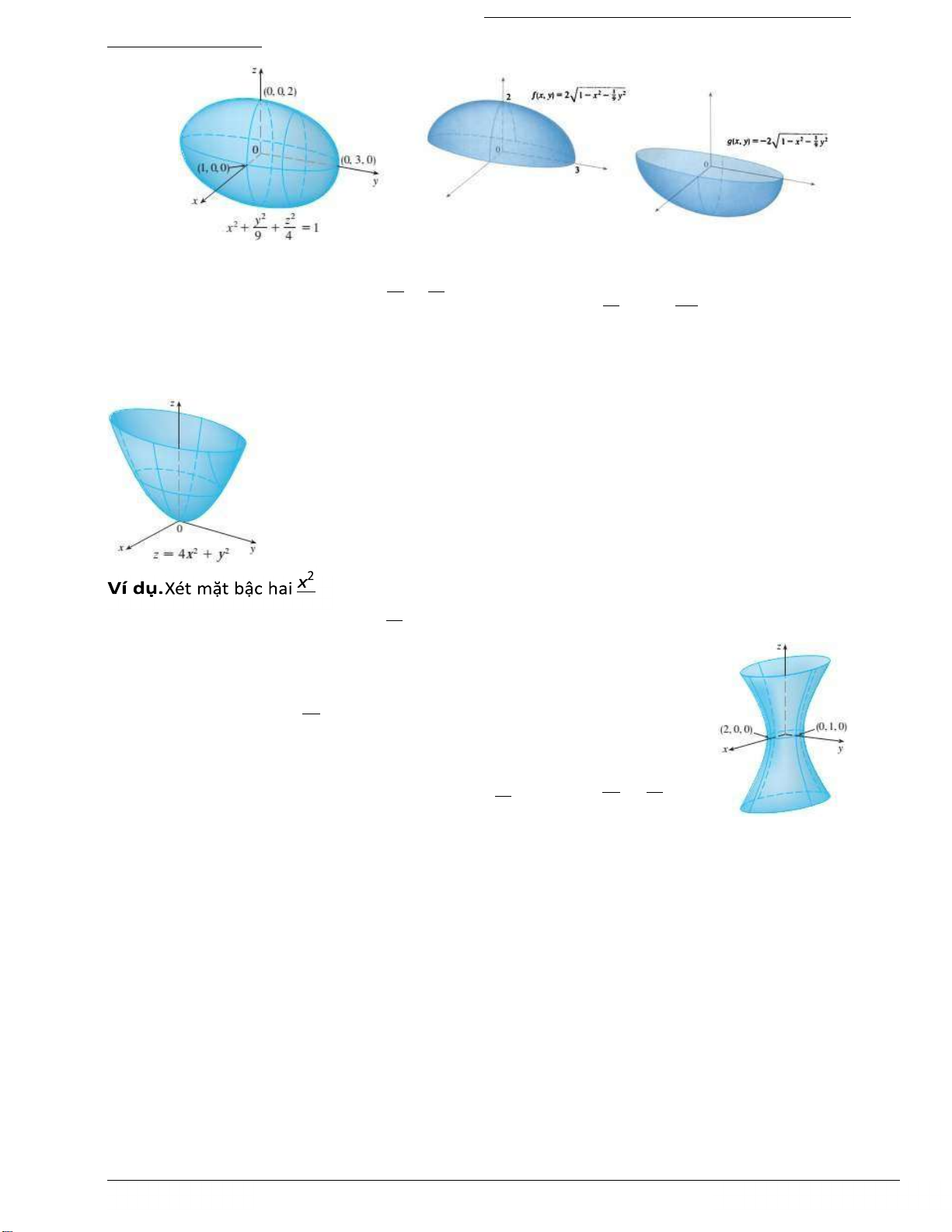
Cho z = 0 ta m vết trong mặt Oxy là el ip x2 + y = 1. Vết trong mặt phẳng z = k là các el ip 9 2 y2 k2 x + = 1 − , −2 ⩽ k ⩽ 2. 9 4
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3
Tương tự, vết dọc cũng là các el ip y2 + z2 = 1−l2 (−1 ⩽ l ⩽ 1), x2 + z2 = 1− m2 (−3 ⩽ m ⩽ 3) . 9 4 4 9
Vì các vết đều là el ip nên mặt có tên là mặt el ipsoid.
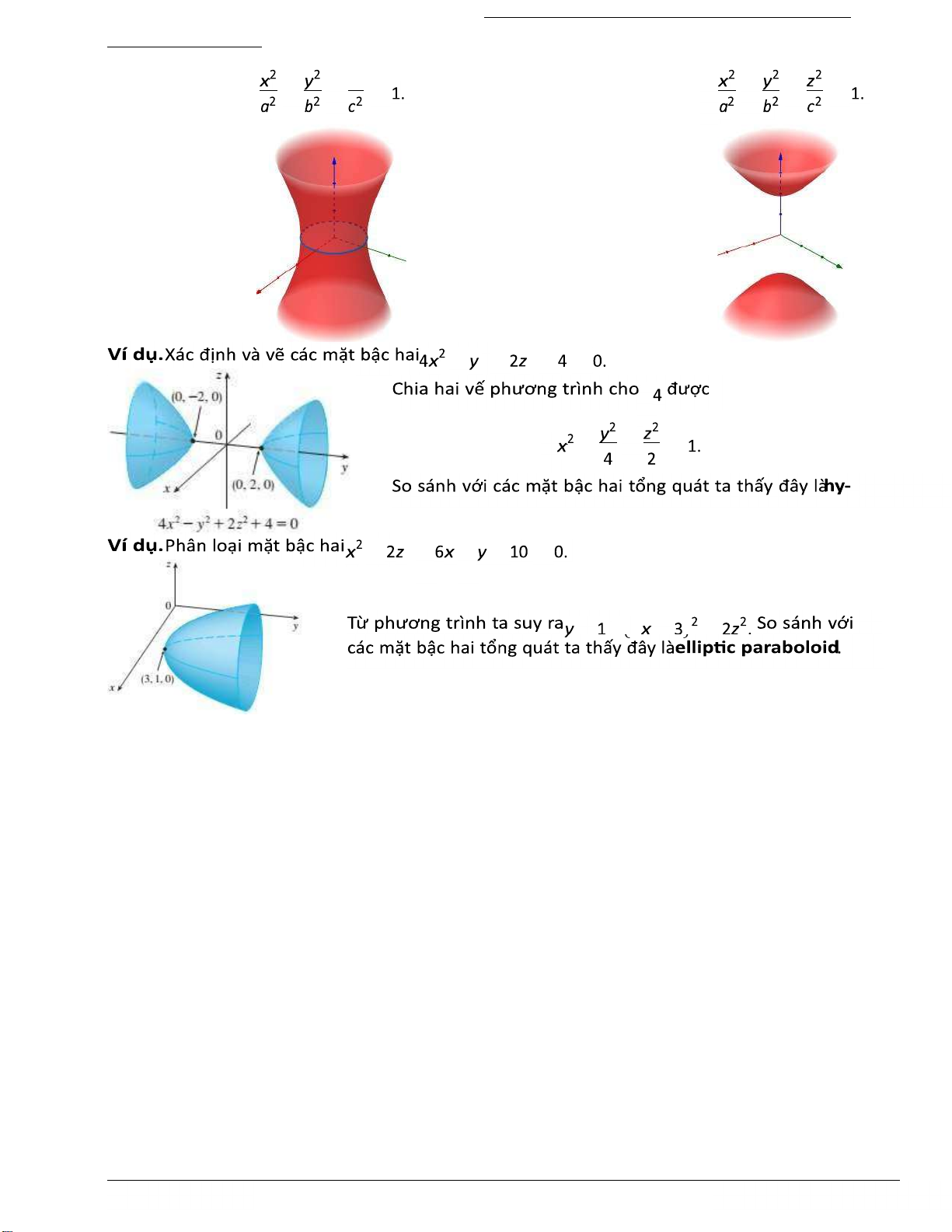
Ví dụ. Xét mặt bậc hai z = 4x2 + y2.
Vết trong mặt z = k là el ip 4x2 + y2 = k. Vết dọc cũng là các parabol z =
4l2 + y2, z = 4x2 + m2. Vết là các parabol và el ip mặt nay có tên ellip c paraboloid. 2 z2 + y − = 1. 4 4 2
Vết trong mặt Oxy là el ip x + y2 = 1. Vết trong mặt Oyz,Oxz là 4 y2 − z2 = 1, x2 − z2 = 1.
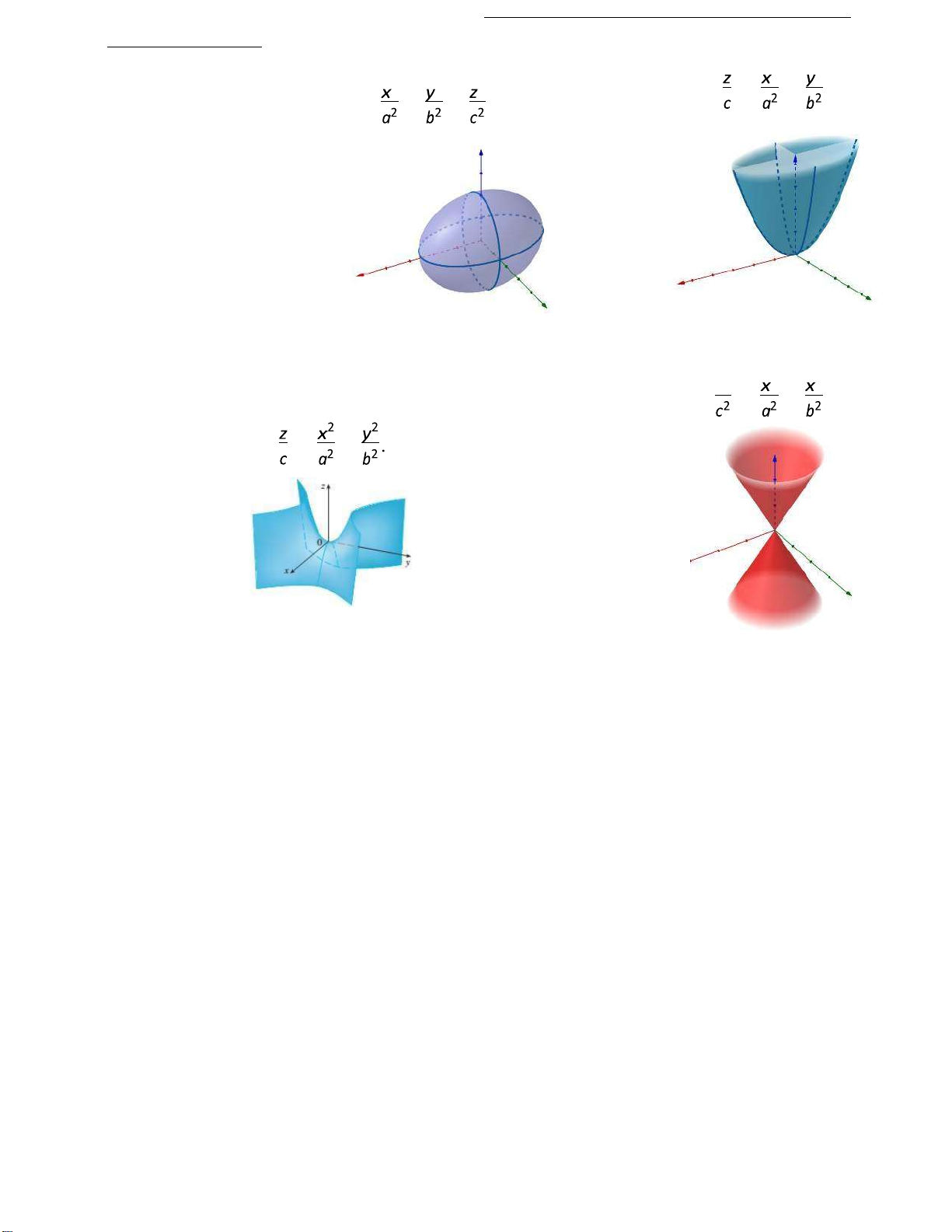
Đồ thị một số mặt bậc hai 4 4 4 El ip c paraboloid: Đây El ipsoid: là
mặt hyperboloid một tầng. Bùi Thanh Duy 3 duy.buithanh@uah.edu.vn
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3 2 2 2 2 2 + + = 1. = + . Nón: = − paraboloid: z = 2 Hyperbolic + 2 . Hyperboloid một tầng: Hyperboloid hai tầng:
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3 + − = − − + = − + + = − − + − = + − − + = − =( − ) + z 2 2 Bùi Thanh Duy 5 duy.buithanh@uah.edu.vn
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3 perboloid hai tầng. 2 1.2 BÀI TẬP 5. xy = 1. 10. y = z2 − x2. 11. 9x2 − y2 + z2 = 0.
Bài 1. Vẽ các mặt bậc hai sau 12. 25x2 + 4y2 + z2 = 100. 1. x2 + z2 = 1. 6. x = y2 + 4z2. 13. 4x2 + 9y2 + z = 0. 2. 4x2 + y2 = 4. 7. x2 = y2 + 4z2. 14. 4x2 − 16y2 + z2 = 16. 3. z = 1 − y2. 8. −x2 + 4y2 − z2 = 4. 15. x = y2 − z2.
4. y = z2. 9. 36x2 + y2 + 36z2 = 36.
Bài 2. Biến đổi phương trình về dạng chuẩn. Phân loại mặt bậc hai. 1. 2. 3.. 4.
5. 4x2 + y2 + 4z2 − 4y − 24z + 36 = 0.
6. 4y2 + z2 − x − 16y − 4z + 20 = 0.
7. x2 − y2 + z2 − 4x − 2y − 2z + 4 = 0.
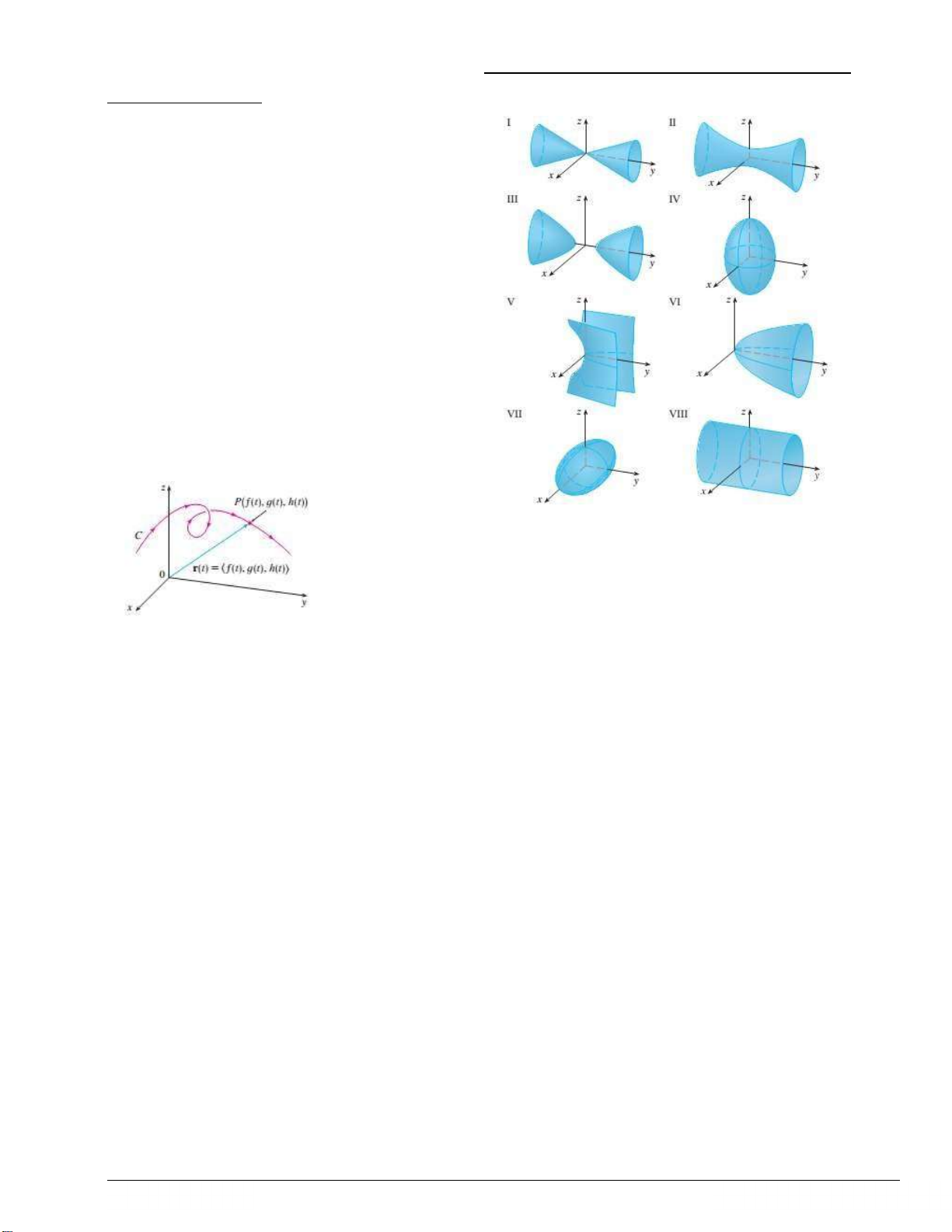
8. x2 − y2 + z2 − 2x + 2y + 4z + 2 = 0. Bài 3. Vẽ hình và xác định các mặt bậc hai sau
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3 1. x2 + 4y2 + 9z2 = 1. 2. x2 − y2 + z2 = 1.
3. y = 2x2 + z2. 4. x2 + 2z2 = 1. 5. 9x2 + 4y2 + z2 = 1. 6. y2 = x2 + 2z2. 7. y = x2 − z2. 8. −x2 + y2 − z2 = 1. 1.3 ĐƯỜNG CONG THAM SỐ Tập hợp các điểm có
tọa độ thỏa phương trình x = f(t), y = g(t), z = h(t), t ∈ I
với f, g, h là hàm liên tục được gọi là đường cong trong không gian. Bùi Thanh Duy 7 duy.buithanh@uah.edu.vn
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3
Ví dụ. Phương trình tham số sau đây là phương trình của một đường thẳng trong không gian x = 1 + t, y = 2 + 5t, z = −1 + 6t. = = = + = + = = = = − ∈ [ ] = ( ) = ( ) = ( ) Z =
q ( ′ ( )) +( ′ ( )) +( ′ ( )) = = = ( ,0, ) ( ,0, )
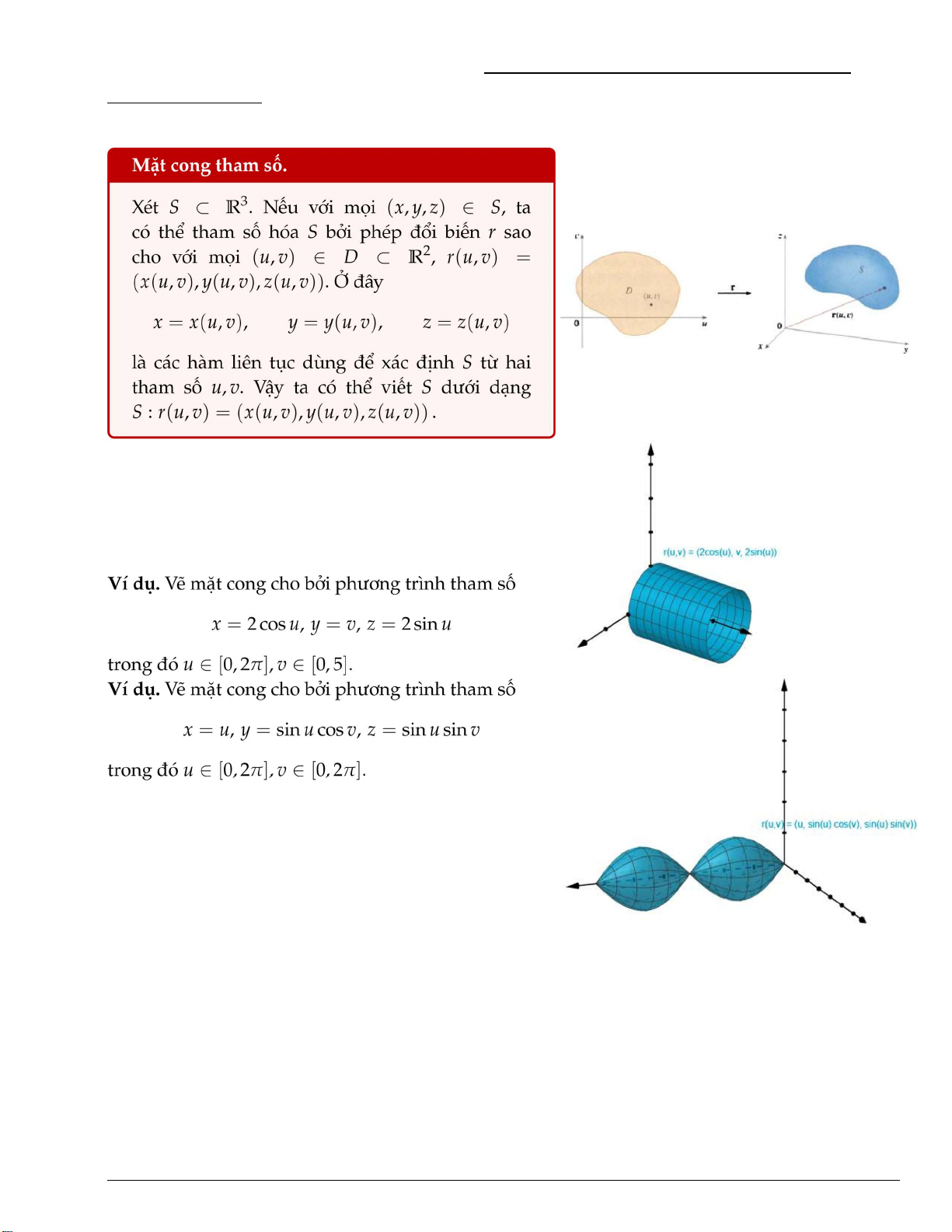
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3 1.4 MẶT CONG THAM SỐ 1.5 BÀI TẬP
Bài 4. Chọn phương trình tham số ứng với đồ thị của nó. Bùi Thanh Duy 9 duy.buithanh@uah.edu.vn
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3
1. x = t cos t, y = t, z = t sin t, t ⩾ 0.
2. x = cos t, y = sin t, z = 1/(1 + t2).
3. x = t, y = 1/(1 + t2), z = t2.
4. x = cos t, y = sin t, z = cos2t.
5. x = cos8t, y = sin8t, z = e0.8t, t ⩾ 0.
6. x = cos2 t, y = sin2 t, z = t.
Bài 5. Chọn phương trình tham số ứng với đồ thị của nó.
1. x = u cos v, y = u sin v, z = v.
2. x = u cos v, y = u sin v, z = sin u, −π ⩽ u ⩽π.
3. x = sin v, y = cos u sin2v, z = sin u sin2v.
4. x = (1 − u)(3 + cos v) cos4πu, y = (1 − u)(3 + cos v)
sin4πu, z = 3u + (1 − u) sin v.
5. x = cos3 u cos3 v, y = sin3 u cos3 v, z = sin3 v.
6. x = (−|u|) cos v, y = (−|u|) sin v, z = u .
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3 1.6 TỌA ĐỘ CỰC ( ) ( − ) ( + )
Ví dụ. Vẽ các điểm sau đây trong tọa độ cực
1. (1,5π/4) 3. (2, −2π/3) 2. (2,3π) 4. (−3,3π/4)
Liên hệ giữa tọa độ Descartes và tọa độ cực có công thức x = r cos θ, y = r sin θ với tan θ = y. x
Ví dụ. Đổi tọa độ điểm (2, π/3) sang tọa độ Descartes. (2, π√/3) → (1, √3 ) Ví dụ.
Đổi tọa độ điểm (1, −1) sang tọa độ cực. (1, −1) → ( 2 , −π/4) Bùi Thanh Duy 11 duy.buithanh@uah.edu.vn
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3
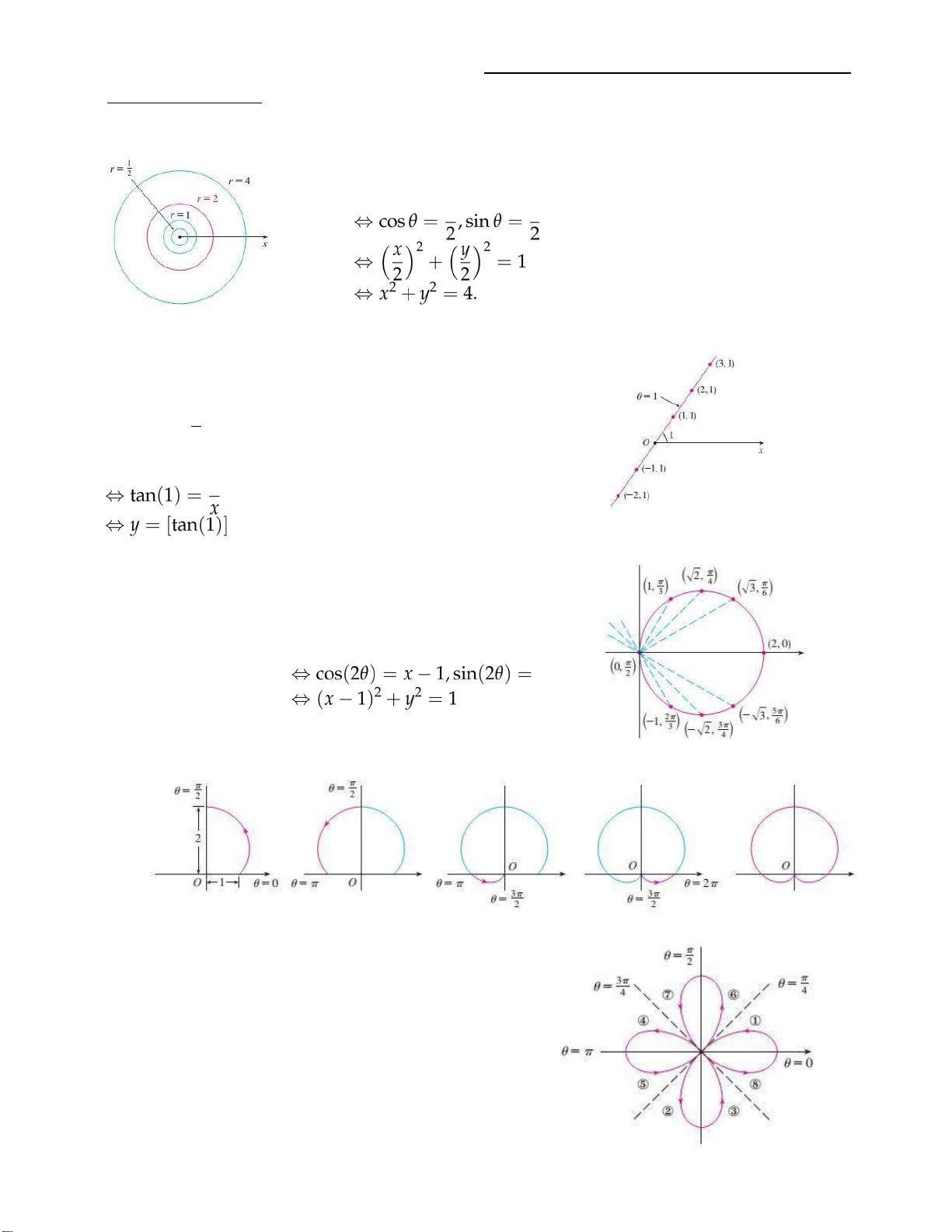
Ví dụ. Vẽ đồ thị đường r = 2 trong tọa cực. Viết phương trình trong tọa độ Descartes. Đổi sang tọa độ cực x = 2cos θ, y = 2sin θ x y Ví dụ.
Vẽ đồ thị đường θ = 1 trong tọa độ cực. Viết
phương trình trong tọa độ Descartes. Đổi sang tọa độ cực x = r cos θ, y = r sin θ y ⇔ tan θ = x y x
Ví dụ. Vẽ đồ thị đường r = 2cos θ trong tọa độ cực. Viết phương trình trong tọa độ Descartes. Đổi sang tọa độ cực
x = r cos θ, y = r sin θ ⇔ x = 2cos θ cos θ, y = 2cos θ sin θ ⇔ x = 1 + cos(2θ), y = sin(2θ) y
Ví dụ. Vẽ đồ thị đường r = 1 + sin θ trong cực.
Ta xem trên từng góc phần tư như hình bên dưới.
Ví dụ. Vẽ đồ thị đường r = 1 + cos2θ trong cực. Ta xem
từng góc phần tám như hình bên.
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3
Ta minh họa cho Ví dụ 1 bằng phần mềm GeoGebra
như sau. Ví dụ. Vẽ đồ thị các hàm số sau bằng Matlab hoặc GeoGebra. 1. r = sin(8θ/5). 2. 3.. 1.7 BÀI TẬP
Bài 6. Đổi từ tọa độ cực sang tọa độ Descartes. 1. (2, π/3). 3. (1, π/2). 5. (3, π/6). 7. (1, π). 2. (1, −3π/4). 4. (1,7π/4). 6. (1, −1). 8. (2, −2π/3).
Bài 7. Đổi từ tọa độ Descartes sang tọa độ cực. 1. (2, −2). 2. (−1, √3 ). 3. (3√3 ,3). 4. (1, −2).
Bài 8. Vẽ hình giới hạn bởi các miền sau đây trong tọa độ cực 1. r ⩾ 1
4. 1 ⩽ r ⩽ 3, π/6 <θ < 5π/6.
2. 0 ⩽ r < 2, π ⩽θ ⩽ 3π/2. 5. 2 < r < 3,5π/3 ⩽θ ⩽ 7π/3.
3. r ⩾ 0, π/4 ⩽θ ⩽ 3π/4. 6. r ⩾ 1, π ⩽θ ⩽ 2π.
Bài 9. Viết phương trình đường cong trong tọa độ Descartes vuông góc. Bùi Thanh Duy 13 duy.buithanh@uah.edu.vn
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3 1. r2 = 5. 2. r = 2cos θ. 3. r2 cos2θ = 1. 4. θ = π/3.
Bài 10. Viết phương trình đường cong trong tọa độ cực. 1. y = 2.
3. y = 1 + 3x. 5. x2 + y2 = 2x. 6. xy = 4. 2. y = x. 4. 4y2 = x. 1.8 TỌA ĐỘ TRỤ Hệ tọa độ trụ.
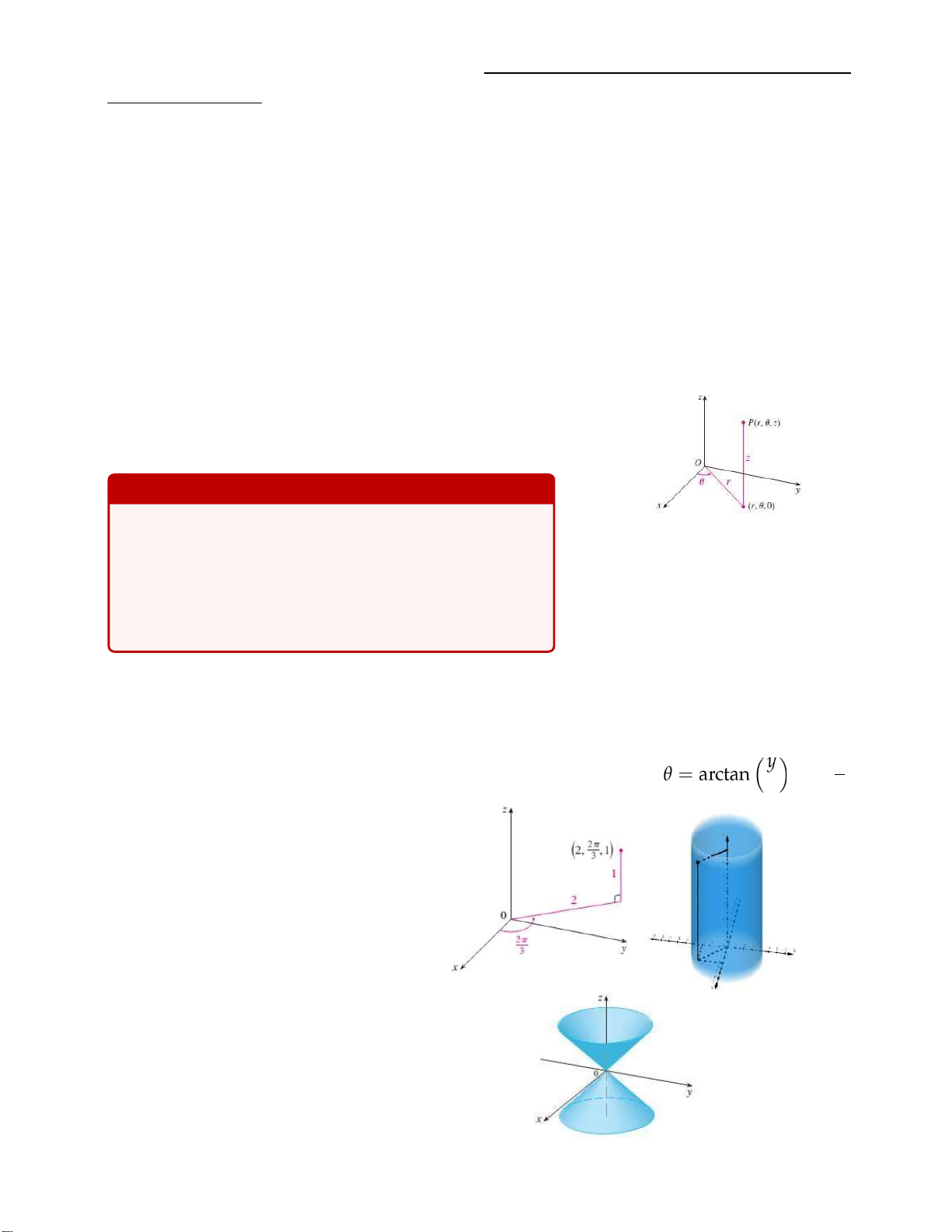
Trong không gian R3 một điểm P xác định duy
nhất bởi bộ ba (r, θ, z) trong đó (r, θ,0) là tọa độ Liên hệ giữa tọa độ trụ và Descartes là cực của hình
chiếu P lên mặt phẳng tọa độ Oxy x = r cos θ,
còn z là khoảng cách từ P tới Oxy. Bộ (r, θ, z) gọi
là tọa độ trụ của điểm P. y = r sin θ, z = z, r2 = x2 + y2, . x Ví dụ. 1. Tìm tọa độ điểm M(2,2π/3,1) trong hệ tọa độ
Descartes. 2. Tìm tọa độ điểm N(3,
−3,7) trong hệ tọa độ trụ. 3. Biểu diễn
mặt có phương trình z2 = r2 trong tọa
độ trụ sang tọa độ Descartes.
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3 1.9 BÀI TẬP
Bài 11. Đổi từ tọa độ trụ sang sang tọa độ Descartes. 3. (√2 ,3π/4,2). 4. (1,1,1).
1. (4, π/3, −2). 2. (2, −π/2,1). Bài 12. Đổi từ tọa
độ Descartes sang tọa độ trụ. 1. (−1,1,1). 2. (−2,2√3 ,3). 3. (2√3 ,2, −1). 4. (4, −3,2).
Bài 13. Mô tả các mặt đã cho trong tọa độ trụ. 1. θ = π/4. 4. 2r2 + z2 = 1. 2. r = 5.
5. 0 ⩽ r ⩽ 2, −π/2 ⩽θ ⩽π/2,0 ⩽ z ⩽ 1. 3. z = 4 − r2.
6. 0 ⩽θ ⩽π/2,r ⩽ z ≤ 2.
Bài 14. Viết phương trình các mặt sau trong tọa độ trụ. 1. z = x2 − y2. 3. 3x + 2y + z = 6.
2. −x2 − y2 + z2 = 1. 4. x2 − x + y2 + z2 = 1.
Bài 15. Vẽ đồ thị khối giới hạn bởi các el ip c paraboloid z = x2 + y2, z = 5 − x2 − y2. 1.10 TỌA ĐỘ CẦU Hệ tọa độ cầu.
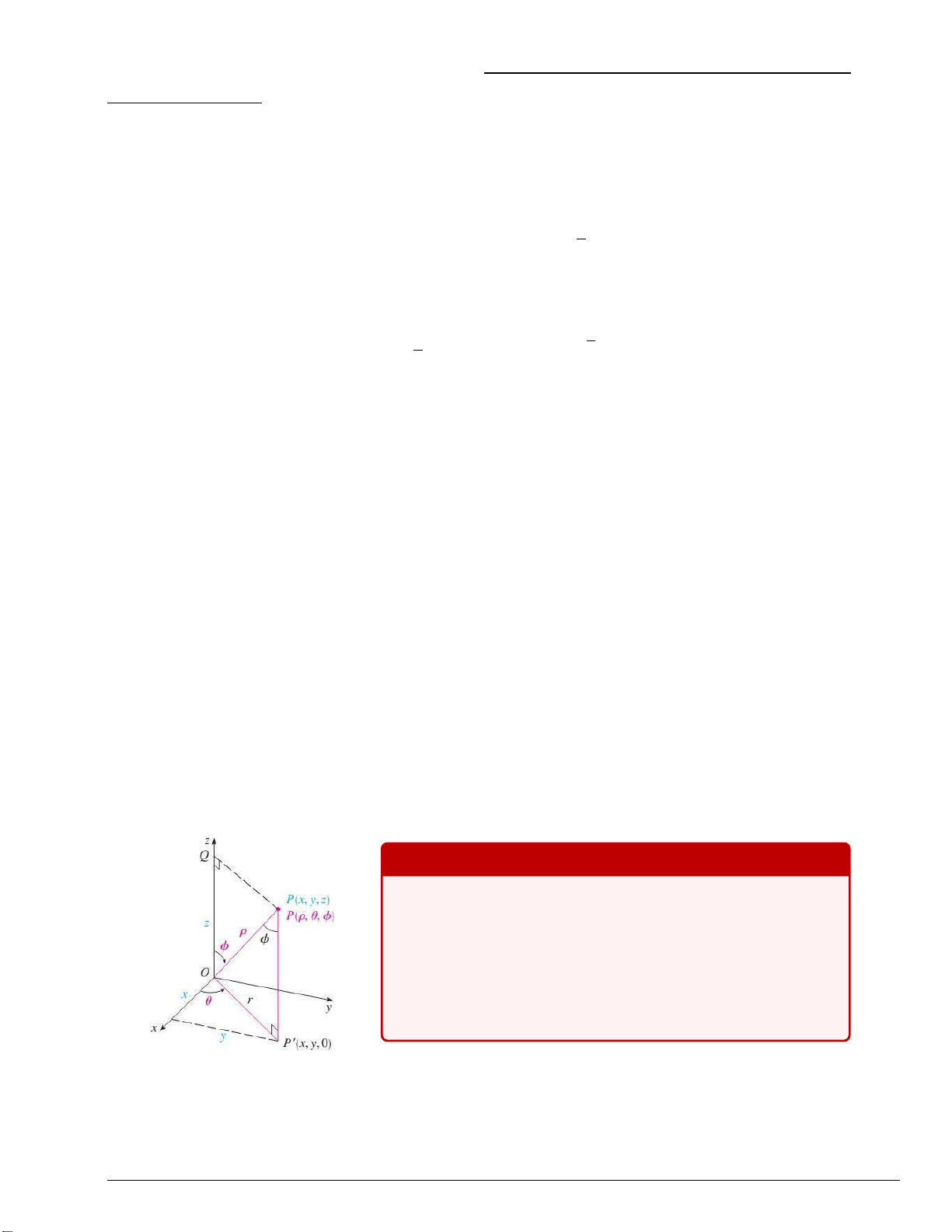
Trong không gian R3 một điểm P xác định duy nhất bởi bộ ba (ρ,
θ, ϕ) trong đó ρ là khoảng cách OP, ϕ là góc mở từ Oz đến OP,
θ là góc cực của hình chiếu P′. Chú ý rằng ρ⩾ 0, 0 ⩽θ < 2π, 0 ⩽ϕ⩽π.
Ta có công thức liên hệ giữa tọa độ cầu và tọa độ Descartes như sau x = ρ cos θ sin ϕ, y = ρ sin θ sin ϕ, z = ρ cos ϕ. Bùi Thanh Duy 15 duy.buithanh@uah.edu.vn
h ps://sites.google.com/uah.edu.vn/b-thanhduy551986 lOMoAR cPSD| 59256994 TOÁNCAOCẤP3
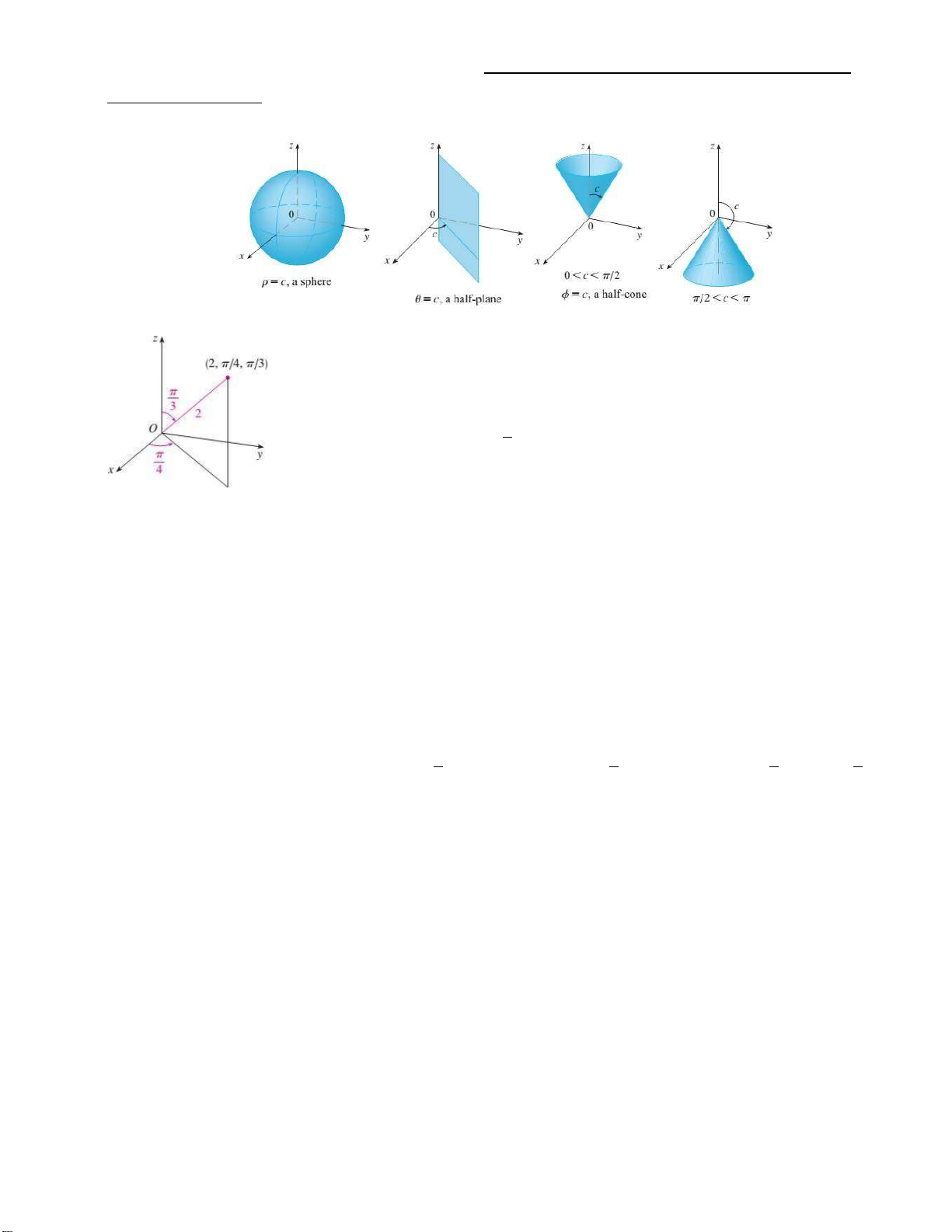
Ta có một số minh họa sau đây khi cố định các biến ρ, θ, ϕ bởi một hằng số c. Ví dụ. 1.
Biễu diễn điểm (2, π/4, π/3) trong tọa độ Descartes. 2.
Biễu diễn điểm (0,2√3 , −2) trong tọa độ cầu. 1.11 BÀI TẬP
Bài 16. Đổi từ tọa độ cầu sang tọa độ Descartes.
1. (6, π/3, π/6). 2. (2, π/2, π/2). Bài 17. Đổi từ tọa 3. (3, π/2,3π/4). 4. (4, −π/4, π/3).
độ Descartes sang tọa độ cầu. 1. (0, −2,0). 2. (−1,1, −√2 ). 3. (1,0, √3 ). 4. (√ 3, −1,2√3 ). Bài 18. Vẽ các mặt sau. 1. ϕ = π/3. 2. ρ = 3.
3. 2 ⩽ρ⩽ 4,0 ⩽ϕ⩽π/3,0 ⩽θ ⩽π.
4. 1 ⩽ρ⩽ 2,0 ⩽ϕ⩽π/2, π/2 ⩽θ ⩽ 3π/2. 5. ρ⩽ 1,3π/4 ⩽ϕ⩽π.
Bài 19. Viết phương trình sau trong tọa độ cầu. 1. z2 = x2 + y2. 3. x2 + z2 = 9.