
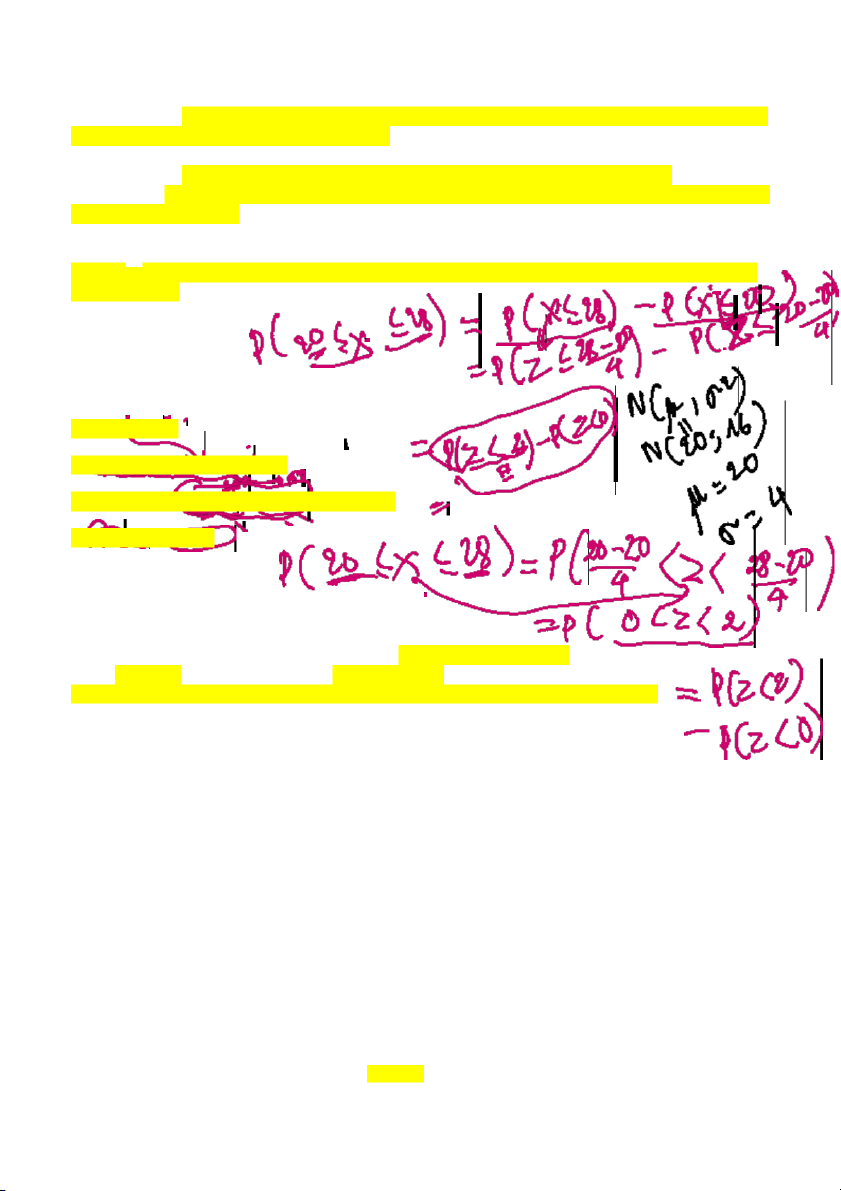


Preview text:
1. (0.250 Point)
Biến “Nhóm máu” là loại biến gì? *A.Biến định tính. B.Biến định lượng.
C. Biến định lượng rời rạc
D.Biến định lượng liên tục. 2. (0.250 Point)
Biến “ Nhóm máu ” là biến được đo bằng thang đo nào sau đây? *A. Thang đo danh nghĩa B. Thang đo thứ hạng C. Thang đo khoảng D. Thang đo tỷ lệ 3. (0.250 Point)
Trong giờ học môn Toán, để biết mức độ hiểu bài của sinh viên, cô giáo đã chọn ngẫu nhiên 5
bạn sinh viên trong danh sách 50 sinh viên của lớp để trả lời câu hỏi, phương pháp lấy mẫu nào được sử dụng: A. Mẫu hệ thống B. Mẫu chùm *C. Mẫu ngẫu nhiên D. Mẫu phân tầng 4. (0.250 Point)
Đối với dữ liệu biến định tính ta nên tổ chức vào bảng phân bố tần số nào?
A. Phân bố tần số không ghép lớp
B. Phân bố tần số ghép lớp
*C. Phân bố tần số phân loại D. Cả A và B 5. (0.250 Point)
Dữ liệu về điểm bài kiểm tra giữa kì môn Xác suất thống kê thang điểm 20 của một lớp như sau:
9;7;8;9;13;15;20;10;7;3;10;16;15;20;15;18;15;17;13 ; 15. Mode của dữ liệu (là giá trị có tần số
lớn nhất, xuất hiện nhiều lần nhất) là ? A. 20 B. 10 *C. 15 D. 7 6. (0.250 Point)
Dữ liệu về điểm bài kiểm tra giữa kì môn Xác suất thống kê thang điểm 20 của một lớp như sau:
9;7;8;9;13;15;20;10;7;3;10;16;15;20;15;18;15;17;13 ; 15. Trung bình mẫu và độ lệch chuẩn mẫu
bằng bao nhiêu? Bấm máy tính
*A. Trung bình: 12.75 và độ lệch chuẩn: 4.67
B. Trung bình: 12.57 và độ lệch chuẩn: 4.76
C. Trung bình: 4.76 và độ lệch chuẩn: 12.57
D. Trung bình: 4.67 và độ lệch chuẩn: 12.75 7. (0.250 Point)
Xác suất xảy ra môt sự kiện là 0.3. Xác suất để sự kiện đó không xảy ra là? A. 0 B. 0.3 *C. 0.7 D. 1 8. (0.250 Point)
Một thiết bị có hai bộ phận hoạt động độc lập. Biết xác suất để bộ phận 1 bị hỏng là 0,5 và xác
suất có ít nhất 1 bộ phận bị hỏng là 0,7. Xác suất để bộ phận 2 bị hỏng là: P(A+B)= P(A)+P(B)-P (A.B) 0.7= 0.5+ P(B)- 0.5 P(B) 0.2=0.5 P(B) P(B)=0.2: 0.5=0.4 A. 0,2 B. 0,3 *C. 0,4 D. 0,5 9. (0.250 Point)
Cho mẫu dữ liệu sau: 209; 223; 211; 227; 213; 240; 240; 211; 229; 212. Tìm trung vị (nhớ phải
sắp xếp trước rồi tìm giá trị ở giữa)của mẫu dữ liệu trên?
209,211,211,212,213,223,227,229,240,240 A. 219 B. 217 C. 220 *D. 218 10. (0.250 Point)
Cho biến ngẫu nhiên X có phương sai là 4. Giá trị độ lệch chuẩn là:
Độ lệch chuẩn là căn bậc 2 của phương sai A. 4 B. 16 *C. 2 D. 0 11. (0.250 Point)
Cho A và B là 2 biến cố xung khắc với P(A)= 0.2 ; P(B)= 0.3. P(A.B) bằng :
2 biến cố xung khắc là không đồng thời xảy ra,P(A.B) là xác suất để A và B cùng xảy ra bằng 0 A. 0,5 B. 0,06 C. 0,6 *D. 0 12. (0.250 Point)
Khảo sát 200 hộ dân ở thành phố A thì thấy có 100 hộ sử dụng dịch vụ truyền hình cáp FPT. Tỉ
lệ mẫu hộ gia đình sử dụng dịch vụ truyền hình cáp của FPT là bao nhiêu? A. 0.2 *B. 0.5 C. 0.3 D. 0.7 13. (0.250 Point)
Cho biến ngẫu nhiên Z có phân phối chuẩn tắc, khi đó giá trị trung bình của Z là:
phân phối chuẩn tắc N(0;1), Có trung bình =0 và độ lệch chuẩn =1 A. 100 B. 1 C. 10 *D. 0 14. (0.250 Point)
Cho A và B là hai biến cố với P(A)= 0.4 ; P(B)= 0.5 ; P(A.B)=0.2. P(B|A) bằng :
P(B|A)= P(A.B) : P(A)= 0.2:0.4 =0.5 A. 0.2 B. 0.4 *C. 0.5 D. 0.67 15. (0.250 Point)
Giá trị Zα/2 với độ tin cậy 99% là. 99% Zα/2=2.58 98% 2.33 96% 2.05 95% 1.96 94% 1.88 90% 1.65 A. 1.96 B. 1.65 *C. 2.58 D. 2.33 16. (0.250 Point)
Có 200 lỗi đánh máy được phân bố đều trong một bản thảo 500 trang. Gọi X là biến ngẫu nhiên
“số lỗi đánh máy trong một trang”. X tuân theo phân phối gì? A. Siêu bội
: trong N phần tử có a phần tử có tính chất A, lấy ngẫu nhiên ra n phần tử trong N, X là
số phần tử có tính chất A trong n phần tử lấy ra B. Chuẩn *C. Poisson
: số lần biến cố A xảy ra trong một khoảng thời gian, một miền, một vùng
D. Nhị thức : dãy phép thử nhị thức, n lần thử độc lập, mỗi lần thử chỉ nhận đươc 2 kết quả, P(A) trong các lần thử như nhau = p 17. (0.250 Point)
Cho X tuân theo phân phối nhị thức B(100; 0.8). Chọn câu đúng trong các câu sau:
B(n, p) n: số lần thử, p= P(A), kỳ vọng hay trung bình E(X)=n.p; phương sai (V arX)= n.p.q. trong đó q=1-p *A. E(X) = 80 B. E(X) = 0.8 C. E(X) = 100 D. E(X) = 16 18. (0.250 Point)
Cho X tuân theo phân phối chuẩn N(20;16). Tính P(20 ≤ X ≤ 28) = ? P(20 ≤ X ≤ 28)
= P ((20-20) :4 ≤ z ≤ (28-20):4)
=P(0 ≤ z ≤ 2) = P( z ≤ 2) - P(z ≤ 0) tra bảng E =0.9772-0.5 =0.4772 A. 0.8234 B. 0.7223 C. 0.5324 *D. 0.4772 19. (0.250 Point)
Ở một cửa hàng người ta theo dõi thấy trong 5 phút có 15 lượt khách vào cửa hàng. Xác suất để
trong một phút bất kì cửa hàng này có 4 lượt khách vào là bao nhiêu?
Phân phối Poisson với lambda (số lần A xuất hiện trung bình)= 15:5=3, P(X=4)=? *A. 0,168 B. 0,832 C. 0,258 D. 0,742 20. (0.250 Point)
Một trang trại có 200 con gà mái, xác suất để mỗi con gà đẻ trứng là 0.6. Gọi X là số gà đẻ trứng
trong 200 con gà đó. Hãy cho biết X tuân theo quy luật phân phối nào? A. Siêu bội B. Poisson *C. Nhị thức D. Chuẩn 21. (0.250 Point)
Một hộp có 20 viên bi, trong đó có 12 viên bi màu đỏ. Rút ngẫu nhiên 8 bi. Gọi X là số bi màu đỏ lấy được
trong 8 bi rút ra. Hãy cho biết X tuân theo quy luật phân phối nào? *A. Siêu bội B. Poisson C. Nhị thức D. Chuẩn 22. (0.250 Point)
Cho đại lượng X tuân theo phân phối chuẩn N (3; 12 ) . Khi đó Var(X), Mode(X) có giá trị:
A. Var(X) = 3, Mode(X) = 1 *B. Var(X) = 1, Mode(X) = 3 C. Var(X) = Mode(X) = 3 D. Var(X) = Mode(X) = 1 23. (0.250 Point)
Cho đại lượng ngẫu nhiên rời rạc X có xác suất: P(X=0) = 0.25; P(X=1)= 0.5; P (X=2)= 0.25
Khi đó P(0 < X ≤ 2) = ? A. 0.25 *B. 0.75 C. 0.5 D. 1 24. (0.250 Point)
Cho P(A) = 0.2; P(B) = 0.7; P(A+B) = 0.9. Vậy:
A. A và B là hai biến cố tùy ý
B. A và B là hai biến cố độc lập
C. A và B là hai biến cố độc lập toàn phần
*D. A và B là hai biến cố xung khắc. 25. (0.250 Point)
Trong một vùng dân cư, tỷ lệ mắc bệnh tim là 9%, mắc bệnh huyết áp là 12%, và mắc cả 2 loại
bệnh trên là 7%. Chọn ngẫu nhiên 1 người trong vùng đó. Xác suất để người đó mắc bệnh tim
hoặc bệnh huyết áp là:
P(T+H)= P(T)+P(H)- P(T.H)=0.09+0.12- 0.07=0.14 A. 0,21 B. 0,28 C. 0,07 *D. 0,14 26. (0.250 Point)
Cho A và B là hai biến cố với P(A)= 0.7 ; P(B)= 0.4 ; P(A.B)= 0.2. P(A+B) bằng : *A. 0,9 B. 0,8 C. 0,7 D. 0,8 27. (0.250 Point)
Cho A và B là hai biến cố với P(A)= 0.7 ; P(B)= 0.4 ; P(A.B)=0.2. P (A|B) bằng : A. 0.2 B. 0.25 C. 0.3 *D. 0.5 28. (0.250 Point)
Trong một hộp kín có 13 viên bi màu đỏ và 7 viên bi màu xanh. Lấy ngẫu nhiên 2 viên bi từ
trong hộp đó. Xác suất để được 2 bi khác màu là: (13C1.7C1): 20C2=91/190 A. 61/190 B. 71/190 C. 81/190 *D. 91/190 29.(0.250 Point)
Một máy bay có 2 động cơ hoạt động độc lập. Xác suất để trong 1 chuyến bay 2 động cơ đó bị
hỏng lần lượt là 0,1 và 0,2. Xác suất để trong 1 chuyến bay cả 2 động cơ đều bị hỏng là:
P(A.B) = P(A). P(B)= 0,1 x 0,2= 0.02 A. 0.3 *B. 0.02 C. 0.002 D. 0.1 30. (0.250 Point)
Cho dãy số liệu sau: 2; 3; 5; 9 ; 12. Trung vị (sắp xếp trước) của dãy số liệu là: *A. 5 B. 9 C. 7 D. 8 31. (0.250 Point)
Hãy nêu bốn phương pháp lấy mẫu được dùng phổ biến trong thống kê? Mẫu hệ thống Mẫu chùm Mẫu ngẫu nhiên Mẫu phân tầng 32. (0.250 Point)
Để phân biệt, phân loại các giá trị trong tập dữ liệu biến định tính ta dùng thang đo nào? Thang đo danh nghĩa 33. (0.250 Point)
Trong một phòng học có 10 bóng đèn. Xác suất để mỗi bóng bị hỏng là 0,25. Tính xác suất để có 5 bóng hỏng. (0.058)
Phân phối nhị thức n=10, p=0,25 P(X=5)= 10C5. (0,25)^5. (0.75)^5=0.058 34. (0.250 Point)
Số lượt xe đi qua trạm thu phí trong 1 giờ là biến ngẫu nhiên tuân theo luật phân phối Poisson , biết số
lượt xe đi qua trạm thu phí trung bình trong một giờ là 30. Tính xác suất để trong một giờ có 20 xe đi qua trạm thu phí? (0.013)
Phân phối poisson P(X=20)= (e^-30* 30^20):20!=0.013 35. (0.250 Point)
Trọng lượng của một gói mỳ ăn liền (gram) là biến ngẫu nhiên tuân theo phân phối chuẩn N(80;16).
Tính xác suất để mua một gói mỳ ăn liền có trọng lượng từ 75 gram đến 90 gram. P(75 ( 0,8882) 36. (0.250 Point)
Cho Z là biến ngẫu nhiên có phân phối chuẩn tắc. Hãy tìm xác suất P(Z > 1.5)? (0.0668) tra bảng E 37. (0.250 Point)
Biến cố đối của biến cố “ Trả lời đúng tất cả câu hỏi” là gì? ( biến cố “Trả lời sai ít nhất một câu” ) 38. (0.250 Point)
Muốn ước lượng số chim trong rừng, người ta bắt 2000 con chim trong rừng đeo khuyên rồi thả lại
trong rừng. Sau đó bắt lại ngẫu nhiên 400 con chim và thấy có 53 con có đeo khuyên. Hãy ước lượng
số chim trong rừng với độ tin cậy là 0,97. (11814; 20896) 39. (0.25 Points)
Khảo sát điểm thi giữa kì của 60 sinh viên lớp STA 151 BJ, ta thu được số liệu như sau: Điểm số [3 ; 4) [4; 5) [5; 6) [6; 7) [7; 8) [8; 9) Số sinh viên 3 8 14 20 11 4
Tính cỡ mẫu, trung bình mẫu và độ lệch chuẩn của mẫu trên. Cỡ mẫu n=60 (Trung bình mẫu là: 6,167
Độ lệch chuẩn mẫu là s= 1,26) 40. (0.25 Points)
Khảo sát điểm thi giữa kì của 60 sinh viên lớp STA 151 BJ ta thu được số liệu như sau: Điểm số [3 ; 4) [4; 5) [5; 6) [6; 7) [7; 8) [8; 9) Số sinh viên 3 8 14 20 11 4 Với độ
tin cậy 95%, hãy ước lượng tỉ lệ sinh viên lớp STA 151 BJ có điểm thi giữa kì thấp hơn 6 điểm. (0.2922 ;0,5417)
Tỷ lệ mẫu p^ = (3+8+14): 60 = q^ =1-p^=
ráp công thức ước lượng cho tỷ lệ




