Toán thực tế 3 đường Conic - Toán ứng dụng | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh

lOMoARcPSD|44744371 lOMoARcPSD|44744371
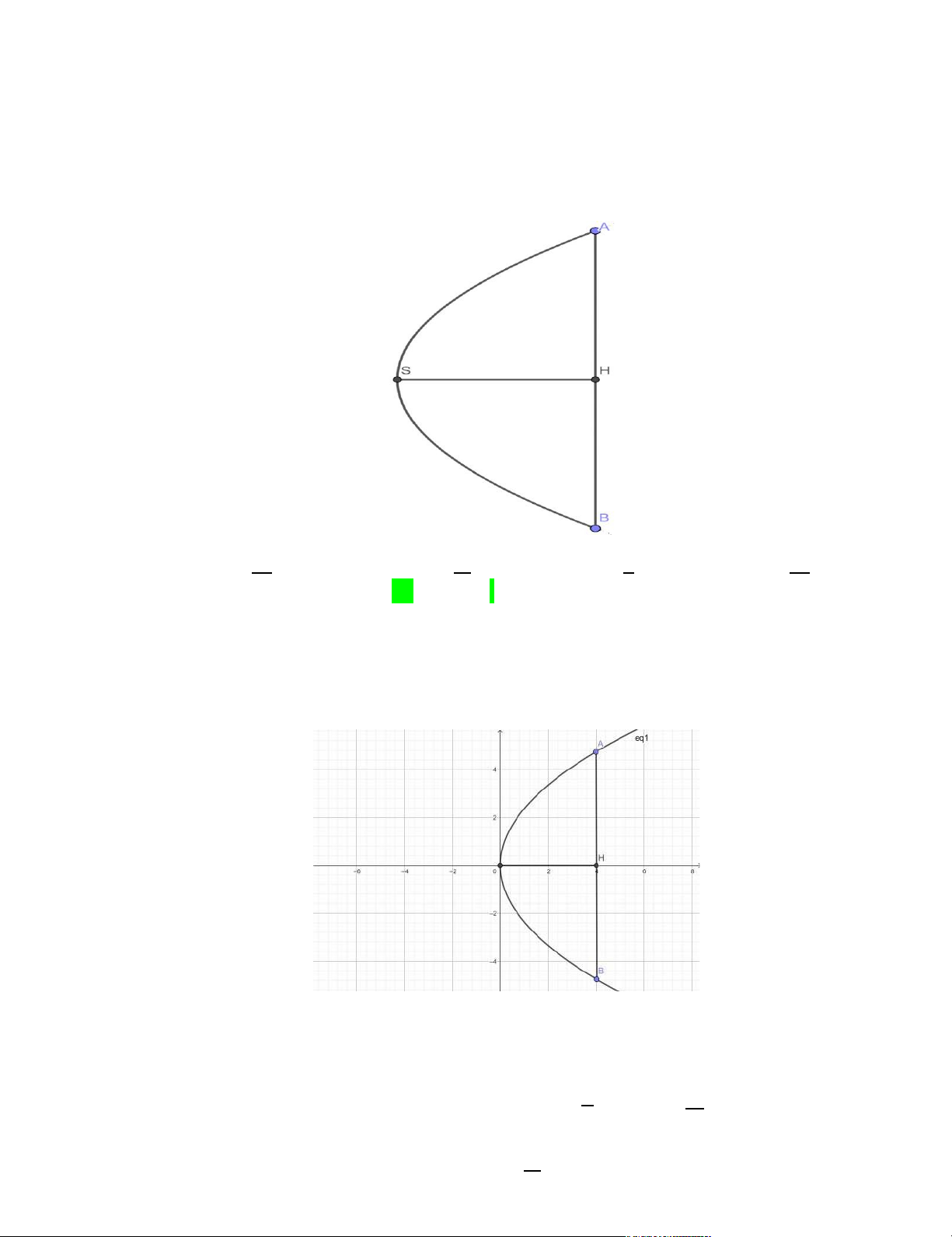
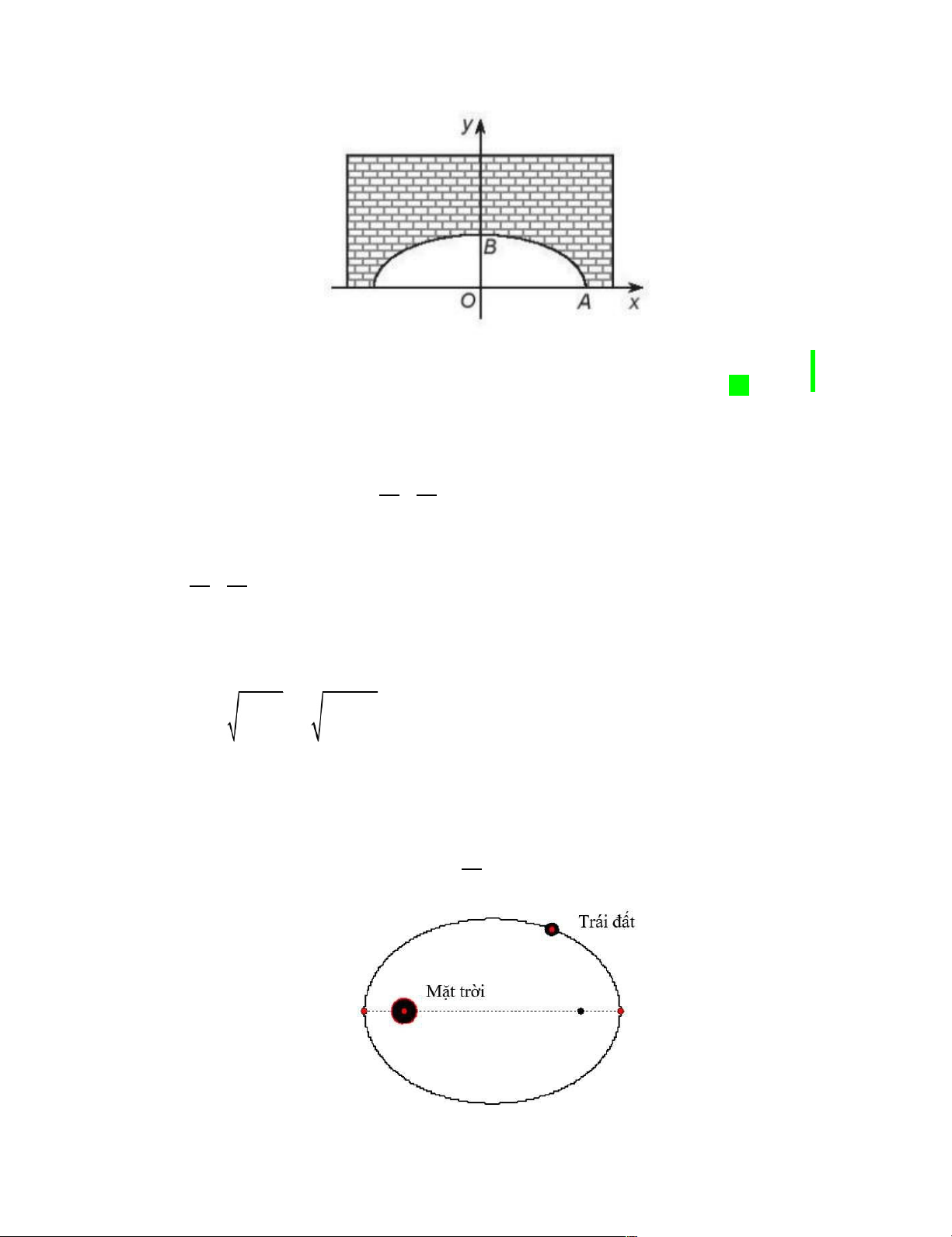
Câu 41. [ Mức độ 3] Môt ̣chiếc cốc nằm ngang, có măt ̣cắt ngang là hình parabol (hình vẽ). Hình
parabol có chiều rông ̣ giữa hai mép cốc là AB 9cm và chiều sâu h 4cm ( h bằng khoảng
cách từ S đến AB , S là điểm chính giữa đáy cốc. Viết phương trình chính tắc parabol đó. y 81 81 9 81 2 x y 2 x y 2 x y 2 x A. 32 . B. 16 . C. 4 . D. 64 . Lời giải
FB tác giả: Xuanhieptienthinh
FB phản biện: Nguyễn Nga
Gắn Parabol vào hê tọa đô ̣như hình vẽ. Gốc tọa độ trùng với điểm S
Gọi phương trình chính tắc của parabol P là y 22 px p 0 . 9 4; 81 A 2 p 4 p 81
Từ giả thiết ta suy ra parabol P đi qua điểm 2nên ta có 4 32 . 81 x
Vâỵtrình chính tắc của parabol P là y 2 16 . lOMoARcPSD|44744371
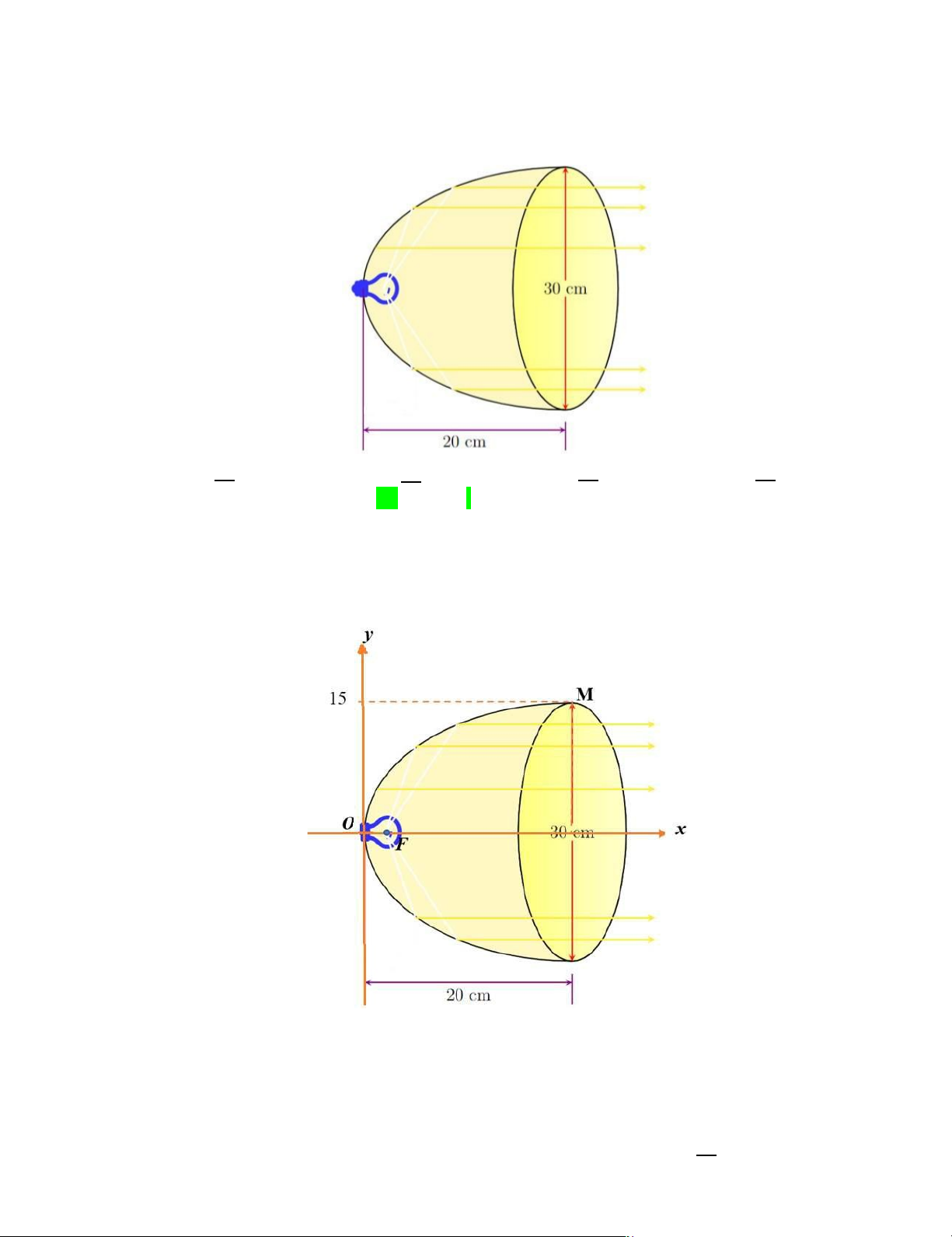
Câu 48. [ Mức độ 4] Cho một cái đèn với chụp bóng đèn có mặt cắt qua trục là parabol với kích thước
được thể hiện trên hình vẽ, giả sử xem dây tóc bóng đèn là một điểm và được đặt ở vị trí
tiêu điểm của parabol. Tính khoảng cách từ dây tóc bóng đèn tới đỉnh của chụp bóng đèn. 45 cm 45 cm 45 cm 45 cm A. 8 16 C. 4 D. 2 . B. . . . Lời giải
FB tác giả: Nguyễn Văn Toàn
FB phản biện: Nga Nguyễn
Chọn hệ trục tọa độ Oxy như hình vẽ.
Gọi P là parabol, với P là mặt cắt qua trục của chụp bóng đèn và P thuộc mặt phẳng tọa
độ Oxy . Phương trình chính tắc của (P): y 2 2 px , p 0. M 20;15 P 152 2 p.20 p 45
Theo đề bài, ta suy ra điểm 8 . lOMoARcPSD|44744371 p 45 OF cm
Khoảng cách từ dây tóc bóng đèn tới đỉnh của chụp bóng đèn là 2 16 .
Câu 49. [ Mức độ 4] Vệ tinh nhân tạo đầu tiên được Liên Xô (cũ) phóng từ Trái Đất năm 1957. Quỹ
đạo của vệ tinh đó là một đường elip nhận tâm Trái Đất là một tiêu điểm có phương trình x 2 y2
1, a 0, b 0,c 2a 2 b2 2 quỹ đạo là a b 2
. Người ta đo được vệ tinh cách bề mặt Trái c
Đất gần nhất là 583 dặm và xa nhất là 1342 dặm (1 dặm xấp xỉ 1,609 km). Tìm tỷ số a ,
biết bán kính của Trái Đất xấp xỉ 4000 dặm. c 0,67 c 0,76 c 0,067 c 0,076 A. a . B. a . C. a . D. a . Lời giải
FB tác giả: Phan Văn Trí
FB phản biện: Nguyễn Văn Toàn
Chọn hệ trục toạ độ sao cho tâm Trái Đất trùng với tiêu điểm F1 của elip.
x 2 y2 1, a 0, b 0 2 2
Khi đó elip có phương trình là: a b 583
Theo đề bài, ta có: vệ tinh cách bề mặt Trái Đất gần nhất là
dặm và xa nhất là 1342 dặm, mà
bán kính của Trái Đất xấp xỉ 4000 dặm nên vệ tinh cách tâm Trái Đất gần nhất là 4583dặm
và xa nhất là 5342 dặm.
Giả sử vệ tinh được biểu thị là điểm M ( x; y ) . MF ac x
Khi đó khoảng cách từ vệ tinh đến tâm Trái Đất là: 1 a
Và ta có a c MF1 a c
( Tính chất bán kính qua tiêu điểm)
Vậy khoảng cách nhỏ nhất và lớn nhất từ vệ tinh đến tâm Trái Đất lần lượt là a c và a c a c 4583 a 4962,5 a c 5342 c 379,5 c 0,076 Suy ra a lOMoARcPSD|44744371
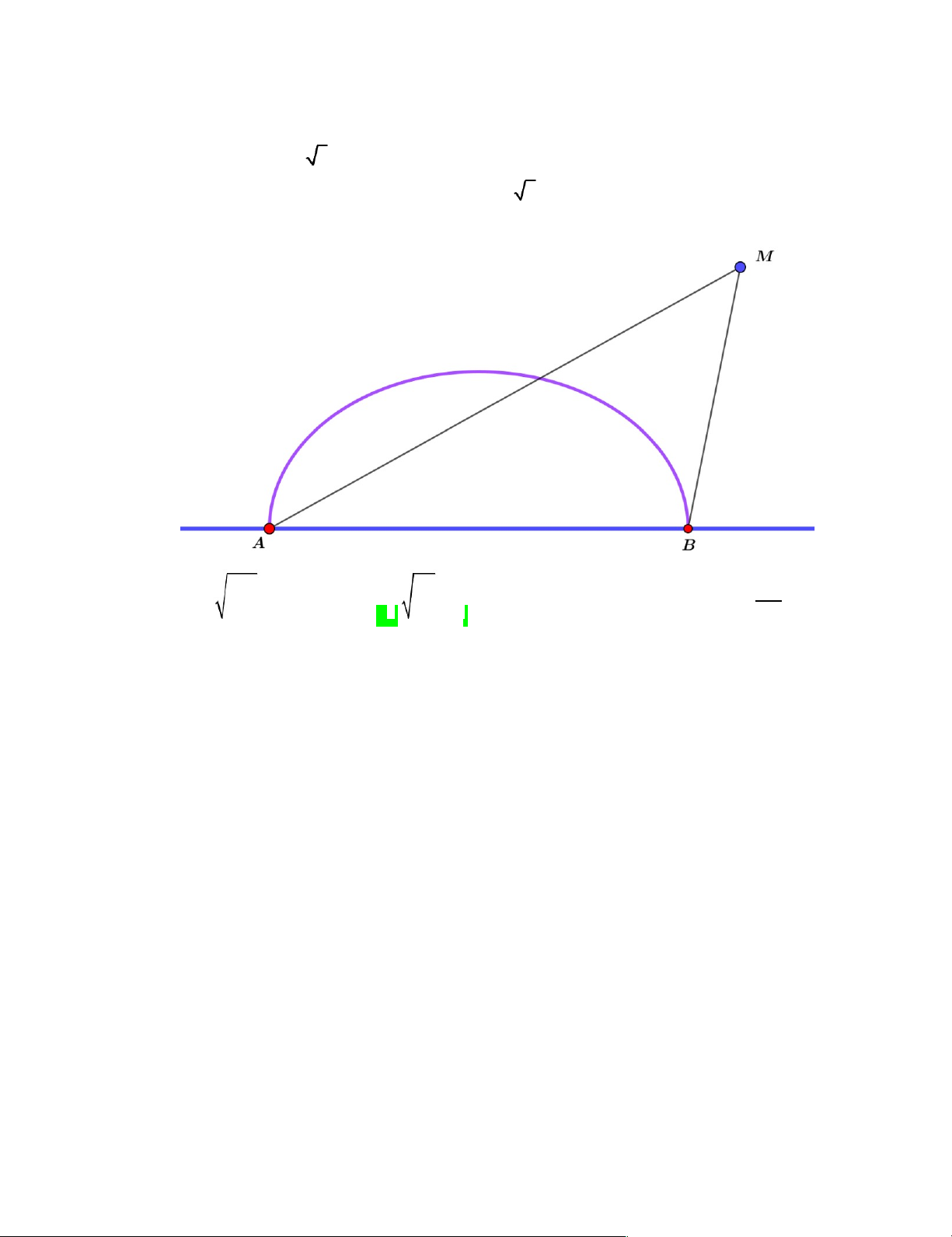
Câu 50. [ Mức độ 4] Trên bờ biển có hai trạm thu phát tín hiệu A và B cách nhau 6 km , người ta xây
một cảng biển cho tàu hàng neo đậu là một nửa hình elip nhận AB làm trục lớn và có
tiêu cự bằng 2 5 km . Một con tàu hàng M nhận tín hiệu đi vào cảng biển sao cho hiệu
khoảng cách từ nó đến A và B luôn là 2 6 km . Khi neo đậu tại cảng thì khoảng cách từ con
tàu đến bờ biển là bao nhiêu? 126 12 12 126 A. 17 km . B . 17 km . C. 17 km . D. 17 km . Lời giải
FB tác giả: Lê Thanh Long lOMoARcPSD|44744371
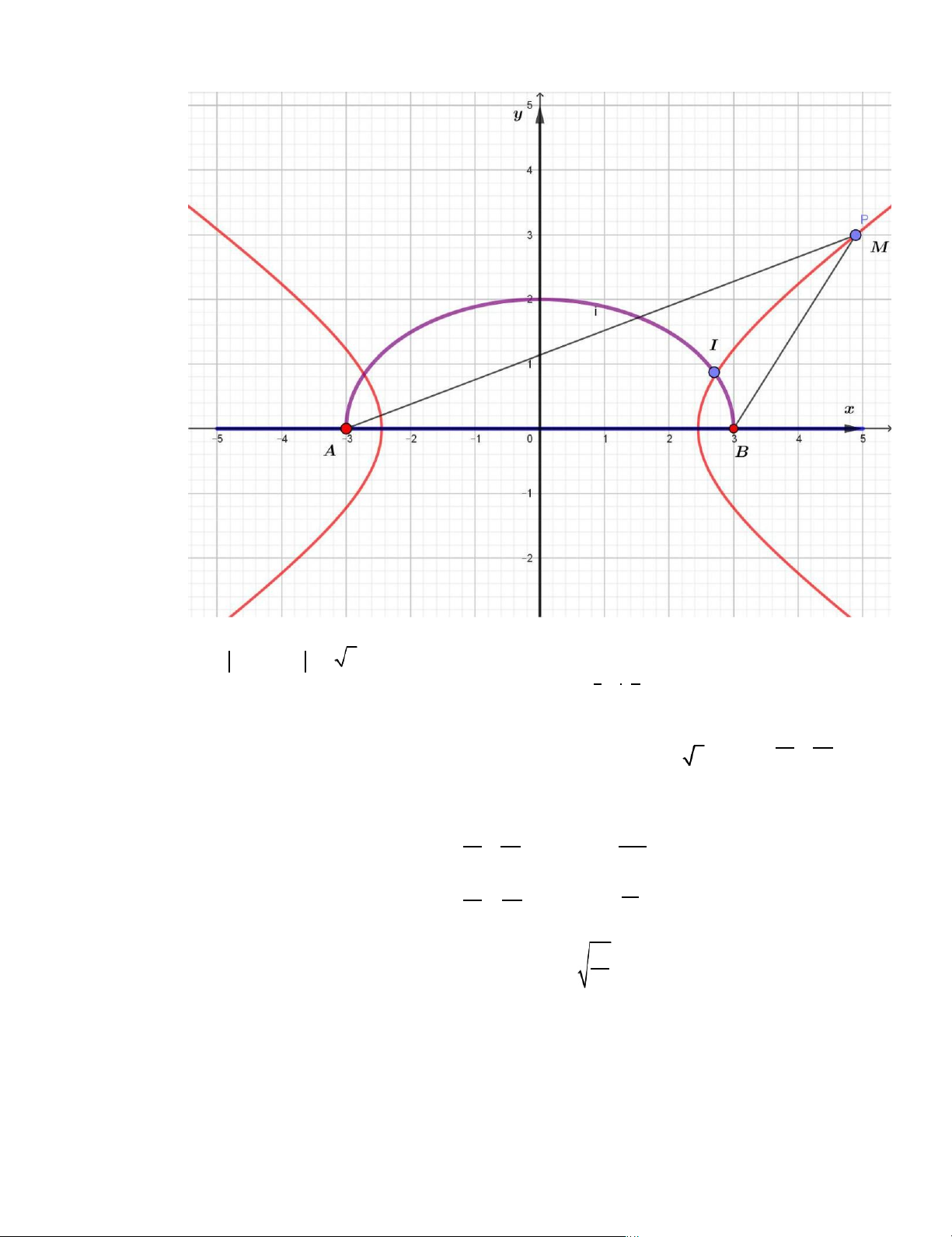
Chọn hệ trục toạ độ Oxy như hình trên, trong đó 1km ứng với 1 đơn vị. MA MB 2 6 2 2 x y A 3;0, B 3;0 H: 1 Do nên M thuộc hypebol 6 3 . E: x 2 y2 1
Cảng biển xây theo hình elip có trục lớn là AB 6 và tiêu cự là 2 5 9 4
Khi con tàu M neo đậu thì chính là tại vị trí I : x 2 y2 126 2 1 x 6 3 17 x 2 y2 y2 12 1
Lúc này toạ độ của I thoả mãn hệ 9 4 17 . 12 Khi đó
khoảng cách từ con tàu M đến bờ biển là 17 km .
Câu 47. [Mức độ 3] Một người kỹỹ ưs thiếết kếếộ m ườtđ
ng hầầmộ m t chiếầuặ có m t cắếtộlàửm t n elip,ahình 12 3
chiếầu ộr ng ủc a hầầm là mét, khoảng cách từ điểm cao nhầết ủc
a elip so ớv i mặ t đườ ng là mét.
Ngườ i kĩ sư nàỹ phải đưa ra cảnh báo cho các loại xe có thể đi qua hầầm. Mộ t chiếếc xe có chiếầuộ r ng 3
bắầng mét thì chiếầu caoớl n nhầết có ểth đi qua hầầm ộthu c khoả ng nào sau đầỹ lOMoARcPSD|44744371 A. 2,6;2,8 2,4;2,6 . B. 2,8;3,00 . C. 3,00;3,20 . D. . Lời giải
FB tác giả: Nguyễễn Quỳnh Châu x 2 y2 là a 2 b2 A 6;0 B 0;3
Phươ ng trình chính tắếc ủc a E
1 , trong đó a b 0 . Do các điểm và a 6; b 3
thuộc E nến thaỹ vào phương trình của E ta có
. Suỹ ra phương trình của E là x 2 y2 1 36 9 . 3 x 1,5
Vớ i những xe tải có chiếầu ộr ng là mét, tương ứng với
. Thaỹ vào phương trình của elip để ta tm ra 1,5
độ cao y của xe tải ( y là tung độ dương của điểm M có hoành độ bắầng
thuộc E ) ta được y 3 1 x2 3 1 1,52 2,781 16 16 . Câu 48.
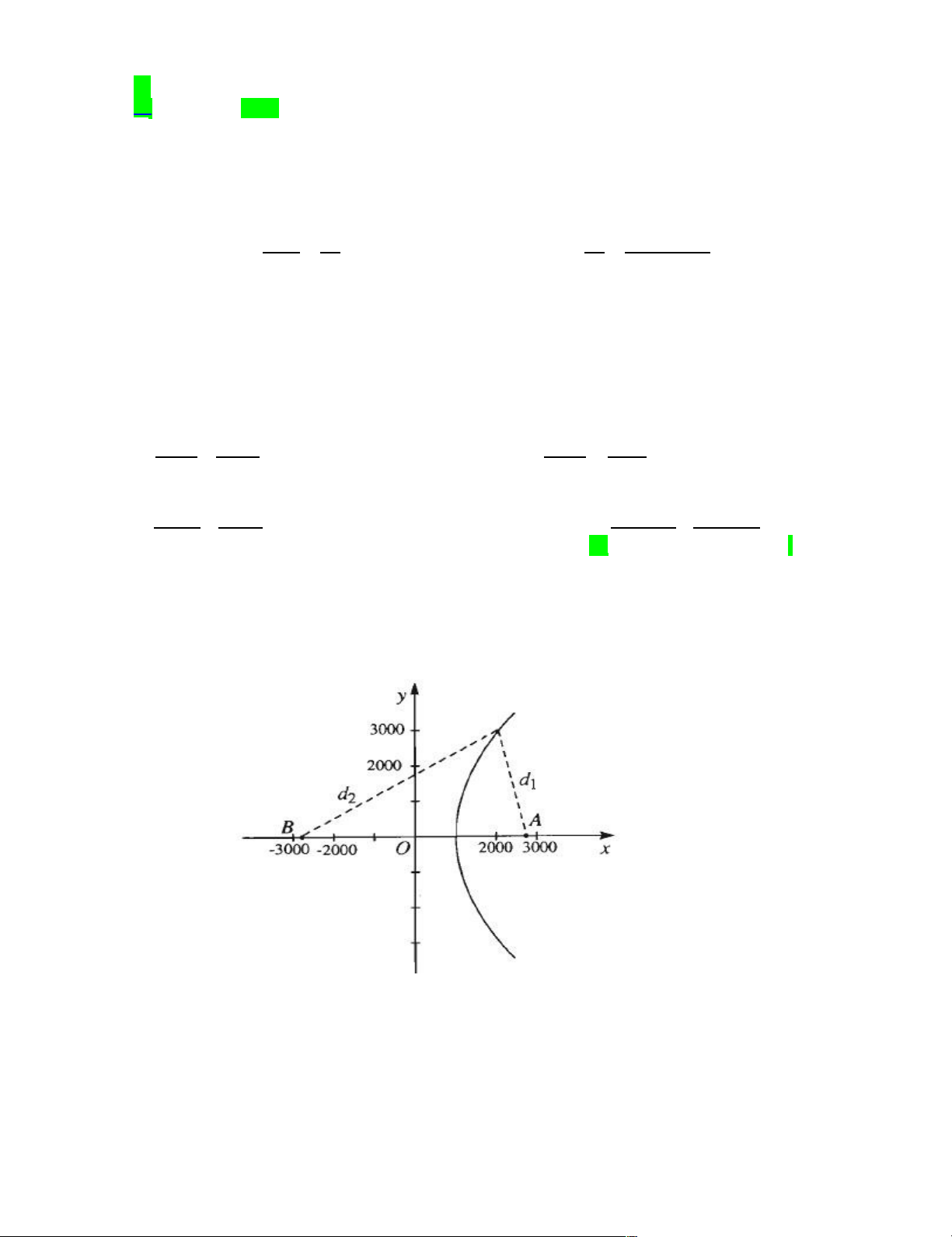
[Mức độ 3] Các hành tnh và các sao chổi khi chuỹển động xung quanh mặt trời có quỹỹđạo là một
đườ ng elip trong đó tầm mặt trời là một tếu điểm. Điểm gầần mặ t trờ i nhầếtọglài điể m cận nhật,
điểm xa mặt trời nhầết ọg i làđiể m viễễn nhậ .tTrái đầết chuỹể n độ ng xung quanh mặ t trờ i theo quỹỹạđ o
là một đường elip có độ dài nửa trục lớn bắầng93.000.000 dặm. Tỉ sốế khoả ng cách giữ a điể m ậc n 59 61
nhật và điểm viếỹn nhậ t đếến ặm tờtr i là (tham khảo hình dưới).
Khoảng cách từ tầm trái đầết đếến tầm ặm tờtr i khi trái đầếtở ể đi ậm c nậnh t bắầng lOMoARcPSD|44744371 A. 91.450.000 dặm. B. 91.455.000 dặm. C. 91.000.000 dặm. D. 91.550.000 dặm. Lời giải
FB tác giả: Nguyễễn Văn Đệ
Ta có a 93.000.000 . Khi đó a c
59 61a 61c 59 a 59 c c a 93.000.000 1.550.000 a c 61 60 60 .
Suỹ ra khoảng cách từ trái đầết đếến ặm tờtr
i khi trái đầếtở ể đi ậm cnhnật là: a c 91.450.000 dặm.
Câu 49. [Mức độ 4] Hai thiếết bị A và B dùng để ghi ầm một vụ nổ đặt cách nhau 1 dặ m, thiếết bị A ghi 1100 feet / s
được ầm thanh trước thiếết bị B là 2 giầỹ, biếết ậv n tốếc ầm thanh là . Tìm các vị trí mà 5280 0,914m
vụ nổ có thể xảỹ ra ( 1 dặm feet; 3 feet ) . x 2 y2 1 x 2 y2 1 A. 5280 2200 . B. 5280 2200 . x 2 y2 1 x 2 y2 1 C. 52802 11002 . D. 1210000 5759600 . Lời giải
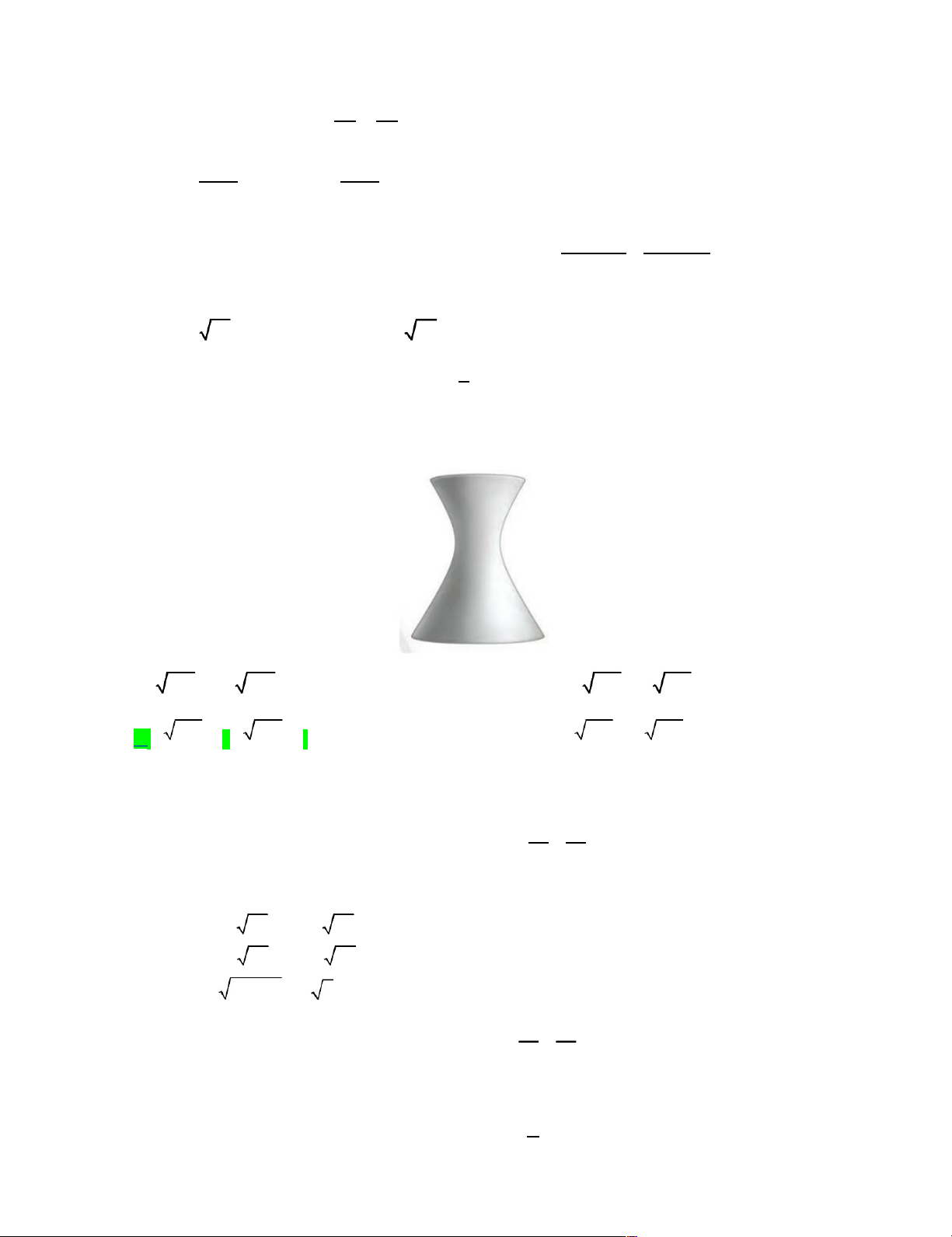
FB tác giả: Vũ Thị Lương Ox
Chọn hệ trục tọa độ Oxy mà
đi qua A và B , Oy là đường trung trực của AB . d1 A d2 Kí hiệu
là quãng đường ầm thanh đi được từ vụ nổ đếến thiếếtị b ,
là quãng đường ầm thanh đi B
được từ vụ nổ đếến thiếếtị b , d1 và d2 tnh theo feet. Khi đó, do thiếết bị A nhận ầm thanh nhanh
hơ n thiếết bị B là 2 giầỹ nến ta có phương trình : d 2 d1 2200 (1)
Các điểm thỏa mãn (1) nắầm trến mộ t nhánh ủc a Hỹpebol có phư ng trình: lOMoARcPSD|44744371 x 2 y2 1 a 2 b 2 c 5280 2640 a
2200 1100, b 2 c 2 a2 5759600 Ta có 2 , 2 , x 2 y2
Vậ ỹ vụ nổ nắầm trến mộ t nhánh ủc a Hỹpebol có phươ ng trình: 1210000 5759600 1 . Câu 50.
[Mức độ 4] Một tháp làm nguội của một nhà máỹ có mặt cắết là hình hỹperbol có tếu ực bắầng 2 70 m 2 42 m 120m
, độ dài trục ảo bắầng
. Biếết chiếầu caoủ c a tháp là và khoảng cách từ nóc 2 3 ứ ủ ả ừ ứ
tháp đếến tầm đốếi x ng c a hỹpebol là kho ng cách t tầm đốếi x ng đếến đáỹ. Bán kính nóc và bán
kính đáỹ của tháp lầầnượl t là A. 391m 2 ; 2 871m . C. 391m ; 871m .
B. 2 391m ; 2 871m. D. 391m ; 871m . Lời giải
FB tác giả: Lễ Thị Như Quỳnh x 2 y2
Phương trình chính tắc của hypebol có dạng a 2
b2 1 , với a c , b 2 c 2 a2 . Ta có: 2c 2 70 c 70 2b 2 42 b 42 a c 2 b2 2 7 x 2 y2 1
Vậy phương trình chính tắc của hypebol là: 28 42 .
Gọi khoảng cách từ tâm đối xứng đến đáy tháp là z. 2
Suy ra khoảng cách từ tâm đối xứng đến nóc tháp là 3 z . lOMoARcPSD|44744371 Ta có
z 2 z 120 z 72 3 . x 2 y2 y 72 1 Thay vào phương trình 28 42 ta tìm được x 2 871. x 2 y2 y 48 1 Thay vào phương trình 28 42 ta tìm được x 2 391.
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là: 2 391m ; 2 871 m. HẾẾT