Tối Ưu Hóa Quá Trình Vận Tải | Tối ưu rời rạc | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội

TỐI ƯU HÓA QUÁ TRÌNH VẬN TẢI
BÀI TOÁN LINEAR PROGRAMMING Bài 1.
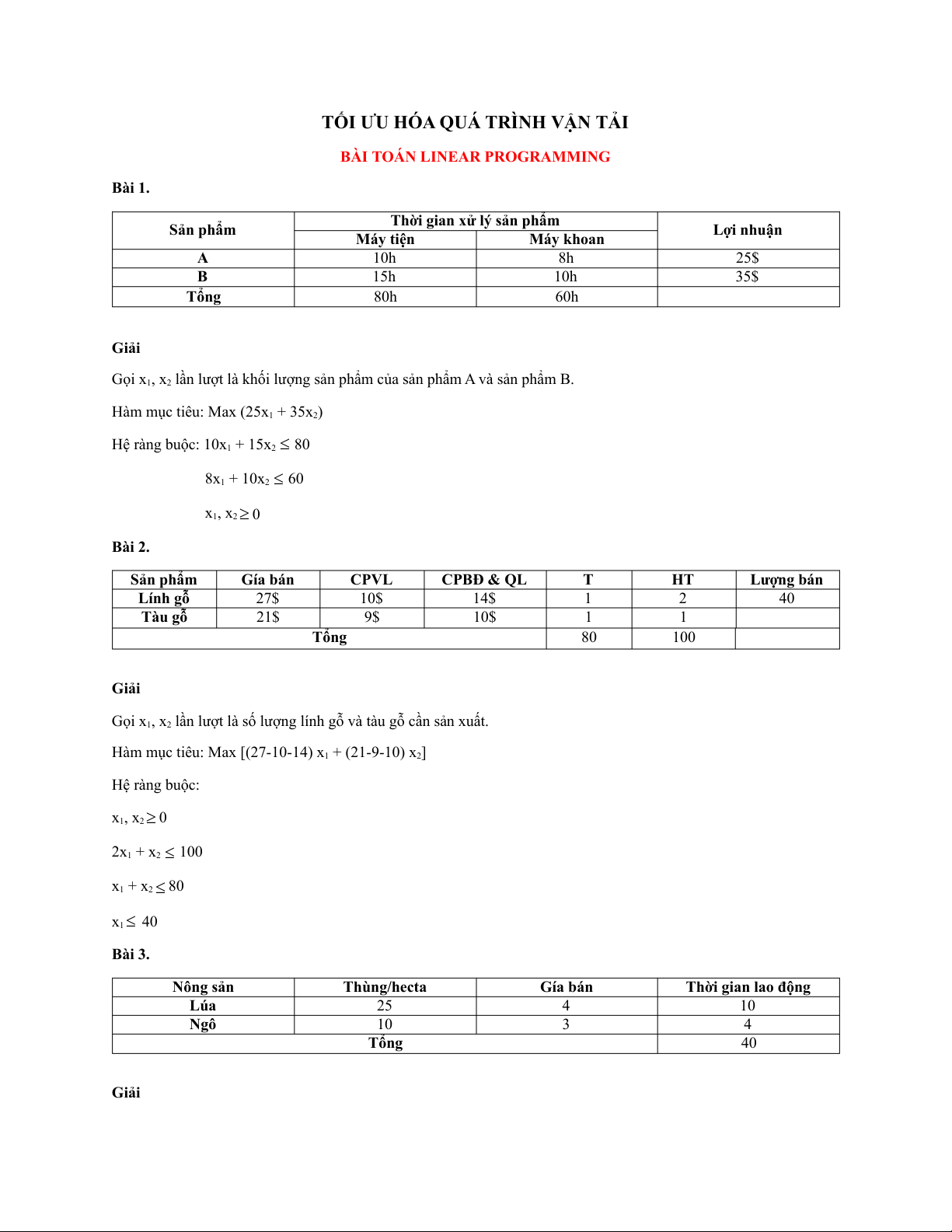
Thời gian xử lý sản phẩm Sản phẩm Lợi nhuận Máy tiện Máy khoan A 10h 8h 25$ B 15h 10h 35$ Tổng 80h 60h Giải
Gọi x1, x2 lần lượt là khối lượng sản phẩm của sản phẩm A và sản phẩm B.
Hàm mục tiêu: Max (25x1 + 35x2)
Hệ ràng buộc: 10x1 + 15x2 ≤ 80 8x1 + 10x2 ≤ 60 x1, x2 ≥ 0 Bài 2. Sản phẩm Gía bán CPVL CPBĐ & QL T HT Lượng bán Lính gỗ 27$ 10$ 14$ 1 2 40 Tàu gỗ 21$ 9$ 10$ 1 1 Tổng 80 100 Giải
Gọi x1, x2 lần lượt là số lượng lính gỗ và tàu gỗ cần sản xuất.
Hàm mục tiêu: Max [(27-10-14) x1 + (21-9-10) x2] Hệ ràng buộc: x1, x2 ≥ 0 2x1 + x2 ≤ 100 x1 + x2 ≤ 80 x1 ≤ 40 Bài 3. Nông sản Thùng/hecta Gía bán Thời gian lao động Lúa 25 4 10 Ngô 10 3 4 Tổng 40 Giải
Gọi x, y lần lượt là số hecta lúa và ngô cần trồng.
Hàm mục tiêu: Max (25.4.x +10.3.y) Hệ ràng buộc: x + y ≤ 7 10x + 4y ≤ 40
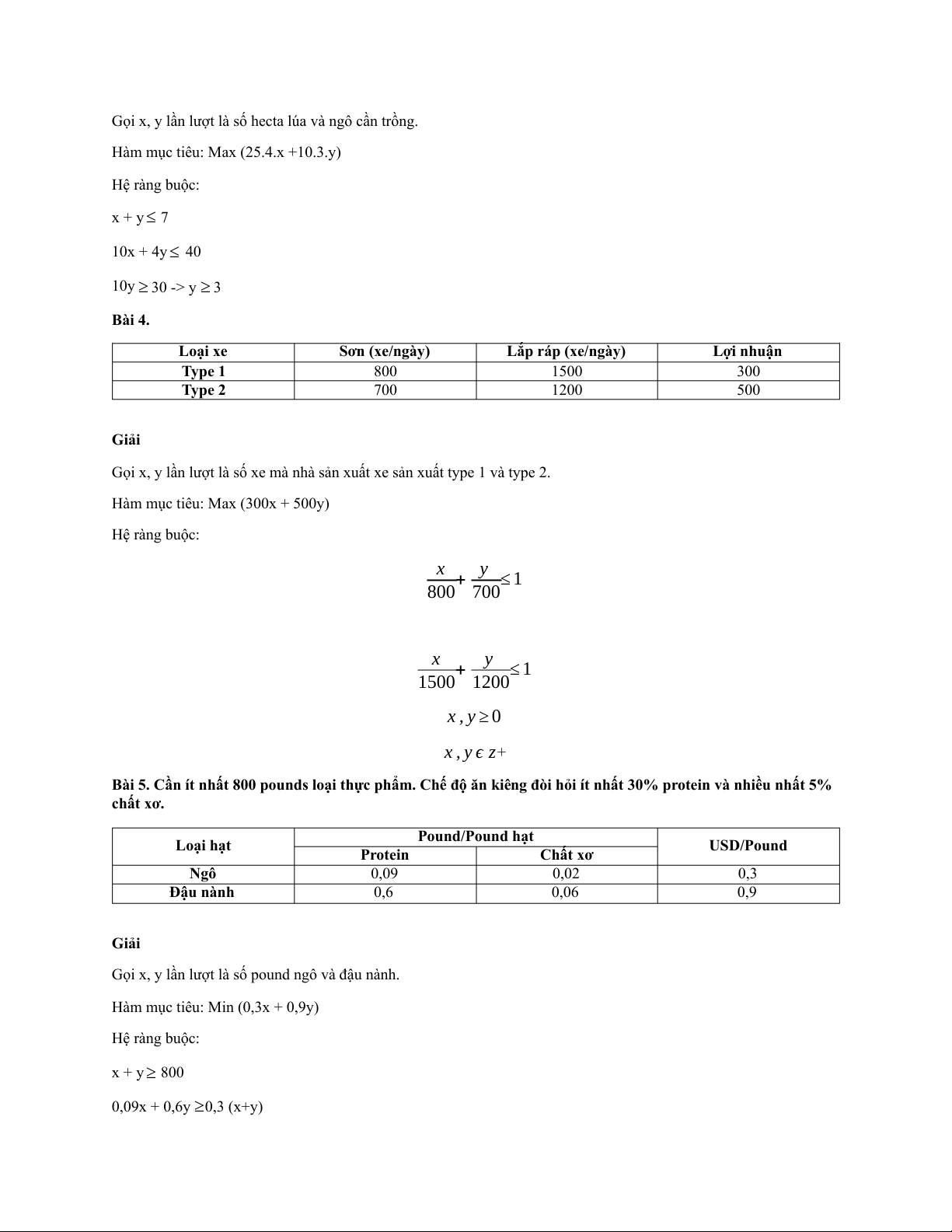
10y ≥ 30 -> y ≥ 3 Bài 4. Loại xe Sơn (xe/ngày) Lắp ráp (xe/ngày) Lợi nhuận Type 1 800 1500 300 Type 2 700 1200 500 Giải
Gọi x, y lần lượt là số xe mà nhà sản xuất xe sản xuất type 1 và type 2.
Hàm mục tiêu: Max (300x + 500y) Hệ ràng buộc: x y + ≤ 1 800 700 x y + ≤ 1 1500 1200 x , y ≥ 0 x , y ϵ z+
Bài 5. Cần ít nhất 800 pounds loại thực phẩm. Chế độ ăn kiêng đòi hỏi ít nhất 30% protein và nhiều nhất 5% chất xơ. Pound/Pound hạt Loại hạt USD/Pound Protein Chất xơ Ngô 0,09 0,02 0,3 Đậu nành 0,6 0,06 0,9 Giải
Gọi x, y lần lượt là số pound ngô và đậu nành.
Hàm mục tiêu: Min (0,3x + 0,9y) Hệ ràng buộc: x + y ≥ 800
0,09x + 0,6y ≥0,3 (x+y)
0,02x + 0,06y ≤ 0,05 (x+y)
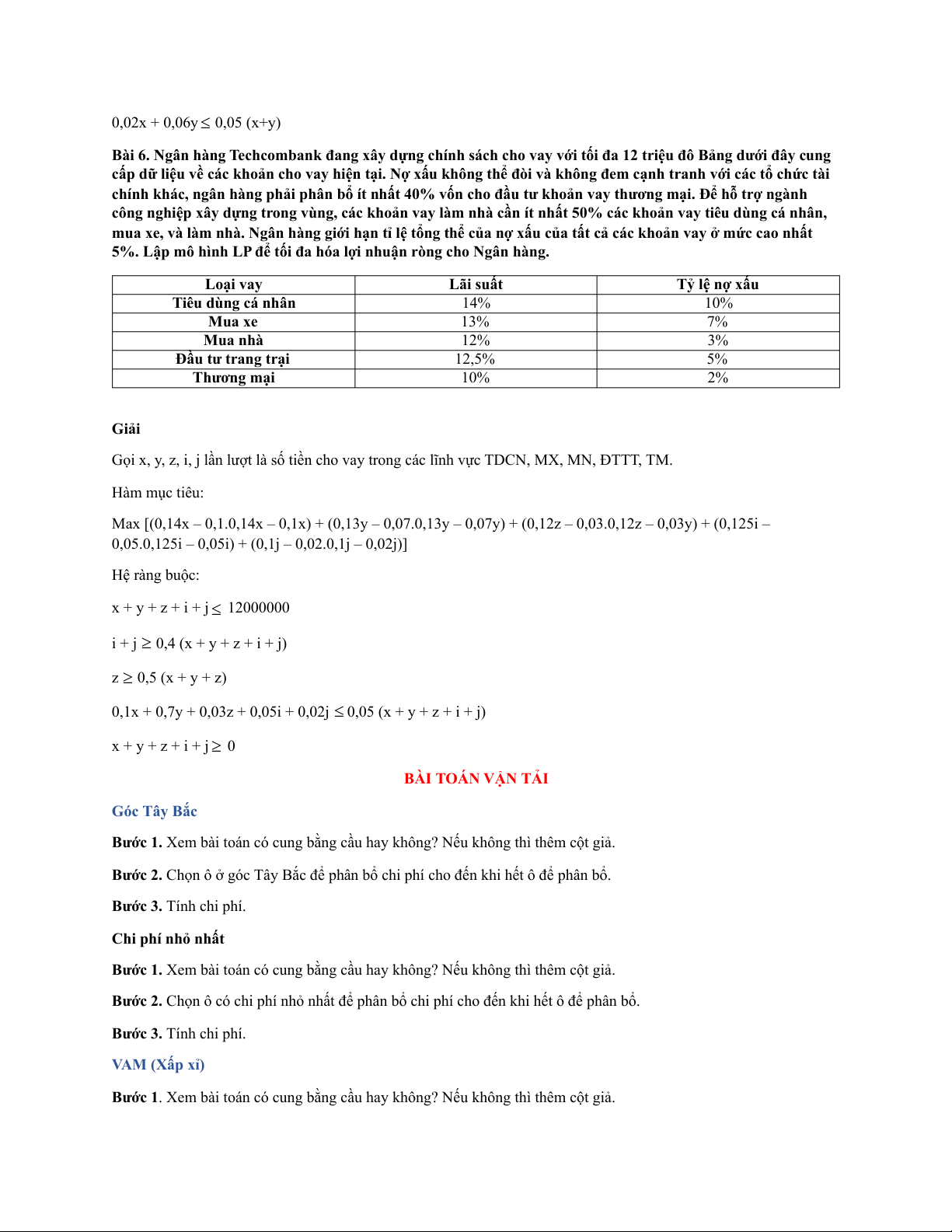
Bài 6. Ngân hàng Techcombank đang xây dựng chính sách cho vay với tối đa 12 triệu đô Bảng dưới đây cung
cấp dữ liệu về các khoản cho vay hiện tại. Nợ xấu không thể đòi và không đem cạnh tranh với các tổ chức tài
chính khác, ngân hàng phải phân bổ ít nhất 40% vốn cho đầu tư khoản vay thương mại. Để hỗ trợ ngành
công nghiệp xây dựng trong vùng, các khoản vay làm nhà cần ít nhất 50% các khoản vay tiêu dùng cá nhân,
mua xe, và làm nhà. Ngân hàng giới hạn tỉ lệ tổng thể của nợ xấu của tất cả các khoản vay ở mức cao nhất
5%. Lập mô hình LP để tối đa hóa lợi nhuận ròng cho Ngân hàng. Loại vay Lãi suất Tỷ lệ nợ xấu Tiêu dùng cá nhân 14% 10% Mua xe 13% 7% Mua nhà 12% 3% Đầu tư trang trại 12,5% 5% Thương mại 10% 2% Giải
Gọi x, y, z, i, j lần lượt là số tiền cho vay trong các lĩnh vực TDCN, MX, MN, ĐTTT, TM. Hàm mục tiêu:
Max [(0,14x – 0,1.0,14x – 0,1x) + (0,13y – 0,07.0,13y – 0,07y) + (0,12z – 0,03.0,12z – 0,03y) + (0,125i –
0,05.0,125i – 0,05i) + (0,1j – 0,02.0,1j – 0,02j)] Hệ ràng buộc:
x + y + z + i + j ≤ 12000000
i + j ≥ 0,4 (x + y + z + i + j) z ≥ 0,5 (x + y + z)
0,1x + 0,7y + 0,03z + 0,05i + 0,02j ≤ 0,05 (x + y + z + i + j)
x + y + z + i + j ≥ 0 BÀI TOÁN VẬN TẢI Góc Tây Bắc
Bước 1. Xem bài toán có cung bằng cầu hay không? Nếu không thì thêm cột giả.
Bước 2. Chọn ô ở góc Tây Bắc để phân bổ chi phí cho đến khi hết ô để phân bổ.
Bước 3. Tính chi phí. Chi phí nhỏ nhất
Bước 1. Xem bài toán có cung bằng cầu hay không? Nếu không thì thêm cột giả.
Bước 2. Chọn ô có chi phí nhỏ nhất để phân bổ chi phí cho đến khi hết ô để phân bổ.
Bước 3. Tính chi phí. VAM (Xấp xỉ)
Bước 1. Xem bài toán có cung bằng cầu hay không? Nếu không thì thêm cột giả.
Bước 2. Tính penalty cost bằng cách lấy hiệu của 2 số nhỏ nhất ở cột hoặc hàng.
Bước 3. Chọn ô có penalty cost lớn nhất, phân phối hàng nhiều nhất có thể vào ô có chi phí thấp nhất trong cột hay hàng đó.
Bước 4. Cứ làm cho tới khi các ô đều được phân bổ.
Bước 5. Tính chi phí.
MODI kiểm tra điều kiện tối ưu
Bước 1. Kiểm tra điều kiện không suy biến:
Số ô được phân bổ = Số hàng + Số cột – 1 thì bài toán không suy biến.
Nếu bài toán suy biến thì sẽ cho giá trị d rất nhỏ vào ô bất kỳ (thường sẽ bỏ vào ô có chi phí nhỏ).
Bước 2. Xác định các giá trị u, v ui + vj = cịj
Cho giá trị u bất kì, u1=0
Tính các u, v còn lại dựa trên cịj tại các ô đã phân bổ trong bảng.
Bước 3. Kiểm tra penalty cost của các ô không được phân bổ: pij = ui + vj – cij
Nếu tất cả pij ≤ 0 thì bài toán đã tối ưu.
Nếu tồn tại giá trị ngược lại thì chọn p lớn nhất và đưa vào ô i, j tương ứng trở thành ô cơ bản và tối ưu tiếp.
Bước 4. Chọn giá trị dương lớn nhất của p làm cơ sở. Vẽ vòng dẫn từ ô cơ sở với hàng và cột đó theo chiều bất kỳ,
miễn là vòng dẫn kết thúc tại điểm xuất phát và có các đỉnh là các ô đã phân bổ.
Thêm dấu (+) cho đỉnh xuất phát, dấu (-) cho đỉnh kế tiếp cho đến khi kết thúc vòng lặp. Sau đó lấy giá trị ở ô có
dấu (-) nhỏ nhất để làm phép tính tương đương với dấu.
Bước 5. Cứ làm lại từ bước 2 cho đến khi mà tất cả pij ≤ 0.
Bước 6. Tính chi phí.
STEPPING STONE kiểm tra điều kiện tối ưu
Bước 1. Kiểm tra điều kiện không suy biến:
Số ô được phân bổ = Số hàng + Số cột – 1 thì bài toán không suy biến.
Nếu bài toán suy biến thì sẽ cho giá trị d rất nhỏ vào ô bất kỳ (thường sẽ bỏ vào ô có chi phí nhỏ).
Bước 2. Tạo các vòng khép kín, xuất phát từ một đỉnh chưa phân phối, đi qua các đỉnh đã phân phối. Đỉnh xuất phát Vòng khép kín Chi phí thay đổi Ghi tên đỉnh xuất phát Ghi vòng lặp Ô1 – ô2 + ô3 – ô4…
Bước 3. Chọn vòng có thay đổi chi phí âm nhiều nhất và thêm các dấu (+), (-) cho các ô đi qua, tương tự như
MODI. Sau đó lấy giá trị ở ô có dấu (-) nhỏ nhất để làm phép tính tương đương với dấu.
Bước 4. Lặp lại bước 2 cho đến khi ở cột chi phí thay đổi đều lớn hơn hoặc bằng 0 thì tối ưu.
Bước 5. Tính chi phí.
BÀI TOÁN NGƯỜI ĐƯA THƯ
Bước 1. Xác định các nút có bậc lẻ.
Bước 2. Lập ma trận chi phí nhỏ nhất giữa các nút bậc lẻ.
Bước 3. Lập bài toán vận tảu với mục tiêu tổng chi phí các nút bậc lẻ là nhỏ nhất.
Min ∑ ∑ cij . xij ∀ i= {Các nút bậc lẻ } , ∀ j= {Các nút bậc lẻ } i j
Bước 4. Bổ sung đường đi.
BÀI TOÁN LẬP MẠNG QUẢN LÝ DỰ ÁN PERT (Trong tập).
BÀI TOÁN QUY HOẠCH TUYẾN TÍNH DẠNG ĐỒ THỊ (Giống MHH) DẠNG ĐƠN HÌNH
Bước 1. Lập mô hình LP cho bài toán. Maximize z = 3x + 2y Hệ ràng buộc: -x + 2y ≤ 4 3x + 2y ≤ 14 x – y ≤ 3 x,y ≥ 0
Bước 2. Chuyển các ràng buộc bất đẳng thức thành ràng buộc đẳng thức (thêm biến giả):
Lưu ý: Đối với max, nếu bất đẳng thức là dấu ≤ thì sẽ cộng cho biến giả, còn ngược lại sẽ trừ cho biến giả.
Đối với min, nếu bất đẳng thức là dấu ≥ thì sẽ cộng cho biến giả, còn ngược lại sẽ trừ cho biến giả.
Maximize z = 3x + 2y + 0s1 + 0s2 + 0s3 Subject to: -x + 2y + s1 = 4 3x + 2y + s2 = 14 x – y + s3 = 3 x,y,s1,s2,s3 ≥ 0 Trong đó: Gọi i là số hàng, i = 3; Gọi j là số cột j = 2;
Hệ số hàm mục tiêu cj: c1 = 3, c2 = 2
oVế phải của ràng buộc bi: b1 = 4, b2 = 14, b3 = 3
Các hệ số vế trái ràng buộc: aij: a11 = -1,…
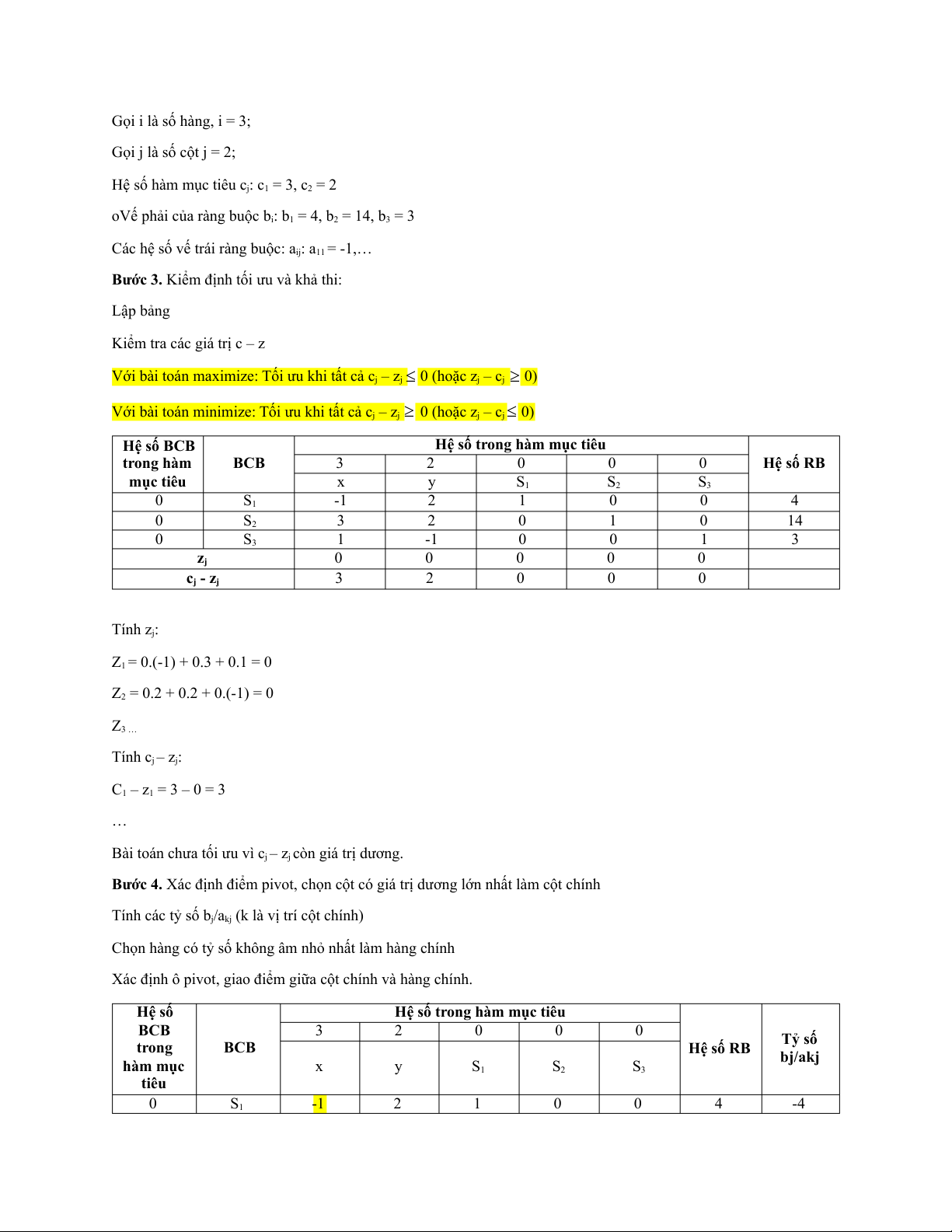
Bước 3. Kiểm định tối ưu và khả thi: Lập bảng
Kiểm tra các giá trị c – z
Với bài toán maximize: Tối ưu khi tất cả cj – zj ≤ 0 (hoặc zj – cj ≥ 0)
Với bài toán minimize: Tối ưu khi tất cả cj – zj ≥ 0 (hoặc zj – cj ≤ 0) Hệ số BCB
Hệ số trong hàm mục tiêu trong hàm BCB 3 2 0 0 0 Hệ số RB mục tiêu x y S1 S2 S3 0 S1 -1 2 1 0 0 4 0 S2 3 2 0 1 0 14 0 S3 1 -1 0 0 1 3 zj 0 0 0 0 0 cj - zj 3 2 0 0 0 Tính zj: Z1 = 0.(-1) + 0.3 + 0.1 = 0 Z2 = 0.2 + 0.2 + 0.(-1) = 0 Z3 … Tính cj – zj: C1 – z1 = 3 – 0 = 3 …
Bài toán chưa tối ưu vì cj – zj còn giá trị dương.
Bước 4. Xác định điểm pivot, chọn cột có giá trị dương lớn nhất làm cột chính
Tính các tỷ số bj/akj (k là vị trí cột chính)
Chọn hàng có tỷ số không âm nhỏ nhất làm hàng chính
Xác định ô pivot, giao điểm giữa cột chính và hàng chính. Hệ số
Hệ số trong hàm mục tiêu BCB 3 2 0 0 0 Tỷ số trong BCB Hệ số RB bj/akj hàm mục x y S1 S2 S3 tiêu 0 S1 -1 2 1 0 0 4 -4 0 S2 3 2 0 1 0 14 14/3 0 S3 1 -1 0 0 1 3 3 zj 0 0 0 0 0 cj - zj 3 2 0 0 0
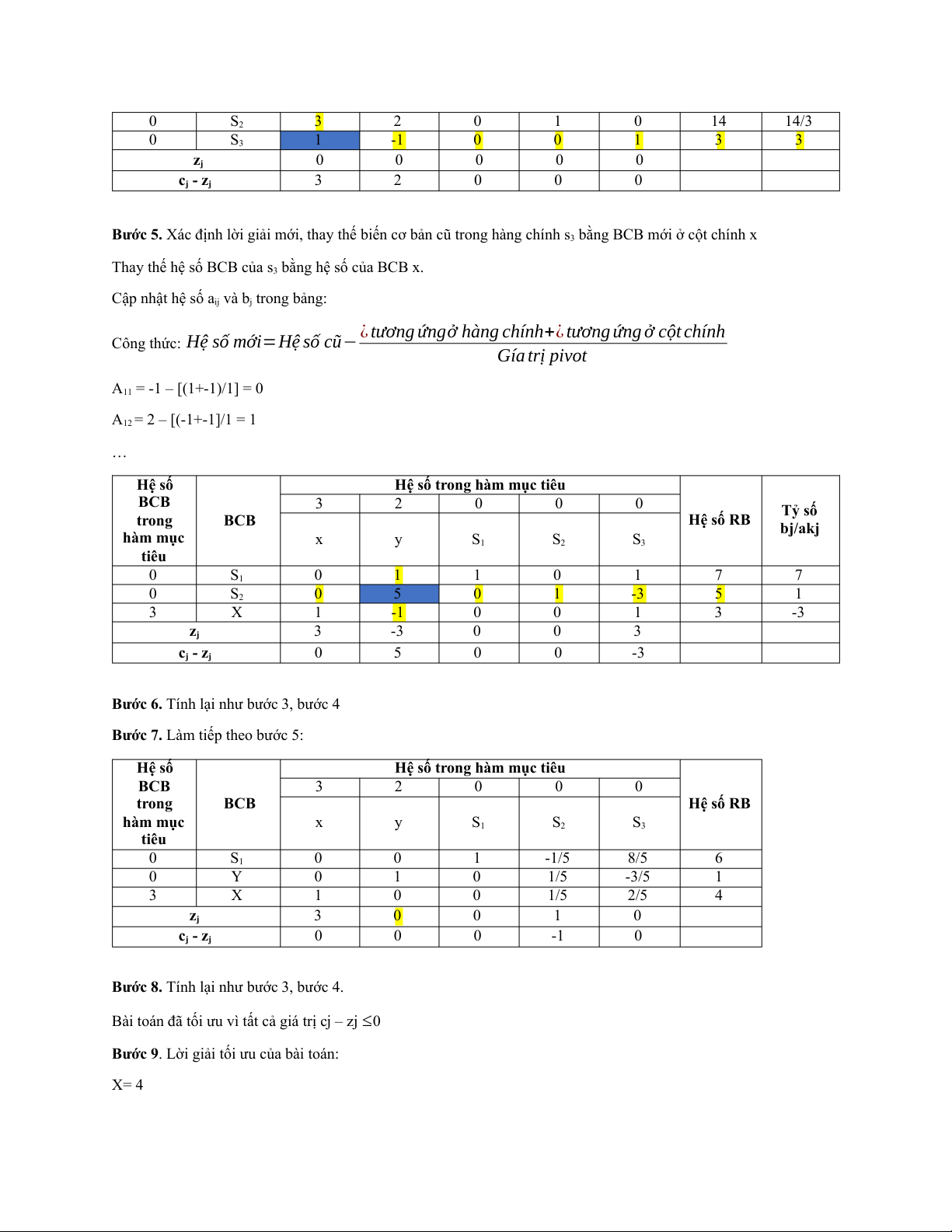
Bước 5. Xác định lời giải mới, thay thế biến cơ bản cũ trong hàng chính s3 bằng BCB mới ở cột chính x
Thay thế hệ số BCB của s3 bằng hệ số của BCB x.
Cập nhật hệ số aij và bj trong bảng:
¿ tương ứngở hàng chính+¿ tương ứng ở cột chính
Công thức: Hệ số mới=Hệ số cũ− Gía trị pivot A11 = -1 – [(1+-1)/1] = 0 A12 = 2 – [(-1+-1]/1 = 1 … Hệ số
Hệ số trong hàm mục tiêu BCB 3 2 0 0 0 Tỷ số trong BCB Hệ số RB bj/akj hàm mục x y S1 S2 S3 tiêu 0 S1 0 1 1 0 1 7 7 0 S2 0 5 0 1 -3 5 1 3 X 1 -1 0 0 1 3 -3 zj 3 -3 0 0 3 cj - zj 0 5 0 0 -3
Bước 6. Tính lại như bước 3, bước 4
Bước 7. Làm tiếp theo bước 5: Hệ số
Hệ số trong hàm mục tiêu BCB 3 2 0 0 0 trong BCB Hệ số RB hàm mục x y S1 S2 S3 tiêu 0 S1 0 0 1 -1/5 8/5 6 0 Y 0 1 0 1/5 -3/5 1 3 X 1 0 0 1/5 2/5 4 zj 3 0 0 1 0 cj - zj 0 0 0 -1 0
Bước 8. Tính lại như bước 3, bước 4.
Bài toán đã tối ưu vì tất cả giá trị cj – zj ≤0
Bước 9. Lời giải tối ưu của bài toán: X= 4 Y = 1
Gía trị của hàm mục tiêu: z = max(3x + 2y) = 3.4 + 2.1 = 14